Лаборатория физики низких температур и магнетизма | Научные отделы и лаборатории | Структура
История создания лаборатории связана с открытием высокотемпературной зависимости в 1986 году. Тогда была создана группа для выращивания сверхпроводников и исследования явления высокотемпературной сверхпроводимости. В 1988 году группа вошла в состав лаборатории физики фазовых переходов. Как отдельное научное подразделение, лаборатория существует с 1993 года.
Основное научное направление лаборатории: Исследование фазовых переходов и магнитотранспортных явлений в сильнокоррелированных электронных системах (высокотемпературные сверхпроводники, легированные манганиты, сплавы со связанными структурными и магнитными фазовыми переходами).
Лаборатория оснащена установками для исследования широкого круга теплофизических и магнитных свойств материалов в области низких температур:
-
Установка для измерения теплоемкости материалов методом а.с.-калоримерии.

- Установка для измерения кинетических свойств (теплопроводность, электросопротивление, термоэдс, эффект Холла). Область температур – 4- 350 К, область магнитных полей 0-30 кЭ.
-
Установки для измерения магнитокалорического эффекта (МКЭ)
a) Установка для измерения МКЭ классическим прямым методом. Область температур – 4- 350 К, область магнитных полей 0-30 кЭ.
b) Установка для прямого измерения МКЭ методом модуляции магнитного поля. Область температур – 80 – 350 К, область магнитных полей 0-18 кЭ. Данная установка позволяет с высокой точностью измерять МКЭ в слабых магнитных полях (от нескольких десятков эрстед и выше). Также на этой установке можно проводить исследования МКЭ малоразмерных образцов (толщиной 10 мкм и больше). -
Вибрационный магнетометр.
 Область температур – 80 – 350 К, область магнитных полей 0-26 кЭ.
Область температур – 80 – 350 К, область магнитных полей 0-26 кЭ. - Установка для измерения магнитной восприимчивости. Область температур – 80 – 350 К, область магнитных полей 0-18 кЭ.
Сотрудники лаборатории
-
Алиев Ахмед Магомедович
Заведующий лабораторией
- Кандидат физико-математических наук
- e-mail: [email protected]; [email protected]
- тел: +7(8722)51-80-35; моб: +7-988-299-40-96
- Skype: akhmedaliev
-
Камилов Ибрагимхан Камилович
Главный научный сотрудник
- Член-корреспондент РАН, доктор физико-математических наук, профессор
- e-mail:
- тел:
-
Главный научный сотрудник
-
Абдулвагидов Шапиулаг Белалович
Ведуший научный сотрудник
-
Алиев Шамиль.
 Микаилович
МикаиловичВедуший научный сотрудник
- Кандидат физико-математических наук
-
Гамзатов Адлер Гудретдинович
Старший научный сотрудник
-
Старший научный сотрудник
- Кандидат физико-математических наук
- e-mail: [email protected]
-
Юсупов Дибир Магомедович
Младший научный сотрудник
-
Мухучев Абдула Ахмедович
Младший научный сотрудник
-
Казанова Эльмира
Младший научный сотрудник
-
Магомедова Лиана Курбановна
Младший научный сотрудник
-
Гусейнов Магомед Магомедович
Научный сотрудник
- Кандидат физико-математических наук
-
e-mail: gusmagm@yandex.
 ru
ru
-
Амиров Абдулкарим Абдулнатипович
Научный сотрудник
-
Черненко Виктория Геннадиевна
Научный сотрудник
-
Ханов Лазер Ниямудинович
Научный сотрудник
Двухступенчатые роторно-пластинчатые насосы EM – Edwards Vacuum
Высокий предельный вакуум и скорость откачки
Эти насосы отличаются широким диапазоном глубины предельного вакуума и высокой скоростью откачки. Насосы EM — отраслевой стандарт в сфере научных и лабораторных исследований, они отлично подходят для использования в качестве форвакуумных насосов для турбомолекулярных насосов небольших типоразмеров.
Насосы EM — прочные, компактные и малошумные механические насосы с масляным уплотнением. Их ключевые преимущества: усовершенствованная контурная смазка, высокая надежность и возможность подобрать вспомогательное оборудование в соответствии с конкретными требованиями.
Насосы EM являются отраслевым стандартом для технологических процессов с нулевым загрязнением и оснащены эффективной системой смазки при высоких газовых нагрузках. Они отлично подходят для эксплуатации в экстремальных газообразных средах, например для сублимационной сушки в фармацевтической промышленности или для откачки газов из системы охлаждения.
Универсальность применения и надежность
Эти компактные, но высокомощные автономные насосы очень просты в установке. Использование электродвигателей, рассчитанных на эксплуатацию в сетях с разным номинальным напряжением, позволяет сократить количество изделий, необходимых для выполнения всех задач.
Использование электродвигателей, рассчитанных на эксплуатацию в сетях с разным номинальным напряжением, позволяет сократить количество изделий, необходимых для выполнения всех задач.
Простота монтажа
Насосы оснащены разъемом стандарта IEC, что позволяет значительно упростить подключение оборудования, не требуют наличия кабеля у заказчика. Впускной присоединительный патрубок с другой стороны позволяет монтировать насос в зонах с ограничением по высоте.
Встроенные системы защиты
Электродвигатель заключен в кожух и охлаждается вентилятором, а защита от перегрева обеспечивается с помощью теплового прерывателя цепи. Насосы EM также оснащены интеллектуальными средствами управления. Он автоматически выполняет сброс и перезапуск насоса после остывания электродвигателя.
Простота технического обслуживания
Наличие смотрового окна с кольцевым уплотнением упрощает проверку уровня масла и состояния насоса.
В поисках кота Шрёдингера. Квантовая физика и реальность
Мир квантов так необычен, что даже Альберт Эйнштейн счел его непонятным и отказался признавать следствия теории, выведенные в 1920-х годах австрийцем Эрвином Шрёдингером и его коллегами. Тем не менее, эта теория и ее уравнения легли в основу всей современной науки,  Вдохновленный собственным открытием, школьник начал «копать дальше» и окончательно убедился в блистательном союзе ума, красоты и простоты, существующем в подлинной науке, которую «слишком многие учителя случайно или нарочно скрывают от своих учеников»
Вдохновленный собственным открытием, школьник начал «копать дальше» и окончательно убедился в блистательном союзе ума, красоты и простоты, существующем в подлинной науке, которую «слишком многие учителя случайно или нарочно скрывают от своих учеников»
 Книга – о том, как возникла и что успела натворить квантовая теория в области компьютеров, телевидения, атомного оружия, молекулярной биологии и т.д.
Книга – о том, как возникла и что успела натворить квантовая теория в области компьютеров, телевидения, атомного оружия, молекулярной биологии и т.д.Логическое и физическое форматирование текста.
Глава 14
В этой главе мы снова будем работать с текстом, и в отличие от материала, изложенного во второй главе: “Редактируем текст” посмотрим на некоторые вещи под другим углом, а так же поговорим о ранее не вошедших в этот учебник тегах, с помощью которых так же можно форматировать текст на страницах сайта.
Дело в том что все теги предназначенные для работы с текстом можно разделить на две группы: “теги физического форматирования текста” и “теги логического форматирования текста”
Теперь по порядку..
О тегах физического форматирования текста речь в этом учебнике шла ранее, поэтому повторятся, не стану, а просто перечислю их:
<b>, <i>, <u>, <strike>, <s>, <tt>, <small>, <big>, <sup>, <sub>, <p>, <font>, <pre>…– всё это теги физического форматирования текста.
Почему их так назвали? Да все просто.. потому что данные теги способны тем или иным способом физически воздействовать на текст.. делать его жирным, курсивом, маленьким, большим.. и т. д. Заключив текст, в какой либо тег из вышеперечисленных, мы получаем ожидаемый результат, который описан в спецификации HTML и в различных браузерах отображается практически одинаково.
На всякий случай вновь покажу старый пример:
<html><head>
<title>Стили текста</title>
</head>
<body>
<big><b><u>Научная статья.</u></b></big>
<br>
<br>
Если разбавить дистиллированную воду Н<sub>2</sub>О сорока процентами этилового спирта С<sub>2</sub>Н<sub>5</sub>ОН то получится жидкость в 40<sup>о</sup> более известную широкой публике под названием <i>– водка.
 </i>
</i><br>
Впервые данную пропорцию <s>придлажил</s> предложил <tt>Дмитрий Иванович МЕНДЕЛЕЕВ.</tt>
<br>
<br>
<br>
<small>Распитие спиртных напитков вредит вашему здоровью.</small>
</body>
</html>
Основная задача тегов физического форматирования текста это выполнение сугубо декоративных функций.
Однако если Вы изучали справочник HTML, то наверняка обратили внимание что выше перечисленные теги это далеко не все инструменты для работы с текстом! А если Вы изучали справочник скрупулезно и пристально, то наверное заметили что некоторые теги выполняют одни и те же действия над текстом..
Например, чем отличается тег <em> от тега <i>? или какая разница между <b> и <strong>? ведь результат и там и там одинаков!
Так да не так. . отличия есть.. и они достаточно существенные!!..
. отличия есть.. и они достаточно существенные!!..
Прежде чем рассказывать о новых тегах расскажу, о том, что следует подразумевать под фразой: “логическая разметка документа”.
Под логической разметкой документа, прежде всего, принято понимать разметку текста тегами направленную на удобство работы поисковых систем и других программ, которые работают с данным документом, а так же придавать тексту в документе некий смысл. Так вот программам абсолютно по барабану как выглядит Ваш документ, красивый он или нет, какой стиль шрифта и текста используется и.т.д. программы в первую очередь пытаются найти логику на Вашей страничке, что бы в дальнейшем использовать её по своему усмотрению, например для более релевантной поисковой выдачи или для автоматического составления содержания Вашего документа…
Теперь давайте опять вернемся к вопросу выше: “Чем отличается тег <em> от тега <i>?” – казалось бы какая разница ведь текст и там и там будет отображаться курсивом .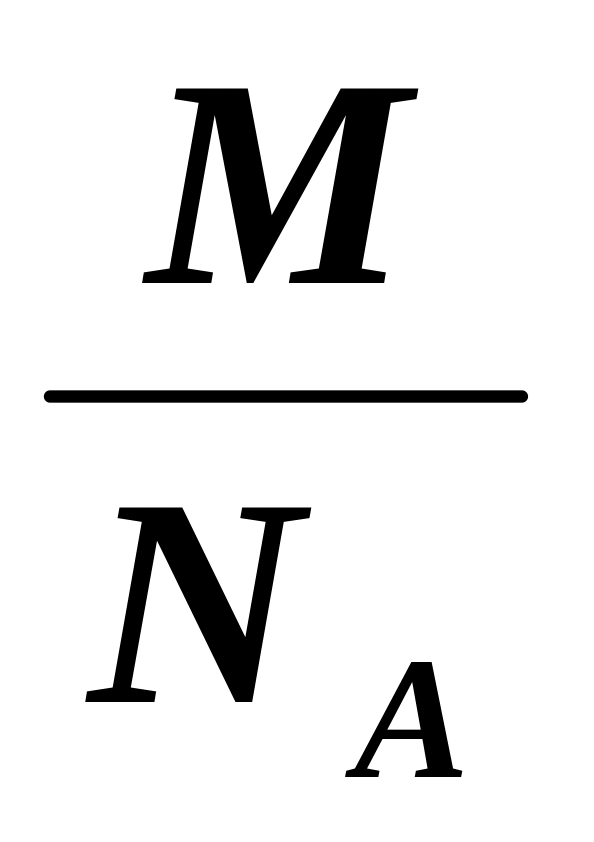 . всё дело в том что тег <i> – (курсив) – является тегом физического форматирования текста и предназначен в первую очередь для людей, а тег <em> (особенно важный текст) – является тегом логического формирования текста и предназначен для машин! А то, что текст, взятый в тег <em>, обычно в браузерах отображается курсивом – это всего лишь, скажем так “мода” и придумка браузеров.
. всё дело в том что тег <i> – (курсив) – является тегом физического форматирования текста и предназначен в первую очередь для людей, а тег <em> (особенно важный текст) – является тегом логического формирования текста и предназначен для машин! А то, что текст, взятый в тег <em>, обычно в браузерах отображается курсивом – это всего лишь, скажем так “мода” и придумка браузеров.
Спецификация HTML не говорит о том, что теги логического форматирования текста должны определённым образом отображаться браузерами, что вот, например тот же тег <em> должен быть отображен именно курсивом и не как иначе, а говорит лишь о том, что такой текст должен отличатся от основного и особым образом выделятся в документе..
Так какие теги лучше использовать? Ну раз уж мы уже заочно познакомились с тегами <em> и <strong> покажу пример, комментарии будут ниже. .
.
<html>
<head>
<title>Как создать сайт</title>
</head>
<body>
<p><strong>Как создать сайт?</strong></p>
<p>Для того, что бы <em>самостоятельно создать сайт</em> для начала в блокноте нужно написать следующие теги:</p>
<b><html></b> – <i>начало документа</i><br>
<b><head></b> – <i>начало головы</i><br>
<b></head></b> – <i>закрытие головы</i><br>
<b><body></b> – <i>начало тела</i><br>
<b></body></b> – <i>закрытие тела</i><br>
<b></html></b> – <i>конец документа</i><br>
</body>
</html>
Теперь объясню, почему на страницах данного сайта, как и в примере выше, в некоторых случаях используются теги <em> и <strong>, а в других случаях <b> и <i>.
Всё дело в том, что мне как создателю данного сайта очень хочется, чтобы люди набрав в том же гугле фразу: “Как создать сайт?” или “Самостоятельное создание сайта” видели в первых строчках поисковой выдачи гугла ссылку: “Как создать сайт?” и переходили по ней на главную страницу моего ресурса 🙂 . Так вот пометив нужные мне куски текста с помощью тегов <em> и <strong>, я тем самым даю понять гуглу что этот текст важный и что на него следует обратить особенное внимание! – конечно, это не залог успеха, тем более для столь популярных (высокочастотных) пользовательских запросов, но при прочих равных условиях, это большой плюс в глазах поисковых систем.
И противоположенный случай..
Как человек старающийся сделать сайт удобным для чтения и восприятия другими людьми, я выделяю некоторые участки текста курсивом (юмор, примечания и прочую отсебятину) и жирным шрифтом (изучаемые теги в примерах), но я не хочу, чтобы поисковые системы обращали сильное внимание на фразы типа: “начало головы” “закрытие тела” – так как сайт написан для начинающих веб-ремесленников, а не для начинающих патологоанатомов, поэтому размечаю такой текст тегами <b> и <i> – они дают нужный результат, собственно полужирный шрифт и курсив, но не являются “красной тряпкой” для программ.
Разобравшись с сутью и предназначением логической разметки текста настало время познакомить Вас с тегами которые способны разбавить сухой текст неким смыслом.
Буду перечислять..
Тег <abbr>
Выделяет в тексте аббревиатуру. Браузерами обычно подчеркивается пунктирной линией.
<abbr>CSS</abbr>
Практически ко всем тегам применим атрибут title – всплывающая подсказка, так вот если Вы в тексте выделяете некую аббревиатуру, старайтесь давать к ней расшифровку, используя данный атрибут.
<abbr title=”Cascading Style Sheets”>CSS</abbr> позволит Вам без труда изменить стиль любого тега логического форматирования текста!
Тег <acronym>
Данный тег выделяет в тексте акроним. Акроним это почти то же самое что и аббревиатура, только образованная из начальных букв, слов или словосочетаний, произносимая как единое слово, а не побуквенно.
Вступай в <acronym title=”коммунистический союз молодёжи”>комсомол</acronym>!!
Так же как и с аббревиатурой для расшифровки текста желательно использовать атрибут title.
Тег <address>
Указывает автора документа и его адрес. Обычно отображается курсивом. Предназначен для поисковых систем для сбора информации об авторе его адресе и прочей информации владельца/цев сайта.
<address>Вася Пупкин г. Урюпинск Макаронная фабрика 2010г.</address>
Тег <cite>
Выделяет в тексте цитату или сноску на другой документ. Обычно браузеры отображают её курсивом.
Как сказал Остап Бендер <cite>Лед тронулся! господа присяжные заседатели!</cite>
Тег <code>
Отмечает текст как некий программный код. Обычно отображается моноширинным шрифтом.
<code>function()</code> – так обозначается функция в PHP
Тег <del>
Выделяет удалённый текст в новой версии документа. Выделенный текст станет перечёркнутым.
Выделенный текст станет перечёркнутым.
Напоминает теги физического форматирования <strike> и сокращённый <s> – перечёркнутый текст.
Использование тега <del>, более предпочтительно, так как помимо того, что он разбавляет текст логикой еще и заменяет собой теги <strike> и <s>, которые помечены спецификацией 4.01 как нежелательные.
<del>Старая цена 1000р.</del> – Новая 999 р.!!!
Тег <dfn>
Выделяет текст как определение. Как правило, когда в тексте встречается новый термин, авторы выделяют его курсивом и дают его определение, собственно для этого и нужен тег <dfn>
<dfn>Акроним</dfn> – аббревиатура, образованная из начальных букв, слов или словосочетаний, произносимая как единое слово, а не побуквенно.
Тег <ins>
Выделяет новый текст в новой версии документа. Выделенный текст в большинстве браузеров станет подчёркнутым.
Выделенный текст в большинстве браузеров станет подчёркнутым.
Противоположен по значению тегу <del> с ним же в паре обычно он и используется.
<del>Старая цена 1000р.</del> – <ins>Новая 999 р.</ins>!!!
Тег <em>
Выделяет особенно важный фрагмент текста. Обычно отображается курсивом.
<em>Как создать сайт?</em> – узнай на Вебремесло.ру!!
Тег <kbd>
От английского keyboard – клавиатура. Указывает текст вводимый с клавиатуры, или для названия клавиш. Обычно отображается моноширинным шрифтом.
Нажмите <kbd>Ctrl + Z</kbd> для того чтобы отменить последнее действие.
Тег <q>
Выделяет в тексте цитату. В отличие от тега <cite> цитата обозначенная тегом <q> автоматически берётся браузерами в кавычки.
Как сказал Остап Бендер <q>Лед тронулся! господа присяжные заседатели!</q>
Кстати, есть еще и тег физического форматирования текста <blockquote> данный тег тоже помечает текст как цитату и при этом выделяет его отступами и переносами строк от остального текста.
Пример:
<!DOCTYPE HTML PUBLIC “-//W3C//DTD HTML 4.01 Transitional//EN” “http://www.w3.org/TR/html4/loose.dtd”><html>
<head>
<title>Цитаты</title>
</head>
<body>
<p>Эта цитата создана с помощью тега <strong>логического</strong> форматирования текста <code><b><q></b></code>: <q>Лед тронулся! господа присяжные заседатели..</q> – браузеры автоматически берут такую цитату в кавычки. Кстати выходя за рамки темы, видом кавычек легко управлять с помощью <abbr title=”Cascading Style Sheets”>CSS</abbr> псевдокласса <code>lang</code> и его значения <code>quotes</code> – кавычки.
 </p>
</p><p>Эта цитата создана с помощью тега <strong>логического</strong> форматирования текста <code><b><cite></b></code>: <cite>Лед тронулся! господа присяжные заседатели.. <a href=”#”>Остап Бендер. 12 стульев.</a></cite> – обычно браузерами она отображается курсивом. Второе призвание такого вида цитаты это выполнение роли сноски на другой документ.</p>
<p>А эта цитата создана с помощью тега <strong>физического</strong> форматирования текста <code><b><blockquote></b></code>: <blockquote>Лед тронулся! господа присяжные заседатели..</blockquote> – в основном тексте она выделяется отступами и переносами строк, как правило, такой цитатой помечают длинные куски текста взятые из других источников.</p>
</body>
</html>
Такие вот различия. .
.
Тег <samp>
Обозначает текст, который выводится на экран в результате работы какой-либо программы. Обычно браузерами отображается моноширинным шрифтом.
В процессе решения задачи 2+2 программа выдаст ответ: <samp>4</samp>
Тег <strong>
Выделяет особенно важный фрагмент текста. Обычно отображается полужирным.
<strong>Как создать сайт?</strong> – узнай на Вебремесло.ру!!
Тег <var>
Выделяет текст, как переменную в работе какой либо программы. Обычно браузерами отображается курсивом.
Данная функция использует переменную <var>$count</var>
Ну вот собственно и все теги созданные для логической разметки текста. Примеры показывать не стану, думаю и так всё понятно, а вот несколько полезных советов по разметке текста в документе дам.
Стиль всех тегов как логического, так и физического форматирования текста, великолепно настраивается с помощью средств CSS! Мой Вам совет учите CSS, если до этого момента ещё незнакомы с ним.
 При использовании свойств CSS в работе с текстом Вы забудете про проблему кроссбраузерности т. е. Ваш текст будет отображаться во всех браузерах именно так как нужно Вам, а не так как вздумается браузеру. Кроме того СSS открывает куда более широкие возможности связанные как со стилем текста, так и с дизайном сайта в целом.
При использовании свойств CSS в работе с текстом Вы забудете про проблему кроссбраузерности т. е. Ваш текст будет отображаться во всех браузерах именно так как нужно Вам, а не так как вздумается браузеру. Кроме того СSS открывает куда более широкие возможности связанные как со стилем текста, так и с дизайном сайта в целом.Старайтесь правильно размечать текст на страницах Вашего сайта.. а именно:
Для начала, разбейте весь Ваш текст на параграфы с помощью тега <p> – это облегчит чтение текста как для людей так и для программ, кроме того, позволит Вам в дальнейшем, легко управлять текстом с помощью CSS. Вообще старайтесь не оставлять “голые” слова и предложения, не взятые в какой либо тег форматирования текста.
Соблюдайте значимость заголовков <h2>-<h6> т. е. допустим заголовок страницы берите в тег <h2> подзаголовки в тег <h3> еще менее значимые подзаголовочки в тег <h4> и т.
 д. В идеале на странице должен быть всего один заголовок <h2>, потом текст разбивается несколькими <h3> и далее по значимости заголовков.
д. В идеале на странице должен быть всего один заголовок <h2>, потом текст разбивается несколькими <h3> и далее по значимости заголовков.Используйте теги логической разметки лишь там где они действительно необходимы т. е. не стоит например выделять аббревиатуру с помощью цитаты и наоборот.. на то она и логика что бы всё было логично!!
Используйте <em> и <strong> в тех случаях, если Вы хотите акцентировать внимание на тексте не только людей, но поисковых систем, в иных ситуациях используйте <b> и <i>.
Когда выучите CSS забудьте и выкиньте из головы тег <font> и все его атрибуты!! Им уже давно никто не пользуется, ну за редким исключением конечно..
Возможно, физики обнаружили новую силу природы | Новости
Стандартная модель (СМ) – лучшая на сегодняшний день теория частиц и взаимодействий. Она касается всего, что мы знаем об окружающем нас физическом мире, и к тому же довольно точна. Но результаты новых испытаний на Большом адронном коллайдере (БАК) могут указывать на ее неполноту. Команда исследователей опубликовала статью на сайте препринтов arXiv.org, и ей еще предстоит рецензирование прежде, чем она будет опубликована в официальном научном издании.
Она касается всего, что мы знаем об окружающем нас физическом мире, и к тому же довольно точна. Но результаты новых испытаний на Большом адронном коллайдере (БАК) могут указывать на ее неполноту. Команда исследователей опубликовала статью на сайте препринтов arXiv.org, и ей еще предстоит рецензирование прежде, чем она будет опубликована в официальном научном издании.
СМ описывает три из четырех фундаментальных взаимодействий. Кроме того, она не предоставляет никакого объяснения темной материи, которая преобладает во Вселенной, согласно последним гипотезам, и также не может объяснить каким образом вещество смогло пережить Большой взрыв.
Прелестные кварки (b-кварки) – нестабильные частицы, в среднем существующие в течение примерно 1,5 триллионной секунды до распада на другие частицы. Распад b-кварков можно связать с воздействием на них других частиц и взаимодействий – они «рассыпаются» на маленькие частицы вроде электронов в частности благодаря слабому взаимодействию. Один из способов обнаружения новой силы природы – незначительное изменение частоты распада b-кварков на различные типы частиц.
В статье, опубликованной в марте 2021 года, обсуждался эксперимент на LHCb – одном из четырех гигантских детекторов частиц, регистрирующих результаты столкновений частиц сверхвысоких энергий на БАК. В ней утверждалось, что b-кварки c разной частотой распадались на электроны и их более тяжелых «родственников» — мюоны. Для СМ это было новшеством, так как мюон – это точная копия электрона, разве что в 200 раз тяжелее. То есть, по идее, все силы должны оказывать на электроны и мюоны взаимодействие с равной силой при распаде на них b-кварка.
Однако выяснилось, что распад на мюоны происходил на 15% реже, чем на электроны. Это предполагает присутствие новой силы природы, по-разному воздействующей на электроны и мюоны и, таким образом, влияющей на распад b-кварков.
Все это звучит очень интригующе, но есть одна оговорка: эти результаты пока не определены окончательно. На данный момент, результаты экспериментов имеют погрешность примерно 1 к 1000. Сами физики, занимающиеся изучением элементарных частиц, называют это «тремя сигмами» и считают, что пока еще далеки от достоверного подтверждения своего открытия.
Тем не менее исследователи, работающие на LHCb уверены, что с марта неплохо продвинулись в разгадке неравномерности распадов. Самые последние результаты экспериментов показывают, что распад на мюоны происходит всего на 30% реже, чем на электроны.
Чтобы новые данные были подтверждены, ученым необходимо снизить погрешность до пяти сигм – менее одного шанса на миллион, что это статистическая аномалия.
Презентация двоекнижия Алексея Цвелика и о. Михаила Аксенова-Меерсона
Дорогие друзья, мы собрались, чтобы высказаться о новой книге, или двоекнижии, физика Алексея Цвелика и философа о. Михаила Аксёнова-Меерсона. Один раз я уже о ней высказался, в предисловии. Хорошие книги, однако, предоставляют возможность дать много предисловий и послесловий, хороших и разных, чем и попытаюсь воспользоваться.Каждая книга имеет информационный объем; в данном случае он весьма скромен, как вы видите, чистого текста ~ 250 килобукв. Объем, однако же, имеет и то, о чем книга, ее предмет—и в данном случае он предельно велик: речь идет об отношении между человеком, Вселенной и Богом. Казалось бы, о столь большом предмете, как этот треугольник, всё давно уже сказано, и на много рядов, так что нам остается лишь цитировать тех или других классиков. Цитат у обоих авторов и правда немало, но они все рабочие, а не авторитарные; цитаты работают на оригинальный замысел двоекнижия, подчинены ему.
Казалось бы, о столь большом предмете, как этот треугольник, всё давно уже сказано, и на много рядов, так что нам остается лишь цитировать тех или других классиков. Цитат у обоих авторов и правда немало, но они все рабочие, а не авторитарные; цитаты работают на оригинальный замысел двоекнижия, подчинены ему.
Если попытаться обозначить этот замысел одним заголовком, то я бы предложил, например — космическое познание как откровение о человеке во Вселенной.
Книга Цвелика рисует картину космогенеза, разворачивания во времени порядков вселенной — рождения и усложнения согласованных физической, биологической и когнитивной подсистем космоса. Вся же эта разворачивающаяся гармония обусловлена тем, что вне времени, атемпорально — то есть фундаментальными физическими законами, логико-математическим каркасом Вселенной, благодаря исключительным свойствам которого возможен не только сам космос, но и его познание.
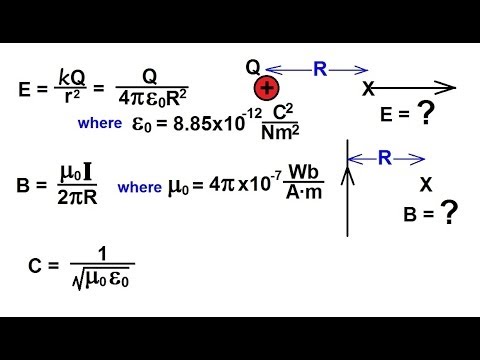
Мы живем в удивительное и странное время—вот что приходит на ум при чтении Цвелика. (-19) метра, т.е. в каком-то невозможном размахе 26+19=45 порядков. Современная физика т.о. демонстрирует, что человек отнюдь не мал во Вселенной, не ничтожен в ней.
(-19) метра, т.е. в каком-то невозможном размахе 26+19=45 порядков. Современная физика т.о. демонстрирует, что человек отнюдь не мал во Вселенной, не ничтожен в ней.
Но это обстоятельство еще надо увидеть. Надо увидеть, что Большому Взрыву, о котором говорит физика, последовали не только появление жизни и мышления, тоже большие взрывы своего рода, но и взрыв 2го уровня, взрыв познания этих больших взрывов. Значение, новизна и сила двоекнижия именно в этой настройке фокуса, на все эти большие взрывы.
Если книга Цвелика посвящена космологии, то книга о. Михаила предлагает историко-философский обзор, каким образом «встреча Нуса и Логоса в премудрости науки» предвосхищалась и отражалась в религиозной и философской мысли. В конце своего размышления о. Михаил выходит к задаче обновленного синтеза веры и разума, задаче для каждого из нас и человечества в целом.
Проблема этого синтеза подчеркивается удивительным и странным характером нашего времени. Самая большая странность, на мой взгляд, состоит в том, что этот неожиданный фантастический успех космического познания не только не привел к общественному осознанию величия человека в космосе, но даже и напротив: влияние учений о бессмысленности мира и ничтожестве человека значительно усилилось среди философов и ученых, включая и ведущих физиков. Этот нигилистический сдвиг не только не идет от научных открытий, но более того — он идет несмотря на них. И книга это замечательно показывает. Книга открывает то великое, что уже произошло и продолжает усиливаться, но свет чего лишь едва начинает доходить до сознания людей, хотя совершили это дело именно они, как говорил по другому случаю Безумец из «Заратустры». Всплеску такого света я и уподобил бы это замечательное двоекнижие.
Этот нигилистический сдвиг не только не идет от научных открытий, но более того — он идет несмотря на них. И книга это замечательно показывает. Книга открывает то великое, что уже произошло и продолжает усиливаться, но свет чего лишь едва начинает доходить до сознания людей, хотя совершили это дело именно они, как говорил по другому случаю Безумец из «Заратустры». Всплеску такого света я и уподобил бы это замечательное двоекнижие.
Электромагнитные волны – Гипертекст по физике
Обсуждение
уравнения Максвелла
Предупреждение: приближается большой, причудливый вывод исчисления. Если вам не нравится векторное исчисление или вы не понимаете его, просто пролистайте все до абзаца перед последним уравнением. Описательный текст довольно легко читать.
Начнем с уравнений Максвелла в производной форме для пустого пространства.
| ∇ · E = 0 | (Гаусс) | |
| ∇ · B = 0 | (без названия) | |
| ∇ × E = | – | ∂ B | (Фарадей) | |
| ∂ т | ||||
| ∇ × B = | мкм 0 ε 0 | ∂ E | (ампер) | |
| ∂ т |
Эти уравнения относятся к первому порядку, что обычно означает, что математика должна быть простой (хорошо!), Но они также связаны, что означает, что это может быть сложно (крысы!). Давайте разделим их, используя этот небольшой трюк. Возьмите завиток обеих сторон законов Фарадея и Ампера. Левая часть каждого уравнения – это ротор ротора, для которого существует особое тождество. С другой стороны, правая часть каждого уравнения представляет собой ротор производной по времени. Мы переключим его на производную локона по времени.
Давайте разделим их, используя этот небольшой трюк. Возьмите завиток обеих сторон законов Фарадея и Ампера. Левая часть каждого уравнения – это ротор ротора, для которого существует особое тождество. С другой стороны, правая часть каждого уравнения представляет собой ротор производной по времени. Мы переключим его на производную локона по времени.
| ∇ × E = | – | ∂ B | ||||
| ∂ т | ||||||
| ∇ × (∇ × E ) = | ∇ × | ⎛ ⎜ ⎝ | – | ∂ B | ⎞ ⎟ ⎠ | |
| ∂ т | ||||||
| ∇ (∇ · E ) – ∇ 2 E = | – | ∂ | (∇ × B ) | |||
| ∂ т | ||||||
| ∇ × B = | мкм 0 ε 0 | ∂ E | |||||
| ∂ т | |||||||
| ∇ × (∇ × B ) = | ∇ × | ⎛ ⎜ ⎝ | мкм 0 ε | 0 | ∂ E | ⎞ ⎟ ⎠ | |
| ∂ т | |||||||
| ∇ (∇ · B ) – ∇ 2 B = | мкм 0 ε 0 | ∂ | (∇ × E ) | ||||
| ∂ т | |||||||
Теперь, если вы посмотрите внимательно, вы увидите, что один член в каждом уравнении равен нулю, а другой можно заменить производной по времени.
| 0 – ∇ 2 E = – | ∂ | ⎛ ⎜ ⎝ | мкм 0 ε | 0 | ∂ E | ⎞ ⎟ ⎠ | |
| ∂ т | ∂ т | ||||||
| 0 – ∇ 2 B = μ 0 ε 0 | ∂ | ⎛ ⎜ ⎝ | – | ∂ B | ⎞ ⎟ ⎠ |
| ∂ т | ∂ т |
Давайте немного очистим его и посмотрим, что у нас получится.
| ∇ 2 E = μ 0 ε 0 | ∂ 2 | E |
| ∂ т 2 |
| ∇ 2 B = μ 0 ε 0 | ∂ 2 | B |
| ∂ т 2 |
Эти уравнения теперь разделены ( E и B имеют свои собственные частные уравнения), что, безусловно, упрощает ситуацию, но в процессе мы изменили их порядок с первого на второй (обратите внимание на все квадраты). Я знаю, что говорил ранее, что с более низким порядком легче работать, но эти уравнения второго порядка не так сложны, как кажутся. Повышение порядка не усложнило дело, а сделало интереснее.
Я знаю, что говорил ранее, что с более низким порядком легче работать, но эти уравнения второго порядка не так сложны, как кажутся. Повышение порядка не усложнило дело, а сделало интереснее.
Вот один набор возможных решений.
| E ( x , t ) = E 0 sin [2π ( футов – | x | + φ)] ĵ |
| λ |
| B ( x , t ) = B 0 sin [2π ( футов – | x | + φ)] k̂ |
| λ |
Этот конкретный пример является одномерным, но есть и двухмерные решения – многие из них.Интересные имеют электрические и магнитные поля, которые меняются во времени. Затем эти изменения распространяются с конечной скоростью. Таким решением является электромагнитная волна .
Таким решением является электромагнитная волна .
Рассмотрим более подробно наше возможное решение. Найти вторые производные электрического поля по пространству и времени…
| ∇ 2 E = – | 4π 2 | E 0 sin [2π ( футов – | х | + φ)] ĵ | |
| λ 2 | λ | ||||
| ∂ 2 | E = – 4π 2 f 2 E 0 sin [2π ( футов – | х | + φ)] ĵ |
| ∂ т 2 | λ |
и подставим их обратно в уравнение в частных производных второго порядка.
| ∇ 2 E = μ 0 ε 0 | ∂ 2 | E |
| ∂ т 2 |
Работайте сначала с левой стороны.
| ∇ 2 E = – | 4π 2 | E 0 sin [2π ( футов – | х | + φ)] ĵ |
| λ 2 | λ |
Работа по правой стороне секунды.
| мкм 0 ε 0 | ∂ 2 | E = μ 0 ε 0 {- 4π 2 f 2 E 0 sin [2π ( футов – | х | + φ)]} ĵ |
| ∂ т 2 | λ |
Отменяет всякую чепуху.
Переставить немного.
Я вижу там скорость волны ( f λ).Мы будем использовать c для этого, поскольку это первая буква латинского слова, обозначающего скорость – celeritas .
Очень интересно.
Учитывая четыре уравнения Максвелла (основанные на наблюдении), мы показали, что как следствие, должны существовать электромагнитные волны. Они могут иметь любую амплитуду E 0 (с B 0 в зависимости от E 0 , как будет показано позже), любую длину волны λ, а также замедляться или опережать любую фазу φ, но они может перемещаться в пустом пространстве только со скоростью одной волны c .
| ||||
|
Говоря словами Максвелла…
Эта скорость настолько близка к скорости света, что кажется, что у нас есть веские основания заключить, что сам свет (включая лучистое тепло и другие излучения, если они есть) является электромагнитным возмущением в форме волн, распространяющихся через электромагнитное поле в соответствии с электромагнитным полем.
законы.
Джеймс Клерк Максвелл, 1865
Это скорость света в вакууме , что означает, что…
- Электромагнитные волны распространяются со скоростью света.
- Свет – это электромагнитная волна.
- Существуют и другие формы электромагнитного излучения.
Это три важных вывода из этого математического экскурса.
история
Давайте вспомним шаги, которые привели к формулировке четырех законов Максвелла.
- Закон Гаусса является расширением закона Кулона и берет свое начало в изучении заряженных объектов и сил притяжения и отталкивания между ними. Говоря обыденным языком, изучение статического прилипания, которое уходит своими корнями в древние времена, когда было замечено, что янтарь, натертый на шерсть животных, притягивает кусочки ткани и бумаги. Греческое слово ηλεκτρον (электрон), обозначающее янтарь, является корнем английских слов «электрический», «электрический», «электричество», «электрик» и т.
 Д.
Д. - Ни один закон не исходит из того факта наблюдений, что у каждого магнита есть как северный, так и южный полюс.Магнитный монополь еще никто не видел. Когда магнит ломается, у него всегда есть северный и южный полюс. Это верно вплоть до субатомного уровня. Из этого наблюдения мы можем сделать вывод, что силовые линии магнитного поля должны образовывать непрерывные петли. Изучение магнетизма восходит к тому времени, когда магнитные породы были впервые обнаружены людьми по всему миру – особенно за пределами древнегреческого города Магнезия, который является корнем английского слова магнетизм.
- Закон Фарадея касается наведенных электрических токов.Имея проволочную петлю и магнит, можно заставить ток течь через петлю, перемещая петлю или перемещая магнит. Статические заряды, изученные Гауссом, Кулоном и Франклином, можно заставить двигаться с помощью необычных камней, найденных на землях старой Греческой Империи.
- Закон Ампера первоначально имел дело с магнетизмом, возникающим из-за движущихся зарядов.
 Пропустите заряды по проводу – и вы сделали магнит – электромагнит. Ключевой вывод Максвелла заключался в том, что пространство между двумя параллельными металлическими пластинами в процессе зарядки будет вести себя так же, как пространство вокруг токоведущего провода.Есть магнетизм, который возникает от электрических токов (например, ток через рабочий электромагнит), и магнетизм, который возникает от токов смещения (например, изменяющееся электрическое поле в конденсаторе, который только что был включен или выключен).
Пропустите заряды по проводу – и вы сделали магнит – электромагнит. Ключевой вывод Максвелла заключался в том, что пространство между двумя параллельными металлическими пластинами в процессе зарядки будет вести себя так же, как пространство вокруг токоведущего провода.Есть магнетизм, который возникает от электрических токов (например, ток через рабочий электромагнит), и магнетизм, который возникает от токов смещения (например, изменяющееся электрическое поле в конденсаторе, который только что был включен или выключен).
Это последний закон в списке – закон Ампера, измененный Максвеллом, – это ключ. Изменяющееся электрическое поле может создавать магнитное поле так же, как электрический ток может создавать магнитное поле. Таким образом, электрические заряды не должны были течь или даже существовать.Изменяющееся электрическое поле само по себе генерирует изменяющееся магнитное поле. Это приведет к изменению электрического поля, что приведет к изменению магнитного поля и так далее – все это улетит в пустое пространство со скоростью света.
Последствия огромны. Возможно, существуют другие формы электромагнитных волн, невидимые человеческому глазу. Уравнения не накладывают ограничений на длину волны или частоту. Единственное требование – они распространяются со скоростью света в вакууме.
Эти выводы были сделаны в 1864 году, еще до появления каких-либо экспериментальных доказательств существования невидимых электромагнитных волн. До Максвелла был свет и ничего больше. Теперь у нас есть неограниченный электромагнитный спектр, который включает радиоволны, микроволны, инфракрасный, видимый свет, ультрафиолет, рентгеновские лучи и гамма-лучи. Возможно, самое удивительное в этой истории не то, что Максвелл показал, что свет был электромагнитной волной, а то, что он наткнулся на нее. Это не было его целью. Это было непредвиденное последствие.Еще раз процитирую Максвелла…
Значение [ c ] было определено путем измерения электродвижущей силы, с которой был заряжен конденсатор известной емкости, и затем разряда конденсатора через гальванометр, чтобы измерить количество электричества в нем в электромагнитном измерении.
Единственное, что использовали свет в эксперименте, – это видеть инструменты . Значение [ c ], найденное М. Фуко, было получено путем определения угла, на который вращается вращающееся зеркало, в то время как отраженный от него свет уходил и возвращался по измеренному курсу. Нет смысла делать что-либо из электричества или магнетизма .
Согласование результатов, кажется, показывает, что свет и магнетизм – это воздействия одного и того же вещества, и что свет – это электромагнитное возмущение, распространяющееся через поле в соответствии с электромагнитными законами. [развернуть]
Янтарь, мех животных, камни из Магнезии, проволочные петли и батареи, соединенные с металлическими пластинами. Что еще я пропустил? Голландские господа заворачивают стеклянные банки металлической фольгой и шокируют друг друга; Франклин запускает воздушного змея в ненастный летний полдень; и китайские моряки, ориентирующиеся по компасам.Возможно, вы не увидите этого сегодня, и вы определенно не заметили бы этого в середине 19-го века, но все эти, казалось бы, несвязанные события связаны скоростью света. Это означает, что мы должны добавить к списку Ньютона, Снеллиуса, Ферма и всех остальных, наблюдающих, как свет преломляется сквозь стекло; Двухщелевой аппарат Юнга; и Галилей со своим телескопом, и это лишь некоторые из них. Хотя никто из них в то время этого не знал, все они работали над одним и тем же огромным проектом – изучением электромагнетизма.
Это означает, что мы должны добавить к списку Ньютона, Снеллиуса, Ферма и всех остальных, наблюдающих, как свет преломляется сквозь стекло; Двухщелевой аппарат Юнга; и Галилей со своим телескопом, и это лишь некоторые из них. Хотя никто из них в то время этого не знал, все они работали над одним и тем же огромным проектом – изучением электромагнетизма.
Остальное уже история…
- Джеймс Клерк Максвелл (1831–1879) Шотландия – Англия
Прогнозирование электромагнитных волн - Генрих Герц (1857–1894) Германия
Экспериментальное подтверждение радиоволн (передатчик-приемник с искровым разрядником) - Гульельмо Маркони (1874–1937) Италия
Первая трансатлантическая передача кода Морзе (из Англии в Ньюфаундленд) - Реджинальд Фессенден (1866–1932) Канада – Бермудские острова
Первое радиовещание с амплитудной модуляцией (AM) - Филон Т.Фарнсворт (1906–1971) США
Первая полностью электронная телевизионная передача - Эдвин Ховард Армстронг (1890–1954) США
Первое радиовещание с частотной модуляцией (FM)
энергия, мощность и давление
Электрическое поле полностью описывает электромагнитную волну в свободном пространстве. Магнитное поле связано с электрическим полем простым соотношением. Начнем с закона Фарадея.
Магнитное поле связано с электрическим полем простым соотношением. Начнем с закона Фарадея.
| ∇ × E = – | ∂ B |
| ∂ t |
Сначала работайте с левой стороны.Подставим одномерное волновое уравнение для электричества и найди его ротор.
| ∇ × E = | ∇ × | { E 0 sin [2π ( футов – | х | + φ)] ĵ } | |
| λ | |||||
| ∇ × E = | – | 2π | E 0 cos [2π ( футов – | х | + φ)] k̂ |
| λ | λ |
Работа по правой стороне секунды.Подставьте одномерное волновое уравнение для магнетизма и найдите его производную по времени.
| ∂ | B | = – | ∂ | { B 0 sin [2π ( футов – | х | + φ)] | k̂ } |
| ∂ т | ∂ т | λ | |||||
| ∂ | B | = – | 2π f | B 0 cos [2π ( футов – | х | + φ)] | k̂ |
| ∂ т | λ |
Уравняйте обе стороны.Отмените косинусные члены и некоторые другие вещи.
Переставить, чтобы он выглядел красиво…
, а затем вспомним, что f λ – это скорость света.
Ну, на самом деле мы исключили слишком много вещей. Это соотношение справедливо для всех значений поля, а не только для максимума. Отношение электрического поля к магнитному в электромагнитной волне в свободном пространстве всегда равно скорости света.
Отношение электрического поля к магнитному в электромагнитной волне в свободном пространстве всегда равно скорости света.
Затем эти знания можно использовать для небольшого упрощения ситуации с плотностью энергии.Начните с плотности магнитной энергии и замените ее выражением, содержащим электрическое поле.
| η B = | 1 | B 2 = | 1 | ⎛ ⎜ ⎝ | E 2 | ⎞ ⎟ ⎠ |
| 2 мкм 0 | 2 мкм 0 | в 2 |
Напомним, что скорость света связана с проницаемостью и константами диэлектрической проницаемости.
Итак…
И таким образом…
| η B = | 1 | мкм 0 ε 0 E 2 = | ε 0 | E 2 |
| 2 мкм 0 | 2 |
Знакомо? Это плотность электрической энергии. Для электромагнитной волны в свободном пространстве половина энергии находится в электрическом поле, а половина – в магнитном поле
Для электромагнитной волны в свободном пространстве половина энергии находится в электрическом поле, а половина – в магнитном поле
| η = | η E | + | η B | |||
| η = | ε 0 | E 2 | + | ε 0 | E 2 | |
| 2 | 2 | |||||
Это дает нам это компактное уравнение для полной плотности энергии электромагнитной волны…
η = ε 0 E 2
или этот, если вы предпочитаете формулировать вещи в терминах магнитного поля…
Это интересный и простой набор соотношений, но имейте в виду, что он работает только для электромагнитных волн в свободном пространстве. В среде все по-другому, и электрическое и магнитное поля могут иметь любые значения, если они статичны (то есть нет ускоряющих зарядов).
В среде все по-другому, и электрическое и магнитное поля могут иметь любые значения, если они статичны (то есть нет ускоряющих зарядов).
Поскольку волны распространяются в пространстве и времени, плотность энергии часто оказывается более полезным понятием, чем энергия. В более широком смысле, мощность волны, вероятно, следует заменить более полезным понятием ее плотности мощности. Поскольку содержание энергии волны заполняет объем пространства, имеет смысл определить плотность энергии как энергию на объем.
Поскольку сила – это энергия в движении, понятие силы, существующей в месте, не имеет особого смысла. Вместо этого мы должны говорить о мощности, доставленной на место. Граница между одним местом и другим описывается областью. В чем разница между пребыванием внутри комнаты и вне комнаты? Ответ в том, на какой стороне дверного проема вы находитесь. Как описывается это открытие? По площади. Разумное определение плотности мощности – это мощность на площадь.
Эта величина также известна как освещенность , поток излучения , мощность излучения , поток энергии или плотность потока энергии . Ни одно из этих слов не начинается с «s», поэтому мне неизвестно, почему в качестве символа был выбран S . Поскольку я также видел это количество, представленное символами q , j и E , возможно, я действительно должен сказать здесь, что я не знаю, почему я выбрал S .Я предполагаю, что это то, как я выучил это давным-давно, и, следовательно, вы тоже должны это изучить.
Единицей этой величины является ватт на квадратный метр, не имеющий специального названия.
| ⎡ ⎢ ⎣ | Вт | = | Вт | ⎤ ⎥ ⎦ |
| м 2 | м 2 |
Мы начнем анализ этой величины с напоминания об определениях мощности (скорости преобразования энергии) и плотности энергии (энергии на единицу объема).
| S = | п | = | 1 | U | = | 1 | η В | ||
| А | А | т | А | т |
А теперь представьте луч света, радиоволны или любой другой вид электромагнитной волны, падающий на поверхность.Энергия, которая падает на эту поверхность за определенный промежуток времени, заполняет столб, который движется в пространстве со скоростью света. Объем этой колонны равен площади ее основания, умноженной на ее длину. Площадь может быть любого произвольного размера, поскольку здесь мы имеем дело с плотностью, а длина этого столбца определяется временем, которое требуется столбцу, чтобы приземлиться на поверхности при движении со скоростью света. Позвольте мне показать вам, о чем я говорю, с помощью математических символов.
| S = | η В | = | η ( Aℓ ) | = | η ( Закон ) | = η с |
| При | при | при |
Следующие шаги включают замену η и c особыми отношениями, описанными ранее.
| S = η c = | ⎛ ⎜ ⎝ | 1 | В 2 | ⎞ ⎟ ⎠ | E | |
| мкм 0 | В |
И вот что у нас получается…
Конечно, не то, что я ожидал, но это традиционный способ записи плотности мощности электромагнитной волны.Ну, почти. Настоящее уравнение записывается в векторной форме так…
и получил странно подходящее имя вектор пойнтинга не потому, что кто-то пошутил о том, как векторы «пойнт», а в честь его первооткрывателя, английского физика Джона Пойнтинга (1852–1914). Вывод Пойнтинга включает векторную математику, которая не подходит для уровня этой книги. (Перевод: я не понимаю.)
Вывод Пойнтинга включает векторную математику, которая не подходит для уровня этой книги. (Перевод: я не понимаю.)
Вектор пойнтинга важен, потому что он выравнивает три вектора электромагнитной волны: электрическое поле, магнитное поле и направление распространения.Эти три вектора взаимно перпендикулярны; то есть каждый перпендикулярен двум другим. Их относительное расположение определяется правилом правой руки перекрестного произведения (то есть; × между E и B в уравнении).
Пример, показанный на диаграмме ниже, соответствует этому правилу. Убедитесь сами. Мысленно выберите пару векторов, выходящих из одной точки на волне. Держите правую руку ровно перед лицом, выставив большой палец сбоку под прямым углом в форме буквы «L».Теперь вращайте руку, пока ваши пальцы не будут указывать в направлении электрического поля, а ладонь – в направлении магнитного поля. Если ваша рука выровнена правильно, вы сможете сложить пальцы так, чтобы они указывали в направлении магнитного поля. (Не двигайте большим пальцем.) Это действие имитирует «пересечение» электрического поля с магнитным полем. Направление этого перекрестного произведения является вектором пойнтинга и указывается большим пальцем. Если вы выполнили это упражнение правильно, ваш большой палец должен быть направлен за пределы экрана к вашему лицу.Ориентация остальной руки зависит от того, совмещали ли вы пальцы с вектором электрического поля, направленным влево или вправо. Один из них удобен для рук, а другой заставляет вас выглядеть так, будто вы занимаетесь какой-то необычной формой йоги.
(Не двигайте большим пальцем.) Это действие имитирует «пересечение» электрического поля с магнитным полем. Направление этого перекрестного произведения является вектором пойнтинга и указывается большим пальцем. Если вы выполнили это упражнение правильно, ваш большой палец должен быть направлен за пределы экрана к вашему лицу.Ориентация остальной руки зависит от того, совмещали ли вы пальцы с вектором электрического поля, направленным влево или вправо. Один из них удобен для рук, а другой заставляет вас выглядеть так, будто вы занимаетесь какой-то необычной формой йоги.
Как мы узнали в предыдущем разделе этой книги, волны передают энергию и импульс, не передавая никакой массы. Это может показаться очевидным для механических волн (особенно если вас когда-либо сбивала с толку сильная океанская волна), но когда в последний раз вы когда-либо чувствовали давление радиоволны или сбивание лучом света? Мы просто не испытываем радиационного давления.Тем не менее, это то, что мы можем вычислить.
Начните с определения давления (сила на площадь) и работы (сила, умноженная на расстояние), и посмотрите, что произойдет.
| п. = | F | = | F | ℓ | = | U | = η | |
| А | А | ℓ | В |
Ну вот интересно.Давление и плотность энергии – это одно и то же. Единственная проблема в том, что для волн не существует единого значения плотности энергии. Это величина, которая колеблется во времени и пространстве. Что нам здесь действительно нужно, так это усредненные по времени значения. Такие количества обозначаются символом между двумя угловыми скобками. Вот так…
| п. = | ⟨ F ⟩ | = | ⟨ F ⟩ | ℓ | = | ⟨ U ⟩ | = η⟩ | |
| А | А | ℓ | В |
Вот как вы это пишете, и вот как вы это делаете для случая простой синусоидальной волны. Интегрируйте уравнение плотности энергии за один период.
Интегрируйте уравнение плотности энергии за один период.
| ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Это может выглядеть как большой средний интеграл, но это не так.Подумайте, как выглядит кривая синус-квадрат. Это волнистая линия, которая идет вверх и вниз между 0 и 1. За один полный цикл она разбивает ящик высотой 1 на T шириной пополам. Это дает нам…
| п. = | ε 0 E 0 2 | т | = ½ε 0 E 0 | |
| т | 2 |
, в котором вы можете распознать половину плотности энергии.
P = ½η
Радиационное давление электромагнитной волны не равно ее плотности энергии, оно равно половине ее плотности энергии. Я верю в эту математику, но думаю, мне еще нужно доказать себе, что это уравнение реально. Как я уже отмечал ранее, я никогда не чувствовал давления радиоволны или падения луча света. Это должен быть исключительно слабый эффект. Мы подтвердим это с помощью вычислений в практических задачах, сопровождающих это обсуждение.
разное
Нужно ли здесь обсуждать импеданс свободного пространства?
| Z = √ | мкм 0 | = мк 0 в |
| ε 0 |
Покажите, что это ом в качестве единицы
Вычислите это.
| Z = μ 0 c Z = (4π × 10 −7 Vs / Am) (299 792 458 м / с) Z = 376. 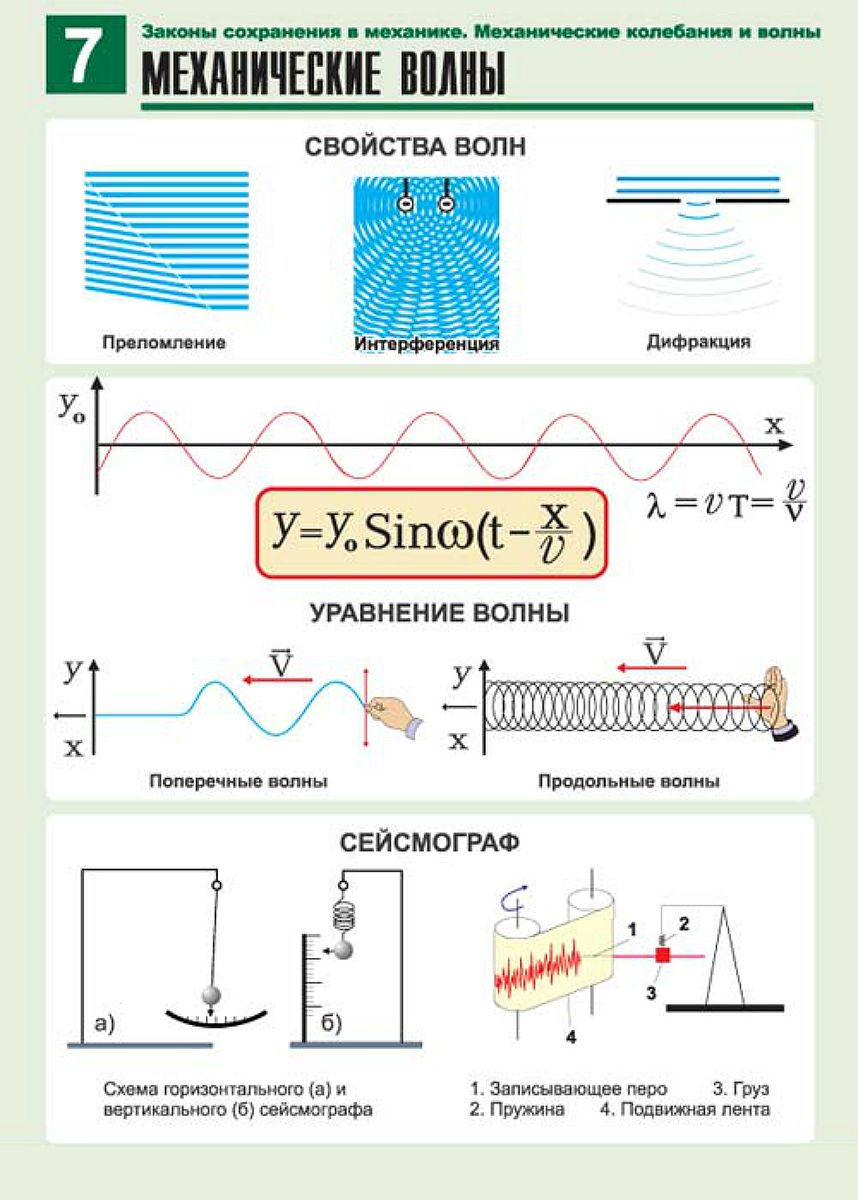 730… Ом 730… Ом |
Электромагнитная физика | geant4.web.cern.ch
НазначениеРабочая группа по электромагнитной (ЭМ) физике разрабатывает и поддерживает подпакеты Geant4 для моделирования электромагнитных взаимодействий заряженных частиц, гамма-излучения и оптических фотонов. Диапазон применимости моделей составляет от порога до 10 ПэВ . «Стандартные» физические подходы оптимальны для приложений с высокими и средними энергиями. Подбиблиотека “low-energy” разработана для приложений с низким энергопотреблением.Группа поддерживает также компоненты для справочных списков Physics Lists и ряд расширенных примеров.
Рабочая группа EM активно разрабатывает физические модели и соответствующее программное обеспечение для приложений физики высоких энергий, прежде всего для экспериментов на LHC (CERN). В июне 2019 года бывшая рабочая группа по низкоэнергетической электромагнитной физике присоединилась к группе EM и продолжает разработку и поддержку различных приложений Geant4. Часть членов рабочей группы EM являются активными разработчиками проекта Geant4-DNA по моделированию биологических эффектов радиации.Другая часть – члены группы тестирования медицинской физики Geant4 (G4MSBG), которая была создана для консолидации системы тестирования Geant4 для приложений медицинской физики. Группа EM также работает в тесном сотрудничестве с ESA-ESTEC над космическими научными приложениями Geant4.
Часть членов рабочей группы EM являются активными разработчиками проекта Geant4-DNA по моделированию биологических эффектов радиации.Другая часть – члены группы тестирования медицинской физики Geant4 (G4MSBG), которая была создана для консолидации системы тестирования Geant4 для приложений медицинской физики. Группа EM также работает в тесном сотрудничестве с ESA-ESTEC над космическими научными приложениями Geant4.
- Джон Апостолакис (ЦЕРН, Женева, Швейцария) – оценка проекта, производительность
- Александр Багуля (Физический институт им. П.Н. Лебедева, Москва, Россия) – валидация, ионизация
- Дени Бернар (IN2P3 / LLR, Париж, Франция) – преобразование гаммы
- Алексей Богданов (МИФИ, Москва, Россия) – мюоны
- Мари-Клод Бордаж (CNRS, Тулуза, Франция) – Geant4-DNA
- Джереми Браун (Технический университет, Делфт, Нидерланды) – Geant4-DNA, Compton
- Игорь Булыженков (МФТИ, Москва, Россия) – высокоэнергетические процессы
- Marilena Bandieramonte (ЦЕРН, Женева, Швейцария) – фотоэффект, векторный прототип
- Helmut Burkhardt (ЦЕРН, Женева, Швейцария) – редкие процессы, заявки на CLIC
- Херардо Депаола (FAMAF, Аргентина) – поляризованные процессы
- Паоло Дондеро (SWHARD, Генуя, Италия) – валидация
- Sabine Elles (LAPP, Анси, Франция) – проверка
- Bruce Faddegon (UCSF, CA, USA) – медицинские приложения
- Зиад Фрэнсис (Университет Св.
 Иосифа, Ливан) – Geant4-DNA
Иосифа, Ливан) – Geant4-DNA - Кшиштоф Гензер (Фермилаб, США) – исследования и разработки в области оптики
- Мигель Антонио Кортес Хиральдо (Севильский университет) – Geant4-DNA, медицинские приложения
- Владимир Гричин (ЦЕРН – Физический институт им. П.Н. Лебедева, Москва, Россия) – Рентгеновские лучи, газовые детекторы
- Susanna Guatelli (Университет Вуллонгонг, Австралия) – медицинское приложение
- Пол Гейе (МГУ, Мичиган, США)
- Peter Gumplinger (TRIUMF, Ванкувер, Канада) – оптический, рентгеновский
- Александр Ховард (Имперский колледж, Лондон, Великобритания) – оптические приложения
- Себастьян Инсерти (CNRS, Париж, Франция) – заместитель координатора, член SB, Geant4-DNA
- Владимир Иванченко (ЦЕРН; РАН, Томский государственный университет, Россия) – координатор , член СО
- Сун Юн Джун (Фермилаб, США) – исследования и разработки в области оптики
- Омран Кадри (Университет короля Сауда, Саудовская Аравия) – множественное рассеяние, проверка
- Матье Карамитрос (Пессак, Франция) – Geant4-DNA
- Иоанна Кириаку (Университет Янины, Греция) – Geant4-DNA
- Натанаэль Лампе (Мельбурн, Австралия) – Geant4-DNA
- Се Бён Ли (NCC, Корея) – медицинские приложения, Geant4-DNA
- Zhuxin Li (IN2P3, Бордо, Франция) – модели с низким энергопотреблением
- Франческо Лонго (INFN, Триест, Италия) – космические приложения
- Мишель Мэр (LAPP, Анси, Франция) – проверка
- Альфонсо Мантеро (SWHARD, Генуя, Италия) – валидация
- Mihaly Novak (ЦЕРН, Женева, Швейцария) – модели EM, проверка TF
- Лучано Пандола (INFN / LNS, Катания, Италия) – заместитель координатора, член SB, Penelope models
- Giada Petringa (INFN / LNS, Катания, Италия) – медицинские приложения
- Ян Перро (IRSN, Париж, Франция) – Geant4-DNA
- Иван Петрович (Институт Винча, Белград, Сербия) – Geant4-DNA
- Mélanie Raine-Theillet (CEA, Париж, Франция) – модели с низким энергопотреблением
- Хосе Рамос-Мендес (UCSF, Калифорния, США) – Geant4-DNA
- Miguel Reis (ITN, Португалия) – модели с низким энергопотреблением
- Александра Ристич-Фира (Институт Винча, Белград, Сербия) – Geant4-DNA
- Джорджио Руссо (INFN / LNS, Катания, Италия) – медицинские приложения
- Доусацу Саката (НИРС, Тиба, Япония) – Geant4-DNA
- Джованни Сантин (ESA / ESTEC, Нидерланды) – Geant4-DNA
- Дарен Соки (Varian Medical Systems, Пало-Альто, США) – заместитель координатора, член SB , валидация, электроны
- Игорь Семенюк (IN2P3 / LLR, Париж, Франция) – преобразование гаммы
- Jae Ik Shin (NCC, Корея) – медицинские приложения
- Ук Гын Шин (Университет Бордо, Франция) – Geant4-DNA
- Тосиюки Тосито (Бюро здравоохранения и социального обеспечения, Нагоя, Япония) – ионы, проверка
- Хоанг Тран (IRSN, Париж, Франция) – Geant4-DNA
- Ласло Урбан (G4AI, Будапешт, Венгрия) – стандартные процессы
- Кармен Виллаграса (IRSN, Париж, Франция) – Geant4-DNA
- Hans-Joachim Wentzel (Fermilab, США) – исследования и разработки в области оптики
- Джулия Ярба (Фермилаб, США) – R&D оптики
- Tomohiro Yamashita (HIBMC, Hyogo, Japan) – валидация
- Анна Заборовска (ЦЕРН) – быстрое моделирование
- Geant4 для VMware и VirtualBox – это ссылка на бесплатный и готовый к использованию программный пакет, позволяющий полностью запускать Geant4 (так называемую виртуальную машину Geant4) и связанные инструменты на ПК с Windows или Mac под VMware или VirtualBox. программное обеспечение без необходимости локальной установки Geant4.
- Следите за обновлениями этой виртуальной машины в Geant4VM в Твиттере.
Группа предоставляет и поддерживает следующие категории расширенных примеров:
- электромагнитный
- экзотическая физика
- медицинский
- оптический
- поляризация
Мы предлагаем нашим пользователям посетить Форум, который является лучшим способом обмена информацией.
Фундаментальная физика электромагнитных волн
\ n \ t \ t \ t2. Предпосылки
\ n \ t \ t \ tЧасто говорят, что для того, чтобы успешно ориентироваться в будущем, нужно понимать прошлое. Фундаментальная физика электромагнитных волн не исключение из этой мудрости. Фактически, понимание истоков физики электромагнитных волн, истоков которой связано с электромагнитными волнами, имеет жизненно важное значение для понимания происходящей в настоящее время научной революции.
\ n \ t \ t \ t \ n \ t \ t \ t \ t2.1. Физика в эпоху разума и просвещения
\ n \ t \ t \ t \ tГалилео Галилей (1564 – 1642) был одним из самых влиятельных ученых тысячелетия, однако он жил во времена протестантской реформации набирала обороты, и Европа была в смятении. Католическая церковь теряла контроль над большей частью северной Европы, и бушевала Тридцатилетняя война. Галилей проживал на итальянском полуострове, где Церковь поддерживала сильную власть, и он не мог полагаться на защиту реформаторов в других частях Европы.Тем не менее, несмотря на то, что «языческие» верования, связанные с частотами и явлениями, связанными с резонансами, были запрещены церковью на протяжении веков, Галилей проводил исследования собственных резонансных частот в маятниковой системе. (Мортенсон, 2010b).
\ n \ t \ t \ t \ tВ 1632 году Галилей опубликовал свой «Диалог» и смелым ходом описал механику собственных резонансных частот, написав: « Маятник совершает свои колебания с одной и той же частотой ». и «у самого маятника есть время своих колебаний… заранее заданное… [и] невозможно заставить его двигаться в любой другой период, кроме того… который для него естественен. »(Галилей, 1632). Он описал резонансные ускоряющие силы, создаваемые точными импульсами его дыхания, заявив:« , дуя на [маятник, который можно] придать Движение, и Движение значительно велико, повторяя взрывы, но только под Временем, собственно принадлежащим его Вибрациям ». Таким образом, Галилей предоставил одно из первых задокументированных описаний резонанса, а именно увеличения амплитуды и энергии колебаний системы, когда приложенная вибрация, движение или энергия соответствуют собственной частоте системы.К сожалению, Церковь оказалась менее любезной, чем ожидал Галилей. Его признали виновным в ереси и поместили под домашний арест на всю оставшуюся жизнь.
\ n \ t \ t \ t \ tПьер де Ферма (1601 – 1665) был французским адвокатом, которому было около тридцати лет, когда Галилея обвинили в ереси. Хотя личным увлечением Ферма была математика, он прекрасно понимал, что изучение определенных математических предметов может быть очень опасным. Таким образом, Ферма тайно занимался своей страстью, делая заметки на полях книг в своей частной библиотеке.Один набор примечаний представлял собой уравнение резонанса, демонстрирующее, что по мере приближения скорости механической вибрации (например, вдоха) к естественной скорости вибрации тела (например, качания маятника) амплитуда колебаний в тело увеличилось (см. также рисунок 1 ниже):
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ ty = 1 / \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t (\ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t1 + x \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t) \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE1
\ n \ t \ t \ t \ tРисунок 1.
Резонансная кривая Ферма показывает увеличение амплитуды колебаний при приложении сил на собственных резонансных частотах («v \ n \ t \ t \ t \ t \ t \ t \ t \ t r »).
\ n \ t \ t \ t \ tБлестящий молодой Исаак Ньютон (1643 – 1727) написал свои знаменитые «Начала », , описывая свои три (3) закона движения примерно во время смерти Ферма. (Ньютон, 1898 г.) Религиозный климат в Англии в то время был довольно хаотичным, и Ньютон ждал еще двадцать (20) лет, чтобы опубликовать свои «Начала ». Его второй закон (сила равна массе, умноженной на ускорение) лег в основу еще одного резонансного уравнения:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tA \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ т \ т \ т \ т \ т \ т \ т \ т \ т | \ п \ т \ т \ т \ т \ т \ т \ т \ т \ т \ т \ п \ т \ т \ т \ т \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t- \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ to \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ т \ т \ т \ т | \ п \ т \ т \ т \ т \ т \ т \ т \ т \ т \ п \ т \ т \ т \ т \ т \ т \ т \ т \ п \ т \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE2
\ n \ t \ t \ t \ tгде «A» i s амплитуда колебаний системы, «a» – это ускорение колебаний системы (вызванное в случае Галилея силой его небольших вдохов), « ν \ n \ t \ t \ t \ t \ t r »- это резонансная или собственная частота системы, а« ν \ n \ t \ t \ t \ t \ t o »- частота внешней силы, приложенной к системе.Как показывает это второе уравнение резонанса, внешняя сила, приложенная с частотой, которая либо намного выше, либо намного ниже, чем собственная резонансная частота системы, дает большой знаменатель и, следовательно, малую амплитуду. И наоборот, чем ближе частота внешней силы к резонансной собственной частоте, тем меньше становится знаменатель. Возникают очень большие амплитуды. Когда внешняя частота точно совпадает с резонансной частотой системы, амплитуда теоретически равна бесконечности (Рисунок 2.).
\ n \ t \ t \ t \ tРисунок 2.
Графическое представление уравнения резонансной амплитуды (уравнение 2). Резонансная частота «v \ n \ t \ t \ t \ t \ t \ t \ t r \ n \ t \ t \ t \ t \ t \ t \ t» находится в начале координат, а входная частота внешняя сила «v \ n \ t \ t \ t \ t \ t \ t \ t o \ n \ t \ t \ t \ t \ t \ t \ t» меняется. Когда входная частота приближается к резонансной частоте, амплитуда приближается к бесконечности.
\ n \ t \ t \ t \ tНьютон отличал силу, прилагаемую ускоряющимся телом, от энергии просто движущегося тела (которое он назвал vis viva) произведением массы и скорости:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ ti \ n \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ t \ п \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ ti \ n \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ t m v \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE3
\ n \ t \ t \ t \ tгде «m» – масса, а v – скорость.Это привело к большой полемике vis viva несколько десятилетий спустя (см. Ниже). К 1704 году Ньютон опубликовал свой трактат « Opticks », в котором он предложил корпускулярную теорию света, а именно, что свет состоит из крошечных частиц, движущихся по прямым линиям. Предвосхищая более поздние работы Эйнштейна, Ньютон заявил, : «Разве грубые тела и свет не могут быть преобразованы друг в друга … и не могут ли тела получать большую часть своей активности от частиц света, которые входят в их состав?» \ n \ t \ t \ t \ t
\ n \ t \ t \ t \ tНесколько десятилетий спустя разгорелась великая полемика vis viva с предложением Джованни Полени (1683–1761) о том, что vis viva energy был пропорционален произведению массы и квадрата скорости, что противоречило Ньютону.Вскоре к дебатам присоединились Лейбниц, Гюйгенс и другие. Голландский физик Виллем Грейвсанде (1688–1742) провел тщательные эксперименты и пришел к выводу, что энергия движения «соответствует [s] Отношению, составленному из масс, и квадратам скоростей» (подчеркнуто добавлено) . (Gravesande, 1747) Известный французский ньютоновский ученый Эмили дю Шатле (1706 – 1749) в своей книге 1740 года «Institutions Physiques» утверждала, что vis viva энергия пропорциональна произведению массы и скорости в квадрате, исходя из о кропотливых экспериментах Грейвсанда.
\ n \ t \ t \ t \ tПока бушевала дискуссия о vis viva , итальянская вундеркинда Мария Гаэтана Агнеси (1718–1799) опубликовала свою книгу 1748 года по исчислению и дифференциальным уравнениям, организовав работу Ферма, Ньютон, Лейбниц и другие. (Agnesi, 1748) Она расширила резонансную кривую Ферма, предоставив подробное геометрическое доказательство и третье уравнение резонанса:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ ty = ha \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t / a \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t + x \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE4
\ n \ t \ t \ t \ t, где «h» – высота кривой, а «a» – полуширина на полувысоте.Ее книга сразу произвела фурор во всей Европе, и резонанс стал широко известным научным принципом, несмотря на ошибку английского перевода, в результате которой кривая резонанса стала известна как «Ведьма Агнеси». (Спенсер, 1940)
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t2.2. Физика девятнадцатого века
\ n \ t \ t \ t \ tК девятнадцатому веку блестящий Жозеф Луи Лагранж (1736 – 1813) организовал работы почти всех известных ученых по вопросам скорости, инерции, силы, энергии и т. Д. и динамика в его «Аналитическая механика» .(Лагранж, 1811 г.) Лагранж заявил, что для тела с постоянной скоростью его энергия ( vis viva ) равна «mv 2 », в результате чего « исчисляется исключительно силами инерции тел». И наоборот, энергия, необходимая для ускорения тела, была функцией расстояния, на котором действовала сила « F δs ». Лагранж объяснил, что все системы демонстрируют динамическое равновесие между vis viva постоянной скорости и силами ускорения : «Сумма этих двух величин, приравнивая их к нулю, составляет общую формулу динамики … когда равновесие не удерживать, тела должны обязательно двигаться из-за всех или некоторых сил, которые действуют на них. В целях систематического объяснения аналитической механики Лагранж заявил, что он предположил, что ускорение всегда происходит в период времени, по крайней мере равный единице времени для скорости. Его предположение эффективно фиксировало временной интервал ускорения на «одной секунде» и исключало ускорения, происходящие менее чем за одну секунду.
\ n \ t \ t \ t \ tЛагранж также обратился к динамике резонанса, используя математическую функцию: «в случае, когда та же функция является максимальной, равновесие не будет устойчивым, и после нарушения системы система начнет с выполнения довольно небольшие колебания, но амплитуда [резонансных] колебаний будет постоянно расти.» Он включил дополнительные разделы на « гармоники [в] узлах колебаний »,« резонанс звучного тела » и резонансную динамику колебаний маятника.
\ n \ t \ t \ t \ tСорок лет спустя Гаспар-Гюстав де Кориолис (1792–1843) много позаимствовал у Лагранжа из его популярного учебника по инженерному делу. (Coriolis, 1829) Кориолис принял предположение Лагранжа относительно временного интервала ускорения для простоты и ясно объяснил, что это предположение исключает рассмотрение «мгновенных» эффектов .Без этого предположения потребовались бы отдельные временные переменные для скорости и ускорения. Кориолис также ввел понятие кинетической энергии как удобство в инженерных приложениях, связанных с гравитационными эффектами: « масса, умноженная на половину квадрата скорости [½mv \ n \ t \ t \ t \ t \ t 2 \ n \ t \ t \ t \ t \ t ] … внесет больше простоты … поскольку множитель ‘½ (v \ n \ t \ t \ t \ t \ t 2 \ n \ t \ t \ t \ t \ t / g) ‘- это не что иное, как высота, с которой тяжелое тело … должно упасть, чтобы набрать скорость’ v ‘». Остро осознавая, что его формула кинетической энергии не применима к объектам, движущимся с постоянной скоростью, Кориолис писал, что когда «скорости стали такими же… [кинетическая энергия] становится [es] нулевой». Однако предостережения Кориолиса вскоре были забыты. К тому времени, когда Джеймс Клерк Максвелл (1831–1879) позже написал свой учебник по основам физики, он ошибочно резюмировал: «Кинетическая энергия тела – это энергия, которой оно обладает благодаря движению…» \ n \ t \ t \ t \ t
\ n \ t \ t \ t \ tМежду тем, междисциплинарный ученый Томас Янг, М.Д. (1773 – 1829) начал анонимно публиковать статьи по физике (чтобы защитить репутацию своей медицинской практики). В конце концов он стал достоянием общественности, и, по словам Янга, его величайшим научным достижением стало создание волновой теории света, основанной на его эксперименте с двойной щелью. Опубликованные ровно через 100 лет после Ньютона Opticks , отчеты Янга о волновой интерференции света в конечном итоге привели к отказу от теории световых корпускул Ньютона. Это привело к развитию веры в то, что материя состоит из мелких частиц, а свет – из непрерывных волн.
\ n \ t \ t \ t \ tДругой междисциплинарный ученый – Герман фон Гельмгольц, доктор медицины (1821 – 1894) – был армейским хирургом, который проводил эксперименты с энергетическими лягушками в своих армейских казармах. Те же самые биомеханические эксперименты привели к его великому трактату о преобразовании и сохранении энергии. (Helmholtz, 1889) Работа Гельмгольца по сохранению энергии стала первым законом термодинамики, а именно, что энергия не создается и не уничтожается, а вместо этого сохраняется и преобразуется из одной формы в другую, «… тепло, электричество, магнетизм, свет, и химическое сродство… от каждого из этих различных проявлений [энергии] мы можем привести в движение любое другое [проявление] ». Гельмгольц тщательно различал между упорядоченной рабочей энергией и неупорядоченной тепловой энергией и учил, что полная энергия системы есть их сумма:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tU \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tA \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t + \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tTS \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ tE5
\ n \ t \ t \ t \ tгде «U» – внутренняя энергия системы, «A» – энергия работы (Гельмгольца), температура «T», энтропия «S» и произведение тепловой энергии «TS».
\ n \ t \ t \ t \ tГельмгольц также много писал о резонансе, который «всегда обнаруживается в тех телах, которые, будучи приведенными в движение любым импульсом, продолжают совершать длинную серию вибраций, прежде чем остановиться. … При условии, что периодичность легких ударов точно такая же, как периодичность собственных колебаний тела, могут возникнуть очень большие и мощные колебания. Но если периодическое время регулярных ударов отличается от периодического времени колебаний, результирующее движение будет слабым или совершенно незаметным.»(Гельмгольц, 1862). Он также описал резонансную связь как« симпатический резонанс ». В конечном итоге Гельмгольц поднялся до самого высокого положения физика в Германии в Берлинском университете, где оказал влияние на многих молодых студентов, включая Макса Планка (1858–1947) и Генриха Герца (1857–1894). (Гельмгольц, 1896 и 1904)
\ n \ t \ t \ t \ tПосле того, как Гельмгольц бросил вызов Герцу, чтобы доказать существование теоретических электромагнитных волн Максвелла, Герцу блестяще это удалось. Новые электромагнитные волны были названы «резонансными волнами Герца» на основе резонансных электрических процессов, которые Герц использовал для их передачи и приема.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t2.3. Квантовая революция
\ n \ t \ t \ t \ tК концу 1800-х годов молодой Макс Планк сам был профессором Берлинского университета и занимался теоретической работой по электромагнитным волнам Герца. (Planck 1896 и 1897) Планк моделировал электромагнитные волны, с одной стороны, как резонансные волны, способные производить упорядоченную рабочую энергию «A», а с другой стороны, как электромагнитные волны, создаваемые случайными хаотическими движениями, основанными исключительно на температуре «TS» (черное тело радиация).(Planck, 1900) В конце 1900 года Планк добился успеха в изучении случайных тепловых электромагнитных волн, когда эмпирически определил правильную формулу для излучения абсолютно черного тела. Однако правильный вывод этого эмпирического уравнения был совершенно другим делом и, согласно Планку, был самой тяжелой работой в его жизни. (Planck, 1901 и 1920)
\ n \ t \ t \ t \ tПланк начал с уравнения Гельмгольца (U = A + TS), а затем представил свою бесспорную резонансную гипотезу: ЭМ «резонансные волны Герца» являются упорядоченными и, таким образом, полностью свободны для преобразования в работу и, таким образом, составляют рабочую энергию «А».Затем Планк объяснил, что, поскольку устройство черного тела, используемое в лаборатории, было специально разработано для исключения всех резонансных электромагнитных волн, он мог предположить, что в устройстве черного тела не было рабочей энергии. Согласно Планку, «А» равнялось нулю, и, таким образом, «вся проблема сводится к определению S как функции от U». Он позаимствовал метод Вильгельма Вина для определения плотности энергии (который устранил временную переменную), а также в конечном итоге прибег к статистическим методам своего заклятого врага Людвига Больцмана (1844–1906).
\ n \ t \ t \ t \ tКинетическая механика Больцмана была основана на ограничивающем предположении, что все элементы (например, молекулы или атомы) в системе движутся беспорядочно, совершенно беспорядочно. Механика Больцмана была ограничена частью тепловой энергии TS уравнения энергии Гельмгольца и не могла быть применена к упорядоченной рабочей энергии A. Однако устройство черного тела и эксперименты были специально разработаны, чтобы исключить рабочую энергию и измерять только беспорядочную, хаотическую тепловую энергию.Этот факт позволил Планку использовать статистические методы Больцмана в своем выводе черного тела и «определить [e] S [исключительно] как функцию от U». Однако также потребовалось, чтобы Планк представил свою квантовую гипотезу, а именно, что энергия квантуется в небольших однородных количествах. Примечательно, что Планк предположил, что эти небольшие однородные количества энергии были разными для каждой частоты, создавая априорное ограничение, исключающее рассмотрение единицы энергии для электромагнитных волн, аналогичной единице заряда для электронов.Математически квантовая гипотеза Планка приняла форму квантовой формулы, которую Планк принял как данность:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t h \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE6
\ n \ t \ t \ t \ tгде «h» – постоянная действия Планка, 6,626 X 10 – 34 Джоуль секунды.
\ n \ t \ t \ t \ tПланк также рассчитал термодинамическую константу, которая теперь называется постоянной Больцмана:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ п \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t k \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tB \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE7
\ n \ t \ t \ t \ tгде «E» – энергия отдельного элемента (т.е.g., одиночный атом или молекула), основываясь исключительно на ее температуре «T», а «k B » – постоянная Больцмана, 1,38 × 10 −23 Джоулей на градус К на элемент. Так же, как уравнение Гельмгольца дает энергию системы на макроуровне, основанную на ее температуре («TS»), термодинамическое уравнение Планка дает энергию отдельного элемента микромасштаба на основе его температуры («k B T»). Таким образом, постоянная Больцмана представляет собой микромасштабный эквивалент энтропии. Однако Планк никогда не вводил микромасштабный эквивалент рабочей энергии «А»: эксперименты с черным телом исключали рабочую энергию.Это привело к формуле микромасштабной энергии, которая обязательно была неполной для любой системы, в которой присутствовала рабочая энергия.
\ n \ t \ t \ t \ tВ то время как некоторые ученые использовали уравнение черного тела Планка в практических приложениях, его революционная квантовая гипотеза не привлекала особого внимания – то есть до тех пор, пока в 1905 году не были опубликованы собственные революционные статьи Альберта Эйнштейна (1879-1955). (Эйнштейн, 1905 г.) Эйнштейн ухватился за квантовую гипотезу Планка и использовал ее для объяснения ряда необъяснимых явлений, таких как фотоэлектрический эффект и ионизация газов.Он предположил, что взаимодействия электромагнитных волн и материи «кажутся более понятными, если предположить, что энергия света неравномерно распределена в пространстве», например, в небольших частицах или пакетах по линиям «световых корпускул» Ньютона, и поглощается «целыми единицами» или «квантами».
\ n \ t \ t \ t \ tХотя работы Эйнштейна весьма противоречивы, они привлекли внимание к квантовой гипотезе и формуле Планка. Несколько лет спустя Нильс Бор (1885–1962) применил квантовую формулу Планка в своей теории атома водорода.(Бор, 1913). Противоречие все еще бушевало, и Роберт Милликен (1858-1963) провел серию тщательных экспериментов, проверяющих справедливость постоянной Планка и того, что он назвал «безрассудными» теориями Эйнштейна относительно квантов энергии и фотоэлектрических явлений. (Милликен, 1916)
\ n \ t \ t \ t \ tМилликен, хорошо знакомый с принятой Планком гипотезой резонанса, различал фотоэлектрический эффект как упорядоченную работу выхода, а не тепловой эффект: «фотоэлектроны не разделяют энергии тепловое возбуждение… поглощение [электромагнитных волн] происходит из-за резонанса (и мы не знаем другого способа понять это…) ».Вторя Галилею, Милликен заявил: «Явления поглощения и излучения показывают, что … генераторы обладают собственными частотами … и характерные волны, которые они излучают, принадлежат к этим частотам … если какая-либо конкретная частота падает на такое вещество, осцилляторы в нем можно предположить, что в гармонии с впечатанными волнами поглощает падающие волны ». Что касается резонансной рабочей природы фотоэлектрического эффекта, он заявил, что «испускание [электронов] из атома … происходит особенно обильно, когда впечатываемая частота совпадает с ‘собственной частотой’ … [Это] предоставляет доказательство, которое совершенно не зависит от факты черного [теплового] излучения, правильности фундаментального предположения квантовой теории, а именно предположения о прерывистой… энергии, поглощаемой электронными составляющими атомов от [ЭМ] волн ».(Подчеркнуто)
\ n \ t \ t \ t \ tКвантовая революция, начатая Планком и Эйнштейном, набирала обороты.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t2.4. Квантовый парадокс
\ n \ t \ t \ t \ tПо мере того, как квантовая революция начала набирать обороты, начали возникать парадоксы и загадки. Простая модель световых волн и частиц материи была нарушена. Луи де Бройль (1892–1987) добавил путаницы в начале 1920-х годов, когда он предположил, что если свет может быть и волной, и частицей, то и материей может быть.(де Бройль, 1924). Следуя этой линии рассуждений, де Бройль обнаружил, что отсутствие единицы энергии для электромагнитных волн, то есть «изолированного количества энергии», особенно беспокоит. Без энергетической постоянной для света (т.е. изолированного количества энергии) де Бройль не смог определить фундаментальную массу света, используя уравнение эквивалентности энергии и массы Эйнштейна «E = mc 2 ». Вместо этого энергия света парадоксальным образом зависела от его частоты. Де Бройль сделал все возможное из концептуально сложной ситуации, и вместо этого установил уравнение эквивалентности масс Эйнштейна, равное квантовой формуле Планка, и решил для массы покоя света на определенной частоте:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t h \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tf \ n \ t \ t \ t \ t \ t \ t \ to \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t h \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ т \ т \ т \ т \ т \ т \ п \ т \ т \ т \ т \ т \ т \ п \ т \ т \ т \ т \ t \ n \ t \ t \ t \ tE8
\ n \ t \ t \ t \ tгде «m 0 » – масса покоя света, а «c» – скорость света в вакууме.Поскольку количество различных частот электромагнитных волн теоретически бесконечно, этот подход дал парадоксально бесконечное количество значений массы покоя света. В отличие от других частиц, таких как электрон или протон, де Бройль не смог найти постоянной массы покоя, связанной с легкими частицами.
\ n \ t \ t \ t \ tОтсутствие каких-либо констант энергии или массы для света действительно озадачивало. Без ведома де Бройля, ограничивающее предположение Планка о разных квантах для каждой частоты исключало само единичное количество энергии, которое искал де Бройль.Однако де Бройль мог, по крайней мере, сделать вывод, что масса покоя света в видимой области довольно мала, и в своей речи на Нобелевской премии объяснил: «Общие формулы … могут быть применены к корпускулам [видимого] света при условии, что здесь масса покоя m 0 бесконечно мала… верхний предел m 0 … составляет примерно 10 -24 грамм. (де Бройль, 1929)
\ n \ t \ t \ t \ tДе Бройль также использовал квантовую формулу Планка, чтобы получить импульс света:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tρ \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ п \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ thv \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ п \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ tλ \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE9
\ n \ t \ t \ t \ tобнаружил, что импульс света оказался прямо пропорционален его частоте и, следовательно, обратно пропорционален его длине волны «λ».И снова Де Бройль получил зоопарк значений – на этот раз для импульса, поскольку диапазон частот и длин волн в спектре ЭМ бесконечен.
\ n \ t \ t \ t \ tТем временем Нилс Бор предпринял свой амбициозный проект моделирования атома водорода на основе квантовой формулы и постоянной Планка. Бор обнаружил, что он не может рассчитать временные интервалы относительно взаимодействий между электромагнитными волнами и электронами. Вместо этого он был вынужден моделировать мгновенно «прыгающие электроны». (Бор, 1913 и 1920) Однако немногие (включая Бора) были удовлетворены прыжками электронов, и в середине 1920-х годов были представлены два новых подхода к квантовой механике.В 1925 году Вернер Гейзенберг ввел матричную механику. (Гейзенберг, 1925) Год спустя Эрвин Шредингер начал публиковать серию статей по волновым уравнениям, предназначенных для представления реальных электронных волн, предложенных де Бройлем. (Schrödinger, 1982)
\ n \ t \ t \ t \ tДаже с этими двумя новыми подходами квантовая механика все еще не имела смысла для многих первых пионеров квантовой теории. Ему не хватало определенности и определенности классической механики. Попытки компенсировать многие парадоксы включали дополнительные принципы, такие как принцип неопределенности Гейзенберга и принцип дополнительности Бора.(Гейзенберг, 1920 и Бор, 1928) Были обнаружены дополнительные переменные и константы необъяснимого происхождения, такие как безразмерная постоянная тонкой структуры. Обсуждения и дебаты продолжались. Школа вероятностей и неопределенности Бора-Гейзенберга боролась со школой реализма и определенности Эйнштейна-Шредингера. Без ответов на такие простые вопросы, как постоянная энергии или масса покоя света, школа Бора-Гейзенберга в конечном итоге возобладала. Ученые пришли к выводу (вопреки яростным возражениям Шредингера), что его волновые уравнения представляют только вероятности, а не реальные физические волны.В конце концов возник консенсус в том, что классическая механика нашего макромасштабного мира просто не может быть применена к калейдоскопическому микромасштабному миру квантов. Согласно Бору, классический предел существовал на самых высоких уровнях энергии электронов в атомах, а ниже этого предела классическая механика просто не могла применяться.
\ n \ t \ t \ t \ tИконоборческий блеск, который изначально привел Эйнштейна к его «безрассудным» квантовым предложениям, не позволял ему присоединиться к квантовой толпе, и он настаивал на том, что кое-что было упущено.Он просто не мог поверить, что Бог и Вселенная настолько извращенно парадоксальны. В 1935 году Эйнштейн опубликовал свою статью «ЭПР», в которой громко провозгласил, что квантовая механика неполна из-за существования «скрытых» квантовых переменных. (Эйнштейн, 1935) Эйнштейн и другие, такие как Бом и Белл, пытались описать скрытые переменные, но такая задача была трудной, если не невозможной. (Бом, 1952) Как математически описать квантовую переменную, когда сама природа переменной неизвестна? Небольшие группы ученых пытались поддержать поиски Эйнштейна, но научное сообщество в целом отказалось от попыток найти какие-либо «скрытые переменные».Вместо этого все соглашались, что парадоксальная природа квантовой механики является неоспоримой реальностью жизни. Затем были приложены невероятные усилия для разработки большего количества квантовых моделей, включающих парадоксы, таких как теории струн, суперсимметрии, мембран и тому подобное.
\ n \ t \ t \ t \ tОднако упорное утверждение Эйнштейна о том, что что-то было упущено, было правильным. Первая из его «скрытых переменных» была открыта почти столетие спустя в результате небольшой математической нити.(\ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tBrooks, 2009 \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t, а) Прослеживание этой нити в исторических записях привело к открытию, что небольшая математическая ошибка в блестящей работе Планка с черным телом побудила его принять неполную и сокращенную версию полной квантовой формулы . Вся квантовая физика была основана на простой квантовой формуле Планка, и это предполагало, что формула была неполной: в ней отсутствовала временная переменная. После восстановления временной переменной постоянная Планка приобрела новый фундаментальный смысл.Появившийся богатый квантовый гобелен показал красиво симметричные квантовые принципы, основанные на реальности и достоверности, с использованием полной квантовой формулы и более всеобъемлющей или полной «термодинамической» формулы. (\ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tBrooks, 2009 \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t, b)
\ n \ t \ t \ t \ n \ t \ t \ n \ t \ t \ t3. Полная квантовая формула
\ n \ t \ t \ tПолная квантовая формула:
\ n \ t \ t \ t\ n \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ n \ t \ t \ tE10
\ n \ t \ t \ tгде «h̃» – постоянная энергии света (6.626 X 10 -34 Джоулей / колебание) и «t м » – это временная переменная измерения.
\ n \ t \ t \ t \ n \ t \ t \ t \ t3.1. Временная переменная
\ n \ t \ t \ t \ tПолная квантовая формула очень похожа на соотношение энергии, обнаруженное в ранней теоретической электромагнитной работе Планка конца 1890-х годов. Он преобразовал основанные на времени измерения мощности «E / t» в общие значения энергии, умножив на время измерения «t m ». Теория ЭМ Планка использовала это простое преобразование в общем соотношении, в котором энергия колебаний системы была пропорциональна произведению общей постоянной «a», переменной времени измерения и частоты:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tδ \ n \ t \ t \ t \ t \ t \ t \ tU \ n \ t \ t \ t \ t \ t \ t \ t≈ \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tδ \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE11
\ n \ t \ t \ t \ tНесколько лет спустя временная переменная была потеряна в сложном выводе Планка для черного тела.Вместо того, чтобы умножать измерения энергии на основе времени на время измерения, Планк использовал математические методы Вина, которые преобразовывали измерения мощности в значения плотности энергии путем деления на скорость света. Это привело к тому, что временная переменная измерения «δt м » была одновременно зафиксирована на значении «одна секунда», а затем «скрыта». Доказательство этих фактов можно найти в статье Планка 1901 года о черном теле, в которой он описал экспериментальные данные и математические методы, которые он использовал:
\ n \ t \ t \ t \ t“§11.Значения обеих универсальных констант h и k могут быть вычислены достаточно точно с помощью имеющихся измерений. Ф. Курлбаум, обозначив полную энергию, излучаемую в воздух с 1 кв. См черного тела при температуре t˚ C за 1 секунду, с помощью S t обнаружил, что:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tS \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t100 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t– \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tS \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t0.0731 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tw \ n \ t \ t \ t \ t \ t \ t \ ta \ п \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t7.31 \ п \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tx \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t105 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ tg \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t ”\ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE12
\ n \ t \ t \ t \ tВместо того, чтобы умножать временные измерения мощности Курлбаума на время измерения для получения полной энергии (как это сделал Планк в своей более ранней работе), он преобразовал измерение мощности в плотность энергии, разделив его на скорость света «c» (3 X 10 10 см / сек) по методу Вина:
\ n \ t \ t \ t \ t«Отсюда можно получить плотность энергии полной энергии излучения в воздухе при абсолютной температуре
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t4 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t · \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t7 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ т.\ n \ t \ t \ t \ t \ t \ t \ t \ t \ t3 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tx \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t5 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t3 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tx \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t (\ n \ t \ t \ t \ t \ t \ t \ t \ t \ t3 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t7 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t3 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t4 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t- \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t7 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t3 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t4 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t) \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t “\ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ п \ т \ т \ т \ т \ т \ т \ т7 \ п \ т \ т \ т \ т \ т \ т \ т.\ n \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t3 \ n \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tx \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t- \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t5 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ tg \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ t3 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ td \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tg \ n \ t \ t \ t \ t \ t \ t \ t \ t4 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE13
\ n \ t \ t \ t \ tВременные переменные в числителе и знаменателе сокращены, и планка казалось бы, мог обращаться с энергией независимо от времени.Однако деление на постоянную скорость света аналогично умножению на время:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tx \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t3 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ т \ т \ т \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE14
\ n \ t \ t \ t \ tгде «s» – расстояние.В этом случае значение времени, на которое умножалось измерение мощности, было постоянной единицей времени «одна секунда» постоянной скорости света. Планк, похоже, не подозревал, что, используя вычисление плотности энергии Вина, он фактически заставлял бесконечно изменяемое время измерения фиксироваться на постоянном значении в одну секунду. Он также, похоже, не знал, что фиксированная временная переменная была впоследствии скрыта в окончательных расчетах его постоянной действия «h»:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t6 \ n \ t \ t \ t \ t \ t \ t \ t.\ n \ t \ t \ t \ t \ t \ t \ t626 X 1 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t− \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t34 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tДжоуль секунд \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE15
\ n \ t \ t \ t \ tЕго постоянная действия на самом деле является произведением истинной универсальной константы – «\ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t˜ \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t »- и фиксированная, скрытая переменная времени измерения« t m ».
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ t˜ \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t; \ n \ t \ t \ t \ t \ t \ t \ tw \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ т \ т; \ п \ т \ т \ т \ т \ т \ т \ т \ п \ т \ т \ т \ т \ т \ т \ т \ тт \ п \ т \ т \ т \ т \ т \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tsecond \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE16
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3 .2. Энергетическая постоянная
\ n \ t \ t \ t \ tКогда пропущенная временная переменная восстанавливается в квантовой формуле, идентичность реальной универсальной постоянной Планка становится очевидной. Скрытая константа, по сути, является универсальной константой энергии, а именно энергией одиночного колебания или электромагнитной волны. Эта универсальная константа энергии света – это то же самое «изолированное количество энергии», которое искал де Бройль, то есть фундаментальный малый квант световой энергии:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ t˜ \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t6 \ n \ t \ t \ t \ t \ t \ t \ т.\ n \ t \ t \ t \ t \ t \ t \ t626 X 1 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t− \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t34 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tДжоуль \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ toscillation \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE17
\ n \ t \ t \ t \ tЭтот факт легко проверяется решением уравнения Планка неполная формула для энергии одиночного колебания света (см. \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tBrooks, 2009 \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ ta для выводов). Числовое значение, вычисленное Планком для его постоянной действия «h», на самом деле является числовым значением средней энергии колебаний отдельных электромагнитных волн.«Изолированное количество энергии», на которое надеялся де Бройль, было найдено.
\ n \ t \ t \ t \ tУниверсальный характер этой постоянной становится ясным из рассмотрения постоянной энергии в широком диапазоне длин волн, периодов времени и частот. Средняя энергия одиночной электромагнитной волны остается постоянной независимо от того, является ли она радиоволной, микроволновой, инфракрасной, видимой или ультрафиолетовой волной. Для низкочастотных и длинноволновых электромагнитных волн, таких как радиоволны, постоянная средняя энергия колебаний распространяется диффузно по большому объему пространства.На более высоких частотах и более коротких длинах волн энергия становится более концентрированной в меньшем объеме пространства. В ультрафиолетовой области энергия колебаний становится чрезвычайно плотной, ограничиваясь очень небольшой областью пространства, размером около 100 нанометров или около того. Однако количество энергии в одном колебании одинаково, независимо от объема или периода времени, которое оно занимает.
\ n \ t \ t \ t \ tПостоянство энергии одиночной электромагнитной волны на разных длинах волн и в разные периоды времени означает, что элементарный квант света постоянен в течение сдвига во времени или пространстве.Когда свойство остается постоянным в течение сдвига во времени или пространстве, это свойство сохраняется и представляет собой универсальное свойство. Теперь фундаментальные отношения ясны. Так же, как у электрона есть фундаментальная единица заряда, которая сохраняется и представляет собой универсальную константу для электронов, у света есть фундаментальная единица энергии, «h̃», которая сохраняется и представляет собой универсальную константу для электромагнитных волн.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3.3. Частотная переменная
\ n \ t \ t \ t \ tКвантовая формула Планка была неполной и, как следствие, не содержала постоянной энергии колебаний.Это, в свою очередь, привело к квантовой формуле, в которой единицы не сбалансированы: \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t (\ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tДжоуль \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t) \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t = h \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t (\ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tДжоуль секунд \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t) \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tv \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t (\ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ toscillations в секунду \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t) \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tb \ n \ t \ t \ t \ t \ t \ t \ t \ tu \ n \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tДжоуль \ n \ t \ t \ t \ t \ t \ t \ t \ t ≠ \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t Джоулевые колебания \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t
\ n \ t \ t \ t \ tУченые обнаружили, что не смогли сбалансировать квантовые уравнения и использовать полные математические обозначения для частоты, а именно циклы, волны или колебания в секунду.В результате вместо этого была принята математически неполная система обозначений, в которой отсутствовали описательные единицы для числителя частоты. Частота в настоящее время описывается в Международной системе единиц («СИ») как «1 / сек» или «сек -1 ». Это неполное обозначение частоты в системе СИ удаляет важный математический элемент реальности в квантовой механике.
\ n \ t \ t \ t \ tНеполное математическое обозначение частоты больше не требуется для компенсации недостатков неполной квантовой формулы.С учетом константы энергии – энергии на одно колебание – частота снова может быть правильно и полностью записана как колебания в единицу времени. Использование полных математических обозначений в квантовой механике восстанавливает жизненно важный аспект математической реальности. Распознавание «колебаний» в числителе измерений частоты дает теоретический элемент, соответствующий каждому элементу реальности в полной квантовой формуле. Как утверждал Эйнштейн, такое соответствие является критическим требованием полной квантовой механики.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3.4. Фотон
\ n \ t \ t \ t \ tВ 1926 году Гилберт Льюис ввел термин «фотон» для кванта света Эйнштейна. Энергия фотона была рассчитана с помощью (неполной) квантовой формулы Планка «E = hv». С тех пор время от времени возникали вопросы, действительно ли «фотон» является неделимой частицей света. Теперь однозначно ответ на этот вопрос: «Нет». Фотон, как было определено ранее, не является неделимой элементарной частицей.
\ n \ t \ t \ t \ tФиксированная переменная времени и постоянная энергии были скрыты в постоянной «действия» Планка, и поэтому для Льюиса или других не было очевидно, что то, что они называли «фотоном», было фактически количество световой энергии, зависящее от времени, которое основывается на фиксированном и произвольном временном интервале измерения в одну секунду. Количество энергии, зависящее от времени, которое зависит от произвольно определенного временного интервала, не может быть фундаментальной или элементарной частицей света. Фотон – не элементарная частица света.
\ n \ t \ t \ t \ tЧто же такое элементарная частица света? Как определяется универсальной энергетической постоянной, элементарная частица света представляет собой единичное колебание электромагнитной энергии, то есть единичный цикл или световую волну. Элементарная частица света обладает постоянной энергией 6,626 X 10 -34 Джоулей. Это самый маленький из известных квантов энергии во Вселенной. То, что физики назвали «фотоном», на самом деле является совокупностью или ансамблем этих маленьких элементарных частиц света.Каждое отдельное колебание представляет собой «целостную единицу» света и может излучаться или поглощаться как единая и незаметная единица.
\ n \ t \ t \ t \ t«Фотон» не является неделимой частицей света, а фактически представляет собой совокупность световых колебаний, которые могут действовать по отдельности и индивидуально как полные единицы энергии. При поглощении детектором или объектом энергия набора дискретных колебаний может распространяться по нескольким атомам или молекулам, что приводит к многоатомному состоянию распределения энергии, известному как «запутанность».(\ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tBrooks, 2009 \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t, c) Это запутывание электромагнитной энергии может иметь место в различных формах или распределениях, в зависимости от природы поглощающего или обнаруживающего материала. Точно так же излучение световой энергии может происходить из «запутанного» энергетического состояния, разделяемого несколькими атомами или молекулами в эмиттере. Ансамбль электромагнитных волн с количеством колебаний меньше «N» (где «v = N / sec») приводит к «субфотонному» набору электромагнитных волн. Конечная субфотонная частица – это элементарная частица света, одиночное электромагнитное колебание.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3.5. Масса света
\ n \ t \ t \ t \ tДе Бройль оплакивал отсутствие «изолированного количества энергии», с помощью которого он мог бы вычислить постоянную массу покоя света. Используя постоянную энергии света, теперь можно завершить вычисления де Бройля и определить массу покоя одиночного кванта света. Согласно первоначальной формулировке де Бройля, использующей уравнение Эйнштейна эквивалентности энергии и массы «E = mc 2 », масса покоя света легко определяется:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t 7 \ n \ t \ t \ t \ t \ t \ т \ т.\ n \ t \ t \ t \ t \ t \ t \ t372 X 1 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t− \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t51 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tkg \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ tocillation \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE18
\ n \ t \ t \ t \ tЭто значение находится в том же порядке, что и величина как самые последние и надежные оценки верхних пределов массы покоя света. Поскольку энергия единичного колебания света постоянна, независимо от его длины волны, периода времени или частоты, его масса также постоянна независимо от его длины волны, периода времени или частоты.Следовательно, масса света постоянна во времени или пространстве. Таким образом, масса света сохраняется и представляет собой еще одну универсальную постоянную для света (\ n \ t \ t \ t \ t \ t \ tMortenson, 2011 \ n \ t \ t \ t \ t \ t).
\ n \ t \ t \ t \ tТак же, как плотность энергии постоянной волны света зависит от длины и объема, который занимает волна, также меняется и плотность ее массы. Масса длинных электромагнитных радиоволн, распространяющихся на расстояние в сотни метров, имеет низкую плотность. Идентичная масса, ограниченная малой длиной волны и объемом рентгеновского колебания (порядка 10 -8 -10 -11 метров), в триллионы раз плотнее.Рентгеновские колебания высокой плотности с их сильно сконцентрированной массой и энергией могут создавать взаимодействия, которые обычно не наблюдаются с радиоволнами низкой плотности, и вызывать такие эффекты, как рассеяние рентгеновских лучей и свойства частиц.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3.6. Импульс света
\ n \ t \ t \ t \ tИмпульс классически рассчитывается как произведение массы объекта на его скорость. Используя постоянную массу электромагнитного колебания, как рассчитано выше, и постоянную скорость света (2.99 X 10 8 м / сек), расчет Де Бройля для импульса света можно завершить:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tρ \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tc \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t2 \ n \ t \ t \ t \ t \ t \ t \ t. \ n \ t \ t \ t \ t \ t \ t \ t21 X 1 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t− \ п \ t \ t \ t \ t \ t \ t \ t \ t \ t42 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tkg m \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ tsec per osc \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE19
\ n \ t \ t \ t \ tКак и в случае с массой, импульс единичного колебания света является постоянным, а не бесконечно переменным.Импульс электромагнитной волны постоянен независимо от ее длины волны, периода времени или частоты. Таким образом, импульс света постоянен во времени или пространстве и является сохраняемым свойством.
\ n \ t \ t \ t \ tС точки зрения более ранних расчетов де Бройля масс и импульсов фотонов, константы массы и импульса для электромагнитных волн не противоречат друг другу и не вводят в заблуждение. Следует помнить, что фотон 20 -го века представлений на самом деле был совокупностью элементарных частиц света, т.е.е., ЭМ колебания. Наборы масс и импульсов могут быть аддитивными. Суммирование постоянной массы и импульса одиночных колебаний (основанное на количестве колебаний «N» в «фотоне» за одну секунду) дает такую же коллективную массу и импульс, которые де Бройль получил с помощью своих расчетов на основе фотонов. Хотя расчеты массы и импульса де Бройля давали бесконечно изменяющиеся результаты, теперь признано, что его переменные результаты были артефактом отсутствующих констант энергии, массы и импульса.Становится очевидной ранее неизвестная симметрия сохранения. Энергия, масса и импульс сохраняются как для света, так и для вещества, завершая триаду соотношений сохранения, описанную ранее Гельмгольцем, Эйнштейном и де Бройлем.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3.7. Сила света
\ n \ t \ t \ t \ tЭнергия, масса и импульс постоянны и сохраняются для света. Однако, используя классическую механику, легко заметить, что сила света непостоянна.Согласно Лагранжу, сила – это произведение массы и изменения скорости «в момент dt» при изменении скорости:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tF \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t m v \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ t dt \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE20
\ n \ t \ t \ t \ tДля изменений в Скорость, возникающая в интервале времени, равном или превышающем единицу времени скорости, может использоваться одна и та же временная переменная как для скорости, так и для ускорения.Если, с другой стороны, ускорение (или замедление) происходит в интервале времени, намного меньшем, чем время единицы скорости (т. Е. «Мгновенное» событие), необходимо использовать вторую временную переменную «t a ». за интервал времени разгона. Когда объект излучает электромагнитное колебание, небольшой кусочек массой 7,372 X 10 -51 кг мгновенно ускоряется до скорости света «c». Точно так же, когда световая волна поглощается объектом, его масса мгновенно замедляется.Ускорение или замедление происходит «в момент dt», который представляет собой период времени «τ» электромагнитной волны. Таким образом, сила, ускоряющая электромагнитное колебание при его излучении (или создаваемое колебанием при его поглощении), равна:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tF \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ т \ т \ т \ т \ т \ т \ т м с \ п \ т \ т \ т \ т \ т \ т \ т / \ п \ т \ т \ т \ т \ т \ т \ т \ п \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ tw \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tτ \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE21
\ n \ t \ t \ t \ tВременные периоды электромагнитных волн бесконечно изменяются, как и их частоты (τ = 1 / v).Таким образом, хотя масса и скорость электромагнитных волн постоянны, силы, которые они оказывают, неизменны. Силы, связанные со световыми колебаниями, изменяются обратно пропорционально их временным периодам и прямо их частотам («F = m c v»).
\ n \ t \ t \ t \ tЭнергия и масса радиоволны, распределенные в течение сравнительно длительного периода времени, оказывают относительно небольшую силу на поглощающий детектор. С другой стороны, энергия и масса колебаний рентгеновских или гамма-лучей сосредоточены в течение минутного периода времени и оказывают чрезвычайно большие силы на поглощающий объект.
\ n \ t \ t \ t \ tЭти силы электромагнитного света являются аддитивными, и при достаточном накоплении силы могут быть довольно большими и приводить к физическому ускорению поглощающей материи. (Лю и др., 2010) Сила света – это рабочий механизм, стоящий за «космическими парусами», которые сейчас используются на космических кораблях. Паруса древних моряков толкались наполнявшим их ветром. Паруса современных исследователей космоса теперь наполнены падающими на них силами света.Точно так же объект, излучающий свет, испытывает силу отдачи, пропорциональную силе излучения электромагнитных волн. (She et al, 2008)
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3.8. Классический предел
\ n \ t \ t \ t \ tПервопроходцы квантовой теории ожидали, что классическая механика будет использоваться для описания физических процессов на очень малых масштабах длины и энергии. Однако возникли многочисленные препятствия из-за скрытых квантовых переменных и констант. Квантовая механика, разработанная Гейзенбергом и Шредингером, предоставила математическую основу для кинетики низких энергий, однако они не смогли получить уверенность и определенность, обеспечиваемые классической механикой.Без массовой постоянной для электромагнитных волн было невозможно использовать классические свойства положения, времени и массы сколько-нибудь значимым образом. Гейзенберг и Бор обнаружили, что они ограничены нахождением только вероятностей и что они могут применять классическую механику только при очень высоких уровнях энергии электронов. Область, где классическая и квантовая механика образует граничную зону, была названа Бором «классическим пределом». (Бор, 1920). Выше предела классическая механика могла применяться с реальностью и уверенностью, в то время как ниже предела все было неопределенным, и могла применяться только квантовая механика.
\ n \ t \ t \ t \ tС использованием новых квантовых переменных и констант исчезает классическая граничная зона между квантовой и классической механикой. (Мортенсон, 2010a) Теперь можно использовать классическую механику на минимально возможных уровнях энергии света, эквивалентных долям процента от самых низких известных уровней энергии электронов. Кинетика поглощения энергии для одиночного электромагнитного колебания, а именно 6,626 · 10 -34 Джоулей, теперь полностью описывается с помощью классической механики.В этом отношении классический предел, ранее теоретизированный Бором, признается артефактом отсутствующих квантовых переменных и констант.
\ n \ t \ t \ t \ tПрименение классической физики на наименьших из известных уровней энергии стало возможным благодаря использованию второй скрытой временной переменной, переменной времени ускорения Лагранжа, «t a ». Поглощение или излучение электромагнитного колебания в видимой области света происходит за 10 -10 секунд. Это приводит к почти мгновенному замедлению или ускорению световой массы.Энергия, необходимая для ускорения тела, является функцией расстояния, на котором действует сила, «F δs». В случае отдельного электромагнитного колебания расстояние, на котором действует сила, является длиной волны «λ» колебания. Умножение переменной силы света на его длину волны, то есть «F δs = (m c v) λ», дает постоянную энергию «mc 2 », или, другими словами, 6,626 × 10 -34 Дж / ос. Таким образом, постоянная энергии света быстро выводится из первых принципов положения, времени и массы.
\ n \ t \ t \ t \ tНедостаток понимания предостережений Лагранжа и Кориолиса относительно временных интервалов ускорения и мгновенных событий способствовал восприятию того, что существует барьер или предел между классической и квантовой механикой. Новая фундаментальная физика электромагнитных волн показывает, что механику частиц можно описать как на макро-, так и на микромасштабе, используя достоверность, реализм и детерминизм классической механики.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3.9.Принцип неопределенности
\ n \ t \ t \ t \ tГейзенберг предложил принцип неопределенности как ответ на неспособность первых пионеров квантовой теории определить квантовые свойства, связанные со временем или энергией, с какой-либо уверенностью. Он предположил, что изменения энергии и времени являются неопределенными до такой степени, что их произведение всегда должно быть больше или равно постоянной Планка (ΔE Δt ≥ h). Этот принцип, конечно же, включал в себя неполную квантовую постоянную «h», которая скрывала постоянную энергии и фиксированную переменную времени.Принцип неопределенности Гейзенберга излечил множество квантовых парадоксов, и, как писал Дэвид Бом поколением позже, «физическая интерпретация квантовой теории сосредоточена вокруг принципа неопределенности». Однако, когда «h» правильно заменяется на энергетическую константу и время измерения, физическая интерпретация квантовой теории резко меняется и сосредотачивается вокруг уверенности и постоянства, где изменение энергии – это энергия одиночной электромагнитной волны, а изменение время «Δt» и время измерения «t м » равны периоду времени «τ» для колебания.:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tΔ \ n \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tΔ \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t≥ \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ t˜ \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ td \ n \ t \ t \ t \ t \ t \ t \ tΔ \ n \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t≥ \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ t˜ \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE22
\ n \ t \ t \ t \ tНаименьшее возможное изменение энергии – это энергия одиночная волна света.
\ n \ t \ t \ t \ tВ прошлом эта концепция была скрыта из-за отсутствия отдельной постоянной энергии и переменной времени в квантовой формуле Планка. В этих условиях неизбежно, что расчеты величин, включающих время и энергию, дадут неопределенные результаты. Теперь неопределенность ушла, ее заменила квантовая механика, которая допускает более определенную и реалистичную физическую интерпретацию.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3.10. Постоянная тонкой структуры
\ n \ t \ t \ t \ tПостоянная тонкой структуры «всегда была загадкой с тех пор, как она была открыта более пятидесяти лет назад, и все хорошие физики-теоретики вывесили это число на свою стену и беспокоиться об этом….Это одна из величайших чертовых загадок физики: магическое число, которое приходит к нам без понимания человеком… »(Фейнман, 1988)
\ n \ t \ t \ t \ tИспользуя недавно открытые квантовые константы и переменные, постоянная тонкой структуры «α» представляет собой гораздо меньшую загадку. Изучение постоянной тонкой структуры в зависимости от действия света «S» и постоянной Планка «h» (т.е. «α h = S») и замена «h» на постоянную энергии «\ n \ t \ t \ t» \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ t˜ \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t ”обнаруживается:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tα \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tS \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t ˜ \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ to \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ ti \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ to \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tw \ n \ t \ t \ t \ t \ t \ t \ to \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ td \ n \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ tα \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t (E \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tt) \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tosc \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ td \ n \ t \ t \ t \ t \ t \ t \ tα \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tosc \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE23
\ n \ t \ t \ t \ tПостоянная тонкой структуры не безразмерна.Он представляет собой масштабную постоянную между временем и одиночным колебанием электромагнитной энергии, то есть «osc t». Таким образом, для постоянной тонкой структуры теперь предусмотрен теоретический элемент, соответствующий элементу реальности. Это критическое требование для полной квантовой механики.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t3.11. Волна – дуальность частиц
\ n \ t \ t \ t \ tДве противоположные модели света – частицы и волны – обсуждались веками. Некоторые исследования предполагают, что свет состоит из волн, в то время как другие предполагают частицы.Эта загадка заставила Эйнштейна возразить: «Но что такое свет на самом деле? Это волна или поток фотонов? Кажется, нет никакой вероятности сформировать последовательное описание явлений света… мы должны иногда использовать одну теорию, а иногда другую… ». (Эйнштейн, 1938) Бор ответил на эти две противоречивые картины реальности своим принципом дополнительности, утверждая, что определенные аспекты света можно рассматривать так или иначе, но никогда оба одновременно.
\ n \ t \ t \ t \ tТеперь нам представлена картина реальности, которая требует, чтобы мы рассматривали свет одновременно как волну и частицу.Элементарная «частица» света – это одиночное электромагнитное колебание или «волна». Хотя время и пространство, которое занимает волна, могут изменяться, это отклонение зависит от постоянного отношения «с», а энергия, масса и импульс элементарной частицы также остаются постоянными.
\ n \ t \ t \ t \ tРасхождения в картинах прошлого возникли из-за относительной разницы в размерах между электромагнитными волнами и веществом, с которым они взаимодействовали. Например, исследования рассеяния сначала были выполнены с использованием мягкого рентгеновского излучения с длинами волн больше, чем у атомов, и не было обнаружено никаких четко выраженных свойств частиц.Однако, когда Артур Комптон использовал ультракороткие жесткие рентгеновские лучи и гамма-лучи (на два порядка меньше атома), он наблюдал свойства частиц. (Комптон, 1923) Концентрированная энергия и масса рентгеновских и гамма-волн выглядели как маленькие точки по сравнению с размером атомов в облучаемых материалах.
\ n \ t \ t \ t \ tС другой стороны, эксперименты с одной и двумя щелями демонстрируют волнообразные свойства света через интерференционные полосы. Однако эти волнообразные свойства также зависят от размеров световых колебаний и вещества, с которым они взаимодействуют.Для щели, ширина которой равна длине волны света, интерференционные полосы не наблюдаются и наблюдается поведение частиц. Только когда ширина щели увеличивается относительно длины волны света, появляются интерференционные полосы и волнообразные свойства.
\ n \ t \ t \ t \ tНедавние эксперименты со световыми щелями и «одиночными фотонами» раскрывают не только сам свет, но и детектирующий материал. «Фотон» – это просто набор отдельных электромагнитных квантов.Когда видимые световые волны (которые намного больше по размеру (400-800 нм) по сравнению с отдельными атомами в детекторе (0,1-0,5 нм)), ударяют в детектор, энергия ансамбля световых волн одновременно падает на несколько атомов детектора. Это вызывает состояние энергетической запутанности в нескольких атомах детектора. (\ N \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tBrooks, 2009 \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t, c) Распределение световой энергии по нескольким атомам возбуждает небольшую точечную часть материала детектора, что приводит к фотонной реакции, и создает в детекторе узор, похожий на частицы.(Roychouhuri, 2009) Хотя полученное изображение детектора, кажется, показывает нарастание с течением времени «фотонных» столкновений, на самом деле они показывают накопление состояний энергетической запутанности в самом детекторе, которые подвергаются положительным и отрицательным интерференциям внутри и между группами запутанные атомы.
\ n \ t \ t \ t \ n \ t \ t \ n \ t \ t \ t4. Энергетическая динамика
\ n \ t \ t \ tЭкспериментальные данные, которые Планк использовал для вывода уравнения черного тела и термодинамики. формула не включала никаких измерений, связанных с упорядоченной рабочей энергией.Следовательно, Планк не включил энергию работы в свою термодинамическую формулу «E = k B T». Вместо этого формулировка Планка ограничивалась исключительно энергией небольшого элемента системы (например, атома, молекулы или иона), основываясь только на его температуре и случайном хаотическом движении.
\ n \ t \ t \ tКогда в системе присутствует упорядоченная рабочая энергия, необходимо использовать более исчерпывающие формулы для представления полной энергии системы или ее элементов. (\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ tBrooks, 2009 \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tb and Mortenson, 2010b) Уравнение энергии Гельмгольца «E = A + TS» воплощает некогда такую инклюзивную формулу на макроуровне и представляет полную энергию системы как сумму ее работы и тепловой энергии.Эта более полная формула охватывает значительно больше, чем простую термодинамику, и ее более уместно назвать формулой динамики энергии.
\ n \ t \ t \ t \ n \ t \ t \ t \ t4.1. Формула динамики энергии
\ n \ t \ t \ t \ tПолная формула динамики энергии для всей системы дается уравнением энергии Гельмгольца «E = A + TS» (уравнение 4 выше). Хотя расчет тепловой энергии системы относительно прост и понятен, определение полной энергии работы может быть значительно сложнее.Рабочие энергии бывают разных форм, включая механическую, химическую, гравитационную и резонансную энергии. Резонансная рабочая энергия – это широкая категория, охватывающая изменяющиеся во времени силы и поля, такие как звуковые волны, электрические или магнитные поля и световые волны. Эти резонансные энергии соединяются с веществом через «симпатический резонанс» и обозначаются в формуле фундаментальной динамики энергии как «A r »:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t A \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t + \ n \ t \ t \ t \ t \ t \ t \ t TS \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE24
\ n \ t \ t \ t \ tФундаментальный принцип, описанный Галилео в его исследованиях маятника, справедлив для резонансных рабочих энергий, т.е.е., «[обеспечивая изменяющуюся во времени энергию, можно] придать Движение и Движение значительно большее, повторяя… но только во Времени, собственно принадлежащем его Вибрациям». Любой, кто толкал ребенка на качелях, приложил резонансную механическую энергию к системе ребенок / качели. Если подтолкнуть ребенка в нужное время (т. Е. Резонансная частота для ансамбля ребенок / качели), это увеличивает скорость, рост и волнение ребенка от езды. Нажатие в неподходящее время, когда ребенок находится на расстоянии нескольких метров, не влияет на систему и может снизить волнение ребенка от езды.
\ n \ t \ t \ t \ tТаким же образом, электромагнитные волны, падающие на материал, передают резонансную электромагнитную энергию поглощающему веществу через свой импульс, силу, скорость и массу. Ускорение колеблющегося элемента в системе является результатом приложенной электромагнитной силы, что приводит к увеличению амплитуды колебаний этого элемента (см. Рис. 1 выше). Таким образом, «толкание» элементов системы электромагнитными волнами в нужный момент увеличивает амплитуду (высоту) колебаний системы и выводит их на более высокие уровни энергии.Величина увеличения амплитуды колебаний системы зависит от того, насколько близка частота резонансной электромагнитной волны к частоте колебаний внутри системы (уравнение 2 и рис. 2 выше).
\ n \ t \ t \ t \ tУвеличенные амплитуды колебаний и уровни энергии в системе могут выполнять работу по-разному, в зависимости от того, какой элемент или амплитуда колебаний увеличивается. Например, изменения в движении, химическом, материальном, организационном или поведенческом состоянии могут быть результатом резонансного энергетического возбуждения в системе.
\ n \ t \ t \ t \ tВыраженная на микромасштабе, формула полной динамики энергии для полной энергии отдельного элемента в системе формулируется параллельно с формулой системы Гельмгольца:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t W \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t + \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tk \ n \ t \ t \ t \ t \ t \ t \ t \ tB \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE25
\ n \ t \ t \ t \ t, где «W e » – переменная полной работы в микромасштабе, представляющая общую работу, выполненную над отдельным элементом.В случае резонансной рабочей энергии можно использовать переменную резонансной работы «r A ». Эта переменная работы резонанса в микромасштабе представляет собой энергию, полученную отдельным элементом в системе в результате энергии работы резонанса, «A r », приложенной к системе в целом:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ tA \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t + \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tk \ n \ t \ t \ t \ t \ t \ t \ t \ tB \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE26
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ т \ т \ т \ т4.2. Определение энергии резонансной работы системы «Ar»
\ n \ t \ t \ t \ tЭнергия резонансной работы (система / макроуровень) и переменная (элемент / микромасштаб) могут быть определены экспериментально. Систему водного растворителя в резонансных условиях сравнивали с идентичной системой в термических условиях (см. Таблицу 1 ниже): \ n \ t \ t \ t \ t \ t \ t
Методика эксперимента – Дистиллированная вода (500 мл при 20 ° C). C) помещали в каждый из двух стаканов по 1000 мл. Один стакан облучали резонансными колебательными электромагнитными частотами воды в течение трех (3) часов источником света с использованием 2.Полная энергия 1 кДж. Другой стакан помещали в непрозрачный инкубатор на три (3) часа. Вода в обоих стаканах по истечении трех (3) часов составляла 23 ° C. В каждый стакан добавляли хлорид натрия (250 г), и стаканы хранились одинаково в затемненном шкафу. Спустя двадцать (20) часов температуры растворов были идентичными (21 ° C / 274 K). Растворы декантировали и измеряли растворенную массу, соленость и концентрацию резонансных и термических солевых растворов, используя стандартные методы.(Brooks et al, 2005)
\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ n \ t \ t \ t \ t| \ n \ t \ t \ t \ t \ t \ t \ t | Резонансная система | \ n \ t \ t \ t \ t \ t \ t \ tТепловая система | \ n \ t \ t \ t \ t \ t \ t
| Масса растворенного раствора (г / 100 мл NaCl) | \ n \ t \ t \ t \ t \ t \ t \ t26,0 | \ n \ t \ t \ t \ t \ t \ t \ t23,8 | \ n \ t \ t \ t \ t \ t \ t
| Растворенные моли (NaCl) | \ n \ t \ t \ t \ t \ t \ t \ t4.65 | \ n \ t \ t \ t \ t \ t \ t \ t4,25 | \ n \ t \ t \ t \ t \ t \ t
| Теплота раствора (кДж) | \ n \ t \ t \ t \ t \ t \ t \ t17,4 | \ n \ t \ t \ t \ t \ t \ t \ t16.0 | \ n \ t \ t \ t \ t \ t \ t
Таблица 1.
Резонансная vs. Система термического водного растворителя
\ n \ t \ t \ t \ tТеплота растворения – это мера работы, выполняемой растворителем над растворяющимся веществом. Работа резонансной системы составила 17,4 кДж, а тепловой системы – всего 16.0 кДж работы с растворенным веществом NaCl. Формулы динамики энергии для обеих систем:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tl \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ ty \ n \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t TS \ n \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ td \ n \ t \ t \ t \ t \ t \ t \ t16 \ n \ t \ t \ t \ t \ t \ t \ t.0 \ n \ t \ t \ t \ t \ t \ t \ t кДж \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ т \ п \ т \ т \ т \ т \ т \ т \ т \ п \ т \ т \ т \ т \ т \ т \ т \ т (\ п \ т \ т \ т \ т \ т \ т \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t274 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t ° \ n \ t \ т \ т \ т \ т \ т \ т \ т \ т К \ п \ т \ т \ т \ т \ т \ т \ т \ т \ п \ т \ т \ т \ т \ т \ т \ т \ t) \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t S \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE27
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tR \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ to \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ ty \ n \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ tR \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t A \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t + \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tTS \ n \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ td \ n \ t \ t \ t \ t \ t \ t \ t17 \ n \ t \ t \ t \ t \ t \ t \ t.\ n \ t \ t \ t \ t \ t \ t \ t4 кДж \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t A \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t + \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t (\ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t274 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t ° \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t K \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t) \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t S \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE28
\ n \ t \ t \ t \ tВычитая, обнаруживаем, что энергия работы резонанса, “A r ”, в резонансной системе равна 1.4 кДж энергии:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tA \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t1 \ n \ t \ t \ t \ t \ t \ t \ t. \ n \ t \ t \ t \ t \ t \ t \ t4 кДж \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE29
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t4.3. Фактор резонанса
\ n \ t \ t \ t \ tОтношение полной энергии в резонансной системе к полной энергии в тепловой системе:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ tR \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t E \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ tf \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE30
\ n \ t \ t \ t \ t– коэффициент резонанса, «r f ».В описанной выше водной системе растворителей коэффициент резонанса составляет 1,09. В резонансной системе было на 9% больше энергии для работы с растворенным веществом и его растворения. Эта резонансная рабочая энергия была добавлена к тепловой энергии, уже присущей системе в результате ее температуры.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t4.4. Определение энергии работы резонанса элемента «r
A » \ n \ t \ t \ t \ tВеличина энергии работы резонанса на микромасштабе является переменной работы резонанса, «r A ».В примере системы растворителей отдельные элементы системы, облученные резонансными электромагнитными волнами, обладали большей энергией, чем элементы тепловой системы. Значение энергии работы микромасштабного резонанса можно вычислить с помощью уравнения 25., приведенного выше:
\ n \ t \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tl \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tl \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tk \ n \ t \ t \ t \ t \ t \ t \ t \ tB \ п \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ td \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t4 \ n \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t5 X 1 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t- \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t23 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tJ на молекулу \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE31
\ n \ t \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tR \ n \ t \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ ts \ n \ t \ t \ t \ t \ t \ t \ to \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tl \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tm \ n \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t r \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tA \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t + \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tk \ n \ t \ t \ t \ t \ t \ t \ t \ tB \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ ta \ n \ t \ t \ t \ t \ t \ t \ tn \ п \ t \ t \ t \ t \ t \ t \ td \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ tE \ п \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t 44 \ п \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t X 1 \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t0 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t− \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t23 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ tJ на молекулу \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE32
\ n \ t \ t \ t \ tВычитание показывает, что каждая молекула воды в резонансной системе совершила дополнительные 35 X 10 -23 J работы над растворенным веществом в результате поглощения резонансных электромагнитных волн.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t4.5. Виртуальные тепловые эффекты резонансных электромагнитных волн
\ n \ t \ t \ t \ tКогда резонансные электромагнитные волны выполняют работу в системе и увеличивают одну или несколько амплитуд колебаний в системе, эта увеличенная энергия колебаний может быть преобразована в работу. внутри системы. В случае водной системы растворителей, описанной в экспериментальном примере выше, возбуждались колебательные колебания молекул растворителя воды. Это, в свою очередь, привело к изменению поведения воды как растворителя.Резонансная вода растворила 26,0 г / 100 мл NaCl, тогда как термальная вода растворила только 23,8 г / 100 мл.
\ n \ t \ t \ t \ tДо какой температуры необходимо поднять тепловую систему, чтобы растворить такое же количество NaCl, что и резонансная система, при прочих равных? Это легко вычислить, установив полную энергию элемента в резонансной системе равной тепловой энергии и решив для температуры «T»:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tk \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tB \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tT \ п \ t \ t \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tt \ n \ t \ t \ t \ t \ t \ t \ t \ t \ th \ n \ t \ t \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tf \ n \ t \ t \ t \ t \ t \ t \ t \ t \ to \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t, \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t E \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ t k \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tB \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t = \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t319 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tº \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tK \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t (\ n \ t \ t \ t \ t \ t \ t \ t \ t \ t46 \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tº \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tC \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t) \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE33
\ n \ t \ t \ t \ tЧтобы растворить такое же количество NaCl в тепловая система, которую резонансная система растворила, тепловая система должна была быть нагрета до 46 ºC.Вода в резонансной системе вела себя так, как если бы она была нагрета до 46 º C, хотя этого не произошло. Электромагнитные волны создавали виртуальный тепловой эффект в резонансной системе растворителей.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t4.6. Энергоэффективность резонансных электромагнитных волн
\ n \ t \ t \ t \ tКак Гельмгольц описал много десятилетий назад, энергия может быть преобразована и преобразована из одной формы в другую: «… тепло, электричество, магнетизм, свет и химическое сродство. «. Эффективность, с которой происходят эти преобразования, не одинакова для всех преобразований энергии.В зависимости от процесса и желаемого конечного результата или продукта эффективность преобразования энергии может широко варьироваться. Например, в примере с водным растворителем, приведенном выше, необходимо нагреть воду до 46 ° C, чтобы растворить такое же количество соли, которое растворила резонансная водная система. Для нагрева 500 мл воды до этой более высокой температуры потребуется не менее 52 кДж энергии.
\ n \ t \ t \ t \ tС другой стороны, источник света, который обеспечивал резонансные колебательные ЭМ волны в резонансной системе, потреблял только 2.1 кДж энергии. (\ n \ t \ t \ t \ t \ t \ tMortenson & George, 2011 \ n \ t \ t \ t \ t \ t). Общая дополнительная энергия, необходимая для достижения желаемого конечного результата или продукта (т. Е. Растворения большего количества соли), намного меньше для резонансных электромагнитных волн: фактически на девяносто шесть процентов (96%) меньше.
\ n \ t \ t \ t \ tОбщая дополнительная теплота работы растворения, выполняемая резонансной водой с растворенным веществом, составляла 1,4 кДж. Эффективность преобразования энергии для резонансной системы составила 67%. Если нагреть термальную воду до повышения ее температуры на 25º, используя 52 кДж энергии, эффективность преобразования тепловой энергии в теплоту растворения составила бы всего 3%.Между эффективностью преобразования энергии резонансной ЭМ-системы и тепловой системы разница более чем на порядок.
\ n \ t \ t \ t \ n \ t \ t \ t \ n \ t \ t \ t \ t4.7. Взвешивание Больцмана
\ n \ t \ t \ t \ tСогласно механике Больцмана для чисто случайных и хаотических тепловых систем, элементы (например, молекулы) в системе придерживаются кривой теплового распределения (рисунок 3.a. ниже) . В общем, при низких температурах большинство элементов или молекул находятся на самом низком уровне энергии или в основном состоянии.По мере увеличения температуры в системе элементы начинают покидать нижние энергетические уровни и заселяют верхние энергетические уровни. При очень высоких температурах может быть заселено несколько верхних энергетических уровней, в результате чего в низшем основном состоянии остается несколько молекул. Распределение элементов по уровням энергии определяется с помощью фактора Больцмана:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t− \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tk \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tB \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE34
\ n \ t \ t \ t \ tЭто весовой коэффициент, который определяет вероятность того, что элемент будет находиться в энергетическом состоянии «n th », когда система находится в термодинамическом равновесии.Фактор Больцмана исключает рассмотрение резонансных рабочих энергий (которые являются упорядоченными) и предполагает полностью случайные движения в системе. Таким образом, при применении механики Больцмана обычно предполагается, что энергии Гельмгольца минимальны.
\ n \ t \ t \ t \ tРисунок 3.
Сравнение состояний заселенности энергетических уровней в тепловых условиях и в условиях резонансной ЭМ. Население верхнего энергетического уровня увеличивается с повышением температуры. Поглощение резонансных электромагнитных волн приводит к нерегулярной кривой распределения резонансной энергии.Это может привести к поведению системы, эквивалентному «виртуальной» кривой теплового распределения.
\ n \ t \ t \ t \ tКогда система подвергается воздействию резонансных электромагнитных волн, может возникать «виртуальный» тепловой эффект, как в примере с водным растворителем выше. В таком случае «виртуальное» тепловое распределение может быть определено с использованием модификации весового коэффициента Больцмана:
\ n \ t \ t \ t \ t\ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ te \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t- \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tE \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tn \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t / \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tr \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tf \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tk \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ tB \ n \ t \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ t \ tT \ n \ t \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ t \ n \ t \ t \ t \ t \ t \ n \ t \ t \ t \ tE35
\ n \ t \ t \ t \ t, в который включен коэффициент резонанса «r f ».Полученная кривая теплового распределения показывает кривую распределения энергетических состояний термодинамической системы, которая приведет к тому же желаемому продукту или поведению, которые производятся системой, поглощающей резонансную энергию.
\ n \ t \ t \ t \ tПредположения о случайности в механике Больцмана неприменимы к резонансным электромагнитным системам с их однородной рабочей энергией, а системы, подверженные воздействию резонансных электромагнитных волн, не следуют плавным кривым теплового распределения, тем не мение. Индивидуальные уровни энергии в системе могут быть выборочно заселены, изменяя форму традиционной плавной кривой на выпуклую или «неровную» кривую распределения энергии.(Рисунок 3b., Выше). Поглощение резонансных электромагнитных волн первоначально приводит к увеличению заселенности верхнего энергетического уровня. По мере того как энергия преобразуется для работы в системе, состояние энергии меняется и расслабляется. Когда вся рабочая энергия израсходована, снова проявляется тепловое распределение. В зависимости от того, какие уровни энергии селективно заселяются, выполняемая работа будет варьироваться и может включать ускорение скорости реакции каталитическим способом, например, виртуальные тепловые эффекты могут заменять энергии химической активации.(\ n \ t \ t \ t \ t \ t \ tФукусима Дж. и др., 2010 \ n \ t \ t \ t \ t \ t)
\ n \ t \ t \ t \ n \ t \ t \ т \ п \ т \ т \ т \ т4.8. Константа равновесия
\ n \ t \ t \ t \ tВ химических и материальных системах работа, выполняемая резонансными электромагнитными волнами, также может сдвинуть равновесие системы и вызвать драматические изменения в ее химической и материальной динамике. В динамическом равновесии химических и материальных систем, в котором реагенты превращаются в продукты с той же скоростью, что продукты превращаются обратно в реагенты, константа равновесия «K» указывает точку динамического равновесия (соотношение концентраций продукта и реагента).Системы с большой константой равновесия содержат в основном продукт, в то время как низкий «K» указывает в основном на реагенты.
\ n \ t \ t \ t \ tРисунок 4.
a) Тепловая система; б) Резонатная система
\ n \ t \ t \ t \ tВ статистической термодинамике константа равновесия пропорциональна другому натуральному логарифму, K ≈ e -ΔE / RT ”(где ΔE – химическая свободная энергия). Когда в системе присутствуют резонансные электромагнитные волны, резонансный коэффициент правильно появляется в знаменателе обозначения мощности, т.е.е., «r f RT», чтобы отразить общее увеличение энергии системы. Если резонансные электромагнитные волны увеличивают химическую свободную энергию, «ΔE», отношение химической свободной энергии к энергии системы остается прежним. Константа равновесия не изменяется, однако электромагнитные волны действуют как катализатор и увеличивают скорость реакции. (Если химическая свободная энергия уменьшается, т. Е. Коэффициент резонанса меньше «единицы», электромагнитные волны будут действовать как отрицательный катализатор и замедлить скорость реакции.)
\ n \ t \ t \ t \ tКогда резонансные электромагнитные волны поглощаются и преобразуются в нечто иное, чем свободная химическая энергия, тогда ΔE / r f RT <ΔE / RT, и константа равновесия будет увеличиваться.Резонансные электромагнитные волны, выполняющие полезную работу в системе, могут, таким образом, увеличивать константу равновесия «K» и увеличивать фактическую концентрацию желаемых продуктов. Резонансные электромагнитные волны могут вызвать сдвиг кривой равновесия. (Рисунок 4.b., выше) Другими словами, резонансные электромагнитные волны могут привести к результатам, недостижимым с помощью классического катализа или термодинамики. (Брукс и Абель, 2007, Блюм и др., 2003, \ n \ t \ t \ t \ t \ t \ tFukushima H., 2010 \ n \ t \ t \ t \ t \ t, и Рой и др., 2002 )
\ n \ t \ t \ t \ n \ t \ t Под редакцией Яна Оксхольма Горделадзе, ISBN 978-953-51-3020-8, ISBN печати 978-953-51-3019-2, 336 страниц,
\ nИздатель: IntechOpen
\ nГлавы опубликованы 22 марта 2017 г. под лицензией CC BY 3.0 лицензия
\ nDOI: 10.5772 / 61430
\ nОтредактированный том
Эта книга служит всесторонним обзором влияния витамина K2 на клеточные функции и системы органов, показывая, что витамин K2 играет важную роль в дифференциации / сохранении различных клеточных фенотипов и как стимулятор и / или посредник межорганного взаимодействия. Витамин K2 связывается с фактором транскрипции SXR / PXR, таким образом действуя как гормон (во многом так же, как витамин A и витамин D). Таким образом, витамин K2 влияет на множество систем органов и считается одним из положительных факторов, обеспечивающих «долголетие» человеческого тела, т.е.g., поддерживая функции / здоровье различных систем органов, а также корректируя функционирование или даже «излечивая» недуги, поражающие несколько органов нашего тела.
Эта книга служит всесторонним обзором влияния витамина K2 на клеточные функции и системы органов, показывая, что витамин K2 играет важную роль в дифференцировке / сохранении различных фенотипов клеток и как стимулятор и / или посредник межорганного взаимодействия. разговаривать. Витамин K2 связывается с фактором транскрипции SXR / PXR, таким образом действуя как гормон (во многом так же, как витамин A и витамин D).Таким образом, витамин K2 влияет на множество систем органов и считается одним из положительных факторов в обеспечении «долголетия» человеческого тела, например, поддерживая функции / здоровье различных систем органов, а также корректируя функционирование или даже «лечить» недуги, поражающие несколько органов нашего тела.
Электромагнитные волны – Physics LibreTexts
Электромагнитная волна состоит из колеблющихся, сопутствующих электрических и магнитных полей, ориентированных перпендикулярно друг другу.
Введение
Электромагнитные волны состоят из двух компонентов: колеблющегося электрического поля и перпендикулярного сопутствующего магнитного поля, которое колеблется с той же частотой, но со сдвигом фазы на 90 °. Они описывают движение пакета энергии между двумя точками. Обсуждая электромагнитные волны, мы обычно обращаем внимание на их волнообразное поведение, а не на их электромагнитные свойства.
Волны – периодические функции, поэтому мы можем определить все свойства волны из одного цикла волны, как на рисунке ниже.Период , T , – это промежуток времени, необходимый для завершения одного цикла, амплитуда (обычно обозначается A), в этом случае – максимальное значение электрического поля волны, а длина волны λ – это расстояние в реальном пространстве, пройденное волной за один цикл.
Мы можем определить некоторые полезные величины из измеримых. Например, частота волны , \ (\ nu \) , просто обратна периоду.
\ [f = 1 / T \]
\ [\ nu = 1 / T \]
Частоту, длину волны и энергию электромагнитной волны можно рассчитать по следующим уравнениям; первое уравнение утверждает, что произведение частоты электромагнитной волны на длину волны постоянно и равно скорости света c. Вторая пара уравнений сообщает нам энергию как функцию длины волны и частоты соответственно. Обратите внимание, что они описывают свет, движущийся через вакуум. {- ik (x- \ nu t)} \]
Электромагнитный спектр
Мы используем множество различных терминов для описания электромагнитного излучения в зависимости от его энергии.Видимый свет, рентгеновские лучи и микроволны – все это электромагнитные волны. Несмотря на названия, все электромагнитное излучение физически одинаково – колеблющиеся электрические и магнитные волны. Однако способ взаимодействия электромагнитных волн разной энергии с веществом заставляет нас называть их по-разному. Например, рентгеновские лучи проходят через многие объекты, недоступные для видимого света, такие как наши тела. Это происходит потому, что атомы могут поглощать электромагнитные волны только с частотами, соответствующими их собственным резонансным частотам.
Инфографика с изображением длины волны, частоты и видимого спектра.Предоставлено Орегонским университетом
ЭМ волны в среде
Когда электромагнитные волны проходят через среду – что угодно, кроме истинного вакуума – они замедляются до скорости, меньшей скорости света в вакууме c, в зависимости от показателя преломления материала n. Их скорость подчиняется простому уравнению \ [v = c / n \]. Показатель преломления – это мера того, как электрические и магнитные поля в среде влияют на бегущие электромагнитные волны. Среды с более высоким показателем преломления сильнее влияют на электромагнитные волны.
Преломление
ЭМ волны, проходящие между двумя средами с разными показателями преломления, преломляются или изменяют направление из-за изменения скорости света в этой среде. Преломление зависит от показателей преломления для обеих сред, а также от угла падения света на вторую среду. На рисунке ниже показано, как свет преломляется водой, исходящей из воздуха. Разница в двух углах определяется формулой, приведенной ниже. В этом случае показатель преломления воздуха фактически равен 1 (точнее, ровно 1.000277), а для воды – 1,33.
\ [\ frac {sin {\ theta_1}} {sin {\ theta_2}} = \ frac {v_1} {v_2} = \ frac {n_1} {n_2} \]
Луч света, проходящий между воздухом и водой. Обратите внимание на изменение углов между падающим и преломленным лучом. Для луча, падающего на воду с воздуха, \ [sin (\ theta_2) = \ frac {1} {1.33} sin (\ theta_1) \]
Домашние задания
1. Похититель драгоценностей, скрывающийся в заброшенном особняке, думает, что он видел, как что-то движется в озере.Подозревая, что дети вмешиваются, он направляет фонарик на грязную, загрязненную воду, но, к его счастью, это просто огромная собака. Если луч света падает на воду под углом 75 градусов, а преломленный свет имеет угол 50 градусов, каков должен быть показатель преломления этого загрязненного озера?
Ответ: n = 1,5
Список литературы
- Джексон, Джон Дэвид. Classical Electrodynamics , John Wiley and Sons, inc, Нью-Джерси 1962
- Гриффитс, Дэвид Дж., Введение в электродинамику, Prentice Hall, inc, Нью-Джерси, 1999 г.
Авторы и авторство
- Майкл Карфункл (Чикаго)
Как развалится физика, если EMdrive работает
Прототип EMdrive в испытательной камере NASA Eagleworks.Изображение предоставлено: H. White et … [+] al., AIAA 2016.
Представьте себе ракету, которая работает без топлива. Вы накачиваете в него энергию и уходите, но с другой стороны не выходит ни тяги, ни выхлопа, ни отходов, ни расходуемого топлива. Это абсолютный вызов Исааку Ньютону: утверждение, что он действует без равной и противоположной реакции. И все же изобретатель EMdrive Роджер Шоуер утверждает, что именно это делает. Он не только говорит, что его устройство работает, он утверждает, что любой может построить его и проверить его на себе.В лаборатории Eagleworks ученые НАСА попытались сделать именно это и просто опубликовали свои выводы в рецензируемом журнале. Результаты, достижения? Они проверяют, что EMdrive работает, как рекламируется.
EMdrive в установке SPR Ltd. Изображение предоставлено: Roger Shawyer / SPR Ltd., через … [+] http://emdrive.com/dynamictests.html.
Если EMdrive действительно является космическим двигателем, который работает без реакции – вы накачиваете в него мощность и получаете тягу без заметного выхлопа – то это крупнейшая революция в физике со времен Исаака Ньютона.Три закона движения Ньютона действовали сотни лет:
- Покоящийся объект остается неподвижным, а объект в движении остается в движении, если на него не действует внешняя сила.
- Сила, действующая на объект, равна скорости изменения его количества движения во времени. ( F = m a для нерелятивистских систем.)
- И на каждое действие есть равная и противоположная реакция.
Этот третий закон известен как сохранение количества движения и верен не только в механике Ньютона, но и в электромагнетизме, общей теории относительности и всей квантовой теории поля.Это единственный закон, который придумал Ньютон, который действует и сегодня без исключений.
Ракета Союз-2.1а стартует 19 апреля 2013 года с Бион-М № 1. Изображение предоставлено Роскосмосом. Обратите внимание … [+] реакция выхлопа на действие ускорения космического корабля.
Но если EMdrive действительно не реагирует, тогда Ньютон ошибается. Кроме того, ошибается Эйнштейн, ошибается Максвелл и ложна вся квантовая физика. Есть фундаментальная симметрия, которая вызывает сохранение импульса: трансляционная симметрия.Это означает, что если моя система находится здесь, в определенной точке пространства, она должна подчиняться тем же законам, как если бы она была там, в другой точке пространства. Но если сохранение импульса не является действительно фундаментальным, то трансляционная симметрия не может быть хорошей симметрией Вселенной. Другими словами, должно быть предпочтительное место, где законы физики в одном месте отличаются от других. Законы физики внезапно зависят от положения.
Различные системы отсчета, включая разные положения и движения, увидят разные законы… [+] физики, если сохранение количества движения неверно. Изображение предоставлено пользователем Wikimedia Commons Krea под c.c.a.-s.a.-3.0.
Это означает, что фундаментальный принцип относительности неверен. Это означает, что если вы находитесь в инерциальной системе отсчета, вы можете увидеть изменение импульса всей системы с течением времени. Более того, это означает, что наблюдатели в разных системах отсчета будут видеть нарушения сохранения импульса на разную величину. Если вы нарушите закон сохранения импульса на разную величину, вы также нарушите закон сохранения энергии; энергия не только не сохраняется, она не сохраняется в разных количествах в разных системах отсчета.Самый священный закон физики элементарных частиц – закон, применимый к каждой системе и каждому взаимодействию, установленному в истории, – будет нарушен.
Треки частиц, исходящие от столкновения с высокой энергией на LHC в 2014 году. Они проверяют … [+] сохранение импульса и энергии гораздо более надежно, чем любой другой эксперимент. Изображение предоставлено пользователем Wikimedia Commons Пчарито, под лицензией c.c.a.-by-s.a.-3.0.
Проблема не в том, что эти законы нельзя опровергнуть экспериментально; конечно могли.Проблема в том, что физики провели так много экспериментов разными способами, так тщательно и с такой точностью проверяя их. Эти законы сохранения были подтверждены для каждого когда-либо наблюдавшегося гравитационного, механического, электромагнитного и квантового взаимодействия. А теперь утверждается, что двигатель, основанный не более чем на простом источнике электромагнитной энергии, опровергает всю физику. И тест NASA Eagleworks в рецензируемой статье подтверждает, что тяга создается без заметной реакции на наблюдаемое действие.
Экспериментальная установка EMdrive. Изображение предоставлено: Х. Уайт и др., «Измерение импульсной … [+] тяги от закрытого радиочастотного резонатора в вакууме», AIAA 2016.
Теперь есть несколько возможностей, которые могут спасти сохранение импульса. Это может спасти законы действия / противодействия. Это может спасти физику в том виде, в каком мы ее знаем. В их числе:
- Что есть выхлоп, который просто не измеряется, в том числе в виде электромагнитного излучения.Это будет означать, что реакция все-таки есть.
- Что существует электромагнитное поле, генерируемое как часть установки, и изменение количества движения поля уравновешивает изменение количества движения двигателя. Опять была бы реакция.
- Или инженеры, проводившие испытание в NASA Eagleworks, были некомпетентны, и либо есть реакция, которую они пропустили, либо наблюдаемая тяга нереальна.
Результаты все еще относятся к очень небольшим толчкам менее 100 микроньютонов с большими входными мощностями от десятков до сотен ватт.Если вы помните нейтрино, превышающие скорость света, результаты BICEP2 для гравитационных волн от инфляции, утверждения о холодном синтезе, вечном движении или любой другой набор результатов, которые позже были опровергнуты большим количеством более точных данных, вы вспомните, что это далеко от слэм-данка. Теоретические утверждения о том, как это могло работать, варьируются от легко опровергнутых до сильно спекулятивных, и все они не имеют никаких доказательств , кроме этого единственного двигателя , которые можно было бы показать.
Это действительно похоже на настоящий эффект, но действительно ли это связано с безреакционным двигателем? Изображение предоставлено :… [+] Х. Уайт и др., “Измерение импульсной тяги от закрытого радиочастотного резонатора в вакууме”, AIAA 2016.
Дело не в том, что физика неверна, и не в том, что команда Eagleworks ошибается. Дело в том, что это начальные этапы реальной науки, проводимой для изучения эффекта. Наиболее вероятный исход состоит в том, что импульс действительно сохраняется и здесь происходит что-то забавное. Для нейтрино быстрее света это был слабый кабель. Для результатов BICEP2 это была неправильная калибровка галактического газа.Для холодного синтеза это была плохая экспериментальная установка, а для вечного двигателя это была афера. Независимо от того, каков будет результат, дальнейшее расследование будет чему-то научным. Будь то новая физика и новый тип двигателя, или это проще, чем это, а причина эффекта просто еще не определена, больше и лучше экспериментов будут окончательным арбитром. Вот почему мы в первую очередь занимаемся наукой.
Действительно ли электромагнитный двигатель нарушил физику в «просочившейся» статье НАСА?
Ионная тяга в настоящее время является самой медленной, но наиболее экономичной формой космических путешествий.Предоставлено: НАСА / Лаборатория реактивного движения.С тех пор, как НАСА объявило о создании прототипа неоднозначного двигателя с резонансным радиочастотным резонатором (также известного как электромагнитный двигатель), все полученные результаты стали предметом споров. И поскольку большинство объявлений принимает форму «утечек» и слухов, все события, о которых сообщается, естественно, были восприняты со скептицизмом.
И все же отчеты продолжают поступать.Последние предполагаемые результаты получены из лабораторий Eagleworks в Космическом центре Джонсона, где “просочившийся” отчет показал, что спорный двигатель способен генерировать тягу в вакууме. Как и в случае с критическим процессом экспертной оценки, вопрос о том, сможет ли двигатель пройти проверку в космосе или нет, оставался неизменным вопросом в течение некоторого времени.
Учитывая преимущества EM Drive, понятно, что люди хотят видеть, как он работает. Теоретически они включают в себя способность генерировать достаточную тягу для полета на Луну всего за четыре часа, на Марс за 70 дней и на Плутон за 18 месяцев, а также возможность делать все это без потребности в топливе.К сожалению, система привода основана на принципах, нарушающих закон сохранения количества движения.
Этот закон гласит, что в системе количество импульса остается постоянным и не создается и не уничтожается, а изменяется только под действием сил. Поскольку EM Drive включает в себя электромагнитные микроволновые резонаторы, преобразующие электрическую энергию непосредственно в тягу, у него нет реактивной массы. Следовательно, это «невозможно» с точки зрения традиционной физики.
Отчет под названием «Измерение импульсной тяги от закрытого радиочастотного резонатора в вакууме», по-видимому, просочился в начале ноября.Его ведущим автором, как и следовало ожидать, является Гарольд Уайт, руководитель группы перспективных двигателей Технического управления НАСА и главный исследователь лаборатории НАСА Eagleworks.
Как он и его коллеги (якобы) сообщают в статье, они выполнили импульсное испытание тяги на «коническом тестовом образце RF». Он состоял из фазы прямой и обратной тяги, маятника малой тяги и трех испытаний тяги на уровнях мощности 40, 60 и 80 Вт. Как указано в отчете:
“Здесь показано, что диалектически нагруженный конический РЧ-образец для испытаний, возбужденный в режиме TM212 на частоте 1937 МГц, способен последовательно генерировать силу на уровне тяги 1.2 ± 0,1 мН / кВт с силой, направленной на узкий конец в условиях вакуума ».
Для ясности, это уровень тяги к мощности – 1,2. миллиньютон на киловатт – совсем несущественно. Фактически, в статье эти результаты помещаются в контекст, сравнивая их с предложениями по ионным двигателям и лазерным парусам:
«Современное состояние тяги к мощности для холловского подруливающего устройства составляет порядка 60 мН / кВт.Это на порядок выше, чем у испытуемого образца, оцененного в ходе этой вакуумной кампании… Параметр производительности 1,2 мН / кВт на два порядка выше, чем у других форм двигателя с «нулевым ракетным топливом», таких как световые паруса, лазерная тяга и фотонные ракеты, имеющие тягу до уровней мощности в диапазоне 3,33-6,67 [микроньютон] / кВт (или 0,0033 – 0,0067 мН / кВт) ».
В настоящее время ионные двигатели считаются наиболее экономичным двигателем. Однако они заведомо медленнее по сравнению с обычными твердотопливными двигателями.Чтобы предложить некоторую перспективу, миссия ESA “Рассвет” опиралась на ксенон-ионный двигатель, который имел тягу для выработки электроэнергии 90 миллиньютон на киловатт. Используя эту технологию, зонду потребовалось почти четыре года, чтобы добраться от Земли до астероида Веста.
Концепция прямой энергии (также известная как лазерные паруса), напротив, требует очень небольшой тяги, поскольку включает в себя аппараты размером с пластину – крошечные зонды, которые весят около грамма и несут все необходимые им инструменты в виде микросхем. Эта концепция в настоящее время изучается с целью совершить путешествие к соседним планетам и звездным системам в рамках нашей собственной жизни.
Два хороших примера – это финансируемая НАСА межзвездная концепция DEEP-IN, которая разрабатывается в UCSB, которая пытается использовать лазеры для приведения корабля в движение со скоростью до 0,25 скорости света. Тем временем Project Starshot (часть Breakthrough Initiatives) разрабатывает корабль, который, как они утверждают, будет развивать скорость в 20% от скорости света и, таким образом, сможет совершить путешествие к Альфе Центавра через 20 лет.
По сравнению с этими предложениями EM Drive может похвастаться тем, что не требует топлива или внешнего источника питания.Но, судя по результатам этих испытаний, количество мощности, которое потребовалось бы для создания значительного количества тяги, сделало бы это непрактичным. Однако следует иметь в виду, что это испытание на малой мощности было разработано для того, чтобы увидеть, может ли какая-либо обнаруженная тяга быть связана с аномалиями (ни одна из которых не была обнаружена).
В отчете также признается, что необходимы дальнейшие испытания, чтобы исключить другие возможные причины, такие как смещение центра тяжести (ЦТ) и тепловое расширение. И если внешние причины снова будут исключены, в будущих тестах, несомненно, будет предпринята попытка максимизировать производительность, чтобы увидеть, какую тягу способен генерировать EM Drive.
Но, конечно, все это предполагает, что “просочившаяся” бумага подлинная. Пока НАСА не подтвердит, что эти результаты действительно реальны, EM Drive застрянет в подвешенном состоянии.
Изображение: запуск ионного двигателя Т6
Цитата : Действительно ли физика нарушена электромагнитным приводом в «просочившейся» статье НАСА? (2016, 11 ноября) получено 27 октября 2021 г. с https: // физ.org / news / 2016-11-Physics-Violated-em-leaked-nasa.html
Этот документ защищен авторским правом. За исключением честных сделок с целью частного изучения или исследования, никакие часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в информационных целях.
2D Азимутальная визуализация коррозии на основе ЭМ с использованием физико-ориентированного машинного обучения PIML | Конференция и выставка SPE Offshore Europe
Вследствие сегодняшней промышленной революции было разработано множество передовых технологий и методов для решения сложных задач при оценке целостности скважин.Одним из наиболее заметных нововведений является интеграция физики данных для надежных внутрискважинных измерений. В этой статье представлен многообещающий прорыв в построении изображений коррозии на основе электромагнетизма с использованием машинного обучения с учетом физики (PIML), протестированных и проверенных на поперечных сечениях реальных металлических обсадных труб / труб с дефектами различных размеров, местоположений и расстояний.
В отличие от существующих инструментов контроля на основе электромагнетизма, в которых измеряется только средняя толщина металла по окружности, это исследование исследует интерпретацию с помощью искусственного интеллекта (AI) уникального расположения электромагнитных (EM) датчиков.Это облегчает разработку нового решения для визуализации коррозии через НКТ, которое улучшает обнаружение дефектов с точностью до пикселя. Разработанный фреймворк включает в себя упреждающий электромагнитный решатель на основе конечных разностей во временной области (FDTD) и искусственную нейронную сеть (ИНС), а именно рекуррентную нейронную сеть с долговременной краткосрочной памятью (LSTM-RNN). ИНС обучается с использованием результатов, сгенерированных решателем FDTD, который моделирует показания датчиков для различных сценариев неисправностей.
Интеграция откликов массива электромагнитных датчиков и ИНС позволила обобщить и точно измерить процент потерь металла по различным экспериментальным дефектам.Это также позволило точно прогнозировать размеры, количество и расположение отверстий дефектов с охватом на 360 градусов. Результаты были нанесены на индивидуальные двухмерные тепловые карты для любого желаемого поперечного сечения испытательной оболочки. Дальнейший анализ различных методов показал, что LSTM-RNN может показать более высокую точность и надежность по сравнению с обычными плотными сетями, особенно в случае множественных дефектов. LSTM-RNN подтверждается с использованием дополнительных данных из смоделированных и экспериментальных данных. Результаты показывают надежные прогнозы даже с ограниченными данными обучения.Модель точно предсказывала дефекты большего и меньшего размера, которые были намеренно исключены из обучающих данных, чтобы продемонстрировать возможность обобщения.


 Область температур – 80 – 350 К, область магнитных полей 0-26 кЭ.
Область температур – 80 – 350 К, область магнитных полей 0-26 кЭ.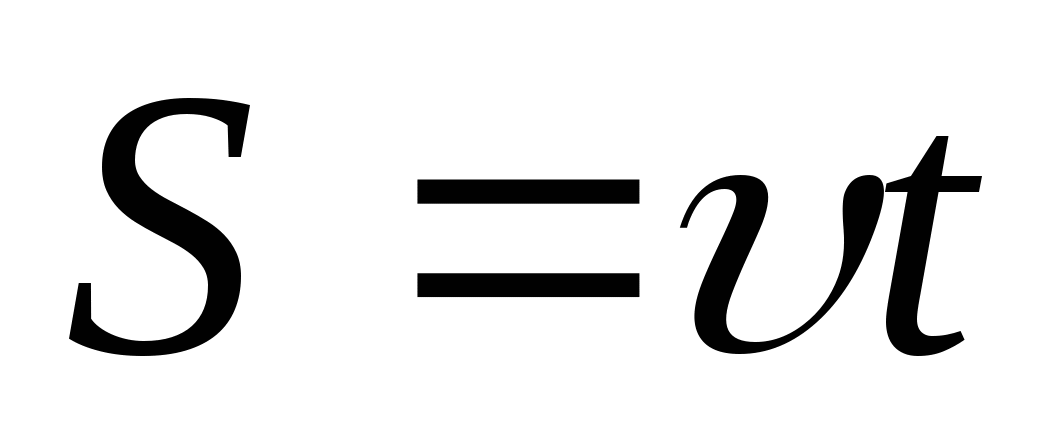 Микаилович
Микаилович ru
ru При использовании свойств CSS в работе с текстом Вы забудете про проблему кроссбраузерности т. е. Ваш текст будет отображаться во всех браузерах именно так как нужно Вам, а не так как вздумается браузеру. Кроме того СSS открывает куда более широкие возможности связанные как со стилем текста, так и с дизайном сайта в целом.
При использовании свойств CSS в работе с текстом Вы забудете про проблему кроссбраузерности т. е. Ваш текст будет отображаться во всех браузерах именно так как нужно Вам, а не так как вздумается браузеру. Кроме того СSS открывает куда более широкие возможности связанные как со стилем текста, так и с дизайном сайта в целом. д. В идеале на странице должен быть всего один заголовок <h2>, потом текст разбивается несколькими <h3> и далее по значимости заголовков.
д. В идеале на странице должен быть всего один заголовок <h2>, потом текст разбивается несколькими <h3> и далее по значимости заголовков. законы.
законы. Д.
Д. Пропустите заряды по проводу – и вы сделали магнит – электромагнит. Ключевой вывод Максвелла заключался в том, что пространство между двумя параллельными металлическими пластинами в процессе зарядки будет вести себя так же, как пространство вокруг токоведущего провода.Есть магнетизм, который возникает от электрических токов (например, ток через рабочий электромагнит), и магнетизм, который возникает от токов смещения (например, изменяющееся электрическое поле в конденсаторе, который только что был включен или выключен).
Пропустите заряды по проводу – и вы сделали магнит – электромагнит. Ключевой вывод Максвелла заключался в том, что пространство между двумя параллельными металлическими пластинами в процессе зарядки будет вести себя так же, как пространство вокруг токоведущего провода.Есть магнетизм, который возникает от электрических токов (например, ток через рабочий электромагнит), и магнетизм, который возникает от токов смещения (например, изменяющееся электрическое поле в конденсаторе, который только что был включен или выключен). Единственное, что использовали свет в эксперименте, – это видеть инструменты . Значение [ c ], найденное М. Фуко, было получено путем определения угла, на который вращается вращающееся зеркало, в то время как отраженный от него свет уходил и возвращался по измеренному курсу. Нет смысла делать что-либо из электричества или магнетизма .
Единственное, что использовали свет в эксперименте, – это видеть инструменты . Значение [ c ], найденное М. Фуко, было получено путем определения угла, на который вращается вращающееся зеркало, в то время как отраженный от него свет уходил и возвращался по измеренному курсу. Нет смысла делать что-либо из электричества или магнетизма . =
= Иосифа, Ливан) – Geant4-DNA
Иосифа, Ливан) – Geant4-DNA