Е от ф как найти: Найти E(f) и D(f). С подробным решением.

Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения

Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.

В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.

Начнем с базовых определений.

Определение 1

Множество значений функции y = f(x) на некотором интервале x представляет собой множество всех значений, которые данная функция принимает при переборе всех значений x∈X.

Определение 2

Область значений функции y=f(x) – это множество всех ее значений, которые она может принять при переборе значений x из области x∈(f).

Область значений некоторой функции принято обозначать E(f).

Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.

 Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y=f(x). Область допустимых значений x для выражения f(x) и будет областью определения данной функции.

Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.

Очевидно, что область значений функции можно получить при проецировании графика функции на ось Oy. При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых промежутков и др.

Рассмотрим основные способы нахождения области значений функции.

Начнем с определения множества значений непрерывной функции y = f(x) на некотором отрезке, обозначенном [a; b]. Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего maxx∈a; bf(x) и наименьшего значения minx∈a; bf(x). Значит, у нас получится отрезок minx∈a; bf(x); maxx∈a; bf(x), в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

Возьмем задачу, в которой нужно определить область значений арксинуса.

Пример 1

Условие: найдите область значений y = arcsin x.

Решение

В общем случае область определения арксинуса располагается на отрезке [-1; 1]. Нам надо определить наибольшее и наименьшее значение указанной функции на нем.

y’ = arcsin x’=11-x2

Мы знаем, что производная функции будет положительной для всех значений x, расположенных в интервале [-1; 1], то есть на протяжении всей области определения функция арксинуса будет возрастать. Значит, самое маленькое значение она примет при x, равном -1, а самое большое – при x, равном 1.

minx∈-1; 1arcsin x=arcsin-1=-π2maxx∈-1; 1arcsin x=arcsin 1=π2

Таким образом, область значений функции арксинус будет равна E(arcsin x)=-π2; π2.

Ответ:  E(arcsin x)=-π2; π2

Пример 2

Условие: вычислите область значений y=x4-5×3+6×2 на заданном отрезке [1; 4].

Решение 

Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.

Для определения точек экстремума надо произвести следующие вычисления:

y’=x4-5×3+6×2’=4×3+15×2+12x=x4x2-15x+12y’=0⇔x(4×2-15x+12)=0x1=0∉1; 4 или 4×2-15x+12=0D=-152-4·4·12=33×2=15-338≈1.16∈1; 4; x3=15+338≈2.59∈1; 4

Теперь найдем значения заданной функции в концах отрезка и точках x2=15-338; x3=15+338:

y(1)=14-5·13+6·12=2y15-338=15-3384-5·15-3383+6·15-3382==117+16533512≈2.08y15+338=15+3384-5·15+3383+6·15+3382==117-16533512≈-1. 62y(4)=44-5·43+6·42=32

Значит, множество значений функции будет определяться отрезком 117-16533512; 32.

Ответ: 117-16533512; 32.

Перейдем к нахождению множества значений непрерывной функции y = f(x) в промежутках (a; b), причем a; +∞, -∞; b, -∞; +∞.

Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.

Пример 3

Условие: вычислите область значений функции y=1×2-4 на интервале (-2; 2).

Решение

Определяем наибольшее и наименьшее значение функции на заданном отрезке

y’=1×2-4’=-2x(x2-4)2y’=0⇔-2x(x2-4)2=0⇔x=0∈(-2; 2)

У нас получилось максимальное значение, равное 0, поскольку именно в этой точке происходит перемена знака функции и график переходит к убыванию. См. на иллюстрацию:

То есть  y(0)=102-4=-14 будет максимальным значений функции.

Теперь определим поведение функции при таком x, который стремится к -2 с правой стороны и к +2 с левой стороны. Иными словами, найдем односторонние пределы:

limx→-2+01×2-4=limx→-2+01(x-2)(x+2)==1-2+0-2-2+0+2=-14·1+0=-∞limx→2+01×2-4=limx→2+01(x-2)(x+2)==12-0-22-0+2=14·1-0=-∞

У нас получилось, что значения функции будут возрастать от минус бесконечности до -14 тогда, когда аргумент изменяется в пределах от -2 до 0. А когда аргумент меняется от 0 до 2, значения функции убывают к минус бесконечности. Следовательно, множеством значений заданной функции на нужном нам интервале будет (-∞; -14].

Ответ: (-∞; -14].

Пример 4

Условие: укажите множество значений y=tg x на заданном интервале -π2; π2.

Решение

Нам известно, что в общем случае производная тангенса в -π2; π2 будет положительной, то есть функция будет возрастать.

Теперь определим, как ведет себя функция в заданных границах:

limx→π2+0tg x=tg-π2+0=-∞limx→π2-0tg x=tgπ2-0=+∞

Мы получили рост значений функции от минус бесконечности к плюс бесконечности при изменении аргумента от -π2 до π2,и можно сказать, что множеством решений данной функции будет множество всех действительных чисел.

Ответ: -∞; +∞.

Пример 5

Условие: определите, какова область значений функции натурального логарифма y = ln x.

Решение

Нам известно, что данная функция является определенной при положительных значениях аргумента D(y)=0; +∞. Производная на заданном интервале будет положительной: y’=ln x’=1x. Значит, на нем происходит возрастание функции. Далее нам нужно определить односторонний предел для того случая, когда аргумент стремится к 0 (в правой  части), и когда x стремится к бесконечности:

limx→0+0ln x=ln(0+0)=-∞limx→∞ln x=ln+∞=+∞

Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.

Ответ: 

множество всех действительных чисел – область значений функции натурального логарифма.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 6

Условие: определите, какова область значений функции y=9×2+1.

Решение

Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:

y’=9×2+1’=-18x(x2+1)2y’=0⇔x=0y’≤0⇔x≥0y’≥0⇔x≤0

В итоге мы определили, что данная функция будет убывать, если x≥0; возрастать, если x≤0; она имеет точку максимума y(0)=902+1=9 при переменной, равной 0.

Посмотрим, как же ведет себя функция на бесконечности:

limx→-∞9×2+1=9-∞2+1=9·1+∞=+0limx→+∞9×2+1=9+∞2+1=9·1+∞=+0

Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.

Подведем итоги: когда аргумент изменяется от минус бесконечности до нуля, то значения функции возрастают от 0 до 9. Когда значения аргумента меняются от 0 до плюс бесконечности, соответствующие значения функции будут убывать от 9 до 0. Мы отобразили это на рисунке:

На нем видно, что областью значений функции будет интервал E(y)=(0; 9]

Ответ: 

E(y)=(0; 9]

Если нам надо определить множество значений функции y = f(x) на промежутках [a; b), (a; b], [a; +∞), (-∞; b], то нам понадобится провести точно такие же исследования. Эти случаи мы пока не будем разбирать: далее они нам еще встретятся в задачах.

А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.

Пример 7

Условие: определите, какова будет область значений y=xx-2.

Решение

Поскольку знаменатель функции не должен быть обращен в 0, то D(y)=-∞; 2∪2; +∞.

Начнем с определения множества значений функции на первом отрезке -∞; 2, который представляет из себя открытый луч. Мы знаем, что функция на нем будет убывать, то есть производная данной функции будет отрицательной.

limx→2-0xx-2=2-02-0-2=2-0=-∞limx→-∞xx-2=limx→-∞x-2+2x-2=limx→-∞1+2x-2=1+2-∞-2=1-0

Тогда в тех случаях, когда аргумент изменяется по направлению к минус бесконечности, значения функции будут асимптотически приближаться к 1. Если же значения x меняются от минус бесконечности до 2, то значения будут убывать от 1 до минус бесконечности, т.е. функция на этом отрезке примет значения из интервала -∞; 1. Единицу мы исключаем из наших рассуждений, поскольку значения функции ее не достигают, а лишь асимптотически приближаются к ней.

Для открытого луча 2; +∞ производим точно такие же действия. Функция на нем также является убывающей:

limx→2+0xx-2=2+02+0-2=2+0=+∞limx→+∞xx-2=limx→+∞x-2+2x-2=limx→+∞1+2x-2=1+2+∞-2=1+0

Значения функции на данном отрезке определяются множеством 1; +∞. Значит, нужная нам область значений функции, заданной в условии, будет объединением множеств -∞; 1 и 1; +∞.

Ответ: E(y)=-∞; 1∪1; +∞.

Это можно увидеть на графике:

Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.

Пример 8

Условие: определите область значений синуса y = sin x.

Решение

Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0; 2π и смотрим, каким будет множество значений на нем.

y’=(sin x)’=cos xy’=0⇔cos x=0⇔x=π2+πk, k∈Z

В рамках 0; 2π у функции будут точки экстремума π2 и x=3π2. Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.

y(0)=sin 0=0yπ2=sin π2=1y3π2=sin3π2=-1y(2π)=sin(2π)=0⇔minx∈0; 2πsin x=sin3π2=-1, maxx∈0; 2πsin x=sinπ2=1

Ответ: E(sin x)=-1; 1.

Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.

Пример 9

Условие: определите область значения y=3arccosx3+5π7-4.

Решение

Нам известно, что отрезок от 0 до пи есть область значений арккосинуса. Иными словами, E(arccos x)=0; π или 0≤arccos x≤π. Мы можем получить функцию arccosx3+5π7 из арккосинуса, сдвинув и растянув ее вдоль оси Ox, но такие преобразования нам ничего не дадут. Значит, 0≤arccosx3+5π7≤π.

Функция 3arccosx3+5π7 может быть получена из арккосинуса arccosx3+5π7 с помощью растяжения вдоль оси ординат, т. е. 0≤3arccosx3+5π7≤3π. Финалом преобразований является сдвиг вдоль оси Oy на 4 значения. В итоге получаем двойное неравенство:

0-4≤3arccosx3+5π7-4≤3π-4⇔-4≤3arccosx3+5π7-4≤3π-4

Мы получили, что нужная нам область значений будет равна E(y)=-4; 3π-4.

Ответ: E(y)=-4; 3π-4.

Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.

Пример 10

Условие: вычислите, какова будет область значений функции y=22x-1+3.

Решение

Перепишем функцию, заданную в условии, как y=2·(2x-1)-12+3. Для степенной функции y=x-12 область значений будет определена на промежутке 0; +∞, т.е. x-12>0. В таком случае:

2x-1-12>0⇒2·(2x-1)-12>0⇒2·(2x-1)-12+3>3

Значит, E(y)=3; +∞.

Ответ: E(y)=3; +∞.

Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.

Пример 11

Условие: дана функция y=2sinx2-4, x≤-3-1, -3<x≤31x-3, x>3. Вычислите область ее значений.

Решение

Данная функция является определенной для всех значений  x. Проведем ее анализ на непрерывность при значениях аргумента, равных -3 и 3:

limx→-3-0f(x)=limx→-32sinx2-4=2sin-32-4=-2sin32-4limx→-3+0f(x)=limx→-3(1)=-1⇒limx→-3-0f(x)≠limx→-3+0f(x)

Имеем неустранимый разрыв первого рода при значении аргумента -3. При приближении к нему значения функции стремятся к -2sin32-4, а при стремлении x к -3 с правой стороны значения будут стремиться к -1.

limx→3-0f(x)=limx→3-0(-1)=1limx→3+0f(x)=limx→3+01x-3=+∞

Имеем неустранимый разрыв второго рода в точке 3. Когда функция стремится к нему, ее значения приближаются к -1, при стремлении к той же точке справа – к минус бесконечности.

Значит, вся область определения данной функции является разбитой на 3 интервала (-∞; -3], (-3; 3], (3; +∞).

На первом из них у нас получилась функция y=2sinx2-4. Поскольку -1≤sin x≤1, получаем:

-1≤sinx2<1⇒-2≤2sinx2≤2⇒-6≤2sinx2-4≤-2

Значит, на данном промежутке (-∞; -3] множество значении функции – [-6;2].

На полуинтервале (-3; 3] получилась постоянная функция y =-1. Следовательно, все множество ее значений в данном случае будет сводится к одному числу -1.

На втором промежутке 3; +∞ у нас есть функция y=1x-3. Она является убывающей, потому что y’=-1(x-3)2<0. Она будет убывать от плюс бесконечности до 0, но самого 0 не достигнет, потому что:

limx→3+01x-3=13+0-3=1+0=+∞limx→+∞1x-3=1+∞-3=1+∞+0

Значит, множество значений исходной функции при x > 3 представляет собой множество 0; +∞. Теперь объединим полученные результаты: E(y)=-6; -2∪-1∪0; +∞.

Ответ: E(y)=-6; -2∪-1∪0; +∞.

Решение показано на графике:

Пример 12

Условие: есть функция y=x2-3ex. Определите множество ее значений.

Решение

Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:

y’=x2-3ex’=2xex-ex(x2-3)e2x=-x2+2x+3ex=-(x+1)(x-3)ex

Мы знаем, что производная обратится в 0, если x=-1 и x=3. Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.

Функция будет убывать на (-∞; -1]∪[3; +∞) и возрастать на [-1; 3]. Точкой минимума будет -1, максимума –3.

Теперь найдем соответствующие значения функции:

y(-1)=-12-3e-1=-2ey(3)=32-3e3=6e-3

Посмотрим на поведение функции на бесконечности:

limx→-∞x2-3ex=-∞2-3e-∞=+∞+0=+∞limx→+∞x2-3ex=+∞2-3e+∞=+∞+∞==limx→+∞x2-3’ex’=limx→+∞2xex=+∞+∞==limx→+∞2x'(ex)’=2limx→+∞1ex=2·1+∞=+0

Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.

На нем видно, что значения функции будут убывать от плюс бесконечности до -2e тогда, когда аргумент меняется от минус бесконечности до -1. Если же он изменяется от 3 до плюс бесконечности, то значения будут убывать от 6e-3 до 0, но при этом 0 достигнут не будет.

Таким образом, E(y)=[-2e; +∞).

Ответ:  E(y)=[-2e; +∞)

Как найти область определения функции?

Понятие области определения функции

Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.

Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.

Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).

Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.

Из понятия функции сформулируем определение области определения функции.

Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох. 

Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

• Например, область значений функции y = x2 — это все числа больше либо равные нулю. Это можно записать так: Е (у): у ≥ 0.

Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.

Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) =  [-1, 1].

Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.

Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:   Через точку с запятой указываем два числа: левую и правую границы промежутка. Если граница входит в промежуток, ставим возле нее квадратную скобку, если не входит — круглую. Если у промежутка нет правой границы, записываем так: ∞ или +∞. Если нет левой границы, пишем -∞. Если нужно описать множество, состоящее из нескольких промежутков, ставим между ними знак объединения: ∪.

Например, все действительные числа от 2 до 5 включительно можно записать так:

Все положительные числа можно описать так:

Ноль не положительное число, поэтому скобка возле него круглая.

Области определения основных элементарных функций

Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.

На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.

Рассмотрим области определения основных элементарных функций.

Область определения постоянной функции

Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа. 

Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.

Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.

Например:

• Область определения постоянной функции y = -3 — это множество всех действительных чисел: D(f) = (−∞, +∞) или D(f) = R.
   
• Область определения функции y = ³√9 является множество R.

Область определения функции с корнем

Функцию с корнем можно определить так: y = ⁿ√x, где n — натуральное число больше единицы.

Рассмотрим две вариации такой функции.

Область определения корня зависит от четности или нечетности показателя:

• Если n — четное число, то есть, n = 2m, где m ∈ N, то ее область определения есть множество всех неотрицательных действительных чисел:
  
• Если показатель корня нечетное число больше единицы, то есть, n = 2m+1, то область определения корня — множество всех действительных чисел:
  

Значит, область определения каждой из функций y = √x, y = ⁴√x, y = ⁶√x,… есть числовое множество [0, +∞). А область определения функций y = ³√x, y = ⁵√x, y = ⁷√x,… — множество (−∞, +∞).

Пример 

Найти область определения функции:

Как решаем:

Так как подкоренное выражение должно быть положительным, то решим неравенство x² + 4x + 3 > 0.

Разложим квадратный трёхчлен на множители:

x² + 4x + 3 > 0

D = 16 – 12 = 4 > 0

Дискриминант положительный. Ищем корни:

Значит парабола a(x) = x² + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x² + 4x + 3 < 0), а другая часть — выше оси (неравенство x² + 4x + 3 > 0).

Поскольку коэффициент a = 1 > 0, то ветви параболы смотрят вверх. Можно сделать вывод, что на интервалах (−∞, -3) ∪ (−1, +∞) выполнено неравенство x² + 4x + 3 > 0 (ветви параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке (-3; -1) ниже оси абсцисс, что соответствует неравенству x² + 4x + 3 < 0.

Ответ: область определения: D(f) = (−∞, -3) ∪ (−1, +∞).

Область определения степенной функции

Степенная функция выглядит так: y = x^a, то есть, f(x) = x^a, где x — переменная в основании степени, a — некоторое число в показателе степени.

Область определения степенной функции зависит от значения показателя степени.

Перечислим возможные случаи:

• Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
• Для нецелых действительных положительных показателей степени: D(f) = [0, +∞).
• Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
• Для остальных действительных отрицательных a область определения степенной функции — числовой промежуток (0, +∞).

При a = 0 степенная функция y = x^a определена для всех действительных значений x, кроме x = 0. Это связано с тем, что мы не определяли 0⁰. А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x⁰ = 1 на области определения (−∞, 0) ∪ (0, +∞).

Рассмотрим несколько примеров.

 

1. Область определения функций y = x⁵, y = x¹² — множество R, так как показатели степени целые положительные.


2. Степенные функции определены на интервале [0, +∞), так как их показатели положительные, но не целые.


3. Область определения функции y = x⁻², как и функции y = x⁻⁵ — это множество (−∞, 0) ∪ (0, +∞), так как показатели степени целые отрицательные.


4. Область определения степенных функций y = x^-√19, y = x^-3e, — открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.

Область определения показательной функции

Показательную функцию можно задать формулой y = a^x, где переменная x — показатель степени, а — больше нуля и не равно единице.

Область определения показательной функции — это множество R.

Примеры показательных функций:

• y = e^x
• y = (√15)^x
• y = 13^x.

Область определения каждой из них (−∞, +∞).

Область определения логарифмической функции

Логарифмическая функция выглядит так: y = log_ax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.

Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:

• D (ln) = (0, +∞) и D (lg) = (0, +∞).

Рассмотрим примеры логарифмических функций: 

• y = log₇x
• y = lnx

Область определения этих функций есть множество (0, +∞).

Пример

Укажите область определения функции:

Как решаем:

Составим и решим систему:

Графическое решение:

Ответ: область определения: D(f) = (−3, -2) ∪ (−2, +∞).

Область определения тригонометрических функций

Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.

• Функция, которая задается формулой y = sinx, называется синусом, обозначается sin и определяется на множестве всех действительных чисел. Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
• Функция, которая задана формулой y = cosx, называется косинусом, обозначается cos и определяется на множестве R. Область определения функции косинус — множество всех действительных чисел: D(cos) = R.
• Функции, которые заданы формулами y = tgx и y = ctgx, называются тангенсом и котангенсом и обозначаются tg и ctg. Область определения тангенса — это множество всех действительных чисел, кроме чисел . Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.

Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и x ∈ r, x ≠ πk, k ∈ Z соответственно.

Пример

Найдите область определения функции f(x) = tg2x.

Как решаем:

Так как a(x) = 2x, то в область определения не войдут следующие точки:

Перенесем 2 из левой части в знаменатель правой части:

В результате . Отразим графически:

Ответ: область определения: .

Область определения обратных тригонометрических функций

Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.

• Функция, которая задается формулой y = arcsinx и рассматривается на отрезке [−1, 1], называется арксинусом и обозначается arcsin.

  Область определения арксинуса — это множество [−1, 1], то есть, D(arcsin) = [−1, 1].

• Функция, которая задается формулой y = arccosx и рассматривается на отрезке [−1, 1], называется арккосинусом и обозначается arccos.

  Область определения функции арккосинус — отрезок [−1, 1], то есть, D(arccos) = [−1, 1].

• Функции, которые задаются формулами вида y = arctgx и y = arcctgx и рассматриваются на множестве всех действительных чисел, называются арктангенсом и арккотангенсом и обозначаются arctg и arcctg.

  Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.

Таблица областей определения функций

Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.

И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните. 

Функция	Область определения функции
Постоянная y = C	R
Корень y = n√x	[0 ; +∞) , если n — четное; (-∞; +∞) , если n  — нечетное.
Степенная y = xa	(-∞; +∞) , если a > 0, a ∈ Z; [0 ; +∞), если a > 0, a ∈ R, a ∉ Z; (-∞; 0) ∪ (0; +∞) , если a < 0, a ∈ Z; (0; +∞), если a ∈ R, a ≠ Z; (-∞; 0) ∪ (0, +∞), если a = 0.
Показательная y = ax	R
Логарифмическая y = lognx	(0; +∞)
Тригонометрические y = sinxy y = cosxy y = tgxy y = ctgx	R R x ∈ R, x ≠ π/2 + πk, k ∈ Z x ∈ R, x ≠ πk, k ∈ Z
Обратные тригонометрические y = arcsinxy  y = arccosxy  y = arctgxy  y = arcctgx	[-1; 1] [-1; 1] R R

Функция, область определения, множество значений, четность, периодичность, график, монотонность: возрастание, убывание, нули. Тесты

Тестирование онлайн

Понятие функции

Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение y.

Обозначение:

Переменную x называют независимой переменной или аргументом, а переменную y – зависимой. Говорят, что y является функцией от x. Значение y, соответствующее заданному значению x, называют значением функции.

Все значения, которые принимает x, образуют область определения функции; все значения, которые принимает y, образуют множество значений функции.

Обозначения:

D(f) – значения аргумента. E(f) – значения функции. Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл.

Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. Если некоторому значению x=x₀ соответствуют несколько значений (а не одно) y, то такое соответствие не является функцией. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая параллельная оси Оу, пересекалась с графиком не более чем в одной точке.

Способы задания функции

1) Функция может быть задана аналитически в виде формулы. Например,

2) Функция может быть задана таблицей из множества пар (x; y).

3) Функция может быть задана графически. Пары значений (x; y) изображаются на координатной плоскости.

Монотонность функции

Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы “взбираться” вверх по графику.

Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы “скатываться” вниз по графику.

Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.

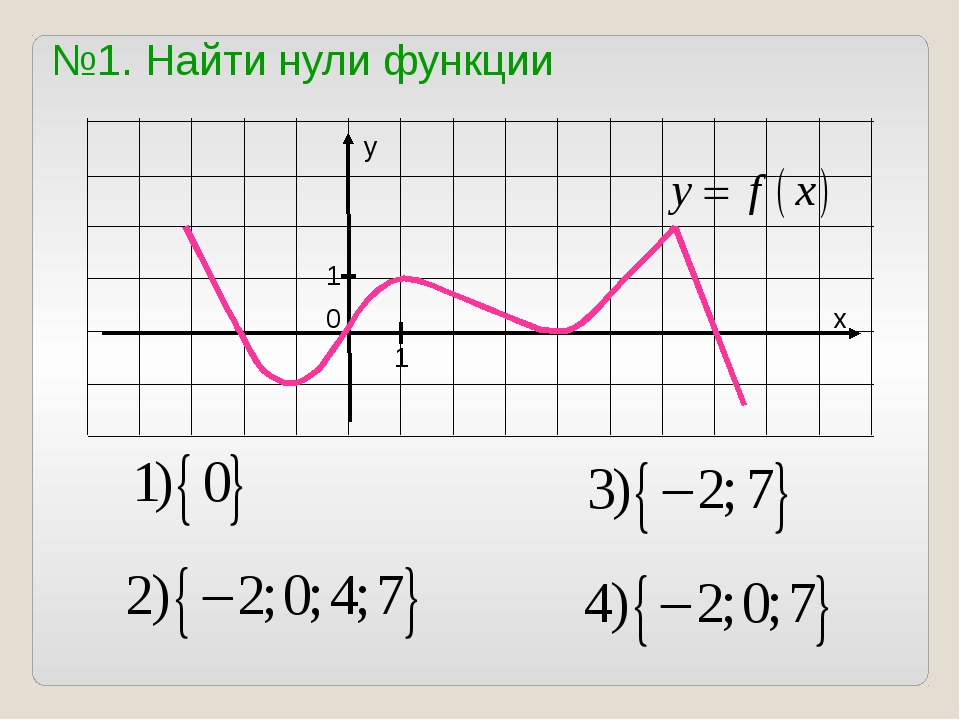
Нули функции и промежутки знакопостоянства

Значения х, при которых y=0, называется нулями функции. Это абсциссы точек пересечения графика функции с осью Ох.

Такие промежутки значений x, на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.

Четные и нечетные функции

Четная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.

Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).

Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.

Периодические функции

Функция f называется периодической, если существует такое число , что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T). T – это период функции.

Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.

Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.

Область определения функции | Онлайн калькулятор

Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. 4)

Jaguar E-PACE | Компактный кроссовер

^†Указанные данные относятся к NEDC2 и рассчитываются по результатам испытаний производителя, проведенных в соответствии с требованиями WLTP и законодательством ЕС при полностью заряженной аккумуляторной батарее. Только для сравнения. Фактические значения могут отличаться. Значения выбросов CO₂, запаса хода, расхода топлива и энергии могут отличаться в зависимости от таких факторов, как стиль вождения, условия окружающей среды, нагрузка на автомобиль, колесные диски и дополнительное оборудование. Значения NEDC2 рассчитываются по официально принятой формуле по данным WLTP и являются эквивалентными показателям используемого ранее цикла NEDC. Исходя из полученных результатов, определяется размер налогообложения.

^±Значение объема Wet определено путем моделирования заполнения багажного отделения жидкостью по соответствующему промышленному стандарту. Объем измеряется до отделки потолка. Конфигурация и общий объем багажного отделения зависят от комплектации автомобиля (версии и силового агрегата), рынка сбыта, а также от того, какое запасное колесо установлено: полноразмерное или уменьшенного размера.

¹Зависит от комплектации.

²В вашем автомобиле можно использовать систему Apple CarPlay. Услуги, предлагаемые системой Apple CarPlay, зависят от доступности функций в вашей стране. Опция не доступна для рынков Армении, Белоруссии и Казахстана.

³В вашем автомобиле можно использовать систему Android Auto. Услуги, предлагаемые системой Android Auto, зависят от доступности функций в вашей стране. Опция не доступна для рынков Армении, Белоруссии и Казахстана.

⁴Приложение Remote включает в себя услуги, требующие подписки. По истечении срока действия подписку можно продлить, обратившись к официальному дилеру Jaguar. Приложение Jaguar Remote необходимо скачать в магазине Apple App Store / Google Play Store.

⁵Для использования подключенной навигационной системы вам потребуется продлить подписку по истечении изначального рекомендованного официальным дилером Jaguar срока.

⁶Может применяться политика правомерного использования. Доступность функций и опций зависит от рынка. Информацию о полных условиях для вашей страны уточняйте у официального дилера Jaguar. Предусмотрена подписка на 1 год. По истечении срока действия подписку можно продлить, обратившись к официальному дилеру Jaguar.

⁷Доступность функций и опций зависит от рынка. Информацию о полных условиях для вашей страны уточняйте у официального дилера Jaguar. Применяется политика правомерного использования. При достижении лимита данных 20 ГБ до окончания месяца скорость передачи данных в автомобиле и функциональность могут быть ограничены. Для получения информации о политике правомерного использования, применяемой к данной функции, см. положения InControl Pivi Pro https://www. jaguar.ru/incontrol/incontrol-support/terms-and-conditions.html.

⁸Время воспроизведения зависит от поставщика потоковой передачи данных и разрешения видеоматериала. Видео в формате HD значительно увеличит объем передачи данных. Включая 1 год подписки, которую можно продлить по истечении срока действия.

⁹Два часа зарядки водонепроницаемого ключа-браслета для доступа в автомобиль Activity Key обеспечивает работу элемента питания до 10 дней.

Дополнительные функции и их доступность могут различаться в зависимости от комплектации автомобиля (модификации и силового агрегата) и рынка сбыта. Для ряда функций требуется установка дополнительных компонентов. Для получения дополнительной информации обратитесь к официальному дилеру или воспользуйтесь онлайн-конфигуратором.

Используйте установленные в автомобиле системы, соблюдая правила безопасности. Водитель обязан непрерывно сохранять полный контроль над автомобилем.

Доступность функций и опций Pivi и InControl, а также услуг сторонних поставщиков зависит от рынка. Информацию о наличии и полных условиях для вашей страны уточняйте у официального дилера Jaguar. Покрытие мобильной сети не гарантируется повсеместно. Информация о технологии InControl и иллюстрирующие ее изображения, включая оформление экрана и последовательность действий, могут быть изменены в зависимости от версии программного обеспечения, обновлений и других системных/визуальных настроек, связанных с выбором различных опций.

Apple CarPlay является зарегистрированным товарным знаком компании Apple Inc. Применяется пользовательское соглашение компании Apple Inc.

Android Auto является зарегистрированным товарным знаком компании Google LLC.

Meridian является зарегистрированным товарным знаком компании Meridian Audio Ltd. Trifield, а устройство «Three fields» является зарегистрированным товарным знаком компании Trifield Productions Ltd.

Nanoe^TM является товарным знаком Panasonic Corporation

Светотехнические параметры и понятия. Часть 1. Справочная информация

Профессиональные светотехники и специалисты, работающие в области освещения, постоянно употребляют разные термины и определения, которые мало о чем говорят простому обывателю, но нужны для правильного описания цветового фона.

Чтобы было проще понимать, о чем идет речь, и что обозначают эти слова, мы подготовили список, объясняющий основные светотехнические термины и характеристики. Его не нужно учить наизусть, можно просто заходить на нужную страницу и освежать в памяти забытый параметр. Говорить «на одном языке» всегда проще.

Светотехнические параметры и понятия.

1 — Видимое и оптическое излучение

Весь окружающий нас мир образуется видимым и оптическим излучением, сосредоточенным в полосе электромагнитных волн от 380 до 760 нм. К ней с одной стороны добавляется ультрафиолетовое излучение (УФ), а с другой инфракрасное (ИК).

УФ-лучи оказывают биологическое воздействия и применяются для уничтожения бактерий. Дозировано они используются для лечебного и оздоровительного эффектов.

ИК-лучи используются для нагрева и сушки в установках, так как в основном производят тепловое воздействие.

2 — Световой поток (Ф)

Световой поток характеризует мощность видимого излучения по воздействию на человеческое зрение. Измеряется в люменах (лм). Величина не зависит от направления. Световой поток — это самая важная характеристика источников света.

Например, лампа накаливания Е27 75 Вт имеет световой поток 935 лм, галогенная G9 на 75 Вт — 1100 лм, люминесцентная Т5 на 35 Вт — 3300 лм, металлогалогенная G12 на 70 Вт (теплая) — 5300 лм, светодиодная Е27 9,5 Вт (теплая) — 800 лм.

3 — Люмен

Люмен (лм) — это световой поток от источника света (лампы) при окружающей температуре 25°, измеренной при эталонных условиях.

 

4 — Освещенность (Е)

Освещенность — это отношение светового потока, подающего на элемент поверхности, к площади этого элемента. Е=Ф/А, где, А -площадь. Единица освещенности — люкс (лк).

Чаще всего нормируется горизонтальная освещенность (на горизонтальной плоскости).

Средние диапазоны освещенности: на улице при искусственном освещении от 0 до 20 лк, в помещении от 20 до 5000 лк, 0,2 лк в полнолуние в природных условиях, 5000 -10000 лк днем при облачности и до 100 000 лк в ясный день.

На картинке представлены: а – средняя освещенность на площади А, б – общая формула для расчета освещенности.

5 — Сила света (I)

Сила света — это пространственная плотность светового потока, ограниченного телесным углом. Т. е. отношение светового потока, исходящего от источника света и распространяющегося внутри малого телесного угла, содержащего рассматриваемое направление.

I=Ф/ω Единица измерения силы света — кандела (кд).

Средняя сила света лампы накаливания в 100 Вт составляет около 100 кд.

КСС (кривая силы света) — распределение силы света в пространстве, это одна из важнейших характеристик светотехнических приборов, необходимая для расчета освещения.

 

6 — Яркость (L)

Яркость (плотность света) — это отношение светового потока, переносимого в элементарном пучке лучей и распространяющемся в телесном угле, к площади сечения данного пучка.

L=I/A (L=I/Cosα) Единица измерения яркости — кд/м2.

Яркость связана с уровнем зрительного ощущения; распространение яркости в поле зрения (в помещении/интерьере) характеризует качество (зрительный комфорт) освещения.

В полной темноте человек реагирует на яркость в одну миллионную долю кд/м2.

Полностью светящийся потолок яркостью боле 500 кд/м2 вызывает у человека дискомфорт.

Яркость солнца примерно миллиард кд/м2, а люминесцентной лампы 5000–11000 кд/м2.

7 — Световая отдача (H)

Световая отдача источника света — это отношение светового потока лампы к ее мощности.

Η=Ф/Р Единица измерения светоотдачи — лм/Вт.

Это характеристика энергоэкономичности источника света. Лампы с высокой световой отдачей обеспечивают экономию электроэнергии.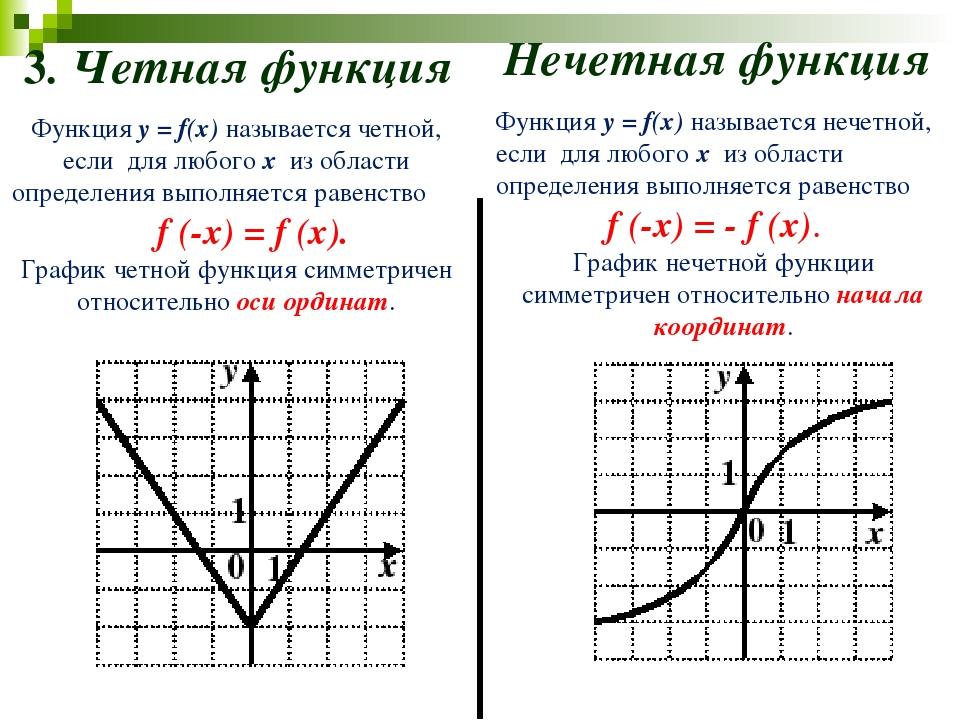 Заменяя лампу накаливания со светоотдачей 7–22 лм/Вт на люминесцентные (50–90 лм/Вт), расход электроэнергии уменьшится в 5–6 раз, а уровень освещенности останется тот же.

 

8 — Цветовая температура (Тц)

Цветовая температура определяет цветность источников света и цветовую тональность освещаемого пространства. При изменении температуры источника света, тональность излучаемого света меняется от красного к синему. Цветовая температура равна температуре нагретого тела (излучатель Планка, черное тело), одинакового по цвету с заданным источником света.

Единица измерения Кельвин (К) по шкале Кельвина: Т — (градусы Цельсия + 273) К.

 

Пламя свечи — 1900 К

Лампа накаливания — 2500–3000 К

Люминесцентные лампы — 2700 — 6500 К

Солнце — 5000–6000 К

Облачное небо — 6000–7000 К

Ясный день — 10 000 — 20 000 К.

9 — Индекс цветопередачи (Ra или CRI)

Индекс цветопередачи характеризует степень воспроизведения цветов различных материалов при их освещении источником света (лампой) при сравнении с эталонным источником.

Максимальное значение индекса цветопередачи Ra =100.

 

Показатели цветопередачи:

Ra = 90 и более — очень хорошая (степень цветопередачи 1А)

Ra = 80–89 — очень хорошая (степень цветопередачи 1В)

Ra = 70–79 — хорошая (степень цветопередачи 2А)

Ra = 60–69 — удовлетворительная (степень цветопередачи 2В)

Ra = 40–59 — достаточная (степень цветопередачи 3)

Ra = менее 39 — низкая (степень цветопередачи 3)

 

Ra он же CRI — color rendering index был разработан для сравнения источников света непрерывного спектра, индекс цветопередачи которых был выше 90, поскольку ниже 90 можно иметь два источника света с одинаковым индексом цветопередачи, но с сильно различающейся передачей цвета.

Комфортное для глаза человека значение CRI = 80–100 Ra

Читайте также:

11.3.1. Показательная функция, ее свойства и график.

Автор Татьяна Андрющенко На чтение 5 мин. Просмотров 11.1k. Опубликовано 26 июня 2012

data-ad-client=”ca-pub-8602906481123293″
data-ad-slot=”8834522701″
data-ad-format=”auto”>

• Функцию вида y=a^x, где а>0, a≠1, х – любое число, называют показательной функцией.
• Область определения показательной функции: D (y)=R – множество всех действительных чисел.
• Область значений показательной функции: E (y)=R₊ – множество всех положительных чисел.
• Показательная функция  y=a^x возрастает при a>1.
• Показательная функция y=a^x убывает при 0<a<1.

Справедливы все свойства степенной функции:

• а⁰=1  Любое число (кроме нуля) в нулевой степени равно единице.
•  а¹=а  Любое число в первой степени равно самому себе.
•  a^x∙a^y=a^x+y   При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
•  a^x:a^y=a^{x- y}  При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
• (a^x)^y=a^xy   При возведении степени в степень основание оставляют прежним, а показатели перемножают
•  (a∙b)^x=a^x∙b^y   При возведении произведения в степень возводят в эту степень каждый из множителей.
• (a/b)^x=a^x/b^y  При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
•   а^-х=1/a^x
•  (a/b)^-x=(b/a)^x.

Примеры.

1) Построить график функции y=2^x. Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=2⁰=1;                   Точка А.

x=1, y=2¹=2;                   Точка В.

x=2, y=2²=4;                   Точка С.

x=3, y=2³=8;                   Точка D.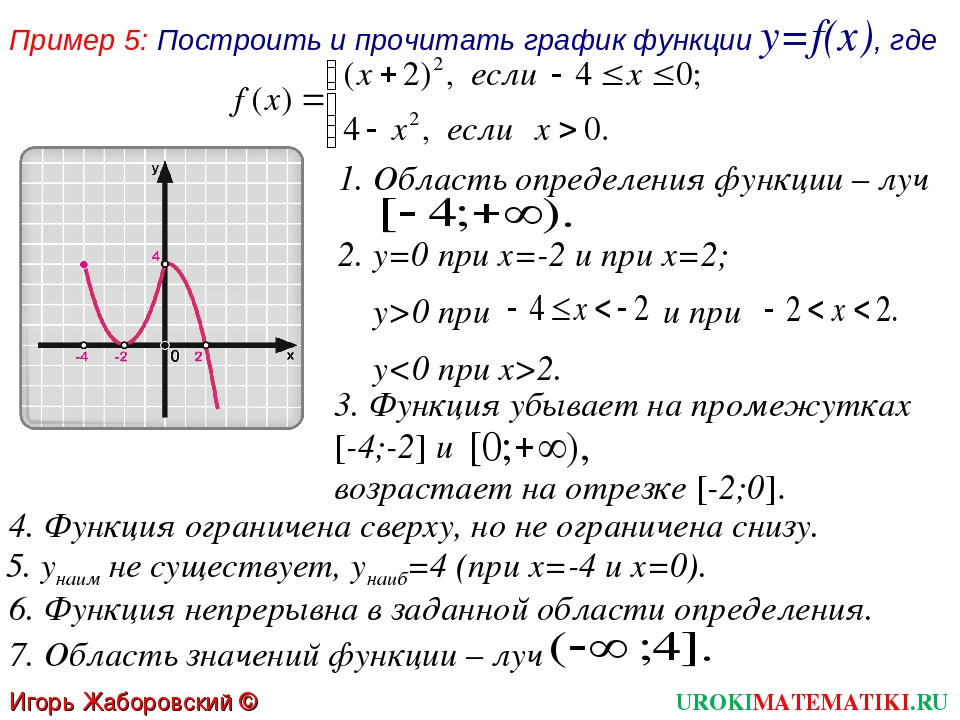              

x=-1, y=2^-1=¹/₂=0,5;       Точка K.

x=-2, y=2^-2=¹/₄=0,25;     Точка M.

x=-3, y=2^-3=¹/₈=0,125;   Точка N.

Большему  значению аргумента х соответствует и большее значение функции у. Функция y=2^x возрастает на всей области определения D (y)=R, так как основание функции 2>1.

2) Построить график функции y=(¹/₂)^x. Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=(½)⁰=1;                  Точка A.

x=1, y=(½)¹=½=0,5;          Точка B.

x=2, y=(½)²=¼=0,25;        Точка C.

x=3, y=(½)³=1/8=0,125;    Точка D.

x=-1, y=(½)^-1=2¹=2;          Точка K.

x=-2, y=(½)^-2=2²=4;          Точка M.

x=-3, y=(½)^-3=2³=8;          Точка N.

 

Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(¹/₂)^x убывает на всей своей области определения: D (y)=R, так как основание функции  0<(¹/₂)<1.

3) В одной координатной плоскости построить графики функций: 

y=2^x, y=3^x, y=5^x, y=10^x. Сделать выводы.

График функции у=2^х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.

Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля  (E (y)=R₊).

Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a>1) показательной функции у=а^х, тем ближе расположена кривая к оси Оу.

Все  данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.

 

4) В одной координатной плоскости построить графики функций:

y=(¹/₂)^x, y=(¹/₃)^x, y=(¹/₅)^x, y=(¹/₁₀)^x. Сделать выводы.

Смотрите построение графика функции y=(¹/₂)^x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.

Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R₊.

Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.

Чем меньше основание а (при 0<a<1) показательной функции у=а^х, тем ближе расположена кривая к оси Оу.

Все  эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.

Решить графически уравнения:

1) 3^x=4-x.

В одной координатной плоскости построим графики функций: у=3^х и у=4-х.

 

Графики пересеклись в точке А(1; 3).

 

Ответ: 1.

 

 

 

 

2) 0,5^х=х+3.

 

В одной координатной плоскости строим графики функций: у=0,5^х

(y=(¹/₂)^x )

 и у=х+3.

Графики пересеклись в точке В(-1; 2).

Ответ: -1.

 

 

Найти область значений функции: 1) y=-2^x; 2) y=(¹/₃)^x+1; 3) y=3^x+1-5.

Решение.

 1) y=-2^x 

Область значений показательной функции y=2^x – все положительные числа, т.е.

0<2^x<+∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем:

— ∞<-2^x<0.

Ответ: Е(у)=(-∞; 0).

 2) y=(¹/₃)^x+1;

0<(¹/₃)^x<+∞, тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:

0+1<(¹/₃)^x+1<+∞+1;

1<(¹/₃)^x+1<+∞.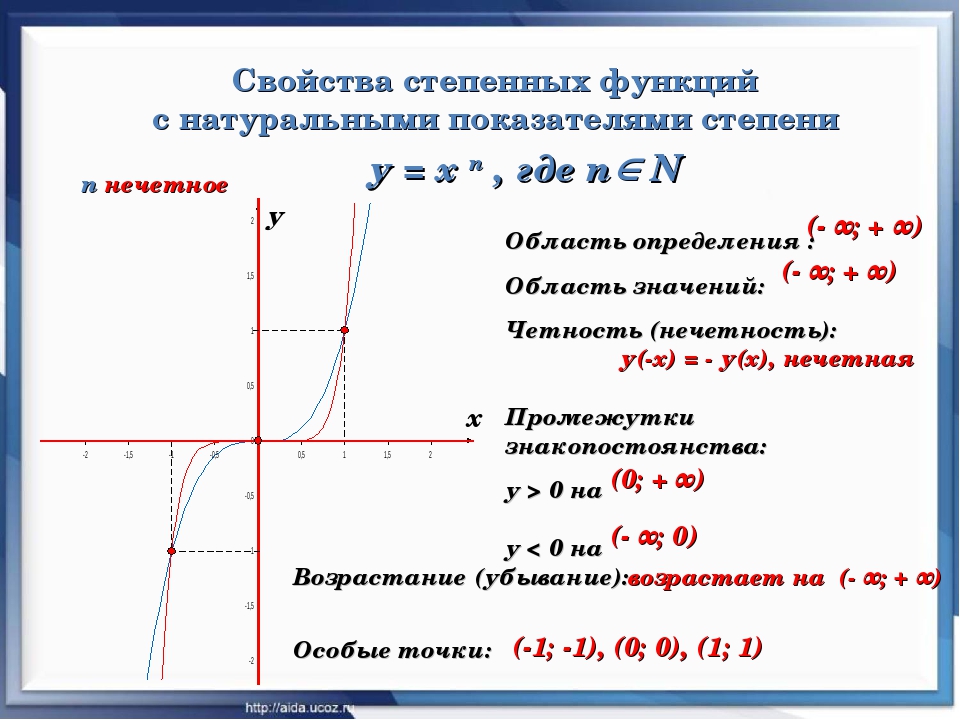

Ответ: Е(у)=(1; +∞).

 3) y=3^x+1-5.

Запишем функцию в виде: у=3^х∙3-5.

0<3^x<+∞;   умножаем все части двойного неравенства на 3:

0∙3<3^x∙3<(+∞)∙3;

0<3^x∙3<+∞;  из всех частей двойного неравенства вычитаем 5:

0-5<3^x∙3-5<+∞-5;

— 5<3^x∙3-5<+∞.

Ответ: Е(у)=(-5; +∞).

Смотрите Карту сайта, и Вы найдете нужные Вам темы!

Найти функцию, обратную экспоненциальной

Пример 1 Найдите обратную функцию, ее область определения и диапазон функции, заданной формулой f (x) = e x-3 Решение для примера 1 Обратите внимание, что данная функция является экспоненциальной функцией с областью определения (-∞, + ∞) и диапазоном (0, + ∞). Сначала запишем функцию в виде уравнения следующим образом y = e x-3 Пройдите по обеим сторонам, чтобы получить x-3 = ln y или x = ln y + 3 Измените x на y и y на x, чтобы получить обратную функцию. f -1 (x) = y = ln x + 3 Область и диапазон обратной функции являются соответственно диапазоном и областью заданной функции f. Следовательно и диапазон f -1 задаются как: домен: (0, + ∞) диапазон: (-∞, + ∞) Пример 2 Найдите обратное, его область определения и диапазон функции, заданной формулой е (х) = 2 е (2 х + 3) + 4 Решение для примера 2 Пример 3 Найдите обратное, его область определения и диапазон функции, заданной формулой f (x) = 2 e (x 2 – 1) + 2, для x ≥ 0 Решение для примера 3 Легко показать, что функция f, заданная приведенной выше формулой, является четной функцией и, следовательно, не взаимно однозначной, если область определения равна R. Однако область в нашем случае задается x ≥ 0, что делает данную функцию взаимно однозначной функцией и, следовательно, имеет обратную. Область f: [0, + ∞), заданная Диапазон: для x в области [0, + ∞) диапазон x 2 задается как [0, + ∞), который можно записать как х 2 ≥ 0 вычтите -1 в обе стороны, чтобы получить: x 2 – 1≥ – 1 возьмите экспоненту с обеих сторон, чтобы получить: e x 2 – 1 ≥ e -1 (экспоненциальная функция является возрастающей функцией) умножьте на +2 к обеим сторонам указанного выше неравенства, чтобы получить: 2 e x 2 – 1 ≥ 2 e -1 прибавьте +2 к обеим сторонам указанного выше неравенства, чтобы получить: 2 e x 2 – 1 + 2 ≥ 2 e -1 + 2 левая часть неравенства выше является заданной функцией, следовательно, диапазон данной функции определяется как: [2 e -1 + 2, + ∞) Найдите обратное к f, запишите f в виде уравнения и решите относительно x. y = 2 e (x 2 – 1) + 2 2 e (x 2 – 1) = y – 2 e (x 2 – 1) = (y – 2) / 2 Пройдите по обеим сторонам, чтобы получить x 2 – 1 = ln ((1/2) (y – 2)) и, наконец, x = + или – sqrt [ln ((1/2) (y – 2)) + 1] Так как x ≥ 0 (заданная область), имеем x = sqrt [ln ((1/2) (y – 2)) + 1] Измените x на y и y на x, чтобы получить обратную функцию. f -1 (x) = y = sqrt [ln ((1/2) (x – 2)) + 1] Домен и диапазон f -1 соответственно задаются диапазоном и доменом f, указанными выше. домен f -1 задается как: [2 e -1 + 2, + ∞), а его диапазон определяется как: [0, + ∞) Упражнения Найдите обратное, его область определения и диапазон функций, приведенных ниже. 1.f (x) = -e x + 4 2. 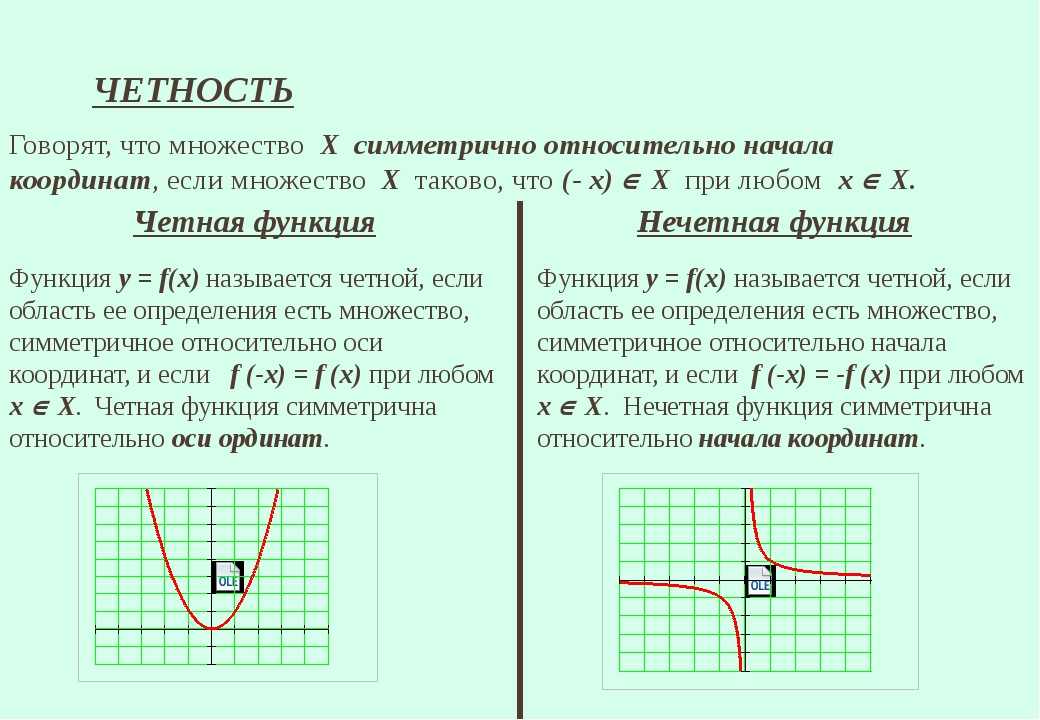g (x) = 2 – e (4x – 2) / 3 3. h (x) = – e (2 x 2 – 5) + 3, для x ≤ 0 Ответы на вышеуказанные упражнения 1. f -1 (x) = ln (-x) – 4; домен: (-∞, 0) Диапазон: (-∞, + ∞) 2. g -1 (x) = (3/4) ln (2 – y) +1/2; домен: (-∞, 2) Диапазон: (-∞, + ∞) 3. h -1 (x) = – sqrt [(1/2) ln (3 – y) + 5/2]; домен: (-∞, – e (-5) + 3) Диапазон: (-∞, + ∞) Дополнительные ссылки и справочные материалы, относящиеся к обратным функциям. Дополнительные ссылки и ссылки на обратные функции Найти обратную рациональную функцию – пошаговый рабочий лист Найти обратные функции – калькулятор Приложения и использование обратных функций Найти обратную функцию – вопросы Найти обратную функцию (1) – Руководство. Определение обратной функции – Интерактивное учебное пособие Поиск функций, обратных корню куба. Найти функции, обратные квадратному корню. Найти обратные логарифмические функции.6 (2n + 2) / ((2n + 1)!) = “ 2,718281828` Графическая демонстрация e Площадь под кривой y = 1 / x между 1 и e равна единице 1 2 . Площадь под кривой `y = 1 / x` между` 1` и `e`. Индивидуальная функция – объяснение и примеры Вы знаете, что изучаете функции, когда слышите «один к одному» чаще, чем когда-либо. Хотите узнать, что делает индивидуальными функциями особенными? Эта статья поможет вам узнать об их свойствах и оценить эти функции.Давайте начнем с этого краткого определения индивидуальных функций: Индивидуальные функции – это функции, которые возвращают уникальный диапазон для каждого элемента в своем домене. Поскольку индивидуальные функции – это особые типы функций, лучше всего проверить наши знания о функциях, их предметной области и их диапазоне. Эта статья поможет нам понять свойства взаимно однозначной функции . Мы также узнаем, как определять индивидуальные функции на основе их выражений и графиков. Давайте продолжим и начнем с определения и свойств взаимно однозначных функций. Что такое функция «один к одному»? Чтобы легко вспомнить, что такое взаимно однозначные функции, попробуйте вспомнить следующее утверждение: «для каждого y существует уникальный x». Следующие два раздела покажут вам, почему эта фраза помогает нам запомнить основную концепцию индивидуальных функций. Определение функции «один к одному» Функция f (x), является функцией «один к одному», когда один уникальный элемент из ее домена будет возвращать каждый элемент своего диапазона.Это означает, что для каждого значения x будет уникальное значение y или f (x). Почему бы нам не визуализировать это, отображая две пары значений для сравнения функций, которые не находятся в однозначном соответствии? Давайте сначала посмотрим на g (x), g (4) и g (-4) имеют общее значение y, равное 16. Это также верно для g (-2) и g (2). Вы правильно угадали; g (x) – функция, не имеющая взаимно однозначного соответствия. Теперь обратите внимание на f (x). Обратите внимание, как для каждого значения f (x) существует только одно уникальное значение x? Когда вы наблюдаете функции, имеющие это соответствие, мы вызываем эти функции один к одному. График функции «один к одному» Чтобы лучше понять концепцию взаимно однозначных функций, давайте изучим индивидуальный график функции. Помните, что для функций «один к одному» каждый x должен иметь уникальное значение y. Поскольку каждый x будет иметь уникальное значение для y, функции один к одному никогда не будут иметь упорядоченных пар, которые имеют одну и ту же координату y. Теперь, когда мы изучили определение взаимно однозначных функций, понимаете ли вы, почему выражение «для каждого y есть уникальный x» полезно запомнить? Индивидуальные свойства функций Какие еще важные свойства взаимно однозначных функций мы должны помнить? Вот некоторые свойства, которые могут помочь вам понять различные типы функций с взаимно однозначным соответствием: Если две функции, f (x) и g (x), взаимно однозначны, f ◦ g взаимно однозначно. функции. Если функция является взаимно однозначной, ее график будет либо всегда увеличиваться, либо всегда уменьшаться. Если g ◦ f взаимно однозначная функция, то f (x) также гарантированно будет взаимно однозначной функцией. Попробуйте самостоятельно изучить две пары графиков и посмотреть, сможете ли вы подтвердить эти свойства. Конечно, прежде чем мы сможем применить эти свойства, нам будет важно узнать, как мы можем подтвердить, является ли данная функция функцией один к одному или нет. Как определить взаимно однозначность функции? Следующие два раздела покажут вам, как мы можем протестировать однозначное соответствие функций.Иногда нам дают выражение или график функции, поэтому мы должны научиться определять однозначные функции алгебраически и геометрически. Давайте начнем с последнего! Тестирование функций один к одному с геометрической точки зрения Помните, что функции должны быть взаимно однозначными. Каждая координата x должна иметь уникальную координату y? Мы можем проверить взаимно однозначные функции с помощью теста горизонтальной линии . При задании функции рисует горизонтальные линии вместе с системой координат. Проверьте, могут ли горизонтальные линии проходить через две точки. Если горизонтальные линии проходят только через одну точку на всем графике, функция является взаимно однозначной функцией . Что делать, если он проходит две или более точки функции? Тогда, как вы уже догадались, они не считаются однозначными функциями. Чтобы лучше понять процесс, давайте продолжим и изучим эти два графика, показанные ниже. Известно, что обратная функция f (x) = 1 / x является взаимно однозначной функцией.Мы также можем проверить это, проведя горизонтальные линии на его графике. Видите, как каждая горизонтальная линия каждый раз проходит через уникальную упорядоченную пару? Когда это происходит, мы можем подтвердить, что данная функция является функцией один к одному. Что происходит, если функция не является взаимно однозначной? Например, квадратичная функция f (x) = x 2 не является взаимно однозначной функцией. Давайте посмотрим на его график, показанный ниже, чтобы увидеть, как тест горизонтальной линии применяется к таким функциям. Как видите, каждая горизонтальная линия, проведенная через график f (x) = x 2 , проходит через две упорядоченные пары. Это еще раз подтверждает, что квадратичная функция не является взаимно однозначной функцией. Алгебраическое тестирование индивидуальных функций Давайте освежим нашу память о том, как мы определяем индивидуальные функции. Напомним, что функции являются взаимно однозначными, если: f (x 1 ) = f (x 2 ) тогда и только тогда, когда x 1 = x 2 f (x 1 ) ≠ f (x 2 ) тогда и только тогда, когда x 1 ≠ x 2 Мы будем использовать это алгебраическое определение, чтобы проверить, является ли функция взаимно однозначной.Как же тогда это сделать? Используйте заданную функцию и найдите выражение для f (x 1 ). Примените тот же процесс и найдите выражение для f (x 2 ). Приравняйте оба выражения и покажите, что x 1 = x 2 . Почему бы нам не попробовать доказать, что f (x) = 1 / x является взаимно однозначной функцией, используя этот метод? Давайте сначала подставим x 1 и x 2 в выражение. У нас будет f (x 1 ) = 1 / x 1 и f (x 2 ) = 1 / x 2 .Чтобы подтвердить взаимно однозначное соответствие функции, приравняем f (x 1 ) и f (x 2 ). 1 / x 1 = 1 / x 2 Перемножьте обе части уравнения, чтобы упростить уравнение. x 2 = x 1 x 1 = x 2 Мы только что показали, что x 1 = x 2 , когда f (x 1 ) = f ( x 2 ), следовательно, обратная функция является взаимно однозначной функцией. Пример 1 Заполните пробелы иногда , всегда или никогда , чтобы следующие утверждения были верными. Отношения могут _______________ быть взаимно однозначными функциями. Индивидуальные функции – это ______________ функции. Когда горизонтальная линия проходит через функцию, которая не является взаимно однозначной, она ____________ будет проходить через две упорядоченные пары. Решение Отвечая на подобные вопросы, всегда возвращайтесь к определениям и свойствам, которые мы только что изучили. Отношения иногда могут быть функциями и, следовательно, иногда представлять функцию один к одному. Так как функции «один к одному» – это особый тип функций, они будут всегда в первую очередь функциями. В нашем примере горизонтальные линии могут проходить через график f (x) = x 2 дважды, но горизонтальные линии могут проходить через большее количество точек. Следовательно, иногда проходит через две упорядоченные пары. Пример 2 Пусть A = {2, 4, 8, 10} и B = {w, x, y, z}. Какой из следующих наборов упорядоченных пар представляет собой функцию один к одному? {(2, w), (2, x), (2, y), (2, z)} {(4, w), (2, x), (10, z), ( 8, y)} {(4, w), (2, x), (8, x), (10, y)} Решение Чтобы функция была взаимно однозначной функцией , каждый элемент из A должен объединяться с уникальным элементом из B. Первый вариант имеет одинаковое значение x для каждого значения y, поэтому это не функция и, следовательно, не взаимно однозначная функция. . Третий вариант имеет разные значения x для каждой упорядоченной пары, но 2 и 8 имеют один и тот же диапазон x. Следовательно, он не представляет собой функцию «один к одному». Второй вариант использует уникальный элемент из A для каждого уникального элемента из B, представляя взаимно однозначную функцию. Это означает, что {(4, w), (2, x), (10, z), (8, y)} представляют собой взаимно однозначную функцию . Пример 3 Какой из следующих наборов значений представляет функцию один к одному? Решение Всегда возвращайтесь к утверждению «для каждого y есть уникальный x.”Для каждого набора давайте проверим, сочетается ли каждый элемент справа с уникальным значением слева. Для первого набора f (x) мы можем видеть, что каждый элемент с правой стороны объединен в пару с уникальным элементом слева. Следовательно, , f (x) взаимно однозначная функция . Набор g (x) показывает разное количество элементов с каждой стороны. Одно это уже говорит нам о том, что функция не является взаимно однозначной. Некоторые значения с левой стороны соответствуют одному и тому же элементу справа, поэтому m (x) также не является взаимно однозначной функцией. Каждый из элементов в первом наборе соответствует уникальному элементу в следующем, поэтому n (x) представляет собой взаимно однозначную функцию. Пример 4 График f (x) = | x | + 1 и определить, является ли функция f (x) взаимно однозначной. Решение Постройте таблицу значений для f (x) и постройте сгенерированные упорядоченные пары. Соединил эти точки с графиком f (x). Сама по себе таблица уже может дать вам представление о том, является ли функция f (x) взаимно однозначной [ Подсказка: f (1) = 2 и f (-1) = 2 ].Но давайте продолжим и построим эти точки на плоскости xy и на графике f (x). После того, как мы построили график f (x) = | x | +1, проведите горизонтальные линии поперек графика и посмотрите, проходит ли он через одну или несколько точек. На графике мы видим, что построенные нами горизонтальные линии проходят через две точки каждая, поэтому функция не является взаимно однозначной функцией . Пример 5 Определите, является ли функция f (x) = -2x 3 -1 взаимно однозначной, используя алгебраический подход. Решение Напомним, что для того, чтобы функция была взаимно однозначной, f (x 1 ) = f (x 2 ) тогда и только тогда, когда x 1 = x 2 . Чтобы проверить, является ли функция f (x) взаимно однозначной, давайте сначала найдем соответствующие выражения для x 1 и x 2 . f (x 1 ) = -2 x 1 3 – 1 f (x 2 ) = -2 x 2 3 – 1 Приравняйте оба выражения и посмотрите, он уменьшается до x 1 = x 2 . -2 x 1 3 – 1 = -2 x 2 3 – 1 -2 x 1 3 = -2 x 2 3 (x 1 ) 3 = (x 2 ) 3 Извлечение кубического корня из обеих частей уравнения приведет нас к x 1 = x 2 . Следовательно, f (x) = -2x 3 – 1 является взаимно однозначной функцией. Пример 6 Покажите, что f (x) = -5x 2 + 1 не является взаимно однозначной функцией. Решение Еще одно важное свойство взаимно однозначных функций заключается в том, что когда x 1 ≠ x 2 , f (x 1 ) не должно быть равно f (x 2 ). Быстрый способ доказать, что f (x) не является взаимно однозначной функцией, – это подумать о контрпримере, показывающем два значения x, где они возвращают одно и то же значение для f (x). Давайте посмотрим, что произойдет, если x 1 = -4 и x 2 = 4. f (x 1 ) = -5 (-4) 2 + 1 = -80 + 1 = -79 f (x 2 ) = -5 (4) 2 + 1 = -80 + 1 = -79 ср. можно видеть, что даже когда x 1 не равно x 2 , он все равно возвращает то же значение для f (x).Это показывает, что функция f (x) = -5x 2 + 1 не является взаимно однозначной функцией. Пример 7 Учитывая, что a и b не равны 0, показывают, что все линейные функции являются взаимно однозначными функциями. Решение Помните, что общий вид линейных функций может быть выражен как ax + b, где a и b ненулевые константы. Мы применяем тот же процесс, подставляя x 1 и x 2 в общее выражение для линейных функций. f (x 1 ) = ax 1 + b f (x 2 ) = ax 2 + b Приравняйте оба уравнения и посмотрите, можно ли их уменьшить до x 1 = х 2 . Поскольку b представляет собой константу, мы можем вычесть b из обеих частей уравнения. ax 1 + b = ax 2 + b ax 1 = ax 2 Разделим обе части уравнения на a, и мы получим x 1 = x 2 .Из этого можно сделать вывод, что все линейные функции взаимно однозначны. Практические вопросы Заполните пропуски иногда , всегда или никогда сделайте следующие утверждения верными. Косинусные функции могут _______________ быть взаимно однозначными функциями. Если функция f (x) взаимно однозначна, ее домен ______________ будет иметь такое же количество элементов, как и диапазон. Когда горизонтальная линия проходит через функцию, которая является функцией один к одному, она ____________ будет проходить через две упорядоченные пары. Пусть M = {3, 6, 9, 12} и N = {a, b, c, d}. Какой из следующих наборов упорядоченных пар представляет собой функцию один к одному? {(6, a), (6, b), (6, c), (6, d)} {(9, d), (12, b), (6, b), (3, c)} {(6, d), (9, c), (12, b), (3, a)} Какой из следующих наборов значений представляет собой взаимно однозначную функцию ? Изобразите следующие функции и определите, являются ли они взаимно однозначными или нет. f (x) = x 2 – 4 g (x) = -4x + 1 h (x) = e x Убедитесь, что следующие функции взаимно однозначны используя алгебраический подход. f (x) = 2x – 1 g (x) = 1 / x 2 h (x) = | x | + 4 Покажите, что g (x) = | x | – 4 не является однозначной функцией. Покажите, что все квадратичные выражения не являются взаимно однозначными функциями. Изображения / математические рисунки создаются с помощью GeoGebra. Предыдущий урок | Главная страница | Следующий урок Что означает E в математике? Обновлено 20 декабря 2020 г. Крис Дезил Буква E может иметь два разных значения в математике, в зависимости от того, заглавная это E или строчная e.Обычно вы видите заглавную букву E на калькуляторе, что означает возведение числа, следующего за ней, в степень 10. Например, 1E6 будет означать 1 × 10 6 , или 1 миллион. Обычно использование E зарезервировано для чисел, которые были бы слишком длинными для отображения на экране калькулятора, если бы они были записаны от руки. Математики используют строчную букву e для гораздо более интересной цели – для обозначения числа Эйлера. Это число, как и π, является иррациональным числом, потому что оно имеет неповторяющуюся десятичную дробь, которая простирается до бесконечности.Как и у иррационального человека, иррациональное число кажется бессмысленным, но число, которое обозначает e, не обязательно должно иметь смысл, чтобы быть полезным. Фактически, это одно из самых полезных чисел в математике. E в экспоненциальной нотации и значение 1E6 Вам не нужен калькулятор, чтобы использовать E для выражения числа в экспоненциальной нотации. Вы можете просто позволить E обозначать базовый корень экспоненты, но только когда база равна 10. Вы не можете использовать E для обозначения базы 8, 4 или любой другой базы, особенно если в основе лежит число Эйлера, e. Когда вы используете E таким образом, вы пишете число x E y , где x – это первый набор целых чисел в числе, а y – показатель степени. . Например, вы можете записать число 1 миллион как 1E6. В обычном научном представлении это 1 × 10 6 , или 1, за которой следуют 6 нулей. Точно так же 5 миллионов будут 5E6, а 42 732 – 4,27E4. При написании числа в научном представлении, независимо от того, используете ли вы E или нет, вы обычно округляете до двух десятичных знаков. Откуда взялось число Эйлера e? Число, представленное буквой e, было обнаружено математиком Леонардом Эйлером как решение проблемы, поставленной другим математиком, Якобом Бернулли, 50 лет назад. 2

Формула Эйлера

Формула Эйлера

---

Многие математические теоремы настолько важны, что неоднократно доказывались удивительно множеством различных способов.Примеры этого включают в существование бесконечного числа простых чисел, оценка дзета (2), фундаментальная теорема алгебры (многочлены имеют корни), квадратичные взаимность (формула для проверки того, является ли арифметическая прогрессия содержит квадрат) и теоремы Пифагора (которая согласно У Уэллса не менее 367 доказательств). Иногда это случается и с несущественными теоремами, например, тот факт, что в любом прямоугольнике, разрезанном на более мелкие прямоугольники, если каждый меньший прямоугольник имеет целочисленную ширину или высоту, то же самое большой.

На этой странице приведены доказательства формулы Эйлера: для любого выпуклого многогранника количество вершин и граней вместе ровно на два больше, чем количество ребер. Символически V − E + F = 2. Например, тетраэдр имеет четыре вершины, четыре грани и шесть ребер; 4-6 + 4 = 2.

Версия формулы датируется Декартом в 1630 году более чем на 100 лет раньше, чем Эйлер. Декарт дает дискретную форму теоремы Гаусса-Бонне, утверждая, что сумма углов граней многогранника равна 2π (V − 2), из чего он делает вывод, что количество плоских углов равно 2F + 2V-4.Число плоских углов всегда в два раза больше числа ребер, поэтому это эквивалентно формуле Эйлера, но более поздние авторы, такие как Лакатос, Малькевич и Поля, не соглашаются, считая, что различие между углами лица и ребрами слишком велико, чтобы это могло быть рассматривается как та же формула. Формула V − E + F = 2 была (повторно) открыта Эйлером; он писал об этом дважды в 1750 году, а в 1752 году опубликовал результат с ошибочным доказательством индукцией для триангулированных многогранников, основанных на удалении вершины и повторной триангуляции дыры, образованной ее удалением.Шаг ретриангуляции не обязательно сохраняет выпуклость или плоскостность полученной формы, поэтому индукция не проходит. Другая ранняя попытка доказательства, выполненная Мейстером в 1784 году, по существу является доказательством удаления треугольника, приведенным здесь, но без обоснования существования треугольника, который необходимо удалить. В 1794 году Лежандр представил полное доказательство, используя сферические углы. Коши вступил в акт в 1811 году, цитируя Лежандра и добавляя неполные доказательства, основанные на удалении треугольника, разложении ушей и удалении тетраэдра из тетраэдрализации разбиения многогранника на более мелкие многогранники.Хилтон и Педерсон предоставляют дополнительные ссылки а также занимательные размышления об открытии формулы Эйлером. Как ни странно, другие уравнения, такие как e ^{i pi} = -1 и a ^{phi ( n )} = 1 (mod n ) также называют «формулой Эйлера»; Эйлер был занятым человеком.

Формулу многогранника, конечно, можно обобщить многими важными способами: некоторые с использованием методов, описанных ниже. Одно важное обобщение – это планарные графы.Чтобы сформировать плоский граф из многогранника, поместите источник света возле одной грани многогранника, а плоскость – на другую.

Тени от ребер многогранника образуют плоский граф, вложенный в таким образом, чтобы края были отрезками прямых линий. Грани многогранника соответствуют выпуклым многоугольники, являющиеся гранями вложения. Лицо, ближайшее к свету источник соответствует внешней грани вложения, которая также выпуклый. И наоборот, любой плоский граф с определенной связностью properties происходит от многогранника таким образом.

Некоторые из приведенных ниже доказательств используют только топологию плоского графа, некоторые используют геометрию его вложения, а некоторые используют трехмерная геометрия исходного многогранника. Графики в этих доказательствах не обязательно будут простыми : ребра могут соединять вершину с собой, а две вершины могут быть соединены несколькими краями. Некоторые доказательства опираются на кривую Жордана. теорема, имеющая множество доказательств; однако это не обычно основывается на формуле Эйлера, поэтому можно использовать кривые Жордана без боязнь циркулярных рассуждений.

Пожалуйста, отправьте электронное письмо если вам известно доказательство, не указанное здесь. Я был бы особенно признателен за доказательства, связанные с теорией когомологий, торические многообразия или другая высшая математика. (Хелена Веррилл показала, что Эйлера формула эквивалентна тому факту, что всякое торическое многообразие над GF [p] имеет количество точек, равное 1 (mod p) но до сих пор отсутствует хорошее некомбинаторное доказательство последнего факта.)

Я полагаю, можно было бы построить индукции основанный на представлении выпуклых многогранников в виде пересечений полупространств или выпуклой оболочки точек, но необходимость обработка входных данных в необщем положении приведет к тому, что в результате Доказательства довольно грязные.

Также есть потенциальная связь к двучленам: если определить многочлен p (t) = 1 + Vt + Et ² + Ft ³ + t ⁴ , Эйлер формулу можно интерпретировать говоря, что p (t) делится на 1 + t. Но для симплексов любого измерения p (t) = (1 + t) ^{d + 1} по биномиальной формуле. Возможно, существует доказательство формулы Эйлера, в которой используется эти многочлены напрямую, а не просто перевод одна из индукций к полиномиальной форме. Джим Пропп задает аналогичные вопросы для бесконечномерных многогранников, интерпретируя p (t) как степенной ряд (см. также его недавний расширение этих идей).

---

Со свалки Геометрии, вычислительный указатели рекреационной геометрии.
Дэвид Эппштейн, Теоретическая группа, ICS, Калифорнийский университет в Ирвине.

Полуавтоматический фильтрованный из общего исходного файла. Последнее обновление: .

E vs F – В чем разница?

е | f | Что касается букв, то разница между e и f заключается в том, что e – пятая буква, а f – шестая буква. В качестве символов разница между e и f заключается в том, что e является ( метка ) основанием натурального логарифма, трансцендентным числом со значением приблизительно 2718281828459, а f – форте. Транслингвальный {{Основная информация о латинских символах, previous = d, next = f, image = ( Википедия E ) Письмо Пятая буква. См. Также ( Латн-скрипт ) * ( выберите похожие буквы и символы ) * ( другие скрипты ) * Видеть Символ ( Неогнутая гласная переднего среднего переднего ряда ) ( глава ) ( метка ) Основание натурального логарифма, трансцендентное число со значением приблизительно 2.718281828459 Знак, отделяющий мантиссу от экспоненты в экспоненциальном представлении. 1,2566e-6 = 1,2566 × 10 -6 ближний средний гласный переднего ряда без округления ( л ) а ”? ” e ” ” ‘=’ ” ” e ‘? ” a ” = ” a ( метка ) электрон Синонимы * ( электрон ) * ( идентификационный элемент ), ( в основном матрицы ) ( l ) См. Также {{Письмо , page = E , НАТО = Эхо , Морс = · , Символ = E5 , Шрифт Брайля =? }} Изображение: Latin E.png, Заглавные и строчные версии E , обычным шрифтом и курсивом Изображение: Fraktur letter E.png, Прописные и строчные буквы E в Fraktur Изображение: Uncial e.png, приблизительная форма заглавной буквы E в шрифте uncial, которая была источником для строчной буквы e —- Транслингвальный {{Основная информация о латинских символах, предыдущий = e, следующий = g, image = ( википедия f ) Письмо Шестая буква. Символ ( Глухой губно-зубной фрикатив ) ( глава ) форте губно-зубной фрикативный глухой См. Также {{Письмо , страница = F , НАТО = Фокстрот , Морс = ·· – · , Символ = F6 , Шрифт Брайля =? }} Изображение: Latin F.png, Заглавные и строчные версии F , обычным шрифтом и курсивом Изображение: Fraktur letter F. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: