NaN все еще может немного удивить / Хабр
Сначала, я подумал, что это очередной вопрос из тех, которые могут задаваться на собеседовании. Наверное, если как следует пораскинуть мозгами, то можно догадаться до того, каким будет результат. Откинувшись на спинку кресла, начал размышлять, включать логику, вспоминать что-нибудь, на что можно опереться в рассуждениях. Но тщетно! Вдруг стало совершенно очевидно, что найти ответ не удается. Но почему? В чем нужно разбираться, чтобы он был найден? В математике? В языке программирования?
Ответ должен быть NaN. Но почему я не уверен в этом? Всю дорогу была уверенность в том, что любые выражения, содержащие NaN, вернут NaN. Ну разве что только если поделить NaN на ноль — в этом случае будет вызвано исключение ZeroDivisionError. Сто процентов NaN!
Ввожу выражение в ячейку блокнота:
>>> 1**nan + 1**nan 2.0
В самом деле? Постойте:
>>> arange(5)**nan array([nan, 1., nan, nan, nan])
То есть, по какой-то причине, единица в степени NaN — это единица, а вот ноль и все остальные числа в степени NaN — это NaN. Где логика? В чем дело?
Так, давайте еще раз:
>>> 0**nan, 1**nan (nan, 1.0)
Может быть я просто из-за отсутствия какой-то практической надобности в глубоких познаниях о NaN, просто о чем-то не подозревал? А может я знал, но забыл? А может еще хуже — я не знал и забыл?
Заходим на Википедию. Там данный вопрос тоже обозначен как проблема, но почему все именно так устроено, никак не объясняется. Зато узнал что:
>>> hypot(inf, nan) inf
Хотя, в то же время:
>>> sqrt(inf**2 + nan**2) nan
Что, согласитесь, тоже немного странно.
Ладно, с Википедии отправляемся в C99 на 182 страницу и наконец-то получаем логическое объяснение, почему pow(x, 0) возвращает 1 для любых x, даже для x равного NaN:
>>> power(nan, 0) 1.0
0Если функция возводится в степень и при этом стремится к 0, то в результате получится 1, вне зависимости от того, какое значение имеет .
А если результат не зависит от числового значения функции , то 1 — является подходящим результатом, даже для NaN. Однако это по-прежнему не объясняет, почему 1 в степени NaN равна 1.
Отыскиваем еще один C99 и на 461 странице не видим никаких объяснений, просто требование того, что pow(+1, y) должно возвращать 1 для всех y, даже равных NaN. Все.
С другой стороны, объяснение, почему pow(NaN, 0)=1 является более предпочтительным, чем pow(NaN, 0)=NaN все-таки наталкивает на мысль о том, что NaN не стоит воспринимать буквально, как Not-a-Number. Допустим, в результате каких- то вычислений мы получили число, превышающее размер памяти, выделенный под данный тип чисел, например:
>>> a = pi*10e307 >>> a inf
В результате мы получили inf, что именно это за число мы не знаем, но все же это какое-то число.
Затем мы снова что-то вычислили и снова получили слишком большое число:
>>> b = e*10e307 >>> b inf
Разность a и b вернет NaN:
>>> c = a - b >>> c nan
Почему же тогда pow(0, NaN)=NaN? Дело в том, что если возвести 0 в любую степень, то мы действительно получим ноль. Кроме одного единственного случая — когда степень равна 0:
>>> 0**0 1
Из-за чего в выражении pow(0, NaN) появляется неопределенность с конкретным значением NaN.
Даже не знаю, что еще сказать… если вы заранее знали ответ, то скорее всего вам можно позавидовать, ведь сферы, где могут пригодиться такие познания, наверняка, переполнены интересными задачами. А может и наоборот. Напишите об этом в комментариях.
P.S. Поскольку NaN относится к числам с плавающей точкой, оно может быть ключом словаря:
>>> d = {0.1: 'a', nan: 'b'}
>>> d[nan]
'b'Имеет ли смысл использовать такое на практике? Думаю, что лучше не стоит.
Многомерные числа или Ноль — имеет значение, а Бесконечность — конечна!
Аннотация: В статье описан принципиально новый метод представления чисел, с помощью которого возможно решить проблему потери данных при умножении на ноль и получения неопределённости при делении на ноль.
Ключевые слова: деление на ноль; оперирование бесконечностью; многомерные числа
Введение
Исторически «ноль» является проблемой в математике: с одной стороны, без ноля невозможно представить современную математику, с другой использование ноля накладывает некоторые ограничения в расчётах (например, деление на ноль).
Актуальность
В большинстве случаев математики и программисты смирились с неудобствами в расчётах, связанных с нолём, получение неопределённости при делении на ноль и потеря данных при умножении на ноль.
Новый метод представления чисел может дать возможность «не смирившимся» делить и умножать на ноль и бесконечность бесконечно много раз и при этом не «терять» результат расчётов.
Научная новизна
Предлагаемое принципиально новое понимание ноля и бесконечности, может раскрыть, для научного мира множество парадоксов и решить до сего момента не решённые задачи.
История ноля и его представление в современной математике
Понятие ноля и бесконечности в истории отлично описана Чарльзом Сейфе [1].
Современное понимание ноля и бесконечности:
Ноль – это «портал» в другие миры
Те, кто из нас помнят начальную школу могут сказать, что там нас учили, что 0 — это пустота или отсутствие чего-либо. Если у Тани 0 яблок, а у Саши 5 яблок, сколько у Тани и Саши яблок?
\( 0 + 5 = 5 ; \)
Нет сомнений, ни у кого не может быть меньше 0 яблок.
Первый портал ноля
Но потом, в средней школе оказалось, что существуют числа меньше ноля.
Появление отрицательных чисел стало логическим продолжением оператора вычитания «-», когда из меньшего числа мы вычитаем большее, само появление отрицательных чисел никого не смутило (за малостью лет мы не задали вопрос Марье Ивановне, мол, а как может быть у Тани меньше 0 яблок), и мы приняли это как данность, и пошли дальше.
Второй портал ноля
Вроде всё ясно, числа могут быть положительными и отрицательными (ты можешь быть в прибыли, а можешь получить убыток), и мы все с этим смирились.
Но вот оказалось, что всё не так просто:
Возведение в степень и извлечение корня из отрицательного числа не давали однозначных решений, и тогда появилась гениальная теория мнимых чисел, она всё нам объяснила.
Корень из отрицательного числа может быть как положительным, так и отрицательным (это число назвали мнимым, оно и существует и нет одновременно).
Прекрасно, мнимые числа описаны Марком Беньевичем Балк [2].
Вроде всё понятно, но…
Третий (крайний) портал ноля
Что делать, когда нам приходиться делить на ноль?
Всё что нам объяснили в школе (кроме примера с калькулятором) так-то что при делении на ноль получается «бесконечность».
Бесконечность? А что это такое? Это не число! Это то что поглощает любые числа, все числа делятся на все, кроме ноля, поделив на ноль мы получаем «бесконечность», то есть «не число»!
Те, кто учился в институте могут вспомнить ещё вот эту картинку:
Но нам никто не рассказал, что делать с вот этими выражениями:
Все эти уравнения не имеют решения.
Те из нас кто глубоко изучал высшую математику ещё вспомнят вот эту картинку:
Это сфера Римана.
Которая объясняет нам проблему деления на ноль и что в итоге получается.
Прежде чем перейти к сути, немного поразмышляем:
Давайте на время забудем о том чему нас учили и попробуем ответить, на несколько вопросов про бесконечность, так как вы это понимаете на житейском уровне.
Вопросы о бесконечности:
| Что больше: | \( \infty \) или \( \infty \) ? Очевидно что они равны? Или нет? |
| Что больше: | \( \infty \) или \( \infty + 100 \) ? или они равны? Или нет? |
| А если так: | \( \infty \) или \( \infty + 10000000000000 \) ? |
| А так?: | \( \infty \) или \( \infty * 2 \) ? Так кажется точно второе значение больше? |
| А если так: | \( \infty \) или \( \infty * \infty \) ? Вот тут, то сто процентов правое выражение больше? |
Классическая математика говорит о том, что все эти выражения не имеют ответа, то есть нельзя поставить ни один из знаков неравенства.
Несмотря на то, что ниже приведённые умозаключения противоречат самому понятию “бесконечности” прошу Вас прочесть их и постараться понять.
Если представить что бесконечность имеет какой-то конечный вид, то было бы логичным заключение о том, что две бесконечности больше чем одна. А бесконечно много бесконечностей, тем более больше, чем просто бесконечность.
Оказывается, если поменять представление о бесконечности, то становиться возможным оперировать ею как обычным числом. При этом изящно решить проблемы деления на ноль и потери данных при умножении на ноль. Для того чтобы числа не растворялись в бесконечности необходимо принять постулат, что бесконечность конечна и она есть обратное от абсолютного ноля.
Многомерные числа и их представление
Для начала дадим некоторые определения, выражениям которыми будем пользоваться в дальнейшем:
Классический ноль – это тот самый ноль (в классической математике) при умножении на который любого числа мы получаем классический ноль, а при делении на него получается неопределённость (классическая бесконечность).
Получаем интересный эффект, если в процессе вычислений мы многократно складываем нули и бесконечности, делим и умножаем, то числовое значение не теряется.
Таким образом, можно число сколь угодно много раз умножить на ноль, а после этого столько же раз разделить на ноль, то мы увидим то самое число.
Реализация в программировании
Прошу прощения за синтаксис, главное понять идею, для примера использован С++.
создаём некий класс или структуру (кому как удобно), например multinumber со следующими членами:
int dimension; // степень бесконечности, по умолчанию для всех чисел кроме ноля степень бесконечности равна 0; для ноля -1.
float value; // собственно само значение числа, может быть отрицательным и положительным,
*multinumber littlenumber // указатель на следующего члена нижнего порядка многомерного числа. На начальном этапе он равен NULL.
Функции:
конструктор по умолчанию, где создаётся объект для классического ноля со следующими значениями
dimension = “-1”; value = “1”; littlenumber = NULL;
конструктор для вводимых данных, где пользователем или программой задаются значения
dimension = “Y”; value = “X”
опять таки если пользователь создаёт ноль то создаём объект по умолчанию.
{-1} $$
, который мы просто игнорируем)
для “*” для старших членов умножаемых multinumber перемножаем value и суммируем dimension, если есть младшие члены то в возвращаемом multinumber добавляем соответствующие littlenumber в соответствии с правилами умножения многочленов.
для “/” для старших членов multinumber соответственно вычитаем dimension и соответственно делим value, если есть младшие члены то в соответствии с правилами деления многочленов делим их.
Можно также прописать функцию отображения значений для пользователя, где у нас три варианта значений
с dimension меньше ноля тогда отображаем “0”;
dimension = 0; тогда отображаем value;
и dimension больше ноля тогда отображаем “infinity”
теперь подставляем вместо обычных float наш multinumber и вуа-ля, наслаждаемся делением на ноль)
эта модель работает на всех видах числовых данных, в том числе опробована на комплексных числах.
Честно признаться, младшими членами можно пренебречь и оперировать только старшими.
Мне пока не довелось, встретится с задачей, где младшие члены многомерного числа играли роль, хотя допускаю, что такие задачи могут быть.
Если пренебрегать младшими членами то класс(структура) multinumber становится ещё проще.
Библиографический список
1. Чарльз Сейфе. Ноль: биография опасной идеи, 2014
2. Балк М.Б. Реальные применения мнимых чисел, 1988
Принцип неопределенности Гейзенберга — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1693
Принцип неопределенности Гейзенберга является одним из самых знаменитых результатов квантовой механики и утверждает, что нельзя (часто, но не всегда) знать все о частице (как это определяется ее волновой функцией) одновременно.
Этот принцип математически проявляется в виде некоммутирующих операторов.
Введение
Принцип неопределенности Гейзенберга утверждает, что акту измерения переменной частицы присуща неопределенность. Обычно применяемый к положению и импульсу частицы, принцип гласит, что чем точнее известно положение, тем более неопределенным является импульс, и наоборот. Это противоречит классической ньютоновской физике, которая считает, что все переменные частиц могут быть измерены с произвольной неопределенностью при наличии достаточно хорошего оборудования. Принцип неопределенности Гейзенберга — это фундаментальная теория квантовой механики, которая объясняет, почему ученый не может одновременно измерять несколько квантовых переменных. До появления квантовой механики считалось, что все переменные объекта могут быть известны с точной точностью одновременно для данного момента. Ньютоновская физика не накладывала ограничений на то, как более совершенные процедуры и методы могут уменьшить неопределенность измерений, так что можно было предположить, что при надлежащей тщательности и точности вся информация может быть определена.
Гейзенберг сделал смелое предположение, что существует нижний предел этой точности, что делает наше знание о частице изначально неопределенным.
Точнее, если известен точный импульс частицы, невозможно узнать точное положение, и наоборот. Это соотношение также применимо к энергии и времени, поскольку невозможно измерить точную энергию системы за конечное время. Неопределенности в произведениях «сопряженных пар» (импульс/позиция) и (энергия/время) были определены Гейзенбергом как имеющие минимальное значение, соответствующее постоянной Планка, деленной на \(4\pi\). Нагляднее:
\[\Delta{p}\Delta{x} \ge \dfrac{h}{4\pi}\]
\[\Delta{t}\Delta{E} \ge \dfrac{h}{4 \pi}\]
Где \(\Delta\) относится к неопределенности этой переменной, а h – постоянная Планка.
Помимо математических определений, можно понять это, представив себе, что чем тщательнее мы пытаемся измерить положение, тем больше нарушений в системе, что приводит к изменениям импульса. Например, сравните влияние измерения положения на импульс электрона и теннисного мяча.
Скажем, для измерения этих объектов требуется свет в виде фотонных частиц. Эти фотонные частицы обладают измеримой массой и скоростью и вступают в контакт с электроном и теннисным мячом, чтобы достичь значения своего положения. Когда два объекта сталкиваются с их соответствующими импульсами (p=m*v), они передают эти импульсы друг другу. Когда фотон контактирует с электроном, часть его импульса передается, и теперь электрон будет двигаться относительно этого значения в зависимости от соотношения их масс. Более крупный теннисный мяч при измерении также будет передавать импульс от фотонов, но эффект будет меньше, поскольку его масса на несколько порядков больше массы фотона. Чтобы дать более практическое описание, представьте себе танк и велосипед, сталкивающиеся друг с другом, причем танк изображает теннисный мяч, а велосипед — фотон. Сама масса танка, хотя он может двигаться с гораздо меньшей скоростью, увеличит его импульс намного выше, чем у велосипеда, фактически заставляя велосипед двигаться в противоположном направлении.
Конечный результат измерения положения объекта приводит к изменению его импульса и наоборот.
Все квантовое поведение следует этому принципу, и это важно при определении ширины спектральной линии, поскольку неопределенность в энергии системы соответствует ширине линии, видимой в областях светового спектра, изучаемых в спектроскопии.
Что это значит?
Трудно представить себе, что нельзя точно знать, где находится частица в данный момент. Интуитивно кажется, что если частица существует в пространстве, то мы можем указать, где она находится; однако принцип неопределенности Гейзенберга ясно показывает обратное. Это связано с волновой природой частицы. Частица рассредоточена по пространству, так что у нее просто нет точного местоположения, которое она занимает, а вместо этого она занимает ряд позиций. Точно так же нельзя точно знать импульс, поскольку частица состоит из пакета волн, каждая из которых имеет свой собственный импульс, так что в лучшем случае можно сказать, что частица имеет диапазон импульсов.
Давайте рассмотрим, можно ли точно измерить квантовые переменные. Волна, положение которой можно точно измерить, схлопывается в одну точку с неопределенной длиной волны и, следовательно, неопределенным импульсом согласно уравнению де Бройля. Точно так же волна с совершенно измеримым импульсом имеет длину волны, которая бесконечно колеблется во всем пространстве и, следовательно, имеет неопределенное положение.
Вы можете провести такой же мысленный эксперимент с энергией и временем. Чтобы точно измерить энергию волны, потребовалось бы бесконечное количество времени, в то время как измерение точного экземпляра волны в пространстве потребовало бы схлопывания в один момент, который имел бы неограниченную энергию.
Последствия
Принцип Гейзенберга имеет большое значение для практической науки и планирования экспериментов. Рассмотрим измерение импульса или положения частицы. Чтобы создать измерение, должно произойти взаимодействие с частицей, которое изменит другие ее переменные.
Например, чтобы измерить положение электрона, должно произойти столкновение между электроном и другой частицей, такой как фотон. Это передаст часть импульса второй частицы измеряемому электрону и тем самым изменит его. Для более точного измерения положения электрона потребуется частица с меньшей длиной волны и, следовательно, более энергичная, но тогда это еще больше изменит импульс во время столкновения. Эксперимент, предназначенный для определения импульса, окажет такое же влияние на положение. Следовательно, эксперименты могут собирать информацию только об одной переменной за раз с любой степенью точности. 9{-31} кг\).
Ответы
9{-31} кг\).
{-30} м\)5
Одним из примеров, который можно использовать, является стакан воды в подстаканнике в движущемся автомобиле. В этом стакане воды несколько молекул воды, каждая из которых состоит из электронов. Вода в стакане — это макроскопический объект, и ее можно увидеть невооруженным глазом. Однако электроны занимают то же пространство, что и вода, но их нельзя увидеть, и поэтому их необходимо измерять под микроскопом. Как сказано выше во введении, эффект измерения крошечной частицы вызывает изменение ее импульса и времени в пространстве, но это не относится к более крупному объекту. Таким образом, принцип неопределенности имеет гораздо большее значение для электронов, чем для макроскопической воды.
Ссылки
- Чанг, Рэймонд. Физическая химия для биологических наук. Саусалито, Калифорния: Университетские научные книги, 2005. .
- Мортимер, Роберт Г. Физическая химия. Сан-Диего: Hardcourt Academic Press, 1993. .
- Найт, Рэндалл. Физика для ученых и инженеров: стратегический подход. Сан-Франциско: Аддисон Уэсли, 2004. .
Физика для ученых и инженеров: стратегический подход. Сан-Франциско: Аддисон Уэсли, 2004.Авторы и ссылки
- Сара Вудс, Крис Баумгартнер (Калифорнийский университет в Дэвисе)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- № на стр.
- Метки
- Принцип неопределенности Гейзенберга
Бесконечность | Encyclopedia.
com Бесконечность этимологически происходит от латинского infinitas, , который представляет собой комбинацию в (что означает «нет») и finis (что означает конец, границу, предел, прекращение и т. д.). В общем, это слово означает состояние или условие, возникающее из-за того, что сущность не имеет какого-либо конца, предела, завершения или определяющего фактора. Он относится как к экстраментальным, реально существующим вещам (таким как Бог, видимая вселенная и материя), так и к интраментальным сущностям (таким как логические понятия и математические конструкции). Состояние, которое оно обозначает в них, может означать либо совершенство, либо несовершенство, в зависимости от того, является ли окончание, которое, таким образом, отсутствует, само по себе совершенством и должна ли рассматриваемая сущность обладать им. Например, когда речь идет о Боге, бесконечность означает совершенство. Это так, потому что это показывает отсутствие в Боге материи и других внутренних факторов, предполагающих простую потенцию, а также отсутствие внешних ограничений, таких как время, место или понимание сотворенным интеллектом, — все это может быть связано с несовершенством.
и ни одно из которых не принадлежит Богу. С другой стороны, применительно к материи бесконечность означает состояние нужды, поскольку она показывает, что материя сама по себе лишена формы и действия; это совершенные факторы, которые должна получить материя, если она должна существовать в реальной вселенной и быть даже косвенно понятной и поддающейся описанию.
В этой статье прослеживается история концепции бесконечности, которая делится на пять основных разделов: (1) у древних греков, (2) у неоплатонизма, (3) у отцов Церкви, (4) у средневековой схоластики и (5) период с 1600 года. В последующем отчете первые два периода рассматриваются как представители греческой и неоплатонической мысли, а последние три – как представители христианской и современной мысли.
Греческая и неоплатоническая мысль
Первый период начинается в Древней Греции Анаксимандром Милетским ( с. 610–546 до н.э.), который утверждал, что «первоначало существующих вещей есть неограниченное» ( Фрагмент 1).
Он «вечный и нестареющий» ( Frag. 2 ), «бессмертный и нерушимый» ( Frag. 3 ) и, скорее всего, является неким основным природным телом, которое безгранично, потому что количественно неисчерпаемо. Пифагорейцы, как сообщает Аристотель ( Meta. 987a 15–19), «думали, что конечность и бесконечность не являются атрибутами некоторых других вещей, например огня, земли или чего-либо еще в этом роде, но что сама бесконечность и единство сами были субстанцией вещей, о которых они говорят». Под их влиянием Платон также сделал бесконечность одним из конституирующих факторов реальности: «Все вещи, о которых когда-либо говорили, что они состоят [так говорят люди древности] из одного и многих, и имеют в своей природе соединение Предела и Безграничность” ( Филебус 16С; также см. 23С). Но Аристотель господствует над этим первым периодом, как и над большинством последующих периодов, в отношении количественной бесконечности. (см. греческую философию.)
Аристотелевское учение.
Согласно Аристотелю (см. Phys. 202b 30-208a 27), количество, движение и время бесконечны ( apeiron или, реже, aoriston ), но бесконечность ( apeiria или аористия ) принадлежит к последним двум только в силу их родства с первым: движение бесконечно, если охватываемая величина так или иначе бесконечна, а время таково только как мера бесконечного движения. Что же тогда апейрия как найти в количестве? В основном это связано с определенными условиями линии.
Количественная бесконечность. Пусть AO — реальная линия определенной длины. Точка A завершает его в начале, а точка O в конце; таким образом, такая линия конечна. Благодаря своим определенным размерам его можно измерить, познать и описать. Соответственно, его статус конечности делает его познаваемым и поддающимся описанию. В ней протяженность относится к конечным точкам примерно так же, как материя по отношению к форме; и оно само представляет собой, так сказать, соединение материи и формы (см.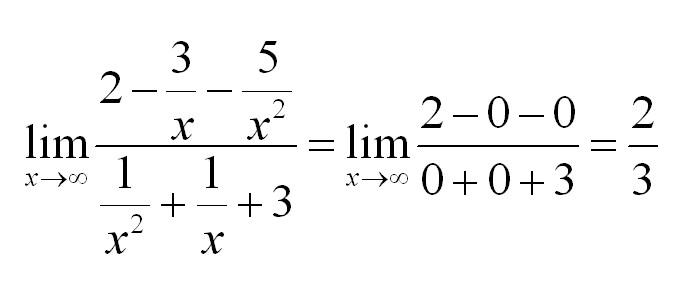
материю и форму). Поскольку совершенство и действительность, не менее чем умопостигаемость, возникают из присутствия формы, AO не только познаваем, но также совершенен и актуален. Следовательно, состояние конечности в АО возникает из-за обладания им определенными размерностями и соотносится с совершенством, действительностью и знанием.
Но как AO бесконечен? Если AO конечен, поскольку имеет определенные размеры благодаря своим начальным и конечным точкам окончания, то он бесконечен, поскольку может быть представлен без того или иного из этих концов. Таким образом AO бесконечен в отношении увеличения, так как независимо от того, какова может быть его действительная длина, всегда можно вообразить, что оно не имеет своей конечной точки и, таким образом, простирается дальше. (То же самое относится и к числу, которое также бесконечно, поскольку независимо от того, какая реальная сумма предлагается, всегда можно подумать о большей). АО также бесконечен в отношении убывания при определенных условиях.
Таким образом, каким бы малым оно ни становилось на самом деле при удалении своей начальной точки к своей конечной, всегда можно представить его меньшим, при условии, что удаление посредством вычитания частей происходит согласно фиксированному соотношению. Итак, пусть AO разделить на B, C, D, и т. д., так что AB = ½ AO, BC = ½ BO, CD = ½ CO, и т. д. Вычитание АВ, ВС, и т. д. из АО может продолжаться бесконечно, и часть АО всегда останется. Какой бы малой ни стала оставшаяся часть, ее можно представить себе еще меньшей, потому что она тоже делима подобным образом. Следовательно, АО бесконечно по убыванию, если смотреть без начальной точки, которую он действительно имеет.
Характеристики. Каковы характеристики такой бесконечности? Конечность, как мы уже видели, связана с умопостигаемостью, актуальностью и совершенством, потому что протяжение в конечной линии связано с ее конечными точками (и, следовательно, с определенными измерениями) как с формой материи.
С другой стороны, линия бесконечна, когда ее продолжение рассматривается как лишенное начальной или конечной точки, и, таким образом, бесконечность указывает на то, что линия в таком состоянии подобна материи без формы. Но форма есть источник познаваемости, актуальности и совершенства. Соответственно, бесконечность связана с состоянием непостижимости, чистой потенциальности и несовершенства. Бесконечная линия, именно как бесконечная, непознаваема, потому что у нее нет определенных измерений, и поэтому ее нельзя измерить или описать. Однако ее бесконечность есть лишь потенциальное условие: каждая линия действительно конечна в силу своей определенной длины, хотя ее можно рассматривать как подверженную бесконечному процессу сложения или деления в силу самой природы количества, подобно тому как первичная материя может принимать бесконечный ряд субстанциальных форм. Бесконечная линия несовершенна, потому что она рассматривается как лишенная определенных размеров, которые она должна иметь и действительно имеет.
Несовершенство Бесконечности. Аристотель часто подчеркивает эту характеристику несовершенства. Бесконечное, поясняет он в важном отрывке ( Phys. 206b 32—207a 2), «оказывается противоположным тому, о чем говорят. Бесконечно не то, что не имеет ничего вне себя, а то, что всегда имеет что-то вне себя». Почему так? Потому что в количестве всегда есть какая-то часть, выходящая за пределы того, чего достигли при его делении или при построении путем прибавления. Количество бесконечно, потому что всегда можно взять часть помимо того, что уже взято. Итак, поскольку бесконечное всегда имеет что-то внешнее и запредельное, в нем всегда чего-то нет или недостает. Таким образом, он не является полным или совершенным. В самом деле, сама бесконечность есть, заключает Аристотель, та самая лишенность целостности и совершенства, субъектом которой является чувственный континуум (9).0170 там же, 207b 35-208a 4).
Последствия. Таким образом, для Аристотеля бесконечность в основном связана с количеством и является синонимом несовершенства.
Эта синонимия имеет два важных следствия. Греческий философ не может предицировать его непосредственно от Самого Бога (для него Перводвигатель и первичный Отдельный Разум), а только от Его силы, и то посредством внешней предикации. То есть Его сила настолько совершенна, что является причиной бесконечного следствия, а именно, бесконечно повторяющегося кругового движения небесных тел через бесконечность времени; только этому непосредственно принадлежит бесконечность и через что божественная сила получает предикацию (9).0170 Мета. 1073а 6–10). Во-вторых, материальная вселенная не может быть на самом деле бесконечной по своим размерам и не является просто одной из бесконечного числа вселенных, поскольку такого рода фактические бесконечности противоречивы и невозможны. Более того, она конечна в силу того, что как «вселенная» она цельна, всеобъемлюща, полна и совершенна; и все, что является целым, завершенным и совершенным, имеет конец, который является его пределом и окончанием ( Phys.
207a).
Неоплатонизм и Плотин. Второй период в истории бесконечности, период неоплатонизма, был начат Плотином (204–270 гг. н.э.). Как и Аристотель до него, Плотин утверждал, что сила Бога (Единого Блага, высшей ипостаси) бесконечна. «Тот, кто способен сотворить все, какое величие имел бы Он? Он бесконечен и, если бы так, то не имел бы физической величины… Принцип был бы велик в том смысле, что нет ничего более могущественного, чем Он, или даже столь же могущественного». ( Энн. 6.7.32.14). «Единый есть величайшее из всех вещей не по физической величине, а по силе, ибо то, что не имеет протяженности, велико благодаря силе… Мы также должны настаивать на том, что Оно не бесконечно, как бы интравертируемо ни по протяженности, ни по числу, а по безграничности. Его могущества» (6.9.6.1–13; см. также 2.4.5.17–20; 5.5.10.20–24). Это утверждение, по-видимому, делается через внешнее наименование: божественная сила настолько велика, что является источником бесконечных эффектов — материальных сущностей, которые бесконечно многочисленны, потому что они непрерывно развертываются в бесконечно повторяющихся мировых циклах (5.
7.1.9–27; 5.7.3.15). 6.2.22.11).
Бесконечность как Совершенство. Однако, в отличие от Аристотеля, Плотин разработал теорию бесконечности, которая является синонимом совершенства и применима к Самому Богу. Эта теория основана на понимании того, что форма и бытие являются определяющими и завершающими факторами, где бы они ни находились (5.1.7.19).–26). Если что-то без формы и бытия, то оно без их определения и, таким образом, неопределенно или бесконечно. Если оно должно обладать ими, но не обладает, то этот статус неопределенности совпадает с несовершенством. Таким образом, материя сама по себе ниже формы и сущности и, соответственно, неопределенна и одновременно несовершенна (1.8.4.14; 2.4.6.17; 2.4.10.1; 2.4.13.26; 2.4.15.16). С другой стороны (и об этом Аристотель явно не сознает), Бог возвышается над бытием и формой, присущими только низшим уровням реальности, а именно умопостигаемой, психической и чувственной вселенной, и тем самым также превосходит любое формальное определение.
Благодаря этой трансцендентности Он бесконечен, и такая бесконечность соответствует абсолютному совершенству и действительному совершенству. «Не замечайте, что [Хорошее] — это таким-то и таким-то образом, потому что такой язык определил бы Это и сделал бы Это конкретной вещью. Тот, кто созерцает Его, не может сказать, что Оно есть или не есть то-то и то-то, ибо тем самым он сказал бы, что Оно есть одно из тех существ, которые можно с полным правом назвать такими-то и такими-то, тогда как Оно действительно иное, чем все подобные существа. Увидев, что Оно неопределенно, он может перечислить все существа, которые приходят после Него, а затем сказать, что Оно есть ничто из них всех, но что Это Тотальная Сила, которая действительно владеет Собой» (6.8.9).0,37; см. также 6.7.17.12–18; 5.1.7.19–26; 5.5.6.1–15; 5.5.11.16–37).
Бесконечность и Небытие. Показав, таким образом, что бесконечность может быть соразмерна совершенству и, таким образом, предсказуема самой божественной реальности, Плотин внес большой вклад в развитие концепции бесконечности. Но следует помнить, что эта предикация только подразумевается в тексте Плотина. Он явно связывает бесконечность с небытием: Единое считается бесконечным, потому что Оно превосходит бытие и форму. Допустим, что эта бесконечность небытия может подразумевать, что Сам Единый бесконечен, тем не менее, это только импликация.
Христианство и современная мысль
Третий период в истории бесконечности занимают Отцы Церкви — СС. Хилари де Пуатье и Августин на Западе; Климент Александрийский, Иоанн Златоуст, Григорий Назианзин, Григорий Нисский, Псевдо-Дионисий и Иоанн Дамаскин на Востоке. Все они находились под влиянием Священного Писания, а также неоплатонизма.
Библейское учение. В Библии есть лишь несколько и (в лучшем случае) косвенных текстов о самой бесконечности. Примером может служить Ps 144.3 Вульгаты: «Magnus Dominus et laudabilis nimis et magnitudinis eius non est finis» (последнее предложение еще менее сильно в современном переводе: «… neque explorari potest magnitudo eius»). Тем не менее Писание подчеркивает ужасающую силу Бога (например, Бытие 17:1; Пс 33:9).; Пс 135,6; Ин 1.3), Его вечность (Втор 32.40; Быт 21.33), Его вездесущность (Втор 4.39; Пс 139.7–12) в сочетании с превосходством любого определенного места (3 Цар 8.27; Джб 11.8; Бар 3.25), Его непохожесть на все остальное ( Ис 46.9), и неспособность любого сотворенного разума адекватно познать Его (Рим. 11.33; Еф. 3.8). В результате латинские и греческие отцы Церкви говорили о Боге как о бесконечном в том смысле, что Он всемогущ, вечен, необъятен, непостижим, а под влиянием неоплатонизма — небытие.
Латинские и греческие отцы. Св. Августин приводит пример учения латинских отцов: «Очевидно, что упорядоченное расположение вселенной осуществляется посредством разума [Бога], и что его можно уместно назвать бесконечным не в пространственных отношениях, а в в силе, которая не может быть понята человеческим мышлением… То, что бестелесно… может быть названо и полным, и бесконечным: полным в силу своей цельности, бесконечным в силу того, что оно не ограничено пространственными границами” (9). 0170 Послание. 118, Отцы Церкви изд., 284–285). Еще: «Что находится в вашем уме и сердце, когда вы думаете об определенной субстанции, которая является живой, вечной, всемогущей, бесконечной, вездесущей, везде полной, нигде не заключенной? сердце” ( В еванг. Иох. 1.8 см. также Нат. бони 3).
Св. Иоанн Дамаскин так же говорит от имени греческих отцов: «[Бога] нельзя найти среди сущего — не потому, что Его нет, но, скорее, потому, что Он выше всех существ и даже выше самого бытия. сущее как его предметы, то то, что выходит за пределы познания, выходит за пределы и сущности, и, наоборот, то, что за пределами сущности, есть и за пределами знания. Поэтому Божество и бесконечно, и непостижимо, и только это постижимо о Нем — самая Его бесконечность и непостижимость» ( Де файд орт. 1.4). «Веруем в единого Бога: единый принцип, безначальный, несотворенный, нерожденный, нерушимый и бессмертный, вечный, безграничный, неограниченный, безграничный, бесконечный по силе, простой, несоставной, бестелесный» ( там же 1. 8). «Из всех имен, данных Богу, более подходящим кажется имя Тот, Кто есть … Ибо, подобно некоему бесконечному и неопределенному морю сущности, Он имеет и содержит в Себе все существа» ( там же 1.9 ).
Другим автором, находящимся под сильным влиянием Ветхого Завета (в версии Септуагинты), который предшествует Отцам и, если на то пошло, также и Плотину, является philo judaeus из Александрии, еврейский богослов и философ. Для него Бог бесконечен трояким образом: как непостижимый, поскольку мы можем знать, что Он существует, но не то, что Он есть; как всемогущий, так как Бог свободно сотворил мир из ничего; и как всеблагий, поскольку Он свободно и любовно заботится даже об отдельных людях (см. H. A. Wolfson, 9).0170 Религиозная философия [Кембридж, Массачусетс, 1961] 5–11).
Средневековая схоластика. 90–197 Четвертый период — период средневековой схоластики. Хотя john scotus erigena придерживался учения о божественной бесконечности, которое кажется почти полностью неоплатоническим (см. De Divisione naturae , 1.56; Patrologia Latina 122; 499D), тем не менее христианские авторы с 10 по середину 13 вв. мало или вообще никакого внимания к божественной бесконечности. Как правило, этот термин даже не может быть причислен теологами к божественным атрибутам (например, абеляровское Ysagoge in theologiam, Robert of Melun, Sententiae, Stephen Langton, Commentarius in sententias, Peter of Poitier, Sententiae, ). Иногда бесконечность применяется к божественной силе или делается синонимом вечности или непостижимости Бога (например, Libri IV sententiarum Петра Ломбардского, Хью Сен-Викторского De sacramentis christianae fidei, Хью Сен-Шера In sententiarum , Александр Хейлз Глосса в сл., Альберта Великого В сл. ). Но нигде она сама подробно не обсуждается.
Бонавентура и Аквинский. Однако после этого периода молчания этой теме уделяют явное и подробное внимание христианские авторы, двое из которых внесли важный вклад в ее развитие и чья позиция до сих пор влияет на многих современных схоластов — С. С. bonaventure (см. его В 1 прислал. 19.2.3 ад 4; 43.1.1 и ад 3; 43.1.2, написано с. 1250) и thomas aquinas (см. его В 1 прил., 43.1.1; писано c. 1254; ST 1a, 7.1–2, писано c. 1267). Их вклад непосредственно касается божественной бесконечности, ибо они вместе со своими современниками приняли аристотелевскую концепцию количественной бесконечности применительно к линиям и числам и, более того, согласились с тем, что мир конечен по протяженности и численно един. Но они порвали с Аристотелем, утверждая бесконечность Самого Бога, как это делал и Плотин. Однако их позиция существенно отличается от позиции неоплатоников, поскольку она опирается на явно иную метафизику.
Фома Аквинский, — чье учение рассматривается здесь для удобства, хотя в этом вопросе позиция Бонавентуры не отличается от позиции Фомы и фактически хронологически предвосхищает ее, — соглашался с Плотином в том, что образует и вообще всякий акт , являются определяющими факторами для всего, что их получает. Соответственно, реципиент, такой как материя, неопределен и бесконечен (а также несовершенен), когда рассматривается сам по себе и как лишенный формы. Но, в отличие от Плотина, Фома также учил, что материя и все другие виды потенций не являются простыми отрицаниями, лишениями или умственными построениями, а являются подлинно реальными и действительно существующими составляющими внутри сущего и обусловливают своего рода детерминацию. Соответственно, субстанциальная форма или акт не имеют ограничивающего определения материи или потенции и, таким образом, бесконечны и бесконечно совершенны.
Бесконечность Бога. Бог такой существующий. Божественная сущность не содержит материи или потенциальности любого рода и, как таковая, полностью свободна от их ограничений. Следовательно, бесконечность есть совершенство самого Его бытия (см. совершенство, онтологическое). В то время как каждое творение является конечным существом, потому что оно представляет собой совокупность актов, полученных и определяемых потенцией, Бог является бесконечным Существом, потому что Он является полностью субстантивным, чистым действием и, следовательно, не имеет какой-либо реципиентной потенции. Совершенное Бытие, потому что Он есть постоянное существование, Бог есть бесконечное Бытие, свободное от ограничивающей детерминации материи и всякой потенции. (см. бесконечность бога.)
Такая ясно изложенная и прочно установленная доктрина была той силой, которая помогла сосредоточить внимание современников Томаса и Бонавентуры и их последователей на бесконечности как на важной теме для обсуждения. Мало кто из последующих философов-схоластов или теологов не смог исследовать, «может ли бесконечность быть приписана как совершенство самому божественному существу», и дать в основном тот же ответ (о duns scotus, см. Bettoni, 132–159).
Современные мыслители. Несхоластические авторы пятого периода, начинающегося в конце XVI века и продолжающегося до наших дней, также сильно озабочены бесконечностью, но разрабатываемые ими учения сильно отличаются от доктрин предшествующих эпох. Что касается божественной бесконечности, то они начинают с доктрины, во многом схожей по содержанию с учением их предшественников-схоластов, отличающейся главным образом терминологией. Например, Р. Декарт считал, что только Бога следует называть «бесконечным», тогда как количественные явления следует называть «неопределенными» (см. 9).0170 Ответ на объект. 1 , перевод Холдейна-Росса, 2:17; Принципы философии, 1.24, 26, 27, 1:229–230).
Бог и Бесконечность. Однако Б. Спиноза ввел совсем иное учение, которого требовал его монизм (и, можно добавить, сохраненное без радикальных изменений Г. В. Ф. Гегелем и последующими монистами). Только Бог действительно реален, а отдельные вещи являются простыми модусами или проявлениями божественной субстанции. Именно как индивидуальное, как определенное, как это, как конечное, они нереальны, так как индивидуальность и конечность суть лишь отрицания. Но Бог есть бесконечность, потому что Он есть тотальная реальность и чистое утверждение: («Под Богом я понимаю Бытие абсолютно бесконечное…. К сущности того, что абсолютно бесконечно, относится все, что выражает сущность и не предполагает отрицания» ( Этика, 1. 6, изд. Дж. Уайлд, 94–95)
Стремясь защитить реальность отдельных вещей, одновременно сохраняя Бога, некоторые последующие философы дошли до противоположной крайности и сделали Бога конечным — Дж. С. Милль, У. Джеймс, А. Н. Уайтхед. (см. Коллинз, 285–324) 9.0024
Революция в космологии. Однако основное отличие этого периода от более ранних усматривается в его космологии. Аристотелевское представление о Вселенной как о конечной по протяженности и количественной единице было заменено, главным образом благодаря открытию и использованию телескопа, совершенно иной концепцией. Например, галактика, видимая в Млечном Пути, крошечной частью которой является Солнечная система, является просто одной из почти бесчисленного множества других галактик. Добавьте к этому тот факт, что галактики, кажется, удаляются друг от друга с огромной скоростью, и можно легко сделать вывод, что Вселенная каким-то образом бесконечна по своим размерам.
Такая доктрина была предвосхищена Джордано Бруно и другими. Их теоретизирование обычно сопровождалось тенденцией говорить о божественной бесконечности в терминах вездесущности и необъятности. Бог бесконечен, поскольку Он присутствует повсюду в этой бесконечной вселенной, которая никоим образом не ограничивает, не содержит и не прекращает Его. К сожалению, в умах некоторых божественная бесконечность настолько тесно связана с бесконечностью абсолютного пространства, что кажется почти идентичной (см. пантеизм; панентеизм).
Современная математика. С этой новой космологией связана современная математика, включая неевклидову геометрию, которая была начата в 17 веке и предложила новый подход к математической бесконечности. Этот подход, разработанный Георгом Кантором, начинается с таких теорем, как: «Существует столько же отрицательных целых чисел, сколько и положительных целых чисел; на отрезке длиной в одну единицу столько же точек, сколько на отрезке длиной в две единицы…, так далее.” Он завершается определением бесконечного множества как множества, обладающего следующим свойством: подходящее подмножество множества может быть поставлено во взаимное соответствие 1-к-1 всему множеству. Короче говоря, множество бесконечно, если часть множества равна целому (см. Hausmann, 76–89).).
Если раньше предполагалось, что сущность математической бесконечности заключается в количестве и изменчивости, то теперь в качестве основных рассматриваются понятия порядка и множественности. Кантор отметил изменение, введя понятие трансфинитных чисел. Что такое трансфинитное число? «Вообще, если мы рассматриваем любой класс множеств элементов, которые могут быть поставлены во взаимно однозначное соответствие, мы определяем свойство, общее для каждого члена класса, как кардинальное число каждого множества Если мы теперь рассмотрим класс всех бесконечных множеств, которые могут быть поставлены во взаимно однозначное соответствие, мы можем определить это свойство этого класса как трансфинитное кардинальное число» ( там же, 86).
Заключение. 90–197 На протяжении всей своей истории бесконечность приписывалась главным образом количественным элементам и Богу; в каждом случае оно претерпело эволюцию значения.
В отношении количества эта эволюция была отложена до самого последнего периода. До этого господствовала концепция Аристотеля. Однако даже сейчас его концепция не полностью отброшена. Действительно, математическая бесконечность по-новому понимается и интерпретируется, и все согласны с тем, что Вселенная не является просто ограниченной системой, какой ее когда-то представляли. Но когда кто-то говорит, что материальный мир бесконечен в своих размерах, не имеет ли он в виду, что каким бы большим он ни был в настоящее время, его все же можно представить себе (и, возможно, он будет расширяться) в еще большей степени? Если так, то это значение бесконечности по-прежнему в основном аристотелевское.
Эволюция относительно бесконечности Бога не терпела отсрочки. Не имея явного основания в Священном Писании и связанного древними греками с несовершенством, бесконечность сначала приписывалась Богу только через внешнее наименование, а именно: Его сила считалась бесконечной, потому что она была способна произвести бесконечное множество действий. Плотин разорвал эту связь с несовершенством, и бесконечность стала божественным атрибутом, хотя и явно связанным с небытием. Используя иную метафизику, Бонавентура и Фома Аквинский отождествляли бесконечность с сущим и всесовершенным бытием. Прибегая к совсем иной метафизике, Спиноза и другие монисты сделали бесконечность синонимом самой реальности и стремились свести все сущее, кроме Бога, к ничтожеству. В ответ на это другие притворялись, что спасают отдельные вещи, низводя Бога до их конечного и несовершенного уровня.
Библиография: л. Суини, «Бесконечность у Плотина», Gregorianum 38 (1957) 515–535, 713–732; «Божественная бесконечность: 1150–1250», Современный школьник 35 (1957–58) 38–51; «Другая интерпретация Эннеад, VI, 7, 32», там же. 38 (1960–61) 289–303; «L’Infini quantitatif chez Aristote», Revue philsophique de Louvain 58 (1960) 504–528; «Некоторые средневековые противники божественной бесконечности», Medieval Studies 19(1957) 233–245; «Ломбард, Августин и бесконечность», Manuscripta 2 (1958) 24–40.