ЭДС. Закон Ома для полной цепи.
Если свободные заряды перемещаются в электрической цепи по замкнутой траектории, то такую цепь называют полной или замкнутой. При этом на каждом из участков такой цепи работа электростатических сил переходит в тепловую, механическую или энергию химических связей. Так как работа электростатических сил, перемещающих заряд по замкнутой траектории, всегда равна нулю, то только силы электростатического поля не могут обеспечить постоянное движение зарядов по замкнутой траектории. Чтобы
электрический ток в замкнутой цепи не прекращался, необходимо включить в неё
источник тока (см. рис. а), внутри которого перемещение свободных
зарядов происходило бы не под действием электростатических сил, а при участии
любых других сил, называемых сторонними. Сторонние силы – силы неэлектростатического
происхождения, действующих на заряды со стороны источника тока. 1) химические реакции – в гальванических элементах (батарейках), аккумуляторах (сторонние силы возникают в результате химических реакций между электродами и жидким электролитом), 2) электромагнитной – в генераторах. При этом генераторы могут использовать а) механическую энергию – ГЭС, б) ядерную – АЭС, в) тепловую – ТЭС, г) приливов и отливов – ПЭС, д) ветровую – ВЭС и т.д. (силы, действующие на свободные заряды, перемещающиеся в магнитном поле). 3) использование фотоэффекта – фото-ЭДС в калькуляторах и солнечных батареях (в фотоэлементах сторонние силы возникают при действии света на электроны атомов, входящих в состав некоторых веществ), 4) пьезоэффект – пьезо-ЭДС, например, в пьезозажигалках, 5) контактная разность потенциалов – термо-ЭДС в термопарах и т.д. Например, в цепи на рис. а, свободные заряды,
перемещаются от тела А к телу Б под
действием электростатических сил, а сторонние силы источника питания заставляют
их возвращаться обратно – от Б к А. Сторонние силы в источнике тока разделяют разноимённые электрические заряды друг от друга, совершая работу против электростатических (кулоновских сил). Контакт (полюс) источника тока, где в результате действия сторонних сил накапливается положительный заряд, называют положительным, а противоположно заряженный полюс – отрицательным, обозначая их так, как изображено на рис. . Как и разность потенциалов, ЭДС в СИ измеряют в вольтах. Сопротивление источника тока или внутреннее сопротивление тоже является его важной характеристикой. Чтобы определить, как зависит сила тока от ЭДС источника в цепи, изображённой на рис. а, нарисуем эквивалентную схему (см. рис. которое называют законом Ома для полной цепи  1) Напряжение на зажимах источника, а соответственно и во внешней цепи где величина Ir– падение напряжения внутри источника тока. 2) Если внешнее сопротивление замкнутой цепи равно нулю, то такой режим источника тока называется коротким замыканием. 3) Для полной цепи закон Джоуля-Ленца Легко показать, что, если полная цепь содержит несколько последовательно соединённых источников тока, то для вычисления силы тока следует вместо Ɛ взять алгебраическую сумму ЭДС всех этих источников, выбрав какое-нибудь направление обхода цепи, например, по часовой стрелке (рис. г). Если при таком обходе мы идём от положительного полюса источника тока к отрицательному, то ЭДС данного источника следует суммировать со знаком минус. Более подробную информацию смотри ЗДЕСЬ. |
Закон Ома для полной цепи
1. Источник тока
При прохождении тока в проводнике выделяется некоторое количество теплоты.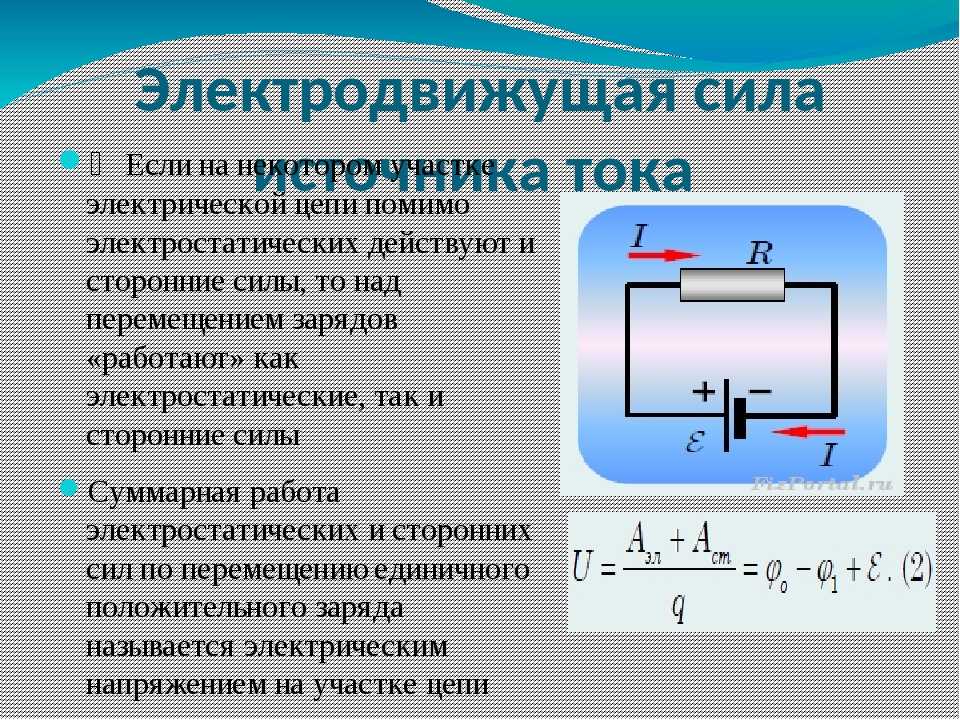 Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.
Согласно закону сохранения энергии при этом в электрическую цепь должна поступать энергия.
Может ли источником этой энергии быть электростатическое поле? Нет, не может, потому что при перемещении заряда вдоль всей цепи, то есть по замкнутой траектории, работа электростатического поля равна кулю.
Следовательно, для существования тока в замкнутой цепи в ней должен быть участок, на котором свободные заряды движутся против сил электростатического поля. Таким участком цепи является источник тока (рис. 59.1).
В источнике тока на свободные заряды действуют силы, которые имеют не электростатическую природу. Их называют сторонними силами. В результате действия сторонних сил происходит разделение зарядов: на одном полюсе источника тока накапливается положительный заряд, а на другом – отрицательный. Вследствие этого возникает электростатическое поле, которое движет свободные заряды в электрической цепи вне источника тока, то есть во внешней цепи.
В химических источниках тока сторонние силы имеют химическую природу. Например, если погрузить цинковый и медный электроды в серную кислоту, то положительные ионы цинка будут чаще покидать электрод, чем положительные ионы меди. В результате между медным и цинковым электродами возникнет разность потенциалов: потенциал медного электрода будет больше, чем цинкового. Медный электрод станет положительным полюсом источника тока, а цинковый – отрицательным.
Например, если погрузить цинковый и медный электроды в серную кислоту, то положительные ионы цинка будут чаще покидать электрод, чем положительные ионы меди. В результате между медным и цинковым электродами возникнет разность потенциалов: потенциал медного электрода будет больше, чем цинкового. Медный электрод станет положительным полюсом источника тока, а цинковый – отрицательным.
В генераторах электростанций сторонними силами являются силы, действующие на свободные электроны в металле со стороны вихревого электрического поля, порождаемого переменным магнитным полем. Работа вихревого электрического поля по перемещению заряда вдоль замкнутого контура не равна нулю. Действие генераторов тока мы рассмотрим в курсе физики 11-го класса.
Электродвижущая сила источника тока
В источнике тока сторонние силы, перемещая свободные заряды против действия сил электростатического поля, совершают работу, которую мы обозначим Aстор.
Эта работа пропорциональна заряду q, который перемещается вдоль цепи за данный промежуток времени. Поэтому отношение работы сторонних сил к величине заряда не зависит ни от Aстор, ни от q. Следовательно, оно является характеристикой источника тока. Это отношение называют электродвижущей силой источника (ЭДС) и обозначают ξ:
Поэтому отношение работы сторонних сил к величине заряда не зависит ни от Aстор, ни от q. Следовательно, оно является характеристикой источника тока. Это отношение называют электродвижущей силой источника (ЭДС) и обозначают ξ:
ξ = Aстор/q. (1)
(Это название не совсем удачно, потому что ЭДС – не «сила» в механическом смысле, а энергетическая характеристика источника.)
ЭДС, как и напряжение, измеряют в вольтах. Например, ЭДС батарейки составляет несколько вольт.
2. Закон Ома для полной цепи
Если сила тока в цепи равна I, то за время t по цепи проходит заряд q = It. Поэтому формулу (1) можно записать в виде
Aстор = ξIt. (2)
При этом во внешней цепи сопротивлением R выделяется количество теплоты
Qвнеш = I2Rt, (3)
а внутри источника тока выделяется количество теплоты
Qвнутр = I2rt, (4)
где r – сопротивление источника, которое называют его внутренним сопротивлением.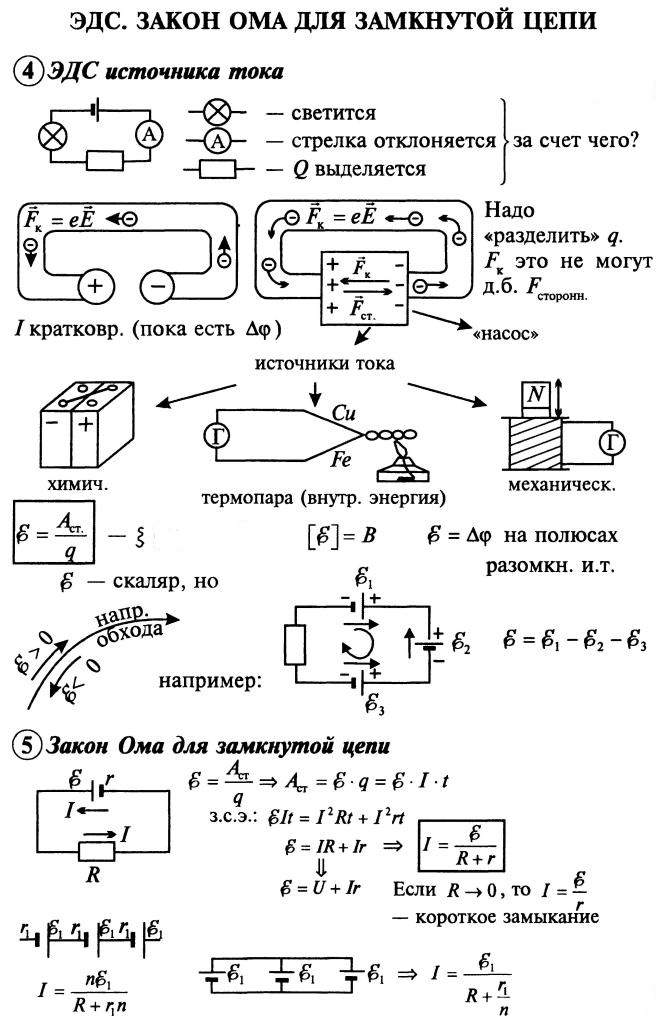
Из закона сохранения энергии следует, что
Qвнеш + Qвнутр = Aстор. (5)
? 1. Докажите, что из формул (2) – (5) следует:
I = ξ / (R + r). (6)
Это соотношение называют законом Ома для полной цепи.
Сумму сопротивлений R + r называют полным сопротивлением цепи.
? 2. ЭДС источника тока 12 В, а его внутреннее сопротивление равно 2 Ом.
а) Чему равна сила тока в цепи, если сопротивление внешней цепи равно 4 Ом?
б) Какова максимально возможная сила тока в цепи? При каком сопротивлении внешней цепи это имеет место?
? 3. При внешнем сопротивлении 2 Ом сила тока в цепи равна 1,5 А, а при внешнем сопротивлении 4 Ом сила тока равна 1 А.
а) Чему равно внутреннее сопротивление источника?
б) Чему равна ЭДС источника?
Напряжение на полюсах источника
Закон Ома для полной цепи можно записать в виде
ξ = IR + Ir. (7)
Первое слагаемое в этой формуле согласно закону Ома для участка цепи равно напряжению U на полюсах источника тока:
IR = U.
Поэтому формулу (7) можно записать в виде
U = ξ – Ir. (8)
Формула (8) выражает зависимость напряжения U на полюсах источника тока от силы тока I в цепи.
Поставим опыт
Зависимость U(I) можно измерить на опыте, изменяя силу тока в цепи с помощью реостата (рис. 59.2, а, б). Красная пунктирная линия на схеме 59.2, б показывает, как идет ток в реостате. Например, если ползунок реостата, изображенного на рисунке 59,2, а, сдвинуть вправо, то сопротивление реостата увеличится, потому что увеличится длина обмотки, по которой идет ток.
? 4. На рисунке 59.3 изображен график зависимости U(I) для некоторого источника тока.
а) Чему равна ЭДС этого источника тока?
б) Чему равна наибольшая сила тока?
в) Чему равно внутреннее сопротивление источника тока?
г) Чему равно внешнее сопротивление, когда сила тока равна нулю?
д) Чему равно внешнее сопротивление, когда сила тока максимальна?
е) Чему равно внешнее сопротивление при I = 1,5 А?
Максимальное напряжение на полюсах источника равно ξ. Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
Следовательно, напряжение между разомкнутыми полюсами источника тока равно ЭДС этого источника.
Минимальное же напряжение между полюсами источника равно нулю. Это имеет место при коротком замыкании, когда внешнее сопротивление R = 0. В этом случае сила тока максимальна. Ее называют силой тока короткого замыкания.
? 5. Покажите, что сила тока короткого замыкания выражается формулой
Iка = ξ/r. (9)
Подсказка. Воспользуйтесь законом Ома для полной цепи.
Из формулы (9) видно, что при очень малом внутреннем сопротивлении источника (как, например, у автомобильного аккумулятора) сила тока короткого замыкания будет очень большой, что может вывести источник тока из строя.
? 6. Сила тока при коротком замыкании батарейки равна 2 А. Когда к батарейке подключили резистор сопротивлением 4 Ом, сила тока стала равной 1 А.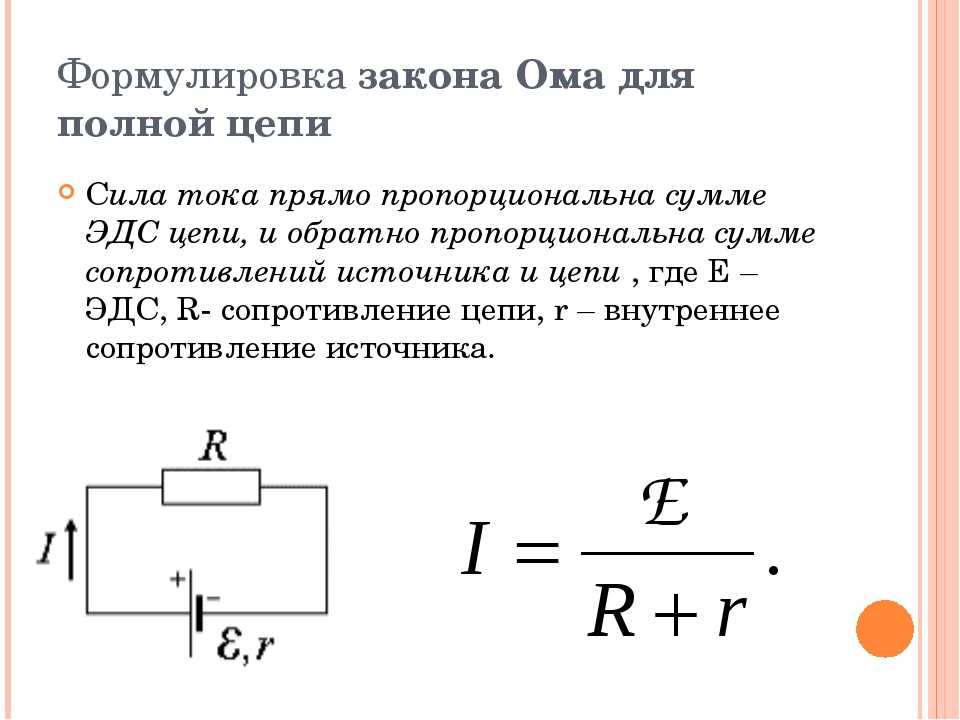
а) Как изменилось полное сопротивление цепи?
б) Чему равно внутреннее сопротивление батарейки?
Измерив напряжение на полюсах источника и силу тока в цепи при двух различных значениях сопротивления внешней цепи, можно найти ЭДС ξ и внутреннее сопротивление r источника тока. Это можно сделать графически и аналитически.
? 7. При силе тока в цепи 2 А напряжение на полюсах источника равно 8 В, а при силе тока 4 А напряжение на полюсах равно 4 В.
а) Постройте систему координат I, U и нанесите две точки графика зависимости U(I) согласно приведенным данным.
б) Проведите прямую через эти точки и отметьте точки пересечения этой прямой с осями координат. Используя этот график, найдите, чему равны ЭДС, сила тока короткого замыкания и внутреннее сопротивление источника тока.
в) Используя уравнение (8), составьте систему двух уравнений с двумя неизвестными ξ и r и решите ее.
3. КПД источника тока
Работу тока во внешней цепи называют полезной работой. Обозначим ее Aпол. Используя формулу для работы тока, получаем:
Используя формулу для работы тока, получаем:
Aпол = I2Rt.
Поскольку источник обладает внутренним сопротивлением, полезная работа меньше работы сторонних сил, потому что часть работы сторонних сил расходуется на выделение в источнике тока количества теплоты I2rt. Поскольку
Aстор = I2Rt + I2rt,
получаем для отношения полезной работы к работе сторонних сил:
η = Aпол / Aстор = (I2Rt) / (I2Rt + I2rt) = R / (R + r).
Это отношение, выраженное в процентах, называют КПД источника тока.
? 8. При каком отношении внешнего сопротивления к внутреннему сопротивлению КПД источника тока равен: 50 %; 80 %? Почему случай, когда КПД источника тока равен 100 %, не представляет практического интереса?
Дополнительные вопросы и задания
9. На рисунке 59.4 изображена схема измерения зависимости напряжения U на полюсах источника тока от силы тока I. Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении – 2 А и 12 В.
Амперметр и вольтметр считайте идеальными. Сопротивление всей обмотки реостата 16 Ом. При первом положении ползунка реостата показания приборов 3 А и 8 В, а при втором положении – 2 А и 12 В.
а) Как сдвинули ползунок реостата между первым и вторым измерениями – влево или вправо?
б) Чему равны ЭДС источника тока и его внутреннее сопротивление?
в) Каковы будут показания приборов, если ползунок реостата передвинуть в крайнее левое положение? в крайнее правое?
10. При силе тока 6 А мощность тока во внешней цепи равна 90 Вт, а при силе тока 2 А она равна 60 Вт.
а) Чему равна ЭДС источника тока?
б) Чему равно внутреннее сопротивление источника тока?
в) Чему равно напряжение на полюсах источника в первом и втором случаях?
г) Чему равен КПД источника тока в первом и втором случаях?
1
Первый слайд презентации: Электродвижущая сила.
 Закон Ома для полной цепи
Закон Ома для полной цепи
Изображение слайда
2
Слайд 2
Чтобы в проводнике электрический ток существовал длительное время, необходимо все это время поддерживать в нем электрическое поле. Электрическое поле в проводниках создается и может длительное время поддерживаться источниками электрического тока.
Изображение слайда
3
Слайд 3
Любой источник тока характеризуется электродвижущей силой (ЭДС). Что это значит?
Изображение слайда
4
Слайд 4
Соединим проводником два металлических шарика, несущих заряды противоположных знаков. Под влиянием электрического поля этих зарядов в проводнике возникает электрический ток.
Но этот ток будет очень кратковременным. Потенциалы шариков станут одинаковыми, электрическое поле исчезнет.
Под влиянием электрического поля этих зарядов в проводнике возникает электрический ток.
Но этот ток будет очень кратковременным. Потенциалы шариков станут одинаковыми, электрическое поле исчезнет.
Изображение слайда
5
Слайд 5: Сторонние силы
Чтобы ток был постоянным, надо поддерживать постоянное напряжение между шариками. Для этого необходимо устройство (источник тока). В таком устройстве на заряды, кроме электрических сил, должны действовать силы неэлектрического происхождения. Одно лишь электрическое поле заряженных частиц (кулоновское поле) не способно поддерживать постоянный ток в цепи.
Изображение слайда
6
Слайд 6
Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительного заряженного электрода к отрицательному), а во всей остальной цепи их приводит в движение электрическое поле.
Изображение слайда
7
Слайд 7: Электродвижущая сила
Действие сторонних сил характеризуется физической величиной, называемой электродвижущей силой (сокращённо ЭДС ). Электродвижущая сила в замкнутом контуре представляет собой отношение работы сторонних сил при перемещении заряда вдоль контура к заряду: ЭДС выражают в вольтах: [Ɛ] = Дж/Кл = В
Изображение слайда
8
Слайд 8
Рассмотрим простейшую полную (замкнутую) цепь, состоящую из источника тока и резистора сопротивлением R.
Ɛ – ЭДС источника тока,
r – внутреннее сопротивление источника тока,
R – внешнее сопротивление цепи,
R + r – полное сопротивление цепи.
C ила тока в полной цепи равна отношению ЭДС цепи к её полному сопротивлению.
Изображение слайда
Слайд 9
Сила тока (А) ЭДС-электродвижущая сила источника тока (В) Сопротивление нагрузки (Ом) Внутреннее сопротивление источника тока (Ом )
Изображение слайда
10
Слайд 10
Изображение слайда
11
Слайд 11
Изображение слайда
12
Слайд 12: Решение задач:
№1 Гальванический элемент с ЭДС E = 5,0 В и внутренним сопротивлением r = 0,2 Ом замкнут на проводник сопротивлением R = 40,0 Ом. Чему равно напряжение U на этом проводнике? Ответ:4,975В
№2 Определить ЭДС источника тока с внутренним
сопротивлением r = 0,3 Ом, если при подключении
к клеммам источника тока параллельно соединенных
резисторов R 1=10 Ом и R 2=6 Ом сила тока в цепи:
I =3 A.
Ответ:12,15В
Чему равно напряжение U на этом проводнике? Ответ:4,975В
№2 Определить ЭДС источника тока с внутренним
сопротивлением r = 0,3 Ом, если при подключении
к клеммам источника тока параллельно соединенных
резисторов R 1=10 Ом и R 2=6 Ом сила тока в цепи:
I =3 A.
Ответ:12,15В
Изображение слайда
13
Слайд 13: В цепи, изображенной на схеме R 1 =2,9Ом, R 2 = 7Ом, R 3 = 3Ом, внутреннее сопротивление источника тока равно 1Ом. Амперметр показывает ток 1А. Определите ЭДС и напряжение на зажимах батареи
Изображение слайда
14
Слайд 14: При разомкнутом ключе амперметр показывает ток 1А. Какой ток покажет амперметр при замкнутом ключе? ЭДС источника 10В, внутреннее сопротивление источника 1Ом, R1= 5Ом, R 2 = 4Ом, R 3 неизвестно
Изображение слайда
15
Слайд 15
ЭДС источника тока 3В, его внутреннее сопротивление 1Ом, сопротивление резисторов R1=R2= 1,75Ом, R 3 = 2Ом, R 4 = 6Ом. Какова сила тока в резисторе R4 ?
Какова сила тока в резисторе R4 ?
Изображение слайда
16
Слайд 16: Короткое замыкание
Короткое замыкание – явление, когда сопротивление во внешней цепи по каким-либо причинам стремится к нулю:
Изображение слайда
17
Слайд 17
Ток короткого замыкания из-за того, что внутреннее сопротивление источников мало по сравнению с сопротивлением внешним, как правило, чрезвычайно велик. Из-за этого выделяется очень большое количество теплоты, что может стать причиной обрывов цепи, пожаров и т. д. Для предотвращения подобного используются предохранители
Изображение слайда
18
Последний слайд презентации: Электродвижущая сила.
 Закон Ома для полной цепи: Домашняя работа
Закон Ома для полной цепи: Домашняя работа
П. 122, 123. Задачи.
Изображение слайда
9B: Электрический ток, ЭДС и закон Ома
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5936
- Джеффри В. Шник
- Колледж Святого Ансельма
Теперь мы приступаем к изучению электрических цепей. Цепь представляет собой замкнутый проводящий путь, по которому течет заряд. В цепях заряд движется по петлям. Скорость потока заряда называется электрическим током. Цепь состоит из элементов цепи, соединенных между собой проводами. Конденсатор — пример элемента схемы, с которым вы уже знакомы. В этой главе мы представим еще несколько элементов схемы. При анализе цепей мы рассматриваем провода как идеальные проводники, а элементы цепи — как идеальные элементы цепи. Существует большое разнообразие цепей по сложности. Компьютер представляет собой сложную схему. Фонарик представляет собой простую схему.
Конденсатор — пример элемента схемы, с которым вы уже знакомы. В этой главе мы представим еще несколько элементов схемы. При анализе цепей мы рассматриваем провода как идеальные проводники, а элементы цепи — как идеальные элементы цепи. Существует большое разнообразие цепей по сложности. Компьютер представляет собой сложную схему. Фонарик представляет собой простую схему.
Элементы схемы, с которыми вы будете иметь дело в этом курсе, представляют собой элементы схемы с двумя клеммами. Существует несколько различных типов двухконтактных элементов схемы, но все они имеют некоторые общие черты. Двухвыводной элемент цепи представляет собой устройство с двумя концами, каждый из которых является проводником. Два проводника называются клеммами. Клеммы могут иметь самые разные формы. Некоторые из проводов, некоторые из металлических пластин, некоторые из металлических кнопок, а некоторые из металлических столбов. Один подключает провода к клеммам, чтобы сделать элемент цепи частью цепи.
Важным элементом двухполюсника является гнездо ЭДС. Вы можете думать о месте EMF как об идеальной батарее или как об идеальном источнике питания. Что он делает, так это поддерживает постоянную разность потенциалов (т. е. постоянное напряжение) между его клеммами. Для представления этой разности потенциалов используется либо имя константы \(\varepsilon\) (сценарий \(E\)) либо имя константы \(V\).
Чтобы достичь разности потенциалов \(E\) между его терминалами, очаг ЭДС, когда он впервые возникает, должен переместить некоторый заряд (мы рассматриваем движение заряда как движение положительного заряда) от одного терминала к другой. «Одна клемма» остается с чистым отрицательным зарядом, а «другая» приобретает чистый положительный заряд. Центр ЭДС перемещает заряд до тех пор, пока потенциал положительной клеммы \(E\) выше, чем у отрицательной клеммы. Обратите внимание, что очаг ЭДС не производит заряда; он просто толкает существующий заряд. Если вы подсоедините изолированный провод к положительной клемме, то он будет иметь тот же потенциал, что и положительная клемма, и, поскольку заряд на положительной клемме будет распространяться по проводу, очаг ЭДС будет иметь чтобы переместить еще немного заряда с клеммы с более низким потенциалом, чтобы сохранить разность потенциалов.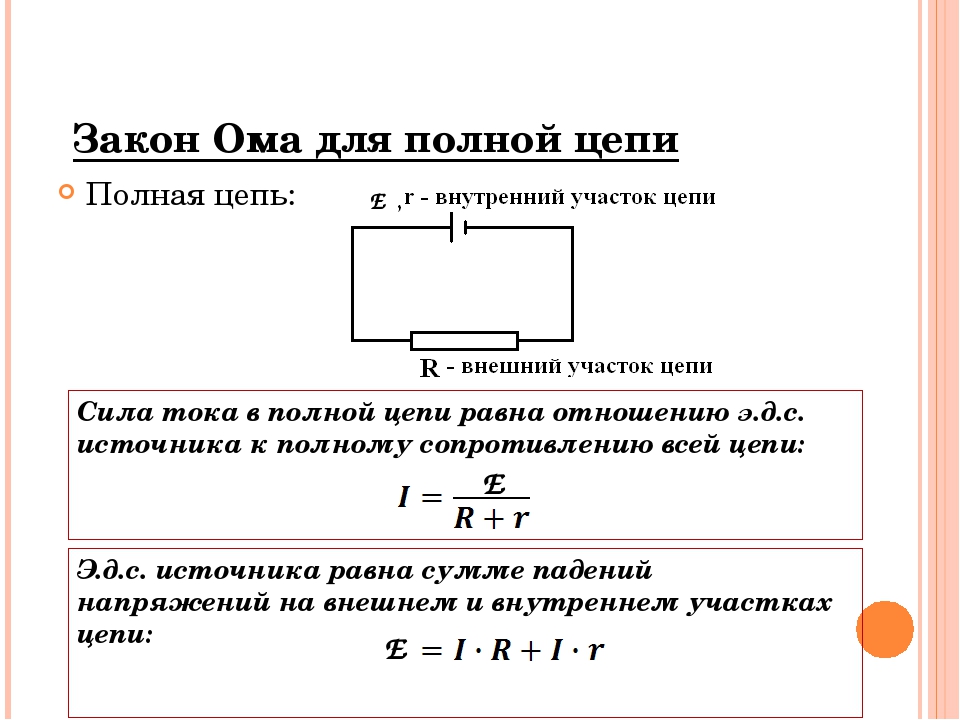 {-12}C\) ). Кроме того, накопление заряда происходит почти мгновенно, поэтому к тому времени, когда вы закончите подключать провод к клемме, этот провод уже имеет заряд, о котором мы говорим. В общем, мы не знаем, сколько заряда на плюсовой клемме и какой провод к ней может быть подключен, и нам все равно. Это мизер. Но достаточно, чтобы разность потенциалов между выводами была номинальным напряжением очага ЭДС.
{-12}C\) ). Кроме того, накопление заряда происходит почти мгновенно, поэтому к тому времени, когда вы закончите подключать провод к клемме, этот провод уже имеет заряд, о котором мы говорим. В общем, мы не знаем, сколько заряда на плюсовой клемме и какой провод к ней может быть подключен, и нам все равно. Это мизер. Но достаточно, чтобы разность потенциалов между выводами была номинальным напряжением очага ЭДС.
Вы помните, что электрический потенциал — это то, что используется для характеристики электрического поля. Вызывая разность потенциалов между его выводами и между любой парой проводов, которые могут быть подключены к его выводам, очаг ЭДС создает электрическое поле. Электрическое поле зависит от расположения проводов, которые подключены к клеммам сиденья ЭДС. Электрическое поле — еще одна величина, которую мы редко обсуждаем при анализе цепей. Обычно мы можем узнать то, что нам нужно, из значения разности потенциалов E, которую местонахождение ЭДС поддерживает между его терминалами. Но электрическое поле действительно существует, и в цепях электрическое поле заряда на проводах, соединенных с очагом ЭДС, вызывает протекание заряда в цепи, а поток заряда в цепи является огромной частью того, что цепь все о.
Но электрическое поле действительно существует, и в цепях электрическое поле заряда на проводах, соединенных с очагом ЭДС, вызывает протекание заряда в цепи, а поток заряда в цепи является огромной частью того, что цепь все о.
Мы используем символ
для представления места ЭДС на принципиальной схеме (также известной как принципиальная схема цепи), где два коллинеарных сегмента линии представляют клеммы места ЭДС, причем тот, который подключен к более короткому из параллельных сегментов линии, является отрицательным, низкопотенциальный, терминальный; а также; тот, который соединен с более длинным из параллельных сегментов линии, является положительным терминалом с более высоким потенциалом.
Другим элементом схемы, который я хочу представить в этой главе, является резистор. Резистор – плохой проводник. Сопротивление резистора является мерой того, насколько плохим проводником является резистор. Чем больше значение сопротивления, тем хуже элемент цепи пропускает через себя заряд. Резисторы бывают разных форм. Нить накала лампочки представляет собой резистор. Элемент тостера (часть, которая светится красным, когда тостер включен) представляет собой резистор. Люди производят небольшие керамические цилиндры (с углеродным покрытием и проволокой, торчащей с каждого конца), чтобы иметь определенные значения сопротивления. Каждый из них имеет свое значение сопротивления, указанное на самом резисторе. Символ
Резисторы бывают разных форм. Нить накала лампочки представляет собой резистор. Элемент тостера (часть, которая светится красным, когда тостер включен) представляет собой резистор. Люди производят небольшие керамические цилиндры (с углеродным покрытием и проволокой, торчащей с каждого конца), чтобы иметь определенные значения сопротивления. Каждый из них имеет свое значение сопротивления, указанное на самом резисторе. Символ
используется для обозначения резистора на принципиальной схеме. Символ R обычно используется для обозначения значения сопротивления резистора.
Теперь мы готовы рассмотреть следующую простую схему:
Вот опять без столько ярлыков:
Верхний провод (проводник) имеет одно значение электрического потенциала (назовем его \(\varphi_{HI}\)) и нижний провод имеет другое значение электрического потенциала (назовем его \(\varphi_{LOW}\)) такой что разница \(\space \varphi_{HI}-\varphi_{LOW}\space\) равна \(\space\varepsilon\).
\[\varphi_{HI}-\varphi_{LOW}=\varepsilon\]
Чтобы поддерживать разность потенциалов \(\varepsilon\) между двумя проводниками, местонахождение ЭДС приводит к тому, что на верхнем проводе появляется незначительное количество положительного заряда, а на нижнем проводе такое же количество отрицательного заряда. Это разделение зарядов вызывает электрическое поле в резисторе.
(Мы проводим это рассуждение в модели положительных носителей заряда. Хотя это не имеет значения для контура, на самом деле это отрицательно заряженные частицы, движущиеся в противоположном направлении. Эффект тот же.)
Важно понимать, что каждая часть цепи заряжена обоими видами заряда. Провод, резистор, все невероятно переполнено как положительным, так и отрицательным зарядом. Один вид заряда может двигаться на фоне другого. Теперь электрическое поле в резисторе толкает положительный заряд в резисторе в направлении от клеммы с более высоким потенциалом к клемме с более низким потенциалом.
Подача положительного заряда на провод с более низким потенциалом приведет к повышению потенциала провода с более низким потенциалом и оставит верхний конец резистора с отрицательным зарядом. Я говорю «будет», потому что любая тенденция к изменению относительного потенциала двух проводов немедленно компенсируется наличием ЭДС. Помните, что это то, что делает место ЭДС, оно поддерживает постоянную разность потенциалов между проводами. Чтобы сделать это в данном случае, очаг ЭДС должен оттянуть некоторые положительные заряды от провода с более низким потенциалом и вытолкнуть их на провод с более высоким потенциалом. Кроме того, любое стремление верхнего конца резистора стать отрицательным немедленно приводит к притяжению положительного заряда в проводе с более высоким потенциалом. Это приводит к тому, что положительный заряд перемещается вниз в резистор вместо заряда, который только что двигался вдоль резистора к проводу с более низким потенциалом. Чистый эффект представляет собой постоянное движение заряда по часовой стрелке вокруг контура, как мы видим на диаграмме, при этом чистое количество заряда на любом коротком участке цепи никогда не меняется. Выберите место в любом месте цепи. Так же быстро, как положительный заряд выходит из этого пятна, в него входит больше положительного заряда из соседнего пятна. У нас есть вся эта скученная масса положительных носителей заряда, движущихся по часовой стрелке вокруг петли, и все из-за электрического поля в резисторе. и «настойчивость» ЭДС в поддержании постоянной разности потенциалов между проводами.
Выберите место в любом месте цепи. Так же быстро, как положительный заряд выходит из этого пятна, в него входит больше положительного заряда из соседнего пятна. У нас есть вся эта скученная масса положительных носителей заряда, движущихся по часовой стрелке вокруг петли, и все из-за электрического поля в резисторе. и «настойчивость» ЭДС в поддержании постоянной разности потенциалов между проводами.
Теперь проведите пунктирную линию поперек цепи в любой точке цепи, как показано ниже.
Скорость, с которой заряд пересекает эту линию, является скоростью потока заряда в этой точке (точке, в которой вы нарисовали пунктирную линию) в цепи. Скорость потока заряда, то есть сколько кулонов заряда в секунду пересекает эту линию, называется электрическим током в этой точке. В данном случае, поскольку вся цепь состоит из одного контура, ток одинаков во всех точках цепи — неважно, где вы «проводите линию». Символ, который обычно используется для обозначения значения тока, – \(I\).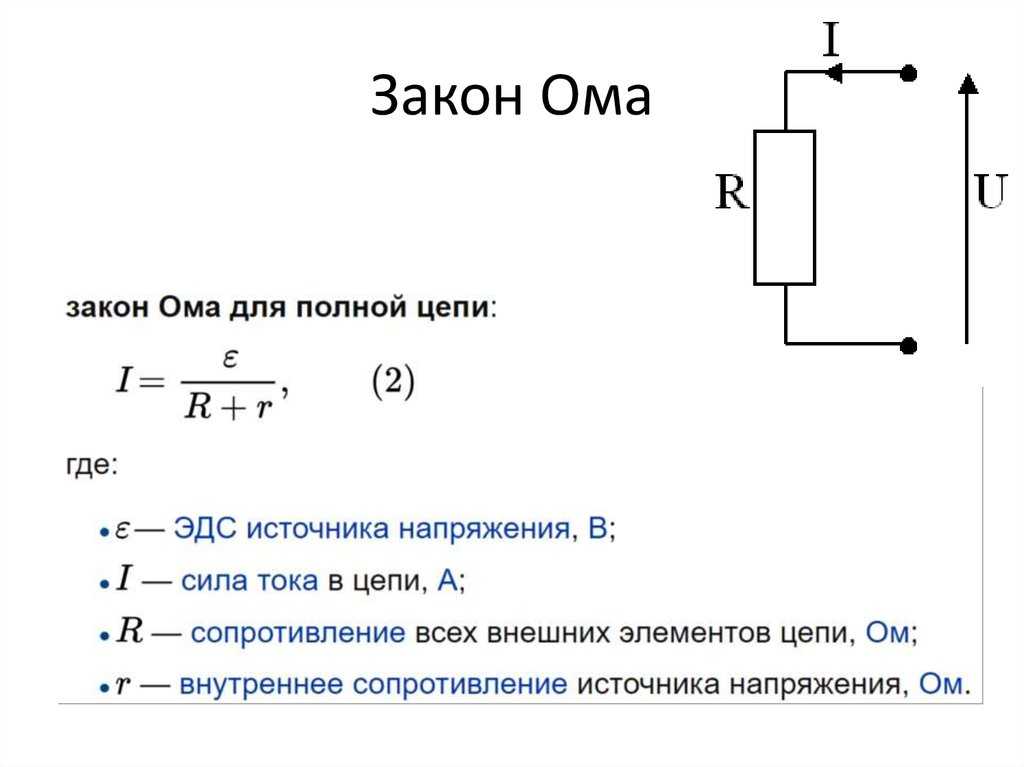
При анализе схемы, если текущая переменная еще не определена для вас, вы должны определить ее
, нарисовав стрелку на схеме и обозначив ее \(I\) или \(I\) нижним индексом.
Единицами тока являются кулоны в секунду (\(Кл/с\)). Этой комбинации единиц дается имя: ампер, сокращенно \(А\).
\[1A=1\frac{C}{s}\]
Теперь об этом резисторе: в нашей модели носителей положительного заряда заряженные частицы, которые могут свободно перемещаться в резисторе, испытывают силу, действующую на них со стороны электрического поля в направлении электрического поля. В результате они испытывают ускорение. Но фоновый материал, составляющий вещество, частью которого являются носители заряда, оказывает на носители заряда тормозящую силу, зависящую от скорости. Чем быстрее они движутся, тем больше тормозящая сила. По завершении цепи (создание этого последнего соединения провода с клеммой) носители заряда в резисторе почти мгновенно достигают предельной скорости, при которой тормозящая сила на данном носителе заряда так же велика, как сила, действующая на него. электрическое поле на этом носителе заряда. Значение конечной скорости, наряду с числом носителей заряда на объем в резисторе и площадью поперечного сечения плохо проводящего материала, из которого состоит резистор, определяют скорость потока заряда, ток , в резисторе. В рассматриваемой простой схеме скорость протекания заряда в резисторе равна скорости протекания заряда по всей цепи.
электрическое поле на этом носителе заряда. Значение конечной скорости, наряду с числом носителей заряда на объем в резисторе и площадью поперечного сечения плохо проводящего материала, из которого состоит резистор, определяют скорость потока заряда, ток , в резисторе. В рассматриваемой простой схеме скорость протекания заряда в резисторе равна скорости протекания заряда по всей цепи.
Само значение конечной скорости зависит от силы электрического поля и от характера тормозящей силы. Характер тормозящей силы зависит от того, из какого материала изготовлен резистор. Один вид материала приведет к большей конечной скорости для того же электрического поля, что и другой вид материала. Даже с одним видом материала возникает вопрос, как тормозящая сила зависит от скорости. Пропорционально ли оно квадрату скорости, логарифму скорости или как? Эксперимент показывает, что в важном подмножестве материалов в определенных диапазонах конечной скорости тормозящая сила пропорциональна самой скорости. Говорят, что такие материалы подчиняются закону Ома и называются омическими материалами.
Говорят, что такие материалы подчиняются закону Ома и называются омическими материалами.
Рассмотрим резистор в простой схеме, с которой мы имели дело.
Если вы удвоите напряжение на резисторе (используя источник ЭДС, который поддерживает двойную разность потенциалов между его клеммами по сравнению с исходным источником ЭДС), вы удвоите электрическое поле в резисторе. Это удваивает силу, действующую на каждый носитель заряда. Это означает, что при предельной скорости любого носителя заряда тормозящая сила должна быть вдвое больше. (Поскольку при выполнении этого последнего соединения цепи скорость носителей заряда увеличивается до тех пор, пока тормозящая сила на каждом из носителей заряда не станет равной по величине приложенной силе.) В омическом материале, если тормозящая сила в два раза больше, то скорость в два раза выше. Если скорость в два раза больше, то и расход заряда, электрический ток, в два раза больше. Таким образом, удвоение напряжения на резисторе удваивает ток. Действительно, для резистора, который подчиняется закону Ома, ток в резисторе прямо пропорционален напряжению на резисторе.
Действительно, для резистора, который подчиняется закону Ома, ток в резисторе прямо пропорционален напряжению на резисторе.
Резюмируя: когда вы подаете напряжение на резистор, в этом резисторе возникает ток. Отношение напряжения к току называется сопротивлением резистора.
\[R=\frac{V}{I}\]
Это определение сопротивления согласуется с нашим пониманием того, что сопротивление резистора является мерой того, насколько паршивым он является проводником. Проверьте это. Если при заданном напряжении на резисторе вы получаете крошечный ток (это означает, что резистор является очень плохим проводником), значение сопротивления \(R=\frac{V}{I}\) при этом небольшом значении ток в знаменателе, очень большой. Если, с другой стороны, при том же напряжении вы получите большой ток (имеется в виду, что резистор является хорошим проводником), то значение сопротивления \(R=\frac{V}{I}\) будет небольшим.
Если материал, из которого изготовлен резистор, подчиняется закону Ома, то сопротивление \(R\) является константой, а это означает, что его значение одинаково для различных напряжений. Отношение \(R=\frac{V}{I}\) обычно записывается в виде \(V=IR\).
Отношение \(R=\frac{V}{I}\) обычно записывается в виде \(V=IR\).
Закон Ома:
Сопротивление \(R\) в выражении \(V = IR\) является константой.
Закон Ома подходит для резисторов, изготовленных из определенных материалов (называемых омическими материалами) в ограниченном диапазоне напряжений.
Учитывая, что сопротивление резистора определяется как отношение напряжения на этом резисторе к результирующему току в этом резисторе,
\[R=\frac{V}{I}\]
Очевидно, что единицей измерения сопротивления является вольт на ампер, \(\frac{V}{A}\). Этому комбинированному устройству дается имя. Мы называем это омом, сокращенно \(\Омега\), заглавной греческой буквой омега.
\[1\Omega=1 \frac{\mbox{вольт}}{\mbox{ампер}}\]
Эта страница под названием 9B: Электрический ток, ЭДС и закон Ома распространяется под лицензией CC BY-SA 2.5 и была создана, изменена и/или курирована Джеффри В. Шником посредством исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джеффри В. Шник
- Лицензия
- CC BY-SA
- Версия лицензии
- 2,5
- Показать оглавление
- нет
- Теги
- цепь
- Текущий
- Закон Ома
- источник@http://www.
 cbphysics.org
cbphysics.org
Куллабс
регистр Логин
Найдите свой запрос
Обзор
ЭДС электрического источника – это скорость, с которой энергия в неэлектрической форме преобразуется в электрическую форму при прохождении через него единичного положительного заряда. Эта заметка содержит информацию о разности потенциалов, электродвижущей силе и законе Ома.- Примечание
- То, что нужно запомнить
- Видео
- Упражнение
- Контрольный опрос
Разность потенциалов, электродвижущая сила и закон Ома
Разность потенциалов и электродвижущая сила
Говорят, что положительно заряженное тело имеет положительный или более высокий потенциал. Говорят, что отрицательно заряженное тело имеет отрицательный или более низкий потенциал.
Говорят, что отрицательно заряженное тело имеет отрицательный или более низкий потенциал.
Разность потенциалов определяется как количество работы, выполненной при перемещении единичного положительного заряда из одной точки в другую в электрической цепи. Единицей p.d (В) является JC-1, который называется вольт.
Разность потенциалов (В) = IR
Электродвижущая сила (Э.Д.С.)
Э.Д.С. электрического источника – это скорость, с которой энергия в неэлектрической форме преобразуется в электрическую форму при прохождении через него единичного положительного заряда.
ВольтметрВольтметр — электрический прибор, измеряющий разность потенциалов между любыми двумя точками электрической цепи.
Разница между ЭДС и фотодиодом
| э.м.ф. | п.д . |
Это мера энергии, подаваемой источником для переноса единичного заряда по цепи. | Это мера работы, выполненной при перемещении единицы заряда из одной точки в другую по цепи. |
| Является причиной p.d. | Это эффект э.д.с. |
| Измеряется в разомкнутой цепи. | Измеряется в замкнутом контуре. |
| Больше p.d. | Меньше э.д.с. |
Электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на двух его концах при постоянном физическом состоянии. (Температура, площадь поперечного сечения, длина, форма, природа материала и т. д.)
Если «I» — это электрический ток в проводе, а «V» — это p.d. через его концы.
I α В
В α I
В= IR………… (i) где R= электрическое сопротивление проводника, используемое как константа.
Из уравнения (i) имеем
R = \(\frac{V}{R}\)
R – электрическое сопротивление проводника, которое считается постоянным.
Здесь I = электрический ток
V = разность потенциалов
R = сопротивление
Согласно приведенному выше соотношению, сопротивление представляет собой отношение разности потенциалов на двух его концах к протекающему через них электрическому току.
Экспериментальная проверка закона Ома
Экспериментальная установка для проверки закона Ома показана на рисунке. Данная фигура состоит из вольтметра (V), который подключен через нихромовый провод ВС. Провод ВС соединен с амперметром (А), ключом К и ячейками. Амперметр измеряет ток (I) в цепи, тогда как вольтметр измеряет p.d. (V) по проводу PQ.
Сначала используйте одну ячейку. Когда ключ К замкнут, в цепи протекает электрический ток. Запишите показания амперметра и вольтметра. Повторите эксперимент, используя две ячейки и соединив M и O. Теперь соедините M и R и запишите показания амперметра и вольтметра. Когда мы строим график между p.d (V) и током (I) и проводим прямую линию через начало координат, как показано на рисунке, это показывает, что ток косвенно пропорционален p. d. что подтверждает закон Ома.
d. что подтверждает закон Ома.
Что следует помнить
- Э.д.с. электрического источника – это скорость, с которой энергия в неэлектрической форме преобразуется в электрическую форму при прохождении через него единичного положительного заряда.
- Вольтметр — электрический прибор, измеряющий разность потенциалов между любыми двумя точками электрической цепи.
- Согласно закону Ома, «электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на двух его концах при постоянном физическом состоянии».
- Сопротивление — это отношение разности потенциалов на двух его концах к электрическому току, протекающему через него.
- Включает в себя все отношения, установившиеся между людьми.
- В обществе может быть более одного сообщества. Сообщество меньше, чем общество.
- Это сеть социальных отношений, которую нельзя увидеть или потрогать.

- общие интересы и общие цели обществу не нужны.
Видеоматериалы о разнице потенциалов, электродвижущей силе и законе Ома
Вопросы и ответы
«60 Вт», написанное на электрической лампочке, 60 Дж электрической энергии преобразуется в тепловую и световую энергию за одну секунду.
До открытия электрона считалось, что существует поток положительного заряда от положительно заряженного тела к отрицательно заряженному телу. Эта концепция все еще используется, которая называется обычным током.
Но на практике направлением потока электронов является фактический поток электрического тока, который противоположен обычному току.
Амперметр — это электронное устройство, измеряющее силу тока, протекающего по цепи.
Вольтметр — это электронное устройство, измеряющее разность потенциалов между любыми двумя точками цепи.
Гальванометр — это электронное устройство, определяющее наличие тока в цепи.
Электрическая цепь, по которой течет электричество, называется замкнутой цепью. Электрическая цепь, по которой не протекает электричество, называется замкнутой цепью.
- Электрическая лампочка
- Сотовый
- Источник переменного тока
- Переключатель
- Вольтметр
- Амперметр
Когда плюсовая клемма одной точки соединена с минусовой клеммой другой точки, это называется последовательной комбинацией. Точно так же, когда положительные клеммы соединены в одной точке, а отрицательные клеммы подключены к другой точке, это называется параллельной комбинацией.
Точно так же, когда положительные клеммы соединены в одной точке, а отрицательные клеммы подключены к другой точке, это называется параллельной комбинацией.
Амперметр включен последовательно, потому что он имеет низкое сопротивление и, следовательно, измеряет ток в цепи без заметного падения потенциала на ней.
Но вольтметр подключается последовательно, потому что он имеет высокое сопротивление и, следовательно, измеряет разность потенциалов на устройстве, не вызывая заметного снижения тока через устройство.
Вольтметр подключен параллельно.
Разность потенциалов определяется как количество работы, совершаемой при перемещении единичного положительного заряда из одной точки в другую в электрической цепи. Его единицей измерения является Вольт (В).
Его единицей измерения является Вольт (В).
Говорят, что разность потенциалов (pd) между любыми двумя точками электрической цепи равна 1 В, если 1 Дж работы совершается при перемещении заряда в 1 Кл между этими двумя точками.
Электродвижущая сила (ЭДС) — это энергия, выделяемая клеткой на единицу заряда, проходящего через цепь. Единицей ЭДС является вольт, но она также описывается как энергия в джоулях, доступная из ячейки на кулон заряда.
| ЭДС | ПД |
| Энергия, выделяемая клеткой на единицу заряда, проходящего через цепь. | Это работа, совершаемая при перемещении единичного положительного заряда из одной точки в другую. |
Больше p. d. d. | Меньше э.д.с. |
Свойство любого материала сопротивляться потоку зарядов через него называется сопротивлением. Его единицей СИ является ом (Ом).
- Длина проводника
- Площадь поперечного сечения проводника
- Материал, из которого изготовлен проводник
- Температура проводника
- Форма проводника
Мы знаем, что сопротивление проводника равно
- прямо пропорционально длине, т.е. R ∝ ρ
- обратно пропорциональна площади его поперечного сечения
R ∝
Комбинируя эти два соотношения,
R ∝
или R = ρ
∴ ρ = .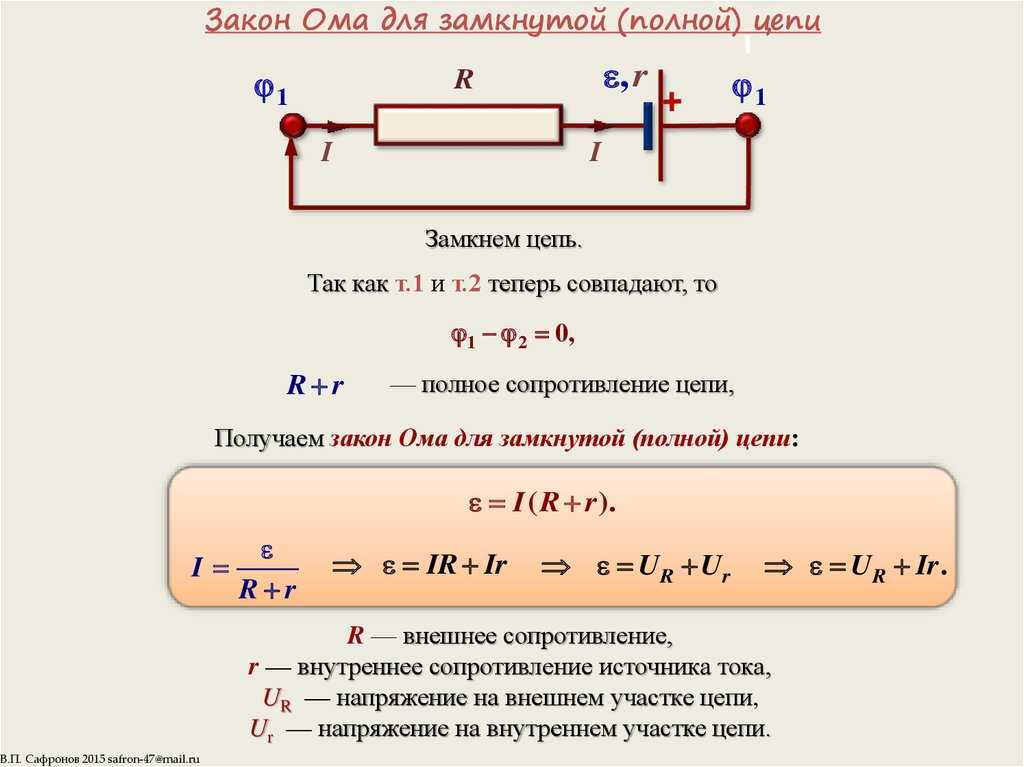
Закон Ома утверждает, что ток, протекающий через резистор, прямо пропорционален приложенной к нему разности потенциалов при условии, что температура и другие физические условия постоянны.
т. е. I ∝ V
или V ∝ I
или V = IR, где «R» — константа пропорциональности, называемая сопротивлением.
Если ток силой 1 А через проводник поддерживает p.d. 1 В на его концах, то его сопротивление называется 1 Ом.
Удельное сопротивление – это характеристика материала провода. Таким образом, он не изменится, даже если его длина увеличится втрое.
Проводники, которые подчиняются закону Ома, известны как омические проводники, тогда как те проводники, которые не подчиняются закону Ома, известны как неомические проводники. Примером омического проводника является медь, а неомического – полупроводник (кремний, германий).
Примером омического проводника является медь, а неомического – полупроводник (кремний, германий).
Несколько резисторов называются последовательно соединенными, если они соединены встык таким образом, что через каждый из них проходит один и тот же ток.
Давайте рассмотрим четыре резистора R1, R2, R3 и R4, соединенные последовательно, так что V1, V2, V3 и V4 представляют собой pds на резисторах R1, R2, R3 и R4 соответственно. Суммарная разность потенциалов равна
В = V1 + V2 + V3 + V4
Предположим, что I — ток в цепи, тогда pd на каждом резисторе равно
V1= IR1
V2= IR2
V3= IR3
V4= IR4
Таким образом, V = IR1 + IR2 + IR3 + IR4
или, = R1 + R2 + R3 + R4
∴ R = R1 + R2 + R3 + R4
Следовательно, эквивалентный резистор в ряду равен сумме всех отдельных резисторов в цепи.
Р = Р1 + Р2 + Р3
Если несколько резисторов соединены с одинаковым потенциалом, говорят, что это параллельная комбинация.
Рассмотрим четыре сопротивления, R1, R2, R3 и R4, соединенные параллельно так, что ток через каждое равен I1, I2, I3, I4
. Здесь общий ток будет равен I = I1 + I2 + I3+ I4. каждый резистор I1 = , I2 = , I3 = , I4 = и
Теперь
I = V (+ + +)
или, = V (+ + +)
или, = + + +
Следовательно, эквивалентное сопротивление в параллельная комбинация
= + + + ………………….+
Название приборов X и Y — амперметр и вольтметр соответственно. Здесь, на рисунке, R — сопротивление, а K — ключ. Направление тока:
Здесь, на рисунке, R — сопротивление, а K — ключ. Направление тока:
Ток (I) = 1 А
Время (t) = 30 мин = 30 x 60 с = 1800 с
Заряд (Q) = ?
Теперь,
Используя формулу,
I =
или, Q = I x t
= 1800 x 1
= 1800 Кл
Следовательно, по цепи протекает заряд 1800 Кл.
Здесь,
Длина (= 5 м
Сопротивление (R) = 2 Ом
Площадь (A) = 0,1 м 2
Удельное сопротивление (ρ) = ?
Проводимость (σ) = ?
А электропроводность( σ) = = 1/0,04 = 25 м/Ом
Сопротивление (R) = 20 Ом
Ток (I) = 0,25 А
Pd батареи (В) = ?
Используя закон Ома,
В = IR
или, V = 0,25 x 20
или, V = 5 В
Следовательно, pd, необходимое для батареи, составляет 5 В.
Разность потенциалов (В) = 30 В
Ток (I) = 5 А
Сопротивление (R) = ?
По закону Ома
В = IR
или, R = = = 6 Ом
Следовательно, между этими двумя точками возникает сопротивление 6 Ом.
Дано,
Первое сопротивление (R1) = 50 Ом
Другое сопротивление (R2) = 10 Ом
Эквивалентное сопротивление (R) = ?
Ток (I) = ?
Питание Pd (В) = 12 В
Как мы знаем, при последовательном соединении
R = R1 + R2
= 50 + 10
= 60 Ом
Теперь, используя закон Ома,
В = IR
или, I =
или I =
или I = 0,2 А
Следовательно, эквивалентное сопротивление равно 60 Ом, а ток равен 0,2 А.
Дано,
Мощность нагревателя (P) = 1000 Вт
Подведенный Pd (V) = 220 В
Ток (I) = ?
Используя формулу,
P = I x V
или 1000 = I x 220
или I =
= 4,54 А
Следовательно, через нагреватель протекает ток 4,54 А.
Дано,
Мощность лампы (P) = 100 Вт
Подведенное Pd (V) = 220 В
Сопротивление лампы (R) = ?
Мы знаем, что
P = I x V
или I = = 0,45 A
Аналогично, используя закон Ома,
V = IR
или 220 = 0,45 x R
или R = 220/0,45
или, R = 488,89 Ом
Следовательно, сопротивление почти 889 Ом.
Здесь
Здесь X — вольтметр, Y — амперметр.
Y подключен таким образом, потому что он имеет низкое сопротивление и не имеет соответствующих потерь по току.
Pd (В) = 20 В
Сопротивление (R) = 3 Ом
Итак, ток, измеряемый Y (I) = ?
Использование V = IR,
I = = = 6,67 А
Следовательно, прибор Y измеряет 6,67 А.
Здесь
Заряд (Q) = 200C
Время (t) = 25 с
Ток (I) = ?
Имеем,
I = \(\frac{Q}{t}\)
= \(\frac{200}{25}\)
= 8A.
Следовательно, ток через проводник равен 8А.
(и). В данном приборе Р есть вольтметр.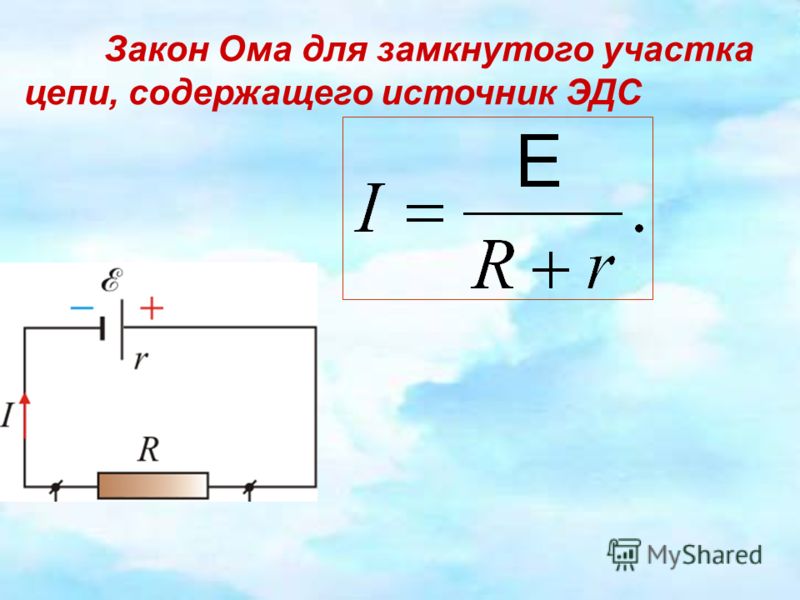 Приборы Q – амперметр.
Приборы Q – амперметр.
(ii). V = 2,4
R = 0,8 Ом
Ток (I) = ?
По закону Ома
В = IR.
\(\следовательно\) 2,4 = I (0,8)
ИЛИ,
I = \(\frac{2.4}{0.8}\)
= 3A
Следовательно, ток в цепи равен 3A.
© 2019-20 Куллабс. Все права защищены.
5.4 Закон Ома – введение в электричество, магнетизм и электрические цепи
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Описать закон Ома
- Распознавать, когда применяется закон Ома, а когда нет
До сих пор в этой главе мы обсуждали три электрических свойства: ток, напряжение и сопротивление. Оказывается, многие материалы демонстрируют простую зависимость между значениями этих свойств, известную как закон Ома. Многие другие материалы не показывают этой взаимосвязи, поэтому, несмотря на то, что он называется законом Ома, он не считается законом природы, как законы Ньютона или законы термодинамики.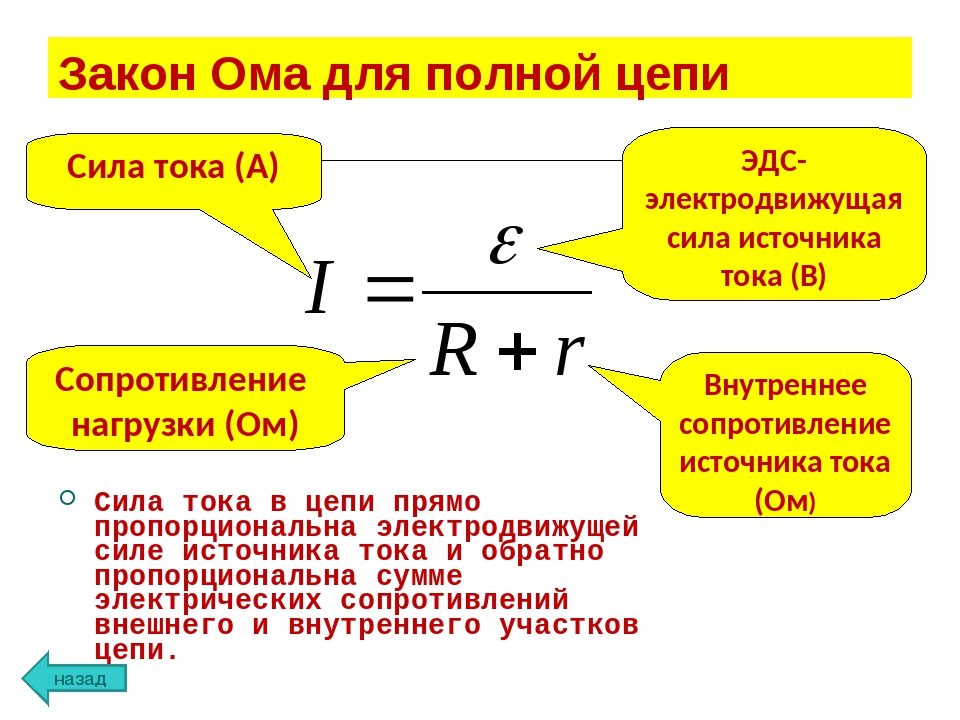 Но это очень полезно для расчетов с материалами, которые подчиняются закону Ома.
Но это очень полезно для расчетов с материалами, которые подчиняются закону Ома.
Описание закона Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению. Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению :
.
Это важное соотношение является основой закона Ома . Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток – следствием. Это эмпирический закон, то есть экспериментально наблюдаемое явление, подобное трению. Такая линейная зависимость не всегда имеет место. Любой материал, компонент или устройство, которые подчиняются закону Ома, где ток через устройство пропорционален приложенному напряжению, называется омический материал или омический компонент. Любой материал или компонент, который не подчиняется закону Ома, известен как неомный материал или неомный компонент.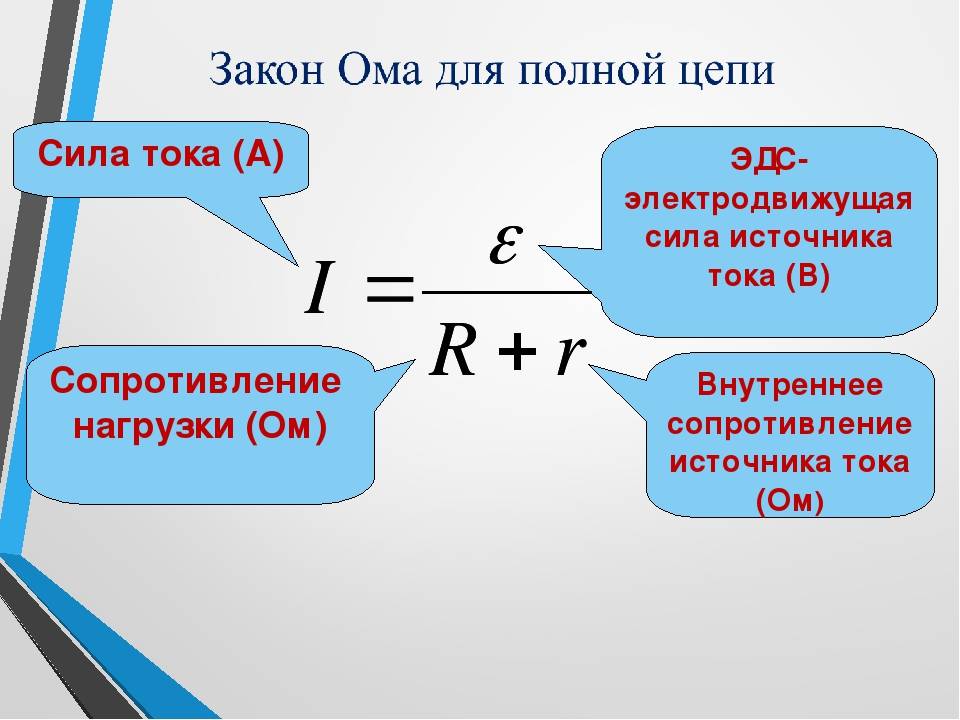
Опыт Ома
В статье, опубликованной в 1827 году, Георг Ом описал эксперимент, в котором он измерял напряжение и ток в различных простых электрических цепях, содержащих провода различной длины. Аналогичный эксперимент показан на рисунке 5.4.1. Этот эксперимент используется для наблюдения за током через резистор, возникающим в результате приложенного напряжения. В этой простой схеме резистор соединен последовательно с батареей. Напряжение измеряется вольтметром, который необходимо поставить на резистор (параллельно резистору). Ток измеряется амперметром, который должен быть подключен к резистору (последовательно с резистором).
(рис. 5.4.1)
Рисунок 5.4.1 Экспериментальная установка, используемая для определения того, является ли резистор омическим или неомическим устройством. (а) Когда батарея присоединена, ток течет по часовой стрелке, а показания вольтметра и амперметра положительны. б) при переключении выводов батареи ток течет против часовой стрелки, а показания вольтметра и амперметра отрицательные.
В этой обновленной версии оригинального эксперимента Ома было выполнено несколько измерений тока для нескольких разных напряжений. Когда батарея была подключена, как показано на рисунке 5.4.1 (а), ток протекал по часовой стрелке, а показания вольтметра и амперметра были положительными. Изменится ли поведение тока, если ток течет в противоположном направлении? Чтобы заставить ток течь в противоположном направлении, выводы батареи можно поменять местами. При переключении выводов батареи показания вольтметра и амперметра были отрицательными, поскольку ток протекал в противоположном направлении, в данном случае против часовой стрелки. Результаты аналогичного эксперимента показаны на рисунке 5.4.2.
(рис. 5.4.2)
Рисунок 5.4.2 Резистор включен в цепь с батареей. Прикладываемое напряжение изменяется от до , увеличиваясь с шагом. На графике показаны значения напряжения в зависимости от тока, типичные для случайного экспериментатора. В этом эксперименте напряжение, прикладываемое к резистору, изменяется от до с шагом . Измеряют ток через резистор и напряжение на резисторе. Строится график зависимости напряжения от тока, и результат приблизительно линейный. Наклон линии – это сопротивление или напряжение, деленное на ток. Этот результат известен как Закон Ома :
Измеряют ток через резистор и напряжение на резисторе. Строится график зависимости напряжения от тока, и результат приблизительно линейный. Наклон линии – это сопротивление или напряжение, деленное на ток. Этот результат известен как Закон Ома :
(5.4.1)
, где это напряжение, измеренное в вольтах на рассматриваемом объекте, это ток, измеренный через объект в амперах, и это сопротивление в единицах Ом. Как указывалось ранее, любое устройство, демонстрирующее линейную зависимость между напряжением и током, известно как омическое устройство. Таким образом, резистор является омическим устройством.
ПРИМЕР 5.4.1
Измерение сопротивления
Угольный резистор при комнатной температуре () подключен к батарее, и ток, измеренный через резистор, равен . а) Чему равно сопротивление резистора в омах? (b) Если температура резистора повышается до за счет нагревания резистора, какова сила тока через резистор?
Стратегия
(а) Сопротивление можно найти по закону Ома.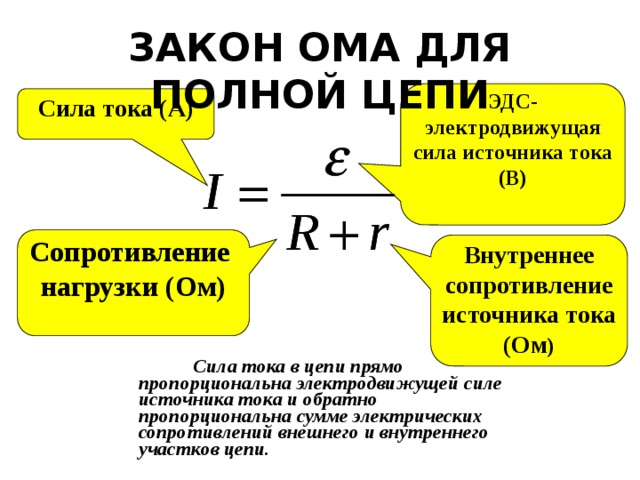 Закон Ома гласит, что сопротивление можно найти, используя .
Закон Ома гласит, что сопротивление можно найти, используя .
(b) Во-первых, сопротивление зависит от температуры, поэтому новое сопротивление после нагревания резистора можно найти с помощью . Силу тока можно найти по закону Ома в виде .
Решение
а. Используя закон Ома и вычислив сопротивление, получаем сопротивление при комнатной температуре:
б. Сопротивление при можно найти, используя где температурный коэффициент для углерода равен .
Ток через нагретый резистор
Значение
Изменение температуры привело к изменению тока. Это может показаться не очень большим изменением, но изменение электрических характеристик может оказать сильное влияние на схемы. По этой причине многие электронные устройства, такие как компьютеры, содержат вентиляторы для отвода тепла, рассеиваемого компонентами электрических цепей.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 5.8
Напряжение, подаваемое в ваш дом, изменяется как . Если к этому напряжению подключить резистор, будет ли действовать закон Ома?
Если к этому напряжению подключить резистор, будет ли действовать закон Ома?
ИНТЕРАКТИВНЫЙ
Посмотрите, как формула закона Ома относится к простой цепи. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Неомические устройства не демонстрируют линейной зависимости между напряжением и током. Одним из таких устройств является полупроводниковый элемент схемы, известный как диод. А диод это схемное устройство, которое позволяет току течь только в одном направлении. Схема простой цепи, состоящей из батареи, диода и резистора, показана на Рисунке 5.4.3. Хотя мы не рассматриваем теорию диода в этом разделе, диод можно проверить, чтобы увидеть, является ли он омическим или неомическим устройством.
(рис. 5.4.3)
Рисунок 5.4.3 Диод — это полупроводниковое устройство, пропускающее ток только в том случае, если диод смещен в прямом направлении, что означает, что анод положительный, а катод отрицательный.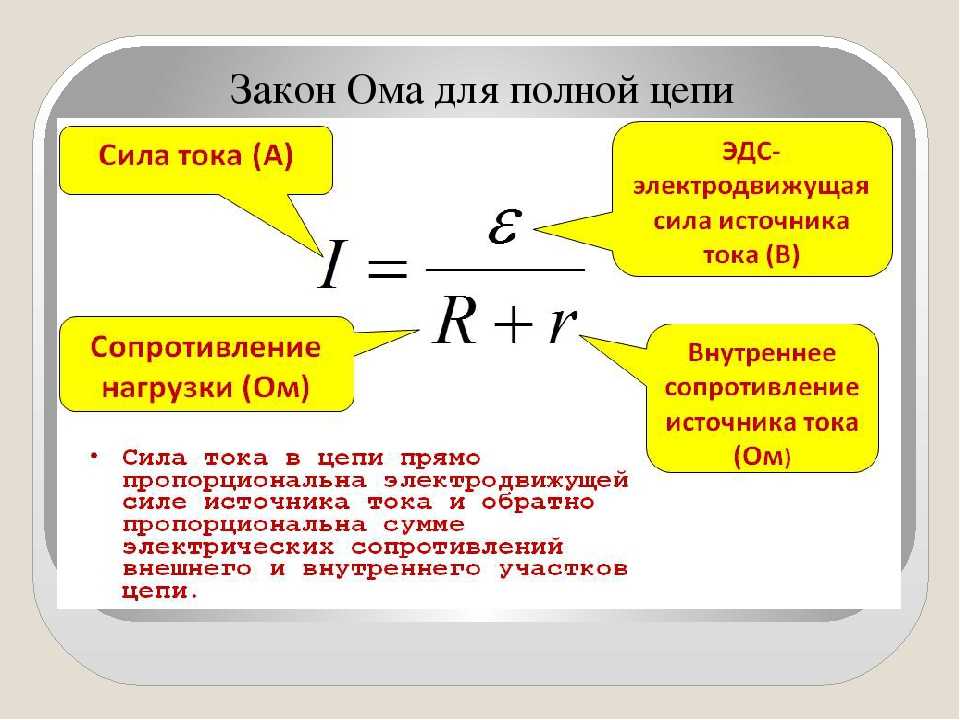
График зависимости тока от напряжения показан на Рисунке 5.4.4. Обратите внимание, что поведение диода показано как зависимость тока от напряжения, тогда как работа резистора показана как зависимость напряжения от тока. Диод состоит из анода и катода. Когда анод имеет отрицательный потенциал, а катод — положительный, как показано в части (а), говорят, что диод имеет обратное смещение. При обратном смещении диод имеет чрезвычайно большое сопротивление, и через диод и резистор протекает очень небольшой ток — практически нулевой ток. По мере увеличения напряжения, приложенного к цепи, ток остается практически нулевым, пока напряжение не достигнет напряжения пробоя и диод не начнет проводить ток, как показано на рисунке 5.4.4. Когда батарея и потенциал на диоде меняются местами, что делает анод положительным, а катод отрицательным, диод проводит ток, и ток течет через диод, если напряжение больше чем . Сопротивление диода близко к нулю. (Это причина резистора в цепи; если бы его не было, ток стал бы очень большим. ) Из графика на рис. 5.4.4 видно, что напряжение и ток не имеют линейной зависимости. Таким образом, диод является примером неомического устройства.
) Из графика на рис. 5.4.4 видно, что напряжение и ток не имеют линейной зависимости. Таким образом, диод является примером неомического устройства.
(рис. 5.4.4)
Рисунок 5.4.4 Когда напряжение на диоде отрицательное и малое, через диод протекает очень небольшой ток. Когда напряжение достигает напряжения пробоя, диод открывается. Когда напряжение на диоде положительное и больше (фактическое значение напряжения зависит от диода), диод проводит. По мере увеличения приложенного напряжения ток через диод увеличивается, но напряжение на диоде остается примерно равным . Закон Ома обычно обозначается как , но первоначально он формулировался как микроскопическое представление с точки зрения плотности тока, проводимости и электрического поля. Этот микроскопический взгляд предполагает, что пропорциональность исходит из скорости дрейфа свободных электронов в металле, возникающей в результате приложенного электрического поля. Как указывалось ранее, плотность тока пропорциональна приложенному электрическому полю.


 Внутренним сопротивлением
гальванического элемента, например, является сопротивление электродов и
электролита, находящегося между ними. Внешним участком замкнутой цепи называют
её участок, подсоединённый снаружи к источнику тока (см. рис. а).
Внутренним сопротивлением
гальванического элемента, например, является сопротивление электродов и
электролита, находящегося между ними. Внешним участком замкнутой цепи называют
её участок, подсоединённый снаружи к источнику тока (см. рис. а).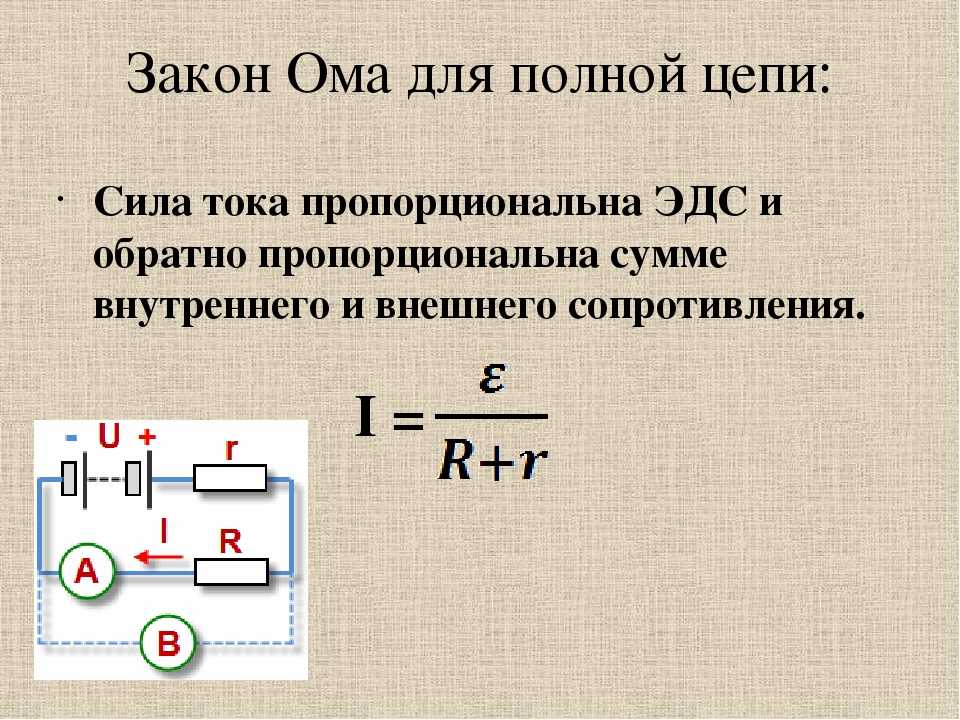 cbphysics.org
cbphysics.org