Эдс и напряжение связь: Формула связи между ЭДС (электродвижущей силой) и напряжением.

5.3. Электродвижущая сила (эдс), напряжение и разность потенциалов. Их физический смысл. Связь между эдс, напряжением и разностью потенциалов

Физическая величина, равная работе сторонних сил по перемещению положительного единичного заряда вдоль всей цепи, включая источник тока, называется электродвижущей силой источника тока (ЭДС) :

. (5.15)

Работа сторонних сил вдоль замкнутой цепи

, (5.16)

где E^* – напряженность поля сторонних сил.

Тогда

. (5.17)

При движении зарядов в проводнике кроме сторонних сил на них действуют силы электростатического поля (). Следовательно, в любой точке цепи на заряд q действует результирующая сила:

. (5.18)

Работа, совершаемая этой силой на участке 1 – 2,

(5. 19)

Физическая величина, численно равная работе сторонних и электрических сил по перемещению положительного единичного заряда на данном участке цепи, называется падением напряжения или напряжением на данном участке цепи:

. (5.20)

Если на участке цепи отсутствует ЭДС (), то

. (5.21)

При ₁ – ₂ = 0,

. (5.22)

Измеряются , U, (₁ – ₂) в системе СИ в вольтах (1 В).

Лекция 6. Классическая электронная теория проводимости металлов. Законы постоянного тока

Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах. Электрическое сопротивление проводников. Изменение сопротивления проводников от температуры и давления. Сверхпроводимость.

Соединения сопротивлений: последовательное, параллельное, смешанное. Шунтирование электроизмерительных приборов. Добавочные сопротивления к электроизмерительным приборам. Правила (законы) Кирхгофа и их применение к расчету простейших электрических цепей. Закон Джоуля-Ленца в дифференциальной и интегральной формах. Энергия, выделяющаяся в цепи постоянного тока. Коэффициент полезного действия (КПД) источника постоянного тока.

6.1. Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах

Классическая электронная теория проводимости металлов объясняет различные электрические свойства веществ существованием и движением в них так называемых квазисвободных электронов проводимости. Электроны проводимости при этом рассматриваются как электронный газ, подобный идеальному газу молекулярной физики.

До открытия электронов было экспериментально показано, что прохождение тока в металлах не связано, в отличие от тока в жидких электролитах, с переносом вещества металла. Опыт состоял в том, что через контакт двух различных металлов, например золота и серебра, в течение времени, исчисляемого многими месяцами, пропускали электрический ток. После чего исследовался материал вблизи контактов. Было показано, что никакого переноса вещества через границу различных металлов не наблюдается и вещество по различные стороны границы раздела имеет тот же состав, что и до пропускания тока. Опыты доказали, что атомы и молекулы металлов не принимают участия в переносе электрического тока, но они не ответили на вопрос о природе носителей заряда в металлах.

Прямым доказательством, что электрический ток в металлах обусловливается движением электронов, были опыты Толмена и Стюарда, проведенные в 1916 г. Идея этих опытов была высказана Мандельштамом и Папалекси в 1913 г.

Представим себе проводящую катушку, которая может вращаться вокруг своей оси. Концы катушки с помощью скользящих контактов замкнуты на гальванометр. Если находящуюся в быстром вращении катушку резко затормозить, то свободные электроны в проволоке продолжают движение по инерции, в результате чего гальванометр должен зарегистрировать импульс тока.

Обозначим линейное ускорение катушки при торможении – a. Оно направлено по касательной к поверхности катушки. При достаточно плотной намотке и тонких проводах можно считать, что ускорение направлено вдоль проводов. При торможении катушки к каждому свободному электрону приложена сила инерции

F_ин = m_ea, направленная противоположно ускорению. Под ее действием электрон ведет себя в металле так, как если бы на него действовало эффективное электрическое поле с напряженностью

. 6.1)

Поэтому эффективная электродвижущая сила в катушке, обусловленная инерцией свободных электронов,

, (6.2)

где L – длина провода на катушке.

Все точки провода тормозятся с одинаковым ускорением, и поэтому ускорение вынесено за знак интеграла.

С учетом формулы (6.2) запишем закон Ома для замкнутой цепи в виде

, (6.3)

где I – сила тока в замкнутой цепи;

R – сопротивление всей цепи, включая сопротивление проводов катушки, проводов внешней цепи и гальванометра.

Количество электричества, протекшее через поперечное сечение проводника в течение времени dt при силе тока I,

. (6.4)

Поэтому в течение времени торможения катушки от начальной линейной скорости v_o

до полной остановки через гальванометр пройдет количество электричества

. (6.5)

Значение q определяется по гальванометру, а значения L, R, v_o известны. Поэтому можно найти как знак, так и абсолютное значение e/m_e.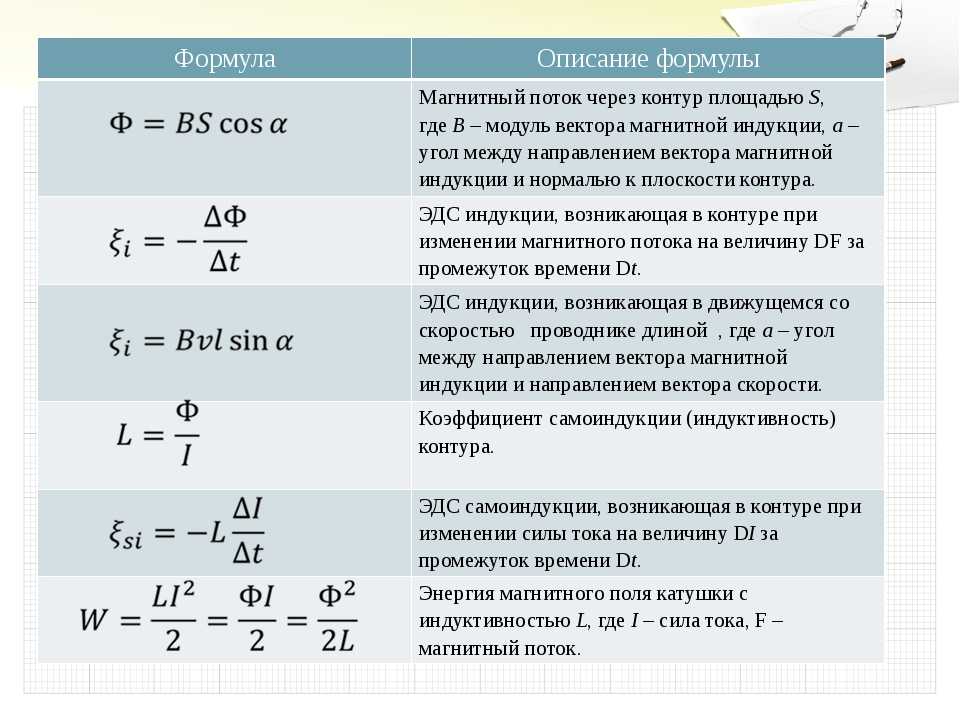 Эксперименты показали, что e/m_e соответствует отношению заряда электрона к его массе. Таким образом, было доказано, что наблюдаемый с помощью гальванометра ток обусловлен движением электронов.

В отсутствие электрического поля в проводниках электроны проводимости движутся хаотично, в произвольных направлениях со скоростями, обусловленными температурой, т.е. с так называемой тепловой скоростью u.

Через определенный промежуток времени t = , двигаясь по прямой, электрон проводимости может провзаимодействовать с ионом кристаллической решетки или с другим электроном проводимости. В результате такого взаимодействия, а оно считается в классической теории проводимости абсолютно упругим, сохраняются полные импульс и энергия, а величина и направление скорости движения могут измениться. Предельным является случай, когда через время, равное  (время свободного пробега), направление скорости теплового движения электрона проводимости изменяется на противоположное.

Время свободного пробега зависит от природы вещества и тем меньше, чем чаще происходят взаимодействия. Между соударениями (взаимодействиями) со скоростью u ничего не происходит.

При наложении электричес-кого поля с напряженностьюE под действием силы F = eE эле-ктроны проводимости приобре-тают некоторое ускорение a и направленное движение с изме-няющейся скоростью от v_o = 0 до v = v_max за время t = .

Изменение скорости направленного движения электрона проводимости происходит до его взаимодействия (рис. 6.1). В результате взаимодействия эта скорость так же может измениться как по величине, так и по направлению.

Если в единице объема проводника n электронов проводимости, которые в некоторый момент времени t обладают скоростью v, то можно определить заряд, прошедший через некоторую площадку S, расположенную перпендикулярно направлению скорости движения электронов проводимости:

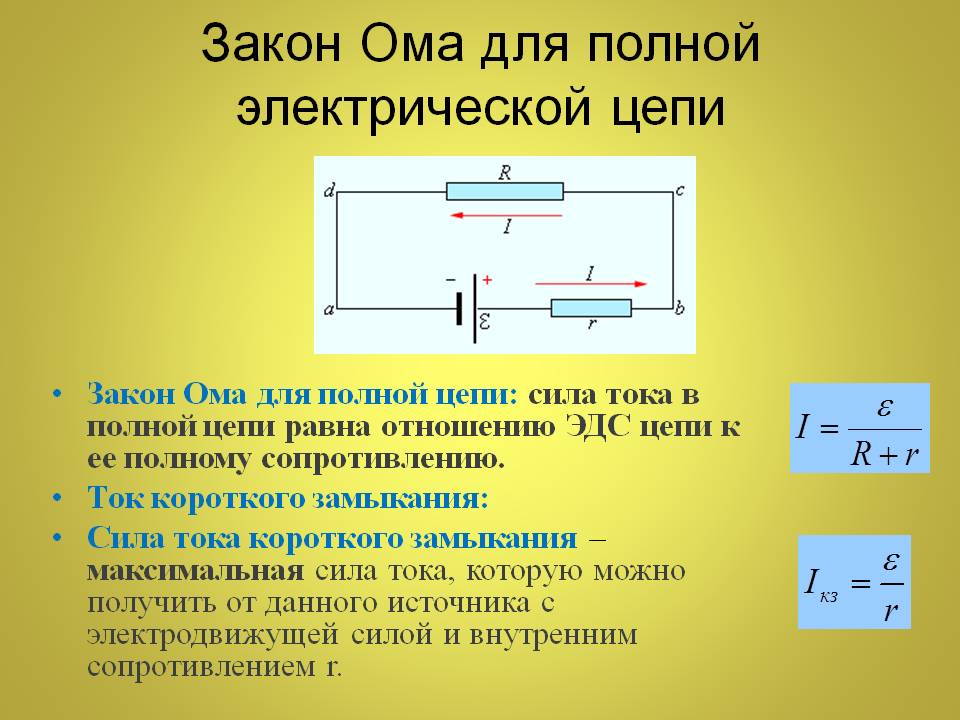, (6. 6)

где <v> – средняя скорость упорядоченного движения электронов проводимости.

Сила (величина) тока в проводнике в этом случае

. (6.7)

Плотность тока проводимости

. (6.8)

В векторной форме

. (6.9)

Согласно (6.8) для определения плотности электрического тока в проводнике необходимо определить среднюю скорость упорядоченного движения электронов проводимости.

Средняя скорость упорядоченного движения в данном случае может быть определена по формуле

, (6.10)

т.к. в начальный момент времени t=0, когда отсутствует электрическое поле, v

o=0.

Максимальная скорость упорядоченного движения, которую приобретает электрон под действием электрического поля за время свободного пробега,

,

где a – ускорение, приобретаемое электроном проводимости под действием электрического поля;

 – время пробега электрона проводимости от взаимодействия до взаимодействия.

На основании второго закона Ньютона F = ma, где F – кулоновская сила,

F = eE.

Имеем:

;

;

. (6.11)

Для средней скорости упорядоченного движения электронов проводимости получим

. (6.12)

Зная среднюю скорость теплового движения электронов проводимости и среднее расстояние, проходимое ими от взаимодействия до взаимодействия, можно определить время между двумя последующими взаимодействиями:

. (6.13)

Сделав подстановку и необходимые преобразования, для плотности тока проводимости будем иметь

, (6.14)

где – удельная электропроводность металла проводника.

В векторной форме

. (6.15)

Выражения (6.14) и (6. 15) являются математической формой записи закона Ома в дифференциальной форме.

Закон Ома в дифференциальной форме справедлив для любых проводников, любых токов, характеризует плотность тока проводимости в любой точке проводника.

Из закона Ома в дифференциальной форме можно получить закон Ома в интегральной форме для замкнутой (или полной) цепи. Для чего выражение (6.15) умножим на величину элементарного участка цепи dl:

,

где ;;.

Таким образом, имеем

или

; . (6.16)

Проинтегрировав выражение (6.16) по замкнутому контуру L, получим

, (6.17)

где – сопротивление внешнего и внутреннего участков цепи;

–ЭДС, действующая в замкнутой цепи, численно равная циркуляции вектора напряженности поля сторонних сил;

–разность потенциалов между двумя рассматриваемыми точками замкнутой цепи.

Для замкнутой цепи

(₁ – ₂) = 0; .

Таким образом, имеем

или , (6.18)

где R₁ – сопротивление внешнего участка цепи;

r – внутреннее сопротивление источника тока.

Из формулы (6.18)

. (6.19)

Следовательно, ЭДС уравновешивает падение напряжения во внешней и внутренней цепи и тем самым обеспечивает непрерывное движение электронов проводимости.

Если цепь не замкнута и в ней отсутствует ЭДС, то

, а . (6.20)

Выражения (6.18) и (6.20) являются математической формой записи закона Ома, соответственно, для полной (замкнутой) цепи и участка цепи, который был открыт им экспериментально. Сила тока в цепи прямопропорциональна ЭДС (напряжению на участке цепи) и обратно пропорциональна сопротивлению цепи.

Связь эдс и напряжения

Мгновенным значением переменного тока называется его значение в фиксированный момент времени. Периодическим называют такой переменный ток, мгновенные значения которого повторяются через равные промежутки времени:. Простейшим типом периодического тока является гармонический ток:. Гармонический ток можно представить в виде проекции на вертикальную ось вращающегося вектора рис. Действующим или эффективным значением гармонического тока называется значение такого постоянного тока, который протекая через одно и тоже неизменное сопротивление за период времени выделяет такое же количество тепла, что и рассматриваемый гармонический ток.

Поиск данных по Вашему запросу:

Связь эдс и напряжения

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Чем отличается ЭДС от напряжения: простое объяснение на примере
• Формула ЭДС
• III. Основы электродинамики
• Эдс и напряжение: что это и в чем разница
• Чем отличается ЭДС от напряжения
• Научный форум dxdy

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Электродвижущая сила (ЭДС)

Чем отличается ЭДС от напряжения: простое объяснение на примере

Любые силы, действующие на заряд, за исключением потенциальных сил электростатического происхождения т. Сторонние силы объясняются электромагнитным взаимодействием между электронами и ядрами. Закон Ома для полной цепи. Опасно, т. Мощность: а Полная.. Соединение источников тока. Если все источники одинаковы и включены в одном направлении, то. Расчет по правилам Кирхгофа см. Правила Кирхгофа. Алгебраическая сумма сил токов в каждом узле точке разветвления равна 0.

В любом замкнутом контуре цепи алгебраическая сумма произведений сил токов в отдельных участках на их сопротивления равна алгебраической сумме ЭДС источников в этих контурах.

Направление токов выбирают произвольно. Если после вычислений значение силы тока отрицательно, то направление противоположно. Замкнутый контур обходят в одном направлении. В полученную систему уравнений должны входить все ЭДС и все сопротивления. Jump to Content. Основные ссылки. Главная Для учителя Архив заданий олимпиад по физике за годы Владимир Анатольевич Зверев предлагает ИКТ на уроке физики История физики на уроке и во внеурочной деятельности Несколько ссылок на работы Анатолия Шперха Общие вопросы методики обучения физике Статьи Александра Борисовича Рыбакова Важнейший общефизический принцип остается непонятым Рыбаков А.

Рыбаков Банджи-джампинг, сохранение импульса и уравнение Мещерского Рыбаков А. Заметки о демоверсии Рыбаков А. Скрябиной Опорные конспекты Н. Опорные конспекты Г. CSS adjustments for Marinelli theme. Объединение учителей Санкт-Петербурга. Форма поиска Поиск. Электродвижущая сила. Словарь Полный список биографий Последние обновления.

Последние публикации. Если Вы или Ваши учителя используют интерактивные доски, то чаще всего доска используется. Ответы как экран для презентаций, фильмов и т. Случайная публикация. Объединение учителей Санкт-Петербурга, При использовании материалов сайта ссылка на www.

Формула ЭДС

Напряжение может быть задано как константа, как функция времени, либо как внешнее управляющее воздействие. В простейшем случае напряжение определено как константа, то есть напряжение источника ЭДС постоянно. Идеальный источник напряжения источник ЭДС является физической абстракцией, то есть подобное устройство не может существовать. Если допустить существование такого устройства, то ток I , протекающий через него, стремился бы к бесконечности при подключении нагрузки, сопротивление R H которой стремится к нулю. Но при этом получается, что мощность источника ЭДС также стремится к бесконечности, так как.

ЭДС и напряжение. Внутреннее сопротивление источников питания. Небольшое дополнение к разговору о батарейках и аккумуляторах, а также – о.

III. Основы электродинамики

Под действием сил внешнего электрического поля и при наличии на концах проводника разности потенциалов — в проводнике возникает электрический ток. Источники электрического тока как раз и являются источниками разности потенциалов. В каждом источнике электрической энергии тока существующая разность потенциалов создаётся и поддерживается сторонними неэлектрическими силами. В источнике электрического тока происходит преобразование неэлектрической формы энергии в электрическую энергию. Эта сила в источнике тока называется — электродвижущая сила. Сокращенное обозначение — ЭДС э. Величина, численно равная работе, совершаемой источником электрической энергии при переносе частицы с зарядом, равной единице, по всей замкнутой цепи, называется электродвижущей силой. Она равна разности потенциалов на зажимах незамкнутого источника. Именно электродвижущая сила является той причиной, по которой в электрической цепи существует электрический ток. В зависимости от типа источника ЭДС, природа сторонних сил, которые рождают электрическую разность потенциалом может быть: электрохимической аккумуляторы, гальванические элементы и т.

Эдс и напряжение: что это и в чем разница

Для того чтобы разобраться что такое электродвижущая сила источника электрической энергии, необходимо вспомнить, что представляет собой электрический ток и за счёт чего происходит его движение в электрической цепи. Известно, электрический ток движется в цепи за счёт разницы потенциалов. Для того чтобы движение тока не прекращалось, нужно непрерывно обеспечивать эту разницу потенциалов между полюсами источника напряжения, к которому подключена цепь. Подобное явление можно сравнить с трубкой, которая соединена с двумя резервуарами с водой.

Сторонние силы. Источники тока.

Чем отличается ЭДС от напряжения

Содержание: Что такое электродвижущая сила Что такое напряжение Так в чем же отличие Вывод. Под ЭДС понимается физическая величина, характеризующая работу каких-либо сторонних сил, находящихся в источниках питания постоянного или переменного тока. При этом, если имеется замкнутый контур, то можно сказать, что ЭДС равна работе сил по перемещению положительного заряда к отрицательному по замкнутой цепи. Или простыми словами, ЭДС источника тока представляет работу, необходимую для перемещения единичного заряда между полюсами. При этом если источник тока имеющего бесконечную мощность, а внутреннее сопротивление будет отсутствовать позиция А на рисунке , то ЭДС можно рассчитать по закону Ома для участка цепи , так как напряжение и электродвижущая сила в этом случае равны. Однако, реальный источник питания имеет конечное внутреннее сопротивление.

Научный форум dxdy

Когда по обмотке катушки проходит электрический ток i , то им формируется в каждом витке магнитное поле, называемое потоком самоиндукции. Для его обозначения принят символ Ф L. Поток индуцирует на выводах обмотки ЭДС, называемую электродвижущей силой самоиндукции, которая обозначается е L. Индуктивность L характеризует пропорциональность между проходящим через обмотку катушки током и потокосцеплением. Она зависима от:.

Электродвижущая сила и напряжение. Для поддержания электрического тока в проводнике необходим какой-то внешний источник энергии, который все.

Последний раз редактировалось Garat Конденсаторы подсоединены в батарее, ЭДС которой равна В. Найдите заряд на каждом конденсаторе и разность потенциалов между обкладками. Для решения данной задачи нужно знать напряжение.

До сих пор, рассматривая генераторы, мы считали, что величина напряжения на их зажимах не зависит от величины тока. Это возможно только при условии дополнительного регулирования работы генератора. В самом деле, проводниковая цепь и внутри генератора обладает сопротивлением, следовательно, часть того общего напряжения, которое создается в генераторе, тратится на сопротивлении самого генератора, если только генератор отдает ток в нагрузку. Напряжение, теряемое в генераторе потеря напряжения , равно произведению внутреннего сопротивления генератора на ток.

Чем отличается ЭДС электродвижущая сила от напряжения?

Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал учтем, что носители тока предполагаются положительными зарядами постоянно убирались доставляемые током заряды, при этом к концу с большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения. Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи или на отдельных участках цепи. Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой ЭДС , действующей в цепи или на участке цепи.

Физическая величина, равная работе сторонних сил по перемещению положительного единичного заряда вдоль всей цепи, включая источник тока, называется электродвижущей силой источника тока ЭДС :. При движении зарядов в проводнике кроме сторонних сил на них действуют силы электростатического поля. Следовательно, в любой точке цепи на заряд q действует результирующая сила:.

Подавление обратного ЭМП – контроль доступа потомства

Введение

Физический электронный контроль доступа почти всегда включает в себя управление каким-либо электромагнитным блокирующим устройством. Это может быть мощный магнит или меньший соленоид внутри защелки или болта. Все эти устройства подчиняются одним и тем же основным законам физики. Электромагнит будет накапливать энергию при подаче питания и будет генерировать «обратную ЭДС» или противоЭДС (CEMF), когда питание отключено.

При подключении питания через обмотки катушки электромагнита протекает ток. Конечный ток покоя определяется сопротивлением постоянному току обмотки катушки и соединительных проводов. Этот ток создает намагничивающее поле, которое выравнивает магнитные домены в металлическом сердечнике электромагнита. Это выравнивание усиливает поле, увеличивая магнитную силу, но при этом сохраняя гораздо больше энергии.

Когда питание отключено, магнитное поле будет стремиться к разрушению и при этом будет генерировать ЭДС или (CEMF) в обмотках катушки электромагнита.

Если эта обратная ЭДС не контролируется или не подавляется, она будет генерировать очень большие напряжения, которые, в свою очередь, могут:

• Вызывать искрение на контактах, сокращая срок службы переключателя
• Генерировать помехи
• Повреждение электроники
• Причина потери данных

EMF — это аббревиатура от Electro-Motive Force. Этот термин немного вводит в заблуждение, поскольку ЭДС на самом деле не является силой. Это напряжение, создаваемое взаимодействием тока в катушке электромагнита с его магнитным полем, когда одно или оба изменяются. Отключенный электромагнит действует как источник тока; создание любого напряжения, необходимого для поддержания исходного тока.

Подавление противо-ЭДС

Противо-ЭДС нельзя предотвратить, но ею можно управлять. При подавлении обратной ЭДС цель состоит в том, чтобы предотвратить очень высокие напряжения и рассеивать накопленную энергию контролируемым образом. Есть несколько способов сделать это, и мы рассмотрим два наиболее распространенных метода, используемых в управлении доступом.

Диод маховика

Термин «маховик» очень уместен. Ток, протекающий в электромагните, очень похож на свободно вращающееся велосипедное колесо. При остановке педали (отключении напряжения питания) колесо продолжает вращаться.

Диод маховика служит средством торможения маховика. При подаче напряжения питания диод смещается в обратном направлении и эффективно размыкается. Когда переключатель размыкается, ток маховика создает обратную ЭДС противоположной полярности, поэтому диод будет проводить. Диод очень хорошо подавляет обратную ЭДС и ограничивает напряжение примерно до одного вольта или около того. Это вполне подходит для небольших соленоидов, таких как те, что используются в забастовках. Однако они не подходят для дверных магнитов.

Почему диоды не подходят для магнитов

Мощность, рассеиваемая диодом, мала, поскольку прямое падение напряжения меньше вольта. Таким образом, скорость отвода энергии от электромагнита мала (Энергия ≈ Мощность x Время). Таким образом:

Таким образом, чем меньше потери мощности через диод, тем больше время рассеяния энергии. Конечным результатом является то, что ток продолжает течь, и магнит дольше держится на якоре. Это может длиться от одной до двух секунд, что приводит к неприятной задержке открывания двери.

Почему MOV подходят для магнитов и защелок

MOV (VDR) имеет номинальное напряжение. Ниже этого напряжения он имеет очень высокое сопротивление. Таким образом, выбрав MOV с номинальным напряжением, немного превышающим нормальное напряжение питания, его можно безопасно подключить через катушку магнита, и, как и диод, он не будет влиять, пока питание подключено.

Металлооксидный варистор (MOV)

При отключении питания противо-ЭДС повышается до номинального напряжения MOV. В этот момент MOV начнет проводить и зафиксирует напряжение чуть выше этого значения.

При ограничении обратной ЭДС падение напряжения обычно составляет порядка 30 В или около того. Используя то же уравнение:

Потери мощности будут в 30 раз больше, чем у диода. В результате энергия теряется примерно в 30 раз быстрее, а магнит освобождает якорь за гораздо меньшее время.

VDR, подходящие для замков на 12 или 24 В, можно приобрести у дистрибьютора, укажите код продукта 0043 (упаковка из 20 шт.).

См. также: Противоэлектродвижущая сила

 

 

Сохр.

Сохр.

Сохр.

Сохр.

электрический ток – Почему ЭДС = напряжению на клеммах в разомкнутой цепи?

спросил 2 года 10 месяцев назад

Изменено 1 год, 9 месяцев назад

Просмотрено 709раз

$\begingroup$

Теперь тривиальным ответом будет то, что ток равен 0.

V= E-Ir (где v — напряжение на клеммах, e — ЭДС, I — ток, r — внутреннее сопротивление) Поскольку i=0, V=E

Но я считаю, что мы упускаем из виду одну вещь: закон Ома не работает, когда любая из трех величин равна 0 (в данном случае ток). Просто потому, что я могу написать V = IR (где R — внешнее сопротивление), это будет означать v = 0, что не так.

Также есть способ решить эту проблему, но в этом случае мы предполагаем, что внешнее сопротивление равно бесконечности в разомкнутой цепи

V=IR –> I=V/R (где R очень близко к бесконечности )

E=I(R+r)–> (V/R)(R+r)

Поскольку R намного больше r, мы можем игнорировать значение r, это будет означать

E= ( V/R)(R) –> E=V

Это правильный способ решения этой проблемы или у меня есть недостаток в моем понимании?

• электрические цепи
• электрический ток
• электрическое сопротивление
• напряжение

$\endgroup$

$\begingroup$

Я не совсем понимаю, к чему вы клоните.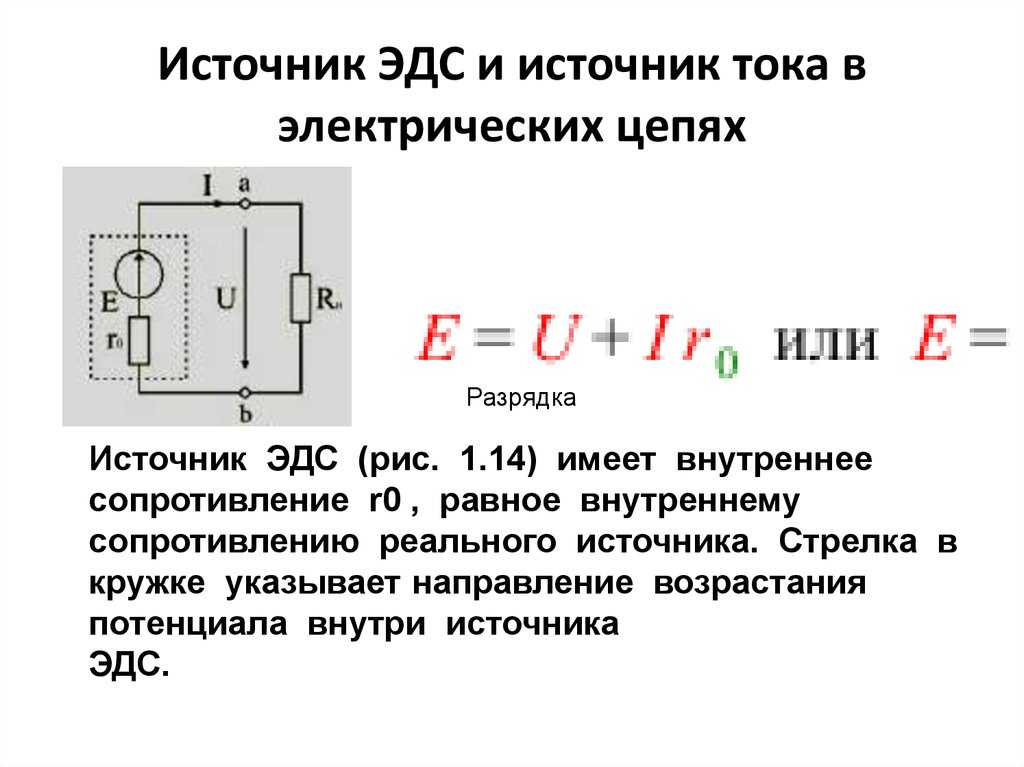 Предположим, мы представляем физическую ячейку в виде идеального источника напряжения с ЭДС $\varepsilon$, последовательно соединенной с резистором $r$.

Если мы ни к чему не подключаем выводы физической ячейки, т.е. имеем разомкнутую цепь, то, как вы говорите, тока через ячейку нет. По закону Ома на резисторе $r$ нет напряжения, так как $v_{r} = ir = 0$, и тогда общее напряжение на физической ячейке равно $\varepsilon$.

Если теперь мы подключим физическую ячейку к нагрузке так, что ток будет ненулевым, то на внутреннем сопротивлении произойдет падение напряжения $v_{r} = ir$. Таким образом, при прохождении через физическую ячейку разность потенциалов между терминалами представляет собой сумму изменений потенциала, а именно $v_{terminal} = -ir + \varepsilon$.

Закон Ома по-прежнему применяется, если $v, i$ или $R$ равны нулю, единственный раз, когда мы должны быть осторожны, это если мы получим форму $\frac{0}{0}$.

Например, по идеальному проводу в цепи протекает ток, но сопротивление равно нулю.