Эдс индукции буква: как найти ЭДС, формулы для источника и внутреннего сопротивления тока

Электротехника

Электротехника

Ломоносов В. Ю. и др. Электротехника/В. Ю. Ломоносов, К. М. Поливанов, О. П. Михайлов. — М.: Энергоатомиздат, 1990. — 400 с. Приводятся основные понятия об элементах электрической цепи, методах расчета простых цепей постоянного и переменного тока. Дается общее описание физических процессов, происходящих в электрическом и магнитном полях. Излагается принцип действия полупроводниковых приборов, электрических машин и аппаратов, электроизмерительных приборов. Приводятся сведения о применении электронных вычислительных устройств в электротехнике. Для читателей, интересующихся основами электротехники и электроники. Оглавление ПРЕДИСЛОВИЕ ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ ГЛАВА ПЕРВАЯ. ТОК И НАПРЯЖЕНИЕ 1.2. ПРОСТЕЙШАЯ ЭЛЕКТРОТЕХНИЧЕСКАЯ УСТАНОВКА 1.3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ 1.4. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ 1.5. ВКЛЮЧЕНИЕ АМПЕРМЕТРА И ВОЛЬТМЕТРА 1.6. МОЩНОСТЬ 1.7. СОПРОТИВЛЕНИЕ ЦЕПИ И ЗАКОН ОМА 1.8. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ 1.9. ПОЧЕМУ ЦЕПИ, ПОДЧИНЯЮЩИЕСЯ ЗАКОНУ ОМА, НАЗЫВАЮТ ЛИНЕЙНЫМИ 1.10. НЕЛИНЕЙНЫЕ ЦЕПИ 1.11. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ 1.12. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА И ЗАКОН ДЖОУЛЯ — ЛЕНЦА 1.13. НАПРАВЛЕНИЕ ТОКА И ЕГО ХИМИЧЕСКОЕ ДЕЙСТВИЕ 1.14. НАПРАВЛЕНИЕ ТОКА И ВЫПРЯМЛЯЮЩИЕ УСТРОЙСТВА 1.15. АККУМУЛЯТОРЫ И ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ 1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ 1.17. ТОК В СЛОЖНЫХ ЦЕПЯХ 1.18. ЭЛЕКТРОДВИЖУЩАЯ СИЛА И ПОТЕРЯ НАПРЯЖЕНИЯ 1.19. ЗАЗЕМЛЕНИЕ И ПОТЕНЦИАЛ 1.20. ЗАКОНЫ КИРХГОФА ГЛАВА ВТОРАЯ. МАГНИТЫ. МАГНИТНОЕ ПОЛЕ. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА 2.1. МАГНИТЫ И МАГНИТНОЕ ПОЛЕ 2.2. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА 2.3. МАГНИТНОЕ ПОЛЕ ДЕЙСТВУЕТ НА ПРОВОДНИК С ТОКОМ 2. 4. МАГНИТНАЯ ИНДУКЦИЯ 2.6. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ 2.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ 2.8. ИЗМЕНЕНИЕ МАГНИТНОГО ПОЛЯ СОЗДАЕТ ЭЛЕКТРОДВИЖУЩУЮ СИЛУ 2.9. ПРАВИЛО ЛЕНЦА 2.10. МАГНИТНЫЙ ПОТОК 2.11. ЗАКОН НАВЕДЕНИЯ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ 2.12. НАВЕДЕНИЕ ЭДС В ПРЯМОЛИНЕЙНОМ ПРОВОДНИКЕ, ДВИЖУЩЕМСЯ В ПОЛЕ 2.13. ВЗАИМНАЯ ИНДУКДИЯ 2.14. САМОИНДУКЦИЯ 2.15. ВЛИЯНИЕ САМОИНДУКЦИИ НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ 2.16. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ ГЛАВА ТРЕТЬЯ. ЖЕЛЕЗО В МАГНИТНОМ ПОЛЕ. МАГНИТНЫЕ ЦЕПИ. ПОСТОЯННЫЕ МАГНИТЫ 3.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ ПРИ ОТСУТСТВИИ ЖЕЛЕЗА 3.2. НАМАГНИЧИВАНИЕ ЖЕЛЕЗНОГО КОЛЬЦА 3.3. ОТНОСИТЕЛЬНАЯ МАГНИТНАЯ ПРОНИЦАЕМОСТЬ 3.4. РАСЧЕТ ПОЛЯ В КОЛЬЦЕВОЙ КАТУШКЕ СО СПЛОШНЫМ СЕРДЕЧНИКОМ ПО МАГНИТНЫМ ХАРАКТЕРИСТИКАМ 3.5. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ОДНОРОДНОГО ПОЛЯ В ФЕРРОМАГНИТНОЙ СРЕДЕ 3.6. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ 3.7. СТАЛЬНОЕ КОЛЬЦО С РАЗРЕЗОМ 3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ 3. 9. НАМАГНИЧЕННОСТЬ ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 4.1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ 4.2. ИЗОЛЯТОРЫ И ПРОВОДНИКИ 4.3. ПРОСТЕЙШИЕ ОПЫТЫ С НЕПОДВИЖНЫМИ ЭЛЕКТРИЧЕСКИМИ ЗАРЯДАМИ (ЭЛЕКТРОСТАТИКА) 4.4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 4.5. НАПРЯЖЕНИЕ (РАЗНОСТЬ ПОТЕНЦИАЛОВ) 4.6. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ 4.7. КОНДЕНСАТОР В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ 4.8. ДВИЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В МАГНИТНОМ ПОЛЕ ГЛАВА ПЯТАЯ. ПЕРЕМЕННЫЙ ТОК 5.1. ЗАЧЕМ НУЖЕН ПЕРЕМЕННЫЙ ТОК? 5.2. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА 5.3. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА 5.4. СИНУСОИДА 5.5. ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА ГЛАВА ШЕСТАЯ. ЦЕПИ ПЕРЕМЕННОГО ТОКА 6.1. КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 6.2. ФАЗОВЫЙ СДВИГ В ИНДУКТИВНОЙ ЦЕПИ 6.3. КОЭФФИЦИЕНТ МОЩНОСТИ 6.4. КОНДЕНСАТОВ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 6.5. КОМПЕНСАЦИЯ СДВИГА ФАЗ 6.6. РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА 6.7. РЕЗОНАНС ТОКОВ 6.8. РЕЗОНАНС НАПРЯЖЕНИЙ ГЛАВА СЕДЬМАЯ. ТРЕХФАЗНЫЙ ТОК 7.1. ТРЕХФАЗНАЯ СИСТЕМА 7.2. РАЗМЕТКА КОНЦОВ ТРЕХФАЗНОЙ СИСТЕМЫ 7.3. СЛОЖЕНИЕ ФАЗНЫХ ЭДС 7.4. СОЕДИНЕНИЕ В ЗВЕЗДУ 7.5. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ 7.6. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА 7.7. ПОТЕРИ МОЩНОСТИ В ТРЕХФАЗНОЙ ЛИНИИ ГЛАВА ВОСЬМАЯ. ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ НА МИКРОКАЛЬКУЛЯТОРАХ 8.1. КАК РАБОТАЕТ МИКРОКАЛЬКУЛЯТОР 8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ 8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ 8.4. ПРОГРАММИРУЕМЫЕ МИКРОКАЛЬКУЛЯТОРЫ 8.5. РАСЧЕТЫ НА ПРОГРАММИРУЕМЫХ МИКРОКАЛЬКУЛЯТОРАХ ГЛАВА ДЕВЯТАЯ. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ 9.1. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 9.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ. ВЫПРЯМИТЕЛИ 9.3. ТРАНЗИСТОРЫ. УСИЛИТЕЛИ ЭЕКТРИЧЕСКИХ СИГНАЛОВ 9.4. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ 9.5. ГЕНЕРАТОРУ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ 9.6. ТИРИСТОРЫ, УПРАВЛЯЕМЫЕ ВЫПРЯМИТЕЛИ 9.7. КЛЮЧИ 9.8. НЕИЗБЕЖНОСТЬ МИКРОЭЛЕКТРОНИКИ 9.9. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ ГЛАВА ДЕСЯТАЯ. МАШИНЫ ПОСТОЯННОГО ТОКА 10.1. НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН 10. 2. МАГНИТНАЯ СИСТЕМА МАШИН ПОСТОЯННОГО ТОМА 10.3. КОЛЛЕКТОР 10.4. ЯКОРНЫЕ ОБМОТКИ 10.5. РАБОЧИЙ РЕЖИМ МАШИН ПОСТОЯННОГО ТОКА 10.6. СПОСОБЫ ВОЗБУЖДЕНИЯ МАШИН 10.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. РАБОТА ДВИГАТЕЛЯ 10.8. ДВИГАТЕЛИ С ПАРАЛЛЕЛЬНЫМ И ПОСЛЕДОВАТЕЛЬНЫМ ВОЗБУЖДЕНИЕМ ГЛАВА ОДИННАДЦАТАЯ. ТРАНСФОРМАТОРЫ 11.1. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА 11.2. РАБОТА ТРАНСФОРМАТОРА 11.3. ТРАНСФОРМАТОР ТРЕХФАЗНОГО ТОКА 11.4. ПОТЕРИ В ТРАНСФОРМАТОРЕ 11.1. АВТОТРАНСФОРМАТОРЫ ГЛАВА ДВЕНАДЦАТАЯ. МАШИНЫ ПЕРЕМЕННОГО ТОКА 12.1. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА 12.2. СИНХРОННЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА 12.3. ТРЕХФАЗНЫЕ МАШИНЫ ПЕРЕМЕННОГО ТОКА 12.4. РАБОТА СИНХРОННЫХ МАШИН 12.5. ПАРАЛЛЕЛЬНАЯ РАБОТА СИНХРОННЫХ ГЕНЕРАТОРОВ 12.6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ 12.7. АСИНХРОННЫЕ ДВИГАТЕЛИ 12.8. КПД ЭЛЕКТРИЧЕСКИХ МАШИН ГЛАВА ТРИНАДЦАТАЯ. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ 13.1. ВЫКЛЮЧАТЕЛИ, КНОПКИ И КЛАВИШИ 13.2. РАБОТА ЭЛЕКТРИЧЕСКИХ КОНТАКТОВ 13. 3. ЭЛЕКТРОМАГНИТЫ 13.4. КОНТАКТОРЫ 13.5. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ 13.6. ПРЕДОХРАНИТЕЛИ, РЕЛЕ ТОКА И ТЕПЛОВЫЕ РЕЛЕ 13.7. ПУТЕВЫЕ ВЫКЛЮЧАТЕЛИ ГЛАВА ЧЕТЫРНАДЦАТАЯ. УПРАВЛЕНИЕ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ 14.1. КАК СОСТАВЛЯЮТСЯ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ 14.2. ДВА ТИПА ЭЛЕКТРИЧЕСКИХ СХЕМ 14.3. КАК ВКЛЮЧИТЬ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ 14.4. СХЕМЫ ТОРМОЖЕНИЯ 14.5. ЗАЩИТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЯ В ЭЛЕКТРОТЕХНИКЕ 15.1. РОЛЬ ИЗМЕРЕНИЙ В ЭЛЕКТРОТЕХНИКЕ 15.2. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ПОСТОЯННОГО ТОКА 15.3. ШУНТЫ И ДОБАВОЧНЫЕ СОПРОТИВЛЕНИЯ 15.4. ИЗМЕРЕНИЕ ОЧЕНЬ МАЛЫХ ТОКОВ. ГАЛЬВАНОМЕТРЫ 15.5. ПРИБОРЫ ПЕРЕМЕННОГО ТОКА 15.6. КАК ИЗМЕРИТЬ МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА 15.7. ЭЛЕКТРИЧЕСКИЙ СЧЕТЧИК ПЕРЕМЕННОГО ТОКА 15.8. ИЗМЕРЕНИЕ МОЩНОСТИ И ЭНЕРГИИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА 15.9. САМОПИСЦЫ И ОСЦИЛЛОГРАФЫ 15.10. ЦИФРОВЫЕ ПРИБОРЫ 15.11. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ЦЕПИ

Вихревые токи

Сердечники якоря и полюсов электрических машин, трансформаторов, дросселей и других аппаратов, по обмоткам которых проходит переменный ток, выполняются обычно из электротехнической стали, представляющей собой ферромагнитный материал и одновременно проводник.

Переменный магнитный поток в каждом сечении сердечника индуктирует ЭДС электромагнитной индукции. Эта ЭДС в каждом слое массивного сердечника создает токи, которые замыкаются в этом слое проводящего материала (рис. 9.10а). Эти токи называются вихревыми токами.

Между вихревыми токами в каждом слое массивного сер­дечника и током I, создаю­щим эти токи, существует не электрическая, а электромаг­нитная связь.

Вихревые токи вызывают нагрев стальных сердечников электромагнитных аппаратов и снижают их КПД за счет потерь энергии, которая тратится на нагрев.

Потери, вызванные вихревыми токами в токопроводящих сердечниках, называются потерями на вихревые токи. Для уменьшения потерь на вихревые токи стальные сердечники, выполняют из листовой стали (рис. 9.106). тонкие листы толщи­ной 0,35 или 0,5 мм. Для уменьшения вихревых токов листы стали изолируются друг от друга специальным лаком.

Вихревые токи применяются для индукционной плавки металла, закалки стальных деталей. В индукционных печах для нагрева заготовок.

ВИХРЕВЫЕ ТОКИ (токи Фуко), замкнутые индукционные токи в массивных проводниках, которые возникают под действием вихревого электрического поля, порождаемого переменным магнитным полем. Вихревые токи приводят к потерям электроэнергии на нагрев проводника, в котором они возникли; для уменьшения этих потерь магнитопроводы машин и аппаратов переменного тока изготовляют из изолированных стальных пластин.

12. Синусоидальный ток, его мгновенное и амплитудное значения. Период, частота, циклическая частота, фаза, начальная фаза.

ОДНОФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

10.1. Основные понятия

Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.

Основное достоинство переменного тока заключается в возмож­ности трансформировать напряжение.

Говоря о переменном токе, обычно имеют в виду синусоидаль­ный переменный ток, т. е. ток, изменяющийся по синусоидально­му закону.

Величины, характеризующие синусоидальную ЭДС

Амплитуда — это максимальное значение периодически изменя­ющейся величины.

Обозначаются амплитуды прописными буквами с индексом m т. е. Е_т, U_m и 1_т.

Тогда

Период — это время, в течение которого переменная величина делает полный цикл своих изменений, после чего изменения по­вторяются в той же последовательности.

Измеряется в секундах, с (сек) т.е. [Т] = с.

Частота — число периодов в единицу времени, т. е. величина, обратная периоду.

Обозначается частота буквой f, и измеряется в герцах (Гц):

Стандартной частотой в электрических сетях России является частота f = 50 Гц.

Угловая частота (угловая скорость) – характеризуется углом поворота

рамки в единицу времени. Обозначается угловая частота буквой ώ (омега):

Измеряется угловая частота в единицах радиан в секунду (рад/с), можно выразить следующим образом:

Мгновенное значение — это значение переменной величины в любой конкретный момент времени. Мгновенные значения обозначаются строчными буквами, т. е. е, i, u.

можно записать так:

Любая синусоидальная величина характеризуется амплитудой и угловой частотой

Характеристики и контроль резонанса в электродвижущей силе электромагнитной индукции

Журнал электромагнитного анализа и приложений
Том 5 № 8 (2013 г.), идентификатор статьи: 35486, 5 страниц DOI: 10. 4236/jemaa.2013.58049

Характеристики и контроль резонанса в электродвижущей силе электромагнитной индукции

Санг Дон Бу, Джин Кю Хан, Джин Ён Хён, Ги Гван Ким

Факультет физики, Национальный университет Чонбук, Чонджу, Южная Корея.

Электронная почта: [email protected]

Copyright © 2013 Sang Don Bu et al. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

Поступила в редакцию 25 апреля ^-го -го, 2013 г.; исправлено 28 мая ^-й , 2013; принята 30 июня ^th , 2013

Ключевые слова: Электромагнитная индукция; Электродвижущая сила; Резонатор, резонансная/антирезонансная частота

АННОТАЦИЯ

Принципы электромагнитной индукции применяются во многих устройствах и системах, включая индукционные плиты, трансформаторы и беспроводную передачу энергии; однако мало данных о резонансе в электродвижущей силе (ЭДС) электромагнитной индукции. Мы изучали электромагнитную индукцию между двумя круглыми катушками провода: одна является катушкой источника, а другая катушкой датчика (или индукции). Измеренные графики зависимости ЭДС от частоты показывают наличие резонанса/антирезонанса в ЭДС электромагнитной индукции в свободном пространстве. Мы обнаружили, что можно управлять резонансными и антирезонансными частотами системы. В некоторых устройствах желаемая резонансная или антирезонансная частота достигается за счет изменения размера резонатора. Здесь, напротив, наши экспериментальные результаты показывают, что резонансную и антирезонансную частоты системы можно регулировать, изменяя расстояние между двумя катушками или число витков индукционной катушки.

1. Введение

1.1. Резонанс

Резонанс широко распространен в природе и используется во многих искусственных устройствах. Электрический резонанс используется во многих схемах [1-5]; например, радио и телевизоры используют резонансные цепи для настройки на станции. В этих устройствах через антенну в цепь одновременно попадают многие частоты, но значительный ток индуцируется только частотами, близкими к резонансной частоте цепи. Изменяя индуктивность или емкость, устройство можно настроить на разные станции. В физике резонанс — это тенденция системы колебаться с большей амплитудой на резонансных частотах системы, чем на других. На этих частотах даже небольшие периодические движущие силы могут вызывать колебания большой амплитуды, поскольку система накапливает энергию колебаний. В этой работе мы изучили электромагнитную индукцию между двумя круглыми катушками провода: одна является катушкой источника, а другая — катушкой датчика (или индукции), и сообщаем о характеристиках и контроле над резонансом и антирезонансом в электродвижущая сила (ЭДС) электромагнитной индукции через свободное пространство.

1.2. Как ведет себя величина электродвижущей силы при увеличении частоты, подаваемой на катушку источника?

Эксперимент проводился по закону Фарадея:

. (1)

где и – ЭДС, индуцируемая в индукционной катушке, и магнитный поток, проходящий через индукционную катушку, соответственно [1,6]. Экспериментальная установка состоит из двух круглых катушек провода, состоящего из электропроводящего медного провода с радиусом поперечного сечения 0,35 мм, туго намотанного в виде ряда петель из 5-320 витков радиусом 7 см и высотой 2 см, как показано на рисунке 1. ● Одна катушка (источник) подключена к генератору сигналов (AFG3021B, Tektronix), а другая (датчик или индукционная катушка) подключена к осциллографу (DSO 5012A, Agilent Technologies). Генератор сигналов подает синусоидальное напряжение на катушку источника, создавая синусоидальное магнитное поле. Магнитное поле переменного тока распространяется в свободном пространстве и достигает приемной катушки. Согласно закону Фарадея, электрическое поле индуцируется в любой области пространства, в которой магнитное поле изменяется

Рис. 1. Схема экспериментальной установки. Экспериментальная установка состоит из двух катушек. Катушка А является катушкой-источником, передающей электромагнитную волну через свободное пространство. Катушка B — это приемная (или индукционная) катушка, которая регистрирует наведенную ЭДС. Катушки А и В выровнены коаксиально, так что расстояние d между двумя катушками можно регулировать от 10 мм до 1000 мм. Катушки неподвижны во время работы.

со временем. Таким образом, в приемной катушке индуцируется ЭДС. Если магнитный поток, проходящий через катушку датчика, равен, то ЭДС индукции равна . Поскольку увеличивается, увеличивается, и величина пропорциональна скорости изменения магнитного потока во времени, так что более быстрые изменения дают более сильные. Здесь наш вопрос: как ведет себя величина при увеличении, особенно в диапазоне высоких частот от 10 кГц до нескольких МГц?

2. Простота использования Свойства электромагнитной индукции

2.1. Сравнение экспериментальной и расчетной электродвижущих сил

На рисунках 2(a) и (b) показаны типичные характеристики 1) среднеквадратичного значения катушки датчика и 2) разности фаз между приложенным напряжением (к катушке источника) и генерируемой (в приемной катушке) соответственно в зависимости от приложенной частоты (к катушке источника). Мы ожидали, что согласно закону Фарадея и радиационному сопротивлению катушки оно будет увеличиваться с ростом и затем, наконец, достигнет нового равновесия, как показано черной пунктирной линией на рис. 2(а). Такой отклик можно смоделировать с помощью функции Ланжевена [7],

. (2)

Однако экспериментальные данные продемонстрировали совсем другое поведение, как показано красными сплошными кружками на рисунке 2(а). Резонансное поведение наблюдалось на высоких частотах, а релаксационное — на низких частотах. Резонансные и антирезонансные пики отчетливо наблюдались на частотах 87 кГц и 285 кГц соответственно.

На рис. 2(b) показано, что при частоте 10 Гц катушка звукоснимателя находилась в противофазе на 78˚ по отношению к волне, подаваемой на катушку источника. По мере увеличения разность фаз уменьшалась до тех пор, пока фазы не совпадали, где фазовое согласование означает, что разность фаз составляет менее 5˚. Между тем, разность фаз сильно изменилась, когда катушка звукоснимателя стала резонансной.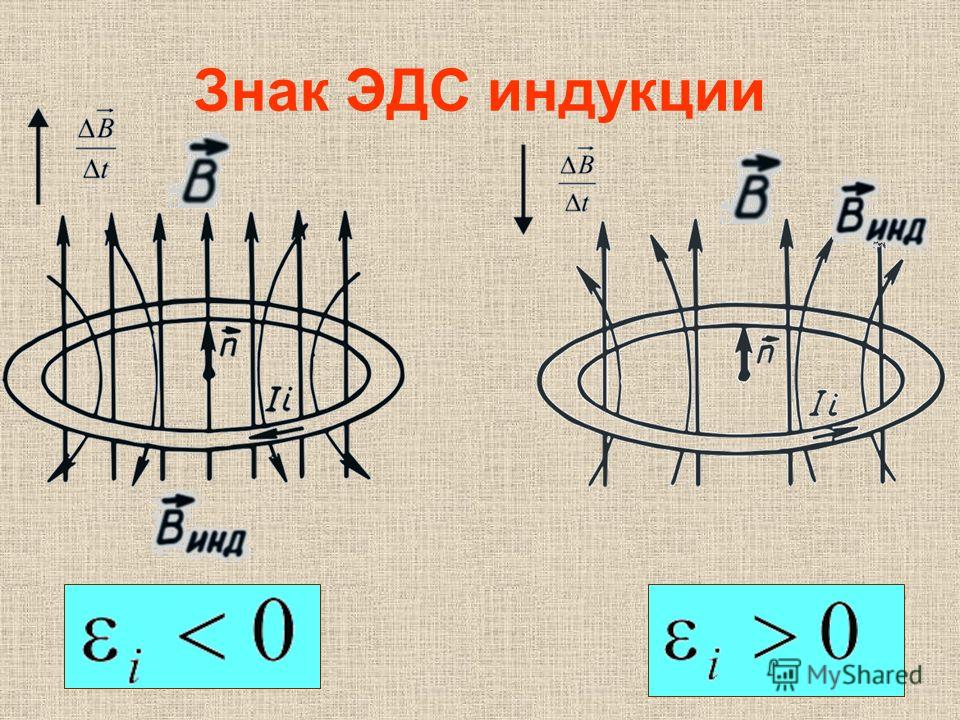 Катушка звукоснимателя была сдвинута по фазе на 176˚ на частотах между резонансным и антирезонансным пиками, то есть в диапазоне частот 87 – 285 кГц.

Резкое изменение разности фаз могло быть вызвано движением зарядов в приемной катушке. Если разность фаз возникла из-за ускорения проводящих электронов, вызванного электромагнитным излучением (генерируемым катушкой источника), разность фаз может быть фактически независимой на высоких частотах. Однако, если бы разность фаз возникла из-за колебаний в электрических/магнитных диполях или тороидальных диполях ¹ [8-14], индуцированных электромагнитным излучением, можно было бы ожидать, что разность фаз будет зависеть от на высоких частотах.

Радиационное сопротивление в катушке с витками, состоящими из электропроводящего медного провода, можно смоделировать следующим образом. Для катушки радиусом 7 см и высотой 2 см, используемой здесь (см. рис. 1), составляющая электрического дипольного излучения в сопротивлении излучения меньше, чем составляющая магнитного дипольного излучения, если предположить, что расстояние от катушки составляет, где скорость света, например; первое порядка, второе порядка, где и – угловая частота и скорость света соответственно. Резонансные частоты, полученные в наших экспериментах, были значительно ниже резонансных частот валентных электронов или электрических/магнитных диполей [6,7]. Следовательно, в рассматриваемой здесь конкретной геометрии резкие изменения разности фаз могли быть преимущественно вызваны колебаниями тороидальных диполей [13,14] в индукционной катушке.

2.2. Настройка резонансной и антирезонансной частот

Для определения резонансной частоты и

Рис. 2. Сравнение экспериментальных и расчетных значений и. Экспериментальные измерения и показаны на (а) и (б) соответственно, обозначены красными и синими сплошными кружками. Амплитуда сигнала, подаваемого на катушку источника, и расстояние между источником и индукционной катушкой затем фиксировались на уровне 14 В и 3 см соответственно. Прогнозируемые значения и показаны на (а) и (б) соответственно черными пунктирными линиями.

антирезонансную частоту можно было регулировать, мы исследовали влияние трех экспериментальных параметров на и. На рисунках 3(a)-(c) показаны зависимости для различных 1) напряжений, подаваемых на катушку источника (= 2, 6, 10 и 14 В), 2) расстояний между двумя катушками (d = 10, 30, 100 В). и 1000 мм) и 3) количество витков приемной катушки (= 5, 50, 150, 250 и 320) соответственно. На рисунках 4(a)-(c) показаны изменения и for и n _B соответственно, полученные из рисунка 3. Резонансные и антирезонансные пики отчетливо видны на большинстве кривых на рисунке 3. или, как показано черными квадратами на рисунках 4(a)-(b). Интервал между и существенно не менялся при увеличении (рис. 4(а)), тогда как резко уменьшался при увеличении (рис. 4(б)). Эти результаты показывают, что можно было контролировать независимо от. С другой стороны, как увеличилось, так и уменьшилось вместе, как показано на рисунке 4(c).

, и каждый из них ведет себя по-своему. Кривые и , показанные на рисунке 4 (b), показывают, что это не зависит от и может быть описано уравнением, включающим логарифм. График в зависимости от давал прямую линию, как показано красной линией на вставке к рисунку 4(b). Таким образом, может иметь вид «», где и – константы пропорциональности и точки пересечения вертикальной оси (или бессмысленные константы), re

Рисунок 3. Графики зависимости от f _A . была измерена как функция напряжения, подаваемого на катушку источника (V _A ), расстояния между двумя катушками (d) и числа витков приемной катушки (n _B ), где количество витков катушки источника (n _A ) было зафиксировано на уровне 320. (a) Графики зависимости f _A для V _A , равного 2, 6, 10 и 14 В, при d и n _B , фиксированном на уровне 30 мм и 320 соответственно; (b) Графики зависимости f _A для d 10, 30, 100 и 1000 мм при V _A и n _B фиксируются на 14 В и 320 В соответственно; (c) Графики зависимости от f _A для n _B , равного 5, 50, 150, 250 и 320, с V _A и d, зафиксированными на уровне 14 В и 100 мм соответственно.

соответственно. Согласно рисунку 4(c), может иметь вид «», а не «», а также может иметь вид «». Экспериментальные результаты, полученные для различных комбинаций и показывают, что можно было описать уравнением вида «» с условием, а можно было описать уравнением вида «» с условием. Отмечено, что в условиях различных поворотов все поведение и с было похоже на результаты, показанные на рисунке 4(b), что указывает на то, что перекрестный член «» может быть незначительным.

Экспериментально мы показали, что катушки звукоснимателя с разными резонансными/антирезонансными частотами можно получить, подобрав подходящие катушки для заданного размера. Эти результаты предполагают возможность «беспроводной станции передачи энергии», которая передает мощность от катушки источника на большое количество приемных катушек

Рис. 4. f _R и f _AR в зависимости от (a) V _A , (b) d и (c) n _B .

через свободное пространство. Если несколько приемных катушек (с разными резонансными/антирезонансными частотами) расположить вокруг катушки-источника (т. е. системы энергоснабжения ближнего действия), мощность можно будет передавать от катушки-источника к приемным катушкам путем модуляции скорости изменения (с течением времени) магнитного потока, проходящего через каждую катушку датчика. Станции беспроводной передачи энергии, аналогичные радиостанциям, могут быть реализованы в ближайшем будущем, чтобы каждый мог использовать энергию в любом месте без необходимости проводной передачи энергии.

3. Заключение

Таким образом, мы изучили электромагнитную индукцию между двумя круглыми витками проволоки и ясно показали наличие резонанса/антирезонанса в ЭДС электромагнитной индукции через свободное пространство. Мы считаем, что наши результаты могут обеспечить конкурентоспособный подход к разработке высокоэффективных систем в устройствах индукционных плит, силовых трансформаторов и беспроводной передачи энергии.

4. Благодарности

Это исследование было поддержано Программой фундаментальных научных исследований через Национальный исследовательский фонд Кореи (NRF), финансируемый Министерством образования, науки и технологий (номер гранта 2012R1A1A 2042743).

ССЫЛКИ

1. Д. К. Джанколи, «Физика: принципы с приложениями», Prentice Hall, Upper Saddle River, 2005, стр. 584–608.
2. А. Курс, А. Каралис, Р. Моффатт, Дж. Д. Джоаннопулос, П. Фишер и М. Солячич, «Беспроводная передача энергии с помощью сильно связанных магнитных резонансов», Science, Vol. 317, № 5834, 2007, стр. 83-86. doi:10.1126/science.1143254
3. Т. Имура, Т. Учида и Ю. Хори, «Гибкость бесконтактной передачи энергии с использованием магнитно-резонансной связи с воздушным зазором и несоосностью для электромобилей», World Electric Vehicle Journal, Vol. 3, 2009 г., стр. 1-10.
4. С. А. Хакворт, X. Лю, К. Ли и М. Сан, «Беспроводная солнечная энергия для домов: магнитно-резонансный подход», Международный журнал инноваций в энергетических системах и энергетике, Vol. 5, № 1, 2010. С. 40-44.
5. Ван Б., Нишино Т. и Тео К. Х., «Повышение эффективности беспроводной передачи энергии с помощью метаматериалов», Материалы Международной конференции IEEE 2010 г. по беспроводным информационным технологиям и системам, Гонолулу, 28 августа — 3 сентября 2010 г., стр. 1–4. . Дои: 10.1109/ICWITS.2010.5612284
6. Джексон Дж.Д. Классическая электродинамика // Wiley. -73.
7. Дубовик В. М., Марценюк М. А., Саха Б. Материальные уравнения для электромагнетизма с тороидальными поляризациями // Physics Review E. Vol. 61, № 6, 2000, стр. 7087-7097. doi: 10.1103/PhysRevE.61.7087
8. В. М. Дубовик, Б. Саха и Дж. Л. Рубин, «Преобразование Лоренца тороидальной поляризации», Секция писем по ферроэлектрикам, Vol. 27, № 1-2, 2000, стр. 1-6. дои: 10.1080/07315170008204647
9. Г. Н. Афанасьев, «Простейшие источники электромагнитных полей как инструмент для проверки теорем взаимности», Journal of Physics D: Applied Physics, Vol. 34, № 4, 2001, стр. 539-559. doi:10.1088/0022-3727/34/4/316
10. Дубовик В.М., Тугушев В.В. Тороидальные моменты в электродинамике и физике твердого тела // Physics Reports. 187, № 4, 1990, стр. 145-202. doi:10. 1016/0370-1573(90)
    -Z
11. Маринов К., Бордман А.Д., Федотов В.А., Желудев Н. Тороидальный метаматериал // Новый журнал физики. 9, № 9, 2007, стр. 324-202. doi:10.1088/1367-2630/9/9/324
12. А.А. Горбацевич, Ю.А. Копаев В. Тороидальный порядок в кристаллах // Сегнетоэлектрики. 161, № 1, 1994, стр. 321-334. doi: 10.1080/00150199408213381
13. Х. Шмид, «Тороидальные моменты в спин-упорядоченных кристаллах», Труды однодневного международного исследовательского семинара по супертороидальной электродинамике, Саутгемптонский университет, Саутгемптон, 2004 г., стр. 108-177.

ПРИМЕЧАНИЯ

¹ Тороидальные моменты были впервые рассмотрены Зельдовичем в 1958. Это фундаментальные электромагнитные возбуждения, которые не могут быть представлены в терминах стандартного мультипольного разложения. Тороидальный дипольный момент представляет собой самый низкий момент третьего независимого семейства электромагнитных мультиполей после электрического и магнитного моментов. Свойства материалов, обладающих тороидальными моментами, и классификация их взаимодействия с внешними электромагнитными полями вызывают растущий интерес [8-14].

Введение в электромагнитный спектр

Электромагнитная энергия распространяется волнами и охватывает широкий спектр от очень длинных радиоволн до очень коротких гамма-лучей. Человеческий глаз может обнаружить только небольшую часть этого спектра, называемого видимым светом. Радио обнаруживает другую часть спектра, а рентгеновский аппарат использует еще одну часть. Научные инструменты НАСА используют весь спектр электромагнитного спектра для изучения Земли, Солнечной системы и Вселенной за ее пределами.

Когда вы настраиваете радио, смотрите телевизор, отправляете текстовое сообщение или готовите попкорн в микроволновой печи, вы используете электромагнитную энергию. Вы зависите от этой энергии каждый час каждого дня. Без него мир, который вы знаете, не мог бы существовать.

 

 

Наша защитная атмосфера

Наше Солнце является источником энергии всего спектра, и его электромагнитное излучение постоянно бомбардирует нашу атмосферу. Однако атмосфера Земли защищает нас от воздействия ряда волн более высокой энергии, которые могут быть опасны для жизни. Гамма-лучи, рентгеновские лучи и некоторые ультрафиолетовые волны являются «ионизирующими», то есть эти волны обладают такой высокой энергией, что могут выбивать электроны из атомов. Воздействие этих высокоэнергетических волн может изменить атомы и молекулы и вызвать повреждение клеток в органическом веществе. Эти изменения в клетках иногда могут быть полезными, например, когда радиация используется для уничтожения раковых клеток, а иногда нет, например, когда мы получаем солнечные ожоги.

Атмосферные окна

Взгляд за пределы нашей атмосферы. Космические корабли НАСА, такие как RHESSI, предоставляют ученым уникальную точку зрения, помогая им «видеть» в высокоэнергетических длинах волн, которые блокируются защитной атмосферой Земли.

Электромагнитное излучение отражается или поглощается главным образом несколькими газами в атмосфере Земли, наиболее важными из которых являются водяной пар, двуокись углерода и озон. Некоторое излучение, например видимый свет, в значительной степени проходит (передается) через атмосферу. Эти области спектра с длинами волн, которые могут проходить через атмосферу, называются «атмосферными окнами». Некоторые микроволны могут даже проходить сквозь облака, что делает их наилучшей длиной волны для передачи сигналов спутниковой связи.

Хотя наша атмосфера необходима для защиты жизни на Земле и поддержания жизни на планете, она не очень полезна, когда дело доходит до изучения источников высокоэнергетического излучения в космосе. Инструменты должны быть расположены над поглощающей энергию атмосферой Земли, чтобы «видеть» более высокие энергии и даже некоторые источники света с более низкими энергиями, такие как квазары.

К началу страницы  | Далее: Анатомия электромагнитной волны

---

Ссылка

APA

Национальное управление по аэронавтике и исследованию космического пространства, Управление научной миссии. (2010). Введение в электромагнитный спектр.