Эдс источника формула: Электродвижущая сила – Умскул Учебник

Определение эдс источника методом компенсации

0

ВЫСШИЙ ГОСУДАРСТВЕННЙ КОЛЛЕДЖ СВЯЗИ

КАФЕДРА МАТЕМАТИКИ И ФИЗИКИ

МЕТОДИЧЕСКОЕ РУКОВОДСТВО

к лабораторной работе № 3.3

по дисциплине «Физика»

для студентов всех специальностей

Минск

2004

Определение электродвижущей силы источника методом компенсации

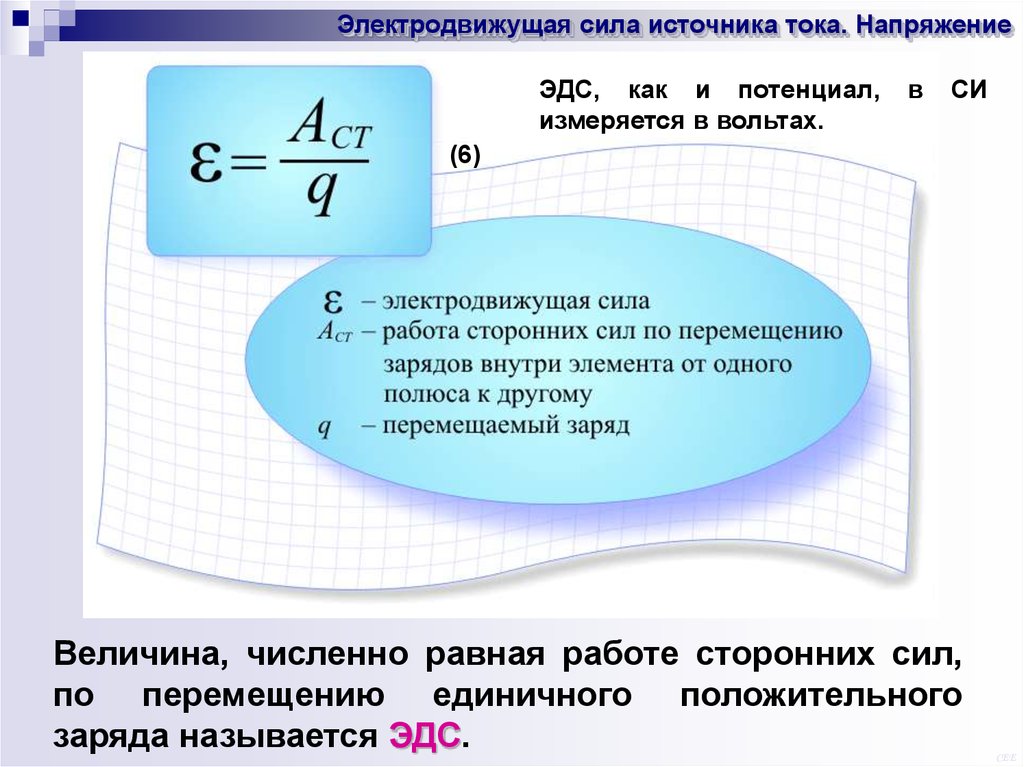
1. Электродвижущая сила

Условием движения электрических зарядов в проводнике является наличие в нем электрического поля, которое создается и поддерживается особыми устройствами, получившими название источники тока.

Основной величиной, характеризующей источник тока, является его электродвижущая сила. Электродвижущей силой (сокращенно ЭДС) называется скалярная физическая величина – количественная мера способности источника создавать на его зажимах (полюсах) разность потенциалов. Она равна работе сторонних сил по перемещению заряженной частицы с положительным единичным зарядом от одного полюса источника к другому, или вдоль замкнутой цепи, т.е.

. (1)

В СИ ЭДС измеряется в вольтах (В) ([ ] = 1 Дж/Кл = 1 В), т.е. в тех же единицах, что и напряжение.

Сторонние силы источника – это силы, которые осуществляют разделение зарядов в источнике и тем самым создают на его полюсах разность потенциалов. Они могут иметь самую различную природу, но только не электрическую (отсюда и название).

Если электрическую цепь разделить на два участка – внешний с сопротивлением и внутренний с сопротивлением , то ЭДС источника тока окажется равной сумме напряжений на внешнем и внутреннем участке цепи:

. (2)

По закону Ома напряжение на любом участке цепи определяется величиной протекающего тока и его сопротивлением:

.

Так как

,

то

, (3)

т.е. напряжение на полюсах источника замкнутой цепи зависит от соотношения сопротивлений внешнего и внутреннего участков цепи. Если , то . На этом основано приблизительное определение ЭДС при помощи вольтметра с большим сопротивлением, подключаемого к полюсам источника.

Только при отсутствии тока в источнике его ЭДС будет равна напряжению на полюсах. Величину ЭДС можно определить точно электростатическим методом или компенсационным методом. При измерении ЭДС электростатическим методом цепь остается разомкнутой, т.к. измерение разности потенциалов на полюсах источника производится прибором, не потребляющим тока (электрометр, электростатический вольтметр).

При применении компенсационного метода цепь источника замкнута, но необходимые отсчеты для определения ЭДС делаются в моменты отсутствия тока в источнике.

2. Компенсационный метод определения эдс

Сущность метода компенсации при измерении ЭДС заключается в подборе и определении напряжения на участке электрической цепи, равного ЭДС исследуемого источника тока.

Схема электрической цепи изображена на рис. 1, где – источник тока, – реостат, – реохорд.

Рис. 1

Параллельно к участку цепи включают исследуемый источник тока с неизвестной ЭДС и чувствительный гальванометр (рис. 1).

При замыкании ключа по ветви потечет ток . Движение электрических зарядов по этому участку обуславливается действием сил электрических полей, создаваемых источниками ₁ и . Если в точке подключен положительный полюс источника ₁, а к точке его отрицательный полюс, то поле, создаваемое в ветви источником ₁ окажется противоположным полю источника и ток будет определяться равенством:

, (4)

где – разность потенциалов точек и ,

₁ – ЭДС источника ₁,

– полное сопротивление ветви .

Разность потенциалов точек и численно равна падению напряжения на отрезке реохорда : .

Если напряжение на участке окажется больше ЭДС источника ₁, то по ветви потечет ток от к через источник ₁, если же будет меньше ₁, то ток потечет в обратную сторону. Стрелка гальванометра в обоих случаях будет отклоняться, но в разные стороны от нулевого деления.

Очевидно, что при полном совпадении значений и ₁ ток будет равен нулю и стрелка гальванометра при замкнутых ключах и совсем не даст отклонения.

Примечание: Равенство ₁ может быть осуществлено лишь при условии, когда ЭДС основного источника будет больше ЭДС исследуемого источника.

Напряжение на отрезке реохорда определяется сопротивлением и величиной тока , текущего по этому участку:

.

При отсутствии тока в ветви по всем участкам цепи течет ток одинаковой величины и его можно определить по закону Ома:

, (5)

где – ЭДС источника;

– полное сопротивление цепи .

Равенство можно практически получить изменением тока при сохранении величины или изменением сопротивлением при постоянном токе (для изменения служит реостат , величину измеряют перемещением движка реохорда).

В том и другом случае задача определения ЭДС сводится к измерению и .

Сопротивление единицы длины реохорда равно ( – длина реохорда , – сопротивление реохорда), поэтому сопротивление отрезка выразится так:

, (6)

где – длина реохорда .

Воспользовавшись формулой (5), выразим ЭДС исследуемого источника следующим образом:

₁ . (7)

Определение величины ЭДС по соотношению (7) требует предварительного измерения многих величин.

Однако задача упрощается при использовании компенсационного метода для сравнения ЭДС двух источников, один из которых является эталонным. Действительно, если вместо источника ₁ подключить источник ₂ с ЭДС ₂ ( ₂< ), то для него найдется такое положение движка реохорда , при котором напряжение на некотором участке реохорда с сопротивлением скомпенсирует ЭДС ₂. При компенсированной ЭДС элемента ₂ величина тока останется прежней, потому что полное сопротивление цепи не изменяется.

Аналогично (7) ЭДС источника ₂ можно выразить так:

₂ .

Отношение ЭДС источников равно отношению сопротивлений соответствующих участков реохорда или прости отношению их длин:

; .

Если ЭДС ₂ считать известной (эталонной), то ₁ определится из равенства:

₁₂. (8)

Путем сравнения чаще определяется ЭДС гальванических элементов. Эталонным источником при этом служит элемент с постоянной ЭДС, величина которой практически не зависит от температуры окружающей среды. Такие элементы называют

нормальными.

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2. 5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

домашнее задание и упражнения – Расчет ЭДС с сопротивлением и без него

спросил 8 лет, 8 месяцев назад

Изменено 3 года, 1 месяц назад

Просмотрено 11 тысяч раз

$\begingroup$

Батарея с внутренним сопротивлением 2 Ом подключена к внешнему сопротивлению 10 Ом. Сила тока 0,5 А. Чему равна ЭДС батареи?

Правильный ответ: 6,0 В. Когда я рассчитал это как последовательную цепь с 2 резисторами, я получил 6 В для ЭДС. Но я думал, что ЭДС не включает внутреннее сопротивление, поэтому я вычислил ее без внутреннего сопротивления и получил 5,0 В. Мне было интересно, может ли кто-нибудь прояснить это для меня?

• домашние задания и упражнения
• электрические цепи
• электрические сопротивления
• напряжение

$\endgroup$

$\begingroup$

При протекании тока внутри источника всегда наблюдается некоторое падение напряжения, поэтому напряжение на клеммах ниже, чем в статической ситуации.

Мы моделируем это поведение простой моделью, изображенной на вашей картинке; мы предполагаем, что реальный источник состоит из идеализированного источника -| |- что дает ЭДС и имеет не сопротивление, а обыкновенное омическое сопротивление (2$\Omega$ в вашем случае).

Под ЭДС источника мы подразумеваем число, дающее напряжение из-за идеализированного источника -||-, а не полное напряжение на реальном источнике при протекании тока, потому что последнее напряжение зависит от тока, а это зависит от того, какие элементы подключен к цепи.

При отсутствии тока нет падения напряжения на внутреннем сопротивлении, поэтому можно сказать, что ЭДС источника равна по величине напряжению, которое источник создает на своих внешних клеммах, когда ток не течет.

$\endgroup$

$\begingroup$

Если $E$ — ЭДС (напряжение холостого хода) батареи, а $r_s$ — внутреннее сопротивление, то уравнение, связывающее последовательный ток $I_S$ через внешнее сопротивление $R_L$, будет иметь вид:

$$I_S = \frac{E}{r_s + R_L}$$

Теперь напряжение на клеммах аккумулятора $V_{BAT}$ определяется как

$$V_{BAT} = E – I_S \ cdot r_s = E\frac{R_L}{r_s + R_L}$$

Таким образом, даже если мы не можем «увидеть» внутреннее сопротивление и измерить напряжение на нем, мы можем сделать вывод о его существовании на основании того факта, что клемма напряжение зависит от тока или, что то же самое, от внешнего резистора.

Конечно, внутри батареи нет резистора, но во многих случаях , моделирующий , такая зависимость напряжения на клеммах от тока с резистором является адекватной.

$\endgroup$

$\begingroup$

Гораздо проще использовать уравнение ЭДС, чтобы вычислить это:

$${\rm ЭДС} = I(R+r)$$

Где ЭДС – это то, что вы вычисляете (в вольтах)

$I = \rm Current$

$R =$ Сопротивление компонента (в данном случае резистора)

$r =$ Внутреннее сопротивление

Подставив числа, вы получите следующее:

$${\rm ЭДС} = 0,5(10+2)$$ $${\rm ЭДС} = 0,5(12)$$ $${\rm ЭДС} = 0,5 \times 12$$ $${\rm EMF} = 6~\rm V$$

Надеюсь, это помогло!

$\endgroup$

1

$\begingroup$

ЭДС=ток x(внутреннее сопротивление+внешнее сопротивление) ЭДС=0,5×[10+2] ЭДС=6В

$\endgroup$

1

15.4 Мощность в цепи переменного тока – University Physics Volume 2

Глава 15. Цепи переменного тока

Цели обучения

К концу этого раздела вы сможете:

• Описать, как можно представить среднюю мощность от цепи переменного тока через пиковый ток и напряжение и среднеквадратичное значение тока и напряжения
• Определить зависимость между фазовым углом тока и напряжения и средней мощностью, известную как коэффициент мощности

Элемент схемы рассеивает или производит мощность в соответствии с [латекс]P=IV,[/латекс], где I — ток через элемент, а В — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность [латекс]p\left(t\right)=i\left(t\right)v\left(t\right)[/latex] также зависит от времени. График p ( t ) для различных элементов схемы показан на рис. 15.16. Для резистора i ( t ) и v ( t ) находятся в фазе и поэтому всегда имеют один и тот же знак (см. рис. 15.5). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. рис. 15.7 и рис. 15.9). Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.

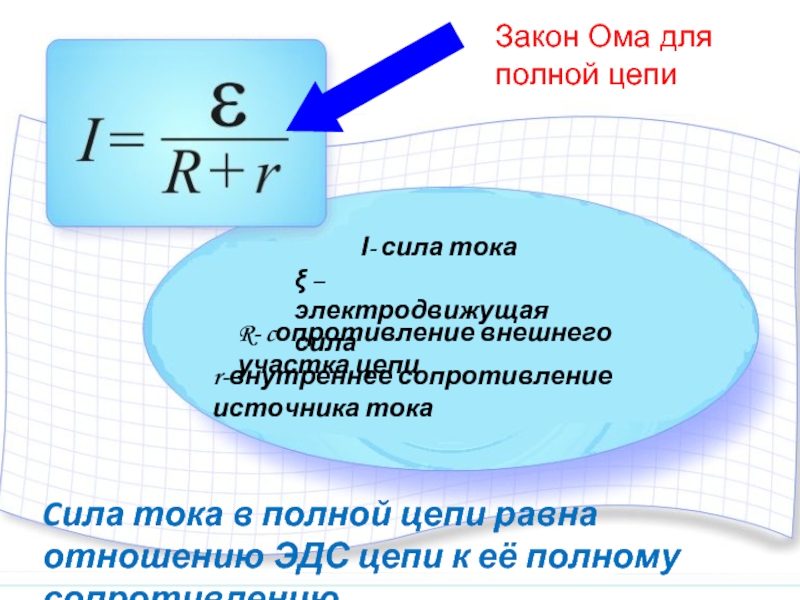Рисунок 15.16  График мгновенной мощности для различных элементов цепи. (a) Для резистора [латекс]{P}_{\text{ave}}={I}_{0}{V}_{0}\text{/}2,[/latex], тогда как для ( б) конденсатор и (в) катушка индуктивности [латекс] {P} _ {\ text {аве}} = 0. [/латекс] (г) для источника [латекс] {P} _ {\ text { ave}}={I}_{0}{V}_{0}\left(\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi \right)\text{/}2 ,[/latex], который может быть положительным, отрицательным или нулевым, в зависимости от [latex]\varphi .[/latex]

Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. Что нас почти всегда интересует, так это мощность, усредненная по времени, которую мы называем 9.{T}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\left(\omega t-\varphi\right)\phantom{\ правило {0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t\phantom{\rule{0.2em}{0ex}}dt.[/latex]

Используя тригонометрическое соотношение [латекс]\фантом{\правило{0.2em}{0ex}}\текст{sin}\фантом{\правило{0.2em}{0ex}}\left(AB\right)=\phantom{ \rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}A\text{cos}\phantom{\rule{0.2em}{0ex}}B-\ фантом {\ правило {0.2em} {0ex}} \ текст {sin} \ фантом {\ правило {0. 2em} {0ex}} B \ фантом {\ правило {0.2em} {0ex}} \ текст {cos} \ phantom{\rule{0.2em}{0ex}}A,[/latex] получаем 9{T}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t\text{cos}\phantom{\rule{0.2em }{0ex}}\omega tdt=0.[/latex]

Следовательно, средняя мощность, связанная с элементом схемы, равна

[латекс] {P} _ {\ text {ave}} = \ frac {1} {2} {I} _ {0} {V} _ {0} \ phantom {\ rule {0.2em} {0ex} }\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi .[/latex]

В инженерных приложениях [латекс]\текст{cos}\фантом{\правило{0.2em}{0ex}}\varphi[/латекс] известен как коэффициент мощности , равный 9.0137 , что является величиной, на которую мощность, подаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе. Для резистора [latex]\varphi =0,[/latex], поэтому средняя рассеиваемая мощность равна

.

[латекс] {P} _ {\ text {ave}} = \ frac {1} {2} {I} _ {0} {V} _ {0}.[/latex]

Сравнение p ( t ) и [latex]{P}_{\text{ave}}[/latex] показано на рис. 15.16(d). Чтобы [латекс]{P}_{\text{ave}}=\left(1\text{/}2\right){I}_{0}{V}_{0}[/latex] выглядел как его аналог на постоянном токе, мы используем среднеквадратичные значения {0ex}}{V}_{\text{rms}}[/latex] тока и напряжения. По определению это 9{2}\влево(т\вправо)дт.[/латекс]

С [латекс] я \ влево (т \ вправо) = {I} _ {0} \ фантом {\ правило {0.2em} {0ex}} \ текст {грех} \ фантом {\ правило {0.2em} {0ex }}\left(\omega t-\varphi\right)\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}v\left(t \right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t,[/latex] получаем

[латекс] {I} _ {\ text {rms}} = \ frac {1} {\ sqrt {2}} {I} _ {0} \ phantom {\ rule {0.2em} {0ex}} \ text {и}\phantom{\rule{0.2em}{0ex}}{V}_{\text{rms}}=\frac{1}{\sqrt{2}}{V}_{0}.[/ латекс] 9{2}Р.[/латекс]

Это уравнение еще раз подчеркивает, почему при обсуждении выбрано среднеквадратичное значение, а не пиковые значения. Оба уравнения для средней мощности верны для уравнения 15. 13, но среднеквадратические значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не нужен.

Переменные напряжения и токи обычно описываются их действующими значениями. Например, 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна [латекс]110\sqrt{2}\phantom{\rule{0.2em}{0ex}}\text{V}=\text{156 В}\text{.}[/latex] Потому что большинство счетчиков переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, подключенный к бытовой розетке, покажет 110 В.

Для конденсатора и катушки индуктивности [латекс]\varphi =\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{ 0ex}}-\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{rad,}[/latex] соответственно. Поскольку [latex]\text{cos}\pi \text{/}2=\text{cos}\left(\text{−}\pi \text{/}2\right)=0,[/latex] мы найдите из уравнения 15.12, что средняя мощность, рассеиваемая любым из этих элементов, равна [латекс] {P} _ {\ text {аве}} = 0. [/латекс] Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода и затем разрядите его обратно в цепь в течение другого полупериода. Это поведение показано на графиках рис. 15.16, (б) и (в), которые показывают p( t) колеблется синусоидально около нуля.

Фазовый угол генератора переменного тока может иметь любое значение. Если [latex]\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi > 0,[/latex] генератор вырабатывает энергию; если [латекс]\текст{cos}\фантом{\правило{0.2em}{0ex}}\varphi

[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ phantom {\ rule {0.2em} {0ex }}\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi .[/latex]

Для генератора в цепи RLC ,

9{2}R,[/латекс]

, что означает, что мощность, вырабатываемая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс. {4} \ текст {рад} \ текст{/} \ текст {s} \ справа) t \ справа][/латекс] 9{-6}\phantom{\rule{0.2em}{0ex}}\text{F}[/latex] и [латекс]R=5.00\phantom{\rule{0.2em}{0ex}}\text{ Ω}[/латекс]. а) Чему равно среднеквадратичное напряжение на генераторе? б) Чему равно сопротивление цепи? в) Какова средняя мощность генератора?

Стратегия

Среднеквадратичное напряжение — это амплитуда напряжения, умноженная на [latex]1\text{/}\sqrt{2}[/latex]. Полное сопротивление цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по уравнению 15.14 или, точнее, по последней части уравнения, потому что у нас есть импеданс цепи Z , среднеквадратичное напряжение [латекс] {V} _ {\ text {среднеквадратичное значение}} [/латекс] и сопротивление R .

Решение

Показать ответ

1. Поскольку [латекс]{V}_{0}=4.00\phantom{\rule{0.2em}{0ex}}\text{V,}[/latex] среднеквадратичное значение напряжения на генератор

   [латекс] {V} _ {\ text {rms}} = \ frac {1} {\ sqrt {2}} \ left (4. {1\text{/}2}\hfill \\ & =7.07\phantom{\rule{0.2em}{0ex }}\text{Ω}\text{.}\hfill \end{массив}[/latex] 9{2}\text{/}R,[/latex], где 90 053 В 90 054 заменяет среднеквадратичное значение напряжения.

   Проверьте свои знания

   Вольтметр переменного тока, подключенный к клеммам генератора переменного тока частотой 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.

   Показать решение

   [латекс]v\left(t\right)=\left(10.0\phantom{\rule{0.2em}{0ex}}\text{V}\right)\phantom{\rule{0.2 em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}90\pi t[/latex]

   Проверьте свои знания

   Покажите, что среднеквадратичное значение напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока со среднеквадратичным значением тока равно [латекс]{I}_{\text{среднеквадратичное значение}}[/латекс] по [латексу] {I} _ {\ text {rms}} R, {I} _ {\ text {rms}} {X} _ {C}, \ phantom {\ rule {0.2em} {0ex}} \ text{and}\phantom{\rule{0.2em}{0ex}}{I}_{\text{rms}}{X}_{L},[/latex] соответственно. Определить эти значения для компонентов Цепь RLC уравнения 15.12.

   Show Solution

   2,00 В; 10,01 В; 8,01 В

   Сводка

   • Средняя мощность переменного тока находится путем умножения среднеквадратичных значений тока и напряжения.
   • Закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.
   • В цепи переменного тока существует угол сдвига фаз между напряжением источника и током, который можно найти, разделив сопротивление на импеданс.
   • Средняя мощность, подаваемая на На цепь RLC влияет фазовый угол.
   • Коэффициент мощности находится в диапазоне от –1 до 1.

   Концептуальные вопросы

   При каком значении фазового угла [latex]\varphi[/latex] между выходным напряжением источника переменного тока и током средняя выходная мощность источника максимальна?

   Обсудите разницу между средней мощностью и мгновенной мощностью.

   Показать решение

   Мгновенная мощность — это мощность в данный момент времени. Средняя мощность — это мощность, усредненная по циклу или количеству циклов.

   Средний переменный ток, подаваемый в цепь, равен нулю. Несмотря на это, мощность рассеивается в цепи. Объяснять.

   Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?

   Показать решение

   Мгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.

   Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?

   Задачи

   ЭДС источника переменного тока определяется выражением [латекс]v\left(t\right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin} \phantom{\rule{0.2em}{0ex}}\omega t,[/latex], где [latex]{V}_{0}=100\phantom{\rule{0. 2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{рад/с}\text{.}[/latex] Вычислить среднюю выходную мощность источника, если он подключен через (a) конденсатор [латекс]20\text{-}\mu \text{F}[/латекс], (б) катушку индуктивности 20 мГн и (в) [латексный ]50\text{-}\text{Ом}[/latex] резистор.

   Расчет среднеквадратичного значения тока для источника переменного тока определяется выражением [латекс]v\left(t\right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin} \phantom{\rule{0.2em}{0ex}}\omega t,[/latex], где [latex]{V}_{0}=100\phantom{\rule{0.2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{rad/s}[/latex] при соединении через (a) [латекс] 20\text{-}\mu \text{F}[/latex] конденсатор, (b) катушка индуктивности 20 мГн и (c) [латекс]50\text{-}\text{Ом}[/latex ] резистор.

   Показать решение

   а. 0,89 А; б. 5,6 А; в. 1,4 А

   Катушка индуктивности 40 мГн подключена к источнику переменного тока частотой 60 Гц, амплитуда напряжения которого составляет 50 В. Если к катушке индуктивности приложить вольтметр переменного тока, что он покажет?

   Для цепи RLC серии амплитуда напряжения и частота источника 100 В и 500 Гц соответственно; [латекс] R = 500 \ фантом {\ правило {0.2em} {0ex}} \ текст {Ω} [/латекс]; и [латекс] L = 0,20 \ фантом {\ правило {0,2em} {0ex}} \ текст {H} [/латекс]. Найдите среднюю мощность, рассеиваемую на резисторе, при следующих значениях емкости: (а) [латекс]С=2,0 мкМ \текст{F}[/латекс] и (б) [латекс]С=0,20\фантом{\ правило{0.2em}{0ex}}\mu \text{F}\text{.}[/latex]

   Показать раствор

   а. 7,3 Вт; б. 6,3 Вт

   Источник переменного тока с амплитудой напряжения 10 В отдает электрическую энергию мощностью 0,80 Вт при выходном токе 2,5 А. Каков фазовый угол [латекс]\varphi[/латекс] между ЭДС и током?

   Цепь серии RLC имеет импеданс [латекс]60\фантом{\правило{0.2em}{0ex}}\текст{Ом}[/латекс] и коэффициент мощности 0,50, при этом напряжение отстает от текущий. а) Следует ли последовательно с элементами включить конденсатор или катушку индуктивности, чтобы повысить коэффициент мощности цепи? б) При каком значении реактивного сопротивления катушки индуктивности коэффициент мощности увеличится до единицы?

   Показать раствор

   а.