Главная
Эдс источника тока определяется выражением: Определите ЭДС источника электрической энергии с внутренним сопротивлением 0,25 Ом, если при замыкании его железным…

Эдс источника тока определяется выражением: Определите ЭДС источника электрической энергии с внутренним сопротивлением 0,25 Ом, если при замыкании его железным…

Содержание

Источник тока. Сторонние силы. Эдс источника тока

Остановимся на отдельных закономерностях тока проводи­мости. Пусть на концах проводника длиной l имеется разность по­тенциалов Δφ=φ1–φ2=U, которая создает внутри него электри­ческое поле напряженностью Е, направленное в сторону падения потенциала (рис. 92), . При этом в проводнике возникнет ток от большего потен­циала φ1 к меньшему φ2.

l

Рис. 92

Движение зарядов от φ1 к φ2 приводит к снижению большего (φ1) и повышению меньшего (φ2) потенциала, т.е. к выравниванию потенциалов. Как только потенциалы выравниваются, электрическое поле в проводнике исчезнет и ток прекратится. Таким образом, для поддержания электрического тока необходимо иметь специальные устройства, которые бы поддерживали на его концах разность по­тенциалов. Такое устройство называется источником тока.

Источ­никами тока являются электрические генераторы, гальванические и термоэлементы, аккумуляторы. Направление тока в устройстве про­тивоположно направлению тока в проводнике. Источник тока вы­полняет и другую роль – он замыкает цепь, по которой осуществля­ется непрерывное движение зарядов. Ток течет по внешней части цепи – проводнику и по внутренней – источнику тока. Источник тока имеет два полюса: положительный с более высоким потенциа­лом и отрицательный – с более низким. При разомкнутой цепи на отрицательном полюсе (выводе) источника тока образуется избыток электронов, а на положительном – недостаток. Разделение зарядов в источнике тока производится с помощью внешних сил, так назы­ваемых сторонних, направленных против кулоновских сил, дейст­вующих на разноименные заряды в проводниках самого источника тока. Природа этих сторонних сил может быть самой различной (химической, механической, электромагнитной).

Рис.93

Если цепь, со­стоящая из проводника и источника тока, замкнута, то по ней про­ходит ток и при этом совершается работа сторонних сил Аст. (рис. 93). Эта работа складывается из работы, совершаемой против сил электрического поля внутри источника тока ( Аист.) и работы, совершаемой против механических сил сопротивления среды ис­точника ( А’ ), т.е. А

ст. = Аист + А’.

Величина, равная отношению работы, которую совершают сторон­ние силы при перемещении точечного положительного заряда Q вдоль всей цепи, (включая и источник тока), к величине заряда Q называют ЭДС источника тока ؏

؏ = .

Работа против сил электрического поля (по определению) равна

Аист. = Q ( φ1 – φ2).

Если полюсы источника разомкнуты, то А’ = 0, и тогда из формулы для ؏

следует ؏ = φ1 – φ2, т.е. ЭДС источника тока при разомкнутой внешней цепи равна раз­ности потенциалов, которая создается на его полюсах.

Электроны проводимости в отсутствие электрического поля внутри металла хаотически движутся и сталкиваются с ионами кри­сталлической решетки металла. При этом в силу хаотичности про­исходит эквивалентный обмен энергией между ними.

При наложении поля электрон приобретает скорость направ­ленного движения и на длине свободного пробега некоторую кине­тическую энергию. При соударении с ионом электрон теряет часть этой энергии, которая преобразуется во внутреннюю энергию про­водника (он нагревается). Другими словами, электрон испытывает сопротивление своему движению под действием поля. Мерой этого сопротивления у каждого вещества является величина удельного сопротивления ρ [Ом·м].

Сопротивление проводника постоянного сечения определя­ется выражением

R = ,

где l – длина проводника, S – площадь поперечного сечения.

Единица измерения – Ом.

Предположим, что два проводника соединены последовательно (рис. 94). Через оба проходит одинаковый заряд за одно и то же время, т.е.

I1 = I2 = I; U1 = φ1 – φ2

; U2 = φ2 – φ3;

Рис. 94

Отсюда U1 =I1 R1 = I R1; U2=I2 R2 =I R2; U1 + U2 = I (R1 + R2). Но U = U1 + U2 = φ1 – φ3, следовательно, U =I (R1 + R2) и R=R1+R2.

Для n последовательно соединенных проводников их суммарное сопротивление R будет равно

.

При параллельном соединении проводников (рис. 95) напряжение на участке АВ для обоих проводников будет оди­наковым U = U1 = U2. На входе в группу параллельных про­водников (в точке А) происхо­дит разветвление тока. Из закона сохранения заряда следует, что ток I равен сумме токов I1 и I2

I = I1 + I2 = .

В свою очередь, на всем участке

,

где R – общее сопротивление проводников.

Откуда

.

Для n проводников при их параллельном соединении суммарное со­противление R определяется из выражения

UNEC – Azərbaycan Dövlət İqtisad Universiteti — Page not found

Why UNEC?

Regionda iqtisad elmini dərindən öyrədən fundamental tədris mərkəzidir;
Tədris prosesi və kadr hazırlığı Amerika və Avropa təhsil sisteminə uyğundur;
İxtisaslar bakalavr, magistr və doktorantura təhsil pillələri üzrə
azərbaycan, ingilis, rus və türk dillərində tədris edilir;
Auditoriyada mərkəz nöqtəsi tələbədir;
Tələbə universiteti iki və daha çox ixtisasla (dual major) bitirə bilər;
Tələbələrin müxtəlif mübadilə proqramlarında iştirak etmək imkanı vardır;

Universitetdə 10 fakültə və 17 kafedra fəaliyyət gös­tərir;
403 professor və dosent çalışır.

Son xəbərlər Elanlar Bütün xəbərlər ALL ANNOUNCEMENTS

The Journal of Economic Sciences: Theory and Practice

№ 2

ECONOMIC HERITAGE OF HEYDAR ALIYEV

Connect with
rector

  • Graduates

    Mikayıl Cabbarov

    İqtisadiyyat naziri

  • Graduates

    Ceyhun Bayramov

    Xarici işlər naziri

  • Graduates

    Şahin Mustafayev

    Azərbaycan Respublikası Baş Nazirinin müavini

  • Graduates

    Muxtar Babayev

    Ekologiya və təbii sərvətlər naziri

  • Graduates

    Fərid Qayıbov

    Gənclər və idman naziri

  • Graduates

    Səttar Möhbalıyev

    Azərbaycan Həmkarlar İttifaqları Konfederasiyasının sədri

  • Graduates

    Vüqar Gülməmmədov

    Hesablama Palatasının sədri

  • Graduates

    Vüsal Hüseynov

    Dövlət Miqrasiya Xidmətinin rəisi

  • Graduates

    Ramin Quluzadə

    Azərbaycan Respublikası Prezidentinin İşlər müdiri

  • Graduates

    Natiq Əmirov

    Azərbaycan Respublikası Prezidentinin İqtisadi islahatlar üzrə köməkçisi

  • Graduates

    Kərəm Həsənov

    Prezident Administrasiyasının Dövlət nəzarəti məsələləri şöbəsinin müdiri

  • Graduates

    Azər Əmiraslanov

    Nazirlər Kabineti Aparatının İqtisadiyyat şöbəsinin müdiri

  • Graduates

    Rövşən Nəcəf

    AR Dövlət Neft Şirkətinin prezidenti

  • Graduates

    Firudin Qurbanov

    Elm və təhsil nazirinin müavini

  • Graduates

    İdris İsayev

    Elm və təhsil nazirinin müavini

  • Graduates

    Sevinc Həsənova

    İqtisadiyyat nazirinin müavini

  • Graduates

    Şirzad Abdullayev

    İqtisadiyyat nazirinin müşaviri

  • Graduates

    Azər Bayramov

    Maliyyə nazirinin müavini

  • Graduates

    Sahib Məmmədov

    İqtisadiyyat nazirinin müavini

  • Graduates

    Məmməd Musayev

    Azərbaycan Respublikası Sahibkarlar (İşəgötürənlər) Təşkilatları Milli Konfederasiyasının prezidenti

  • Graduates

    Vüsal Qasımlı

    İqtisadi İslahatların Təhlili və Kommunikasiya Mərkəzinin direktoru

  • Graduates

    İlqar Rəhimov

    Milli Paralimpiya Komitəsinin prezidenti

  • Graduates

    Rüfət Rüstəmzadə

    Qida Təhlükəsizliyi Agentliyinin sədr müavini

  • Graduates

    Rəşad Mafusov

    Qida Təhlükəsizliyi Agentliyinin sədr müavini

  • Graduates

    Rauf Səlimov

    Dövlət Statistika Komitəsi sədrinin müavini

  • Graduates

    Cabbar Musayev

    Dövlət Statistika Komitəsinin Aparat rəhbəri

  • Graduates

    Fərhad Hacıyev

    Gənclər və idman nazirinin müavini

  • Graduates

    Süleyman Qasımov

    AR Dövlət Neft Şirkətinin iqtisadi məsələlər üzrə vitse-prezidenti

  • Graduates

    Fərhad Tağı-zadə

    General-leytenant

  • Graduates

    Ziyad Səmədzadə

    Millət vəkili

  • Graduates

    Xanhüseyn Kazımlı

    Azərbaycan Sosial Rifah Partiyasının sədri

  • Graduates

    Mikayıl İsmayılov

    AR Dövlət Neft Şirkətinin vitse-prezidenti

  • Graduates

    Vahab Məmmədov

    Dövlət Statistika Komitəsi sədrinin birinci müavini

  • Graduates

    Yusif Yusifov

    Dövlət Statistika Komitəsi sədrinin müavini

  • Graduates

    Fəxrəddin İsmayılov

    Auditorlar Palatası sədrinin müavini

  • Graduates

    Xalid Əhədov

    Birinci vitse-prezidentin köməkçisi

  • Graduates

    Emin Hüseynov

    Birinci vitse-prezidentin köməkçisi

  • Graduates

    Qəşəm Bayramov

    Auditorlar Palatası aparatının rəhbəri

  • Graduates

    Rafiq Aslanov

    Meliorasiya və Su Təsərrüfatı Açıq Səhmdar Cəmiyyətinin sədr müavini

  • Graduates

    Tahir Mirkişili

    Millət vəkili, Milli Məclisin İqtisadi siyasət, sənaye və sahibkarlıq komitəsinin sədri

  • Graduates

    Əli Məsimli

    Millət vəkili

  • Graduates

    Vüqar Bayramov

    Millət vəkili

  • Graduates

    Eldar Quliyev

    Millət vəkili

  • Graduates

    Əli Nuriyev

    AMEA-nın müxbir üzvü

  • Graduates

    İqbal Məmmədov

    Millət vəkili

  • Graduates

    Şahin Əliyev

    Nəqliyyat, Rabitə və Yüksək Texnologiyalar Nazirliyi yanında Elektron Təhlükəsizlik Xidmətinin rəisi

  • Graduates

    Şahin Bayramov

    Mingəçevir Dövlət Universitetinin rektoru

  • Graduates

    Balakişi Qasımov

    İctimai Televiziya və Radio Yayımları Şirkətinin baş direktoru

  • Graduates

    Elnur Rzayev

    Xaçmaz Rayon İcra Hakimiyyətinin başçısı

  • Graduates

    Kamran İbrahimov

    “Azərpoçt” MMC-nin baş direktor müavini

  • Graduates

    Alim Quliyev

    Mərkəzi Bankın sədrinin birinci müavini

  • Graduates

    Vadim Xubanov

    Mərkəzi Bankın sədrinin müavini

  • Graduates

    Aftandil Babayev

    Mərkəzi Bankın sədrinin müavini

  • Graduates

    Mehman Məmmədov

    “Expressbank” ASC-nin İdarə Heyətinin sədri

  • Graduates

    Anar Həsənov

    AccessBankın İdarə Heyətinin Sədri

  • Graduates

    Fərid Hüseynov

    “Kapital Bank”ın İdarə Heyəti sədrinin I müavini

  • Graduates

    Rövşən Allahverdiyev

    Kapital Bankın İdarə Heyətinin sədri

  • Graduates

    Rza Sadiq

    “Bank BTB” Müşahidə Şurasının Sədri

  • Graduates

    Elnur Qurbanov

    “AFB Bank” ASC-nin Müşahidə Şurasının Sədri

  • Graduates

    Zaur Qaraisayev

    “AFB Bank” ASC-nin İdarə Heyətinin Sədri

  • Graduates

    Kamal İbrahimov

    “Baku Steel Company” şirkətinin direktoru

  • Graduates

    Vaqif Həsənov

    “Qarant Sığorta” ASC-nin İdarə Heyətinin sədri

Elektron Kitabxana

ABCÇDEƏFGĞHXIİJKQLMNOÖPRSŞTUÜVYZ0-9

Налоги и налогообложение в Азербайджане

460 PAGES | DOWNLOAD

Dördüncü sənaye inqilabı

204 PAGES | DOWNLOAD

Mühasibat hesabatı

258 PAGES | DOWNLOAD

İaşə məhsullarının texnologiyası kursundan laboratoriya praktikumu

219 PAGES | DOWNLOAD

Susuz həyat yoxdur

215 PAGES | DOWNLOAD

Elektron kommersiya

212 PAGES | DOWNLOAD

www. president.az www.mehriban-aliyeva.org www.heydar-aliyev-foundation.org www.azerbaijan.az www.edu.gov.az www.tqdk.gov.az www.economy.gov.az www.science.gov.az www.azstat.org www.atgti.az www.virtualkarabakh.az www.ecosciences.edu.az www.polpred.com

15.2: Источники переменного тока – Physics LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    4442
    • OpenStax
    • OpenStax
    Цели обучения

    К концу раздела вы сможете:

    • Объяснять разницу между постоянным (постоянным) и переменным током (переменный)
    • Определение характеристик переменного тока и напряжения, таких как амплитуда или пик и частота

    Большинство примеров, рассмотренных до сих пор в этой книге, особенно те, которые используют батареи, имеют источники постоянного напряжения. Таким образом, как только ток установлен, он является постоянным. Постоянный ток (пост. ток) — это поток электрического заряда только в одном направлении. Это устойчивое состояние цепи постоянного напряжения.

    Однако в большинстве известных приложений используется переменный во времени источник напряжения. Переменный ток (ac) — это поток электрического заряда, который периодически меняет направление. Переменный ток создается переменной ЭДС, которая генерируется на электростанции, как описано в Индуцированных электрических полях. Если источник переменного тока периодически меняется, особенно синусоидально, цепь называется цепью переменного тока. Примеры включают коммерческую и жилую энергию, которая удовлетворяет многие из наших потребностей.

    Напряжение и частота переменного тока, обычно используемые на предприятиях и дома, различаются по всему миру. В типичном доме разность потенциалов между двумя сторонами электрической розетки меняется синусоидально с частотой 60 или 50 Гц и амплитудой 170 или 311 В, в зависимости от того, живете ли вы в США или Европе соответственно.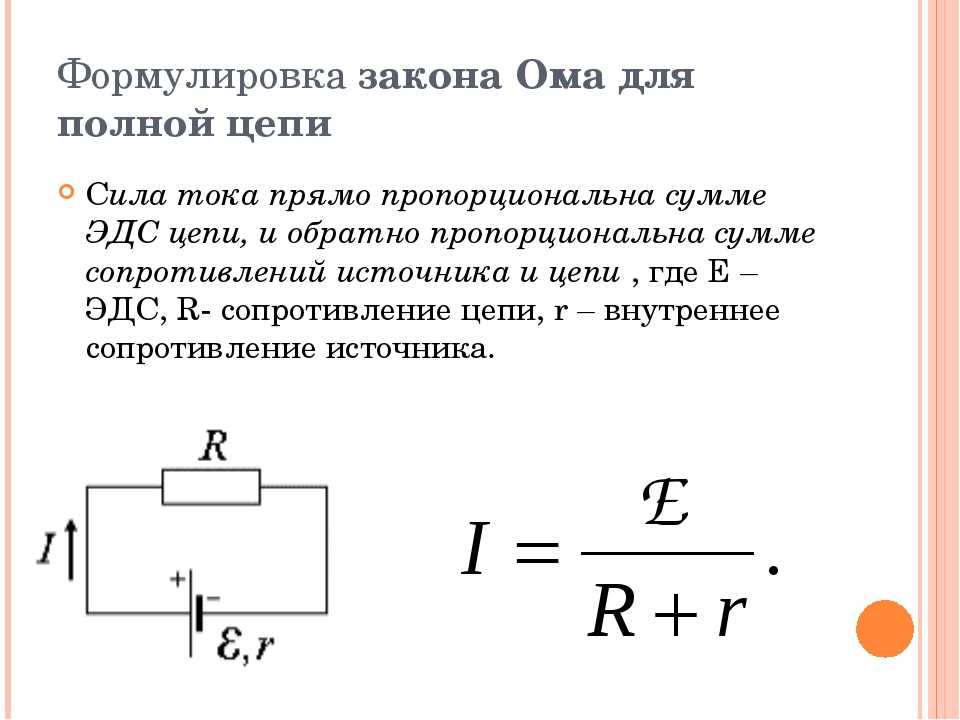 Большинство людей знают, что разность потенциалов для электрических розеток составляет 120 В или 220 В в США или Европе, но, как поясняется далее в этой главе, эти напряжения не являются пиковыми значениями, приведенными здесь, а скорее связаны с обычными напряжениями, которые мы видим в нашей таблице. электрические розетки. На рисунке \(\PageIndex{1}\) показаны графики зависимости напряжения и силы тока от времени для типичной мощности постоянного и переменного тока в США.

    Рисунок \(\PageIndex{1}\): (a) Напряжение и ток постоянного тока постоянны во времени после установления тока. (b) Зависимость напряжения и тока от времени для переменного тока сильно различается. В этом примере, который показывает мощность переменного тока 60 Гц и время t в миллисекундах, напряжение и ток синусоидальны и находятся в фазе для простой цепи сопротивления. Частоты и пиковые напряжения источников переменного тока сильно различаются.

    Предположим, мы подключаем резистор к источнику переменного напряжения и определяем, как во времени меняются напряжение и ток на резисторе. На рисунке \(\PageIndex{2}\) показана схема простой цепи с источником переменного напряжения. Напряжение колеблется синусоидально во времени с фиксированной частотой, как показано, либо на клеммах батареи, либо на резисторе. Следовательно, напряжение переменного тока или «напряжение на вилке» может быть указано как

    \[v(t) = V_0 \, \sin\, \omega t,\]

    где

    • \(v\) – напряжение в момент времени \(t\),
    • \(V_0\) – пиковое напряжение, а
    • \(\omega\) – угловая частота в радианах в секунду.

    Для типичного дома в США \(V_0 = 156 \, V\) и \(\omega = 120 \pi \, рад/с\), тогда как в Европе \(V_0 = 311 \, V \) и \(\omega = 100 \pi \, рад/с\).

    Рисунок \(\PageIndex{2}\): Разность потенциалов В между клеммами источника переменного напряжения колеблется, поэтому источник и резистор имеют синусоидальные волны переменного тока друг над другом. Математическое выражение для v имеет вид \(v = V_0 \, sin \, \omega t\).

    Для этой простой цепи сопротивления \(I = V/R\), поэтому переменный ток , то есть ток, синусоидально колеблющийся со временем на фиксированной частоте, равен

    \[i(t) = I_0 \, \sin \, \omega t,\]

    где

    • \(i(t)\) – ток в момент времени \(t\) и
    • \(I_0\) – пиковый ток, равный \(V_0/R\).

    В этом примере говорят, что напряжение и ток находятся в фазе, что означает, что их синусоидальные функциональные формы имеют пики, впадины и узлы в одном и том же месте. Они колеблются синхронно друг с другом, как показано на рисунке \(\PageIndex{1b}\). В этих уравнениях и во всей этой главе мы используем строчные буквы (например, \(i\)) для обозначения мгновенных значений и заглавные буквы (например, \(I\)) для обозначения максимальных или пиковых значений.

    Ток в резисторе колеблется туда-сюда точно так же, как управляющее напряжение, поскольку \(I = V/R\). Например, если резистор представляет собой люминесцентную лампочку, она становится ярче и тускнеет 120 раз в секунду, поскольку ток многократно проходит через ноль. Мерцание с частотой 120 Гц слишком быстрое для ваших глаз, но если вы помашете рукой туда-сюда между лицом и флуоресцентным светом, вы увидите стробоскопический эффект переменного тока.

    Упражнение \(\PageIndex{1}\)

    Если рассматривается европейский источник переменного напряжения, какова разница во времени между переходами через нуль на графике зависимости переменного напряжения от времени?

    Решение

    10 мс

    Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими соавторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

    Эта страница под названием 15.2: AC Sources распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        ОпенСтакс
        Лицензия
        СС BY
        Версия лицензии
        4,0
        Программа OER или Publisher
        ОпенСтакс
        Показать оглавление
        нет
      2. Теги
        1. Переменный ток
        2. Напряжение переменного тока
        3. переменный ток
        4. постоянный ток
        5. источник@https://openstax. org/details/books/university-physics-volume-2

      15.4 Мощность в цепи переменного тока – University Physics Volume 2

      Глава 15. Цепи переменного тока

      Цели обучения

      К концу этого раздела вы сможете:

      • Описывать, как можно представить среднюю мощность в цепи переменного тока через пиковый ток и напряжение и среднеквадратичное значение тока и напряжения
      • Определить зависимость между фазовым углом тока и напряжения и средней мощностью, известную как коэффициент мощности

      Элемент схемы рассеивает или производит мощность в соответствии с [латекс]P=IV,[/латекс], где I — ток через элемент, а В — напряжение на нем. Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность [латекс]p\left(t\right)=i\left(t\right)v\left(t\right)[/latex] также зависит от времени. Сюжет р ( т ) для различных элементов схемы показан на рисунке 15.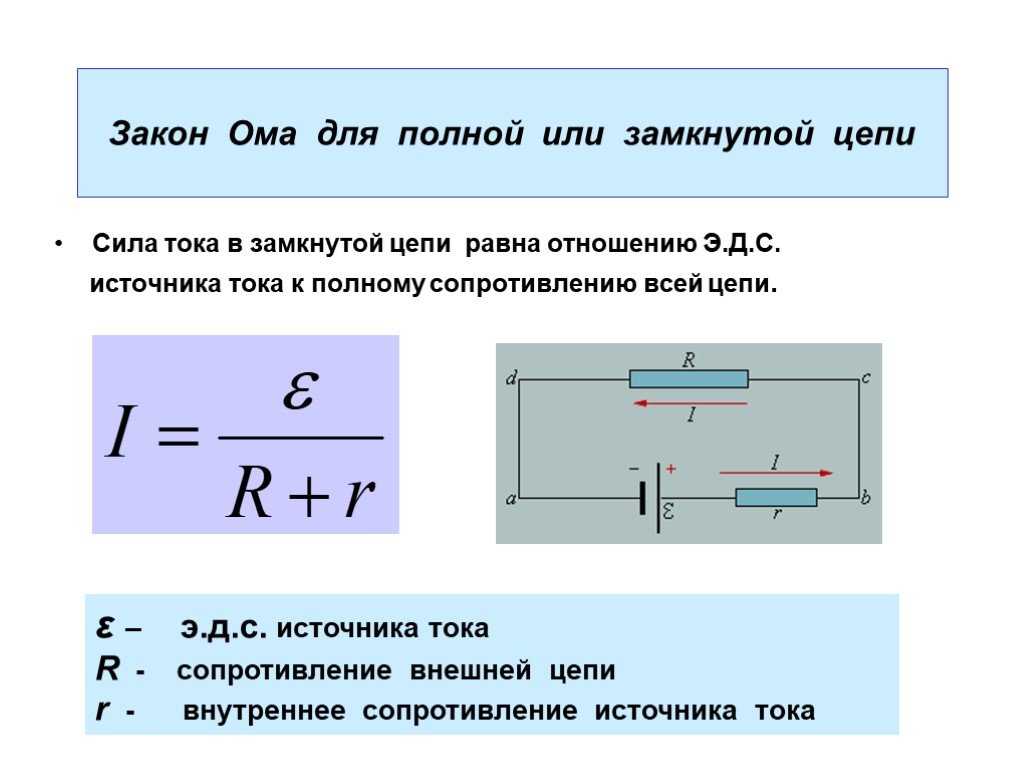 16. Для резистора i ( t ) и v ( t ) совпадают по фазе и поэтому всегда имеют один и тот же знак (см. рис. 15.5). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разности фаз (см. рис. 15.7 и рис. 15.9). Следовательно, p ( t ) в одни моменты времени положителен, а в другие отрицателен, указывая на то, что емкостные и индуктивные элементы производят мощность в одни моменты времени и поглощают ее в другие.

      Рисунок 15.16  График мгновенной мощности для различных элементов цепи. (a) Для резистора [латекс]{P}_{\text{ave}}={I}_{0}{V}_{0}\text{/}2,[/latex], тогда как для ( б) конденсатор и (в) катушка индуктивности [латекс] {P} _ {\ text {аве}} = 0. [/латекс] (г) для источника [латекс] {P} _ {\ text { ave}}={I}_{0}{V}_{0}\left(\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi \right)\text{/}2 ,[/latex], который может быть положительным, отрицательным или нулевым, в зависимости от [latex]\varphi . [/latex]

      Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. Что нас почти всегда интересует, так это мощность, усредненная по времени, которую мы называем 9.{T}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\left(\omega t-\varphi\right)\phantom{\ правило {0.2em} {0ex}} \ text {sin} \ phantom {\ правило {0.2em} {0ex}} \ omega t \ phantom {\ правило {0.2em} {0ex}} дт. [/латекс]

      Использование тригонометрического соотношения [латекс]\фантом{\правило{0.2em}{0ex}}\текст{sin}\фантом{\правило{0.2em}{0ex}}\left(AB\right)=\phantom{ \rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}A\text{cos}\phantom{\rule{0.2em}{0ex}}B-\ фантом {\ правило {0.2em} {0ex}} \ текст {sin} \ фантом {\ правило {0.2em} {0ex}} B \ фантом {\ правило {0.2em} {0ex}} \ текст {cos} \ phantom{\rule{0.2em}{0ex}}A,[/latex] получаем 9{T}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t\text{cos}\phantom{\rule{0. 2em }{0ex}}\omega tdt=0.[/latex]

      Следовательно, средняя мощность, связанная с элементом схемы, равна

      .

      [латекс] {P} _ {\ text {ave}} = \ frac {1} {2} {I} _ {0} {V} _ {0} \ phantom {\ rule {0.2em} {0ex} }\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi .[/latex]

      В инженерных приложениях [латекс]\текст{cos}\фантом{\правило{0.2em}{0ex}}\varphi[/латекс] известен как коэффициент мощности , равный 9.0043 , что является величиной, на которую мощность, подаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе. Для резистора [latex]\varphi =0,[/latex], поэтому средняя рассеиваемая мощность равна

      .

      [латекс] {P} _ {\ text {ave}} = \ frac {1} {2} {I} _ {0} {V} _ {0}.[/latex]

      Сравнение p ( t ) и [латекс]{P}_{\text{ave}}[/latex] показано на рис. 15.16(d). Чтобы [латекс]{P}_{\text{ave}}=\left(1\text{/}2\right){I}_{0}{V}_{0}[/latex] выглядел как его аналог на постоянном токе, мы используем среднеквадратичные значения {0ex}}{V}_{\text{rms}}[/latex] тока и напряжения. По определению это 9{2}\влево(т\вправо)дт.[/латекс]

      С [латекс]i\left(t\right)={I}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex }}\left(\omega t-\varphi\right)\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}v\left(t \right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\omega t,[/latex] получаем

      [латекс] {I} _ {\ text {rms}} = \ frac {1} {\ sqrt {2}} {I} _ {0} \ phantom {\ rule {0.2em} {0ex}} \ text {и}\phantom{\rule{0.2em}{0ex}}{V}_{\text{rms}}=\frac{1}{\sqrt{2}}{V}_{0}.[/ латекс] 9{2}Р.[/латекс]

      Это уравнение еще раз подчеркивает, почему при обсуждении выбрано среднеквадратичное значение, а не пиковые значения. Оба уравнения для средней мощности верны для уравнения 15.13, но среднеквадратические значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не нужен.

      Переменные напряжения и токи обычно описываются их действующими значениями. Например, 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника составляет [латекс]110\sqrt{2}\phantom{\rule{0.2em}{0ex}}\text{V}=\text{156 В}\text{.}[/latex] Потому что большинство счетчиков переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, подключенный к бытовой розетке, покажет 110 В.

      Для конденсатора и катушки индуктивности [латекс]\varphi =\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{ 0ex}}-\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{rad,}[/latex] соответственно. Поскольку [latex]\text{cos}\pi \text{/}2=\text{cos}\left(\text{−}\pi \text{/}2\right)=0,[/latex] мы найдите из уравнения 15.12, что средняя мощность, рассеиваемая любым из этих элементов, равна [латекс] {P} _ {\ text {аве}} = 0. [/латекс] Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода и затем разрядите его обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках рис. 15.16, (б) и (в), которые показывают p( t) колеблется синусоидально около нуля.

      Фазовый угол генератора переменного тока может иметь любое значение. Если [latex]\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi > 0,[/latex] генератор вырабатывает энергию; если [латекс]\текст{cos}\фантом{\правило{0.2em}{0ex}}\varphi

      [латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ phantom {\ rule {0.2em} {0ex }}\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi .[/latex]

      Для генератора в цепи RLC ,

      9{2}R,[/латекс]

      , что означает, что мощность, вырабатываемая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.

      Пример

      Выходная мощность генератора

      Генератор переменного тока, ЭДС которого определяется выражением

      [латекс]v\left(t\right)=\left(4.00\phantom{\rule{0.2em}{0ex}} \text{V}\right)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0. {4} \ текст {рад} \ текст{/} \ текст {s} \ справа) t \ справа][/латекс] 9{-6}\phantom{\rule{0.2em}{0ex}}\text{F}[/latex] и [латекс]R=5.00\phantom{\rule{0.2em}{0ex}}\text{ Ω}[/латекс]. а) Чему равно среднеквадратичное напряжение на генераторе? б) Чему равно сопротивление цепи? в) Какова средняя мощность генератора?

      Стратегия

      Среднеквадратичное значение напряжения равно амплитуде напряжения, умноженной на [latex]1\text{/}\sqrt{2}[/latex]. Полное сопротивление цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по уравнению 15.14 или, точнее, по последней части уравнения, потому что у нас есть импеданс цепи Z , среднеквадратичное значение напряжения [латекс] {V} _ {\ text {среднеквадратичное значение}} [/латекс] и сопротивление R .

      Решение
      Показать ответ
      1. Поскольку [латекс]{V}_{0}=4.00\phantom{\rule{0.2em}{0ex}}\text{V,}[/latex] среднеквадратичное значение напряжения на генератор

        [латекс] {V} _ {\ text {rms}} = \ frac {1} {\ sqrt {2}} \ left (4. {1\text{/}2}\hfill \\ & =7.07\phantom{\rule{0.2em}{0ex }}\text{Ω}\text{.}\hfill \end{массив}[/latex] 9{2}\text{/}R,[/latex], где 90 198 В 90 199 заменяет среднеквадратичное значение напряжения.

        Проверьте свои знания

        Вольтметр переменного тока, подключенный к клеммам генератора переменного тока частотой 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.

        Показать решение

        [латекс]v\left(t\right)=\left(10.0\phantom{\rule{0.2em}{0ex}}\text{V}\right)\phantom{\rule{0.2 em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}90\pi t[/latex]

        Проверьте свои знания

        Покажите, что среднеквадратичное значение напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока со среднеквадратичным значением тока равно [латекс]{I}_{\text{среднеквадратичное значение}}[/латекс] по [латексу] {I} _ {\ text {rms}} R, {I} _ {\ text {rms}} {X} _ {C}, \ phantom {\ rule {0.2em} {0ex}} \ text{and}\phantom{\rule{0.2em}{0ex}}{I}_{\text{rms}}{X}_{L},[/latex] соответственно. Определить эти значения для компонентов Цепь RLC уравнения 15.12.

        Показать раствор

        2,00 В; 10,01 В; 8,01 В

        Резюме

        • Средняя мощность переменного тока находится путем умножения среднеквадратичных значений тока и напряжения.
        • Закон Ома для среднеквадратичного значения переменного тока находится путем деления среднеквадратичного значения напряжения на импеданс.
        • В цепи переменного тока существует угол сдвига фаз между напряжением источника и током, который можно найти, разделив сопротивление на импеданс.
        • Средняя мощность, подаваемая на На цепь RLC влияет фазовый угол.
        • Коэффициент мощности находится в диапазоне от –1 до 1.

        Концептуальные вопросы

        При каком значении фазового угла [latex]\varphi[/latex] между выходным напряжением источника переменного тока и током средняя выходная мощность источника максимальна?

        Обсудите разницу между средней мощностью и мгновенной мощностью.

        Показать решение

        Мгновенная мощность — это мощность в данный момент времени. Средняя мощность — это мощность, усредненная по циклу или количеству циклов.

        Средний переменный ток, подаваемый в цепь, равен нулю. Несмотря на это, мощность рассеивается в цепи. Объяснять.

        Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?

        Показать решение

        Мгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.

        Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?

        Задачи

        ЭДС источника переменного тока определяется выражением [латекс]v\left(t\right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin} \phantom{\rule{0.2em}{0ex}}\omega t,[/latex], где [latex]{V}_{0}=100\phantom{\rule{0. 2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{рад/с}\text{.}[/latex] Вычислить среднюю выходную мощность источника, если он подключен через (a) конденсатор [латекс]20\text{-}\mu \text{F}[/латекс], (б) катушку индуктивности 20 мГн и (в) [латексный ]50\text{-}\text{Ом}[/latex] резистор.

        Расчет среднеквадратичного значения тока для источника переменного тока определяется выражением [латекс]v\left(t\right)={V}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin} \phantom{\rule{0.2em}{0ex}}\omega t,[/latex], где [latex]{V}_{0}=100\phantom{\rule{0.2em}{0ex}}\text{ V}[/latex] и [latex]\omega =200\pi \phantom{\rule{0.2em}{0ex}}\text{rad/s}[/latex] при соединении через (a) [латекс] 20\text{-}\mu \text{F}[/latex] конденсатор, (b) катушка индуктивности 20 мГн и (c) [латекс]50\text{-}\text{Ом}[/latex ] резистор.

        Показать решение

        а. 0,89 А; б. 5,6 А; в. 1,4 А

        Катушка индуктивности 40 мГн подключена к источнику переменного тока частотой 60 Гц, амплитуда напряжения которого составляет 50 В. Если к катушке индуктивности приложить вольтметр переменного тока, что он покажет?

        Для цепи РЛК серии амплитуда напряжения и частота источника 100 В и 500 Гц соответственно; [латекс] R = 500 \ фантом {\ правило {0.2em} {0ex}} \ текст {Ω} [/латекс]; и [латекс] L = 0,20 \ фантом {\ правило {0,2em} {0ex}} \ текст {H} [/латекс]. Найдите среднюю мощность, рассеиваемую на резисторе, при следующих значениях емкости: (а) [латекс]С=2,0 мкМ \текст{F}[/латекс] и (б) [латекс]С=0,20\фантом{\ правило{0.2em}{0ex}}\mu \text{F}\text{.}[/latex]

        Показать раствор

        а. 7,3 Вт; б. 6,3 Вт

        Источник переменного тока с амплитудой напряжения 10 В отдает электрическую энергию мощностью 0,80 Вт при выходном токе 2,5 А. Каков фазовый угол [латекс]\varphi[/латекс] между ЭДС и током?

        Цепь серии RLC имеет импеданс [латекс]60\фантом{\правило{0.2em}{0ex}}\текст{Ом}[/латекс] и коэффициент мощности 0,50, при этом напряжение отстает от текущий. а) Следует ли последовательно с элементами включить конденсатор или катушку индуктивности, чтобы повысить коэффициент мощности цепи? б) При каком реактивном сопротивлении катушки индуктивности коэффициент мощности увеличится до единицы?

        Показать раствор

        а.

      Оставить комментарий