Эдс равно напряжению когда: Формула связи между ЭДС (электродвижущей силой) и напряжением.

Индуктивность / Хабр

Выше мы рассматривали два основных понятия в электротехнике — идеальный генератор напряжения и идеальный генератор тока.

Идеальный генератор напряжения выдает заданное напряжения U (давление в водопроводной аналогии) на любой нагрузке (сопротивлении внешней цепи).

При этом в соответствии с законом Ома I=U/R, даже если R стремится к нулю, а ток возрастает до бесконечности.

Внутренне сопротивление идеального генератора напряжения равно 0.

Идеальный генератор тока выдает заданный ток I (поток в водопроводной аналогии), даже если сопротивление внешней цепи стремится к бесконечности. Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.

Внутреннее сопротивление идеального генератора тока равно ∞.

Тут можно увидеть определенную симметрию, дуализм.

Мы рассматривали конденсатор С который может накапливать заряд (потому и называется — емкость) С=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление) при закачке в конденсатор заряда U=Q/C.

Если емкость заряда очень большая (стремится к бесконечности), то такой конденсатор бесконечной емкости будет являться идеальным генератором напряжения. Он никогда не разрядится и при этом может выдать ток любой величины, и напряжение на нем будет оставаться постоянным.

Симметричным (дуальным) к конденсатору элементом будет являться индуктивность. Индуктивность обозначается буквой L (см схему ниже).

Обычно сам электронный компонент называется катушка индуктивности, а его параметр — индуктивность L.

рис 13. Подключение катушки индуктивности к генератору напряжения.

Если конденсатор является генератором напряжения, то индуктивность является генератором тока. Индуктивность стремиться поддерживать ток в цепи постоянным, то есть препятствует изменению тока в цепи.

Индуктивность бесконечной величины является идеальным генератором тока, то есть будет бесконечно гнать заданный ток I независимо от сопротивления нагрузки.

Как хорошо сказано в wiki – “При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с 

силой инерции.”

Это похоже как если вы подойдете к стоящей на рельсах вагонетке и станете ее толкать (приложите к ней силу). Вагонетка начнет медленно разгоняться и «ток все быстрее и быстрее побежит по проводам». А потом попробуйте вагонетку тормозить и она будет медленно останавливаться.

Так и в индуктивности, после подачи напряжения ток будет постепенно расти (вагонетка разгоняется), а при подаче напряжения другой полярности — постепенно уменьшаться (вагонетка тормозится).

Отсюда следует вывод «Поезд мгновенно остановить нельзя!»

«Ток в индуктивности мгновенно остановить нельзя!»

То есть даже если щелкнуть выключателем S4 на схеме и разомкнуть цепь, ток в первый момент после этого будет продолжать идти! На практике это приводит к тому, что в момент размыкания контактов в выключателе между ними будет проскакивать искра.

Сопротивление при размыкании контактов увеличивается до бесконечности (в реальности до очень больших величин) и протекающий ток создаст на этом сопротивлении напряжение очень большой величины, так что воздушный промежуток между контактами будет пробит.

В водопроводной аналогии этому явлению можно сопоставить гидравлический удар, когда масса воды в водопроводе набирает скорость, и при резком закрытии крана вода, продолжая двигаться по инерции, создает высокое давление, что может привести к разрыву трубы.

Причины по которой индуктивность имеет такие свойства (поддержание тока в цепи) хорошо описаны в wiki – https://ru.wikipedia.org/wiki/Самоиндукция

“При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током).

Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока.”

По отношению к конденсатору , основным отличием индуктивности, если говорить простыми словами, является то, что конденсатор пропускает переменный ток и не пропускает постоянный, а индуктивность наоборот — пропускает постоянный ток и не пропускает переменный.

Тут есть некий момент — постоянный ток это ток, который не меняется со временем, то, что называется «постоянная составляющая» частотой равной 0 Гц. Ее конденсатор не пропускает. Совсем.

А вот индуктивность совсем не пропускает переменный ток бесконечной частоты. А просто переменный ток любой конечной частоты немножко пропускает.

Но к понятию напряжения переменного тока мы вернемся позже.

Рассмотрим цепь на рис. 13 – подключение катушки индуктивности к генератору напряжения.
Ниже представлен график тока в индуктивности при подаче на нее постоянного напряжения от генератора напряжения.

рис. 14 График тока в индуктивности при подаче на нее постоянного напряжения.

При подаче на индуктивность постоянного напряжения ток в ней линейно возрастает со временем.

Мы помним аналогичную картину для конденсатора.

Напряжение на конденсаторе линейно возрастает при его заряде постоянным током.

А что будет, если запитать индуктивность от генератора тока?

рис 15. Подключение индуктивности к генератору тока.

Ну тут из серии «кто кого заборет — слон или кит».

Попробуйте проанализировать работу схемы (hint – вообще схема изображена с ошибкой. В чем она заключается? Как нарисовать схему правильно?)

Цепи, содержащие конденсатор и индуктивность

Как было отмечено выше, индуктивность в электротехнике играет ту же роль, что масса в механике. А что является аналогом конденсатора в механике? Конденсатор является генератором напряжения, то есть создает силу, которая двигает поток заряда по проводам. Выше мы приводили аналог конденсатора в виде водонапорной башни, которая заполняется водой (зарядом) и давление (напряжение) в ней увеличивается.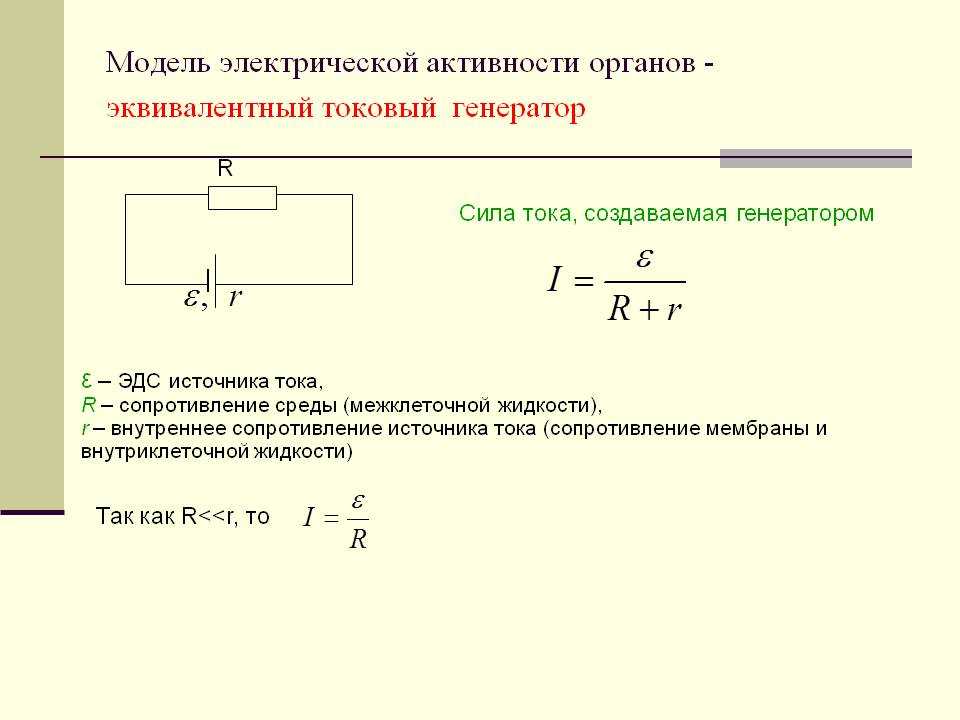

Но можно также представить конденсатор в виде пружины — при заряде пружина сжимается и сила сжатия (напряжение) увеличивается. Емкость в этом случае величина обратная жесткости пружины. Чем пружина жестче, тем быстрее возрастает сила при сжатии. То есть соединение конденсатора и индуктивности эквивалентно вагонетке закрепленной на пружине. )

Что же будет происходить, если конденсатор соединить с индуктивностью, например как в схеме на рис. 16

рис 16. Параллельное включение конденсатора и катушки индуктивности.

Пусть конденсатор С заряжен до напряжения U. Ключ S2 замыкается и в цепи начинает течь ток. Это эквивалентно тому, как если бы мы сжали пружину и затем в какой-то момент отпустили (замкнули ключ S2).

В первый момент после замыкания ключа ток в цепи будет равен 0, так как индуктивность препятствует изменению тока. К вагонетке приложили силу, но в первый момент времени ее скорость равна 0. Затем ток начинает возрастать (вагонетка разгоняется). Пружина разжимается все больше и больше, скорость вагонетки (ток) растет и в какой-то момент времени пружина оказывается не сжата.

Конденсатор разрядился до 0. Но. Мы помним что «ток в индуктивности мгновенно остановить нельзя!» Вагонетка разогналась и даже если мы не будем ее толкать, она будет двигаться по инерции. То есть индуктивность будет поддерживать ток и при этом заряжать конденсатор, но уже в другой полярности – заряды теперь будут скапливаться на другой обкладке конденсатора. Растущее напряжение противоположного знака на конденсаторе будет препятствовать движению зарядов, и в конце концов ток в цепи станет равным нулю. Но при этом конденсатор уже зарядился напряжением U другой полярности!

То есть цепь пришла в состояние когда конденсатор заряжен, ток в ней равен нулю.
Хм.. но это то же состояние, с которого мы начали, только полярность напряжения противоположная. Следовательно процесс повторится, только ток потечет уже в другую сторону и система вернется в исходное состояние. Вагонетка поедет обратно, проедет положение равновесия и по инерции снова сожмет пружину.

Возникнет колебательный процесс.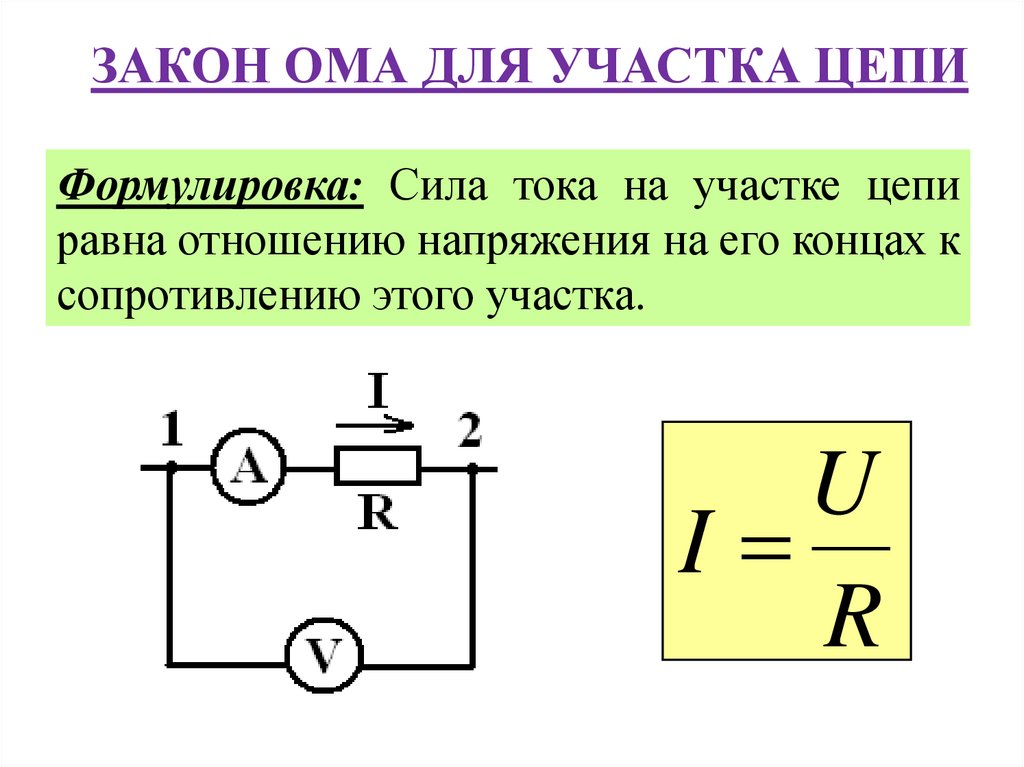 То есть вагонетка на пружине так и будет кататься туда-сюда и в отсутствие потерь энергии (трения) этот процесс будет длиться бесконечно.

Таким образом соединение конденсатора с индуктивностью образует колебательное звено. Такие звенья широко используются в электротехнике для создания генераторов и фильтров напряжения переменного тока.

Понятие переменного тока рассмотрим в следующей статье.

UPD.
Поскольку возник диспут экспоненциально ли растет ток при подключении катушки индуктивности к генератору напряжения или линейно, скажу еще пару слов по этому вопросу.

Откуда же берется экспонента роста тока в схеме на рис.13?
Ответ- ниоткуда. Ее там нет. Ток растет линейно и зависимость тока от напряжения описывается формулой

ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения силы тока в этой цепи.
Чтобы обеспечить U=const (а U – это производная от тока в катушке), ток должен линейно расти.

А откуда тогда вообще зашел разговор об экспоненте? А зашел он потому, что ток линейно растет только в идеальном случае — в схеме с идеальным генератором напряжения (бесконечной мощности и с нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением).
В реальном случае с учетом внутреннего сопротивления схема будет выглядеть так.

рис 17. Подключение катушки индуктивности к генератору напряжения с учетом внутреннего сопротивления.

На схеме рис.17 R символизирует собой внутреннее сопротивление генератора и катушки индуктивности. (они все равно включены последовательно, поэтому можно обойтись одним R, как суммой этих сопротивлений)

В этом случае процесс разворачивается следующим образом. При замыкании ключа S4 цепь замкнется и должен был бы пойти ток. Однако, катушка индуктивности препятствует изменению тока, и в первый момент времени после замыкания ключа ток останется равным 0! По сути дела катушка в этот момент представляет собой разрыв цепи с бесконечным сопротивлением. Поэтому напряжение U будет приложено к катушке целиком. Можно и по другому подойти – Ur=I*R. Падение напряжения на резисторе равно I*R, I у нас равен 0, поэтому напряжение на резисторе тоже равно 0, и к катушке будет приложено полное напряжение U. Дальше ток в катушке будет расти. В области 0 линейно кстати (см рис 19 «Переход Суворова через Альпы» «Экспонента проходит через 0 под углом 45 градусов»). Ток будет расти и падение напряжения на резисторе тоже будет расти. А на катушке соответственно падать, потому что часть напряжения будет забирать на себя резистор. Поэтому со временем линейность роста тока в цепи будет нарушаться. Когда падение напряжения на резисторе I*R сравняется с напряжением генератора U рост тока прекратится совсем, потому что напряжение на катушке будет равно 0 (все напряжение будет падать на резисторе).

Вот в этом случае и получится такой экспоненциальный график роста тока в индуктивности.

Рис. 18 Экспоненциальный график роста тока в индуктивности.ис 19 «Экспонента проходит через 0 под углом 45 градусов»

зы. В интернете столько разнообразной ереси на тему катушек индуктивности. Просто диву даешься.
«Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения.»
Ну.. поскольку про резистор в цепи ничего не сказано, то не на короткий промежуток, а пока входное напряжение не будет снято. Вторая часть звучит бредово, но направление верное — ток с цепи растет от нуля до.. без резистора до бесконечности, с резистором до I=Uвх/R.

Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:

VL = – L*(di/dt), (1)
где:
VL – напряжение (обратная ЭДС), индуцированная на катушке;
L – индуктивность катушки;
di/dt – скорость изменения тока во времени.

Видимо здесь попытались описать начальный момент возникновения ЭДС самоиндукции, но получилась ерунда. Говорить, что «индуцированное напряжение противоположно по полярности приложенному напряжению» это то же самое, что “падение напряжения на резисторе противоположно по полярности приложенному напряжению.” Ага, точно, приложенное напряжение сложили с падением напряжения и после резистора получили 0. Так и есть, лол.
«ЭДС самоиндукции» в катушке это аналог «падения напряжения» на резисторе. Только в резисторе электрическая энергия рассеивается, переходит в тепло, а в индуктивности — накапливается, переходит в энергию магнитного поля.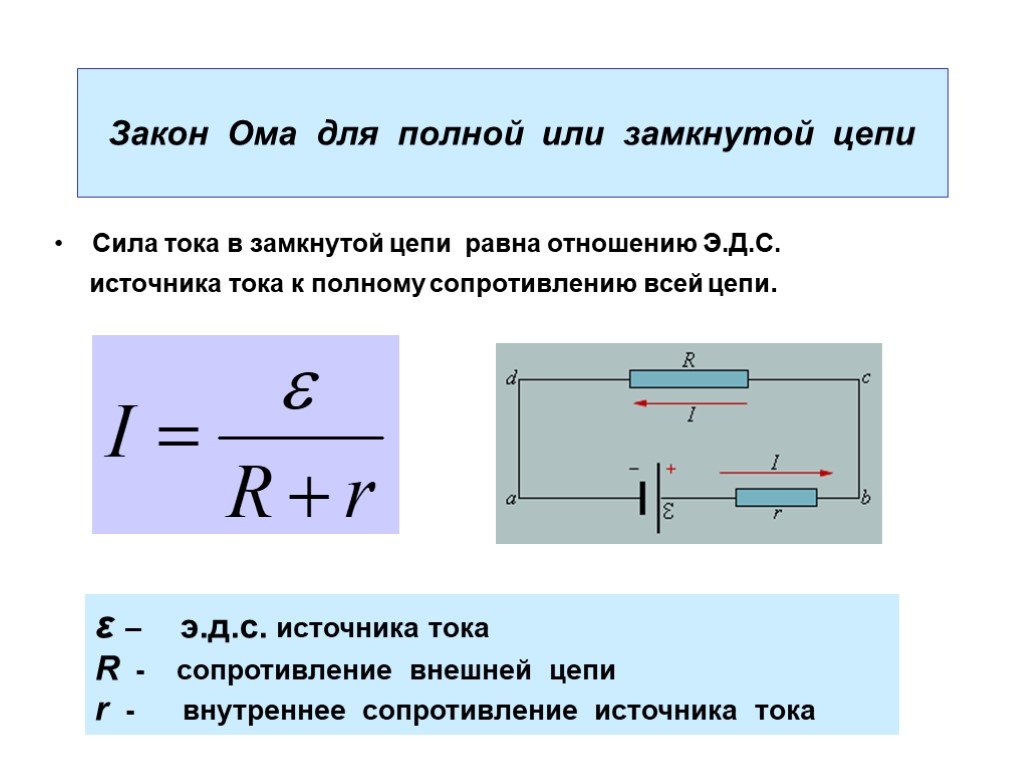 В водопроводной аналогии индуктивность это такая турбинка, вставленная в водопроводную трубу, и которая имеет момент инерции. Турбинка пропускает воду только когда вращается. И вот крантель открыли, давление к турбинке приложили, она начала вращаться и пошел ток дальше по трубе. И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.

Рис.20 Переходной процесс в цепи с индуктивностью

Картинка неправильная. В правильном варианте при отключении источника, подключался резистор и цепь оставалась замкнутой.

Рассмотрим следующую цепь

Рис.21 Цепь с индуктивностью и переключателем

Вопрос на засыпку: Чему будет равно напряжение на индуктивности в первый момент после переключения ключа S из верхнего положения в нижнее?

Hint: Не надо выносить себе мозг, пытаясь сообразить с каким там знаком возникнет ЭДС самоиндукции и что с ней будет дальше. Надо применять простое правило:
Ток в индуктивности в первый момент времени после переключения сохраняется неизменным.
Дальше применять закон Ома.

Помогите решить / разобраться (Ф)

Garat	Как найти напряжение зная ЭДС и емкость конденсатора? 15.01.2013, 07:59
15/01/13 7	Два конденсатора емкостью С1 = 3 мкФ и С2 = 6 мкФ соединены между собой параллельно. Конденсаторы подсоединены в батарее, ЭДС которой равна 120 В. Найдите заряд на каждом конденсаторе и разность потенциалов между обкладками. Для решения данной задачи нужно знать напряжение. Не могу найти связь между ЭДС и напряжением, подскажите пожалуйста. Видел на форумах что ЭДС = напряжению (U) это неверно на мой взгляд, ЭДС всегда меньше напряжения, но вот насколько в данном случае? — 15.01.2013, 11:18 — ЭДС=А/q A=q(φ1-φ2)=qU ЭДС=qU/q=U правильно ли ЭДС считать равным напряжению?

miflin	Re: Как найти напряжение зная ЭДС и емкость конденсатора? 15. 01.2013, 08:46
27/02/12 2959	Garat в сообщении #671802 писал(а): ЭДС всегда меньше напряжения, но вот насколько в данном случае? Напряжение всегда меньше ЭДС, хотели вы сказать… Это верно для замкнутой цепи. Замкнутой активным сопротивлением (резистором). Конденсатор же цепь с источником постоянной ЭДС не замыкает. Ток в этой цепи не течет. Точнее, он течет весьма короткое время, пока конденсатор заряжается. Но в задаче речь об установившихся параметрах. Garat в сообщении #671802 писал(а): правильно ли ЭДС считать равным напряжению? В данном случае правильно.

Евгений Машеров	Re: Как найти напряжение зная ЭДС и емкость конденсатора? 15.01.2013, 09:21
Заслуженный участник 11/03/08 8545 Москва	Э. Д.С. батареи отличается от напряжения на её клеммах на величину падения напряжения на внутреннем сопротивлении батареи. Оно равно току, умноженному на внутреннее сопротивление. Поскольку ток нулевой (переходной процесс закончился), падение напряжения отсутствует.

Garat	Re: Как найти напряжение зная ЭДС и емкость конденсатора? 15.01.2013, 13:44
15/01/13 7	Чему будет равна разность потенциалов? ЭДС=A/q A=q(φ1-φ2)=qU т. е. ЭДС=q(φ1-φ2)/q=(φ1-φ2) ЭДС=(φ1-φ2)=U В данной задачи получается что ЭДС равно напряжению и разности потенциалов т.е 120 В так получается?

miflin	Re: Как найти напряжение зная ЭДС и емкость конденсатора? 15.01.2013, 14:04
27/02/12 2959	Garat в сообщении #671883 писал(а): В данной задачи получается что ЭДС равно напряжению и разности потенциалов т. е 120 В так получается? Почему Вы пытаетесь обосновать значение ЭДС как следствие из каких-то соотношений? Причину и следствие меняете местами. ЭДС в задаче – это данность , в обоих смыслах. Вам нужно обосновать, почему разность потенциалов на обкладках конденсатора равна ЭДС, а не наоборот – почему ЭДС равна разности потенциалов. Но это обоснование Вам уже сообщили. Ну вот ещё. Вы, думаю, знаете, что вольтметр (идеальный), подсоединённый к батарее, показывает разность потенциалов, равную ЭДС батареи. Представьте, что в качестве подводящих проводов взяты две пластины. Сближаем их, не соприкасая, в цепи появляется конденсатор. Изменятся ли показания вольтметра?

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 5 ]

Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы

Индуктивность

.

Если индуктивное напряжение (противо-ЭДС) равно и противоположно приложенному напряжению, что управляет током?

спросил 7 лет, 7 месяцев назад

Изменено 6 месяцев назад

Просмотрено 17 тысяч раз

$\begingroup$

Предположим, у нас есть цепь с источником напряжения, разомкнутым переключателем и катушкой индуктивности, соединенными последовательно. Если мы замкнем переключатель, разность потенциалов источника напряжения мгновенно приложится к индуктору. Когда ток начинает нарастать, наведенное напряжение от индуктивности противодействует ему. Если индуцированное напряжение (противо-ЭДС) равно и противоположно приложенному напряжению, а чистое напряжение равно нулю, что тогда управляет током? Все, что я мог найти в Интернете, было это:

“. ..трудно понять, что может быть ток без “результирующей” ЭДС. Закон Фарадея утверждает $e = LdI/dt$ и если нет сопротивления $e = E$. Это электрическая аналогия постоянной скорости без необходимости в равнодействующей силе. Если есть сопротивление, то $e = LdI/dt = E – Ir$ … ‘результирующая’ $\text{ЭДС} = e$”

Не могли бы вы немного расширить эту идею?

• напряжение
• индуктивность

$\endgroup$

4

$\begingroup$

Ответ на ваш вопрос заключается в том, что вы имеете дело с двумя различными типами электрического поля (консервативным и неконсервативным) и что неконсервативное электрическое поле обязано своим существованием изменяющемуся магнитному потоку, создаваемому изменяющимся током. .

Определение собственной индуктивности: $L=\dfrac {\Phi}{I}$, где $\Phi$ — магнитный поток, а $I$ — ток.

Дифференцирование определяющего уравнения по времени и последующее преобразование уравнения дает $$\dfrac{d\Phi}{dt} = L\dfrac{dI}{dt} \Rightarrow \mathcal E_{\rm L} = – L\dfrac{dI}{dt} $$ после применения закона Фарадея, где $\mathcal E_{\rm L}$ — ЭДС индукции, создаваемая изменяющимся током.
Электрическое поле, связанное с изменяющимся магнитным потоком, не является консервативным.

Рассмотрим цепь, состоящую из идеальной ячейки с ЭДС $V{\rm s}$, переключателя и идеальной катушки индуктивности, последовательно соединенных друг с другом.

В момент времени $t=0$ переключатель замкнут.
Начальный ток должен быть равен нулю, что вы можете понять, учитывая тот факт, что подвижные носители заряда обладают инерцией и, следовательно, не могут подвергаться бесконечному ускорению.

Консервативное поле, создаваемое ячейкой, пытается увеличить ток от нуля, но неконсервативное поле, создаваемое индуктором, пытается остановить изменение тока.
Какое поле выигрывает?
При $t=0$ тока нет, поэтому может показаться, что между двумя полями есть ничья, но неконсервативное поле может остановить ток только при $t=0$ при условии изменения тока . 2}{L}$, а площадь под графиком зависимости мощности от времени (заштрихована зеленым).

$\endgroup$

9

$\begingroup$

Если предполагается, что ЭДС соленоида противодействует приложенному напряжению и имеет одинаковую величину (в вольтах), то результирующая интенсивность электродвижущей силы в проводе, действующем на ток, равна нулю. Поскольку предполагается, что некоторый ток присутствует, это означает, что ток течет, даже когда чистая электродвижущая сила (результат как консервативной, так и индуцированной электрической силы) равна нулю.

Это возможно для провода из идеального проводника (сверхпроводника). На практике всегда существует некоторое сопротивление току, поэтому ЭДС индукции вдоль катушек индуктивности не может всегда точно компенсировать приложенное напряжение.

$\endgroup$

7

$\begingroup$

В резисторе $I=\frac{V}{R}$. Если каким-то образом ток был меньше, то есть переключатель был просто замкнут, он увеличивался до тех пор, пока не соответствовал уравнению. Это связано с тем, что если бы ток был меньше, то обратная ЭДС резистора не равнялась бы ЭДС возбуждения, и, таким образом, ток хотел бы увеличиться. Поскольку в этой модели нет индуктивности, ничто не препятствует мгновенному изменению тока, поэтому цепь может мгновенно уравновеситься.

Теперь рассмотрим индуктор. До замыкания ключа нет тока, нет ЭДС и, что важно, нет изменения тока. Когда переключатель замыкается, тока по-прежнему нет, но есть приложенная ЭДС. Предположим, изменение тока постаралось остаться меньше $\frac{V}{L}$. Теперь обратная ЭДС от индуктора будет меньше, чем ЭДС, поэтому будет чистая ЭДС, увеличивающая ток. Таким образом, скорость увеличения тока увеличивается до тех пор, пока обратная ЭДС индуктора не сравняется с приложенной ЭДС. Кроме того, поскольку ничто не препятствует мгновенным изменениям скорости изменения тока, схема может мгновенно уравновеситься до устойчивого состояния (постоянно увеличивающегося тока).

$\endgroup$

1

$\begingroup$

(1) Магнитное поле возникает при прохождении тока по проводу. Этот ток может быть неизменен. В качестве примера (на данный момент не обращайте внимания на то, что происходит изначально, и сосредоточьтесь на устойчивом состоянии), обернув провод вокруг гвоздя и подключив концы к источнику постоянного тока, магнитное поле будет проходить через гвоздь, создавая магнит. Магнитное поле постоянно, как и ток.

(2) Когда магнитное поле пересекает провод, оно индуцирует ЭДС.

Если проволока намотана в виде катушки, по мере увеличения тока через проволоку магнитное поле будет увеличиваться, разрезая витки катушки, что будет индуцировать ЭДС в проволоке. Эта индуцированная ЭДС противостоит приложенной ЭДС. Вы это уже знаете. Ключевым моментом является то, что по проводу должен течь ток из-за пункта 1) выше. Индуктивная противо-ЭДС и создаваемый ею ток уступают приложенному току на бесконечно малую величину по мере увеличения приложенного тока.

Поскольку этот ток бесконечно мал, вы не увидите его на графике зависимости переменного напряжения от силы тока для чисто индуктивной цепи. Вместо этого на графике не будет протекать ток, поскольку приложенное переменное напряжение изменяется от 0 до 90 градусов. Но между 0 и 90 градусами течет бесконечно малый ток, иначе у вас не было бы изменения тока через индуктор.

Когда уравнение является производной $V=L\dfrac{\mathrm d i}{\mathrm d t}$, вы смотрите на касательную к функции и выбираете две точки на этой линии, бесконечно близкие друг к другу. Когда вы берете среднее значение этих двух точек, вы можете игнорировать бесконечно малое расстояние между точками и считать, что у вас есть точка в данный момент. Но пространство между точками реальное. Я хочу сказать, что каждый раз, когда речь идет об исчислении, у вас могут возникнуть эти умственные конфликты, и это помогает думать о «бесконечно малом изменении».

$\endgroup$

$\begingroup$

Ну… Когда противо-ЭДС равна напряжению, выдаваемому батареей, несложно понять, как в таком случае возникает ток. Видите, все, что вам нужно понять, это то, что на самом деле является обратной ЭДС? Когда заряды в движении, пытаются пройти через индуктор – индуктор преобразует свою кинетическую энергию в магнитную энергию и замедляет движущиеся заряды. Фактическая сила, которая действует на заряды, чтобы замедлить их, представляет собой наведенное электрическое поле из-за изменяющегося магнитного поля, связанного с индуктором. Что такое обратная ЭДС? Это просто энергия, потребляемая индуктором на единицу заряда. Согласно закону Кирхгофа (сохранения энергии), движущаяся заряженная частица затрачивает на свое движение вне батареи столько же энергии, сколько приобретает внутри батареи. Таким образом, вся энергия, которую электрон наберет в батарее, будет передана магнитной энергии индуктора. Итак, обратная ЭДС = напряжение источника. Но, очевидно, ток существует, потому что заряд сначала ускоряется внутри батареи, а потом замедляется, работая против противо-ЭДС.

$\endgroup$

2

$\begingroup$

Краткий ответ: вы правы – они НЕ МОГУТ быть равными, даже несмотря на то, что каждый петлевой закон, проходящий через индуктор, предполагает, что это так.

Вот как я об этом думаю: поскольку обратная ЭДС катушки индуктивности является следствием закона Фарадея, она подчиняется тому же условию отрицательной обратной связи, что и закон Ленца. То есть: обратная ЭДС не может когда-либо соответствует или превышает ∆V, которое может изменить ток через него.

Роль катушки индуктивности в цепи аналогична инерционной массе в пружинной системе. Масса сопротивляется любому изменению своей скорости, положительной или отрицательной, но любая конечная масса не может ПОЛНОСТЬЮ уменьшить силу d v /d t до нуля; для этого потребовалась бы бесконечная масса. Аналогично, я думаю об индуктивности ( L ) как о инерции тока. Следовательно, для создания противо-ЭДС 9 потребуется бесконечная индуктивность.0107 точно равны по величине приложенному напряжению.

(Кроме того, «бесконечная катушка индуктивности» всегда идеально поддерживает мгновенный ток, протекающий через нее.)

Вы наткнулись на одно из многих предположений об удобстве электрических цепей; это только вопли о том, что Кирхгоф НИКОГДА не ошибается (предупреждение о спойлере: да, иногда это так) отсюда и вниз.

$\endgroup$

Общая физика II

Вопросы 2, 4, 5, 6, 8, 9, 28

Проблемы 1, 2, 14, 15, 19, 20, 28, 41, 42, 45, 50

---

Q2 При каком условии разность потенциалов на клеммах батареи равна ее ЭДС? Может ли терминал напряжение когда-либо превышало ЭДС?

При отсутствии нагрузки напряжение на клеммах то же, что и ЭДС. Напряжение на клеммах может никогда превышать эдс.

Q4 Доступны два комплекта елочных огней. За комплект А , при извлечении (или перегорании) одной лампочки остальные лампочки продолжают гореть. Для комплекта B , когда один лампочка удалена, остальные лампочки не работают. Объясните разница в проводке двух наборов.

Набор А подключен параллельно.

Набор B соединен последовательно.

 

Q5 Как бы вы соединили резисторы, чтобы эквивалентное сопротивление на 90 129 больше, чем на 90 130, чем индивидуальное сопротивление?

Резисторы, включенные последовательно, обеспечат эквивалентную сопротивление, превышающее наибольшую индивидуальную сопротивление.

Q6 Как бы вы соединили резисторы, чтобы эквивалентное сопротивление меньше чем человек сопротивление?

Резисторы, включенные параллельно, обеспечивают эквивалент сопротивление меньше, чем у наименьшего индивидуума сопротивление.

Q8 Когда резисторы соединены последовательно , которые из следующего будет одинаковых для каждого резистора: разность потенциалов, ток, мощность?

Резисторы, соединенные последовательно, имеют общий ток.

Q9 Когда резисторы соединены параллельно , что из следующего будет таким же для каждого резистора: разность потенциалов, ток, мощность?

Резисторы, включенные параллельно, имеют общее напряжение или разность потенциалов.

Q28 Последовательная цепь состоит из трех одинаковых ламп подключен к батарее, как показано на рис. 28.29. Когда переключатель S закрыто, что происходит

(а) к силам света ламп А и В;

(б) к силе света лампы С;

(в) к току в цепи; и

(г) к падению напряжения на трех лампах?

(e) Мощность, рассеиваемая в цепи, увеличивается, уменьшается или остаться прежним?

Когда переключатель S замкнут, ток протекает через сначала две лампочки, а затем течет через выключатель и обратно в батарея. Третья лампочка гаснет.

(a) Лампы A и B (две слева) испытывают полное напряжение вместо 2/3, поэтому их интенсивность УВЕЛИЧИВАТЬ.

(b) Яркость лампы C становится НУЛЕВОЙ.

(c) Ток УВЕЛИЧИВАЕТСЯ, так как эквивалентное сопротивление контура теперь составляет всего 2/3 от того, что было до переключения был закрыт.

(d) Падение напряжения на каждой из ламп в начальный момент было [(1/3) E] . После замыкания ключа напряжение падение на каждой из первых двух ламп составляет [(1/20) E] при этом напряжение на третьей лампе равно нулю.

(e) Ток увеличивается, поэтому мощность тоже УВЕЛИЧИВАЕТ.

---

28,1 Батарея с ЭДС 12 В и внутренней сопротивление 0,90 Ом подключено через нагрузочный резистор R.

(a) Если сила тока в цепи равна 1,4 А, какова величина Р?

(b) Какая мощность рассеивается на внутреннем сопротивлении батарея?

I = 1,4 А = 12 В / [R + 0,90 ]

[R + 0,90] = 12 В/1,4 А

Р + 0,90 = 8,57

R = (8,57 – 0,90)

R = 7,67

28,2 Батарея 9,00 В выдает 117 мА при подключении к 72,0 Ом Определить внутреннее сопротивление батареи.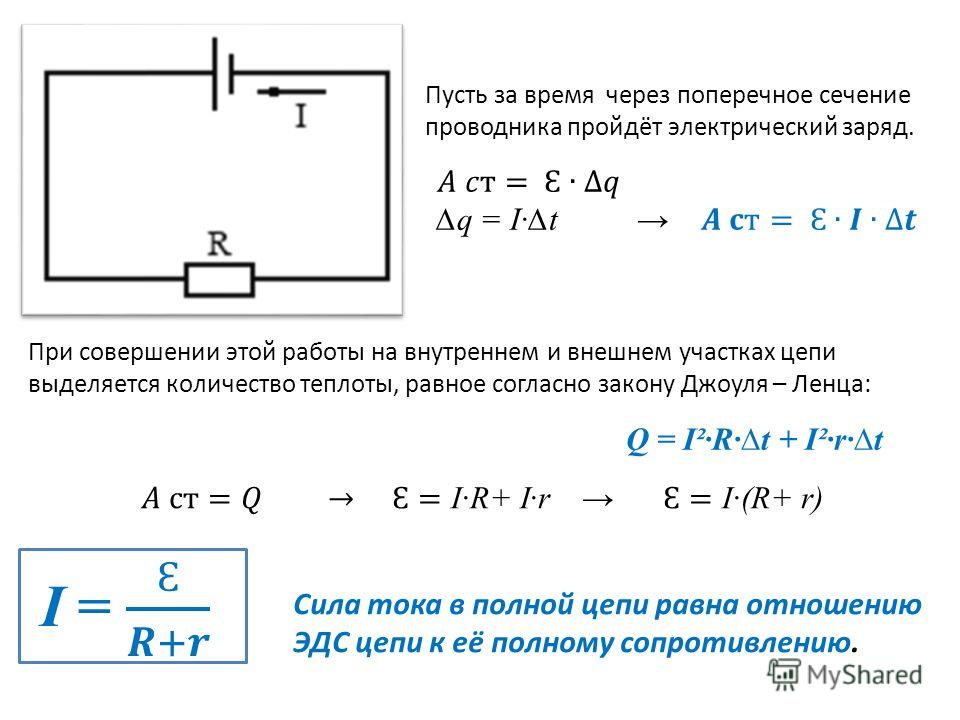

0,117 А = 9,0 В / [72,0 + Ринт]

[72,0 + R _{целое число} ] = 9,0 В / 0,117 А

72,0 + R _{целое число} = 76,9

R _{целое число} = (76,9 – 72,0)

R _{целое число} = 4,9

28,14 (a) Найдите эквивалентное сопротивление между точками а и б на рисунке P28.14

(b) Если между точками приложена разность потенциалов 34 В a и b, рассчитайте ток в каждом резисторе .

Сначала замените 7- и 10- резистор с одним эквивалентным резистором Req1. 7- и 10- резистор подключен в параллельно:

1/R _экв1 = 1/7 + 1/10

1/R _экв1 = (0,143 + 0,100)(1/)

1/R _экв1 = 0,243 (1/)

R _экв1 = (1/0,243 ) = 4,12

Теперь эти три резистора входят в серию , поэтому мы можем заменить их одним эквивалентным резистором Req2;

R _экв2 = 4 + 4. 12 + 9

Ч _экв2 = 17,12

Теперь мы знаем эквивалентное сопротивление. Если разница в напряжении 34 В подается на клеммы a и b, ток

И = В/Р

I = 34 В / 17,12

I = 1,986 А

вытечет из аккумулятора. Этот же ток протекает через 4- резистор и 9- резистор. Тот же самый ток течет (или будет течь) через первый эквивалентный резистор Req1. Это означает потенциал разница между концами этого эквивалентного резистора Req1 должна быть

В = I R _eq2

В = (1,986 А)(4,12 )

В = 8,18 В

Это напряжение также является общим напряжением на концах 7- резистор и на концах 10- резистор. Таким образом, мы можем найти ток через каждый из этих резисторы;

И = В / Р

я(7) = 8,18 В/7 = 1,17 А

Я(10) = 8,18 В/10 = 0,82 А

Обратите внимание, что сумма из этих двух напряжений, I _Сумма = 1,17 А + 0,82 А = 1,99 А (по существу) такой же, как ток через 4- и 9- резисторы (как это должно быть , конечно)!

 

28,15 Сопротивление между клеммами a и b на рис. P28.15 — 75 Ом. Если резисторы с маркировкой R имеют одинаковое значение, определить Р.

Сначала замените R и 5.0 с одним эквивалентным резистором R _экв1 ,

Поскольку они входят в серию , этот эквивалентный резистор имеет стоимость

R _eq1 = R + 5,0

Теперь у нас есть три резистора параллельно .

Эти резисторы 120-мм. резистор, 40- резистор, и этот эквивалентный резистор Req1 = R + 5,0 . Рассчитайте этот новый эквивалентный резистор Req2, который заменит эти три;

1/R _eq2 = [1/120 + 1/40 + 1/(R + 5)][1/]

1/R _экв.2 = [0,00833 + 0,025 + 1/(R + 5)][1/]

1/R _экв.2 = [0,0333 + 1/(R + 5)][1/]

R _eq2 = (1/[0,0333 + 1/(R + 5)])

Теперь у нас есть R и R _eq2 в серии , так что это очень легко вычислить этот окончательный эквивалентный резистор, Req3;

Р _экв3 = R + R _экв2

Это сопротивление равно 75 Ом. Теперь мы можем использовать немного алгебры;

R _экв.3 = R + R _экв.2

R _экв.2 = (1/[0,0333 + 1/(R + 5)])

75 = R + (1/[0,0333 + 1/(R + 5)])

28,19 Рассчитайте мощность, рассеиваемую на каждом резисторе в схема рисунка П28.19.

Чтобы найти мощность нам сначала нужно найти ток через каждый резистор и напряжение через каждый резистор. Это значит найти эквивалент резистора а затем возвращаемся обратно.

1/R _экв1 = 1/3 + 1/1

1/R _экв1 = 4/3

R _экв1 = (3/4)

R _экв1 = 0,75

85

Теперь они в серии, поэтому мы можем заменить их окончательными эквивалент резистора Треб.

Ч _экв. = 2 + 0,75 + 4

R _экв = 6,75

Ток, поступающий от аккумулятора,

I = V/R _eq

I = 18 В / 6,75

I = 2,67 А

Это также ток через 2- резистор и 4- резистор.

Р = I В = I ² Р

P ₂ = I ₂ ² R ₂

P ₂ = (2,67 А) ² (2 ) = 14,26 Вт

П ₄ = И ₄ ² Р

P ₄ = (2,67 А) ² (4 ) = 28,52 Вт

Мы можем легко найти напряжение на Req1, которое также является напряжение на 1- резистор и 3- резистор.

В = I R _eq1

В = (2,67 А) (0,75 Ом) = 2,00 В

P = I V = (V/R) V = V ² /Р

P ₁ = (2 В) ² /1 = 4 Вт

P ₃ = (2 В) ² /3 = 1,25 Вт

Теперь мы закончили. Но все же “приятно” проверить наши ответы или проверить физику мощности, производимой батареей и суммарная мощность, рассеиваемая всеми резисторами.

P _bat = I В = (2,67 А)(18 В) = 48,06 Вт

P _до = P1 + P2 + P3 + P4

P _to = 4 Вт + 14,26 Вт + 1,25 Вт + 28,52 Вт

P _до = 48,03 Вт

И те же (с точностью до «ошибки округления»), что и должно быть.

 

28,20 Определите эквивалентное сопротивление между клеммы a и b для сети, показанной на рисунке P28.20.

Три резистора в правом нижнем углу находятся в параллель . Иногда помогает просто перерисовать а схема.

Перерисовал вот так, должно быть понятно, что три резистора в правом нижнем углу параллельны . Начнем с заменив их эквивалентным резистором R _eq1 .

1/R _экв1 = 1/2 + 1/2 + 1/1

1/R _eq1 = (0,5 + 0,5 + 1,0)(1/)

1/R _экв.1 = 2,0 (1/)

Ч _экв1 = 0,5

Ч _экв2 = 2,0 + 0,5

R _экв2 = 2,5

Теперь обратим внимание на 3.0- и 5.0- резисторы в верхней части схемы, которые подключены в параллели.

1/R _экв3 = 1/3 + 1/5

1/R _eq3 = (0,33 + 0,20)(1/)

1/R _экв3 = 0,53 (1/)

R _eq3 = (1/0.53)

R _eq3 = 1.89

R _eq4 = R _eq3 + 1

R _eq4 = 1.89 + 1,0

R _EQ4 = 2,89

1/R _EQ5 = 1/R _EQ4 + 1/R _EQ2

+ 1/R _EQ2

1/R _EQ2

+ 1/R _EQ2

+ 1/R _eq2 9000 . + 1/2,5

1/R _eq5 = (0,346 + 0,4)(1/)

1/Р _экв5 = 0,746 (1/)

R _экв5 = (1/0,746)

R _экв5 = 1,34

R _экв = 2,0289 + R _экв5

R _экв = 2,0 + 1,34

R _экв = 3,34

R _экв = 3,34

 

28,28 В схеме рисунка П28. 28 определить ток в каждом резисторе и напряжение на 200-омной резистор.

Хорошо, вот оно! Это требует применения Правила Кирхгофа . Начните с назначения тока через каждый резисторов.

 

Примените правило Кирхгофа для перекрестков на двух перекрестках.

J1: I ₁ + I ₂ = I ₅

J2: I ₅ + Я ₃ + Я ₄ = 0

I ₁ + I ₂ + I ₃ + I ₄ = 0

Безусловно, один или несколько наших токов окажутся минус . (Это хорошо! ) У нас есть четыре неизвестные и только одно уравнение. Нам нужно будет получить три больше уравнений из правила цикла Кирхгофа.

L1: – 40 В = I ₂ (80 ) – я ₁ (200 )

L2: 40 В – 360 В = I ₃ (20 ) – I ₂ (80 )

L3: – 360 В – 80 В = I ₄ (70 ) – Я ₃ (20)

---

Мы закончили с “Физикой” этой задачи. Это “просто” математика с этого момента. У нас есть четыре неизвестных так что теперь нам нужно всего четыре уравнения ,

Я ₁ + Я ₂ + Я ₃ + Я ₄ = 0

– 40 В = I ₂ (80 ) – I ₁ (200 )

40 В – 360 В = I ₃ (20 ) – I ₂ (80 )

– 360 В – 80 В = I ₄ (70 ) – I ₃ (20 )

80 В = I ₄ (70 ) – I ₁ (200 )

---

Принятие решения о выборе «петли» иногда кажется трудным. Любая непрерывная петля является кандидатом. Мы могли бы использовать петля вокруг снаружи всей схемы.

L4: 80 В = I ₄ (70 ) – I ₁ (200 )

 

28,41 Полностью заряженный конденсатор хранит 12 Дж энергии. Сколько энергии останется, когда его заряд уменьшится до половины своего исходное значение?

Э = ( ¹ / ₂ ) Q ² / С

Когда груз уменьшается до половины , энергия уменьшилось до четверти .

28,42 Рассмотрим последовательную RC-цепь (рис. 28.15) для где R = 1,0 МОм, C = 5,00 мкФ и E = 30,0 В. Найти

(а) постоянная времени цепи и

(b) максимальный заряд конденсатора после переключения закрыто.

в) Если ключ замкнут в момент времени t = 0, найти ток в резистор через 10,0 с.

(а) постоянная времени цепи

= Р С

= (1 x 10 ⁶ )(5 x 10 ^{– 6} ) с

= 5 с

(б) максимальный заряд конденсатора после выключения закрыто.

С = Q/V

Q _f = C V
Q _f = (5 х 10 ^{– 6} f)(30 В) [ ^(В/П) / _ф ]

Q _f = 0,00015 С

Q _f = 1,5 x 10 ^{– 4} C

(в) Если ключ замкнут в момент времени t = 0, найти ток в резистор через 10,0 с.

Io = V/R = 30 В/1 x 10 ⁶

Io = 3 x 10 ^{– 5} A

I(5s) = (3 x 10 ^{– 5} A) EXP[ – (5s/10s)]

I(5s) = (3 x 10 ^{– 5} A) EXP[ – 2]

I(5s) = (3 x 10 ^{– 5} А) (0,135)

I(5s) = 4,05 x 10 ^{– 6} А

I(5с) = 4,05 А

 

28,45 Резистор 4,00 МОм и 3,00 мкФ Конденсатор соединен последовательно с источником питания 12,0 В.

а) Какова постоянная времени цепи?

(b) Выразите ток в цепи и заряд на конденсатор как функция времени.

= Р С

= (4 x 10 ⁶ )(3 x 10 ^{– 6} ) с

= 12 с

Io = V/R = 12 В/4 x 10 ⁶

Io = 3 x 10 ^{– 6} A

Io = 3 А

i(t) = (3 А) ОПЫТ(- т/12с)

С = Q/V

Q _f = C V

Q _f = (3 x 10 ^{– 6} f)(12 В) [(С/В)/ф]

Q _f = 36 х 10 ^{– 6} С

Q _f = 36 С

q(t) = (36 С) [ 1 – ОПЫТ (- t/12s)

 

28,50 Конденсатор в RC-цепи заряжается до 60 % его максимальное значение через 0,90 с.