Эффект Доплера — Википедия
Материал из Википедии — свободной энциклопедии
Источник волн перемещается влево. Тогда слева частота волн становится выше (больше), а справа — ниже (меньше). Другими словами, если источник волн догоняет испускаемые им волны, то длина волны уменьшается. Если удаляется — длина волны увеличивается.Эффе́кт До́плера — изменение частоты и, соответственно, длины волны излучения, воспринимаемой наблюдателем (приёмником), вследствие движения источника излучения и/или движения наблюдателя (приёмника)[1]. Эффект назван в честь австрийского физика Кристиана Доплера.
Причина эффекта Доплера заключается в том, что когда источник волн движется в направлении наблюдателя, каждый последующий гребень волны выходит из положения, более близкого к наблюдателю, чем гребень предыдущей волны[2][3]. Таким образом, каждой последующей волне необходимо немного меньше времени, чтобы добраться до наблюдателя, чем предыдущей волне. Следовательно, время между приходом последовательных гребней волн на наблюдателя сокращается, вызывая увеличение частоты.
Исходя из собственных наблюдений за волнами на воде, Доплер предположил, что подобные явления происходят в воздухе с другими волнами. На основании волновой теории он в 1842 году вывел, что приближение источника света к наблюдателю увеличивает наблюдаемую частоту, отдаление уменьшает её (статья «О цветном свете двойных звезд и некоторых других звезд на небесах (англ.)русск.»). Доплер теоретически обосновал зависимость частоты звуковых и световых колебаний, воспринимаемых наблюдателем, от скорости и направления движения источника волн и наблюдателя относительно друг друга. Это явление впоследствии было названо его именем.
Доплер использовал этот принцип в астрономии и провёл параллель между акустическим и оптическим явлениями. Он полагал, что все звёзды излучают белый с
ru.wikipedia.org
Эффект Доплера
Его суть заключается в изменении частоты звука, воспринимаемого наблюдателем, вследствие относительного движения источника и приемника звука. Когда звук отражается от движущегося объекта, частота отраженного сигнала изменяется (происходит сдвиг частоты).
Частота колебаний воспринимаемых наблюдателем, определяется выражением
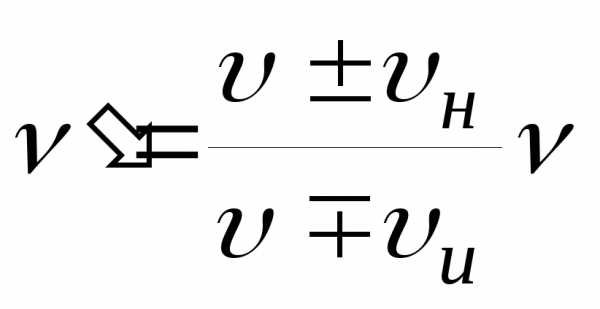 ,
,
где 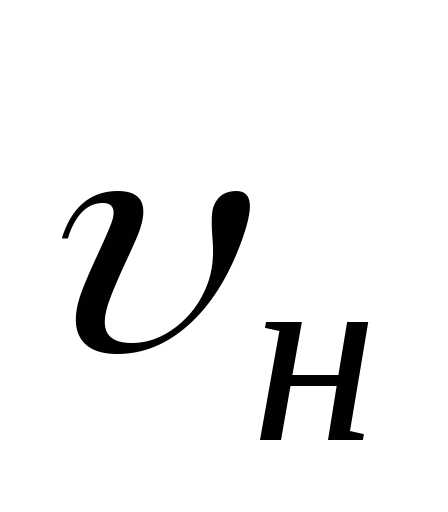 и-
скорости наблюдателя и источника упругой
волны относительно среды,
и-
скорости наблюдателя и источника упругой
волны относительно среды,
– скорость распространения волны в этой
среде,  -частота
испускаемых колебаний. Верхние знаки
соответствуют встречному движению
наблюдателя и источника, нижние – в
противоположные стороны.
-частота
испускаемых колебаний. Верхние знаки
соответствуют встречному движению
наблюдателя и источника, нижние – в
противоположные стороны.
Доплеровский сдвиг частоты определяется выражением
 ,
где
,
где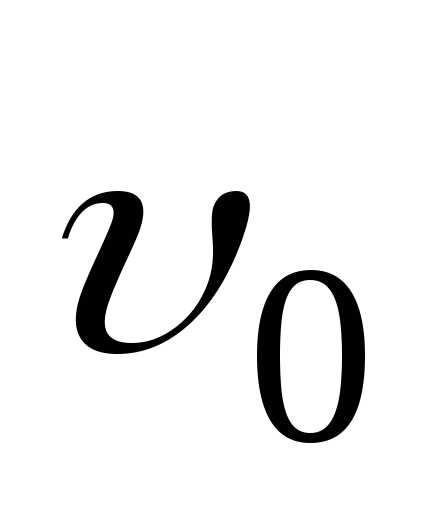 – скорость движущегося объекта,
– скорость движущегося объекта, – скорость волны (ультразвука),
– скорость волны (ультразвука),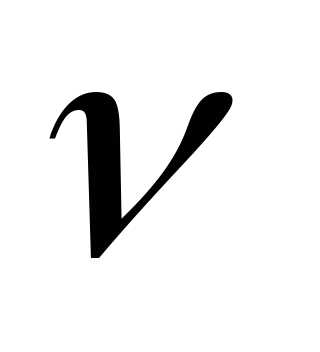 -частота
сигнала.
-частота
сигнала.
Диагностическое применение эффекта Доплера
В ультразвуковой доплеркардиогрфии в качестве объекта исследования выступает сердце, на движущиеся элементы которого (клапаны, миокард, предсердия, желудочки) направляется УЗ-пучок в непрерывном режиме. Регистрируя доплеровский сдвиг частот, можно определить скорость движения элементов сердца.
УЗ доплеровская локация сердца позволяет судить о клапанных нарушениях и диссоциации фаз сердечного цикла раздельно для каждой полости сердца.
УЗ эффект Доплера применяется в клинической практике для определения скорости кровотока (УЗ-флоуметрия)
Примеры решения задач
1. Доплеровский сдвиг частоты при отражении ультразвукового импульса от движущихся эритроцитов равен 50 Гц. Частота излучения УЗ-сигнала равна 105 Гц. Определить скорость кровотока в сосуде.
Решение:
Как известно сдвиг частот при эф.Доплера представляет собой изменение частоты УЗ-сигнала при отражении от эритроцитов, т.е.
,
здесь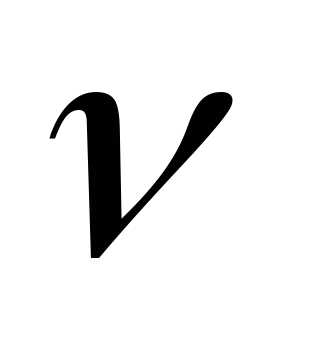 –
частота излучения генератора,
–
частота излучения генератора,
 -скорость
кровотока,
-скорость
кровотока, -скорость
распространения УЗ в крови
-скорость
распространения УЗ в крови Отсюда легко найти 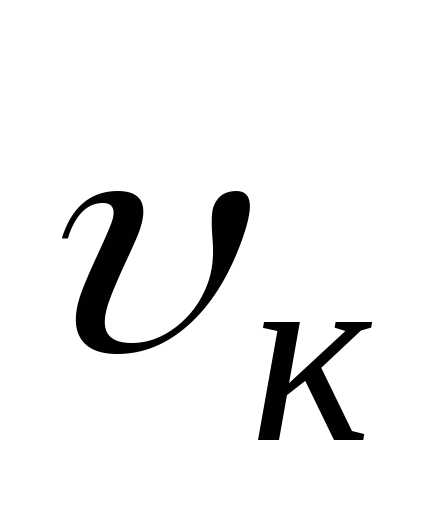 :
:

Лекция №2 Течение и свойства жидкостей
1. Идеальная жидкость. Основные определения. Движение идеальной жидкости. Уравнение неразрывности. Уравнение Бернулли.
2. Движение вязкой жидкости. Уравнение Ньютона. Формула Пуазейля.
3. Модель кровообращения Франка. Электрическая модель кровообращения. Пульсовая волна. Формула Моенса-Кортевега.
1. Система кровообращения служит для постоянного снабжения клеток питательными веществами и газами, для обмена продуктами жизнедеятельности клеток, а также переноса тепла. Она представляет собой разветвленную и замкнутую цепь сосудов различного калибра. В этом она сходна с водопроводной системой, также предназначена для обмена водой и теплом между источником и многочисленными потребителями. В обеих системах движущей силой является давление, создаваемое на входе в систему и в участках выхода. Этой цели служит генератор давления, которым в системе кровообращения является сердце, а в водопроводной системе – насос.
Движение жидкости или крови всегда происходит от участка с более высоким давлением к участку со сниженным давлением, поэтому движение крови подчиняется тем же закономерностям, которые определяют движение жидкости в любой гидродинамической системе.
Воображаемая жидкость, совершенно не обладающая вязкостью называется идеальной.Уравнение неразрывности:произведение площади поперечного сечения трубки на скорость движения жидкости есть величина постоянная
(1)
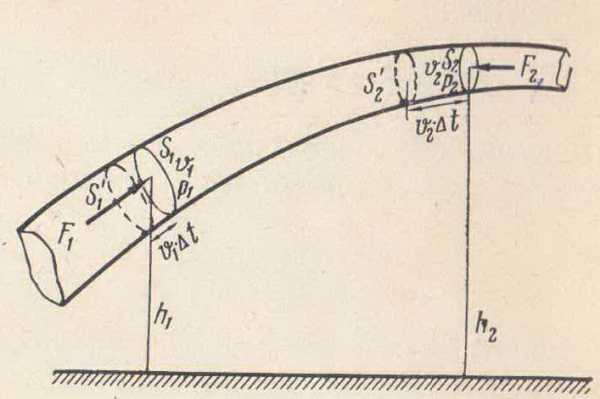
Пусть по наклонной трубке тока переменного
сечения движется жидкость в направлении
слева направо. Мысленно выделим область
трубки, ограниченную сечениями  и
и
 и
и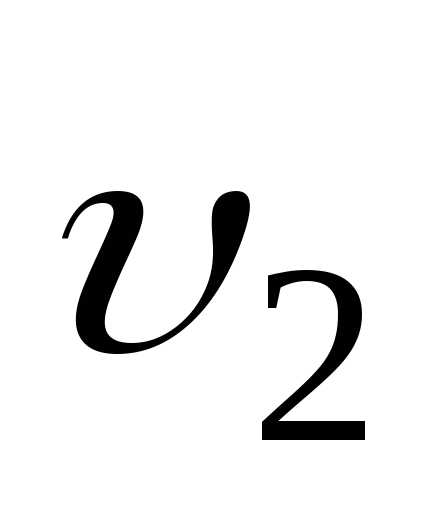 .
. 
Определим изменение полной энергии в
этой области за промежуток времени  .
За это время масса жидкости заключенная
между сечениями
.
За это время масса жидкости заключенная
между сечениями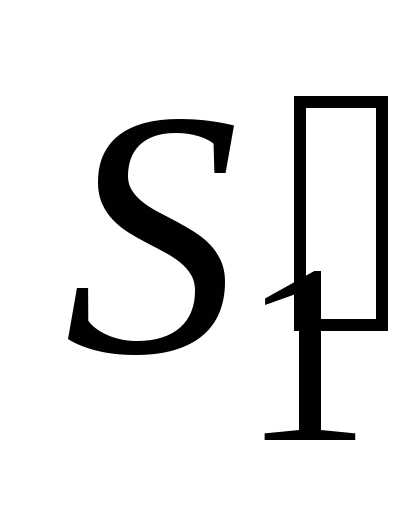 и
и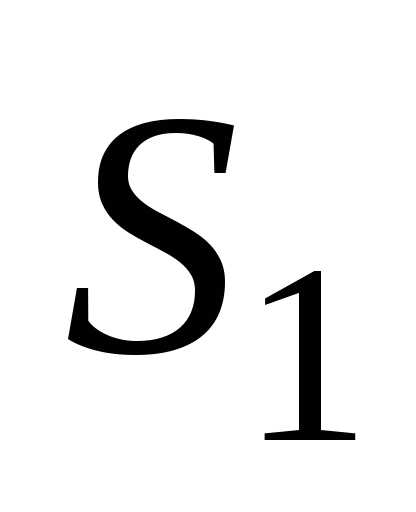 ,
втекает в рассматриваемую область, а
масса, заключенная между
,
втекает в рассматриваемую область, а
масса, заключенная между
 ,
вытекает из нее.
,
вытекает из нее.Полная энергия жидкости
(2)
Или (3)
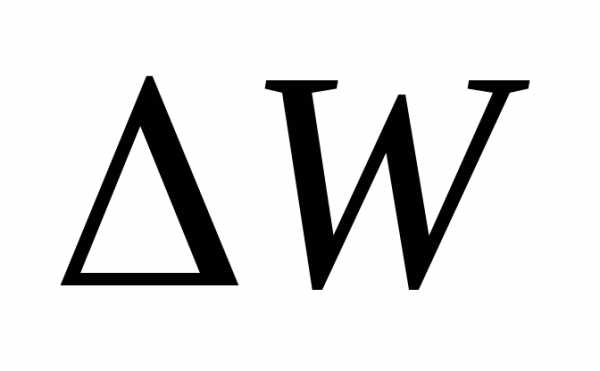 должна
равняться работе
должна
равняться работе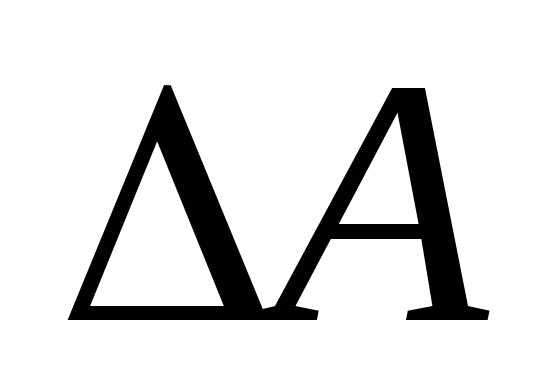 внешних сил по перемещению массы
внешних сил по перемещению массы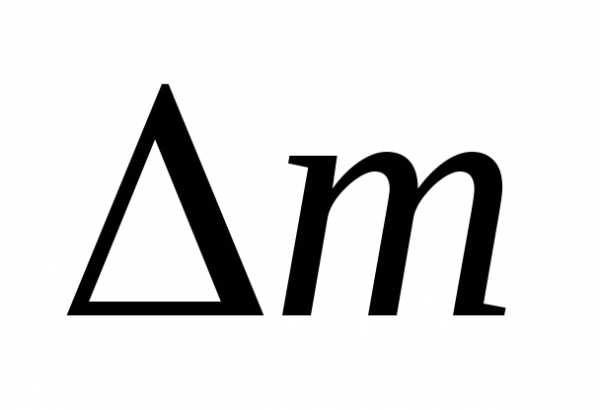
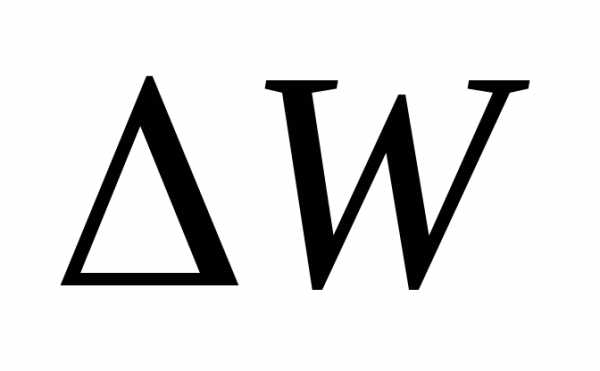 =
=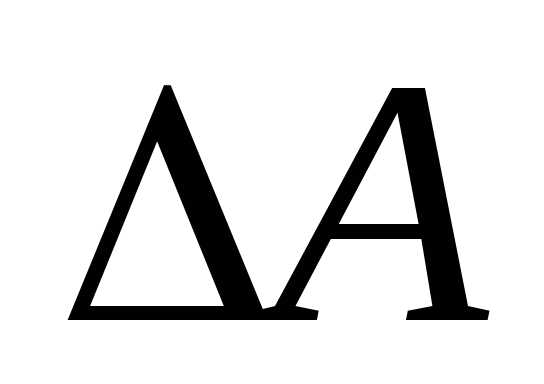 (4)
(4)
Определим  .
Внешняя сила давленияF1 совершает работу
.
Внешняя сила давленияF1 совершает работу
 ;
в то же время вытекающая масса совершает
работу
;
в то же время вытекающая масса совершает
работу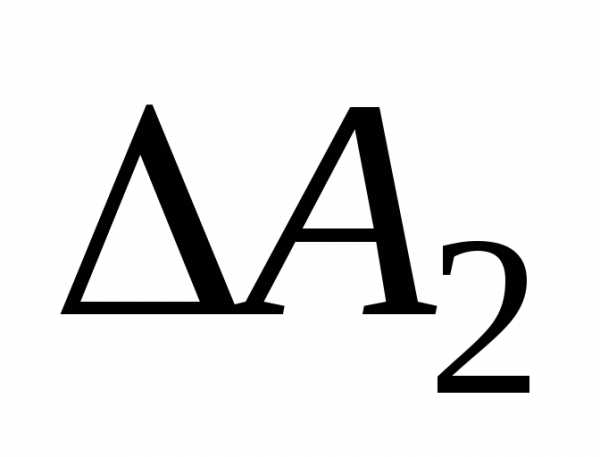 против
внешней силыF2 на
путипоэтому
против
внешней силыF2 на
путипоэтому,,
Учитывая, что 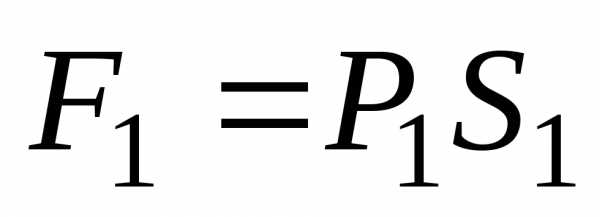 и,
гдеP1иP2-давления
на сеченияхS1 иS2,
получим,
но
и,
гдеP1иP2-давления
на сеченияхS1 иS2,
получим,
но
Где  -объем
каждой из рассматриваемых масс, поэтому(5)
-объем
каждой из рассматриваемых масс, поэтому(5)
Объединяя формулы 3, 4, 5, получим:
Поделив обе части на 
 ,
получим
,
получимПосколькуS1 иS2 выбраны произвольно
–уравнение Бернулли
В идеальной несжимаемой жидкости сумма динамического, гидравлического и статического давлений постоянна на любом поперечном сечении потока.
Для горизонтальной трубки уравнение
Бернулли принимает вид 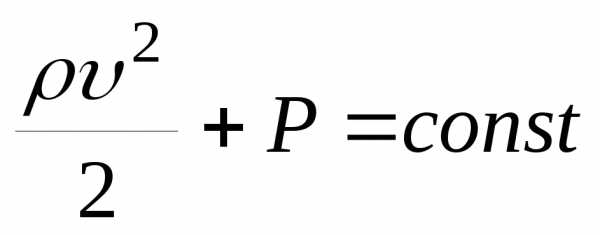
Из уравнения Бернулли и неразрывности следует, что в местах сужения трубопровода скорость течения жидкости возрастает, а давление понижается.
При течении реальной жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к слоям. Это явление называется
Рассмотрим движение жидкости между
двумя твердыми пластинками, из которых
нижняя неподвижна, а верхняя движется
со скоростью 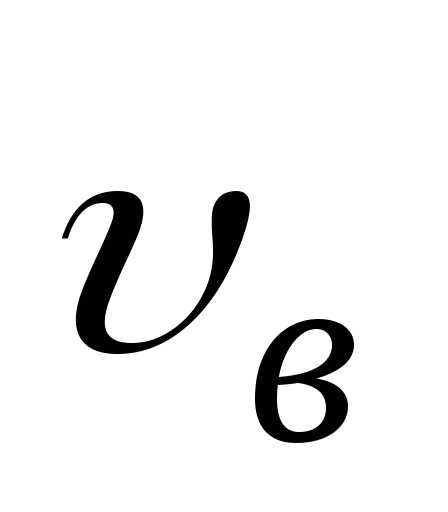 .
Слой, прилипший ко дну, неподвижен.
Максимальная скорость
.
Слой, прилипший ко дну, неподвижен.
Максимальная скорость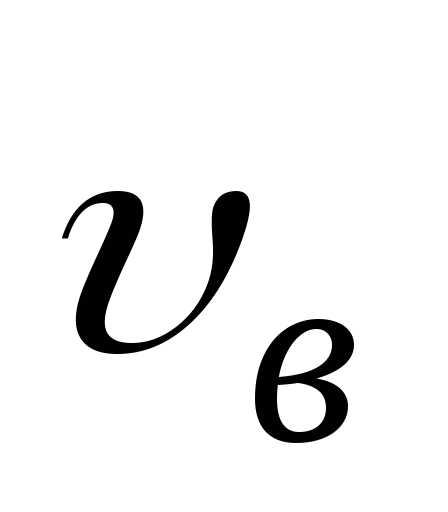 будет у слоя, «прилипшего» к верхней
пластинке.
будет у слоя, «прилипшего» к верхней
пластинке.

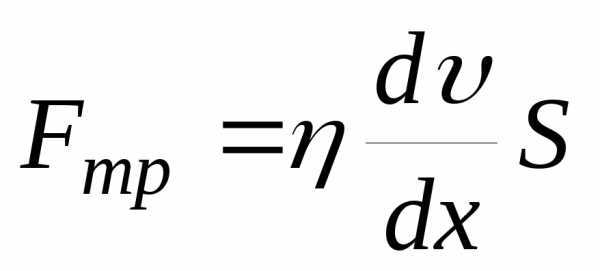 – уравнение Ньютона.
– уравнение Ньютона.
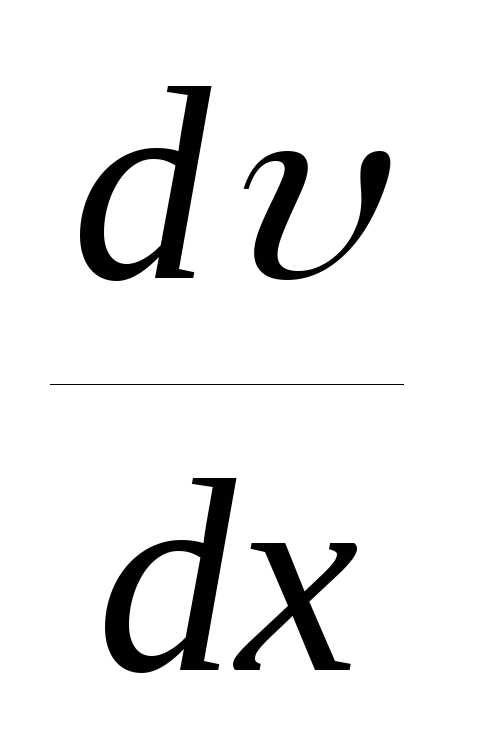 -градиент
скорости,S- площадь
соприкасающихся слоев жидкости,
-градиент
скорости,S- площадь
соприкасающихся слоев жидкости, -коэффициент
вязкости.
-коэффициент
вязкости.
Жидкости, подчиняющиеся уравнению Ньютона, называются ньютоновскими. Жидкости, не подчиняющиеся уравнению Ньютона, называются неньютоновскими. Вязкость ньютоновских жидкостей называют нормальной, неньютоновских – аномальной.
Кровь является неньютоновской жидкостью.
studfiles.net
Эффект Доплера • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Вам, наверняка, хоть раз в жизни доводилось стоять у дороги, по которой проносится машина со спецсигналом и включенной сиреной. Пока вой сирены приближается, его тон выше, затем, когда машина поравняется с вами, он понижается, и, наконец, когда машина начинает удаляться, он понижается еще, и получается знакомое: ййййииииээээЭААААОоооуууумммм — такой примерно звукоряд. Сами того, возможно, не сознавая, вы при этом наблюдаете фундаментальнейшее (и полезнейшее) свойство волн.
Волны — вообще вещь странная. Представьте себе пустую бутылку, болтающуюся неподалеку от берега. Она гуляет вверх-вниз, к берегу не приближаясь, в то время как вода, казалось бы, волнами набегает на берег. Но нет — вода (и бутылка в ней) — остаются на месте, колеблясь лишь в плоскости, перпендикулярной поверхности водоема. Иными словами, движение среды, в которой распространяются волны, не соответствует движению самих волн. По крайней мере, футбольные болельщики хорошо это усвоили и научились использовать на практике: пуская «волну» по стадиону, они сами никуда не бегут, просто встают и садятся в свой черед, а «волна» (в Великобритании это явление принято называть «мексиканской волной») бежит вокруг трибун.
Волны принято описывать их частотой (число волновых пиков в секунду в точке наблюдения) или длиной (расстояние между двумя соседними гребнями или впадинами). Эти две характеристики связаны между собой через скорость распространения волны в среде, поэтому, зная скорость распространения волны и одну из главных волновых характеристик, можно легко рассчитать другую.
Как только волна пошла, скорость ее распространения определяется только свойствами среды, в которой она распространяется, — источник же волны никакой роли больше не играет. По поверхности воды, например, волны, возбудившись, далее распространяются лишь в силу взаимодействия сил давления, поверхностного натяжения и гравитации. Акустические же волны распространяются в воздухе (и иных звукопроводящих средах) в силу направленной передачи перепада давлений. И ни один из механизмов распространения волн не зависит от источника волны. Отсюда и эффект Доплера.
Давайте еще раз задумаемся над примером с воющей сиреной. Предположим для начала, что спецмашина стоит. Звук от сирены доходит до нас потому, что упругая мембрана внутри нее периодически воздействует на воздух, создавая в нем сжатия — области повышенного давления, — чередующиеся с разрежениями. Пики сжатия — «гребни» акустической волны — распространяются в среде (воздухе), пока не достигнут наших ушей и не воздействуют на барабанные перепонки, от которых поступит сигнал в наш головной мозг (именно так устроен слух). Частоту воспринимаемых нами звуковых колебаний мы по традиции называем тоном или высотой звука: например, частота колебаний 440 герц в секунду соответствует ноте «ля» первой октавы. Так вот, пока спецмашина стоит, мы так и будем слышать неизмененный тон ее сигнала.
Но как только спецмашина тронется с места в вашу сторону, добавится новый эффект. За время с момента испускания одного пика волны до следующего машина проедет некоторое расстояние по направлению к вам. Из-за этого источник каждого следующего пика волны будет ближе. В результате волны будут достигать ваших ушей чаще, чем это было, пока машина стояла неподвижно, и высота звука, который вы воспринимаете, увеличится. И, наоборот, если спецмашина тронется в обратном направлении, пики акустических волн будут достигать ваших ушей реже, и воспринимаемая частота звука понизится. Вот и объяснение тому, почему при проезде машины со спецсигналами мимо вас тон сирены понижается.
Мы рассмотрели эффект Доплера применительно к звуковым волнам, но он в равной мере относится и к любым другим. Если источник видимого света приближается к нам, длина видимой нами волны укорачивается, и мы наблюдаем так называемое фиолетовое смещение (из всех видимых цветов гаммы светового спектра фиолетовому соответствуют самые короткие длины волн). Если же источник удаляется, происходит кажущееся смещение в сторону красной части спектра (удлинение волн).
Этот эффект назван в честь Кристиана Иоганна Доплера, впервые предсказавшего его теоретически. Эффект Доплера меня на всю жизнь заинтересовал благодаря тому, как именно он был впервые проверен экспериментально. Голландский ученый Кристиан Баллот (Christian Buys Ballot, 1817–1870) посадил духовой оркестр в открытый железнодорожный вагон, а на платформе собрал группу музыкантов с абсолютным слухом. (Идеальным слухом называется умение, выслушав ноту, точно назвать её.). Всякий раз, когда состав с музыкальным вагоном проезжал мимо платформы, духовой оркестр тянул какую-либо ноту, а наблюдатели (слушатели) записывали слышащуюся им нотную партитуру. Как и ожидалось, кажущаяся высота звука оказалась в прямой зависимости от скорости поезда, что, собственно, и предсказывалось законом Доплера.
Эффект Доплера находит широкое применение и в науке, и в быту. Во всем мире он используется в полицейских радарах, позволяющих отлавливать и штрафовать нарушителей правил дорожного движения, превышающих скорость. Пистолет-радар излучает радиоволновой сигнал (обычно в диапазоне УКВ или СВЧ), который отражается от металлического кузова вашей машины. Обратно на радар сигнал поступает уже с доплеровским смещением частоты, величина которого зависит от скорости машины. Сопоставляя частоты исходящего и входящего сигнала, прибор автоматически вычисляет скорость вашей машины и выводит ее на экран.
Несколько более эзотерическое применение эффект Доплера нашел в астрофизике: в частности, Эдвин Хаббл, впервые измеряя расстояния до ближайших галактик на новейшем телескопе, одновременно обнаружил в спектре их атомного излучения красное доплеровское смещение, из чего был сделан вывод, что галактики удаляются от нас (см. Закон Хаббла). По сути, это был столь же однозначный вывод, как если бы вы, закрыв глаза, вдруг услышали, что тон звука двигателя машины знакомой вам модели оказался ниже, чем нужно, и сделали вывод, что машина от вас удаляется. Когда же Хаббл обнаружил к тому же, что чем дальше галактика, тем сильнее красное смещение (и тем быстрее она от нас улетает), оно понял, что Вселенная расширяется. Это стало первым шагом на пути к теории Большого взрыва — а это вещь куда более серьезная, чем поезд с духовым оркестром.
elementy.ru
Эффект Доплера
Если источник звука и наблюдатель движутся друг относительно друга, частота звука, воспринимаемого наблюдателем, не совпадает с частотой источника звука. Это явление, открытое в 1842 г., носит название эффекта Доплера.
Звуковые волны распространяются в воздухе (или другой однородной среде) с постоянной скоростью, которая зависит только от свойств среды. Однако, длина волны и частота звука могут существенно изменяться при движении источника звука и наблюдателя.
Рассмотрим простой случай, когда скорость источника υИ и скорость наблюдателя υН относительно среды направлены вдоль прямой, которая их соединяет. За положительное направление для υИ и υН можно принять направление от наблюдателя к источнику. Скорость звука υ всегда считается положительной.
|
Рисунок 2.8.1. Эффект Доплера. Случай движущегося наблюдателя. Последовательные положения наблюдателя показаны через период TН звука, воспринимаемого наблюдателем |
Рис. 2.8.1 иллюстрирует эффект Доплера в случае движущегося наблюдателя и неподвижного источника. Период звуковых колебаний, воспринимаемых наблюдателем, обозначен через TН. Из рис. 2.8.1 следует:
υНTН + υTН = λ. |
Принимая во внимание
получим:
Если наблюдатель движется в направлении источника (υН > 0), то fН > fИ, если наблюдатель движется от источника (υН < 0), то fН < fИ.
|
Рисунок 2.8.2. Эффект Доплера. Случай движущегося источника. Последовательные положения источника показаны через период T звука, излучаемого источником |
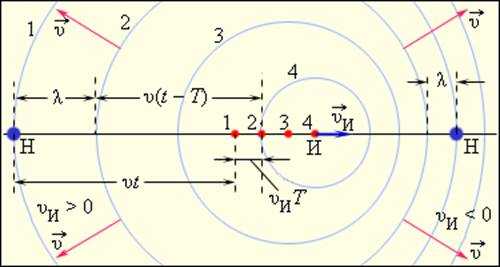
На рис. 2.8.2 наблюдатель неподвижен, а источник звука движется с некоторой скоростью υИ. В этом случае согласно рис. 2.8.2 справедливо соотношение:
υt + υИT = υ(t – T) + λ или (υИ + υ)T = λ, |
где и
Отсюда следует:
Если источник удаляется от наблюдателя, то υИ > 0 и, следовательно, fН < fИ. Если источник приближается к наблюдателю, то υИ < 0 и fН > fИ.
В общем случае, когда и источник, и наблюдатель движутся со скоростями υИ и υН, формула для эффекта Доплера приобретает вид:
Это соотношение выражает связь между fН и fИ. Скорости υИ и υН всегда измеряются относительно воздуха или другой среды, в которой распространяются звуковые волны. Это так называемый нерелятивистский Доплер-эффект.
 |
Модель. Эффект Доплера. |
В случае электромагнитных волн в пустоте (свет, радиоволны) также наблюдается эффект Доплера. Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость υ источника и наблюдателя.
Выражение для релятивистского Доплер-эффекта имеет вид
где c – скорость света. Когда υ > 0, источник удаляется от наблюдателя и fН < fИ, в случае υ < 0 источник приближается к наблюдателю, и fН > fИ.
Доплер-эффект широко используется в технике для измерения скоростей движущихся объектов («доплеровская локация» в акустике, оптике и радио).
questions-physics.ru
13.1. Эффект Доплера | Политех в Сети
При рассмотрении интерференции света указывалось, что во многих практически важных случаях (например, при свечении плазмы низкого давления) уширение спектральной линии в основном определяется изменением наблюдаемой частоты, связанным с хаотическим движением излучающих атомов. Такое уширение линии, легко наблюдаемое на опыте, является, следствием эффекта, играющего существенную роль в современной физике и по-разному проявляющегося при изменении условий эксперимента. Этот эффект был предсказан Х. Доплером (1842 г.) для сугубо частного случая распространения акустических волн, целиком объясненного с позиций классической физики. В оптическом диапазоне его впервые наблюдал Физо, заметивший смещение спектральных линий в излучении некоторых небесных светил. В лабораторных условиях первые наблюдения изменения частоты спектральных линий при отражении света от движущегося зеркала были осуществлены А. А. Белопольским. Значительно позже был обнаружен поперечный эффект Доплера и тем самым получено экспериментальное доказательство этого явления, предсказанного теорией относительности.
Мы получим здесь общее выражение для преобразования частоты и рассмотрим принципиальное различие эффекта Доплера в оптике и акустике.
Исследуем относительное движение источника электромагнитных волн и приемника, которое всегда можно разложить на продольное движение и движение, направление которого перпендикулярно линии, соединяющей исследуемые два тела. Вычисления ведут в предположении, что излучатель и приемник движутся равномерно и прямолинейно, т. е. рассматривают две связанные с ними инерциальные системы X, Y, Z и X¢, Y¢, Z¢. Дисперсия среды не учитывается, волна распространяется в вакууме (N = 1). Эти упрощения не снижают общности вывода и соответствуют условиям, обычно реализующимся при астрономических измерениях.
Проведем расчет продольного эффекта Доплера, используя преобразования Лоренца, связывающие координаты в двух инерциальных системах, движущихся одна относительно другой равномерно и прямолинейно с относительной скоростью V, направленной вдоль оси OX (O¢X¢), а именно:
. (1)
Преобразования Лоренца получены как прямое следствие постулатов специальной теории относительности.
Согласно первому постулату утверждается, что никакими физическими опытами нельзя установить, какая из двух инерциальных систем покоится, а какая движется.
Второй постулат сводится к утверждению, что существует конечная максимальная скорость распространения любого взаимодействия, которая равна C — скорости света в вакууме. По принципу относительности эта скорость одинакова во всех инерциальных системах и не зависит от длины волны, интенсивности и относительной скорости движения источника и приемника света. В нашем случае относительная скорость движения приёмника света и излучателя и нормаль к плоской волне направлены вдоль одной прямой, которая совпадает с направлением оси Ox (рис. 1). Уравнение плоской волны в связанной с излучателем в системе X, У, Z имеет вид
. (2)
В системе X¢, Y¢, Z¢, связанной с приёмником света, это выражение преобразуется:
(3)
Но очевидно, что в системе x¢, y¢, z¢ уравнение для плоской волны, распространяющейся вдоль оси O¢X¢, должно иметь вид
(4)
Сравнивая последние два соотношения, получим закон преобразования частоты для случая, когда нормаль к фронту волны и относительная скорость движения направлены, вдоль одной прямой (продольный эффект Доплера)
(5)
Это выражение также можно записать в виде
(6)
Если относительная скорость n мала (n << c) в достаточно точном приближении можно пренебречь членом порядка b2. Тогда для изменения частоты получается следующая простая формула, которой обычно и пользуются при физических измерениях:
(7)
Соотношение (7) устанавливает линейную зависимость между n¢/n и b = n/c. Следовательно, продольный эффект Доплера является эффектом первого порядка. Пользуясь упрощенным соотношением (7) и вводя обозначение Dn = n¢ — n, получаем выражение, в котором в явном виде фигурирует доплеровский сдвиг частоты Dn как функция b = V/C, а именно
(8)
Учитывая, что
,
Его можно записать в виде
, (9)
Где Dl =l¢ — l.
Очевидно, что сдвигу фаз в область более длинных волн (n¢ < n, l¢ < l, так называемое красное смещение) соответствует положительная относительная скорость приемника и излучателя (n > 0), т. е. источник и приемник электромагнитных волн удаляются один от другого. При фиолетовом смещении (n¢ > n, l¢ > l) имеет место сближение источника и приемника света. Ниже эти соотношения будут проиллюстрированы примерами из астрофизики.
Рассмотрим теперь возникновение поперечного эффекта Доплера. Пусть плоская волна распространяется вдоль OZ¢, а относительная скорость двух инерциальных систем направлена вдоль OX (OX¢). Предположим, что в системе X, Y, Z, связанней с излучателем, нормаль к исследуемой волне будет составлять некоторый угол g с направлением OZ (рис. 2). Запишем уравнение волны в системах X, Y, Z и X¢, Y¢, Z¢.
, (10)
. (11)
Применяя к соотношению (10) преобразования Лоренца, имеем
. (12)
Сравнивая (12) и (11), получаем закон преобразования частоты в данных условиях в виде
или . (13)
Разлагая правую часть (13) в ряд и, ограничиваясь членом второго порядка по b, находим Dn/n = — b2/2, где Dl = l¢ — l. Следовательно, смещение спектральной линии равно
или , (14)
Где Dn = n¢ — n, Dl = l¢ — l.
Соотношение (14) показывает, что при фиксации прямого угла между и g в системе, связанной с приёмником света, поперечный эффект Доплера должен приводить к красному смещению (Dl > 0).
Проведенное выше рассмотрение, которое и привело нас к выражениям (13) и (14), базировалось на исходном положении, что направление распространения волны перпендикулярно скорости приемника или излучателя при измерении этого угла в системе X¢, Y¢, Z¢, связанной с приемником, что обычно удобно при сравнении теории с данными опыта. Если потребовать, чтобы угол между и был прямым в системе X, Y, Z, связанной с излучателем, то получится другой результат.
Действительно, запишем снова уравнение волны в системе координат x, y, z при :
Если, используя преобразования Лоренца, перейти от системы X, Y, Z к X¢, Y¢, Z¢, то получится
или . (15)
Тогда
или . (16)
Очевидно, что при задании прямого угла между и g в системе связанной с излучателем, должно наблюдаться фиолетовое смещение.
Поперечный эффект Доплера — это эффект второго порядка относительно b = V/C (Dn ~ b2), тогда как для продольного характерна линейная зависимость смещения от b. Нетрудно заметить, что поперечный эффект не меняет знака при замене +V на –V. Он много меньше продольного, но само его существование представляется очень важным, так как в данном случае имеется качественное отличие от акустики, где никакого поперечного эффекта Доплера нет.
Введем угол y, который составляет (в системе, связанной с излучателем) направление нормали к волне с линией, соединяющей излучатель и приемник света. Тогда для продольного эффекта cosy = 1 а для поперечного cosy = 0. Формулы (7) и (15) можно объединить в одно выражение, описывающее эффект Доплера в оптике, а именно
(17)
Заметим, что при вычислении поперечного эффекта мы фактически решили еще одну задачу, представляющую интерес для обсуждаемого круга вопросов. Речь идет о явлении звездной аберрации, которое давно известно в астрономии и даже может служить одним из методов измерения скорости света. При наблюдении в телескоп неподвижных звезд приходиться наклонять его ось относительно истинного направления на угол g, который зависит от модуля и направления скорости орбитального движения Земли в момент измерения и испытывает годичные изменения. Выполняя измерения в разное время года, можно найти угол g, под которым должна быть наклонена ось телескопа. Наибольшее его значение g = V/C.
Действительно, из выражения (12) следует, что или sing = b = V/C. Если V << C, то можно считать sing » g = V/C что и оправдывается при астрономических измерениях.
Вернемся к рассмотрению полученных основных результатов. Интересно провести сравнение изменения частоты при относительном движении излучателя и приемника, наблюдающегося при оптических измерениях, с аналогичным акустическим эффектом. Выше уже указывалось, что само существование поперечного эффекта позволяет различить эти два явления. Но даже в том случае, когда исследуется эффект первого порядка (т. е. пренебрегают членами, содержащими b2), можно обнаружить принципиальную разницу между акустическим и оптическим явлениями. В акустике можно опытным путем определить как скорость приемника, так и скорость излучателя относительно среды, в которой происходит их движение. В оптике же в соответствии с постулатами Эйнштейна речь может идти только об измерении относительной скорости приемника света и излучателя, и никакими дополнительными экспериментами нельзя установить их абсолютные скорости. По образному выражению А. Зоммерфельда, природа не знает абсолютного движения ни источника света, ни наблюдателя. Она поступает проще и красивее, объединяя их в выражение типа (7).
Перейдем к исследованию того, как проявляется эффект Доплера при оптических экспериментах. Укажем, что следует различать направленное и хаотическое движение излучающих частиц, в котором они могут одновременно участвовать. К сдвигу частоты V/C приводит лишь направленное движение ансамбля атомов, и прежде всего мы проанализируем те эксперименты, где проявляется именно этот вид движения.
Практически всегда учитывается лишь продельный эффект, т. е. определяется проекция относительной скорости на линию, соединяющую источник и приемник света. В частности, именно такая лучевая скорость звезд измерялась в классических опытах Физо, где сравнивалось положение спектральных линий от звезд и земных источников. По сей день измерение доплеровских сдвигов является основным методом, определения относительных лучевых скоростей Земли и небесных светил.
Продольный эффект Доплера обусловливает также расщепление на две компоненты спектральных линий, излучаемых двойными звездами, т. е. системой из двух тел, вращающихся вокруг одного центра. Расстояние между звездами может быть столь мало, что обычными методами их нельзя разрешить, даже используя самые большие телескопы.
При проведении астрономических измерений, основанных на эффекте Доплера, был обнаружен ряд явлений, истолкование которых вызвало широкую дискуссию, ещё не исчерпавшую круг рассматриваемых вопросов. Дело в том, что при наблюдении спектров удаленных скоплений звезд (галактик) всегда фиксируется красное смещение, что соответствует удалению исследуемых светил. В некоторых случаях скорость удаления галактик, определенная из доплеровского смещения, была очень велика и достигала 0,3–0,4 скорости света в вакууме (сине-зеленые линии попадали в красную область спектра).
Эти наблюдения качественно подтверждали высказанную ученым А. А. Фридманом гипотезу о расширяющейся Вселенной, которая может рассматриваться как следствие общей теории относительности, но грандиозные масштабы явления требуют его детального осмысления и обсуждения, как в физическом, так и в философском плане.
www.webpoliteh.ru
ДОПЛЕРА ЭФФЕКТ | Энциклопедия Кругосвет
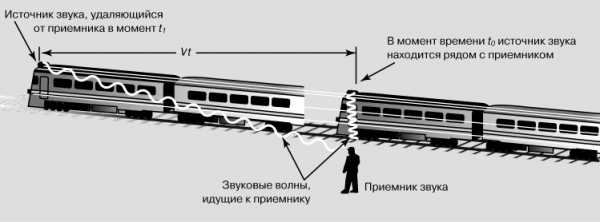
ДОПЛЕРА ЭФФЕКТ, изменение воспринимаемой частоты колебаний, обусловленное движением источника или приемника волн, либо и того и другого; впервые теоретически обоснован в 1842 К.Доплером (1803–1853). Данный эффект особенно заметен в случае звуковых волн, примером чему может служить изменение воспринимаемой высоты тона гудка проходящего мимо поезда. Возникновение эффекта поясняется рисунком, на котором источник волн движется влево со скоростью v относительно неподвижного наблюдателя («приемника»). За время t = t1 – t0 источник проходит расстояние vt. Если l – длина волны испускаемого звука, то число волн, укладывающихся в промежутке между источником и приемником, увеличивается на vt/l. Если частота звука fe, то за время t испускается fet волн. Но число frt волн, достигших приемника, меньше, чем испущено источником, на величину vt/l. Отсюда следует, что
Это соотношение справедливо и в том случае, когда приемник движется, а источник неподвижен. Если скорость v значительно меньше скорости звука c, то величину l можно заменить величиной c/fe, не совершив большой ошибки. Принимаемая частота оказывается ниже излучаемой, если источник и приемник удаляются друг от друга, и выше излучаемой, если они сближаются. Движение среды, в которой распространяются звуковые волны, например, ветер, дующий в направлении приемника или от него, также приводит к изменению регистрируемой приемником частоты.
Эффект Доплера имеет важное значение в астрономии, гидролокации и радиолокации. В астрономии по доплеровскому сдвигу определенной частоты испускаемого света можно судить о скорости движения звезды вдоль линии ее наблюдения. Наиболее удивительный результат дает наблюдение доплеровского сдвига частот света удаленных галактик: так называемое красное смещение свидетельствует о том, что все галактики удаляются от нас со скоростями примерно до половины скорости света, возрастающими с расстоянием. Вопрос о том, расширяется ли Вселенная подобным образом или красное смещение обусловлено чем-то иным, а не «разбеганием» галактик, остается открытым.
Радиолокация – это определение местоположения объекта, обычно самолета или ракеты, путем облучения его высокочастотными радиоволнами и последующей регистрации отраженного сигнала. Если объект движется с большой скоростью в направлении радиолокатора или от него, то сигнал будет принят со значительным доплеровским сдвигом частоты, и по этому сдвигу можно вычислить скорость объекта. Точно так же доплеровский сдвиг частоты ультразвукового сигнала используется для определения скорости движения подводных лодок.
См. также РАДИОЛОКАЦИЯ; ЗВУК И АКУСТИКА.
Проверь себя!
Ответь на вопросы викторины «Физика»
Что такое изотоп, чему равно число Авогадро и что изучает наука реология?
www.krugosvet.ru
Эффект Доплера – Формулы по физике.рф
Эффект Доплера — Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается. Если удаляется — длина волны увеличивается.
Частота волны в общем виде, зависит только от того, с какой скоростью двигается приемник
Как только волна пошла от источника, скорость ее распространения определяется только свойствами среды, в которой она распространяется, — источник же волны никакой роли больше не играет. По поверхности воды, например, волны, возбудившись, далее распространяются лишь в силу взаимодействия сил давления, поверхностного натяжения и гравитации. Акустические же волны распространяются в воздухе (и иных звукопроводящих средах) в силу направленной передачи перепада давлений. И ни один из механизмов распространения волн не зависит от источника волны. Отсюда и эффект Доплера.
Для того чтоб Эффект Доплера был более понятным, рассмотрим пример на машине с сиреной.
Предположим для начала, что машина стоит. Звук от сирены доходит до нас потому, что упругая мембрана внутри нее периодически воздействует на воздух, создавая в нем сжатия — области повышенного давления, — чередующиеся с разряжениями. Пики сжатия — «гребни» акустической волны — распространяются в среде (воздухе), пока не достигнут наших ушей и не воздействуют на барабанные перепонки. Так вот, пока машина стоит, мы так и будем слышать неизмененный тон ее сигнала.
Но как только машина тронется с места в вашу сторону, добавится новый эффект. За время с момента испускания одного пика волны до следующего машина проедет некоторое расстояние по направлению к вам. Из-за этого источник каждого следующего пика волны будет ближе. В результате волны будут достигать ваших ушей чаще, чем это было, пока машина стояла неподвижно, и высота звука, который вы воспринимаете, увеличится. И, наоборот, если машина с звуковым сигналом поедет в обратном направлении, пики акустических волн будут достигать ваших ушей реже, и воспринимаемая частота звука понизится.
Эффект Доплера имеет важное значение в астрономии, гидролокации и радиолокации. В астрономии по доплеровскому сдвигу определенной частоты испускаемого света можно судить о скорости движения звезды вдоль линии ее наблюдения. Наиболее удивительный результат дает наблюдение доплеровского сдвига частот света удаленных галактик: так называемое красное смещение свидетельствует о том, что все галактики удаляются от нас со скоростями примерно до половины скорости света, возрастающими с расстоянием. Вопрос о том, расширяется ли Вселенная подобным образом или красное смещение обусловлено чем-то иным, а не «разбеганием» галактик, остается открытым.
В формуле мы использовали :
— Длина волны
— Частота, с которой источник испускает волны
— Частота, регистрируемая приёмником
— Скорость распространения волн в среде
— Скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).
xn--e1adcbkcgpcji1bjh6h.xn--p1ai