Эффект доплера в радиолокации: Эффект доплера в радиолокации формула. Что такое эффект Доплера? Иллюзия, вызванная движением

Эффект доплера в радиолокации формула. Что такое эффект Доплера? Иллюзия, вызванная движением

Эффект Доплера описывается формулой:

где – частота волны, регистрируемой приемником; – частота волны, испускаемой источником; – в среде; и – скорости приемника и источника относительно упругой среды соответственно.

Если источник звука приближается к приемнику, то его скорость имеет знак «плюс». Если источник удаляется от приемника, его скорость имеет знак «минус».

Из формулы видно, что при таком движении источника и приемника, при котором расстояние между ними уменьшается, воспринимаемая приемником частота оказывается больше частоты источника . Если расстояние между источником и приемником увеличивается, будет меньше, чем .

Эффект Доплера лежит в основе радаров, с помощью которых сотрудники ГАИ определяют скорость автомобиля. В медицине используют эффект Доплера для того, чтобы с помощью ультразвукового прибора отличить вены от артерий при проведении инъекций.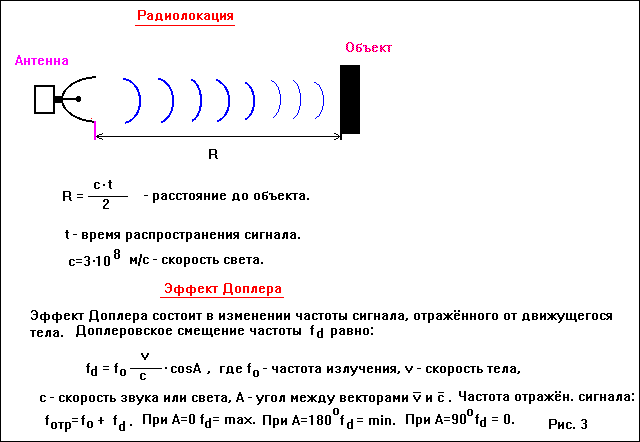 Благодаря эффекту Доплера, астрономы установили, что Вселенная расширяется — галактики разбегаются друг от друга. С помощью эффекта Доплера определяются параметры движения планет и космических аппаратов.

Примеры решения задач

ПРИМЕР 1

Задание	На шоссе сближаются два автомобиля со скоростями м/с и м/с. Первый из них подает звуковой сигнал частотой 600 Гц. Определить частоту сигнала, который услышит водитель второго автомобиля: а) до встречи; б) после встречи. Скорость звука принять равной 348 м/с.
Решение	До встречи автомобили сближаются т.е. расстояние между ними уменьшается и источник звука (первый автомобиль) приближается к приемнику звука (второму автомобилю), поэтому скорость первого автомобиля войдет в формулу со знаком «плюс». Вычислим: Гц После встречи автомобили будут удаляться друг от друга, т.е. источник звукового сигнала будет удаляться от приемника, поэтому скорость источника войдет в формулу со знаком «минус»: Гц
Ответ	Частота сигнала, который услышит водитель второй автомашины до встречи с первой, составит 732 Гц, а после встречи – 616 Гц.

ПРИМЕР 2

Задание	Скорый поезд приближается к стоящему на путях электропоезду со скоростью 72 км/ч. Электропоезд подает звуковой сигнал частотой 0,6 кГц. Определить кажущуюся частоту звукового сигнала, который услышит машинист скорого поезда. Скорость звука принять равной 340 м/с.
Решение	Запишем формулу для эффекта Доплера: В системе отсчета, связанной со скорым поездом, машинист скорого поезда (приемник сигнала) неподвижен, поэтому , а электропоезд (источник сигнала) движется навстречу скорому поезду со скоростью , которая имеет знак «плюс», так как расстояние между источником и приемником звукового сигнала уменьшается. Переведем единицы в систему СИ: скорость движения электропоезда относительно скорого поезда км/ч м/с; частота звукового сигнала электропоезда кГц Гц. Вычислим: Гц
Ответ	Кажущаяся частота , который услышит машинист скорого поезда, 638 Гц.

ПРИМЕР 3

Задание	Мимо железнодорожной платформы проходит электропоезд. Наблюдатель, стоящий на платформе, слышит звук сирены поезда. Когда поезд приближается? наблюдатель слышит звук частотой 1100 Гц, когда поезд удаляется, кажущаяся частота звука 900 Гц. Найти скорость электровоза и частоту звука, издаваемого сиреной. Скорость звука в воздухе принять равной 340 м/с.
Решение	Так как наблюдатель, стоящий на платформе, неподвижен, скорость приемника . Запишем формулу для эффекта Доплера для обоих случаев. а) когда поезд приближается: б) когда поезд удаляется: Выразим частоты звукового сигнала сирены и приравняем правые части полученных равенств:

Эффект Доплера – это хорошо знакомое изменение звука, происходящее при перемещении источника звука относительно слушателя. Неподвижному слушателю кажется, что звук становится более высоким по мере приближения его источника и более низким по мере его удаления.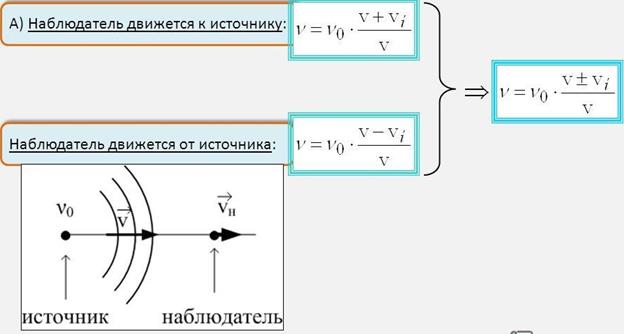

Это так называемое доплеровское смещение вызывается звуковыми волновыми фронтами, которые по мере приближения источника к слушателю достигают его с постепенно увеличивающейся частотой. Возрастание частоты сопровождается уменьшением длины волны. Ученые установили, что чем больше частота звука, тем выше его тон. Когда объект удаляется от слушателя, направленность изменений меняется на противоположную. Частота уменьшается, длина волны увеличивается, а кажущийся тон звука, воспринимаемого слушателем, становится все более низким.

С эффектом Доплера можно легко познакомиться, если прислушаться к свистку проходящего поезда, сиренам медицинских и полицейских машин или гулу реактивных двигателей самолетов.

Прибывающий поезд свистит более пронзительно

Удаляющийся поезд

Когда поезд удаляется, волновым фронтам его свистка требуется больше времени для достижения слушателя, поэтому тот слышит снижение тона.

Приближающийся поезд

Когда поезд приближается, звуковые волны достигают слушателя быстрее и кажутся более высокими в тоне.

Иллюзия, вызванная движением

Для слушателя на поезде тон свистка неизменен. Однако для слушателя, находящегося сзади или впереди поезда (рисунок справа), тон изменяется из-за неодинаковости расстояния между волновыми фронтами.

Альтернативный взгляд на проблему

Другой способ рассмотрения эффекта Доплера заключается в представлении слушателя приближающимся к источнику звука. Чем ближе пешеход подходит к колоколу, тем быстрее волновые фронты достигают его ушей и тем выше для него тон колокольного звона.

Два вида сверху

Звуковые волны от неподвижного источника распространяются в виде концентрических окружностей (рисунок вверху). Волны от движущегося источника (рисунок вверху справа), концентрируются впереди источника. Длины волн уменьшаются и тон становится более высоким.

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам – очень круто.

Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите

Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается. Если удаляется – длина волны увеличивается.

Частота волны в общем виде, зависит только от того, с какой скоростью двигается приемник

Как только волна пошла от источника, скорость ее распространения определяется только свойствами среды, в которой она распространяется, – источник же волны никакой роли больше не играет. По поверхности воды, например, волны, возбудившись, далее распространяются лишь в силу взаимодействия сил давления, поверхностного натяжения и гравитации. Акустические же волны распространяются в воздухе (и иных звукопроводящих средах) в силу направленной передачи перепада давлений.

И ни один из механизмов распространения волн не зависит от источника волны. Отсюда и эффект Доплера .

Для того чтоб был более понятным, рассмотрим пример на машине с сиреной.

Предположим для начала, что машина стоит. Звук от сирены доходит до нас потому, что упругая мембрана внутри нее периодически воздействует на воздух, создавая в нем сжатия – области повышенного давления, – чередующиеся с разряжениями. Пики сжатия – «гребни» акустической волны – распространяются в среде (воздухе), пока не достигнут наших ушей и не воздействуют на барабанные перепонки. Так вот, пока машина стоит, мы так и будем слышать неизмененный тон ее сигнала.

Но как только машина тронется с места в вашу сторону, добавится новый эффект . За время с момента испускания одного пика волны до следующего машина проедет некоторое расстояние по направлению к вам. Из-за этого источник каждого следующего пика волны будет ближе. В результате волны будут достигать ваших ушей чаще, чем это было, пока машина стояла неподвижно, и высота звука, который вы воспринимаете, увеличится.

И, наоборот, если машина с звуковым сигналом поедет в обратном направлении, пики акустических волн будут достигать ваших ушей реже, и воспринимаемая частота звука понизится.

Имеет важное значение в астрономии, гидролокации и радиолокации. В астрономии по доплеровскому сдвигу определенной частоты испускаемого света можно судить о скорости движения звезды вдоль линии ее наблюдения. Наиболее удивительный результат дает наблюдение доплеровского сдвига частот света удаленных галактик: так называемое красное смещение свидетельствует о том, что все галактики удаляются от нас со скоростями примерно до половины скорости света, возрастающими с расстоянием. Вопрос о том, расширяется ли Вселенная подобным образом или красное смещение обусловлено чем-то иным, а не «разбеганием» галактик, остается открытым.

Звук может восприниматься человеком по-разному, если источник звука и слушатель движутся относительно друг друга. Он может казаться более высоким или более низким, чем есть на самом деле.

Если источник звуковых волн и приёмник находятся в движении, то частота звука, которую воспринимает приёмник, отличается от частоты источника звука. При их сближении частота увеличивается, а при удалении уменьшается. Это явление называется эффектом Доплера , по имени учёного, его открывшего.

Эффект Доплера в акустике

Многим из нас приходилось наблюдать, как изменяется тон гудка поезда, двигающегося с большой скоростью. Он зависит от частоты звуковой волны, которую улавливает наше ухо. При приближении поезда эта частота увеличивается, и сигнал становится более высоким. При удалении от наблюдателя частота уменьшается, и мы слышим более низкий звук.

Такой же эффект наблюдается, когда движется приёмник звука, а источник неподвижен, или когда в движении находятся оба.

Почему изменяется частота звуковой волны, объяснил австрийский физик Кристиан Доплер. В 1842 г. он впервые описал эффект изменения частоты, названный эффектом Доплера .

Когда приёмник звука приближается к неподвижному источнику звуковых волн, за единицу времени он встречает на своём пути больше волн, чем если бы он находился в неподвижном состоянии. То есть он воспринимает более высокую частоту и слышит более высокий тон. Когда же он удаляется, число пересечённых в единицу времени волн уменьшается. И звук кажется более низким.

При движении источника звука к приёмнику он словно догоняет волну, созданную им же. Её длина уменьшается, следовательно, увеличивается частота. Если же он удаляется, то длина волны становится больше, а частота меньше.

Как вычислить частоту принимаемой волны

Звуковая волна способна распространяться только в среде. Её длина λ зависит от скорости и направления её движения.

где ω 0 – круговая частота, с которой источник испускает волны;

с – скорость распространения волн в среде;

v – скорость, с которой движется источник волн относительно среды.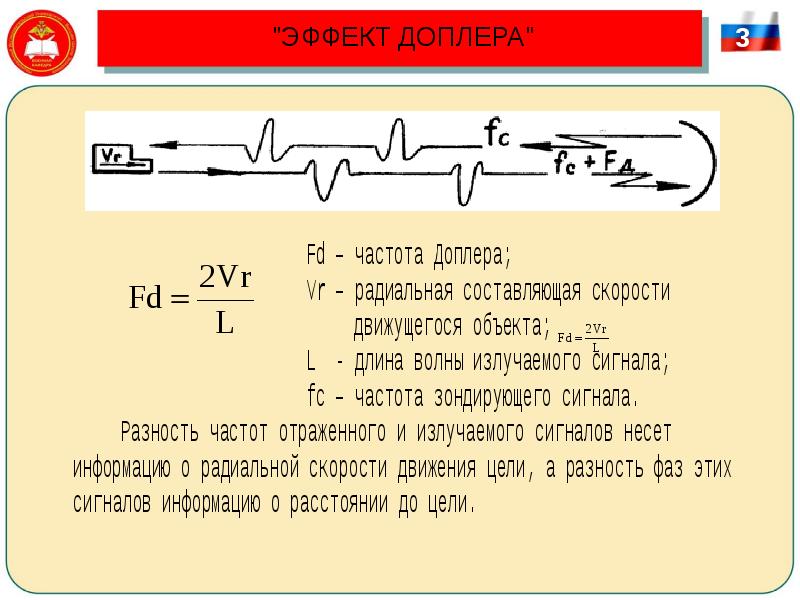 Её значение положительно, если источник движется навстречу приёмнику, и отрицательно, если он удаляется.

Неподвижный приёмник воспринимает частоту

Если же источник звука неподвижен, а приёмник движется, то частота, которую он будет воспринимать, равна

где u – скорость приёмника относительно среды. Она имеет положительное значение, если приёмник движется навстречу источнику, и отрицательное, если он удаляется.

В общем случае формула частоты, воспринимаемой приёмником, имеет вид:

Эффект Доплера наблюдается для волн любой частоты, а также электромагнитного излучения.

Где применяется эффект Доплера

Эффект Доплера используют везде, где нужно измерить скорость объектов, которые способны излучать или отражать волны. Главное условие для появления этого эффекта – движение источника волн и приёмника относительно друг друга.

Радар Доплера – это прибор, испускающий радиоволну, а затем измеряющий частоту отражённой от движущегося объекта волны. По изменению частоты сигнала он определяет скорость объекта. Такие радары используют сотрудники ГИБДД, чтобы выявить нарушителей, превышающих допустимую скорость. Применяют эффект Доплера в морской и воздушной навигации, в детекторах движения в охранных системах, для измерения скорости ветра и облаков в метеорологии и др.

Мы часто слышим о таком исследовании в кардиологии, как доплеровская эхокардиография. Эффект Доплера используют в этом случае для определения скорости движения клапанов сердца, скорости кровотока.

И даже скорость движения звёзд, галактик и других небесных тел научились определять по смещению спектральных линий с помощью эффекта Доплера.

Регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Его легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, тот услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.

Для волн, распространяющихся в какой-либо среде (например, звука) нужно принимать во внимание движение как источника так и приёмника волн относительно этой среды. Для электромагнитных волн (например, света), для распространения которых не нужна никакая среда, имеет значение только относительное движение источника и приёмника.

Также важен случай, когда в среде движется заряженная частица с релятивистской скоростью. В этом случае в лабораторной системе регистрируется черенковское излучение , имеющее непосредственное отношение к эффекту Доплера.

где f 0 – частота, с которой источник испускает волны, c – скорость распространения волн в среде, v – скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).

Частота, регистрируемая неподвижным приёмником

u – скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).

Подставив значение частоты из формулы (1) в формулу (2), получим формулу для общего случая.

(3)

Релятивистский эффект Доплера

В случае электромагнитных волн формулу для частоты выводят из уравнений специальной теории относительности .Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость источника и наблюдателя.

где с – скорость света, v – относительная скорость приёмника и источника (положительная в случае их удаления друг от друга).

Как наблюдать эффект Доплера

Поскольку явление характерно для любых колебательных процессов, то его очень легко наблюдать для звука. Частота звуковых колебаний воспринимается на слух как высота звука . Надо дождаться ситуации, когда быстро движущийся автомобиль будет проезжать мимо вас, издавая звук, например, сирену или просто звуковой сигнал. Вы услышите, что когда автомобиль будет приближаться к вам, высота звука будет выше, потом, когда автомобиль поравняется с вами, резко понизится и далее, при удалении, автомобиль будет сигналить на более низкой ноте .

Применение

Доплеровский радар

Ссылки

• Применение эффекта Доплера для измерения течений в океане

Wikimedia Foundation . 2010 .

Смотреть что такое “Доплеровское смещение” в других словарях:

доплеровское смещение – Doplerio poslinkis statusas T sritis fizika atitikmenys: angl. Doppler displacement; Doppler shift vok. Doppler Verschiebung, f rus. доплеровский сдвиг, m; доплеровское смещение, n pranc. déplacement Doppler, m; déviation Doppler, f … Fizikos terminų žodynas

доплеровское смещение частоты – Doplerio dažnio poslinkis statusas T sritis radioelektronika atitikmenys: angl. Doppler frequency displacement; Doppler frequency shift vok. Doppler Frequenzverschiebung, f rus. доплеровский сдвиг частоты, m; доплеровское смещение частоты, n… … Radioelektronikos terminų žodynas

Красное смещение сдвиг спектральных линий химических элементов в красную (длинноволновую) сторону. Это явление может быть выражением эффекта Доплера или гравитационного красного смещения, или их комбинацией. Сдвиг спектра … Википедия

Увеличение длин волн (l) линий в эл. магн. спектре источника (смещение линий в сторону красной части спектра) по сравнению с линиями эталонных спектров. Количественно К. с. характеризуется величиной z=(lприн lисп)/lисп, где lисп и lприн… … Физическая энциклопедия

Гравитационное синее смещение кванта (фотона) или иной элементарной частицы (такой как электрон, или протон) при её падении в гравитационное поле (создаваемое жёлтой звездой в нижней части … Википедия

Понижение частот электромагнитного излучения, одно из проявлений Доплера эффекта. Название «К. с.» связано с тем, что в видимой части спектра в результате этого явления линии оказываются смещенными к его красному концу; К. с. наблюдается… … Большая советская энциклопедия

Изменение частоты колебаний w или длины волны l, воспринимаемой наблюдателем, при движении источника колебаний и наблюдателя относительно друг друга. Возникновение Д. э. проще всего объяснить на след. примере. Пусть неподвижный источник испускает … Физическая энциклопедия

Теории относительности образуют существенную часть теоретического базиса современной физики. Существуют две основные теории: частная (специальная) и общая. Обе были созданы А.Эйнштейном, частная в 1905, общая в 1915. В современной физике частная… … Энциклопедия Кольера

Раздел астрономии, изучающий космические объекты путем анализа приходящего от них радиоизлучения. Многие космические тела излучают радиоволны, достигающие Земли: это, в частности, внешние слои Солнца и атмосфер планет, облака межзвездного газа. … … Энциклопедия Кольера

Горячие светящиеся небесные тела, подобные Солнцу. Звезды различаются по размеру, температуре и яркости. По многих параметрам Солнце типичная звезда, хотя кажется гораздо ярче и больше всех остальных звезд, поскольку расположено намного ближе к… … Энциклопедия Кольера

Рекомендуем также

Где же эффект Доплера при радиолокации Венеры?

Планеты покоятся в своих планетарных частотных воронках, поэтому локально-абсолютные скорости планет тождественно равны нулю. Отсюда, на основе выражения

следует фантастический вывод: допплеровский сдвиг в условиях, когда излучатель и приёмник находятся на разных планетах, должен иметь составляющие, обусловленные лишь движениями излучателя и приёмника в своих планетоцентрических системах отсчёта – но должна отсутствовать составляющая, которая соответствует взаимному сближению или удалению этих планет. Планета, при проведении её радиолокации, может приближаться к Земле, или удаляться от неё, со скоростью в десятки километров в секунду – но это приближение-удаление не должно вызывать соответствующий допплеровский сдвиг!

Именно этот феномен и обнаружился при проведении радиолокации Венеры в 1961 г. -5.

Абсолютная же величина этого сдвига, при несущей частоте излучаемого сигнала в 700 МГц, составила бы 11.6 кГц. Поскольку ширина полосы, в которой велись поиски эхо-сигнала, не превышала 600 Гц, то, по традиционной логике, непременно требовалась компенсация эффекта Допплера, чтобы несущая эхо-сигнала попадала в полосу анализа. Для этой компенсации не перенастраивался приёмный тракт, а сдвигалась несущая излучаемого сигнала на предвычисленную величину. Конечно, не могло быть и речи о прямом наблюдении эффекта Допплера, т.е. смешении отправляемой и принимаемой частот с выделением их разностной частоты. Для такой методики требовалась широкая полоса пропускания приёмного тракта, в которой эхо-сигнал было невозможно выделить из шумов.

Применялся же многоступенчатый перенос спектра принимаемого зашумлённого сигнала в низкочастотную область, в которой делалась запись на магнитную ленту, а затем эта запись анализировалась. Принцип выделения сигнала из шумов был основан на том, что излучаемый сигнал имел прямоугольную амплитудную модуляцию с глубиной 100%.

Таким образом, в одной половине такта модуляции должны были приниматься как полезный сигнал, так и шумы, а в другой – только шумы. При правильно выбранном моменте начала обработки магнитной записи, систематическое превышение принятой мощности в первых половинах тактов модуляции, по сравнению со вторыми, свидетельствовало бы о детектировании полезного сигнала.

Анализ проводился в«широкой» полосе (600 Гц) и в«узкой» полосе (40 Гц). В
полученных спектрах широкополосной составляющей(см.[К2]) не просматривается никакой систематики, похожей на продетектированный сигнал. Особенное же недоумение вызывает тот факт, что на всех спектрах широкополосной составляющей отсутствует узкополосная составляющая, которая, по традиционной логике, непременно должна была попасть в широкую полосу анализа. Поразительно: в той же статье приведены
великолепные спектры узкополосной составляющей, положения энергетических максимумов которых позволили уточнить значение астрономической единицы, т. е. среднего радиуса орбиты Земли, на два порядка! Почему же спектры узкополосной составляющей, благодаря которым оказался возможен этот прорыв, не обнаруживались при анализе в широкой полосе?

Ответ на этот вопрос подсказывает статья[К3], где написано буквально следующее:
«Под узкополосной составляющей понимается составляющая эхо-сигнала, соответствующая отражению от неподвижного точечного отражателя»(курсив наш).
Надо полагать, что на этой фразе читатели спотыкались: какой, спрашивается, неподвижный отражатель может быть на удаляющейся вращающейся планете? И почему он точечный – какая, спрашивается, мощность может отразиться от точечного отражателя?
Дело, по-видимому, в том, что термин«точечный» употреблён здесь не для описания размеров отражателя, а для того, чтобы исключить возможность понимания термина «неподвижный» в смысле«не вращающийся». Т.е.,«неподвижный» – означает«не удаляющийся». Но каким образом можно было получить эхо-сигнал,«соответствующий»
«не удаляющемуся» отражателю, если на самом деле он удалялся? Искушённые в тонкостях
физической терминологии специалисты должны согласиться с тем, что подлинный смысл процитированной фразы таков:«Узкополосная составляющая – это эхо-сигнал, который наблюдался, когда компенсация эффекта Допплера, соответствующего удалению планеты, не проводилась». Но это означает, что когда в несущую излучаемого сигнала вносилась допплеровская поправка на удаление планеты, эхо-сигнал не обнаруживался, а когда эта поправка не вносилась – эхо-сигнал обнаруживался! Это с очевидностью свидетельствует о том, что эффект Допплера, который должен был вызываться удалением Венеры, в действительности отсутствовал. Согласно нашей модели, так и должно было быть; с официальной же теорией эти результаты несовместимы.

Добавим, что радиолокация Венеры узкополосным сигналом проводилась также зарубежными группами исследователей, и, по-видимому, всем им пришлось решать одну и ту же задачу: представить свои результаты так, чтобы прорыв не был омрачён скандалом.
Впоследствии, впрочем, были обнаружены допплеровские сдвиги у эхо-сигналов, отражённых от западного и восточного краёв диска Венеры – из-за её медленного вращения вокруг своей оси. Но главная составляющая допплеровского сдвига, из-за приближения-удаления Венеры, упорно не обнаруживалась(см. также 2. 13).
В дальнейшем, благодаря быстрому развитию экспериментальной техники, при радиолокации планет стало возможно обнаружение эхо-импульсов в реальном времени, что позволило измерять временные задержки на движение радиоимпульсов до планеты и обратно. Однако, при такой методике, экспериментаторы имеют дело с широкополосными сигналами, когда принципиально исключается нахождение допплеровских сдвигов – и проблема этих сдвигов перешла в разряд«неактуальных». Секрет успешной радиолокации
Венеры в 1961 г. так и остался неизвестен для широкой научной общественности.

Пояснения

Из книги “ЭТОТ«ЦИФРОВОЙ» ФИЗИЧЕСКИЙ МИР”, А.А. Гришаев.

Допплеровский измеритель скорости / Хабр

Принципы частотно-модулированной радиолокации с постоянной частотой несущей используются в интерферометрии для измерения расстояния до объектов и их скорости. Это достигается путём передачи ЧМ сигнала и измерения разницы в частоте между задержанным принятым и передаваемым согналами. Основное внимание в этом проекте было уделено разработке и внедрению схем делителя мощности и микшера. Архитектура радара показана ниже.

Архитектура радара на допплеровском эффекте

Разветвитель представляет собой направленный ответвитель со связанными медными микрополосковыми линиями. Когда электрический ток проходит по микрополосковой линии печатной платы, появляются электрическое и магнитное поля между микрополосковой и заземляющей плоскостями на противоположной стороне диэлектрической подложки. В центре микрополоски электрическое поле однородно, но по направлению к краю микрополосковой линии оно перетекает наружу, распространяясь через её границу. Этот эффект позволяет объединять энергию двух микрополосковых линий, физически расположенных близко друг к другу. В случае силовых ответвителей и сплиттеров это весьма выгодно, и, регулируя расстояние между ними, можно отрегулировать количество энергии, проходящее между ними, до желаемой величины.

Используя Qucs — универсальный симулятор цепи, авторы рассчитали размеры для микрополоскового соединителя и самих микрополосок на печатной плате. Часть из них выполняли роль трансформаторов волнового сопротивления 50 Ом.

Вертикальная ось — это величина затухания в дБ, а горизонтальная ось — это частота в Гц.

Синяя кривая (S11) — это мощность, отражаемая соединителем, минимизируемая вокруг основной частоты радара 2,4 ГГц. Красная кривая (S13) — это передаваемая мощность, подключённая через ответвитель, -12 дБ соответствует примерно 6% мощности. Почти вся мощность передаётся, как показано розовой кривой (S12).

Авторы изготовили опытный образец на подложке из СВЧ стеклотекстолита FR-1 и измерили параметры рассеяния с помощью сетевого анализатора. Прототип показан ниже.

Прототип разветвителя

Созданный прототип не был точно настроен на частоту 2,4 ГГц и имел достаточно высокий коэффициент отражения (-10 дБ), однако связь по мощности (-17 дБ) и передача (-7 дБ) были очень приличными. Часть потерь очевидно определялась слабой связью между разъёмами SMA и PCB.

Схема микшера состоит из суммирующего микшера и RC-цепи полуволнового выпрямителя для выделения огибающей. Суммирующий микшер — это силовой сумматор Уилкинсона, который обладает прекрасным свойством изоляции портов, два входных порта (справа на рисунке) разделены на полволны (1,2 ГГц) через сумматор и резистор.

Прототип, изображенный ниже, был также изготовлен из того же СВЧ стеклотекстолита FR-1. И он каким-то образом оказался намного более эстетичным, чем приведённый выше разветвитель, ослабление сигнала достигла -25 дБ на частоте 2,4 ГГц, максимальное значение ослабления сигнала около -35 дБ наблюдалась ближе к частоте 3,5 ГГц, что указывает на то, что длина петли была физически слишком мала для свойств нашего прототипа, она получилась не совсем равной четверти длины волны на частоте 2,4 ГГц.

Прототип микшера

После тестирования прототипов авторы разработали плату, объединяющую все модули, показанные выше на структурной схеме. Плата была вытравлена на подложке из стеклотекстолита FR-4, которая имеет примерно такую же относительную диэлектрическую проницаемость, как и FR-1.

Изображение платы после травления с тонером

Доработка горячим воздухом для удаления тонера

Когда авторы наконец закончили монтаж платы и подключили её к функциональному генератору, подающему напряжение настройки на ГУН и к осциллографу, измеряющему напряжение на выходе микшера, они не смогли измерить никакого тона биений, даже с высокоотражающим металлическим угловым «кубом» (показан ниже).

Угловой «куб» для отражения волны

В конечном итоге после проверки практически всех возможных частот модуляции и размещения платы в экранирующую коробку, было установлено, что перемещение отражателя приводило к биению с частотой, прямо пропорциональной скорости движения отражателя.

Этот результат подтвердил, что делитель мощности и микшер работали, таким образом был спроектирован допплеровский радар. Движущийся отражатель создает допплеровский сдвиг, так что принимаемый сигнал имеет частоту, отличную от передаваемого сигнала, которую авторы смогли измерить с помощью микшера.

Радарные системы – эффект Доплера

В этой главе мы узнаем об эффекте Доплера в радиолокационных системах.

Если цель не является стационарной, то произойдет изменение частоты сигнала, который передается с радара и который принимается радаром. Этот эффект известен как эффект Доплера .

В соответствии с эффектом Доплера мы получим два возможных случая:

• Частота принимаемого сигнала будет увеличиваться , когда цель движется в направлении радара.

• Частота принимаемого сигнала будет уменьшаться , когда цель удаляется от радара.

Частота принимаемого сигнала будет увеличиваться , когда цель движется в направлении радара.

Частота принимаемого сигнала будет уменьшаться , когда цель удаляется от радара.

Теперь давайте выведем формулу для доплеровской частоты.

Вывод доплеровской частоты

Расстояние между радаром и целью является ничем иным, как дальностью цели или просто дальностью R. Следовательно, общее расстояние между радаром и целью на двусторонней линии связи будет равно 2R, поскольку радар передает сигнал к цели и соответственно цель посылает эхо-сигнал на радар.

Если  lambda — одна длина волны, то число длин волн N, которые присутствуют в двухстороннем пути связи между радаром и целью, будет равно 2R/ lambda.

Мы знаем, что одной длине волны  lambda соответствует угловая экскурсия в 2 pi радиан. Таким образом, общий угол отклонения, создаваемого электромагнитной волной во время двусторонней связи между радаром и целью, будет равен 4 piR/ lambda радиан.

Ниже приводится математическая формула для угловой частоты ,  omega —

 omega=2 pifEquation1

Следующее уравнение показывает математическое соотношение между угловой частотой  omega и фазовым углом  phi —

 omega= fracd phidtEquation2

Выравнивайте правые члены уравнения 1 и 2, поскольку левые члены этих двух уравнений одинаковы.

2 pif= fracd phidt

 Rightarrowf= frac12 pi fracd phidtEquation3

Замените f=fd и  phi=4 piR/ lambda в уравнении 3.

fd= frac12 pi fracddt left( frac4 piR lambda right)

 Rightarrowfd= frac12 pi frac4 pi lambda fracdRdt

 Rightarrowfd= frac2Vr lambdaEquation4

Куда,

fd — доплеровская частота

Vr — относительная скорость

Мы можем найти значение доплеровской частоты fd, подставив в уравнение 4 значения Vr и  lambda.

Замените  lambda=C/f в уравнении 4.

fd= frac2VrC/f

 Rightarrowfd= frac2VrfCEquation5

Куда,

f — частота передаваемого сигнала

C — это скорость света, и она равна 3 times108m/sec

Мы можем найти значение доплеровской частоты fd, подставив в уравнение 5 значения Vr,f и C.

Примечание. Как в уравнении 4, так и в уравнении 5 показаны формулы доплеровской частоты fd. Мы можем использовать уравнение 4 или уравнение 5 для нахождения доплеровской частоты , fd, основываясь на данных.

Пример задачи

Если радар работает на частоте 5 ГГц, найдите доплеровскую частоту самолета, движущегося со скоростью 100 км / ч.

Решение

Дано,

Частота передаваемого сигнала, f=5ГГц

Скорость самолета (цель), $ V_r = 100 км / ч

 RightarrowVr= frac100 times1033600м/с

 RightarrowVr=27,78м/с

Мы конвертировали заданную скорость самолета (цель), которая присутствует в км / ч, в эквивалентную м / с.

Мы знаем, что скорость света, C=3 умножитьна108м/с

Теперь следующая формула для доплеровской частоты —

fd= гидроразрыва2VrfC

Подставим значения ??, Vr,f и C в вышеприведенное уравнение.

 Rightarrowfd= frac2 left(27.78 right) left(5 times109 right)3 times108

 Rightarrowfd=926HZ

Поэтому значение доплеровской частоты fd составляет 926 Гц $ для данных спецификаций.

Исследование частотного метода измерения дальности с использованием пачечного ЛЧМ-сигнала | Зайцев

Посредством режима «Сопровождение на проходе» (СНП) можно организовать много­целевое сопровождение в зоне обзора с ко­личеством до 100 целей. Однако в режиме квазинепрерывного излучения зондирующих импульсов возникает неоднозначность по частоте Доплера, когда доплеровский сдвиг частоты отраженного от объекта сигнала пре­вышает частоту повторения импульсов. Так­же возникает неоднозначность по дальности, связанная с тем, что период повторения зон­дирующих импульсов меньше реальной за­держки принятого сигнала.

В связи с этим для измерения коорди­нат происходит одновременное излучение не­скольких пачек сигналов с различными зна­чениями частоты повторения в каждой пачке. Путем корреляционной обработки по неодно­значным координатам, измеренным при при­еме каждой пачки, вычисляют однозначные координаты целей – дальность и скорость. Данный метод требует 8-10 излучений в од­ной угловой позиции на разных частотах по­вторения.

В режиме СНП можно уменьшить время измерения однозначной дальности. Для этого необходимо провести излучение и обработку сигнала в двух тактах обзора подряд с пачеч­ным линейно-частотно-модулированным сиг­налом (ЛЧМ-сигналом).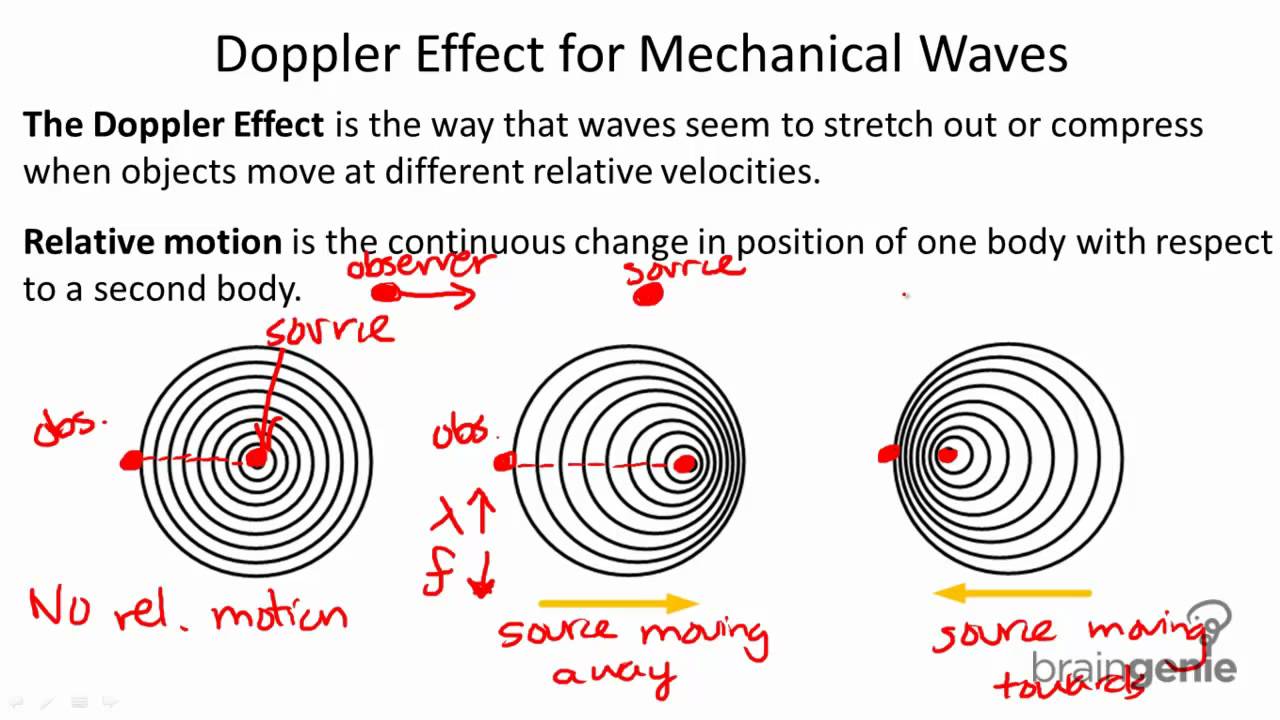

Использование частотной модуляции внутри пачки когерентно излучаемых импуль­сов позволяет применять доплеровскую об­работку отраженных сигналов с измерением частоты Доплера [1]. Изменение девиации от пачки к пачке позволяет измерить зависимость частоты Доплера от значения девиации и даль­ности до цели. Частотный метод позволяет за короткое время получить однозначное измере­ние дальности [2-4].

В данной статье методом математическо­го моделирования исследована зависимость точности измерения дальности до цели:

• от полосы пропускания и расстановки доплеровских фильтров;
• девиации частоты;
• шум-фактора (С/Ш) при измерении ча­стоты Доплера.

Структурная схема дальномера представ­лена на рис. 1.

 

Рис. 1. Структурная схема дальномера:

БПФ – быстрое преобразование Фурье; АЦП – аналого-цифровой преобразователь

 

Передатчик, состоящий из частотного модулятора и генератора высокой частоты, генерирует колебания, частота которых меняет­ся по пилообразному периодическому закону. Аналитическая запись ЛЧМ-сигнала имеет вид:

где U₀ – амплитуда;

f₀ – несущая частота; t – время, изменяющееся в диапазоне 0…T_signal с периодом дискретизации Δt

T_signal – длительность тактов обзора;

k – девиация частоты.

Таким образом, мгновенная частота в сигнале изменяется по линейному закону:

f_и = f₀ + kt                                                           (2)

В случае отраженного сигнала мгновен­ная частота будет иметь следующий вид:

f_c = f₀ + k (t – τ_D)                                                  (3)

где  –  время  задержки;

D – дальность;

с – скорость света.

Учитывая эффект Доплера, получим:

Здесь V_radial – радиальная скорость цели.

Измерив разность частот излучаемых и принимаемых колебаний, получим значение частоты Доплера:

При излучении сигнала в двух тактах обзора подряд на одной несущей частоте, но с разными девиациями частот к₁ и к₂, вычислим разность между значениями частот Доплера:

f_Д1 — f_Д1 = k₁ τ_D — k₂ τ_D D (k₁ — k₂ ).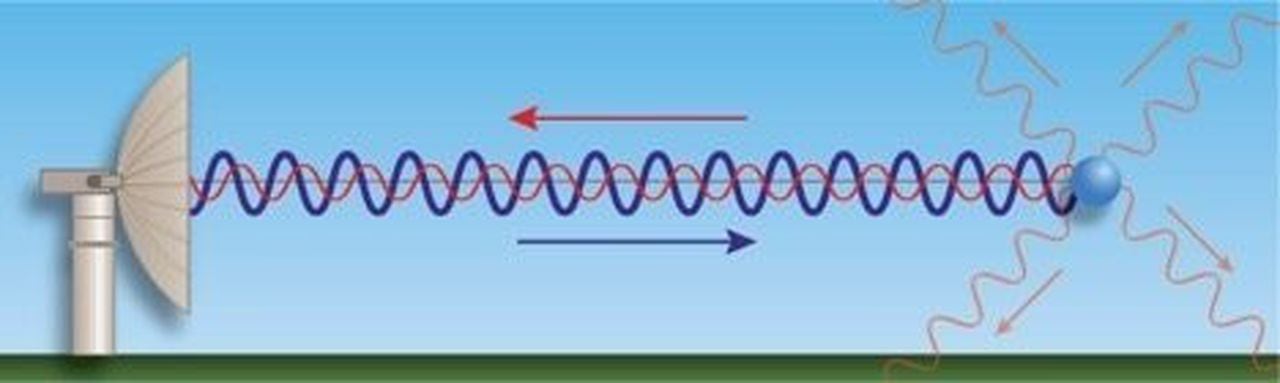                                   (6)

Затем, измерив значения частот Доплера сигнала в двух тактах обзора, можно получить дальность до цели. Кроме того, точность изме­рения будет зависеть не от скорости цели, а от разности частот Доплера.

Зная излучаемый сигнал при нулевой дальности, можно вычислить зависимость сдвига автокорреляционной функции от те­кущей дальности. Для отраженного сигнала с временн0й задержкой строится взаимно кор­реляционная функция по излучаемому и при­нимаемому сигналам [5, 6].

По максимальным значениям функций, зная разницу на частотной оси, можно опре­делить частоты Доплера f_Д1 и fД₂ для двух значений девиации.

Таким образом, дальность до цели рас­считывается по формулам:

Для построения модели использован программный пакет MATLAB с расширени­ем Simulink. В качестве входного воздействия имитирована траектория движения точечной цели в прямоугольной системе координат. На траектории были выбраны значения дальности до цели D = 1. ..220 км с шагом 500 м.

На первом этапе моделирования была ис­следована зависимость среднеквадратическо­го отклонения (СКО) от значения дисперсии шума для следующих значений девиации для первого и второго тактов обзора соответственно:

• _k1 = 40 кГц, k₂ = 60 кГц;
• _k2 = 300 кГц, k₂ = 500 кГц;
• _k3 = 3 МГц, k₂ = 5 МГц.

Для пачки длительностью T_signal = 10 мс шаг расстановки доплеровских фильтров со­ставляет 1/T_signal, т. е. 100 Гц. Были получены ошибки измерения дальности для разных зна­чений девиации. На каждой позиции цели с шагом 500 м была последовательно проведена серия численных опытов на дальностях в диа­пазоне 1…220 км. Всего было проведено 440 опытов. Статистическая обработка чис­ленных опытов дает следующие погрешности измерений дальности:

• для девиаций 40 и 60 кГц – 1500 м;
• для девиаций 300 и 500 кГц – 100 м;
• для девиаций 3 и 5 МГц – 10 м.

Радиолокационным измерениям сопут­ствует флюктуационная составляющая. В ма­тематической модели в качестве источника шума использован генератор случайных чисел с нормальным распределением. СКО случай­ного числа σ выбрано в диапазоне с шагом 5 Гц. Для каждого значения дисперсии шума была последовательно проведена серия чис­ленных опытов на дальностях в диапазоне 1…220 км с шагом 500 м. Общее количество выборок на каждом значении дисперсии шума составило 4400 численных опытов.

По результатам статистической обработ­ки измерения дальности был проведен расчет СКО. На рис. 2 приведены зависимости СКО измерения дальности от дисперсии шума для разных значений выбранных девиаций частот.

 

Рис. 2. Зависимости СКО от значения дисперсии шума:

а – девиации 40/60 кГц; б – девиации 300/500 кГц; в – девиации 3/5 МГц

 

На основании полученных результатов можно сделать вывод, что увеличение девиа­ции частоты приводит к уменьшению погреш­ности измерения дальности.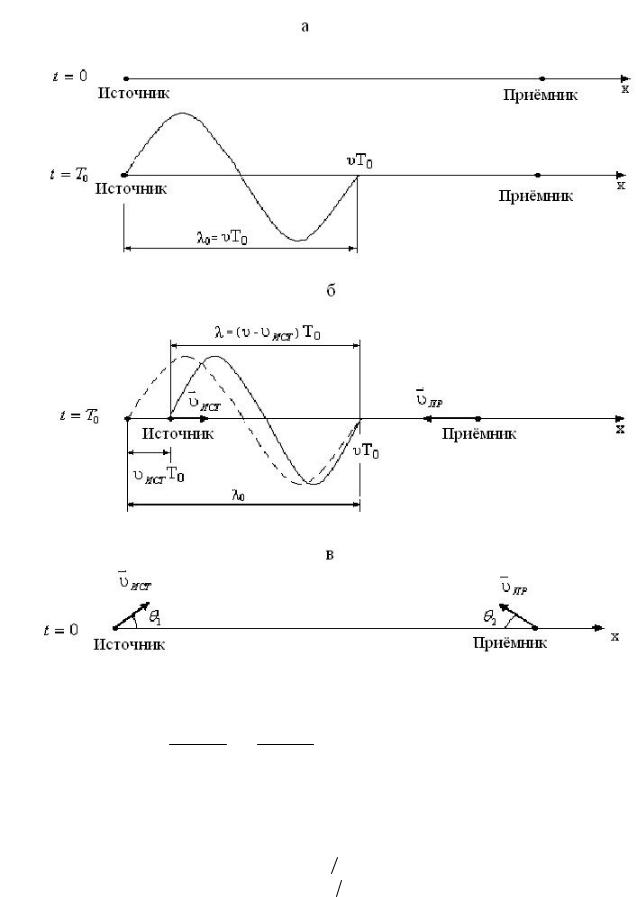

На втором этапе моделирования был уменьшен шаг расстановки доплеровского фильтра со 100 до 20 Гц. Были выбраны сле­дующие значения девиации к. 40 кГц для пер­вого и 60 кГц для второго тактов обзора.

Аналогично на каждой позиции цели с шагом 500 м была последовательно проведена серия численных опытов на дальностях в диа­пазоне 1.220 км. При отсутствии шум-фактора по полученным 440 измерениям дальности погрешность уменьшается с 1500 до 400 м.

СКО случайного числа σ было выбрано в диапазоне 0.100 Гц с шагом 1 Гц. Для каждого значения дисперсии шума была последователь­но проведена серия численных опытов на даль­ностях в диапазоне 1…220 км с шагом 500 м.

На рис. 3 представлены результаты ста­тистической обработки измерения дальности в зависимости от дисперсии шума. Общее ко­личество выборок на каждом значении диспер­сии шума составило 4400 численных опытов.

 

Рис. 3. Зависимость СКО от значения дисперсии шума с уменьшенным шагом расстановки доплеровских фильтров (девиации 40/60 кГц)

 

Из рис. 2 и 3 следует, что точность из­мерения можно повысить, не только увеличив девиацию частоты, но и уменьшив шаг расста­новки доплеровских фильтров.

В данной статье проведено численное моделирование измерения дальности частот­ным методом с использованием пачечного ЛЧМ-сигнала. Установлено, что погрешность измерения дальности до цели можно умень­шить, увеличив девиацию и уменьшив шаг расстановки доплеровских фильтров.

Для реализации данного метода измере­ния дальности с учетом возможности техни­ческой реализации в РЛС оптимальными зна­чениями девиации оказались частоты порядка 40 и 60 кГц.

При отсутствии шум-фактора погреш­ность измерения дальности определяется раз­решающей способностью по частоте Доплера.

Для частот девиации 40 и 60 кГц при дли­тельности накопления сигнала 10 мс погреш­ность измерения дальности составляет 1500 м.

Для типовых значений соотношения С/Ш ≥ 15.20 дБ в режиме СНП дисперсия доплеровского шума менее 30 Гц, СКО изме­рения дальности составит не более 1700 м.

При значении девиации, превышающем частоту повторения импульсов в пачке, возникает неоднозначность по частоте Доплера, что стоит учитывать при выборе частот.

Полученные этим методом однозначные значения координат целей позволяют выпол­нить процедуру сопоставления вновь измерен­ных значений координат с координатами уже сопровождаемых целей в режиме СНП, при этом уменьшается время измерения однознач­ной дальности. При работе радиолокационных станций в автоматическом режиме это един­ственный метод организации обзора заданно­го сектора ответственности с формированием трасс по многим целям.

Сборник тезисов докладов шестнадцатой Всероссийской открытой конференции “Современные проблемы дистанционного зондирования Земли из космоса”

Сборник тезисов докладов шестнадцатой Всероссийской открытой конференции “Современные проблемы дистанционного зондирования Земли из космоса”

Ермошкин А.В. (1)

(1) Институт прикладной физики РАН, Нижний Новгород, Россия

Работа направлена на развитие методов дистанционного радиолокационного (РЛ) зондирования водной поверхности, связанных с использованием когерентного радиоизлучения сверхвысокочастотного (СВЧ) диапазона, которое позволяет получать амплитудные и скоростные характеристики рассеяния и изучение их связи с физическими параметрами границы системы океан-атмосфера.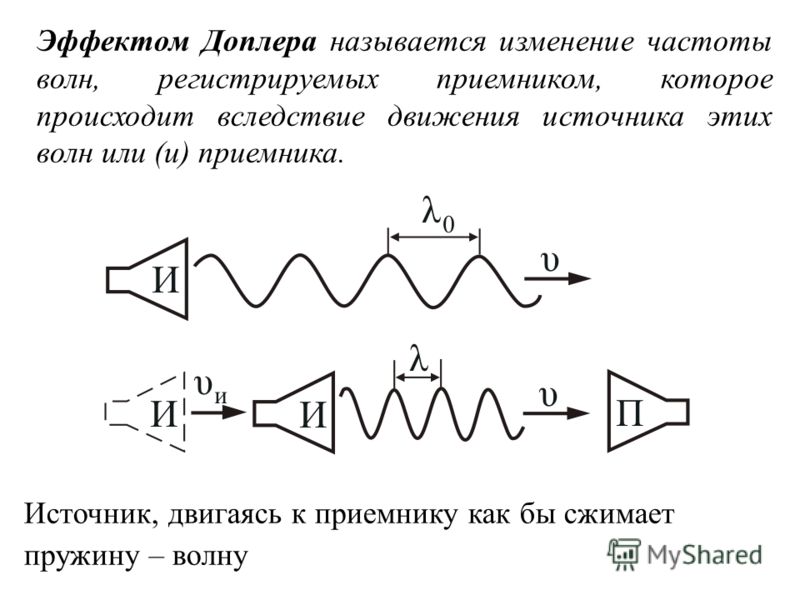 К настоящему времени подавляющее большинство работ по радиолокации морской поверхности, посвященных решению океанологических задач, опираются на данные некогерентного РЛ зондирования. При этом возникает ряд ограничений, например алгоритм определения высоты волнения нуждается в калибровке по данным контактных измерений, а скорость приповерхностного течения определяется на основе теоретического дисперсионного соотношения, которое не всегда справедливо. Появление новых инструментов дистанционного зондирования позволяет получать качественно новые знания об исследуемых процессах. Такими средствами могут выступать когерентные радиолокаторы, которые наряду с амплитудными характеристиками рассеяния позволяют получать информацию и о скоростных параметрах рассеивающей поверхности. Использование метода когерентного РЛ зондирования существенно увеличивает объем получаемой информации о подстилающей поверхности, следовательно, и о протекающих физических процессах на границе системы океан-атмосфера. Совместный анализ результатов экспериментальных исследований, включающий данные когерентного зондирования в СВЧ диапазоне обладающие высоким пространственным и временным разрешением, позволил рассмотреть протекающие физические процессы на границе системы океан-атмосфера, такие как модуляция поля коротких ветровых волн в поле орбитальных скоростей длинной волны, проявления внутренних волн, неоднородных течений и пленочных загрязнений на морской поверхности. Данные результаты позволят развить метод дистанционного когерентного РЛ зондирования морской поверхности в СВЧ диапазоне.
Работа выполнена при поддержке гранта РНФ № 18-77-00072.

Ключевые слова: когерентная радиолокация, эффект Доплера, морское волнение, течения, слики, длинные волны

Дистанционные исследования поверхности океана и ледяных покровов

262

Научная группа «Оптоэлектронные и микроволновые устройства дистанционного зондирования»

Актуальность:

Современные технологии предполагают создание, развитие и совершенствование средств дистанционного определения параметров наземных и летательных беспилотных транспортных средств (БТС). Летательные БТС осуществляют мониторинг важных городских промышленных объектов, автомагистралей на наличие пробок, состояние объектов жилищно-коммунального хозяйства, доставляют почту и посылки, участвуют в обслуживании туристического сектора. Вместе с тем, летательные БТС могут также нести угрозу нормальному функционированию объектов народного хозяйства, для противодействия которой требуется определение параметров беспилотных летательных аппаратов (БПЛА). Наземные БТС, в основном транспортные средства передвижения, используют радары для автоматического контроля дистанции между движущимися средствами, предупреждения о перекрестном движении, помощи в смене полосы движения, парковке и обнаружения препятствий, пешеходов и слепых зон. Кроме того, радары используют службы автоинспекции для обеспечения безопасности движения с использованием административных мер воздействия.

Среди дистанционно определяемых параметров наземных и летательных БТС наиболее важными являются: дальность, радиальная скорость, направление движения, эффективная площадь рассеивания (ЭПР), азимут и угол места. Для определения местоположения и радиальной скорости объектов могут быть использованы различные методы: ультразвуковой, лидарный оптический, использование видеокамер и микроволновый. Первые три перечисленных принципа имеют существенный недостаток – сильную зависимость от погодных условий (осадков, тумана), имеют малую обнаружимую дальность до объекта (ультразвуковой и видекамерный), имеют высокую стоимость (лидарный оптический). В определённой степени перечисленные методы дополняют друг друга, но вследствие указанных причин, предпочтительным методом повсеместно признаётся микроволновый радарный метод.

Научная значимость:

Ориентированные фундаментальные исследования по разработке новых систем дистанционного определения параметров наземных БТС и БПЛА микроволновыми радарами включают следующие задачи: разработка и применение радиочастотных сигналов специальной формы, устранение неоднозначности определения скоростей в широком диапазоне, устранение ложных целей в режиме регистрации параметров множества целей (multi-target), выделение и группировка точек отражения по дистанции и скорости, сопровождение объектов, повышение чувствительности радиочастотных трактов радаров для измерения параметров БТС с очень низкими ЭПР за счет применения многоканальных структур радаров.

Основные направления исследований:

Выявление фундаментальных аналитических закономерностей, соотношений для построения математических моделей, лежащих в основе новых алгоритмов дистанционного определения параметров наземных БТС и БПЛА микроволновыми радарами, а также моделирование выявленных закономерностей в вычислительных экспериментах и апробирование их на экспериментальных образцах радаров.

Краткое описание результатов:

Результатом научно-исследовательской деятельности группы являются фундаментальные аналитические закономерности и соотношения, используемые для построения математических моделей. Разработанные модели служат основой новых алгоритмов дистанционного определения параметров наземных БТС и БПЛА микроволновыми радарами и проходят проверку на экспериментальных образцах оптоэлектронных и микроволновых устройств дистанционного зондирования.

Используемые ресурсы и оборудование:

Выявление фундаментальных аналитических закономерностей, соотношений и математических моделей, лежащих в основе новых алгоритмов дистанционного определения параметров наземных БТС и БПЛА микроволновыми радарами, основано на применении разделов радиофизики (распространение, отражение и поглощение радиоволн различными средами, частотно-временной анализ, модуляция сигналов, СВЧ-электроника), радиолокации (эффект Доплера), радиотехники (оптимальный приём и фильтрация сигнала, статистическая теория принятия решений, теория помехоустойчивости), информатики (анализ алгоритмов, протоколов передачи данных, базы данных). Моделирование выявленных закономерностей в вычислительных экспериментах проводится в программных пакетах LabVIEW, MatLab, MathCAD, обладающих поддержкой всех необходимых функций. Апробирование выявленных закономерностей и моделей проводится на экспериментальных образцах радаров.

Участие студентов в выполняемых проектах:

К научно-исследовательским работам группы «Оптоэлектронные и микроволновые устройства дистанционного зондирования» привлекаются студенты, обучающиеся по программам подготовки как бакалавров, так и магистров. В научной группе защищают выпускные квалификационные работы в том числе и иностранные обучающиеся.

Эффект Доплера – обзор

2.2.4.7 Лазерный датчик Доплера

Эффект Доплера, открытый в 1842 году австрийским ученым Кристианом Допплером, представляет собой эффект в физике, согласно которому частота движения любой гармонической волны в приемнике отличается от частоты в его источнике всякий раз, когда приемник, источник или оба находятся в движении относительно друг друга.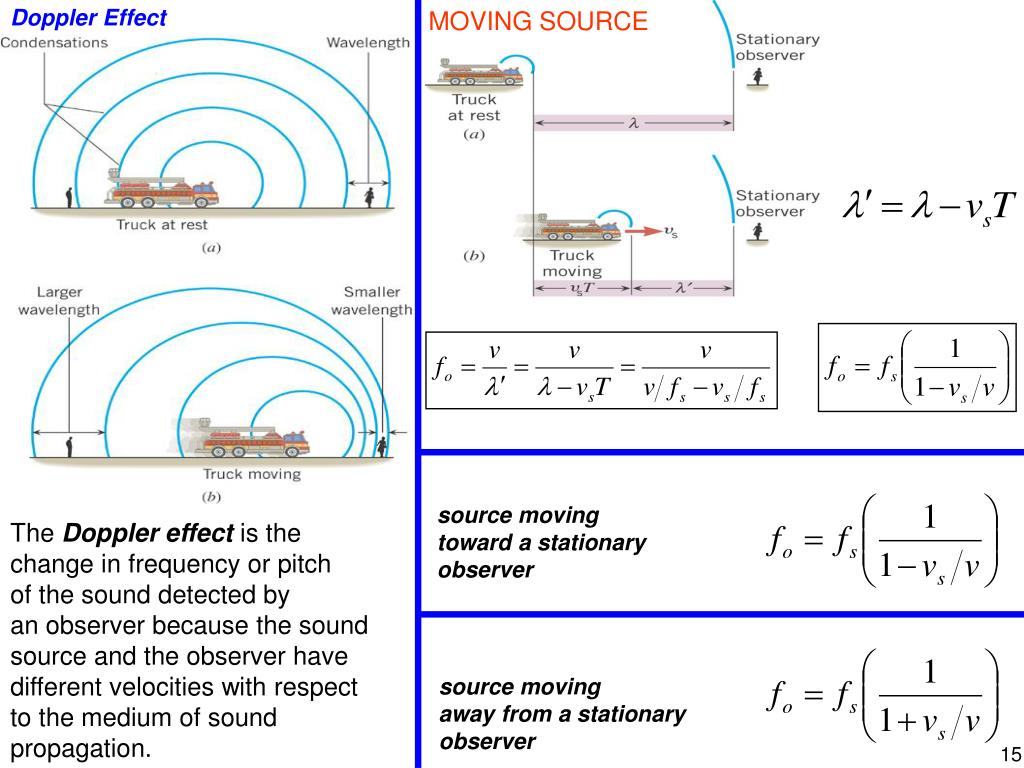 Впоследствии этот эффект стал использоваться для разнообразных приложений в различных областях, представляющих практический интерес.В областях океанографических исследований и оперативной океанографии эффект Доплера широко используется для дистанционного измерения океанских течений.

Методы лазерного доплера применялись для измерения потока жидкости еще в 1964 году. Однако его морское применение началось только в 1980 году. освещенные монохроматическим световым излучением, вносят частотные сдвиги в рассеянное световое излучение благодаря эффекту Доплера.Предполагается, что рассеивающие частицы являются пассивными индикаторами скорости воды. Введенный таким образом доплеровский сдвиг частоты линейно связан со скоростью потока воды, полностью определяемой геометрией системы. Доплеровский сдвиг частоты измеряется по гетеродинированному сигналу, полученному в результате фотосмешения полученного рассеянного излучения с прямым излучением или с другим рассеянным излучением.

Широко используются два типа лазерных доплеровских систем: система прямого рассеяния и система обратного рассеяния. Для системы прямого рассеяния требуется два водонепроницаемых кожуха, в одном из которых находится источник лазерного излучения, а в другом – приемник. Эти ограждения должны поддерживаться в строгом оптическом выравнивании. Рассеяние света от природных частиц гораздо сильнее в прямом направлении. С сильными оптическими сигналами прямого рассеяния можно получать как непрерывные, так и периодические выборки скорости потока воды. Недостатком системы прямого рассеяния является то, что распорки, соединяющие лазерный источник и приемник, могут мешать потоку, который предполагается измерять.Конфигурация обратного рассеяния допускает «моностатическую» конструкцию (т. е. источник и приемник в одном и том же месте), что позволяет проводить измерения расхода удаленно, не нарушая потока. Таким образом, для системы обратного рассеяния потребуется только один корпус, но более мощный лазер. Это связано с тем, что отношение сигнал/шум для системы обратного рассеяния обычно хуже, чем для системы прямого рассеяния.

В системе прямого рассеяния, описанной Fowlis et al. (1974), исходный лазерный луч разделяется на два параллельных луча светоделителем.Чтобы определить величину, а также направление потока, необходимо ввести известное смещение частоты, скажем, f _R , в один из лазерных лучей. Один из способов введения такого сдвига частоты состоит в вращении радиальной дифракционной решетки в одном из лучей. В зависимости от скорости вращения и общего количества линий на решетке частота дифрагированного света смещается на постоянное кратное исходной частоте в зависимости от того, какой порядок дифракции наблюдается.

Другим методом, используемым для создания известного сдвига частоты, является введение ячейки Брэгга в один из двух параллельных лучей. Затем линза фокусирует два параллельных луча, один с исходной частотой, а другой с искусственно введенным смещением частоты, в общую точку в поле потока. Точка пересечения (известная как точка пересечения ) этих двух лучей определяет положение рассеивающего объема. Это место является местом измерения расхода воды.Эта геометрия создает интерференционные полосы в общем объеме пересечения двух лучей. Объем пересечения лучей, часто называемый зондовым объемом или интерференционной областью , связан с пространственным разрешением. Частицы в поле течения, проходя через пересекающийся объем, рассеивают свет от обоих падающих лучей. Когда одна рассеивающая частица проходит через синусоидальную оптическую интерференционную картину, интенсивность рассеянного света изменяется синусоидально во времени с частотой, пропорциональной скорости частицы.Когда более чем одна частица проходит через интерференционную картину одновременно, между рассеянными сигналами, соответствующими каждой частице, возникают фазовые сдвиги. Когда сигнал велик, многочастичные фазовые сдвиги не имеют значения (Стачник и Мэйо, 1977). Поскольку между двумя падающими лучами существует угол, рассеянный свет от каждого луча смещается по частоте (доплеровский сдвиг) на разную величину. Затем два направленных вперед световых луча направляются на вторую собирающую линзу, которая фокусирует рассеянный свет на фотодетектор.Эта компоновка известна как система двойного рассеяния или интерференционная система . Световые лучи, рассеянные частицами в воде, смешиваются (то есть гетеродинируются) на поверхности фотодетектора, что приводит к генерации частот биений. Поскольку выходное напряжение фотодетектора представляет собой суперпозицию большого числа импульсов, рассеянных частицами разного размера и пространственного разнесения, этот сигнал будет иметь случайно меняющуюся амплитуду и случайно флуктуирующую фазу (Greated and Durrani, 1971), фронт Концевая электронная схема выделяет, обычно методом «частотной области», разностную частоту (f _R ± f _D ), где f _D — доплеровский сдвиг, вызванный потоком воды.Знак f _D зависит от направления потока. В геометрии двойного рассеяния скорость потока связана с f _D формулой

(2. 3)fD=2μvsinθλ

где μ — показатель преломления жидкости, λ — длина волны лазерного излучения в вакууме , θ — половина угла между двумя сходящимися падающими лучами, а v — составляющая потока, перпендикулярная плоскости, содержащей оптическую ось и два луча системы. В практических проектах (Fowlis et al., 1974), этот угол меньше 6°. Заметим, что если бы в один из падающих лучей не было введено дополнительное смещение частоты f _R , то было бы невозможно определить знак f _D , и тогда система была бы чувствительна только к скорости потока и не его направление.

Один набор падающих лучей может обнаруживать только один компонент водного потока. Поворот светоделителя на 90° вокруг оптической оси или установка второго светоделителя с оптической осью, параллельной исходной системе, но повернутой на 90° по отношению к ней, сделает комбинированную систему чувствительной к двум взаимно ортогональные компоненты потока.Первый метод будет включать временное разделение измерения двух компонентов потока, тогда как последний метод будет включать пространственное разделение.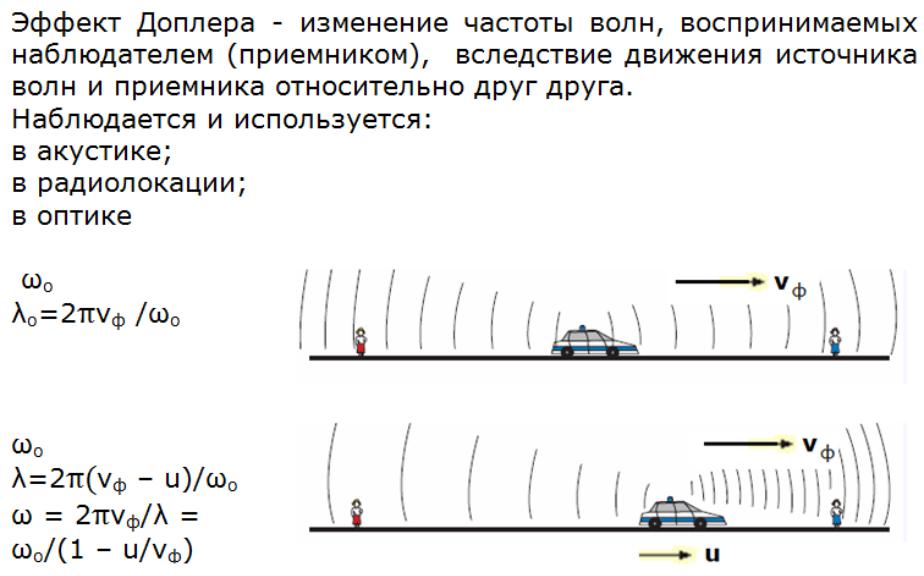 Для большинства измерений океанского стока такие незначительные разнесения не будут приводить к каким-либо существенным ошибкам. Для одновременных измерений двух ортогональных компонентов потока в одном и том же месте в пространстве потребуется многокомпонентная лазерная доплеровская система.

Оригинальный подход, использованный Agrawal and Belting (1988) для получения двух отдельных компонентов скорости с использованием системы прямого рассеяния, заключается в использовании трех лучей от одного лазера, но с сильно различающимися смещениями (рис. 2.12). Затем фототок от детектора усиливается и смешивается с локальными генераторами, частоты которых очень близки к частотам смещения лазера, и подвергается полосовой фильтрации для разделения двух осей скорости.

РИСУНОК 2.12. (а) Система прямого и (б) обратного рассеяния лазерного доплеровского измерителя скорости (LDV).

(Источник: Agrawal and Belting, 1988.)

В системах обратного рассеяния лазерные лучи с разным частотным сдвигом, полученные от одного и того же источника, фокусируются в точке измерения через стеклянное окно.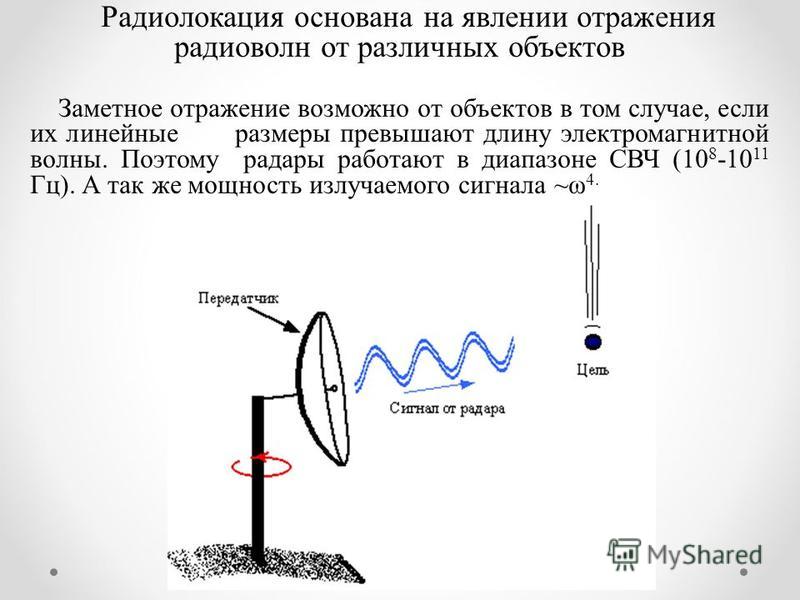 Обратно-рассеянное излучение из объема кроссовера затем направляется на фотодетектор с последующей обработкой сигнала. Преимущество системы обратного рассеяния заключается в том, что с помощью процесса оптического масштабирования можно дистанционно измерять профили скорости течения воды (Agrawal and Belting, 1988). Оптическое масштабирование точки измерения вдоль оптической оси достигается поворотом фокусирующей линзы падающего луча с помощью шагового двигателя. Такое расположение, используемое в геометрии обратного рассеяния, создает геометрию зонд-объем, зависящую от дальности.

Примечательным достоинством лазерных доплеровских измерителей скорости является то, что они могут достигать чрезвычайно малых объемов измерения (часто менее одного кубического миллиметра) и могут дистанционно (порядка метра) измерять скорости потока, не воздействуя на поле потока. Они также обладают высокой точностью и стабильностью и не требуют повторной калибровки. У них чрезвычайно низкие пороги скорости потока, а их отклики по своей сути линейны. Можно точно измерить скорость потока 0,1 см/с или меньше.Их пространственное и временное разрешение хорошее, и они способны работать с высокой частотой дискретизации. Способность лазерного допплеровского метода обнаруживать медленные потоки предполагает его пригодность в конструкциях измерителей скорости вертикального потока. Эти характеристики возникают из-за того, что короткая длина волны когерентного лазерного излучения позволяет сфокусировать его на очень малые воспринимаемые объемы, а высокая стабильность частоты лазерных источников позволяет оптически интерферирующим лучам формировать устойчивые интерференционные картины в пространстве и во времени (Стачник, 1977).

Недостатком LDCM является то, что, хотя они не имеют внешних движущихся частей, многие практические конструкции должны иметь внутренние движущиеся части. Вращение светоделителя и радиальной решетки, оптическое масштабирование и т. д. — вот некоторые из областей, где использование двигателя становится неизбежным. Кроме того, для работы лазера, ячейки Брэгга, фотоумножителя и т.п. требуется относительно высокая мощность. В результате этих логистических ограничений лазерные доплеровские измерители скорости потока в настоящее время используются только для специализированных приложений, таких как изучение переноса наносов в глубоком море и полей турбулентных скоростей ближе к морскому дну, где другие типы измерителей течений могут оказаться непригодными. .

Полицейский доплеровский радар

Полицейский доплеровский радар предыдущий | Следующий

Полицейские микроволновые радары используют принцип Доплера для измерения скорости. Радар передает непрерывный микроволновый сигнал и одновременно измеряет эхо-сигнал, частота которого сдвинута пропорционально скорости, т. е. доплеровский сдвиг. Сдвиг частоты измеряется в циклах в секунду и имеет единичную размерность Герц (Гц).

Звук движущегося поезда — хороший пример эффекта Доплера. Когда поезд приближается к неподвижному слушателю, частота свистка звучит выше, чем когда поезд идет ровно со слушателем. По мере удаления поезда от слушателя высота звука уменьшается. Автомобильные гудки демонстрируют то же явление, что и все звуки.

В приведенном выше примере, если автомобильный гудок не работает, а слушатель находится в поезде, принцип Доплера все еще применяется. По мере того, как слушатель в поезде приближается к стационарному гудку, высота гудка звучит выше, когда поезд удаляется от стационарного гудка, высота звука для всех в поезде снижается.

Стационарный радар
Микроволновые сигналы распространяются со скоростью света, но подчиняются принципу Доплера.Микроволновые радары принимают отражение с доплеровским сдвигом частоты от движущегося объекта. Частота смещается выше для приближающихся объектов и ниже для удаляющихся объектов. Сдвиг частоты пропорционален скорости.

Рекламные ссылки

Сдвиг частоты эха
Приближающийся трафик		Отступающий трафик
ф т = ф о + ф д		ф т = ф о – ф д

f _t = Частота эха трафика (возврата)
f _o = Частота передачи
f _d = Доплеровский сдвиг радара

Сигнал радара

Доплеровский сдвиг радара (f _d ) является функцией частоты передачи (f _o ), скорости волны (c = скорость света) и скорости целевого транспортного средства (v). Скорость положительна (+v) для приближающегося транспорта и отрицательна (-v) для удаляющегося.

Уравнение радиолокационного доплеровского сдвига

f d = Доплеровский сдвиг радара f o = Частота передачи

v = скорость автомобиля c = скорость света

Радиолокационный доплеровский сдвиг

Движущееся транспортное средство с радар-детектором будет получать сигнал радара, сдвинутый в доплеровском режиме пропорционально скорости.Радар снова получит отражение, сдвинутое пропорционально скорости. Эхо-сигнал, который принимает радар, имеет вдвое больший доплеровский сдвиг, который получает радар-детектор целевого транспортного средства.

Стационарный радар с доплеровским сдвигом

Измеренная скорость
v = f _d c / (2 f _o )

v = Скорость движения (-v для удаляющегося транспорта) f d = Доплеровский сдвиг радара (-f d для удаляющегося транспорта) f o = Частота передачи c = Скорость света

Рекламные ссылки

Доплеровский сдвиг радара на полицейских частотах
В таблице ниже показано доплеровское смещение радара на единицу скорости (1 единица) для обычных частот полицейских радаров. Доплеровский сдвиг радара равен сдвиг единиц умноженный на скорость . Например, доплеровский сдвиг радара X-диапазона для автомобиля со скоростью 100 миль в час составляет 31,39 Гц/миль/час, умноженное на 100 миль/час, и равняется 3139 Герц.

Доплеровский сдвиг скорости единицы измерения

Передающий радар Частота		Радар Доплеровский сдвиг
Лента	ГГц	Гц/км/ч	Гц/м/ч	Гц/узел
С	2.455	4,53	7,29	8,39
Х	9.410	17,44	28.06	32,30
Х	9.900	18,34	29,53	33,98
Х	10,525	19,50	31,39	36,12
Ку	13. 450	24,92	40.11	46.16
К	24.125	44,71	71,95	82,80
К	24.150	44,75	72,02	82,88
Ка	33,4 – 36,0	61,89 – 66,71	99,61 – 107,36	114,63 – 123,55

Доплеровский сдвиг радара в зависимости от скорости
Рекламные ссылки

Частотный спектр
Передаваемый сигнал имеет несколько шумовых юбок, которые мешают отражению от медленно движущихся объектов.Большинство радаров имеют минимальную скорость цели, как правило, 10-15 миль в час. Некоторые радары имеют минимальную скорость 1–3 мили в час.

Доплеровский сдвиг радара в зависимости от скорости

Помехи от отражения от земли обычно являются самым сильным отражением сигнала, но, поскольку земля не движется, она не имеет доплеровского сдвига. В радаре с движущимся режимом эхо-сигнал от земли смещается по частоте в зависимости от скорости патрульной машины, как и все другие отражения, кроме тех, которые имеют ту же скорость, что и радар.

kTBF представляет собой средний уровень шума приемника и является функцией температуры (T), ширины полосы шума радиолокационного приемника (B), коэффициента шума приемника (F) и постоянной Больцмана (k).

---

CopRadar.com
Информационный центр полицейских радаров
Доплеровский радар
Предыдущая | Топ | Следующий

Как звучит эффект Доплера? Мы исследуем эту историю доплеровского радара в Южной Дакоте

.

Эта история взята из ежедневной передачи SDPB по связям с общественностью In the Moment , которую ведет Лори Уолш.

В этот день в 1995 году Национальная служба погоды в Су-Фолс ввела в эксплуатацию новый доплеровский радар. Это было провозглашено важной вехой для Национальной метеорологической службы.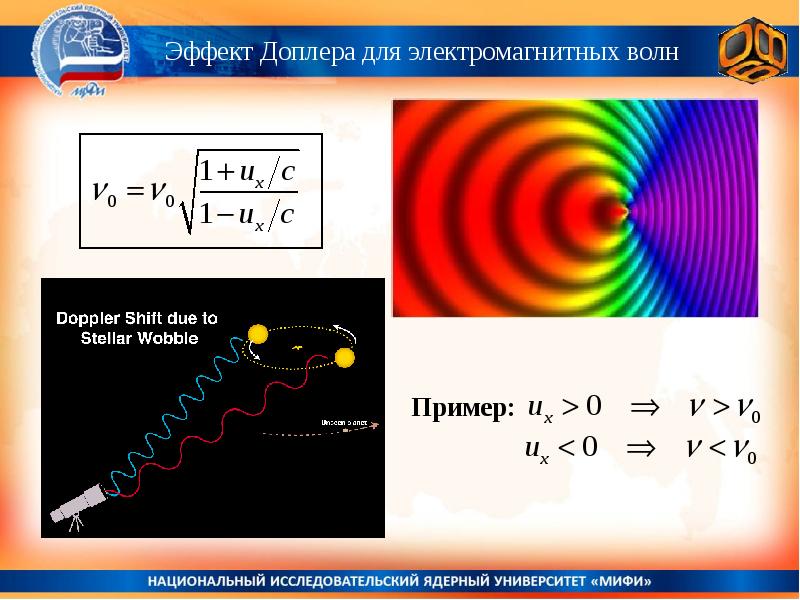

Радары имеют решающее значение и позволяют наблюдателям «видеть» внутри облаков и помогают понять, что происходит. Доплеровские метеорологические радары — это приборы дистанционного зондирования, способные обнаруживать типы частиц… например, дождя, снега, града и даже насекомых. Кроме того, они могут обнаруживать интенсивность и движение.Данные доплеровского радара можно использовать для определения структуры штормов и прогнозирования силы штормов.

Текущая версия доплеровского радара Национальной метеорологической службы называется NEX-RAD или Next-Generation-Radar. Радар испускает всплеск энергии. Если энергия попадает на объект, такой как капля дождя, снежинка или град, энергия рассеивается, но небольшая часть излучаемой энергии направляется обратно к радару.

Компьютеры анализируют силу возвращенного импульса, время, затраченное на путь до объекта и обратно, а также фазу или доплеровский сдвиг импульса.И этот процесс происходит до 1300 раз в секунду.

Способность обнаруживать так называемый «сдвиг фазы» импульса энергии делает NEX-RAD доплеровским радаром. Этот эффект Доплера был назван в честь австрийского физика Кристиана Доплера, открывшего его. Фаза возвращаемого сигнала обычно изменяется в зависимости от движения капель дождя.

Скорее всего, вы испытали на себе эффект Доплера от проезжающих мимо поездов или автомобилей. Когда поезд или автомобиль проезжает мимо вашего местоположения, вы, возможно, замечали, что высота гудка поезда или шума двигателя автомобиля меняется с высокой на более низкую.При приближении звуковые волны сжимаются, повышая высоту тона. Когда объект удаляется от вас, звуковые волны растягиваются, понижая высоту звука.

Тот же эффект имеет место в атмосфере, когда импульс энергии от NEX-RAD поражает объект и отражается обратно к радару. Компьютеры радара измеряют изменение фазы отраженного импульса энергии, которое затем преобразует это изменение в скорость и направление объекта.

В этот день в 1995 году Национальная метеорологическая служба Су-Фолс ввела в эксплуатацию новую радиолокационную систему.

Помощь в производстве благодаря Брэду Теннанту, доктору философии, профессору истории в Presentation College.

Применение доплеровского радара

RADAR, что означает «Радио». Обнаружение и определение дальности – это распространенный метод обнаружения движущиеся объекты. Например, полиция использует доплеровский радар для определять скорость движущегося автомобиля.австрийский физик. по имени Доплер впервые описал эту концепцию в 19 ^-й -й век. Эффект Доплера описывает то, что происходит, когда волна (звуковая, радио и т. д.) попадает на движущуюся объект.

Например, полиция использовать радар-детектор для определения скорости автомобиля он движется по шоссе. Радиолокационные волны передаются от полицейская машина на определенной частоте.Напомним, что волны имеют как амплитуду, так и частоту. Когда волны отскакивают на движущийся объект влияет их частота. Как радио волны отскакивают от автомобиля, который движется к детектору частота волны уменьшается. Если волны отскакивают от машина удаляется от детектора частота волны увеличивается. Детектор использует разницу в частоты передаваемых и принимаемых волн для определения скорость автомобиля.

Радарная технология теперь встроенный в новый фонарик устройство, которое может обнаруживать движение человека через дверь или стена. Устройство может обнаруживать движение из-за человеческого дыхание на расстоянии до трех метров. Устройство будет оказаться полезным для полиции в обнаружении преступников в засаде ситуации, при проверке постели в тюрьмах или для определение местонахождения заложников в здании.То Устройство также может быть использовано для обнаружения выживших после теракта. землетрясение или лавина.

Радиолокационная технология также может быть используется для обнаружения мин. НАТО тратит миллионы на разработать устройство для обнаружения и обезвреживания фугасов. То базовая технология состоит из двух антенн, которые фокусируют радар энергии в точку чуть ниже земли в нескольких футах от человек, несущий антенну.Устройство запрограммировано на игнорировать сигналы, отражающиеся от поверхности, и зарытые предметы светятся ярче на радиолокационном изображении.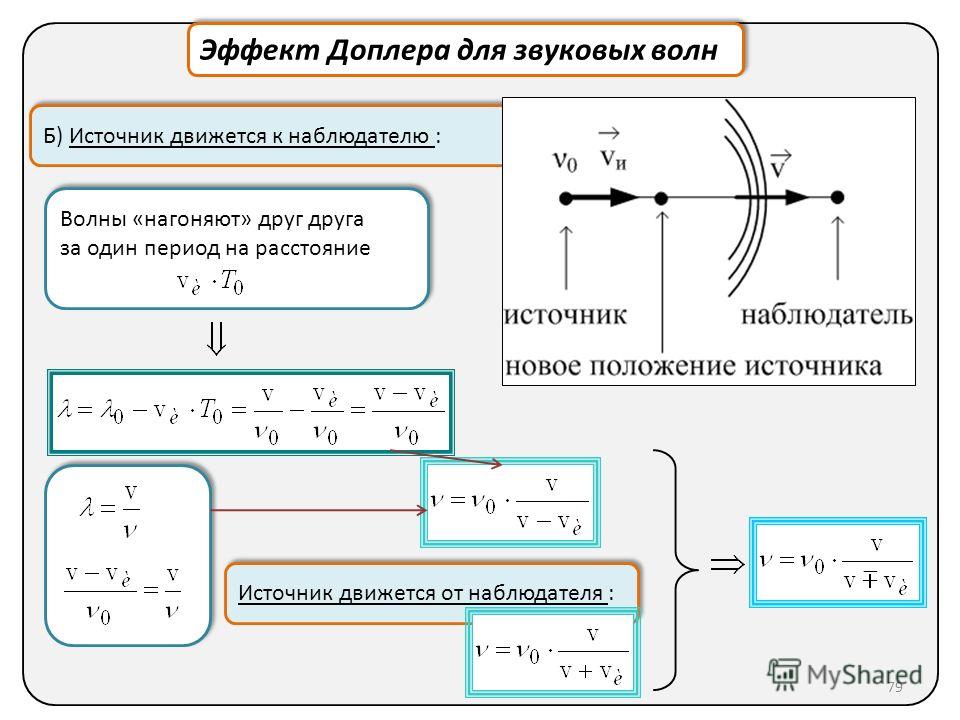 Этот позволяет оператору фактически обнаруживать наземные мины никогда не касаясь земли.

Эффект Доплера для сигналов Рона Куртуса

SfC Home > Физика > Волновое движение >

Рона Куртуса

Эффект Доплера — это изменение наблюдаемой длины волны или частоты формы волны по сравнению с излучаемой источником, когда источник и/или наблюдатель перемещаются относительно волновой среды.

Например, вы слышите изменение звука сирены, когда к вам приближается машина скорой помощи, и наблюдаете за изменением цвета — или красным смещением — звезды, которая движется в направлении от Земли.

Этот эффект был назван в честь австрийского ученого Кристиана Доплера, открывшего явление света в 1842 году. Голландский химик Байс Баллот подтвердил эффект Доплера для звука в 1845 году.

Возможные вопросы:

• Почему возникает эффект Доплера?
• Как это влияет на звук?
• Как эффект используется в астрономии?

Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц измерения

---

---

Что вызывает эффект Доплера?

Эффект Доплера возникает, когда источник волны, такой как звук или свет, излучает волны с постоянной скоростью или частотой, но между источником и наблюдателем существует постоянное относительное движение, вызывающее изменение наблюдаемой частоты.

Связь между

λ и f

Связь между длиной волны и частотой видна из:

с = λf

где

• c — постоянная скорость волны (например, звука или света)
• λ длина волны
• f это частота

Таким образом, когда λ уменьшается, f увеличивается, и наоборот.

Примечание : Скорость звука может варьироваться в зависимости от условий, но мы предполагаем, что ничего не меняется, поэтому она постоянна.

Если источник движется

Если этот источник движется относительно неподвижного наблюдателя, скорость волны остается постоянной, но расстояние между излучаемыми волнами уменьшается в направлении движения источника и увеличивается в противоположном направлении.

Эффект Доплера, вызванный движущимся источником

На рисунке показано, что когда источник волн перемещается вправо, частота волн в этом направлении выше.Длина волны в обратном направлении меньше.

Если наблюдатель движется

Если вы движетесь к стационарному источнику, вы получаете волны с большей скоростью, чем частота их излучения. Таким образом, наблюдаемая длина волны укорачивается, а частота увеличивается. Точно так же, если вы удаляетесь от источника, наблюдаемая длина волны удлиняется, а частота уменьшается.

Помните, что движение относительно, поэтому нас не волнует, движется ли источник или наблюдатель.Вместо этого беспокоит то, движутся ли они друг к другу или от друг друга.

Отражение от движущегося объекта

Если и источник волны, и наблюдатель неподвижны, но волна отражается от движущегося объекта, это как если бы объект был движущимся источником. Наблюдаемая длина волны и частота изменятся в соответствии с эффектом Доплера.

Этот принцип используется в доплеровском радаре.

Звуковые волны

Эффект Доплера возникает при движении источника и отражении звука от движущегося объекта.

( См. Эффект Доплера для звука для получения информации о расчете эффекта. )

Обратите внимание , что скорость источника или движущегося объекта должна быть на меньше скорости звука на . При скоростях, равных или превышающих скорость звука, имеет место несколько иной эффект.

( Для получения дополнительной информации см. Путешествие быстрее звука. )

Источник перемещается

Когда вы слышите звук движущегося к вам объекта, например, сирены из машины скорой помощи, высота этого звука выше, чем если бы машина стояла на месте.Точно так же, когда автомобиль удаляется от вас, сирена будет звучать тише.

Отражение от движущегося объекта

Если стационарный источник посылает звуковые волны и они отражаются от движущегося объекта, звуковые волны, слышимые от источника, будут иметь различную высоту тона в зависимости от направления объекта. Это как если бы движущийся объект излучал звуковые волны. В то время как гидролокатор использует звуковые волны для измерения расстояния до объекта, доплеровский гидролокатор также измеряет скорость объекта.

Электромагнитные волны

Астрономы используют эффект Доплера для измерения скоростей галактик относительно Земли. Кроме того, доплеровский радар использует электромагнитные волны для измерения скорости транспортных средств и штормов.

( См. Уравнения эффекта Доплера для света для получения информации о расчете эффекта. )

Измерить скорость галактики

Большинство звезд и галактик имеют высокую концентрацию водорода, который, в свою очередь, имеет специфический спектр цветов, когда он очень горячий, например, на нашем Солнце и в других звездах.При измерении длин волн света от далеких галактик оказалось, что спектр немного сместился в красную сторону. Это означает, что длины волн длиннее, чем они должны быть обычно, что указывает на эффект Доплера, вызванный удалением источника света от Земли.

Это называется красным смещением. Из измерений можно подсчитать, насколько быстро галактики удаляются от нас. Это также показывает, что Вселенная расширяется.

Галактики и звезды, движущиеся к нашей Солнечной системе, испускают более короткие волны в виде синего смещения.

Доплеровский радар

Доплеровский радар излучает электромагнитные волны — обычно в микроволновом диапазоне — для расчета скорости движущихся объектов путем измерения эффекта Доплера, вызванного отражением от движущегося объекта.

Полиция использует радарные устройства для отправки электромагнитного луча определенной длины волны. Когда эта форма волны отражается от движущегося автомобиля, движение вызывает увеличение длины волны отражения, что позволяет доплеровскому радиолокационному устройству рассчитать скорость автомобиля.

Резюме

Эффект Доплера — это воспринимаемое изменение частоты или длины волны, вызванное перемещением источника сигнала.

Длина волны кажется короче, когда источник движется к вам, и длиннее, когда источник удаляется. Вы могли слышать, как звук сирены становится выше, когда автомобиль движется к вам, а затем становится ниже, когда он удаляется.

Эффект Доплера также используется в астрономии для измерения движения галактик по мере их удаления от Земли.

---

Двигайтесь по течению

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Веб-сайты

Волны, движение и частота: эффект Доплера — Хороший обзор с анимацией от Einstein Online

Ресурсы Wave Motion

Книги

(Примечание: Школа чемпионов может получать комиссионные за покупку книг)

Лучшие книги по эффекту Доплера

---

Поделиться этой страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.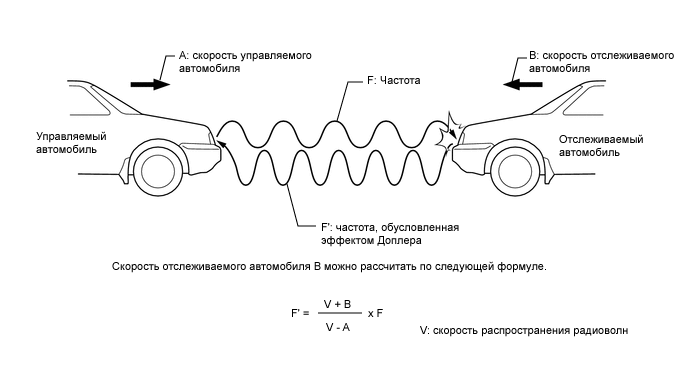 com/science/
wave_doppler_effect.htm

Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.

Copyright © Ограничения

---

Где ты сейчас?

Школа чемпионов

Темы по физике

Эффект Доплера для сигналов

---

Что такое доплеровский радар? – Определение и использование

Доплеровский радар Определение

Радар — это любая система, которая излучает радиоволны, которые отражаются от поверхностей и возвращаются для обнаружения тем же устройством.Первоначально радар был сокращением от радио обнаружения и диапазона . Цель состоит в том, чтобы выяснить наличие, скорость, расстояние или направление объектов, особенно транспортных средств. Например, радар можно использовать для отслеживания самолетов. Это похоже на то, как подводные лодки отслеживают другие подводные объекты, за исключением того, что подводный гидролокатор использует звук вместо радиоволн.

Изображение военного радара

Доплеровский радар – это специальный радар , используемый для определения скорости объекта ‘.Доплеровский радар работает, используя знания о том, что волны, создаваемые объектом, будут сжиматься ближе друг к другу, если он движется к вам, или распространяться дальше, если он удаляется. Вот почему полицейская сирена звучит так, как будто ее тон падает по мере того, как машина удаляется от вас: по мере того, как создается каждая волна, машина удаляется все дальше и дальше, увеличивая расстояние между каждым фронтом волны. С другой стороны, если автомобиль движется к вам, у него есть шанс догнать созданную им предыдущую волну, сдавливая волны вместе.Сжатые волны имеют более высокую частоту, а более высокая частота — более высокий тон. Распространенные волны имеют более низкую частоту, а более низкая частота – более низкий тон. Таким образом, сирена полицейской машины, движущейся к вам, будет иметь более высокий тон, а сирена полицейской машины, удаляющейся от вас, будет иметь сирену более низкого тона.

Автомобильные сирены звучат выше, если машина движется к вам из-за эффекта Доплера.

Доплеровский радар работает аналогичным образом.Доплеровский радар отражает импульс радиоволн от целевого объекта. Когда волна отскакивает, она действует так же, как звуковые волны полицейской сирены. А измерив, насколько изменится частота радиоволн после отражения от объекта, вы сможете рассчитать скорость этого объекта.

Иллюстрация эффекта Доплера

Но как это использовать? Когда нам нужно знать скорость объекта?

17.7 Эффект Доплера. Общая физика с использованием исчисления I

Цели обучения

К концу этого раздела вы сможете:

• Объясните изменение наблюдаемой частоты при приближении или удалении движущегося источника звука от неподвижного наблюдателя
• Объясните изменение наблюдаемой частоты по мере того, как наблюдатель движется к стационарному источнику звука или от него

Характерный звук проезжающего мимо мотоцикла является примером эффекта Доплера . В частности, если вы стоите на углу улицы и наблюдаете, как машина скорой помощи со звуком сирены проезжает с постоянной скоростью, вы заметите два характерных изменения в звуке сирены. Во-первых, громкость звука увеличивается по мере приближения машины скорой помощи и уменьшается по мере ее удаления, что и ожидалось. Но, кроме того, высокий звук сирены резко меняется на более низкий звук. Когда машина скорой помощи проезжает, частота звука, слышимого стационарным наблюдателем, изменяется с постоянной высокой частоты на постоянную более низкую частоту, даже если сирена излучает постоянную частоту источника.Чем ближе проезжает скорая помощь, тем резче сдвиг. Кроме того, чем быстрее движется машина скорой помощи, тем больше смещение. Мы также слышим этот характерный сдвиг частоты для проезжающих автомобилей, самолетов и поездов.

Эффект Доплера — это изменение наблюдаемой частоты звука из-за движения либо источника, либо наблюдателя. Хотя этот эффект менее известен, он легко заметен для стационарного источника и движущегося наблюдателя. Например, если вы проедете в поезде мимо стационарного звукового сигнала, вы услышите, как частота звукового сигнала смещается с высокой на низкую, когда вы проходите мимо.Фактическое изменение частоты из-за относительного движения источника и наблюдателя называется доплеровским сдвигом . Эффект Доплера и доплеровский сдвиг названы в честь австрийского физика и математика Кристиана Иоганна Доплера (1803–1853), который проводил эксперименты как с движущимися источниками, так и с движущимися наблюдателями. Допплер, например, заставил музыкантов играть в движущемся открытом вагоне поезда, а также играть стоя рядом с железнодорожными путями, когда поезд проезжал мимо. Их музыку наблюдали как в поезде, так и вне его, и измеряли изменения частоты.

Что вызывает доплеровский сдвиг? На рисунке показаны звуковые волны, излучаемые стационарными и движущимися источниками в неподвижной воздушной массе. Каждое возмущение распространяется сферически от точки, в которой излучается звук. Если источник неподвижен, то центр всех сфер, представляющих сжатие воздуха в звуковой волне, находится в одной точке, и неподвижные наблюдатели с обеих сторон слышат ту же длину волны и частоту, что и источник (случай а). Если источник движется, ситуация иная.Каждое сжатие воздуха движется по сфере из точки, в которой он был выпущен, но точка выброса движется. Эта движущаяся точка выброса заставляет сжатия воздуха быть ближе друг к другу с одной стороны и дальше друг от друга с другой. Таким образом, длина волны меньше в направлении движения источника (вправо в случае б) и длиннее в противоположном направлении (влево в случае б). Наконец, если наблюдатели перемещаются, как в случае (с), частота, с которой они получают сжатия, изменяется.Наблюдатель, движущийся к источнику, принимает их с более высокой частотой, а человек, удаляющийся от источника, принимает их с более низкой частотой.

Рисунок 17.30 Звуки, излучаемые источником, распространяющимся в виде сферических волн. (а) Когда источник, наблюдатели и воздух неподвижны, длина волны и частота одинаковы во всех направлениях и для всех наблюдателей. (б) Звуки, излучаемые источником, движущимся вправо, распространяются от точек, в которых они излучались. Длина волны уменьшается, и, следовательно, частота увеличивается в направлении движения, так что наблюдатель справа слышит более высокий звук.Противоположное верно для наблюдателя слева, где длина волны увеличивается, а частота уменьшается. в) Тот же эффект возникает при движении наблюдателей относительно источника. Движение к источнику увеличивает частоту, поскольку наблюдатель справа проходит через большее количество гребней волны, чем если бы он оставался неподвижным. При движении от источника частота уменьшается, поскольку наблюдатель слева проходит через меньшее количество гребней волны, чем если бы он оставался неподвижным.

Мы знаем, что длина волны и частота связаны соотношением [latex]v=f\lambda ,[/latex], где v — фиксированная скорость звука. Звук движется в среде и имеет в этой среде одну и ту же скорость v независимо от того, движется источник или нет. Таким образом, f , умноженное на [латекс]\лямбда[/латекс], является константой. Поскольку наблюдатель справа в случае (b) получает более короткую длину волны, частота, которую он принимает, должна быть выше. Точно так же наблюдатель слева получает более длинную волну и, следовательно, слышит более низкую частоту. То же самое происходит и в случае (с). Наблюдатель, движущийся к источнику, принимает более высокую частоту, а наблюдатель, удаляющийся от источника, принимает более низкую частоту.В общем, относительное движение источника и наблюдателя друг к другу увеличивает принимаемую частоту. Относительное движение врозь снижает частоту. Чем больше относительная скорость, тем больше эффект.

Эффект Доплера возникает не только для звука, но и для любой волны, когда существует относительное движение между наблюдателем и источником. Доплеровские сдвиги возникают, например, в частоте звуковых, световых и водных волн. Доплеровские сдвиги можно использовать для определения скорости, например, когда ультразвук отражается от крови при медицинской диагностике.Относительные скорости звезд и галактик определяются сдвигом частот света, получаемого от них, и многое говорят о происхождении Вселенной. На современную физику глубоко повлияли наблюдения доплеровских сдвигов.

Получение наблюдаемой частоты из-за доплеровского сдвига

Рассмотрим двух стационарных наблюдателей X и Y на рисунке, расположенных по обе стороны от стационарного источника. Каждый наблюдатель слышит одну и ту же частоту, и эта частота является частотой, создаваемой стационарным источником.

Рисунок 17.31 Неподвижный источник излучает звуковые волны с постоянной частотой [латекс] {f} _ {\ текст {s}}, [/латекс] с постоянной длиной волны [латекс] {\ лямбда} _ {\ текст { s}},[/latex] со скоростью звука v. Два стационарных наблюдателя X и Y по обе стороны от источника наблюдают частоту [латекс]{f}_{\text{o}}={f} _{\text{s}}[/latex], с длиной волны [латекс]{\lambda}_{\text{o}}={\lambda}_{\text{s}}. [/latex]

Теперь рассмотрим стационарного наблюдателя X с источником, удаляющимся от наблюдателя с постоянной скоростью [latex]{v}_{\text{s}} \lt v[/latex] (рисунок).В момент времени [latex]t=0[/latex] источник посылает звуковую волну, обозначенную черным цветом. Эта волна движется со скоростью звука v . Положение звуковой волны в каждом временном интервале периода [латекс]{Т}_{\текст{с}}[/латекс] показано пунктирными линиями. После одного периода источник переместился [латекс]\Delta x={v}_{\text{s}}{T}_{\text{s}}[/latex] и испускает вторую звуковую волну, которая движется выходит со скоростью звука. Источник продолжает двигаться и производить звуковые волны, на что указывают кружки с номерами 3 и 4.Обратите внимание, что по мере того, как волны удаляются, они остаются центрированными в своей соответствующей точке происхождения.

Рис. 17.32 Источник, движущийся с постоянной скоростью [латекс]{v}_{\text{s}}[/латекс] от наблюдателя X. Движущийся источник посылает звуковые волны с постоянной частотой [латекс]{ f}_{\text{s}},[/latex] с постоянной длиной волны [латекс]{\lambda }_{\text{s}}[/latex], со скоростью звука v.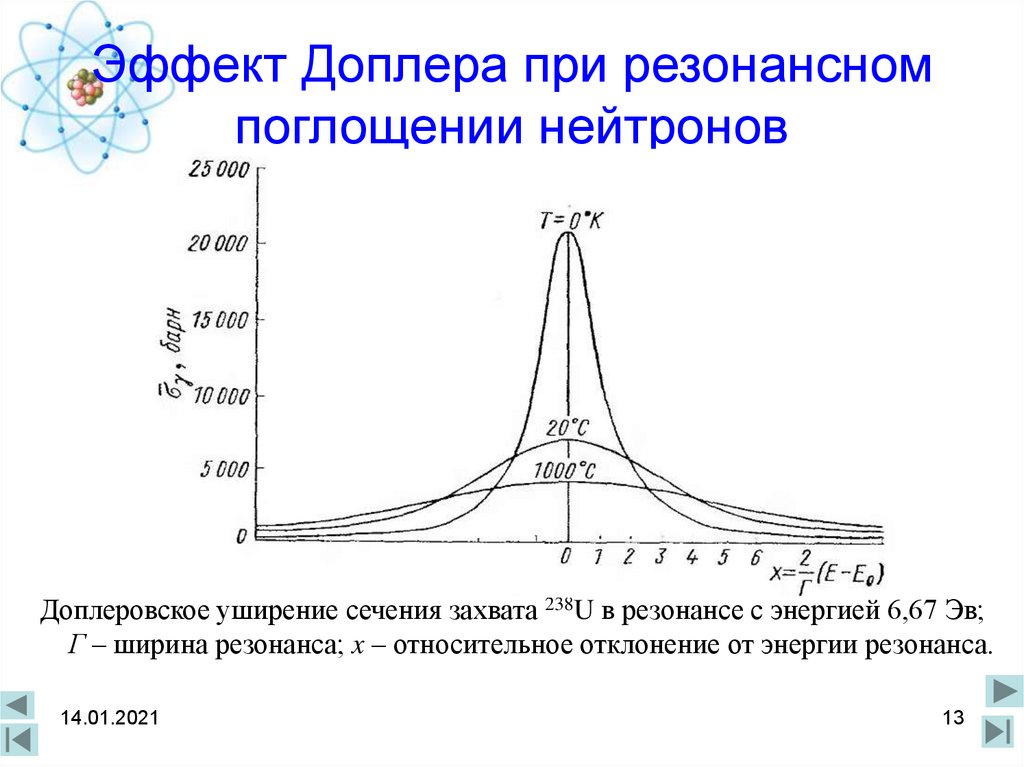 Моментальные снимки источника с интервалом [latex]{T}_{\text{s}}[/latex] показаны по мере удаления источника от неподвижного наблюдателя X.Сплошные линии представляют положение звуковых волн через четыре периода от начального времени. Пунктирные линии используются для отображения положения волн в каждый период времени. Наблюдатель слышит длину волны [латекс] {\ lambda} _ {\ text {o}} = {\ lambda} _ {\ text {s}} + \ Delta x = {\ lambda} _ {\ text {s} }+{v}_{\text{s}}{T}_{\text{s}}[/латекс].

Используя тот факт, что длина волны равна произведению скорости на период, а период обратно пропорционален частоте, мы можем получить наблюдаемую частоту:

[латекс] \ begin {массив} {ccc} \ hfill {\ lambda} _ {\ text {o}} & = \ hfill & {\ lambda} _ {\ text {s}} + \ Delta x \ hfill \ \ \ hfill v {T} _ {\ text {o}} & = \ hfill & v {T} _ {\ text {s}} + {v} _ {\ text {s}} {T} _ {\ text{s}}\hfill \\ \hfill \frac{v}{{f}_{\text{o}}}& =\hfill & \frac{v}{{f}_{\text{s} }}=\frac{{v}_{\text{s}}}{{f}_{\text{s}}}=\frac{v+{v}_{\text{s}}}{{ f} _ {\ text {s}}} \ hfill \\ \ hfill {f} _ {\ text {o}} & = \ hfill & {f} _ {\ text {s}} (\ frac {v} {v+{v}_{\text{s}}}). \hfill \end{массив}[/латекс]

Когда источник удаляется от наблюдателя, наблюдаемая частота становится ниже частоты источника.

Теперь рассмотрим источник, движущийся с постоянной скоростью [latex]{v}_{s},[/latex] движущийся к неподвижному наблюдателю Y , также показанному на рисунке. Длина волны определяется Y как [латекс] {\ lambda} _ {\ text {o}} = {\ lambda} _ {\ text {s}} – \ Delta x = {\ lambda} _ {\ text {s}}-{v}_{\text{s}}{T}_{\text{s}}.[/latex] Еще раз, используя тот факт, что длина волны равна скорости, умноженной на период, и период обратно пропорционален частоте, мы можем получить наблюдаемую частоту:

[латекс] \ begin {массив} {ccc} \ hfill {\ lambda} _ {\ text {o}} & = \ hfill & {\ lambda} _ {\ text {s}} – \ Delta x \ hfill \ \ \ hfill v {T} _ {\ text {o}} & = \ hfill & v {T} _ {\ text {s}} – {v} _ {\ text {s}} {T} _ {\ text{s}}\hfill \\ \hfill \frac{v}{{f}_{\text{o}}}& =\hfill & \frac{v}{{f}_{\text{s} }} – \ frac {{v} _ {\ text {s}}} {{f} _ {\ text {s}}} = \ frac {v- {v} _ {\ text {s}}} { {f} _ {\ text {s}}} \ hfill \\ \ hfill {f} _ {\ text {o}} & = \ hfill & {f} _ {\ text {s}} (\ frac {v }{v-{v}_{\text{s}}}). \hfill \end{массив}[/латекс]

Когда источник движется, а наблюдатель неподвижен, наблюдаемая частота равна

[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v} {v \ mp {v} _ {\ text {s}}}) \текст{‘}[/латекс]

, где [latex]{f}_{\text{o}}[/latex] — частота, наблюдаемая неподвижным наблюдателем, [latex]{f}_{\text{s}}[/latex] — частота создаваемого движущимся источником, v — скорость звука, [латекс] {v} _ {\ текст {s}} [/латекс] — постоянная скорость источника, а верхний знак соответствует приближающемуся источнику. наблюдатель, а нижний знак — источник, уходящий от наблюдателя.

Что произойдет, если наблюдатель движется, а источник неподвижен? Если наблюдатель движется к стационарному источнику, наблюдаемая частота выше, чем частота источника. Если наблюдатель удаляется от стационарного источника, наблюдаемая частота ниже частоты источника. Рассмотрим наблюдателя X на рисунке, когда наблюдатель движется к стационарному источнику со скоростью [латекс]{v}_{\text{о}}[/латекс]. Источник излучает тон с постоянной частотой [latex]{f}_{\text{s}}[/latex] и постоянным периодом [latex]{T}_{\text{s}}.[/latex] Наблюдатель слышит первую волну, излучаемую источником. Если бы наблюдатель был неподвижен, время прохождения одной длины волны звука должно быть равно периоду источника [латекс]{Т}_{\текст{с}}.[/латекс] Поскольку наблюдатель движется к источник, время прохождения одной длины волны меньше [латекс]{Т}_{\текст{с}}[/латекс] и равно наблюдаемому периоду [латекс]{Т}_{\текст{о} }={T}_{\text{s}}-\Delta t.[/latex] В момент времени [latex]t=0,[/latex] наблюдатель начинает с начала длины волны и движется ко второй длине волны по мере удаления длины волны от источника.Длина волны равна расстоянию, пройденному наблюдателем, плюс расстояние, пройденное звуковой волной до встречи с наблюдателем:

[латекс] \ begin {массив} {ccc} \ hfill {\ lambda} _ {\ text {s}} & = \ hfill & v {T} _ {\ text {o}} + {v} _ {\ text {o}} {T} _ {\ text {o}} \ hfill \\ \ hfill v {T} _ {\ text {s}} & = \ hfill & (v + {v} _ {\ text {o }}){T}_{\text{o}}\hfill \\ \hfill v(\frac{1}{{f}_{\text{s}}})& =\hfill & (v+{v }_{\text{o}})(\frac{1}{{f}_{\text{o}}})\hfill \\ \hfill {f}_{\text{o}}& =\ hfill & {f} _ {\ text {s}} (\ frac {v + {v} _ {\ text {o}}} {v}). \hfill \end{массив}[/латекс]

Рисунок 17.33 Неподвижный источник излучает звуковую волну с постоянной частотой [латекс] {f} _ {\ текст {s}} [/латекс], с постоянной длиной волны [латекс] {\ лямбда} _ {\ текст { s}}[/latex] движется со скоростью звука v. Наблюдатель X движется к источнику с постоянной скоростью [latex]{v}_{\text{o}}[/latex], а на рисунке показана начальная и конечное положение наблюдателя X. Наблюдатель X наблюдает частоту выше, чем частота источника. Сплошные линии показывают положение волн при [latex]t=0[/latex].Пунктирные линии показывают положение волн в точке [latex]t={T}_{\text{o}}[/latex].

Если наблюдатель удаляется от источника (рисунок), можно найти наблюдаемую частоту:

[латекс] \ begin {массив} {ccc} \ hfill {\ lambda} _ {\ text {s}} & = \ hfill & v {T} _ {\ text {o}} – {v} _ {\ text {o}} {T} _ {\ text {o}} \ hfill \\ \ hfill v {T} _ {\ text {s}} & = \ hfill & (v- {v} _ {\ text { o}}){T}_{\text{o}}\hfill \\ \hfill v(\frac{1}{{f}_{\text{s}}})& =\hfill & \hfill ( v-{v}_{\text{o}})(\frac{1}{{f}_{\text{o}}})\\ \hfill {f}_{\text{o}}& =\hfill & {f}_{\text{s}}(\frac{v-{v}_{\text{o}}}{v}). \hfill \end{массив}[/латекс]

Рисунок 17.34 Неподвижный источник излучает звуковую волну с постоянной частотой [латекс] {f} _ {\ текст {s}} [/латекс], с постоянной длиной волны [латекс] {\ лямбда} _ {\ текст { s}}[/latex] движется со скоростью звука v. Наблюдатель Y удаляется от источника с постоянной скоростью [latex]{v}_{\text{o}}[/latex], а на рисунке показана начальная и конечное положение наблюдателя Y. Наблюдатель Y наблюдает частоту ниже частоты источника. Сплошные линии показывают положение волн при [latex]t=0[/latex].Пунктирные линии показывают положение волн в точке [latex]t={T}_{\text{o}}[/latex].

Уравнения для наблюдателя, движущегося к стационарному источнику или от него, можно объединить в одно уравнение:

[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v \ pm {v} _ {\ text {o}}} {v}) ,[/латекс]

, где [latex]{f}_{\text{o}}[/latex] — наблюдаемая частота, [latex]{f}_{\text{s}}[/latex] — исходная частота, [latex ]{v}_{\text{w}}[/latex] – скорость звука, [latex]{v}_{\text{o}}[/latex] – скорость наблюдателя, верхний знак для наблюдателя, приближающегося к источнику, а нижний знак — для наблюдателя, удаляющегося от источника.

Рисунок и рисунок могут быть суммированы в одном уравнении (верхний знак означает приближение) и дополнительно проиллюстрирован на рисунке:

[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v \ pm {v} _ {\ text {o}}} {v \ mp {v}_{\text{s}}}),[/латекс]

” The fourth row contains “source moving away from observer”, “f subscript o equals f subscript s times v over v plus v subscript s”, “f subscript o equals f subscript s times v plus v subscript o over v plus v subscript s”, and f subscript o equals f subscript s times v minus v subscript o over v plus v subscript s.””>

Доплеровский сдвиг [латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v \ pm {v} _ {\ text {o}}} {v \ mp {v}_{\text{s}}})[/латекс]	Стационарный наблюдатель	Наблюдатель движется к источнику	Наблюдатель удаляется от источника
Стационарный источник	[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} [/ латекс]	[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v + {v} _ {\ text {o}}} {v}) [/ латекс]	[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v- {v} _ {\ text {o}}} {v}) [ /латекс]
Источник движется к наблюдателю	[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v} {v- {v} _ {\ text {s}}}) [ /латекс]	[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v + {v} _ {\ text {o}}} {v- {v} _{\текст{ы}}})[/латекс]	[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v- {v} _ {\ text {o}}} {v- {v }_{\text{s}}})[/латекс]
Источник удаляется от наблюдателя	[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v} {v + {v} _ {\ text {s}}}) [/ латекс]	[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v + {v} _ {\ text {o}}} {v + {v} _ {\текст{ы}}})[/латекс]	[латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v- {v} _ {\ text {o}}} {v + {v} _{\текст{ы}}})[/латекс]

где [латекс]{f}_{o}[/латекс] — наблюдаемая частота, [латекс]{f}_{s}[/латекс] — исходная частота, [латекс]{v}_ {w}[/latex] — скорость звука, [latex]{v}_{o}[/latex] — скорость наблюдателя, [latex]{v}_{s}[/latex] — скорость звука.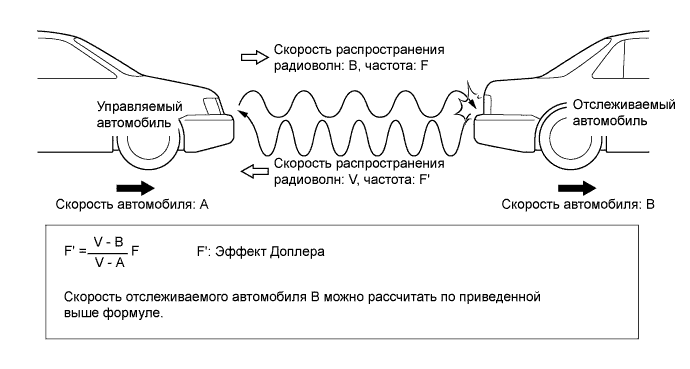 скорость источника, верхний знак соответствует приближению, а нижний — удалению.

Пример

Расчет доплеровского сдвига

Предположим, что поезд со звуковым сигналом частотой 150 Гц движется со скоростью 35,0 м/с в неподвижном воздухе в день, когда скорость звука составляет 340 м/с.

а) Какие частоты наблюдает человек, стоящий на обочине пути, при приближении поезда и после его прохождения?

(b) Какую частоту наблюдает машинист, едущий в поезде?

Стратегия

Чтобы найти наблюдаемую частоту в (а), мы должны использовать [латекс] {f} _ {\ text {obs}} = {f} _ {\ text {s}} (\ frac {v} {v \ mp {v}_{\text{s}}})[/latex], потому что источник движется.Знак «минус» используется для приближающегося поезда, а знак «плюс» — для удаляющегося поезда. В (b) есть два доплеровских смещения — одно для движущегося источника и другое для движущегося наблюдателя.

Решение

1. Введите известные значения в [латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v} {v- {v} _ {\ text {s }}}):[/латекс]

   [латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v} {v- {v} _ {\ text {s}}}) = (150\,\text{Гц})(\frac{340\,\text{м/с}}{340\,\text{м/с}-35,0\,\text{м/с}}). [/латекс]

   Вычислите частоту, наблюдаемую неподвижным человеком при приближении поезда:

   [латекс] {f} _ {\ text {o}} = (150 \, \ text {Гц}) (1.11)=167\,\текст{Гц}\текст{.}[/латекс]

   Используйте то же уравнение со знаком плюс, чтобы найти частоту, слышимую неподвижным человеком при удалении поезда:

   [латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}} (\ frac {v} {v + {v} _ {\ text {s}}}) = ( 150\,\text{Гц})(\frac{340\,\text{м/с}}{340\,\text{м/с}+35,0\,\text{м/с}}).[ /латекс]

   Вычислить вторую частоту:

   [латекс] {f} _ {\ text {o}} = (150 \, \ text {Гц}) (0,907) = 136 \, \ text {Гц} \ text {.} [/latex]

2. Определить известные:
   • Кажется разумным, что инженер получит ту же частоту, что и рупор, потому что относительная скорость между ними равна нулю.
   • Относительно среды (воздуха) скорость составляет [латекс]{v}_{\text{s}}={v}_{\text{o}}=35,0\,\text{м/с}\ текст{.}[/латекс]
   • Первое доплеровское смещение для движущегося наблюдателя; второй для движущегося источника.

   Используйте следующее уравнение:

   [латекс] {f} _ {\ text {o}} = [{f} _ {\ text {s}} (\ frac {v \ pm {v} _ {\ text {o}}} {v} )](\frac{v}{v\mp {v}_{\text{s}}}).[/latex]

   Величина в квадратных скобках представляет собой частоту, сдвинутую Доплером из-за движущегося наблюдателя.Фактор справа — это эффект движущегося источника.

   Поскольку машинист движется в направлении к звуковому сигналу, мы должны использовать знак плюс для [latex]{v}_{\text{obs}};[/latex] однако, поскольку звуковой сигнал также движется в направлении звукового сигнала. направление от машиниста, мы также используем знак плюс для [латекс]{v}_{\text{s}}.[/латекс] Но поезд несет и машиниста, и гудок с одинаковой скоростью, поэтому [ латекс] {v}_{\text{s}}={v}_{\text{o}}.[/latex] В результате все, кроме [латекса]{f}_{\text{s}} [/latex] отменяет, возвращая

   [латекс] {f} _ {\ text {o}} = {f} _ {\ text {s}}.[/латекс]

Значение

Для случая, когда источник и наблюдатель не движутся вместе, рассчитанные числа действительны, когда источник (в данном случае поезд) находится достаточно далеко, чтобы движение происходило почти вдоль линии, соединяющей источник и наблюдатель. В обоих случаях сдвиг значителен и легко заметен. Обратите внимание, что сдвиг составляет 17,0 Гц для движения вперед и 14,0 Гц для движения назад. Сдвиги не симметричны.

Для машиниста, едущего в поезде, мы можем ожидать, что частота не изменится, потому что источник и наблюдатель движутся вместе.Это соответствует вашему опыту. Например, нет доплеровского сдвига частоты разговоров водителя и пассажира на мотоцикле. Люди, разговаривающие, когда ветер перемещает воздух между ними, также не наблюдают в своем разговоре доплеровского сдвига. Важным моментом является то, что источник и наблюдатель не движутся друг относительно друга.

Проверьте свое понимание

Опишите ситуацию в вашей жизни, когда вы могли бы положиться на доплеровский сдвиг, чтобы помочь вам, когда вы ведете машину или идете рядом с транспортным средством.

Показать решение

Если я за рулем и слышу доплеровский сдвиг в сирене скорой помощи, я могу сказать, когда она приближалась, а также прошла ли она мимо. Это помогло бы мне узнать, нужно ли мне остановиться и пропустить скорую помощь.

Эффект Доплера и сдвиг Доплера имеют множество важных применений в науке и технике. Например, доплеровский сдвиг в ультразвуке можно использовать для измерения скорости кровотока, а полиция использует доплеровский сдвиг в радаре (микроволне) для измерения скорости автомобиля.В метеорологии доплеровский сдвиг используется для отслеживания движения грозовых облаков; такой «доплеровский радар» может определить скорость и направление дождя или снега на погодном фронте. В астрономии мы можем исследовать свет, излучаемый далекими галактиками, и определять их скорость относительно нашей. По мере того, как галактики удаляются от нас, их свет смещается в сторону более низкой частоты и, следовательно, в сторону большей длины волны — так называемое красное смещение. Такая информация от далеких-далеких галактик позволила нам оценить возраст Вселенной (с момента Большого взрыва) примерно в 14 миллиардов лет.

Резюме

• Эффект Доплера — это изменение наблюдаемой частоты звука из-за движения либо источника, либо наблюдателя.
• Фактическое изменение частоты называется доплеровским сдвигом.

Концептуальные вопросы

Доплеровский сдвиг реален или это просто сенсорная иллюзия?

Три стационарных наблюдателя наблюдают доплеровское смещение от источника, движущегося с постоянной скоростью. Наблюдатели располагаются, как показано ниже.Какой наблюдатель будет наблюдать наибольшую частоту? Какой наблюдатель будет наблюдать самую низкую частоту? Что можно сказать о частоте, наблюдаемой наблюдателем 3?

Показать ответ

Наблюдатель 1 будет наблюдать самую высокую частоту. Наблюдатель 2 будет наблюдать за самой низкой частотой. Наблюдатель 3 будет слышать более высокую частоту, чем частота источника, но ниже частоты, наблюдаемой наблюдателем 1, по мере приближения источника и более низкую частоту, чем частота источника, но выше частоты, наблюдаемой наблюдателем 1, по мере удаления источника. от наблюдателя 3.

Ниже показан стационарный источник и движущиеся наблюдатели. Опишите частоты, наблюдаемые наблюдателями для этой конфигурации.

До 1980 года синоптики использовали обычный радар. В 1960-х синоптики начали экспериментировать с доплеровским радаром. Как вы думаете, в чем преимущество использования доплеровского радара?

Show Solution

Доплеровский радар может определять не только расстояние до грозы, но также скорость и направление, с которой движется гроза.

Проблемы

(a) Какую частоту воспринимает человек, наблюдающий за приближающейся машиной скорой помощи, движущейся со скоростью 110 км/ч и излучающей сиреной ровный звук частотой 800 Гц? Скорость звука в этот день 345 м/с. б) Какую частоту она получает после того, как проехала машина скорой помощи?

Показать решение

а. 878 Гц; б. 735 Гц

(a) На авиашоу реактивный самолет летит прямо к трибунам со скоростью 1200 км/ч, излучая частоту 3500 Гц, в день, когда скорость звука составляет 342 м/с. {3}\,\текст{Гц}[/латекс]

Зритель на параде слышит сигнал частотой 888 Гц от приближающегося трубача, который играет ноту частотой 880 Гц. С какой скоростью приближается музыкант, если скорость звука 338 м/с?

Пригородный поезд гудит в гудок на 200 Гц, приближаясь к переезду. Скорость звука 335 м/с. (a) Наблюдатель, ожидающий на перекрестке, принимает частоту 208 Гц. Какова скорость поезда? б) Какую частоту получает наблюдатель при удалении поезда?

Показать решение

а.12,9 м/с; б. 193 Гц

Можете ли вы ощутить сдвиг частоты, возникающий, когда вы тянете на себя камертон со скоростью 10,0 м/с в день, когда скорость звука составляет 344 м/с? Чтобы ответить на этот вопрос, рассчитайте коэффициент, на который смещается частота, и посмотрите, больше ли он 0,300%.

Два орла летят прямо навстречу друг другу, первый со скоростью 15,0 м/с, а второй со скоростью 20,0 м/с. Оба визжат, первый издает частоту 3200 Гц, а второй – частоту 3800 Гц. {3}\,\текст{Гц}.[/латекс]

Ученик A бежит по коридору школы со скоростью [латекс]{v}_{\text{o}}=5,00\,\text{м/с,}[/латекс], неся звон 1024,00 -Гц камертон в сторону бетонной стены. Скорость звука [латекс]v=343,00\,\текст{м/с}\текст{.}[/латекс] Студент B стоит неподвижно у стены. (a) Какую частоту слышит студент B ? (b) Какую частоту ударов слышит учащийся A ?

Машина скорой помощи с сиреной [латекс](f=1.00\text{кГц})[/latex] рев приближается к месту аварии. Машина скорой помощи движется со скоростью 70,00 миль в час. Медсестра приближается к месту происшествия с противоположной стороны, бежит со скоростью [latex]{v}_{o}=7.00\,\text{м/с}\text{.}[/latex] Какую частоту наблюдает медсестра? Предположим, что скорость звука равна [латекс]v=343,00\,\текст{м/с}\текст{.}[/латекс]

Показать решение

[латекс]\begin{array}{cc} {v}_{\text{s}}=31,29\,\text{м/с}\hfill \\ {f}_{\text{o} }=1.12\,\text{кГц}\hfill \end{массив}[/latex]

Частота сигнала сирены скорой помощи составляет 900 Гц, и она приближается к вам. Вы стоите на углу и наблюдаете частоту 960 Гц. Какова скорость машины скорой помощи (в милях в час), если скорость звука [латекс]v=340,00\,\текст{м/с?}[/латекс]

Какова минимальная скорость, с которой источник должен двигаться к вам, чтобы вы могли услышать, что его частота сдвинута по Доплеру? То есть какая скорость производит сдвиг [латекс]0,300\текст{%}[/латекс] в день, когда скорость звука равна 331 м/с?

Показать решение

Слышимый сдвиг происходит, когда [latex]\frac{{f}_{\text{obs}}}{{f}_{\text{s}}}\ge 1.003[/латекс]; [латекс] \ begin {array} {cc} {f} _ {\ text {obs}} = {f} _ {\ text {s}} \ frac {v} {v- {v} _ {\ text { s}}} \ Rightarrow \ frac {{f} _ {\ text {obs}}} {{f} _ {\ text {s}}} = \ frac {v} {v- {v} _ {\ text {s}}}\Rightarrow \hfill \\ {v}_{\text{s}}=0,990\,\text{м/с}\hfill \end{массив}[/latex]

Глоссарий

Эффект Доплера

изменение наблюдаемой частоты звука из-за движения либо источника, либо наблюдателя

Доплеровский сдвиг

фактическое изменение частоты из-за относительного движения источника и наблюдателя

.