Эксперимент бела по определению спина частицы: Эксперимент, который навсегда изменил наше представление о реальности / Хабр

Эксперимент, который навсегда изменил наше представление о реальности / Хабр

Принцип неопределенности говорит, что мы не можем знать определённые свойства квантовой системы в один и тот же момент времени. Например, мы не можем одновременно узнать положение частицы и ее скорость. Но что это говорит нам о реальном мире? Если бы мы могли заглянуть за кулисы квантовой теории, обнаружили бы мы, что объекты действительно обладают определенным положением и скоростью? Или принцип неопределенности означает, что на фундаментальном уровне объекты просто не имеют четкой координаты и импульса одновременно. Другими словами, неполна ли наша теория или реальность «размыта» на самом деле?

Вариант 1: Мутные очки, чёткая реальность

Первая перспектива такова, что использование квантовой механики — как ношение мутных очков. Если бы мы могли как-то снять эти очки и заглянуть за кулисы на фундаментальную реальность, то, конечно, частица должна иметь некоторую определенную координату и импульс. В конце концов, это вещь в нашей Вселенной и Вселенная должна знать, где эта вещь и в какую сторону она движется, даже если мы не знаем этого. Согласно этой точке зрения, квантовая механика не является полным описанием реальности — мы исследуем всю тонкость природы тупым инструментом и поэтому несомненно пропускаем некоторые детали.

Это соответствует тому, как все остальное в нашем мире работает. Когда я снимаю свою обувь, и вы видите, что я надел красные носки, вы не думаете, что мои носки были в состоянии неопределенного цвета, пока мы не наблюдали их, с тем шансом, что они могли бы быть синие, желтые или розовые. Вместо этого вы (правильно) предполагаете, что мои носки всегда были красные. Так почему же частицы должны работать по-другому? Очевидно, что свойства вещей в природе должны существовать независимо от того, измеряем ли мы их, правда?

Вариант 2: Чёткие очки, мутная реальность

С другой стороны, может оказаться, что наши очки совершенно четки, но реальность размыта. Согласно этой точке зрения, квантовая механика является полным описанием реальности на этом уровне и все объекты во Вселенной просто не имеют определенного положения и импульса. Это мнение, которого большинство квантовых физиков придерживаются. Это не инструменты тупые, а реальность туманна по своей сути. В отличие от случая с моими красными носками, когда вы измеряете позицию частицы, она не имеет определенного положения до того момента, как вы измерили его. Акт измерения позиции

вынуждает частицу иметь определенную позицию.

Теперь вы можете подумать, что это один из тех «если-дерево-падает-в-лесу» метафизических вопросов, которые не могут иметь определенный ответ. Тем не менее, в отличие от большинства философских вопросов есть фактический эксперимент, который вы можете сделать, чтобы разрешить этот спор. Более того, этот эксперимент был проделан множество раз. На мой взгляд, это одна из самых недооцененных идей в нашем понимании физики. Эксперимент является довольно простым и чрезвычайно глубоким, потому что объясняет нам кое-что удивительное о природе реальности.

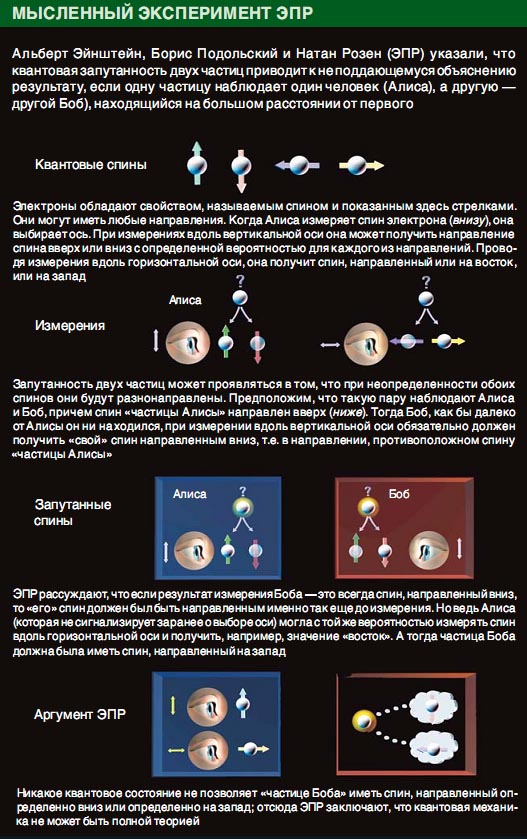
Вот установка. Есть источник света в середине комнаты. Каждую минуту он посылает два фотона в противоположных направлениях. Эти пары фотонов создаются в особом состоянии, известном как квантовая запутанность. Это означает, что они оба связаны квантовым образом — если вы делаете измерения одного фотона, вы не просто меняете его квантовое состояние, но сразу же влияете на квантовое состояние другого фотона.

Слева и справа в этой комнате два одинаковых ящика, предназначенных для приема фотонов. На каждом ящике есть лампочка-индикатор. Каждый раз, когда фотон попадает в устройство, индикатор мигает одним из двух цветов — красным или зеленым. Каждый раз цвет лампочки оказывается случайным — без какой-либо закономерности. По всей видимости эта коробка измеряет некоторое свойство фотона.

Вы можете только догадываться о том, какой цвет зажжётся следующим. Но вот действительно странная вещь: всякий раз, когда одна коробка мигает определенным цветом, другая коробка мигает тем же самым. Независимо от того, как далеко вы пытаетесь переместить коробки от детектора, даже если бы они находились в противоположных концах нашей Солнечной системы, они будут мигать и одним и тем же цветом без сбоев.

Это похоже на то, как если бы эти ящики были в сговоре с целью дать один и тот же результат. Как это возможно? (Если у вас есть собственная теория о том, как эти коробки работают, придержите её и скоро вы сможете сравнить свою идею с экспериментом.)

«Ага! — скажет квантовый энтузиаст. — Я могу объяснить, что здесь происходит. Каждый раз, когда фотон попадает в один из ящиков, устройство измеряет его квантовое состояние, которое сообщается миганием красным или зеленым цветом. Но два фотона квантово сцеплены, поэтому когда мы измерили, что один фотон находится, скажем, в „красном состоянии“, мы вынуждаем другой фотон быть в том же самом состоянии! Вот почему два ящика всегда мигают одним и тем же цветом».

«Подожди-ка, — говорит классический физик. — Частицы — это бильярдные шары, а не куклы вуду. Это абсурд, что измерение в одном месте пространства может мгновенно повлиять на что-то в совершенно другом месте. Когда я замечаю, что один из моих носков красный, это не меняет состояние моего другого носка, заставляя его быть также красным. Простое объяснение в том, что фотоны в этом эксперименте, как и носки, создаются парами. Иногда они оба в красном состоянии, в остальных случаях — в зеленом. Эти коробки просто измеряют „скрытые параметры“ фотонов».

Эксперимент и рассуждения, изложенные здесь, являются версией мысленного эксперимента, впервые сформулированного Эйнштейном, Подольским и Розеном, и известным как парадокс ЭПР. Решающим моментом их аргументов является то, что абсурдным кажется тот факт, что измерение в одном месте может мгновенно повлиять на измерение в совершенно другом месте. Более логичное объяснение в том, что ящики детектируют некоторые скрытые свойства, которыми обладают оба фотона. С момента их создания эти фотоны имеют какой-то скрытый штамп, как паспорт, который относит их к красному или зеленому состоянию.

Коробки, должно быть, определяют этот штамп. Эйнштейн, Подольский и Розен утверждали, что случайность, которую мы наблюдаем в этих экспериментах, является нашим пробелом в теории природы. По их словам — наши очки мутны. В терминологии теорий поля эта идея известна как Теория скрытых параметров.

Казалось бы, классическая физика выиграл этот раунд, с объяснением, что проще и имеет больше смысла.

На следующий день новая пара ящиков приходит по почте. Новая версия коробки имеет три встроенных двери. Вы можете открыть только одну дверь за один раз. За каждой дверью индикатор, который как и прежде, может светиться красным или зеленым.

Оба физика играются с этими новыми девайсами, ловя фотоны и наблюдая, что происходит, когда они открывают двери. Через несколько часов возни они выясняют:

1. Если они открывают одну и ту же дверь на обоих коробках, лампочки горят всегда одним и тем же цветом.

2. Если они открывают двери двух коробок случайно, то один и тот же цвет появляется ровно в половине случаев.

После некоторых размышлений классический физик придумывает простое объяснение этому эксперименту. «В принципе, это не очень отличается от вчерашних коробок. Это можно объяснить так. Предположим, что вместо одного штампа каждый фотон из пары теперь имеет три штампа, как наличие нескольких паспортов. Каждая дверь коробки соответствует одному из таких штампов. Так, например, три штампа могут быть красным, зеленым, красным. Это будет значить, что индикатор за первой дверью будет мигать красным, за второй зеленым и за третьей тоже красным».

«Эта идея объясняет, что, когда мы открываем ту же дверь на обоих коробках, мы получаем тот же цвет, потому что обе коробки читают один и тот же штамп. Но когда мы открываем разные двери, устройства читают разные штампы, поэтому они могут давать разные результаты».

И снова объяснение классического физика просто и не касается никаких модных понятий, как квантовая запутанность или принцип неопределенности.

«Не так быстро, — говорит квантовый физик, который только что закончил строчить расчет в своем блокноте.

— Когда мы открываем двери наугад, то обнаруживаем, что в половине раз огни мигают одним и тем же цветом. Это число — 0.5 — в точности совпадает с предсказаниями квантовой механики. Но согласно вашей „теории скрытых параметров“, лампочки должны мигать одним и тем же цветом больше половины раз!»

«Согласно идее скрытых параметров, есть 8 возможных комбинаций штампов, которые фотоны могут иметь. Давайте называть их по первым буквам цветов для краткости, так RRG = красный, красный, зеленый (red, red, green)».

RRG
RGR
GRR
GGR
GRG
RGG
RRR
GGG

«Теперь, если мы выбираем двери рандомно, то в трети случаев мы выберем одну и ту же дверь и увидим тот же цвет».

«Остальные две трети времени мы выбираем разные двери. Скажем, мы имеем дело с фотонами со следующей конфигурацией штампов»:

RRG

«В такой конфигурации, если мы выбрали дверь 1 на одной коробке и дверь 2 на другой, индикаторы светятся одинаковыми цветами (красный и красный). Но если мы выбрали двери 1 и 3 или двери 2 и 3 — цвета разные (красный и зеленый). Таким образом, в одной трети таких случаев коробки дают один и тот же цвет».

«Подводя итог. В трети случаев коробки имеют одинаковые цвета, потому что мы выбрали одинаковые двери. Две трети времени мы выбираем разные двери, и в одной трети этих случаев мы получим один и тот же цвет».

«Посчитаем»:

⅓ + ⅔ ⅓ = 3/9 + 2/9 = 5/9 = 55.55%

«55.55% — вероятность того, что ящики зажгутся одним и тем же цветом, когда мы выбираем две двери наугад, в соответствии с теорией скрытых параметров».

«Но подождите! Мы разобрали только одну комбинацию — RRG. А как же остальные? Быстро взглянув, можно заметить, что математика остаётся точно такой же во всех следующих случаях»:

RRG
RGR
GRR
GGR
GRG
RGG

«Остаётся два варианта»:

RRR
GGG

«В этих ситуациях мы получим одинаковые цвета независимо от того, какие двери мы выберем. Таким образом, шансы выбрать один и тот же цвет только увеличиваются».

«Кульминацией является то, что согласно идее скрытых параметров, шансы коробок мигать одним и тем же цветом, когда мы открываем двери наугад — не менее 55.55%. Но согласно квантовой механике, ответ составляет 50%. Экспериментальные данные согласуются с квантовой механикой, и это исключает теорию скрытых параметров».

Можно сделать паузу и подумать, что мы только что показали.

Мы рассмотрели новаторский аргумент в квантовой механике, известный как Теорема Белла. Черные ящики в действительности не мигают красными и зелеными огнями, но ключевые детали совпадают с реальными экспериментами, которые измеряют поляризацию спутанных фотонов.

Теорема Белла рисует линию на песке между странным квантовым миром и классическим миром, который мы знаем и любим. Это доказывает, что теории скрытых параметров и схожие с ними теории, которые Эйнштейн и его приятели придумали, не отображают реальный мир. Вместо этого появляется квантовая механика с её частицами, которые могут быть сцеплены на огромных расстояниях. Когда вы возмущаете квантовое состояние одной из этих запутанных частиц, вы мгновенно возмущаете состояние другой независимо от того, где во Вселенной она находится.

Отрадно думать, что мы могли бы объяснить странности квантовой механики, если бы вообразили повседневные частицы с маленькими невидимыми механизмами внутри или невидимыми штампами, или спрятанными записными книжками, или чем-то ещё — некоторыми скрытыми переменными, к которым мы не имеем доступа и которые хранят «реальные» координаты и импульс, и другие подробности о частице. Комфортно думать, что на фундаментальном уровне реальность ведет себя классически и что наша неуклюжая теория не позволяет нам заглянуть в этот скрытый регистр. Но Теорема Белла лишает нас этого комфорта. Реальность размыта, и мы просто должны привыкнуть к этому факту.

Первый эксперимент, который корректно доказывает нарушение неравенства Белла

Ведущий автор научной работы Бас Хенсен (Bas Hensen) и профессор Рональд Хансон (Ronald Hanson) настраивают установку для эксперимента Белла в точке А, откуда эмитируются электроны

В 1935 году Альберт Эйнштейн поставил под сомнение принцип квантовой теории о том, что наблюдение одной частицы мгновенно влияет на состояние связанной с ней частицы, где бы она ни находилась. Это означает, что информация от частицы к частице передаётся быстрее скорости света, что Эйнштейн считал невозможным и несовместимым с теорией относительности.

Физики с 70-х гг пытались проверить данное свойство частиц. Для этого были сформулированы так называемые неравенства Белла и условия эксперимента Белла. Но учёным никак не удавалось избавиться от проблем экспериментальной установки или «лазеек» (loopholes), которые не позволяли назвать эксперимент чистым и корректным, действительно опровергающим теорию относительности и демонстрирующим передачу информации быстрее скорости света. Эти лазейки позволяли объяснить передачу информации якобы быстрее скорости света другими локальными факторами.

Только сейчас исследователям из технологического университета Делфта (Нидерланды) удалось впервые в истории провести корректный эксперимент Белла, избавленный от обеих известных проблем экспериментальной установки: лазейки местоположения (locality loophole) и лазейки обнаружения (detection loophole).

Экспериментаторы из технологического университета Делфта проверили состояние частиц на расстоянии 1,3 км (на территории кампуса) и зарегистрировали совпадение ~96%. Это больше, чем предсказано теоремой Белла.

Результаты и техника эксперимента опубликованы в статье “Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres”, журнал Nature, дата публикации 21 октября 2015 года (pdf).

На иллюстрации: слева точка А с одним из двух алмазов, другой алмаз находится на противоположном конце кампуса справа. Между ними — точка С, где располагается сплитер (разделитель) луча.

Теорема Белла показывает, что вне зависимости от реального наличия в квантово-механической теории неких скрытых параметров, влияющих на любую физическую характеристику квантовой частицы, можно провести серийный эксперимент, статистические результаты которого подтвердят либо опровергнут наличие таких скрытых параметров в квантово-механической теории. Условно говоря, в одном случае статистическое соотношение составит не более 2:3, а в другом — не менее 3:4.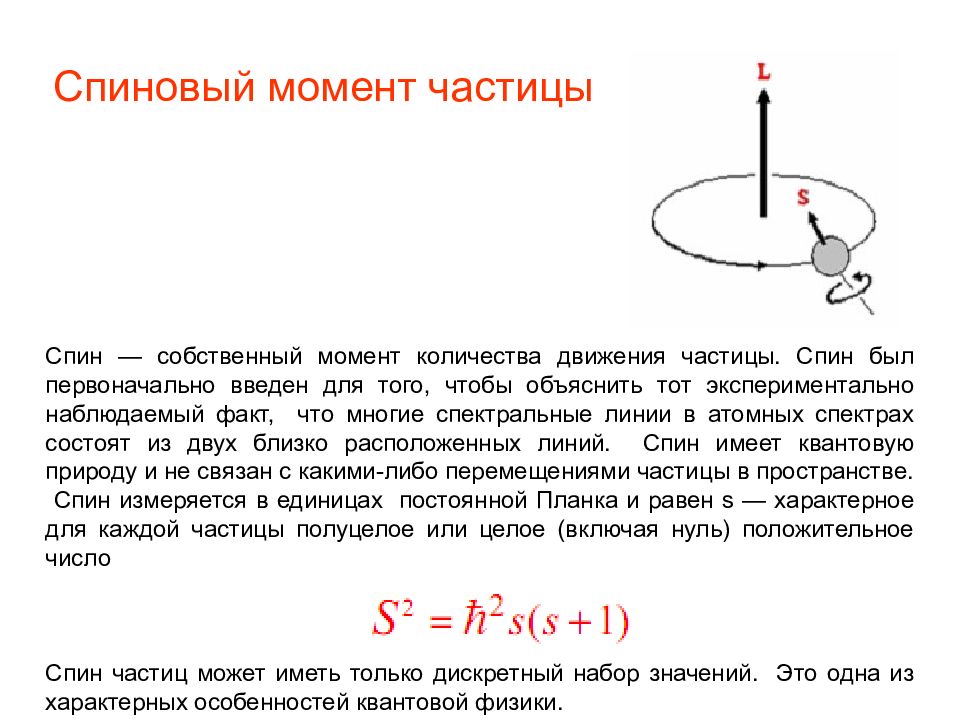

Условия эксперимента Белла объясняются на видео на примере пары «связанных» любовными узами посетителей ресторана, которые должны заказать разное вино в бокале и бутылке. Они могут заранее договориться о стратегии, но не могут обмениваться информацией во время «игры».

Главным достижением группы экспериментаторов в последнем эксперименте является продвинутая техника, которая позволила избавиться от лазеек местоположения и обнаружения. Для этого они использовали два алмазных детектора (в точках А и С на схеме вверху) и разделитель сигнала посередине между ними. Спины электронов измерялись с помощью микроволновых и лазерных импульсов в детекторах на противоположных сторонах кампуса. Архитектура установки с разделением луча и детектированием спина связанных электронов спроектирована таким образом, что связанные электроны не могли обмениваться информацией с помощью никакой из известных лазеек во время измерения.

Эксперимент доказал нарушение концепции локального реализма, который сочетает принцип локальности с «реалистичным» предположением, что все объекты обладают «объективно существующими» значениями своих параметров и характеристик для любых возможных измерений, могущих быть произведенными над этими объектами, перед тем как эти измерения производятся.

В реальности же подтвердился принцип квантовой механики, что у электронов нет характеристик до тех пор, пока их не наблюдают с помощью детектора. До этого момента частицы существуют в нескольких состояниях одновременно.

Правда, некоторые независимые эксперты говорят, что есть ещё третья лазейка, от которой во время эксперимента не избавились. Дело в том, что случайное разделение электронов с разными спинами может быть не совсем случайным, а происходить с некоей скрытой закономерностью. Так что о нарушении теории относительности и неправоте Эйнштейна пока рано говорить с полной уверенностью.

В следующем году в Массачусетском технологическом институте пройдёт более продвинутый эксперимент, в котором детекторы будут проверять характеристики фотонов с разных частей Галактики — там уже наверняка не будет действовать никакая из трёх лазеек.

Теорема Белла • Джеймс Трефил, энциклопедия «Двести законов мироздания»

«Бог не играет в кости со Вселенной».

Этими словами Альберт Эйнштейн бросил вызов коллегам, разрабатывавшим новую теорию — квантовую механику. По его мнению, принцип неопределенности Гейзенберга и уравнение Шрёдингера вносили в микромир нездоровую неопределенность. Он был уверен, что Создатель не мог допустить, чтобы мир электронов так разительно отличался от привычного мира ньютоновских бильярдных шаров. Фактически, на протяжении долгих лет Эйнштейн играл роль адвоката дьявола в отношении квантовой механики, выдумывая хитроумные парадоксы, призванные завести создателей новой теории в тупик. Тем самым, однако, он делал доброе дело, серьезно озадачивая теоретиков противоположного лагеря своими парадоксами и заставляя глубоко задумываться над тем, как их разрешить, что всегда бывает полезно, когда разрабатывается новая область знаний.

Есть странная ирония судьбы в том, что Эйнштейн вошел в историю как принципиальный оппонент квантовой механики, хотя первоначально сам стоял у ее истоков. В частности, Нобелевскую премию по физике за 1921 год он получил вовсе не за теорию относительности, а за объяснение фотоэлектрического эффекта на основе новых квантовых представлений, буквально захлестнувших научный мир в начале ХХ века.

Больше всего Эйнштейн протестовал против необходимости описывать явления микромира в терминах вероятностей и волновых функций (см. Квантовая механика), а не с привычной позиции координат и скоростей частиц. Вот что он имел в виду под «игрой в кости». Он признавал, что описание движения электронов через их скорости и координаты противоречит принципу неопределенности. Но, утверждал Эйнштейн, должны существовать еще какие-то переменные или параметры, с учетом которых квантово-механическая картина микромира вернется на путь целостности и детерминизма. То есть, настаивал он, нам только кажется, будто Бог играет с нами в кости, потому что мы не всё понимаем. Тем самым он первым сформулировал гипотезу скрытой переменной в уравнениях квантовой механики. Она состоит в том, что на самом деле электроны имеют фиксированные координаты и скорость, подобно ньютоновским бильярдным шарам, а принцип неопределенности и вероятностный подход к их определению в рамках квантовой механики — результат неполноты самой теории, из-за чего она и не позволяет их доподлинно определить.

Теорию скрытой переменной можно наглядно представить примерно так: физическим обоснованием принципа неопределенности служит то, что измерить характеристики квантового объекта, например электрона, можно лишь через его взаимодействие с другим квантовым объектом; при этом состояние измеряемого объекта изменится. Но, возможно, есть какой-то иной способ измерения с использованием неизвестных нам пока что инструментов. Эти инструменты (назовем их «субэлектронами»), возможно, будут взаимодействовать с квантовыми объектами, не изменяя их свойств, и принцип неопределенности будет неприменим к таким измерениям. Хотя никаких фактических данных в пользу гипотез такого рода не имелось, они призрачно маячили на обочине главного пути развития квантовой механики — в основном, я полагаю, по причине психологического дискомфорта, испытываемого многими учеными из-за необходимости отказа от устоявшихся ньютоновских представлений об устройстве Вселенной.

И вот в 1964 году Джон Белл получил новый и неожиданный для многих теоретический результат. Он доказал, что можно провести определенный эксперимент (подробности чуть позже), результаты которого позволят определить, действительно ли квантово-механические объекты описываются волновыми функциями распределения вероятностей, как они есть, или же имеется скрытый параметр, позволяющий точно описать их положение и импульс, как у ньютоновского шарика. Теорема Белла, как ее теперь называют, показывает, что как при наличии в квантово-механической теории скрытого параметра, влияющего на любую физическую характеристику квантовой частицы, так и при отсутствии такового можно провести серийный эксперимент, статистические результаты которого подтвердят или опровергнут наличие скрытых параметров в квантово-механической теории. Условно говоря, в одном случае статистическое соотношение составит не более 2:3, а в другом — не менее 3:4.

(Тут я хочу в скобках заметить, что в том году, когда Белл доказал свою теорему, я был студентом-старшекурсником в Стэнфорде. Рыжебородого, с сильным ирландским акцентом Белла было трудно не заметить. Помню, я стоял в коридоре научного корпуса Стэнфордского линейного ускорителя, и тут он вышел из своего кабинета в состоянии крайнего возбуждения и во всеуслышание заявил, что только что обнаружил по-настоящему важную и интересную вещь. И, хотя доказательств на этот счет у меня нет никаких, мне очень хотелось бы надеяться, что я в тот день стал невольным свидетелем его открытия.)

Однако опыт, предлагаемый Беллом, оказался простым только на бумаге и поначалу казался практически невыполнимым. Эксперимент должен был выглядеть так: под внешним воздействием атом должен был синхронно испустить две частицы, например два фотона, причем в противоположных направлениях. После этого нужно было уловить эти частицы и инструментально определить направление спина каждой и сделать это тысячекратно, чтобы накопить достаточную статистику для подтверждения или опровержения существования скрытого параметра по теореме Белла (выражаясь языком математической статистики, нужно было рассчитать коэффициенты корреляции).

Самым неприятным сюрпризом для всех после публикации теоремы Белла как раз и стала необходимость проведения колоссальной серии опытов, которые в ту пору казались практически невыполнимыми, для получения статистически достоверной картины. Однако не прошло и десятилетия, как ученые-экспериментаторы не только разработали и построили необходимое оборудование, но и накопили достаточный массив данных для статистической обработки. Не вдаваясь в технические подробности, скажу лишь, что тогда, в середине шестидесятых, трудоемкость этой задачи казалась столь чудовищной, что вероятность ее реализации представлялась равной тому, как если бы кто-то задумал посадить за пишущие машинки миллион дрессированных обезьян из пословицы в надежде отыскать среди плодов их коллективного труда творение, равное Шекспиру.

Когда в начале 1970-х годов результаты экспериментов были обобщены, всё стало предельно ясно. Волновая функция распределения вероятностей совершенно безошибочно описывает движение частиц от источника к датчику. Следовательно, уравнения волновой квантовой механики не содержат скрытых переменных. Это единственный известный случай в истории науки, когда блестящий теоретик доказал возможность экспериментальной проверки гипотезы и дал обоснование метода такой проверки, блестящие экспериментаторы титаническими усилиями провели сложный, дорогостоящий и затяжной эксперимент, который в итоге лишь подтвердил и без того господствующую теорию и даже не внес в нее ничего нового, в результате чего все почувствовали себя жестоко обманутыми в ожиданиях!

Однако не все труды пропали даром. Совсем недавно ученые и инженеры к немалому собственному удивлению нашли теореме Белла весьма достойное практическое применение. Две частицы, испускаемые источником на установке Белла, являются когерентными (имеют одинаковую волновую фазу), поскольку испускаются синхронно. И это их свойство теперь собираются использовать в криптографии для шифровки особо секретных сообщений, направляемых по двум раздельным каналам. При перехвате и попытке дешифровки сообщения по одному из каналов когерентность мгновенно нарушается (опять же в силу принципа неопределенности), и сообщение неизбежно и мгновенно самоуничтожается в момент нарушения связи между частицами.

А Эйнштейн, похоже, был неправ: Бог все-таки играет в кости со Вселенной. Возможно, Эйнштейну все-таки следовало прислушаться к совету своего старого друга и коллеги Нильса Бора, который, в очередной раз услышав старый припев про «игру в кости», воскликнул: «Альберт, перестань же ты, наконец, указывать Богу, что ему делать!»

Теорема Белла для чайников, как она работает?

Теорема Белла показывает, что стандартное управление качеством несовместимо с локальным реализмом . Локальный реализм – это очень общий принцип, который изначально не предполагал каких-либо проверяемых физических предсказаний. Основная часть достижений Белла заключалась в том, что неравенство Белла подразумевается локальным реализмом , в то время как стандартные предсказания КМ нарушают его .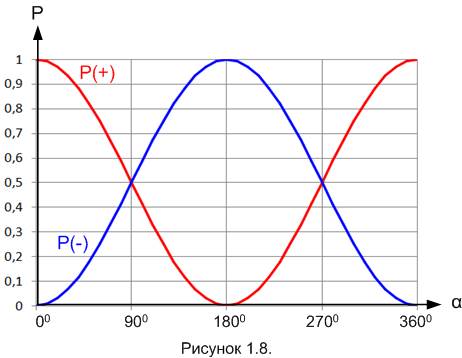 Эксперименты, подобные Аспекту, с тех пор показали, что неравенства Белла в действительности нарушаются, опровергая местный реализм, в соответствии со стандартным QM.

Я думаю, что ваша проблема с определением местного реализма:

при измерении на одной и той же оси состояния вращения всегда должны быть противоположными (.5 + -.5 = 0, т.е. сохранение) при измерении на противоположной оси состояния вращения должны всегда быть одинаковыми (.5 – .5 = 0) и при измерении на 90 градусов значения абсолютно случайны.

Это именно то, что предсказывает стандартная КМ для запутанных частиц.

Локальный реализм утверждает, что на то, что происходит в любой точке, может непосредственно влиять только состояние в его непосредственной близости, любые дальнодействующие эффекты должны опосредоваться частицами или возмущениями поля, движущимися с (суб) люминальными скоростями, и что все поведение является детерминированным.

Если запутанные частицы находятся достаточно далеко друг от друга, чтобы можно было проводить измерения на обоих из них таким образом, чтобы гарантировать, что события измерения разделены пространственно-подобным интервалом, тогда локальный реализм потребовал бы, чтобы частицы имели достаточно скрытых переменных, чтобы предопределить результат каждого из них. возможное измерение, поскольку любой эффект от одного измерения не успеет распространиться на другое измерение, чтобы обеспечить коррелированные наблюдения.

Локальный реализм и неравенства Белла не нарушаются, если рассматривать только измерения, разделенные целыми числами, кратными 90 градусам, как в вашем описании. Расхождение между QM и локальным реализмом проявляется только при рассмотрении углов наклона, достигая максимума, когда угол между измерениями составляет 45 градусов (плюс несколько кратных 90 градусов), когда корреляция между измерениями становится 2 – √ 2 больше, чем допускается неравенством Белла и, следовательно, местным реализмом.

Сохранение спина – это действительно отдельная проблема. Это просто говорит о том, что если бы полное вращение изолированной системы было Икс Икс в какой-то момент в прошлом, это всегда будет Икс Икс и наоборот. Entanglemnt обеспечивает способ соблюдения законов сохранения без назначения определенных значений сохраняемых величин отдельным компонентам.

Теорема Белла действительно о местном реализме, а не о QM. Экспериментальные результаты могут в принципе нарушить неравенство Белла, но также не согласуются с предсказаниями КМ. Это все равно исключает местный реализм и все теории, удовлетворяющие его. Тот факт, что QM предсказывает корреляции выше, чем это допускается неравенством Белла, и экспериментальные результаты согласуются с этими предсказаниями, является своего рода случайным.

КВАНТОВАЯ МЕХАНИКА • Большая российская энциклопедия

КВА́НТОВАЯ МЕХА́НИКА, раз­дел тео­ре­тич. фи­зи­ки, пред­став­ляю­щий со­бой сис­те­му по­ня­тий и ма­те­ма­тич. ап­па­рат, не­об­хо­ди­мые для опи­са­ния фи­зич. яв­ле­ний, обу­слов­лен­ных су­ще­ст­во­ва­ни­ем в при­ро­де наи­мень­ше­го кван­та дей­ст­вия $h$ (План­ка по­сто­ян­ной). Чис­лен­ное зна­че­ние $h=$6,62607·10^–34 Дж·с (и дру­гое, час­то ис­поль­зуе­мое зна­че­ние $\hbar=h/2\pi=$1,05457·10 –34 Дж·с) чрез­вы­чай­но ма­ло, но тот факт, что оно ко­неч­но, прин­ци­пи­аль­но от­ли­ча­ет кван­то­вые яв­ле­ния от всех дру­гих и оп­ре­де­ля­ет их осн. осо­бен­но­сти. К кван­то­вым яв­ле­ни­ям от­но­сят­ся про­цес­сы из­лу­че­ния, яв­ле­ния атом­ной и ядер­ной фи­зи­ки, фи­зи­ки кон­ден­си­ров. сред, хи­мич. связь и др.

История создания квантовой механики

Ис­то­ри­че­ски пер­вым яв­ле­ни­ем, для объ­яс­не­ния ко­то­ро­го в 1900 бы­ло вве­де­но по­ня­тие кван­та дей­ст­вия $h$, был спектр из­лу­че­ния аб­со­лют­но чёр­но­го те­ла, т. е. за­ви­си­мость ин­тен­сив­но­сти те­п­ло­во­го из­лу­че­ния от его час­то­ты $\nu$ и темп-ры $T$ на­гре­то­го те­ла. Пер­во­на­чаль­но связь это­го яв­ле­ния с про­цес­са­ми, про­ис­хо­дя­щи­ми в ато­ме, не бы­ла яс­на; в то вре­мя не бы­ла об­ще­при­знан­ной и са­ма идея ато­ма, хо­тя уже то­гда бы­ли из­вест­ны на­блю­де­ния, ко­то­рые ука­зы­ва­ли на слож­ную внут­ри­атом­ную струк­ту­ру.

В 1802 У. Вол­ла­стон об­на­ру­жил в спек­тре из­лу­че­ния Солн­ца уз­кие спек­траль­ные ли­нии, ко­то­рые в 1814 под­роб­но опи­сал Й. Фра­ун­го­фер. В 1859 Г. Кирх­гоф и Р. Бун­зен ус­та­но­ви­ли, что ка­ж­до­му хи­мич. эле­мен­ту при­сущ ин­ди­ви­ду­аль­ный на­бор спек­траль­ных ли­ний, а швейц. учё­ный И. Я. Баль­мер (1885), швед. фи­зик Й. Рид­берг (1890) и нем. учё­ный В. Ритц (1908) об­на­ру­жи­ли в их рас­по­ло­же­нии оп­ре­де­лён­ные за­ко­но­мер­но­сти. В 1896 П. Зее­ман на­блю­дал рас­ще­п­ле­ние спек­траль­ных ли­ний в маг­нит­ном по­ле (эф­фект Зее­ма­на), ко­то­рое Х. А. Ло­ренц в сле­дую­щем го­ду объ­яс­нил дви­же­ни­ем элек­тро­на в ато­ме. Су­ще­ст­во­ва­ние элек­тро­на экс­пе­ри­мен­таль­но до­ка­зал в 1897 Дж. Дж. Том­сон.

Су­ще­ст­вую­щие фи­зич. тео­рии ока­за­лись не­до­ста­точ­ны­ми для объ­яс­не­ния за­ко­нов фо­то­эф­фек­та: ока­за­лось, что энер­гия элек­тро­нов, вы­ле­таю­щих из ве­ще­ст­ва при об­лу­че­нии его све­том, за­ви­сит толь­ко от час­то­ты све­та $v$, а не от его ин­тен­сив­но­сти (А. Г. Сто­ле­тов, 1889; Ф. фон Ле­нард, 1904). Этот факт пол­но­стью про­ти­во­ре­чил об­ще­при­ня­той в то вре­мя вол­но­вой при­ро­де све­та, но ес­те­ст­вен­но объ­яс­нял­ся в пред­по­ло­же­нии, что свет рас­про­стра­ня­ет­ся в ви­де кван­тов энер­гии $E=h \nu$(А.  Эйн­штейн, 1905), на­зван­ных впо­след­ст­вии фо­то­на­ми (Г. Льюис, 1926).

В те­че­ние 10 лет по­сле от­кры­тия элек­тро­на бы­ло пред­ло­же­но неск. мо­де­лей ато­ма, не под­кре­п­лён­ных, од­на­ко, экс­пе­ри­мен­та­ми. В 1909–11 Э. Ре­зер­форд, изу­чая рас­сея­ние $\alpha$-час­тиц на ато­мах, ус­та­но­вил су­ще­ст­во­ва­ние ком­пакт­но­го по­ло­жи­тель­но за­ря­жен­но­го яд­ра, в ко­то­ром со­сре­до­то­че­на прак­ти­че­ски вся мас­са ато­ма. Эти экс­пе­ри­мен­ты ста­ли ос­но­вой пла­не­тар­ной мо­де­ли ато­ма: по­ло­жи­тель­но за­ря­жен­ное яд­ро, во­круг ко­то­ро­го вра­ща­ют­ся от­ри­ца­тель­но за­ря­жен­ные элек­тро­ны. Та­кая мо­дель, од­на­ко, про­ти­во­ре­чи­ла фак­ту ста­биль­но­сти ато­ма, по­сколь­ку из клас­сич. элек­тро­ди­на­ми­ки сле­до­ва­ло, что че­рез вре­мя по­ряд­ка 10^–9 с вра­щаю­щий­ся элек­трон упа­дёт на яд­ро, по­те­ряв энер­гию на из­лу­че­ние.

В 1913 Н. Бор пред­по­ло­жил, что ста­биль­ность пла­не­тар­но­го ато­ма объ­яс­ня­ет­ся ко­неч­но­стью кван­та дей­ст­вия $h$. 2$ ($e$ – элект­рич. за­ряд эле­кт­ро­на) ста­цио­нар­ных со­стоя­ний, а так­же диа­метр ато­ма во­до­ро­да (по­ряд­ка 10^–8 cм) – в пол­ном со­от­вет­ст­вии с вы­во­да­ми ки­не­тич. тео­рии ма­те­рии.

Вто­рой по­сту­лат Бо­ра ут­вер­ждал, что из­лу­че­ние про­ис­хо­дит толь­ко при пе­ре­хо­дах элек­тро­нов с од­ной ста­цио­нар­ной ор­би­ты на дру­гую, при­чём час­то­та из­лу­че­ния $\nu_{nk}$ пе­ре­хо­дов из со­стоя­ния $E_n$ в со­стоя­ние $E_k$ рав­на $\nu_{nk}=(E_k-E_n)/h$ (см. Атом­ная фи­зи­ка). Тео­рия Бо­ра ес­те­ст­вен­ным об­ра­зом объ­яс­ня­ла за­ко­но­мер­но­сти в спек­трах ато­мов, од­на­ко её по­сту­ла­ты на­хо­ди­лись в оче­вид­ном про­ти­во­ре­чии с клас­сич. ме­ха­ни­кой и тео­ри­ей элек­тро­маг­нит­но­го по­ля.

В 1922 А. Комп­тон, изу­чая рас­сея­ние рент­ге­нов­ских лу­чей на элек­тро­нах, ус­та­но­вил, что па­даю­щий и рас­се­ян­ный рент­ге­нов­ские кван­ты энер­гии ве­дут се­бя как час­ти­цы. В 1923 Ч. Т. Р. Виль­сон и Д. В. Ско­бель­цын на­блю­да­ли элек­трон от­да­чи в этой ре­ак­ции и тем са­мым под­твер­ди­ли кор­пус­ку­ляр­ную при­ро­ду рент­ге­нов­ских лу­чей (ядер­но­го $\gamma$-из­лу­че­ния). Это, од­на­ко, про­ти­во­ре­чи­ло опы­там М. Ла­уэ, ко­то­рый ещё в 1912 на­блю­дал ди­фрак­цию рент­ге­нов­ских лу­чей и тем са­мым до­ка­зал их вол­но­вую при­ро­ду.

В 1921 нем. фи­зик К. Рам­зау­эр об­на­ру­жил, что при оп­ре­де­лён­ной энер­гии элек­тро­ны про­хо­дят сквозь га­зы, прак­ти­че­ски не рас­сеи­ва­ясь, по­доб­но све­то­вым вол­нам в про­зрач­ной сре­де. Это бы­ло пер­вое экс­пе­рим. сви­де­тель­ст­во о вол­но­вых свой­ст­вах элек­тро­на, ре­аль­ность ко­то­рых в 1927 бы­ла под­твер­жде­на пря­мы­ми опы­та­ми К. Дж. Дэ­вис­со­на, Л. Джер­ме­ра и Дж. П. Том­со­на.

В 1923 Л. де Бройль ввёл по­ня­тие о вол­нах ма­те­рии: ка­ж­дой час­ти­це с мас­сой $m$ и ско­ро­стью $v$ мож­но со­пос­та­вить вол­ну с дли­ной $\lambda=h/mv$, точ­но так же как ка­ж­дой вол­не с час­то­той $\nu=c/\lambda$ мож­но со­пос­та­вить час­ти­цу с энер­ги­ей $E=h \nu$. Обоб­ще­ние этой ги­по­те­зы, из­вест­ное как кор­пус­ку­ляр­но-вол­но­вой дуа­лизм, ста­ло фун­да­мен­том и уни­вер­саль­ным прин­ци­пом кван­то­вой фи­зи­ки. Суть его со­сто­ит в том, что од­ни и те же объ­ек­ты ис­сле­до­ва­ния про­яв­ля­ют се­бя двоя­ко: ли­бо как час­ти­ца, ли­бо как вол­на – в за­ви­си­мо­сти от ус­ло­вий их на­блю­де­ния.

Рис. 1. Интерференция рентгеновского излучения (а) и электронов (б). (На рис. б приведена оригинальная фотография, полученная Дж. П. Томсоном.)

Со­от­но­ше­ния ме­ж­ду ха­рак­те­ри­сти­ка­ми вол­ны и час­ти­цы бы­ли ус­та­нов­ле­ны ещё до соз­да­ния К. м.: $E=h \nu$ (1900) и $\lambda=h/mv=h/p$ (1923), где час­то­та $\nu$ и дли­на вол­ны $\lambda$ – ха­рак­те­ри­сти­ки вол­ны, а энер­гия $E$ и мас­са $m$, ско­рость $v$ и им­пульс $p=mv$ – ха­рак­те­ри­сти­ки час­ти­цы; связь ме­ж­ду эти­ми дву­мя ти­па­ми ха­рак­те­ри­стик осу­ще­ст­в­ля­ет­ся че­рез по­сто­ян­ную План­ка $h$. Наи­бо­лее от­чёт­ли­во со­от­но­ше­ния ду­аль­но­сти вы­ра­жа­ют­ся че­рез кру­го­вую час­то­ту $\omega=2 \pi \nu$ и вол­но­вой век­тор $\boldsymbol k=2\pi/\lambda$: $$E=\hbar \omega, \boldsymbol p =\hbar \boldsymbol k. $$На­гляд­ная ил­лю­ст­ра­ция дуа­лиз­ма вол­на-час­ти­ца пред­став­ле­на на рис. 1: ди­фрак­ци­он­ные коль­ца, на­блю­дае­мые при рас­сея­нии элек­тро­нов и рент­ге­нов­ских лу­чей, прак­ти­че­ски иден­тич­ны.

К. м. – тео­ре­тич. ба­зис всей кван­то­вой фи­зи­ки – бы­ла соз­да­на за не­пол­ных три го­да. В 1925 В. Гей­зен­берг, опи­ра­ясь на идеи Бо­ра, пред­ло­жил мат­рич­ную ме­ха­ни­ку, ко­то­рая к кон­цу то­го же го­да при­об­ре­ла вид за­кон­чен­ной тео­рии в тру­дах М. Бор­на, нем. фи­зи­ка П. Йор­да­на и П. Ди­ра­ка. Осн. объ­ек­та­ми этой тео­рии ста­ли мат­ри­цы спец. ви­да, ко­то­рые в К. м. пред­став­ля­ют фи­зич. ве­ли­чи­ны клас­сич. ме­ха­ни­ки.

В 1926 Э. Шрё­дин­гер, ис­хо­дя из пред­став­ле­ний Л. де Брой­ля о вол­нах ма­те­рии, пред­ло­жил вол­но­вую ме­ха­ни­ку, где осн. роль иг­ра­ет вол­но­вая функ­ция кван­то­во­го со­стоя­ния, ко­то­рая под­чи­ня­ет­ся диф­фе­рен­ци­аль­но­му урав­не­нию 2-го по­ряд­ка с за­дан­ны­ми гра­нич­ны­ми ус­ло­вия­ми. Обе тео­рии оди­на­ко­во хо­ро­шо объ­яс­ня­ли ус­той­чи­вость пла­не­тар­но­го ато­ма и по­зво­ля­ли вы­чис­лить его осн. ха­рак­те­ри­сти­ки. В том же го­ду М. Борн пред­ло­жил ста­ти­стич. ин­тер­пре­та­цию вол­но­вой функ­ции, Шрё­дин­гер (а так­же не­за­ви­си­мо В. Пау­ли и др.) до­ка­зал ма­те­ма­тич. эк­ви­ва­лент­ность мат­рич­ной и вол­но­вой ме­ха­ник, а Борн совм. с Н. Ви­не­ром ввёл по­ня­тие опе­ра­то­ра фи­зич. ве­ли­чи­ны.

В 1927 В. Гей­зен­берг от­крыл со­от­но­ше­ние не­оп­ре­де­лён­но­стей, а Н. Бор сфор­му­ли­ро­вал прин­цип до­пол­ни­тель­но­сти. От­кры­тие спи­на элек­тро­на (Дж. Улен­бек и С. Га­уд­смит, 1925) и вы­вод урав­не­ния Пау­ли, учи­ты­ваю­ще­го спин элек­тро­на (1927), за­вер­ши­ли ло­ги­че­скую и рас­чёт­ную схе­мы не­ре­ля­ти­ви­ст­ской К. м., а П. Ди­рак и Дж. фон Ней­ман из­ло­жи­ли К. м. как за­кон­чен­ную кон­цеп­ту­аль­но не­за­ви­си­мую тео­рию на ба­зе ог­ра­ни­чен­но­го на­бо­ра по­ня­тий и по­сту­ла­тов, та­ких как опе­ра­тор, век­тор со­стоя­ния, ам­пли­ту­да ве­ро­ят­но­сти, су­пер­по­зи­ция со­стоя­ний и др. *(x)$ – функ­ция, ком­плекс­но со­пря­жён­ная к функ­ции $f(x)$.

Ор­то­го­наль­ным ба­зи­сом в этом про­стран­ст­ве яв­ля­ет­ся на­бор собств. функ­ций $|n\rangle=|f_n(x)\rangle$, $n=1,2,3,\dots$, для ко­торых дей­ст­вие опе­ра­то­ра $\hat A$ сво­дит­ся к ум­но­же­нию на чис­ло (собств. зна­че­ние $a_n$ опе­ра­то­ра $\hat A$): $$\hat A|n\rangle=a_n| n\rangle.$$Ба­зис функ­ций $|n\rangle$ нор­ми­ро­ван ус­ло­ви­ем $$\langle n|n’\rangle=\delta_{nn’} = \begin{cases} 1 & \quad \text{при } n=n’\\ 0 & \quad \text{при } n \neq n’\\ \end{cases}, $$а чис­ло ба­зис­ных функ­ций (в от­ли­чие от ба­зис­ных век­то­ров трёх­мер­но­го про­стран­ст­ва клас­сич. фи­зи­ки) бес­ко­неч­но, при­чём ин­декс $n$ мо­жет из­ме­нять­ся как дис­крет­но, так и не­пре­рыв­но. Все воз­мож­ные зна­че­ния на­блю­дае­мой $a$ со­дер­жат­ся в на­бо­ре $\{a_n\}$ собств. зна­че­ний со­от­вет­ст­вую­ще­го ей опе­ра­то­ра $\hat A$, и толь­ко эти зна­че­ния мо­гут стать ре­зуль­та­та­ми из­ме­ре­ний.

Осн. 2=1$, т. е. пол­ная веро­ят­ность най­ти сис­те­му в од­ном из кван­то­вых со­стоя­ний $n$ рав­на еди­ни­це.

В К. м. Гей­зен­бер­га опе­ра­то­ры $\hat A$ и со­от­вет­ст­вую­щие им мат­ри­цы под­чи­ня­ют­ся урав­не­нию $$i\hbar \frac{\partial \hat A}{\partial t}=[\hat A,\hat H],$$где $|\hat A, \hat H|=\hat A\hat H-\hat H\hat A$ – ком­му­та­тор опе­ра­то­ров $\hat A$ и $\hat H$. В от­ли­чие от схе­мы Шрёдин­ге­ра, где от вре­ме­ни за­ви­сит вол­но­вая функ­ция $\psi$, в схе­ме Гей­зен­бер­га вре­мен­нáя за­ви­си­мость от­не­се­на к опе­ра­то­ру $\hat A$. Оба эти под­хо­да ма­те­ма­ти­че­ски эк­ви­ва­лент­ны, од­на­ко в мно­го­числ. при­ло­же­ни­ях К. м. под­ход Шрё­дин­ге­ра ока­зал­ся пред­поч­ти­тель­нее.

Собств. зна­че­ние опе­ра­то­ра Га­миль­то­на $\hat H$ есть пол­ная энер­гия сис­те­мы $E$, не за­ви­ся­щая от вре­ме­ни, ко­то­рая на­хо­дит­ся как ре­ше­ние ста­цио­нар­но­го урав­не­ния Шрё­дин­ге­ра $$\hat H\psi=E\psi.$$Его ре­ше­ния под­раз­де­ля­ют­ся на два ти­па в за­ви­си­мо­сти от ви­да гра­нич­ных ус­ло­вий. 2/2m$, а ин­декс $p$ ре­ше­ния $\psi_p(x)$ при­ни­ма­ет не­пре­рыв­ный ряд зна­че­ний.

Опе­ра­то­ры ко­ор­ди­на­ты и им­пуль­са (и лю­бой др. па­ры ка­но­ни­че­ски со­пря­жён­ных пе­ре­мен­ных) под­чи­ня­ют­ся пе­ре­ста­но­воч­но­му (ком­му­та­ци­он­но­му) со­от­но­ше­нию: $$[\hat x, \hat p]=\hat x \hat p-\hat p \hat x=i\hbar.$$Об­ще­го ба­зи­са собств. функ­ций для пар та­ких опе­ра­то­ров не су­ще­ст­ву­ет, а со­от­вет­ст­вую­щие им фи­зич. ве­ли­чи­ны не мо­гут быть оп­ре­де­ле­ны од­но­вре­мен­но с про­из­воль­ной точ­но­стью. Из со­от­но­ше­ния ком­му­та­ции для опе­ра­то­ров $\hat x$ и $\hat p$ сле­ду­ет ог­ра­ни­че­ние на точ­ность $\Delta x$ и $\Delta p$ оп­ре­де­ле­ния ко­ор­ди­на­ты $x$ и со­пря­жён­но­го ей им­пуль­са $p$ кван­то­вой сис­те­мы (со­от­но­ше­ние не­оп­ре­де­лён­но­стей Гей­зен­бер­га): $$\Delta x\cdot \Delta p \geq \frac {\hbar}{2}.$$От­сю­да, в ча­ст­но­сти, сра­зу сле­ду­ет вы­вод об ус­той­чи­во­сти ато­ма, по­сколь­ку со­от­но­ше­ние $\Delta x=\Delta p=0$, со­от­вет­ст­вую­щее па­де­нию элек­тро­на на яд­ро, в этой схе­ме за­пре­ще­но. *_mA_{mn}\psi_n.$$Это со­от­но­ше­ние спра­вед­ли­во для чис­тых со­стоя­ний, т. е. для изо­ли­ро­ван­ных кван­то­вых сис­тем. В об­щем слу­чае сме­шан­ных со­стоя­ний мы все­гда име­ем де­ло с боль­шой со­во­куп­но­стью (ста­ти­стич. ан­самб­лем) иден­тич­ных сис­тем (напр., ато­мов), свой­ст­ва ко­то­рой оп­ре­де­ля­ют­ся пу­тём ус­ред­не­ния по это­му ан­самб­лю. В этом слу­чае ср. зна­че­ние $\bar A$ опе­ра­то­ра $\hat A$ при­ни­ма­ет вид $$\bar A=\sum_{m,n}\rho_{nm}A_{mn},$$где $\rho_{nm}$ – мат­ри­ца плот­но­сти (Л. Д. Лан­дау, Дж. фон Ней­ман, 1929) с ус­ло­ви­ем нор­ми­ров­ки $\sum_n\rho_{nn}=1$. Фор­ма­лизм матри­цы плот­но­сти по­зво­ля­ет объ­е­ди­нить кван­то­во­ме­ха­нич. ус­ред­не­ние по со­стоя­ни­ям и ста­ти­стич. ус­ред­не­ние по ан­самб­лю. Мат­ри­ца плот­но­сти иг­ра­ет важ­ную роль так­же в тео­рии кван­то­вых из­ме­ре­ний, суть ко­то­рых все­гда со­сто­ит во взаи­мо­дей­ст­вии кван­то­вой и клас­сич. под­сис­тем. По­ня­тие мат­ри­цы плот­но­сти яв­ля­ет­ся ос­но­вой кван­то­вой ста­ти­сти­ки и ба­зи­сом для од­ной из аль­тер­на­тив­ных фор­му­ли­ро­вок К.  м. Ещё од­ну фор­му К. м., ос­но­ван­ную на по­ня­тии кон­ти­ну­аль­но­го ин­те­гра­ла (или ин­те­гра­ла по тра­ек­то­ри­ям), пред­ло­жил Р. Фейн­ман в 1948.

Принцип соответствия

К. м. име­ет глу­бо­кие кор­ни как в клас­си­че­ской, так и в ста­ти­стич. ме­ха­ни­ке. Уже в сво­ей пер­вой ра­бо­те Н. Бор сфор­му­ли­ро­вал прин­цип со­от­вет­ст­вия, со­глас­но ко­то­ро­му кван­то­вые со­от­но­ше­ния долж­ны пе­ре­хо­дить в клас­си­че­ские при боль­ших кван­то­вых чис­лах $n$. П. Эрен­фест в 1927 по­ка­зал, что с учё­том урав­не­ний К. м. ср. зна­че­ние $\bar A$ опе­ра­то­ра $\hat A$ удов­ле­тво­ря­ет урав­не­нию дви­же­ния клас­сич. ме­ха­ни­ки. Тео­ре­ма Эрен­фе­ста есть ча­ст­ный слу­чай об­ще­го прин­ци­па со­от­вет­ст­вия: в пре­де­ле $h \to 0$ урав­не­ния К. м. пе­ре­хо­дят в урав­не­ния клас­сич. ме­ха­ни­ки. В ча­ст­но­сти, вол­но­вое урав­не­ние Шрё­дин­ге­ра в пре­де­ле $h \to 0$ пе­ре­хо­дит в урав­не­ние гео­мет­рич. оп­ти­ки для тра­ек­то­рии све­то­во­го лу­ча (и лю­бо­го из­лу­че­ния) без учё­та его вол­но­вых свойств. Пред­ста­вив ре­ше­ние $\psi(x)$ урав­не­ния Шрё­дин­ге­ра в ви­де $\psi(x)=\exp\{iS/\hbar\}$, где $S=\int p(x)dx$ – ана­лог клас­сич. ин­те­гра­ла дей­ст­вия, мож­но убе­дить­ся, что в пре­де­ле $\hbar \to 0$ функ­ция $S$ удов­ле­тво­ря­ет клас­сич. урав­не­нию Га­миль­то­на – Яко­би. Кро­ме то­го, в пре­де­ле $h \to 0$ опе­ра­то­ры $\hat x$ и $\hat p$ ком­му­ти­ру­ют и со­от­вет­ст­вую­щие им зна­че­ния ко­ор­ди­на­ты и им­пуль­са мо­гут быть оп­ре­де­ле­ны од­но­вре­мен­но, как это и пред­по­ла­га­ет­ся в клас­сич. ме­ха­ни­ке.

Наи­бо­лее су­ще­ст­вен­ные ана­ло­гии ме­ж­ду со­от­но­ше­ния­ми клас­сич. и кван­то­вой ме­ха­ник для пе­рио­дич. дви­же­ний про­сле­жи­ва­ют­ся на фа­зо­вой плос­ко­сти ка­но­ни­че­ски со­пря­жён­ных пе­ре­мен­ных, напр. ко­ор­ди­на­ты $x$ и им­пуль­са $p$ сис­те­мы. Ин­те­гра­лы ти­па $\oint p(x)dx$, взя­тые по замк­ну­той тра­ек­то­рии (ин­те­граль­ные ин­ва­ри­ан­ты Пу­ан­ка­ре), из­вест­ны в пре­д­ыс­то­рии К. м. как адиа­ба­тич. ин­ва­ри­ан­ты Эрен­фе­ста. 2/2$ (гар­мо­нич. ос­цил­ля­тор с собств. час­то­той $\omega_0$) из ус­ло­вия кван­то­ва­ния $\oint p(x)dx=n h$ сле­ду­ет ряд зна­че­ний энер­гии $E_n=\hbar \omega_0n$, в то вре­мя как точ­ное ре­ше­ние кван­то­вых урав­не­ний для ос­цил­ля­то­ра при­во­дит к по­сле­до­ва­тель­но­сти $E_n=\hbar \omega_0(n+1/2)$. Этот ре­зуль­тат К. м., впер­вые по­лу­чен­ный В. Гей­зен­бер­гом, прин­ци­пи­аль­но от­ли­ча­ет­ся от при­бли­жён­но­го на­ли­чи­ем ну­ле­вой энер­гии ко­ле­ба­ний $E_0=\hbar \omega_0/2$, ко­то­рая име­ет чис­то кван­то­вую при­ро­ду: со­стоя­ние по­коя $(x=0, p=0)$ в К. м. за­пре­ще­но, по­сколь­ку оно про­ти­во­ре­чит со­от­но­ше­нию не­оп­ре­де­лён­но­стей $\Delta x\cdot\Delta p \geq \hbar/2$.

Принцип суперпозиции состояний и вероятностная интерпретация

Ос­нов­ное и на­гляд­ное про­ти­во­ре­чие ме­ж­ду кор­пус­ку­ляр­ной и вол­но­вой кар­ти­на­ми кван­то­вых яв­ле­ний уда­лось уст­ра­нить в 1926, по­сле то­го, как М. Борн пред­ло­жил ин­тер­пре­ти­ро­вать ком­плекс­ную вол­но­вую функ­цию $\psi_n(x)=|\psi_n(x)|\cdot \exp(i \phi_n)$ как ам­пли­ту­ду ве­ро­ят­но­сти со­стоя­ния $n$, а квад­рат её мо­ду­ля $|\psi_n(x)|^2$ – как плот­ность ве­ро­ят­но­сти об­на­ру­жить со­стоя­ние $n$ в точ­ке $x$. 2$ – в со­от­вет­ст­вии с из­ме­не­ни­ем раз­но­сти фаз $\Delta \phi$ от 0 до $\pi/2$. В ча­ст­но­сти, при этом мо­жет ока­зать­ся, что при двух от­кры­тых ще­лях на мес­те изо­бра­же­ния оди­ноч­ной ще­ли мы не об­на­ру­жим ни­ка­ко­го сиг­на­ла, что с кор­пус­ку­ляр­ной точ­ки зре­ния аб­сурд­но.

Су­ще­ст­вен­но, что эта кар­ти­на яв­ле­ния не за­ви­сит от ин­тен­сив­но­сти пуч­ка элек­тро­нов, т. е. это не ре­зуль­тат их взаи­мо­дей­ст­вия ме­ж­ду со­бой. Ин­тер­фе­рен­ци­он­ная кар­ти­на воз­ни­ка­ет да­же в пре­де­ле, ко­гда элек­тро­ны про­хо­дят че­рез ще­ли в пе­ре­го­род­ке по­оди­ноч­ке, т. е. ка­ж­дый элек­трон ин­тер­фе­ри­ру­ет сам с со­бой. Та­кое не­воз­мож­но для час­ти­цы, но впол­не ес­те­ст­вен­но для вол­ны, напр. при её от­ра­же­нии или ди­фрак­ции на пре­пят­ст­вии, раз­ме­ры ко­то­ро­го срав­ни­мы с её дли­ной. В этом опы­те дуа­лизм вол­на-час­ти­ца про­яв­ля­ет­ся в том, что один и тот же элек­трон ре­ги­ст­ри­ру­ет­ся как час­ти­ца, но рас­про­стра­ня­ет­ся как вол­на осо­бой при­ро­ды: это вол­на ве­ро­ят­но­сти об­на­ру­жить элек­трон в к. -л. точ­ке про­стран­ст­ва. В та­кой кар­ти­не про­цес­са рас­сея­ния во­прос: «Че­рез ка­кую из ще­лей про­шёл элек­трон-час­ти­ца?» те­ря­ет смысл, по­сколь­ку со­от­вет­ст­вую­щая ему вол­на ве­ро­ят­но­сти про­хо­дит че­рез обе ще­ли сра­зу.

Дру­гой при­мер, ил­лю­ст­ри­рую­щий ве­ро­ят­но­ст­ный ха­рак­тер яв­ле­ний К. м., – про­хо­ж­де­ние све­та че­рез по­лу­про­зрач­ную пла­стин­ку. По оп­ре­де­ле­нию, ко­эф. от­ра­же­ния све­та ра­вен от­но­ше­нию чис­ла фо­то­нов, от­ра­жён­ных от пла­стин­ки, к чис­лу па­даю­щих. Од­на­ко это есть не ре­зуль­тат ус­ред­не­ния боль­шо­го чис­ла со­бы­тий, а ха­рак­те­ри­сти­ка, из­на­чаль­но при­су­щая ка­ж­до­му фо­то­ну.

Прин­цип су­пер­по­зи­ции и кон­цеп­ция ве­ро­ят­но­сти по­зво­ли­ли осу­ще­ст­вить не­про­ти­во­ре­чи­вый син­тез по­ня­тий «вол­на» и «час­ти­ца»: ка­ж­дое из кван­то­вых со­бы­тий и его ре­ги­ст­ра­ция дис­крет­ны, но их рас­пре­де­ле­ние дик­ту­ет­ся за­ко­ном рас­про­стра­не­ния не­пре­рыв­ных волн ве­ро­ят­но­сти. 2/r-e \boldsymbol E r$, уров­ни энер­гии ато­ма $E_{nlm}$ при этом сме­ща­ют­ся, что при­во­дит к из­ме­не­нию час­тот $\nu_{nk}$ пе­ре­хо­дов ме­ж­ду ни­ми (эф­фект Штар­ка). Кро­ме то­го, ка­че­ст­вен­но этот по­тен­ци­ал ста­но­вит­ся по­доб­ным по­тен­циа­лу $\alpha$-рас­па­да, вслед­ст­вие че­го воз­ни­ка­ет ко­неч­ная ве­ро­ят­ность тун­не­ли­ро­ва­ния элек­тро­на че­рез по­тен­ци­аль­ный барь­ер (Р. Оп­пен­гей­мер, 1928). При дос­ти­же­нии кри­тич. зна­че­ний $\boldsymbol E$ барь­ер по­ни­жа­ет­ся на­столь­ко, что элек­трон по­ки­да­ет атом (т. н. ла­вин­ная ио­ни­за­ция).

Аль­фа-рас­пад есть ча­ст­ный слу­чай рас­па­да ква­зи­ста­цио­нар­но­го со­стоя­ния, ко­то­рый тес­но свя­зан с по­ня­ти­ем кван­то­во­ме­ха­нич. ре­зо­нан­са и по­зво­ля­ет по­нять до­пол­нит. ас­пек­ты не­ста­цио­нар­ных про­цес­сов в К. м. Из урав­не­ния Шрё­дин­ге­ра сле­ду­ет за­ви­си­мость его ре­ше­ний от вре­ме­ни: $$\psi(x,t)=\exp \left\{ -\frac{i}{\hbar}Et \right\}\psi(x),$$где $E$ – собств. зна­че­ние га­миль­то­ниа­на $\hat H$, ко­то­рое для эр­ми­то­вых опе­ра­то­ров К. 2_0$. В ядер­ной фи­зи­ке имен­но от этих се­че­ний за­ви­сит ра­бо­та ядер­но­го и тер­мо­ядер­но­го ре­ак­то­ров. В атом­ной фи­зи­ке это яв­ле­ние впер­вые на­блю­да­ли Дж. Франк и Г. Герц (1913) в опы­тах по ре­зо­нанс­но­му по­гло­ще­нию элек­тро­нов ато­ма­ми рту­ти. В про­ти­во­по­лож­ном слу­чае $(\delta_0=0)$ се­че­ние рас­сея­ния ано­маль­но ма­ло (эф­фект Рам­зау­эра, 1921).

Функ­ция $W(E)$ из­вест­на в оп­ти­ке как ло­рен­цев­ский про­филь ли­нии из­лу­че­ния и име­ет вид ти­пич­ной ре­зо­нанс­ной кри­вой с мак­си­му­мом при $E=E_0$, а ши­ри­на ре­зо­нан­са $Г=2\Delta E=2(E-E_0)$ оп­ре­де­ля­ет­ся из со­от­но­ше­ния $W(E_0 \pm \Delta E)=W(E_0)/2$. Фу­нк­ция  но­сит уни­вер­саль­ный ха­рак­тер и опи­сы­ва­ет как рас­пад ква­зи­ста­цио­нар­но­го со­стоя­ния, так и ре­зо­нанс­ную за­ви­си­мость се­че­ния рас­сея­ния от энер­гии столк­но­ве­ния $E$, а в яв­ле­ни­ях из­лу­че­ния оп­ре­де­ля­ет ес­теств. ши­ри­ну Γ спек­траль­ной ли­нии, ко­то­рая свя­за­на с вре­ме­нем жиз­ни $\tau$ из­лу­ча­те­ля со­от­но­ше­ни­ем $\tau=\hbar/Г$. Это со­от­но­ше­ние оп­ре­де­ля­ет так­же вре­мя жиз­ни эле­мен­тар­ных час­тиц.

Из оп­ре­де­ле­ния $\tau=\hbar/Г$ с учё­том ра­вен­ст­ва $Г=2\Delta E$ сле­ду­ет со­от­но­ше­ние не­опре­де­лён­но­стей для энер­гии и вре­ме­ни: $\Delta E \cdot \Delta t \geq\hbar/2$, где $\Delta t \geq \tau$. По фор­ме оно ана­ло­гич­но со­от­но­ше­нию $\Delta x \cdot \Delta p \geq \hbar/2$, од­на­ко он­то­ло­гич. ста­тус это­го не­ра­вен­ст­ва дру­гой, по­сколь­ку в К. м. вре­мя $t$ не яв­ля­ет­ся ди­на­мич. пе­ре­мен­ной. По­это­му со­от­но­ше­ние $\Delta E \cdot \Delta t \geq \hbar/2$ не сле­ду­ет не­по­сред­ст­вен­но из осн. по­сту­ла­тов ста­цио­нар­ной К. м. и, стро­го го­во­ря, име­ет смысл толь­ко для сис­тем, энер­гия ко­то­рых ме­ня­ет­ся во вре­ме­ни. Его фи­зич. смысл со­сто­ит в том, что за вре­мя $\Delta t$ энер­гия сис­те­мы не мо­жет быть из­ме­ре­на точ­нее, чем ве­ли­чи­на $\Delta E$, оп­ре­де­ляе­мая со­от­но­ше­ни­ем $\Delta E \cdot \Delta t \geq \hbar/2$. Ста­цио­нар­ное со­стоя­ние $(\Delta E \to 0)$ су­ще­ст­ву­ет бес­ко­неч­но дол­го $(\Delta t \to \infty)$.

Спин, тождественность частиц и обменное взаимодействие

По­ня­тие «спин» ут­вер­ди­лось в фи­зи­ке тру­да­ми В. Пау­ли, ни­дерл. фи­зи­ка Р. Кро­ни­га, С. Га­уд­сми­та и Дж. Улен­бе­ка (1924–27), хо­тя экс­пе­рим. сви­де­тель­ст­ва о его су­ще­ст­во­ва­нии бы­ли по­лу­че­ны за­дол­го до со­зда­ния К. м. в опы­тах А. Эйн­штей­на и В. Й. де Хаа­за (1915), а так­же О. Штер­на и нем. фи­зи­ка В. Гер­ла­ха (1922). Спин (соб­ст­вен­ный ме­ха­нич. мо­мент час­ти­цы) для элек­тро­на ра­вен $S=\hbar/2$. Это та­кая же важ­ная ха­рак­те­ри­сти­ка кван­то­вой час­ти­цы, как и за­ряд и мас­са, ко­то­рая, од­на­ко, не име­ет клас­сич. ана­ло­гов.

Опе­ра­тор спи­на  $\hat S=\hbar \hat\sigma/2$, где $\hat\sigma=(\hat\sigma_x, \hat\sigma_y,\hat\sigma_z)$ – дву­мер­ные мат­ри­цы Пау­ли, оп­ре­де­лён в про­стран­ст­ве двух­ком­по­нент­ных собств. функ­ций $u=(u_+, u_-)$ опе­ра­то­ра $\hat S_z$ про­ек­ции спи­на на ось $z$: $\hat\sigma_zu=\sigma u, \sigma=\pm 1/2$. Собств. 2$, $\hat S_z$. Эти ре­ше­ния опи­сы­ва­ют са­мые тон­кие осо­бен­но­сти на­блю­дае­мых спек­тров ато­мов, в ча­ст­но­сти рас­ще­п­ле­ние спек­траль­ных ли­ний в маг­нит­ном по­ле (нор­маль­ный и ано­маль­ный эф­фект Зее­ма­на), а так­же их муль­ти­плет­ную струк­ту­ру в ре­зуль­та­те взаи­мо­дей­ст­вия спи­на элек­тро­на с ор­би­таль­ным мо­мен­том ато­ма (тон­кая струк­ту­ра) и спи­ном яд­ра (сверх­тон­кая струк­ту­ра).

В 1924, ещё до соз­да­ния К. м., В. Пау­ли сфор­му­ли­ро­вал прин­цип за­пре­та: в ато­ме не мо­жет быть двух элек­тро­нов с од­ним и тем же на­бо­ром кван­то­вых чи­сел $i=(nlm\sigma)$. Этот прин­цип по­зво­лил по­нять струк­ту­ру пе­рио­дич. сис­те­мы хи­мич. эле­мен­тов и объ­яс­нить пе­рио­дич­ность из­ме­не­ния их хи­мич. свойств при мо­но­тон­ном уве­ли­че­нии за­ря­да их ядер.

Прин­цип за­пре­та есть ча­ст­ный слу­чай бо­лее об­ще­го прин­ци­па, ко­то­рый ус­та­нав­ли­ва­ет связь ме­ж­ду спи­ном час­ти­цы и сим­мет­ри­ей её вол­но­вой функ­ции. В за­ви­си­мо­сти от зна­че­ния спи­на все эле­мен­тар­ные час­ти­цы раз­де­ля­ют­ся на два клас­са: фер­мио­ны – час­ти­цы с по­лу­це­лым спи­ном (элек­трон, про­тон, $\mu$-ме­зон и т.  д.) и бо­зо­ны – час­ти­цы с ну­ле­вым или це­лым спи­ном (фо­тон, $\pi$-ме­зон, K-ме­зон и т. д.). В 1940 Пау­ли до­ка­зал об­щую тео­ре­му о свя­зи спи­на со ста­ти­сти­кой, из ко­то­рой сле­ду­ет, что вол­но­вые функ­ции лю­бой сис­те­мы фер­мио­нов об­ла­да­ют от­ри­ца­тель­ной чёт­но­стью (ме­ня­ют знак при их по­пар­ной пе­ре­ста­нов­ке), а чёт­ность вол­но­вой функ­ции сис­те­мы бо­зо­нов все­гда по­ло­жи­тель­на. В со­от­вет­ст­вии с этим су­ще­ст­ву­ют два ти­па рас­пре­де­ле­ний час­тиц по энер­ги­ям: рас­пре­де­ле­ние Фер­ми – Ди­ра­ка и рас­пре­де­ле­ние Бо­зе – Эйн­штей­на, ча­ст­ным слу­ча­ем ко­то­ро­го яв­ля­ет­ся рас­пре­де­ле­ние План­ка для сис­те­мы фо­то­нов.

Од­но из след­ст­вий прин­ци­па Пау­ли – су­ще­ст­во­ва­ние т. н. об­мен­но­го взаи­мо­дей­ст­вия, ко­то­рое про­яв­ля­ет­ся уже в сис­те­ме двух элек­тро­нов. В ча­ст­но­сти, имен­но это взаи­мо­дей­ст­вие обес­пе­чи­ва­ет ко­ва­лент­ную хи­мич. связь ато­мов в мо­ле­ку­лах Н₂, N₂, О₂ и т. *(r_1)\psi_n(r_2)\psi_m(r_2)$, воз­ни­каю­щие как след­ст­вие прин­ци­па су­пер­по­зи­ции, ко­то­рый по­зво­ля­ет ка­ж­до­му элек­тро­ну на­хо­дить­ся од­но­вре­мен­но в разл. кван­то­вых со­стоя­ни­ях $n$ и $m$ обо­их ато­мов. Кро­ме то­го, в си­лу прин­ци­па Пау­ли, спи­но­вая часть вол­но­вой функ­ции мо­ле­ку­лы долж­на быть ан­ти­сим­мет­рич­ной по от­но­ше­нию к пе­ре­ста­нов­ке элек­тро­нов, т. е. хи­мич. связь ато­мов в мо­ле­ку­ле осу­ще­ст­в­ля­ет­ся па­рой элек­тро­нов с про­ти­во­по­лож­но на­прав­лен­ны­ми спи­на­ми. Вол­но­вая функ­ция слож­ных мо­ле­кул мо­жет быть пред­став­ле­на как су­пер­по­зи­ция вол­но­вых функ­ций, со­от­вет­ст­вую­щих разл. воз­мож­ным кон­фи­гу­ра­ци­ям мо­ле­ку­лы (тео­рия ре­зо­нан­са, Л. По­линг, 1928).

Раз­ви­тые в К. м. ме­то­ды рас­чё­та (ме­тод Хар­три – Фо­ка, ме­тод мо­ле­ку­ляр­ных ор­би­та­лей и др.) по­зво­ля­ют вы­чис­лить на совр. ком­пь­ю­те­рах все ха­рак­тери­сти­ки ус­той­чи­вых кон­фи­гу­ра­ций слож­ных мо­ле­кул: по­ря­док за­пол­не­ния элек­трон­ных обо­ло­чек в ато­ме, рав­но­вес­ные рас­стоя­ния ме­ж­ду ато­ма­ми в мо­ле­ку­лах, энер­гию и на­прав­ле­ние хи­мич. свя­зей, рас­по­ло­же­ние ато­мов в про­стран­ст­ве, а так­же по­стро­ить по­тен­ци­аль­ные по­верх­но­сти, ко­то­рые оп­ре­де­ля­ют на­прав­ле­ние хи­мич. ре­ак­ций. Та­кой под­ход по­зво­ля­ет так­же вы­чис­лить по­тен­циа­лы меж­атом­ных и меж­мо­ле­ку­ляр­ных взаи­мо­дей­ст­вий, в ча­ст­но­сти си­лы Ван дер Ва­аль­са, оце­нить проч­ность во­до­род­ных свя­зей и др. Тем са­мым про­бле­ма хи­мич. свя­зи сво­дит­ся к за­да­че рас­чё­та кван­то­вых ха­рак­те­ри­стик сис­те­мы час­тиц с ку­ло­нов­ским взаи­мо­дей­ст­ви­ем, и с этой точ­ки зре­ния струк­тур­ную хи­мию мож­но рас­смат­ри­вать как один из раз­де­лов кван­то­вой ме­ха­ни­ки.

Об­мен­ное взаи­мо­дей­ст­вие су­ще­ст­вен­но за­ви­сит от ви­да по­тен­ци­аль­но­го взаи­мо­дей­ст­вия ме­ж­ду час­ти­ца­ми. В ча­ст­но­сти, в не­ко­то­рых ме­тал­лах имен­но бла­го­да­ря ему бо­лее ус­той­чи­вым яв­ля­ет­ся со­стоя­ние пар элек­тро­нов с па­рал­лель­ны­ми спи­на­ми, что объ­яс­ня­ет яв­ле­ние фер­ро­маг­не­тиз­ма.

Приложения квантовой механики

К.  м. – тео­ре­тич. ба­зис кван­то­вой фи­зи­ки. Она по­зво­ли­ла по­нять строе­ние элек­трон­ных обо­ло­чек ато­мов и за­ко­но­мер­но­сти в их спек­трах из­лу­че­ния, струк­ту­ру ядер и за­ко­ны их ра­дио­ак­тив­но­го рас­па­да, про­ис­хо­ж­де­ние хи­мич. эле­мен­тов и эво­лю­цию звёзд, вклю­чая взры­вы но­вых и сверх­но­вых звёзд, а так­же ис­точ­ник энер­гии Солн­ца. К. м. объ­яс­ни­ла смысл пе­рио­дич. сис­те­мы эле­мен­тов, при­ро­ду хи­мич. свя­зи и строе­ние кри­с­тал­лов, те­п­ло­ём­кость и маг­нит­ные свой­ст­ва ве­ществ, яв­ле­ния сверх­про­во­ди­мо­сти и сверх­те­ку­че­сти и др. К. м. – фи­зич. ос­но­ва мно­го­числ. тех­нич. при­ло­же­ний: спек­траль­но­го ана­ли­за, ла­зе­ра, тран­зи­с­то­ра и ком­пь­ю­те­ра, ядер­но­го ре­ак­то­ра и атом­ной бом­бы и т. д.

Свой­ст­ва ме­тал­лов, ди­элект­ри­ков, по­лу­про­вод­ни­ков и др. ве­ществ в рам­ках К. м. так­же по­лу­ча­ют ес­теств. объ­яс­не­ние. В кри­стал­лах ато­мы со­вер­ша­ют око­ло по­ло­же­ний рав­но­ве­сия ма­лые ко­ле­ба­ния с час­то­той $\omega$, ко­то­рым со­пос­тав­ля­ют­ся кван­ты ко­ле­ба­ний кри­стал­лич. ре­шёт­ки и со­от­вет­ст­вую­щие им ква­зи­ча­сти­цы – фо­но­ны с энер­ги­ей $E=\hbar \omega$. Те­п­ло­ём­кость кри­стал­ла в зна­чит. сте­пе­ни оп­ре­де­ля­ет­ся те­п­ло­ём­ко­стью га­за его фо­но­нов, а его те­п­ло­про­вод­ность мож­но трак­то­вать как те­п­ло­про­вод­ность фо­нон­но­го га­за. В ме­тал­лах элек­тро­ны про­во­ди­мо­сти пред­став­ля­ют со­бой газ фер­мио­нов, а их рас­сея­ние на фо­но­нах яв­ля­ет­ся осн. при­чи­ной элек­трич. со­про­тив­ле­ния про­вод­ни­ков, а так­же объ­яс­ня­ет по­до­бие те­п­ло­вых и элек­трич. свойств ме­тал­лов (см. Ви­де­ма­на – Фран­ца за­кон). В маг­ни­то­упо­ря­до­чен­ных струк­ту­рах воз­ни­ка­ют ква­зи­ча­сти­цы – маг­но­ны, ко­то­рым со­от­вет­ст­ву­ют спи­но­вые вол­ны, в кван­то­вых жид­ко­стях воз­ни­ка­ют кван­ты вра­ща­тель­но­го воз­бу­ж­де­ния – ро­то­ны, а маг­нит­ные свой­ст­ва ве­ществ оп­реде­ля­ют­ся спи­на­ми элек­тро­нов и ядер (см. Маг­не­тизм). Взаи­мо­дей­ст­вие спи­нов элек­тро­нов и ядер с маг­нит­ным по­лем – ос­но­ва прак­тич. при­ло­же­ний яв­ле­ний элек­трон­но­го па­ра­маг­нит­но­го и ядер­но­го маг­нит­но­го ре­зо­нан­сов, в част­но­сти в мед. то­мо­гра­фах.

Упо­ря­до­чен­ная струк­ту­ра кри­стал­лов по­ро­ж­да­ет до­пол­нит. сим­мет­рию га­миль­то­ниа­на по от­но­ше­нию к сдви­гу $x \to x+a$, где $a$ – пе­ри­од кри­стал­лич. ре­шёт­ки. Учёт пе­рио­дич. струк­ту­ры кван­то­вой сис­те­мы при­во­дит к рас­ще­п­ле­нию её энер­ге­тич. спек­тра на раз­ре­шён­ные и за­пре­щён­ные зо­ны. Та­кая струк­ту­ра уров­ней энер­гии ле­жит в ос­но­ве ра­бо­ты тран­зи­сто­ров и всей ба­зи­рую­щей­ся на них элек­тро­ни­ки (те­ле­ви­зор, ком­пь­ю­тер, со­то­вый те­ле­фон и др.). В нач. 21 в. дос­тиг­ну­ты су­ще­ст­вен­ные ус­пе­хи в соз­да­нии кри­стал­лов с за­дан­ны­ми свой­ст­ва­ми и струк­ту­рой энер­ге­тич. зон (сверх­ре­шёт­ки, фо­тон­ные кри­стал­лы и ге­те­ро­ст­рук­ту­ры: кван­то­вые точ­ки, кван­то­вые ни­ти, на­нот­руб­ки и др.).

При по­ни­же­нии темп-ры не­ко­то­рые ве­ще­ст­ва пе­ре­хо­дят в со­стоя­ние кван­то­вой жид­ко­сти, энер­гия ко­то­рой при темп-ре $T \to 0$ при­бли­жа­ет­ся к энер­гии ну­ле­вых ко­ле­ба­ний сис­те­мы. В не­ко­то­рых ме­тал­лах при низ­ких темп-рах об­ра­зу­ют­ся ку­пе­ров­ские па­ры – сис­те­мы из двух элек­т­ро­нов с про­ти­во­по­лож­ны­ми спи­на­ми и им­пуль­са­ми. При этом элек­трон­ный газ фер­мио­нов транс­фор­ми­ру­ет­ся в газ бо­зо­нов, что вле­чёт за со­бой бо­зе-кон­ден­са­цию, ко­то­рая объ­яс­ня­ет яв­ле­ние сверх­про­во­ди­мо­сти.

При низ­ких темп-рах дли­на вол­ны де Брой­ля те­п­ло­вых дви­же­ний ато­мов ста­но­вит­ся срав­ни­мой с меж­атом­ны­ми рас­стоя­ния­ми и воз­ни­ка­ет кор­ре­ля­ция фаз вол­но­вых функ­ций мн. час­тиц, что при­во­дит к мак­ро­ско­пич. кван­то­вым эф­фек­там (эф­фект Джо­зеф­со­на, кван­то­ва­ние маг­нит­но­го по­то­ка, дроб­ный кван­то­вый эф­фект Хол­ла, ан­д­ре­ев­ское от­ра­же­ние).

На ос­но­ве кван­то­вых яв­ле­ний соз­да­ны наи­бо­лее точ­ные кван­то­вые эта­ло­ны разл. фи­зич. ве­ли­чин: час­то­ты (ге­лий-не­оно­вый ла­зер), элек­трич. на­пря­же­ния (эф­фект Джо­зеф­со­на), со­про­тив­ле­ния (кван­то­вый эф­фект Хол­ла) и т.  д., а так­же при­бо­ры для разл. пре­цизи­он­ных из­ме­ре­ний: скви­ды, кван­то­вые ча­сы, кван­то­вый ги­ро­скоп и т. д.

К. м. воз­ник­ла как тео­рия для объ­яс­не­ния спе­ци­фич. яв­ле­ний атом­ной фи­зи­ки (её вна­ча­ле так и на­зы­ва­ли: атом­ная ди­на­ми­ка), но по­сте­пен­но ста­ло яс­но, что К. м. об­ра­зу­ет так­же ос­но­ву всей суб­атом­ной фи­зи­ки, и все её осн. по­ня­тия при­ме­ни­мы для опи­са­ния яв­ле­ний фи­зи­ки яд­ра и эле­мен­тар­ных час­тиц. Пер­во­на­чаль­ная К. м. бы­ла не­ре­ля­ти­вист­ской, т. е. опи­сы­ва­ла дви­же­ние сис­тем со ско­ро­стя­ми мно­го мень­ши­ми ско­ро­сти све­та. Взаи­мо­дей­ст­вие час­тиц в этой тео­рии по-преж­не­му опи­сы­ва­лось в клас­сич. тер­ми­нах. В 1928 П. Ди­рак на­шёл ре­ля­ти­ви­ст­ское урав­не­ние К. м. (урав­не­ние Ди­ра­ка), ко­то­рое при со­хра­не­нии всех её по­ня­тий учи­ты­ва­ло тре­бо­ва­ния тео­рии от­но­си­тель­но­сти. Кро­ме то­го, был раз­вит фор­ма­лизм вто­рич­но­го кван­то­ва­ния, ко­то­рый опи­сы­ва­ет ро­ж­де­ние и унич­то­же­ние час­тиц, в ча­ст­но­сти ро­ж­де­ние и по­гло­ще­ние фо­то­нов в про­цес­сах из­лу­че­ния. На этой ос­но­ве воз­ник­ла кван­то­вая элек­тро­ди­на­ми­ка, ко­то­рая по­зво­ли­ла с боль­шой точ­но­стью рас­счи­ты­вать все свой­ст­ва сис­тем с элек­тро­маг­нит­ным взаи­мо­дей­ст­ви­ем. В даль­ней­шем она раз­ви­лась в кван­то­вую тео­рию по­ля, объ­е­ди­няю­щую в еди­ном фор­ма­лиз­ме час­ти­цы и по­ля, по­сред­ст­вом ко­то­рых они взаи­мо­дей­ст­ву­ют.

Для опи­са­ния эле­мен­тар­ных час­тиц и их взаи­мо­дей­ст­вий ис­поль­зу­ют­ся все осн. по­ня­тия К. м.: ос­та­ёт­ся спра­вед­ли­вым дуа­лизм вол­на-час­ти­ца, со­хра­ня­ет­ся язык опе­ра­то­ров и кван­то­вых чи­сел, ве­ро­ят­но­ст­ная трак­тов­ка на­блю­дае­мых яв­ле­ний и т. д. В ча­ст­но­сти, для объ­яс­не­ния взаи­мо­пре­вра­ще­ния трёх ти­пов ней­три­но: $\nu_e$, $\nu_\mu$ и $\nu_\tau$ (ос­цил­ля­ции ней­три­но), а так­же ней­траль­ных K-ме­зо­нов ис­поль­зу­ет­ся прин­цип су­пер­по­зи­ции со­стоя­ний.

Интерпретация квантовой механики

Спра­вед­ли­вость урав­не­ний и за­клю­че­ний К. м. мно­го­крат­но под­твер­жде­на мно­го­числ. опы­та­ми. Сис­те­ма её по­ня­тий, соз­дан­ная тру­да­ми Н. Бо­ра, его уче­ни­ков и по­сле­до­ва­те­лей, из­вест­ная как «ко­пен­га­ген­ская ин­тер­пре­та­ция», яв­ля­ет­ся ны­не об­ще­при­ня­той, хо­тя ряд соз­да­те­лей К. м. (М. Планк, А. Эйн­штейн и Э. Шрё­дин­гер и др.) до кон­ца жиз­ни ос­та­лись в убе­ж­де­нии, что К. м. – не­за­вер­шён­ная тео­рия. Спе­ци­фич. труд­ность вос­при­я­тия К. м. обу­слов­ле­на, в ча­ст­но­сти, тем об­стоя­тель­ст­вом, что бóльшая часть её осн. по­ня­тий (вол­на, час­ти­ца, на­блю­де­ние и т. д.) взя­ты из клас­сич. фи­зи­ки. В К. м. их смысл и об­ласть при­ме­ни­мо­сти ог­ра­ни­че­ны в си­лу ко­неч­но­сти кван­та дей­ст­вия $h$, а это, в свою оче­редь, по­тре­бо­ва­ло ре­ви­зии ус­то­яв­ших­ся по­ло­же­ний фи­ло­со­фии по­зна­ния.

Пре­ж­де все­го в К. м. из­ме­нил­ся смысл по­ня­тия «на­блю­де­ние». В клас­сич. фи­зи­ке пред­по­ла­га­ли, что воз­му­ще­ния изу­чае­мой сис­те­мы, вы­зван­ные про­цес­сом из­ме­ре­ния, мо­гут быть кор­рект­но уч­те­ны, по­сле че­го мож­но вос­ста­но­вить ис­ход­ное со­стоя­ние сис­те­мы, не­за­ви­си­мое от средств на­блю­де­ния. В К. м. со­от­но­ше­ние не­оп­ре­де­лён­но­стей ста­вит на этом пу­ти прин­ци­пи­аль­ный пре­дел, ко­то­рый ни­как не свя­зан с ис­кус­ст­вом экс­пе­ри­мен­та­то­ра и тон­ко­стью ис­поль­зуе­мых ме­то­дов на­блю­де­ния. Квант дей­ст­вия $h$ оп­ре­де­ля­ет гра­ни­цы К. м., по­доб­но ско­ро­сти све­та в тео­рии элек­тро­маг­нит­ных яв­ле­ний или аб­со­лют­но­му ну­лю темп-р в тер­мо­ди­на­ми­ке.

При­чи­ну не­при­ятия со­от­но­ше­ния не­оп­ре­де­лён­но­стей и спо­соб пре­одо­ле­ния труд­но­стей вос­при­ятия его ло­гич. след­ст­вий пред­ло­жил Н. Бор в кон­цеп­ции до­пол­ни­тель­но­сти (см. До­пол­ни­тель­но­сти прин­цип). Со­глас­но Бо­ру, для пол­но­го и аде­к­ват­но­го опи­са­ния кван­то­вых яв­ле­ний не­об­хо­ди­ма па­ра до­пол­нит. по­ня­тий и со­от­вет­ст­вую­щая им па­ра на­блю­дае­мых. Для из­ме­ре­ния этих на­блю­дае­мых не­об­хо­ди­мы два раз­ных ти­па при­бо­ров с не­со­вмес­ти­мы­ми свой­ст­ва­ми. Напр., для точ­но­го из­ме­ре­ния ко­ор­ди­на­ты ну­жен ста­биль­ный, мас­сив­ный при­бор, а для из­ме­ре­ния им­пуль­са, на­обо­рот, лёг­кий и чув­ст­ви­тель­ный. Оба эти при­бо­ра не­со­вмес­ти­мы, но они до­пол­ни­тель­ны в том смыс­ле, что обе ве­ли­чи­ны, из­ме­ряе­мые ими, рав­но не­об­хо­ди­мы для пол­ной ха­рак­те­ри­сти­ки кван­то­во­го объ­ек­та или яв­ле­ния. Бор объ­яс­нил, что «яв­ле­ние» и «на­блю­де­ние» – до­пол­нит. по­ня­тия и не мо­гут быть оп­ре­де­ле­ны по­рознь: про­цесс на­блю­де­ния уже есть не­кое яв­ле­ние, а без на­блю­де­ния яв­ле­ние есть «вещь в се­бе». В дей­ст­ви­тель­но­сти мы все­гда име­ем де­ло не с яв­ле­ни­ем са­мим по се­бе, а с ре­зуль­та­том на­блю­де­ния яв­ле­ния, и ре­зуль­тат этот за­ви­сит в т. ч. от вы­бо­ра ти­па при­бо­ра, ис­поль­зуе­мо­го для из­ме­ре­ния ха­рак­те­ри­стик кван­то­во­го объ­ек­та. Ре­зуль­та­ты та­ких на­блю­де­ний К. м. объ­яс­ня­ет и пред­ска­зы­ва­ет без вся­ко­го про­из­во­ла.

Важ­ное от­ли­чие кван­то­вых урав­не­ний от клас­си­че­ских со­сто­ит так­же в том, что вол­но­вая функ­ция кван­то­вой сис­те­мы са­ма не на­блю­дае­ма, а все ве­ли­чи­ны, вы­чис­лен­ные с её по­мо­щью, име­ют ве­ро­ят­но­ст­ный смысл. Кро­ме то­го, по­ня­тие ве­ро­ят­но­сти в К. м. в кор­не от­ли­ча­ет­ся от при­выч­но­го по­ни­ма­ния ве­ро­ят­но­сти как ме­ры на­ше­го не­зна­ния де­та­лей про­цес­сов. Ве­ро­ят­ность в К. м. – это внутр. свой­ст­во ин­ди­ви­ду­аль­но­го кван­то­во­го яв­ле­ния, при­су­щее ему из­на­чаль­но и не­за­ви­си­мо от из­ме­ре­ний, а не спо­соб пред­став­ле­ния ре­зуль­та­тов из­ме­ре­ний. В со­от­вет­ст­вии с этим прин­цип су­пер­по­зи­ции в К. м. от­но­сит­ся не к ве­ро­ят­но­стям, а к ам­пли­ту­дам ве­ро­ят­но­сти. Кро­ме то­го, в си­лу ве­ро­ят­но­ст­но­го ха­рак­те­ра со­бы­тий су­пер­по­зи­ция кван­то­вых со­стоя­ний мо­жет вклю­чать в се­бя со­стоя­ния, не­со­в­ме­с­ти­мые с клас­сич. точ­ки зре­ния, напр. со­стоя­ния от­ра­жён­но­го и про­шед­ше­го фо­то­нов на гра­ни­це по­лу­про­зрач­но­го эк­ра­на или аль­тер­на­тив­ные со­стоя­ния элек­тро­на, про­хо­дя­ще­го че­рез лю­бую из ще­лей в зна­ме­ни­том ин­тер­фе­рен­ци­он­ном опы­те.

Не­при­ятие ве­ро­ят­но­ст­ной трак­тов­ки К.  м. по­ро­ди­ло мас­су по­пы­ток мо­ди­фи­ци­ро­вать осн. по­ло­же­ния К. м. Од­на из та­ких по­пы­ток – вве­де­ние в К. м. скры­тых па­ра­мет­ров, ко­то­рые из­ме­ня­ют­ся в со­от­вет­ст­вии со стро­ги­ми за­ко­на­ми при­чин­но­сти, а ве­ро­ят­но­ст­ный ха­рак­тер опи­са­ния в К. м. воз­ни­ка­ет как ре­зуль­тат ус­ред­не­ния по этим па­ра­мет­рам. До­ка­за­тель­ст­во не­воз­мож­но­сти вве­де­ния в К. м. скры­тых па­ра­мет­ров без на­ру­ше­ния сис­те­мы её по­сту­ла­тов бы­ло да­но Дж. фон Ней­ма­ном ещё в 1929. Бо­лее де­таль­ный ана­лиз сис­те­мы по­сту­ла­тов К. м. был пред­при­нят Дж. Бел­лом в 1965. Экс­пе­рим. про­вер­ка т. н. не­ра­венств Бел­ла (1972) ещё раз под­твер­ди­ла об­ще­при­ня­тую схе­му кван­то­вой ме­ха­ни­ки.

Ны­не К. м. пред­став­ля­ет со­бой за­кон­чен­ную тео­рию, ко­то­рая все­гда да­ёт пра­виль­ные пред­ска­за­ния в гра­ни­цах её при­ме­ни­мо­сти. Все из­вест­ные по­пыт­ки её мо­ди­фи­ка­ции (их из­вест­но око­ло де­ся­ти) не из­ме­ни­ли её струк­ту­ры, но по­ло­жи­ли на­ча­ло но­вым от­рас­лям на­ук о кван­то­вых яв­ле­ни­ях: кван­то­вой элек­тро­ди­на­ми­ке, кван­то­вой тео­рии по­ля, тео­рии элек­тро­сла­бо­го взаи­мо­дей­ст­вия, кван­то­вой хро­мо­ди­на­ми­ке, кван­то­вой тео­рии гра­ви­та­ции, тео­рии струн и су­пер­струн и др.

К. м. сто­ит в ря­ду та­ких дос­ти­же­ний нау­ки, как клас­сич. ме­ха­ни­ка, уче­ние об элек­три­че­ст­ве, тео­рия от­но­си­тель­но­сти и ки­не­тич. тео­рия. Ни од­на фи­зич. тео­рия не объ­яс­ни­ла та­ко­го ши­ро­ко­го кру­га фи­зич. яв­ле­ний при­ро­ды: из 94 Но­бе­лев­ских пре­мий по фи­зи­ке, при­су­ж­дён­ных в 20 в., толь­ко 12 не свя­за­ны на­пря­мую с кван­то­вой фи­зи­кой. Зна­че­ние К. м. во всей сис­те­ме зна­ний об ок­ру­жаю­щей при­ро­де вы­хо­дит да­ле­ко за рам­ки уче­ния о кван­то­вых яв­ле­ни­ях: она соз­да­ла язык об­ще­ния в совр. фи­зи­ке, хи­мии и да­же био­ло­гии, при­ве­ла к пе­ре­смот­ру фи­ло­со­фии нау­ки и тео­рии по­зна­ния, а её тех­но­ло­гич. след­ст­вия до сих пор оп­ре­де­ля­ют на­прав­ле­ние раз­ви­тия совр. ци­ви­ли­за­ции.

Характер физических законов на пальцах™ — (3/3) — Проверяя непроверяемое: sly2m — LiveJournal

Мы добрались до заключительной части обсуждения характера физических законов на пальцах™, где читателя ждет самое интересное, самая вкуснота. Можно сказать, что две предыдущие части (первая и вторая) были лишь приготовлением, являлись очень растянутым лирическим вступлением к обсуждению основного научного вопроса, рассматриваемого на пальцах™ — что такое “неравенства Белла” и почему эти два слова являются не только разрешением векового спора гениальнейших ученых планеты, но и определяют истинное устройство Вселенной вокруг нас.

Быстренько напомню, в чем заключалась суть спора. Нильс Бор и сотоварищи говорят нам — неопределенность есть истинное положение вещей в окружающем нас мире. У Вселенной и ее частей (частиц) вообще нет никаких определенных свойств до тех пор, как мы эту частицу не поймали и не измерили те самые свойства. А Луны не существует, покуда на нее никто не смотрит.

Эйнштейн же с друзьями (в основном П и Р) твердят обратное — невозможно поступиться принципами! Мы итак отдали целую руку на растерзание — принцип неопределенности работает и неоднократно экспериментально проверен, мы с этим даже уже почти не спорим. Но оставьте нам хотя бы какой–то островок стабильности в океане бушующего хаоса случайностей! Пусть мы никогда одновременно не сможем узнать всех свойств какой–то частицы, но давайте признаем, что они у частицы все–таки есть! До измерения или после — частица обладает своими внутренними свойствами, то, что мы их не можем узнать, это наша, человеческая проблема. То, что их изначально не было до момента измерения — это уже проблема Вселенной, проблема Бога, который играет в кости и сам не знает, какая комбинация выпадет следующей — а это, уже, извините как минимум богохульство и научная ересь…

Как я уже говорил, и Эйнштейн, и Бор умерли так и не дождавшись разрешения этого фундаментального научного конфликта. Четкое, простое и оттого гениальное решение пришло в голову ирландскому ученому Джону Беллу в виде одноименных неравенств лишь в 1964м году и еще 20 лет после этого ждало своего экспериментального подтверждения.

Обязательно должен предупредить. Этот пост технически и научно потяжелее двух предыдущих. Чуть–чуть все же придется пораскинуть мозгами. Но не такой, чтобы прям совсем сложный, доступный для понимания вполне себе на пальцах™.

Вот, что удивительно, оказалось не так–то легко найти информацию на русском языке, что же это за зверь такой — “неравенства Белла”. Вроде бы такое эпохальное открытие, лежащее в фундаменте определения сути устройства окружающего мира, разрешающее вековой спор ученых светил и определяющее, чем наши знания о реальности отличаются от того, какова реальность есть на самом деле. Но попробуйте поискать и разобраться в этом вопросе сами, скорее всего вас ждет разочарование.

Нет, вы попробуйте, попробуйте, я серьезно!

Википедия, луркоморье, просто тупой перебор выдачи гугла по ключевой фразе мало чем помогут. Кругом либо расплывчатые описания из серии “как показал Белл в своих неравенствах…”, и дальше идут выводы и следствия без четкого определения — что же это были за неравенства, в чем была их суть и что там конкретно в эксперименте мерили, либо разговор резко уходит в область матана волновой функции, где 300 формул на одной странице и вообще ничего не понятно.

Позвольте изложить свою версию сущности идей, предложенных Беллом, и в миллионный раз напомнить — далее последуют объяснения на пальцах™ в виде набора несложных аналогий, которые, хоть и верны в принципе, тем не менее остаются всего лишь аналогиями, не более, ведь суть неравенств Белла можно выразить очень по–разному.

Скажу больше. То, как Белл изначально записал свои неравенства, вообще экспериментальной проверке не поддается. Однако это был действительный прорыв научной мысли, ибо хоть теоретически, хоть и оставаясь в философско–рассуждательной области, Белл все равно показал, что спор Эйшнтейна с Бором можно было разрешить хотя бы в принципе. А это многого стоит.

Экспериментально, как я уже сказал, проверялись совсем другие вещи. Причем по–разному, несколькими физическими экспериментами с разными выкладками и аппаратом.

Я же и вовсе буду рассказывать третью историю. В науке так бывает — если невозможно что–то проверить напрямую, есть шансы построить логическую цепочку в сторону, посмотреть, какие выводы нас ожидают в этом случае и проверить результаты подобных выводов. Математически все четко и последовательно вытекает друг из друга, но физические проявления и аспекты могут сильно разниться. Настоящий физик при всем богатстве выбора всегда предпочтет тот аспект, который легче всего экспериментально проверить, я же выбираю такой, который легче всего объяснить на пальцах™. Лишь бы все они математически (и, что важно — физически) оставались эквивалентны друг другу, это главное.

Мы помним, что в случае двух противоположных (некоммутирующих) параметров, например, координата частицы и ее скорость, или энергия и время, или когда спины “вверх–вниз” — никаким образом невозможно понять, были ли у частицы (в смысле у двух запутанных частиц) эти свойства изначально, или они появились одновременно у обоих в процессе измерения. Эйнштейн говорит, что были раньше, хоть и были скрыты от нашего знания (теория скрытых параметров), Бор говорит, что происходит “жуткое дальнодействие” и все всем платится прямо на месте. Когда мы измеряли состояние одной частицы, это тут же в мгновение ока сказывалось на поведении второй.

Экспериментально обе ситуации абсолютно идентичны. Чего гадать, было что–то у частицы или не было до того, как мы ее поймали и измерили. Вопрос скорее философский, чем научный, ибо физика занимается тем, что можно непосредственно пощупать и измерить. Фантазировать о том, что могло бы произойти в случае, о котором мы никогда ничего не узнаем — антинаучная ерунда, не так ли?

Очень может быть. Но давайте сперва рассмотрим поближе, что же представляет собой спин частицы или системы.

Согласно википедии спин (англ. spin — вращение) определяет угловой момент вращения частицы вокруг своей оси.

И сразу стоп!

Тут важно уяснить раз и навсегда. Ничего на самом деле никуда и нигде не вращается. По всем современным понятиям, скажем, элементарная частица электрон не имеет пространственных размеров и представляет собой реальную, хоть и математическую точку. Что не мешает ей в то же время быть одновременно и волной (ну, корпускулярно–волновой дуализм же!).

Спин это просто очередная характеристика частицы, рассуждать о спине как о реальном вращении лишь помогает проводить параллели с привычным нам миром, но не более. Легко и удобно думать о пути перемещения баскетбольного мяча (сопоставляя с путем перемещения частицы, что не совсем верно, ибо как говорилось выше, у нее нет пути в нашем человеческом понимании), так и о вращении мяча вокруг своей оси (сопоставляя со спином частицы, что тоже неверно, ибо нет там никакого вращения!).

Ближе всего к спину можно подобраться со стороны симметрии и ее нарушения. Ведь когда мяч (электрон) просто сам по себе мяч (электрон) он со всех сторон симметричен. Мяч со всех сторон круглый, электрон со всех сторон точка.

Но когда у мяча появляется вращение (а у электрона спин) симметрия нарушается. Например, если мяч вращается вокруг вертикальной оси, он не вращается вокруг горизонтальной — симметрия нарушена. Мяч не может одновременно вращаться и так и так. Он может вращаться в наклоненном состоянии, т.е. как бы “по диагонали”, но это ведь не совсем то же самое, что одновременное вращение сразу по вертикали и по горизонтали.

То же самое и со спином электрона. Спин — мера его симметрии. И эту симметрию можно разложить на оси координат X и Y (точнее на оси X, Y и Z, все ведь трехмерное, но для простоты останемся пока в двух координатах, чтобы заранее не усложнять).

Сначала посмотрим на классический объект (мяч) и его спин. Пусть у нас есть баскетбольный мяч, который вращается со скоростью 8.12 оборотов в минуту. Если ось вращения расположена вертикально, можно считать, что мяч “весь” вращается вокруг оси Y, его Y–спин, или спин относительно оси Y равен 8.12 об/мин, и при этом он совершенно не вращается вокруг оси X (его X–спин равняется нулю). Ну, или если он вращается вокруг горизонтально расположенной оси, будет все то же самое, только наоборот.

Если ось вращения расположена под углом к горизонту, допустимо разложить спин мяча на Y — и X–компоненты, Y — и X–спины. Напомню, мяч не вращается одновременно вокруг осей Y и Х, он вращается вокруг своей собственной оси L, наклоненной под некоторым углом к горизонту, но момент его вращения можно разложить на Y — и X — составляющие. Тут все просто. Спин мяча остается 8.12 оборотов в минуту, на приведенном рисунке это получается гипотенуза, а Y — и X — спины вычисляются через синус (косинус) угла, ну, или по теореме Пифагора.

В квантовом мире все одновременно проще и сложней. Проще, потому что мир квантовый, и подчиняется законам квантовой механики, а это, кроме всего прочего, чисто по названию означает, что все в этом мире квантуется. И спин в том числе. Вращение обычного предмета вокруг своей оси (спин этого предмета) может быть любым. Он может совершать 1 оборот в минуту, может полтора, может 8.12 (как в случае с нашим баскетбольным мячом), может даже крутиться 100500 оборотов в минуту — никаких проблем.

В мире элементарных частиц спин может занимать только вполне конкретные, квантованные числа. Скажем, у электрона он может иметь только два значения или +1/2 или –1/2. И ничего больше.

Почему + и — понятно. Это просто смотря в какую сторону электрон “вращается”, вправо или влево. С мячом была та же история, если оставить его вращаться, но перевернуть вверх ногами, спин получится –8.12 оборотов в минуту, что по сути то же самое вращение, только в другую сторону.

С 1/2 чуточку сложнее. Во–первых, это уже никакие не “обороты в минуту”. Это вообще не обороты, если вы помните, электрон на самом деле не вращается, и уж тем более не “в минуту”. Это просто некая удобная для записи величина, некоторое безразмерное число. Можно было бы принять спин электрона за +10 и –10. Или +100 и –100. Как вы догадываетесь, лучше всего было тупо принять спин электрона за +1 и –1, но ученые, как истинные комсомольцы, любят некоторые трудности. Были исторические причины, почему спин электрона оказался 1/2 а не 1, но так как величина все равно формальная и безразмерная, это все не суть. Главное, что спин любой частицы может изменяться только квантованными порциями–половинками — 0 (нет вращения, нет спина), 1/2, 1, 3/2, 2, 5/2 и т.д. И то же самое, но со знаком минус, если вращение в другую сторону.

Читателю со звездочкой^(*) наверняка будет интересно узнать, что все частицы, имеющие полуцелый спин (кратный 1/2), составляют нашу материю и их называют фермионами за то, что они подчиняются статистике Ферми–Дирака.
Это уже знакомые нам электроны, а также протоны, нейтроны, кварки и прочие нейтрино — т.н. “материальные частицы”. В 1925м году Вольфганг Паули запретил фермионам занимать одно квантовое состояние (грубо говоря — садиться друг другу на шею) и с тех пор электроны не падают на ядра атомов, а наша Вселенная получила законное основание занимать некий объем в пространстве.

Частицы с целым спином называют бозоны, они статистике Ферми–Дирака не подчиняются, у них своя статистика — Бозе–Эйнштейна. (Да, этот хитрый еврей и сюда пролез. Всю жизнь он ненавидел “жуткие дальнодействующие” кванты, хотя в свое время лично положил начало всему этому беспределу, отчего его имя встречается не только в законах теории относительности, но и в законах квантовой механики). Бозонам (“полевым частицам”, “частицам энергии”) пофигу на законодательные запреты Паули, наоборот, они любят занимать одинаковые квантовые состояния (садиться друг другу на голову), тем самым поддерживая и усиливая друг друга, именно поэтому лазерный луч может легко резать стальные листы.

Лазер — ни что иное как физическое воплощение квантовых микроэффектов статистики Бозе–Эйнштейна в нашем макромире, вот и все описание его работы на пальцах™.

Но это я отвлекся, так вот. С одной стороны ситуация со спином в квантовом мире гораздо проще, чем в мире реальном, значения спина все сплошь квантовые и их буквально всего несколько штук, максимальный спин самого замороченного бариона вроде бы 15/2 и баста. У электрона их вообще может быть всего два, +1/2 и –1/2, или как я их называл в прошлой части “вверх” и “вниз”. Теперь понятно, кстати, почему? Только там не просто “вверх” и “вниз”, эти “вверх–вниз” (+1/2 или –1/2) могут быть вдоль любой из осей X и Y (еще и Z, не забываем про Z!), или вообще вдоль любой “неперпендикулярной” оси, но зато на любой оси их может поместиться всего два, они всегда будут противоположны, потому–то и “вверх–вниз”.

С другой стороны, все сильно сложнее, потому что спин–компоненты вдоль разных осей — некоммутирующие параметры.

Задумайтесь над предыдущей фразой. Помните, что такое некоммутирующие параметры? Это те, что Гейзенберг запрещает одновременно измерять, вроде координаты и скорости частицы.

В нашем мире, если мы знаем X–спин (Х–компоненту вращения), то Y–спин элементарно вычисляется по теореме Пифагора. В квантовом мире, если мы знаем X–спин, мы абсолютно ничего не знаем про его Y–спин, он может оказаться каким угодно. Ну, как сказать “каким угодно”… Я же только что заявил, спин электрона бывает лишь или +1/2 или –1/2 (или “вверх” или “вниз”). Но какой он окажется конкретно, померить и узнать (одновременно с первым измерением) совершенно невозможно. Такая вот несправедливость, такая вот неопределенность.

И тут начинается самое интересное. Помните суть грызни Эйнштейна с Бором насчет запутанных частиц? У запутанных частиц спин всегда занимает противоположные значения. Если у одной он “вниз”, то у другой обязательно “вверх”. Или же один сапог правый, а второй левый, помните? И невозможно узнать, какой был какой, покуда не было произведено измерения. Но вся фишка в том, что в отличие от правых–левых сапогов, спин у электронов может быть так сказать “вдоль любых осей”.

Нет, все предыдущие выкладки пока в силе. Если у первого из запутанных электронов X-спин был “вверх”, значит у второго X-спин будет “вниз”. Если у первого Y-спин был “вниз”, значит у второго Y-спин будет “вверх”. Но одновременно получить X- и Y-спин у любой из частиц мы не можем. Тут покуда никаких новостей, Эйнштейн все это знал и учитывал, что теперь при измерении нам придется не только говорить какой у электрона спин, “вверх” или “вниз”, но и сообщать вдоль какой оси мы его мерили. Необязательно X или Y, кстати, можно измерить спин вдоль оси под углом 17.5 градусов к горизонту, почему нет? И у второй частицы по этой же оси будет противоположный спин.

А вот теперь хитрый финт ушами, который провернул Белл. Для начала продолжим оставаться лишь в трех перпендикулярных осях X, Y и Z, чтобы не морочиться с дробными вероятностями. Напомню, что если мы знаем спин электрона относительно оси X (скажем “вверх”), то мы понятия не имеем, каким он будет относительно оси Y, может быть “вверх”, а может быть “вниз” с одинаковой вероятностью 50% на 50%. Вдоль же оси, расположенной под углом 45^о к X, вероятность “вверх–вниз” будет не 75% на 25%, как казалось бы (ведь 45^о это половина от 90^о), а ~86% на ~14%. Там сложная формула, не будем забивать ей голову.

Далее представим себе, что мы меряем спин у первой частицы по произвольной оси, а потом у второй частицы, опять таки по случайно выбранной произвольной оси. Какова вероятность, что и там и там мы обнаружим, что спины совпадают (окажутся оба вверх или оба вниз)?

Напомню, если мы меряем спины у этих частиц по одинаковым осям, они всегда будут противоположны, частицы же запутаны. Если у одной из них спин “вверх” у второй запутанной частицы по этой оси спин будет “вниз”, а значит вероятность обнаружения одинакового спина — 0%.

Несложно догадаться, что в варианте истинно случайного квантового мира, в котором каждый раз спин (и любая другая характеристика) появляется у частицы лишь в непосредственный момент измерения, если мы случайным образом выбираем ось измерения у первой частицы, и случайным образом выбираем ось измерения второй частицы вероятность обнаружить два одинаковых спина у этих двух частиц по разным осям равна 50%. Все это в истинно случайном квантовом мире Бора.

В мире скрытых переменных Эйнштейна оказывается совсем другая песня. Эксперимент протекает точно так же — мы случайным образом выбираем направления осей, что будем мерить, и мы заранее наперед не знаем, что за параметры были у частицы, которую мы будем измерять. Но главное, мы верим, что они у нее заранее были.

Если вам действительно интересно разобраться во всей этой хитрости, обратите, пожалуйста пристальное внимание на следующие несколько абзацев. Ничего сложного там нет, никаких формул и подавно, но чуть–чуть мозг и немножко логики таки придется напрячь, читайте внимательно, можно даже и два раза.

Предположим, к нам в руки попала частица, у которой заранее были предопределены спины по осям X, Y и Z. Пусть это были спины “вниз”, “вниз” и “вверх” вдоль этих осей соответственно. Это все равно, что сказать, что в первой коробке–частице лежали левый, левый и правые сапоги. В то же время вторая запутанная частица имеет спины наоборот “вверх”, “вверх” и “вниз” вдоль этих осей, или же вторая коробка–частица содержит правый, правый и левый сапог. Мы всего этого пока не знаем (и никогда полностью не узнаем), но если верить Эйнштейну, эти свойства у частиц уже есть, хоть они и скрытые и навсегда останутся скрытыми.

Посмотрим, какие варианты опытов у нас могут получиться с этими (конкретно этими) частицами. Всего мы можем выбрать 9 вариантов проведения эксперимента. Тут внимательный читатель можно взять две реальные коробки, положить в них указанные правые и левые сапоги и начать случайным образом доставать по одному из каждой коробки, пытаясь не наткнуться на пару.

Измерять спин у первой частицы вдоль одной оси, а у второй вдоль другой, дозволено в комбинациях осей:

X1 и X2, X1 и Y2, X1 и Z2
Y1 и X2, Y1 и Y2, Y1 и Z2
Z1 и X2, Z1 и Y2, Z1 и Z2

Все девять, других вариантов нет.

Если оси у частиц совпадают, спины точно не совпадают и будут противоположны, мы это помним, они же запутанные! Значит варианты X1 и X2, Y1 и Y2, Z1 и Z2 заведомо дадут отрицательный результат несовпадения спинов или же совпадения пар обуви, что в данном случае нам не нужно, мы ищем когда спины–сапоги совпадают, т.е. когда встретятся два левых или два правых, а не когда получается пара.

Так же у этих (у конкретных этих!) частиц не совпадут спины при измерении X1 и Y2, а так же при измерении Y1 и Х2, потому что состояние конкретно этой пары частиц мы написали (поглядите!) абзацем ранее, где было предопределено — у первой было X1–”вниз” Y1–”вниз”, а у второй X2–”вверх” Y2–”вверх”.

Выходит, что в пяти случаях из девяти возможных вариантов, результаты эксперимента по поиску одинаково направленных спинов (хоть и по разным осям) дадут отрицательный ответ! Пять из девяти это больше половины, значит более чем в половине случаев мы не найдем, что хотели, а найдем это лишь в 4х из 9ти, что составляет вероятность примерно в 44%. Вместо вероятности в 50%, что была у нас при истинно случайном квантовом распределении.

Да, мы все еще не забываем, что это только лишь в конкретном случае двух конкретно сконфигурированных заранее частиц “вниз”, “вниз”, “вверх” и “вверх”, “вверх”, “вниз”. Ведь при другой конфигурации все может оказаться иначе!

Неа. Не может. И тут вторая фишка (или вторая часть фишки) придуманной Беллом. Как бы мы ни конфигурировали частицы, в смысле, как бы они сами не конфигурировались изначально и скрыто от нас, все равно это будут некие наборы из “два плюс один”. Например “два вверха” плюс “вниз” и “два вниза” плюс “вверх”, или “вверх” плюс “два вниза” и “вниз” плюс “два вверха” или какая–то другая комбинация из “два чего–то плюс один”. Данная ситуация абсолютно идентична уже рассмотренному случаю. Все выкладки окажутся теми же самыми, можете сами проверить, а можете поверить мне на слово. Все равно в случайном квантовом мире вероятность успеха будет 50%, а в мире скрытых параметров — 44%.

Встречается, правда, еще один вариант, когда все три спина у частицы совпадают, т.е. редкий случай “три против трех”. Например “вверх”, “вверх”, “вверх” против “вниз”, “вниз”, “вниз” или наоборот. Но тут даже считать ничего не придется. Итак понятно, что если в первой коробке лежат все левые сапоги, а во второй все правые, доставая случайным образом по одному сапогу из каждой коробки мы всегда будем получать пару, что в нашем случае означает — спины никогда не будут совпадать и всегда будут противоположными. Вероятность совпадения ровно 0%.

Теперь нужно просуммировать вероятности, когда у нас получается конфигурация “два плюс один” и когда конфигурация “три против трех”. Потому что в мире Эйнштейна частицы могут случайно, но заранее быть сконфигурированными либо так, либо так. Причем вариант “два плюс один” встречается чаще, чем “три против трех”, от чего суммарная вероятность будет где-то между 44% и 0%, но не ровно посредине, а ближе к 44%, ибо “два плюс один” встречается чаще. Итого 50% в одном случае и что–то среднее между 44% и 0%, мне уже влом считать, пусть будет где–то около 33% во втором. Такова разница вариантов исхода одинаковых экспериментов, проведенных в мирах Бора и Эйнштейна.

Конечно же, все это точно весьма теоретически, практически нужно проводить сотни и тысячи экспериментов, набирать статистику, потому что оборудование не идеальное, погрешности всегда есть, плюс все же статистическое, можем не точно 50% вероятности получить, а сначала примерно 52%, а потом 48% и т.д. Опять таки, это всего лишь один из вариантов проведения эксперимента (точнее даже его аналогия), у самого Белла все было чуточку иначе, а реальный эксперимент и вовсе был в другую степь. Например, помните я говорил, что это упрощение — пользоваться лишь осями X, Y и Z. Если мерить спины по осям “под углом”, начинаются сложные формулы расчета вероятностей, но зато, кстати, можно обойтись всего двумя некоммутирующими осями (а они там все относительно друг друга некоммутирующие). Угол между осями будет выступать в качестве “третьей составляющей” конфигурации частиц, ибо от него по хитрой формуле зависит конкретный процент вероятности в итоге.

Это все математические, технические и ситуационные детали. Основная идея всей затеи такова — если мы проведем тысячи и тысячи опытов и в итоге получим одну вероятность какого–то искомого результата, значит, мы имеем дело с квантовым миром Бора. Если же получим другую вероятность (а еще точнее убедимся, что эта вероятность никогда не превышает или наоборот всегда превышает какое–то определенное значение, всегда чего–то больше или всегда меньше, отсюда и “неравенства Белла”, кстати, разные для каждого конкретного эксперимента), следовательно, мы живем в детерминистическом мире Эйнштейна, где истинных случайностей не случается (каламбур), все заранее предопределено, хоть мы этого никогда и не узнаем.

Опыты были поставлены. Тысячи и тысячи их, разной аппаратурой в разных конфигурациях для разных неравенств Белла. Прав оказался Бор. Природа нашего мира абсолютно случайна на квантовом уровне, нет никакой возможности предсказать результат следующего эксперимента, любое событие во Вселенной может произойти лишь с некой долей вероятности, чисто статистически, а может не произойти вовсе.

Характер физических законов природы оказался истинно случаен.
Нет судьбы.
Так и живем.

Квантовая запутанность

За последние полтора века произошел значительный скачок в развитии человечества, в особенности в области фундаментальной физики. Не успели ученые окунуться в физику атома, как уже начали строиться атомные станции; научный переворот, совершённый Эйнштейном в скором времени привел нас к полной глобализации с более чем тысячью спутниками на орбите Земли. Примеров – масса, однако осталось еще немало нерешенных задач и необъясненных явлений. Одно из таких явлений скрывается в микромире квантовых процессов, а именно – квантовая запутанность. Что это такое, почему это важно и какие исследования ведутся для решения этого вопроса – разбираем в данной статье.

Основные сведения

Прежде всего, определим само понятие «квантовая запутанность». Вся информация об объекте в микромире описывается неким абстрактным (математическим) состоянием, которое включает, например, вероятность обнаружения частицы в данном объеме, импульс частицы, ее заряд или спин, и тп. Подобное «состояние» может быть описано физическими уравнениями, которые, несмотря на свою абстрактность и сложность, все же способны предсказывать результаты экспериментов.

Квантовой запутанностью называют такое явление, когда квантовые состояния двух и более частиц оказываются взаимосвязаны. То есть, определив состояние одной частицы, можно предсказать некоторые характеристики другой. Примечательно, что изменение некоторого параметра одной частицы приводит к изменению некоторого параметра другой частицы, независимо от расстояния.

Противоречие с «принципом локальности»

Как известно из работ Эйнштейна, в природе имеет место так называемый «принцип локальности», согласно которому любое взаимодействие между телами не может происходить мгновенно, а передается через посредника. Скорость передачи этого взаимодействия не должна превышать скорость света в вакууме. В то же время, как было упомянуто ранее, квантовая запутанность может наблюдаться на огромных расстояниях с «мгновенной передачей информации», что является прямым нарушением принципа локальности.

Эйнштейн, Нильс Бор и квантовая механика

В 1927-м году в Брюсселе состоялся Пятый Сольвеевский конгресс — международная конференция на тему актуальных проблем в области физики и химии. Одна из состоявшихся дискуссий была на тему так называемой Копенгагенской интерпретации квантовой механики.

Нильс Бор и Альберт Эйнштейн

Данная теория была разработана Нильсом Бором и Вернером Гейзенбергом и  утверждает о вероятностной природе волновой функции. Несмотря на решение некоторых тогдашних проблем физики, например, связанных с корпускулярно-волновым дуализмом, данная теория также вызывала и ряд вопросов. В первую очередь, само представление объекта с известным импульсом, не имеющего определенной координаты, а лишь вероятность обнаружения в данной точке, — противоречит нашему опыту жизни в макромире. Кроме того, эта теория подразумевала неопределенность в расположении частицы, до тех пор, пока не будет произведено измерение.

Совместное фото участников Пятого Сольвеевского конгресса

Альберт Эйнштейн не мог принять такую интерпретацию, в результате чего и зародилась его известная фраза «Бог не играет в кости», на что Нильс Бор ответил «Альберт, не указывай Богу, что ему делать». Так начался длительный спор Эйнштейна и Бора.

Ответ Эйнштейна последовал в 1935-м году, когда он, вместе с Борисом Подольским и Натаном Розеном опубликовал работу, носившую название «Можно ли считать квантово-механическое описание физической реальности полным?». В данной статье был представлен мысленный эксперимент под названием «парадокс Эйнштейна — Подольского — Розена» (ЭПР-парадокс).

ЭПР-парадокс

Эксперимент был направлен на опровержение такого фундаментального для квантовой механики утверждения, как принцип неопределенности Гейзенберга, который гласит, что нельзя одновременно измерить две характеристики частицы, зачастую имеют ввиду – импульс и координату.

ЭПР-парадокс звучит следующим образом. Пусть две частицы одного сорта образовались вследствие распада третьей частицы. Тогда сумма их импульсов будет равна импульсу исходной частицы, согласно закону сохранения импульса. Далее, зная импульс исходной частицы (которую заранее подготовят экспериментаторы), и измерив импульс второй частицы, можно рассчитать импульс первой. То есть в результате измерения мы получили такую характеристику первой частицы как импульс. Теперь измерим координату второй частицы, и в итоге будем иметь две измеренные характеристики одной частицы, что прямо противоречит принципу неопределенности Гейзенберга.

Однако в самой же квантовой механике есть средства для разрешения этого парадокса. Согласно законам квантового мира – любое измерение приводит к изменению характеристик измеряемого тела. Тогда до измерения координаты второй частицы, действительно, может иметь место определенный импульс. Но в момент измерения координаты состояние частицы меняется и нельзя утверждать, что эти характеристики были измерены одновременно.

Тем не менее, в результате корпускулярно-волнового дуализма, находясь на некотором расстоянии, эти возникшие частицы имеют состояния, описываемые одной волновой функцией. Из этого вытекает, что измерение (а значит и изменение) импульса одной частицы приводит и к измерению импульса другой. Причем увеличение расстояния между этими частицами не запрещается, что опять же противоречит принципу локальности.

Теорема Белла

Человеку, существующему всю свою историю в масштабах макромира, сложно понять законы квантовой механики, которые часто противоречат наблюдениям в макромире. Так зародилась теория скрытых параметров, согласно которой, упомянутое ранее дальнодействие между частицами, может быть вызвано наличием неких изначально скрытых параметров частиц. Проще говоря – измерение одной частицы не приводит к изменению состояния другой, и оба эти состояния возникли вместе с этими частицами, в момент распада исходной частицы. Такое интуитивно понятное объяснение удовлетворило бы человеческий ум.

В 1964-м году Джон Стюарт Белл сформулировал свои неравенства, позже называемые теоремой, которые позволяют провести эксперимент, позволяющий точно определить – имеют ли место некие скрытые параметры. То есть если частицы имели скрытые параметры до своего разделения, то выполнилось бы одно неравенство, а если их состояния связаны и неопределенны до измерения одной из частиц – другое неравенство Белла.

В 1972-м году подобный эксперимент был проведен Фридманом и Клаузером, и результаты указывали на существования неопределенности состояний до измерения. Впрочем, данное явление воспринималось научным сообществом как некий конфуз, который рано или поздно будет разрешен. Однако в 1981-м году был нанесен второй удар по физической теории – эксперимент Аллена Аспе. Этот весьма популярный эксперимент стал последним аргументом в пользу существования квантовой запутанности и так называемого «жуткого дальнодействия». И хотя окончательно поставить точку в этом вопросе не получилось, результаты были настолько убедительны, что ученым пришлось принять такую особенность квантового мира.

Исследования в области квантовой запутанности

Почему вновь поднимается эта давно известная тема? Дело в том, что за последние несколько лет разработки в области квантовых компьютеров, работающих на основе квантовой запутанности, заметно шагнули вперед. Так в марте 2018-го года Google заявила об успешном создании 72-кубитного квантового процессора под названием Bristlecone, который достигает «квантового превосходства». То есть  способен выполнять задачи, которые недоступны для обычных компьютеров.

Квантовый процессор Bristlecone компании Google (слева) и схематическое изображение кубитов, где каждый кубит связан с соседними (справа)

Также летом 2018-го года в журнале Nature была опубликована научная работа, которая рассказывает о создании первого квантового процессора с долговременной памятью. Ранее, в 2015-м году, эта же исследовательская группа из Делфтского технического университета вместе с главой организации QUTech — Рональдом Хэнсоном представили еще более убедительные доказательства существования квантовой запутанности.

Об эксперименте в Делфтском техническом университете

Эксперимент, результаты которого были опубликованы в 2015-м году, происходил следующим образом. В эксперименте использовались алмазные листы с решеткой полостей, которые заполняются азотом.  Такая технология была разработана исследователями Калифорнийского университета в Санта-Барбаре и Национальной лаборатории Лоуренса в Беркли в 2010-м году. Два таких кристалла алмаза расположили на расстоянии 1.3 км друг от друга. В результате облучения обоих пластин микроволновым излучением и лазерами электроны этих «алмазных ловушек» переходили в возбужденное состояние и испускали пару фотонов, которые взаимодействовали друг с другом. Как следствие этого взаимодействия – возникала квантовая запутанность между электронами, которые излучали эти фотоны.

Точки расположения алмазных листов на территории кампуса Делфтского технического университета

Для обнаружения данного явления ученые проводили измерение спинов электронов с разных пластин практически одновременно, что не допустило бы обмен информацией между ними со скоростью света. Однако, как оказалось, спины двух электронов были синхронизированы, что говорит о передачи информации неким образом, который позволяет превысить скорость света. Конечно, сама процедура определения характеристик электронов намного сложнее, и потребовалось провести немало расчетов и сравнить их волновые функции. Несмотря на все сложности эксперимента, он проводился 245 раз в течение 18-ти дней, и был запланирован таким образом, чтобы избежать всех возможных ошибок, как со стороны измерительных приборов, так и со стороны окружающей среды.

Бас Хенсен и Рональд Хэнсон устанавливают оборудование для эксперимента по проверке неравенств Белла

Окончательно закроет эту тему будущий крупный эксперимент в Массачусетском технологическом институте в течение ближайших трех лет. Исследовательская группа планирует собирать электромагнитное излучение пульсаров, а также свет, приходящий из дальних галактик. Подобный эксперимент позволит избежать какой-либо связи измерительных приборов и источников сигнала, тем самым устраняя последнюю возможность наличия скрытых параметров.

Схематическое изображение пульсара

Квантовый компьютер и интернет

Разработки QUTech вышли далеко за пределы теоретической физики и двинулись в сторону квантового компьютера. Так в 2012-м году несколько научных групп разработали двухкубитный квантовый процессор на основе вышеупомянутых кристаллов, а в 2018-м – была опубликована работа, в которой исследователи описали созданный ими квантовый процессор с долговременной памятью. Проблема создания такого процессора состояла в том, что связи между квантовыми битами («кубитами») пропадали быстрее, чем ученым удавалось их обнаружить. Очередной эксперимент в Делфтском техническом университете показал, что новый процессор не обладает данной проблемой.

Исследовательская группа использовала вышеупомянутые алмазные пластины, где среди атомов углерода «спрятался» атом азота. Место, в котором располагается атом азота, обладает специфическими свойствами, как если бы в этой ячейке кристаллической решетки находился атом углерода, но в неком «замороженном» состоянии. Такой подход заметно продлевает жизнь алмазным кубитам (300-500 миллисекунд). Кроме того, был разработан и новый метод «запутывания» электронов в этих дефектных точках.

Данная технология не только является прорывной в области квантовых компьютеров, но и приближает нас на шаг к квантовому интернету. Взаимодействие нескольких отдельных квантовых компьютеров позволит организовать между ними сеть, работающую посредством передачи запутанных кубитов. Преимущество состоит в скорости: пусть имеется k квантовых компьютеров, каждый из которых состоит из n кубитов. Тогда для передачи по обычной сети полного состояния одного такого компьютера понадобится 2n бит данных, в то время как для квантовой сети потребуется лишь n кубитов. Запутанность между всеми компьютерами в масштабах целой сети дает преимущество в скорости передачи информации на несколько порядков.

Итоги

Несмотря на квантовый мир, будоражащий множество умов по всему миру, квантовая запутанность сегодня является общепризнанным явлением, которое не только наблюдается экспериментально, но и используется в технологических процессах. Дальнейшее применение квантовой запутанности может вывести человечество на совсем иной уровень развития, с суперкомпьютерами и невообразимо быстрым интернетом.

Понравилась запись? Расскажи о ней друзьям!

Просмотров записи: 23561

Запись опубликована: 17.04.2019
Автор: Владимир Соловьев

Больше доказательств в поддержку «жуткого действия на расстоянии» квантовой теории | Наука

Это одна из самых странных концепций в и без того странной области квантовой физики: измерение состояния или состояния квантовой частицы, такой как электрон, может мгновенно изменить состояние другого электрона, даже если он находится на расстоянии световых лет. Эта идея раздражала таких, как Альберт Эйнштейн, поскольку она предполагает, что что-то может двигаться быстрее света, и что реальность так или иначе определяется измерениями, которые мы проводим.Но теперь группа экспериментаторов утверждает, что доказала правильность этой концепции, заполнив лазейки в предыдущих демонстрациях.

«Это абсолютно знаковая статья в квантовой физике», – говорит Говард Вайзман, физик из Университета Гриффита, Натан, Австралия, который не принимал участия в работе. «Больше не может быть никаких разумных сомнений в том, что физический мир глубоко отличается от нашей повседневной интуиции». Кристофер Ферри, физик из Сиднейского университета в Австралии, отмечает, что для многих физиков этот вопрос был давно решен.«Опросите любых физиков моего поколения или позже, и они будут совершенно не обеспокоены [этим]», – говорит он. По его словам, настоящий прорыв заключается в том, чтобы открыть путь для сверхбезопасных технологий квантовой связи.

Эксперимент был проведен Рональдом Хансоном, физиком из Делфтского технологического университета в Нидерландах, и его коллегами. Хэнсон отказался обсуждать статью, которая размещена на сервере препринтов arXiv, поскольку она находится на рассмотрении в нераскрытом журнале.

Эксперимент включает концепцию запутанности.Рассмотрим электрон. Как волчок, он может вращаться в одну сторону (вверх) или в другую (вниз). Как ни странно, квантовая теория утверждает, что электрон также может вращаться одинаково в обе стороны одновременно – хотя, если вы его измерите, квантовое состояние «схлопнется», так что вы обнаружите, что электрон вращается вверх или вниз с равной вероятностью. Важно то, как производится такое измерение. Согласно квантовой теории, вы не можете просто прочитать спин напрямую; вы должны использовать анализатор, который можно настроить, наподобие шкалы, на определенную ориентацию, чтобы увидеть, вращается ли электрон в ту или иную сторону.В случае двухстороннего спина установка анализатора вертикально приводит к коллапсу электрона с результатом 50-50.

Еще более странно то, что два электрона могут быть запутаны, так что спин каждого электрона совершенно не определен, но два спина полностью связаны друг с другом и коррелированы. Предположим, что Алиса и Боб разделяют два запутанных электрона, и у каждого есть анализатор, установленный вертикально. Если Алиса измеряет свой электрон и обнаруживает, что он вращается, она сразу же узнает, что электрон Боба вращается вниз, даже если он находится на расстоянии галактики.Это «жуткое действие на расстоянии» обеспокоило Эйнштейна, поскольку оно предполагает, что квантовая волна, описывающая электроны, коллапсирует со скоростью, превышающей скорость света. Это также предполагает, что «реальность» спинового состояния электрона – то, что о нем известно, – не определяется до тех пор, пока электрон не будет измерен и квантовая волна не схлопнется.

Эйнштейн счел эту идею неприятной. Вместо этого он утверждал, что квантовая механика неполна – по сути, что «скрытые переменные», закодированные в каждом электроне, но выходящие за рамки теории, определяют результаты измерений Боба.Эта концепция позволяет избежать коллапса, превышающего скорость света, поскольку определяющий фактор движется вместе с электроном Боба. Это также согласуется с представлением о том, что измерения раскрывают некий аспект мира, существующий независимо от них – точно так же, как мы предполагаем, что цвет теннисного мяча существует, прежде чем мы смотрим на него.

Однако в 1964 году британский теоретик Джон Белл нашел способ проверить разницу между коллапсирующими квантовыми волнами и скрытыми переменными. Согласно квантовой теории, если Алиса и Боб наклоняют свои анализаторы под разными углами, они больше не должны видеть идеальной корреляции в своих измерениях.Например, предположим, что Алиса держит свой анализатор вертикально, а Боб наклоняет его на 45 °. Тогда, если Алиса обнаружит, что ее электрон вращается вверх, вероятность того, что Боб обнаружит, что его электрон вращается вниз, – определенная в его новой ориентации – составляет всего 71%. Белл представил, что Алиса и Боб неоднократно меняли ориентацию своих анализаторов. Он математически доказал, что скрытые переменные будут производить корреляции слабее определенного предела, что было записано в формуле, называемой неравенством Белла. Коллапсирующие квантовые волны могут давать более сильные корреляции.Формула предлагала лакмусовую бумажку для определения, действительно ли скрытые переменные присутствовали.

Белл также объяснил, что коллапс волн со скоростью, превышающей скорость света, не обязательно нарушает запрет теории относительности на путешествия со скоростью, превышающей скорость света. Поскольку Алиса не может контролировать результаты своих измерений, она не может использовать их для отправки информации Бобу быстрее света. Она и Боб могут просто подтвердить корреляцию постфактум. Теперь это стандартная интерпретация теории относительности.

В 1970-х годах экспериментаторы начали проводить измерения, чтобы проверить, выполняется ли неравенство Белла. Они постоянно находили корреляции более сильные, чем позволяют скрытые переменные. Эти результаты в целом убедили физиков в том, что Эйнштейн был неправ. Либо квантовые волны действительно должны коллапсировать быстрее света, либо результаты измерений не могут быть предопределены скрытыми переменными: пока электрон, вращающийся в обе стороны, не будет измерен, он буквально вращается в обе стороны.

Однако провести герметичную проверку теоремы Белла сложно, и в последние годы физики беспокоились о «лазейках», которые позволили бы некоторому эффекту, отличному от мгновенного коллапса квантовых волн, исказить результаты.Теперь Хэнсон и 18 его коллег утверждают, что провели первую безошибочную проверку теоремы Белла.

Чтобы проверить идею Белла, физики должны убедиться, что никакое влияние, кроме влияния измерений, не может распространяться между электронами за время, необходимое для выполнения измерений. Это сложная задача, поскольку свет проходит 299 792 километра в секунду. Хэнсон и его коллеги разделяли две станции с их электронами на 1,28 километра в кампусе Делфта. Это дало им 4,27 микросекунды на выполнение обоих измерений, прежде чем сигнал скорости света от одной станции достигнет другой.

Исследователям еще предстояло запутать далекие электроны. Для этого они сначала запутали каждый вращающийся электрон с состоянием фотона, который затем отправили по оптическому волокну на третью станцию ​​между двумя другими. Только в том случае, если два фотона прибыли одновременно и правильно интерферируют друг с другом, электроны запутаются в результате процесса, называемого обменом запутывания. Менее одной из 150 миллионов пар фотонов зарегистрировали правильный интерференционный сигнал.Тем не менее, исследователи могли начать измерения электронов до встречи фотонов, а потом просмотреть данные, чтобы найти испытания, которые сработали. В препринте они сообщают о 245 успешных испытаниях за 22 часа сбора данных.

Наконец, физики должны закрыть лазейку, которая открывается, если они не могут надежно прочитать состояние электронов. Такое неудачное измерение могло скрыть истинную корреляцию между спинами электронов. Чтобы преодолеть это, команда Хэнсона использовала отдельные электроны, захваченные дефектами атомного размера в алмазах, охлажденных почти до абсолютного нуля.В дефектах электроны легко сохраняют свои тонкие спиновые состояния и ими можно манипулировать с помощью микроволн и света. Физики измерили спин каждого электрона с эффективностью более 95%.

Когда обе лазейки закрыты, исследователи видят явное нарушение неравенства Белла – торпедирование скрытой переменной Эйнштейна и подтверждение схлопывающихся квантовых волн. «Единственное, что может вызвать серьезную озабоченность по поводу этой статьи, – это небольшой набор данных, а это означает, что результат не так надежен, как хотелось бы в идеале», – говорит Уайзман.«Но я уверен, что это скоро будет исправлено».

«Всегда можно придумать еще более дикие лазейки», – говорит Ферри. Но эксперимент закрывает те, которые могут быть использованы для атаки на определенные развивающиеся квантовые технологии, такие как схемы использования запутанных частиц для безопасного распространения ключей для кодирования секретных сообщений в так называемых «аппаратно-независимых квантовых распределениях ключей». «Это огромная техническая веха, – говорит Ферри, – и предпосылка для многих будущих квантовых технологий, которые, несомненно, позволят исследовать и в конечном итоге понять новую физику.«

* Исправление, 30 августа, 9:47 ,: История была изменена, чтобы исправить математическую ошибку в объяснении аргумента Белла.

В поисках квантовой запутанности

Более 12 миллиардов лет назад летящие частицы света покинули чрезвычайно яркий небесный объект, называемый квазаром, и начали долгое путешествие к планете, которой еще не было. Более чем 4 миллиарда лет спустя еще больше фотонов покинули другой квазар и отправились в похожий путь.Когда Земля и ее солнечная система сформировались, жизнь эволюционировала, и люди начали изучать физику, частицы продолжали свой путь. В конце концов, они приземлились на Канарском острове Ла-Пальма в паре телескопов, установленных для эксперимента, проверяющего саму природу реальности.

Эксперимент был разработан для изучения квантовой запутанности, явления, которое связывает квантовые системы способами, невозможными в нашем макро-классическом мире. Когда две частицы, такие как пара электронов, запутаны, невозможно измерить одну, не узнав что-то о другой.Их свойства, такие как импульс и положение, неразрывно связаны.

«Квантовая запутанность означает, что вы не можете описать вашу совместную квантовую систему только с помощью локальных описаний, по одному для каждой системы», – говорит Майкл Холл, физик-теоретик из Австралийского национального университета.

Запутанность впервые возникла в результате мысленного эксперимента, проведенного не кем иным, как Альбертом Эйнштейном. В статье 1935 года Эйнштейн и двое его коллег показали, что если квантовая механика полностью описывает реальность, то проведение измерения на одной части запутанной системы мгновенно повлияет на наши знания о будущих измерениях на другой части, по-видимому, посылая информацию быстрее, чем скорость свет, что невозможно по всем известным физикам.Эйнштейн назвал этот эффект «жутким действием на расстоянии», подразумевая что-то в корне неправильное с зарождающейся наукой квантовой механикой.

Спустя десятилетия квантовая запутанность неоднократно подтверждалась экспериментально. Хотя физики научились контролировать и изучать квантовую запутанность, им еще предстоит найти механизм, чтобы объяснить ее или прийти к консенсусу относительно того, что она означает в отношении природы реальности.

«Сама запутанность проверялась на протяжении многих-многих десятилетий», – говорит Эндрю Фридман, астрофизик из Калифорнийского университета в Сан-Диего, который работал над экспериментом с квазаром, также известным как «испытание космического Белла».«Настоящая проблема в том, что, хотя мы знаем, что это экспериментальная реальность, у нас нет убедительной истории о том, как это работает».

Предположения Белла

Мир квантовой механики – физики, которая управляет поведением Вселенной в самых маленьких масштабах – часто описывается как чрезвычайно странный. Согласно ее законам, строительные блоки природы одновременно являются волнами и частицами, не имеющими определенного места в пространстве. Требуется внешняя система, наблюдающая или измеряющая их, чтобы подтолкнуть их к «выбору» окончательного состояния.И запутанные частицы, кажется, мгновенно влияют на «выбор» друг друга, независимо от того, насколько они удалены друг от друга.

Эйнштейн был настолько недоволен этими идеями, что постулировал классические «скрытые переменные» вне нашего понимания квантовой механики, что, если бы мы их поняли, запутанность не была бы такой пугающей. В 1960-х годах физик Джон Белл разработал тест для моделей с такими скрытыми переменными, известный как «неравенство Белла».

Белл обрисовал в общих чертах три предположения о мире, каждое с соответствующим математическим утверждением: реализм, который утверждает, что объекты обладают свойствами, которые они поддерживают независимо от того, наблюдаются они или нет; местность, где говорится, что ничто не может повлиять на что-то достаточно далеко, чтобы сигнал между ними должен был распространяться быстрее света; и свобода выбора, согласно которой физики могут проводить измерения свободно и без влияния скрытых переменных.Зондирование запутанности – ключ к проверке этих предположений. Если эксперименты показывают, что природа подчиняется этим предположениям, тогда мы живем в мире, который можем понять классически, а скрытые переменные создают только иллюзию квантовой запутанности. Если эксперименты показывают, что мир не следует за ними, тогда квантовая запутанность реальна, а субатомный мир действительно столь же странен, как кажется.

«Белл показал, что если мир подчиняется этим предположениям, существует верхний предел того, насколько могут быть коррелированы измерения запутанных частиц», – говорит Фридман.

Физики могут измерять свойства частиц, такие как их спин, импульс или поляризация. Эксперименты показали, что когда частицы запутаны, результаты этих измерений более статистически коррелированы, чем можно было бы ожидать в классической системе, что нарушает неравенства Белла.

В одном из тестов Белла ученые отправляют два запутанных фотона на детекторы, расположенные далеко друг от друга. Достигнут ли фотоны детекторов, зависит от их поляризации; если они идеально выровнены, они пройдут, но в противном случае существует некоторая вероятность того, что они будут заблокированы, в зависимости от угла выравнивания.Ученые чаще пытаются выяснить, имеют ли запутанные частицы одну и ту же поляризацию, чем это можно объяснить классической статистикой. Если они это сделают, то по крайней мере одно из предположений Белла не может быть истинным по своей природе. Если мир не подчиняется реализму, тогда свойства частиц не будут четко определены до измерений. Если бы частицы могли влиять друг на друга мгновенно, то они каким-то образом взаимодействовали бы друг с другом со скоростью, превышающей скорость света, нарушая локальность и специальную теорию относительности Эйнштейна.

Ученые давно предполагают, что предыдущие экспериментальные результаты можно лучше всего объяснить, если мир не подчиняется одному или обоим из первых двух предположений Белла – реализму и локальности. Но недавняя работа показала, что виновником может быть его третье предположение – свобода выбора. Возможно, решение ученых о том, под каким углом впустить фотоны, не такое свободное и случайное, как они думали.

Эксперимент с квазаром был последним, кто проверил предположение о свободе выбора.Ученые определили угол, под которым они будут пропускать фотоны в свои детекторы, на основе длины волны света, обнаруженного ими от двух далеких квазаров, что было определено 7,8 и 12,2 миллиарда лет назад соответственно. Длинно перемещающиеся фотоны заняли место физиков или обычных генераторов случайных чисел в решении, устраняя земное влияние на эксперимент, будь то человеческое или иное.

В конце теста команда обнаружила гораздо более высокую корреляцию между запутанными фотонами, чем теорема Белла могла бы предсказать, если бы мир был классическим.

Это означает, что, если бы какая-то скрытая классическая переменная действительно определяла результаты эксперимента, в самом экстремальном сценарии выбор измерения должен был бы быть сделан задолго до человеческого существования – подразумевая, что квантовая «странность» на самом деле является определяющей. результат вселенной, где все предопределено.

«Многих это не устраивает, – говорит Холл. «Они на самом деле говорят, что если бы это было так давно, вам пришлось бы попытаться объяснить квантовые корреляции с помощью предопределенного выбора.Жизнь потеряет всякий смысл, и мы перестанем заниматься физикой ».

Конечно, физика идет вперед, и запутанность сохраняет много загадок, которые нужно исследовать. Помимо отсутствия причинного объяснения запутанности, физики не понимают, как измерение запутанной системы внезапно возвращает ее в классическое, незапутанное состояние или действительно ли запутанные частицы каким-то образом сообщаются, загадки, которые они продолжают исследовать с помощью новых экспериментов. .

«Никакая информация не может перейти отсюда туда мгновенно, но разные интерпретации квантовой механики согласятся или не согласятся с тем, что существует какое-то скрытое влияние», – говорит Габриэла Баррето Лемос, научный сотрудник Международного института физики в Бразилии.«Но мы все согласны с этим определением с точки зрения корреляции и статистики».

Ищу что-то странное

Более глубокое понимание запутанности может помочь решить проблемы как практического, так и фундаментального характера. Квантовые компьютеры полагаются на запутанность. Квантовое шифрование – теоретическая мера безопасности, взломать которую, согласно прогнозам, невозможно, – также требует полного понимания квантовой запутанности. Если скрытые переменные действительны, квантовое шифрование может быть взломано.

И запутанность может содержать ключ к некоторым из самых фундаментальных вопросов физики. Некоторые исследователи изучали материалы с большим количеством запутанных частиц, а не просто пары. Когда происходит это многочастичное запутывание, физики наблюдают новые состояния материи, выходящие за рамки привычных твердого тела, жидкости и газа, а также новые паттерны запутывания, которые больше нигде не наблюдаются.

«Одна вещь, которую он говорит вам, – это то, что Вселенная богаче, чем вы предполагали ранее», – говорит Брайан Суингл, физик из Мэрилендского университета, исследующий такие материалы.«То, что у вас есть скопление электронов, не означает, что результирующее состояние вещества должно быть электронным».

Такие интересные свойства проявляются в этих материалах, что физики начинают понимать, что запутанность может фактически сшить воедино само пространство-время – несколько иронический поворот, поскольку Эйнштейн, впервые связавший пространство и время в своей теории относительности, так не любил квантовую механику. . Но если теория окажется верной, запутанность может помочь физикам наконец достичь одной из своих конечных целей: создать теорию квантовой гравитации, которая объединяет релятивистский мир Эйнштейна с загадочным и, казалось бы, противоречивым квантовым миром.

«Очень важно проводить эти эксперименты, даже если мы не верим, что обнаружим что-нибудь странное», – говорит Лемос. «В физике революция наступает, когда мы думаем, что не обнаружим чего-то странного, и тогда мы это делаем. Так что ты должен это сделать ».

Корреляции Белла между пространственно разделенными парами атомов

Запутывание пар атомов, вызванное столкновениями

Наш эксперимент начинается с магнитно-захваченного БЭК атомов гелия-4 в долгоживущем метастабильном состоянии \ ({2} ^ {3} {{ \ rm {S}}} _ {1} \) (подробности см. в разделе «Методы»).Переход {3} {{\ rm {P}}} _ {0} \) (см. Рис. 1b) одновременно переворачивает половину спина атомов на \ (| {\!} {\!} \ Downarrow {\! } {\!} \ rangle \) и сообщает скорость \ (\ sim {\! \!} 120 \ {\ rm {мм / с}} \) вдоль оси \ (z \), противоположной силе тяжести. (см. рис. 1а). В системе центра масс два конденсата разделяются на \ ({v} _ {{\ rm {r}}} \ приблизительно \ pm60 \ {\ rm {mm / s}} \) и спонтанно разбрасывают атомы на коррелированные пары противоположного импульса и спина через двойные \ (s \) – столкновения волн, образующие равномерно распределенное сферическое гало в импульсном пространстве с радиусом \ ({k} _ {{\ rm {r}}} = 2 \ pi / \ sqrt {2} \ lambda \) (коэффициент \ (1 / \ sqrt {2} \) обусловлен углом пересечения рамановских лучей 90 °) ³⁰ .По аналогии с гиперзапутанными парами фотонов (запутанными как по поляризации, так и по импульсу), генерируемым SPDC ³¹ , встречно-поляризованное столкновение БЭК запутывает пары атомов по спину (см. Вставку на рис. 1a), а также по импульсу, из сохранения полного углового (\ ({m} _ {J} \)) и количества движения. С импульсами каждой пары, заданными как \ (({\ bf {k}}, – {\ bf {k}} = A, B) \), состояние симметрично относительно обмена разметкой по импульсу и антикоррелировано в закрутите в исходную основу.{+} \ rangle = \ left (| {\ uparrow} {\ rangle} _ {A} \ otimes | {\ downarrow} {\ rangle} _ {B} + | {\ downarrow} {\ rangle} _ {A } \ otimes | {\ uparrow} {\ rangle} _ {B} \ right) / \ sqrt {2} $$

(1)

(см. Дополнительное примечание 1). Такое состояние максимально запутано, полезно в различных задачах квантовой информации ³ и, что более важно для данной работы, является жизнеспособным кандидатом для демонстрации нелокальности ¹⁸ .

Равномерное вращение спина и обнаружение одиночного атома

После импульса столкновения гало рассеяния свободно эволюционирует в однородном магнитном поле \ (\ sim {\!} 0. {(B)} \) представляют \ (y \) – составляющая матриц Паули для спинов в \ (A \) и \ (B \), не сообщая при этом никакого чистого изменения импульса атомам.Состояние {+} \ rangle \) состоит в том, что оно не инвариантно относительно вращения при равномерном вращении обоих атомов в паре на один угол \ (\ theta \), что позволяет нам измерить запутанность состояния.

Сразу после импульса вращения создается градиент магнитного поля в направлении \ (z \) (см. Рис. 1c). Это проецирует атомы в \ ({\ hat {\ sigma}} _ {z} \) собственные состояния \ (\ left \ {| {\ uparrow} \ rangle, | {\ downarrow} \ rangle \ right \} \) с помощью эффекта Штерна-Герлаха (SG), разделяющего два спиновых состояния в вертикальном направлении.Поскольку только состояние \ ({m} _ {J} = 1 \) имеет ненулевой магнитный момент, только \ (| {\ uparrow} \ rangle \) ощущает магнитную силу, заставляя состояние пространственно отделиться от \ (| {\ downarrow} \ rangle \) атомов в детекторе, что позволяет обнаружение с разрешением по состоянию.

Затем атомы падают под действием силы тяжести на микроканальную пластину-детектор линии задержки (MCP-DLD), расположенный \ (0.848 \ {\ rm {m}} \) ниже центра ловушки, что позволяет провести важную часть этого эксперимента: детектирование одиночного атома с полным 3D разрешением ³³ .Трехмерный импульс \ ({\ bf {k}} \) каждого атома восстанавливается из пространственных положений (2D) и времени прибытия, записанных MCP – DLD, в то время как \ ({m} _ {J} \) Состояние отличается от большого расстояния между временем прихода различных спиновых состояний из-за эффекта SG (см. дополнительное примечание 2). На рис. 1с показано типичное изображение из в среднем 1000 экспериментальных снимков, на котором показаны два полностью разделенных ореола, когда для равномерного смешивания спинов применялось \ (\ pi / 2 \) – вращение. Атомы в состоянии \ (| {\!} {\!} \ Uparrow {\!} {\!} \ Rangle \) образуют нижний гало, слегка несферический из-за неоднородности градиента магнитного поля, вызывающего пространственно-зависимая сила вокруг гало (см. {(2)} (\ Delta {\ bf {k}}) = \ frac {{\ sum} _ {{\ bf {k}} \ in V} \ langle {\ hat {n}} _ {{\ bf {k}}, i} {\ hat {n}} _ {- {\ bf {k}} + \ Delta {\ bf {k}}, j} \ rangle} { {\ sum} _ {{\ bf {k}} \ in V} \ langle {\ hat {n}} _ {{\ bf {k}}, i} \ rangle \ langle {\ hat {n}} _ {- {\ bf {k}} + \ Delta {\ bf {k}}, j} \ rangle}, $$

(3)

где \ (i, j \ in \ {\ uparrow, \ downarrow \} \) обозначают состояния вращения, \ ({\ hat {n}} _ {{\ bf {q}}, m} \) число атомов с импульсом \ ({\ bf {q}} \) и спином \ (m \), а \ (V \) объем в импульсном пространстве, занимаемый гало \ (s \) – волнового рассеяния ³⁴ ( схематически изображенный на рис.{(2)} \) в гало спонтанного рассеяния задается заселенностью моды \ (n \), определяемой средним числом атомов в рассеянной моде, причем каждая мода имеет объем, приблизительно равный объему исходного конденсата по импульсу. площадь ³⁴ . Амплитуда корреляции обратно пропорциональна занятости мод для спонтанного парного источника ³⁴ , который мы экспериментально настраиваем путем изменения начального числа атомов в БЭК до столкновения. Эта связь подтверждается на рис.{(2)} (\ Delta {\ bf {k}} = 0) \ приблизительно 30 \), амплитуда, достаточная для демонстрации нарушения неравенства Белла в описании КМ ¹⁸ . Соответствующая средняя занятость мод в гало рассеяния \ (\ sim {\!} 0,03 \) означает, что мы работаем в режиме низкого усиления, где преобладающий вклад в гало вносит рассеяние одиночных пар. За один прогон эксперимента, который занимает \ (\ приблизительно {\!} 30 \) с, это привело к тому, что в гало рассеяния было обнаружено в среднем \ (\ приблизительно 8,3 \) атомов, и, таким образом, общая скорость обнаружения \ (\ приблизительно {\!} 2 \) пар / мин при эффективности обнаружения \ (\ приблизительно {\!} 10 \% \).{(2)} \> \ 3 + 2 \ sqrt {2} \) (заштрихованная область) на основе полностью QM-прогноза нарушения неравенства CHSH ¹⁸ . Все полосы погрешностей указывают на стандартную ошибку в среднем

Для характеристики вращения спина изначально был \ (| {\!} {\!} \ Uparrow {\!} {\!} \ Rangle \) – поляризованный ореол рассеяния подготовлен из рамановской последовательности, подобной нашей предыдущей работе, для генерации гало \ ({m} _ {J} = 0 \) (см. { (2)} \) условия).Полученный таким образом коррелятор (интегрированный по всем модам рассеяния \ ({\ bf {k}}}) рассматривает несколько рассеянных пар в одном гало как параллельные реализации одного и того же состояния в одном кадре эксперимента. Это воплощает неотъемлемое преимущество в скорости сбора данных за счет использования многомодового ореола рассеяния в качестве парного источника по сравнению с маломодовыми аналогами, такими как двухлучевой ²⁸ . Мы подтвердили, что многократно рассеянные пары действительно идентичны по спиновой степени свободы, показав, что двухчастичные корреляционные функции, локализованные по импульсу ³² , не зависят от угла рассеяния.{+} \ rangle \). Это первое убедительное свидетельство того, что два атома сильно перепутаны.

Рис. 4

Неклассические корреляции в гало рассеяния. a Сильная корреляция \ ({\ mathcal {B}} \), превышающая \ (1 / \ sqrt {2} \) (заштрихованная область), сигнализирует о возможности наблюдать нарушение неравенства Белла, основанного на квантовой механическая модель. Предсказание КМ о нарушении наблюдалось как \ ({\ mathcal {B}} (\ pi / 2) = 0.90 (1) \) со значимостью 18 \ (\ sigma \) из 18 000 экспериментальных запусков, когда спины были повернут на \ (\ pi / 2 \).{+} \ rangle \), а сплошная линия – ориентир для глаз для обеих фигур. b Прямое наблюдение неклассичности парных корреляций на основе КМ-свидетельства корреляций Белла \ ({\ mathcal {S}} \). Корреляции, расположенные в заштрихованных и заштрихованных областях, указывают на наличие квантовой запутанности и нелокальности Белла соответственно. 6 \ (\ sigma \) нарушение неравенства свидетеля Белла (уравнение (6)) наблюдается при \ ({\ mathcal {S}} (0, \, \ pi / 2) \, = \, 1.77 (6 ) \). Все планки ошибок соответствуют стандартной ошибке, полученной при начальной загрузке

Квантовые корреляции

Чтобы доказать неклассические свойства нашей двухатомной системы, мы сначала покажем, что пары запутаны.{\ prime}) | \, \ le \, 1. $$

(5)

Мы обнаруживаем явное нарушение этого ограничения на рис. 4b, которое доказывает, что система запутана – необходимый ингредиент для нарушения неравенства Белла для любой квантовой системы.

Поскольку мы показали, что атомные спины являются векторными величинами при вращении (см. Рис. 3 и дополнительное примечание 2), теперь мы можем исключить широкий класс теорий локальных скрытых переменных. Нарушение неравенства

$$ {\ mathcal {S}} \ left (\ theta, \ theta + \ frac {\ pi} {2} \ right) = \ left | {\ mathcal {B}} (\ theta ) – {\ mathcal {B}} \ left (\ theta + \ frac {\ pi} {2} \ right) \ right | \ leq \ sqrt {2}, $$

(6)

из двух дополнительных измерений удостоверяет исключение ситуаций, в которых одна подсистема дает двоичные результаты, а вторая состоит из векторной величины (см. Дополнительное примечание 1).Это нарушается в нашей системе, как показано на рис. 4b, поскольку для \ (\ theta = 0 \) мы наблюдаем \ ({\ mathcal {S}} (0, \, \ pi / 2) \, = \, 1,77 (6) \).

Наконец, мы сравниваем наши результаты с предсказаниями теории Боголюбова, примененной к процессу рассеяния (см. Дополнительное примечание 1), который был протестирован для широкого диапазона процессов образования пар, от SPDC фотонов до излучения запутанных атомы из сталкивающихся БЭК (как в нашем случае). В частности, эта теория предсказывает, что \ ({\ mathcal {B}} (\ theta) = – {\!} \ Cos 2 \ theta \).Кроме того, модель Боголюбова обеспечивает необходимое условие для нарушения неравенства CHSH в нашей системе ²⁹ , а именно \ (| {\ mathcal {B}} (\ theta) | \> \ \ frac {1} {\ sqrt { 2}} \). Оба эти утверждения подтверждаются экспериментальными данными на рис. 4а.

Электронный спин – Университетская физика, том 3

Цели обучения

К концу этого раздела вы сможете:

• Выразите состояние электрона в атоме водорода через пять квантовых чисел
• Используйте квантовые числа для вычисления величины и направления спина и магнитного момента электрона
• Объясните тонкую и сверхтонкую структуру спектра водорода с точки зрения магнитных взаимодействий внутри атома водорода

В этом разделе мы рассмотрим эффекты электронного спина.Спин вводит два дополнительных квантовых числа в нашу модель атома водорода. Оба были открыты путем изучения тонкой структуры атомных спектров. Спин является фундаментальной характеристикой всех частиц, а не только электронов, и аналогичен собственному вращению протяженных тел вокруг их собственных осей, например суточному вращению Земли.

Спин квантуется так же, как орбитальный угловой момент. Было обнаружено, что величина собственного спинового углового момента S электрона определяется выражением

, где s определяется как квантовое число спина.Это похоже на квантование L , приведенное на (Рисунок), за исключением того, что единственное допустимое значение для s для электрона – Электрон называется «частица с половинным спином». Квантовое число проекции спина связано с z -компонентами спина, выраженными как

.

Как правило, допустимые квантовые числа –

.

Для частного случая электрона (),

Направления собственного спина квантуются так же, как они были для орбитального углового момента.Состояние называется состоянием «спин вниз» и имеет z -компонент вращения,; Состояние называется состоянием «со спином вверх» и имеет z -компонент спина. Эти состояния показаны на (Рисунок).

Два возможных состояния спина электрона.

Собственный магнитный дипольный момент электрона также можно выразить через квантовое число спина. По аналогии с орбитальным угловым моментом величина магнитного момента электрона равна

.

Согласно специальной теории относительности, это значение мало в два раза.Таким образом, в векторной форме спиновый магнитный момент равен

z -компонента магнитного момента

Квантовое число проекции спина имеет всего два значения, поэтому компонент магнитного момента z- также имеет два значения:

где – один магнетон Бора. Электрон является магнитным, поэтому мы ожидаем, что электрон будет взаимодействовать с другими магнитными полями. Мы рассматриваем два частных случая: взаимодействие свободного электрона с внешним (неоднородным) магнитным полем и электрон в атоме водорода с магнитным полем, создаваемым орбитальным угловым моментом электрона.

В атоме водорода магнитный момент электрона может взаимодействовать с магнитным полем, создаваемым орбитальным угловым моментом электрона, это явление называется спин-орбитальной связью. Векторы орбитального углового момента (), орбитального магнитного момента (), спинового углового момента () и спинового магнитного момента () показаны вместе на (Рисунок).

Подобно тому, как уровни энергии атома водорода могут быть разделены внешним магнитным полем , , так же уровни энергии атома водорода расщепляются внутренними магнитными полями атома .Если магнитный момент электрона и орбитальный магнитный момент электрона антипараллельны, потенциальная энергия от магнитного взаимодействия относительно высока, но когда эти моменты параллельны, потенциальная энергия относительно мала. Переход из каждого из этих двух состояний на уровень с более низкой энергией приводит к испусканию фотона немного другой частоты. То есть спин-орбитальная связь «расщепляет» спектральную линию, ожидаемую от бесспинового электрона. Тонкая структура спектра водорода объясняется спин-орбитальной связью.

Спин-орбитальная связь – это взаимодействие спинового магнитного момента электрона с его орбитальным магнитным моментом.

Эксперимент Штерна-Герлаха предоставляет экспериментальные доказательства того, что электроны обладают спиновым угловым моментом. В эксперименте поток атомов серебра (Ag) пропускается через внешнее неоднородное магнитное поле. Атом Ag имеет нулевой орбитальный угловой момент и содержит единственный неспаренный электрон во внешней оболочке. Следовательно, полный угловой момент атома Ag полностью обусловлен спином внешнего электрона (.Из-за электронного спина атомы Ag действуют как крошечные магниты, проходя через магнитное поле. Эти «магниты» имеют две возможные ориентации, которые соответствуют состояниям электрона со спином вверх и вниз. Магнитное поле отклоняет атомы со спином вверх в одном направлении, а атомы со спином вниз – в другом. Это создает две отдельные полосы на экране ((Рисунок)).

В эксперименте Штерна-Герлаха внешнее неоднородное магнитное поле отклоняет пучок электронов в двух разных направлениях.Этот результат связан с квантованием спинового углового момента.

Согласно классическим предсказаниям, угловой момент (и, следовательно, магнитный момент) атома Ag может указывать в любом направлении, поэтому вместо этого ожидается непрерывное пятно на экране. Полученные в результате две полосы эксперимента Штерна-Герлаха предоставляют поразительную поддержку идеям квантовой механики.

Проверьте свое понимание Если эксперимент Штерна-Герлаха дал четыре различных полосы вместо двух, какой можно сделать вывод о квантовом числе спина заряженной частицы?

Протон, как и электрон, имеет спин 1/2 и магнитный момент.(Согласно теории ядра, этот момент обусловлен орбитальным движением кварков внутри протона.) Сверхтонкая структура спектра водорода объясняется взаимодействием между магнитным моментом протона и магнитным моментом электрона, взаимодействием известное как спин-спиновая связь. Энергия системы электрон-протон различается в зависимости от того, совмещены ли моменты или нет. Переходы между этими состояниями (переходы с переворотом спина) приводят к испусканию фотона с длиной волны (в радиодиапазоне).Линия 21 см в атомной спектроскопии – это «отпечаток пальца» газообразного водорода. Астрономы используют эту спектральную линию, чтобы нанести на карту спиральные рукава галактик, которые в основном состоят из водорода ((Рисунок)).

Магнитное взаимодействие между электроном и протоном в атоме водорода используется для картирования спиральных рукавов Галактики Вертушка (NGC 5457). а) галактика в видимом свете; (б) галактика, видимая в излучении водорода 21 см; (c) составное изображение (a) и (b). Обратите внимание, как излучение водорода проникает в пыль в галактике, чтобы очень четко показать спиральные рукава, тогда как ядро ​​галактики лучше видно в видимом свете (предоставлено: модификация работы ЕКА и НАСА; кредит b: модификация работы Фабиана Уолтера) .

Для полного описания состояния электрона в атоме водорода требуется пять квантовых чисел: n , l , m , s и. Имена, символы и допустимые значения этих квантовых чисел приведены на (Рисунок).

Сводка квантовых чисел электрона в атоме водорода

Имя	Символ	Допустимые значения
Главное квантовое число	n	1, 2, 3,…
Угловой момент	л	0, 1, 2,… n – 1
Проекция углового момента	м
Отжим	с	1/2 (электроны)
Проекция вращения

Обратите внимание, что внутренние квантовые числа, введенные в этом разделе ( s и m _s ), действительны для многих частиц, а не только для электронов.Например, кварки в атомном ядре также являются частицами с половинным спином. Как мы увидим позже, квантовые числа помогают классифицировать субатомные частицы и вводить научные модели, которые пытаются объяснить, как устроена Вселенная.

Сводка

• Состояние электрона в атоме водорода можно выразить пятью квантовыми числами.
• Квант спинового углового момента электрона равен = . Квантовое число проекции спинового углового момента составляет м _с (вращение вверх или вниз).
• Тонкие и сверхтонкие структуры спектра водорода объясняются магнитными взаимодействиями внутри атома.

Концептуальные вопросы

Объясните, как атом водорода в основном состоянии может магнитно взаимодействовать с внешним магнитным полем.

Даже в основном состоянии () атом водорода обладает магнитными свойствами из-за собственного (внутреннего) спина электрона. Магнитный момент электрона пропорционален его спину.

Сравните орбитальный угловой момент со спиновым угловым моментом электрона в атоме водорода.

Выровнены ли векторы углового момента и?

Что такое спин-орбитальная связь?

У электрона есть магнитный момент, связанный с его собственным (внутренним) спином. Спин-орбитальная связь возникает, когда она взаимодействует с магнитным полем, создаваемым орбитальным угловым моментом электрона.

Проблемы

Какова величина спинового момента электрона? (Выразите свой ответ в цифрах

Каковы возможные полярные ориентации вектора спинового момента электрона?

Вращение вверх (относительно положительной оси z ):

Вращение вниз (относительно положительной оси z ):

Для записи всех возможных наборов квантовых чисел ( n , l , m ,).

Атом водорода помещен во внешнее однородное магнитное поле (). Вычислите длину волны света, возникающего при переходе из состояния вращения вверх в состояние вращения вниз.

Если магнитное поле в предыдущей задаче умножается в четыре раза, что происходит с длиной волны света, возникающей при переходе из состояния вращения вверх в состояние вращения вниз?

Если магнитный момент в предыдущей задаче удвоится, что произойдет с частотой света, возникающей при переходе из состояния вращения вверх в состояние вращения вниз?

Увеличивается в 2 раза.

Для запишите все возможные наборы квантовых чисел ( n , l , m ,).

Глоссарий

тонкая структура

подробная структура атомных спектров, созданных спин-орбитальной связью

сверхтонкая структура

подробная структура атомных спектров, созданных спин-орбитальной связью

переходы с переворотом спина

атомные переходы между состояниями системы электрон-протон, в которых магнитные моменты выровнены, а не выровнены

спин-орбитальная муфта

взаимодействие между магнитным моментом электрона и магнитным полем, создаваемым орбитальным угловым моментом электрона

квантовое число проекции спина ()

Квантовое число

, связанное с z -компонентой спинового углового момента электрона

спиновое квантовое число ( с )

Квантовое число

, связанное со спиновым угловым моментом электрона

Статистика, причинность и теорема Белла в JSTOR

Abstract

Теорема Белла [Physics 1 (1964) 195-200], как широко предполагается, устанавливает нелокальность квантовой физики.Нарушение неравенства Белла в таких экспериментах, как Аспект, Далибард и Роджер [Phys. Rev. Lett. 49 (1982) 1804-1807] дает эмпирическое доказательство нелокальности в реальном мире. В этой статье рассматривается недавняя работа по теореме Белла, связывая ее с проблемами причинно-следственной связи, как они понимаются статистиками. Статья начинается с доказательства сильной конечной выборки, версии неравенства Белла и, следовательно, теоремы Белла, в которой утверждается, что квантовая теория несовместима с сочетанием трех ранее неоспоримых физических принципов, здесь называемых локальностью, реализмом и свободой. .Локальность – это принцип, согласно которому направление причинности совпадает с направлением времени и что причинным влияниям требуется время для распространения в пространстве. Реализм и свобода напрямую связаны со статистическим мышлением о причинности: они связаны с контрфактическими рассуждениями и рандомизацией соответственно. Экспериментальные лазейки в современных экспериментах типа Белла связаны со статистическими проблемами пост-отбора в наблюдательных исследованиях и случайным отсутствием допущения. Их можно избежать, правильно сопоставив статистический анализ с фактическим планом эксперимента, вместо того, чтобы делать непроверяемые предположения о независимости между наблюдаемыми и ненаблюдаемыми переменными.Обсуждаются методологические и статистические вопросы при разработке квантовых задач Рэнди (QRC). В статье утверждается, что теорема Белла (и ее экспериментальное подтверждение) должны привести нас к отказу не от локальности, а от реализма.

Информация журнала

Цель статистической науки – представить полный спектр современная статистическая мысль на техническом уровне, доступном широкому кругу лиц. сообщество практиков, учителей, исследователей и студентов, изучающих статистику и вероятность.В журнале публикуются обсуждения методологических и теоретических тем. актуальные и актуальные, обзоры основных направлений исследований с перспективными статистическими приложениями, подробными обзорами книг, обсуждениями классических статей из статистической литературы и интервью с известными статистики и вероятностники.

Информация об издателе

Целью Института математической статистики (IMS) является содействие развитие и распространение теории и приложений статистики и вероятность.Институт сформирован на встрече заинтересованных лиц. 12 сентября 1935 года в Анн-Арборе, штат Мичиган, вследствие чувства что теория статистики будет продвинута с образованием организации тех, кто особенно интересуется математическими аспектами предмета. Летопись статистики и Анналы вероятности (которые заменяют “Анналы математической статистики”), Статистические Наука и Анналы прикладной вероятности – это научные журналы института.Они и Бюллетень IMS включают официальные журналы института. Институт имеет индивидуальное и организационное членство. Сборы оплачиваются ежегодно и включают подписку на информационный бюллетень организации, Бюллетень IMS. Участники также получают приоритетные цены на все другие публикации IMS.

Структура раствора дискоидных частиц липопротеинов высокой плотности с укороченным аполипопротеином AI

Родственные концепции

Белок APOA1, человеческая альфа-спиральная конформация, белок-альфа-1 липопротеин Растворы Про-аполипопротеин Спектроскопия A-IP-протеина Спектроскопия бета-аполипопротеина А-IP-спектроскопия

Связанные корма

АпоЕ, липиды и холестерин

сывороточный холестерин, триглицериды, аполипопротеин b (апоб) -содержащие липопротеины (липопротеины очень низкой плотности [vldl], липопротеины немедленной плотности [idl] и липопротеин [ldl]), липопротеин (a) (lp [a]) и соотношение общий холестерин / холестерин липопротеинов высокой плотности (hdl) – все они связаны между собой при заболеваниях.Узнайте о последних исследованиях этих молекул здесь.

Липиды и гомеостаз мембраны

Клеточная мембрана состоит из различных липидных молекул, которые помогают поддерживать целостность и гомеостаз мембраны. Узнайте о последних исследованиях липидов и мембранного гомеостаза

Ганглиозиды и абсорбция холестерина

Ганглиозиды – это гликосфинголипиды, содержащие сиаловую кислоту, сконцентрированные на поверхности клеток и в большом количестве обнаруженные в нервной системе. Ганглиозиды выполняют несколько функций, включая роль в абсорбции холестерина.Вот последнее исследование.

Статьи по теме

Тенденции в сердечно-сосудистой медицине

V Koppaka, PH Axelsen

The Journal of Biological Chemistry

Jere P SegrestS C Harvey

Biochemistry

Public Proteeis A Schne of the Protein Society

Bin ChenJianjun Wang

Journal of the Royal Society, Interface

Amy Y ShihKlaus Schulten

Индикатор быстро сходящегося хаоса для изучения динамической апертуры в накопительном кольце с пространственным зарядом (журнальная статья)

Хван, Килин, Митчелл, Чад и Райн, Роберт.Индикатор быстро сходящегося хаоса для исследования динамической апертуры в накопителе с объемным зарядом. США: Н. п., 2020. Интернет. https://doi.org/10.1103/physrevaccelbeams.23.084601.

Хван, Килин, Митчелл, Чад и Райн, Роберт. Индикатор быстро сходящегося хаоса для исследования динамической апертуры в накопителе с объемным зарядом. Соединенные Штаты. https://doi.org/10.1103/physrevaccelbeams.23.084601

Хван, Килин, Митчелл, Чад и Райн, Роберт. Пн. «Быстро сходящийся индикатор хаоса для исследования динамической апертуры в накопителе с объемным зарядом». Соединенные Штаты. https://doi.org/10.1103/physrevaccelbeams.23.084601.

@article {osti_1656690,
title = {Индикатор быстро сходящегося хаоса для изучения динамической апертуры в накопительном кольце с пространственным зарядом},
author = {Hwang, Kilean and Mitchell, Chad and Ryne, Robert},
abstractNote = {Определение динамическая апертура в накопителях и коллайдерах - процедура, требующая больших количественных затрат.Когда принимаются во внимание реалистичные силы пространственного заряда, численная нагрузка становится еще больше. Кроме того, динамическая оценка апертуры с использованием индикаторов хаоса, таких как анализ частотной карты (FMA), поднимает проблемы надежности, когда динамическая система имеет зависящее от времени возмущение, такое как сила пространственного заряда. В этой статье мы применяем быстро сходящийся индикатор хаоса, называемый методом ошибки обратимости (REM), для изучения вклада пространственного заряда в динамическую апертуру накопительного кольца интегрируемого оптического ускорителя (IOTA) при небольшом значении сдвига настройки пространственного заряда. .Сила REM рассматривается с помощью примеров, в том числе модели образования гало на основе частиц ядра. Мы также разрабатываем игрушечную модель решетки IOTA, чтобы еще больше сократить время вычислений, необходимое для оценки динамической апертуры, и сравниваем эту модель с реалистичным моделированием пространственного заряда для проверки.