Электрические цепи физика: Электрические цепи — урок. Физика, 8 класс.

Электрическая цепь и ее составные части | 8 класс

Содержание

Из прошлых уроков вы уже знаете, что для возникновения электрического тока должны выполняться определенные условия.

Во-первых, необходимо наличие зарядов в проводнике — свободных электронов или ионов. А во-вторых, обязательно наличие источника тока, который создает в проводнике электрическое поле, что и приводит к возникновению тока.

Все ли это необходимые условия? Нет, нам осталось изучить всего еще одно — наличие электрической цепи. Именно о ней и пойдет речь на данном уроке.

Необходимые части электрической цепи

Итак, первое, что должно обязательно присутствовать в электрической цепи — это источник тока.

Он создаст электрическое поле и будет его поддерживать, возникнет электрический ток. Мы же можем использовать его энергию.

Каким образом? Для этого нам нужен потребитель или приемник электрической энергии. Так называют все электрические приборы, которые мы используем, начиная от простых лампочек и фонариков, заканчивая компьютерами, электродвигателями, различной бытовой техникой.

Источник тока и его потребитель необходимо соединить друг с другом проводами. По ним ток от источника будет достигать потребителя.

{"questions":[{"content":"В электрической цепи ток[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["От источника подается к потребителю электрической энергии","От потребителя электрической энергии подается на источник тока","Существует независимо от наличия источника и потребителя"],"explanations":["","Наличие потребителя электрической энергии не может привести к возникновению тока в цепи. Для этого изначально нужен источник тока.","Наличие источника тока является обязательным условием возникновения самого тока."],"answer":[0]}}}]}

Обозначения частей электрической цепи

Электрические цепи принято изображать с помощью специальных схем.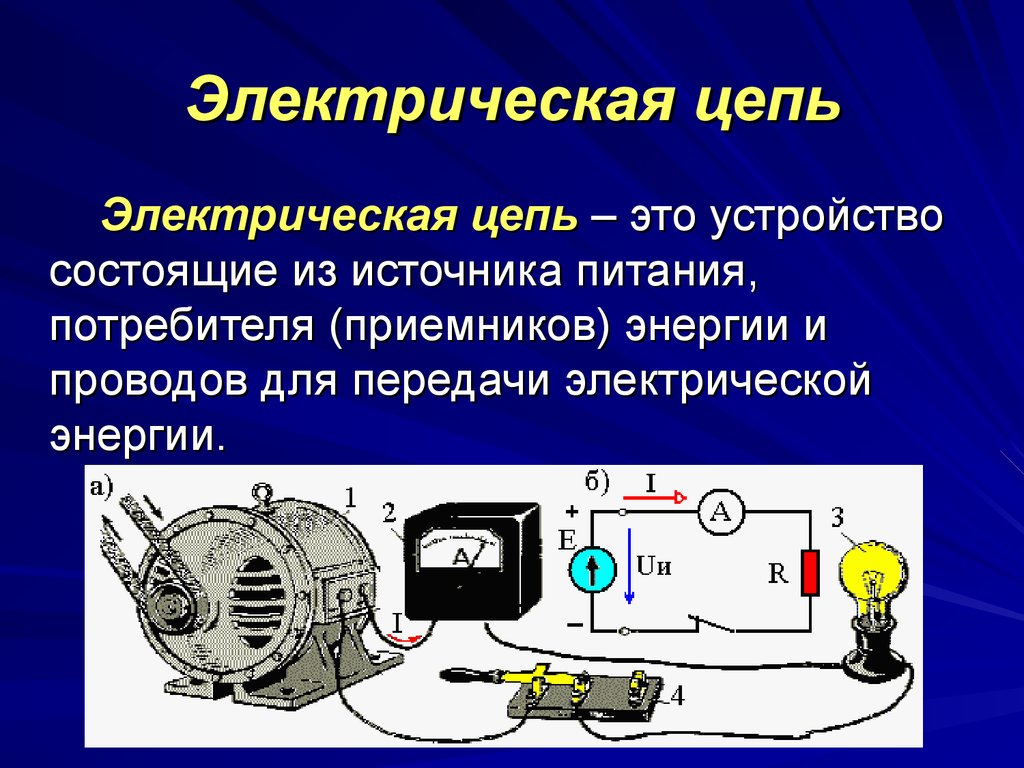 На них все элементы обозначаются специальными условными знаками.

На рисунке 1 изображены такие знаки для источников тока и их систем, таких потребителей тока, как лампа и электрический звонок.

Рисунок 1. Условные обозначения, применяемые на схемах электрической цепи

Также на рисунке 1 изображен условный знак для ключа. Его (а также рубильники, кнопки и различные выключатели) используют для того, чтобы включать или выключать приемники электрической энергии. Такие устройства называют замыкающими или размыкающими устройствами (рисунок 2).

Рисунок 2. Замыкающее устройство (ключ)

{"questions":[{"content":"В электрической цепи кнопка является[[choice-12]]","widgets":{"choice-12":{"type":"choice","options":["Замыкающим устройством","Источником тока","Приемником тока","Видом соединительного провода"],"answer":[0]}}}]}

В ходе изучения материала данного раздела вы будете знакомиться с различными новыми устройствами, которые используют в электричестве. При этом для каждого так же будет специальный условный знак. Так, вы познакомитесь с реостатами, конденсаторами, электрическими лампами и предохранителями.

Схема простейшей электрической цепи

Итак, самый простой вариант электрической цепи изображен на рисунке 3.

Рисунок 3. Схема простейшей электрической цепи

Из каких частей она состоит?

1. Источник тока
2. Приемник тока
3. Замыкающее устройство
4. Соединяющие провода

В данном случае источником тока является гальванический элемент или аккумулятор, приемником — лампочка, замыкающим устройством — ключ. Все эти элементы соединены между собой проводами.

{"questions":[{"content":"Условное обозначение, показанное на рисунке, используется для изображения на схеме электрической цепи[[image-1]][[choice-5]]","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/01/obozn-klyucha.svg","width":"200"},"choice-5":{"type":"choice","options":["ключа/кнопки/выключателя","аккумулятора/гальванического элемента","электрической лампочки","системы аккумуляторов"],"answer":[0]}}}]}

Замкнутость электрической цепи

Чтобы в цепи был ток, она должна быть замкнутой.

Что это означает? Цепь должна состоять только из проводников электричества.

Если в каком-то месте соединительный провод будет поврежден или оборван, то тока в цепи не будет. Именно на этом основывается действие замыкающих устройств.

{"questions":[{"content":"В электрической цепи, в которой существует ток, ее составные элементы[[choice-6]]","widgets":{"choice-6":{"type":"choice","options":["Соединены между собой проводами","Могут иметь разрывы","Соединены между собой любыми материалами"],"explanations":["","Наличие разрывов приводит к исчезновению тока.","Электрическая цепь может состоять только из проводников."],"answer":[0]}}}]}

Упражнения

Упражнение №1

Начертите схему цепи, содержащей один гальванический элемент и два звонка, каждый из которых можно включать отдельно.

Что будет отвечать в цепи за включение звонка? Ключ. А так как у нас два звонка и каждый нужно включать независимо от другого, то и ключа должно быть два (рисунок 4).

Рисунок 4. Схема электрический цепи с двумя звонками, каждый из которых можно включать отдельно

Обратите внимание на расположение звонков. Если мы соединим их просто один друг за другом, это будет неверным вариантом решения. Ведь если тогда выключим один звонок, он будет являться для второго своеобразным «оборванным проводом», и второй звонок работать не будет. 

Упражнение №2

Придумайте схему соединения гальванического элемента, звонка и двух кнопок, расположенных так, чтобы можно было позвонить из двух разных мест.

Чтобы звонить из двух разных мест мы можем разместить кнопки, как показано на рисунке 5.

Рисунок 5. Схема электрической цепи со звонком и двумя кнопками

Второй ключ (кнопку) можно разместить и с другой стороны цепи похожим способом.

Упражнение №3

На рисунке 6 дана схема соединения лампы и двух переключателей. Рассмотрите схему и подумайте, где можно применить такую проводку.

Рисунок 6. Схема электрической цепи с лампой и двумя переключателями

Обратите внимание, таким способом изображают ключи\переключатели, связанные между собой. Т.е. при замыкании одного замыкается и другой, и наоборот.

Такую проводку удобно использовать в больших помещениях. Например, заходя в длинный коридор, вы включаете свет рядом с дверью. Идете в другой конец коридора до другого помещения, и нужно выключить за собой свет. Рядом с вами находится вторая кнопка. Нажав на нее, вы выключаете свет.

Также можно использовать такой вариант электрической цепи, если включать/выключать свет необходимо разным людям из разных мест помещения.

Упражнение №4

Нарисуйте схему цепи карманного фонаря (рисунок 7) и назовите части этой цепи. Какие элементы фонаря отмечены цифрами?

Рисунок 7. Устройство карманного фонаря

На рисунке 6 под цифрой 1 обозначены два источника тока (гальванических элемента или аккумулятора). Цифрой 2 обозначена лампа, а цифрой 3 — кнопка включения/выключения (замыкающее устройство).

Нарисуем схему цепи такого фонаря (рисунок 8).

Рисунок 8. Схема электрической цепи карманного фонаря

На схеме у нас расположены все вышеперечисленные элементы, соединенные между собой проводами.

Электрические цепи — что это, определение и ответ

Через конденсатор постоянный ток не течёт.

Напряжение на параллельных участках цепи одинаково.

В системе отключенных конденсаторов заряд всегда остаётся постоянным. Напряжение и ёмкость может меняться.

Выделившееся количество теплоты равно разности начальной и конечной энергии:

Q = E_н – Е_к ¸ где

Q ― выделившееся тепло [Дж];

E_н ― начальная энергия системы [Дж];

Е_к ― конечная энергия системы [Дж].

Начальные и конечные энергии определяются энергиями конденсаторов и катушек индуктивности входящих в цепь.

Плоский конденсатор представляет собой пластинки, на которых может скапливаться заряд. Между пластинками находится пространство, заполненное диэлектриком (или воздухом в роли диэлектрика). Поскольку диэлектрики ― вещества, плохо проводящие ток, от одной пластины конденсатора через слой диэлектрика на другую пластину заряд перейти не может, а значит, через конденсатор ток не проходит. Если на участке цепи находится такой конденсатор ― этот участок «заблокирован», тока в нем нет.

Если на участке цепи находится конденсатор не заряженный, или заряженный частично, а цепь подключают к источнику тока ― на обкладках конденсатора начинает скапливаться заряд. Это означает, что на этом участке цепи до конденсатора есть ток ― до тех пор, пока конденсатор не заряжен полностью.

Если цепь от источника тока отключить, и в ней есть заряженный конденсатор ― конденсатор начинает разряжаться. Заряды с одной обкладки конденсатора пытаются перейти на другую, по «длинному пути» ― через всю цепь, создавая, таким образом, ток. Ток в такой цепи будет до тех пор, пока конденсатор не разрядится.

Пусть в цепи есть два резистора с сопротивлениями R₁ и R₂, источник ЭДС ε, и конденсатор емкостью C:

Конденсатор C полностью заряжен. В этом случае токи в цепи не проходят через участок цепи FG ― его словно нет в цепи, и в расчетах параметров цепи он не учитывается. Ток считается выходящим из положительно заряженной клеммы источника ЭДС (тонкая и длинная) к входящим в отрицательно заряженную клемму (жирная короткая черта):

Конденсатор разряжен или заряжен не док конца. В этом случае конденсатор только заряжается, и ток в цепи через точку F проходит – вплоть до обкладки конденсатора – но дальше, в точку G ток не проходит.

Конденсатор заряжен, но от источника ЭДС цепь отключена. В этом случае ток идет через всю цепь ― пока конденсатор может служить источником зарядов и пока полностью не разрядится. Когда конденсатор разрядится ― ток в цепи прекратится.

Напряжения на всех параллельных участках цепи равны ― это основное свойство параллельного подключения. Вне зависимости от того, находится на ветви резистор, или конденсатор. Таким образом, во всех случаях для примера выше, напряжение на конденсаторе C равно напряжению на резисторе R₁, и равно напряжению на резисторе R₂. Благодаря этому свойству, зная, например, энергию, скопившуюся на заряженном конденсаторе, или его заряд, можно вычислить напряжение на резисторах.

После установления равновесия, напряжение есть только на конденсаторах, не подключенных параллельно к резисторам.

В цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R₁ и R₂, оба конденсатора емкостями C₁ и C₂ разряжены.

Ток от источника ЭДС до конденсатора C₁ будет идти до тех пор, пока конденсатор C₁ не будет полностью заряжен. При этом от конденсатора C₁ дальше заряды не проходят ― ни на резисторы R₁ и R₂, ни на конденсаторC₂. Как только конденсатор C₁ полностью заряжается, в системе наступает состояние равновесия ― напряжение на конденсаторе становится равным ЭДС, весь возможный заряд конденсатор принял. Поскольку ток через него не прошел до конденсатора C₂ ― этот конденсатор так и остался незаряженным. Напряжение есть лишь на конденсаторе C₁, а на конденсаторе C₂ напряжение равно нулю. Зарядка конденсатораC₁:

После того, как конденсатор C₁ заряжен, ток в цепи прекращается.

В цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R₁ и R₂, все три конденсатора емкостями C₁, C₂ и C₃ разряжены.

Ток, выходя из источника ЭДС, разделяется на два тока ― один питает подзарядку конденсатораC₁, а другой ― конденсатораC₂. Состояние равновесия наступает, когда оба конденсатора полностью заряжены ― в цепи ток больше не проходит. Но так как ток дальше конденсаторов не проходит ― конденсатор C₃ не получает заряд, и остается разряженным. Напряжение на конденсаторе C₃ равно нулю.

Зарядка конденсаторов C₁ иC₂:

После того, как конденсаторыC₁ и C₂ заряжены, ток в цепи прекращается.

Учебное пособие по физике: последовательные цепи

Как упоминалось в предыдущем разделе урока 4, два или более электрических устройства в цепи могут быть соединены последовательно или параллельно. Когда все устройства соединены с помощью последовательных соединений, цепь называется последовательной цепью . В последовательной цепи каждое устройство подключено таким образом, что существует только один путь, по которому заряд может пройти через внешнюю цепь. Каждый заряд, проходящий через петлю внешней цепи, будет последовательно проходить через каждый резистор.


В предыдущем разделе урока 4 было проведено краткое сравнение и противопоставление последовательной и параллельной цепей. В этом разделе было подчеркнуто, что добавление большего количества резисторов в последовательную цепь приводит к довольно ожидаемому результату в виде увеличения общей сопротивление. Поскольку в цепи есть только один путь, каждый заряд сталкивается с сопротивлением каждого устройства; поэтому добавление большего количества устройств приводит к увеличению общего сопротивления. Это повышенное сопротивление служит для уменьшения скорости протекания заряда (также известной как ток).

 

Эквивалентное сопротивление и ток

Заряды протекают вместе через внешнюю цепь со скоростью, которая везде одинакова. Ток в одном месте не больше, чем в другом. Фактическая величина тока обратно пропорциональна величине общего сопротивления. Существует четкая зависимость между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Что касается батареи, которая качает заряд, наличие двух 6-омных резисторов, соединенных последовательно, будет эквивалентно наличию в цепи одного 12-омного резистора.

Наличие трех последовательно соединенных резисторов сопротивлением 6 Ом будет эквивалентно наличию в цепи одного резистора сопротивлением 18 Ом. А наличие четырех резисторов на 6 Ом последовательно было бы эквивалентно наличию в цепи одного резистора на 24 Ом.

Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи представляет собой величину сопротивления, которая потребуется одному резистору, чтобы уравнять общий эффект набора резисторов, присутствующих в цепи. Для последовательных цепей математическая формула для расчета эквивалентного сопротивления (R

экв. ) выглядит следующим образом:
R _экв. = R ₁ + R ₂ + R ₃ + …

, где R ₁ , R ₂ и R ₃ — значения сопротивления отдельных резисторов, соединенных последовательно.

Больше практики

Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже.

Составьте себе задачу с любым количеством резисторов и любых номиналов. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.

Ток в последовательной цепи везде одинаков. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами так, что в одном месте его меньше, чем в другом. Заряды можно представить себе как марширующие вместе по проводам электрической цепи, везде марширующие с одинаковой скоростью. Ток — скорость, с которой течет заряд, — везде одинакова. Это то же самое на первом резисторе, что и на последнем резисторе, как и в батарее. Математически можно написать

I _{Аккумулятор} = I ₁ = I ₂ = I ₃ = …

, где I ₁ , I ₂ и I ₃ , Iccount Thurn. Thuousth Ara The Arach значения в отдельных местах резисторов.

Эти значения тока легко рассчитать, если известно напряжение батареи и известны значения отдельных сопротивлений. Используя значения отдельных резисторов и приведенное выше уравнение, можно рассчитать эквивалентное сопротивление. А используя закон Ома (ΔV = I • R), можно определить ток в батарее и, следовательно, через каждый резистор, найдя соотношение напряжения батареи и эквивалентного сопротивления.

 

I _battery = I ₁ = I ₂ = I ₃ = ΔV _battery / R _eq

 

 

Electric Potential Difference and Voltage Drops

Как обсуждалось в Уроке 1, электрохимическая ячейка цепи подает энергию заряду для его перемещения через ячейку и создания разности электрических потенциалов на двух концах внешней цепи. Ячейка на 1,5 вольта создаст разность электрических потенциалов во внешней цепи 1,5 вольта. Это означает, что электрический потенциал на положительной клемме на 1,5 вольт больше, чем на отрицательной клемме. Когда заряд движется по внешней цепи, он теряет 1,5 вольта электрического потенциала. Эта потеря электрического потенциала называется падение напряжения

. Это происходит, когда электрическая энергия заряда преобразуется в другие формы энергии (тепловую, световую, механическую и т. д.) внутри резисторов или нагрузок. Если электрическая цепь, питаемая от 1,5-вольтовой ячейки, оснащена более чем одним резистором, то суммарная потеря электрического потенциала составляет 1,5 вольта. На каждом резисторе есть падение напряжения, но сумма этих падений напряжения составляет 1,5 вольта – столько же, сколько номинальное напряжение источника питания. Эта концепция может быть выражена математически следующим уравнением:
ΔV _{батарея} = ΔV ₁ + ΔV ₂ + ΔV ₃ + …

Чтобы проиллюстрировать этот математический принцип в действии, рассмотрим две схемы, показанные ниже на диаграммах A и B.

что вас попросили определить два неизвестных значения разности электрических потенциалов между лампочками в каждой цепи. Чтобы определить их значения, вам придется использовать приведенное выше уравнение. Батарея изображается своим обычным схематическим символом, а ее напряжение указывается рядом с ним. Определите падение напряжения для двух лампочек, а затем нажмите кнопку «Проверить ответы», чтобы убедиться, что вы правы.
 

 

 

Ранее в Уроке 1 обсуждалось использование диаграммы электрического потенциала. Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим принципиальную схему ниже и соответствующую ей диаграмму электрических потенциалов.

Схема, показанная на схеме выше, питается от 12-вольтового источника питания. В цепи последовательно соединены три резистора, каждый из которых имеет свое падение напряжения.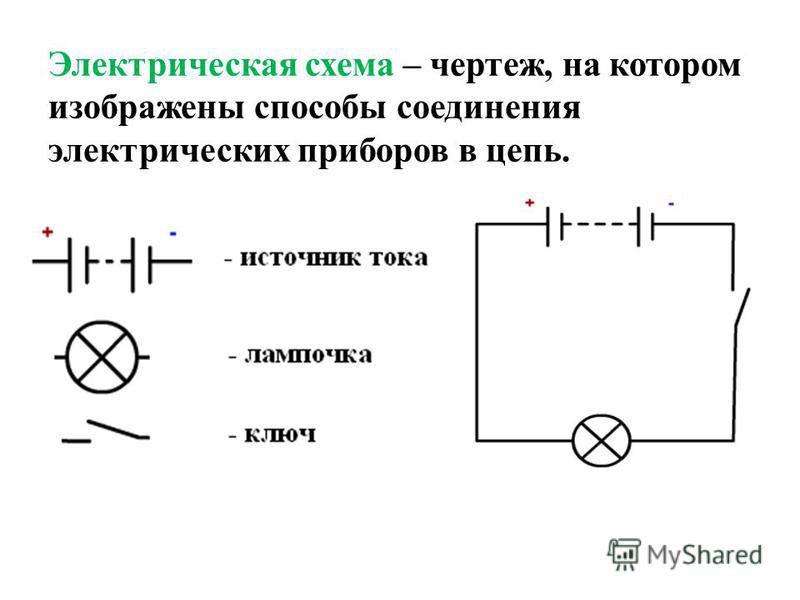 Отрицательный знак разности электрических потенциалов просто означает, что при прохождении через резистор происходит потеря электрического потенциала. Обычный ток направляется по внешней цепи от положительного вывода к отрицательному. Поскольку схематический символ источника напряжения использует длинную полосу для обозначения положительной клеммы, место А на схеме соответствует положительной клемме или клемме с высоким потенциалом. Место A находится под напряжением 12 вольт, а место H (отрицательная клемма) находится под напряжением 0 вольт. Проходя через аккумулятор, заряд приобретает 12 вольт электрического потенциала. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются за три этапа, каждый из которых соответствует протеканию через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда.

Поскольку точки А и В разделены проводом, они имеют практически одинаковый электрический потенциал 12 В. Когда заряд проходит через его первый резистор, он теряет 3 В электрического потенциала и падает до 9 В.V в точке C. Поскольку точка D отделена от точки C простым проводом, она имеет фактически тот же электрический потенциал 9 В, что и C. Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает вниз. до 2 В в точке E. Поскольку точка F отделена от точки E простым проводом, она имеет фактически тот же электрический потенциал 2 В, что и E. Наконец, когда заряд проходит через последний резистор, он теряет 2 В электрического тока. потенциала и падает до 0 В в точке G. В точках G и H заряду не хватает энергии, и ему требуется повышение энергии, чтобы снова пройти через внешнюю цепь. Повышение энергии обеспечивается аккумулятором по мере того, как заряд перемещается от H к A.

В уроке 3 закон Ома (ΔV = I • R) был представлен как уравнение, связывающее падение напряжения на резисторе с сопротивлением резистора и током на резисторе.

Уравнение закона Ома можно использовать для любого отдельного резистора в последовательной цепи. При объединении закона Ома с некоторыми принципами, уже обсуждавшимися на этой странице, возникает большая идея.

В последовательных цепях резистор с наибольшим сопротивлением имеет наибольшее падение напряжения.

Поскольку ток в последовательной цепи везде одинаков, значение I ΔV = I • R одинаково для каждого из резисторов последовательной цепи. Таким образом, падение напряжения (ΔV) зависит от изменения сопротивления. Везде, где сопротивление наибольшее, падение напряжения будет наибольшим на этом резисторе. Уравнение закона Ома можно использовать не только для прогнозирования того, что резистор в последовательной цепи будет иметь наибольшее падение напряжения, но и для расчета фактических значений падения напряжения.

Δ В 1 = I • R 1

Δ В 2 = I • R 2

Δ В 3 = I • R 3

 

Математический анализ последовательных цепей

Приведенные выше принципы и формулы можно использовать для анализа последовательной цепи и определения значений тока при и разности электрических потенциалов на каждом из резисторов в последовательной цепи. Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R _eq ), тока в батарее (I _tot ), а также падения напряжения и тока для каждого из трех резисторов.

 

Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.

R _eq = R ₁ + R ₂ + R ₃ = 17 Ом + 12 Ом + 11 Ом = 40 Ом

Теперь, когда известно эквивалентное сопротивление батареи можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в цепи важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R. Расчет показан здесь:

I _tot = ΔV _{батареи} / R _eq = (60 В) / (40 Ом) = 1,5 ампера

Значение тока 1,5 ампера — это ток в месте расположения батареи. Для последовательной цепи без мест разветвления ток везде одинаков. Ток в месте расположения батареи такой же, как ток в каждом месте резистора. Следовательно, 1,5 ампера — это значение I ₁ , I ₂ и I ₃ .

I _{аккумулятор} = I ₁ = I ₂ = I ₃ = 1,5 А

Осталось определить три значения — падение напряжения на каждом из отдельных резисторов. Закон Ома снова используется для определения падения напряжения на каждом резисторе – это просто произведение тока на каждом резисторе (рассчитанного выше как 1,5 ампера) и сопротивления каждого резистора (указанного в условии задачи). Расчеты показаны ниже.

ΔV 1 = I 1 • R 1 ΔV 1 = (1,5 А) • (17 Ом) ΔV 1 = 25,5 В

ΔV 2 = I 2 • R 2 ΔV 2 = (1,5 А) • (12 Ом) ΔV 2 = 18 В

ΔV 3 = I 3 • R 3 ΔV 3 = (1,5 А) • (11 Ом) ΔV 3 = 16,5 В

Для проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли рассчитанные значения принципу, согласно которому сумма падений напряжения на каждом отдельном резисторе равна номинальному напряжению батареи. Другими словами, является ли ΔV _{батарея} = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Является ли батарея ΔV = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Является ли 60 В = 25,5 В + 18 В + 16,5 В?

Является ли 60 В = 60 В?

Да!!

 

Математический анализ этой последовательной цепи включал сочетание концепций и уравнений. Как это часто бывает в физике, отрыв понятий от уравнений при решении физической задачи — опасный поступок. Здесь необходимо учитывать понятия, что ток везде одинаков и что напряжение батареи эквивалентно сумме падений напряжения на каждом резисторе, чтобы завершить математический анализ. В следующей части урока 4 параллельные цепи будут проанализированы с использованием закона Ома и концепций параллельных цепей. Мы увидим, что подход смешивания понятий с уравнениями будет столь же важен для этого анализа.

 

 

Мы хотели бы предложить . ..

Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).


Посетите:  DC Circuit Builder




Проверьте свое понимание

1. Используйте свое понимание эквивалентного сопротивления, чтобы завершить следующие утверждения:

a. Два последовательно соединенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное одному резистору сопротивлением _____ Ом.

б. Три последовательно соединенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное одному резистору сопротивлением _____ Ом.

с. Три последовательно соединенных резистора сопротивлением 5 Ом обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

д. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.

эл. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.

ф. Три резистора с сопротивлением 12 Ом, 3 Ом и 21 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.

 

 

2. При увеличении количества резисторов в последовательной цепи общее сопротивление __________ (увеличивается, уменьшается, остается неизменным) и ток в цепи __________ (увеличивается, уменьшается, остается неизменным).




3. Рассмотрим следующие две схемы последовательных цепей. Для каждой диаграммы используйте стрелки, чтобы указать направление условного тока. Затем сравните напряжение и ток в обозначенных точках для каждой диаграммы.

 

 




4. Три одинаковые лампочки подключены к D-ячейке, как показано справа. Какое из следующих утверждений верно?

а. Все три лампочки будут иметь одинаковую яркость.

б. Лампочка между X и Y будет самой яркой.

в. Лампочка между Y и Z будет самой яркой.

д. Лампочка между Z и батареей будет самой яркой.

 

 

 

5. Три одинаковые лампочки подключены к батарейке, как показано справа. Какие корректировки можно внести в схему, чтобы увеличить ток, измеряемый в точке X? Перечислите все, что применимо.

а. Увеличьте сопротивление одной из лампочек.

б. Увеличьте сопротивление двух лампочек.

в. Уменьшите сопротивление двух лампочек.

д. Увеличьте напряжение батареи.

эл. Уменьшите напряжение батареи.

ф. Снимите одну из лампочек.

 

 




6. Три одинаковые лампочки подключены к батарейке, как показано справа. W, X, Y и Z обозначают местоположения вдоль цепи. Какое из следующих утверждений верно?

а. Разность потенциалов между X и Y больше, чем между Y и Z.

б. Разность потенциалов между X и Y больше, чем между Y и W.

в. Разность потенциалов между Y и Z больше, чем между Y и W.

д. Разность потенциалов между X и Z больше, чем между Z и W.

эл. Разность потенциалов между X и W больше, чем на аккумуляторе.

ф. Разность потенциалов между X и Y больше, чем между Z и W.

 




7. Сравните схемы X и Y ниже. Каждый питается от 12-вольтовой батареи. Падение напряжения на резисторе 12 Ом в цепи Y равно ____ падению напряжения на одном резисторе в цепи X.

a. меньше чем

б. больше

в. то же, что

 

 

 

8. Батарея 12 В, резистор 12 Ом и лампочка подключены, как показано на схеме X ниже. Резистор на 6 Ом добавляется к резистору на 12 Ом и лампочке, чтобы создать цепь Y, как показано на рисунке. Лампочка появится ____.

а. диммер в контуре X

б. диммер в цепи Y

в. одинаковая яркость в обоих контурах

 

 




9. Три резистора соединены последовательно. Если поместить в цепь с 12-вольтовым источником питания. Определить эквивалентное сопротивление, общий ток цепи, падение напряжения и ток на каждом резисторе.

 

 

Следующий раздел:

Electric Circuits — Physics Video by Brightstorm

Давайте поговорим об электрических цепях. Что такое электрическая цепь? Ну, электрическая цепь — это одна или несколько петель провода, которые соединяют кучу элементов цепи. Обычно ток может течь по всей цепи. Если ток не может протекать через него полностью, я не буду называть это цепью. Хорошо.

Цепи обычно питаются от батареи. То, как мы представляем батареи, таково: у нас есть такая длинная полоса, это положительная сторона батареи, а затем у нас есть короткая полоса, это отрицательная сторона батареи. Резисторы — это еще один элемент схемы, о котором я буду говорить в этой статье, и они представлены этой маленькой странной волнистой линией.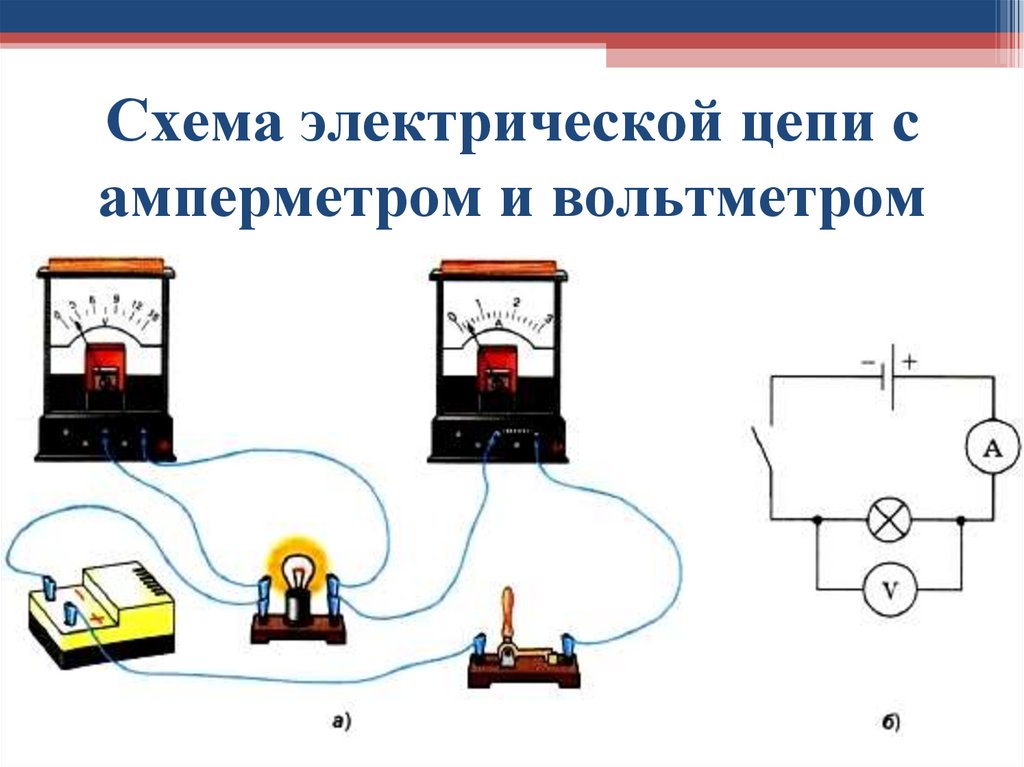 Таким образом, важная вещь в рисовании волнистой линии заключается в том, что вы должны двигаться ниже и выше прямой линии. Прямая линия просто представляет провод. На самом деле ничего не делает, кроме подключения элементов схемы. Так что у него нет никакой разности потенциалов, никакого сопротивления или чего-то в этом роде. Он просто соединяет различные элементы схемы. Говорит вам, где вещи связаны. Хорошо. Таким образом, цель батареи – управлять цепью, а цель резистора – использовать энергию.

Итак, какие есть примеры резисторов? Ну, по сути, все, что вы хотите подключить, это резистор. Лампочка, резистор. Телевидение, резистор. Автомобиль, резистор. Микроволновка, резистор, все резисторы. Все, что вы подключаете для использования энергии, является резистором. Вот как это будет представлено на принципиальной схеме, подобной этой. Хорошо. Итак, давайте посмотрим, как мы можем на самом деле решить схему.

Итак, предположим, что у меня есть схема, похожая на эту. Хорошо. У меня аккумулятор на 20 вольт. Заметьте, я не поставил плюс и минус. Я поставил длинную и короткую, и вы должны знать, что длинная — это плюс, а короткая — минус. И я хочу знать, какой ток через эту цепь? Хорошо. Мы собираемся сделать это двумя разными способами. Первый способ несколько прямолинейный, и в этом случае он даст нам довольно быстрый ответ. второй способ немного сложнее, но он гораздо более широко применим. Хорошо. Итак, пойдем по первому пути.

Так что я хочу сказать, смотрите. Эти провода — идеальные проводники, вот что они представляют. Это означает, что между ними не может быть никакой разности потенциалов. Итак, если между ними нет разности потенциалов, разность потенциалов здесь составляет 20 вольт, тогда разность потенциалов здесь должна быть 20 вольт. Итак, пришло время для закона Ома. Итак, мы скажем, дельта v равно минус ir, разность потенциалов -20 вольт равна минус i, умноженная на то, что это, 4 Ом делят, и все готово. я равен 5 ампер. Итак, через эту цепь проходит ток 5 ампер.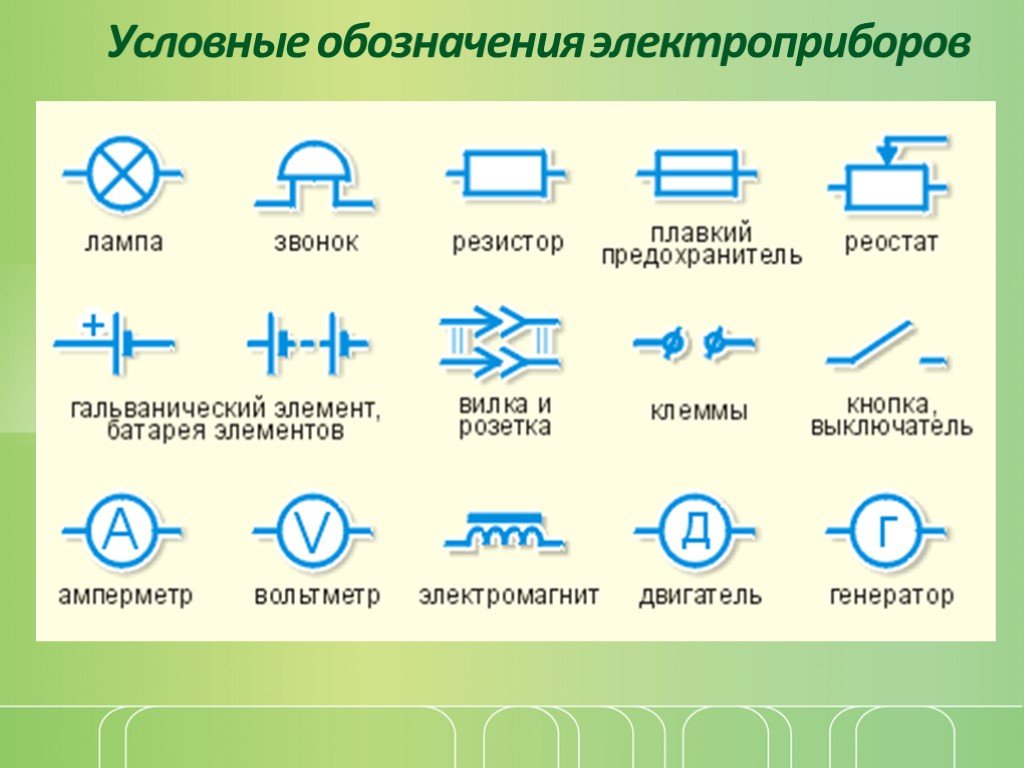 Хорошо.

Пойдем вторым путем. Второй способ связан с так называемым законом Кирхгофа. Кирхгоф сказал, что если вы проходите по петле в цепи и отслеживаете все разности потенциалов по мере прохождения, то к тому времени, когда вы вернетесь к тому, с чего начали, результирующая разность потенциалов должна быть равна нулю. Хорошо. Итак, мы начнем, и мы начнем прямо здесь, и мы просто пойдем по цепи в направлении тока. Так пройди через аккумулятор, какая разница потенциалов? Ну я набрал 20 вольт, так у меня получилось +20. Хорошо. Перейдите через провод здесь. Ничего не произошло. Перебери резистор, теперь закон Ома говорит мне, что я получаю падение потенциала ir. Итак, минус ir, и теперь я здесь, а потом снова иду через провод. И снова ничего не происходит. Теперь я вернулся к тому, с чего начал. Так что это означает, что все это привело меня к нулю. Так что теперь я перенесу этого парня на другую сторону уравнения и разделю. Таким образом, 20 вольт равны i для омов, и я разделю, и я получу 5 ампер, равных i. Тот же ответ, который я получил раньше, конечно, должен быть, не может быть двух разных действительных методов, дающих вам разные ответы. Хорошо.

Так зачем мне этот метод Кирхгофа? Ну, это гораздо более широко применимо к другим ситуациям, когда я не могу привести такие простые аргументы разности потенциалов. Итак, давайте посмотрим на эту схему здесь.

У меня тут два резистора. Итак, теперь я хочу запустить лампочку и телевизор, верно? И я хочу запустить их на одной и той же схеме. Хорошо. Так что я собираюсь использовать Кирхгофа, потому что пока не знаю, как привести эти потенциальные аргументы. Хорошо. Итак, мы начнем, и у нас есть 16 вольт, ничего, минус 5i минус 3i. И теперь мы вернулись к началу, так что у нас есть ноль. Сложив 5 и 3, мы получили 16=8i и, следовательно, ток равен 2 ампера. Но это не то, о чем просила проблема. Проблема тока не просила. Он хочет знать, какова разность потенциалов на резисторе 3 Ом? Боже, я не знаю. Ну вот теперь у меня тока 2 ампера.