формулы расчета мощности в проводнике
Прохождение электрического тока через любую проводящую среду объясняется наличием в ней некоторого количества носителей заряда: электронов – для металлов, ионов – в жидкостях и газах. Как найти её величину, определяет физика силы тока.
Электрический ток в проводнике
В спокойном состоянии носители движутся хаотично, но при воздействии на них электрического поля движение становится упорядоченным, определяемым ориентацией этого поля – возникает сила тока в проводнике. Количество носителей, участвующих в переносе заряда, определяется физической величиной – силой тока.
От концентрации и заряда частиц-носителей, или количества электричества, напрямую зависит сила тока, проходящего через проводник. Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:
Зависимость силы тока от электрического заряда
Входящие в формулу величины:
- I – сила электрического тока, единицей измерения является ампер, входит в семь основных единиц системы Си.
 Понятие «электрический ток» ввёл Андре Ампер, единица названа в честь этого французского физика. В настоящее время определяется как ток, вызывающий силу взаимодействия 2×10-7 ньютона между двумя параллельными проводниками, при расстоянии 1 метр между ними;
Понятие «электрический ток» ввёл Андре Ампер, единица названа в честь этого французского физика. В настоящее время определяется как ток, вызывающий силу взаимодействия 2×10-7 ньютона между двумя параллельными проводниками, при расстоянии 1 метр между ними; - Величина электрического заряда, применённая здесь для характеристики силы тока, является производной единицей, измеряется в кулонах. Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;
- Время в секундах.
Сила тока через заряд может вычисляться с применением данных о скорости и концентрации частиц, угла их движения, площади проводника:
I = (qnv)cosαS.
Также используется интегрирование по площади поверхности и сечению проводника.
Определение силы тока с использованием величины заряда применяется в специальных областях физических исследований, в обычной практике не используется.
Связь между электрическими величинами устанавливается законом Ома, который указывает на соответствие силы тока напряжению и сопротивлению:
Сила тока участка цепи и цепи с источником тока
Сила электрического тока здесь как отношение напряжения в электрической цепи к её сопротивлению, эти формулы используются во всех областях электротехники и электроники. Они верны для постоянного тока с резистивной нагрузкой.
Они верны для постоянного тока с резистивной нагрузкой.
В случае косвенного расчета для переменного тока следует учитывать, что измеряется и указывается среднеквадратичное (действующее) значение переменного напряжения, которое меньше амплитудного в 1,41 раза, следовательно, максимальная сила тока в цепи будет больше во столько же раз.
При индуктивном или емкостном характере нагрузки вычисляется комплексное сопротивление для определённых частот – найти силу тока для такого рода нагрузок, используя значение активного сопротивления постоянному току, невозможно.
Так, сопротивление конденсатора постоянному току практически бесконечно, а для переменного:
RC = 1/ FC.
Здесь RC – сопротивление того же конденсатора ёмкостью С, на частоте F, которое во многом зависит от его свойств, сопротивления разных типов ёмкостей для одной частоты значительно различаются. В таких цепях сила тока по формуле, как правило, не определяется – используются различные измерительные приборы.
Для нахождения значения силы тока при известных значениях мощности и напряжения, применяются элементарные преобразования закона Ома:
Тут сила тока – в амперах, сопротивление – в омах, мощность – в вольт-амперах.
Электрический ток имеет свойство разделяться по разным участкам цепи. Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.
I = I1 + I2 + I3
Общий ток цепи равен сумме токов на её участках – при полном проходе через электрическую замкнутую цепь ток разветвляется, затем принимает исходное значение.
Видео
Оцените статью:Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца
Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.
Рассмотрим эти вопросы.
Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени
(21.1) |
Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита.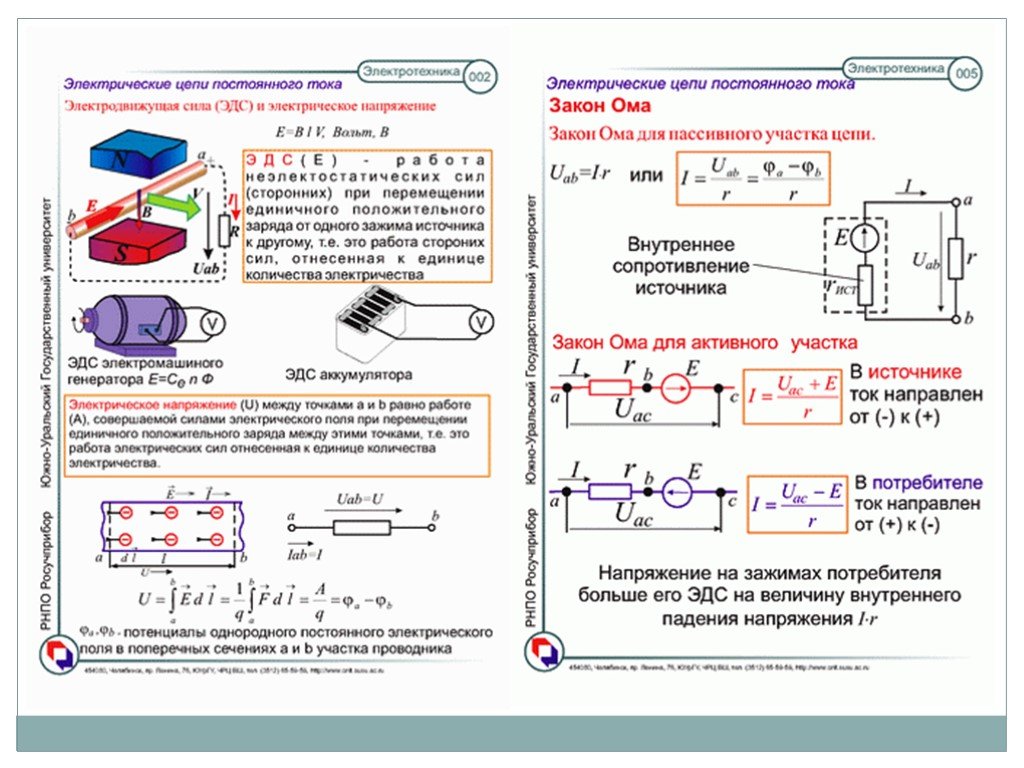
Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то
(21.2) |
Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид
(21.3) |
Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова

Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения
(21.4) |
где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.
Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников
(21.4) |
Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см.
(21.5) |
Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
(21.6) |
В этом случае сила тока в цепи равна
(21. |
Формула (21.7) называется законом Ома для замкнутой электрической цепи.
При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно
(21.8) |
(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение
(21.9) |
которое называется мощностью тока, не зависит от времени наблюдения.
Рассмотрим теперь задачи.
Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).
Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21.1.2)
(ответ 2).
Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).
По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21. 1.4)
1.4)
Таким образом, сила тока уменьшилась в 4 раза (ответ 3).
(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.
Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6
где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
(ответ 3).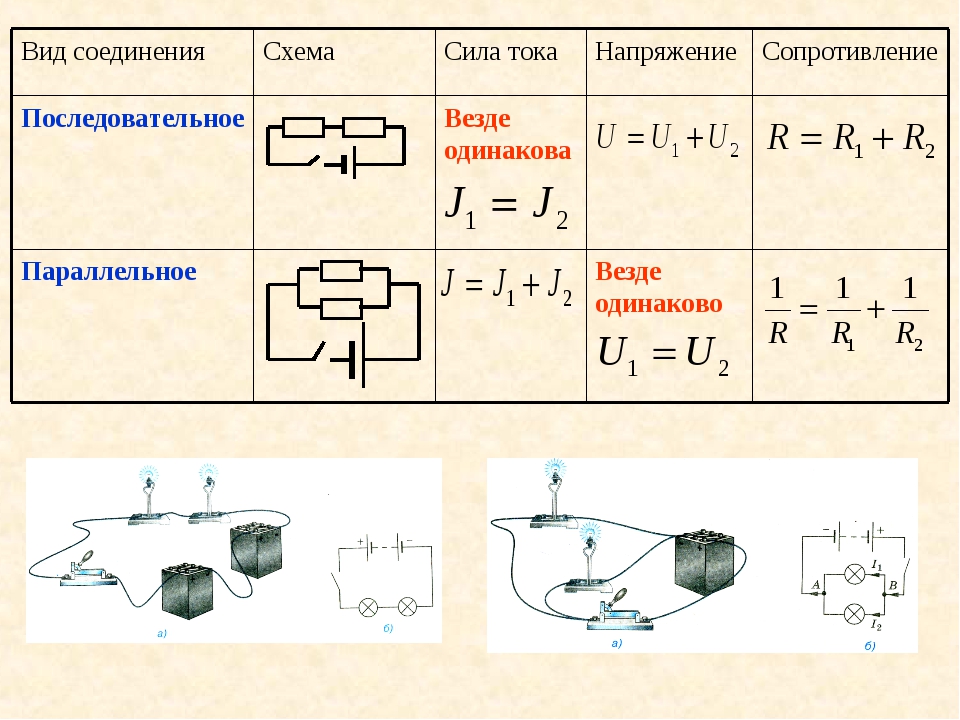
Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).
В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем
где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).
В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
где — внутреннее сопротивление источника (ответ 3).
Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).
В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).
Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21.2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно
Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно
(ответ 2).
Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что
(ответ 2).
При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что
(ответ 1).
Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка
По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка
а затем и эквивалентное сопротивление всей цепи
(ответ 3).
При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).
Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна
где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:
Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:
(ответ 2).
Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
(ответ 1).
Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22. 8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).
§ 7. Закон Ома | Электротехника
Закон Ома для электрической цепи.
Согласно этому закону сила тока I в электрической цепи равна э. д. с. Е источника, поделенной на сопротивление цепи Rц, т. е.
I = E / Rц (7)
Полное сопротивление замкнутой электрической цепи (рис. 13) можно представить в виде суммы сопротивления внешней цепи R (например, какого-либо приемника электрической энергии) и внутреннего сопротивления Ro источника. Поэтому сила тока
I = E / (R+Ro) (8)
Чем больше э. д. с. Е источника и чем меньше сопротивление электрической цепи, тем больший ток проходит по этой цепи.
Из формулы (7) следует, что э. д. с. источника электрической энергии равна произведению силы тока на полное сопротивление электрической цепи:
E = IRц (7)
Закон Ома для участка электрической цепи.
Закон Ома может быть применен не только ко всей цепи, но и к любому ее участку, например между точками а и б (см. рис. 13).
Рис. 13. Схема простейшей электрической цепи и Рис 14. Прохождение электрического тока по проводникам аналогично прохождению воды по трубам
В этом случае э.
 д. с. Е источника в формуле (7) должна быть заменена разностью потенциалов между началом и концом рассматриваемого участка, т. е. напряжением U, а вместо сопротивления всей цепи в формулу должно быть подставлено сопротивление R данного участка. В этом случае закон Ома формулируется следующим образом. Сила тока I на данном участке электрической цепи равна напряжению U, приложенному к участку, поделенному на сопротивление R этого участка:
д. с. Е источника в формуле (7) должна быть заменена разностью потенциалов между началом и концом рассматриваемого участка, т. е. напряжением U, а вместо сопротивления всей цепи в формулу должно быть подставлено сопротивление R данного участка. В этом случае закон Ома формулируется следующим образом. Сила тока I на данном участке электрической цепи равна напряжению U, приложенному к участку, поделенному на сопротивление R этого участка:I = U / R (9)
Прохождение электрического тока по проводникам полностью аналогично прохождению воды по трубам (рис. 14).
Чем больше разность уровней воды при входе и выходе из трубы (напор) и чем больше поперечное сечение трубы, тем больше воды протекает сквозь трубу в единицу времени. Точно так же, чем больше разность электрических потенциалов (напряжение) на зажимах источника или приемника электрической энергии и чем меньше его сопротивление (т. е. чем больше площадь поперечного сечения проводника), тем больший ток проходит по нему.
Из формулы (9) следует, что напряжение U, действующее на некотором участке цепи, равно произведению силы тока I на сопротивление R этого участка:
U = IR (10)
Так как потенциал электрического поля в начале участка электрической цепи больше, чем в конце, разность потенциалов, или напряжение U, приложенное к участку электрической цепи, часто называют падением напряжения на данном участке.
Сопротивление R участка цепи равно напряжению, приложенному к данному участку, поделенному на силу тока на этом участке, т. е.
R = U / I (11)
Если сопротивление R не зависит от проходящего по нему тока и приложенного к нему напряжения, то его вольт-амперная характеристика, т. е. зависимость силы тока I от напряжения U, представляет собой прямую линию 1 (рис. 15).
Рис. 15. Вольт-амперные характеристики линейных и нелинейных сопротивлений
Такие сопротивления называют линейными, а электрические цепи, в которых включены подобные сопротивления,— линейными цепями.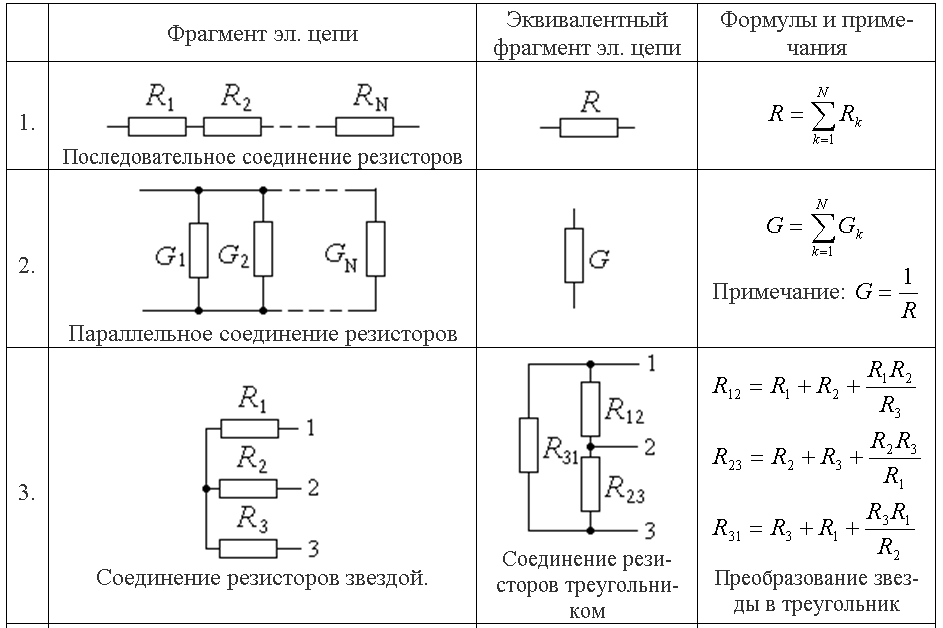
Однако в электротехнике широко применяют и такие устройства, сопротивление которых резко изменяется в зависимости от силы или направления проходящего через них тока либо приложенного напряжения. Подобные сопротивления имеют вольт-амперную характеристику, отличающуюся от прямой (кривая 2 на рис. 15), и называются поэтому нелинейными сопротивлениями.
Простейшим нелинейным сопротивлением является электрическая лампа накаливания. При протекании тока по металлической нити лампа нагревается и сопротивление ее возрастает. Следовательно, при увеличении приложенного к лампе напряжения сила тока будет возрастать не прямо пропорционально напряжению, а в несколько меньшей степени.
В принципе большинство электрических устройств может быть представлено в виде нелинейного сопротивления, так как при изменении силы тока меняется температура данного устройства, а следовательно, и его сопротивление. Однако у многих из них вольт-амперные характеристики в рабочем диапазоне изменений напряжения и тока мало отличаются от прямой, поэтому приближенно можно их считать линейными сопротивлениями.
К сопротивлениям с нелинейной вольт-амперной характеристикой относятся электрические лампы накаливания, термисторы (полупроводниковые резисторы, сопротивление которых сильно изменяется при изменении температуры), полупроводниковые диоды, тиристоры и транзисторы, электронные лампы и пр. Нелинейные сопротивления широко используют в электротехнике для автоматического регулирования силы тока и напряжения в электрических цепях, электрических измерений, выпрямления тока и пр.
РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ОНЛАЙН – ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ, ТОКА, МОЩНОСТИ И СЕЧЕНИЯ ПРОВОДНИКА
Наверное, каждый кто делал или делает ремонт электрики сталкивался с проблемой определения той или иной электрической величины. Для кого-то это становится настоящим камнем преткновения, а для кого-то все предельно ясно и каких-либо сложностей при определении той или иной величины нет. Данная статья посвящена именно первой категории – то есть для тех, кто не очень силен в теории электрических цепей и тех показателей, которые для них характерны.
Итак, для начала вернемся немного в прошлое и постараемся вспомнить школьный курс физики, касательно электрики. Как мы помним, основные электрические величины определяются на основании всего одного закона – закона Ома. Именно этот закон является базой проведения абсолютно для любых расчетов и имеет вид:
Отметим, что в данном случае речь идет о расчете самой простейшей электрической цепи, которая выглядит следующим образом:
Подчеркнем, что абсолютно любой расчет ведется именно посредством этой формулы. То есть путем не сложных математических вычислений можно определить ту или иную величину зная при этом два иных электрических параметра. Как бы там ни было, наш ресурс призван упростить жизнь тому кто делает ремонт, а поэтому мы упростим решение задачи определения электрических параметров, вывив основные формулы и предоставив возможность произвести расчет электрических цепей онлайн.
Как узнать ток зная мощность и напряжение?
В данном случае формула вычисления выглядит следующим образом:
Расчет силы тока онлайн:
(Не целые числа вводим через точку. Например: 0.5)
Например: 0.5)
Как узнать напряжение зная силу тока?
Для того, чтобы узнать напряжение, зная при этом сопротивление потребителя тока можно воспользоваться формулой:
Расчет напряжения онлайн:
Если же сопротивление неизвестно, но зато известна мощность потребителя, то напряжение вычисляется по формуле:
Определение величины онлайн:
Как рассчитать мощность зная силу тока и напряжения?
Здесь необходимо знать величины действующего напряжения и действующей силы тока в электрической цепи. Согласно формуле предоставленной выше, мощность определяется путем умножения силы тока на действующее напряжение.
Расчет цепи онлайн:
Как определить потребляемую мощность цепи имея тестер, который меряет сопротивление?
Этот вопрос был задан в комментарие в одном из материалов нашего сайта. Поспешим дать ответ на этот вопрос. Итак, для начала измеряем тестером сопротивление электроприбора (для этого достаточно подсоединить щупы тестера к вилке шнура питания). Узнав сопротивление мы можем определить и мощность, для чего необходимо напряжение в квадрате разделить на сопротивление.
Узнав сопротивление мы можем определить и мощность, для чего необходимо напряжение в квадрате разделить на сопротивление.
Онлайн расчет:
Формула расчета сечения провода и как определяется сечение провода
Довольно много вопросов связано с определением сечения провода при построении электропроводки. Если углубиться в электротехническую теорию, то формула расчета сечения имеет такой вид:
Конечно же, на практике, такой формулой пользуются довольно редко, прибегая к более простой схеме вычислений. Эта схема довольно проста: определяют силу тока, которая будет действовать в цепи, после чего согласно специальной таблице определяют сечение. Более детально по этому поводу можно почитать в материале – «Сечение провода для электропроводки»
Приведем пример. Есть бойлер мощностью 2000 Вт, какое сечение провода должно быть, чтобы подключить его к бытовой электропрводке? Для начала определим силу тока, которая будет действовать в цепи:
I=P/U=2000/220В = 9А
Как видим, сила тока получается довольно приличной. Округляем значение до 10 А и обращаемся к таблице:
Округляем значение до 10 А и обращаемся к таблице:
Таким образом, для нашего бойлера потребуется провод сечением 1,7 мм. Для большей надежности используем провод сечением 2 или 2,5 мм.
Рекомендуем ознакомиться:
— БЛОК ПИТАНИЯ ДЛЯ СВЕТОДИОДНЫХ ЛЕНТ
— ЗАЩИТНОЕ ЗАНУЛЕНИЕ
— СВЕТОДИОДНЫЕ СВЕТИЛЬНИКИ — ЛУЧШЕ НЕ ПРИДУМАЕШЬ!
— АЛМАЗНАЯ РЕЗКА БЕТОНА И ЖБ КОНСТРУКЦИЙ
Автор — Антон Писарев
Урок 29. закон ома для участка цепи. соединения проводников – Физика – 10 класс
Физика, 10 класс
Урок 29. Закон Ома для участка цепи. Соединения проводников
Перечень вопросов, рассматриваемых на уроке:
- условия, необходимые для существования электрического тока;
- постоянный электрический ток;
- закон Ома для участка цепи;
- формула расчета сопротивления проводника с учетом свойств материала проводника и его геометрических размеров;
- типы соединений проводников и формулы расчета параметров электрической цепи для каждого типа.

Глоссарий по теме.
Сила тока I – скалярная величина, равная отношению заряда q, прошедшего через поперечное сечение проводника, к промежутку времени t, в течение которого шёл ток.
Постоянный ток – электрический ток, не изменяющийся со временем.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом.
Параллельное соединение проводников. При параллельном соединении концы проводников присоединены к одной и той же паре точек.
Смешанное соединение проводников – это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.
Узел – это точка электрической цепи, где сходится не менее трех ветвей.
Свойство проводника ограничивать силу тока в цепи, то есть противодействовать электрическому току, называют электрическим сопротивлением проводника.
Резистор или проводник – элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления.
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 335 – 340.
2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. – М.: Дрофа, 2009. – С. 105 – 109.
3. Элементарный учебник физики. Учебное пособие в 3 томах под редакцией академика Ландсберга Г.С.: Т.2. Электричество и магнетизм. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 110 – 115.
4. Тульчинский М.Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 83 – 87.
5. Савельев И.В. Курс общей физики, том II. Электричество. М.: Изд. «Наука», 1970 г. С. 108.
Открытые электронные ресурсы:
http://kvant.mccme. ru/1979/02/elektrichestvo_ie_temperatura.htm
ru/1979/02/elektrichestvo_ie_temperatura.htm
Теоретический материал для дополнительного изучения
Сложно представить нашу жизнь без электрического тока. Каждый день, не задумываясь, мы используем различные электрические приборы, в основе работы которых лежат простые и сложные электрические цепи. Какому закону подчиняются основные параметры электрических цепей? Как рассчитать эти цепи, чтобы приборы работали исправно?
Вы уже знаете, электрическим током называют упорядоченное (направленное) движение заряженных частиц.
Для возникновения и существования электрического тока в проводнике необходимо:
- наличие свободных заряженных частиц;
- сила, действующая на них в определённом направлении, то есть наличие электрического поля в проводнике.
Различают следующие действия электрического тока:
- тепловое ;
- химическое ;
- магнитное .
Постоянный ток — электрический ток, у которого сила тока и направление не изменяются со временем.
Сила тока I равна отношению электрического заряда q, прошедшего через поперечное сечение проводника, ко времени его прохождения t:
За направление электрического тока условно выбрано направление движения положительно заряженных частиц, то есть в сторону, противоположную направлению движения электронов.
Для каждого проводника – твердого, жидкого и газообразного – существует определённая зависимость силы тока от приложенной разности потенциалов (напряжения) на концах проводника. Эту зависимость выражает, так называемая, вольт-амперная характеристика проводника.
Для широкого класса проводников (в т. ч. металлов ) при неизменной температуре справедлив закон Ома для участка цепи:
Сила тока на участке цепи прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению этого участка цепи:
Закон имеет простую форму, но доказать экспериментально его справедливость довольно трудно.
Закон Ома является основой всей электротехники постоянных токов. Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно.
Основная электрическая характеристика проводника – сопротивление. От этой величины зависит сила тока в проводнике при заданном напряжении. Причиной электрического сопротивления является взаимодействие электронов при их движении по проводнику с ионами кристаллической решетки. Сопротивление проводника зависит от свойств материала проводника и его геометрических размеров.
Электрическое сопротивление металлов прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения:
где величина ρ – удельное сопротивление проводника – величина, зависящая от рода вещества и его состояния (от температуры в первую очередь). Удельное сопротивление веществ приводятся в справочных таблицах.
Омметр – прибор для измерения сопротивления.
От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию.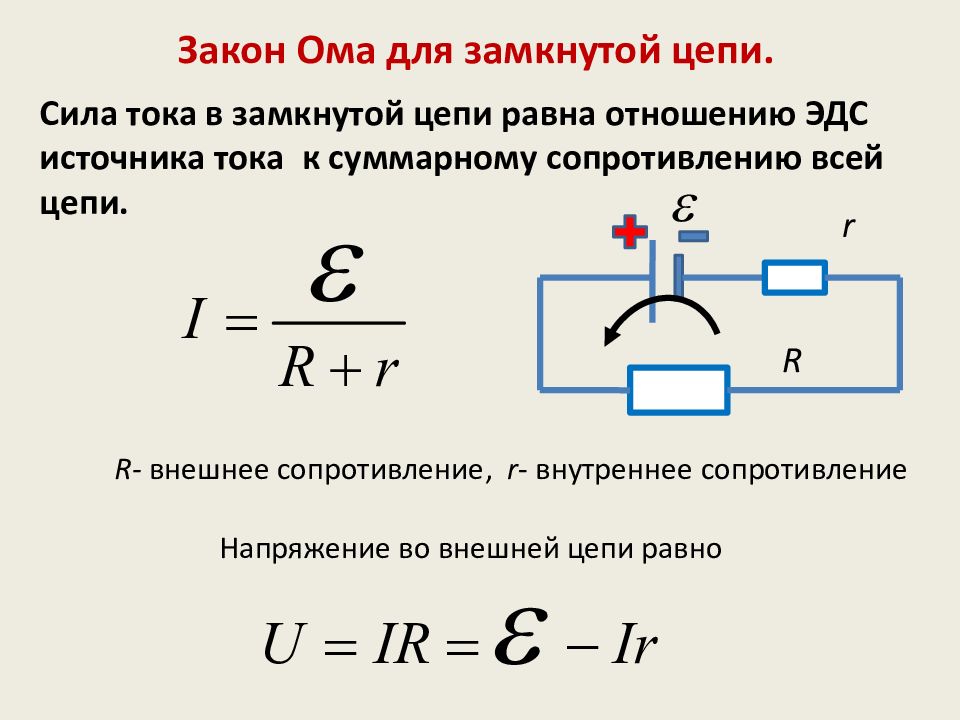 Для этого составляют электрические цепи различной сложности. Различают последовательное, параллельное, смешанное соединения проводников.
Для этого составляют электрические цепи различной сложности. Различают последовательное, параллельное, смешанное соединения проводников.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом. Главная особенность последовательного соединения заключается в том, что через все проводники протекает одинаковый ток. Если через один проводник протекает ток определенной величины, то такой же ток протекает и через все остальные. Если хотя бы в одном проводнике отсутствует ток, то он обязательно отсутствует и во всех остальных. Напряжение на концах последовательно соединенных проводников складывается. Полное сопротивление всего участка цепи при последовательном соединении равно сумме сопротивлений всех проводников.
Последовательное соединение | |
Физическая величина | Формула |
Сила тока | I = I1 = I2 |
Напряжение | U = U1 + U2 |
Сопротивление | R = R1 + R2 |
Параллельное соединение проводников. При параллельном соединении концы проводников присоединены к одной и той же паре точек.
При параллельном соединении концы проводников присоединены к одной и той же паре точек.
Параллельное соединение | |
Физическая величина | Формула |
Сила тока | I = I1 + I2 |
Напряжение | U = U1 = U2 |
Сопротивление | |
Узел – это точка электрической цепи, где сходится не менее трех ветвей.
Узел обозначается на схеме жирной точкой в том месте, где ветви соединяются между собой.
Смешанное соединение проводников.
Смешанным соединением проводников называют такое соединение, при котором в цепи присутствует и последовательное, и параллельное соединение.
Метод эквивалентных преобразований заключается в том, что электрическую цепь или ее часть заменяют более простой по структуре электрической цепью.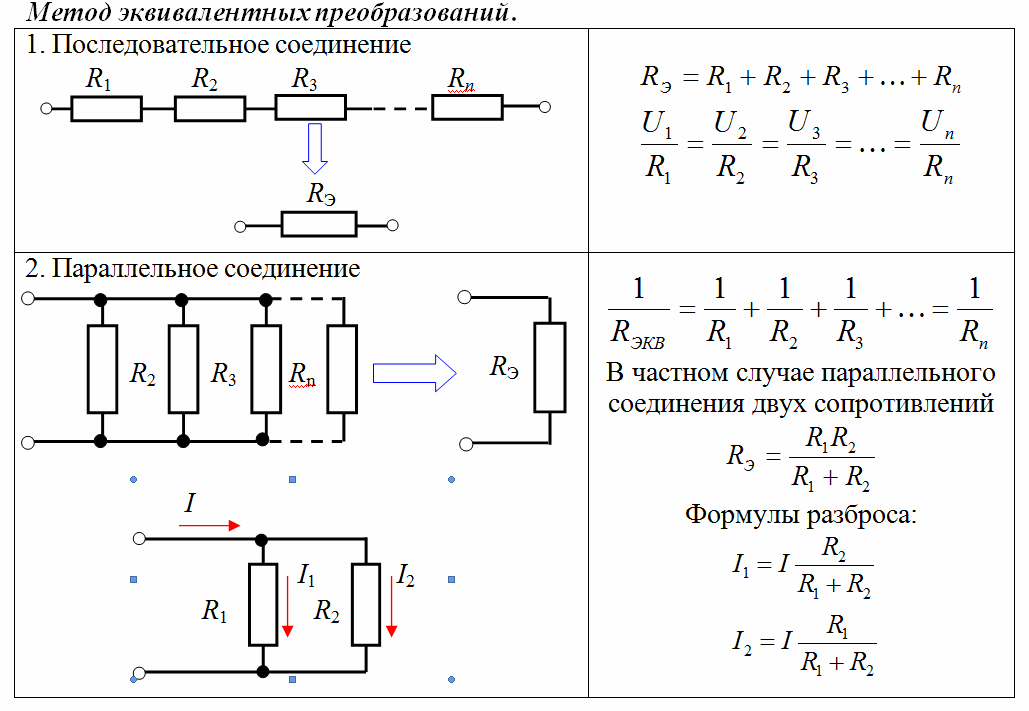 При этом токи и напряжения в непреобразованной части цепи должны оставаться неизменными, т.е. такими, какими они были до преобразования. В результате преобразований расчет цепи упрощается и часто сводится к элементарным арифметическим операциям.
При этом токи и напряжения в непреобразованной части цепи должны оставаться неизменными, т.е. такими, какими они были до преобразования. В результате преобразований расчет цепи упрощается и часто сводится к элементарным арифметическим операциям.
Расчет сопротивления сложной цепи:
Рези́стор или проводник – пассивный элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления.
Примеры и разбор решения заданий
1. Выберите один из 3 вариантов ответа:
При параллельном соединении проводников…
1) напряжение зависит от сопротивления на данном участке цепи
2) напряжение везде разное
3) напряжение везде одинаковое
Ответ: 3) напряжение везде одинаковое.
2. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно 24 Ом. Чему равно полное сопротивление участка при замкнутом ключе К?
Решение.
После замыкания ключа схема будет представлять собой параллельное соединение резистора с двумя последовательно соединенными резисторами.
Полное сопротивление участка при замкнутом ключе равно
(R+R)R/((R+R) + R) = 2R/3 = 16 Ом.
Ответ: 16 Ом.
Электрическая цепь и электрическое сопротивление
Электрической цепью называется путь, по которому проходит электрический ток. Чтобы по электрической цепи проходил ток, она должна быть замкнутой. Простейшая электрическая цепь состоит из трех основных частей: источника электрического тока, приемника (потребителя) электрического тока и системы соединительных проводов с вспомогательными приборами (включатели и переключатели тока, измерительные приборы и т. п.).
В качестве источников электрического тока могут служить: механические — электрические генераторы, в которых механи¬ческая энергия преобразуется в электрическую; химические— гальванические элементы и аккумуляторы, в которых химическая энергия преобразуется в электрическую; тепловые — термоэлементы, преобразующие тепловую энергию в электрическую; лучевые — фотоэлементы, преобразующие световую энергию в электрическую.
Приемниками электрического тока могут служить электродвигатели, электролампы, электронагревательные приборы и т. п. Часть электрической цепи, состоящая из приемников электрической энергии и соединительных проводов, называется внешней цепью. Токопроводящие пути самого источника электрической энергии называются внутренней цепью.
Если оборвать электрическую цепь на каком-либо участке, то ток по всей цепи прекращается. Замыкание и размыкание цепи осуществляется выключателем или рубильником.
Для измерения величин, характеризующих электрический ток, в цепь могут быть включены измерительные приборы.
Все вещества обладают различной способностью оказывать сопротивление прохождению электрического тока. Эта способность веществ оказывать сопротивление прохождению электрического тока называется электрическим сопротивлением.
Величина сопротивления измеряется в омах и обозначается буквой R или r. За 1 ом принято сопротивление ртутного столба длиной 106,3 см и поперечным сечением 1 мм2 при 0°С.
В практике применяются также единицы электрического сопротивления килоом (1 ком=1000 ом) и мегом (1 Мом=1 000 000 ом).
Величина сопротивления зависит от длины, поперечного сечения и материала, из которого изготовлен проводник. Эта зависимость выражается следующей формулой:
где R — сопротивление проводника, ом;
р — удельное сопротивление материала проводника, ом мм2/м;
I — длина проводника, м;
S — поперечное сечение проводника, мм2.
Как видно из формулы, чем длиннее проводник и меньше его поперечное сечение, тем больше его сопротивление.
Удельным сопротивлением материала называется сопротивление проводника из данного материала длиной в 1 м и поперечным сечением 1 мм2 при 0°С. Обычно различные проводники сравниваются по этому показателю. Например, серебро, медь, алюминий обладают небольшим сопротивлением, а такие сплавы, как константан (сплав меди, никеля и марганца), нихром (сплав никеля, хрома, железа, марганца), никелин и другие обладают сопротивлением значительно большим.
Помимо размеров и материала, на сопротивление проводника влияет его температура. Так, почти у всех металлических проводников при повышении температуры сопротивление увеличивается. И только вышеперечисленные сплавы: константан, нихром, никелин и другие практически почти не изменяют своего сопротивления при нагревании и способны выдерживать высокие температуры, благодаря чему эти сплавы и получили широкое применение в электротехнике.
Закон ома. Соединение сопротивлений
Зависимость между величинами, характеризующими электрическую цепь, т.е. силой тока, э. д. с. и сопротивлением, устанавливается законом Ома, который формулируется следующим образом:
сила тока в замкнутой неразветвленной цепи прямо пропорциональна электродвижущей силе и обратно пропорциональна сопротивлению цепи.
Закон Ома выражается формулой:
где I — сила тока, а;
Е — э. д. с. источника электрической энергии, в;
R — сопротивление внешнего участка цепи, ом;
r— сопротивление внутреннего участка цепи, ом.
Эта формула может быть записана и в таком виде:
т. е. электродвижущая сила, создаваемая источником электрической энергии, равна величине тока, умноженной на общее сопротивление цепи, и складывается из двух слагаемых, из которых первое (IR) представляет собой разность потенциалов на зажимах внешнего сопротивления, называется напряжением на зажимах внешней цепи и обозначается через U, а второе слагаемое (Ir) носит название падения напряжения на внутреннем участке цепи.
Для внешней цепи и для отдельных ее участков закон Ома обычно записывается в следующем виде:
т. е. сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению данного участка цепи.
Различные сопротивления в электрическую цепь можно включить последовательно, параллельно и смешанным способом (рис. 159).
Последовательным соединением сопротивлений называют такое соединение, когда конец одного сопротивления соединяют с началом второго, конец второго с началом третьего и т. д., а конец последнего и начало первого сопротивлений подключаются к зажимам источника тока (см. 159, а). Основным свойством последовательного соединения является то, что при таком соединении сила тока во всех сопротивлениях внешней и внутренней цепи одинакова и согласно закону Ома
д., а конец последнего и начало первого сопротивлений подключаются к зажимам источника тока (см. 159, а). Основным свойством последовательного соединения является то, что при таком соединении сила тока во всех сопротивлениях внешней и внутренней цепи одинакова и согласно закону Ома
Общее сопротивление последовательной цепи равно сумме всех соединенных сопротивлений, т. е.
Напряжение на зажимах источника тока при последовательно соединенных сопротивлениях равно произведению величины тока на сопротивление внешнего участка цепи. Обозначив через U1, U2, U3, U4, напряжения на концах каждого сопротивления, получим:
а следовательно,
Напряжение на полюсах источника тока при последовательном соединении сопротивлений равно сумме напряжений на отдельных участках цепи.
Параллельным, соединением сопротивлений называется такое соединение, при котором начала всех сопротивлений соединяются в один общий узел, а концы — в другой.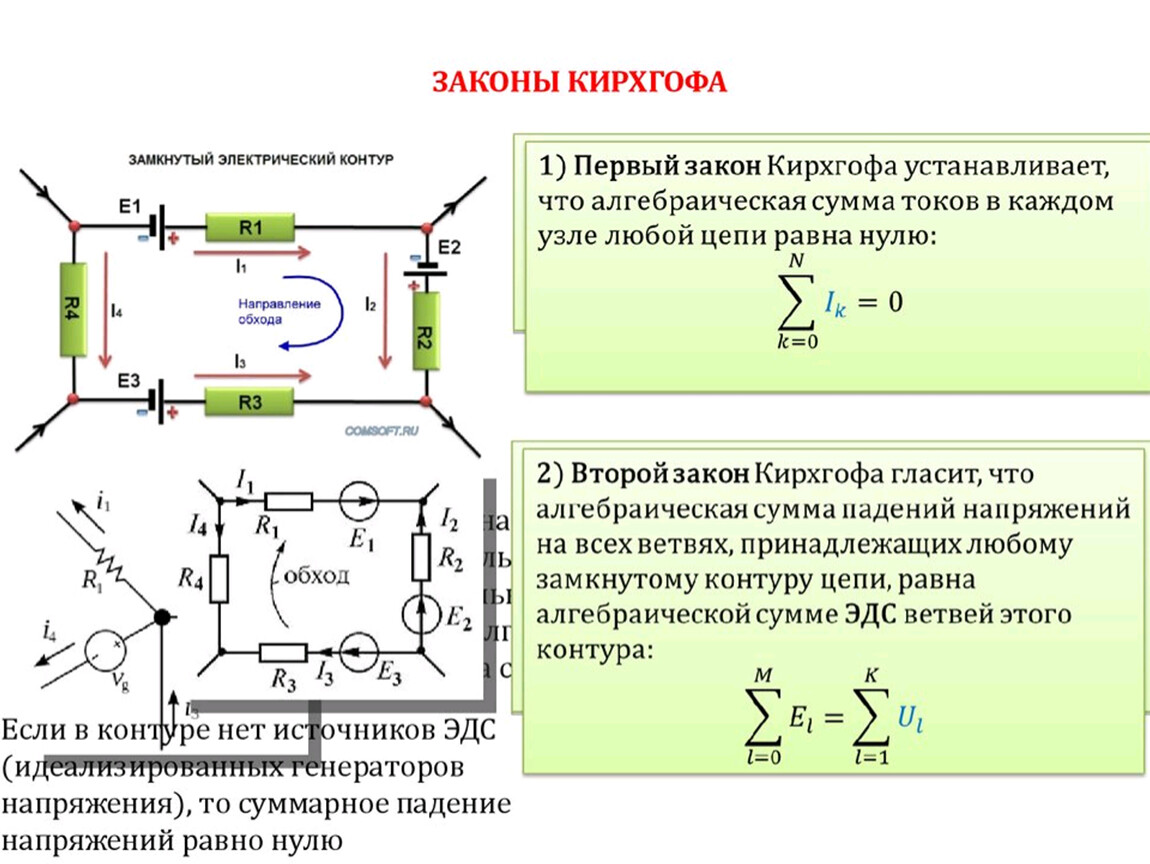 При этом зажимы источника тока включаются к узлам цепи А и В (рис. 159, б).
При этом зажимы источника тока включаются к узлам цепи А и В (рис. 159, б).
Если напряжение между точками А и В равно U, то такое же напряжение будет между началом и концом каждого сопротивления. Тогда для каждого участка цепи по закону Ома можно написать:
т. е. при параллельно соединенных сопротивлениях ток будет больше там, где меньше сопротивление.
Основным свойством параллельного соединения является то, что в каждом разветвлении цепи устанавливается своя сила тока, обратно пропорциональная сопротивлению данного участка цепи.
В точке В ток разветвляется в нескольких направлениях (на несколько ветвей), а в сумме он равен I. Поэтому при параллельном соединении нескольких сопротивлений ток, подведенный к этим сопротивлениям, равен сумме токов во всех сопротивлениях:
Для определения общего сопротивления параллельной цепи пользуются следующим соотношением: общая проводимость (обратная величина сопротивлению) параллельной цепи равна сумме проводимостей отдельных разветвлений цепи, т. е.
е.
Если в электрической цепи часть сопротивлений включена последовательно, а часть параллельно, то такое соединение называется смешанным. На рис. 159, в сопротивления R 1и R2 соединены последовательно, a R3 и R4 — параллельно.
Похожие статьи
Расчет простых цепей постоянного тока
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1 Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
А затем напряжение
Зная напряжения, найдем токи, протекающие через резисторы
Как видите, токи получились теми же.
Пример 3 В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи
Отсюда мощность, выделяемая на R1
Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
Таким образом производится расчет простых цепей постоянного тока.
резисторов последовательно и параллельно
Цели обучения
К концу этого раздела вы сможете:
- Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Contrast (Контраст), как рассчитывается общее сопротивление для резисторов, включенных последовательно и параллельно.
- Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Вычислить общее сопротивление цепи, которая содержит смесь резисторов, включенных последовательно и параллельно.
Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов – это последовательное и параллельное соединение, показанное на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Рис. 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, тогда R 1 на Рисунке 1 (а) может быть сопротивлением вала отвертки, R 2 сопротивлением ее ручки , R 3 сопротивление тела человека и R 4 сопротивление его обуви.На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с резиновыми подошвами с высоким сопротивлением. прибор, уменьшающий рабочий ток.)
Рис. 2. Три резистора, подключенных последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на рисунке 2. Согласно закону Ома, падение напряжения, В, , на резистор, когда через него протекает ток, рассчитывается по формуле V = IR , где I равно току в амперах (A), а R – сопротивление в омах (Ω).Другой способ представить это: В, – это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , что на R 2 составляет В 2 = IR 2 и что для R 3 это V 3 = IR 3 . Сумма этих напряжений равна выходному напряжению источника; то есть
Сумма этих напряжений равна выходному напряжению источника; то есть
В = В 1 + В 2 + В 3 .
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV , где q – электрический заряд, а V – напряжение. Таким образом, энергия, отдаваемая источником, составляет кв.кв. , а энергия, рассеиваемая резисторами, составляет
.qV 1 + qV 2 + qV 3 .
Установление связей: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые гласят, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии.Таким образом, qV = qV 1 + qV 2 + qV 3 . Плата q аннулируется, давая V = V 1 + V 2 + V 3 , как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.) Теперь подстановка значений для отдельных напряжений дает
В = IR 1 + IR 2 + IR 3 = I ( R 1 + R 2 + R 3 ).
Обратите внимание, что для эквивалентного сопротивления одной серии R с , мы имеем
В = ИК с .
Это означает, что полное или эквивалентное последовательное сопротивление R с трех резисторов составляет R с = R 1 + R 2 + R 3 .Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление R с последовательного соединения составляет
R с = R 1 + R 2 + R 3 +…,
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 1. Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 2 равно 12.0 В, а сопротивления равны R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите ток. (c) Вычислите падение напряжения на каждом резисторе и покажите, как полученная сумма равна выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
а) Каково полное сопротивление? (б) Найдите ток. (c) Вычислите падение напряжения на каждом резисторе и покажите, как полученная сумма равна выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Общее сопротивление – это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
[латекс] \ begin {array} {lll} {R} _ {\ text {s}} & = & {R} _ {1} + {R} _ {2} + {R} _ {3} \ \ & = & 1.00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].
Стратегия и решение для (b)Ток определяется по закону Ома: В = IR . Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
[латекс] I = \ frac {V} {{R} _ {\ text {s}}} = \ frac {12. 0 \ text {V}} {20.0 \ text {} \ Omega} = 0.60 \ text {A }\\[/латекс].
0 \ text {V}} {20.0 \ text {} \ Omega} = 0.60 \ text {A }\\[/латекс].
Напряжение – или падение IR – на резисторе определяется законом Ома.Ввод тока и значения первого сопротивления дает
.В 1 = IR 1 = (0,600 A) (1,0 Ом) = 0,600 В.
Аналогично
В 2 = IR 2 = (0,600 A) (6,0 Ом) = 3,60 В
и
V3 = IR 3 = (0,600 A) (13,0 Ом) = 7,80 В.
Обсуждение для (c)Три капли IR добавляют к 12.0 В, прогноз:
В 1 + В 2 + В 3 = (0,600 + 3,60 + 7,80) В = 12,0 В.
Стратегия и решение для (d) Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, – это использовать закон Джоуля , P = IV , где P – электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток.Подставляя закон Ома V = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
В этом случае через каждый резистор протекает одинаковый полный ток.Подставляя закон Ома V = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
P 1 = I 2 R 1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт
Аналогично
P 2 = I 2 R 2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт
и
P 3 = I 2 R 3 = (0.{2}} {R} \\ [/ latex], где В, – это падение напряжения на резисторе (а не полное напряжение источника). Будут получены те же значения.
Стратегия и решение для (e)Самый простой способ рассчитать выходную мощность источника – использовать P = IV , где В, – напряжение источника. Это дает
P = (0,600 A) (12,0 В) = 7,20 Вт.
Обсуждение для (e) Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7. 20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
P 1 + P 2 + P 3 = (0,360 + 2,16 + 4,68) W = 7,20 Вт.
Мощность – это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Последовательные сопротивления добавить: R с = R 1 + R 2 + R 3 +….
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
На рисунке 3 показаны резисторы , включенные параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника. Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)
Таким образом, к каждому резистору приложено полное напряжение источника. Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)
Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления R p , давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} \\ [/ latex] , [латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} \\ [/ latex] и [латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} \\ [/ латекс]. Сохранение заряда подразумевает, что полный ток I , производимый источником, является суммой этих токов:
Сохранение заряда подразумевает, что полный ток I , производимый источником, является суммой этих токов:
I = I 1 + I 2 + I 3 .
Подстановка выражений для отдельных токов дает
[латекс] I = \ frac {V} {{R} _ {1}} + \ frac {V} {{R} _ {2}} + \ frac {V} {{R} _ {3}} = V \ left (\ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} \ справа) \\ [/ латекс].
Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
[латекс] I = \ frac {V} {{R} _ {p}} = V \ left (\ frac {1} {{R} _ {p}} \ right) \\ [/ latex].
Члены в круглых скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление R p параллельного соединения связано с отдельными сопротивлениями на
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ гидроразрыв {1} {{R} _ {\ text {. } 3}} + \ text {.} \ Text {…} \\ [/ latex]
} 3}} + \ text {.} \ Text {…} \\ [/ latex]
Это соотношение приводит к общему сопротивлению R p , которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: В = 12.0 В, R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
(e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения.Ввод известных значений дает
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} = \ frac {1} {1 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {6 \ text {. } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} \\ [/ latex].
Таким образом,
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1.00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой. ) Мы должны перевернуть это, чтобы найти полное сопротивление R p . Это дает
) Мы должны перевернуть это, чтобы найти полное сопротивление R p . Это дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {1 \ text {.} \ Text {2436}} \ text {} \ Omega = 0 \ text {.} \ Text { 8041} \ text {} \ Omega \\ [/ latex].
Суммарное сопротивление с правильным количеством значащих цифр составляет R p = 0,804 Ом
Обсуждение для (а)R p , как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)Полный ток можно найти из закона Ома, заменив полное сопротивление R p . Это дает
[латекс] I = \ frac {V} {{R} _ {\ text {p}}} = \ frac {\ text {12.0 V}} {0.8041 \ text {} \ Omega} = \ text {14} \ text {.} \ text {92 A} \\ [/ latex].
Обсуждение для (б) Ток I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
[латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} = \ frac {12.0 \ text {V}} {1.00 \ text {} \ Omega} = 12.0 \ text {A} \\ [/ латекс].
Аналогично
[латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} = \ frac {12.0 \ text {V}} {6.00 \ text {} \ Omega} = 2 \ text {.} \ text {00} \ text {A} \\ [/ latex]
и
[латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} = \ frac {\ text {12} \ text {.} 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].
Обсуждение для (c)Общий ток складывается из отдельных токов:
I 1 + I 2 + I 3 = 14,92 A.
Это соответствует сохранению заряда.{2}} {13.0 \ text {} \ Omega} = 11.1 \ text {W} \\ [/ latex].
Обсуждение для (d)Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)Общую мощность также можно рассчитать несколькими способами. Выбрав P = IV и введя полный ток, получим
P = IV = (14,92 A) (12,0 В) = 179 Вт.
Обсуждение для (e)Общая мощность, рассеиваемая резисторами, также составляет 179 Вт:
P 1 + P 2 + P 3 = 144 Вт + 24,0 Вт + 11,1 Вт = 179 Вт
Это соответствует закону сохранения энергии.
Общее обсуждениеОбратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики резисторов, подключенных параллельно- Параллельное сопротивление определяется из [latex] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {1}} + \ frac {1} { {R} _ {2}} + \ frac {1} {{R} _ {3}} + \ text {…} \\ [/ latex], и оно меньше любого отдельного сопротивления в комбинации.
- На каждый параллельно включенный резистор подается такое же полное напряжение источника. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они делят это.
Сочетания последовательного и параллельного
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учесть сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно свести к одному эквивалентному сопротивлению, используя методику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Рис. 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.
Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 4, также является наиболее поучительной, поскольку она используется во многих приложениях.Например, R 1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R 2 и R 3 могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 3. Расчет сопротивления,
IR Падение, ток и рассеиваемая мощность: объединение последовательных и параллельных цепейНа рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом – сочетание последовательного и параллельного.Можно считать R 1 сопротивлением проводов, ведущих к R 2 и R 3 . (а) Найдите полное сопротивление. (b) Что такое падение IR в R 1 ? (c) Найдите текущие значения от I 2 до R 2 . (d) Какую мощность рассеивает R 2 ?
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация включена последовательно с R 1 .
Стратегия и решение для (а)Чтобы найти полное сопротивление, отметим, что R 2 и R 3 находятся параллельно, и их комбинация R p находится последовательно с R 1 . Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет
.R до = R 1 + R p .
Сначала мы находим R p , используя уравнение для параллельных резисторов и вводя известные значения:
[латекс] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3 }} = \ frac {1} {6 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].
Инвертирование дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {0,2436} \ text {} \ Omega = 4.11 \ text {} \ Omega \\ [/ latex].
Таким образом, общее сопротивление равно
.R до = R 1 + R p = 1,00 Ом + 4,11 Ом = 5,11 Ом.
Обсуждение для (а)Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чистой параллели (20.0 Ом и 0,804 Ом соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)Чтобы найти падение IR в R 1 , отметим, что полный ток I протекает через R 1 . Таким образом, его падение IR составляет
В 1 = ИК 1
Мы должны найти I , прежде чем сможем вычислить V 1 .Полный ток I находится с помощью закона Ома для схемы. То есть
[латекс] I = \ frac {V} {{R} _ {\ text {tot}}} = \ frac {\ text {12.0} \ text {V}} {5.11 \ text {} \ Omega} = 2.35 \ text {A} \\ [/ latex].
Вводя это в выражение выше, мы получаем
В 1 = IR 1 = (2,35 A) (1,00 Ом) = 2,35 В.
Обсуждение для (б)Напряжение, приложенное к R 2 и R 3 , меньше полного напряжения на величину В 1 .Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R 2 и R 3 .
Стратегия и решение для (c)Чтобы найти ток через R 2 , мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение В p , потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное как к R 2 , так и к R 3 , уменьшается на величину В 1 , и поэтому оно составляет
В p = V – V 1 = 12.0 В – 2,35 В = 9,65 В.
Теперь ток I 2 через сопротивление R 2 находится по закону Ома:
[латекс] {I} _ {2} = \ frac {{V} _ {\ text {p}}} {{R} _ {2}} = \ frac {9.65 \ text {V}} {6.00 \ текст {} \ Omega} = 1,61 \ text {A} \\ [/ latex].
Обсуждение для (c)Ток меньше 2,00 А, которые протекали через R 2 , когда он был подключен параллельно к батарее в предыдущем примере параллельной цепи.
Стратегия и решение для (d)Мощность, рассеиваемая R 2 равна
P 2 = ( I 2 ) 2 R 2 = (1,61 A) 2 (6,00 Ом) = 15,5 Вт
Обсуждение для (d)Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное номером R 3 , имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, представленных R 1 , уменьшая напряжение на лампе (которое составляет R 2 ), которое затем заметно гаснет.
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
Проверьте свое понимание
Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.
Решение Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут включены в Правила Кирхгофа, позволят вам проанализировать схему. Стратегии решения проблем для последовательных и параллельных резисторов- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой – для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при обнаружении R необходимо проявлять осторожность.
- Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Сводка раздела
Концептуальные вопросы
1. Переключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и очень большое в разомкнутом, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.
Рис. 7. Переключатель обычно включается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
2. Какое напряжение на разомкнутом переключателе на Рисунке 7?
3. На разомкнутом переключателе есть напряжение, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?
4. Почему мощность, рассеиваемая замкнутым переключателем, как на Рисунке 7, мала?
5. Студент в лаборатории физики по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рисунке 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и гаснет, когда выключатель замкнут. (Не пытайтесь – батарея сильно разряжается!)
Рис. 8. Ошибка подключения. Включите этот переключатель параллельно устройству, обозначенному [латекс] R [/ латекс].(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
6. Зная, что сила удара зависит от величины тока, протекающего через ваше тело, вы бы предпочли, чтобы он был включен последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он поражен им? Объяснять.
7. Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.
8. Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?
9.Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
10. Предположим, вы проводите физическую лабораторию, в которой вас просят вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?
11. Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление.Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.
12. У некоторых лампочек есть три уровня мощности (не включая ноль), получаемые от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей нити необходимо для трех режимов мощности?
Задачи и упражнения
Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.
1. (a) Каково сопротивление десяти последовательно соединенных резисторов сопротивлением 275 Ом? (б) Параллельно?
2. (a) Каково сопротивление последовательно соединенных резисторов 1,00 × 10 2 Ом, 2,50 кОм и 4,00 кОм? (б) Параллельно?
3. Какое наибольшее и наименьшее сопротивление можно получить, соединив резисторы на 36,0 Ом, 50,0 Ом и 700 Ом?
4. Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5. Фара мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)
6.(a) Учитывая батарею на 48,0 В и резисторы на 24,0 и 96,0 Ом, найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.
7. Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите I 3 двумя следующими способами: (a) по известным значениям I и I 2 ; (б) используя закон Ома для R 3 . В обеих частях явно показано, как вы следуете шагам, описанным выше в стратегии решения проблем для последовательных и параллельных резисторов .
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация включена последовательно с R 1 .
8. Ссылаясь на рисунок 5: (a) Вычислите P 3 и обратите внимание на его сравнение с P 3 , найденным в первых двух примерах задач в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
9. См. Рисунок 6 и обсуждение затемнения света при включении тяжелого прибора. (a) Учитывая, что источник напряжения составляет 120 В, сопротивление провода составляет 0,400 Ом, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя через провода пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
10. Линия электропередачи на 240 кВ, имеющая 5,00 × 10 2 , подвешена к заземленным металлическим опорам с помощью керамических изоляторов, каждый из которых имеет сопротивление 1,00 × 10 9 Ом (рис. 9 (а)). Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы следуете шагам, описанным выше в стратегии решения проблем для последовательных и параллельных резисторов .
Рис. 9. Высоковольтная (240 кВ) линия электропередачи 5,00 × 10 2 подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает сопротивление 1,00 × 10 9 Ом каждый.
11. Покажите, что если два резистора R 1 и R 2 объединены, и один из них намного больше другого ( R 1 >> R 2 ): (a ) Их последовательное сопротивление почти равно большему сопротивлению R 1 .(б) Их параллельное сопротивление почти равно меньшему сопротивлению R 2 .
12. Необоснованные результаты Два резистора, один из которых имеет сопротивление 145 Ом, подключены параллельно, чтобы получить общее сопротивление 150 Ом. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
13. Необоснованные результаты Два резистора, один из которых имеет сопротивление 900 кОм, соединены последовательно, чтобы получить общее сопротивление 0.500 МОм. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Глоссарий
- серия:
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор:
- компонент, обеспечивающий сопротивление току, протекающему через электрическую цепь
- сопротивление:
- вызывает потерю электроэнергии в цепи
- Закон Ома:
- соотношение между током, напряжением и сопротивлением в электрической цепи: В = IR
- напряжение:
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором
- падение напряжения:
- потеря электроэнергии при прохождении тока через резистор, провод или другой компонент
- ток:
- поток заряда через электрическую цепь мимо заданной точки измерения
- Закон Джоуля:
- взаимосвязь между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемая следующим образом: [latex] {P} _ {e} = \ text {IV} [/ latex]
- параллельно:
- разводку резисторов или других компонентов в электрической цепи, так что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
Избранные решения проблем и упражнения
1.(а) 2,75 кОм (б) 27,5 Ом
3. (а) 786 Ом (б) 20,3 Ом
5. 29,6 Вт
7. (а) 0,74 А (б) 0,742 А
9. (а) 60,8 Вт (б) 3,18 кВт
11. (a) [латекс] \ begin {array} {} {R} _ {\ text {s}} = {R} _ {1} + {R} _ {2} \\ \ Rightarrow {R} _ {\ text {s}} \ приблизительно {R} _ {1} \ left ({R} _ {1} \ text {>>} {R} _ {2} \ right) \ end {array} \\ [/ латекс]
(b) [латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2} } = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ [/ latex],
, так что
[латекс] \ begin {array} {} {R} _ {p} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ приблизительно \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1}} = {R} _ {2} \ left ({R} _ {1 } \ text {>>} {R} _ {2} \ right) \ text {.} \ end {array} \\ [/ latex]
13. (a) –400 кОм (b) Сопротивление не может быть отрицательным. (c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.
Калькулятор закона Ома
Наш калькулятор закона Ома – это удобный небольшой инструмент, который поможет вам найти взаимосвязь между напряжением, током и сопротивлением в данном проводнике. Формула закона Ома и формула напряжения в основном используются в электротехнике и электронике.Кроме того, если вы знаете, как рассчитать мощность, вы можете найти его очень полезным при изучении электронных схем. Все эти расчеты вы производите с помощью нашего Калькулятора Ом.
В оставшейся части статьи вы найдете:
- Формула закона Ома
- Как использовать формулу напряжения
- Что такое уравнение мощности
- Как рассчитать мощность
- Закон Ома для анизотропных материалов
Формула закона Ома
Закон Ома – один из основных законов физики.Он описывает взаимосвязь между напряжением, силой тока (также известной как ток) и сопротивлением. Напряжение означает разность потенциалов между двумя точками электрического поля. Сила тока связана с потоком носителей электрического заряда, обычно электронов или электронодефицитных атомов. Последний термин, сопротивление, – это сопротивление вещества потоку электрического тока.
ЗаконОма гласит, что ток течет через проводник со скоростью, пропорциональной напряжению между концами этого проводника.Другими словами, соотношение между напряжением и током постоянно:
I / V = const
Формулу закона Ома можно использовать для вычисления сопротивления как отношения напряжения и тока. Это может быть записано как:
R = V / I
Где:
- R – сопротивление
- В – напряжение
- I – Текущий
Сопротивление выражается в омах. И устройство, и правило названы в честь Георга Ома – физика и изобретателя закона Ома.
Помните, что формула закона Ома относится только к веществам, которые способны вызывать энергию. такие как металлы и керамика. Однако есть много других материалов, для которых нельзя использовать формулу закона Ома, например, полупроводники и изоляторы. Закон Ома также действует только при определенных условиях, например, при фиксированной температуре.
Ищете практическое применение закона Ома? Обязательно ознакомьтесь с калькулятором светодиодного резистора!
Формула напряжения
Формула напряжения – это одно из трех математических уравнений, связанных с законом Ома.Это формула, приведенная в предыдущем абзаце, но переписанная так, чтобы вы могли рассчитать напряжение на основе тока и сопротивления, то есть формула напряжения является произведением тока и сопротивления. Уравнение:
В = ИК
Это значение измеряется в вольтах.
Какое уравнение для мощности?
Другая величина, которую вы можете вычислить на основании закона Ома, – это мощность. Мощность – это произведение напряжения и тока, поэтому уравнение выглядит следующим образом:
P = V x I
С помощью этой формулы вы можете рассчитать, например, мощность лампочки.Если вы знаете, что напряжение батареи составляет 18V , а ток 6A , вы можете, что мощность будет 108, со следующим расчетом:
P = 6A x 18V = 108 Вт
Как рассчитать мощность?
Если вы все еще не знаете, как рассчитать мощность по приведенным формулам, или просто хотите сэкономить время, вы можете использовать наш калькулятор закона Ома. Структура этого инструмента не слишком сложна, просто введите любые два из четырех значений, чтобы получить два других.Калькулятор закона Ома основан на формуле мощности вместе с формулой закона Ома. Все, что вам нужно сделать, чтобы получить значение мощности, это набрать:
- Напряжение (в вольтах)
- Ток (выраженный в амперах)
Тогда калькулятор закона Ома выдаст вам два значения – сопротивление, выраженное в омах, и мощность, выраженное в ваттах. Если вам нужен этот результат в другом устройстве, вы можете использовать наш калькулятор ватт в ампер.
Закон Ома для анизотропных материалов
Существует еще одна версия закона Ома, в которой используются электрические свойства проводника.Некоторые предпочитают его предыдущей формуле из-за его размерного вида. Электропроводящие материалы подчиняются закону Ома, когда удельное сопротивление материалов не зависит от величины и направления приложенного электрического поля.
Вы можете найти следующую формулу, если нажмете на кнопку Расширенный режим :
ρ = E / J , где
ρ– удельное сопротивление проводящего материала.E– вектор электрического поля.J– вектор плотности тока.
Что касается изотропных материалов, лучше использовать первую формулу, поскольку она намного менее сложна. Изотропные материалы – это материалы с одинаковыми электрическими свойствами во всех направлениях, например металлы и стекло. Эта формула может пригодиться при работе с анизотропными материалами, такими как дерево или графит.
Формулы мощности в однофазных и трехфазных цепях постоянного и переменного тока
Формулы и уравнения мощности в цепях постоянного и переменного тока 1-Φ и 3-Φ
Возвращаясь к основам, ниже приведены простые формулы электрической мощности для одиночных Цепи фазного переменного тока, трехфазные цепи переменного тока и цепи постоянного тока.Вы можете легко найти электрическую мощность в ваттах , используя следующие формулы электрической мощности в электрических цепях .
Базовая формула мощности в цепях переменного и постоянного тока
Формула мощности в цепях постоянного тока- P = V x I
- P = I 2 x R
- P = V 2 / R
- P = V x I x Cos Ф
- P = I 2 x R x Cos Ф
- P = V 2 / R (Cos Ф)
- P = √3 x V L x I L x Cos Ф
- P = 3 x V Ph x I Ph x Cos Ф
- P = 3 x I 2 x R x Cos Ф
- P = 3 (V 2 / R) x Cos Ф
Где:
Формулы питания переменного тока в сложных схемах: Комплексная мощность и полная мощность:Когда в цепи есть индуктор или конденсатор, wer становится комплексной степенью «S» , что означает, что он состоит из двух частей i.е. реальная и мнимая часть. Величина комплексной мощности называется полной мощностью | S |.
Где
- P – активная мощность
- Q – реактивная мощность
Действительная часть – Комплексная мощность «S» известна как активная или реальная мощность «P» , а мнимая часть известна как реактивная мощность «Q» .
- S = P + jQ
- P = V I cosθ
- Q = V I sinθ
Где
θ – фазовый угол между напряжением и током.
Коэффициент мощности:Коэффициент мощности «PF» – это отношение активной мощности «P» к полной мощности «| S |» . Математически коэффициент мощности – это косинус угла θ между активной и полной мощностью.
Где
| S | = √ (P 2 + Q 2 )
Другие формулы, используемые для коэффициента мощности, следующие:
Cosθ = R / Z
Где:
- Cosθ = коэффициент мощности
- R = сопротивление
- Z = импеданс (сопротивление в цепях переменного тока i.е. X L , X C и R , известные как Индуктивное реактивное сопротивление , емкостное реактивное сопротивление и сопротивление соответственно).
Cosθ = кВт / кВА
Где
- Cosθ = коэффициент мощности
- кВт = фактическая мощность в ваттах
- кВА = полная мощность в вольт-амперах или ваттах
Для определения коэффициента мощности используются дополнительные формулы.
Реальная мощность однофазного и трехфазного токаГде
- В действующее значение и I среднеквадратичное значение – среднеквадратичное значение напряжения и тока соответственно.
- В L-N & I L-N – это напряжение и ток между фазой и нейтралью соответственно.
- В L-L & I L-L – линейное напряжение и ток соответственно.
- Cosθ – коэффициент мощности PF.
Где
θ = – фазовый угол, т.е. разность фаз между напряжением и током.
В следующей таблице показаны различные формулы мощности для цепей переменного и постоянного тока.
| Количество | Постоянный ток | Переменный ток (1-фазный) | Переменный ток (3 фазы) |
Вт |
Сопутствующие формулы and Equations Posts:
[PDF] Расчеты электрических цепей – Скачать бесплатно PDF
1 Расчет электрических цепей Последовательные цепи Во многих цепях имеется более одного преобразователя (т.е. тост…
Вычисление электрических цепей Последовательные цепи Во многих цепях имеется более одного устройства преобразования (например, тостер, нагреватель, лампы и т. Д.), А в некоторых имеется более одного источника электроэнергии. Если компоненты схемы соединены встык, образуя единую петлю, это последовательная схема.Помните, что ток – это скорость, с которой электроны движутся по цепи. Так же, как в нескольких шлангах, соединенных последовательно, чтобы сформировать одну длинную линию, вода может выходить только на дальнем конце с той же скоростью, с которой она поступает (без учета трения).На каждом компоненте есть падение напряжения (и это сила, необходимая для преобразования электрической энергии в какую-либо другую форму). Все падения напряжения в цепи складываются в ЭДС. (Напряжение) источника питания. В приведенной выше схеме E = V1 + V2 (предполагается, что соединительные провода имеют очень маленькое сопротивление, что не является необоснованным предположением.) Амперметры Амперметры – это инструменты, которые измеряют ток и поэтому должны находиться на пути тока, то есть , последовательно с устройством, ток которого измеряется.
Падение напряжения на каждом компоненте можно рассчитать с помощью закона Ома, если известны ток цепи и значение сопротивления каждого компонента. (Помните, что ЭДС источника питания распространяется на всю цепь, а не только на какой-либо из компонентов.)
Рабочий пример: • Если показанная схема потребляет 10 ампер от источника питания, рассчитайте падение напряжения на каждом резисторе и объем ЭДС питания Обратите внимание, что поскольку это последовательная схема, ток на всех резисторах одинаков.
V1 = IR1 = 10 x 10 = 100 В V2 = IR2 = 10 x 20 = 200 В V3 = IR3 = 10 x 5 = 50 В При падении напряжения все складывается с напряжением питания EE
= V1 + V2 + V3 = 100 + 200 + 50 =
Если бы в приведенной выше схеме было задано напряжение питания, но не текущий объем, мы могли бы рассчитать его, потому что полное сопротивление последовательной цепи Rtotal – это просто сумма сопротивлений
Это общее сопротивление в цепи питания, поэтому эту схему можно заменить одним резистором на 35 Ом.
350 В
Ток питания
I
= E / Rt = 350/35 = 10 ампер
Посмотрите на схему ниже. Несмотря на то, что мы соединили два резистора, вы сможете сразу определить, какое падение напряжения на двух резисторах вместе.
Падение напряжения конечно 24 вольта.
Если указаны ЭДС E и отдельные сопротивления, рассчитайте ток цепи и напряжение на каждом резисторе упадет. 1 Сложите сопротивления, чтобы получить общее сопротивление 2 Рассчитайте ток цепи, разделив мощность E на RT 3 Рассчитайте падение напряжения на каждом резисторе по формуле: V1 = I x R1 V2 = I x R2 V3 = I x R3 и т. Д. .
A Рабочий пример • Рассчитав приведенную ниже схему, I Общее сопротивление 2 Ток. 3 Падение напряжения на каждом резисторе –
1. Общее сопротивление:
R всего
2. Ток (I) определяется с помощью закона Ома: I
Следовательно, ток цепи I
= = =
R1 + R2 + R3 40 + 5 + 80 125 Ом
=
E / RT
=
250/125
=
2 ампера
(3)
Падение напряжения на каждом резисторе: падение напряжения на R1 :
Падение напряжения на R2:
Падение напряжения на R3:
V1
V2
V3
=
I x R1
=
2 x 40
=
=
=
I x R2
=
2×5
=
10 вольт
=
I x R3
=
2 x 80
=
160 вольт As check
9000 вольт на резисторах должно составлять напряжение питания.т.е.= VD1 + VD2 + VD3 = 80 + 10 + 160 = 250 вольт.
Параллельная цепь Когда каждый из ряда компонентов схемы подключен к одному источнику питания или между одними и теми же двумя точками в цепи, они считаются подключенными параллельно.
Когда резисторы включены параллельно, на каждом из них наблюдается одинаковое падение напряжения. На рисунке 1 падение напряжения на R1, R2 и R3 будет одинаковым и будет напряжением питания. На рисунке 2 падение напряжения на E2, R3 и R4 будет одинаковым и составит V2
В отличие от последовательного соединения, ток в параллельных резисторах не такой же (если только они не имеют одинаковое значение сопротивления).
Вольтметры Вольтметры – это приборы, которые используются для измерения напряжений либо ЭДС, либо падений напряжения. Так как на резисторе (или на выводах батареи или генератора) происходит падение напряжения, вольтметр всегда подключается параллельно нагрузке
Другой Рабочий пример • Чтобы измерить ток на каждом резисторе, нам необходимо знать падение напряжения на каждом резисторе.
Какой ток в IMS? Ответ:
Другой рабочий пример Изучите эту схему:
Рассчитайте величину тока в R1.I2
=
V2 R2
=
100 10
=
10A
I3
=
V2 R3
=
100 5
000=
0005
= 200004
V2 R4
=
100 5
=
20A
I5
=
V2 R5
=
100 25
=
00040004 I2 + I3 + I4 + I5 10 + 20 + 20 + 4 54A
Эквивалентное сопротивление Есть еще одна вещь, которую мы можем узнать о параллельной цепи, ее эквивалентное комбинированное сопротивление. параллельна и заставит тот же комбинированный ток потребляться от источника питания.
Экспериментально можно показать, что два резистора на 6 Ом и 12 Ом, включенные параллельно, могут быть заменены одним резистором на 4 Ом для измерения тока.
Расчет эквивалентного сопротивления Если мы подключим омметр к цепи, как показано ниже, он будет измерять эквивалентное комбинированное сопротивление резисторов 6 Ом и 12 Ом, включенных параллельно. Как вы можете видеть, он показывает четыре Ом
120
Итак, с параллельными цепями вы не добавляете сопротивления.Чтобы подтвердить показания счетчика, мы можем вычислить эквивалентное сопротивление, используя закон Ома.
Мы уже нашли полный ток, который будет протекать через эквивалентное сопротивление, и знаем напряжение на нем.
Использование формулы закона Ома: RT
=
EI
=
24 6
=
4 Ом
Таким образом, мы заключаем, что параллельное сопротивление 6 Ом и 12 Ом будет действовать как если бы они были единичным сопротивлением 4 Ом. Важно отметить, что величина эквивалентного сопротивления.(4 Ом) ниже наименьшего параллельного сопротивления (6 Ом). В параллельной цепи полное сопротивление всегда меньше наименьшего сопротивления.
Метод 2 Другой способ вычисления параллельного сопротивления ряда резисторов, включенных параллельно, основан на формуле 1 Эквивалентное сопротивление
=
1 + R1
1 R2
+
1 R3
Два резистора, R1 2 Ом и резистор 3 Ом подключены параллельно к источнику питания 100 В. Какой ток будет потребляться этой комбинацией от источника питания?
A Рабочий пример • Изучите принципиальную схему ниже и сравните ее со схемой на странице 17
Вы можете видеть, что добавление еще одного резистора на 12 Ом параллельно привело к увеличению общего тока до 8A.Определите эквивалентное сопротивление сейчас. 1 RT
=
1 R1
+
1 R2
+
1 R3
1 RT
=
1 6
+
1 12
120004 +
+
1 RT
=
4 12
RT
3 Ом
Или, для расчета по закону Ома: =
E IT
=
24 8
=
3 Ом
RT
Эквивалент сопротивление было 4 Ом до того, как в параллель был добавлен резистор на 12 Ом.Таким образом, добавление резистора снизило эквивалентное сопротивление. Например, если добавить еще один турникет на футбольном поле, толпа будет быстрее перемещаться по площадке, или, другими словами, весь поток людей будет испытывать меньшее сопротивление движению со стороны добавление дополнительного турникета В таблице ниже указан порядок, в котором вы должны работать при работе с простыми обычными цепями, в которых указаны значения напряжения питания и отдельных сопротивлений. 1 Определите падение напряжения на каждом параллельном сопротивлении.Падение напряжения на каждом сопротивлении одинаковое. 2 Рассчитайте ток в каждом параллельном сопротивлении, используйте формулу закона Ома: I = V R Двумя известными значениями являются падение напряжения на резисторе и сопротивление резистора.3 Определите полный ток, протекающий в цепи. Полный ток равен сумме токов в параллельных резисторах.
4 Рассчитайте эквивалентное сопротивление Используйте формулу закона Омов: I = V R Два известных значения – это падение напряжения на резисторе и 1T – общий ток.
Чтобы сложить дроби Для сложения или вычитания дробей (что часто приходится делать для решения проблем параллельной цепи) будут полезны следующие рекомендации:
Параллельные цепи сериисерия с одной или несколькими параллельными комбинациями
В приведенной выше схеме ток будет течь через последовательный резистор, а затем делиться на A и течь через обе ветви параллельной комбинации. Поскольку через последовательный резистор прошел ток, на нем произойдет падение напряжения.Следовательно, напряжение на параллельных резисторах не будет таким же, как напряжение, приложенное к цепи. Это будет ЭДС. напряжение минус падение напряжения на последовательном резисторе. Чтобы вычислить полное сопротивление в цепи, сначала уменьшите параллельную часть цепи до эквивалентного значения сопротивления, а затем рассмотрите всю цепь как последовательную цепь. Это эквивалентное значение сопротивления представляет собой значение сопротивления, которое заменит подключенные параллельно резисторы.
• Два резистора R1 и R2 на два Ом и четыре Ом подключаются параллельно, а затем последовательно соединяются с резистором R3 на 4 Ом 1
Рассчитайте общее сопротивление цепи.
Эквивалентное сопротивление параллельной ветви = RP 1 = RP
1 + R1
1 R2
1 = RP
1 2
1 4
RP
=
3 4
=
4 3=
+
1,3 Ом
Общее сопротивление цепи = RT RT = R3 + RP = 1,3 + 4 = 5,3 Ом 2
Если бы эта цепь была теперь подключена к источнику питания 100 В, какой бы на ней ток? брать.
IT = E RT = 100 5,3 = 18.9A
2
V1
V2
V2
Каким будет падение напряжения на каждом резисторе.
=
IT x эквивалент R R1 и R2
=
18,9 x 1,3
=
24,6V
=
IT x R3
=
18,9 x 4
V=
E – V1
=
100 – 24,6
=
75,4 V
(Небольшая разница в ответах связана с точностью в десятичных разрядах, но не существенна.)
Резюме В этом модуле рассмотрены последовательные цепи, в которых резисторы соединены встык, а особенности последовательной цепи: (a) Ток имеет одинаковое значение во всей цепи. (b) «Общее сопротивление последовательной цепи – это сумма сопротивлений. (c) Падение напряжения на каждом резисторе может быть рассчитано с использованием закона Ома, т.е.Падение напряжения = ток цепи x сопротивление (d) Падение напряжения на каждом резисторе при сложении равно напряжению питания (E).Затем была рассмотрена параллельная схема, в которой два или более резистора подключены к источнику питания или между одними и теми же двумя точками в цепи. A
Падение напряжения на всех резисторах, включенных параллельно, одинаковое.
B
Общее сопротивление параллельной цепи RT можно рассчитать по формуле: 1 RP
=
1 R1
+
1 R2
+
1 R3
C Ток в каждой Резистор можно рассчитать из падения напряжения на резисторе, деленного на его сопротивление (обратите внимание, что падение напряжения на резисторах будет одинаковым для всех резисторов в параллельной ветви).Если параллельная ветвь – единственное, что есть в цепи, падение напряжения на ней будет таким же, как и напряжение питания E. D Полный ток цепи входит в ветвь, а затем разделяется, чтобы пройти через параллельные резисторы пропорционально их значениям. Таким образом, полный ток цепи – это сумма всех токов в параллельном банке.
Третий тип схемы – это последовательно-параллельная схема, в которой некоторые резисторы соединены последовательно с параллельными рядами резисторов. В последовательной / параллельной цепи следует помнить следующее: A Общее сопротивление цепи – это сумма резисторов, включенных последовательно, плюс эквивалентные сопротивления всех параллельных групп.B Общий ток в цепи можно рассчитать, разделив напряжение питания E на общее сопротивление цепи или вычислив все токи в любом параллельном блоке и сложив их вместе, или разделив падение напряжения на любом последовательном резисторе на его сопротивление. . C Общее напряжение источника питания E можно рассчитать, сложив все падения напряжения в цепи (помня, что на каждом последовательном резисторе есть падение напряжения, но только у каждой параллельной группы есть падение напряжения на одно вольт).
Калькулятор закона Ома и электрические формулы
Используйте закон Ома для расчета напряжения, тока, сопротивления или мощности в электрической цепи.Введите любые два известных значения, чтобы найти два других.
Например, введите напряжение и мощность, чтобы найти ток и сопротивление.
Что такое закон Ома?
Закон Ома определяет соотношение между электрическим током, сопротивлением и напряжением. Более конкретно, в нем говорится, что ток через элемент схемы прямо пропорционален приложенной к нему разности потенциалов и обратно пропорционален сопротивлению . [1]
Закон Ома позволяет рассчитать напряжение, ток, мощность и сопротивление электрической цепи, если вы знаете хотя бы два других значения.
Например, если вы знаете напряжение и сопротивление, воспользуйтесь калькулятором выше, чтобы найти мощность и ток по закону Ома. Кроме того, вы можете использовать калькулятор для вычисления мощности и сопротивления, если вы знаете напряжение и ток.
Формула закона Ома
Формула закона Ома: I = E / R, где I – ток через проводник, измеренный в амперах, E – разность потенциалов на проводе, измеренная в вольтах, а R – измеренное сопротивление проводника. в ом. [2]
I = ER
Формула утверждает, что ток I равен напряжению E , деленному на сопротивление R .
Треугольник закона Ома
Треугольник закона Ома показывает, как рассчитать напряжение, ток или сопротивление. Чтобы использовать его, накройте единицу, которую вы хотите вычислить, чтобы открыть формулу для ее решения.
Треугольник закона Ома, где E представляет напряжение, I представляет ток, а R представляет сопротивление.Например, чтобы найти вольты, прикройте E большим пальцем, и это покажет, что напряжение равно I × R.
Что означают буквы в формуле закона Ома?
В формуле закона Ома E представляет электродвижущую силу или напряжение, I представляет силу или ток, а R представляет сопротивление.
Георг Симон Ом создал закон Ома в статье, опубликованной в 1827 году, [3] задолго до того, как были определены единицы измерения напряжения, тока и сопротивления.
Вольт, ампер и ом были определены только в 1881 году, спустя более 50 лет после того, как был опубликован закон Ома. Это объясняет, почему буквы не относятся к современным единицам, используемым в формуле.
Формула силы
Формула мощности гласит, что электрическая мощность, измеренная в ваттах, равна току в цепи, умноженному на напряжение. Эта формула очень похожа на закон Ома и может помочь найти мощность или мощность.
Мы часто используем формулу мощности в сочетании с законом Ома для определения электрических свойств, когда мощность цепи известна.
P = I × E
Таким образом, формула мощности утверждает, что мощность P равна току I, , умноженному на напряжение E . [4]
Треугольник силы
Треугольник мощности иллюстрирует формулу для определения ватт, вольт или ампер. Как и в случае с другим треугольником, накройте единицу измерения, которую вы хотите решить, чтобы открыть формулу для ее решения.
Например, чтобы найти усилители, прикройте I большим пальцем, чтобы увидеть, что ток равен P / E.
Формула мощности, где P представляет мощность, I представляет ток, а E представляет напряжение.Наш калькулятор ватт в ампер использует эту формулу, например, для преобразования мощности в ток в электрических цепях.
Колесо закона Ома
Мы можем использовать закон Ома для расчета вольт, ватт, ампер или ом, если известны как минимум два измерения. Формула позволяет нам вывести уравнения для расчета любого измерения с учетом двух других известных значений.
Колесо закона Ома показывает все формулы, которые вы можете использовать для определения вольт, ватт, ампер или ом. См. Все производные формулы ниже.
Колесо закона Ома со всеми формулами, которые можно использовать для расчета вольт, ампер, ом или ватт.Формулы напряжения
Найдите напряжение, используя следующие формулы:
Напряжение = ток × сопротивление
Напряжение = мощность ÷ ток
Напряжение = мощность × сопротивление
Формулы мощности
Найдите мощность по этим формулам:
Мощность = Напряжение × Ток
Мощность = Напряжение 2 ÷ Сопротивление
Мощность = Ток 2 × Сопротивление
Текущие формулы
Решите для тока, используя эти формулы:
Ток = Напряжение ÷ Сопротивление
Ток = Мощность ÷ Напряжение
Ток = мощность ÷ сопротивление
Формулы сопротивления
Найдите сопротивление, используя следующие формулы:
Сопротивление = Напряжение ÷ Ток
Сопротивление = Напряжение 2 ÷ Мощность
Сопротивление = мощность ÷ ток 2
Мы используем закон Ома для многих вещей, таких как определение максимального размера микроволн или максимального количества осветительных приборов, с которыми цепь может безопасно обращаться, не создавая опасности возгорания.
Наш калькулятор затрат на освещение может помочь определить потребление энергии на освещение, а наш калькулятор затрат на электроэнергию поможет определить затраты на питание электрических устройств.
Используйте закон Ома, чтобы определить размер электрической цепи или выяснить, какой размер нагревателя можно безопасно использовать в обычной розетке. Вы также можете найти наш калькулятор падения напряжения, чтобы определить падение напряжения, необходимый минимальный размер провода и максимальную длину провода для вашего следующего электрического проекта.
Расчет мощности схемы – Высшая школа физики
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Калькулятор законаОм
Укажите любые 2 значения и нажмите «Рассчитать», чтобы получить другие значения в уравнениях закона Ома V = I × R и P = V × I.
Закон Ома
ЗаконОма гласит, что ток через проводник между двумя точками прямо пропорционален напряжению.Это верно для многих материалов в широком диапазоне напряжений и токов, а сопротивление и проводимость электронных компонентов, изготовленных из этих материалов, остаются постоянными. Закон Ома верен для цепей, содержащих только резистивные элементы (без конденсаторов или катушек индуктивности), независимо от того, является ли управляющее напряжение или ток постоянным (DC) или изменяющимся во времени (AC). Его можно выразить с помощью ряда уравнений, обычно всех трех вместе, как показано ниже.
Где:
В – напряжение в вольтах
R – сопротивление в Ом
Я ток в амперах
Электроэнергетика
Мощность – это скорость, с которой электрическая энергия передается по электрической цепи в единицу времени, обычно выражается в ваттах в Международной системе единиц (СИ).Электроэнергия обычно вырабатывается электрическими генераторами и поставляется предприятиям и домам через электроэнергетику, но также может поставляться от электрических батарей или других источников.
В резистивных цепях закон Джоуля можно объединить с законом Ома для получения альтернативных выражений для количества рассеиваемой мощности, как показано ниже.
Где:
P – мощность в ваттах
Колесо формул закона Ома
Ниже приведено колесо формул для соотношений по закону Ома между P, I, V и R.По сути, это то, что делает калькулятор, и это просто представление алгебраической манипуляции с уравнениями выше. Чтобы использовать колесо, выберите переменную для поиска в середине колеса, затем используйте соотношение для двух известных переменных в поперечном сечении круга.
.
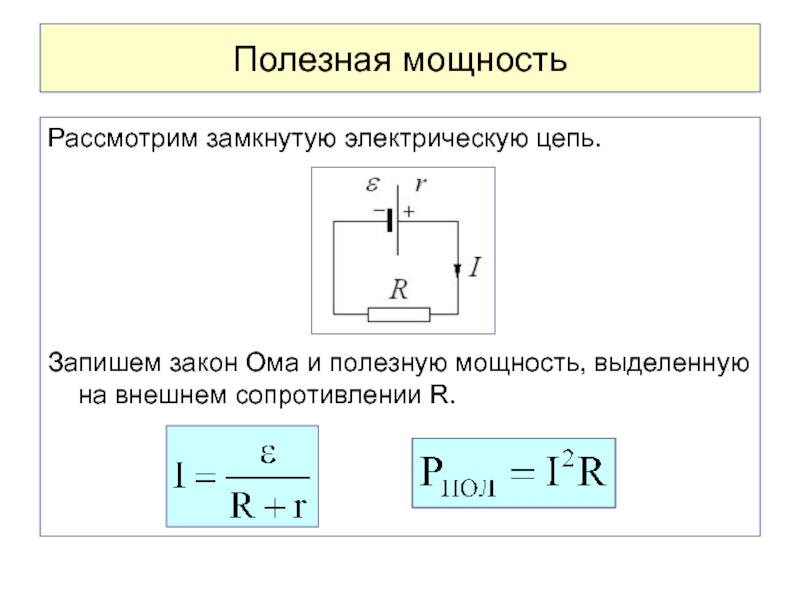 7)
7)