Электромагнетизм в физике: основные формулы
Основные формулы электромагнетизма
Кратность электрического заряда
Здесь q — заряд (Кл), N — число не скомпенсированных элементарных зарядов в заряде q (безразмерное), — элементарный заряд (Кл).
Поверхностная плотность заряда
Здесь — поверхностная плотность заряда , q — заряд на поверхности (Кл), S — площадь этой поверхности .
Закон Кулона
Здесь F — сила взаимодействия точечных зарядов (Н), — коэффициент пропорциональности, и — модули взаимодействующих зарядов (Кл), — относительная диэлектрическая проницаемость среды (безразмерная), —электрическая постоянная, r — расстояние между зарядами (м).
Напряженность электрического поля
Здесь Е — напряженность электрического поля (Н/Кл или В/м), F — сила, действующая на заряд (Н), q — заряд (Кл).
Напряженность поля точечного заряда
Здесь Е — напряженность поля (Н/Кл или В/м), k — коэффициент пропорциональности , q — модуль заряда (Кл), — относительная диэлектрическая проницаемость среды (безразмерная), — электрическая постоянная (Ф/м), r — расстояние от точки с напряженностью Е до заряда q (м).
Напряженность поля бесконечной равномерно заряженной плоскости
Здесь Е — напряженность электрического поля (В/м), — поверхностная плотность зарядов на плоскости , £0— электрическая постоянная (Ф/м), — диэлектрическая проницаемость среды (безразмерная).
Напряженность поля двух разноименно и равномерно заряженных плоскостей с одинаковой поверхностной плотностью зарядов (напряженность поля плоского конденсатора)
Все величины те же, что и в предыдущей формуле.
Работа перемещения заряда в однородном электрическом поле
Здесь А — работа перемещения заряда (Дж), Е — напряженность однородного поля (Н/Кл или В/м), q — перемещаемый заряд (Кл), d — проекция перемещения на силовую линию однородного поля (м).
Потенциал электрического поля
Здесь — потенциал электрического поля (В), — потенциальная энергия заряда (Дж), q — заряд, обладающий этой энергией в электрическом поле (Кл).
Потенциал поля точечного заряда
Все величины те же, что и в аналогичной формуле напряженности.
Разность потенциалов
Здесь — разность потенциалов между двумя точками поля (В), U — напряжение (В), А — работа перемещения заряда (Дж), q — перемещаемый заряд (Кл).
Связь напряженности с разностью потенциалов в однородном электрическом поле
Здесь Е — напряженность электрического поля (Н/Кл или В/м), — разность потенциалов между двумя точками поля (В), U — напряжение между этими точками (В), d — проекция расстояния между этими точками на силовую линию поля (м).
Электроемкость проводника
Здесь С — емкость проводника (Ф), q — заряд проводника (Кл), — его потенциал (В).
Емкость сферического проводника
Здесь С — емкость сферического проводника (Ф), — электрическая постоянная (Ф/м), — относительная диэлектрическая проницаемость среды (безразмерная), R — радиус сферы (м).
Емкость конденсатора
Здесь С — емкость конденсатора (Ф), q — его заряд (Кл), — разность потенциалов между его обкладками (В), U — напряжение между обкладками (В).
Емкость плоского конденсатора
Здесь С — емкость плоского конденсатора (Ф), — электрическая постоянная (Ф/м), — относительная диэлектрическая проницаемость среды (безразмерная), S — площадь обкладок конденсатора , d — расстояние между обкладками (м).
Последовательное соединение конденсаторов
q — одинаков на всех конденсаторах
Если все конденсаторы имеют одинаковую емкость С, то
Здесь q — заряд конденсаторов (Кл), — общее напряжение на батарее конденсаторов (В), — напряжения на отдельных конденсаторах (В), N — число конденсаторов (безразмерное), — общая емкость батареи конденсаторов (Ф), — емкости отдельных конденсаторов (Ф).
Параллельное соединение конденсаторов
U — одинаково на всех конденсаторах
Если все конденсаторы имеют одинаковую емкость С, то
Здесь U — напряжение на конденсаторах (В), — общий заряд батареи конденсаторов (Кл), — заряды отдельных конденсаторов (Кл), N — число конденсаторов (безразмерное), — емкость батареи конденсаторов (Ф), , — емкости отдельных конденсаторов (Ф).
Формулы энергии электрического поля проводника
Здесь — энергия электрического поля (Дж), С — емкость проводника (Ф), — потенциал проводника (В), q — заряд проводника (Кл).
Формулы энергии электрического поля конденсатора
Здесь — энергия электрического поля конденсатора (Дж), С — емкость конденсатора (Ф), q — заряд на его обкладках (Кл), U — напряжение на обкладках конденсатора (В).
Формула энергии системы точечных зарядов
Здесь — энергия системы N точечных зарядов (Дж), — заряды, входящие в систему (Кл), — потенциалы полей, созданных в точке, где находится один из зарядов, остальными зарядами системы (В).
Формулы силы тока
Здесь I — сила постоянного тока (A), q — заряд, прошедший через поперечное сечение проводника (Кл), t — время прохождения заряда (с), n — концентрация свободных электронов , е — модуль заряда электрона (Кл), v — скорость упорядоченного движения электронов по проводнику (м/с), S — площадь поперечного сечения проводника .
Формулы плотности тока
Здесь j — плотность тока , I — сила тока (A), S — площадь поперечного сечения проводника , п — концентрация свободных электронов в проводнике , е — модуль заряда электрона (Кл), v — скорость упорядоченного движения свободных электронов (м/с).
Формулы сопротивления проводника
Здесь R — сопротивление проводника (Ом), U — напряжение на нем (В), I — сила тока в проводнике (А), — удельное сопротивление (Ом • м),
Зависимость сопротивления металлического проводника от температуры
Здесь R — сопротивление проводника при температуре t °C (Ом), — сопротивление проводника при О °C (Ом), а — температурный коэффициент сопротивления , t — температура по шкале Цельсия, — изменение абсолютной температуры проводника при нагревании от О °C = 273 К до абсолютной температуры Т (К).
Закон Ома для однородного участка цепи
Здесь I — сила тока (A), U — напряжение (В), R — сопротивление участка (Ом).
Последовательное соединение проводников
I — одинакова во всех проводниках
Если все проводники имеют одинаковое сопротивление, то
для двух последовательных проводников
Здесь I — сила тока (А), — общее напряжение на всех последовательно соединенных проводниках (В), ,…, — напряжения на отдельных проводниках (В), — общее сопротивление всех последовательно соединенных проводников (Ом), — сопротивления отдельных проводников (Ом), N — количество проводников (безразмерное).
Параллельное соединение проводников
U — одинаково на всех проводниках
Если все проводники имеют одинаковое сопротивление, то
общее сопротивление двух параллельных проводников
общее сопротивление трех параллельных проводников
— для двух параллельных проводников
Здесь U — напряжение на проводниках (В), — сила тока в неразветвленном участке цепи (А), — сила тока в отдельных проводниках (А), — общее сопротивление параллельных проводников (Ом), — сопротивления отдельных проводников (Ом), N — количество проводников (безразмерное).
Закон Ома для неоднородного участка цепи
Здесь I — сила тока (А), — разность потенциалов на концах участка (В), — ЭДС, действующая в участке (В), R — сопротивление участка (Ом).
Формула ЭДС
Здесь — ЭДС (В), — работа сторонних сил (Дж), q — перемещаемый заряд (Кл).
Закон Ома для всей цепи
в случае соединенных последовательно одинаковых источников тока
в случае соединенных параллельно одинаковых источников тока
Здесь I — сила тока в цепи (А), — ЭДС источника тока (В), R — сопротивление внешней части цепи (Ом), r — внутреннее сопротивление или сопротивление источника тока (Ом), N — количество одинаковых источников тока (безразмерное).
Сила тока короткого замыкания
Все величины названы в предыдущей формуле.
Расчет сопротивления шунта к амперметру
Здесь — сопротивление шунта (Ом), — сопротивление амперметра (Ом), — число, показывающее, во сколько раз измеряемая амперметром сила тока I больше силы тока , на которую он рассчитан (безразмерное число).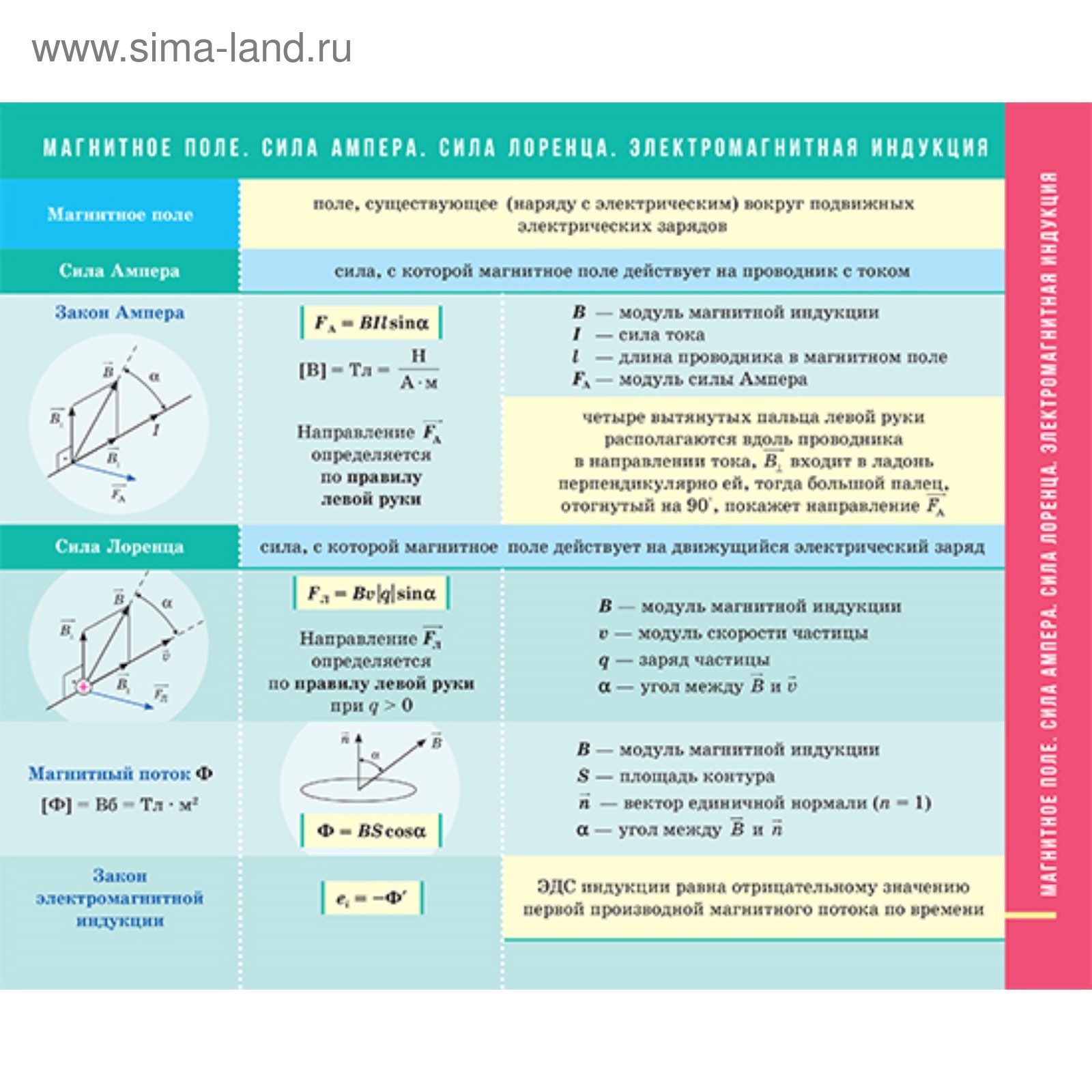
Расчет добавочного сопротивления к вольтметру
Здесь — добавочное сопротивление (Ом), — сопротивление вольтметра (Ом), — число, показывающее, во сколько раз измеряемое напряжение U больше напряжения , на которое рассчитан вольтметр (безразмерное число).
Работа тока
Здесь А — работа тока (Дж), U — напряжение на участке цепи (В), I — сила тока в цепи (A), t — время прохождения тока (с), q — прошедший по цепи заряд (Кл), — разность потенциалов на концах участка цепи (В), R — сопротивление участка цепи (Ом), — ЭДС источника тока (В), Р — мощность тока (Вт).
Мощность тока
Здесь Р — мощность тока (Вт), U — напряжение (В), I — сила тока (A), R — сопротивление (Ом), — ЭДС источника тока (В), А — работа тока (Дж), t — время (с).
Закон Джоуля — Ленца
Здесь Q — количество теплоты (Дж). Остальные величины названы в предыдущей формуле.
Коэффициент полезного действия (КПД) электрической цепи
Здесь — КПД электрической цепи (% или безразмерный), U — напряжение на внешнем участке цепи (В), R — сопротивление внешнего участка цепи (Ом), r — внутреннее сопротивление или сопротивление источника тока (Ом), — ЭДС источника тока (В).
Закон Фарадея для электролиза
Здесь m — масса вещества, выделившегося на электроде (кг), k — электрохимический эквивалент этого вещества (кг/Кл), q — заряд, прошедший через электролит, I — сила тока в электрохимической ванне (A), t — время электролиза (с), F — число Фарадея (Кл/моль), М — молярная масса выделившегося вещества (кг/моль, n — валентность этого вещества (безразмерная).
Формулы индукции магнитного поля
Здесь В — индукция магнитного поля (Тл), — максимальный момент сил, вращающих контур с током в магнитном поле (Н • м), I — сила тока в контуре (A), S — площадь контура — максимальная сила Ампера, действующая на проводник с током в магнитном поле (Н), l — длина проводника в магнитном поле (м).
Формула силы Ампера
Здесь — сила Ампера, действующая на проводник с током в магнитном поле (Н), В — индукция магнитного поля (Тл), I — сила тока в проводнике (А), l — длина проводника в магнитном поле (м), — угол между направлением тока в проводнике и вектором магнитной индукции (рад).
Формула момента сил, вращающих контур с током в магнитном поле
Здесь М — момент сил, вращающих контур с током в магнитном поле (Н • м), В — индукция магнитного поля (Тл), I — сила тока в контуре (A), S — площадь контура — угол между нормалью к плоскости контура и вектором магнитной индукции (рад).
Формула силы Лоренца, действующей на заряд, движущийся в магнитном попе
Здесь — сила Лоренца, действующая на заряд, движущийся в магнитном поле (Н), В — индукция магнитного поля (Тл), q — заряд (Кл), v — скорость заряда (м/с), — угол между векторами магнитной индукции и скорости (рад).
Формула магнитного потока
Здесь Ф — магнитный поток сквозь поверхность (Вб), S — площадь поверхности — угол между нормалью к поверхности и вектором магнитной индукции (рад), L — индуктивность контура (Гн), I — сила тока в контуре (А).
Формула ЭДС электромагнитной индукции
Здесь — ЭДС индукции в контуре (В), — скорость изменения магнитного потока, пересекающего контур (Вб/с), N — число витков в контуре (безразмерное), — первая производная магнитного потока по времени (Вб/с).
Формула ЭДС индукции в проводнике, движущемся поступательно в магнитном поле
Здесь — ЭДС индукции в проводнике (В), В — индукция магнитного поля (Тл), v — скорость проводника в магнитном поле (м/с), l — длина проводника в магнитном поле (м), — угол между векторами скорости и магнитной индукции (рад), — максимальная ЭДС индукции, когда проводник движется перпендикулярно линиям магнитной индукции.
Формула ЭДС индукции в контуре, вращающемся в магнитном поле
Здесь — ЭДС индукции во вращающемся контуре (В), В — индукция магнитного поля (Тл), — угловая скорость вращения (рад/с), S — площадь контура, N — число витков в контуре (безразмерное), — угол между вектором индукции и нормалью к плоскости контура, —максимальная ЭДС индукции, когда угол между нормалью к плоскости контура и вектором магнитной индукции равен 90°, т.е. когда плоскость контура параллельная линиям магнитной индукции.
Формула ЭДС самоиндукции
Здесь — ЭДС самоиндукции в контуре (В), L — индуктивность контура (Гн), — скорость изменения силы тока в контуре (А/с), — первая производная силы тока по времени.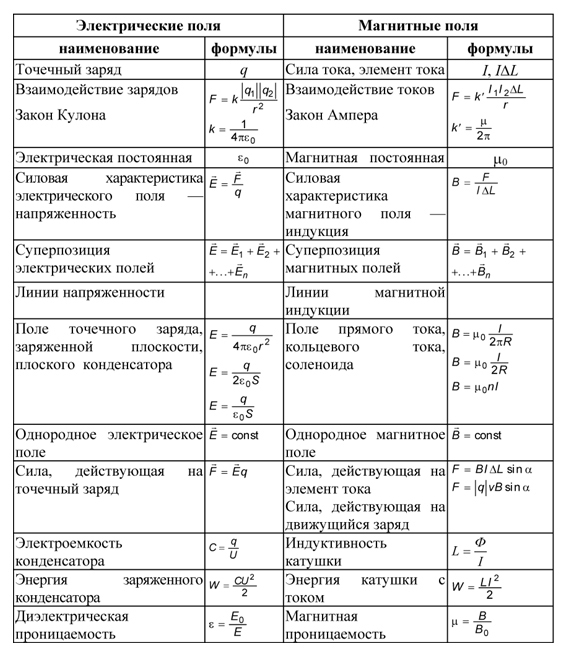
Формула магнитной проницаемости магнетика
Здесь — магнитная проницаемость магнетика (безразмерная), В — индукция магнитного поля в магнетике (Тл), — индукция магнитного поля в вакууме (Тл).
Формула энергии магнитного поля
Здесь — энергия магнитного поля (Дж), L — индуктивность контура (Гн), I — сила тока в контуре (А).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Все формулы электромагнетизма. Основные формулы по физике
Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем . Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).
Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл). Если в магнитное поле с индукцией B поместить проводник длиной l с током I , то на него будет действовать сила, называемая силой Ампера , которая вычисляется по формуле:
где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.
Для определения направления силы Ампера обычно используют правило «Левой руки» : если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).
рисунок).
Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.
Момент сил, действующих на рамку с током
Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера. Вращательный момент сил Ампера равен:
где: S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции (нормаль – вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.
Сила Лоренца
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I , находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца . Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B , двигающуюся со скоростью v , вычисляется по следующей формуле:
Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет отрицательный заряд, то направление силы Лоренца, найденное по правилу левой руки, надо будет заменить на противоположное.
Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает . Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:
Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R .
Теория о магнитном поле
Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I 1 и I 2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:
Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I 1 и I 2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:
где: μ 0 – постоянная величина, которую называют магнитной постоянной . Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:
μ 0 = 4π ·10 –7 H/A 2 ≈ 1,26·10 –6 H/A 2 .
Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:
где: μ – магнитная проницаемость вещества (об этом чуть ниже).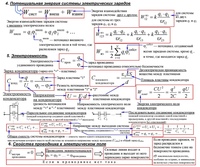 Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:
Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:
Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй – на юг. Отсюда название полюсов: северный (N ) и южный (S ). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N ) и южный (красным цветом или буквой S ). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.
Вектор магнитной индукции
Вектор магнитной индукции – векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику. Обозначается В , единица измерения – 1 Тесла. 1 Тл – очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Обозначается В , единица измерения – 1 Тесла. 1 Тл – очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.
Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:
В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки» : если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:
В случае прямого тока линии магнитной индукции – окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.
Вектора магнитной индукции направлены по касательной к окружности.
Соленоид – намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):
Линии магнитного поля имеют вид замкнутых линий – это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.
Магнитные свойства вещества
Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ , для которой верно следующее:
Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики – кислород, платина, магний – несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков – железо, никель, кобальт – μ >> 1. Например, у железа μ ≈ 25000.
В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики – кислород, платина, магний – несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков – железо, никель, кобальт – μ >> 1. Например, у железа μ ≈ 25000.
Магнитный поток. Электромагнитная индукция
Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:
где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).
Единица магнитного потока в системе СИ называется Вебером (Вб).
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции ε инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.
- Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
- Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
При решении задач важно сразу определить за счет чего меняется магнитный поток.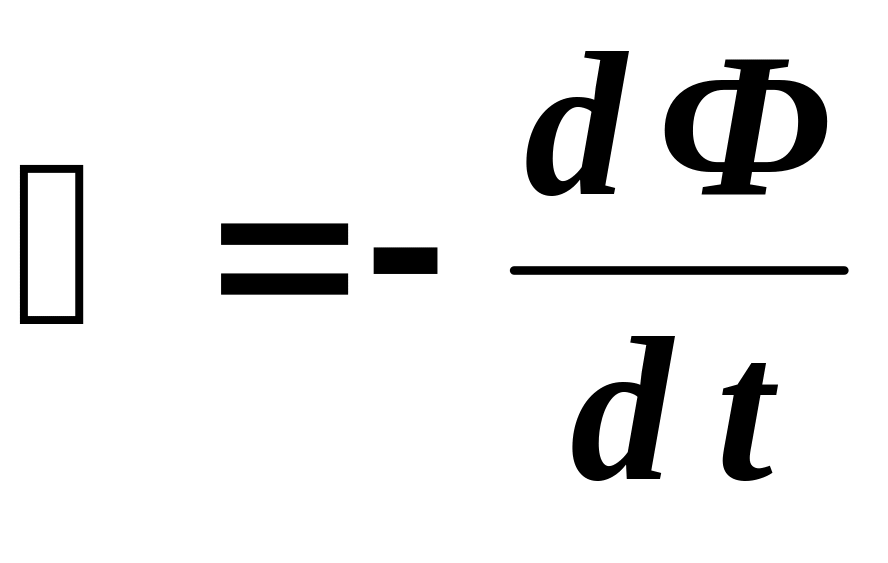 Возможно три варианта:
Возможно три варианта:
- Меняется магнитное поле.
- Меняется площадь контура.
- Меняется ориентация рамки относительно поля.
При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S , вращающемся с угловой скоростью ω в магнитном поле с индукцией В :
Движение проводника в магнитном поле
При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:
где: α – угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.
Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω , то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:
Индуктивность.
 Самоиндукция. Энергия магнитного поля
Самоиндукция. Энергия магнитного поляСамоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ , пронизывающий контур или катушку с током, пропорционален силе тока I :
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).
Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:
Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:
где: n – концентрация витков на единицу длины катушки:
ЭДС самоиндукции , возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:
Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия W м магнитного поля катушки с индуктивностью L , создаваемого током I , может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI ):
Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):
Правило Ленца
Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.
В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.
На этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
 В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
В проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током . За направление электрического тока принято направление движения положительных свободных зарядов, хотя в большинстве случае движутся электроны – отрицательно заряженные частицы.
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда q , переносимого через поперечное сечение проводника за интервал времени t , к этому интервалу времени:
Если ток не постоянный, то для нахождения количества прошедшего через проводник заряда рассчитывают площадь фигуры под графиком зависимости силы тока от времени.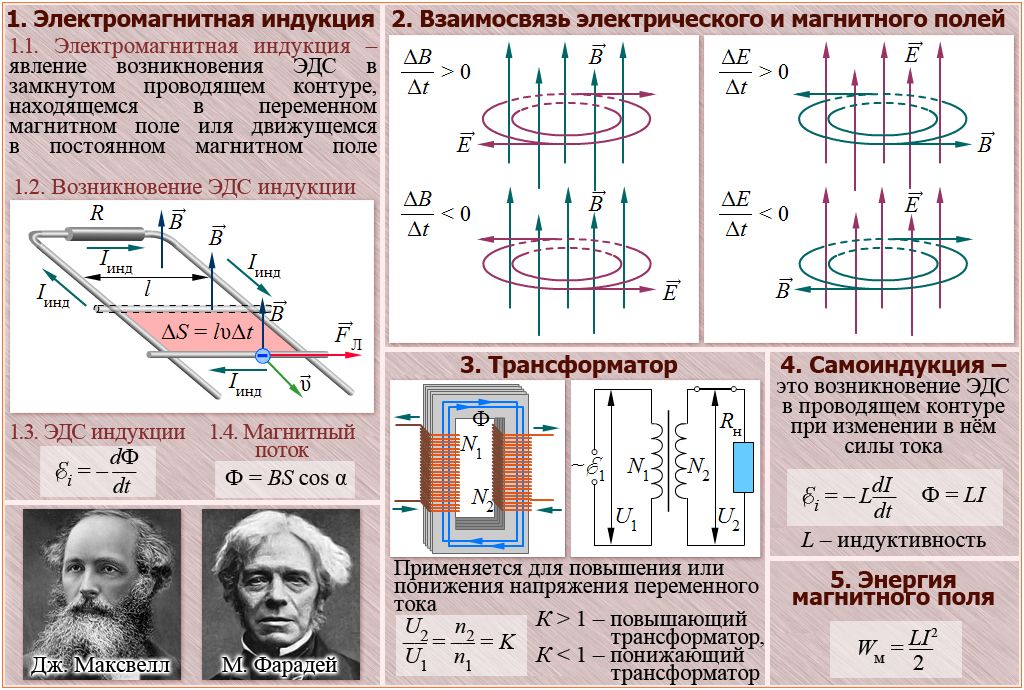
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным . Сила тока измеряется амперметром, который включается в цепь последовательно. В Международной системе единиц СИ сила тока измеряется в амперах [А]. 1 А = 1 Кл/с.
Находится как отношение всего заряда ко всему времени (т.е. по тому же принципу, что и средняя скорость или любая другая средняя величина в физике):
Если же ток равномерно меняется с течением времени от значения I 1 до значения I 2 , то можно значение среднего тока можно найти как среднеарифметическое крайних значений:
Плотность тока – сила тока, приходящаяся на единицу поперечного сечения проводника, рассчитывается по формуле:
При прохождении тока по проводнику ток испытывает сопротивление со стороны проводника. Причина сопротивления – взаимодействие зарядов с атомами вещества проводника и между собой. Единица измерения сопротивления 1 Ом. Сопротивление проводника R определяется по формуле:
где: l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника (будьте внимательны и не перепутайте последнюю величину с плотностью вещества), которое характеризует способность материала проводника противодействовать прохождению тока. То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества – табличная величина.
То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества – табличная величина.
Сопротивление проводника зависит и от его температуры:
где: R 0 – сопротивление проводника при 0°С, t – температура, выраженная в градусах Цельсия, α – температурный коэффициент сопротивления. Он равен относительному изменению сопротивления, при увеличении температуры на 1°С. Для металлов он всегда больше нуля, для электролитов наоборот, всегда меньше нуля.
Диод в цепи постоянного тока
Диод – это нелинейный элемент цепи, сопротивление которого зависит от направления протекания тока. Обозначается диод следующим образом:
Стрелка в схематическом обозначении диода показывает, в каком направлении он пропускает ток. В этом случае его сопротивление равно нулю, и диод можно заменить просто на проводник с нулевым сопротивлением. Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.
Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.
Закон Ома. Последовательное и параллельное соединение проводников
Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I , текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением R , пропорциональна напряжению U на концах проводника:
Величину R принято называть электрическим сопротивлением . Проводник, обладающий электрическим сопротивлением, называется резистором . Это соотношение выражает закон Ома для однородного участка цепи : сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Проводники, подчиняющиеся закону Ома, называются линейными . Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно . У каждого способа есть свои закономерности.
1. Закономерности последовательного соединения:
Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено n одинаковых сопротивлений R , то общее сопротивление R 0 находится по формуле:
2. Закономерности параллельного соединения:
Закономерности параллельного соединения:
Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R , то общее сопротивление R 0 находится по формуле:
Электроизмерительные приборы
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры .
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением R B . Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.
Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением R A . В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.
Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением R A . В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.
ЭДС. Закон Ома для полной цепи
Для существования постоянного тока необходимо наличие в электрической замкнутой цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока . Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами .
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы A ст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС) :
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
Закон Ома для полной (замкнутой) цепи: сила тока в замкнутой цепи равна электродвижущей силе источника, деленной на общее (внутреннее + внешнее) сопротивление цепи:
Сопротивление r – внутреннее (собственное) сопротивление источника тока (зависит от внутреннего строения источника). Сопротивление R – сопротивление нагрузки (внешнее сопротивление цепи).
Сопротивление R – сопротивление нагрузки (внешнее сопротивление цепи).
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника ):
Важно понять и запомнить: ЭДС и внутреннее сопротивление источника тока не меняются, при подключении разных нагрузок.
Если сопротивление нагрузки равно нулю (источник замыкается сам на себя) или много меньше сопротивления источника, то тогда в цепи потечет ток короткого замыкания :
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ε и внутренним сопротивлением r . У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
Несколько источников ЭДС в цепи
Если в цепи присутствует несколько ЭДС подключенных последовательно , то:
1. При правильном (положительный полюс одного источника присоединяется к отрицательному другого) подключении источников общее ЭДС всех источников и их внутреннее сопротивление может быть найдено по формулам:
Например, такое подключение источников осуществляется в пультах дистанционного управления, фотоаппаратах и других бытовых приборах, работающих от нескольких батареек.
2. При неправильном (источники соединяются одинаковыми полюсами) подключении источников их общее ЭДС и сопротивление рассчитывается по формулам:
В обоих случаях общее сопротивление источников увеличивается.
При параллельном подключении имеет смысл соединять источники только c одинаковой ЭДС, иначе источники будут разряжаться друг на друга. Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:
Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:
В этом и состоит смысл параллельного соединения источников. В любом случае при решении задач сначала надо найти суммарную ЭДС и полное внутреннее сопротивление получившегося источника, а затем записать закон Ома для полной цепи.
Работа и мощность тока. Закон Джоуля-Ленца
Работа A электрического тока I , протекающего по неподвижному проводнику с сопротивлением R , преобразуется в теплоту Q , выделяющееся на проводнике. Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.Джоулем и Э.Ленцем и носит название закона Джоуля–Ленца .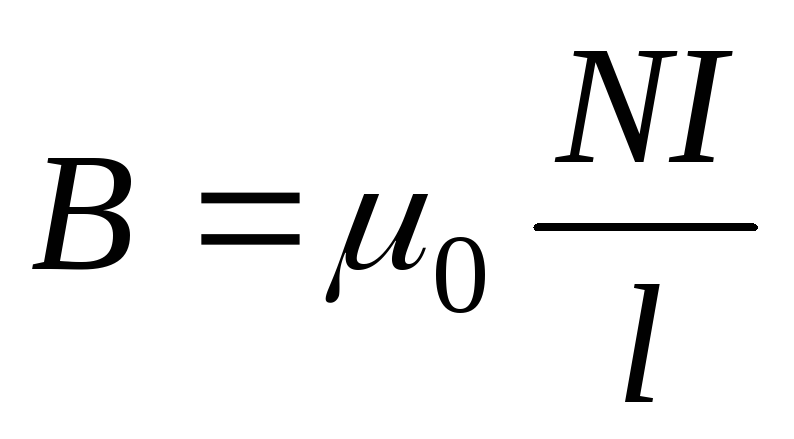 Мощность электрического тока равна отношению работы тока A к интервалу времени Δt , за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:
Мощность электрического тока равна отношению работы тока A к интервалу времени Δt , за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:
Работа электрического тока в СИ, как обычно, выражается в джоулях (Дж), мощность – в ваттах (Вт).
Энергобаланс замкнутой цепи
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ε и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R . В этом случае полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R 1 и R 2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
Электролитами принято называть проводящие среды, в которых протекание электрического тока сопровождается переносом вещества. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы. К электролитам относятся многие соединения металлов с металлоидами в расплавленном состоянии, а также некоторые твердые вещества. Однако основными представителями электролитов, широко используемыми в технике, являются водные растворы неорганических кислот, солей и оснований.
Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы. К электролитам относятся многие соединения металлов с металлоидами в расплавленном состоянии, а также некоторые твердые вещества. Однако основными представителями электролитов, широко используемыми в технике, являются водные растворы неорганических кислот, солей и оснований.
Прохождение электрического тока через электролит сопровождается выделением вещества на электродах. Это явление получило название электролиза .
Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду ), отрицательные ионы – к положительному электроду (аноду ). Ионы обоих знаков появляются в водных растворах солей, кислот и щелочей в результате расщепления части нейтральных молекул. Это явление называется электролитической диссоциацией .
Закон электролиза был экспериментально установлен английским физиком М. Фарадеем в 1833 году. Закон Фарадея определяет количества первичных продуктов, выделяющихся на электродах при электролизе. Итак, масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q , прошедшему через электролит:
Фарадеем в 1833 году. Закон Фарадея определяет количества первичных продуктов, выделяющихся на электродах при электролизе. Итак, масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q , прошедшему через электролит:
Величину k называют электрохимическим эквивалентом . Он может быть рассчитан по формуле:
где: n – валентность вещества, N A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Электрический ток в газах и в вакууме
Электрический ток в газах
В обычных условиях газы не проводят электрический ток. Это объясняется электрической нейтральностью молекул газов и, следовательно, отсутствием носителей электрических зарядов. Для того чтобы газ стал проводником, от молекул необходимо оторвать один или несколько электронов. Тогда появятся свободные носителя зарядов – электроны и положительные ионы. Этот процесс называется ионизацией газов .
Этот процесс называется ионизацией газов .
Ионизировать молекулы газа можно внешним воздействием – ионизатором . Ионизаторами может быть: поток света, рентгеновские лучи, поток электронов или α -частиц. Молекулы газа также ионизируются при высокой температуре. Ионизация приводит к возникновению в газах свободных носителей зарядов – электронов, положительных ионов, отрицательных ионов (электрон, объединившийся с нейтральной молекулой).
Если создать в пространстве, занятом ионизированным газом, электрическое поле, то носители электрических зарядов придут в упорядоченное движение – так возникает электрический ток в газах. Если ионизатор перестает действовать, то газ снова становится нейтральным, так как в нем происходит рекомбинация – образование нейтральных атомов ионами и электронами.
Электрический ток в вакууме
Вакуумом называется такая степень разрежения газа, при котором можно пренебречь соударением между его молекулами и считать, что средняя длина свободного пробега превышает линейные размеры сосуда, в котором газ находится.
Электрическим током в вакууме называют проводимость межэлектродного промежутка в состоянии вакуума. Молекул газа при этом столь мало, что процессы их ионизации не могут обеспечить такого числа электронов и ионов, которые необходимы для ионизации. Проводимость межэлектродного промежутка в вакууме может быть обеспечена лишь с помощью заряженных частиц, возникших за счет эмиссионных явлений на электродах.
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности.
 Последнему научиться можно только решив тысячи задач.
Последнему научиться можно только решив тысячи задач. - Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию.
 Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
При изучении темы “Постоянный ток” необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца При изучении “Магнетизма” необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.
Электрические и магнитные явления связаны особой формой существования материи – электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.
Основой теории электромагнитного поля является теория Максвелла.
Таблица основных формул электричества и магнетизма
Физические законы, формулы, переменные | Формулы электричество и магнетизм | ||||||||
Закон Кулона: | |||||||||
Напряженность электрического поля: где Ḟ – сила, действующая на заряд q 0 , находящийся в данной точке поля. | |||||||||
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями | |||||||||
Потенциал электрического поля: где W – потенциальная энергия заряда
q
0 . | |||||||||
Потенциал поля точечного заряда на расстоянии r от заряда: | |||||||||
По принципу суперпозиции полей, напряженность: | |||||||||
Потенциал: где Ē i и ϕ i – напряженность и потенциал в данной точке поля, создаваемый i-м зарядом. | |||||||||
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ 1 в точку с потенциалом ϕ 2 : | |||||||||
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля: | |||||||||
Электроемкость уединенного проводника: | |||||||||
Электроемкость конденсатора: | |||||||||
Электроемкость плоского конденсатора: где S – площадь пластины (одной) конденсатора, d – расстояние между пластинами. | |||||||||
Энергия заряженного конденсатора: | |||||||||
Сила тока: | |||||||||
Плотность тока: где S – площадь поперечного сечения проводника. | |||||||||
Сопротивление проводника: l – длина проводника; S – площадь поперечного сечения. | |||||||||
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС: Где ε – ЭДС источника тока, R и r – внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи: | |||||||||
Закон Джоуля-Ленца 1) для однородного участка цепи постоянного тока: 2) для участка цепи с изменяющимся со временем током: | |||||||||
Мощность тока: | |||||||||
Связь магнитной индукции и напряженности магнитного поля: где B – вектор магнитной индукции, | |||||||||
Магнитная индукция (индукция магнитного поля): 2) поля бесконечно длинного прямого тока 3) поля, созданного отрезком проводника с током |
Электричество и магнетизм формулы.
Закон Кулона
1. закон Кулона
2 . напряженность электрического поля
3. модуль напряженности поля точечного заряда
4 . принцип суперпозиции
5. -вектор электрического момента диполя – дипольный момент
6.
2. Теорема Гаусса
7
8.
9. теорема Гаусса
теорема Гаусса
10. теорема Гаусса
11.
12. – дивергенция поля
13
Потенциал электростатического поля
14. -работа сил электростатического поля по перемещению пробного заряда q в электрическом поле точечного заряда Q
15. – интегральный признак потенциальности электростатического поля
16. – приращение потенциала электростатического поля
17 . – убыль потенциала электростатического поля
18 . – нормировка потенциала (выбор начала отсчета)
19 . – принцип суперпозиции для
20. – квазистатическая работа сил поля при перемещении
по произвольному пути из т.1 в т.2
21. – локальное соотношение между и
22. – потенциал точечного заряда
23. – потенциал диполя
24. – дифференциальный оператор Гамильтона («набла») в полярной системе координат
25 . – оператор Лапласа или лапласиан
– оператор Лапласа или лапласиан
26. – уравнение Лапласа
27. – уравнение Пуассона
4. Энергия в электростатике.
28. – энергия электростатического взаимодействия зарядов друг с другом
29 . – полная электростатическая энергия заряженного тела
30. – объемная плотность энергии (энергия, локализованная в единичном объеме)
31. – энергия взаимодействия точечного диполя с внешним полем
5. Проводники электростатике
32. – поле вблизи поверхности проводника
33. – электроемкость уединенного проводника
34. – емкость плоского конденсатора
35 . – емкость сферического конденсатора, образованного сферическими проводящими поверхностями радиусов а и b
36 . – энергия конденсатора
6. Электростатическое поле в диэлектриках
37. , – диэлектрическая восприимчивость вещества
38.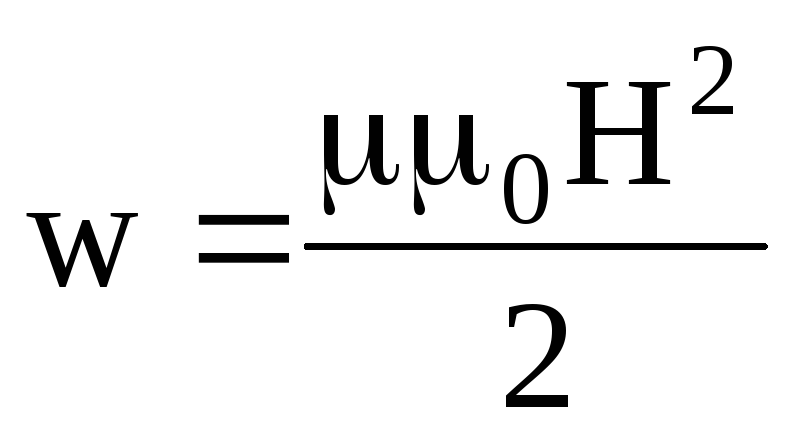 – поляризованность (электрический дипольный момент единицы объема вещества)
– поляризованность (электрический дипольный момент единицы объема вещества)
39. – связь между напряженностью и поляризованностью
40 . теорема Гаусса для вектора в интегральной форме
41. – теорема Гаусса для вектора в дифференциальной форме
42. – граничные условия для вектора
43. – теорема Гаусса для вектора в диэлектриках
44 . – электрическое смещение
45. – интегральная и локальная теорема Гаусса для вектора
46. – граничные условия для вектора , где – поверхностная плотность сторонних зарядов
47. – связь и для изотропных сред
Постоянный ток
48. – сила тока
49 . – заряд, проходящий через сечение проводника
50. – уравнение непрерывности (закон сохранения заряда)
51. – уравнение непрерывности в дифференциальной форме
52 . – разность потенциалов для проводника, в котором не действуют сторонние силы, отождествляется с падением напряжения
53. – закон Ома
– закон Ома
54. – закон Джоуля -Ленца
55. – сопротивление провода из однородного материала одинаковой толщины
56. – закон Ома в дифференциальной форме
57 . – величина, обратная удельному сопротивлению называется удельной электрической проводимостью
58 . – закон Джоуля –Ленца в дифференциальной форме
59. -интегральная форма закона Ома с учетом поля сторонних сил для участка цепи, содержащего ЭДС.
60 . – первый закон Кирхгофа. Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю.
61. -второй закон Кирхгофа. Сумма напряжений вдоль любого замкнутого контура цепи равна алгебраической сумме ЭДС, действующих в этом контуре.
62 . – удельная тепловая мощность тока в неоднородной проводящей среде
Закон Био-Савара
63 . – сила Лоренца
64 . – если в некоторой системе отсчета электромагнитное поле является электрическим
(т.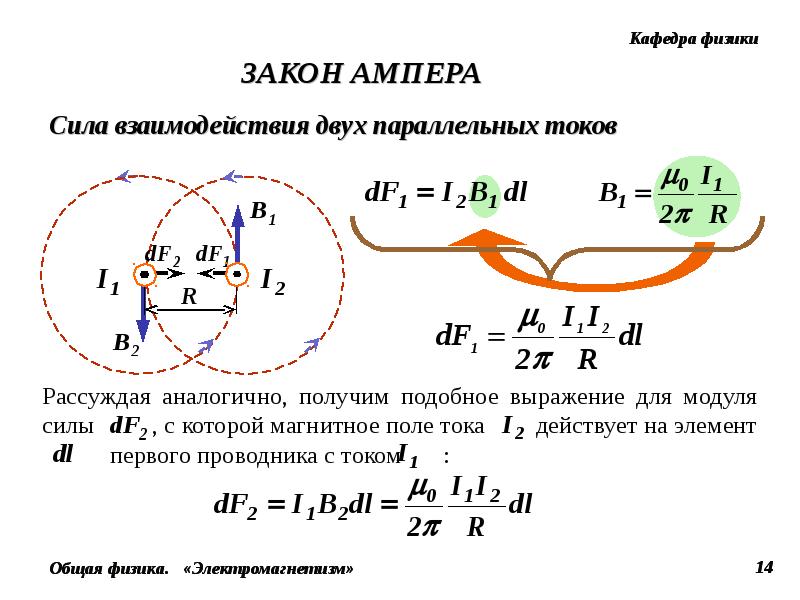 е. ), то в другой системе отсчета , движущейся относительно К со скоростью , компоненты электромагнитного поля отличны от нуля и связаны соотношением 64
е. ), то в другой системе отсчета , движущейся относительно К со скоростью , компоненты электромагнитного поля отличны от нуля и связаны соотношением 64
65 . – если в некоторой системе отсчета электрически заряженное тело имеет скорость , то электрическая и магнитная компоненты электромагнитного поля, создаваемого его зарядом, связаны в этой системе отсчета соотношением
66 . – если в некоторой системе отсчета электромагнитное поле является магнитным (), то в любой другой системе отсчета, движущейся со скоростью относительно первой, компоненты и электромагнитного поля отличны от нуля и связаны соотношением
67. – индукция магнитного поля движущегося заряда
68 . – магнитная постоянная
6.
2. Теорема Гаусса
7 . – поток поля через произвольную поверхность
8. – принцип аддитивности потоков
9. теорема Гаусса
10. теорема Гаусса
11. – дифференциальный оператор Гамильтона («набла»)в декартовой системе координат
– дифференциальный оператор Гамильтона («набла»)в декартовой системе координат
12. – дивергенция поля
13 . локальная (дифференциальная) теорема Гаусса
Электромагнетизм — Викизнание… Это Вам НЕ Википедия!
См. также[править]
Начальный вариант статьи, взят из Большого энциклопедического словаря Брокгауза Ф.А., Ефрона И.А. http://www.cultinfo.ru/fulltext/1/001/007/121/[править]
Электромагнетизм*
– Начало учению об электромагнитных явлениях положено открытием Эрстеда. В 1820 г. Эрстед показал, что проволока, по которой течет электрический ток, вызывает отклонение магнитной стрелки. Он подробно исследовал это отклонение с качественной стороны, но не дал общего правила, по которому можно было бы определять направление отклонения в каждом отдельном случае. Вслед за Эрстедом открытия пошли одно за другим. Ампер (1820) опубликовал свои работы о действии тока на ток или тока на магнит. Амперу принадлежит общее правило для действия тока на магнитную стрелку: если вообразить себя расположенным в проводнике лицом к магнитной стрелке и притом так, чтобы ток имел направление от ног к голове, то северный полюс отклоняется влево.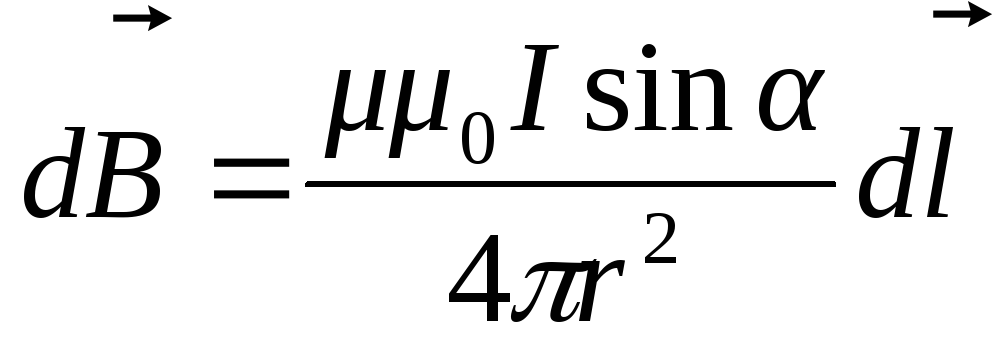 Далее мы увидим, что Ампер свел явления электромагнитные к явлениям электродинамическим (1823). К 1820 г. относятся также работы Араго, который заметил, что проволока, по которой течет электрический ток, притягивает к себе железные опилки. Он же намагнитил впервые железные и стальные проволоки, помещая их внутрь катушки медных проволок, по которым проходил ток. Ему же удалось намагнитить иглу, поместив ее в катушку и разрядив лейденскую банку через катушку. Независимо от Араго намагничивание стали и железа током было открыто Дэви.
Далее мы увидим, что Ампер свел явления электромагнитные к явлениям электродинамическим (1823). К 1820 г. относятся также работы Араго, который заметил, что проволока, по которой течет электрический ток, притягивает к себе железные опилки. Он же намагнитил впервые железные и стальные проволоки, помещая их внутрь катушки медных проволок, по которым проходил ток. Ему же удалось намагнитить иглу, поместив ее в катушку и разрядив лейденскую банку через катушку. Независимо от Араго намагничивание стали и железа током было открыто Дэви.
Первые количественные определения действия тока на магнит точно так же относятся к 1820 г. и принадлежат Био и Савару. Эти ученые из своих опытов вывели следующее:
Если укрепить маленькую магнитную стрелку sn вблизи длинного вертикального проводника AB и астазировать земное поле магнитом NS (фиг. 1), то можно обнаружить следующее:
1. При прохождении тока через проводник магнитная стрелка устанавливается своей длиной под прямым углом к перпендикуляру, опущенному из центра стрелки на проводник.
2. Сила, действующая на тот или другой полюс n и s перпендикулярна к плоскости, проведенной через проводник и данный полюс
3. Сила, с которой действует на магнитную стрелку данный ток, проходящий по очень длинному прямолинейному проводнику, обратно пропорциональна расстоянию от проводника до магнитной стрелки.
Все эти наблюдения и другие могут быть выведены из следующего элементарного количественного закона, известного под именем закона Лапласа-Био-Савара:
dF = k(imSin θ ds)/r2, (1),
где dF – действие элемента тока на магнитный полюс; i – сила тока; m – количество магнетизма, θ – угол, составляемый направлением тока в элементе с линией, соединяющей полюс с элементом тока; ds – длина элемента тока; r -расстояние рассматриваемого элемента от полюса; k – коэффициент пропорциональности.
На основании закона действие равно противодействию, Ампер заключил, что магнитный полюс должен действовать на элемент тока с такой же силой
dФ = k(imSin θ ds)/r2, (2)
прямо противоположной по направлению силе dF, точно также действующей по направлению, составляющему прямой угол с плоскостью, проходящей через полюс и данный элемент. Хотя выражения (1) и (2) хорошо согласуются с опытами, тем не менее на них приходится смотреть не как на закон природы, а как на удобное средство описывать количественную сторону процессов. Главная причина этого в том, что мы не знаем никаких токов, кроме замкнутых, и, следовательно, допущение элемента тока в сущности неправильно. Далее, если мы прибавим к выражениям (1) и (2) какие-нибудь функции, ограниченные только условием, что интеграл их по замкнутому контуру равен нулю, то согласие с опытами будет не менее полное.
Хотя выражения (1) и (2) хорошо согласуются с опытами, тем не менее на них приходится смотреть не как на закон природы, а как на удобное средство описывать количественную сторону процессов. Главная причина этого в том, что мы не знаем никаких токов, кроме замкнутых, и, следовательно, допущение элемента тока в сущности неправильно. Далее, если мы прибавим к выражениям (1) и (2) какие-нибудь функции, ограниченные только условием, что интеграл их по замкнутому контуру равен нулю, то согласие с опытами будет не менее полное.
Все факты вышеуказанные приводят к выводу, что электрический ток вызывает вокруг себя магнитное поле. Для магнитной силы этого поля должны быть справедливы все законы, справедливые для магнитного поля вообще. В частности, вполне уместно введением понятия о силовых линиях магнитного поля, вызываемого электрическим током. Направление силовых линий в этом случае может быть обнаружено обычным способом при посредстве железных опилок. Если пропустить вертикальную проволоку с током через горизонтальный лист картона и насыпать на картон опилок, то при легком постукивании опилки расположатся концентрическими кругами, если только проводник достаточно длинен.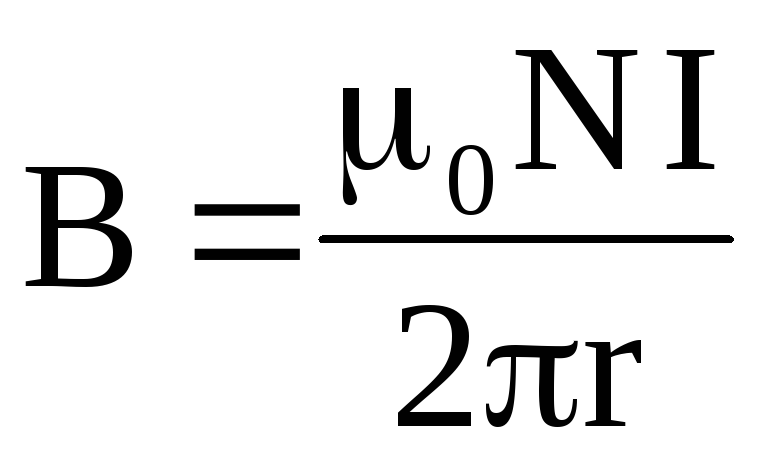 Если проводник имеет форму замкнутого вертикального круга, то на горизонтальном сечении опилки расположатся приблизительно так, как показано на фиг. 2.
Если проводник имеет форму замкнутого вертикального круга, то на горизонтальном сечении опилки расположатся приблизительно так, как показано на фиг. 2.
Так как силовые линии вокруг проволоки замыкаются и так как силовая линия определяет путь, по которому двигалась бы единица магнетизма в данном поле, то ясно, что можно вызвать вращение магнитного полюса вокруг тока. Первый прибор, в котором подобное вращение было осуществлено, был построен Фарадеем. Очевидно, что по силе магнитного поля можно судить о силе тока. К этому вопросу мы сейчас и подойдем.
Рассматривая магнитный потенциал очень длинного прямолинейного тока, мы легко можем доказать, что этот потенциал многозначен. В данной точке он может иметь бесконечно большое число различных значений, разнящихся одно от другого на 4 kmi π , где k – коэффициент, остальные буквы известны. Этим и объясняется возможность непрерывного вращения магнитного полюса вокруг тока. 4 kmi π и есть работа, совершаемая при одном обороте полюса; она берется за счет энергии источника тока. Особый интерес представляет случай замкнутого тока. Замкнутый ток мы можем себе представить в виде петли, сделанной на проволоке, по которой течет ток. Петля имеет произвольную форму. Два конца петли свернуты в жгут (шнур) и идут к далеко поставленному элементу. Опыт показывает, что жгут, составленный из двух проводников, по которым ток течет в противоположных направлениях и которые навиты один на другой, не производит магнитного поля. Элемент предполагается далеко расположенным. Следовательно, остается только петля, которую можно рассматривать, как замкнутый ток. Рассматривая магнитный потенциал такого замкнутого тока в какой-нибудь точке P и сравнивая его с потенциалом в той же точке двойного магнитного слоя, ограниченного тем же контуром, что и наш ток, мы придем к такому выводу (как известно, двойным магнитным слоем называется бесконечно тонкий листок, ограниченный данным контуром и намагниченный перпендикулярно к своей поверхности; произведение σε – поверхностной плотности намагничивания на толщину слоя – называется магнитной силой листка; обозначим ее через ф).
Особый интерес представляет случай замкнутого тока. Замкнутый ток мы можем себе представить в виде петли, сделанной на проволоке, по которой течет ток. Петля имеет произвольную форму. Два конца петли свернуты в жгут (шнур) и идут к далеко поставленному элементу. Опыт показывает, что жгут, составленный из двух проводников, по которым ток течет в противоположных направлениях и которые навиты один на другой, не производит магнитного поля. Элемент предполагается далеко расположенным. Следовательно, остается только петля, которую можно рассматривать, как замкнутый ток. Рассматривая магнитный потенциал такого замкнутого тока в какой-нибудь точке P и сравнивая его с потенциалом в той же точке двойного магнитного слоя, ограниченного тем же контуром, что и наш ток, мы придем к такому выводу (как известно, двойным магнитным слоем называется бесконечно тонкий листок, ограниченный данным контуром и намагниченный перпендикулярно к своей поверхности; произведение σε – поверхностной плотности намагничивания на толщину слоя – называется магнитной силой листка; обозначим ее через ф).
Если сила двойного магнитного слоя численно равна ki и если двойной магнитный слой расположен на поверхности S (фиг. 3) таким образом, что его положительная сторона (сев. магнетизм) приходится с той стороны, откуда ток представляется идущим обратно часовой стрелке, то потенциал в каких-либо точках P и Р’ от двойного магнитного слоя и от замкнутого тока отличается только на величину постоянную, т. е. не зависящую от координат.
Обозначим потенциалы от замкнутого тока через Ω и Ω’, а от двойного магнитного слоя через V и V’; телесный угол, под которым из точек P и P’ виден контур, обозначим через ω и ω ‘.
Тогда мы будем иметь
Ω = ki ω + С, Ω ‘ = ki ω ‘ + C, (3)
V = фω, W’ = фω ‘
Итак, силы, с которыми действуют на данное количество магнетизма замкнутый ток и двойной магнитный слой, ограниченный тем же контуром, что и ток, и удовлетворяющий указанным выше двум условиям, равны и по величине и по направлению. Следовательно, любой замкнутый ток можно заменить эквивалентным ему двойным магнитным слоем. Такой способ рассмотрения замкнутых токов приводит к установлению электромагнитной единицы силы тока.
Следовательно, любой замкнутый ток можно заменить эквивалентным ему двойным магнитным слоем. Такой способ рассмотрения замкнутых токов приводит к установлению электромагнитной единицы силы тока.
Условие эквивалентности есть ф = ki приняв k = 1, получим i = 1, если ф = 1. Это и есть электромагнитная единица. Словами эта теорема может быть выражена так.
Электромагнитная единица силы тока есть сила такого тока, которые, проходя по замкнутому контуру, оказывает на данное внешнее количество магнетизма то же действие, что и двойной магнитный слой, ограниченный тем же контуром и обладающий силой ф = 1. Отсюда сейчас получаются измерения электромагнитной единицы силы тока.
[i] = [ ф ] = [m] ε / S = [L3/2M ½T–1] / [L] = [L½M ½T–1] (4)
Рассматривая работу, совершаемую при передвижении единицы количества северного магнетизма в магнитном поле замкнутого тока по замкнутой кривой из данной точки снова в первоначальное положение, можно убедиться в том, что эта работа равна 0, когда кривая движения единицы магнетизма не охватывает собой линии тока (фиг. 4, кривые РР 1P2 Р , РР 1‘ Р 2 ‘Р ) и равна ± 4 π i, когда кривая движения охватывает собой линию тока (кривая QQ’Q2Q1Q).
4, кривые РР 1P2 Р , РР 1‘ Р 2 ‘Р ) и равна ± 4 π i, когда кривая движения охватывает собой линию тока (кривая QQ’Q2Q1Q).
Это происходит от того, что, переходя через двойной магнитный слой, потенциал меняется не непрерывно, а скачком на ± 4 π i. Следовательно, если единица количества магнетизма n раз обернется вокруг тока, то работа будет ± 4π ni. Мы видим, что и потенциал замкнутого тока есть функция многозначная с периодом ± 4 π i . Общее выражением для потенциала замкнутого тока, т. е. для величины работы, необходимой для переведения единицы северного магнетизма из бесконечности в данную точку, равно
Ω = ± i ω + п4π i. (5)
Прежде, чем пойти дальше в рассмотрении электромагнитных явлений, нам надо установить понятие о магнитном потоке.
Пусть H есть нормальная к элементу поверхности dS слагающая магнитной силы поля. Тогда через элемент поверхности dS проходит, как говорят, магнитный силовой поток HdS.
Тогда через элемент поверхности dS проходит, как говорят, магнитный силовой поток HdS.
Выражение это требует введения еще одного множителя, если мы примем во внимание магнитную проницаемость среды и если нам надо обобщить вывод на случай нескольких сред. В таком случае его пишут так: μ HdS, и называют потоком магнитной индукции, или просто магнитным потоком через элемент поверхности. Если мы от элемента поверхности перейдем к определенной площади, то надо взять двойной интеграл от выражения μ HdS. Условимся говорить, что из данной поверхности исходит одна силовая трубка, если
∫∫ μ HdS = 1.
Тогда вообще μ HdS = dN
и
∫∫ μ HdS = N (6)
прямо дают число силовых трубок N, проходящих через данную поверхность. Выражение μ HdS не теряет свойства непрерывности при переходе из одной среды в другую.
Далее, в данном магнитном потоке для любого сечения S справедливо соотношение ∫∫ μ HndS = const, где Hn – нормальная производящая магнитной силы. Это свойство уподобляет магнитный поток потоку несжимаемой жидкости. О силовых трубках магнитного потока прежде всего предполагают, что они не начинаются у одного полюса и кончаются у другого; а что они внутри магнита идут от второго полюса к первому и, следовательно, замкнуты сами на себя (фиг. 5). Следовательно, мы имеем замкнутую магнитную цепь.
Это свойство уподобляет магнитный поток потоку несжимаемой жидкости. О силовых трубках магнитного потока прежде всего предполагают, что они не начинаются у одного полюса и кончаются у другого; а что они внутри магнита идут от второго полюса к первому и, следовательно, замкнуты сами на себя (фиг. 5). Следовательно, мы имеем замкнутую магнитную цепь.
Рассмотрим одну силовую трубку этой цепи. Пусть её сечение dq. Возьмем элемент силовой линии dl в этой трубке. Работа необходимая, чтобы обвести вокруг по этой силовой линии единицу количества магнетизма пусть будет равна А. Она называется магнитодвижущей силой.
Очевидно,
А = ∫Hdl. (7)
С другой стороны, магнитный поток равняется
N = μ Hdq или H = N/ μ dq, (8)
отсюда
A = N∫(dl/ μ dq),
или
N = А/(∫dl/μ dq) = [∫Hdl] /[ ∫(1/ μ )(dl/ dq)]. (9)
(9)
Формула полученная весьма похожа на формулу Ома. Магнитный поток играет роль силы тока ∫ Hdl – магнитодвижущая сила, аналогичная электродвижущей силе в формуле Ома ∫(1/μ)(dl/ dq), играет роль магнитного сопротивления. Оно, подобно электрическому, прямо пропорционально длине и обратно пропорционально поперечному сечению. 1/μ – удельное магнитное сопротивление.
Хевисайд предложил называть величину ∫(1/μ)(dl/ dq) магнитной неподатливостью. Обозначая ее одной буквой W, мы получаем известное соотношение A = NW,т. е. магнитодвижущая сила равна произведению магнитного потока на магнитное сопротивление.
Перейдем теперь снова к Э. Определим магнитную силу внутри соленоида. Вообразим себе тонкостенную трубку сечения q и длины l; q предполагается малым сравнительно с l. В стенках течет ток; направление токовых линий перпендикулярно к направлению оси трубки. Осуществить этот случай можно, свив проволоку в спираль и пропуская через нее ток (соленоид, фиг. 6).
6).
Если у соленоида на длину l приходится n витков и по нему течет ток i, то это равносильно тому, как если бы обороты соленоида не были изолированы один от другого и если бы в образованной при этом сплошной металлической трубке протекал ток равный ni. Внутри соленоида магнитные силовые линии будут параллельны оси соленоида. Применим к магнитному потоку соленоида только что полученное выражение для магнитной цепи. Мы видели, что если провести единицу магнетизма по замкнутой кривой вокруг проволоки с током i, то производится работа 4π i. Следовательно, магнитодвижущая сила соленоида из n оборотов и с силой тока i будет равна 4π ni.
Что касается сопротивления магнитной цепи, то трубки магнитной индукции, выйдя из соленоида, где они параллельны оси соленоида, замкнутся через внешнее пространство. При этом сечение сильно возрастет и, следовательно, сопротивление будет мало по сравнению с сопротивлением внутри соленоида.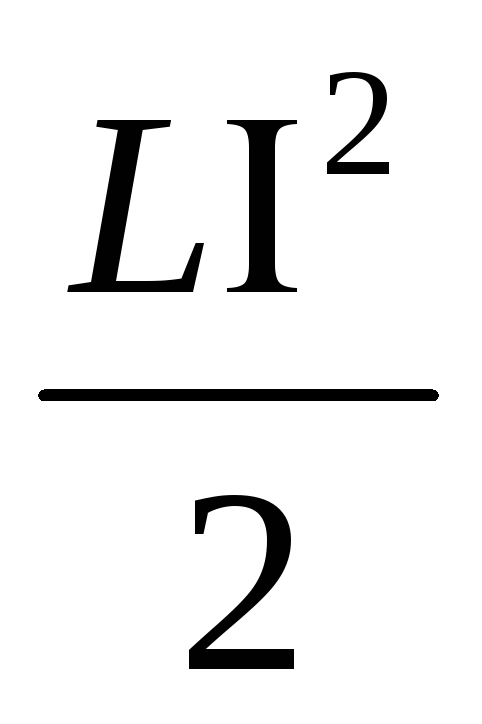 Мы можем пренебречь первым сравнительно со вторым. Тогда выражение для магнитного потока напишется так: N = A/W, A = 4 π ni,
Мы можем пренебречь первым сравнительно со вторым. Тогда выражение для магнитного потока напишется так: N = A/W, A = 4 π ni,
W = l/q, N = 4 π niq/l.
Магнитная сила внутри соленоида
H = N/q = 4 π ni/l. (10)
Если оба конца соленоида свести и устроить замкнутый соленоид, то силовые линии вовсе не выйдут наружу, и вышенаписанные формулы становятся строго верными. Внешнего действия такой соленоид не обнаружит, так как для каждой внешней замкнутой кривой магнитодвижущая сила = 0.
Если оба конца свободны, то соленоид должен действовать как магниты. Количество магнетизма полюса может быть измерено таким образом m = N/4 π = niq/l.
Эти формулы есть следствие формулы (2). Число силовых линий значительно возрастет, если ввести в соленоид железный сердечник, так как тогда уменьшится сопротивление магнитной цепи.
Соответственно этому получатся и более мощные магниты. На этом основано устройство электромагнитов. Внутри катушки из изолированной проволоки (соленоида) помещается сердечник из мягкого железа.
На этом основано устройство электромагнитов. Внутри катушки из изолированной проволоки (соленоида) помещается сердечник из мягкого железа.
Число линий сил внутри соленоида будет
4 π ni /(1/ μ) (l/q). (11)
Заметим, что только что написанная формула в несколько более общем виде
N = (Σ 4 π ni)/ [ Σ (1/ μ) (l /q)] играет большую роль в электротехнике. Она известна под именем формулы Каппа и братьев Гопкинсонов. Итак, соленоид с железным сердечником есть электромагнит. Э. придается самая разнообразная форма. Фиг. 7 изображает прямой электромагнит, фиг. 8 обыкновенный большой подковообразный магнит; на таблице Электромагнит, фиг. 5 представлен горизонтальный электромагнит Румкорфа, особенно удобный для исследования магнитооптических явлений; фиг. 9 – электромагнит Джоуля, очень большой подъемной силы, так как в нем сердечник очень широкий и очень короткий, т. е. очень малого сопротивления.
Электромагниты значительно превосходят все другие магниты по силе, и только благодаря им и стало возможно исследование многих свойств и явлений в магнитном поле, напр.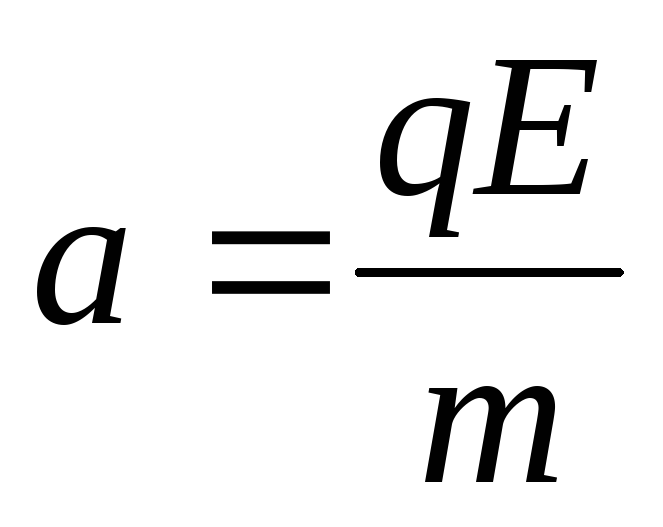 , магнитных свойств всех тел (пара- и диамагнетизм), магнитного вращения плоскости поляризации, магнитострикция, явления Керра, Зеемана, Холля, гистерезис etc.
, магнитных свойств всех тел (пара- и диамагнетизм), магнитного вращения плоскости поляризации, магнитострикция, явления Керра, Зеемана, Холля, гистерезис etc.
Магнитные свойства соленоида привели Ампера к выводу, что все электромагнитные явления в сущности суть электродинамические и что всякий магнит есть соленоид. Именно Ампер предположил, что можно каждый кусок железа или стали представлять себе состоящим из маленьких молекулярных магнитов, которые суть не что иное как частицы того же железа или стали, но вокруг которых течет ток в определенном направлении. Явление намагничивания и состоит в ориентировке всех этих магнитиков параллельно друг другу. Тогда внутри магнита токи никакого действия не окажут, так как рядом с каждым током, текущим справа налево, непременно будет ток обратного направления. Токи же на поверхности сложатся в один соленоидальный. Следовательно, магнит есть соленоид. Многие, хотя не все, явления магнетизма хорошо объясняются теорией Ампера. Однако мы видели, что удобен и вполне возможен и обратный путь, когда замкнутые токи рассматриваются как двойные магнитные слои, следовательно, явления электродинамические сводятся к электромагнитным. Таким образом, можно выяснить все явления электромагнетизма, не прибегая к действию на расстояние. Выводится и правило Ампера и его же закон элементарного действия магнитного поля на элемент тока. В заключение укажу на выражение потенциальной энергии двойного магнитного слоя или замкнутого тока.
Таким образом, можно выяснить все явления электромагнетизма, не прибегая к действию на расстояние. Выводится и правило Ампера и его же закон элементарного действия магнитного поля на элемент тока. В заключение укажу на выражение потенциальной энергии двойного магнитного слоя или замкнутого тока.
P = – фN для двойного магнитного слоя.
P = – iN для замкнутого тока. Именно из этого выражения исходя и выводится увеличение параметра тока в магнитном поле и элементарный закон действия магнитного ноля на ток.
К. Баумгарт.
“Электромагнетизм” – Физика – Уроки
Название предмета | Физика |
Класс | 11 |
УМК | Физика. |
Уровень обучения | базовый |
Тема урока | Электромагнетизм. |
Общее количество часов, отведённое на изучение темы | 1 |
Место урока в системе уроков по теме | 3 урок по теме «Повторение 11 класс», 6 часов |
Цель урока | закрепить первоначальные сведения о явлении электромагнитной индукции |
Задачи урока | Обучающие: повторить основные величины, понятия и формулы по электромагнитным колебаниям при помощи фронтального опроса; совершенствовать навык решения задач. |
Развивающие: развить умение решать задачи по физике | |
Воспитательные: повысить интерес к предмету | |
Планируемые результаты | Знания о явлении электромагнетизм, понимание смысла и связи между электричеством и магнетизмом. Умение пользоваться методами научного познания. Овладение навыками самостоятельного приобретения новых знаний. Формирование умений работать в паре, представлять свои взгляды, вести диалог. Убежденность в возможности познания природы. Уважение к творцам науки и техники. |
Техническое обеспечение урока | мультимедиа проектор; экран; компьютер с выходом в Интернет, компьютерная презентация, раздаточный материал Электронные пособия.
2.Электронное пособие. Физика. Библиотека наглядных пособий. 7—11 классы (под |
Дополнительное методическое и дидактическое обеспечение урока |
|
Содержание урока
Организационный этап.

Звучит музыка ( по принципу телевизионной игры «Угадай мелодию»)
Обобщение и систематизация знаний. Подготовка обучающихся к обобщенной деятельности. Воспроизведение на новом уровне (переформулированные вопросы).
Игра по теме «Электромагнетизм»:
С правилами игры знакомит учитель и сам выступает в роли ведущего:
1,2 туры играются по табло, 3-ий тур – аукционный , 4-ый тур – супер игра.
В 1,2 турах играет весь ряд, отвечающего определяет капитан; время на обдумывание ответа 5 с.
В случае отсутствия ответа у отвечающей команды, право ответа переходит к следующей.
За каждый правильный ответ начисляется 1 балл.
В аукционе участвуют капитаны двух команд, набравших наибольшее количество баллов по итогам 1,2 туров.

Правила 3,4 туров: за 2 мин необходимо ответить на 6 вопросов, если нет ответа на какой-либо вопрос, то к нему можно вернуться в оставшееся время.
1,2 туры проводятся с выбором соответствующей категории (крайняя левая колонка табло; числа в последующих колонках, указывают на количество букв в слове или словосочетаниях ответа).
Готовое табло 1,2 туров содержат только числа, так как вопросы задаются ведущим устно.
1 тур
Величина | 8 показывающая, какой заряд проходит через поперечное сечение проводника в единицу времению Сила тока | 13 электрическая характеристика проводника. Сопротивление | 8 характеристика устройства, показывает, какая работа совершается в единицу времени. Мощность | 10 показывающая, какую работу совершает ЭП по перемещению электрического заряда. Напряжение |
Частица | 8 элементарная частица, имеющая самый малый заряд, далее уже неделимый. Электрон | 7 не имеющая электрического заряда. Нейтрон | 8 наимельчайшая частица вещества. Молекула | 3 имеющая либо недостаток, либо избыток электронов Ион |
В портретной галлерее | 6 Итальянский физик, один из основателей учения об электрическом токе, создатель первого гальванического элемента, положившего начало учению об электрическом токе. Вольт | 9 Английский физик, предложил планетную модель атома, впервые осуществил расщепление ядра атома. Резерфорд | 5 Русский физик, прославился открытием гальванопластики, построил первый электрический двигатель и телеграфный аппарат, печатающий буквы. Якоби | 6 Английский физик, открыл закон сохранения энергии; установил закон, определяющий тепловое действие тока, вычислил скорость движения молекул газа и её зависимость от температуры. Джоуль |
2 тур
Явление | 10 превращении световой энергии в электрическую. Фотоэффект | 12 возникает при натирании тел друг о друга, после чего они могут притягивать другие маленькие тела. Электризация | 16 упорядоченное движение электрических частиц под воздействием электрического поля. Электрический ток | 13 кратковременное возмущение магнитного поля земли, связанное с солнечной активностью. Магнитная буря |
Устройство | 9 Генератор | 12 Гальванометр | 11 Потребитель | 7 Реостат |
Полиглот | 8 Как с греческого языка переводится слово «изоляро». Уединять | 9 Как с греческого языка переводится слово «скопео» Наблюдать | 8 Как с греческого языка переводится слово «янтарь» Электрон | 9 Что означает латинское слово «аккумуляре». Накоплять |
Физминутка
Решение задачи:
Колебательный контур содержит конденсатор электроемкостью С=8 пФ и катушку индуктивностью L=0,5 мГн. Максимальная сила тока в катушке 1т=40 мА. Определите максимальное напряжение на обкладках конденсатора.
Дано: СИ
С=8 пФ 8∙10-12Ф
L=0,5 мГн 0,5∙10-3Гн
1т=40 мА 40∙10-3 А
Найти:
Um-?
Решение:
WЭ=WМ
Ответ : Um=317В
3 тур (аукционный)
Правила проведения:
Тур проводится до трех побед одного из участников.
Торги начинаются со слов «Я отвечу на этот вопрос за… секунд (максимальная цена- 5 сек, минимальная- 30 сек; цена торга кратна 5 сек; по истечении указанного времени выигравший торг должен дать ответ).
Вопросы для аукциона:
Электрический ток в металлах представляет собой упорядоченное движение ….
Формула закона Ома для участка цепи ….

Вещество, не проводящее электрический ток, называется ….
Французский физик и математик, создал первую теорию, которая выражала связь электрических и магнитных явлений, выдвинул гипотезу о природе магнетизма, ввел в физику понятие электрический ток .
Назвать все элементы электрической цепи.
Решение задачи:
Колебательный контур имеет индуктивность L=1,6 мГн и электроемкость С=0,04 мкФ, максимальное напряжение на конденсаторе Um=200 В. Определите максимальную силу тока в контуре, считая его идеальным.
Дано: СИ
С=0,04 мкФ 0,04∙10-6Ф
L=1,6 мГн 1,6∙10-3Гн
Uт=300В
Найти:
Im-?
Решение:
WЭ=WМ
Ответ : Im=1А
4 тур – Суперигра
Вопросы:
1. То, из чего состоят молекулы.
То, из чего состоят молекулы.
2. За направление тока, принимается направленные движения …
3. Ядро атома заряжено…
4. Прибор для измерения силы тока, называется…
5. Закон, выражающий зависимость от , сопротивления проводника и температуры его протекания, называется законом…
6. Соленоид, это …
Информация о домашнем задании, инструктаж по его выполнению.
§20 – 27, повторить
Рефлексия (подведение итогов занятия)
В той атмосфере и обстановке, в которой мы сегодня работали, каждый из вас чувствовал себя по-разному. И сейчас мне бы хотелось, чтобы вы оценили, насколько внутренне комфортно ощущал себя на этом уроке каждый из вас, и понравилось ли вам дело, которым мы с вами сегодня занимались.
Вы видите рисунок, на котором изображен сосуд с водой. При выходе из кабинета поставьте в нем, пожалуйста, магнит на той глубине, которая соответствовала бы глубине вашего погружения в тему «Электромагнетизм».
При выходе из кабинета поставьте в нем, пожалуйста, магнит на той глубине, которая соответствовала бы глубине вашего погружения в тему «Электромагнетизм».
5.Анализ активности обучающихся
Основные формулы электродинамики таблица. Электромагнетизм
Определение 1
Электродинамика – это огромная и важная область физики, в которой исследуются классические, неквантовые свойства электромагнитного поля и движения положительно заряженных магнитных зарядов, взаимодействующих друг с другом с помощью этого поля.
Рисунок 1. Коротко про электродинамику. Автор24 – интернет-биржа студенческих работ
Электродинамика представляется широким комплексом разнообразных постановок задач и их грамотных решений, приближенных способов и частных случаев, которые объединены в одно целое общими начальными законами и уравнениями. Последние, составляя основную часть классической электродинамики, подробно представлены в формулах Максвелла. В настоящее время ученые продолжают изучать принципы указанной области в физике, скелет ее построения взаимоотношения с другими научными направлениями.
В настоящее время ученые продолжают изучать принципы указанной области в физике, скелет ее построения взаимоотношения с другими научными направлениями.
Закон Кулона в электродинамике обозначается таким образом: $F= \frac {kq1q2} {r2}$, где $k= \frac {9 \cdot 10 (H \cdot m)} {Кл}$. Уравнение напряженности электрического поля записывается так: $E= \frac {F}{q}$, а поток вектора индукции магнитного поля $∆Ф=В∆S \cos {a}$.
В электродинамике в первую очередь изучаются свободные заряды и системы зарядов, которые содействуют активизации непрерывного энергетического спектра. Классическому описанию электромагнитного взаимодействия благоприятствует то, что оно является эффективным уже в низкоэнергетическом пределе, когда энергетический потенциал частиц и фотонов мал по сравнению с энергией покоя электрона.
В таких ситуациях зачастую отсутствует аннигиляция заряженных частиц, так как присутствует только постепенное изменение состояния их нестабильного движения в итоге обмена большим количеством низкоэнергетических фотонов.
Замечание 1
Однако и при высоких энергиях частиц в среде, несмотря на существенную роль флуктуации, электродинамика может быть использована с успехом для комплексного описания среднестатистических, макроскопических характеристик и процессов.
Основные уравнения электродинамики
Основными формулами, которые описывают поведение электромагнитного поля и его прямое взаимодействие с заряженными телами, являются уравнения Максвелла, определяющие вероятные действия свободного электромагнитного поля в среде и вакууме, а также общую генерацию поля источниками.
Среди этих положений в физике возможно выделить:
- теорема Гаусса для электрического поля – предназначена для определения генерации электростатического поля положительными зарядами;
- гипотеза замкнутости силовых линий – содействует взаимодействию процессов внутри самого магнитного поля;
- закон индукции Фарадея – устанавливает генерацию электрического и магнитного поля переменными свойствами окружающей среды.

В целом, теорема Ампера – Максвелла – это уникальная идея о циркуляции линий в магнитном поле с постепенным добавлением токов смещения, введенных самим Максвеллом, точно определяет трансформацию магнитного поля движущимися зарядами и переменным действием электрического поля.
Заряд и сила в электродинамике
В электродинамике взаимодействие силы и заряда электромагнитного поля исходит из следующего совместного определения электрического заряда $q$, энергии $E$ и магнитного $B$ полей, которые утверждаются в качестве основополагающего физического закона, основанного на всей совокупности экспериментальных данных. Формулу для силы Лоренца (в пределах идеализации точечного заряда, движущегося с определенной скоростью), записывают с заменой скорости $v$.
В проводниках зачастую содержится огромное количество зарядов, следовательно, эти заряды достаточно хорошо скомпенсированы: число положительных и отрицательных зарядов всегда равны между собой. Следовательно, суммарная электрическая сила, которая постоянно действует на проводник, равна также нулю. Магнитные же силы, функционирующие на отдельных зарядов в проводнике, в итоге не компенсируются, ведь при наличии тока скорости движения зарядов всегда различны. Уравнение действия проводника с током в магнитном поле можно записать так: $G = |v ⃗ |s \cos{a} $
Магнитные же силы, функционирующие на отдельных зарядов в проводнике, в итоге не компенсируются, ведь при наличии тока скорости движения зарядов всегда различны. Уравнение действия проводника с током в магнитном поле можно записать так: $G = |v ⃗ |s \cos{a} $
Если исследовать не жидкость, а полноценный и стабильный поток заряженных частиц в качестве тока, то весь энергетический потенциал, проходящий линейно через площадку за $1с$,- и будет являться силой тока, равной: $I = ρ| \vec {v} |s \cos{a} $, где $ρ$ – плотность заряда (в единице объема в общем потоке).
Замечание 2
Если магнитное и электрическое поле систематически меняется от точки к точке на конкретной площадке, то в выражениях и формулах для частичных потоков, как и в случае с жидкостью, в обязательном порядке проставляются средние показатели $E ⃗ $и $B ⃗$ на площадке.
Особое положение электродинамике в физике
Значимое положение электродинамики в современной науке возможно подтвердить посредством известного произведения А. Эйнштейна, в котором были детально изложены принципы и основы специальной теории относительности. Научный труд выдающегося ученого называется «К электродинамике подвижных тел», и включает в себя огромное количество важных уравнений и определений.
Эйнштейна, в котором были детально изложены принципы и основы специальной теории относительности. Научный труд выдающегося ученого называется «К электродинамике подвижных тел», и включает в себя огромное количество важных уравнений и определений.
Как отдельная область физики электродинамика состоит из таких разделов:
- учение о поле неподвижных, но электрически заряженных физических тел и частиц;
- учение о свойствах электрического тока;
- учение о взаимодействии магнитного поля и электромагнитной индукции;
- учение об электромагнитных волнах и колебаниях.
Все вышеуказанные разделы в одно целое объединяет теорема Д. Максвелла, который не только создал и представил стройную теорию электромагнитного поля, но и описал все его свойства, доказав его реальное существование. Работа именно этого ученого показала научному миру, что известные на тот момент электрическое и магнитное поля являются всего лишь проявлением единого электромагнитного поля, функционирующего в различных системах отсчета.
Существенная часть физики посвящена изучению электродинамики и электромагнитных явлений . Эта область в значительной мере претендует на статус отдельной науки, так как она не только исследует все закономерности электромагнитных взаимодействий, но и детально описывает их посредством математических формул. Глубокие и многолетние исследования электродинамики открыли новые пути для использования электромагнитных явлений на практике, для блага всего человечества.
Закон Кулона:
где F – сила электростатического взаимодействия между двумя заряженными телами;
q 1 , q 2 – электрические заряды тел;
ε – относительная, диэлектрическая проницаемость среды;
ε 0 =8,85·10 -12 Ф/м – электрическая постоянная;
r – расстояние между двумя заряженными телами.
Линейная плотность заряда:
где dq – элементарныйзаряд, приходящийся на участок длины dl.
Поверхностная плотность заряда:
где dq – элементарныйзаряд, приходящийся на поверхность ds.
Объемная плотность заряда:
где dq – элементарныйзаряд, в объеме dV.
Напряженность электрического поля:
где F – сила действующая на заряд q .
Теорема Гаусса:
где Е – напряженность электростатического поля;
dS – вектор, модуль которого равен площади пронизываемой поверхности, а направление совпадает с направлением нормали к площадке;
q – алгебраическая сумма заключенных внутри поверхности dS зарядов.
Теорема о циркуляции вектора напряженности:
Потенциал электростатического поля:
где W p – потенциальная энергия точечного заряда q .
Потенциал точечного заряда:
Напряженность поля точечного заряда:
.
Напряженность поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром:
где τ – линейная плотность заряда;
r – расстояние от нити или оси цилиндра до точки, напряженность поля в которой определяется.
Напряженность поля, создаваемого бесконечной равномерной заряженной плоскостью:
где σ – поверхностная плотность заряда.
Связь потенциала с напряженностью в общем случае:
E= – gradφ= .
Связь потенциала с напряженностью в случае однородного поля:
E = ,
где d – расстояние между точками с потенциалами φ 1 и φ 2 .
Связь потенциала с напряженностью в случае поля, обладающего центральной или осевой симметрией:
Работа сил поля по перемещению заряда q из точки поля с потенциалом φ 1 в точку с потенциалом φ 2:
A=q(φ 1 – φ 2).
Электроемкость проводника:
где q – заряд проводника;
φ – потенциал проводника при условии, что в бесконечности потенциал проводника принимается равным нулю.
Электроемкость конденсатора:
где q – заряд конденсатора;
U – разность потенциалов между пластинами конденсатора.
Электроемкость плоского конденсатора:
где ε – диэлектрическая проницаемость диэлектрика, расположенного между пластинами;
d – расстояние между пластинами;
S – суммарная площадь пластин.
Электроемкость батареи конденсаторов:
б) при параллельном соединении:
Энергия заряженного конденсатора:
,
где q – заряд конденсатора;
U – разность потенциалов между пластинами;
C – электроемкость конденсатора.
Сила постоянного тока:
где dq – заряд, протекший через поперечное сечение проводника за время dt .
Плотность тока:
где I – сила тока в проводнике;
S – площадь проводника.
Закон Ома для участка цепи, не содержащего ЭДС:
где I – сила тока на участке;
U
R – сопротивление участка.
Закон Ома для участка цепи, содержащего ЭДС:
где I – сила тока на участке;
U – напряжение на концах участка;
R – полное сопротивление участка;
ε – ЭДС источника.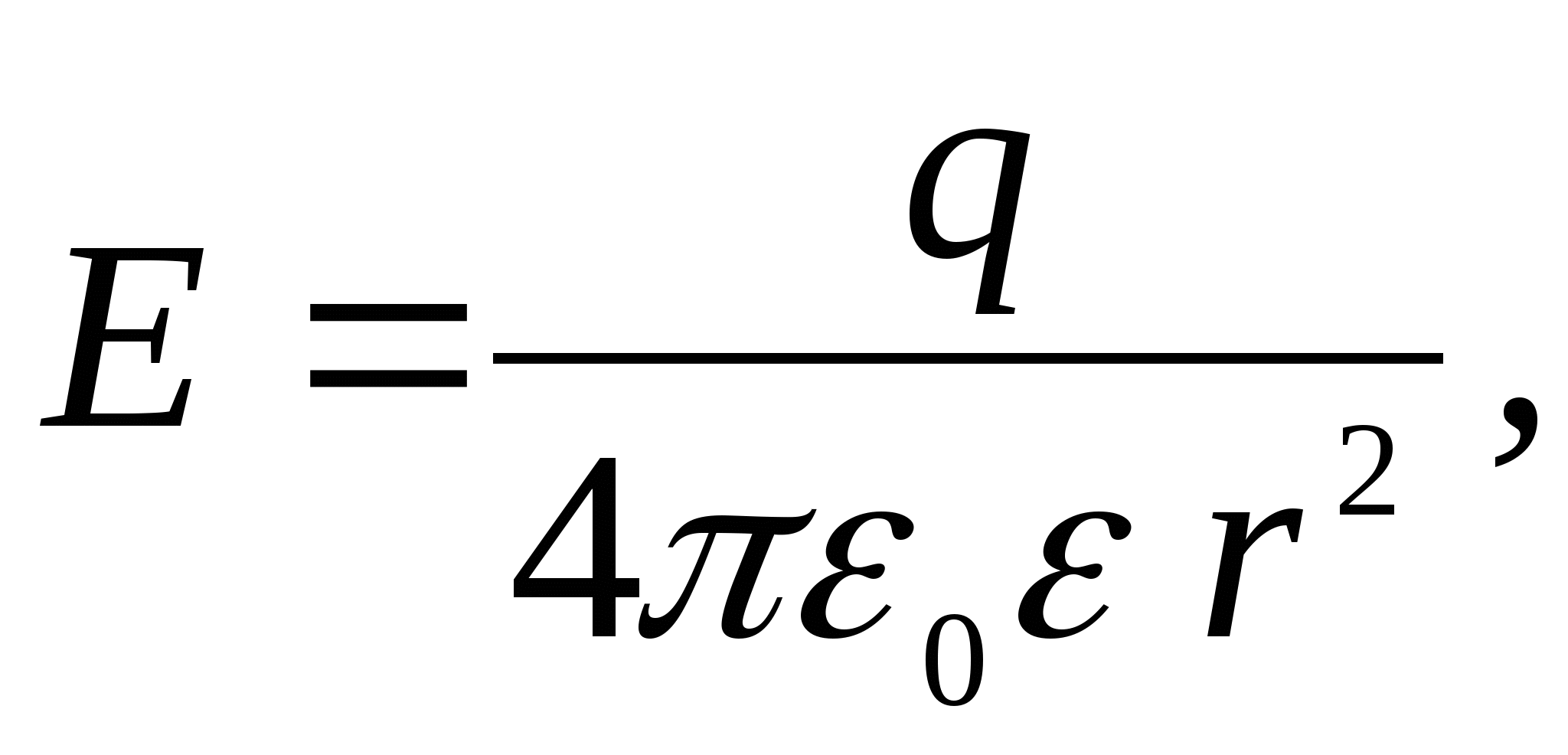
Закон Ома для замкнутой (полной) цепи:
где I – сила тока в цепи;
R – внешнее сопротивление цепи;
r – внутреннее сопротивление источника;
ε – ЭДС источника.
Законы Кирхгофа:
2. ,
где – алгебраическая сумма сил токов, сходящихся в узле;
– алгебраическая сумма падений напряжений в контуре;
– алгебраическая сумма ЭДС в контуре.
Сопротивление проводника:
где R – сопротивление проводника;
ρ – удельное сопротивление проводника;
l – длина проводника;
S
Проводимость проводника:
где G – проводимость проводника;
γ – удельная проводимость проводника;
l – длина проводника;
S – площадь поперечного сечения проводника.
Сопротивление системы проводников:
а) при последовательном соединении:
а) при параллельном соединении:
Работа тока:
,
где A – работа тока;
U – напряжение;
I – сила тока;
R – сопротивление;
t – время.
Мощность тока:
.
Закон Джоуля – Ленца
где Q – количество выделившейся теплоты.
Закон Ома в дифференциальной форме:
j =γE ,
где j – плотность тока;
γ – удельная проводимость;
E – напряженность электрического поля.
Связь магнитной индукции с напряженность магнитного поля:
B =μμ 0 H ,
где B – вектор магнитной индукции;
μ– магнитная проницаемость;
H – напряженность магнитного поля.
Закон Био – Савара – Лапласа:
,
где dB – индукция магнитного поля, создаваемая проводником в некоторой точке;
μ – магнитная проницаемость;
μ 0 =4π·10 -7 Гн/м – магнитная постоянная;
I – сила тока в проводнике;
dl – элемент проводника;
r – радиус-вектор, проведенный из элемента dl проводника в точку, в которой определяется индукция магнитного поля.
Закон полного тока для магнитного поля (теорема о циркуляции вектора B ):
,
где n – число проводников с токами, охватываемых контуром L произвольной формы.
Магнитная индукция в центре кругового тока:
где R – радиус кругового витка.
Магнитная индукция на оси кругового тока:
,
где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока:
где r 0 – расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля соленоида:
B= μμ 0 nI,
где n – отношение числа витков соленоида к его длине.
Сила Ампера:
dF =I,
где dF – сила Ампера;
I – сила тока в проводнике;
dl – длина проводника;
B – индукция магнитного поля.
Сила Лоренца:
F =qE +q [v B ],
где F – сила Лоренца;
q – заряд частицы;
E – напряженность электрического поля;
v – скорость частицы;
B – индукция магнитного поля.
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности:
Φ=B n S ,
где Φ –магнитный поток;
B n – проекция вектора магнитной индукции на вектор нормали;
S – площадь контура;
б) в случае неоднородного магнитного поля и произвольной проекции:
Потокосцепления (полный поток) для тороида и соленоида:
где Ψ – полный поток;
N – число витков;
Φ – магнитный поток, пронизывающий один виток.
Индуктивность контура:
Индуктивность соленоида:
L= μμ 0 n 2 V,
где L – индуктивность соленоида;
μ – магнитная проницаемость;
μ 0 – магнитная постоянная;
n – отношение числа витков к его длине;
V – объем соленоида.
Закон электромагнитной индукции Фарадея:
где ε i – ЭДС индукции;
– изменение полного потока в единицу времени.
Работа по перемещению замкнутого контура в магнитном поле:
A=I ΔΦ,
где A – работа по перемещению контура;
I – сила тока в контуре;
ΔΦ – изменение магнитного потока, пронизывающего контур.
ЭДС самоиндукции:
Энергия магнитного поля:
Объемная плотность энергии магнитного поля:
,
где ω – объемная плотность энергии магнитного поля;
B – индукция магнитного поля;
H – напряженность магнитного поля;
μ – магнитная проницаемость;
μ 0 – магнитная постоянная.
3.2. Понятия и определения
? Перечислите свойства электрического заряда.
1. Существуют заряды двух типов – положительные и отрицательные.
2. Одноименные заряды отталкиваются, разноименные притягиваются.
3.Заряды обладают свойством дискретности – все кратны наименьшему элементарному.
4. Заряд инвариантен, его величина не зависит от системы отсчета.
5. Заряд аддитивен – заряд системы тел равен сумме зарядов всех тел системы.
6. Полный электрический заряд замкнутой системы есть величина постоянная
7. Неподвижный заряд – источник электрического поля, движущийся заряд – источник магнитного поля.
? Сформулируйте закон Кулона.
Сила взаимодействия двух точечных неподвижных зарядов пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними. Направлена сила вдоль линии, соединяющей заряды.
? Что такое электрическое поле? Напряженность электрического поля? Сформулируйте принцип суперпозиции напряженности электрического поля.
Электрическое поле – вид материи, связанный с электрическими зарядами и передающий действие одних зарядов на другие. Напряженность – силовая характеристика поля, равная силе, действующий на единичный положительный заряд, помещенный в данную точку поля. Принцип суперпозиции – напряженность поля, создаваемая системой точечных зарядов, равна векторной сумме напряженностей поля каждого заряда.
Напряженность – силовая характеристика поля, равная силе, действующий на единичный положительный заряд, помещенный в данную точку поля. Принцип суперпозиции – напряженность поля, создаваемая системой точечных зарядов, равна векторной сумме напряженностей поля каждого заряда.
? Что называют силовыми линиями напряженности электростатического поля? Перечислите свойства силовых линий.
Линия, касательная в каждой точке которых совпадает с направлением вектора напряженности поля называется силовой. Свойства силовые линии – начинаются на положительных, заканчиваются на отрицательных зарядах, не прерываются, не пересекаются друг с другом.
? Дайте определение электрического диполя. Поле диполя.
Система из двух равных по модулю, противоположных по знаку точечных электрических зарядов, расстояние между которыми мало по сравнению с расстоянием до точек, где наблюдается действие этих зарядов.Вектор напряженности имеет направление, противоположное вектору электрического момента диполя (который, в свою очередь, направлен от отрицательного заряда к положительному).
? Что такое потенциал электростатического поля? Сформулируйте принцип суперпозиции потенциала.
Скалярная величина, численно равная отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к величине этого заряда. Принцип суперпозиции – потенциал системы точечных зарядов в некоторой точке пространства равен алгебраической сумме потенциалов, которые создали бы по отдельности эти заряды в этой же точке пространства.
? Какова связь между напряженностью и потенциалом?
E =- (E -напряженность поля в данной точке поля, j – потенциал в этой точке.)
? Определите понятие «поток вектора напряженности электрического поля». Сформулируйте электростатическую теорему Гаусса.
Для произвольной замкнутой поверхности поток вектора напряженности E электрического поля Ф Е = . Теорема Гаусса:
= (здесь Q i – заряды, охваченные замкнутой поверхностью). Справедлива для замкнутой поверхности любой формы.
Справедлива для замкнутой поверхности любой формы.
? Какие вещества называют проводниками? Как распределены заряды и электростатическое поле в проводнике? Что такое электростатическая индукция?
Проводники -вещества, в которых под действием электрического поля могут двигаться упорядоченно свободные заряды. Под действием внешнего поля заряды перераспределяются, создавая собственное поле, равное по модулю внешнему и направленное противоположно. Поэтому результирующая напряженность внутри проводника равна 0.
Электростатическая индукция – вид электризации, при котором под действием внешнего электрического поля происходит перераспределение зарядов между частями данного тела.
? Что такое электроемкость уединенного проводника, конденсатора. Как определить емкость плоского кондесатора, батареи конденсаторов, соединенных последовательно, параллельно? Единица измерения электроемкости.
Уединенный проводник: где С –емкость, q – заряд, j – потенциал. Единица измерения – фарад [Ф ]. (1 Ф – емкость проводника, у которого потенциал возрастает на 1 В при сообщении проводнику заряда 1 Кл).
Единица измерения – фарад [Ф ]. (1 Ф – емкость проводника, у которого потенциал возрастает на 1 В при сообщении проводнику заряда 1 Кл).
Емкость плоского конденсатора . Последовательное соединение: . Параллельное соединение: С общ =С 1 +С 2 +…+С n
? Какие вещества называют диэлектриками? Какие типы диэлектриков вы знаете? Что такое поляризация диэлектриков?
Диэлектрики – вещества, в которых при обычных условиях нет свободных электрических зарядов. Существуют диэлектрики полярные, неполярные, сегнетоэлектрики. Поляризацией называется процесс ориентации диполей под воздействием внешнего электрического поля.
? Что такое вектор электрического смещения? Cформулируйте постулат Максвелла.
Вектор электрического смещения D характеризует электростатическое поле, создаваемое свободными зарядами (т.е. в вакууме), но при таком распределении в пространстве, какое имеется при наличии диэлектрика. Постулат Максвелла: . Физический смысл – выражает закон создания электрических полей действием зарядов в произвольных средах.
Постулат Максвелла: . Физический смысл – выражает закон создания электрических полей действием зарядов в произвольных средах.
? Сформулируйте и поясните граничные условия для электростатического поля.
При переходе электрического поля через границу раздела двух диэлектрических сред вектор напряженности и смещения скачкообразно меняются по величине и направлению. Соотношения, характеризующие эти изменения, называются граничными условиями. Их 4:
(3), (4)
? Как определяется энергия электростатического поля? Плотность энергии?
Энергия W= (E- напряженность поля, e-диэлектрическая проницаемость, e 0 -электрическая постоянная, V – объем поля), плотность энергии
? Определите понятие «электрический ток». Виды токов. Характеристики электрического тока. Какое условие необходимо для его возникновения и существования?
Ток – упорядоченное движение заряженных частиц. Виды – ток проводимости, упорядоченное движение свободных зарядов в проводнике, конвекционный – возникает при перемещении в пространстве заряженного макроскопического тела. Для возникновения и существования тока необходимо наличие заряженных частиц, способных перемещаться упорядоченно, и наличие электрического поля, энергия которого восполняясь, расходовалась бы на это упорядоченное движение.
Виды – ток проводимости, упорядоченное движение свободных зарядов в проводнике, конвекционный – возникает при перемещении в пространстве заряженного макроскопического тела. Для возникновения и существования тока необходимо наличие заряженных частиц, способных перемещаться упорядоченно, и наличие электрического поля, энергия которого восполняясь, расходовалась бы на это упорядоченное движение.
? Приведите и поясните уравнение непрерывности. Сформулируйте условие стационарности тока в интегральной и дифференциальной формах.
Уравнение непрерывности . Выражает в дифференциальной форме закон сохранения заряда. Условие стационарности (постоянства) тока в интегральной форме: и дифференциальной – .
? Запишите закон Ома в интегральной и дифференциальной формах.
Интегральная форма – (I –ток, U – напряжение, R -сопротивление). Дифференциальная форма – (j -плотность тока, g- удельная электрическая проводимость, E – напряженность поля в проводнике).
? Что такое сторонние силы? ЭДС?
Сторонние силы разделяют заряды на положительные и отрицательные. ЭДС- отношение работы по перемещению заряда вдоль всей замкнутой цепи к его величине
? Как определяется работа и мощность тока?
При перемещении заряда q по электрической цепи, на концах которой действует напряжение U , электрическим полем совершается работа , мощность тока (t-время)
? Сформулируйте правила Кирхгофа для разветвленных цепей. Какие законы сохранения заложены в правилах Кирхгофа? Сколько независимых уравнений надо составить на основе первого и второго законов Кирхгофа?
1. Алгебраическая сумма токов, сходящихся в узле, равна 0.
2. В любом произвольно выбранном замкнутом контуре алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС, встречающихся в этом контуре. Первое правило Кирхгофа вытекает из закона сохранения электрического заряда.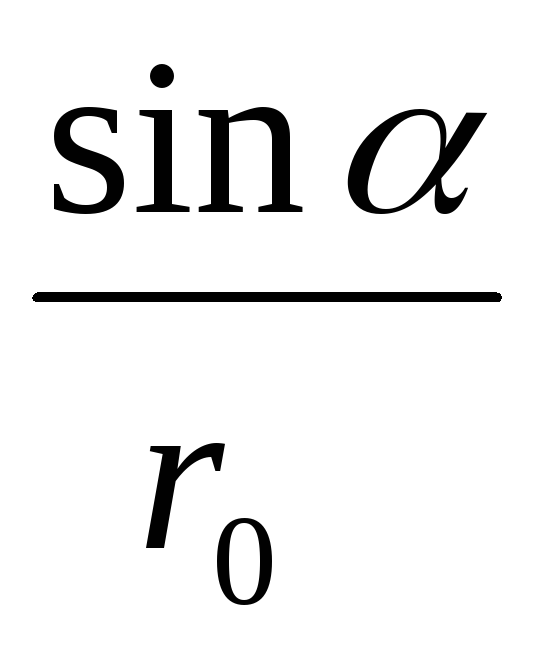 Число уравнений в сумме должно быть равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС).
Число уравнений в сумме должно быть равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС).
? Электрический ток в газе. Процессы ионизации и рекомбинации. Понятие о плазме.
Электрический ток в газах – направленное движение свободных электронов и ионов. При нормальных условиях газы – диэлектрики, проводниками становятся после ионизации. Ионизация – процесс образования ионов путем отделения электронов от молекул газа. Происходит вследствие воздействия внешнего ионизатора – сильного нагрева, рентгеновского или ультрафиолетового облучения, бомбардировки электронами. Рекомбинация – процесс, обратный ионизации. Плазма – представляет собой полностью или частично ионизированный газ, в котором концентрации положительных и отрицательных зарядов равны.
? Электрический ток в вакууме. Термоэлектронная эмиссия.
Носители тока в вакууме – электроны, вылетевшие вследствие эмиссии с поверхности электродов. Термоэлектронная эмиссия – испускание электронов нагретыми металлами.
Термоэлектронная эмиссия – испускание электронов нагретыми металлами.
? Что вы знаете о явлении сверхпроводимости?
Явление, при котором сопротивление некоторых чистых металлов (олово, свинец, алюминий) падает до нуля при температурах, близких к абсолютному нулю.
? Что вы знаете об электрическом сопротивлении проводников? Что такое удельное сопротивление, зависимость его от температуры, удельная электрическая проводимость? Что вы знаете о последовательном и параллельном соединении проводников. Что такое шунт, дополнительное сопротивление?
Сопротивление – величина, прямо пропорциональная длине проводника l и обратно пропорциональная площади S поперечного сечения проводника: (r-удельное сопротивление). Проводимость- величина, обратная сопротивлению. Удельное сопротивление (сопротивление проводника длиной 1 м сечением 1 м 2). Удельное сопротивление зависит от температуры , здесь a – температурный коэффициент, R и R 0 , r и r 0 –сопротивления и удельные сопротивления при t и 0 0 С. Параллельное – , последовательное R=R 1 +R 2 +…+R n . Шунт- резистор, подключаемый параллельно электроизмерительному прибору, для отведения части электрического тока, чтобы расширить пределы измерений.
Параллельное – , последовательное R=R 1 +R 2 +…+R n . Шунт- резистор, подключаемый параллельно электроизмерительному прибору, для отведения части электрического тока, чтобы расширить пределы измерений.
? Магнитное поле. Какие источники могут создавать магнитное поле?
Магнитное поле – особый вид материи, посредством которой взаимодействуют движущиеся электрические заряды. Причина существования постоянного магнитного поля неподвижный проводник с постоянным электрическим током, или постоянные магниты.
? Сформулируйте закон Ампера. Как взаимодействуют проводники, по которым ток течет в одном (противоположном) направлении?
На проводник с током действует сила Ампера, равная .
B – магнитная индукция, I- ток в проводнике, Dl –длина участка проводника, a-угол между магнитной индукцией и участком проводника. В одном направлении -притягиваются, в противоположном – отталкиваются.
? Дайте определение силы Ампера. Как определить ее направление?
Это сила, действующая на проводник с током, помещенный в магнитное поле. Направление определяем так: ладонь левой руки располагаем так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца были направлены по току в проводнике. Отогнутый большой палец покажет направление силы Ампера.
? Поясните движение заряженных частиц в магнитном поле. Что такое сила Лоренца? Как находится ее направление?
Движущаяся заряженная частица создает свое собственное магнитное поле. Если ее поместить во внешнее магнитное поле, то взаимодействие полей проявится в возникновении силы, действующей на частицу со стороны внешнего поля – силы Лоренца. Направление – по правилу левой руки. Для положительного заряда- вектор B входит в ладонь левой руки, четыре пальца направлены по движению положительного заряда (вектору скорости), отогнутый большой палец показывает направление силы Лоренца. На отрицательный заряд та же сила действует в обратном направлении.
На отрицательный заряд та же сила действует в обратном направлении.
(q -заряд, v -скорость, B – индукция, a- угол между направлением скорости и магнитной индукции).
? Рамка с током в однородном магнитном поле. Как определяется магнитный момент?
Магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая ее определенным образом. Вращающий момент определяется формулой: M =p m xB , где p m – вектор магнитного момента рамки с током, равный ISn (ток на площадь поверхности контура, на единичную нормаль к контуру), B -вектор магнитной индукции, количественная характеристика магнитного поля.
? Что такое вектор магнитной индукции? Как определить его направление? Как графически изображают магнитное поле?
Вектор магнитной индукции – это силовая характеристика магнитного поля.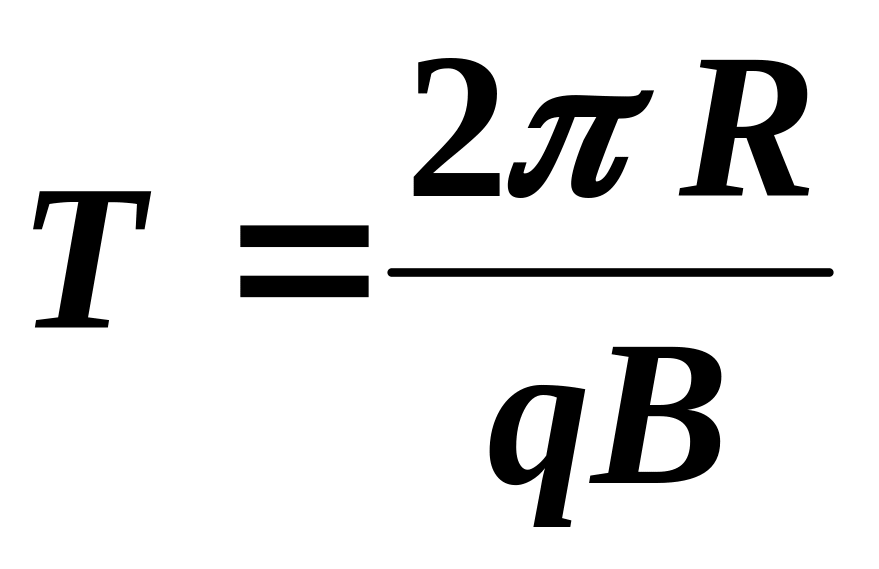 Магнитное поле наглядно изображают с помощью силовых линий. В каждой точке поля касательная к силовой линии совпадает с направлением вектора магнитной индукции.
Магнитное поле наглядно изображают с помощью силовых линий. В каждой точке поля касательная к силовой линии совпадает с направлением вектора магнитной индукции.
? Сформулируйте и поясните закон Био – Савара – Лапласа.
Закон Био – Савара – Лапласа позволяет рассчитать для проводника с током I магнитную индукцию поля dB , создаваемого в произвольной точке поля dl проводника: (здесь m 0 -магнитная постоянная, m-магнитная проницаемость среды). Направление вектора индукции определяется по правилу правого винта, если поступательное движение винта соответствует направлению тока в элементе.
? Сформулируйте принцип суперпозиции для магнитного поля.
Принцип суперпозиции – магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
? Поясните основные характеристики магнитного поля: магнитный поток, циркуляция магнитного поля, магнитная индукция.
Магнитным потоком Ф через какую-либо поверхность S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и косинус угла a между векторами B и n (внешней нормалью к поверхности). Циркуляцией вектора B по заданному замкнутому контуру называется интеграл вида , где dl – вектор элементарной длины контура. Теорема о циркуляции вектора B : циркуляция вектора B по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром. Вектор магнитной индукции – это силовая характеристика магнитного поля. Магнитное поле наглядно изображают с помощью силовых линий. В каждой точке поля касательная к силовой линии совпадает с направлением вектора магнитной индукции.
? Запишите и прокомментируйте условие соленоидальности магнитного поля интегральной и дифференциальной формах.
Векторные поля, в которых отсутствуют источники и стоки, называют соленоидальными. Условие соленоидальности магнитного поля в интегральной форме: и дифференциальной форме:
? Магнетики. Виды магнетиков. Феромагнетики и их свойства. Что такое гистерезис?
Вещество является магнетиком, если оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками.Намагничивающиеся во внешнем магнитном поле по направлению поля – парамагнетиками. Эти два класса называют слабомагнитными веществами. Сильномагнитные вещества, намагниченные даже при отсутствии внешнего магнитного поля, называют ферромагнетиками. Магнитный гистерезис – различие в значениях намагниченности ферромагнетика при одной и той же напряженности Н намагничивающего поля в зависимости от значения предварительной намагниченности. Такая графическая зависимость называется петлей гистерезиса.
? Сформулируйте и поясните закон полного тока в интегральной и дифференциальной формах (основные ур-я магнитостатики в веществе).
? Что такое электромагнитная индукция? Сформулируйте и поясните основной закон электромагнитной индукции (закон Фарадея). Сформулируйте правило Ленца.
Явление возникновения электродвижущей силы (ЭДС индукции) в проводнике, находящемся в переменном магнитном поле или движущемся в постоянном в постоянном магнитном поле называют электромагнитной индукцией. Закон Фарадея: какова бы не была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре ЭДС
Знак минус определяется правилом Ленца – индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.
? В чем заключается явление самоиндукции? Что такое индуктивность, единицы измерения? Токи при замыкании и размыкании электрической цепи.
Возникновение ЭДС индукции в проводящем контуре под действием собственного магнитного поля при его изменении, происходящем в результате изменения в проводнике силы тока. Индуктивность – коэффициент пропорциональности, зависящий от формы и размеров проводника или контура, [Гн]. В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи. Поэтому величина силы тока не может меняться мгновенно (механический аналог – инертность).
? Явление взаимной индукции. Коэффициент взаимной индукции.
Если два неподвижных контура расположены близко друг к другу, то при изменении силы тока в одном контуре, возникает ЭДС в другом контуре. Это явление называется взаимной индукцией. Коэффициенты пропорциональности L 21 и L 12 называют взаимной индуктивностью контуров, они равны.
? Запишите уравнения Максвелла в интегральной форме. Поясните их физический смысл.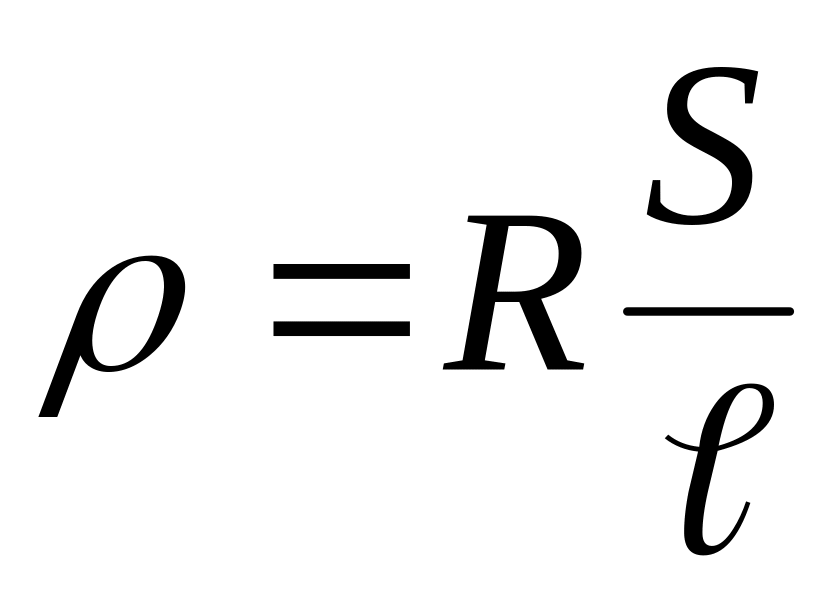
; ;
; .
Из теории Максвелла следует, что электрическое и магнитное поле нельзя рассматривать как независимые – изменение во времени одного приводит к изменению другого.
? Энергия магнитного поля. Плотность энергии магнитного поля.
Энергия , L –индуктивность, I – сила тока.
Плотность , В – магнитная индукция, Н – напряженность магнитного поля, V -объем.
? Принцип относительности в электродинамике
Общие закономерности электромагнитных полей описываются уравнениями Максвелла. В релятивистской электродинамике установлено, что релятивистская инвариантность этих уравнений имеет место только при условии относительности электрических и магнитных полей, т.е. при зависимости характеристик этих полей от выбора инерциальных систем отсчета. В подвижной системе электрическое поле такое же, как в неподвижной, но в подвижной системе имеется магнитное поле, которого в неподвижной системе нет.
Колебания и волны
Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
При изучении темы “Постоянный ток” необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца При изучении “Магнетизма” необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.
Электрические и магнитные явления связаны особой формой существования материи – электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.
Основой теории электромагнитного поля является теория Максвелла.
Таблица основных формул электричества и магнетизма
Физические законы, формулы, переменные | Формулы электричество и магнетизм | ||||||||
Закон Кулона: | |||||||||
Напряженность электрического поля: где Ḟ – сила, действующая на заряд q 0 , находящийся в данной точке поля. | |||||||||
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями | |||||||||
Потенциал электрического поля: где W – потенциальная энергия заряда
q
0 . | |||||||||
Потенциал поля точечного заряда на расстоянии r от заряда: | |||||||||
По принципу суперпозиции полей, напряженность: | |||||||||
Потенциал: где Ē i и ϕ i – напряженность и потенциал в данной точке поля, создаваемый i-м зарядом. | |||||||||
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ 1 в точку с потенциалом ϕ 2 : | |||||||||
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля: | |||||||||
Электроемкость уединенного проводника: | |||||||||
Электроемкость конденсатора: | |||||||||
Электроемкость плоского конденсатора: где S – площадь пластины (одной) конденсатора, d – расстояние между пластинами. | |||||||||
Энергия заряженного конденсатора: | |||||||||
Сила тока: | |||||||||
Плотность тока: где S – площадь поперечного сечения проводника. | |||||||||
Сопротивление проводника: l – длина проводника; S – площадь поперечного сечения. | |||||||||
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС: Где ε – ЭДС источника тока, R и r – внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи: | |||||||||
Закон Джоуля-Ленца 1) для однородного участка цепи постоянного тока: 2) для участка цепи с изменяющимся со временем током: | |||||||||
Мощность тока: | |||||||||
Связь магнитной индукции и напряженности магнитного поля: где B – вектор магнитной индукции, | |||||||||
Магнитная индукция (индукция магнитного поля): 2) поля бесконечно длинного прямого тока 3) поля, созданного отрезком проводника с током |
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Электродинамика –
это наука о свойствах и закономерностях
особого вида материи – электромагнитного
поля, которое осуществляет взаимодействие
между электрическими заряженными телами
или частицами.
Ква́нтовая электродина́мика (КЭД) – квантовополевая теория электромагнитных взаимодействий; наиболее разработанная часть квантовой теории поля. Классическая электродинамика учитывает только непрерывные свойства электромагнитного поля, в основе же квантовой электродинамики лежит представление о том, что электромагнитное поле обладает также и прерывными (дискретными) свойствами, носителями которых являются кванты поля -фотоны. Взаимодействие электромагнитного излучения с заряженными частицами рассматривается в квантовой электродинамике как поглощение и испускание частицами фотонов.
2.Характеристики электромагнитного поля
Электромагнитное поле – Е = Н/Кл = В/М
E = F / q – отношение силы, действующей со стороны поля к величине этого заряда.
D – индукция электрического поля – называется вектор пропорциональный вектору напряженности, но независящий от свойств среды
D = 𝞮 E ; 𝞮 = 𝞮 0 𝞮 ’ 0 =
8.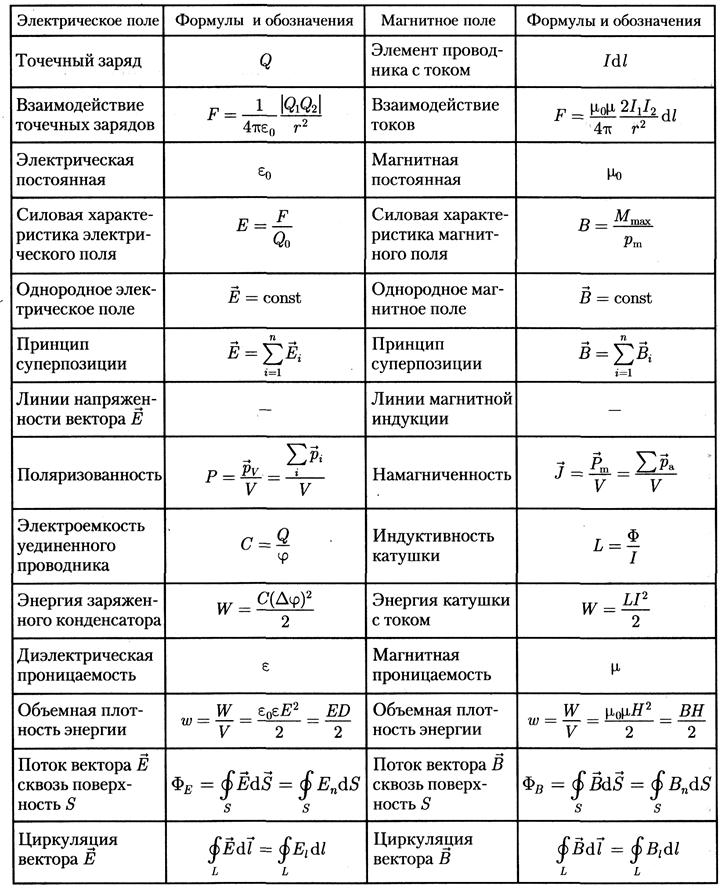 85 * 10 -12 Ф/м
85 * 10 -12 Ф/м
В- вектор индукции магнитного поля = Н/А*м= 1Тл
Индукцией называется вектор, модуль которого есть отношение модуля силы действующий со стороны поля на проводник с током, на силу тока в проводнике и его длину. B = | F |/ I * l (Н/ А*м) Н – напряженность магнитного поля (А/м) = 80 эрстед =) 80 Гаусс, называется вектор параллельный вектору индукции, но независящий от свойств среды. Н= 1/µ, где µ = µ 0* µ’
3.Векторные поля.Интегральные и дифферциальные характеристики векторного поля
4.ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА И СТОКСА
5.ЗАКОН КУЛОНА
6.ТЕОРЕМА ГАУССА
7.ПОТОК ВЕКТОРА
8.УРАВНЕНИЯ НЕПРЕРЫВНОСТИ
9.ТОК СМЕЩЕНИЯ
10.ЗАКОН ПОЛНОГО ТОКА
11. ЗАКОН
НЕПРЕРЫВНОСТИ МАГНИТНОГО ПОТОКА
ЗАКОН
НЕПРЕРЫВНОСТИ МАГНИТНОГО ПОТОКА
12.ГРАНИЧНЫЕ УСЛОВИЯ
13.ЗАКОНЫ ДЖОУЛЯ-ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
Количество теплоты, выделяющееся в единицу времени в проводнике с сопротивлением R при силе тока I, по закону Джоуля-Ленца, равно:
Применив этот закон к бесконечно малому цилиндру, ось которого совпадает с направлением тока, получаем
Учитывая что – обьем бесконечно малого цилиндра, а– количество теплоты, выделенной в единице обьема за единицу времени, находим
,
Где выражается в ватах на кубический метр. Учитывая, что j 2 =j*j и используя для j выражение можно записать соотношение в виде:
Это равенство выражает закон Джоуля-Ленца в дифференциальной форме.
14.Полная система уравнений максвелла в веществе
В
среде сторонние электрические и магнитные
поля вызывают поляризацию и намагничивание
вещества, которые макроскопически
описываются соответственно вектором
поляризации P и вектором
намагниченности M вещества,
и вызваны появлением связанных зарядов и
токов . В результате поле в среде оказывается
суммой внешних полей и полей, вызванных
связанными зарядами и токами.
В результате поле в среде оказывается
суммой внешних полей и полей, вызванных
связанными зарядами и токами.
Поляризация P и намагниченность вещества M связаны с векторами напряжённости и индукции электрического и магнитного поля следующими соотношениями:
Поэтому, выражая векторы D и H через E, B, и , можно получить математически эквивалентную систему уравнений Максвелла:
Индексом здесь обозначены свободные заряды и токи. Уравнения Максвелла в такой форме являются фундаментальными, в том смысле, что они не зависят от модели электромагнитного устройства вещества. Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в ,, а затем в P, M и, следовательно, в D, B сложный микроскопический характер электромагнитного поля в среде.
16.1 Уравнения Максвелла и электромагнитные волны — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните поправку Максвелла к закону Ампера, включив ток смещения
- Сформулируйте и примените уравнения Максвелла в интегральной форме
- Опишите, как симметрия между изменяющимися электрическими и изменяющимися магнитными полями объясняет предсказание Максвелла об электромагнитных волнах
- Опишите, как Герц подтвердил предсказание Максвелла об электромагнитных волнах
Джеймс Клерк Максвелл (1831–1879) внес значительный вклад в физику девятнадцатого века (рис.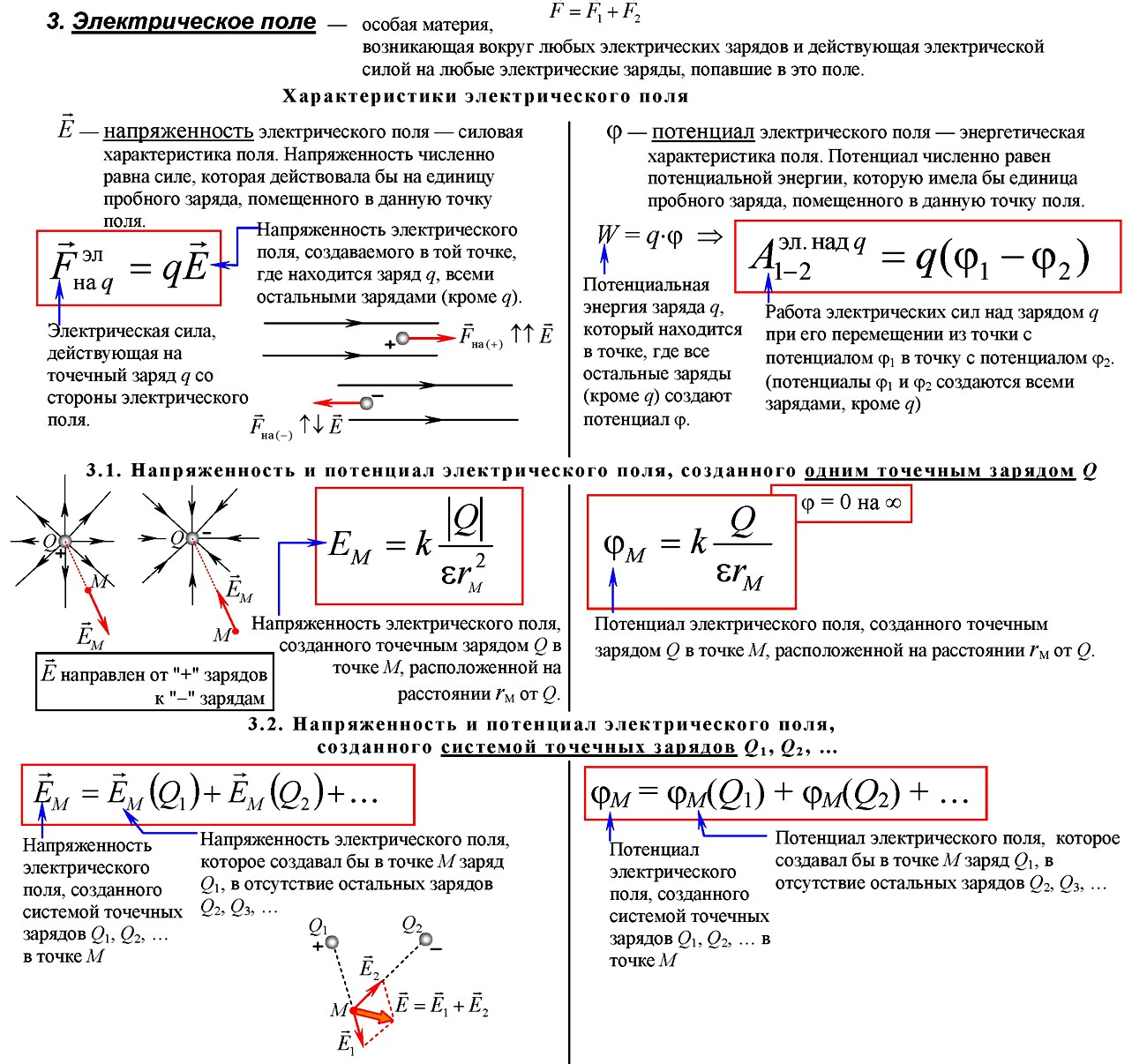 16.2). Хотя он умер молодым, он внес большой вклад в развитие кинетической теории газов, в понимание цветового зрения и в природу колец Сатурна. Он, вероятно, наиболее известен тем, что объединил существующие знания о законах электричества и магнетизма с собственными открытиями в полной всеобъемлющей электромагнитной теории, представленной уравнениями Максвелла.
16.2). Хотя он умер молодым, он внес большой вклад в развитие кинетической теории газов, в понимание цветового зрения и в природу колец Сатурна. Он, вероятно, наиболее известен тем, что объединил существующие знания о законах электричества и магнетизма с собственными открытиями в полной всеобъемлющей электромагнитной теории, представленной уравнениями Максвелла.
Фигура 16,2 Джеймс Клерк Максвелл, физик девятнадцатого века, разработал теорию, объясняющую взаимосвязь между электричеством и магнетизмом, и правильно предсказал, что видимый свет состоит из электромагнитных волн.
Поправка Максвелла к законам электричества и магнетизма
Четыре основных закона электричества и магнетизма были открыты экспериментально благодаря работам таких физиков, как Эрстед, Кулон, Гаусс и Фарадей. Максвелл обнаружил логические противоречия в этих более ранних результатах и назвал их причиной неполноту закона Ампера.
Напомним, что по закону Ампера интеграл магнитного поля вокруг замкнутого контура C пропорционален току I , проходящему через любую поверхность, границей которой является сам контур C :
∮CB→·ds→=µ0I. ∮CB→·ds→=µ0I.
∮CB→·ds→=µ0I.16.1
Существует бесконечно много поверхностей, которые можно присоединить к любой петле, и закон Ампера, сформулированный в уравнении 16.1, не зависит от выбора поверхности.
Рассмотрим настройку на рис. 16.3. Источник ЭДС резко подключается к пластинчатому конденсатору так, что в проводе возникает зависящий от времени ток I . Предположим, мы применяем закон Ампера к петле C , показанной до того, как конденсатор полностью заряжен, так что I≠0I≠0.Поверхность S1S1 дает ненулевое значение для замкнутого тока I , тогда как поверхность S2S2 дает нулевое значение для замкнутого тока, потому что через нее не проходит ток:
∮CB→·ds→={µ0Iесли используется поверхность S10если используется поверхность S2. ∮CB→·ds→={µ0Iесли используется поверхностьS10если используется поверхностьS2. Понятно, что закон Ампера в его обычном виде здесь не работает. Это внутреннее противоречие теории, которое требует модификации самой теории, закона Ампера.
Как изменить закон Ампера, чтобы он работал во всех ситуациях? Максвелл предложил включить в действительный ток I ,
дополнительный вклад, называемый током смещения IdId. ∮CB→·ds→=µ0(I+Id)∮CB→·ds→=µ0(I+Id)16,2
, где ток смещения определен как
Id=ε0dΦEdt.Id=ε0dΦEdt.16,3
Здесь ε0ε0 — диэлектрическая проницаемость свободного пространства, а ΦEΦE — электрический поток, определяемый как
ΦE=∬SurfaceSE→·dA→.ΦE=∬SurfaceSE→·dA→. Ток смещения аналогичен реальному току в законе Ампера, входя в закон Ампера таким же образом. Однако он создается изменяющимся электрическим полем. Он объясняет изменяющееся электрическое поле, создающее магнитное поле, как это делает реальный ток, но ток смещения может создавать магнитное поле даже там, где нет реального тока. Когда этот дополнительный член включен, уравнение модифицированного закона Ампера становится равным
Когда этот дополнительный член включен, уравнение модифицированного закона Ампера становится равным
16.4
и не зависит от поверхности S , через которую измеряется ток I .
Теперь мы можем изучить эту модифицированную версию закона Ампера, чтобы подтвердить, что он выполняется независимо от того, выбрана ли поверхность S1S1 или поверхность S2S2 на рис. 16.3. Электрическое поле E→E→, соответствующее потоку ΦEΦE в уравнении 16.3, находится между пластинами конденсатора. Следовательно, поле E→E→ и ток смещения через поверхность S1S1 равны нулю, и уравнение 16.2 принимает вид
∮CB→·ds→=µ0I. ∮CB→·ds→=µ0I.16,5
Теперь мы должны показать, что для поверхностей S2,S2, через которые фактически не протекает ток, ток смещения приводит к тому же самому значению µ0Iµ0I для правой части уравнения закона Ампера. Для поверхности S2,S2 уравнение принимает вид
∮CB→·ds→=µ0ddt[ε0∬SurfaceS2E→·dA→]. ∮CB→·ds→=µ0ddt[ε0∬SurfaceS2E→·dA→].
∮CB→·ds→=µ0ddt[ε0∬SurfaceS2E→·dA→].16,6
Закон Гаусса для электрического заряда требует замкнутой поверхности и обычно не может быть применен к поверхности, такой как только S1S1 или только S2S2.Но две поверхности S1S1 и S2S2 образуют замкнутую поверхность на рис. 16.3 и могут использоваться в законе Гаусса. Поскольку электрическое поле равно нулю на S1S1, вклад потока через S1S1 равен нулю. Это дает нам
∯SurfaceS1+S2E→·dA→=∬SurfaceS1E→·dA→+∬SurfaceS2E→·dA→=0+∬SurfaceS2E→·dA→=∬SurfaceS2E→·dA→.∯SurfaceS1+S2E→·dA→=∬SurfaceS1E →·dA→+∬SurfaceS2E→·dA→=0+∬SurfaceS2E→·dA→=∬SurfaceS2E→·dA→.Следовательно, мы можем заменить интеграл по S2S2 в уравнении 16.6 замкнутой гауссовой поверхностью S1+S2S1+S2 и применить закон Гаусса, чтобы получить
∮S1B→·ds→=μ0dQindt=μ0I.∮S1B→·ds→=μ0dQindt=μ0I.16,7
Таким образом, модифицированное уравнение закона Ампера одинаково для поверхности S2,S2, где правая часть является результатом тока смещения, как и для поверхности S1,S1, где вклад исходит от фактического потока электрического заряда .
Пример 16.1
Ток смещения в зарядном конденсаторе
Плоский конденсатор емкостью Кл , пластины которого имеют площадь А и расстояние между ними d , подключен к резистору R и батарее напряжением В .Ток начинает течь при t=0t=0. а) Найдите ток смещения между пластинами конденсатора в момент времени t . (b) По свойствам конденсатора найдите соответствующий реальный ток I=dQdtI=dQdt и сравните ответ с ожидаемым током в проводах соответствующей цепи RC .Стратегия
Мы можем использовать уравнения из анализа цепи RC (цепи переменного тока) плюс максвелловскую версию закона Ампера.Решение
- Напряжение между пластинами в момент времени t определяется выражением
VC=1CQ(t)=V0(1−e−t/RC).
 VC=1CQ(t)=V0(1−e−t/RC).
Пусть ось z указывает от положительной пластины к отрицательной пластине. Тогда z -компонента электрического поля между пластинами как функция времени t равна
Ez(t)=V0d(1−e−t/RC).Ez(t)=V0d(1−e−t/RC).
Следовательно, z-составляющая тока смещения IdId между пластинами равна
Id(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC=V0Re−t/RC,Id(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC= V0Re-t/RC,
где мы использовали C=ε0AdC=ε0Ad для емкости.
VC=1CQ(t)=V0(1−e−t/RC).
Пусть ось z указывает от положительной пластины к отрицательной пластине. Тогда z -компонента электрического поля между пластинами как функция времени t равна
Ez(t)=V0d(1−e−t/RC).Ez(t)=V0d(1−e−t/RC).
Следовательно, z-составляющая тока смещения IdId между пластинами равна
Id(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC=V0Re−t/RC,Id(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC= V0Re-t/RC,
где мы использовали C=ε0AdC=ε0Ad для емкости. - Из выражения для VC,VC заряд конденсатора равен Q(t)=CVC=CV0(1-e-t/RC).Q(t)=CVC=CV0(1-e-t/RC). Таким образом, ток в конденсаторе после замыкания цепи равен I=dQdt=V0Re-t/RC.I=dQdt=V0Re-t/RC. Этот ток такой же, как IdId, найденный в (а).
Уравнения Максвелла
С поправкой на ток смещения уравнения Максвелла принимают вид
∮E→·dA→=Qinε0(закон Гаусса)∮E→·dA→=Qinε0(закон Гаусса)16,8
∮B→·dA→=0(закон Гаусса для магнетизма)∮B→·dA→=0(закон Гаусса для магнетизма) 16. 9
9
16.10
∮B→·ds→=µ0I+ε0µ0dΦEdt(закон Ампера-Максвелла).∮B→·ds→=µ0I+ε0µ0dΦEdt(закон Ампера-Максвелла).16.11
После расчета полей с использованием этих четырех уравнений уравнение силы Лоренца
F→=qE→+qv→×B→F→=qE→+qv→×B→16,12
дает силу, с которой поля действуют на частицу с зарядом q , движущуюся со скоростью v→v→. Уравнение силы Лоренца объединяет силу электрического поля и магнитного поля, действующую на движущийся заряд.Магнитные и электрические силы рассматривались в предыдущих модулях. Эти четыре уравнения Максвелла равны соответственно
Уравнения Максвелла
1. Закон Гаусса
Электрический поток через любую замкнутую поверхность равен электрическому заряду QinQin , заключенному в этой поверхности. Закон Гаусса [уравнение 16.7] описывает связь между электрическим зарядом и создаваемым им электрическим полем. Это часто изображают в виде силовых линий электрического поля, исходящих из положительных зарядов и заканчивающихся отрицательными зарядами и указывающих направление электрического поля в каждой точке пространства.
Это часто изображают в виде силовых линий электрического поля, исходящих из положительных зарядов и заканчивающихся отрицательными зарядами и указывающих направление электрического поля в каждой точке пространства.
2. Закон Гаусса для магнетизма
Поток магнитного поля через любую замкнутую поверхность равен нулю [уравнение 16.8]. Это эквивалентно утверждению, что силовые линии магнитного поля непрерывны, не имеют ни начала, ни конца. Любая линия магнитного поля, входящая в область, ограниченную поверхностью, также должна покинуть ее. Известно, что не существует магнитных монополей, где линии магнитного поля заканчивались бы (см. Магнитные поля и линии).
3. Закон Фарадея
Изменяющееся магнитное поле индуцирует электродвижущую силу (ЭДС) и, следовательно, электрическое поле.Направление ЭДС противоположно изменению. Это третье уравнение Максвелла, уравнение 16.9, представляет собой закон индукции Фарадея и включает в себя закон Ленца. Электрическое поле от изменяющегося магнитного поля имеет силовые линии, которые образуют замкнутые петли без начала и конца.
Электрическое поле от изменяющегося магнитного поля имеет силовые линии, которые образуют замкнутые петли без начала и конца.
4. Закон Ампера-Максвелла
Магнитные поля генерируются движущимися зарядами или изменяющимися электрическими полями. Это четвертое уравнение Максвелла, уравнение 16.10, включает в себя закон Ампера и добавляет еще один источник магнитных полей, а именно изменяющиеся электрические поля.
Уравнения Максвелла и закон силы Лоренца вместе охватывают все законы электричества и магнетизма. Симметрия, которую Максвелл ввел в свою математическую структуру, может быть не сразу очевидна. Закон Фарадея описывает, как изменяющиеся магнитные поля создают электрические поля. Вместо этого введенный Максвеллом ток смещения является результатом изменяющегося электрического поля и объясняет изменяющееся электрическое поле, создающее магнитное поле. Уравнения для эффектов как изменяющихся электрических полей, так и изменяющихся магнитных полей различаются по форме только там, где отсутствие магнитных монополей приводит к пропущенным членам. Эта симметрия между эффектами изменения магнитного и электрического полей имеет важное значение для объяснения природы электромагнитных волн.
Эта симметрия между эффектами изменения магнитного и электрического полей имеет важное значение для объяснения природы электромагнитных волн.
Последующее применение теории относительности Эйнштейна к полной и симметричной теории Максвелла показало, что электрические и магнитные силы не являются отдельными, а являются разными проявлениями одного и того же — электромагнитной силы. Электромагнитное взаимодействие и слабое ядерное взаимодействие так же объединены, как и электрослабое взаимодействие. Это объединение сил было одним из мотивов попыток объединить все четыре основных взаимодействия в природе — гравитационное, электрическое, сильное и слабое ядерное взаимодействие (см. Физика элементарных частиц и космология).
Механизм распространения электромагнитных волн
Чтобы увидеть, как введенная Максвеллом симметрия объясняет существование комбинированных электрических и магнитных волн, распространяющихся в пространстве, представьте себе изменяющееся во времени магнитное поле B→0(t)B→0(t), создаваемое высокочастотным переменным полем. ток показан на рис. 16.4. Мы представляем B→0(t)B→0(t) на диаграмме одной из ее силовых линий. Согласно закону Фарадея, изменение магнитного поля через поверхность индуцирует изменяющееся во времени электрическое поле E→0(t)E→0(t) на границе этой поверхности.Источник тока смещения для электрического поля, как и источник закона Фарадея для магнитного поля, создает только замкнутые петли силовых линий из-за математической симметрии, связанной с уравнениями для индуцированного электрического и индуцированного магнитного полей. Представление линии поля E→0(t)E→0(t) показано. В свою очередь изменяющееся электрическое поле E→0(t)E→0(t) создает магнитное поле B→1(t)B→1(t) по модифицированному закону Ампера. Это изменяющееся поле индуцирует E→1(t), E→1(t), что индуцирует B→2(t), B→2(t) и так далее.Затем мы имеем самопродолжающийся процесс, который приводит к созданию изменяющихся во времени электрических и магнитных полей в областях, все дальше и дальше от O . Этот процесс можно представить себе как распространение электромагнитной волны в пространстве.
ток показан на рис. 16.4. Мы представляем B→0(t)B→0(t) на диаграмме одной из ее силовых линий. Согласно закону Фарадея, изменение магнитного поля через поверхность индуцирует изменяющееся во времени электрическое поле E→0(t)E→0(t) на границе этой поверхности.Источник тока смещения для электрического поля, как и источник закона Фарадея для магнитного поля, создает только замкнутые петли силовых линий из-за математической симметрии, связанной с уравнениями для индуцированного электрического и индуцированного магнитного полей. Представление линии поля E→0(t)E→0(t) показано. В свою очередь изменяющееся электрическое поле E→0(t)E→0(t) создает магнитное поле B→1(t)B→1(t) по модифицированному закону Ампера. Это изменяющееся поле индуцирует E→1(t), E→1(t), что индуцирует B→2(t), B→2(t) и так далее.Затем мы имеем самопродолжающийся процесс, который приводит к созданию изменяющихся во времени электрических и магнитных полей в областях, все дальше и дальше от O . Этот процесс можно представить себе как распространение электромагнитной волны в пространстве.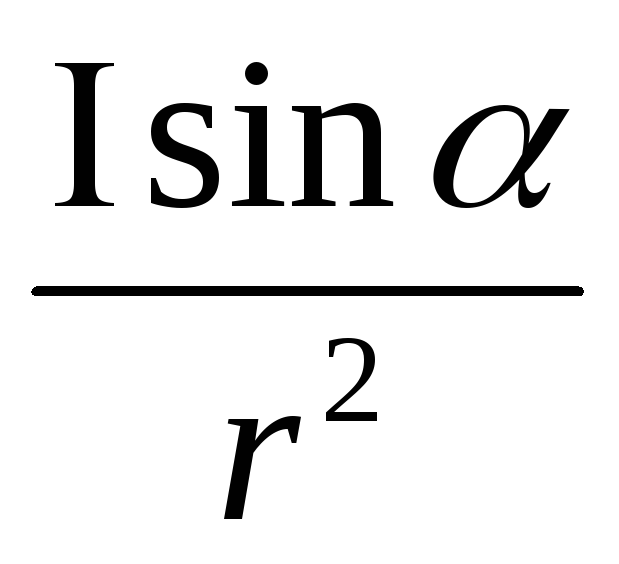
В следующем разделе мы покажем в более точных математических терминах, как уравнения Максвелла приводят к предсказанию электромагнитных волн, которые могут распространяться в пространстве без материальной среды, подразумевая скорость электромагнитных волн, равную скорости света.
До работы Максвелла эксперименты уже указывали на то, что свет представляет собой волновое явление, хотя природа волн была еще неизвестна. В 1801 году Томас Юнг (1773–1829) показал, что, когда световой луч разделяется двумя узкими щелями, а затем снова объединяется, на экране образуется рисунок, состоящий из ярких и темных полос. Янг объяснил это поведение, предполагая, что свет состоит из волн, которые складываются конструктивно в одних точках и разрушительно в других (см. Интерференция).Впоследствии Жан Фуко (1819–1868) с измерениями скорости света в различных средах и Огюстен Френель (1788–1827) с подробными экспериментами, связанными с интерференцией и дифракцией света, предоставили дополнительные убедительные доказательства того, что свет представляет собой волну. Итак, свет был волной, и Максвелл предсказал существование электромагнитных волн, распространяющихся со скоростью света. Вывод казался неизбежным: свет должен быть формой электромагнитного излучения. Но теория Максвелла показала, что для электромагнитных волн возможны другие длины волн и частоты, отличные от световых.Он показал, что электромагнитное излучение с теми же фундаментальными свойствами, что и видимый свет, должно существовать на любой частоте. Другим оставалось проверить и подтвердить это предсказание.
Итак, свет был волной, и Максвелл предсказал существование электромагнитных волн, распространяющихся со скоростью света. Вывод казался неизбежным: свет должен быть формой электромагнитного излучения. Но теория Максвелла показала, что для электромагнитных волн возможны другие длины волн и частоты, отличные от световых.Он показал, что электромагнитное излучение с теми же фундаментальными свойствами, что и видимый свет, должно существовать на любой частоте. Другим оставалось проверить и подтвердить это предсказание.
Проверьте свое понимание 16.1
Проверьте свое понимание Когда ЭДС на конденсаторе включена и конденсатор заряжается, когда магнитное поле, вызванное током смещения, имеет наибольшую величину?
Наблюдения Герца
Немецкий физик Генрих Герц (1857–1894) первым сгенерировал и обнаружил определенные типы электромагнитных волн в лаборатории.Начиная с 1887 года, он провел серию экспериментов, которые не только подтвердили существование электромагнитных волн, но и подтвердили, что они распространяются со скоростью света.
Герц использовал цепь переменного тока RLC (резистор-индуктор-конденсатор), которая резонирует на известной частоте f0=12πLCf0=12πLC и соединила ее с проволочной петлей, как показано на рис. 16.5. Высокое напряжение, индуцированное через разрыв в петле, вызывало искры, которые были видимым свидетельством тока в цепи и помогали генерировать электромагнитные волны.
Через лабораторию Герц разместил еще одну петлю, присоединенную к другой цепи RLC , которую можно было настроить (как циферблат на радио) на ту же резонансную частоту, что и первую, и, таким образом, можно было настроить на прием электромагнитных волн. В этой петле также был зазор, через который генерировались искры, что давало убедительные доказательства того, что электромагнитные волны были получены.
Фигура 16,5 Аппарат, использованный Герцем в 1887 году для генерации и обнаружения электромагнитных волн.
Герц также изучил картины отражения, преломления и интерференции генерируемых им электромагнитных волн, подтвердив их волновой характер. Он смог определить длины волн по интерференционным картинам и, зная их частоты, рассчитать скорость распространения по уравнению v=fλv=fλ, где v — скорость волны, f — ее частота, λλ – его длина волны. Таким образом, Герц смог доказать, что электромагнитные волны распространяются со скоростью света.Единица СИ для частоты, герц (1 Гц = 1 цикл / с, 1 Гц = 1 цикл / с), названа в его честь.
Он смог определить длины волн по интерференционным картинам и, зная их частоты, рассчитать скорость распространения по уравнению v=fλv=fλ, где v — скорость волны, f — ее частота, λλ – его длина волны. Таким образом, Герц смог доказать, что электромагнитные волны распространяются со скоростью света.Единица СИ для частоты, герц (1 Гц = 1 цикл / с, 1 Гц = 1 цикл / с), названа в его честь.
Проверьте свое понимание 16,2
Проверьте свои знания Может ли чисто электрическое поле распространяться в виде волны в вакууме без магнитного поля? Обосновать ответ.
Единая теория – электричество, магнетизм, гравитация, механика
Единая теория – электричество, магнетизм, гравитация, механикаarXiv:physics/9
4v1 [physics.gen-ph] 12 августа 1999 г.Единая теория – электричество, магнетизм, гравитация и механика
Юлиус Преттеребнер, Im Rank 10, D-71570 Oppenweiler, Германия
Контактное лицо: Julius@Pretterebner.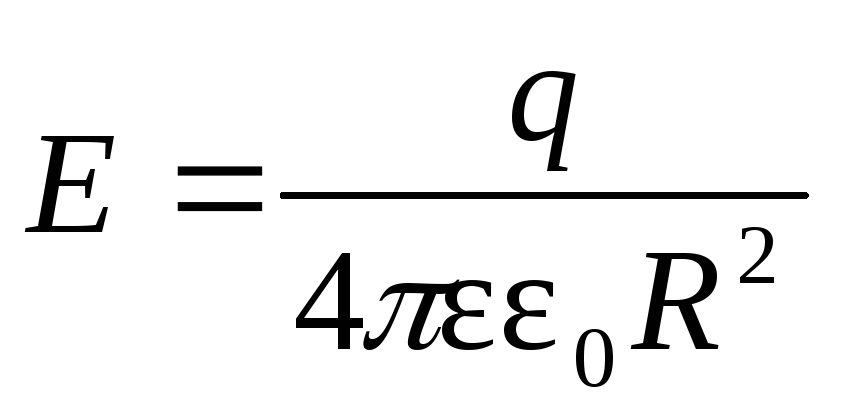 DE
DE
Аннотация
В этой статье показаны отношения между электричеством, магнетизмом,
гравитацию и механику, представляя существующую скрытую структуру в уравнениях Максвелла.
Эта скрытая структура позволяет открыть классическую физику с новой точки зрения.
ведущая к единой теории (UT).В этом UT магнетизм представляет собой вращающееся электрическое
импульс поля, а механический импульс – это импульс гравитационного поля. Смешивание
теория точек – т.е. массовые точки – и теория поля – т.е.
электромагнитные волны – не допускает УТ. Строгое использование теории поля
преодолевает эту проблему и приводит к UT. В первом разделе этой статьи речь
теория представлена как редукция теории поля. Отношение между точкой
импульс и импульс поля является ключевым моментом для УТ.Во втором разделе
электрические уравнения Максвелла выводятся из скалярного волнового уравнения, показывающего скрытую
структура и объединение электричества и магнетизма.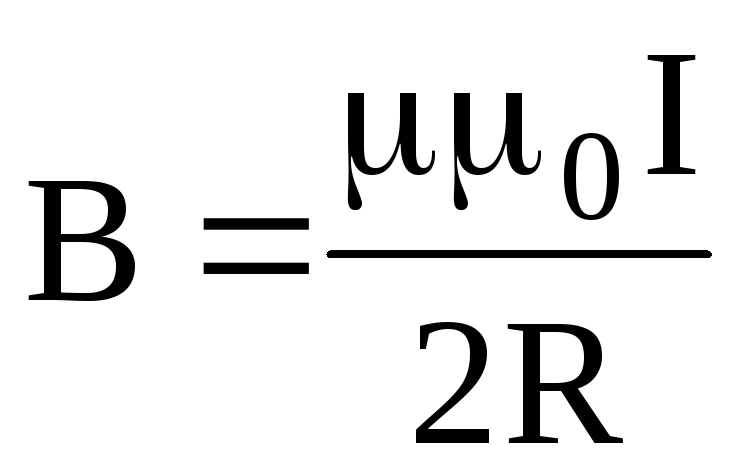 Использование этой конструкции для
гравитационное поле сочетает в себе классическую механику с гравитацией. Все электрические и
магнитный эффект можно наблюдать для гравитации и наоборот. Определение
электричество как вариации плотности гравитационного поля позволяет определить UT. В
в конце статьи представлены некоторые результаты УТ.Сила Лоренца
и закон Ньютона рассмотрены. Теория относительности и квантовая теория
описывается волновым эффектом UT. Эта статья написана для моей жены Андреа и
мой брат Берт.
Использование этой конструкции для
гравитационное поле сочетает в себе классическую механику с гравитацией. Все электрические и
магнитный эффект можно наблюдать для гравитации и наоборот. Определение
электричество как вариации плотности гравитационного поля позволяет определить UT. В
в конце статьи представлены некоторые результаты УТ.Сила Лоренца
и закон Ньютона рассмотрены. Теория относительности и квантовая теория
описывается волновым эффектом UT. Эта статья написана для моей жены Андреа и
мой брат Берт.
Введение
Иоганн Кеплер обнаружил, что форма движения Земли
вокруг солнца эллипсоид. Исаак Ньютон рассчитал эту форму, приняв гравитацию
сила . Нефизическая бесконечная скорость силы тяжести для любого расстояния d
делает невозможным закрытое решение для трех и более планет.Дополнительная масса земли m E и масса солнца m S описываются массовыми точками, что также неверно. в
по механическому закону Ньютона объект описывается точкой массы m. Сила между двумя
электрически заряженные частицы описываются заряженными точками. Майкл Фарадей
представил и продемонстрировал свои идеи деформированного поля в пространстве между двумя
заряженные частицы. Джеймс Кларк Максвелл ввел в 1864 году ток смещения в первое из четырех уравнений электрического поля, которое стало так
называются уравнениями Максвелла (Maxeq).Электрическое или магнитное влияние материала
описывается тремя материальными уравнениями (Mateq). Эти уравнения описывают структуру
между электрическим и магнитным полем.
Сила между двумя
электрически заряженные частицы описываются заряженными точками. Майкл Фарадей
представил и продемонстрировал свои идеи деформированного поля в пространстве между двумя
заряженные частицы. Джеймс Кларк Максвелл ввел в 1864 году ток смещения в первое из четырех уравнений электрического поля, которое стало так
называются уравнениями Максвелла (Maxeq).Электрическое или магнитное влияние материала
описывается тремя материальными уравнениями (Mateq). Эти уравнения описывают структуру
между электрическим и магнитным полем.
С помощью этих уравнений все электромагнитные эффекты описываются формулой поведение поля. Первые четыре уравнения могут быть выведены из одного волнового уравнения по формуле использование скрытой структуры.
Теория точек против теории поля
Классическая физика использует дискретные значения для положений объектов
и определить такие параметры, как скорость, импульс, сила и т.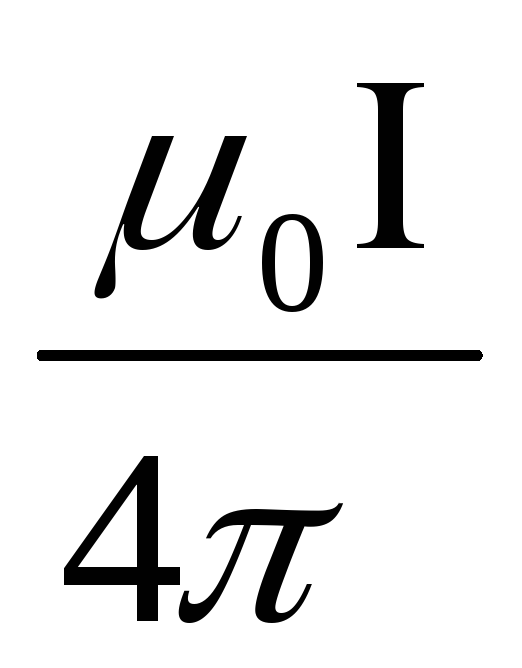 д.. Очевидно, что геометрия
реальный объект имеет конечные размеры и не является математической точкой. Теория поля
определяет, что воздействие на объект определяется окружающим его полем. Это означает, что
объект P деформирует пространство, вызывая «поле», и любой новый объект S, проходящий через
это пространство будет подвержено влиянию, как это происходит со спутником, проходящим мимо планеты. Это значит в
подробно, что объект P вызывает поле F P и
объект S вызывает поле F S , а эти два поля F P и F S вызывают
реакция.Реакция между P и S не идет напрямую, она осуществляется над полем
деформации. Это означает, что пространство характеризуется физическими величинами, поле
ценности. Общая сила F PS , реагирующая на S, оценивается с помощью
замкнутый поверхностный интеграл, содержащий весь объект S. После этого шага сила F PS можно считать находящимся в одной точке, центре тяжести S.
д.. Очевидно, что геометрия
реальный объект имеет конечные размеры и не является математической точкой. Теория поля
определяет, что воздействие на объект определяется окружающим его полем. Это означает, что
объект P деформирует пространство, вызывая «поле», и любой новый объект S, проходящий через
это пространство будет подвержено влиянию, как это происходит со спутником, проходящим мимо планеты. Это значит в
подробно, что объект P вызывает поле F P и
объект S вызывает поле F S , а эти два поля F P и F S вызывают
реакция.Реакция между P и S не идет напрямую, она осуществляется над полем
деформации. Это означает, что пространство характеризуется физическими величинами, поле
ценности. Общая сила F PS , реагирующая на S, оценивается с помощью
замкнутый поверхностный интеграл, содержащий весь объект S. После этого шага сила F PS можно считать находящимся в одной точке, центре тяжести S.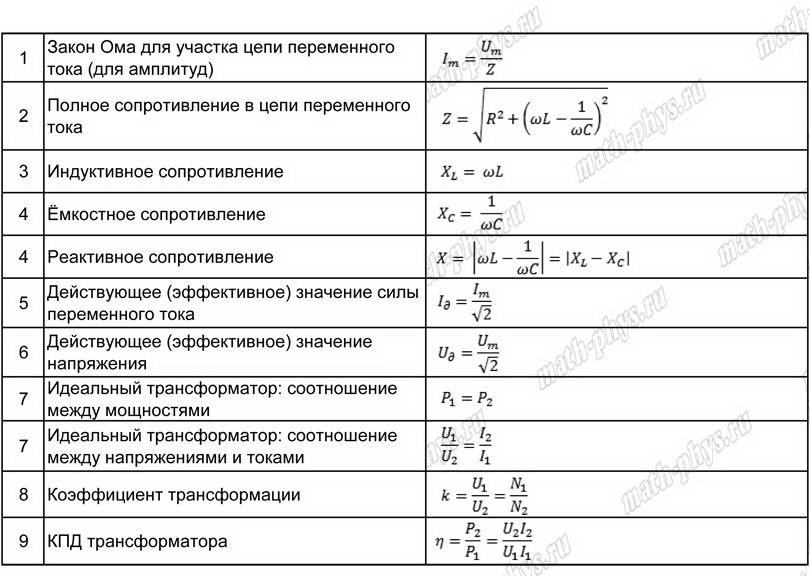 Это означает, что
теория поля включает точечную классическую теорию.Значения полей переносятся в
пространство с конечной скоростью c. Если бы планета P исчезла – т.е. взорваться – в
расстоянии d спутник S заметит за время
исчезновение гравитации. Это тормозящее t планетарной силы не было включено в
Классическая теория точек. Структура поля в пространстве описывается тремя
размерное волновое уравнение: . Поле F S , заданное дифференциальным уравнением второго порядка, может быть решено, если
начальные значения для поля F S и импульс
поля F S v S даны.Если объект S движется с постоянной скоростью v S , то поле F S следует за S со скоростью v S .
В следующей таблице показаны определения:
Это означает, что
теория поля включает точечную классическую теорию.Значения полей переносятся в
пространство с конечной скоростью c. Если бы планета P исчезла – т.е. взорваться – в
расстоянии d спутник S заметит за время
исчезновение гравитации. Это тормозящее t планетарной силы не было включено в
Классическая теория точек. Структура поля в пространстве описывается тремя
размерное волновое уравнение: . Поле F S , заданное дифференциальным уравнением второго порядка, может быть решено, если
начальные значения для поля F S и импульс
поля F S v S даны.Если объект S движется с постоянной скоростью v S , то поле F S следует за S со скоростью v S .
В следующей таблице показаны определения:
| Теория точек | Количество баллов | Значение поля | Теория поля |
точка массы S | м С | Ж С | потенциал поля S |
массовая скорость S | v С | v С | скорость поля S |
массовый импульс S | p S = m S v S | Р С = F S v S | Импульс поля S |
Инерционная масса и гравитационная масса используют одну и ту же среду –
сила тяжести. Если объект S меняет скорость — он ускоряется, — то поле F S производит волны, известные как инерционное поведение S. При
высокие скорости v S c поле будет ограничивать из-за эффекта Маха дальнейшее увеличение скорости v S известный как релятивистский дефект массы.
Если объект S меняет скорость — он ускоряется, — то поле F S производит волны, известные как инерционное поведение S. При
высокие скорости v S c поле будет ограничивать из-за эффекта Маха дальнейшее увеличение скорости v S известный как релятивистский дефект массы.
Теория электрического поля – электричество и магнетизм
В связи с широким распространением применения в электричестве электрические
поле анализируется во многих деталях.Независимо от этого знания существует скрытое
структура в уравнениях Максвелла, показывающая связь между электричеством и
магнетизм. Сначала исследуют одиночный электрический провод, по которому течет ток J. Провод
электрически нейтрален, так как количество положительных и отрицательных атомов одинаково.
электроны. Суммарный потенциал F total равен нулю, поскольку
потенциал, исходящий от атомов, компенсируется потенциалом электронов: .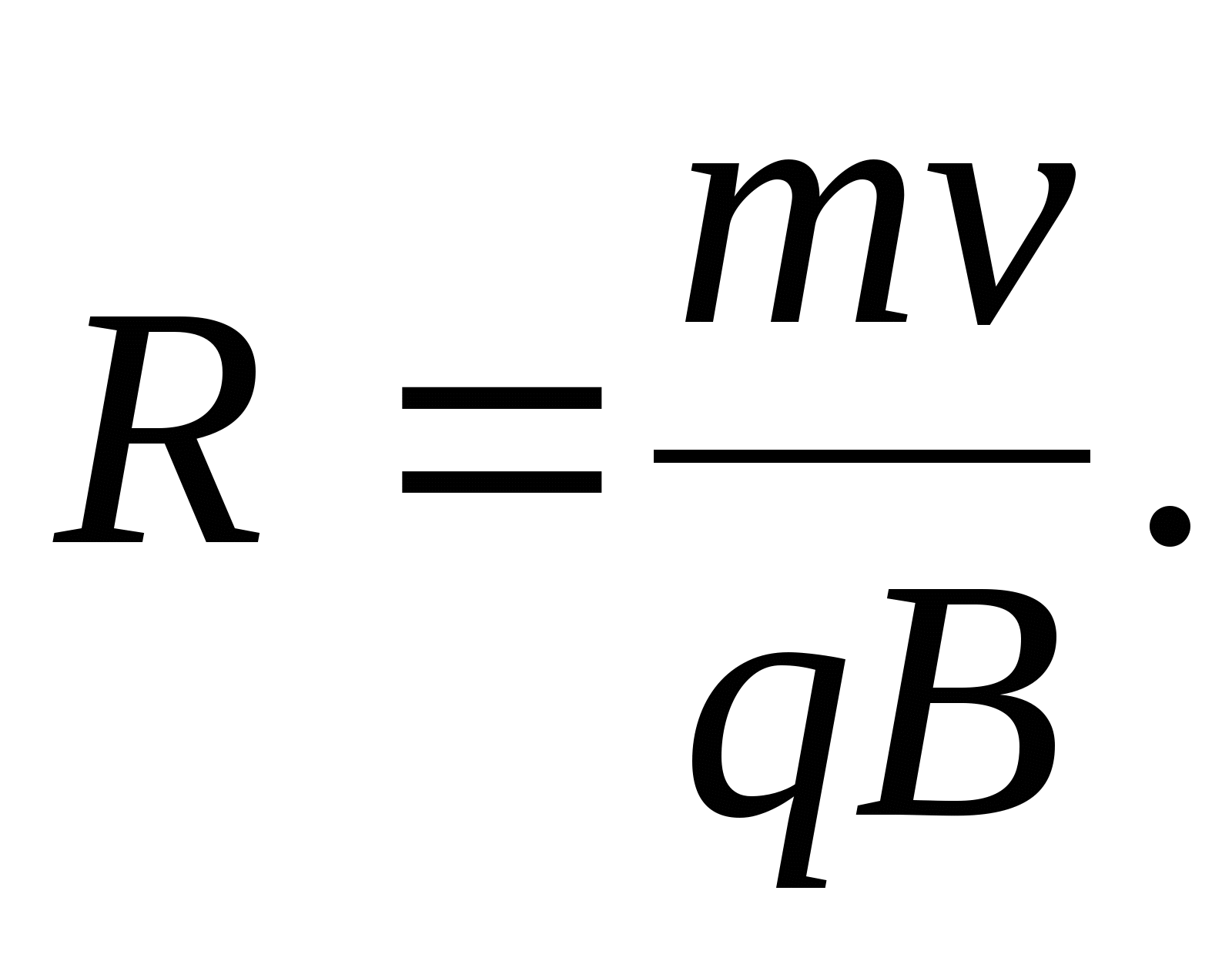 Суммарный импульс поля P total составляет
не равно нулю, так как отрицательные электроны движутся, а атомы неподвижны.
должность: .Математически точный перенос этого результата на
электрический потенциал позволяет увидеть новую структуру в уравнениях Максвелла.
Суммарный импульс поля P total составляет
не равно нулю, так как отрицательные электроны движутся, а атомы неподвижны.
должность: .Математически точный перенос этого результата на
электрический потенциал позволяет увидеть новую структуру в уравнениях Максвелла.
Трехмерное уравнение Гельмгольца для потенциала:
.
Теперь определим для импульса поля A также называемый вектором потенциал:
.
Если мы умножим обе части уравнения Гельмгольца на скорость v потенциала получаем волновое уравнение для импульса поля:
.
Уравнение Лоренца для A означает, что поле потенциал — или, в более общем смысле, энергия — может уйти, но не может исчезнуть.
Мы определяем B , называемую индукцией, как:
Поскольку мы определили A , мы можем вычислить
Волновое уравнение для B оценивается по волновому уравнение для А :
Мы определяем E , называемую напряженностью электрического поля, как:
, что означает, что E индуцируется изменением плотности и ускоренным импульсом поля.
Определение трех уравнений материалов приводит к:
Для нормализации материальных констант мы определяем:
Из определения Е-поля получаем секунды Максвелл уравнение:
и четвертое уравнение Максвелла:
Из определения B-поля получаем третье Максвелла уравнение:
Путем применения отношения оператора:
следует, что:
и последний:
получаем первое уравнение Максвелла:
Наконец, мы можем рассчитать силу Лоренца, которая обычно используется для
определить поле B . Для вращательного движения центробежное ускорение a дано:
Для вращательного движения центробежное ускорение a дано:
Сила, действующая на заряженную частицу, движущуюся во вращающемся поле, определяется автор:
Теория гравитационного поля. Гравитация и механика
Классическая теория гравитации предполагает мгновенное движение гравитационное поле при движении массивного объекта. Внедрение замедленного движения гравитация ведет к объединению гравитации и механики.математический эквивалентностью этого эффекта является трехмерное волновое уравнение, уравнение Гельмгольца для гравитационное поле
Обычно коэффициент g вводится в
классической физики, чтобы иметь правильное соотношение между силой, исходящей от
статическая сила тяжести и сила инерции, исходящая от массы. Для того, чтобы использовать тот же
в математической системе для электричества и механики этот коэффициент использоваться не будет.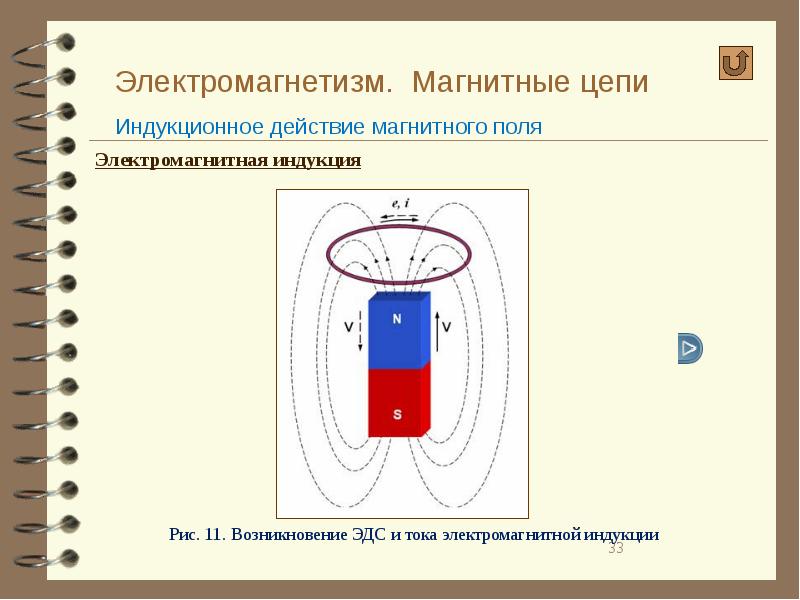 По аналогии с импульсом электрического поля мы можем определить импульс механического поля
По аналогии с импульсом электрического поля мы можем определить импульс механического поля
Для источника импульса поля можно определить механическую массу импульс плотности P M аналог импульса плотности электрического заряда P E также называется плотностью электрического тока S .
Если мы умножим уравнение Гельмгольца для гравитационного поля на скорости гравитационного поля получаем волновое уравнение для импульса механического поля:
Для напряженности гравитационного поля g имеем то же самое определение как для напряженности электрического поля E :
, что означает, что g индуцируется
изменение плотности M гравитации и ускоренным импульсом поля.Любое ускорение массового объекта приводит к возбуждению гравитационных волн в виде , известному как инерционное действие массы –
Закон Ньютона.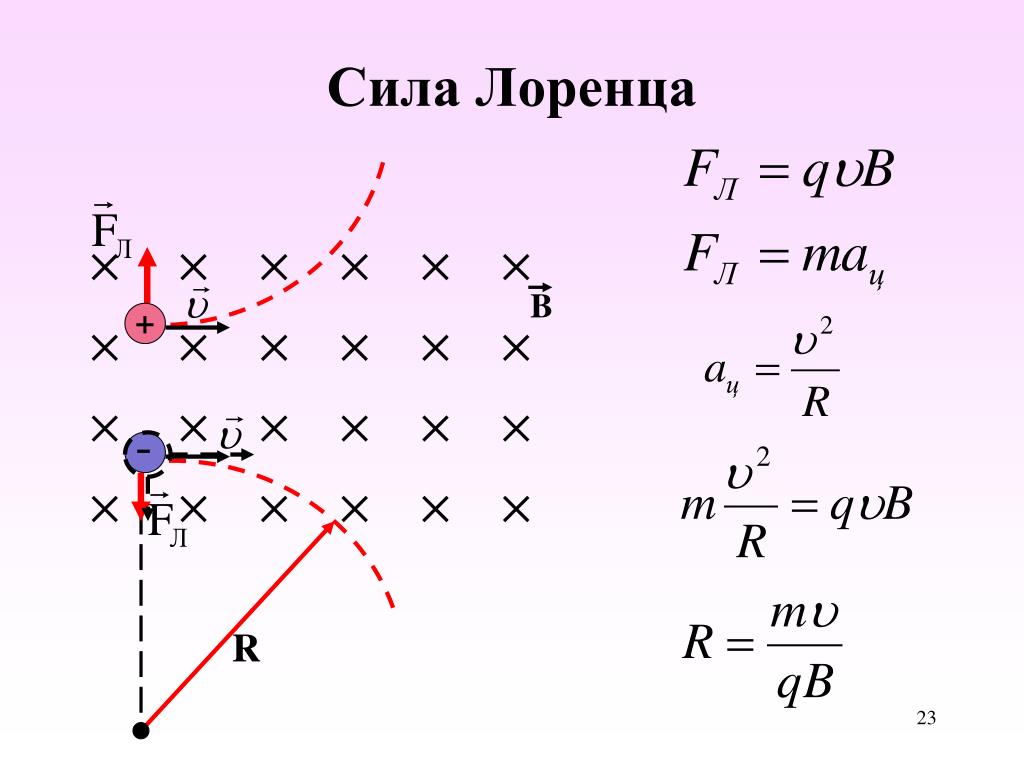 Аналоговый эквивалент поля B дает уравнение для
вращательные механические движения.
Аналоговый эквивалент поля B дает уравнение для
вращательные механические движения.
Единая теория
Для того, чтобы объединить гравитационное поле и электрическое поле отношение
между гравитацией и электричеством должно быть определено. Гравитация похожа на жидкое пространство
плотность энергии – давление свободного пространства.Гравитация существует в более низкой плотности
– «пустое пространство» – или в более высокой плотности – «материал».
Электричество должно быть произведено и не существует постоянно. Электричество является синонимом
неустойчивая гравитационная ситуация – колебания гравитации. «отрицательный
заряд» — это избыточное давление силы тяжести, а «положительный заряд» — это
под давлением стабильного давления – гравитация. Если положить отрицательные частицы
вместе, то положительное давление увеличивается, а отрицательные частицы пытаются избежать
это.По той же причине положительные частицы стараются избегать сбора с них. Если
Положительные и отрицательные частицы складываются вместе, затем создается избыточное и пониженное давление.
компенсируется. Когда электричество вырабатывается всегда одинаковое количество под давлением –
отрицательная плотность энергии – и избыточное давление – положительная плотность энергии – генерируется
так как полное давление – энергия – постоянна. Поскольку электричество является
изменение плотности гравитации, гравитация и электричество имеют одинаковую сигнализацию
скорость c 0 .Это можно резюмировать: когда у вас есть гравитационная масса, вы можете
увидеть объект благодаря его электрическим волнам. Для единой теории только одна энергетическая волна
уравнение, состоящее из двух составляющих: гравитационной волны и
электрическая волна.
Если
Положительные и отрицательные частицы складываются вместе, затем создается избыточное и пониженное давление.
компенсируется. Когда электричество вырабатывается всегда одинаковое количество под давлением –
отрицательная плотность энергии – и избыточное давление – положительная плотность энергии – генерируется
так как полное давление – энергия – постоянна. Поскольку электричество является
изменение плотности гравитации, гравитация и электричество имеют одинаковую сигнализацию
скорость c 0 .Это можно резюмировать: когда у вас есть гравитационная масса, вы можете
увидеть объект благодаря его электрическим волнам. Для единой теории только одна энергетическая волна
уравнение, состоящее из двух составляющих: гравитационной волны и
электрическая волна.
С введением тензора импульса поля:
можно рассчитать волновое уравнение для импульса поля и других величин.
Результаты Единой Теории
Единая теория объясняет физические величины, такие как B -поле. Некоторые физические законы, такие как сила Ньютона, сила Лоренца, дефект массы, время и
расширение длины можно понять.
Некоторые физические законы, такие как сила Ньютона, сила Лоренца, дефект массы, время и
расширение длины можно понять.
Сила Лоренца
наблюдается, если заряженная частица проходит вращающееся поле. Это значит что поле вращается, даже если там нет заряженных частиц. Вращение поля можно наблюдать при эффекте Майснера-Оксенфельда.
Причина, по которой два магнита могут притягиваться или отталкиваться, находится в двух невидимые вращающиеся завитки электрического поля, определяемые B -полем.
Закон Ньютона
является результатом гравитационной волны, вызванной ускорением
объект. Действующая сила, используемая для ускорения массы, создает гравитационную волну. Реакция
гравитационной волны является реактивной силой, которая точно так же велика, как ускоряющая
сила есть. Закон Ньютона также является индикатором того, что наш гравитационный материал состоит из атомов.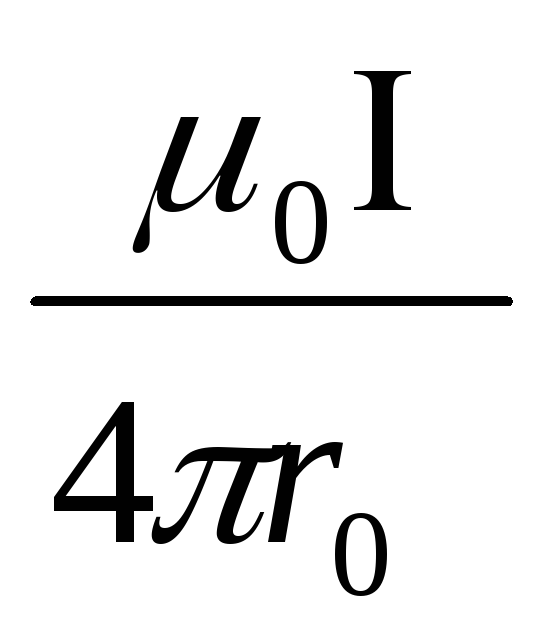 и есть широкое пустое пространство между атомами.
и есть широкое пустое пространство между атомами.
Теория относительности
Теория относительности берет свое начало при высоких скоростях около c 0 объектов.Действительная единая теория должна быть в состоянии объяснить влияние теория относительности. При высоких скоростях масса увеличивается, так как гравитационные волны могут не «убежать» впереди объекта – эффект Маха. Это увеличение инерционная масса создает больший эффект. Электроны, движущиеся вокруг атомов, увеличиваются их масса – они становятся тяжелее. Более тяжелые электроны уменьшат свое расстояние до атомное ядро, так как полная энергия электронов постоянна, атом будет усадка, которая является релятивистским сокращением длины.Более тяжелые электроны будут замедляться в их скоростях, так как полная энергия электронов постоянна, атом будет замедлить его реакции, что является релятивистским дефектом времени.
Квантовая теория
Для объектов небольших размеров гравитационные волны будут двигаться более прямолинейно.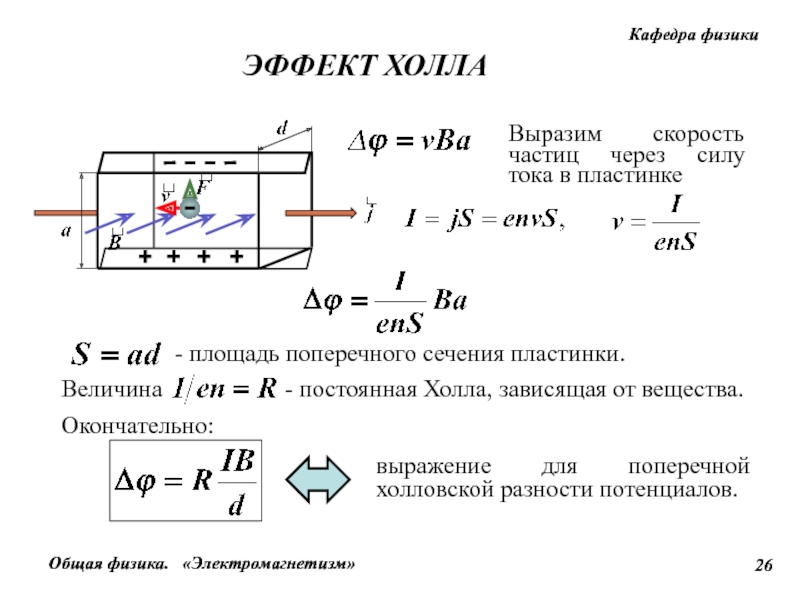 объект. Волновое поведение гравитационной волны становится более доминирующим, поскольку частица может
не интегрировать по многим гравитационным импульсам. Математический способ описать это поведение
есть уравнение Шредингера.Тот же эффект происходит для небольшого корабля в море в
отличие от океанского парохода.
объект. Волновое поведение гравитационной волны становится более доминирующим, поскольку частица может
не интегрировать по многим гравитационным импульсам. Математический способ описать это поведение
есть уравнение Шредингера.Тот же эффект происходит для небольшого корабля в море в
отличие от океанского парохода.
Резюме
Представлена единая теория. Электричество и магнетизм
представлены в новом понимании. Показана связь между гравитацией и механикой.
Многие из хорошо известных классических эффектов рассматриваются с новой точки зрения. Некоторые из
физические законы, ранее считавшиеся догмами, подобно силе Ньютона, теперь являются результатом
уравнение. Использовались только простые математические методы.Никаких новых “размеров”
или были представлены новые «странные идеи», поскольку лишь скрытая структура в нашем
была проанализирована классическая физика. Классическая физика до и после единой теории
то же самое, только точка зрения изменилась.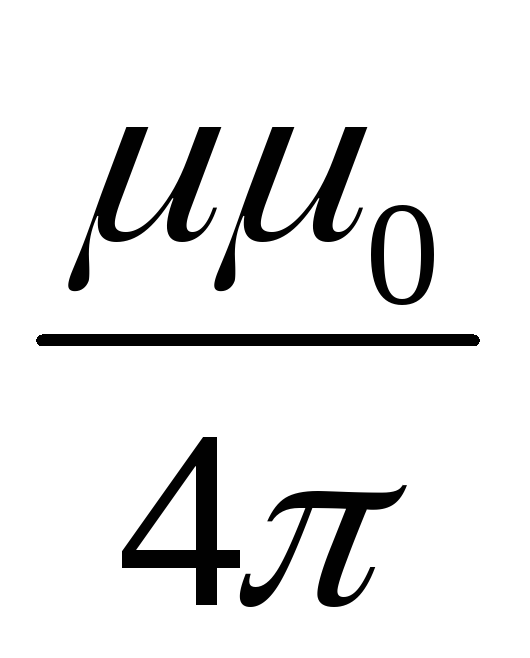 Более глубокие вопросы, такие как: Почему у нас есть
космическая энергия? все еще открыты, но они также несут ответственность.
Более глубокие вопросы, такие как: Почему у нас есть
космическая энергия? все еще открыты, но они также несут ответственность.
Список используемых уравнений
F …сила, Q…заряд, v …скорость заряда, B …магнитная индукция
F …сила, м…масса, а …ускорение
F… скалярная сила тяжести, г … гравитационная постоянная, м E … масса земли,
m S …масса солнца, d…расстояние от земли до солнца
F…скалярная электрическая сила, м …проницаемость, Q A …заряженный частица А,
Q B …заряженная частица B, d…расстояние между двумя заряженными частицами
S D … плотность тока смещения, D … диэлектрик водоизмещение
Первое уравнение Максвелла.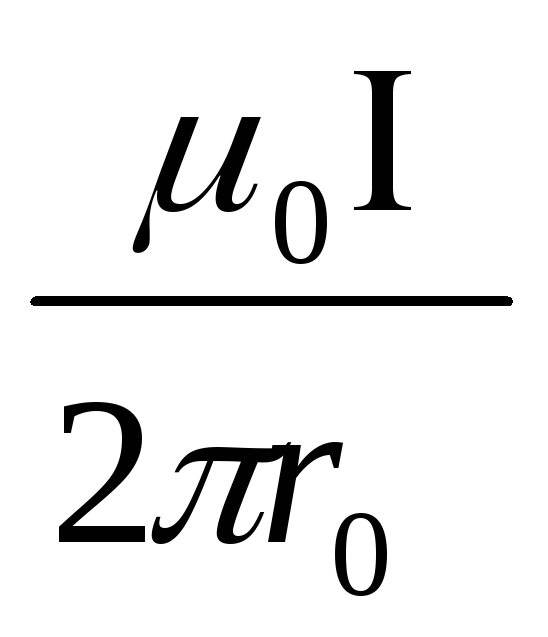 Генерируется вращательная часть поля H по плотности электрического тока и по
Генерируется вращательная часть поля H по плотности электрического тока и по
плотность тока смещения
Н …напряженность магнитного поля, S …плотность электрического тока, D …диэлектрик водоизмещение, т…час
Второе уравнение Максвелла. Генерируется вращательная часть поля E повышенным вращением электрического поля.
E…напряженность электрического поля, B …магнитная индукция, т…время
Третье уравнение Максвелла.Вращение поля не имеет начальной точки
B…магнитная индукция
Четвертое уравнение Максвелла. Источники диэлектрического смещения
— это «истинные» заряженные частицы, а не поляризованные частицы.
D…смещение, r …плотность электрического заряда
S. ..плотность электрического тока, с …проводимость, E …электрический
напряженность поля
..плотность электрического тока, с …проводимость, E …электрический
напряженность поля
D…смещение, e 0 ..диэлектрический вакуум постоянная, E … напряженность электрического поля, P … электрическая поляризация
B…магнитная индукция, м 0 ..магнитная константа вакуума,
H… напряженность магнитного поля, M …магнитная поляризация
t…время, c 0 …вакуумная скорость света, d…расстояние до
F S …потенциал гравитационного поля, c 0 …вакуум скорость света, t…время, r S …плотность массы
F всего …общий электрический потенциал, F P …потенциал положительного электрического заряда,
Ф Н . ..потенциал отрицательного электрического заряда
..потенциал отрицательного электрического заряда
P всего …общего импульса поля, P P …положительного импульса поля,
P N …импульс отрицательного поля, F N …потенциал отрицательного электрического заряда,
v N …скорость отрицательного электрического заряда
F …электрический потенциал, c 0 …вакуумная скорость свет, т…время,
r …плотность электрического заряда, э 0 … диэлектрическая постоянная вакуума
A… импульс поля, F … электрический потенциал, v … поле скорость, c 0 …вакуумная скорость света
А…импульс электрического поля, c 0 …вакуумная скорость света, t…время,
r …плотность электрического заряда, v . ..поле
скорость,
..поле
скорость,
e 0 …диэлектрическая постоянная вакуума, с 0 …вакуум скорость света, м 0 ..постоянная магнитного вакуума
А… импульс электрического поля, c 0 … скорость света в вакууме,
F …электрический потенциал, v …скорость поля, т… время
B…магнитная индукция, А …импульс электрического поля
B… магнитная индукция, A … импульс электрического поля, F … электрический потенциал,
w …угловая скорость поля, с 0 …вакуум скорость света
А…импульс электрического поля, т…время, с 0 …вакуумная скорость света, B … магнитная индукция,
м 0 ..магнитная постоянная вакуума, S .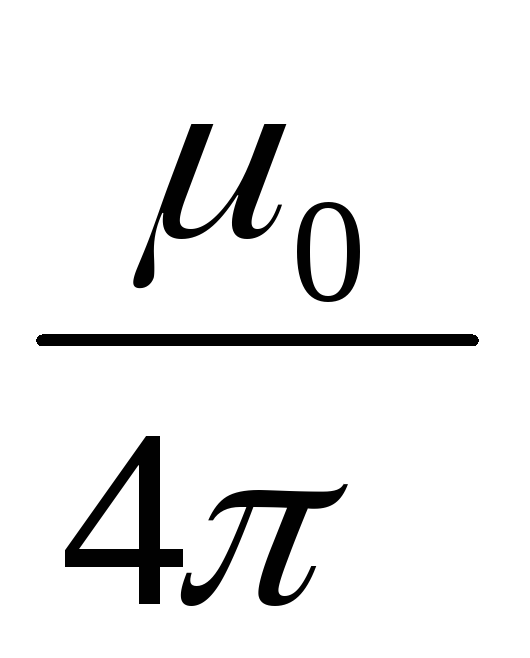 ..электрическая
плотность тока
..электрическая
плотность тока
E…напряженность электрического поля, F…электрический потенциал, А …импульс электрического поля, т…время
S… плотность электрического тока, с … проводимость, E …электрический напряженность поля
Д…смещение, e 0 ..диэлектрический вакуум постоянная, E … напряженность электрического поля, P … электрическая поляризация
B…магнитная индукция, м 0 ..магнитная константа вакуума,
H… напряженность магнитного поля, M … магнитная поляризация
m 0 ..постоянная магнитного вакуума, e 0 …диэлектрическая постоянная вакуума, c 0 …вакуум скорость света
E. ..напряженность электрического поля, F…электрический
потенциал,
..напряженность электрического поля, F…электрический
потенциал,
А…импульс электрического поля, т…время, В …магнитная индукция
E… напряженность электрического поля, F … электрическое поле потенциал,
А…импульс электрического поля, t…время, c 0 …вакуумная скорость света,
r …плотность электрического заряда, э 0 … диэлектрическая постоянная вакуума
B… магнитная индукция, А … импульс электрического поля
B… магнитная индукция, А … импульс электрического поля
м 0 ..магнитная постоянная вакуума, S …электрическая плотность тока,
А…импульс электрического поля, т…время, с 0 . ..вакуумная скорость света,
..вакуумная скорость света,
B…магнитная индукция, м 0 ..магнитная константа вакуума,
e 0 … диэлектрическая константа вакуума, E … электрическая напряженность поля
Б…магнитная индукция, м 0 ..магнитная вакуумная постоянная, e 0 …диэлектрическая вакуумная постоянная,
t…время, E …напряженность электрического поля, S …электрический ток плотность
H… напряженность магнитного поля, S … плотность электрического тока,
D…диэлектрическое смещение, t…время
а…ускорение, v …скорость, t…время, w …угловая скорость поля
F…сила, Q…электрический заряд, E . ..напряженность электрического поля, A …электрический
импульс поля, т…время,
..напряженность электрического поля, A …электрический
импульс поля, т…время,
F …электрический потенциал, v …скорость поля, c 0 …вакуум скорость света,
ш …угловая скорость поля, B …магнитная индукция
F M … потенциал гравитационного поля, с 0 … вакуум скорость света,
t…время, r M …плотность массы, e 0 … диэлектрическая постоянная вакуума
A M …импульс гравитационного поля, F M … гравитационный потенциал,
v М …скорость гравитационного поля, c 0 …вакуумная скорость свет
P M …импульс плотности массы, г M …масса плотность, v M …массовая скорость
P E . ..импульс плотности электрического заряда, r E …электрический
плотность заряда,
..импульс плотности электрического заряда, r E …электрический
плотность заряда,
v E …скорость заряда, S …плотность электрического тока
A M …импульс гравитационного поля c 0 …вакуумная скорость свет, т…время,
F M … потенциал гравитационного поля, v M … гравитация скорость поля, r M …плотность массы,
m 0 ..постоянная магнитного вакуума, P M …масса импульс плотности
g… напряженность гравитационного поля, A M … гравитационное поле импульс, т…время
F M … потенциал гравитационного поля, F E … потенциал электрического поля,
c 0 …вакуумная скорость света, t. ..время, r M …масса
плотность,
..время, r M …масса
плотность,
r E …плотность электрического заряда, e 0 … диэлектрическая постоянная вакуума
A G …тензор импульса гравитационного поля, c 0 …скорость вакуума света,
F M … потенциал гравитационного поля, v M … гравитация скорость поля,
F E … потенциал электрического поля, v E … электрический скорость поля,
Ф…сила, м…масса, a …ускорение
Что такое электромагнитные волны – определения, примечания, формулы, уравнения и книги
Волна — это не что иное, как образец возмущения, которое распространяется и несет с собой энергию. Вы можете создать волну на веревке, перемещая один конец веревки вверх и вниз. Волне, создаваемой на веревке, нужна среда для распространения, и здесь средой является сама веревка. Этот тип волн известен как механические волны.Но в случае электромагнитных волн им не нужна среда для распространения. Электромагнитные волны — это волны, возникающие в результате вариаций электрического поля и магнитного поля. Или мы можем сказать, что электромагнитные волны есть не что иное, как изменяющиеся магнитные и электрические поля. Известно также, что электромагнитные волны являются решениями уравнений Максвелла. А уравнения Максвелла являются фундаментальными уравнениями электродинамики. Электромагнитные волны могут передавать энергию и проходить через вакуум.световые волны являются примерами электромагнитных волн. Обычно электромагнитные волны изображаются синусоидальным графиком.
Волне, создаваемой на веревке, нужна среда для распространения, и здесь средой является сама веревка. Этот тип волн известен как механические волны.Но в случае электромагнитных волн им не нужна среда для распространения. Электромагнитные волны — это волны, возникающие в результате вариаций электрического поля и магнитного поля. Или мы можем сказать, что электромагнитные волны есть не что иное, как изменяющиеся магнитные и электрические поля. Известно также, что электромагнитные волны являются решениями уравнений Максвелла. А уравнения Максвелла являются фундаментальными уравнениями электродинамики. Электромагнитные волны могут передавать энергию и проходить через вакуум.световые волны являются примерами электромагнитных волн. Обычно электромагнитные волны изображаются синусоидальным графиком.
Как показано на рисунке Электромагнитные волны состоят из изменяющихся во времени электрического и магнитного полей и они перпендикулярны друг другу И эти оба поля также перпендикулярны направлению распространения волн.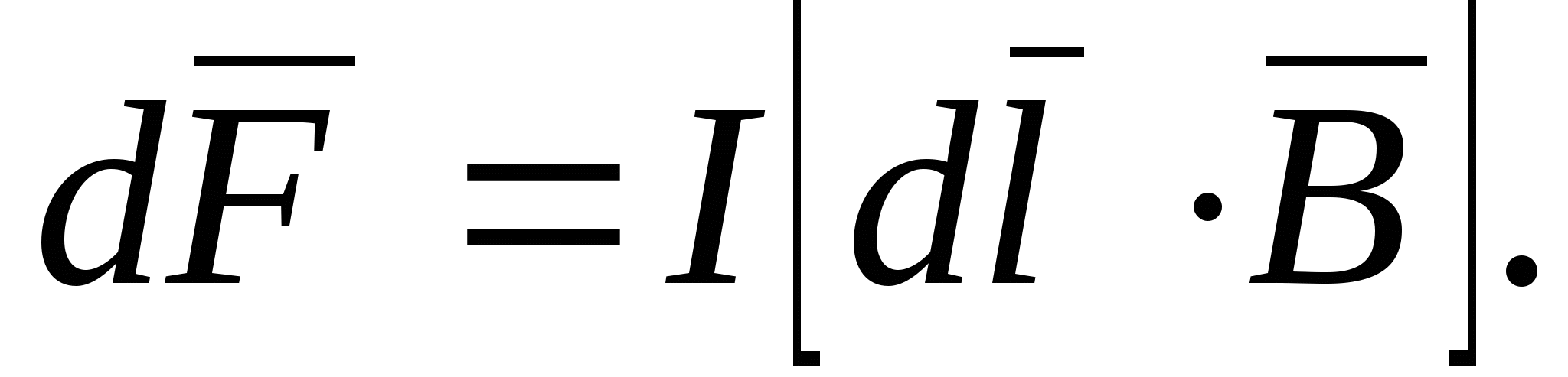 И из-за этого Электромагнитные волны имеют поперечный характер.
И из-за этого Электромагнитные волны имеют поперечный характер.
Электромагнитные волны — одна из самых важных глав современной физики при подготовке ко всем конкурсным экзаменам, потому что она помогает понять важные свойства электромагнитных волн.Эта глава также поможет вам понять различные типы электромагнитных волн и их применение. Это простая для понимания и высоко оцениваемая тема. Иногда Концепция электромагнитных волн и другие разделы физики смешиваются с разными вопросами, которые задают на различных конкурсных экзаменах.
Онлайн-подготовка к JEE Main/NEETCrack JEE 2021 с онлайн-программой подготовки к JEE/NEET
Начинай сейчас Заметки об электромагнитных волнахИтак, мы шаг за шагом обсудим важные темы этой главы, а затем сделаем обзор этой главы.Тогда мы поймем важные формулы из этой главы. Запоминание этих формул повысит вашу скорость при решении вопросов.
Электромагнитные волны ТемыЭлектромагнитные волны и их характеристики.
 Поперечный характер электромагнитных волн.
Поперечный характер электромагнитных волн.Электромагнитный спектр (микроволновые, инфракрасные, видимые, радиоволны, рентгеновские лучи, ультрафиолетовые, гамма-лучи). Приложения эл.м. волны.
Электромагнитные волны Обзор
В главе «Электромагнитные волны» мы узнаем об электромагнитных волнах, их всех важных свойствах, типах и приложениях. Так мы узнаем о
Уравнения Максвелла- Поскольку электромагнитные волны также являются решениями уравнений Максвелла. Поэтому важно узнать о них. Джеймс С. Максвелл заметил непоследовательность в законе Ампера и асимметрию в законах электромагнетизма.Таким образом, он представил некоторые предложения в этих законах. Например, он предложил идею тока смещения, чтобы устранить это противоречие в законе Ампера. Таким образом, он представил модифицированную версию этих законов с помощью уравнений Максвелла, которые приведены ниже.

Первое уравнение Максвелла – Закон Гаусса для электростатики
Второе уравнение Максвелла: закон Гаусса в магнетизме
3-е уравнение Максвелла-закон Фарадея
4-е уравнение Максвелла-закон Ампера
Эти волны не требуют среды для распространения и имеют поперечный характер.
Эти волны распространяются в пространстве со скоростью света в вакууме.
Волна, имеющая более высокую частоту, будет иметь более высокую энергию, связанную с ней.
Может использоваться для переноса информации.
Он движется по прямой.
Его можно разделить и рекомбинировать для формирования интерференционной/дифракционной картины.

Может отражаться или преломляться.
Одним из очень важных типов электромагнитных волн являются синусоидальные плоские волны. Все электромагнитные волны можно рассматривать как линейную суперпозицию синусоидальных плоских волн, распространяющихся в произвольных направлениях.
Например- Плоская волна, распространяющаяся в направлении x, имеет форму
А если E находится в плоскости y-z, то
Где E – электрическое поле при (x,t)
– Амплитуда электрического поля
= Угловая частота
c = скорость света в вакууме
Аналогично, B находится в плоскости y-z
Где B = магнитное поле при (x,t)
= Амплитуда магнитного поля
Вы узнаете о некоторой физической величине, приведенной ниже-
Интенсивность электромагнитной волны
Импульс электромагнитной волны
Плотность энергии электромагнитной волны
Длина волны электромагнитной волны
Частота электромагнитной волны
Типы электромагнитных волн и их применение
В зависимости от диапазона частот волны существуют различные типы электромагнитной волны. И эти волны имеют различное применение в нашей повседневной жизни. Ниже приведены некоторые типы электромагнитной волны
И эти волны имеют различное применение в нашей повседневной жизни. Ниже приведены некоторые типы электромагнитной волны
γ – луч (гамма-луч) – полезен при обнаружении дефектов, трещин, дефектов, отверстий в металлах.
Рентгеновские лучи — полезны при рентгенотерапии.
Ультрафиолетовое излучение — помогает в изучении молекулярной структуры.
Инфракрасные волны — помогают фотографировать в тумане или дыму
Микроволны — используются в радио- и телекоммуникациях.
Формулы электромагнитных волн
E находится в плоскости y-z
B находится в плоскости y-z
- Ток смещения Максвелла-
- Закон Гаусса для электричества-
- Закон Гаусса для магнетизма-
- Связь между и –
- Плотность энергии ЭМ волны-
- Интенсивность электромагнитной волны-
- Во-первых, вы должны хорошо разбираться в концепциях электромагнитных волн, а также уметь применять их во время вступительного экзамена или при решении вопросов.

- Пожалуйста, постарайтесь понять каждое понятие из этой главы с помощью теории, вопросов с решениями и видеолекций по каждому важному понятию.
- Для каждой концепции попрактикуйтесь в достаточном количестве задач, чтобы у вас было полное понимание концепции.
- Решите все вопросы дома с должной концентрацией и попробуйте сделать все расчеты самостоятельно, не видя сначала решения.
- При решении вопросов волнового уравнения необходимо также учитывать направление соответствующих векторов.
- Пожалуйста, хорошо разбирайтесь в спектре электромагнитных волн и применении различных электромагнитных волн.
- Вспомните все формулы Энергии, импульса, частоты Электромагнитных волн. Это поможет вам при решении вопросов.
Наконечники для электромагнитных волн
- Составьте план подготовки к этой главе и придерживайтесь расписания.
- Ставьте умные и реалистичные цели и старайтесь их достичь.

- Сначала изучите концепцию, а затем начинайте решать вопросы. Не задавайте вопросы напрямую, не зная концепции.
- Формулы из этой главы очень важны с точки зрения конкурсного экзамена. Поэтому, пожалуйста, запомните их и решите множество вопросов на основе этих формул.
- Решить вопрос предыдущего года различных экзаменов из этой главы.
- Используйте умные методы для решения вопросов.
Книги об электромагнитных волнах
Для Электромагнитных волн понятий главы в NCERT достаточно, но вам придется практиковать множество вопросов, включая вопросы предыдущего года, и вы можете следовать другим стандартным книгам, доступным для подготовки к конкурсным экзаменам, таким как Concepts of Physics (HC Verma) и Understanding Physics by DC Pandey. (Арихант Публикации).
Примечания по главам физики для технических и медицинских экзаменов
В: Каковы уравнения электромагнетизма? Что все они нам описывают?
Физик : Электромагнетизм и вся связанная с ним математика – удивительно наглядные науки. Понимание уравнений Максвелла (уравнений электромагнетизма) требует множества картинок.
Понимание уравнений Максвелла (уравнений электромагнетизма) требует множества картинок.
В этих уравнениях и являются физическими константами, которые определяют, насколько сильны электрические и магнитные силы, но при выполнении расчетов (или вообще когда угодно) их трудно отслеживать. Так что впредь я их игнорирую:
Где:
Электрические и магнитные поля, «» и «», подобны ветру или текущей воде; в каждом месте они указывают в каком-то направлении, с некоторой силой.
Кстати, можно было бы ожидать, что «М» будет использоваться для обозначения магнитного поля, но оно уже используется для обозначения массы, поэтому какой-то гений решил, что «В» — хорошая буква для магнитов. В этих уравнениях есть два странных символа (операции): «» и ««. Первый называется «дивергенция», а второй – «завиток». Вот что они означают.
Дивергенция () — это мера того, насколько поле сближается или разлетается. В дальнейшем «» — это течение воды или ветра.
Ограничьте свое внимание только поверхностью раковины. Положительная дивергенция означает, что поле «вытекает» из области. Отрицательная дивергенция означает, что поле «втекает» в область. Когда дивергенция равна нулю, тогда сумма, которая «втекает», должна быть равна сумме, которая вытекает.
Положительная дивергенция означает, что поле «вытекает» из области. Отрицательная дивергенция означает, что поле «втекает» в область. Когда дивергенция равна нулю, тогда сумма, которая «втекает», должна быть равна сумме, которая вытекает.
Curl — насколько поле «закручивается». Некоторое представление о том, что curl делает с полем; в водовороте или торнадо вся завихренность находится в центральной воронке, а поле (ветер) обвивает место завихрения.
Если W — это то, как дует ветер, то торнадо — это завиток W.Завиток – это «извилистость» поля, которое направлено вокруг завитка. Хотя ветер вокруг смерча движется, все завихрения происходят только на самом смерче.
и) :
Вы можете изобразить магнитные и электрические поля в терминах «силовых линий». Чем больше линий поля, тем сильнее поле. Вы можете использовать эту метафору, например, чтобы изобразить, почему поля теряют силу по мере того, как вы удаляетесь все дальше и дальше от их источника (линии расходятся).
Это первое уравнение просто утверждает, что силовые линии электрического поля () начинаются только с положительных зарядов () и заканчиваются только с отрицательными зарядами ().
Линии электрического поля начинаются и заканчиваются только зарядами. Любая область, не содержащая зарядов (или равное количество положительных и отрицательных зарядов), будет иметь такое же количество линий поля, входящих в нее, как и выходящих.
Если область не содержит зарядов, то количество линий поля, входящих в нее, равно количеству линий поля, выходящих из нее.Опять же, «линий поля» не существует. Это просто очень полезная метафора.
ii) :
Это магнитная версия приведенного выше электрического уравнения. Это утверждает, что силовые линии магнитного поля никогда не начинаются и не заканчиваются. Вместо этого они всегда должны образовывать замкнутые петли.
Если бы каким-то образом существовали магнитные монополи («магнитные заряды»), то это уравнение выглядело бы точно так же, как (i).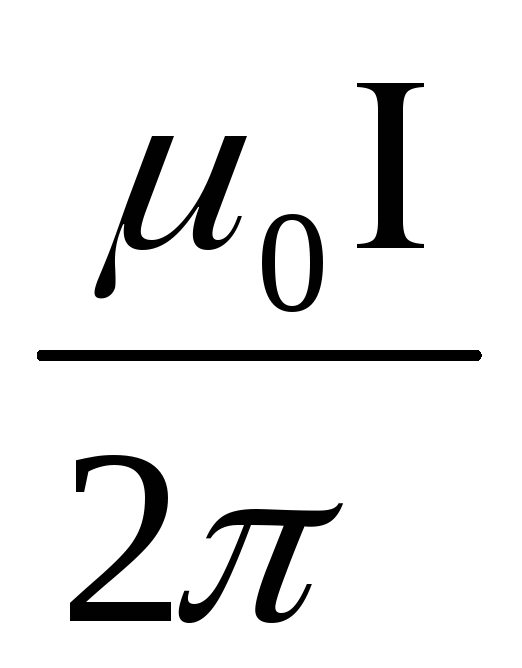 Однако магнитных монополей не существует.
Однако магнитных монополей не существует.
iii) :
Сначала часть «J»: Это уравнение утверждает, что магнитные поля (B) буквально закручиваются вокруг электрических токов (J).
«Магнитные поля закручиваются вокруг тока». Это проводник с током, проходящий через лист бумаги с железными наполнителями на нем. Железные пломбы обладают прекрасным свойством выстраиваться вдоль магнитных полей.
Итак, в терминах приведенных выше метафор электрический ток подобен воронке торнадо, а магнитное поле подобно ветру, хлещущему вокруг воронки.
Другой, но эквивалентный способ формулировки этого уравнения: «если есть магнитное поле, бегущее по петле, то должен быть ток, протекающий через петлю».
Допустим, у вас есть ферма, и она полностью огорожена забором. Тогда это утверждение эквивалентно высказыванию «если вокруг забора дует ветер в одном направлении, то на моей ферме должно быть торнадо». По сути, если ветер движется по кругу, в какой-то момент он должен закручиваться, и это завихрение.
Обратите внимание, что слово «через» было подчеркнуто (для акцента!). Когда ученый говорит о прохождении цикла, важно иметь строгое определение.В конце концов, что, если петля действительно странной формы? Таким образом, вы найдете «охватывающую поверхность». Охватывающая поверхность — это любая поверхность, которая имеет петлю в качестве границы.
Пример странной петли и столь же странной связующей поверхности.
Ток определяется как «проходящий через петлю», если он проходит через охватывающую поверхность этой петли. Это может показаться бесполезным, случайным способом определения «через», но оказывается, что математике это нравится. Это вытекает из теоремы под названием «теорема Стокса».Что очень важно, так это то, что ток должен проходить через любую связующую поверхность.
Что подводит нас ко второй части уравнения:
Что делать, если в проводе есть конденсатор? Конденсатор (по своей сути) представляет собой провод, идущий к пластине, затем разрыв, затем еще одна пластина, затем провод продолжается (верхняя диаграмма на рисунке ниже). Ток, который просто перемещает заряд, заставляет эти заряды накапливаться с одной стороны, а противоположный заряд — с другой.Но реальный заряд не перемещается с одной пластины на другую.
Ток, который просто перемещает заряд, заставляет эти заряды накапливаться с одной стороны, а противоположный заряд — с другой.Но реальный заряд не перемещается с одной пластины на другую.
Выберите петлю в космосе. Если ток проходит через поверхность, охватывающую эту петлю, то ток заставляет магнитное поле бегать по этой петле. Но в конденсаторе переменное электрическое поле заменяет ток.
Итак, если бы вы были достаточно жестоки, чтобы выбрать связующую поверхность, которая проходит через конденсатор, где нет тока (средняя диаграмма выше), а не через провод, где есть ток (верхняя диаграмма), вы получите новый и противоречивый результат.
Но сама ситуация не изменилась! Независимо от того, какую поверхность вы выберете, магнитное поле вокруг петли должно быть одинаковым. Это не может быть просто ток, который заставляет магнитное поле вращаться. Так что же происходит в конденсаторе?
Итак, когда ток течет в одну сторону, накапливается положительный заряд, а когда ток выходит из другой стороны, накапливается отрицательный заряд. В результате между пластинами конденсатора возникает нарастающее электрическое поле (нижняя диаграмма).
В результате между пластинами конденсатора возникает нарастающее электрическое поле (нижняя диаграмма).
Заключение состоит в том, что ток () и изменяющиеся электрические поля () создают завихрения в магнитных полях;
iv) :
С точки зрения современного общества это, возможно, самое важное уравнение, поскольку поведение электрических турбин определяется этим уравнением. Как и последнее уравнение, это уравнение утверждает, что изменяющееся магнитное поле создает завихрение в электрическом поле.
Если у вас есть электрическое поле, которое закручивается по кругу, то вы можете генерировать ток и электрическую энергию.
Изменяющееся магнитное поле создает завиток в электрическом поле. Итак, если вы увеличите магнитное поле через петлю из провода, вдоль провода возникнет электрическое поле (торнадо создает ветер вдоль забора). Когда электрическое поле движется вдоль провода, оно выталкивает по нему заряды. Наведенный ток!
Итак, если у вас есть петля из проволоки рядом с магнитом, тока не будет. Но если вы переместите этот магнит, магнитное поле в петле изменится, и появится ток.
Но если вы переместите этот магнит, магнитное поле в петле изменится, и появится ток.
Автомобильный генератор. При вращении он изменит магнитное поле через эти петли провода и создаст ток.
Большинство электростанций (гидро, атомных, газовых, угольных, ветряных) просто вращают генераторы, которые (в основном) двигают большие магниты вперед и назад, изменяя магнитное поле с помощью проволочных петель и создавая ток. Фактически, магнитное поле через эти петли меняется 60 раз в секунду, поэтому электрическая мощность в вашей розетке, в свою очередь, также переключается 60 раз в секунду (переменный ток).
Солнечные панели являются ярким исключением, но в остальном вся энергия производится одинаково:
Обратите внимание, кстати, что, в отличие от уравнения (iii), здесь нет члена «J». J движется электрический заряд. Если бы существовала такая вещь, как «магнитный заряд», то у вас мог бы быть «магнитный ток», и в уравнении (iv) был бы член магнитного тока.
Но нет.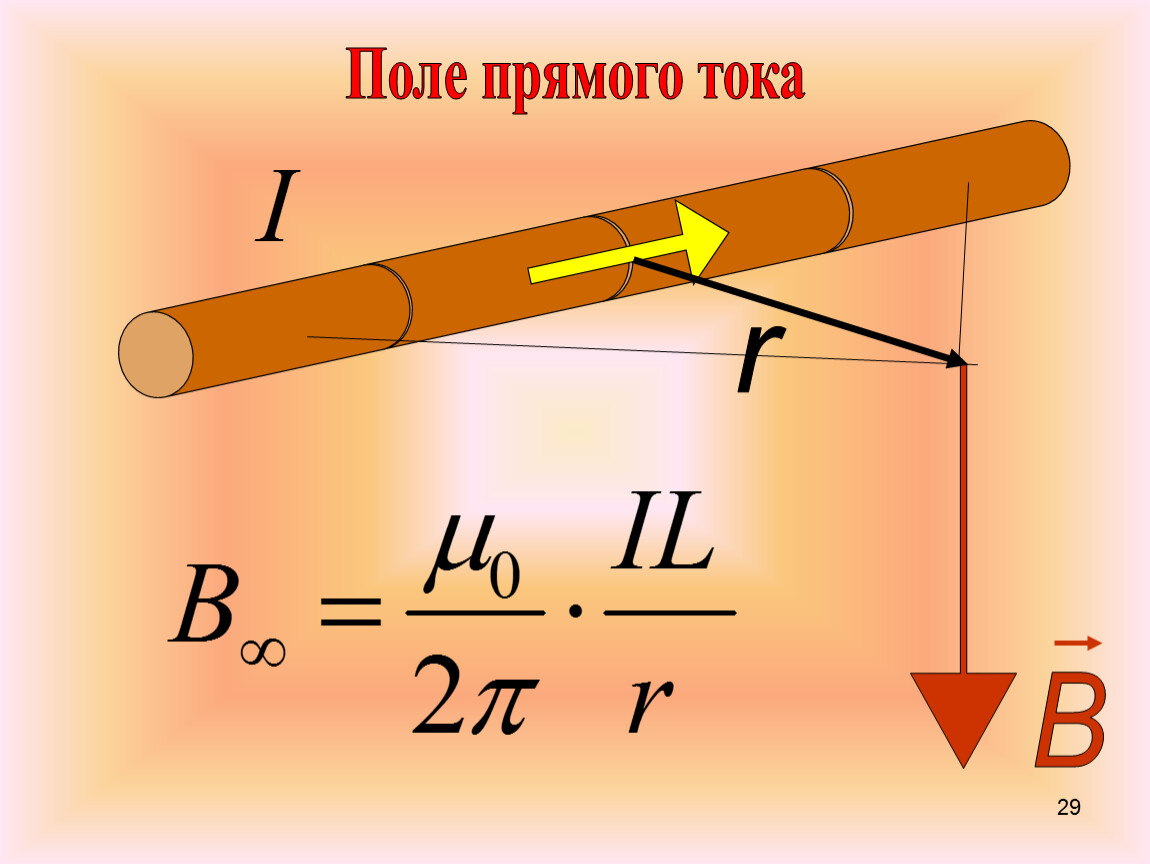
Скорость света : На рубеже прошлого века (1900 год) некоторые умные люди заметили, что уравнения Максвелла подразумевают, что изменение электрических полей создает магнитные поля (iii), а изменение магнитных полей создает электрические поля (iv).Они начали задаваться вопросом, могут ли электрические и магнитные поля поддерживать друг друга без необходимости в электрических зарядах или токах.
Короткий ответ – да. Эти самоподдерживающиеся поля на самом деле легкие (не правда ли, странно?). Итак, когда вы видите кусок солнечного света, вы видите просто движущийся заряд на поверхности солнца, который создает изменяющееся электрическое поле, которое создает изменяющееся магнитное поле, которое создает… до тех пор, пока эти поля не взаимодействуют с химическими веществами. в вашем глазу и зарегистрируйтесь как «легкий» через 93 миллиона миль.
Ответ подливка :
Длинный ответ требует некоторого векторного исчисления. Возьмем уравнения Мауэлла в вакууме (без зарядов, без токов):
Возьмем уравнения Мауэлла в вакууме (без зарядов, без токов):
Я просто попытаюсь найти электрическое поле, поэтому, взяв производную по времени от (iii) и затем подставив (iv), мы получим:
Векторное исчисление — это один из тех уголков математики, которые славятся удивительным набором тождеств, которые вы притворяетесь, что запоминаете, но тайком просматриваете книги за 3 минуты до того, как будете тестироваться.Вот один из них:
. Я немного подумал о том, как вывести это число, но если вы знаете (математически), что означают эти символы, вы можете доказать это сами (это довольно просто). Если нет, то просто страшно. Вернемся к делу:
Здесь я использовал, что никаких сборов нет, так что .
Последнее уравнение кажется очень странным, но проверьте! Общее волновое уравнение записывается: , где A — волна, а v — скорость распространения этой волны. Итак, электрическое поле E распространяется как волна со скоростью света.
Я подозреваю, что, когда это впервые выяснилось, чуваки сами влипли в дерьмо. В то время не было никаких предыдущих (прямых) указаний на то, что электричество и магнетизм имеют какое-либо отношение к свету.
В то время не было никаких предыдущих (прямых) указаний на то, что электричество и магнетизм имеют какое-либо отношение к свету.
Что еще более важно, поскольку все законы физики не зависят от того, как быстро вы движетесь (физика одинакова, двигаетесь вы или сидите на месте), теперь появилась скорость, которая не зависела от того, как быстро вы двигаетесь. Относительность!
Amazon.com: Электронная книга по физике (Qucik Study Academic): BarCharts, Inc.: Kindle Store
Студенты и исследователи в области физики, техники и других наук найдут этот сборник из более чем 3000 физических формул и таблиц бесценным. Вся включенная информация является практической, исключены редко используемые результаты. Темы варьируются от элементарных до продвинутых – от классической механики, термодинамики и электромагнетизма до оптики и атомной физики. Большое внимание было уделено тому, чтобы представить все результаты кратко и ясно. Отлично держать в качестве удобного справочника! Если у вас мало времени, но вы хотите преуспеть в учебе, эта книга поможет вам: Освежиться перед тестами Быстро найти ответы Выучить ключевые формулы и таблицы Учиться быстрее и эффективнее Учащиеся любят учебные пособия MobileReference! Каждый год сотни тысяч студентов улучшают свои результаты тестов и итоговые оценки с помощью этих незаменимых учебных пособий. Повышайте свои оценки с помощью персонального репетитора на вашем портативном компьютере — загрузите MobileReference Quick Study Guides на свое мобильное устройство. В этом руководстве вы найдете: Более 3000 формул и таблиц Четкие и краткие объяснения всех результатов Формулы и таблицы от элементарных до сложных тем Полный указатель ко всем темам Законы науки Классическая механика Теплота, газ и термодинамика Электромагнетизм Оптика Атомная физика Веса и Измерения Физические константы Переменные (символы), обычно используемые в физике Делайте то, что уже сделали большинство ваших одноклассников — скачивайте пособия на мобильное устройство и готовьтесь к экзаменам в любое время и в любом месте — дома, в автобусе, в метро.Нам доверяют миллионы — учебные пособия от MobileReference. Больше электронных книг от MobileReference – Лучшие книги. Лучшая цена. Лучший поиск и навигация (TM) Все художественные книги стоят всего 0,99 доллара. Все коллекции стоят всего $5,99. Предназначены для оптимальной навигации на Kindle и других электронных устройствах.
Повышайте свои оценки с помощью персонального репетитора на вашем портативном компьютере — загрузите MobileReference Quick Study Guides на свое мобильное устройство. В этом руководстве вы найдете: Более 3000 формул и таблиц Четкие и краткие объяснения всех результатов Формулы и таблицы от элементарных до сложных тем Полный указатель ко всем темам Законы науки Классическая механика Теплота, газ и термодинамика Электромагнетизм Оптика Атомная физика Веса и Измерения Физические константы Переменные (символы), обычно используемые в физике Делайте то, что уже сделали большинство ваших одноклассников — скачивайте пособия на мобильное устройство и готовьтесь к экзаменам в любое время и в любом месте — дома, в автобусе, в метро.Нам доверяют миллионы — учебные пособия от MobileReference. Больше электронных книг от MobileReference – Лучшие книги. Лучшая цена. Лучший поиск и навигация (TM) Все художественные книги стоят всего 0,99 доллара. Все коллекции стоят всего $5,99. Предназначены для оптимальной навигации на Kindle и других электронных устройствах. Поиск по любому названию: введите mobi (сокращенно MobileReference) и ключевое слово; например: mobi ShakespeareЧтобы просмотреть все книги, щелкните ссылку MobileReference рядом с названием книги Литературная классика: более 10 000 полных собраний сочинений Шекспира, Джейн Остин, Марка Твена, Конан Дойля, Жюля Верна, Диккенса, Толстого и других авторов.Все книги снабжены гиперссылками на содержание, сноски и биографию автора. Книги также доступны в виде коллекций, организованных автором. Коллекции упрощают доступ к книгам с помощью категорийных, алфавитных и хронологических указателей. Они предлагают более низкую цену, удобство однократной загрузки и уменьшают беспорядок в вашей цифровой библиотеке. Религия: Иллюстрированная Библия короля Иакова, Американская стандартная Библия, Всемирная английская Библия (современный перевод), Священные тексты мормонской церкви Философия: Руссо, Спиноза, Платон, Аристотель, Маркс, Энгельс Путеводители и разговорники для всех крупных городов: Нью-Йорк, Париж , Лондон, Рим, Венеция, Прага, Пекин, Греция.
Поиск по любому названию: введите mobi (сокращенно MobileReference) и ключевое слово; например: mobi ShakespeareЧтобы просмотреть все книги, щелкните ссылку MobileReference рядом с названием книги Литературная классика: более 10 000 полных собраний сочинений Шекспира, Джейн Остин, Марка Твена, Конан Дойля, Жюля Верна, Диккенса, Толстого и других авторов.Все книги снабжены гиперссылками на содержание, сноски и биографию автора. Книги также доступны в виде коллекций, организованных автором. Коллекции упрощают доступ к книгам с помощью категорийных, алфавитных и хронологических указателей. Они предлагают более низкую цену, удобство однократной загрузки и уменьшают беспорядок в вашей цифровой библиотеке. Религия: Иллюстрированная Библия короля Иакова, Американская стандартная Библия, Всемирная английская Библия (современный перевод), Священные тексты мормонской церкви Философия: Руссо, Спиноза, Платон, Аристотель, Маркс, Энгельс Путеводители и разговорники для всех крупных городов: Нью-Йорк, Париж , Лондон, Рим, Венеция, Прага, Пекин, Греция. Медицинские учебные пособия: анатомия и физиология, фармакология, сокращения и терминология, нервная система человека, биохимия. , Языки, Философия, Психология, Мифология, История: История искусств, Американские президенты, У.S. История, Энциклопедии Римской империи, Древнего Египта. Здоровье: Руководство по точечному массажу, Руководство по оказанию первой помощи, Искусство любви, Поваренная книга, Коктейли, Астрология. Справочник: Самая большая в мире мобильная энциклопедия; CIA World Factbook, Иллюстрированные энциклопедии птиц, млекопитающих
Медицинские учебные пособия: анатомия и физиология, фармакология, сокращения и терминология, нервная система человека, биохимия. , Языки, Философия, Психология, Мифология, История: История искусств, Американские президенты, У.S. История, Энциклопедии Римской империи, Древнего Египта. Здоровье: Руководство по точечному массажу, Руководство по оказанию первой помощи, Искусство любви, Поваренная книга, Коктейли, Астрология. Справочник: Самая большая в мире мобильная энциклопедия; CIA World Factbook, Иллюстрированные энциклопедии птиц, млекопитающих
Что такое уравнения Максвелла? | Физика
Уравнения Максвелла впервые появились в «Динамической теории электромагнитного поля» Философских трудов Лондонского королевского общества в 1865 году. Это уравнения света, математические соотношения, которые показали нам, как электрифицировать наш мир и передавать энергия и информация по воздуху.
В начале 19 века мы освещали наши дома и офисы свечами и масляными лампами. Сообщения принимали форму рукописных писем, которые путешествовали по стране за несколько дней, а через океаны — за несколько недель. Сегодня мы используем электричество для питания всего и радиоволны, чтобы мгновенно общаться друг с другом в любой точке мира.
Сегодня мы используем электричество для питания всего и радиоволны, чтобы мгновенно общаться друг с другом в любой точке мира.
Семена этого огромного изменения были посеяны в 1830-х годах, когда британский физик Майкл Фарадей построил электрические двигатели и показал, что две силы природы, электричество и магнетизм, связаны между собой.Он предположил, что эти силы существуют как «поля», пронизывающие пространство. Во второй половине XIX века шотландский физик Джеймс Клерк Максвелл сформулировал уравнения, описывающие эти поля.
Максвелл смоделировал поля, как если бы они были невидимыми жидкостями, заполняющими пространство. В каждой точке пространства электрическое поле имеет направление и силу, которые можно измерить, если поместить туда что-то, что может чувствовать воздействие поля, — скажем, электрон. Если бы вы могли каким-то образом измерить поле в каждой точке пространства, вы бы знали, как оно течет и изменяется.
Два уравнения слева на рисунке показывают, что суммарный поток электрического (E) и магнитного (H) полей из замкнутого объема пространства, вдали от любых электрических зарядов или магнитных материалов, равен нулю.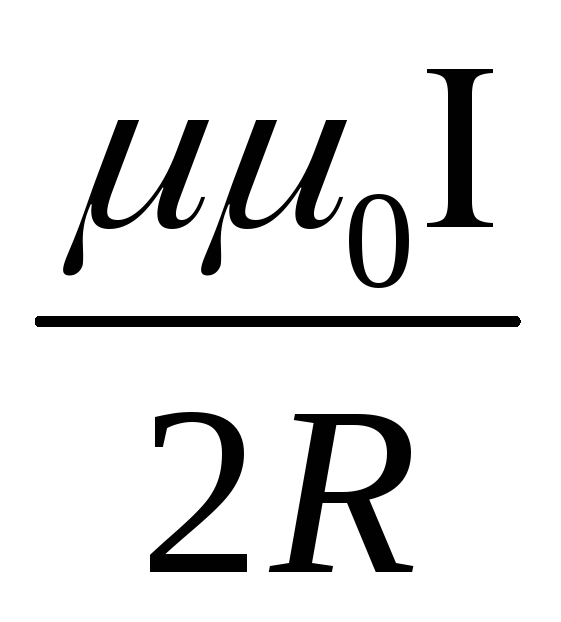 Символ треугольника и точки перед символами поля (называемый оператором «дивергенции») — это математический способ измерения того, ведет ли себя поле как источник или сток в определенной точке пространства.
Символ треугольника и точки перед символами поля (называемый оператором «дивергенции») — это математический способ измерения того, ведет ли себя поле как источник или сток в определенной точке пространства.
Уравнение для магнитного поля (H) остается тем же, даже когда вокруг есть магнит — подумайте о стержневом магните, линии магнитного поля вокруг него начинаются от северного полюса и идут по окружности к южному полюсу.И эти силовые линии всегда будут останавливаться и начинаться на магнитном объекте, они не появляются и не исчезают в пустом пространстве.
Уравнение для электрического поля (E) немного отличается, когда вокруг есть электрические заряды. Положительный заряд является чистым источником электрических полей, а отрицательный заряд — стоком. В этом случае чистая величина поля, выходящего из объема или входящего в него, пропорциональна заряду, содержащемуся в нем.
Два уравнения справа объясняют, что происходит, когда вы перемещаете электрическое или магнитное поле. Оператор «завиток» (сочетание треугольника и символа x) слева от каждого уравнения — это способ измерения поля, движущегося по крошечному кругу. Изменяющееся электрическое поле (Е) создает изменяющееся магнитное поле (Н). И наоборот. Фигурные d/dts справа измеряют скорость изменения, крошечное изменение в поле (E или H), деленное на крошечное изменение во времени (t).
Оператор «завиток» (сочетание треугольника и символа x) слева от каждого уравнения — это способ измерения поля, движущегося по крошечному кругу. Изменяющееся электрическое поле (Е) создает изменяющееся магнитное поле (Н). И наоборот. Фигурные d/dts справа измеряют скорость изменения, крошечное изменение в поле (E или H), деленное на крошечное изменение во времени (t).
Эти уравнения лежат в основе электромагнитной индукции, идеи о том, что если вы перемещаете магнит рядом с электрическим проводником (или наоборот), вы генерируете электричество.Электричество, которое вы используете каждый день, производится с помощью генераторов, работающих по этим уравнениям.
Что оставляет нам букву “с” в правой части вторых двух уравнений. Это константа со значением около 300 000 километров в секунду, что как раз и является скоростью света.
Имейте в виду, что Максвелл поместил это туда не потому, что изучал свет; число просто неожиданно выскочило из математики материалов, которые он изучал.
Максвелл начал с изучения свойств электричества и магнетизма и наткнулся на гораздо более глубокую истину о них: электромагнитное поле было средой для волн, которые, подобно ряби по поверхности пруда, двигались со скоростью «с». И свет, который мы видим, является одной из этих электромагнитных волн.
Значит, должны быть другие электромагнитные волны. Длины волн, которые мы можем обнаружить глазами, воспринимаются нами как цвета. К более коротким длинам волн света относятся ультрафиолетовые и гамма-лучи.
Более длинные волны включают тепло (инфракрасные волны), микроволны и радиоволны. Последние, конечно же, являются методом связи 20-го века — все, от радиоприемников и телевизоров до радаров и мобильных телефонов, основано на наших манипуляциях с электромагнитным полем, как описано уравнениями Максвелла.
Уравнения Максвелла: определение и применение — видео и расшифровка урока
Приложения Максвелла
Вариантов использования и приложений уравнений Максвелла слишком много, чтобы сосчитать. Поняв электромагнетизм, мы можем создавать изображения тела с помощью МРТ-сканеров в больницах; мы создали магнитную ленту, произвели электричество и построили компьютеры. Любое устройство, использующее электричество или магниты, на фундаментальном уровне построено на первоначальном открытии уравнений Максвелла.
Поняв электромагнетизм, мы можем создавать изображения тела с помощью МРТ-сканеров в больницах; мы создали магнитную ленту, произвели электричество и построили компьютеры. Любое устройство, использующее электричество или магниты, на фундаментальном уровне построено на первоначальном открытии уравнений Максвелла.
Хотя использование уравнений Максвелла часто связано с исчислением, существуют упрощенные версии уравнений, которые мы можем изучать. Эти версии работают только в определенных обстоятельствах, но могут быть полезными и избавить от многих проблем.Давайте рассмотрим один из них — упрощенную версию закона Фарадея.
Напоминаем, что закон Фарадея гласит, что любое изменение магнитной среды катушки с проводом вызовет наведение напряжения в катушке. И мы можем количественно оценить эти изменения с помощью простого уравнения. Это дает вам следующее уравнение, приведенное ниже, где N — число витков на катушке провода, дельта BA — это изменение магнитного поля, умноженное на площадь катушки провода, а дельта t — это время, в течение которого происходит это изменение.
Это уравнение даст вам напряжение, создаваемое в катушке. Если что-либо изменит значения B или A , будет произведено напряжение.
Пример
Давайте рассмотрим пример использования упрощенной версии закона Фарадея. Катушка с проводом помещена во внешнее магнитное поле напряженностью 0,1 тесла. Катушка имеет 50 витков и площадь поперечного сечения 0,05 квадратных метра.Какое напряжение будет индуцироваться в катушке провода, если постепенно, в течение 3 секунд, изменить напряженность поля до 0,4 тесла?
Прежде всего, следует записать то, что мы знаем: начальное магнитное поле Bi равно 0,1; число витков N равно 50; площадь A равна 0,05; конечное магнитное поле Bf равно 0,4; а время t равно 3.
Поскольку в уравнении есть дельта B , нам нужно найти изменение поля.Изменением поля будет разница между начальным и конечным значениями, которая равна 0,4 минус 0,1, что равно 0,3.
Наконец, мы просто подставляем наши числа в уравнение и решаем. 50 умножить на 0,3 умножить на 0,05 (поскольку площадь не изменилась) разделить на 3 равно 0,25 вольта. И это все; это наш ответ.
Итоги урока
Уравнения Максвелла представляют собой серию из четырех дифференциальных уравнений в частных производных, описывающих силу электромагнетизма.Уравнения выглядят так:
Закон Гаусса связывает распределение электрического заряда с полем, которое создает заряд. Если вы знаете форму объекта и, следовательно, как распределяется заряд, вы можете использовать закон Гаусса, чтобы найти выражение для электрического поля. Закон Гаусса для магнетизма говорит, что магнитных монополей не существует.
Закон Фарадея гласит, что любое изменение магнитной среды катушки с проводом вызовет наведение напряжения в катушке. Если изменяется напряженность магнитного поля, или магнит перемещается, или катушка движется, или катушка вращается – любое из этих событий создаст напряжение в катушке. И Закон Ампера говорит, что магнитное поле, создаваемое электрическим током, пропорционально величине этого электрического тока, с константой пропорциональности, равной проницаемости свободного пространства.
Если изменяется напряженность магнитного поля, или магнит перемещается, или катушка движется, или катушка вращается – любое из этих событий создаст напряжение в катушке. И Закон Ампера говорит, что магнитное поле, создаваемое электрическим током, пропорционально величине этого электрического тока, с константой пропорциональности, равной проницаемости свободного пространства.
Вариантов использования и приложений уравнений Максвелла слишком много, чтобы сосчитать. Понимая электромагнетизм, мы можем создавать изображения тела с помощью МРТ-сканеров в больницах; мы создали магнитную ленту, произвели электричество и построили компьютеры.
Мы можем упростить закон Фарадея и количественно определить индуцированное напряжение, которое он описывает. Это дает нам приведенное ниже уравнение, где N — число витков на катушке провода, дельта BA — изменение магнитного поля, умноженное на площадь катушки провода, а дельта t — это время, в течение которого происходит это изменение:
Это уравнение даст нам напряжение, создаваемое в катушке.

 Последнему научиться можно только решив тысячи задач.
Последнему научиться можно только решив тысячи задач. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.


 11 класс. В.А.Касьянов (базовый уровень), 2014 год
11 класс. В.А.Касьянов (базовый уровень), 2014 год










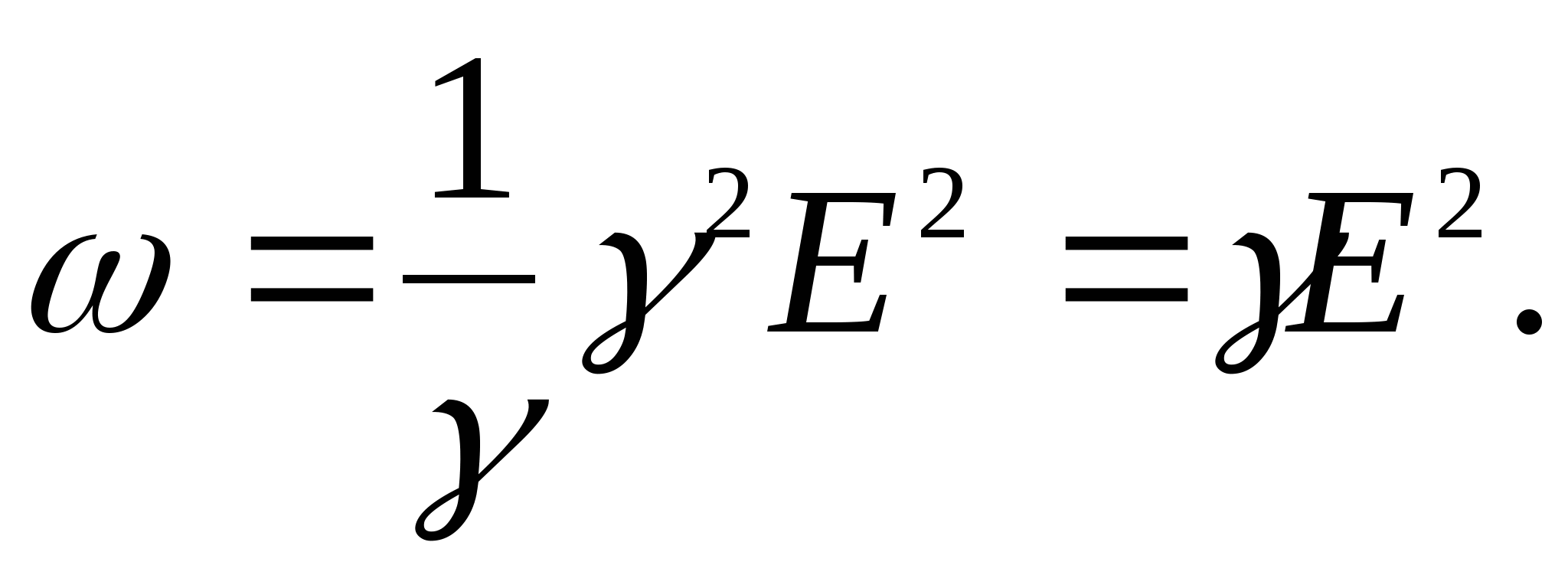

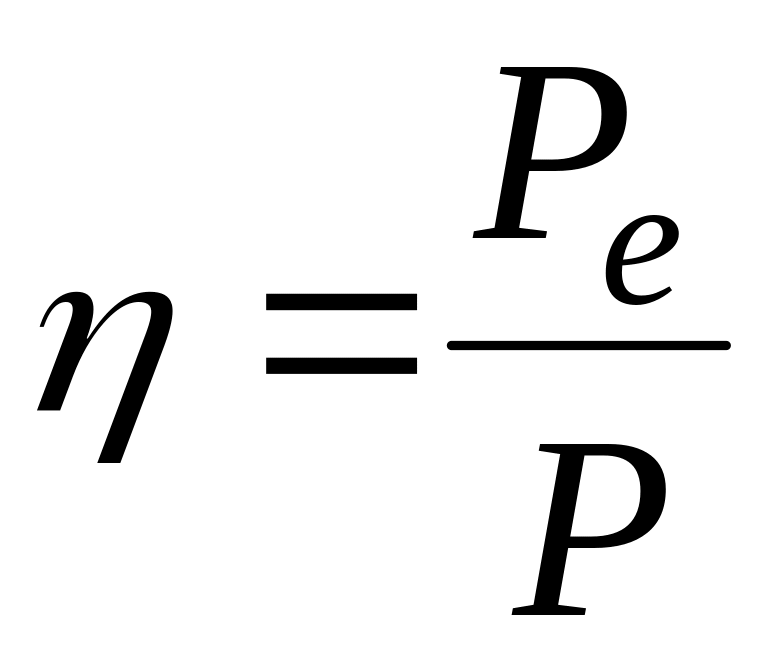
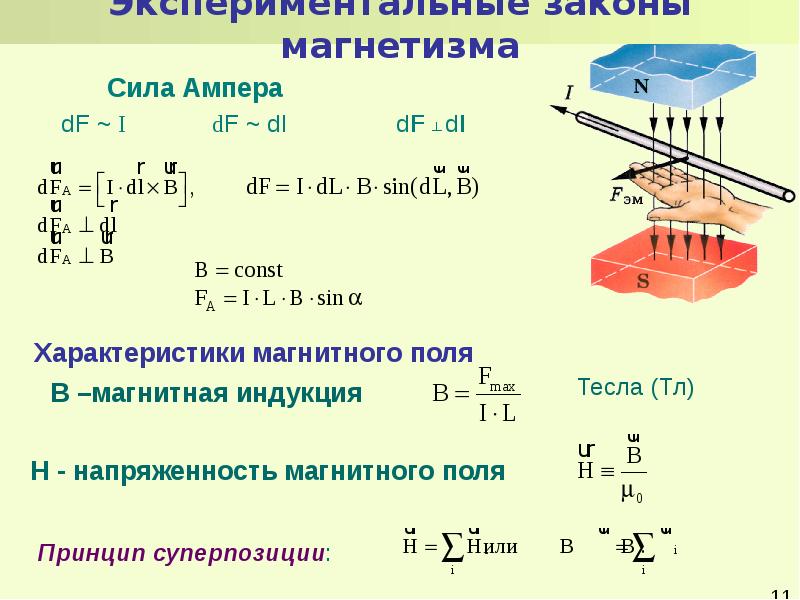 VC=1CQ(t)=V0(1−e−t/RC).
Пусть ось z указывает от положительной пластины к отрицательной пластине. Тогда z -компонента электрического поля между пластинами как функция времени t равна
Ez(t)=V0d(1−e−t/RC).Ez(t)=V0d(1−e−t/RC).
Следовательно, z-составляющая тока смещения IdId между пластинами равна
Id(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC=V0Re−t/RC,Id(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC= V0Re-t/RC,
где мы использовали C=ε0AdC=ε0Ad для емкости.
VC=1CQ(t)=V0(1−e−t/RC).
Пусть ось z указывает от положительной пластины к отрицательной пластине. Тогда z -компонента электрического поля между пластинами как функция времени t равна
Ez(t)=V0d(1−e−t/RC).Ez(t)=V0d(1−e−t/RC).
Следовательно, z-составляющая тока смещения IdId между пластинами равна
Id(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC=V0Re−t/RC,Id(t)=ε0A∂Ez(t)∂t=ε0AV0d×1RCe−t/RC= V0Re-t/RC,
где мы использовали C=ε0AdC=ε0Ad для емкости.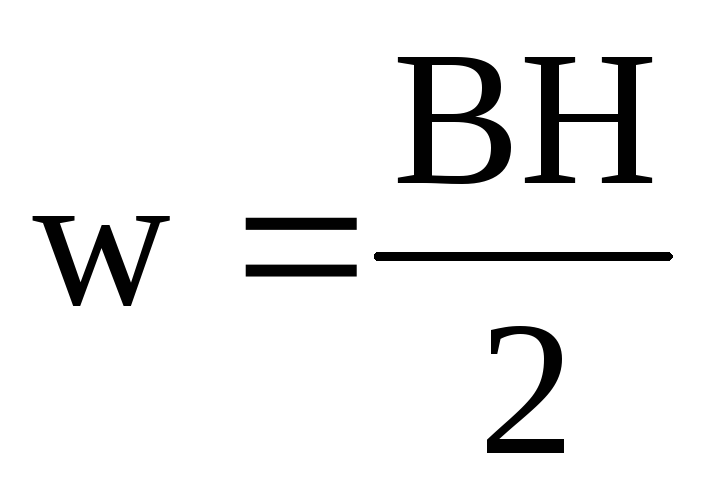 Поперечный характер электромагнитных волн.
Поперечный характер электромагнитных волн.