Задачи на трехфазные цепи
ТОЭ примеры решения
Трехфазные электрические цепи получили широкое распространение в промышленности, благодаря своим немалым преимуществам перед другими системами электрических цепей. К ним относятся – экономичность передачи энергии, относительная простота создания вращающегося магнитного поля, а также возможность получения двух значений напряжения. Основными потребителями трехфазных систем являются асинхронные двигатели, а основными источниками – трехфазные генераторы.
В разделе электротехники трехфазным цепям переменного тока посвящено немало задач, рассмотрим решение некоторых из них.
Задача 1
Обмотки трехфазного генератора соединены по схеме “звезда”, э.д.с. в них 220 В. Построить векторные диаграммы и определить линейные напряжения для схемы соединения, в которой в одной точке сходятся: a) X Y Z б) X B Z в) X B C . Начала обмоток – A,B,C, концы обмоток – X,Y,Z. Принять нагрузку на генераторе равной нулю.
а) Для данной схемы соединения векторная диаграмма будет выглядеть следующим образом
Линейные напряжения в данном случае будут равны и определяться как
б) Так как обмотка BY подключена началом в нейтральную точку, то вектор напряжения оказывается повернутым на 180 относительно нормального положения.
Линейные напряжения в данном примере будут разными по значению
в) В данном случае относительно нормального положения повернуты вектора двух обмоток – BY и CZ.
Как и в предыдущем примере, линейные напряжения не будут равны
Задача 2
К зажимам приемника подсоединён трехфазный генератор, как показано на схеме. Определить показания амперметров A1,A2 и фазные токи зная, что Uл=380В, R=50 Ом, xL=35 Ом.
Определим комплексные значения сопротивления (для удобства вычислений будем переводить в показательную форму)
Напряжения в фазах будет равно
Токи в фазах
Ток в нейтральном проводе равен (для удобства сложения сначала переведем из показательной формы в алгебраическую, а затем наоборот)
Соответственно, показания амперметров будут следующими:
Задача 3
К зажимам приемника, подсоединён трехфазный генератор, обмотки которого соединены по схеме “треугольник”. Определить фазные и линейные токи, показания вольтметра, зная, что линейное напряжение равно 220 В, R=25 Ом, xL=xC=10 Ом.
Определить фазные и линейные токи, показания вольтметра, зная, что линейное напряжение равно 220 В, R=25 Ом, xL=xC=10 Ом.
Как и в предыдущей задаче, в первую очередь определим комплексы сопротивлений
Фазное напряжение при данном соединении будет равно линейному, следовательно
Фазные токи при несимметричной нагрузке не равны
Для определения линейных токов представим фазные токи в алгебраической форме комплексного числа
Сумма линейных токов
Равенство нулю суммы линейных токов является свойством любой трёхфазной системы.
Чтобы определить показания вольтметра, найдём сумму падений напряжения на xL и R в соответствующих обмотках.
Так решаются задачи на трехфазные цепи. Спасибо за внимание! Читайте также – задачи на цепи переменный ток
1.
 3.2 Решение типовых задач
3.2 Решение типовых задачПримеры решения типовых задач
Задача 1.3.1 Трехфазный асинхронный двигатель включен в сеть 380 В по схеме «звезда». Параметры обмоток следующие: Rф = 2 Ом, Хф = 8 Ом.
Требуется: изобразить схему включения двигателя в сеть; определить фазные и линейные токи; определить потребляемую активную мощность; построить векторную диаграмму токов и напряжений; рассмотреть два аварийных режима – обрыв и короткое замыкание фазы А.
Решение:
Трехфазный асинхронный двигатель является симметричной активно-индуктивной нагрузкой, поэтому включается в сеть по схеме «звезда» без нейтрального провода. Его схема замещения представлена на рис. 1.3.8
Номинальное напряжение сети является линейным напряжением, т. е. , тогда фазное напряжение
Поскольку
нагрузка симметричная, то расчет можно
проводить для одной фазы.
Полное сопротивление фазы
Ф
А(а)
азный ток
.
Для схемы «звезда» линейный ток . Потребляемая активная мощность
где – фазовый угол,
Векторная диаграмма токов и напряжений показана на рис. 1.3.9. Для построения векторной диаграммы необходимо выбрать масштабы напряжений и токов .
Рассмотрим аварийный режим работы– обрыв фазы А (рис.1.3.10).
В этом случае трехфазная цепь превращается в однофазную , причем фазы b и с оказываются включенными последовательно на линейное напряжение , т. е. на каждую из этих фаз падает напряжение
Фазные и линейные токи
.
Потребляемая мощность Рис. Если обрыв фазы произошел внутри самого двигателя (обрыв обмотки), то эта обмотка оказывается под повышенным напряжением , что видно из векторной диаграммы (рис.1.3.11). Неповрежденные обмотки находятся под пониженным напряжением, что не опасно для них. |
Рассмотрим аварийный режим работы – короткое замыкание фазы «а»
При коротком замыкании фазы нейтральная точка оказывается связана с питающей точкой А, значит, неповрежденные фазы b и с окажутся включенными на линейное напряжение , что видно из векторной диаграммы.
Токи в неповрежденных фазах
.
а | б |
Рис.
Ток в фазе а равен геометрической сумме токов и ( по векторной диаграмме составляет примерно 69 А).
Задача 1.3.2. Три однофазных приемника включены в трехфазную сеть с напряжением 380 В по схеме “звезда с нейтральным проводом”. Сопротивления приемников: Ом; Ом; Ом.
Требуется изобразить схему включения приемников; определить токи в проводах сети; построить векторную диаграмму токов и напряжений; вычислить активную, реактивную и полную (кажущуюся) мощности.
Решение:
Схема включения приемников принципиальная и расчетная представлены на рис. 1.3.13, а,б.
а | б |
Рис. | |
Наличие нейтрального провода обеспечивает симметричную систему фазных напряжений на приемниках. Напряжение сети – линейное напряжение
В.
Система фазных напряжений в комплексной форме
Сопротивления фаз
Для схемы “звезда“ фазные и линейные токи равны между собой и составляют
Ток в нейтральном проводе
При построении
векторных диаграмм фазные и линейные
напряжения и токи строятся относительно
комплексных осей откладываются с
учетом начальных фаз. Ток в нейтральном
проводе – это результат геометрического
сложения векторов фазных токов, и его
расположение и длина должны
соответствовать расчетному значению
(рис. | Рис. 1.3.13 |
Задача 1.3.3. К трехфазной системе напряжением 380 В подключены три одинаковых приемника (RФ = 3 Ом, XLФ = 4 Ом), соединенные по схеме “треугольник“ (рис.1.3.14). Определить токи в фазных и линейных проводах и потребляемую мощность (активную, реактивную, полную). Построить векторную диаграмму токов и напряжений.
Рассмотреть аварийные режимы – обрывы фазного и линейных проводов.
Решение:
Нагрузка фаз одинакова, поэтому расчет проводится для одной фазы. Напряжение сети – это линейное напряжение, в схеме “треугольник “ Uф = Uл = 380 В. Комплексное сопротивление фазы: где | Рис. |
Фазные токи:
линейные токи (только для симметричной нагрузки):
Активная мощность, потребляемая нагрузкой:
реактивная мощность:
полная мощность:
Векторная диаграмма может быть построена в двух вариантах в зависимости от изображения системы напряжений (рис.1.3.15 ). Предварительно выбирают масштабы тока и напряжения.
Рис. 1.3.15 | |
Фазные токи отстают от соответствующих напряжений на угол Ф = 53. Линейные токи находятся из соотношений:
Рассмотрим обрыв
фазы “аb”
(рис. 1.3.16,а). Определим токи в неповрежденных
фазах и в линии, построим векторную
диаграмму токов и напряжений.
1.3.16,а). Определим токи в неповрежденных
фазах и в линии, построим векторную
диаграмму токов и напряжений.
а) | б) |
Рис. 1.3.16 | |
Токи в неповрежденных фазах не изменяются, так как не изменяются напряжения:
Линейные токи по первому закону Кирхгофа (с учетом ):
.
Из этих уравнений следует, что действующие значения линейных токов и равны действующим значениям фазных токов, а у линейного тока действующее значение не изменяется
Векторная диаграмма токов и напряжений строится аналогично симметричному режиму и приведена на рис.1.3.16,б.
Рассмотрим обрыв
линейного провода А (рис. 1.3.17,а). Определим фазные и линейные
токи и построим векторную диаграмму
токов и напряжений.
1.3.17,а). Определим фазные и линейные
токи и построим векторную диаграмму
токов и напряжений.
К приемнику подводится только напряжение
Сопротивление фазы “bс” включено на полное напряжение , а равные сопротивления фаз “аb” и ”са” включены последовательно друг с другом, причем к каждому из них подведена половина напряжения .
а) б) Рис.1.3.17 |
Сеть становится аналогичной однофазной с двумя параллельными ветвями:
Ток фазы “bс” не изменяется:
токи других фаз :
линейные токи ( при ) :
Векторная
диаграмма токов и напряжений представлена
на рис. 1.3.17,б.
1.3.17,б.
Задача 1.3.4 В трехфазную сеть напряжением 380 В, частотой f = 50 Гц включен трехфазный асинхронный двигатель по схеме “треугольник“. Потребляемая активная мощность P = 1,44 кВт, коэффициент мощности cos = 0,85. Определить потребляемый двигателем ток, токи в обмотках двигателя, активное и индуктивное сопротивления, индуктивность катушек, полную и реактивную потребляемые мощности.
Решение:
Двигатель является симметричной нагрузкой, поэтому расчет ведем на фазу.
Сеть маркируется линейным напряжением, поэтому UЛ = 380 В.
При соединении по схеме “треугольник“ UЛ = UФ= 380 В.
Активная мощность, потребляемая нагрузкой,
отсюда фазный ток, протекающий в обмотках двигателя:
Потребляемые двигателем токи – линейные токи:
Полное сопротивление фазы обмотки двигателя:
Ом,
активное сопротивление
Ом,
индуктивное сопротивление
Ом.
Индуктивность обмотки определяется из выражения
,
Гн.
Полная потребляемая мощность:
кВА;
реактивная мощность:
Задача 7.3 К трехпроводной трехфазной линии с напряжением 380 В подключены три однофазных приемника с параметрами: R1= 5 Ом, R2= 6 Ом, XL2= 8 Ом, R3=4 Ом, XC3= 3 Ом. Определить токи в фазах и линейных проводах, активную, реактивную и полную мощности и построить векторную диаграмму токов и напряжений.
Решение:
Однофазные приемники к трехпроводной сети подключаются по схеме “треугольник“ (рис.1.3.18). Нагрузка
несимметричная, ток каждой фазы нужно
считать отдельно. Комплексные сопротивления фаз: Ом; | |
Ом;
Ом;
Фазные токи:
Линейные токи:
Сумма линейных токов должна равняться нулю, и действительно,
Активная мощность:
Реактивная мощность:
здесь знак “минус” показывает, что преобладает емкостная нагрузка.
Полная мощность:
Векторные диаграммы
токов и напряжений в двух вариантах
(для разного представления исходной
системы напряжений) приведены на
рис. 1.3.19.
1.3.19.
Предварительно выбирают масштабы тока и напряжения. Векторы фазных токов откладывают относительно векторов соответствующих напряжений под углами , , или в соответствии с полученными их начальными фазами ; ; . Затем по первому закону Кирхгофа строят векторы линейных токов , длина и направление которых должны соответствовать расчетным данным.
Рис.1.3.19 Векторные диаграммы токов и напряжений несимметричной нагрузки | |
Решенные задачи: анализ трехфазных цепей
Проблемы
1. двигатель измеряется как 5кВт. Если напряжение и ток двигателя составляют 400 В и 8,6 А соответственно, определите коэффициент мощности системы?
Мощность P =5000 Вт,
напряжение сети
1 В, 2 L = 20002 линейный ток, I L = 8 . 6A and
6A and
power, P =√3 V L I L cos φ
Hence
power factor = cos φ = P √3 V L I L
= 5000 √3 (400) (8 . 6)
.0002 = 0,839
2. Два ваттметра подключены для измерения входной мощности на сбалансированную трехфазную нагрузку методом двух ваттметров. Если показания прибора равны 8 кВт и 4 кВт, определите (а) общую потребляемую мощность и (б) коэффициент мощности нагрузки.
(A) Общая входная мощность,
P = P 1 + P 2 = 8 + 4 = 12KW
P 2 = 8 + 4 = 12KW .0002(b) TAN φ = √3 ( P 1 – P 2) / ( P 1 + P 2)
= √3 (8 – 4) / ( 8 + 4)
= √3 (4/12)
= √3 (1/3)
= 1/√3
Отсюда φ = TAN – 1 10005
. √3 =30◦
√3 =30◦
Коэффициент мощности= cos φ = cos 30◦ = 0,866
9 0003 3
04
Два ваттметра, подключенных к трехфазному двигателю, показывают, что общая потребляемая мощность составляет 12 кВт. Коэффициент мощности 0,6. Определить показания каждого ваттметра.
If the two wattmeters indicate P 1 and P 2 respectively
Then P 1 + P 2 = 12kW | —(1) |
тангенс φ =√3( P 1 − P 2)/( P 1 + P 2)
И коэффициент мощности=0 . 6 = cos φ .
Угол φ = cos−10 . 6=53 . 13◦ и
загар 53 . 13◦ =1 . 3333.
Отсюда
1 . 3333 =√3( P 1 − P 2)/12
3333 =√3( P 1 − P 2)/12
Из чего
P 1 − P 2 = 12(1 . 3333) /√3
т. е. P 1 − P 2 =9 . 237кВт —-(2)
Сложение уравнений (1) и (2) дает:
2 P 1 = 21 . 237
т. е. P 1 = 21 . 237/2
= 10 . 62 кВт Следовательно, ваттметр 1 показывает 10,62 кВт Из уравнения (1) ваттметр 2 показывает
(12−10,62)=1,38 кВт
4. Три нагрузки, каждая с сопротивлением 30 Ом, подключены звездой к трехфазной сети 415 В. Определите
(a) фазное напряжение системы, (b) фазный ток и (c) линейный ток.
A «415 В, 3-фазное питание» означает, что 415 В является линейным напряжением, VL
(a) Следовательно, для фазного напряжения, VL =√3Vp = ВЛ/√3
= 415/√3
= 239,6 В или 240 В
Правильно до 3 значащих рисунков
(b) Фазовый ток, IP = VP/RP
= 240/30.
= 8 A
(C) для звездного соединения, IP = IL Следовательно, ток линии, IL = 8 A
5.
Три одинаковые катушки сопротивлением 10 9 каждая.0021 Ом и индуктивность 42 мГн подключены (а) по схеме «звезда» и (б) по схеме «треугольник» к 3-фазному источнику питания 415 В, 50 Гц. Определить общую мощность, рассеиваемую в каждом случае.
(A) Звездное соединение
Индуктивное реактивное сопротивление,
x L = 2 πf L = 2 π (50) (42 × 10-3) = 13 . 19
Полное сопротивление фазы,
Z p =√( R 2 + X L2)
=√(102 +13 . 192) =16 . 55
Line voltage, V L =415 V
And phase voltage,
V P = V L / √3=415 / √3=240 V.
Фазовый ток,
I P = V P / Z P = 240 / 16 . 55=14 . 50 А. Линейный ток,
55=14 . 50 А. Линейный ток,
I L = I p =14 . 50 A.
Коэффициент мощности = cos φ = R p /Z p =10 1 902 / 90 55 =0,6042 отставание.
Power dissipated,
P =√3 V L I L cos φ =√3 (415) (14 . 50)(0 . 6042) = 6.3kW (Alternatively,
P =3 I 2 R = 3 (14 . 50) 2 (10) = 6,3 кВт )
(B) Delta Connection
V L = V .
V L = V .
V L = v .
V L = V 959
V L = V
V L = V
V L = V
V L = . = 415 В,
= 415 В,
Z p = 16 . 55 _ , cos φ = 0 . 6042 отставание (сверху). Ток фазы,
I p = В p /Z p =415 / 16 . 55=25 . 08А . Линейный ток,
I L =√3 I p =√3(25 . 08)=43 . 44А .
Рассеиваемая мощность,
P = √3 V L I L COS φ
= √3 (415) (43 . 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442 442. ) = 18.87kW
(Alternatively,
P =3 I 2R
=3(25 . 08)2(10) = 18.87 kW)
6. A 415 В, 3 фазы переменного тока двигатель имеет выходную мощность 12,75 кВт и работает с коэффициентом мощности 0,77 отставания и с КПД 85 процентов. Если двигатель соединен треугольником, определите (а) потребляемую мощность, (б) линейный ток и (в) фазный ток.
Если двигатель соединен треугольником, определите (а) потребляемую мощность, (б) линейный ток и (в) фазный ток.
(a) Эффективность = выходная мощность / потребляемая мощность.
Следовательно,
(85 / 100) = 12,750 Вход мощности, из которого Вход мощности = 12. 750 × 10085
= 15 000 Вт или 15KW
00009
0909
0909
0909
0 9000 9000 9000 9000 Вт 9000 Вт. (b) Мощность, P =√3 В L I L cos φ , следовательно,
(c) Ток линии ,
I L = P/ √3 (415) (0 . 77)
= 15 000/ a ) (0 . 77)
= 27.10A
(D) для Delta Connection, I L = √3 I P,
HARE
599595995992992929292929299292992992992992929292955595992929292929292929292929
29
Фазный ток , I p = IL/√3
= 27 . 10 /√3
10 /√3
= 15,65A
7. А. из 30 _ и индуктивное сопротивление 40 _ . Рассчитайте (а) ток, подаваемый генератором переменного тока и (б) выходную мощность и кВА генератора переменного тока, пренебрегая потерями в линии между генератором переменного тока и нагрузкой.
Диаграмма схемы генератора и нагрузки показана на рис.
(а) Учитывая нагрузку:
Фазовый ток, I P = V 299
, I P = V 229992 p /Z p
V p = V L для соединения треугольником,
Отсюда V p = 400 В.
Полное сопротивление фазы,
Z p =√ ( R 2+ x L2)
= √ (302 +402) = 50
Рисунок
ОСНОВАЯ / 50=8А.
Для соединения треугольником,
Линейный ток, I L =√3 I p =√3 (8) =13 . 86 А.
86 А.
Следовательно 13,86 А – это ток, подаваемый генератором .
(b) Выходная мощность генератора равна мощности, рассеиваемой нагрузкой
Т.е. P = √3 V L I L COS φ , где COS φ = R P / Z P = 30 / 50 = 0 . 6 .
Отсюда P =√3 (400) (13 . 86) (0 . 6) = 9,704 кВт
Alternator output kVA,
S =√3 V L I L =√3 (400) (13 . 86)
9.60 кВА .
Объяснение электрической мощности. Часть 3: Сбалансированная трехфазная сеть переменного тока
Большие трехфазные двигатели и оборудование, которое они приводят в действие, должны потреблять мощность в равной степени от каждой из трех фаз сети. Однако часто этого не происходит. Дисбаланс и гармоники могут вызвать нестабильность, а вибрация двигателя снижает как эффективность, так и срок службы. Дисбаланс также может вызвать неисправности в однофазных нагрузках. Все это может снизить качество электроэнергии, что приведет к штрафным санкциям со стороны коммунальных служб.
Дисбаланс и гармоники могут вызвать нестабильность, а вибрация двигателя снижает как эффективность, так и срок службы. Дисбаланс также может вызвать неисправности в однофазных нагрузках. Все это может снизить качество электроэнергии, что приведет к штрафным санкциям со стороны коммунальных служб.
В этом блоге мы опишем сбалансированные трехфазные системы питания, в которых каждая фаза потребляет одинаковый ток. В следующих статьях блога, опубликованных позже, мы представим несбалансированную мощность.
В нашем предыдущем блоге было показано, как бесконечно изменяющиеся мгновенные формы тока и мощности могут быть просто представлены одним числом: параметрами. Возможно, наиболее полезными являются активная, реактивная и полная мощности.
Активная мощность совершает полезную работу, протекая через резистивную часть сети и имея то же среднее значение, что и мгновенная мощность. Реактивная мощность протекает по индуктивной части цепи 9на 0° позже и имеет среднее значение, равное нулю. Кажущаяся мощность – это общая мощность, видимая коммунальным предприятием. Коэффициент мощности представляет собой активную над полной мощностью.
Кажущаяся мощность – это общая мощность, видимая коммунальным предприятием. Коэффициент мощности представляет собой активную над полной мощностью.
Сбалансированные индуктивные/резистивные нагрузки
Трехфазные резистивные нагрузки просты, поэтому мы сразу перейдем к индуктивным нагрузкам (которые также включают резистивную составляющую).
В сбалансированной системе полная активная/реактивная/полная мощность представляет собой просто сумму их соответствующих фазных мощностей.
Базовая трехфазная система питания с тремя индуктивными нагрузками по 600 ВА. (Красный, зеленый и синий цвета фазы приведены только для демонстрации и не соответствуют никакому стандарту)
Сумма всех напряжений (и токов) в точке звезды всегда равна нулю. В сбалансированной системе ток нейтрали и мощность нейтрали равны нулю. Вы можете думать о сбалансированной трехфазной системе как о трех однофазных системах, подключенных к нейтральной линии.
Кривые напряжения и тока в сбалансированной системе
Трехфазные кривые напряжения и тока
Каждое напряжение отстает от предыдущего на 120° (посмотрите на пересечение нуля). Двигатель также снова вводит свой собственный 30-градусный фазовый сдвиг между напряжением и током.
Векторная (фазорная) диаграмма показывает ту же информацию, что и кривые
Эта векторная диаграмма показывает только основные значения. Длины линий представляют среднеквадратичные значения, а их высота над началом координат показывает мгновенные значения. Все это вращается со скоростью 60 раз в секунду против часовой стрелки. Опять же, напряжения фаз B и C отстают на 120° и 240°, а токи фаз A, B и C отстают на 30°, 150° и 270°.
Вы также можете нарисовать векторную диаграмму для каждой гармонической составляющей (но только основная составляющая обычно переносит полезную энергию).
09
0909
0 9000 9000 9000 9000 Вт 9000 Вт. (b) Мощность, P =√3 В L I L cos φ , следовательно,
(c) Ток линии ,
I L = P/ √3 (415) (0 . 77)
= 15 000/ a ) (0 . 77)
= 27.10A
(D) для Delta Connection, I L = √3 I P,
HARE
599595995992992929292929299292992992992992929292955595992929292929292929292929
29
Фазный ток , I p = IL/√3
= 27 . 10 /√3
10 /√3
= 15,65A
7. А. из 30 _ и индуктивное сопротивление 40 _ . Рассчитайте (а) ток, подаваемый генератором переменного тока и (б) выходную мощность и кВА генератора переменного тока, пренебрегая потерями в линии между генератором переменного тока и нагрузкой.
Диаграмма схемы генератора и нагрузки показана на рис.
(а) Учитывая нагрузку:
Фазовый ток, I P = V 299
, I P = V 229992 p /Z p
V p = V L для соединения треугольником,
Отсюда V p = 400 В.
Полное сопротивление фазы,
Z p =√ ( R 2+ x L2)
= √ (302 +402) = 50
Рисунок
ОСНОВАЯ / 50=8А.
Для соединения треугольником,
Линейный ток, I L =√3 I p =√3 (8) =13 . 86 А.
86 А.
Следовательно 13,86 А – это ток, подаваемый генератором .
(b) Выходная мощность генератора равна мощности, рассеиваемой нагрузкой
Т.е. P = √3 V L I L COS φ , где COS φ = R P / Z P = 30 / 50 = 0 . 6 .
Отсюда P =√3 (400) (13 . 86) (0 . 6) = 9,704 кВт
Alternator output kVA,
S =√3 V L I L =√3 (400) (13 . 86)
9.60 кВА .
Объяснение электрической мощности. Часть 3: Сбалансированная трехфазная сеть переменного тока
Большие трехфазные двигатели и оборудование, которое они приводят в действие, должны потреблять мощность в равной степени от каждой из трех фаз сети. Однако часто этого не происходит. Дисбаланс и гармоники могут вызвать нестабильность, а вибрация двигателя снижает как эффективность, так и срок службы. Дисбаланс также может вызвать неисправности в однофазных нагрузках. Все это может снизить качество электроэнергии, что приведет к штрафным санкциям со стороны коммунальных служб.
Дисбаланс и гармоники могут вызвать нестабильность, а вибрация двигателя снижает как эффективность, так и срок службы. Дисбаланс также может вызвать неисправности в однофазных нагрузках. Все это может снизить качество электроэнергии, что приведет к штрафным санкциям со стороны коммунальных служб.
В этом блоге мы опишем сбалансированные трехфазные системы питания, в которых каждая фаза потребляет одинаковый ток. В следующих статьях блога, опубликованных позже, мы представим несбалансированную мощность.
В нашем предыдущем блоге было показано, как бесконечно изменяющиеся мгновенные формы тока и мощности могут быть просто представлены одним числом: параметрами. Возможно, наиболее полезными являются активная, реактивная и полная мощности.
Активная мощность совершает полезную работу, протекая через резистивную часть сети и имея то же среднее значение, что и мгновенная мощность. Реактивная мощность протекает по индуктивной части цепи 9на 0° позже и имеет среднее значение, равное нулю. Кажущаяся мощность – это общая мощность, видимая коммунальным предприятием. Коэффициент мощности представляет собой активную над полной мощностью.
Кажущаяся мощность – это общая мощность, видимая коммунальным предприятием. Коэффициент мощности представляет собой активную над полной мощностью.
Сбалансированные индуктивные/резистивные нагрузки
Трехфазные резистивные нагрузки просты, поэтому мы сразу перейдем к индуктивным нагрузкам (которые также включают резистивную составляющую).
В сбалансированной системе полная активная/реактивная/полная мощность представляет собой просто сумму их соответствующих фазных мощностей.
Базовая трехфазная система питания с тремя индуктивными нагрузками по 600 ВА. (Красный, зеленый и синий цвета фазы приведены только для демонстрации и не соответствуют никакому стандарту)
Сумма всех напряжений (и токов) в точке звезды всегда равна нулю. В сбалансированной системе ток нейтрали и мощность нейтрали равны нулю. Вы можете думать о сбалансированной трехфазной системе как о трех однофазных системах, подключенных к нейтральной линии.
Кривые напряжения и тока в сбалансированной системе
Трехфазные кривые напряжения и тока
Каждое напряжение отстает от предыдущего на 120° (посмотрите на пересечение нуля). Двигатель также снова вводит свой собственный 30-градусный фазовый сдвиг между напряжением и током.
Векторная (фазорная) диаграмма показывает ту же информацию, что и кривые
Эта векторная диаграмма показывает только основные значения. Длины линий представляют среднеквадратичные значения, а их высота над началом координат показывает мгновенные значения. Все это вращается со скоростью 60 раз в секунду против часовой стрелки. Опять же, напряжения фаз B и C отстают на 120° и 240°, а токи фаз A, B и C отстают на 30°, 150° и 270°.
Вы также можете нарисовать векторную диаграмму для каждой гармонической составляющей (но только основная составляющая обычно переносит полезную энергию).
(c) Ток линии ,
I L = P/ √3 (415) (0 . 77)
= 15 000/ a ) (0 . 77)
= 27.10A
(D) для Delta Connection, I L = √3 I P,
HARE
599595995992992929292929299292992992992992929292955595992929292929292929292929 10 /√3
10 /√3 86 А.
86 А.  Дисбаланс и гармоники могут вызвать нестабильность, а вибрация двигателя снижает как эффективность, так и срок службы. Дисбаланс также может вызвать неисправности в однофазных нагрузках. Все это может снизить качество электроэнергии, что приведет к штрафным санкциям со стороны коммунальных служб.
Дисбаланс и гармоники могут вызвать нестабильность, а вибрация двигателя снижает как эффективность, так и срок службы. Дисбаланс также может вызвать неисправности в однофазных нагрузках. Все это может снизить качество электроэнергии, что приведет к штрафным санкциям со стороны коммунальных служб. Кажущаяся мощность – это общая мощность, видимая коммунальным предприятием. Коэффициент мощности представляет собой активную над полной мощностью.
Кажущаяся мощность – это общая мощность, видимая коммунальным предприятием. Коэффициент мощности представляет собой активную над полной мощностью.


 1.3.11
1.3.11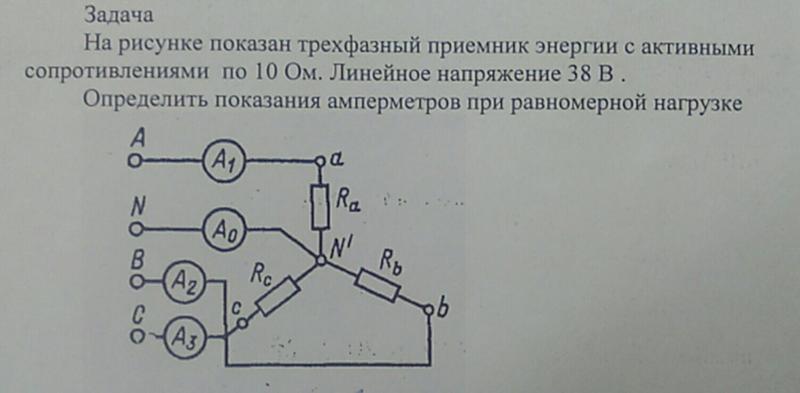 1.3.13
1.3.13
 1.3.14
1.3.14 Исходная система
напряжений:
Исходная система
напряжений: