Элементарные производные: Производные основных элементарных функций

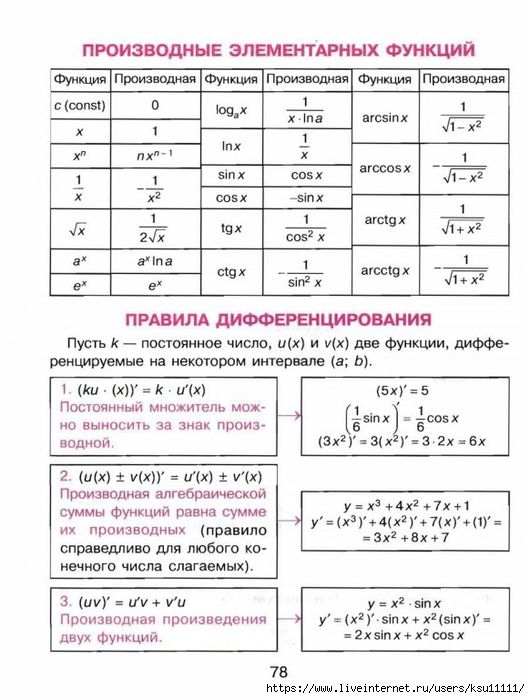
Производные основных элементарных функций

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

К элементарным функциям относятся основные элементарные функции и те, которые можно образовать из них с помощью конечного числа операций (сложения, вычитания, умножения и деления) и суперпозиций.

Из определения производной следует следующий алгоритм вычислений:

1. Составить приращение $\Delta $y, $\Delta $x функции
\[\frac{f(x+\Delta x)-f(x)}{\Delta x} \]
2. Найти частное приращение функции и аргумента
\[\frac{\Delta y}{\Delta x} =\frac{f(x+\Delta x)-f(x)}{\Delta x} \]
3. Найти предел отношения, при стремлении независимой переменной к 0
\[\mathop{\lim }\limits_{\Delta x\to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \]

Пример 1

Найти производную постоянной y = c

Решение. {n-1} \]

Частный вывод: Если y = x, то y` = 1.

Ответ: Производная степенной функции равна $nx_n-1$.

Пример 3

Найти производную тригонометрической функции y = sinx

Решение.

1. Составим приращение и найдем предел отношения
\[y`=\mathop{\lim }\limits_{\Delta x\to 0} \frac{\sin (x+\Delta x)-\sin x}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0} \frac{2\cos (x+\frac{\Delta x}{2} )\sin x\frac{\Delta x}{2} }{\Delta x} =\]
2. Упростим дробь
\[=\mathop{\lim }\limits_{\Delta x\to 0} \cos (x+\frac{\Delta x}{2} )\frac{\sin \frac{\Delta x}{2} }{\frac{\Delta x}{2} } =\cos x\]
Ответ: Производная sinx = cosx

Пример 4

Найти производную тригонометрической функции y = cosx

Решение.

1. Составим приращение и найдем предел отношения
\[y`=\mathop{\lim }\limits_{\Delta x\to 0} \frac{\cos (x+\Delta x)-\cos x}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0} -\frac{2\sin (x+\frac{\Delta x}{2} )\sin x\frac{\Delta x}{2} }{\Delta x} =\]
2. Упростим дробь
\[=-\mathop{\lim }\limits_{\Delta x\to 0} \sin (x+\frac{\Delta x}{2} )\frac{\sin \frac{\Delta x}{2} }{\frac{\Delta x}{2} } =-\sin x\]

Ответ: Производная cosx = – sinx

Пример 5

Найти производную логарифмической функции $y = logx (x > 0)$

Решение.

Составим приращение и найдем предел отношения

\[y`=\mathop{\lim }\limits_{\Delta x\to 0} \frac{\log (x+\Delta x)-\log x}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0} \frac{\log (1+\frac{\Delta x}{x} )}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0} \frac{1}{x} \frac{\log (1+\frac{\Delta x}{x} )}{\frac{\Delta x}{x} } =\frac{1}{x} \]

Ответ: Производная logx = 1/x

Пример 6

Найти производную функции y = cf(x), где с — постоянная, f(x) — функция.

Решение.

\[y`=\mathop{\lim }\limits_{\Delta x\to 0} \frac{cf(x+\Delta x)-cf(x)}{\Delta x} =c\mathop{\lim }\limits_{\Delta x\to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} =cf`(x)\]

Вывод: производная от производной постоянной величины на переменную равна произведению этой постоянной на производную от переменной функции. Т.е. постоянный множитель выносится за знак производной!

Пример 7

Найти производную логарифмической функции $y = log_a x$

Решение. 2 x$

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 10.12.2021

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Производные некоторых основных элементарных функций (Лекция №5)

1. y = xⁿ.
   Если n – целое положительное число, то, используя формулу бинома Ньютона:

   (a + b)ⁿ = aⁿ+n·a^n-1·b + 1/2∙n(n – 1)a^n-2∙b²+ 1/(2∙3)∙n(n – 1)(n – 2)a^n-3b³+…+ bⁿ,

   можно доказать, что

   Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)ⁿ, и, следовательно,

   Δy=(x+Δx)ⁿ – xⁿ

   =n·x^n-1·Δx + 1/2·n·(n–1)·x^n-2·Δx² +…+Δxⁿ.

   Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3.

   Найдем предел

   Мы доказали эту формулу для n Î N. Далее увидим, что она справедлива и при любом n Î R.

2. y= sin x. Вновь воспользуемся определением производной.

   Так как, f(x+Δx)=sin(

   x+Δx), то

   Таким образом,

3. Аналогично можно показать, что

4. Рассмотрим функцию y= ln x.

   Имеем f(x+Δx)=ln(x+Δx). Поэтому

   Итак,

5. Используя свойства логарифма можно показать, что

Формулы 3 и 5 докажите самостоятельно.

ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x)

– две дифференцируемые функции от переменной x.

2. .
3. (справедлива для любого конечного числа слагаемых).
4. .
5. .

   а) .

   б) .

Формулы 1 и 2 докажите самостоятельно.

Доказательство формулы 3.

Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).

Тогда

Δy=y(x+Δx) – y(x) = u(x+Δ

x) + v(x+Δx) – u(x) – v(x) = Δu +Δv.

Следовательно,

.

Доказательство формулы 4.

Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому

Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).

Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0.

Поэтому можем записать

На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.

Пусть, например, y=u·v·w. Тогда,

y ‘ = u ‘·(v·w) + u·(v ·w) ‘ = u ‘·v·w + u·(v ‘·w +v·w ‘) = u ‘·v·w + u·v ‘·w + u·v·w ‘.

Доказательство формулы 5.

Пусть . Тогда

При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.

Примеры.

1. Если , то
2. y = x³ – 3x² + 5x + 2. Найдем y ‘(–1).

   y ‘ = 3x² – 6x+ 5. Следовательно, y ‘(–1) = 14.

3. y = ln x · cos x, то y ‘ = (ln x) ‘ cos x + ln x (cos x) ‘ =1/x∙cos x – ln x · sin x.

5. Таким образом,

6. Аналогично для y= ctgx,

ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ

Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.

Областью определения функции y = f(u(x)) является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области определения функции y= f(u).

Операция “функция от функции” может проводиться не один раз, а любое число раз.

Установим правило дифференцирования сложной функции.

Теорема. Если функция u= u(x) имеет в некоторой точке x₀ производную и принимает в этой точке значение u₀ = u(x₀), а функция y= f(u) имеет в точке u₀ производную y ‘_u= f ‘(u₀), то сложная функция y = f(u(x)) в указанной точке x₀ тоже имеет производную, которая равна y ‘_x= f ‘(u₀)·u ‘(x₀), где вместо u должно быть подставлено выражение u= u(x).

Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.

Доказательство. При фиксированном значении х₀ будем иметь u₀=u(x₀), у₀=f(u₀). Для нового значения аргумента x₀+Δx:

Δu= u(x₀ + Δx) – u(x₀), Δy=f(u₀+Δu) – f(u₀).

Т.к. u – дифференцируема в точке x₀, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0.

По условию . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)

,

где α→0 при Δu→0, а, следовательно, и при Δx→0.

Перепишем это равенство в виде:

Δy= y ‘_uΔu+α·Δu.

Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx

.

По условию . Поэтому, переходя к пределу при Δx→0, получим y ‘_x= y ‘_u·u ‘_x . Теорема доказана.

Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от “внешней” функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от “внутренней” функции по независимой переменной.

Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y ‘_x осуществляется последовательным применением предыдущей теоремы.

По доказанному правилу имеем y ‘_x= y ‘_u·u ‘_x . Применяя эту же теорему для u ‘_x получаем , т.е.

y ‘_x = y ‘_x· u ‘_v· v ‘_x = f ‘_u (u)·u ‘_v (v)·v ‘_x (x).

Примеры.

1. y = sin x². Тогда .

ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ

Начнем с примера. Рассмотрим функцию y= x³. Будем рассматривать равенство y= x³ как уравнение относительно x. Это уравнение для каждого значения у определяет единственное значение x: . Геометрически это значит, что всякая прямая параллельная оси Oxпересекает график функции y= x³ только в одной точке. Поэтому мы можем рассматривать x как функцию от y. Функция называется обратной по отношению к функции y= x³.

Прежде чем перейти к общему случаю, введем определения.

Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x₂>x₁, то f(x₂) > f(x₁).

Аналогично функция называется убывающей, если меньшему значению аргумента соответствует большее значение функции, т.е. еслих₂ < х₁ , то f(x₂) > f(х₁).

Итак, пусть дана возрастающая или убывающая функция y= f(x), определенная на некотором отрезке [a; b]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).

Рассмотрим два различных значения х₁ и х₂. Пусть y₁=f(x₁), y₂=f(x₂). Из определения возрастающей функции следует, что если x₁<x₂, то у₁<у₂. Следовательно, двум различным значениям х₁ и х₂ соответствуют два различных значения функции у₁ и у₂. Справедливо и обратное, т.е. если у₁<у₂, то из определения возрастающей функции следует, чтоx₁<x₂. Т.е. вновь двум различным значениям у₁ и у₂ соответствуют два различных значенияx₁ и x₂. Т.о., между значениями x и соответствующими им значениями y устанавливается взаимно однозначное соответствие, т. е. уравнение y=f(x) для каждого y (взятого из области значений функции y=f(x)) определяет единственное значение x, и можно сказать, что x есть некоторая функция аргумента y: x= g(у).

Эта функция называется обратной для функции y=f(x). Очевидно, что и функция y=f(x) является обратной для функции x=g(у).

Заметим, что обратная функция x=g(y) находится путем решения уравнения y=f(x) относительно х.

Пример. Пусть дана функция y = e^x. Эта функция возрастает при –∞ < x <+∞. Она имеет обратную функцию x = lny. Область определения обратной функции 0 < y < + ∞.

Сделаем несколько замечаний.

Замечание 1. Если возрастающая (или убывающая) функция y=f(x) непрерывна на отрезке [a; b], причем f(a)=c, f(b)=d, то обратная функция определена и непрерывна на отрезке [c; d].

Замечание 2. Если функция y=f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.

Пример. Функция y=x² определена при –∞<x<+∞. Она не является ни возрастающей, ни убывающей и не имеет обратной функции. Однако, если мы рассмотриминтервал 0≤x<+∞, то здесь функция является возрастающей и обратной для нее будет . На интервале – ∞ <x≤ 0 функция – убывает и обратная для нее .

Замечание 3. Если функции y=f(x) и x=g(y) являются взаимно обратными, то они выражают одну и ту же связь между переменными x и y. Поэтому графикомих является одна и та же кривая. Но если аргумент обратной функции мы обозначим снова через x, а функцию через y и построим их в одной системе координат, то получим уже два различных графика. Легко заметить, что графики будут симметричны относительно биссектрисы 1-го координатного угла.

ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ

Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции.

Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у₀ имеет производную g ‘(v₀), отличную от нуля, то в соответствующей точке x₀=g(x₀) функция y=f(x) имеет производную f ‘(x₀), равную , т.е. справедлива формула.

Доказательство. Т.к. x=g(y) дифференцируема в точке y₀, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x₀=g(y₀). Следовательно, при Δx→0 Δy→0.

Покажем, что .

Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. .

Следовательно,

,

что и требовалось доказать.

Эту формулу можно записать в виде .

Рассмотрим применение этой теоремы на примерах.

Примеры.

1. y = e^x. Обратной для этой функции является функция x= ln y. Мы уже доказали, что . Поэтому согласно сформулированной выше теореме

   Итак, (e^x) ‘ = e^x

2. Аналогично можно показать, что (a^x) ‘ = a^x·lna. Докажите самостоятельно.
3. y = arcsin x. Рассмотрим обратную функцию x = sin y. Эта функция в интервале – π/2<y<π/2 монотонна. Ее производная x ‘ = cos y не обращается в этом интервале в нуль. Следовательно, по теореме о производной обратной функции

   .

   Но на (–π/2; π/2) .

   Поэтому

4. Аналогично

   Докажите самостоятельно.

5. y = arctg x. Эта функция по определению удовлетворяет условию существования обратной функции на интервале –π/2< y < π/2. При этом обратная функция x = tg y монотонна. По ранее доказанному .

   Следовательно, y ‘ = cos²y . Но .

   Поэтому

6.  

7. Используя эти формулы, найти производные следующих функций:

Производные элементарных функций – eMathHelp

Начнем с простейшей функции, а именно постоянного многочлена $$${f{{\left({x}\right)}}}={c}$$$.

Производная постоянной функции. $$$\frac{{d}}{{{d}{x}}}{\left({c}\right)}={0}$$$.

Действительно, $$${f{‘}}{\left({x}\right)}=\lim_{{{h}\to{0}}}\frac{{{f{{\left( {x}+{h}\right)}}}-{f{{\left({x}\right)}}}}}{{h}}=\lim_{{{h}\to{0} }}\frac{{{c}-{c}}}{{h}}=\lim_{{{h}\to{0}}}{0}={0}$$$. {{\frac{{x}}{{h}}}}\right)}$$$. 9{{t}}\right)}=$$$

$$$=\frac{{1}}{{x}}{\log}_{{a}}{\left({e}\right )}=\frac{{1}}{{x}}\frac{{{\ln{{\left({e}\right)}}}}}{{\ln{{\left({a}} \right)}}}}=\frac{{1}}{{{x}{\ln{{\left({a}\right)}}}}}$$$.

Производная логарифмической функции. $$${\log}_{{a}}{\left({x}\right)}=\frac{{1}}{{{x}{\ln{{\left({a}\) правильно)}}}}}$$$.

В частности, если $$${a}={e}$$$, мы имеем $$${\left({\ln{{\left({x}\right)}}}\right) }’=\frac{{1}}{{x}}$$$.

Теперь найдем производные тригонометрических функций.

Пусть $$${y}={\sin{{\left({x}\right)}}}$$$.

По определению $$${f{‘}}{\left({x}\right)}=\lim_{{{h}\to{0}}}\frac{{{\sin{{\ влево({x}+{h}\right)}}}-{\sin{{\left({x}\right)}}}}}{{h}}$$$.

Здесь нам нужно преобразовать разность синусов в произведение: $$${\sin{{\left({x}+{h}\right)}}}-{\sin{{\left({ x}\right)}}}={2}{\sin{{\left(\frac{{{x}+{h}-{x}}}{{2}}\right)}}}{\ cos{{\left(\frac{{{x}+{h}+{x}}}{{2}}\right)}}}=$$$

$$$={2}{\sin {{\ left (\ frac {{h}} {{2}} \ right)}}} {\ cos {{\ left ({x} + \ frac {{h}} {{2}} \ right) }}}$$$.

Теперь предел можно переписать как $$$\lim_{{{h}\to{0}}}\frac{{{2}{\sin{{\left(\frac{{h}}{ {2}}\right)}}}{\cos{{\left({x}+\frac{{h}}{{2}}\right)}}}}}{{h}}=\lim_ {{{h}\to{0}}}\frac{{{\sin{{\left(\frac{{h}}{{2}}\right)}}}}}{{\frac{{ h}}{{2}}}}{\cos{{\left({x}+\frac{{h}}{{2}}\right)}}}=$$$

$$$= \lim_{{{h}\to{0}}}\frac{{{\sin{{\left(\frac{{h}}{{2}}\right)}}}}}{{\frac {{h}}{{2}}}}\lim_{{{h}\to{0}}}{\cos{{\left({x}+\frac{{h}}{{2}} \right)}}}={1}\cdot{\cos{{\left({x}+\frac{{0}}{{2}}\right)}}}={\cos{{\left ({х}\справа)}}}.$$$

Производная синуса. $$${\left({\sin{{\left({x}\right)}}}\right)}’={\cos{{\left({x}\right)}}}$$ $.

Точно так же можно найти, что $$${\left({\cos{{\left({x}\right)}}}\right)}’=-{\sin{{\left({x }\справа)}}}$$$.

Производная косинуса. $$${\left({\cos{{\left({x}\right)}}}\right)}’=-{\sin{{\left({x}\right)}}}$ $$.

Мы можем найти производную тангенса, используя определение, но проще использовать правило частных:

$$${\left({\tan{{\left({x}\right)}}}\ справа)} ‘= {\ влево (\ гидроразрыва {{{\ грех {{\ влево ({х} \ вправо)}}}}} {{{\ соз {{\ влево ({х} \ вправо)}} }}}\right)}’=\frac{{{\left({\sin{{\left({x}\right)}}}\right)}'{\cos{{\left({x}) \right)}}}-{\sin{{\left({x}\right)}}}{\left({\cos{{\left({x}\right)}}}\right)}’ }}{{{{\cos}}^{{2}}{\left({x}\right)}}}=\frac{{{\cos{{\left({x}\right)}} }{\cos{{\left({x}\right)}}} – {\sin{{\left({x}\right)}}}}{\left(-{\sin{{\left({ x}\right)}}}\right)}}}{{{{\cos}}^{{2}}{\left({x}\right)}}}=$$$ 9{{2}}{\left({x}\right)}}}=\frac{{{\sin{{\left({x}\right)}}}}}}{{{\cos{{\ влево ({x} \ вправо)}}}}} \ cdot \ frac {{1}} {{\ cos {{\ влево ({x} \ вправо)}}}}} = {\ tan {{\ влево ( {x}\right)}}}{\sec{{\left({x}\right)}}}$$$.

Производная от секущей. $$${\left({\sec{{\left({x}\right)}}}\right)}’={\tan{{\left({x}\right)}}}{\ сек {{\ влево ({x} \ вправо)}}} $ $ $.

Производная косеканса. $$${\left({\csc{{\left({x}\right)}}}\right)}’=-{\cot{{\left({x}\right)}}}{ \csc{{\left({x}\right)}}}$$$.

Для нахождения производных обратных тригонометрических функций проще использовать неявное дифференцирование.

По определению, если $$${y}={\operatorname{asin}{{\left({x}\right)}}}$$$, можно утверждать, что $$${\sin{{ \left({y}\right)}}}={x}$$$ для $$$-\frac{\pi}{{2}}\le{y}\le\frac{\pi}{{ 2}}$$$.

Теперь продифференцируем $$${\sin{{\left({y}\right)}}}={x}$$$ относительно $$${x}$$$: $$${\ cos{{\left({y}\right)}}}\cdot{y}’={x}’$$$ или $$${\cos{{\left({y}\right)}} }{y}’={1}$$$.

9{{2}}+{1}}}}}$$$.

Производные элементарных функций можно найти в таблице производных.

Задачи на элементарные производные — Math Insight

Задача 1

Ниже приведен график функции $h(p)$.

1. При каких значениях $p$ равно $\diff{h}{p}$
   1. отрицательный?
   2. положительный?
   3. ноль?
   4. не определено?
2. Найдите все критические точки $h$.
3. При каких значениях $p$ $\diffn{h}{p}{2}$
   1. отрицательный?
   2. положительный?
   3. ноль?
   4. не определено?
4. Найдите все точки перегиба кривой $h$.

Задача 2

Ниже приведен график функции $r(z)$.

1. Для каких значений $z$ есть $r'(z)$
   1. отрицательный?
   2. положительный?
   3. ноль?
   4. не определено?
2. Найдите все критические точки $r$.
3. При каких значениях $z$ есть $r”(z)$
   1. отрицательный?
   2. положительный?
   3. ноль?
   4. не определено?
4. Найдите все точки перегиба кривой $r$.