Энергия в Полевой физике
Энциклопедия Полевой физики
Понятия и термины
«Энергия» – очень емкое и разнородное понятие, которому сложно дать единое определение. В одних случаях под энергией понимают одну из характеристик механического движения, в других – универсальную величину, способную связать все разделы физики в рамках единого закона сохранения энергии, в третьих – некую мистическую силу, ответственную за все непонятные и необъяснимые явления. Наиболее употребительные понятия – кинетическая энергия и потенциальная энергия, внутренняя энергия, энергия массы и другие. Согласно современной физике, понятие энергии эквивалентно понятию массы согласно известной формуле E = mc2.
В связи с большой путаницей, возникшей вокруг понятия энергия, полевая физика относится к нему очень осторожно. Так в полевой физике энергия возникает как одна из характеристик движения, которая в процессе него остается постоянной. Фактически речь идет о возможности проинтегрировать уравнение движения в общем виде, в результате чего в процессе движения остается неизменной некая величина, которую можно назвать энергией.
В общем случае величина энергии E в полевой физике определяется функцией связи частиц в полевой среде W и относительной скоростью их движения u:
В некоторых случаях, например, в классическом приближении выражение для энергии можно разделить на два слагаемых, одно из которых зависит от скорости и носит название кинетическая энергия, а второе – совпадает с выражением для функции полевой связи W и соответствует классическому понятию потенциальной энергии. Однако такое разделение возможно далеко не всегда, например, его нельзя произвести в случае квантового движения. В квантовых условиях формула энергии в полевой физике автоматически приводит к выражению Де-Бройля
Полевая физика также приводит к связи энергии и массы, только в совершено ином виде, нежели современная физика. В полевой физике масса каждого тела определяется согласно формуле полевой массы потенциальной энергией связи этого тела со всеми остальными телами.
Более того, активно используемая в теории относительности формула E = mc2 численно совпадает с выражением для кинетической энергии в релятивистском приближении полевой механики. А огромная энергия массы покоя оказывается ни чем иным, как потенциальной энергией взаимодействия тела со всей остальной Вселенной, и она может выделиться только в случае падения тела на основные гравитирующие объекты, например, на центр нашей Галактики.
- Полевая физика за 5 минут Самое краткое изложение основных идей и результатов полевой физики
- Полевая физика за час Краткое содержание I тома книги «Полевая физика или как устроен Мир?»
- Сущность Полевой физики Основные принципы и логический «фундамент» полевой физики
формула, формулировка простыми словами, кто открыл, задачи с решением, примеры из жизни
Энергия — одно из сложнейших понятий современной физики. И закон сохранения энергии относится к числу ее основополагающих принципов.
Вместе с экспертом разберем задачи с решением этого фундаментального закона природы и узнаем, кто его открыл
Андрей Найденов Преподаватель математики и физики онлайн-школы TutorOnline Борис Михеев Автор КП
Содержание
- Формулировка закона
- Формула
- История
- Задачи с решениями
- Вопросы и ответы
Физика ставит своей целью понимание самых общих закономерностей материального мира. Имена Архимеда, Ньютона, Эйнштейна знакомы каждому школьнику.
Но великое множество ученых вложили по кирпичику в здание современной науки и ускорили развитие человеческой цивилизации. Ее современный уровень был бы недостижим без понимания природы энергии и ее законов прежде всего в механике, самом доступном для наблюдений и экспериментов разделе физики.
Формулировка закона сохранения энергии простыми словами в механике
Закон сохранения энергии действует повсеместно и незаметно. В механике он срабатывает в замкнутой системе под воздействием консервативных сил – то есть сил тяжести и упругости, зависящих только от стартового и финального положения тела и не зависящих от траектории движения. При таких условиях энергия тел никуда не исчезает, а лишь переходит из кинетической в потенциальную и наоборот – из потенциальной в кинетическую. Это и есть самая простая формулировка закона сохранения энергии для механических систем.
Формула закона сохранения энергии
E=Ep+Ek=const
Где:
Ep — потенциальная энергия;
Ek — кинетическая энергия;
Фото pixabay.comИстория открытия закона сохранения энергии
Закономерности взаимодействия физических тел интересовали ученых с античных времен. Но описать их в виде формулы или хотя бы принципа они не сумели. Первым это попытался сделать Рене Декарт в своем труде «Начала философии», изданном в середине XVII века. Он указал, что если одно тело сталкивается с другим, то может отдать ему только такое количество движения, сколько второе у него отнимет. Идею Декарта развил Лейбниц, введя понятие «живой силы», которую мы называем кинетической энергией. Поддержал его рассуждения Михайло Ломоносов в своем «всеобщем естественном законе», но все формулировки были скорее принципом, а не законом, формул не было.
От «живой силы» физики перешли к «кинетической энергии» только в середине XIX столетия, накопив опыт работы с тепловыми и электрическими машинами. Немалый экспериментальный вклад сделал в понимание этого закона Джеймс Джоуль и Роберт Майер. Самую полную математическую формулировку дал Герман Гельмгольц, который ввел понятие потенциальной энергии и обобщил закон сохранения энергии на все разделы физики – даже на те, которые в его время не существовали.
Например, на теорию относительности и квантовую механику.
Задачи на закон сохранения энергии
Самый общий физический закон используется при решении совершенно практических задач.
Задача 1
Некое тело подбросили вверх вертикально с начальной скоростью 15 м/с. На какую высоту оно поднимется? Сопротивление воздуха при решении задачи не учитывать.
Решение: полученная при броске кинетическая энергия будет постепенно преобразовываться в потенциальную энергию:
Ep=Ek
То есть: mgh=(m*V2)/2
Где:
m – масса тела;
V – начальная скорость;
g – ускорение свободного падения;
h – высота подъема.
После преобразований получаем формулу для высоты подъема:
h= V2/(2*g)=225/(2*9,8)=11,47 м.
Ответ: тело поднимется на высоту 11,47 м.
это интересно
Сила Архимеда
Формула и определение силы Архимеда простыми словами
подробнее
Задача 2
Пружину растянули на 15 см.
Известно, что она получила потенциальную энергию 24 Дж. Какова жесткость пружины?
Решение: формула потенциальной энергии упруго деформированного тела:
Ep=(k*x2)/2
Где:
k – коэффициент жесткости;
x – величина деформации.
Преобразуем формулу для расчета:
k=(2*Ep)/x2=(2*24)/225=2133,33 Н/м
Ответ: жесткость пружины равна 2133,33 Н/м.
Популярные вопросы и ответы
Отвечает Андрей Найденов, преподаватель математики и физики онлайн-школы TutorOnline.
Кто открыл закон сохранения энергии?
В открытии закона сохранения энергии участвовали многие ученые. Некоторые из них были очень близки, чтобы сформулировать его. Например, Майер и Джоуль своими работами показали, что количество выделяемой теплоты равно совершенной работе и наоборот. Однако наиболее полную формулировку первым дал в своих работах Гельмгольц.
Какие примеры из жизни на закон сохранения энергии существуют?
Таких примеров множество.
Пример с молотком и гвоздем хорошо иллюстрирует переход механической энергии от молотка к гвоздю. Закон сохранения энергии здесь в том, что сколько молоток при ударе энергии отдал, столько же энергии гвоздь и получил. Ни больше ни меньше.
Другой пример. Кубики льда, взятые при температуре 0º С и опущенные в бокал с газированной водой, растаят, если им сообщить столько же Джоулей тепла, сколько забрали тепла у воды, взятой при температуре 0º С, когда ее замораживали, чтобы она перешла в твердое агрегатное состояние – лед. А если газированная вода будет недостаточно теплой, то лед не растает. Однако если этот бокал оставить на столе надолго, лед все равно растает, так как он получит необходимое количество тепла из окружающего воздуха.
Еще пример. Когда болит горло, есть хороший бабушкин рецепт. Надо пить теплое молоко. Молоко прогревает горло, отдает тепло, что помогает лечению. Молоко при этом остывает в горле и не греет желудок, что тоже важно.
Во всех этих примерах можно наблюдать большие потери тепла на нагрев окружающих тел.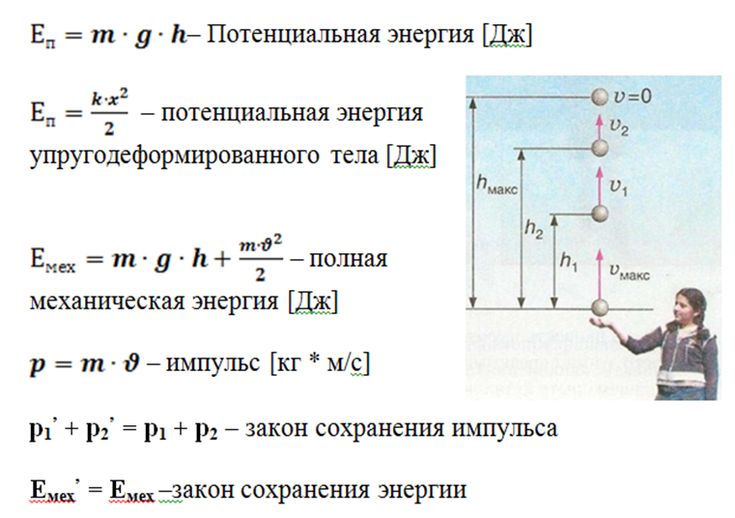
Но основная часть энергии идет на полезное действие. Сколько энергии отдает одно тело, столько же получает и другое, минус потери тепла на нагрев окружающих тел.
Если исключить потери тепла, можно добиться очень высокой эффективности процесса. Это возможно в системах, где энергия не выходит наружу и не рассеивается, поэтому ее потери минимальные. Примером такой системы может служить термос. Горячая вода в термосе долго не остывает, потому что потери тепла минимальные.
Когда сохраняется полная механическая энергия?
Полная механическая энергия сохраняется в системах, которые называются изолированными. Получить полностью изолированную систему достаточно сложно. Всегда найдутся силы, которые будут действовать на тело или систему из нескольких тел извне.
Хорошим примером может стать жизнь космонавтов на орбитальном комплексе, вращающемся вокруг Земли. Если космонавт оттолкнется от пола на Земле, то сила притяжения быстро вернет его обратно на пол.
В орбитальном комплексе сила притяжения к Земле скомпенсирована движением корабля по круговой орбите. Состояние невесомости позволяет космонавту оттолкнутся от пола и лететь вверх неопределенно долго, пока он не столкнется с потолком. Тело космонавта можно считать изолированной системой, так как на него не действуют силы извне, а силы сопротивления движению со стороны воздуха в корабле минимальны.
В каком классе изучают закон сохранения энергии?
Здесь есть одна тонкость. Закон сохранения механической энергии изучают на уроках физики в седьмом классе. А закон сохранения энергии, применительно к тепловым процессам, с использованием понятия внутренней энергии тела, изучают уже в восьмом классе.
Кинетическая и потенциальная энергия – Уроки Византа
Написал преподаватель Герман К.
Закон сохранения энергии гласит, что энергия не может быть создана или уничтожена. Другими словами, полная энергия системы остается постоянной. Это важная концепция, которую следует помнить при решении энергетических проблем.
Двумя основными формами энергии, на которых мы сосредоточимся, являются кинетическая энергия и потенциальная энергия.
Кинетическая энергия
Кинетическая энергия — это энергия, возникающая в результате движения. Другими словами, движущиеся объекты обладают так называемой кинетической энергией. Поскольку кинетическая энергия основана на движении, она всегда положительна. Если он не движется, кинетическая энергия этого объекта равна нулю. Кинетическая энергия никогда не может быть отрицательной величиной. Кинетическая энергия может быть определена как половина произведения массы на квадрат скорости (KE = 1 / 2 *m*v²). В единицах СИ масса должна быть в килограммах (кг), а скорость в метрах в секунду (м/с). В английских единицах измерения масса должна быть выражена либо в фунтах (lbm), либо в slug, а скорость – в футах в секунду (ft/sec).
Потенциальная Энергия
Потенциальная Энергия, как это и звучит, это энергия, связанная с потенциалом объекта.
Потенциальная энергия может быть количественно выражена как масса, умноженная на силу тяжести, умноженная на высоту (PE=m*g*h). Единицей массы должен быть либо килограмм, либо фунт массы в зависимости от системы единиц. Гравитация постоянна, 90,81 м / с² в единицах СИ или 32,2 фут/сек² в английских единицах. Гравитация — это ускорение, его можно описать как метры или футы в секунду за секунду или изменение скорости в секунду. Наконец, высота измеряется в метрах в единицах СИ и в футах в английских единицах. Важно отметить, что высота считается относительной величиной. Другими словами, при рассмотрении потенциальной энергии первым шагом является установление данных или источника. Это означает, что необходимо определить отметку, где высота равна нулю. Например, пол можно определить как высоту, равную нулю. Однако нулевая точка (датум) не обязательно должна быть полом, это может быть любая точка, но ее нельзя изменять после ее определения. Также важно отметить, что потенциальная энергия может быть положительной, нулевой или отрицательной.
Например, если исходная точка определяется как верхняя часть стола, а объект находится на полу, этот объект имеет отрицательную потенциальную энергию, поскольку высота ниже верхней части стола.
Теперь, когда определены кинетическая и потенциальная энергии, мы можем применить Закон сохранения энергии. Другими словами, кинетическая энергия плюс потенциальная энергия равняются константе (KE+PE=Constant).
Давайте представим себе простую энергетическую задачу. Есть объект, который перемещается из одной точки в другую. Назовем первую точку начальной точкой (1), а вторую точку конечной точкой (2). Не принимая во внимание ничего другого, мы можем составить основное уравнение как KE 1 +PE 1 =KE 2 +PE 2 . Давайте упростим это еще больше; допустим, объект начинается в состоянии покоя (KE 1 =0), и допустим, мы определяем датум в конечной точке (PE 2 =0). Теперь мы можем сказать, что PE 1 =KE 2 .
Энергия буквально была преобразована из потенциальной энергии в кинетическую энергию. Обратите внимание, что полная энергия в точке 1 равна энергии в точке 2, энергия изменила форму, но не была создана или уничтожена.
Также полезно знать, что энергия считается независимой от пути. Другими словами, не имеет значения, какой путь прошел объект, чтобы попасть из точки 1 в точку 2, энергия в точке 1 и точке 2 не изменилась. Единственное, что имеет значение, это разница в высоте двух точек; пока высота не меняется от сценария к сценарию, решение не меняется.
Примеры кинетической и потенциальной энергии
Представьте себе мяч, катящийся по полу из одной точки в другую.
Допустим, мяч массой 3 кг движется со скоростью 2 м / с
В точке 1:
кинетическая энергия = 2 / / 9 м В 1 2 = 1 / 2 (3 кг)(2 м / s ) 2
=6 кг 901 901
, где м = масса в килограммах
v = скорость в м / с
м = единица длины, метр
с = единица времени, секунда
Н = единица силы, ньютон
1 Н = 1 кг* м / с 2 Дж = единица энергии, Джоуль
1 Дж = 1 Н*м
Также потенциальная энергия = м гх 1 = 0, так как h = 0
g = ускорение свободного падения = 9,8 м / s 2
h 1 = высота относительно исходной точки, в метрах
В точке 1 полная энергия = KE 1 + PE 1 = 6 + 0
= 6 Дж
Примечание к пункту 2:
PE 2 также = 0, поэтому KE 2 0 90 1 90 014 = 16 014 = 0, потому что ч 2 = 0, так как пол ровный.
Если КЕ 2 = КЕ 1 и масса не меняется,
v 2 = v 1 = 2 м / с 5 Другой пример 04 Теперь допустим ч
1 ≠ч 2 , допустим ч 2 = -2 м
h 2 = -2 м означает, что точка 2 находится на 2 метра ниже точки 1.
A, B и C представляют три возможных пути. Примечание: выбранный путь не влияет на решение.
Напомним, что KE = 6 Дж, PE = 0 Дж.
Поскольку полная энергия остается постоянной 2 + PE 2
Мы можем найти PE 2 начиная с h 2 = -2 м
PE 2 = м гх 2 = (3 кг)(9,8 м / с )(-2 м) = -58,8 Дж
KE 014 – 58,8
Теперь решите для KE 2
6 + 58,8 = KE 2
KE 2 = 64,8 Дж
Чтобы найти v 1 = KE 2 3 2
1 / 2 м v 2 2 = 1 / 2 (3 кг)(v 2 ) 2 = 64,8
v 2 2 = 2 / 3 (64,8) = 43,2
v 2 = 6,57 м / увеличение с 7 м / с
Другое Типы энергии
Энергия не ограничивается только кинетической и потенциальной энергией.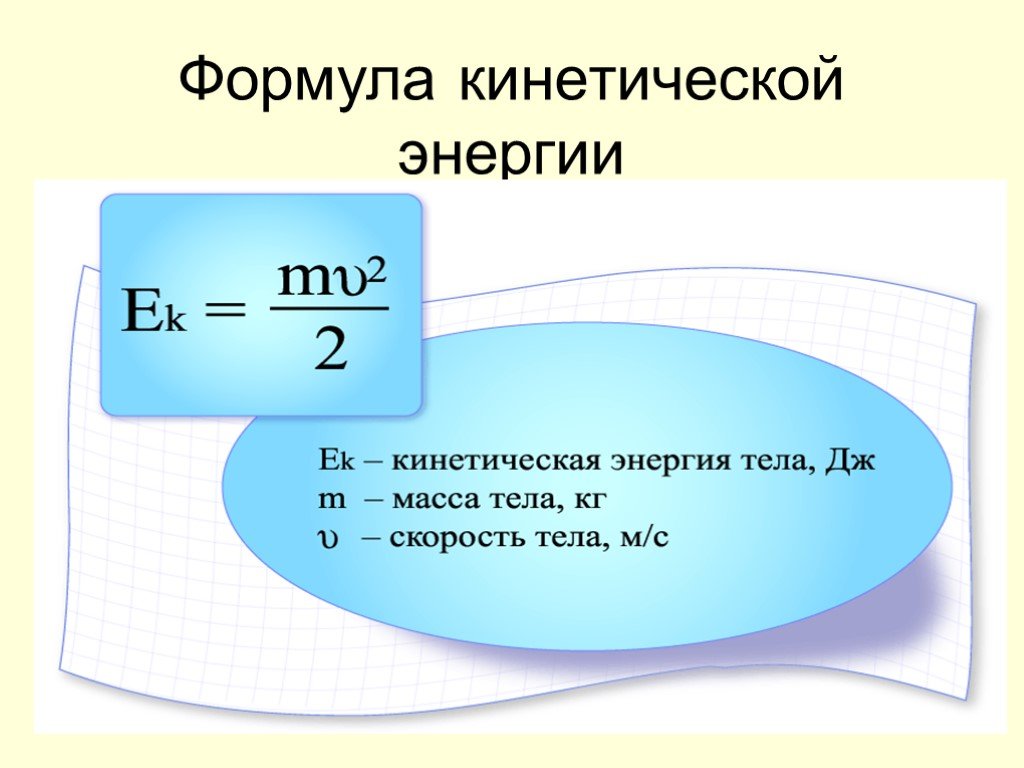
Существует множество различных форм энергии. Однако в базовой физике другие формы игнорируются, чтобы упростить предмет уравнений энергии. Другие формы энергии обычно вводятся на уровне колледжа.
Например, работа, вносимая в систему, может влиять на общую энергию этой системы. Например, представьте себе мебель на заднем дворе. Вот сидит и не шевелится. Поскольку он не движется, он не имеет кинетической энергии. Кроме того, поскольку он находится на земле, он не может опускаться ниже. В этом случае и потенциальная, и кинетическая энергия равны нулю. Теперь, что произойдет, если кто-то придет и заберет диван. Потенциальная энергия этой кушетки изменилась, но не из-за кинетической энергии. Так откуда же берется эта энергия? Был ли он создан? Нарушили ли мы закон сохранения энергии? Ответ — нет, мы не нарушили никаких законов физики. Изначально в нашем примере кушетка рассматривается как изолированная система. Человек — это внешняя сущность, которая привнесла энергию в эту систему, подняв кушетку.
С точки зрения физики, человек действительно работал над системой. Работа рассматривается как форма энергии. Работу можно выразить как силу, умноженную на расстояние.
Однако не все так просто. Сила и расстояние должны быть направлены в одном направлении. Например, вес есть сила. Например, работа может совершаться под действием силы тяжести. На самом деле работа, совершаемая гравитацией, — это еще один способ определения потенциальной энергии. Вес равен массе, умноженной на гравитацию. Гравитация всегда направлена вниз, поэтому и сила направлена вниз. Чтобы гравитация совершала работу, объект должен либо подняться, либо опуститься. В этом случае работа не выполняется, если объект перемещается из стороны в сторону. Эту концепцию лучше понять, разобравшись с векторами.
Чтобы прояснить вектор, мы сравним скорость со скоростью. Скорость есть величина, например 60 миль в час. Обратите внимание, что скорость не определяет направление. Скорость — это вектор, то есть она имеет величину и направление.
Например, скорость может быть 60 миль в час в направлении Y. Векторы лучше всего определяются в задачах о снарядах, также называемых уравнениями кинематики.
Еще один случай, когда энергия может не оставаться постоянной, — это проблема столкновения. Допустим, человек держит яблоко на уровне плеч. В этот момент у яблока есть потенциальная энергия, но нет кинетической энергии. Затем человек отпускает яблоко, позволяя ему начать падать. По мере падения энергия преобразуется из потенциальной в кинетическую. Непосредственно перед тем, как он ударится о землю, почти вся потенциальная энергия была преобразована в кинетическую энергию. Но что произойдет, когда он действительно упадет на землю? Когда яблоко падает на землю, оно на самом деле сталкивается с землей, и эта кинетическая энергия поглощается землей во время столкновения.
Во время столкновения сохраняется импульс. В зависимости от коэффициента восстановления два объекта, участвующие в столкновении, фактически распределяют момент до и после столкновения в зависимости от свойств их материала.
Например, представьте, что человек держит в руках два предмета. В одной руке человек держит баскетбольный мяч. В другой руке человек держит мешок с песком. Если человек уронит оба предмета на бетонный пол, баскетбольный мяч отскочит, а мешок с песком просто плюхнется на землю и останется лежать там. Во время столкновения баскетбольный мяч сохраняет большую часть своего импульса, в то время как мешок с песком теряет его. Есть причина, по которой это происходит; коэффициент восстановления между бетоном и баскетбольным мячом отличается от коэффициента восстановления между бетоном и мешком с песком.
Пример с использованием работы
Теперь давайте снова посмотрим на исходный пример, за исключением того, что сила будет приложена из точки 1 в точку 2, как будто кто-то привязал веревку к мячу.
Допустим, расстояние от точки 1 до точки 2 равно 20 метрам, а сила равна 7 ньютонам.
*Обратите внимание, что угол между силой и траекторией движения составляет 35°.
Также напомним KE 1 = 6 Дж, PE 1 = 0
Опять же, поскольку плоский, PE 1 = PE 2 = 0
Очень важно: полная энергия непостоянна из-за приложенной силы. Эта приложенная сила вводит новую энергию через работу.
где
w = работа в джоулях
F = приложенная сила в ньютонах
d = расстояние от точки 1 до точки 2 в метрах
· = скалярное произведение
-> = определяет значения как векторы
Следовательно:
где Θ = угол между силой и путем.
Наконец W 1-2 = [7(cos(35°))N](20m) = 114,68J
Новое уравнение
KE 1 + PE 1 + W 1-2 = KE 2 + PE 2
6 + 0 + 290 0 3 KE
120,68 Дж = KE 2
Наконец, найти v 2
KE 2 = 1 / 2 m v 2 2 0061 120,68 = 1 / 2 (3 кг) (v 2 ) 2
80,45 = v 2 2
v 2 = 8,97 м / с
Увеличение на 6,97 м / с за счет приложенной силы через 20 м из точки 1 в точку 2.
Ньютон формула взялась?
Хорошо, вывод теоремы о работе-энергии из F=ma
Уточнение «теорема» действительно уместно.
Если мы примем второй закон Ньютона как аксиому и примем как аксиому, что пространство евклидово, то теорема о работе-энергии логически следует. 92$, это выражение можно определить как «кинетическую энергию».
В динамике мы привыкли думать с точки зрения накопления времени . Уравнение движения есть функция времени
Теорема о работе-энергии не подходит под эту форму. Теорема о работе-энергии описывает накопление на расстоянии .
В истории физики теорема о работе-энергии была признана довольно поздно. Я думаю, что это было впервые заявлено около 1800 года или около того.
Обобщение
Использование (4), конечно, не является общим способом вывода теоремы о работе-энергии. Используемые кинематические отношения относятся к равномерному ускорению.