значение в термодинамике, правила определения, формулы
Физика
12.11.21
14 мин.
Тепловые явления можно описать при помощи специальных макроскопических параметров, измеряемых термометром либо манометром. Эти приборы не реагируют на воздействие отдельных частиц. Термодинамикой называется теоретическая часть тепловых процессов, когда не берётся во внимание молекулярное строение тел. На уроках физики в 10 классе изучают внутреннюю энергию идеального газа, которая позволяет определить скорость движения молекул.
Оглавление:
- Краткое описание
- Свойства газа
- Использование высоких температур
- Особенности теплообмена
- Макроскопические параметры
- Воздействие внешних факторов
- Принцип определения ВЭ
Краткое описание
На уроках физики можно узнать, что основной функцией состояния термодинамической системы является внутренняя энергия (ВЭ) идеального газа.
В физике описывается только два варианта изменения внутренней энергии тела:
- Теплопередача.
- Выполнение механической работы.
Потенциальная энергия взаимодействия частиц идеального газа равна нулю. По этой причине итоговые параметры одноатомного идеального газа будут сведены к суммарной кинетической энергии поступательного движения атомов. Если речь касается многоатомного агрегатного состояния, тогда дополнительно должно быть учтено вращение молекул и колебания атомов. В противном случае результат будет ошибочным.
Когда нужно найти энергию, то число атомов необходимо умножить на кинетическую энергию. На этот случай в физике существует специальная формула: U = NE = N *(3/2) kT = vNa * 3/2 kT = 3/2 vRT либо U = 3 m /2M RT. Химический состав и масса идеального газа останутся неизменными. Полученный результат можно рассматривать только как показатель температуры. У твёрдого тела, жидкости либо газа итоговая величина ВЭ во многом зависит от объёма, при изменении которого меняется расположение входящих в состав частиц.
Свойства газа
В физике газ описывается как агрегатное состояние какого-либо вещества, для которого свойственна большая подвижность входящих в состав частиц. Дополнительно можно выделить минимальную связь между атомами и молекулами. Вещество не имеет определённой формы в газообразном состоянии. Из-за чего стандартные способы решения сложных задач являются неактуальными. Если правильно подобрать температурный режим и параметры давления, то практически любое вещество можно будет перевести в газообразное состояние.
Идеальным можно назвать только тот газ, который обладает следующими свойствами:
- Молекулы не взаимодействуют между собой. Это связано с тем, что отсутствуют силы притяжения и отталкивания.
- Молекулы отличаются небольшим размером.
- Движение частиц происходит по принципу закона Ньютона.
- Молекулы могут отталкиваться друг от друга и от стенок ёмкости, в которую они помещены. Такие соударения подробно описаны формулами из раздела механики.
- Расстояние между молекулами существенно превышает их размер.
Если присутствуют все эти свойств, тогда можно говорить, что работать предстоит с идеальным газом.
Использование высоких температур
Многочисленные эксперименты доказали, что при нагревании частицы газа начинают двигаться гораздо быстрее. Изобретение термометров и введение величины температуры позволило учёным наблюдать за различными явлениями, которые связаны с нагревом и охлаждением. В результате усердной работы физикам удалось получить уравнение состояния идеальных газов: p*V = (m/µ) * (R * T).
Речь касается соотношения между давлением, объёмом и абсолютной температурой по шкале Кельвина.
- Молярная масса — µ (R = 8.3157).
- Температура — T.
- Объём — V.
- Давление — p.
Это уравнение можно использовать только тогда, когда речь касается одноатомного газа. У молекул с большим количеством атомов дополнительно присутствуют колебательные и вращательные движения. К примеру, молекула О2 (кислорода) имеет энергию (7/2) * k * T, что существенного превышает стандартное значение одноатомного газа.
Особенности теплообмена
Перенос внутренней энергии в газах или жидкостях под воздействием циркуляции потоков называется конвекцией. Вблизи отопительных радиаторов воздух постепенно нагревается и расширяется. В действие вступает сила тяжести, не меняющая своих значений, а вот выталкивающие способности постепенно увеличиваются, из-за чего воздух поднимается.
Смена потоков задаёт темп циркуляции воздуха, что и является примером конвекции. Тепло распространяется по комнате благодаря воздушным потокам. Аналогичный процесс можно наблюдать и в случае использования жидкостей. Например, если поставить на плиту кастрюлю с водой, то её нагрев будет происходить благодаря конвекции. Многое зависит от теплопроводности используемой жидкости.
Конвекции невозможно добиться в том случае, если используются твёрдые тела. Силы взаимодействия частиц настолько велики, что они колеблются вблизи фиксированных пространственных точек.
Если циркуляция конвекционных потоков будет использоваться для отопления помещения, тогда нужно позаботиться о том, чтобы нагретому воздуху было куда подниматься. Если попробовать установить радиатор под потолком, то тепло не опустится. Отопительные приборы должны быть расположены максимально близко к полу. А вот климатическое оборудование нужно фиксировать как можно выше.
Макроскопические параметры
Чтобы на практике использовать формулу изменения внутренней энергии, нужно учесть, что итоговый результат во многом зависит от температуры. Средняя потенциальная энергия взаимодействия молекул у реальных газов, твёрдых тел и жидкостей не равна нулю. Всё зависит от объёма вещества. В каждой ситуации можно наблюдать разное расстояние между молекулами. В термодинамике ВЭ реального газа зависит от объёма V и температуры T. Аналогичное правило действует и по отношению к макроскопическим телам.
Невозможно правильно вычислить внутреннюю энергию, если брать во внимание только движение отдельных молекул и их расположение относительно друг друга. Это связано с тем, что в макроскопических телах слишком много молекул.
Нужно уметь определять значение ВЭ с использованием тех параметров, которые можно измерить при помощи термометра или манометра.
Воздействие внешних факторов
Если по отношению к объекту были совершены какие-либо действия, тогда показатель ВЭ возрастёт. В качестве примера можно рассмотреть ситуацию, когда после нескольких ударов молотком гвоздь нагревается, а также немного деформируется.
Такой результат свидетельствует об увеличении кинетической энергии. Микроскопические частицы разгоняются от удара молотком и трения гвоздя о материал.
Деформацию можно расценивать как элементарное смещение частиц относительно друг друга. После удара молотком происходит сжатие. Частицы постепенно сближаются, из-за чего между ними возрастает сила отталкивания, что приводит к приращению потенциальной энергии. Так как над гвоздём была совершена работа, его ВЭ возросла.
В других ситуациях внутренняя энергия тела может существенно уменьшиться
Например, в теплоизолированной трубе сжатый воздух под поршнем постепенно расширяется, из-за чего поднимается определённый груз, совершая тем самым работу. Этот процесс отличается тем, что молекулы будут ударяться о стены, отдавая при этом часть своей кинетической энергии. ВЭ будет постепенно уменьшаться. Определённую работу совершает только воздух, у которого имеется достаточный запас энергии. Так как труба теплоизолированная, отсутствует приток кислорода, который мог бы пополнить запасы ВЭ.Принцип определения ВЭ
Используя формулы внутренней энергии газа, нужно учитывать, что полученное значение будет прямо пропорционально его абсолютной температуре. Чёткое понимание концепции идеального газа важно при решении задач с системами, находящимися в этом агрегатном состоянии. На уроках физики в 10 классе чаще всего используют следующую формулу: U = Ek + En.
- ВЭ газа — U.
- Кинетическая энергия хаотичного теплового движения — Ek.
- Показатель потенциальной энергии взаимодействия присутствующих в составе молекул — En.
Если по условиям задачи нужно правильно определить ВЭ газа (Ud), тогда в используемой формуле можно убрать потенциальную составляющую энергии. К примеру: Ud = Ek. Только благодаря сложению всех отдельных частиц рассчитывается кинетическая энергия вещества Eew. Если всё сделать правильно, то в итоге формула будет выглядеть так: Eew = E1 + E2 + E3 + E4 +… En. Буква n обозначает общее количество частиц в идеальном газе.
В разделе механики используется следующая формула: Ek = (m*v2)/2. Для обозначения массы используется буква m, скорость — v, а кинетическая энергия — Ek. Такой подход актуален на уроках физики, когда не подразумевается углублённое изучение темы. Но если нужно будет максимально точно рассчитать ВЭ частиц газа, тогда должен быть применён немного другой подход.
Для решения более сложных задач необходимо знать массу всех частиц, а также их суммарное количество.
Но даже в одном моле вещества содержится большое количество молекул, которых просто не сосчитать. Именно поэтому понадобятся такие макроскопические параметры, как температура и давление.
Формула расчета внутренней энергии идеального газа. Изменение внутренней энергии газа: формула расчета
Изучая поведение газов в физике, часто возникают задачи на определение запасенной в них энергии, которую теоретически можно использовать для совершения некоторой полезной работы. В данной статье рассмотрим вопрос, по каким формулам внутренняя энергия идеального газа может быть рассчитана.
Понятие о газе идеальном
Четкое понимание концепции идеального газа важно при решении задач с системами, находящимися в этом агрегатном состоянии. Любой газ принимает форму и объем сосуда, в который его помещают, однако, не всякий газ является идеальным. Например, воздух можно считать смесью идеальных газов, в то же время водяной пар не является таковым.
В чем же заключается принципиальная разница между реальными газами и их идеальной моделью?
Ответом на поставленный вопрос будут две следующие особенности:
- соотношение между кинетической и потенциальной энергией молекул и атомов, составляющих газ;
- соотношение между линейными размерами частиц газа и средним расстоянием между ними.
Газ считается идеальным только в том случае, когда средняя кинетическая энергия его частиц несоизмеримо больше энергии связи между ними. Разница между этими энергиями такова, что можно считать, что взаимодействие между частицами полностью отсутствует. Также для идеального газа характерно отсутствие размеров у его частиц, вернее эти размеры можно не учитывать, поскольку они намного меньше средних межчастичных расстояний.
Хорошими эмпирическими критериями, позволяющими определить идеальность газовой системы, являются такие ее термодинамические характеристики, как температура и давление. Если первая больше 300 К, и второе меньше 1 атмосферы, то любой газ может полагаться идеальным.
Что это внутренняя энергия газа?
Прежде чем записать формулу внутренней энергии газа идеального, необходимо познакомится с этой характеристикой ближе.
В термодинамике внутреннюю энергию, как правило, обозначают латинской буквой U. Определяется в общем случае она по следующей формуле:
U = H – P*V
Где H – энтальпия системы, P и V – давление и объем.
По своему физическому смыслу внутренняя энергия состоит из двух составляющих: кинетической и потенциальной. Первая связана с различного рода движением частиц системы, а вторая – с силовым взаимодействием между ними. Если применить это определение к концепции газа идеального, у которого отсутствует потенциальная энергия, то величина U при любом состоянии системы будет точно равна его кинетической энергии, то есть:
U = Ek.
Вывод формулы внутренней энергии
Выше мы установили, что для ее определения у системы с идеальным газом необходимо рассчитать его кинетическую энергию.
Из курса общей физики известно, что энергия частицы массой m, которая поступательно движется в некотором направлении со скоростью v, определяется по формуле:
Ek1 = m*v2/2.
Ее также можно применить для газовых частиц (атомов и молекул), однако, необходимо сделать некоторые замечания.
Во-первых, под скоростью v следует понимать некоторую среднюю величину. Дело в том, что газовые частицы движутся с разными скоростями согласно распределению Максвелла-Больцмана. Последнее позволяет определить среднюю скорость, которая с течением времени не изменяется, если отсутствуют внешние воздействия на систему.
Во-вторых, формула для Ek1 предполагает энергию на одну степень свободы. Газовые частицы могут двигаться во всех трех направлениях, а также вращаться в зависимости от их строения. Чтобы учесть величину степени свободы z, следует ее умножить на Ek1, то есть:
Ek1z = z/2*m*v2.
Кинетическая энергия всей системы Ek в N раз больше, чем Ek1z, где N – общее число газовых частиц. Тогда для U получаем:
U = z/2*N*m*v2.
Согласно этой формуле, изменение внутренней энергии газа возможно только в том случае, если поменять число частиц N в системе, либо их среднюю скорость v.
Внутренняя энергия и температура
Применяя положения молекулярно-кинетической теории идеального газа, можно получить следующую формулу связи между средней кинетической энергией одной частицы и абсолютной температурой:
m*v2/2 = 1/2*kB*T.
Здесь kB – постоянная Больцмана. Подставляя это равенство в формулу для U, полученную в пункте выше, приходим к следующему выражению:
U = z/2*N*kB*T.
Данное выражение можно переписать через количество вещества n и газовую постоянную R в следующем виде:
U = z/2*n*R *T.
В соответствии с этой формулой, изменение внутренней энергии газа возможно, если поменять его температуру. Величины U и T зависят друг от друга линейно, то есть график функции U(T) представляет собой прямую линию.
Как строение газовой частицы влияет на внутреннюю энергию системы?
Под строением частицы газа (молекулы) имеется в виду количество атомов, которое ее составляет. Оно играет определяющую роль при подстановке соответствующей степени свободы z в формулу для U. Если газ является одноатомным, формула внутренней энергии газа принимает такой вид:
U = 3/2*n*R*T.
Откуда взялась величина z=3? Ее появление связано всего с тремя степенями свободы, которыми обладает атом, поскольку он может двигаться только в одном из трех пространственных направлений.
Если рассматривается двухатомная молекула газа, то внутреннюю энергию следует вычислять по такой формуле:
U = 5/2*n*R*T.
Как видим, двухатомная молекула уже имеет 5 степеней свободы, 3 из которых являются поступательными и 2 вращательными (в соответствии с геометрией молекулы, она может вращаться вокруг двух взаимно перпендикулярных осей).
Наконец, если газ является трех- и более атомным, то справедливо следующее выражение для U:
U = 3*n*R*T.
Сложные молекулы имеют 3 поступательных и 3 вращательных степени свободы.
Пример задачи
Под поршнем находится одноатомный газ при давлении 1 атмосфера. В результате нагрева газ расширился так, что его объем увеличился от 2-х литров до 3-х. Как при этом изменилась внутренняя энергия газовой системы, если процесс расширения был изобарным.
Чтобы решить эту задачу, недостаточно приведенных в статье формул. Необходимо вспомнить об уравнении состояния идеального газа. Оно имеет вид, представленный ниже.
Поскольку поршень закрывает цилиндр с газом, то в процессе расширения количество вещества n остается постоянным. Во время изобарного процесса температура изменяется прямо пропорционально объему системы (закон Шарля). Это означает, что формула выше запишется так:
P*ΔV = n*R*ΔT.
Тогда выражение для внутренней энергии одноатомного газа примет форму:
ΔU = 3/2*P*ΔV.
Подставляя в это равенство значения давления и изменения объема в единицах СИ, получаем ответ: ΔU ≈ 152 Дж.
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
-
3. 1 МКТ
- 3.2 Термодинамика
-
3.
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
-
5. 2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
1 МКТ
2 Волновая оптика
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
2.2 Давление, температура и среднеквадратическая скорость – University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объяснить соотношение между микроскопическими и макроскопическими величинами в газе
- Решение задач на смеси газов
- Решение задач на расстояние и время между столкновениями молекул газа
Мы исследовали давление и температуру на основе их макроскопических определений.
Давление — это сила, деленная на площадь, на которую действует сила, а температура измеряется термометром. Мы можем лучше понять давление и температуру из кинетической теории газов, теории, которая связывает макроскопические свойства газов с движением молекул, из которых они состоят. Во-первых, мы делаем два предположения о молекулах в идеальном газе.
- Существует очень большое количество N молекул, все они идентичны и каждая имеет массу m .
- Молекулы подчиняются законам Ньютона и находятся в непрерывном движении, которое является случайным и изотропным, то есть одинаковым во всех направлениях.
Чтобы вывести закон идеального газа и связь между микроскопическими величинами, такими как энергия типичной молекулы, и макроскопическими величинами, такими как температура, мы анализируем образец идеального газа в жестком контейнере, относительно которого мы делаем два дополнительных предположения:
- Молекулы намного меньше среднего расстояния между ними, поэтому их общий объем намного меньше, чем объем их контейнера (объем которого V ). Другими словами, мы принимаем постоянную Ван-дер-Ваальса b , объем моля молекул газа, пренебрежимо малым по сравнению с объемом моля газа в сосуде.
- Молекулы совершают абсолютно упругие столкновения со стенками сосуда и друг с другом. На них действуют другие силы, включая гравитацию и притяжение, представленное постоянной Ван-дер-Ваальса 9.0018 a пренебрежимо малы (что необходимо для предположения изотропности).
Другими словами, мы принимаем постоянную Ван-дер-Ваальса b , объем моля молекул газа, пренебрежимо малым по сравнению с объемом моля газа в сосуде.Столкновения между молекулами не учитываются при выводе закона идеального газа. Они также не мешают выводу, так как столкновения молекул, движущихся со случайными скоростями, дают новые случайные скорости. Кроме того, если скорости молекул газа в сосуде изначально не случайны и не изотропны, столкновения молекул делают их случайными и изотропными.
Сделаем еще предположения, упрощающие расчеты, но не влияющие на результат. Во-первых, пусть контейнер будет прямоугольной коробкой. Во-вторых, мы начнем с рассмотрения одноатомные газы, молекулы которых состоят из отдельных атомов, например гелий.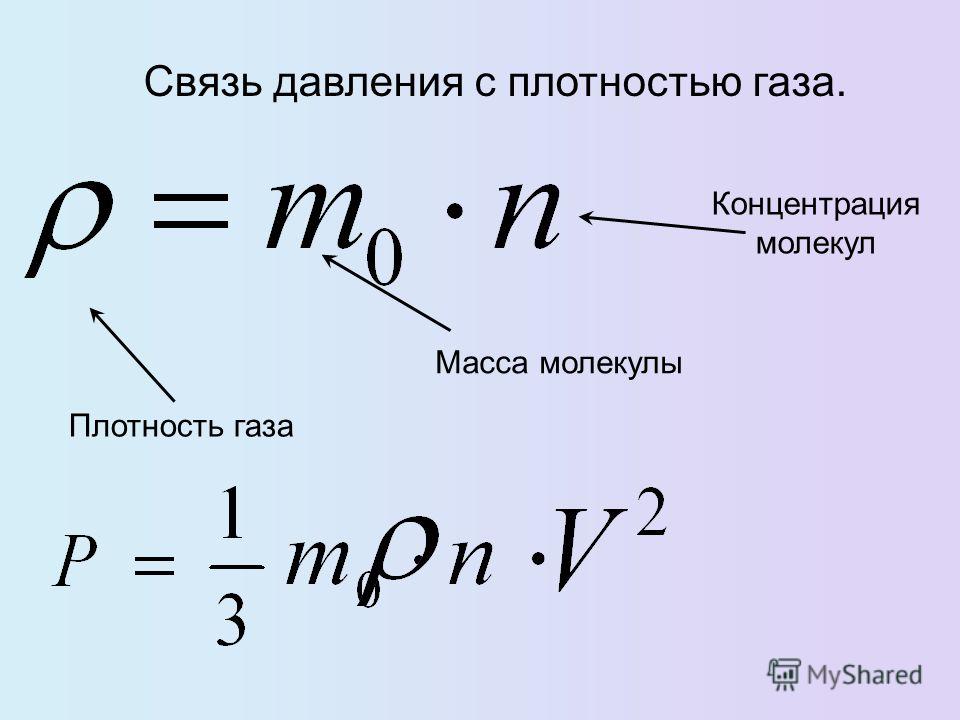
Тогда мы можем предположить, что у атомов нет энергии, кроме их поступательной кинетической энергии; например, они не имеют ни вращательной, ни колебательной энергии. (Позже мы обсудим справедливость этого предположения для реальных одноатомных газов и обойдемся без него для рассмотрения двухатомных и многоатомных газов.)
На рис. на стене (по третьему закону Ньютона). Эти столкновения являются источником давления в газе. По мере увеличения числа молекул увеличивается число столкновений и, следовательно, давление. Точно так же, если средняя скорость молекул выше, давление газа выше.
Рисунок 2,9 Когда молекула сталкивается с твердой стенкой, составляющая ее импульса, перпендикулярная стенке, меняется на противоположную. Таким образом, на стену действует сила, создающая давление.
В образце газа в контейнере хаотичность молекулярного движения приводит к колебаниям числа столкновений молекул с любой частью стенки в заданное время. Однако из-за того, что за короткое время со стенкой сталкивается огромное количество молекул, количество столкновений в масштабах времени и пространства, которые мы измеряем, колеблется лишь на крошечную, обычно ненаблюдаемую долю от среднего значения.
Мы можем сравнить эту ситуацию с ситуацией в казино, где результаты ставок случайны, а доходы казино колеблются по минутам и часам. Тем не менее, в течение длительного времени, такого как год, доходы казино очень близки к средним значениям, ожидаемым от шансов. В баллоне с газом неимоверно больше молекул, чем игроков в казино за год, а за секунду молекулы совершают гораздо больше столкновений, чем ставок в казино.
Вычисление средней силы, с которой молекулы действуют на стенки ящика, приводит нас к закону идеального газа и к связи между температурой и молекулярной кинетической энергией. (На самом деле мы возьмем два средних значения: одно по времени, чтобы получить среднюю силу, действующую на одну молекулу с заданной скоростью, а затем другое среднее значение по молекулам с разными скоростями.) Этот подход был разработан Даниэлем Бернулли (1700–1782). , который наиболее известен в физике своими работами по течению жидкости (гидродинамике). Примечательно, что Бернулли проделал эту работу до того, как Дальтон установил представление о материи, состоящей из атомов.
На рис. 2.10 показан сосуд, наполненный газом, и увеличенный вид упругого столкновения молекулы газа со стенкой сосуда, разбитого на составляющие. Мы предположили, что молекула мала по сравнению с расстоянием между молекулами в газе и что ее взаимодействием с другими молекулами можно пренебречь. В этих условиях закон идеального газа является экспериментально верным. Поскольку мы также предположили, что стена жесткая, а частицы — точки, столкновение является упругим (по закону сохранения энергии — кинетической энергии частицы некуда деваться). Следовательно, кинетическая энергия молекулы остается постоянной, а значит, ее скорость и величина импульса также остаются постоянными. Это предположение не всегда верно, но результаты в остальной части этого модуля также получены в моделях, которые позволяют молекулам обмениваться энергией и импульсом со стенкой.
Рисунок
2.10
Газ в ящике оказывает внешнее давление на его стенки. Молекула, сталкивающаяся с твердой стенкой, имеет обратную скорость и импульс в направлении x .
Это направление перпендикулярно стене. Составляющие его импульса скорости в направлениях y и z не меняются, а значит, сила, параллельная стенке, отсутствует.
Если скорость молекулы изменяется в направлении x , ее импульс изменяется от −mvx−mvx до +mvx.+mvx. Таким образом, его изменение импульса равно Δmv=+mvx−(−mvx)=2mvx.Δmv=+mvx−(−mvx)=2mvx. Согласно теореме об импульсе-импульсе, приведенной в главе о линейном количестве движения и столкновениях, сила, действующая на i -я молекула, где i обозначает молекулы от 1 до N , определяется как
Fi=ΔpiΔt=2mvixΔt.Fi=ΔpiΔt=2mvixΔt.
(Только в этом уравнении p представляет импульс, а не давление.) Между стенкой и молекулой нет никакой силы, за исключением момента, когда молекула касается стенки. В течение короткого времени столкновения сила между молекулой и стенкой относительно велика, но это не та сила, которую мы ищем.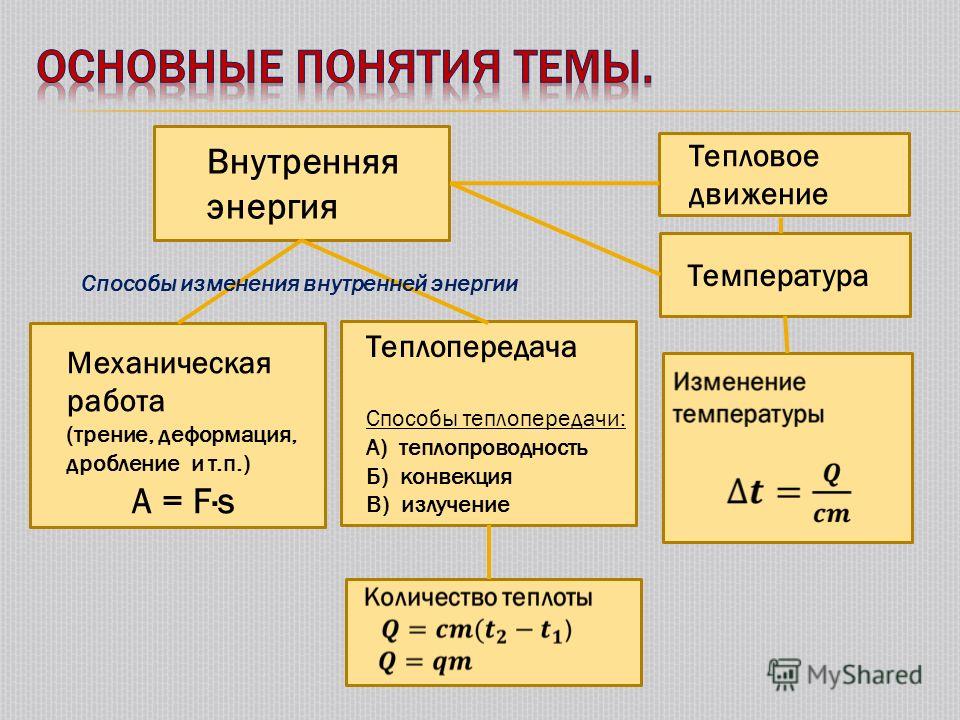
Мы ищем среднюю силу, поэтому мы принимаем ΔtΔt как среднее время между столкновениями данной молекулы с этой стенкой, то есть время, за которое мы ожидаем найти одно столкновение. Пусть l представляют собой длину коробки в направлении x . Тогда ΔtΔt — это время, за которое молекула пройдет через коробку и обратно на расстояние 2 l со скоростью vx.vx. Таким образом, Δt=2l/vx, Δt=2l/vx, и выражение для силы принимает вид
Fi=2mvix2l/vix=mvix2l.Fi=2mvix2l/vix=mvix2l.
Эта сила обусловлена одной молекулой. Чтобы найти общую силу, действующую на стенку, F , нам нужно сложить вклады всех N молекул:
F=∑i=1NFi=∑i=1Nmvix2l=ml∑i=1Nvix2.F=∑i=1NFi=∑i=1Nmvix2l=ml∑i=1Nvix2.
Теперь воспользуемся определением среднего, которое мы обозначили чертой, чтобы найти силу: –л.
Нам нужна сила с точки зрения скорости v , а не x -компонента скорости.
Заметим, что квадрат полной скорости есть сумма квадратов ее составляющих, так что
v2–=vx2–+vy2–+vz2–.v2–=vx2–+vy2–+vz2–.
В предположении изотропии три средних в правой части равны, поэтому
v2–=3vix2–.v2–=3vix2–.
Подстановка этого выражения для F дает
F=Nmv2–3l.F=Nmv2–3l.
Давление равно F / A , поэтому получаем
p=FA=Nmv2–3Al=Nmv2–3V,p=FA=Nmv2–3Al=Nmv2–3V,
где использовали V=AlV =Al для громкости. Это дает важный результат
pV=13Nmv2–.pV=13Nmv2–.
2,5
Объединение этого уравнения с pV=NkBTpV=NkBT дает
13Nmv2–=NkBT.13Nmv2–=NkBT.
Мы можем получить среднюю кинетическую энергию молекулы, 12mv2–12mv2–, из левой части уравнения, разделив N и умножив на 3/2.
Средняя кинетическая энергия на молекулу
Средняя кинетическая энергия молекулы прямо пропорциональна ее абсолютной температуре:
K–=12mv2–=32kBT.
K–=12mv2–=32kBT.
2,6
Уравнение K–=32kBTK–=32kBT представляет собой среднюю кинетическую энергию на молекулу. Обратите внимание, в частности, что ничто в этом уравнении не зависит от молекулярной массы (или любого другого свойства) газа, давления или чего-либо еще, кроме температуры. Если образцы газообразного гелия и ксенона с очень разными молекулярными массами находятся при одинаковой температуре, молекулы имеют одинаковую среднюю кинетическую энергию.
Внутренняя энергия термодинамической системы представляет собой сумму механических энергий всех молекул в ней. Теперь мы можем дать уравнение для внутренней энергии одноатомного идеального газа. В таком газе единственная энергия молекул — это их поступательная кинетическая энергия. Поэтому, обозначая внутреннюю энергию через Eint,Eint, имеем просто Eint=NK–,Eint=NK–, или
Eint=32NkBT.Eint=32NkBT.
2,7
Часто мы хотели бы использовать это уравнение в молях:
Eint=32nRT.
Eint=32nRT.
Мы можем решить K–=12mv2–=32kBTK–=12mv2–=32kBT для типичной скорости молекулы в идеальном газе в терминах температуры, чтобы определить то, что известно как среднеквадратичное значение ( среднеквадратичное значение ) скорость молекулы.
Среднеквадратичная скорость молекулы
Среднеквадратическая (среднеквадратическая) скорость молекулы, или квадратный корень из среднего квадрата скорости v2–v2–, равна
vrms=v2–=3kBTm.vrms=v2–=3kBTm.
2,8
Среднеквадратическая скорость не является средней или наиболее вероятной скоростью молекул, как мы увидим в разделе «Распределение молекулярных скоростей», но обеспечивает легко вычисляемую оценку скорости молекул, связанную с их кинетической энергией. Снова мы можем записать это уравнение в терминах газовой постоянной R и молекулярной массы M в кг/моль:
vrms=3RTM.
vrms=3RTM.
2,9
Мы отвлеклись на мгновение, чтобы ответить на вопрос, который мог возникнуть у вас: когда мы применяем модель к атомам вместо теоретических точечных частиц, меняет ли кинетическая энергия вращения наши результаты? Чтобы ответить на этот вопрос, мы должны обратиться к квантовой механике. В квантовой механике кинетическая энергия вращения не может принимать любое значение; оно ограничено дискретным набором значений, а наименьшее значение обратно пропорционально инерции вращения. Вращательная инерция атома ничтожно мала, потому что почти вся его масса находится в ядре, которое обычно имеет радиус менее 10-14м10-14м. Таким образом, минимальная энергия вращения атома намного превышает 12kBT12kBT при любой достижимой температуре, а доступной энергии недостаточно, чтобы заставить атом вращаться. Мы вернемся к этому вопросу при обсуждении двухатомных и многоатомных газов в следующем разделе.
Пример 2,4
Расчет кинетической энергии и скорости молекулы газа
а) Какова средняя кинетическая энергия молекулы газа при температуре 20,0°C20,0°C (комнатная температура)? б) Найдите среднеквадратичную скорость молекулы азота (N2)(N2) при этой температуре.
Стратегия
а) Известная в уравнении для средней кинетической энергии температура:
К–=12мв2–=32кБТ.К–=12мв2–=32кБТ.
Прежде чем подставить значения в это уравнение, мы должны перевести заданную температуру в кельвины: T=(20,0+273)K=293К.Т=(20,0+273)К=293К. Мы можем найти среднеквадратичную скорость молекулы азота, используя уравнение
vrms=v2–=3kBTm,vrms=v2–=3kBTm,
, но сначала мы должны найти массу молекулы азота. Получив молярную массу азота N2N2 из таблицы Менделеева, находим
m=MNA=2(14,0067)×10−3кг/моль)6,02×1023моль-1=4,65×10−26кг.m=MNA=2(14,0067 )×10-3кг/моль)6,02×1023моль-1=4,65×10-26кг.
Решение
- Одной температуры достаточно, чтобы найти среднюю поступательную кинетическую энергию. Подстановка температуры в уравнение поступательной кинетической энергии дает
K–=32kBT=32(1,38×10–23 Дж/К)(293K)=6,07×10–21 Дж. K–=32kBT=32(1,38×10–23 Дж/K)(293K)=6,07×10–21 Дж .
- Подстановка этой массы и значения kBkB в уравнение для vrmsvrms дает
vrms=3kBTm=3(1,38×10-23 Дж/K)(293K)4,65×10-26кг=511м/с.vrms=3kBTm=3(1,38×10-23J/K)(293K)4,65×10-26кг =511 м/с.
Значение
Обратите внимание, что средняя кинетическая энергия молекулы не зависит от типа молекулы. Средняя поступательная кинетическая энергия зависит только от абсолютной температуры. Кинетическая энергия очень мала по сравнению с макроскопическими энергиями, поэтому мы не чувствуем, когда молекула воздуха попадает на нашу кожу. С другой стороны, это намного больше, чем типичная разница в гравитационной потенциальной энергии, когда молекула движется, скажем, от верха до низа комнаты, так что наше пренебрежение гравитацией оправдано в типичных реальных ситуациях. Среднеквадратичная скорость молекулы азота удивительно велика. Эти большие молекулярные скорости не дают макроскопического движения воздуха, так как молекулы движутся во всех направлениях с равной вероятностью.
средний свободный пробег (расстояние, которое молекула проходит в среднем между столкновениями, обсуждаемое чуть позже в этом разделе) молекул в воздухе очень мал, поэтому молекулы движутся быстро, но не уходят очень далеко за секунду. Высокое значение среднеквадратичной скорости отражено в скорости звука, которая составляет около 340 м/с при комнатной температуре. Чем выше среднеквадратическая скорость молекул воздуха, тем быстрее звуковые колебания могут передаваться по воздуху. Скорость звука увеличивается с температурой и больше в газах с малой молекулярной массой, таких как гелий (см. рис. 2.11).
Рисунок 2.11 а) В обычном газе так много молекул движутся так быстро, что сталкиваются миллиарды раз каждую секунду. (б) Отдельные молекулы не перемещаются очень далеко за небольшой промежуток времени, но возмущения, подобные звуковым волнам, передаются со скоростями, связанными со скоростями молекул.
Пример 2,5
Расчет температуры: скорость убегания атомов гелия
Чтобы избежать гравитации Земли, объект в верхней части атмосферы (на высоте 100 км) должен удалиться от Земли со скоростью 11,1 км/с.
Эта скорость называется скорость убегания . При какой температуре атомы гелия будут иметь среднеквадратичную скорость, равную скорости убегания?
Стратегия
Определите известные и неизвестные и определите, какие уравнения использовать для решения задачи.
Решение
- Определите известные числа: v – скорость убегания, 11,1 км/с.
- Определите неизвестные: Нам нужно найти температуру, T . Нам также нужно найти массу m атома гелия.
- Определите, какие уравнения необходимы.
- Чтобы получить массу m атома гелия, мы можем использовать информацию из периодической таблицы:
м=МНА.м=МНА.
- Чтобы определить температуру T , мы можем переставить
12mv2–=32kBT12mv2–=32kBT
уступатьT=mv2–3kB.
T=mv2–3kB.
- Чтобы получить массу m атома гелия, мы можем использовать информацию из периодической таблицы:
- Подставьте известные значения в уравнения и найдите неизвестные,
m=MNA=4,0026×10-3 кг/моль6,02×1023моль=6,65×10-27кгm=MNA=4,0026×10-3кг/моль6,02×1023моль=6,65×10-27кг
а такжеT=(6,65×10-27кг)(11,1×103м/с)23(1,38×10-23Дж/К)=1,98×104K.T=(6,65×10-27кг)(11,1×103м/с)23( 1,38×10-23Дж/К)=1,98×104К.
T=mv2–3kB.Значение
Эта температура намного выше атмосферной температуры, которая составляет примерно 250 К (-25 ° C или -10 ° F) (-25 ° C или -10 ° F) на большой высоте. В атмосфере осталось очень мало атомов гелия, но многие из них присутствовали при формировании атмосферы, и все больше атомов гелия всегда создается в результате радиоактивного распада (см. главу о ядерной физике). Причина потери атомов гелия заключается в том, что небольшое количество атомов гелия имеет скорости выше скорости убегания Земли даже при нормальных температурах. Скорость атома гелия меняется от одного столкновения к другому, так что в любой момент существует небольшая, но ненулевая вероятность того, что скорость атома больше скорости убегания.
Шанс достаточно высок, чтобы за время существования Земли почти все атомы гелия, побывавшие в атмосфере, достигли космической скорости на больших высотах и вырвались из-под земного притяжения. Более тяжелые молекулы, такие как кислород, азот и вода, имеют меньшую среднеквадратичную скорость, поэтому маловероятно, что какая-либо из них будет иметь скорость, превышающую скорость убегания. На самом деле вероятность настолько мала, что требуются миллиарды лет, чтобы потерять значительное количество более тяжелых молекул из атмосферы. На рис. 2.12 показано влияние отсутствия атмосферы на Луне. Поскольку гравитационное притяжение Луны намного слабее, она потеряла почти всю свою атмосферу. В упражнениях этой главы сравниваются атмосферы Земли и других тел.
Рисунок
2.12
Эта фотография командира «Аполлона-17» Юджина Сернана за рулем лунохода на Луне в 1972 году выглядит так, как будто она была сделана ночью с большим прожектором. На самом деле свет исходит от Солнца. Поскольку ускорение силы тяжести на Луне очень низкое (около 1/6 земного), скорость убегания Луны намного меньше.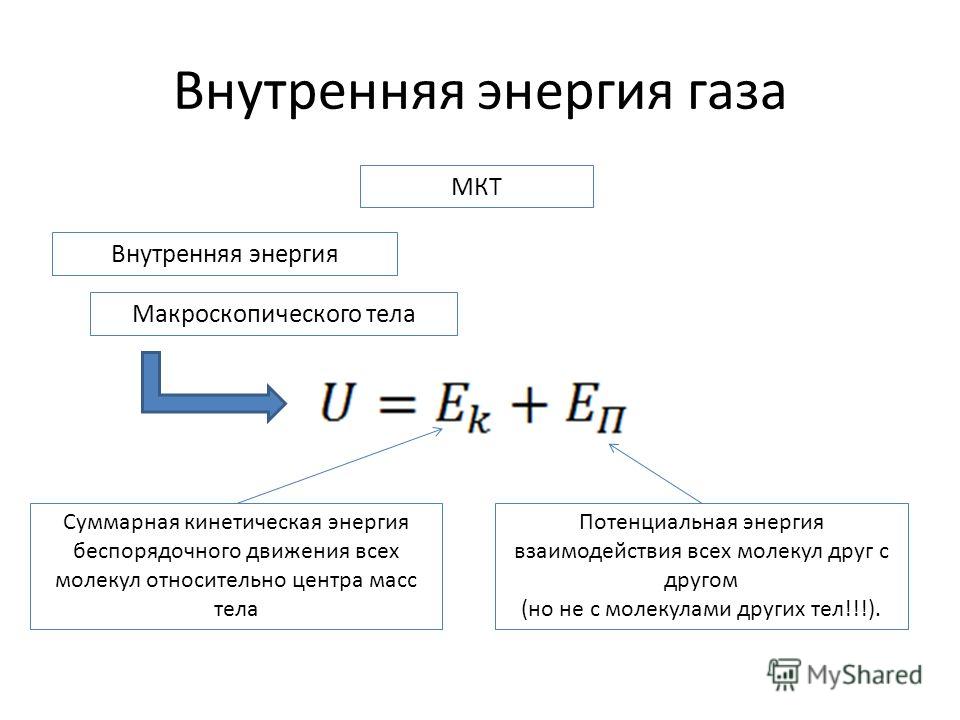
В результате молекулы газа очень легко покидают Луну, оставляя ее практически без атмосферы. Даже днем небо черное, потому что нет газа, рассеивающего солнечный свет. (кредит: Харрисон Х. Шмитт/НАСА)
Проверьте свое понимание 2,4
Проверьте свое понимание Если рассмотреть очень маленький объект, например пыльцу, в газе, то количество молекул, ударяющихся о его поверхность, также будет относительно небольшим. Можно ли ожидать, что пыльцевое зерно испытывает какие-либо колебания давления из-за статистических колебаний числа молекул газа, сталкивающихся с ним за заданный промежуток времени?
Давление пара, парциальное давление и закон Дальтона
Давление, которое создал бы газ, если бы он занимал весь доступный объем, называется парциальным давлением газа. Если смешать два или более газа, они придут к тепловому равновесию в результате столкновений между молекулами; процесс аналогичен теплопроводности, описанной в главе о температуре и теплоте.
Как мы видели из кинетической теории, когда газы имеют одинаковую температуру, их молекулы имеют одинаковую среднюю кинетическую энергию. Таким образом, каждый газ по отдельности подчиняется закону идеального газа и оказывает такое же давление на стенки сосуда, как если бы он был один. Следовательно, в смеси газов общее давление представляет собой сумму парциальных давлений составляющих газов при условии идеального поведения газа и отсутствии химических реакций между компонентами. Этот закон известен как закон парциальных давлений Дальтона по имени английского ученого Джона Дальтона (1766–1844), который предложил его. Закон Дальтона согласуется с тем фактом, что давления складываются в соответствии с принципом Паскаля.
В смеси идеальных газов, находящихся в тепловом равновесии, число молекул каждого газа пропорционально его парциальному давлению. Этот результат следует из применения к каждому закону идеального газа в виде p/n=RT/V.p/n=RT/V. Поскольку правая часть одинакова для любого газа при данной температуре в сосуде данного объема, то и левая часть одинакова.
- Парциальное давление — это давление, которое создал бы газ, если бы он существовал один.
- Закон Дальтона гласит, что общее давление равно сумме парциальных давлений всех присутствующих газов.
- Для любых двух газов (обозначенных цифрами 1 и 2), находящихся в равновесии в сосуде, p1n1=p2n2.p1n1=p2n2.
Важным применением парциального давления является то, что в химии оно действует как концентрация газа при определении скорости реакции. Здесь упомянем только, что парциальное давление кислорода в легких человека имеет решающее значение для жизни и здоровья. Вдыхание воздуха с парциальным давлением кислорода ниже 0,16 атм может ухудшить координацию и суждение, особенно у людей, не привыкших к большой высоте. Более низкие парциальные давления O2O2 имеют более серьезные последствия; парциальное давление ниже 0,06 атм может быстро привести к летальному исходу, и вероятны необратимые повреждения, даже если человека спасут.
Однако ощущение необходимости дышать, как и при задержке дыхания, вызвано в большей степени высокой концентрацией углекислого газа в крови, чем низкой концентрацией кислорода. Так, если маленькое помещение или чулан наполнить воздухом с низкой концентрацией кислорода, возможно, из-за того, что там хранится негерметичный баллон с каким-то сжатым газом, то человек не почувствует ощущения «удушья» и может впасть в судороги или потерять сознание. не замечая ничего плохого. Инженеры по технике безопасности уделяют этой опасности значительное внимание.
Другим важным применением парциального давления является давление пара, которое представляет собой парциальное давление пара, при котором он находится в равновесии с жидкой (или твердой, в случае сублимации) фазой того же вещества. При любой температуре парциальное давление воды в воздухе не может превышать давление пара над водой при этой температуре, потому что всякий раз, когда парциальное давление достигает давления пара, вода конденсируется из воздуха.
Роса является примером такой конденсации. Температура, при которой происходит конденсация пробы воздуха, называется точка росы . Его легко измерить, медленно охлаждая металлический шарик; точка росы – это температура, при которой на шаре впервые появляется конденсат.
Давление паров воды при некоторых температурах, представляющих интерес для метеорологии, приведены в таблице 2.2.
| Т (°С)(°С) | Давление паров (Па) |
|---|---|
| 0 | 610,5 |
| 3 | 757,9 |
| 5 | 872,3 |
| 8 | 1073 |
| 10 | 1228 |
| 13 | 1497 |
| 15 | 1705 |
| 18 | 2063 |
| 20 | 2338 |
| 23 | 2809 |
| 25 | 3167 |
| 30 | 4243 |
| 35 | 5623 |
| 40 | 7376 |
Стол
2.
2
Давление паров воды при различных температурах
Относительная влажность (R.H.) при температуре T определяется
R.H.= парциальное давление водяного пара при T или давление воды при T×100%. R.H.= парциальное давление водяного пара при T или давление воды при T×100%.
Относительная влажность 100 %100 % означает, что парциальное давление воды равно давлению пара; другими словами, воздух насыщен водой.
Пример 2,6
Расчет относительной влажности
Какова относительная влажность воздуха при температуре воздуха 25ºC25ºC и точке росы 15ºC15ºC?
Стратегия
Мы просто смотрим давление пара при заданной температуре и точке росы и находим соотношение.
Solution
R.H.=Парциальное давление водяного пара при 15°CПарциальное давление водяного пара при 25°C×100%=1705Pa3167Pa×100%=53,8%.
R.H.=Парциальное давление водяного пара при 15°CПарциальное давление водяного пара при 25°C С×100%=1705Па3167Па×100%=53,8%.
Значение
RH важен для нашего комфорта. Значение 53,8%53,8% находится в диапазоне от 40% до 60% от 40% до 60%, рекомендованном для комфортного помещения.
Как отмечалось в главе о температуре и тепле, температура редко падает ниже точки росы, потому что, когда она достигает точки росы или точки замерзания, вода конденсируется и высвобождает относительно большое количество скрытой теплоты парообразования.
Средний свободный пробег и среднее время свободного хода
Теперь мы явно рассматриваем коллизии. Обычный первый шаг (это все, что мы предпримем) — вычислить длину свободного пробега, λ, λ, среднее расстояние, которое проходит молекула между столкновениями с другими молекулами, и среднее время свободного пробега ττ, среднее время между столкновениями молекулы.
Если считать все молекулы сферами радиусом r , то одна молекула столкнется с другой, если их центры находятся на расстоянии 2 r друг от друга. Для данной частицы мы говорим, что площадь круга с этим радиусом, 4πr24πr2, является «поперечным сечением» для столкновений. При движении частица движется по цилиндру с такой площадью поперечного сечения. Средняя длина свободного пробега — это длина λλ, при которой ожидаемое число других молекул в цилиндре длины λλ и поперечного сечения 4πr24πr2 равно 1. Если мы временно проигнорируем движение молекул, отличных от той, которую мы рассматриваем, ожидаемое число – это числовая плотность молекул, N / V , умноженный на объем, а объем равен 4πr2λ4πr2λ, поэтому мы имеем (N/V)4πr2λ=1, (N/V)4πr2λ=1 или
λ=V4πr2N.λ=V4πr2N.
Учет движения всех молекул значительно усложняет расчет, но единственное изменение — коэффициент 2,2.
Результат
λ=V42πr2N.λ=V42πr2N.
2.10
В идеальном газе мы можем заменить V/N=kBT/pV/N=kBT/p, чтобы получить
λ=kBT42πr2p.λ=kBT42πr2p.
2.11
Среднее время свободного пробега ττ — это просто длина свободного пробега, деленная на типичную скорость, и обычно выбирают среднеквадратичную скорость. Затем
τ=kBT42πr2pvrms.τ=kBT42πr2pvrms.
2.12
Пример 2,7
Расчет среднего времени простоя
Найти среднее время свободного пробега атомов аргона (М=39,9г/моль)(М=39,9г/моль) при температуре 0°С0°С и давлении 1,00 атм. Примем радиус атома аргона равным 1,70×10-10 м. 1,70×10-10 м.
Раствор
- Определить известные значения и преобразовать их в единицы СИ. Мы знаем, что молярная масса 0,0399 кг/моль, температура 273 К, давление 1,01×105 Па, 1,01×105 Па и радиус 1,70×10-10 м. 1,70×10-10 м.
- Найдите среднеквадратичную скорость: vrms=3RTM=413msvrms=3RTM=413ms.
- Подставить в уравнение для среднего времени простоя: 90 004 10-23 Дж/К)(273К)42π(1,70×10-10м)2(1,01×105Па)(413м/с)=1,76×10-10с.
1,70×10-10 м.Значение
Мы вряд ли можем сравнить этот результат с нашими интуитивными представлениями о молекулах газа, но он дает нам картину столкновения молекул с чрезвычайно высокой частотой.
Проверьте свое понимание 2,5
Проверьте свое понимание Что имеет большую длину свободного пробега, жидкая вода или водяной пар в воздухе?
Расчет внутренней энергии идеальных газов
Подробнее о расчете внутренней энергии идеальных газов читайте в этой статье.
- 1 Первый закон термодинамики
- 2 Предварительные соображения для определения изменения внутренней энергии
- 3 Вывод соотношения на примере изохорного процесса
- 4 Замечание к формуле
- 5 Внутренняя энергия идеальных газов
- 6 Аналогия между внутренней энергией и гравитационной потенциальной энергией
Первый закон термодинамики
В статье Внутренняя энергия идеальных газов было подробно объяснено, что в идеальных газах только кинетическая энергия молекул газа существует как внутренняя энергия (тепловая энергия).
Согласно первому закону термодинамики эту внутреннюю энергию можно изменить, передав энергию в виде работы W или в виде теплоты Q:
\begin{align}
&\boxed{\Delta U = W + Q } ~~~~~\text{изменение внутренней энергии} \\[5px]
\end{align}
Согласно распределению Максвелла-Больцмана кинетическая энергия молекул, в свою очередь, напрямую связана с температурой газа. Таким образом, изменение внутренней энергии (изменение кинетической энергии) неизбежно означает изменение температуры. В связи с этим возникает вопрос, как изменение внутренней энергии ΔU связано с изменением температуры ΔT.
Предварительные соображения для определения изменения внутренней энергии
Как уже говорилось, кинетическая теория газов показывает прямую зависимость между средней кинетической энергией молекул в газе и его температурой. Так что если вы знаете температуру газа (и количество частиц), то с ним напрямую связана определенная внутренняя энергия.
Это не зависит от давления или объема газа. Поэтому изменение внутренней энергии зависит только от изменение температуры.
Таким образом, изменение внутренней энергии во время термодинамического процесса ясно определяется в идеальных газах, если известны начальная температура (и, следовательно, начальная энергия) и конечная температура (и, следовательно, конечная энергия). Поэтому для изменения внутренней энергии не имеет значения, является ли это изобарным, изохорным, изоэнтропическим или любым другим процессом. Только изменение температуры определяет изменение внутренней энергии!
Тот факт, что внутренняя энергия зависит только от состояния газа (с точки зрения температуры), а не от типа процесса, делает внутреннюю энергию переменная состояния . В противоположность этому теплота и работа зависят от термодинамического процесса (будь то изохорный, изотермический, изобарический или изоэнтропический) и поэтому считаются величинами процесса .
Итак, если кто-то хочет исследовать взаимосвязь между изменением внутренней энергии и изменением температуры, это можно сделать в принципе для любого термодинамического процесса. Результаты, полученные в результате этого процесса, затем справедливы и для любого другого термодинамического процесса, то есть вообще для идеальных газов. В этот момент изохорный процесс особенно подходит для исследования взаимосвязи, поскольку при таком процессе над газом или газом не совершается никакой работы. Таким образом, подвод тепла увеличивает внутреннюю энергию на ту же величину, и поэтому его относительно легко исследовать. Это будет обсуждаться более подробно в следующем разделе.
Вывод зависимости на примере изохорного процесса
Для определения зависимости между изменением внутренней энергии и изменением температуры проводится следующий эксперимент. Газ массой m находится в сосуде постоянного объема. Передавая тепло, температура газа увеличивается, а вместе с ней и внутренняя энергия.
Поскольку объем газа не может измениться во время такого изохорного процесса, энергия не может передаваться в виде работы при расширении или сжатии (W=0). Согласно первому закону термодинамики теплота Q, переданная газу, таким образом, полностью увеличивает внутреннюю энергию ΔU:
\begin{align}
& \Delta U = \underbrace{W}_{=0}+Q= Q \\[5px]
\label{u}
& \underline{\Delta U = Q} \\[5px]
\end{align}
Таким образом, чтобы установить связь между изменением внутренней энергии и изменением температуры, нет необходимости проводить сложные исследования кинетической энергии отдельных молекул. Согласно уравнению (\ref{u}) необходимо исследовать только взаимосвязь между тепловложением Q изохорного процесса (которое тогда непосредственно соответствует изменению внутренней энергии ΔU) и результирующим повышением температуры ΔT.
При использовании электрического нагревателя подводимую энергию можно определить относительно легко («тепло = электрическая мощность x время»).
Эксперимент показывает, что изменение температуры ΔT пропорционально переданному теплу Q, т.е. для увеличения в два раза изменения температуры требуется в два раза больше тепла:
\begin{align}
\label{q}
& Q \sim \ Delta T \\[5px]
\end{align}
Также наблюдается, что чем больше теплоты требуется, тем большую массу газа нужно нагреть. При вдвое большей массе для нагревания газа требуется в два раза больше теплоты Q. Следовательно, теплота Q и масса m также пропорциональны друг другу:
\begin{align}
\label{m}
& Q \sim m \\[5px]
\end{align}
В целом, переданное тепло Q пропорционален массе m и изменению температуры ΔT газа.
Константа пропорциональности между этими величинами называется удельной изохорной теплоемкостью c v и зависит только от типа газа:
\begin{align}\;\;\;\;\;
& Q \sim m \cdot \Delta T \\[5px]
\label{c}
& \underline {Q = c_\text{v} \cdot m \cdot \Delta T} ~~~~~ [ c_\text{v}]=\frac{\text{J}}{\text{kg} \cdot \text{K}} ~~~\text{удельная изохорная теплоемкость} \\[5px]
\end {align}
Удельная теплоемкость показывает, сколько энергии требуется для изменения температуры вещества массой 1 кг на 1 К. Или в этом случае: на сколько изменяется внутренняя энергия на единицу массы при изменении температуры на 1 K. Согласно уравнению (\ref{u}) теперь найдена искомая связь между изменением внутренней энергии ΔU и изменением температуры ΔT для идеального газа:
\begin{align}\;\;\;\;\;
\label{d}
& \boxed{ \Delta U = c_\text{v} \cdot m \cdot \Delta T} ~~~\text{где } \Delta T = T_2-T_1~~~\text {относится вообще к идеальным газам!} \\[5px]
\end{align}
Замечание к формуле
Здесь не следует вводить в заблуждение термином «удельная изохорная теплоемкость » c v , который появляется в формуле (\ref{d}).
В связи с изменением внутренней энергии величину c v следует рассматривать только как константу пропорциональности между изменением внутренней энергии и изменением температуры.
Эта константа пропорциональности называется удельной изохорной теплоемкостью только потому, что для изохорного процесса (и только для изохорного процесса!) эта величина описывает переданное тепло – см. уравнение (\ref{c}). Но когда дело доходит до изменения внутренней энергии, уравнение (\ref{d}) применимо к любому термодинамическому процессу идеальных газов – см. раздел «Предварительные соображения для определения изменения внутренней энергии»!
Внутренняя энергия идеальных газов
Хотя в термодинамике часто имеет значение только изменение внутренней энергии ΔU, для идеальных газов также может быть определена абсолютная внутренняя энергия U. Для этого представьте себе газ, находящийся в цилиндре постоянного объема, который охлаждается до абсолютного нуля.
В этом состоянии все молекулы покоятся, поэтому газ не имеет внутренней энергии. Теперь теплота Q передается газу в постоянном объеме до тех пор, пока он не достигнет температуры T. Все тепло, необходимое для нагревания газа, в конечном итоге присутствует в виде внутренней энергии U. Таким образом, при температуре T газ имеет следующую внутреннюю энергию U :
\begin{align}
\label{t}
& \boxed{ U = c_v \cdot m \cdot T} ~~~\text{обычно применимо к идеальным газам!} \\[5px]
\end {align}
Примечание : Строго говоря, удельная изохорная теплоемкость c v для идеальных газов также может зависеть от температуры. А именно, когда степени свободы замораживаются при понижении температуры из-за квантово-механических эффектов. Уравнения (\ref{d}) и (\ref{t}) больше недействительны без ограничений. Однако если предположить, что такой температурной зависимости не существует, то часто говорят о идеальные газы и уравнения (\ref{d}) и (\ref{t}) по-прежнему применяются без ограничений.
Аналогия между внутренней энергией и гравитационной потенциальной энергией
Внутреннюю энергию идеальных газов можно очень четко сравнить по аналогии с гравитационной потенциальной энергией объекта. В то время как гравитационная потенциальная энергия представляет собой энергетическое (гравитационное) состояние объекта на заданной высоте h, внутренняя энергия представляет собой энергетическое (кинетическое) состояние идеального газа при данной температуре T.
Рис.: Аналогия между потенциальной энергией и внутренней энергией Заданной высоте h можно присвоить определенную потенциальную энергию через массу m объекта. Точно так же некоторая внутренняя энергия может быть соотнесена с данной температурой T через массу m газа. Точная связь между потенциальной энергией и высотой h устанавливается ускорением свободного падения g (зависит от положения!). В случае внутренней энергии связь между внутренней энергией U и температурой T устанавливается удельной изохорной теплоемкостью c v (зависит от типа газа!).
| Gravitational potential energy | Internal energy |
|---|---|
| height h | temperature T |
| mass of the object m | mass of the gas m |
| gravitational acceleration g | specific изохорная теплоемкость c v |
| гравитационная потенциальная энергия Вт = м⋅г⋅ч | внутренняя энергия U = m⋅c v ⋅T |
| change of potential energy ΔW = m⋅g⋅Δh | change of internal energy ΔU = m⋅c v ⋅ΔT |
The Энергетическое состояние объекта, расположенного на высоте h, можно изменить путем передачи энергии – его можно поднять на большую высоту. Точно так же энергетическое состояние газа при температуре T можно изменить путем передачи энергии — довести до более высокой температуры.
Энергия, необходимая для подъема предмета с высоты h 1 на высоту h 2 зависит только от разности высот Δh = h 2 – h 1 и не зависит от пути! Точно так же энергия, необходимая для повышения температуры идеального газа с T 1 до T 2 , зависит только от разности температур ΔT = T 2 – T 1 , а не от термодинамического процесса.
Закон идеального газа
Закон идеального газаИдеальный газ определяется как газ, в котором все столкновения между атомами или молекулами абсолютно упругие и в котором нет сил межмолекулярного притяжения. Можно представить себе это как набор совершенно твердых сфер, которые сталкиваются, но в остальном не взаимодействуют друг с другом. В таком газе вся внутренняя энергия находится в виде кинетической энергии, и любое изменение внутренней энергии сопровождается изменением температуры. Идеальный газ можно охарактеризовать тремя переменными состояния: абсолютным давлением (P), объемом (V) и абсолютной температурой (T). Отношение между ними может быть выведено из кинетической теории и называется
Закон идеального газа можно рассматривать как результат кинетического давления молекул газа, сталкивающихся со стенками сосуда в соответствии с законами Ньютона.
| Индекс Концепции газового закона Концепции кинетической теории | ||||||||||||||||||||||||||||||||||
|
Но есть и статистический элемент в определении средней кинетической энергии этих молекул. Температура считается пропорциональной этой средней кинетической энергии; это вызывает идею кинетической температуры. Один моль идеального газа при СТП занимает 22,4 литра.
Оно должно быть однозначно однозначным, чтобы характеризовать состояние. Например, в примере с тепловой работой конечное состояние
характеризуется определенной температурой (переменной состояния) независимо от
было ли оно доведено до этого состояния нагреванием или совершением работы над
это, или оба.
Чтобы быть уверенным, в нем нулевое полезное давление, и ваш шинный манометр покажет ноль фунтов на квадратный дюйм. Большинство манометров показывают превышение давления над атмосферным давлением, и это превышение называется «манометрическим давлением». Хотя это полезное измерение для многих практических целей, оно должно быть преобразовано в абсолютное давление для таких приложений, как закон идеального газа.
На этом изображении система открыта и находится в равновесии с атмосферой. На правом изображении система закрыта, а поршень нажат до тех пор, пока давление не станет около 15 фунтов/дюйм 2 . Это означает, что абсолютное давление увеличилось примерно вдвое за счет сжатия газа до половины его объема (закон идеального газа). Стандартное атмосферное давление в этих общепринятых единицах измерения США составляет 14,7 фунта/дюйм 9 .0737 2 , так что это нужно добавить к манометрическому давлению выше, чтобы получить абсолютное давление.