Энергия и масса в релятивистской механике: 6. 6. Взаимосвязь массы и энергии. Закон сохранения энергии в релятивистской механике. @ - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

6. 6. Взаимосвязь массы и энергии. Закон сохранения энергии в релятивистской механике. @

Исследуя следствия основного закона релятивистской динамики, Эйнштейн пришел к выводу о том, что полная энергия двигающейся частицы равна . Из этого уравнения следует, что даже неподвижная частица (когда=0) обладает энергией Е₀ = m₀с², эту энергию называют энергией покоя (или собственной энергией).

Итак, универсальная зависимость полной энергии частицы от ее массы: Е = mс². Это фундаментальный закон природы – закон взаимосвязи массы и энергии. Согласно этому закону масса, находящаяся в покое, обладает огромным запасом энергии и любое изменение массы Δm сопровождается изменением полной энергии частицы ΔE=c²Δm.

Например, 1кг речного песка должен содержать 1(3,0∙10⁸м/c)²=9∙10¹⁶Дж энергии. Это вдвое больше еженедельного потребления энергии в США.

Однако большая часть этой энергии недоступна, так как закон сохранения материи требует, чтобы общее число барионов (так называются элементарные частицы – нейтроны и протоны) в любой замкнутой системе оставалось постоянным. Отсюда следует, что суммарная масса барионов не меняется и, соответственно, она не может быть преобразована в энергию.

Но внутри атомных ядер нейтроны и протоны кроме энергии покоя обладают большой энергией взаимодействия друг с другом. В ряде таких процессов как синтез и деление ядер, часть этой потенциальной энергии взаимодействия может превращаться в добавочную кинетическую энергию, получаемых в реакциях, частиц. Это превращение и служит источником энергии ядерных реакторов и атомных бомб.

Правильность соотношения Эйнштейна можно доказать на примере распада свободного нейтрона на протон, электрон и нейтрино (с нулевой массой покоя): n → p + e^– + ν. При этом суммарная кинетическая энергия конечных продуктов равна 1,25∙10^-13 Дж. Масса покоя нейтрона превышает суммарную массу протона и электрона на 13,9∙10^-31 кг. Этому уменьшению массы должна соответствовать энергия ΔE=c²Δm=(13,9∙10^-31)(3,0∙10⁸)²=1,25∙10^-15Дж. Она совпадает с наблюдаемой кинетической энергией продуктов распада.

В релятивистской механике не соблюдается закон сохранения массы покоя, но выполняется закон сохранения энергии: полная энергия замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Спустя несколько лет после опубликования специальной теории относительности, Эйнштейном была разработана и окончательно сформулирована в 1915 г. общая теория относительности, которая представляет собой современную физическую теорию пространства, времени и тяготения.

Главным предметом общей теории относительности является гравитационное взаимодействие, или тяготение

. В законе всемирного тяготения Ньютона подразумевается, что сила тяготения действует мгновенно.

Такое утверждение противоречит одному из основных принципов теории относительности, а именно: ни энергия, ни сигнал не могут распространяться быстрее скорости света. Таким образом, Эйнштейн столкнулся с проблемой релятивистской теории тяготения. Для решения этой проблемы необходимо было также ответить на вопрос: различаются ли гравитационная масса (входящая в закон Всемирного тяготения) и инертная масса (входящая во второй закон Ньютона )? Ответ на этот вопрос может дать только опыт. Вся совокупность опытных фактов указывает на то, что инертная и гравитационная массы тождественны. Известно, что силы инерции аналогичны силам тяготения: находясь внутри закрытой кабины, никакими опытами нельзя установить, чем вызвано действие на тело силы mg – тем ли, что кабина движется с ускорением g, либо тем, что неподвижная кабина находится вблизи поверхности Земли. Вышесказанное представляет собой так называемый принцип эквивалентности: поле тяготения по своему проявлению тождественно ускоряющейся системе отсчета.

Это утверждение и было положено Эйнштейном в основу общей теории относительности.

В своей теории Эйнштейн получил, что свойства пространства и времени связаны более сложными соотношениями, чем соотношения Лоренца. Вид этих связей зависит от распределения материи в пространстве, часто образно говорят, что материя искривляет пространство и время. Если материи нет на больших расстояниях от точки наблюдения или искривление пространства‑времени мало, то можно с удовлетворительной точностью использовать соотношения Лоренца.

Явление гравитации (притяжение тел имеющих массу) Эйнштейн объяснил тем, что массивные тела так искривляют пространство, что естественное движение других тел по инерции происходит по тем же траекториям, как если бы существовали силы притяжения.

Таким образом, Эйнштейн решил проблему совпадения гравитационной и инертной массы путем отказа от использования понятия сил гравитации.

Следствия, полученные из общей теории относительности (теории гравитации), предсказали наличие новых физических явлений вблизи массивных тел: изменение хода времени; изменение траекторий других тел, не объясняемое в классической механике; отклонение лучей света; изменение частоты света; необратимое притяжение всех форм материи к достаточно массивным звездам и др. Все эти явления были обнаружены: изменение хода часов наблюдали при полете самолета вокруг Земли; траектория движения самой близкой к Солнцу планеты – Меркурия объясняется только этой теорией, отклонение лучей света наблюдается для лучей, идущих от звезд к нам вблизи Солнца; изменение частоты или длины волны света также обнаружено, этот эффект называется гравитационным красным смещением, он наблюдается в спектральных линиях Солнца и тяжелых звезд; необратимым притяжением материи к звездам объясняют наличие «черных дыр» ‑ космических звездных объектов, поглощающих даже свет. Кроме этого, множество космологических вопросов находит объяснение в общей теории относительности.

Масса, импульс и энергия в специальной теории относительности. Школьный курс физики

Главная | Физика 11 класс | Масса, импульс и энергия в специальной теории относительности

Релятивистский импульс.

Согласно второму закону Ньютона, постоянная сила, действуя на тело продолжительное время, может сообщить ему сколь угодно большую скорость. Но в действительности скорость света в вакууме является предельной, и ни при каких условиях тело не может двигаться со скоростью, превышающей скорость света в вакууме.

Таким образом, СТО требует пересмотра и уточнения законов механики. При этом должны выполняться закон сохранения импульса и закон сохранения механической энергии в замкнутых системах. Для того чтобы закон сохранения импульса выполнялся во всех ИСО, необходимо изменить определение импульса тела. В рамках СТО релятивистский импульс тела массой m, движущегося со скоростью , имеет вид

При скоростях движения, много меньших скорости света (υ << с), релятивистский импульс переходит в классический. Обратим внимание, что масса m, входящая в выражение (1), является фундаментальной характеристикой тела, не зависящей от выбора системы отсчёта.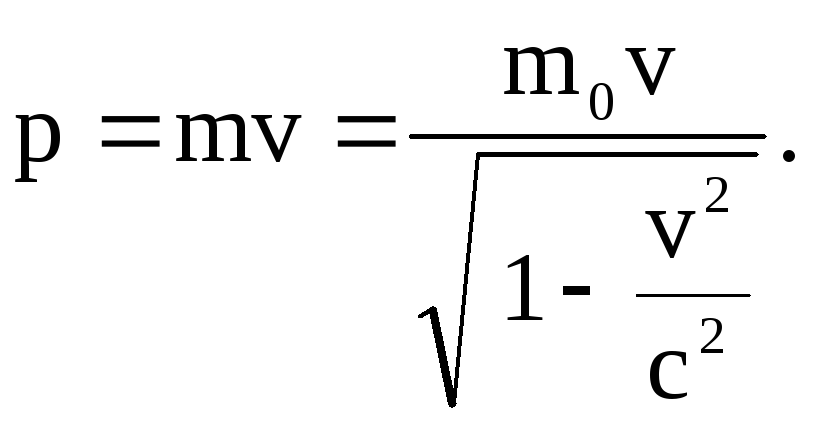

Основной закон релятивистской динамики.

В курсе физики 10 класса мы использовали запись второго закона динамики Ньютона в форме

Основной закон релятивистской динамики записывается так же, однако под следует понимать релятивистский импульс:

Связь между энергией и массой.

Как уже было сказано, в релятивистской механике выполняется закон сохранения механической энергии. Для того чтобы разогнать частицу массой m из состояний покоя до некоторой скорости υ, сила F должна совершить работу

А, которая будет равна кинетической энергии E_k частицы. Основной закон релятивистской динамики позволяет получить для работы следующее выражение:

Эйнштейн интерпретировал первый член в правой части формулы (2) как полную энергию E движущейся частицы:

а второй член — как энергию покоя E₀:

При малых скоростях (υ << с) формула (2) переходит в классическое выражение для кинетической энергии¹E_k = mυ² / 2.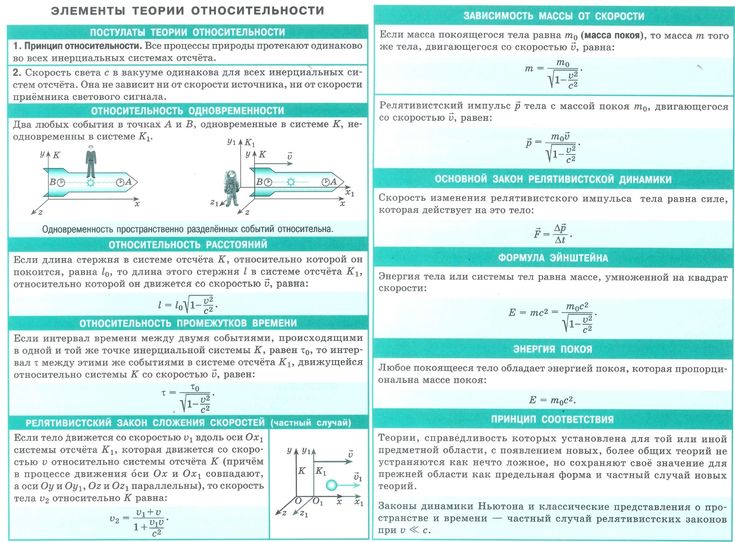

¹ Это можно показать, воспользовавшись приближёнными равенствами , справедливыми при ∣ x∣ ≪ 1.

Формула Эйнштейна (4) выражает фундаментальный закон природы, который называют законом взаимосвязи массы и энергии. Во всей физике найдётся совсем немного столь же простых и универсальных формул, связывающих фундаментальные физические величины.

Согласно формуле Эйнштейна, любое тело обладает энергией уже только благодаря факту своего существования. Так, в 1 кг вещества содержится энергия E₀ = 1 • (3 ∙ 10⁸) Дж = 9 ∙ 10¹⁶ Дж. Для того чтобы выделилась такая энергия, потребовалось бы сжечь 9 млн т древесины!

Почему же в задачах классической механики и термодинамики, применяя закон сохранения энергии, мы не учитывали энергию покоя? При малых скоростях движения тела формулу (3) можно записать в виде E ≈ mс² + mυ² / 2, т. е. энергия покоя входит в качестве слагаемого в полную энергию. Однако изменения энергии, возникающие в этих задачах, настолько малы по сравнению с энергиями покоя взаимодействующих тел, что изменениями масс тел можно пренебречь. Но так бывает не всегда. Далее мы увидим, что в ядерных реакциях относительное изменение массы достигает величин, с которыми необходимо считаться. Например, при делении ядра урана-235 масса продуктов распада примерно на 0,1% меньше массы исходного ядра. При этом выделяется огромная энергия.

Релятивистское соотношение между энергией и импульсом.

C помощью формул (1) и (3) можно получить соотношение, связывающее энергию и импульс релятивистской частицы. Возводя обе части этих формул в квадрат и преобразовывая разность E² – p²c², получим

Таким образом,

E² = m²c⁴ + p²c².

Данное соотношение показывает, что частица может иметь энергию и импульс, но при этом не иметь массы.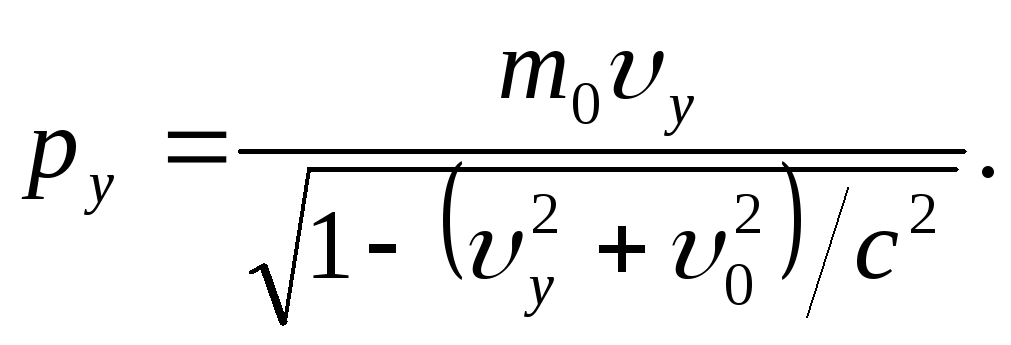 Для безмассовой частицы (например, фотона) связь между энергией и импульсом имеет вид

E = pc.

Безмассовая частица не может существовать в состоянии покоя. В любой ИСО она движется со скоростью света.

Общая теория относительности.

Закон всемирного тяготения фактически утверждает, что если изменить распределение вещества в одном месте пространства, то изменения гравитационного поля мгновенно проявятся во всей Вселенной. Это не только означает возможность передавать сигналы со сверхсветовой скоростью (что невозможно в рамках СТО), но и требует существования абсолютного времени (что также противоречит основным положениям СТО). В связи с этим Эйнштейном в 1915—1916 гг. была создана новая теория пространства-времени, которая получила название общей теории относительности (ОТО). Она является обобщением СТО для гравитационных полей. Согласно ОТО, свойства пространства обусловлены находящейся в нем материей. При этом чем больше массы тел, тем более искривлено пространство вокруг них. Следовательно, вблизи тяготеющей массы (например, Солнца) должно наблюдаться искривление луча света.

В обычных условиях наблюдать этот эффект очень трудно, поскольку свет Солнца затмевает звёзды, расположенные вблизи него. Однако такие наблюдения можно выполнить во время солнечных затмений. В 1919 г. британская экспедиция, наблюдавшая солнечное затмение в Западной Африке, обнаружила, что световые лучи действительно отклоняются Солнцем. Отметим, что гравитационное отклонение света, наряду с другими эффектами ОТО, является экспериментальным подтверждением справедливости данной теории.

Вопросы:

1. Как можно определить релятивистский импульс тела?

2. Как записывается формула Эйнштейна?

3. Что называют энергией покоя (собственной энергией)?

4. Как связаны между собой энергия и импульс в СТО?

Упражнения:

1. Вычислите энергию покоя электрона.

2. На сколько увеличивается масса воды в озере объёмом 10⁶ м³ при её нагревании на 22 °C?

3. Общая мощность излучения Солнца составляет около 3,8 ∙ 10²⁶ Вт. На сколько уменьшается масса Солнца за 1 с?

4. На сколько увеличится масса пружины жёсткостью 10 кН/м при её растяжении на 3 см?

5. При какой скорости кинетическая энергия частицы равна её энергии покоя?

Предыдущая страницаСледующая страница

Специальная теория относительности — релятивистская масса, энергия и импульс

Поскольку вся ньютоновская физика опирается на время и расстояние, мы правильно предполагаем, что концепции, зависящие от времени и расстояния, также меняются. Как изменяются энергия, работа, сила и импульс в специальной теории относительности? Пристегнитесь: релятивистские аттракционы не из этого мира. Мы имеем в виду это буквально.

Коробка Эйнштейна

В ньютоновской механике мы определили импульс как произведение массы и скорости, p = мю . Мы также связали массу с некоторой инерцией, склонностью объекта оставаться в покое или двигаться с постоянной скоростью. Чем больше масса, тем больше инерция.

Закон инерции применим и к энергии? Другими словами, имеет ли энергия инертную массу?

Самое известное уравнение Эйнштейна E = mc ² описывает именно это. Энергия просто равна массе, умноженной на скорость света в квадрате. Это соотношение мы используем, когда объясняем ядерные реакции ⁸ .

Есть мысленный эксперимент («мысленный эксперимент» Эйнштейна), который позволяет нам самим прийти к такому выводу.

Представьте себе следующий сценарий. У нас есть ящик массой M и длиной L , который изначально покоится. Ящик испускает всплеск фотонов с одного конца:

Мы знаем из физики элементарных частиц, где релятивистские скорости являются нормой, что импульс фотона определяется выражением , где E — это энергия этого фотона. По закону сохранения импульса общий импульс системы, состоящей из ящика и фотонов, должен быть равен нулю. Это означает, что коробка приобретает импульс, равный фотонам и противоположный ему, при каждом столкновении, и отскакивает на небольшое расстояние Δ x на каждое столкновение, как и отдача распадающихся частиц.

Поскольку импульс равен p = Mv и , мы можем написать это и решить для скорости отдачи v , так что .

Фотоны достигают конца ящика, преодолев расстояние, равное его длине L . Это происходит в интервале времени Δ t , равном .

Когда фотоны достигают конца ящика, ящик снова отскакивает на расстояние Δ x и возвращается в исходное положение. Поскольку смещение равно скорости, умноженной на время, или Δ x = v Δ t , мы можем написать, что .

Но действительно ли перемещался центр масс ящика и его содержимого? Маловероятно. А фотоны? Что, если бы со светом была связана небольшая масса m , так что центр масс системы не изменился? В этом случае центр масс коробки C будет равен . Центр масс фотонов, C (фотонов), будет равен . Поскольку общий центр масс не меняется, мы можем сложить их вместе и установить к нулю, как это было бы, если бы центр масс всей системы остался прежним. :

Другими словами, E = mc ² .

Это известно как принцип эквивалентности массы и энергии. Энергия в любой форме имеет массовый эквивалент. А если что-то имеет массу, то и энергия имеет инерцию.

Релятивистская масса, кинетическая энергия и импульс

Уравнение E = mc ² подразумевает, что масса связана с относительностью, не так ли? Давайте поговорим об этом подробнее.

Если энергия релятивистской частицы увеличивается, то должна увеличиваться и масса. Как бы странно это ни было, это также защита. Чтобы разогнать массивный объект до релятивистской скорости, потребуется – столько энергии, что это нереально. Следовательно, сегодняшние космические челноки путешествуют со скоростью всего 0,00005 c .

В любом случае, поскольку масса также увеличивается с релятивистскими скоростями вместе с полной энергией, мы имеем релятивистскую массу m и массу покоя, или собственную массу, m _o . Как мы уже могли догадаться, они связаны нашим другом γ уравнением m = γm _o , где γ как обычно равно и .

Поскольку энергия E определяется выражением E = mc ² , нам также придется различать релятивистскую энергию E и энергию покоя E _{5 o _{. Но что такое релятивистская энергия, как не энергия, связанная с движением? Да, мы видели это раньше. Это называется кинетической энергией, или К . В классической механике кинетическая энергия равна } . В специальной теории относительности полная энергия E определяется как энергия покоя плюс кинетическая энергия, так что K = E − E _o = mc 0 2}}

0 о с ² = ( γ −1) м _о с ² .

Наконец, в классической механике мы узнали, что импульс объекта равен его скорости, умноженной на его массу, или p = mv и этот импульс сохраняется. Сохранение импульса означает, что он не должен меняться в зависимости от системы отсчета. Как это может быть верным, если мы только что узнали, что скорости будут трансформироваться от одного кадра к другому?

Поскольку p = mv справедливо только тогда, когда v << c , когда скорость объекта намного, намного меньше скорости света, как и в остальной ньютоновской физике, мы должны учитывать возросшую массу на релятивистских скоростях, или p = γm _o v .

Сведем все это в список. Кто не любит списки? О, опусти руку.

P = γM _O V
M = γ M _O
E = K + E _{7 e = k + E _{7 = = 079007}}

0707070707078. 07070707070707070707.9007 = 07070707070707078 = 077070707. . 0707070707070707078 = = 079007. E _o = m _o c ² K = ( γ – 1) m _o c ²
На приведенном ниже графике показано, что взаимосвязь между кинетической энергией и скоростью различна для ньютоновской механики и специальной теории относительности, где скорость выражается в долях скорости света, β . В специальной теории относительности кинетическая энергия асимптотически возрастает до бесконечности, поскольку из-за второго постулата Эйнштейна предел скорости Вселенной составляет c .
На любое явление, связанное со скоростью в физике, повлияет приближение скоростей к скорости света. Это означает, что у величины или вектора будет две «стороны»: одна измеряется в состоянии покоя, например, масса покоя, а другая измеряется во время движения, например, релятивистская масса.
Специалисты по физике элементарных частиц постоянно учитывают теорию относительности, как и астрономы, как и все устройства GPS. Читайте все об относительности для системы GPS и многое другое.
Распространенные ошибки
Еще раз обратите внимание на разницу между массой покоя и энергией покоя и релятивистскими версиями. Подумайте, должно ли число быть больше или меньше другого, чтобы распознать, когда вычисления пойдут наперекосяк.
Мозговая закуска
Для получения E = mc ² , уравнение источника ядерной энергии, Альберта Эйнштейна назвали «отцом атомной бомбы». В ответ на эти обвинения он сказал: «Высвобождение атомной энергии не создало новой проблемы. Оно просто сделало более насущной необходимость решения существующей».
Релятивистское увеличение массы
Майкл Фаулер, УФа Физика.
Импульс имеет направление
Как мы обсуждали в прошлой лекции, даже до того, как Ньютон сформулировал свою законы, Декарт с небольшой помощью Гюйгенса открыл глубокую динамическая истина: в любом столкновении или фактически в любом взаимодействии любого рода общее количество «импульса» — мера из движение —всегда остался прежним. Импульс движущегося объекта определяется как произведение масса и скорость, и поэтому вектор : он имеет величину и направление . Если вы стоите на коньки без трения, и вы бросаете мяч, вы двигаетесь назад: у вас есть импульс равны по величине, но напротив по направление к направлению движения мяча, поэтому общий импульс (ваш плюс импульс мяча) остается нулевым. Ракеты работают так же, путем выбрасывания материала на высокой скорости. они делают , а не работают, «отталкиваясь от воздуха», они работают толкать то, что они выталкивают, так же, как вы толкаете мяч вы бросаете, и это толкает вас назад, вызывая ваше ускорение.
Если вы все еще подозреваете, что действительно ракеты толкают против воздуха, помните, что они работают так же хорошо в космосе! На самом деле, было широко распространено мнение, когда Годдард, ранний американец ракетчик (его именем назван Центр космических полетов имени Годдарда) рассказывал о ракеты в космосе, он зря терял время. Цитата из New York Times Редакционная статья, написанная в 1921 году: « Профессор Годдард не знает отношения между действием и противодействием и необходимости есть что-то лучше, чем вакуум, против которого можно реагировать. Кажется, ему не хватает базовых знаний ежедневно в наших средних школах. ” Очевидно, редакционных писателей New York Times того времени не хватало базовых знаний, выложенных в этом курсе!
На самом деле, как мы обсуждали, сохранение импульса в столкновения следует из законов Ньютона. Однако это более общая и простая концепция — она не никак не зависят от деталей взаимодействий и т. д. Эта простота, очевидно, обратился к Эйнштейну, который был убежден, что когда динамика переформулируется в включают новые представления о времени и пространстве, закон сохранения импульса должен остаются верными в любой инерциальной системе отсчета . Как мы увидим, это привело его к некоторым неожиданным выводам.
Сохранение импульса на бильярдном столе
В качестве разминки рассмотрим сохранение импульса при столкновении двух шаров на бильярдном столе. Проводим мелом линию посередине бильярдный стол и бросайте шары рядом с мелом, но с противоположных сторон линии с обоих концов с одинаковой скоростью, поэтому они попадут в середину с скользящий удар, который повернет их скорости на небольшой угол. В других слова, если изначально мы говорим их (равная величина, противоположное направление) скорости были параллельны x -направление—мел линия – затем после при столкновении они также будут иметь равные и противоположно малые скорости в направлении 90 275 y 90 276 . (Скорости в направлении x уменьшатся очень незначительно).
Симметричное столкновение космического корабля
Теперь давайте повторим упражнение в большом масштабе. Предположим, где-то в космосе, вдали от гравитационные поля, мы натянули струну длиной в миллион миль. (Это может быть между нашими двумя часами в эксперимент с замедлением времени). Эта строка соответствует меловой линии на бильярдном столе. Допустим теперь у нас есть два одинаковых космических корабля сближаются с равными и противоположными скоростями параллельно струна с двух концов струны, направленная так, чтобы они слегка скользящее столкновение, когда они встречаются посередине. Это видно из симметрии ситуации этот импульс сохраняется в обоих направлениях. В частности, скорость, с которой один космический корабль удаляется от строка после столкновения — это y -скорость—равна и противоположно скорости, с которой другой удаляется от струны.
Но теперь представьте, что это столкновение наблюдал кто-то в один из космических кораблей, назовите его A . Перед столкновением он видит у окна очень быстро движущуюся струну, скажем, в нескольких метрах. После столкновения, он видит, что струна удаляется, скажем, на 15 метров в секунду. второй. Это потому, что космический корабль A набрал скорость перпендикулярно струне 15 м/с. второй. Между тем, поскольку это полностью симметричная ситуация, наблюдатель на космическом корабле B бы конечно сделать вывод, что ее космический корабль удалялся от струны на 15 метров в секунду так же.
Насколько он симметричен?
Ключевой вопрос: как быстро наблюдатель в космический корабль А видите космический корабль Б, удаляющийся от струны? Предположим, что относительно космического корабля A , космический корабль B удаляется (в направлении x ) на 0,6 c . Во-первых, напомним, что расстояния, перпендикулярные направление движения не лоренцево сокращение. Поэтому, когда наблюдатель на космическом корабле Б говорит, что она переместилась на 15 метров дальше от веревки за одну секунду интервал, наблюдатель, наблюдающий за этим движением с космического корабля A , будет согласен насчет 15 метров, но не соглашусь на одну секунду! Он скажет ее часы идут медленно, так что по его часам 1,25 секунды придется прошло 15 метров в y -направлении.
Отсюда следует, что в результате замедления времени этот столкновение, если смотреть с космического корабля А делает не причина равная и противоположные скорости для двух космических кораблей в y -направлении. Первоначально оба космических корабля двигались параллельно оси x было ноль импульс в направлении y . Так как мы можем утверждать, что общий импульс равен нулю в y -направлении после столкновение, когда одинаковые космические корабли , а не имеют равные и противоположные скорости?
Эйнштейн спасает сохранение импульса
Эйнштейн был так уверен, что сохранение импульса всегда должно считают, что он спас его смелой гипотезой: масса объекта должна зависит от его скорости! На самом деле масса должно увеличиваться со скоростью именно таким образом, чтобы компенсировать нижнее y -направление скорость в результате замедления времени. То есть, если покоящийся объект имеет массу m, двигаясь со скоростью v, он будет иметь инерцию, соответствующую «релятивистская масса» mотн=m/1−(v2/c2). Тогда импульс становится
                                               p→=mrelv→=mv→/1−(v2/c2).
Обратите внимание, что это релятивистское увеличение массы является необнаружимым небольшой эффект на обычных скоростях, но когда объект приближается к скорости свет, масса увеличивается без ограничений!
Реальная масса
Увеличивается ли со скоростью
Решение о том, что массы объектов должны зависеть от скорости, как это кажется высокой ценой за спасение сохранения импульса! Тем не менее, это прогноз, который не трудно проверить опытным путем. первое подтверждение пришло в 1908, отклоняющий быстрые электроны в вакуумной трубке. На самом деле, электроны в старом цвете Телевизионная трубка имеет примерно на полпроцента большую инерцию, чем покоящиеся электроны, и это необходимо учитывать при расчете магнитных полей, используемых для направления экран.
Гораздо важнее то, что в современных ускорителях частиц очень мощные электрические поля используются для ускорения электронов, протонов и других частицы. На практике обнаруживается, что эти частицы нуждаются во все больших и больших силах для дальнейшего ускорения по мере того, как приближается скорость света. Следовательно, скорость света является естественным абсолютным пределом скорости. Частицы разгоняются до скоростей, при которых их релятивистская масса в тысячи раз превышает их массу, измеренную в состоянии покоя, обычно называемая «массой покоя».
…Или?
На самом деле среди физиков продолжаются споры относительно этой концепции релятивистской массы. Спор во многом семантический: никто не сомневается в правильности выражение для импульса частицы с массой покоя m , движущейся со скоростью v→ , равно p→=m1−v2/c2v→. Но особенно физики элементарных частиц, многие из которые проводят свою жизнь, измеряя массы покоя частиц с большой точностью, не хочется писать это как p→=mrelv→. Им не нравится идея переменной масса. С одной стороны, это может дать такое впечатление, что по мере ускорения частица раздувается в размерах или, по крайней мере, ее внутренняя структура как-то видоизменяется. Фактически, релятивистская частица как раз подвергается лоренцеву сжатию вдоль направления движения, как и все остальное. Он переходит от сферической формы к диску подобная форма с одинаковым поперечным радиусом.
Как может эта «масса увеличить» понимать? По-прежнему, Эйнштейн был прав: он заметил, что каждая форма энергии обладает инерция. Сама кинетическая энергия имеет инерцию . Теперь «инерция» является определяющим свойством масса. Другое фундаментальное свойство масса заключается в том, что она притягивается гравитационно. Делает ли это кинетическая энергия? Чтобы увидеть ответ, рассмотрим сферу, заполненную газ. Он будет генерировать сферически симметричное гравитационное поле снаружи. сам по себе силой, пропорциональной общей массе. Если теперь нагреть газ, частицы газа будет иметь эту увеличенную (релятивистскую) массу, соответствующую их увеличенной кинетической энергии, а внешнее гравитационное поле увеличится пропорционально. (Никто не сомневается в этом либо. )
Итак, «релятивистская масса» действительно обладает двумя основными свойствами массы: инерцией и гравитационным Привлечение. (Как станет ясно в после лекций эта релятивистская масса есть не что иное, как полная энергия, при этом сама масса покоя теперь рассматривается как энергия.)
На более тривиальном уровне некоторые учителя возражают против введения относительной массы, потому что они опасаются, что студенты примут кинетическую энергию релятивистски движущаяся частица всего лишь 12mv→2, используя релятивистскую массу — это не так, как мы вскоре увидим.
Сноска : Для тех, кто может когда-нибудь перейти к более математически сложной обработки, следует добавить, что масса покоя играет важную роль как i nвариант при переходе от одного кадра ссылка на другой, но “ релятивистский Используемая здесь масса 90 276 — это всего лишь первая составляющая (энергия) четырехмерный вектор энергии-импульса частицы, поэтому , а не , является инвариантом.
Кинетическая энергия и масса очень быстрых частиц
Давайте подумаем о кинетической энергии одного из этих частицы, движущиеся со скоростью, близкой к скорости света. Вспомним, что в предыдущей лекции мы нашли кинетическая энергия обычной нерелятивистской (т.е. медленно движущейся) массы m составляла 12mv2. Мы сделали это, рассмотрев, как нам пришлось проделать большую работу, чтобы поднять его на определенную высоту: нам пришлось приложить силу, равную его весу W, чтобы поднять его на высоту h, при этом общая выполненная работа или затраченная энергия составляет сила х расстояние, Втч. Как это упал обратно, сила тяжести W совершила точно равную работу Wh над падающим объектом, но на этот раз работа пошел на ускорение объекта, чтобы дать ему кинетическую энергию. Поскольку мы знаем, как быстро падают падающие предметы, увеличив скорость, мы смогли сделать вывод, что кинетическая энергия равна 12 мВ2. (Подробности см. в предыдущей лекции.)
В более общем смысле мы могли бы ускорить массу любым постоянная сила F, и нашли работу, совершаемую силой (сила x расстояние), чтобы разогнать его до скорости v с места. Кинетическая энергия массы, E=12mv2, точно равна работе, совершаемой силой в доведении массы до этой скорости. (Аналогичным образом можно показать, что если сила приложена к Если частица уже движется со скоростью u, скажем, и разгоняется до скорости v, необходимая работа составляет 12mv2−12mu2. )
Интересно попробовать повторить упражнение частица, движущаяся очень близко к скорости света , подобно частицам в ускорители, упомянутые в предыдущем абзаце. Второй закон Ньютона в форме
Сила = скорость изменение импульса
по-прежнему верно, но близка к скорости света скорость изменяется незначительно, так как сила продолжает работать — вместо этого, масса увеличивается! Поэтому мы может писать в отличном приближении,
Сила = (коэффициент изменение массы) x c
, где, как обычно, c – скорость света. Чтобы получить более конкретную информацию, предположим, что у нас есть константа сила F, толкающая частицу. В какой-то момент частица имеет массу M и скорость, чрезвычайно близкую к c. Один секундой позже, так как сила продолжает действовать на частицу, и, таким образом, увеличить свой импульс в соответствии со вторым законом Ньютона, частица будет иметь массу, скажем, M + m, где m — увеличение массы в результате работа, совершаемая силой.
Каково увеличение кинетической энергии E частицы в течение этой одной секунды? период? По точной аналогии с рассмотренном выше нерелятивистском случае, это просто работа, совершаемая силой в тот период. Теперь, поскольку масса частицы изменяется на m за одну секунду, m также является 90 275 скоростью изменения 90 276 масса. Следовательно, из второго Ньютона Закон в форме
Сила = (скорость изменения массы) x c,
мы можем написать
Сила =mc.
Увеличение кинетической энергии E за период в одну секунду — это просто работа сила ,
E = сила x расстояние.
Поскольку частица движется практически со скоростью свет, расстояние сила действует в течение одной секунды просто с метров, с=3×108.
Таким образом, общая работа, которую сила совершает за эту секунду, равна силе x расстояние =mc×c=mc2.
Отсюда связь между увеличением массы релятивистской частицы и ее увеличение кинетической энергии составляет:
                                                             E=mc2.
Кинетическая энергия и масса медленных частиц
Вспомните это, чтобы получить Чтобы законы были верны во всех инерциальных системах отсчета, мы должны были предположить увеличение массы со скоростью в 1/1−(v2/c2). Это означает, что даже медленно движущийся объект имеет крошечное увеличение массы при движении!
Как это крошечное увеличение связано с кинетическим энергия? Рассмотрим массу M, движущуюся со скоростью v, намного меньше скорости света. Его кинетическая энергия E=12Mv2, как обсуждалось выше. Его масса равна M/1−(v2/c2), которую мы можем записать как M+m. Что м?
Поскольку мы говорим о скоростях, с которыми мы знакомы, например реактивный самолет, где v/c действительно мало, мы можем использовать некоторые простые математические трюки, чтобы упростить задачу.
Первое является хорошим приближением для квадратного корня из 1−x, когда x намного меньше единицы:
                                                 1−x≅1−12x для x≪1.
Вы можете легко проверить это с помощью своего калькулятора: попробуйте x=1100, вы найдете 99100=0,994987… что очень близко к 1−121100=0,9.95!
Следующее приближение:
                                                   11−x≅1+x для x≪1.
Это тоже легко проверить: снова возьмем x=1100: 11−х=199100=10099=1,01010…, и 1+х=101100=1,01.
Используя эти приближения с x=v/c, мы можем аппроксимировать 1−(v2/c2) как 1−12(v2/c2), а затем 1/(1−12(v2/c2)) как 1+12(v2/c2).
Это означает полную массу при скорости v
                                           M1−(v2/c2)≅M(1+12(v2/c2)),
и записывая это как M+m, мы видим, что увеличение массы m равно 12Mv2/c2.
Это означает, что снова масса увеличение m связано с кинетической энергией E соотношением E=mc2.
На самом деле это не сложно показать, используя немного исчисление, что во всем диапазоне скоростей от нуля до сколь угодно близкого до скорости света движущаяся частица испытывает увеличение массы, связанное с его кинетическая энергия через E=mc2. К понять, почему этого не замечают в повседневной жизни, попробуйте пример, такой как реактивный самолет массой 100 тонн, движущийся со скоростью 2000 миль в час. 100 тонн это 100000 кг, 2000 миль в час это около 1000 метров в секунду. Это кинетическая энергия 12Mv2 ½×10 ¹¹ Дж, но соответствующее изменение массы самолета уменьшается в c2, 9×1016 раз, что дает фактическое увеличение массы примерно на полмиллиграмма, что не так-то просто обнаружить!
E = mc ²
Выше мы видели, что когда сила совершает работу, ускоряя тело, чтобы сообщить ему кинетическую энергию, масса тела увеличивается на величину равна общей работе, выполненной силой, переданной энергии E, деленной на c2. Как насчет того, когда сила действует на тело это , а не ускоряет его, поэтому нет увеличения кинетики энергия? Например, что, если я просто подниму что-то с постоянной скоростью, придающее ему потенциальную энергию? Оказывается, и в этом случае есть увеличение массы, определяемое как E=mc2, конечно, неизмеримо малое для повседневного объекты.
Однако этот является измеримым и важным эффектом в ядерная физика. Например, гелий атом имеет ядро, в котором два протона и два нейтрона связаны друг с другом очень плотно сильной ядерной силой притяжения. Если приложена достаточная внешняя сила, это можно разделить на два ядра «тяжелого водорода», каждое из которых имеет один протон и один нейтрон. Для этого нужно затратить много внешней энергии. добиться этого разделения, и оказывается, что общая масса двух тяжелых ядер водорода составляет измеримо (около половины процента) тяжелее , чем исходное ядро гелия. Это дополнительное масса, умноженная на c2, равна энергии, необходимой для расщепления ядро гелия на два.