Энтропия это в термодинамике простыми словами: Энтропия? Это просто! / Хабр - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Энтропия? Это просто! / Хабр

Этот пост является вольным переводом ответа, который Mark Eichenlaub дал на вопрос What’s an intuitive way to understand entropy?, заданный на сайте Quora

Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.

Если в двух словах, то

Энтропия — это то, как много информации вам не известно о системе

Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна.

Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации.

Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём).

Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).

А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.

Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.

Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:

S = log Ω

Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B.

Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.

Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.

Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере.

Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях.

Величины, описывающие макросостояние, могут быть связаны друг с другом через так называемое «уравнение состояния». Именно наличие этой связи позволяет, не зная микросостояний, предсказывать, что будет с нашей системой, если начать её нагревать или перемещать поршень. Для идеального газа уравнение состояния имеет простой вид:

p = ρT

хотя вы, скорее всего, лучше знакомы с уравнением Клапейрона — Менделеева pV = νRT — это то же самое уравнение, только с добавлением пары констант, чтобы вас запутать. Чем больше микросостояний отвечают данному макросостоянию, то есть чем больше частиц входят в состав нашей системы, тем лучше уравнение состояния её описывают. Для газа характерные значения числа частиц равны числу Авогадро, то есть составляют порядка 10

23.

Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.

Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.

Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия.

Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.

Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.

Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад.

Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.

И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.

Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).

Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа.

Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?

Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.

Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.

Энтропия простыми словами с формулами

Понятие энтропии ввел Р. Клаузиус в 1865 г.

Энтропия – функция состояния

Для того чтобы выяснить в чем состоит физический смысл энтропии, рассмотрим изотермический процесс и приведенное количество теплоты в этом процессе на очень малом участке этого процесса -$\frac{\delta Q}{T}$, где $\delta Q$ – количество теплоты, которое получает тело, $T$ – температура тела.

Приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе:

$\oint {\frac{\delta Q}{T}=0\left( 1 \right).}$

Равенство нулю левой части выражения (1), который берут по замкнутому контуру, означает, что отношение δQ/T – это полный дифференциал некоторой функции состояния системы, которая не зависит от формы пути перехода системы из начального состояния в конечное.

Введем следующее обозначение:

$\frac{\delta Q}{T}=dS\left( 2 \right)$.

Определение 1

Энтропией ($S$) называют функцию состояния, дифференциал которой равен приведенному количеству тепла на малом участке термодинамического процесса, которое передано системе в этом процессе.

Для обратимых процессов изменение энтропии равно нулю:

$\Delta S=0\left( 3 \right)$.

Если выполняется необратимый процесс, то энтропия системы увеличивается:

$\Delta S$>$0\, \left( 4 \right)$.

Все реальные процессы являются необратимыми, поэтому в реальности энтропия изолированной системы способна только расти. Она становится максимальной в состоянии термодинамического равновесия.

Замечание 1

Формулы (3) и (4) выполняются только в том случае, если система замкнута. В том случае, если термодинамическая система может обмениваться теплом с внешней средой, то поведение энтропии может быть любым.

Готовые работы на аналогичную тему

Неравенство Клаузиуса

Выражения (3) и (4) объединяются в неравенство, которое называется неравенством Клаузиуса:

$\Delta S\ge \left( 5 \right)$. 2{\frac{dU+\delta A}{T}\left( 6 \right),} }$

где $dU$ – изменение внутренней энергии в рассматриваемом процессе; $\delta A$ – работа, выполняемая в этом процессе.

Выражение (6) способно определить энтропию с точностью до аддитивной константы. Это означает то, что физическим смыслом обладает не энтропия, а ее разность.

$S=\int\limits_{обр} {\frac{\delta Q}{T}+const\, \left( 7 \right).}$

Свойства энтропии

Замечание 2

Энтропия – аддитивная величина. Это означает, что энтропию системы можно найти как сумму энтропий тел, которые эту систему образуют.

Свойство аддитивности имеют:

масса;
внутренняя энергия;
количество теплоты.

Аддитивными не являются:

объем,
температура,
давление.

Определение 2

Термодинамический процесс, в котором энтропия остается постоянной, называется изоэнтропийным процессом.

Так, при обратимом адиабатном процессе мы имеем:

$\delta Q=0\to S=const. T {C_{p}\frac{dT}{T}}$ – вычисляют для обратимого изохорного процесса, при изменении температуры от 0К до $T$; $C_V$ – теплоемкость изохорного процесса; $C_p$ – теплоемкость при изобарном процессе; $S_{01 }=S(V,0)$ ; $S_{02 }=S(p,0).$

Статистический смысл энтропии

Допустим, что энтропия в обратимом процессе претерпевает изменения под воздействием внешних условий, которые оказывают влияние на систему. Механизм действия этих условий на энтропию можно сформулировать так:

Внешние условия определяют микросостояния, которые доступны системе, а также их количество.
В рамках доступных для системы микросостояний, она приходит в состояние равновесия.
Энтропия получает соответствующее значение. Получается, что величина энтропии идет за изменением внешних условий, принимая наибольшую величину, совместимую с внешними условиями.

Глубокий смысл энтропии раскрывается в статистической физике. Энтропия связана с термодинамической вероятностью состояния системы.

Определение 3

Термодинамическая вероятность ($W$) – количество способов, реализации данного состояния термодинамической системы. Или иначе, это число микросостояний, реализующих данное макросостояние.

Термодинамическая вероятность всегда больше или равна единице.

Энтропия системы и термодинамическая вероятность связаны между собой формулой Больцмана:

$S=k ln⁡(W) (10),$

где $k$ – постоянная Больцмана.

Формула (10) означает, что энтропия определена натуральным логарифмом количества микросостояний, которые реализуют рассматриваемое макросостояние.
Согласно формуле Больцмана, энтропия – это мера вероятности состояния термодинамической системы.
Говорят, что энтропия – мера беспорядка системы. Это статистическая интерпретация энтропии. Большее количество микросостояний, которое осуществляет макросостояние, соответствует большей энтропии.
Если система находится в состоянии термодинамического равновесия, что соответствует наиболее вероятному состоянию системы, количество микросостояний наибольшее, энтропия в этом случае максимальна.
Поскольку при необратимых процессах энтропия увеличивается, при статистическом толковании это значит, процессы в замкнутой системе проходят в направлении роста количества микросостояний. Это означает, что процессы идут от менее вероятных к более вероятным, до достижения вероятностью максимальной величины.

Замечание 3

Все статистические законы справедливы для систем, которые составлены из огромного количества частиц. Но эти законы могут нарушаться с небольшим числом частиц. Для систем с малым количеством частиц возможны флуктуации, это значит, что энтропия и термодинамическая вероятность состояний замкнутой системы на некотором временном отрезке могут убывать, а не расти или не изменяться.

«Как бы вы объяснили простыми словами, что такое энтропия?» – Яндекс.Кью

Если применительно к быту человека, “энтропия“, по сути, характеризует конкретность информации, или, можно сказать, является мерой неопределённости. Если мы знаем о чем то точно – то энтропия этого события низкая. Если же мы в чем то не уверены и у нас мало информации – энтропия высокая.

Впервые термин «энтропия» в 1865 году ввел немецкий физик Рудольф Клаузиус, для оценки меры необратимого рассеяния энергии. За эти полтора века понятие энтропии прочно закрепилось во всех языках и оказалось востребованным и удобным в теориях, как естественнонаучных, так и гуманитарных. А сейчас уже стало вполне универсальным, так как в целом, энтропия тесно связана с мерой и степенью неопределенности, хаоса, беспорядка в любой системе.

В естественных науках (физика, химия, биология, география…) это мера беспорядка системы, состоящей из большого количества отдельных элементов;

В математике — мера сложности объекта или процесса;

В экономике – энтропия – это количественный показатель беспорядка, мера излишней работы при достижении поставленной финансовой цели, доля неполезных побочных процессов или явлений, сопровождающих какую-либо деятельность (неэффективность хозяйственной деятельности, конкуренция и пр. )

В гуманитарных науках – в области психологии, и социологии выделяют энтропию личности:

неопределенность состояния личности в психологии – психическая энтропия – беспорядок сознания, когда наше внутреннее внимание, сосредоточенное на какой-то цели, перемешивается с разными мыслями, которые отвлекают нас от нашей цели.

социальную энтропию:

это мера отклонения социальной системы от эталонного состояния, когда отклонение проявляется в снижении уровня организации, эффективности функционирования, темпов развития системы, а значит и уровня жизни.

В теории информации — мера неопределённости какого-либо опыта, процесса или испытания, которые могут иметь разные исходы (по сути – мера количества недостающей информации)

что это простыми словами в жизни и физике

Понятие энтропии — одно из наиболее сложных и многогранных. Постараемся разобраться, что это такое.

Что такое энтропия

Понятие энтропии используется в различных областях знаний. Наиболее общее ее определение можно выразить следующим образом:

Энтропия — мера хаоса, беспорядка, степень неопределенности.

Впервые этот термин был использован немецким физиком Рудольфом Клаузиусом в 1865 году. Тогда он имел узкое значение одной из физических переменных.

Источник: pexels.com

Энтропия в термодинамике

Термодинамическая энтропия — физическая величина, которая описывает термодинамическую систему, термические явления и свойства макроскопических объектов.

Энтропия — это переменная, описывающая физическое состояние системы (обозначается буквой S).

Объяснить понятие энтропии можно на следующем примере. Представьте кусок горячего металла, чье тепло распространяется по окружающей среде. Также рядом с этим металлом витают пять молекул газа. Металл передаст пять квантов тепла. Значит ли это, что каждая молекула газа получит по одному кванту? Нет. Возможно, три молекулы получат по одному кванту, одна — два, а последняя — ни одного. Или двум молекулам перейдут два кванта, одной — один, а две другие не получат ни одной. Вариантов развития событий в таком случае 126.

Каждая из возможных комбинаций называется микросостоянием, а общий уровень энергии — макросостоянием. Тогда энтропия — значение числа способов, мера вероятностей распределения энергии между молекулами в системе.

Формулировка закона энтропии в термодинамике

Исходным положением термодинамики является постулат о равновесии, суть которого заключается в том, что любая изолированная система со временем приходит в состояние термодинамического равновесия и самопроизвольно выйти из него не может.

Второй закон термодинамики связан с понятием энтропии. Он говорит о том, что энтропия Вселенной возрастает.

Есть два классических определения второго закона:

Кельвина и Планка. Нет циклического процесса, который мог бы извлекать количество теплоты при определенной температуре и полностью превращает эту теплоту в работу.
Клаузиуса. Нет процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому.

Оба определения основываются на первом законе термодинамики, согласно которому энергия убывает.

Можно сделать следующие выводы:

100% энергии не может быть преобразовано в работу;
энтропия может быть выработана, но не может быть уничтожена.

Энтропия в экономике

В экономике понятие энтропии объясняет непредвиденное развитие рынка. То есть экономическая цель не достигнута по причине того, что система оказалось неупорядоченной, неинформативной и так далее.

Энтропия — количественный показатель беспорядка, мера излишне выполненной работы для достижения цели, доля побочных явлений и процесс какой-либо деятельности.

Движение денег в экономике происходит ассиметрично. Также если предположить, что деньги являются аналогом энергии, то второй закон термодинамики можно адаптировать следующим образом: не существует такой экономической системы, единственным итогом деятельности которой будет переход денег от рынка производителей к рынку потребителей.

Общая формула для экономической энтропии выглядит так:

$dS = d Financial Resources / Price For The Resources $

Энтропия в коммуникации

Понятие энтропии в коммуникации тесно связано с шумами. Шумы в коммуникации преодолеваются либо через многократное повторение одного и того же сообщения, либо через дублирование его через другие каналы связи.

Энтропия — информационная неопределенность в системе.

Информация — противоположность энтропии, возможность уменьшения беспорядка. То есть чем более информации содержит система, тем более она является упорядоченной.

Источник: pexels.com

Примеры энтропии в разных сферах жизни

Рассмотрим данное понятие на примерах из жизни.

Представьте, что у вашего друга в руках десять игральных кубиков. Он их бросил и сказал вам, что сумма всех выпавших чисел равна 30. Но вы не знаете, какие конкретно числа ему выпали. Именно этой информации вам не хватает.

Тогда общая сумма в этом случае будет макросостоянием, а возможные комбинации чисел — микросостоянием. Для данной ситуации существует 2 930 455 микросостояний.

Частично снять вашу энтропию друг сможет, если сообщит, например, что сумма первой половины чисел равна 17, а второй — 13. Для первой половины есть 720 возможных комбинаций, а для второй — 420. Тогда для всего макросостояния существует 327 600 вариантов.

Как пример системы, увеличивающей энтропию, можно рассмотреть шкаф. Вы аккуратно сложили в него вещи, то есть упорядочили систему. Но даже если шкаф будет закрыт на долгие годы, одежда начнет разлагаться. То есть система будет увеличивать показатель своей энтропии.

Если нужна работа, связанная с понятием энтропии, или по какой-либо другой теме, обращайтесь в ФениксХелп.

Энтропия что это такое простыми словами

Простыми словами про энтропию можно сказать так:энтропия-это беспорядок,хаос.Но это очень грубо,просто неграмотно.Поэтому надо всё-таки надо поднапрячься и разобраться посеръёзней.

Обратимся ко второму началу термодинамики.Оно утверждает:

В изолированной системе самопроизвольно могут протекать только такие процессы,которые ведут к увеличению неупорядоченности системы,т.е.к росту энтропии.

И это подтверждает,что энтропия-хаос.Но есть нюансы.Совершенно строго энтропия была введена в термодинамике как функция состояния системы S,изменение которой определяется отношением количества теплоты Q,полученной (или отданной) системой при температуре T, к этой температуре:

S=Q/T

Если изолированная система получает некоторое количество теплоты при постоянной температуре,то вся теплота идёт на увеличение беспорядочного,хаотичного движения частиц,то есть на увеличение энтропии. Так происходит при плавлении вещества или при его испарении,например при кипении(лёд плавится и вода и кипит при постоянной температуре).Наоборот,порядок увеличивается,например при кристаллизации(замерзании) жидкости,энтропия системы уменьшается и выделяется скрытая теплота плавления.

В газе,где частицы движутся независимо,неупорядоченность гораздо больше,чем в кристалле.Жидкость занимает промежуточное положение.Соответственно,и энтропия вещества в газообразном состоянии больше,чем в жидком,а в жидком больше,чем в твердом.

При обсуждении химических проблем удобно пользоваться определением энтропии,данном Больцманом.

Энтропия ( S ) пропорциональна логарифму термодинамической вероятности ( W ) состояния системы: S = k lnW,

где k — постоянная Больцмана,а термодинамическая вероятность W определяется числом микросостояний,которыми может осуществляться рассматриваемое (макро)состояние.

Вот простой пример соотношения макро- и микросостояния системы. Система-кинозал с 10 рядами по 10 кресел и 100 зрителей.Для наилучшего обзора экрана зрители должны быть рассажены строго по росту с первого по 100 место.Это единственное микросостояние.Если рассадить зрителей по росту в только колонках,то число микросостояний будет равно числу сочетаний из 100 по 10,что составляет 10¹³

Но если зрители будут рассаживаться произвольно,число микростояний будет равно 100! и это будет самая неупорядоченная система.

В химии же системы такие,что число частиц очень велико.Например,один моль составляет 6·10²³

частиц и число микросостояний становится невообразимо большим.

Увеличение энтропии означает возможность самопроизвольного протекания таких процессов,как диффузия газов и жидкостей,любой процесс растворения,осмос.

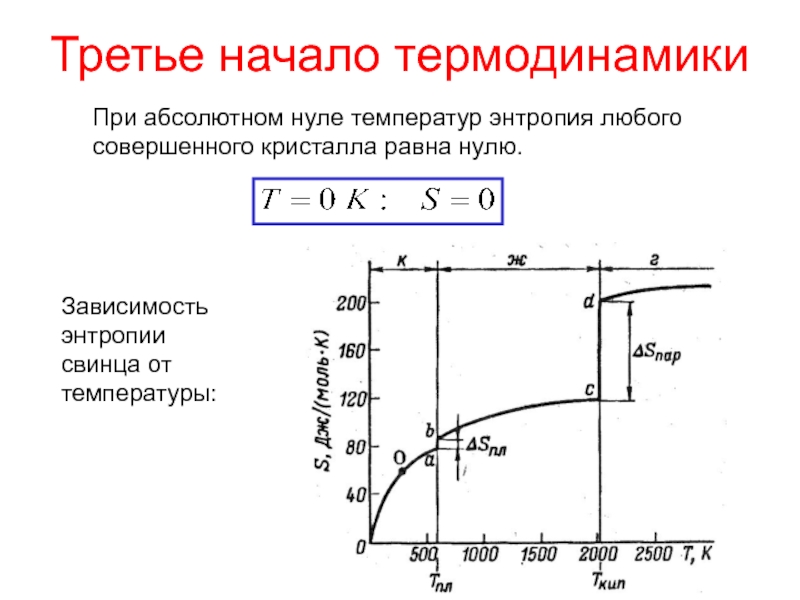
Второе начало термодинамики говорит только о направлении изменения энтропии в процессе,но ничего не говорит об абсолютном значении энтропии.В 19 столетии путем экспериментов были установлены температурные зависимости энтропии для газов и жидкостей при фазовых переходах. При понижении температуры энтропия медленно уменьшается,а при конденсации газа и при кристаллизации жидкости уменьшается резко, скачком.

В 1911 году М.Планк постулировал:

Для идеального кристалла при стремлении температуры к абсолютному нулю,энтропия также стремится к нулю.

Третье начало термодинамики гласит:

Энтропия идеального кристалла при 0 K равна нулю.

Таким образом,значения энтропии отсчитываются от нуля и могут быть найдены для любого состояния вещества и любых условий.

Энтропия измеряется в единицах Дж/K и относится к определённому количеству вещества,обычно к 1 моль.Для веществ в одинаковых состояниях энтропия увеличивается с ростом молярной массы.

Значения энтропии для некоторых веществ при обычной температуре.

Таким образом,появилась ещё одна характеристика химической реакции-изменение энтропии и ещё один критерий-стремление системы к максимуму энтропии.

Итак,ещё раз,энтропия простыми словами-это функция состояния системы (системой может быть простое вещество).

Что такое энтропия простыми словами. Энтропия – что это такое: объяснение термина простыми словами

Довольно быстро вы поймете, что ничего у вас не получится, но не расстраивайтесь: вы не собрали кубик Рубика, зато проиллюстрировали второе начало термодинамики:

Энтропия изолированной системы не может уменьшаться.

Героиня фильма Вуди Аллена Whatever Works дает такое определение энтропии: это из-за чего тяжело засунуть обратно в тюбик зубную пасту. Она еще интересно объясняет принцип неопределенности Гейзенберга, еще один повод посмотреть фильм.

Энтропия – это мера беспорядка, хаоса. Вы пригласили друзей на новогоднюю вечеринку, прибрались, помыли пол, разложили на столе закуску, расставили напитки. Одним словом, все упорядочили и устранили столько хаоса, сколько смогли. Это система с маленькой энтропией.

Вы все, наверное, представляете, что происходит с квартирой, если вечеринка удалась: полный хаос. Зато у вас утром есть в распоряжении система с большой энтропией.

Для того, чтобы привести квартиру в порядок, надо прибраться, то есть потратить на это много энергии. Энтропия системы уменьшилась, но никакого противоречия со вторым началом термодинамики нет – вы же добавили энергию извне, и эта система уже не изолированная.

Неравный бой

Один из вариантов конца света – тепловая смерть Вселенной вследствие второго начала термодинамики. Энтропия вселенной достигнет своего максимума и ничего в ней больше происходить не будет.

В общем случае звучит все довольно уныло: в природе все упорядоченные вещи стремятся к разрушению, к хаосу. Но откуда тогда на Земле жизнь? Все живые организмы невероятно сложные и упорядоченные и каким-то образом всю свою жизнь борются с энтропией (хотя в конце концов она всегда побеждает).

Все очень просто. Живые организмы в процессе жизнедеятельности перераспределяют энтропию вокруг себя, то есть отдают свою энтропию всему, чему только могут. Например, когда мы едим бутерброд, то красивый упорядоченный хлеб с маслом мы превращаем известно во что. Получается, что свою энтропию мы отдали бутерброду, а в общей системе энтропия не уменьшилась.

А если взять Землю в целом, то она вообще не является замкнутой системой: Солнце снабжает нас энергией на борьбу с энтропией.

Энтропия – это мера усложнения системы. Не беспорядка, а усложнения и развития. Чем больше энтропия, тем труднее понять логику этой конкретной системы, ситуации, явления. Принято считать, что чем больше проходит времени, тем менее упорядоченной становится Вселенная. Причина этого – неравномерная скорость развития Вселенной в целом и нас, как наблюдателей энтропии. Мы, как наблюдатели, являемся на огромное число порядков проще Вселенной. Поэтому она кажется нам чрезмерно избыточной, мы не в состоянии понять большинство причинно-следственных связей, её составляющих. Важен и психологический аспект – людям трудно свыкнуться с тем, что они не уникальны. Поймите, тезис о том, что люди – венец эволюции, недалеко ушёл от более раннего убеждения в том, что Земля является центром мироздания. Человеку приятно верить в свою исключительность и неудивительно, что структуры, которые сложнее нас, мы склонны видеть беспорядочными и хаотическими.

Выше есть очень хорошие ответы, объясняющие энтропию, исходя из современной научной парадигмы. На простых примерах отвечающие объясняют это явление. Разбросанные по комнате носки, разбитые стаканы, игра обезьян в шахматы и т.д. Но если приглядеться, то понимаешь – порядок здесь выражается в истинно человеческом представлении. К доброй половине таких примеров применимо слово “лучше”. Лучше сложенные в шкафу носки, чем разбросанные носки на полу. Лучше целый стакан, чем стакан разбитый. Тетрадь, написанная красивым почерком лучше тетради с кляксами. В человеческой логике непонятно, что делать с энтропией. Дым, вылетающий из трубки не утилитарен. Разорванная на мелкие кусочки книга бесполезна. Из многоголосого говора и шума в метро трудно выудить хотя бы минимум информации. В этом смысле очень интересным будет вернуться к определению энтропии, введённому физиком и математиком Рудольфом Клаузиусом, видевшему это явление, как меру необратимого рассеяния энергии. От кого уходит эта энергия? Кому становится труднее ей воспользоваться? Да человеку же! Пролитую воду очень трудно (если не невозможно) всю, до капли снова собрать в стакан. Чтобы починить старую одежду, нужно воспользоваться новым материалом (тканью, нитками и т.д.). При этом не учитывается смысл, который данная энтропия может нести не для людей. Приведу пример, когда рассеяние энергии для нас будет нести прямо противоположный смысл для другой системы:

Вы знаете, что ежесекундно огромное количество информации с нашей планеты улетает в космос. Например, в виде радиоволн. Для нас эта информация кажется абсолютно потерянной. Но если на пути радиоволн окажется достаточно развитая инопланетная цивилизация, её представители могут принять и расшифровать часть этой потерянной для нас энергии. Услышать и понять наши голоса, увидеть наши телевизионные и радио передачи, подключиться к нашему интернет-траффику))). В таком случае, нашу энтропию могут упорядочить другие разумные существа. И чем больше рассеяние энергии будет для нас, тем больше энергии смогут собрать они.

Энтропия – термин, который используется не только в точных науках, но и в гуманитарных. В общем случае – это мера хаотичности, неупорядоченности некоторой системы.

Как известно, человечество всегда стремилось к тому, чтобы переложить как можно больше работы на плечи машинам и механизмам, используя для этого как можно меньше ресурсов. Упоминания о вечном двигателе впервые обнаружены в арабских рукописях XVI в. С тех пор было предложено немало конструкций для потенциально вечного двигателя. Вскоре, после множества неудачных экспериментов, ученые поняли некоторые особенности природы, которые впоследствии определили основы термодинамики.

Рисунок вечного двигателя

Первое начало термодинамики говорит следующее: для выполнения работы термодинамической системой потребуется либо внутренняя энергия системы, либо внешняя энергия из дополнительных источников. Это утверждение является термодинамическим законом сохранения энергии и запрещает существование вечного двигателя первого рода – системы, совершающей работу без затрачивания энергии. Механизм одного из таких двигателей основывался на внутренней энергии тела, которая может перейти в работу. К примеру, это может происходить за счет расширения. Но человечеству неизвестны тела либо системы, которые могут бесконечно расширяться, а значит рано или поздно их внутренняя энергия закончится и двигатель остановится.

Несколько позже появился так называемый вечный двигатель второго рода, который не перечил закону сохранения энергии, и основывался на механизме передачи тепла, требуемого для работы, окружающими телами. В пример брали океан, охлаждая который, предположительно, можно было бы получить внушительный запас тепла. Однако, в 1865-м году немецкий ученый, математик и физик Р. Клаузиус определил второе начало термодинамики: «повторяющийся процесс не может существовать, если в результате произойдет лишь передача тепла от менее нагретого тела к более нагретому, и только». Позднее он ввел понятие энтропии — некоторой функции, изменение которой равно отношению количества переданного тепла к температуре.

После чего альтернативой второму началу термодинамики стал закон неубывания энтропии: «в замкнутой системе энтропия не уменьшается».

Простыми словами

Так как энтропия имеет место быть в самых различных областях деятельности человека, ее определение является несколько расплывчатым. Однако на простейших примерах можно понять суть этой величины. Энтропия – это степень беспорядка, другими словами – неопределенности, неупорядоченности. Тогда система из разбросанных клочьев бумаги на улице, которые еще периодически подбрасывает ветер, имеет высокую энтропию. А система из сложенных в стопку бумаг на рабочем столе имеет минимальную энтропию. Чтобы понизить энтропию в системе с клочьями бумаги, Вам придется затратить немало времени и энергии на склеивание клочков бумаги в полноценные листы, и складывание их в стопку.

В случае с закрытой системой так же все просто. К примеру, Ваши вещи в закрытом шкафу. Если Вы не будете действовать на них извне, то вещи долгое время будут, вроде бы, сохранять свое значение энтропии. Но рано или поздно они разложатся. Например, шерстяной носок будет разлагаться до пяти лет, а вот кожаной обуви потребуется около сорока лет. В описанном случае шкаф – изолированная система, а разложение вещей – переход от упорядоченных структур к хаосу.

Подводя итоги, следует отметить, что минимальная энтропия наблюдается у разнообразных макроскопических объектов (тех, которые можно наблюдать невооруженным глазом), имеющих определенную структуру, а максимальная — у вакуума.

Энтропия Вселенной

В результате возникновения такого понятия как энтропия появилось множество других утверждений и физических определений, которые позволили подробнее описать законы природы. Одним из них есть такое понятие как «обратимые/необратимые процессы». К первым относят процессы, энтропия системы которых не возрастает и остается постоянной. Необратимые – такие процессы, в замкнутой системе которых энтропия растет. Вернуть замкнутую систему в состояние до процесса невозможно, т.к. в таком случае энтропия должна была бы понижаться.

По мнению Клаузиуса, необратимым процессом является существование Вселенной, в конце которого ее ждет так называемая «Тепловая смерть», иначе – термодинамическое равновесие, существующее для закрытых систем. То есть энтропия достигнет максимального показателя, а все процессы просто затухнут. Но, как вскоре оказалось, Рудольф Клаузиус не учитывал силы гравитации, которые присутствуют повсеместно во Вселенной. К примеру, благодаря ним распределение частиц при максимальной энтропии не обязано быть однородным.

Также к другим недостаткам теории о «тепловой смерти Вселенной» можно отнести тот факт, что нам неизвестно действительно ли она конечна, и можно ли к ней применить понятие «замкнутая система». Стоит учитывать и то, что состояние максимальной энтропии, как собственно и абсолютный вакуум – такие же теоретические понятия, как и идеальный газ. Это означает, что в реальности энтропия не будет достигать максимального значения, из-за различных случайных отклонений.

Примечательно то, что видимая в своем объеме сохраняет значение энтропии. Причиной тому служит уже известный для многих феномен – Вселенной. Это интересное совпадение в очередной раз доказывает человечеству то, что в природе ничего не происходит просто так. Согласно подсчетам ученых, по порядку величины значение энтропии равняется количеству существующих фотонов.

Словом «хаос» называют изначальное состояние Вселенной. В этот момент она представляла собой лишь не имеющую форму совокупность пространства и материи.
Согласно исследованиям одних ученых, наибольшим источником энтропии являются сверхмассивные . Но другие считают, что благодаря мощным гравитационным силам, притягивающим все к массивному телу, мера хаоса передается в окружающее пространство в незначительном количестве.
Интересно то, что жизнь и эволюция человека направлены в противоположную сторону от хаоса. Ученые утверждают, что это возможно из-за того, что на протяжении своей жизни человек, как и другие живые организмы, принимает на себя меньшее значение энтропии, нежели отдает в окружающую среду.

Введение 4

Понятие энтропии 5

Измерение энтропии 8

Понятия и примеры возрастания энтропии 9

Заключение 13

Список литературы 14

Введение

Естествознание – это раздел науки основанный на воспроизводимой эмпирической проверке гипотез и создании теорий или эмпирических обобщений, описывающих природные явления.

Предмет естествознания – факты и явления, воспринимаемые нашими органами чувств. Задача ученого обобщить эти факты и создать теоретическую модель изучаемого явления природы включающую законы управляющие им. Явления, например, закон всемирного тяготения, даются нам в опыте; один из законов науки – закон всемирного тяготения, представляет собой варианты объяснения этих явлений. Факты, будучи установлены, сохраняют свою актуальность всегда, законы могут быть пересмотрены или скорректированы в соответствии с новыми данными или новой концепцией их объясняющей. Факты действительности являются необходимой составляющей научного исследования.

Основной принцип естествознания гласит 1: знания о природе должны допускать эмпирическую проверку. Это не означает, что научная теория должна немедленно подтверждаться, но каждое ее положение должно быть таким, чтобы такая проверка была возможна в принципе.

От технических наук естествознание отличает то, что оно преимущественно направлено не на преобразование мира, а на его познание. От математики естествознание отличает то, что оно исследует природные, а не знаковые системы. Попробовать связать естествознание, технические и математическую науки попробуем с помощью понятия – «энтропия».

Таким образом, целью данной работы является рассмотрение и решение следующих задач:

Понятие энтропии;

Измерение энтропии;

Понятия и примеры возрастания энтропии.

Понятие энтропии

Понятие энтропии было введено Р. Клаузиусом 2 , сформулировавшим второе начало термодинамики, согласно которому переход теплоты от более холодного тела к более теплому не может происходить без затраты внешней работы.

Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла ΔQ к величине абсолютной температуры T:

Рудольф Клаузиус дал величине S имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование).

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

где dS – приращение (дифференциал) энтропии, а δQ – бесконечно малое приращение количества теплоты.

Заметим, что энтропия является функцией состояния, поэтому в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты являетсяфункцией процесса, в котором эта теплота была передана, поэтому δQ ни в коем случае нельзя считать полным дифференциалом.

Энтропия, таким образом, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамикипозволяет определить её точно: при этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.

Энтропия – это количественная мера той теплоты, которая не переходит в работу.

S 2 -S 1 =ΔS=

Или, другими словами, энтропия – мера рассеивания свободной энергии. А ведь нам уже известно, что любая открытая термодинамическая система в стационарном состоянии стремится к минимальному рассеиванию свободной энергии. Поэтому если в силу причин система отклонилась от стационарного состояния, то вследствие стремления системы к минимальной энтропии, в ней возникают внутренние изменения, возвращающие ее в стационарное состояние.

Как видно из выше написанного, энтропия характеризует определенную направленность процесса в замкнутой системе. В соответствии со вторым началом термодинамики 3 возрастанию энтропии соответствует направление теплового потока от более горячего тела к менее горячему. Непрерывное возрастание энтропии в замкнутой системе происходит до тех пор, пока температура не выровняется по всему объему системы. Наступает, как говорят, термодинамическое равновесие системы, при котором исчезают направленные тепловые потоки и система становится однородной.

Абсолютное значение энтропии зависит от целого ряда физических параметров. При фиксированном объеме энтропия увеличивается с увеличением температуры системы, а при фиксированной температуре увеличивается с увеличением объема и уменьшением давления. Нагревание системы сопровождается фазовыми превращениями и снижением степени упорядоченности системы, поскольку твердое тело переходит в жидкость, а жидкость превращается в газ. При охлаждении вещества происходит обратный процесс, упорядоченность системы возрастает. Эта упорядоченность проявляется в том, что молекулы вещества занимают все более определенное положение относительно друг друга. В твердом теле их положение фиксировано структурой кристаллической решетки.

Другими словами – энтропия выступает мерой хаоса 4 (споры определения которого ведутся уже давно).

Все процессы в природе протекают в направлении увеличения энтропии. Термодинамическому равновесию системы соответствует состояние с максимумом энтропии. Равновесие, которому соответствует максимум энтропии, называется абсолютно устойчивым. Таким образом, увеличение энтропии системы означает переход в состояние, имеющее большую вероятность. То есть энтропия характеризует вероятность, с которой устанавливается то или иное состояние, и является мерой хаотичности или необратимости. Это мера хаоса в расположении атомов, фотонов, электронов и других частиц. Чем больше порядка, тем меньше энтропия. Чем больше информации поступает в систему, тем система более организована, и тем меньше её энтропия:

(По теории Шеннона 5)

Энтропия – что это такое простыми словами в химии, физике и каков ее коэффициент

Понятие энтропии используется в различных науках: физике, химии, математике, биологии, социологии. Само слово произошло от греческого и обозначает «превращение, изменение». Что это такое простыми словами? Можно сказать, что это мера беспорядка, хаотичности в любой системе. Чем меньше порядка, тем больше ее значение. Если книги стоят на полке, неупорядоченность у них меньше, чем если они лежат кучей.

Что означает термин

Определение данного термина зависит от сферы его применения. В общих словах можно сказать, что это мера беспорядка и необратимого рассеяния энергии. Чем более упорядочена какая-то система, тем энергия более сконцентрирована. Например, если мы поместим горячий предмет в холодную воду, постепенно он остынет, а вода нагреется. Во втором случае энтропия больше.

Важно! Энтропия характеризует беспорядок. Чем она больше, тем меньше система упорядочена.

В качестве системы может выступать что угодно. В физике или химии это обычно газ, жидкость, твердое тело, набор определенного числа частиц. В информатике это может быть текст, в социологии группа людей.

Термин энтропия

В физике

Этот термин используется в таких разделах физики, как термодинамика и статистическая физика. Термодинамика изучает способы передачи и превращения энергии. Она имеет дело с процессами, в которых можно использовать понятие температуры. Именно в термодинамике впервые начали использовать это понятие. Ввел его немецкий ученый Рудольф Клаузиус. Статистическая механика изучает поведение систем из конечного количества частиц, используя для этого методы теории вероятности.

В разных разделах физики этот термин означает несколько разные вещи. В термодинамике это характеристика необратимого рассеяния энергии. В статистической физике эта величина показывает вероятность какого-то состояния.

Это интересно! В чем заключается принцип теории Гюйгенса Френеля

В термодинамике

Энтропия — единственная величина, показывающая направление физических процессов. Что это значит?

В изолированной системе, то есть той, которая не обменивается ни веществом, ни энергией с окружающими предметами, процессы всегда идут так, что неупорядоченность увеличивается. Достигнув максимума, она остается постоянной. В этом суть второго начала термодинамики.
Обратимые процессы не меняют неупорядоченность.
Необратимые процессы всегда идут так, что беспорядок увеличивается.
В открытой системе эта величина может возрастать или оставаться постоянной, возможны и такие процессы, при которых беспорядок уменьшается. То есть вмешательством извне мы можем уменьшить неупорядоченность.

Всякая система, находящаяся в неизменных внешних условиях, со временем приходит в состояние равновесия и не может самостоятельно из него выйти. При этом все ее части будут иметь одинаковую температуру. Это нулевое начало термодинамики.

В равновесии беспорядок больше всего. Например, есть сосуд, разделенный перегородкой. С одной стороны находится один газ, с другой — другой. Если убрать перегородку, постепенно газы смешаются и самостоятельно уже не разделятся снова. Такое состояние будет более беспорядочным, чем состояние, когда газы были разделены.

В физике эта величина — функция состояния системы. Это значит, что она зависит от параметров системы:

температуры;
давления;
объема;
внутренней энергии.

Это интересно! Формула закона полного отражения и преломления света

В статистической механике

В статистической механике это понятие связано с вероятностью получить определенное состояние. Например, для нескольких предметов или частиц она зависит от числа способов их расположить.

Есть несколько определений этой величины. Наиболее простое определение Больцамана. Она равна логарифму вероятности состояния, умноженному на постоянную Больцмана: S=k*ln(W).

Полезное видео: что такое энтропия

Абсолютное значение

Энтропия — величина неотрицательная (больше или равна нулю). Чем ближе температура к абсолютному нулю, тем она тоже ближе к нулю. Это третье начало термодинамики. В первоначальном виде его сформулировал Макс Планк в 1911 году.

Также третье начало термодинамики называют принципом недостижимости абсолютного нуля. Это значит, что при любых процессах, связанных с изменением неупорядоченности, невозможно достигнуть абсолютного нуля (0К, или -273,15 С). Можно только бесконечно приближаться к этой температуре. Ученые договорились, что при 0 К неупорядоченность равна 0.

Важно! Абсолютное значение неупорядоченности можно посчитать как изменение энергии при данной температуре.

В термодинамике обычно не имеет значения абсолютная величина, важно только ее изменение. Однако можно найти и абсолютное значение. Оно вычисляется по разным формулам для твердого, жидкого и газообразного состояния вещества. Эта величина измеряется в Дж/К или Дж/градус, то есть в тех же единицах, что и теплоемкость. Удобно поделить эту величину на массу или количество моль вещества. Поэтому используют единицы Дж/(моль*К) или Дж/(моль*градус) в зависимости от того, в чем измеряется температура — в кельвинах или градусах.

Это интересно! Формулировки законов Исаака Ньютона: кратко и понятно

В химии

Что такое, к примеру, энтропия в химии? Это понятие применяется в химической термодинамике. Здесь важно изменение этой величины. Если оно положительно, то и система становится менее упорядоченной. Знать это важно для определения направления химических реакций и изменения химического равновесия. Этот термин связан с понятием энтальпии — энергии, которую можно превратить в тепло при определенном постоянном давлении.

По изменению неупорядоченности можно определить, может ли реакция протекать самопроизвольно. Этого нельзя сделать только по изменению энергии, так как существуют и реакции, протекающие с поглощением тепла, и реакции, протекающие с его выделением. Согласно второму началу термодинамики, состояние с наибольшей неупорядоченностью — это наиболее устойчивое состояние замкнутой системы. Также любая замкнутая система стремится к наименее упорядоченному состоянию. Поэтому при самопроизвольных процессах беспорядок возрастает.

Это интересно! Квантовые постулаты Нильса Бора: кратко об основных положениях

В теории информации

Информационная энтропия характеризует непредсказуемость какой-либо системы. Например, это может быть вероятность появления какого-то символа из алфавита в тексте. При этом эта функция равна количеству информации, которое приходится на один символ. Клод Шеннон — ученый, который ввел этот термин в теории информации, — даже сначала хотел называть эту величину информацией.

Шеннон предположил, что, увеличивая количество информации, мы уменьшаем неопределенность. Упорядочивая систему, мы также уменьшаем неопределенность.

Важно! Чем более предсказуемо какое-то событие, тем оно менее информативно, и тем меньше беспорядок.

С помощью этой неопределенности можно предсказывать события, например, исход какого-то эксперимента. Для этого события делят на отдельные части и считают неопределенность для них.

Информационная энтропия связана с числом доступных состояний. Чем это число больше, тем она больше. Например, если мы будем играть в шахматы по правилам, для шахматной доски эта величина будет меньше, чем если переставлять фигуры хаотически. Неопределенность для монетки, которая может упасть только на одну или другую сторону, меньше, чем у игральной кости с 6 гранями, а у кости с 20 гранями эта величина еще больше.

Существует также энтропия языка. Это понятие обозначает количество информации на единицу текста на этом языке (одни символ) и измеряется в битах на букву. Для разных языков она разная.

В языке одни символы появляются чаще, другие реже, также есть определенные часто встречающиеся сочетания символов. Проводя анализ вероятности появления того или иного символа, можно декодировать зашифрованный текст. Информационная неупорядоченность также помогает устанавливать необходимую пропускную способность каналов для передачи зашифрованных сообщений.

Для анализа данных в самых разных сферах, от медицины до социологии, используется информационно-энтропийный анализ. Простыми словами можно сказать, что, анализируя увеличение или уменьшение беспорядка, можно установить связи между явлениями.

Понятие «информационная энтропия» используется также в математической статистике и статистической физике. Эти науки также имеют дело с вероятностью различных состояний и используют методы теории вероятности.

Это интересно! Какие бывают системы отсчета в физике и что это такое

В экономике

В экономике используется понятие «коэффициент энтропии». Он связан с концентрацией продавцов на рынке. Чем больше концентрация, тем меньше этот коэффициент, или индекс. Он зависит от распределения долей между фирмами на рынке, и чем больше разница в величине этих долей, тем больше и коэффициент энтропии.

Если поделить этот индекс на количество фирм на рынке, получится относительный показатель. Он обозначается буквой Е. Его значение находится между 0 и 1. Значение Е=0 соответствует монополии, а Е=1 — совершенной конкуренции.

Что говорит википедия

В википедии можно найти разные определения этого понятия. Самое общее — это мера необратимого рассеяния энергии, отклонения реального процесса от идеального. Также в википедии можно найти:

статьи об этом термине в классической термодинамике;
в биологической экологии;
энтропию Вселенной;
языка;
дифференциальную;
топологическую;
информационную.

Полезное видео: представление об энтропии

Заключение

Термин «энтропия» впервые был использован в термодинамике Рудольфом Клаузиусом. Из физики он пришел и в другие науки. Это понятие обозначает неупорядоченность, хаотичность, непредсказуемость и тесно связано с вероятностью. Энтропийный анализ помогает изучать данные и находить связи между явлениями, определять направления физических и химических процессов.

Вконтакте

Одноклассники

Facebook

Мой мир

Twitter

Энтропия и второй закон термодинамики: беспорядок и недоступность энергии

Цели обучения

К концу этого раздела вы сможете:

Определите энтропию.
Вычислить увеличение энтропии в системе с обратимыми и необратимыми процессами.
Объясните ожидаемую судьбу Вселенной в энтропийных терминах.
Вычислить нарастающий беспорядок в системе.

Рисунок 1.Лед в этом напитке медленно тает. В конце концов жидкость достигнет теплового равновесия, как предсказывает второй закон термодинамики. (Источник: Джон Салливан, PDPhoto.org)

Есть еще один способ выразить второй закон термодинамики. Эта версия относится к концепции под названием энтропия . Изучив его, мы увидим, что направления, связанные со вторым законом – например, теплопередача от горячего к холодному – связаны с природной тенденцией к тому, что системы становятся неупорядоченными и меньше энергии доступно для использования в качестве работы.Фактически можно показать, что энтропия системы является мерой ее беспорядка и недоступности энергии для выполнения работы.

Установление связей: энтропия, энергия и работа

Напомним, что простое определение энергии – это способность выполнять работу. Энтропия – это мера того, сколько энергии недоступно для выполнения работы. Хотя все формы энергии взаимопревращаемы, и все они могут быть использованы для работы, не всегда возможно, даже в принципе, преобразовать всю доступную энергию в работу.Эта недоступная энергия представляет интерес для термодинамики, потому что область термодинамики возникла из попыток преобразовать тепло в работу.

Мы можем увидеть, как определяется энтропия, вспомнив наше обсуждение двигателя Карно. Мы отметили, что для цикла Карно и, следовательно, для любых обратимых процессов

[латекс] \ displaystyle \ frac {Q _ {\ text {c}}} {Q _ {\ text {h}}} = \ frac {T _ {\ text {c}}} {T _ {\ text {h}} }\\[/латекс].

Перестановка условий дает

[латекс] \ displaystyle \ frac {Q _ {\ text {c}}} {T _ {\ text {c}}} = \ frac {Q _ {\ text {h}}} {T _ {\ text {h}} } \\ [/ latex]

для любого обратимого процесса. Q _c и Q _h – абсолютные значения теплоотдачи при температурах T _c и T _h соответственно. Это соотношение [латекс] \ frac {Q} {T} \\ [/ latex] определяется как изменение энтропии Δ S для обратимого процесса, [латекс] \ Delta {S} = \ left (\ frac {Q} {T} \ right) _ {\ text {rev}} \\ [/ latex], где Q – теплопередача, положительная для теплопередачи в и отрицательная для теплопередачи из , а T – абсолютная температура, при которой имеет место обратимый процесс.Единица измерения энтропии в системе СИ – джоули на кельвин (Дж / К). Если температура изменяется во время процесса, то обычно хорошим приближением (для небольших изменений температуры) будет принять T в качестве средней температуры, избегая необходимости использовать интегральное исчисление для определения Δ S .

Определение Δ S действительно только для обратимых процессов, например, используемых в двигателе Карно. Однако мы можем найти Δ S точно даже для реальных, необратимых процессов.Причина в том, что энтропия S системы, как и внутренняя энергия U , зависит только от состояния системы, а не от того, как она достигла этого состояния. Энтропия – это свойство состояния. Таким образом, изменение энтропии Δ S системы между состоянием 1 и состоянием 2 одинаково, независимо от того, как происходит изменение. Нам просто нужно найти или представить себе обратимый процесс, который переводит нас из состояния 1 в состояние 2, и вычислить Δ S для этого процесса. Это будет изменение энтропии для любого процесса, переходящего из состояния 1 в состояние 2.(См. Рисунок 2.)

Рис. 2. Когда система переходит из состояния 1 в состояние 2, ее энтропия изменяется на ту же величину Δ S независимо от того, идет ли гипотетический обратимый путь или выбирается реальный необратимый путь.

Теперь давайте посмотрим на изменение энтропии двигателя Карно и его тепловых резервуаров за один полный цикл. Горячий резервуар имеет потерю энтропии [латекс] \ Delta {S} _ {\ text {h}} = \ frac {-Q _ {\ text {h}}} {T _ {\ text {h}}} \\ [/ latex], потому что теплообмен происходит из него (помните, что когда тепло передается, то Q имеет отрицательный знак). Холодный резервуар имеет прирост энтропии [латекс] \ Delta {S} _ {\ text {c}} = \ frac {Q _ {\ text {c}}} {T _ {\ text {c}}} \\ [ / латекс], потому что в него происходит теплопередача. (Мы предполагаем, что резервуары достаточно велики, чтобы их температура была постоянной.) Таким образом, полное изменение энтропии составляет Δ S _до = Δ S _h + Δ S _c.

Таким образом, поскольку мы знаем, что [латекс] \ frac {Q _ {\ text {h}}} {T _ {\ text {h}}} = \ frac {Q _ {\ text {c}}} {T _ {\ text {c}}} \\ [/ latex] для двигателя Карно, [latex] \ Delta {S} _ {\ text {tot}} = \ frac {Q _ {\ text {h}}} {T _ {\ text {h}}} = \ frac {Q _ {\ text {c}}} {T _ {\ text {c}}} = 0 \\ [/ latex].

Этот результат, имеющий общую силу, означает, что полное изменение энтропии для системы в любом обратимом процессе равно нулю.

Энтропия различных частей системы может изменяться, но общее изменение равно нулю. Кроме того, система не влияет на энтропию своего окружения, поскольку теплообмен между ними не происходит. Таким образом, обратимый процесс не изменяет ни общую энтропию системы, ни энтропию ее окружения. Иногда об этом говорят так: Обратимые процессы не влияют на полную энтропию Вселенной. Однако реальные процессы необратимы, и они действительно изменяют общую энтропию. Однако мы можем использовать гипотетические обратимые процессы для определения значения энтропии в реальных необратимых процессах. Пример 1 иллюстрирует это.

Пример 1. Увеличение энтропии в необратимом (реальном) процессе

Самопроизвольная передача тепла от горячего к холодному – необратимый процесс. Вычислите полное изменение энтропии, если теплопередача 4000 Дж происходит от горячего резервуара при T _h = 600 K (327ºC) к холодному резервуару при T _c = 250 K (-23ºC), предполагая нет изменения температуры ни в одном из резервуаров.(См. Рисунок 3.)

Рис. 3. (a) Передача тепла от горячего объекта к холодному – это необратимый процесс, который приводит к общему увеличению энтропии. (b) То же самое конечное состояние и, следовательно, такое же изменение энтропии достигается для объектов, если между двумя объектами происходят обратимые процессы теплопередачи, температура которых совпадает с температурами соответствующих объектов в необратимом процессе.

Стратегия

Как мы можем рассчитать изменение энтропии для необратимого процесса, если Δ S _tot = Δ S _h + Δ S _c действительно только для обратимых процессов? Помните, что полное изменение энтропии горячего и холодного резервуаров будет одинаковым независимо от того, идет ли речь об обратимом или необратимом процессе в передаче тепла от горячего к холодному.Таким образом, мы можем рассчитать изменение энтропии горячего резервуара для гипотетического обратимого процесса, в котором от него происходит передача тепла 4000 Дж; затем мы делаем то же самое для гипотетического обратимого процесса, в котором происходит передача тепла в холодный резервуар 4000 Дж. Это вызывает те же изменения в горячем и холодном резервуарах, которые произошли бы, если бы теплопередача между ними происходила необратимо, и, таким образом, это также вызывает такие же изменения энтропии.

Решение

Теперь вычислим два изменения энтропии, используя Δ S _tot = Δ S _h + Δ S _c.Во-первых, для передачи тепла от горячего резервуара

[латекс] \ displaystyle \ Delta {S} _ {\ text {h}} = \ frac {-Q _ {\ text {h}}} {T _ {\ text {h}}} = \ frac {-4000 \ текст {J}} {600 \ text {K}} = – 6,67 \ text {J / K} \\ [/ latex]

А для холодного резервуара,

[латекс] \ displaystyle \ Delta {S} _ {\ text {c}} = \ frac {-Q _ {\ text {c}}} {T _ {\ text {c}}} = \ frac {4000 \ text {J}} {250 \ text {K}} = 16,0 \ text {J / K} \\ [/ latex]

Таким образом, всего

[латекс] \ begin {array} {lll} \ Delta {S} _ {\ text {tot}} & = & \ Delta {S} _ {\ text {h}} + \ Delta {S} _ {\ текст {c}} \\\ text {} & = & \ left (-6. 67 + 16.0 \ right) \ text {J / K} \\\ text {} & = & 9.33 \ text {J / K} \ end {array} \\ [/ latex]

Обсуждение

Существует увеличение на энтропии для системы из двух тепловых резервуаров, подвергающихся этой необратимой теплопередаче. Мы увидим, что это означает потерю способности работать с переданной энергией. Энтропия увеличилась, и энергия стала недоступной для работы.

Разумно, что энтропия увеличивается при передаче тепла от горячего к холодному.Поскольку изменение энтропии составляет [латекс] \ frac {Q} {T} \\ [/ latex], при более низких температурах наблюдается большее изменение. Таким образом, уменьшение энтропии горячего объекта меньше, чем увеличение энтропии холодного объекта, что приводит к общему увеличению, как и в предыдущем примере. Это очень общий результат:

Существует увеличение энтропии для любой системы, в которой происходит необратимый процесс.

Что касается энтропии, есть только две возможности: энтропия постоянна для обратимого процесса и увеличивается для необратимого процесса. Существует четвертая версия второго закона термодинамики, выраженная в терминах энтропии :

Полная энтропия системы либо увеличивается, либо остается постоянной в любом процессе; он никогда не уменьшается.

Например, передача тепла не может происходить самопроизвольно от холода к горячему, потому что энтропия уменьшится.

Энтропия сильно отличается от энергии. Энтропия не сохраняется, а увеличивается во всех реальных процессах. Обратимые процессы (например, в двигателях Карно) – это процессы, в которых происходит наибольшая теплопередача к работе, а также те, которые поддерживают постоянную энтропию.Таким образом, мы вынуждены установить связь между энтропией и доступностью энергии для выполнения работы.

Энтропия и недоступность энергии для работы

Что означает изменение энтропии и почему это должно нас интересовать? Одна из причин заключается в том, что энтропия напрямую связана с тем, что не вся теплопередача может быть преобразована в работу. Пример 2 дает некоторое представление о том, как увеличение энтропии приводит к уменьшению теплопередачи при работе.

Пример 2. При данном теплопередаче меньше работы производится, когда изменение энтропии больше

Рассчитайте рабочую мощность двигателя Карно, работающего в диапазоне температур от 600 K до 100 K, для передачи тепла к двигателю 4000 Дж.
Теперь предположим, что теплопередача 4000 Дж происходит сначала из резервуара 600 K в резервуар 250 K (без выполнения какой-либо работы, и это приводит к увеличению энтропии, вычисленному выше), а затем передается в двигатель Карно, работающий от 250 K до 100 K. K. Какие результаты работы производятся? (См. Рисунок 4.)

Рис. 4. (a) Двигатель Карно, работающий при температуре от 600 K до 100 K, имеет 4000 Дж теплопередачи и выполняет 3333 Дж работы. (b) Теплопередача 4000 Дж сначала происходит необратимо в резервуар 250 К, а затем переходит в двигатель Карно.Увеличение энтропии, вызванное теплопередачей в более холодный резервуар, приводит к меньшей выходной мощности – 2400 Дж. Постоянная потеря энергии на выполнение работы составляет 933 Дж.

Стратегия

В обеих частях мы должны сначала рассчитать КПД Карно, а затем объем работы.

Решение части 1

Эффективность Карно определяется выражением [латекс] \ mathit {Eff} _ {\ text {C}} = 1- \ frac {T _ {\ text {c}}} {T _ {\ text {h}}} \\ [/латекс].

Подстановка заданных температур дает [латекс] \ mathit {Eff} _ {\ text {C}} = 1- \ frac {100 \ text {K}} {600 \ text {K}} = 0.833 \ [/ латекс].

Теперь объем работы можно рассчитать, используя определение эффективности для любого теплового двигателя в виде [latex] \ mathit {Eff} = \ frac {W} {Q _ {\ text {h}}} \\ [/ latex] .

Решение W и замена известных терминов дает

[латекс] \ begin {array} {lll} W & = & \ mathit {Eff} _ {\ text {C}} Q _ {\ text {h}} \\\ text {} & = & \ left (0.833 \ right) \ left (4000 \ text {J} \ right) = 3333 \ text {J} \ end {array} \\ [/ latex]

Решение части 2

Аналогично [латекс] \ mathit {Eff} \ prime _ {\ text {C}} = 1- \ frac {T _ {\ text {c}}} {T \ prime _ {\ text {c}}} = \ frac {100 \ text {K}} {250 \ text {K}} = 0. 600 \ [/ латекс]

, так что

[латекс] \ begin {array} {lll} W & = & \ mathit {Eff} \ prime _ {\ text {C}} Q _ {\ text {h}} \\\ text {} & = & \ left (0,600 \ right) \ left (4000 \ text {J} \ right) = 2400 \ text {J} \ end {array} \\ [/ latex]

Обсуждение

При том же теплопередаче во втором процессе работы на 933 Дж меньше. Этот результат важен. Одна и та же теплопередача в двух совершенных двигателях дает разные результаты работы, потому что изменение энтропии в этих двух случаях разное.Во втором случае энтропия больше, и работы производится меньше. Энтропия связана с доступностью и энергии для выполнения работы.

Когда энтропия увеличивается, определенное количество энергии становится навсегда недоступным для работы. Энергия не теряется, но ее характер изменяется, так что некоторая ее часть никогда не может быть преобразована для выполнения работы, то есть в организованную силу, действующую на расстоянии. Например, в Примере 2 работа была сделана на 933 Дж меньше после увеличения энтропии на 9. 33 Дж / К произошло при передаче тепла 4000 Дж от резервуара 600 К к резервуару 250 К. Можно показать, что количество энергии, которое становится недоступным для работы, составляет Вт _{недоступно} = Δ S ⋅ T ₀, где T ₀ – самая низкая используемая температура. В примере 2 Вт _{отсутствует} = (9,33 Дж / К) (100 К) = 933 Дж, как было найдено.

Тепловая смерть Вселенной: передозировка энтропии

В ранней, энергичной Вселенной вся материя и энергия были легко взаимозаменяемыми и идентичными по своей природе.Гравитация сыграла жизненно важную роль в молодой Вселенной. Хотя могло казаться беспорядочным и, следовательно, внешне энтропийным, на самом деле для совершения работы имелась огромная потенциальная энергия – вся будущая энергия во Вселенной.

По мере того, как Вселенная созревала, возникали разницы температур, что создавало больше возможностей для работы. Например, звезды горячее планет, которые теплее ледяных астероидов, которые еще теплее вакуума в пространстве между ними.

Большинство из них остывают после своего обычно бурного рождения, когда им была предоставлена собственная энергия – ядерная энергия в случае звезд, вулканическая энергия на Земле и других планетах и так далее. Однако без дополнительных затрат энергии их дни сочтены.

По мере увеличения энтропии все меньше и меньше энергии во Вселенной становится доступной для работы. На Земле у нас все еще есть большие запасы энергии, такой как ископаемое и ядерное топливо; крупномасштабные перепады температур, которые могут дать энергию ветра; геотермальная энергия из-за разницы температур в слоях Земли; и приливная энергия из-за нашего обилия жидкой воды.Когда они используются, определенная часть содержащейся в них энергии никогда не может быть преобразована в выполнение работы. В конце концов, все виды топлива будут исчерпаны, все температуры выровняются, и тепловые двигатели не смогут работать или выполнять работу.

Энтропия увеличивается в замкнутой системе, такой как вселенная. Но в некоторых частях Вселенной, например, в Солнечной системе, это не локально замкнутая система. Энергия течет от Солнца к планетам, пополняя запасы энергии Земли.Солнце будет продолжать снабжать нас энергией еще около пяти миллиардов лет. Мы будем наслаждаться прямой солнечной энергией, а также побочными эффектами солнечной энергии, такими как энергия ветра и энергия биомассы от фотосинтезирующих растений. Энергия Солнца будет поддерживать нашу воду в жидком состоянии, а гравитационное притяжение Луны будет продолжать обеспечивать приливную энергию. Но геотермальная энергия Земли будет медленно истощаться и не будет пополняться.

Но с точки зрения Вселенной и очень долгосрочной, очень крупномасштабной картины, энтропия Вселенной увеличивается, и поэтому доступность энергии для выполнения работы постоянно уменьшается.В конце концов, когда все звезды умерли, все формы потенциальной энергии были использованы, и все температуры выровнялись (в зависимости от массы Вселенной, либо при очень высокой температуре после универсального сжатия, либо при очень низкой температуре непосредственно перед вся деятельность прекращается) работать не будет.

В любом случае Вселенная предназначена для термодинамического равновесия – максимальной энтропии. Это часто называют тепловой смертью вселенной , и это будет означать конец всей деятельности.Однако независимо от того, сжимается и нагревается Вселенная или продолжает расширяться и остывать, конец еще не близок. Расчеты черных дыр предполагают, что энтропия может легко продолжаться как минимум 10 ¹⁰⁰ лет.

Порядок беспорядка

Энтропия связана не только с недоступностью энергии для выполнения работы – она также является мерой беспорядка. Это понятие изначально было высказано Людвигом Больцманом в 1800-х годах. Например, таяние глыбы льда означает преобразование сильно структурированной и упорядоченной системы молекул воды в неупорядоченную жидкость, в которой молекулы не имеют фиксированных положений.(См. Рис. 5.) Как видно из следующего примера, в процессе происходит значительное увеличение энтропии.

Рис. 5. Когда лед тает, он становится более неупорядоченным и менее структурированным. Систематическое расположение молекул в кристаллической структуре заменяется более случайным и менее упорядоченным движением молекул без фиксированных положений или ориентации. Его энтропия увеличивается, потому что в него происходит передача тепла. Энтропия – это мера беспорядка.

Пример 3. Энтропия, связанная с расстройством

Найдите увеличение энтропии на 1.00 кг льда первоначально при 0 ° C, который тает с образованием воды при 0 ° C.

Стратегия

Как и раньше, изменение энтропии может быть вычислено из определения Δ S , как только мы найдем энергию Q , необходимую для таяния льда.

Решение

Изменение энтропии определяется как: [latex] \ Delta {S} = \ frac {Q} {T} \\ [/ latex].

Здесь Q – теплопередача, необходимая для плавления 1,00 кг льда, и определяется как Q = мл _f, где м – масса, а L _f – скрытая теплота слияние. 3 \ text {J / K} \ end {array} \\ [/ latex]

Обсуждение

Это значительное увеличение энтропии, сопровождающее увеличение беспорядка.

В другом легко вообразимом примере предположим, что мы изначально смешали равные массы воды при двух разных температурах, скажем, 20,0 ° C и 40,0 ° C. В результате получается вода с промежуточной температурой 30,0 ° C. В результате были получены три результата: энтропия увеличилась, некоторая энергия стала недоступной для выполнения работы, и система стала менее упорядоченной.Давайте подумаем о каждом из этих результатов.

Во-первых, энтропия увеличилась по той же причине, что и в Примере 3. Смешивание двух водоемов имеет тот же эффект, что и передача тепла от горячего, и такая же теплопередача в холодный. Смешивание уменьшает энтропию горячей воды, но увеличивает энтропию холодной воды на большее количество, производя общее увеличение энтропии.

Во-вторых, когда две массы воды смешиваются, остается только одна температура – с ними нельзя запустить тепловую машину. Энергия, которая могла быть использована для запуска теплового двигателя, теперь недоступна для работы.

В-третьих, смесь менее упорядоченная или, используя другой термин, менее структурированная. Вместо того, чтобы иметь две массы при разных температурах и с различным распределением молекулярных скоростей, теперь у нас есть одна масса с однородной температурой.

Эти три результата – энтропия, недоступность энергии и беспорядок – не только связаны, но и фактически эквивалентны.

Жизнь, эволюция и второй закон термодинамики

Некоторые люди неправильно понимают второй закон термодинамики, выраженный в терминах энтропии, говоря, что процесс эволюции жизни нарушает этот закон.Со временем сложные организмы произошли от гораздо более простых предков, что привело к значительному уменьшению энтропии биосферы Земли. Это факт, что живые организмы эволюционировали до высоко структурированных и гораздо более низких по энтропии веществ, чем вещества, из которых они выросли. Но всегда возможно, чтобы энтропия одной части Вселенной уменьшилась, при условии, что общее изменение энтропии Вселенной увеличивается. В форме уравнения мы можем записать это как Δ S _tot = Δ S _syst + Δ S _envir> 0.

Таким образом, Δ S _syst может быть отрицательным, пока Δ S _envir является положительным и большим по величине.

Как система может уменьшить свою энтропию? Передача энергии необходима. Если я беру шарики, разбросанные по комнате, и кладу их в чашку, моя работа уменьшала энтропию этой системы. Если я собираю с земли железную руду, превращаю ее в сталь и строю мост, моя работа уменьшала энтропию этой системы.Энергия, приходящая от Солнца, может уменьшать энтропию локальных систем на Земле, то есть Δ S _syst отрицательна. Но общая энтропия остальной Вселенной увеличивается на большую величину, то есть Δ S _envir положительна и больше по величине. Таким образом, Δ S _tot = Δ S _syst + Δ S _envir> 0, и второй закон термодинамики не нарушается.

Каждый раз, когда растение накапливает солнечную энергию в виде потенциальной химической энергии или восходящий поток теплого воздуха поднимает парящую птицу, Землю можно рассматривать как тепловую машину, работающую между горячим резервуаром, питаемым Солнцем, и холодным резервуаром. обеспечивается темным космическим пространством – тепловым двигателем высокой сложности, вызывающим локальное уменьшение энтропии, поскольку он использует часть теплопередачи от Солнца в глубокий космос.В результате такой массивной теплопередачи происходит большое общее увеличение энтропии. Небольшая часть этой теплопередачи хранится в структурированных системах на Земле, вызывая гораздо меньшее локальное уменьшение энтропии. (См. Рисунок 6.)

Рис. 6. Энтропия Земли может уменьшаться в процессе перехвата небольшой части теплопередачи от Солнца в глубокий космос. Энтропия всего процесса значительно возрастает, в то время как Земля становится более структурированной с живыми системами и накопленной энергией в различных формах.

Исследования PhET: обратимые реакции

Наблюдайте за реакцией, протекающей с течением времени. Как общая энергия влияет на скорость реакции? Варьируйте температуру, высоту барьера и потенциальную энергию. Запишите концентрации и время, чтобы извлечь коэффициенты скорости. Проведите температурно-зависимые исследования, чтобы извлечь параметры Аррениуса. Эту симуляцию лучше всего использовать под руководством учителя, поскольку она представляет собой аналог химических реакций.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

Энтропия – это потеря энергии, доступной для выполнения работы.
Другая форма второго закона термодинамики гласит, что полная энтропия системы либо увеличивается, либо остается постоянной; он никогда не уменьшается.
Энтропия в обратимом процессе равна нулю; он увеличивается в результате необратимого процесса.
Окончательной судьбой Вселенной, вероятно, будет термодинамическое равновесие, при котором универсальная температура постоянна и для работы нет энергии.
Энтропия также связана с тенденцией к беспорядку в закрытой системе.

Концептуальные вопросы

Женщина закрывает дачу в сентябре и возвращается в июне. Тем временем в коттедж никто не заходил. Объясните, что она может найти, с точки зрения второго закона термодинамики.
Рассмотрим систему с определенным содержанием энергии, из которой мы хотим извлечь как можно больше работы. Энтропия системы должна быть высокой или низкой? Это порядок или беспорядок? Структурированный или равномерный? Кратко объясните.
Становится ли газ более упорядоченным при сжижении? Меняется ли его энтропия? Если да, энтропия увеличивается или уменьшается? Поясните свой ответ.
Объясните, как энтропия воды может уменьшаться при замерзании без нарушения второго закона термодинамики. В частности, объясните, что происходит с энтропией окружающей среды.
Является ли газ с однородной температурой более или менее упорядоченным, чем газ с несколькими разными температурами? Что более структурировано? Что может привести к передаче тепла при работе, выполняемой без передачи тепла от другой системы?
Приведите пример спонтанного процесса, в котором система становится менее упорядоченной, а энергия становится менее доступной для выполнения работы.Что происходит с энтропией системы в этом процессе?
Каково изменение энтропии в адиабатическом процессе? Означает ли это, что адиабатические процессы обратимы? Может ли процесс быть точно адиабатическим для макроскопической системы?
Энтропия звезды увеличивается или уменьшается по мере ее излучения? Увеличивается или уменьшается энтропия пространства, в которое он излучается (имеющего температуру около 3 К)? Что это делает с энтропией Вселенной?
Объясните, почему здание из кирпичей имеет меньшую энтропию, чем такие же кирпичи в неорганизованной куче.Сделайте это, рассмотрев количество способов, которыми каждый может быть сформирован (количество микросостояний в каждом макросостоянии).

Задачи и упражнения

(a) Зимним днем какой-то дом теряет 5,00 × 10 ⁸ Дж тепла снаружи (около 500 000 британских тепловых единиц). Каково полное изменение энтропии только за счет этой теплопередачи, принимая среднюю температуру в помещении 21,0 ° C и среднюю температуру наружного воздуха 5,00 ° C? (б) Это большое изменение энтропии означает, что большое количество энергии стало недоступным для выполнения работы.Где мы можем найти больше энергии, если она потеряна для нас?
В жаркий летний день происходит передача тепла 4,00 × 10 ⁶ Дж в припаркованный автомобиль, повышая его температуру с 35,0 ° C до 45,0 ° C. Каково увеличение энтропии автомобиля только за счет этой теплопередачи?
Горячий камень, выброшенный из лавового фонтана вулкана, охлаждается с 1100ºC до 40,0ºC, а его энтропия уменьшается на 950 Дж / К. Сколько тепла происходит от камня?
Когда 1,60 × 10 ⁵ Дж теплопередачи происходит в мясной пирог первоначально при 20.0ºC его энтропия увеличивается на 480 Дж / К. Какова его конечная температура?
Солнце излучает энергию со скоростью 3,80 × 10 ²⁶ Вт со своей поверхности 5500ºC в темное пустое пространство (ничтожно малая часть излучается на Землю и другие планеты). Эффективная температура глубокого космоса -270ºC. (а) Каково увеличение энтропии за один день из-за этой теплопередачи? б) Сколько работы стало недоступно?
(a) При достижении равновесия, сколько тепла происходит от 1.00 кг воды при 40,0ºC, когда он находится в контакте с 1,00 кг воды 20,0ºC для достижения равновесия? (б) Каково изменение энтропии из-за этой теплопередачи? (c) Сколько работы становится недоступной, если принять самую низкую температуру 20,0 ° C? Ясно покажите, как вы следуете шагам, указанным в Стратегиях решения проблем для энтропии.
Каково уменьшение энтропии 25,0 г воды, которая конденсируется на зеркале в ванной при температуре 35,0 ° C, при условии отсутствия изменений температуры и при условии, что скрытая теплота испарения составляет 2450 кДж / кг?
Найдите увеличение энтропии на 1.00 кг жидкого азота, который начинается при температуре кипения, закипает и нагревается до 20,0 ° C при постоянном давлении.
Крупная электростанция вырабатывает 1000 МВт электроэнергии с КПД 35,0%. (a) Рассчитайте теплопередачу на электростанцию, Q _h, за один день. (б) Сколько тепла передается в окружающую среду за один день Q _c? (c) Если теплопередача в градирнях составляет от 35,0 ° C воды в местную воздушную массу, температура которой увеличивается с 18 ° C.От 0 ° C до 20,0 ° C, каково общее увеличение энтропии из-за этой теплопередачи? (d) Сколько энергии становится недоступной для работы из-за этого увеличения энтропии, если предположить, что самая низкая температура составляет 18,0 ° C? (Часть Q _c может использоваться для работы тепловых двигателей или для простого обогрева окружающей среды, но это редко.)
(a) Сколько тепла происходит от 20,0 кг воды с температурой 90,0 ° C, помещенных в контакт с 20,0 кг воды с температурой 10,0 ° C, с получением конечной температуры 50 ° C.0ºC? (b) Сколько работы мог бы проделать двигатель Карно с такой теплопередачей, если предположить, что он работает между двумя резервуарами при постоянных температурах от 90,0 ° C до 10,0 ° C? (c) Какое увеличение энтропии происходит при смешивании 20,0 кг воды с температурой 90,0 ° C и 20,0 кг воды с температурой 10,0 ° C? (d) Рассчитайте объем работы, недоступной из-за этого перемешивания, используя низкую температуру 10,0 ° C, и сравните ее с работой, выполненной двигателем Карно. Ясно покажите, как вы следуете шагам, указанным в Стратегиях решения проблем для энтропии.(e) Обсудите, как повседневные процессы делают все больше энергии недоступной для работы, что подразумевается этой проблемой.

Глоссарий

энтропия: измерение неупорядоченности системы и ее неспособности выполнять работу в системе

изменение энтропии: отношение теплопередачи к температуре [латекс] \ frac {Q} {T} \\ [/ latex]

второй закон термодинамики, выраженный в терминах энтропии: полная энтропия системы либо увеличивается, либо остается постоянной; никогда не уменьшается

Избранные решения проблем и упражнения

1.(а) 9,78 × 10 ⁴ Дж / К; б) Чтобы получить больше энергии, мы должны генерировать ее из вещей в доме, таких как тепловой насос, человеческие тела и другие приборы. Как вы знаете, мы тратим много энергии на поддержание тепла в наших домах зимой из-за потери тепла наружу.

3. 8.01 × 10 ⁵ Дж

5. (а) 1.04 × 10 ³¹ Дж / К; (б) 3,28 × 10 ³¹ Дж

7. 199 Дж / К

9. (а) 2,47 × 10 ¹⁴ Дж; (б) 1,60 × 10 ¹⁴ Дж; (в) 2.85 × 10 ¹⁰ Дж / К; (г) 8,29 × 10 ¹² Дж

энтропия | Определение и уравнение

энтропия , мера тепловой энергии системы на единицу температуры, которая недоступна для выполнения полезной работы. Поскольку работа получается из упорядоченного молекулярного движения, количество энтропии также является мерой молекулярного беспорядка или случайности системы. Концепция энтропии позволяет глубже понять направление спонтанных изменений для многих повседневных явлений.Его введение немецким физиком Рудольфом Клаузиусом в 1850 году стало ярким событием в физике XIX века.

Идея энтропии предоставляет математический способ закодировать интуитивное представление о том, какие процессы невозможны, даже если они не нарушают фундаментальный закон сохранения энергии. Например, кусок льда, поставленный на горячую плиту, обязательно тает, а плита остывает. Такой процесс называется необратимым, потому что никакие незначительные изменения не заставят талая вода снова превратиться в лед, пока плита нагревается.Напротив, кусок льда, помещенный в ванну с ледяной водой, либо немного оттает, либо немного замерзнет, в зависимости от того, добавлено ли небольшое количество тепла к системе или отнято от нее. Такой процесс обратим, потому что требуется лишь бесконечно малое количество тепла, чтобы изменить его направление с постепенного замораживания на постепенное оттаивание. Точно так же сжатый газ, заключенный в цилиндр, мог либо свободно расширяться в атмосферу, если клапан был открыт (необратимый процесс), либо он мог выполнять полезную работу, толкая подвижный поршень против силы, необходимой для удержания газа.Последний процесс обратим, потому что только небольшое увеличение удерживающей силы может изменить направление процесса от расширения к сжатию. Для обратимых процессов система находится в равновесии с окружающей средой, а для необратимых – нет.

Подробнее по этой теме

термодинамика: энтропия

Понятие об энтропии было впервые введено в 1850 году Клаузиусом как точный математический способ проверки того, является ли второе…

энтропия и стрела времени

Альберт Эйнштейн говорил об энтропии и втором законе термодинамики как о единственном способе проникновения в суть устройства мира, который никогда не будет опровергнут. Это видео является эпизодом из серии Daily Equation Брайана Грина.

© World Science Festival (издательский партнер Britannica) Посмотреть все видео к этой статье
Чтобы количественно измерить направление спонтанных изменений, Клаузиус ввел понятие энтропии как точный способ выражения второго закона термодинамики.Форма Клаузиуса второго закона гласит, что спонтанное изменение необратимого процесса в изолированной системе (то есть в системе, которая не обменивается теплом и не работает с окружающей средой) всегда происходит в направлении увеличения энтропии. Например, ледяной блок и плита составляют две части изолированной системы, общая энтропия которой увеличивается по мере таяния льда.
Согласно определению Клаузиуса, если количество тепла Q течет в большой тепловой резервуар при температуре T выше абсолютного нуля, то увеличение энтропии составляет Δ S = Q / T .Это уравнение эффективно дает альтернативное определение температуры, которое согласуется с обычным определением. Предположим, что имеется два резервуара тепла R ₁ и R ₂ при температурах T ₁ и T ₂ (например, плита и глыба льда). Если количество тепла Q течет от R ₁ к R ₂, то чистое изменение энтропии для двух резервуаров будет положительным при условии, что T ₁> T ₂.Таким образом, наблюдение, что тепло никогда не перетекает самопроизвольно от холода к горячему, эквивалентно требованию, чтобы изменение чистой энтропии было положительным для спонтанного потока тепла. Если T ₁ = T ₂, то резервуары находятся в равновесии, тепловые потоки отсутствуют, и Δ S = 0.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Условие Δ S ≥ 0 определяет максимально возможную эффективность тепловых двигателей, то есть таких систем, как бензиновые или паровые двигатели, которые могут работать циклически.Предположим, что тепловая машина поглощает тепло Q ₁ из R ₁ и отводит тепло Q ₂ до R ₂ для каждого полного цикла. За счет сохранения энергии работа, выполненная за цикл, составляет Вт = Q ₁ – Q ₂, а чистое изменение энтропии должно сделать Вт как можно больше, Q ₂ должен быть как можно меньше по сравнению с Q ₁.Однако Q ₂ не может быть нулевым, потому что это сделало бы Δ S отрицательным и таким образом нарушило бы второй закон. Наименьшее возможное значение Q ₂ соответствует условию Δ S = 0, что является основным уравнением, ограничивающим эффективность всех тепловых двигателей. Процесс, для которого Δ S = 0, является обратимым, поскольку бесконечно малого изменения было бы достаточно, чтобы тепловой двигатель работал в обратном направлении, как холодильник.
По тем же соображениям можно определить изменение энтропии рабочего вещества в тепловом двигателе, например газа в цилиндре с подвижным поршнем.Если газ поглощает дополнительное количество тепла d Q из теплового резервуара при температуре T и обратимо расширяется против максимально возможного сдерживающего давления P , то он выполняет максимальную работу d W = P d V , где d V – изменение объема. Внутренняя энергия газа также может измениться на величину d U по мере его расширения.Тогда по сохранению энергии d Q = d U + P d V . Поскольку чистое изменение энтропии для системы плюс резервуар равно нулю, когда выполняется максимальная работа, а энтропия резервуара уменьшается на величину d S _{резервуар} = – d Q / T , это должен уравновешиваться увеличением энтропии рабочего газа так, чтобы d S _{система} + d S _{резервуар} = 0.Для любого реального процесса будет выполнено меньше, чем максимальная работа (например, из-за трения), и поэтому фактическое количество тепла d Q ′, поглощенное из теплового резервуара, будет меньше максимального количества d Q . Например, газ может свободно расширяться в вакуум и вообще не работать. Следовательно, можно констатировать, что с d Q ′ = d Q в случае максимальной работы, соответствующей обратимому процессу.
Это уравнение определяет S _{система} как термодинамическую переменную состояния, что означает, что ее значение полностью определяется текущим состоянием системы, а не тем, как система достигла этого состояния. Энтропия – это обширное свойство, поскольку ее величина зависит от количества материала в системе.
В одной статистической интерпретации энтропии обнаружено, что для очень большой системы в термодинамическом равновесии энтропия S пропорциональна натуральному логарифму величины Ω, представляющей максимальное количество микроскопических способов, в которых макроскопическое состояние, соответствующее S может быть реализовано; то есть S = k ln Ω, где k – постоянная Больцмана, связанная с молекулярной энергией.
Все спонтанные процессы необратимы; следовательно, было сказано, что энтропия Вселенной увеличивается: то есть все больше и больше энергии становится недоступным для преобразования в работу. Из-за этого вселенная, как говорят, «истощается».
Энтропия проста … Если вы избегаете вересковых пятен!
Энтропия проста – если избегать шиповника Патчи!
Фрэнк Л. Ламберт, почетный профессор (химия)
Западный колледж, Лос-Анджелес
августа 2013
Авторское право 2013 Фрэнк Л.Ламберт
Воспроизведение или выдержки разрешены
если запрос сделан на [email protected]
Введение
Секунда закон термодинамики является мощным подспорьем, помогающим понять, почему мир работает так, как работает – почему горячие сковороды остывают, почему наши тела остаются тепло даже на морозе, почему бензин заставляет моторы работать. Это окончательный основа химических производств, спасших мир от голода за последние полвека (производство удобрений с использованием азота из воздух) и сохранил нас здоровыми и менее болезненными в то время (через процессы для спасающих жизни и обезболивающих фармацевтических препаратов).
Энтропия также просто описать и качественно объяснить. (Энтропия в количественном термодинамика более трудна и часто сложна.) Однако для начала наш качественный подход, мы должны избегать пятен шиповника, вовлекающих второй закон и энтропия, посаженные на акрах книжных страниц и веб-сайты.
Для тех, кто предпочитает выводы, а не объяснения:
Второй закон термодинамики гласит, что энергия всего виды в нашем материальном мире рассеиваются или распространяются, если они ничто не препятствует этому.Энтропия – количественная мера такого спонтанного процесса: сколько энергии от локализации к более широкому распространению выход (при определенной температуре).
В этой статье будет использоваться множество повседневных примеров, чтобы проиллюстрировать эти выводы и кратко связать их с атомным и молекулярным поведением.
Нашивка из шиповника №1. Писатели, которые не ученые и математики-шутники
К сожалению, идеи энтропии и второго закона были почти безнадежно перепутаны благонамеренными, но наивными с научной точки зрения философами и писателями художественной и научно-популярной литературы.Поисковые системы правильно назвали популярный сайт об энтропийном «загадывании». Его автор – архитектор, не ученый. Единственная из когда-либо опубликованных бестселлеров по энтропии, наполненный ошибками, ведущими к абсурдным заявлениям, был написан человеком со степенями в области экономики и международных отношений, но без научных фон.
Дополнительный источник путаницы для кого-либо, кроме химии или физики, связан с блестящим, но легкомысленным математикам.Они решили, что это будет будет забавно назвать очень важную новую математическую функцию связи «энтропия», потому что «никто не знает, что [термодинамическая] энтропия на самом деле есть, поэтому в дебатах у вас всегда будет преимущество “. (Эта цитата разговора Джона фон Неймана с Клодом Шенноном ( Sci. Am. 1971 , 225 , 180.) За последние полвека это оказалось жестоким практическим шутка навязывается поколениям ученых и не-ученых, потому что многие авторы полностью перепутали информационную «энтропию» и термодинамическую энтропию.Они не такие же ! От 1860-е годы до настоящего времени, в физике и химии (две науки, зародившиеся в и наиболее широко используя эту концепцию) энтропия применила только к ситуации, связанные с потоком энергии, который можно измерить как изменение “тепла”, как указано в описании из двух слов, термодинамический (“ тепло действие или поток “) энтропия. Только термодинамическая энтропия будет рассматриваются в этой статье.
Когда бы то ни было Обсуждается информационная «энтропия» – особенно когда она в той же статье, что и термодинамическая энтропия – та математическая «энтропия» следует заключать в кавычки, чтобы четко отличать его от энтропии, т.е. термодинамической энтропия.
Научная записка (для химиков, физиков, математиков): Термодинамическое изменение энтропии складывается из двух факторов. Изменение энтропии включен дюйм химии за счет энергии движения молекул (или из-за изменения энергии связи в химической реакции), но термодинамическая энтропия только актуализируется , если сам процесс (расширение, нагрев, перемешивание, реакция) делает доступным большее количество микросостояний, максимальная вероятность Больцмана на определенная температура.(Информационная «энтропия» состоит только из последних фактор вероятности. «Сигма-энтропия» физики, равная S / k _B, имеет только ln W, не имеющую отношения ни к какому виду энергии.)
Нашивка из шиповника №2. «Изолированные системы»
В статьях и веб-страницы, знакомящие с энтропией не ученых, что является самым ненужным из всех вводящих в заблуждение акцентов, которые появляются в них, – это развернутое обсуждение “изолированных систем” физиков.Эти теоретические системы не только бесполезны для новичка, но и то, что в них происходит, может глубоко запутать любого, кто пытается понять энтропию и второй закон в реальный мир. Мы, люди, живем в открытой системе Земли, Солнца и внешнего мира. Космос. Мы сталкиваемся со вторым законом и энтропией внутри этой открытой системы. Следовательно, полезные для нас соотношения энергия-энтропия исследовать находятся в этой реальной системе.
Нашивка из шиповника №3.«Энтропия – это беспорядок» (Энтропия – это НЕ беспорядок!)
Эта путаница о беспорядке и энтропии взято из заявления 1898 года блестящего физик-теоретик, чей математический вклад в термодинамику и энтропия по-прежнему полностью действительны. Однако его попытка интерпретировать энтропия простым языком была неправильной, потому что только после его смерти в 1906 году пришло понимание молекулярного поведения. Порядок / беспорядок стал все более устаревает применять к энтропии и второму закону, когда существование квантованных уровней энергии в физике и химии обычно принят после середины 1920-х гг.
Хотя порядок / беспорядок все еще присутствует в некоторых текстах по элементарной химии как уловка для предположений об изменениях энтропии (и полезна для экспертов в некоторых области термодинамики), это вводит в заблуждение и анахронизм для новички в химии. Он был удален из большинства университетов первого года обучения. учебники химии в США .. По гуманитарным наукам и популярной литературе, многократное использование энтропии в связи с «беспорядком» (в множество его различных общих значений) вызвало огромные интеллектуальные вред.Таким образом, энтропия была отделена от квинтэссенциальной связи. с его атомно-молекулярной энергетической основой. В результате девятнадцатый ошибка века относительно значения энтропии была в целом и ошибочно применяется к беспорядочным вечеринкам, неблагополучной личной жизни и даже срывам в международных мероприятиях. Это может сделать страницы метафоры, но это полностью не связаны с термодинамической энтропией в физико-химической науке, что на самом деле действительно влияет на нашу жизнь.Это так же смешно, как говорить о том, как Эйнштейн Теория относительности может быть применена к нежелательным родственникам человека в Чикаго.
| наверх |

Второй закон термодинамики
Предупреждение о научно неправильном словоблудии в следующих разделах: Для удобства слово «тепло» иногда используется в ошибочном смысле “что-то”, вещество в объекте.(См. Полное объяснение в Приложении.)
Второй закон термодинамики – какой запретный набор слов! Тем не мение, любой страх перед этой фразой или тем, что за ней скрывается, исчезает, когда мы понимаем что второй закон мы уже хорошо знаем из повседневного опыта. Мы просто не осознавали, что такие разнообразные события, как следующие все это примеры второго закона: горячая сковорода остывает; вода самопроизвольно стекает с Ниагарского водопада; воздух в наших шинах улетит в атмосферу если стенки покрышки проколоты; когда бензин смешивается с воздухом в цилиндры автомобиля, при попадании искры взрывается; мчащаяся машина удар о кирпичную стену не останавливается пассивно.Раздается громкий треск поскольку металл машины погнут, пластик и стекло разбиты, а кирпичи (слегка подогретые) облетайте всю территорию. Сливки, добавленные в кофе, не остается сам по себе, но вместо этого распространяется по всему кофе. Как все эти разные события описываются одним законом, особенно законом с сложное имя?
В горячем металле атомы очень быстро вибрируют (потому что тепло распространилось в сковороде от более горячего пламени).Эти атомы будут рассеивать энергию их энергичных, но ограниченных движений, до менее быстро движущихся молекулы – тем, кто находится в прохладной столешнице, или более свободно, но менее энергично движущиеся молекулы азота и кислорода в прохладном воздухе комната. Молекулы воды на вершине Ниагарского водопада обладают относительно большим потенциалом энергия; они рассеивают его, если упадут далеко в реку. Молекулы в воздухе, ограниченном небольшим объемом автомобильной шины, немедленно выходят в больший объем наружного воздуха, распространяя свои энергия более широко в атмосфере, если шина пробита или проступь отделяется от стен.
Молекулы бензин с кислородом (в воздухе) имеют большую энергию во внутренних связях которые удерживают свои атомы вместе, чем углекислый газ и вода, которые образуются при реакции бензина с кислородом. Следовательно, газ и кислород самопроизвольно стремятся к к реагируют и производят углекислый газ и воду, потому что тогда энергия будет рассеиваться к окружающей среде в процессе. Однако так же, как воздух в шине физически заблокирован или “ препятствует ” более широкому распространению энергии его молекул в большем объеме атмосферы прочными стенками и протектором шины, бензином и воздух химически заблокированы от немедленного рассеивания их энергии за счет барьер называется энергией активации .(См. Приложение для Детали.) Таким образом, бензин и кислород воздуха могут оставаться в контакте друг с другом. неизменным годами и столетиями. Однако, дав искру преодолеть активацию энергия, которая препятствует их реакции, бензин и кислород будут сильно реагируют на распространение большого количества тепла в результате трансформации части их высокоэнергетических связей как низкоэнергетических связей углекислого газа и воды образуются.
В примере мчащегося автомобиля, все молекулы его пластика и его атомы стекла и металла имеют большую кинетическую энергию в том направлении, в котором мчится.Чтобы он остановился, необходимо рассеять кинетическую энергию. как-то где-то. Если его останавливает кирпичная стена, большое количество кинетической энергии в автомобиле изменяется. в звук, кинетическую энергию кирпичей, летящих после того, как их оторвали от стены, тепло кирпичей и битые теплые кусочки пластика, стекла и скрученного металла – очень широкое распространение энергии, прежде всего сконцентрированной в движущейся машине.
Наконец, и на первый взгляд совершенно не имеющий отношения к предыдущим примерам, это случай сливок самопроизвольно смешивается с кофе (даже если они не перемешаны и предотвращены конвекционные токи).Это прообраз всех стихийных смешивание жидкостей и растворение (хотя растворение твердых веществ в жидкостях имеет факторы в дополнение к простому смешиванию).
Все мельчайших частиц, атомы или молекулы в этих примерах, находятся в постоянном сильное случайное движение. (Молекулы кислорода в нашем воздухе в среднем движутся около тысячи миль в час при обычных температурах, но меняется от 0 до почти 3000 миль в час, поскольку они врезаются в другие молекулы после движения около 15 миллионных дюйма.В твердых телах частицы танцуют на месте (вибрируют) с энергиями, зависящими от температуры.) Все энергичные атомы и молекулы будут распространяют свою двигательную энергию, если им дается возможность сделать это – в больший объем, чтобы другие молекулы не двигались так быстро (т.е. температура) .. Второй закон термодинамики просто резюмирует факт такая молекулярная энергия движения рассеивает , если ей не препятствуют в этом. Намного более обширно, чем эти несколько примеров: Все спонтанные события в материальном мире (те, которые продолжаются без посторонней помощи, за исключением возможно, для начала) являются примерами второго закона, потому что они включают рассеивание энергии .Энергия, которая находится в быстро движущемся, непрерывно сталкивающиеся мельчайшие частицы материи (в том числе более доступны химическими реакциями, такими как бензин с кислородом, которые содержат связи с более высокой энергией внутри них, чем их возможные продукты) будут диффундировать, рассредоточиться, рассредоточиться, если есть какой-то способ, чтобы это происходило беспрепятственно.
Секунда закон термодинамики настолько вошел в наш повседневный опыт, что это адекватно резюмируется в простых примерах, которые мы видели, трех архетипы, являющиеся:
“горячие сковороды остывают”, случай немедленного разгона энергии,
, потому что они склонны рассеивать энергию своего быстро движущегося частицы [которые мы обычно называем теплом] в их металлических или стеклянных контейнерах к чему-либо они контактируют, например, с более прохладным воздухом в комнате [более медленно движущиеся молекулы, которые затем немного увеличьте их скорость],
или «взрывается бензин», случай затрудненного рассеивания энергии от химической реакции,
потому что он имеет тенденцию реагировать с кислородом воздуха, но делает это только в том случае, если смесь воспламеняется, т.е.е. получил немного дополнительной энергии от искры или крошечного пламени. Затем бензин и кислород могут распределять часть энергии в своих связях. (химические связи удерживают атомы в молекулах) при образовании углекислого газа и вода, у которой меньше энергии в своих связях. Разница в энергии равна диспергировали до все молекул в газообразном паре (оставшийся кислород, азот, углекислый газ, H ₂ O, CO и др.). Это заставляет их двигаться очень быстро (характеристика молекул / атомов во всем очень горячем) и давление в замкнутом пространстве сразу возрастает.Такое высокое давление в малый объем цилиндра, `еще больше распределяет энергию горячих молекул (снова второй закон), с силой толкая поршни автомобиля вниз так, чтобы поршневые штоки рассеивают свою кинетическую энергию за счет поворота коленчатого вала и т. д.
“лопаются шины” и “смесь сливок в кофе”, когда вещества распространяют свою энергию в пространстве без каких-либо изменений в этой первоначальной энергии.
, потому что эти, казалось бы, несопоставимые примеры не предполагают изменения температуры или изменения их начальной энергии.(На самом деле, это идеализация, потому что реальный воздух охлаждается при расширении.) С научной точки зрения эти спонтанные события относятся к той же категории – расширение газа, такого как воздух, влечет за собой увеличение объема (распространение исходной энергии в большем пространстве) смешивание включает в себя отделение молекул одного типа от его вида (своего рода рассредоточение начальной энергии, потому что все молекулы одного типа больше не примыкают друг к другу).
Смысл слова «если ничто не препятствует» в вышеизложенном невозможно переоценить.Это упущение идеи “препятствия” или “препятствия”, на мгновение или на долгое время », что сбивает с толку большинство не ученых читают или пишут о втором законе. Так много стресса обычно ставится на непосредственность и неизбежность ужасных последствий второй закон (и его предполагаемая сложность), что его можно заставить казаться неоправданно угрожает почти каждому аспекту нашей жизни.
Второй закон термодинамики ни в коем случае нельзя считать мгновенным повиновением.Он точно предсказывает вероятность рассеивания энергии. который локализован или «сконцентрирован» в группе молекул или атомов – и это может привести к нежелательным событиям, начиная от серьезных аварий. к разрушительным лесным пожарам или к нашей окончательной смерти. В этом смысле второй закон – наш “самый плохой плохой”. Однако в законе совершенно ничего не говорится о сколько времени может потребоваться, чтобы его прогнозы сбылись.
| наверх |

Что такое энтропия? Как это связано со вторым закон?
Энтропия просто количественная мера того, что второй закон термодинамики описывает: распространение энергии в процессе в нашем материальном мире .Энтропия качественно не сложно. Конечно, энтропия – это не беспорядок ни в какой мере хаос – хотя он, таким образом, ошибочно определен в словари или источники до 2002 года.
Потому что энтропия – это показатель предсказаний второго закона об энергии, краткий слово энтропия часто используется как синоним громоздкой фразы ” второй закон термодинамики ». Краткое изложение природы энтропии: Энтропия изменение измеряет рассредоточение энергии: насколько распределяется энергии в конкретном процессе, или как широко распределяется становится (при определенная температура).Теперь вы видите, как горячие сковороды охлаждаются и химические реакции принадлежат к категории «сколько», куда передается энергия. Кофе в сливках и газе, а также в парфюмерии в воздухе – это процессы «насколько широко», где начальная энергия молекул остается прежней, но объем, занимаемый молекул увеличивается. Рассеивание энергии может легко увидеть любой в сотни распространенных явлений, подобных тем, которые мы здесь представили, потому что Второй закон – это не какая-то экзотическая или абстрактная математическая теория.Второй закон на самом деле просто резюме обычного человеческого опыта. Подробности того, как энергия растекается или расходится в таких повседневных практических мероприятиях, можно элегантно соотнести с вероятное поведение атомов и молекул.
| наверх |

Наше самое большое благо, второй закон термодинамики
В Второй закон – постоянная угроза для нас. Наши тела состоят из десятков тысяч химических веществ («соединений»), которые необходимы для нашего функционирования.Однако кислород в нашей атмосфере, который нам необходим для жизни, также имеет тенденцию разрушать почти все эти важные биохимические соединения. Почему? Кислород плюс любое из наших незаменимых органических соединений имеет более высокое содержание энергии, чем окисленные соединения диоксида углерода и воды (CO ₂ и H ₂ O) что будет сформировано из них. Таким образом, если бы второму закону не было препятствий, почти все вещества в нашем организме немедленно вступают в реакцию с кислородом в воздухе, так что некоторая энергия связи в этих важных веществах будет распространяться как тепло.Концентрированная или локализованная энергия для рассеянной или рассредоточенной энергия – это закономерность в природе, которую резюмирует второй закон.
Этот точно подобен бензину и кислороду, имеющему более высокую энергию в своих связях чем их продукты, углекислый газ и вода. Однако поверхностная причина что мы никогда не могли бы спонтанно окисляться («сгорать») так быстро, как бензин в кислороде – это большое количество воды в наших клетках, сдерживающее такой процесс. (Древесина в стволах живых деревьев горит (окисляется) медленно и с трудом, потому что он и твердая, и влажная – в отличие от более быстрых сжигание листьев и веток с меньшей влажностью и большей площадью поверхности.) Тем не менее, даже если бы все наше тело не окислилось быстро, у нас могло бы быть достаточное количество клеток в нас, скажем, сотые доли процента от общего количества критических клеток для продолжения нашей жизни, которая может случайным образом окисляться и подчиняться второму закону в рассеивании их концентрированной энергии. Этого могло быть достаточно, чтобы вызвать серьезные дисфункция и смерть.
К счастью, есть серьезная причина того, что наши клетки и их химические составляющие сопротивляются угроза второго закона (т.е., что они «должны» реагировать с кислородом потому что тогда они будут следовать закону, рассеивая свою энергию.) Причина наличие энергий активации, врожденное препятствие второму закону термодинамики в химических реакциях. Мы видели это в наших часто используемых иллюстрация бензина и кислорода: реакция не происходит, пока не возникнет искра или пламя сначала вводится в смесь, чтобы дать небольшой энергетический “толчок” Начни это. Это типично почти для всех реакций кислорода с биохимическими веществами. внутри нас.. Таким образом, хотя второй закон является фундаментальной угрозой для нашей живет в нашей атмосфере, содержащей кислород, второй закон не менее фундаментален заблокирован. на с энергией активации , вызывающей наше окисление и смерть. (См. Приложение или http://secondlaw.oxy.edu/three.html для подробности об энергиях активации. Сайт http://shakespeare2ndlaw.oxy.edu описывает важность энергии активации в нашу жизнь.)
В то же время, что мы осознаем, что второй закон термодинамики представляет собой постоянную угрозу, мы также должны понимать, что это наше «величайшее благо»: что, если направление потока энергии было , а не всегда от сосредоточенного разогнать? Что, если бы процесс был часто беспорядочным или точно 50 на 50? – с обратным потоком энергии от рассредоточенной к концентрированной половине время? Ни один организм не мог жить в такой хаотичной вселенной.Как организмы мы в основном это машины для обработки энергии. Чтобы поддерживать множество различные «автоматические» биохимические процессы в нашем организме, которые требуют энергия, чтобы заставить вещества “подняться на энергетический холм”, чтобы они были более концентрированными энергии внутри них, мы должны постоянно получать энергию от вне нас в виде кислорода и пищи. Это всегда надежный направление спонтанного рассеивания энергии от окисления пищи что делает возможным весь спектр нашей энергоемкой деятельности которые составляют сами наши жизни.
Этот процесс окисления происходит поразительно сложными способами и во многих шагов (так что любая энергия, которая распространяется в виде тепла, медленно и умеренно выпущен, в отличие от, казалось бы, мгновенного “одношагового” взрывного устройства. рассеивание энергии при реакции бензина с кислородом). Кроме того, любые тепло, которое рассеивается в наших телах, не тратится зря, потому что оно сохраняет наши тела теплые, чтобы оптимально функционировать даже в холодных условиях. Некоторые из энергия, текущая вниз от окисления пищевых продуктов, улавливается «связанными реакции », так что вещество средней энергии, АДФ, получает повышенную энергию чтобы стать более энергоемким веществом, таким как АТФ.АТФ есть в каждом клетка в нашем теле, чтобы рассеивать энергию для множества различных реакций в то время как он становится АДФ, а затем регенерируется сопряженной реакцией. Из Конечно, хранение АТФ противоречит прогнозам второго закон, но мы знаем, как он «побеждает» второй закон:: Энергия внутри связи этих молекул АТФ и аналогичных разновидностей не допускаются рассеиваются за счет энергетических барьеров активации до тех пор, пока, конечно, нам неизвестно, нашим клеткам он нужен для каких-то действий.СПС и аналогичные источники хранения энергии то, что дает нам мгновенный осознанный выбор в пользу использования мышц рук для работы или наших глазных мышц для того, чтобы смотреть в определенном направлении – или наш мозг для размышлений. Многие из наших ~ 30 000 химических веществ и сложные клетки, из которых они сделаны, должны постоянно разрушаться и остатки, выводимые из организма, синтезируются как новые. (Например, В каждом эритроците содержится около 250 миллионов молекул гемоглобина.В каждом гемоглобине есть четыре атома железа, которые отвечают за улавливание кислород в наших легких, транспортируя его ко всем клеткам нашего тела и высвобождая его там для производства энергии в процессе окисления. Персона средней массы синтезирует примерно 500 трлн молекул железосодержащего гемоглобина в секунду в костном мозге. Каждую секунду разрушается одинаковое количество молекул гемоглобина. затем выводится с калом, придавая ему цвет одной формы оксида железа (ржавчина.) Не может быть минут, в которые кислород не поступает к энергозатратным клеткам сердца или перекачивается к энергозатратным мозг: мы умираем от сердечного приступа, если его клетки и мозг будут либо необратимо повреждены, либо, если их слишком много минуты проходят без кислорода для рассеивания энергии и синтеза АТФ, приводит к смерти .. Второй закон – или, лучше сказать, предсказанный поток энергии по второму закону – необходим для всей жизни.
(Несколько дополнительных деталей можно найти на http://secondlaw.oxy.edu/five.html) Тысячи раз в день в нашей обычной деятельности (и неисчислимые триллионы раз триллионы раз в биохимии нашего тела), мы неосознанно используем второй закон направленности потока энергии к нашему большому преимуществу.
В наша открытая система Земли, Солнца и космоса у нас есть огромная привилегия использования второго закона для блага человека, как и природа для поддержание на Земле ее высокоэнергетической экологии.Мы делаем это путем отклонения части энергии для наших целей, так как она составляет , рассеивая , когда самопроизвольно процесс следует второму закону. Ярким примером является использование нами горения. или окисление в наших машинах .. Горение – это спонтанная реакция углеродсодержащих такие вещества, как древесина, уголь, газ или масло с кислородом – после того, как реакция был инициирован пламенем или искрой. Потому что это спонтанно, по мнению второй закон, помимо новых низкоэнергетических химических соединений, образованных (в основном углекислый газ и вода), окисление рассеивает большое количество энергии в виде тепла (то есть на самом деле очень быстро движущиеся молекулы углерода диоксид + вода + воздух) и немного света.Затем наступает выигрыш: наши используют второй закон для наших человеческих целей. Сегодня это не просто отвлекает это рассеивание энергии от горящих дров костра в пещере для обогрева мы сами и готовим еду, как это делалось тысячелетия, но поток энергии ископаемого топлива для нашей деятельности, которая заставляет двигатели и машины, которые работают преобразовать наш материальный мир.
Очевидно, если мы подумаем о быть благодарным за природные явления, такие как слава теплого солнца каждый день и благо дождя на плодородной почве, мы должны быть благодарны действительно для второго закона.Как мы могли переоценить огромную диверсию энергии, которую мы можем получить за счет рассеивания энергии, которая второй закон благоприятствует сжиганию ископаемого топлива? Уголь, и особенно нефтяное топливо для автомобилей, самолетов, грузовиков, землеройных машин, поездов, корабли и электростанции – это кровь, руки и ноги и поддержка нервной системы современного общества. Конечно, мы не способный отводить больше, чем часть энергии, полученной при сгорании для нашего использования.Некоторая часть любого рассеивания энергии немедленно продолжается на своем способ полного рассеивания в окружающей среде и окончательной потери внешнего Космос. Большая часть энергии не «запружена» синтезом новых высших энергетические долгоживущие соединения (как в фотосинтезе), но просто используемые в движении машины или аналогичные временные функции просто рассредоточены позже, чем отходящее тепло, теряемое из выхлопной трубы после первоначального взрыва топливо. Второй закон часто откладывается, но его никогда не нарушают.
В равной степени очевидно, что наши истинные Наибольшую благодарность за второй закон следует выразить за постоянный разгон солнечной энергии, которая давным-давно помогала различным формам жизни, которые в конечном итоге образовалось ископаемое топливо, такое как нефть и уголь – та же солнечная энергодисперсионный процесс, который делает возможной сегодня жизнь растений и человека. Из огромного количества солнечной энергии, рассеянной в космическом пространстве, только одна миллиардная его ударяет в крошечный объем Земли.Около 30% из этого немедленно отражается и разносится в космическое пространство и 70% временно поглощается облаками и земной поверхностью. Только о 0,02% одной миллиардной солнечной энергии, поступающей на Землю, составляет захвачены для фотосинтеза. (Эти цифры устанавливают в контексте иррациональность писателей, которые, по сути, говорят, что Вселенная движется к ” цветение увеличенной жизни и сложной организации [растений и оживляет] “.Такое цветение, хотя для нас крайне важен, он ультрамикроскопичен до тех пор, пока Вселенная обеспокоен.)
| наверх |
Нарушение второго закона
Энергия распространение может быть отложено от микросекунд до тысячелетий или эонов из-за барьеров которые описаны в текстах по химии или http://secondlaw.oxy.edu/three.html или очевидны. У объектов, которые находятся высоко над уровнем земли, есть потенциал энергия.Второй закон предсказывает, что они склонны рассеивать эту энергию упав на землю. Очевидно, что горы не быстро уносят из этого предсказания второго закона. Самые высокие каменные вершины просто поскольку все опорные камни горы удерживаются на месте твердыми химические связи, соединяющие кремний и кислород, кальций и магний и другие атомы на месте. (Причем эти облигации нисколько не повлияли на кислородом – в отличие от бензина – потому что они уже в низкоэнергетическом полностью окисленном состоянии.) Таким образом, никаких изменений в высоких горный камень до внешних источников энергии, таких как чрезвычайно сильные бури или многочисленные циклы замерзания и оттаивания сначала физически прерываются или расколоть части скалы и куски горы, чтобы они могли разойтись их потенциальная энергия за счет падения на более низкие уровни. Второй закон может действительно быть заблокированным на миллионы лет в некоторых веществах и некоторых механизмах из них.
Мы, люди разрабатывать всевозможные методы для создания препятствий или «загромождения» второй закон в течение значительных периодов времени.Обыденный пример: мы рисуем утюг, чтобы предотвратить его ржавчину. Живопись таким образом эффективна не из-за сложной химии, а просто потому, что он сохраняет кислород вдали от железа, поэтому реакция не может произойти. (Ржавчина, оксид железа, имеет тенденцию образовываться из металлического железа и газообразного кислорода, потому что, как и в большинстве самопроизвольных химические реакции, реагенты, железо и кислород, имеют большую внутреннюю энергии, чем продукт, оксид железа. Концентрированная энергия в менее концентрированную энергия по второму закону.) Хромирование стали методом препятствовать второму закону, препятствуя окислению стали. Термос для горячих или холодных жидкостей (как совсем другой изолирующий контейнер из этого белого пенополистирола) является простым примером препятствовать быстрому рассеиванию тепла, которое предсказывается второй закон. (Вакуум термоса между двумя стенками не иметь много молекул воздуха, которые могут переносить энергию от горячей жидкости к более прохладная атмосфера – или от более теплой атмосферы к холодным жидкостям внутри.Плохая передача энергии пенополистиролом также препятствует тому, что второй закон предсказывает – распространение энергии.)
Некоторые системы распространяют свои энергия быстро, например, тепловая энергия в горячих объектах в более прохладную комнату. Однако, к счастью, большинство делает это очень медленно. Как уже указывалось – тоже часто (!) но это жизненно важный момент, малоизвестный тем не в химии о действии второго закона – – некоторые системы и формы энергии, такие как энергия, содержащаяся в химических связях, остаются «запруженными» и не могут рассеивать свою энергию в химическом реакции до тех пор, пока им не будет передана дополнительная энергия, энергия активации. начать процесс.Энергия в целлюлозе и других химических веществах в деревьях, окруженных кислородом воздуха, остается неизменным в течение многих лет или столетия, но через короткое время горячее пламя может начать высвобождение эта энергия в виде тепла, углекислого газа и воды – и количества выделяемой энергии может хватить на распространение лесного пожара. (Дым и большая часть золы являются результатом неполного окисления химикаты в деревьях.)
Солнце потребуется в общей сложности около 5 000 000 000 лет, чтобы высвободить ядерный энергия в его водороде, который плавится, образуя гелий.Некоторые люди видят это повод для отчаяния даже с точки зрения наших 12000 летняя цивилизация. Остальные не возмущены.
Нашивка из шиповника №4. Путаница (бумаги на столе, одежда в спальню)
В процессе естественного самопроизвольного «распространения энергии», видимые объекты от гальки до бумаги и камней пирамид можно перемещать в случайные места, если величина и тип рассеиваемой энергии воздействует на объекты, чтобы воздействовать на них.Распространенная ошибка в интерпретации изменение энтропии означает увеличение энтропии в объектах когда вещи, которые мы определяем как «упорядоченные» подталкиваются к случайным или «беспорядочным» порядкам. Это неверно. Вместо этого он смотрит на пассивную половину изображения, на объекты. энергии, которая толкает вещи и распространяется в процессе! Изменение энтропии связано с распространением энергии , а не с узоры.У объектов не происходит изменения энтропии, если их энергия не равна изменяется после перемещения, таким образом, увеличение энтропии не происходит в их, если от них или к ним не было разогнано энергия . Грязный Комната ученика может показаться нечетким узором, но она не представляет любое увеличение энтропии в объектах по сравнению с изначально опрятной комнатой. Единственное изменение энергии, которое произошло, – это энергия, рассеянная в теле ученика. мышцы во время подбрасывания или падения вещей здесь или там, а не в предметах самих себя.
в случайном порядке карты, классический ошибочный пример увеличения энтропии, становятся «беспорядочными» из-за того, что энергия рассеивается в мышцах шаффлера, чей АТФ используется для перемещения карт (наряду с производством небольшого количества тепла). Сами карты не претерпевают никаких изменений энтропии, потому что в них не происходит рассеивания энергии. Чрезмерно развернутое обсуждение этой ошибки находится в http: // secondlaw.oxy.edu/six.html и последующие страницы. А более научный анализ находится на http://www.jce.divched.org/Journal/Issues/1999/Oct/abs1385.html
Земля выигрывает от второго закона – использования энергии расходится от солнца
В природе лучистая энергия солнца рассеивается, когда оно ударяет по молекулам воды в океане и заставляет их двигаться быстрее, т.е. вода становится теплее и легче испаряется.В этом процессе рассеивания солнечного энергии, несметные тонны воды поднимаются в воздух, создавая облака как некоторые молекулы воды передают часть своей энергии охладителю верхняя атмосфера. Когда солнечная энергия рассеивается, ударяясь о землю поверхность и нагревает ее, часть ее затеняется облаками. Неравномерное потепление земли и воды вызывает переменные столбы теплого воздуха, поднимающиеся и увеличивающиеся случайное движение воздуха. Результатом являются ветры, которые еще больше рассеивают исходный энергия массового движения воздуха.Вода в воздухе, которая была в форма облаков, радикально остывает, когда начинает течь по высоким горам или встречает холодный воздух и выпадает в виде дождя, увеличивая количество озер и создавая источники потока на больших высотах. Конечно, это дает потенциальную энергию к таким ручьям, потому что они находятся намного выше уровня моря. Вода течет из высоты рассеивает свою потенциальную энергию (если она не загорожена, и второму закону таким образом препятствует) течением вниз, прорезая овраги и, с поднятием земли (вызванным рассеянием энергии глубоко под поверхность), образуя как небольшие, так и грандиозные каньоны.
ср использовать движение воды в реках (рассеивая их потенциальную энергию по мере того, как они стекают к уровню моря), чтобы включить турбины, подключенные к электрическому генераторы, которые производят для нас электроэнергию (дальнейшее распространение потенциала энергия текущей воды). Ветры рассеивают свою энергию в вращении ветряных мельниц присоединенные к генераторам также производят некоторую электрическую мощность. Это некоторые из действия, посредством которых природа, следуя второму закону, дает нам свежие вода, с переменным ветром, с заснеженными горами и с уровнем выше уровня моря вода, которая приводит в движение наши турбины и производит электричество.
Иногда и по совпадению, движение ветра и теплой влаги из тропического океана может вызвать концентрацию энергии для образования урагана. (Ураганов нет больше нарушение второго закона, чем автомобиль с кривошипным двигателем, который случается выпрыгивает в гору и умирает, поэтому без тормозов превращается в ракету мчится назад вниз по склону и въезжает в дом .. Больше тепла в поднимающейся влажности с теплой поверхности океана был подан в зарождающийся кружащийся туманный ветер и случайно слабая сила Кориолиса от вращения Земли помогает немного кружится и всасывается больше влаги.Так начинается огромный вихрь. и сметает в него больше теплой влаги .. Конечно, наблюдатель разрушительного ураган не может ощутить основной вклад солнечной энергии или сложного рассеяние энергии от теплой поверхности океана к более прохладным верхним слоям атмосферы, что по совпадению сформировал его.) “Смерть” урагана – более очевидный пример второй закон в действии: если такой шторм, порождаемый океаном, не будет продолжаться питается тепловой энергией из теплой воды для поддержания своего высокоэнергетического существования, ураган распространяет свою энергию и стихает.Второй закон всегда действует тенденция и – в динамических случаях, подобных этому – демонстрирует эту тенденцию в относительно короткое время, а не годы или эоны.
| наверх |

Фотосинтез, еще один пример взаимодействия энергии рассредоточение с отвлечением части этого потока энергии для получения нового, более концентрированное состояние энергии
В целом фотосинтетический процесс использует второй закон распределения солнечной энергии аналогично тому, что мы, люди, делаем с ископаемым топливом.Мы берем энергию, которая есть в химических связях топлива и кислорода, чтобы двигатели выполняли то, что мы хотим – за счет распределения части химической энергии в топливо и кислород в виде отработанного тепла и углекислый газ плюс вода в атмосферу. Растения принимают некоторые длины волн солнечной энергии рассеяния (плюс углекислый газ). из воздуха и воды из воздуха или земли) и создавать новые химические соединения в растении, которые более сложные и более энергоемкие, чем исходные углекислый газ и вода.(Тем временем выделяется кислород, и большая часть этого солнечная энергия, падающая на растение, распространяется по окружающей среде в виде тепла).
Впоследствии эти новые активные химические вещества в растении, невероятно сложные процессы образуют углеводы, некоторые аминокислоты, жирные кислоты и тысячи другие соединения посредством множества других реакций – но также рассеивают некоторую энергию во всех этих вторичных синтезах в виде тепла. В целом на заводе процесс «под гору» энергии, рассеиваемой от Солнца, отвлекается и затем соединяется с процессом “в гору” концентрации энергии в новых растительных веществах, но нет нарушения второй закон: улавливается только около 30% солнечной энергии, падающей под гору. синтезировать новые вещества в первичном процессе фотосинтеза. г. чистая общая дисперсия, «потеря» энергии (70%) все еще превышает концентрация, «прирост» энергии (30%) .
(Общая энергетическая схема похожа на то, как мы ведем машину. в гору. На мгновение это может показаться противоречащим второму закону. потому что мы «создали» огромную потенциальную энергию, закончив с тяжелой машиной на вершине холма. Однако расчеты быстро показать, что на больше энергии было рассеяно из-за изменения химические связи в бензине и кислороде с углекислым газом, водой и нагреть (чтобы заставить поршни, шестерни и колеса двигаться), чем потенциальная энергия, которую автомобиль получает, находясь на вершине холм.В огромном количестве процессов сложнее вождения автомобиль в гору, фотосинтез использует или отвлекает только часть нисходящий поток энергии второго закона для создания «восходящих» веществ и снабжают энергией растущее растение, чтобы оно продолжало функционировать.
Точно сказать что мы используем или используем второй закон отводя энергию из своего «нисходящего» (рассеивающего) поток для запуска двигателей, которые помогают нам перемещаться по земле и в космос, чтобы изменить топографию Земли для нашего удовольствия и для нашей повышенной безопасности (плотины, дамбы, водозабор), сделать полезные вещи от лыж до небоскребов или просто переставить маленькие и массивные предметы, чтобы доставить удовольствие нашему чувству красоты или порядка.Однако ни мы, ни фотосинтез природы на самом деле никогда не побеждают второй закон. Энергия самопроизвольно рассеивается, если ей не препятствовать – или переадресовано нами или по своей природе так.
Что случилось с энтропией?
Где был энтропии во всех предыдущих обсуждениях нашего и естественного участия со вторым законом? Мы исследовали многие аспекты расселения энергия, фундаментальный процесс, предсказываемый вторым законом.Энтропия количественная мера этого процесса. Говоря о втором права, мы говорили в целом качественно. Любой пример спонтанное физическое или химическое изменение (кроме гравитационного потенциала изменение энергии) включает в себя увеличение энтропии, поэтому в каждом из этих многих в предшествующих спонтанных случаях наблюдалось увеличение энтропии. (Это само по себе качественное предложение, конечно. Количественный расчет изменение количества энтропии иногда бывает непростым.)
Распространенная ошибка в неформальной обсуждение энтропии включает изменения энтропии в фотосинтезе. Это только что было проанализировано с точки зрения второго закона и энергии. В Ниже приводится краткое изложение энтропии.
Потому что сложный и высокоэнергетический соединения (по сравнению с исходными материалами диоксида углерода и воды) образуются в процессе фотосинтеза, часто делается вывод, что там это уменьшение на энтропии на в процессе.Это смотрит только на половину участников реакции – атомы углекислого газа и вода, которая была реорганизована. Но это изменение / рассеяние энергии в вся система завода и его окружения , определяющая изменение энтропии! (Вот где точка зрения “изолированной системы” of Briar Patch # 2 часто вводит в заблуждение. Фотосинтез в растении не состоит из одной изолированной системы завода.) Мы не можем пропустить учитывая, что случилось с солнечным светом, который рассеивает энергию и управляя всеми огромными изменениями в листьях растений.
Как мы видели, эксперименты и расчеты показывают, что максимальная эффективность фотосинтеза у большинства растений находится в пределах 30%. Это означает, что из солнечного света попадает в растение, 70% рассеивается в окружающей среде (энтропия увеличение при небольшом нагревании листа и атмосферы), а 30% поглощается растением на начальных этапах фотосинтеза новых комплекс “высокоэнергетический” вещества (у растения уменьшилась энтропия).Конечно, это меньше, чем увеличение энтропии на 100%, которое происходит, когда солнечный свет просто ударяет по песку (и просто согревает его, воздух и излучается обратно в космос) вместо того, чтобы ударить по листу. Тем не менее фотосинтез по-прежнему чистое увеличение энтропии и не уменьшение энтропии для всего процесса, который включает как растения, так и падающий солнечный свет, как часто упоминается в печати.
Второй закон – точный описание того, как устроен мир.Это было основано на обычном человеческом опыте. и было подтверждено в бесчисленных случаях, включая фотосинтез, точным научным наблюдением.
Энтропия увеличение без энергии увеличение
Много повседневные примеры увеличения энтропии включают простое увеличение энергии в особая «система» (часть совокупности «система плюс окружение»).. Это увеличение энергии обычно проявляется в повышении температуры (вызванном более быстро движущиеся молекулы) в системе после некоторого появления, чем прежде, например, когда кастрюля или вода в кастрюле нагреваются, или когда нагревается комната, их энтропия увеличивается. В них была рассеяна дополнительная энергия извне. источник, «окружение». Внешним источником часто является горение, химическое реакция нефтепродуктов – природного газа или мазута – с кислородом на дают менее энергичный углекислый газ и воду плюс тепло.Энергия разошлась от г. химические связи газа или масла и кислорода распределяются от до медленнее движущиеся молекулы кастрюли, воды или воздуха в комнате. Если энергия увеличение происходит внутри системы, в ней должно происходить увеличение энтропии. Более энергия была рассредоточена внутри системы, и это то, что измеряет энтропия.
Таким образом, мы можем анализировать множество простых ситуаций с точки зрения энергии и энтропии. Почему тает лед в теплом помещении? В первом приближении это просто.В быстрее движущиеся («более горячие») молекулы в комнате могут рассеиваться их энергия, заставляя более медленно движущиеся («более холодные») молекулы во льду ускоряться. Это было бы следствием второго закона и следовательно, это должен быть спонтанный процесс, связанный с увеличением энтропия льда, когда он тает с образованием воды. Более сложный вид включает в себя тот факт, что жидкая вода может иметь гораздо больше способов распространения энергии, чем лед – молекулы воды быстро разрывают свои связи с соседними молекулами и могут перемещаться на небольшое расстояние, создавая новые связи с другими молекулами.Это движение, хотя и незначительное, намного сильнее предыдущего «танца в точке» в кристаллическом льду. Следовательно, если вода более эффективно рассеивает энергию, чем лед, когда они вместе при температуре чуть выше равновесной температуры, жидкая вода будет предпочтительнее, потому что она лучше рассеивает доступную энергию в системе чем лед.
В мудрый наблюдатель спросит: «Разве теплая комната не уменьшает в своей энтропии ? когда его молекулы должны немного замедлиться в результате передачи некоторых их энергии на более медленные во льду и на более подвижные в воде? »Ответ – да, в комнате действительно уменьшается энтропия, но окончательно состояние комнаты ПЛЮС от нагретого и растаявшего льда приводит к чистой энтропии увеличивать.Чтобы правильно оценить изменение энтропии, нужно всегда проверять оба систему и ее окружение. [Ниже приводится краткое описание для тех, кто с некоторыми предварительными знаниями энтропии: напомним, что энтропия равна q / T и, следовательно, при более низком T во льду, чем в комнате, количество энтропии увеличивается в лед больше, чем уменьшение q / T в помещении с более высокой температурой. Генерал вывод: любая передача энергии из-за разницы T приводит к чистой энтропии увеличьте в совокупности системы плюс окружение .])
В тот же мудрый наблюдатель мог бы задать аналогичный вопрос в начале этого статья, когда упоминались горячие сковороды, охлаждающиеся на воздухе в помещении. Сковорода уменьшается в энтропии, но полное изменение энтропии в кастрюле + комнате представляет собой чистое увеличение энтропия. Системы с более высокими температурами / окружающая среда уменьшаются на меньше дюймов энтропия, чем более низкотемпературные системы / окружающая среда, увеличивается в энтропии.
И наоборот, почему снежинки образуются, когда в воздухе присутствует влага (вода), более холодная, чем замерзшая вода температура? Если энергия может легко распространяться, она будет.Это второй закон! Поэтому, если что-то теплее другого и два находятся в контакте, теплее будет распространяться или рассеиваться часть его энергия к более холодным. Вот почему вода рассеивает свою энергию в более холодный воздух и тогда температура воды упадет до нуля и вода начнет формировать кристаллы льда, которые мы узнаем как снежинки. (Молекулы воды в воздухе образуют снежинки, лед, гексагональные узоры, потому что энергии в этой форме кристалла самые низкие – большее количество энергии будет рассеиваться по второму закону, если формируются эти шестиугольные узоры, а не другие возможные формы.)
Некоторые, казалось бы, более сложные оценки энергии и энтропии используются даже в обыденных ситуациях встречаются ежедневно. Однако, сделав несколько подсказок, мы можем прийти к общему ответы на все подобные события.
1. Почему газы смешиваются самопроизвольно? Ставится тот же основной вопрос в “Почему вы могли быстро почувствовать запах духов, которые выпущены в одном углу большой комнаты в дальнем углу, даже если воздух в комнате может быть “абсолютно” неподвижным? ” (В этом процессе НЕТ изменений энергии, и все же это происходит спонтанно.Где здесь такое рассредоточение энергии, которое, согласно второму закону, является характерным? всех стихийных происшествий?)
2. Почему жидкости смешиваются самопроизвольно? Тот же вопрос: “Почему крем смешать с кофе той же температуры? “(БЕЗ изменения энергии. Где это какой-то рассредоточение энергии ?!)
3. Зачем ароматизировать пар, кислород, азот или гелий самопроизвольно? и мгновенно перетекать в откачанную камеру? (НИКАКОГО изменения энергии.Где второй закон здесь?)
Быстрый, простой и правильный качественный ответ: эти примеры смешивания или увеличения объема – это просто иллюстрации того, что происходит при быстром движении, случайно сталкивающиеся молекулы делают, когда им задано возможность распространить свою энергию в большем пространстве .
[Ниже приводится более подробная информация, чем в любом другом случайный читатель должен быть обеспокоен.Это несколько более сложный изучение научных основ рассредоточения энергии по объему расширение и смешивание, хотя это более низкий уровень, чем окончательное утверждение второго закона, представленного в «Коробке» возле старта этой статьи, которая включает микросостояния.]
Чтобы разобраться в этих случаях нам нужно рассказать о том, как уровни энергии участвуют в поведении энергичных молекул. (Рисунки 1 и 2 в http: // 2ndlaw.oxy.edu/entropy.html .) В любой группе есть широкий диапазон скорости и видов движения. молекул, что выше абсолютного нуля. Молекулы движутся (переводить), кувыркаться (вращаться) и вибрировать (атомы в молекулах действуют так, как будто они связаны с пружинами, растягивая вперед и назад, или виляние париком). Все этих движений увеличиваются по мере увеличения содержания энергии (обозначено температура). Каждый тип движения связан с определенной энергией. уровни от более низкого до более высокого содержания энергии.Для более точного понимание, рассеяние энергии, которое мы рассмотрели скорее с научной точки зрения, как просто распространение на другие молекулы и т. д., следует интерпретировать с точки зрения того, что энергичные молекулы находятся или «занимают» определенные уровни энергии или группы уровней. Эти уровни дискретны, т.е. молекулы не могут находиться в каком-либо промежуточном энергетическом состоянии. Энергия «квантуется» и рассмотрение их энергетических отношений является частью квантовой механики.
чем больше энергетических уровней могут занимать энергичные молекулы, тем шире энергия может быть рассредоточена и тем больше энтропия. Но во многих случаях как мы уже говорили, дополнительные энергетические уровни могут быть заняты только в том случае, если системы были нагреты так, чтобы более медленные молекулы ускорились, и будет намного больше быстро движущихся молекул, чтобы занять доступные более высокие уровни. Тем не мение, это не единственный способ сделать доступными дополнительные уровни энергии.
Когда молекулам позволяют расширяться в больший объем (в трехмерном космос), квантовая механика показывает, что интересное изменение в возможном происходит сближение уровней энергии: уровни энергии становятся ближе друг к другу. (Технически, мы должны сказать, что плотность занятых уровней в любой выбранной энергии диапазон больше.) Это фактически означает, что молекулы, если им позволено занимают больший объем даже без увеличения своей энергии , может распространяться, чтобы занять гораздо больше уровней энергии.Это означает больший разброс энергии и увеличение энтропии просто благодаря большему трехмерному объем, в котором могут двигаться молекулы. (Далее, поскольку любое изменение в увеличение энтропии является спонтанным изменением. Это происходит без каких-либо внешняя помощь, энергозатраты и т. д.)
Как это применимо к (1) духам в комнате? Самопроизвольно смешивается с газами в большой комнате , потому что его энергия перераспределяется между больше уровней энергии , чем в небольшом паровом пространстве бутылки.Это то же самое, что и большее рассеяние энергии = увеличение энтропии = спонтанность.
А (2) сливки в кофе? (Или любые другие виды смешивания жидкостей?) То же, что и выше. Поскольку энергия движения в молекулах вещества в сливках могут быть более распределены между молекулами в кофе, энергия сливок или любой другой жидкости, смешивающейся с другой, перераспределяется между еще энергией уровень в смеси, чем сам по себе = больший разброс энергии = увеличение энтропии = самопроизвольное перемешивание.
(3) Газ самопроизвольно устремляется в пространство, которое было вакуумом? Тем же объяснение как (1) выше. Увеличение объема = больше энергии доступно для вещества с той же энергией, что и в меньшем объеме = перераспределение энергии между большим количеством уровней энергии = повышенная энергия рассеяние = увеличение энтропии = самопроизвольный процесс.
В этом примере газу «позволено» попасть в откачанный бутылки, коробки или камеры, мы считаем, что это не только быть спонтанным (происходить само по себе), но мгновенным (происходить очень быстро).Но чувства ненадежны. Наука требует причин (и, как мы осведомлены, второй закон делает предсказания только о спонтанности событий, а не их темпов или скорости их протекания). К счастью, сейчас есть прочная теоретическая основа для наших практических внутреннее чувство, что “из Конечно, газ автоматически заполнит вакуум! ». Квантовая механика дает неоспоримые расчеты, которые являются разумное основание, не только для газа, расширяющегося в вакуум, но для всех результатов второго закона, представленных в этой статье.В наука, это даже лучше, чем чувство.
Перорация
W Мы видели ряд примеров важности второго закона термодинамики. в корреляции, если не в объяснении, почему и сколько видов событий происходит. Там опубликовано не менее 30 различных авторитетных положений второго закона выдающимися физиками и химиками за последние 130 лет. Никто не помогает понять общая направленность закона лучше, чем “Второй закон термодинамики” говорит, что энергия всех видов в нашем материальном мире спонтанно рассеивается или распространяется, если этому не препятствуют.”” Его количественное codicil: «Изменение энтропии измеряет рассеивание энергии: сколько сколько энергии распространяется в конкретном процессе, или насколько широко, распространяется становится (при определенной температуре). Энтропия действительно проста, качественно!
Приложение
Жара
В отличие от большинства обыкновенных терминов, в науке слово «тепло» не означает вещество, вещь или товар. Строго говоря, поэтому невозможно иметь тепло в объекте, потому что тепло – это не сгусток или какая-то более достойная единица вида энергии.Тепло – это имя для процесс передачи энергии от тела при более высокой температуре к телу то есть при более низкой температуре. С молекулярной точки зрения тепло – это передача энергии через хаотическое / случайное движение молекул – более быстро движущиеся молекулы ударяя по менее быстро движущимся молекулам и увеличивая скорость помедленнее.
«Эта комната полна тепла» – это неверно с научной точки зрения (и, по общему признанию, невероятное в разговоре).«В комнате жарко» – правильный ощущение и заявление. “Я обогрел комнату” правильно, потому что это подразумевает процесс передачи энергии.
Однако часто бывает крайне неудобно уточнять наука или беседа, и поэтому слово “тепло” часто используется вне термодинамики (и во многих текстах), как если бы это была субстанция – зная, что это не так! «Тепло моей газовой горелки использовалось для …» может быть технически некорректным, но это четкое сообщение.Это конечно предпочтительнее «Тепловое движение продуктов окисления метан с кислородом (в результате энергии, выделенной из-за энергии связи углекислого газа и воды намного меньше, чем у реагентов) частично передано… ». 🙂
Энергия активации
Причина «энергии активации» кроется в природе химического вещества. связей и как сила связи влияет на химическую реакцию происходит.Следовательно, нам нужно сначала поговорить о связях в химии.
Химические связи – это силы, которые удерживают атомы вместе в молекуле. На схеме молекулы водорода HH штрих представляет собой связь между двумя атомами, который прочно удерживает их в единое целое. Большинство связей между атомы в молекулах довольно сильны; обычно требуется много энергии на перерыв им. (И наоборот, когда облигации образуются , между из отдельных атомов в молекулу обычно выделяется много энергии.) Связи в воде, h3O или, более подробно, H-O-H (которые должны иметь угол 105 ° между H-O и O-H), не допускайте попадания воды на отдельные атомов не только при температуре кипения 212 ° F, но даже намного выше 2000 ° F, где энергия в молекулах воды была бы очень большой. (Они бы не только быстро двигались, но и вибрировали, растягивая связи. между атомами O и H.)
В химической реакции, скажем, водорода с кислородом с образованием воды (H-H и O-O дают H-O-H), связи между атомами водорода в двух молекулы и между атомами кислорода должны быть разорваны и новые связи между водородом и кислородом должны образоваться две молекулы воды.Но процесс не может быть пошаговым в таком порядке – чтобы все связи должны быть сломаны до того, как будут сформированы новые – потому что обычно это занимает много времени. много энергии, чтобы разорвать химическую связь. Чтобы разорвать все или многие связи в реакции смеси, прежде чем могут образоваться какие-либо новые, потребует огромного количества внешних поставляемая энергия.
Вот почему для большинства реакций требуется относительно небольшой энергетический «толчок». начать. Например, искра должна быть внесена в смесь водород и кислород до того, как реакция начнет образовывать воду, но затем сразу становится взрывом.Почему это странное сочетание молекулярных непокорность, сопровождаемая фантастически быстрой реакцией? Нарушение старого связи (требующие энергии) обычно должны возникать немного до образования новых (развивающаяся энергия). Таким образом, даже если вода имеет более низкую энергию в своих связях, чем молекулы водорода плюс молекулы кислорода в их, так что большое количество энергии выделяется в целом, когда происходит реакция, ни одна из этой энергии может быть выпущен без начального “толчка”, чтобы помочь разорвать несколько водородных и кислородных связей непосредственно перед тем, как они образуют несколько молекул воды.Как только этот “толчок” происходит, энергия выделяется по мере того, как вода формируется обратная связь, чтобы сделать многие из непрореагировавших молекул водорода и кислорода двигаться гораздо быстрее и сталкиваться с силой, чтобы они реагировали на дальнейшее развитие энергия и так далее и так далее.
Первоначальный “толчок”, описанный в предыдущем абзаце, – это то, что химики вызовите энергию активации . Большинство спонтанных реакций требуют этого начального ввод количества энергии, энергии активации, чтобы помочь первому несколько молекул реагируют, поэтому они возвращают свою эволюционировавшую энергию, чтобы служить в качестве энергии активации для последующих молекул, чтобы повторить цикл.(Видеть http://shakespeare2ndlaw.oxy.edu для диаграмм энергий активации, E _ACT, то есть обозначается правильно как E _a в текстах и научных публикациях.)
Именно эта «второстепенная» деталь химических реакций, активация энергия, препятствующая мгновенному выполнению предсказаний второго закона и, таким образом, защищает биохимические вещества нашего организма и наши разлагаемые артефакты. от мгновенного окисления и других вредных реакций
| наверх |
Академическая и профессиональная биография
Что такое энтропия?
Энтропия – важное понятие в физике и химии, плюс его можно применять к другим дисциплинам, включая космологию и экономику.В физике это часть термодинамики. В химии это ключевое понятие физической химии.
Ключевые выводы: энтропия
Энтропия – это мера случайности или беспорядка системы.
Значение энтропии зависит от массы системы. Он обозначается буквой S и измеряется в джоулях на кельвин.
Энтропия может иметь положительное или отрицательное значение. Согласно второму закону термодинамики, энтропия системы может уменьшаться только в том случае, если энтропия другой системы увеличивается.
Определение энтропии
Энтропия – это мера беспорядка в системе. Это обширное свойство термодинамической системы, что означает, что его значение изменяется в зависимости от количества присутствующего вещества. В уравнениях энтропия обычно обозначается буквой S и измеряется в джоулях на кельвин (J⋅K ⁻¹) или кг⋅m ² ⋅s ⁻² K ⁻¹. Высокоупорядоченная система имеет низкую энтропию.
Уравнение и расчет энтропии
Существует несколько способов вычисления энтропии, но два наиболее распространенных уравнения относятся к обратимым термодинамическим процессам и изотермическим (с постоянной температурой) процессам.
Энтропия обратимого процесса
При расчете энтропии обратимого процесса делаются определенные допущения. Вероятно, наиболее важным предположением является то, что каждая конфигурация в рамках процесса равновероятна (чего на самом деле может не быть). При равной вероятности исходов энтропия равна постоянной Больцмана (k _B), умноженной на натуральный логарифм количества возможных состояний (W):
S = k _B ln Вт
Постоянная Больцмана равна 1.38065 × 10−23 Дж / К.
Энтропия изотермического процесса
Расчет может использоваться для нахождения интеграла dQ / T от начального состояния до конечного состояния, где Q – тепло, а T – абсолютная (Кельвиновская) температура системы.
Другой способ заявить об этом состоит в том, что изменение энтропии ( ΔS ) равно изменению тепла ( ΔQ ), деленному на абсолютную температуру ( T ):
ΔS = ΔQ / T
Энтропия и внутренняя энергия
В физической химии и термодинамике одно из наиболее полезных уравнений связывает энтропию с внутренней энергией (U) системы:
dU = T dS – p dV
Здесь изменение внутренней энергии dU равно абсолютной температуре T , умноженной на изменение энтропии за вычетом внешнего давления p и изменение объема V .
Энтропия и второй закон термодинамики
Второй закон термодинамики гласит, что полная энтропия замкнутой системы не может уменьшаться. Однако внутри системы энтропия одной системы может уменьшаться за счет увеличения энтропии другой системы.
Энтропия и тепловая смерть Вселенной
Некоторые ученые предсказывают, что энтропия Вселенной возрастет до такой степени, что случайность создаст систему, неспособную к полезной работе.Когда осталась только тепловая энергия, можно было бы сказать, что Вселенная умерла от тепловой смерти.
Однако другие ученые оспаривают теорию тепловой смерти. Некоторые говорят, что Вселенная как система все дальше отдаляется от энтропии, даже когда энтропия в ее областях увеличивается. Другие считают Вселенную частью более крупной системы. Третьи говорят, что возможные состояния не имеют равной вероятности, поэтому обычные уравнения для вычисления энтропии не верны.
Пример энтропии
Энтропия ледяной глыбы будет увеличиваться по мере таяния.Легко представить себе увеличение беспорядка в системе. Лед состоит из молекул воды, связанных друг с другом в кристаллической решетке. По мере таяния льда молекулы получают больше энергии, расходятся дальше друг от друга и теряют структуру, образуя жидкость. Точно так же фазовый переход от жидкости к газу, как от воды к водяному пару, увеличивает энергию системы.
С другой стороны, энергия может уменьшаться. Это происходит, когда пар превращается из фазы в воду или когда вода превращается в лед. Второй закон термодинамики не нарушается, потому что дело не в замкнутой системе.В то время как энтропия изучаемой системы может уменьшаться, энтропия окружающей среды увеличивается.
Энтропия и время
Энтропию часто называют стрелой времени, потому что материя в изолированных системах имеет тенденцию двигаться от порядка к беспорядку.
Источники
Аткинс, Питер; Хулио де Паула (2006). Физическая химия (8-е изд.). Издательство Оксфордского университета. ISBN 978-0-19-870072-2.
Чанг, Раймонд (1998). Химия (6-е изд.). Нью-Йорк: Макгроу Хилл. ISBN 978-0-07-115221-1.
Клаузиус, Рудольф (1850). О движущей силе тепла и о законах, которые могут быть выведены из нее для теории тепла . Poggendorff’s Annalen der Physick , LXXIX (Dover Reprint). ISBN 978-0-486-59065-3.
Landsberg, P.T. (1984). «Могут ли энтропия и« порядок »расти вместе?». Письма по физике . 102А (4): 171–173. DOI: 10.1016 / 0375-9601 (84) -4
Уотсон, Дж.Р.; Карсон, Э.М. (май 2002 г.). «Понимание студентами энтропии и свободной энергии Гиббса». Университетское химическое образование . 6 (1): 4. ISSN 1369-5614
Три закона термодинамики
Цель обучения
Обсудите три закона термодинамики.
Ключевые моменты
Первый закон, также известный как Закон сохранения энергии, гласит, что энергия не может быть создана или уничтожена в изолированной системе.
Второй закон термодинамики гласит, что энтропия любой изолированной системы всегда увеличивается.
Третий закон термодинамики гласит, что энтропия системы приближается к постоянному значению, когда температура приближается к абсолютному нулю.
Условия
абсолютный ноль Наименьшая теоретически возможная температура.
энтропия – термодинамическое свойство, которое является мерой тепловой энергии системы на единицу температуры, недоступной для выполнения полезной работы.
Система или окружение
Чтобы избежать путаницы, ученые обсуждают термодинамические величины применительно к системе и ее окружению. Все, что не является частью системы, составляет ее окружение. Система и окружение разделены границей. Например, если система представляет собой один моль газа в контейнере, то граница – это просто внутренняя стенка самого контейнера. Все, что находится за пределами границы, считается окружающей средой, включая сам контейнер.
Граница должна быть четко определена, чтобы можно было четко сказать, находится ли данная часть мира в системе или в ее окружении. Если материя не может пройти через границу, то система называется закрытой ; в противном случае это открытый . Замкнутая система все еще может обмениваться энергией с окружающей средой, если система не является изолированной, и в этом случае ни материя, ни энергия не могут проходить через границу.
Термодинамическая система Схема термодинамической системы
Первый закон термодинамики
Первый закон термодинамики, также известный как закон сохранения энергии, гласит, что энергия не может быть ни создана, ни разрушена; энергия может только передаваться или изменяться из одной формы в другую.Например, включение света производит энергию; однако преобразуется именно электрическая энергия.
Один из способов выразить первый закон термодинамики состоит в том, что любое изменение внутренней энергии (∆E) системы определяется суммой тепла (q), протекающего через ее границы, и работы (w), совершаемой над система по окрестностям:
[латекс] \ Delta E = q + w [/ латекс]
Этот закон гласит, что есть два вида процессов, тепло и работа, которые могут привести к изменению внутренней энергии системы.Поскольку и тепло, и работа могут быть измерены и количественно определены, это то же самое, что сказать, что любое изменение энергии системы должно приводить к соответствующему изменению энергии окружающей среды вне системы. Другими словами, энергия не может быть создана или уничтожена. Если тепло поступает в систему или окружающая среда работает над ней, внутренняя энергия увеличивается, а знаки q и w положительны. И наоборот, тепловой поток из системы или работа, выполняемая системой (в окружающей среде), будет происходить за счет внутренней энергии, и поэтому q и w будут отрицательными.
Второй закон термодинамики
Второй закон термодинамики гласит, что энтропия любой изолированной системы всегда увеличивается. Изолированные системы спонтанно эволюционируют к тепловому равновесию – состоянию максимальной энтропии системы. Проще говоря: энтропия Вселенной (конечной изолированной системы) только увеличивается и никогда не уменьшается.
Простой способ представить себе второй закон термодинамики состоит в том, что комната, если ее не убирать и не прибирать, со временем неизменно становится более беспорядочной и беспорядочной – независимо от того, насколько осторожно нужно содержать ее в чистоте.Когда комната убирается, ее энтропия уменьшается, но усилия по ее очистке привели к увеличению энтропии за пределами комнаты, которое превышает потерянную энтропию.
Третий закон термодинамики
Третий закон термодинамики гласит, что энтропия системы приближается к постоянному значению, когда температура приближается к абсолютному нулю. Энтропия системы при абсолютном нуле обычно равна нулю и во всех случаях определяется только количеством различных основных состояний, которые она имеет.В частности, энтропия чистого кристаллического вещества (совершенный порядок) при абсолютной нулевой температуре равна нулю. Это утверждение верно, если в идеальном кристалле есть только одно состояние с минимальной энергией.
Показать источники
Boundless проверяет и курирует высококачественный контент с открытой лицензией из Интернета. Этот конкретный ресурс использовал следующие источники:
12.3 Второй закон термодинамики: энтропия – физика
Цели обучения секции
К концу этого раздела вы сможете делать следующее:
Опишите энтропию
Опишите второй закон термодинамики
Решение задач, связанных со вторым началом термодинамики
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
(6) Научные концепции.Учащийся знает, что в физической системе происходят изменения, и применяет законы сохранения энергии и количества движения. Ожидается, что студент:
(ГРАММ) анализировать и объяснять повседневные примеры, которые иллюстрируют законы термодинамики, включая закон сохранения энергии и закон энтропии
Раздел Ключевые термины
энтропия второй закон термодинамики
Энтропия
Поддержка учителей
Поддержка учителей
[BL] [OL] [AL] Проверить температуру и абсолютную температуру.Вспомните предыдущие дискуссии об эффективности двигателя. Оцените понимание учащимися эффективности.
Вспомните из введения к главе, что даже теоретически невозможно, чтобы двигатели были на 100 процентов эффективными. Это явление объясняется вторым законом термодинамики, который основан на концепции, известной как энтропия. Энтропия – это мера беспорядка системы. Энтропия также описывает, сколько энергии , а не доступно для выполнения работы. Чем более неупорядоченная система и выше энтропия, тем меньше энергии доступно системе для выполнения работы.
Поддержка учителей
Поддержка учителей
Значение энтропии трудно понять, поскольку это может показаться абстрактным понятием. Однако мы видим примеры энтропии в нашей повседневной жизни. Например, при проколе автомобильной шины воздух рассеивается во всех направлениях. Когда вода в посуде ставится на стойку, она в конечном итоге испаряется, а отдельные молекулы распространяются в окружающем воздухе. Когда в комнате помещается горячий предмет, он быстро распределяет тепловую энергию во всех направлениях.Энтропию можно рассматривать как меру рассеивания энергии. Он измеряет, сколько энергии было распределено в процессе. Поток любой энергии всегда идет снизу вверх. Следовательно, энтропия всегда имеет тенденцию к увеличению.
Хотя для работы можно использовать все формы энергии, невозможно использовать всю доступную энергию для работы. Следовательно, не вся энергия, передаваемая посредством тепла, может быть преобразована в работу, и некоторая ее часть теряется в виде отработанного тепла, то есть тепла, которое не идет на выполнение работы.Недоступность энергии важна в термодинамике; Фактически, это поле возникло из-за попыток преобразовать тепло в работу, как это делают двигатели.
Уравнение изменения энтропии, ΔSΔS, равно
, где Q – это тепло, которое передает энергию во время процесса, а T – абсолютная температура, при которой происходит процесс.
Q положительно для энергии, переданной в системе посредством тепла, и отрицательно для энергии, переданной из системе посредством тепла.В системе СИ энтропия выражается в джоулях на кельвин (Дж / К). Если температура изменяется во время процесса, то обычно хорошим приближением (для небольших изменений температуры) является средняя температура T , чтобы избежать сложных математических расчетов (расчетов).
Советы для успеха
Абсолютная температура – это температура, измеряемая в Кельвинах. Шкала Кельвина – это шкала абсолютной температуры, которая измеряется числом градусов выше абсолютного нуля.Таким образом, все температуры положительные. Использование температуры по другой, неабсолютной шкале, например по Фаренгейту или Цельсию, даст неправильный ответ.
Второй закон термодинамики
Вы когда-нибудь играли в карточную игру «52 пикапа»? Если это так, то вы были объектом розыгрыша и в процессе извлекли ценный урок о природе Вселенной, описанной вторым законом термодинамики. В игре «52 подбора» шутник бросает на пол всю колоду игральных карт, а вы можете их поднять.В процессе подбора карт вы, возможно, заметили, что объем работы, необходимый для восстановления упорядоченного состояния карт в колоде, намного превышает объем работы, необходимый для того, чтобы подбросить карты и создать беспорядок.
Второй закон термодинамики утверждает, что полная энтропия системы либо увеличивается, либо остается постоянной в любом спонтанном процессе; он никогда не уменьшается. Важным следствием этого закона является то, что тепло передает энергию спонтанно от объектов с более высокой температурой к объектам с более низкой температурой, но никогда самопроизвольно в обратном направлении.Это связано с тем, что энтропия увеличивается при передаче тепла от горячей к холодной (рис. 12.9). Поскольку изменение энтропии составляет Q / T , существует большее изменение ΔSΔS при более низких температурах (меньшее T ). Таким образом, уменьшение энтропии горячего (больший T ) объекта меньше, чем увеличение энтропии холодного (меньшего T ) объекта, что приводит к общему увеличению энтропии для системы.
Рисунок 12.9 Лед в этом напитке медленно тает.В конце концов, компоненты жидкости достигнут теплового равновесия, как предсказывает второй закон термодинамики, то есть после того, как тепло передает энергию от более теплой жидкости к более холодному льду. (Джон Салливан, PDPhoto.org)
Другой способ думать об этом заключается в том, что ни один процесс не может иметь своим единственным результатом теплопередачу энергии от холодильника к более горячему объекту. Тепло не может спонтанно передавать энергию от более холодной к более горячей, потому что энтропия всей системы уменьшится.
Предположим, мы смешиваем равные массы воды, которые изначально имеют две разные температуры, скажем 20,0 ° C 20,0 ° C. и 40,0 ° С – 40,0 ° С. В результате получится вода с промежуточной температурой 30,0 ° C30,0 ° C. В результате были получены три результата: энтропия увеличилась, некоторая энергия стала недоступной для выполнения работы, и система стала менее упорядоченной. Давайте подумаем о каждом из этих результатов.
Во-первых, почему увеличилась энтропия? Смешивание двух водоемов имеет тот же эффект, что и теплопередача энергии от вещества с более высокой температурой к веществу с более низкой температурой.Смешивание уменьшает энтропию более горячей воды, но увеличивает энтропию более холодной воды на большее количество, производя общее увеличение энтропии.
Во-вторых, как только две массы воды смешиваются, больше не остается разницы температур для передачи энергии за счет тепла и, следовательно, для выполнения работы. Энергия все еще находится в воде, но сейчас недоступно для работы .
В-третьих, смесь менее упорядоченная или, используя другой термин, менее структурированная.Вместо того, чтобы иметь две массы при разных температурах и с различным распределением молекулярных скоростей, теперь у нас есть одна масса с широким распределением молекулярных скоростей, среднее из которых дает промежуточную температуру.
Эти три результата – энтропия, недоступность энергии и беспорядок – не только связаны, но и фактически эквивалентны. Теплопередача энергии от горячей к холодной связана с природной тенденцией к тому, что системы становятся неупорядоченными и меньше энергии становится доступным для использования в качестве работы.
Чего не может быть на основании этого закона? Холодный объект, соприкасающийся с горячим, никогда самопроизвольно не передает энергию посредством тепла горячему объекту, становясь холоднее, в то время как горячий объект становится горячее. Горячий неподвижный автомобиль никогда не остывает и не трогается с места.
Другой пример – расширение клубка газа, введенного в один угол вакуумной камеры. Газ расширяется и заполняет камеру, но никогда не собирается самостоятельно в углу. Случайное движение молекул газа могло бы вернуть их всех в угол, но этого никогда не происходит (рис.12.10).
Рисунок 12.10 Примеры односторонних процессов в природе. (а) Передача тепла происходит самопроизвольно от горячего к холодному, но не от холодного к горячему. (б) Тормоза этого автомобиля преобразуют кинетическую энергию для увеличения внутренней энергии (температуры), а тепло передает эту энергию в окружающую среду. Обратный процесс невозможен. (c) Выброс газа в эту вакуумную камеру быстро расширяется, чтобы равномерно заполнить каждую часть камеры. Беспорядочные движения молекул газа не позволят им вообще вернуться в угол.
Мы объяснили, что тепло никогда не передает энергию спонтанно от более холодного объекта к более горячему. Ключевое слово здесь – спонтанно . Если мы действительно работаем с в системе, то будет возможным передавать энергию посредством тепла от более холодного объекта к более горячему. Мы узнаем об этом больше в следующем разделе, в котором холодильники рассматриваются как одно из приложений законов термодинамики.
Иногда люди неправильно понимают второй закон термодинамики, думая, что, исходя из этого закона, энтропия не может уменьшаться в каком-либо конкретном месте.Но на самом деле – это возможно, чтобы энтропия одной части Вселенной уменьшилась, пока общее изменение энтропии Вселенной увеличивается. В форме уравнения мы можем записать это как
ΔStot = ΔSsyst + ΔSenvir> 0. ΔStot = ΔSsyst + ΔSenvir> 0.
На основании этого уравнения мы видим, что ΔSsystΔSsyst может быть отрицательным, пока ΔSenvirΔSenvir положительна и больше по величине.
Как может энтропия системы уменьшаться? Передача энергии необходима.Если вы возьмете разбросанные по комнате шарики и поместите их в чашку, ваша работа уменьшит энтропию этой системы. Если вы собираете железную руду с земли, превращаете ее в сталь и строите мост, ваша работа уменьшит энтропию этой системы. Энергия, исходящая от Солнца, может уменьшить энтропию локальных систем на Земле, то есть ΔSsystΔSsyst отрицательна. Но общая энтропия остальной части Вселенной увеличивается на большую величину, то есть ΔSenvirΔSenvir положительна и больше по величине.В случае с железной рудой, хотя вы сделали систему моста и стали более структурированной, вы сделали это за счет Вселенной. В целом энтропия Вселенной увеличивается из-за беспорядка, создаваемого выкапыванием руды и превращением ее в сталь. Следовательно,
ΔStot = ΔSsyst + ΔSenvir> 0, ΔStot = ΔSsyst + ΔSenvir> 0,
12,14
и второй закон термодинамики не нарушается.
Каждый раз, когда растение накапливает некоторую солнечную энергию в виде химической потенциальной энергии или восходящий поток теплого воздуха поднимает парящую птицу, Земля испытывает локальное уменьшение энтропии, поскольку она использует часть энергии, передаваемой от Солнца в глубокий космос, для этого. Работа.Существует большое общее увеличение энтропии в результате такой массивной передачи энергии. Небольшая часть этой передачи энергии посредством тепла накапливается в структурированных системах на Земле, что приводит к гораздо меньшему локальному уменьшению энтропии.
Поддержка учителей
Поддержка учителей
[AL] Спросите учащихся, что бы произошло, если бы второй закон термодинамики не выполнялся. Что, если направление потока энергии было непредсказуемым? Сможет ли жизнь на Земле функционировать?
Решение задач, связанных со вторым началом термодинамики
Энтропия связана не только с недоступностью энергии для выполнения работы; это также показатель беспорядка.Например, в случае тающего блока льда высокоструктурированная и упорядоченная система молекул воды превращается в неупорядоченную жидкость, в которой молекулы не имеют фиксированных положений (рис. 12.11). Энтропия этого процесса сильно увеличилась, как мы увидим в следующем рабочем примере.
Рис. 12.11 Эти льдины тают во время арктического лета. Некоторые из них повторно замерзают зимой, но второй закон термодинамики предсказывает, что крайне маловероятно, что молекулы воды, содержащиеся в этих льдинах, превратятся в характерную форму аллигатора, которой они обладали, когда этот снимок был сделан летом этого года. 2009 г.(Патрик Келли, Береговая охрана США, Геологическая служба США)
Рабочий пример
Энтропия, связанная с расстройством
Найдите увеличение энтропии 1,00 кг льда при исходной температуре 0 ° C0 ° C. и плавится с образованием воды при 0 ° C0 ° C.
Стратегия
Изменение энтропии может быть вычислено из определения ΔSΔS, как только мы найдем энергию Q , необходимую для таяния льда.
Решение
Изменение энтропии определяется как
Здесь Q – тепло, необходимое для плавления 1.00 кг льда и выдается
, где м – масса, а LfLf – скрытая теплота плавления. Lf = 334 кДж / кг Lf = 334 кДж / кг для воды, поэтому
Q = (1,00 кг) (334 кДж / кг) = 3,34 × 105 Дж. Q = (1,00 кг) (334 кДж / кг) = 3,34 × 105 Дж.
12,17
Поскольку Q – это количество энергии, которое тепло добавляет ко льду, его значение положительное, а T – это температура таяния льда, T = 273 KT = 273 K Таким образом, изменение энтропии составляет
. ΔS = QT = 3,34 × 105J273 K = 1,22 × 103Дж / К. ΔS = QT = 3.34 × 105J273 K = 1,22 × 103 Дж / К.
12,18
Обсуждение
Рис. 12.12 Когда лед тает, он становится более неупорядоченным и менее структурированным. В систематическое расположение молекул в кристаллической структуре заменяется более случайное и менее упорядоченное движение молекул без фиксированных положений или ориентации. Его энтропия увеличивается, потому что в него происходит передача тепла. Энтропия – это мера беспорядок.
Изменение энтропии положительное, потому что тепло передает энергию льду , вызывая фазовый переход.{8} \, \ text {J / K}
Проверьте свое понимание
Поддержка учителей
Поддержка учителей
Используйте эти вопросы, чтобы оценить достижения учащимися учебных целей раздела. Если учащиеся борются с какой-то конкретной целью, эти вопросы помогут определить, какие учащиеся, и направят их к соответствующему содержанию.
13.
Что такое энтропия?
Энтропия – это мера потенциальной энергии системы.
Энтропия – это мера чистой работы, проделанной системой.
Энтропия – это мера неупорядоченности системы.
Энтропия – это мера теплопередачи энергии в системе.
14.
Какие формы энергии можно использовать для работы?
Работать может только работа.
Только тепло может делать работу.
Только внутренняя энергия может делать работу.
Тепло, работа и внутренняя энергия – все способны на работу.
15.
Каково утверждение второго закона термодинамики?
Все спонтанные процессы приводят к снижению общей энтропии системы.
Все спонтанные процессы приводят к увеличению общей энтропии системы.
Все спонтанные процессы приводят к пониженной или постоянной общей энтропии системы.
Все спонтанные процессы приводят к увеличению или постоянству общей энтропии системы.
16.
Что обычно происходит с энтропией всей системы при передаче энергии от высокой к низкой температуре?
Уменьшается.
Он должен оставаться постоянным.
Энтропию системы невозможно предсказать без конкретных значений температур.
Увеличивается.
Энтропия – Химия LibreTexts
Последнее обновление
Сохранить как PDF
Без заголовков
Энтропия – это функция состояния, которую часто ошибочно называют «состоянием беспорядка» системы.Качественно энтропия – это просто мера того, насколько энергия атомов и молекул становится более разбросанной в процессе, и может быть определена в терминах статистических вероятностей системы или в терминах других термодинамических величин. Энтропия также является предметом Второго и Третьего законов термодинамики, которые описывают изменения энтропии Вселенной по отношению к системе и окружающей среде, а также энтропию веществ, соответственно.
«Беспорядок» в термодинамической энтропии
Смысл Больцмана «повышенной случайности» как критерия конечного состояния равновесия для системы по сравнению с начальными условиями не был ошибочным.; это был его удивительно упрощенный вывод: если конечное состояние случайно, то исходная система должна быть противоположной, то есть упорядоченной. «Беспорядок» был для Больцмана следствием первоначального «порядка», а не – как это очевидно сегодня – того, что можно назвать только «предшествующим, меньшим, но все еще невообразимым для человека, большим количеством доступных микросостояний
Микросостояния
Словари определяют «макросостояние» как большое, а «микро» как очень маленькое, но макросостояние и микросостояние в термодинамике – это не просто определения больших и малых размеров химических систем.Напротив, это два совершенно разных взгляда на систему. Микросостояние – это одно из огромного количества различных доступных конфигураций энергии движения молекул * для конкретного макросостояния.
Простые изменения энтропии – примеры
Несколько примеров приведены для демонстрации того, как можно применить статистическое определение энтропии и 2-й закон. Фазовое изменение, расширение газа, разбавление, коллигативные свойства и осмос.
Статистическая энтропия
Энтропия – это функция состояния, которую часто ошибочно называют «состоянием беспорядка» системы.Качественно энтропия – это просто мера того, насколько энергия атомов и молекул становится более разбросанной в процессе, и может быть определена в терминах статистических вероятностей системы или в терминах других термодинамических величин.
Статистическая энтропия – масса, энергия и свобода
Энергия или масса части Вселенной может увеличиваться или уменьшаться, но только если есть соответствующее уменьшение или увеличение где-то еще во Вселенной.