Если предел стремится к нулю: Что такое предел функции как его найти - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Что такое предел функции как его найти

При каком условии Вам будут совсем не страшны любые задачи, где требуется найти предел функции? Условие следующее: у Вас есть базовый навык деления одних чисел на другие, на очень-очень маленькие числа и на очень-очень большие числа. Успех придет в процессе решения.

А теперь посмотрим, что о пределе функции гласит теория. Впрочем, можно зайти чуть-чуть вперед и сразу перейти к задачам, а потом вернуться к теории. Как удобнее.

Обобщённое понятие предела: число a есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.

Поясним это на примере, который также проиллюстрируем. А после примера приведём общий алгоритм решения пределов.

Запишем приведённый пример на языке формул. Итак, номер окружности возрастает и стремится к бесконечности, то есть .

Допустим, существует такой равнобедренный треугольник, что длина диаметра каждой вписанной в него окружности расчитывается по формуле

Величина, которую нам требуется найти, будет записана так:

Lim это и есть предел, а под ним указывается переменная, которая стремится к определённому значению – нулю, любому другому числу, бесконечности.

Теперь вычислим предел, присвоив переменной x значение бесконечность (в более строгом определении это называется “доопределить функцию”, с этим определением вы можете ознакомиться в последующих частях главы “Предел”). Примем, что конечная величина, поделенная на бесконечность, равна нулю:

С рассмотренной последовательностью окружностей свяжем другую переменную величину – последовательность сумм их диаметров:

Рассмотрев рисунок снова, обнаружим, что предел последовательности равен h – высоте равнобедренного треугольника. Вообще, предел может быть равен нулю, любому другому числу или бесконечности.

Теперь более строгие определения предела функции, которые Вас могут спросить на экзамене, и для понимания которых потребуется чуть больше внимания.

Предел функции при

Пусть функция f(x) определена на некотором множестве X и пусть дана точка . Возьмём из X последовательность точек, отличных от :

(1)

сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность

(2)

и можно ставить вопрос о существовании её предела.

Это означает: чтобы найти предел функции, нужно в функцию вместо

x подставить то значение, к которому стремится x.

Пример 1. Найти предел функции при .

Решение. Подставляем вместо x значение 0. Получаем:

Итак, предел данной функции при равен 1.

Предел функции при , при и при

Кроме рассмотренного понятия предела функции при существует также понятие предела функции при стремлении аргумента к бесконечности.

Определение 2.

Число A называется пределом функции f(x) при , если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к A.

Символически это записывается так: .

Определение 3. Число A называется пределом функции f(x) при (), если для любой бесконечно большой последовательности значений аргумента, элементы которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.

Символически это записывается так: ().

Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо x подставить бесконечность, плюс бесконечность или минус бесконечность.

Пример 2. Найти предел функции при .

Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:

Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.

Теорема 2.

Если функции f(x) и g(x) имеют пределы в точке , то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

(3)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

(4)

3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.

(5)

Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций.

Следствие 1. Предел постоянной равен самой постоянной, т.е.

Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.

Пример 3. Найти предел:

Решение.

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 4. Найти предел:

Решение. Предварительно убедимся, что предел делителя не равен нулю:

Таким образом, формула (5) применима и, значит,

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Теорема 3 (о пределе сложной функции).

Если существует конечный предел

а функция f(u) непрерывна в точке , то

Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.

Пример 5. Найти предел:

Решение. Теорема о пределе частного здесь неприменима, так как

Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим

где

корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:

При решении примеров 5 и 8 нам уже встретилась неопределённость вида . Эта неопределённость и неопределённость вида – самые распространённые неопределённости, которые требуется раскрывать при решении пределов.

БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.

Освоим эти приёмы на примерах.

Для преобразования выражений потребуются пособия Действия со степенями и корнями и Действия с дробями.

Неопределённость вида

Пример 12. Раскрыть неопределённость и найти предел .

Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :

Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или “супермалому числу”.

Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 13. Раскрыть неопределённость и найти предел .

Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:

Комментарий к ходу решения. В числителе загоняем “икс” под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо “икса”.

Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Неопределённость вида

Пример 14. Раскрыть неопределённость и найти предел .

Решение. В числителе – разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:

В знаменателе – квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):

Запишем выражение, полученное в результате преобразований и найдём предел функции:

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 15. Раскрыть неопределённость и найти предел

Решение. Теорема о пределе частного здесь неприменима, поскольку

Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:

Пример 16. Раскрыть неопределённость и найти предел

Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:

Продолжение темы “Предел”

Поделиться с друзьями

Mathway | Популярные задачи

1	Trovare la Derivata – d/dx	натуральный логарифм x
2	Вычислим интеграл	интеграл натурального логарифма x по x
3	Trovare la Derivata – d/dx	e^x
4	Вычислим интеграл	интеграл e^(2x) относительно x
5	Trovare la Derivata – d/dx	1/x
6	Trovare la Derivata – d/dx	x^2
7	Trovare la Derivata – d/dx	1/(x^2)
8	Trovare la Derivata – d/dx	sin(x)^2
9	Trovare la Derivata – d/dx	sec(x)
10	Вычислим интеграл	интеграл e^x относительно x
11	Вычислим интеграл	интеграл x^2 относительно x
12	Вычислим интеграл	интеграл квадратного корня x по x
13	Trovare la Derivata – d/dx	cos(x)^2
14	Вычислим интеграл	интеграл 1/x относительно x
15	Вычислим интеграл	интеграл sin(x)^2 относительно x
16	Trovare la Derivata – d/dx	x^3
17	Trovare la Derivata – d/dx	sec(x)^2
18	Вычислим интеграл	интеграл cos(x)^2 относительно x
19	Вычислим интеграл	интеграл sec(x)^2 относительно x
20	Trovare la Derivata – d/dx	e^(x^2)
21	Вычислим интеграл	интеграл в пределах от 0 до 1 кубического корня 1+7x по x
22	Trovare la Derivata – d/dx	sin(2x)
23	Trovare la Derivata – d/dx	tan(x)^2
24	Вычислим интеграл	интеграл 1/(x^2) относительно x
25	Trovare la Derivata – d/dx	2^x
26	График	натуральный логарифм a
27	Trovare la Derivata – d/dx	cos(2x)
28	Trovare la Derivata – d/dx	xe^x
29	Вычислим интеграл	интеграл 2x относительно x
30	Trovare la Derivata – d/dx	( натуральный логарифм x)^2
31	Trovare la Derivata – d/dx	натуральный логарифм (x)^2
32	Trovare la Derivata – d/dx	3x^2
33	Вычислим интеграл	интеграл xe^(2x) относительно x
34	Trovare la Derivata – d/dx	2e^x
35	Trovare la Derivata – d/dx	натуральный логарифм 2x
36	Trovare la Derivata – d/dx	-sin(x)
37	Trovare la Derivata – d/dx	4x^2-x+5
38	Trovare la Derivata – d/dx	y=16 корень четвертой степени 4x^4+4
39	Trovare la Derivata – d/dx	2x^2
40	Вычислим интеграл	интеграл e^(3x) относительно x
41	Вычислим интеграл	интеграл cos(2x) относительно x
42	Trovare la Derivata – d/dx	1/( квадратный корень x)
43	Вычислим интеграл	интеграл e^(x^2) относительно x
44	Вычислить	e^infinity
45	Trovare la Derivata – d/dx	x/2
46	Trovare la Derivata – d/dx	-cos(x)
47	Trovare la Derivata – d/dx	sin(3x)
48	Trovare la Derivata – d/dx	1/(x^3)
49	Вычислим интеграл	интеграл tan(x)^2 относительно x
50	Вычислим интеграл	интеграл 1 относительно x
51	Trovare la Derivata – d/dx	x^x
52	Trovare la Derivata – d/dx	x натуральный логарифм x
53	Trovare la Derivata – d/dx	x^4
54	Оценить предел	предел (3x-5)/(x-3), если x стремится к 3
55	Вычислим интеграл	интеграл от x^2 натуральный логарифм x по x
56	Trovare la Derivata – d/dx	f(x) = square root of x
57	Trovare la Derivata – d/dx	x^2sin(x)
58	Вычислим интеграл	интеграл sin(2x) относительно x
59	Trovare la Derivata – d/dx	3e^x
60	Вычислим интеграл	интеграл xe^x относительно x
61	Trovare la Derivata – d/dx	y=x^2
62	Trovare la Derivata – d/dx	квадратный корень x^2+1
63	Trovare la Derivata – d/dx	sin(x^2)
64	Вычислим интеграл	интеграл e^(-2x) относительно x
65	Вычислим интеграл	интеграл натурального логарифма квадратного корня x по x
66	Trovare la Derivata – d/dx	e^2
67	Trovare la Derivata – d/dx	x^2+1
68	Вычислим интеграл	интеграл sin(x) относительно x
69	Trovare la Derivata – d/dx	arcsin(x)
70	Оценить предел	предел (sin(x))/x, если x стремится к 0
71	Вычислим интеграл	интеграл e^(-x) относительно x
72	Trovare la Derivata – d/dx	x^5
73	Trovare la Derivata – d/dx	2/x
74	Trovare la Derivata – d/dx	натуральный логарифм 3x
75	Trovare la Derivata – d/dx	x^(1/2)
76	Trovare la Derivata – d/d@VAR	f(x) = square root of x
77	Trovare la Derivata – d/dx	cos(x^2)
78	Trovare la Derivata – d/dx	1/(x^5)
79	Trovare la Derivata – d/dx	кубический корень x^2
80	Вычислим интеграл	интеграл cos(x) относительно x
81	Вычислим интеграл	интеграл e^(-x^2) относительно x
82	Trovare la Derivata – d/d@VAR	f(x)=x^3
83	Вычислим интеграл	интеграл 4x^2+7 от 0 до 10 относительно x
84	Вычислим интеграл	интеграл от ( натуральный логарифм x)^2 по x
85	Trovare la Derivata – d/dx	логарифм x
86	Trovare la Derivata – d/dx	arctan(x)
87	Trovare la Derivata – d/dx	натуральный логарифм 5x
88	Trovare la Derivata – d/dx	5e^x
89	Trovare la Derivata – d/dx	cos(3x)
90	Вычислим интеграл	интеграл x^3 относительно x
91	Вычислим интеграл	интеграл x^2e^x относительно x
92	Trovare la Derivata – d/dx	16 корень четвертой степени 4x^4+4
93	Trovare la Derivata – d/dx	x/(e^x)
94	Оценить предел	предел arctan(e^x), если x стремится к 3
95	Вычислим интеграл	интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x
96	Trovare la Derivata – d/dx	3^x
97	Вычислим интеграл	интеграл xe^(x^2) относительно x
98	Trovare la Derivata – d/dx	2sin(x)
99	Вычислить	sec(0)^2
100	Trovare la Derivata – d/dx	натуральный логарифм x^2

Второй замечательный предел.

n, на него и упрощаем
Далее оцениваем вклад каждого слагаемого
Слагаемые 3/8 стремятся к нулю при переменной направляюейся к бесконечности, поскольку 3/8<1 (свойство степенно-показательной функции).

Пример 37.Предел последовательности с факториалами раскрывается розписанням факториала к наибольшему общему множителю для числителя и знаменателя.
Далее на него сокращаем и оцениваем лимит по значению показателей номера в числителе и знаменателе.
В нашем примере знаменатель быстрее растет, поэтому предел равен нулю.

Здесь использована следующее

свойство факториала.

Пример 38.Не применяя правила Лопиталя сравниваем максимальные показатели переменной в числителе и знаменателе дроби.
Так как знаменатель содержит старший показатель переменной 4>2 то и растет он быстрее.
Отсюда делаем вывод, что предел функции стремится к нулю.

Пример 39.Раскрываем особенность вида бесконечность разделить на бесконечность методом вынесения x^4 с числителя и знаменателя дроби. 3 и выполним предельный переход

Пример 41.Имеем особенность типа единица в степени бесконечность.
А это значит, что выражение в скобках и сам показатель надо свести под вторую важную границу.
Распишем числитель, чтобы выделить в нем выражение идентичное знаменателе.
Далее переходим к выражению, содержащем единицу плюс слагаемое.
В степени нужно выделить множителем 1/(слагаемое).
Таким образом получим экспоненту в степени предела дробной функции.
Для раскрития особенности использовали второй предел:

Пример 42.Имеем особенность типа единица в степени бесконечность.
Для ее раскрытия следует свести функцию под второй замечатеьный предел.
Как это сделать подробно показано в приведенной далее формуле

Подобных задач Вы можете найти очень много. Их суть в том, чтобы в показателе получить нужный степень, а он равен обратному значению слагаемого в скобках при единицы.
Таким методом получаем экспоненту. Дальнейшее вычисление сводится к вичислению предела степени экспоненты.
Здесь экспоненциальная функция стремится к бесконечности , поскольку значение больше единицы e=2.72>1.

Пример 43 В знаменателе дроби имеем неопределенность типа бесконечность минус бесконечность, фактически равное делению на ноль.
Чтобы избавиться корня домножим на сопряженное выражение, а дальше по формуле разности квадратов перепишем знаменатель.
Получим неопределенность бесконечность разделить на бесконечность, поэтому выносим переменную в наибольшей степени и сокращаем на нее.
Далее оцениваем вклад каждого слагаемого и находим предел функции на бесконечности

Пример 44.Найти повторные границы

Решение: Вычисляем предел функции двух переменных сначала по y, а дальше – x)
a)
б)

Пример 45. Вычислить повторные границы

Решение: Методика вычисления повторных границ не сложна:
сначала находим границу по одной переменной, считая вторую переменную постоянной.
Далее остается функция от одной переменной, а таких пределов мы разобрали очень много.
а)
б)
В этом задании предел по первой переменной равен нулю, поэтому повторные записываем только для формальности.
Предел в данном случае от порядка нахождения не зависит.
Однако, если взглянуть ответ из предыдущего примера то такое утверждение не всегда выполняется.

Ищите эффективные схемы вычисления пределов на страницах сайта, если возникают проблемы с пределами на экзаменах и модулях – обращайтесь за помощью!

Подготовка школьников к ЕГЭ (Справочник по математике – Элементы математического анализа

Предел функции

В ряде разделов нашего справочника, где требуется применение понятия предела функции, встречаются несколько ситуаций в зависимости от того, куда стремится аргумент функции x , и того, куда при этом стремится значение функции. Определения предела функции для этих случаев удобно представить в форме таблицы. Однако таблица, описывающая все возможные случаи, должна содержать 24 строки и является слишком громоздкой. Для удобства читателей мы привели в таблице только те определения предела функции, которые использованы в нашем справочнике.

Название

Обозначение

Определение

Предел функции f (x) при x, стремящемся к числу a, равен числу A

Число A называют пределом функции f (x) при x, стремящемся к числу a, если для любого положительного числа ε найдется такое положительное число δ , что при всех , удовлетворяющих неравенству

| x – a | < δ ,

будет выполняться неравенство

| f (x) – A | < ε .

f (x) → A

при x → a

Предел функции f (x) при x, стремящемся к , равен числу A

Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству

x > C ,

будет выполняться неравенство

| f (x) – A | < ε .

f (x) → A

при

Предел функции f (x) при x, стремящемся к , равен числу A

Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству

x < C ,

будет выполняться неравенство

| f (x) – A | < ε .

f (x) → A

при

Предел функции f (x) при x, стремящемся к , равен числу A

| x | > C ,

будет выполняться неравенство

| f (x) – A | < ε .

f (x) → A

при x →

Предел функции f (x) при x, стремящемся к , равен

Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству

| x | > C ,

будет выполняться неравенство

| f (x)| > D .

f (x) →

при x →

Предел функции f (x) при x, стремящемся к , равен

x > C ,

будет выполняться неравенство

| f (x)| > D .

f (x) →

при

Предел функции f (x) при x, стремящемся к , равен

Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству

x < C ,

будет выполняться неравенство

| f (x)| > D .

f (x) →

при

Предел функции f (x) при x, стремящемся к числу a слева, равен

Замечание. Когда говорят, что x стремится к a слева, то это означает, что при определении предела функции рассматриваются только те значения x , которые меньше a .

Функция f (x) стремится к , при x, стремящемся к числу a слева, если для любого положительного числа С найдется такое положительное число δ что при всех x, удовлетворяющих неравенству

a – δ < x < a ,

будет выполняться неравенство

| f (x)| > C .

f (x) →

при x → a – 0

Предел функции f (x) при x, стремящемся к числу a справа, равен

Замечание. Когда говорят, что x стремится к a справа, то это означает, что при определении предела функции рассматриваются только те значения x , которые больше a .

Функция f (x) стремится к , при x , стремящемся к числу a справа, если для любого положительного числа С, найдется такое положительное число δ что при всех x, удовлетворяющих неравенству

a < x < a + δ ,

будет выполняться неравенство

| f (x)| > C .

f (x) →

при x → a + 0

Название:

Предел функции f (x) при x, стремящемся к числу a, равен числу A

Обозначения:

или

f (x) → A при x → a

Определение:

| x – a | < δ ,

будет выполняться неравенство

| f (x) – A | < ε .

Название:

Предел функции f (x) при x, стремящемся к , равен числу A

Обозначения:

или

f (x) → A при

Определение:

Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству

x > C ,

будет выполняться неравенство

| f (x) – A | < ε .

Название:

Предел функции f (x) при x, стремящемся к , равен числу A

Обозначения:

или

f (x) → A при

Определение:

Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству

x < C ,

будет выполняться неравенство

| f (x) – A | < ε .

Название:

Предел функции f (x) при x, стремящемся к , равен числу A

Обозначения:

или

f (x) → A при x →

Определение:

| x | > C ,

будет выполняться неравенство

| f (x) – A | < ε .

Название:

Предел функции f (x) при x, стремящемся к , равен

Обозначения:

или

f (x) → при x →

Определение:

| x | > C ,

будет выполняться неравенство

| f (x)| > D .

Название:

Предел функции f (x) при x, стремящемся к , равен

Обозначения:

или

f (x) → при

Определение:

x > C ,

будет выполняться неравенство

| f (x)| > D .

Название:

Предел функции f (x) при x, стремящемся к , равен

Обозначения:

или

f (x) → при

Определение:

x < C ,

будет выполняться неравенство

| f (x)| > D .

Название:

Предел функции f (x) при x, стремящемся к числу a слева, равен

Обозначения:

или

f (x) → при x → a – 0 .

Определение:

a – δ < x < a ,

будет выполняться неравенство

| f (x)| > C .

Название:

Предел функции f (x) при x, стремящемся к числу a справа, равен

Обозначения:

или

f (x) → при x → a + 0 .

Определение:

a < x < a + δ ,

будет выполняться неравенство

| f (x)| > C .

Свойства пределов функций

Если у функций f (x) и g (x) при x , стремящемся к a , существуют пределы

и ,

где A и B – некоторые числа, то при x , стремящемся к a , существуют также и пределы суммы, разности и произведения этих функций, причем

Если, кроме того, выполнено условие

то при x , стремящемся к a , существует предел дроби

причем

Для любой непрерывной функции F (x) справедливо равенство

Раскрытие неопределенностей типа

Определение 1 . Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .

Часто неопределенность типа удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменале дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.

Пример 1. Найти предел функции предел функции

Решение. Вынесем за скобки «самое большое» слагаемое в каждой из скобок числителя и знаменателя дроби и, используя свойства пределов функций, получим

Ответ.

Пример 2. Найти предел функции предел функции

Решение. Преобразуем выражение, стоящее под знаком предела, к более удобному виду:

Далее, используя свойства пределов функций, находим

Ответ. 3 .

Раскрытие неопределенностей типа

Определение 2 . Если при нахождении предела дроби выясняется, что пределы числителя и знаменателя дроби равны 0 , то вычисление такого предела называют раскрытием неопределенности .

В алгебраических дробях неопределенность при x → a раскрывается при помощи разложения на множители числителя и знаменателя дроби с последующим сокращением на соответствующую степень множителя (x – a) .

Пример 3. Найти предел функции

Решение. Поскольку и числитель, и знаменатель дроби стремятся к 0 при x → – 2 , то для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе применим формулу сокращенного умножения «сумма кубов», а в знаменателе – разложение квадратного трехчлена на множители, а затем сократим дробь на (x + 2) :

Теперь предел знаменателя дроби равен – 11 , и, воспользовавшись свойствами пределов функций, получаем

Ответ.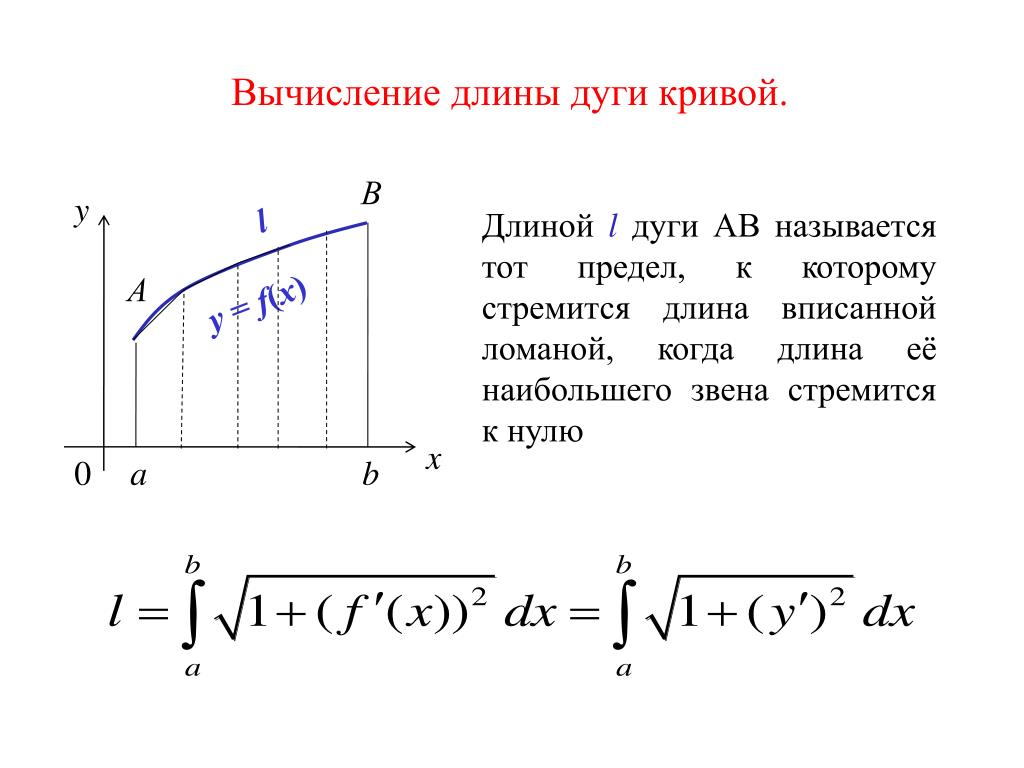

Пример 4. Найти предел функции

Решение. В этом примере также возникает неопределенность типа .

К сожалению, из-за большого размера формул для расчета подробные вычисления на Вашем мобильном устройстве не видны. Их можно посмотреть только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах).

Указания к решению примера. Поскольку знаменатель дроби является разностью двух квадратных корней, каждый из которых стремится к одному и тому же числу 5 при x → 5 , то сначала необходимо домножить и числитель, и знаменатель дроби на сумму этих квадратных корней и применить формулу сокращенного уножения «разность квадратов». Затем, разложив квадратный трехчлен 4x² – 9x – 55 на множители, сократить числитель и знаменатель на (x – 5) .

После этого, воспользовавшись свойствами пределов функций, получить ответ.

На Вашем мобильном устройстве отображается только результат описанных операций.

Ответ.

Первый замечательный предел

В пределах, содержащих тригонометрические функции, неопределенность раскрывается с помощью первого замечательного предела

Пример 5. Найти предел функции

Решение. Числитель и знаменатель дроби стремятся к 0 при x → 0 , поэтому для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе вынесем за скобки x², а в знаменателе воспользуемся формулой «разность косинусов»:

Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем

Ответ.

Пример 6. Найти предел функции

Решение. Чтобы вычислить данный предел, перейдем от переменной x к новой переменной z по формуле

Поскольку

то предел можно преобразовать к виду

Применяя формулы приведения и формулу для косинуса двойного угла, получаем

Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем

Ответ.

Раскрытие неопределенности типа . Второй замечательный предел

Определение 3. Если при нахождении предела степени некоторого выражения выясняется, что предел основания степени равен 1, а предел показателя степени равен , то вычисление такого предела называют раскрытием неопределенности .

Неопределенность раскрывается с помощью второго замечательного предела:

(1)

Если взять натуральный логарифм от обеих частей формулы (1), то второй замечательный предел примет вид:

(2)

Пример 7. Найти предел функции предел функции

Решение. Рассмотрим функцию

и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x →. Применяя свойства логарифмов, получаем

Преобразуем выражение, стоящее под знаком логарифма к виду, удобному для применения второго замечательного предела,

и заметим, что

В пределе

и числитель, и знаменатель дроби стремятся к стремятся к, поэтому для раскрытия неопределенности вынесем за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби и, используя свойства пределов функций, получим

Следовательно,

Таким образом,

Ответ.

Пример 8. Найти предел функции

Решение. Рассмотрим функцию

и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x → – 6 . Применяя свойства логарифмов, получаем

Чтобы вычислить предел функции y = ln f (x) при x → – 6 , перейдем от переменной x к новой переменной z по формуле

x = – 6 + z .

Поскольку

то предел (3) можно преобразовать к виду, с помощью формулы (3), получаем

Воспользовавшись вторым замечательным пределом в виде (2) и свойствами пределов функций, получаем

Следовательно,

Ответ.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Предел функции – rajak.rs

Предел функции в бесконечности

Число $A$ называется пределом функции $y = f\left( x \right)$ при $x$ стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного $\varepsilon $, найдется такое число $M$ (зависящее от $\varepsilon $), что для всех $x$ таких, что $\left| x \right| > M$,выполнено неравенство: \[\left| {f\left( x \right) – A} \right| < \varepsilon .\]

На языке кванторов определение предела функции в бесконечности запишется следующим образом:

$A = \mathop {\lim }\limits_{x \to \infty } f\left( x \right),$ если $\forall \varepsilon > 0\exists M:\forall \left| x \right| > M\left| {f\left( x \right) – A} \right| < \varepsilon $

Предел функции в точке

Число $A$ называется пределом функции $y = f\left( x \right)$ при $x$ стремящемся к определенному значению $a$ если для любого, даже сколь угодно малого положительного $\varepsilon $, найдется такое число $\delta > 0$ (зависящее от $\varepsilon $), что для всех $x$ из $\delta$-окрестности точки $a$, выполнено неравенство: \[\left| {f\left( x \right) – A} \right| < \varepsilon . \]

Запишем на языке кванторов определение предела функции в точке:

$A = \mathop {\lim }\limits_{x \to \ a } f\left( x \right)$, если $\forall \delta \left( \varepsilon \right) > 0:\left| {x – a} \right| < \delta \Rightarrow \left| {f\left( x \right) – A} \right| < \varepsilon $

Критерий Коши существования предела функции

Будем говорить, что функция $f$ удовлетворяет в точке ${x_0}$ условию Коши, если для любого положительного числа $\varepsilon > 0$, найдётся отвечающее ему положительное число $\delta$ такое, что для любых двух значений аргумента ${x_1}$ и ${x_2}$, удовлетворяющих условиям

$\left| {{x_1} – {x_0}} \right| < \delta $ и $\left| {{x_2} – {x_0}} \right| < \delta $,

справедливо неравенство

$\left| {f\left( {{x_1}} \right) – f\left( {{x_2}} \right)} \right| < \varepsilon$.

Для того чтобы функция $f$ имела в точке ${x_0}$ конечный предел, необходимо и достаточно, чтобы функция $f$ удовлетворяла в точке ${x_0}$ условию Коши.

Односторонние пределы

Кроме определения обычного предела функции в точке возможно также дать определение понятия одностороннего предела.

Пределом функции $f$ в точке ${x_0}$ слева называется предел, вычисляемый в предположении, что $x \to {x_0}$, оставаясь всё время меньше значения ${x_0}$.

Аналогично, пределом справа называется предел функции $f$ при $x \to {x_0}$, при том, что $x > {x_0}$. Односторонние пределы обозначаются так:

$\mathop {\lim }\limits_{x \to {x_0} + 0} f\left( x \right) = L$, $\left( {\mathop {\lim }\limits_{x \to {x_0} – 0} f\left( x \right) = L} \right)$

Функция $f$ имеет предел в точке ${x_0}$ тогда т только тогда, когда она имеет в этой точке правый и левый предел и они равны.

Пределы на бесконечности

Пусть числовая функция $f$ задана на множестве $Х$, в котором отыщется сколь угодно большой элемент, то есть для всякого положительного $\delta $ в нём найдётся элемент, лежащий за границами отрезка $\left[ { – \delta , + \delta } \right]$. В этом случае число $L$ называется пределом функции $f$ на бесконечности, если для произвольного положительного числа $\varepsilon > 0$ отыщется отвечающее ему положительное число $\delta $ такое, что для всех точек, превышающих $\delta $ по абсолютному значению, справедливо неравенство $|f\left( x \right) – L| < \varepsilon $.

Обозначается: $\mathop {\lim }\limits_{x \to \infty } f(x) = L$

Пусть числовая функция $f$ задана на множестве $Х$, в котором для любого числа $\delta $ найдётся элемент, лежащий правее него. В этом случае число $L$ называется пределом функции $f$ на плюс бесконечности, если для произвольного положительного числа $\varepsilon > 0$ отыщется отвечающее ему положительное число $\delta $ такое, что для всех точек, лежащих правее $\delta $, справедливо неравенство $|f\left( x \right) – L| < \varepsilon $.

Обозначается: $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L$

Пусть числовая функция $f$ задана на множестве $Х$, в котором для любого числа $\delta $ найдётся элемент, лежащий правее него. В этом случае число $L$ называется пределом функции $f$ на минус бесконечности, если для произвольного положительного числа $\varepsilon > 0$ отыщется отвечающее ему положительное число $\delta $ такое, что для всех точек, лежащих левее $\-delta $, справедливо неравенство $|f\left( x \right) – L| < \varepsilon $.

Обозначается: $\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = L$

Основные теоремы о пределе

Если для случаев
$x \to {x_0}$, $x \to {x_0} \pm 0$, $x \to {x_0} \pm 0$,

существуют пределы

$\lim f\left( x \right) = a$ и $\lim g\left( x \right) = b$,

тогда

$\lim \left( {f\left( x \right) \pm g\left( x \right)} \right) = a \pm b$,
$\lim \left( {C \cdot f\left( x \right)} \right) = Ca,{\text{ }}S \in \mathbb{R}$,
$\lim \left( {f\left( x \right) \cdot g\left( x \right)} \right) = ab$ ,
$\lim \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{a}{b}$, ако је $b \ne 0$,
Если $\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = a$ и $\mathop {\lim }\limits_{x \to a} g\left( x \right) = b$, тогда
$\mathop {\lim }\limits_{x \to {x_0}} \left( {g \circ f} \right)\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} g\left( {f\left( x \right)} \right) = b$. { – x}} = 0,a = 0$.

Бесконечно большие и бесконечно малые функции (Лекция №2)

БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Примеры.

Функция f(x)=(x-1)² является бесконечно малой при x→1, так как (см. рис.).
Функция f(x) = tgx – бесконечно малая при x→0.
f(x) = ln (1+x)– бесконечно малая при x→0.
f(x) = 1/x– бесконечно малая при x→∞.

Установим следующее важное соотношение:

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Доказательство.

Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что .
Если , то при любом ε>0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.

Рассмотрим основные свойства бесконечно малых функций.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство. Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где и . Нам нужно доказать, что при произвольном как угодно малом ε>0 найдется δ>0, такое, что для x, удовлетворяющих неравенству |x – a|<δ, выполняется |f(x)|< ε.

Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ₁>0, что при |x – a|<δ₁ имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ₂>0, что при |x – a|<δ₂ имеем | β(x)|< ε/2.

Возьмем δ=min{ δ₁, δ₂}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2.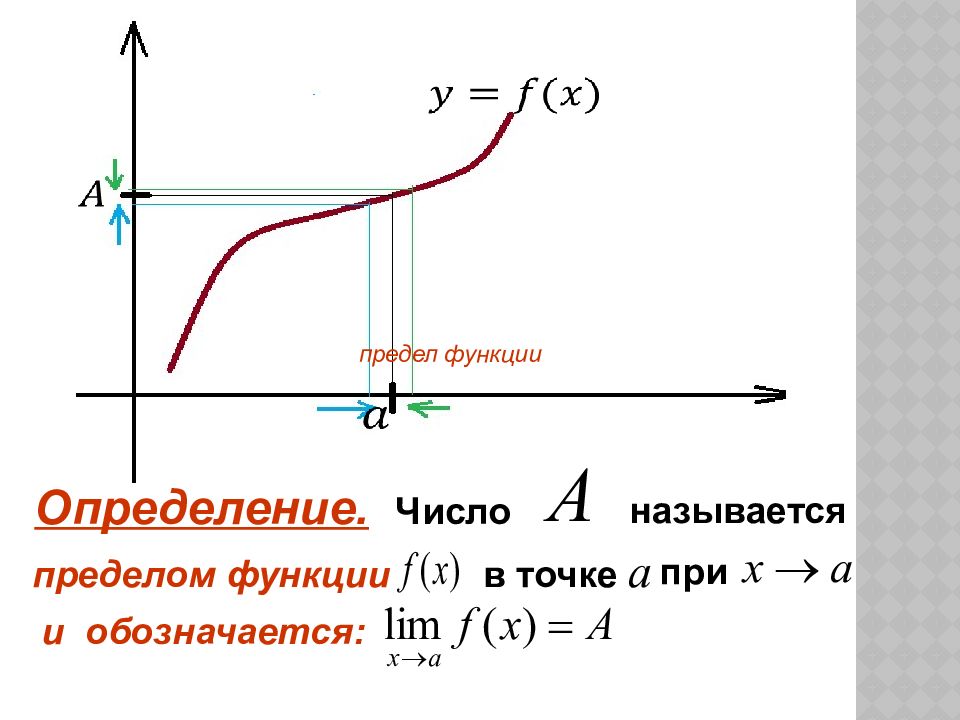 Следовательно, в этой окрестности будет

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,

т.е. |f(x)|<ε, что и требовалось доказать.

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

Из доказанной теоремы вытекают:

Следствие 1. Если и , то .

Следствие 2. Если и c=const, то .

Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Доказательство. Пусть . Тогда 1/f(x) есть ограниченная функция. Поэтому дробь есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.

СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ

Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.

Доказательство. Возьмем произвольное число ε>0 и покажем, что при некотором δ>0 (зависящим от ε) при всех x, для которых |x – a|<δ, выполняется неравенство , а это и будет означать, что 1/f(x) – бесконечно малая функция. Действительно, так как f(x) – бесконечно большая функция при x→a, то найдется δ>0 такое, что как только |x – a|<δ, так |f(x)|>1/ ε. Но тогда для тех же x.

Примеры.

Ясно, что при x→+∞ функция y=x²+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция – бесконечно малая при x→+∞, т.е. .
.

Можно доказать и обратную теорему.

Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.

Доказательство теоремы проведите самостоятельно.

Примеры.

.
.
, так как функции и – бесконечно малые при x→+∞, то , как сумма бесконечно малых функций есть функция бесконечно малая. Функция же является суммой постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для бесконечно малых функций получаем нужное равенство.

Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0

ТЕОРЕМЫ О ПРЕДЕЛАХ

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть .Тогда f(x)=b+α(x) и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

Пример. .

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .

Следствие 1. Постоянный множитель можно выносить за знак предела:

Следствие 2. Предел степени равен степени предела:

Пример..

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное

Дробь является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c²≠0.

Примеры.

.
.
Рассмотрим . При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как , т.е. есть бесконечно малая функция при x→1, то .

Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если

, то .

Смысл этой теоремы понятен из рисунка.

Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.

Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.

Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы , то имеет место неравенство b≥c.

Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5 , или .

ОДНОСТОРОННИЕ ПРЕДЕЛЫ

До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a, оставаясь с одной стороны от а, слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.

Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что xпринимает только значения, меньшие a, то пишут и называют bпределом функции f(x) в точке a слева.

Таким образом, число b называется пределом функции y=f(x) при x→aслева, если каково бы ни было положительное число ε, найдется такое число δ (меньшее a), что для всех выполняется неравенство .

Аналогично, если x→a и принимает значения большие a, то пишут и называют b пределом функции в точке а справа. Т.е. число b называется пределом функции y=f(x) при x→a справа, если каково бы ни было положительное число ε, найдется такое число δ (большее а), что для всех выполняется неравенство .

Заметим, что если пределы слева и справа в точке a для функции f(x) не совпадают, то функция не имеет предела (двустороннего) в точке а.

Примеры.

Рассмотрим функцию y=f(x), определенную на отрезке [0,1] следующим образом

Найдем пределы функции f(x) при x→3. Очевидно, , а .
.
.

ТИПЫ НЕОПРЕДЕЛЕННОСТЕЙ И СПОСОБЫ ИХ РАСКРЫТИЯ

Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.

Условные выражения

характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов.

Рассмотрим некоторые приемы раскрытия неопределенностей.

I. Неопределенность .

.
.
При разложении числителя на множители воспользовались правилом деления многочлена на многочлен «углом». Так как число x=1 является корнем многочлена x³ – 6x² + 11x– 6, то при делении получим
.

II. Неопределенность .

.
При вычислении предела числитель и знаменатель данной дроби разделили на x в старшей степени.
.
.
.

При вычислении предела воспользовались равенством ,если x<0.

Следующие виды неопределенностей с помощью алгебраических преобразований функции, стоящей под знаком предела, сводят к одному из рассмотренных выше случаев или .

III. Неопределенность 0 ·∞.

IV. Неопределенность ∞ –∞.

Исчисление – Пределы

Пределы, когда x стремится к бесконечности

Интуитивно мы можем понять, что по мере того, как \ (x \) становится все больше и больше, 1 \ (/ x \) становится все меньше и меньше. Предел 1 \ (/ x \) при \ (x \) стремится к бесконечности, равна нулю. Мы пишем это как:

\ [\ lim_ {x \ rightarrow \ infty} \ frac {1} {x} = 0 \]

Обратите внимание, что используется знак равенства, предел равен нулю.

Другой способ записи:

\ [\ frac {1} {x} \ rightarrow 0 \ text {as} x \ rightarrow \ infty \]

Здесь мы используем стрелки, 1 \ (/ x \) никогда не равно нулю, но имеет тенденцию к нуль.

Не , а не смешивать “lim” и стрелки, или выражения и знак равенства; выберите одну из форм выше!

В общем случае мы называем предел \ (A \) и записываем его как

\ [\ lim_ {x \ rightarrow \ infty} f (x) = A \]

Точного определения лимита нет в программе. Неформально это означает что значение \ (f (x) \) можно сделать как можно ближе к \ (A \) мы хотим, если мы просто выберем \ (x \) достаточно большим.

Горизонтальные асимптоты

Если функция \ (f (x) \) имеет предел \ (A \) при стремлении \ (x \) до бесконечности, то график \ (f (x) \) будет приближаться к линия \ (y = A \).2 + 1}} \)

\ (\ Displaystyle {е (х) = 2 + \ гидроразрыва {\ грех х} {х}} \)

\ (\ Displaystyle {е (х) = 2 + \ гидроразрыва {х} {\ грех х}} \)

\ (\ Displaystyle {е (х) = 2 + \ гидроразрыва {х} {2+ \ грех х}} \)

\ (\ Displaystyle {е (х) = 2 + \ гидроразрыва {1} {\ sqrt {x} -100 \ соз х}} \)

Есть ли способ найти горизонтальную асимптоту рациональной функции (что такое рациональная функция?) без использования электронного устройства?

Можете ли вы определить пределы 7-10 без построения графиков?

Пределы, поскольку x стремится к

Функция

\ [f (x) = \ frac {x ^ 2 + 4x-12} {x ^ 2-2x} \]

не определяется, когда \ (x = 2 \), однако имеет предел как \ (x \ rightarrow 2 \), предел равен \ (4 \).2 + 2x-8} \]

Знаменатель равен нулю, когда \ (x = 2 \) и когда \ (x = -4 \). Функция имеет две вертикальные асимптоты.

Мы можем приблизиться к значению \ (x = 2 \) с двух сторон, либо \ (x \ lt 2 \) или \ (2 \ lt x \). Чтобы предел существовал, пределы, которые мы получаем от два направления должны быть одинаковыми. В этом случае не существует предела, даже бесконечности. Функция однако имеет вертикальную асимптоту. Иногда мы хотим указать, что выражение имеет разные пределы в зависимости от того, приближаемся ли мы к пределу слева или справа.2 + 2x-8} = – \ infty \]

Сложные пределы

В некоторых случаях вы пользуетесь здравым смыслом, чтобы найти пределы:

\ [\ frac {1} \ infty = 0 \ hspace {1 см} \ frac {1} {0} = \ infty \ hspace {1 см} 1+ \ infty = \ infty \ hspace {1 см} 2 \ cdot \ infty = \ infty \]

(Не пишите так на ↑ экзамене)

В некоторых случаях сложно:

\ [\ frac {\ infty} \ infty =? \ hspace {1 см} \ frac {0} {0} =? \ hspace {1 см} \ infty- \ infty =? \ hspace {1 см} 0 \ cdot \ infty =? \]

Упражнение 2

Изобразите следующие функции, чтобы найти пределы, если они существуют.

\ (\ displaystyle {\ lim_ {x \ rightarrow 0} \ sin \ left (\ frac {1} {x} \ right)} \)
\ (\ Displaystyle {\ lim_ {х \ rightarrow 0} х \ CDOT \ грех \ влево (\ гидроразрыва {1} {х} \ вправо)} \)
\ (\ displaystyle {\ lim_ {x \ rightarrow 0} \ frac {\ sin x} {x}} \)
\ (\ Displaystyle {\ lim_ {х \ rightarrow 0} \ гидроразрыва {\ соз х -1} {х}} \)

Последовательности

Последовательность – это функция, доменом которой являются натуральные числа \ (\ mathbb {N} \).п} \)

Предел sin (x) / x, доказательство

Лимит найти легко

\ [\ lim_ {x \ rightarrow 0} \ frac {\ sin x} {x} \]

численно. Если вы хотите доказать, каков предел, вы должны использовать геометрию.

Чтобы предел стал простым числом, вы должны использовать радианы для измерения углов, это это причина, по которой градусы никогда не используются при расчетах. Этот предел используется для нахождения производная тригонометрических функций.

Двигайся P!

Упражнение 4

Используя обозначения в таблице выше:

Найдите площади треугольников \ (\ Delta OAP \), \ (\ Delta OAB \) и площадь сектора \ (OAP \). Опишите области в терминах \ (\ alpha \), \ (\ sin (\ alpha) \) и \ (\ cos (\ alpha) \).

Используйте неравенства \ (\ Delta OAP \ lt OAP \ lt \ Delta OAB \), чтобы найти предел

\ [\ lim _ {\ alpha \ rightarrow 0} \ frac {\ alpha} {\ sin {\ alpha}} \]

Переставьте неравенства, чтобы найти предел

\ [\ lim _ {\ alpha \ rightarrow 0} \ frac {\ sin \ alpha} {\ alpha} \]

, автор – Малин Кристерсон, лицензия Creative Commons Attribution-Noncommercial-Share Подобно 2.5 Лицензия Швеции

www.malinc.se

MathScene – Пределы – Урок 1

2008 Rasmus ehf og Jhann sak

Урок 1.

Пределы и функции, определяемые интервалом

Что происходит со значением функции как x становится бесконечно большим? Неужели функция тоже становится бесконечно большой? Делает он достигает максимума или минимума? Что на самом деле происходит? Это то, что мы собираемся для размышления в следующем тексте.

Мы знаем, что не можем делим на ноль, но что произойдет, если мы разделим на число, очень близкое к нулю? Мы увидим, что иногда график функция идет вверх или вниз почти перпендикулярно около этой точки, а иногда график не может пройти через точку, оставив бесконечно малую дыру.

Математика использует концепция пределов для рассмотрения проблем такого рода.

Посмотрите на функцию

Калькулятор Casio, кажется, рисует прямую линии, когда вас попросят построить график этой функции (см. диаграмму).Если вы выберете большой масштаб, например INIT в V-Window, вы можете заметить крошечный разрыв на графике, когда x = 1. Это потому, что, когда x = 1, мы делим на ноль, и функция не определено в этом пункте. Область определения функции – D _f = R \ {1}.

А теперь попробуем отработать что происходит как x приближается к 1. Математически это записывается следующим образом:

Лим – это аббревиатура от латинского слова “лаймы”. что означает предел.Приведенное выше обозначение означает значение, до которого функция стремится по мере приближения x к 1.

Мы можем использовать алгебру, чтобы упростить функцию но не следует упускать из виду исходную функцию и проблему деления на нуль.

Теперь у нас больше нет проблема деления на ноль, поэтому мы можем поместить значение x = 1 в выражение ( вычислитьf (1)).

= 1 + 1 = 2

Это показывает нам, что функция стремится к значению 2, когда x стремится к 1.

На графике f (x) действительно есть дыра, где x = 1 (см. График)

Мы можем заполнить эту дыру, если определим непрерывная функция с тем же алгебраическим выражением, но с добавлением значения что функция может принимать при x = 1. Эта новая функция g (x) определена следующим образом:

Таким образом получаем показан непрерывный график .

Функции, которые определены таким образом, с дополнительными чем одно выражение, в зависимости от значений, которые принимает x, называются интервальные определенные функции.

Пример 1

Найдите значение

В этом случае нет проблема деления на ноль, поэтому мы можем поместить число 2 в выражение вместо x.

2 ³ 2 ² = 8 4 = 4

Функция f (x) = x ³ x ² становится все ближе и ближе к 4 по мере того, как x становится все ближе и ближе к 2.

Пример 2

Находить Лимит

В этом случае мы не можем дать x значение 3, так как это будет означать деление на ноль. Однако мы можем факторизовать выражение в числителе и исключить множитель x 3

Положите значение 3 дюйма для x.

Пример 3

Найдите предел

Теперь мы не можем упростить выражение, поэтому мы пытаемся найти решение, подставляя значения x, близкие к 1.Мы выбираем значения как немного больше, так и немного меньше 1.

См. Следующую таблицу значений.

График состоит из двух частей. с вертикальной асимптотой по x = 1.

Давайте посмотрим, что происходит когда x приближается к значению 1. Из графика видно, что мы должны рассматривать отдельно значения выше и ниже x = 1.2 / (D11). Обе формулы скопировал.

Мы видим, что когда x равно меньше 1, то есть когда x приближается к значению 1 слева (слева от число 1 на оси x) значения f (x) (столбец B) все ближе и ближе к ∞. Когда x больше чем 1, который приближается к 1 справа, функция f (x) стремится к + ∞. Конечно, бесконечности не существует, как бы большое число вы ни вообразили. всегда существует еще больший.

Рисуем следующие вывод:

Предел не существует.

Снидми 4

Учтите предел.

Мы не можем ввести значения x которые меньше нуля, потому что квадратный корень отрицательного числа не существовать.
В этих условиях мы можем говорить только о пределе справа, то есть когда x больше 0.

Следующие обозначения используемый:

The + Знак показывает, что x приближается к 0 справа (x> 0).

Калькулятор CASIO показывает следующий график:

График спускается с ось y, а затем идет вправо по оси x. Ни x, ни f (x) не принимают отрицательные значения. Для малых значений x значения y большие
и для больших значений x значения y малы.Очевидно, что f (x) стремится к бесконечность, когда x стремится к нулю, поэтому не существует.

Пример 5

Находить если он существует.

Не очевидно, как мы можем отменить это выражение, но тот факт, что значение x = 1 делает как числитель и нулевой знаменатель говорят нам, что факторизация возможна. Использование правила (a b) (a + b) = a ² b ² дает следующий.

Найти предел функции f (x), когда x стремится к a, существует три различные ситуации, которые могут возникнуть:

1. Вычисляем f (a) (a подставляется в выражение вместо x).

2. Если числитель и знаменатель f (x) равен нулю, когда x = a, тогда f (x) может быть факторизован и упрощается за счет отмены.Затем, если возможно, вычисляется f (a).

3. Если, когда x = a, знаменатель равен нулю, а числитель не равен ноль, то предел не существует.

Пример 6

Рассмотрим следующий интервал определенная функция:

График показан здесь. Прямая
y = x + 3 заканчивается точкой (1, 4) (не доходя до точки).Линия
y = x + 1 начинается в точке (1, 2)
(включая эту точку, которая показана на графике сплошной точкой)

В этом примере предел f (x) поскольку x стремится к 1, не существует, поскольку это зависит от того, больше ли x или менее 1.

Говорят, что функция f (x) быть непрерывным в точке (a, f (a)), если оно существует в интервале около x = a и

Если это верно для всех значений x в области определения f (x), то мы говорим, что функция непрерывный.

Наоборот, если функция непрерывна, то она непрерывна во всех точка своего домена.

Теперь посмотрим на пределы когда x стремится к + или бесконечность.

Это не проблема при рассмотрении полиномиальных функций. Поскольку x стремится к бесконечности (+ или), функция также стремится к бесконечности. Будет ли это + или бесконечность, зависит на срок с наибольшей мощностью. Ни логарифм функции, экспоненциальные функции или функции квадратного корня представляют любые проблема.

Это другое дело однако с рациональными функциями (функции в виде f (x) / g (x)).

При рассмотрении нам нужно посмотреть, числитель или знаменатель увеличивает быстрее.

Если числитель, f (x), увеличивается быстрее, чем x стремится к бесконечности, тогда предел не существует, но стремится к + или бесконечности.

Однако, если знаменатель g (x) увеличится больше быстро, то ограничение, вероятно, будет стремиться к определенному значению.

Пример 7

А теперь давайте посмотрим на некоторые примеры, где x стремится к бесконечности.

а)
Здесь знаменатель стремится к бесконечности, а числитель не меняется. Когда мы делим на число, которое становится все больше и больше, результат становится меньше и
меньшее стремится к нулю. Так что предел равен нулю.

б)

Здесь знаменатель увеличивается быстрее, чем числитель, поэтому дробь становится меньше и меньшее стремится к нулю.

в)

Это противоположно пункту b). Числитель увеличивается быстрее, а результат становится все больше и больше. стремится к бесконечности. Мы говорим, что предела не существует.
(NB. В некоторых текстах предел называется бесконечностью).

г)

В этом примере знаменатель имеет более высокую степень, чем числитель, и поэтому увеличивает больше быстро.Дробь стремится к нулю, поэтому

0, если g (x) увеличивается быстрее, чем f (x)

. Это произойдет, если для Например, степень знаменателя g (x) больше, чем степень числителя f (x).

Пример 8

Находить .

Что происходит, когда числитель и знаменатель – многочлены одной степени? Оба увеличивают одинаково быстро. Если мы разделим все на наивысшую степень x (в этот чехол x ²) мы можем найти решение.

Поскольку x стремится к бесконечности, два члены в числителе x / x ² и 2 / x ² стремятся к нулю, оставляя us с 1 в числителе и 2 в знаменателе.Таким образом, результат:

Проблемы с пределами рациональных функций, где числитель и знаменатель – многочлены одинаковой степени, могут быть решается делением всего на наивысшую степень x.

Попрактикуйтесь в этих методах, затем возьмите тест 1 по пределам.

шт. не забудьте заполнить свой контрольный список.

Предел «бесконечности» – подход к исчислению

Определение «становится бесконечным»

Пределы рациональных функций

Изменение переменной

БЕСКОНЕЧНОСТЬ вместе со своим символом ∞ не является числом и не местом.Когда мы говорим в математике, что что-то «бесконечно», мы просто имеем в виду, что у его значений нет предела.

Пусть, например, f ( x ) будет. Затем, когда значения x становятся все меньше и меньше, значения f ( x ) становятся все больше и больше. Независимо от того, какое большое число мы назовем, можно будет назвать значение x таким образом, чтобы значение f ( x ) было больше, чем это число, которое мы назвали.

Затем мы говорим, что значения f ( x ) становятся бесконечными или стремятся к бесконечности. Мы говорим, что когда x приближается к 0, предел f ( x ) равен бесконечности.

Теперь предел – это число – граница. Поэтому, когда мы говорим, что предел равен бесконечности, мы имеем в виду, что не существует числа , которое мы можем назвать.

Учащийся должен знать, что слово «бесконечный» в том виде, в котором оно используется и исторически использовалось в исчислении, не имеет того же значения, что и в теории бесконечных множеств.См. Это из Википедии, особенно взгляды Карла Фридриха Гаусса в разделе «Прием аргументов».

ОПРЕДЕЛЕНИЕ 4. становится бесконечным. Мы говорим, что переменная «становится бесконечной» или «стремится к бесконечности», если, начиная с определенного члена в последовательности его значений, абсолютное значение этого термина и любого последующего термина, который мы называем, больше любого положительного числа, которое мы называем. , каким бы большим он ни был.

Когда переменная имеет размер x и принимает только положительные значения, тогда x становится положительно бесконечным.Мы пишем

Если x принимает только отрицательные значения, оно становится отрицательно бесконечным, и в этом случае мы пишем

В обоих случаях мы имеем в виду: независимо от того, какое большое число M мы назовем, мы добираемся до точки в последовательности значений x , в которой их абсолютные значения становятся больше, чем M.

Когда переменная является функцией f ( x ), и она становится положительно или отрицательно бесконечной, когда x приближается к значению c , тогда мы пишем

Хотя мы пишем символ «lim» для обозначения лимита, эти алгебраические утверждения означают: Предел f ( x ), поскольку x приближается к c , не существует.Опять же, предел – это число. (Определение 2.1.)

Определение 4 – это определение «становится бесконечным»; это не определение предела.

Что касается символа ∞, мы используем его в алгебраических утверждениях, чтобы показать, что определение становится бесконечным. Сам по себе этот символ не имеет значения.

Вот для примера график функции

1
x

Давайте посмотрим, что происходит со значениями y , когда x приближается к 0 справа:

Поскольку последовательность значений x становится очень маленькими числами, тогда последовательность значений y , обратных величин, становится очень большими числами.Значения y станут и останутся больше, например, чем 10 ^100000000. y становится бесконечным.

Пишем:

Если x приближается к 0 слева, то значения становятся большими отрицательными числами. В этом случае мы пишем

Когда функция становится бесконечной, когда x приближается к значению c , тогда функция является прерывистой при x = c , и прямая линия x = c представляет собой вертикальную асимптоту графика.(Тема 18 Precalculus.) Таким образом, график y = прерывистый при x = 0, а прямая линия x = c представляет собой вертикальную асимптоту.

Далее, давайте рассмотрим случай, когда x становится бесконечным, то есть когда его значения становятся большими положительными числами в крайнем правом углу от 0.

В этом случае число становится очень маленьким, а именно 0. Мы пишем

.
Мы должны читать, что как «предел x становится бесконечным», а не как « x приближается к бесконечности», потому что снова бесконечность не является ни числом, ни местом.С другой стороны, мы могли бы прочитать это, как бы нам ни хотелось («предел x становится головокружительным»), если любое используемое нами выражение относится к условию из определения 4.
См. Первые принципы элементов Евклида, комментарий к определениям. Обратите особое внимание на то, что определение: номинал ; он утверждает только то, как слово или имя будут использоваться; и мы должны согласиться с этим.
Наконец, когда x становится бесконечно отрицательным, то есть когда принимает значения, лежащие в крайнем левом углу от 0 (-∞), тогда снова p приближается к 0.Пишем
Другими словами, всякий раз, когда x становится бесконечным положительно или отрицательно, значения y = приближаются к горизонтальной линии y = 0. Эта линия называется горизонтальной асимптотой графика.
Задача 1. Оценить
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
At, tan x не существует. (Тема 15 и тема 18 тригонометрии.)
По мере приближения x слева, загар x становится больше, чем любое число, которое мы могли бы назвать. (Определение 4.)
Пределы рациональных функций
Рациональная функция – это частное от многочленов (Тема 6 Precalculus). Он будет иметь такую форму:
, где f и g – полиномы ( g 0).
Помимо постоянного члена, каждый член полинома будет иметь множитель x ⁿ ( n ≥ 1). Поэтому давайте исследуем следующие ограничения.
c может быть любой положительной константой. Студент должен заполнить каждую правую часть.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала сделай сам!
1) = 0
2a) = ∞
n чет.
2b) = ∞
n нечет.
2c) = −∞
n нечет.
Сравнить y = 1
x выше, где n = 1.
3) = ∞
4) = ∞
Пример. Доказательство:
Решение . Разделите числитель и знаменатель на наибольшую степень x .В этом случае разделите их на x ²:
Согласно пункту 1), предел каждого члена, который содержит x , равен 0. Следовательно, по теоремам темы 2 мы имеем требуемый ответ.
В аналогичных случаях первый шаг: Разделите числитель и знаменатель на степень x , которая появляется в главном члене любого из них.
Проблема 2. = 4
Результат следует после деления числителя и знаменателя на x .
Задача 3. =
Другими словами: Когда числитель и знаменатель равны,
тогда предел, когда x становится бесконечным, равен частному первых коэффициентов.
Проблема 4.
Далее рациональная функция является обратной функцией приведенной выше:
= = ∞
Эта проблема иллюстрирует:
Когда степень знаменателя больше степени числителя, то есть когда знаменатель доминирует, тогда предел, когда x становится бесконечным, равен 0.Но когда числитель доминирует – когда степень числителя больше – тогда предел, когда x становится бесконечным, равен .
Изменение переменной
Учтите этот предел:
Вместо того, чтобы использовать переменную, приближающуюся к 0, мы иногда предпочитаем, чтобы она стала бесконечной. В этом случае мы меняем переменную. Ставим х = или, неважно. Для x , приближающегося к 0, эквивалентно z , становящемуся бесконечным.Тогда
При замене x на, мы позволяем z стать бесконечным. Лимит остается 1.
Где это появится? В пределе, из которого мы вычисляем число e:
(Урок 15.)
Проблема 5. В приведенном выше пределе измените переменную на n , и пусть она станет бесконечной.
Следующий урок: производная
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]

Исчисление I – Пределы вычислений
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с “узкой” шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-5: Пределы вычислений
В предыдущем разделе мы видели, что существует большой класс функций, который позволяет нам использовать
\ [\ mathop {\ lim} \ limits_ {x \ to a} f \ left (x \ right) = f \ left (a \ right) \]
для вычисления пределов.2} – 2x}} & = \ mathop {\ lim} \ limits_ {x \ to 2} \ frac {{\ left ({x – 2} \ right) \ left ({x + 6} \ right)}} {{x \ left ({x – 2} \ right)}} \\ & = \ mathop {\ lim} \ limits_ {x \ to 2} \ frac {{x + 6}} {x} \ end {align *} \]
Итак, разложив на множители, мы увидели, что можем сократить \ (x – 2 \) как из числителя, так и из знаменателя. После этого у нас теперь есть новое рациональное выражение, в которое мы можем вставить \ (x = 2 \), потому что мы потеряли проблему деления на ноль. Таким образом, ограничение составляет
\ [\ mathop {\ lim} \ limits_ {x \ to 2} \ frac {{{x ^ 2} + 4x – 12}} {{{x ^ 2} – 2x}} = \ mathop {\ lim} \ limits_ {x \ to 2} \ frac {{x + 6}} {x} = \ frac {8} {2} = 4 \]
Обратите внимание, что это на самом деле то, что мы предполагали.2} – 2x}} = \ frac {{x + 6}} {x} \ hspace {0,25 дюйма} {\ mbox {provided}} x \ ne 2 \]
Другими словами, два уравнения дают одинаковые значения, за исключением точки \ (x = 2 \), и поскольку пределы касаются только того, что происходит вокруг точки \ (x = 2 \), предел двух уравнений будет равен . Что еще более важно, в упрощенной версии мы получаем «достаточно хорошее» уравнение, и поэтому то, что происходит вокруг \ (x = 2 \), идентично тому, что происходит в \ (x = 2 \).
Таким образом, мы можем взять предел упрощенной версии, просто подставив \ (x = 2 \), даже если мы не могли вставить \ (x = 2 \) в исходное уравнение и значение предела упрощенного уравнения будет таким же, как предел исходного уравнения.
Кстати, 0/0, которое мы изначально получили в предыдущем примере, называется неопределенной формой . Это означает, что мы действительно не знаем, что это будет, пока мы не продолжим работу. Обычно ноль в знаменателе означает, что он не определен. Однако это будет верно только в том случае, если числитель также не равен нулю. Кроме того, ноль в числителе обычно означает, что дробь равна нулю, если знаменатель также не равен нулю. Точно так же все, что делится само по себе, равно 1, если мы не говорим о нуле.
Итак, здесь действительно есть три конкурирующих «правила», и неясно, какое из них победит. Также возможно, что ни один из них не выиграет, и мы получим что-то совершенно отличное от undefined, нуля или единицы. Мы могли бы, например, получить из этого значение 4, чтобы выбрать число наугад.
При простой оценке уравнения 0/0 не определено. Однако, принимая предел, если мы получим 0/0, мы можем получить множество ответов, и единственный способ узнать, какой из них правильный, – это фактически вычислить предел.2}}} {h} \\ & = \ mathop {\ lim} \ limits_ {h \ to 0} \ frac {{h \ left ({- 12 + 2h} \ right)}} {h} \\ & = \ mathop {\ lim} \ limits_ {h \ to 0} \, \, – 12 + 2h = – 12 \ end {align *} \] Пример 3 Оцените следующий предел. \ [\ mathop {\ lim} \ limits_ {t \ to 4} \ frac {{t – \ sqrt {3t + 4}}} {{4 – t}} \] Показать решение
Этот предел требует немного больше усилий, чем два предыдущих. Однако еще раз обратите внимание, что мы получаем неопределенную форму 0/0, если пытаемся просто оценить предел.2} \]
Итак, если в первом и / или втором члене есть квадратный корень, рационализация устранит корень (и). Этот может помочь в оценке предела .
Давайте попробуем рационализировать числитель в этом случае.
\ [\ mathop {\ lim} \ limits_ {t \ to 4} \ frac {{t – \ sqrt {3t + 4}}} {{4 – t}} = \ mathop {\ lim} \ limits_ {t \ на 4} \ frac {{\ left ({t – \ sqrt {3t + 4}} \ right)}} {{\ left ({4 – t} \ right)}} \, \ frac {{\ left ( {t + \ sqrt {3t + 4}} \ right)}} {{\ left ({t + \ sqrt {3t + 4}} \ right)}} \]
Помните, что для обоснования мы просто берем числитель (поскольку это то, что мы рационализируем), меняем знак у второго члена и умножаем числитель и знаменатель на этот новый член.2} – 3t – 4}} {{\ left ({4 – t} \ right) \ left ({t + \ sqrt {3t + 4}} \ right)}} \ end {align *} \]
Обратите внимание, что мы также не умножали знаменатель. Большинство студентов заканчивают занятия по алгебре, и им в голову приходит мысль постоянно умножать эти вещи. Однако в этом случае умножение сделает задачу очень сложной, и в конце концов вы все равно ее вычтите обратно.
На этом мы почти закончили. Обратите внимание, что числитель можно разложить на множители, так что давайте сделаем это.
\ [\ mathop {\ lim} \ limits_ {t \ to 4} \ frac {{t – \ sqrt {3t + 4}}} {{4 – t}} = \ mathop {\ lim} \ limits_ {t \ до 4} \ frac {{\ left ({t – 4} \ right) \ left ({t + 1} \ right)}} {{\ left ({4 – t} \ right) \ left ({t + \ sqrt {3t + 4}} \ right)}} \]
Теперь все, что нам нужно сделать, это заметить, что если мы вычленим «-1» из первого члена знаменателя, мы можем произвести некоторое сокращение. В этот момент проблема деления на ноль исчезнет, и мы сможем оценить предел.
\ [\ begin {align *} \ mathop {\ lim} \ limits_ {t \ to 4} \ frac {{t – \ sqrt {3t + 4}}} {{4 – t}} & = \ mathop {\ lim} \ limits_ {t \ to 4} \ frac {{\ left ({t – 4} \ right) \ left ({t + 1} \ right)}} {{- \ left ({t – 4} \ right) \ left ({t + \ sqrt {3t + 4}} \ right)}} \\ & = \ mathop {\ lim} \ limits_ {t \ to 4} \ frac {{t + 1}} {{ – \ left ({t + \ sqrt {3t + 4}} \ right)}} \\ & = – \ frac {5} {8} \ end {align *} \]
Обратите внимание, что если бы мы умножили знаменатель, мы не смогли бы выполнить это отмену и, по всей вероятности, даже не увидели бы, что какое-то сокращение могло быть выполнено.2} + 5 & \ hspace {0.25in} {\ mbox {if}} y
Вычислите следующие ограничения.
\ (\ mathop {\ lim} \ limits_ {y \ to 6} g \ left (y \ right) \)
\ (\ mathop {\ lim} \ limits_ {y \ to – 2} g \ left (y \ right) \)
Показать все решения Скрыть все решения a \ (\ mathop {\ lim} \ limits_ {y \ to 6} g \ left (y \ right) \) Показать решение
В этом случае действительно особо нечего делать. Делая ограничения, помните, что мы всегда должны смотреть на то, что происходит по обе стороны от рассматриваемой точки, когда мы приближаемся к ней.В этом случае \ (y = 6 \) полностью находится внутри второго интервала для функции, поэтому есть значения \ (y \) по обе стороны от \ (y = 6 \), которые также находятся внутри этого интервала. Это означает, что мы можем просто использовать этот факт для оценки этого предела.
\ [\ begin {align *} \ mathop {\ lim} \ limits_ {y \ to 6} g \ left (y \ right) & = \ mathop {\ lim} \ limits_ {y \ to 6} (1 – 3y ) \\ & = – 17 \ end {align *} \]
b \ (\ mathop {\ lim} \ limits_ {y \ to – 2} g \ left (y \ right) \) Показать решение
В этой части и есть суть проблемы.В этом случае точка, для которой мы хотим взять предел, – это точка отсечки для двух интервалов. Другими словами, мы не можем просто вставить \ (y = – 2 \) во вторую часть, потому что этот интервал не содержит значений \ (y \) слева от \ (y = – 2 \), и нам нужно чтобы знать, что происходит по обе стороны от точки зрения.
Для выполнения этой части нам нужно помнить факт из раздела об односторонних ограничениях, в котором говорится, что если два односторонних ограничения существуют и одинаковы, то нормальный предел также будет существовать и иметь такое же значение.+}} g \ left (y \ right) \]
и так как два односторонних ограничения не совпадают
\ [\ mathop {\ lim} \ limits_ {y \ to – 2} g \ left (y \ right) \]
не существует.
Обратите внимание, что очень простое изменение функции приведет к существованию предела в \ (y = – 2 \), поэтому не вдавайтесь в голову, что ограничения в этих точках отсечки в кусочной функции никогда не существуют, как следующие пример покажет.
Пример 5 Оцените следующий предел.-} {\ mbox {подразумевает}} y – 2 \\ & = 9 \ end {align *} \]
Односторонние ограничения такие же, поэтому получаем
\ [\ mathop {\ lim} \ limits_ {y \ to – 2} g \ left (y \ right) = 9 \]
Нам нужно сделать еще одно ограничение. Однако нам понадобится новый факт об ограничениях, который поможет нам в этом.
Факт
Если \ (f \ left (x \ right) \ le g \ left (x \ right) \) для всех \ (x \) на \ ([a, b] \) (кроме, возможно, в \ (x = c \)) и \ (a \ le c \ le b \), то
\ [\ mathop {\ lim} \ limits_ {x \ to c} f \ left (x \ right) \ le \ mathop {\ lim} \ limits_ {x \ to c} g \ left (x \ right) \]
Обратите внимание, что этот факт должен иметь некоторый смысл для вас, если мы предположим, что обе функции достаточно хороши.Если обе функции «достаточно хороши», чтобы использовать факт оценки предела, то у нас есть
\ [\ mathop {\ lim} \ limits_ {x \ to c} f \ left (x \ right) = f \ left (c \ right) \ le g \ left (c \ right) = \ mathop {\ lim} \ limits_ {x \ to c} g \ left (x \ right) \]
Неравенство верно, потому что мы знаем, что \ (c \) находится где-то между \ (a \) и \ (b \), и в этом диапазоне мы также знаем \ (f \ left (x \ right) \ le g \ left (х \ право) \).
Обратите внимание, что на самом деле нам не нужно, чтобы две функции были достаточно точными, чтобы факт был правдой, но это действительно хороший способ дать быстрое «обоснование» факту.
Также обратите внимание, что мы сказали, что мы предполагали, что \ (f \ left (x \ right) \ le g \ left (x \ right) \) для всех \ (x \) на \ ([a, b] \) (кроме, возможно, точки \ (x = c \)). Поскольку ограничения не заботятся о том, что на самом деле происходит в \ (x = c \), нам действительно не нужно, чтобы неравенство сохранялось в этой конкретной точке. Нам нужно только, чтобы он держался около \ (x = c \), так как это то, о чем заботится предел.
Мы можем пойти еще дальше и получить следующую теорему.
Теорема сжатия
Предположим, что для всех \ (x \) на \ ([a, b] \) (кроме, возможно, в \ (x = c \)) имеем
\ [е \ влево (х \ вправо) \ ле ч \ влево (х \ вправо) \ ле г \ влево (х \ вправо) \]
Также предположим, что,
\ [\ mathop {\ lim} \ limits_ {x \ to c} f \ left (x \ right) = \ mathop {\ lim} \ limits_ {x \ to c} g \ left (x \ right) = L \ ]
для некоторых \ (a \ le c \ le b \).Затем
\ [\ mathop {\ lim} \ limits_ {x \ to c} h \ left (x \ right) = L \]
Как и в случае с предыдущим фактом, нам нужно только знать, что \ (f \ left (x \ right) \ le h \ left (x \ right) \ le g \ left (x \ right) \) истинно вокруг \ (x = c \), потому что мы работаем с ограничениями, и их интересует только то, что происходит вокруг \ (x = c \), а не то, что на самом деле происходит в \ (x = c \).
Теперь, если мы снова предположим, что все три функции достаточно хороши (опять же, это не требуется, чтобы сделать теорему сжатия истинной, это только помогает с визуализацией), тогда мы можем получить быстрый набросок того, что говорит нам теорема сжатия. .На следующем рисунке показано, что происходит в этой теореме.
Из рисунка видно, что если пределы \ (f (x) \) и \ (g (x) \) равны при \ (x = c \), то значения функций также должны быть равны при \ ( x = c \) (здесь мы используем тот факт, что мы предполагали, что функции «достаточно хороши», что на самом деле не требуется для теоремы). Однако, поскольку в этой точке \ (h (x) \) «зажато» между \ (f (x) \) и \ (g (x) \), то \ (h (x) \) должно иметь такое же значение. .2} \ cos \ left ({\ frac {1} {x}} \ right) \] Показать решение
В этом примере нам не поможет ни один из предыдущих примеров. Здесь нет необходимости в факторинге или упрощении. Мы не можем рационализировать, и односторонние ограничения не работают. Есть даже вопрос, будет ли существовать этот предел, поскольку у нас есть деление на ноль внутри косинуса в \ (x = 0 \).
Первое, на что следует обратить внимание, это то, что мы знаем следующий факт о косинусе.
\ [- 1 \ le \ cos \ left (x \ right) \ le 1 \]
В нашей функции не просто \ (x \) в косинусе, но пока мы избегаем \ (x = 0 \), мы можем сказать то же самое для нашего косинуса.2} \ cos \ left ({\ frac {1} {x}} \ right) = 0 \]
Мы можем проверить это с помощью графика трех функций. Это показано ниже.
В этом разделе мы рассмотрели несколько инструментов, которые мы можем использовать, чтобы помочь нам вычислить пределы, в которых мы не можем просто оценить функцию в рассматриваемой точке. Как мы увидим, многие ограничения, которые мы будем делать в следующих разделах, потребуют одного или нескольких из этих инструментов.
Calculus – Нормально ли предел функции -1/0?
исчисление – Предел функции -1/0 в порядке? – Обмен стеками математики
Сеть обмена стеком
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
0
+0
Авторизоваться Зарегистрироваться
Mathematics Stack Exchange – это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил 5 лет, 3 месяца назад
Просмотрено 7к раз
$ \ begingroup $
Быстрый вопрос, определяю лимит этой функции:
$$ \ lim_ {x → 1} \ frac {x ^ 2 – 2x} {x ^ 2 -2x +1} $$
Когда я делю числитель и знаменатель на $ x ^ 2 $ и заполняю $ 1 $, я получаю $ -1 / 0 $. + \; $ (что означает: приближается к нулю с положительной стороны), поэтому ваш предел – отрицательная бесконечность.
Кто-то может определить это как «предел не существует», но я думаю, что более правильным будет сказать «предел не существует бесконечно» и / или «предел существует в широком смысле слова», » функция расходится к $ \; – \ infty \; $ “или чему-то подобному.

Создан 04 марта ’16 в 15: 142016-03-04 15:14
ДонАнтониоДонАнтонио
1k1717 золотых знаков115115 серебряных знаков266266 бронзовых знаков
$ \ endgroup $ 4 $ \ begingroup $
Нет ничего противозаконного в форме. 2-2x + 1} _ {\ to 0 +}} = \ color {red} { – \ infty}
$
Создан 04 марта ’16 в 15: 592016-03-04 15:59
3САТ 3САТ
7,38222 золотых знака2121 серебряный знак4040 бронзовых знаков
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Бесконечные ограничения
Некоторые функции «взлетают» в положительном или отрицательном направлении (неограниченное увеличение или уменьшение) около определенных значений независимой переменной.Когда это происходит, говорят, что функция имеет бесконечный предел ; значит, вы пишите. Также обратите внимание, что функция имеет вертикальную асимптоту при x = c , если выполняется любой из вышеуказанных пределов.
В общем случае дробная функция будет иметь бесконечный предел, если предел знаменателя равен нулю, а предел числителя не равен нулю. Знак бесконечного предела определяется знаком частного числителя и знаменателя при значениях, близких к числу, к которому приближается независимая переменная.
Пример 1: Оценить.
Поскольку x приближается к 0, числитель всегда положителен, а знаменатель приближается к 0 и всегда положителен; следовательно, функция неограниченно возрастает и. Функция имеет вертикальную асимптоту при x = 0 (см. Рисунок).
Рисунок 1 График y = 1/ x ².
Пример 2: Оценить.
Поскольку x приближается к 2 слева, числитель приближается к 5, а знаменатель приближается к 0 через отрицательные значения; следовательно, функция неограниченно убывает и.Функция имеет вертикальную асимптоту при x = 2.
Пример 3: Оценить.
Перезапись 1/ x ² – 1/ x ³ как эквивалентное дробное выражение ( x – 1) / x ³, числитель приближается к -1, а знаменатель приближается к 0 через положительные значения, когда x приближается к 0 справа; следовательно, функция неограниченно убывает и. Функция имеет вертикальную асимптоту при x = 0.
Предупреждение: не оценивайте пределы по отдельности и вычитайте их, потому что ± ∞ не являются действительными числами. В этом примере
, что бессмысленно.
Когда предел f (x) не определен?
Привет Николаса,
Существует техническое определение предела функции, которое обычно выражается греческими буквами дельта и эпсилон. Ответ на ваш вопрос заключается в том, что предел не определен, если предел не существует, как описано в этом техническом определении.Однако я думаю, что это не тот ответ, который вы ищете. Что я сделаю, так это приведу вам три примера ситуаций, когда предел не существует.
Пример 1.
f (x) = ¹/_{x ²}
Эта функция существует для всех ненулевых значений x.

f (x) = ¹/_{x ²}
В этом примере предел f (x), когда x приближается к нулю, не существует, поскольку, когда x приближается к нулю, значения функции неограниченно увеличиваются.Значения функции «приближаются к бесконечности», я имею в виду, что они становятся большими и не приближаются к действительному числу.
Пример 2.
f (t) = 0, если t <0
f (t) = 1, если t = 0
f (t) = 1, если t> 0
Это функция, которая представляет ток, протекающий по проводу, соединяющему лампу на вашем столе с настенной розеткой. Здесь переменная t – время.Лампа изначально выключена, и в нулевой момент времени вы включаете лампу, так что в этот момент ток перескакивает с нуля на единицу и остается на этом значении до тех пор, пока вы не выключите лампу.
Здесь снова не существует предела f (t), когда t приближается к нулю. Причина на этот раз в том, что если t приближается к нулю с левой стороны, кажется, что предел должен быть равен нулю, но если t приближается к нулю справа, кажется, что предел должен быть 1. Когда возникает такая ситуация, предел не существует. .
Пример 3.
f (x) = 0, если x <0
f (x) = 0, если x = 0
f (x) = sin (¹/_x), если x> 0
Для x больше нуля эта функция имеет «дикое» поведение. Он колеблется между -1 и 1, и колебания происходят тем быстрее, чем ближе вы приближаетесь к нулю. Я только попытался нарисовать график для x от 0,01 до 0,15.
В этом случае, когда x приближается к нулю справа, значения функции кажутся близкими к каждому числу от -1 до 1 на оси y.Опять же, в этой ситуации ограничения не существует.
Надеюсь, это поможет,
Пенни
.

1)		=	0

2a)		=	∞
	n чет.

2b)		=	∞
	n нечет.
2c)		=	−∞
	n нечет.

Что такое предел функции как его найти

Mathway | Популярные задачи

Второй замечательный предел.

Подготовка школьников к ЕГЭ (Справочник по математике – Элементы математического анализа

Предел функции

Свойства пределов функций

Раскрытие неопределенностей типа

Раскрытие неопределенностей типа

Первый замечательный предел

Раскрытие неопределенности типа . Второй замечательный предел

Предел функции – rajak.rs

Предел функции в бесконечности

Предел функции в точке

Критерий Коши существования предела функции

Односторонние пределы

Пределы на бесконечности

Основные теоремы о пределе

Бесконечно большие и бесконечно малые функции (Лекция №2)

Исчисление – Пределы

Пределы, когда x стремится к бесконечности

Горизонтальные асимптоты

Пределы, поскольку x стремится к

Сложные пределы

Упражнение 2

Последовательности

Предел sin (x) / x, доказательство

Упражнение 4

MathScene – Пределы – Урок 1

Пример 1

Пример 2

Пример 3

Снидми 4

Пример 5

Пример 6

Пример 7

Пример 8

Предел «бесконечности» – подход к исчислению

Исчисление I – Пределы вычислений

Раздел 2-5: Пределы вычислений

Факт

Теорема сжатия

Calculus – Нормально ли предел функции -1/0?

Сеть обмена стеком

Бесконечные ограничения

Когда предел f (x) не определен?

Оставить комментарий Отменить ответ