Глава 2. Ускорение. Равноускоренное движение
Характеристикой изменения скорости является ускорение. Эта величина определяется как отношение изменения скорости тела к тому интервалу времени, за который это изменение произошло
(2.1) |
где и — скорости тела в конце и начале интервала времени .
Из определения (2.1) следует, что вектор ускорения тела отличен от нуля только в том в случае, когда изменяется вектор скорости.
При этом направление вектора определяется направлением разности , и может не совпадать с направлениями векторов и .
Поэтому в задаче 2.1.1 ситуации, перечисленные в ответах 1, 3 и 4, возможны в следующих случаях. В 1 — когда тело, поворачивая на восток, в некоторый момент времени имеет вектор скорости, направленный на север. В 3 — при равноускоренном движении. В 4 — например, в такой ситуации:
тело бросили вертикально вверх и в верхней точке траектории оно имеет нулевую скорость и ускорение, равное ускорению свободного падения.
В задаче 2.1.2 вектор скорости в конце любого интервала времени меньше вектора скорости в начале этого интервала. Поэтому при направлении вектора скорости на юг вектор изменения скорости, а, следовательно, и вектор ускорения направлены на север (ответ 3).
Если тело движется с постоянной скоростью, координата линейно зависит от времени, причем наклон графика определяется скоростью. Поэтому скорость тела уменьшается, если уменьшается угол наклона графика зависимости координаты от времени к оси времени (задача
Движение тела, при котором его ускорение (как величина, так и направление) не изменяется, называется равноускоренным (задача 2.1.4 — ответ 4). Из определения ускорения (2.1) следует, что при равноускоренном движении зависимость скорости от времени является линейной. Поэтому равноускоренному движению в задаче 2.1.5 отвечает график 1 (несмотря на то, что скорость тела убывает). В этой связи отметим, что равноускоренность означает не то, что тело постоянно разгоняется, а то, что оно имеет «равное ускорение».
Поэтому равноускоренному движению в задаче 2.1.5 отвечает график 1 (несмотря на то, что скорость тела убывает). В этой связи отметим, что равноускоренность означает не то, что тело постоянно разгоняется, а то, что оно имеет «равное ускорение».
При равноускоренном движении зависимости радиус-вектора тела по отношению к произвольной системе координат и скорости тела от времени даются соотношениями
(2.2) |
(2.3) |
где и — радиус-вектор и скорость тела в момент времени , — ускорение тела. После проецирования на оси координат зависимости (2.2) и (2.3) позволяют находить координаты тела и проекции его скорости на оси в любые моменты времени.
В задаче 2.1.6 зависимость (2.2) в проекциях на ось , которая направлена параллельно ускорению и начало которой находится в точке начала движения, дает
Поскольку тело движется из начала координат и только в одну сторону, то, очевидно, координата тела совпадает с пройденным путем. Поэтому при ускорении через 20 с после начала движения пройденный путь будет равен 100 м (ответ 2). Из этого результата следует, что задача 2.1.7 является обратной по отношению к задаче 2.1.6, поэтому правильный ответ для времени, за которое тело пройдет путь 100 м — 20 с (ответ
Поэтому при ускорении через 20 с после начала движения пройденный путь будет равен 100 м (ответ 2). Из этого результата следует, что задача 2.1.7 является обратной по отношению к задаче 2.1.6, поэтому правильный ответ для времени, за которое тело пройдет путь 100 м — 20 с (ответ
В задаче 2.1.8 необходимо использовать зависимость (2.3) для скорости. Так как по условию автомобиль движется из состояния покоя, проекция зависимости (2.3) на ось , направленную вдоль вектора ускорения, имеет вид
где – проекция вектора скорости тела на ось . Так как в момент времени , находим (правильный ответ – 2).
Сравнивая данную в задаче 2.1.9 зависимость координаты от времени с законом (2.2), заключаем, что начальная скорость тела , проекция ускорения тела на ось – . Поэтому из (2.3) получаем зависимость скорости тела от времени .
 Можно было также найти скорость как производную координаты по времени. Дифференцируя данную в условии функцию, получим тот же ответ
Можно было также найти скорость как производную координаты по времени. Дифференцируя данную в условии функцию, получим тот же ответЗависимость проекции скорости от времени на ось, направленную вертикально вверх, для тела из задачи 2.1.10 имеет вид
где — начальная скорость тела. Подставляя в эту формулу время , находим скорость тела через 0,5 с после броска (ответ 3). Знак «плюс» для проекции скорости на рассматриваемую ось показывает, что через 0,5 c после броска вектор скорости тела все еще направлен вверх.
Чтобы найти время подъема тела, брошенного вертикально вверх, на максимальную высоту (задача 2.2.1) используем то обстоятельство, что в верхней точке траектории скорость тела равна нулю. Поэтому подстановка времени подъема в зависимость скорости от времени дает
где — начальная скорость тела. Отсюда получаем для времени подъема (ответ 4). А самую максимальную высоту подъема (задача 2.2.2) можно найти, подставляя найденное время подъема в зависимость координаты тела по вертикальной оси от времени
А самую максимальную высоту подъема (задача 2.2.2) можно найти, подставляя найденное время подъема в зависимость координаты тела по вертикальной оси от времени
Подстановка в эту формулу числовых значений дает (ответ 1).
Пусть время, затраченное телом на прохождение участка пути длиной , отсчитанного от начальной точки, равно , а время, затраченное телом на прохождение участка пути длиной , отсчитанного от этой же точки, равно (задача 2.2.3). Тогда из уравнения движения (2.2) в проекции на ось, направленную вдоль вектора ускорения тела, имеем
Равноускоренное движение, вектор ускорения, направление, перемещение. Формулы, определение, законы
Тестирование онлайн
Равноускоренное движение
В этой теме мы рассмотрим очень особенный вид неравномерного движения. Исходя из противопоставления равномерному движению, неравномерное движение – это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое “равно ускоряется”. Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово “равно”, получим равное увеличение скорости. А как понимать “равное увеличение скорости”, как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.
Исходя из противопоставления равномерному движению, неравномерное движение – это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое “равно ускоряется”. Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово “равно”, получим равное увеличение скорости. А как понимать “равное увеличение скорости”, как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.
Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.
Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7км/ч, во вторую – 9км/ч, в третью 12км/ч? Нельзя! Велосипедист ускоряется, но не одинаково, сначала ускорился на 7км/ч (7-0), потом на 2 км/ч (9-7), затем на 3 км/ч (12-9).
Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение же с убывающей скоростью – замедленным движением. Но физики любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в любом случае он движется с ускорением.
Равноускоренное движение – это такое движение тела, при котором его скорость за любые равные промежутки времени изменяется (может увеличиваться или уменьшаться) одинаково
Ускорение тела
Ускорение характеризует быстроту изменения скорости. Это число, на которое изменяется скорость за каждую секунду. Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении). Ускорение – это физическая векторная величина, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Определим ускорение в следующей задаче. В начальный момент времени скорость теплохода была 3 м/с, в конце первой секунды скорость теплохода стала 5 м/с, в конце второй – 7м/с, в конце третьей 9 м/с и т.д. Очевидно, . Но как мы определили? Мы рассматриваем разницу скоростей за одну секунду. В первую секунду 5-3=2, во вторую секунду 7-5=2, в третью 9-7=2. А как быть, если скорости даны не за каждую секунду? Такая задача: начальная скорость теплохода 3 м/с, в конце второй секунды – 7 м/с, в конце четвертой 11 м/с.В этом случае необходимо 11-7= 4, затем 4/2=2. Разницу скоростей мы делим на промежуток времени.
Эту формулу чаще всего при решении задач применяют в видоизмененном виде:
Формула записана не в векторном виде, поэтому знак “+” пишем, когда тело ускоряется, знак “-” – когда замедляется.
Направление вектора ускорения
Направление вектора ускорения изображено на рисунках
На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо).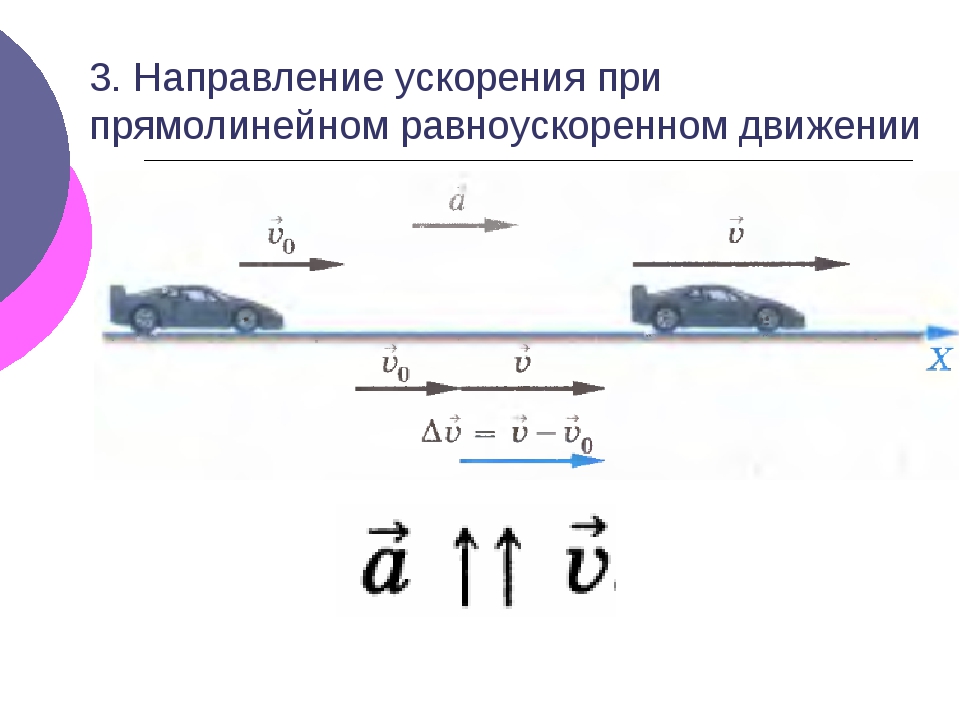 Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.
Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.
При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.
На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.
При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.
Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на “-2м/с”. 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.
При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком “минус”!!!
Перемещение при равноускоренном движении
Дополнительная формула, которую называют безвременной
Формула в координатах
Связь со средней скоростью
При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости
Из этого правила следует формула, которую очень удобно использовать при решении многих задач
Соотношение путей
Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.
Главное запомнить
1) Что такое равноускоренное движение;
2) Что характеризует ускорение;
3) Ускорение – вектор. Если тело разгоняется ускорение положительное, если замедляется – ускорение отрицательное;
3) Направление вектора ускорения;
4) Формулы, единицы измерения в СИ
Упражнения
Два поезда идут навстречу друг другу: один – ускоренно на север, другой – замедленно на юг. Как направлены ускорения поездов?
Одинаково на север. Потому что у первого поезда ускорение совпадает по направлению с движением, а у второго – противоположное движению (он замедляется).
Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?
Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.
Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.
Какие из приведенных зависимостей описывают равноускоренное движение?
Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?
*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?
В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.
Равнопеременное движение (равноускоренное, равнозамедленное)
Рассмотрим прямолинейное движение тела вдоль оси (одномерный случай) и пусть при этом скорость тела изменяется.
Когда скорость изменяется, появляется ускорение. Ускорение, в свою очередь, тоже может меняться.
Если изменяется и ускорение, и скорость тела – движение сложное, например, колебательное;
Движение равнопеременное — если изменяется только скорость, а ускорение постоянное.
Термин «равнопеременное» применяют потому, что за одинаковые интервалы времени перемещение изменяется на одну и ту же величину.
При этом, если скорость увеличивается – движение называют равноускоренным, а если скорость уменьшается – равнозамедленным.
Примечание: Вместо слов «ускорение постоянное» можно произнести «ускорение не меняется», или «ускорение одно и то же».
Рекомендую предварительно ознакомиться с основными терминами для описания движения.
Будем выбирать направления для векторов скорости и ускорения относительно оси. Разберем несколько возможных вариантов.
Равноускоренное движение
Пусть при движении по прямой скорость тела увеличивается. Обратим внимание на перемещение тела.
Примечание: Движение равноускоренное, значит, за одинаковые интервалы времени перемещение будет увеличиваться на одну и ту же величину.
Этот факт иллюстрирует рисунок 1. Из рисунка видно: по сравнению с первой секундой, за вторую секунду пути перемещение увеличивается на небольшой отрезок, а за третью секунду – на два таких отрезка. 2}{2} \end{cases} } \]
2}{2} \end{cases} } \]
Примечание: Перемещение тела можно вычислить, не обладая информацией о времени движения, зная только начальную и конечную скорость тела и его ускорение. Об этом подробно написано в статье о формуле пути без времени.
Равнозамедленное движение
Пусть теперь тело движется по прямой и его скорость уменьшается. Рассмотрим перемещение тела.
Примечание: Движение равнозамедленное, значит, за одинаковые интервалы времени перемещение будет уменьшаться. При чем, на одну и ту же величину.
Рис. 3. Перемещение уменьшается на одну и ту же величину при равнозамедленном движении
На рисунке 3 представлено изменение перемещения. Видно, что по сравнению с первой секундой, за вторую секунду перемещение уменьшается на небольшой отрезок, а за третью секунду – на два таких отрезка.
Примечание: Скорость будет уменьшаться, когда вектор ускорения направлен противоположно вектору скорости. 2}{2} \end{cases} } \]
2}{2} \end{cases} } \]
Расшифруем теперь, к примеру, словосочетание «прямолинейное равнозамедленное движение» — это движение по прямой, ускорение есть, оно не меняется. Скорость тела уменьшается, так как вектор ускорения направлен противоположно вектору скорости.
Примечание: Перемещение замедляющегося тела можно вычислить не используя время. Потому, что существует запись формулы пути без времени для случая, когда скорость тела уменьшается.
Скорость направлена против оси, а ускорение – по оси
Дополнительно рассмотрим случай, когда скорость и ускорение направлены в противоположные стороны, ускорение – по оси, а скорость – против оси (рис. 5).
Рис. 5. Векторы скорости и ускорения направлены в противоположные стороны, скорость направлена против оси, модуль скорости уменьшается
При такой направленности векторов \(\vec{v}\) и \(\vec{a}\), с течением времени модуль скорости будет уменьшаться до нуля. Это движение будет равнозамедленным.
2}{2} \end{cases} } \]
Решая задачи на движение, иногда вычисляют мгновенную и среднюю скорости.
Термины «мгновенная скорость» и «средняя скорость» применяют для случаев, когда скорость изменяется – то есть, для неравномерного движения.
Мгновенная скорость
Мгновенная скорость – это скорость тела в какое-то мгновение. Когда скорость тела меняется, то в различные мгновения (моменты времени) скорости будут различаться.
Мгновенную скорость v вычисляют, вместо символа t подставляя в формулу интересующее нас время:
\[ v = v_{0} \pm a \cdot t \]
Знак ускорения зависит его направления.
Средняя скорость
Средняя скорость тела – скорость, с которой нужно двигаться равномерно, чтобы пройти тот же путь за то же время.
Другими словами, средняя скорость помогает понять, с какой постоянной скоростью могло бы двигаться тело, чтобы пройти весь пройденный путь за такое же время.
Примечания:
- Выражение «скорость постоянная» можно заменить словами «неизменная», «одна и та же».
- Вместо фразы «за такое же время» в учебниках напишут «за выделенный интервал времени».
- Если скорость изменяется, появляется ускорение.
Формула для расчета средней скорости:
\[ \large \boxed { v_{\text{средняя}} = \frac{S_{\text{весь}}}{t_{\text{полное}}}} \]
\( S_{\text{весь}}(\text{м}) \)– полный путь, пройденный телом;
\( t_{\text{полное}} \left( c \right)\) – время, за которое тело прошло весь путь.
Ускорение
всем привет меня зовут владимир романов тема урока ускорения ускорение это физическая величина показывающая как быстро меняется скорость ускорение будем обозначать буквой а и ускорение равняется изменение скорости в 2 минус в 1 разделить на время за которое произошло это изменение скорости ускорение также как и скорость имеет направление следовательно эта величина векторная если векторы скорости и ускорение направлены в одну сторону то тогда скорость тела будет возрастать с течением времени если же векторы скорости и ускорения направлены в разные стороны то скорость тела будет уменьшаться с течением времени и в первом случае мы скажем что тело ускоряется во втором случае у нас тело замедляется если в начальный момент времени у тела была какая-то скорость b1 то тогда зависимость скорости тела от времени будет изображаться прямой линии направленный вверх и это значение и будет начальной скоростью v1 если же начальная скорость была равна нулю то график зависимости скорости от времени будет выглядеть так и если у нас в 1 равняется нулю то ускорение мы можем вычислить по формуле а равняется в разделить на t скорость тела увеличивается с течением времени только тогда когда у нас вектор ускорения и вектор скорости направлены в одну сторону если же у нас вектор скорости и вектор ускорения направлены в разные стороны то тогда зависимость скорости от времени будет изображаться прямой направленный вниз это значение скорости также будет начальной скоростью v1 теперь давайте вернемся к этой формуле скорость тела мы измеряем в метрах делённые на секунды делим это еще на секунды так как здесь мы скорость делим на время разделить на секунды это то же самое что умножить на единицу деленное на секунду итак мы получим метр и деленное на секунды в квадрате это и будет единицы измерения ускорения в системе sim теперь рассмотрим задачу лифт когда начинает движение увеличивает свою скорость на 3,3 метров в секунду за время равное трем секундам найдите ускорение лифта ускорение это скорость разделить на время а точнее изменение скорости разделить на изменение времени за которое произошло это изменение скорости этот треугольник буква дельта и означает изменение физической величины дельта v это изменение скорости дельта т это изменение времени изменение скорости у нас 3,3 метров в секунду разделить на изменение времени и мы получим одну целую одну десятую метра на секунду в квадрате это и будет ускорение лифта и еще раз дельта v это изменение скорости и будет равняться конечное значение скорости в 2 минус начальное значение скорости в один точно также и изменение времени это конечное значение времени t 2 минус начальное значение времени t1 задача номер два поезд подходя к станции сбросил скорость 70 километров в час до 50 двух километров в час потратив на это 10 секунд определите ускорение поезда ускорение у нас равняется изменения скорости ведь на время или дельта v разделить на время время у нас здесь 10 секунд давайте найдем чему будет равняться изменения скорости конечная скорость 52 километра в час начальная скорость 70 и так мы получим минус 18 километров в час давайте переведем эту скорость в метры в секунду для этого умножим минус 18 на дробь 1036 их сократим эту дробь на два и числитель и знаменатель получим 5 18 итак у нас останется минус 5 метров в секунду и это будет дельта v подставляем значения минус 5 делим на 10 это будет минус 0,5 метра в секунду в квадрате как вы видите мы получили здесь отрицательное ускорение это значит что векторы скорости поезда и ускорения были направлены в разные стороны и поезд у нас замедлялся поэтому мы получили отрицательное ускорение на сегодня это все вопросы и пожелания по урокам пишите в комментариях получайте только хорошие оценки всем пока
Куда направлено ускорение
☰
Ускорение — это быстрота изменения скорости.
В системе СИ ускорение измеряется в метрах за секунду в квадрате (м/с2), то есть показывает, на сколько изменяется скорость тела за одну секунду.
Если, например, ускорение тела равно 10 м/с2, то это значит, что за каждую секунду скорость тела увеличивается на 10 м/с. Так, если до начала ускорения тело двигалось с постоянной скоростью 100 м/с, то после первой секунды движения с ускорением его скорость составит 110 м/с, после второй — 120 м/с и т. д. В данном случае скорость тела постепенно увеличивалась.
Но скорость тела может постепенно и уменьшаться. Обычно так происходит при торможении. Если то же тело, двигавшееся с постоянной скоростью 100 м/с, начинает уменьшать свою скорость на 10 м/с в каждую секунду, то через две секунды его скорость будет равна 80 м/с. А через 10 с тело вообще остановится.
Во втором случае (при торможении) мы можем сказать, что ускорение является отрицательной величиной. Действительно, чтобы найти текущую скорость после начала торможения, надо из начальной скорости вычесть ускорение умноженное на время.
Например, какова скорость тела через 6 секунд после торможения? 100 м/с – 10 м/с2 · 6 с = 40 м/с.
Поскольку ускорение может принимать как положительные, так и отрицательные значения, то это значит, что ускорение является векторной величиной.
Из рассмотренных примеров мы могли бы сказать, что при разгоне (увеличении скорости) ускорение положительная величина, а при торможении — отрицательная. Однако не так все просто, когда мы имеем дело с системой координат. Здесь скорость тоже оказывается величиной векторной, способной быть как положительной, так и отрицательной. Поэтому то, куда направлено ускорение, зависит от направления скорости, а не от того, уменьшается скорость или увеличивается под действием ускорения.
Если скорость тела направлена в положительном направлении оси координат (скажем, X), то тело за каждую секунду времени увеличивает свою координату. Так, если в момент начала измерения тело находилось в точке с координатой 25 м и начало двигаться с постоянной скоростью 5 м/с в положительном направлении оси X, то через одну секунду тело будет находиться в координате 30 м, через 2 с — 35 м.
Вообще, чтобы найти координату тела в определенный момент времени, надо к начальной координате прибавить скорость умноженную на количество прошедшего времени. Например, 25 м + 5 м/с · 7 с = 60 м. В данном случае тело через 7 секунд окажется в точке с координатой 60. Здесь скорость — положительная величина, так как координата увеличивается.
Скорость отрицательна, когда ее вектор направлен в отрицательном направлении оси координат. Пусть тело из предыдущего примера начало двигаться не в положительном, а в отрицательном направлении оси X с постоянной скоростью. Через 1 с тело будет в точке с координатой 20 м, через 2 с — 15 м и т. д. Теперь чтобы найти координату, надо из начальной вычесть скорость умноженную на время. Например, где будет тело через 8 с? 25 м – 5 м/с · 8 с = -15 м. То есть тело окажется в точке с координатой x, равной -15. В формуле перед скоростью мы ставим знак минус (-5 м/с), значит скорость – отрицательная величина.
Назовем первый случай (когда тело двигается в положительном направлении оси X) A, а второй случай B.
Рассмотрим, куда будет направлено ускорение при торможении и разгоне в обоих случаях.
В случае A при разгоне ускорение будет направлено в ту же сторону, что и скорость. Поскольку скорость положительна, то и ускорение будет положительно.
В случае A при торможении ускорение направлено в противоположном скорости направлении. Так как скорость положительная величина, то ускорение — будет отрицательной, то есть вектор ускорения будет направлен в отрицательном направлении оси X.
В случае B при разгоне направление ускорения будет совпадать с направлением скорости, а значит ускорение будет направлено в отрицательном направлении оси X (ведь туда же направлена и скорость). Обратите внимание, несмотря на то, что ускорение отрицательно, оно все же увеличивает модуль скорости.
В случае B при торможении ускорение направлено противоположно скорости. Так как скорость имеет отрицательное направление, то ускорение окажется положительной величиной. Но при этом будет уменьшать модуль скорости.
Например, начальная скорость была -20 м/с, ускорение равно 2 м/с2. Скорость тела через 3 с, окажется равной -20 м/с + 2 м/с2 · 3 с = -14 м/с.
Таким образом, ответ на вопрос «куда направлено ускорение» зависит от того, по отношению к чему оно рассматривается. По отношению к скорости ускорение может быть направлено в ту же сторону, что и скорость (при разгоне), или в противоположную сторону (при торможении).
В системе координат положительное и отрицательное ускорение само по себе ничего не говорит от том, тормозило ли тело (уменьшало свою скорость) или разгонялось (увеличивало скорость). Надо смотреть на то, куда направлена скорость.
Занятие 2. Ускорение. Равноускоренное движение
/ /15
1.
ПодробнееЗадание 1 7777 Вариант 3580273 Небольшое тело движется в пространстве. На рисунке показаны графики зависимости от времени t проекций V x, V y и V z скорости этого тела на оси OX, OY и OZ от времени
Зависимость скорости от времени
И В Яковлев Материалы по физике MathUsru Равноускоренное движение Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное
ПодробнееКИНЕМАТИКА задания типа В Стр. 1 из 5
КИНЕМТИК задания типа В Стр. 1 из 5 1. Тело начало движение вдоль оси OX из точки x = 0 с начальной скоростью v0х = 10 м/с и с постоянным ускорением a х = 1 м/c 2. Как будут меняться физические величины,
ПодробнееЦДО «Уникум» РУДН ОЛИМПИАДА ПО ФИЗИКЕ
ЦДО «Уникум» РУДН ОЛИМПИАДА ПО ФИЗИКЕ Задание 1.
ПодробнееДальность полета снаряда, летящего по навесной траектории, равна максимальной высоте подъема. Какова максимальная высота настильной траектории при той же
Кинематика 1 1) 1 2) 2 3) 3 4) 4
Кинематика 1 1 Точка движется по окружности радиусом 2 м, и ее перемещение равно по модулю диаметру. Путь, пройденный телом, равен 1) 2 м 2) 4 м ) 6,28 м 4) 12,56 м 2 Камень брошен из окна второго этажа
ПодробнееКИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ПРЕДИСЛОВИЕ Физика является одной из тех наук, знание которой необходимо для успешного изучения общенаучных и специальных дисциплин При изучении курса физики студенты
ПодробнееДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Министерство образования Российской Федерации Государственное образовательное учреждение высшего профессионального образования «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «МЕХАНИКА» ДИНАМИКА
ПодробнееПРОБНЫЙ ЭКЗАМЕН по теме 1.
КИНЕМАТИКА
ПРОБНЫЙ ЭКЗАМЕН по теме. КИНЕМАТИКА Внимание: сначала попытайтесь ответить на вопросы и решить задачи самостоятельно, а потом проверьте свои ответы. Указание: ускорение свободного падения принимать равным
Подробнееуч. год. 3, 9 кл. Физика. Динамика.
006-007 уч. год. 3, 9 кл. Физика. Динамика. 6. Примеры решения задач Приступая к решению задач, сделаем несколько общих замечаний. Во-первых, при решении задач нужно прежде всего выяснить, какие силы действуют
ПодробнееИТТ Вариант 1 ОСНОВЫ КИНЕМАТИКИ
ИТТ- 10.1.1 Вариант 1 ОСНОВЫ КИНЕМАТИКИ 1.Предложены две задачи: 1) Рассчитать период обращения вокруг Земли искусственного спутника шара радиусом 20 м. 2) Рассчитать силу Архимеда, действующую в воде
ПодробнееЭлементы высшей математики
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
Подробнее= 1 е) f(9) = 27; f(1) = 3
Глава 8 ФУНКЦИИ И ГРАФИКИ Алгоритмы А- Задание стандартных функций А- Понятие функции.
ПодробнееГрафик функции А-3 Каноническая запись зависимостей А- Задание стандартных функций. К стандартным функциям отнесем
ИТТ Вариант 2 ОСНОВЫ КИНЕМАТИКИ
ИТТ- 10.1.2 Вариант 2 ОСНОВЫ КИНЕМАТИКИ 1.Предложены две задачи: 1) Определить среднюю скорость самолёта по известному расстоянию между двумя городами и времени полёта. 2) Определить путь, пройденный самолётом
ПодробнееКинематика точки. Задачи. – орты осей X, Y и Z) (A, B, C положительные постоянные, ex. 3. Материальная точка движется вдоль оси x по закону: x( t)
1 Кинематика точки Задачи (,, положительные постоянные, e, e, ez – орты осей X, Y и Z) 1 Материальная точка движется вдоль оси по закону: ( ) cos ω Найдите проекцию скорости V () Материальная точка движется
ПодробнееЗанятие 1. Вариант t
Занятие.
ПодробнееВариант… Тело движется равномерно по окружности. Найти отношение пройденного пути к величине перемещения тела за четверть периода движения… 3. 4. 3… Движение тела является равномерным, если:.
ВАРИАНТ Дано: Решение
ВАРИАНТ 0 Дано: Решение V 0 =0м/ c h = 30 м t п -? s -? Тело движется свободно под действием силы тяжести Сначала мяч летит вверх и поднимается на максимальную высоту а затем падает вниз двигаясь при этом
ПодробнееПРЕДИСЛОВИЕ генератором тестов
ПРЕДИСЛОВИЕ Пособие предназначено для учащихся средних школ, колледжей и техникумов и может быть использовано как при изучении физики, так и при подготовке к ЕГЭ. В пособии представлено 816 разноуровневых
ПодробнееПримерные практические задания:
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА класс (профиль) Учащиеся должны знать/понимать: Понятие производной.
ПодробнееОпределение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Лабораторная работа 113
Лабораторная работа 113 Изучение законов равномерного и равноускоренного движения. Цель работы : изучение законов равномерного и равноускоренного движения на машине Атвуда. Краткая теория работы. Машина
ПодробнееЛОМОНОСОВ МЕХАНИКА.
ЛОМОНОСОВ МЕХАНИКА классы Краткие решения и критерии оценки задач Задача (вариант ) Перворазрядник Чуков пробегает один круг по пересеченной местности на три минуты быстрее, чем его одноклассник Геков
ПодробнееЗадачи 29 и 30 (бывшие С2 и С3)
Задачи 29 и 30 (бывшие С2 и С3) Задача 29 (по новой нумерации, которую вводят в ЕГЭ с 2015 года) это расчетная задача на механику. До 2014 года включительно она фигурировала под номером «С2».
ПодробнееЭто может
если υ 0 а – движение ускоренное
Кинематика Механическое движение изменение положения тела в пространстве с течением времени относительно других тел. Поступательное движение движение, при котором все точки тела проходят одинаковые траектории.
ПодробнееМЕТОДИЧЕСКИЕ УКАЗАНИЯ
Министерство общего и профессионального образования Российской Федерации ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра физики Т.М. Чмерева М.Р. Ишмеев МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторной работе 104
Подробнее(c) О производной.
О производной. Начиная разговор о производной, я допускаю, что читателю известно, что такое функция, что он не путает таких два понятия, как функция и график функции, что он также знает, что такое область
ПодробнееПодготовка к ОГЭ ЧАСТЬ 1
Подготовка к ОГЭ ЧАСТЬ 1 МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ-1 1.
ПодробнееКинематика 1. Буксирный катер за ч проплыл 5 км. Определите скорость катера..тело, двигаясь из состояния покоя, равноускоренно за первую секунду проходит
Районный тур 2018/ класс. I вариант
Районный тур 018/19. 11 класс. I вариант Задача 1. Поскольку на систему не действует никаких внешних сил в горизонтальном направлении, выполняется закон сохранения полного импульса системы в проекции на
ПодробнееКурсы подготовки к ЕГЭ по физике
Курсы подготовки к ЕГЭ по физике Механика. Задание 9 Учитель физики: Бабчик И.И. Учебное заведение: МБОУ лицей 1 г. Сургут, 019 г. Задание 9. Основные вопросы 1 1. Кинематика Задача 1 Задача 7. Движение
ПодробнееКинематика материальной точки.
Кинематика материальной точки. : Скорость материальной точки.
Подробнее… Ускорение материальной точки…. 3 Тангенциальное и нормальное ускорение…. 4 Проекции скорости и ускорения… 5 График скорости… 6 Вращательное
Урок 4. равномерное движение точки по окружности – Физика – 10 класс
Физика, 10 класс
Урок 04.Равномерное движение точки по окружности
Перечень вопросов, рассматриваемых на уроке:
- Равномерное движение точки по окружности и его характеристики.
- Центростремительное ускорение.
Глоссарий по теме
Криволинейное движение – это движение по дугам окружностей разных радиусов.
Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0
Равномерное движение точки по окружности – движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.
Ключевые слова
Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.
Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение.
Напомним, что траектория – это линия, вдоль которой двигалось тело.
При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.
Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.
Возьмем разные точки на линии и нарисуем векторы скорости . Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.
Векторы и не лежат на одной прямой, угол между ними не равен нулю.
Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.
2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.
Равномерное движение точки по окружности – это движение точки с постоянной по модулю скоростью (v = const) по траектории, представляющей собой окружность. Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение
Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.
Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.
Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была.
Модули скоростей равны:
но вектора скоростей не равны.
Поэтому построим вектор для тела, движущегося по окружности. Перенесем вектор в начало вектораи найдем разность векторов.
направлен в сторону.
Вспомним, что векторнаправлен по касательной, а касательная перпендикулярна радиусу окружности. Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
Что можно сказать об угле между векторами ? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.
Рассмотрим равнобедренный треугольник со сторонами , . Углы у основания равны.
Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 900
Вектор будет перпендикулярен вектору в пределе, а значит вектор ускорения тоже перпендикулярен т.е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением
Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами и треугольник, образованный радиусами и хордой.
У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.
Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю. Тогда можно сказать, что длина хорды s равна длине дуги АВ при
Длина дуги АВ это путь, пройденный точкой от А до В,
тогда запишем:
Умножим наи получим:
В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:
Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными
- Криволинейное движение – это движение по дугам окружностей разных радиусов.
А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.
Всегда при равномерном криволинейном движении вектор ускорения перпендикулярен вектору скорости, поэтому центростремительное ускорение иногда называют нормальным ускорением, от слова нормаль, т.е. перпендикуляр.
Основные выводы:
– движение криволинейное, так как траекторией является окружность;
– движение равномерное, так как модуль скорости не меняется;
– вектор скорости направлен по касательной к окружности;
-вектор ускорения направлен к центру окружности;
– модуль центростремительного ускорения равен:
Примеры и разбор решения заданий
1. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением
где R = 50 м; υ= км/ч = 10 м/с.
Тогда ac = (10 м/с)2 / 50 м = 2 м/с2.
Ответ: 2 м/с2
2. Две материальные точки движутся по окружностям радиусами R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
Дано:
R1 =10см = 0,10 м
R2 = 30см = 0,30 м
Найти –
Задано два объекта:
1) материальная точка, которая движется по окружности R1;
2) материальная точка, которая движется по окружности R2.
При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением
Для тела 1 уравнение (1) примет вид:
для тела 2:
Тогда
Центростремительное ускорение тела (2) меньше ускорения тела (1) в 3 раза.
Веб-сайт класса физики
Объект движется по кругу с постоянной скоростью «по часовой стрелке».
Показан вид круга “глазами Бога”. Для указанного положения направление вектора скорости показано стрелкой ____; направление вектора ускорения обозначено ____; и направление вектора чистой силы представлено стрелкой ____.
На схеме большая точка обозначает определенное место по кругу, по которому движется объект.Вы должны выбрать три стрелки, которые представляют направления векторов скорости, ускорения и результирующей силы в этом месте. Используйте информацию в разделах Physics Rules ниже, чтобы ответить на этот вопрос.
Равномерное круговое движение и скорость:
Скорость – это вектор и направление. Направление скорости объекта всегда совпадает с направлением движения объекта.Для объекта, движущегося по кругу с постоянной скоростью, вектор скорости всегда направлен в направлении, касательном к окружности.Равномерное круговое движение и ускорение:
Ускоряющиеся объекты меняют свою скорость – либо величину, либо направление скорости. Объекты, движущиеся по кругу с постоянной скоростью, ускоряются из-за изменения направления.Направление ускорения направлено к центру круга, вокруг которого движется объект. Такое направление описывается как центростремительное направление .Равномерное круговое движение и полезная сила:
Объект, который движется по кругу, ускоряется. Ускорения вызваны неуравновешенной или чистой силой.Чистая сила всегда совпадает с направлением ускорения. Для объектов, движущихся по кругу с постоянной скоростью, результирующая сила направлена к центру круга, вокруг которого движется объект. Такое направление описывается как центростремительное направление .Каково направление вектора скорости для кругового движения?
Каково направление вектора ускорения при круговом движении?
Каково направление вектора чистой силы для кругового движения?
Разгон | Физика
Цели обучения
К концу этого раздела вы сможете:
- Определение и различие между мгновенным ускорением, средним ускорением и замедлением.
- Рассчитайте ускорение с учетом начального времени, начальной скорости, конечного времени и конечной скорости.
Рис. 1. Самолет замедляется или замедляется при посадке на острове Сен-Мартен. Его ускорение противоположно его скорости. (Источник: Стив Конри, Flickr)
В повседневном разговоре ускорять означает ускоряться. Фактически, ускоритель в автомобиле может заставить его разогнаться. Чем больше ускорение , тем больше изменение скорости за заданный промежуток времени.
Среднее ускорениеФормальное определение ускорения согласуется с этими понятиями, но является более всеобъемлющим.
Среднее ускорение – это скорость, с которой изменяется скорость ,
[латекс] \ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {f} – {v} _ {0}} {{t} _ {f} – {t} _ {0}} [/ latex]
, где [latex] \ bar {a} [/ latex] – среднее ускорение, v – скорость, а t – время.(Полоса над и означает среднее ускорение .)
Поскольку ускорение – это скорость в м / с, деленная на время в секундах, единицами измерения ускорения в системе СИ являются м / с 2 , квадратные метры в секунду или метры в секунду в секунду, что буквально означает, сколько метров в секунду скорость меняется каждую секунду.
Напомним, что скорость – это вектор, у нее есть величина и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но это также может быть изменение в направлении , .
Ускорение как векторНапример, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение возникает, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по обоим направлениям.
Ускорение – это вектор в том же направлении, что и , изменение скорости , Δ v . Поскольку скорость – это вектор, она может меняться по величине или по направлению.Таким образом, ускорение – это изменение скорости или направления, либо и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости на , оно не всегда происходит в направлении движения . Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление .
Мгновенное ускорение
Мгновенное ускорение a , или ускорение в определенный момент времени , получается с помощью того же процесса, который обсуждался для мгновенной скорости во времени, скорости и скорости, то есть путем рассмотрения бесконечно малого интервала время.
Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рисунке 6 показаны графики мгновенного ускорения в зависимости от времени для двух очень разных движений. На Рисунке 6 (а) ускорение незначительно меняется, и среднее значение за весь интервал почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1.8 м / с 2 ). На рисунке 6 (b) ускорение резко меняется со временем. В таких ситуациях лучше всего рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, мы можем рассматривать движение во временных интервалах от 0 до 1,0 с и от 1,0 до 3,0 с как отдельные движения с ускорениями +3,0 м / с 2 и –2,0 м / с 2 соответственно.
В следующих нескольких примерах рассматривается движение поезда метро, показанного на рисунке 7.
В (а) волан движется вправо, а в (б) – влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые рассуждения, которые используются при решении проблем.
Пример 2. Расчет смещения: поезд метро
Каковы величина и знак смещений при движении поезда метро, показанных в частях (a) и (b) рисунка 7?
СтратегияЧертеж с системой координат уже предоставлен, поэтому нам не нужно делать набросок, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает.Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение Δ x = x f – x 0 . Это просто, поскольку даны начальная и конечная позиции.
Раствор1. Определите известные. На рисунке мы видим, что x f = 6,70 км и x 0 = 4,70 км для части (a), а x ′ f = 3,75 км и x ′ 0 = 5.
25 км по части (б).
2. Найдите смещение в части (а).
[латекс] \ Delta x = {x} _ {f} – {x} _ {0} = 6,70 \ text {km} -4,70 \ text {km} = \ text {+} 2,00 \ text {km} [ / латекс]
3. Найдите смещение в части (b).
[латекс] \ Delta x ′ = {x ′} _ {f} – {x ′} _ {0} = \ text {3,75 км} – \ text {5,25 км} = – \ text {1,50 км} [/ латекс]
ОбсуждениеНаправление движения в (a) – вправо, и поэтому его смещение имеет положительный знак, тогда как движение в (b) – влево и, следовательно, имеет отрицательный знак.
Пример 3. Сравнение пройденного расстояния и перемещения: поезд метро
Каковы расстояния, пройденные за движения, показанные в частях (a) и (b) поезда метро на Рисунке 7?
СтратегияЧтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, которая была найдена в Примере 1.Пройденное расстояние – это общая длина пути, пройденного между двумя позициями. (См. Смещение.) В случае поезда метро, показанного на рисунке 7, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.
Раствор1. Смещение для части (а) составило +2,00 км. Таким образом, расстояние между начальной и конечной позициями составило 2,00 км, а пройденное расстояние – 2,00 км.
2. Смещение для части (b) было -1.5 км. Таким образом, расстояние между начальной и конечной позициями составляло 1,50 км, а пройденное расстояние – 1,50 км.
ОбсуждениеРасстояние – скаляр. У него есть величина, но нет знака, указывающего направление.
Пример 4. Расчет ускорения: поезд метро набирает скорость
Предположим, поезд на Рисунке 7 (a) ускоряется из состояния покоя до 30,0 км / ч за первые 20,0 с своего движения. Каково его среднее ускорение за этот промежуток времени?
СтратегияЗдесь стоит сделать простой набросок:
Раствор1.Определите известные. v 0 = 0 (поезда запускаются в состоянии покоя), v f = 30,0 км / ч, а Δ t = 20,0 с.
2. Вычислить Δ v . Поскольку поезд трогается с места, его скорость изменяется на [latex] \ Delta v \ text {=} \ text {+} \ text {30,0 км / ч} [/ latex], где знак плюса означает скорость вправо. .
3. Подставьте известные значения и решите неизвестное, [latex] \ bar {a} [/ latex].
[латекс] \ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {+ \ text {30.{2} [/ латекс]
ОбсуждениеЗнак плюс означает, что ускорение направо. Это разумно, потому что поезд стартует из состояния покоя и заканчивает со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и , изменяя скорость на , как всегда.
Пример 5. Расчет ускорения: замедление поезда метро
Теперь предположим, что в конце поездки поезд на рис. 7 (а) замедляется до остановки со скорости 30.0 км / ч за 8.00 с. Какое у него среднее ускорение при остановке?
Стратегия Раствор1. Определите известные. v 0 = 30,0 км / ч, v f = 0 км / ч (поезд остановлен, поэтому его скорость равна 0), и Δ t = 8,00 с.
2. Найдите изменение скорости Δ v .
Δ v = v f – v 0 = 0 – 30.{2} \ text {.} [/ Latex]
ОбсуждениеЗнак минус указывает на то, что ускорение происходит влево. Этот знак разумен, потому что поезд изначально имеет положительную скорость в этой задаче, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости на , которое здесь отрицательно. Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости.
Графики положения, скорости и ускорения отВремя для поездов в Примере 4 и Примере 5 показано на Рисунке 10. (Мы приняли скорость постоянной от 20 до 40 с, после чего поезд замедляется.)
Пример 6. Расчет средней скорости: поезд метро
Какова средняя скорость поезда в части b примера 2, снова показанной ниже, если поездка занимает 5,00 минут?
СтратегияСредняя скорость – это смещение, разделенное на время. Здесь он будет отрицательным, так как поезд движется влево и имеет отрицательное смещение.
Раствор1. Определите известные. x ′ f = 3,75 км, x ′ 0 = 5,25 км, Δ t = 5,00 мин.
2. Определите перемещение Δ x ′. В примере 2 мы обнаружили, что Δ x ′ составляет −1,5 км.
3. Найдите среднюю скорость.
[латекс] \ bar {v} = \ frac {\ Delta x ′} {\ Delta t} = \ frac {- \ text {1,50 км}} {\ text {5,00 мин}} [/ latex]
4. Перевести единицы.
[латекс] \ bar {v} = \ frac {\ Delta x ′} {\ Delta t} = \ left (\ frac {-1 \ text {.} \ text {50 км}} {5 \ text {.} \ text {00 min}} \ right) \ left (\ frac {\ text {60 min}} {1 h} \ right) = – \ text { 18} \ text {.0 км / ч} [/ latex]
ОбсуждениеОтрицательная скорость указывает на движение влево.
Пример 7. Расчет замедления: поезд метро
Наконец, предположим, что поезд на Рисунке 2 замедляется до остановки со скорости 20,0 км / ч за 10,0 с. Какое у него среднее ускорение?
СтратегияЕще раз нарисуем набросок:
Как и раньше, мы должны найти изменение скорости и изменение во времени, чтобы вычислить среднее ускорение.
Раствор1. Определите известные. v 0 = −20 км / ч, v f = 0 км / ч, Δ t = 10,0 с.
2. Вычислить Δ v . Изменение скорости здесь действительно положительное, так как
[латекс] \ Delta v = {v} _ {f} – {v} _ {0} = 0- \ left (- \ text {20 км / ч} \ right) \ text {=} \ phantom {\ правило {0.25} {0ex}} \ text {+} \ text {20 км / ч} [/ latex]
3. Решите для [латекс] \ bar {a} [/ latex].
[латекс] \ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {+ \ text {20} \ text {.{2} [/ латекс]
ОбсуждениеЗнак плюс означает, что ускорение направо. Это разумно, потому что у поезда изначально отрицательная скорость (слева) в этой задаче, а положительное ускорение противодействует движению (то есть справа). Опять же, ускорение происходит в том же направлении, что и изменение скорости на , что здесь положительно. Как и в примере 5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости.
Возможно, самое важное, что нужно отметить в этих примерах, – это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус – слева. Это легко представить для смещения и скорости. Но для разгона это немного менее очевидно. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Этого не было в Примере 2, где положительное ускорение замедляло отрицательную скорость. Решающее различие заключалось в том, что ускорение происходило в направлении, противоположном скорости.Фактически, отрицательное ускорение увеличит отрицательную скорость. Например, поезд, движущийся влево на рисунке 11, ускоряется за счет ускорения влево. В этом случае и v , и a отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и изменение скорости, объект ускоряется. Если ускорение имеет знак, противоположный изменению скорости, объект замедляется.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, летящей на восток.Опишите его ускорение.
РастворЕсли принять восток за положительное значение, то самолет имеет отрицательное ускорение, поскольку он ускоряется в сторону запада. Он также замедляется: его ускорение противоположно направлению его скорости.
Исследования PhET: моделирование движущегося человека
Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка взад и вперед мышью и наметьте его движение. Задайте положение, скорость или ускорение и позвольте симуляции перемещать человека за вас.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
Концептуальные вопросы
1. Возможно ли, чтобы скорость была постоянной при ненулевом ускорении? Приведите пример такой ситуации.
2. Возможно ли, чтобы скорость была постоянной, если ускорение не равно нулю? Объяснять.
3. Приведите пример, в котором скорость равна нулю, а ускорение – нет.
4. Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное?
5.Знаки плюс и минус используются в одномерном движении для обозначения направления. Каков знак ускорения, уменьшающего величину отрицательной скорости? Положительной скорости?
Задачи и упражнения
1. Гепард может разогнаться от состояния покоя до скорости 30,0 м / с за 7,00 с. Какое у него ускорение?
2. Профессиональное приложение. Доктор Джон Пол Стэпп был офицером ВВС США, изучавшим влияние экстремального замедления на человеческое тело.10 декабря 1954 года Стапп ездил на ракетных санях, разгоняясь из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с, и был резко остановлен всего за 1,40 с! Вычислите его (а) ускорение и (б) замедление. Выразите каждое значение кратным г (9,80 м / с 2 ), взяв его отношение к ускорению свободного падения.
3. Пассажир выезжает на машине задним ходом из гаража с ускорением 1,40 м / с 2 . (A) Сколько времени ему нужно, чтобы набрать скорость 2.00 м / с? (b) Если она затем тормозит до остановки через 0,800 с, каково ее замедление?
4. Предположим, что межконтинентальная баллистическая ракета переходит из состояния покоя в суборбитальную скорость 6,50 км / с за 60,0 с (фактическая скорость и время засекречены). Каково его среднее ускорение в м / с 2 и кратное g (9,80 м / с 2 ).
Глоссарий
- ускорение:
- скорость изменения скорости; изменение скорости с течением времени
- среднее ускорение:
- изменение скорости, деленное на время, в течение которого оно изменяется
- мгновенное ускорение:
- ускорение в определенный момент времени
- замедление:
- ускорение в направлении, противоположном скорости; ускорение, которое приводит к уменьшению скорости
Избранные решения проблем и упражнения
1.4,29 м / с 2
3. (а) 1,43 с (б) -2,50 м / с 2
Скорость, ускорение и сила | Безграничная физика
Угол вращения и угловая скорость
Угол поворота – это мера того, как далеко вращается объект, а угловая скорость – это скорость его вращения.
Цели обучения
Выразите взаимосвязь между углом поворота и расстоянием
Основные выводы
Ключевые моменты
- Когда объект вращается вокруг оси, точки на краю объекта перемещаются по дугам.
- Угол, выходящий за пределы этих дуг, называется углом поворота и обычно обозначается символом theta .
- Мера того, насколько быстро объект вращается относительно времени, называется угловой скоростью. Обычно он представлен греческим символом омега . Как и его аналог линейной скорости, это вектор.
Ключевые термины
- радиан : угол, образуемый в центре окружности дугой той же длины, что и радиус окружности.
Угол вращения и угловая скорость
Когда объект вращается вокруг оси, как в случае с шиной на автомобиле или с записью на поворотной платформе, движение можно описать двумя способами. Точка на краю вращающегося объекта будет иметь некоторую скорость и будет перенесена по дуге на вращающемся объекте. Точка пройдет расстояние [latex] \ Delta \ text {S} [/ latex], но часто удобнее говорить о степени поворота объекта. Величина поворота объекта называется углом поворота и может измеряться в градусах или радианах.Поскольку угол поворота связан с расстоянием [latex] \ Delta \ text {S} [/ latex] и с радиусом [latex] \ text {r} [/ latex] уравнением [latex] \ Delta \ theta = \ frac {\ Delta \ text {S}} {\ text {R}} [/ latex], обычно удобнее использовать радианы.
Угол θ и длина дуги s : Радиус круга поворачивается на угол [латекс] \ дельта \ тета [/ латекс]. Длина дуги [латекс] \ Delta \ text {s} [/ latex] указывается на окружности.
Скорость вращения объекта определяется угловой скоростью, которая представляет собой скорость изменения угла поворота во времени.Хотя сам угол не является векторной величиной, угловая скорость – это вектор. Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно задается правилом правой руки. Угловое ускорение дает скорость изменения угловой скорости. Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.
Направление угловой скорости : Угловая скорость описывает скорость вращения и ориентацию мгновенной оси, вокруг которой происходит вращение.Направление угловой скорости будет вдоль оси вращения. В этом случае (вращение против часовой стрелки) вектор направлен вверх.
Когда ось вращения перпендикулярна вектору положения, угловую скорость можно вычислить, взяв линейную скорость [latex] \ text {v} [/ latex] точки на краю вращающегося объекта и разделив на радиус. Это даст угловую скорость, обычно обозначаемую [latex] \ omega [/ latex], в радианах в секунду.
Угловая скорость : Муха на краю вращающегося объекта фиксирует постоянную скорость [latex] \ text {v} [/ latex]. Объект вращается с угловой скоростью, равной [latex] \ frac {\ text {v}} {\ text {r}} [/ latex].
Центробежное ускорение
Центростремительное ускорение – это постоянное изменение скорости, необходимое объекту для поддержания круговой траектории.
Цели обучения
Выразите центростремительное ускорение через скорость вращения
Основные выводы
Ключевые моменты
- Для того, чтобы объект сохранял круговое движение, он должен постоянно менять направление.
- Поскольку скорость является вектором, изменения направления представляют собой изменения скорости.
- Изменение скорости называется ускорением. Изменение скорости из-за кругового движения известно как центростремительное ускорение.
- Центростремительное ускорение можно рассчитать, разделив квадрат линейной скорости на радиус круга, по которому движется объект.
Ключевые термины
- ускорение : величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).
- круговое движение : движение таким образом, что выбранная траектория представляет собой круговую траекторию.
- скорость : векторная величина, которая обозначает скорость изменения положения относительно времени или скорость с направленным компонентом.
Обзор
Как упоминалось в предыдущих разделах по кинематике, любое изменение скорости определяется ускорением. Часто изменения скорости являются изменениями по величине. Когда объект ускоряется или замедляется, это изменение скорости объекта.Изменения в величине скорости соответствуют нашему интуитивному и повседневному использованию термина «ускорение». Однако, поскольку скорость является вектором, у нее также есть направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Равномерное круговое движение означает, что объект движется по круговой траектории с постоянной скоростью. Поскольку скорость постоянна, обычно не думается, что объект ускоряется. Однако направление постоянно меняется, когда объект пересекает круг.Таким образом, говорят, что он ускоряется. Это ускорение можно почувствовать, катаясь на американских горках. Даже если скорость постоянная, быстрый поворот вызовет у гонщика чувство силы. Это ощущение ускорения.
Центростремительное ускорение : Краткий обзор центростремительного ускорения для школьников-физиков.
Расчет центростремительного ускорения
Для расчета центростремительного ускорения объекта, совершающего равномерное круговое движение, необходимо иметь скорость, с которой движется объект, и радиус круга, вокруг которого происходит движение.2 \ text {r} [/ latex]
, где омега – это скорость вращения, заданная [latex] \ frac {\ text {v}} {\ text {r}} [/ latex].
Центростремительное ускорение : Когда объект движется по окружности, направление вектора скорости постоянно меняется.
Центростремительная сила
Сила, которая вызывает движение по криволинейной траектории, называется центростремительной силой (равномерное круговое движение является примером центростремительной силы).
Цели обучения
Выразите уравнения для центростремительной силы и ускорения
Основные выводы
Ключевые моменты
- Когда объект находится в равномерном круговом движении, он постоянно меняет направление и, следовательно, ускоряется.Это угловое ускорение.
- Сила, действующая на объект при равномерном круговом движении (называемая центростремительной силой), действует на объект из центра круга.
Ключевые термины
- центростремительный : Направлен или движется к центру.
- угловая скорость : векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой. Равномерное круговое движение является примером действия центростремительной силы. Это можно увидеть на орбите спутников вокруг Земли, натяжении веревки в игре с тросом, в петле-петле на американских горках или в ведре, вращающемся вокруг тела.
Обзор центростремительной силы : Краткий обзор центростремительной силы.
Ранее мы узнали, что любое изменение скорости – это ускорение.По мере того, как объект движется по круговой траектории, он постоянно меняет направление и, следовательно, ускоряется, вызывая постоянное воздействие на объект силы. Эта центростремительная сила действует по направлению к центру кривизны, по направлению к оси вращения. Поскольку объект движется перпендикулярно силе, путь, по которому он движется, является круговым. Именно эта сила удерживает мяч от выпадения из ведра, если вы непрерывно раскачиваете его по кругу.
Центростремительная сила : Когда объект движется по круговой траектории с постоянной скоростью, он испытывает центростремительную силу, ускоряющую его к центру.2 [/ латекс]
3.1 Разгон | Texas Gateway
Определение ускорения
В этой главе мы будем использовать следующие термины: время , смещение , скорость и ускорение . Напомним, что у каждого из этих терминов есть обозначенная переменная и единица измерения СИ следующим образом:
- Время: t , измеряется в секундах (с)
- Смещение: Δ d , измеряется в метрах (м)
- Скорость: v , измеряется в метрах в секунду (м / с)
- Ускорение: a , измеряется в метрах в секунду в секунду (м / с 2 , также называется метрами в секунду в квадрате)
- Также обратите внимание на следующее:
- Δ означает изменение в
- Нижний индекс 0 относится к начальному значению; иногда индекс i используется для обозначения начального значения.
- Нижний индекс f относится к окончательному значению
- Полоса над символом, например ¯a¯, означает в среднем
Ускорение – это изменение скорости, деленное на период времени, в течение которого это изменение происходит. В системе СИ единицами измерения скорости являются м / с, а единицей СИ для времени – с, поэтому единицами СИ для ускорения являются м / с 2 . Среднее ускорение дает
a¯ = ΔvΔt = vf − v0tf − t0.a¯ = ΔvΔt = vf − v0tf − t0.Среднее ускорение отличается от мгновенного ускорения, которое представляет собой ускорение в определенный момент времени.Величина ускорения часто не постоянна во времени. Например, бегуны, участвующие в гонке, ускоряются в первую секунду гонки с большей скоростью, чем в последующие секунды. Вам не нужно постоянно знать все мгновенные ускорения, чтобы рассчитать среднее ускорение. Все, что вам нужно знать, это изменение скорости (то есть конечная скорость минус начальная скорость) и изменение во времени (то есть конечное время минус начальное время), как показано в формуле. Обратите внимание, что среднее ускорение может быть положительным, отрицательным или нулевым.Отрицательное ускорение – это просто ускорение в отрицательном направлении.
Имейте в виду, что хотя ускорение указывает в том же направлении, что и , изменение скорости на , оно не всегда происходит в направлении самой скорости. Когда объект замедляется, его ускорение противоположно направлению его скорости. На обыденном языке это называется замедлением; но в физике это ускорение, направление которого противоположно направлению скорости. А пока предположим, что движение вправо по оси x – это положительное значение , а движение влево – отрицательное значение .
На рис. 3.2 показан автомобиль с положительным ускорением в (a) и отрицательным ускорением в (b). Стрелки представляют собой векторы, показывающие направление и величину скорости и ускорения.
Рис. 3.2 Автомобиль ускоряется на (a) и замедляется на (b).
Скорость и ускорение являются векторными величинами. Напомним, что векторы имеют как величину, так и направление. Объект, движущийся с постоянной скоростью – следовательно, не имеющий ускорения – действительно ускоряется, если он меняет направление.Итак, поворот рулевого колеса движущегося автомобиля заставляет автомобиль ускоряться, потому что скорость меняет направление.
Virtual Physics
The Moving Man
С помощью этой анимации на рисунке 3.3 вы можете создать как вариации ускорения, так и скорости, показанные на рисунке 3.2, а также еще несколько вариаций. Изменяйте скорость и ускорение, перемещая красный и зеленый маркеры по шкале. Удержание маркера скорости около нуля сделает эффект ускорения более очевидным.Попробуйте изменить ускорение с положительного на отрицательное, пока мужчина движется. Мы вернемся к этой анимации и посмотрим на представление Charts , когда будем изучать графическое представление движения.
Проверка захвата
Какая часть (a) или (b) представлена, когда вектор скорости находится на положительной стороне шкалы, а вектор ускорения установлен на отрицательной стороне шкалы? Как выглядит движение автомобиля для данного сценария?
- Часть (а).Автомобиль замедляется, потому что векторы ускорения и скорости действуют в противоположном направлении.
- Часть (а). Автомобиль ускоряется, потому что векторы ускорения и скорости действуют в одном направлении.
- Часть (б). Автомобиль замедляется, потому что векторы ускорения и скорости действуют в противоположных направлениях.
- Часть (б). Автомобиль ускоряется, потому что векторы ускорения и скорости действуют в одном направлении.
вектор | Определение, физика и факты
Вектор , в физике величина, имеющая как величину, так и направление. Обычно он представлен стрелкой, направление которой совпадает с направлением количества, а длина пропорциональна величине величины. Хотя вектор имеет величину и направление, у него нет позиции. То есть, пока его длина не изменяется, вектор не изменяется, если он смещается параллельно самому себе.
В отличие от векторов, обычные величины, которые имеют величину, но не направление, называются скалярами.Например, смещение, скорость и ускорение – векторные величины, а скорость (величина скорости), время и масса – скаляры.
Чтобы считаться вектором, величина, имеющая величину и направление, также должна подчиняться определенным правилам комбинирования. Одним из них является сложение векторов, символически записываемое как A + B = C (векторы обычно обозначаются жирным шрифтом). С геометрической точки зрения векторную сумму можно визуализировать, поместив хвост вектора B в начало вектора A и нарисовав вектор C, начиная с хвоста A и заканчивая в голове B, так, чтобы он завершал треугольник.Если A, B и C – векторы, должна быть возможность выполнить ту же операцию и получить тот же результат (C) в обратном порядке, B + A = C. Величины, такие как смещение и скорость, обладают этим свойством (закон коммутативности). , но есть величины (например, конечные вращения в пространстве), которые не являются векторами и поэтому не являются векторами.
Векторный параллелограмм для сложения и вычитанияОдин из методов сложения и вычитания векторов состоит в том, чтобы соединить их хвосты вместе, а затем подвести еще две стороны, чтобы сформировать параллелограмм.Вектор от их хвостов к противоположному углу параллелограмма равен сумме исходных векторов. Вектор между их головами (начиная с вычитаемого вектора) равен их разности.
Encyclopdia Britannica, Inc.Другими правилами обработки векторов являются вычитание, умножение на скаляр, скалярное умножение (также известное как скалярное произведение или внутреннее произведение), векторное умножение (также известное как перекрестное произведение) и дифференцирование. .Нет операции, соответствующей делению на вектор. См. Векторный анализ для описания всех этих правил.
Правило правой руки для векторного векторного произведенияОбычное, или точечное, произведение двух векторов – это просто одномерное число или скаляр. Напротив, перекрестное произведение двух векторов приводит к другому вектору, направление которого ортогонально обоим исходным векторам, как показано правилом правой руки. Величина или длина вектора векторного произведения задается следующим образом: v w sin θ , где θ – это угол между исходными векторами v и w .
Британская энциклопедия, Inc. Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасХотя векторы математически просты и чрезвычайно полезны при обсуждении физики, они не были разработаны в их современной форме до конца XIX века, когда Джозайя Уиллард Гиббс и Оливер Хевисайд (из США и Англии соответственно) применили векторный анализ в своих исследованиях. чтобы помочь выразить новые законы электромагнетизма, предложенные Джеймсом Клерком Максвеллом.
Кинематика – скорость в зависимости от ускорения
Кинематика – скорость в зависимости от ускорения
Глава 2 Цели]BHS -> Физика -> Механика -> Кинематика -> эта страница
Скорость и ускорение
Понятия скорости и ускорения взаимосвязаны, но они связаны неправильно в сознании многих людей. Многие люди думают, что если объект имеет большую скорость, он должен иметь большое ускорение – если у него небольшая скорость, у него должно быть небольшое ускорение – если его скорость равна нулю, его ускорение должно быть ноль тоже. ЭТО НЕПРАВИЛЬНО !!
Ускорение – это скорость изменения скорости, что означает это ускорение говорит вам , насколько быстро скорость меняется. Большое ускорение говорит о том, что скорость равна быстро меняется – небольшое ускорение говорит о том, что скорость меняется медленно – нулевое ускорение говорит о том, что скорость вообще не меняется.
Acceleration говорит вам, как изменяется скорость, но не говорит какая скорость! Объект может иметь большую скорость и небольшое (или нулевое) ускорение – и наоборот.
Ускорение и замедление
Многие люди также ошибочно полагают, что «положительный ускорение означает ускорение, отрицательное ускорение означает замедление вниз. “Извините! Изучая примеры Из расчета ускорений можно сделать вывод, что:
- Если скорость и ускорение в одном направлении (оба имеют одинаковый знак – оба положительные или оба отрицательные) объект ускоряется.
- Если скорость и ускорение противоположны (у них противоположные знаки), объект замедляется.
Цели главы 2] BHS -> Физика -> Механика -> Кинематика -> эта страница
, последнее обновление 31 августа 2009 г., автор: JL Stanbrough6.2 Равномерное круговое движение – Физика
Задачи обучения секции
К концу этого раздела вы сможете делать следующее:
- Описывать центростремительное ускорение и связывать его с линейным ускорением
- Опишите центростремительную силу и свяжите ее с линейной силой
- Решение проблем, связанных с центростремительным ускорением и центростремительной силой
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и кругов.
- (D) вычислить влияние сил на объекты, включая закон инерции, соотношение между силой и ускорением и характер пар сил между объектами.
Кроме того, руководство лаборатории физики средней школы рассматривает содержание этого раздела лаборатории под названием «Круговое и вращательное движение», а также следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и кругов.
Раздел Основные термины
центробежная сила центростремительное ускорение центростремительная сила равномерное круговое движение Центростремительное ускорение
Поддержка учителя
Поддержка учителя
[BL] [OL] Проверьте равномерное круговое движение.Попросите учащихся привести примеры кругового движения. Просмотрите линейное ускорение.
В предыдущем разделе мы определили круговое движение. Простейшим случаем кругового движения является равномерное круговое движение, когда объект движется по круговой траектории с постоянной скоростью . Обратите внимание, что, в отличие от скорости, линейная скорость объекта при круговом движении постоянно меняется, потому что он всегда меняет направление. Из кинематики мы знаем, что ускорение – это изменение скорости либо по величине, либо по направлению, либо по обоим направлениям.Следовательно, объект, совершающий равномерное круговое движение, всегда ускоряется, даже если величина его скорости постоянна.
Вы сами испытываете это ускорение каждый раз, когда едете в машине на повороте. Если вы держите рулевое колесо неподвижно во время поворота и двигаетесь с постоянной скоростью, вы совершаете равномерное круговое движение. Вы замечаете ощущение скольжения (или отбрасывания, в зависимости от скорости) от центра поворота. На вас действует не настоящая сила – это происходит только потому, что ваше тело хочет продолжать движение по прямой (согласно первому закону Ньютона), в то время как машина сворачивает с этого прямолинейного пути.Внутри машины создается впечатление, что вас оттесняют от центра поворота. Эта фиктивная сила известна как центробежная сила. Чем резче кривая и чем выше ваша скорость, тем заметнее становится этот эффект.
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Продемонстрируйте круговое движение, привязывая груз к веревке и вращая ее. Спросите студентов, что произойдет, если вы внезапно перережете веревку? В каком направлении движется объект? Почему? Что это говорит о направлении ускорения? Попросите учащихся привести примеры, когда они столкнулись с центростремительным ускорением.
На рис. 6.7 показан объект, движущийся по круговой траектории с постоянной скоростью. Направление мгновенной тангенциальной скорости показано в двух точках вдоль пути. Ускорение происходит в направлении изменения скорости; в этом случае он указывает примерно на центр вращения. (Центр вращения находится в центре круговой траектории). Если мы представим, что ΔsΔs становится все меньше и меньше, тогда ускорение будет направлять точно на к центру вращения, но этот случай трудно изобразить.Мы называем ускорение объекта, движущегося в равномерном круговом движении, центростремительным ускорением a c , потому что центростремительное означает центростремительное движение .
Рисунок 6.7 Показаны направления скорости объекта в двух разных точках, и видно, что изменение скорости ΔvΔv указывает приблизительно на центр кривизны (см. Маленькую вставку). При очень малом значении ΔsΔs ΔvΔv указывает точно на центр круга (но это трудно изобразить).Поскольку ac = Δv / Δtac = Δv / Δt, ускорение также направлено к центру, поэтому a c называется центростремительным ускорением.Поддержка учителей
Поддержка учителей
Обратите внимание на рисунок 6.7. На рисунке показан объект, движущийся по круговой траектории с постоянной скоростью, и направление мгновенной скорости двух точек на траектории. Ускорение происходит в направлении изменения скорости и указывает на центр вращения. Это строго верно только при стремлении ΔsΔs к нулю.
Теперь, когда мы знаем, что центростремительное ускорение направлено к центру вращения, давайте обсудим величину центростремительного ускорения. Для объекта, движущегося со скоростью по круговой траектории с радиусом , величина центростремительного ускорения составляет
.Центростремительное ускорение больше на высоких скоростях и на крутых поворотах (меньший радиус), как вы могли заметить при вождении автомобиля, потому что автомобиль фактически толкает вас к центру поворота.Но немного удивительно, что a c пропорционально квадрату скорости. Это означает, например, что при повороте на скорости 100 км / ч ускорение в четыре раза больше, чем при 50 км / ч.
Мы также можем выразить a c через величину угловой скорости. Подставляя v = rωv = rω в приведенное выше уравнение, мы получаем ac = (rω) 2r = rω2ac = (rω) 2r = rω2. Следовательно, величина центростремительного ускорения с точки зрения величины угловой скорости составляет
Советы для успеха
Уравнение, выраженное в форме a c = rω 2 , полезно для решения задач, где вам известна угловая скорость, а не тангенциальная скорость.
Виртуальная физика
Движение божьей коровки в 2D
В этом моделировании вы экспериментируете с положением, скоростью и ускорением божьей коровки при круговом и эллиптическом движении. Переключите тип движения с линейного на круговое и наблюдайте за векторами скорости и ускорения. Затем попробуйте эллиптическое движение и обратите внимание, как векторы скорости и ускорения отличаются от векторов кругового движения.
Проверка захвата
Какой угол между ускорением и скоростью при равномерном круговом движении? Какое ускорение испытывает тело при равномерном круговом движении?
- Угол между ускорением и скоростью равен 0 °, и тело испытывает линейное ускорение.
- Угол между ускорением и скоростью равен 0 °, и тело испытывает центростремительное ускорение.
- Угол между ускорением и скоростью составляет 90 °, и тело испытывает линейное ускорение.
- Угол между ускорением и скоростью составляет 90 °, и тело испытывает центростремительное ускорение.
Центростремительная сила
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Используя ту же демонстрацию, что и раньше, попросите учащихся предсказать отношения между величинами угловой скорости, центростремительного ускорения, массы, центростремительной силы.Предложите студентам поэкспериментировать, используя веревки разной длины и веса.
Поскольку объект при равномерном круговом движении испытывает постоянное ускорение (за счет изменения направления), мы знаем из второго закона движения Ньютона, что на объект должна действовать постоянная чистая внешняя сила.
Любая сила или комбинация сил могут вызвать центростремительное ускорение. Вот лишь несколько примеров: натяжение веревки на шаре троса, сила притяжения Земли на Луне, трение между дорогой и шинами автомобиля при движении по кривой или нормальная сила американских горок. следите за тележкой во время петли.
Любая чистая сила, вызывающая равномерное круговое движение, называется центростремительной силой. Направление центростремительной силы – к центру вращения, такое же, как и для центростремительного ускорения. Согласно второму закону движения Ньютона, чистая сила вызывает ускорение массы согласно F net = м a . Для равномерного кругового движения ускорение является центростремительным: a = a c . Следовательно, величина центростремительной силы F c равна Fc = macFc = mac.
Используя две различные формы уравнения для величины центростремительного ускорения, ac = v2 / rac = v2 / r и ac = rω2ac = rω2, мы получаем два выражения, включающих величину центростремительной силы F c . Первое выражение относится к тангенциальной скорости, второе – к угловой скорости: Fc = mv2rFc = mv2r и Fc = mrω2Fc = mrω2.
Обе формы уравнения зависят от массы, скорости и радиуса круговой траектории. Вы можете использовать любое более удобное выражение для центростремительной силы.Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и чистая сила. По определению центростремительная сила направлена к центру вращения, поэтому объект также будет ускоряться к центру. Прямая линия, проведенная от круговой траектории к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для r , вы получите
Из этого выражения мы видим, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть резкую кривую.
Рисунок 6.8 На этом рисунке сила трения f служит центростремительной силой F c . Центростремительная сила перпендикулярна тангенциальной скорости и вызывает равномерное круговое движение. Чем больше центростремительная сила F c , тем меньше радиус кривизны r и тем острее кривизна. Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F c дает меньший радиус r’r ‘.Watch Physics
Центростремительная сила и ускорение Intuition
В этом видео объясняется, почему центростремительная сила создает центростремительное ускорение и равномерное круговое движение. Он также охватывает разницу между скоростью и скоростью и показывает примеры равномерного кругового движения.
Поддержка учителей
Предупреждение о неправильном представлении
Поддержка учителей
Некоторые студенты могут запутаться между центростремительной силой и центробежной силой. Центробежная сила – это не реальная сила, а результат ускоряющейся системы отсчета, такой как вращающийся автомобиль или вращающаяся Земля.Центробежная сила относится к вымышленному центру , убегающему от силы .
Проверка захвата
Представьте, что вы качаете йойо по вертикальному кругу по часовой стрелке перед собой, перпендикулярно направлению, в которое вы смотрите. Если веревка порвется, когда йо-йо достигнет самого нижнего положения, ближайшего к полу. Что будет с йо-йо после разрыва струны?
- Йо-йо полетит внутрь в направлении центростремительной силы.
- Йо-йо полетит наружу в направлении центростремительной силы.
- Йо-йо полетит влево в направлении тангенциальной скорости.
- Йо-йо полетит вправо в направлении тангенциальной скорости.
Решение проблем центростремительного ускорения и центростремительной силы
Чтобы получить представление о типичных величинах центростремительного ускорения, мы проведем лабораторию по оценке центростремительного ускорения теннисной ракетки, а затем, в нашем первом рабочем примере, сравним центростремительное ускорение автомобиля, огибающего кривую, с ускорением свободного падения.Для второго рабочего примера мы вычислим силу, необходимую для поворота автомобиля на повороте.
Snap Lab
Оценка центростремительного ускорения
В этом упражнении вы будете измерять качание клюшки для гольфа или теннисной ракетки, чтобы оценить центростремительное ускорение конца клюшки или ракетки. Вы можете сделать это в замедленном режиме. Напомним, что уравнение центростремительного ускорения: ac = v2rac = v2r или ac = rω2ac = rω2.
- Одна теннисная ракетка или клюшка для гольфа
- Один таймер
- Одна линейка или рулетка
Порядок действий
- Работа с партнером.Стойте на безопасном расстоянии от вашего партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой.
- Опишите движение качелей – это равномерное круговое движение? Почему или почему нет?
- Постарайтесь сделать свинг как можно ближе к равномерному круговому движению. Какие корректировки пришлось внести вашему партнеру?
- Измерьте радиус кривизны. Что вы измерили физически?
- Используя таймер, найдите либо линейную, либо угловую скорость, в зависимости от того, какое уравнение вы решите использовать.
- Каково примерное центростремительное ускорение на основе этих измерений? Как вы думаете, насколько они точны? Почему? Как вы и ваш партнер можете сделать эти измерения более точными?
Подставка для учителя
Подставка для учителя
Размах клюшки или ракетки можно сделать очень близким к равномерному круговому движению. Для этого человек должен двигать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки – это радиус кривизны.Точность измерения угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки наблюдения человека. Размах клюшки или ракетки может быть очень близок к равномерному круговому движению. Для этого человек должен двигать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерения угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки наблюдения человека.
Проверка захвата
Было ли более полезным использовать в этом упражнении уравнение ac = v2rac = v2r или ac = rω2ac = rω2? Почему?
- Должно быть проще использовать ac = rω2ac = rω2, потому что измерение угловой скорости путем наблюдения было бы проще.
- Должно быть проще использовать ac = v2rac = v2r, потому что измерение тангенциальной скорости посредством наблюдения было бы проще.
- Должно быть проще использовать ac = rω2ac = rω2, потому что измерение угловой скорости путем наблюдения было бы затруднительно.
- Должно быть проще использовать ac = v2rac = v2r, потому что измерение тангенциальной скорости посредством наблюдения было бы затруднительно.
Рабочий пример
Сравнение центростремительного ускорения автомобиля, огибающего кривую, с ускорением под действием силы тяжести
Автомобиль следует кривой радиусом 500 м со скоростью 25,0 м / с (около 90 км / ч). Какова величина центростремительного ускорения автомобиля? Сравните центростремительное ускорение для этой довольно пологой кривой, снятой на скорости шоссе, с ускорением свободного падения ( g ).
Стратегия
Поскольку дана линейная, а не угловая скорость, наиболее удобно использовать выражение ac = v2rac = v2r, чтобы найти величину центростремительного ускорения.
Решение
Ввод данных значений v = 25,0 м / с и r = 500 м в выражение для a c дает
ac = v2r = (25,0 м / с) 2500 м = 1,25 м / с 2. ac = v2r = (25,0 м / с) 2500 м = 1,25 м / с2.Обсуждение
Для сравнения с ускорением свободного падения ( g = 9.80 м / с 2 ), берем соотношение ac / g = (1,25 м / с2) / (9,80 м / с2) = 0,128 ac / g = (1,25 м / с2) / (9,80 м / с2) = 0,128. Следовательно, ac = 0,128gac = 0,128g, что означает, что центростремительное ускорение составляет примерно одну десятую ускорения свободного падения.
Рабочий пример
Сила трения на шинах автомобиля, огибающих кривую
- Рассчитайте центростремительную силу, действующую на автомобиль массой 900 кг, который движется по кривой радиусом 600 м на горизонтальной поверхности со скоростью 25,0 м / с.
- Статическое трение предотвращает скольжение автомобиля.Найдите величину силы трения между шинами и дорогой, которая позволяет автомобилю обогнуть поворот, не соскальзывая по прямой.
Стратегия и решение для (а)
Мы знаем, что Fc = mv2rFc = mv2r. Следовательно,
Fc = mv2r = (900 кг) (25,0 м / с) 2600 м = 938 Н. Fc = mv2r = (900 кг) (25,0 м / с) 2600 м = 938 Н.Стратегия и решение для (b)
На изображении выше показаны силы, действующие на автомобиль при повороте кривой. На этой диаграмме автомобиль движется по странице, как показано, и поворачивает налево.Трение действует влево, ускоряя автомобиль к центру поворота. Поскольку трение – единственная горизонтальная сила, действующая на автомобиль, в этом случае оно обеспечивает всю центростремительную силу. Следовательно, сила трения является центростремительной силой в этой ситуации и направлена к центру кривой.
Обсуждение
Поскольку мы нашли силу трения в части (b), мы также можем найти коэффициент трения, поскольку f = μsN = μsmgf = μsN = μsmg.
Практические задачи
9.Какое центростремительное ускорение ощущают пассажиры автомобиля, движущегося со скоростью 12 м / с по кривой радиусом 2,0 м?
10.
- 3 м / с 2
- 6 м / с 2
- 36 м / с 2
- 72 м / с 2
Вычислить центростремительное ускорение объекта, движущегося по траектории с радиусом кривизны 0,2 м и угловой скоростью 5 рад / с.
- 1 м / с
- 5 м / с
- 1 м / с 2
- 5 м / с 2
Проверьте свое понимание
11.Что такое равномерное круговое движение?
12.
- Равномерное круговое движение – это когда объект ускоряется по круговой траектории с постоянно увеличивающейся скоростью.
- Равномерное круговое движение – это когда объект движется по круговой траектории с переменным ускорением.
- Равномерное круговое движение – это когда объект движется по круговой траектории с постоянной скоростью.
- Равномерное круговое движение – это когда объект движется по круговой траектории с переменной скоростью.
Что такое центростремительное ускорение?
13.
- Ускорение объекта, движущегося по круговой траектории и радиально направленного к центру круговой орбиты
- Ускорение объекта, движущегося по круговой траектории и тангенциально направленного по круговой траектории
- Ускорение объекта, движущегося по линейной траектории и направленного в направлении движения объекта
- Ускорение объекта, движущегося по линейной траектории и направленного в направлении, противоположном движению объекта
Существует ли чистая сила, действующая на объект при равномерном круговом движении?
14.
- Да, объект ускоряется, поэтому на него должна действовать чистая сила.
- Да потому что разгона нет.
- Нет, потому что есть ускорение.
- Нет, потому что нет разгона.
Укажите два примера сил, которые могут вызвать центростремительное ускорение.
- Сила притяжения Земли на Луну и нормальная сила
- Сила притяжения Земли на Луну и натяжение веревки на вращающемся тросболе
- Нормальная сила и сила трения, действующие на движущийся автомобиль
- Нормальная сила и натяжение веревки на тезерболе
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, усвоили ли учащиеся учебные цели этого раздела.Если учащиеся борются с определенной целью, формирующая оценка поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
.

 Например, в задаче 2.2.4 зависимости координаты тела по вертикальной оси и проекции скорости на эту ось имеют вид
Например, в задаче 2.2.4 зависимости координаты тела по вертикальной оси и проекции скорости на эту ось имеют вид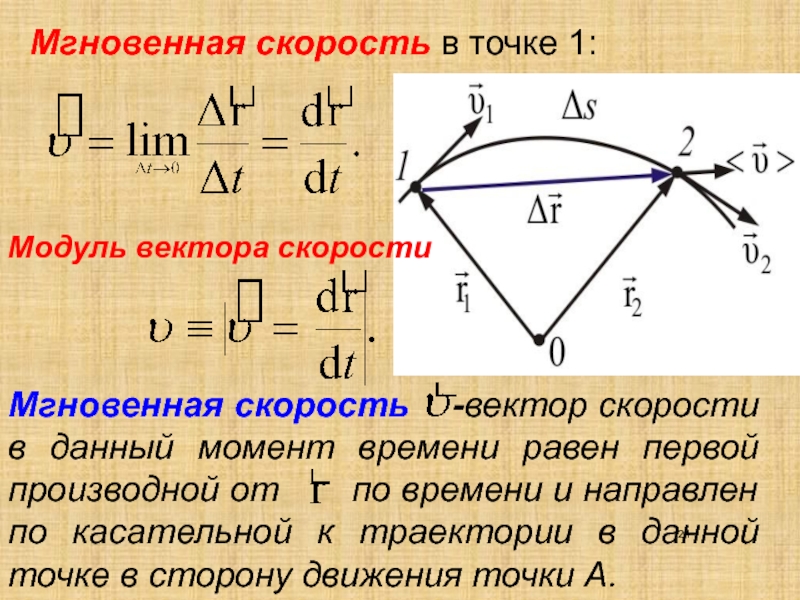
 2.7 следует из зависимости скорости от времени найти время падения, а затем подставить его в зависимость координаты от времени. Правильный ответ — 1.
2.7 следует из зависимости скорости от времени найти время падения, а затем подставить его в зависимость координаты от времени. Правильный ответ — 1.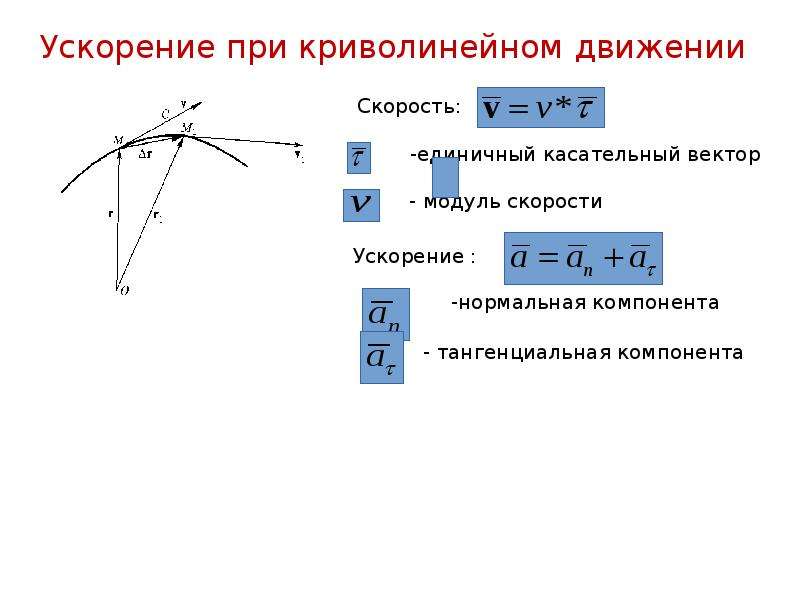 По условию задачи 2.2.9 проекции векторов начальной скорости тел на горизонтальную ось одинаковы (это подчеркнуто на рисунке в условии с помощью вертикальной пунктирной прямой).
Поэтому дальше улетит то из них, у которого больше время движения. А оно, в свою очередь, определяется проекцией уравнения (2.2) на вертикальную ось
По условию задачи 2.2.9 проекции векторов начальной скорости тел на горизонтальную ось одинаковы (это подчеркнуто на рисунке в условии с помощью вертикальной пунктирной прямой).
Поэтому дальше улетит то из них, у которого больше время движения. А оно, в свою очередь, определяется проекцией уравнения (2.2) на вертикальную ось В нашем же случае тело движется сначала вверх, потом вниз.
Действительно, время подъема для тела, брошенного вертикально вверх со скоростью 20 м/с, равно 2 с. А пройденный путь нужно найти за 3 с после броска.
Поэтому пройденный путь складывается из максимальной высоты подъема (для тела, брошенного со скоростью 20 м/с, она равна 20 м) и длины участка пути от верхней точки траектории до точки, в которой тело окажется через 3 с после броска.
Координату этой точки в системе координат, начало которой расположено на земле, а ось направлена вертикально вверх, можно найти, подставляя это значение времени в уравнение
В нашем же случае тело движется сначала вверх, потом вниз.
Действительно, время подъема для тела, брошенного вертикально вверх со скоростью 20 м/с, равно 2 с. А пройденный путь нужно найти за 3 с после броска.
Поэтому пройденный путь складывается из максимальной высоты подъема (для тела, брошенного со скоростью 20 м/с, она равна 20 м) и длины участка пути от верхней точки траектории до точки, в которой тело окажется через 3 с после броска.
Координату этой точки в системе координат, начало которой расположено на земле, а ось направлена вертикально вверх, можно найти, подставляя это значение времени в уравнение
 2}{2} \end{cases} } \]
2}{2} \end{cases} } \]
 В системе СИ ускорение измеряется в метрах за секунду в квадрате (м/с2), то есть показывает, на сколько изменяется скорость тела за одну секунду.
В системе СИ ускорение измеряется в метрах за секунду в квадрате (м/с2), то есть показывает, на сколько изменяется скорость тела за одну секунду.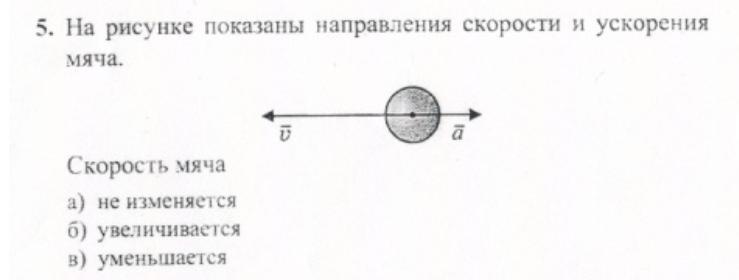 Например, какова скорость тела через 6 секунд после торможения? 100 м/с – 10 м/с2 · 6 с = 40 м/с.
Например, какова скорость тела через 6 секунд после торможения? 100 м/с – 10 м/с2 · 6 с = 40 м/с. Вообще, чтобы найти координату тела в определенный момент времени, надо к начальной координате прибавить скорость умноженную на количество прошедшего времени. Например, 25 м + 5 м/с · 7 с = 60 м. В данном случае тело через 7 секунд окажется в точке с координатой 60. Здесь скорость — положительная величина, так как координата увеличивается.
Вообще, чтобы найти координату тела в определенный момент времени, надо к начальной координате прибавить скорость умноженную на количество прошедшего времени. Например, 25 м + 5 м/с · 7 с = 60 м. В данном случае тело через 7 секунд окажется в точке с координатой 60. Здесь скорость — положительная величина, так как координата увеличивается. Рассмотрим, куда будет направлено ускорение при торможении и разгоне в обоих случаях.
Рассмотрим, куда будет направлено ускорение при торможении и разгоне в обоих случаях. Например, начальная скорость была -20 м/с, ускорение равно 2 м/с2. Скорость тела через 3 с, окажется равной -20 м/с + 2 м/с2 · 3 с = -14 м/с.
Например, начальная скорость была -20 м/с, ускорение равно 2 м/с2. Скорость тела через 3 с, окажется равной -20 м/с + 2 м/с2 · 3 с = -14 м/с.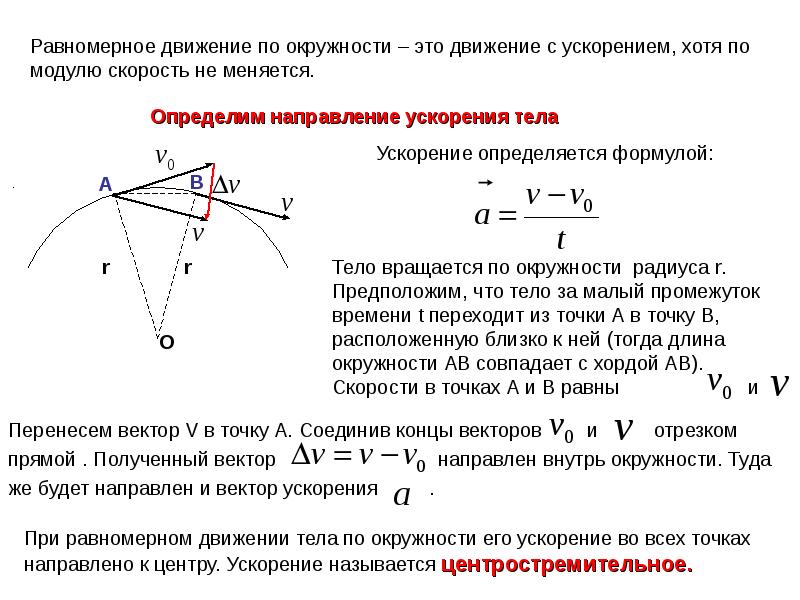 Задание 1 7777 Вариант 3580273 Небольшое тело движется в пространстве. На рисунке показаны графики зависимости от времени t проекций V x, V y и V z скорости этого тела на оси OX, OY и OZ от времени
Задание 1 7777 Вариант 3580273 Небольшое тело движется в пространстве. На рисунке показаны графики зависимости от времени t проекций V x, V y и V z скорости этого тела на оси OX, OY и OZ от времени Дальность полета снаряда, летящего по навесной траектории, равна максимальной высоте подъема. Какова максимальная высота настильной траектории при той же
Дальность полета снаряда, летящего по навесной траектории, равна максимальной высоте подъема. Какова максимальная высота настильной траектории при той же КИНЕМАТИКА
КИНЕМАТИКА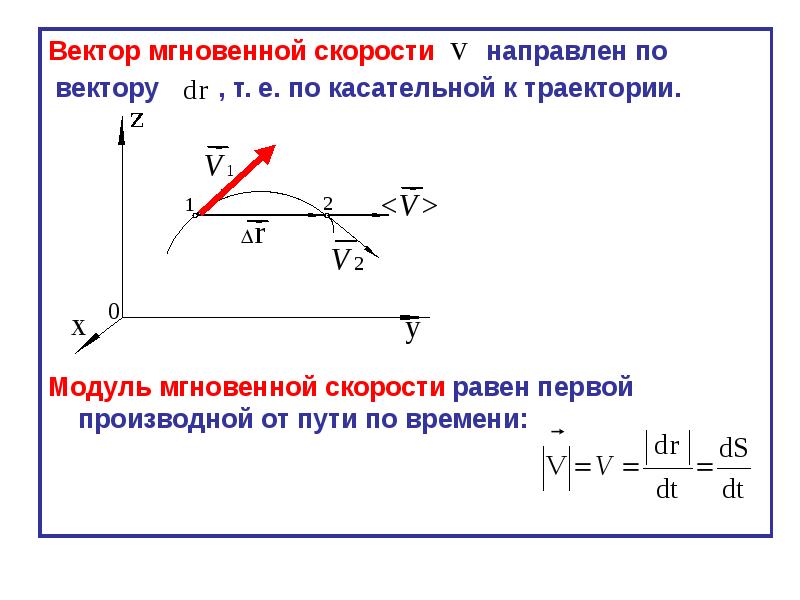 График функции А-3 Каноническая запись зависимостей А- Задание стандартных функций. К стандартным функциям отнесем
График функции А-3 Каноническая запись зависимостей А- Задание стандартных функций. К стандартным функциям отнесем Вариант… Тело движется равномерно по окружности. Найти отношение пройденного пути к величине перемещения тела за четверть периода движения… 3. 4. 3… Движение тела является равномерным, если:.
Вариант… Тело движется равномерно по окружности. Найти отношение пройденного пути к величине перемещения тела за четверть периода движения… 3. 4. 3… Движение тела является равномерным, если:. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения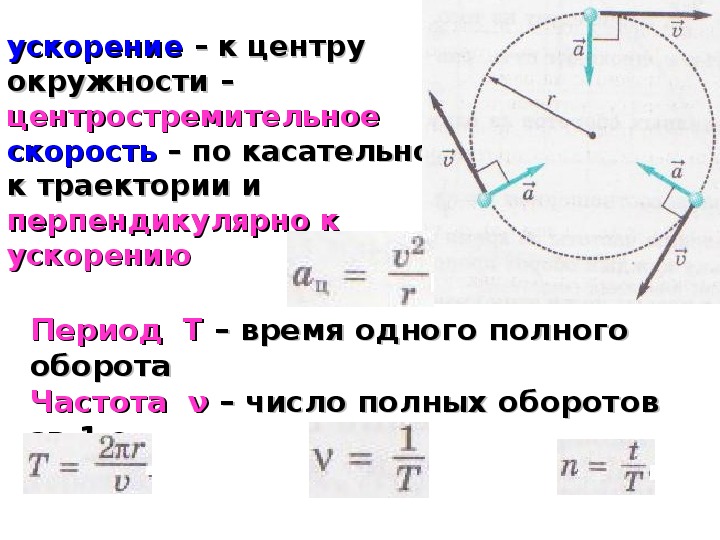 Это может
Это может Кинематика 1. Буксирный катер за ч проплыл 5 км. Определите скорость катера..тело, двигаясь из состояния покоя, равноускоренно за первую секунду проходит
Кинематика 1. Буксирный катер за ч проплыл 5 км. Определите скорость катера..тело, двигаясь из состояния покоя, равноускоренно за первую секунду проходит … Ускорение материальной точки…. 3 Тангенциальное и нормальное ускорение…. 4 Проекции скорости и ускорения… 5 График скорости… 6 Вращательное
… Ускорение материальной точки…. 3 Тангенциальное и нормальное ускорение…. 4 Проекции скорости и ускорения… 5 График скорости… 6 Вращательное
 Напомним, что траектория – это линия, вдоль которой двигалось тело.
Напомним, что траектория – это линия, вдоль которой двигалось тело.

 У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.
У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.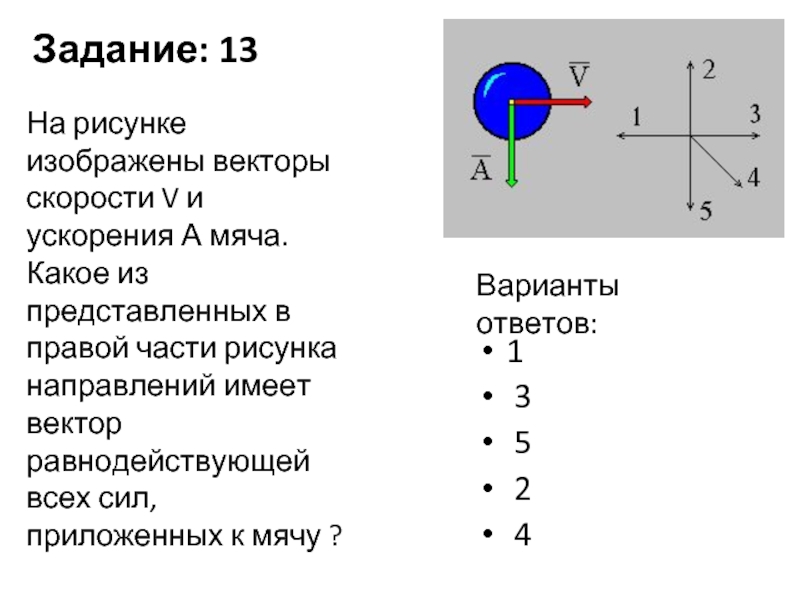
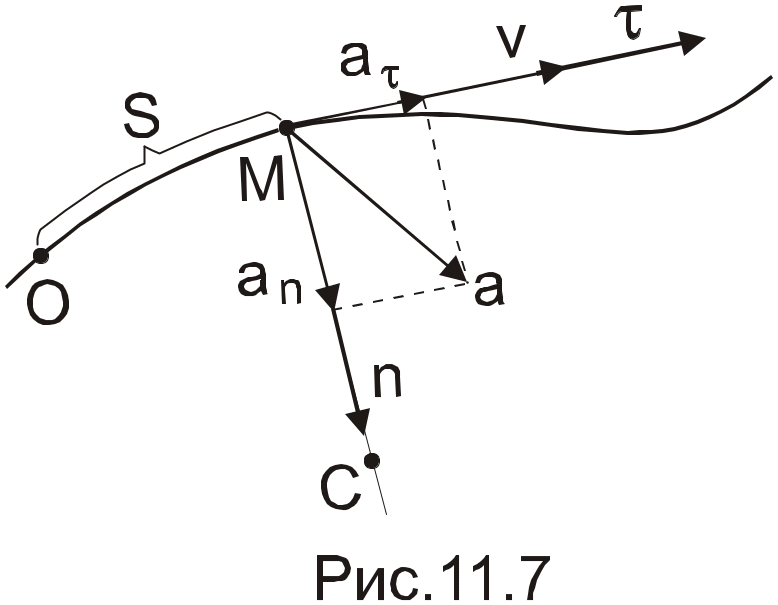
 Показан вид круга “глазами Бога”. Для указанного положения направление вектора скорости показано стрелкой ____; направление вектора ускорения обозначено ____; и направление вектора чистой силы представлено стрелкой ____.
Показан вид круга “глазами Бога”. Для указанного положения направление вектора скорости показано стрелкой ____; направление вектора ускорения обозначено ____; и направление вектора чистой силы представлено стрелкой ____.

 Формальное определение ускорения согласуется с этими понятиями, но является более всеобъемлющим.
Формальное определение ускорения согласуется с этими понятиями, но является более всеобъемлющим.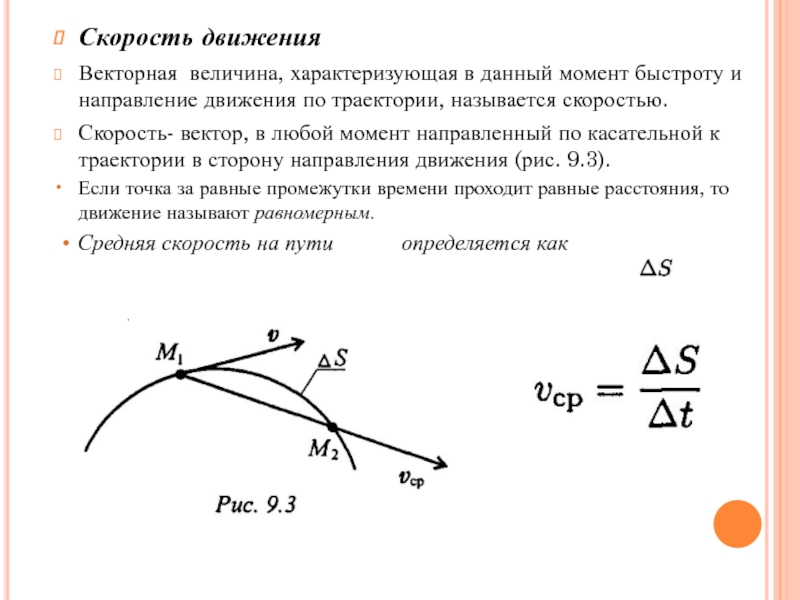 Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение возникает, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по обоим направлениям.
Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение возникает, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по обоим направлениям.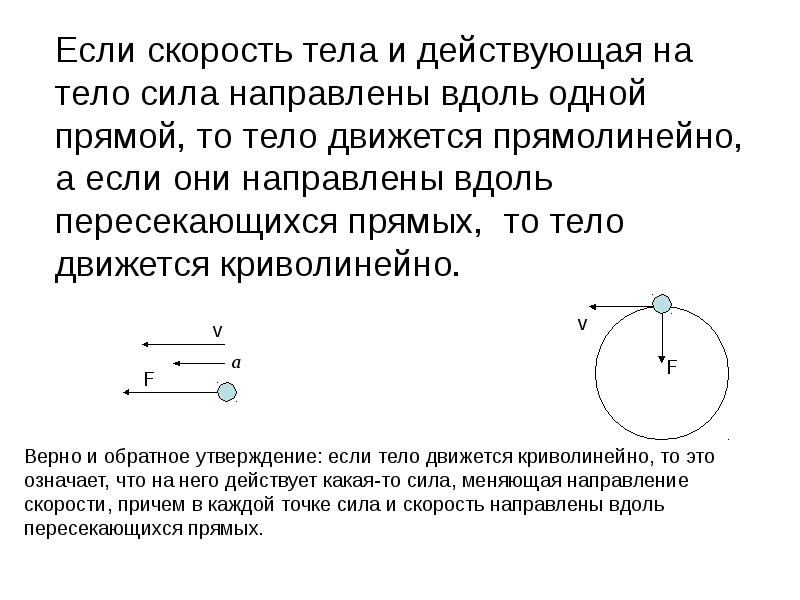 Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рисунке 6 показаны графики мгновенного ускорения в зависимости от времени для двух очень разных движений. На Рисунке 6 (а) ускорение незначительно меняется, и среднее значение за весь интервал почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1.8 м / с 2 ). На рисунке 6 (b) ускорение резко меняется со временем. В таких ситуациях лучше всего рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, мы можем рассматривать движение во временных интервалах от 0 до 1,0 с и от 1,0 до 3,0 с как отдельные движения с ускорениями +3,0 м / с 2 и –2,0 м / с 2 соответственно.
Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рисунке 6 показаны графики мгновенного ускорения в зависимости от времени для двух очень разных движений. На Рисунке 6 (а) ускорение незначительно меняется, и среднее значение за весь интервал почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1.8 м / с 2 ). На рисунке 6 (b) ускорение резко меняется со временем. В таких ситуациях лучше всего рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, мы можем рассматривать движение во временных интервалах от 0 до 1,0 с и от 1,0 до 3,0 с как отдельные движения с ускорениями +3,0 м / с 2 и –2,0 м / с 2 соответственно.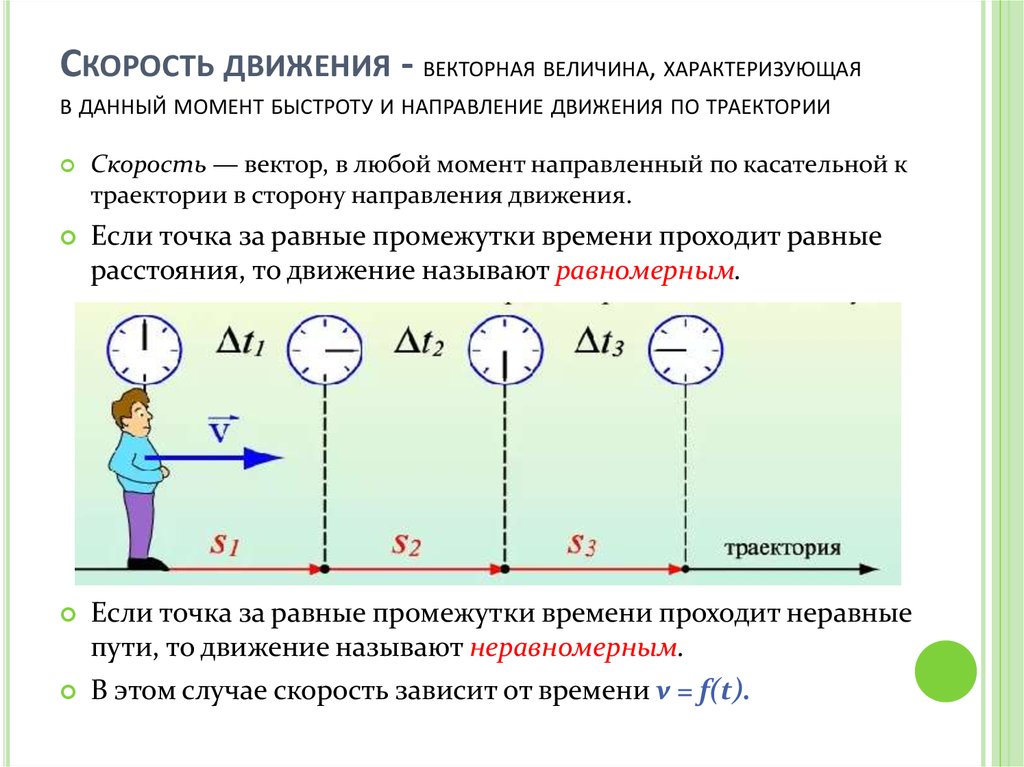 В (а) волан движется вправо, а в (б) – влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые рассуждения, которые используются при решении проблем.
В (а) волан движется вправо, а в (б) – влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые рассуждения, которые используются при решении проблем. 25 км по части (б).
25 км по части (б).