Формула смысла, радио, шоу, слушать онлайн // Смотрим
Формула смысла, радио, шоу, слушать онлайн // СмотримПрофиль
программа
12+ шоу
Смотрим всё
Смотрим всё
Мир сошел с ума? Возможно.
.. Но даже самым безумным событиям и явлениям найдется разумное объяснение. Смысл есть, его не может не быть. Новое прочтение знакомых сюжетов. Трактовки. Интерпретации. Толкования.
Что происходит и как это понимать?! Утреннее шоу “Формула смысла” с Дмитрием Куликовым.
По понедельникам и пятницам с 7 до 11. На радио “Вести FM”.
Железная логика
Новостные выпуски
- общество
- шоу
- передача/программа
- Россия
- Украина
- радио
- политика
- новости
- Европа
- история
- Запад
- популярное
- политические радиошоу
- Вести FM: политические шоу
- Вести FM: все программы
Авто-геолокация
Flexmetal
Сетка
Список
Сортировка: По умолчаниюНазвание (А > Я)Название (Я > А)Цена (Низкая > Высокая)Цена (Высокая > Низкая)Рейтинг (Высокий)Рейтинг (Низкий)Модель (А > Я)Модель (Я > А)
Показать: 255075100
22,68 грн.
Без налога: 22,68 грн.
22,68 грн. Без налога: 22,68 грн.
22,68 грн. Без налога: 22,68 грн.
39,46 грн. Без налога: 39,46 грн.
39,46 грн. Без налога: 39,46 грн.
39,46 грн. Без налога: 39,46 грн.
47,88 грн. Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
47,88 грн. Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
47,88 грн.
Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
47,88 грн. Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
47,88 грн. Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
47,88 грн. Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
47,88 грн. Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
47,88 грн.
Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
58,8 грн. Без налога: 58,8 грн.
47,88 грн. Без налога: 47,88 грн.
60,06 грн. Без налога: 60,06 грн.
47,88 грн. Без налога: 47,88 грн.
22,68 грн. Без налога: 22,68 грн.
22,68 грн. Без налога: 22,68 грн.
22,68 грн. Без налога: 22,68 грн.
22,68 грн. Без налога: 22,68 грн.
22,68 грн. Без налога: 22,68 грн.
22,68 грн. Без налога: 22,68 грн.
39,48 грн. Без налога: 39,48 грн.
11,76 грн. Без налога: 11,76 грн.
39,48 грн.
Без налога: 39,48 грн.
39,48 грн. Без налога: 39,48 грн.
40,74 грн. Без налога: 40,74 грн.
39,48 грн. Без налога: 39,48 грн.
40,74 грн. Без налога: 40,74 грн.
39,48 грн. Без налога: 39,48 грн.
40,74 грн. Без налога: 40,74 грн.
New
39,48 грн. Без налога: 39,48 грн.
22,68 грн. Без налога: 22,68 грн.
39,48 грн. Без налога: 39,48 грн.
40,74 грн. Без налога: 40,74 грн.
39,48 грн. Без налога: 39,48 грн.
11,76 грн. Без налога: 11,76 грн.
39,48 грн. Без налога: 39,48 грн.
11,76 грн. Без налога: 11,76 грн.
39,48 грн.
Без налога: 39,48 грн.
39,48 грн. Без налога: 39,48 грн.
39,48 грн. Без налога: 39,48 грн.
39,48 грн. Без налога: 39,48 грн.
20,41 грн. Без налога: 20,41 грн.
40,82 грн. Без налога: 40,82 грн.
20,41 грн. Без налога: 20,41 грн.
40,82 грн. Без налога: 40,82 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
40,82 грн. Без налога: 40,82 грн.
52,16 грн. Без налога: 52,16 грн.
20,41 грн. Без налога: 20,41 грн.
40,82 грн.
Без налога: 40,82 грн.
40,82 грн. Без налога: 40,82 грн.
52,16 грн. Без налога: 52,16 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
40,82 грн. Без налога: 40,82 грн.
20,41 грн. Без налога: 20,41 грн.
5,44 грн. Без налога: 5,44 грн.
5,44 грн. Без налога: 5,44 грн.
5,44 грн. Без налога: 5,44 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
40,82 грн. Без налога: 40,82 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн.
Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
20,41 грн. Без налога: 20,41 грн.
40,82 грн. Без налога: 40,82 грн.
52,16 грн. Без налога: 52,16 грн.
20,41 грн. Без налога: 20,41 грн.
40,82 грн. Без налога: 40,82 грн.
20,41 грн. Без налога: 20,41 грн.
Показаны с 1 по 100 из 714 (8 страниц)
Уравнения частотной модуляции
FM (частотная модуляция) существует уже давно. Эта система существовала наряду с AM (амплитудной модуляцией) и имела несколько недостатков.
Несмотря на то, что мы не могли дифференцировать потенциал FM-передатчика, с самим FM проблем не было. Но когда беспроводная связь была новой концепцией, потребности людей не удовлетворялись только за счет использования FM. Это произошло потому, что требовалась более узкая полоса пропускания, которая была полезна для снижения шума. Итак, чтобы преодолеть все эти препятствия, они начали использовать амплитудную модуляцию сигнала. В этой статье подробно рассматриваются уравнения частотной модуляции, свойства частотной модуляции, их преимущества и недостатки, а также вопросы, относящиеся к частотной модуляции.
В соответствии с уравнением частотной модуляции, которое отмечает UPSC, частота несущего сигнала регулируется (по ширине линии) амплитудой входного модулирующего сигнала при частотной модуляции. Однотональная синусоидальная волна также используется в качестве входа для усиления требуемых сигналов. Если модулирующий (входной) сигнал увеличивается, будет увеличиваться только несущая частота (fc).
Кроме того, входной сигнал достигает своего пика, когда несущая частота (fc )max максимальна.
Несущая частота будет только отклоняться от своего начального значения. По мере уменьшения амплитуды модулирующего (входного) сигнала уменьшаются и сигналы несущей частоты. Когда входной сигнал самый низкий, несущая частота минимальна (fc)min. Несущая лишь незначительно отклоняется от своего типичного значения. Когда значение входного сигнала равно 0 В, несущая частота будет равна ее нормальному значению (свободная работа) fc.
Сигнал сообщения будет содержать указанные данные, но несущий сигнал не будет содержать ничего. Модулированные FM-сигналы будут исходить из модуляции этих сигналов. Этот сигнал необходим, поскольку частота этого сигнала колеблется в зависимости от амплитуды сигнала. Этот частотный сдвиг также может быть выражен в кГц (килогерцах). Например, если изменение частоты составляет 6 кГц вверх и вниз, это записывается как 6 кГц.
Вывод напряжения частотной модуляции Частотная модуляция происходит, когда частота несущего сигнала изменяется в ответ на мгновенную амплитуду модулирующего сигнала.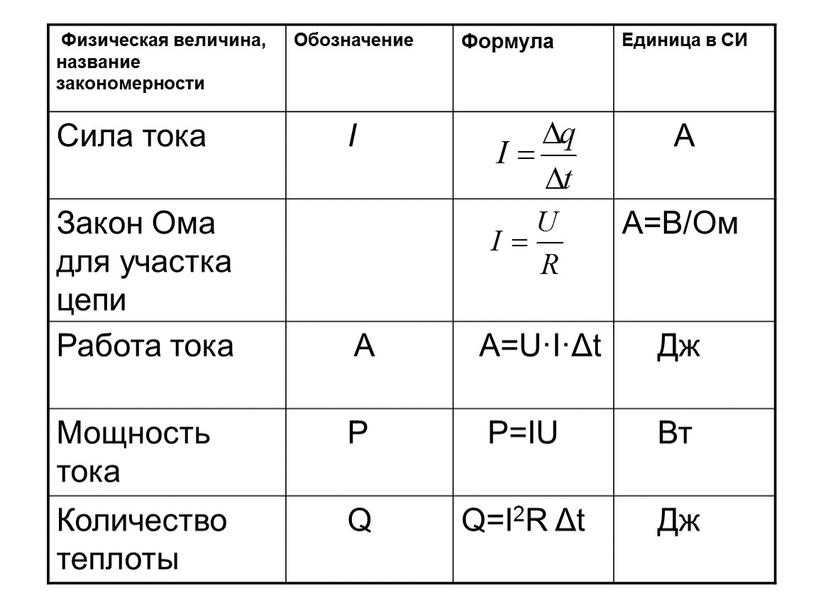
При этом амплитуда несущей в ЧМ останется постоянной. Девиация частоты ((δ)) — это разница в несущей частоте. В этом разница между модулированными и немодулированными несущими.
ЧМ – это нелинейный процесс, содержащий девиацию частоты.
Математический вывод частотной модуляцииПусть мгновенная частота модулированной волны будет: kVm cos Wmt
Здесь k представляет чувствительность частотной модуляции к девиации частоты.
Тогда мгновенная частота будет:
Wi = Wc+δ
Wi = Wc+kVm cos Wmt (i)
Модулированный сигнал будет представлен математически как:
Wi = dθ /dt
Wi dt = dθ
∫dθ= ∫Wi dt
Теперь подставим значения уравнения (1) в приведенное выше выражение:
θ= ∫ (Wc+kVm cos dt Wmt )
θ= Wct+ (KVm/Wm) sin Wmt
θ= Wct+Mf sin Wmt (iii)
Здесь Mf будет индексом частотной модуляции, равным (KVm/Wm)
Теперь мы можем подставить значения уравнения (3) в уравнение (2)
Vfm=Vc sin (Wct+Mf sin Wmt)
Это искомое уравнение частотной модуляции
Математическое уравнение частотной модуляцииУравнение частотной модуляции включает: ,
A – амплитуда сигналов частотной модуляции.
∆f — девиация частоты.
Mf — индекс частотной модуляции.
mf = ∆f/fm
wm = 2π fm WC = 2π fC
Это требуемое математическое уравнение для представления важности уравнений частотной модуляции.
FM также известен как система с постоянной полосой пропускания. Но почему?Постоянная ЧМ известна как система с постоянной полосой пропускания. Давайте разберемся, почему это так, на этом простом примере:
9009.8 Из приведенных выше примеров видно, что частота увеличилась в 20 раз с 50 Гц до 5000 Гц. Но отклонение увеличилось лишь незначительно со 151 Гц до 170 Гц.
Поэтому эта система частотной модуляции известна как система с постоянной полосой пропускания.
- Основным преимуществом частотной модуляции является ее устойчивость к изменениям сигнала любой величины. Это достигается таким образом, что любое отклонение сигнала не влияет на звук. И сигнал не на уровне, с которым приемник не может справиться. Благодаря этому FM-модулированные передачи являются отличным вариантом для мобильной и радиосвязи, а также для множества других портативных применений.
- Также сигналы с частотной модуляцией не подвержены каким-либо искажениям и идеально подходят для улучшения качества передачи вещания.
- Еще одним преимуществом является возможность использования модуляции уже на самых ранних этапах разработки передатчика. Но нет необходимости использовать линейное усиление для усиления мощности сигнала.
- Еще более вероятно использование нелинейных ВЧ-усилителей для объединения ЧМ-сигналов в передатчике. Но они более эффективны, чем линейные, необходимые для сигналов с вариациями амплитуды.
- ЧМ-демодуляторы немного сложнее в изготовлении, чем радиоинтегральные схемы. Это также не самый большой недостаток, потому что в настоящее время в радиоприемниках есть встроенные демодуляторы.
- Поскольку сигналы частотной модуляции могут быть продлены на неопределенный срок, иногда требуются фильтры для уменьшения расширяемости боковой полосы. Фильтры могут вызывать искажения. Это может быть одним из недостатков использования частотной модуляции.
Частотная модуляция — это метод кодирования информации о сигнале (аналоговом или цифровом) путем сдвига несущей частоты волны в соответствии с частотой модулирующего сигнала. Здесь мы узнали, как вывести уравнение вместе с математическим выражением.
Уравнения частотной модуляции Формулы Бесселя
Частота модуляция использует мгновенную амплитуду модулирующего сигнала (голос, музыка, данных и т. д.) для прямого изменения частоты несущего сигнала. Индекс модуляции, β используется для описания отношения максимальной девиации частоты несущей к максимальная девиация частоты модулирующего сигнала. Концепция была впервые применена Эдвин Х. Армстронг в конце 1920-х годов и запатентован в начале 1930-е годы.
В зависимости от выбранного индекса модуляции несущая и определенные боковые частоты действительно могут быть подавлены. Пересечения нулей функций Бесселя, J n (β), происходят, когда соответствующая боковая полоса n исчезает для данного индекса модуляции, β. Полный спектр одного тона состоит из линий на несущей и верхняя и нижняя боковые полосы (противофазные), с амплитудами, определяемыми Значения функции Бесселя на этих частотах.
Узкополосная ЧМ определяется как условие, при котором β достаточно мало, чтобы все
члены после первых двух в ряду разложения уравнения ФМ пренебрежимо малы.
Узкополосное приближение: β = Δω/Ω м < 0,2 (хотя может достигать 0,5)
Ширина полосы ~ 2ω м
Широкополосный FM определяется как когда значительное количество боковых полос имеют значительные амплитуды.
Ширина полосы ~ 2Δω
Дж. Р. Карсон показал в 1920-х годах, что хорошее малый и очень большой β,
BW ~ 2 (Δω + Ом м )) = 2*Ом м (1 + β)
В следующих примерах несущая частота в одиннадцать раз больше модуляции частота. Красные (пунктирные) линии представляют огибающую модуляции. Синие (сплошные) линии представляют модулированную несущую.
Здесь максимальная частота (f max ) вызывает максимальное отклонение 1*f max в перевозчике. Из формулы индекса модуляции:
Здесь максимальная частота (f max ) вызывает максимальное отклонение 5*f max в перевозчике.