Калькулятор онлайн – Найти (с решением) производную функции
Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.
Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.
Примеры подробного решения >>
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Определение производной
Определение. Пусть функция \( y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \( x_0 \).
Дадим аргументу приращение \( \Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
\( \Delta y \) (при переходе от точки \( x_0 \) к точке \( x_0 + \Delta x \) ) и составим отношение
\( \frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \( \Delta x \rightarrow 0 \), то
указанный предел называют производной функции \( y=f(x) \) в точке \( x_0 \) и обозначают \( f'(x_0) \).
Если существует предел этого отношения при \( \Delta x \rightarrow 0 \), то
указанный предел называют производной функции \( y=f(x) \) в точке \( x_0 \) и обозначают \( f'(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x_0) $$
Для обозначения производной часто используют символ \( y’ \). Отметим, что \( y’ = f(x) \) – это новая функция, но, естественно, связанная с функцией \( y = f(x) \), определенная во всех точках \(x\), в которых существует указанный выше предел. Эту функцию называют так: производная функции \( y = f(x) \).
Геометрический смысл производной состоит в следующем. Если к графику функции \( y = f(x) \) в точке с абсциссой \( x=a \) можно
провести касательную, непараллельную оси \(y\), то \( f(a) \) выражает угловой коэффициент касательной:
\( k = f'(a) \)
Поскольку \( k = tg(a) \), то верно равенство \( f'(a) = tg(a) \) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. 2 \) справедливо приближенное равенство \( \Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 \) справедливо приближенное равенство \( \Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \( x \), найти \( f(x) \)
2. Дать аргументу \( x \) приращение \( \Delta x \), перейти в новую точку \( x+ \Delta x \), найти \( f(x+ \Delta x) \)
4. Составить отношение \( \frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке \(x\).
Если функция \(y=f(x)\) имеет производную в точке \(x\), то ее называют дифференцируемой в точке \(x\). Процедуру нахождения производной
функции \(y=f(x)\) называют дифференцированием функции \(y=f(x)\).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция \(y=f(x)\) дифференцируема в точке \(x\). Тогда к графику функции в точке \( M(x; \; f(x)) \) можно провести касательную, причем, напомним, угловой коэффициент касательной равен \( f'(x) \). Такой график не может «разрываться» в точке \(M\), т. е. функция обязана быть непрерывной в точке \(x\).
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция \(y=f(x)\) дифференцируема в точке \(x\), то выполняется приближенное равенство \( \Delta y \approx f'(x) \cdot \Delta x \). Если в этом равенстве \( \Delta x \) устремить к нулю, то и \( \Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция \( y=|x|\) непрерывна везде, в частности в точке \(x=0\), но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция \( y=\sqrt[3]{x} \) непрерывна на всей числовой прямой, в том числе в точке \(x=0\). И касательная к графику функции существует в любой точке, в том числе в точке \(x=0\). Но в этой точке касательная совпадает с осью \(y\), т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид \(x=0\). Углового коэффициента у такой прямой нет, значит, не существует и \( f'(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси
абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она
перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Сложная функция
Сложная функцияПример 1. Дана функция f(x) = 3x2 – 4. Найти:
Решение: f(4) = 3•42 – 4 = 48 – 4 = 44;
f(a3 + 1) = 3(a3 + 1)2 – 4 = 3(a6 + 2a3 + 1) – 4 =
= 3a6 + 6a3 – 1;
f(t) = 3t2 – 4;
Пример 2. Найти функцию f(x), если f(x + 1) = x2 + 2x + 2.
Решение. Пусть x + 1 = a,
тогда x = a – 1; f(a) = (a – 1)2 + 2(a – 1) + 2 = a2 – 2a + 1 + 2a – 2 + 2 = a2 + 1.
Ответ: f(x) = x2 + 1.
Пример 3. F(2x – 1) = 4x – 7;
Решение. Пусть 2x – 1 = a, тогда
т. е. F(x) = 2x – 5. Значит,
F(g(x)) = 2g(x) – 5. 2g(x) – 5 = x3.
Ответ:
Пример № 229г (из учебника «алгебра, 10–11» А.Н. Колмогорова). Найти такую функцию f, что
f(g(x)) = x, g(x) = x2 + 1, x Ј 0.
Решение. По условию f
Пусть x2 + 1 = t, тогда
Ответ:
Пример 4. Найти F(x),
если F(sin x) + F(cos x) = 3.
Найти F(x),
если F(sin x) + F(cos x) = 3.
Решение. Перепишем данное уравнение в виде
F(sin x) + F(cos x) = 3(sin2 x + cos2 x).
В выражении sin x заменим букву x на m, получим sin m. Допустим, что cos x = sin m, выразим x через
x = arccos (sin m).
Уравнение примет вид
F(sin m) + F(cos (arccos (sin m))) = 3(sin2 m + sin2 m),
2F(sin m) = 3•2sin2 m,
т. е. F(sin m) = 3sin2 m; F(x) = 3x2.
Ответ: F(x) = 3x2.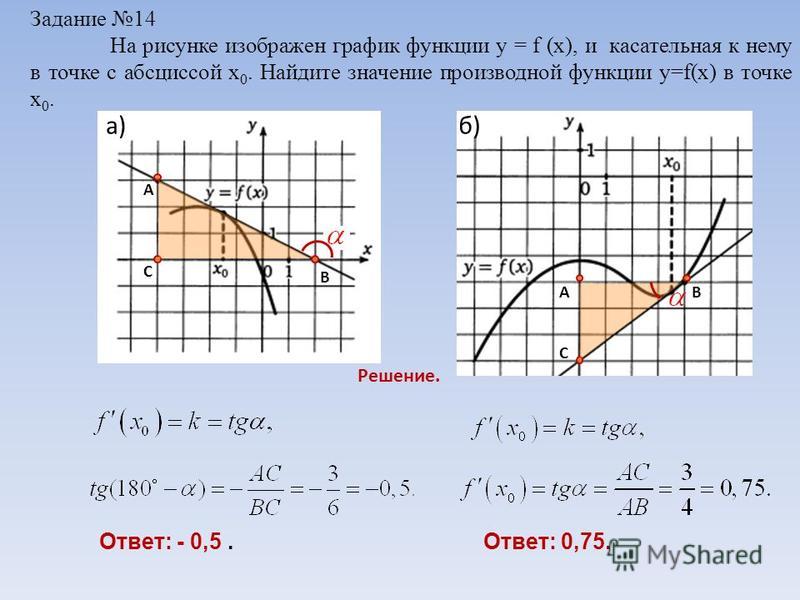
Пример 5. Найти функцию f(x), если
Решение. В дроби
заменив x на m, получим
Пусть
Выразим x через m, получим
Найдем значение дроби через m:
и значение дроби в правой части данного уравнения тоже при
Получим новое уравнение (при аргументе m)
или, заменив букву m на x,
Вместе с данным уравнением составим систему
Эта система, линейная относительно неизвестных
и
решается любым из возможных способов. Ее решение (после упрощения):
или
Найдем f(t), если допустим, что
Выразим x через t:
Тогда
Аналогичный результат
получим из первого уравнения последней системы.
Ответ:
Пример 6. Найти функцию f(x), если
Решение. Пусть
тогда
Получим новое уравнение с переменной t
Заменив t на x, запишем
Составим систему с данным уравнением, переставив слагаемые
Исключим из системы неизвестное
Ответ:
Пример 7. Найти функции F(x) и g(x) из системы уравнений
Решение. Пусть
Тогда
и первое уравнение примет вид
Заменим t на x. Получим систему
Вычитая уравнения почленно, находим
а затем и
Пусть 2x + 1 = a, тогда
Следовательно,
Ответ:
Пример 8. Найти функции F(x)
и g(x) из системы уравнений
Найти функции F(x)
и g(x) из системы уравнений
Решение. Пусть
откуда
и второе уравнение перепишется в виде
Система примет вид
Исключим функцию F(•):
Значит,
Пусть
тогда
F(a) = 2a + 3.
Ответ: F(x) = 2x + 3, g(x) = 0.
Упражнения для самостоятельной работы
1. Найдите функцию F(x) из уравнений:
2. Найдите g(x), если
1) F(x – 1) = 2x – 3, F(g(x)) = 3x – 4.

2) F(x) = x3, F(g(x)) = 2x + 1.
3. Найдите F(x) и g(x) из систем уравнений:
Ответы
М Селиванова,
г. Реутов
Построение и решение графиков Функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.

- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Чтобы ребенок разобрался в теории и чувствовал себя увереннее на школьных контрольных, запишите его на современные уроки математики в онлайн-школу Skysmart.
Интерактивные задания, математические комиксы и карта прогресса в личном кабинете — математика еще никогда не была таким увлекательным приключением!
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
Задача 2. Построим график функции
Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 4. Построить графики функций:
а) y = 3x – 1
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x – 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5.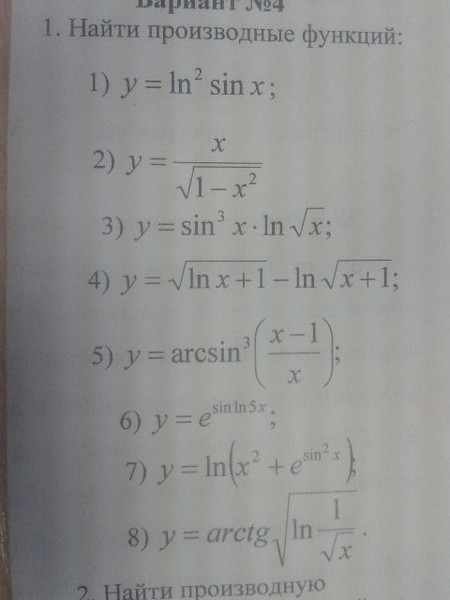 Построить график функции
Построить график функции
Как решаем:
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
а) y = x² + 1
б)
в) y = (x – 1)² + 2
г)
д)
Как решаем:
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x – a).
y = √x
Сдвигаем график вправо на 1:
y = √x – 1
в) y = (x – 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x – a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x – 1)²
Сдвигаем график вверх на 2:
y = (x – 1)² + 2
г)
Преобразование в одно действие типа
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
В детской школе Skysmart учиники чертят графики на специальной онлайн-доске. Учитель видит, как размышляет ученик и может вовремя его направить в нужную сторону.
Запишитесь на бесплатный вводный урок математики и занимайтесь в современном формате и с поддержкой заботливых учителей.
Формулы для первой производной функции
y есть функция y = y(x)
C = постоянная, производная (y’) постоянной есть 0
y = C => y’ = 0
пример: y = 5, y’ = 0
Если y есть функцией типа y = xn, формула для производной есть:
y = xn => y’ = nxn-1
пример: y = x3 y’ = 3x3-1 = 3x2
y = x-3 y’ = -3x-4
Из вышеприведенной формулы мы можем сказать, что для производной y’ функции y = x = x1 that:
если y = x тогда y’=1
y = f1(x) + f2(x) + f3(x) …=>
y’ = f’1(x) + f’2(x) + f’3(x) …
Эта формула представляет производную функции, являющейся суммой функций.
Пример: Если мы имеем две функции f(x) = x2 + x + 1 и
g(x) = x5 + 7 и y = f(x) + g(x) тогда y’ = f'(x) + g'(x) =>
y’ = (x2 + x + 1)’ + (x5 + 7)’ = 2x1 + 1 + 0 + 5x4 + 0 = 5x4 + 2x + 1
Если функция есть произведением двух функций, формула производной выглядит так:
y = f(x). g(x) => y’ = f'(x)g(x) + f(x)g'(x)
g(x) => y’ = f'(x)g(x) + f(x)g'(x)
Если f(x) = C(C есть постоянной) и y = f(x)g(x)
y = Cg(x) y’=C’.g(x) + C.g'(x) = 0 + C.g'(x) = C.g'(x)
y = Cf(x) => y’ = C.f'(x)
Формулы вычисления производной
| y = | y’ = |
|
y = ln x => y’ = 1/x
y = ex => y’ = ex
y = sin x => y’ = cos x
y = cos x => y’ = -sin x
y = tg x => y’ = 1/cos2x
y = ctg x => y’ = –1/sin2x
если функция есть функцией функции: u = u(x)
y = f(u) => y’ = f'(u).u’
Пример. Пусть у нас есть функция y = sin(x2)
в этом случае u = x2, f(u) = sin(u), производные есть f'(u) = cos(u), u’ = 2x
y’ = (sin(u))’.u’ = cos(x2). 2x = 2.x.cos(x2)
2x = 2.x.cos(x2)
Задачи с производными
1) f(x) = 10x + 4y. Найдите первую производную f'(x)
ОТВЕТ: Мы можем использовать формулу нахождения производной для суммы функций
f(x) = f1(x) + f2(x), f1(x) = 10x, f2(x) = 4y
для функции f2(x) = 4y, y есть постоянной, потому что аргумент f2(x) есть x.
Поэтому f’2(x) = (4y)’ = 0. Отсюда производная функции f(x) есть: f'(x) = 10 + 0 = 10.
| 2) Вычислите производную f(x) = |
ОТВЕТ: у нас есть две функции h(x) = x10 и g(x) = 4.15 + cos x
функция f(x) есть h(x), разделенная на g(x). h'(x) = 10x9 g'(x) = 0 – sin x = -sin x
| f'(x) = |
|
| f'(x) = |
| = |
|
3) f(x) = ln(sinx). Какая производная функции f(x)?
ОТВЕТ: Чтобы решить эту задачу, мы можем использовать последнюю формулу.
Как мы видим, f(x) есть функцией двух функций:
f(x) = h(g(x)), где h = ln и g = sin x
Подробнее о производных на страницах математического форума
Форум о производных
Урок 10. определение производной. физический смысл производной – Алгебра и начала математического анализа – 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №10. Определение производной. Физический смысл производной.
Перечень вопросов, рассматриваемых в теме
1) Определение производной;
2) Физический смысл производной;
2) Приращение функции;
3) Скорость материальной точки в заданный момент времени по данному закону движения.
Глоссарий по теме
Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Изучая поведение функции y=f(x) около конкретной точки x0, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.
Для этого используют понятия приращений аргумента и функции.
Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.
Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита “дельта”; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.
Итак, x1-x0=Δx, значит, x1=x0+Δx.
f(x1)-f(x0)=Δy, значит,
Δy=f(x0+Δx)-f(x0). (1)
Нельзя истолковывать термин “приращение” как “прирост”.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=1,9
Решение:
Δx= x1−x0=1,9-2=-0,1
Δf= f(1,9) –f(2)=1,92-22=-0,39
Ответ: Δx=-0,1; Δf =-0,39
Пример 2.
Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=2,1
Решение:
Δx= x1−x0=2,1-2=0,1
Δf= f(1,9) –f(2)=2,12-22=0,41
Ответ: Δx=0,1; Δf =0,41
Пример 3.
Найдем приращение Δf функции в точке x0,если приращение аргумента равно x0.
Решение:
по формуле (1) находим:
.
Ответ: .
С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t0; t0+∆t]. Если точка движется по прямой и известна ее координата x(t), то
Эта формула верна и для ∆t<0 (для промежутка [t0+∆t; t0]).
Аналогично выражение называют средней скорость изменения функции на промежутке с концами х0 и х0+∆х.
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Обозначение: y’ или f’(x)
Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.
Схема вычисления производной функции
- Найти приращение функции на отрезке [x; x+Δx]:
∆y=y(x+∆x)-y(x)
- Разделить приращение функции на приращение аргумента:
- Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Пример 4.
Вычислить производную функции y=x2
Решение: Используем схему вычисления производной по действиям:
- ∆y=y(x+∆x)-y(x)= (х+∆х)²-х²= х²+2х·∆х+ ∆х²-х²= 2х·∆х+ ∆х²
Ответ: y’=2x.
Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).
Таким образом, скорость – есть производная от пути по времени.
Пример 5.
Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.
Решение:
найдем ∆t= 1-0,8=0,2
S(0,8)= 1-2·0,8= -0,6=S(t)
S(1)= 1-2·1= -1=S(t+∆t)
.
Ответ: .
Необходимое и достаточное условие дифференцируемости
Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.
Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx.
Область определения функции | Онлайн калькулятор
Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма.4))
Итак, восьмое задание в общей семе исследования функции решено. На очереди 9-е задание: Определить интервалы монотонности функции f(x). Как его решить? Об этом – в следующем посте.
Как найти f (x) – Алгебра 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Обозначение функций: Определения и оценка по номеру
Purplemath
Вы уже некоторое время играете с уравнениями типа “ y =”.И вы видели, что «красивые» уравнения (скажем, прямые линии, а не эллипсы) – это те уравнения, которые вы можете решить для « y =», а затем подключить к графическому калькулятору. Эти уравнения « y =» являются функциями. Но в настоящее время вы сталкиваетесь с вопросом: «Зачем мне нужна эта нотация функции, особенно когда у меня есть совершенно хорошее ‘ y =’, и как эта нотация работает?»
Вспомните, когда вы учились в начальной школе. Ваш учитель дал вам рабочие листы, содержащие такие утверждения, как «[] + 2 = 4», и сказал вам заполнить поле.Когда вы стали старше, ваш учитель начал давать вам рабочие листы, содержащие такие утверждения, как « x + 2 = 4», и предлагал вам «решить для x ».
MathHelp.com
Почему ваши учителя перешли от ящиков к переменным? Что ж, подумайте: сколько форм вы бы использовали для формул, подобных формуле для площади A трапеции с верхним основанием a , нижним основанием b и высотой h ? Формула выглядит следующим образом:
Если вы попытаетесь выразить вышеупомянутое или что-то более сложное, используя прямоугольники различной формы, вы быстро потеряете формы.Кроме того, вы знаете по опыту, что « A » означает «площадь», « h » означает «высоту», а « a » и « b » обозначают длины параллельной вершины и нижние стороны. Только небо знает, что может означать квадратная или треугольная коробка!
Другими словами, они перешли с ящиков на переменные, потому что, хотя прямоугольники и буквы означают одно и то же (а именно, слот, ожидающий заполнения значения), переменные лучше.Переменные более гибкие, их легче читать, и они могут дать вам больше информации.
То же самое верно для « y » и « f ( x )» (произносится как «эфф-оф-экс»). Для функций два обозначения означают одно и то же, но « f ( x )» дает вам больше гибкости и больше информации. Раньше вы говорили: « y = 2 x + 3; найдите y , когда x = –1». Теперь вы говорите: « f ( x ) = 2 x + 3; найдите f (–1)» (произносится как « f -of- x равно 2 x плюс три; найти f -of-negative-one “).В любой форме вы делаете одно и то же: подставляете –1 для x , умножаете на 2, а затем прибавляете 3, упрощая, чтобы получить окончательное значение +1.
Но обозначение функций дает большую гибкость, чем использование просто « y » для каждой формулы. Например, ваш графический калькулятор будет перечислять различные функции, такие как y1, y2 и т. Д., Поэтому вы можете различать уравнения, когда, скажем, просматриваете их значения в «ТАБЛИЦЕ».
Точно так же в учебниках и при написании вещей мы используем разные названия функций, такие как f ( x ), g ( x ), h ( x ), s ( t ) и т. Д., Чтобы отслеживать и работать с более чем одной формулой в любом контексте.С обозначением функций теперь мы можем использовать более одной функции одновременно, не запутываясь и не путая формулы, заставляя себя задаться вопросом: «Хорошо, что ‘ y ‘ – это , а это ?» И обозначения могут быть полезными для пояснения.
Из геометрии вы знаете, что « A ( r ) = π r 2 » обозначает площадь круга, выраженную через значение радиуса r , а « C ( r ) = 2π r “обозначает длину окружности, выраженную в виде радиуса r .Обе функции имеют одну и ту же переменную плагина (« r »), но « A » напоминает вам, что первая функция является формулой для «площади», а « C » напоминает вам, что вторая функция – это формула для «окружности».
Помните: обозначение « f ( x )» в точности то же, что и « y ». Вы даже можете обозначить ось y на своих графиках « f ( x )», если хотите.
Позвольте мне прояснить еще один момент. В то время как круглые скобки до сих пор всегда указывали на умножение, это не относится к обозначениям функций. Вопреки всему предыдущему опыту, круглые скобки для обозначения функции не , а не указывают на умножение.
Выражение « f ( x )» означает «формула с именем f имеет x в качестве входной переменной».Это означает, что , а не означает «умножить на и x »!
Не смущайте себя, произнося (или думая) « f ( x )» как « f умножить на x », а никогда не пытайтесь «умножить» имя функции с помощью скобок. Вход.
В обозначении функции « x » в « f ( x )» называется «аргументом функции» или просто «аргументом».Поэтому, если они дадут вам выражение « f (2)» и спросят «аргумент», ответ будет просто «2».
В сторону: Почему ввод называется «аргументом»? Термин «аргумент» имеет давнюю историю. Первоначально это был логический термин, относящийся к утверждению, содержащему доказательство или, в менее формальном смысле, утверждению, которое использовалось, чтобы попытаться кого-то в чем-то убедить. В конце концов, этот термин стал обозначать в раннем научном контексте любое математическое значение, которое требовалось в качестве входных данных для других вычислений, или любое значение, от которого зависели последующие результаты.
В двадцатом веке, когда компьютерное кодирование стало обычным явлением, кодировщики приняли математическое значение для обозначения входных данных для своего кодирования. В нашем математическом контексте «аргумент» – это независимая переменная (та, для которой вы выбираете значение, обычно это значение x ), а вывод функции – это зависимая переменная (та, значение которой зависит от того, что было подключено. в, обычно это значение y ).
Учитывая
h ( s ), каково имя функции и какой аргумент?
Сначала сделаю вторую часть.Аргумент – это то, что находится в круглых скобках, поэтому здесь аргумент s .
Имя функции – это переменная, которая стоит перед круглыми скобками. В этом случае имя функции – h .
название функции: h
аргумент: с
Каков аргумент
f ( y )?
Аргумент – это то, что подключено.В этом частном (необычном) случае подключаемая переменная – « y ». (В конце концов, не существует правила, согласно которому y не может быть независимой переменной.) Итак:
Учитывая
г ( т ) = т 2 + т , как называется функция? В г (–1), какой аргумент?
Имя функции – это то, что стоит перед круглыми скобками, поэтому здесь имя функции – g .
Во второй части вопроса меня просят аргументировать. В первой части, где они дали мне имя функции и аргумент (часть « g ( t )») и формулу (часть « t 2 + t »), аргумент был т . Но во второй части ввели конкретную стоимость т . Итак, во второй части аргументом является число –1.
название функции: г
аргумент г (–1): –1
Оценка по номеру
Вы оцениваете « f ( x )» точно так же, как вы всегда оценивали « y ».А именно, вы берете число, которое они дают вам, в качестве входной переменной, вы подключаете его к переменной, и вы упрощаете получение ответа. Например:
Учитывая
f ( x ) = x 2 + 2 x – 1, найдите f (2).
Чтобы оценить f ( x ) при x = 2, я вставлю 2 для каждого экземпляра x в правило функции:
f (2) = (2) 2 +2 (2) – 1
Чтобы держать все в голове (и прояснить в своей работе), я заключил в круглые скобки каждый экземпляр аргумента 2 в формуле для f .Теперь я могу упростить:
Тогда мой ответ:
Дано
f ( x ) = x 2 + 2 x – 1, найдите f (–3).
Для оценки делаю то, что делал всегда. Я подставлю данное значение (–3) для указанной переменной ( x ) в данную формулу:
f (–3) = (–3) 2 + 2 (–3) – 1
Я снова использовал круглые скобки, чтобы четко обозначить значение, вводимое в формулу.В данном случае круглые скобки помогают мне отслеживать знаки «минус». Теперь я могу упростить:
Тогда мой ответ:
Если вы испытываете трудности при работе с негативами, попробуйте использовать круглые скобки, как я сделал выше. Это помогает отслеживать такие вещи, как то, стоит ли показатель степени на знаке «минус». И это просто хорошая привычка.
Важный тип функции называется «кусочной» функцией, потому что, ну, она состоит из частей.Например, это кусочная функция:
Как видите, эта функция разделена на две половины: половину, которая идет перед x = 1, и половину, которая идет от x = 1 до бесконечности. Какую половину функции вы используете, зависит от значения x . Давайте рассмотрим это:
Учитывая функцию
f ( x ), как определено выше, оцените функцию при следующих значениях: x = –1, x = 3 и x = 1.
Эта функция поставляется по частям; отсюда и название «кусочная» функция. Когда я оцениваю его при различных значениях x , я должен быть осторожен, чтобы вставить аргумент в правильную часть функции.
Сначала они хотят, чтобы я оценил значение x = –1. Поскольку это меньше 1, то этот аргумент переходит в первую часть функции. Для обновления используется следующая функция:
Затем я вставлю –1 в правило 2 x 2 – 1:
f (–1) = 2 (–1) 2 – 1
= 2 (1) – 1
= 2 – 1 = 1
Затем они хотят, чтобы я нашел значение f (3).Поскольку 3 больше 1, мне нужно подключить вторую часть функции, поэтому:
Наконец, они хотят, чтобы я оценил f ( x ) при x = 1. Это единственное значение x , которое немного сложно. Какую половину использовать?
Внимательно глядя на правила для функций, я вижу, что первая часть – это правило для значений x , которые строго меньше единицы; правило не применяется, если x равно 1.С другой стороны, вторая фигура применяется, когда x больше или равно 1. Поскольку здесь я имею дело с x = 1, то применяется правило второй части.
Тогда мой ответ:
f (–1) = 1
f (3) = 7
f (1) = 5
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении функций по заданному числовому значению.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Оценить», чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/fcnnot.htm
Функции– Алгебра – Математика A-Level Revision
В этом разделе рассматриваются функции в рамках более широкой темы алгебры.
Функцию можно рассматривать как правило, которое берет каждый элемент x набора и присваивает ему то же самое значение y , известное на его изображении.
x → Функция → y
Буква f, g или h часто используется для обозначения функции. Функция, которая возводит число в квадрат и добавляет 3, может быть записана как f (x) = x 2 + 5 . Это же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.
Пример
f (4) = 4 2 + 5 = 21, f (-10) = (-10) 2 +5 = 105 или, альтернативно, f : x → x 2 + 5 .
Фраза «y является функцией x» означает, что значение y зависит от значения x, поэтому:
- y можно записать через x (например, y = 3x).
- Если f (x) = 3x, а y является функцией x (т.е. y = f (x)), то значение y, когда x равно 4, равно f (4), которое находится путем замены x “s на 4. “с.
Пример
Если f (x) = 3x + 4, найти f (5) и f (x + 1).
f (5) = 3 (5) + 4 = 19
f (x + 1) = 3 (x + 1) + 4 = 3x + 7
Домен и диапазон
Область функции – это набор значений, которые вам разрешено вводить в функцию (то есть все значения, которые может принимать x). Диапазон функции – это набор всех значений, которые функция может принимать, другими словами, все возможные значения y, когда y = f (x).Итак, если y = x 2 , мы можем выбрать в качестве домена все действительные числа. Диапазон – это все действительные числа, большие (или равные) нулю, поскольку, если y = x 2 , y не может быть отрицательным.
Индивидуальные переговоры
Мы говорим, что функция является взаимно однозначной , если для каждой точки y в диапазоне функции существует только одно значение x такое, что y = f (x). f (x) = x 2 не один к одному, потому что, например, есть два значения x, такие что f (x) = 4 (а именно –2 и 2).На графике функция взаимно однозначна, если любая горизонтальная линия разрезает график только один раз.
Составные функции
fg означает выполнение функции g, затем функции f. Иногда fg записывается как fog
.Пример
Если f (x) = x 2 и g (x) = x – 1, то
gf (x) = g (x 2 ) = x 2 – 1
fg (x) = f (x – 1) = (х – 1) 2
Как видите, fg не обязательно равно gf
Обратная функция
Обратной функцией является функция, которая обращает эффект исходной функции.Например, y = 2x, обратный y = ½ x.
Чтобы найти обратную функцию, поменяйте местами x “s и y” s и сделайте y объектом формулы.
Пример
Найдите обратное к f (x) = 2x + 1
Пусть y = f (x), поэтому y = 2x + 1
поменяет местами x “s и y” s:
x = 2y + 1
Сделайте y темой формулы:
2y = x – 1, поэтому y = ½ (x – 1)
Следовательно, f -1 (x) = ½ (x – 1)
f -1 (x) – стандартное обозначение, обратное к f (x).Обратное считается существующим тогда и только тогда, когда существует функция f -1 с ff -1 (x) = f -1 f (x) = x
.Обратите внимание, что график f -1 будет отражением f в линии y = x.
Это видео объясняет больше об обратной функции
Графики
Функции можно изобразить в виде графиков. Функция является непрерывной , если ее график не имеет разрывов. Пример прерывистого графа y = 1 / x, поскольку граф нельзя нарисовать, не отрывая карандаш от бумаги:
Функция является периодической , если ее график повторяется через равные промежутки времени, этот интервал известен как период.
Функция равна и даже , если она не меняется при замене x на -x. График такой функции будет симметричным по оси ординат. Даже функции, которые являются полиномами, имеют четные степени (например, y = x²).
Функция равна нечетным , если знак функции изменяется при замене x на -x. График функции будет иметь симметрию вращения относительно начала координат (например, y = x³).
Функция модуля
Модуль числа – это величина этого числа.Например, модуль -1 (| -1 |) равен 1. Модуль x, | x |, равен x для значений x, которые положительны, и -x для значений x, которые отрицательны. Итак, график y = | x | y = x для всех положительных значений x и y = -x для всех отрицательных значений x:
Преобразование графиков
Если y = f (x), график y = f (x) + c (где c – константа) будет графиком y = f (x), сдвинутым на c единиц вверх (в направлении y- ось).
Если y = f (x), график y = f (x + c) будет графиком y = f (x), сдвинутым на c единиц влево.
Если y = f (x), график y = f (x – c) будет графиком y = f (x), сдвинутым на c единиц вправо.
Если y = f (x), график y = af (x) представляет собой отрезок графика y = f (x), масштабный коэффициент (1 / a), параллельный оси x. [Масштабный коэффициент 1 / a означает, что “растяжение” фактически приводит к сжатию графика, если a – число больше 1]
Пример
График y = | x – 1 | будет таким же, как на приведенном выше графике, но со смещением на одну единицу вправо (так что точка V попадет на ось x в 1, а не в 0).
Обратные функции
Обратная функция – наоборот!
Начнем с примера:
Здесь у нас есть функция f (x) = 2x + 3 , записанная в виде блок-схемы:
Обратная функция идет другим путем:
Итак, обратное: 2x + 3: (y-3) / 2
Обратное значение обычно отображается путем добавления небольшого «-1» после имени функции, например:
ф -1 (г)
Мы говорим “ f инверсия y”
Итак, обратное к f (x) = 2x + 3 записывается:
f -1 (y) = (y-3) / 2
(я также использовал y вместо x , чтобы показать, что мы используем другое значение.)
Вернуться туда, где мы начали
Самое замечательное в обратном преобразовании состоит в том, что он должен вернуть нам исходное значение:
.
Когда функция f превращает яблоко в банан,
Затем функция, обратная f -1 превращает банан обратно в яблоко
Пример:
Используя приведенные выше формулы, мы можем начать с x = 4:
f (4) = 2 × 4 + 3 = 11
Затем мы можем использовать обратное для 11:
f -1 (11) = (11-3) / 2 = 4
И мы волшебным образом снова получаем 4 !
Мы можем написать это одной строкой:
f -1 (f (4)) = 4
“f, обратное f 4, равно 4”
Таким образом, применение функции f, а затем ее обратной f -1 возвращает нам исходное значение снова:
f -1 (f (x)) = x
Мы могли бы также расположить функции в другом порядке, и он все еще работает:
f (f -1 (x)) = x
Пример:
Начать с:
f -1 (11) = (11-3) / 2 = 4
А потом:
f (4) = 2 × 4 + 3 = 11
Итак, мы можем сказать:
f (f -1 (11)) = 11
“f f, обратное 11, равно 11”
Решить с помощью алгебры
Мы можем вычислить обратное, используя алгебру. Положите y вместо f (x) и решите относительно x:
| Функция: | f (x) | = | 2x + 3 | |
| Положите “y” вместо “f (x)”: | y | = | 2x + 3 | |
| Вычтем 3 с обеих сторон: | г-3 | = | 2x | |
| Разделите обе стороны на 2: | (у-3) / 2 | = | x | |
| Поменять стороны: | x | = | (у-3) / 2 | |
| Решение (вместо «x» подставьте «f -1 (y)»): | ф -1 (у) | = | (у-3) / 2 |
Этот метод хорошо подходит для более сложных инверсий.
Фаренгейта в Цельсия
Полезный пример – преобразование между градусами Фаренгейта и Цельсия:
Для преобразования Фаренгейта в Цельсия: f (F) = (F – 32) × 5 9
Обратная функция (градусы Цельсия обратно по Фаренгейту): f -1 (C) = (C × 9 5 ) + 32
Для вас: посмотрите, сможете ли вы сделать шаги, чтобы создать инверсию!
Инверсия общих функций
До сих пор это было легко, потому что мы знаем, что обратное к умножению – это деление, а обратное к сложению – вычитание, но как насчет других функций?
Вот список, который вам поможет:
(Примечание: вы можете узнать больше об обратном синусе, косинусе и тангенсе.)
Осторожно!
Вы видели “Осторожно!” столбец выше? Это потому, что некоторые инверсии работают только с определенными значениями .
Пример: квадрат и квадратный корень
Когда мы возводим в квадрат отрицательное число , а затем делаем обратное, происходит следующее:
Квадрат: (- 2) 2 = 4
Обратная величина (квадратный корень): √ (4) = 2
Но мы не вернули исходное значение! Мы получили 2 вместо −2 .Наша вина в том, что мы не были осторожны!
Таким образом, квадратная функция (как она есть) не имеет обратной
Но мы можем это исправить!
Ограничить домен (значения, которые могут входить в функцию).
Пример: (продолжение)
Только убедитесь, что мы не используем отрицательные числа.
Другими словами, ограничьте его до x ≥ 0 , и тогда мы сможем получить обратное.
Итак, мы имеем такую ситуацию:
- x 2 не имеет ли инверсия
- но {x 2 | x ≥ 0} (в котором говорится, что «x возведен в квадрат, такой, что x больше или равен нулю», используя нотацию создателя множеств) имеет ли обратное.
Нет обратного?
Давайте посмотрим наглядно, что здесь происходит:
Чтобы иметь возможность иметь инверсию, нам нужно уникальных значений .
Подумайте … если есть два или более значений x для одного значения y , как мы узнаем, какое из них выбрать, когда вернемся?
| Общие функции |
| Нет обратного |
Представьте, что мы перешли от x 1 к определенному значению y, куда мы вернемся? x 1 или x 2 ?
В этом случае у нас не может быть обратного.
Но если мы можем иметь ровно один x для каждого y, мы можем получить обратное.
Это называется “однозначным соответствием” или биективным, например
| Биективная функция |
| Имеет инверсию |
Функция должна быть «биективной», чтобы иметь инверсию.
Таким образом, биективная функция подчиняется более строгим правилам, чем общая функция, что позволяет нам иметь обратную функцию.
Домен и диапазон
Так что же все эти разговоры о «, ограничение домена »?
В простейшей форме область – это все значения, которые входят в функцию (а диапазон – это все значения, которые выходят).
В его нынешнем виде функция , а не , имеет инверсию, потому что некоторые значения y будут иметь более одного значения x.
Но мы могли бы ограничить домен так, чтобы для каждого y было уникальных x…
… и теперь у нас может быть обратное:
Также примечание:
- Функция f (x) переходит из области в диапазон,
- Обратная функция f -1 (y) переходит из диапазона обратно в домен.
Давайте изобразим их оба в терминах x … так что теперь это f -1 (x) , а не f -1 (y) :
f (x) и f -1 (x) похожи на зеркальные изображения
(перевернут по диагонали).
Другими словами:
График f (x) и f -1 (x) симметричны по линии y = x
Пример: квадрат и квадратный корень (продолжение)
Сначала , мы ограничиваем Домен до x ≥ 0 :
- {x 2 | x ≥ 0} “x в квадрате, так что x больше или равно нулю”
- {√x | x ≥ 0} “квадратный корень из x такой, что x больше или равен нулю”
И вы видите, что это “зеркальные отражения”
друг от друга по диагонали y = x.
Примечание: когда мы ограничиваем область до x ≤ 0 (меньше или равно 0), обратное значение будет f -1 (x) = −√x :
- {x 2 | х ≤ 0}
- {−√x | x ≥ 0}
Которые тоже обратные.
Не всегда разрешимо!
Иногда невозможно найти обратную функцию.
Пример: f (x) = x / 2 + sin (x)
Мы не можем вычислить обратное, потому что мы не можем решить для «x»:
у = х / 2 + грех (х)
г …? = х
Примечания к обозначениям
Несмотря на то, что мы пишем f -1 (x), «-1» – это , а не показатель степени (или степени):
| f -1 (x) | … отличается от … | f (x) -1 |
| Функция, обратная f | f (x) -1 = 1 / f (x) (Взаимное) |
Сводка
- Значение, обратное f (x), равно f -1 (y)
- Мы можем найти обратное, перевернув “блок-схему”
- Или мы можем найти обратное с помощью алгебры:
- Положите “y” вместо “f (x)” и
- Решить относительно x
- Нам может потребоваться ограничить домен , чтобы функция имела инверсию
– пояснения и примеры
Концепция функций была разработана в семнадцатом веке, когда Рене Декарт использовал эту идею для моделирования математических отношений в своей книге Geometry .Термин «функция» был введен Готфридом Вильгельмом Лейбницем через пятьдесят лет после публикации «Геометрии ».
Позже Леонард Эйлер формализовал использование функций, когда ввел понятие обозначения функций; у = f (х). Так продолжалось до 1837 года, когда немецкий математик Петер Дирихле дал современное определение функции.
Что такое функция?
В математике функция – это набор входных данных с одним выходом в каждом случае.У каждой функции есть домен и диапазон. Область – это набор независимых значений переменной x для определенного отношения или функции. Проще говоря, домен – это набор значений x, которые генерируют реальные значения y при подстановке в функцию.
С другой стороны, диапазон – это набор всех возможных значений, которые может выдать функция. Диапазон функции может быть выражен в виде интервалов или содержать информацию о неравенствах.
Что такое обозначение функций?
Обозначение можно определить как систему символов или знаков, обозначающих такие элементы, как фразы, числа, слова и т. Д.
Следовательно, обозначение функции – это способ, которым функция может быть представлена с помощью символов и знаков. Обозначение функций – это более простой способ описания функции без подробного письменного объяснения.
Чаще всего используется обозначение функции f (x), которое читается как «f» или «x». В этом случае буква x, помещенная в круглые скобки, и весь символ f (x) обозначают набор доменов и набор диапазонов соответственно.
Хотя f – самая популярная буква, используемая при написании обозначений функций, любая другая буква алфавита также может использоваться как в верхнем, так и в нижнем регистре.
Преимущества использования обозначения функций
- Поскольку большинство функций представлены различными переменными, такими как; a, f, g, h, k и т. д., мы используем f (x), чтобы избежать путаницы относительно того, какая функция оценивается.
- Обозначение функций позволяет легко идентифицировать независимую переменную.
- Обозначение функции также помогает нам идентифицировать элемент функции, который необходимо исследовать.
Рассмотрим линейную функцию y = 3x + 7. Чтобы записать такую функцию в обозначении функции, мы просто заменяем переменную y фразой f (x), чтобы получить;
f (x) = 3x + 7.Эта функция f (x) = 3x + 7 читается как значение f для x или как f для x.
Типы функций
В алгебре есть несколько типов функций.
К наиболее распространенным типам функций относятся:
Линейная функция – это многочлен первой степени. Линейная функция имеет общий вид f (x) = ax + b, где a и b – числовые значения, а a 0.
Полиномиальная функция второй степени известна как квадратичная функция. Общая форма квадратичной функции: f (x) = ax 2 + bx + c, где a, b и c – целые числа и a 0.
Это полиномиальная функция от 3 rd градуса, которая имеет форму f (x) = ax 3 + bx 2 + cx + d
Логарифмическая функция – это уравнение, в котором переменная отображается как аргумент логарифма. Общая функция функции f (x) = log a (x), где a – основание, а x – аргумент.
Экспоненциальная функция – это уравнение, в котором переменная появляется как показатель степени. Экспоненциальная функция представлена как f (x) = a x .
f (x) = sin x, f (x) = cos x и т. Д. Являются примерами тригонометрических функций
Identity Function:
Идентификационная функция такова, что f: A → B и f (x ) = x, ∀ x ∈ A
Rational Function:
Функция называется рациональной, если R (x) = P (x) / Q (x), где Q (x) ≠ 0.
Как оценивать функции?
Оценка функции – это процесс определения выходных значений функции. Это делается путем подстановки входных значений в обозначение данной функции.
Пример 1
Запишите y = x 2 + 4x + 1, используя обозначение функции, и оцените функцию при x = 3.
Решение
Учитывая, y = x 2 + 4x + 1
Применяя обозначение функции, получаем
f (x) = x 2 + 4x + 1
Evaluation:
Заменить x на 3
f (3) = 3 2 + 4 × 3 + 1 = 9 + 12 + 1 = 22
Пример 2
Вычислите функцию f (x) = 3 (2x + 1), когда x = 4.
Решение
Подставьте x = 4 в функцию f (x).
f (4) = 3 [2 (4) + 1]
f (4) = 3 [8 + 1]
f (4) = 3 x 9
f (4) = 27
Пример 3
Запишите функцию y = 2x 2 + 4x – 3 в обозначении функции и найдите f (2a + 3).
Решение
y = 2x 2 + 4x – 3 ⟹ f (x) = 2x 2 + 4x – 3
Заменить x на (2a + 3).
f (2a + 3) = 2 (2a + 3) 2 + 4 (2a + 3) – 3
= 2 (4a 2 + 12a + 9) + 8a + 12-3
= 8a 2 + 24a + 18 + 8a + 12-3
= 8a 2 + 32a + 27
Пример 4
Представьте y = x 3 – 4x, используя обозначение функции, и решите для y при x = 2.
Решение
Учитывая функцию y = x 3 – 4x, замените y на f (x), чтобы получить;
f (x) = x 3 – 4x
Теперь оцените f (x), когда x = 2
⟹ f (2) = 2 3 – 4 × 2 = 8-8 = 0
Следовательно , значение y при x = 2 равно 0
Пример 5
Найдите f (k + 2) при условии, что f (x) = x² + 3x + 5.
Решение
Чтобы оценить f (k + 2), замените x на (k + 2) в функции.
⟹ f (k + 2) = (k + 2) ² + 3 (k + 2) + 5
⟹ k² + 2² + 2k (2) + 3k + 6 + 5
⟹ k² + 4 + 4k + 3k + 6 + 5
= k² + 7k + 15
Пример 6
Учитывая обозначение функции f (x) = x 2 – x – 4. Найдите значение x, когда f ( x) = 8
Решение
f (x) = x 2 – x – 4
Заменить f (x) на 8.
8 = x 2 – x – 4
x 2 – x – 12 = 0
Решите квадратное уравнение путем разложения на множители, чтобы получить;
⟹ (x – 4) (x + 3) = 0
⟹ x – 4 = 0; x + 3 = 0
Следовательно, значения x при f (x) = 8 равны;
х = 4; x = -3
Пример 7
Вычислите функцию g (x) = x 2 + 2 при x = −3
Решение
Замените x на -3.
г (−3) = (−3) 2 + 2 = 9 + 2 = 11
Примеры обозначений функций из реальной жизни
Обозначения функций можно применять в реальной жизни для оценки математических задач, как показано ниже Примеры:
Пример 8
Для производства определенного продукта компания тратит x долларов на сырье и y долларов на рабочую силу. Если себестоимость продукции описывается функцией f (x, y) = 36000 + 40x + 30y + xy / 100.Рассчитайте стоимость производства, если фирма тратит 10 000 и 1 000 долларов на сырье и рабочую силу соответственно.
Решение
Дано x = 10000 долларов США и y = 1000 долларов США
Подставьте значения x и y в функцию производственных затрат
⟹f (10000, 1000) = 36000 + 40 (10000) + 30 (1000) + (10000) (1000) / 100.
⟹ f (10000, 1000) = 36000 + 4000000 + 30000 + 100000
⟹ 4136000 долларов.
Пример 9
Мэри экономит 100 долларов в неделю на предстоящий день рождения.Если у нее уже есть 1000 долларов, сколько у нее будет через 22 недели.
Решение
Пусть x = количество недель, а f (x) = общая сумма. Мы можем записать эту проблему в обозначении функции как;
f (x) = 100x + 1000
Теперь оцените функцию, когда x = 22
f (22) = 100 (22) +1000
f (22) = 3200
Таким образом, общая сумма составит 3200 долларов.
Пример 10
Стоимость разговора в двух мобильных сетях A и B составляет 34 доллара плюс 0.05 / мин и 40 долларов плюс 0,04 / мин соответственно.
- Представьте эту проблему в обозначении функций.
- Какая мобильная сеть является доступной с учетом того, что в среднем каждый месяц используется 1 160 минут.
- Когда ежемесячные счета двух сетей равны?
Решение
- Пусть x будет количеством минут, используемых в каждой сети.
Следовательно, функция сети A равна f (x) = 0,05x + 34, а функция сети B – f (x) = 0.04x + 40 долларов.
- Чтобы определить, какая сеть является доступной, подставьте x = 1160 в каждую функцию
A ⟹ f (1160) = 0,05 (1160) + 34
= 58 + 34 = 92 доллара
B f (1160) = 0,04 (1160) + 40
= 46,4 + 40
= 86,4 долл. США
Следовательно, сеть B является доступной, поскольку ее общая стоимость времени разговора меньше, чем у A.
- Приравняйте две функции и решите x
⟹ 0,05x +34 = 0,04x + 40
⟹ 0,01x = 6
x = 600
Ежемесячный счет A и B будет равен, когда среднее количество минут составляет 600.
Доказательство:
A ⟹ 0,05 (600) +34 = 64 доллара США
B ⟹ 0,04 (600) + 40 = 64 доллара США
Пример 11
Определенное число такое, что при его добавлении к 142, результат на 64 раза больше исходного числа. Найдите номер.
Решение
Пусть x = исходное число, а f (x) будет результатом сложения 142.
f (x) = 142 + x = 3x + 64
2x = 78
x = 39
Пример 12
Если произведение двух последовательных положительных целых чисел равно 1122, найдите два целых числа.
Решение
Пусть x будет первым целым числом;
второе целое число = x + 1
Теперь сформируйте функцию как;
f (x) = x (x + 1)
найти значение x, если f (x) = 1122
Заменить функцию f (x) на 1122
1122 = x (x + 1)
1122 = x 2 + 1
x 2 = 1121
Найдите квадрат обеих сторон функции
x = 33
x + 1 = 34
Целые числа 33 и 34.
Предыдущий урок | Главная страница | Следующий урокОпределение функций с помощью графиков | Колледж алгебры
Результаты обучения
- Проверьте работу с помощью теста вертикальной линии
- Проверьте однозначное соответствие с помощью теста горизонтальной линии
- Определить графики функций инструментария
Как мы видели в примерах выше, мы можем представить функцию с помощью графика. Графики отображают множество пар ввода-вывода на небольшом пространстве.Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Наиболее распространенные графики называют входное значение [latex] x [/ latex] и выходное значение [latex] y [/ latex], и мы говорим, что [latex] y [/ latex] является функцией [latex] x [ / latex] или [latex] y = f \ left (x \ right) [/ latex], если функция называется [latex] f [/ latex]. График функции – это набор всех точек [латекс] \ left (x, y \ right) [/ latex] в плоскости, которая удовлетворяет уравнению [латекс] y = f \ left (x \ right) [/ latex ].Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующее выходное значение. Например, черные точки на графике на графике ниже говорят нам, что [латекс] f \ left (0 \ right) = 2 [/ latex] и [latex] f \ left (6 \ right) = 1 [/ latex ]. Однако набор всех точек [latex] \ left (x, y \ right) [/ latex], удовлетворяющих [latex] y = f \ left (x \ right) [/ latex], является кривой.Показанная кривая включает [латекс] \ left (0,2 \ right) [/ latex] и [latex] \ left (6,1 \ right) [/ latex], потому что кривая проходит через эти точки.
Тест вертикальной линии может использоваться для определения того, представляет ли график функцию. Вертикальная линия включает все точки с определенным значением [latex] x [/ latex]. Значение [latex] y [/ latex] точки, где вертикальная линия пересекает график, представляет собой выход для этого входного значения [latex] x [/ latex]. Если мы можем нарисовать любую вертикальную линию , которая пересекает график более одного раза, тогда график , а не определяет функцию, потому что это значение [latex] x [/ latex] имеет более одного вывода.Функция имеет только одно выходное значение для каждого входного значения.
Практическое руководство. Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
- Проверьте график, чтобы увидеть, пересекает ли нарисованная вертикальная линия кривую более одного раза.
- Если такая линия есть, график не представляет функцию.
- Если ни одна вертикальная линия не может пересекать кривую более одного раза, график действительно представляет функцию.
Пример: применение теста вертикальной линии
Какой из графиков представляет функцию [латекс] y = f \ left (x \ right)? [/ Latex]
Показать решениеЕсли какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией.Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) графика выше. Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что при максимальном значении x вертикальная линия будет пересекать график более чем в одной точке.
Попробуй
Представляет ли приведенный ниже график функцию?
Тест горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли он взаимно однозначной функцией, – это использовать тест горизонтальной линии .Проведите через график горизонтальные линии. Горизонтальная линия включает все точки с определенным значением [latex] y [/ latex]. Значение [latex] x [/ latex] точки, где вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex] y [/ latex]. Если мы можем нарисовать любую горизонтальную линию , которая пересекает график более одного раза, тогда график , а не представляет функцию, потому что это значение [latex] y [/ latex] имеет более одного входа.
Практическое руководство. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию.
- Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
- Если такая строка есть, функция не взаимно однозначная.
- Если ни одна горизонтальная линия не может пересекать кривую более одного раза, функция взаимно однозначна.
Пример: применение теста горизонтальной линии
Рассмотрим функции (a) и (b), показанные на графиках ниже.
Являются ли какие-либо функции взаимно однозначными?
Показать решениеФункция в (а) не является взаимно однозначной.Горизонтальная линия, показанная ниже, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках).
Функция в (b) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную линию не более одного раза.
Определение основных функций набора инструментов
В этом тексте мы исследуем функции – формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем.Когда учимся читать, мы начинаем с алфавита. Когда мы учимся арифметике, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор базовых именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать [latex] x [/ latex] в качестве входной переменной и [latex] y = f \ left (x \ right) [/ latex] в качестве выходной переменной.
Мы будем часто видеть эти функции набора инструментов, комбинации функций набора инструментов, их графики и их преобразования на протяжении всей этой книги. Будет очень полезно, если мы сможем быстро распознать эти функции набора инструментов и их возможности по имени, формуле, графику и основным свойствам таблицы. Графики и примерные значения таблицы включены в каждую функцию, показанную ниже.
Попробуй
В этом упражнении вы построите график функций инструментария с помощью онлайн-инструмента построения графиков.
- Изобразите каждую функцию набора инструментов, используя обозначение функций.
- Создайте таблицу значений, которая ссылается на функцию и включает как минимум интервал [-5,5].
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Что на самом деле означает y = f (x)?
Привет, Джон,
Я считаю, что иногда полезно думать о функции как о машине, когда вы вводите число в качестве входных данных для машины и получаете число в качестве выходных данных.Имя функции $ f, $ вход $ x $ и выход $ f (x), $ read “$ f $ of $ x”. $ Выход $ f (x) $ иногда получает дополнительное имя $ y $ на $ y = f (x). $
На ум приходит функция вычисления квадратного корня на вашем калькуляторе. Имя функции – $ \ sqrt {\; \;} $, и мы обычно пишем функцию как $ f (x) = \ sqrt {x}. $ На моем калькуляторе я ввожу $ x $, например, нажимая 2, затем 5. Затем я вызываю функцию, нажимая кнопку $ \ sqrt {\; \;} $ I, и получаю 5 на дисплее калькулятора.2 – 4 = 9 – 4 = 5. $ Чтобы построить график этой функции, я бы начал с выбора некоторых значений $ x $, и, поскольку у меня есть выбор, я бы выбрал значения, которые упрощают арифметику. Например, $ x = 0, x = 1, x = -1 $ и так далее. Я собираюсь отслеживать, что я делаю, с помощью таблицы.
x | y = f (x) |
|---|---|
0 | -4 |
1 | -3 |
-1 | -3 |
2 | 0 |
3 | 5 |
Добавьте еще несколько строк в таблицу, выбрав собственные значения $ x.$ Изобразите значения в своей таблице $ (0, -4), (1, -3) $ и т. Д. На миллиметровой бумаге, а затем посмотрите, сможете ли вы нарисовать график, проходящий через эти точки.
Напишите ответ, если вам нужна дополнительная помощь,
Пенни




 15 + cos x) – x10(-sin x)
15 + cos x) – x10(-sin x)