Динамика | Формулы по физике
Инертность, масса, ускорение
Найти
Известно, что:
a1a2m2m1 =
Вычислить ‘a1’Сила, масса, ускорение
Найти
Известно, что:
Fma =
Вычислить ‘F’Сила тяжести
Найти
Известно, что:
Nmg =
Вычислить ‘N’Сила трения
Найти
F_трμN =
Вычислить ‘F_тр’Сила трения
Найти
Известно, что:
F_трμmg =
Вычислить ‘F_тр’Закон всемирного тяготения
Найти
Известно, что:
FGm1m2r =
Вычислить ‘F’Центростремительное ускорение спутника
Найти
Известно, что:
avRh =
Вычислить ‘a’Скорость спутника
Найти
Известно, что:
vGMRh =
Вычислить ‘v’Первая космическая скорость (движение по круговой орбите)
Найти
Известно, что:
vgR =
Вычислить ‘v’Вторая космическая скорость (преодоление гравитации)
Найти
Известно, что:
vgR =
Вычислить ‘v’Третий закон Кеплера
Найти
Известно, что:
T1T2a1a2 =
Вычислить ‘T1’Найти
Известно, что:
gGMR =
Вычислить ‘g’Вес тела
Найти
Известно, что:
Pmg =
Вычислить ‘P’Вес тела: невесомость
Найти
Pmga =
Вычислить ‘P’Вес тела: перегрузка
Найти
Известно, что:
Pmga =
Вычислить ‘P’Время торможения
Найти
Известно, что:
tmvF_тр =
Вычислить ‘t’Время торможения
Известно, что:
tvμg =
Вычислить ‘t’Путь торможения
Найти
Известно, что:
smvF_тр =
Вычислить ‘s’Путь торможения
Найти
Известно, что:
svμg =
Сила трения качения
Найти
Известно, что:
F_трμNR =
Вычислить ‘F_тр’Сила упругости
Найти
Известно, что:
F_упругkx =
Вычислить ‘F_упруг’Кинетическая энергия вращающегося тела
Найти
Известно, что:
W_kJω =
Вычислить ‘W_k’Основные формулы по физике – ОПТИКА
Оптика – это раздел физики, изучающий природу светового излучения, его распространение и взаимодействие с веществом. Световые волны – это электромагнитные волны. Длина волны световых волн заключена в интервале [0,4·10-6 м ÷ 0,76·10-6 м]. Волны такого диапазона воспринимаются человеческим глазом.
Световые волны – это электромагнитные волны. Длина волны световых волн заключена в интервале [0,4·10-6 м ÷ 0,76·10-6 м]. Волны такого диапазона воспринимаются человеческим глазом.
Свет распространяется вдоль линий, называемых лучами. В приближении лучевой (или геометрической) оптики пренебрегают конечностью длин волн света, полагая, что λ→0. Геометрическая оптика во многих случаях позволяет достаточно хорошо рассчитать оптическую систему. Простейшей оптической системой является линза.
При изучении интерференции света следует помнить, что интерференция наблюдается только от когерентных источников и что интерференция связана с перераспределением энергии в пространстве. Здесь важно уметь правильно записывать условие максимума и минимума интенсивности света и обратить внимание на такие вопросы, как цвета тонких пленок, полосы равной толщины и равного наклона.
При изучении явления дифракции света необходимо уяснить принцип Гюйгенса-Френеля, метод зон Френеля, понимать, как описать дифракционную картину на одной щели и на дифракционной решетке.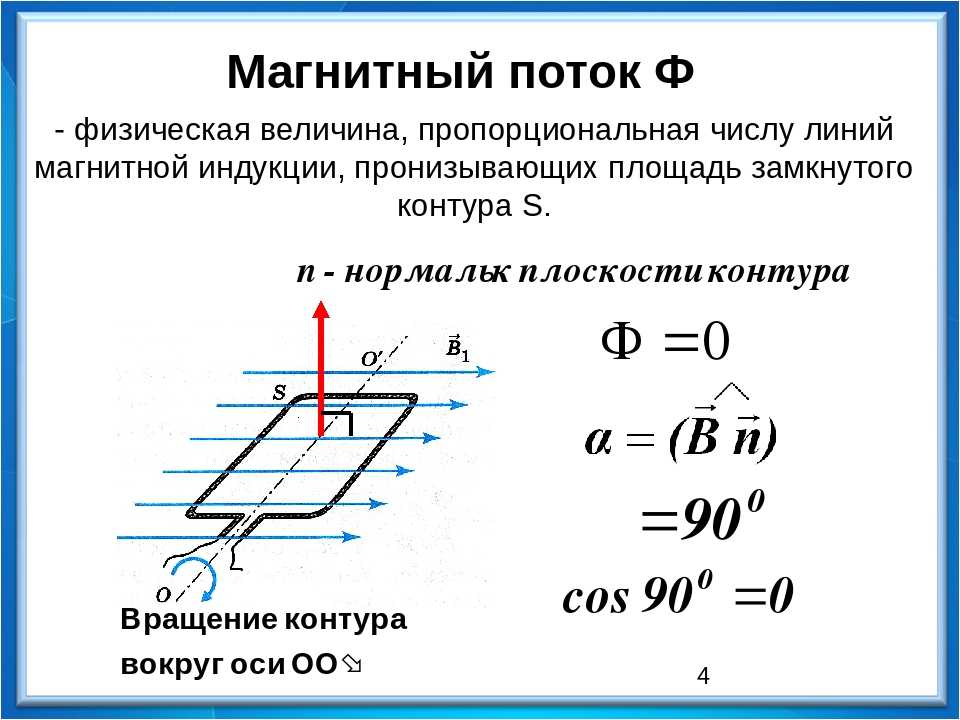
При изучении явления поляризации света нужно понимать, что в основе этого явления лежит поперечность световых волн. Следует обратить внимание на способы получения поляризованного света и на законы Брюстера и Малюса.
Смотрите также основные формулы по физике – колебания и волны
Таблица основных формул по оптике
|
Физические законы, формулы, переменные |
Формулы оптики |
|
Абсолютный показатель преломления где с – скорость света в вакууме, с=3·108 м/с, v – скорость распространения света в среде. |
|
|
Относительный показатель преломления |
|
|
Закон преломления где i – угол падения, r – угол преломления. |
|
|
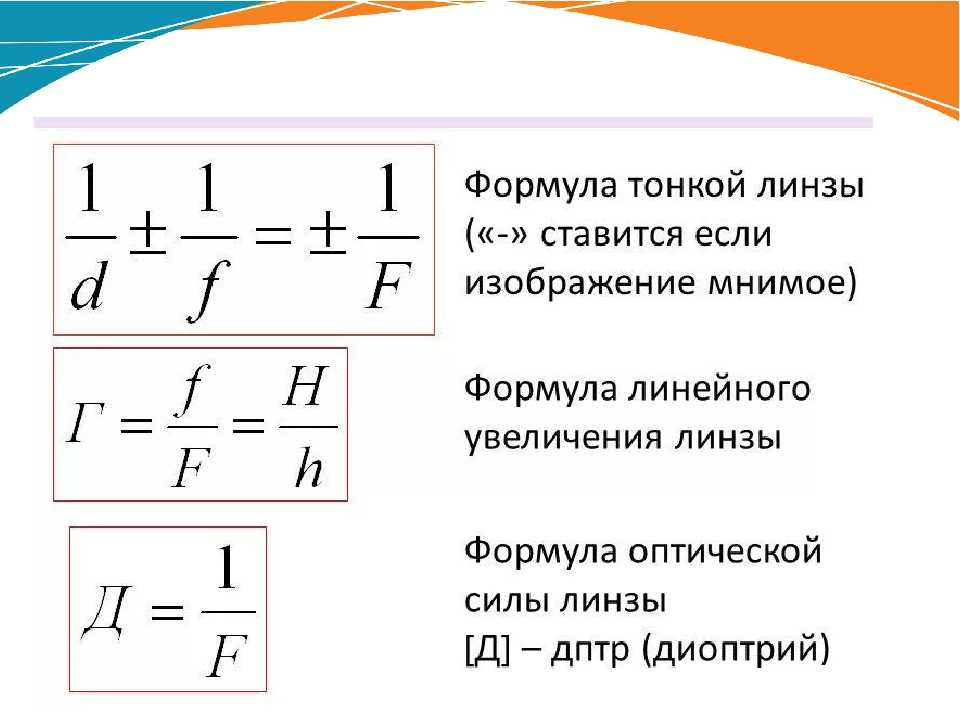
Формула тонкой линзы где F – фокусное расстояние линзы, d – расстояние от предмета до линзы, f – расстояние от линзы до изображения. |
|
|
где R1 и R2 – радиусы кривизны сферических поверхностей линзы. Для выпуклой поверхности R>0. Для вогнутой поверхности R<0. |
|
|
Оптическая длина пути: где n – показатель преломления среды; r – геометрическая длина пути световой волны. |
|
|
Оптическая разность хода: L1 и L2 – оптические пути двух световых волн. |
|
|
Условие интерференционного максимума: минимума: где λ0 – длина световой волны в вакууме; m – порядок интерференционного максимума или минимума. |
|
|
Оптическая разность хода в тонких пленках в отраженном свете: в проходящем свете: где d – толщина пленки; i – угол падения света; n – показатель преломления. |
|
|
Ширина интерференционных полос в опыте Юнга: где d – расстояние между когерентными источниками света; L – расстояние от источника до экрана. |
|
|
Условие главных максимумов дифракционной решетки: где d – постоянная дифракционной решетки; φ – угол дифракции. |
|
|
Разрешающая способность дифракционной решетки: где Δλ – минимальная разность длин волн двух спектральных линий, разрешаемых решеткой; m – порядок спектра; N – общее число щелей решетки. |
|
|
Закон Малюса: где I0 – интенсивность плоско-поляризованного света, падающего на анализатор; I – интенсивность света, прошедшего через анализатор; α – угол между плоскостью поляризации падающего света и главной плоскостью анализатора. |
|
|
Связь интенсивности естественного света Iест с интенсивностью света, прошедшего поляризатор (и падающего на анализатор): где k – относительная потеря интенсивности света в поляризаторе. |
|
|
Дисперсия вещества |
|
|
Средняя дисперсия |
|
|
Групповая скорость света |
|
|
Фазовая скорость света |
Урок 14.
 статика. равновесие абсолютно твердых тел – Физика – 10 класс
статика. равновесие абсолютно твердых тел – Физика – 10 классФизика, 10 класс
Урок 14. Статика. Равновесие абсолютно твёрдых тел
Перечень вопросов, рассматриваемых на уроке:
1.Условия равновесия тела
2.Момент силы
3.Плечо силы
4. Центр тяжести
Глоссарий по теме
Статика – раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой
Абсолютно твердое тело – модельное понятие классической механики, обозначающее совокупность точек, расстояния между текущими положениями которых не изменяются.
Центр тяжести – центром тяжести тела называют точку, через которую при любом положении тела в пространстве проходит равнодействующая сил тяжести, действующих на все частицы тела.
Плечо силы – это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы – это физическая величина, равная произведению модуля силы на ее плечо.
Устойчивое равновесие – это равновесие, при котором тело, выведенное из состояния устойчивого равновесия, стремится вернуться в начальное положение.
Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.
Безразличное равновесие системы — равновесие, при котором после устранения причин, вызвавших малые отклонения, система остается в покое в этом отклоненном состоянии
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017.– С. 165 – 169.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. – М.: Дрофа, 2009.
Степанова Г.Н. Сборник задач по физике. 10-11 класс. – М.: Просвещение. 1999 г. С.48- 50.
Теоретический материал для самостоятельного изучения
Равновесие – это состояние покоя, т. е. если тело покоится относительно инерциальной системы отсчета, то говорят, что оно находится в равновесии. Вопросы равновесия интересуют строителей, альпинистов, артистов цирка и многих-многих других людей. Любому человеку приходилось сталкиваться с проблемой сохранения равновесия. Почему одни тела, выведенные из состояния равновесия, падают, а другие – нет? Выясним, при каком условии тело будет находиться в состоянии равновесия.
е. если тело покоится относительно инерциальной системы отсчета, то говорят, что оно находится в равновесии. Вопросы равновесия интересуют строителей, альпинистов, артистов цирка и многих-многих других людей. Любому человеку приходилось сталкиваться с проблемой сохранения равновесия. Почему одни тела, выведенные из состояния равновесия, падают, а другие – нет? Выясним, при каком условии тело будет находиться в состоянии равновесия.
Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой. Статика является частным случаем динамики. В статике твердое тело рассматривается как абсолютно твердое, т.е. недеформируемое тело. Это означает, что деформация так мала, что её можно не учитывать.
Центр тяжести существует у любого тела. Эта точка может находиться и вне тела. Как же подвесить или подпереть тело, чтобы оно находилось в равновесии.
Подобную задачу в свое время решил Архимед. Им же были введены понятие плеча силы и момента силы.
Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
После своих исследований Архимед сформулировал условие равновесия рычага и вывел формулу:
Это правило является следствием 2-го закона Ньютона.
Первое условие равновесия
Для равновесия тела необходимо, чтобы сумма всех сил, приложенных к телу была равна нулю.
формула должна быть в векторном виде и стоять знак суммы
Второе условие равновесия
При равновесии твердого тела сумма моментов вcех внешних сил, действующих на него относительно любой оси, равна нулю.
Не менее важен случай, когда тело имеет площадь опоры. Тело, имеющее площадь опоры, находится в равновесии, когда вертикальная прямая, проходящая через центр тяжести тела, не выходит за пределы площади опоры этого тела. Известно, что в городе Пизе в Италии существует наклонная башня. Несмотря на то, что башня наклонена, она не опрокидывается, хотя ее часто называют падающей. Очевидно, что при том наклоне, которого башня достигла к настоящему времени, вертикаль, проведенная из центра тяжести башни, все еще проходит внутри ее площади опоры.
Очевидно, что при том наклоне, которого башня достигла к настоящему времени, вертикаль, проведенная из центра тяжести башни, все еще проходит внутри ее площади опоры.
В практике большую роль играет не только выполнение условия равновесия тел, но и качественная характеристика равновесия, называемая устойчивостью.
Различают 3 вида равновесия: устойчивое, неустойчивое, безразличное.
Если при отклонении тела от положения равновесия, возникают силы или моменты сил, стремящиеся вернуть тело в положение равновесия, то такое равновесие называется устойчивым.
Неустойчивое равновесие — это противоположный случай. При отклонении тела от положения равновесия, возникают силы или моменты сил, которые стремятся увеличить это отклонение.
Наконец, если при малом отклонении от положения равновесия тело все равно остается в равновесии, то такое равновесие называется безразличным.
Чаще всего необходимо, чтобы равновесие было устойчивым. Когда равновесие нарушается, то сооружение становится опасным, если его размеры велики.
Примеры и разбор решения заданий
1. Чему равен момент силы тяжести груза массой 40 кг, подвешенного на кронштейне АВС, относительно оси, проходящей через точку В, если АВ=0,5 м и угол α=450
Решение:
Момент силы – это величина равная произведению модуля силы на её плечо.
Сначала найдём плечо силы, для этого нам надо опустить перпендикуляр из точки опоры на линию действия силы. Плечо силы тяжести равно расстоянию АС. Так как угол равен 45°, то мы видим, что АС=АВ
Модуль силы тяжести находим по формуле:
После подстановки числовых значений величин мы получим:
F=40×9,8 =400 Н, М= 400 ×0,5=200 Н м.
Ответ: М=200 Н м.
2. Приложив вертикальную силу F, груз массой М — 100 кг удерживают на месте с помощью рычага (см. рис.). Рычаг состоит из шарнира без трения и однородного массивного стержня длиной L=8 м. Расстояние от оси шарнира до точки подвеса груза равно b=2 м. Чему равен модуль силы F, если масса рычага равна 40 кг.
Решение:
По условию задачи рычаг находится в равновесии. Напишем второе условие равновесия для рычага:
.
После подстановки числовых значений величин получим
F= (100×9,8 ×2 + 0,5×40×9,8×8)/8=450 Н
Ответ: 450 Н.
Силы, действующие в простом механизме блок
Автор: Шумейко Алёна Витальевна
Научный руководитель: Веташенко Олег Георгиевич
Рубрика: Физика
Опубликовано в
Юный учёный
№2 (32) февраль 2020 г.
Дата публикации: 04.02.2020 2020-02-04
Статья просмотрена: 2320 раз
Скачать электронную версию
Библиографическое описание:Шумейко, А. В. Силы, действующие в простом механизме блок / А. В. Шумейко, О. Г. Веташенко. — Текст : непосредственный // Юный ученый. — 2020. — № 2 (32). — С. 38-42. — URL: https://moluch.ru/young/archive/32/1875/ (дата обращения: 18.09.2022).
В учебниках физики для 7 класса при изложении материала о подъёме груза простым механизмом блок авторы учебников рассматривают разное количество сил, действующих на блок или трос. Для выяснения, что за силы и на какие предметы они действуют в простом механизме блок при подъёме груза, и написана эта статья.
Ключевые слова: неподвижный блок, подвижный блок, сила упругости троса, сила трения.
В учебнике физики для 7 класса автора А. В. Пёрышкина на рис.177 нарисован подъём груза простым механизмом неподвижный блок и на рис.178 силы F 1 и F 2 действуют на блок в точках А и В , а в учебнике О. Ф. Кабардина на рис.22.3 нарисован неподвижный блок, с тросом и сила F действует на трос, а сила тяжести mg действует на груз.
То же самое происходит и в изложении материала о подвижном блоке: в учебнике А. В. Пёрышкина рис.179, на блок действуют две силы Р и F рис.180, а в учебнике О. Ф. Кабардина на том же самом подвижном блоке три силы: сила тяжести mg на грузе и две силы F натяжения троса рис. 22.4.
22.4.
Выяснение сил, действующих в простом механизме блок, начнём с неподвижного блока, изображенного на рис.1. Груз висит на одном из концов троса, далее трос огибает верхнюю полуокружность блока и за второй конец троса происходит подъём груза. На груз действует сила притяжения Земли F тяж г , которая направлена вертикально вниз. Под действием силы тяжести груза в тросу возникает сила упругости F упр т , направленная по тросу и одинаковая по всей длине троса рис.2.
Рис.1. Рис.2. Рис.3. Рис.4.
На рис.3 трос огибает верхнюю полуокружность блока и по всей длине этой полуокружности действуют силы тяжести: груза и троса, а также сила необходимая для подъёма груза. При сложении всех этих параллельных сил равнодействующая сила тяжести F тяж б приложена к центру блока и направлена вертикально вниз, одновременно создавая силу упругости обоймы блока F упр б , направленную по обойме блока вверх. На рис.4, при подъёме груза, трос движется по верхней полуокружности вращая блок и создавая силу трения скольжения F тр между тросом и блоком.
На рис.4, при подъёме груза, трос движется по верхней полуокружности вращая блок и создавая силу трения скольжения F тр между тросом и блоком.
На рис.5 для определения силы, необходимой для поднятия груза, уберём силу тяжести блока F тяж б и силу упругости блока F упр б , так как они не влияют на величину силы поднятия груза . Остались три силы: сила тяжести груза F тяж г , сила упругости троса F упр т и сила трения F тр . Вспомним, что в покое или при равномерном подъёме сила упругости троса равна силе тяжести груза F упр т = F тяж г , а сила трения F тр препятствует подъёму. Поэтому для равномерного подъёма груза необходима сила F п, равная сумме сил упругости троса и силы трения F п = F упр т + F тр . Это равенство справедливо для поднятия груза полной силой , а на рис.142 в Элементарном учебнике физики под редакцией академика Л. Г. Ландсберга маляры и альпинисты поднимают себя половинной силой .
Поэтому для равномерного подъёма груза необходима сила F п, равная сумме сил упругости троса и силы трения F п = F упр т + F тр . Это равенство справедливо для поднятия груза полной силой , а на рис.142 в Элементарном учебнике физики под редакцией академика Л. Г. Ландсберга маляры и альпинисты поднимают себя половинной силой .
Рис. 5.Рис. 142Рис. 6Рис. 7
На рис.142 человек сидит на сидении, которое прикреплено к тросу, огибающему верхнюю часть неподвижного блока, за второй конец троса человек руками поднимает себя. На рис.6 нарисуем действующие силы подъёма человека. Земля притягивает человека, поэтому на сидение действует половина веса тела человека Р ч, вторая половина веса приходится на руки, которые производят подъём человека. Под действием деления веса человека в тросу возникают силы упругости F упр 1 и F упр 2 , каждая из которых будет в 2 раза меньше веса человека F упр = Р ч. Наглядно это можно представить как на рис.7, груз поднимают за два независимых троса, и вес груза разделится между тросами, и сила упругости каждого троса будет в два раза меньше веса груза. F упр = Р г .
Под действием деления веса человека в тросу возникают силы упругости F упр 1 и F упр 2 , каждая из которых будет в 2 раза меньше веса человека F упр = Р ч. Наглядно это можно представить как на рис.7, груз поднимают за два независимых троса, и вес груза разделится между тросами, и сила упругости каждого троса будет в два раза меньше веса груза. F упр = Р г .
Подведём итог по силам, действующим на неподвижном блоке:
- Сила необходимая для подъёма груза на неподвижном блоке равна сумме силы упругости троса и силе трения F п = F упр + F тр .

- Величина силы упругости троса зависит от способа крепления поднимаемого груза. Если груз закреплён за один из концов троса (за одну ветвь троса) то сила упругости равна весу груза F упр = Р г , а если груз закреплён за оба конца троса (за две ветви троса) то сила упругости равна половине веса груза F упр = Р г . Выигрыш в силе в 2 раза при подъёме груза половинной силой с помощью неподвижного блока даёт трос, а не неподвижный блок.
- На рис.178 неподвижный блок нельзя рассматривать как равноплечий рычаг из-за того, что при изменении направления действия силы F 2 меняется длина рычага ОВ на рис.
 8 (видоизменённом рис.178).
8 (видоизменённом рис.178).
Рис. 178.Рис. 8.
Рассмотрим силы, действующие на подвижный блок рис.9. Груз висит на подвижном блоке, который своей нижней полуокружностью висит на тросу, один конец этого троса закреплён, а подъём подвижного блока с грузом происходит за второй конец троса. На рис.10 обозначим действующие силы на подвижный блок: Земля притягивает груз висящий на подвижном блоке и поэтому в центре подвижного блока действует сила веса груза Р г, а на концах троса силы упругости F упр 1 и F упр 2 , каждая из которых в 2 раза меньше веса груза из-за того, что вес груза распределился поровну между концами (ветвями) троса, как будто груз висит на двух отдельных тросах рис.11.
Рис. 9.Рис.10.Рис.11.Рис. 12.
12.
При подъёме груза блок будет вращаться и создавать силу трения скольжения между подвижным блоком и тросом рис.12, из которого видно, что поднимая груз за один конец троса мы прикладываем силу упругости (которая в 2 раза меньше веса груза) и силу трения F п = F упр 2 + F тр . Выигрыш в силе в 2 раза даёт трос, а не подвижный блок и это можно проверить с помощью рис.181 из учебника А. В. Пёрышкина, на котором нарисован неподвижный блок, который не даёт выигрыша в силе и подвижный блок — дающий выигрыш в силе в 2 раза. Общий выигрыш в силе этой комбинации блоков при подъёме груза 2 раза.
Рис.181. Выигрыш в силе 2 разаРис.13 (изменённый рис.181). Выигрыш в силе 3 раза.
Выигрыш в силе 2 разаРис.13 (изменённый рис.181). Выигрыш в силе 3 раза.
Если в этот рисунок добавить еще один неподвижный блок (не дающий выигрыш в силе) и закрепить конец троса за груз рис.13 (изменённый рис.181), то выигрыш в силе данной комбинации блоков при подъёме груза будет равен трем, потому что вес груза разделится на три части, так как висит на трёх частях (ветвях) троса. Отсюда следует, что доказательство в учебнике А. В. Пёрышкина о том, что неподвижный блок не даёт выигрыша в силе, а подвижный блок даёт выигрыш в силе является ошибочным, так как выигрыш в силе при подъёме груза на простом механизме блок даёт сила упругости троса (верёвки, цепи), а модуль выигрыша равен количеству частей (ветвей) троса, на которых висит груз, так как вес груза делится на их количество.
Литература:
- Кабардин О. Ф. Физика. 7 класс: учеб.
 для общеобразоват. организаций /О. Ф. Кабардин, — 6-е изд. — М.: Просвещение, 2018, — 174 с.: ил. — ISBN 978–5–09–060739–1.
для общеобразоват. организаций /О. Ф. Кабардин, — 6-е изд. — М.: Просвещение, 2018, — 174 с.: ил. — ISBN 978–5–09–060739–1. - Ландсберг Г. С.(ред). Элементарный учебник физики, том 1. Механика. Теплота. Молекулярная физика. М. Наука 1985 г.
- Пёрышкин А. В. Физика 7 кл.; учебник / А. В. Пёрышкин, — 9-е изд., пер. — М.: Дрофа, 2019, — 224 с.: ил. ISВN 978–5–358–09796–4.
Основные термины (генерируются автоматически): неподвижный блок, подъем груза, сила, вес груза, трос, конец троса, подвижной блок, подвижный блок, сила трения, сила упругости.
Ключевые слова
неподвижный блок, подвижный блок, сила упругости троса, сила трениянеподвижный блок, подвижный блок, сила упругости троса, сила трения
Похожие статьи
Современный взгляд на простой механизм «
блок», изучаемый по. ..
..Ключевые слова: блок, двойной блок, неподвижный блок, подвижный блок, полиспаст. Сначала ознакомимся и сравним как получают
На рис. 4 груз закреплён на одном конце троса и если поднимать груз за другой конец троса, то для подъёма этого груза потребуется сила…
Переименование и исключение
силы упругости в учебниках…Ключевые слова: сила упругости, сила натяжения, сила нормальной реакции, половинная сила, неподвижный блок, подвижный блок.
Внимательно смотрим на рис. 179 и видим, что груз висит на оси подвижного блока и вес груза действует на колесо блока деформируя его…
179 и видим, что груз висит на оси подвижного блока и вес груза действует на колесо блока деформируя его…
Ошибки в учебниках физики для 7 класса при изучении механизма…
Ключевые слова: блок, рычаг, подвижный блок, ось вращения, сила упругости троса. Рисунки физических моделей подвижного блока из 6
Вывод: В учебниках, где выигрыш в силе в 2 раза подвижным блоком при подъёме груза доказывается с помощью рычага второго рода…
«Вечный двигатель» в учебниках физики для 7 класса
В подвижном блоке при подъёме груза существует сила упругости колеса блока и сила упругости подвеса, на котором висит подвижный блок с грузом и если анализировать работу подвижного блока с учётом этих сил упругости, то о представлении подвижного блока как. ..
..
Демонстрация
веса тела и состояния его невесомости с помощью…подъёме груза [1, с.182]. Опыт № 2 начнём с крепления динамометров на концы троса, на который повесим подвижный блок с грузом весом 102 г, что соответствует силе тяжести 1 Н. Один из концов троса закрепим на подвесе…
Конспект урока по физике для 7 класса по теме «
Сила трения»Вид урока: комбинированный урок с использованием игровых и ИКТ технологий. Тип урока: систематизации и обобщения знаний и умений. Технология: личностно-ориентированная, информационно-коммуникативная, исследовательская деятельность.
«Наглядные» задачи в процессе обучения физике
Найти работу равнодействующей всех сил, действующих на брусок с грузом при перемещении бруска на 20 см. Задача: На рисунке 2 изображена установка для исследования
Задача: На рисунке 2 изображена установка для исследования
Зависимость упругости р насыщающих паров воды от абсолютной температуры Т. Т, К.
Равновесие: определение, виды, примеры | Статья в журнале…
Равновесие — это комплекс сил, которые действуя на одну систему, компенсируют друг друга и система не получает ускорение.
При небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю.
Летательные аппараты нетрадиционных схем | Статья в журнале…
В результате уменьшается подъемная сила всего самолета, причем потери в подъемной силе особенно велики на режимах взлета и посадки.
В этом случае переднее горизонтальное оперение (ПГО), состоящее обычно из неподвижных (стабилизаторы) и подвижных (рули…
- Как издать спецвыпуск?
- Правила оформления статей
- Оплата и скидки
Похожие статьи
Современный взгляд на простой механизм «
блок», изучаемый по. ..
..Ключевые слова: блок, двойной блок, неподвижный блок, подвижный блок, полиспаст. Сначала ознакомимся и сравним как получают
На рис. 4 груз закреплён на одном конце троса и если поднимать груз за другой конец троса, то для подъёма этого груза потребуется сила…
Переименование и исключение
силы упругости в учебниках…Ключевые слова: сила упругости, сила натяжения, сила нормальной реакции, половинная сила, неподвижный блок, подвижный блок.
Внимательно смотрим на рис. 179 и видим, что груз висит на оси подвижного блока и вес груза действует на колесо блока деформируя его…
179 и видим, что груз висит на оси подвижного блока и вес груза действует на колесо блока деформируя его…
Ошибки в учебниках физики для 7 класса при изучении механизма…
Ключевые слова: блок, рычаг, подвижный блок, ось вращения, сила упругости троса. Рисунки физических моделей подвижного блока из 6
Вывод: В учебниках, где выигрыш в силе в 2 раза подвижным блоком при подъёме груза доказывается с помощью рычага второго рода…
«Вечный двигатель» в учебниках физики для 7 класса
В подвижном блоке при подъёме груза существует сила упругости колеса блока и сила упругости подвеса, на котором висит подвижный блок с грузом и если анализировать работу подвижного блока с учётом этих сил упругости, то о представлении подвижного блока как. ..
..
Демонстрация
веса тела и состояния его невесомости с помощью…подъёме груза [1, с.182]. Опыт № 2 начнём с крепления динамометров на концы троса, на который повесим подвижный блок с грузом весом 102 г, что соответствует силе тяжести 1 Н. Один из концов троса закрепим на подвесе…
Конспект урока по физике для 7 класса по теме «
Сила трения»Вид урока: комбинированный урок с использованием игровых и ИКТ технологий. Тип урока: систематизации и обобщения знаний и умений. Технология: личностно-ориентированная, информационно-коммуникативная, исследовательская деятельность.
«Наглядные» задачи в процессе обучения физике
Найти работу равнодействующей всех сил, действующих на брусок с грузом при перемещении бруска на 20 см. Задача: На рисунке 2 изображена установка для исследования
Задача: На рисунке 2 изображена установка для исследования
Зависимость упругости р насыщающих паров воды от абсолютной температуры Т. Т, К.
Равновесие: определение, виды, примеры | Статья в журнале…
Равновесие — это комплекс сил, которые действуя на одну систему, компенсируют друг друга и система не получает ускорение.
При небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю.
Летательные аппараты нетрадиционных схем | Статья в журнале…
В результате уменьшается подъемная сила всего самолета, причем потери в подъемной силе особенно велики на режимах взлета и посадки.
В этом случае переднее горизонтальное оперение (ПГО), состоящее обычно из неподвижных (стабилизаторы) и подвижных (рули..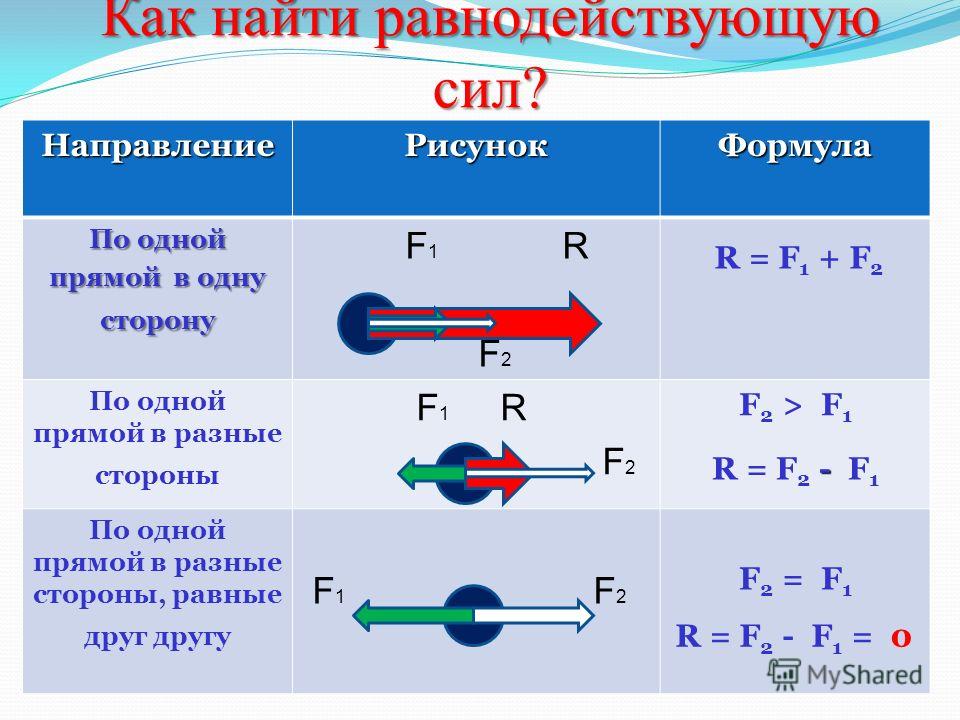 .
.
Формулы по физике
Механика
Давление Р=F/S
Плотность ρ=m/V
Давление на глубине жидкости P=ρ∙g∙h
Сила тяжести Fт=mg
Архимедова сила Fa=ρж∙g∙Vт
Уравнение движения при равноускоренном движении
X=X0+υ0∙t+(a∙t2)/2 S= (υ2–υ02)/2а S= (υ+υ0) ∙t /2
Уравнение скорости при равноускоренном движении υ=υ0+a∙t
Ускорение a=(υ–υ 0)/t
Скорость при движении по окружности υ=2πR/Т
Центростремительное ускорение a=υ2/R
Связь периода с частотой ν=1/T=ω/2π
II закон Ньютона F=ma
Закон Гука Fy=-kx
Закон Всемирного тяготения F=G∙M∙m/R2
Вес тела, движущегося с ускорением а↑ Р=m(g+a)
Вес тела, движущегося с ускорением а↓ Р=m(g-a)
Сила трения Fтр=µN
Импульс тела p=mυ
Импульс силы Ft=∆p
Момент силы M=F∙ℓ
Потенциальная энергия тела, поднятого над землей Eп=mgh
Потенциальная энергия упруго деформированного тела Eп=kx2/2
Кинетическая энергия тела Ek=mυ2/2
Работа A=F∙S∙cosα
Мощность N=A/t=F∙υ
Коэффициент полезного действия η=Aп/Аз
Период колебаний математического маятника T=2π√ℓ/g
Период колебаний пружинного маятника T=2 π √m/k
Уравнение гармонических колебаний Х=Хmax∙cos ωt
Связь длины волны, ее скорости и периода λ= υТ
Молекулярная физика и термодинамика
Количество вещества ν=N/ Na
Молярная масса М=m/ν
Cр.
 кин. энергия молекул одноатомного газа
Ek=3/2∙kT
кин. энергия молекул одноатомного газа
Ek=3/2∙kTОсновное уравнение МКТ P=nkT=1/3nm0υ2
Закон Гей – Люссака (изобарный процесс) V/T =const
Закон Шарля (изохорный процесс) P/T =const
Относительная влажность φ=P/P0∙100%
Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
Работа газа A=P∙ΔV
Закон Бойля – Мариотта (изотермический процесс) PV=const
Количество теплоты при нагревании Q=Cm(T2-T1)
Количество теплоты при плавлении Q=λm
Количество теплоты при парообразовании Q=Lm
Количество теплоты при сгорании топлива Q=qm
Уравнение состояния идеального газа PV=m/M∙RT
Первый закон термодинамики ΔU=A+Q
КПД тепловых двигателей η= (Q1 – Q2)/ Q1
КПД идеал.
 двигателей
(цикл Карно) η= (Т1 – Т2)/
Т1
двигателей
(цикл Карно) η= (Т1 – Т2)/
Т1
Электростатика и электродинамика
Закон Кулона F=k∙q1∙q2/R2
Напряженность электрического поля E=F/q
Напряженность эл. поля точечного заряда E=k∙q/R2
Поверхностная плотность зарядов σ = q/S
Напряженность эл. поля бесконечной плоскости E=2πkσ
Диэлектрическая проницаемость ε=E0/E
Потенциальная энергия взаимод. зарядов W= k∙q1q2/R
Потенциал φ=W/q
Потенциал точечного заряда φ=k∙q/R
Напряжение U=A/q
Для однородного электрического поля U=E∙d
Электроемкость C=q/U
Электроемкость плоского конденсатора C=S∙ε∙ε0/d
Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
Сила тока I=q/t
Сопротивление проводника R=ρ∙ℓ/S
Закон Ома для участка цепи I=U/R
Законы послед.
 соединения I1=I2=I,
U1+U2=U,
R1+R2=R
соединения I1=I2=I,
U1+U2=U,
R1+R2=RЗаконы паралл. соед. U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R
Мощность электрического тока P=I∙U
Закон Джоуля-Ленца Q=I2Rt
Закон Ома для полной цепи I=ε/(R+r)
Ток короткого замыкания (R=0) I=ε/r
Вектор магнитной индукции B=Fmax/ℓ∙I
Сила Ампера Fa=IBℓsin α
Сила Лоренца Fл=Bqυsin α
Магнитный поток Ф=BSсos α Ф=LI
Закон электромагнитной индукции Ei=ΔФ/Δt
ЭДС индукции в движ проводнике Ei=Вℓυsinα
ЭДС самоиндукции Esi=-L∙ΔI/Δt
Энергия магнитного поля катушки Wм=LI2/2
Период колебаний кол. контура T=2π ∙√LC
Индуктивное сопротивление XL=ωL=2πLν
Емкостное сопротивление Xc=1/ωC
Действующее значение силы тока Iд=Imax/√2,
Действующее значение напряжения Uд=Umax/√2
Полное сопротивление Z=√(Xc-XL)2+R2
Оптика
Закон преломления света n21=n2/n1= υ 1/ υ 2
Показатель преломления n21=sin α/sin γ
Формула тонкой линзы 1/F=1/d + 1/f
Оптическая сила линзы D=1/F
max интерференции: Δd=kλ,
min интерференции: Δd=(2k+1)λ/2
Диф.
 решетка
d∙sin
φ=k
λ
решетка
d∙sin
φ=k
λ
Квантовая физика
Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=Uзе
Красная граница фотоэффекта νк = Aвых/h
Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
Закон радиоактивного распада N=N0∙2–t/T
Энергия связи атомных ядер
ECB=(Zmp+Nmn-Mя)∙c2
СТО
t=t1/√1-υ2/c2
ℓ=ℓ0∙√1-υ2/c2
υ2=(υ1+υ)/1+ υ1∙υ/c2
Е = mс2
Азбука физики…
Нижний регистрационные буквы | Верхний чехол Буквы | NB всегда предшествует символу единицы | ||||||
| альфа | А = площадь А = нуклон число (атомная масса) а = ускорение а = Постоянная Вейна а = альфа-частица | а = атто | х 10 -18 | |||||
| бета | Б = плотность магнитного потока б = бета-частица | Б = звонок (сила звука) Бк = беккерель (активность) | ||||||
| х | С = емкость c = скорость света c = удельная теплоемкость | или С = градус Цельсия (температура) | с = | сантих 10 -2 | ||||
| дельта | д = диаметр d = расстояние D = расстояние от экрана бахрома узор D = поглощенная доза Δ = изменение δ = небольшое изменение | Д = диоптрия (сила линзы) дБ = децибел (сила звука) | д = деци да = дека (или дека) | х 10 -1 x 10 1 | ||||
| ε | e = заряд электрона Э = энергия E k = кинетическая энергия E = напряженность электрического поля E = Модуль Юнга ε = ЭДС ε = деформация растяжения ε o = диэлектрическая проницаемость свободного пространства | эВ = электрон-вольт (энергия) | Э = экса | х 10 18 | ||||
| фи | F = усилие f = частота f = фокусное расстояние f e = фокусное расстояние линзы окуляра f o = фокусное расстояние объектива Φ = поток φ = работа выхода | Ф = фарад (емкость) | ф = фемто | х 10 -15 | ||||
| гамма | г = напряженность гравитационного поля g = ускорение свободного падения G = гравитационная постоянная Г = проводимость γ = гамма-излучение | Гр = серый (поглощенная доза) | Г = гига | x 10 9 | ||||
| эта | h = высота ч = постоянная Планка H = эквивалент дозы> H = постоянная Хаббла Η = коэффициент вязкости | Гн = Генри (индуктивность) Гц = герц (частота) | ч = гекто | x 10 2 | ||||
| йота | I = ток I 0 = пиковый ток I = сила звука I = момент инерции | |||||||
| тета | Дж = плотность тока Дж = момент инерции Θ = угол | Дж = джоуль (энергия) | ||||||
| каппа | k = постоянная Больцмана k = жесткость пружины | K = кельвин (абсолютная температура) кг = килограмм (масса) | к = килограмм | x 10 3 | ||||
| лямбда | л = длина л = удельная скрытая теплота λ = длина волны λ = постоянная затухания L = собственная индуктивность L = угловой момент ln = натуральный логарифм log = логарифм с основанием 10 | л = литр (= 1000 см 3 ) – измерение объема | ||||||
| мю | м = масса М = увеличение мк = проницаемость μ = коэффициент трения | м = метр (длина) м 2 = метр в квадрате (площадь) м 3 = кубический метр (объем) | М = мега м = милли мк = микро | x 10 6 x 10 -3 x 10 -6 | ||||
| ну | N = номер N O = оригинальный номер Н А = постоянная Авогадро N = количество витков провода n = количество молей n= порядок дифракции n = количество носителей заряда на единицу объема n = показатель преломления | Н = ньютон (сила или вес) | н = нано | х 10 -9 | ||||
| омикрон |  | |||||||
| пи | Р = мощность р = давление р = импульс π = 3,14 | Па = паскаль (давление) | р = пико P = пета | х 10 -12 x 10 15 | ||||
В = заряд Q = тепло энергия Q = качество фактор | ||||||||
| ро | r = радиус R = сопротивление R = молярная газовая постоянная R = реактивная сила ρ = плотность ρ = удельное сопротивление рад = | радиан|||||||
| сигма | с = смещение (векторная версия расстояния) с = ширина щели σ = проводимость σ = растягивающее напряжение σ = постоянная Стефана Σ = сумма | с = секунда (время) Зв = зиверт (эквивалент дозы) S = Сименс (проводимость) | ||||||
| тау | т = время Т = температура T = период сигнала T 1/2 = период полураспада T E = эффективный период полураспада T B = период полураспада T P = физический период полураспада | T = тесла (плотность магнитного потока) | Т = тера | х 10 12 | ||||
| ипсилон | u = начальная скорость u = расстояние до изображения U = значение U U = внутреннее тепло системы | u = атомная единица массы (масса на атомном уровне) | ||||||
v = скорость v = конечная скорость (при использовании вместе с ‘u’) v = расстояние до изображения В = объем В = разность потенциалов В 0 = пиковое напряжение | В = вольт (электрический потенциал) | |||||||
| омега | Вт = выполненная работа ω = угловая скорость w = ширина бахромы | Ом = Ом (электрическое сопротивление) Вт = ватт (мощность) Wb =вебер (магнитный поток) | ||||||
| Чи | х = ширина X = реактивное сопротивление | |||||||
| и | г = рост | г = октябрь годаY = йотта | x 10 -24 x 10 24 | |||||
| дзета | z = глубина Z = номер протона (атомный номер) | г = зепто Z = дзета | х 10 -21 х 10 21 | |||||
NB А Кандидаты уровня должны: | ||||||||
LOJ ноябрь
1999 г.
пересмотренный 2021 г.
ньютоновская механика – Что означает $F=ma$? Значит ли это, что тело с массой $m$ будет иметь ускорение $a$, если к нему приложить внешнюю силу $F$?
спросил
Изменено 1 год, 7 месяцев назад
Просмотрено 239 раз
$\begingroup$
Я знаю, что это очень простой вопрос, но я только изучаю физику. Я вижу основы того, как блок на горизонтальной поверхности без трения ускоряется силой F в любом направлении. Тем не менее, я спрашиваю себя, используется ли F=ma только для объекта, к которому прикладывается сила, а не для источника силы (который может быть пальцем, другим блоком или чем-либо, что толкает)
Можно ли использовать F=ma, чтобы вычислить силу, которую объект массой M будет производить сам по себе, если он уже имеет ускорение. Заранее спасибо за полезные ответы
Заранее спасибо за полезные ответы
- ньютоновская механика
- силы
- масса
- ускорение
$\endgroup$
$\begingroup$
Замечательно, что вы задаете концептуальные вопросы, а не просто используете формулы.
Значит ли это, что тело массой М будет иметь ускорение а, если к нему приложить внешнюю силу?
Да.
Однако я задаюсь вопросом, применяется ли F=ma только к объекту, к которому прикладывается сила, а не к источнику силы (которым может быть палец, другой блок или что-либо, что толкает)
Верно, он используется только таким образом, а не для источника.
Можно ли использовать F=ma, чтобы вычислить силу, которую объект массой M произвел бы сам по себе, если бы он уже имел ускорение.
№
(1) Нет смысла говорить о том, что объект уже имеет ускорение. Когда мы говорим о том, что объект уже имеет, мы описываем его текущее состояние. Его состояние — это информация, которую, если бы объект оставили в покое, мы впоследствии смогли бы реконструировать. Он сохраняет информацию о своем положении (x) и скорости (v). Он не сохраняет информацию об ускорениях. Например, если я вижу хоккейную шайбу, скользящую по льду, я могу увидеть ее текущие x и v, а также могу реконструировать ее прошлые x и v, возвращаясь назад во времени, пока ее не трогали. Я ничего не могу восстановить о его прошлых ускорениях.
Когда мы говорим о том, что объект уже имеет, мы описываем его текущее состояние. Его состояние — это информация, которую, если бы объект оставили в покое, мы впоследствии смогли бы реконструировать. Он сохраняет информацию о своем положении (x) и скорости (v). Он не сохраняет информацию об ускорениях. Например, если я вижу хоккейную шайбу, скользящую по льду, я могу увидеть ее текущие x и v, а также могу реконструировать ее прошлые x и v, возвращаясь назад во времени, пока ее не трогали. Я ничего не могу восстановить о его прошлых ускорениях.
(2) Сила — это всегда взаимодействие между двумя объектами, поэтому говорить о том, что объект сам по себе обладает силой, не имеет смысла.
$\endgroup$
2
$\begingroup$
Если объект уже имеет ускорение, то да на него действует ( всего ) сила, определяемая формулой
$$F=ма$$
Не имеет значения, откуда исходит сила: если общая действующая сила, независимо от происхождения, равна $F$, то ускорение объекта будет равно $ma$. Если на вас действует несколько сил одновременно (например, вы сталкиваетесь с другим человеком), то вам нужно сумма таких сил.
Если на вас действует несколько сил одновременно (например, вы сталкиваетесь с другим человеком), то вам нужно сумма таких сил.
Однако непонятно, что вы имеете в виду под “силой, созданной самой по себе”. Массы не «производят» силу сами по себе. Если у вас есть кусок какого-то материала, движущийся с ускорением $a$, то должна быть сила, толкающая его, это все, что вы знаете.
Если вы имеете в виду автомобиль, или мотор, или что-то, способное двигать предметы, то да, сила $F$ может быть связана с каким-то процессом, происходящим «внутри» объекта. Но то, что на самом деле толкает объект, обычно является силой реакции из-за третьего закона Ньютона (действие/противодействие): например, если вы идете, вы толкаете землю, а земля отталкивает вас назад. Таким образом, сила, которую вы должны учитывать, это сила , действующая на объект, а не сила, которую оказывает объект.
Некоторые примеры (все объекты в этих примерах имеют массу $m$):
объект падает с ускорением $a$.
. Тогда гравитация действует на объект с силой, определяемой выражением $F=ma$
Тогда гравитация действует на объект с силой, определяемой выражением $F=ma$вы толкаете объект с силой $F$ по поверхности с трением и замечаете, что объект движется с постоянной скоростью ($a=0$). Это означает, что трение противодействует силе $F-f$, точно такой же, как ваша, но в противоположном направлении, так что общая сила равна $F_{tot}=F-F_f=ma=0$
Автомобиль движется с ускорением $a$. Это означает, что автомобиль воздействует на землю через колеса так, что земля отвечает силой $F$.
Продолжая учиться, вы научитесь описывать все такие процессы, но итог этого ответа таков:
в $F=ma$ сила $F$ в этом уравнении относится к сумме всех сил. силы, действующие на объект
$\endgroup$
1
$\begingroup$
Тем не менее, я спрашиваю себя, используется ли F=ma только на объекте, сила которого применяется, а не к источнику силы (который может быть палец, другой блок или что-то, что толкает)
$F_{net}=ma$ — второй закон Ньютона. Третий закон Ньютона гласит, что объект, к которому приложена сила $F$, оказывает равную и противоположную силу $F$ на объект, применяющий эту силу (палец, другой блок или что-либо, что толкает). Воздействие на объект, применяющий силу, будет зависеть от чистой силы, которую он испытывает, в соответствии со вторым законом Ньютона, примененным к нему.
Третий закон Ньютона гласит, что объект, к которому приложена сила $F$, оказывает равную и противоположную силу $F$ на объект, применяющий эту силу (палец, другой блок или что-либо, что толкает). Воздействие на объект, применяющий силу, будет зависеть от чистой силы, которую он испытывает, в соответствии со вторым законом Ньютона, примененным к нему.
Можно ли использовать F=ma для вычисления силы объекта массой M произвел бы сам по себе, если бы у него уже было ускорение.
“… имел ускорение” означает, что объект массы M больше не ускоряется, то есть на него больше не действует результирующая сила, т. е. $F_{net}=0$. Следовательно, он продолжает двигаться со скоростью, которая была у него, когда сила была удалена, и, следовательно, не создает и не испытывает силы (при условии отсутствия трения или сопротивления воздуха). Однако такой объект может воздействовать на другой объект при столкновении с другим объектом.
Надеюсь, это поможет.
$\endgroup$
$\begingroup$
Ответы здесь уже замечательные, но вот небольшое предложение, которое я могу добавить: при изучении законов Ньютона, я думаю, легче начать с размышлений о втором законе Ньютона как о $$ а = \ гидроразрыва {F} {м} $$ Математически это то же самое, что и $F = ma$, но я заметил, что студенты склонны думать, что уравнение $X = Y$ означает, что $Y$ вызывает $X$ — вероятно, потому, что они привыкли подставляя значения в правую сторону чтобы получить значение на левой стороне Я думаю, именно это стоит за вашим вопросом о том, означает ли $F=ma$, что масса с ускорением может генерировать силу. Однако это неправильный причинно-следственный порядок; это сила, которая вызывает ускорение. Крайне важно помнить об этом и быть знакомым с ним при решении задач, и представление о законе как $a = F/m$ может помочь в этом.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
| любой символ¯любой символ¯ | среднее (обозначается чертой над символом — например, v¯v¯ — средняя скорость) |
| °С°С | Градусов Цельсия |
| °F°F | 9 градусов по Фаренгейту0009 |
| //// | параллельный |
| ⊥⊥ | перпендикулярно |
| ∝∝ | пропорционально |
| ±± | плюс-минус |
| 00 | ноль в качестве нижнего индекса обозначает начальное значение |
| αα | альфа-лучи |
| αα | угловое ускорение |
| αα | температурный коэффициент(ы) удельного сопротивления |
| ββ | бета-лучи |
| ββ | уровень звука |
| ββ | объемный коэффициент расширения |
| β-β- | электронов, испускаемых при ядерном бета-распаде |
| β+β+ | позитронный распад |
| γγ | гамма-лучи |
| γγ | поверхностное натяжение |
| γ=1/1−v2/c2γ=1/1−v2/c2 | константа, используемая в теории относительности |
| ΔΔ | изменение любого количества, следующего за |
| δδ | неопределенность в любой величине, следующей за |
| ΔЕΔЕ | изменение энергии между начальной и конечной орбитами электрона в атоме |
| ΔЕΔЕ | неопределенность в энергии |
| ΔmΔm | разница в массе между исходным и конечным продуктами |
| ΔNΔN | количество распадов |
| ΔpΔp | изменение импульса |
| ΔpΔp | неопределенность в импульсе |
| ΔPEgΔPEg | изменение потенциальной энергии гравитации |
| ΔθΔθ | угол поворота |
| ΔsΔs | расстояние, пройденное по круговой траектории |
| ΔtΔt | неопределенность во времени |
| Δt0Δt0 | собственное время, измеренное неподвижным наблюдателем относительно процесса |
| ΔVΔV | разность потенциалов |
| ΔxΔx | неопределенность в позиции |
| ε0ε0 | диэлектрическая проницаемость свободного пространства |
| ηη | вязкость|
| θθ | угол между вектором силы и вектором смещения |
| θθ | угол между двумя линиями |
| θθ | Угол контакта |
| θθ | направление результирующего |
| Угол Брюстера | |
| критический угол | |
| кк | диэлектрическая проницаемость |
| λλ | постоянная распада нуклида |
| λλ | длина волны|
| λnλn | длина волныв среде |
| μ0μ0 | проницаемость свободного пространства |
| мккк | коэффициент кинетического трения |
| мксмкс | коэффициент статического трения |
| веве | электронное нейтрино |
| п+п+ | положительный пион |
| π−π− | отрицательный пион |
| π0π0 | нейтральный пион |
| рр | плотность |
| ρcρc | критическая плотность, плотность, необходимая только для того, чтобы остановить универсальное расширение |
| ρflρfl | плотность жидкости |
| ρ¯objρ¯obj | средняя плотность объекта |
| ρ/ρwρ/ρw | удельный вес |
| ттт | характеристическая постоянная времени для цепи сопротивления и индуктивности (RL)(RL) или сопротивления и емкости (RC)(RC) |
| ттт | характеристическое время для цепи резистора и конденсатора (RC)(RC) |
| ттт | крутящий момент |
| йен | ипсилон-мезон |
| ФФ | магнитный поток |
| фф | фазовый угол |
| Ом | Ом (ед. ) ) |
| ωω | угловая скорость |
| АА | ампер (текущая единица измерения) |
| АА | район |
| АА | площадь поперечного сечения |
| АА | общее количество нуклонов |
| аа | ускорение |
| аБаБ | Боровский радиус |
| акак | центростремительное ускорение |
| номер | тангенциальное ускорение |
| АСАС | переменный ток |
| АМАМ | амплитудная модуляция |
| атматм | атмосфера |
| ББ | барионное число |
| ББ | синий кварк цвет |
| Б¯Б¯ | антисиний (желтый) антикварковый цвет |
| бб | дно со вкусом творога или красотка |
| ББ | объемный модуль |
| ББ | напряженность магнитного поля |
| БинтБинт | собственное магнитное поле электрона |
| БорбБорб | орбитальное магнитное поле |
| БЕБЕ | энергия связи ядра — это энергия, необходимая для его полной разборки на отдельные протоны и нейтроны |
| ВЕ/АБЭ/А | энергии связи на нуклон |
| БкБк | беккерелей — один распад в секунду |
| СС | емкость (количество заряда на вольт) |
| СС | кулон (основная единица заряда в системе СИ) |
| CPCP | общая емкость параллельно |
| КСК | общая емкость в серии |
| CGCG | центр тяжести |
| СМСМ | центр масс |
| копия | Шарм со вкусом творога |
| копия | удельная теплоемкость |
| копия | скорость света |
| Калкал | килокалорий |
| известковый | калорий |
| COPhCOPhp | КПД теплового насоса |
| COPrefCOPref | КПД холодильников и кондиционеров |
| cosθcosθ | косинус |
| детская кроватка | котангенс |
| cscθcscθ | косеканс |
| ДД | константа диффузии |
| дд | рабочий объем |
| дд | творог со вкусом пуха |
| дБдБ | децибел |
| диди | расстояние изображения от центра объектива |
| додо | расстояние объекта от центра линзы |
| DCDC | постоянный ток |
| ЕЕ | напряженность электрического поля |
| εε | ЭДС (напряжение) или ЭДС Холла |
| эмфемф | электродвижущая сила |
| ЕЕ | энергия одного фотона |
| ЕЕ | энергия ядерной реакции |
| ЕЕ | релятивистская полная энергия |
| ЕЕ | общая энергия |
| E0E0 | энергия основного состояния для водорода |
| E0E0 | энергия покоя |
| ЕСЕС | электронный захват |
| ЭкапЭкап | энергия, запасенная в конденсаторе |
| ЭффЭфф | КПД — выход полезной работы, деленный на подводимую энергию | .
| EffCEffC | Эффективность Карно |
| ЭйнЭйн | потребляемая энергия (пища переваривается человеком) |
| ЭйндЭйнд | энергия, запасенная в катушке индуктивности |
| EoutEout | выход энергии |
| ее | коэффициент излучения объекта |
| е+е+ | антиэлектрон или позитрон |
| эВэВ | электрон-вольт |
| ФФ | фарад (единица измерения емкости, кулон на вольт) |
| ФФ | фокус объектива |
| ФФ | сила |
| ФФ | величина силы |
| ФФ | восстанавливающая сила |
| ФБФБ | выталкивающая сила |
| FcFc | центростремительная сила |
| Фифи | принудительный ввод |
| ФнетФнет | чистая сила |
| ФоФо | силовой выход |
| ФМФМ | частотная модуляция |
| иф | фокусное расстояние |
| иф | частота |
| f0f0 | резонансная частота последовательной цепи сопротивления, индуктивности и емкости (RLC)(RLC) |
| f0f0 | пороговая частота для конкретного материала (фотоэффект) |
| f1f1 | основной |
| f2f2 | первый обертон |
| f3f3 | второй обертон |
| фбфб | частота ударов |
| фкфк | величина кинетического трения |
| фсфс | величина статического трения |
| ГГ | гравитационная постоянная |
| ГГ | зеленый кварк цвет |
| Г¯Г¯ | антизеленый (пурпурный) антикварковый цвет |
| гг | ускорение свободного падения |
| гг | глюоны (частицы-носители сильного ядерного взаимодействия) |
| чч | изменение вертикального положения |
| чч | высота над некоторой контрольной точкой |
| чч | максимальная высота снаряда |
| чч | постоянная Планка |
| хфхф | энергия фотона |
| привет | высота изображения |
| хохо | высота объекта |
| II | электрический ток |
| II | интенсивность |
| II | интенсивность прошедшей волны |
| II | момент инерции (также называемый вращательной инерцией) |
| I0I0 | интенсивность поляризованной волны перед прохождением через фильтр |
| средняя интенсивность непрерывной синусоидальной электромагнитной волны | |
| ИрмсИрмс | средний ток |
| JJ | джоулей |
| Дж/ΨДж/Ψ | Джоули/пси-мезон |
| КК | кельвин |
| кк | постоянная Больцмана |
| кк | силовая постоянная пружины |
| КаКа | рентгеновских лучей, возникающих при падении электрона на вакансию оболочки n=1n=1 из оболочки n=3n=3 |
| KβKβ | рентгеновских лучей, возникающих при падении электрона на вакансию оболочки n=2n=2 из оболочки n=3n=3 |
| ккалкал | килокалорий |
| КЕКЕ | поступательная кинетическая энергия |
| КЭ + ПЭКЕ + ПЭ | механическая энергия |
| КЕИКЕ | кинетическая энергия выбитого электрона |
| KErelKErel | релятивистская кинетическая энергия |
| KErotKErot | вращательная кинетическая энергия |
| КЕ¯КЕ¯ | тепловая энергия |
| кгкг | килограмм (основная единица массы в системе СИ) |
| ЛЛ | угловой момент |
| ЛЛ | литр |
| ЛЛ | величина углового момента |
| ЛЛ | самоиндукция |
| ℓℓ | угловой момент импульса квантовое число |
| Лала | рентгеновских лучей, возникающих при падении электрона на оболочку n=2n=2 |
| ЛеЛе | электрон общий семейный номер |
| LмкLмк | семейство мюонов общее количество |
| LτLτ | общее количество членов семьи тау |
| LfLf | теплота плавления |
| Lf и LvLf и Lv | коэффициенты скрытой теплоты |
| ЛорбЛорб | орбитальный угловой момент |
| LsLs | теплота сублимации |
| Уровень | теплота парообразования |
| ЛзЛз | z – составляющая углового момента |
| ММ | угловое увеличение |
| ММ | взаимная индуктивность |
| мм | указывает на метастабильное состояние |
| мм | увеличение |
| мм | масса |
| мм | масса объекта, измеренная покоящимся человеком относительно объекта |
| мм | метр (основная единица длины в системе СИ) |
| мм | приказ о вмешательстве |
| мм | общее увеличение (произведение отдельных увеличений) |
| МАКСМАКС | атомная масса нуклида |
| МАМА | механическое преимущество |
| мем | увеличение окуляра |
| мем | масса электрона |
| мℓмℓ | квантовое число проекции углового момента |
| минмн | масса нейтрона |
| момо | увеличение объектива |
| молмол | моль |
| пмп | масса протона |
| смс | квантовое число проекции спина |
| NN | величина нормальной силы |
| NN | ньютон |
| NN | нормальное усилие |
| NN | количество нейтронов |
| № | показатель преломления |
| № | количество бесплатных сборов на единицу объема |
| НАНА | Номер Авогадро |
| №№ | Номер Рейнольдса |
| Н⋅мН⋅м | ньютон-метр (единица работы-энергии) |
| Н⋅мН⋅м | ньютонов на метр (единица крутящего момента в СИ) |
| ОЕОЕ | прочая энергия |
| ПП | сила |
| ПП | сила линзы |
| ПП | давление |
| стр | импульс |
| стр | магнитуда импульса |
| стр | релятивистский импульс |
| пттоптот | общий импульс |
| птот’птот | общий импульс некоторое время спустя |
| ПабсПабс | абсолютное давление |
| PatmPatm | атмосферное давление |
| PatmPatm | стандартное атмосферное давление |
| ПЕПЕ | потенциальная энергия |
| PEelPEel | упругая потенциальная энергия |
| PEelecPEelec | электрическая потенциальная энергия |
| ПЭСП | потенциальная энергия пружины |
| ПГГ | манометрическое давление |
| ПинПин | потребляемая мощность или вход |
| выходная полезная мощность, превращающаяся в полезную работу или желаемую форму энергии | |
| скрытая теплота | |
| полезное тепло, переданное в систему | |
| расход — объем в единицу времени, протекающий через точку | .|
| +Q+Q | положительный заряд |
| −Q−Q | отрицательный заряд |
| кв | заряд электрона |
| qpqp | заряд протона |
| кв | испытательный заряд |
| QFQF | добротность |
| руб. | активность, скорость распада |
| руб. | радиус кривизны сферического зеркала |
| 9 руб.0009 | красный кварк цвет |
| Р¯Р¯ | антикрасный (голубой) кварковый цвет |
| руб. | сопротивление |
| руб. | Результирующее или полное водоизмещение |
| руб. | постоянная Ридберга |
| 9 руб.0009 | универсальная газовая постоянная |
| руб. | расстояние от точки вращения до точки приложения силы |
| руб. | внутреннее сопротивление |
| р⊥р⊥ | перпендикулярный рычаг |
| руб. | радиус ядра |
| руб. | радиус кривизны |
| руб. | удельное сопротивление |
| р или радр или рад | Единица дозы облучения |
| ремрем | рентген эквивалент человека |
| радрад | радиан |
| РБЕРБЕ | относительная биологическая эффективность |
| РЦКР | резистор и конденсатор схема |
| СКРМ | среднеквадратичное значение |
| ррн | радиус n -й орбиты H-атома |
| рупий | полное сопротивление параллельного соединения |
| рупий | полное сопротивление последовательного соединения |
| рупий | Радиус Шварцшильда |
| СС | энтропия |
| СС | собственный спин (собственный угловой момент) |
| СС | величина собственного (внутреннего) спинового углового момента |
| СС | модуль сдвига |
| СС | квантовое число странности |
| СС | вкус творога странный |
| СС | секунд (основная единица времени СИ) |
| СС | спин квантовое число |
| СС | полное водоизмещение |
| сек | секанс |
| sinθsinθ | синус |
| сзз | z -компонент спинового углового момента |
| ТТ | период — время совершения одного колебания |
| ТТ | температура |
| ТкТк | критическая температура — температура, ниже которой материал становится сверхпроводником |
| ТТ | натяжение |
| ТТ | тесла (напряженность магнитного поля B ) |
| тт | Топ со вкусом творога или правда |
| тт | время |
| т1/2т1/2 | Период полураспада— время, за которое распадается половина исходных ядер |
| tanθtanθ | тангенс |
| УУ | внутренняя энергия |
| уу | вкус творога до |
| уу | единая атомная единица массы |
| уу | скорость объекта относительно наблюдателя |
| у’у’ | скорость относительно другого наблюдателя |
| ВВ | электрический потенциал |
| ВВ | клеммное напряжение |
| ВВ | вольт (ед. ) ) |
| ВВ | том |
| вв | относительная скорость между двумя наблюдателями |
| вв | скорость света в материале |
| вв | скорость |
| в¯в¯ | средняя скорость жидкости |
| ВБ-ВАВБ-ВА | изменение потенциала |
| вдвд | скорость дрейфа |
| ВпВп | трансформатор входного напряжения |
| VrmsVrms | среднеквадратичное значение напряжения |
| ВсВс | Трансформатор выходного напряжения |
| втотвот | общая скорость |
| вввв | скорость распространения звука или другой волны |
| вввв | скорость волны |
| WW | работа |
| 9 мировая война0009 | чистая работа, выполненная системой |
| WW | Вт |
| вв | вес |
| вфлвфл | вес жидкости, вытесненной объектом |
| туалет | общая работа, проделанная всеми консервативными силами |
| ВнкВнк | общая работа, выполненная всеми неконсервативными силами |
| полезный результат работы | |
| ХХ | амплитуда |
| ХХ | символ элемента |
| AZXNAZXN | обозначение конкретного нуклида |
| хх | деформация или смещение от равновесия |
| хх | смещение пружины из недеформированного положения |
| хх | горизонтальная ось |
| ССХС | емкостное реактивное сопротивление |
| XLXL | индуктивное сопротивление |
| ксрмксрмс | среднеквадратичное расстояние диффузии |
| год | вертикальная ось |
| ГГ | модуль упругостиили модуль Юнга |
| ЗЗ | атомный номер (количество протонов в ядре) |
| ЗЗ | импеданс |
Сила и мощность – разница и сравнение
Понятия сила и мощность , похоже, имеют схожие значения и часто путаются друг с другом. Но в физике они не взаимозаменяемы. Сила — это фундаментальный результат взаимодействия двух объектов, а мощность — это выражение потребляемой во времени энергии (работы), элементом которой является сила. Силу и мощность можно и описать, и измерить, но сила — это реальный физический феномен, а сила сама по себе — нет.
Но в физике они не взаимозаменяемы. Сила — это фундаментальный результат взаимодействия двух объектов, а мощность — это выражение потребляемой во времени энергии (работы), элементом которой является сила. Силу и мощность можно и описать, и измерить, но сила — это реальный физический феномен, а сила сама по себе — нет.
Сравнительная таблица
| Сила | Мощность | |
|---|---|---|
| Определение | Толчок или притяжение в результате взаимодействия между объектами. | Мощность — это скорость выполнения работы или передачи энергии. |
| Блок | ньютонов | ватт = | джоулей в секунду
| Символ | F | Р |
| Назван в честь | Исаака Ньютона | Джеймс Ватт |
| Производные от других величин | F = m a (сила = масса, умноженная на ускорение) | P = Вт/т (мощность = работа, деленная на время) |
| Отношение к «Работе» | Сила, приложенная на расстоянии, создает работу. | Скорость выполнения работы. |
| Повседневный пример | Гравитация, трение, магнетизм. | лошадиных сил (1 лошадиная сила = 750 Вт). |
Основная концепция
Сила может возникнуть только при взаимодействии объектов. Всякий раз, когда объекты взаимодействуют, они толкают или притягивают друг друга, будь то прямой контакт или контакт на расстоянии. Примеры сил прямого контакта включают трение автомобильных шин о дорогу или сопротивление воздуха движущемуся автомобилю. Взаимодействие на расстоянии происходит за счет таких сил, как гравитация и магнетизм. Сила является фундаментальным выражением физических событий, так же как время и расстояние.
Мощность определяется как количество энергии, потребляемой в единицу времени. Другой способ выразить это так: скорость, с которой выполняется «работа». Работа происходит, когда есть сила, вызывающая движение объекта. Например, человек, прижимающийся к кирпичной стене, потребляет энергию, но не совершает никакой работы и не создает энергии, потому что стена не движется. Но если человек толкает стол и двигает его, то работа есть. Мощность показывает, насколько быстро выполняется эта работа.
Таким образом, сила является одним из элементов уравнения мощности, наряду с другими основными элементами, такими как расстояние и время.
Например, человек, прижимающийся к кирпичной стене, потребляет энергию, но не совершает никакой работы и не создает энергии, потому что стена не движется. Но если человек толкает стол и двигает его, то работа есть. Мощность показывает, насколько быстро выполняется эта работа.
Таким образом, сила является одним из элементов уравнения мощности, наряду с другими основными элементами, такими как расстояние и время.
Формулы
Сила рассчитывается как произведение массы и ускорения свободного падения и обычно обозначается как
где F — сила, м — масса и a — ускорение свободного падения.
В качестве скорости изменения выполненной работы или энергии подсистемы мощность рассчитывается как:
где P мощность, Вт работа и т 904:10 время.
Пример
Сила присуща взаимодействию любых и всех объектов. Когда бейсболист ударяет по мячу, бита действует на мяч (и наоборот). Планеты вращаются вокруг Солнца из-за силы. Чтобы рассчитать силу в ньютонах бейсбольного мяча весом 146 г, вы просто умножаете массу (в килограммах, то есть 0,146) на ускорение (земное притяжение составляет 9,8 метра в секунду), что равняется 1,43 ньютона.
Планеты вращаются вокруг Солнца из-за силы. Чтобы рассчитать силу в ньютонах бейсбольного мяча весом 146 г, вы просто умножаете массу (в килограммах, то есть 0,146) на ускорение (земное притяжение составляет 9,8 метра в секунду), что равняется 1,43 ньютона.
Если человек бежит, а затем поднимается по одному и тому же лестничному пролету, оба раза выполняется один и тот же объем работы, но во время бега вырабатывается больше энергии, поскольку тот же объем работы выполняется за меньшее время.
Единицы измерения
В научных приложениях сила измеряется в ньютонах, а в английской системе она выражается в фунтах. Единицей силы в системе СИ является ньютон (Н). Один ньютон — это сила, необходимая для ускорения массы в один килограмм со скоростью один метр в секунду в квадрате, или кг·м·с−2. Один ньютон равен 100 000 дин.
Единицей мощности в системе СИ является ватт (Вт). Один ватт равен одному джоулю в секунду, где джоуль — единица измерения энергии. Это стандартная единица измерения, но мощность может быть выражена любым способом энергии во времени. Другим распространенным выражением мощности является лошадиная сила, где 1 лошадиная сила равна 746 Вт.
Другим распространенным выражением мощности является лошадиная сила, где 1 лошадиная сила равна 746 Вт.
Ученые-тезки
Силы вызывают ускорение (изменение скорости). Стандартная единица силы была названа в честь Исаака Ньютона в честь его 2-го закона, который гласит: «Ускорение объекта прямо пропорционально приложенной силе…». 1 ньютон — это сила, необходимая для ускорения массы 1 килограмм со скоростью 1 метр в секунду.
Джеймс Уатт был шотландским изобретателем и инженером. Уатт создал единицу измерения лошадиных сил, чтобы объяснить увеличение мощности своего парового двигателя. Из-за его большого вклада в повышение эффективности паровых двигателей научное сообщество решило почтить его память, назвав в его честь единицу мощности. Ватт был добавлен в СИ как единица мощности в 19 г.60.
Список литературы
- Сила и ее представление – Кабинет физики
- Определение и математика работы – Кабинет физики
- Мощность – Кабинет физики
- Википедия: Сила (физика)
- Как работают сила, мощность, крутящий момент и энергия — HowStuffWorks
- Википедия: Ватт
- Википедия: Джеймс Уатт
- Подписаться
- Поделиться
- Ссылка
- Авторов
Поделитесь этим сравнением:
Если вы дочитали до этого места, подписывайтесь на нас:
«Сила против власти». Diffen.com. Diffen LLC, nd Веб. 18 сентября 2022 г. < >
Diffen.com. Diffen LLC, nd Веб. 18 сентября 2022 г. < >
Физические символы — список физических символов и имен
В физике существует большое количество физических величин, которые мы учитываем при выполнении расчетов. Чтобы сделать их более удобными для пользователей, а также более простыми в использовании и запоминании, мы часто используем обозначения/символы для представления этих физических величин. Эти обозначения/символы, которые мы используем для представления физических величин при решении связанных с ними задач или для других целей, являются символами.
В физике все обозначается английским/греческим алфавитом, например, скорость света, длина волны, скорость и так далее.
Предположим, женщина едет на машине со скоростью 30 км/ч и добирается до родного города за 2 часа, а если она едет со скоростью 50 км/ч, то добирается за 1,5 часа. Итак, если нам нужно представить эти единицы в виде символов, как мы можем это сделать?
В этой статье вы найдете самые популярные физические символы, а также те, которые мы обычно используем в физике, с их названиями, типом величин и соответствующими единицами измерения в табличном формате.
Примеры физических символов
Кроме того, символы, используемые для физических величин, сильно различаются. Иногда символ может быть первой буквой физических величин, которые они представляют, например «d», что означает расстояние. В других случаях они могут быть совершенно не связаны с названием физических величин, например, c символизирует скорость света. Они также могут быть в виде греческих символов, таких как λ, что означает длину волны.
Ниже приведен подробный список наиболее часто используемых символов в физике с их единицами СИ. Обратите внимание, что один и тот же символ может относиться к нескольким величинам.
Symbols for Physical Quantities Related to Space and Time
Symbols | Quantity/ Coefficients | S.I. Unit | Physical Quantity (Scalar/Vector) | |
r | Радиус, радиус кривизны | Метр | Функции как скалярные, так и векторные | |
s | Displacement | Metre | Vector | |
d | Distance | Metre | Scalar | |
θ | Угловое смещение, | Радиан | Вектор | |
φ3 0009 | Угол поворота | Радиан | Уникально определенная величина и направление, но не векторная величина. (Does Not obey commutative law) | |
x, y, z | Cartesian Coordinates | Unitless | Scalar | |
î, ĵ, k̂ | Декартовы единичные векторы | Unitless | Vector | |
r, θ, φ | Spherical coordinates | Metre/Radian | Vector | |
r̂, θ̂, φ̂ | Сферические векторы | Unitless | Vector | |
R, θ, Z | CINDINDRCALINATS | .0009 | Metre/Radian | Scalar |
r̂, θ̂, ẑ | Cylindrical vectors | Unitless | Vector | |
n̂ | Normal вектор | Безразмерный | Вектор | |
t̂ | 3596 Unitless | Vector | ||
h | Height, Depth | Metre | Scalar | |
ℓ, L | Length | Metre | Scalar | |
T | Время | Second | Скалар | |
D (= 2 r) | Diameter | Metre | Scalar | |
C | Circumference | Metre | Scalar | |
A | Площадь | Квадратный метр | Функции как скалярные, так и векторные (аналогично вектору площади в формуле магнитного потока) | |
V | Volume | Cubic Metre (m3) | Scalar | |
τ | Time Constant | Second (s) | Scalar | |
T | Периодическое время | Second (S) | Scalar | 9 9336 | 90009 | 9 9336 | 90009 | 9336 3596 f | Frequency | 1/second or (1/s) | Scalar |
ω | Angular frequency | Rad/s | Scalar |
Ниже приведены некоторые символы, часто используемые в физике, с их названиями, типом величин и соответствующими единицами СИ в табличном формате.
Физические символы, относящиеся к механике
Symbols | Quantity/ Coefficients | S.I. Unit | Physical Quantity (Scalar/Vector) | ||||
v | Velocity, скорость | метр/сек (м/с) | Скорость = скаляр Скорость = вектор1336 Acceleration | metre/square second (m/s2) | Vector | ||
g | Acceleration due to gravity | metre/square second | Vector | ||||
ac | Центростремительное/центробежное ускорение | метр/кв. | m | Mass | Kilogram (kg) | Scalar | |
F | Force | Newton (N) | Vector | ||||
W/FG | Сила из -за гравитации/веса | Newton | Vector | ||||
FG/N | |||||||
FG/N | |||||||
.0009 | Normal force | N | Vector | ||||
Ff | Force of friction | N | Vector | ||||
µ | Коэффициент трения | Безразмерный | Скаляр | ||||
p | Импульс 93 | Kg. | Vector | ||||
J | Impulse | N/s | Vector | ||||
E | Energy | Joule (J) | Scalar | ||||
K | Kinetic energy | J | Scalar | ||||
U | Potential Energy | J | Scalar | ||||
Vg | Gravitational potential | J/kg | Scalar | ||||
η | Эффективность | Безразмерная | Скаляр | 9006 3 9006 90009 | Power | Watt | Scalar |
α | Rotational acceleration | Radian per second squared (Rad/s2) | Vector | ||||
ω | Скорость вращения | Рад/с | Вектор | ||||
N/m | Vector | ||||||
L | Angular momentum | Kilogram meter squared per second Kg. | Vector | ||||
ρ | Плотность Том Массовая плотность | к килограмму на кубический метр | Скалар | 99999999Scalar | 999999999999999999999. | ||
I | Moment of inertia | Kg.m2 | Scalar |
Physical Symbols Related to Fluid Mechanics
Symbols | Количество/Коэффициенты | Единица S.I.3596 λ | Linear mass density | kg/m | Scalar | |||||||||
σ | Area mass density | Kilogram per square meter (kg/m2) | Scalar | |||||||||||
FB, B | Blueancy | N | 9999 | 39999 | 999 | 99999 | 999 900399 | 999 900399 | 9000 | 9393999000 | 99999000 9000 9003 | Mass flow rate | kg/s | Scalar |
qV | Volume flow rate | m3/s | Scalar | |||||||||||
FD, R | Перетаскивание или сопротивление воздуха | N | Vector | |||||||||||
CD | COEFTAIT CD | 0003 | Unitless | Scalar | ||||||||||
η | Viscosity | Pascal-second | Scalar | |||||||||||
v | Kinematic Viscosity | м2/с | Скаляр | |||||||||||
σ | Плотность площади | 0003 | Scalar | |||||||||||
Re | Reynolds number | Unitless | Scalar | |||||||||||
Fr | Froude number | Unitless | Скалярное | |||||||||||
Ма | Число Маха | Безразмерное | Скалярное 0009 |
Symbols Related to Solid Mechanics
Symbols | Quantity/ Coefficients | S. | Physical Quantity (Scalar/Vector) |
P | Давление | Паскаль Или Н/м2 | S0calar |
σ | Stress | Pascal | Scalar |
τ | Shear stress | Pascal | Scalar |
k | Жесткость пружины | Н/м | Скаляр |
E | 3333596 Young’s modulus of elasticityPascal | Scalar | |
G | Shear modulus of rigidity | Pascal | Scalar |
ε | Линейная деформация | Безразмерная | Скалярная |
γ | Деформация сдвига 0003 | Unitless | Scalar |
θ | Volume strain | Unitless | Scalar |
S | Surface Tension | Н/м | Скаляр |
K | Объемный модуль сжатия | Pascal | Scalar |
Physical Quantities Related to Thermal Physics
Symbols | Quantity/ Coefficients | S. | Physical Количество (скаляр/вектор) |
k | Теплопроводность | Вт/м.К | Scalar |
P | Heat flow rate | Watt | Scalar |
N | Number of particles | Unitless | Скаляр |
n | Количество вещества | Моль | |
L | Latent heat/specific latent heat | J/kg | Scalar |
c | Specific heat capacity | J/kg. | Scalar |
Q | Heat | J | Scalar |
B | Volume expansivity, coefficient of volume thermal expansion | 1/K (inverse Kelvin) | Scalar |
α | Linear expansivity, coefficient of thermal expansion | 1/k (обратный кельвин) | Скаляр |
T | Температура | Kelvin | Scalar |
Physical Symbol Related to Wave and Optics
Symbol | Quantity/Coefficients | S. | Physical Quantity ( Скаляр/вектор) |
M | Увеличение | Долесс | Скаляр0003 |
f | Focal length | Metre | Scalar |
n | Index of refraction | Unitless | Scalar |
L | Уровень | Децибел (дБ), decineper | Скаляр |
I | Intensity | W/m2 | Scalar |
v, c | Wave speed | m/s | Scalar |
λ | Wavelength | Metre (m) | Scalar |
P | Power of a lens | Dioptre (D) | Scalar |
Physics Symbols Related to Electricity and Magnetism
Symbol | Quantity/Coefficients | Единица S. | Физическая величина (скаляр/вектор) |
S | Вектор Пойнтинга, интенсивность | W/m2 | Vector |
η | Energy density | J/m3 | Scalar |
n | Turns per Длина блока | 1/M | Скаляр |
N | Количество | Unitless 96 9000 9.0009 | Scalar |
φB | Magnetic flux | Weber | Vector |
B | Magnetic field | Tesla | Vector |
FB | Магнитная сила | Н | Vector 39 |
σ | Conductivity | Siemens/m (S/m) | Scalar |
G | Conductance | Siemens | Scalar |
ρ | Resistivity | Ohm-m | Scalar |
R, r | Electric resistance/internal resistance | Ohm | Scalar |
I | Electric current | Ampere (A) | Scalar |
ϵ | Диэлектрическая проницаемость | Безразмерная | Скаляр |
Electromotive Force | Volt (V) | Scalar | |
C | Capacitance | Farad (F) | Scalar |
V | Напряжение, электрический потенциал | В | Скаляр |
УЭ | 3 3 9 15 96 30003J | Scalar | |
φE | Electric flux | Newton meter squared per coulomb (N/m2. | Vector |
E | Электрическое поле | N/C или V/M | Vector |
FE | Электростатический0003 | N | Vector |
λ | Linear charge density | kg/m | Scalar |
σ | Area charge density | кг/м2 | Скаляр |
ρ | Плотность заряда | KG/M3 3 | Scalar |
q, Q | Electric charge | Coulomb (C) | Scalar |
Symbols Used in Modern Physics
Символ | Количество/коэффициенты | Единица измерения S. | Физическая величина (Скаляр V)0003 |
D | Dose/ dose absorbed | Gray (Gy) | Scalar |
t1⁄2 | Half-life | Second | Vector |
ψ(r,t), ψ(r)φ(t) | Wave function | Unitless | Scalar |
W | Work function | J | Scalar |
H | Effective Dose | Sievert | Scalar |
Γ | Lorentz Factor/Lorentz Gamma | Unitless | Скаляр |
Из вышеуказанного текста на физических символах, мы понимаем, что мы используем, что мы используем, что мы используем, что мы используем, что мы используем, мы не понимаем, что мы используем, что мы используем, что мы используем. Обозначения облегчают представление величин.
Обозначения облегчают представление величин.
Было также интересно увидеть, что некоторые физические символы были очень связаны (например, «d» для расстояния), а некоторые не связаны (например, «c» для скорости света или «λ» для длины волны). Кроме того, мы заметили, что конкретный символ связан с более чем одной величиной.
Forces — Физика для старших классов
Все ресурсы по физике для старших классов
6 диагностических тестов 233 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 5 6 7 8 9 … 13 14 Следующая →
Справка по физике для старших классов » Силы
Две собаки, одна и одна, тянут кость. Каждый из них тянет с одинаковой силой, но в противоположных направлениях. Чему равно ускорение кости?
Возможные ответы:
Кость будет ускоряться по направлению к собаке
Кость будет иметь положительное, а затем отрицательное ускорение
Кость взлетит в воздух
Кость будет ускоряться по направлению к собаке
Кость будет иметь нулевое ускорение
Правильный ответ:
Кость будет иметь нулевое ускорение
Объяснение:
В этой задаче мы рассматриваем результирующую силу, действующую на кость. Поскольку обе собаки тянут с одинаковой силой, мы можем сказать, что величина силы собаки 1 равна величине силы собаки 2, но в противоположных направлениях. Математически, .
Поскольку обе собаки тянут с одинаковой силой, мы можем сказать, что величина силы собаки 1 равна величине силы собаки 2, но в противоположных направлениях. Математически, .
Чтобы найти результирующую силу, действующую на кость, мы суммируем отдельные силы.
Мы можем подставить наши силы в уравнение чистой силы.
Чистая сила равна нулю. Каждая собака тянет с одинаковой силой в противоположных направлениях, что позволяет уравновешивать общую силу.
Согласно второму закону Ньютона, . Если результирующая сила равна нулю, то ускорение кости также должно быть равно нулю.
Сообщить об ошибке
Мужчина красит дом. Он замечает маленькую каплю краски, которая совершенно неподвижна на вертикальной стене. Какой вывод он может сделать о краске?
Возможные ответы:
Краска на водной основе
Нам нужно знать массу капли, чтобы делать какие-либо выводы
Капля краски находится очень близко к земле, что придает ей низкую потенциальную энергию
Чтобы делать выводы, нужно знать плотность капли
Сила трения о каплю равна силе тяжести на ней
Правильный ответ:
Сила трения о каплю равна к силе тяжести на нем
Пояснение:
Если капля покоится, то это означает, что суммарные силы, действующие на нее, равны нулю. На каплю действуют две силы: сила тяжести и сила трения краски о стену.
На каплю действуют две силы: сила тяжести и сила трения краски о стену.
Математически мы можем составить уравнение для результирующей силы:
Силы трения и гравитации будут равны и противоположны, в результате чего капля останется на стене.
Сообщить об ошибке
Как возможно, что две силы равной величины могут привести к нулевой результирующей силе?
Возможные ответы:
Силы действуют на разные объекты
Силы противоположно направлены
Силы параллельны друг другу круг
Правильный ответ:
Силы противоположно направлены
Пояснение:
Если на один объект действуют две силы, то результирующая сила, действующая на объект, равна сумме сил, действующих на него.
Однако силы являются векторными величинами. Это означает, что все силы имеют величину и направление действия. Добавляя силы, мы должны учитывать их направления. Направления разбиваются на горизонтальные и вертикальные части для добавления векторов и могут быть положительными или отрицательными в зависимости от направления вдоль оси.
Добавляя силы, мы должны учитывать их направления. Направления разбиваются на горизонтальные и вертикальные части для добавления векторов и могут быть положительными или отрицательными в зависимости от направления вдоль оси.
Чтобы результирующая сила была равна нулю, одна сила должна быть положительной, а другая отрицательной вдоль заданной оси. Если силы равны по величине, то они должны действовать в противоположных направлениях, чтобы компенсировать друг друга.
Сообщить об ошибке
Что из перечисленного не является видом силы?
Возможные ответы:
Выталкивающая сила
Сила трения
Сопротивление (сопротивление воздуха)
Кинетическая сила
Нормальная сила
Правильный ответ:
Кинетическая сила
Пояснение:
Кинетическая сила не является технически правильным свойством. Кинетическая энергия может использоваться для создания силы, но сама по себе силой не является. Силы требуют ненулевого ускорения, а это означает, что они существуют только при изменении скорости. Изменение кинетической энергии может указывать на изменение скорости, что приводит к ненулевому значению силы.
Кинетическая энергия может использоваться для создания силы, но сама по себе силой не является. Силы требуют ненулевого ускорения, а это означает, что они существуют только при изменении скорости. Изменение кинетической энергии может указывать на изменение скорости, что приводит к ненулевому значению силы.
Нормальная сила — это сила поверхности, действующая на объект, часто противодействующая гравитации. Сила трения представляет собой сопротивление между объектом и поверхностью и действует в направлении, противоположном направлению движения объекта. Выталкивающая сила — это восходящая сила жидкости, действующей на погруженный в воду объект. Сопротивление, или сопротивление воздуха, представляет собой особую форму силы трения для объекта, движущегося в жидкости.
Сообщить об ошибке
Двое детей, стоящих на гладкой поверхности, с силой отталкиваются друг от друга. Если масса одного ребенка в два раза больше массы другого ребенка, каково отношение более легкого ребенка к более тяжелому?
Возможные ответы:
Правильный ответ:
Пояснение:
Во-первых, поймите, что сила, с которой более легкий ребенок действует на более тяжелого ребенка, равна и противоположна силе, с которой более тяжелый ребенок действует на более легкого ребенка, согласно третьему закону Ньютона.
Используя второй закон Ньютона, мы можем переписать это уравнение.
Вопрос говорит нам об этом, делая ребенка более тяжелым и более легким. Мы также можем использовать это в нашем уравнении.
Мы ищем отношение к , поэтому нам нужно изменить уравнение.
Во-первых, массы компенсируются.
Затем разделите обе части на .
Отношение к .
Сообщить об ошибке
Ящик скользит по полу с постоянной скоростью. Какова результирующая сила, действующая на ящик?
Возможные ответы:
Правильный ответ:
Объяснение:
Связь между силой и ускорением такова.
Поскольку скорость ящика постоянна, ускорение отсутствует.
Если ускорение равно нулю, это означает, что на объект не действует результирующая сила или .
Сообщить об ошибке
Ящик скользит по гладкой поверхности. Если он поддерживает постоянную скорость , какова результирующая сила, действующая на объект?
Возможные ответы:
Правильный ответ:
Пояснение:
Второй закон Ньютона утверждает, что . Мы знаем массу, но нам нужно вычислить ускорение.
Ускорение — это изменение скорости в единицу времени.
Поскольку скорость не меняется от одного момента к другому, то у объекта не должно быть результирующего ускорения.
Возвращаясь ко второму закону Ньютона, мы видим, что если нет ускорения, то нет результирующей силы.
Сообщить об ошибке
Одна и та же сила приложена к двум различным объектам. Один объект имеет массу , а другой имеет массу . Какой из них имеет большее ускорение?
Возможные ответы:
Нам нужно знать значение приложенной силы, чтобы решить
Нам нужно знать значение приложенной силы, чтобы решить
Ускорения равны
21153
Объяснение:
Уравнение для силы:
Мы можем записать это уравнение в терминах каждого объекта:
Мы знаем, что сила, приложенная к каждому объекту, будет одинаковой, поэтому мы можем установить эти уравнения равны друг другу.
Мы знаем, что второй объект в два раза тяжелее первого.
Мы можем исключить массу с каждой стороны, оставив связь между двумя ускорениями.
Ускорение первой массы вдвое превышает ускорение второй; таким образом, ускорение более легкой массы больше.
Сообщить об ошибке
Лэнс толкает ящик массы с силой в ньютоны. Каково результирующее ускорение?
Возможные ответы:
Правильный ответ:
Пояснение:
Формула силы — второй закон Ньютона:
В вопросе сказано использовать для массы и для силы.
Теперь мы можем изолировать ускорение.
Это также имеет смысл с точки зрения единиц измерения. Единицами силы являются ньютоны, которые можно записать как:
В нашем уравнении мы видим, что ньютоны делятся на массу:
Это приведет к единицам ускорения.
Сообщить об ошибке
Мяч начинает катиться со скоростью . Если на него не действуют никакие внешние силы, какова будет его скорость в ?
Возможные ответы:
Правильный ответ:
Пояснение:
Если на объект не действуют никакие силы, то нет и ускорения. Если ускорения нет, то тело будет двигаться с постоянной скоростью.
Математически мы можем посмотреть на второй закон Ньютона и формулу ускорения.
Мы знаем, что сила равна нулю.
Поскольку мы знаем, что масса не может быть равна нулю, ускорение должно быть равно нулю.
Теперь мы можем использовать формулу для ускорения, чтобы увидеть влияние на скорость.
Мы знаем, что ускорение равно нулю, а время равно десяти секундам.
Чтобы это было правдой, начальная и конечная скорости должны быть равны.


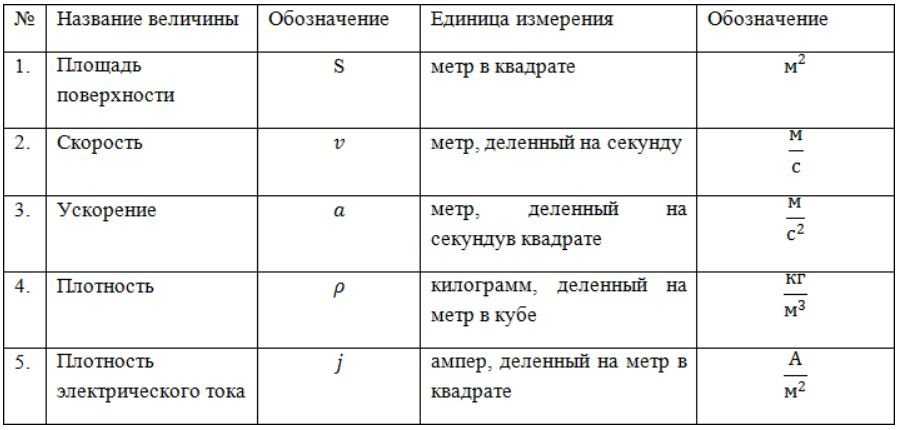
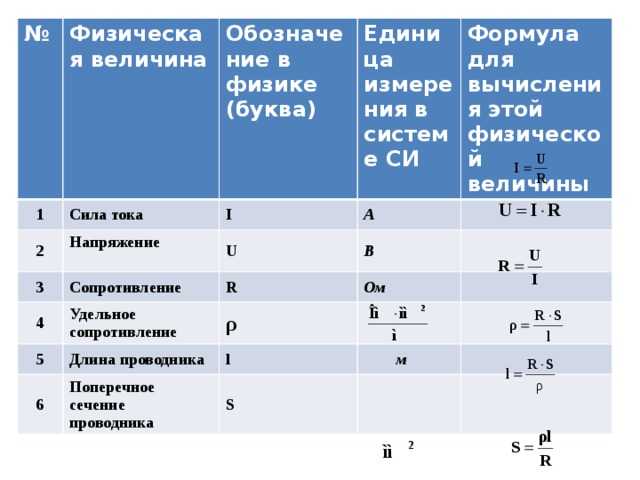
 8 (видоизменённом рис.178).
8 (видоизменённом рис.178). для общеобразоват. организаций /О. Ф. Кабардин, — 6-е изд. — М.: Просвещение, 2018, — 174 с.: ил. — ISBN 978–5–09–060739–1.
для общеобразоват. организаций /О. Ф. Кабардин, — 6-е изд. — М.: Просвещение, 2018, — 174 с.: ил. — ISBN 978–5–09–060739–1. кин. энергия молекул одноатомного газа
Ek=3/2∙kT
кин. энергия молекул одноатомного газа
Ek=3/2∙kT двигателей
(цикл Карно) η= (Т1 – Т2)/
Т1
двигателей
(цикл Карно) η= (Т1 – Т2)/
Т1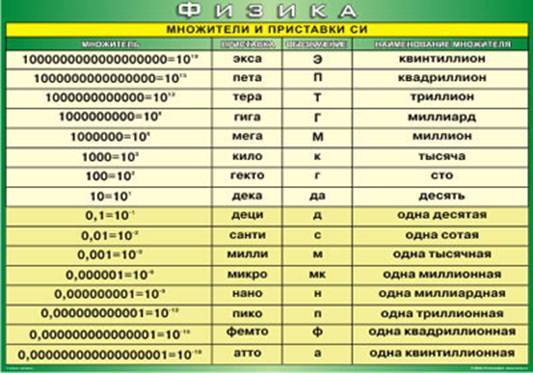 соединения I1=I2=I,
U1+U2=U,
R1+R2=R
соединения I1=I2=I,
U1+U2=U,
R1+R2=R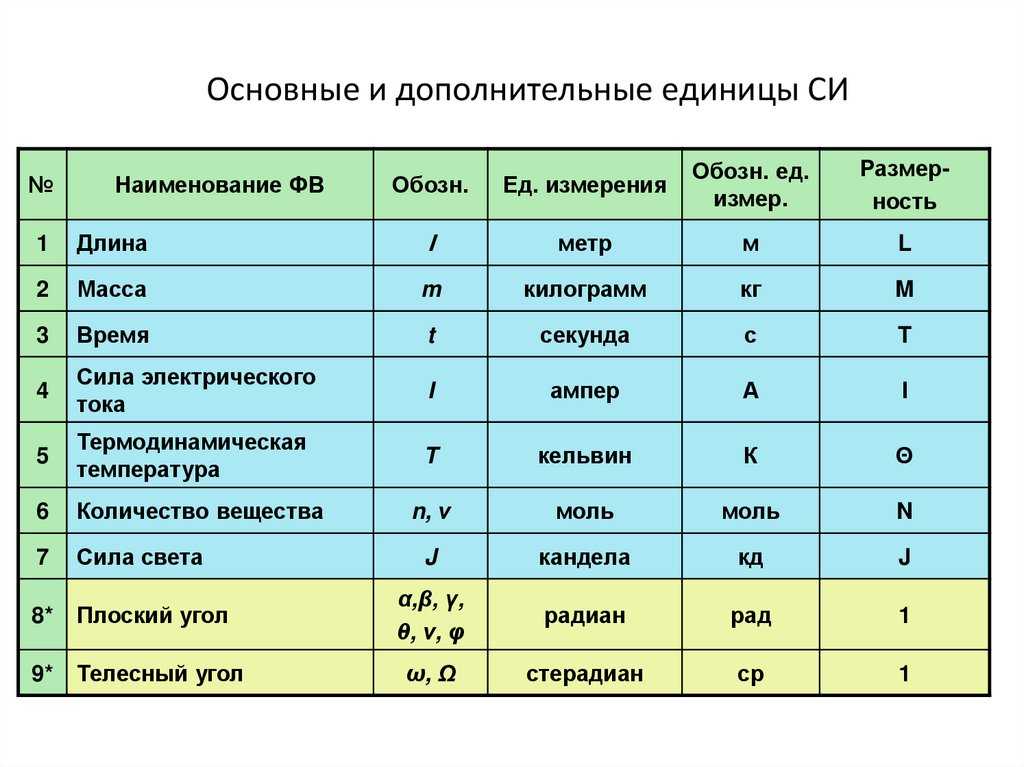 решетка
d∙sin
φ=k
λ
решетка
d∙sin
φ=k
λ Тогда гравитация действует на объект с силой, определяемой выражением $F=ma$
Тогда гравитация действует на объект с силой, определяемой выражением $F=ma$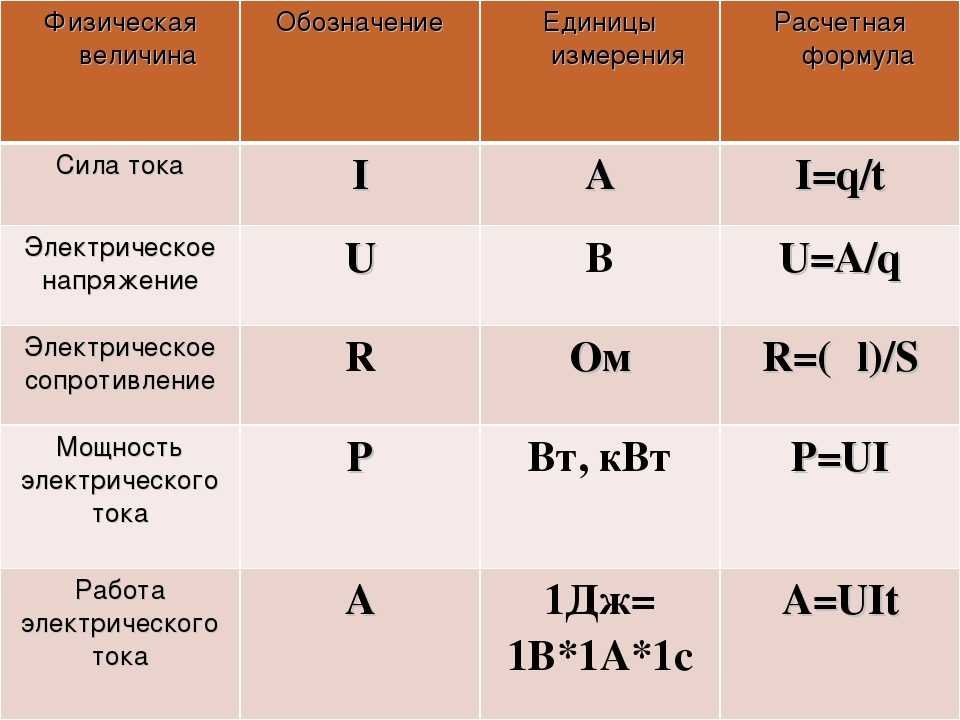


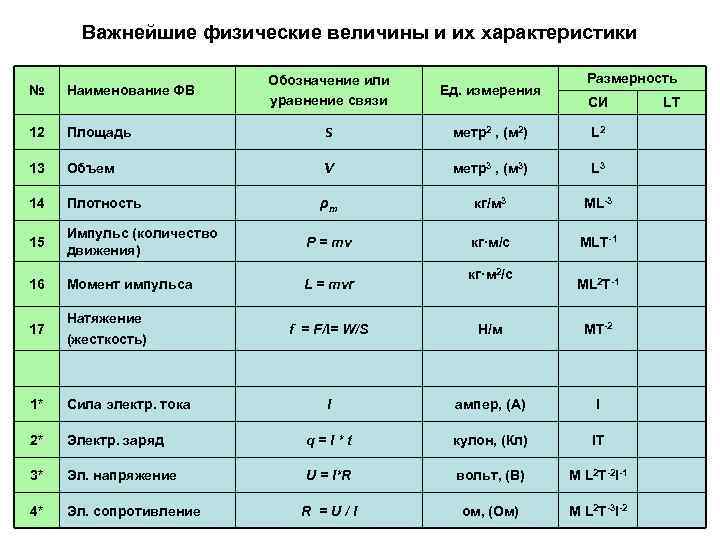
 сек0005
сек0005 m/s
m/s