Помощь с учёбой от преподавателя Натальи Брильёновой
Обо мнеЗдравствуйте, я, Брильёнова Наталья Валерьевна, бывший преподаватель кафедры информатики и электроники Екатеринбургского государственного института. С 2014 года занимаюсь онлайн образованием. У меня работает большая команда бывших преподавателей с огромным опытом и квалификацией.
Мы за этот месяц выполнили:заказов.
Мы помогаем с предметами любого уровня сложности из разных учебных заведений: средняя школа, колледж или университет. Независимо от темы, объёма – задание в одну формулу или большая расчётная работа от 80 страниц, я и моя команда всегда выполняем высококачественно. Каждый день я и моя команда преподавателей помогаем ученикам и студентам учиться лучше.
Мы всегда соблюдаем сроки. Наша цель – чтобы вы учились на хорошие оценки! Нет времени, но хотите хорошую оценку? Попросите меня вам помочь! Согласуем с вами требования и сроки и через 1-4 дня всё будет на “отлично”.
Любой срок – любой предмет:
- Я и моя профессиональная команда поможем с любым предметом, независимо от темы или сложности.
Telegram чат 24/7:
- Общайтесь со мной в любое время чтобы обсудить детали заказа и т. д.
Оригинальность:
- У меня разработан эффективный алгоритм проверки на плагиат. Я проверяю каждую работу через различные инструменты обнаружения плагиата для получения оригинального текста. Оригинальность наших работ от 88%.
Доступные цены:
- Я предлагаю самую лучшую цену. У меня есть скидки от 20% для тех, кто сделает больше пяти заказов.
Напишите мне в Telegram и прикрепите своё задание и методические материалы (лекции) и укажите сроки выполнения.
Я изучу ваш заказ и рассчитаю стоимость.
Как только вы оплатите свой заказ, я и моя команда преподавателей его выполняем.
В указанную вами дату или, возможно, раньше получаете свой заказ!
Часто задаваемые вопросыСколько стоит помощь?
- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам – я изучу и оценю.
Какой срок выполнения?
- Нам под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые заказы раньше срока.
Если требуется доработка, это бесплатно?
- Доработка заказ бесплатна. Срок выполнения от 1 до 2 дней.
Могу ли я не платить, если меня не устроит стоимость?
- Оценка стоимости вашего задания бесплатна.
Каким способом можно оплатить?
- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.
 д.
д.
В какое время я вам могу написать и прислать задание на выполнение
- Присылайте в любое время!
Помощь с учёбой от преподавателя Натальи Брильёновой
Обо мнеЗдравствуйте, я, Брильёнова Наталья Валерьевна, бывший преподаватель кафедры информатики и электроники Екатеринбургского государственного института. С 2014 года занимаюсь онлайн образованием. У меня работает большая команда бывших преподавателей с огромным опытом и квалификацией.
Мы за этот месяц выполнили:заказов.
Мы помогаем с предметами любого уровня сложности из разных учебных заведений: средняя школа, колледж или университет. Независимо от темы, объёма – задание в одну формулу или большая расчётная работа от 80 страниц, я и моя команда всегда выполняем высококачественно. Каждый день я и моя команда преподавателей помогаем ученикам и студентам учиться лучше.
Мы всегда соблюдаем сроки. Наша цель – чтобы вы учились на хорошие оценки! Нет времени, но хотите хорошую оценку? Попросите меня вам помочь! Согласуем с вами требования и сроки и через 1-4 дня всё будет на “отлично”.
Мои особенностиЛюбой срок – любой предмет:
- Я и моя профессиональная команда поможем с любым предметом, независимо от темы или сложности.
Telegram чат 24/7:
- Общайтесь со мной в любое время чтобы обсудить детали заказа и т. д.
Оригинальность:
- У меня разработан эффективный алгоритм проверки на плагиат. Я проверяю каждую работу через различные инструменты обнаружения плагиата для получения оригинального текста. Оригинальность наших работ от 88%.
Доступные цены:
- Я предлагаю самую лучшую цену. У меня есть скидки от 20% для тех, кто сделает больше пяти заказов.
Напишите мне в Telegram и прикрепите своё задание и методические материалы (лекции) и укажите сроки выполнения.
Я изучу ваш заказ и рассчитаю стоимость.
Как только вы оплатите свой заказ, я и моя команда преподавателей его выполняем.
В указанную вами дату или, возможно, раньше получаете свой заказ!
Часто задаваемые вопросыСколько стоит помощь?
- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам – я изучу и оценю.
Какой срок выполнения?
- Нам под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые заказы раньше срока.
Если требуется доработка, это бесплатно?
- Доработка заказ бесплатна. Срок выполнения от 1 до 2 дней.
Могу ли я не платить, если меня не устроит стоимость?
- Оценка стоимости вашего задания бесплатна.

Каким способом можно оплатить?
- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.
В какое время я вам могу написать и прислать задание на выполнение?
- Присылайте в любое время!
Что такое ферма? – Учебник по гражданскому строительству
доктора Шона Кэрролла
|
Обновлено: 5 января 2019 г.
|
Учебник
Ферма представляет собой конструкцию, состоящую из набора конструктивных элементов, соединенных шарнирными соединениями или узлами
 Это делает фермы особенно эффективной структурной формой. В этом уроке мы обсудим распространенные формы ферм, их особенности, приблизительные методы анализа и ключевые допущения, относящиеся к нашему анализу. Если вы хотите узнать, как мы можем вручную анализировать фермы, чтобы определить силы, возникающие в каждом элементе, я написал руководство по этому вопросу здесь.
Это делает фермы особенно эффективной структурной формой. В этом уроке мы обсудим распространенные формы ферм, их особенности, приблизительные методы анализа и ключевые допущения, относящиеся к нашему анализу. Если вы хотите узнать, как мы можем вручную анализировать фермы, чтобы определить силы, возникающие в каждом элементе, я написал руководство по этому вопросу здесь.Если вас интересует поведение фермы, ознакомьтесь с нашим бесплатным набором инструментов для анализа ферм ниже. Нет никакой замены для понимания фундаментальной механики фермы, но доступ к простому в использовании калькулятору фермы делает жизнь немного проще!
ОНЛАЙН TRUSS TOOLBOX 🛠️
Воспроизвести видео о Truss-toolbox | DegreeTutors.com
Предыдущий
Следующий
Попробуйте наш бесплатный набор инструментов для анализа ферм для расчета реакций, осевых усилий и прогибов.
Мы видим фермы повсюду вокруг застройки. Это простые, но невероятно эффективные конструкции, способные преодолевать очень большие расстояния при использовании относительно небольшого количества материала. Это означает, что они легкие с очень хорошим соотношением прочности и веса. Именно эта эффективность делает их хорошо подходящими в качестве конструкций крыш и мостов.
Распространенные типы ферм
Существует множество распространенных форм или моделей ферм, появившихся в результате различных вариантов использования. Одними из наиболее распространенных являются Pratt, Howe, Warren и Modified Warren. Схема фермы относится к расположению внутренних вертикальных и диагональных элементов. Верхние и нижние горизонтальные элементы часто называют поясами ферм или стрелами.
Верхние и нижние горизонтальные элементы часто называют поясами ферм или стрелами.
Pratt
Ферма Пратта (впервые предложенная Томасом Праттом в 1844 г.) является одной из наиболее распространенных форм ферм и состоит из вертикальных и диагональных элементов, образующих форму или форму буквы «N». Диагональные элементы расположены так, что они развивают только растягивающие усилия. Как таковые, они могут быть спроектированы так, чтобы противостоять только осевому растяжению, что позволяет избежать необходимости анализа потери устойчивости при сжатии. Вертикальные элементы фермы Пратта развивают силы сжатия. Это означает, что они, как правило, будут более прочными и способными противостоять изгибу. Простота фермы Пратта позволяет использовать методы ручного анализа.
Ферма Пратта: зеленых элементов в растяжении, красные элементы в сжатии, серые элементы с нулевой силой ферма Пратта (перевернутая ферма Пратта). В результате в ответ на вертикальную или гравитационную нагрузку вертикальные элементы обычно растягиваются, а диагональные элементы сжимаются. Это немного менее выгодно, чем конфигурация фермы Пратта, поскольку теперь более длинные диагональные элементы должны сопротивляться изгибу при сжатии. Ферма Howe: зеленых элементов в состоянии растяжения, красные элементы в сжатом состоянии, серые элементы с нулевой нагрузкой
Это немного менее выгодно, чем конфигурация фермы Пратта, поскольку теперь более длинные диагональные элементы должны сопротивляться изгибу при сжатии. Ферма Howe: зеленых элементов в состоянии растяжения, красные элементы в сжатом состоянии, серые элементы с нулевой нагрузкойWarren
Ферма Warren полностью обходится без внутренних вертикальных элементов и состоит из ряда равносторонних треугольников. За счет исключения вертикальных элементов ферма Уоррена относительно экономична с точки зрения использования материалов. Внутренние диагональные элементы попеременно сопротивляются силам растяжения и сжатия. Джеймс Уоррен предложил свою ферму Уоррена в 1848 году.
Ферма Уоррена: зеленых элементов в растяжении, красные элементы в сжатии, серые элементы с нулевой силой Неслучайно три наиболее распространенных формы ферм появились менее чем за десятилетие. 1840-е годы — это период, который характеризуется Железнодорожной манией . Это был период интенсивных инвестиций и развития железнодорожных сетей. Это привело к инновациям в конструкции мостов, которые дали нам фермы Уоррена, Хоу и Пратта, которые мы так часто видим сегодня.
Это был период интенсивных инвестиций и развития железнодорожных сетей. Это привело к инновациям в конструкции мостов, которые дали нам фермы Уоррена, Хоу и Пратта, которые мы так часто видим сегодня.
Модифицированный Уоррен
Одним из последствий отсутствия вертикальных элементов в ферме Уоррена является то, что верхний и нижний горизонтальные пояса должны охватывать относительно большое расстояние между узлами (или соединениями). Это может стать проблемой, когда горизонтальный элемент сжимается. Модифицированная ферма Уоррена повторно вводит вертикальные элементы, уменьшая вдвое расстояние между узлами в верхнем (обычно сжатом) поясе. Это также особенно полезно, когда ферма должна поддерживать второстепенные конструкции, такие как, например, прогоны крыши. Одним из важных условий, которое следует соблюдать при проектировании фермы, является обеспечение приложения любой внешней нагрузки в узловой точке. Этому способствуют вертикальные элементы модифицированной фермы Уоррена.
Ферма Вирендела
Существует множество вариаций распространенных типов ферм, рассмотренных выше. Тем не менее, стоит упомянуть одну конкретную ферму, которая значительно отличается от фермы Vierendeel. Этот тип ферм принципиально отличается тем, как он передает усилия. Общей чертой всех ферм с шарнирным соединением является то, что они состоят из треугольных форм. Это продиктовано их штифтовыми соединениями, не оказывающими сопротивления вращению.
Однако ферма Vierendeel имеет прямоугольные или квадратные «проемы». Это стало возможным благодаря тому, что все элементы соединены жестко. В результате элементы, составляющие ферму Виренделя, развивают как осевые силы, так и изгибающие моменты. Фермы Vierendeel обычно представляют собой гораздо более прочные конструкции из-за необходимости выдерживать осевые и нормальные напряжения из-за изгиба.
Проектирование фермы на самом деле является относительно простым процессом; определение приблизительных (схемных) деталей фермы может быть достигнуто с использованием некоторого очень элементарного анализа. Расчет приблизительного размера горизонтальных элементов заключается в определении осевой силы, развивающейся в точке максимального изгибающего момента.
Быстрый ручной расчет для определения максимальной силы, развиваемой в поясах фермыДопустим, момент
развивается в середине пролета свободно опертой фермы. Мы можем найти осевую силу в верхнем и нижнем поясах, разделив момент на доступное плечо рычага, скажем, .
Предполагая, что случай сжатия будет определять размер обоих поясов, мы можем просто указать элемент, который имеет сопротивление продольному изгибу, превышающее осевую нагрузку, возникающую из-за изгибающего момента, которому мы должны сопротивляться. Способность к продольному изгибу сильно зависит от расстояния между боковыми ограничителями. То, как ферма удерживается «вне плоскости», является важным соображением, которое нельзя упускать из виду.
Точно так же просто определить размер внутренних элементов, если определена величина внутренних сил в каждом элементе. В большинстве случаев (статически определимые фермы) этого можно легко добиться, выполнив метод соединений и/или метод анализа сечений . Этот анализ позволяет нам быстро спроектировать ряд вариантов фермы в соответствии с конкретным требованием конструкции.
Этот анализ позволяет нам быстро спроектировать ряд вариантов фермы в соответствии с конкретным требованием конструкции.
Сравнение моделей конструкций с поведением в реальном мире
Важно понимать некоторые общие предположения, которые часто применяются при анализе ферм. На самом деле, эти предположения говорят о более фундаментальном моменте, который применим к структурному анализу в целом и, в частности, к «ручным» методам анализа, в отличие от компьютерного анализа.
Дело в том, что… когда мы приступаем к анализу фермы, мы сначала должны построить модель, на которой будет основываться наш анализ. Эта модель вполне может быть линейной диаграммой, нарисованной на странице. Но мы всегда должны помнить, что модель является несовершенным представлением структуры реального мира . Это наша аппроксимация реальной структуры, и она почти никогда не захватит 100% деталей реальной структуры.
Иногда эти различия между моделью и структурой довольно малы, и в этом случае мы можем быть более уверены в нашем анализе. Однако, если мы не будем осторожны, упрощающие допущения, которые облегчают наш анализ, могут быть настолько ограничивающими, что поведение модели не будет хорошим представлением структуры. Чрезвычайно важно иметь представление о том, как ваши предположения ухудшают точность вашей модели.
Однако, если мы не будем осторожны, упрощающие допущения, которые облегчают наш анализ, могут быть настолько ограничивающими, что поведение модели не будет хорошим представлением структуры. Чрезвычайно важно иметь представление о том, как ваши предположения ухудшают точность вашей модели.
Предположения по анализу ферм
Итак, какие допущения применимы к анализу ферм? О первом уже упоминалось; мы предполагаем, что узлы или соединения, соединяющие элементы, ведут себя как штифты. Другими словами, если мы рассмотрим два элемента, соединяющихся в суставе, они будут свободно вращаться относительно друг друга. Из этого следует, что через соединение не могут передаваться никакие изгибающие моменты, только сила.
Это приводит ко второму предположению; элементы внутри фермы подвергаются только осевым нагрузкам, растяжению, сжатию или не подвергаются воздействию силы. При условии, что все внешние нагрузки приложены к соединениям, ни один из элементов не будет изгибаться. Конечно, если бы к элементу между соединениями была приложена внешняя сила, в этом элементе возникли бы нормальные напряжения из-за изгиба, но обычно мы пытаемся по возможности избегать этой «межузловой» нагрузки в фермах.
Возникает очевидный вопрос: насколько верны эти предположения? Что касается штифтовых соединений, то на самом деле настоящие штифты, допускающие свободное вращение, встречаются очень редко. Это в основном обусловлено относительно высокой стоимостью изготовления таких соединений. В стальной ферме соединения почти всегда болтовые или сварные. Таким образом, изгибающие моменты будут в некоторой степени передаваться через соединения и, следовательно, внутри конструкции.
Однако геометрия соединений обычно такова, что их способность передавать крутящий момент весьма ограничена. Таким образом, наше предположение обычно приводит к тому, что модельное поведение относительно мало отклоняется от фактического структурного поведения. Что касается элементов, развивающих только осевые нагрузки, то из нашего обсуждения соединений следует, что если межузловая нагрузка сведена к минимуму, то преобладающим действием, испытываемым на элементы, будет осевая сила. Таким образом, в целом наши модели ферм, которые мы используем для проведения метода сечений и метода анализа соединений, являются довольно разумными приближениями к реальным ферменным конструкциям.
Таким образом, наше предположение обычно приводит к тому, что модельное поведение относительно мало отклоняется от фактического структурного поведения. Что касается элементов, развивающих только осевые нагрузки, то из нашего обсуждения соединений следует, что если межузловая нагрузка сведена к минимуму, то преобладающим действием, испытываемым на элементы, будет осевая сила. Таким образом, в целом наши модели ферм, которые мы используем для проведения метода сечений и метода анализа соединений, являются довольно разумными приближениями к реальным ферменным конструкциям.
Линкедин Твиттер YouTube
Автор
Д-р Шон Кэрролл
Бакалавр искусств (с отличием), MSc, PhD, CEng MIEI, FHEA
Привет, я Шон, основатель DegreeTutors.com. Я надеюсь, что вы нашли этот урок полезным. Проведя 10 лет в качестве преподавателя в университете по проектированию конструкций, я запустила DegreeTutors.com, чтобы помочь большему количеству людей понять инженерию и получить такое же удовольствие от ее изучения, как и я. Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
Подпишитесь на обновления учебников и курсов
© 2023 DegreeTutors & Mind Map Media Ltd. Все права защищены
Учебное пособие по анализу ферм| Метод соединений и сечений
доктора Шона Кэрролла
|
Обновлено: 14 апреля 2021 г.
|
Учебник
В этом уроке мы сосредоточимся на фермах, также известных как шарнирные конструкции. Мы обсудим их сильные стороны и распространенные методы ручного анализа ферм. Мы собираемся начать с самого начала, кратко рассмотрев, что такое ферма, но мы быстро перейдем к анализу фермы. Более широкий контекст здесь заключается в том, что прежде чем можно будет спроектировать ферму и указать размеры элементов, требуется полный анализ фермы, чтобы мы могли определить силы, возникающие в каждом элементе.
Если вы только начинаете изучать анализ ферм, будет полезно иметь возможность проверить результаты ручного анализа. Ознакомьтесь с нашим бесплатным набором инструментов для анализа ферм ниже. Очень важно понимать методы, которые мы обсуждаем в этом посте, но иметь под рукой «калькулятор ферм» будет огромным подспорьем на этом пути.
Ознакомьтесь с нашим бесплатным набором инструментов для анализа ферм ниже. Очень важно понимать методы, которые мы обсуждаем в этом посте, но иметь под рукой «калькулятор ферм» будет огромным подспорьем на этом пути.
ОНЛАЙН TRUSS TOOLBOX 🛠️
Воспроизвести видео о Truss-toolbox | DegreeTutors.com
Предыдущий
Следующий
Попробуйте наш бесплатный набор инструментов для анализа ферм для расчета реакций, осевых усилий и прогибов. Удобный инструмент для студентов и профессиональных инженеров.
Фермы — один из первых типов конструкций, с которыми столкнется новичок в инженерии. Для этого есть несколько причин; во-первых, ферма — это очень простая конструкция, которую относительно легко понять и проанализировать. Используя некоторые простые механизмы, наш анализ фермы позволяет нам проследить траекторию нагрузки через ферму и визуализировать, как силы передаются через конструкцию и возвращаются к ее опорам.
Другая причина, по которой мы сосредотачиваемся на фермах в начале изучения инженерии, заключается в их повсеместном распространении. Мы видим их повсюду в застроенной среде. Это простые, но невероятно эффективные конструкции, которые могут охватывать очень большие расстояния с относительно небольшим количеством материала. Именно эта эффективность делает их хорошо подходящими в качестве конструкций крыш и мостов. После прочтения этого руководства, если вы хотите работать с другими примерами, вы можете пройти мой курс на Основы структурного анализа .
Основы расчета конструкций
Раз и навсегда освойте расчет строительных конструкций.
После завершения этого курса…
- Вы поймете такие ключевые понятия, как момент силы, статическое равновесие и детерминированность.
- Вы сможете определить опорные реакции для конструкций, подверженных различным условиям нагрузки.

- Вы научитесь использовать метод разрешения соединений и метод сечений для анализа ферменных конструкций с шарнирным соединением.
Подробнее
1.0 Что такое ферма?
Давайте начнем с определения того, что такое ферма. Ферма — это конструкция, состоящая из набора элементов, соединенных штифтовыми соединениями или узлами. Теоретически штифтовые соединения не создают сопротивления вращению и ведут себя как шарниры. Преимущество фермы заключается в том, что ее элементы нагружаются преимущественно в осевом направлении. Это означает, что они находятся либо в сжатии, либо в растяжении, либо не имеют силы, так называемые элементы с нулевой силой. Это делает фермы особенно эффективной структурной формой.
Конструктивная эффективность ферм подтверждается тем фактом, что мы видим, что ферменные конструкции обычно используются для покрытия больших расстояний и эффективно выдерживают высокие нагрузки. В этом уроке мы рассмотрим двухмерные ферменные конструкции, но все, что мы обсуждаем, в равной степени применимо и к трехмерным фермам, иногда называемым пространственными каркасами. Обычный башенный кран является хорошим примером трехмерной ферменной конструкции.
Обычный башенный кран является хорошим примером трехмерной ферменной конструкции.
1.1 Теоретическое поведение фермы и траектории нагрузки
Как мы уже говорили, по крайней мере теоретически, все узлы фермы фактически являются штифтами или шарнирами. Это означает, что элементы, встречающиеся в узле, могут свободно вращаться относительно друг друга. Таким образом, моменты не могут передаваться от одного элемента к соседним элементам. Через узлы могут передаваться только силы.
⚠️ В этом посте я рассказал о различиях между теоретическим и фактическим поведением фермы. Чтобы полностью понять предположения, присущие нашим методам анализа ферм, обсуждаемым ниже, обязательно прочитайте этот пост.
С инженерной точки зрения, ферма, как и любая конструкция, имеет одну цель – передавать внешние силы через конструкцию и обратно на опоры или фундаменты этой конструкции. В качестве примера возьмем простейшую форму фермы.
В качестве примера возьмем простейшую форму фермы.
Сила
, приложенная в узле B, должна передаваться через конструкцию обратно на штифтовые опоры в точках A и C соответственно. Мы можем думать о внешних нагрузках, перемещающихся по путь загрузки . Задача инженера состоит в том, чтобы оценить траекторию нагрузки и убедиться, что элементы конструкции вдоль этой траектории могут выдерживать напряжения, вызванные передаваемыми нагрузками.
Используя три уравнения статики (
,, и ), реакции в A и C легко оцениваются;
(1)
Подтвердите эти значения самостоятельно путем расчета. Чтобы эти реакции развивались на опорах, стержень АВ должен передавать усилие сжатия
в то время как стержень BC передает усилие натяжения . Это показано на правой схеме пути нагрузки ниже. К концу этого учебного курса вы научитесь определять эти пути нагрузки для статически определимых ферменных конструкций.
К концу этого учебного курса вы научитесь определять эти пути нагрузки для статически определимых ферменных конструкций.
2.0 Метод совместного разрешения для анализа фермы
Теперь, когда мы выяснили, что такое ферма, и понятие пути нагрузки, описывающее передачу сил через конструкцию, следующая задача состоит в том, чтобы определить, как определить силы вдоль путь загрузки. Другими словами, мы хотим иметь возможность рассчитать силы, возникающие в каждом из элементов в ответ на внешнюю нагрузку.
Мы сосредоточимся на двух похожих методах, использующих уравнения статического равновесия. Это:
- метод совместного разрешения
- метод секций
В обоих случаях мы должны сначала определить опорные реакции конструкции. Только тогда мы можем использовать метод совместного разрешения, метод сечений или их комбинацию.
Мы начнем с рассмотрения метода разрешения соединений, который включает в себя оценку равновесия сил в каждом соединении или узле и использование уравнений статики для решения неизвестных сил стержня. Снова рассмотрим двухстержневую ферму, показанную ниже как диаграмму свободного тела.
Диаграмма свободного тела двухстержневой фермыМетод разрешения соединений требует, чтобы мы оценили сумму сил, встречающихся в соединении. Эти силы можно разложить на два ортогональных (взаимно перпендикулярных) направления, что позволяет оценить два уравнения силового равновесия. Таким образом, у нас есть два уравнения, из которых мы можем определить два неизвестных. Таким образом, используя метод суставов, мы можем начать только с сустава, который имеет максимум две неизвестные силы стержня . Для этой простой структуры мы можем рассмотреть любой из трех узлов, начнем с узла B.
Мы изолируем соединение, вырезая членов, собравшихся в этом месте. Делая эти разрезы, мы обнаруживаем внутренние силы стержня, на данный момент обозначенные как
, и где указывает, что мы предполагаем (пока не доказано обратное), что силы являются силами растяжения.
Диаграмма свободного тела сустава затем оценивается путем взятия суммы сил в горизонтальном и вертикальном направлениях и приравнивания их к нулю, чтобы выявить неизвестные силы стержня (помните два неизвестных, поэтому два уравнения обязательный). В следующем анализе обратите внимание, что базовая геометрия дает нам угол
. Теперь рассмотрим равновесие сил шарнира B:
(2)
Обратите внимание, что
оценивается как положительное число, и поэтому наше предположение о том, что сила в стержне BC является силой растяжения, верно. Теперь, оценивая равновесие горизонтальной силы,
(3)
Здесь отрицательное значение говорит нам о том, что сила в стержне BA на самом деле противоположна нашему первоначальному предположению и, следовательно, представляет собой силу сжатия. На этом анализ этой простой фермы завершен. Стоит задуматься над направлением стрелок, указывающих на растяжение и сжатие внизу.
Для элемента AB, находящегося в сжатом состоянии, желтые стрелки силы направлены наружу, как если бы они сопротивлялись силе, сжимающей элемент. По той же аналогии стрелки силы для стержня BC направлены внутрь, как будто сопротивляясь силе, пытающейся разорвать или растянуть стержень. Поначалу это может показаться нелогичным, поэтому убедитесь, что вы довольны этим соглашением, прежде чем продолжить, иначе позже вы ужасно запутаетесь.
В двух словах это метод совместного решения. Пока мы продемонстрировали это только для очень простой фермы, но процесс точно такой же, независимо от того, насколько велика ваша ферма. Пока вы можете идентифицировать узел в вашей конструкции фермы, через который проходит не более двух неизвестных сил-членов, вы можете применить метод совместного решения. Чуть позже мы снова увидим это в действии!
3.0 Метод сечений для анализа ферм
Теперь мы можем рассмотреть другой инструмент в нашем распоряжении, метод сечений. Вместо того, чтобы изолировать один стык, метод сечений предполагает выполнение воображаемого разреза через всю конструкцию . При этом мы раскрываем внутренние силы стержня в стержнях, через которые проходит наша плоскость. Затем мы можем оценить равновесие любой из двух подструктур, созданных разрезом.
Вместо того, чтобы изолировать один стык, метод сечений предполагает выполнение воображаемого разреза через всю конструкцию . При этом мы раскрываем внутренние силы стержня в стержнях, через которые проходит наша плоскость. Затем мы можем оценить равновесие любой из двух подструктур, созданных разрезом.
Этот метод структурного анализа приводит в действие третье уравнение равновесия; поскольку все силы, действующие на подконструкцию, больше не проходят через одну и ту же точку, теперь мы можем рассмотреть сумму моментов относительно любой точки, которая является нашим третьим уравнением.
Поскольку конструкция находится в состоянии статического равновесия, сумма моментов (как и сил) должна равняться нулю. Итак, теперь у нас есть три уравнения статики. Главное, что нужно помнить при использовании метода сечений, это то, что наша плоскость не может разрезать более трех стержней с неизвестными силами на стержнях.
Как обычно, лучше всего понять эту технику можно на примере. Итак, рассмотрим приведенную ниже простую ферму Уоррена, на которую действуют точечные нагрузки в узлах B и D.
Итак, рассмотрим приведенную ниже простую ферму Уоррена, на которую действуют точечные нагрузки в узлах B и D.
Реакции
Как и при любом статически определимом анализе, первой задачей является определение опорных реакций. Начнем с рассмотрения суммы моментов относительно точки А, которая должна быть равна нулю. Предположим, что моменты по часовой стрелке положительны.
(4)
(5)
(6)
Далее мы можем оценить сумму сил в вертикальном или
направлении, чтобы определить оставшуюся неизвестную вертикальную реакцию. Предполагая, что направленные вверх силы положительны, мы имеем,
(7)
(8)
(9)
Наконец, путем рассмотрения мы можем сказать, что горизонтальная реакция,
(10)
Раздел 1, давайте начнем с рассмотрения вертикального сечения, разрезающего структуру между узлами G и C. Это прорежет элементы BC, CG и GF, что покажет внутренние силы в этих элементах. Как и в случае метода соединений, мы предполагаем, что эти силы являются силами растяжения, и поэтому стрелки сил указывают в сторону от разрезаемого элемента.
Это прорежет элементы BC, CG и GF, что покажет внутренние силы в этих элементах. Как и в случае метода соединений, мы предполагаем, что эти силы являются силами растяжения, и поэтому стрелки сил указывают в сторону от разрезаемого элемента.
Подконструкция слева от разреза (на фото ниже) теперь должна находиться в состоянии статического равновесия под влиянием внешних сил, реакций в точке А и внутренних сил стержня,
и . Итак, у нас есть три неизвестных и три уравнения, которые мы теперь можем решить для сил-членов.
Ферма Уоррена с вертикальным разрезом, обнажающим три неизвестные силыМы начнем с использования уравнения моментов и оценки суммы моментов относительно точки G. Точка G является хорошей отправной точкой, потому что через нее проходят два наших неизвестных, и поэтому исчезают из уравнения моментов, остается только
, которые мы можем решить напрямую.
(11)
(12)
(13)
Теперь тот факт, что
оценивается как отрицательное число, означает, что стрелка силы на самом деле указывает в противоположном направлении, что означает, что это сила сжатия,
(14)
Далее, если мы оцениваем сумму сил в вертикальном
направлении, мы можем решить для ,
(15)
(16)
(17)
И, наконец, мы можем определить оставшиеся неизвестные
, рассмотрев равновесие горизонтальных сил и предполагая, что силы справа положительны,
(18)
(19)
(20)
(21)
Метод сечений является полезным методом, поскольку мы можем сделать разрез в любом месте конструкции, чтобы определить усилия стержня. Нам не нужно знать какие-либо другие внутренние силы членов. Так, например, нам не нужно было знать, какие силы были в членах AB, AG или BG, прежде чем мы сделали наше сокращение.
Нам не нужно знать какие-либо другие внутренние силы членов. Так, например, нам не нужно было знать, какие силы были в членах AB, AG или BG, прежде чем мы сделали наше сокращение.
Если бы мы использовали только метод совместного разрешения, нам пришлось бы двигаться от опорных узлов к интересующей области и оценивать силы в каждом узле по пути, что может стать утомительным для более крупной структуры.
Давайте попробуем другой разрез, на этот раз с секущей плоскостью между D и F и с учетом несущей конструкции справа от секущей плоскости.
Ферма Уоррена с вертикальным разрезом, обнажающим три неизвестных силы стержня Снова обратите внимание, что наша секущая плоскость разрезала не более трех стержней с неизвестными внутренними силами стержня. Это ключевой момент, если наш разрез обнаружит больше трех неизвестных, у нас не будет достаточно уравнений, чтобы решить их все. Разумной отправной точкой на этот раз является рассмотрение суммы моментов относительно точки D, исключая два неизвестных из уравнения моментов.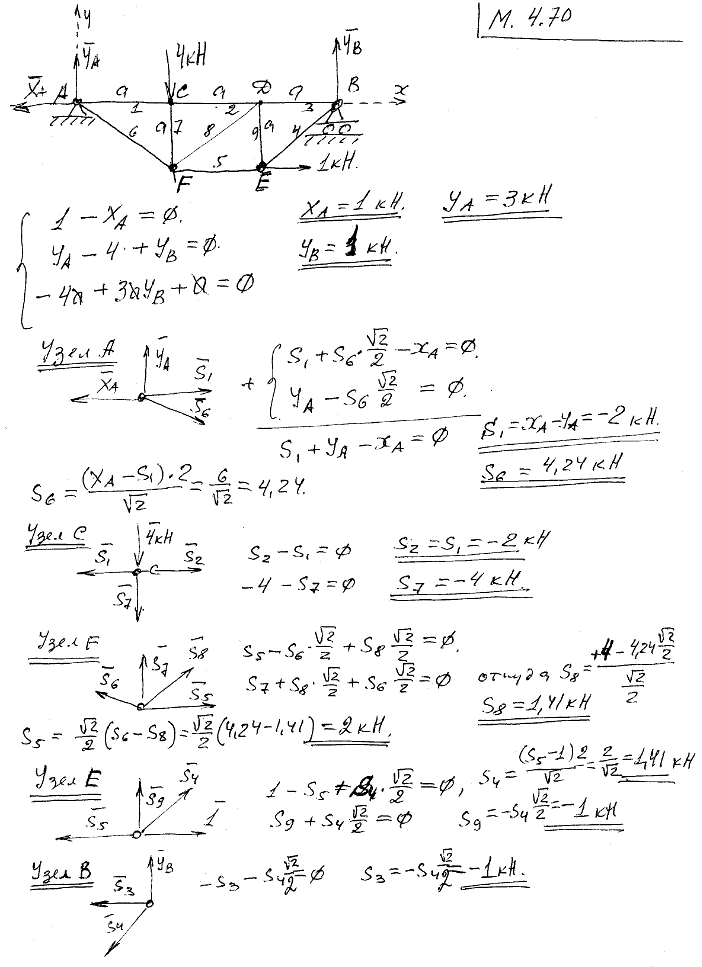
(22)
(23)
(24)
Оценка равновесия вертикальной силы. 28)
(29)
(30)
(31)
Теперь самое время подвести итоги, где мы находимся в анализе,
Сводка внутренних сил элементов до сих пор с оставшимися неизвестными силами, выделенными краснымМы могли бы продолжить использовать метод сечений и сделать больше разрезов в конструкции или мы могли бы использовать метод соединений, чтобы закончить наш анализ. Ради разнообразия мы будем использовать метод суставов с этого момента.
Соединение A
Начиная с соединения A, мы разрезаем элементы, соединяющиеся в стыке, чтобы выявить их неизвестные внутренние силы,
Соединение фермы AПомните из нашего обсуждения выше, у нас есть только 2 уравнения для работы, и поэтому мы может оценивать только суставы с максимум двумя неизвестными силами члена. Оценка равновесия вертикальной силы в первую очередь,
(32)
(33)
(34)
(35)
В настоящее время учитывая равновесие горизонтальной силы,
(36)
(37)
(38)
(39)
. Соединение B
Соединение B
Переходим к соединению B,
Соединение фермы BНам нужно только оценить равновесие вертикальной силы, чтобы определить наше единственное неизвестное здесь,
.
(40)
(41)
(42)
(43)
Соединение C
Рассмотрение равновесия горизонтальной силы соединения C далее.
Торс -сустав C(44)
(45)
(46)
(47)
Состав E.
и, наконец, равновесие вертикального силы E.
(49)
(50)
(51)
Теперь, когда мы оценили все силы внутренних элементов, мы можем обобщить их ниже.
Сводка всех внутренних сил стержня, представляющих полный путь нагрузки для конструкции при этих внешних нагрузках. Надеемся, что эти несколько примеров дали вам четкое представление о том, как именно проводить анализ статически определимой фермы. Шаги высокого уровня каждый раз одинаковы; сначала определите свои опорные реакции, а затем начните прорабатывать структуру, используя метод совместного решения, метод разделов или и то, и другое.
Помните, что при использовании метода разрешения соединений у вас есть два уравнения для работы, поэтому анализируйте соединения, в которых есть до двух элементов с неизвестными силами, действующими на соединение. При использовании метода сечений вы разблокируете третье уравнение для работы, уравнение моментов. Так что теперь, какое бы сечение вы ни проходили через структуру, она не может прорезать более трех членов с неизвестными внутренними силами.
При попытке выполнить анализ фермы вы можете обнаружить, что не можете начать анализ или на полпути вы не можете двигаться дальше. Может не оказаться подходящих разрезов или соединений для анализа. В этом случае вы, вероятно, имеете дело со статически неопределимой фермой, и обсуждаемые здесь методы не сработают.
В этом посте я написал немного больше о концепции неопределенности фермы, а в этом посте я написал полное руководство по альтернативному методу решения, применимому к неопределенным фермам. Так что проверьте их для получения дополнительной информации.
Это анализ фермы в этом посте, увидимся в следующем.
Линкедин Твиттер YouTube
Автор
Д-р Шон Кэрролл
Бакалавр искусств (с отличием), MSc, PhD, CEng MIEI, FHEA
Привет, я Шон, основатель DegreeTutors.com. Я надеюсь, что вы нашли этот урок полезным. Проведя 10 лет в качестве преподавателя в университете по проектированию конструкций, я запустила DegreeTutors.com, чтобы помочь большему количеству людей понять инженерию и получить такое же удовольствие от ее изучения, как и я. Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
Подпишитесь на обновления учебников и курсов
© 2023 DegreeTutors & Mind Map Media Ltd. Все права защищены
Раз и навсегда освойте расчет строительных конструкций
Воспроизвести видео
Предыдущий
Следующий
Этот курс охватывает основные концепции и методы статического расчета конструкций. Начиная с самых основ, мы рассматриваем сил, моментов и как использовать принцип статического равновесия . Затем мы переходим к изучению конструкций или ферм с шарнирным соединением; что это такое и как их анализировать? Мы подробно рассмотрим метод совместного разрешения и метод разделов . Рабочие примеры широко используются для демонстрации практического применения теории.
Начиная с самых основ, мы рассматриваем сил, моментов и как использовать принцип статического равновесия . Затем мы переходим к изучению конструкций или ферм с шарнирным соединением; что это такое и как их анализировать? Мы подробно рассмотрим метод совместного разрешения и метод разделов . Рабочие примеры широко используются для демонстрации практического применения теории.
Основываясь на моем опыте преподавания студентам инженерных специальностей, курс фокусируется на тех областях, которые студенты считают особенно сложными в начале. Связь между теорией и практикой усиливается благодаря моему опыту инженера-конструктора.
Акцент делается на проработанных примерах, а учащимся предлагается попробовать ответить на вопросы до того, как будет представлено подробное решение. Философия преподавания – «учись на практике!».
Этот курс подходит для студентов инженерных специальностей , которые считают свои лекции по конструкциям запутанными и чувствуют себя немного потерянными, когда дело доходит до структурного анализа.

 д.
д.