Формулы по Оптике | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Формулы по Оптике
Основные формулы школьного курса оптики | ||
Формула | Обозначения | Комментарий |
Геометрическая оптика | ||
α – угол падения; β – угол отражения; с – скорость света в вакууме; υ – скорость света в среде; n – абсолютный показатель преломления; n2,1 – относительный показатель преломления; α0 – предельны угол полного отражения; D F – фокусное расстояние линзы; d – расстояние от предмета до линзы; f – расстояние от линзы до изображения; H – размер изображения; h – размер предмета; Г – линейное увеличение линзы | Закон преломления | |
Абсолютный показатель преломления | ||
Относительный показатель преломления второй среды относительно первой; | ||
Условие полного внутреннего отражения | ||
Оптическая сила линзы | ||
Формула тонкой линзы | ||
Линейное увеличение тонкой линзы | ||
Волновая и квантовая оптика | ||
d – период дифракционной решетки; k – порядок спектра; λ – длина волны; ν – частота; Δd – разность хода волн;
ε – энергия; h – постоянная Планка; p – импульс;
А – работа выхода; m – масса электрона; υ – скорость электрона | Формула дифракционной решетки | |
Скорость волны | ||
Условия максимума и минимума интерференции | ||
Энергия кванта (фотона) | ||
Импульс кванта (фотона) | ||
Уравнение Эйнштейна для фотоэффекта | ||
Теги:
конспект
формулы
Физика Влажность воздуха и её измерение
youtube.com/embed/kjJVrM1VLqQ” frameborder=”0″ allowfullscreen=””>Материалы к уроку
Конспект урока
Вода занимает около 70,8% поверхности земного шара. Живые организмы содержат от 50 до 99,7% (пятидесяти до девяноста девяти целых семи десятых процента) воды. В атмосфере находится около 13-15 тыс. км3 воды в виде капель, кристаллов снега и водяного пара. Атмосферный водяной пар влияет на погоду Земли.
Водяной пар в воздухе не всегда является насыщенным, несмотря на огромные поверхности океанов, морей, озер и рек. Перемещению воздушных масс способствует ветер. Это приводит к тому, что в одних местах нашей планеты в данный момент испарение воды преобладает над конденсацией, а в других, наоборот, преобладает конденсация. Но в воздухе практически всегда имеется некоторое количество водяного пара и для каждой территории оно различно.
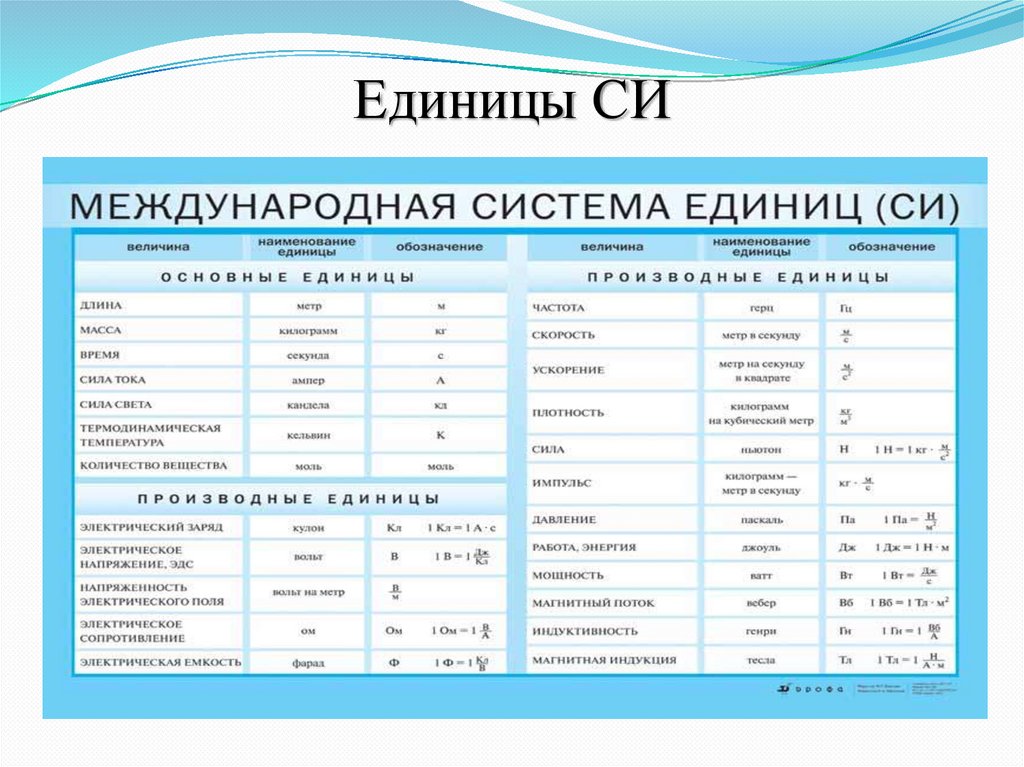
1. Абсолютная влажность ρ (ро)– плотность водяного пара в воздухе измеряется в килограммах на метр кубический (кг/м3), т.е. показывает, сколько граммов водяного пара содержится в воздухе объёмом 1 м³ при данных условиях.
Чем выше температура воздуха, тем больше в нем может быть пара;
Степень насыщения водяного пара зависит от
• количества водяных паров,
• давления,
• температуры.
В окружающем нас воздухе практически всегда находится водяной пар. Влажность воздуха зависит от количества водяного пара, содержащегося в нем.
Сырой воздух содержит больший процент молекул воды, чем сухой.
Например, в центральной части России воздух сухой по сравнению с островом Сахалин. Там воздух настолько влажный, что одежда всегда кажется тоже влажной.

2. Атмосферный воздух представляет собой смесь различных газов и водяного пара, имеющих свои определенные величины давления. Однако, давление, производимое воздухом на находящиеся в нем тела равно суммарному давлению. Парциальным давлением водяного пара называют давление, которое производил бы водяной пар, если бы все остальные газы отсутствовали, т.е. если создать идеальные условия. Парциальное давление водяного пара является одним из показателей влажности воздуха. Его выражают в единицах давления – паскалях или миллиметрах ртутного столба.
3. Относительная влажность – это величина, показывающая, насколько водяной пар при данной температуре близок к насыщению. Так как по парциальному давлению водяного пара и абсолютной влажности нельзя судить о том, насколько водяной пар в данных условиях близок к насыщению.
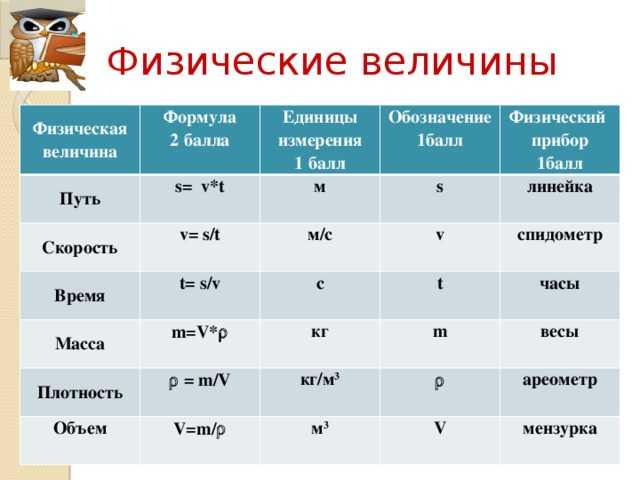 А от этого зависит интенсивность испарения воды и потеря влаги живыми организмами.
А от этого зависит интенсивность испарения воды и потеря влаги живыми организмами. Относительной влажностью воздуха ФИ называют отношение парциального давления р (П) водяного пара, содержащегося в воздухе при данной температуре, к давлению р
Для определения влажности воздуха используют несколько приборов.
ПсихрОметр. Состоит из двух термометров. Резервуар одного из них остается сухим, и он показывает температуру воздуха. Резервуар другого окружен полоской ткани, конец которой опущен в воду. Вода испаряется, и благодаря этому термометр охлаждается. Чем больше относительная влажность, тем менее интенсивно идет испарение, так как в воздухе много водного пара. Температура, показываемая термометром, окруженным влажной тканью, ближе к температуре сухого термометра.
 По разности температур этих термометров с помощью специальных таблиц можно определить влажность воздуха.
По разности температур этих термометров с помощью специальных таблиц можно определить влажность воздуха. Гигрометр.
Существует несколько видов гигрометров:
1. волосной,
2. конденсационный,
3. психрометрический.
Волосной гигрометр состоит из рамки, волоса, стрелки, ролика и груза. Принцип его действия основан на свойстве обезжиренного волоса изменять свою длину в зависимости от влажности воздуха, в котором он находится. Волос натянут на металлическую рамку. Изменение длины волоса передаётся стрелке, перемещающейся вдоль шкалы.
Компенсационный гигрометр – прибор для определения влажности воздуха путем охлаждения последнего до точки росы. Прибор сотоит из термометра, металлической трубки с эфиром и груши, для накачивания воздуха. При испарении эфира на отполированной стенке появляются капли воды.
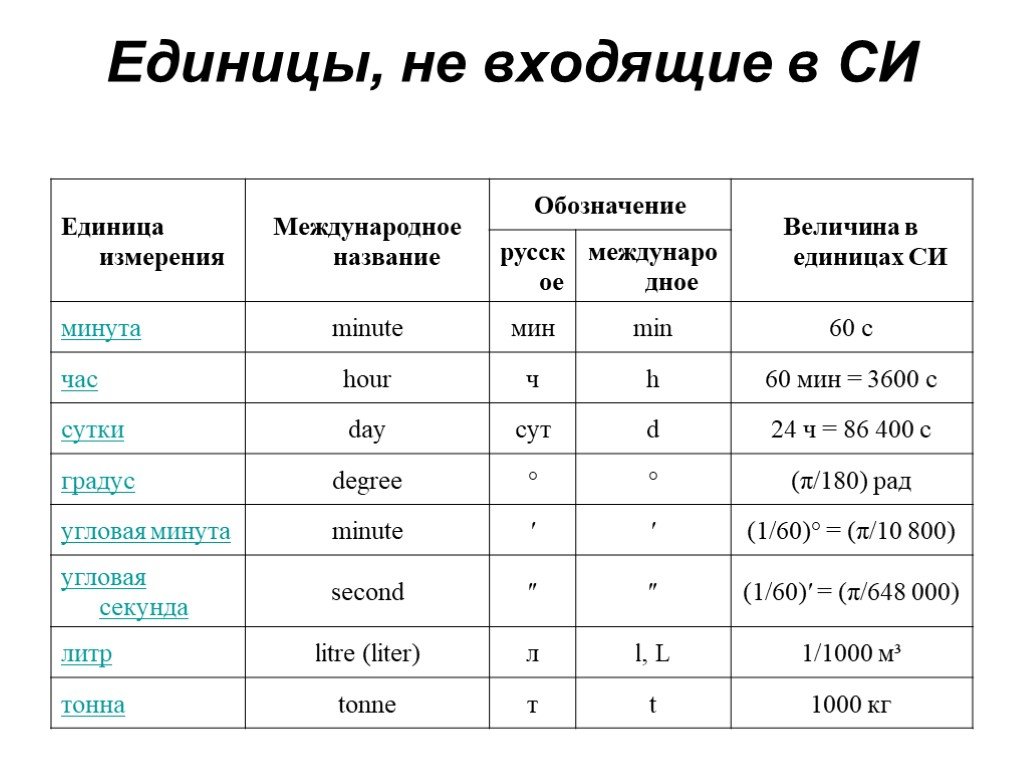
По точке росы находят соответствующую ей плотность насыщенного пара.
По таблице плотности насыщенного пара находят относительную влажность воздуха.
Для ускорения процесса испарения эфира через него с помощью груши прогоняется воздух.
В конденсационном гигрометре М. И. ГОльцмана температура металлического зеркала, измеряемая электрически, может быть понижена до —150°С (минус) с помощью обтекающего его жидкого кислорода или жидкого воздуха.
Воздух просасывается через прибор и проходит мимо зеркала, где и происходит конденсация.
Точка росы также характеризует влажность воздуха:
• выпадение росы под утро,
• запотевание холодного стекла, если на него подышать,
• образование капли воды на холодной водопроводной трубе,
• сырость в подвалах домов.

Наиболее комфортная влажность воздуха для человека лежит в пределах 40—60%.
Высокую температуру легче переносить в сухом воздухе. Жара в сухой пустыне может не так сильно изнурять, как 25 градусов после сильного дождя, когда влажность воздуха очень высока. Чтобы не перегреться, организму в жару надо сильно потеть. Однако при высокой влажности пот не будет высыхать и не даст охлаждения тела.
При высокой температуре воздуха и низкой влажности человек, потея, выводит влагу из организма в основном через кожу, а не через почки. Это свойство организма используется в медицине при заболеваниях почек.
От влажности также зависит интенсивность испарения влаги с поверхности кожи человека. Испарение влаги имеет большое значение для поддержания температуры тела постоянной. В космических кораблях поддерживается наиболее благоприятная для человека относительная влажность воздуха (40-60%).
Очень важно знать влажность в метеорологии – в связи с предсказанием погоды.
 Хотя относительное количество водяного пара в атмосфере сравнительно невелико (около 1%), роль его в атмосферных явлениях значительна. Конденсация водяного пара приводит к образованию облаков и последующему выпадению осадков. При этом выделяется большое количество теплоты. И наоборот, испарение воды сопровождается поглощением теплоты.
Хотя относительное количество водяного пара в атмосфере сравнительно невелико (около 1%), роль его в атмосферных явлениях значительна. Конденсация водяного пара приводит к образованию облаков и последующему выпадению осадков. При этом выделяется большое количество теплоты. И наоборот, испарение воды сопровождается поглощением теплоты.Определенная влажность необходима в ткацком, кондитерском и других производствах для нормального течения процесса.
Хранение произведений искусства и книг требует поддержания влажности воздуха на необходимом уровне. Поэтому в музеях на стенах вы можете видеть психрометры.
Рассмотрим решение задачи.
Найдите относительную влажность воздуха в комнате при температуре 18 °С, если при 10°С образуется роса.
По таблице зависимости давления насыщенных водяных паров от температуры найдем нужные нам значения: при температуре 18 градусов цельсия парциальное давление водяного пара равно одна целая, 23 сотых килопаскаля, а давление насыщенного пара равно две целых семь сотых килопаскаль.
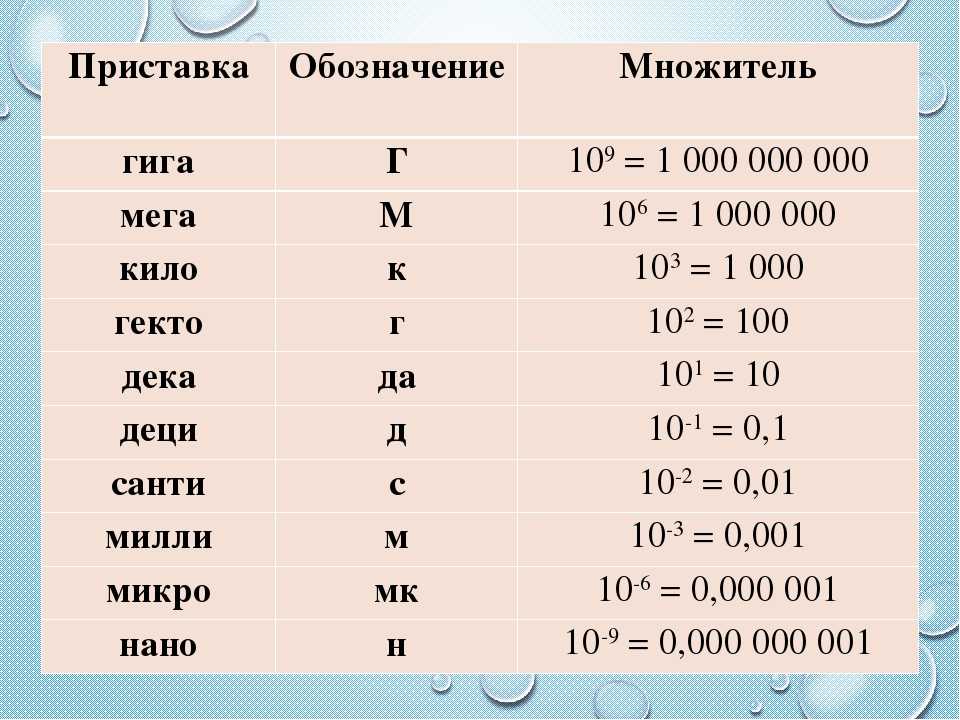 Переведем килопаскали в паскали, и подставив значение величин в формулу, получим: фи равно парциальное давление водяного пара разделить на давление насыщенного пара и умножить на 100 процентов равно 1230 паскаль разделить на 2070 паскаль и умножить на 100 процентов равно 59 процентов.
Переведем килопаскали в паскали, и подставив значение величин в формулу, получим: фи равно парциальное давление водяного пара разделить на давление насыщенного пара и умножить на 100 процентов равно 1230 паскаль разделить на 2070 паскаль и умножить на 100 процентов равно 59 процентов.Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Пи против Фи, Магия и Тайна – Шастра Снехи
Пи и Фи, что это такое? Что у них общего и чего нет? Ни один студент-математик не закончил бы свой курс, не встретившись с числом пи хотя бы раз. И фи, если вы восхищаетесь красотой, то все благодаря ей. Они веками заставляли ученых работать над ними, время от времени разгадывая тайны праведникам. У нас уже есть статья о золотом сечении, известном как фи. Если вы не читали это, вы можете найти это здесь: Интригующее божественное соотношение природы
У нас уже есть статья о золотом сечении, известном как фи. Если вы не читали это, вы можете найти это здесь: Интригующее божественное соотношение природы
«Вероятно, ни один символ в математике не вызывал столько тайн, романтизма, заблуждений и человеческого интереса, как число пи»
Уильям Л. Шааф, Природа и история числа Пи
Что такое Пи?
Отношение длины окружности к ее диаметру , обозначаемое строчной греческой буквой 𝜋 , является одной из известных математических констант. Для любого идеального круга отношение его длины окружности к диаметру является константой, то есть числом пи, независимо от того, рассматривается ли большой или маленький круг. 3.141592654… это то, что вы получаете в калькуляторе не потому, что это значение. Но дисплей калькуляторов часто ограничен десятью цифрами. Пи — это иррациональное число, бесконечное и неповторяющееся десятичное число . 22/7, 3.14 и 3 — несколько часто используемых приближений.
22/7, 3.14 и 3 — несколько часто используемых приближений.
Математики и их одержимость числом Пи:
Поиск значения числа Пи начался давно, и вы не поверите, если я скажу когда. Многие известные математики, в том числе Фибоначчи, Лейбниц, Гаусс, Ньютон, Иоганн Генрих Ламберт и несколько других менее известных математиков, внесли свой вклад в поиск значений числа Пи. Это началось 4000 лет назад, когда Древние вавилоняне использовали приблизительное значение длины окружности круга, т. е. умноженное на 3 его диаметра. Свидетельства утверждают, что они использовали 3,125, что является близким приближением. Греки использовали формулу, которая аппроксимирует число Пи как (16/9) 2 = 3,165.
Стих 1 Царств 7:23 из Библии говорит:
Он сделал море из литого металла, круглой формы, размером десять локтей от края до края и пять локтей высотой. Чтобы измерить его, потребовалась линия в тридцать локтей.

Архимед , греческий математик, использовал интересный алгоритмический подход, чтобы доказать, что значение числа пи должно быть не меньше 221/73 и не больше 22/7. Только в 1600-х годах у него было глобальное название. Перенесемся вперед, теперь мы приблизили число пи к 31 415 926 535 897 цифр (~ 31 триллион !). Для меня самое удивительное приближение получено с помощью Арьябхаты , индийского математика и астронома, который приблизил это число к 3,1416. Впечатляет, не так ли? Поклонники числа Пи установили мировые рекорды, запоминая значения числа Пи. Вы спросите, много ли я знаю? 100 цифр, я уже горжусь собой. Но все, что вам нужно, это 39 цифр или около того, чтобы практически не было ошибки .
Храм Пи в ЭксплораториумеГде находится число Пи?
Повсюду вокруг тебя! Круги, треугольники, конусы, сферы, цилиндры, дуги, назовите это, я вижу это. Пи широко используется в математике и физике, например, для нахождения площади и объема, в квантовой механике, в строительстве, в теории музыки, в авиаперелетах и во многих других областях. Благодаря технологическим достижениям последних дней их применение в реальных системах значительно расширилось. При расчете траекторий НАСА использует технику под названием Передача Пи на космическом корабле «Кассини» для завершения маневра полета к Титану, спутнику Сатурна. От отслеживания динамики населения, изучения структуры глаза до расчета площадей обшивки самолетов широко используется значение числа Пи. В измерении волн число пи.
Благодаря технологическим достижениям последних дней их применение в реальных системах значительно расширилось. При расчете траекторий НАСА использует технику под названием Передача Пи на космическом корабле «Кассини» для завершения маневра полета к Титану, спутнику Сатурна. От отслеживания динамики населения, изучения структуры глаза до расчета площадей обшивки самолетов широко используется значение числа Пи. В измерении волн число пи.
Почему это так важно?
Когда люди запоминают тысячи цифр просто для развлечения, в этом нет ничего необычного. Из определения числа пи следует новый взгляд на Вселенную, в которой мы живем, новый подход к измерению углов (9).0003 радиан, мера ), более полезный способ, чем привычная градусная мера , связывающая угол с длиной . 360° = 2𝜋. Включая принцип неопределенности Гейзенберга , он используется во многих важных формулах. Вероятность того, что любые два случайных числа взаимно просты, равна 6/𝜋 2 . Странный! Будь то лучи или волны, вы измеряете их числом Пи. Из-за своей важности у него есть день, посвященный ему самому! Угадайте, когда? 14 марта -й (3.14).
Странный! Будь то лучи или волны, вы измеряете их числом Пи. Из-за своей важности у него есть день, посвященный ему самому! Угадайте, когда? 14 марта -й (3.14).
Пилиш , форма письма, разработанная поклонниками числа Пи, основанная на длине слов, соответствует числам, записанным в последовательности цифр числа Пи. Есть рассказы, стихи (пиэмы), пи-кус, а также роман. Максимальная длина пилишской строки, найденной в других писаниях, на данный момент составляет 8.
Что такое фи?
Обозначается как 21 st Греческая буква – фи, отношение, полученное при делении отрезка линии особым образом. Отношение между двумя отрезками отрезка называется фи, если их отношение равно отношению их суммы к большей из двух величин. Также называется Золотое сечение, Золотое сечение, Золотое число, Золотое сечение, Золотая пропорция, Божественная пропорция и Божественное сечение ; это объясняет совершенную красоту природы. Как и пи, это тоже иррациональное число. Оно приблизительно равно 1,618 .
Как и пи, это тоже иррациональное число. Оно приблизительно равно 1,618 .
Золотое сечение используется даже в фотографии для визуальной композиции. Изображение разделено на девять частей с помощью двух горизонтальных и вертикальных линий, известных как фи-сетка. Затем объекты размещаются близко к пересечению линий.«Последовательность Фибоначчи оказывается ключом к пониманию того, как природа проектирует… и является… частью той же вездесущей музыки сфер, которая встраивает гармонию в атомы, молекулы, кристаллы, оболочки, солнца и галактики и создает Вселенная поет».
― Гай Мерчи, Семь тайн жизни: исследование науки и философии.
Ретроспективный кадр:
От Да Винчи до соседского фотографа, все восхищаются золотым сечением за то, что оно делает вещи красивыми. Никто не изобретал золотое сечение, они просто открыли то, что уже было распространено в природе. Ряд Фибоначчи тесно связан с золотым сечением. Чем больше члены, тем ближе их отношение к фи. В рукотворных чудесах золотое сечение можно широко наблюдать в искусстве и архитектуре. Датируется Парфенон греков , Пирамиды египтян , мы видим Золотое сечение. В 1900-х годах американский математик Марк Барр впервые обозначил золотое сечение символом фи (𝜙). Евклид был первым, кто использовал число 0,618… для деления линии на основе отношения ее крайних значений к среднему. Хотя его близкий родственник ряд Фибоначчи был обнаружен в 1175 году нашей эры, его связь с золотым сечением может оказаться неожиданной.
Чем больше члены, тем ближе их отношение к фи. В рукотворных чудесах золотое сечение можно широко наблюдать в искусстве и архитектуре. Датируется Парфенон греков , Пирамиды египтян , мы видим Золотое сечение. В 1900-х годах американский математик Марк Барр впервые обозначил золотое сечение символом фи (𝜙). Евклид был первым, кто использовал число 0,618… для деления линии на основе отношения ее крайних значений к среднему. Хотя его близкий родственник ряд Фибоначчи был обнаружен в 1175 году нашей эры, его связь с золотым сечением может оказаться неожиданной.
Код Да Винчи говорит Фи:
Леонардо да Винчи использовал фи во многих своих картинах, включая самую известную Мону Лизу. Не только он, но и многие другие художники эпохи Возрождения. Хотя это ярко видно во многих чудесах искусства и архитектуры, мы не совсем уверены, думали ли они об этом. Многие картины эпохи Возрождения демонстрируют фи в той или иной форме, в том числе знаменитые Мона Лиза и Тайная вечеря Леонардо да Винчи . Его появление в нас и вокруг нас побудило многих писателей отвести ему ключевую роль в своих книгах. Дэн Браун не исключение. Его роман «Код да Винчи» вращается вокруг этого загадочного числа фи. Хотя не все, что он упомянул в своей книге, правда, факт, что семена в подсолнухе, листья вокруг стебля связаны с золотым сечением, верен. Но наличие числа у людей (отношение роста тела к расстоянию от пупка до пола) на самом деле неверно. И не для других животных тоже.
Его появление в нас и вокруг нас побудило многих писателей отвести ему ключевую роль в своих книгах. Дэн Браун не исключение. Его роман «Код да Винчи» вращается вокруг этого загадочного числа фи. Хотя не все, что он упомянул в своей книге, правда, факт, что семена в подсолнухе, листья вокруг стебля связаны с золотым сечением, верен. Но наличие числа у людей (отношение роста тела к расстоянию от пупка до пола) на самом деле неверно. И не для других животных тоже.
Его присутствие в чудесах вселенной могло заставить его поверить, что это правда. Хотя Евклид впервые использовал это число, дело не в том, что другие не столкнулись бы с ним. Есть много других констант, таких как постоянная Эйлера, натуральный логарифм (e) и многие другие, которые играют ключевую роль в жизни этой вселенной. В самовоспроизведении появляется золотое сечение, но также появляются и некоторые другие, что не делает его особенным. При выводе характеристического уравнения для моделирования самовоспроизводства корнями являются алгебраические числа. Если вы думаете, что золотая середина — единственная, у которой есть название драгоценного металла, посмотрите другие металлические средства .
Если вы думаете, что золотая середина — единственная, у которой есть название драгоценного металла, посмотрите другие металлические средства .
Все еще думаешь о том, что общего? Я бы ничего не сказал, кроме того факта, что они оба являются иррациональными десятичными числами и играют важную роль в своих таинственных способах.
Ссылка :
- Вычисление рекордных 31,4 трлн знаков постоянной Архимеда в Google Cloud
- Веб-сайт, посвященный Pi 0002 Сферические координаты могут быть сначала немного сложно понять. Сферические координаты определяют положение точки в трехмерном пространстве на основе расстояния $\rho$ от начала координат и двух углов $\theta$ и $\phi$. Если кто-то знаком с полярными координатами, то угол $\theta$ понять несложно, так как он практически такой же, как угол $\theta$ в полярных координатах. Но некоторым людям трудно понять, что
угол $\phi$ это все о.
Следующая графика и интерактивные апплеты могут помочь вам понять сферические лучше координирует.
 На этой странице мы выводим взаимосвязь между сферическими и декартовыми координатами, показываем апплет, позволяющий исследовать влияние каждой сферической координаты, и иллюстрируем простые сферические координатные поверхности.
На этой странице мы выводим взаимосвязь между сферическими и декартовыми координатами, показываем апплет, позволяющий исследовать влияние каждой сферической координаты, и иллюстрируем простые сферические координатные поверхности.Связь между сферическими и декартовыми координатами
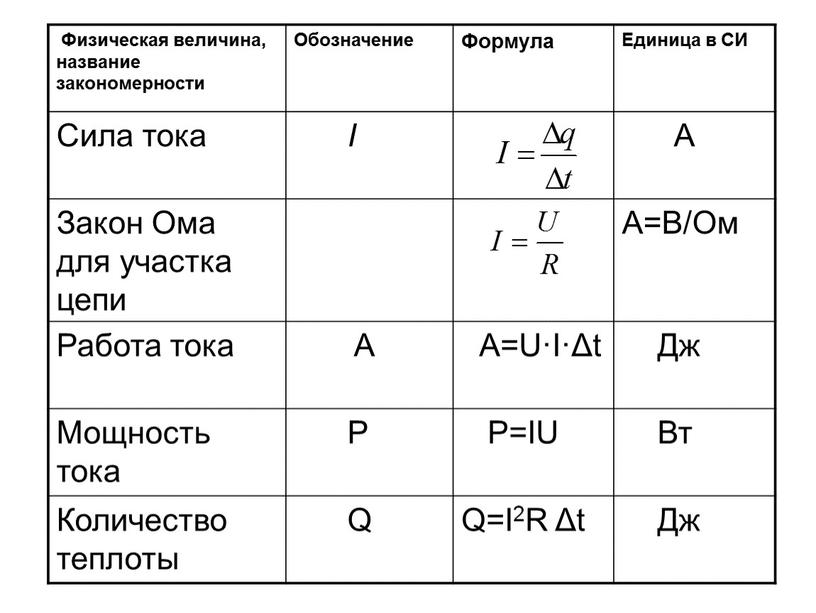
Сферические координаты определяются, как указано в следующий рисунок, который иллюстрирует сферические координаты точка $P$.
Координата $\rho$ — это расстояние от $P$ до начала координат. Если точка $Q$ является проекцией $P$ на плоскость $xy$, тогда $\theta$ угол между положительной осью $x$ и отрезком от начала координат до $Q$. Наконец, $\phi$ — это угол между положительной осью $z$ и отрезок прямой от начала координат до $P$.
Связь между декартовыми координатами $(x,y,z)$ точки $P$ и ее сферическими координатами $(\rho,\theta,\phi)$ можно вычислить с помощью тригонометрии. Розовый треугольник вверху — это прямоугольный треугольник, вершинами которого являются начало координат, точка $P$ и ее проекция на ось $z$.
 Поскольку длина гипотенузы равна $\rho$, а $\phi$ – это угол, который гипотенуза образует с катетом прямоугольного треугольника по оси $z$, координата $z$ точки $P$ (т. е. высота треугольника) равно $z=\rho\cos\phi$. Длина другого катета прямоугольного треугольника — это расстояние от $P$ до оси $z$, равное $r=\rho\sin\phi$. Столько же находится и расстояние точки $Q$ от начала координат.
Поскольку длина гипотенузы равна $\rho$, а $\phi$ – это угол, который гипотенуза образует с катетом прямоугольного треугольника по оси $z$, координата $z$ точки $P$ (т. е. высота треугольника) равно $z=\rho\cos\phi$. Длина другого катета прямоугольного треугольника — это расстояние от $P$ до оси $z$, равное $r=\rho\sin\phi$. Столько же находится и расстояние точки $Q$ от начала координат.Голубой треугольник, показанный как в исходной трехмерной системе координат слева, так и в плоскости $xy$ справа, представляет собой прямоугольный треугольник, вершинами которого являются начало координат, точка $Q$ и ее проекция на $x$-ось. На правом графике расстояние от $Q$ до начала координат, которое является длиной гипотенузы прямоугольного треугольника, обозначено как $r$. Поскольку $\theta$ — это угол, который эта гипотенуза образует с осью $x$, $x$- и $y$-компоненты точки $Q$ (которые совпадают с $x$- и $y$-компонентами точки $Q$ $-компоненты точки $P$) задаются выражениями $x=r\cos\theta$ и $y=r\sin\theta$.
 Поскольку $r=\rho\sin\phi$, эти компоненты можно переписать как $x=\rho\sin\phi\cos\theta$ и $y=\rho\sin\phi\sin\theta$. Таким образом, формулы для декартовых координат в терминах сферических координат:
\начать{выравнивать}
x &= \rho\sin\phi\cos\theta\notag\\
y &= \rho\sin\phi\sin\theta\label{spherical_cartesian}\tag{1}\\
z &= \rho\cos\phi\notag.
\end{выравнивание}
Поскольку $r=\rho\sin\phi$, эти компоненты можно переписать как $x=\rho\sin\phi\cos\theta$ и $y=\rho\sin\phi\sin\theta$. Таким образом, формулы для декартовых координат в терминах сферических координат:
\начать{выравнивать}
x &= \rho\sin\phi\cos\theta\notag\\
y &= \rho\sin\phi\sin\theta\label{spherical_cartesian}\tag{1}\\
z &= \rho\cos\phi\notag.
\end{выравнивание}Изучение влияния каждой сферической координаты
Приведенный ниже апплет позволяет увидеть, как положение точки изменяется при изменении вы меняете $\rho$, $\theta$ и $\phi$. Точка $P$, соответствующая значению координат, показана большой фиолетовой точкой. Зеленая точка — это точка $Q$, т. е. проекция $P$ на $xy$-плоскость.
Загрузка апплета
Сферические координаты. Учитывая значения сферических координат $\rho$, $\theta$ и $\phi$, которые можно изменить, перетаскивая точки на ползунках, большая красная точка показывает соответствующее положение в Декартовы координаты.
 Зеленая точка — это проекция точки на $xy$-плоскость. Вы можете визуализировать каждую из сферических координат с помощью геометрических структур, которые окрашены в соответствии с цветами ползунка. Длина отрезка красной линии от начала координат равна $\rho$. Угол зеленой части диска в плоскости $xy$ равен $\theta$. Угол синей части вертикального диска равен $\phi$. Вы также можете перемещать большую красную точку и зеленую проекцию этой точки непосредственно с помощью мыши.
Зеленая точка — это проекция точки на $xy$-плоскость. Вы можете визуализировать каждую из сферических координат с помощью геометрических структур, которые окрашены в соответствии с цветами ползунка. Длина отрезка красной линии от начала координат равна $\rho$. Угол зеленой части диска в плоскости $xy$ равен $\theta$. Угол синей части вертикального диска равен $\phi$. Вы также можете перемещать большую красную точку и зеленую проекцию этой точки непосредственно с помощью мыши.Дополнительная информация об апплете.
Обратите внимание, как вы можете получить любую точку, даже если мы ограничиваем $\rho \ge 0$, $0 \le\тета
Эти ограничения устранили большую часть неуникальности сферических координаты. Обратите внимание, что в точке $\rho =0$ все еще присутствует неединственность, в точке $\phi = 0$ и при $\phi=\pi$. Когда любое из этих условий верно, вы можете изменить значение одной или нескольких других координат без перемещения точки.
К сожалению, соглашение об обозначении сферических координат не стандартизировано в разных дисциплинах.
 Например, в физике роли $\theta$ и $\phi$ обычно меняются местами. Чтобы правильно понять, как кто-то использует сферические координаты, вы должны сначала определить, какие обозначения используются при этом. Вы не можете предположить, что они следуют соглашению, используемому здесь.
Например, в физике роли $\theta$ и $\phi$ обычно меняются местами. Чтобы правильно понять, как кто-то использует сферические координаты, вы должны сначала определить, какие обозначения используются при этом. Вы не можете предположить, что они следуют соглашению, используемому здесь.Простые сферические координатные поверхности
Эти три следующих апплета могут помочь вам понять, что представляет собой каждый из трех значит сферические координаты. Они показывают, какие поверхности $\phi=$ константа, константа $\theta=$ и константа $\rho=$ выглядят так. значение константы определяется положением ползунков. Во всех случаях мы ограничиваем поверхности областью $\rho
Константа $\phi$
Что означает, что точка имеет сферическую координату $\phi=\pi/3$? Взгляните на поверхности, которые определяется уравнением $\phi=$ постоянная.
Загрузка апплета
Поверхности постоянных $\phi$ в сферических координатах. Показана коническая поверхность константы $\phi=$, где значение $\phi$ определяется синей точкой на бегунке.
 Только часть поверхности где $\rho
Только часть поверхности где $\rhoПодробнее о апплете.
Поверхностная константа $\phi=$ представляет собой просто одиночный конус, направленный либо вверх или вниз. Если вы знаете, что $\phi=\pi/3$, то вы знаете точка находится где-то на (широком) единственном конусе, который открывается вверх, т. е. Уравнение $\phi=\pi/3$ задает поверхность, которая представляет собой одно конусное отверстие вверх. Уравнение $\phi=\pi/2$ соответствует плоскости $xy$. 92}$$ где $C=1/\tan \phi$, что действительно является уравнением для конуса.
Постоянная $\theta$
Поверхностная постоянная $\theta=$ представляет собой полуплоскость вне оси $z$. (Это отображается как полукруг только потому, что мы ограничиваем график $\ро
Загрузка апплета
Поверхности постоянных $\theta$ в сферических координатах. Показана полуплоская поверхность константы $\theta=$, где значение $\theta$ определяется синей точкой на бегунке. Только часть поверхности, где $\rho
Дополнительная информация об апплете.

Если точка имеет $\theta=\pi/2$, то вы знаете, что точка находится на половина плоскости $yz$, где значения $y$ положительны. Уравнение $\theta=\pi/2$ — уравнение для этой полуплоскости.
Из отношения \eqref{spherical_cartesian} отношение между $x$ и $y$ можно записать, например, как $y/x = \tan \theta$. Если $\theta$ поддерживается постоянным, то отношение между $x$ и $y$ остается постоянным. Таким образом, константа $\theta=$ дает прямую, проходящую через начало координат в плоскости $xy$. Так как $z$ не имеет ограничений, мы получаем вертикальную плоскость. Оглядываясь назад на отношение \eqref{spherical_cartesian}, мы видим, что это всего лишь полуплоскость, потому что $\rho\sin\phi$ не может быть отрицательным.
Константа $\rho$
У большинства людей нет проблем с пониманием того, что означает $\rho=3$. Это сфера радиуса 3 с центром в начале координат. В общем, поверхность Константа $\rho=$ — это сфера радиуса $\rho$ с центром в начале координат.



 На этой странице мы выводим взаимосвязь между сферическими и декартовыми координатами, показываем апплет, позволяющий исследовать влияние каждой сферической координаты, и иллюстрируем простые сферические координатные поверхности.
На этой странице мы выводим взаимосвязь между сферическими и декартовыми координатами, показываем апплет, позволяющий исследовать влияние каждой сферической координаты, и иллюстрируем простые сферические координатные поверхности. Поскольку длина гипотенузы равна $\rho$, а $\phi$ – это угол, который гипотенуза образует с катетом прямоугольного треугольника по оси $z$, координата $z$ точки $P$ (т. е. высота треугольника) равно $z=\rho\cos\phi$. Длина другого катета прямоугольного треугольника — это расстояние от $P$ до оси $z$, равное $r=\rho\sin\phi$. Столько же находится и расстояние точки $Q$ от начала координат.
Поскольку длина гипотенузы равна $\rho$, а $\phi$ – это угол, который гипотенуза образует с катетом прямоугольного треугольника по оси $z$, координата $z$ точки $P$ (т. е. высота треугольника) равно $z=\rho\cos\phi$. Длина другого катета прямоугольного треугольника — это расстояние от $P$ до оси $z$, равное $r=\rho\sin\phi$. Столько же находится и расстояние точки $Q$ от начала координат.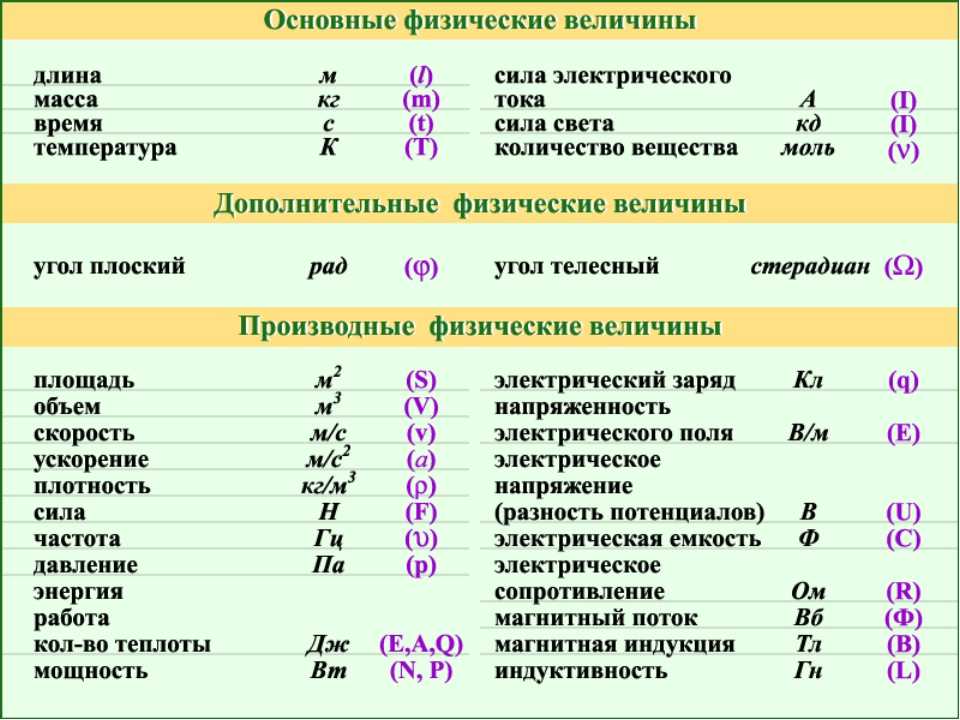 Поскольку $r=\rho\sin\phi$, эти компоненты можно переписать как $x=\rho\sin\phi\cos\theta$ и $y=\rho\sin\phi\sin\theta$. Таким образом, формулы для декартовых координат в терминах сферических координат:
\начать{выравнивать}
x &= \rho\sin\phi\cos\theta\notag\\
y &= \rho\sin\phi\sin\theta\label{spherical_cartesian}\tag{1}\\
z &= \rho\cos\phi\notag.
\end{выравнивание}
Поскольку $r=\rho\sin\phi$, эти компоненты можно переписать как $x=\rho\sin\phi\cos\theta$ и $y=\rho\sin\phi\sin\theta$. Таким образом, формулы для декартовых координат в терминах сферических координат:
\начать{выравнивать}
x &= \rho\sin\phi\cos\theta\notag\\
y &= \rho\sin\phi\sin\theta\label{spherical_cartesian}\tag{1}\\
z &= \rho\cos\phi\notag.
\end{выравнивание} Зеленая точка — это проекция точки на $xy$-плоскость. Вы можете визуализировать каждую из сферических координат с помощью геометрических структур, которые окрашены в соответствии с цветами ползунка. Длина отрезка красной линии от начала координат равна $\rho$. Угол зеленой части диска в плоскости $xy$ равен $\theta$. Угол синей части вертикального диска равен $\phi$. Вы также можете перемещать большую красную точку и зеленую проекцию этой точки непосредственно с помощью мыши.
Зеленая точка — это проекция точки на $xy$-плоскость. Вы можете визуализировать каждую из сферических координат с помощью геометрических структур, которые окрашены в соответствии с цветами ползунка. Длина отрезка красной линии от начала координат равна $\rho$. Угол зеленой части диска в плоскости $xy$ равен $\theta$. Угол синей части вертикального диска равен $\phi$. Вы также можете перемещать большую красную точку и зеленую проекцию этой точки непосредственно с помощью мыши.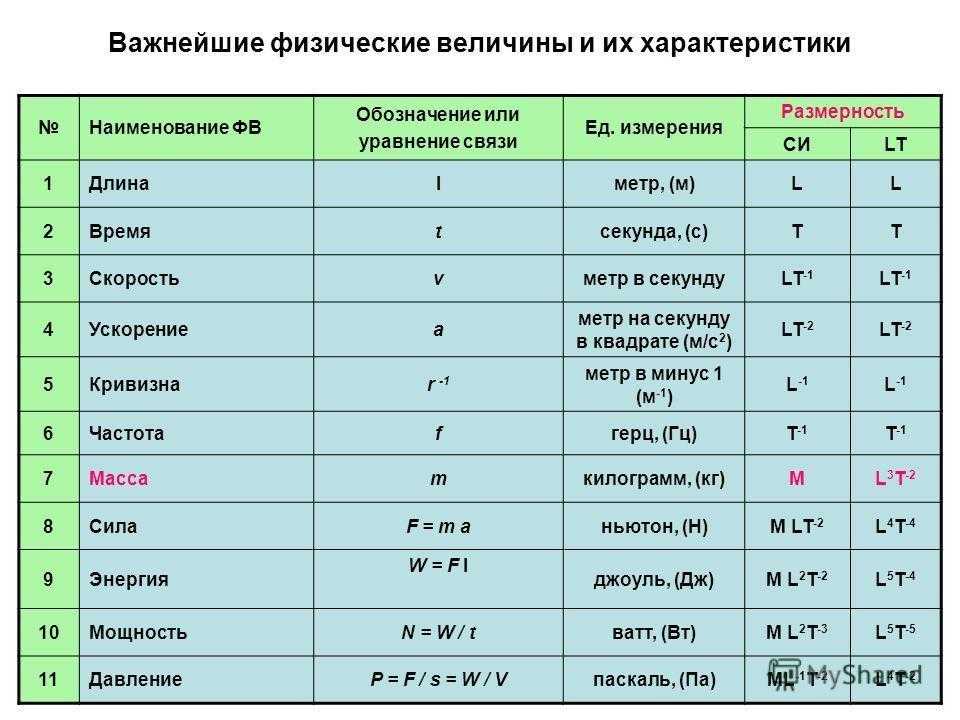 Например, в физике роли $\theta$ и $\phi$ обычно меняются местами. Чтобы правильно понять, как кто-то использует сферические координаты, вы должны сначала определить, какие обозначения используются при этом. Вы не можете предположить, что они следуют соглашению, используемому здесь.
Например, в физике роли $\theta$ и $\phi$ обычно меняются местами. Чтобы правильно понять, как кто-то использует сферические координаты, вы должны сначала определить, какие обозначения используются при этом. Вы не можете предположить, что они следуют соглашению, используемому здесь. Только часть поверхности где $\rho
Только часть поверхности где $\rho
