Физическая формула объема: Меры объёма — урок. Физика, 7 класс. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

формула через ребро и диагональ грани

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение объема куба: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.

Формула вычисления объема куба
Примеры задач

Формула вычисления объема куба

1. Через длину ребра

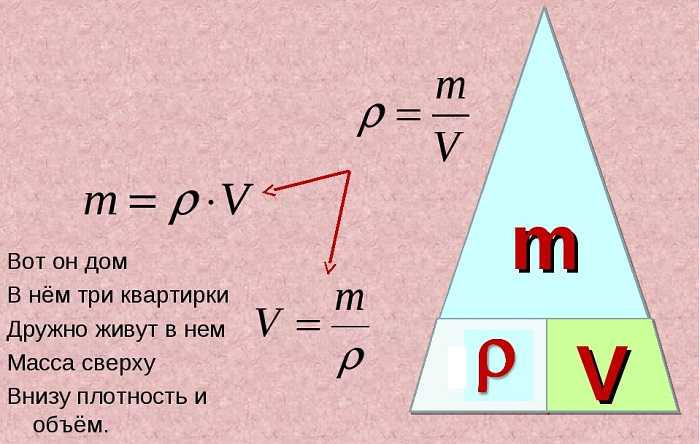
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.

V = a ⋅ a ⋅ a = a³

2. Через длину диагонали грани

Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.

Следовательно, вычислить объем куба можно так:

Примеры задач

Задание 1
Вычислите объем куба, если его ребро равняется 5 см.

Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см³.

Задание 2
Известно, что объем куба равен 512 см³. Найдите длину его ребра.

Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:

Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.

Решение:
Применим формулу, в которой используется диагональ грани:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

способы нахождения, формула, единицы измерения, свойства объема тела

Содержание:

Понятие объема тела
Свойства объема тела
Как вычислить объем тела: все формулы
Примеры решения задач
Задания для самостоятельной работы

Содержание

Понятие объема тела

Свойства объема тела
Как вычислить объем тела: все формулы
Примеры решения задач
Задания для самостоятельной работы

Понятие объема тела

Объем является количественным параметром пространства, занятого телом или веществом.

Термин объема можно рассматривать совместно с понятием вместимости. Это обозначение для объема какого-то внутреннего пространства сосуда, коробки и тому подобного. Объем тела, как и вместимость некой емкости, зависит от таких характеристик, как:

форма;
линейные размеры.

Главным свойством объема принято считать аддитивность.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Аддитивность означает равенство объема какого-либо тела сумме объемов частей этого тела, которые не пересекаются между собой.

Согласно СИ, единицей измерения объема является метр кубический (м³). В процессе решения задач можно встретить единицы измерения объемов тел в виде см³, дм³, или литров. В иностранной литературе также используются указания объемов веществ, находящихся в жидком или сыпучем состоянии, в таких единицах измерения, как, например, галлон, баррель и другие.

Величина объема используется при составлении различных уравнений и неравенств. При этом данный параметр обозначают с помощью буквы V. Это сокращение от латинского слова volume, которое в переводе означает объем или наполнение.

Свойства объема тела

В процессе решения разнообразных задач по физике, алгебре и геометрии целесообразно использовать свойства, которыми обладает объем тела. Перечислим основные из них:

Объем тела не может быть отрицательной величиной.
В том случае, когда некое геометрическое тело состоит из определенного количества геометрических тел, не обладающих едиными внутренними точками, объем такого тела складывается из объемов составляющих его тел.
Объем фигуры в виде куба с ребром, значение которого равно единице измерения длины, равен единице.
Аналогичные друг другу геометрические тела обладают одинаковыми объемами.

В том случае, когда тело имеет объем V1 и расположено в другом теле с объемом V2, справедливо следующее соотношение: \(V1<V2 \). 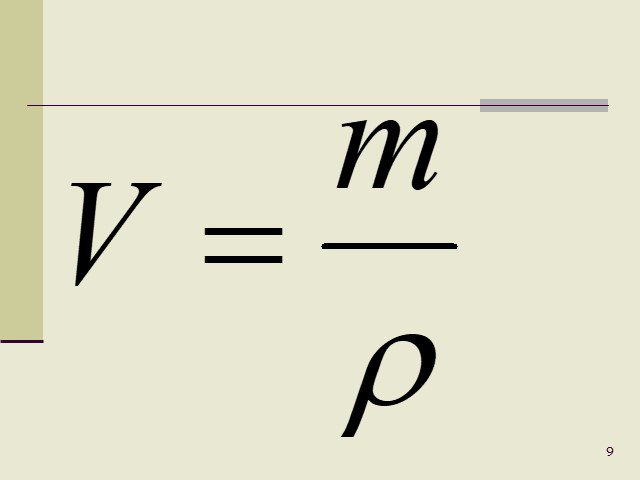2}=25\)
Таким образом, первый шар имеет площадь поверхности, которая в 25 раз больше по сравнению с аналогичной характеристикой второго шара.
Ответ: 25.
Задача 2
На рисунке изображены конусы. Назовем их \(K_1\) и \(K_2\).
Полная поверхность \(K_1\) по площади относится к площади полной поверхности \(K_2\) как 4:1.
Фигура \(K_1\) обладает радиусом, который в 4 раза больше образующей \(K_1\) и в 2 раза больше радиуса \(K_2\).

Требуется вычислить, как относится образующая \(K_2\) к образующей \(K_1.\)
Источник: shkolkovo.net
Решение
Представим, что образующая конуса равна 1, а радиус основания обозначим, как R. Тогда можно записать следующее соотношение:
\(S=\pi R (R+l)\)
Запишем отношения площадей полной поверхности заданных конусов:
\(\dfrac41=\dfrac{\pi \,R_1\cdot (R_1+l_1)}{\pi \, R_2\cdot (R_2+l_2)}\)
Согласно условию задачи, имеем:
\(R_1=4l_1, R_2=\frac12R_1=2l_1\)
В результате:
\(\dfrac41=\dfrac{4l_1\cdot (4l_1+l_1)}{2l_1\cdot (2l_1+l_2)} \quad\Rightarrow\quad \dfrac{l_2}{l_1}=\dfrac12=0,5\)

Ответ: 0,5.
Задача 3
Даны два прямоугольных параллелепипеда. Объем первой фигуры равен 105. Известно, что первый параллелепипед по высоте превышает второй в 7 раз. Ширина второй фигуры в 2 раза больше по сравнению с аналогичным параметром первой фигуры. Первый параллелепипед длиннее в три раза, чем второй. Необходимо вычислить объем, который имеет второй параллелепипед.
Источник: shkolkovo.net
Решение
Обозначим высоту, ширину и длину геометрических фигур с помощью букв а, b,

с соответственно. Вспомним формулу, по которой можно найти объем прямоугольного параллелепипеда:
V=abc
Применительно к нашей задаче, запишем:
\(\dfrac{105}{V_2}=\dfrac{V_1}{V_2}=\dfrac{a_1b_1c_1}{a_2b_2c_2}\)
Известно, что:
\(a_1=7a_2, b_2=2b_1, c_1=3c_2\)
В результате:
\(\dfrac{105}{V_2}=\dfrac{7a_2\cdot b_1\cdot 3c_2}{a_2\cdot 2b_1\cdot c_2}= \dfrac{7\cdot 3}2 \quad\Rightarrow\quad V_2=\dfrac{105\cdot 2}{21}=10\)
Ответ: 10.
Задача 4
Даны два конуса. Площадь боковой поверхности первой геометрической фигуры относится к площади боковой поверхности второй фигуры как 3:7. Первый конус обладает радиусом, который относится к радиусу второго конуса, как 15:7. Необходимо определить, как относится образующая первого конуса к образующей второго конуса.
Источник: shkolkovo.net
Решение
Составим формулу для расчета площади боковой поверхности конуса:
\(S=\pi Rl\)
Запишем отношения площадей боковых поверхностей для первого и второго конусов:
\(\dfrac 37=\dfrac{S_1}{S_2}=\dfrac{\pi R_1\,l_1}{\pi R_2\,l_2}\)
Зная, что отношение радиусов двух геометрических фигур равно 15:7, получим:
\(\frac{R_1}{R_2}=\frac{15}7, то \dfrac37=\dfrac {15}7\cdot \dfrac{l_1}{l_2} \quad\Rightarrow\quad \dfrac{l_1}{l_2}=\dfrac37\cdot \dfrac7{15}=\dfrac15=0,2\)
Ответ: 0,2.
Задача 5
Имеется пара шаров. 2\cdot \rho\right)=8\cdot 75=600 \ {\small{\text{грамм}}}\)
Таким образом, потребуется долить в емкость:
\(600-75=525 \ {\small{\text{грамм}}}\)
Ответ: 525.
Задача 7
Изображена четырехугольная пирамида. Ее высота равна h. Отметим точку сбоку на ребре геометрической фигуры так, чтобы она была удалена на \frac13h от плоскости основания. Данную точку пересекает плоскость, которая параллельна плоскости основания и отделяет от пирамиды аналогичную фигуру меньшего размера. Объем начальной пирамиды равен 54. Требуется вычислить объем меньшей пирамиды, которая получилась в результате.
Источник: shkolkovo.net
Решение
Назовем точку, через которую проведена плоскость, A’ на ребре AS. Параллельность плоскости и основания является причиной пересечения боковых граней по прямым A’B’, \ B’C’, \ C’D’, \ D’A’, параллельным соответственно AB, \ BC, \ CD, \ DA. В этом случае SA’B’C’D’ является правильной четырехугольной пирамидой. 3 \quad\Rightarrow\quad \dfrac{R_1}{R_2}=\sqrt[3]{343}=7\)
Сделаем вывод, что радиус первого шара в 7 раз больше по сравнению с радиусом второго шара.
Ответ: 7.
Задание 3
На рисунке изображены два цилиндра. Первый из них обладает площадью боковой поверхности, равной 16. Радиус второй фигуры больше в 4 раза по сравнению с радиусом первой фигуры. Второй цилиндр ниже, чем первый цилиндр, в 5 раз. Требуется вычислить площадь боковой поверхности второго цилиндра.
Источник: shkolkovo.net
Решение
Запишем формулу для вычисления площади боковой поверхности цилиндра, которую уже проходили ранее:
\(S=2\pi RH\)
Составим отношение площадей боковых поверхностей двух фигур:
\(\dfrac{16}{S_2}=\dfrac{S_1}{S_2}=\dfrac{2\pi \,R_1\,H_1}{2\pi \,R_2\,H_2}= \dfrac{R_1}{R_2}\cdot \dfrac{H_1}{H_2}\)
В результате:
\(R_2=4R_1, H_1=5H_2\)
Таким образом:
\(\dfrac{16}{S_2}=\dfrac{R_1}{4R_1}\cdot \dfrac{5H_2}{H_2}= \dfrac14\cdot 5=\dfrac54\)
Получим, что:
\(S_2=\dfrac{16\cdot 4}5=12,8\)
Ответ: 12,8. 3=27\)
В результате объем первого шара в 27 раз больше по сравнению с объемом второго шара.
Ответ: 27.

Насколько полезной была для вас статья?
У этой статьи пока нет оценок.

Расчет объема | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых предметов, т.е. сколько вы могли бы вместить в предмет, если, например, вы наполнили его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (дополнительную информацию см. на нашей странице: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница о трехмерных фигурах объясняет основы таких фигур.
В реальном мире вычисление объема, вероятно, не будет использоваться так часто, как вычисление площади.
Тем не менее, это может быть важно. Возможность рассчитать объем позволит вам, например, определить, сколько места у вас есть для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете поместить в банку.
Это также может быть полезно для понимания того, что имеют в виду СМИ, когда говорят о мощности плотины или расходе реки.
Примечание по единицам измерения
Площадь выражается в квадратных единицах ( ² ), поскольку она измеряется в двух измерениях (например, длина × ширина).
Объем выражается в кубических единицах ( ³ ), поскольку он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы. Кубические единицы включают ³ см, ³ м и кубические футы.
ВНИМАНИЕ!
Объем также может быть выражен как емкость по жидкости.
Метрическая система
В метрической системе вместимость жидкости измеряется в литрах, что напрямую сравнимо с кубическим измерением, поскольку 1 мл = 1 см ³ . 1 литр = 1000 мл = 1000 см ³ .
Имперская/английская система
В имперской/английской системе эквивалентными единицами измерения являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема.
Для получения дополнительной информации см. нашу страницу о системах измерения.
Основные формулы для вычисления объема
Объем тел, основанных на прямоугольниках

В то время как основная формула площади прямоугольной формы равна длине × ширине, основная формула для объема равна длине × ширине
6 ×
высота.
То, как вы ссылаетесь на различные измерения, не влияет на расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, поскольку это не изменит ответ (см. нашу страницу на умножить на для большего).
Коробка с размерами 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см для покрытия объема цилиндров и призм тоже. Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем равен площади одной стороны, умноженной на глубину или высоту формы.
Таким образом, основная формула для объема призм и цилиндров:
Площадь торца × высота/глубина призмы/цилиндра.
Остерегайтесь несовместимых единиц!
Прямой отрезок круглой трубы имеет внутренний диаметр 2 см и длину 1,7 м. Рассчитайте объем воды в трубе.
В этом примере вам нужно рассчитать объем очень длинного тонкого цилиндра, образующего внутреннюю часть трубы. Площадь одного конца можно рассчитать по формуле площади круга πr ² . Диаметр 2см, значит радиус 1см. Таким образом, площадь равна π × 1 ² , что составляет 3,14 см ² .
Длина трубы 1,7 м, поэтому вам нужно умножить площадь конца на длину, чтобы найти объем.
Остерегайтесь несовместимых юнитов! Площадь в сантиметрах, а длина в метрах. Сначала преобразуйте длину в см 1,7 × 1000 = 1700 см.
Таким образом, объем равен 3,14 × 1700 = 5338 см ³ . Это эквивалентно 5,338 литра или 0,0053 м ³ .
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они сходятся в точке, объем составляет лишь долю сумма, которая была бы, если бы они продолжали иметь ту же форму (поперечное сечение) насквозь.
Объем конуса или пирамиды составляет ровно одну треть объема коробки или цилиндра с таким же основанием.
Таким образом, формула выглядит следующим образом:
Площадь основания или торца × высота конуса/пирамиды × ¹ / ₃
Если не можете, вернитесь на нашу страницу
0 0 Расчет площади помните, как вычислить площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:
Площадь внутри круга = πr ² (где π (пи) приблизительно равно 3,14, а r — радиус круг).
В этом примере площадь основания (круга) = πr ² = 3,14 × 5 × 5 = 78,5 см ² .
78,5 × 10 = 785
785 × 1/3 = 261,6667 см ³
Объем сферы
Как и в случае с кругом, для вычисления объема сферы требуется π (пи).
Формула 4/3 × π × радиус ³ .
Вам может быть интересно, как можно вычислить радиус мяча. Если не считать протыкания вязальной спицы (эффективно, но смертельно для мяча!), есть более простой способ.
Расстояние вокруг самой широкой точки сферы можно измерить напрямую, например, рулеткой. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности рассчитывается как 2 x π x радиус.
Чтобы вычислить радиус по длине окружности:
Разделите длину окружности на (2 x π) .
Примеры работы: Расчет объема

Расчет объема неправильных тел
Точно так же, как вы можете рассчитать площадь неправильных двумерных фигур, разбив их на правильные, вы можете сделать то же самое для расчета объема неправильных тел. Просто разделите тело на более мелкие части, пока не получите только многогранники, с которыми вам будет легко работать.

Дальнейшее чтение из книги «Навыки, которые вам нужны»
Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»
В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства фигур, линий и твердых тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем почти всего в вашей жизни, будь то упаковочный ящик, комната или цилиндр с водой.
Том: определение, примеры и формула
Сколько места занимает ручка или слон? Сколько места вы занимаете? Мы часто можем ссылаться на объем объекта, но что такое объем, как мы измеряем объемы и какие единицы измерения мы используем для описания объема?
Определение объема
Хотя объем чего-либо является интуитивно понятным понятием, может быть трудно точно описать, что такое объем. Ниже приводится возможное описание тома.
объем объекта является мерой объема трехмерного пространства, которое он занимает.
Это означает, что объем слона больше объема комара.
Один из способов представить объем — это спросить, сколько кубиков сахара поместилось бы внутри предмета, если бы он был полым. Если объект гипотетически содержит кубики сахара, а объект будет содержать, то объем объекта будет в два раза больше объема объекта.
Другой (неисчисляемый, но более точный) способ представления объема – сколько воды поместилось бы внутри объекта, если бы он был полым. Если вы наполните водой два предмета, и предмет будет в два раза тяжелее предмета, то предмет будет иметь вдвое больший объем, чем предмет.
Так же, как масса, заряд и форма, объем является физическим свойством объекта.
Формула для объема
Не существует общей формулы для объема объектов (если мы не хотим использовать исчисление), но давайте рассмотрим очень простой объект: прямоугольный параллелепипед. Это трехмерная версия прямоугольника, см. рисунок ниже.
Прямоугольный параллелепипед со сторонами a , b и c , Арьян ван Дензен – StudySmarter Originals.
Он имеет длину сторон, и. Если мы удвоим, то внутри прямоугольного параллелепипеда поместится в два раза больше кубиков сахара, чем раньше, потому что у нас фактически есть две копии исходного прямоугольного параллелепипеда друг над другом. Это означает, что объем прямоугольного параллелепипеда удваивается, если мы удваиваем длину. То же самое касается длины песка. Эти длины являются единственными факторами, влияющими на объем прямоугольного параллелепипеда, потому что они содержат всю информацию, необходимую для определения этого объекта. Таким образом, объем прямоугольного кубоида должен быть постоянным, умноженным на произведение длин всех сторон . Бывает, что константа isso наша формула принимает вид:
.
Объем всех других объектов теперь можно определить с помощью этого прямоугольного параллелепипеда: мы создаем объект, объем которого хотим узнать. Делаем объект полым и заливаем водой. Затем мы наливаем эту воду в резервуар с прямоугольным основанием, чтобы вода приняла форму прямоугольного куба. Мы измеряем три стороны кубоида, созданного водой, и умножаем их, чтобы получить объем нашего объекта.
Объем куба со сторонами длины представляет собой длину одной стороны в кубе, так как куб представляет собой просто прямоугольный параллелепипед с.
Измерение объемов
Мы также можем использовать воду для измерения объема объектов на практике. Мы начинаем с полностью заполненного прямоугольно-кубовидного резервуара с водой и опускаем наш объект в воду. Часть воды будет переливаться в этом процессе, потому что вода должна освободить место для объекта внутри резервуара. Это количество комнаты является объемом объекта. Если теперь мы снова вытащим объект из воды, уровень воды в резервуаре упадет, потому что мы удалили объем нашего объекта из резервуара. Незаполненная часть бака теперь имеет тот же объем, что и объект, потому что мы только что вынули объект из бака! Эта незаполненная часть бака будет иметь форму прямоугольного параллелепипеда, поэтому этот объем легко измерить по формуле, которую мы приводили ранее. Вуаля, этот измеренный объем и есть объем нашего объекта. См. иллюстрацию ниже для схематического представления этого процесса.
Способ измерения объема предметов, Арьян ван Дензен – StudySmarter Originals.
Размеры объема в физике
Каковы размеры объема? Давайте посмотрим на формулу объема нашего прямоугольного параллелепипеда. Мы умножаем три расстояния (из 3 измерений в 3-мерном пространстве, упомянутом в определении объема) друг на друга, чтобы получить объем, поэтому размеры объема прямоугольного параллелепипеда должны быть равными. Это автоматически означает, что размеры всех томов должны быть. Стандартной единицей измерения расстояния является метр, поэтому стандартной единицей измерения объема является девятка.0005 кубометр .
Другой часто используемой единицей объема является литр. Он имеет символ и определяется как.
Куб со сторонами имеет объем потому что. Это.
Вычисление объемов
Существуют фигуры, для которых достаточно легко вычислить объем, т. е. без необходимости использования какой-либо сложной математики, такой как исчисление, каждый раз, когда вы сталкиваетесь с такой формой.
Пирамиды имеют основание и высоту, перпендикулярную этому основанию, см. рисунок ниже для иллюстрации. Если основание пирамиды имеет площадь, а пирамида имеет высоту, то объем пирамиды всегда определяется выражением.
Пирамида высотой h и площадью основания A , Арьян ван Дензен – StudySmarter Originals.
Объем шара с радиусом.
Обратите внимание на то, как работают измерения объема в обоих приведенных выше примерах.
Если вы когда-либо вычисляли объем и замечали, что он имеет неправильные размеры, вы сделали что-то не так. Объем всегда имеет размеры .
Примеры объемов в физике
Объем объектов важен во многих вопросах физики.
Знание объема газа (например, газа, находящегося в закрытом сосуде) необходимо для заключения о его плотности, давлении и температуре. Если мы сожмем газ до меньшего объема, его давление возрастет: он будет отталкивать нас.
Попробуйте сжать закрытую бутылку с водой. Вы не уйдете очень далеко, потому что уменьшение объема воздуха в бутылке вызовет увеличение давления, отталкивающего вас. Это уменьшение объема необходимо для увеличения отталкивающей силы.
Принимая ванну, вы должны учитывать объем своего тела. Поскольку ваше тело занимает место воды в ванне, ванна переполнится, если ваш объем больше, чем объем незаполненной части ванны. Подсознательно вы учитываете собственный объем, когда наполняете ванну.
Объем — основные выводы
Объем объекта — это мера объема трехмерного пространства, которое он занимает.
Один из способов представить объем — сколько воды поместилось бы внутри объекта, если бы он был полым.
Объем прямоугольного кубоида со сторонами и определяется как.
Мы можем использовать резервуар с водой для измерения объема объектов.
Стандартной единицей объема является кубический метр (). Литр () — это кубический метр.