Физическая природа интерференции примеры: Интерференция света – примеры кратко, формулы, определение (9 класс)

Интерференция света – примеры кратко, формулы, определение (9 класс)

4.5

Средняя оценка: 4.5

Всего получено оценок: 223.

Обновлено 18 Декабря, 2020

4.5

Средняя оценка: 4.5

Всего получено оценок: 223.

Обновлено 18 Декабря, 2020

Свет — это электромагнитная волна определенного диапазона частот, распространяющаяся в пространстве. И как волновое явление, свет демонстрирует все признаки волны. Одним из таких признаков является интерференция. Кратко поговорим на эту тему, дадим определение интерференции, рассмотрим ее механизм.

Явление интерференции

Большинство сред, где происходит распространение волн, подчиняется принципу суперпозиции, известного из курса физики 9 класса. Поэтому, если в такой среде распространяются волны от двух и более источников, то в точке встречи мгновенное значение амплитуд волн складывается. При этом, если частоты волн одинаковы, то происходит интересное явление, называемое интерференцией.

Если на воде возбуждать две волны одинаковой частоты, то, глядя на расходящиеся круги, можно заметить, что там, где круги от разных источников начинают сливаться, на кругах появляются участки, где высота волны усиливается, и участки, где, наоборот, волна практически исчезает. Распространяющиеся «суммарные» круги получаются пересечены линиями отсутствия волн, которые радиально расходятся от источников.

Рис. 1. Интерференционная картина на воде.

Почему происходит интерференция?

Условия максимумов и минимумов

Вкратце, схема образования интерференционной картины следующая. В момент встречи двух волн одинаковой амплитуды их сложение дает некоторое значение амплитуды: от нуля до двойной амплитуды.

Для того чтобы в данной точке суммарная волна колебалась с удвоенной амплитудой, необходимо, чтобы разность фаз в этой точке была равна нулю, а это возможно, если в разность хода волн $Δd$ укладывается целое число волн (четное число полуволн):

$$Δd_{max} = \pm k\lambda$$

Для того чтобы суммарная волна имела нулевую амплитуду, необходимо, чтобы фаза одной волны отличалась от другой на половину периода. То есть в разность хода должно укладываться нечетное число полуволн:

$$Δd_{min} = \pm (2k+1){\lambda \over 2}$$

Если разность хода имеет величину, в которую не укладывается целое число полуволн, то результирующая амплитуда будет иметь некоторое промежуточное значение.

Рис. 2. Условия максимума и минимума интерференции.

Когерентность

Для появления интерференционной картины необходимо, чтобы условия минимумов и максимумов в данной точке не менялись. То есть чтобы разность хода двух волн всегда содержала одинаковое число полуволн. Это условие выполняется в том случае, если источники волн не перемещаются, а возбуждаемые волны имеют одинаковую частоту и постоянную разность фаз.

Источники, отвечающие этому условию, называются когерентными. Только волны когерентных источников дают устойчивую интерференционную картину.

Если источники некогерентны, то во всех точках среды условия минимумов и максимумов начинают постоянно меняться, и устойчивая интерференционная картина сменяется хаотичным волновым процессом.

Интерференция света

В обычной жизни наблюдать интерференцию света от двух источников невозможно. Происходит это потому, что обычные источники света некогерентны: у них, как правило, неодинакова частота, и фаза излучения меняется со временем.

Однако, если две световых волны будут являться частями одного светового пучка, можно добиться, чтобы возникла интерференционная картина.

Наиболее частым примером интерференции света, доказывающим волновую его природу, является появление радуги на тонкой поверхности мыльного пузыря или масла на воде. Луч света, попавший в тонкую пленку, отражается от двух ее поверхностей, образуя внутри пленки два когерентных луча. При сложении эти лучи образуют чередование светлых и темных полос. При этом еще играет роль и разность толщины пленки: условия чередования в разных местах выполняются для света разной длины. В результате на тонкой пленке суммарная интерференционная картина складывается из интерференционных картин разных длин волн, образуя радужные переливы.

Рис. 3. Радужные переливы на воздушных пузырях.

Что мы узнали?

Интерференция — это явление сложения двух волн, в результате которого в среде появляются участки волны с двойной и с нулевой амплитудой. Условия максимумов и минимумов описываются специальными формулами. Появление интерференционной картины на тонких пленках доказывает волновую природу света.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

• Андрей Иванов

  10/10

Оценка доклада

4.5

Средняя оценка: 4.5

Всего получено оценок: 223.

---

А какая ваша оценка?

ИНТЕРФЕРЕНЦИОННЫЕ ТАЙНЫ ПРИРОДЫ | Наука и жизнь

В течение нескольких сотен лет физики пытались понять, что же такое свет — волны или поток частиц, названных позднее фотонами, и в конце концов выяснили, что слово «или» употреблять нельзя.

В одних случаях свет ведёт себя как волна, в других — как поток фотонов, проявляя квантовый, то есть дискретный характер излучения. Другими словами, свет имеет двойственную природу. На научном языке это называется «корпускулярно-волновой дуализм» (слово «корпускула» означает «частица»). Интерференция считается одним из нагляднейших проявлений волновых свойств: ведь интерферировать могут только волны. Казалось бы, и спорить не о чем. Однако всё не так просто. Недаром существует весьма выразительное изречение: «Свет — самое тёмное место в физике»…

Наука и жизнь // Иллюстрации

Фото Н. Домриной.

Рис. 1. Схема опыта для наблюдения интерференции.

Рис. 2. К опыту Юнга с одиночными фотонами.

Существует множество конструкций приборов для сложения электромагнитных волн светового диапазона — интерферометров.

‹

›

Открыть в полном размере

Интерференция — замечательное явление, имеющее множество применений. Оно прояв-Лж. ляется как в оптическом, так и в радиодиапазоне. Особенно впечатляюща интерференция света, так как мы можем её наблюдать непосредственно, в то время как радиоволны невидимы глазом. Часто интерференцию света характеризуют такой «парадоксальной» фразой: свет плюс свет может давать темноту. Человеку, совершенно незнакомому с физической оптикой, это может показаться очень странным: как это так — если к свету прибавить ещё свет, то должно стать ещё светлее! Правда, все мы изучали физику в школе, и, наверное, всё-таки у каждого остались хотя бы какие-то смутные воспоминания о том, что такое интерференция («Да… что-то связанное со светом… не очень помню, но вроде бы это какое-то наложение световых волн…»). Уже хорошо! Давайте же начнём с того, что освежим эти полузабытые знания, которые позволят нам побеседовать о крайне удивительных и интересных явлениях, связанных с интерференцией света.

Возьмём более или менее «направленный» источник света, например карманный фонарик (с галогенной лампочкой, дающей яркий свет, а ещё лучше — со светодиодом), и направим его на белый экран.

На экране возникнет пятно света. Теперь возьмём второй такой же фонарик и направим его свет на то же место экрана. «И что, мы получим темноту?» — иронически спросит читатель, прочитавший преды-дущий абзац, но настолько позабывший школьную физику, что слово «оптика» ассоциируется у него лишь с очками и лупами. Нет, конечно, никакой темноты мы не получим, световое пятно станет ещё ярче. «Ну и что в этом удивительного?» — заметит наш скептик. В этом — ничего. Но теперь сделаем следующее: возьмём лист плотного картона, проколем в нём иголкой две дырочки как можно ближе одну к другой (скажем, на расстоянии 0,5 миллиметра), поставим лист перед экраном (на расстоянии около 20—30 см) и осветим эти дырочки одним фонариком (см. рис. 1). Возможно, придётся немного порегулировать расстояние между фонариком и картоном, но мы обязательно найдём положение, при котором на экране светлое пятно будет пересекаться тёмными участками. Вот мы и получили темноту!

Почему же возникают эти тёмные участки? Почему их не было в случае двух фонариков, а появились они только при освещении отверстий в картоне одним фонариком?

Зададим такой «нелепый» вопрос.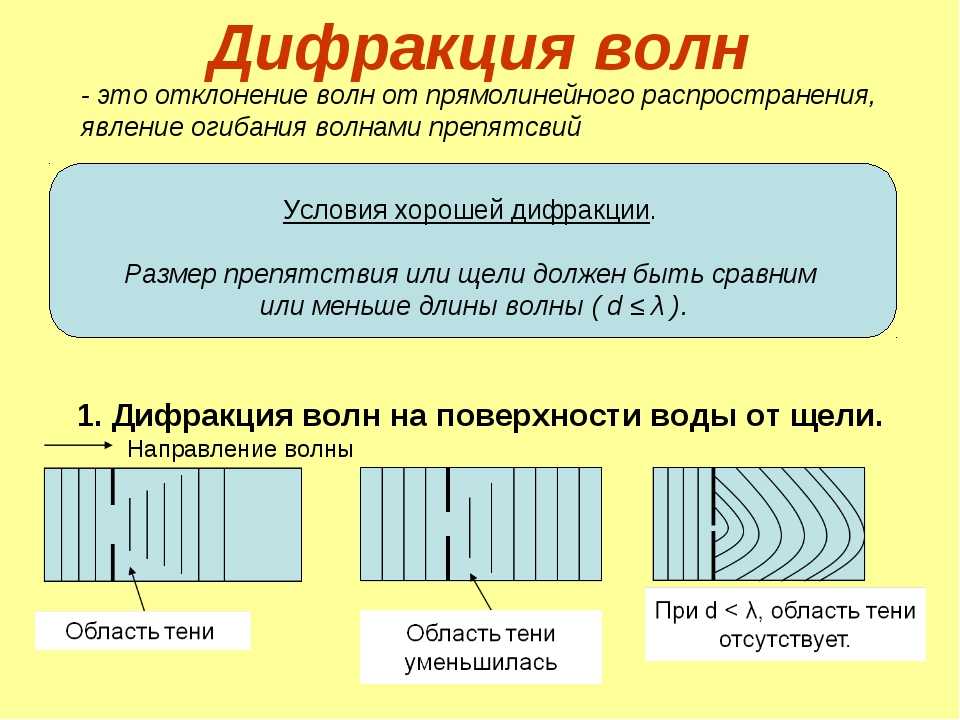

Сколько источников света было в этих двух случаях? Я назвал этот вопрос «нелепым» потому, что он может вызвать недоумение: как сколько? В первом случае мы включали оба фонарика, значит, было два источника света, а во втором светил только один фонарик, один источник света. Разве не так?

Нет, не так. Во втором случае было тоже два источника, которыми стали два отверстия в картоне (1 и 2, рис.1). То есть исходный источник был, конечно, один, но свет на экран шёл из этих двух дырочек, которые играли роль вторичных источников света. А вот то, что свет этих вторичных источников образовался от одного исходного, сыграло фундаментальную роль.

Используя картон с дырочками, изображённый на рис.1, мы воспроизвели (с некоторыми несущественными отличиями) знаменитый опыт Т. Юнга, впервые наблюдавшего интерференцию света от двух щелей в 1802 году.

Интерференция — это такое сложение волн, при котором происходит не просто суммирование интенсивностей этих волн, а их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от разности фаз волн в этих точках.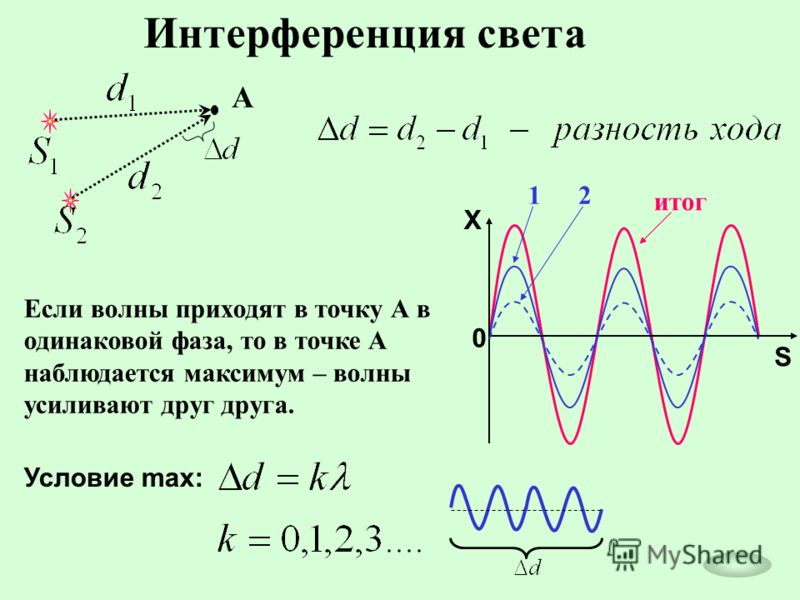

Но прежде чем рассматривать интерференцию, необходимо поговорить об одном фундаментальном понятии, играющем ключевую роль.

Почему в случае с двумя фонариками происходило только суммирование интенсивностей (яркостей), а в случае с картоном мы могли наблюдать интерференцию? Потому, что в первом случае световые волны от двух источников были некогерентны, а во втором — когерентны, так как порождены одним источником. Следовательно, необходимым условием образования интерференции является когерентность волн. Что это такое?

Слово «когерентность» — греческого происхождения и в наиболее общем смысле означает «согласованность». Простейший пример: когда по улице прогуливается толпа людей, она идёт некогерентно, а когда марширует рота солдат, то она идёт когерентно.

Когерентные волны — это волны одинаковой частоты, между которыми сохраняется постоянная разность фаз (то есть они согласованы по фазе). При сложении двух когерентных волн одинаковой поляризации (с одним и тем же направлением колебаний напряженности электрического поля) амплитуда суммарной волны зависит от разности фаз складываемых волн — это и есть интерференция.

При интерференции световых волн удобнее иметь дело не с амплитудами, а с интенсивностями. Это не меняет существа дела, так как интенсивность пропорциональна квадрату амплитуды. Если в какую-либо точку приходят две волны с интенсивностями I₁ и I₂ и фазами φ₁ и φ₂ соответственно, то результирующая интенсивность в этой точке определяется выражением

где ∆φ = | φ ₁ – φ ₂ | — разность фаз, а множитель у отражает степень когерентности волн. Из этой формулы наглядно видна зависимость результирующей интенсивности от разности фаз ∆φ и от величины γ.

В тех местах, куда волны приходят в одинаковой фазе, то есть «гребни» и «впадины» одной волны совпадают с «гребнями» и «впадинами» другой (∆φ =0 , cos ∆φ = 1), волны усиливают одна другую и наблюдается максимальная интенсивность (I _max). В тех местах, куда волны приходят в противофазе, «гребни» одной волны совпадают со «впадинами» другой ( ∆φ = 180^о, cos ∆φ = —1), волны гасят одна другую и результирующая интенсивность становится минимальной (I_min ). Таким образом, образуется интерференционная картина, состоящая из чередующихся светлых и тёмных участков.

Когерентность волн определяет их способность к интерференции. Практическим критерием степени постоянства разности фаз, то есть мерой степени когерентности у, является контраст (видность, резкость, чёткость) интерференционных полос — важнейший параметр интерференционной картины. Если условие ∆φ = const не соблюдается, то, как видно из вышеприведённой формулы, изменяется и результирующая интенсивность I_рез, что приводит к «размытию» интерференционных полос — уменьшению контраста К. В общем случае контраст определяется выражением

K=(I_max – I_min) / (I_max + I_min).

При этом 0 1 = I₂ = I), то К = γ, то есть значение γ непосредственно равно величине контраста К.

Теперь, прояснив наиболее существенные моменты, касающиеся интерференции, перейдём к нашей основной теме, сформулированной в заголовке статьи.

Существует множество интерференционных схем (интерферометров), но достаточно рассмотреть только одну из них. Вернёмся к уже знакомой схеме интерферометра Юнга (рис.1). На экране наблюдается интерференционная картина. Будем постепенно уменьшать интенсивность света. Освещённость экрана станет падать, но интерференционная картина сохранится. Продолжим уменьшать интенсивность света, а вместо экрана поставим фотопластинку, потому что глазом уже ничего не видно (рис. 2). Увеличив время экспозиции и проявив пластинку, обнаружим на ней всё ту же интерференционную картину (на рис. 2 это показано кривой D, отображающей интерференционное распределение полос). Уже интересно: значит, интерференция не зависит от интенсивности света? Продолжаем опыт, все больше уменьшая интенсивность и соответственно увеличивая время экспозиции. Короче говоря, при достаточно длительной экспозиции можно обнаружить интерференционную кривую D в принципе при сколь угодно малой интенсивности света. Но с уменьшением интенсивности светового пучка уменьшается число фотонов в нем, и наступит такой момент, когда вместо световых волн в интерферометр Юнга будут поступать отдельные фотоны. Вот излучился один фотон, за ним другой и т.д. — фотоны поступают в интерферометр сугубо поодиночке. Но при этом сохраняется интерференционный характер кривой D, на фотопластинке получается такая же интерференционная картина, как и от световых волн!

Как же это может быть? Ведь для получения интерференции необходимо, чтобы свет поступал на пластинку одновременно от двух отверстий 1 и 2. Но отдельный фотон не может пройти сразу через оба отверстия. Он проходит либо через отверстие 1, либо через отверстие 2. Очевидно также, что он не может разделиться на две «половинки». И вот тут мы сталкиваемся с совершенно мистической ситуацией. Фотон проходит через одно отверстие, но эффект такой, как будто он прошёл через оба. Это приводит к парадоксальному утверждению: нельзя считать, что фотон проходит через одно отверстие независимо от другого. Если бы это было так, то при прохождении, скажем, через отверстие 1 было бы совершенно безразлично, открыто или закрыто отверстие 2. Но если мы закроем отверстие 2, то, как показывает опыт, интерференционная картина немедленно исчезнет!

Всё это очень странно. Более того — непостижимо. Но вернёмся к схеме Юнга — нас ждёт ещё много интересного.

Итак, мы имеем дело с отдельными фотонами. Закроем отверстие 2. Теперь мы точно знаем, что фотоны проходят только через отверстие 1. Интерференция исчезает, и распределение попаданий фотонов на фотопластинку за некоторый достаточно большой интервал времени описывается кривой А (рис. 2). Теперь откроем отверстие 2 и закроем 1. Фотоны будут проходить только через открытое отверстие 2, и их распределение отобразится кривой В. Теперь откроем оба отверстия. Если, как этого требует логика, считать, что каждый фотон проходит либо через одно, либо через другое отверстие, то на фотопластинке-детекторе должна зафиксироваться сумма этих распределений, то есть кривая С (обозначенная на рис. 2 пунктиром). Но возникает не суммарное, а интерференционное распределение D. То есть фотон при прохождении того или другого отверстия каким-то образом «ощущает» соседнее отверстие; в противном случае, как уже говорилось, фотону было бы «безразлично», открыто или закрыто это соседнее отверстие, и при обоих открытых отверстиях должна была бы фиксироваться суммарная кривая С. Это удивительное появление интерференции при прохождении фотонов через одно отверстие – чисто квантовый эффект, один из парадоксов квантовой механики, который невозможно объяснить на основе классической теории.

Но пойдём дальше. Описанный эффект наблюдается не только с фотонами, но и с электронами, протонами, нейтронами, то есть с микрообъектами (подобные эксперименты производились неоднократно). Особенно наглядными были опыты с электронами, которые вроде бы уж точно «частицы», а не волны. И вот физики придумали, как «подглядеть», каким образом электрон проходит через отверстия. Они поместили вблизи каждого отверстия по источнику света и фотоприёмнику, расположив их так, что фотоприёмники регистрируют свет, рассеянный электроном. Если электрон проходит через одно отверстие, сработает один фотоприёмник, и мы узнаем, через какое именно отверстие прошёл электрон; если же он непостижимым образом пройдет сразу через оба отверстия, то сработают оба фотоприемника. Что же дал такой опыт?

Оказалось, что всегда срабатывает только один фотоприёмник и никогда не срабатывают оба одновременно. Значит, электрон всегда проходит только через одно отверстие, и мы всегда можем сказать, через какое именно. Что же получается? Что электрон, проходя через одно отверстие, каким-то образом «ощущает» другое? Но давайте наберём достаточно большое число попаданий электронов на разные места экрана и посмотрим, как распределятся эти попадания. (В случае электронов вместо фотопластинки используется передвижной детектор, например счётчик Гейгера или другое устройство, откликающееся при попадании на него электрона, скажем, щелчком в динамике.) И вот тут обнаруживается совершенно неожиданная вещь. Кривая распределения оказывается не интерференционной, а суммарной! А если мы уберём источники света и фотоприёмники, то получится интерференционная кривая. Другими словами, попытка «подглядеть» за электронами разрушает интерференцию!

Но может быть, освещая электроны, мы изменили их движение? Вполне возможно: ведь фотоны света, сталкиваясь с электронами, оказывают на них какое-то воздействие. Наверное, надо как-то уменьшить это воздействие до практически пренебрегаемого, чтобы интерференционная картина не разрушалась. Но как? Уменьшить интенсивность подсветки? Это ничего не даст, так как при этом будет уменьшаться число фотонов в пучке, и если мы добьёмся испускания света отдельными фотонами, то просто возрастёт количество «незарегистрированных» электронов. Нужно уменьшать не интенсивность, а энергию фотонов. Однако для этого есть только один путь — увеличивать длину волны света или, что то же, уменьшать частоту световых колебаний: энергия фотона (кванта света) Е связана с оптической частотой ν соотношением Е = hν, где h — постоянная Планка. Значит, чем больше длина волны, тем меньше её энергия и тем слабее воздействие на электрон. Самый длинноволновый свет в видимой области — красный; ещё лучше взять инфракрасное излучение, у которого длина волны может быть гораздо больше. Но — увы! — этот путь тоже оказывается тупиковым. Ибо, как только длина волны сравняется с расстоянием между отверстиями, невозможно будет разобрать, возле какого отверстия произошла вспышка. Если длина волны будет намного превышать расстояние между отверстиями — вот тогда возмущение, оказываемое светом, станет настолько слабым, что снова появится интерференционная кривая, но при этом не окажется никакой возможности установить, куда прошёл электрон.

Предпринималось ещё много попыток придумать опыт, который позволил бы «наблюдать» за электронами без разрушения интерференции, но ни одна из них не увенчалась успехом.

Мы рассмотрели эту проблему с чисто качественной стороны, ибо строгое аналитическое рассмотрение требует знакомства с математическим аппаратом квантовой механики. Поэтому ограничимся сказанным, из которого следует вывод: при интерференции отдельных фотонов, электронов и прочих микробъектов любые попытки проследить, как она образуется, немедленно разрушают интерференционную картину. Почему природа не позволяет нам понять механизм подобного явления — на этот вопрос не может ответить никто, по крайней мере в настоящее время. И здесь уместно привести слова выдающегося американского физика Ричарда Фейнмана: «Мы говорим «в настоящее время», но мы очень серьёзно подозреваем, что всё это — уже навсегда и разгрызть этот орешек человеку не по зубам, ибо такова природа вещей».

ПОДРОБНОСТИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫX

Кривые А и В на рис.2 отражают распределение вероятностей попадания микрообъектов (фотонов, электронов) в ту или иную точку вдоль экрана (фотопластинки, детектора). При открытом отверстии 1 и закрытом 2 вероятность описывается кривой А; обозначим эту вероятность Р₁. При открытом отверстии 2 и закрытом 1 вероятность описывается аналогичной кривой В; эту вероятность обозначим Р₂. Если открыты оба отверстия, то логично ожидать, что результирующая вероятность Р будет суммой вероятностей Р₁ и Р₂, то есть Р = Р₁+ Р₂, что соответствует кривой С. Но опыт показывает, что этого не происходит: результирующая вероятность Р соответствует не суммарному, а интерференционному распределению, описываемому кривой D. Вероятность, соответствующую этому распределению, обозначим Р₁₂. Таким образом, при обоих открытых отверстиях получаем Р = Р₁₂ ≠ Р₁+ Р₂. Как это можно интерпретировать?

В квантовой механике вводят понятие комплексной волновой функции ψ описывающей микрообъект и связанной с вероятностью таким образом, что вероятность есть квадрат модуля (абсолютной величины) волновой функции, то есть | ψ |². Термин «волновая функция» впоследствии заменили термином «амплитуда вероятности», чтобы подчеркнуть вероятностный характер описания микробъекта. Итак, для нашего случая имеем: Р₁ = | ψ ₁ |², Р₂ = | ψ ₂|². А далее надо учесть принципиальное обстоятельство, связанное с различимостью взаимоисключающих событий. Что под этим понимается?

У микрообъекта — скажем, у электрона — имеется возможность альтернативной реализации двух вариантов (событий): пройти либо через отверстие 1, либо через отверстие 2. Когда подсветка выключена, то есть мы не наблюдаем за электроном, то эти события являются неразличимыми. Как только мы включаем свет, они становятся различимыми. Ничего подобного нет в классической физике (там все события всегда различимы), такая ситуация возможна только в микромире. Так вот, в квантовой механике справедливо такое правило: если события различимы, складываются соответствующие им вероятности; если же события неразличимы, складываются амплитуды вероятностей. В первом случае (с подсветкой) мы имеем Р = Р₁+ Р ₂ = | ψ ₁ |² + | ψ ₂ |², интерференция отсутствует. Во втором случае (без подсветки) получаем: ψ = ψ ₁ + ψ ₂ и P = | ψ ₁ + ψ ₂| ². Возникает интерференция.

Учебное пособие по физике: Интерференция двухточечных источников

Интерференция волн — это явление, возникающее при встрече двух волн, распространяющихся в одной и той же среде. Интерференция волн заставляет среду принимать форму, которая является результатом суммарного воздействия двух отдельных волн на частицы среды. Интерференция волн может быть конструктивной или деструктивной по своей природе. Конструктивная интерференция возникает в любом месте среды, где две интерферирующие волны смещаются в одном направлении. Например, если в данный момент времени и в заданном месте в среде гребень одной волны встречается с гребнем второй волны, они будут интерферировать таким образом, что получится «супергребень». Точно так же интерференция впадины и впадины конструктивно интерферирует, образуя «супер-впадину». Деструктивная интерференция возникает в любом месте среды, где две интерферирующие волны имеют смещение в противоположном направлении. Например, интерференция гребня с желобом является примером деструктивной интерференции. Деструктивное вмешательство имеет тенденцию уменьшать результирующую величину смещения среды. Принципы интерференции были впервые представлены в Разделе 10 учебного пособия по физике. Впоследствии эти принципы были применены к интерференции звуковых волн в Разделе 11 Учебного пособия по физике.

Определяющий момент в истории споров о природе света произошел в первые годы девятнадцатого века. Томас Янг показал, что интерференционная картина возникает, когда свет от двух источников встречается при прохождении через одну и ту же среду. Чтобы понять эксперимент Юнга, важно вернуться на несколько шагов назад и обсудить интерференцию волн на воде, исходящих из двух точек.

В блоке 10 была представлена ​​и обсуждена ценность волнового резервуара для изучения поведения волн на воде. Если объект качается вверх и вниз в воде, в воде будет производиться серия водяных волн в форме концентрических кругов. Если два объекта качаются вверх и вниз с одинаковой частотой в двух разных точках, то на поверхности воды будут возникать два набора концентрических круговых волн. Эти концентрические волны будут мешать друг другу, когда они проходят по поверхности воды. Если вы когда-нибудь одновременно бросали в озеро два камешка (или как-то одновременно взбалтывали озеро в двух местах), вы, несомненно, замечали интерференцию этих волн. Гребень одной волны будет конструктивно мешать гребню второй волны, вызывая большое смещение вверх. А впадина одной волны будет конструктивно мешать впадине второй волны, вызывая большое смещение вниз. И, наконец, гребень одной волны будет разрушительно мешать впадине второй волны, не вызывая смещения. В пульсирующем резервуаре это конструктивное и деструктивное вмешательство можно легко контролировать и наблюдать. Он представляет собой базовое поведение волны, которое можно ожидать от волны любого типа.

 

Картины интерференции двухточечных источников

Интерференция двух наборов периодических и концентрических волн с одинаковой частотой создает интересную картину в пульсирующем резервуаре. Диаграмма справа изображает интерференционную картину, создаваемую двумя периодическими возмущениями. Гребни обозначены толстыми линиями, а впадины – тонкими линиями. Таким образом, конструктивная интерференция возникает везде, где толстая линия встречается с толстой линией или тонкая линия встречается с тонкой линией; этот тип интерференции приводит к образованию пучность . Пучности обозначены красной точкой. Деструктивное вмешательство происходит везде, где толстая линия встречается с тонкой; этот тип интерференции приводит к образованию узла . Узлы обозначены синей точкой. Паттерн представляет собой паттерн стоячей волны, характеризующийся наличием узлов и пучностей, которые «стоят на месте», т. е. всегда находятся в одном и том же месте на среде. Пучности (точки, где волны всегда конструктивно интерферируют) кажутся расположенными вдоль линий — креативно называемых пучностные линии . Узлы также располагаются вдоль линий, называемых узловыми линиями . Интерференционная картина двухточечного источника характеризуется чередованием узловых и промежуточных линий. В шаблоне есть центральная линия – линия, которая делит пополам отрезок, проведенный между двумя источниками, является пучностью. Эта центральная пучностная линия представляет собой линию точек, где волны от каждого источника всегда усиливают друг друга посредством конструктивной интерференции.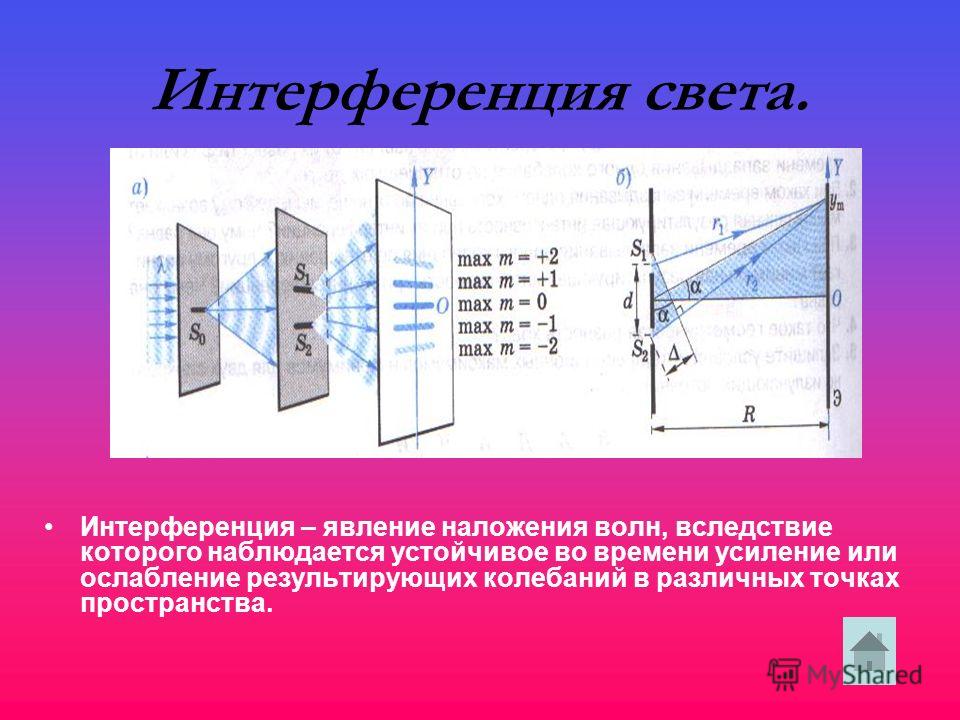 Узловые и пучностные линии показаны на диаграмме ниже.

Интерференционная картина от двухточечного источника всегда имеет чередующийся рисунок узловых и промежуточных линий. Однако есть некоторые особенности шаблона, которые можно изменить. Во-первых, изменение длины волны (или частоты) источника изменит количество линий в узоре и изменит близость или близость линий. Увеличение частоты приведет к большему количеству линий на сантиметр и меньшему расстоянию между каждой последующей строкой. А уменьшение частоты приведет к меньшему количеству линий на сантиметр и большему расстоянию между каждой последующей строкой.

Во-вторых, изменение расстояния между двумя источниками также изменит количество линий и близость или близость линий. Когда источники раздвигаются дальше друг от друга, на сантиметр создается больше линий, и линии сближаются. Эти две общие причинно-следственные связи применимы к любой интерференционной картине двухточечного источника, вызванной волнами на воде, звуковыми волнами или волнами любого другого типа.

Изменение разделения источника	Изменение длины волны

 

Картины интерференции света от двухточечных источников

Волны любого типа, будь то волны на воде или звуковые волны, должны создавать интерференционные картины двухточечных источников, если два источника периодически возмущают среду на той же частоты. Такой узор всегда характеризуется чередованием узловых и пучностных линий. Конечно, должен был возникнуть вопрос, и он действительно возник в начале девятнадцатого века: может ли свет создавать интерференционную картину из двух точек? Если обнаружится, что свет создает такую ​​картину, то это даст больше доказательств в поддержку волнообразной природы света.

Перед тем, как мы подробно рассмотрим доказательства, давайте обсудим, что можно было бы наблюдать, если бы свет подвергался интерференции двухточечного источника. Что произойдет, если «гребень» одной световой волны перемешается с «гребнем» второй световой волны? А что было бы, если бы «впадина» одной световой волны пересекалась с «впадиной» второй световой волны? И, наконец, что произойдет, если «гребень» одной световой волны натолкнется на «впадину» второй световой волны?

Всякий раз, когда свет конструктивно интерферирует (например, когда гребень встречается с гребнем или впадина встречается с впадиной), две волны усиливают друг друга и создают «суперсветовую волну». С другой стороны, всякий раз, когда свет деструктивно интерферирует (например, когда гребень встречается с впадиной), две волны разрушают друг друга и не производят световой волны. Таким образом, интерференционная картина двухточечного источника по-прежнему будет состоять из чередующейся картины пучностных и узловых линий. Однако для световых волн пучности эквивалентны ярким линиям, а узловые линии эквивалентны темным линиям. Если бы такая интерференционная картина могла быть создана двумя источниками света и спроецирована на экран, то на экране должна была бы быть чередующаяся картина из темных и светлых полос. А так как центральная линия в таком узоре является пучностью, то и центральная полоса на экране должна быть яркой полосой.

В 1801 году Томас Янг успешно показал, что свет создает интерференционную картину двухточечного источника. Для создания такого рисунка необходимо использовать монохроматический свет. Монохроматический свет — это свет одного цвета; при использовании такого света два источника будут вибрировать с одинаковой частотой. Также важно, чтобы две световые волны колебались в фазе друг с другом; то есть гребень одной волны должен образоваться в то же самое время, что и гребень второй волны. (Это часто упоминается как когерентный свет .) Для этого Томас Янг использовал один источник света и проецировал свет на два точечных отверстия. Затем свет от источника дифрагирует через отверстия, и рисунок можно спроецировать на экран. Поскольку есть только один источник света, набор двух волн, исходящих из отверстий, будет находиться в фазе друг с другом. Как и ожидалось, использование монохроматического источника света и точечных отверстий для генерации синфазных световых волн привело к появлению на экране узора из чередующихся ярких и темных полос. Типичный вид паттерна показан ниже.

 

Эксперимент Янга с двухточечной интерференцией часто проводится в курсе физики с использованием лазерного излучения. Обнаружено, что те же самые принципы, которые применимы к волнам воды в резервуаре с пульсацией, применимы и к световым волнам в эксперименте. Например, источник света с более высокой частотой должен создавать интерференционную картину с большим количеством линий на сантиметр рисунка и меньшим расстоянием между линиями. Действительно, это наблюдается. Кроме того, большее расстояние между щелями должно создавать интерференционную картину с большим количеством линий на сантиметр рисунка и меньшим расстоянием между линиями. Опять же, это наблюдается.

 

Самое удивительное, что Томас Янг смог использовать волновые принципы для измерения длины волны света. Подробная информация о разработке уравнения Юнга и дополнительная информация о его эксперименте представлены в уроке 3 этого раздела. На данный момент основное внимание уделяется тому, как те же характеристики, которые наблюдаются у волн на воде в резервуаре с пульсацией, также наблюдаются у световых волн. Открытия Томаса Янга предоставляют ученым того времени еще больше доказательств того, что свет ведет себя как волна. Ведь может ли все это делать поток частиц?

Следующий раздел:

Перейти к следующему уроку:

Помехи | Интерференция света | Учебник по микроскопии

Интерференция света — это явление интерференции нескольких световых волн друг с другом при определенных обстоятельствах, в результате чего суммарная амплитуда волн либо увеличивается, либо уменьшается. В этой части мы обсуждаем как конструктивную, так и деструктивную интерференцию световых волн, причины интерференции, а также некоторые примеры и эксперименты из реальной жизни, демонстрирующие это явление.

Что такое интерференция световых волн?

Важной характеристикой световых волн является их способность при определенных обстоятельствах интерферировать друг с другом. Определение интерференции в физике – это суперпозиция волн, вызывающая увеличение или уменьшение амплитуды результирующей волны. Большинство людей каждый день наблюдают оптические помехи того или иного типа, но не понимают, что вызывает это явление. Один из лучших примеров интерференции света демонстрирует свет, отраженный от масляной пленки, плавающей на воде. Другим примером является мыльный пузырь, показанный на рисунке 1, который отражает множество красивых цветов при освещении естественными или искусственными источниками света.

В чем разница между конструктивным и деструктивным вмешательством?

Эта динамичная игра цветов происходит из-за одновременного отражения света как от внутренней, так и от внешней поверхности пузырька. Две поверхности расположены очень близко друг к другу (их толщина составляет всего несколько микрон), и свет, отраженный от внутренней поверхности, интерферирует как конструктивно , так и деструктивно  со светом, отраженным от внешней поверхности.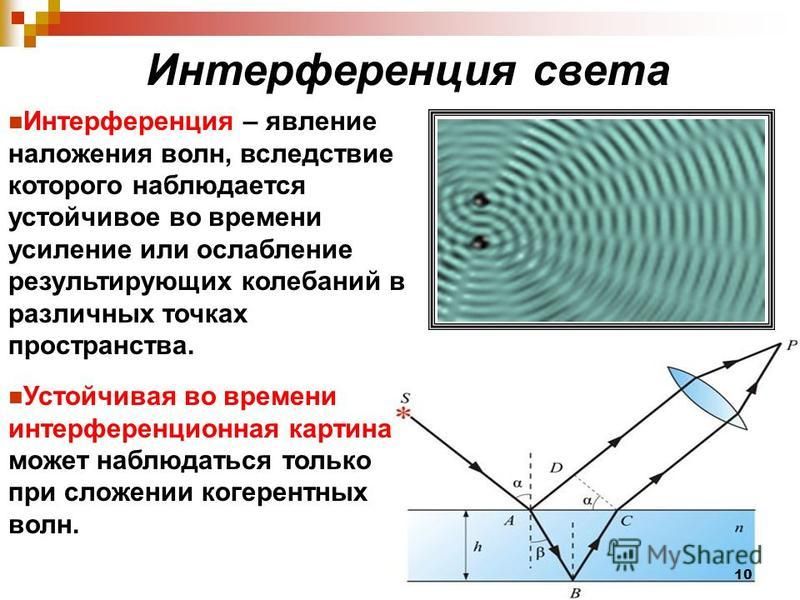 Это связано с тем, что свет, отраженный от внутренней поверхности пузыря, должен распространяться дальше, чем свет, отраженный от внешней поверхности. Когда световые волны, отраженные от внутренней и внешней поверхности, объединяются, они будут интерферировать друг с другом, удаляя или усиливая некоторые части белого света за счет деструктивной или созидательной интерференции. Это приводит к цвету. Если дополнительное расстояние, пройденное внутренними световыми волнами, точно равно длине волны внешних световых волн, то они будут рекомбинировать конструктивно, и будут получены яркие цвета этих длин волн. В местах, где волны идут не в ногу, возникнут деструктивные интерференции, нейтрализующие отраженный свет (и цвет).

Как происходит интерференция света?

Ниже приводится объяснение того, как световые волны интерферируют друг с другом. Рассмотрим пару световых волн от одного и того же источника, которые движутся, например, в направлении D . Это направление распространения (как показано на рисунке 2), и если колебания (которые перпендикулярны направлению распространения, обозначенному C на рисунке 2) параллельны друг другу, а также параллельны относительно направления вибрации, то световые волны могут интерферировать друг с другом. Если колебания не в одной плоскости и колеблются на 90 градусов друг к другу, то они не могут мешать друг другу.

Конструктивное вмешательство

Если предположить, что все перечисленные выше критерии соблюдены, то волны могут конструктивно или деструктивно интерферировать друг с другом. Если гребни одной из волн совпадают с гребнями другой, то амплитуды аддитивны. Если амплитуды обеих волн равны, результирующая амплитуда удвоится. Имейте в виду, что интенсивность света напрямую зависит от  квадрат амплитуды. Таким образом, если амплитуда удваивается, интенсивность увеличивается в четыре раза. Такая аддитивная интерференция называется конструктивной интерференцией   (показана на рисунке 2).

Разрушительное вмешательство

Если гребни одной волны совпадают с впадинами другой волны, результирующая амплитуда уменьшается или может даже полностью аннулироваться, как показано на рисунке 3. Это называется деструктивной интерференцией . Результатом является падение интенсивности или, в случае полной отмены, чернота.

Интерференция света

Узнайте, как две световые волны могут объединяться, создавая интерференцию друг с другом.

Начало обучения

Примеры помех

Томас Янг был физиком начала 19 века, который продемонстрировал интерференцию, показав, что свет является волновым явлением, а также постулировал, что разные цвета света образуются из волн разной длины. Это противоречило распространенному в то время мнению, которое склонялось к теории о том, что свет представляет собой поток частиц. В 1801 году Янг провел эксперимент, давший важные доказательства того, что видимый свет обладает волнообразными свойствами. В этом классическом эксперименте, который часто называют «экспериментом с двумя щелями», первоначально в качестве источника света использовался солнечный свет, который сначала дифрагировал через одну щель, но мы опишем эксперимент с использованием когерентного красного лазерного излучения.

Эксперимент с двумя щелями

Базовая схема эксперимента с двумя щелями показана на рис. 4. Когерентный лазерный свет освещает барьер, содержащий два точечных отверстия, через которые проходит только часть света. В область за щелями помещается экран, и на экране становится видна картина из ярко-красных и темных интерференционных полос. Ключом к этому эксперименту является взаимная когерентность между светом, дифрагированным от двух щелей на барьере. Юнг достиг этой когерентности за счет дифракции солнечного света от первой щели, и мы используем когерентный лазерный источник для целей этого обсуждения.

Эксперимент Янга с двумя щелями

Узнайте, как интерференционные картины меняются в зависимости от длины волны и размера щели.

Начало обучения

Что такое интерференционные полосы?

Когда лазерный свет дифрагирует через две щели барьера, каждая дифрагированная волна встречается с другой в последовательности шагов, как показано на рис. 4 (и графически в интерактивном руководстве  , описанном выше). Иногда волны встречаются в такт (или в фазе, конструктивная интерференция), иногда они встречаются не в такт (или не в фазе, деструктивная интерференция), а иногда встречаются частично в такт. Когда волны встречаются в шаге, они складываются за счет конструктивной интерференции, и на экране отображается яркая область. В областях, где волны встречаются совершенно не в ногу, они будут вычитаться друг из друга, вызывая разрушительную интерференцию, и в этой части экрана появится темная область. Образующиеся на экране узоры, являющиеся результатом интерференции двух дифрагированных лучей лазерного света, часто называют интерференцией 9.0156 бахрома .

Другие типы экспериментов были разработаны для демонстрации волнообразной природы световых и интерференционных эффектов. Наиболее примечательны эксперимент Ллойда с одним зеркалом и эксперименты с двойным зеркалом и бипризмой, разработанные Огюстеном Френелем. Эти эксперименты подробно описаны во многих книгах по физике, перечисленных в нашей библиографии.

Эксперимент с кольцами Ньютона

Сэр Исаак Ньютон, знаменитый математик и физик XVII века, был одним из первых ученых, изучавших явление интерференции. В своей знаменитой 9В эксперименте 0156 Кольца Ньютона он поместил выпуклую линзу большого радиуса кривизны на плоскую стеклянную пластину и приложил давление, чтобы скрепить линзу и стеклянную пластину. Когда он рассматривал пластины в отраженном солнечном свете, он заметил серию концентрических светлых и темных ярко окрашенных световых полос, подобных показанным на рис. 5. Ньютон понял, что кольца указывают на наличие некоторой степени периодичности, и использовал это наблюдение, чтобы предположить волновая теория света. Несмотря на это, Ньютон рассматривал свет как поток частиц.

Кольца возникают из-за тонкого слоя воздуха, который существует между изогнутыми выпуклыми и плоскими стеклянными поверхностями. Свет, отраженный от верхней и нижней поверхностей стекла, накладывается (объединяется) и создает интерференционные картины, которые выглядят как цветные кольца. Этот принцип часто используется производителями линз для проверки однородности больших полированных поверхностей.

Интенсивность помех и распределение интерференционных полос

Полосы распределения интенсивности интерференции (например, наблюдаемые в эксперименте Юнга с двумя щелями) различаются по интенсивности, когда они представлены на однородном фоне. Видимость ( В ) интенсивности было определено Альбертом Майкельсоном, физиком начала 20-го века, как разность между максимальной и минимальной интенсивностью полосы, деленная на их сумму:

В = I(max) – I(min)/ I(max) + I(min)

, где I(max) — максимальная интенсивность, а I(min) — минимальная интенсивность. Из уравнения идеализированная интенсивность интерференционных полос всегда находится между нулем и единицей, однако на практике видимость интерференционных полос зависит от геометрического плана эксперимента и используемого спектрального диапазона. Это является причиной множества интерференционных картин, наблюдаемых в естественных явлениях.

Интерференционные цвета, возникающие из-за областей напряжения в материалах, можно легко наблюдать в поляризованном свете. Линейка на Рисунке 6 изготовлена ​​из пластика и наблюдается через скрещенные поляризаторы. При обычном освещении линейка кажется полупрозрачной, а ее градуировка хорошо видна. Однако при просмотре линейки в поляризованном свете на линейке проявляются узоры напряжения, которые проявляются более глубоко в областях, которые более сильно деформированы. Это связано с высокой степенью выравнивания молекул длинноцепочечного полимера, из которых состоит линейка. Обратите внимание, что наибольшая степень двойного лучепреломления возникает вблизи отверстия на левой стороне линейки.

Реальное использование помех

Другим применением интерференции света являются измерения, проводимые на больших расстояниях с помощью лазеров. В этом случае лазеры можно использовать для измерения очень малых расстояний в диапазоне многих миль. Это достигается путем разделения лазерного луча и его отражения от разных поверхностей. Анализ результирующих интерференционных полос (при рекомбинации отдельных лазерных лучей) даст удивительно точное вычисление расстояния между двумя объектами.

Голограммы также зависят от интерференции света для создания своих трехмерных изображений. В отражательных голограммах как опорный, так и освещающий объект луч отражаются на толстой пленке с противоположных сторон. Эти лучи интерферируют, создавая светлые и темные области, которые соответствуют изображению, которое кажется трехмерным. Пропускающие голограммы используют как опорный луч, так и луч, освещающий объект, на одной стороне пленки для создания эффекта аналогичного типа.

Интерференция также возникает со звуковыми волнами и волнами, возникающими в стоячем бассейне с водой. Очень краткий и простой эксперимент с интерференцией можно провести дома, используя раковину, полную воды, и два шарика. Сначала дайте воде стать очень тихой, затем одновременно бросьте шарики в воду (на расстоянии около 10-14 дюймов друг от друга) с высоты около фута.