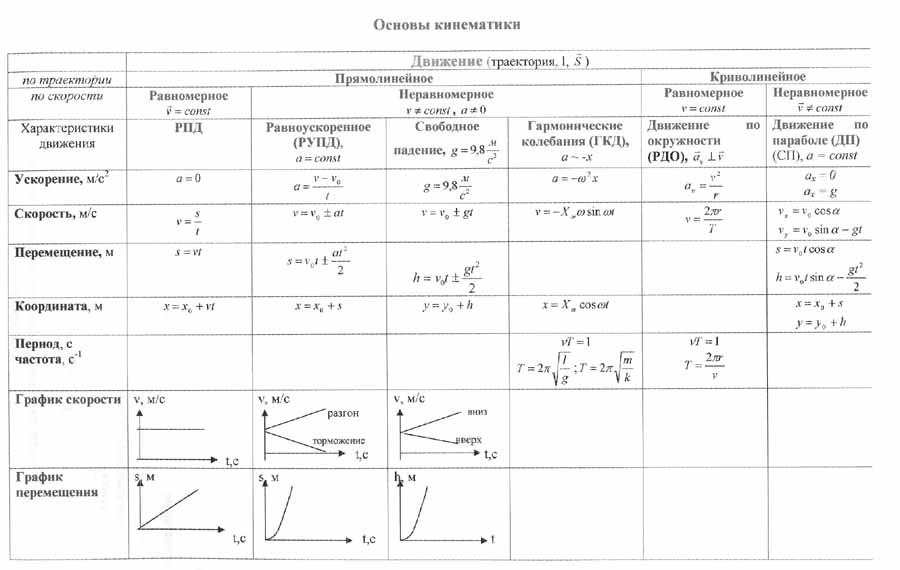
Основные кинематические величины.
Перемещение— векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:
.
Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени.
Средняя скорость— векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:
.
Скорость— векторная физическая величина, равная первойпроизводнойот радиус-вектора по времени:
.
Характеризует быстроту перемещения материальной точки.
Единица измерения скорости в системе СИ—м/с, в системеСГС— см/с. Мгновенная скорость всегда направлена по касательной к траектории.
Ускорение— векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:
.
Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормального и тангенциального ускорения:
.
Здесь — единичныйвектор нормали,— единичный вектор касательной. Величинаназываетсянормальным ускорениеми характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость ирадиус кривизнытраектории:
.
В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности.
Величина называетсятангенциальным ускорениеми характеризует величину изменения модуля скорости:
.
Вопрос №3)Законы динамики материальной точки.
Дина́мика —
раздел механики,
в котором изучаются причины
возникновения
Все задачи в динамике делятся на прямую и обратную задачи..
Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.
Обратная задача динамики: по заданным силам определить характер движения тела.
Классическая динамика основана на трёх основных законах Ньютона:
I закон Ньютона:
Существуют такие системы отсчета,
относительно которых поступательно
движущееся тело сохраняет свою скорость
постоянной, если на него не действуют
другие тела или их действие скомпенсировано.
II закон Ньютона: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой,прямо пропорциональновызывающей его силе, совпадает с ней по направлению иобратно пропорциональномассе материальной точки.
где — ускорениетела, — силы, приложенные к материальной точке, а — её масса.
Также второй закон можно записать в виде:
В классической (ньютоновской) механикемасса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами.
Второй закона Ньютона можно также сформулировать с использованием понятия импульса:
скорость изменения импульса материальной точки равна действующей на точку силе
где —
импульс (количество движения) точки, —
её скорость,
а — время.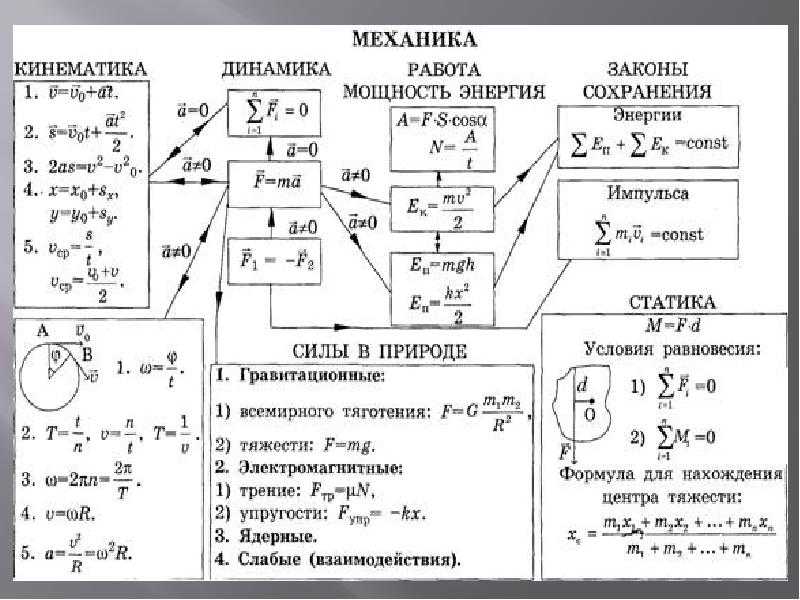 При такой формулировке, как и ранее,
полагают, что масса материальной точки
неизменна во времени.
При такой формулировке, как и ранее,
полагают, что масса материальной точки
неизменна во времени.
III закон Ньютона: Силы, с которыми тела действуют друг на друга, лежат на одной прямой, имеют противоположные направления и равные модули
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульсасистемы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохраненияимпульсаимомента импульса
В динамике существует инерциальная и неинерциальная система отсчета.
Инерциа́льная
систе́ма отсчёта (ИСО)
— система
отсчёта,
в которой все свободные тела
движутся прямолинейно и равномерно или покоятся. Иногда также говорят что: «Инерциальной
называется система отсчёта, по отношению
к которой пространство является однородным и изотропным,
а время — однородным». Законы
Ньютона,
а также все остальные аксиомы динамики в классической
механике формулируются
по отношению к инерциальным системам
отсчёта.
Иногда также говорят что: «Инерциальной
называется система отсчёта, по отношению
к которой пространство является однородным и изотропным,
а время — однородным». Законы
Ньютона,
а также все остальные аксиомы динамики в классической
механике формулируются
по отношению к инерциальным системам
отсчёта.
Неинерциа́льная
систе́ма отсчёта — система
отсчёта, в которой не выполняется
первыйзакон
Ньютона— «законинерции»,
говорящий о том, что каждое тело, в
отсутствие действующих на него сил,
покоится либо движется по прямой и с
постоянной скоростью. Всякая система
отсчета, движущаяся с ускорением или
поворачивающаяся относительно
инерциальной, является неинерциальной.Второй
закон Ньютонатакже не выполняется
в неинерциальных системах отсчёта. Для
того чтобы уравнение движения материальной
точки в неинерциальной системе отсчёта
по форме совпадало с уравнением второго
закона Ньютона, дополнительно к «обычным»
силам, действующим в инерциальных
системах, вводятсилы
инерции.
Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.
Вопрос№4) Импульс материальной точки.
И́мпульс (Коли́чество движе́ния) — векторнаяфизическая величина, являющаяся мероймеханического движениятела. В классической механике импульс тела равен произведениюмассыm этого тела на его скоростьv, направление импульса совпадает с направлением вектора скорости:
По II закону Ньютона скорость изменения импульса материальной точки равна действующей на точку силе
Это формула носит название закона изменения импульса материальной точки.
Для системы материальных точек вышеуказанная формула принимает вид:
Закон
изменения импульса для системы,где Fik –
внутренние силы взаимодействия i-й и
k-й частиц системы
между собой; Fi –
равнодействующая внешних сил, приложенных
к i-й частице.
Свойства импульса.
Аддитивность. Это свойство означает, что импульс механической системы, состоящей из материальных точек, равен сумме импульсов всех материальных точек, входящих в систему.
Инвариантность по отношению к повороту системы отсчета.
Сохранение. Импульс не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Свойства сохранения кинетической энергии, сохранения импульса и второго закона Ньютона достаточно, чтобы вывести математичекую формулу импульса.
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) – импульс замкнутой системы тел не меняется с течением времени.
Σp = const т.е. m1v1+m2v2=m1‘v1‘+m2‘v2‘
Замкнутая
система сил–
система на которую не действуют внешние
силы. Закон сохранения импульса
является следствием из второго и третьего
законов Ньютона.
Закон сохранения импульса
является следствием из второго и третьего
законов Ньютона.
Закон сохранения импульса выполняется не только для систем, на которые не действуют внешние силы, но и для систем, сумма всех внешних сил которых равна нулю. Равенство нулю всех внешних сил достаточно, но не необходимо для выполнения закона сохранения импульса.
Вопрос№5)Механическая работа.
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещенияточки (точек), тела или системы.
Обычно обозначается символом A.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силыработа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения:
Здесь
точкой обозначено скалярное
произведение, — вектор
перемещения; подразумевается, что
действующая сила постоянна
в течение всего того времени, за которое
вычисляется работа.
В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго родапо траектории точки:
Если существует зависимость силы от координат, интеграл определяется следующим образом:
,
где и—радиус-векторыначального и конечного положения тела соответственно.
ЛК_№1-Кинематика
3
ЛИТЕРАТУРА.
И.В.Савельев, Курс общей физики. М: Изд. «Наука».1970г.
Т.И.Трофимова, Курс физики. М: Изд.«Высшая школа».2001г.
А.И.Черноуцан, Краткий курс физики. М: Изд.«Высшая школа».2004г.
Б.М.Яворский, А.А.Детлаф, Справочник по физике для инженеров и студентов ВУЗов. М: Изд.»Наука».1978. – 939с.
Раздел. МЕХАНИКА
Тема 1. Кинематика.
Лекция_№1.
Физические величины, основные свойства.
Кинематика материальной точки,общие определения.
Физические величины, основные свойства.
Что такое физическая величина? В чём её основные отличительные свойства?
Критерием достоверности знаний о материальном мире является опыт.
Проведение опыта – это определение физической величины, то есть её наблюдение и измерение. Таким образом физическая величина должна обладать свойством быть наблюдаемой и измеряемой.
Требование достоверности означает, что физический опыт должен быть повторяемым. Это значит, что при повторении опыт, проведенный в равных условиях, должен приводить всякий раз к одинаковому результату. Таким образом, физическая величина должна обладать свойством повторяемости.
Наконец, физические
величины должны обладать свойством
размерности.
Под размерностью физической величины понимают совокупность параметров, необходимых для ее определения. Например, простые физические величины — это длина, время и масса. Они имеют собственные размерности, обозначаемые соответственно буквами [L], [T] и [M], потому что для их определения никаких других измерений производить не нужно. Но для определения скорости тела необходимо произвести два независимых измерения — длины L и времени T. Поэтому размерность скорости есть отношение [L/T] .
Подчеркнем,
что размерность физической величины и
единицы ее измерения — это разные
понятия. Например, скорость может
измеряться в см/с, или в м/с,
или в км/ч,
а размерность ее при этом не меняется
— она всегда есть [L/T],
потому что независимо от того, в каких
единицах мы измеряем скорость, мы всегда
производим измерения одних и тех же
двух параметров — длины L, и времени T.
Размерность физической величины представляет ее важнейшее свойство. Часто приходится сравнивать между собой различные величины. Физические величины можно сравнивать, только если они обладают одинаковой размерностью. Например, нельзя сравнивать между собой длину пути и отрезки времени: это бессмысленно — они обладают разной размерностью.
Итак, важнейшими свойствами физических величин являются:
Материальная точка – это идеализация реальных физических объектов.
Определение 1.
Материальная точка – это физическое тело, обладающее массой, размерами которого можно пренебречь при рассмотрении его движения.
При движении пространственное положение материальной точки фиксируется
тройкой
чисел в какой-либо системе координат.
Кроме системы координат, необходимо
устройство для измерения времени.
Образно говоря, такое устройство назовем
часами.
Итак, выбранная система координат и связанные с ней часы образуют систему отсчета.
Например, в декартовой прямоугольной системе координат {X,Y,Z} радиус-вектор описывает траекторию материальной точки. Длина траектории точки представляет собой величину пройденного пути S(t).
Путь S(t)— скалярная величина.
Наряду с величиной пройденного пути, перемещение точки характеризуется направлением, в котором она движется. В отличие от пути перемещение есть векторная величина.
Определение 2.
Разность двух радиус-векторов, взятых в различные моменты времени, образует вектор
перемещения точки (см. рис.), .
Изменение
положения точки в пространстве
характеризуется её скоростью.
Определение 3.
Под средней скоростью движения по траектории за конечное время t понимают отношение пройденного за это время конечного пути S ко времени:
. (1)
Определение 4.
В терминах дифференциального исчисления мгновенная скорость точки определяется соотношением:
. (2)
Скорость движения точки по траектории — скалярная величина. Наряду с ней в механике вводится средняя скорость перемещения точки.
Определение 5.
Средняя скорость перемещения — это величина, направленная вдоль вектора перемещения,
. (3)
Определение 6.
Производная радиус-вектора по времени определяет мгновенную скорость перемещения точки.
. (4)
Поскольку перемещение совпадает с бесконечно малым элементом траектории , то вектор скорости направлен по касательной к траектории, а его величина (модуль вектора!):
. (5)
Интегрируя выражение (5) в интервале времени от t0 до t, можно вычислить путь, пройденный телом за время t–t0 , если известна зависимость от времени его скорости v(t) (точнее приращение пути!)
. (6)
(6)
В случае равномерного движения, когда скорость сохраняет свое постоянное значение во все время движения, v=const; следует выражение
. (6а)
Если к начальному моменту времени – был пройден путь – , то
, (7)
Определение 7.
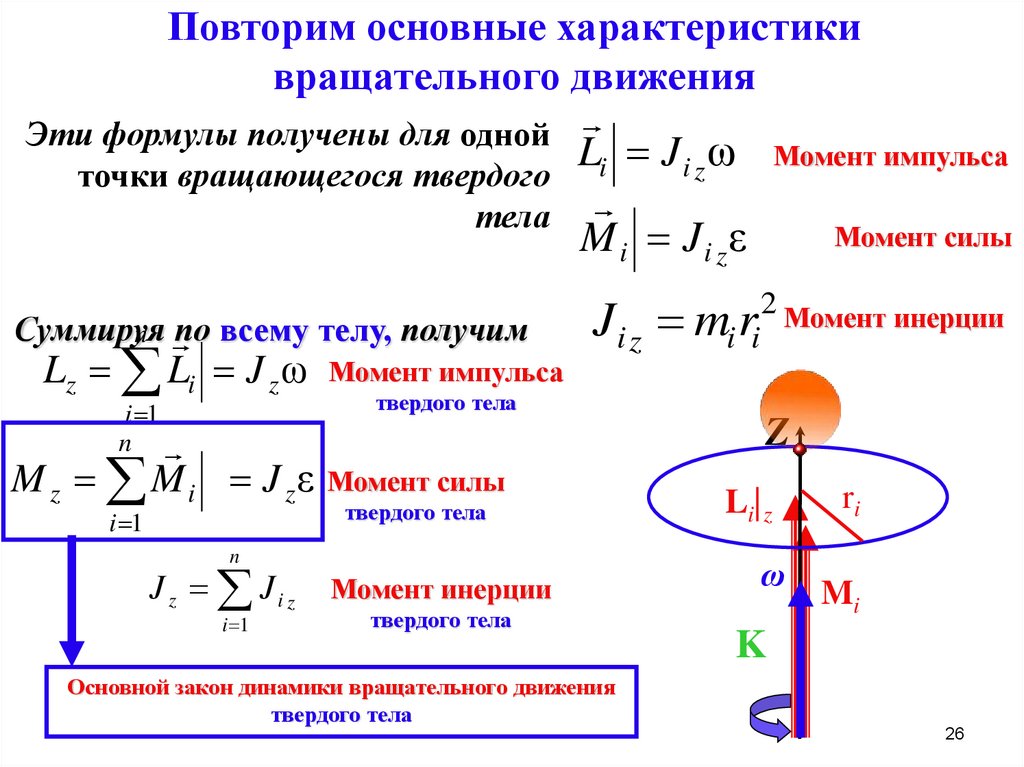
Производную скорости по времени, которая является второй производной по времени от радиус-вектора, называют ускорением точки:
. (8)
Вектор ускорения а направлен вдоль вектора приращения скорости dv.
Пусть.
Этот важный и часто встречаемый случай
носит название равноускоренного
или равнозамедленного движения (в
зависимости от знака ускорения
–
!)
.
Проинтегрируем выражение (8) в пределах от t = 0 до t, получим, что
(9)
. (10)
Кинематические величины Определения/Примечания – IB Physics HL/SL
- Кинематические величины описывают движение объектов.
- Они зависят от системы отсчета.
- Это либо векторные, либо скалярные значения.
- Основными кинематическими величинами являются: перемещение, расстояние, скорость, скорость и время.
- Ускорение обсуждается на странице примечаний «равномерно ускоренное движение».
Кинематика – изучение движения. Что такое кинематические величины? Это меры, которые предоставляют информацию о движении объекта.
- Позиция – место, где объект находится относительно других объектов (Вектор Количество).

- Требуется направление и величина.
- «Человек находится в 5 метрах левее маркера положения».
- Система координат должна быть определена (или подразумеваться), чтобы определить положение объекта.
- В примере маркер положения — это система отсчета, необходимая для обсуждения положения человека и Луны.
- Время – сколько времени требуется для выполнения определенного действия?
- Скалярное значение, для которого требуется только величина
- Смещение — общее изменение положения объекта.
- Описывает, как далеко по сравнению с исходным положением продвинулся данный объект.
- Векторная величина, для которой необходимы как величина, так и направление.
- Расстояние — длина пройденного пути.
- Описывает, «сколько земли покрыл объект»
- Скалярная величина, нужна только величина
- В примере слева зеленая линия — смещение, а черная линия — расстояние.

- Обе величины измеряются в метрах.
- Расстояние может быть равно или больше смещения, но не меньше.
- Скорость — изменение положения (перемещения) за изменение во времени.
- Векторная величина, требуется как величина, так и направление.
- Скорость это расстояние во времени.
- Скалярная величина, требуется только величина, но не направление.
- Оба измеряются в м/с (метры в секунду).
- Скорость: объект движется со скоростью 200 м/с.
- Скорость: объект движется на север со скоростью 200 м/с.
- Оба описывают «скорость изменения положения в единицу времени»
В равномерном движении скорость/скорость постоянны.
- Нет ускорения.
- При условии, что на объект не действуют внешние силы.
Это наиболее часто используемое уравнение для равномерного движения:
- Используется для связи скорости (или скорости) с перемещением (или расстоянием) и временем.
- Нижний индекс f используется для обозначения окончательных значений, тогда как нижний индекс i используется для обозначения начальных значений.
- Вычитание начального из конечного дает нам изменение значения, которое используется в уравнении.
- Нижний индекс f используется для обозначения окончательных значений, тогда как нижний индекс i используется для обозначения начальных значений.
Часто задаваемые вопросы:
- В чем разница между скалярными и векторными величинами?
- Скалярные величины (время, расстояние, скорость) используют только величину для описания движения объекта.
- Векторные величины (смещение, скорость, ускорение) имеют не только величину, но и направление, поэтому они предоставляют больше информации о движении объекта.
- Благодаря этой дополнительной информации они используются чаще.
Физический модуль 1: Кинематика | HSCOne
Пранав Шарма
Последнее обновление: 24 августа 2021 г. 4 минуты чтения 11 класс, физика
СодержаниеДвижение
- Движение — фундаментальное наблюдаемое явление.
- Изучение кинематики включает описание, измерение и анализ движения без учета задействованных сил и масс.
Скаляры и векторы
- Скаляры — это физические величины, которые могут быть описаны как величина с единицей измерения (например, 60 км/ч)
- Примеры скаляров включают время, расстояние, объем и скорость
- Скаляры представлен простым курсивом, например, t для времени или d для расстояния
- Векторы — это физические величины, которые можно описать как величину, единицу измерения и направление (например, 20 м на запад)
- Примеры векторов включают положение, смещение, скорость , ускорение и сила
- Векторы представляются с помощью ВЕКТОРНОЙ ОБОЗНАЧЕНИЯ.
- Наиболее распространенный тип векторной записи использует стрелку над символом, например \(\vec{v}\) для скорости
Сложение и вычитание векторов с помощью алгебры (одно измерение)
- При сложении или вычитании векторов с помощью алгебры необходимо установить соглашение о знаках для представления направления используя соглашение о знаках, ВАЖНО предоставить ключ, объясняющий используемое соглашение.

- Использование знака позволяет вводить направления и величины в калькулятор. Знак конечной величины указывает направление полного вектора.
Шаги для добавления:
- Примените правило знаков, чтобы изменить каждое из направлений на знаки
- Сложите их величины и их знаки вместе
- Обратитесь к правилу знаков, чтобы определить направление результирующего вектора
- Укажите результирующий вектор
- Пример:
- Ученик прошел 25 м вперед, затем 16 м назад, затем 44 м вперед, затем 12 м назад. Определить полное перемещение.
- Вперед положительна
- 25m ВЕРНАЯ = 25M
- 16M назад = -16 м
- 44M вперед = 44M
- 12m назад = -12M
- \ (25-16 +44-12 =41. \)
- Положительный вперед
- Следовательно, полное перемещение равно 41 м вперед.
Шаги для вычитания
- Применение правил знаков для изменения каждого из направлений на знаки
- Изменение направления исходного вектора на противоположное путем изменения знака
- Выполните сложение векторов с результатами
- Пример:
- Самолет меняет курс с 255 м/с на запад на 160 м/с на восток.
 Определить изменение скорости.
Определить изменение скорости.
- Запад отрицательный
- 225 м/с Запад = -255 м/с \(\vec{v}_1\)
- 160 м/с Восток = 160 м/с \(\vec{v}_2\)
- Обратить исходный вектор: \(-\vec{v}_1\) = 255 м/с
- Сложить векторы: \(-\vec{v}_1 + \vec{v}_2 = 225+160 = 415 м/с\)
- Положительное значение указывает на восток, поэтому изменение скорости составляет 415 м/с на восток
- Самолет меняет курс с 255 м/с на запад на 160 м/с на восток.
Перемещение, скорость и скорость
- , перемещение, скорость и скорость.
Центр масс
- Движение объекта описывается с точки зрения его ЦЕНТРА МАССЫ, единственной точки, которая является точкой баланса объекта.
Позиция
- Позиция описывает положение объекта в определенный момент времени относительно начала координат.
- Позиция является векторной величиной и поэтому требует направления. Абсолютная система отсчета для направления является источником объекта.

- Положение измеряется в метрах.
Пройденное расстояние
- Пройденное расстояние описывает, какое расстояние проходит тело во время путешествия.
- Расстояние является скалярной величиной и измеряется в метрах.
Смещение
- Смещение — это изменение положения объекта, представленное символом \(\vec{s}\)
- Смещение учитывает только начальную и конечную точки
- Другими словами, смещение объекта — это расстояние по прямой между его начальной и конечной точками
- Смещение рассчитывается путем вычитания начального положения из конечного положения
- Смещение — это ВЕКТОР, поэтому оно должно иметь направление, а также величину
Графики перемещения-времени
- Графики перемещения-времени можно использовать для обобщения движения объекта
- Градиент графика в любой точке представляет собой скорость в этой точке
Скорость и скорость
- это скорость, с которой пройдено расстояние
- скорость это СКАЛЯР
- скорость это скорость изменения перемещения
- скорость это ВЕКТОР
- скорость и скорость измеряются в \(м/с^2\ )
Мгновенная скорость и скорость
- Скорость движения объекта в определенный момент времени
- Мгновенная скорость ВСЕГДА равна величине мгновенной скорости
Средняя скорость и скорость
Преобразование км/ч в м/с
- Чтобы преобразовать км/ч в м/с, разделите на 3,6
- Чтобы преобразовать из м/с в км/ч, умножьте на 3,6
Уравнения SUVAT
- Они также могут быть выражены с помощью различных предметов:
Кинематика 11 год Физика
Пранав Шарма
Владелец сайта
Университет Нового Южного Уэльса Студент, владелец сайта и разработчик.
