Физический смысл производной
Физический смысл производной обозначился ещё с практических задач мгновенной скорости, прямолинейного движения и даже свободного падения.
Всё дело в том, что любое тело при движении или падении перемещается неравномерно. Скорость (v) может постепенно возрастать или наоборот уменьшаться (в случае падения, конечно, только возрастать).
Поэтому смотрим на две точки во времени:
Момент времени: t1 = t
Другой момент времени (и другая точка нахождения тела): t2 = t +
За это время был пройден путь:
И s мы выражаем в виде функции от времени – s(t)
или проще:
Но брать в физике среднюю скорость стало не совсем удобно, так как требовались более точные измерения (привет физическому смыслу производной).
В общем, появляется понятие о мгновенной скорости прямолинейного движения (по сути, скорости в конкретный момент времени t). Так средняя скорость в пределе, при получает значение:
по сути,
Теперь ясно, что мгновенная скорость – это предел приращения функции s(t) деленный на приращение аргумента t (с ).
А вот и производная в её общем виде, где производная ф-ции y=f(x) в точке x является пределом (при условии его существования и конечности) приращения самой функции деленным на приращение аргумента, который стремится к нулю:
или же:
Решение этой задачи и становится физическим смыслом производной.
Решим простой пример
Начнем с приращения :
Раскрываем скобки:
Ищем приращение функции:
Находим приращение ф-ции к приращению аргумента:
И мы дошли до предела при (по сути, производной):
И еще немного о физическом смысле производной
По примерам выше можно понять варианты физических переменных и производных указанных ниже (просто в формате шпаргалки):
Скорость и ускорение тела:
Находим скорость от времени: v(t) = x'(t)
Ускорение по функции скорости от времени: a(f) = v'(t)
Или еще вариант ускорения по времени: a(t) = x”(t)
Угловая скорость и угловое ускорение при вращательном движении:
Угол от времени: φ = φ(t)
Угловая скорость по времени: ω = φ'(t)
Угловое ускорение: ε = φ'(t) или ε = φ”(t).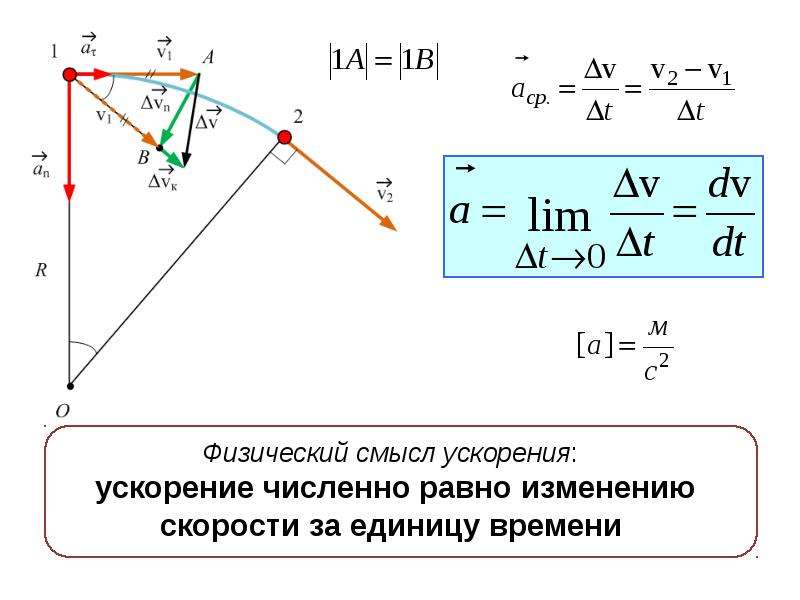
Решение для гармонических колебаний:
у” = Asin(ωt + φ0) или у = Acos(ωt + φ
А – амплитуда колебаний
ω – циклическая частота
φ0 – начальная фаза
Редактировать этот урок и/или добавить задание Добавить свой урок и/или заданиеДобавить интересную новость
Точка движется прямолинейно. Физический смысл производной
Точка движется прямолинейно по закону S = t 4 +2t (S – в метрах, t – в секундах). Найти ее среднее ускорение в промежутке между моментами t 1 = 5 с, t 2 = 7 с , а также ее истинное ускорение в момент t 3 = 6 с.
Решение.
1. Находим скорость движения точки как производную от пути S по времени t, т.е.
2. Подставляя вместо t его значения t 1 = 5 с и t 2 = 7 с, находим скорости:
V 1 = 4 5 3 + 2 = 502 м/с; V 2 = 4 7 3 + 2=1374 м/с.
3. Определяем приращение скорости ΔV за время Δt = 7 – 5 =2 с:
ΔV = V 2 – V 1 = 1374 – 502 = 872 м/с.
4. Таким образом, среднее ускорение точки будет равно
5. Для определения истинного значения ускорения точки берем производную скорости по времени:
6. Подставляя вместо t значение t 3 = 6 с, получим ускорение в этот момент времени
a ср =12-6 3 =432 м/с 2 .
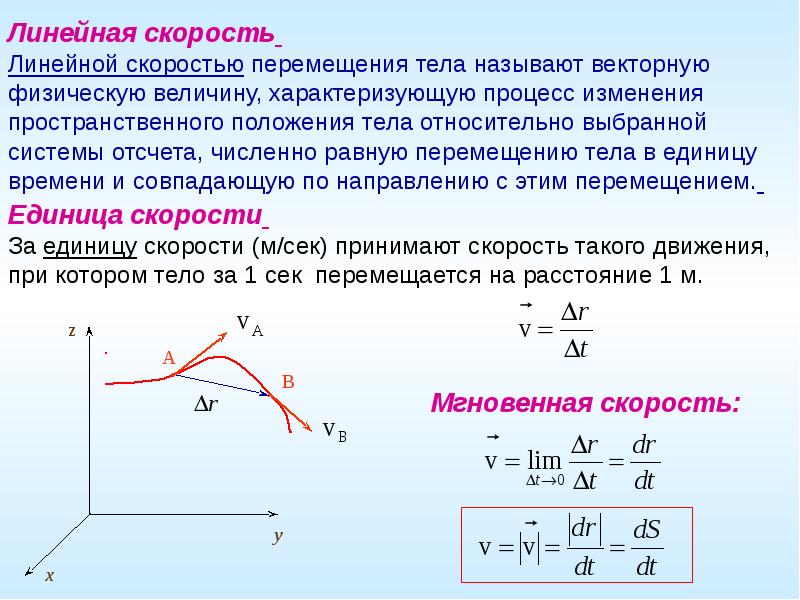
Криволинейное движение. При криволинейном движении скорость точки изменяется по величине и направлению.
Представим себе точку М, которая за время Δt, двигаясь по какой-то криволинейной траектории, переместилась в положение М 1 (рис. 6).
Вектор приращения (изменения) скорости ΔV будет
Для нахождения вектора ΔV перенесем вектор V 1 , в точку М и построим треугольник скоростей. Определим вектор среднего ускорения:
Вектор а ср параллелен вектору ΔV , так как от деления вектора на скалярную величину направление вектора не изменяется.
Такой предел называют векторной производной.
Таким образом, истинное ускорение точки при криволинейном движении равно векторной производной по скорости.
Из рис. 6 видно, что вектор ускорения при криволинейном движении всегда направлен в сторону вогнутости траектории.
Для удобства расчетов ускорение раскладывают на две составляющие к траектории движения: по касательной, называемое касательным (тангенциальным) ускорением а , и по нормали, называемое нор-мальным ускорением а n (рис. 7).
В этом случае полное ускорение будет равно
Касательное ускорение совпадает по направлению со скоростью точки или противоположно ей. Оно характеризует изменение величины скорости и соответственно определяется по формуле
Нормальное ускорение перпендикулярно к направлению скорости точки, а численное значение его определяется по формуле
где r – радиус кривизны траектории в рассматриваемой точке.
Так как касательное и нормальные ускорения взаимно перпендикулярны, поэтому величина полного ускорения определяется по формуле
а направление его
Если , то векторы касательного ускорения и скорости направлены в одну сторону и движение будет ускоренным.
Если , то вектор касательного ускорения направлен в сторону, противоположную вектору скорости, и движение будет замедленным.
Вектор нормального ускорения всегда направлен к центру кривизны, поэтому оно называется центростремительным.
Физический смысл производной. В состав ЕГЭ по математике входит группа задач для решения которых необходимо знание и понимание физического смысла производной. В частности, есть задачи, где дан закон движения определённой точки (объекта), выраженный уравнением и требуется найти его скорость в определённый момент времени движения, либо время, через которое объект приобретёт определённую заданную скорость.
Задачи очень простые, решаются они в одно действие.
Пусть задан закон движения материальной точки x (t) вдоль координатной оси, где x координата движущейся точки, t – время.
Скорость в определённый момент времени – это производная координаты по времени. В этом и состоит механический смысл производной.
Аналогично, ускорение – это производная скорости по времени:
Таким образом, физический смысл производной это скорость. Это может быть скорость движения, скорость изменения какого-либо процесса (например роста бактерий), скорость совершения работы (и так далее, прикладных задач множество).
Кроме того, необходимо знать таблицу производных (знать её нужно также, как таблицу умножения) и правила дифференцирования. Если конкретно, то для решения оговоренных задач необходимо знание первых шести производных (см. таблицу):
Рассмотрим задачи:
x (t) = t 2 – 7t – 20
где x t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 5 c.
Физический смысл производной это скорость (скорость движения, скорость изменения процесса, скорость работы и т.д.)
Найдем закон изменения скорости: v (t) = x′(t) = 2t – 7 м/с.
При t = 5 имеем:
Ответ: 3
Решить самостоятельно:
Материальная точка движется прямолинейно по закону x (t) = 6t 2 – 48t + 17, где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 c.
Материальная точка движется прямолинейно по закону x (t) = 0,5t 3 – 3t 2 + 2t, где x t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
Материальная точка движется прямолинейно по закону
x (t) = –t 4 + 6t 3 + 5t + 23
где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.
Материальная точка движется прямолинейно по закону
x (t) = (1/6) t 2 + 5t + 28
где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с?
Найдем закон изменения скорости:
Для того, чтобы найти, в какой момент времени
Ответ: 3
Решите самостоятельно:
Материальная точка движется прямолинейно по закону x (t) = t 2 – 13t + 23, где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Материальная точка движется прямолинейно по закону
x (t) = (1/3) t 3 – 3t 2 – 5t + 3
где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Отмечу, что ориентироваться только на такой тип задач на ЕГЭ не стоит. Могут совершенно неожиданно ввести задачи обратные представленным. Когда дан закон изменения скорости и будет стоять вопрос о нахождении закона движения.
Могут совершенно неожиданно ввести задачи обратные представленным. Когда дан закон изменения скорости и будет стоять вопрос о нахождении закона движения.
Подсказка: в этом случае необходимо найти интеграл от функции скорости (это так же задачи в одно действие). Если потребуется найти пройденное расстояние за определённый момент времени, то необходимо подставить время в полученное уравнение и вычислить расстояние. Впрочем, мы такие задачи тоже будем разбирать, не пропустите! Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
«Материальная ответственность сторон трудового договора» – Материальная ответственность работодателя. Если сумма взыскания не превышает среднего заработка за 1 месяц. Добровольный по заявлению или письменному обязательству. Для работника. Материальная ответственность работника Ограниченная Полная Индивидуальная Коллективная (бригадная). Путем удержания из заработной платы по распоряжению работодателя.
«Колебание точки» – 5. Линейные колебания. 7. Свободные колебания с вязким сопротивлением. 4. Примеры колебаний. Биение. 3. Примеры колебаний. Движение является затухающим и апериодичным. Показывает во сколько раз амплитуда колебаний превосходит статическое отклонение. Свободные колебания, вызванные вынуждающей силой. 4) Период затухающих колебаний больше чем у незатухающих.
«Прямолинейное движение» – Графики для ПРД. Прямолинейное равномерное движение (ПРД). Sx =X – X0= vx t – проекция перемещения на ось X. Прямолинейное равноускоренное движение (ПРУД). Пруд. X = X0 + sx – закон движения. Графики ПРУД. То есть изменяется скорость?. – Закон движения. Пример: X = X0 + Vx t – закон движения для ПРД.
«Точки небесной сферы» – Дни солнцестояния, как и дни равноденствия, могут меняться. В 1 радиане 57°17?45″. градус – центральный угол, соответствующий 1/360 части окружности. В точке летнего солнцестояния 22 июня Солнце имеет максимальное склонение. Перемещение Солнца по эклиптике вызвано годовым движением Земли вокруг Солнца.
«Расстояние от точки до прямой» – В единичном кубе A…D1 найдите расстояние от точки A до прямой CB1. Нахождение расстояний 2. В единичном кубе A…D1 точка E – середина ребра C1D1. В единичном кубе A…D1 найдите расстояние от точки A до прямой CD. В единичном кубе A…D1 найдите расстояние от точки A до прямой CD1. В единичном кубе A…D1 найдите расстояние от точки A до прямой BD.
«Четыре замечательные точки треугольника» – Высотой треугольника. Медианой треугольника. Отрезок АН – перпендикуляр, опущенный из точки А на прямую а, если. Медиана. Отрезок, соединяющий вершину с серединой противолежащей стороны, называется. Биссектрисой треугольника. Задача №2. Задача № 1. Перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону, называется.
Физика – 10
В СИ за единицу ускорения принят 1 м
с2 – ускорение такого равнопеременного движения, при котором материальная точка за 1 секунду изменяет свою скорость на 1 м
с
[a] [Δv]
[Δt] = 1 м/с
c = 1 м
с2
Знаете ли вы? Ускорение — одна из наиболее значимых величин, используемых в физике и технике. Известно, что при постепенном торможении автомобиля, автобуса и поезда
Известно, что при постепенном торможении автомобиля, автобуса и поезда
пассажиры не чувствуют дискомфорта, однако при резком торможении для них возникает серьезная опасность. Значит, важно не просто изменение скорости, а быстрота изменения скорости. Для контроля за изменением скорости машин и механизмов используется прибор, измеряющий ускорение – акселерометр (лат.: ассеlero – “ускоряю” и греч.: metreo – “измеряю”) (d).
Применение. Исследование-2. Чему равна средняя скорость?Задача: Велосипедист первую половину прямолинейного пути проходит с постоянной по 4 м
с, а вторую половину — с постоянной по модулю скоростью 6 м
с. Определите среднюю скорость велосипедиста на всем пути.
| Дано | Решение |
| v1 = 4 м/с v2 = 6 м/с vср-? | vср = l Поскольку l1 = l Аналогично: t2=l |
| Вычисление | |
| … | |
- Какой формулой определяется средняя скорость на пути, состоящем из двух равных участков?
- Какой формулой определяется средняя скорость велосипедиста, движущегося в течение двух равных последовательных промежутков времени (t1 = t2), соответственно, со скоростями v1 и v2 ?
- Какую скорость измеряет спидометр автомобиля: среднюю или мгновенную? Ответ обоснуйте.

- Какие понятия повторили на уроке? Что из этого вы хорошо поняли, а что осталось вам не ясным?
- Чем отличаются друг от друга средняя путевая скорость и средняя скорость перемещения?
- Каков физический смысл ускорения?
- Чему равны, соответственно, ускорения при равномерном и неравномерном прямолинейном движении? Почему?
- Как направлен вектор ускорения автомобиля, если он начинает прямолинейное движение из состояния покоя? Почему?
- Как направлен вектор ускорения автомобиля, если он начинает тормозить? Почему?
Вторая производная и ее физический смысл
Тема: «Втораяпроизводная и ее
физический смысл».

2. Цели занятия:
• 1. Формирование знаний опроизводных второго порядка;
• 2. Формирование навыков
применения второй производной к
решению задач.
3. Повторение
Определение. Производной функции y f ( x) называется конечный пределотношения приращения функции f f ( x x) f ( x) к приращению
независимой переменной x при стремлении последнего к нулю:
y
f ( x x) f ( x)
lim
.
x 0 x
x 0
x
y f lim
Производная от первой производной
называется производной второго
порядка или второй производной и
2
обозначается:
d y
у , f ( x),
dx
2
6. Физический смысл производной второго порядка.
Пусть тело движется по закону S f (x) .Как известно, скорость v движения тела
в данный момент времени равна
производной пути по времени, т.е.
v S (t )
Если тело движется неравномерно, то
скорость v с течением времени
изменяется и является функцией от
времени.
 И, следовательно, от нее также
И, следовательно, от нее такжеможно найти производную, т.е.
v
а lim
v ( S ) S
t 0 t
Эта величина называется ускорением в
данный момент времени и обозначается
буквой а.
Таким образом, ускорение
прямолинейного движения тела
в данный момент времени равно
второй производной пути по
времени, вычисленной для
данного момента.
В этом и заключается физический
смысл второй производной.
9. 3. Применение понятия производной функции при решении задач.
Тело движется прямолинейно по закону:S 3t 3t 8
2
Найти скорость и ускорение тела в
момент времени t = 4 c.
Решение.
Для определения скорости движения
тела нужно найти первую производную
от данной функции при t = 4 с.
v S (3t 3t 8) 6t 3
2
vt 4 6 4 3 21( м / с)
Ускорение тела равно второй
производной от функции при t = 4 c.
a S ( S ) (6t 3) 6( м / с )
2
Величина ускорения оказалась
постоянной для любого значения t,
следовательно движение тела по
заданному закону происходит с
постоянным ускорением.

2
Ответ: v = 21 м/с, а = 6 м/с .
12. 1. . Найти вторую производную .
1. y x ln x . Найти вторую производную.
Решение.
1. Находим первую производную:
1
y x ln x x (ln x) ln x x ln x 1
x
2. Находим вторую производную:
1
y (ln x 1) x 1
x
13. 2. Найти
2. y e2 x 1
1
Найти y 2
Решение.
y 2e 2 x 1 y 4e 2 x 1
Вычислим значение второй
1
производной при
x
2
Подставим во вторую производную:
1
y 4e1 1 4e 0 4
2
14. Тело движется прямолинейно по закону км. Определить скорость и ускорение движения тела через 6 часов после начала движения.
Тело движется прямолинейно по законуS (t 2 2)t 1 км. Определить скорость и
ускорение движения тела через 6 часов после
начала движения.
Решение.
v S 3t 2 2 v(6) 3 36 2 110км / час
2
a v S 6t a(6) 6 6 36км / час
Самостоятельная работа
Найти производные второго порядка
от заданных функций:
1.

3.
y x sin x
3
y cos x
2.
y e ln 2
4.
y x ln x
x
5. Тело движется прямолинейно по
закону S 1 2t t 3 . Определить
скорость и ускорение в момент
времени t 3 .
17. Критерии оценки:
• «5» – решены правильно все задачи;• «4» – решены все задачи, но в одной из
них допущена ошибка;
• «3» – решены правильно три задачи.
«При движении любых тел их скорости обычно меняются либо по модулю, либо по направлению или же одновременно и по модулю и по направлению». Это цитата из современного учебника по физике (Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика, Учебник для 10 класса, 2005). Так, там начинается 13 параграф – «Ускорение». Ну, во-первых, при движении любых тел их скорости обычно не меняются, пока нет внешних сил, во-вторых, очень символично, что именно в 13-ом параграфе объясняют про ускорение, именно 13. Нужно заметить, что ускорение это особенное понятие, наверно самое главное, именно из него определяются, вычисляются, формулируются все другие понятия в механике, как в базовом разделе физики. Кроме того, в предыдущей статье мы выяснили, что определять скорость по модулю неверно, правильнее говорить про, просто скорость, и единичный вектор направления – ё. В учебнике рассматривают ускорение как изменение скорости тела за единицу времени, и определяют так: где V – скорость, м/с; t – время, с; a – ускорение, соответственно м/с2 . Таким образом, ускорение имеет размерность – м / с 2 , т.е. метры разделить на секунды в квадрате. А что такое секунда в квадрате, какой физический смысл это имеет. Какой смысл возводить в квадрат слова, не цифры и числа, а простые слова? Есть только один случай, когда это имеет смысл, это квадратный метр – м2. А какой смысл в с2, зачем это? 25 с2 = 5 с × 5 с ; Т.е. степень два означает умножение какого-то числа или цифры на такое же число или цифру. В свою очередь операция умножения означает многократное сложение: 5 с + 5 с + 5 с + 5 с + 5 с = 25 с, И в этом случае никакой квадратной степени не образуется, и секунды остаются секундами, а не секунда в квадрате. И это правильно, все компьютеры мира умеют только складывать, правда, с учетом знака, и ни каких других операций делать не умеют. Значит, при компьютерном вычислении секунды в квадрате не образуются, а если они там и появляются, то это искусственно создается внешним программированием. С учетом всей этой математики ускорение должно иметь размерность в виде м / с, и никакого отличия от скорости иметь не будет. Как так? В физике, в ее разделе под названием механика, почти все понятия и определения вычисляются через ускорение, например скорость при движении с постоянным ускорением: V = Vo + a t. Кстати, в жизни такого движения практически не бывает, точнее, бывает только на очень коротких дистанциях. Разгон, как правило, бывает нелинейным, потом равномерное движение без ускорения и торможение тоже нелинейное. Получается, что все понятия, определения и выражения в механике неправильные. Они выведены с использованием такого понятия, как ускорение, а его в действительности нет. В жизни изменяется всё: время, энергия, мощность, температура, давление, скважность, сила, возраст, влажность, мнение, кэш, отношение между людьми и многое, многое. Но почему-то только у скорости имеется такое понятие, как ускорение? Попробуем тогда рассмотреть всю эту историю по-другому, с другого ракурса. Материальное тело движется прямолинейно и постепенно увеличивает свою скорость, например с использованием электромотора. В какой-то точке, назовем ее начальной, скорость составляет Vн, через метр, в следующей точке, назовем ее конечной, скорость составляет Vк. Таким образом, на дистанции в один метр скорость изменилась от Vн до Vк: Vк – Vн, и это произошло на дистанции S, длиной 1 метр: (Vк – Vн) / S = ΔV / S . Вот это и есть ускорение, оно определяется не через равные промежутки времени, а через равные промежутки дистанции. Размерность в этом случае; м / с / м = 1 / с. Вот такое должно быть ускорение, т.е. ускорение это изменение скорости на какую-то величину, т.е. это – разы. На сколько то, или во столько то раз. Вот в этом физический смысл 1/с, в отличие от м/с2 , где физического смысла нет. Чтобы отличать наше новое понятие об ускорении от старого и неправильного будем обозначать его не буквой «а», а например буквой «у» – ускорение: у = ΔV / S, [ 1 / c ]. Вот это представление будет правильным, оно не содержит размерностей в степенях и имеет простой и понятный физический смысл; при движении с постоянным ускорением скорость точки меняется на постоянную величину через каждый метр, ну или через каждый миллиметр, километр. Формула для определения скорости с постоянным ускорением будет иметь вид: V = Vo + S у, Где Vo – скорость в начальной точке , [ м / c ] , S – перемещение , [ м ], у – ускорение , [ 1 / c ]. Например, начальная скорость 10 м/с, перемещение 4 метра, ускорение 2 (1/с): V = 10 м/с + 4 × 2 [м × 1/с] = 10 м/с + 8 м/с = 18 м/с. Вот так вот, … и всё! Это продолжение темы об ошибках физиков и не только, начало см: «Нет, ребята, все не так,…» см также: “Ошибка Ньютона”, “Картина мира”, др., по этой теме. |
Математика онлайн
Решение математики онлайн
Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.
Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.
Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.
О калькуляторах
По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.
Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту [email protected]
Преимущества
1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.
3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.
4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.
5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.
Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.
4. ЯВЛЕНИЕ КОРИОЛИСА – ФИЗИЧЕСКИЙ СМЫСЛ . Физика. Порядок вещей, или Осознание знаний. Книга 2
Густав Гаспар Кориолис (1792—1843 гг.) – французский математик и механик открыл силу инерции, названную впоследствии его именем. Она возникает в неинерциальной вращающейся системе отсчета. Он также вывел ее формулу.
Кориолис Г. Г.
Сила Кориолиса равна удвоенной радиальной скорости (Vр), умноженной на угловую скорость вращения (?) и умноженную на синус угла между ними, а так же на испытуемую массу (M).
В классической физике описаны два варианта проявления силы и ускорения Кориолиса.
В первом варианте относительная скорость направлена вдоль радиуса вращающейся системы. Здесь действительно проявляется достаточно выраженное явление, которое в классической физике ассоциируют с ускорением Кориолиса. Однако в классической физике за силу и ускорение Кориолиса фактически принимается противо реакция на обычную тангенциальную силу, которая поддерживает угловую скорость переносного вращения. Поддерживающая сила – это либо сила, действующая на движущееся радиально тело со стороны вращающихся масс системы, которые не изменяют своего радиального положения, либо любая внешняя сила, которая поддерживает переносную угловую скорость на постоянном уровне.
В отсутствие поддерживающей силы происходит естественное уменьшение угловой скорости при радиальном движении от центра вращения и естественное увеличение угловой скорости при радиальном движении к центру вращения. Это явление в классической физике называется законом сохранения углового момента, который якобы выполняется в отсутствие тангенциальных сил. Однако в реальной действительности угловой момент сохраняется именно за счёт тангенциальной составляющей радиальной силы. Это и есть основа явления Кориолиса. Поэтому тангенциальную составляющую радиальной силы мы называем истинной силой Кориолиса-Кеплера.
Однако в реальной действительности угловой момент сохраняется именно за счёт тангенциальной составляющей радиальной силы. Это и есть основа явления Кориолиса. Поэтому тангенциальную составляющую радиальной силы мы называем истинной силой Кориолиса-Кеплера.
Проявляясь совместно с «обычной» истинной силой Кориолиса, фиктивная сила инерции Кориолиса одновременно противоречит, как физическому смыслу обычных сил, так и фиктивных сил инерции. Поскольку в классической динамике вращательного движения понятие об обычной истинной силе Кориолиса-Кеплера отсутствует, то в классической физике родилась самая странная сила не только из всех сил инерции, но и самая странная из всех обычных сил!!!
Классическая сила Кориолиса – это либо, полу фиктивная обычная сила, либо, полу обычная фиктивная сила. Недаром физики всех народов, начиная со времён Кориолиса, и до сих пор спорят, реальна ли сила Кориолиса или же это только иллюзорная сила инерции.
Поскольку истинная сила Кориолиса-Кеплера в классической модели явления Кориолиса полностью скомпенсирована, то природа этого явления принципиально не может быть раскрыта в классической физике. В частности реальное ускорение и сила Кориолиса за счёт компенсации истинной силы Кориолиса-Кеплера вдвое меньше классического ускорения и силы Кориолиса. При этом классической силе Кориолиса соответствует только общее силовое напряжение, возникающее при противодействии поддерживающей силы и истинной силы Кориолиса-Кеплера.
В частности реальное ускорение и сила Кориолиса за счёт компенсации истинной силы Кориолиса-Кеплера вдвое меньше классического ускорения и силы Кориолиса. При этом классической силе Кориолиса соответствует только общее силовое напряжение, возникающее при противодействии поддерживающей силы и истинной силы Кориолиса-Кеплера.
Во втором варианте относительная скорость направлена перпендикулярно постоянному радиусу вращающейся системы. При этом абсолютная линейная скорость является величиной постоянной. Но это есть не что иное, как равномерное вращательное движение, динамику которого с классической же точки зрения определяет исключительно только центростремительное ускорение. Следовательно, либо никакого ускорения Кориолиса при тангенциальном относительном движении нет, либо классической физике следует пересмотреть свои взгляды, как на явление Кориолиса, так и на классическую модель вращательного движения.
Явление Кориолиса – Кеплера играет очень важную роль в природе. Например, А. И. Андреев в работе «Основы естественной энергетики», Санкт-Петербург, 2004, г. на стр. 181 пишет:
Например, А. И. Андреев в работе «Основы естественной энергетики», Санкт-Петербург, 2004, г. на стр. 181 пишет:
«Поскольку образование и существование вихрей элементарных частиц и гравитации происходит за счёт кориолисовых сил и самовращения, то кориолисово самовращение, именно в этом смысле является основой природы».
В реальной действительности никакого самовращения вихрей за счёт силы Кориолиса нет, и не может быть в принципе. Самовращение есть только в равномерном вращательном движении. Тем не менее, явление Кориолиса – Кеплера заслуживает того, чтобы уделить ему особое внимание при рассмотрении вопросов физики движения, тем более что в классической физике оно не имеет непротиворечивого объяснения.
Рассмотрим эти вопросы подробнее.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесУскорение: определение и концепция | Study.
 com
comПримеры ускоренного движения
Каждый раз, когда ваша скорость изменяется, вы ускоряетесь. Например, когда вы едете на работу утром, вам постоянно приходится останавливаться и начинать движение, когда вы сталкиваетесь со светофором или знаками остановки. Каждый раз, когда вам нужно завести машину, вы ускоряетесь, и каждый раз, когда вам нужно останавливать машину перед светофором или знаком «стоп», вы ускоряетесь (более известное как замедление, хотя в физике ускорение просто означает, что ваша скорость изменяется, но не изменяется). обязательно означает, что вы едете быстрее).Главной особенностью ускоренного движения является то, что скорость разная каждую секунду и пройденное расстояние тоже каждую секунду меняется. В первой таблице ниже показано движение, которое НЕ ускорено, поэтому вы можете сравнить его со второй таблицей, показывающей ускоренное движение.
| Время (в секундах) | Скорость (в метрах/сек) | Расстояние (в метрах) |
|---|---|---|
| 1 | 2,0 | 2,0 |
| 2 | 2. 0 0 | 4,0 |
| 3 | 2,0 | 6,0 |
| 4 | 2,0 | 8,0 |
| 5 | 2,0 | 10,0 |
Обратите внимание, что скорость одна и та же каждую секунду, а пройденное расстояние увеличивается на одну и ту же величину каждую секунду; в этом случае расстояние увеличивается на 2,0 метра каждую секунду. Сравните эту таблицу с таблицей ниже.
| Время (в секундах) | Скорость (в метрах/сек) | Расстояние (в метрах) |
|---|---|---|
| 1 | 1,0 | 0,5 |
| 2 | 2,0 | 2,0 |
| 3 | 3,0 | 4,5 |
| 4 | 4,0 | 8,0 |
| 5 | 5.0 | 12,5 |
Обратите внимание, что скорость увеличивается на 1 метр в секунду каждую секунду, а пройденное расстояние увеличивается от секунды к секунде. Вторая таблица представляет собой пример ускоренного движения. Чтобы дополнительно проиллюстрировать ускорение, будут показаны два набора графиков. Первый набор графиков показывает графики зависимости скорости от времени и положения от времени неускоренного движения, а второй набор графиков показывает ускоренное движение.
Вторая таблица представляет собой пример ускоренного движения. Чтобы дополнительно проиллюстрировать ускорение, будут показаны два набора графиков. Первый набор графиков показывает графики зависимости скорости от времени и положения от времени неускоренного движения, а второй набор графиков показывает ускоренное движение.
Обратите внимание, что график расстояния представляет собой прямую линию, а график скорости — горизонтальную линию, что указывает на отсутствие ускорения в данном случае.
На этом графике график расстояний больше не является прямым, что указывает на то, что расстояние увеличивается на разную величину каждую секунду. График скорости показывает скорость, увеличивающуюся каждую секунду, в отличие от предыдущего графика, который представляет собой горизонтальную линию. Это указывает на то, что этот объект ускоряется.
График скорости показывает скорость, увеличивающуюся каждую секунду, в отличие от предыдущего графика, который представляет собой горизонтальную линию. Это указывает на то, что этот объект ускоряется.
Резюме урока
Когда объект ускоряется, с ним происходят две вещи.Во-первых, скорость объекта меняется от секунды к секунде независимо от того, ускоряется объект или замедляется. Во-вторых, расстояние, проходимое объектом каждую секунду, также меняется. Итак, пока ваша скорость меняется, вы ускоряетесь, ускоряетесь ли вы или замедляетесь. В результате вашей переменной скорости расстояние, пройденное вами каждую секунду, также меняется.
Проверьте свою память
| Термины, выделенные жирным шрифтом | Пояснения |
|---|---|
| Ускорение | скорость изменения скорости или скорости |
| Без ускорения | показатель скорости не меняется |
| Замедление | замедление скорости (т. е. при приближении к знаку стоп) е. при приближении к знаку стоп) |
Результаты обучения
Этот урок может дать вам ясность, необходимую для:
- Запишите определение ускорения
- График ускорения, отсутствия ускорения и замедления
- Укажите примеры ускоренного движения
Каков физический смысл ускорения? – Легче с практикой.ком
Каков физический смысл ускорения?
В физике или физических науках ускорение (символ: а) определяется как скорость изменения (или производная по времени) скорости. Каждый раз, когда знак (+ или -) ускорения совпадает со знаком скорости, объект будет ускоряться. Если знаки противоположны, объект будет замедляться.
Каков физический смысл ускорения свободного падения?
Когда объект свободно падает на поверхность земли с определенной высоты, его скорость изменяется.Это изменение скорости вызывает ускорение объекта, известное как ускорение силы тяжести, обозначаемое буквой g.
Какое ускорение вызывает гравитация?
Числовое значение ускорения свободного падения наиболее точно известно как 9,8 м/с/с.
Почему ускорение свободного падения положительное?
Если тело движется вниз, ускорение свободного падения направлено вниз и, следовательно, оно действует в том же направлении, что и скорость. Таким образом, он считается положительным.
Чему будет равно ускорение свободного падения на высоте?
Величина ускорения свободного падения на поверхности Земли составляет 9,8 мс−2. Высота над его поверхностью, на которой ускорение свободного падения уменьшается до 4,9 мс-2, близка к: (Радиус Земли = 6,4×106 м)
Что такое ускорение под действием силы тяжести и чем оно отличается от ускорения?
Когда гравитация притягивает объекты к земле, они всегда ускоряются со скоростью 9,8 м/с2.Независимо от различий в массе все объекты ускоряются с одинаковой скоростью из-за гравитации, если только сопротивление воздуха не влияет на один больше, чем на другой.
Может ли ускорение под действием силы тяжести измениться?
Ускорение объекта изменяется с высотой. Изменение гравитационного ускорения по мере удаления от центра Земли подчиняется закону обратных квадратов. Это означает, что гравитационное ускорение обратно пропорционально квадрату расстояния от центра Земли.
Почему ускорение увеличивается с увеличением высоты?
Ускорение свободного падения зависит от силы тяжести.Итак, если сила тяжести, действующая на объект, меньше, когда он находится на большей высоте, то это означает, что на большей высоте ускорение, которое испытывает объект, также будет меньше.
Ускорение – обзор | ScienceDirect Topics
Детерминанты травмы, связанной с ускорением
Несколько простых характеристик ускорения — величина и тип ускорения, его продолжительность и скорость, с которой ускорение прикладывается к голове, — взаимосвязаны и вместе способствуют картине повреждения, наблюдаемого в каждый индивидуум. Безусловно, эти параметры связаны; например, для постоянного уровня ускорения по мере увеличения продолжительности скорость головы и движение также увеличиваются. В прошлых попытках описать толерантность головы к различным формам черепно-мозговой травмы исследователи использовали два основных показателя — (1) ускорение и (2) скорость/продолжительность ускорения головы — чтобы отразить эту сложную взаимосвязь между движением и полученным повреждением. . Структурное повреждение поверхностных сосудистых тканей, особенно соединительных вен и пиальных сосудов, происходит в условиях высокого ускорения и кратковременности, в то время как повреждение мозговой ткани происходит в условиях высоких ускорений с более длительными импульсами и, следовательно, более высокими скоростями (как описано в более подробности далее в этой главе).
Безусловно, эти параметры связаны; например, для постоянного уровня ускорения по мере увеличения продолжительности скорость головы и движение также увеличиваются. В прошлых попытках описать толерантность головы к различным формам черепно-мозговой травмы исследователи использовали два основных показателя — (1) ускорение и (2) скорость/продолжительность ускорения головы — чтобы отразить эту сложную взаимосвязь между движением и полученным повреждением. . Структурное повреждение поверхностных сосудистых тканей, особенно соединительных вен и пиальных сосудов, происходит в условиях высокого ускорения и кратковременности, в то время как повреждение мозговой ткани происходит в условиях высоких ускорений с более длительными импульсами и, следовательно, более высокими скоростями (как описано в более подробности далее в этой главе).
Количество повреждений, вызванных инерцией, зависит не только от типа ускорения головы, но и от ряда других факторов. Величину ускорения можно рассматривать как пропорциональную величине напряжения, прикладываемого к мозгу, а скорость ускорения пропорциональна скорости напряжения. Как деформация, так и скорость деформации являются факторами, влияющими на структурные или функциональные ограничения внутричерепных тканей. Если величина ускорения постоянна, скорость ускорения изменяется обратно пропорционально продолжительности, в течение которой происходит ускорение.И наоборот, если продолжительность ускорения постоянна, скорость ускорения напрямую зависит от величины ускорения.
Как деформация, так и скорость деформации являются факторами, влияющими на структурные или функциональные ограничения внутричерепных тканей. Если величина ускорения постоянна, скорость ускорения изменяется обратно пропорционально продолжительности, в течение которой происходит ускорение.И наоборот, если продолжительность ускорения постоянна, скорость ускорения напрямую зависит от величины ускорения.
Когда величина ускорения постоянна и изменяется только продолжительность, в течение которой происходит ускорение, встречаются три зоны клинического интереса (рис. 337-5). Во-первых, при очень коротких ускорениях многие инерционные эффекты в мозге гасятся, и в результате мозг испытывает очень мало напряжения. В результате для получения травмы требуются чрезвычайно высокие ускорения.Во-вторых, если продолжительность акселерации немного больше, напряжения начинают появляться внутри мозга, но ограничиваются преимущественно периферией. Более того, поверхность мозга может скользить по отношению к поверхности черепа/твердой мозговой оболочки. Повреждения, возникающие в этих условиях, ограничиваются периферией головного мозга и сосудами (например, мостовидными венами). В-третьих, по мере увеличения продолжительности акселерации деформации распространяются вглубь мозга и могут вызывать диффузное аксональное повреждение, которое в тяжелой форме проявляется в виде длительной травматической комы.
Повреждения, возникающие в этих условиях, ограничиваются периферией головного мозга и сосудами (например, мостовидными венами). В-третьих, по мере увеличения продолжительности акселерации деформации распространяются вглубь мозга и могут вызывать диффузное аксональное повреждение, которое в тяжелой форме проявляется в виде длительной травматической комы.
В первой описанной зоне скорость деформации уже настолько высока, что увеличение ускорения мало что добавляет к картине повреждения. Во второй зоне поражения явно поражены сосудистые ткани поверхности головного мозга; следовательно, дальнейшее увеличение скорости деформации за счет увеличения уровней ускорения головы вызывает нарушение большего количества сосудов на поверхности мозга. В третьей зоне, в которой скорость деформации вызывает повреждение мозговой ткани, но недостаточна для повреждения сосудов, увеличение величины ускорения может увеличить напряжение в достаточной степени, чтобы вызвать повреждение сосудов.Результатом может быть сочетание диффузного повреждения аксонов с кровоизлияниями в разрыв ткани, субдуральной гематомой или тем и другим. Эти примеры подчеркивают сложность сопоставления профилей ускорения с точными моделями повреждений мозга.
Эти примеры подчеркивают сложность сопоставления профилей ускорения с точными моделями повреждений мозга.
№ 1534: Ускорение
Сегодня давайте подумаем о падении. Университет Инженерный колледж Хьюстона представляет это сериал о машинах, которые делают наши цивилизация управляется, и люди, чья изобретательность создал их.
Концепция чего-либо ускорение плохо видно без
вычисления и графики. Но ускорение с нами
каждое мгновение бодрствования. Мы все плаваем в одном море
равномерное гравитационное ускорение. Мы чувствуем все это
время. Каждый раз, когда мы роняем или бросаем предмет,
гравитация действует на него таким же образом.Прыгать с
высотой пять футов, и вы ударитесь о землю на
восемнадцать футов в секунду. С десятифутовой стены,
это становится двадцать пять футов в секунду.
С десятифутовой стены,
это становится двадцать пять футов в секунду.
Поэтому, когда вы удваиваете высоту, вы не удваиваете скорость, которую вы достигаете. Скорость растет только как квадрат корень высоты падения. Кстати, ты начните подвергать опасности свои конечности примерно на двадцати футах в секунду (в зависимости от вашего возраста и физической условие).
Гравитация ускорит любой объект со скоростью 32
футов в секунду в секунду. Но что нам делать с
этот номер? Это означает, что если мы попадемся на
одну секунду мы достигнем скорости 32 фута в секунду
второй. Через две секунды мы достигаем 64 фута в секунду.
второй. Скорость возрастает как квадратный корень из высоты, а в прямо пропорциональна времени.
Таким образом, ускорение сложнее, чем могло бы сначала казаться. Ничто не ускоряется, пока на него не действует сила Это. Но мы не чувствуем силы, когда падаем. Сила есть гравитация, действующая на каждую молекулу в нашем тела, но сила не встречает сопротивления, поэтому мы чувствуем ничего. Пока мы не встанем на твердый пол, мы почувствовать силу тяжести.пол это что сопротивляется гравитации и действует только на наши ноги.
Таким образом, орбитальный астронавт, не чувствующий гравитации,
в вечном свободном падении, постоянно ускоряющемся
к Земле и одновременно устремляясь вперед.
Космический шаттл продолжает падать с
прямой путь, но достаточно быстрый, чтобы оставаться
постоянная высота над Землей при падении – и
падает и падает.
Качайте камень на веревке, и он следует за тем же своего рода круговой путь, как это делает космический шаттл. Но нет значительной силы тяжести, чтобы притягивать камень к себе. Вот почему вы должны были замените гравитацию строкой. Теперь ты чувствуешь сколько силы нужно, чтобы разогнать камень от прямого полета.
Конечно, большинство ускорений не имеют равномерность гравитации. Поднимающийся лифт сначала разгоняется, и мы чувствуем свой вес увеличиться на несколько фунтов. Когда мы замедляемся на 18-й этаж, наш вес чуть-чуть падает. (Это может быть приятным чувством.)
Но слишком многие этого не понимают, например автомобилисты.
кто задним бортом или не замедляется для кривой на
ледяная дорога. Ускорение может обмануть нас. Поэтому
Исаак Ньютон, который впервые объяснил, как сила и
связаны с ускорением, был также изобретателем
исчисление — особый язык для объяснения
как вещи меняются во времени и пространстве. Ускорение
намного яснее, когда у нас есть этот новый язык
чтобы описать это. И я слышу отголоски прекрасного старого
высказывание о языке математики:
«Математика позволяет дуракам делать то, что без нее могли бы делать только гении.”
Ускорение может обмануть нас. Поэтому
Исаак Ньютон, который впервые объяснил, как сила и
связаны с ускорением, был также изобретателем
исчисление — особый язык для объяснения
как вещи меняются во времени и пространстве. Ускорение
намного яснее, когда у нас есть этот новый язык
чтобы описать это. И я слышу отголоски прекрасного старого
высказывание о языке математики:
«Математика позволяет дуракам делать то, что без нее могли бы делать только гении.”
Я Джон Линхард из Хьюстонского университета. где нас интересует, как изобретательные умы работай.
(Музыкальная тема)определение ускорения по The Free Dictionary
Отсюда они достаточно логически заключили, что ускорение движения должно сопровождаться соответствующим уменьшением расстояния, разделяющего два тела; и что, если предположить, что двойной эффект будет продолжаться до бесконечности, Луна в конце концов упадет на Землю за один день. Этот зов снова вызвал неизбежное ускорение перехода субботы в пятницу; пятница несчастного случая со смертельным исходом, пятница, когда он пошел на смерть. Физический закон не говорит нам, что «за А последует Б», но говорит нам, какое ускорение будет иметь частица при данных обстоятельствах, т. е. я почувствовал резкое ослабление шхуна, потеря на данный момент всего напряжения и давления, соединенного с быстрым ускорением скорости. Все, что я хотел бы сказать, это то, что я могу отправиться за границу без того, чтобы ваша семья выступила вперед, чтобы поддержать меня, – короче говоря, с прощальным толчком их холодных плеч; и что, в целом, я предпочел бы покинуть Англию с тем импульсом, который у меня есть, чем получить какое-либо ускорение из этой стороны.Они говорят, что с помощью электромагнетизма ваш салат будет выращен из семян, пока ваша птица будет жариться на обед; это символ наших современных целей и усилий, нашего уплотнения и ускорения объектов, но ничего не достигается; природу нельзя обмануть; человеческая жизнь состоит всего лишь из семидесяти салатов, растут они быстро или растут медленно.
Этот зов снова вызвал неизбежное ускорение перехода субботы в пятницу; пятница несчастного случая со смертельным исходом, пятница, когда он пошел на смерть. Физический закон не говорит нам, что «за А последует Б», но говорит нам, какое ускорение будет иметь частица при данных обстоятельствах, т. е. я почувствовал резкое ослабление шхуна, потеря на данный момент всего напряжения и давления, соединенного с быстрым ускорением скорости. Все, что я хотел бы сказать, это то, что я могу отправиться за границу без того, чтобы ваша семья выступила вперед, чтобы поддержать меня, – короче говоря, с прощальным толчком их холодных плеч; и что, в целом, я предпочел бы покинуть Англию с тем импульсом, который у меня есть, чем получить какое-либо ускорение из этой стороны.Они говорят, что с помощью электромагнетизма ваш салат будет выращен из семян, пока ваша птица будет жариться на обед; это символ наших современных целей и усилий, нашего уплотнения и ускорения объектов, но ничего не достигается; природу нельзя обмануть; человеческая жизнь состоит всего лишь из семидесяти салатов, растут они быстро или растут медленно. С облегчением от того, что у него есть этот спутник, и от ощущения, что он может доверять ему, он перешел к обоим, и оба снова привели его в чувство, с увеличением и ростом. ускорение силы, к его исходной точке.Тем не менее, он ощущал ускорение в биении своего сердца. Дата выпуска – 05082019 – Плата программируемого ускорения Intel FPGA D5005 является второй картой в портфолио Intel PAC. Базовая тригонометрия наклонной плоскости позволяет рассчитать скорость ускорения как синус базового угла. Исследование показывает, что каждое увеличение стандартного отклонения индекса апноэ-гипопноэ, меры тяжести нарушений дыхания во сне, было связано с ускорением биологического возраста, эквивалентным 215 дням.Точно так же каждое увеличение стандартного отклонения в индексе возбуждения, показателе нарушения сна, было связано с эквивалентом 321 дня ускорения возраста. уведомление об ускорении или даже когда истек 29-дневный период лечения, который сделал возможным ускорение.
С облегчением от того, что у него есть этот спутник, и от ощущения, что он может доверять ему, он перешел к обоим, и оба снова привели его в чувство, с увеличением и ростом. ускорение силы, к его исходной точке.Тем не менее, он ощущал ускорение в биении своего сердца. Дата выпуска – 05082019 – Плата программируемого ускорения Intel FPGA D5005 является второй картой в портфолио Intel PAC. Базовая тригонометрия наклонной плоскости позволяет рассчитать скорость ускорения как синус базового угла. Исследование показывает, что каждое увеличение стандартного отклонения индекса апноэ-гипопноэ, меры тяжести нарушений дыхания во сне, было связано с ускорением биологического возраста, эквивалентным 215 дням.Точно так же каждое увеличение стандартного отклонения в индексе возбуждения, показателе нарушения сна, было связано с эквивалентом 321 дня ускорения возраста. уведомление об ускорении или даже когда истек 29-дневный период лечения, который сделал возможным ускорение.| При замене напряжение эквивалентно умножению времени до отказа на константу, мы имеем истинное (физическое) ускорение | Физическое ускорение (иногда называемое Истинное ускорение или просто Ускорение) означает, что работа устройства в условиях высокой нагрузки
(я. Отказ может быть вызван механической усталостью, коррозией, химической реакцией, диффузия, миграция и т. д. Это те же причины разрушения при нормальном напряжении; шкала времени просто отличается. | Фактор ускорения — это постоянный множитель между двумя уровнями напряжения | При истинном ускорении изменение напряжения
эквивалентно преобразованию временной шкалы, используемой для регистрации отказов
происходить.Обычно используемые преобразования линейные , что означает
что время до отказа при высоких нагрузках просто нужно умножить на постоянную
(коэффициент ускорения ), чтобы получить эквивалентное время до отказа при
использовать стресс. Мы используем следующие обозначения:
Тогда коэффициент ускорения \(AF\) между стрессом и использованием средств имеют место следующие соотношения: Зависимости линейного ускорения
| Каждый режим отказа имеет собственное ускорение
фактор Данные об отказах должны быть разделены по видам отказа при анализе, если ускорение актуально Графики вероятности данных из разных ячеек стресса имеют одинаковый наклон (если есть ускорение) | Примечание : Ускорение требует наличия
зависимый от стресса физический процесс, вызывающий изменения или деградацию, которые
приводит к неудаче. В общем разные
режимы отказа будут по-разному зависеть от напряжения и иметь разные
факторы ускорения. Поэтому маловероятно, что единичное ускорение
фактор будет применяться к более чем одному механизму отказа. В общем разные
режимы отказа будут по-разному зависеть от напряжения и иметь разные
факторы ускорения. Разделяйте различные типы отказов при анализе
данные об отказе. В общем разные
режимы отказа будут по-разному зависеть от напряжения и иметь разные
факторы ускорения. Поэтому маловероятно, что единичное ускорение
фактор будет применяться к более чем одному механизму отказа. В общем разные
режимы отказа будут по-разному зависеть от напряжения и иметь разные
факторы ускорения. Разделяйте различные типы отказов при анализе
данные об отказе.Кроме того, следствие отношений линейного ускорения, показанных выше (что непосредственно следует из «истинного ускорения») состоит в следующем: Параметр формы для ключевых моделей распределения срока службы (Weibull, Логнормальный) не меняется для агрегатов, работающих при разных нагрузках.Графики вероятности данных из разных клеток стресса выстроятся в линию примерно параллельно.Эти распределения и вероятность построение графиков будет обсуждаться в последующих разделах. |
Различия между ускорением и скоростью
Чтобы изучить скорость, ускорение и различия между ними, во-первых, необходимо подробно изучить концепцию движения. Не только это, но и другие основные определения, такие как скалярные и векторные величины, единицы измерения и т. д., должны быть известны.Во-первых, давайте посмотрим на движение объекта, которое также называют смещением.
Не только это, но и другие основные определения, такие как скалярные и векторные величины, единицы измерения и т. д., должны быть известны.Во-первых, давайте посмотрим на движение объекта, которое также называют смещением.
Движение объекта
Рассмотрим объект, перемещающийся из фиксированной известной точки (а также его положения) относительно внешнего воздействия, тогда говорят, что объект совершил движение.
Различные типы движения
Существует четыре типа движения. Они бывают вращательными, колебательными, возвратно-поступательными и линейными. Во всех этих типах движение должно происходить во времени.Хотя вариация движения незначительна, все они имеют разное понятие. Например, для вращательного движения смещение называется угловым смещением, а также для скорости — угловой скоростью и т. д.
Скалярные и векторные величины
Скалярные величины
Скалярная величина есть мера величины, которая является одномерной, т. е. только ее величина; например, температура, работа, масса и т.д.
е. только ее величина; например, температура, работа, масса и т.д.
Векторные величины
Векторная величина является мерой двумерной величины, т.е.е., как его величина, так и направление; например, смещение, скорость, ускорение и так далее.
Единицы
Единицей измерения является определенная величина величины. Все измерения и их выражение единиц выполняются на основе Международной системы единиц. Есть семь основных единиц. Они следующие:
S.No. | физических величин | 9 | 7|
килограмма ( кг) | |||
| 7 | |||
5 | Температура7 | ||
06 Kelvin (K) | |||
Прочие наборы кв.
Смещение объекта определяется как разность векторов между начальной и конечной точками смещаемого объекта. Перемещение не всегда равно пройденному расстоянию.
Перемещение d = P – O = x m (м, единица длины)
Определение скорости Скорость изменения смещения – это скорость.
Другими словами, это перемещение, производимое в единицу времени.
Скорость = Перемещение / Время = x / t
Где x — расстояние, пройденное в заданном направлении, т. е. перемещение. Рассчитывается как разница между позициями.
x = Конечная точка – Начальная точка = v – u t, время прохождения пути. V = d / t
Скорость V рассчитывается как изменение смещения во времени. Это векторная величина, поскольку она зависит как от величины, так и от направления.
Например, путешествие в автомобиле со скоростью 20 м/с на север за 2 минуты; этим объясняется, с какой скоростью, в каком направлении двигался автомобиль и сколько времени потребовалось на это перемещение.
Следовательно, скорость является векторной величиной. Векторная величина включает в себя не только величину, но и направление, т. е. двумерность. Единицей скорости в СИ является м/с или мс–1.
Определение скорости Скорость — это расстояние, пройденное объектом за заданное время. Скорость является скалярной величиной, поскольку она выражает только величину, а не направление. Скорость = Расстояние / Время
Скорость и скорость подобны относительно движения объекта.Проще говоря, скорость — это скорость с направлением. Скорость включает в себя направление со смещением, тогда как скорость включает только пройденное расстояние.
Определение ускорения Обычно слово «ускорение» относится к движению или увеличению с высокой скоростью. Но фактический смысл есть изменение скорости, т. е. изменение скорости (за счет увеличения или уменьшения скорости). Скорость изменения скорости есть ускорение.
Как мы уже видели, скорость называется скоростью с направлением.Другими словами, когда есть изменение скорости, следовательно, существует ускорение.
Например, рассмотрим камешек, брошенный в воду. При падении камешка его начальная скорость равна нулю, при ударе о воду его скорость увеличивается за счет силы тяжести Земли. Итак, вода плещется. Следовательно, ускорение определяется как скорость изменения скорости. Если скорость тела изменяется от «u» до «v» за время «t», то ускорение определяется следующим образом. 06Ускорение = Изменение скорости / Время принимается = конечная скорость – начальная скорость / время принимается A = D (U-V) / DT , так как он имеет величину, так и направление, это является векторной величиной. Разница между скоростью и ускорением между скоростью и ускорением
|



 Ну, может быть и не все, но многие и основные, да. Поэтому параграф с номером 13 – это как бы знак, что наука наткнулась на закопанный лом и, не поняв, что произошло, продолжает пахать это поле, просто разрушая его.
Ну, может быть и не все, но многие и основные, да. Поэтому параграф с номером 13 – это как бы знак, что наука наткнулась на закопанный лом и, не поняв, что произошло, продолжает пахать это поле, просто разрушая его. Здесь просто, краткое обозначения площади (территории) в форме квадрата со стороной в один метр. Здесь не метр в квадрате, а квадрат со стороной в один метр. Вот и все.
Здесь просто, краткое обозначения площади (территории) в форме квадрата со стороной в один метр. Здесь не метр в квадрате, а квадрат со стороной в один метр. Вот и все. Вот поэтому, строго говоря, ускорение в том виде, которое дается в учебниках по физике, которое было выведено Ньютоном триста лет назад вот такого ускорения и не существует и это понимание неправильное. Оно существует только на страницах учебников по физике.
Вот поэтому, строго говоря, ускорение в том виде, которое дается в учебниках по физике, которое было выведено Ньютоном триста лет назад вот такого ускорения и не существует и это понимание неправильное. Оно существует только на страницах учебников по физике. С другой стороны, скорость тела действительно меняется под воздействием каких либо внешних сил. Неважно, какую природу имеют эти силы, но скорость меняется, и мы имеем право назвать это изменение ускорением, ну или замедлением. Почему нет?
С другой стороны, скорость тела действительно меняется под воздействием каких либо внешних сил. Неважно, какую природу имеют эти силы, но скорость меняется, и мы имеем право назвать это изменение ускорением, ну или замедлением. Почему нет?

 е., более высокая температура или напряжение, влажность или рабочий цикл и т. д.) производит
те же отказы, которые произошли бы при типичных нагрузках, за исключением того, что
они происходят гораздо быстрее.
е., более высокая температура или напряжение, влажность или рабочий цикл и т. д.) производит
те же отказы, которые произошли бы при типичных нагрузках, за исключением того, что
они происходят гораздо быстрее. там есть античности, которые называются производными величинами.Они представляют собой комбинацию семи основных единиц. Просто они выводятся из фундаментальных величин. Скажем, например, единицей силы является м/с2, или мс–2, или ньютон, сокращенно Н. Здесь «м» — это сокращение от метра длины физической величины, а «с» — это сокращение от секунды физическая величина время. Другим примером производной величины является плотность. Выражается в кг/м3 или кгм–3. Здесь «кг» — это аббревиатура килограмма массы физической величины, а «м» — аббревиатура метра длины физической величины.
там есть античности, которые называются производными величинами.Они представляют собой комбинацию семи основных единиц. Просто они выводятся из фундаментальных величин. Скажем, например, единицей силы является м/с2, или мс–2, или ньютон, сокращенно Н. Здесь «м» — это сокращение от метра длины физической величины, а «с» — это сокращение от секунды физическая величина время. Другим примером производной величины является плотность. Выражается в кг/м3 или кгм–3. Здесь «кг» — это аббревиатура килограмма массы физической величины, а «м» — аббревиатура метра длины физической величины. Когда объект движется в определенном направлении во времени, говорят, что это скорость, т.е.т. е. величина, определяющая как расстояние, так и время, называется скоростью. Скорость объекта можно изменить, изменив скорость, направление или и то, и другое этого объекта.
Когда объект движется в определенном направлении во времени, говорят, что это скорость, т.е.т. е. величина, определяющая как расстояние, так и время, называется скоростью. Скорость объекта можно изменить, изменив скорость, направление или и то, и другое этого объекта.

 Единицей ускорения в СИ является м/с2 или мс–2.
Единицей ускорения в СИ является м/с2 или мс–2.