Физика блоки формулы: Формулы неподвижного блока - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Простые механизмы. Блок.. Блоки бывают подвижные и неподвижные… | by maxim | dx/dy

Одним из простых механизмов является блок. Блок — это колесо с желобом, по которому пропущена веревка или трос. Используется блок, как и все простые механизмы, для преобразования силы — т.е. изменения направления и модуля приложенной силы.

Блоки бывают подвижные и неподвижные. Рассмотрим каждый случай подробно.

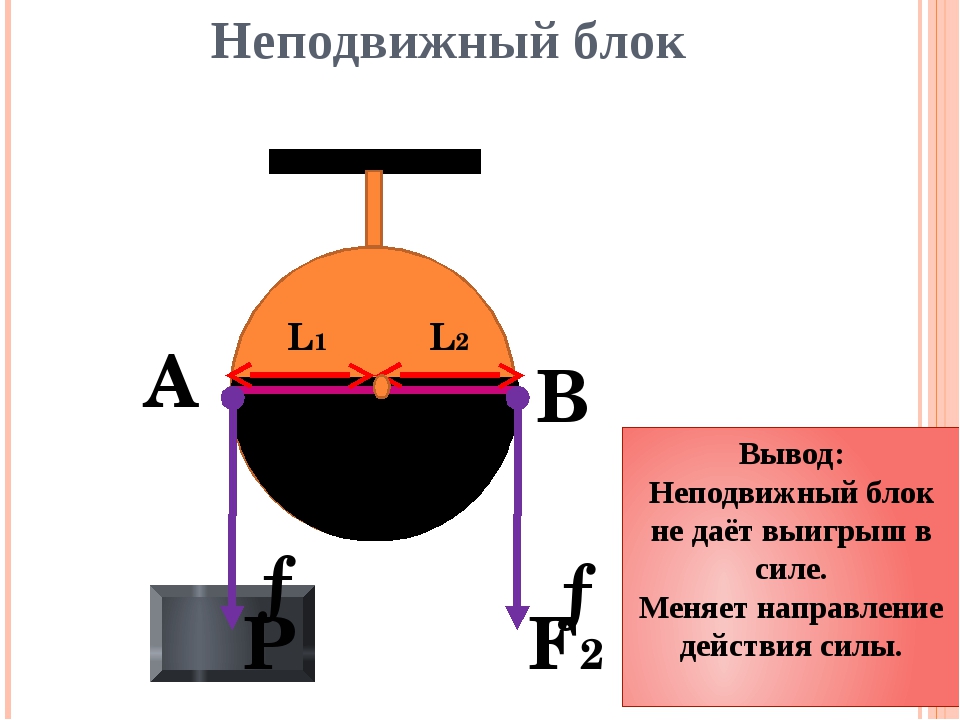
Неподвижный блок — это блок, ось которого (точка О на рисунке) закреплена, и блок при подъеме грузов не опускается и не поднимается.

Такой блок можно рассматривать как рычаг первого рода, у которого оба плеча равны между собой, и равны радиусу колеса блока:

Так как плечи рычага равны, то мы не получим выигрыша в силе. Проверим это, используя формулу равновесия рычага:

плечи рычага

В нашем случае неподвижного блока:

значит:

а следовательно:

Действительно, для того чтобы уравновесить силу на одном конце веревки, перекинутой через блок, нам необходимо приложить такую же силу на другом конце. Поэтому неподвижные блоки используют в том случае, если удобнее изменить направление силы, для совершения работы. Например, удобнее поднимать груз, удерживая веревку при помощи своего веса, поэтому на рисунке экспериментатор использует неподвижный блок.

Используя комбинации из неподвижных блоков можно менять направление силы как угодно:

И в этом случае, используя уже два неподвижных блока — мы не получаем выигрыша в силе, зато изменили направление приложения силы, теперь для поднятия груза силу мы должны приложить в горизонтальном направлении.

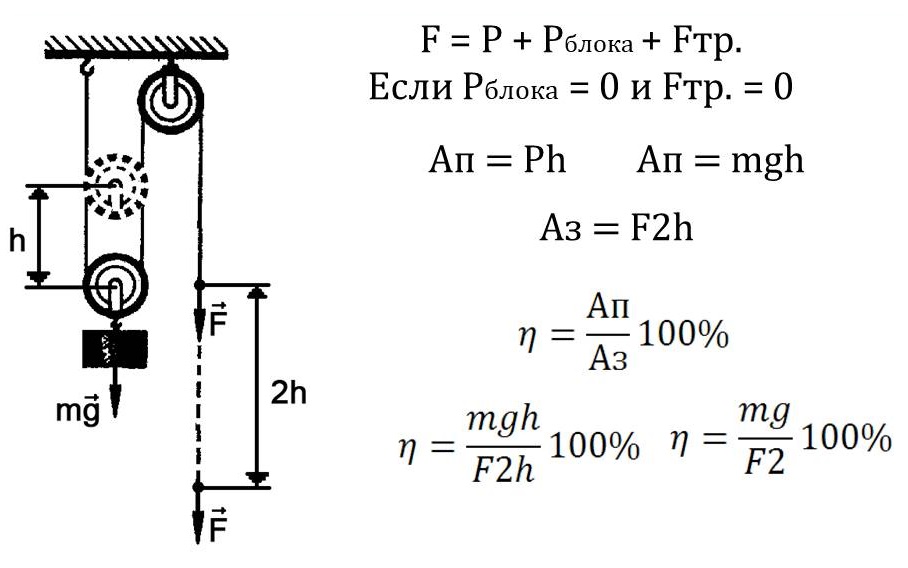
Подвижный блок — это блок, ось которого не закреплена, а поднимается вместе с грузом. Изобразим подвижный блок находящийся в равновесии, отметим на рисунке силы, действующие на систему, а также плечи приложения этих сил:

Подвижный блок можно сравнить с рычагом второго рода. Действительно: точка опоры О лежит по одну сторону от точки приложения сил, отрезок ОА — плечо силы P

отрезок:

– плечо силы F

Рассчитаем, какой выигрыш в силе мы получим от использования подвижного блока.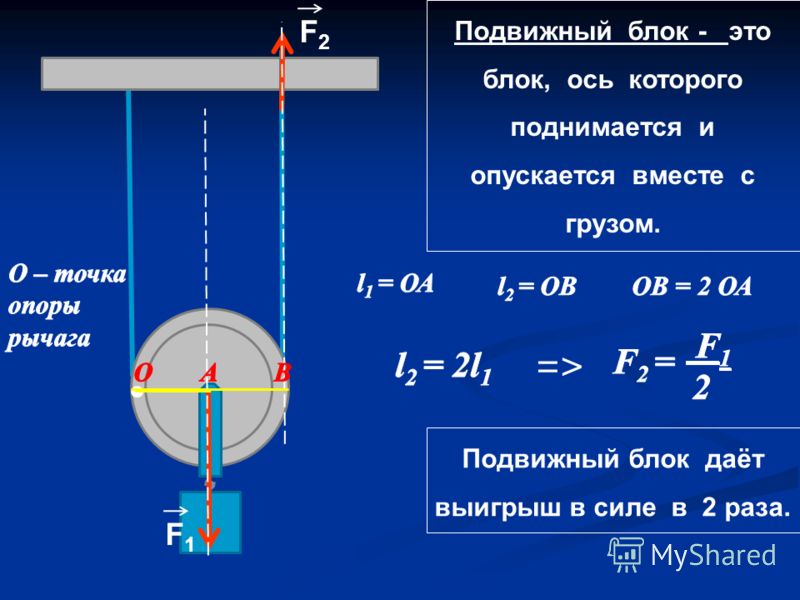 Для этого воспользуемся формулой равновесия рычага:

а следовательно

Получается, для удержания груза весом Р необходимо приложить в два раза меньшую силу. Таким образом, при использовании подвижного блока мы получаем двукратный выигрыш в силе.

Отлично, мы можем поднять груз в два раза тяжелее, чем без использования подвижного блока. Но как же золотое правило механики? Проверим, нарушается ли оно. Изобразим груз, поднятый на высоту h:

Из рисунка видно, что для поднятия груза на высоту h нам необходимо вытянуть веревку длиной

А так как

, очевидно, что для вытягивания груза на высоту h нам необходимо будет вытянуть веревку длиной 2h.

Таким образом, золотое правило механики (действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути) не нарушается, мы произведем такую же работу, как если бы поднимали груз без использования блока.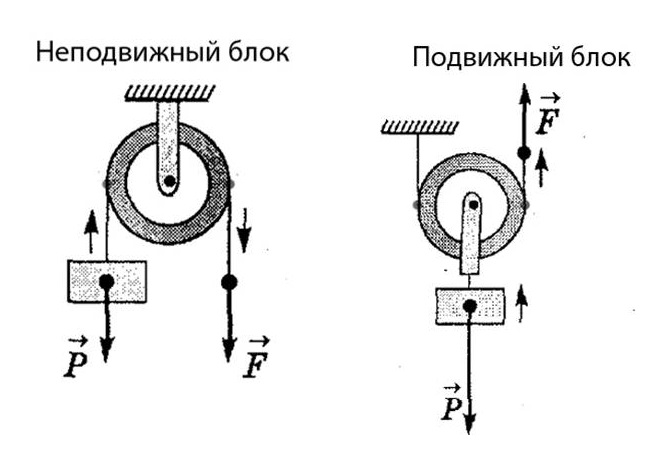

Физика 7 класс. Простые механизмы. Блок :: Класс!ная физика

Физика 7 класс. ПРОСТЫЕ МЕХАНИЗМЫ

В современной технике для переноса грузов на стройках и предприятиях широко используются грузоподъемные механизмы, незаменимыми составными частями которых можно назвать простые механизмы. Среди них древнейшие изобретения человечества: блок и рычаг. Древнегреческий ученый Архимед облегчил труд человека, дав ему при использовании своего изобретения выигрыш в силе, и научил менять направление действия силы.

Блок – это колесо с желобом по окружности для каната или цепи, ось которого жестко прикреплена к стене или потолочной балке. Грузоподъемные устройства обычно используют не один, а несколько блоков. Система блоков и тросов, предназначенная для повышения грузоподъемности, называется полиспаст.

Подвижный и неподвижный блок – такие же древнейшие простые механизмы, как и рычаг. Уже в 212 г.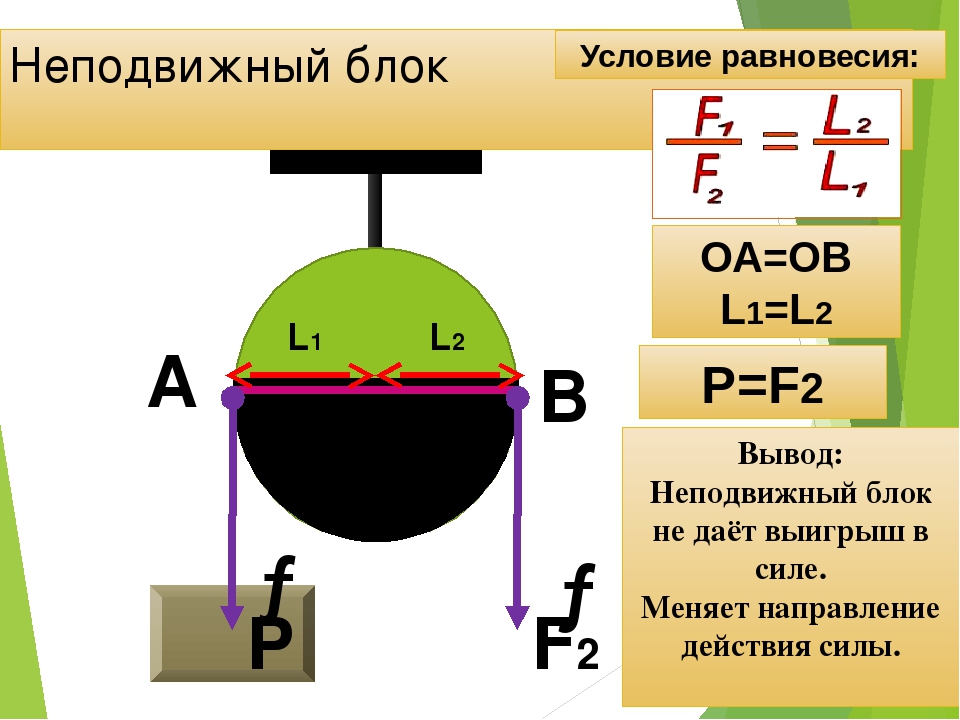

до н.эры с помощью крюков и захватов, соединенных с блоками, сиракузцы захватывали у римлян средства осады. Сооружением военных машин и обороной города руководил Архимед.

Неподвижный блок Архимед рассматривал как равноплечий рычаг.
Момент силы, действующей с одной стороны блока, равен моменту силы, приложенной с другой стороны блока. Одинаковы и силы, создающие эти моменты.
Выигрыш в силе при этом отсутствует, но такой блок позволяет изменить направление действия силы, что иногда необходимо.

Подвижный блок Архимед принимал за неравноплечий рычаг, дающий выигрыш в силе в 2 раза. Относительно центра вращения действуют моменты сил, которые при равновесии должны быть равны.

Архимед изучил механические свойства подвижного блока и применил его на практике. По свидетельству Афинея, “для спуска на воду исполинского корабля, построенного сиракузским тираном Гиероном, придумывали много способов, но механик Архимед, применив простые механизмы, один сумел сдвинуть корабль с помощью немногих людей.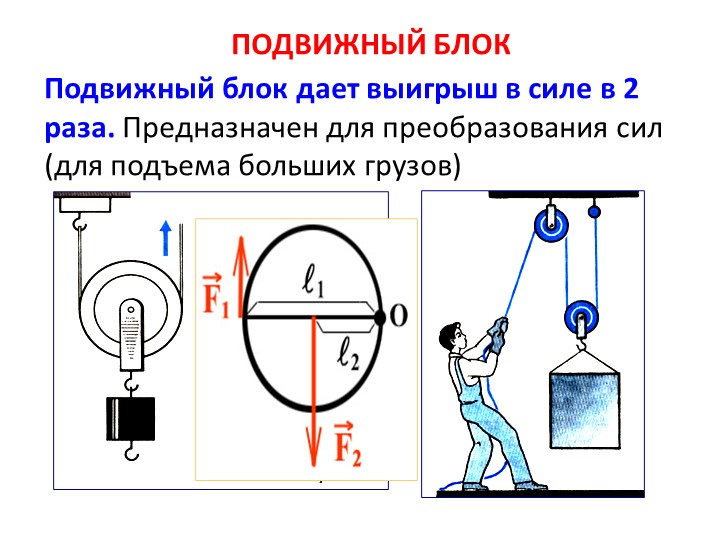 Архимед придумал блок и посредством него спустил на воду громадный корабль”.

Блок не дает выигрыша в работе, подтверждая “золотое правило” механики. В этом легко убедиться, обратив внимание на расстояния, пройденные рукой и гирей.

Спортивные парусные суда, как и парусники прошлого,

Устали? – Отдыхаем!

Идеальный блок дает выигрыш. Блоки как простые механизмы

Блок представляет собой устройство, имеющее форму колеса с желобом, по которому пропускают веревку, трос или цепь. Различают два основных вида блоков – подвижный и неподвижный. У неподвижного блока ось закреплена и при подъеме грузов не поднимается и не опускается (рис. 54), а у подвижного блока ось перемещается вместе с грузом (рис. 55).

Неподвижный блок не дает выигрыша в силе.

Его применяют для того, чтобы изменить направление действия силы.

Так, например, прикладывая к веревке, перекинутой через такой блок, силу, направленную вниз, мы заставляем груз подниматься вверх (см. Рис. 54). Иначе обстоит дело с подвижным блоком. Этот блок позволяет небольшой силой уравновесить силу, в 2 раза большую. Для доказательства этого обратимся к рисунку 56. Прикладывая силу F , мы стремимся повернуть блок вокруг оси, проходящей через точку О . Момент этой силы равен произведению Fl , где l – плечо силы F , равное диаметру блока ОВ . Одновременно с этим прикрепленный к блоку груз своим весом Р создает момент, равный, где – плечо силы Р , равное радиусу блока ОА . Согласно правилу моментов (21.2)

что и требовалось доказать.

Из формулы (22.2) следует, что P/F = 2. Это означает, что выигрыш, в силе, получаемый с помощью подвижного блока, равен 2 . Опыт, изображенный на рисунке 57, подтверждает этот вывод.

На практике часто применяют комбинацию подвижного блока с неподвижным (рис. 58). Это позволяет изменить направление силового воздействия с одновременным двукратным выигрышем в силе.

Для получения большего выигрыша в силе применяют грузоподъемный механизм, называемый

полиспастом . Греческое слово «полиспаст» образовано из двух корней: «поли» – много и «спао» – тяну, так что в целом получается «многотяг».

Полиспаст представляет собой комбинацию из двух обойм, одна из которых состоит из трех неподвижных блоков, а другая – из трех подвижных блоков (рис. 59). Поскольку каждый из подвижных блоков удваивает силу тяги, то в целом полиспаст дает шестикратный выигрыш в силе.

1. Какие два вида блоков вы знаете? 2. Чем отличается подвижный блок от неподвижного? 3. Для какой цели применяют неподвижный блок? 4. Для чего используют подвижный блок? 5. Что представляет собой полиспаст? Какой выигрыш в силе он дает?

Под термином “блок” понимается некоторое механическое устройство, представляющее из себя ролик, который закреплен на перпендикулярной оси.

Этот ролик или может свободно перемещаться, или напротив – закреплен жестко. Упростим определение – если ось вращения ролика перемещается в пространстве, то блок подвижный.

На ролике есть желобок, в который вставляется веревка или трос. Картинка ниже демонстрирует внешний вид блока.

Если ролик закреплен, например, на потолке – это неподвижный блок. Если ролик перемещается вместе с грузом – это подвижный блок. В общем смысле разница только в этом.

Смысл использования подвижного блока – выигрыш в силе при подъеме или перемещении грузов и физических тел. Неподвижный же блок выигрыша не даёт, однако часто сильно упрощает перемещение тела и используется в системах совместно с подвижным блоком.

Применение подвижного и неподвижного блоков

Система блоков встречается повсеместно. Это и подъемные краны, и различные устройства для перемещения грузов в гараже, и даже приводные ремни в современном автомобиле. Часто блок используется даже без четкого понимания того, что это тот самый механизм.

Наверняка на строительных площадках вам встречались подвижные колесики, закрепленные на верхних этажах строящегося дома. Через такое колесо перекинута веревка или цепь и рабочий, закрепляя ведро на первом этаже, поднимает его на верхний этаж, перемещая веревку. Это простой пример использования неподвижного блока. Если же к ведру добавить ещё одно колесико, то получится система блоков – подвижный и неподвижный.

Ещё один более редкий пример использования неподвижного блока. Когда человек вытаскивает из грязи автомобиль, обернув буксировочный трос вокруг ствола дерева. Делается это для большего удобства, поскольку буксировочная лебедка легко зацепится за небольшой конец троса, обернутого вокруг ствола. От самого такого блока выигрыша нет, да и поскольку дерево не вращается вокург своей оси, сила сопротивления увеличивает нагрузку.

Примеров использования этих простых механизмов вокруг нас очень много.

Самое известное устройство, которое работает на принципе блоков – это полиспаст. Оно активно применяется в подъемных механизмах. Система блоков уменьшает силу и общая работа сокращается в 4-8 раз.

Решение задач с подвижным и неподвижным блоками

В задачах по физике часто необходимо определить, какой суммарный выигрыш в силе будет получен при использовании блоков. Ученику предлагается сложная схема, где соединены подряд несколько блоков разного типа.

Ключ к решению подобных задач лежит в умении разобраться во взаимодействии этих устройств. Каждый блок рассчитывается отдельно, а затем добавляется в общую формулу. Расчётная формула для всей задачи составляется согласно схеме, которую нарисовал ученик, читая условие.

Для лучшего понимания подобных задач следует помнить, что блок – это своеобразный рычаг . Выигранная сила даёт потерю в расстоянии (в случае подвижного блока).

Расчётная формула очень простая.

Для неподвижного блока F=fmg, где F – это сила, f – коэффициент сопротивления блока, m – масса груза, g – гравитационная постоянная. Иными словами, F – это та сила, которую нужно приложить, чтобы поднять, например, ящик с земли с использованием неподвижного блока. Как видите, зависимость прямая и коэффициента нет.

Для подвижного блока мы имеем двукратный выигрыш в силе. Расчётная формулаF=0,5fmg, где буквенные обозначения аналогичны формуле чуть выше.

Соответственно, при использовании подвижного блока, такой ящик с массой m будет поднять в два раза легче с блоком, чем с использованием одной лишь только собственной спины.

Обратите внимание, что коэффициент сопротивления – это то противодействие, которое возникает в блоке при перемещении по нему веревки. Обычно эти величины заданы в условии задачи или являются табличной величиной. Иногда в школьных задачах эти коэффициенты вовсе опускаются и не учитываются.

Кроме того, не нужно забывать, что если сила прилагается под углом, то нужно использовать стандартную методику расчёта треугольника сил

. Если в задаче сказано, что человек тянет груз за веревку, которая находится под 30 градусами к линии горизонта, то это безусловно должно быть учтено и обозначено на расчётной схеме.

Блок – это разновидность рычага, представляет собой колесо с желобом (рис.1), через желоб можно пропустить веревку, трос, канат или цепь.

Рис.1. Общий вид блока

Блоки подразделяют на подвижные и неподвижные.

У неподвижного блока ось закреплена, при подъеме или опускании груза она не поднимается и не опускается. Вес груза, который поднимаем, обозначим P, прикладываемую силу обозначим F, точку опоры – O (рис.2).

Рис.2. Неподвижный блок

Плечом силы P будет отрезок OA (плечо силы l 1 ), плечом силы F отрезок OB (плечо силы l 2 ) (рис.3). Эти отрезки являются радиусами колеса, тогда плечи равны радиусу . Если плечи равны, то вес груза и сила, которую мы прикладываем для подъёма, численно равны .

Рис.3. Неподвижный блок

Такой блок не дает выигрыша в силе.Из этого можно сделать вывод, что неподвижный блок применять целесообразно для удобства подъема, проще поднимать груз вверх, применяя силу, которая направлена вниз.

Устройство, в котором ось может подниматься и опускаться вместе с грузом. Действие аналогично действию рычага (рис.4).

Рис. 4. Подвижный блок

Для работы этого блока один конец веревки закрепляется, ко второму концу приложим силу F, чтобы поднять груз весом P, груз прикреплен к точке A. Точкой опоры при вращении будет точка О, потому что в каждый момент движения блок поворачивается и точка O служит точкой опоры (рис.5).

Рис. 5. Подвижный блок

Значения плеча силы F составляет два радиуса .

Значение плеча силы P составляет один радиус.

Плечи сил отличаются в два раза, по правилу равновесия рычага, силы отличаются в два раза. Сила, которая необходима, чтобы поднять груз весом P, будет в два раза меньше, чем вес груза . Подвижный блок дает преимущество в силе в два раза.

На практике применяют комбинации блоков для изменения направления действия применяемой силы для подъема и ее уменьшения в два раза (рис.6).

Рис. 6. Комбинация подвижного и неподвижного блоков

На занятие мы познакомились с устройством неподвижного и подвижного блока, разобрали, что блоки – это разновидности рычагов. Для решения задач по этой теме необходимо помнить правило равновесия рычага: отношение сил обратно пропорционально отношению плеч этих сил.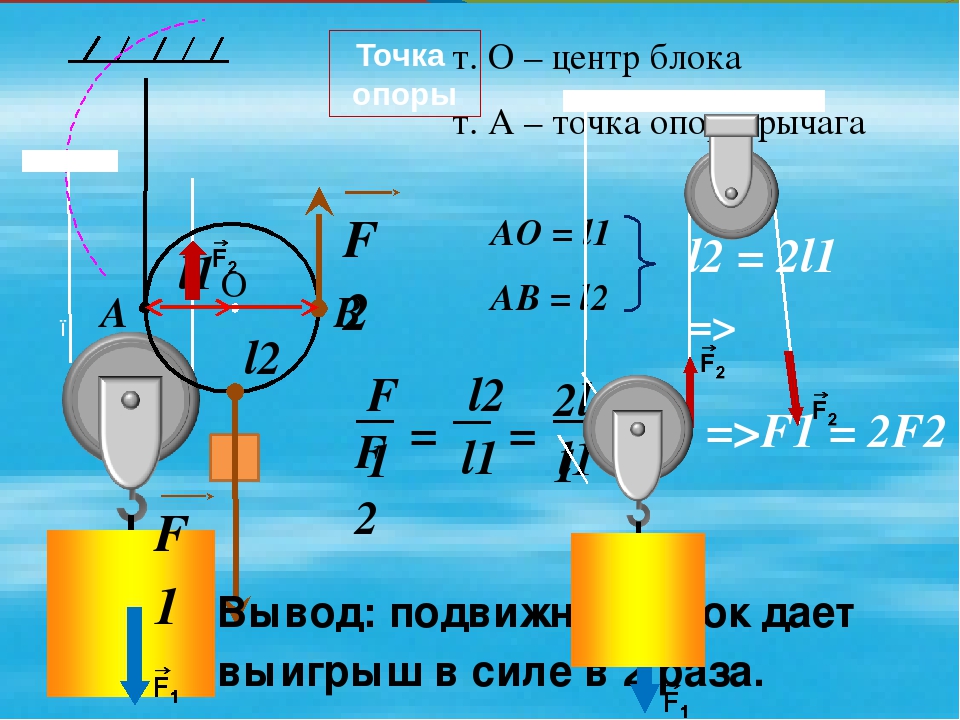

Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7-9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.
Перышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
Перышкин А.В. Сборник задач по физике, 7-9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.

Class-fizika.narod.ru ().
School.xvatit.com ().
Scienceland.info ().

Домашнее задание

Узнайте самостоятельно, что собой представляет полиспаст и какой выигрыш в силе он дает.
Где применяют в быту неподвижные и подвижные блоки?
Как легче подниматься вверх: лезть по веревке или подниматься при помощи неподвижного блока?

Будем пока считать, что массой блока и троса, а также трением в блоке можно пренебречь. В таком случае можно считать силу натяжения троса одинаковой во всех его частях. Кроме того, трос будем считать нерастяжимым, а его массу – пренебрежимо малой.

Неподвижный блок

Неподвижный блок используют для того, чтобы изменить направление действия силы. На рис. 24.1, а показано, как с помощью неподвижного блока изменить направление силы на противоположное. Однако с его помощью можно изменить направление действия силы как угодно.

Нарисуйте схему использования неподвижного блока, с помощью которого можно повернуть направление действия силы на 90°.

Дает ли неподвижный блок выигрыш в силе? Рассмотрим это на примере, показанном на рис. 24.1, а. Трос натянут силой, приложенной рыбаком к свободному концу троса. Сила натяжения троса остается постоянной вдоль троса, поэтому со стороны троса на груз (рыбу) действует такая же по модулю сила. Следовательно, неподвижный блок не дает выигрыша в силе.

При использовании неподвижного блока груз поднимается на столько же, на сколько опускается конец троса, к которому прикладывает силу рыбак. Это означает, что, используя неподвижный блок, мы не выигрываем и не проигрываем в пути.

Подвижный блок

Поставим опыт

Поднимая груз с помощью легкого подвижного блока, мы заметим, что, если трение мало, то для подъема груза надо прикладывать силу, которая примерно в 2 раза меньше веса груза (рис. 24.3). Таким образом, подвижный блок дает выигрыш в силе в 2 раза.

Рис. 24.3. При использовании подвижного блока мы выигрываем в силе в 2 раза, но во столько же раз проигрываем в пути

Однако за двойной выигрыш в силе приходится платить таким же проигрышем в пути: чтобы поднять груз, например, на 1 м, надо поднять конец переброшенного через блок троса на 2 м.

То, что подвижный блок дает двойной выигрыш в силе, можно доказать и не прибегая к опыту (см. ниже раздел «Почему подвижный блок дает выигрыш в силе в два раза?»).

Физика 7 класс. ПРОСТЫЕ МЕХАНИЗМЫ

В современной технике для переноса грузов на стройках и предприятиях широко используются грузоподъемные механизмы, незаменимыми составными частями которых можно назвать простые механизмы . Среди них древнейшие изобретения человечества: блок и рычаг . Древнегреческий ученый Архимед облегчил труд человека, дав ему при использовании своего изобретения выигрыш в силе, и научил менять направление действия силы.

Подвижный и неподвижный блок – такие же древнейшие простые механизмы, как и рычаг. Уже в 212 г.до н.эры с помощью крюков и захватов, соединенных с блоками, сиракузцы захватывали у римлян средства осады. Сооружением военных машин и обороной города руководил Архимед.

Физика подвижный и неподвижный блок. Простые механизмы. Золотое правило механики

Применение подвижного блока даёт двукратный выигрыш в силе, применение неподвижного – позволяет изменить направление прилагаемой силы. На практике используются комбинации подвижных и неподвижных блоков . При этом каждый подвижный блок позволяет вдвое уменьшить прилагаемое усилие или вдвое увеличить скорость перемещения груза. Неподвижные блоки используют для связи подвижных блоков в единую систему. Такая система подвижных и неподвижных блоков называется полиспаст.

Определение

Полиспаст – система подвижных и неподвижных блоков, соединенных гибкой связью (канаты, цепи) используемая для увеличения силы или скорости подъема грузов.

Используется полиспаст в случаях, если необходимо прилагая минимальные усилия поднять или переместить тяжелый груз, обеспечить натяжение и т.п. Простейший полиспаст состоит всего из одного блока и каната, при этом позволяет в два раза снизить тяговое усилие, необходимое для подъема груза.

Рисунок 1. Каждый подвижный блок в полиспасте даёт двукратный выигрыш в силе или скорости

Обычно в грузоподъемных механизмах применяют силовые полиспасты, позволяющие уменьшить натяжение каната, момент от веса груза на барабане и передаточное число механизма (тали, лебедки). Скоростные полиспасты, позволяющие получить выигрыш в скорости перемещения груза при малых скоростях приводного элемента, применяются значительно реже. Они используются в гидравлических или пневматических подъемниках, погрузчиках, механизмах выдвижения телескопических стрел кранов.

Основной характеристикой полиспаста является кратность. Это отношение числа ветвей гибкого органа, на котором подвешен груз, к числу ветвей наматываемых на барабан (для силовых полиспастов), либо отношение скорости ведущего конца гибкого органа к ведомому (для скоростных полиспастов). Условно говоря, кратность это теоретически рассчитанный коэффициент выигрыша в силе или скорости при использовании полиспаста. Изменение кратности полиспаста происходит путем введения или удаления из системы дополнительных блоков, при этом конец каната при четной кратности крепится на неподвижном элементе конструкции, а при нечетной кратности – на крюковой обойме.

Рисунок 2. Крепление каната при чётной и нечётной кратности полиспаста

Выигрыш в силе при применении полиспаста с $n$ подвижных и $n$ неподвижных блоков определяется по формуле: $P=2Fn$, где $Р$ – вес груза, $F$ – сила, прилагаемая на входе полиспаста, $n$ – число подвижных блоков.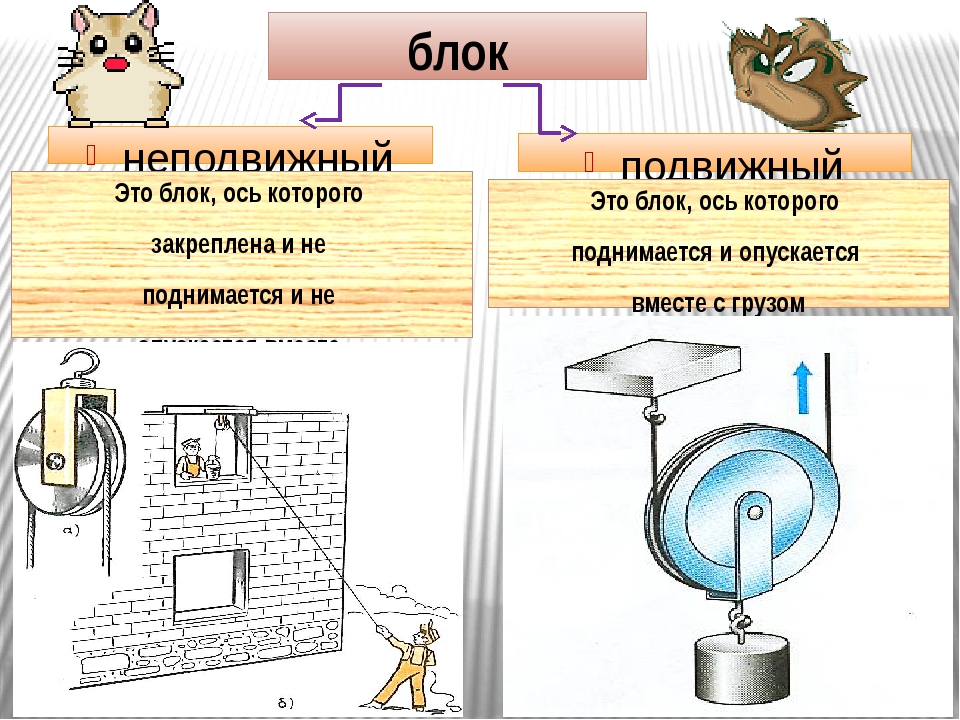

В зависимости от количества ветвей каната, закрепленных на барабане грузоподъемного механизма, можно выделить одинарные (простые) и сдвоенные полиспасты. В одинарных полиспастах, при наматывании или сматывании гибкого элемента вследствие его перемещения вдоль оси барабана, создается нежелательное изменение нагрузки на опоры барабана. Также в случае отсутствия в системе свободных блоков (канат с блока крюковой подвески непосредственно переходит на барабан) происходит перемещение груза не только в вертикальной, но и в горизонтальной плоскости.

Рисунок 3. Одинарные и сдвоенные полиспасты

Для обеспечения строго вертикального подъема груза применяют сдвоенные полиспасты, (состоящие из двух одинарных), в этом случае на барабане закрепляются оба конца каната. Для обеспечения нормального положения крюковой подвески при неравномерной вытяжке гибкого элемента обоих полиспастов применяют балансир или уравнительные блоки.

Рисунок 4. Способы обеспечения вертикальности подъёма груза

Скоростные полиспасты отличаются от силовых тем, что в них рабочая сила, обычно развиваемая гидравлическим или пневматическим цилиндром, прикладывается к подвижной обойме, а груз подвешивается к свободному концу каната или цепи.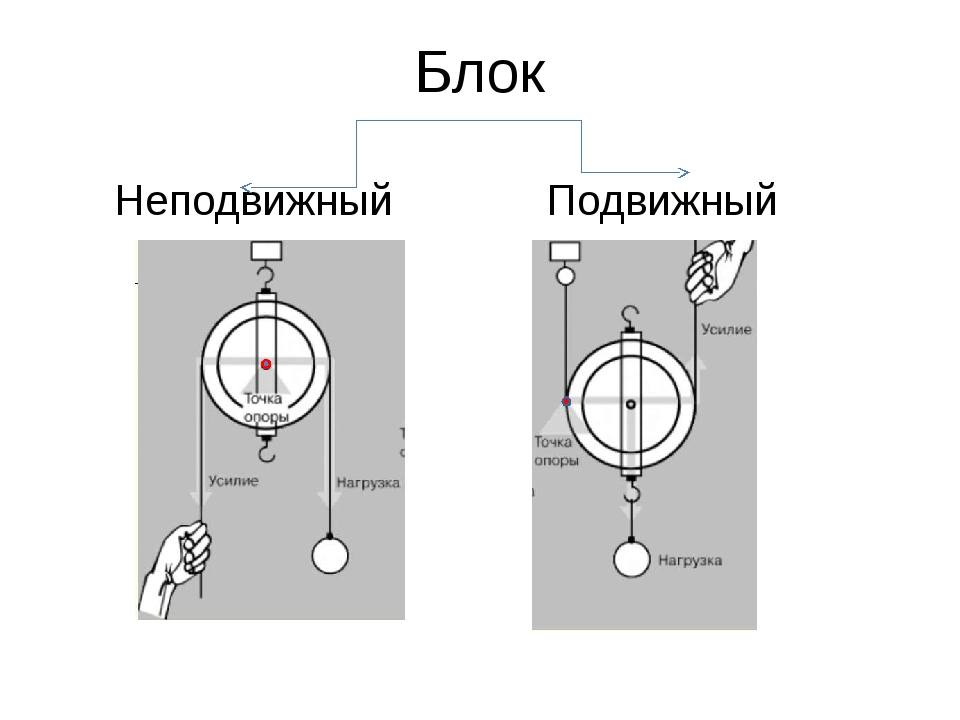 Выигрыш в скорости при использовании такого полиспаста получается в результате увеличения высоты подъёма груза.

При использовании полиспастов следует учитывать, что используемые в системе элементы не являются абсолютно гибкими телами, а имеют определенную жесткость, поэтому набегающая ветвь не сразу ложится в ручей блока, а сбегающая ветвь не сразу выпрямляется. Это наиболее заметно при использовании стальных канатов.

Вопрос: почему у подъемных строительных кранов крюк, который переносит груз, закреплен не на конце троса, а на обойме подвижного блока?

Ответ: для обеспечения вертикальности подъёма груза.

На рис.5 изображён степенной полиспаст, в котором несколько подвижных блоков, а неподвижный – только один. Определите, какой вес можно поднять, приложив к неподвижному блоку усилие $F$ = 200 H?

Рисунок 5

Каждый из подвижных блоков степенного полиспаста удваивает прилагаемое усилие. Вес, который может поднять степенной полистпаст третьей степени (без учёта поправок на силы трения и жёсткость троса), определяется формулой:

Ответ: полиспаст может поднять груз весом 800 Н.

Неподвижный блок не дает выигрыша в силе. Его применяют для того, чтобы изменить направление действия силы. Так, например, прикладывая к веревке, перекинутой через такой блок, силу, направленную вниз, мы заставляем груз подниматься вверх (см. Рис. 54). Иначе обстоит дело с подвижным блоком. Этот блок позволяет небольшой силой уравновесить силу, в 2 раза большую. Для доказательства этого обратимся к рисунку 56. Прикладывая силу F , мы стремимся повернуть блок вокруг оси, проходящей через точку О . Момент этой силы равен произведению Fl , где l – плечо силы F , равное диаметру блока ОВ . Одновременно с этим прикрепленный к блоку груз своим весом Р создает момент, равный, где – плечо силы Р , равное радиусу блока ОА . Согласно правилу моментов (21.2)

что и требовалось доказать.

Для получения большего выигрыша в силе применяют грузоподъемный механизм, называемый полиспастом . Греческое слово «полиспаст» образовано из двух корней: «поли» – много и «спао» – тяну, так что в целом получается «многотяг».

Блоки используют для поднятия грузов. Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускают веревку, трос или цепь. Неподвижным называют такой блок, ось которого закреплена и при подъеме грузов она не поднимается и не опускается (рис. 1, а, б).

Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи приложенных сил равны радиусу колеса. Следовательно, из правила моментов вытекает, что неподвижный блок выигрыша в силе не дает . Он позволяет менять направление действия силы.

На рисунке 2, а, б изображен подвижный блок (ось блока поднимается и опускается вместе с грузом). Такой блок поворачивается около мгновенной оси О. Правило моментов для него будет иметь вид

Таким образом, подвижный блок дает выигрыш в силе в два раза.

Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис. 3). Неподвижный блок применяется только для удобства. Он, изменяя направление действия силы, позволяет, например, поднимать груз, стоя на земле.

Блок состоит из одного или нескольких колес (роликов), огибаемых цепью, ремнем или тросом. Так же, как и рычаг, блок уменьшает усилие, необходимое для подъема груза, но плюс к этому может изменять направление прикладываемой силы.

За выигрыш в силе приходится расплачиваться расстоянием: чем меньшее усилие требуется для подъема груза, тем больше путь, который должна пройти точка приложения этого усилия. Система блоков увеличивает выигрыш в силе за счет использования большего количества грузонесущих цепей. Подобные силосберегающие устройства имеют очень широкий диапазон применения – от перемещения на высоту массивных стальных балок на строительных площадках до подъема флагов.

Как и в случае других простых механизмов, изобретатели блока неизвестны. Хотя, возможно, блоки существовали и раньше, первое упоминание о них в литературе относится к пятому веку до нашей эры и связано с использованием блоков древними греками на кораблях и в театрах.

Установленные на подвесном рельсе подвижные системы блоков (рисунок сверху) широко распространены на сборочных линиях, поскольку существенно облегчают перемещение тяжелых деталей. Прикладываемая сила (F) равна частному от деления веса груза (W) на используемое количество поддерживающих его цепей (n).

Одинарные неподвижные блоки

Этот простейший тип блока не уменьшает усилие, необходимое для подъема груза, но зато изменяет направление прикладываемой силы, как это показано на рисунках сверху и справа вверху. Неподвижный блок на верхней части флагштока облегчает подъем флага, позволяя тянуть шнур, к которому привязан флаг, вниз.

Одинарные подвижные блоки

Одинарный блок, имеющий возможность перемещения, уменьшает наполовину усилие, требующееся для подъема груза. Однако уменьшение вдвое прикладываемой силы означает, что точка ее приложения должна пройти в два раза больший путь. В данном случае сила равна половине веса (F=1/2W).

Системы блоков

При использовании комбинации неподвижного блока с подвижным прикладываемая сила кратна общему количеству грузонесущих цепей. В данном случае сила равна половине веса (F=1/2W).

Груз , подвешенный через блок вертикально, позволяет туго натягивать горизонтальные электрические провода.

Подвесной подъемник (рисунок сверху) состоит из цепи, обвитой вокруг одного подвижного и двух неподвижных блоков. Подъем груза требует прикладывания силы, составляющей всего лишь половину от его веса.

Полиспаст , обычно используемый в больших подъемных кранах (рисунок справа), состоит из комплекта подвижных блоков, к которому подвешивается груз, и комплекта неподвижных, прикрепленного к стреле крана. Получая выигрыш в силе от столь большого количества блоков, кран может поднимать очень тяжелые грузы, например, стальные балки. В данном случае сила (F) равна частному от деления веса груза (W) на количество поддерживающих тросов (n).

Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость.

ОПРЕДЕЛЕНИЕ

Блок – твердое тело, которое имеет возможность вращаться вокруг неподвижной оси.

Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).

Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.

Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:

Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны:

так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу.

Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:

при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:

Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.

Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.

Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в таком случае будут неравными. Двойной блок действует как рычаг с плечами разной длины. На рис.2 изображена схема двойного блока.

Условие равновесия для рычага на рис.2 станет формула:

Двойной блок может преобразовывать силу. Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.

Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Рассмотрим рис. 3. Плечо силы в два раза больше, чем плечо силы , следовательно, для равновесия необходимо, чтобы величина силы F была в два раза меньше, чем модуль силы P:

Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как:

Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:

Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.

Золотое правило механики

Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.

В виде формулы «золотое правило№ можно записать так:

где – путь, который проходит точка приложения силы – путь проходимый точкой приложения силы .

Золотое правило является самой простой формулировкой закона сохранения энергии. Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( и ) как:

Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:

Если силы и уравновешены, то блок покоится или движется равномерно.

Примеры решения задач

ПРИМЕР 1

Задание

Используя систему из двух подвижных и двух неподвижных блоков, рабочие поднимают строительные балки, при этом прикладывают силу равную 200 Н. Чему равна масса (m) балок? Трение в блоках не учитывайте.

Решение

Сделаем рисунок.

Вес груза, приложенный к системе грузов, будет равен силе тяжести, которая приложена к поднимаемому телу (балке):

Неподвижные блоки выигрыша в силе не дают. Каждый подвижный блок дает выигрыш в силе в два раза, следовательно, при наших условиях мы получим выигрыш в силе в четыре раза. Это значит, что можно записать:

Получаем, что масса балки равна:

Вычислим массу балки, примем :

Ответ

m=80 кг

ПРИМЕР 2

Задание

Пусть высота, на которую поднимают балки рабочие, в первом примере равна м. Чему равна работа, которую совершают рабочие? Какова работа груза по перемещению на заданную высоту?

Решение

В соответствии с «золотым правилом» механики, если мы, используя имеющуюся систему блоков, получили выигрыш в силе в четыре раза, то проигрыш в перемещении составит тоже четыре. В нашем примере это означает, что длина веревки (l) которую рабочим следует выбрать составит длину в четыре раза большую, чем расстояние, которое пройдет груз, то есть:

Блоки. Золотое правило механики

Конспект урока по теме: «Блоки. Золотое правило механики».

Тип урока: урок формирования новых знаний.

Цель урока: Формирование понятий блок и его применение. Ввести понятие «Золотого правила» механики; выяснить, как оно выполняется для простых механизмов.

Задачи урока:

доказать, что условие равновесия рычага применимо к блоку, сформировать знание «золотого правила механики», проверить, как оно выполняется для простых механизмов, показать практические применения рычага, используя ИКТ, объяснительно-иллюстративный метод с элементами проблемно-поискового обучения, экспериментальные навыки учащихся.

Ход урока

Организационный момент. Вводное слово учителя.

Здравствуйте ребята. Садитесь. Очень часто вы меня спрашиваете, нужна ли вам будет физика, после окончания школы. А я вам отвечаю, что мы в повседневной жизни живем по законам этой науки, даже и не задумываясь об этом. Вот на последних уроках мы говорили о простых механизмах и их назначении. Откройте ваши тетради и запишите тему урока: «Блоки. «Золотое правило» механики».

Эпиграфом нашего урока являются слова Яна Полонского

Царство науки не знает предела –

Всюду следы ее вечных побед,

Разума слово и дело,

Сила и свет.

Актуализация знаний.

Для чего нам нужны простые механизмы.

Перечислите известные вам простые механизмы.

Что называют рычагом?

Что называют плечом силы?

Как найти плечо силы? (Рисунок на доске)

В чем заключается правило равновесия рычага? (Формула на доске)

Что называют моментом силы? (Формула на доске)

Найдите ошибку на рисунке. (На доске рисунок на котором неверно изображена плечи сил)

Качественные задачи

Почему ручку располагают у края двери как можно дальше от петель?

Чтобы увеличить плечо действующей силы.

Груз несут на палке, перекинутой через плечо. Как влияет положение груза на величину силы, с которой груз действует на плечо?

Чем ближе груз расположен к плечу, тем меньше сила, с которой рука удерживает палку.

Расчетные задачи.

С какой силой натянута мышца человека при подъёме гири весом 50 Н, если расстояние от гири до локтя равно 40 см, а от локтя до места закрепления мышцы – 4 см?

это пропорция 50*40=х*4
40х=200
х=5 (Н)

Экспериментальная задача.

На рычаге уравновешенны две гири одинакового объема, но из различных материалов, причем одна гиря легче другой. Изменится ли равновесие рычага, если гири погрузить в воду.

Равновесие нарушится, та гиря, которая тяжелее перевесит, так как на гири, которые находятся в жидкости, действуют силы Архимеда и силы тяжести, Архимедовы силы одинаковы, так как одинаковы объемы тел и жидкости в сосудах, а вот силы тяжести не равны.

II. Изучение нового материала.

1. Блоки.

Итак, с правилами равновесия рычага вы знакомы, можете применять их на практике. Познакомимся еще с одним видом простого механизма блоком. Вернее с блоками.

Что же такое блок и для чего он нам необходим?

Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускают веревку, трос или цепь.

Являясь разновидностью рычага, блок служит для преобразования силы. Каким же образом? Дело в том, что блоки бывают двух видов подвижные и неподвижные. Чтобы понять, в чем их разница дадим характеристику каждого вида в отдельности.

Вначале рассмотрим неподвижный блок.

Неподвижным называется блок, ось которого закреплена, то есть она не поднимается и не опускается при поднятии груза.

Какое же преобразование силы дает нам этот блок?

Блок это рычаг, определим его плечи, (возьмите карандаши и линейки) обозначим центр – ось вращения буквой О. Проведем диаметр через центр и обозначим его АВ. Укажем силы, приложенные к блоку. Сила тяжести, действующая на груз, направлена вниз, и сила удерживающая груз тоже направлена вниз.

Скажите, пожалуйста, чему равно плечо силы тяжести груза F1?

Плечо силы F1 равно ОА, а плечо приложенной силы F2? ОВ, верно. АВ это диаметр, а что такое ОА и ОВ? Верно радиусы. Итак? у неподвижного блока плечи сил равны радиусу колеса. ОА = ОВ = r. А по условию равновесия рычага, если равны плечи сил, то и сами силы будут также равны F1 = F2..

Значит, неподвижный блок не дает выигрыша в силе, но позволяет менять направление действия силы. Подпишите этот вывод под чертежом неподвижного блока

Рассмотрим теперь подвижный блок.

Подвижный это блок, ось которого поднимается и опускается вместе с грузом. Обозначим точку опоры О. На рисунке видно, что у подвижного блока она переместилась на обод блока. Р –э то вес тела, поднимаемого блоком, F – приложенная к нему сила.

ОА — плечо силы Р и ОВ — плечо силы F. Так как плечо ОВ в 2 раза больше плеча ОА, ОА это радиус, а ОВ диаметр значит, ОВ = 2 ОА то сила F в 2 раза меньше силы Р, Р = 2 F

Таким образом, подвижный блок дает выигрыш в силе в 2 раза. Подпишите этот вывод под чертежом подвижного блока.

Действие неподвижного и подвижного блоков аналогично действию рычага, так же есть точка опоры, отношение сил характеризуется отношением плеч.

Неподвижный блок не дает выигрыша в силе, но позволяет менять направление ее действия.

Подвижный блок дает выигрыш в силе в 2 раза.

2. Демонстрация действия неподвижного и подвижного блоков.

Обычно на практике применяют комбинацию неподвижного блока с подвижным. Неподвижный блок применяется только для удобства. Он не дает выигрыша в силе, но изменяет направление действия силы, например, позволяет поднимать груз, стоя на земле, а используя вместе с ним и подвижный блок, мы получаем еще и выигрыш в силе в 2 раза.

Итак, мы с вами выясняли, что правило равновесия рычага справедливо и для блока.

«Золотое правило механики»

Когда люди начали использовать рычаги, блоки они обнаружили одну интересную особенность …перемещения, совершаемые при работе простых механизмом оказались связанными с силами, развиваемыми этими механизмами.

То, что мы выигрываем в силе, то же мы и проигрываем в пути.

Данное положение столь общее и одновременно столь важное, что получило название «золотое правило» механики.

Итак, сделаем вывод: ни один механизм не дает выигрыша в работе, во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии.

Великий физик – Архимед Сегодня мы познакомились с «золотым правилом» механики. Это положение, общее для всех разновидностей простых механизмов. Оно было установлено еще в древности – великим ученым древнегреческим ученым, математиком и физиком – Архимедом.

Рефлексия. Достигли целей поставленных в начале урока?

Что нового, интересного и важного вы узнали на уроке?

III. Итог урока.

Физика наука, подарившая нам много открытий, но непознанного вокруг еще много. Какое поле деятельности для пытливого ума, умелых рук и любознательных натур. Пусть сегодняшний урок разбудит у вас жажду новых познаний, ведь великий океан истины, по-прежнему, простилается перед вами, не исследованный до конца.

Домашнее задание.

Момент силы — как найти? В чем измеряется? Формулы

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Плечо силы

Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.

Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.

Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Момент силы

При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.

Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.

Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.

Момент силы

M = Fl

M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]

Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.

Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.

На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.

То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.

Расчет момента силы

Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.

Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

МА=F×AB=F×3м

Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.

Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

Момент силы относительно точки B:

MB=F×cos30×AB=F×cos30×3м

Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

Момент силы относительно точки B:

MB=F×3м

Правило моментов

Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов

M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n

M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:

По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

|OA|=FB/FA)*|OB|=30/80*80=30 см

Ответ: расстояние ОА равно 30 см

Задача 3

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:

По правилу рычага m1g*l1=m2g*l2

Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг

Ответ: Масса груза равна 0,3 кг

Задача 4

На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.

Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н

Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно

4T = 4*100= 400 Н

Ответ: натяжение провода равно 400 Н

Задача 5 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

mg=F*5/0,8=120*5/0,8=750Н

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Статика – Физика – Теория, тесты, формулы и задачи

Основные теоретические сведения

Основы статики

К оглавлению…

Статикой называется раздел механики, изучающий условия равновесия тел. Равновесием называют такое состояние тела или системы тел, в котором оно не движется в данной системе отсчета. Различают три вида равновесия:

Устойчивое равновесие. Если систему вывести из состояния устойчивого равновесия, то она самопроизвольно в него вернется, то есть при выведении из положения равновесия возникает сила, возвращающая систему к равновесию. Для этого необходимо, чтобы потенциальная энергия системы в состоянии устойчивого равновесия имела минимальное значение. Любая физическая система стремится к состоянию устойчивого равновесия. Это значит, что любой самопроизвольный процесс всегда проходит с уменьшением потенциальной энергии.
Неустойчивое равновесие. В данном случае при выведении из состояния равновесия возникают силы, уводящие систему от равновесия, и система самопроизвольно не может в него вернуться. В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
Безразличное равновесие. При выведении из состояния равновесия в системе не возникает ни возвращающих, ни уводящих в сторону сил.

Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение (действительно, ведь ускорение тела при этом равно нулю). В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей силы все силы, действующие на тело, можно прикладывать к центру масс. Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело.

Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. Иными словами, векторная сумма всех сил, приложенных к телу должна быть равна нолю:

Момент силы. Правило моментов

К оглавлению…

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.

Для описания причин вызывающих вращения и условия равновесия тела в статике вводится новое понятие – момент силы. Произведение модуля силы F на плечо d и называется моментом силы M. Таким образом момент силы в статике вычисляется по формуле:

Обычно в физике используется следующее правило знаков: если сила поворачивает тело по часовой стрелке, то ее момент считается положительным, а если против – то отрицательным. Момент силы может и равняться нулю, если сила проходит (сама или продолжением) через ось. Обратите внимание: если Вы перепутаете, и возьмете знаки моментов наоборот (по часовой стрелке со знаком минус, а против часовой со знаком плюс), то ничего страшного не произойдет. Поэтому, важно запомнить, что моменты сил, вращающих тело в различных направлениях относительно часовой стрелки, берутся с различными знаками.

Обратите внимание, что момент силы зависит не только от величины силы, но и от ее плеча. Следовательно, одно и то же значение момента можно получить двумя способами: взять большую силу и малое плечо или взять малую силу и большое плечо. Вывод: чем больше плечо, тем меньшую силу необходимо прилагать для получения одного и того же результата.

Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

При записи этого условия в ходе решения конкретной задачи по статике моменты сил необходимо записывать с учётом их знаков. В Международной системе единиц (СИ) моменты сил измеряются в ньютоно-метрах (Н∙м).

Обратите внимание: в общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов.

Алгоритм решения задач на правило моментов (задач по статике):

Нарисовать рисунок. Следует помнить, что сила тяжести, действующая на тело изображается один раз. Если же в задаче идет речь об изломанной палочке, то удобнее рисовать отдельно силы тяжести, действующие на каждую часть палочки, считая массы частей пропорциональными их длинам. В отличие от динамики, где силы изображаются из одной точки, в статике важно точно указать точку приложения силы.
Выбрать ось вращения в точке приложения самой ненужной в задаче силы или сил (той силы, которую определять не надо и не хочется из-за природного чувства лени). При этом плечо (и, следовательно, момент) этой силы обратится в нуль независимо от ее величины, и в дальнейших вычислениях эту силу можно не учитывать совсем.
Записать правило моментов относительно данной оси, на забывая про правило знаков.
При необходимости записать также условие согласно которому равнодействующая сила равна нолю.
Выразить искомую силу.

Рычаги и блоки

К оглавлению…

Как вы знаете из практики, иногда необходимо изменить направление силы, увеличить или уменьшить ее величину. Этой цели служат простые механизмы: устройства, преобразующие величину или направление силы с помощью механических явлений. Для всех простых механизмов справедливо золотое правило механики: выиграл в силе – проиграл в перемещении (или наоборот). Это значит, что при увеличении силы за счет некоторого механизма неизбежно будет уменьшено и перемещение. Рассмотрим основные типы простых механизмов изучаемых в школьной физике:

Равноплечий рычаг (весы). Рычаг, ось вращения которого проходит через его геометрический центр.
Неравноплечий рычаг. Рычаг ось вращения которого проходит через произвольную точку.
Неподвижный блок. Это диск с закрепленной осью, через который переброшена нить. Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.
Подвижный блок. Это диск, ось которого может двигаться поступательно. Подвижный блок позволяет уменьшить силу в два раза, одновременно с этим вдвое увеличивая перемещение.
Наклонная плоскость. Это устройство применяется для поднятия тяжестей. При достаточно малых значениях угла наклона и небольшом коэффициенте трения сила, которую необходимо приложить чтобы поднимать некоторое тело вдоль наклонной плоскости может быть значительно меньше веса тела. Таким образом, подъем становится легче. Естественно, при этом в полном соответствии с «золотым правилом» увеличивается перемещение тела.

Центр тяжести тела

К оглавлению…

Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело. В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее).

Рассмотрим основные методы определения положения центра масс тел для некоторых конкретных случаев, возникающих при решении задач по статике:

1. У однородных тел правильной формы (шары, прямоугольники, стержни) центр тяжести совпадает с геометрическим центром. Следует запомнить, что центр тяжести однородной треугольной пластины лежит в точке пересечения ее медиан. Для однородных симметричных тел центр тяжести всегда расположен на оси симметрии.

2. Определение положения центра тяжести системы из двух тел с известными центрами тяжести. Здесь можно использовать замечательное свойство центра тяжести. Подперев центр тяжести, мы обеспечим равновесие тела. Таким образом, центр тяжести системы из двух тел лежит на отрезке, соединяющем их центры тяжести, и делит его в отношении, обратном отношению масс тел:

где: l₁ – расстояние от центра масс до тела с массой m₁, а l₂ – до тела с массой m₂.

3. Определение положения центра тяжести любой системы тел с известными положениями центров тяжести. Необходимо ввести систему координат (естественно, начало координат выбрать в точке, относительно которой необходимо рассчитать положение центра тяжести), определить в ней координаты центров тяжести всех тел и найти координаты центра тяжести системы по формуле:

Аналогичные уравнения получаются для остальных координатных осей, если таковые необходимо рассматривать в задаче (просто переменная x меняется на y или z соответственно).

4. Однородное тело правильной формы с вырезом правильной формы. Проще всего свести задачу к обратной: мысленно вставить вырез обратно и получить тело правильной формы с известным положением центра тяжести. Далее представить его в виде двух тел: страшного с вырезом и самого выреза. А теперь все просто. У одного из тел (выреза) мы знаем положения центра тяжести. У другого – нет. Зато знаем положение центра тяжести системы двух тел. Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ.

5. Теорема Паппа. Применяется для определения положения центра тяжести плоской пластины, которая при вращении вокруг некоторой оси образует тело с легко вычисляемым объемом. Необходимо мысленно повернуть пластину на один оборот, нарисовать рисунок и применить теорему:

Формулировка теоремы: объем тела, полученного при вращении пластины, равен произведению ее площади на путь, пройденный центром тяжести при вращении:

Контактные силы – Высшая школа физики

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

6.2 Трение – Университетская физика, Том 1

Цели обучения

К концу этого раздела вы сможете:

Опишите общие характеристики трения
Перечислите различные типы трения
Рассчитайте величину статического и кинетического трения и используйте их в задачах, связанных с законами движения Ньютона.

Когда тело находится в движении, оно имеет сопротивление, потому что оно взаимодействует с окружающей средой.Это сопротивление – сила трения. Трение противодействует относительному движению между контактирующими системами, но также позволяет нам двигаться – концепция, которая становится очевидной, если вы пытаетесь ходить по льду. Трение – обычная, но сложная сила, и ее поведение до сих пор полностью не изучено. Тем не менее, можно понять обстоятельства, в которых он ведет себя.

Статическое и кинетическое трение

Основное определение трения относительно просто сформулировать.

Трение

Трение – это сила, которая препятствует относительному движению между контактирующими системами.

Есть несколько форм трения. Одна из более простых характеристик трения скольжения состоит в том, что оно параллельно контактным поверхностям между системами и всегда находится в направлении, противоположном движению или попытке движения систем относительно друг друга. Если две системы находятся в контакте и движутся относительно друг друга, то трение между ними называется кинетическим трением. Например, трение замедляет скольжение хоккейной шайбы по льду. Когда объекты неподвижны, между ними может действовать статическое трение; статическое трение обычно больше кинетического трения между двумя объектами.

Статическое и кинетическое трение

Если две системы находятся в контакте и неподвижны относительно друг друга, то трение между ними называется трением покоя. Если две системы находятся в контакте и движутся относительно друг друга, то трение между ними называется кинетическим трением.

Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу – вы можете очень сильно надавить на ящик и вообще не сдвинуть его. Это означает, что статическое трение реагирует на ваши действия – оно увеличивается, чтобы быть равным вашему толчку и в противоположном ему направлении.Если вы, наконец, достаточно сильно надавите, ящик, кажется, внезапно соскользнет и начнет двигаться. Теперь статическое трение уступает место кинетическому трению. Находясь в движении, легче удерживать его в движении, чем начать, что указывает на то, что кинетическая сила трения меньше, чем сила статического трения. Если вы добавите массу в ящик, скажем, поставив на него коробку, вам нужно будет еще сильнее толкнуть его, чтобы он завелся, а также чтобы он продолжал двигаться. Кроме того, если вы смазываете бетон маслом, вам будет легче запустить ящик и продолжать работу (как и следовало ожидать).

Рисунок 6.10 представляет собой грубое графическое представление того, как возникает трение на границе раздела между двумя объектами. Осмотр этих поверхностей крупным планом показывает, что они шероховатые. Таким образом, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет проскочить, ударяясь только кончиками поверхности, отламывая точки или и то и другое. Существенной силе можно противостоять трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик ставится еще одна коробка), тем больше силы требуется для их перемещения.Частично трение происходит из-за сил сцепления между поверхностными молекулами двух объектов, что объясняет зависимость трения от природы веществ. Например, обувь на резиновой подошве скользит меньше, чем на кожаной. Адгезия зависит от контактирующих веществ и является сложным аспектом физики поверхности. Когда объект движется, остается меньше точек соприкосновения (меньше прилипающих молекул), поэтому требуется меньшая сила, чтобы удерживать объект в движении. На малых, но ненулевых скоростях трение практически не зависит от скорости.

Фигура 6.10 Силы трения, такие как f →, f →, всегда препятствуют движению или попытке движения между соприкасающимися объектами. Трение возникает частично из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде. Чтобы объект переместился, он должен подняться до того места, где пики верхней поверхности могут проплывать по нижней поверхности. Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые вершины будут сломаны, что также потребует силы для поддержания движения.Большая часть трения на самом деле возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже идеально гладкие поверхности не свободны от трения. (Фактически, идеально гладкие, чистые поверхности из аналогичных материалов будут прилипать, образуя соединение, называемое «холодной сваркой».)

Величина силы трения имеет две формы: одна для статических ситуаций (статическое трение), другая для ситуаций, связанных с движением (кинетическое трение). Далее следует лишь приблизительная эмпирическая (экспериментально определенная) модель.Эти уравнения статического и кинетического трения не являются векторными уравнениями.

Величина статического трения

Величина статического трения fsfs составляет

, где μsμs – коэффициент трения покоя, а N – величина нормальной силы.

Символ ≤≤ означает, что меньше или равно , подразумевая, что статическое трение может иметь максимальное значение мксН.мксН. Статическое трение – это сила реакции, которая увеличивается, чтобы быть равной и противоположной любой приложенной силе, вплоть до своего максимального предела.Как только приложенная сила превышает

fs (max), fs (max), объект перемещается. Таким образом,

fs (max) = μsN.fs (max) = μsN.

Величина кинетического трения

Величина кинетического трения fkfk определяется как

где μkμk – коэффициент кинетического трения.

Система, в которой fk = μkNfk = μkN, описывается как система, в которой трение ведет себя просто . Переход от статического трения к кинетическому трению показан на рисунке 6.11.

Фигура 6.11 (a) Сила трения f → f → между блоком и шероховатой поверхностью противоположна направлению приложенной силы F → .F →. Величина статического трения уравновешивает приложенную силу. Это показано в левой части графика в (c). (b) В какой-то момент величина приложенной силы превышает силу кинетического трения, и блок перемещается вправо. Это показано в правой части графика. (c) график зависимости силы трения от приложенной силы; обратите внимание, что fs (max)> fk.fs (макс)> fk. Это означает, что μs> μk.μs> μk.

Как видно из таблицы 6.1, коэффициенты кинетического трения меньше, чем их статические аналоги. Приблизительные значения μμ состоят из одной или двух цифр, чтобы указать приблизительное описание трения, даваемое двумя предыдущими уравнениями.

Система	Статическое трение мкс мкс	Кинетическое трение μkμk
Резина на сухом бетоне	1.0	0,7
Резина на мокром бетоне	0,5-0,7	0,3-0,5
Дерево по дереву	0,5	0,3
Вощеное дерево по мокрому снегу	0,14	0,1
Металл по дереву	0,5	0,3
Сталь по стали (сухая)	0,6	0,3
Сталь на стали (промасленная)	0.05	0,03
Тефлон на стали	0,04	0,04
Кость смазана синовиальной жидкостью	0,016	0,015
Туфли по дереву	0,9	0,7
Обувь на льду	0,1	0,05
Лед на льду	0,1	0,03
Сталь на льду	0,4	0.02

Стол 6.1 Приблизительные коэффициенты статического и кинетического трения.

Уравнение 6.1 и 6.2 включают зависимость трения от материалов и нормальной силы. Направление трения всегда противоположно направлению движения, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с силой, параллельной полу), имеет массу 100 кг, то нормальная сила равна его весу,

. w = мг = (100 кг) (9.80 м / с2) = 980 Н, w = mg = (100 кг) (9.80 м / с2) = 980 Н,

перпендикулярно полу. Если коэффициент трения покоя равен 0,45, вам придется приложить силу, параллельную полу, более

. fs (макс.) = μsN = (0,45) (980N) = 440Nfs (макс.) = μsN = (0,45) (980N) = 440N

, чтобы переместить ящик. Когда есть движение, трение меньше, и коэффициент кинетического трения может быть 0,30, так что сила только

fk = μkN = (0,30) (980N) = 290N fk = μkN = (0,30) (980N) = 290N

позволяет ему двигаться с постоянной скоростью. Если пол смазан, оба коэффициента будут значительно меньше, чем без смазки.Коэффициент трения – это безразмерная величина с величиной обычно от 0 до 1,0. Фактическое значение зависит от двух соприкасающихся поверхностей.

Многие люди испытывали скользкость при ходьбе по льду. Однако многие части тела, особенно суставы, имеют гораздо меньшие коэффициенты трения – часто в три или четыре раза меньше, чем у льда. Сустав образован концами двух костей, которые соединены толстыми тканями. Коленный сустав образован костью голени (большеберцовая кость) и бедренной костью (бедренная кость).Бедро представляет собой шарообразный (на конце бедренной кости) и суставную впадину (часть таза). Концы костей в суставе покрыты хрящом, который обеспечивает гладкую, почти стеклянную поверхность. Суставы также производят жидкость (синовиальную жидкость), которая снижает трение и износ. Поврежденный или артритный сустав можно заменить искусственным суставом (рис. 6.12). Эти заменители могут быть изготовлены из металла (нержавеющая сталь или титан) или пластика (полиэтилен), также с очень малым коэффициентом трения.

Фигура 6,12 Замена искусственного колена – это процедура, которая проводится более 20 лет. Эти послеоперационные рентгеновские снимки показывают замену правого коленного сустава. (кредит: модификация работы Майка Бэрда)

Натуральные лубриканты включают слюну, вырабатываемую во рту, чтобы помочь в процессе глотания, и скользкую слизь, находящуюся между органами в теле, позволяющую им свободно перемещаться друг мимо друга во время сердечных сокращений, во время дыхания и при движении человека.Больницы и врачебные клиники обычно используют искусственные смазки, такие как гели, для уменьшения трения.

Уравнения статического и кинетического трения представляют собой эмпирические законы, описывающие поведение сил трения. Хотя эти формулы очень полезны для практических целей, они не имеют статуса математических утверждений, которые представляют общие принципы (например, второй закон Ньютона). Фактически, есть случаи, когда эти уравнения даже не являются хорошими приближениями.Например, ни одна из формул не является точной для смазанных поверхностей или для двух поверхностей, пересекающих друг друга на высоких скоростях. Если не указано иное, мы не будем касаться этих исключений.

Пример 6.10

Статическое и кинетическое трение

Ящик весом 20,0 кг стоит на полу, как показано на рис. 6.13. Коэффициент статического трения между обрешеткой и полом составляет 0,700, а коэффициент кинетического трения составляет 0,600. К обрешетке прилагается горизонтальная сила P → P →.. Фигура 6,13 (а) Ящик на горизонтальной поверхности толкает с силой P → .P →. (б) Силы, действующие на ящик. Здесь f → f → может представлять либо статическую, либо кинетическую силу трения.

Стратегия

Схема ящика со свободным телом показана на Рисунке 6.13 (b). Мы применяем второй закон Ньютона в горизонтальном и вертикальном направлениях, включая силу трения, противоположную направлению движения коробки.

Решение

Второй закон Ньютона ДАЕТ∑Fx = max∑Fy = mayP − f = maxN − w = 0.∑Fx = max∑Fy = mayP − f = maxN − w = 0.

Здесь мы используем символ f для обозначения силы трения, поскольку мы еще не определили, подвержен ли ящик трению станции или кинетическому трению. Мы делаем это всякий раз, когда не уверены, какой тип трения действует. Теперь вес ящика

w = (20,0 кг) (9,80 м / с2) = 196N, w = (20,0 кг) (9,80 м / с2) = 196N,

, что также равно N . Таким образом, максимальная сила трения покоя составляет (0,700) (196 Н) = 137 Н. (0,700) (196 Н) = 137 Н.Пока P → P → меньше 137 Н, сила статического трения удерживает ящик в неподвижном состоянии и fs = P → .fs = P →. Таким образом, (a) fs = 20.0N, fs = 20.0N, (b) fs = 30.0N, fs = 30.0N и (c) fs = 120.0N.fs = 120.0N.

(d) Если P → = 180,0 Н, P → = 180,0 Н, приложенная сила больше максимальной силы статического трения (137 Н), поэтому ящик больше не может оставаться в покое. Когда ящик находится в движении, действует кинетическое трение. Тогда

fk = μkN = (0,600) (196N) = 118N, fk = μkN = (0,600) (196N) = 118N,

и ускорение

ах = P − fkm = 180.0N − 118N20,0 кг = 3,10 м / с 2.ax = P − fkm = 180,0 N − 118N20,0 кг = 3,10 м / с2.

Значение

Этот пример показывает, как мы рассматриваем трение в задаче динамики. Обратите внимание, что статическое трение имеет значение, соответствующее приложенной силе, пока мы не достигнем максимального значения статического трения. Кроме того, движение не может происходить до тех пор, пока приложенная сила не сравняется с силой статического трения, но тогда сила кинетического трения станет меньше.

Проверьте свое понимание 6,7

Блок массы 1.0 кг лежит на горизонтальной поверхности. Коэффициенты трения для блока и поверхности составляют μs = 0,50 μs = 0,50 и μk = 0,40.μk = 0,40. а) Какая минимальная горизонтальная сила требуется для перемещения блока? (б) Каково ускорение блока при приложении этой силы?

Трение и наклонная плоскость

Одна из ситуаций, в которой трение играет очевидную роль, – это объект на склоне. Это может быть ящик, который поднимают по пандусу к погрузочной платформе, или скейтбордист, спускающийся с горы, но основная физика остается той же.Обычно мы обобщаем наклонную поверхность и называем ее наклонной плоскостью, но затем делаем вид, что поверхность плоская. Давайте посмотрим на пример анализа движения на наклонной плоскости с трением.

Пример 6,11

Скоростной спуск

Лыжник массой 62 кг скользит по снежному склону с постоянным ускорением. Найдите коэффициент кинетического трения лыжника, если известно, что трение составляет 45,0 Н.

Стратегия

Величина кинетического трения равна 45.0 Н. Кинетическое трение связано с нормальной силой NN соотношением fk = μkNfk = μkN; таким образом, мы можем найти коэффициент кинетического трения, если сможем найти нормальную силу, действующую на лыжника. Нормальная сила всегда перпендикулярна поверхности, и поскольку нет движения перпендикулярно поверхности, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону. (См. Рис. 6.14, на котором повторяется фигура из главы о законах движения Ньютона.) Фигура 6,14 Движение лыжника и трение параллельны склону, поэтому наиболее удобно проецировать все силы в систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника).Нормальная сила N → N → перпендикулярна склону, а трение f → f → параллельно склону, но вес лыжника w → w → имеет компоненты вдоль обеих осей, а именно w → yw → y и w → xw → Икс. Нормальная сила N → N → равна по величине w → y, w → y, поэтому нет движения перпендикулярно склону.

У нас

N = wy = wcos25 ° = mgcos25 ° .N = wy = wcos25 ° = mgcos25 °.

Подставляя это в выражение для кинетического трения, получаем

fk = μkmgcos25 °, fk = μkmgcos25 °,

, который теперь можно решить для коэффициента кинетического трения μk.мкк.

Решение

Решение относительно μkμk дает μk = fkN = fkwcos25 ° = fkmgcos25 ° .μk = fkN = fkwcos25 ° = fkmgcos25 °.

Подставляя известные значения в правую часть уравнения,

μk = 45,0 Н (62 кг) (9,80 м / с2) (0,906) = 0,082. μk = 45,0 Н (62 кг) (9,80 м / с2) (0,906) = 0,082.

Значение

Этот результат немного меньше, чем коэффициент, указанный в таблице 6.1 для вощеной древесины на снегу, но он все же разумен, поскольку значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой м скользит по склону, составляющему угол θθ с горизонтом, трение определяется как fk = μkmgcosθ.fk = μkmgcosθ. В этих условиях все объекты скользят по склону с постоянным ускорением.

Мы обсуждали, что когда объект лежит на горизонтальной поверхности, нормальная сила, поддерживающая его, равна по величине его весу. Кроме того, простое трение всегда пропорционально нормальной силе. Когда объект находится не на горизонтальной поверхности, как в случае с наклонной плоскостью, мы должны найти силу, действующую на объект, которая направлена перпендикулярно поверхности; это составляющая веса.

Теперь мы выведем полезное соотношение для расчета коэффициента трения на наклонной плоскости. Обратите внимание, что результат применим только к ситуациям, когда объект скользит по рампе с постоянной скоростью.

Объект скользит по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в Примере 6.11, кинетическое трение на склоне равно fk = μkmgcosθfk = μkmgcosθ.Компонент веса вниз по склону равен mgsinθmgsinθ (см. Диаграмму свободного тела на рис. 6.14). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Выписывая их, получаем

μkmgcosθ = mgsinθ.μkmgcosθ = mgsinθ.

Решая для μk, μk, находим

μk = mgsinθmgcosθ = tanθ.μk = mgsinθmgcosθ = tanθ.

Поместите монету в книгу и наклоните ее, пока монета не будет скользить по книге с постоянной скоростью. Возможно, вам придется слегка постучать по книге, чтобы монета двинулась.Измерьте угол наклона относительно горизонтали и найдите μk.μk. Обратите внимание, что монета вообще не начинает скользить, пока не будет достигнут угол, превышающий θθ, поскольку коэффициент статического трения больше, чем коэффициент кинетического трения. Подумайте, как это может повлиять на значение μkμk и его неопределенность.

Объяснение трения в атомном масштабе

Наиболее простые аспекты трения, о которых до сих пор говорилось, – это его макроскопические (крупномасштабные) характеристики. За последние несколько десятилетий в объяснении трения в атомном масштабе были достигнуты большие успехи.Исследователи обнаруживают, что атомная природа трения, по-видимому, имеет несколько фундаментальных характеристик. Эти характеристики не только объясняют некоторые из более простых аспектов трения – они также содержат потенциал для развития среды, почти свободной от трения, которая могла бы сэкономить сотни миллиардов долларов энергии, которая в настоящее время преобразуется (без необходимости) в тепло.

Рисунок 6.15 иллюстрирует одну макроскопическую характеристику трения, которая объясняется микроскопическими (мелкомасштабными) исследованиями.Мы отметили, что трение пропорционально нормальной силе, но не площади соприкосновения, что несколько противоречит здравому смыслу. Когда две шероховатые поверхности соприкасаются, фактическая площадь контакта составляет крошечную долю от общей площади, потому что соприкасаются только высокие точки. Когда прикладывается большая нормальная сила, фактическая площадь контакта увеличивается, и мы обнаруживаем, что трение пропорционально этой площади.

Фигура 6,15 Две соприкасающиеся шероховатые поверхности имеют гораздо меньшую площадь фактического контакта, чем их общая площадь.Когда нормальная сила больше в результате большей приложенной силы, площадь фактического контакта увеличивается, как и трение.

Однако представление в атомном масштабе обещает объяснить гораздо больше, чем более простые особенности трения. Механизм генерации тепла сейчас определяется. Другими словами, почему при трении поверхности нагреваются? По сути, атомы связаны друг с другом, образуя решетки. Когда поверхность трутся, поверхностные атомы прилипают и заставляют атомные решетки вибрировать, по сути создавая звуковые волны, проникающие в материал.Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с трением, также могут происходить между атомами и молекулами на поверхностях. На рис. 6.16 показано, как острие зонда, проведенного по другому материалу, деформируется трением атомного масштаба. Можно измерить силу, необходимую для перетаскивания наконечника, и оказалось, что она связана с напряжением сдвига, которое обсуждается в разделе «Статическое равновесие и упругость». Изменение напряжения сдвига замечательно (более чем в 1012 · 1012 раз) и его трудно предсказать теоретически, но напряжение сдвига дает фундаментальное понимание крупномасштабного явления, известного с древних времен – трения.

Фигура 6,16 Наконечник зонда деформируется вбок под действием силы трения, когда зонд волочится по поверхности. Измерения того, как сила изменяется для разных материалов, дают фундаментальное представление об атомной природе трения.

Пример 6,12

Блоки сдвижные

Два блока на рис. 6.17 прикреплены друг к другу безмассовой струной, которая обернута вокруг шкива без трения. Когда внизу 4.Блок массой 00 кг тянется влево постоянной силой P →, P →, верхний блок массой 2,00 кг скользит по нему вправо. Найдите величину силы, необходимой для перемещения блоков с постоянной скоростью. Предположим, что коэффициент кинетического трения между всеми поверхностями равен 0,400.

Фигура 6,17 (а) Каждый блок движется с постоянной скоростью. (б) Диаграммы свободного тела для блоков.

Стратегия

Мы анализируем движения двух блоков по отдельности. На верхний блок действует контактная сила со стороны нижнего блока.Составляющими этой силы являются нормальная сила N1N1 и сила трения −0,400N1. − 0,400N1. Другими силами, действующими на верхний блок, являются натяжение TiTi в струне и вес самого верхнего блока, 19,6 Н. На нижний блок действуют контактные силы из-за верхнего блока и из-за пола. Первая контактная сила имеет компоненты -N1-N1 и 0,400N1,0,400N1, которые представляют собой просто силы реакции на контактные силы, которые нижний блок оказывает на верхний блок. Составляющие силы контакта пола равны N2N2 и 0.400N2.0.400N2. Другие силы на этот блок: -P, -P, натяжение Ti, Ti и вес -39,2 Н.

Решение

Поскольку верхний блок движется горизонтально вправо с постоянной скоростью, его ускорение равно нулю как в горизонтальном, так и в вертикальном направлениях. Из второго закона Ньютона ∑Fx = m1ax∑Fy = m1ayT − 0.400N1 = 0N1−19.6N = 0.∑Fx = m1ax∑Fy = m1ayT − 0.400N1 = 0N1−19.6N = 0.

Решая для двух неизвестных, получаем N1 = 19,6NN1 = 19,6N и T = 0,40N1 = 7,84N.T = 0,40N1 = 7,84N. Нижний блок также не ускоряется, поэтому применение второго закона Ньютона к этому блоку дает

∑Fx = m2ax∑Fy = m2ayT − P + 0.400N1 + 0,400N2 = 0N2−39,2N − N1 = 0.∑Fx = m2ax∑Fy = m2ayT − P + 0,400N1 + 0,400N2 = 0N2−39,2N − N1 = 0.

Значения N1N1 и T были найдены с помощью первой системы уравнений. Когда эти значения подставляются во вторую систему уравнений, мы можем определить N2N2 и P . Их

N2 = 58,8N и P = 39,2N, N2 = 58,8NandP = 39,2N.

Значение

Часто бывает сложно понять, в каком направлении рисовать силу трения. Обратите внимание, что каждая сила трения обозначена на рисунке 6.17 действует в направлении, противоположном движению соответствующего блока.

Пример 6,13

Ящик на грузовике-ускорителе

Ящик весом 50,0 кг стоит на платформе грузовика, как показано на рис. 6.18. Коэффициенты трения между поверхностями равны μk = 0,300μk = 0,300 и μs = 0,400.μs = 0,400. Найдите силу трения обрешетки, когда грузовик ускоряется вперед относительно земли: (a) 2,00 м / с ² и (b) 5,00 м / с ².

Фигура 6.18 (а) Ящик стоит на платформе грузовика, который ускоряется вперед. (б) Схема ящика со свободным телом.

Стратегия

Силы, действующие на ящик, – это его вес, а также нормальные силы и силы трения, возникающие при контакте с кузовом грузовика. Мы начинаем с , предполагая, что , что ящик не скользит. В этом случае на обрешетку действует статическая сила трения fsfs. Кроме того, ускорения ящика и грузовика одинаковы.

Решение

Применение второго закона Ньютона к ящику с использованием системы отсчета, прикрепленной к земле, дает
∑Fx = max∑Fy = mayfs = (50.0 кг) (2,00 м / с2) N − 4,90 × 102N = (50,0 кг) (0) = 1,00 × 102NN = 4,90 × 102 Н.∑Fx = max∑Fy = mayfs = (50,0 кг) (2,00 м / с2) N −4,90 × 102N = (50,0 кг) (0) = 1,00 × 102NN = 4,90 × 102N. Теперь мы можем проверить справедливость нашего предположения об отсутствии проскальзывания. Максимальное значение силы статического трения –
мксН = (0,400) (4,90 × 102Н) = 196Н, мксН = (0,400) (4,90 × 102Н) = 196Н, тогда как фактическая сила трения , которая действует, когда грузовик ускоряется вперед со скоростью 2,00 м / с22,00 м / с2, составляет всего 1,00 × 102Н. 1,00 × 102Н. Таким образом, предположение об отсутствии проскальзывания остается в силе.
Если ящик должен двигаться вместе с грузовиком при ускорении 5,0 м / с2,5,0 м / с2, сила статического трения должна составлять
fs = макс = (50,0 кг) (5,00 м / с2) = 250 Н. fs = макс = (50,0 кг) (5,00 м / с2) = 250 Н. Поскольку это превышает максимальное значение 196 Н, обрешетка должна соскользнуть. Таким образом, сила трения кинетическая и составляет
fk = μkN = (0,300) (4,90 × 102N) = 147N. fk = μkN = (0,300) (4,90 × 102N) = 147N. Горизонтальное ускорение ящика относительно земли теперь определяется по
. ∑Fx = max147N = (50,0 кг) топор, soax = 2.94 м / с2. Fx = max147N = (50,0 кг) топор, soax = 2,94 м / с2.

Значение

Относительно земли грузовик ускоряется вперед со скоростью 5,0 м / с25,0 м / с2, а ящик ускоряется вперед со скоростью 2,94 м / с22,94 м / с2. Следовательно, ящик скользит назад относительно платформы грузовика с ускорением 2,94 м / с2-5,00 м / с2 = -2,06 м / с2,2,94 м / с2-5,00 м / с2 = -2,06 м / с2.

Пример 6,14

Сноуборд

Ранее мы проанализировали ситуацию, когда горнолыжник движется с постоянной скоростью, чтобы определить коэффициент кинетического трения.Теперь давайте проведем аналогичный анализ, чтобы определить ускорение. Сноубордист, изображенный на рис. 6.19, скользит по склону, наклоненному под углом θ = 130θ = 130 к горизонтали. Коэффициент кинетического трения между доской и снегом составляет μk = 0,20, μk = 0,20. Какое ускорение у сноубордиста?

Фигура 6,19 (a) Сноубордист спускается по склону с уклоном 13 ° к горизонтали. (б) Схема свободного тела сноубордиста.

Стратегия

Силы, действующие на сноубордиста, – это ее вес и сила контакта на склоне, которая имеет составляющую, перпендикулярную склоне, и составляющую вдоль склона (сила кинетического трения).Поскольку она движется по склону, наиболее удобной системой отсчета для анализа ее движения является система с осью x вдоль и осью y , перпендикулярной наклонной плоскости. В этой системе координат и нормальная сила, и сила трения лежат вдоль координатных осей, компоненты веса – это mgsinθ вдоль наклона и mgcosθ под прямым углом к наклону, mgsinθ вдоль наклона и mgcosθ под прямым углом к наклону, и единственное ускорение идет вдоль x -ось (ay = 0).(ау = 0).

Решение

Теперь мы можем применить второй закон Ньютона к сноубордисту: ∑Fx = max∑Fy = maymgsinθ − μkN = maxN − mgcosθ = m (0) .∑Fx = max∑Fy = maymgsinθ − μkN = maxN − mgcosθ = m (0).

Из второго уравнения N = mgcosθ.N = mgcosθ. Подставив это в первое уравнение, находим

ax = g (sinθ − μkcosθ) = g (sin13 ° −0.20cos13 °) = 0,29 м / с 2.ax = g (sinθ − μkcosθ) = g (sin13 ° −0,20cos13 °) = 0,29 м / с2.

Значение

Обратите внимание на это уравнение: если θθ достаточно мало или μkμk достаточно велико, axax отрицательна, то есть сноубордист замедляется.

Проверьте свое понимание 6,8

Сноубордист спускается с холма с уклоном 10,0 ° 10,0 °. Какое ускорение у лыжника?

Урок 6: Работа с уравнениями

Управление уравнениями, вероятно, один из самых важных навыков, которым нужно овладеть в школьном курсе физики.

Хотя он основан на знакомых (и довольно простых) математических концепциях, он все еще остается камнем преткновения для большинства начинающих студентов-физиков.
Управление уравнением означает, что вы переставляете уравнение так, чтобы неизвестное, которое вы пытаетесь вычислить, находилось само по себе на одной стороне уравнения.
Не используйте для формулы v = d / t какие-либо методы, такие как «треугольник», который вы выучили в младших классах. Это отлично подходит для простой формулы, но попробуйте использовать ее для v _f ² = v _i ² + 2ad.
Позже в ходе курса вы также сможете комбинировать формулы (что необходимо) для решения более сложных задач.
Изучение того, как манипулировать формулами сейчас (пока формулы еще простые!) Окупится позже.

Всегда помните два основных математических правила …

Чтобы переместить что-либо на другую сторону, просто выполните математическую операцию, противоположную этому.
Если вы сделаете это с одной стороны, сделайте то же с другой.

Пример 1: Основная формула для расчета скорости объекта: v = d / t , где «v» – скорость, «d» – смещение, а «t» – время. Эта формула хороша «как есть», если мы собираемся вычислить скорость, но что, если мне нужно рассчитать смещение, и мне даны скорость и время? Нам нужно манипулировать формулой, чтобы найти « d ».

В формуле v = d / t «d» делится на «t». Чтобы перевести «t» на другую сторону, нам нужно сделать обратное … умножить на «t»!

но то, что мы делаем с одной стороной, мы делаем с другой …

буквы “т” справа компенсируют друг друга …

последний шаг (и это, по сути, просто традиция) – поместить наше неизвестное в левую часть уравнения. Итак, давайте перевернем все это, чтобы получить окончательное уравнение!

d = t v

И все! Это не новая формула, которую нужно запоминать; это формула, которая уже есть в вашем листе данных, которую вы изменили, чтобы упростить ее использование для конкретного вопроса.

Теперь попробуйте решить ту же формулу для «t». У вас должно получиться …

Будьте осторожны с формулами со сложением, вычитанием, квадратными корнями и квадратами.

В основном вам нужно следовать правилу BEDMAS (скобки, экспоненты, деление, умножение, сложение, вычитание) из математики, но в обратном порядке. Всегда сначала заботьтесь о сложении и вычитании, затем об умножении и делении и, наконец, о показателях (помните, что квадратный корень – это просто показатель степени).

Пример 2: Решите следующую формулу для v _i

Прежде чем делать что-либо еще, позаботьтесь о том, чтобы что-либо добавлялось или вычиталось из v _i, выполнив обратное …

, что оставляет нам …

переверните всю формулу (так v _i находится слева) и извлеките квадратный корень из обеих частей …

и готово!

4.3: Momenta of Systems – Physics LibreTexts

Сохранение импульса

Наша причина изучения центра масс заключалась в том, чтобы понять его роль в сохранении импульса.Теперь мы можем распаковать “\ (\ Delta \ overrightarrow p_ {cm} \)” из уравнения 4.1.5. Мы знаем, что дельта означает «после минус до», поэтому давайте сосредоточимся на остальном:

\ [\ overrightarrow p_ {cm} = M \ overrightarrow v_ {cm} = M \ dfrac {d} {dt} \ overrightarrow r_ {cm} = \ cancel {M} \ dfrac {d} {dt} \ left [ \ dfrac {m_1 \ overrightarrow r_1 + m_2 \ overrightarrow r_2 + \ dots} {\ cancel {M}} \ right] = m_1 \ dfrac {d} {dt} \ overrightarrow r_1 + m_2 \ dfrac {d} {dt} \ overrightarrow r_2 + \ dots = m_1 \ overrightarrow v_1 + m_2 \ overrightarrow v_2 + \ dots = \ overrightarrow p_1 + \ overrightarrow p_2 + \ dots \]

Итак, мы видим очень важный результат:

Импульс системы, определяемый как полная масса системы, умноженная на скорость центра масс этой системы, равняется (векторной) сумме импульсов отдельных объектов, содержащихся в системе.

Предупреждение

Повторяем предыдущее предупреждение … Скорость центра масс системы – это скорость математической конструкции, а не определенного куска материи. Объекты внутри системы движутся так же, как и они, и центр масс определяется из всех этих движений. В самом деле, центр масс может оставаться неподвижным, даже если каждый объект в системе движется, если их импульсы сокращаются до нуля.

Если теперь снова ввести дельту и предположить, что сумма внешних импульсов равна нулю, мы получим следующее выражение сохранения импульса системы:

\ [0 = \ Delta \ overrightarrow p_ {cm} = \ Delta \ overrightarrow p_1 + \ Delta \ overrightarrow p_2 + \ dots \]

Когда мы говорим о нескольких объектах, вероятно, более интуитивно понятнее будет принять эквивалентную точку зрения «до = после».Это состоит из разбивки всех \ (\ Delta \ overrightarrow p \) на \ (\ overrightarrow p_ {after} – \ overrightarrow p_ {before} \) и сбора всех “befores” на одной стороне уравнение, а с другой – «афтеры». Это выглядит так:

\ [\ underbrace {\ overrightarrow p_1 + \ overrightarrow p_2 + \ dots} _ {before} = \ underbrace {\ overrightarrow p_1 + \ overrightarrow p_2 + \ dots} _ {after} \]

Сумма с каждой стороны превышает несколько объектов в системе. Таким образом, сложение векторов импульса всех объектов перед некоторым событием, а затем повторение этого снова после события дает тот же вектор.Это, конечно, предполагает, что «событие» не связано с внешним импульсом, хотя оно может включать в себя любое количество внутренних импульсов.

Предупреждение

Важно помнить, что это уравнение не означает, что каждый из членов остается неизменным. Скорее, они изменяются таким образом, что все изменения компенсируют друг друга, и сумма совершенно новых векторов импульса возвращается к той же сумме, что и раньше.

Пример \ (\ PageIndex {2} \)

А 30.Ребенок весом 0 кг сидит на заднем конце саней длиной 12,0 кг и 3,50 м (масса которой равномерно распределена по длине) с блоком замороженного снега весом 18 кг, лежащим у нее на коленях. Сани скользят вперед по горизонтальному снегу без трения с постоянной скоростью 1,60 м / с, когда девушка внезапно толкает блок вперед в салазках (она остается твердо стоящей на салазках). По прошествии 2,50 с блок останавливается в передней части салазок.

Найдите скорость салазок после того, как блок перестанет скользить вперед.
Найдите положение центра масс девушки + сани + блока до того, как блок будет вытолкнут. Обозначьте это положение с задней стороны салазок.
Найдите расстояние (относительно земли), на которое центр масс девушки + сани + блок перемещается в течение периода времени, когда блок скользит вперед.
Найдите расстояние, на которое салазки перемещаются за период времени, когда блок скользит вперед.

Решение

а.Чтобы получить этот ответ, можно проделать все «промежуточные» вычисления, но самый простой способ – это отметить, что все силы между ребенком, снегом и салазками являются внутренними по отношению к системе, и система не испытывает чистой внешней силы. это означает, что движение его центра масс остается неизменным. Центр масс системы перемещался со скоростью 1,60 м / с до того, как ребенок толкнул ребенка, и он будет двигаться с той же скоростью, что и снег, и с такой же скоростью после того, как снег остановится. Сани будут двигаться медленнее, чем его начальная скорость, поскольку снег движется вперед, потому что сани движутся не вместе с центром масс системы, но когда снег достигает передней части, вся система снова движется вместе.

г. Чтобы найти центр масс системы, мы рассматриваем каждый объект в системе как точечную массу, существующую в его собственном центре масс, и включаем уравнение центра масс. Выбирая заднюю часть санок в качестве исходной точки (наша контрольная точка), девушка и снег находятся в исходной точке, в то время как центр масс саней находится на половине ее длины от начала координат, что дает:

\ [x_ {cm} = \ dfrac {m_ {girl} x_ {girl} + m_ {snow} x_ {snow} + m_ {sled} x_ {sled}} {m_ {girl} + m_ {snow} + m_ {sled}} = \ в коробке {0.350м} \ nonumber \]

г. Скорость системы остается неизменной в течение этого времени (как указано в части a), поэтому расстояние, на которое перемещается центр масс в течение этого периода, равно скорости, умноженной на время:

\ [\ Delta x_ {cm} = v_ {cm} t = \ boxed {4,00m} \ nonumber \]

г. Как бы далеко ни проехали сани, девочка проходит такое же расстояние, а снег проходит это расстояние плюс длина саней.Подставив все эти изменения в уравнение изменения центра масс (всей системы), получим:

\ [\ Delta x_ {cm} = \ dfrac {m_ {girl} \ Delta x_ {girl} + m_ {snow} \ Delta x_ {snow} + m_ {sled} \ Delta x_ {sled}} {m_ { girl} + m_ {snow} + m_ {sled}} = \ dfrac {m_ {girl} \ Delta x_ {sled} + m_ {snow} \ left (\ Delta x_ {sled} + L \ right) + m_ {sled } \ Delta x_ {sled}} {M} \ nonumber \]

Решение для перемещения салазок дает:

\ [\ Delta x_ {sled} = \ Delta x_ {cm} – \ dfrac {m_ {snow} L} {M} = \ boxed {2.95m} \ nonumber \]

Использование центра масс

Давайте рассмотрим пример того, как мы можем использовать то, что мы знаем о центре масс, для анализа случая двух блоков разной массы, которые сжимают (безмассовую) пружину между собой, пока они не выйдут из состояния покоя.

Рисунок 4.3.1 – отталкивающие Массы

Интуитивно, наверное, можно сказать, что для данной ситуации \ (m_2> m_1 \).Когда легкий объект отталкивается от тяжелого (блоха, спрыгивающая с собаки, пуля, вылетающая из пистолета и т. Д.), Движение более легкого объекта всегда изменяется в большей степени. С нашей физической подготовкой мы можем объяснить это вторым и третьим законами Ньютона: блоки толкают друг друга с равными силами (третий закон), и при равных силах блок с меньшей массой будет ускоряться больше. Оба они начинают из состояния покоя и толкаются в течение равных периодов времени, поэтому тот, у кого больше ускорение, будет двигаться быстрее, когда они разделятся, отправив его на большее расстояние за тот же период времени.

Хорошо, теперь давайте посмотрим на это с точки зрения сохранения импульса. Если рассматривать два блока как единую систему, сила пружины производит только внутренние импульсы, а это означает, что импульс системы сохраняется. Импульс перед разгрузкой пружины равен нулю, поэтому после этого он должен быть равен нулю. Если \ (v_1 \) и \ (v_2 \) – скорости двух блоков (т.е. это положительные числа), то для нашего уравнения сохранения имеем:

\ [импульс \; before = импульс \; после \;\;\; \Правая стрелка \;\;\; 0 = m_1 v_1 \ left (- \ widehat i \ right) + m_2 v_2 \ left (+ \ widehat i \ right) \; \; \; \Правая стрелка \;\;\; v_1 = \ dfrac {m_2} {m_1} v_2 \]

Поскольку из диаграммы ясно, что \ (v_1> v_2 \), должно быть это \ (m_2> m_1 \).Мы также можем использовать здесь то, что мы знаем о центре масс. Система не испытывает внешнего сетевого импульса, и ее центр масс неподвижен, поэтому он должен оставаться неподвижным! Мы не знаем точно, где находится центр масс до отталкивания, но поскольку он остается на месте, мы можем провести вертикальную линию вниз на второй диаграмме, чтобы найти, где он находится после отталкивания. Это явно приводит к тому, что центр масс находится ближе к \ (m_2 \), что означает, что это большая масса.

Центр ускорения масс

Давайте посмотрим, сможем ли мы включить то, что мы узнали о центре масс, чтобы понять второй закон Ньютона.Рассмотрим две системы, показанные на рисунке 4.3.2. Каждая состоит из набора из 8 идентичных частиц, находящихся в непосредственной близости друг от друга (показанные прямоугольники используются только в качестве ориентира для последующего движения – они не являются физическими объектами). В левой системе частицы плавают свободно (нет гравитации или других сил), в то время как на правой диаграмме частицы связаны вместе жесткими безмассовыми стержнями. Две системы идентичны во всех отношениях, за исключением наличия этих стержней – все частицы имеют те же положения и массы, что и их аналоги, и все они находятся в состоянии покоя.

Теперь об эксперименте: предположим, что мы прилагаем одинаковую силу к одной и той же частице в обеих системах. Ясно, что в этих двух случаях реакция различна – в левом случае только частица, получившая толчок, ускоряется, в то время как в правых случаях ускоряется вся группа частиц. Возникает вопрос, в каком случае центр масс системы частиц ускоряется на больше ?

Рисунок 4.3.2 – Нагрузки на свободных и жестких систем

Вот краткий ответ: силы, которые существуют (или не существуют) между частицами, определяющими систему, являются внутренними и, следовательно, не влияют на скорость центра масс системы.Единственная внешняя сила, действующая на каждую систему, – это \ (\ overrightarrow F \), и каждая система имеет одинаковую массу, поэтому второй закон Ньютона гласит, что обе системы должны реагировать с одинаковым ускорением своего центра масс.

Но это неубедительно, когда мы видим, что в одном случае движется только одна частица, а в другом – весь конгломерат! Предположим, силы действуют в течение некоторого небольшого промежутка времени. Ускорение отдельной частицы будет в восемь раз больше, чем у конгломерата, поэтому за тот же интервал времени она переместится в восемь раз дальше конгломерата.Назовем начальное положение центра масс началом координат. Семь частиц, оставшихся позади, не претерпевают никаких изменений в своем положении относительно этого источника, и положение одной частицы относительно начала координат перемещается на восемь единиц расстояния, в то время как все восемь частиц в другой системе перемещаются только на одну единицу от своих исходных положений относительно к происхождению. Рассматривая направление движения как направление \ (+ x \) и подставляя массы и расстояния в уравнение 4.2.1, сразу должно быть ясно, что оба центра масс перемещаются на одинаковую величину.Как ни странно это звучит, второй закон Ньютона работает для любой системы частиц, независимо от того, связаны ли они вместе, образуя твердый объект, или полностью независимы друг от друга, как частицы в газе.

Рама центра масс

Иногда анализ проблем, связанных с взаимодействием нескольких объектов друг с другом, упрощается за счет использования так называемой системы координат центра масс . Вот пример.

Детская игрушка «горячий картофель» состоит из двух полусферических раковин, которые закрываются на пружине и удерживаются вместе защелкой на таймере.Когда время истекает, защелка освобождается, и пружина может расшириться, стреляя двумя снарядами в противоположных направлениях, подвергая игрушечную компанию иску об ответственности за качество продукции от семьи ребенка, который держит горячий картофель, когда он срабатывает.

Предположим, что ребенок бросает эту горячую картошку в воздух, и на пике ее движения снаряда он взрывается так, что два снаряда летят горизонтально, как показано на рисунке 4.3.3. Отмечается точка приземления снаряда, который приземляется ближе всего к тому месту, где была брошена игрушка, но другой снаряд улетает в высокую траву и теряется.Естественно, ребенок знает начальную скорость, которую он дал игрушке, а также угол выхода, и он может легко измерить расстояние, которое проходит более близкий снаряд от точки запуска. Основываясь на этой информации и своих обширных познаниях в физике, она придумывает план по поиску другой оболочки, которая намного элегантнее, чем ее поиск в высокой траве.

Рисунок 4.3.3 – взрывающаяся Метательный

Силы, действующие на оболочки со стороны пружины, являются внутренними по отношению к системе с двумя оболочками, поэтому при условии, что сопротивление воздуха незначительно, центр масс системы будет вести себя точно так же, как если бы внутренние силы не существовали.Зная начальный угол и скорость, ребенок может использовать уравнение дальности (см. Пример 1.7.4) для вычисления точки приземления центра масс системы. Затем, используя фактическую точку приземления одной детали игрушки, она может использовать формулу центра масс для вычисления точки приземления другой детали.

Вы можете подумать, что мы можем сделать то же самое, даже если пружина разгружается в ориентации, отличной от горизонтальной, но это не так. Движение центра масс по-прежнему следует той же параболической траектории, но, естественно, центр масс всегда находится между двумя оболочками.В приведенном выше случае снаряды приземляются одновременно (оба они начинают с нулевой вертикальной составляющей скорости, когда происходит взрыв), поэтому центр масс приземляется одновременно между снарядами. Когда взрыв не горизонтальный, один снаряд приземляется раньше другого, тогда трение прекращается – это горизонтальное движение, в то время как другой снаряд продолжает двигаться горизонтально. Это делает невозможным вычисление точки приземления центра масс с использованием обычного уравнения дальности.

Пример \ (\ PageIndex {3} \)

А 1.Блок весом 4 кг скользит по горизонтальной поверхности без трения со скоростью v = 4,8 м / с, начиная с положения x = 0 и времени t = 0. В момент времени t = 2,0 с идентичный блок приземляется прямо на него. Поверхности блоков являются липкими, поэтому верхний блок прилипает к нижнему блоку, когда он приземляется на него, и они продолжают движение вместе. Блоки скользят вместе в закрытое занавесом место, после чего вы слышите шум пружины и «глухой удар». В момент времени t = 5,0 с нижний блок выходит из завесы в положении x = 18.0 м без верхнего блока, после того, как верхняя крышка откинулась изнутри. Найдите положение x другого блока в это время (который, как предполагается, находится на поверхности без трения, все еще в пределах завешенной области).

Раствор

При столкновении двух блоков вертикальный импульс не сохраняется (гравитация и нормальная сила от пола не компенсируются во время столкновения, поэтому возникает чистый вертикальный импульс), но горизонтальный импульс сохраняется.Это потому, что горизонтальное трение (или «сила сцепления», если хотите) является внутренним по отношению к двухблочной системе. Блоки имеют равную массу, поэтому установка входящего горизонтального импульса одного блока, равного исходящему горизонтальному импульсу обоих блоков, дает:

\ [mv_o + 0 = 2mv_f \; \; \; \Правая стрелка \;\;\; v_f = \ frac {1} {2} v_o = 2,4 \ dfrac {m} {s} \ nonumber \]

Горизонтальный импульс двухблочной системы остается постоянным в течение всего времени, что означает, что центр масс этой системы продолжает двигаться с постоянной горизонтальной скоростью.Эта скорость центра масс, несомненно, является «конечной» скоростью, вычисленной выше, поскольку при \ (t = 2,0 с \) два блока движутся вместе. Поэтому все, что нам нужно, это начальное \ (x \) – положение центра масс системы и прошедшее время, и мы можем определить новое положение центра масс. Начальным положением центра масс двухблочной системы является \ (x \) – положение на полпути между блоками (поскольку они имеют равные массы), и мы можем установить начальное положение скользящего блока как начало координат, но каково \ (x \) – положение падающего блока?

Нам дано время, которое требуется скользящему блоку, чтобы достичь падающего блока, и у нас есть его скорость, поэтому мы знаем, как далеко эти два блока разделены в направлении \ (x \), и вместе с этим, исходное положение центра масс:

\ [x_ {cm} \ left (t = 0s \ right) = \ frac {1} {2} v_o t = 4.80м \ nonumber \]

С помощью скорости центра масс двухблочной системы, начального положения центра масс и прошедшего времени мы знаем, где находится центр масс позже:

\ [x_ {см} \ left (t \ right) = x_ {cm} \ left (t = 0s \ right) + v_ {cm} t = 16,8 м \ nonumber \]

Блоки имеют равную массу, поэтому это положение центра масс находится на полпути между двумя блоками, и, поскольку мы знаем положение скользящего блока, мы можем получить положение падающего блока:

\ [x_ {cm} = \ frac {1} {2} \ left (x_ {скольжение} + x_ {падение} \ right) \; \; \; \Правая стрелка \;\;\; х_ {падение} = \ в коробке {15.6м} \ nonumber \]

Ракетная техника

Пока мы обсуждаем тему двух частей системы, идущих разными путями, отталкиваясь друг от друга, это подводит нас к теме ракетной техники. Ракета, которая неподвижна в космосе, каким-то образом способна ускоряться за счет запуска своих двигателей. Как центр масс ракетной системы может ускоряться без воздействия на него внешних сил? Ну, конечно, не может, но ракета (точнее, ее фюзеляж) – это не изолированная система.Он выталкивает топливо (в виде очень горячего газа) назад. Если включить топливо как часть системы, то центр масс системы вообще не будет ускоряться! В конечном итоге имеет значение только то, что фюзеляж ракеты продвигается вперед. Также обратите внимание, что ракета имеет большую массу, чем топливо, но воспламененное топливо отсылает частицы с очень высокой скоростью, и этот импульс уравновешивает импульс фюзеляжа в противоположном направлении (который имеет большую массу и меньшую скорость).

Калькулятор плотности p = m / V

Использование калькулятора

Выберите расчет для плотности p, массы m или объема V.Введите два других значения, и калькулятор найдет третье в выбранных единицах. Вы также можете ввести научную нотацию, например, 3.45e22.

Уравнение плотности для этих расчетов:

\ (p = \ dfrac {m} {V} \)

Где:
p = плотность
м = масса
В = объем

Калькулятор плотности использует формулу p = m / V, или плотность (p) равна массе (m), деленной на объем (V).Калькулятор может использовать любые два значения для вычисления третьего. Плотность определяется как масса на единицу объема. Наряду со значениями введите известные единицы измерения для каждого, и этот калькулятор будет преобразовывать единицы измерения.

Значимые цифры

Для значения 165778 выбор 4 значащих цифр вернет 165800. Для значения 0,00165778 выбор 4 значащих цифр вернет 0,001658. См. Также наши справочные примечания по значимые фигуры.

Расчет плотности:

Решая для плотности, массы или объема, мы можем использовать следующие формулы:

Вычислить p по m и V
Рассчитайте плотность по массе и объему.

\ (p = \ dfrac {m} {V} \)

Вычислить m по заданным p и V
Рассчитайте массу с учетом плотности и объема.

\ (m = pV \)

Вычислить V для заданных p и m
Рассчитайте объем с учетом плотности и массы.

\ (V = \ dfrac {m} {p} \)

Кубический корень из объема показан для помощи в мысленной визуализации реального объема. Еще раз спасибо пользователю, который предложил этот калькулятор!

\ (\ sqrt [3] {V} \)

Физика скользящего блока

Блок на наклонной плоскости будет ускоряться вниз по плоскости. В величина ускорения определяется ускорением свободного падения, угол наклона плоскости и коэффициент трения блока с самолетом.

Коэффициент трения – это мера силы трения. который существует между двумя материалами, когда один скользит по другому. это ноль, если нет трения, и бесконечно, если нет движения возможный. Коэффициент трения лыж по снегу 0,01; из латунь на стекле – 0,1; и о растирании двух рук 0,5.

Вот еще один рисунок, который поможет вам познакомиться со значением векторы, которые также будут появляться в Лаборатории 4 (корова скользит вниз наклон).

В случае, если вы тянете объект по горизонтали поверхность, вы должны преодолеть статическое трение, чтобы получить объект движется. То есть приложенная сила должна преодолевать сила трения:

Максимальная сила статического трения между двумя поверхностями. пропорциональна нормальной силе и в основном не зависит от площади контакт. Эта ситуация показана здесь: N = полная нормальная сила (сила, перпендикулярная горизонтальной поверхности), которая по существу вес объекта.Коэффициент в этом уравнении называется коэффициент трения покоя, который зависит от материала:

Когда объект действительно движется, трение считается кинетическим. трение, которое обычно меньше трения покоя. Если мы добавляем больше массы, мы увеличиваем нормальную силу (Н) (потому что вес увеличилась) и, следовательно, мы увеличили общую силу трения. Это показано здесь, где видно, что необходимо вдвое большее усилие. применяется для перемещения двух кирпичей вместо одного (измеритель силы показывает вдвое больше).Обычно силы трения не зависят от площади контакта. хотя это эмпирическое наблюдение, а не теория. Рассмотрим металлический кирпич и металлический стол. Причина того, что трение почти не зависит от площади поверхности, заключается в если «микроскопическая» площадь контакта кирпича со столом независимо от ориентации кирпича. Если это не так, тогда трение будет иметь небольшую зависимость от площади. В нормальном обстоятельства, при которых наибольшая площадь поверхности кирпича соприкасается со столом имеется большое количество «контактных» точек, которые поддерживать нагрузку.При наименьшей площади соприкосновения (кирпичная кладка на конце) контактов меньше, но пока площадь каждого контакт больше из-за более высокого давления (та же сила, меньшая единица площадь), то разницы в величине статического трения не будет. В широких пределах большинство материалов следуют этому, и, следовательно, трение в значительной степени не зависит от площади поверхности. если у вас есть ситуация, когда площадь микроскопического контакта не масштабируется в соответствии с давление, то статическое трение будет зависеть от ориентации.
Потери энергии на трение
В общем, в реальном мире трение есть везде (к счастью) и почти любая макроскопическая система теряет энергию в виде ТЕПЛО от трения. Типичный пример – когда вы применяете ваши тормоза во время движения. Если вы едете со скоростью 80 миль в час на автострада (и, конечно, вы), а затем снизьте скорость до 0 миль в час тогда было потеряно очень много кинетической энергии. Эта потерянная энергия рассеивается в виде тепла. Теоретически, если бы ваша скорость была достаточно высокой и вы нажали на тормоза, чтобы достичь скорости = 0; ваши шины будут таять.
Формула натяжения | Проблемы с решенными примерами
На атомном уровне, когда атомы или молекулы отделяются друг от друга и получают потенциальную энергию с сохраняющейся восстанавливающей силой, восстанавливающая сила может создавать напряжение. Каждый конец струны или стержня при таком натяжении может тянуть за объект, к которому он прикреплен, чтобы вернуть струну / стержень к ее расслабленной длине.
Натяжение можно легко объяснить в случае подвешивания тел на цепи, тросе, веревке и т. Д.Он обозначается буквой T (иногда также обозначается Ft).
Если такое подвешенное тело движется вертикально с ускорением a, то;
T = W ± ma
Где W – вес тела, а m – масса тела
Случай (i) Если тело движется вверх, с ускорением a, натяжение; T = W + ma
Случай (ii) Если тело движется вниз с ускорением a, натяжение; T = W – ma
Случай (iii) Если тело просто подвешено (не движется), напряжение; Т = W.
Случай (iv) Если тело движется вверх или вниз с одинаковой скоростью, напряжение; T = W
Вес объекта W = мг.
Следовательно, формула натяжения может быть изменена как:
T = m (g ± a)
Где m = масса тела, g = ускорение свободного падения, a = ускорение движущегося тела.
Поскольку натяжение – это сила, ее единицей СИ является ньютон (Н).
Пример:
Легкая и нерастяжимая веревка поддерживает тело массой 15 кг, свисающее с нижнего конца.Если верхний конец тетивы надежно прикреплен к крючку на крыше, то каково натяжение тетивы?
Решение:
Поскольку тело не движется, а просто подвешено, натяжение тетивы будет равно весу тела. m = 15 кг
T = W = mg = 15 × 9,8 = 147 Н
Пример:
Обезьяна массой 10 кг поднимается по легкой вертикальной веревке, подвешенной к крюку с ускорением 2 м / с2. . Найдите натяжение струны (возьмите g = 10 м / с2)
Решение:
м = 10 кг, g = 10 м / с2, a = 2 м / с2
По мере того, как обезьяна движется вверх с При ускорении натяжение тетивы будет равно кажущемуся весу обезьяны.

Простые механизмы. Блок.. Блоки бывают подвижные и неподвижные… | by maxim | dx/dy

Физика 7 класс. Простые механизмы. Блок :: Класс!ная физика

Устали? – Отдыхаем!

Идеальный блок дает выигрыш. Блоки как простые механизмы

Применение подвижного и неподвижного блоков

Решение задач с подвижным и неподвижным блоками

Неподвижный блок

Подвижный блок

Поставим опыт

Физика подвижный и неподвижный блок. Простые механизмы. Золотое правило механики

Одинарные неподвижные блоки

Одинарные подвижные блоки

Системы блоков

Золотое правило механики

Примеры решения задач

Блоки. Золотое правило механики

Момент силы — как найти? В чем измеряется? Формулы

Сила: что это за величина

Плечо силы

Рычаг

Момент силы

Расчет момента силы

Правило моментов

Статика – Физика – Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Основы статики

Момент силы. Правило моментов

Рычаги и блоки

Центр тяжести тела

Контактные силы – Высшая школа физики

6.2 Трение – Университетская физика, Том 1

Цели обучения

Статическое и кинетическое трение

Трение

Статическое и кинетическое трение

Величина статического трения

Величина кинетического трения

Пример 6.10

Статическое и кинетическое трение

Стратегия

Решение

Значение

Проверьте свое понимание 6,7

Трение и наклонная плоскость

Пример 6,11

Скоростной спуск

Стратегия

Решение

Значение

Объяснение трения в атомном масштабе

Пример 6,12

Блоки сдвижные

Стратегия

Решение

Значение

Пример 6,13

Ящик на грузовике-ускорителе

Стратегия

Решение

Значение

Пример 6,14

Сноуборд

Стратегия

Решение

Значение

Проверьте свое понимание 6,8

Урок 6: Работа с уравнениями

4.3: Momenta of Systems – Physics LibreTexts

Сохранение импульса

Использование центра масс

Центр ускорения масс

Рама центра масс

Ракетная техника

Калькулятор плотности p = m / V

Использование калькулятора

Уравнение плотности для этих расчетов:

Значимые цифры

Расчет плотности:

Физика скользящего блока