Физика что такое давление: Недопустимое название — Викиверситет - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Закон Паскаля — для жидкостей и газов

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Давление

Идущий по рыхлому снегу человек будет в него постоянно проваливаться. А вот на лыжах он сможет передвигаться по тому же самому снегу спокойно. Казалось бы, ничего не меняется — человек воздействует на снег с одинаковой силой и на лыжах, и без них.

Дело в том, что «проваливание» в снег характеризуется не только силой — оно также зависит от площади, на которую эта сила воздействует. Площадь поверхности лыжи в 20 раз больше площади поверхности подошвы, поэтому человек, стоя на лыжах, действует на каждый квадратный сантиметр с силой в 20 раз меньшей, чем без них.

Или, например, если вы будете с одинаковой силой втыкать кнопки в пробковую доску, легче войдет та кнопка, у которой более заостренный конец, так как его площадь меньше.

Резюмируем: результат действия силы зависит не только от ее модуля, направления и точки приложения, но и от площади поверхности, к которой эта сила приложена.

А теперь подтвердим этот вывод опытами, как настоящие физики.

Возьмем небольшую доску и вобьем гвозди в ее углы. Также возьмем емкость с песком и поставим конструкцию из доски и гвоздей в эту емкость. Сначала расположим конструкцию шляпками вниз и поставим на нее гирю. Конструкция не утонет в песке, а только чуть-чуть углубится в него.

Затем перевернем конструкцию так, чтобы шляпки гвоздей оказались сверху и также поставим на доску гирю. Теперь конструкция утонет в песке.

От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия силы.

Во всех примерах мы говорили о действии силы, перпендикулярной поверхности. Чтобы охарактеризовать это действие, используется величина давление.

Давление

p = F/S

p — давление [Па]

F — сила [Н]

S — площадь [м²]

Как уменьшить или увеличить давление

Тяжелый гусеничный трактор производит давление на почву, равное 40–50 кПа. Мальчик массой 45 кг производит давление всего лишь в 3 раза меньше, чем такой трактор. Это связано с большой площадью гусениц трактора.

В зависимости от того, какое давление хотят получить, площадь опор уменьшают или увеличивают. Например, чтобы уменьшить давление здания на грунт, в процессе строительства увеличивают площадь нижней части фундамента.

Шины грузовых автомобилей делают значительно шире легковых автомобилей.

Чтобы убедиться в этом, обратите внимание на колеса какой-нибудь большой фуры. Самые широкие шины можно увидеть на автомобилях, предназначенных для передвижения в пустыне. Тот же лайфхак используется в шасси самолетов.

Обратную зависимость тоже применяют, например, при создании лезвий колющих и режущих инструментов. Острое лезвие имеет малую площадь, поэтому даже при небольшом нажатии создается большое давление.

Задачка раз

Книга лежит на столе. Масса книги равна 0,6 кг. Площадь ее соприкосновения со столом равна 0,08 м2. Определите давление книги на стол.

Решение

На стол будет давить сила, равная весу книги. Так как она покоится, ее вес будет равен силе тяжести. Следовательно:

p = mg/S = 0,6 × 10 / 0,08 = 75 Па

Ответ: давление книги на стол будет равно 75 Па.

Задачка два

Гусеничный трактор ДТ-75М массой 6 610 кг имеет опорную площадь обеих гусениц 1,4 м². Определите давление этого трактора на почву.

Решение:

p = mg/S = 6 610 × 10 / 1,4 = 47 214 Па = 47,2 кПа

Ответ: давление трактора на почву составляет 47,2 кПа.

Задачка три

Человек массой 80 кг с сумкой весом 100 Н стоит неподвижно на полу. Сила давления подошв его ботинок на пол равномерно распределена по площади 600 см2. Какое давление человек оказывает на пол?

Решение

Масса человека: m = 80 кг.

Вес сумки, которую держит человек: P_c = 100 Н.

Площадь соприкосновения подошвы ботинок с полом: S = 600 см².

600 см² = 600 / 10 000 м² = 0,06 м²

Давление — это отношение силы к площади, на которую она действует. В данном случае на площадь действует сила, равная сумме силы тяжести человека и веса сумки:

F = mg + P_с

Поэтому давление, оказываемое человеком с сумкой на пол, равно:

p = (mg + P_с) / S = (80 × 10 + 100) / 0,06 = 15 000 Па = 15 кПа

Ответ: давление человека с сумкой на пол равно 15 кПа.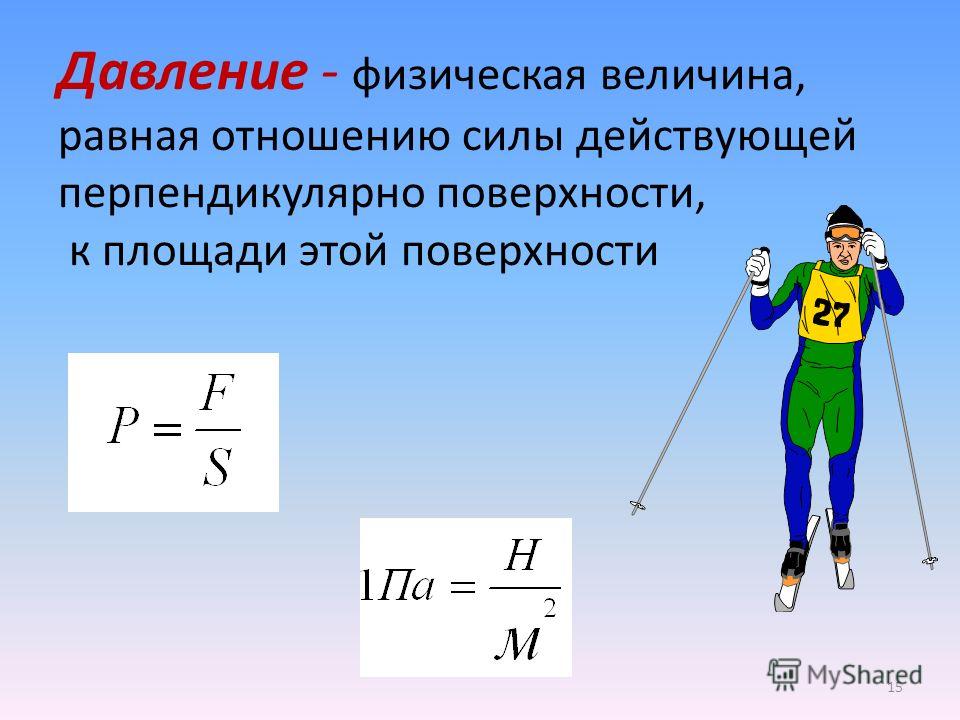

Еще больше интересной практики — на элективном курсе по физике для 10 класса.

Определение закона Паскаля

Итак, мы подошли к формулировке закона Паскаля, и звучит она так:

Давление, производимое на жидкость или газ, передается в любую точку одинаково во всех направлениях.

Обратите внимание — закон работает только с жидкостями и газами. Дело в том, что молекулы жидких и газообразных веществ под давлением ведут себя совсем не так, как молекулы твердых тел. Если молекулы жидкости и газа движутся почти свободно, то молекулы твердых тел так не умеют. Они могут лишь колебаться, немного отклоняясь от исходного положения. Именно благодаря свободному передвижению молекулы газа и жидкости оказывают давление во всех направлениях.

Рассмотрим опыт с шаром Паскаля, чтобы стало понятнее.

Присоединим к трубе с поршнем полый шар со множеством небольших отверстий. Зальем в шар воду и будем давить на поршень.

Давление в трубе вырастет и вода будет выливаться через отверстия, причем напор всех струй будет одинаковым. Такой же результат получится, если вместо воды в шарике будет газ.

Важный момент

У Земли есть атмосфера. Эта атмосфера создает давление, которое добавляется ко всем другим. То есть если мы давим рукой на стол, то давление, которое испытывает стол — это давление нашей руки плюс атмосферное.

Давление жидкости

Из закона Паскаля следует, что раз давление передается одинаково во всех направлениях, то верхние слои жидкости давят на средние, средние — на нижние, нижние — на дно сосуда.

Давление внутри жидкости на одном и том же уровне одинаково по всем направлениям. С глубиной давление увеличивается.

Это утверждение проверяется с помощью манометра — прибора для измерения давления. Чем глубже мы измеряем давление, тем больше показания.

Давление столба жидкости

p = ρgh

ρ — плотность [кг/м³]

h — высота столба жидкости [м]

g — ускорение свободного падения [м/с

На Земле g = 9,8 м/с²

Формула давления столба жидкости часто требуется в задачах.

Задачка раз

На горизонтальном столе стоят два цилиндрических сосуда — узкий и широкий (см. рисунок). В узкий сосуд налита вода, в широкий — керосин. Уровень жидкости в сосудах одинаковый. Сравните давления p жидкостей в точках A, B, C, D и выберите правильную пару утверждений.

Решение

Давление столба жидкости прямо пропорционально ее плотности и высоте столба. Плотность воды больше плотности керосина, следовательно, давление в точке

A больше давления в точке C. Давления в точках B и D равны.

Правильный ответ указан под номером 4.

Задачка два

В сосуд с водой плотностью ρ = 998 кг/м³ опущена вертикальная стеклянная пробирка, целиком заполненная водой (см. рисунок). Высота h₁ равна 0,3 м. Найдите давление, оказываемое водой на дно сосуда в точке

А. Ускорение свободного падения примите равным 10 м/с².

Решение

Поскольку вода не вытекает из пробирки, давление столба высотой h₂ на жидкость в сосуде высотой h₁ уравновешено давлением, которое оказывает вода в сосуде на столб воды в пробирке. Сосуд открытый, поэтому на него действует внешнее давление, которое и передается столбу воды. В результате столб воды в пробирке не оказывает дополнительного давления на точку А, поэтому давление, оказываемое водой на дно сосуда в точке А, равно p = ρgh2. Тогда:

p = ρgh₁ = 998 × 10 × 0,3 = 2 994 Па

Ответ: 2 994 Па.

Академия занимательных наук. Физика – Формула давления твёрдых тел. Видеоуроки физики

Формула давления твёрдых тел.

Видеоуроки физики Выпуск 16

В видеоуроке физики от Академии занимательных наук профессор Даниил Эдисонович познакомит юных телезрителей с новой физической величиной, которая служит для измерения давления — Паскалем. Посмотрев передачу вы узнаете, какое значение имеет площадь опоры твёрдого тела, как не провалиться под лёд или снег, а также познакомитесь с формулой давления твёрдых тел.

Формула давления твёрдых тел

Как вы наверное помните из прошлой передачи, вес — это сила, с которой тело давит на опору. Почему же один и тот же человек, идя по снегу в ботинках проваливается, а идя на лыжах — нет? Чтобы разобраться в этом вопросе профессор Даниил Эдисонович научит вас формуле давления твёрдых тел. Трактор весит гораздо больше автомобиля, а в рыхлой почве не вязнет. В то же время лёгкий автомобиль попав на такую почву скорее всего застрянет и его придётся вытаскивать трактором. Результат действия силы на поверхность зависит не только от величины этой силы, но и от площади, к которой приложена эта сила. Когда человек наступает в снег, вес его тела распределяется по площади его ступней. А если человек обут в лыжи, то вес распределяется по их площади, которая намного больше площади ступней. Поскольку площадь приложения стала больше, человек не провалится в снег. Давление – это скалярная физическая величина, равная отношению силы давления, приложенной к данной поверхности, к площади этой поверхности. Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь этой поверхности. Формула давления твёрдых тел записывается так: p=F/S, где р – это давление, F – сила давления, S – площадь опоры. За единицу давления принимается давление, которое производит сила в 1 ньютон, действующая на поверхность площадью 1м2 перпендикулярно этой поверхности. Измеряется давление в паскалях. Таким образом, по формуле давления твёрдых тел, 1 паскаль равен 1 ньютону на квадратный метр. Между силой давления и давлением существует прямо пропорциональная зависимость, то есть чем больше сила, тем больше давление и наоборот, чем меньше сила, тем меньше давление. Если говорить о зависимости давления от площади опоры, то здесь наблюдается обратно пропорциональная зависимость, то есть чем больше площадь опоры, тем меньше давление и наоборот, чем меньше площадь соприкосновения тел, тем давление больше. Величина давления имеет большое значение не только в жизни человека, но и в жизни животных. Например, заяц, оказывающий давление в 1,2 кПа может сравнительно легко убежать от волка, который оказывает давление 12 кПа, по рыхлому снегу, но не спасется от него на твердой почве.

Давление твердых тел – Класс!ная физика

Давление твердых тел

Действие силы на поверхность тела характеризуется давлением.

Давление – величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности.

где
p – давление, Па
F – приложенная сила давления, Н
S – площадь поверхности / иначе площадь опоры тела /, м2

Давление – величина скалярная , у давления нет направления. .
В качестве силы давления чаще всего выступает вес тела. Числовое значение давления показывает силу, приходящуюся на единицу площади ее приложения. Например, при давлении 2 Паскаля на 1 м2 площади будет действовать сила 2 Ньютона.

От чего зависит давление тела на поверхность?
Почему заостренные предметы / иглы, зубы, клыки, когти, жала, ножи / очень хорошо колют и режут? Результат действия силы на поверхность зависит не только от ее величины, направления , точки приложения, но и от площади опоры давящего тела.

КНИЖНАЯ ПОЛКА

Почему заостренные предметы колючи? ……….смотреть
Наподобие Левиафана ………. смотреть

ЗНАЕШЬ ЛИ ТЫ

… давление гусеничного трактора массой 6,7 тонны на почву составляет 47000 Па

… втыкая пальцем иглу или булавку в ткань, мы создаем давление около 100 000 000 Па

… когда жалит оса, то она оказывает на кожу человека давление 30 000 000 000 Па

. .. давление в центре Земли в 3 миллиона раз выше, чем давление земной атмосферы.

… что очень высокие давления существуют в глубинах небесных тел!

… давление в центре земного шара равно приблизительно 300 млрд Па / т.е. 300 000 000 000 Па /.

… в Африке хирурги народности банту зашивают раны с помощью муравьев. Прижимают края раны друг к другу, а затем на пораненное место помещают несколько муравьев определенного вида. Муравьи кусают кожу пациента, после чего медики отрезают грудь и заднюю часть муравья, а рана остается плотно закрытой, словно на нее наложили скобки.

МОЖНО ЛИ СТОЯТЬ НА ЛАМПОЧКАХ?

Если взять 4 маленьких стеклянных банки из-под майонеза, поставить их на пол, в каждую банку вставить обычную электрическую лампу накаливания цоколем вниз, сверху положить фанерку в виде квадрата так, чтобы банки располагались в углах фанерки / как ножки у стола / и осторожно встать на середину фанерки, то лампочки не лопнут! Такая конструкция выдерживает даже взрослого человека. Аналогичный опыт можно провести и с однойлампочкой, поставленной посредине!
Меры предосторожности: зашлифовать края банок, убрав все неровности, подошва обуви тоже должна максимально соприкасаться с фанерой / долой рифленую подошву/, поверхность лампочек протереть, удалив возможные песчинки, и, конечно, подстелить что-нибудь , чтобы в случае неудачи было мягче падать и удобнее собирать осколки.

ПРОЧНА ЛИ ЯИЧНАЯ СКОРЛУПА ?

Если вылить содержимое яйца, а для опыта оставить скорлупу, то можно попробовать проткнуть ее иголкой изнутри и снаружи. Изнутри – легче, снаружи – тяжелее. Результат при одинаковых усилиях будет зависить от формы скорлупы: выпуклая или вогнутая.

Поэтому малеький цыпленок легко разбивает скорлупу изнутри, а снаружи он защищен более надежно. Свойство выпуклых форм лучше выдерживать нагрузку позволяет архитекторам проектировать куполообразные крыши, мосты, потолки, т.к. они прочнее плоских!

ТЫ СЧИТАЕШЬ, ЧТО УЖЕ ПОРА ЛОВИТЬ “ПЯТЕРКУ”?

Вперед!

1. Что произойдет, если шарики в шариковых ручках будут делать меньшего размера? Почему?

2. Может ли быть человеку на каменном ложе так же комфортно, как и на пуховой перине?
На твердых камнях возлегает
И твердость оных презирает
Для крепости великих сил,
Считая их за мягкий ил…
/М.В.Ломоносов/

3. Вспомни ” Принцессу на горошине”, почему она испытывала неудобство, лежа на перине, под которой были положены горошины?

4. Почему буря, которая летом валит живые деревья, часто не может свалить стоящее рядом сухое дерево без листьев, если оно не подгнило?

5. Почему при постройке дома все его стены выводят одновременно почти до одинаковой высоты?

6. Попробуй рассчитать наибольшую высоту бетонной колонны, которая не разрушалась бы под действием собственной силы тяжести. Допустимое давление бетона составляет 5 000 кПа.

Александр Ржевский. Физика, 7 класс.

Давление

Давление Что такое давление? Как зависит давление от силы и от площади опоры? Какие способы уменьшения и увеличения давления вы знаете? Закон Паскаля Как передается давление жидкостями и газами? Как называется закон, описывающий этот процесс? Где и как используется это явление в жизни человека? Сообщающиеся сосуды Садовая лейка – это сообщающийся или несообщающийся сосуд? Какие еще сообщающиеся сосуды вы знаете? Атмосферное давление Мы живем на дне воздушного океана и постоянно испытываем давление воздуха, хотя не чувствуем его. Почему? Как измеряется давление воздуха? Закон Архимеда Почему одни тела тонут, а другие нет? В чём причина плавучести тел? Почему возможно воздухоплавание?
Что такое давление? 1. Давление = отношение силы, действующей на поверхность перпендикулярно этой поверхности, к площади этой поверхности. Единица давления в СИ = 1Па (паскаль). Обиходная (особенно в технике) единица давления = 1атм (примерно, давление земной атмосферы) = 100000Па.
2. Сила давления – это сила, которая оказывает давление на какую-либо поверхность. Для уменьшения давления в том случае, если силу уменьшить невозможно, увеличивают площадь опоры. В тех случаях, когда бывает необходимо увеличить давление, уменьшают площадь поверхности, на которую действует сила давления.
Закон Паскаля 3. Закон Паскаля: “жидкости и газы передают оказываемое на них давление без изменения в каждую точку жидкости или газа”.
4. Основное свойство жидкостей и газов – передавать давление без изменения по всем направлениям – лежит в основе конструкции гидравлических и пневматических устройств и машин. Во сколько раз площадь одного поршня больше площади другого, во столько же раз гидравлическая машина дает выигрыш в силе.
5. Давление на глубине жидкости не зависит от площади поверхности, а зависит от плотности жидкости и от глубины: р = ρgh
Сообщающиеся сосуды 6. Свойство сообщающихся сосудов: поверхности жидкости в сообщающихся сосудах устанавливаются на одном уровне. Но поверхности разных жидкостей, плотности которых отличаются, устанавливаются в сообщающихся сосудах на разных уровнях! Сосуды, соединенные между собой, называются сообщающимися.
7. Действие простейшего U-образного жидкостного манометра основано на свойстве сообщающихся сосудов. Он позволяет сравнивать давление в присоединенном к нему сосуде с атмосферным давлением.
Атмосферное давление 8. Итальянский физик Торричелли (1608-1647) первым измерил атмосферное давление с помощью ртутного барометра. На практике для измерения атмосферного давления чаще всего применяют барометры-анероиды. Нормальным атмосферным давлением принято считать давление, равное давлению столба ртути высотой 760 мм при температуре 0 градусов по шкале Цельсия.
9. Поскольку мы живем на дне воздушного океана, на нас постоянно действует атмосферное давление. Оно не может нас сплюснуть в лепешку потому, что действует и изнутри нас, даже изнутри клеток. Но пожилые и другие метеочувствительные люди болезненно реагируют на быстрые перепады внешнего давления, поскольку они не успевают компенсироваться внутренним давлением.
10. Атмосферное давление убывает с увеличением высоты над уровнем моря. Для определения изменения высоты используют высотомеры.
Закон Архимеда 11. Закон Архимеда (около 287-212 до н.э.) гласит: на тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и численно равная весу вытесненной жидкости или газа. Эту силу называют архимедовой силой. Вес равен массе на ускорение свободного падения. Масса жидкости, вытесненной телом, = произведение плотности жидкости на объем тела.
12. Условие плавания тел таково: если плотность тела больше плотности жидкости, то тело в ней тонет, если же плотность тела меньше плотности жидкости, то тело в ней всплывает. При равенстве плотностей жидкости и тела, тело плавает.
<< На старт! \|\| НАВЕРХ \|\| Введение >> Движение и взаимодействие тел >> Силы >> Работа и энергия >> Строение вещества >> Давление >>

Атомная физика

При падении электромагнитных волн на какую-нибудь поверхность они оказывают давление на эту поверхность. Давление света может быть объяснено как с электромагнитной точки зрения, так и в рамках квантовой теории.

Пусть на поверхность металла падает нормально плоская электромагнитная волна, тогда векторы электрического и магнитного поля такой волны параллельны поверхности. Под действием электрического поля Е электроны начинают двигаться параллельно поверхности. При этом на каждый электрон, движущийся со скоростью , со стороны магнитного поля световой волны с индукцией действует сила Лоренца

направленная внутрь металла перпендикулярно его поверхности. Таким образом, световая волна должна производить давление на поверхность металла.

В рамках квантовой фотонной теории световое давление обусловлено тем, что каждый фотон не только несет энергию , но и обладает импульсом . Каждый поглощенный фотон передает поверхности свой импульс

(2. 18)

а каждый отраженный — удвоенный импульс

(2.19)

Пусть на поверхность некоторого тела падает по нормали поток фотонов N_ф (N_ф — число фотонов, падающих на единичную площадку в единицу времени). Если поверхность тела имеет коэффициент отражения , то в единицу времени фотонов отразится от нее, а фотонов поглотится поверхностью. Импульс, получаемый единицей площади поверхности тела за единицу времени, равен

(2. 20)

Согласно второму закону Ньютона, есть нормальная к поверхности сила (в данном случае это сила давления), а величина — давление. Таким образом, световое давление равно

(2.21)

Величина, равная произведению энергии фотона ħw на число фотонов N_ф, падающих на единицу площади тела в единицу времени, есть плотность потока световой энергии R. Эту же величину можно получить, умножая среднюю плотность энергии <w> в волне на скорость света:

(2. 22)

Поэтому

(2.23)

Эту формулу при и мы уже обсуждали ранее, когда рассматривали давление электромагнитных волн.

Видео 2.4. Вертушка. Давление света на преграду и конкурирующие эффекты

Пример. Определим давление Р солнечного света на зачерненную пластинку, расположенную перпендикулярно солнечным лучам и находящуюся вне земной атмосферы вблизи Земли.

Солнечная постоянная, то есть плотность потока энергии солнечного электромагнитного излучения вблизи Земли вне её атмосферы, примерно равна . Зачерненная пластинка поглощает практически всё, то есть, для оценки, можно положить . Отсюда давление

Давление света играет огромную роль в ориентации кометных хвостов относительно Солнца. Пылевидные частицы и молекулы газов, имеющиеся в кометах, испытывают световое давление со стороны солнечных лучей, в результате которого и образуются своеобразные формы кометных хвостов, ориентированных в противоположную сторону от Солнца. (В настоящее время предполагается, что явление образования хвостов комет частично определяется «протонным» ветром, исходящим от Солнца.)

Рис. 2.20. Давление света отклоняет хвост кометы от Солнца

Рис. 2.21. Проект солнечного паруса на орбите Земли, движимого давлением света

Таким образом, и электромагнитная (волновая), и фотонная (квантовая) теории с одинаковым успехом решают вопрос о механизме и закономерностях светового давления.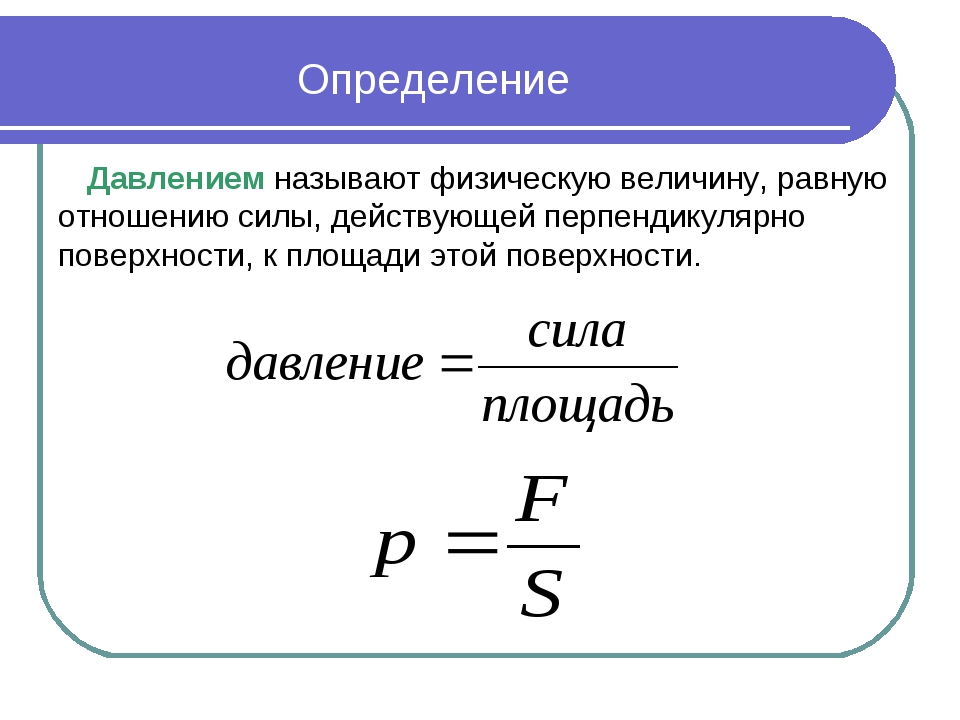

Подведем итоги:

1. В явлениях распространения и отражения света (дифракция и интерференция) свет ведет себя как волна с такими типично волновыми характеристиками, как частота и длина волны .

2. В явлениях испускания и передачи энергии свет ведет себя как частица, характеризуемая энергией и импульсом .

3. Постоянная Планка численно связывает корпускулярные характеристики с волновыми.

Поэтому приходится признать за фотоном двойственную природу. Пока в нашем курсе это необычное свойство — корпускулярно-волновой дуализм — установлено только для света.

Явления высокого давления | физика

Явления высокого давления , изменения физических, химических и структурных характеристик, которым подвергается вещество при воздействии высокого давления. Таким образом, давление служит универсальным инструментом в исследованиях материалов, и оно особенно важно при исследовании горных пород и минералов, которые образуют глубокие недра Земли и других планет.

Давление, определяемое как сила, приложенная к области, является термохимической переменной, которая вызываетфизические и химические изменения, сравнимые с более знакомыми эффектамитемпература . Жидкая вода, например, превращается в твердый лед при охлаждении до температуры ниже 0 ° C (32 ° F), ноЛед также можно производить при комнатной температуре путем сжатия воды до давления, примерно в 10 000 раз превышающего атмосферное . Точно так же вода превращается в газообразную форму при высокой температуре или при низком давлении .

Несмотря на внешнее сходство между температурой и давлением, эти две переменные фундаментально различаются способами, которыми они влияют на внутреннюю энергию материала . Вариации температуры отражают изменения кинетической энергии и, следовательно, термодинамического поведения колеблющихся атомов. С другой стороны, повышенное давление изменяет энергию атомных связей, заставляя атомы сближаться в меньшем объеме. Таким образом, давление служит мощным зондом атомных взаимодействий и химической связи . Кроме того, давление является важным инструментом для синтеза плотных структур, включая сверхтвердые материалы, новые затвердевшие газы и жидкости, а также минералоподобные фазы, которые, как предполагается, находятся глубоко внутри Земли и других планет.

Были введены многочисленные единицы измерения давления, которые иногда путают в литературе. Ватмосферы (атм; приблизительно 1,034 килограмма на квадратный сантиметр [14,7 фунтов на квадратный дюйм], что эквивалентно весу около 760 миллиметров [30 дюймов] ртутного столба) ибар (эквивалент одного килограмма на квадратный сантиметр) часто упоминается. По совпадению, эти единицы практически идентичны (1 бар = 0,987 атм). Впаскаль , определяемый как один ньютон на квадратный метр (1 Па = 0,00001 бар), является официальной единицей давления в системе СИ (Système International d’Unités). Тем не менее, паскаль не получил всеобщего признания среди исследователей высокого давления, возможно, из-за неудобной необходимости использовать гигапаскаль (1 ГПа = 10 000 бар) и терапаскаль (1 ТПа = 10 000 000 бар) для описания результатов высокого давления.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

В повседневной практике давление выше атмосферного встречается, например, в скороварках (около 1,5 атм), пневматических шинах легковых и грузовых автомобилей (обычно от 2 до 3 атм) и паровых системах (до 20 атм). Однако в контексте исследования материалов под «высоким давлением» обычно понимают давления в диапазоне от тысяч до миллионов атмосфер.

Исследования вещества под высоким давлением особенно важны в планетарном контексте. Объекты в самой глубокой впадине Тихого океана подвергаются воздействию давления около 0,1 ГПа (примерно 1000 атм), что эквивалентно давлению под трехкилометровым столбом породы. Давление нацентр Земли превышает 300 ГПа, а давление внутри крупнейших планет -Сатурн иЮпитер – примерно 2 и 10 ТПа соответственно. На верхнем пределе давление внутризвезды могут превышать 1 000 000 000 ТПа.

Производство высокое давление

Ученые изучают материалы под высоким давлением, помещая образцы в специально разработанные машины, которые прикладывают силу к области образца. До 1900 г. эти исследования проводились в цилиндрах из довольно грубого чугуна или стали, обычно с относительно неэффективными винтовыми уплотнениями. Максимальные лабораторные давления были ограничены примерно 0,3 ГПа, и взрывы цилиндров были обычным и иногда опасным явлением. Кардинальные усовершенствования аппаратов высокого давления и методов измерения были внесены американским физиком.Перси Уильямс Бриджман из Гарвардского университета в Кембридже, штат Массачусетс. В 1905 году Бриджмен открыл метод упаковки образцов под давлением, включая газы и жидкости, таким образом, что уплотнительная прокладка всегда испытывала более высокое давление, чем исследуемый образец, тем самым ограничивая образец и снижение риска неудачи эксперимента. Бриджмен не только обычно достигал давления выше 30 000 атм, но также мог изучать жидкости и другие трудные образцы.

Аппараты большого объема

Устойчиво высокий давление и температура в настоящее время обычно производятся на массивных прессах, которые фокусируют большие усилия (до тысяч тонн) за счет двух или более сильныхнаковальни для сжатия образца. В простейшем из этих устройств, представленных Бриджменом в 1930-х годах, используются две конические наковальни, которые сжимают образец, как тиски. Несмотря на то, что сжиматель способен выдерживать очень высокие давления – более 50 ГПа в конструкциях с достаточной боковой опорой, осевое усилие сжимающего устройства имеет тенденцию деформировать образцы в чрезвычайно сплющенные и сильно деформированные диски.

В Конструкция « поршень в цилиндре» , используемая более века, включает в себя прочный металлический или карбидный поршень, который забивается в цилиндр для удержания образца. В принципе, поршень может быть довольно длинным, поэтому конструкция поршневой цилиндр может вместить гораздо больший объем образца, чем сжиматель, в зависимости от размеров цилиндра для хранения образца. Эти устройства редко используются при давлениях выше примерно 10 ГПа из-за вероятности бокового разрушения (а именно взрывного разрыва) металлического цилиндра.

В ленточный аппарат, изобретенный в 1954 г. ученым Трейси Холл из компании General Electric, предназначенная для использования в программе алмазодобычи компании, включает в себя элементы конструкции как с противоположной опорой, так и с поршневым цилиндром. Две сильно заостренные поршневые наковальни сжимают образец, заключенный в торе, что очень похоже на цилиндр, открытый с обоих концов. Сотни устройств ленточного типа используются во всем мире для синтеза алмазов.

Многие исследователи высокого давления теперь используют устройства с разделенной сферой или множеством опор, которые равномерно сжимают образец со всех сторон. Широко используются версии с шестью наковальнями, которые прижимаются к шести граням образца кубической формы, или с восемью наковальнями, которые сжимают октаэдрический образец. В отличие от простых сжимающих устройств, поршневых цилиндров и ленточных устройств, устройства с несколькими подпорками могут сжимать образец равномерно со всех сторон, достигая диапазона давлений с верхним пределом не менее 30 ГПа. Все эти типы аппаратов высокого давления могут быть оснащены резистивным нагревателем, обычно цилиндром из графита, окружающим образец, или другим электропроводящим нагревательным элементом, для исследований при температурах до 2000 ° C.

Давление – Гиперучебник по физике

дневное время

3,4 × 10 ¹¹	3,4 × 10 ¹⁶	центр Солнца
????	????	центр Юпитера
10 ¹⁰	10 ¹⁵	алмазная наковальня, рекордно высокая
3,6 × 10 ⁶	3,6 × 10 ¹¹	центр Земли
1080	1.1 × 10 ⁸	Марианская впадина, Тихий океан (−10 924 м)
160	1,6 × 10 ⁷	Озеро Байкал, Азия (−1620 м)
140	1,4 × 10 ⁷	Озеро Танганьика, Африка (−1470 м)
90	9,0 × 10 ⁶	поверхность Венеры
40	4,0 × 10 ⁶	Озеро Верхнее, Северная Америка (−406 м)
????	????	рекордное погружение человека
26	2. 6 × 10 ⁶	гелий замерзает при температуре около 1 К
>3	>300 000	кислородное отравление и азотный наркоз при погружениях > 30 м
	108 380	Атмосфера Земли, рекордно высокая, с поправкой на высоту (Сибирь, 1968)
	106 000	Атмосфера Земли, Мертвое море (−400 м)
1	101 325	Атмосфера Земли, уровень моря, стандартная атмосфера
	90 000	Атмосфера Земли на высоте 1000 м, внутренняя часть Concorde
	87 000	Земная атмосфера, рекордно низкая, с поправкой на высоту (Typhoon Tip, 1979)
	80 000	Атмосфера Земли на высоте 2000 м, салон коммерческого реактивного самолета
	65 000	Земная атмосфера, Ла-Пас, Боливия (3650 м)
~½	53 000	Земная атмосфера, самый высокий постоянно населенный пункт (5100 м)
	~40 000~	Атмосфера Земли, вертикальный предел живучести человека (~7000 м)
~⅓	31 000	Земная атмосфера, гора Эверест (8848 м)
~⅕	19 000	Атмосфера Земли, высота коммерческого реактивного самолета (12 000 м)
0. 063	6400	Земная атмосфера, предел Армстронга, открытое кипение жидкостей тела (19 000 м)
>0,033	>3300>	низкий вакуум (LV)
<0,033	<3300<	средний вакуум (MV)
0,025	2200	Атмосфера Земли, высота полета самолета-разведчика (26000 м)
0,007	700	поверхность Марса
0.002	230	Атмосфера Земли, высота наибольшего прыжка с парашютом (41 422 м)
0,0006	60	Атмосфера Земли, высота наибольшего полета беспилотного аэростата (52 000 м)
~10 ⁻⁵	~1	поверхность Плутона, максимум
<10 ⁻⁶	<0,1	высокий вакуум (ВВ)
<10 ⁻⁹	<0.0001	очень высокий вакуум (VHV)
<10 ⁻¹²	<10 ⁻⁷	сверхвысокий вакуум (СВВ)
~10 ⁻¹³	~10 ⁻⁸	поверхность Луны,
~10 ⁻¹⁵	~10 ⁻¹⁰	поверхность Луны, ночь
<10 ⁻¹⁵	<10 ⁻¹⁰	сверхвысокий вакуум (XHV)
~10 ⁻¹⁷	~10 ⁻¹²	Мне сказали, что ниже этого значения все вакуумное оборудование негерметично.

15.1: Давление — Физика LibreTexts

Давление, оказываемое силой $\vec F$ на поверхность площадью $A$, является скалярной величиной $P$, определяемой как:

\[\begin{align} P=\frac{F_{\perp}}{A}\end{align}\]

, где $F_{⊥}$ — составляющая силы, перпендикулярная поверхности. Единицей давления в системе СИ является Паскаль (Па). Давление связано с площадью $A$, на которую действует сила, и может рассматриваться как мера концентрации этой силы.Например, сила $10\text{ Н}$, приложенная через иглу (небольшая площадь), приведет к гораздо большему давлению, чем если бы эта сила была приложена плоской рукой (большая площадь).

Когда сила воздействует на жидкость, она создает давление, которое мы моделируем как везде в жидкости . Для каждого элемента в жидкости давление окружающей жидкости оказывает внутреннюю силу на элемент со всех сторон (см. рисунок $\PageIndex{1}$). В ответ элемент оказывает внешнее усилие во всех направлениях, и эти силы действуют на соседние элементы.

Это в некоторой степени аналогично натяжению, существующему повсюду в веревке, когда каждый элемент веревки испытывает силы от соседних элементов веревки, которые пытаются «разорвать его». Давление можно рассматривать как «отрицательное» напряжение, поскольку на материал, находящийся под давлением, воздействуют силы, пытающиеся сжать элемент на себя, а не разорвать его на части. Чтобы создать натяжение в веревке, нужно приложить внешнюю силу к веревке (чтобы растянуть ее), так что веревка в ответ приложит внутреннюю силу.Чтобы создать давление в жидкости, нужно приложить внутреннюю силу к жидкости, которая затем в ответ воздействует на внешнюю силу.

Если мы рассмотрим небольшой кубический объем жидкости, как показано в центре рисунка $\PageIndex{1}$, на этот элемент жидкости будут воздействовать внутренние силы во всех направлениях от давления в окружающей жидкости, как показано на рисунке стрелки. Если силы от давления не приводят к результирующей силе на жидкий элемент, то мы говорим, что жидкость находится в гидростатическом равновесии, а жидкий элемент будет покоиться в инерциальной системе отсчета.

Рисунок $\PageIndex{1}$: Небольшой элемент внутри жидкости под давлением не будет подвергаться результирующей силе от давления в жидкости, поскольку сила, связанная с давлением в жидкости, действует во всех направлениях.

Вместо этого рассмотрим элемент жидкости, который находится на краю емкости для жидкости (например, чашки с водой), как показано на рисунке $\PageIndex{2}$.

Рисунок $\PageIndex{2}$: На краю контейнера небольшой элемент жидкости будет оказывать внешнее усилие на контейнер, а контейнер будет оказывать внутреннее усилие на элемент жидкости.

В этом случае на правой стороне жидкостного элемента нет жидкости, которая могла бы оказывать усилие влево. Если жидкий элемент находится в равновесии, тогда это должен быть контейнер, который воздействует на жидкость этой силой, контейнером $\vec F$. Согласно третьему закону Ньютона элемент жидкости оказывает внешнее воздействие на сосуд. Это верно для всех точек на поверхности контейнера, которые будут испытывать внешнюю силу от давления жидкости. Если давление над поверхностью постоянно, величина внешней силы на поверхности будет равна давлению жидкости, умноженному на площадь этой поверхности.

Если вы поместите пустую запечатанную жестяную банку под воду, вода будет оказывать давление на все поверхности жестяной банки, что приведет к общей внутренней силе на всех поверхностях жестяной банки. Если давление воды достаточно высокое, консервная банка раздавится. С другой стороны, если консервную банку наполнить водой, она не раздавится, так как вода внутри консервной банки будет иметь то же давление, что и вода снаружи консервной банки, и будет оказывать равную чистую внешнюю силу. на всех поверхностях консервной банки.Суммарная сила, действующая на каждую поверхность банки, будет равна нулю, и консервная банка не раздавится, каким бы высоким ни было давление воды.

В общем случае, если есть поверхность раздела с жидкостью по обе стороны от нее с разным давлением, именно разность давления по обе стороны от границы раздела определяет результирующую силу, действующую на поверхность раздела, а не абсолютное давление.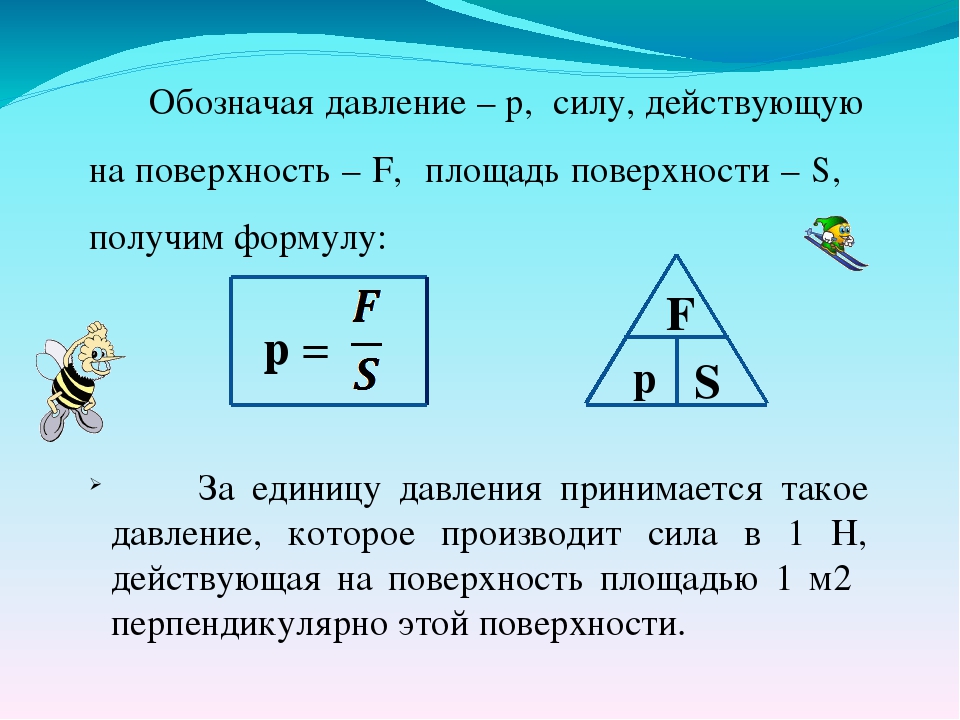

Упражнение $\PageIndex{1}$

Вы ставите консервную банку на стол и с помощью насоса создаете вакуум внутри банки.Вы замечаете, что консервная банка раздавливается. Какое объяснение верное?

Высасывая воздух из банки, вы также всасываете стенки банки.
Вы снижаете давление внутри банки, так что воздух снаружи банки оказывает большее внутреннее усилие на банку, чем направленная наружу сила воздуха внутри банки.
Вы понижаете давление внутри банки, чтобы воздух внутри банки притягивал стенки банки.
Все вышеперечисленное является допустимым способом моделирования этого.

Ответить

Эффект гравитации

При обсуждении рисунка $\PageIndex{1}$ мы утверждали, что жидкость оказывает равную силу со всех направлений на жидкий элемент, так что результирующая сила, действующая на жидкий элемент, равна нулю. Это не совсем правильно при наличии гравитации, когда жидкий элемент будет иметь вес. Таким образом, если жидкий элемент должен находиться в равновесии, направленная вверх сила (и давление) со стороны жидкости внизу должна быть выше, чем со стороны жидкости над жидким элементом.

На рисунке $\PageIndex{3}$ показан элемент жидкости, имеющий высоту $h$ и площадь поверхности $A$ в горизонтальной плоскости. Давление $P_{2}$ в жидкости под элементом жидкости должно быть выше, чем давление $P_{1}$ над элементом жидкости, если элемент жидкости находится в равновесии.

Рисунок $\PageIndex{3}$: При наличии гравитации давление под элементом жидкости должно быть выше, если элемент жидкости должен оставаться в равновесии.

Элемент жидкости имеет общую массу $m$, определяемую как:

\[\begin{align} m = \rho V = \rho Ah \end{align}\]

, где $V = Ah$ — объем жидкости, а $ρ$ — ее плотность.

Суммарная (горизонтальная) сила, действующая со стороны внешней жидкости на элемент жидкости, равна нулю вдоль вертикальных поверхностей. Пусть $P_{1}$ будет давлением в жидкости над жидким элементом, а $P_{2}$ будет давлением под жидким элементом. Если мы выберем ось y, которая направлена положительно вверх, а элемент жидкости не ускоряется в вертикальном направлении, то компонент y второго закона Ньютона, записанный для элемента жидкости, будет равен:

\[\begin{align} &\sum F_{y} =F_{2}-F_{1}-mg=0 \\ &P_{2}AP_{1}A-mg=0 \\ &P_{ 2}A-P_{1}A-\rho Ahg=0 \\ &\поэтому P_{2}-P_{1}=\rho gh \end{выровнено}\]

, где мы использовали тот факт, что сила, возникающая в результате давления, определяется давлением, умноженным на площадь, на которую оно воздействует.Таким образом, мы находим, что разница в давлении из-за силы тяжести в жидкости между двумя положениями, $y_{2}$ и $y_{1}$, определяется как:

\[P(y_{2})-P(y_{1})=-\rhog(y_{2}-y_{1})\]

, где ось $y$ определяется как увеличение в направлении вверх. Поскольку давление в жидкости зависит от местоположения в жидкости, мы говорим, что в жидкости существует «градиент давления».

Упражнение $\PageIndex{2}$

Рисунок $\PageIndex{4}$: Держит воду в вертикальной соломинке.

Вы перекрываете пальцем верхний конец соломинки, а затем вынимаете соломинку из стакана с водой. Какое наиболее правильное описание того, почему вода остается в соломинке (рис. $\PageIndex{4}$) до того, как вы отпустите палец?

Внутри соломинки не может быть вакуума; если палец не убрать, чтобы впустить воздух вместо воды, вода останется в соломинке.
Над водой создается небольшой вакуум, который всасывает воду вверх и предотвращает ее падение.
Давление воздуха в соломинке под водой выше, чем давление воздуха в соломинке над водой.
Давление воздуха в соломинке под водой ниже, чем давление воздуха в соломинке над водой.

Ответить

. Мы предположили, что плотность жидкости $ρ$ постоянна и что жидкость не может быть сжата. Это очень хорошее приближение для такой жидкости, как вода, но не для газа, плотность которого будет зависеть от его давления.Если бы жидкостью был газ (например, столб воздуха в нашей атмосфере), плотность и давление изменялись бы в зависимости от высоты. Мы можем легко учесть это в нашей модели, если будем считать, что жидкий элемент имеет очень маленькую высоту $dy$, а не конечную высоту $h$, как в приведенном выше выводе. Элемент жидкости бесконечно малой высоты $dy$ показан на рисунке $\PageIndex{5}$.

Рисунок $\PageIndex{5}$: Градиент давления от силы тяжести на бесконечно малый элемент жидкости.

На очень малой высоте $dy$ плотность жидкости $ρ$ можно считать постоянной, и бесконечно малый элемент жидкости будет иметь массу $dm$:

\[\begin{aligned} dm=\rho Ady \end{aligned}\]

Мы можем смоделировать давление, оказываемое жидкостью над жидким элементом, как $P + dP$, а давление, оказываемое жидкостью ниже, как $P$, где $dP$ — небольшое (отрицательное) изменение давления ¹ . Компонент $y$ второго закона Ньютона, записанный для бесконечно малого жидкого элемента, равен:

\[\begin{aligned} \sum F_{y} = PA-(P+dP)A-dmg &=0 \\ PA-PA-dPA-\rho Адыг&=0 \\ \следовательно – dP – \rho gdy &=0 \end{выровнено}\]

Таким образом, мы можем определить, как давление изменяется с высотой, $y$:

\[\frac{dP}{dy}=-\rho g\]

Это говорит нам о том, что скорость изменения давления с увеличением $у$ отрицательна; другими словами, давление уменьшается по мере увеличения высоты, как мы уже заключили.{y_{2}}\rho gdy\end{выровнено}\]

Если плотность $ρ$ постоянна, то это приводит к Уравнению 15.1.1 . Обратите внимание, что до сих пор мы только моделировали изменение давления в жидкости с высотой, но не определяли абсолютное давление в жидкости.

Пример $\PageIndex{1}$

Если предположить, что плотность воздуха пропорциональна его давлению, то как изменится плотность воздуха с высотой?

Решение :

Мы знаем, что скорость изменения давления с высотой (положение $y$, где положительное $y$ определяется как направленное вверх) определяется выражением:

\[\begin{aligned}\frac{dP}{dy}=-\rho g \end{align}\]

Поскольку мы можем предположить, что плотность пропорциональна давлению, мы можем ввести произвольную константу $a$ и заявить, что:

\[\begin{aligned} \rho &=aP \\ \следовательно \frac{dP}{dy}&=\frac{d}{dy}\frac{1}{a}\rho = \frac{1 }{a}\frac{d\rho}{dy} \end{aligned}\]

, где константу $a$ можно вычислить, если мы знаем давление и плотность в какой-то точке. {- agy} \end{выровнено}\]

Таким образом, мы находим, что плотность воздуха экспоненциально уменьшается с высотой.{-agy} \end{выровнено}\]

, где $P_{0}$ — давление на высоте $y = 0$. Если мы знаем $P_{0}$ и $ρ_{0}$, то константа $a$ определяется как:

\[\begin{align} a=\frac{\rho _{0}}{P_{0}} \end{align}\]

Обсуждение :

Если бы мы применили эту модель к атмосфере Земли, наша модель дала бы только качественное согласие, так как плотность воздуха также зависит от его температуры и других факторов. Тем не менее интересно, что, основываясь на простом требовании, чтобы элемент воздуха находился в гидростатическом равновесии, мы можем получить разумное описание того, как давление и плотность изменяются с высотой в земной атмосфере.

Принцип Паскаля

Принцип Паскаля утверждает, что если внешнее давление воздействует на жидкость, давление во всем пространстве жидкости увеличивается на эту величину . {5}\text{Па}\).Если атмосферное давление равно $P_{0}$ на поверхности океана, то давление на некоторой глубине $h$ определяется как:

\[\begin{выровнено} P(h)=P_{0}+\rho gh \end{выровнено}\]

, где $ρ$ — плотность воды. Как следствие, давление в жидкости на любой глубине \(h) одинаково везде на этой глубине в жидкости.

Упражнение $\PageIndex{3}$

Рисунок $\PageIndex{7}$: Три стакана разной формы.

Вы наполняете три стакана на рисунке $\PageIndex{7}$ так, чтобы уровень жидкости достигал высоты h над дном стакана.Что вы можете сказать о давлении жидкости на дно каждого стакана?

Наибольшее значение имеет стекло $A$.
Наибольшее значение имеет стекло $B$.
Наибольшее значение имеет стекло $C$.
Одинаков для всех очков.
Это одинаково для всех стекол, только если мы можем пренебречь атмосферным давлением.

Ответить

Пример $\PageIndex{2}$

Рисунок $\PageIndex{8}$: Сила, действующая на поршень гидравлического подъемника, чтобы привести в движение массу $M$.

{2}=4F\ конец {выровнено}\]

Таким образом, сила, действующая на большой поршень, будет в четыре раза больше силы, действующей на маленький поршень.Нужно только приложить силу величиной $Mg/4$, чтобы поднять массу $M$.

Измерение давления

В этом разделе мы опишем, как можно разработать приборы для измерения давления. Наиболее простым устройством является манометр, который представляет собой U-образную трубку, заполненную жидкостью с известной плотностью $ρ$, как показано на рисунке $\PageIndex{9}$.

Рисунок $\PageIndex{9}$: Манометр может измерять разницу между давлением $P$ и атмосферным давлением, $P_{0}$.Эта разница называется «манометрическим давлением».

Манометр можно использовать для измерения давления $P$ относительно атмосферного давления, $P_{0}$. Один конец трубки открыт для атмосферного давления, а другой соединен с жидкостью (например, газом), для которой мы хотим измерить давление. Если измеряемое давление больше атмосферного, жидкость в манометре будет подвергаться большей направленной вниз силе со стороны измеряемого давления, чем со стороны, открытой для атмосферного давления, как показано на рисунке $\PageIndex{9 }$. Будет разница $h$ в уровне жидкости на каждой стороне трубы, которая прямо пропорциональна разнице давлений между двумя сторонами трубы.

Рассмотрим точку жидкости в точке $B$ на рисунке $\PageIndex{9}$, где давление равно $P_{B} = P$, давление, которое необходимо измерить. Точка в жидкости в точке $A$, которая находится на той же высоте в жидкости, должна иметь то же давление, что и точка $B$. Мы можем записать давление в точке $A, P_{A}$ как сумму атмосферного давления и давления водяного столба высотой $h$:

\[\begin{выровнено} P_{A}=P_{0}+\rho gh \end{выровнено}\]

Поскольку оно также должно быть равно давлению в точке $B$, мы можем найти разницу между давлением, которое мы хотим измерить, и атмосферным давлением:

\[\begin{выровнено} P_{A}&=P_{B} \\ P_{0}+\rho gh &=P \\ \следовательно PP_{0}&=\rho gh \end{выровнено }\]

Разница между давлением и атмосферным давлением называется «манометрическим давлением», и это все, что мы можем измерить, если не знаем абсолютного значения атмосферного давления.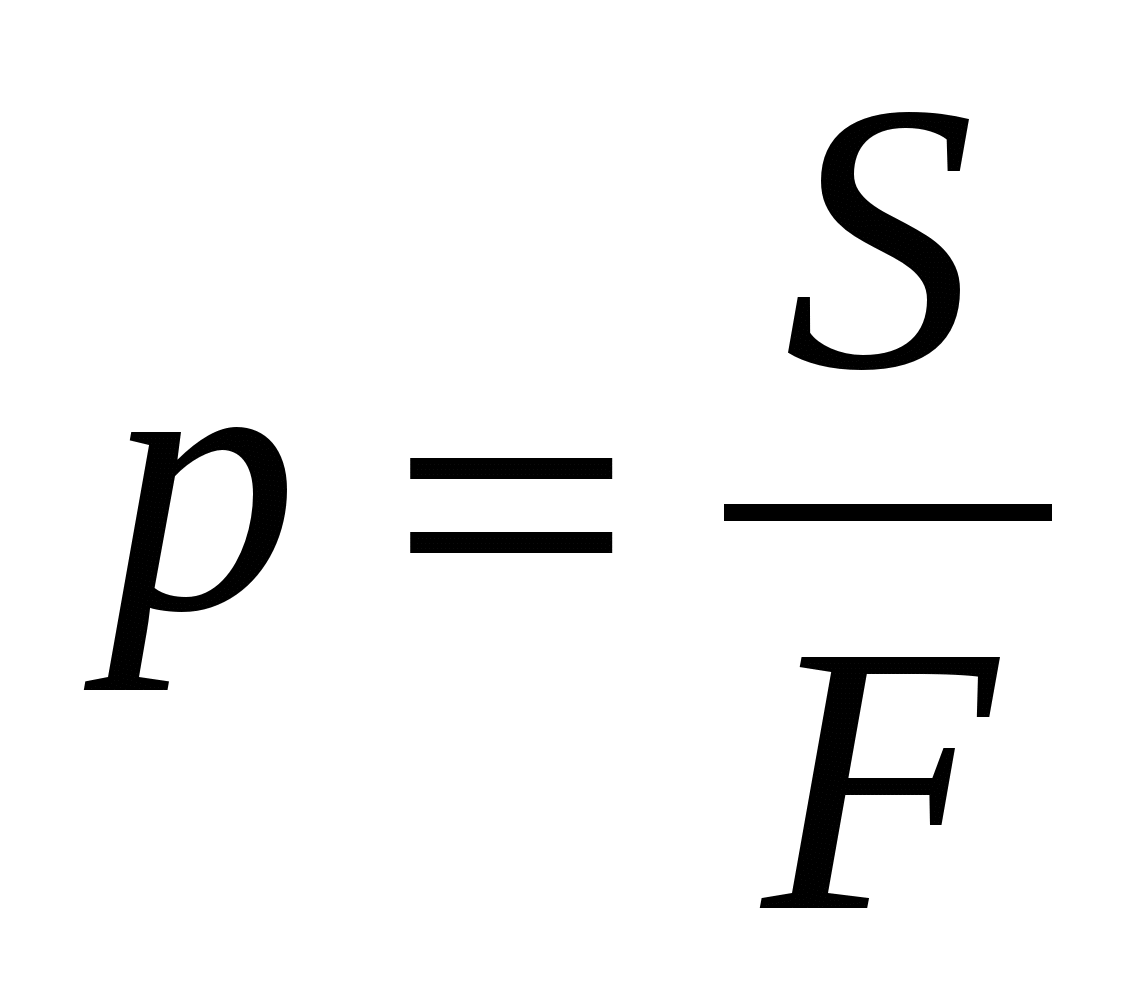 При использовании манометра манометрическое давление определяется как $ρgh$, тогда как «абсолютное давление» $P$ определяется добавлением атмосферного давления к манометрическому давлению, $P = P_{0} + рг$. Большинство устройств для измерения давления («манометры») измеряют давление относительно атмосферного давления, используя аналогичный механизм.

Атмосферное давление в определенном месте на Земле зависит от погоды. Барометр – прибор, предназначенный для измерения атмосферного давления. Простой барометр можно построить из манометра с закрытым одним концом, как показано на рисунке $\PageIndex{10}$.

Рисунок $\PageIndex{10}$: барометр, созданный на основе мамометра для измерения относительных изменений атмосферного давления.

Один конец манометра запаивают в день, когда атмосферное давление равно, скажем, $P_{0}$, а другой конец трубки оставляют открытым. Разница высот $h$ между жидкостью по обеим сторонам трубки является мерой того, насколько текущее атмосферное давление $P_{1}$ отличается от давления, $P_{0 }$, когда манометр был опломбирован. На рисунке $\PageIndex{10}$ показан барометр в день, когда атмосферное давление ниже, чем в день, когда манометр был опломбирован.Разница в давлении определяется как:

\[\begin{выровнено} P_{1}=P_{0}+\rho gh \end{выровнено}\]

, если мы определим $h$ как положительное, когда сторона с давлением $P_{0}$ выше (поэтому $h$ отрицательно на рисунке $\PageIndex{10}$ и \ (P_{1}\) меньше, чем $P_{0}$).

Мы также можем измерить абсолютное атмосферное давление, если откачиваем воздух из запаянного конца трубы, так что $P_{0} = 0$. При этом разница в высоте между жидкостью по обе стороны от манометра является мерой абсолютного атмосферного давления.{2})}=10,3\текст{м} \конец{выровнено}\]

Обсуждение :

Разница в высоте составляет около $10\text{ м}$ при номинальном атмосферном давлении. Это означает, что манометр должен быть как минимум такой высоты, чтобы измерять абсолютное атмосферное давление, что нецелесообразно строить! Если вместо этого использовать жидкость с более высокой плотностью, чем у воды, то эту высоту можно существенно уменьшить. Традиционно барометры строились с использованием ртути, которая имеет плотность ($ρ_{Hg} = 13.{3}$), так что перепад высот при номинальном атмосферном давлении составляет $760\text{ мм}$. Это гораздо более простой в изготовлении прибор (помимо соображений безопасности при использовании ртути). По этой причине часто используемой единицей давления является «мм ртутного столба», что соответствует перепаду высот в манометре, построенном с использованием ртути.

Упражнение $\PageIndex{4}$

Рисунок $\PageIndex{12}$: барометр Торричелли.

Вы строите барометр Торричелли, как показано на рисунке $\PageIndex{12}$, для измерения абсолютного атмосферного давления.Герметичная вертикальная трубка имеет вакуумированное верхнее пространство (давление равно нулю), так что атмосферное давление на контейнер с жидкостью выталкивает жидкость вверх по трубе на высоту $h$, которая пропорциональна атмосферному давлению. давление. Если вы используете оливковое масло в качестве жидкости, что вы можете сказать о высоте $h$ при номинальном атмосферном давлении?

Больше $10,3\текст{м}$.
Равно $10.3\text{ m}$.
Меньше $10.3\текст{м}$.
Недостаточно информации.

Ответить

Сноски

1. Мы разместили $dP$ в верхней части жидкости, хотя давление в нижней части жидкости выше, потому что ось $y$ возрастает вверх. Нас действительно интересует изменение давления $dP$, которое соответствует изменению высоты $dy$ в положительном направлении $y$.

Давление — это сила на единицу площади Рон Куртус

SfC Главная > Физика > Сила >

Рона Куртуса

Давление – это сила , воздействующая на объект, которая распределяется по площади поверхности .

Уравнение давления представляет собой силу, деленную на площадь, на которую действует сила. Хотя это измерение является простым, когда твердое тело давит на твердое тело, в случае, когда твердое тело давит на жидкость или газ, требуется, чтобы жидкость была заключена в контейнер.

Сила также может создаваться весом объекта.

Возможные вопросы:

Какое давление возникает, когда одно твердое тело давит на другое твердое тело?
Что происходит, когда твердое тело давит на замкнутую жидкость?
Что происходит, когда сила исходит от гравитации?

Этот урок ответит на эти вопросы.Полезный инструмент: Преобразование единиц

Давление твердого тела на твердое тело

Когда вы прикладываете силу к твердому объекту, давление определяется как приложенная сила, деленная на площадь приложения. Уравнение для давления:

П = F/A

где

P давление
F приложенная сила
A — площадь поверхности, на которую действует сила
F/A равно F , разделенному на A

Например, если вы давите рукой на предмет с силой 20 фунтов, а площадь вашей руки составляет 10 квадратных дюймов, то оказываемое вами давление составляет 20/10 = 2 фунта на квадратный дюйм.

Давление равно силе, деленной на площадь

Вы можете видеть, что для данной силы, чем меньше площадь поверхности, тем больше давление. Если вы используете большую площадь, вы распределяете силу, и давление (или сила на единицу площади) становится меньше.

Твердое давление на замкнутую жидкость

Когда жидкость или газ находятся в контейнере или цилиндре, вы можете создать давление, приложив усилие с помощью твердого поршня. Давление, создаваемое в цилиндре, равно приложенной силе, деленной на площадь поршня: P = F/A .

В замкнутой жидкости, если пренебречь действием силы тяжести на жидкость, давление одинаково во всем сосуде, оказывая одинаковое давление на все стенки. В случае с велосипедным насосом давление, создаваемое внутри насоса, будет передаваться по шлангу в велосипедную шину. Но воздух по-прежнему замкнут.

Давление во всех направлениях в жидкости

Увеличение силы увеличивает давление внутри цилиндра.

Вызвано гравитацией

Поскольку вес объекта является силой, вызванной гравитацией, мы можем подставить вес в уравнение давления.Таким образом, давление ( P ), вызванное весом ( W ) объекта, равно весу, деленному на площадь ( A ), к которой приложен вес.

П = Б/Д

Если положить на пол твердый предмет, давление на пол в области контакта будет равно весу предмета, деленному на площадь пола.

Давление равно весу, деленному на площадь

Пример с туфлями

Хорошим примером того, как сила на небольшой площади может привести к очень высокому давлению, является женская обувь на высоких каблуках с шипами.Эти типы обуви могут повредить некоторые полы из-за очень высокого давления на пол в области пятки.

Средний ботинок распределяет вес человека на 20 квадратных дюймов. Таким образом, человек весом 100 фунтов прикладывает к полу 100/20 = 5 фунтов на квадратный дюйм.

Поскольку площадь каблука-шпильки составляет всего 0,25 квадратных дюйма, человек весом 100 фунтов будет прикладывать 100/0,25 = 400 фунтов на квадратный дюйм к полу в районе пятки! В некоторых случаях этого достаточно, чтобы повредить пол.

Жидкий груз

Если вы поместите жидкость в сосуд, вес этой жидкости будет давить на дно сосуда подобно весу твердого предмета. Давление на дно сосуда было бы таким же, как если бы вес был из твердого тела:

P = W/A .

Единственная разница в том, что давление в жидкости идет во всех направлениях. Так что давление по бокам внизу будет одинаковым.

Газы и жидкости испытывают давление из-за своего веса в каждой точке жидкости.

Резюме

Давление — это сила, действующая на объект, распределенная по площади поверхности. Уравнение для давления: P = F/A . Давление можно измерить, если твердое тело давит на твердое тело, но в случае, когда твердое тело давит на жидкость или газ, требуется, чтобы жидкость была заключена в контейнер. Сила также может быть создана весом объекта.

Заставьте себя преуспеть

Ресурсы и ссылки

Полномочия Рона Куртуса

веб-сайтов

Ресурсы по физике

Книги

(Примечание: Школа чемпионов может получать комиссионные за покупку книг)

Лучшие книги по физике силы

Поделиться этой страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
давление.htm

Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.

Где ты сейчас?

Школа Чемпионов

Темы физики
Давление — это сила на единицу площади

Давление жидкости, Рон Куртус

SfC Home > Physics > Matter > Fluids >

Рона Куртуса

Давление жидкости — это измерение силы на единицу площади объекта в жидкости или на поверхности закрытого контейнера. Это давление может быть вызвано гравитацией, ускорением или силами вне закрытого контейнера.

Поскольку жидкость не имеет определенной формы, ее давление действует во всех направлениях. Давление жидкости также может быть усилено с помощью гидравлических механизмов и изменения скорости жидкости.

Возможные вопросы:

Как гравитация влияет на давление жидкости?
Как действует давление воздуха и воды во всех направлениях?
Каковы другие области применения давления жидкости?

Этот урок ответит на эти вопросы.Полезный инструмент: Преобразование единиц

Давление жидкости под действием силы тяжести или ускорения

Вес жидкости может оказывать давление на все, что находится под ней. Кроме того, относительное движение жидкости или газа может оказывать давление.

Давление

Давление определяется как сила, деленная на площадь, на которую действует сила. ( Подробности см. в уроке о давлении. ) Вы можете записать это в виде уравнения, если хотите произвести некоторые вычисления:

П = F/A

где

P = давление
F = сила
А = площадь
F/A = F разделить на A

Давление под действием силы тяжести

Поскольку вес предмета или материала равен силе, действующей на него под действием силы тяжести,

Объект может оказывать давление вниз из-за своего веса и силы тяжести.Давление, которое вы оказываете на пол, равно вашему весу, деленному на площадь подошвы вашей обуви. Если сила обусловлена весом ( Вт ) объекта, уравнение будет таким: P = Вт/A

Давление воды

Давление воды на дне озера равно весу столба воды над ним, деленному на площадь этого столба.

Давление на глубине Вес/Площадь

Колонка на макушке

Если бы вы стояли на дне бассейна (при условии, что вы не начнете плавать), столб воды диаметром с вашу голову на всем пути до поверхности воды будет давить на вас. Если вы возьмете этот столб воды и взвесите его, а затем разделите этот вес на площадь вашей макушки, вы получите значение давления воды на вашу голову.

Причина, по которой это не влияет на вас, заключается в том, что ваше внутреннее давление тела увеличивается, чтобы нейтрализовать большую часть давления воды. Но на больших глубинах давление воды может стать настолько большим, что может навредить дайверу.

Демонстрация с банкой

Демонстрацию того, как давление воды увеличивается с глубиной воды, можно продемонстрировать с помощью большой консервной банки.Пробейте отверстия для гвоздей по вертикали вверх по стенке банки через каждые дюйм или несколько сантиметров. Затем наполните банку водой. Вода может просто вытекать из верхних отверстий, но увеличение давления с глубиной приводит к тому, что вода выбрасывается с большим давлением в нижние отверстия.

Давление воздуха

Точно так же давление воздуха на макушку равно весу столба воздуха (высотой в несколько миль), деленному на площадь макушки. Среднее давление воздуха на голову 14.7 фунтов за квадратный дюйм! Это большой вес, который вы держите.

Атмосферное давление при погоде

Если в метеосводке указано высокое давление, это означает, что столб воздуха поднимается выше, чем для считывателя низкого давления. Барометр измеряет давление воздуха или вес столба воздуха.

Атмосферное давление возникает из-за веса всего воздуха, идущего на несколько миль выше вас. Это примерно 16 фунтов на квадратный дюйм во всех направлениях вашего тела.К счастью, в наших телах есть внутреннее давление, которое уравнивает давление воздуха.

Воздушные шары

Давление воздуха внутри воздушного шара выбрасывается наружу во всех направлениях. Когда давление увеличивается, размер воздушного шара увеличивается, пока он, наконец, не лопнет. Внутреннее давление воздуха намного больше, чем внешнее давление воздуха.

Различные высоты

Нормальное атмосферное давление в Денвере, штат Колорадо, меньше, чем в Денвере. Это связано с тем, что большая высота Денвера означает, что его столб воздуха не такой высокий, как в Милуоки.

Поскольку многие закуски запечатаны в пакеты под давлением, пакет, запечатанный в Милуоки, требует более высокого внутреннего давления, чем пакет, изготовленный в Денвере. Таким образом, пакет с закусками из Милуоки расширится, если его довести до более низкого давления воздуха, чем в Денвере, и даже может взорваться.

Направление давления жидкости

Давление, создаваемое жидкостью или газом, отличается тем, что не только давление давит вниз в данной точке, но и то же давление толкает вверх и в стороны.

Все направления

Давление в жидкости в данной точке одинаково во всех направлениях. Это верно из-за свойства жидкостей и газов принимать форму своего сосуда.

Давление воды одинаково во всех направлениях

Что это также означает, что любой полый контейнер, погруженный в жидкость, оказывает давление на каждый квадратный сантиметр своей поверхности, сверху и снизу.

Плавание под водой

Когда вы плаваете под водой, чем глубже вы погружаетесь, тем больше давление воды на ваше тело.Теперь вопрос: “Почему тебя не раздавил весь этот вес?”

Причина в том, что ваше тело компенсирует это, создавая внутреннее давление, равное давлению воздуха или воды. Вы чем-то похожи на воздушный шар, наполненный жидкостью под давлением. Теперь, когда вы уходите очень глубоко под воду, давление воды может стать больше, чем ваше тело может компенсировать, и вы почувствуете дискомфорт.

Другие эффекты давления

Другими эффектами давления жидкости являются движение, нагревание и химические эффекты, а также применение в области гидравлики и в авиации.

( Подробности см. в Applications of Fluid Principles. )

Ветер и течение

Движение жидкости, такое как ветер или течение реки, может оказывать давление на объект на его пути, пропорциональное площади поверхности, перпендикулярной направлению движения.

Обтекаемость объекта снижает это давление.

Нагревание и химическое воздействие

Когда вы нагреваете жидкость, она обычно расширяется.Если вы нагреете жидкость, находящуюся в закрытом контейнере, расширение приведет к увеличению внутреннего давления. Например, нагрев воздушного шара приведет к его расширению.

Точно так же химические реакции, в результате которых выделяются газы, повышают давление внутри контейнера. Например, встряхивание бутылки с газированным напитком приводит к выделению большего количества газа и повышению внутреннего давления. Это можно ощутить, когда вы открываете бутылку и напиток разбрызгивается.

Гидравлика

Когда жидкость, особенно жидкость, находится в частично закрытом контейнере, сила, приложенная в одной области, может привести к большей силе в другой области.Этот эффект используется в гидравлике для создания механического преимущества за счет того, что сила, приложенная к маленькому поршню, приводит к большей силе, приложенной к большому поршню.

Самолет

Ученый Бернулли обнаружил, что давление воздуха в трубе падает, когда скорость воздуха в трубе увеличивается. Это открытие стало известно как Принцип Бернулли .

Наибольшее применение этого принципа используется в самолетах. Крыло самолета обычно изогнуто сверху и плоско снизу.Когда воздух движется над изогнутой верхней частью крыла, он ускоряется из-за формы. Это снижает давление по отношению к нижней части крыла. Меньшее давление на верхнюю часть приводит к подъемной силе, необходимой для удержания самолета в воздухе.

Резюме

Давление жидкости под действием силы тяжести представляет собой вес жидкости выше, деленный на площадь, на которую она давит. Давление жидкости действует во всех направлениях. Внутреннее давление объекта равно внешнему давлению жидкости, иначе объект может быть раздавлен.Ветер и отопление также могут создавать давление.

Способность работать под давлением

Ресурсы и ссылки

Полномочия Рона Куртуса

веб-сайтов

Материальные ресурсы

Ресурсы по физике

Книги

(Примечание: Школа чемпионов может получать комиссионные за покупку книг)

Книги с самым высоким рейтингом по Материи

Лучшие книги по физике

Лучшие книги по физике жидкостей

Гидромеханика Ира М. Коэн и Пиюш К. Кунду, Academic Press (2004) $ 74,95

Векторы, тензоры и основные уравнения гидромеханики Резерфорд Арис, Dover Publications (1990) $14,95

Основы гидромеханики Брюс Р. Мансон, Дональд Ф. Янг, Теодор Х. Окииши; Уайли (2001) $37,95

Вопросы и комментарии

У вас есть вопросы, комментарии или мнения по этому вопросу? Если это так, отправьте электронное письмо с вашим отзывом.Я постараюсь вернуться к вам как можно скорее.

Поделиться этой страницей

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
Fluid_Pressure.htm

Где ты сейчас?

Школа Чемпионов

Темы физики
Давление жидкости

Давление | Encyclopedia.

com

ПОНЯТИЕ

Давление — это отношение силы к площади поверхности, на которую она воздействует. Хотя твердые тела оказывают давление, самые интересные примеры давления связаны с жидкостями, то есть газами и жидкостями, и в частности с водой и воздухом.Давление играет ряд важных ролей в повседневной жизни, в том числе его роль в работе насосов и гидравлических прессов. Поддержание обычного атмосферного давления необходимо для здоровья и благополучия человека: тело идеально приспособлено к обычному атмосферному давлению, и если это давление значительно изменится, у человека могут возникнуть вредные или даже фатальные побочные эффекты.

КАК ЭТО РАБОТАЕТ

Сила и площадь поверхности

Когда сила приложена перпендикулярно площади поверхности, она оказывает давление на эту поверхность, равное отношению F к A, , где F — сила и A площадь поверхности.Следовательно, формула для давления ( p ) имеет вид p = F / A.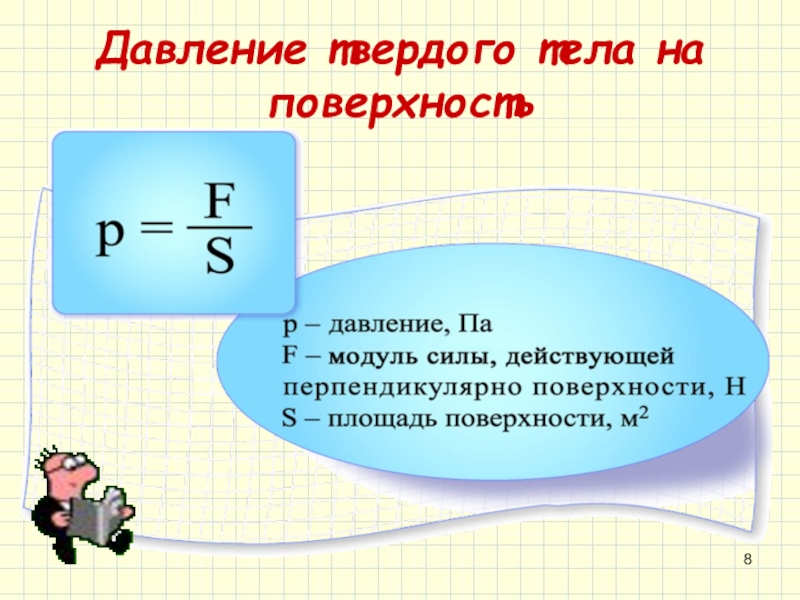 Одним интересным следствием этого отношения является тот факт, что давление может увеличиваться или уменьшаться без какого-либо изменения силы, другими словами, если поверхность становится меньше, давление становится больше, и наоборот.

Если бы одна чирлидерша держала на плечах другую чирлидершу, а девушка сверху стояла бы на лопатках девушки снизу, то ноги верхней девушки оказывали бы определенное давление на плечи нижней девушки.Это давление будет равно весу верхней девушки ( F, , что в данном случае является ее массой, умноженной на нисходящее ускорение под действием силы тяжести), деленному на площадь поверхности ее ступней. Предположим, что верхняя девушка выполняет сложное акробатическое движение, поднимая левую ногу и упираясь ею в правое колено, так что только ее правая нога оказывает всю силу своего веса. Теперь площадь поверхности, на которую действует сила, уменьшилась вдвое, и, таким образом, давление на нижнее плечо девушки увеличилось в два раза.

По той же причине — а именно, что уменьшение площади поверхности увеличивает чистое давление — хорошо поставленный удар карате гораздо эффективнее, чем шлепок открытой ладонью. Если бы кто-то ударил ладонью прямо по доске, единственным вероятным результатом была бы сильная жалящая боль в руке. Но если вместо этого нанести удар по доске, держа руку перпендикулярно — при условии, конечно, что вы являетесь знатоком карате, — доска может расколоться надвое. В первом случае площадь приложения силы велика, а чистое давление на доску относительно невелико, тогда как в случае удара карате площадь поверхности намного меньше, а, следовательно, давление намного больше.

Иногда предпочтительна большая площадь поверхности. Таким образом, снегоступы гораздо эффективнее для ходьбы по снегу, чем обычные туфли или ботинки. Обычная обувь ненамного больше поверхности стопы и идеально подходит для ходьбы по тротуару или траве. Но при глубоком снегу эта относительно небольшая площадь поверхности увеличивает давление на снег и заставляет ноги тонуть. Снегоступы, поскольку их площадь поверхности значительно больше, чем у обычной обуви, уменьшают отношение силы к площади поверхности и, следовательно, снижают чистое давление.

Тот же принцип применим к зимним лыжам и водным лыжам. Как и снегоступы, лыжи позволяют лыжнику оставаться на поверхности. снегу, но, в отличие от снегоступов, лыжи длинные и тонкие, что позволяет лыжнику более эффективно скользить по заснеженному склону. Что касается катания на воде, то люди, имеющие опыт в этом виде спорта, могут кататься босиком, но это сложно. Большинству новичков требуются водные лыжи, которые еще раз уменьшают чистое давление, оказываемое весом лыжника на поверхность воды.

Измерение давления

Давление измеряется рядом единиц в английской и метрической, или, как это называется в научном сообществе, системе СИ. Поскольку p = F / A , все единицы давления представляют собой некоторое отношение силы к площади поверхности. Основная единица СИ называется паскаль (Па) или 1 Н/м ² . Ньютон (Н), единица силы в СИ, равен силе, необходимой для ускорения 1 килограмма массы со скоростью 1 метр в секунду в квадрате. Таким образом, Паскаль равен давлению в 1 ньютон на поверхности площадью 1 квадратный метр.

В английской или британской системе давление измеряется в фунтах на квадратный дюйм, сокращенно фунт/дюйм ² . Это равно 6,89 · 10 ³ Па, или 6890 Па. Ученые — даже в США, где преобладает британская система единиц, — предпочитают пользоваться единицами СИ. Тем не менее, британская единица давления является знакомой частью повседневной жизни американского водителя, потому что давление в шинах в Соединенных Штатах обычно измеряется в фунтах на квадратный дюйм.(Рекомендуемое давление в шинах для автомобилей среднего размера обычно составляет 30-35 фунтов/дюйм ² .)

Другой важной мерой давления является атмосфера (атм), представляющая собой среднее давление воздуха на уровне моря. В английских единицах это равно 14,7 фунта/дюйм ² , а в единицах СИ 1,013 · 10 ⁵ Па, т. е. 101 300 Па. В системе СИ есть еще две специализированные единицы измерения давления. : бар, равный 10 ⁵ Па, и торр, равный 133 Па.Метеорологи, ученые, изучающие погодные условия, используют миллибар (мб), который, как следует из его названия, равен 0,001 бар. На уровне моря атмосферное давление составляет примерно 1013 мб.

БАРОМЕТР.

Торр, когда-то известный как «миллиметр ртутного столба», равен давлению, необходимому для поднятия столбика ртути (химический символ ртутного столба) на 1 мм. Он назван в честь итальянского физика Евангелиста Торричелли (1608-1647), который изобрел барометр, прибор для измерения атмосферного давления.

Барометр, сконструированный Торричелли в 1643 году, состоял из длинной стеклянной трубки, наполненной ртутью. Трубка была открыта с одного конца и перевернута вверх дном в чашу, содержащую больше ртути: следовательно, открытый конец был погружен в ртуть, а закрытый конец наверху представлял собой вакуум, т. е. область, в которой давление значительно ниже 1 атм.

Давление окружающего воздуха давило на поверхность ртути в чаше, а вакуум в верхней части трубки создавал область практически без давления, в которую могла подниматься ртуть. Таким образом, высота, на которую поднималась ртуть в стеклянной трубке, представляла собой нормальное давление воздуха (т. е. 1 атм.). Торричелли обнаружил, что при нормальном атмосферном давлении столбик ртути поднимается до 760 миллиметров.

Таким образом, значение 1 атм было установлено равным давлению, оказываемому на столбик ртути высотой 760 мм при температуре 0°C (32°F). Более того, изобретение Торричелли со временем стало неотъемлемой частью обеих научных лабораторий. и домохозяйств. Поскольку изменения атмосферного давления влияют на погодные условия, сегодня многие домашние и наружные термометры также включают барометр.

Давление и жидкости

С точки зрения физики и газы, и жидкости называются жидкостями, то есть веществами, которые соответствуют форме своего сосуда. Таким образом, давление воздуха и давление воды являются особыми предметами под более широким заголовком «давление жидкости». Жидкость реагирует на давление совершенно иначе, чем твердое тело. Плотность твердого тела делает его устойчивым к небольшим приложениям давления, но если давление увеличивается, оно испытывает растяжение и, в конечном счете, деформацию.Однако в случае жидкости напряжение заставляет ее течь, а не деформироваться.

Существуют три важные характеристики давления, оказываемого на жидкости контейнером. Во-первых, жидкость в сосуде, не испытывающая внешнего движения, прикладывает силу, перпендикулярную стенкам сосуда. Точно так же стенки контейнера воздействуют на жидкость, и в обоих случаях сила всегда перпендикулярна стенкам.

В каждой из этих трех характеристик предполагается, что емкость конечна: другими словами, жидкости некуда больше деваться.Отсюда второе утверждение: внешнее давление, действующее на жидкость, передается равномерно. Обратите внимание, что предыдущее утверждение было квалифицировано термином «внешнее»: сама жидкость оказывает давление, составляющая силы которого равна ее весу. Следовательно, жидкость на дне имеет гораздо большее давление, чем жидкость наверху, из-за веса жидкости над ней.

В-третьих, давление на любую маленькую поверхность жидкости одинаково, независимо от ориентации этой поверхности. Другими словами, область жидкости, перпендикулярная стенкам контейнера, испытывает такое же давление, как и область, параллельная или расположенная под углом к стенкам.Может показаться, что это противоречит первому принципу, согласно которому сила перпендикулярна стенкам сосуда. На самом деле сила является векторной величиной, что означает, что она имеет как величину, так и направление, тогда как давление является скаляром, что означает, что оно имеет величину, но не имеет определенного направления.

ПРИМЕНЕНИЕ В РЕАЛЬНОЙ ЖИЗНИ

Принцип Паскаля и гидравлический пресс

Три характеристики давления жидкости, описанные выше, имеют ряд следствий и приложений, среди которых так называемый принцип Паскаля.Как и единица давления в системе СИ, принцип Паскаля назван в честь французского математика и физика Блеза Паскаля (1623–1662), сформулировавшего второе из трех утверждений: внешнее давление, приложенное к жидкости, передается равномерно по всему объему тела. эта жидкость. Принцип Паскаля лег в основу одной из важнейших когда-либо разработанных машин — гидравлического пресса.

Простой гидравлический пресс, используемый для подъема автомобиля в автомастерской, обычно состоит из двух больших цилиндров, расположенных рядом.Каждый цилиндр содержит поршень, и цилиндры соединены в нижней части каналом, содержащим жидкость. Клапаны регулируют поток между двумя цилиндрами. Когда кто-то прикладывает усилие, нажимая на поршень в одном цилиндре (входном цилиндре), это дает равномерное давление, которое вызывает выход в второй цилиндр, толкая вверх поршень, который поднимает автомобиль.

В соответствии с принципом Паскаля давление во всем гидравлическом прессе одинаково и всегда будет равно отношению силы к давлению.Пока это соотношение одинаково, значения F и A могут различаться. В случае автомобильного домкрата входной цилиндр имеет относительно небольшую площадь поверхности, и, следовательно, сила, которая должна быть приложена, также относительно невелика. Выходной цилиндр имеет относительно большую площадь поверхности и, следовательно, прилагает относительно большую силу для подъема автомобиля. Это, в сочетании с разницей в высоте между двумя цилиндрами (обсуждаемой в контексте механических преимуществ в другом месте этой книги), позволяет поднимать тяжелый автомобиль с относительно небольшим усилием.

ГИДРАВЛИЧЕСКИЙ ТАРАНТ.

Автомобильный домкрат представляет собой простую модель гидравлического пресса в действии, но на самом деле принцип Паскаля имеет гораздо больше применений. Среди них гидравлический цилиндр, используемый в различных машинах, от бульдозеров до гидравлических подъемников, используемых пожарными и коммунальными службами для подъема на высоту. Однако в гидроцилиндре характеристики входного и выходного цилиндров противоположны характеристикам автомобильного домкрата.

Входной цилиндр, называемый главным цилиндром, имеет большую площадь поверхности, тогда как выходной цилиндр (называемый рабочим цилиндром) имеет небольшую площадь поверхности. Кроме того, хотя опять же, это фактор, связанный с механическим преимуществом, а не с давлением как таковым, главный цилиндр короткий, а рабочий цилиндр высокий. Из-за большей площади поверхности главного цилиндра по сравнению с рабочим цилиндром гидроцилиндр не считается эффективным с точки зрения механического преимущества: другими словами, входная сила намного больше, чем выходная сила.

Тем не менее, гидроцилиндр так же хорошо подходит для своей цели, как автомобильный домкрат.В то время как домкрат предназначен для подъема тяжелого автомобиля на небольшое расстояние по вертикали, гидроцилиндр поднимает гораздо более легкий груз (обычно всего одного человека) на гораздо большее расстояние по вертикали — например, на вершину дерева или здания.

Использование разницы давлений

НАСОСЫ.

В насосе используется принцип Паскаля, но вместо того, чтобы удерживать жидкость в одном контейнере, насос позволяет жидкости вытекать. В частности, насос использует разницу давлений, заставляя жидкость перемещаться из области более высокого давления в область более низкого давления. Очень простым примером этого является сифонный шланг, используемый для забора бензина из бензобака автомобиля. Всасывание на одном конце шланга создает область низкого давления по сравнению с областью относительно высокого давления бензобака. В конце концов, бензин выйдет из конца шланга низкого давления. (И если повезет, человек, перекачивающий воду, сможет это предвидеть, чтобы не получить полный рот бензина!)

Поршневой насос, более сложный, но все же довольно простой, состоит из вертикального цилиндра, вдоль которого расположен поршень. поднимается и опускается.Рядом с дном цилиндра расположены два клапана: впускной клапан, через который жидкость поступает в цилиндр, и выпускной клапан, через который жидкость вытекает из него. На такте всасывания, когда поршень движется вверх, впускной клапан открывается и позволяет жидкости поступать в цилиндр. При ходе вниз впускной клапан закрывается, а выпускной клапан открывается, и давление, создаваемое поршнем на жидкость, выталкивает ее через выпускной клапан.

Одним из наиболее очевидных применений поршневого насоса является двигатель автомобиля.В этом случае, конечно, перекачиваемой жидкостью является бензин, который толкает поршни, обеспечивая серию контролируемых взрывов, создаваемых воспламенением газа от свечи зажигания. В другой разновидности поршневых насосов, используемых для накачивания баскетбольных мячей или велосипедных шин, перекачиваемой жидкостью является воздух. Затем есть насос для воды, который качает питьевую воду из-под земли. Его также можно использовать для удаления желаемой воды из места, где она является помехой, например, со дна лодки.

ПРИНЦИП БЕРНУЛЛИ.

Хотя Паскаль дал ценные сведения об использовании давления для выполнения работы, мыслителем, первым сформулировавшим общие принципы взаимосвязи между жидкостями и давлением, был швейцарский математик и физик Даниэль Бернулли (1700–1782). Бернулли считается отцом гидромеханики, изучения поведения газов и жидкостей в состоянии покоя и в движении.

Проводя эксперименты с жидкостями, Бернулли заметил, что при уменьшении диаметра трубы вода течет быстрее.Это навело его на мысль, что какая-то сила должна действовать на воду сила, как он рассуждал, должна возникать из-за разности давлений. В частности, более медленно движущаяся жидкость в более широкой части трубы имеет большее давление, чем часть жидкости, движущейся через более узкую часть трубы. В результате он пришел к выводу, что давление и скорость обратно пропорциональны, другими словами, при увеличении одного уменьшается другое.

Отсюда он сформулировал принцип Бернулли, который гласит, что при всех изменениях движения сумма статического и динамического давления в жидкости остается неизменной.Жидкость в состоянии покоя оказывает статическое давление, которое обычно подразумевается под «давлением», как и под «давлением воды». Однако, когда жидкость начинает двигаться, часть статического давления, пропорциональная скорости жидкости, преобразуется в так называемое динамическое давление или давление движения. В цилиндрической трубе статическое давление действует перпендикулярно поверхности сосуда, а динамическое давление параллельно ей.

Согласно принципу Бернулли, чем больше скорость потока в жидкости, тем больше динамическое давление и меньше статическое давление: другими словами, более медленно движущаяся жидкость оказывает большее давление, чем более быстро движущаяся.Открытие этого принципа в конечном итоге сделало возможным создание самолета.

При движении жидкости из более широкой трубы в более узкую объем этой жидкости, перемещающейся на заданное расстояние за заданный период времени, не изменяется. Но поскольку ширина более узкой трубы меньше, жидкость должна двигаться быстрее (то есть с большим динамическим давлением), чтобы переместить то же количество жидкости на то же расстояние за то же время. Один из способов проиллюстрировать это — понаблюдать за поведением реки: в широкой, свободной области она течет медленно, но если ее поток сужается стенами каньона, то она резко ускоряется.

Принцип Бернулли в конечном итоге стал основой аэродинамического профиля, конструкции крыла самолета, если смотреть с торца. Аэродинамический профиль имеет форму асимметричной капли, лежащей на боку, «толстым» концом к воздушному потоку. Когда воздух попадает на переднюю часть аэродинамического профиля, воздушный поток разделяется, часть его проходит над крылом, а часть проходит под ним. Однако верхняя поверхность аэродинамического профиля изогнута, тогда как нижняя поверхность намного прямее.

В результате воздуху, протекающему сверху, приходится преодолевать большее расстояние, чем воздуху, протекающему под крылом.Поскольку жидкости имеют тенденцию компенсировать все объекты, с которыми они вступают в контакт, воздух вверху будет течь быстрее, чтобы встретиться с воздухом внизу в задней части крыла. Более быстрый поток воздуха, как продемонстрировал Бернулли, указывает на более низкое давление, а это означает, что давление на нижнюю часть крыла удерживает самолет в воздухе.

Плавучесть и давление

За сто двадцать лет до первого успешного полета на самолете братьев Райт в 1903 году другая пара братьев — французские гольфисты — разработали еще одно средство полета.Это был воздушный шар, который опирался на совершенно другой принцип отрыва от земли: плавучесть или стремление объекта, погруженного в жидкость, всплывать. Однако, как и в случае с принципом Бернулли, понятие плавучести связано с давлением.

В третьем веке до нашей эры греческий математик, физик и изобретатель Архимед (ок. 287–212 до н. э.) открыл так называемый принцип Архимеда, согласно которому выталкивающая сила объекта, погруженного в жидкость, равна вес жидкости, вытесненной телом.Вот почему корабли плавают: потому что их выталкивающая, или подъемная, сила меньше, чем равна весу вытесняемой ими воды.

Корпус корабля предназначен для вытеснения или перемещения количества воды, вес которого превышает вес самого судна. Вес вытесненной воды, то есть ее масса, умноженная на нисходящее ускорение, вызванное силой тяжести, равна выталкивающей силе, действующей на корабль со стороны океана. Если корабль весит меньше, чем вытесняемая им вода, он будет плавать; но если он будет весить больше, он утонет.

Факторы, связанные с принципом Архимеда, зависят от плотности, гравитации и глубины, а не от давления. Однако чем больше глубина внутри жидкости, тем больше давление, которое давит на объект, погруженный в жидкость. Более того, общее давление жидкости на заданной глубине частично связано как с плотностью, так и с гравитацией, составляющими выталкивающей силы.

ДАВЛЕНИЕ И ГЛУБИНА.

Давление, которое жидкость оказывает на дно сосуда, равно dgh, , где d — плотность, g — ускорение свободного падения и h — глубина сосуда.Для любой порции жидкости 90 654 ч 90 655 равно ее глубине внутри контейнера, а это означает, что чем глубже человек идет, тем больше давление. Кроме того, полное давление внутри жидкости равно dgh + p _{внешнее,}, где p _{внешнее} — давление, оказываемое на поверхность жидкости. В поршне-цилиндровом узле это давление исходит от поршня, а в воде – из атмосферы.

В этом контексте океан можно рассматривать как своего рода «контейнер».«На ее поверхности воздух оказывает направленное вниз давление, равное 1 атм. Плотность самой воды одинакова, как и ускорение вниз под действием силы тяжести; тогда единственной переменной является 90 654 ч, 90 655 или расстояние под поверхностью. … В самых глубоких частях океана давление невероятно велико – намного больше, чем может выдержать любой человек. Это огромное давление толкает вверх, сопротивляясь нисходящему давлению объектов на его поверхности. В то же время, если лодка вес правильно распределяется вдоль его корпуса, корабль увеличивает площадь и минимизирует силу, тем самым оказывая нисходящее давление на поверхность воды, которое меньше, чем восходящее давление самой воды.Следовательно, он плавает.

Давление и тело человека

ДАВЛЕНИЕ ВОЗДУХА.

Монгольфы использовали принцип плавучести не для того, чтобы плыть по воде, а для того, чтобы парить в небе на корабле легче воздуха. Подробности этого достижения обсуждаются в другом месте в контексте плавучести; но тема полета легче воздуха предполагает еще одну концепцию, которая несколько раз упоминалась в этом эссе: атмосферное давление.

Точно так же, как давление воды самое большое на дне океана, давление воздуха самое большое на поверхности Земли, которая фактически находится на дне «океана» воздуха.И давление воздуха, и давление воды являются примерами гидростатического давления — давления, которое существует в любом месте тела жидкости из-за веса жидкости над ним. В случае давления воздуха воздух тянется вниз силой земного притяжения, а воздух вдоль поверхности имеет большее давление из-за веса (функции силы тяжести) воздуха над ним. Однако на больших высотах над поверхностью Земли сила гравитации уменьшается, и, следовательно, атмосферное давление намного меньше.

При обычном опыте тело человека подвергается внушительному давлению.Учитывая значение атмосферного давления, обсуждавшееся ранее, если вытянуть руку — предполагая, что поверхность составляет около 20 дюймов ² (0,129 м ² ) — сила воздуха, воздействующая на нее, составляет почти 300 фунтов (136 кг). )! Как же это руку не раздавит весь этот вес? Причина в том, что само человеческое тело находится под давлением, и что внутренняя часть тела оказывает давление, равное давлению воздуха.

РЕАКЦИЯ НА ИЗМЕНЕНИЕ ДАВЛЕНИЯ ВОЗДУХА.

Человеческое тело приспособлено к нормальному атмосферному давлению в 1 атм, и если это внешнее давление изменить, в организме происходят изменения, которые могут быть вредными или даже фатальными.Незначительным примером этого является «хлопанье» в ушах, которое происходит, когда кто-то едет через горы или едет в самолете. С изменением высоты меняется давление, и, следовательно, давление в ушах также меняется.

Как отмечалось ранее, на больших высотах атмосферное давление снижается, что затрудняет дыхание. Поскольку воздух — это газ, его молекулы имеют тенденцию не притягиваться: другими словами, когда давление низкое, они стремятся удалиться друг от друга, и в результате человеку, находящемуся на большой высоте, трудно достичь цели. достаточное количество воздуха в его легкие. Бегуны, участвовавшие в Олимпийских играх 1968 года в Мехико, городе в горах, должны были тренироваться в высокогорных условиях, чтобы они могли дышать во время соревнований. Для бейсбольных команд, соревнующихся в Денвере, штат Колорадо (известном как «Город на высоте мили»), этот недостаток дыхания компенсируется тем фактом, что пониженное давление и сопротивление позволяют бейсбольному мячу легче двигаться по воздуху.

Если человек вырос в такой высокогорной среде, конечно, он привыкает дышать в условиях низкого давления воздуха.В перуанских Андах, например, люди проводят всю свою жизнь на высоте, более чем в два раза превышающей денверскую, но человеку из низкогорной местности следует посещать такие места только после принятия мер предосторожности. На очень больших высотах, конечно, человек не может дышать: поэтому кабины самолетов герметизированы. Большинство самолетов оснащены кислородными масками, которые падают с потолка, если внутри салона происходит перепад давления. Без этих масок все в салоне погибли бы.

КРОВЯНОЕ ДАВЛЕНИЕ.

Еще одним аспектом давления и человеческого организма является кровяное давление. Точно так же, как идеальное зрение 20/20, врачи рекомендуют целевое кровяное давление «120 на 80» — но что это значит? Когда у человека измеряют артериальное давление, на плечо на уровне сердца наматывают надувную манжету. В то же время стетоскоп помещают вдоль артерии в нижней части руки для контроля звука кровотока. Манжета надувается, чтобы остановить кровоток, затем давление высвобождается до тех пор, пока кровь снова не начнет течь, производя булькающий звук в стетоскопе.

Давление, необходимое для остановки кровотока, известно как систолическое давление, которое равно максимальному давлению, создаваемому сердцем. После уменьшения давления на манжету до тех пор, пока кровь не начнет нормально течь, что отражается в прекращении булькающего звука в стетоскопе, вновь измеряется давление в артерии. Это диастолическое давление, или давление, существующее в артерии между ударами сердца. Для здорового человека систолическое давление должно быть 120 торр, а диастолическое давление 80 торр.

ГДЕ УЗНАТЬ БОЛЬШЕ

«Атмосферное давление: сила, действующая под действием веса воздуха» (веб-сайт). (7 апреля 2001 г.).

Бейсер, Артур. Физика, 5-е изд. Чтение, Массачусетс: Addison-Wesley, 1991.

«Кровяное давление» (веб-сайт). (7 апреля 2001 г.).

Кларк, Джон Оуэн Эдвард. Атмосфера. Нью-Йорк: Gloucester Press, 1992.

Кобб, Аллан Б. Супер научные проекты об океанах. New York: Rosen, 2000.

«Физика подводного плавания: урок давления» (веб-сайт). (7 апреля 2001 г.).

Провензо, Юджин Ф. и Астери Бейкер Провензо. 47 простых классических экспериментов. Иллюстрации Питера А. Цорна-младшего. Нью-Йорк: Dover Publications, 1989.

«Понимание атмосферного давления» USA Today (веб-сайт). (7 апреля 2001 г.).

Зубровски, Берни. Воздушные шары: сборка и эксперименты с надувными игрушками. Иллюстрировано Роем Доти. New York: Morrow Junior Books, 1990.

КЛЮЧЕВЫЕ ТЕРМИНЫ

АТМОСФЕРА:

Мера давления, обозначаемая аббревиатурой «атм» и равная среднему давлению воздуха на уровне моря. В английских единицах это равно 14,7 фунтов на квадратный дюйм, а в единицах СИ — 101 300 паскалей.

БАРОМЕТР:

Прибор для измерения атмосферного давления.

ПЛАВУЧОСТЬ:

Тенденция объекта, погруженного в жидкость, плавать.

ЖИДКОСТЬ:

Любое вещество, будь то газ или жидкость, которое соответствует форме своего сосуда.

МЕХАНИКА ГИДРОИЗОЛЯЦИИ:

Изучение поведения газов и жидкостей в состоянии покоя и в движении.

ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ:

давление, существующее в любом месте тела жидкости из-за веса жидкости над ним.

ПАСКАЛЬ:

Основная СИ или метрическая единица давления, сокращенно «Па» и равная 1 Н/м ² .

ПРИНЦИП ПАСКАЛЯ:

Утверждение, сформулированное французским математиком и физиком Блезом Паскалем (1623-1662), согласно которому внешнее давление, приложенное к жидкости, передается равномерно по всему телу этой жидкости.

ДАВЛЕНИЕ:

Отношение силы к площади поверхности, когда сила приложена в направлении, перпендикулярном этой поверхности.Формула давления ( p ) выглядит следующим образом: p = F / A , где F — сила, а A — площадь поверхности.

Но что такое давление? Думая о частицах

Давление

Свойства материи

Но что такое давление? Думая о частицах

Рассказ о физике за 11-14

Что такое давление?

Здесь макроскопическое явление давления связано с действиями частиц.

Жидкости – жидкости и газы – состоят из множества мелких частиц, находящихся в постоянном беспорядочном движении. Эти частицы воздействуют на любые поверхности, с которыми им приходится сталкиваться. Таким образом, сила, возникающая из-за давления, возникает из-за бомбардировки частицами поверхностей. Давление является мерой состояния жидкости: давление в жидкости . Одна вещь, которую может предсказать эта мера, – это сила, которая будет действовать на область, ограничивающую жидкость.

Обратите внимание, что направление силы задается ориентацией области.Сила действует на площадь из-за дифференциальной бомбардировки частицами внутри и снаружи (поэтому разность давлений). Мы считаем полезным поговорить о давлении жидкости и силе, действующей на площадь.

Это бомбардировка ваших ушей молекулами воды, которая создает силу на ваших барабанных перепонках. Если давление воды велико (потому что вы погружаетесь на дно океана), столкновения молекул воды с барабанными перепонками происходят чаще, и создается большая сила.

Нам нужно представить действие давления (всегда в жидкости) как результат столкновения частиц с поверхностями. Уменьшение объема приводит к большему количеству столкновений, следовательно, к большему давлению.

Давление – Давление – GCSE Physics (Single Science) Revision

Давление – это сила на единицу площади .

Это означает, что давление, которое твердый объект оказывает на другую твердую поверхность, равно его весу в ньютонах, деленному на его площадь в квадратных метрах.

\[давление=\frac{сила}{площадь}\]

\[p=\frac{f}{a}\]

0.0.0.1:0.1.0.$0.$1.$4″> где:

p – единица измерения давления в паскалях. Один паскаль равен 1 Н/м. = длина × ширина

Единицами длины и ширины являются метры.

Вопрос

Сила 20 Н действует на площадь 2 м ² . Какое давление?

Показать ответ

сила ÷ площадь = давление

Закон Паскаля — для жидкостей и газов

Давление

Как уменьшить или увеличить давление

Задачка раз

Задачка два

Задачка три

Определение закона Паскаля

Давление жидкости

Задачка раз

Задачка два

Академия занимательных наук. Физика – Формула давления твёрдых тел. Видеоуроки физики

Формула давления твёрдых тел.

Формула давления твёрдых тел

Давление твердых тел – Класс!ная физика

Давление твердых тел

Александр Ржевский. Физика, 7 класс.

Давление

Что такое давление?

Закон Паскаля

Сообщающиеся сосуды

Атмосферное давление

Закон Архимеда

Атомная физика

Явления высокого давления | физика

Производство высокое давление

Аппараты большого объема

Давление – Гиперучебник по физике

15.1: Давление — Физика LibreTexts

Эффект гравитации

Принцип Паскаля

Измерение давления

Сноски

Давление — это сила на единицу площади Рон Куртус

Давление твердого тела на твердое тело

Твердое давление на замкнутую жидкость

Вызвано гравитацией

Пример с туфлями

Жидкий груз

Резюме

Ресурсы и ссылки

веб-сайтов

Книги

Поделиться этой страницей

Студенты и исследователи

Где ты сейчас?

Давление — это сила на единицу площади

Давление жидкости, Рон Куртус

Давление жидкости под действием силы тяжести или ускорения

Давление

Давление под действием силы тяжести

Давление воды

Колонка на макушке

Демонстрация с банкой

Давление воздуха

Атмосферное давление при погоде

Воздушные шары

Различные высоты

Направление давления жидкости

Все направления

Плавание под водой

Другие эффекты давления

Ветер и течение

Нагревание и химическое воздействие

Гидравлика

Самолет

Резюме

Ресурсы и ссылки

веб-сайтов

Книги

Вопросы и комментарии

Поделиться этой страницей

Студенты и исследователи

Где ты сейчас?

Давление жидкости

Давление | Encyclopedia.

ПОНЯТИЕ

КАК ЭТО РАБОТАЕТ

Сила и площадь поверхности

Измерение давления

БАРОМЕТР.