Физика электромагнетизм формулы: Основные формулы Электромагнетизм

Основные формулы Электромагнетизм

МАГНЕТИЗМ

Методические указания и контрольные задания для самостоятельной работы студентов

Дарибазарон Э.Ч., Санеев Э.Л., Шагдаров В.Б.

Редактор Т.Ю.Артюнина

Подготовлено в печать 2001 г. Формат 6080 1/16

Усл.п.л. 3,72; уч.-изд.л. 3,2; Тираж 150 экз.

___________________________________________________

РИО ВСГТУ, Улан-Удэ, Ключевская, 40а

Отпечатано на ротапринте ВСГТУ, Улан-Удэ,

Ключевская, 42.

 Восточно-Сибирский государственный

технологический университет

Министерство образования РФ

ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

ЗАДАНИЯ ПО ФИЗИКЕ

ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ

РАЗДЕЛ: ”МАГНЕТИЗМ”

Составители: Дарибазарон Э. Ч.,

Санеев Э.Л.,

Шагдаров В.Б.

Улан-Удэ 2002

Связь магнитной индукции B с напряженностью H магнитного поля:

где  – магнитная проницаемость изотропной среды; ₀ – магнитная постоянная.

В вакууме  = 1, и тогда магнитная индукция в вакууме

Закон Био-Савара-Лапласа:

или

где – магнитная индукция поля, создаваемого элементом проводника длинойdl с током I;

– радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция;  – угол между радиусом-вектором и направлением тока в элементе проводника.

Магнитная индукция в центре кругового тока:

где R – радиус кругового витка.

Магнитная индукция на оси кругового тока:

где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока

где r_o – расстояние от оси проводника до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током (рис.I,a):

Обозначения ясны из рисунка. Направление вектора магнитной индукции обозначено точкой – это значит, что направлен перпендикулярно плоскости чертежа к нам.

При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (рис.I,б):

-cos₂ = cos₁=cos,

тогда

Рис.1

Магнитная индукция поля соленоида

где n – отношение числа витков соленоида к его длине.

Сила, действующая на проводник с током в магнитном поле (закон Ампера):

где l – длина проводника;  – угол между направлением тока в проводнике и вектором магнитной индукции . Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямым, то закон Ампера можно применить к каждому элементу проводника в отдельности:

Магнитный момент плоского контура с током:

где – единичный вектор нормали (положительный) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.

Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:

, или

где  – угол между векторами и .

Потенциальная энергия (механическая) контура с током в магнитном поле:

, или

Отношение магнитного момента к механическому (моменту импульса) заряженной частицы, движущейся по круговой орбите:

где Q – заряд частицы; m – масса частицы.

Сила Лоренца:

, или

где – скорость заряженной частицы;  – угол между векторами и.

Магнитный поток:

а) в случае однородного магнитного поля и плоской поверхности

или

где S – площадь контура;  – угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности

(интегрирование ведется по всей поверхности).

Потокосцепление (полный поток):

Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

Работа по перемещению контура в магнитном поле:

Э.д.с. индукции:

Разность потенциалов на концах проводника, движущегося со скоростью

в магнитном поле:

где l – длина проводника;  – угол между векторами и.

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:

или

где R – сопротивление контура.

Индуктивность контура:

Э.д.с. самоиндукции:

Индуктивность соленоида:

где n – отношение числа витков соленоида к его длине; V – объем соленоида.

Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:

а) (при замыкании цепи), где E – э.д.с. источника тока; t – время, прошедшее после замыкания цепи;

б) (при размыкании цепи), где I_o – сила тока в цепи приt = 0; t – время, прошедшее с момента размыкания цепи.

Энергия магнитного поля:

Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему):

, или , или

где B – магнитная индукция; H – напряженность магнитного поля.

Электромагнетизм в физике: основные формулы

Основные формулы электромагнетизма

Кратность электрического заряда

Здесь q — заряд (Кл), N — число не скомпенсированных элементарных зарядов в заряде q (безразмерное), — элементарный заряд (Кл).

Поверхностная плотность заряда

Здесь — поверхностная плотность заряда , q — заряд на поверхности (Кл), S — площадь этой поверхности .

Закон Кулона

Здесь F — сила взаимодействия точечных зарядов (Н), — коэффициент пропорциональности, и — модули взаимодействующих зарядов (Кл), — относительная диэлектрическая проницаемость среды (безразмерная), —электрическая постоянная, r — расстояние между зарядами (м).

Напряженность электрического поля

Здесь Е — напряженность электрического поля (Н/Кл или В/м), F — сила, действующая на заряд (Н), q — заряд (Кл).

Напряженность поля точечного заряда

Здесь Е — напряженность поля (Н/Кл или В/м), k — коэффициент пропорциональности , q — модуль заряда (Кл), — относительная диэлектрическая проницаемость среды (безразмерная), — электрическая постоянная (Ф/м), r — расстояние от точки с напряженностью Е до заряда q (м).

Напряженность поля бесконечной равномерно заряженной плоскости

Здесь Е — напряженность электрического поля (В/м), — поверхностная плотность зарядов на плоскости , £0— электрическая постоянная (Ф/м), — диэлектрическая проницаемость среды (безразмерная).

Напряженность поля двух разноименно и равномерно заряженных плоскостей с одинаковой поверхностной плотностью зарядов (напряженность поля плоского конденсатора)

Все величины те же, что и в предыдущей формуле.

Работа перемещения заряда в однородном электрическом поле

Здесь А — работа перемещения заряда (Дж), Е — напряженность однородного поля (Н/Кл или В/м), q — перемещаемый заряд (Кл), d — проекция перемещения на силовую линию однородного поля (м).

Потенциал электрического поля

Здесь — потенциал электрического поля (В), — потенциальная энергия заряда (Дж), q — заряд, обладающий этой энергией в электрическом поле (Кл).

Потенциал поля точечного заряда

Все величины те же, что и в аналогичной формуле напряженности.

Разность потенциалов

Здесь — разность потенциалов между двумя точками поля (В), U — напряжение (В), А — работа перемещения заряда (Дж), q — перемещаемый заряд (Кл).

Связь напряженности с разностью потенциалов в однородном электрическом поле

Здесь Е — напряженность электрического поля (Н/Кл или В/м), — разность потенциалов между двумя точками поля (В), U — напряжение между этими точками (В), d — проекция расстояния между этими точками на силовую линию поля (м).

Электроемкость проводника

Здесь С — емкость проводника (Ф), q — заряд проводника (Кл), — его потенциал (В).

Емкость сферического проводника

Здесь С — емкость сферического проводника (Ф), — электрическая постоянная (Ф/м), — относительная диэлектрическая проницаемость среды (безразмерная), R — радиус сферы (м).

Емкость конденсатора

Здесь С — емкость конденсатора (Ф), q — его заряд (Кл), — разность потенциалов между его обкладками (В), U — напряжение между обкладками (В).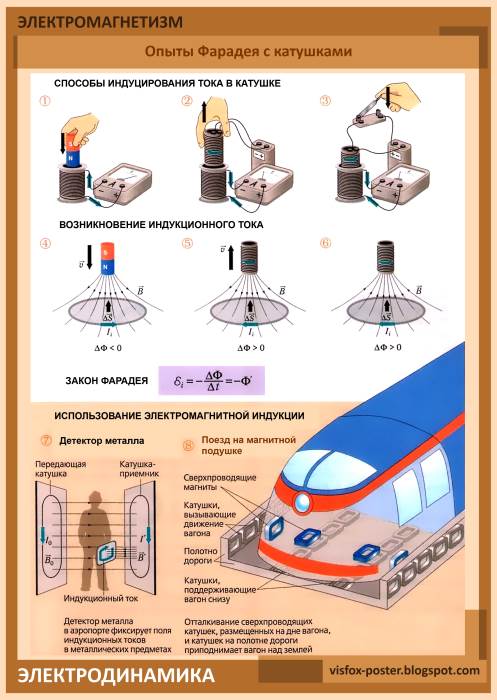

Емкость плоского конденсатора

Здесь С — емкость плоского конденсатора (Ф), — электрическая постоянная (Ф/м), — относительная диэлектрическая проницаемость среды (безразмерная), S — площадь обкладок конденсатора , d — расстояние между обкладками (м).

Последовательное соединение конденсаторов

q — одинаков на всех конденсаторах

Если все конденсаторы имеют одинаковую емкость С, то

Здесь q — заряд конденсаторов (Кл), — общее напряжение на батарее конденсаторов (В), — напряжения на отдельных конденсаторах (В), N — число конденсаторов (безразмерное), — общая емкость батареи конденсаторов (Ф), — емкости отдельных конденсаторов (Ф).

Параллельное соединение конденсаторов

U — одинаково на всех конденсаторах

Если все конденсаторы имеют одинаковую емкость С, то

Здесь U — напряжение на конденсаторах (В), — общий заряд батареи конденсаторов (Кл), — заряды отдельных конденсаторов (Кл), N — число конденсаторов (безразмерное), — емкость батареи конденсаторов (Ф), , — емкости отдельных конденсаторов (Ф).

Формулы энергии электрического поля проводника

Здесь — энергия электрического поля (Дж), С — емкость проводника (Ф), — потенциал проводника (В), q — заряд проводника (Кл).

Формулы энергии электрического поля конденсатора

Здесь — энергия электрического поля конденсатора (Дж), С — емкость конденсатора (Ф), q — заряд на его обкладках (Кл), U — напряжение на обкладках конденсатора (В).

Формула энергии системы точечных зарядов

Здесь — энергия системы N точечных зарядов (Дж), — заряды, входящие в систему (Кл), — потенциалы полей, созданных в точке, где находится один из зарядов, остальными зарядами системы (В).

Формулы силы тока

Здесь I — сила постоянного тока (A), q — заряд, прошедший через поперечное сечение проводника (Кл), t — время прохождения заряда (с), n — концентрация свободных электронов , е — модуль заряда электрона (Кл), v — скорость упорядоченного движения электронов по проводнику (м/с), S — площадь поперечного сечения проводника .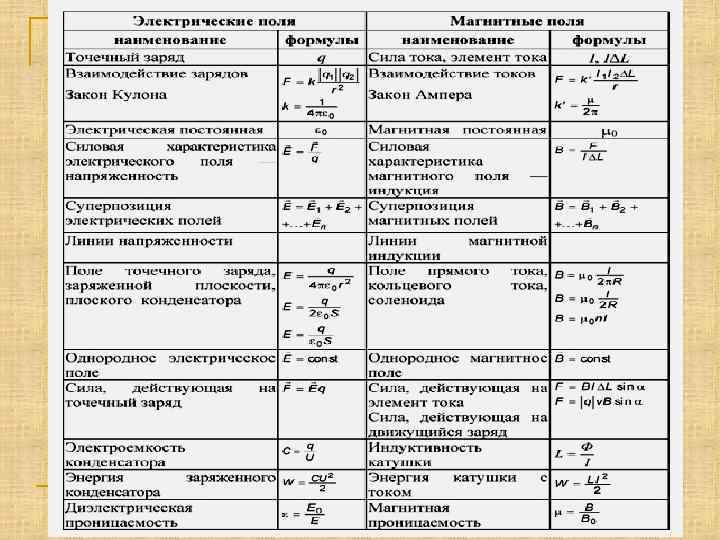

Формулы плотности тока

Здесь j — плотность тока , I — сила тока (A), S — площадь поперечного сечения проводника , п — концентрация свободных электронов в проводнике , е — модуль заряда электрона (Кл), v — скорость упорядоченного движения свободных электронов (м/с).

Формулы сопротивления проводника

Здесь R — сопротивление проводника (Ом), U — напряжение на нем (В), I — сила тока в проводнике (А), — удельное сопротивление (Ом • м), l — длина проводника (м), S — площадь поперечного сечения проводника .

Зависимость сопротивления металлического проводника от температуры

Здесь R — сопротивление проводника при температуре t °C (Ом), — сопротивление проводника при О °C (Ом), а — температурный коэффициент сопротивления , t — температура по шкале Цельсия, — изменение абсолютной температуры проводника при нагревании от О °C = 273 К до абсолютной температуры Т (К).

Закон Ома для однородного участка цепи

Здесь I — сила тока (A), U — напряжение (В), R — сопротивление участка (Ом).

Последовательное соединение проводников

I — одинакова во всех проводниках

Если все проводники имеют одинаковое сопротивление, то

для двух последовательных проводников

Здесь I — сила тока (А), — общее напряжение на всех последовательно соединенных проводниках (В), ,…, — напряжения на отдельных проводниках (В), — общее сопротивление всех последовательно соединенных проводников (Ом), — сопротивления отдельных проводников (Ом), N — количество проводников (безразмерное).

Параллельное соединение проводников

U — одинаково на всех проводниках

Если все проводники имеют одинаковое сопротивление, то

общее сопротивление двух параллельных проводников

общее сопротивление трех параллельных проводников

— для двух параллельных проводников

Здесь U — напряжение на проводниках (В), — сила тока в неразветвленном участке цепи (А), — сила тока в отдельных проводниках (А), — общее сопротивление параллельных проводников (Ом), — сопротивления отдельных проводников (Ом), N — количество проводников (безразмерное).

Закон Ома для неоднородного участка цепи

Здесь I — сила тока (А), — разность потенциалов на концах участка (В), — ЭДС, действующая в участке (В), R — сопротивление участка (Ом).

Формула ЭДС

Здесь — ЭДС (В), — работа сторонних сил (Дж), q — перемещаемый заряд (Кл).

Закон Ома для всей цепи

в случае соединенных последовательно одинаковых источников тока

в случае соединенных параллельно одинаковых источников тока

Здесь I — сила тока в цепи (А), — ЭДС источника тока (В), R — сопротивление внешней части цепи (Ом), r — внутреннее сопротивление или сопротивление источника тока (Ом), N — количество одинаковых источников тока (безразмерное).

Сила тока короткого замыкания

при R = О

Все величины названы в предыдущей формуле.

Расчет сопротивления шунта к амперметру

Здесь — сопротивление шунта (Ом), — сопротивление амперметра (Ом), — число, показывающее, во сколько раз измеряемая амперметром сила тока I больше силы тока , на которую он рассчитан (безразмерное число).

Расчет добавочного сопротивления к вольтметру

Здесь — добавочное сопротивление (Ом), — сопротивление вольтметра (Ом), — число, показывающее, во сколько раз измеряемое напряжение U больше напряжения , на которое рассчитан вольтметр (безразмерное число).

Работа тока

Здесь А — работа тока (Дж), U — напряжение на участке цепи (В), I — сила тока в цепи (A), t — время прохождения тока (с), q — прошедший по цепи заряд (Кл), — разность потенциалов на концах участка цепи (В), R — сопротивление участка цепи (Ом), — ЭДС источника тока (В), Р — мощность тока (Вт).

Мощность тока

Здесь Р — мощность тока (Вт), U — напряжение (В), I — сила тока (A), R — сопротивление (Ом), — ЭДС источника тока (В), А — работа тока (Дж), t — время (с).

Закон Джоуля — Ленца

Здесь Q — количество теплоты (Дж). Остальные величины названы в предыдущей формуле.

Коэффициент полезного действия (КПД) электрической цепи

Здесь — КПД электрической цепи (% или безразмерный), U — напряжение на внешнем участке цепи (В), R — сопротивление внешнего участка цепи (Ом), r — внутреннее сопротивление или сопротивление источника тока (Ом), — ЭДС источника тока (В).

Закон Фарадея для электролиза

Здесь m — масса вещества, выделившегося на электроде (кг), k — электрохимический эквивалент этого вещества (кг/Кл), q — заряд, прошедший через электролит, I — сила тока в электрохимической ванне (A), t — время электролиза (с), F — число Фарадея (Кл/моль), М — молярная масса выделившегося вещества (кг/моль, n — валентность этого вещества (безразмерная).

Формулы индукции магнитного поля

Здесь В — индукция магнитного поля (Тл), — максимальный момент сил, вращающих контур с током в магнитном поле (Н • м), I — сила тока в контуре (A), S — площадь контура — максимальная сила Ампера, действующая на проводник с током в магнитном поле (Н), l — длина проводника в магнитном поле (м).

Формула силы Ампера

Здесь — сила Ампера, действующая на проводник с током в магнитном поле (Н), В — индукция магнитного поля (Тл), I — сила тока в проводнике (А), l — длина проводника в магнитном поле (м), — угол между направлением тока в проводнике и вектором магнитной индукции (рад).

Формула момента сил, вращающих контур с током в магнитном поле

Здесь М — момент сил, вращающих контур с током в магнитном поле (Н • м), В — индукция магнитного поля (Тл), I — сила тока в контуре (A), S — площадь контура — угол между нормалью к плоскости контура и вектором магнитной индукции (рад).

Формула силы Лоренца, действующей на заряд, движущийся в магнитном попе

Здесь — сила Лоренца, действующая на заряд, движущийся в магнитном поле (Н), В — индукция магнитного поля (Тл), q — заряд (Кл), v — скорость заряда (м/с), — угол между векторами магнитной индукции и скорости (рад).

Формула магнитного потока

Здесь Ф — магнитный поток сквозь поверхность (Вб), S — площадь поверхности — угол между нормалью к поверхности и вектором магнитной индукции (рад), L — индуктивность контура (Гн), I — сила тока в контуре (А).

Формула ЭДС электромагнитной индукции

Здесь — ЭДС индукции в контуре (В), — скорость изменения магнитного потока, пересекающего контур (Вб/с), N — число витков в контуре (безразмерное), — первая производная магнитного потока по времени (Вб/с).

Формула ЭДС индукции в проводнике, движущемся поступательно в магнитном поле

Здесь — ЭДС индукции в проводнике (В), В — индукция магнитного поля (Тл), v — скорость проводника в магнитном поле (м/с), l — длина проводника в магнитном поле (м), — угол между векторами скорости и магнитной индукции (рад), — максимальная ЭДС индукции, когда проводник движется перпендикулярно линиям магнитной индукции.

Формула ЭДС индукции в контуре, вращающемся в магнитном поле

Здесь — ЭДС индукции во вращающемся контуре (В), В — индукция магнитного поля (Тл), — угловая скорость вращения (рад/с), S — площадь контура, N — число витков в контуре (безразмерное), — угол между вектором индукции и нормалью к плоскости контура, —максимальная ЭДС индукции, когда угол между нормалью к плоскости контура и вектором магнитной индукции равен 90°, т.е. когда плоскость контура параллельная линиям магнитной индукции.

Формула ЭДС самоиндукции

Здесь — ЭДС самоиндукции в контуре (В), L — индуктивность контура (Гн), — скорость изменения силы тока в контуре (А/с), — первая производная силы тока по времени.

Формула магнитной проницаемости магнетика

Здесь — магнитная проницаемость магнетика (безразмерная), В — индукция магнитного поля в магнетике (Тл), — индукция магнитного поля в вакууме (Тл).

Формула энергии магнитного поля

Здесь — энергия магнитного поля (Дж), L — индуктивность контура (Гн), I — сила тока в контуре (А).

Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти страницы:

16.2: уравнения Максвелла и электромагнитные волны

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4449

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Объяснять поправку Максвелла к закону Ампера, включая ток смещения
• Сформулируйте и примените уравнения Максвелла в интегральной форме
• Опишите, как симметрия между изменяющимися электрическими и изменяющимися магнитными полями объясняет предсказание Максвелла электромагнитных волн
• Опишите, как Герц подтвердил предсказание Максвелла об электромагнитных волнах

Джеймс Клерк Максвелл (1831–1879) был одним из основных авторов физики девятнадцатого века (рис. \(\PageIndex{1}\)). Хотя он умер молодым, он внес большой вклад в развитие кинетической теории газов, в понимание цветового зрения и в природу колец Сатурна. Он, вероятно, наиболее известен тем, что объединил существующие знания о законах электричества и магнетизма с собственными открытиями в полную всеобъемлющую электромагнитную теорию, представленную Уравнения Максвелла .

Рисунок \(\PageIndex{1}\): Джеймс Клерк Максвелл, физик девятнадцатого века, разработал теорию, объясняющую взаимосвязь между электричеством и магнетизмом, и правильно предсказал, что видимый свет состоит из электромагнитных волн.

Поправка Максвелла к законам электричества и магнетизма

Четыре основных закона электричества и магнетизма были открыты экспериментально благодаря работам таких физиков, как Эрстед, Кулон, Гаусс и Фарадей. Максвелл обнаружил логические противоречия в этих более ранних результатах и ​​назвал их причиной неполноту закона Ампера.

Напомним, что по закону Ампера интеграл магнитного поля вокруг замкнутого контура C пропорционален току I , проходящему через любую поверхность, границей которой является сам контур C :

\[\oint\ vec{B} \cdot d\vec{s} = \mu_0 I. \label{Eq1}\]

Существует бесконечно много поверхностей, которые можно присоединить к любой петле, и закон Ампера сформулирован в уравнении \ref{Eq1} не зависит от выбора поверхности.

Рассмотрим настройку на рисунке \(\PageIndex{2}\). Источник ЭДС резко подключается к пластинчатому конденсатору так, что ток 9 зависит от времени.0046 I развивается в проводе. Предположим, мы применяем закон Ампера к контуру C , показанному до того, как конденсатор полностью заряжен, так что \( I \neq 0\). Поверхность \(S_1\) дает ненулевое значение для замкнутого тока I , тогда как поверхность \(S_2\) дает нулевое значение для замкнутого тока, потому что через нее не проходит ток:

\[\underbrace{\oint_C \vec{ B} \cdot d\vec{s} = \mu_0 I}_{\text{если используется поверхность} S_1 \text{используется}}\]

\[\underbrace{ \, =0 }_{\text{ если поверхность } S_2 \text{используется}}\]

Понятно, что закон Ампера в его обычном виде здесь не работает. В этом нет ничего удивительного, поскольку закон Ампера, примененный в предыдущих главах, требовал постоянного тока, тогда как в этом эксперименте ток меняется со временем и вовсе не является постоянным.

Рисунок \(\PageIndex{2}\): Токи через поверхность \(S_1\) и поверхность \(S_2\) неодинаковы, несмотря на то, что они имеют один и тот же граничный контур C .

Как изменить закон Ампера, чтобы он работал во всех ситуациях? Максвелл предложил включить дополнительный вклад, называемый током смещения \(I_d\), в действительный ток I ,

\[\boxed{\oint_S \vec{B} \cdot d\vec{s} = \mu_0 (I + I_d)} \label{EQ4}\]

где определяется ток смещения быть

\[\boxed{I_d = \epsilon_0 \dfrac{d\Phi_E}{dt}.} \label{EQ5}\]

Здесь \(\epsilon_0\) – диэлектрическая проницаемость свободного пространства и \(\Phi_E\) – электрический поток, определяемый как

\[\Phi_E = \iint_{Surface \, S} \vec{E} \cdot d\vec{A}. \]

Ток смещения аналогично реальному току в законе Ампера, входя таким же образом в закон Ампера. Однако он создается изменяющимся электрическим полем. Он объясняет изменяющееся электрическое поле, создающее магнитное поле, как это делает реальный ток, но ток смещения может создавать магнитное поле даже там, где нет реального тока. Когда этот дополнительный член включен, модифицированное уравнение закона Ампера становится равным

\[\oint_C \vec{B} \cdot d\vec{s} = \mu_0 I + \epsilon_0 \mu_0 \dfrac{d\Phi_E}{dt}\]

и не зависит от поверхности S через который измеряется ток I .

Теперь мы можем изучить эту модифицированную версию закона Ампера, чтобы подтвердить, что он выполняется независимо от того, выбрана ли поверхность \(S_1\) или поверхность \(S_2\) на рисунке \(\PageIndex{2}\). Электрическое поле \(\vec{E}\), соответствующее потоку \(\Phi_E\) в уравнении \ref{EQ5}, находится между пластинами конденсатора. Следовательно, поле \(\vec{E}\) и ток смещения через поверхность \(S_1\) равны нулю, и уравнение \ref{EQ4} принимает вид

\[\oint_C \vec{B} \cdot d\vec{s} = \mu_0 I. \label{16.5}\]

Теперь мы должны показать, что для поверхности \(S_2\), через которую нет фактического течет ток, то ток смещения приводит к тому же значению \(\mu_0 I\) для правой части уравнения закона Ампера. Для поверхности \(S_2\) уравнение принимает вид

\[\oint_C \vec{B} \cdot d\vec{s} = \mu_0 \dfrac{d}{dt} \left[ \epsilon_0 \iint_{Surface \ , S_2} \vec{E} \cdot d\vec{A} \right].\]

Закон Гаусса для электрического заряда требует замкнутой поверхности и обычно не может быть применен к такой поверхности, как \(S_1\) отдельно или \ (S_2\) один. Но две поверхности \(S_1\) и \(S_2\) образуют замкнутую поверхность на рисунке \(\PageIndex{2}\) и могут использоваться в законе Гаусса. Поскольку электрическое поле равно нулю на \(S_1\), вклад потока через \(S_1\) равен нулю. Это дает нам

\[ \begin{align} \oint_{Поверхность \, S_1 + S_2} \vec{E} \cdot d\vec{A} &= \iint_{Поверхность \, S_1} \vec{E} \cdot d \vec{A} + \iint_{Поверхность \, S_2} \vec{E} \cdot d\vec{A} \\[4pt] &= 0 + \iint_{Поверхность \, S_2} \vec{E} \ cdot d\vec{A} \\[4pt] &= \iint_{Поверхность \, S_2} \vec{E} \cdot d\vec{A}. \end{align}\]

Следовательно, мы можем заменить интеграл по \(S_2\) в уравнении \ref{16.5} замкнутой гауссовой поверхностью \(S_1 + S_2\) и применить закон Гаусса, чтобы получить

\ [\oint_{S_1} \vec{B} \cdot d\vec{s} = \mu_0 \dfrac{dQ_{in}}{dt} = \mu_0 I.\]

Таким образом, модифицированное уравнение закона Ампера с использованием поверхности \(S_2\), где правая часть является результатом тока смещения, такое же, как и для поверхности \(S_1\), где вклад исходит от реальный поток электрического заряда.

Ток смещения в зарядном конденсаторе

Плоский конденсатор емкостью C , пластины которого имеют площадь A и расстояние между пластинами d , соединенный с резистором R и аккумулятор напряжением В . Ток начинает течь при \(t = 0\).

1. Найти ток смещения между пластинами конденсатора в момент времени t .
2. По свойствам конденсатора найдите соответствующий действительный ток \(I = \dfrac{dQ}{dt}\) и сравните ответ с ожидаемым током в проводах соответствующей RC-цепи .

Стратегия

Мы можем использовать уравнения из анализа 9{-t/RC}. \nonumber\] Этот ток такой же, как \(I_d\), найденный в (a).

Уравнения Максвелла

С поправкой на ток смещения уравнения Максвелла принимают вид

\[ \begin{align} \oint \vec{E} \cdot d\vec{A} &= \dfrac{Q_{ in}}{\epsilon_0} \, (\text{закон Гаусса}) \label{eq1} \\[4pt] \oint \vec{B} \cdot d\vec{A} &= 0 \, (\text {Закон Гаусса для магнетизма}) \label{eq2} \\[4pt] \oint \vec{E} \cdot d\vec{s} &= – \dfrac{d\Phi_m}{dt} \, (\text {Закон Фарадея}) \label{eq3} \\[4pt] \oint \vec{B} \cdot d\vec{s} &= \mu_0 I + \epsilon_0I + \epsilon_0 \mu_0 \dfrac{d\Phi_E} {dt} (\text{Закон Ампера-Максвелла}). \label{eq4} \end{align}\]

После того, как поля были рассчитаны с использованием этих четырех уравнений, уравнение силы Лоренца

\[\vec{F} = q\vec{E} + q\vec{v} \times \vec{B}\ ]

дает силу, с которой поля действуют на частицу с зарядом q , движущуюся со скоростью \(\vec{v}\). Уравнение силы Лоренца объединяет силу электрического поля и магнитного поля, действующую на движущийся заряд. Магнитные и электрические силы рассматривались в предыдущих модулях. Эти четыре уравнения Максвелла, соответственно, таковы:

Уравнения Максвелла

1. Закон Гаусса

Электрический поток через любую замкнутую поверхность равен электрическому заряду \(Q_{in}\), заключенному в этой поверхности. Закон Гаусса (уравнение \ref{eq1}) описывает связь между электрическим зарядом и создаваемым им электрическим полем. Это часто изображают в виде силовых линий электрического поля, исходящих из положительных зарядов и заканчивающихся отрицательными зарядами и указывающих направление электрического поля в каждой точке пространства.

2. Закон Гаусса для магнетизма

Поток магнитного поля через любую замкнутую поверхность равен нулю (уравнение \ref{eq2}). Это эквивалентно утверждению, что силовые линии магнитного поля непрерывны, не имеют ни начала, ни конца. Любая линия магнитного поля, входящая в область, ограниченную поверхностью, также должна покинуть ее. Известно, что не существует магнитных монополей, где линии магнитного поля заканчивались бы (см. Раздел о магнитных полях и линиях).

3. Закон Фарадея

Изменяющееся магнитное поле индуцирует электродвижущую силу (ЭДС) и, следовательно, электрическое поле. Направление ЭДС противоположно изменению. Уравнение \ref{eq3} представляет собой закон индукции Фарадея и включает в себя закон Ленца. Электрическое поле от изменяющегося магнитного поля имеет силовые линии, которые образуют замкнутые петли без начала и конца.

4. Закон Ампера-Максвелла

Магнитные поля генерируются движущимися зарядами или изменяющимися электрическими полями. Это четвертое уравнение Максвелла, уравнение \ref{eq4}, включает в себя закон Ампера и добавляет еще один источник магнитных полей, а именно изменяющиеся электрические поля.

Уравнения Максвелла и закон силы Лоренца вместе охватывают все законы электричества и магнетизма. Симметрия, которую Максвелл ввел в свою математическую структуру, может быть не сразу очевидна. Закон Фарадея описывает, как изменяющиеся магнитные поля создают электрические поля. Вместо этого введенный Максвеллом ток смещения является результатом изменяющегося электрического поля и объясняет изменяющееся электрическое поле, создающее магнитное поле. Уравнения для эффектов как изменяющихся электрических полей, так и изменяющихся магнитных полей различаются по форме только там, где отсутствие магнитных монополей приводит к пропущенным членам. Эта симметрия между эффектами изменения магнитного и электрического полей имеет важное значение для объяснения природы электромагнитных волн.

Позднее применение теории относительности Эйнштейна к полной и симметричной теории Максвелла показало, что электрические и магнитные силы не являются отдельными, а являются разными проявлениями одного и того же — электромагнитной силы. Электромагнитное взаимодействие и слабое ядерное взаимодействие так же объединены, как и электрослабое взаимодействие. Это объединение сил было одним из мотивов попыток объединить все четыре основных взаимодействия в природе — гравитационное, электрическое, сильное и слабое ядерное взаимодействие (см. Физика элементарных частиц и космология).

Механизм распространения электромагнитных волн

Чтобы увидеть, как симметрия, введенная Максвеллом, объясняет существование комбинированных электрических и магнитных волн, распространяющихся в пространстве, представьте себе изменяющееся во времени магнитное поле \(\vec{B}_0(t )\), создаваемый высокочастотным переменным током, показанным на рисунке \(\PageIndex{3}\). Мы представляем \(\vec{B}_0(t)\) на диаграмме одной из его линий поля. Согласно закону Фарадея, изменение магнитного поля через поверхность индуцирует изменяющееся во времени электрическое поле \(\vec{E}_0(t)\) на границе этой поверхности. Источник тока смещения для электрического поля, как и источник закона Фарадея для магнитного поля, создает только замкнутые петли силовых линий из-за математической симметрии, связанной с уравнениями для индуцированного электрического и индуцированного магнитного полей. Представление линии поля \(\vec{E}_0(t)\) показано. В свою очередь изменяющееся электрическое поле \(\vec{E}_0(t)\) создает магнитное поле \(\vec{B}_1(t)\) по модифицированному закону Ампера. Это изменяющееся поле индуцирует \(\vec{E}_1(t)\), которое индуцирует \(\vec{B}_2(t)\) и так далее. Затем мы имеем самопродолжающийся процесс, который приводит к созданию изменяющихся во времени электрических и магнитных полей в регионах, все дальше и дальше от О . Этот процесс можно представить себе как распространение электромагнитной волны в пространстве.

Рисунок \(\PageIndex{3}\): Как изменяющиеся поля \(\vec{E}\) и \(\vec{B}\) распространяются в пространстве.

В следующем разделе мы покажем в более точных математических терминах, как уравнения Максвелла приводят к предсказанию электромагнитных волн, которые могут распространяться в пространстве без материальной среды, подразумевая скорость электромагнитных волн, равную скорости света.

До работы Максвелла эксперименты уже указывали на то, что свет является волновым явлением, хотя природа волн была еще неизвестна. В 1801 году Томас Янг (1773–1829 гг.) показал, что когда световой пучок разделялся двумя узкими щелями, а затем рекомбинировался, на экране образовывался узор из светлых и темных полос. Янг объяснил это поведение, предполагая, что свет состоит из волн, которые складываются конструктивно в одних точках и разрушительно в других (см. Интерференция). Впоследствии Жан Фуко (1819–1868) с измерениями скорости света в различных средах и Огюстен Френель (1788–1827) с подробными экспериментами, связанными с интерференцией и дифракцией света, предоставили дополнительные убедительные доказательства того, что свет представляет собой волну. Итак, свет был волной, и Максвелл предсказал существование электромагнитных волн, распространяющихся со скоростью света. Вывод казался неизбежным: свет должен быть формой электромагнитного излучения. Но теория Максвелла показала, что для электромагнитных волн возможны другие длины волн и частоты, отличные от световых. Он показал, что электромагнитное излучение с теми же фундаментальными свойствами, что и видимый свет, должно существовать на любой частоте. Другим оставалось проверить и подтвердить это предсказание.

Упражнение \(\PageIndex{1}\)

Когда ЭДС на конденсаторе включена и конденсатор заряжается, когда магнитное поле, вызванное током смещения, имеет наибольшую величину?

Решение

Максимальное значение сразу после включения тока. Ток смещения и магнитное поле от него пропорциональны скорости изменения электрического поля между пластинами, которая наибольшая, когда пластины впервые начинают заряжаться.

Наблюдения Герца

Немецкий физик Генрих Герц (1857–1894) первым сгенерировал и обнаружил определенные типы электромагнитных волн в лаборатории. Начиная с 1887 года, он провел серию экспериментов, которые не только подтвердили существование электромагнитных волн, но и подтвердили, что они распространяются со скоростью света.

Герц использовал цепь переменного тока RLC (резистор-индуктор-конденсатор), которая резонирует на известной частоте \(f_0 = \dfrac{1}{2\pi \sqrt{LC}}\) и подключил ее к проволочную петлю, как показано на рисунке \(\PageIndex{4}\). Высокое напряжение, индуцированное через разрыв в петле, вызывало искры, которые были видимым свидетельством тока в цепи и помогали генерировать электромагнитные волны.

Через лабораторию Герц поместил еще одну петлю, присоединенную к другой цепи RLC , которую можно было настроить (как циферблат на радио) на ту же резонансную частоту, что и первую, и таким образом можно было настроить на прием электромагнитных волн. В этой петле также был зазор, через который генерировались искры, что давало убедительные доказательства того, что электромагнитные волны были получены.

Рисунок \(\PageIndex{4}\): Устройство, которое Герц использовал в 1887 году для генерации и обнаружения электромагнитных волн.

Герц также изучил картины отражения, преломления и интерференции генерируемых им электромагнитных волн, подтвердив их волновой характер. Он смог определить длины волн по интерференционным картинам, а зная их частоты, рассчитать скорость распространения по уравнению \(v = f\lambda\), где v — скорость волны, f — ее частота, а \(\lambda\) — ее длина волны. Таким образом, Герц смог доказать, что электромагнитные волны распространяются со скоростью света. Единица СИ для частоты, герц \((1 \, Гц = 1 \, цикл/секунда)\), названа в его честь.

Упражнение \(\PageIndex{2}\)

Может ли чисто электрическое поле распространяться в виде волны через вакуум без магнитного поля? Обосновать ответ.

Решение

Нет. Изменение электрического поля в соответствии с модифицированной версией закона Ампера обязательно индуцирует изменение магнитного поля.

---

Эта страница под названием 16.2: уравнения Максвелла и электромагнитные волны распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. Ток смещения
   2. сила Лоренца
   3. уравнения Максвелла
   4. источник@https://openstax. org/details/books/university-physics-volume-2

Уравнения Максвелла и свет

Уравнения Максвелла и свет

Уравнения Максвелла и свет

Мы завершили изучение законов электричества и магнетизма. Все, что мы узнали можно резюмировать в уравнениях, известных как уравнений Максвелла , вместе с формулами для электрических и магнитных сил, действующих на заряд. Один из нескольких способов, которыми уравнения Максвелла могут быть написано справа, чтобы вы могли сказать, что видели их. Первое уравнение — это закон Ампера (включая член в правой части, который мы не обсуждали). в этом курсе). Второе уравнение представляет собой закон Фарадея в сочетании с законом Ленца. Третье уравнение – это закон Гаусса, который выражает тот факт, что силовые линии электрического поля начинаются и заканчиваются только на зарядке. Четвертое уравнение является магнитным эквивалентом закона Гаусса, который выражает тот факт, что магнитное силовые линии никогда не начинаются и не заканчиваются (т. е. нет свободных магнитных зарядов).

Используя некоторые не очень простые вычисления, уравнения Максвелла могут быть используется, чтобы показать, что электрические и магнитные поля подчиняются волновым уравнениям. скорость c электромагнитной волны определяется константами электричество и магнетизм, которые вы так хорошо знаете:
&nbsp в = 1/( е ₀ м ₀ ) ^{870 1/2 2,998 х 10 8 м/с .}

Свет — это электромагнитная волна: это понял Максвелл примерно в 1864 г., как только уравнение с = 1/(е ₀ м ₀ ) ^1/2 = 2,998 X 10 ⁸ м/с была открыта, так как к тому времени скорость света была точно измерена, и ее согласие с c вряд ли было совпадением. Радиосигналы также являются электромагнитными волнами; после открытия уравнений Максвелла потребовалось меньше века, чтобы выяснить, как производить и обнаруживать их до такой степени, что произвело революцию в нашей технологической цивилизации. Инфракрасный свет, ультрафиолетовый свет, рентгеновские лучи и гамма-лучи также являются примерами электромагнитных волн; подобно радиоволнам, они были неизвестны в то время, когда были открыты уравнения Максвелла.

Детали электромагнитной волны довольно сложный. Векторы электрического и магнитного полей указывают направления, перпендикулярны друг другу и перпендикулярны направлению распространения волны. Если волна движется в z -направлении, а электрическое поле колеблется в направлении x , то магнитное поле колеблется в y -направлении. Такая волна называется поляризованной в х -направление. (Поляризация описывается в терминах электрического поля, а не магнитного поля, потому что электрическое поле легче взаимодействует с большинством материалов.) На рисунке ниже показано поведение электромагнитной волны, поляризованной вдоль оси x и путешествуя по з -направление.