Физика энергии формула: Ошибка: 404 Материал не найден

Формула потенциальной энергии в физике

Содержание:

Определение и формула потенциальной энергии

Определение

Потенциальной энергией называют часть механической энергии совокупности тел (тела), которая зависит от взаимного расположения частей системы (конфигурации) и положения во внешнем поле сил.

Потенциальная энергия определяется работой, совершаемой потенциальными силами, которые действуют на все части системы, если система переходит из исследуемой конфигурации к состоянию, в котором считают потенциальную энергию равной нулю.А именно работа консервативных сил равна убыли потенциальной энергии. Начало отсчета потенциальной энергии делают произвольно. Эмпирически представляется возможным измерение только изменения потенциальной энергии. Начало отсчета потенциальной энергии делают так, чтобы упрощалось решение конкретной задачи.

Потенциальная энергия является скаляром. Чаще всего потенциальную энергию обозначают: E_p,W_p, U.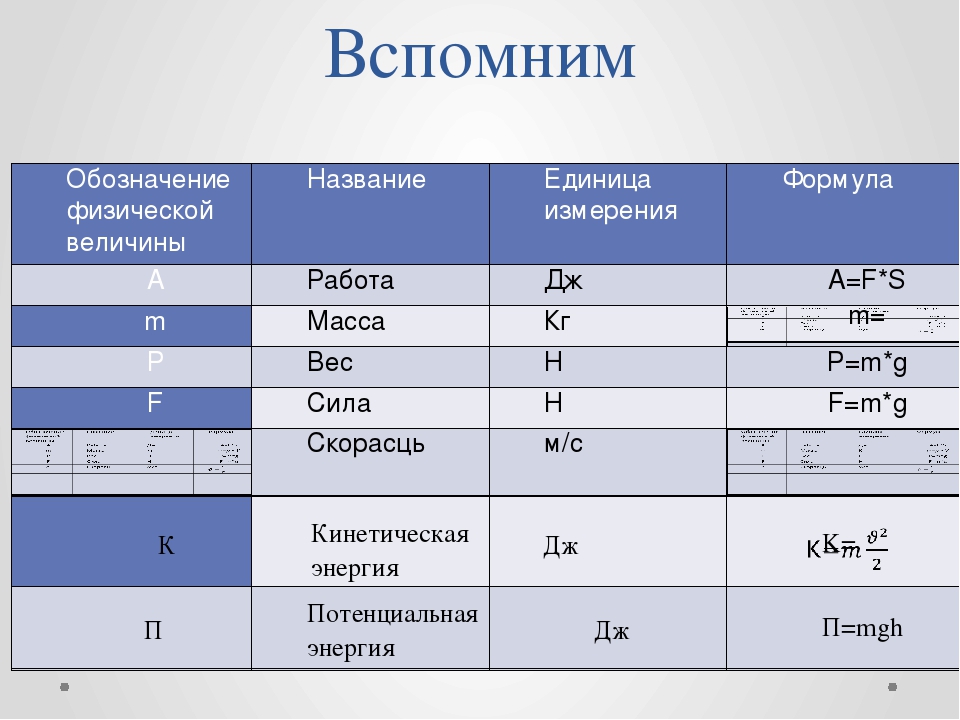

{\text {vnutr}}(1)$$

где E_p^vnesh получается как результат воздействия на систему со стороны тел, которые в рассматриваемую систему не входят. E_p^vnutr – вызвана взаимодействием разных частей составляющих систему.

E_p^vnutr является функцией координат всех материальных точек системы; E_p^vnesh помимо координат может в явном виде зависеть от времени.

Выражения для потенциальной энергии

Потенциальная энергия материальной точки находящейся в потенциальном поле сил определяют формулой:

$$d E_{p}=-d Y \rightarrow E_{p}=-Y+C$$

где Y – силовая функция, C – постоянная интегрирования.

Консервативная сила ($\bar{F}$), которая действует на материальную точку связана с потенциальной энергией соотношением:

$$\bar{F}=-g \operatorname{rad} E_{p}=-\left(\frac{\partial E_{p}}{\partial x} \bar{i}+\frac{\partial E_{p}}{\partial y} \bar{j}+\frac{\partial E_{p}}{\partial z} \bar{k}\right)=-\bar{\nabla} E_{p}(3)$$

где $\bar{\nabla}$ или $\nabla$ – оператор Гамильтона (оператор набла).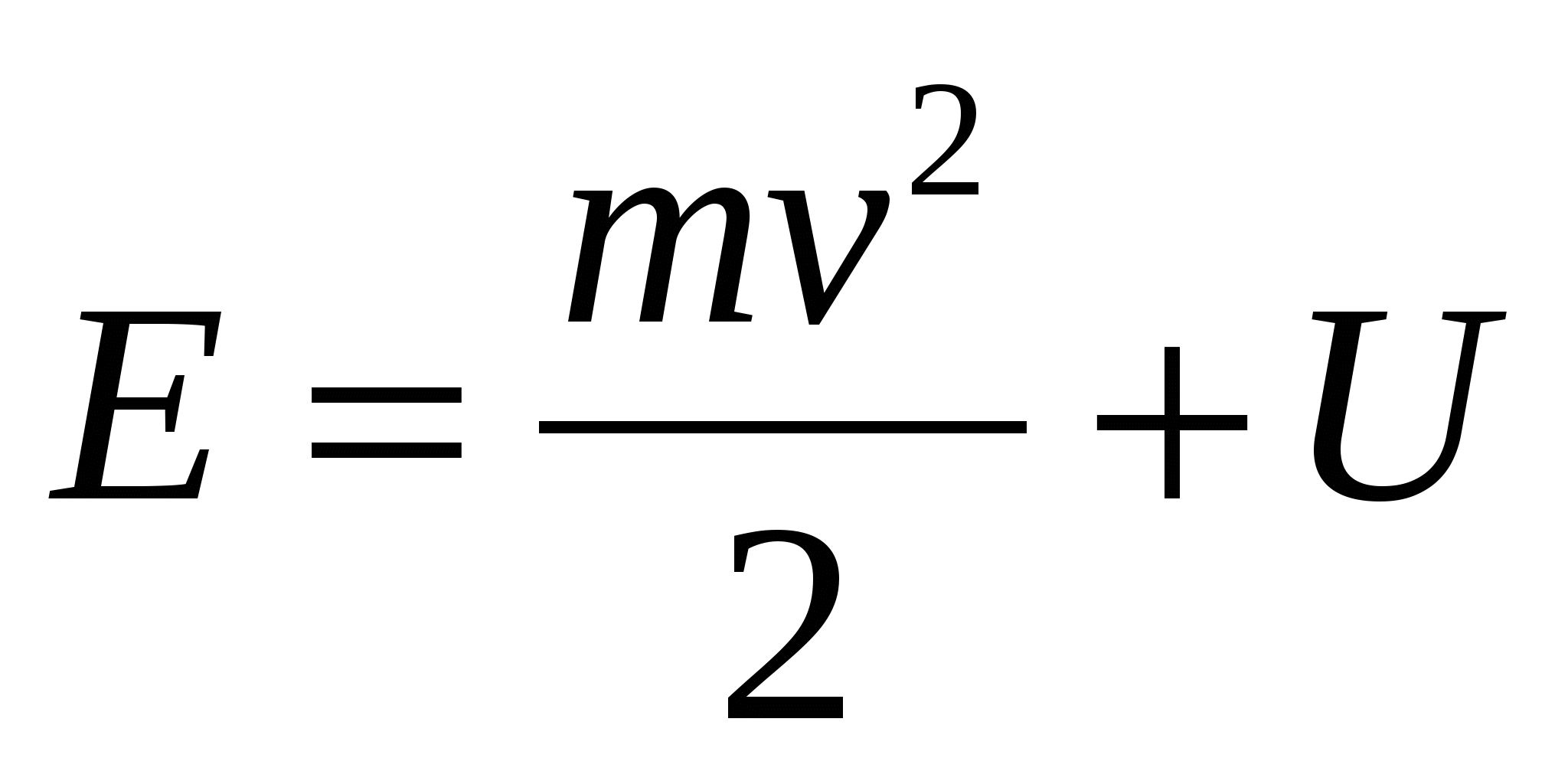 {2}}{2}(6)$$

где k – коэффициент упругости.

Потенциальная энергия точки в поле гравитации Земли:

$$E_{p}=-\frac{G m M}{r}(r>R)(7)$$

где m – масса материальной точки, M – масса Земли, R – радиус Земли. G – гравитационная постоянная. При этом полагают, что при $r \rightarrow \infty$ потенциальная энергия равна нулю $\left(E_{p}(\infty)=0\right)$.

Потенциальная энергия тела поднятого над Землей на расстояние много меньшее, чем радиус Земли равна:

$$E_{p}=m g h(8)$$

где m – масса тела, g- ускорение свободного падения, h – высота поднятия тела ( от некоторого условно нулевого уровня, где потенциальная энергия считается равной нулю).

Единицы измерения потенциальной энергии

Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит Дж (джоуль), в системе СГС – эрг. При этом: 1 дж = 10⁷ эрг.

Примеры решения задач

Пример

Задание. Материальная точка перемещается в положительном направлении оси X (x>0)в поле консервативных сил, потенциальная энергия которых задана графиком (рис. 1). Как изменится в процессе движения модуль ускорения?

Решение. Исходя из графика на рис.1 можно записать уравнение, которое свяжет потенциальную энергию и координату материальной точки в ходе перемещения:

$$E_{p}=B x$$

где A – некоторая постоянная.

В качестве основы для решения задачи используем формулу, связывающую консервативную силы и потенциальную энергию:

$$\bar{F}=-g r a d E_{p}(1.2)$$

Для движения по оси X, которое представлено в нашей задаче выражение (1.2) примет вид:

$$\bar{F}=-\frac{d E_{p}}{d x} \bar{i}(1.3)$$

Соответственно (1.1) и (1.3) модуль силы, действующей на материальную точку равен:

$$F=\frac{d}{d x}(B x)=B(1.4)$$

По второму закону Ньютона модуль силы может быть найден как:

$$F = ma (1.5)$$

Значит, получим выражение для ускорения рассматриваемой материальной точки:

$$a=\frac{B}{m}$$

Ответ. Из полученного выражения для ускорения материально точки в заданном поле можно сделать вывод, что ускорение по модулю не изменяется.

{3}=22 \end{array} $$

Получаем:

$A = 4 – 22 = -18$ (Дж)

Ответ. A = -18 (Дж)

Читать дальше: Формула силы притяжения.

Физика микромира

Семинар 1. Введение. Физика микромира

Во введении рассматриваются основные составляющие новой физики, возникшей на рубеже XIX и XX столетий:

• Теория относительности, изменившая существующие в классической физике представления о пространстве и времени.
• Квантовая теория, изменившая представление о структуре материи. Явление радиоактивности, открытие электрона, сложная структура атома, протон-нейтронная структура атомного ядра, открытие фундаментальных частиц и взаимодействий привели к современному представлению об окружающем мире.
• Открытия в области физики частиц, коренным образом повлиявшие на понимание процессов, происходящих во Вселенной.

1.1.     Масштабы явлений в физике

1.2.     Упругое рассеяние α-частиц. Формула Резерфорда

1.3.     Сечение реакции

1.4.     Размер ядра

1.5.     Радиоактивность

1.6.     Преобразования Лоренца

1.7.     Эффект Доплера

1.8.     Системы отсчета

1.9.     Основные формулы релятивистской физики

1.10.   Система единиц Гаусса

1.11.   Энергия и порог реакции

1.12.   Энергии частиц в двухчастичном распаде

           Задачи

1.1. Масштабы явлений в физике

Диапазон временных интервалов во Вселенной
Возраст Вселенной	13.8 млрд. лет
Возраст Солнца	4.6 млрд. лет
Возраст Земли	4. 5 млрд. лет
Появление жизни на Земле	~3.5 млрд. лет
Время прохождения светом расстояния Солнце–Земля	~5·102 с
Время прохождения светом расстояния 1 метр	3·10–9 с
Время прохождения светом расстояния, равного радиусу атома	~10–19 с
Время прохождения светом расстояния, равного радиусу атомного ядра	~10–24 с

 

Диапазон расстояний во Вселенной
Видимая граница Вселенной	~1010 св. лет
Ближайшая галактика (Магеллановы облака)	163 000 св. лет
Диаметр галактики Млечный путь	100 000 св. лет
Ближайшая звезда Проксима Центавра	4·1018 см = 4.2 св. года
Расстояние Земля–Солнце (астрономические единицы)	1.5·1013 см
Радиус Солнца	6.9·1010 см
Радиус Земли	6.4·108 см
Радиус Луны	1.7·108 см
Радиус атома водорода	~0.5·10–8 см
Радиус атомного ядра водорода	~0.8·10–13 см
Размеры лептонов, кварков	<10–17 см
1 световой год (расстояние, которое проходит свет за 1 год)	~9. 5·1017 см
1 парсек	3.1·1018 см = = 3.26 светового года

 

Диапазон масс во Вселенной
Масса видимого вещества во Вселенной	~1056 г
Масса видимого вещества нашей галактики Млечный путь	~1012 масс Солнца
Масса Солнца	1.99·1033 г
Масса Земли	5.98·1027 г
Масса Луны	7.35·1025 г
Масса 1 куб. м свинца	1.135·107 г
Масса 1 куб. м воздуха (20°C, 1 атм.)	1.204·103 г
Масса атома свинца	3.45·10−22 г
Масса протона	1.67·10–24 г
Масса электрона	9.11·10–28 г

1.2. Упругое рассеяние α-частиц. Формула Резерфорда

    Классическая физика основана на ряде блестящих экспериментов, среди которых особое место занимают эксперименты Г. Кавендиша и Ш. Кулона. С помощью крутильных весов ими были установлены законы гравитационного и электрического взаимодействий макроскопических тел. Однако метод эксперимента, который использовался Кавендишем и Кулоном, не может использоваться в микрофизике из-за малых размеров исследуемых объектов.
    Новый метод изучения микроскопических систем, был предложен Э. Резерфордом. Он первым разработал и применил метод исследования с помощью рассеяния пробной «частицы-снаряда» на исследуемом объекте. В своем первом эксперименте Резерфорд использовал рассеяние α-частиц на атомах для того, чтобы изучить атомную структуру. Выяснив, что вероятность рассеяния α-частиц на атоме, как функция угла рассеяния θ, подчиняется формуле Резерфорда для рассеяния ее на точечном кулоновском центре

вероятность рассеяния ~ ,

(1.1)

где Z_α, Z_я – заряды (в единицах элементарного заряда) α-частицы и ядра-мишени, Т – кинетическая энергия α-частицы, он установил, что в атоме имеется ядро размером менее 5·10^–12 см, сосредотачивающее в себе почти всю массу атома.

Рис. 1.1 Рассеяние α-частицы на ядре мишени с зарядом Zя. Угол рассеяния θ зависит от прицельного параметра b: tg(θ/2) = ZαZяe2/(2bT).

Атом состоит из ядра и связанных с ним электронов. Атомное ядро состоит из нуклонов: Z протонов и N нейтронов. Массовое число А = Z + N соответствует суммарному числу протонов и нейтронов. В нейтральном атоме число электронов равно числу протонов Z.

1.3. Сечение реакции

    Для характеристики вероятности процессов в микромире пользуются понятиями полного эффективного сечения σ и дифференциального эффективного сечения dσ/dΩ. Дифференциальное сечение используется для описания вероятности процесса взаимодействия частиц. Если мишень содержит N_М ядер и вся находится в пучке падающих частиц плотностью
j (j – число частиц, падающих в единицу времени на единицу поперечной площади мишени), то число dN(0)/dΩ частиц, рассеиваемых мишенью в единицу времени на угол θ в пределах телесного угла dΩ, определяется соотношением:

(1. 2)

Полное число частиц, рассеиваемых мишенью в единицу времени под всеми углами, определяется соотношением

(1.3)

σ − полное эффективное сечение, N_М = nSd − характеристика мишени (n − число ядер мишени в единице объёма, S − облучаемая поперечная площадь мишени, d − толщина мишени в направлении падающего пучка частиц). Полное сечение измеряется в барнах (1 барн = 10^–24см²).

1.4. Размер ядра

    Наиболее распространенный метод исследования атомных ядер – это рассеяние на ядрах различных частиц и ядер, ускоренных до высоких энергий. Точные данные по размерам атомных ядер были получены из экспериментов по рассеянию электронов. Радиусы ядер R растут с увеличением массового числа А и хорошо описываются соотношением

R ≈ 1. 3·10-13·A1/3 см = 1.3·A1/3 Фм.

(1.4)

Численный коэффициент в (1.4) зависит от методики определения радиуса ядра и меняется в пределах 1.1÷1.4. Здесь и далее будет использоваться значение 1.3.

1.5. Радиоактивность

    Радиоактивность – свойство атомных ядер самопроизвольно (спонтанно) изменять свой состав (заряд Z, массовое число A) в результате испускания частиц или ядерных фрагментов. К явлению радиоактивности относится также испускание атомным ядром гамма-квантов, но при этом ни заряд Z, ни массовое число A не изменяются.

Основные виды радиоактивных распадов:(A,Z) → (A-4,Z-2) + α из атомного ядра испускается α-частица – ядро атома 4He. β–-распад: (A,Z) → (A,Z+1) + e– + e из атомного ядра испускаются электрон e– и антинейтрино e, один из нейтронов ядра превращается в протон. β+-распад: (A,Z) → (A,Z-1) + e+ + νe из атомного ядра испускаются позитрон e+ и нейтрино νe, один из протонов ядра превращается в нейтрон. e-захват: (A,Z) + e– → (A,Z-1) + νe в результате взаимодействия между протоном и электроном атомной оболочки из ядра испускается нейтрино, один из протонов ядра превращается в нейтрон γ-распад: (A,Z)* → (A,Z) + γ из возбужденного атомного ядра испускается один или несколько гамма-квантов.

Рис. 1.2. Зависимость активности от времени (слева). Данная зависимость в логарифмическом масштабе отображается прямой, тангенс угла наклона которой равен постоянной распада λ. Справа приведена кривая активации (наведенной радиоактивности) в зависимости от времени. Рост числа радиоактивных ядер практически прекращается при достижении активации насыщения за время t ≈ 5T_1/2

    Процесс радиоактивного распада, как и все процессы в микромире, – это случайный (статистический) процесс.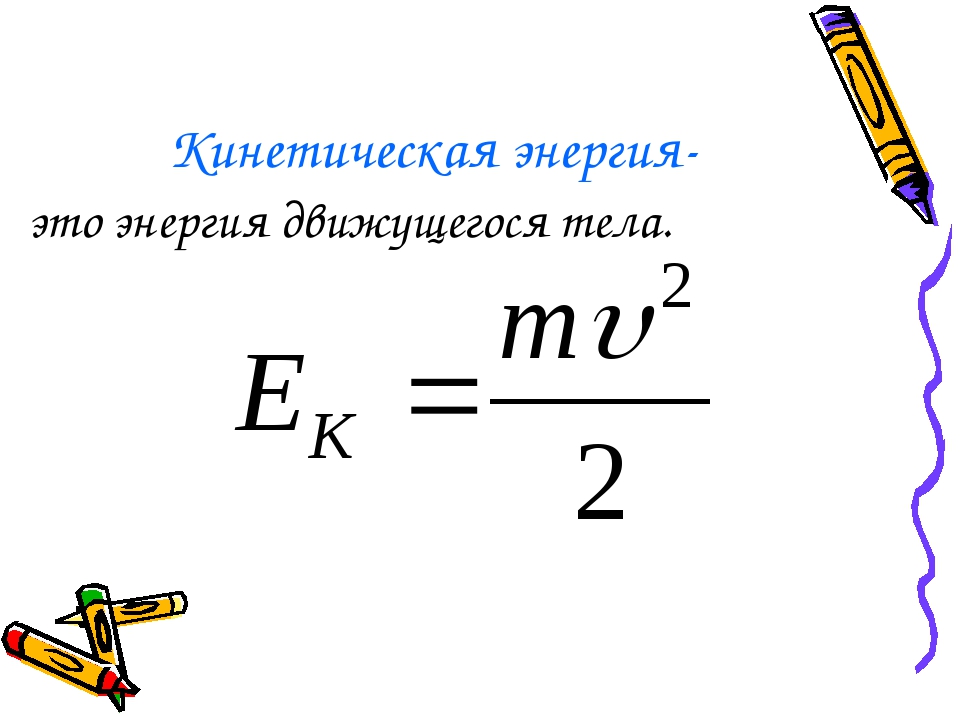 Атомные ядра одного сорта распадаются за разное время. Однако среднее время жизни τ ядер, вычисленное по наблюдению большого числа распадов, оказывается не зависящим от способа получения этих ядер и от внешних условий. Среднее время жизни τ ядра характеризует скорость их распада. Постоянная распада λ:

Физический смысл λ – это вероятность распада радиоактивного ядра в единицу времени.
    Закон радиоактивного распада показывает, как со временем изменяется в среднем число радиоактивных ядер в образце. Если в момент времени t имеется большое число N радиоактивных ядер, то к моменту t + dt распад испытают в среднем λNdt ядер. Поэтому изменение их числа dN определяется соотношением

Знак минус означает, что общее число радиоактивных ядер (частиц) уменьшается в процессе распада. Интегрируя соотношение (1.6), получим закон радиоактивного распада:

где N₀ − число радиоактивных ядер в начальный момент t = 0. Закон радиоактивного распада относится к статистическим средним и справедлив лишь при достаточно большом числе распадающихся ядер.
    Среднее время жизни τ ядра вычисляется по формуле

.

(1.8)

    Часто для характеристики скорости радиоактивного распада атомных ядер используют величину, называемую периодом полураспада – T_1/2. Период полураспада – это время, за которое число радиоактивных ядер уменьшается вдвое:  N₀/2 = N₀, откуда

T1/2 = ln2/λ ≈ 0.693/λ = 0.693τ.

(1.9)

    Активность образца А – число распадов в единицу времени, является производной от N по времени, взятой с обратным знаком:

Активность образца уменьшается со временем по тому же экспоненциаль­ному закону, что и число нестабильных ядер. Активность измеряют в беккерелях или в кюри.

1 Бк (беккерель) = 1 распад в секунду, 1 Ки (кюри) = 3.7·1010 Бк. 1 Ки – это активность 1 г радия вместе с продуктами его распада.

    Энергия распадающейся системы в соответствии с принципом неопределенностей Гейзенберга, не может быть точно определена. Всякое распадающееся состояние, имеющее среднее время жизни τ, описывается волновой функцией ψ(t), квадрат модуля которой убывает со временем по экспоненциальному закону радиоактивного распада

|ψ(t)|² = |ψ(0)|²e^-t/τ.

Ядро в любом состоянии с τ ≠ ∞ имеет энергетическую неопределённость ΔE ≈ Г, которая связана с τ соотношением неопределённостей Г·τ ≈ ћ , где Г – ширина уровня на половине высоты.
    Подавляющее число частиц также являются нестабильными и распадаются по тем же законам радиоактивного распада, как и атомные ядра. Традиционно радиоактивность атомных ядер описывают, используя период полураспада T_1/2, а распады частиц описывают, использую среднее время жизни τ

1.6. Преобразования Лоренца

    Основные положения специальной теории относительности изучались в разделе «Механика» общего курса физики. Здесь лишь напомним основные соотношения релятивистской физики.

Принцип относительности – все законы природы должны быть одинаковыми для всех наблюдателей, двигающихся друг относительно друга с постоянной скоростью. Специальная теория относительности была построена на двух постулатах, сформулированных Эйнштейном в 1905 году: 1. Законы физики одинаковы во всех инерциальных системах отсчета. 2. Скорость света в вакууме равна постоянной величине с независимо от скорости движения источника.

 

Рис. 1.3. Штрихованная система S’ движется относительно системы S со скоростью вдоль оси z.

    Рассмотрим материальную точку с массой покоя m. Ее координаты в инерциальной системе отсчета S определяются как (t,) = (t,x,y,z), а скорость v = ||. Координаты той же точки в другой инерциальной системе отсчета S’ (t’,x’,y’,z’), движущейся относительно S вдоль оси z с постоянной скоростью , связаны с координатами в системе S преобразованиями Лоренца. В случае, если координатные оси систем z и z’ сонаправлены с вектором и в начальный момент времени t = t’ = 0 начала координат обеих систем совпадали, то преобразования Лоренца даются выражениями:

x’ = x, y’ = y, z’ = γ(z − βct), ct’ = γ(ct − βz),

(1. 11)

где β = v/c  (0 < β < 1), а  γ = 1/(1 – β²)^1/2 – лоренц-фактор.

Скорость частицы ‘ в системе S’ связана со скоростью в системе S соотношением:

(1.12)

Обратные преобразования Лоренца получаются взаимной заменой координат r_i → r_i‘, v_i  → v_i‘ и учетом изменения направления скорости v → -v:

x = x’, y = y’, z = γ(z’ + βct’), ct = γ(ct’ + βz’)

(1.13)

При малых скоростях преобразования Лоренца совпадают с выражениями для нерелятивистских преобразований Галилея:

Преобразования Лоренца	Преобразования Галилея
x’ = x, y’ = y	x’ = x, y’ = y
z’ = γ(z − vt)	z’ = z – vt
ct’ = γ(ct − βz)	t’ = t

Относительность пространственных расстояний (Сокращение Лоренца-Фитцджеральда):

Относительность промежутков времени между событиями  (релятивистское замедление времени):

Относительность одновременности событий. Если в системе S для событий A и B t_A = t_B и x_A ≠ x_B, то в системе S’

t’A = t’B + γv/c2 (xB − xA).

(1.16)

    В общем случае преобразования Лоренца записываются в терминах
4-векторов a = (a⁰,) = (a⁰,a¹,a²,a³). При относительном движении систем S и S’, как на рис. 1.2, 4-вектор a преобразуется следующим образом:

a’0 = γ(a0 − βa3), a’1 = a1, a’2 = a2, a’3 = γ(a3 − βa0),

(1.17)

 

Скалярное произведение двух 4-векторов a и b в 4-мерном пространстве времени определяется как: и является инвариантом, т. е. сохраняется во всех инерциальных системах отсчета.

Таким образом, квадрат 4-вектора также является инвариантом. Например, квадрат 4-вектора координаты

(X)2 = (ct,)2 = c2t2 − ()2 = τ2

(1.18)

определяет “собственное” время частицы (т.е. время в ее системе отсчета). 4-вектор скорости
u = γ(c,) вводится таким образом, чтобы (u)² = c². 4-импульс, определяется как произведение массы на скорость

P = mu = mγ(c,) = (E/c,).

(1.19)

Так как u² = c², то (P)² = m²c² = (E/c)² − ()², или

Следовательно,

E = γmc2, = γm, = c2/E.

(1.21)

Преобразования Лоренца для 4-импульса (1.17):

E’/c = γ(E/c − βpz),   p’x = px,   p’y = py,   p’z = γ(p’z − βE/c).

(1.22)

Скалярное произведение 4-импульсов является инвариантом по определению. Вместо произведения 4-импульсов двух частиц, например P₁P₂, обычно используют квадрат инвариантной массы двух частиц (s-инвариант):

(1.23)

или квадрат переданного импульса (t-инвариант)

1.

7. Эффект Доплера

    Если в системе S (рис. 1.2) в направлении оси z испущен фотон энергии E₀ = p₀c, то его энергия E, длина волны λ и частота ν в системе отсчета S’ (наблюдатель удаляется от источника света) составит

E = γ(E₀ − βp₀c) = γE₀(1 − β),

(1.24)

Параметр смещения z в этом случае z = (λ − λ₀)/λ₀ = (ν₀ − )/ν > 0, что соответствует красному смещению λ > λ₀, ν < ν₀. Если скорость системы S’ направлена в противоположную сторону (наблюдатель приближается к источнику света), то знаки изменяются на противоположные:

(1.25)

В данном случае наблюдается синее смещение: λ < λ₀. Поскольку в общем случае преобразование Лоренца записывается как E = γ(E₀ − ()/c², то, в отличие от классической физики, в релятивистском случае наблюдается поперечный эффект Доплера: v/v₀ = γ.
    Из формул, соответствующих синему смещению, можно получить классическую формулировку эффекта Доплера, используя разложение в ряд:

 

Тогда для относительного изменения частоты излучения: Δν/ν₀ = β = v/c, что соответствует классической формулировке эффекта Доплера (без учета среды):

ν = ν₀(1 + ν/ν_звук).

1.8. Системы отсчета

    Рассмотрим двухчастичный процесс a + b → c + d. 4-х импульсы сталкивающихся частиц
P_a = (E_a/c,_a) и P_b = (E_b/c,_b) соответственно.
    При описании взаимодействий частиц и атомных ядер, как и в классической физике, обычно используются две системы отсчета: система покоя мишени и система центра инерции (рис. 1.4).

Рис. 1.4. Определение некоторых систем отсчета

1. Система покоя мишени – система, в которой частица b (мишень) покоится, p_b = 0, E_b =  m_bc². Обычно под лабораторной системой (ЛС) отсчета подразумевается система покоя мишени. В данной системе s-инвариант:

(1.26)

Энергия налетающей частицы, выраженная через s-инвариант:

(1.27)

2. Система центра инерции (СЦИ) – система, в которой ^*_a = ^*_b = 0. Величины в СЦИ в дальнейшем будут отмечаться звездочкой. В СЦИ . s-инвариант в СЦИ:

(1.28)

В экспериментах физики высоких энергий часто используется система встречных пучков – система, в которой частицы равной массы и равных по абсолютной величине импульсов сталкиваются под углом π − θ. При θ = 0 система встречных пучков совпадает с СЦИ.

1.9. Основные формулы релятивистской физики

    Универсальность законов сохранения приводит к необходимости установить для релятивистской кинематики такие уравнения, которые удовлетворяли бы к законам сохранения энергии и импульса и были инвариантны относительно преобразований Лоренца:

1. E = (m²c⁴ + p²c²)^1/2 = γmc² = mc² + T,
   E – полная энергия частицы, m – масса частицы,
   с – скорость света в вакууме,
   = γm – релятивистский импульс частицы,
   β = v/c, γ = (1 – β²)^-1/2 – Лоренц-фактор, – скорость частицы,
   T = mc²(γ – 1) – релятивистская кинетическая энергия частицы.
2. p²c² = T(2mc² + T).
3. τ = γτ₀ – релятивистское замедление времени,
   τ₀ – время жизни частицы в состоянии покоя,
   τ – времени жизни частицы, движущейся со скоростью .
4. l = l₀/γ,
5. E² – p²c² = inv = m²c⁴,
   E – полная энергия частицы или системы частиц,
   p – импульс частицы или суммарный импульс системы частиц.
6. Энергия налетающих частиц Е в ускорителе с неподвижной мишенью, эквивалентном коллайдеру с пучками частиц массы m и энергии E*:

   (1.29)

7. Порог реакции. Если на неподвижной мишени b под действием налетающих частиц a происходит реакция a + b → c + d +… и энергия реакции (изменение суммарной массы частиц) Q = (∑m_i – ∑m_f)c² < 0, то минимальная кинетическая энергия частицы а, необходимая для осуществления такой реакции

   (1.30)

1.10. Система единиц Гаусса

Время	1 с
Энергия, масса E = mc2	1 эВ (электрон-Вольт) = 1.6·10-19 эрг = = 1.6·10-19 Дж. 1эВ = 10-3 кэВ = 10-6 МэВ = 10-9 ГэВ =  = 10-12 ТэВ
Энергия покоя электрона протона нейтрона	0.511 МэВ 938.3 МэВ 939.6 МэВ
Длина	1 Фм (ферми, фемтометр) = 10-13 см 1 Å (ангстрем) = 10-8 см
Скорость света в вакууме	с = 3·1010 см/с
Заряд электрона	e = 4.8·10-10 ед. СГС
Приведенная постоянная Планка Константы	ћ = h/2π = 6.58·10-22 Мэв·с
	ћс = 197 МэВ·Фм; α = e2/ћс = 1/137

    При решении задач будет использоваться система единиц Гаусса, в которой основными единицами являются сантиметр, грамм и секунда. В данной системе диэлектрическая и магнитная проницаемости являются безразмерными величинами, причём для вакуума они приняты равными единице. В качестве единицы измерения энергии используется внесистемная единица 1 эВ (электрон-Вольт) – энергия, приобретаемая электроном при прохождении потенциала в 1 Вольт.

1.11. Энергия и порог реакции

    Частица массы m_a налетает на покоящуюся частицу массы m_b. В результате реакции в конечном состоянии образуется n частиц с массами m’₁,…m’_n Определить энергию и порог реакции.
    Обозначим суммарную массу взаимодействующих частиц m_a + m_b = ∑m_i (индекс i соответствует начальному состоянию (initial)), суммарную массу образовавшихся частиц  m’₁ + m’₂ +… m’_n = ∑m_f (индекс f обозначает конечное состояние (final)). Энергия реакции Q соответствует изменению суммарной массы частиц:

Q = (∑mi − ∑mf )c2.

(1.31)

Пороговая энергия реакции – это дополнительная кинетическая энергия, необходимая для осуществления эндотермической реакции (Q < 0). Данное значение энергии соответствует предельному случаю, когда продукты реакции образуются с нулевыми импульсами в СЦИ и s-инвариант в конечном состоянии равен квадрату суммы масс конечных продуктов: . В начальном состоянии в СЦИ . Следовательно, необходимая суммарная энергия сталкивающихся частиц должна быть .
    Пороговая кинетическая энергия в СЦИ:

    В лабораторной системе отсчета частица-мишень покоится: |_b| = 0, E_b = m_bc². Соответственно, s-инвариант в лабораторной системе в начальном состоянии равен:

Приравнивая s в начальном и конечном состояниях, получаем:

(1.32)

(1.33)

Раскладывая разность квадратов и выделяя Q, получим (1.31):

(1.34)

    Значение пороговой энергии реакции в лабораторной системе всегда больше соответствующего значения в системе центра инерции. Их разность определяет ту часть энергии, которая идет на движение центра инерции в лабораторной системе.

1.12. Энергии частиц в двухчастичном распаде

    Получим выражение для энергий и импульсов продуктов распада C → A + B через массы частиц в релятивистском случае в СЦИ.
    СЦИ связана с распадающейся частицей С, ее энергия в данной системе E_С = m_Сc², продукты распада разлетаются под углом 180°. Законы сохранения энергии и импульса:

Учитывая, что (pc)² = E² − (mc²)² и подставляя выражение E_B через E_A во второе уравнение, получим:

E²_A − (m_Ac²)² = (m_Сc² −  E_A)² − (m_Bc²)².

Отсюда для частицы A:

(1.35)

Выражения для частицы B получаются перестановкой соответствующих индексов.
    Полезно выписать выражения для энергий продуктов распада в некоторых частных случаях:
а) распад на частицы равной массы m_A = m_B.

(1.36)

б) образование безмассовой частицы m_A = 0.

(1.37)

в) нерелятивистский случай: Q << m_Cc², m_C ≈ m_A + m_B

(1.38)

Задачи

1.1. Альфа-частица (Z_α = 2) с кинетической энергией T = 5 МэВ испытывает лобовое столкновение с ядром золота (Z_я = 79). Рассчитать расстояние максимального сближения α-частицы с ядром золота.

1.2. Протон с кинетической энергией Т = 2 МэВ налетает на неподвижное ядро ¹⁹⁷Au. Определить дифференциальное сечение рассеяния dσ/dΩ на угол θ = 60° . Как изменится величина дифференциального сечения рассеяния, если в качестве рассеивающего ядра выбрать ²⁷Al?

1.3. Частица массы m_a налетает на покоящуюся частицу массы m_b. В результате реакции в конечном состоянии образуется n частиц с массами m’₁,…m’_n. Определить энергию и порог реакции.

    Обозначим суммарную массу взаимодействующих частиц m_a + m_b = ∑_im_i  (индекс i соответствует начальному состоянию (initial)),  суммарную массу образовавшихся частиц
m’₁ + m’₂ + …+ m’_n = ∑_f m_f  (индекс f обозначает конечное состояние (final)). Энергия реакции Q соответствует изменению суммарной массы частиц:

Q = (∑imi − ∑fmf )c2.

(1.31)

    Пороговая энергия реакции – это дополнительная кинетическая энергия, необходимая для осуществления эндотермической реакции (Q < 0). Данное значение энергии соответствует предельному случаю, когда продукты реакции в СЦИ образуются с нулевыми импульсами и s-инвариант в конечном состоянии равен квадрату суммы масс конечных продуктов:
s = (∑_f P_f )/c² = (∑_fm_f ). В начальном состоянии в СЦИ s = (∑_i P*_i )/c² = (E*_a + E*_b)²/c⁴. Следовательно, необходимая суммарная энергия сталкивающихся частиц должна быть E*_a + E*_b = ∑_fm_f c².
    Пороговая кинетическая энергия в СЦИ:

T*_a +T*_b = ∑_fm_f c² − ∑_im_ic² = |Q|.

    В лабораторной системе отсчета частица-мишень покоится: |_b| = 0, E_b = m_bc². Соответственно, s-инвариант в лабораторной системе в начальном состоянии равен:

s = (P_a + P_b)/c² = (E_a/c² + E_b/c²) − (_a/c − _b/c)² = m_a² + m_b2 − 2E_am_b/c².

Приравнивая s в начальном и конечном состояниях, получаем:

(1.32)

(1.33)

Раскладывая разность квадратов и выделяя Q, получим (1.30):

(1.30)

    Значение пороговой энергии реакции в лабораторной системе всегда больше соответствующего значения в системе центра инерции. Их разность определяет ту часть энергии, которая идет на движение центра инерции в лабораторной системе.

1.4. Получим выражение для энергий и импульсов продуктов распада C → A + B через массы частиц в релятивистском случае в СЦИ.
    СЦИ связана с распадающейся частицей С, ее энергия в данной системе E_С = m_Сc², продукты распада разлетаются под углом 180°. Законы сохранения энергии и импульса:

Учитывая, что (pc)² = E² − (mc²)² и подставляя выражение E_B через E_A во второе уравнение, получим:

E²_A − (m_Ac²)² = (m_Сc² −  E_A)² − (m_Bc²)².

Отсюда для частицы A:

(1.35)

Выражения для частицы B получаются перестановкой соответствующих индексов.
    Полезно выписать выражения для энергий продуктов распада в некоторых частных случаях:
а) распад на частицы равной массы m_A = m_B.

(1.36)

б) образование безмассовой частицы m_A = 0.

(1.37)

в) нерелятивистский случай: Q << m_Cc², m_C ≈ m_A + m_B

(1.38)

1.5. Рассчитать кинетические энергии α-частицы и ядра ²²²Rn, образующихся при распаде
²²⁶Ra → ²²²Rn + α.
(m_Rn = 206764.10 МэВ, m_Ra = 210496.35 МэВ, m_α = 3727.38 МэВ.)
Ответ: Q_α = 4.87 МэВ, T_α = 4.78 МэВ, T_Rn = 0.086 МэВ

1.6. Рассчитать дифференциальное сечение рассеяния α-частицы с кинетической энергией 10 МэВ
1) на ядре кальция ⁴⁰Ca на угол 60°,
2) на ядре меди ⁶³Cu на угол 90°,
3) на ядре молибдена ⁹⁶Mo на угол 120°,
4) на ядре серебра ⁷⁹Ag на угол 180°.
Ответ: 1) 0.33 барн/стер, 2) 0.17 б/стер, 3) 0.16 б/стер, 4) 0.11 б/стер

1.7. Рассчитать отношение сечений рассеяния α-частиц с кинетической энергиями 10 МэВ на ядре ¹⁹⁷Au под углами 6° и 180°.
Ответ: W = 13.3·10⁴

1.8. Рассчитать расстояния максимального сближения R
1) α-частицы с кинетической энергией 5 МэВ с ядром ¹⁹⁷Au и ⁷Li,
2) α-частицы с кинетической энергией 10 МэВ с ядром ⁴⁰Ca,
3) протона с кинетической энергией 7 МэВ с ядром ¹⁹⁷Au,
4) α-частицы с кинетической энергией 5 МэВ с ядром ²⁰⁸Pb.
Ответ: 1) R = 1.7 Фм, 2) R = 5.8 Фм, 3) R = 16.2 Фм, 4) R = 47.2 Фм

1.9.Пучок α-частиц с энергией T_α = 5 МэВ падает перпендикулярно на фольгу из серебра толщиной 1 мг/см². α-частицы, рассеянные под углом 60°, регистрируются детектором площадью 1 см², расположенном на расстоянии 20 см от мишени. Какая доля от полного числа рассеянных α-частиц ΔN/N будет зарегистрирована детектором?
Ответ: ∆N(60º)/N = 4·10^–10

1.10. В ходе эксперимента медная фольга (Z = 29, M_mol = 63.55 г/моль) толщиной 2 мг/см² облучается пучком α-частиц с с кинетической энергией Т_α = 5 МэВ и интенсивностью 10⁵ частиц в секунду. Сколько α-частиц в минуту ∆N будет регистрировать детектор площадью 1 см², расположенный на расстоянии 10 см от мишени под следующими углами к направлению падающего пучка: 1) 30°, 2) 90°, 3) 120°?
Ответ: 1) ∆N(30º) ≈ 44 част., 2) ∆N(90º) ≈ 0.8 част., 3) ∆N(120º) ≈ 0.4 част.

1.11. Почему из экспериментов по упругому рассеянию α-частиц следовало, что в атоме расположено положительно заряженное атомное ядро размером < 5·10^–12 см? Почему полученные результаты нельзя было объяснить на основании модели Томсона?

1.12. Во сколько раз число распадов ядер радиоактивного изотопа йода ¹³¹I в течение первых суток больше числа распадов в течение вторых суток? Период полураспада изотопа  T_1/2(¹³¹I) = 193 часа.

1.13. Пучок π^–-мезонов движется со скоростью v = 0.9c. Среднее время жизни π^–-мезонов составляет τ = 2.6·10^–8 с. Какое расстояние в среднем они пройдут до своего распада?
Ответ: L_π = 16 м

1.14. На каком расстоянии интенсивность пучка мюонов с кинетической энергией T = 0.5 ГэВ, движущихся в вакууме, уменьшается до половины первоначального значения?
m_μ = 105.66 МэВ, τ_μ = 2.197·10^-6 сек.
Ответ: L  = 2.6 км

1.15. Полная энергия электрона составляет 2.5 МэВ. Определите его импульс и скорость в лабораторной системе отсчета.
Ответ: p = 2.45 МэВ/c, v = 0.989c

1.16. Электрон и протон ускоряются разностью потенциалов 10⁷ В. Рассчитайте фактор γ, скорость, импульс и полную энергию каждой частицы.
Ответ: 1) E ≈ pc = 10.5 МэВ, γ = 20.57, v = 0.999c; 2) E = 948.27 МэВ, pc = 137.35 МэВ, γ = 1.01, v = 0.147c

1.17. Какую энергию надо затратить, чтобы электрон достиг скорости а) 0.5 c, б) 0.9 c, в) 0.99 c.
Какая энергия необходима, чтобы протон достиг тех же скоростей?
Ответ: а) T_e = 0.08 МэВ, T_p = 145.2 МэВ; б) T_e = 0.66 МэВ, T_p = 1.2 ГэВ;
в) T_e = 3.11 МэВ, T_p = 5.7  ГэВ.

1.18. Какую энергию надо затратить, чтобы увеличить скорость протона а) от 0.20 c до 0.21 c,
б) от 0.80 c до 0.81 c, в) от 0.90 c до 0.91 c, г) от 0.98 c до 0.99 c.
Ответ: а) T_p = 2.05 МэВ, б) T_p = 36.2 МэВ, в) T_p = 110.5 МэВ, г) T_p = 1 936 МэВ

1.19. Полная энергия частицы в два раза больше ее энергии покоя. Рассчитайте отношение v/c для этой частицы и определите ее импульс.

1.20. Определите массу частицы если известно, что ее импульс равен 500 МэВ/c,
а энергия – 1746 МэВ.

1.21. Рассчитайте скорость уменьшения массы Солнца, если известно, что плотность лучистой энергии Солнца на Земле в среднем равна 1.37·10³ Вт/м².

1.22. Энергия связи электрона в атоме водорода составляет 13.6 эВ. Насколько масса атома водорода меньше суммы масс электрона и протона?

1.23. Энергия связи дейтрона (система, состоящая из протона и нейтрона) составляет 2.224 МэВ. Насколько масса ядра дейтрона меньше суммы масс составляющих его нуклонов?

1.24. Энергия, выделяющаяся при делении одного ядра ²³⁵U, составляет ~200 МэВ. Какое количество массы ядра урана превращается в энергию?

1.25. Какой должна быть относительная скорость двух наблюдателей, чтобы измеряемые ими интервалы времени различались на 5 %?
Ответ: υ = 0.33с

1.26. На какое время разойдутся показания часов земного наблюдателя и наблюдателя на спутнике Земли с периодом обращения 90 мин через 5 лет?
Ответ: ∆t = 0.05 с

1.27. Используя разложение в ряд, получите следующие формулы для приближенного вычисления релятивистских поправок в случае
v << c: ; ; .

1.28. Исходя из релятивистского соотношения между энергией и импульсом, покажите, что в нерелятивистском пределе выполняется соотношение для кинетической энергии T = mv²/2.

1.29. Длина волны, излучаемая атомом водорода, составляет λ₀ = 6560 Å. Измерение длины волны этого же излучения из удаляющейся галактики составляет λ₁ = 14580 Å. Определите скорость, с которой галактика удаляется от Земли.
Ответ: υ = 2·10⁸ м/с

1.30. Галактика удаляется от земного наблюдателя со скоростью 1.9·10⁷ м/с. Определите относительную величину красного смещения (λ₁ − λ₀)/λ₀ для света этой галактики.
Ответ: z = 0.065 ≈ β

1.31. Измерение гравитационного потенциала ∆φ при удалении на бесконечность с расстояния R от центра сферического не вращающегося тела массы M составляет При этом величина красного смещения света определяется соотношением . Оцените величину красного смещения линии водорода в гравитационном поле Солнца. Оцените величину синего смещения этой линии в гравитационном поле Земли.

1.32. Видимый свет от близкой звезды смещен в фиолетовую часть спектра на 5 %. С какой лучевой скоростью движется звезда?
Ответ: β = 0.05c, v = 1.5·10⁷ м/с

1.33. С какой скоростью должен двигаться автомобиль, чтобы красный свет светофора выглядел зеленым? Сравните результат с космическими скоростями.

1.34. Определить порог реакции α + α → ⁷Li + p. Определить долю кинетической энергии налетающей частицы, идущую на движение центра инерции. m_α = 3727.38 МэВ, m_p = 938.27 МэВ,
m_Li = 6533.83 МэВ.

1.35. Рассчитать порог реакции ¹⁴N + α → ¹⁷O + p в двух случаях:

• налетающей частицей является ядро азота ¹⁴N,
• налетающей частицей является α-частица.

Объяснить полученный результат.

1.36. 1) В коллайдере LHC энергия пучков протонов составляет E*_p = 7 ТэВ. Определите энергию столкновения √s в системе центра инерции. Какая энергия протонного пучка E_p потребовалась бы для достижения данной энергии в ускорителе с неподвижной мишенью? Сравните результат с энергией протонов космических лучей.
2) В условии задачи 1) рассмотрите столкновение пучков электронов и позитронов с энергиями
E*_e = 500 ГэВ (проект ILC).
3) В условии задачи 1) рассмотрите столкновение пучков протонов с энергиями E*_p = 1 ТэВ (коллайдер TEVATRON).
4) В условии задачи 1) рассмотрите столкновение пучков электронов с энергиями E*_e =  100 ГэВ (коллайдер LEP)
Ответ: 1) E_p = 10⁸ ГэВ, 2) E_e = 10⁹ ГэВ, 3) E_p = 2·10⁶ ГэВ, 4) E_e = 4·10⁷ ГэВ

26.10.2016

Закон сохранения механической энергии в физике

Содержание:

Закон сохранения механической энергии:

Любое тело может обладать одновременно и кинетической, и потенциальной энергией. Тело, падающее с определенной высоты, имеет потенциальную энергию в поле силы тяжести и кинетическую энергию, поскольку оно движется с определенной скоростью относительно Земли.

Сумму потенциальной и кинетической энергий тела называют полной механической энергией:

Кинетическая и потенциальная энергии тела могут изменяться, но в замкнутой системе их сумма остается постоянной. В этом состоит суть закона сохранения и превращения механической энергии: если в замкнутой системе действуют только силы упругости и тяжести, то полная механическая энергия системы остается неизменной – взаимные превращения происходят с кинетической и потенциальной энергией:

Если в замкнутой системе действуют только силы упругости и тяжести, то полная механическая энергия системы остается постоянной.

Действие силы трения приводит к увеличению внутренней энергии тела. Точные экспериментальные исследования показали, что все «потери» механической энергии равны увеличению внутренней энергии. Это говорит о том, что энергия не возникает из ничего и не исчезает бесследно.

Она только переходит из одного вида в другой.

Этот вывод отражает суть общего закона природы – закона сохранения и превращения энергии, открытого в 1840 г. Р. Майером. Несмотря на то что ученый совершил это открытие в процессе медицинских наблюдений над организмом человека, закон оказался всеобщим и был проверен и подтвержден в процессе многочисленных исследований.

Если в системе действует и сила трения то полная механическая энергия претерпевает изменения.

Определения и формулы

В механике различают и изучают силы упругости, трения, всемирного тяготения. Сила упругости возникает в результате взаимодействия микрочастиц, из которых состоят тела.

Сила трения также имеет электромагнитную природу.
Сила всемирного тяготения действует между всеми без исключения телами. Она пропорциональна произведению масс взаимодействующих тел и обратно пропорциональна квадрату расстояния между ними:

Первый закон динамики: любое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные к нему силы не выведут его из этого состояния.

Второй закон динамики: ускорение, полученное телом в результате взаимодействия, прямо пропорционально силе, действующей на тело, обратно пропорционально его массе и имеет то же направление, что и сила:

Третий закон динамики: любое действие порождает равное по величине и противоположное по направлению противодействие:

Равновесие – это состояние тела, при котором под действием приложенных к нему сил отсутствует перемещение любых его точек. При равновесии тел выполняются такие два условия:

1)    геометрическая сумма приложенных к телу сил равна нулю:

2)    алгебраическая сумма моментов сил, приложенных к телу относительно какой-либо неподвижной оси, равна нулю:

Каждое движущееся тело имеет импульс: и кинетическую энергию:

В замкнутой системе сумма импульсов тел при любых взаимодействиях между ними остается постоянной (закон сохранения импульса).

В общем случае механическая работа: Она характеризует изменение энергии тела.

Взаимодействующие тела имеют потенциальную энергию. В поле силы тяжести:

Полная механическая энергия замкнутой системы остается постоянной, если в ней действуют лишь силы тяжести или упругости: изменяются только кинетическая и потенциальная энергия (закон сохранения механической энергии):

Закон сохранения механической энергии

В предыдущих параграфах мы познакомились с двумя видами механической энергии тел: кинетической и потенциальной. Кинетическая энергия — это энергия тела, движущегося с некоторой скоростью относительно выбранной системы отсчета. Потенциальная энергия — это энергия взаимодействия. Естественно, при движении некоторого тела могут изменяться и кинетическая, и потенциальная энергии. Рассмотрим этот вопрос более подробно на примере тела массой m, брошенного под углом к горизонту. На такое тело действуют две силы — сила тяжести и сила сопротивления воздуха . (рис. 145).

Равнодействующая этих сил:

Рис. 145

Предположим, что в положении 1 тело имеет скорость и находится на высоте h₁, а в точке 2 имеет скорость и находится на высоте h₂ относительно некоторого уровня, принятого за нулевой. При движении тела из начального положения 1 в конечное положение 2, как уже было раньше показано, работа равнодействующей (результирующей) силы равна сумме работ всех сил, действующих на тело. В нашем случае

     (1)

Работа результирующей силы равна изменению кинетической энергии тела:
     (2)

В тоже время, как мы знаем, работа силы тяжести равна убыли потенциальной энергии тела:

     (3)

Поэтому выражение (1) с учетом (2) и (3) можно переписать в следующем

   (4)

В полученном выражении в скобках стоит сумма кинетической и потенциальной энергии тела в конечном и начальном положениях тела. Эта величина называется полной механической энергией тела или просто механической энергией W:

Используя понятие полной механической энергии, выражению (4) можно придать вид:
   (5)

Сила трения не является потенциальной, поэтому из (5) следует, что изменение механической энергии тела равно работе непотенциальных сил. Если сил трения нет, то A_с = 0, мы приходим к закону сохранения механической энергии:

т. е. для тел, движущихся под действием силы тяжести в отсутствие сил сопротивления, полная механическая энергия сохраняется.

При движении тела вверх его потенциальная энергия увеличивается, а кинетическая энергия уменьшается. И наоборот, при движении вниз его потенциальная энергия уменьшается, зато увеличивается кинетическая. Например, такое превращение энергии происходит при раскачивании на качелях (рис. 146). Причем изменение одной в точности равно изменению другой, если пренебречь сопротивлением воздуха и трением в подвесе качелей.
Это следует из формулы (6), которую можно переписать в виде:

Рис. 146

Если на тело, кроме силы тяжести, действует еще и сила упругости пружины, то можно ввести полную механическую энергию системы в виде:
    (7)

и она будет сохраняться при движении тела, если работа всех других сил, действующих на него, равна нулю.

Закон сохранения полной механической энергии является частным случаем общего закона сохранения и превращения энергии.

Если работа сил трения не равна нулю, то механическая энергия системы изменяется. Мы показали раньше, что работа этих сил идет на изменение внутренней энергии тел: тела нагреваются. Если все тщательно подсчитать, то сумма кинетической, потенциальной и внутренней энергии всех взаимодействующих тел остается неизменной. При движении тел происходит взаимное превращение одного вида энергии в другой. Но полная энергия остается постоянной.

Закон сохранения и превращения энергии является одним из важнейших законов не только физики, но и всех других наук о природе. На его основе строятся новые научные теории.
Любой теоретический вывод следует проверить «испытанием» на совместимость с этим законом. Если вывод не согласуется с законом сохранения и превращения энергии, то он неверен.

Главные выводы:

1. Полная механическая энергия равна сумме кинетической и потенциальной энергии тела.
2. Если на тело действуют сила тяжести и сила упругости, которые являются потенциальными силами, то изменение полной механической энергии, определенной равенством (7), равно работе непотенциальных сил, действующих на тело.
3. Если диссипативные силы не действуют или работой этих сил можно пренебречь, то выполняется закон сохранения энергии в виде W₁ = W₂, т. е. полная механическая энергия системы есть величина постоянная.
4. Закон сохранения полной механической энергии является частным случаем общего закона сохранения и превращения энергии.

Потенциальная энергия Рона Куртуса

SfC Home> Физика> Энергия>

Рона Куртуса

Потенциальная энергия – это состояние объекта или частицы, при котором они могут стать кинетической энергией или родственными формами энергии. Объект остается в состоянии равновесия, когда существует сила, которая пытается переместить материю, и такая же другая сила, препятствующая этому движению.

Освобождение силы, препятствующей движению, или добавление внешней силы может преобразовать потенциальную энергию в кинетическую.

Хорошим примером этого равновесия является сила, сжимающая пружину, и внутренняя сила, пытающаяся расширить пружину. Эта внутренняя сила считается потенциальной энергией сжатой пружины.

Общие типы потенциальной энергии – упругая, гравитационная, химическая, электрическая и ядерная. Когда потенциальная энергия высвобождается, ее можно использовать для работы.

Вопросы, которые могут у вас возникнуть:

• Какое состояние равновесия?
• Какие виды потенциальной энергии?
• Как можно применить потенциальную энергию?

Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц

---

---

Равновесие и потенциальная энергия

Потенциальная энергия – это когда к объекту прикладываются две равные силы в противоположных направлениях.

Сила вызывает ускорение

Когда вы прикладываете силу к объекту, он будет ускоряться, пока действует эта сила, в соответствии со Вторым законом Ньютона и уравнением:

F = ma

где

• F – приложенная сила в ньютонах (Н)
• м – масса в килограммах (кг)
• a – результирующее ускорение в метрах на секунду в квадрате (м / с ² )

Примечание : 1 Н = 1 кг-м / с².

Сила сопротивления может привести к появлению потенциальной энергии

Но это простое уравнение или взаимосвязь основаны на предположении, что нет других сил, препятствующих этому движению. Если есть сила, такая как трение, которая сопротивляется движению, ускорение будет:

a = (F – F _r ) / м

, где F _r – сила сопротивления.

Теперь, если F _r равно приложенной силе F , ускорение и движение будут равны нулю.Но если сила F все еще применяется, тогда существует потенциальная энергия, которая высвободится, как только F _r будет убрана или уменьшена.

Пример

Например, если вы находитесь в машине на холме, сила тяжести F _g пытается скатить машину с холма. Но если у вас есть тормоза, сила сопротивления F _r будет сдерживать вас. F _г – потенциальная энергия.Теперь, если вы медленно отпустите тормоза, эта потенциальная энергия изменится на кинетическую, когда вы начнете катиться с холма. Повторное нажатие на тормоза вернет вас в состояние потенциальной энергии, пока вы находитесь на холме.

Виды потенциальной энергии

Бывают ситуации, когда объект может начать движение и получить кинетическую энергию. Часто на объект действуют силы, но этих сил еще недостаточно для перемещения объекта. Общие типы потенциальной энергии:

• эластичный
• Гравитация
• Химическая промышленность
• Электрооборудование
• Ядерная

Упругая потенциальная энергия

Когда вы сжимаете пружину, вы создаете потенциальную энергию.Сила сжатия пропорциональна сжатию согласно закону Гука. При отпускании пружины потенциальная энергия превращается в кинетическую. затем пружину можно использовать для приведения в движение некоторого объекта.

Воздушный шар – еще один пример упругой потенциальной энергии, когда воздух сжимается внутри воздушного шара. Разрыв шара иглой превратит потенциальную энергию в кинетическую энергию быстро движущихся молекул воздуха.

Потенциальная энергия гравитации

У объекта, удерживаемого над землей, есть потенциальная энергия, связанная с высотой, на которой он удерживается, в соответствии с уравнением

PE = mgh

где:

• PE – потенциальная энергия в джоулях (Дж)
• м – масса объекта в кг
• g – постоянная ускорения свободного падения (9.8 м / с²)
• h – высота над землей или расстояние, на которое объект падает в м
• мг составляет м раз г раза ч

Примечание : 1 Дж = 1 кг-м ² / с ²

Если вы уроните объект, его потенциальная энергия станет кинетической энергией движения:

KE = ½ мв²

где

• KE – кинетическая энергия в Дж или кг-м ² / с ²
• v – скорость в м / с

Так как PE = и KE = ½ мв² , тогда мгв = ½ мв² .

Вы можете определить скорость, с которой он будет двигаться после падения с высоты h , решив уравнение для v :

½ mv² = mgh

v² = 2 мг / м

v² = 2gh

v = SQRT (2gh) = √ (2gh)

Примечание: SQRT (2gh) и √ (2gh) означает квадратный корень из 2gh . Обратите внимание, что масса м не входит в уравнение, что означает, что все объекты падают с одинаковой скоростью.

Таким образом, если h = 1 фут, а поскольку g = 32 фут / с², то v² = 2 * 32 * 1 = 64 и
v = 8 футов / с.

Химическая потенциальная энергия

Некоторые нестабильные молекулы, такие как нитроглицерин, обладают потенциальной энергией, готовой к высвобождению при правильных условиях. Выброс может быть взрывом с выделением кинетической энергии в виде света, тепла и движущихся частиц.

Некоторые смеси химикатов могут реагировать – хотя и не так бурно – с выделением тепла и других форм кинетической энергии.

Потенциальная электрическая энергия

Электрическая розетка в вашем доме имеет потенциальную энергию 110 В или 220 В, в зависимости от страны, в которой вы живете. Как только электрическая цепь установлена, эта потенциальная энергия становится кинетической энергией движения электронов, а также тепла и других эффектов.

Ядерная потенциальная энергия

Некоторые атомы имеют нестабильное ядро, которое может расщепляться и высвобождать кинетическую энергию. Например, уран-235 нестабилен и может расщепляться на две части, высвобождая высокоскоростные субатомные частицы и радиацию.Его потенциальная энергия превращается в кинетическую энергию.

Приложения потенциальной энергии

Контроль высвобождения потенциальной энергии может привести к выполнению им полезной работы. Мы используем пружины, чтобы закрывать двери в наших домах. Плотины и электрические генераторы используют потенциальную энергию воды для производства электроэнергии. Мы сжигаем топливо, чтобы приводить в движение автомобили и обогревать дома. Мы высвобождаем потенциальную энергию электричества для работы наших приборов. Ядерная потенциальная энергия также используется для производства электроэнергии.

Сводка

Потенциальная энергия – это когда объект может создавать кинетическую энергию или связанные с ней формы энергии. Объект находится в состоянии равновесия, где есть сила, которая пытается переместить материю, и такая же другая сила, препятствующая этому движению. Общие типы потенциальной энергии – упругая, гравитационная, химическая, электрическая и ядерная. Когда потенциальная энергия высвобождается, ее можно использовать для работы.

---

У вас большой потенциал

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайтов

Физические ресурсы

Книги

(Примечание: Школа чемпионов может получать комиссионные от покупки книг)

Книги по физике энергетики с самым высоким рейтингом

---

Поделиться страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
energy_potential.htm

Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.

Авторские права © Ограничения

---

Где ты сейчас?

Школа чемпионов

По физике

Потенциальная энергия

---

Работа, энергия и мощность

Эта страница дает представление о некоторых клипах, показанных в мультимедийном руководстве. Мы все знаем о физической работе, поэтому мы начали учебное пособие с этого примера, который также дает представление о размерах задействованных количеств. Начнем с расчетов за гистограммами, которые мы показали. Это мешки по 20 кг, поэтому вес каждого составляет около 200 ньютонов вниз , это серая стрелка. Обычно мы не говорим «вниз» в этом контексте, потому что вес всегда имеет направление, близкое к вниз .Я сделал это здесь, чтобы напомнить вам, что вес – это вектор. Итак, напишем, для одной сумки, W = – мг j = – (200 Н) j . Убедитесь, что обозначение: вес, W , является вектором, а работа, W, является скаляром. (Иногда нам также понадобится W для величины W , но вы узнаете из контекста, что есть что.) Движение мешков медленное, их ускорение мало по сравнению с g, поэтому сила, необходимая для их ускорения, мала по сравнению с их весом. Поэтому, когда я их поднимаю, я прилагаю усилие F ≅ – W = (200 Н) j , это черная стрелка. Если вы помните скалярное произведение, вы знаете, что ij = 0, но jj = 1. Итак, если я приложу эту постоянную силу к смещению Δ s = Δx i + Δy j , работа (W), которую я выполняю, W = F . Δ с = (мг j ) . (Δx i + Δy j ) = мг Δy (что, как мы показываем в мультимедийном руководстве, представляет собой увеличение потенциальной энергии массы m в гравитационном поле с величиной g при поднятии на высоту Δy). Итак, для первого мешка усилие 200 Н, я поднимаю его примерно на 0,7 м (красная стрелка), поэтому делаю 140 Дж работы. Джоуль (символ J) – единица работы в системе СИ: один ньютон умножить на один метр.Джоуль невелик в человеческом масштабе: поднимите маленькое яблоко (весом около 1 Н) на высоту 1 м, и вы проделали 1 джоуль работы с персиком – но, скорее, больше, чем двигая рукой! Точно так же, хотя я использую только 140 Дж на сумке, я больше работаю над движением рук и туловища. Здоровый человек может выполнить мегаджоуль работы за час. Куча теперь короче, поэтому я должен поднять вторую сумку через большее увеличение высоты: это напоминает мне, что работа пропорциональна смещению! Работа также пропорциональна силе, поэтому для подъема двух сумок требуется вдвое больше усилий, а я выполняю в два раза больше работы, чем над первой сумкой. Хм, я не спланировал это хорошо и должен поднять последние два мешка дальше: 400 N умножить на 1,5 м – это 600 Дж. Посмотрите на большой объем тележки и насколько она легкая. Тележка поддерживает шесть мешков, поэтому сила, которую она прилагает вверх, имеет величину 1,2 кН ​​(черная стрелка), и она перемещается на несколько метров (красная стрелка). Но сила находится в направлении j (или y), а смещение – в направлении i (или x): они расположены под прямым углом.Помнить i.j = 0. Или F . Δcos θ = 0. Таким образом, работа не выполняется. Поднять мешки по 20 кг (вес = 200 Н) не так уж и сложно. Поднятие собственной массы 70 кг (вес W = 700 Н) требует большего усилия. Но только не, если мы будем использовать шкивы (которые более подробно обсуждаются в физике блоков и шкивов). Здесь одна веревка идет от опоры вниз к моей подвеске, вокруг шкива, обратно к опоре, вокруг другого шкива и обратно в мои руки.Шкивы вращаются легко, поэтому натяжение Т на каждом участке каната одинаково. Меня тянут вверх три секции. Согласно второму закону Ньютона, общая сила, действующая на меня, равна моей массе, умноженной на мое ускорение. По сравнению с g мое ускорение здесь незначительно. Так 3 T + W = m a ≅ 0 Итак, если пренебречь моим (скромным) ускорением, сила, тянущая на меня вверх трех секций, равна моему весу: величина напряжения T = | W | / 3 = (700 Н) / 3. Значит, сила, которую мне нужно снабдить руками, уменьшена. Однако, чтобы поднять свое тело, скажем, на высоту 2 м, мне все равно нужно сделать (700 Н) (2 м) = 1,4 кДж работы. Как это возможно? Ну, по каждая из трех секций каната укорачивается на 2 м. Так руки тянут веревку 6 м. Я выполняю работу (6 м) (700 Н) / 3 = 1,4 кДж работы (плюс еще немного для преодоления трения в шкивах). Как и рычаги, блоки и шкивы не спасают вашу работу, но они могут уменьшить (или увеличить) усилие, что может сделать задачу более удобной и комфортной. Кинетическая энергия и теорема об энергии работы Мультимедийный учебник представляет эту теорему, но, возможно, вы захотите увидеть ее здесь снова. Давайте приложим постоянную силу F к массе m, когда она перемещается в одном измерении на расстояние x. (Это может быть, например, магнитная сила, которую мы использовали в нашем разделе о законах Ньютона.) Сила постоянна по x, x увеличивается линейно по x, поэтому проделанная работа ∫ F.dx линейно возрастает по x. Как только мы свяжем это со временем и скоростью, нам нужно будет выполнить интегрирование. (Помните, что есть помощь с расчетом.) Итак, давайте рассмотрим случай – все еще одномерный – в котором сила приложена на коротком расстоянии dx, и что масса m увеличивается со скоростью от v до v + dv. Общая работа, проделанная с массой, составляет где F – общая сила , действующая на массу.Подставляя второй закон Ньютона, F = ma = m (dv / dt), дает: dW = m (dv / dt) dx = m * dx * dv / dt где мы явно написали мультипликацию и деление. dx, dv и dt – все маленькие величины, но нет причин, по которым мы не можем изменить порядок умножения. Итак, напишем: dW = m * dv * dx / dt = m * v * dv Преимущество этой перестановки в том, что теперь мы можем легко выполнить интеграл: W = ∫ dW = ∫ mv.dv Предположим, мы начали с v = 0, тогда общая работа, проделанная для ускорения массы m от состояния покоя до скорости v, равна: W = ∫ mv.dv = ½mv 2 Эта величина настолько полезна, что мы даем ей имя кинетическая энергия и записываем Значит, вам не нравится исчисление? Воспользуемся уравнениями одномерной кинематики (для которой есть мультимедийный учебник). Предположим, что тело начинает движение в состоянии покоя и что мы применяем постоянную (общую) силу F в течение определенного времени T в одном примере и в течение удвоенного времени (2T) в более позднем примере (черные графики справа). Окончательная скорость будет v = aT = (F / m) T в первом примере и вдвое больше значения во втором примере (красные графики справа). Пройденное расстояние при действии силы , то есть расстояние, пройденное во время ускорения, теперь в четыре раза больше, как показано на фиолетовых графиках справа. Таким образом, постоянная сила была приложена на четырехкратном расстоянии и выполнила четырехкратную работу. Итак, несмотря на то, что скорость только удвоилась, мы проделали в четыре раза больше работы (синий график справа). Это важное следствие: при удвоении скорости масса имеет , в четыре раза превышающую кинетическую энергию . Как мы увидим далее, это имеет важные последствия для безопасности дорожного движения. Тормозной путь и теорема об энергии работы Если я еду на велосипеде в два раза быстрее, сколько еще нужно, чтобы остановиться? (Я включаю только расстояние после торможения, а не время, необходимое мне, чтобы среагировать на опасность и задействовать тормоза. При удвоении скорости моя кинетическая энергия K = ½ мв 2 в четыре раза больше. Итак, чтобы выполнить в четыре раза больше (отрицательной) работы, тормозная сила (предполагаемая постоянная) должна быть приложена на четырехкратном расстоянии. Пожалуйста, помните об этом в дороге. . Предположим, я медленно поднимаю массу в гравитационном поле. В этом клипе из мультимедийного руководства веревка с небольшой помощью с моей стороны медленно поднимает емкость с водой.Сила натяжения F выполняет работу W над контейнером, но не увеличивает его кинетическую энергию. Причина, конечно же, в том, что вес контейнера m g тянет в другую сторону: он отрицательно воздействует на контейнер. Однако работа W не потеряна: мы можем восстановить ее: мы можем медленно опустить контейнер и, таким образом, поднять кирпич на другом конце веревки. Итак, где работа F , когда мы поднимаем контейнер? В каком-то смысле он хранится в гравитационном взаимодействии между контейнером и землей.Эта «сохраненная работа» может работать на нас. Это пример потенциальной энергии – в данном случае потенциальной энергии гравитации. Итак, сколько потенциальной энергии мы храним в этом случае? Мы используем силу F для перемещения объекта массы m смещение ds в гравитационном поле, поэтому мы работаем (где вы, возможно, захотите изменить векторы). Предположим, что мы перемещаем его таким образом, что мы не меняем его скорость (и поэтому не меняем его кинетическую энергию).Тогда общая сила, действующая на него, равна нулю, поэтому F + m g = 0, поэтому Однако g находится в отрицательном вертикальном направлении, скажем, в направлении минус y, поэтому Для смещений в планетарном масштабе мы должны учитывать изменение гравитационного поля с высотой, что мы и делаем в разделе о гравитации. Для более скромных смещений g является однородным, и интегрирование дает нам . ∫ dU grav = ∫ dW = ∫ мг dy = mgΔy = mgΔh , где h обычно используется для вертикальной координаты.U определяется интегралом, а для интегралов требуется постоянная интегрирования. Для потенциальной энергии эта постоянная является точкой отсчета для нуля потенциальной энергии. Если мы определим U grav равным нулю при h = 0 , то мы можем написать Как мы увидим, не все силы позволяют определить потенциальную энергию. Однако другой пример – Потенциальная энергия пружины. Если мы медленно сжимаем или растягиваем пружину из положения покоя, мы снова работаем, не создавая кинетической энергии.Но опять же, он «хранится» – мы можем вернуть его. Согласно закону Гука, сила, прилагаемая пружиной, равна F пружина = – kx, где x – это смещение от ее длины в нерастянутом состоянии, а k – жесткость пружины для этой конкретной пружины. Поскольку мы ничего не ускоряем, мы должны приложить силу F = – F , пружина , поэтому ∫ dU пружина = ∫ dW = ∫ F dx = −∫ F пружина dx = ∫ kx dx = Δ (½kx 2 ) Опять же, нам нужно определить постоянную интегрирования и ноль потенциальной энергии.Обычно мы устанавливаем U = 0 при x = 0, поэтому Обратите внимание, что при этом эталонном значении пружина U всегда положительна: относительно ненапряженного состояния и растяжение (x> 0), и сжатие (x <0) требуют работы, поэтому потенциальная энергия в каждом случае положительна. . В клипе я работаю, чтобы сохранить потенциальную энергию пружины, затем пружина воздействует на массу, передавая ей кинетическую энергию. Биохимическая энергия в моей руке была преобразована весной в потенциальную, а затем в кинетическую. Консервативные и неконсервативные силы Давайте посмотрим на мою работу по перемещению массы в гравитационном поле. Мы сделаем вид, что я делаю это с таким медленным ускорением, что масса всегда находится в механическом равновесии, то есть сила, действующая моей рукой, плюс вес массы прибавляются к нулю, поэтому работа, которую я выполняю против силы тяжести, – ∫ F рука . ds , который показан в виде гистограммы коричневого цвета. Когда я поднимаю груз, F рука идет вверх (положительно) и s также положительно, итак проделанная мной работа положительная: Когда я уменьшаю массу, F рука все еще вверх (положительная), но теперь s отрицательная, так что проделанная мной работа отрицательная: Следовательно, выполните полный цикл, который возвращает массу в ее начальную точку, ∫ F hand . DS = 0. Точно так же работа, совершаемая силой тяжести вокруг цикла, равна нулю (потому что F грав = – F рука ). Это делает гравитацию консервативной силой: Определение : Консервативная сила – это сила, которая совершает нулевую работу вокруг замкнутого контура в пространстве. Отсюда следует, что для консервативной силы F мы можем определить потенциальную энергию как функцию положения r : Если работа, выполняемая вокруг замкнутого цикла, не равна нулю, тогда мы не можем определить такую ​​функцию: ее значение должно было бы меняться со временем, если бы мы обошли такой цикл.Силы с этим свойством называются, очевидно, неконсервативными силами. Итак, какую силу оказывает идеальная пружина? Опять же, давайте представим, что я делаю это так медленно, что пружина находится в механическом равновесии: F рука = – F пружина . Движу рукой вправо, растягивая пружину. F hand положительный, а ds положительный. Я выполняю положительную работу (показано на гистограмме), а пружина выполняет отрицательную работу. Затем я двигаю рукой влево, но продолжаю тянуть, чтобы сохранить растяжку весной. По мере того как пружина укорачивается, F hand все еще положительный, но теперь ds отрицательный. Я выполняю отрицательную работу (показано на гистограмме), а пружина – положительно. Для пружины ∫ F . dr вокруг замкнутого пути равен нулю. Сила, создаваемая идеальной пружиной, является консервативной силой . Что за сила трения? Опять же, давайте представим, что я делаю это так медленно, что масса находится в механическом равновесии: F рука = – F трение .Двигаясь вправо, я прилагаю силу вправо, и объект перемещается вправо: F рука и ds оба положительные: я выполняю положительную работу (показано на гистограмме) и трение делает отрицательную работу. Двигаясь влево, я прилагаю силу влево, и объект перемещается влево: F рука и ds оба положительные: я выполняю положительную работу (показано на гистограмме) и трение делает отрицательную работу.Итак, вокруг замкнутого контура работа против трения больше нуля, поэтому трение является неконсервативной силой . Сохранение механической энергии В теореме об энергии работы мы видели выше, что полная работа ΔW, совершенная над объектом, равна увеличению ΔK его кинетической энергии. Но рассмотрим случай, когда все силы, выполняющие работу ΔW – консервативные силы: здесь работа, совершаемая этими силами, равна минус 1, умноженная на работу, совершаемую против них, другими словами, это −ΔU.Итак, если действуют только консервативные силы, тогда ΔU + ΔK = 0, Определите механическую энергию : E ≡ U + K. Так , если действуют только консервативные силы, механическая энергия сохраняется. Мы сделаем это сильнее ниже, но прежде давайте рассмотрим пример, в котором механическая энергия (почти) сохраняется. Кинетическая и потенциальная энергия в маятнике В этом видеоролике показан пример обмена кинетической и потенциальной энергией в маятнике.Предупреждение, однако: ради сокращения времени загрузки эти видеоклипы повторяются за один цикл. В оригинальном фильме маятник постепенно теряет энергию: в каждом цикле теряется небольшая часть энергии, частично из-за выталкивания воздуха. Кинетическая энергия K показана красным цветом: как функция от x на графике и в виде гистограммы, которая изменяется со временем. Обратите внимание, что K стремится к нулю в крайних точках движения. Потенциальная энергия U показана фиолетовым цветом.Он имеет максимумы в крайних точках движения, когда масса наибольшая. Поскольку ноль потенциальной энергии является произвольным, значит, это ноль полной механической энергии E = U + K. Здесь E (показано белым) является постоянным. В разделе «Волны и звук» Physclips есть глава о механике колебаний и раздел о механической энергии в простом гармоническом движении. Сохранение механической энергии: заявление Мы видели, что если единственные присутствующие силы консервативны, то механическая энергия сохраняется.Однако можно пойти дальше. При условии, что неконсервативные силы не работают, тогда увеличение ΔK кинетической энергии тела по-прежнему является работой консервативных сил, равной −ΔU. Таким образом, можно сделать вывод, что Если неконсервативные силы не работают, сохраняется механическая энергия (E ≡ U + K) . Это утверждение можно записать несколькими способами, из которых можно выделить два: Если неконсервативные силы не работают, ΔU + ΔK = 0 или U i + K i = U f + K f , где i и f означают начальное и конечное.Я настоятельно рекомендую вам всегда писать оговорки, потому что, как правило, механическая энергия не сохраняется. (И никогда, никогда не пишите «кинетическая энергия равна потенциальной энергии». Это неправда, и вы не должны лгать.) На катящемся колесе трение не работает. Здесь я еду медленно, так что давайте пренебрежем сопротивлением воздуха и сопротивлением качению. Существует значительная сила трения: именно трение между шинами и дорожным покрытием ускоряет меня по кругу.В этом случае сила трения находится под прямым углом к ​​смещению, поэтому трение не работает. Итак, пока я не крутил педали, (приблизительно) работа не выполняется, а моя механическая энергия (приблизительно) постоянна. Работа и мощность Мощность определяется как скорость выполнения работы или скорость преобразования или передачи энергии: P = dW / dt. В этом примере моя кинетическая энергия примерно постоянна. Однако моя потенциальная энергия увеличивается.Поскольку я лазаю, я иду не очень быстро, поэтому скорость, с которой я работаю против неконсервативных сил, таких как сопротивление воздуха, мала. Приведенные ниже уравнения позволяют нам рассчитать скорость, с которой я работаю против силы тяжести (что является недооценкой скорости, с которой я работаю). Моя высота увеличивается на 1 мс -1 , а мой вес составляет 700 Н, поэтому P = dW / dt ≅ dU / dt = mg (dh / dt) = 700 Вт. Задача скольжения Вот проблема из учебника: работать против неконсервативной силы.Здесь я прилагаю силу F через натяжение струны. Работа, которую я делаю, это dW = F . ds = F ds cos θ Теперь v = ds / dt, поэтому мощность, которую я применяю, т.е. скорость, с которой я выполняю работу, составляет: P = dW / dt = F v cos θ Я предоставлю читателю возможность нарисовать свободную диаграмму тела. Затем воспользуйтесь вторым законом Ньютона и свяжите P с m, g, v и μ k . Проблема петли Это классическая проблема.Маленькая игрушечная машинка движется на колесах, которые, как предполагается, вращаются свободно и масса которых незначительна, поэтому мы можем рассматривать ее как частицу. С какой высоты я должен отпустить его, чтобы он замкнул петлю, оставаясь полностью контактировать с дорожкой? Если автомобиль сохраняет контакт с гусеницей, то в верхней части петли, которая является круговой, центростремительное ускорение будет направлено вниз и его величина будет равна v 2 / r. Силами, обеспечивающими это ускорение, являются его вес mg (действующий вниз) и нормальная сила N от пути, также действующая вниз в этой точке. Итак, если N> 0, нам требуется v 2 / r> g, или, для критического состояния, при котором он просто теряет контакт, нам требуется v крит 2 / r = g или v крит 2 = rg Мы можем решить эту задачу, используя сохранение механической энергии. U начальный + K начальный = U конечный + K конечный Выбрав нижнюю часть дорожки в качестве нуля для U, мы могли бы написать, мг начальный + 0 = мг.(2р) + ½мв финал и, если v окончательный = v критический = √ (rg) мг начальная = 2 мг + ½ мг Итак, критический высота на 5r / 2 выше низа дорожки. Проблема плотины ГЭС Уровень воды в плотине гидроэлектростанции на 100 м выше высоты выхода воды из труб. Предполагая, что турбины и генераторы эффективны на 100%, и пренебрегая вязкостью и турбулентностью, рассчитайте расход воды, необходимый для выработки 10 МВт мощности.Выходные трубы имеют сечение 5 м 2 . Эта задача имеет теорему работы-энергии, использует мощность и требует некоторого размышления. Давай сделаем это. Давайте рассмотрим, что происходит в устойчивом состоянии для этой системы. Через время dt некоторое количество воды массой dm выходит из нижней трубы со скоростью v. Эта вода доставляется к вершине плотины с незначительной скоростью. Таким образом, чистый эффект состоит в том, чтобы взять dm неподвижной воды на высоте h и доставить ее на дно плотины на нулевой высоте и скорости v.Выглядит просто. Пойдем. Пусть поток равен dm / dt. Работа, совершаемая водой, dW, является минусом увеличения энергии воды, поэтому dW = – dE = – dK – dU = – (½dm.v 2 – 0) – (0 – dm.gh) = dm (gh – ½v 2 ) Доставляемая мощность составляет всего P = dW / dt. так P = (gh – ½v 2 ) дм / дт Конечно расход dm / dt зависит от v.Давайте посмотрим, как: За время dt вода течет по трубе на расстояние vdt. Поперечное сечение трубы – A, поэтому объем воды, прошедшей через данную точку, равен dV = A (vdt). Используя определение плотности, ρ = dm / dV, имеем dm / dt = ρdV / dt = ρA. (Vdt) / dt = ρAv. Подстановка в приведенное выше уравнение дает нам P = ρAv (gh – ½v 2 ) или ½v 3 – ghv + P / ρA = 0. Как ни крути, это кубическое уравнение, которое звучит как запутанное решение.Однако давайте подумаем о том, что термины означают. Первый произошел от термина кинетической энергии. Второй – это работа, совершаемая под действием силы тяжести. Третий – это работа над турбинами. Если бы я спроектировал эту плотину, я бы хотел преобразовать как можно больше гравитационной потенциальной энергии в работу, выполняемую на турбинах, поэтому я бы сделал трубы достаточно широкими, чтобы кинетическая энергия, теряемая при оттоке воды, была быть незначительным. Посмотрим, верна ли моя догадка. Если первый член пренебрежимо мал, то мы просто имеем hgv = P / ρA. Таким образом, v = P / ρghA = 2 м.с −1 . Таким образом, первый член будет 4 m 3 .s −3 , второй будет – 2000 m 3 .s −3 , а третий будет 2000 m 3 .s −3 . . Итак, да, предположение было правильным, и с точностью, необходимой для решения этой задачи, ответ будет v = 2 м.с -1 . Уравнение Бернулли Уравнение Бернулли является примером теоремы работы-энергии.На анимации жидкость течет с постоянной скоростью в трубу с поперечным сечением A 1 и высотой h 1 , где она имеет скорость v 1 и давление P 1 . Жидкость выходит из трубы с поперечным сечением A 2 и высотой h 2 , где она имеет скорость v 2 и давление P 2 . Жидкость имеет постоянную плотность ρ, и мы предполагаем, что ее вязкость незначительна и что турбулентность отсутствует, поэтому неконсервативные силы не действуют. Какая связь между скоростью, высотой и давлением? Какая связь между скоростью, высотой и давлением? Прежде чем делать это количественно, мы можем спросить, как связаны давление и скорость. На той же высоте, и если у нас нет турбулентности или вязкости, то единственное, что ускоряет жидкость, – это разница в давлении. Жидкость будет ускоряться от высокого к низкому давлению, поэтому, когда P высокое, v должно быть низким, а – наоборот .Посмотрим: За короткое время dt масса dm входит в трубу слева, и, поскольку поток является постоянным, такая же масса dm вытекает справа. Поскольку поток постоянный, общая энергия воды в трубе не изменяется. Таким образом, общая работа, проделанная над dm, по теореме работы-энергии, равна dW всего = ½ дм.в 2 2 – ½ дм.в 1 2 . Работа совершается двумя силами: гравитацией, которая совершает работу – dU grav , и давлением.dU grav равно dm.gΔh, поэтому Итак, сколько работы совершает разница в давлении, действующем в трубе? По определению, давление – это сила на единицу площади, поэтому сила, действующая со стороны P на площадь поперечного сечения A, равна PA. Если эта сила приложена на расстоянии ds под прямым углом к ​​A, она действительно сработает. Но перемещаемый объем равен dV = Ads, поэтому работа, выполняемая давлением, равна PdV. Работа, проделанная P 1 , является положительной, а работа P 2 – отрицательной, поэтому P 1 dV – P 2 dV = ½ дм.v 2 2 + dm.gh 2 – ½ dm.v 1 2 – dm.gh 2 . Теперь воспользуемся определением плотности: ρ = dm / dV. Итак, если мы разделим обе части уравнения на dV и переставим члены, P 1 + ½ρv 1 2 + ρgh 1 = P 2 + ½ρv 2 2 + ρgh 2 . Конечно, мы могли бы применить этот анализ к любым двум точкам в трубе, поэтому при условии, что поток является устойчивым, несжимаемым, невязким и не турбулентным, мы имеем уравнение Бернулли P + ½ρv 2 + ρgh = постоянная . Помня, что ρ = dm / dV, мы можем увидеть значение каждого из этих терминов: P – это работа, совершаемая давлением на единицу объема, ½ρv 2 – кинетическая энергия на единицу объема, а ρgh – гравитационная потенциальная энергия на единицу объема. Уравнение Бернулли – это просто теорема об энергии работы, записанная на единицу объема e. При отсутствии потока это просто дает изменение давления с глубиной : . ΔP = – ρgΔh , если нет потока. Если высота постоянна, имеем ΔP = – Δ (½ρv 2 ), если нет изменения высоты. Это последнее наблюдение говорит нам, что (на одинаковой высоте) давление будет высоким при низкой скорости и , наоборот, . В этом есть смысл: если скорость увеличилась при постоянном h, значит, должно было действовать давление, ускоряющее жидкость. Жидкость, конечно, течет от высокого давления к низкому, поэтому она должна быть медленнее при высоком давлении и быстрее при низком давлении.(Напомним, что мы пренебрегаем вязкостью и турбулентностью: здесь не действуют неконсервативные силы.) Это прекрасная демонстрация: шланг подает высокоскоростную струю воздуха. Что держит мяч в воздухе? Сопротивление воздушной струи, когда она проходит мимо мяча, заставляет его вращаться, поэтому мы можем сделать вывод, исходя из направления вращения, что большая часть струи проходит над мячом . Мяч имеет вес, и единственные силы, действующие на него, связаны с давлением воздуха вокруг него. Таким образом, мы можем сделать вывод, что давление над мячом существенно меньше, чем под ним. Однако это не простая демонстрация эффекта, описываемого уравнением Бернулли. Несомненно, что быстро движущийся воздух, выходящий из шланга, имеет давление несколько меньшее, чем давление в неподвижном воздухе. Поскольку струя воздуха, выходящая из шланга, в основном отклоняется над шаром, это делает давление над шаром меньше атмосферного.Однако в этом случае сама струя отклоняется присутствием шара, поэтому есть также вклад от изменения количества движения струи. (Кроме того, сопротивление, вызывающее вращение, говорит нам о наличии неконсервативной силы, и поэтому уравнение Бернулли здесь не применимо.) Центр масс работы Когда мы пишем W = ∫ F . ds , для расширенного объекта, что такое F , а что ds ? F – это общая внешняя сила, действующая на объект, которая, согласно третьему закону Ньютона, равна общей силе, действующей на объект. ds в данном случае это смещение центра масс, ds CoM . В этой простой демонстрации сила, ускоряющая меня, – это сила, которую стена прилагает к моей руке. Однако стена не двигается. Во время ускорения движется мой центр масс, поэтому кинетическая энергия, связанная с движением моего центра масс, увеличивается на ∫ F external . DS CoM . Мы оставим вывод этого раздела на центр масс. Работа, выполняемая трением Трение сложно, и расчет работы, выполняемой трением, требует некоторых приближения и тонкости. Предположим, мы рассматриваем блок, скользящий по поверхности с постоянной скоростью, и что мы рассматриваем блок как точечную массу. Если мы посмотрим на блок отдельно, на него действуют две силы: внешняя приложенная сила, которая работает W, и трение с поверхности.Поскольку объект не ускоряется, эти силы равны и противоположны, поэтому общая работа, выполняемая на блоке, равна нулю, а трение действительно работает W на блоке (сила той же величины, противоположное направление по сравнению с тем же смещением). На макроскопическом изображении с блоком не происходит никакой работы, поэтому согласно теореме работы-энергии его кинетическая энергия не изменяется. Работа –W, совершаемая трением, преобразуется в тепло (и небольшой звук и некоторая пластическая деформация поверхности). Вот одна сложность: в системе отсчета поверхности блок движется, поэтому –W создается силой трения, которую поверхность оказывает на блок (который движется), а нулевая работа выполняется силой трения, которую блок воздействует на нижнюю поверхность (которая не двигается).В качестве альтернативы, в системе отсчета блока поверхность движется, поэтому –W создается силой трения, которую блок оказывает на поверхность (которая движется), а нулевая работа выполняется силой трения, которую поверхность оказывает на блок (который не двигается). А в симметричной системе отсчета, движущейся со скоростью v / 2 по поверхности, –W / 2 будет вычисляться для каждого. На практике большая часть –W превращается в тепло, части которого передаются в оба, хотя обычно не симметрично.Микроскопическая картина намного сложнее, потому что трение часто включает временные пятна слипания крошечных точек соприкосновения и микроскопические деформации двух сторон с неоднородными движениями ползучести и ускорениями. Почему устают мышцы, не выполняя работу Вопрос студента: Если я держу объект, не перемещая его, я не выполняю работу (по определению физики), но все равно устаю . Почему так? Короткий ответ заключается в том, что мышцам требуется биохимическая энергия для приложения силы, даже если нет движения.Таким образом, мы используем биохимическую энергию, что утомительно, даже если эта энергия не работает. Об этом есть отдельная страница.

25A: потенциальная энергия, сохранение энергии, мощность

Работа, совершаемая над частицей силой, действующей на нее, когда эта частица перемещается из точки A в точку B под действием этой силы, для некоторых сил , не зависит от пути, пройденного частицей. Для такой силы есть простой способ вычислить работу, совершаемую частицей при ее движении от точки A к точке B .Просто нужно присвоить значение потенциальной энергии (частицы) точке A (назовите это значение \ (U_A \)) и значение потенциальной энергии точке B (назовите это значение \ (U_B \) ). Выбираются значения таким образом, чтобы работа, выполняемая рассматриваемой силой, была просто отрицательной величиной разницы между двумя значениями.

\ [W = – (U_B-U_A) \]

\ [W = – \ треугольник U \ label {25-1} \]

\ (\ треугольник U = U_B-U_A \) – это изменение потенциальной энергии, испытываемой частицей при движении от точки A к точке B .Знак минус в уравнении 25-1 гарантирует, что увеличение потенциальной энергии соответствует отрицательной работе, совершаемой соответствующей силой. Например, в случае потенциальной энергии гравитации у поверхности Земли, связанной с ней силой является сила тяжести, также известная как гравитационная сила. Если мы поднимаем объект вверх около поверхности земли, гравитационная сила оказывает отрицательное воздействие на объект, поскольку (направленная вниз) сила имеет направление, противоположное (восходящему) смещению.В то же время мы увеличиваем способность частицы выполнять работу, поэтому мы увеличиваем потенциальную энергию. Таким образом, нам нужен знак «-» в \ (\ omega = – \ треугольник U \), чтобы гарантировать, что метод вычисления работы с изменением потенциальной энергии дает тот же алгебраический знак для значения работы, что и сила-вдоль -путь, умноженный на длину пути, дает.

Обратите внимание, что для того, чтобы этот метод расчета работы был полезен в любом случае, который может возникнуть, необходимо присвоить значение потенциальной энергии каждой точке в пространстве, где сила может действовать на частицу, чтобы можно было использовать этот метод. для расчета работы, совершаемой над частицей при движении частицы из любой точки A в любую точку B .В общем, это означает, что нам нужно значение для каждой из бесконечного набора точек в пространстве.

Это присвоение значения потенциальной энергии каждой из бесконечного набора точек в пространстве может показаться пугающим, пока вы не поймете, что это можно сделать с помощью простого алгебраического выражения. Например, мы уже написали задание для частицы массы \ (m_2 \) для случая универсальной гравитационной силы, создаваемой частицей массы \ (m_1 \). Это было уравнение \ (\ ref {17-5} \):

\ [U \ space = \ space – \ dfrac {Gm_1m_2} {r} \]

, в котором G – всемирная гравитационная постоянная \ (G = 6.2} \), а r – расстояние, на котором частица 2 находится от частицы 1. Обратите внимание, что, учитывая, что частица 1 находится в начале системы координат, это уравнение присваивает значение потенциальной энергии каждой точке Вселенной! Значение для любой точки просто зависит от расстояния, на котором точка находится от начала координат. Предположим, мы хотим найти работу, совершаемую гравитационной силой из-за частицы 1 над частицей 2, когда частица 2 движется из точки A , расстояние \ (r_A \) от частицы 1 до точки B , расстояние \ ( r_B \), от частицы 1.Гравитационная сила, действующая на нее (частицу 2) гравитационным полем частицы 1, выполняет определенную работу с частицей 2, определяемую (начиная с уравнения \ (\ ref {25-1} \)):

\ [W = \ треугольник U \]

\ [W = – (U_B-U_A) \]

\ [W = – \ Big [(- \ dfrac {Gm_1m_2} {r_B}) – (- \ dfrac {Gm_1m_2} {r_A}) \ Big] \]

\ [W = Gm_1m_2 (\ dfrac {1} {r_B} – \ dfrac {1} {r_A}) \]

Связь между консервативной силой и соответствующим потенциалом

Хотя процесс вычисления работы, проделанной над частицей, как отрицательного значения изменения ее потенциальной энергии, действительно значительно упрощает вычисление работы, мы должны быть осторожны, чтобы определить потенциал таким образом, чтобы этот метод был эквивалентен вычисление работы как сила на пути, умноженная на длину пути.Вместо того, чтобы вдаваться в проблему нахождения потенциальной энергии во всех точках трехмерной области пространства для силы, известной как существующая во всех точках этой трехмерной области пространства, давайте рассмотрим более простую задачу нахождения потенциал вдоль линии. Мы определяем систему координат, состоящую из одной оси, назовем ее осью x, с началом координат и положительным направлением. Мы помещаем частицу на линию, частицу, которая может двигаться вдоль линии. Мы предполагаем, что у нас есть сила, которая действует на частицу, где бы частица ни находилась на линии, и что сила направлена ​​вдоль линии.Хотя мы также рассмотрим случай силы, которая имеет одинаковое значение в разных точках на линии, мы предполагаем, что в целом сила зависит от положения. \ (\ leftarrow \) Запомните этот факт, чтобы вы могли найти недостаток, обсуждаемый ниже. Поскольку мы хотим определить для него потенциал, важно, чтобы работа, выполняемая над частицей силой, действующей на частицу, когда частица движется из точки A в точку B, не зависела от того, как частица попадает из точки A до точки B .Наша цель – определить функцию потенциальной энергии для силы так, чтобы мы получали одно и то же значение для работы, совершаемой с частицей силой, независимо от того, используем ли мы метод силы вдоль пути для ее вычисления или отрицательное значение изменения. метода потенциальной энергии. Предположим, что частица под действием силы перемещается \ (\ треугольник x \) вдоль линии. Посмотрите, видите ли вы недостаток в следующем, прежде чем я укажу на него: Мы пишем \ (W = F \ треугольник x \) для работы, выполняемой силой, рассчитанной с использованием силы на пути, умноженной на длину идеи пути, а затем \ (W = – \ треугольник U \) для работы, совершаемой силой, рассчитанной с использованием отрицательного значения концепции изменения потенциальной энергии.Приравнивая два выражения друг к другу, получаем \ (F \ треугольник x = – \ треугольник U \), который мы можем записать как \ (F = – \ dfrac {\ треугольник U} {\ треугольник x} \) для связь между потенциальной энергией и x-составляющей силы.

Вы видите, в чем мы ошиблись? Хотя этот метод будет работать в частном случае, в котором сила является постоянной, мы должны были придумать соотношение, которое было бы хорошо для общего случая, в котором сила изменяется в зависимости от положения. Это означает, что для каждого значения x в диапазоне значений, простирающихся от начального значения, назовем его \ (x_A \) до значения в конце смещения \ (x_A + \ треугольник x \), существует другой значение силы.Так что выражение \ (W = F \ треугольник x \) неуместно. Учитывая числовую задачу, нет единого значения, которое можно было бы подставить для F, потому что F изменяется вдоль \ (\ треугольника x \).

Чтобы исправить ситуацию, мы можем уменьшить \ (\ треугольник x \) до бесконечно малого размера, настолько маленького, что \ (x_A \) и \ (x_A + \ треугольник x \) будут для всех практических целей одной и той же точкой. . То есть мы берем предел как \ (\ треугольник x \ rightarrow 0 \). Тогда наше отношение становится

\ [F_x = \ lim \ limits _ {\ треугольник x \ to 0} (- \ dfrac {\ треугольник U} {\ треугольник x}) \]

, что то же самое, что

\ [F_x = – \ lim \ limits _ {\ треугольник x \ rightarrow 0} (- \ dfrac {\ треугольник U} {\ треугольник x}) \]

Предел \ (\ frac {\ треугольник U} {\ треугольник x} \), который появляется справа, есть не что иное, как производная \ (\ frac {dU} {dx} \), поэтому:

\ [F_x = – \ dfrac {dU} {dx} \ label {25-2} \]

Чтобы подчеркнуть тот факт, что сила является вектором, мы записываем его в обозначении единичного вектора как:

\ [\ vec {F} = – \ dfrac {dU} {dx} \ hat {i} \ label {25-3} \]

Давайте сделаем это более конкретным, используя его для определения потенциальной энергии из-за силы, с которой вы знакомы, – силы из-за пружины.

Рассмотрим блок на горизонтальной поверхности без трения. Блок прикреплен к одному концу пружины. Другой конец пружины прикреплен к стене. Пружина проходит горизонтально от стены под прямым углом к ​​стене. Определите ось x с началом в положении равновесия того конца пружины, который прикреплен к блоку. Считайте, что направление от стены является положительным направлением оси x. Экспериментально выяснилось, что сила, прилагаемая пружиной к блоку, равна:

\ [\ vec {F} = – kx \ hat {i} \ label {25-4} \]

где \ (k \) – силовая постоянная пружины.(Примечание: положительное значение \ (x \), соответствующее тому, что блок был оторван от стены, таким образом растягивая пружину, приводит к возникновению силы в отрицательном направлении \ (x \). Отрицательное значение \ (x \), сжатая пружина приводит к возникновению силы в направлении \ (+ x \) в соответствии со здравым смыслом.) По сравнению с уравнением \ (\ ref {25-3} \) (тем, которое читается как \ (\ vec {F}) = – \ dfrac {dU} {dx} \ hat {i} \)) отметим, что функция потенциальной энергии должна быть определена так, чтобы

\ [\ dfrac {dU} {dx} = kx \]

Это настолько простой случай, что мы можем в значительной степени догадаться, что должно быть \ (U \).2 \ label {25-5} \]

– это действительно потенциальная энергия силы пружины. Вы использовали это выражение еще в главе \ (2 \). Теперь вы знаете, откуда это взялось.

Мы рассмотрели две другие консервативные силы. Для каждого найдем функцию потенциальной энергии \ (U \), которая соответствует критерию, который мы записали как \ (\ vec {F} = – \ dfrac {dU} {dx} \ hat {i} \).

Во-первых, давайте рассмотрим гравитационную силу у поверхности Земли, действующую на объект массы m со стороны Земли.Мы выбираем нашу единственную ось, направленную вертикально вверх с началом отсчета на произвольной, но четко определенной и фиксированной высоте для всей проблемы, которую можно было бы решить, используя концепции, рассматриваемые здесь. По соглашению мы называем такую ​​ось осью y, а не осью x. Теперь мы знаем, что гравитационная сила задается просто (опять же, это экспериментальный результат)

\ [\ vec {F} = \ space -mg \ hat {j} \]

, где mg – известная величина гравитационной силы, а \ (- \ hat {j} \) – направление вниз.

Уравнение \ (\ ref {25-3} \), записанное для рассматриваемого случая:

\ [\ vec {F} = – \ dfrac {dU} {dy} \ hat {j} \]

Чтобы последние два уравнения согласовывались друг с другом, нам нужно определить \ (U \) так, чтобы

\ [\ dfrac {dU} {dy} = \ space mg \]

Чтобы производная \ (U \) по y была константой « mg », \ (U \) должно быть задано как

\ [U = \ space mgy \ label {25-6} \]

, и это действительно уравнение для потенциальной энергии гравитации у поверхности Земли.Пожалуйста, убедитесь, что когда вы берете производную по y, вы действительно получаете величину гравитационной силы \ (mg \).

Теперь давайте обратим наше внимание на Всемирный закон тяготения. Частица номер 1 массы \ (m_1 \) создает гравитационное поле в области пространства вокруг себя. Давайте определим положение частицы номер 1 как начало трехмерной декартовой системы координат. Теперь предположим, что частица номер 2 находится в некотором положении в пространстве, на расстоянии r от частицы 1.{-1}} {- 1} \]

, что можно записать

\ [U = – \ dfrac {Gm_1m_2} {r} \ label {25-7} \]

Это действительно выражение для гравитационного потенциала, которое мы дали вам (без какого-либо обоснования) еще в главе 17, главе о Всеобщем законе тяготения.

Новый взгляд на сбережение энергии

Вспомните соотношение работы и энергии, уравнение \ (\ ref {24-2} \) из предыдущей главы,

\ [W = \ треугольник K, \]

утверждение, что работа вызывает изменение кинетической энергии.Теперь рассмотрим случай, когда вся работа выполняется консервативными силами, поэтому работу можно выразить как отрицательное изменение потенциальной энергии.

\ [- \ треугольник U = \ треугольник K \]

Далее предположим, что мы имеем дело с ситуацией, когда частица движется из точки A в точку B под действием силы или сил, соответствующих потенциальной энергии \ (U \).

Тогда предыдущее выражение можно записать как:

\ [- (U_B-U_A) = K_B-K_A \]

\ [- U_B + U_A = K_B-K_A \]

\ [K_A + U_A = K_B + U_B \]

Переключившись на обозначение, в котором мы используем переменные со штрихом для характеристики частицы, когда она находится в точке B , и переменные без штрихов в точке A , мы имеем:

\ [K + U = K ‘+ U’ \]

Интерпретируя \ (E = K + U \) как энергию системы в момент «до», а \ (E ‘= K’ + U ‘\) как энергию системы в момент «после», мы видим, что мы вывели утверждение о сохранении механической энергии для особого случая, когда чистая энергия не передается в окружающую среду или из нее, а энергия внутри системы не преобразуется из механической энергии в другие формы или наоборот.В форме уравнения:

.

\ [E = E ‘\ label {25-8} \]

– уравнение, с которым вы познакомились в главе 2. Обратите внимание, что вам стоит просмотреть главу 2 сейчас, потому что в текущей главе вы снова несете ответственность за решение любой из проблем типа «главы 2» (вспоминая включить и правильно использовать диаграммы до и после) и ответить на любой из вопросов типа «глава 2».

Мощность

В этом последнем разделе об энергии мы обращаемся к новой теме.Как отдельная и важная концепция, она заслуживает отдельной главы, за исключением того факта, что это такая простая и понятная концепция. Мощность – это скорость передачи энергии, преобразования энергии и, в некоторых случаях, скорость, с которой передача и преобразование энергии происходят одновременно. Когда вы работаете с объектом, вы передаете ему энергию. Предположим, например, что вы толкаете блок по горизонтальной поверхности без трения. Вы работаете над объектом. Кинетическая энергия объекта увеличивается.2 \]

\ [P = \ dfrac {1} {2} m \ space 2v \ space \ dfrac {dv} {dt} \]

\ [P = m \ dfrac {dv} {dt} v \]

\ [P = m \, a _ {\ parallel} v \]

\ [P = F _ {\ parallel} \, v \]

\ [P = \ vec {F} \ cdot \ vec {v} \ label {25-10} \]

где \ (a _ {\ parallel} \) – составляющая ускорения, параллельная вектору скорости. Перпендикулярный компонент изменяет направление скорости, но не величину.

Помимо скорости изменения кинетической энергии, мощность – это скорость, с которой работа выполняется с объектом.В бесконечно малом интервале времени dt вы выполняете бесконечно малый объем работы

\ [dW = \ vec {F} \ cdot \ vec {dx} \]

на объекте. Разделив обе стороны на dt, получим

\ [\ dfrac {dW} {dt} = \ vec {F} \ cdot \ dfrac {\ vec {dx}} {dt} \]

, что снова равно

, как и должно быть, поскольку в соответствии с соотношением работа-энергия скорость, с которой вы работаете с объектом, должна быть скоростью, с которой увеличивается кинетическая энергия объекта.

Если вы работаете с постоянной скоростью в течение конечного временного интервала, мощность будет постоянной и может быть просто рассчитана как количество работы, выполненной в течение временного интервала, деленное на сам временной интервал.Например, поднимаясь по лестнице, вы преобразуете химическую энергию, хранящуюся в вашем теле, в потенциальную энергию гравитации. Скорость, с которой вы это делаете, и есть мощность. Если вы поднимаетесь с постоянной скоростью для общего увеличения гравитационной потенциальной энергии \ (\ треугольника U \) за временной интервал \ (\ треугольник t \), то постоянное значение вашей силы в течение этого временного интервала составляет

.

\ [P = \ dfrac {\ треугольник U} {\ треугольник t} \ label {25-11} \]

Если вы знаете, что мощность постоянна, вам известно значение мощности P , и вас попросят найти общий объем выполненной работы, общее количество переданной энергии и / или общее количество преобразованной энергии. в течение определенного промежутка времени \ (\ треугольник t \) вам просто нужно умножить мощность P на временной интервал \ (\ треугольник t \).

\ [\ mbox {Энергия} = P \ треугольник t \ label {25-12} \]

Можно включить как минимум дюжину формул в таблицу формул мощности, но все они настолько просты, что, если вы понимаете, что такое мощность, вы можете придумать конкретную формулу, которая вам нужна для случая, над которым вы работаете. Мы включаем только одну формулу в лист формул,

\ [P = \ dfrac {dE} {dt} \ label {25-13} \]

, который должен напомнить вам, что такое мощность. Поскольку мощность – это скорость изменения энергии, единицы мощности в системе СИ должны быть \ (\ frac {j} {s} \).Этому комбинированному блоку присвоено название ватт, сокращенно Вт .

\ [1W = 1 \ dfrac {J} {s} \ label {25-14} \]

Авторы и авторство

Вывод формулы кинетической энергии

Что такое кинетическая энергия?

Слово «кинетическая энергия» произошло от французского слова travail mécanique (механическая работа) или Quantité de travail (количество работы). Кинетическая энергия тела – это энергия, которой тело обладает благодаря его движению.

Например, кинетическая энергия может применяться по-разному:

• Гвоздь забивается в деревянный брусок в зависимости от кинетической энергии удара молотка по гвоздю.

• Бейсбольный мяч, брошенный питчером, имеет небольшую массу, но большое количество кинетической энергии из-за высокой скорости.

На этой странице мы узнаем о следующем:

• Формула кинетической энергии

• Вывести формулу кинетической энергии

• Вывод уравнения кинетической энергии

• Расчет кинетической энергии

• Вычисление кинетической энергии с помощью алгебры

Формула кинетической энергии

Говорят, что танцующий более энергичен, чем храпящий.2

i

Кинетическая энергия частицы или системы частиц может увеличиваться, уменьшаться или оставаться постоянной с течением времени.

Получение формулы кинетической энергии с помощью алгебры

Кинетическая энергия может быть получена одним из следующих способов:

Рассмотрим второй случай:

Предположим, что m = масса тела в состоянии покоя.

u = Начальная скорость тела.

F = сила, приложенная к телу

a = ускорение, создаваемое телом в направлении приложенной силы

v = скорость, приобретаемая телом при перемещении на расстояние s.2

Эта работа над телом осуществляется за счет кинетической энергии (K.E) тела.

Получение формулы кинетической энергии расчетным путем

Формула для кинетической энергии может быть получена расчетным методом:

Предположим, что

m = масса тела

u = Начальная скорость тела

→

F = Сила, приложенная к телу в направлении движения

→

ds = Небольшое смещение тела в направлении движения

Небольшое количество работы, выполняемой силой, будет:

→ →

dW = F. 2 – 0

K.2

Резюме

• Сила выполняет некоторую работу с телом, кинетическая энергия увеличивается на ту же величину. Таким образом, согласно этому принципу работа и энергия эквивалентны друг другу.

• Сила необходима для изменения кинетической энергии частицы. Если результирующая сила, действующая на частицу, перпендикулярна ее скорости, скорость не изменяется и, следовательно, кинетическая энергия не изменяется.

SAQ

Q1: Рассчитайте среднюю силу трения, необходимую для остановки автомобиля весом 600 кг на расстоянии 35 м, если начальная скорость составляет 36 км / ч.

Решение: Учитывая m = 600 кг, s = 35 м

v = конечная скорость = 0 (Так как тело окончательно остановится)

u = 36 км / ч

u = 36 км / ч = 10 м / с

Согласно принципу работы-энергии,

W = изменение K.2)

Решая, получаем:

Средняя сила трения (F) = 857 Н

22,5 Сохранение механической энергии | Механическая энергия

До сих пор мы рассматривали два типа энергии: гравитационная потенциальная энергия и кинетическая энергия. Сумма гравитационная потенциальная энергия и кинетическая энергия называется механической энергией. В закрытой системе та, где отсутствуют внешние диссипативные силы, механическая энергия останется постоянной.Другими словами, это не изменится (станет более-менее). Это называется законом сохранения механической энергии.

Это означает, что потенциальная энергия может стать кинетической или наоборот, но энергия не может “пропадать”. Например, при отсутствии сопротивления воздуха механическая энергия движущегося объекта через воздух в гравитационном поле Земли остается постоянным (сохраняется).

Использование закона сохранения энергии (ESAHP)

Механическая энергия сохраняется (при отсутствии трения). {- 1} $} \).

Отсюда мы видим, что когда объект поднимается, например чемодан в нашем примере, он получает потенциальную энергию. В виде он падает обратно на землю, он теряет эту потенциальную энергию, но приобретает кинетическую энергию. Мы знаем эту энергию не может быть создан или уничтожен, а только преобразован из одной формы в другую. В нашем примере потенциал энергия, которую теряет чемодан, превращается в кинетическую энергию.

Чемодан будет иметь максимальную потенциальную энергию в верхней части шкафа и максимальную кинетическую энергию в верхней части шкафа. дно шкафа.На полпути вниз он будет иметь половину кинетической энергии и половину потенциальной энергии. Как он движется вниз, потенциальная энергия будет преобразована (изменена) в кинетическую энергию до тех пор, пока вся потенциальная энергия не будет ушел, и осталась только кинетическая энергия. \ (\ Text {19,6} \) \ (\ text {J} \) потенциальной энергии наверху будет стать \ (\ text {19,6} \) \ (\ text {J} \) кинетической энергии внизу.

Преобразование энергии

Материалы

Отрезок пластиковой трубы диаметром примерно 20 мм, мрамор, клейкая лента и измерительная Лента.

Сделать (1)

Сначала поместите один конец трубы на столешницу так, чтобы он был параллелен верхней части стола, и закрепите его скотчем. на место с помощью малярной ленты.

Поднимите другой конец трубы вверх и удерживайте его на устойчивой высоте не слишком высоко над столом.

Измерьте высоту по вертикали от столешницы до верхнего отверстия трубы.

Теперь поместите шарик в верхнюю часть трубы и отпустите его, чтобы он прошел через трубу и вышел из нее. другой конец.

Вопросы

• Какова скорость (т.е. быстро, медленно, неподвижно) шарика, когда вы впервые помещаете его в верхнюю часть труба и что это означает для ее гравитационного потенциала и кинетической энергии?

• Какова скорость (т.е. быстро, медленно, неподвижно) шарика, когда он достигает другого конца трубку и катит на стол? Что это означает для его гравитационного потенциала и кинетической энергии?

Сделать (2)

Теперь поднимите верхнюю часть трубы как можно выше.

Измерьте вертикальную высоту верха трубы над столешницей.

Поместите шарик в верхнее отверстие и позвольте ему катиться по трубе на стол.

Вопросы

• Какова скорость (т.е. быстро, медленно, неподвижно) шарика, когда вы помещаете его в верхнюю часть труба, и что это означает для ее гравитационного потенциала и кинетической энергии?

• Чем изменилась высота верха трубки по сравнению с первой попыткой? Как ты думаете, что это влияет на гравитационную потенциальную энергию мрамора?

• По сравнению с вашей первой попыткой, шарик двигался быстрее или медленнее, когда он выходил из-под дна. трубы второй раз? Что это означает для кинетической энергии мрамора?

Движение мрамора, катящегося по трубе, очень хорошо показывает преобразование гравитационного потенциальная энергия и кинетическая энергия.В первом случае труба держалась относительно низко, и поэтому гравитационная потенциальная энергия также была относительно низкой. Кинетическая энергия в этой точке была равна нулю, так как мрамор еще не двигался. Когда мрамор выкатился из другого конца трубы, он двигался относительно медленно, и поэтому его кинетическая энергия также была относительно низкой. В этот момент его гравитационный потенциал энергия была равна нулю, так как она находилась на нулевой высоте над столешницей.

Во втором случае шарик стартовал выше и, следовательно, его гравитационная потенциальная энергия была равна выше.К тому времени, когда он достиг дна трубы, его гравитационная потенциальная энергия была равна нулю (нулевая высота над столом), но его кинетическая энергия была высокой, поскольку он двигался намного быстрее, чем в первый раз. Следовательно, гравитационная потенциальная энергия была полностью преобразована в кинетическую энергию (если не учитывать трение о трубка).

В случае, когда труба находится выше, гравитационная потенциальная энергия в начале была выше, и кинетическая энергия (и скорость) шарика в конце была выше.Другими словами, полная механическая энергия был выше и зависел только от высоты, на которой вы держали трубку над столешницей, а не от расстояния до мрамор должен был пройти через трубу.

Рабочий пример 7: Использование закона сохранения механической энергии

Во время наводнения ствол дерева массой \ (\ text {100} \) \ (\ text {kg} \) падает с водопадом. Водопад \ (\ text {5} \) \ (\ text {m} \) высокий.

Если сопротивление воздуха не учитывается, рассчитайте:

• потенциальная энергия ствола дерева на вершине водопада.

• кинетическая энергия ствола дерева у подножия водопада.

• величина скорости ствола дерева у подножия водопада.

Проанализируйте вопрос, чтобы определить, какая информация предоставляется

• Масса ствола дерева \ (m = \ text {100} \ text {kg} \)

• Высота водопада \ (h = \ text {5} \ text {m} \).{-2} $} \ right) \ left (\ text {5} \ text { m} \ right) \\ & = \ текст {4 900} \ текст {J} \ end {выровнять *}

  Рассчитайте кинетическую энергию внизу водопада.

  Полная механическая энергия должна быть сохранена.

  \ [{E} _ {K1} + {E} _ {P1} = {E} _ {K2} + {E} _ {P2} \]

  Поскольку скорость ствола на вершине водопада равна нулю, \ ({E} _ {K1} = 0 \).

  Внизу водопада \ (h = \ text {0} \ text {m} \), поэтому \ ({E} _ {P2} = 0 \).

  Следовательно \ ({E} _ {P1} = {E} _ {K2} \) или прописью:

  Кинетическая энергия ствола дерева у подножия водопада равна его потенциальной энергии. на вершине водопада. Следовательно, \ ({E} _ {K} = \ text {4 900} \ text {J} \)

  Рассчитайте скорость на дне водопада.

  Чтобы вычислить скорость ствола дерева, нам нужно использовать уравнение для кинетической энергии.{-1} $} \ end {выровнять *}

  Рабочий пример 8: Маятник

  Металлический шар \ (\ text {2} \) \ (\ text {kg} \) подвешен на веревке как маятник. Если он выпущен из точка A и поворачивается вниз к точке B (нижняя часть дуги):

  1. показывают, что скорость мяча не зависит от его массы,

  2. рассчитать скорость мяча в точке B. {2} \ end {выровнять *}

     Это доказывает, что скорость мяча не зависит от его массы.{-1} $} \ end {выровнять *}

     Сработанный пример 9: Американские горки

     Поездка на американских горках в парке развлечений начинается с отдыха на высоте \ (\ text {50} \) \ (\ text {m} \) выше землю и быстро падает вниз по своему следу. В какой-то момент трек делает полный цикл на 360 °, который имеет высоту \ (\ text {20} \) \ (\ text {m} \) перед тем, как закончить на уровне земли. Поезд американских горок сам с полной загрузкой людей на нем имеет массу \ (\ text {850} \) \ (\ text {kg} \).

     Американские горки

     Если американские горки и их гусеница не имеют трения, рассчитайте:

     1. скорость американских горок, когда они достигают вершины петли

     2. скорость американских горок в нижней части контура (т. {- 1} $} \)

     3. Высота петли \ ({h} _ {2} = \ text {20} \ text {m} \)

     4. Высота в нижней части петли на уровне земли, \ ({h} _ {3} = \ text {0} \ text {m} \)

Нам не нужно переводить единицы, так как они уже находятся в правильном виде.

Проанализируйте вопрос, чтобы определить, что задают

Рассчитайте скорость в верхней части контура

Из закона сохранения механической энергии мы знаем, что в любых двух точках системы общая механическая энергия должна быть такой же. Сравним ситуацию в начале американских горок с положение в верхней части петли:

\ begin {align *} {E} _ {M1} & = {E} _ {M2} \\ {E} _ {K1} + {E} _ {P1} & = {E} _ {K2} + {E} _ {P2} \\ 0 + mg {h} _ {1} & = \ frac {1} {2} m {\ left ({v} _ {2} \ right)} ^ {2} + mg {h} _ {2} \ end {выровнять *}

Мы можем исключить массу \ (m \) из уравнения, разделив обе части на \ (m \). {- 1} $} \ end {выровнять *}

Рабочий пример 10: Наклонная плоскость

Альпинист, поднимающийся на гору в Драконовом озере зимой, по ошибке роняет воду. бутылка, которая затем скользит \ (\ text {100} \) \ (\ text {m} \) вниз по крутому ледяному склону к точке, которая На 10 м ниже положения альпиниста.Масса альпиниста \ (\ text {60} \) \ (\ text {kg} \) и его вода бутылка имеет массу \ (\ text {500} \) \ (\ text {g} \).

1. Если бутылка запускается в состоянии покоя, как быстро она движется к тому времени, когда достигает дна емкости? склон? (Трением пренебречь.)

2. Каково полное изменение потенциальной энергии альпиниста, когда она спускается с горы, чтобы забрать ее? упавшая бутылка с водой? я.е. в чем разница между ее потенциальной энергией на вершине склона а внизу скат?

Проанализируйте вопрос, чтобы определить, какая информация предоставляется

• расстояние, пройденное бутылкой с водой вниз по склону, \ (d = \ text {100} \ text {m} \)

• разница в высоте между исходным положением и конечным положением бутылки с водой составляет \ (h = \ text {10} \ text {m} \)

• бутылка начинает скользить из состояния покоя, поэтому ее начальная скорость равна \ ({v} _ {1} = \ text {9,8} \ text { м · с $ ^ {- 1} $} \)

• масса альпиниста \ (\ text {60} \) \ (\ text {kg} \)

• масса бутылки с водой равна \ (\ text {500} \) \ (\ text {g} \). {- 2} $} \ right) \ left (\ text {0} \ text { m} \ right) \\ & = \ текст {0} \ текст {J} \ end {выровнять *}

  Следовательно, разница в ее потенциальной энергии при движении от вершины склона к основанию составляет:

  \ [{E} _ {P1} – {E} _ {P2} = \ text {5 880} – 0 = \ text {5 880} \ text {J} \]

  Потенциальная энергия

  Учебное упражнение 22.3

  Теннисный мяч массой \ (\ text {120} \) \ (\ text {kg} \) падает с высоты \ (\ text {5} \) \ (\ текст {м} \). Не обращайте внимания на трение воздуха.

  1. Какова потенциальная энергия мяча, когда он упал \ (\ text {3} \) \ (\ text {m} \)?

  2. Какова скорость мяча, когда он падает на землю?

  Решение пока недоступно

  Мяч катится с холма, высота которого по вертикали составляет \ (\ text {15} \) \ (\ text {m} \). {- 1} $} \).Используйте принцип сохранения механической энергии, чтобы определить высоту, на которую достигнет пуля. Не обращайте внимания на трение воздуха.

  Решение пока недоступно

  Лыжник массой \ (\ text {50} \) \ (\ text {kg} \) находится на вершине \ (\ text {6,4} \) \ (\ text {m} \) лыжный склон.

  1. Определите максимальную скорость, которую она может достичь, спускаясь на лыжах со дна склона.{-1} $} \). Рассчитайте высоту A из который был выпущен на свободу. Не обращайте внимания на трение воздуха.

     Решение пока недоступно

     Докажите, что скорость объекта при свободном падении в замкнутой системе не зависит от его массы.

     Решение пока недоступно

     Закон сохранения энергии

     Закон сохранения энергии гласит, что энергия не может быть ни создана, ни уничтожена – только преобразована из одной формы энергии в другую.Это означает, что система всегда имеет одинаковое количество энергии, если только она не добавляется извне. Это особенно сбивает с толку в случае неконсервативных сил, когда энергия преобразуется из механической энергии в тепловую, но общая энергия остается неизменной. Единственный способ использовать энергию – это преобразовывать энергию из одной формы в другую.

     Таким образом, количество энергии в любой системе определяется по следующему уравнению:

     [математика] U_ {T} = U_ {i} + W + Q [/ математика]

     • [математика] U_T [/ математика] – это полная внутренняя энергия системы.
     • [math] U_i [/ ​​math] – начальная внутренняя энергия системы.
     • [математика] W [/ математика] – это работа, выполняемая системой или в ней.
     • [math] Q [/ math] – это тепло, добавляемое к системе или отводимое от нее.

     Также можно определить изменение внутренней энергии системы, используя уравнение: [математика] \ Дельта U = W + Q [/ математика]

     Это также утверждение первого закона термодинамики. {2} [/ математика]

     • [математика] E [/ математика] – это количество энергии в объекте или системе.8 м / с [/ математика].

     Для дальнейшего чтения

     Чтобы узнать больше о физике закона сохранения энергии, см. Гиперфизику, а о том, как это связано с химией, см. Вики по химии Калифорнийского университета Дэвиса.

     Уравнение работы / энергии

     Уравнение работы / энергии

     ---

     ---

     Уравнение Работа / Энергия:

     Уравнение работы / энергии:

     (деривация доступный.)

     И что?

     Предположим, мы называем величину “половину массы, умноженной на скорость”. в квадрате “ Кинетическая энергия объекта. Тогда это конечная кинетическая энергия объекта и равна начальная кинетическая энергия объекта. Если мы назовем количество “сила, умноженная на расстояние” Работа выполнена на объекте, то это работа, выполняемая над объектом чистой силой. Следовательно предыдущее уравнение говорит:

     Работа, выполненная чистой силой = окончательная кинетическая энергия – начальная кинетическая энергия

     или:

     ---

     Работа, проделанная над объектом чистой силой = изменение кинетической энергии объекта.

     ---

     Очень Важно “Мелкий шрифт!”
     1. Следует подчеркнуть, что только уравнение работа / энергия применяется к работе, выполняемой чистой силой в механической системе – работа, выполненная любой старой силой, может проявиться или не проявиться как кинетическая энергии, но работа, совершаемая чистой силой, всегда отображается как кинетическая энергия .
        
     2. Эта версия уравнения работы-энергии () была получена для одномерного движения и действительна только в том случае, если (1) чистая сила, действующая на объект, постоянна, и (2) чистая сила и смещение объекта находятся вдоль та же линия.Если ситуация включает два или более измерения или если результирующая сила непостоянна, уравнение работы-энергии по-прежнему остается в силе, но выглядит более сложным.
        
     3. Иногда люди думают, что уравнение работы-энергии () говорит, что чистая сила на объекте всегда действительно работает, поскольку левая часть уравнения никогда не равна нулю, пока чистая сила и смещение не равны нулю. Если результирующая сила постоянна, а результирующая сила и смещение лежат на одной линии, это верно, но в целом это не так!

     ---

     ---

     последнее обновление 21 ноября 2007 г., автор: JL Stanbrough
     .