Физика энергия формула: Ошибка: 404 Материал не найден

Кинетическая энергия — урок. Физика, 8 класс.

Энергию, которой обладают только движущиеся тела, называют кинетической энергией.

Если тело находится в состоянии покоя, его кинетическая энергия равна нулю. 

Кинетическая энергия тела (Eкин) зависит от массы тела (m) и от скорости его движения (v).

Кинетическая энергия прямо пропорциональна массе тела и квадрату его скорости.

Определяют кинетическую энергию по формуле:

 

Eкин=m⋅v22.

 

Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом:

 

m=2⋅Eкинv2 и v=2⋅Eкинm.

 

С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия. 

Если масса увеличивается в \(2\) раза, тогда кинетическая энергия увеличивается также в \(2\) раза.

Зависимость кинетической энергии от массы можно отобразить на данном графике, если принять скорость тела постоянной и равной \(2  м/с\).

 

 

Рис. \(1\). График, зависимость кинетической энергии от массы

 

С увеличением скорости движения тела увеличивается также и его кинетическая энергия в квадратичной зависимости.

Если скорость увеличивается в \(2\) раза, тогда кинетическая энергия увеличивается в \(4\) раза.  

Зависимость кинетической энергии от скорости движения можно отобразить на данном графике, если принять массу тела постоянной и равной \(2  кг\).

 

 

Рис. \(2\). График, зависимость кинетической энергии от скорости движения

 

Пример:

Автомобиль, масса которого \(1400  кг\), из состояния покоя развивает скорость до значения \(5  м/с\).

Какова кинетическая энергия автомобиля на конечном этапе движения?

 

Eкин=m⋅v22=1400⋅522=17500Дж.

Источники:

Рис. 1. График, зависимость кинетической энергии от массы. © ЯКласс.
Рис. 2. График, зависимость кинетической энергии от скорости движения. © ЯКласс.

Потенциальная и кинетическая энергия.

7 класс

Потенциальная и кинетическая энергия. 7 класс

Подробности

Просмотров: 373

 

Существуют два вида механической энергии: потенциальная и кинетическая.

1. Какую энергию называют потенциальной?

Потенциальной энергией называется энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.

а). Потенциальной энергией обладает тело, поднятое относительно поверхности Земли.
Здесь потенциальная энергия тела зависит от взаимного положения тела и Земли и их взаимного притяжения.
Потенциальная энергия тела, поднятого на какую-то высоту, определится работой, которую совершит сила тяжести при падении тела на Землю.

где
Еп — потенциальная энергия (Дж),
F — сила тяжести (Н),
g — ускорение свободного падения (м/с2),

m — масса тела (кг),
h — высота, на которую поднято тело (м).

Например:

Потенциальную энергию молота копра используют в строительстве для забивания свай.

Каждый кубический метр текущей воды в реке обладает потенциальной энергией.
Ведь течение воды в реке возможно, если уровень поверхности земли у истока (в начале реки) выше, чем уровень поверхности земли в устье, т.е. вода течет под горку. Этот перепад высот и определяет величину потенциальной энергии воды. В истоках каждый кубометр воды будет обладать большей потенциальной энергией, чем в устье.

Огромной потенциальной энергией обладает вода в реках, удерживаемая плотинами. Падая вниз, вода совершает работу, приводя в движение мощные турбины электростанций.

б). Потенциальной энергией обладает всякое упругое деформированное тело.

Например:

Дверная пружина при открывании двери растягивается (деформируется) и за счет приобретенной потенциальной энергии, сокращаясь, совершает работу, т.е. закрывает дверь.

Энергию пружин используют в ручных часах и заводных игрушках.

Потенциальную энергию сжатого газа используют в тепловых двигателях, в отбойных молотках.

2. От каких величин зависит потенциальная энергия?

Потенциальная энергия тела зависит от массы тела и высоты подъема над поверхностью земли.
(смотри формулу)

Например:

Сосулька, падающая с крыши пятиэтажного дома, будет обладат большим запасом потенциальной энергии, чем такая же, падающая с балкона второго этажа.

Большой камень и маленький камушек, поднятые на одинаковую высоту, в результате падения на землю совершат разную работу, один пробьет глубокую яму, а другой – лишь незначительную вмятину. Из-за разной массы они будут обладать различной потенциальной энергией.

3. Когда потенциальная энергия тела равна нулю?

Если тело лежит на поверхности Земли, то его потенциальная энергия равна нулю.
Если тело (например, пружина, кусок резины или резиновый мяч) упруго не деформировано, то его потенциальная энергия тоже равна нулю.

4. Какую энергию называют кинетической?

Энергия, которой обладает тело вследствие своего движения, называется кинетической энергией ( кинема — движение).

Любое движущееся тело обладает кинетической энергией.

где
Ек — кинетическая ээнергия (Дж),

m — масса тела (кг),
v — скорость движения тела ((м/с).

Например:

Движущаяся молекула обладает кинетической энергией.

Едущий автомобиль, идущий человек обладают кинетической энергий.

Кинетической энергией обладает движущаяся вода в реке.

Кинетической энергией обладает и движущийся воздух — ветер.

5. От каких величин зависит кинетическая энергия?

Кинетическая энергия зависит от массы тела и его скорости.
(смотри формулу)

Чем больше масса тела и скорость, с которой оно движется, тем больше его кинетическая энергия.

Например:

При одинаковой скорости полета большей кинетической энергией будет обладать птица по сравнению с мухой, ведь масса птицы больше, чем масса мухи.

Если сравнить кинетическую энергию кубического метра текущей воды в равнинной и горной реке, то понятно, что за счет большей скорости течения воды в горной реке, эта вода будет обладать большей кинетической энергией, чем вода в равнинной реке.

5. В каком случае кинетическая энергия тела равна нулю?

Кинетическая энергия тела в состоянии покоя равна нулю.

6. Может ли тело одновременно обладать и потенциальной, и кинетической ээнергией?

Все тела в природе обладают либо потенциальной, либо кинетической энергией, а иногда той и другой вместе.

Например:

Летящий самолет обладает относительно Земли и кинетической и потенциальной энергией.

Следующая страница – смотреть

Назад в “Оглавление” – смотреть

Энергия – Физика

Маркиза Эмили дю Шатле в книге «Учебник физики»  объединила идею Лейбница с практическими наблюдениями Виллема Гравезанда.

В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия живая сила. Гаспар-Гюстав Кориолис раскрыл связь между работой и кинетической энергией в 1829 году. Уильям Томсон (будущий лорд Кельвин) впервые использовал термин «кинетическая энергия» не позже 1851 года, а в 1853 году Уильям Ренкин впервые ввёл понятие «потенциальная энергия».

Несколько лет велись споры, является ли энергия субстанцией (теплород) или только физической величиной.

Развитие паровых двигателей требовало от инженеров разработать понятия и формулы, которые позволили бы им описать механический и термический КПД своих систем. Инженеры (Сади Карно), физики (Джеймс Джоуль, Эмиль Клапейрон и Герман Гельмгольц), математики — все развивали идею, что способность совершать определённые действия, называемая работой, была как-то связана с энергией системы. В 1850-х годах, профессор натурфилософии из Глазго Уильям Томсон и инженер Уильям Ренкин начали работу по замене устаревшего языка механики с такими понятиями как «кинетическая и фактическая (actual) энергии». Уильям Томсон соединил знания об энергии в законы термодинамики, что способствовало стремительному развитию химии. Рудольф Клаузиус, Джозайя Гиббс и Вальтер Нернст объяснили многие химические процессы, используя законы термодинамики. Развитие термодинамики было продолжено Клаузиусом, который ввёл и математически сформулировал понятие энтропии, и Джозефом Стефаном, который ввёл закон излучения абсолютно чёрного тела. В 1853 году Уильям Ренкин ввёл понятие «потенциальная энергия». В 1881 году Уильям Томсон заявил перед слушателями:

Особенности преобразования тепла и работы были показаны в первых двух законах термодинамики. Наука об энергии разделилась на множество различных областей, таких как биологическая термодинамика и термоэкономика. Параллельно развивались связанные понятия, такие как энтропия, мера потери полезной энергии, мощность, поток энергии за единицу времени, и так далее. В последние два века использование слова энергия в ненаучном смысле широко распространилось в популярной литературе. В течение следующих тридцати лет эта новая наука имела несколько названий, например, «динамическая теория тепла»  и «энергетика» . В 1920-х годах общепринятым стало название «термодинамика» — наука о преобразовании энергии.

В 1918 году было доказано, что закон сохранения энергии есть математическое следствие трансляционной симметрии времени, величины сопряжённой энергии. То есть энергия сохраняется, потому что законы физики не отличают разные моменты времени .

“Механическая энергия. Закон сохранения механической энергии”

Цели урока

Образовательная:

Развивающая:

• уметь творчески интерпретировать имеющуюся информацию, обогащать словарный запас учащихся, отрабатывать вычислительные навыки.

Воспитывающая:

• воспитание доброжелательности, сотрудничества, сотворчества;

• воспитание профориентационной направленности.

Тип урока: комбинированный.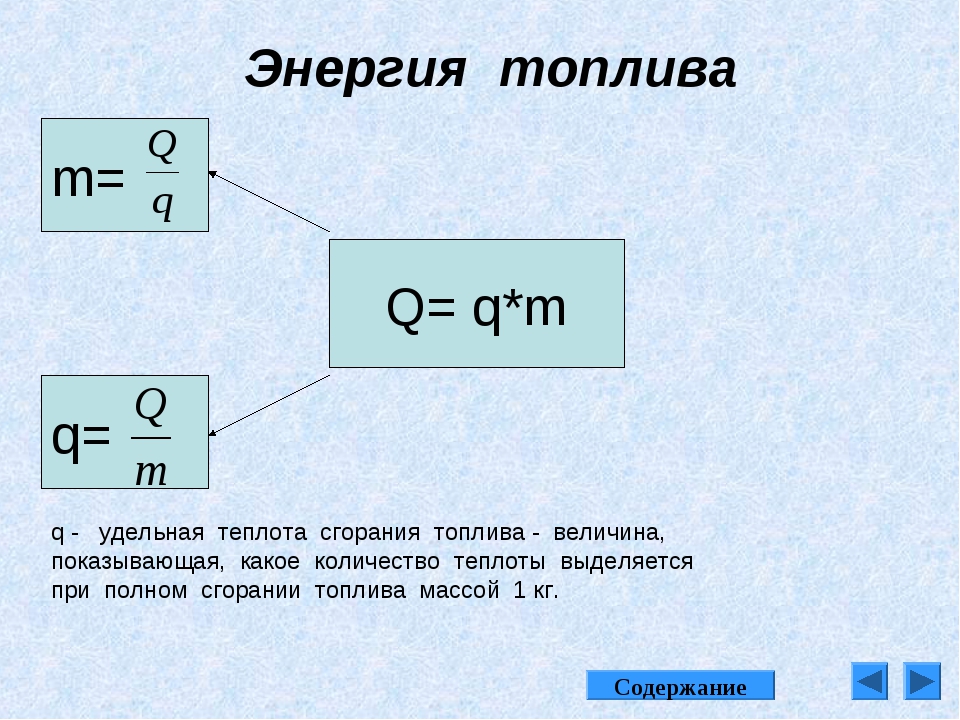

Продолжительность занятия – 45 минут.

Материалы и оборудование:

План урока:

1. Организационный момент;

2. Постановка темы и целей урока;

3. Проверка домашнего задания;

4. Изучение нового материала;

5. Закрепление нового материала;

6. Подведение итогов урока.

7. Домашнее задание.
   

Ход урока:

I. Организационный момент:

1. Приветствие и настрой на урок.

II. Постановка темы и целей урока.

III. Проверка домашнего задания: Фронтальный опрос: Что такое работа? По какой формуле вычисляется работа? В каких единицах измеряется работа? Что характеризует мощность? В каких единицах измеряется мощность? По какой формуле вычисляется мощность?

III. Изучение нового материала:

Мы с вами повторили основные две физические величины это работа и мощность. Следующая физическая величина которую мы будим проходить – это

энергия. Итак, мы вводим новое понятие энергия. Как Вы думаете, какова цель нашего сегодняшнего урока. Для чего мы должны изучать энергию?

Какие виды энергии вы знаете? Приведите примеры?

Ребята! Сегодня мы с вами познакомимся с механической энергией. Механическая энергия – физическая величина, показывающая какую работу может совершить тело.

Она обозначается: W

Рассмотрим теперь несколько ситуаций, которые помогут нам ввести понятие «энергия», которое чрезвычайно важно в физике и технике. Им мы будем пользоваться вплоть до 11 класса.

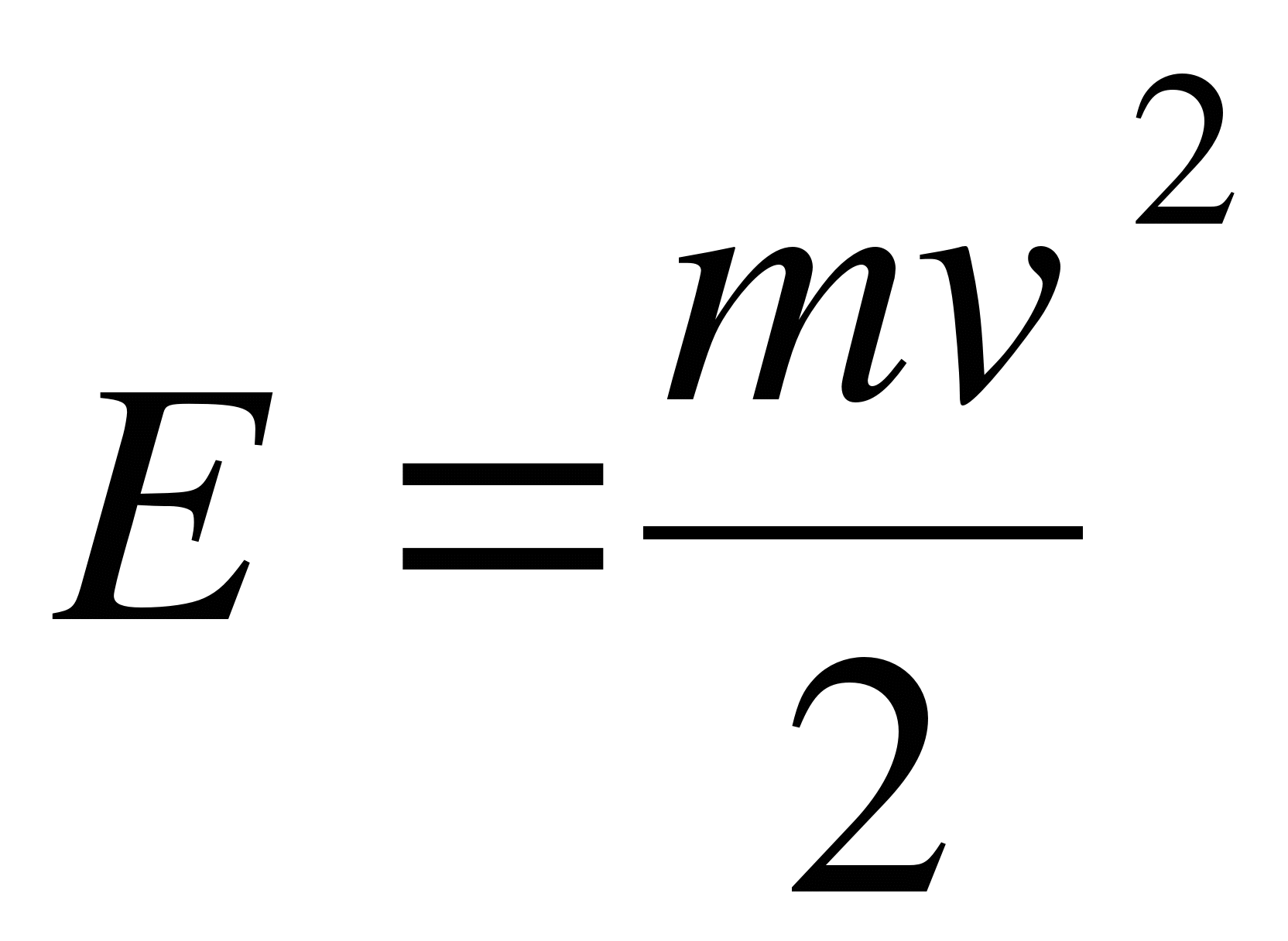Двое грузчиков работают на стройке. Ребята, а какие Вы знаете строительные профессии, кто хочет стать строителем? Вы знаете, что сейчас много грантов и рабочих мест выделено именно строительным специальностям. Посмотрите на рисунок. Ситуация первая – грузчики поднимают кирпичи на второй этаж. Посмотрите на рисунок. Один из них может носить по десятку кирпичей, а другой – только по два кирпича. У какого рабочего больше энергии? Какой рабочий может выполнить большее количество работы? Обратим внимание, что грузчики совершают над кирпичами механическую работу. Говорят, что у толстячка больше 

энергии, так как он способен выполнить больше работы. Тем не менее, даже упитанный персонаж не может работать бесконечно – через некоторое время оба грузчика утомятся. Итак, по мере совершения грузчиками работы их способность совершать новую работу (то есть их энергия) уменьшается. Обобщённо мы скажем: при совершении телом работы его собственная энергия уменьшается. Как вы думаете почему? Это означает, что в их мышцах иссякла энергия. После отдыха (или лучше – после принятия пищи и отдыха) мышцы вновь будут способны совершать работу, так как кровь доставляет питательные вещества, за счёт которых энергия пополняется.

Ситуация вторая. Первобытный человек совершает механическую работу над камнем – поднимает его. В отличие от первой ситуации, в качестве рассматриваемого тела выберем теперь не человека, а камень. То есть теперь работу совершает не само тело, а кто-то над телом. В результате этого энергия тела увеличивается. Теперь камень может, например, упасть и разбить орех, то есть совершить работу, на выполнение которой прежней энергии камня было недостаточно.

Итак, энергия – физическая величина, характеризующая способность тела (или нескольких тел) совершать работу. Поэтому, как и работа энергия измеряется джоулями. Чем больше работы может совершить тело, тем больше его энергия. И наоборот.

Слово «энергия» мы используем очень часто. Так, для работы электродвигателей нужна электрическая энергия. Двигатели автомобилей работают, используя энергию, выделяющуюся при сгорании топлива. Живые организмы (в том числе человек) могут совершать работу, так как используют энергию пищи. При работе гидроэлектростанций используется энергия падающей воды. При совершении механической работы энергия тел обязательно изменяется: у одних тел уменьшается, у других – увеличивается.

Например, при подъёме кирпичей энергия грузчика уменьшается, а энергия кирпичей увеличивается. Это подтверждается тем, что чем выше они подняты, тем большую механическую работу смогут произвести (например, когда упадут, подобно камню на рисунке с орехом). Энергия грузчика уменьшается, так как его способность поднимать новые кирпичи всё меньше.

Рассмотрим два вида механической энергии:

1. Потенциальная энергия (от латинского «потенция» – возможность) – это энергия взаимодействия. Потенциальной энергией, например, обладает тело, поднятое относительно Земли, потому что энергия зависит от взаимного положения его и Земли и их взаимного притяжения. Если считать потенциальную энергию тела, лежащего на Земле равной нулю, то энергия тела, поднятого на какую-то высоту, определяется той работой, которую совершит сила тяжести при падении тела на Землю. Любое тело, поднятое над поверхностью Земли, обладает относительно неё потенциальной энергией. Кроме того, потенциальной энергией обладает натянутая тетива лука, пружина заведенного механизма, т.е. всякое упругое деформированное тело.

Найдем потенциальную энергию тела, поднятого над Землей. Чтобы поднять яблоко надо совершить работу, кроме того на яблоко будит действовать сила тяжести

A = Fтяж h

От чего зависит потенциальная энергия? Таким образом, потенциальная энергия зависит от силы взаимодействия тел и расстояния между ними.

2. Кинетическая энергия(от латинского «кинетикос» – движение) – это энергия движущихся тел. Кинетическая энергия тем больше, чем больше масса тела и скорость его движения.

Таким образом, в общем случае тело обладает одновременно как кинетической, так и потенциальной энергией. Их сумму называют полной механической энергией.

Давайте рассмотрим превращение энергии:

Яблоко свободно падает с дерева. Найдите его кинетическую и потенциальную энергию тела в точках 1, 2 и 3.

Ep переходит в Ek

Укажите превращения одного вида энергии в другой:

1. При бросании мяча вертикально вверх

2. При спуске велосипедиста с горы.

Делаем вывод: Энергия не исчезает и не возникает из ничего, она переходит из одного вида в другой и передаётся от одного тела к другому.

IV. Закрепление нового материала:

Задача

Найдите потенциальную энергию тела массой 3 кг на высоте 6м и 4м от поверхности земли. Сравните их потенциальные энергии.

Сравни кинетические энергии следующих тел:

1. Грузовой и легковой автомобили, движущиеся со скоростью 60 км/ч.

2. Бегущий слон и пуля, вылетевшая из ружья.

3. Два самолета равной массы, летящие с одинаковой скоростью на разных высотах.

4. Автомобиль, обгоняющий другой автомобиль такой же массы.

Тест:

1. Какой энергией обладает растянутая или сжатая пружина?

2. Камень, падающий на землю, непосредственно перед ударом о землю обладает ………энергией.

3. Пружина заведенных часов обладает …….. энергией.

4. Какой энергией относительно земли обладает летящий самолет?

5. От чего зависит потенциальная энергия тела, поднятого над Землей ?

Вопросы:

1. Какие виды энергий существуют?

2. Какую энергию называют потенциальной?

3. По какой формуле можно вычислить потенциальную энергию?

4. От каких величин зависит потенциальная энергия тела?

5. В каком случае потенциальная энергия тела равна нулю?

6. Какую энергию называют кинетической?

7. По какой формуле можно вычислить кинетическую энергию?

8. От каких величин зависит кинетическая энергия тела?

9. Каковы единицы измерения энергии?

10. В каком случае кинетическую энергию тела считают равной нулю?

X. Подведение итогов урока

XI. Домашнее задание: § 68 стр 168 учить, упражнение № 40 (1,2)

Работа, энергия и сила – IB Physics Stuff

2.5.1 Определение работы

Работа – это не энергия, это средство передачи энергии посредством силы, приложенной к движущемуся объекту. Если объект не движется или сила направлена ​​не в направлении движения, то сила не передает энергию объекту, или мы говорим: «Сила не выполняет работу с объектом». Математически мы определяем работу как:

(1)

\ begin {align} W = \ vec F \ bullet s \ end {align}

Или в мире IB:

(2)

\ begin {align} W = Fs \ cos {\ theta} \ end {align}

Где W – работа, F – сила, s – смещение, а θ – угол между силой и смещением.Вторая формула – это формула, которую дает IB, и вы должны ее понять. Первое – это «реальное» уравнение, это векторное скалярное произведение, но его можно упростить до второго уравнения.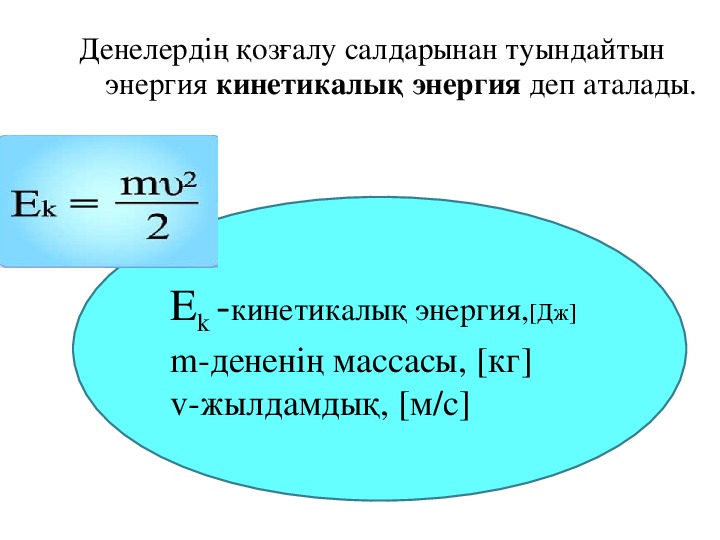

Обратите внимание, что если сила и смещение перпендикулярны, то сила не совершает никакой работы. Если угол равен 180 °, сила выполняет отрицательную работу, примером этого может быть автомобиль, движущийся вперед, в то время как водитель нажимает на тормоза…

2.5.2 Определите работу, совершаемую непостоянной силой, интерпретируя график силы смещения

Приведенное выше уравнение хорошо работает, если сила постоянна, но в большинстве случаев сила непостоянна… Таким образом, мы можем либо выполнить некоторые вычисления, либо посмотреть на график (фактически, все еще выполняя вычисления).

Представьте, что к тележке прилагается сила в том же направлении, что и перемещение. Если сила меняется со временем, и мы строим график зависимости силы от смещения:

В этом случае формулу использовать нельзя, по крайней мере, не просто. Однако площадь под кривой зависимости силы от смещения – это работа, совершаемая на тележке силой.

2.5.4 Определить кинетическую энергию

Если масса m ускоряется силой F от начальной скорости u до конечной скорости v. 2

Это последнее выражение определяется как кинетическая энергия.2 \ end {align}

Первый член справа – это начальная кинетическая энергия, а последний член – конечная кинетическая энергия. Таким образом, работа, выполняемая при ускорении объекта, равна изменению кинетической энергии.

2.5.5 Опишите концепции гравитационной потенциальной энергии и упругой потенциальной энергии

Если объект массы m поднимается вертикально на расстояние h, то работа, выполненная над объектом, составляет:

(9)

\ begin {уравнение} W = Fs \ end {уравнение}

(10)

\ begin {уравнение} W = Fh \ end {уравнение}

Сила, необходимая для подъема объекта:

(11)

\ begin {уравнение} F = мг \ end {уравнение}

Или вес объекта, мы можем описать проделанную работу как:

(12)

\ begin {уравнение} W = mgh \ end {уравнение}

Последнее выражение – это гравитационная потенциальная энергия объекта.Потенциальная энергия – это энергия, которую объект имеет исключительно из-за его положения или конфигурации.

Если объект поднимается с начальной высоты hI до конечной высоты hf. Тогда водоизмещение будет:

(13)

\ begin {уравнение} s = h_f – h_i \ end {уравнение}

А по объекту выполнено работ:

(14)

\ begin {уравнение} W = мг (h_f – h_i) \ end {уравнение}

(15)

\ begin {уравнение} W = mgh_f – mgh_i \ end {уравнение}

Другими словами, работа, выполняемая при поднятии объекта, равна изменению потенциальной энергии.2 \ end {формула}

Это также потенциальная энергия растяжения пружины.

2.5.6 Изложить принцип сохранения энергии

Энергосбережение – это принцип, согласно которому в замкнутой системе энергия не приобретается и не теряется. В открытой системе энергия может добавляться или теряться. Это определение также можно перевернуть. Если система набирает или теряет энергию, то это открытая система. Единственная действительно открытая система во Вселенной, Земля постоянно получает энергию от солнца в течение дня и излучает энергию обратно ночью.

Можно сказать, что полная энергия перед событием равна полной энергии после события или:

(18)

\ begin {формула} Начальная энергия = Конечная энергия \ end {формула}

По кинетической и потенциальной энергии:

(19)

\ begin {уравнение} KE_i + PE_i = KE_f + PE_f \ end {уравнение}

Итак, для закрытой системы падающий шар является хорошим приближением, поскольку по мере падения шара его потенциальная энергия уменьшается, но его кинетическая энергия увеличивается с той же, но противоположной скоростью.

Примечание: потенциальная и кинетическая энергия являются примерами механической энергии, они не единственные типы энергии.

Это видео показывает два пути (или пути) преобразования потенциальной энергии в кинетическую. Начальные потенциальные энергии одинаковы, поскольку оба шара падают с одинаковой высоты. Конечная кинетическая энергия “показана” временем, когда мяч прошел через фотозатвор. Время, необходимое для прохождения фотозатвора, зависит только от скорости и, следовательно, от кинетической энергии. Поскольку два времени одинаковы, две конечные кинетические энергии одинаковы.

2.5.7 Перечислите различные формы энергии и опишите примеры преобразования энергии из одной формы в другую

Украдено из Advanced Physics, Стив Адамс и Джонатан Аллдей

2.5.8 Определить мощность

Мощность – это скорость выполнения работы или скорость передачи энергии.

(20)

\ begin {align} P = {W \ over t} \ end {align}

Единица измерения мощности – Ватты, $ Ватт = {Нм \ over s} $.Это тот же блок, что и у ваших лампочек и электроприборов.

Мы также можем переписать мощность как:

(21)

\ begin {align} P = {Fs \ over t} = Fv \ end {align}

Где F – приложенная сила, s – смещение, t – время, а v – скорость.

2.5.9 Определение и применение концепции эффективности

Когда работа выполняется с объектом, иногда энергия преобразуется в нежелательные или бесполезные формы (часто в тепло). Отношение полезной энергии к количеству приложенной энергии – это КПД, его также можно определить в единицах мощности:

(22)

\ begin {align} КПД \% = {Полезная энергия \ над общей энергией} \ times 100 \% = {Полезная мощность \ над общей мощностью} \ times 100 \% \ end {align}

---

Хотите добавить или прокомментировать эти заметки? Сделайте это ниже.

Формула упругой потенциальной энергии

Формула упругой потенциальной энергии

Упругая потенциальная энергия – это запасенная энергия сжимаемого или растягиваемого объекта, такого как пружина, резинка или молекула. Упругая потенциальная энергия равна силе, умноженной на расстояние перемещения.

Упругая потенциальная энергия = сила x расстояние смещения.

Вт =

фунтов стерлингов

W = упругая потенциальная энергия, в Джоулях

F = сила в Ньютонах

с = водоизмещение, м

Поскольку сила равна постоянной пружины x смещению, тогда упругая потенциальная энергия = постоянная пружины x смещение в квадрате.

F = 1/2 шт.

k = жесткость пружины, Ньютон / м

Таким образом, W = (1/2 ks) с

Вт = 1 / 2кс ² = ПЭ

Вопросы по формуле упругой потенциальной энергии:

1) У вас есть упругая пружина с жесткостью пружины 1,5 x 10 ^-2 Ньютон на метр, и пружина сжимается на 15,0 см. Что такое ПЭ весны?

Жесткость пружины k = 1,5 x 10 ^-2 Ньютон / м и Δs = 15,0 см = 0.15 мес.

PE = 1/2 шт. ²

PE = [1/2 x (1,5 x 10 ^-2 ) Ньютонов / м] (0,15 м) ²

PE = 1,69 x10 ^-4 Ньютон-м =

Дж

2) Вы прикрепляете к доске пружину закона Гука и растягиваете пружину на 99 см за 3 J. Какое значение жесткости пружины?

Мы знаем, что W = 3 Дж и s = 99 см = 0,99 м. Исходя из этого, определите k, жесткость пружины.

W = [1/2 k] с ²

1/2 k = Вт / с ²

k = Вт / (1/2 с ² )

k = (3J / [0.5 x 0,99 м ² ])

k = 3J / 0,49 м ²

k = 3 Н / м / 0,49 м ²

k = 6,122 Н / м

Связанные темы
Потенциальная энергия: формула упругости
Факты о потенциальной энергии
Примеры потенциальной энергии
Формула электрической потенциальной энергии
Потенциальная энергия и сохранение энергии
Формулы: физические формулы и математические формулы
Формула сохранения энергии
Физические формулы
Физические формулы
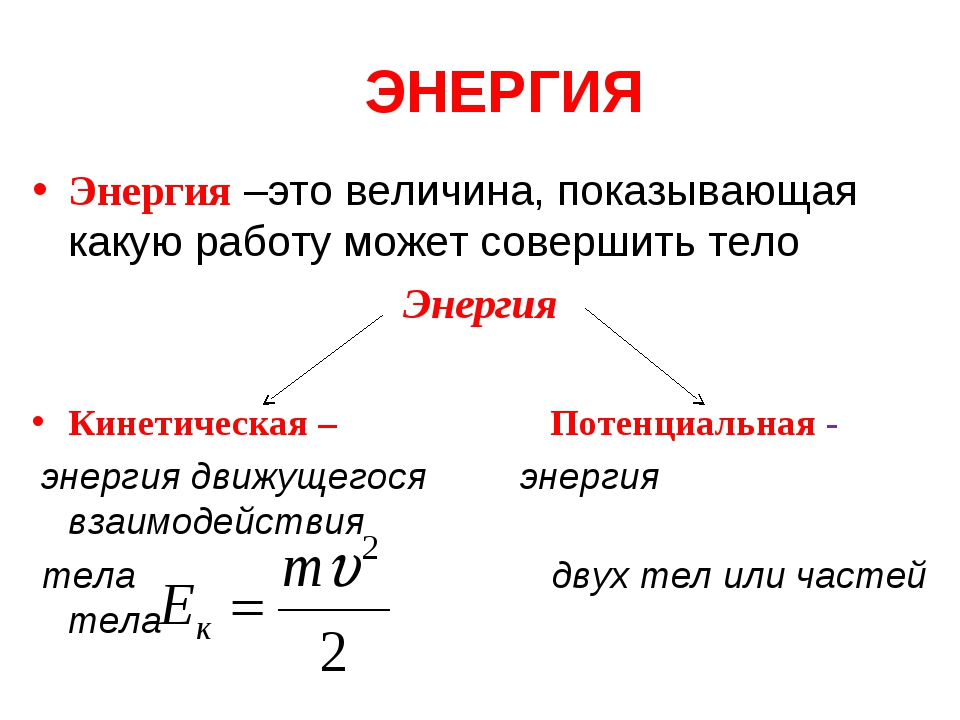
. {2} \]

\ [KE = \ frac {1} {2} \ times 30 \ times 16 \]

\ [KE = 240 \\ J \]

Расчет гравитационной потенциальной энергии

количество гравитационной потенциальной энергии, запасенной объектом на высоте, можно рассчитать с помощью уравнения:

изменение гравитационной потенциальной энергии = масса × напряженность гравитационного поля × изменение вертикальной высоты

\ [∆GPE = m \ times g \ times ∆ h \]

Это когда:

• изменение гравитационной потенциальной энергии ( 1ww8rc37hr8.0.0.0.1:0.1.0.$0.$4.$5.$0.$1″> ∆GPE ) измеряется в джоулях (Дж)
• масса ( м ) измеряется в килограммах (кг)
• напряженность гравитационного поля ( м ) измеряется в ньютонах на килограмм (Н / кг)
• Изменение вертикальной высоты (∆ℎ) измеряется в метрах (м)

Пример

Галилео поднимает 5-килограммовое пушечное ядро ​​на вершину Пизанская башня для одного из его экспериментов.Высота башни 56 метров. Сколько гравитационной потенциальной энергии накопило пушечное ядро? (г = 10 Н / кг)

$2″> \ [∆GPE = m \ times g \ times ∆h \]

\ [∆GPE = 5 \ times 10 \ times 56 \]

\ [∆GPE = 2,800 \ \ J \]

Вопрос

Сколько гравитационной потенциальной энергии приобретает книга весом 500 г, когда ее поднимают на полку на 1,5 м?

Показать ответ

\ [∆GPE = m \ times g \ times ∆h \]

\ [∆GPE = 0,5 \ times 10 \ times 1.5 \]

\ [∆GPE = 7,5 \\ J \]

1ww8rc37hr8.0.0.0.1:0.1.0.$0.$6.$1″> Для любого из этих уравнений может потребоваться изменить тему формулы.

Формула механической энергии – Уравнение

Формула механической энергии

В физике механическая энергия (E _mech ) – это энергия, связанная с движением и положением объекта, обычно в некотором силовом поле (например, гравитационное поле). Механическая энергия (а также тепловая энергия) может быть разделена на две категории: переходная и накопленная.Переходная энергия – это энергия в движении, то есть энергия, передаваемая из одного места в другое. Сохраненная энергия – это энергия, содержащаяся в веществе или объекте. Переходная механическая энергия обычно обозначается как , работа . Сохраненная механическая энергия существует в одной из двух форм: кинетическая или потенциальная :

• Потенциальная энергия . Потенциальная энергия U определяется как энергия, запасенная в объекте, подверженном действию консервативной силы. Общие типы включают гравитационную потенциальную энергию объекта, которая зависит от его массы и расстояния от центра масс другого объекта.
• Кинетическая энергия . Кинетическая энергия, K , определяется как энергия, запасенная в объекте из-за его движения. Это зависит от скорости объекта и способности движущегося объекта работать с другими объектами при столкновении с ними.

См. Также: Сохранение механической энергии

Изолированная система – это система, в которой никакая внешняя сила не вызывает изменения энергии. Если на объект действуют только консервативных сил и U является функцией потенциальной энергии для общей консервативной силы, то

E _мех = U + K

потенциальная энергия, U , зависит от положения объекта, на который действует консервативная сила.

Определяется как способность объекта выполнять работу и увеличивается по мере того, как объект перемещается в направлении, противоположном направлению силы.

Потенциальная энергия , связанная с системой, состоящей из Земли и ближайшей частицы, равна гравитационной потенциальной энергии .

Кинетическая энергия, K , зависит от скорости объекта и представляет собой способность движущегося объекта выполнять работу с другими объектами при столкновении с ними.

K = ½ mv ²

Вышеупомянутое определение ( E _mech = U + K ) предполагает, что система свободна от трения и других non- консервативные силы . Разница между консервативной и неконсервативной силой состоит в том, что когда консервативная сила перемещает объект из одной точки в другую, работа, выполняемая консервативной силой, не зависит от пути.

8.3 Сохранение энергии – Университетская физика, том 1

Цели обучения

К концу этого раздела вы сможете:

• Сформулируйте принцип сохранения механической энергии с наличием или без наличия неконсервативных сил
• Использование принципа сохранения механической энергии для расчета различных свойств простых систем

В этом разделе мы разрабатываем и расширяем результат, который мы получили в статье «Потенциальная энергия системы», где мы переписали теорему о работе-энергии в терминах изменения кинетической и потенциальной энергий частицы.Это приведет нас к обсуждению важного принципа сохранения механической энергии. По мере того, как вы продолжаете изучать другие темы физики, в последующих главах этой книги вы увидите, как этот закон сохранения обобщается на другие типы энергии и передачи энергии. В последнем разделе этой главы представлен предварительный просмотр.

Термины «сохраняемая величина» и «закон сохранения» имеют в физике специфические научные значения, которые отличаются от повседневных значений, связанных с использованием этих слов. (То же самое относится и к научному и повседневному использованию слова «работа».) В повседневном использовании вы можете сэкономить воду, не используя ее, или используя меньше, или повторно используя ее. Вода состоит из молекул, состоящих из двух атомов водорода и одного атома кислорода. Соедините эти атомы вместе, чтобы сформировать молекулу, и вы создадите воду; диссоциируйте атомы в такой молекуле, и вы разрушите воду. Однако в научном использовании сохраненное количество для системы остается постоянным, изменяется на определенную величину, которая передается в другие системы и / или преобразуется в другие формы этого количества.Сохраняемое количество в научном смысле может быть преобразовано, но не может быть создано или уничтожено строго. Таким образом, нет физического закона сохранения воды.

Системы с одной частицей или объектом

Сначала рассмотрим систему с одной частицей или объектом. Возвращаясь к нашему развитию (рисунок), напомним, что мы сначала разделили все силы, действующие на частицу, на консервативные и неконсервативные типы, и записали работу, выполняемую каждым типом силы, как отдельный член в теореме работы-энергии. Затем мы заменили работу, выполняемую консервативными силами, изменением потенциальной энергии частицы, объединив ее с изменением кинетической энергии частицы, чтобы получить (рисунок). Теперь мы запишем это уравнение без среднего шага и определим сумму кинетической и потенциальной энергий,

– это механическая энергия частицы.

Сохранение энергии

Механическая энергия E частицы остается постоянной, если на нее не действуют силы вне системы или неконсервативные силы; в этом случае изменение механической энергии равно работе, совершаемой неконсервативными силами:

Это утверждение выражает концепцию сохранения энергии для классической частицы до тех пор, пока нет неконсервативной работы.Напомним, что классическая частица – это просто точечная масса, она нерелятивистская и подчиняется законам движения Ньютона. В теории относительности мы увидим, что закон сохранения энергии все еще применяется к неклассической частице, но для того, чтобы это произошло, мы должны внести небольшую поправку в определение энергии.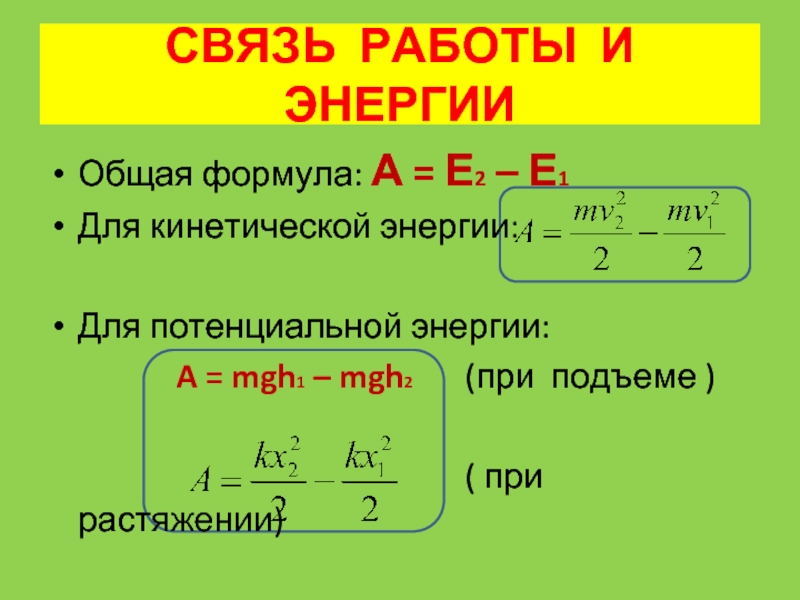

Иногда удобно выделить случай, когда работа, выполняемая неконсервативными силами, равна нулю, либо потому, что такие силы не предполагаются присутствующими, либо, как и нормальная сила, они не выполняют нулевую работу, когда движение параллельно поверхности.Тогда

В этом случае сохранение механической энергии можно выразить следующим образом: механическая энергия частицы не изменяется, если все неконсервативные силы, которые могут на нее действовать, не действуют. Важно понимать концепцию энергосбережения, а не конкретное уравнение, которое вы используете для ее выражения.

Стратегия решения проблем: сохранение энергии

1. Укажите тело или тела, которые необходимо изучить (систему).Часто, применяя принцип сохранения механической энергии, мы изучаем более одного тела одновременно.
2. Определите все силы, действующие на тело или тела.
3. Определите, является ли каждая действующая сила консервативной. Если неконсервативная сила (например, трение) выполняет работу, то механическая энергия не сохраняется. Затем система должна быть проанализирована неконсервативной работой (рисунок).
4. Для каждой действующей силы выберите точку отсчета и определите функцию потенциальной энергии для силы.Контрольные точки для различных потенциальных энергий не обязательно должны находиться в одном и том же месте.
5. Примените принцип сохранения механической энергии, установив сумму кинетической энергии и потенциальной энергии равной в каждой точке интереса.

Пример

Простой маятник

Частица массой м. подвешена к потолку на безмассовой веревке длиной 1,0 м, как показано на (Рисунок). Частица выходит из состояния покоя, когда угол между струной и вертикальным направлением вниз составляет

.

Какова его скорость, когда он достигает самой нижней точки своей дуги?

Рисунок 8.7 Частица, подвешенная на веревке, представляет собой простой маятник. Он отображается после выхода из состояния покоя вместе с некоторыми расстояниями, используемыми для анализа движения.

Стратегия

Используя нашу стратегию решения проблем, первый шаг – определить, что нас интересует система частица-Земля. Во-вторых, на частицу действует только гравитационная сила, что является консервативным (шаг 3). Мы пренебрегаем сопротивлением воздуха в задаче, и натяжение струны, перпендикулярное дуге движения, не выполняет никакой работы.Следовательно, механическая энергия системы сохраняется, как показано (рисунок),

. Поскольку частица стартует из состояния покоя, увеличение кинетической энергии – это просто кинетическая энергия в самой низкой точке. Это увеличение кинетической энергии равно уменьшению гравитационной потенциальной энергии, которую мы можем вычислить из геометрии. На шаге 4 мы выбираем точку отсчета для нулевой гравитационной потенциальной энергии, которая должна находиться в самой низкой вертикальной точке, которую достигает частица, то есть в середине колебания.Наконец, на шаге 5 мы устанавливаем сумму энергий от наивысшей точки (начальной) поворота до самой низкой (конечной) точки поворота, чтобы в конечном итоге определить конечную скорость.

Решение

Мы пренебрегаем неконсервативными силами, поэтому запишем формулу сохранения энергии, связывающую частицу в наивысшей точке (начальной) и самой низкой точке колебания (конечная точка) как

Поскольку частица выходит из состояния покоя, начальная кинетическая энергия равна нулю.В самой нижней точке мы определяем гравитационную потенциальную энергию равной нулю. Следовательно, наша формула сохранения энергии сводится к

.

Вертикальная высота частицы прямо в задаче не указывается. Это можно решить, используя тригонометрию и два заданных значения: длину маятника и угол, под которым частица поднимается вверх по вертикали. На диаграмме вертикальная пунктирная линия обозначает длину струны маятника. Высота по вертикали обозначена h .Другая частичная длина вертикальной струны может быть рассчитана с помощью тригонометрии. Эта часть решена на

Следовательно, глядя на две части строки, мы можем найти высоту h ,

Мы подставляем эту высоту в предыдущее выражение для скорости, чтобы вычислить наш результат:

Значение

Мы нашли скорость непосредственно из закона сохранения механической энергии, без необходимости решать дифференциальное уравнение движения маятника (см. Колебания).Мы можем подойти к этой проблеме с точки зрения гистограмм полной энергии . Первоначально частица имеет всю потенциальную энергию, находясь в наивысшей точке, и не имеет кинетической энергии. Когда частица пересекает самую низкую точку в нижней части качелей, энергия перемещается из столбца потенциальной энергии в столбец кинетической энергии. Следовательно, мы можем вообразить прогрессию этого переноса, когда частица перемещается между своей наивысшей точкой, самой низкой точкой поворота и обратно к самой высокой точке ((Рисунок)).По мере того, как частица перемещается от самой низкой точки колебания к самой высокой точке в дальнем правом углу диаграммы, столбики энергии меняются в обратном порядке от (c) до (b) до (a).

Рис. 8.8 Гистограммы, представляющие полную энергию (E), потенциальную энергию (U) и кинетическую энергию (K) частицы в различных положениях. (а) Полная энергия системы равна потенциальной энергии, а кинетическая энергия равна нулю и находится в наивысшей точке, которой достигает частица. (b) Частица находится на полпути между самой высокой и самой низкой точкой, поэтому столбиковые диаграммы кинетической энергии плюс потенциальной энергии равны полной энергии.(c) Частица находится в самой низкой точке поворота, поэтому столбик кинетической энергии является самым высоким и равен полной энергии системы.

Проверьте свое понимание

Насколько высоко над дном его дуги находится частица в простом маятнике наверху, когда его скорость равна

[show-answer q = ”fs-id1165036877134 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1165036877134 ″]

[/ hidden-answer]

Пример

Сопротивление воздуха падающему объекту

Вертолет парит на высоте

, когда панель с нижней стороны вырывается и падает на землю ((Рисунок)).Масса панели

, и он ударяется о землю со скоростью

. Сколько механической энергии было рассеяно сопротивлением воздуха во время спуска панели?

Рис. 8.9 Вертолет теряет панель, которая падает, пока не достигает предельной скорости 45 м / с. Насколько сопротивление воздуха способствовало рассеянию энергии в этой задаче?

Стратегия

Шаг 1: Здесь исследуется только одно тело.

Шаг 2: На панель действует сила тяжести и сопротивление воздуха, указанное в задаче.

Шаг 3: Сила тяготения консервативна; однако неконсервативная сила сопротивления воздуха оказывает негативное воздействие на падающую панель, поэтому мы можем использовать закон сохранения механической энергии в форме (рисунок), чтобы найти рассеиваемую энергию. Эта энергия и есть величина работы:

Шаг 4: Начальная кинетическая энергия на

равно нулю.Для удобства мы установили нулевую гравитационную потенциальную энергию на уровне земли.

Шаг 5: Неконсервативная работа устанавливается равной энергии, которую необходимо решить для работы, рассеиваемой сопротивлением воздуха.

Решение

Механическая энергия, рассеиваемая сопротивлением воздуха, представляет собой алгебраическую сумму увеличения кинетической энергии и потери потенциальной энергии. Следовательно, расчет этой энергии равен

.

Значение

Большая часть начальной механической энергии панели

, 147 кДж, было потеряно из-за сопротивления воздуха.Обратите внимание, что мы смогли вычислить рассеиваемую энергию, не зная, какова сила сопротивления воздуха, только то, что она была рассеивающей.

Проверьте свое понимание

Вы, наверное, помните, что если пренебречь сопротивлением воздуха, если вы бросите снаряд прямо вверх, время, необходимое для достижения его максимальной высоты, равно времени, необходимому для падения с максимальной высоты обратно на стартовую высоту. Предположим, вы не можете пренебречь сопротивлением воздуха, как на (Рисунок). Время, необходимое снаряду, чтобы взлететь, (а) больше, (б) меньше, или (в), равно времени, необходимому для возврата снаряда? Объяснять.

[показывать-ответ q = ”fs-id1165036750131 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165036750131 ″]

г.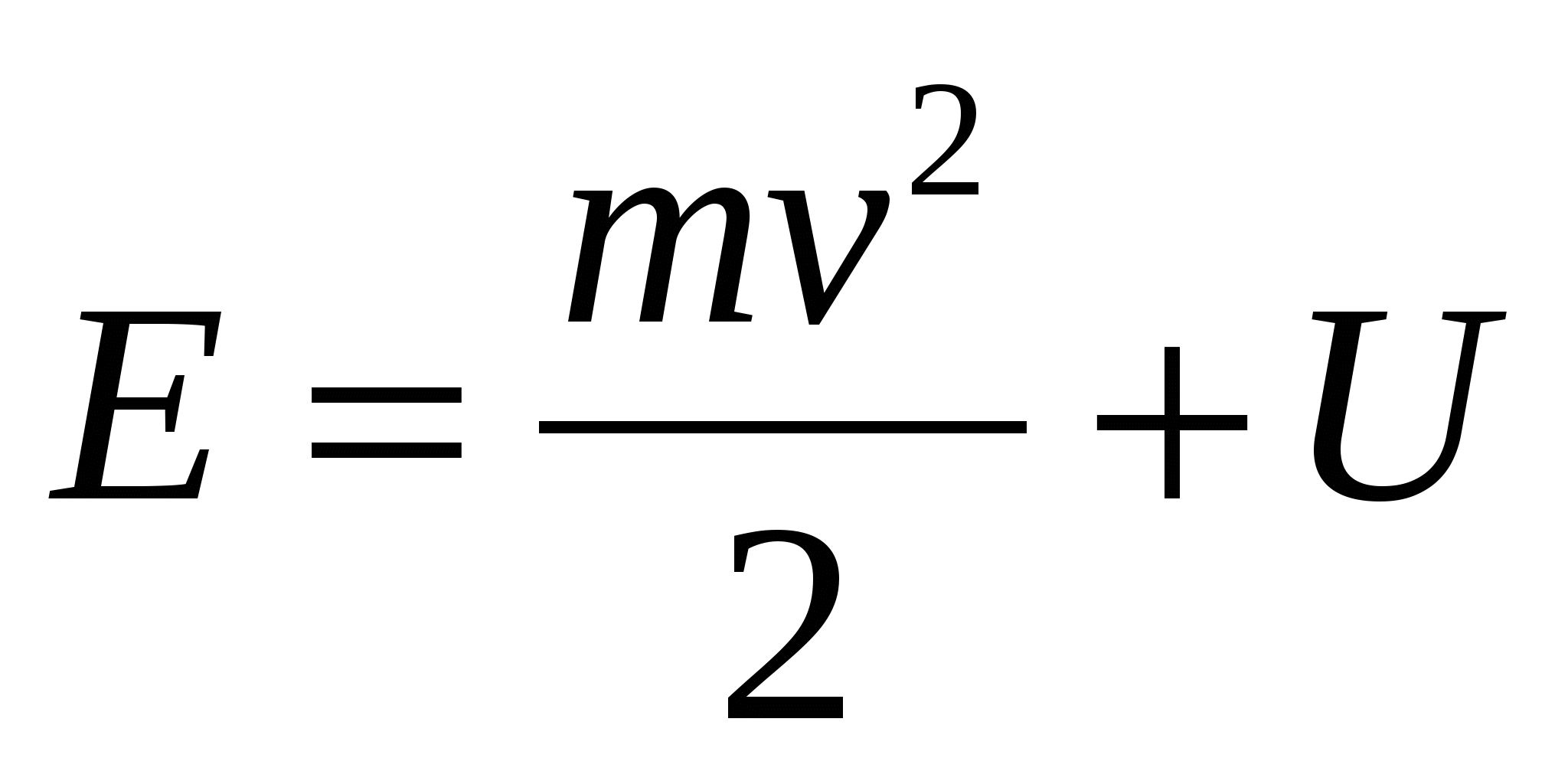 На любой заданной высоте гравитационная потенциальная энергия одинакова при движении вверх или вниз, но кинетическая энергия меньше понижается, чем поднимается, поскольку сопротивление воздуха является диссипативным и выполняет отрицательную работу. Следовательно, на любой высоте скорость на спуске меньше, чем на подъеме, поэтому для спуска требуется больше времени, чем для подъема.

[/ hidden-answer]

В этих примерах мы смогли использовать закон сохранения энергии для вычисления скорости частицы только в определенных точках ее движения.Но метод анализа движения частиц, начиная с сохранения энергии, более мощный, чем это. Более продвинутые подходы к теории механики позволяют рассчитать полную временную зависимость движения частицы для заданной потенциальной энергии. Фактически, часто бывает, что лучшая модель движения частицы обеспечивается формой ее кинетической и потенциальной энергии, а не уравнением силы, действующей на нее. (Это особенно верно для квантово-механического описания частиц, таких как электроны или атомы. )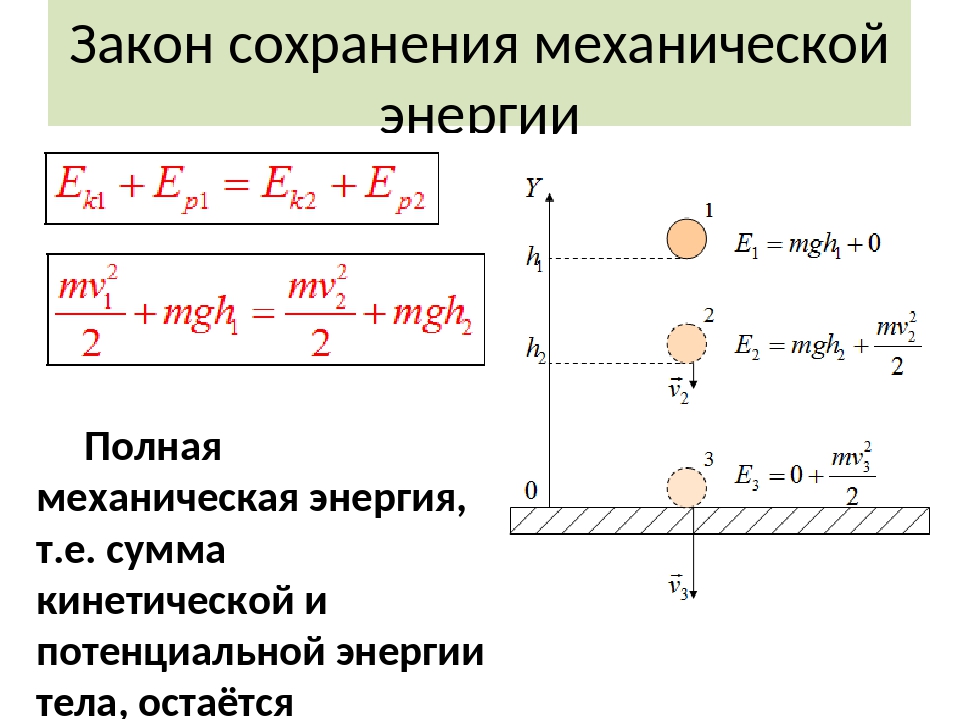

Мы можем проиллюстрировать некоторые из простейших особенностей этого основанного на энергии подхода, рассматривая частицу в одномерном движении с потенциальной энергией U ( x ) и отсутствием неконсервативных взаимодействий. (Рисунок) и определение скорости требуют

Разделить переменные x и t и интегрировать, начиная с начального времени

к произвольному времени, чтобы получить

Если вы можете выполнить интеграл на (Рисунок), то вы можете найти x как функцию от t .

Пример

Постоянное ускорение

Используйте потенциальную энергию

для

на (рисунок), чтобы найти положение частицы x как функцию времени t .

Стратегия

Поскольку мы знаем, как изменяется потенциальная энергия в зависимости от x , мы можем заменить

на (рисунок), проинтегрируйте, а затем решите для x . Это приводит к выражению x как функции времени с константами энергии E , массы m и начального положения

Решение

Следуя первым двум предложенным шагам в приведенной выше стратегии,

Решая позицию, получаем

.

Значение

Положение как функция времени для этого потенциала представляет одномерное движение с постоянным ускорением,

запуск в состоянии покоя из положения

Это не так уж удивительно, поскольку это потенциальная энергия для постоянной силы,

и

Проверьте свое понимание

Какая потенциальная энергия

Можете ли вы заменить на (Рисунок), что приведет к движению с постоянной скоростью 2 м / с частицу массой 1 кг и механической энергией 1 Дж?

[показывать-ответ q = ”fs-id1165037977079 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165037977079 ″]

постоянная

[/ hidden-answer]

Мы рассмотрим другой, более физически подходящий пример использования (Рисунок) после того, как изучим некоторые дальнейшие выводы, которые можно извлечь из функциональной формы потенциальной энергии частицы.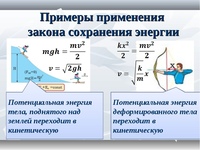

8. СОХРАНЕНИЕ ЭНЕРГИИ

8. СОХРАНЕНИЕ ЭНЕРГИИ

---

В этой главе мы обсудим сохранение энергии. Законы сохранения в физике можно выразить в очень простой форме:

«Рассмотрим систему частиц, полностью изолированную от внешнего воздействия. Поскольку частицы движутся и взаимодействуют друг с другом, возникают определенные свойства системы, которые не меняются “

Вкратце мы можем выразить это как

X = константа

в котором X – сохраняющееся свойство.

Масса, свисающая с потолка, будет иметь кинетическую энергию, равную нулю. Если шнур рвется, масса быстро увеличивает свою кинетическую энергию. Этот кинетическая энергия каким-то образом накапливалась в массе, когда она висела на потолок: энергия была скрыта, но может снова появиться в виде кинетической энергия. Накопленная энергия называется потенциальной энергией . Сохранение энергия говорит нам, что полная энергия системы сохраняется , а в в этом случае сумма кинетической и потенциальной энергии должна быть постоянной.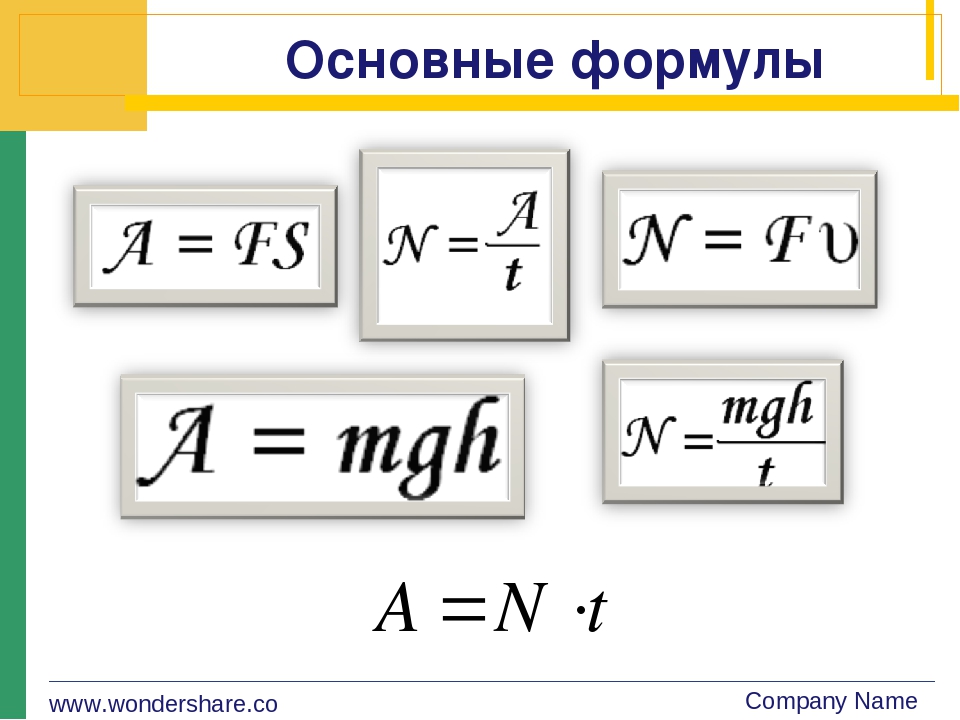 Этот означает, что каждое изменение кинетической энергии системы должно быть с равным, но противоположным изменением потенциальной энергии :

[Дельта] U + [Дельта] K = 0

и

E = U + K = постоянная

Теорема работы-энергии, обсуждаемая в главе 7, связывает количество работа W на изменение кинетической энергии системы

W = [Delta] K

Изменение потенциальной энергии системы теперь можно связать с объем работы, проделанной в системе

[Delta] U = – [Delta] K = – W

что будет определением потенциальной энергии.Единица потенциальная энергия – Джоуль (Дж).

Потенциальная энергия U может быть получена из приложенной силы F

и

где U (x ₀ ) – потенциальная энергия системы на ее выбранная эталонная конфигурация. Получается, что меняется только в потенциальная энергия важна , и мы можем присвоить произвольную нулевое значение потенциальной энергии системы, когда она находится в эталонном состоянии. конфигурация .

Иногда функция потенциальной энергии U (x) известна. Сила ответственный за этот потенциал может быть получен

Мы продолжим обсуждение некоторых примеров сохранения энергия.

8.2.1. Пружина усилие

Силу, прилагаемую пружиной к массе m, можно рассчитать с помощью Закон Гука

F (x) = – k x

где k – жесткость пружины, а x – величина, на которую пружина растягивается (x> 0) или сжимается (x <0).Когда движущийся объект впадает в расслабленную пружину, она замедляется, на мгновение останавливается, прежде чем ускорение в направлении, противоположном его первоначальному направлению (см. рис. 8.1). Пока объект замедляется, он сжимает пружину. Как пружина сжимается, кинетическая энергия блока постепенно передается к источнику, где он хранится как потенциальная энергия. Потенциальная энергия пружина в расслабленном положении считается нулевой. Потенциальная энергия пружины в любом другом состоянии можно получить из закона Гука

Предположим, что полная энергия системы шарик-пружина равна E. Сохранение энергии сообщает нам

Обратите внимание, что объем работы, выполняемой пружиной на блоке после нее возвращается в исходное положение – ноль.

Рисунок 8.1. Преобразование кинетической энергии в потенциальную и наоборот.

Пример задачи 8-4

Пружина пружинного пистолета сжимается на расстояние d от своего расслабленного состояния. А мяч, если в ствол вложена масса m.С какой скоростью мяч покинет ствол после выстрела?

Предположим, что E _i – это механическая энергия системы, когда пружина сжат. Поскольку система изначально находится в состоянии покоя, полная энергия равна потенциальная энергия сжатой пружины:

В тот момент, когда шар покидает ствол, пружина находится в своем положении. расслабленное положение, и его потенциальная энергия равна нулю. Полная энергия при этом точка – это просто кинетическая энергия движущейся массы:

Для сохранения энергии требуется, чтобы E _i = E _f . Это означает

Теперь мы можем вычислить скорость мяча

Пример задачи 1

Предположим, что шар на рисунке 8.1 имеет начальную скорость v ₀ . и масса m. Если жесткость пружины равна k, то каково максимальное сжатие весна ?

В исходной ситуации пружина находится в расслабленном положении (U = 0).В полная энергия системы шарик-пружина равна

Максимальное сжатие пружины произойдет, когда шар находится в отдыхать. В этот момент кинетическая энергия системы равна нулю (K = 0) и общая энергия системы равна

Сохранение энергии говорит нам, что E _i = E _f , и таким образом

и

8.2.2. Гравитационная сила

Шар, движущийся вверх в гравитационном поле Земли потеряет кинетическую энергию и на мгновение остановится в своей наивысшей точке. Затем мяч меняет направление, постепенно восстанавливая свою кинетическую энергию. что было потеряно на пути вверх. Когда мяч достигает начальной точки, он будет иметь кинетическую энергию, равную его начальной кинетической энергии. Проделанная работа сила тяжести на шаре отрицательна при движении вверх пока он идет вниз.Работа, выполненная, когда мяч возвращается в его исходное положение равно нулю.

Потенциальная энергия за счет силы тяжести может быть вычислена

где потенциальная энергия при y = 0 определена равной нулю. Сохранение энергии для системы земля-шар теперь показывает

Это уравнение справедливо также для шара, движущегося в двух или трех измерениях. Поскольку F _g перпендикулярно горизонтальному направлению, работа проделана эта сила на шаре равна нулю для смещения по оси x и / или z-направление.При расчете изменения гравитационного потенциала энергии объекта, необходимо только смещение в вертикальном направлении. быть на рассмотрении.

Пример задачи 8-3

Ребенок с массой m выходит из состояния покоя на вершине изогнутой водной горки, высота h над уровнем бассейна. Какая скорость у ребенка при она проецируется в бассейн? Предположим, что ползун не имеет трения.

Начальная энергия состоит только из потенциальной энергии (так как ребенок находится на в остальном кинетическая энергия равна нулю)

E _i = m g h

где мы приняли потенциальную энергию на уровне бассейна равной нулю.В внизу слайда потенциальная энергия равна нулю, а конечная энергия состоит только из кинетической энергии

Для сохранения энергии необходимо, чтобы

E _i = E _f

Таким образом

или

8.2.3. Сила трения

Блок массы m, спроецированный на шероховатую поверхность, будет остановлено кинетической силой трения. Нет возможности вернуть первоначальная кинетическая энергия блока после того, как сила трения довела его до отдыхать. Направленное крупномасштабное движение блока преобразовано в кинетическая энергия беспорядочно направленных движущихся атомов, составляющих блок, и самолет. Мы не можем связать потенциальную энергию с силой трения.

Если потенциальная энергия может быть связана с силой, мы называем силу консервативный .Примерами консервативных сил являются сила пружины и гравитационная сила. Если потенциальная энергия не может быть связана с силу, мы называем эту силу неконсервативной . Пример – трение сила. Альтернативные тесты консервативного характера силы:

1. Сила консервативна, если работа, которую она совершает с частицей, которая движется через поездка туда и обратно равна нулю; в противном случае сила неконсервативна. В Требование нулевой работы для поездки туда и обратно не выполняется за счет силы трения.

2. Сила консервативна, если работа, совершаемая ею над движущейся частицей между двумя точками одинаков для всех путей, соединяющих эти точки; в противном случае это неконсервативно.

Тест 1 и тест 2 эквивалентны. Например, предположим, что работа, проделанная для путь туда и обратно от A до B и обратно до A (см. рисунок 8.2) равен нулю. Это означает что

Рисунок 8.2. Частица в пути туда и обратно из А в Б обратно в А и из А в пункт B двумя разными маршрутами.

W _{AB, 1} + W _{BA, 2} = 0

или

W _{AB, 1} = – W _{BA, 2}

Работа, выполняемая силой на каждом сегменте, меняет знак, если мы вернемся направление

W _{AB, 2} = – W _{BA, 2}

Это соотношение можно использовать, чтобы показать, что

W _{AB, 1} = W _{AB, 2}

это именно то, что утверждает тест 2 (работа, выполняемая силой на объект зависит только от начальной и конечной позиции объекта, а не от выбранный путь).

На рис. 8.3 показаны две возможные траектории, чтобы добраться из пункта А в пункт Б. работа, совершаемая на объекте силой тяжести для траектории 1 и для траектория 2? Произведенная работа при перемещении массы по маршруту 1 равна

.

Альтернативный маршрут (маршрут 2) состоит из движения по горизонтали. направление, за которым следует один в вертикальном направлении. Для любого движения в В горизонтальной плоскости сила тяжести перпендикулярна смещению.Таким образом, работа, совершаемая гравитационной силой, равна нулю. Для движения по вертикали движению противостоит сила тяжести. Работа под действием силы тяжести

Рисунок 8.3. Две возможные траектории из пункта А в пункт Б.

Суммарная работа, совершаемая гравитационной силой над объектом, когда он перемещен из A в B по маршруту 2, поэтому

что равно W ₁ .

График потенциальной энергии как функции координаты x говорит нам о многом. о движении объекта (см., например, рис. 8.12 в книге Халлидея, Резник и Уокер). Дифференцируя U (x), мы можем получить силу, действующую на объект

В отсутствие трения сохраняется сохранение механической энергии. и

U (x) + K = E

Поскольку кинетическая энергия не может быть отрицательной, частица может быть только в тех регионах, для которых E – U равно нулю или положительно.Точки, в которых E – U = K = 0 называются поворотными точками. Кривая потенциальной энергии (Рисунок 8.12 у Холлидея, Резника и Уолкера) показывает несколько локальных максимумов и минимумы. Сила в каждом из этих максимумов и минимумов равна нулю. Точка – это положение устойчивого равновесия, если потенциальная энергия при этом имеет минимум точки (в этом случае небольшие смещения в любом направлении приведут к сила, которая толкает частицу обратно в положение стабильной равновесие).Точки неустойчивого равновесия проявляются как максимумы в потенциале кривая энергии (если частица немного смещена от положения неустойчивое равновесие, силы, действующие на него, будут стремиться толкать частицу еще дальше).

Если мы посмотрим на систему блок-пружина, колеблющуюся на шероховатой поверхности, мы видим, что амплитуда движения непрерывно уменьшается. Из-за сила трения, механическая энергия больше не сохраняется.Если мы посмотрим на система, на которую действуют несколько консервативных сил, помимо трения сила. Всего по системе проделано

что равно изменению кинетической энергии системы (теорема работы-энергии). Каждую консервативную силу можно отождествить с потенциальная энергия и

Теперь мы можем переписать выражение для изменения кинетической энергии системы

Работа, совершаемая силой трения, равна изменению механическая энергия системы.

При наличии неконсервативных сил механическая энергия преобразуется во внутреннюю энергию U _int (или тепловую энергию):

[Delta] U _int = – W _f

При таком определении внутренней энергии работа-энергия теорему можно переписать как

что является законом сохранения энергии. Прописью

“Энергия может быть преобразована из одного вида в другой в изолированной системе. но его нельзя создать или уничтожить; полная энергия системы всегда остается постоянным.”

Пример задачи 8-8

Шарикоподшипник массой m запускается вертикально вниз с высоты h. с начальной скоростью v ₀ (см. рисунок 8.4). Он зарывается в песок на глубине d. Какая средняя восходящая сила сопротивления f действует на песок воздействовать на мяч, когда дело касается отдыха?

Рисунок 8.4. Пример задачи 5.

Работа, совершаемая силой трения f, определяется по формуле

.

Начальная механическая энергия системы равна

.

Конечная механическая энергия системы состоит только из потенциальная энергия (K _f = 0)

E _f = U _f = m g (- d) = – m g d

Изменение механической энергии

которая должна быть равна работе, совершаемой на подшипнике фрикционным сила

Теперь можно рассчитать силу трения f

Пример задачи 2

Блок массой m запускается по наклонной плоскости (см. Рис. 8.5) с начальной скоростью v ₀ . Он проходит расстояние d вверх по плоскости, на мгновение останавливается, а затем скользит обратно в нижнюю часть самолет. Какова величина кинетической силы трения, действующей на блок, пока он движется? Какая будет скорость, когда блок возвращается в исходное положение.

Работа, совершаемая силой трения, равна изменению механической энергия системы. Потенциальная энергия в начале координат принимается равной нулю.Следовательно, начальная механическая энергия системы – это просто кинетическая энергия. энергия блока

Рисунок 8.5. Пример задачи 2.

Конечная механическая энергия (на максимальной высоте) – это всего лишь потенциальная энергия блока на высоте h:

E _f = m g h = m g d sin ([theta])

Изменение механической энергии

Работа, совершаемая на блоке силой трения, составляет

W _f = – f d

и должен быть равен [Delta] E. Таким образом

Теперь можно получить силу трения f

Когда блок возвращается в исходное положение, сила трения снова действует. работа на блоке. Суммарная работа силы трения на блоке равна сейчас

W _f = – 2 f d

Это должно быть равно изменению механической энергии системы. Когда блок возвращается в начало координат, его потенциал не меняется. энергия.Изменение механической энергии системы происходит из-за изменения в скорости блока:

Теперь можно рассчитать конечную скорость блока

---

Отправляйте комментарии, вопросы и / или предложения по электронной почте на адрес [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса.

Энергия от силы тяжести падающих предметов, Рон Куртус

SfC Home> Физика> Гравитация>

Рона Куртуса

Объект, удерживаемый на заданной высоте над землей, имеет начальную потенциальную энергию ( PE ) в соответствии с его массой и начальной высотой.

Когда объект отпускается, его скорость увеличивается при падении. Это увеличение скорости приводит к увеличению кинетической энергии объекта ( KE ). Но это также приводит к снижению PE .

Из-за Закона сохранения энергии полная энергия ( TE ) объекта остается постоянной. Это позволяет рассчитать скорость объекта в любой момент его падения.

Вопросы, которые могут у вас возникнуть:

• Какова потенциальная энергия падающего предмета?
• Какова его кинетическая энергия?
• Какова полная энергия и конечная скорость падающего объекта?

Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц

---

---

Потенциальная энергия объекта

Потенциальная энергия объекта на некоторой высоте относительно силы тяжести:

PE = mgh

где

• PE – начальная потенциальная энергия в джоулях (Дж) или фут-фунтах (фут-фунтах)
• м – масса объекта в кг-масса или фунт-масса
• g – ускорение свободного падения (9. 8 м / с ² или 32 фут / с ² )
• h – высота над землей в м или футах

Примечание : Возможная энергия также иногда сокращается как U .

Когда объект достигает земли, h = 0 и, таким образом, конечная потенциальная энергия равна:

PE _f = 0

Примечание : На самом деле гравитационная сила все еще действует на объект на поверхности Земли, поэтому объект имеет гравитационную потенциальную энергию в этой точке.Но поскольку объект не может никуда уйти, мы говорим, что его PE от силы тяжести равен нулю.

Кинетическая энергия падающего объекта

Кинетическая энергия ( KE ) – это энергия движения. Поскольку объект не движется в исходном положении, исходное значение KE составляет:

KE _i = 0

Как только объект выпущен, он ускоряется вниз. Когда объект достигает земли, его кинетическая энергия составляет:

KE _f = mv _f ² /2

где

• KE _f – кинетическая энергия у земли в джоулях (Дж) или фут-фунтах (фут-фунтах)
• v _f – скорость объекта, падающего на землю, в м / с или фут / с

Полная энергия падающего объекта

Суммарная энергия объекта:

TE = PE + KE

Полная энергия является постоянной величиной при условии, что на объект не действуют никакие внешние силы, кроме гравитации.Таким образом, начальная полная энергия равна конечной полной энергии:

TE _i = TE _f

PE _i + KE _i = PE _f + KE _f

Когда объект просто уронили,

mgh + 0 = 0 + mv _f ² /2

mgh = mv _f ² /2

Конечная скорость падающего объекта

Исходя из этого эквивалента, вы можете определить конечную скорость падающего объекта. Разделите на м и умножьте на 2:

v _f ² = 2gh

v _f = √ (2gh)

Это эквивалентно v = √ (2gy) , которое дается в уравнениях скорости падающих предметов.

Сводка

Потенциальная энергия относительно силы тяжести составляет PE = mgh . Когда объект падает, бросается вниз или проецируется вверх, его кинетическая энергия становится равной KE = mv ² /2 вместе с коэффициентом начальной скорости.

Сумма PE и KE – это полная энергия ( TE ), которая является постоянной величиной. Приравнивая начальную полную энергию к конечной полной энергии, вы можете определить конечную скорость объекта.

---

Вы можете добиться успеха

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайтов

Гравитация и потенциальная энергия – Университет Аляски

Калькулятор потенциальной энергии

Гравитационные ресурсы

Книги

(Примечание: Школа чемпионов может получать комиссионные от покупки книг)

Книги с самым высоким рейтингом по простой науке о гравитации

Книги с самым высоким рейтингом по продвинутой физике гравитации

---

Вопросы и комментарии

Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.