Физика формула ax: Формулы равноускоренного прямолинейного движения в физике

2.
5. Характеристика движения. Судя по уравнению, с уверенностью можно сказать, что это равноускоренное прямолинейное движение, так как присутствует квадрат времени.
6. График. Я бы нарисовала график, но у меня слишком плохая камера, чтобы сфотографировать. Надеюсь ты построишь график по формуле: Vx=2-2t. 

Квадратичная функция, как построить Параболу

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax² + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

a — старший коэффициент, который отвечает за ширину параболы. Большое значение a — парабола узкая, небольшое — парабола широкая. b — второй коэффициент, который отвечает за смещение параболы от центра координат. с — свободный член, который соответствует координате пересечения параболы с осью ординат.

График квадратичной функции — парабола, которая имеет следующий вид для y = x²:

 

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x², нужно составить таблицу:

x	-2	-1	0	1	2
y	4	1	0	1	4

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x² при любых значениях остальных коэффициентов.

График функции y = –x² выглядит, как перевернутая парабола:

 

Зафиксируем координаты базовых точек в таблице:

x	-2	-1	0	1	2
y	-4	-1	0	-1	-4

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.

Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.

Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.

Для наглядности возьмем функцию y = ax² + bx + c, для построения которой нужно решить квадратное уравнение ax² + bx + c = 0. В процессе найдем дискриминант D = b² – 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1.  Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
   

2. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
3. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:



Если a > 0, то график выглядит как-то так:

 

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax² + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c.

То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

 

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax

² + bx + c.

Разберем общий алгоритм на примере y = 2x² + 3x – 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x² + 3x – 5.

D = b² – 4ac = 9 – 4 * 2 * (-5) = 49 > 0

√D = 7

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

2x² + 3x – 5 = 0

3. Координаты вершины параболы:

4. Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
5. Нанести эти точки на координатную плоскость и построить график параболы:
   

Уравнение квадратичной функции имеет вид y = a * (x – x₀)

² + y₀

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x²

+ 3x – 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x – 1)² + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить y = x²,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

2. Построить график параболы для каждого случая.

Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)

Рассмотрим следующий пример: y = (x – 2) * (x + 1).

Как строим:

1. Данный вид уравнения позволяет быстро найти нули функции:

(x – 2) * (x + 1) = 0, отсюда х₁ = 2, х₂ = -1.

2. Определим координаты вершины параболы:

3. Найти точку пересечения с осью OY:

с = ab =(-2) * (1)= -2 и ей симметричная.

4. Отметим эти точки на координатной плоскости и соединим плавной прямой.

Колебания – Физика – Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Гармонические колебания

К оглавлению…

В технике и окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют

колебательными. Колебаниями называют изменения физической величины, происходящие по определенному закону во времени. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.

Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Для существования в системе

гармонических колебаний необходимо, чтобы у нее было положение устойчивого равновесия, то есть такое положение, при выведении из которого на систему начала бы действовать возвращающая сила.

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.

Простейшим видом колебательного процесса являются колебания, происходящие по закону синуса или косинуса, называемые гармоническими колебаниями. Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω₀ задаётся следующим образом:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний, которое имеет вид:

где: x – смещение тела от положение равновесия, A – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний (ω = 2Π/T), t – время. Величина, стоящая под знаком косинуса: φ = ωt + φ₀, называется фазой гармонического процесса. Смысл фазы колебаний: стадия, в которой колебание находится в данный момент времени. При t = 0 получаем, что φ = φ₀, поэтому φ₀ называют начальной фазой (то есть той стадией, из которой начиналось колебание).

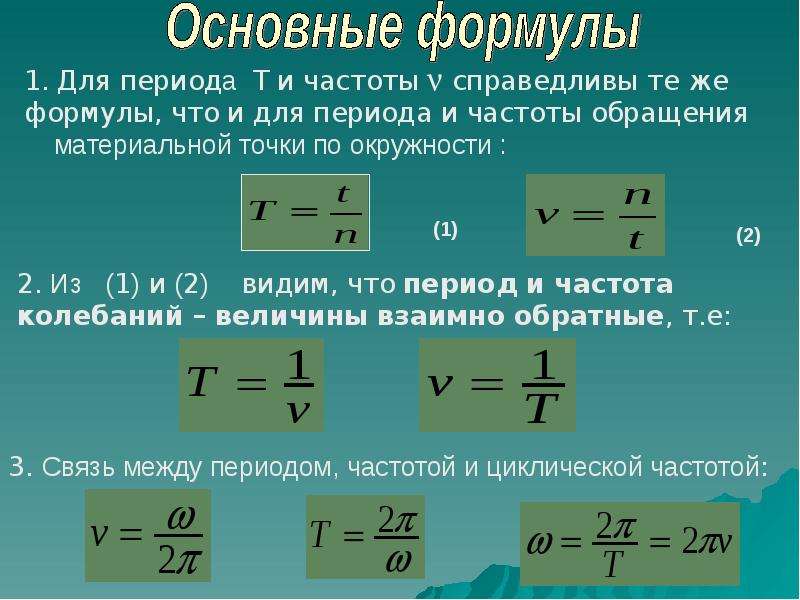
Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Если же количество колебаний N, а их время t, то период находится как:

Физическая величина, обратная периоду колебаний, называется частотой колебаний:

Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота колебаний связана с циклической частотой ω и периодом колебаний T соотношениями:

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Максимальные по модулю значения скорости υ_m = ωA достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = a_x тела при гармонических колебаниях.  Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Знак минус в предыдущем выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, возвращает тело в начальное положение (x = 0), т.е. заставляет тело совершать гармонические колебания.

Следует обратить внимание на то, что:

• физические свойства колебательной системы определяют только собственную частоту колебаний ω₀ или период T.
• Такие параметры процесса колебаний, как амплитуда A = x_m и начальная фаза φ₀, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени, т.е. начальными условиями.
• При колебательном движении тело за время, равное периоду, проходит путь, равный 4 амплитудам. При этом тело возвращается в исходную точку, то есть перемещение тела будет равно нулю. Следовательно, путь равный амплитуде тело пройдет за время равное четверти периода.

Чтобы определить, когда в уравнение колебаний подставлять синус, а когда косинус, нужно обратить внимание на следующие факторы:

• Проще всего, если в условии задачи колебания названы синусоидальными или косинусоидальными.
• Если сказано, что тело толкнули из положения равновесия – берем синус с начальной фазой, равной нулю.
• Если сказано, что тело отклонили и отпустили – косинус с начальной фазой, равной нулю.
• Если тело толкнули из отклоненного от положения равновесия состояния, то начальная фаза не равна нолю, а брать можно и синус и косинус.

 

Математический маятник

К оглавлению…

Математическим маятником называют тело небольших размеров, подвешенное на тонкой, длинной и нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела.  Только в случае малых колебаний математический маятник является гармоническим осциллятором, то есть системой, способной совершать гармонические (по закону sin или cos) колебания. Практически такое приближение справедливо для углов порядка 5–10°. Колебания маятника при больших амплитудах не являются гармоническими.

Циклическая частота колебаний математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Полученная формула называется формулой Гюйгенса и выполняется, когда точка подвеса маятника неподвижна. Важно запомнить, что период малых колебаний математического маятника не зависит от амплитуды колебаний. Такое свойство маятника называется изохронностью. Как и для любой другой системы, совершающей механические гармонические колебания, для математического маятника выполняются следующие соотношения:

1. Путь от положения равновесия до крайней точки (или обратно) проходится за четверть периода.
2. Путь от крайней точки до половины амплитуды (или обратно) проходится за одну шестую периода.
3. Путь от положения равновесия до половины амплитуды (или обратно) проходится за одну двенадцатую долю периода.

 

Пружинный маятник

К оглавлению…

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению. Таким свойством обладает сила упругости.

Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную совершать в отсутствие трения свободные гармонические колебания. Груз на пружине называют пружинным маятником.

Циклическая частота колебаний пружинного маятника рассчитывается по формуле:

Период колебаний пружинного маятника:

При малых амплитудах период колебаний пружинного маятника не зависит от амплитуды (как и у математического маятника). При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x₀, равную:

А колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты ω₀ и периода колебаний T справедливы и в этом случае. Таким образом, полученная формула для периода колебаний груза на пружине остается справедливой во всех случаях, независимо от направления колебаний, движения опоры, действия внешних постоянных сил.

При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются.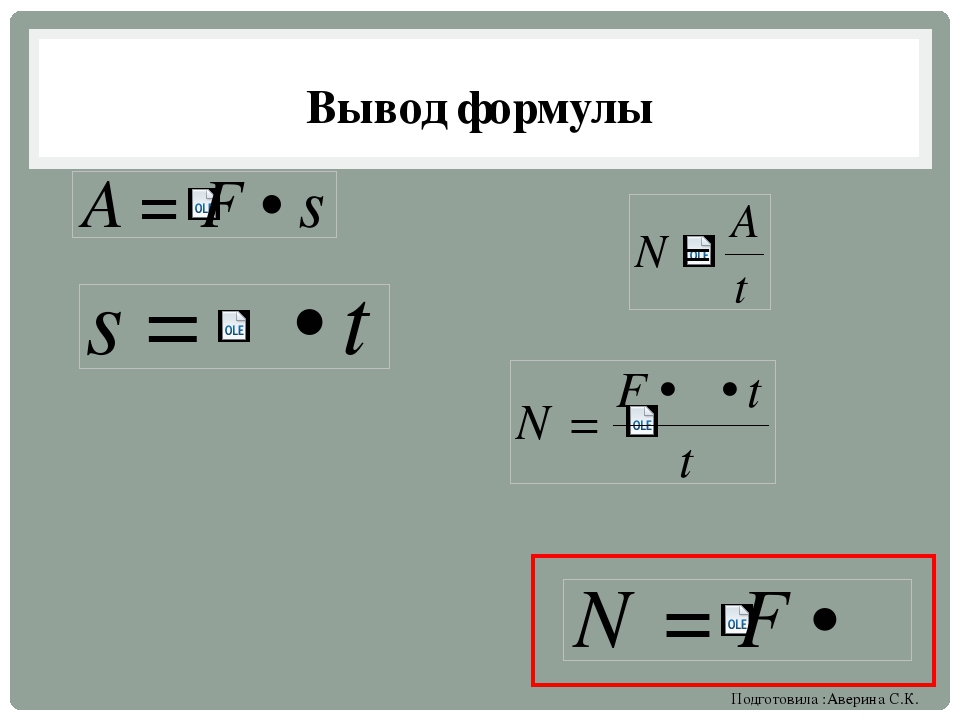 При максимальном отклонении тела от положения равновесия его скорость, а, следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругой деформации пружины. Для математического маятника – это энергия в поле тяготения Земли.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией (как правило, потенциальную энергию в положении равновесия полагают равной нулю). Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и так далее.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.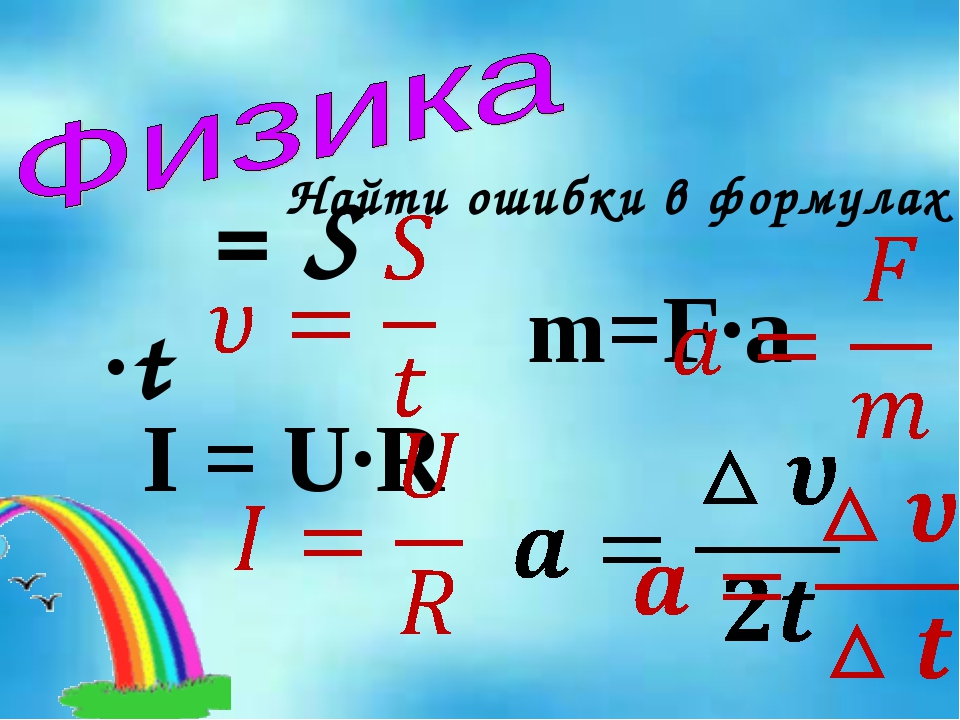  Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. При этом, максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса (полная механическая энергия равна максимальным значениям кинетической и потенциальной энергий, а также сумме кинетической и потенциальной энергий в произвольный момент времени):

 

Механические волны

К оглавлению…

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной.

Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют немеханические волны, которые способны распространяться и в пустоте (например, световые, т.е. электромагнитные волны могут распространяться в вакууме).

• Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
• Поперечные волны не могут существовать в жидкой или газообразной средах.

Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой ν и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.

Длиной волны λ называют расстояние между двумя соседними точками, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за время равное периоду T, следовательно, длина волны может быть рассчитана по формуле:

где: υ – скорость распространения волны. При переходе волны из одной среды в другую длина волны и скорость ее распространения меняются. Неизменными остаются только частота и период волны.

Разность фаз колебаний двух точек волны, расстояние между которыми l рассчитывается по формуле:

 

Электрический контур

К оглавлению. ..

В электрических цепях, так же, как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный LC-контур. В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими. Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:

Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:

Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:

Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:

Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:

Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в теплоту, выделяющуюся на резисторе, и колебания становятся затухающими.

 

Переменный ток. Трансформатор

К оглавлению…

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими синусоидальное напряжение. Они позволяют наиболее просто и экономно осуществлять передачу, распределение и использование электрической энергии.

Устройство, предназначенное для превращения механической энергии в энергию переменного тока, называется генератором переменного тока. Он характеризуется переменным напряжением U(t) (индуцированной ЭДС) на его клеммах. В основу работы генератора переменного тока положено явление электромагнитной индукции.

Переменным током называется электрический ток, который изменяется с течением времени по гармоническому закону.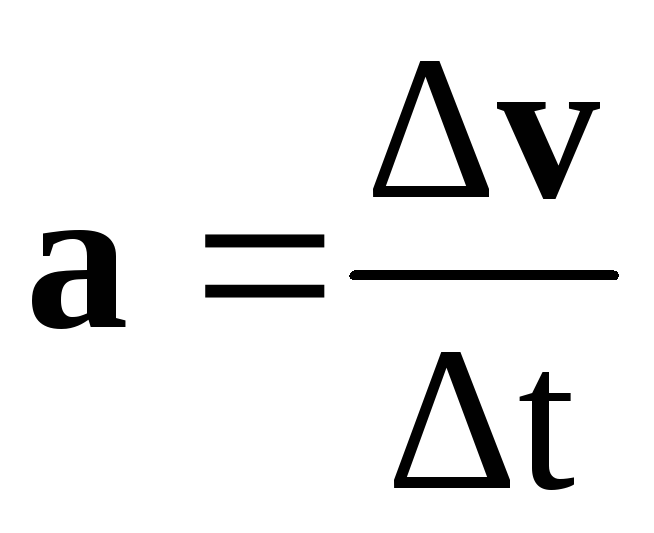 Величины U₀, I₀ = U₀/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.

Переменный ток характеризуется действующими значениями силы тока и напряжения. Действующим (эффективным) значением переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы в единицу времени такое же количество теплоты, что и данный переменный ток. Для переменного тока действующее значение силы тока может быть рассчитано по формуле:

Аналогично можно ввести действующее (эффективное) значение и для напряжения, рассчитываемое по формуле:

Таким образом, выражения для мощности постоянного тока остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

Обратите внимание, что если идет речь о напряжении или силе переменного тока, то (если не сказано иного) имеется в виду именно действующее значение. Так, 220В – это действующее напряжение в домашней электросети.

Конденсатор в цепи переменного тока

Строго говоря, конденсатор ток не проводит (в том смысле, что носители заряда через него не протекают). Поэтому, если конденсатор подключен в цепь постоянного тока, то сила тока в любой момент времени в любой точке цепи равна нулю. При подключении в цепь переменного тока из-за постоянного изменения ЭДС конденсатор перезаряжается. Ток через него по-прежнему не течет, но ток в цепи существует. Поэтому условно говорят, что конденсатор проводит переменный ток. В этом случае вводится понятие сопротивления конденсатора в цепи переменного тока (или емкостного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что емкостное сопротивление зависит от частоты переменного тока. Оно в корне отличается от привычного нам сопротивления R. Так, на сопротивлении R выделяется теплота (поэтому его часто называют активным), а на емкостном сопротивлении теплота не выделяется. Активное сопротивление связано со взаимодействием носителей заряда при протекании тока, а емкостное – с процессами перезарядки конденсатора.

Катушка индуктивности в цепи переменного тока

При протекании переменного тока в катушке возникает явление самоиндукции, и, следовательно, ЭДС. Из-за этого напряжение и сила тока в катушке не совпадают по фазе (когда сила тока равна нулю, напряжение имеет максимальное значение и наоборот). Из-за такого несовпадения средняя тепловая мощность, выделяющаяся в катушке, равна нулю. В этом случае вводится понятие сопротивления катушки в цепи переменного тока (или индуктивного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что индуктивное сопротивление зависит от частоты переменного тока. Как и емкостное сопротивление, оно отличается от сопротивления R. Как и на емкостном сопротивлении, на индуктивном сопротивлении теплота не выделяется. Индуктивное сопротивление связано с явлением самоиндукции в катушке.

Трансформаторы

Среди приборов переменного тока, нашедших широкое применение в технике, значительное место занимают трансформаторы. Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении электромагнитной индукции. Простейший трансформатор состоит из сердечника замкнутой формы, на который намотаны две обмотки: первичная и вторичная. Первичная обмотка подсоединяется к источнику переменного тока с некоторым напряжением U₁, а вторичная обмотка подключается к нагрузке, на которой появляется напряжение U₂. При этом, если число витков в первичной обмотке равно n₁, а во вторичной n₂, то выполняется следующее соотношение:

Коэффициент трансформации вычисляется по формуле:

Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):

В неидеальном трансформаторе вводится понятие КПД:

 

Электромагнитные волны

К оглавлению. ..

Электромагнитные волны – это распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Электромагнитные волны распространяются в веществе с конечной скоростью, которая может быть рассчитана по формуле:

где: ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10^–12 Ф/м, μ₀ = 1,25664·10^–6 Гн/м. Скорость электромагнитных волн в вакууме (где ε = μ = 1) постоянна и равна с = 3∙10⁸ м/с, она также может быть вычислена по формуле:

Скорость распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных. Если электромагнитная волна распространяется в какой-либо среде, то скорость ее распространения также выражается следующим соотношением:

где: n – показатель преломления вещества – физическая величина, показывающая во сколько раз скорость света в среде меньше чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:

• Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии.
• Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с неизменной скоростью, не являются источником электромагнитных волн. А вот цепи, в которых протекает переменный ток, т.е. такие цепи в которых носители заряда постоянно меняют направление своего движения, т.е. двигаются с ускорением – являются источником электромагнитных волн. В современной радиотехнике излучение электромагнитных волн производится с помощью антенн различных конструкций, в которых возбуждаются быстропеременные токи.

v 2 = 2ax v2 ​​= 2ax или v 2 = axe v2 = ax?

Насколько я знаю, v 2 = 2 х х v 2 знак равно 2 Икс это формула, чтобы найти скорость в различных вопросах.

Если кинетическая энергия = работа,

1 2 м в 2 = F Икс 1 2 м v 2 знак равно F Икс

м в 2 = 2 м х х м v 2 знак равно 2 м Икс

v 2 = 2 х х v 2 знак равно 2 Икс

Мы используем эту формулу, чтобы решить некоторые вопросы в школе. Но когда я просто играю с основными формулами, я получаю это.

х / в = т Икс / v знак равно T

v / a = t v / знак равно T

т = т T знак равно T

x / v = v / a Икс / v знак равно v /

v 2 = х v 2 знак равно Икс

И это меня просто смущает. Я предполагаю что х / в = т Икс / v знак равно T и v / a = t v / знак равно T на самом деле отчасти упрощенный, иначе я не могу понять, почему v 2 v 2 равно х Икс на одном и 2 х х 2 Икс с другой.

Может кто-нибудь объяснить мне, что я делаю не так?

Дэвид З

В вашем втором выводе правильные формулы

Δx v ≈ Δ т V ≈ Δ т Δ Икс v ≈ Δ T Δ v ≈ Δ T

Я уверен, что вы можете легко найти несколько примеров, чтобы показать вам, почему х / в = т Икс / v знак равно T и v / a = t v / знак равно T не имеет никакого смысла. Во всяком случае, когда вы кладете их вместе, вы получаете v Δ v ≈ a Δ x v Δ v ≈ Δ Икс с приближением становится более точным, чем меньше Δ Δ с.

Обратите внимание, что если вы берете лимит как V Δ v и Δx Δ Икс перейти к нулю, затем интегрировать, вы получите

∫ v е v я v д V v 2 е – v 2 я 2 v 2 е = ∫ Икс е Икс я д х = а ( х е – х я ) = V 2 я + 2 а Δ х ∫ v я v е v d v знак равно ∫ Икс я Икс е d Икс v е 2 – v я 2 2 знак равно ( Икс е – Икс я ) v е 2 знак равно v я 2 + 2 Δ Икс

это точно правильная формула.

Внеклассный урок – Построение графика квадратичной функции

Построение графика квадратичной функции

Возьмем формулу квадратичной функции y = ax² + bx + c. Проведя вычисления, можно прийти к другому виду этой формулы (можете вычислить сами):

                b          b² – 4ac
y = a(x + — )² – ————.
                2a            4a

 

Заменим полученные дроби буквами m и n. Тогда мы получим формулу, которая уже известна нам из предыдущего раздела:

y = a(x – m)² + n,  где

              b
 m = – ——,
             2a

           b² – 4ac
n = – ————
               4a

 

Вывод:

Графиком функции y = ax² + bx + c является парабола, которую можно получить из графика функции y = ax² с помощью двух параллельных переносов – сдвига вдоль оси x вправо или влево, а вдоль оси y – вверх или вниз.
                                                                                                 b                 b² – 4ac
Вершиной этой параболы является (m; n), где m = – ——,   n = – ————.
                                                                                                2a                    4a

Три особенности этой параболы:

1) x = m (пояснение: ось симметрии параболы параллельна оси y)

2) y = n (пояснение: y = ax² + bx + c = a(x – m)² + n = n)

3) при a > 0 ветви параболы направлены вверх, при a<0 – вниз.

 

Чтобы построить график квадратичной функции, надо в первую очередь найти координаты вершины параболы.

 

Пример.

Надо построить график функции y = –2x² + 12x – 19.

Начинаем решать. Для этого отметим, что a = –2, b = 12, c = –19.

Мы видим, что a < 0. Значит, графиком данной функции является парабола, ветви которой направлены вниз.

Найдем координаты ее вершины – то есть значения m и n:

              b                12
 m = – —— = – ———— = 3
             2a            2 · (–2)

Значение n можно вычислить двумя способами. Один из них – формула, приведенная выше. Но поскольку x = m, а y = n (см.выше), то можно найти n более простым способом – непосредственно с помощью нашего выражения –2x² + 12x – 19, вставляя вместо x значение m, равное 3:

n = –2 · 3² + 12 · 3 – 19 = –1

 

Итак, вершина параболы имеет координаты (3; –1).

Далее с помощью приведенных формул просто находим координаты еще нескольких точек, отмечаем их на оси координат, соединяем точки – и получаем нашу параболу.

 
 

 

Равноускоренное движение

Равноускоренным называют движение с постоянным ускорением. Простейшим примером такого движения является свободное падение тел, изучением которых занимался ещё Галилео Галилей. Скорость движения при этом не остаётся постоянной: в общем случае она меняется и по модулю, и по направлению. Описание данного движения значительно сложнее по сравнению с равномерным прямолинейном. Действия с числами здесь заменяют на действия с векторами, так как векторы содержат в себе информацию о направлений величин, характеризующих движение (о скорости, ускорений, перемещений).
Ускорение при равноускоренном движений показывает, на сколько изменяется скорость тела за каждую секунду движения:

(1)

Где V₀ – начальная скорость тела, а V скорость того же тела спустя некоторое время t.
Ускорение показывает изменение скорости за единицу времени.
Из определения ускорения следует, что мгновенная скорость тела при равноускоренном движении изменяется с течением времени по линейному закону:

(2)

Эта формула позволяет по начальной скорости и ускорению тела вычислить его скорость в любой момент времени t. Между тем основная задача механики заключается в определении того, где будет находиться тело спустя заданное время. Для её решения необходимо знать перемещение, совершённое телом за это время. Перемещение можно найти, умножив среднюю скорость на время движения:

s=v_cpt

При равноускоренном движении средняя скорость равна полусумме начальной и конечной скоростей движения:

Поэтому:

Подставляя сюда выражения (2), получаем:

s=v₀t +at²/2(3)

Именно это уравнение является обобщением формулы:s=vt на случай движения с постоянным ускорением.
Уравнения (1),(2),(3) – векторные. Действия с векторами отличаются от действий с числами, поэтому никакие числовые значения перемещения, скорости и ускорения в такие уравнения подставлять нельзя. Между тем любые расчёты требуют проведений операций именно с числами. Чтобы это стало возможным, необходимо от векторного способа описания движения перейти к координатному. При координатном описаний движения вместо векторов используют проекций на оси координат. Поскольку любой вектор характеризуется тремя проекциями на оси X,Y и Z, следовательно каждому вектору уравнению в общем случае будут соответствовать три уравнения в координатной форме. Для плоского (двухмерного) движения таких уравнений только два. Если же движение является прямолинейным, то для его описания достаточно одного уравнения в проекций на ось X(при условии, что эта ось направлена параллельно вектору скорости частицы). Тогда уравнения (2) и (3).например, можно записать следующим образом:

v_x=v_0x+a_xt

s_x=v_0xt+a_xt²/2(4)

При координатном описаний движения, координота тела будет равна:

x=x₀+v_0xt+a_xt²/2(5)

Угловое ускорение | Безграничная физика

Постоянное угловое ускорение

Постоянное угловое ускорение описывает взаимосвязь между угловой скоростью, углом поворота и временем.

Цели обучения

Связать угол поворота, угловую скорость и угловое ускорение с их эквивалентами в линейной кинематике

Основные выводы

Ключевые моменты

• Приведенные здесь кинематические уравнения для вращательного и / или линейного движения могут использоваться для решения любой задачи вращательной или поступательной кинематики, в которой a и α постоянны.
• Используя соотношения между скоростью и угловой скоростью, расстоянием и углом поворота, а также ускорением и угловым ускорением, кинематические уравнения вращения могут быть получены из их аналогов линейного движения.
• Чтобы вывести уравнения вращения из линейных аналогов, мы использовали соотношения a = rα , v = rω и x = rθ .

Ключевые термины

• кинематика : Раздел механики, имеющий отношение к движущимся объектам, но не к задействованным силам.
• угловой : относящийся к углу или углам; имеющий угол или углы; образующий угол или угол; остроугольный; заостренный; как в угловой фигуре.

Просто используя нашу интуицию, мы можем начать видеть взаимосвязь таких величин вращения, как θ (угол поворота), ω (угловая скорость) и α (угловое ускорение). Например, если колесо мотоцикла имеет большое угловое ускорение в течение довольно долгого времени, оно в конечном итоге быстро вращается и совершает много оборотов.2 + 2 \ text {ax} [/ latex]

Аналогичным образом кинематика вращательного движения описывает отношения между углом вращения, угловой скоростью, угловым ускорением и временем. Начнем с нахождения уравнения, связывающего ω , α и t . Чтобы определить это уравнение, мы используем соответствующее уравнение для линейного движения:

[латекс] \ text {v} = \ text {v} _0 + \ text {at} [/ latex].

Как и в линейной кинематике, где мы предполагали, что a является постоянным, здесь мы предполагаем, что угловое ускорение α является постоянным, и можем использовать соотношение: [latex] \ text {a} = \ text {r} \ alpha [ / latex] Где r – радиус закругления. 2 + 2 \ альфа \ тета [/ латекс]

Уравнения, приведенные выше, могут использоваться для решения любой задачи вращательной или поступательной кинематики, в которой a и α постоянны. показывает взаимосвязь между некоторыми величинами, обсуждаемыми в этом атоме.

Линейное и угловое : На этом рисунке показано равномерное круговое движение и некоторые из его определенных величин.

Физические формулы Physic 1201 ЗАКЛЮЧИТЕЛЬНЫЙ ЭКЗАМЕН ФОРМУЛА ЛИСТ Величина векторов A Ax Ay Ax Acos Ay Asin tan Ax Ay Rx Ax Bx Ry Ay By AB cos AB Kinematics Dimension vave

Текст для предварительного просмотра

Physic 1201 ФОРМУЛА ЗАКЛЮЧИТЕЛЬНОГО ЭКЗАМЕНА

Векторы

Величина A A A

руб. = =

А Б Б А

r r r r + = +

(А Б) С А (В С)

r r r r r r + + = + +

Топор Ay

р р р = +

Ax = Acosθ

Ay = Asinθ

х

г A

A

tanθ =

2 2 А = Топор + Ay

Rx = Ax + Bx

Ry = Ay + By

A⋅B = AB cosθAB

г

Кинематика – 1 измерение

т

х

т т

х х ваве ∆

∆

=

–

–

=

2 1

2 1

т

х v т ∆

∆

=

∆ → 0

лим

т

v

т т

в в Aave ∆

∆

=

–

–

=

2 1

2 1

т

v а т ∆

∆

=

∆ → 0

лим

v = v 0 + при

2 0 0 2

1

x = x + vt + при

2 (0)

2 0

2 v = v + a x − x

т

в в х х 2

0 0

+

– =

Кинематика – 2 размера

т

руб. ваве ∆

∆

=

r

т

руб. v т ∆

∆

=

∆ →

руб. r

0

лим

т

х v т

х ∆

∆

=

∆ → 0

лим

т

г v т

г ∆

∆

=

∆ → 0

лим

т

v Aave ∆

∆

=

г r

т

v а т ∆

∆

=

∆ →

руб. r

0

лим

т

v

х

т

х ∆

∆

=

∆ → 0

лим

r

т

v

л

т

г ∆

∆

=

∆ → 0

лим

r

R

и

2

⊥ =

т

πR v

2

=

Законы Ньютона

1 ст: ∑F = 0

r

2-я: ∑F = ma

r r

3

-й : П 12 Ж 21

р р = –

∑Fx = макс

∑Fy = май

R

v Ф м м

2

∑ ⊥ = ⊥ =

масс. Мг

р р =

Силы

Fk = мккН

Фс ≤ мксН

Fspring = −kx

Вт =

мг

2

1 2

r

мм Fg = G

2 E

E

R

Гм г =

Константы и математика

5.7 10 ()

8. 314 ()

6. 67 10 (/)

9. 8 (/)

8 2 4

1 1

11 2 2

2

– – –

– –

–

= × ⋅ ⋅

= ⋅ ⋅

= ×

=

Вт м K

R Дж моль K

G Нм кг

г м с

σ

а

b b ac х

топор bx c

2

4

0

2

2

– ± –

⇒ =

+ + =

θ

θ θ

θ θ

cos

грех загар

cos /

грех /

sin cos 1

2 2

=

=

=

+ =

прил. Гипп

OPP

Работа, энергия и сила

2

2

1

K = mv

Вт = F⋅s = FscosθFs

г

Вт = Γ (θ 2 −θ 1)

Wобщ = ∆K = K 2 −K 1

Юграв = mgh

r

ГМм Уграв = –

2

2

1

Uspring = kx

Wgrav = −∆Ugrav

Wspring = −∆Uspring

Эмех = К + У

Wother = ∆U + ∆K

Fv т

Вт

P = ||

∆

∆

=

P = Γω

Кинематика вращения

т т т

пр. ∆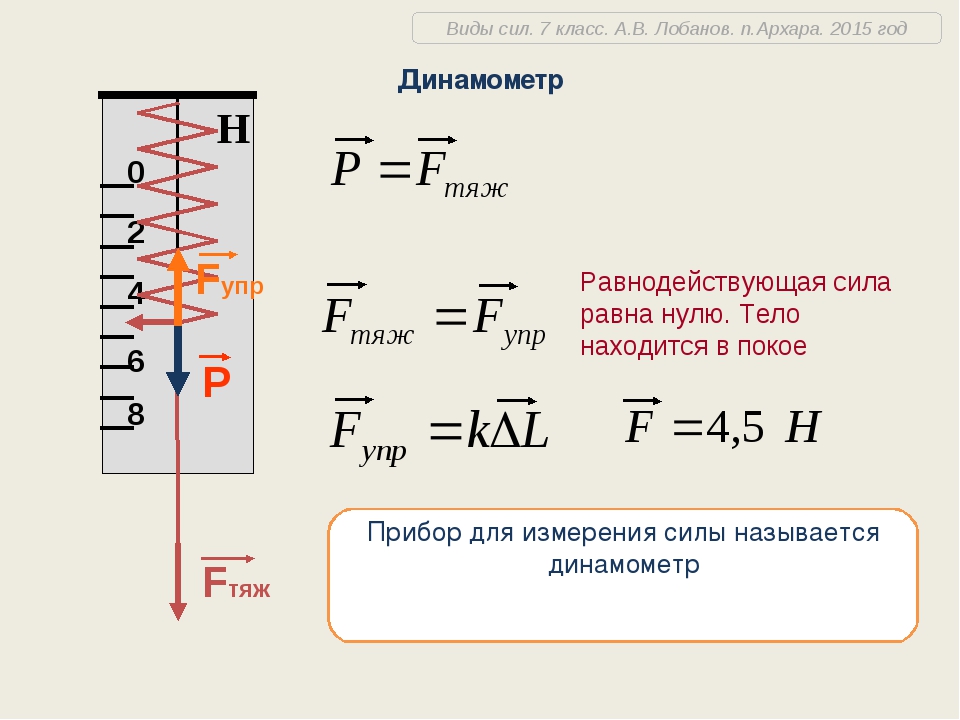

∆

=

–

–

=

θ θ θ ω

2 1

2 1

т ∆t

∆

=

∆ →

θ ω 0

лим

т т т

пр. ∆

∆

=

–

–

=

ω ω ω α

2 1

2 1

т ∆t

∆

=

∆ →

θ α 0

лим

ω = ω 0 + αt

2 0 0 2

1

θ = θ + ω t + αt

2 (0)

2 0

2 ω = ω + α θ −θ

т 2

0 0

ω ω θ θ

+

– =

Импульс, Импульс и CM

п мв

р р =

Дж = F t −t = F∆t

р р р (2 1)

Дж с

р р = ∆

П 1 л 2

р р р = +

т

п.

т

v Ф м м ∆

∆

=

∆

∆

= =

r r r r

.

..

…

1 2

1 1 2 2

+ +

=

м м

м x м x

х

…

…

1 2

1 1 2 2

+ +

=

м м

м г м г Y

…

…

1 2

11 2 2

+ +

=

м м

мв м в V

х х х

…

…

1 2

1 1 2 2

мв м в V

г г y

…

…

1 2

1 1 2 2

+ +

=

м м

м м а A

х х х

…

…

1 2

1 1 2 2

м м а A

г г y

∑Fext = MA

r r

Вращательное и линейное движение

с = θR

v || = ωR

а || = αR

R

R

v

2

2 || ⊥ = = ω

τ = 2 π / ω

Импульс вращения и

Momentum, крутящий момент

L = Iω 2 L = pr⊥ = mvr⊥ = mωr⊥

= ∑ ⊥

2 L mωr

Jθ = Γ (t 2 −t 1) = Γ∆t

Jθ = ∆L

т

л

т

I I

∆

∆

=

∆

∆

∑Γ = =

ω α

Γ = Fl = Frsinθ

R

и

2 ⊥ =

т

πR v

2

=

Инерция вращения и энергия

∑

=

=

n

и

I мрий

1

2

2 _ 2

1

Изолирующий цилиндр = MR

2 Ithin_walled_cyl = MR

2

5

2

Isphere = MR

2

2

1

К = Iω

Равновесие

∑Fx = 0

∑Fy = 0

∑Γ =

any_axis

0

.

..

…

1 2

1 1 2 2

+ +

=

w w

ш x ш x Xcog

…

…

1 2

1 1 2 2

в г г у Иког

Формула перекрестного произведения

Векторное произведение или перекрестное произведение – это бинарная операция между двумя векторами в трехмерном пространстве. В результате получается вектор, перпендикулярный векторам, которые умножаются, и, следовательно, нормальный к плоскости, которая их содержит.Благодаря способности получать вектор, перпендикулярный двум другим векторам, направление которых изменяется в зависимости от угла, образованного между этими двумя векторами, эта операция часто применяется для решения математических, физических или инженерных задач.

вектор a X вектор b = модуль вектора a * модуль вектора b * синус угла между векторами a и b * нормаль плоскости, образованной векторами a и b.

Уравнение:

,

у нас,

вектор а.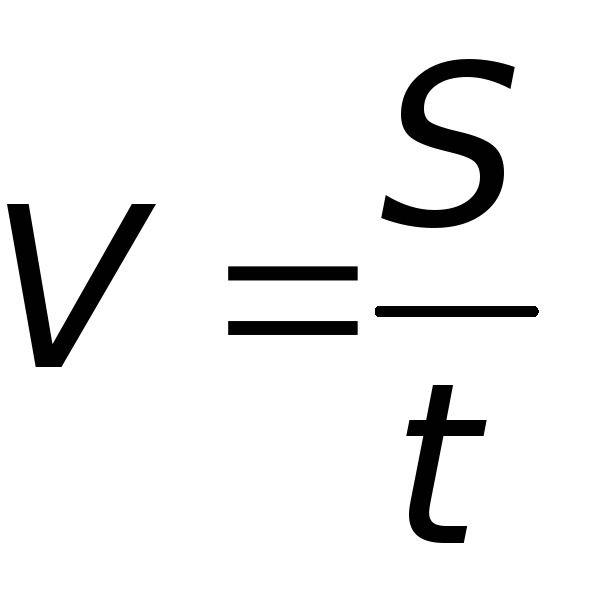

вектор б.

модуль вектора a.

модуль вектора b.

= угол между векторами a и b.

= * нормаль к плоскости, образованной векторами a и b.

Другой способ вычисления векторного произведения в декартовом пространстве R3 – через определитель следующей матрицы.

| I j k |

| a _x a _y a _z |

| b _x b _y b _z |

И определитель:

= (a _y * b _z – a _z * b _y ) i + (a _z * b _x – a _x * b _z ) j + (a _x * b _y – a _y * b _x ) k

Вопросы по перекрестному продукту:

1) Учитывая вектор a = 1i-3j и вектор b = -3i + 2, и угол между ними равен 134.69 °, вычислите векторное произведение между a и b.

Ответ: Первое, что нужно сделать, это вычислить модуль обоих векторов.

| а | = ((1) ² + (- 3) ² ) ^-1/2 = 3,16

| b | = ((- 3) ² + (2) ² ) = 3,6

, то нормаль к плоскости, образованной векторами a и b, равна k, потому что они находятся в плоскости xy. Затем мы вычисляем перекрестное произведение между a и b:

= 3,16 * 3,6 * sin (134,69 °) k = 8.09 к.

а х б = 8,09 к.

2) Учитывая вектор a = 4i + 3j-2k и вектор b = i-2j-4k, вычислите векторное произведение между a и b.

Ответ: поскольку мы не знаем угол, образованный векторами a и b, воспользуемся формулой определителя:

a _x = 4.

a _y = 3.

a _z = -2.

b _x = 1.

b _y = -2.

b _z = -4.

= (a _y * b _z – a _z * b _y ) i + (a _z * b _x – a _x * b _z ) j + (a _x * b _y – a _y * b _x ) k = (3 * (- 4) – (-2) * (- 2)) i + ((-2) * 1-4 * (-4)) j + (4 * (- 2) – 3 * 1) k = -16i + 14j-11k.

axb = -16i + 14j – 11k.

Проблемы с горизонтально запущенными снарядами

Одна из сильных сторон физики – это ее способность использовать принципы физики для предсказания конечного результата движения объекта.Такие прогнозы делаются путем применения физических принципов и математических формул к заданному набору начальных условий. В случае снарядов студент-физик может использовать информацию о начальной скорости и положении снаряда, чтобы предсказать такие вещи, как, сколько времени снаряд находится в воздухе и как далеко снаряд уйдет. Физические принципы, которые необходимо применять, обсуждались ранее в Уроке 2. Используемые математические формулы обычно называются кинематическими уравнениями.Объединение этих двух параметров позволяет делать прогнозы относительно движения снаряда. На типичном уроке физики предсказательная способность принципов и формул чаще всего демонстрируется в задачах словесного рассказа, известных как задачи со снарядами.

В этом курсе мы обсудим два основных типа проблем со снарядами. Хотя общие принципы одинаковы для каждого типа задач, подход будет отличаться из-за того, что задачи различаются по своим начальным условиям.Есть два типа проблем:

Тип проблемы 1:

Снаряд запускается с начальной горизонтальной скоростью из возвышенного положения и следует параболической траектории к земле. Предсказуемые неизвестные включают начальную скорость снаряда, начальную высоту снаряда, время полета и горизонтальное расстояние снаряда.

Примеры проблем этого типа:

1. Мяч для пула оставляет 0.Стол высотой 60 метров с начальной горизонтальной скоростью 2,4 м / с. Предскажите время, необходимое для того, чтобы шар для пула упал на землю, и расстояние по горизонтали между краем стола и местом приземления мяча.
2. Футбольный мяч отбрасывается горизонтально с холма высотой 22 метра и приземляется на расстоянии 35 метров от края холма. Определите начальную горизонтальную скорость футбольного мяча.

Тип проблемы 2:

Снаряд запускается под углом к ​​горизонтали и поднимается вверх до пика при движении по горизонтали.Достигнув пика, снаряд падает с движением, симметричным его траектории вверх к пику. Предсказуемые неизвестные включают время полета, горизонтальную дальность и высоту снаряда, когда он находится на пике.

Примеры проблем этого типа:

1. Футбольный мяч бьет ногой с начальной скоростью 25 м / с под углом 45 градусов к горизонтали. Определите время полета, горизонтальное расстояние и максимальную высоту футбольного мяча.
2. Прыгун в длину отрывается от земли с начальной скоростью 12 м / с под углом 28 градусов относительно горизонтали. Определите время полета, горизонтальное расстояние и максимальную высоту прыгуна в длину.

Второй тип проблем будет предметом следующей части Урока 2. В этой части Урока 2 мы сосредоточимся на первом типе проблем, которые иногда называют проблемами снарядов, запускаемых горизонтально.Три общих кинематических уравнения, которые будут использоваться для обоих типов задач, включают следующее:

d = v _i • t + 0,5 * a * t ²

v _f = v _i + a • t

v _f ² = v _i ² + 2 * а • д

где	d = смещение	a = ускорение	t = время
	v f = конечная скорость	v i = начальная скорость

Уравнения горизонтального движения снаряда

Приведенные выше уравнения хорошо подходят для движения в одном измерении, но снаряд обычно движется в двух измерениях – как горизонтально, так и вертикально.Поскольку эти две составляющие движения не зависят друг от друга, необходимы две четко отдельных системы уравнений – одна для горизонтального движения снаряда, а другая – для его вертикального движения. Таким образом, три приведенных выше уравнения преобразуются в две системы из трех уравнений. Для горизонтальных составляющих движения уравнения:

x = v _{i x} • t + 0,5 * a _x * t ²

v _{f x} = v _{i x} + a _x • t

v _{f x} ² = v _{i x} ² + 2 * a _x • x

где	x = горизонт.смещение	a x = горизонт. разгон	t = время
	v f x = конечный горизонт. скорость	v i x = начальный горизонт. скорость

Из этих трех уравнений чаще всего используется верхнее уравнение.Применение концепции снаряда к каждому из этих уравнений также привело бы к заключению, что любой член с _x в нем будет сокращаться из уравнения, поскольку _x = 0 м / с / с. После отмены терминов топор единственное уравнение полезности будет:

.

x = v _{i x} • t

Уравнения вертикального движения снаряда

Для вертикальных составляющих движения три уравнения:

y = v _iy • t + 0.5 * ау * т ²

v _fy = v _iy + ay • t

v _fy ² = v _iy ² + 2 * ay • y

где	y = верт. смещение	ау = верт. разгон	t = время
	v fy = финальная верт.скорость	v iy = начальная верт. скорость

В каждом из приведенных выше уравнений вертикальное ускорение снаряда составляет -9,8 м / с / с (ускорение свободного падения). Кроме того, для частного случая проблем первого типа (проблемы с снарядами горизонтального запуска) v _iy = 0 м / с. Таким образом, любой член с v _iy будет сокращаться из уравнения.

Два набора из трех приведенных выше уравнений являются кинематическими уравнениями, которые будут использоваться для решения задач движения снаряда.

Решение проблем с снарядами

Чтобы проиллюстрировать полезность приведенных выше уравнений при прогнозировании движения снаряда, рассмотрим решение следующей проблемы.

Пример Шарик для пула оставляет 0.Стол высотой 60 метров с начальной горизонтальной скоростью 2,4 м / с. Предскажите время, необходимое для того, чтобы шар для пула упал на землю, и расстояние по горизонтали между краем стола и местом приземления мяча.

Решение этой проблемы начинается с приравнивания известных или заданных значений к символам кинематических уравнений – x, y, v _ix , v _iy , a _x , a _y и t. Поскольку горизонтальная и вертикальная информация используется отдельно, разумно организовать данную информацию в два столбца – один столбец для горизонтальной информации и один столбец для вертикальной информации.В этом случае в постановке задачи либо дается, либо подразумевается следующая информация:

Информация по горизонтали	Вертикальная информация
х = ??? v ix = 2,4 м / с a x = 0 м / с / с	y = -0.60 кв.м. v iy = 0 м / с a y = -9,8 м / с / с

Как указано в таблице, неизвестная величина – это горизонтальное смещение (и время полета) шара для пула. Решение проблемы теперь требует выбора соответствующей стратегии использования кинематических уравнений и известной информации для решения неизвестных величин.Почти всегда такая стратегия требует, чтобы одно из вертикальных уравнений использовалось для определения времени полета снаряда, а затем одно из горизонтальных уравнений использовалось для нахождения других неизвестных величин (или наоборот – сначала используйте уравнение по горизонтали, а затем по вертикали). Организованный список известных количеств (как в таблице выше) дает подсказки для выбора стратегии. Например, таблица выше показывает, что о вертикальном движении шара для пула известно три величины.Поскольку каждое уравнение содержит четыре переменных, знание трех переменных позволяет вычислить четвертую переменную. Таким образом, было бы разумно использовать вертикальное уравнение с вертикальными значениями для определения времени, а затем использовать горизонтальные уравнения для определения горизонтального смещения (x). Первое вертикальное уравнение (y = v _iy • t + 0,5 • a _y • t ² ) позволит определить время. Как только соответствующее уравнение выбрано, физическая проблема трансформируется в проблему алгебры.Путем подстановки известных значений уравнение принимает вид

-0,60 м = (0 м / с) • т + 0,5 • (-9,8 м / с / с) • т ²

Поскольку первый член в правой части уравнения сводится к 0, уравнение можно упростить до

-0,60 м = (-4,9 м / с / с) • т ²

Если обе части уравнения разделить на -5,0 м / с / с, уравнение станет

0,122 с ² = т ²

Получив квадратный корень из обеих частей уравнения, можно определить время полета. .

t = 0,350 с (округлено от 0,3499 с)

После определения времени можно использовать уравнение по горизонтали для определения горизонтального смещения шара для пула. Напомним, из приведенной информации, v _ix = 2,4 м / с и _x = 0 м / с / с. Затем первое горизонтальное уравнение (x = v _ix • t + 0,5 • a _x • t ² ) можно использовать для решения относительно «x». После выбора уравнения физическая проблема снова превращается в проблему алгебры.Путем подстановки известных значений уравнение принимает вид

x = (2,4 м / с) • (0,3499 с) + 0,5 • (0 м / с / с) • (0,3499 с) ²

Поскольку второй член в правой части уравнения сводится к 0, уравнение можно упростить до

x = (2,4 м / с) • (0,3499 с)

Таким образом,

x = 0,84 м (округлено от 0,8398 м)

Ответ на поставленную проблему заключается в том, что мяч для пула находится в воздухе в течение 0,35 секунды и приземляется на горизонтальном расстоянии 0.84 м от края бильярдного стола.

Следующая процедура резюмирует описанный выше подход к решению проблем.

1. Внимательно прочтите проблему и перечислите известную и неизвестную информацию в терминах символов кинематических уравнений. Для удобства сделайте таблицу с горизонтальной информацией с одной стороны и вертикальной информацией с другой стороны.
2. Укажите неизвестное количество, для устранения которого требуется проблема.
3. Выберите горизонтальное или вертикальное уравнение для определения времени полета снаряда.
4. Определив время, используйте одно из других уравнений, чтобы найти неизвестное. (Обычно, если для определения времени используется горизонтальное уравнение, то для определения окончательной неизвестной величины можно использовать вертикальное уравнение.)

Одно предупреждение. Использование только четырех- и пятиэтапных процедур для решения физических задач – всегда опасный подход. Проблемы физики обычно просто проблемы! Хотя проблемы часто можно упростить, используя короткие процедуры, подобные описанной выше, не все проблемы можно решить с помощью описанной выше процедуры.Хотя шаги 1 и 2, указанные выше, имеют решающее значение для вашего успеха в решении проблем с снарядами, запускаемыми горизонтально, всегда будет проблема, которая не подходит для формы . Решение проблем – это не приготовление пищи; это не просто следование рецепту. Скорее, решение проблем требует внимательного чтения, твердого понимания концептуальной физики, критического мышления и анализа и большого количества дисциплинированной практики. Никогда не отделяйте концептуальное понимание и критическое мышление от своего подхода к решению проблем.

Проверьте свое понимание

Футбольный мяч отбрасывается горизонтально с холма высотой 22 метра и приземляется на расстоянии 35 метров от края холма. Определите начальную горизонтальную скорость футбольного мяча.

Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно.Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо Turd the Target Interactive, либо нашего симулятора движения снаряда. Вы можете найти их обоих в разделе Physics Interactives на нашем веб-сайте. В игре Turd the Target Interactive учащиеся пытаются помешать Birdman решить школьное футбольное поле, точно решая задачу с горизонтально запущенным снарядом.Симулятор движения снаряда позволяет учащемуся изучать концепции движения снаряда в интерактивном режиме. Измените высоту, измените угол, измените скорость и запустите снаряд.

Негоризонтально запущенные проблемы снарядов

В предыдущей части Урока 2 было представлено и продемонстрировано использование кинематических уравнений для решения задач о снарядах. Эти уравнения использовались для решения задач, связанных с запуском снарядов в горизонтальном направлении с высоты.В этом разделе Урока 2 будет продемонстрировано использование кинематических уравнений для решения не горизонтально запускаемых снарядов. Снаряд, запускаемый негоризонтально, – это снаряд, который начинает свое движение с начальной скоростью, которая является как горизонтальной, так и вертикальной. Чтобы решить такие проблемы, те же принципы, которые обсуждались ранее в Уроке 2, должны быть объединены с кинематическими уравнениями для движения снаряда. Как вы могли вспомнить ранее, существует два набора кинематических уравнений – набор уравнений для горизонтальных компонентов движения и аналогичный набор для вертикальных компонентов движения.Для горизонтальных составляющих движения уравнения:

x = v _{i x} • t + 0,5 * a _x * t ²

v _{f x} = v _{i x} + a _x • t

v _{f x} ² = v _{i x} ² + 2 * a _x • x

где	x = горизонт.смещение	a x = горизонт. разгон	t = время
	v f x = конечный горизонт. скорость	v i x = начальный горизонт. скорость

Из этих трех уравнений чаще всего используется верхнее уравнение.Два других уравнения используются редко (если вообще когда-либо). Применение концепции снаряда к каждому из этих уравнений также привело бы к заключению, что любой член с _x в нем будет сокращаться из уравнения, поскольку _x = 0 м / с / с.

Для вертикальных составляющих движения три уравнения:

y = v _iy • t + 0,5 * ay * t ²

v _fy = v _iy + ay • t

v _fy ² = v _iy ² + 2 * ay • y

где	y = верт.смещение	ау = верт. разгон	t = время
	v fy = финальная верт. скорость	v iy = начальная верт. скорость

В каждом из приведенных выше уравнений вертикальное ускорение снаряда составляет -9,8 м / с / с (ускорение свободного падения).

Как обсуждалось ранее в Уроке 2, значения v _ix и v _iy в каждом из приведенных выше наборов кинематических уравнений можно определить с помощью тригонометрических функций. Начальная скорость по оси x (v _ix ) может быть найдена с помощью уравнения v _ix = v _i • косинус (Theta), где Theta – это угол, который вектор скорости образует с горизонталью. Начальная скорость по оси y (v _iy ) может быть найдена с помощью уравнения v _iy = v _i • sine (Theta), где Theta – это угол, который вектор скорости образует с горизонталью.Тема компонент вектора скорости обсуждалась ранее в Уроке 2.

Чтобы проиллюстрировать полезность приведенных выше уравнений при прогнозировании движения снаряда, рассмотрим их использование при решении следующей задачи.

Пример Футбольный мяч бьет ногой с начальной скоростью 25 м / с под углом 45 градусов к горизонтали.Определите время полета, горизонтальное смещение и максимальную высоту футбольного мяча.

Решение любой задачи о снаряде, выпущенном не по горизонтали (в котором даны v _, и Theta), должно начинаться с разделения начальной скорости на горизонтальную и вертикальную составляющие с использованием тригонометрических функций, описанных выше. Таким образом,

Горизонтальный компонент	Вертикальный Компонент
v ix = v i • cos (тета) v ix = 25 м / с • cos (45 градусов) v ix = 17.7 м / с	v iy = v i • sin (Theta) v iy = 25 м / с • sin (45 градусов) v iy = 17,7 м / с

В этом случае случается, что значения v _ix и v _iy совпадают, как всегда, когда угол составляет 45 градусов.

Решение продолжается объявлением значений известной информации в терминах символов кинематических уравнений – x, y, v _ix , v _iy , a _x , a _y и t.В этом случае в формулировке проблемы явно или подразумевается следующая информация:

Информация по горизонтали	Вертикальная информация
х = ??? v ix = 17,7 м / с v FX = 17,7 м / с a x = 0 м / с / с	y = ??? v iy = 17.7 м / с v fy = -17,7 м / с a y = -9,8 м / с / с

Как указано в таблице, конечная x-скорость (v _fx ) такая же, как начальная x-скорость (v _ix ). Это связано с тем, что горизонтальная скорость снаряда постоянна; нет горизонтального ускорения. Таблица также показывает, что конечная y-скорость (v _fy ) имеет ту же величину и противоположное направление, что и начальная y-скорость (v _iy ).Это связано с симметричным характером траектории снаряда.

Неизвестными величинами являются горизонтальное смещение, время полета и высота футбольного мяча на пике. Решение проблемы теперь требует выбора соответствующей стратегии использования кинематических уравнений и известной информации для решения неизвестных величин. Существует множество возможных стратегий решения проблемы. Организованный список известных количеств в двух столбцах таблицы дает подсказки для выбора полезной стратегии.

Из информации по вертикали в таблице выше и второго уравнения, указанного среди уравнений вертикальной кинематики (v _fy = v _iy + a _y * t), становится очевидным, что время полета снаряда может определяется. Путем подстановки известных значений уравнение принимает вид

-17,7 м / с = 17,7 м / с + (-9,8 м / с / с) • t

Проблема физики теперь принимает форму проблемы алгебры.Вычитая 17,7 м / с из каждой части уравнения, уравнение принимает вид

. -35,4 м / с = (-9,8 м / с / с) • t

Если обе части уравнения разделить на -9,8 м / с / с, уравнение станет

3,61 с = т

(округлено от 3,6077 с)

Общее время полета футбольного мяча 3,61 секунды.

После определения времени информация в таблице и уравнения горизонтальной кинематики могут использоваться для определения горизонтального смещения (x) снаряда.Первое уравнение (x = v _ix • t + 0,5 • a _x • t ² ), перечисленное среди горизонтальных кинематических уравнений, подходит для определения x. После выбора уравнения физическая проблема снова превращается в проблему алгебры. Путем подстановки известных значений уравнение принимает вид

x = (17,7 м / с) • (3,6077 с) + 0,5 • (0 м / с / с) • (3,6077 с) ²

Поскольку второй член в правой части уравнения сводится к 0, уравнение можно упростить до

х = (17.7 м / с) • (3,6077 с)

Таким образом,

x = 63,8 м

Горизонтальное смещение снаряда 63,8 м.

Наконец, в постановке задачи задается максимальная высота снаряда. Это то же самое, что спросить: «Каково вертикальное смещение (y) снаряда, когда он проходит половину своей траектории?» Другими словами, найдите y, когда t = 1,80 секунды (половина общего времени). Для определения максимальной высоты снаряда (y при t = 1.80 секунд), можно использовать первое уравнение (y = v _iy • t + 0,5 • a _y • t ² ), указанное среди вертикальных кинематических уравнений. Подставив известные значения в это уравнение, оно принимает вид

y = (17,7 м / с) • (1,80 с) + 0,5 * (- 10 м / с / с) • (1,80 с) ²

С помощью калькулятора это уравнение можно упростить до

y = 31,9 м + (-15,9 м)

И, таким образом,

y = 15,9 м

Решение задачи дает следующие ответы: время полета футбольного мяча равно 3.61 с, горизонтальное перемещение футбольного мяча составляет 63,8 м, а максимальная высота футбольного мяча – 15,9 м.

(Обратите внимание, что во всех выполненных выше расчетах использовались неокругленные числа. Числа, указанные на предварительных этапах и в окончательном ответе, были округленной формой фактических неокругленных значений.)

Типичный подход к решению проблем

Следующая процедура резюмирует описанный выше подход к решению проблем.

1. Используйте заданные значения начальной скорости (величина и угол) для определения горизонтальной и вертикальной составляющих скорости (v _ix и v _iy ).
2. Внимательно прочтите проблему и перечислите известную и неизвестную информацию в терминах символов кинематических уравнений. Для удобства сделайте таблицу с горизонтальной информацией с одной стороны и вертикальной информацией с другой стороны.
3. Укажите неизвестное количество, для устранения которого требуется проблема.
4. Выберите горизонтальное или вертикальное уравнение для определения времени полета снаряда. Для снарядов, запускаемых не горизонтально, второе уравнение, указанное среди вертикальных уравнений (v _fy = v _iy + a _y * t), обычно является наиболее полезным уравнением.
5. Определив время, используйте горизонтальное уравнение (обычно x = v _ix * t + 0,5 * a _x * t ² ), чтобы определить горизонтальное смещение снаряда.
6. Наконец, максимальная высота снаряда может быть найдена с использованием значения времени, которое составляет половину общего времени полета. Наиболее полезным уравнением для этого обычно является y = v _iy * t + 0,5 * a _y * t ² .

Одно предостережение: полагаться только на 4- и 5-ступенчатые процедуры для решения физических задач всегда опасно. Проблемы физики обычно просто проблемы! И проблемы часто можно упростить, используя короткие процедуры, подобные описанной выше.Однако не все проблемы можно решить с помощью описанной выше процедуры. Хотя шаги 1, 2 и 3, указанные выше, имеют решающее значение для вашего успеха в решении проблем со снарядами, запускаемыми негоризонтально, всегда будет проблема, которая «не соответствует форме». Решение проблем – это не приготовление пищи; это не просто следование рецепту. Скорее, решение проблем требует внимательного чтения, твердого понимания концептуальной физики, критического мышления и анализа и большого количества дисциплинированной практики. Никогда не отделяйте концептуальное понимание и критическое мышление от своего подхода к решению проблем.

Ваша очередь попробовать! Используйте виджет Range of an Angle-Launched Projectile , чтобы отработать задачу со снарядом (или двумя) (или тремя). Используя заданные скорость запуска и угол запуска, определите ожидаемое горизонтальное смещение (d _x ). После завершения расчета нажмите кнопку Отправить , чтобы проверить свой ответ.

Проверьте свое понимание

Прыгун в длину отрывается от земли с начальной скоростью 12 м / с под углом 28 градусов относительно горизонтали.Определите время полета, горизонтальное расстояние и максимальную высоту прыгуна в длину.

Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо Turd the Target 2 Interactive, либо нашего симулятора движения снаряда.Вы можете найти их обоих в разделе Physics Interactives на нашем веб-сайте. В интерактивном режиме Turd the Target 2 учащиеся пытаются предотвратить столкновение Birdman с школьным футбольным полем, точно решая задачу о снаряде, выпущенном под углом. Симулятор движения снаряда позволяет учащемуся изучать концепции движения снаряда в интерактивном режиме. Измените высоту, измените угол, измените скорость и запустите снаряд.

Физика – Интерференция – Бирмингемский университет

В 1672 году Исаак Ньютон опубликовал свою теорию о том, что свет состоит из частиц материи, но в 1678 году Христиан Гюйгенс утверждал, что опровергает Ньютона доказательствами того, что свет на самом деле был волной.Только после открытия квантовой физики около 100 лет назад мы начали точно определять, что такое свет.

Так свет – это волна или частица?

В 1801 году Томас Янг провел очень простой эксперимент, чтобы определить это. Используя источник видимого света, он сначала сделал свет когерентным, сначала пропустив его через одинарную щель, а затем через двойную щель. Таким образом, он успешно продемонстрировал волновую природу света – поскольку полученная интерференционная картина может быть объяснена принципом суперпозиции и .Волны, выходящие из любой щели, рекомбинируют либо конструктивно (создавая пики света), либо деструктивно (создавая впадины).

Используя только лазер и двойную щель, мы можем воспроизвести эксперимент Юнга с двойной щелью, поскольку лазер уже является источником когерентного света.

Как воспроизвести эксперимент Юнга со щелью?

Как мы можем воссоздать эксперимент Юнга со щелью?

Как получить наилучшие измерения?

Помните, что точность и аккуратность – разные вещи.В лабораторных условиях точность – это разница между вашим измерением и истинным значением, тогда как точность описывает изменение вашего измерения при повторных измерениях одного и того же значения. Для точных измерений важно использовать прибор с наименьшей шкалой – микрометр даст вам значение, более близкое к истинной длине, чем метрическая линейка. Однако, если вы попытаетесь измерить расстояние в десятки или сотни сантиметров с помощью микрометра, ваш инструмент будет неточным – каждый раз, когда вы измеряете это расстояние, вы будете получать совершенно разные показания.Это означает, что обычно существует компромисс между точностью и точностью при попытке получить наилучшие измерения.

Очень точные инструменты, такие как микрометры и штангенциркуль, полезны на небольших расстояниях, но они имеют разные действия и могут быть более или менее точными в зависимости от их конструкции. Например, микрометр, который Мэгги использует на картинке, очень хорош для измерения размеров объектов, которые помещаются в ее челюсти, например, диаметра проволоки. Однако они намного менее точны, если их использовать для измерения расстояния между чем-то вроде интерференционных пиков в эксперименте Юнга со щелью – вам следует подумать о том, насколько точно вы записываете свои показания соответственно.

Все переменные в этом эксперименте – это расстояния, и поэтому источники ошибок сводятся к нашей способности точно и точно измерить эти расстояния. Чтобы ваши результаты были максимально надежными, должно быть ясно, что выбор прибора соответствует требуемому диапазону измерений. При измерении длины волны света повторение эксперимента несколько раз для различных расстояний между прорезями и экраном, а также диапазон расстояний между прорезями должны дать вам более надежный набор результатов.Не забудьте также сделать повторные измерения и вычислить среднее значение. Повторные измерения важны даже для очень опытных исследователей-экспериментаторов, поскольку они не только улучшают точность и точность результата, но также демонстрируют, что эксперимент можно воспроизвести.

Что мы можем узнать из эксперимента Янга?

Эксперимент Юнга демонстрирует волновую природу света, поскольку полученную интерференционную картину нельзя легко объяснить, если бы свет был только подобен частицам.Теперь мы знаем, что узор, созданный наложением световых волн, может использоваться либо для определения длины волны света, когда длина / расстояния известны, либо для определения размера небольших разделений, когда длина волны известна. Ключевое уравнение в этом расчете: λ, = осей / D , где λ – длина волны света, a – расстояние между щелями, x – расстояние между полосами и D, – расстояние. между щелью и экраном, всего метра .

Результаты щелевого эксперимента Янга по-прежнему лежат в основе многих физических исследований, проводимых сегодня в университетах, в которых используется свет и другие виды электромагнитного излучения. В последнее время при обнаружении гравитационных волн наше понимание света используется для обнаружения интерференции лазерного луча, когда гравитационная волна проходит через детектор. Лазерные лучи в детекторах лазерной интерферометрической обсерватории гравитационных волн (LIGO) распространяются на расстояние 4 км, но проходящая гравитационная волна вызовет возмущение, намного меньшее, чем размер атома! Так что в этом случае убедиться, что измерение расстояния является точным и точным, является довольно сложной задачей.

Первоначальный эксперимент Юнга со щелью подтвердил первоначальную идею Гюйгенса о свете как о волне, однако можно сделать еще один шаг, чтобы показать дуальность света волна / частица. Если вы повторите этот эксперимент с источником света, который испускает одиночные фотоны света, постепенно нарастает та же интерференционная картина, даже если детекторы показывают, что только одиночный фотон проходит через ту или иную щель в любой момент времени. Для этого требуется, чтобы фотон находился в состоянии квантовой суперпозиции , и эксперимент с двойной щелью является непосредственно наблюдаемым примером этого явления – вы, возможно, знакомы с концепцией суперпозиции из мысленного эксперимента Эрвина Шредингера, обычно называемого « Кот Шредингера ».

Следующие шаги

Эти ссылки предоставляются только для удобства и в информационных целях; они не означают одобрения или одобрения Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте. Бирмингемский университет не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок. Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы относительно его содержания.

% PDF-1.3 % 63 0 объект > эндобдж xref 63 83 0000000016 00000 н. 0000002008 00000 н. 0000002589 00000 н. 0000002801 00000 п. 0000003111 00000 п. 0000003329 00000 н. 0000003554 00000 н. 0000004041 00000 н. 0000004565 00000 н. 0000004605 00000 н. 0000004626 00000 н. 0000005282 00000 н. 0000005691 00000 п. 0000005950 00000 н. 0000006426 00000 н. 0000006633 00000 н. 0000008724 00000 н. 0000009064 00000 н. 0000009291 00000 п. 0000009312 00000 п. 0000010125 00000 п. 0000010295 00000 п. 0000010520 00000 п. 0000010599 00000 п. 0000011142 00000 п. 0000011163 00000 п. 0000011744 00000 п. 0000011914 00000 п. 0000011996 00000 п. 0000012225 00000 п. 0000012448 00000 п. 0000012618 00000 п. 0000012847 00000 п. 0000013070 00000 п. 0000013293 00000 п. 0000013522 00000 п. 0000013604 00000 п. 0000013686 00000 п. 0000013857 00000 п. 0000013879 00000 п. 0000014599 00000 п. 0000014682 00000 п.