Персональный сайт – Закон сохранения механической энергии
Рассмотрим пример проявления этого закона. Пусть тело, поднятое над Землей, обладает потенциальной энергией Е1 = mgh1 и скоростью v1 направленной вниз. В результате свободного падения тело переместилось в точку с высотой h2 (E2 = mgh2), при этом скорость его возросла от v1 до v2. Следовательно, его кинетическая энергия возросла от
Запишем уравнение кинематики:
Умножим обе части равенства на mg, получим:
mgh1 – mgh2 = A = mv22/2 – mv12/2
После преобразования получим:
mgh1 + mv12/2 = A = mv22/2 + mgh2
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости. Рис. 1.20.1 поясняет решение этой задачи.
Рисунок 1.20.1.
– сила натяжения нити в нижней точке траектории
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
Обратим внимание на то, что сила натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.
При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:
Из этих соотношений следует:
v12min = 5gl |
Центростремительное ускорение в нижней точке создается силами и mg направленными в противоположные стороны:
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
F = 6mg. |
Прочность нити должна, очевидно, превышать это значение.
Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.
Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
Потенциальная энергия. | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Потенциальная энергия.
| Потенциальная энергия. | |
Потенциальная энергия – энергия взаимодействия тел или частей тела.Потенциальная энергия (от латинского potentia – возможность) определяется взаимным расположением тел или частей тела, т.е. расстояниями между ними. |
|
Потенциальная энергия тела, поднятого над Землей. Работа силы тяжести. | |
Пусть тело свободно падает с высоты h1 над уровнем Земли на уровень h2. Тогда: При падении сила тяжести совершает положительную работу, при движении тела вверх – отрицательную. Величину Eз = mgh называют потенциальной энергией взаимодействия тела и Земли. | |
Т.о. A = – (Ep2 – Ep1) = –ΔEp Работа сила тяжести равна изменению потенциальной энергии, взятому с противоположным знаком. Т.е., если потенциальная энергия увеличивается (тело поднимается), то сила тяжести совершает отрицательную работу и наоборот. | Eз = mgh
A = – (Ep2 – Ep1) = –ΔEp |
Т. |
|
Если тело движется под углом к направлению вектора силы тяжести, то, как видно из рисунка, работа силы тяжести независимо от траектории определяется изменением положения тела (на рис. – высотой наклонной плоскости h). Если тело движется по произвольной траектории, то ее можно представить в виде суммы горизонтальных участков, на которых работа силы тяжести равна нулю, и вертикальных, на которых суммарная работа будет равна А=mgh. Работа силы тяжести не зависит от формы траектории и определяется только начальным и конечным положением тела. На замкнутой траектории работа силы тяжести равна нулю, | |
Потенциальная энергия тел, взаимодействующих посредством гравитационных сил. | |
, где r- расстояние между взаимодействующими телами. Знак “-” говорит о том, что это энергия притягивающихся тел. При сближении тел потенциальная энергия увеличивается по модулю. Работа по сближению двух астрономических объектов: . | |
Потенциальная энергия упруго деформированного тела. Работа силы упругости. | |
Для вывода формулы используем, что работа численной равна площади под графиком зависимости силы от координаты. При малых упругих деформациях сила упругости прямо пропорциональна абсолютной деформации (з-н Гука) – см. рис. Тогда работа при изменении деформации от х1 до х2 равна: .
| |
Т.о., если принять за потенциальную энергию упруго деформированного тела величину ,
где k – коэффициент жесткости, а х – абсолютная деформация тела, то можно сделать вывод , что , т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком. |
|
Работа силы упругости зависит только от координат (начальной и конечной деформаций) тела и, следовательно, не зависит от траектории. Работа по замкнутой траектории равна нулю. |
|
Консервативные силы. Консервативными (сохраняющими) наз. |
|
Диссипативные силы Диссипативными (рассеивающими) наз. силы, работа которых зависит от траектории и по замкнутой траектории не равна нулю (такие силы зависят от скорости). Пример: сила трения. |
|
Теги:
конспект
7.3 Гравитационная потенциальная энергия – биомеханика движения человека
Резюме
- Объясните гравитационную потенциальную энергию с точки зрения работы, совершаемой против силы тяжести.
- Покажите, что гравитационная потенциальная энергия объекта массой м на высоте ч на Земле равна PE г = mgh .
- Покажите, как знание потенциальной энергии в зависимости от положения можно использовать для упрощения вычислений и объяснения физических явлений.

Подъем по лестнице и подъем предметов — это работа как в научном, так и в повседневном смысле — это работа, совершаемая против силы гравитации. Когда есть работа, есть преобразование энергии. Работа, совершаемая против силы гравитации, превращается в важную форму накопленной энергии, которую мы рассмотрим в этом разделе.
Рассчитаем работу, совершаемую при подъеме объекта массой м на высоту h , как показано на рисунке 1. Если объект поднимается прямо вверх с постоянной скоростью, то сила, необходимая для подъема он равен его весу мг . Тогда работа над массой равна  Для удобства мы обозначаем это как PE g , полученное объектом, признавая, что это энергия, хранящаяся в гравитационном поле Земли. Почему мы используем слово «система»? Потенциальная энергия является свойством системы, а не отдельного объекта из-за его физического положения. Гравитационный потенциал объекта обусловлен его положением относительно окружающей среды в системе Земля-объект. Сила, приложенная к объекту, является внешней силой, находящейся вне системы. Когда он совершает положительную работу, он увеличивает гравитационную потенциальную энергию системы. Поскольку потенциальная энергия гравитации зависит от относительного положения, нам нужен опорный уровень, на котором можно установить потенциальную энергию равной 0. Мы обычно выбираем эту точку как поверхность Земли, но эта точка произвольна; главное
Для удобства мы обозначаем это как PE g , полученное объектом, признавая, что это энергия, хранящаяся в гравитационном поле Земли. Почему мы используем слово «система»? Потенциальная энергия является свойством системы, а не отдельного объекта из-за его физического положения. Гравитационный потенциал объекта обусловлен его положением относительно окружающей среды в системе Земля-объект. Сила, приложенная к объекту, является внешней силой, находящейся вне системы. Когда он совершает положительную работу, он увеличивает гравитационную потенциальную энергию системы. Поскольку потенциальная энергия гравитации зависит от относительного положения, нам нужен опорный уровень, на котором можно установить потенциальную энергию равной 0. Мы обычно выбираем эту точку как поверхность Земли, но эта точка произвольна; главное 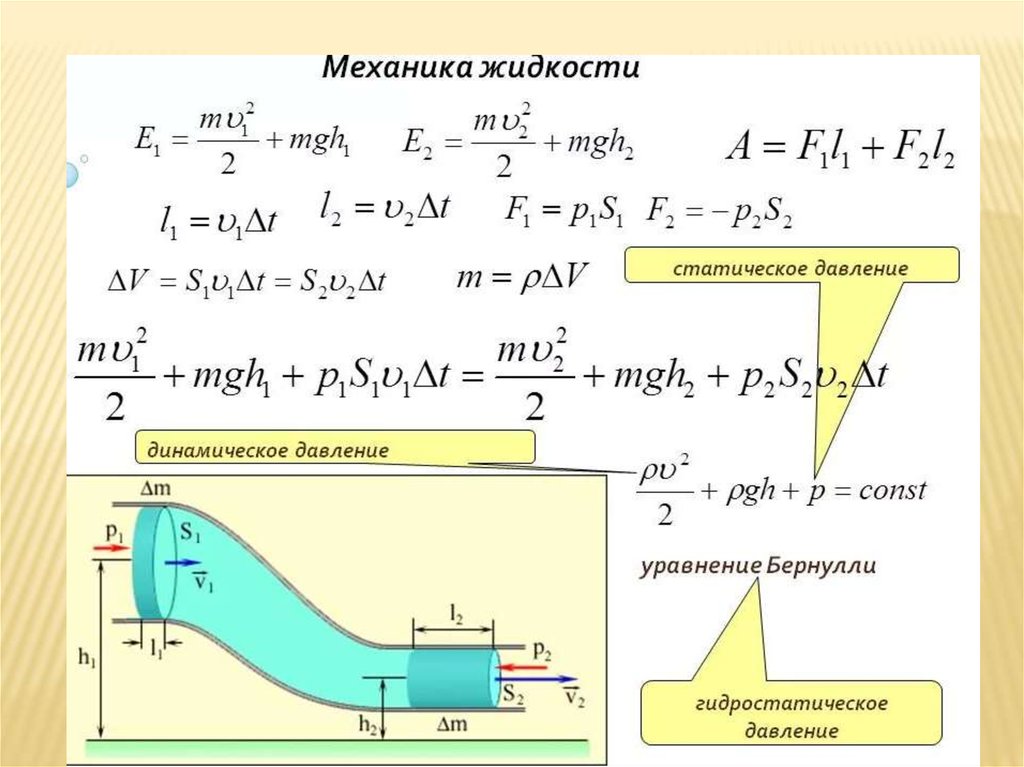
Гравитационная потенциальная энергия может быть преобразована в другие формы энергии, такие как кинетическая энергия. Если мы отпустим массу, гравитационная сила совершит работу, равную mgh на него, тем самым увеличив его кинетическую энергию на ту же величину (по теореме о работе-энергии). Мы найдем более полезным рассмотреть просто преобразование PE g в KE без явного рассмотрения промежуточного шага работы. (См. пример 2.) Этот ярлык упрощает решение задач с использованием энергии (если это возможно), а не с явным использованием сил.
Точнее, мы определяем изменение гравитационной потенциальной энергии ΔPE g как
[латекс]\boldsymbol{\Delta\textbf{PE}_{\textbf{g}}=mgh,}[/latex]
где для простоты мы обозначаем изменение высоты как h вместо обычного Δ h .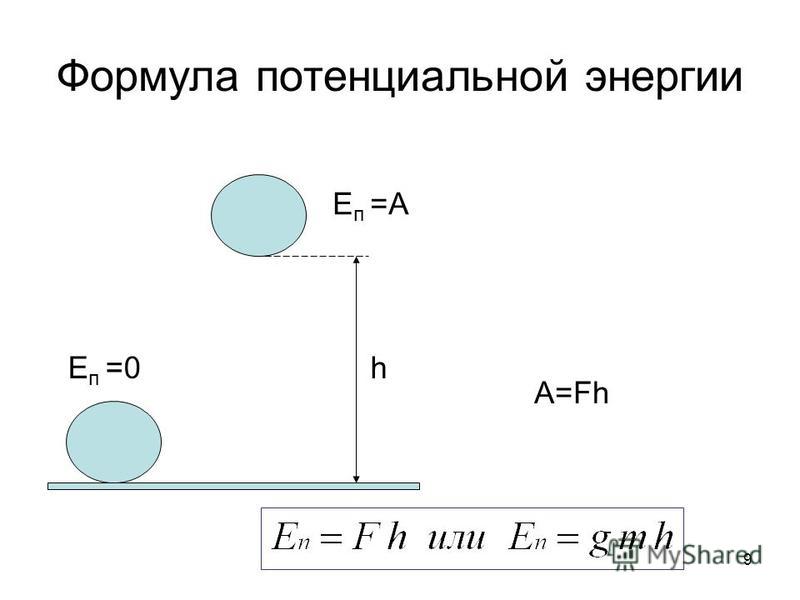 Обратите внимание, что h положительно, когда конечная высота больше начальной, и наоборот. Например, если груз массой 0,500 кг, подвешенный к часам с кукушкой, поднять на 1,00 м, то его изменение потенциальной энергии гравитации составит 92=4.90\textbf{ J.}} \end{массив}[/latex]
Обратите внимание, что h положительно, когда конечная высота больше начальной, и наоборот. Например, если груз массой 0,500 кг, подвешенный к часам с кукушкой, поднять на 1,00 м, то его изменение потенциальной энергии гравитации составит 92=4.90\textbf{ J.}} \end{массив}[/latex]
Обратите внимание, что единицами гравитационной потенциальной энергии оказались джоули, такие же, как для работы и других форм энергии. По мере хода часов масса опускается. Мы можем думать о массе как о постепенном отказе от своих 4,90 Дж гравитационной потенциальной энергии без непосредственного учета силы гравитации, совершающей работу .
Уравнение ΔPE g = mgh применимо для любого пути с изменением высоты на h , а не только когда груз поднимают прямо вверх. (См. рис. 2.) Гораздо проще вычислить mgh (простое умножение), чем вычислить работу, выполненную на сложном пути. Идея гравитационной потенциальной энергии имеет двойное преимущество: она очень широко применима и упрощает расчеты. С этого момента будем считать, что любое изменение вертикального положения h массы m сопровождается изменением потенциальной энергии гравитации mgh , и мы избежим эквивалентной, но более сложной задачи вычисления работы, совершаемой силами гравитации или против них.
Идея гравитационной потенциальной энергии имеет двойное преимущество: она очень широко применима и упрощает расчеты. С этого момента будем считать, что любое изменение вертикального положения h массы m сопровождается изменением потенциальной энергии гравитации mgh , и мы избежим эквивалентной, но более сложной задачи вычисления работы, совершаемой силами гравитации или против них.
Пример 1: Сила, препятствующая падению
Человек массой 60,0 кг прыгает на пол с высоты 3,00 м. Если он туго приземляется (со сжатием коленных суставов на 0,500 см), рассчитайте силу, действующую на коленные суставы.
Если он туго приземляется (со сжатием коленных суставов на 0,500 см), рассчитайте силу, действующую на коленные суставы.
Стратегия
Энергия этого человека в этой ситуации сводится к нулю из-за работы, проделанной над ним полом, когда он останавливается. Начальный PE g трансформируется в KE при падении. Работа, совершаемая полом, сводит эту кинетическую энергию к нулю.
Решение
Работа, совершаемая полом над человеком, когда он останавливается, равна
[латекс]\boldsymbol{W=Fd\:\textbf{cos}\:\theta=-Fd},[ /латекс]
со знаком минус, потому что смещение при остановке и сила от пола направлены в противоположные стороны ( cos θ = cos 180° = 1 ). Пол забирает энергию из системы, поэтому совершает отрицательную работу.
Кинетическая энергия, которой обладает человек при достижении пола, представляет собой количество потенциальной энергии, потерянной при падении с высоты h :
[латекс]\boldsymbol{\textbf{KE}=-\Delta\textbf{PE}_{\textbf{g}}=-mgh,}[/latex]
Расстояние d того, что колени человека сгибаются, намного меньше, чем высота h падения, поэтому дополнительное изменение гравитационной потенциальной энергии при сгибании колена игнорируется.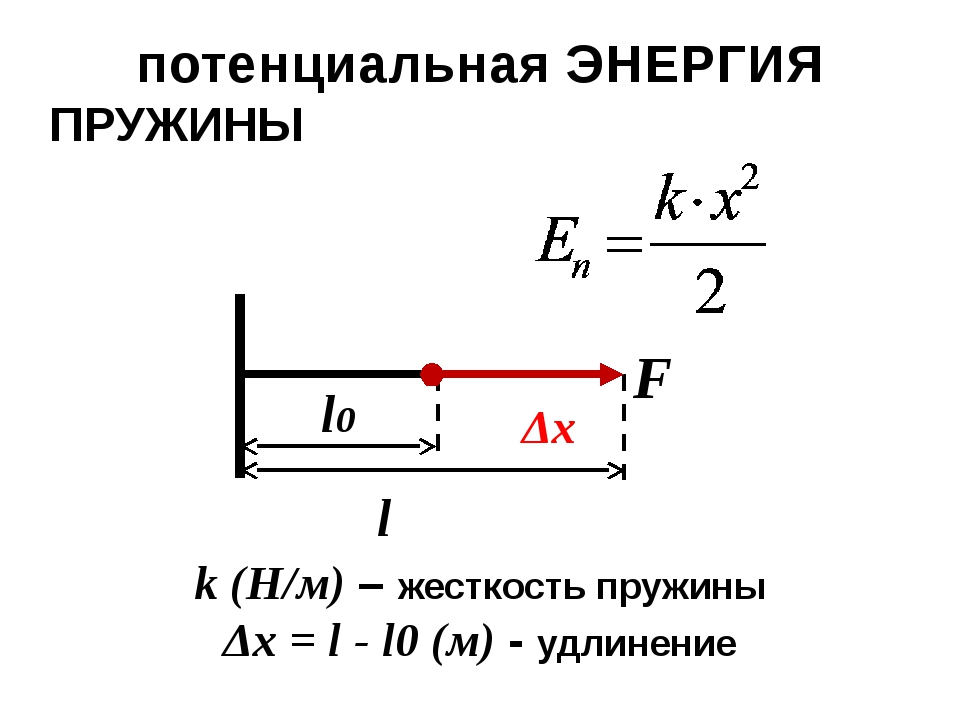
Работа Вт , совершаемая полом на человеке, останавливает человека и сводит кинетическую энергию человека к нулю: 95\textbf{ N.}}[/latex]
Обсуждение
Такой большой силы (в 500 раз превышающей вес человека) за короткое время удара достаточно, чтобы сломать кости. Гораздо лучший способ смягчить удар — согнуть ноги или покататься по земле, увеличивая время действия силы. Таким образом, изгибающее движение на 0,5 м дает силу в 100 раз меньшую, чем в примере. Прыжки кенгуру демонстрируют этот метод в действии. Кенгуру — единственное крупное животное, использующее прыжки для передвижения, но шок при прыжках смягчается сгибанием задних ног при каждом прыжке (см. рис. 3).
Рисунок 3. Работа, совершаемая землей над кенгуру, уменьшает его кинетическую энергию до нуля, когда он приземляется. Однако за счет приложения силы земли к задним ногам на более длинном расстоянии воздействие на кости уменьшается.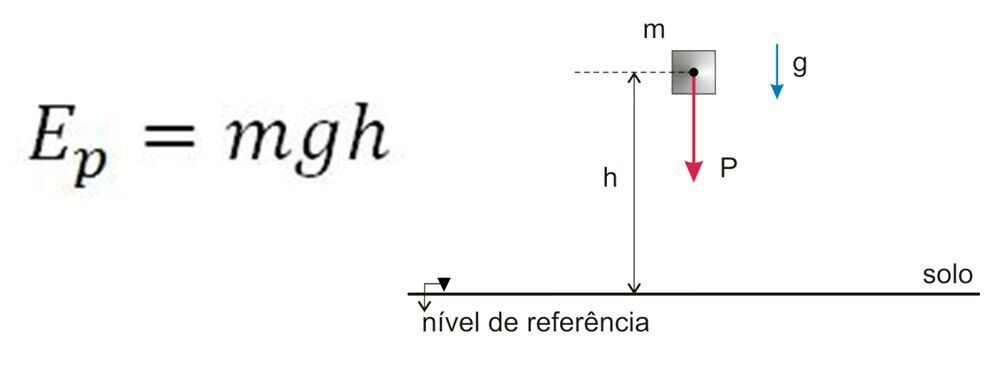 (кредит: Крис Самуэль, Flickr)
(кредит: Крис Самуэль, Flickr)Пример 2: определение скорости американских горок по их высоте
(a) Какова конечная скорость американских горок, показанных на рисунке 4, если они стартуют из состояния покоя в верхней части Холм высотой 20 м и работа сил трения пренебрежимо мала? б) Какова его конечная скорость (опять же в предположении пренебрежимо малого трения), если его начальная скорость равна 5,00 м/с?
Рисунок 4. Скорость американских горок увеличивается по мере того, как гравитация тянет их вниз по склону, и достигает наибольшего значения в самой нижней точке. С точки зрения энергии потенциальная гравитационная энергия системы «американские горки-Земля» преобразуется в кинетическую энергию. Если работа трения незначительна, все ΔPE g преобразуются в KE .Стратегия
Американские горки теряют потенциальную энергию при спуске. Мы пренебрегаем трением, так что оставшаяся сила, действующая на гусеницу, является нормальной силой, которая перпендикулярна направлению движения и не совершает работы. 2}.[/ латекс] Уравнение изменения потенциальной энергии утверждает, что 92}.[/latex]
2}.[/ латекс] Уравнение изменения потенциальной энергии утверждает, что 92}.[/latex]
Решая для v , мы находим, что масса сокращается и что
[latex]\boldsymbol{v=\sqrt{2g|h|}}.[/latex]
Подставляя известные значения,
[латекс]\begin{array}{lcl} \boldsymbol{v} & \boldsymbol{=} & \boldsymbol{\sqrt{2(9.80\textbf{ м/с})(20.0\textbf { m})}} \\ {} & \boldsymbol{=} & \boldsymbol{19.8\textbf{ м/с.}} \end{array}[/latex]
Решение для (b)
Снова -ΔPE г 92}} \\ {} & \boldsymbol{=} & \boldsymbol{20.4\textbf{ м/с.}} \end{array}[/latex]
Обсуждение и последствия
Во-первых, обратите внимание, что масса отменяет. Это вполне согласуется с наблюдениями, сделанными в главе 2.7 «Падающие предметы», о том, что все объекты падают с одинаковой скоростью, если трением можно пренебречь. Во-вторых, учитывается только скорость американских горок; нет информации о его направлении ни в одной точке.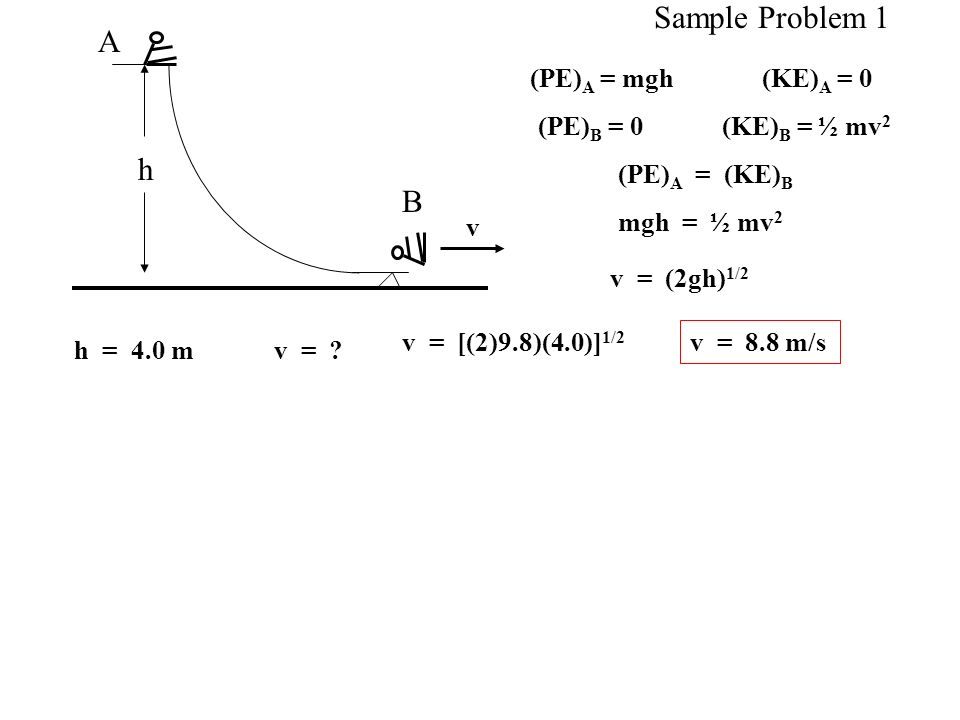 Это раскрывает еще одну общую истину. Когда трением можно пренебречь, скорость падающего тела зависит только от его начальной скорости и высоты, а не от его массы или пройденного пути. Например, американские горки будут иметь одинаковую конечную скорость независимо от того, падают ли они с высоты 20,0 м прямо вниз или движутся по более сложной траектории, как показано на рисунке. В-третьих, и, возможно, неожиданно, конечная скорость в части (b) больше, чем в части (а), но намного меньше, чем 5,00 м/с. Наконец, обратите внимание, что скорость можно найти в любую высоту по пути, просто используя соответствующее значение h в точке интереса.
Это раскрывает еще одну общую истину. Когда трением можно пренебречь, скорость падающего тела зависит только от его начальной скорости и высоты, а не от его массы или пройденного пути. Например, американские горки будут иметь одинаковую конечную скорость независимо от того, падают ли они с высоты 20,0 м прямо вниз или движутся по более сложной траектории, как показано на рисунке. В-третьих, и, возможно, неожиданно, конечная скорость в части (b) больше, чем в части (а), но намного меньше, чем 5,00 м/с. Наконец, обратите внимание, что скорость можно найти в любую высоту по пути, просто используя соответствующее значение h в точке интереса.
Мы видели, что работа, совершаемая силой гравитации или против нее, зависит только от начальной и конечной точек, а не от пути между ними, что позволяет нам определить упрощающую концепцию гравитационной потенциальной энергии. Мы можем сделать то же самое для некоторых других сил, и мы увидим, что это приводит к формальному определению закона сохранения энергии.
УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: ВЫНОСНОЕ ИССЛЕДОВАНИЕ — ПРЕОБРАЗОВАНИЕ ПОТЕНЦИАЛА В КИНЕТИЧЕСКУЮ ЭНЕРГИЮ
В этом эксперименте можно изучить преобразование гравитационной потенциальной энергии в кинетическую. На гладкой ровной поверхности используйте линейку с желобком по всей длине и книгу, чтобы сделать наклон (см. рис. 5). Поместите шарик на расстоянии 10 см от линейки и дайте ему скатиться по линейке. Когда он упадет на ровную поверхность, измерьте время, за которое катится один метр. Теперь поместите шарик в положения 20 см и 30 см и снова измерьте время, необходимое для того, чтобы перекатить 1 м по ровной поверхности. Найдите скорость шарика на ровной поверхности во всех трех положениях. Постройте квадрат скорости в зависимости от расстояния, пройденного шариком. Какова форма каждого участка? Если форма представляет собой прямую линию, график показывает, что кинетическая энергия шарика на дне пропорциональна его потенциальной энергии в точке выброса.
Рис. 5. Шарик скатывается по линейке и измеряется его скорость на ровной поверхности.
5. Шарик скатывается по линейке и измеряется его скорость на ровной поверхности.- Работа, совершаемая против силы тяжести при подъеме объекта, становится потенциальной энергией системы объект-Земля.
- Изменение гравитационной потенциальной энергии, ΔPE г , равно ΔPEg = mgh , где ч является увеличением высоты и 901 g из-за ускорения силы тяжести.
- Гравитационная потенциальная энергия объекта у поверхности Земли обусловлена его положением в системе масса-Земля. Различия только в гравитационной потенциальной энергии, ΔPE g , имеют физическое значение.
- Когда объект опускается без трения, его гравитационная потенциальная энергия превращается в кинетическую энергию, соответствующую увеличению скорости, так что ΔKE = -ΔPE g .
- гравитационная потенциальная энергия
- энергия объекта из-за его положения в гравитационном поле
ньютонов гравитации – Потенциальная энергия $= mgh$, что такое $h$?
Это первый. Это действительно отличное наблюдение! Это увлекательный факт физики.
Это действительно отличное наблюдение! Это увлекательный факт физики.
Абсолютная потенциальная энергия – глупая идея. Если вы возьмете кучу разных объектов, перечислите их потенциальные энергии, а затем добавите к каждому из них по 100 долларов, ничего не изменится в поведении системы. Мы говорим только об относительной потенциальной энергии.
Кинетическая энергия, которую объект приобретает при падении с определенной высоты, равна потенциальной энергии, которую он теряет. Если мы позволим объекту упасть с $h_1$ на $h_2$, мы обнаружим, что изменение его кинетической энергии равно $\Delta KE = m g h_1 – m g h_2.$ Если мы добавим произвольное число $C$ к каждому из этих потенциалов энергий разница та же: $\Delta KE = (m g h_1 + C) – (m g h_2 + C) = m g h_1 – m g h_2.$
Мы часто используем высоту над землей, потому что это означает, что на уровне земли $PE = mgh = mg \cdot 0 = 0$ для всех объектов, а поскольку ничто не может быть ниже уровня земли в простой системе, это делает смысла говорить, что $0$ — это наименьшая возможная потенциальная энергия, которую можно достичь.
РЕДАКТИРОВАТЬ:
Чтобы добавить к этому, давайте рассмотрим еще немного математического формализма. Оказывается, в классической механике отсутствие «абсолютной потенциальной энергии» — это частный случай того, что называется калибровочная инвариантность .
Для простоты поговорим об одномерной системе — у нас есть шарик, который может двигаться вперед и назад только по одной линии. Пусть $x$ будет положением шара.
Пусть $U(x)$ — потенциальная энергия системы как функция положения шарика. Это может быть, например, простая гравитационная задача — $x$ — это высота мяча над землей, а $U(x) = m g x.$ Но для общности мы не будем указывать, в каком виде $U$ есть.
Мы скажем, что потенциальная энергия является результатом действия некоторой силы на объект. Мы знаем, что потенциальная энергия объекта в определенном положении, возникающая под действием данной силы, представляет собой работу, необходимую для того, чтобы привести этот объект в это положение. Таким образом, если на тело действует сила $F(x)$, потенциальная энергия в точке $x$ равна $U(x) = W = – \int F(x)\, dx$ (знак минус получается из тот факт, что мы должны работать в направлении, противоположном силе).
Таким образом, если на тело действует сила $F(x)$, потенциальная энергия в точке $x$ равна $U(x) = W = – \int F(x)\, dx$ (знак минус получается из тот факт, что мы должны работать в направлении, противоположном силе).
Итак, из основной теоремы исчисления, если $U(x) = – \int F(x)\, dx$, то
$F(x) = – \frac{d U(x)}{d x}.$
Хорошо, это интересно. В классической механике мы можем полностью описать движение системы, если знаем действующие на нее силы (так как тогда мы можем использовать закон Ньютона $F = ma$). Но поскольку мы знаем $F(x) = – \frac{d U(x)}{d x}$, мы можем полностью описать движение системы, зная потенциальную энергию.
Вот выигрыш:
Если силы одинаковы для двух различных функций потенциальной энергии, то эти функции потенциальной энергии приводят к одному и тому же физическому поведению.
Математически:
Если $U_1(x)$ и $U_2(x)$ — две функции потенциальной энергии такие, что $- \frac{d U_1(x)}{dx} = – \frac{d U_2(x) )}{dx}$, то функции потенциальной энергии приводят к такому же физическому поведению.
Что значит, если две функции имеют одну и ту же производную? Ну, значит, они отличаются на константу.
О! Вот куда мы хотели попасть, не так ли? Если две функции потенциальной энергии отличаются на константу, то они приводят к одному и тому же физическому поведению. Так что не имеет смысла говорить об «абсолютной потенциальной энергии», потому что независимо от того, что мы можем добавить любую постоянную, которую мы хотим, мы получим те же самые силы и, таким образом, то же самое физическое поведение.
Следовательно, имеет смысл говорить только об изменении потенциальной энергии, а не об абсолютной потенциальной энергии.
(ранее я говорил, что это пример калибровочной инвариантности — выбор другой константы для добавления к вашей функции потенциальной энергии может называться выбором другого «калибра» [это физический термин]. принцип калибровочной инвариантности утверждает, что физическое поведение системы одинаково независимо от того, какую калибровку вы выберете.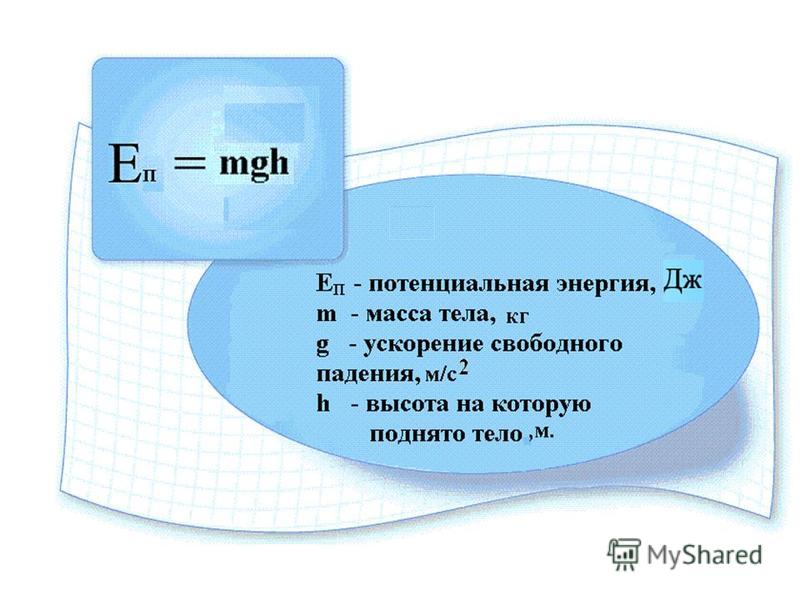

 к. потенциальная энергия определяется координатой, то величина потенциальной энергии определяется выбором системы координат (выбором нулевого уровня). Т.е. она определяется с точностью до постоянной величины. В данной задаче удобно за точку отсчета выбирать уровень Земли.
к. потенциальная энергия определяется координатой, то величина потенциальной энергии определяется выбором системы координат (выбором нулевого уровня). Т.е. она определяется с точностью до постоянной величины. В данной задаче удобно за точку отсчета выбирать уровень Земли. к. потенциальная энергия не меняется.
к. потенциальная энергия не меняется.
 силы, работа которых не зависит от траектории и по замкнутой траектории равна нулю (эти силы не зависят от скоростей). Примеры: гравитационные, упругие.
силы, работа которых не зависит от траектории и по замкнутой траектории равна нулю (эти силы не зависят от скоростей). Примеры: гравитационные, упругие.