Физика формула ньютона: www.webmath.ru | 523: Origin is unreachable

6. \]

Всё очень несложно и запоминается на всю жизнь. Кстати, самостоятельно вспомнить и вывести формулу бинома Ньютона, нарисовав на черновике треугольник Паскаля, тоже намного проще.

Некоторые историки науки приписывают Блезу Паскалю авторство не только треугольника, позволяющего находить биномиальные коэффициенты, но и самой формулы бинома. Они считают, что Паскаль вывел её несколько раньше Ньютона, а тот лишь обобщил формулу для разных показателей степеней.

Простая физика – EASY-PHYSIC

В этой статье предлагаю вспомнить (или познакомиться) с геометрическим смыслом интеграла, формулой Ньютона-Лейбница, и научиться определять площади различных фигур, ограниченных теми или иными кривыми.

Дадим определение определенного интеграла: пусть функция ) определена и интегрируема на отрезке [a,b] и пусть – некоторая ее первообразная. Тогда число называется интегралом от а до b функции и обозначается

Равенство называется формулой Ньютона–Лейбница.

Площадь криволинейной трапеции, ограниченной графиком функции (), прямыми , равна разности значений первообразной для функции в точках b и a:  .

Формула Ньютона–Лейбница связывает задачу нахождения площади плоской фигуры с интегралом.

В общем случае, если фигура ограничена графиками функций () и прямыми, то ее площадь равна:

 

Теперь решим несколько задач.

Задача 1.

Найти площадь фигуры, ограниченной заданными линиями: параболой и прямой, проходящей через точки и .

Про параболу все более-менее понятно, займемся сначала прямой. Найдем ее уравнение. Для этого запишем общее уравнение прямой: и подставим в него координаты точек. Получим систему:

То есть , . Таким образом, искомое уравнение .

Теперь надо построить обе функции.

– парабола с ветвями вниз, вершина расположена: , .

Определим сразу, где пересекутся наши функции (это будут пределы вычисления интеграла). Для этого приравняем

И решим уравнение:

Точки пересечения , .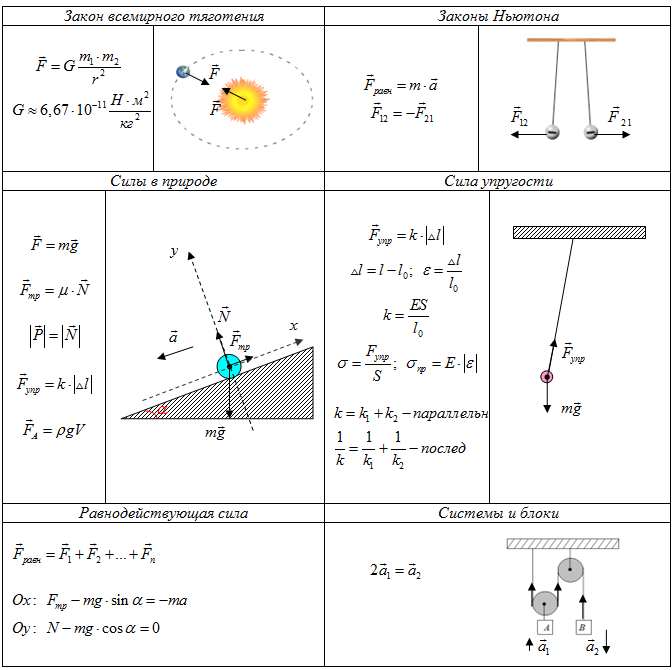 4)=1-frac{1}{4}+2+frac{16}{4}=6frac{3}{4}

Ответ: .

Задача 5.

Найти площадь фигуры, ограниченной линиями , , .

Итак, имеем две параболы и прямую. Первая парабола имеет абсциссу вершины , ординату вершины:

. Определим также корни уравнения

Сумма коэффициентов уравнения равна 0, поэтому , .

Вторая парабола имеет абсциссу вершины , ординату вершины:

. Определим также корни уравнения

Сумма коэффициентов уравнения равна 0, поэтому , .

Строим:

К задаче 5

Чтобы определить площадь фигурки, нужно разбить ее на удобные куски. Два возможных варианта разбиения показаны на рисунке, возможно, вы найдете еще какие-то.

Первый вариант разбиения

Второй вариант разбиения

Считаем площадь (с использованием разбиения на две части). Для этого определим пределы интегрирования. Точка пересечения парабол:

Точка пересечения параболы и прямой :

Корни по Виету: , . Нас сейчас интересует точка с абсциссой 4.

Точка пересечения параболы и прямой :

Корни по Виету: , . Нас сейчас интересует точка с абсциссой 5.

Тогда:

Ответ: .

Броуновское движение | физика | Британика

Броуновская частица

Посмотреть все СМИ

Ключевые люди:

Альберт Эйнштейн Роберт Браун Венделин Вернер Жан Перрен

Похожие темы:

движение кинетическая теория

Просмотреть весь соответствующий контент →

Резюме

Прочтите краткий обзор этой темы

Броуновское движение , также называемое Броуновское движение

, любое из различных физических явлений, при котором некоторая величина постоянно подвергается небольшим случайным колебаниям. Он был назван в честь шотландского ботаника Роберта Брауна, который первым изучил такие колебания (1827 г. ).

Если в данной среде присутствует некоторое количество частиц, подверженных броуновскому движению, и нет предпочтительного направления для случайных колебаний, то с течением времени частицы будут иметь тенденцию равномерно распределяться по среде. Таким образом, если A и B являются двумя смежными областями, и в момент времени t

A содержит в два раза больше частиц, чем B , в этот момент вероятность того, что частица покинет A и войдет в B , равна вдвое больше, чем вероятность того, что частица покинет B и войдет в A . Физический процесс, при котором вещество имеет тенденцию к устойчивому распространению из областей с высокой концентрацией в области с более низкой концентрацией, называется диффузией. Таким образом, диффузию можно рассматривать как макроскопическое проявление броуновского движения на микроскопическом уровне. Таким образом, можно изучать диффузию, моделируя движение броуновской частицы и вычисляя ее среднее поведение. Несколько примеров бесчисленных диффузионных процессов, которые изучаются с точки зрения броуновского движения, включают диффузию загрязняющих веществ через атмосферу, диффузию «дырок» (мельчайших областей, в которых потенциал электрического заряда положителен) через полупроводник и диффузию. кальция через костную ткань в живых организмах.

Ранние исследования

Термин «классическое броуновское движение» описывает беспорядочное движение микроскопических частиц, взвешенных в жидкости или газе. Браун исследовал процесс оплодотворения Clarkia pulchella , недавно открытого вида цветковых растений, когда заметил под микроскопом «быстрое колебательное движение» микроскопических частиц внутри пыльцевых зерен, взвешенных в воде. Другие исследователи заметили это явление и раньше, но первым его изучил Браун. Первоначально он полагал, что такое движение является жизненной деятельностью, свойственной мужским половым клеткам растений, но затем проверил, проявляет ли такое же движение пыльца растений, умерших более века. Браун назвал это «очень неожиданным фактом сохранения кажущейся жизнеспособности этих «молекул» так долго после смерти растения». Дальнейшее исследование показало, что такое же движение можно было наблюдать не только с частицами других органических веществ, но даже с осколками стекла или гранита и частицами дыма. Наконец, бесспорно подтверждая неживую природу этого явления, он продемонстрировал его на заполненных жидкостью пузырьках в скале Великого Сфинкса.

Ранние объяснения объясняли движение потоками тепловой конвекции в жидкости. Однако, когда наблюдения показали, что близлежащие частицы проявляют совершенно некоррелированную активность, от этого простого объяснения отказались. К 1860-м годам физики-теоретики заинтересовались броуновским движением и искали последовательное объяснение его различных характеристик: казалось, что данная частица с одинаковой вероятностью будет двигаться в любом направлении; дальнейшее движение казалось совершенно не связанным с прошлым движением; и движение никогда не прекращалось.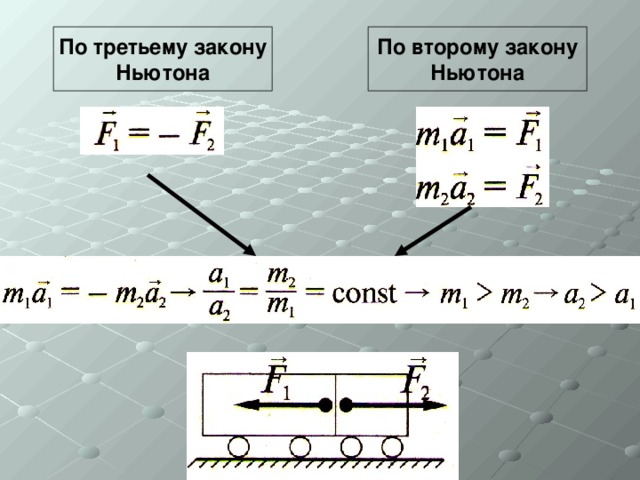 Опыт (1865 г.), в котором суспензию запечатывали в течение года в стекле, показал, что броуновское движение сохраняется. Более систематическое исследование 1889 г.определили, что малый размер частиц и низкая вязкость окружающей жидкости приводят к более быстрому движению.

Теория броуновского движения Эйнштейна

Поскольку более высокие температуры также приводили к более быстрому броуновскому движению, в 1877 г. было высказано предположение, что его причина кроется в «тепловом молекулярном движении в жидкой среде». Представление о том, что молекулы жидкости или газа постоянно находятся в движении, сталкиваясь друг с другом и отскакивая назад и вперед, составляет видную часть кинетической теории газов, разработанной в третьей четверти XIX в.физиками Джеймсом Клерком Максвеллом, Людвигом Больцманом и Рудольфом Клаузиусом в объяснении тепловых явлений. Согласно теории, температура вещества пропорциональна средней кинетической энергии, с которой движутся или колеблются молекулы вещества.

Было естественно предположить, что каким-то образом это движение могло быть сообщено более крупным частицам, которые можно было наблюдать под микроскопом; если это правда, это был бы первый непосредственно наблюдаемый эффект, подтверждающий кинетическую теорию. Эта линия рассуждений привела немецкого физика Альберта Эйнштейна в 1905 для создания своей количественной теории броуновского движения. Подобные исследования броуновского движения были проведены независимо и почти одновременно польским физиком Марианом Смолуховским, который использовал методы, несколько отличные от эйнштейновских.

Узнайте о теории Альберта Эйнштейна о броуновском движении и о том, как он определил размер атомов на основе скорости движения броуновских частиц

Просмотреть все видео к этой статье возможно существование атомов определенного размера. В разгар этой работы он обнаружил, что согласно атомной теории должно наблюдаться движение взвешенных микроскопических частиц. Эйнштейн не осознавал, что наблюдения, касающиеся броуновского движения, уже давно известны. Рассуждая на основе статистической механики, он показал, что для такой микроскопической частицы случайная разница между давлением молекулярной бомбардировки с двух противоположных сторон заставит ее постоянно раскачиваться вперед и назад. Частица меньшего размера, жидкость с меньшей вязкостью и более высокая температура увеличивают количество движения, которое можно было бы наблюдать. Через какое-то время частица будет иметь тенденцию дрейфовать от своей начальной точки, и на основе кинетической теории можно вычислить вероятность (

P ) перемещения частицы на определенное расстояние ( x ) в любом заданном направлении (общее расстояние, которое она пройдет, будет больше, чем x ) за определенный интервал времени ( t ) в среде, коэффициент которой диффузия ( D ) известна, D равна половине среднего квадрата смещения в направлении x . Эта формула для «плотности» вероятности позволяет нанести P на график против x . График представляет собой знакомую колоколообразную «нормальную» кривую Гаусса, которая обычно возникает, когда случайная величина представляет собой сумму многих независимых, статистически идентичных случайных величин, в данном случае множества небольших толчков, которые складываются в общее движение. Уравнение для этой связи

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Появление ультрамикроскопа в 1903 году помогло количественным исследованиям, делая видимыми маленькие коллоидные частицы, чью большую активность было легче измерить. Несколько важных измерений такого рода было сделано с 1905 по 1911 год. В этот период французский физик Жан-Батист Перрен успешно проверил анализ Эйнштейна, и за эту работу он был удостоен Нобелевской премии по физике в 1919 году.26. Его работа установила физическую теорию броуновского движения и положила конец скептицизму относительно существования атомов и молекул как реальных физических объектов.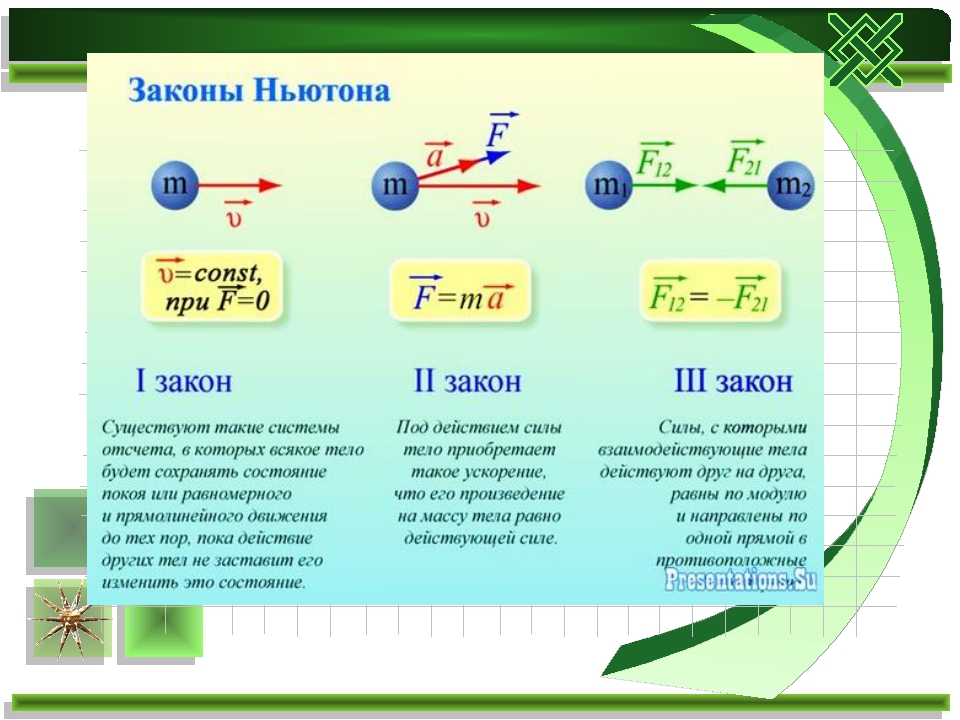

Эта статья была недавно отредактирована и обновлена ​​Эриком Грегерсеном.

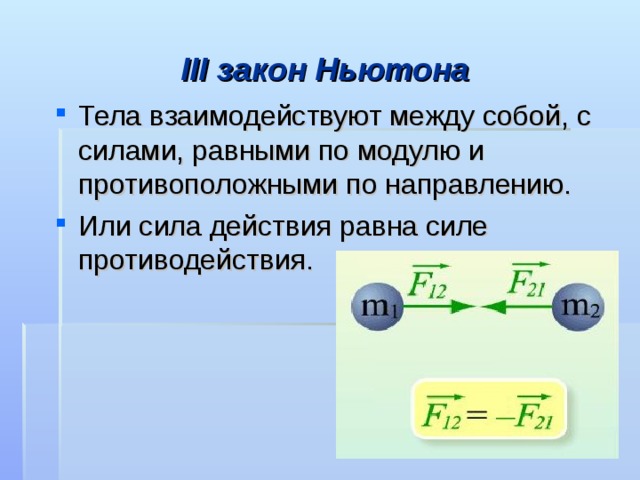
4.3: Второй закон Ньютона. Концепция системы

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1499

• OpenStax
• OpenStax

 

Цели обучения

К концу этого раздела вы сможете:

• Определить результирующую силу, внешнюю силу и систему.
• Поймите второй закон движения Ньютона.
• Примените второй закон Ньютона, чтобы определить вес объекта.

Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона носит более количественный характер и широко используется для расчета того, что происходит в ситуациях, связанных с силой. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, определяющего точное соотношение между силой, массой и ускорением, нам нужно уточнить некоторые уже упомянутые идеи.

Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорений . Первый закон Ньютона гласит, что результирующая внешняя сила вызывает изменение движения; таким образом, мы видим, что суммарная внешняя сила

вызывает ускорение .

Сразу возникает другой вопрос. Что мы понимаем под внешней силой? Интуитивное представление о внешнем верное — внешняя сила действует снаружи системы интереса. Например, на рис. \(\PageIndex{1a}\) интересующая нас система — это фургон плюс ребенок в нем. Две силы, действующие со стороны других детей, являются внешними силами. Между элементами системы действует внутренняя сила. Снова взглянув на рисунок \(\PageIndex{1a}\), сила, которую ребенок в тележке прилагает, чтобы повиснуть на тележке, является внутренней силой между элементами интересующей системы. Только внешние силы влияют на движение системы в соответствии с первым законом Ньютона. (Внутренние силы на самом деле компенсируются, как мы увидим в следующем разделе.)

Вы должны определить границы системы, прежде чем сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы является более тонким. Понятие системы является фундаментальным для многих областей физики, как и правильное применение законов Ньютона. К этой концепции мы будем возвращаться много раз в нашем путешествии по физике.

Рисунок \(\PageIndex{1}\): разные силы, действующие на одну и ту же массу, вызывают разные ускорения. а) Двое детей толкают тележку с ребенком. Показаны стрелки, представляющие все внешние силы. Система интереса — это повозка и ее всадник. Вес \(w\) системы и опора основания \(N\) также показаны для полноты и предполагаются сокращающимися. Вектор \(f\) представляет трение, действующее на вагон, причем он действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, складываются вместе, чтобы создать результирующую силу \(F_{net} \). Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая результирующая внешняя сила создает большее ускорение \((al>a)\), когда взрослый толкает ребенка.

Теперь кажется разумным, что ускорение должно быть прямо пропорционально и направлено в том же направлении, что и чистая (полная) внешняя сила, действующая на систему. Это предположение было проверено экспериментально и показано на рис. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (в). Для полноты показаны также вертикальные силы; предполагается, что они компенсируются, поскольку ускорение в вертикальном направлении отсутствует. Вертикальные силы – это вес \(w\) и опора земли \(N\), а горизонтальная сила \(f\) представляет собой силу трения. Они будут обсуждаться более подробно в следующих разделах. Сейчас мы определим трение как сила, противодействующая движению друг относительно друга соприкасающихся объектов. На рисунке \(\PageIndex{1b}\) показано, как векторы, представляющие внешние силы, складываются вместе, образуя результирующую силу \(F_{net}\).

Чтобы получить уравнение для второго закона Ньютона, мы сначала запишем отношение ускорения и чистой внешней силы в виде пропорциональности

\[ a \propto F_{net} \]

, где символ \(\propto\) означает «пропорционально», а \(F_{net} \) — это чистая внешняя сила . (Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод «голова к хвосту», или аналитически, используя компоненты. Методы такие же, как и для добавления других векторов, и рассматриваются в разделе главы о двумерной кинематике.) Эта пропорциональность утверждает то, что мы сказали словами: ускорение прямо пропорционально суммарной внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние. Не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о бесчисленных силах между атомами в объектах, — это огромное упрощение, но, делая это, мы можем легко решить некоторые очень сложные задачи с минимальной ошибкой благодаря нашему упрощению

Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой.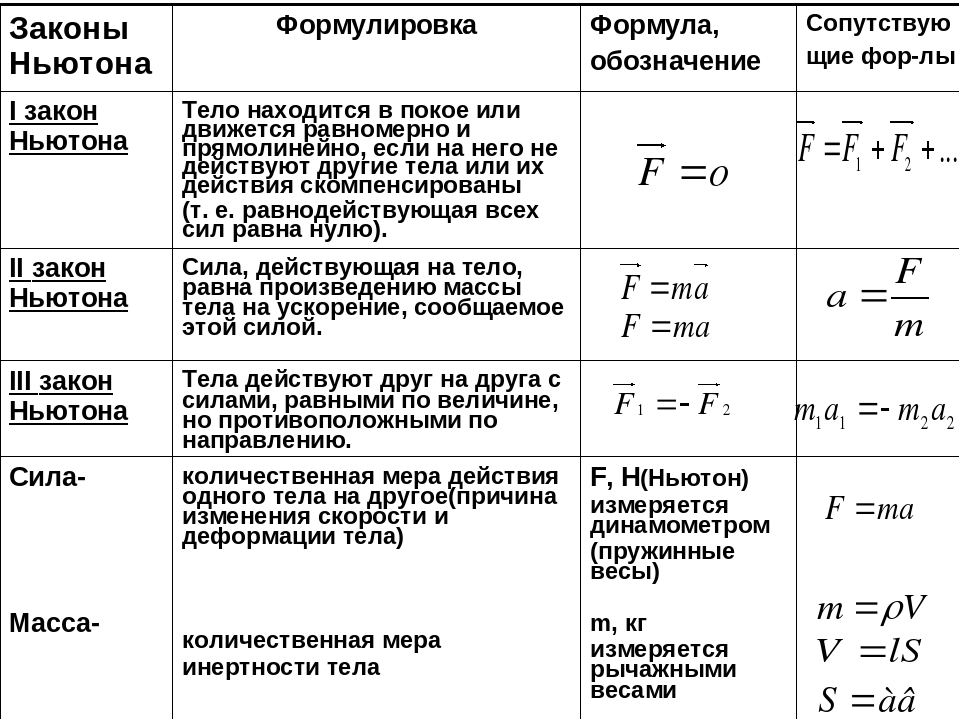 И действительно, как показано на рисунке, та же внешняя сила, приложенная к автомобилю, создает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как

\[ a \propto \dfrac{1}{m}, \]

, где \(m\) – масса системы. Эксперименты показали, что ускорение точно обратно пропорционально массе, точно так же, как оно точно линейно пропорционально суммарной внешней силе.

Рисунок \(\PageIndex{2}\): Одна и та же сила, действующая на системы с разной массой, создает разные ускорения. а) Баскетболист толкает мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (b) Тот же игрок прикладывает такую ​​же силу к заглохшему внедорожнику и создает гораздо меньшее ускорение (даже если трением можно пренебречь). (c) Диаграммы свободного тела идентичны, что позволяет проводить прямое сравнение двух ситуаций. Ряд паттернов для диаграммы свободного тела появится по мере того, как вы будете решать больше задач.

Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта. Сочетание двух только что приведенных пропорций дает второй закон движения Ньютона.

Второй закон движения Ньютона

Ускорение системы прямо пропорционально внешней силе, действующей на систему, и направлено в том же направлении, что и обратно пропорционально ее массе. В форме уравнения второй закон Ньютона равен 9.0003

\[ a = \dfrac{F_{net}}{m}\]

Это часто записывается в более знакомой форме

\[ F_{net} = ma. \]

Когда учитываются только величина силы и ускорения, это уравнение просто

\[ F_{net} = ma. \]

Хотя последние два уравнения на самом деле одинаковы, первое дает более полное представление о том, что означает второй закон Ньютона. Закон представляет собой причинно-следственную связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке. 92 \]

В то время как почти во всем мире в качестве единицы силы используется ньютон, в Соединенных Штатах наиболее распространенной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.

Вес и гравитационная сила

Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что результирующая сила, действующая на объект, отвечает за его ускорение. Если сопротивлением воздуха можно пренебречь, результирующая сила, действующая на падающий объект, представляет собой гравитационную силу, обычно называемую ее вес \(w\). Вес можно обозначить как вектор \(w\), потому что он имеет направление; вниз по определению является направлением силы тяжести, и, следовательно, вес является направленной вниз силой. Величина веса обозначается как \(w\). Галилей сыграл важную роль в том, чтобы показать, что в отсутствие сопротивления воздуха все тела падают с одинаковым ускорением \(w\). Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.

Рассмотрим объект массой \(m\), падающий вниз к Земле. Он испытывает только направленную вниз силу тяжести, которая имеет величину \(w\). Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна \(F_{net} = ma\). 92) = 9,8 Н. \]

Напомним, что \(g\) может принимать положительное или отрицательное значение в зависимости от положительного направления в системе координат. Обязательно учитывайте это при решении задач с весом.

Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении . То есть единственная сила, действующая на объект, — это сила тяжести. В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует восходящая сила воздуха. 92\). Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.

Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это гравитационная сила, действующая на него со стороны ближайшего крупного тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно резко отличается от определения веса, используемого НАСА и популярными средствами массовой информации в связи с космическими путешествиями и исследованиями. Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике называется «свободным падением». Мы воспользуемся приведенным выше определением веса и проведем тщательное различие между свободным падением и фактической невесомостью.

Важно знать, что вес и масса — очень разные физические величины, хотя и тесно связанные между собой. Масса — это количество материи (сколько «вещества») и не меняется в классической физике, тогда как вес — это гравитационная сила, которая зависит от гравитации. Заманчиво приравнять их, поскольку большинство наших примеров происходят на Земле, где вес объекта лишь немного зависит от местоположения объекта. Кроме того, термины масса и вес взаимозаменяемы в повседневном языке; например, наши медицинские записи часто показывают наш «вес» в килограммах, но никогда в правильных единицах измерения — ньютонах.

РАСПРОСТРАНЕННЫЕ ЗАБЛУЖДЕНИЯ: МАССА ПРОТИВ. ВЕС

Масса и вес часто используются как синонимы в повседневном языке.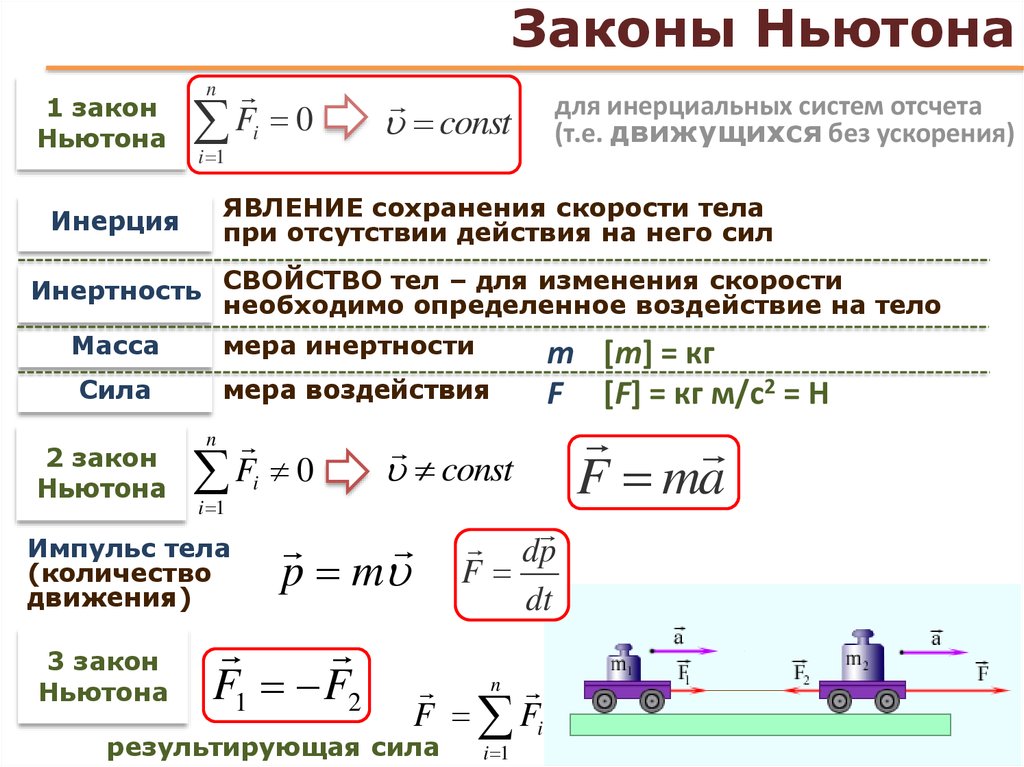 Однако в науке эти термины резко отличаются друг от друга. Масса — это мера того, сколько материи содержится в объекте. Типичной мерой массы является килограмм (или «слаг» в английских единицах измерения). Вес, с другой стороны, является мерой силы тяжести, действующей на объект. Вес равен массе объекта \((m)\), умноженной на ускорение свободного падения \((g)\). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах измерения). 92\) ). Если вы измерите свой вес на Земле, а затем измерите свой вес на Луне, вы обнаружите, что «весите» намного меньше, даже если вы не выглядите стройнее. Это связано с тем, что на Луне сила гравитации слабее. На самом деле, когда люди говорят, что они «теряют вес», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, приводит к тому, что они весят меньше) мера? Когда вы встаете на напольные весы, что происходит с весами? Это слегка угнетает. Весы содержат пружины, которые сжимаются пропорционально вашему весу, подобно резиновым лентам, которые растягиваются при натяжении. Пружины обеспечивают меру вашего веса (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран измерение делится на 9.80, чтобы дать показание в единицах массы килограммов. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на стол рядом с вами. Что происходит с чтением? Почему? Измерят ли ваши весы ту же «массу» на Земле, что и на Луне?

Пример \(\PageIndex{1}\): Какое ускорение может создать человек, толкая газонокосилку?

Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, равна 51 Н (около 11 фунтов) параллельно земле. Масса косилки 24 кг. Каково его ускорение?

Рисунок \(\PageIndex{3}\): Чистая сила, действующая на газонокосилку, составляет 51 Н вправо. С какой скоростью газонокосилка ускоряется вправо?

Стратегия

Поскольку \( F_{net} \) и \( m \) заданы, ускорение можно рассчитать непосредственно из второго закона Ньютона, как указано в \( F_{net} = ma \).

Решение

Величина ускорения \(a\) равна \(a = \frac{F_{net}}{m}\). Ввод известных значений дает \[ a = \dfrac{51 \, N}{24 \, кг} \] 92 \]

Обсуждение

Направление ускорения совпадает с направлением чистой силы, которая параллельна земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, действующая на человека, толкающего косилку, должна быть больше, чем трение, противодействующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны уравновешиваться, если не должно быть ускорения в вертикальном направлении (ускорение в вертикальном направлении). косилка движется только горизонтально). Найденное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро достигнет максимальной скорости.

Пример \(\PageIndex{2}\): Какая реактивная тяга ускоряет эти сани?

До пилотируемых космических полетов ракетные салазки использовались для испытаний самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, установленной на одном или двух рельсах и приводившейся в движение несколькими ракетами. Вычислите величину силы, действующей на каждую ракету, называемую ее тягой \(Т\), для четырехракетной двигательной установки, показанной на рисунке. Начальное ускорение саней равно \(492\) масса системы 2100 кг, а сила трения, противодействующая движению, известна как 650 Н.

Рис. 4.4.4. Сани испытывают реактивную тягу, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу \(Т\). Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы компенсируются. Земля воздействует на систему направленной вверх силой \(N\), равной по величине и противоположной по направлению ее весу \(w\). Система здесь — это сани, их ракеты и всадник, поэтому никакие силы между этими объектами не учитываются. Стрелка, обозначающая трение \((f)\), нарисована больше масштаба.

Стратегия

Хотя существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления обозначаются знаками плюс или минус, где право считается положительным направлением. См. диаграмму свободного тела на рисунке.

Решение

Поскольку ускорение, масса и сила трения известны, начнем со второго закона Ньютона и будем искать способы найти тягу двигателей. Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин. Следовательно, мы начинаем с \[ F_{net} = ma. \], где \(F_{net}\) – результирующая сила в горизонтальном направлении. Из рисунка видно, что тяги двигателя складываются, а трение противодействует тяге. В форме уравнения чистая внешняя сила равна \[ F_{net} = 4T – f. \] 92\) ). В то время как живые объекты больше не используются, с помощью ракетных саней была достигнута наземная скорость 10 000 км/ч. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.

Второй закон движения Ньютона — это больше, чем определение; это отношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждая из этих физических величин может быть определена независимо, поэтому второй закон говорит нам нечто основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.

Резюме

• Ускорение, \(a\), определяется как изменение скорости, то есть изменение ее величины или направления, или того и другого.
• Внешняя сила — это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.
• Второй закон Ньютона гласит, что ускорение системы прямо пропорционально внешней силе, действующей на систему, и направлено в том же направлении, что и обратно пропорционально ее массе.
• В форме уравнения второй закон движения Ньютона имеет вид \( a = \frac{F_{net}}{m} \)
• Это часто записывается в более привычной форме: \( F_{net} = ma.