СЛОБОДСКОВ БОРИС АНАТОЛЬЕВИЧ – ФИЗИКА (КУРС ЛЕКЦИЙ)
СЛОБОДСКОВ БОРИС АНАТОЛЬЕВИЧ – ФИЗИКА (КУРС ЛЕКЦИЙ)|
ЛЕКЦИИ
ПО ФИЗИКЕ |
|
|
|
© Лопатин
Павел Борисович |
 Равнозамедленное
движение. Формула пути Равнозамедленное
движение. Формула пути
1. Понятие равнозамедленного движения. Формула пути.
Это
движение также является частным
случаем движения с постоянным
ускорением, поэтому любую задачу на это
движение можно решать с помощью
известных формул проекций скорости и
координат движения с постоянным
ускорением.
Получим теперь формулу модуля скорости равнозамедленного движения. ,
где ,
то есть . Из формулы координаты движения с постоянным ускорением можно получить формулу пути равнозамедленного движения.
, где . 2. График пути равнозамедленного движения. Графиком пути при равнозамедленном движении является ветвь параболы; вершина параболы расположена в конце времени движения. 2а. График пути в этом случае будет выглядеть так.
|
|
< Предыдущий параграф < Оглавление |
|
|
© Лопатин Павел Борисович
|
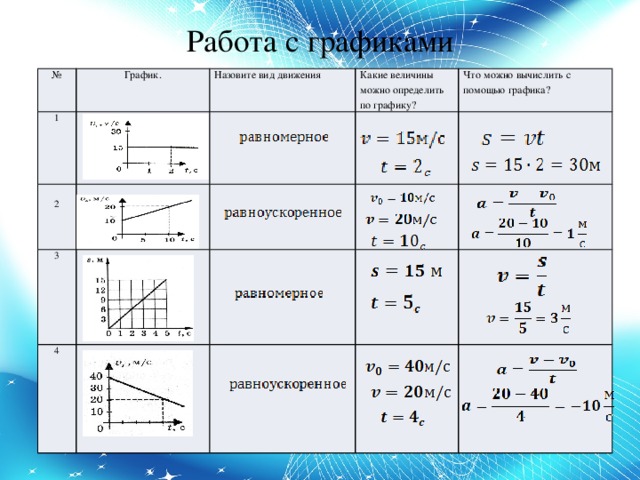
Скорость в физике – это… Формула скорости
Эта тема будет полезна не только учащимся средней школы, но даже взрослым. Кроме того, статья будет интересна родителям, желающим объяснить своим детям простые вещи из естественных наук. Среди очень важных тем – это скорость в физике.
Довольно часто ученики не могут разобраться в решении задач, отличить имеющиеся виды скоростей, а еще сложнее понять научные определения. Здесь мы рассмотрим все на более доступном языке, чтобы было не только все ясно, но даже интересно. А вот запомнить некоторые вещи все же придется, так как технические науки (физика и математика) требуют заучивать наизусть формулы, единицы измерения и, конечно же, значения символов в каждой формуле.
Где встречается?
Для начала вспомним, что данная тема относится к такому разделу физики как механика, подразделу «Кинематика». Кроме того, изучение скорости на этом не заканчивается, оно будет и в последующих разделах:
- оптика,
- колебания и волны,
- термодинамика,
- квантовая физика и так далее.

Также понятие скорость встречается в химии, биологии, географии, информатике. В физике тема «скорость» встречается чаще всего и изучается углубленно.
Кроме того, данное слово употребляется в повседневной жизни всеми нами, особенно среди автомобилистов, водителей транспортной техники. Даже опытные кулинары иногда используют фразу, например, «взбить яичные белки миксером на средней скорости».
Что такое скорость?
Скорость в физике – это кинематическая величина. Означает расстояние, которое преодолевается телом за какой-то промежуток времени. Допустим, молодой человек движется от дома к магазину, преодолевая двести метров за одну минуту. Напротив, его старенькая бабушка пройдет тем же маршрутом за шесть минут мелкими шажками. То есть парень перемещается намного быстрее своей пожилой родственницы, так как развивает скорость гораздо больше, делая очень быстрые длинные шаги.
То же самое стоит сказать про автомобиль: одна машина едет быстрее, а другая медленнее, потому что скорости движения разные. Позднее мы рассмотрим многочисленные примеры, связанные с этим понятием.
Позднее мы рассмотрим многочисленные примеры, связанные с этим понятием.
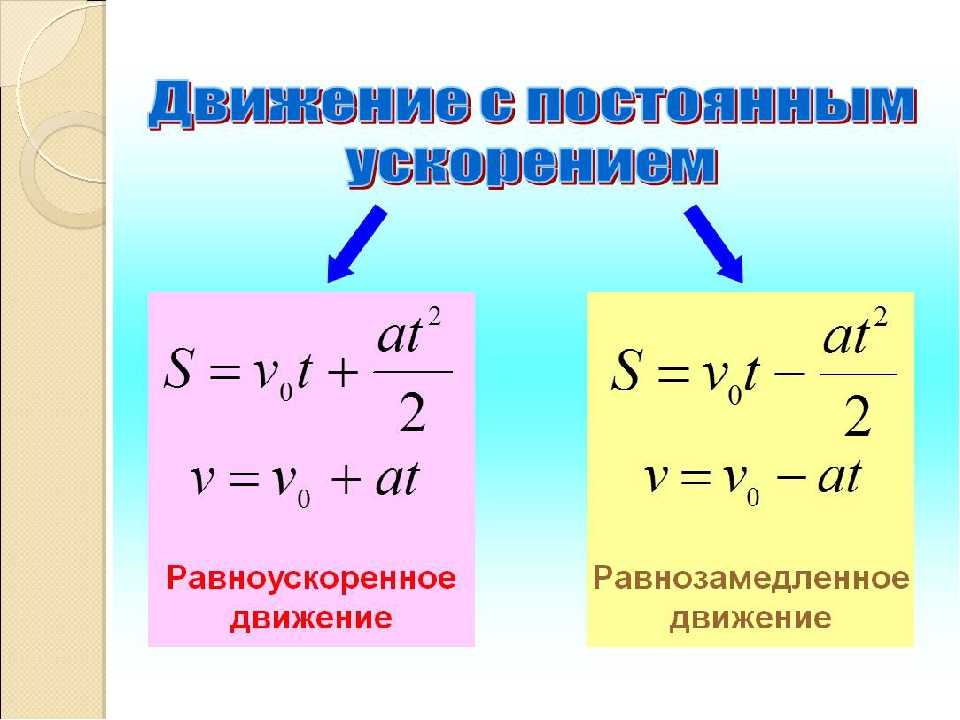
Формула
На уроке в школе обязательно рассматривается формула скорости в физике для того, чтобы было удобно решать задачи.
- V – это, соответственно, скорость движения;
- S – расстояние, которое преодолевается телом при перемещении от одной точки в пространстве до другой;
- t – время перемещения.
Следует запомнить формулу, потому что она пригодится в будущем при решении множества задач и не только. Например, вам может стать интересно, с какой скоростью дойдете от дома до работы или места учебы. Но вы заранее можете узнать расстояние по карте в смартфоне или на компьютере, либо по бумажному варианту, зная масштаб и имея при себе линейку. Далее вы засекаете время, перед тем, как начать движение. Придя на место назначения, смотрите, сколько минут или часов потребовалось пройти без остановки.
В чем измеряется?
Скорость чаще всего измеряется по системе единиц СИ. Ниже представлены не только единицы, но и примеры того, где они применяются:
Ниже представлены не только единицы, но и примеры того, где они применяются:
- км/ч (километр в час) – транспорт;
- м/с (метр в секунду) – ветер;
- км/с (километр в секунду) – космические объекты, ракеты;
- мм/ч (миллиметр в час) – жидкости.
Давайте для начала разберемся, откуда взялась дробная черта и почему единица измерения именно такая. Обратите внимание по физике на формулу скорости. Что вы видите? В числителе стоит S (расстояние, путь). В чем измеряется расстояние? В километрах, метрах, миллиметрах. В знаменателе, соответственно, t (время) – часы, минуты, секунды. Отсюда и единицы измерения величины именно такие, как представлены в начале данного раздела.
Закрепим с вами изучение формулы скорости в физике следующим образом: какое расстояние преодолеет тело за конкретный промежуток времени? Например, человек пройдет 5 километров за 1 час. Итого: скорость движения человека – 5 км/ч.
От чего зависит?
Нередко учителя задают ученикам вопрос: “От чего зависит скорость?”. Школьники часто теряются и не знают, что сказать. На самом деле, все очень просто. Достаточно посмотреть на формулу, чтобы всплыла подсказка. Скорость тела в физике зависит от времени движения и расстояния. Если неизвестен хотя бы один из этих параметров, решить задачу будет невозможно. Кроме того, в примере можно встретить другие виды скоростей, о которых речь пойдет в следующих разделах этой статьи.
Школьники часто теряются и не знают, что сказать. На самом деле, все очень просто. Достаточно посмотреть на формулу, чтобы всплыла подсказка. Скорость тела в физике зависит от времени движения и расстояния. Если неизвестен хотя бы один из этих параметров, решить задачу будет невозможно. Кроме того, в примере можно встретить другие виды скоростей, о которых речь пойдет в следующих разделах этой статьи.
Во многих задачах по кинематике приходится строить графики зависимости, где по оси Х – время, а по оси Y – расстояние, путь. По таким изображениям можно легко оценить характер скорости движения. Стоит отметить, что во многих профессиях, связанных с транспортом, электрическими машинами часто применяются графики. Например, на железной дороге.
В нужный момент измеряем скорость
Есть еще одна тема, которая пугает учеников средней школы, – мгновенная скорость. В физике это понятие встречается как определение величины скорости в мгновенный промежуток времени.
Давайте рассмотрим простой пример: машинист ведет поезд, его помощник наблюдает за скоростью движения время от времени. Вдалеке виднеется знак ограничения скорости. Следует проконтролировать, с какой скоростью движется поезд именно сейчас. Помощник машиниста сообщает в 16 часов 00 минут, что скорость равна 117 км/ч. Это и есть мгновенная скорость, зафиксированная ровно в 4 часа вечера. Через три минуты скорость стала 98 км/ч. Это тоже мгновенная скорость относительно 16 часов 03 минут.
Вдалеке виднеется знак ограничения скорости. Следует проконтролировать, с какой скоростью движется поезд именно сейчас. Помощник машиниста сообщает в 16 часов 00 минут, что скорость равна 117 км/ч. Это и есть мгновенная скорость, зафиксированная ровно в 4 часа вечера. Через три минуты скорость стала 98 км/ч. Это тоже мгновенная скорость относительно 16 часов 03 минут.
Начало движения
Без начальной скорости физика не представляет практически ни одно движение транспортной техники. Что это за параметр? Это скорость, с которой начинает движение объект. Допустим, машина не может начинать движение моментально со скоростью 50 км/ч. Ей нужно разогнаться. Когда водитель нажимает педаль, автомобиль плавно начинает движение, например, со скоростью сначала 5 км/ч, потом постепенно 10 км/ч, 20 км/ч и так далее (5 км/ч и есть начальная скорость).
Конечно, можно совершить резкий старт, какой бывает у бегунов-спортсменов, при ударе теннисного мяча ракеткой, но все равно всегда существует начальная скорость. Ее нет по нашим меркам только у звезд, планет и спутников нашей Галактики, так как мы не знаем, когда началось движение и каким образом. Ведь до самой смерти космические объекты не могут останавливаться, они всегда в движении.
Ее нет по нашим меркам только у звезд, планет и спутников нашей Галактики, так как мы не знаем, когда началось движение и каким образом. Ведь до самой смерти космические объекты не могут останавливаться, они всегда в движении.
Равномерная скорость
Скорость в физике – это совокупность отдельных явлений и характеристик. Различают также равномерное и неравномерное движение, криволинейное и прямолинейное. Давайте приведем пример: человек идет по прямой дороге с одинаковой скоростью преодолевая из точки А в точку В расстояние 100 метров.
С одной стороны, это можно назвать прямолинейной и равномерной скоростью. Но если присоединить человеку очень точные датчики скорости, маршрута, то можно заметить, что разница все же есть. Неравномерная скорость – это когда скорость регулярно или постоянно меняется.
В быту и технике
Скорость движения в физике существует всюду. Даже микроорганизмы перемещаются, пусть и с очень медленной скоростью. Стоит отметить, что существует вращение, которое характеризуется также скоростью, но имеет единицу измерения – об/мин (обороты в минуту). Например, скорость вращения барабана в стиральной машине. Данная единица измерения употребляется всюду, где есть механизмы и машины (двигатели, моторы).
Например, скорость вращения барабана в стиральной машине. Данная единица измерения употребляется всюду, где есть механизмы и машины (двигатели, моторы).
В географии и химии
Даже вода имеет скорость движения. Физика всего лишь является дочерней наукой в сфере процессов, происходящих в природе. Допустим, скорость ветра, волны в море – это все измеряется привычными физическими параметрами, величинами.
Наверняка, многие из вас знакомы с фразой «скорость химической реакции». Только в химии это имеет иное значение, так как имеется в виду, за какое время произойдет тот или иной процесс. Например, марганцовка быстрее растворится в воде, если взболтать сосуд.
Скорость-невидимка
Существуют невидимые явления. Например, мы не можем видеть, как перемещаются частицы света, различных излучений, как распространяется звук. Но если бы не было движения их частиц, то никакое бы из этих явлений не существовало в природе.
Информатика
Практически каждый современный человек сталкивается с понятием «скорость» во время работы на компьютере:
- скорость Интернета;
- скорость загрузки страниц;
- быстрота загрузки процессора и так далее.

Примеров скорости движения в физике можно привести огромное множество.
Внимательно прочитав статью, вы познакомились с понятием скорости, узнали, что она из себя представляет. Пусть данный материал поможет вам углубленно изучить раздел «Механика», проявить к нему интерес и побороть страх при ответах на уроках. Ведь скорость в физике – это часто встречающееся понятие, которое легко запомнить.
7.2: Работа – Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4006
- OpenStax
- OpenStax
Цели обучения
- Представление работы любой силы
- Оценить работу, совершаемую различными силами
В физике работа представляет собой тип энергии.
\[dW = \vec{F} \cdotp d \vec{r} = |\vec{F}||d \vec{r}| \cos\тета\ldotp\метка{7.1}\]
Затем мы можем сложить вклады для бесконечно малых перемещений вдоль пути между двумя положениями, чтобы получить общую работу.
Работа, совершаемая силой
Работа, совершаемая силой, представляет собой интеграл силы по перемещению вдоль пути перемещения:
\[W_{AB} = \int_{path\; AB} \vec{F} \cdotp d \vec{r} \ldotp \label{7.2}\]
Векторы, участвующие в определении работы силы, действующей на частицу, показаны на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Векторы, используемые для определения работы. Сила, действующая на частицу, и ее бесконечно малое перемещение показаны в одной точке на пути между А и В. Бесконечно малая работа есть скалярное произведение этих двух векторов; общая работа является интегралом скалярного произведения вдоль пути.
Сила, действующая на частицу, и ее бесконечно малое перемещение показаны в одной точке на пути между А и В. Бесконечно малая работа есть скалярное произведение этих двух векторов; общая работа является интегралом скалярного произведения вдоль пути.
Напомним, что произведение величины силы на косинус угла, образуемого силой с данным направлением, является составляющей силы в данном направлении. Компоненты вектора могут быть положительными, отрицательными или нулевыми, в зависимости от того, находится ли угол между вектором и компонентом-направлением между 0° и 90° или между 90° и 180° или равен 90°. В результате работа, совершаемая силой, может быть положительной, отрицательной или нулевой, в зависимости от того, направлена ли сила обычно в направлении смещения, обычно противоположно смещению или перпендикулярно смещению. Максимальная работа совершается данной силой, когда она действует вдоль направления перемещения (cos \(\theta\) = ± 1), а нулевая работа совершается, когда сила перпендикулярна перемещению (cos \(\theta \) = 0).
Единицы работы – это единицы силы, умноженные на единицы длины, которые в системе СИ равны ньютонам, умноженным на метры, Н • м. Эта комбинация называется джоулем по историческим причинам, о которых мы упомянем позже, и обозначается аббревиатурой J. В английской системе, до сих пор используемой в Соединенных Штатах, единицей силы является фунт (lb), а единицей расстояния является фут (фут), поэтому единицей работы является фут-фунт (фут • фунт).
В английской системе, до сих пор используемой в Соединенных Штатах, единицей силы является фунт (lb), а единицей расстояния является фут (фут), поэтому единицей работы является фут-фунт (фут • фунт).
Работа, выполняемая постоянными силами и контактными силами
9{B} dz \\ & = F_{x} (x_{B} – x_{A}) + F_{y} (y_{B} – y_{A}) + F_{z} (z_{B} – z_{A}) = \vec{F} \cdotp (\vec{r}_{B} – \vec{r}_{A}) \ldotp \end{split} \nonumber\]Рисунок \( \PageIndex{2a}\) показывает человека, прилагающего постоянную силу \(\vec{F}\) к ручке газонокосилки, которая образует угол \(\theta\) с горизонтом. Горизонтальное перемещение газонокосилки, на которое действует сила, равно \(\vec{d}\). Работа, выполненная газонокосилкой, равна
\[W = \vec{F} \cdotp \vec{d} = Fd \cos \theta,\nonumber \]
, который на рисунке также показан как горизонтальная составляющая силы, умноженная на величину смещения.
Рисунок \(\PageIndex{2}\): Работа, совершаемая постоянной силой. а) Человек толкает газонокосилку с постоянной силой. Составляющая силы, параллельная смещению, представляет собой выполненную работу, как показано в уравнении на рисунке. б) Человек держит портфель. Работа не совершается, так как перемещение равно нулю. (c) Человек в (b) идет горизонтально, держа портфель. Работа не совершается, потому что cos \(\theta\) равен нулю.
Составляющая силы, параллельная смещению, представляет собой выполненную работу, как показано в уравнении на рисунке. б) Человек держит портфель. Работа не совершается, так как перемещение равно нулю. (c) Человек в (b) идет горизонтально, держа портфель. Работа не совершается, потому что cos \(\theta\) равен нулю. На рисунке \(\PageIndex{2b}\) изображен человек с портфелем. Человек должен приложить направленную вверх силу, по величине равную весу портфеля, но эта сила не работает, потому что перемещение, на которое она действует, равно нулю. Так почему же вы в конечном итоге чувствуете усталость, просто держа портфель, если вы не выполняете с ним никакой работы? Ответ заключается в том, что мышечные волокна вашей руки сокращаются и выполняют работу внутри вашей руки, хотя сила, которую ваши мышцы воздействуют снаружи на портфель, не выполняет над ней никакой работы. (Часть силы, которую вы прикладываете, может также быть напряжением костей и связок вашей руки, но другие мышцы вашего тела будут выполнять работу, чтобы поддерживать положение вашей руки. )
)
На рисунке \(\PageIndex{2c}\), где человек в (b) идет горизонтально с постоянной скоростью, работа, выполняемая человеком с портфелем, по-прежнему равна нулю, но теперь, поскольку угол между приложенной силой и смещение равно 90° (\(\vec{F}\) перпендикулярно \(\vec{d}\)) и cos 90° = 0.
Пример \(\PageIndex{1}\): Расчет Работа, которую вы совершаете, чтобы толкнуть газонокосилку
Какую работу совершает на газонокосилке человек на рисунке \(\PageIndex{2a}\), если он прикладывает постоянную силу 75,0 Н под углом 35° ниже горизонтали и толкает косилку на 25,0 м по ровной поверхности?
Стратегия
Мы можем решить эту задачу, подставив данные значения в определение работы, совершаемой над объектом постоянной силой, выраженной в уравнении W = Fd cos \(\theta\). Сила, угол и перемещение известны, так что неизвестна только работа W.
Решение
Уравнение для работы:
\[W = Fd \cos \theta \ldotp \nonumber \]
Подстановка известных значений дает
\[W = (75,0\; N)(25,0\ m) \cos(35,0^{o}) = 1,54 \times 10^{3}\; J \ldotp\номер\]
Значение
Несмотря на то, что полтора килоджоуля могут показаться большой работой, мы увидим в книге «Потенциальная энергия и сохранение энергии», что это примерно столько же работы, сколько вы могли бы выполнить, сожгая одну шестую грамма. жира.
жира.
Когда вы косите траву, помимо вашей силы на газонокосилку действуют и другие силы, а именно контактная сила земли и сила гравитации Земли. Рассмотрим работу этих сил в общем виде. Для объекта, движущегося по поверхности, смещение d \(\vec{r}\) касается поверхности. Часть контактной силы на объекте, которая перпендикулярна поверхности, является нормальной силой \(\vec{N}\). Поскольку косинус угла между нормалью и касательной к поверхности равен нулю, имеем
\[dW_{N} = \vec{N} \cdotp d \vec{r} = \vec{0} \ldotp \nonumber \]
Обычная сила никогда не работает в этих обстоятельствах. (Обратите внимание, что если бы смещение d \(\vec{r}\) действительно имело бы относительную составляющую, перпендикулярную поверхности, объект либо покинул бы поверхность, либо прорвался бы сквозь нее, и нормальной контактной силы больше не было бы. Однако , если объект больше, чем частица, и имеет внутреннюю структуру, нормальная контактная сила может совершать над ним работу, например, смещая его или деформируя его форму (об этом будет сказано в следующей главе). {B} |др| = – f_{k} |l_{AB}| \ldotp \label{7.3}\]
{B} |др| = – f_{k} |l_{AB}| \ldotp \label{7.3}\]
, где |l AB | длина пути на поверхности. (Обратите внимание, что, особенно если работа, совершаемая силой, отрицательна, люди могут ссылаться на работу, совершенную против этой силы, где dW против = -dW на . Работа, совершенная против силы, также может рассматриваться как работа, совершаемая против этой силы. работа, необходимая для преодоления этой силы, как в «Сколько работы требуется, чтобы преодолеть…?») Сила трения покоя, однако, может выполнять положительную или отрицательную работу. Когда вы идете, сила статического трения, оказываемая землей на заднюю ногу, ускоряет вас на части каждого шага. Если вы замедляетесь, сила земли на вашей передней ноге замедляет вас. Если вы едете на своем автомобиле с предельной скоростью по прямому ровному участку шоссе, отрицательная работа, выполняемая кинетическим трением сопротивления воздуха, уравновешивается положительной работой, выполняемой статическим трением дороги на ведущих колесах. Вы можете вытащить коврик из-под предмета таким образом, чтобы он скользил назад относительно коврика, но вперед относительно пола. В этом случае кинетическое трение, оказываемое ковриком на объект, может иметь то же направление, что и смещение объекта относительно пола, и совершать положительную работу. Суть в том, что вам нужно анализировать каждый конкретный случай, чтобы определить работу, совершаемую силами, будь то положительная, отрицательная или нулевая.
Вы можете вытащить коврик из-под предмета таким образом, чтобы он скользил назад относительно коврика, но вперед относительно пола. В этом случае кинетическое трение, оказываемое ковриком на объект, может иметь то же направление, что и смещение объекта относительно пола, и совершать положительную работу. Суть в том, что вам нужно анализировать каждый конкретный случай, чтобы определить работу, совершаемую силами, будь то положительная, отрицательная или нулевая.
Пример \(\PageIndex{2}\): Перемещение дивана
Вы решили переместить диван в новое место на горизонтальном полу гостиной. Нормальная сила на кушетке равна 1 кН, а коэффициент трения равен 0,6. (a) Сначала вы толкаете кушетку на 3 м параллельно стене, а затем на 1 м перпендикулярно стене (от A до B на рисунке \(\PageIndex{3}\)). Какую работу совершает сила трения? (b) Вам не нравится новое положение, поэтому вы возвращаете диван в исходное положение (от B к A на рисунке \(\PageIndex{3}\)). Какова была полная работа, совершенная против трения, перемещающего кушетку из исходного положения и обратно?
Рисунок \(\PageIndex{3}\): Вид сверху на пути для перемещения кушетки.
Стратегия
Величина силы кинетического трения о кушетку постоянна и равна произведению коэффициента трения на нормальную силу, f K = \(\mu_{K}\)N. Следовательно, работа, совершаемая им, равна W fr = −f K d, где d — длина пройденного пути. Сегменты путей являются сторонами прямоугольного треугольника, поэтому длину путей легко вычислить. В части (b) вы можете использовать тот факт, что работа, совершаемая против силы, является отрицательной по отношению к работе, совершаемой этой силой.
Решение
- Работа трения равна $$W = − (0,6)(1\; кН)(3\; m + 1\; m) = − 2,4\; кДж \ldotp\номер $$
- Длина пути по гипотенузе равна \(\sqrt{10}\) м, поэтому общая работа, совершаемая против трения, равна $$W = (0,6)(1\; кН)(3\; m + 1\). m + \sqrt{10}\ m) = 4,3\; кДж \ldotp\номер $$
Значение
Полный путь, на котором оценивалась работа трения, начинался и заканчивался в одной и той же точке (это был замкнутый путь), так что полное перемещение кушетки было равно нулю.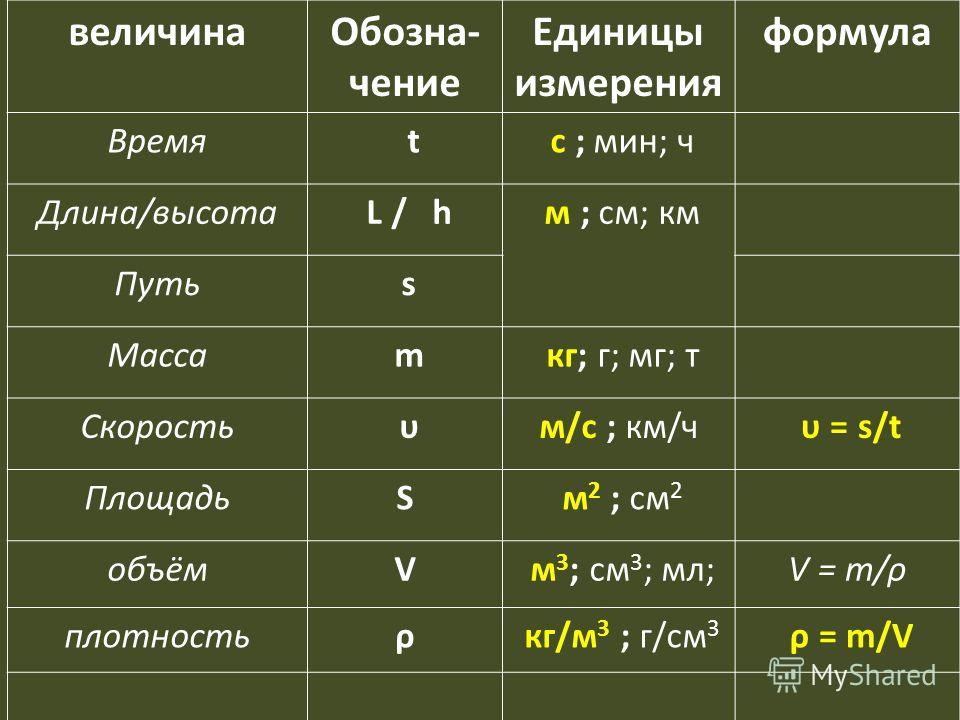 Однако общая работа была не нулевой. Причина в том, что такие силы, как трение, классифицируются как неконсервативные силы или диссипативные силы, как мы обсудим в следующей главе.
Однако общая работа была не нулевой. Причина в том, что такие силы, как трение, классифицируются как неконсервативные силы или диссипативные силы, как мы обсудим в следующей главе.
Упражнение 7.1
Может ли кинетическое трение быть постоянной силой для всех путей?
Другой силой, действующей на газонокосилку, о которой говорилось выше, была сила земного притяжения, или вес косилки. Вблизи поверхности Земли гравитационная сила, действующая на объект массы m, имеет постоянную величину mg и постоянное направление вертикально вниз. Таким образом, работа, совершаемая силой тяжести над объектом, является скалярным произведением его веса и его смещения. Во многих случаях скалярное произведение гравитационной работы удобно выражать через x-, y- и z-компоненты векторов. В типичной системе координат ось x горизонтальна, а ось y вертикально вверх. Тогда гравитационная сила равна −mg \(\hat{j}\), поэтому работа, совершаемая гравитацией на любом пути из A в B, равна
\[W_{грав,\; AB} = -mg \hat{j} \cdotp (\vec{r}_{B} – \vec{r}_{A}) = -mg (y_{B} – y_{A}) \ldotp \ label{7. 4}\]
4}\]
Работа, совершаемая постоянной силой тяжести над объектом, зависит только от веса объекта и разницы высот, на которую перемещается объект. Гравитация совершает отрицательную работу над объектом, который движется вверх (y B > y A ), или, другими словами, вы должны совершить положительную работу против силы тяжести, чтобы поднять объект вверх. С другой стороны, гравитация совершает положительную работу над объектом, который движется вниз (y B < y A ), или вы выполняете отрицательную работу против гравитации, чтобы «поднять» объект вниз, контролируя его опускание, чтобы он не упал на землю. («Подъем» используется вместо «падение».)
Пример \(\PageIndex{3}\): Установка книги на полку
Вы поднимаете негабаритную библиотечную книгу весом 20 Н на 1 м вертикально вниз с полки , и перенесите его на 3 м горизонтально к столу (рис. \(\PageIndex{4}\)). Какую работу совершает гравитация над книгой? (б) Когда вы закончите, вы вернете книгу по прямой линии на прежнее место на полке. Какая общая работа была совершена против силы тяжести, когда книга перемещалась от ее первоначального положения на полке и обратно?
Какая общая работа была совершена против силы тяжести, когда книга перемещалась от ее первоначального положения на полке и обратно?
Стратегия
Мы только что видели, что работа, совершаемая постоянной силой тяжести, зависит только от веса перемещаемого объекта и разности высот на пройденном пути, W AB = −mg(yB − y А ). Мы можем оценить разницу в росте для ответов (а) и (б).
Решение
- Поскольку книга начинается на полке и поднимается вниз y B − y A = −1 m, имеем $$W = −(20\; N)( − 1\; m) = 20 J \ldotp \nonumber$$
- Существует нулевая разница в высоте для любого пути, который начинается и заканчивается в одном и том же месте на полке, поэтому W = 0,
Значение
Сила тяжести совершает положительную работу (20 Дж), когда книга опускается с полки. Гравитационная сила между двумя объектами — это сила притяжения, которая совершает положительную работу, когда объекты сближаются. Гравитация совершает нулевую работу (0 Дж), когда книга перемещается горизонтально с полки на стол, и отрицательную работу (-20 Дж), когда книга перемещается со стола обратно на полку. Суммарная работа силы тяжести равна нулю [20 Дж + 0 Дж + (-20 Дж) = 0].
Гравитационная сила между двумя объектами — это сила притяжения, которая совершает положительную работу, когда объекты сближаются. Гравитация совершает нулевую работу (0 Дж), когда книга перемещается горизонтально с полки на стол, и отрицательную работу (-20 Дж), когда книга перемещается со стола обратно на полку. Суммарная работа силы тяжести равна нулю [20 Дж + 0 Дж + (-20 Дж) = 0].
В отличие от трения или других диссипативных сил, описанных в примере \(\PageIndex{2}\), полная работа, совершаемая против силы тяжести на любом замкнутом пути, равна нулю. Положительная работа совершается против силы тяжести на восходящих частях замкнутого пути, но такая же отрицательная работа совершается против силы тяжести на нисходящих частях. Другими словами, работа, выполненная против силы тяжести , при подъеме объекта вверх , «возвращается», когда объект возвращается вниз. Такие силы, как гравитация (те, которые совершают нулевую работу на любой замкнутой траектории), классифицируются как консервативные силы и играют важную роль в физике.
Упражнение 7.2
Может ли гравитация Земли быть постоянной силой для всех путей?
Работа, выполняемая изменяющимися силами
В общем, силы могут различаться по величине и направлению в точках пространства, а пути между двумя точками могут быть кривыми. Бесконечно малая работа, совершаемая переменной силой, может быть выражена через компоненты силы и перемещения по пути:
\[dW = F_{x} dx + F_{y} dy + F_{z} dz \ ldotp \nonumber\]
Здесь компоненты силы являются функциями положения вдоль пути, а перемещения зависят от уравнений пути. (Хотя мы решили проиллюстрировать dW в декартовых координатах, другие координаты лучше подходят для некоторых ситуаций.) Уравнение \ref{7.2} определяет общую работу как линейный интеграл или предел суммы бесконечно малых объемов работы. Физическая концепция работы проста: вы вычисляете работу для крошечных перемещений и суммируете их. Иногда математика может показаться сложной, но следующий пример демонстрирует, насколько чисто они могут работать.
Пример \(\PageIndex{4}\): Работа переменной силы по криволинейному пути
Объект движется по параболическому пути y = (0,5 м −1 )x 2 от начала координат A = (0, 0) в точку B = (2 м, 2 м) под действием силы \(\vec{F}\) = (5 Н/м)y \(\hat{i}\) + (10 Н/м)x \(\hat{j}\) (рисунок \(\PageIndex{5}\)). Вычислить выполненную работу.
Рисунок \(\PageIndex{5}\): Параболический путь частицы под действием заданной силы.Стратегия 9{2}) \влево(\dfrac{8}{3}\вправо) = 33,3\; J \ldotp \nonumber\]
Значимость
Этот интеграл не составило труда. Вы можете выполнить те же шаги, что и в этом примере, чтобы вычислить линейные интегралы, представляющие работу для более сложных сил и траекторий. В данном примере все было дано с точки зрения x- и y-компонент, которые проще всего использовать при оценке работы в данном случае. В других ситуациях величины и углы могут быть проще.
Упражнение \(\PageIndex{4}\)
Найдите работу, совершаемую той же силой в примере \(\PageIndex{4}\) на кубическом пути, y = (0,25 м −2 )x 3 , между теми же точками A = (0, 0) и B = (2 м, 2 м).
В примере \(\PageIndex{4}\) вы видели, что для вычисления линейного интеграла его можно свести к интегралу по одной переменной или параметру. Обычно для этого есть несколько способов, которые могут быть более или менее удобными, в зависимости от конкретного случая. В примере \(\PageIndex{4}\) мы свели линейный интеграл к интегралу по x, но с тем же успехом мы могли бы свести все к функции от y. Мы этого не сделали, потому что функции в y включают квадратный корень и дробные показатели степени, что может быть менее знакомо, но для наглядности мы делаем это сейчас. Решая x и dx через y по параболическому пути, мы получаем 9{2/3} = 33,3\; J \ldotp \nonumber\]
Как и ожидалось, результат точно такой же, как и раньше.
Одной из очень важных и широко применяемых переменных сил является сила, действующая на абсолютно упругую пружину, которая удовлетворяет закону Гука \(\vec{F}\) = −k\(\Delta \vec{x}\), где k – постоянная пружины, а \(\Delta \vec{x}\) = \(\vec{x}\) – \(\vec{x}_{eq}\) – смещение от нерастянутой (равновесной) пружины ) положение (законы движения Ньютона). Обратите внимание, что нерастянутое положение совпадает с положением равновесия только в том случае, если никакие другие силы не действуют (или, если они действуют, они компенсируют друг друга). Силы между молекулами или в любой системе, претерпевающей небольшие отклонения от устойчивого равновесия, ведут себя примерно как сила пружины.
Обратите внимание, что нерастянутое положение совпадает с положением равновесия только в том случае, если никакие другие силы не действуют (или, если они действуют, они компенсируют друг друга). Силы между молекулами или в любой системе, претерпевающей небольшие отклонения от устойчивого равновесия, ведут себя примерно как сила пружины.
Чтобы рассчитать работу силы пружины, мы можем выбрать ось x вдоль длины пружины в направлении увеличения длины, как показано на рисунке \(\PageIndex{6}\), с началом в точке положение равновесия x eq = 0. (Тогда положительный x соответствует растяжению, а отрицательный x – сжатию.) При таком выборе координат сила пружины имеет только x-компоненту, F x = −kx, а работа, выполненная при изменении x с x A на x B , равна 9.{2} \big) \ldotp \label{7.5}\]
Рисунок \(\PageIndex{6}\): (a) Пружина не действует в положении равновесия. Пружина оказывает усилие в направлении, противоположном (b) растяжению или растяжению и (c) сжатию.
Обратите внимание, что W AB зависит только от начальной и конечной точек A и B и не зависит от фактического пути между ними, если он начинается в A и заканчивается в B. То есть фактический путь может включать переходя туда и обратно, прежде чем закончить.
Еще одна интересная вещь, которую следует отметить в уравнении \ref{7.5}, заключается в том, что для этого одномерного случая вы можете легко увидеть соответствие между работой, совершаемой силой, и площадью под кривой силы в зависимости от ее смещения. Напомним, что в общем случае одномерный интеграл является пределом суммы бесконечно малых f(x)dx , представляющих площадь полос, как показано на рисунке \(\PageIndex{7}\). В уравнении \ref{7.5}, поскольку F = −kx представляет собой прямую линию с наклоном −k, при построении графика зависимости от x «площадь» под линией представляет собой просто алгебраическую комбинацию треугольных «площадей», где «площади» выше ось x положительна, а нижняя — отрицательна, как показано на рисунке \(\PageIndex{8}\). Величина одной из этих «площадей» равна половине основания треугольника по оси x, умноженной на высоту треугольника по оси силы. (Вокруг слова «площадь» заключены кавычки, потому что в этом продукте базовой высоты используются единицы работы, а не квадратные метры.)
Величина одной из этих «площадей» равна половине основания треугольника по оси x, умноженной на высоту треугольника по оси силы. (Вокруг слова «площадь» заключены кавычки, потому что в этом продукте базовой высоты используются единицы работы, а не квадратные метры.)
Пример \(\PageIndex{5}\): работа, совершаемая силой пружины
Совершенно упругая пружина требует работы 0,54 Дж, чтобы растянуться на 6 см от положения равновесия, как показано на рисунке \(\PageIndex{6b}\) . а) Какова его жесткость k? б) Какую работу необходимо совершить, чтобы растянуть его еще на 6 см?
Стратегия
«Необходимая» работа означает работу, выполняемую против силы пружины, которая является отрицательной работой в уравнении \ref{7.5}, то есть 9{2}],\; так\; к = 1,62\; J \ldotp\nonumber$$
Значимость
Поскольку работа силы пружины не зависит от пути, вам нужно было только вычислить разницу в количестве \(\frac{1}{2}\)kx 2 в конце точки. Обратите внимание, что работа, необходимая для растяжения пружины от 0 до 12 см, в четыре раза больше работы, необходимой для ее растяжения от 0 до 6 см, потому что эта работа зависит от квадрата степени растяжения от равновесия, \(\frac{1} {2}\)кх 2 . В этом случае работа по растяжению пружины от 0 до 12 см также равна работе для составного пути от 0 до 6 см с последующим дополнительным растяжением от 6 до 12 см. Следовательно, 4W(0 см до 6 см) = W(0 см до 6 см) + W(6 см до 12 см) или W(6 см до 12 см) = 3W(0 см до 6 см), так как мы нашел выше.
В этом случае работа по растяжению пружины от 0 до 12 см также равна работе для составного пути от 0 до 6 см с последующим дополнительным растяжением от 6 до 12 см. Следовательно, 4W(0 см до 6 см) = W(0 см до 6 см) + W(6 см до 12 см) или W(6 см до 12 см) = 3W(0 см до 6 см), так как мы нашел выше.
Упражнение \(\PageIndex{5}\)
Пружина в примере \(\PageIndex{5}\) сжата на 6 см от ее равновесной длины. (а) Сила пружины совершает положительную или отрицательную работу и (б) какова ее величина?
Эта страница под заголовком 7.2: Работа публикуется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- source@https://openstax.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1 - работа
- работа, совершаемая силой
- source@https://openstax.
Формула траектории – GeeksforGeeks
Снарядное движение — это тип движения, при котором объект движется в двусторонне симметричном параболическом направлении. Путь, по которому движется объект, называется его траекторией. Траектория — это кривая маршрута предмета в зависимости от его скорости и силы тяжести. Это тип движения, при котором объект, запущенный в воздух, движется по извилистому маршруту под действием силы тяжести. Он также включает компоненты положения по вертикали (y) и по горизонтали (x). Формула траектории помогает нам определить гравитационную силу, действующую на объект. Он используется для расчета траектории или траектории полета движущегося объекта, на который действует сила тяжести.
Формула
Примеры задачy = x tan θ – gx 2 /2V 2 Cos 2 θ
, где
,,,,,,,,,,,,,, 2 θ , 2 .составляющая,
θ — угол, под которым снаряд выбрасывается от горизонтали,
g — постоянная, называемая ускорением свободного падения,
v — начальная скорость снаряда.
Задача 1. Снаряд брошен с начальной скоростью 10 м/с и углом 60 o . Найдите горизонтальную составляющую снаряда, если его вертикальная составляющая равна 4 м. Используйте g = 9,8 м/с 2 .
Решение:
Мы имеем,
V = 10, θ = 60 O , x = 4 и G = 9,8
Использование формулы траектории,
y = x = x = x = x = x = x = x = x = x. gx 2 /2v 2 cos 2 θ
= 4 (тангенс 60) − (9,8) (4) 2 /2(10) 2 (cos 2 60)
= 1,73 (4) – 4,903 (190/252)
= 3,78 м
Задача 2. Снаряд брошен под углом 30 o . Найти начальную скорость снаряда, если его горизонтальная составляющая 9 м, а вертикальная 5 м. Используйте g = 9,8 м/с 2 .
Используйте g = 9,8 м/с 2 .
Решение:
Имеем,
θ = 30 o , x = 5, y = 9 и g = 9,8
Используя формулу траектории, имеем (tan 30) − (9,8) (5) 2 /2v 2 (cos 2 30)
=> 9 = 2,88 – 4,903(5)² / v 2 (1,5)
2 =
> v 2 = 25=> v = 5 м/с
Задача 3. Снаряд брошен под углом 45 o и имеет начальную скорость 12 м/с. Найдите вертикальную составляющую снаряда, если его горизонтальная составляющая равна 15 м. Используйте g = 10 м/с 2 .
Решение:
Мы имеем,
V = 12, θ = 45 O , Y = 15 и G = 9,8
Используя формулу траектории,
y = x = x = x = GX 2 /2V 2 COS 2 θ
=> 15 = X (TAN 45) – (10) x 2 /2 (12) 2 (COS 2 45) 2 (COS 2 45) 2 (COS 2 45) 2 (COS 2 45) 2 (COS 2 45) 2 .
=> 15 = x – 10x 2 /144
Решите квадратное уравнение относительно x.
=> x = 1,175, -1,275
Отбросив отрицательное значение, так как расстояние не может быть меньше нуля, получим
=> x = 1,175 м
Задача 4. Снаряд брошен под углом 30 o и начальной скоростью 6 м/с. Найдите уравнение траектории снаряда. Используйте g = 9,8 м/с 2 .
Решение:
Имеем,
θ = 30 o , v = 6 и g = 9,8
Используя формулу траектории, имеем,
y = x tan θ − gx 2 /2v 2 cos 2 θ
y = x (tan 30) − (9,8) x 2 /2(6) 29026 2 30)
y = 0,58 x – 4,9(x)²/(72) (1,5)
y = 0,58x – 4,9x²/27
Задача 5. Снаряд брошен под углом 60 o и начальной скоростью 9 м/с. Найдите уравнение траектории снаряда. Используйте g = 9,8 м/с 2 .
Решение:
Мы имеем,
θ = 60 O , V = 9 и G = 9,8
с использованием формулы Trauctory, мы имеем
Y = X Tan θ – GX 2 /2V
2626 26267 2626 2626 2626 26267 2. 2 θ
y = x (tan 60) − (9,8) x 2 /2(9) 2 (cos 2 60)
y = 1,73 x – ²/4,9 81) (1/4)
y = 1,73x – 4,903x² / 20,25
Задача 6. Снаряд брошен под углом 45 o с начальной скоростью 12 м/с. Найдите уравнение траектории снаряда. Используйте г = 9.8 м/с 2 .
Решение:
У нас есть,
? = 45 O , V = 12 и G = 9,8
Используя формулу траектории. y = x (tan 45) – (9,8) x 2 /2(12) 2 (cos 2 45)
y = x – 4,9(x)²/(144) (1/ 2)
y = x – 4,9x²/72
Задача 7.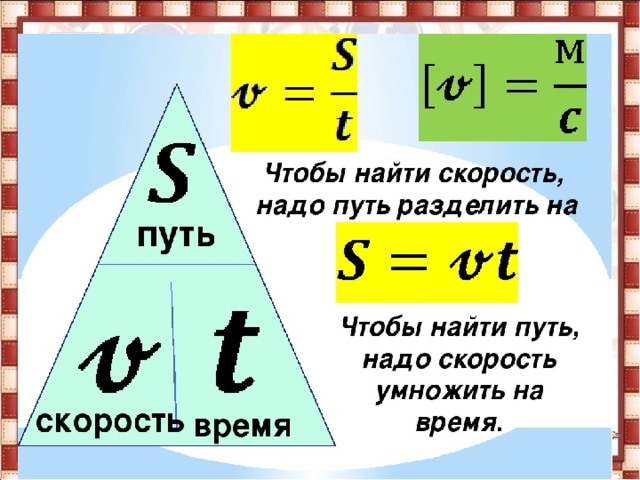

 Но иногда для более
быстрого решения задач можно
использовать формулы модуля скорости и
пути.
Но иногда для более
быстрого решения задач можно
использовать формулы модуля скорости и
пути.
 Тело
двигалось равнозамедленно,
остановилось, а затем вновь начало
двигаться (равноускоренно) в противоположном
направлении: например, мяч, брошенный
вертикально вверх.
Тело
двигалось равнозамедленно,
остановилось, а затем вновь начало
двигаться (равноускоренно) в противоположном
направлении: например, мяч, брошенный
вертикально вверх.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1 составляющая,
составляющая, => 15 = x – 10x 2 /144
=> 15 = x – 10x 2 /144