Как найти радиус окружности – Лайфхакер
20 февраля 2020ЛикбезОбразование
Лайфхакер собрал девять способов, которые помогут справиться с геометрическими задачами.
Поделиться
0Выбирайте формулу в зависимости от известных величин.
Через площадь круга
- Разделите площадь круга на число пи.
- Найдите корень из результата.
- R — искомый радиус окружности.
- S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
Сейчас читают 🔥
- ТЕСТ: Сможете ли вы решить простейшие уравнения?
Через длину окружности
- Умножьте число пи на два.
- Разделите длину окружности на результат.
- R — искомый радиус окружности.

- P — длина окружности (периметр круга).
- π (пи) — константа, равная 3,14.
Через диаметр окружности
Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.
Иллюстрация: Лайфхакер- R — искомый радиус окружности.
- D — диаметр.
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
Иллюстрация: Лайфхакер- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Через стороны и площадь вписанного треугольника
- Перемножьте три стороны треугольника.
- Разделите результат на четыре площади треугольника.
- R — искомый радиус окружности.
- a, b, с — стороны вписанного треугольника.
- S — площадь треугольника.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
Иллюстрация: Лайфхакер- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Через площадь сектора и его центральный угол
- Умножьте площадь сектора на 360 градусов.
- Разделите результат на произведение пи и центрального угла.

- Найдите корень из полученного числа.
- R — искомый радиус окружности.
- S — площадь сектора круга.
- α — центральный угол.
- π (пи) — константа, равная 3,14.
Через сторону вписанного правильного многоугольника
- Разделите 180 градусов на количество сторон многоугольника.
- Найдите синус полученного числа.
- Умножьте результат на два.
- Разделите сторону многоугольника на результат всех предыдущих действий.
- R — искомый радиус окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✂️📌
- Как найти периметр прямоугольника
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
-
2.
 1 Кинематика
1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
2.
-
3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
-
4 Электродинамика
-
4.
 1 Электростатика
1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
4.
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
-
5.
 5 Излучение и спектры
5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| Icarus |
| ||
07/12/16 |
| ||
| |||
| Eule_A |
| |||
30/09/17 |
| |||
| ||||
| iifat |
| |||
16/02/13 |
| |||
| ||||
| pogulyat_vyshel |
| ||
31/08/17 |
| ||
| |||
| iifat |
| |||
16/02/13 |
| |||
| ||||
| pogulyat_vyshel |
| ||
31/08/17 |
| ||
| |||
| Icarus |
| ||
07/12/16 |
| ||
| |||
| iifat |
| |||
16/02/13 |
| |||
| ||||
| pogulyat_vyshel |
| ||
31/08/17 |
| ||
| |||
| Icarus |
| ||
07/12/16 |
| ||
| |||
| iifat |
| |||
16/02/13 |
| |||
| ||||
| Pphantom |
| |||
09/05/12 |
| |||
| ||||
| Icarus |
| ||
07/12/16 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 13 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
6.
 3 Центростремительная сила | University Physics Volume 1
3 Центростремительная сила | University Physics Volume 1Цели обучения
К концу раздела вы сможете:
- Объяснить уравнение центростремительного ускорения
- Примените второй закон Ньютона, чтобы составить уравнение для центростремительной силы
- Использовать концепции кругового движения при решении задач, связанных с законами движения Ньютона
В книге “Движение в двух и трех измерениях” мы рассмотрели основные понятия кругового движения. Объект, совершающий круговое движение, например один из гоночных автомобилей, показанных в начале этой главы, должен ускоряться, потому что он меняет направление своей скорости. Мы доказали, что это центральное ускорение, называемое 9{2}. [/latex]
Угловая скорость показывает скорость, с которой объект вращается по кривой, в рад/с. Это ускорение действует по радиусу криволинейной траектории и поэтому также называется радиальным ускорением.
Ускорение должно создаваться силой. Любая сила или комбинация сил может вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение веревки на тросовом шаре, сила земного притяжения на Луне, трение между роликовыми коньками и полом катка, сила наклона проезжей части, действующая на автомобиль, и силы на трубе вращающейся центрифуги. . Любая результирующая сила, вызывающая равномерное круговое движение, называется центростремительная сила . Направление центростремительной силы совпадает с направлением центростремительного ускорения к центру кривизны. Согласно второму закону движения Ньютона, результирующая сила равна массе, умноженной на ускорение: [латекс] {F}_{\text{net}}=ma. [/latex] Для равномерного кругового движения ускорение равно центростремительному ускорению: . [латекс] a={a}_{\text{c}}. [/latex] Таким образом, величина центростремительной силы [латекс] {F}_{\text{c}} [/латекс] равна 9{2}}{{F}_{\text{c}}}. [/latex]
Любая сила или комбинация сил может вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение веревки на тросовом шаре, сила земного притяжения на Луне, трение между роликовыми коньками и полом катка, сила наклона проезжей части, действующая на автомобиль, и силы на трубе вращающейся центрифуги. . Любая результирующая сила, вызывающая равномерное круговое движение, называется центростремительная сила . Направление центростремительной силы совпадает с направлением центростремительного ускорения к центру кривизны. Согласно второму закону движения Ньютона, результирующая сила равна массе, умноженной на ускорение: [латекс] {F}_{\text{net}}=ma. [/latex] Для равномерного кругового движения ускорение равно центростремительному ускорению: . [латекс] a={a}_{\text{c}}. [/latex] Таким образом, величина центростремительной силы [латекс] {F}_{\text{c}} [/латекс] равна 9{2}}{{F}_{\text{c}}}. [/latex]
Это означает, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть крутую кривую, как на (рис.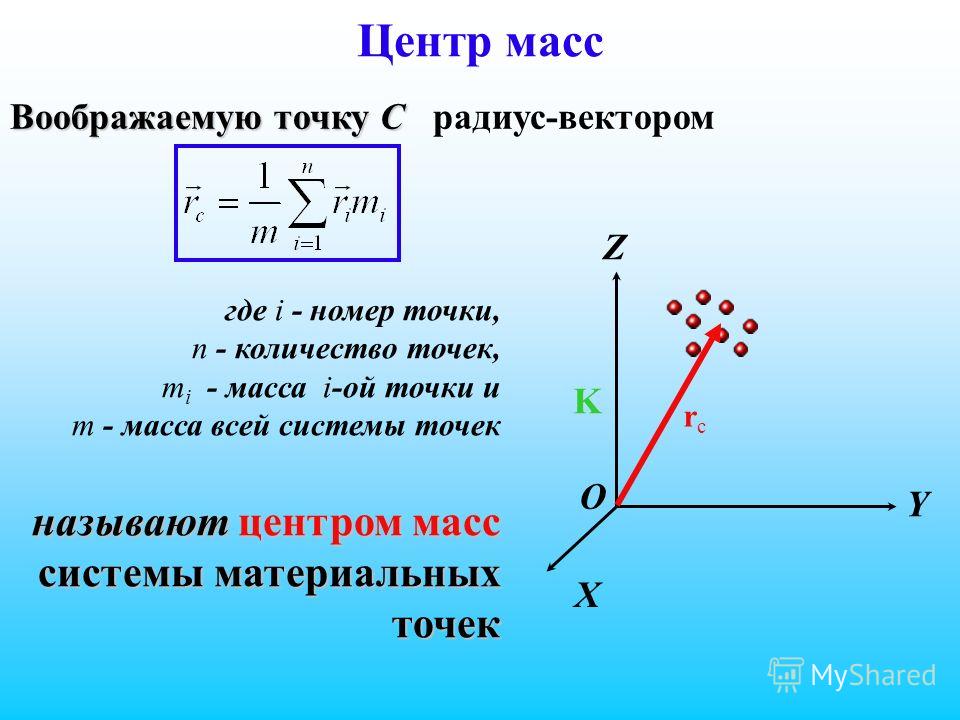 ).
).
Рисунок 6.20 Сила трения дополняет центростремительную силу и численно равна ей. Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше [латекс] {F}_{\text{c}}, [/латекс], тем меньше радиус кривизны r и тем острее кривая. Вторая кривая имеет такое же значение v, но чем больше [латекс] {F}_{\text{c}} [/латекс], тем меньше r’.
Пример
Какой коэффициент трения нужен автомобилям на плоской кривой?
(a) Рассчитайте центростремительную силу, действующую на автомобиль массой 900,0 кг, который движется по кривой радиусом 500,0 м со скоростью 25,00 м/с. (b) Предполагая, что кривая не имеет наклона, найдите минимальный статический коэффициент трения между шинами и дорогой, причем статическое трение является причиной, удерживающей автомобиль от проскальзывания ((Рисунок)).
Рисунок 6.21 Этот автомобиль на ровной поверхности удаляется и поворачивает влево. Центростремительная сила, заставляющая автомобиль поворачивать по круговой траектории, возникает из-за трения между шинами и дорогой.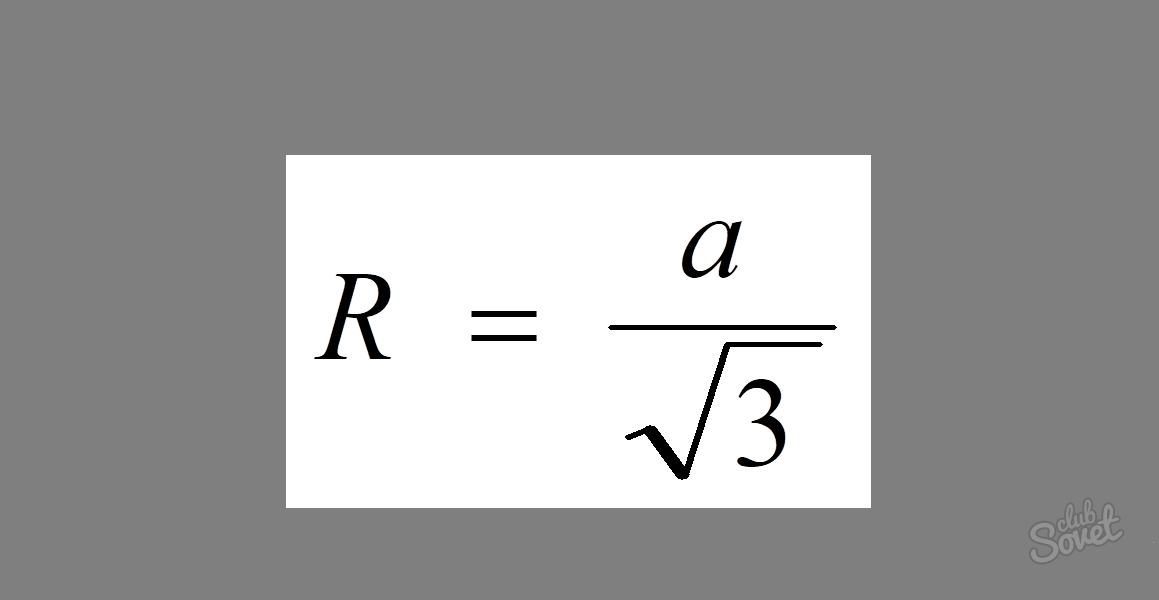 Необходим минимальный коэффициент трения, иначе автомобиль будет двигаться по кривой с большим радиусом и сойдет с проезжей части. 9{2}}{(500.0\,\text{m})}=1125\,\text{N}\text{.} [/latex]
Необходим минимальный коэффициент трения, иначе автомобиль будет двигаться по кривой с большим радиусом и сойдет с проезжей части. 9{2}}{(500.0\,\text{m})}=1125\,\text{N}\text{.} [/latex]
(Поскольку коэффициенты трения являются приблизительными, ответ дается только двумя цифрами.)
Значение
Коэффициент трения, показанный на (Рисунок)(b), намного меньше, чем обычно наблюдается между шинами и дорогами. Автомобиль все еще преодолевает кривую, если коэффициент больше 0,13, потому что статическое трение – это реактивная сила, способная принимать значение меньше, но не больше, чем [латекс] {\ mu } _ {\ text {s}} Н. [/latex] Более высокий коэффициент также позволит автомобилю проходить поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет меньше 25 м/с. Обратите внимание, что масса отменяется, а это означает, что в этом примере не имеет значения, насколько сильно загружена машина для преодоления поворота. Масса компенсируется, потому что предполагается, что трение пропорционально нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы меньше, как обсуждается далее.
Автомобиль все еще преодолевает кривую, если коэффициент больше 0,13, потому что статическое трение – это реактивная сила, способная принимать значение меньше, но не больше, чем [латекс] {\ mu } _ {\ text {s}} Н. [/latex] Более высокий коэффициент также позволит автомобилю проходить поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет меньше 25 м/с. Обратите внимание, что масса отменяется, а это означает, что в этом примере не имеет значения, насколько сильно загружена машина для преодоления поворота. Масса компенсируется, потому что предполагается, что трение пропорционально нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы меньше, как обсуждается далее.
Проверьте свои знания
Автомобиль, движущийся со скоростью 96,8 км/ч, движется по кривой окружности радиусом 182,9 м по ровной проселочной дороге. Каким должен быть минимальный коэффициент трения покоя, чтобы автомобиль не скользил?
Показать раствор
Кривые с виражами
Теперь рассмотрим кривых с виражами , где наклон дороги помогает вам преодолевать кривую ((Рисунок)). Чем больше угол [латекс]\тета[/латекс], тем быстрее вы сможете взять кривую. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. В «идеально наклонной кривой» угол [латекс]\тета[/латекс] таков, что вы можете преодолевать кривую на определенной скорости без помощи трения между шинами и дорогой. Мы выведем выражение для [латекс] \тета [/латекс] для идеально изогнутой кривой и рассмотрим пример, связанный с ним.
Чем больше угол [латекс]\тета[/латекс], тем быстрее вы сможете взять кривую. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. В «идеально наклонной кривой» угол [латекс]\тета[/латекс] таков, что вы можете преодолевать кривую на определенной скорости без помощи трения между шинами и дорогой. Мы выведем выражение для [латекс] \тета [/латекс] для идеально изогнутой кривой и рассмотрим пример, связанный с ним.
Рисунок 6.22 Автомобиль на этой кривой с наклоном удаляется и поворачивает влево.
Для идеального крена чистая внешняя сила равна горизонтальной центростремительной силе при отсутствии трения. Составляющие нормальной силы Н в горизонтальном и вертикальном направлениях должны быть равны центростремительной силе и весу автомобиля соответственно. В случаях, когда силы не параллельны, удобнее всего рассматривать составляющие вдоль перпендикулярных осей — в данном случае вертикального и горизонтального направлений.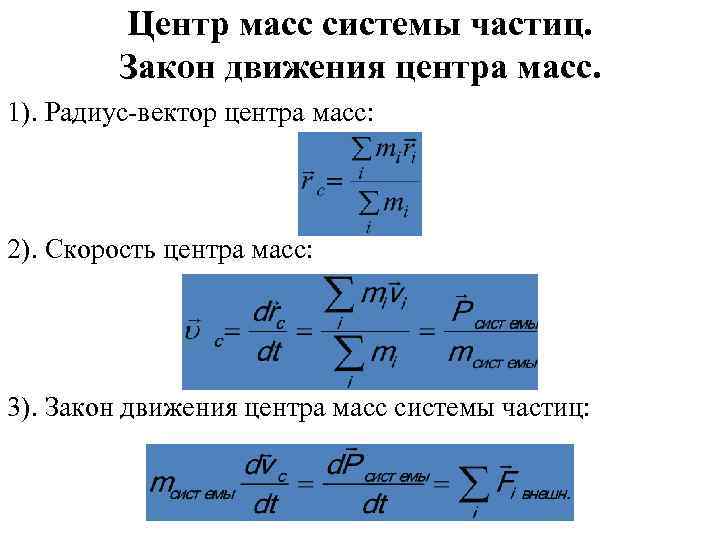 {2}\text{/}r. [/latex] Поскольку это решающая сила, и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, то есть 9{2}}{р}. [/latex]
{2}\text{/}r. [/latex] Поскольку это решающая сила, и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, то есть 9{2}}{р}. [/latex]
Поскольку автомобиль не отрывается от поверхности дороги, результирующая вертикальная сила должна быть равна нулю, а это означает, что вертикальные составляющие двух внешних сил должны быть равны по величине и противоположны по направлению. Из (рис.) мы видим, что вертикальная составляющая нормальной силы равна [латекс] Н\,\текст{cos}\,\theta , [/латекс], а единственная другая вертикальная сила – это вес автомобиля. Они должны быть равны по величине; таким образом,
[латекс] N\,\text{cos}\,\theta = мг. [/латекс] 9{2}}{рг}). [/latex]
Это выражение можно понять, если рассмотреть, как [латекс] \тета [/латекс] зависит от v и r . Большой [латекс]\тета[/латекс] получается для большого v и маленького r. То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам проходить кривую с большей или меньшей скоростью, чем если бы кривая была без трения. Обратите внимание, что [латекс]\тета[/латекс] не зависит от массы транспортного средства.
То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам проходить кривую с большей или меньшей скоростью, чем если бы кривая была без трения. Обратите внимание, что [латекс]\тета[/латекс] не зависит от массы транспортного средства.
Пример
Какова идеальная скорость для крутого крутого поворота?
Кривые на некоторых тестовых трассах и гоночных трассах, таких как Daytona International Speedway во Флориде, очень крутые. Этот крен с помощью трения шин и очень стабильной конфигурации автомобиля позволяет проходить повороты на очень высокой скорости. Чтобы проиллюстрировать это, рассчитайте скорость, с которой следует двигаться по кривой радиусом 100,0 м с уклоном [latex] 31,0\text{°} [/latex], если бы на дороге не было трения. 9{2})(0,609)}=24,4\,\text{м/с}\text{.} [/latex]
Значимость
Это примерно 165 км/ч, что соответствует очень крутому склону и довольно резкий изгиб. Трение в шинах позволяет автомобилю проходить поворот на значительно более высоких скоростях.
Трение в шинах позволяет автомобилю проходить поворот на значительно более высоких скоростях.
Самолеты также совершают повороты по крену. Подъемная сила из-за силы воздуха, действующей на крыло, действует под прямым углом к крылу. Когда самолет кренится, пилот получает большую подъемную силу, чем необходимо для горизонтального полета. Вертикальная составляющая подъемной силы уравновешивает вес самолета, а горизонтальная составляющая ускоряет его. Угол крена, показанный на (Рисунке), определяется как [латекс] \тета [/латекс]. Мы анализируем силы так же, как рассматривали случай, когда автомобиль огибает кривую с креном.
Рисунок 6.23 В повороте с креном горизонтальная составляющая подъемной силы выходит из равновесия и ускоряет самолет. Нормальная составляющая подъемной силы уравновешивает вес самолета. Угол крена задается как [латекс] \тета [/латекс]. Сравните векторную диаграмму с представленной на (Рисунок).
Вместе с божьей коровкой исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол или выбрать постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой xy – положение, скорость и ускорение с использованием векторов или графиков.
Вращайте карусель, чтобы изменить ее угол или выбрать постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой xy – положение, скорость и ускорение с использованием векторов или графиков.
Круговое движение требует силы, так называемой центростремительной силы, которая направлена к оси вращения. Эта упрощенная модель карусели демонстрирует эту силу.
Силы инерции и неинерциальные (ускоренные) системы отсчета: сила Кориолиса
Что имеют в виду взлет реактивного самолета, поворот на автомобиле, катание на карусели и круговое движение тропического циклона? общий? Каждая проявляет силы инерции — силы, которые просто кажутся возникающими из-за движения, потому что система отсчета наблюдателя ускоряется или вращается. Большинство людей согласятся, что при взлете в реактивном самолете вас как будто вдавливают обратно в сиденье, когда самолет ускоряется на взлетно-посадочной полосе. Однако физик сказал бы, что вы склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более распространенный опыт возникает, когда вы делаете крутой поворот на своей машине, скажем, вправо ((Рисунок)). Вы чувствуете, как будто вас отбрасывает (то есть принудительно ) влево относительно автомобиля. Опять же, физик сказал бы, что вы едете по прямой (вспомните первый закон Ньютона), но машина движется вправо, а не то, что вы испытываете силу слева.
Еще более распространенный опыт возникает, когда вы делаете крутой поворот на своей машине, скажем, вправо ((Рисунок)). Вы чувствуете, как будто вас отбрасывает (то есть принудительно ) влево относительно автомобиля. Опять же, физик сказал бы, что вы едете по прямой (вспомните первый закон Ньютона), но машина движется вправо, а не то, что вы испытываете силу слева.
Рисунок 6.24 (a) Водитель автомобиля чувствует себя вынужденным сместиться влево относительно автомобиля, когда он поворачивает направо. Это сила инерции, возникающая из-за использования автомобиля в качестве системы отсчета. б) В земной системе отсчета водитель движется прямолинейно, подчиняясь первому закону Ньютона, а машина движется вправо. Слева на водителя относительно Земли силы нет. Вместо этого справа на автомобиль действует сила, заставляющая его поворачиваться.
Мы можем согласовать эти точки зрения, исследуя используемые системы отсчета. Давайте сосредоточимся на людях в машине. Пассажиры инстинктивно используют автомобиль в качестве системы отсчета, тогда как физик может использовать Землю. Физик может сделать такой выбор, потому что Земля представляет собой почти инерциальную систему отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в законах движения Ньютона. Машина неинерциальная система отсчета , потому что она ускоряется в сторону. Сила слева, воспринимаемая пассажирами автомобиля, представляет собой инерционную силу , не имеющую физического происхождения (она обусловлена исключительно инерцией пассажира, а не какой-либо физической причиной, такой как напряжение, трение или гравитация). Автомобиль, как и водитель, фактически ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.
Пассажиры инстинктивно используют автомобиль в качестве системы отсчета, тогда как физик может использовать Землю. Физик может сделать такой выбор, потому что Земля представляет собой почти инерциальную систему отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в законах движения Ньютона. Машина неинерциальная система отсчета , потому что она ускоряется в сторону. Сила слева, воспринимаемая пассажирами автомобиля, представляет собой инерционную силу , не имеющую физического происхождения (она обусловлена исключительно инерцией пассажира, а не какой-либо физической причиной, такой как напряжение, трение или гравитация). Автомобиль, как и водитель, фактически ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.
Физик выберет любую систему отсчета, наиболее удобную для анализируемой ситуации. Для физика не проблема включить силы инерции и второй закон Ньютона, как обычно, если это удобнее, например, на карусели или на вращающейся планете. Неинерциальные (ускоренные) системы отсчета используются, когда это полезно. При обсуждении движения астронавта в космическом корабле, летящего со скоростями, близкими к скорости света, необходимо учитывать различные системы отсчета, как вы оцените при изучении специальной теории относительности.
Для физика не проблема включить силы инерции и второй закон Ньютона, как обычно, если это удобнее, например, на карусели или на вращающейся планете. Неинерциальные (ускоренные) системы отсчета используются, когда это полезно. При обсуждении движения астронавта в космическом корабле, летящего со скоростями, близкими к скорости света, необходимо учитывать различные системы отсчета, как вы оцените при изучении специальной теории относительности.
Теперь давайте мысленно прокатимся на карусели, а именно на быстро вращающейся игровой карусели ((Рисунок)). Вы принимаете карусель за систему отсчета, потому что вращаетесь вместе. При вращении в этой неинерциальной системе отсчета вы чувствуете силу инерции, которая стремится сбить вас с толку; это часто называют центробежной силой (не путать с центростремительной силой). Центробежная сила является широко используемым термином, но на самом деле его не существует. Вы должны крепко держаться, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В земной системе отсчета нет силы, пытающейся сбросить вас; подчеркнем, что центробежная сила — фикция. Вы должны цепляться за то, чтобы заставить себя двигаться по кругу, потому что иначе вы пойдете по прямой, сразу же с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.
В земной системе отсчета нет силы, пытающейся сбросить вас; подчеркнем, что центробежная сила — фикция. Вы должны цепляться за то, чтобы заставить себя двигаться по кругу, потому что иначе вы пойдете по прямой, сразу же с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.
Рисунок 6.25 (a) Всадник на карусели чувствует, как будто его сбрасывают. Эту силу инерции иногда ошибочно называют центробежной силой, пытаясь объяснить движение всадника во вращающейся системе отсчета. б) В инерциальной системе отсчета и по законам Ньютона его увлекает инерция (у незаштрихованного всадника [латекс] {F}_{\text{net}}=0 [/латекс] и головы по прямой). Сила [латекс] {F} _ {\ text {центростремительная}} [/латекс] необходима, чтобы вызвать круговой путь.
Этот инерционный эффект, уносящий вас от центра вращения, если нет центростремительной силы, вызывающей круговое движение, хорошо используется в центрифугах ((Рисунок)). Как упоминалось ранее в этой главе, центрифуга очень быстро вращает образец. Если смотреть со стороны вращающейся системы отсчета, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц несет их вдоль линии, касательной к окружности, в то время как пробирка движется по круговой траектории под действием центростремительной силы.
Как упоминалось ранее в этой главе, центрифуга очень быстро вращает образец. Если смотреть со стороны вращающейся системы отсчета, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц несет их вдоль линии, касательной к окружности, в то время как пробирка движется по круговой траектории под действием центростремительной силы.
Рисунок 6.26 Центрифуги используют инерцию для выполнения своей задачи. Частицы в жидком осадке оседают, потому что их инерция уносит их от центра вращения. Большая угловая скорость центрифуги ускоряет седиментацию. В конечном итоге частицы вступают в контакт со стенками пробирки, которые затем создают центростремительную силу, необходимую для того, чтобы заставить их двигаться по окружности постоянного радиуса.
Давайте теперь рассмотрим, что происходит, если что-то движется во вращающейся системе отсчета. Например, что, если вы сдвинете мяч прямо от центра карусели, как показано на (рис.)? Мяч движется по прямой относительно Земли (при условии пренебрежимо малого трения) и по кривой вправо на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а карусель вращается под ним. В системе отсчета карусели мы объясняем кажущуюся кривую вправо с помощью силы инерции, называемой 9.0015 Сила Кориолиса , которая заставляет мяч искривляться вправо. Любой человек в этой системе отсчета может использовать силу Кориолиса, чтобы объяснить, почему объекты следуют кривым траекториям, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.
Например, что, если вы сдвинете мяч прямо от центра карусели, как показано на (рис.)? Мяч движется по прямой относительно Земли (при условии пренебрежимо малого трения) и по кривой вправо на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а карусель вращается под ним. В системе отсчета карусели мы объясняем кажущуюся кривую вправо с помощью силы инерции, называемой 9.0015 Сила Кориолиса , которая заставляет мяч искривляться вправо. Любой человек в этой системе отсчета может использовать силу Кориолиса, чтобы объяснить, почему объекты следуют кривым траекториям, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.
Рис. 6.27 Глядя вниз на вращение карусели против часовой стрелки, мы видим, что мяч, скользящий прямо к краю, следует по кривой вправо. Человек двигает мяч к точке B, начиная с точки A. Обе точки поворачиваются к заштрихованным позициям (A’ и B’), показанным во времени, когда мяч следует по кривой траектории во вращающейся системе отсчета и по прямой траектории в системе Земли. .
.
До сих пор мы считали Землю инерциальной системой отсчета, практически не беспокоясь о последствиях ее вращения. Однако такие эффекты существуют, например, при вращении погодных систем. Большинство последствий вращения Земли можно качественно понять по аналогии с каруселью. Если смотреть сверху на Северный полюс, Земля вращается против часовой стрелки, как и карусель на (рис.). Как и на карусели, любое движение в Северном полушарии Земли вызывает действие силы Кориолиса вправо. Как раз обратное происходит в Южном полушарии; там сила слева. Поскольку угловая скорость Земли невелика, сила Кориолиса обычно незначительна, но для крупномасштабных движений, таких как ветры, она оказывает существенное влияние.
Сила Кориолиса заставляет ураганы в северном полушарии вращаться против часовой стрелки, тогда как тропические циклоны в южном полушарии вращаются по часовой стрелке. (Термины ураган, тайфун и тропический шторм являются региональными названиями циклонов, представляющих собой штормовые системы, характеризующиеся центрами низкого давления, сильными ветрами и проливными дождями. ) (Рисунок) помогает показать, как происходят эти вращения. Воздух течет к любой области низкого давления, а тропические циклоны содержат особенно низкое давление. Таким образом, ветры направляются к центру тропического циклона или к погодной системе низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с восходящим воздухом, что также приводит к охлаждению и образованию облаков, что делает модели низкого давления хорошо видимыми из космоса. И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, поскольку высокое давление связано с опусканием воздуха, что приводит к чистому небу.
) (Рисунок) помогает показать, как происходят эти вращения. Воздух течет к любой области низкого давления, а тропические циклоны содержат особенно низкое давление. Таким образом, ветры направляются к центру тропического циклона или к погодной системе низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с восходящим воздухом, что также приводит к охлаждению и образованию облаков, что делает модели низкого давления хорошо видимыми из космоса. И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, поскольку высокое давление связано с опусканием воздуха, что приводит к чистому небу.
Рис. 6.28 (a) Вращение этого урагана в северном полушарии против часовой стрелки является основным следствием действия силы Кориолиса. (b) Без силы Кориолиса воздух попадал бы прямо в зону низкого давления, например, в тропических циклонах. (c) Сила Кориолиса отклоняет ветры вправо, вызывая вращение против часовой стрелки. (d) Ветер, идущий от зоны высокого давления, также отклоняется вправо, создавая вращение по часовой стрелке. (e) Противоположное направление вращения создается силой Кориолиса в Южном полушарии, что приводит к тропическим циклонам. (кредит a и кредит e: модификации работы НАСА)
(b) Без силы Кориолиса воздух попадал бы прямо в зону низкого давления, например, в тропических циклонах. (c) Сила Кориолиса отклоняет ветры вправо, вызывая вращение против часовой стрелки. (d) Ветер, идущий от зоны высокого давления, также отклоняется вправо, создавая вращение по часовой стрелке. (e) Противоположное направление вращения создается силой Кориолиса в Южном полушарии, что приводит к тропическим циклонам. (кредит a и кредит e: модификации работы НАСА)
Вращение тропических циклонов и движение шарика на карусели с таким же успехом можно объяснить инерцией и вращением системы под ними. Когда используются неинерциальные системы отсчета, необходимо изобрести силы инерции, такие как сила Кориолиса, чтобы объяснить кривую траекторию. Не существует идентифицируемого физического источника этих сил инерции. В инерциальной системе отсчета инерция объясняет траекторию, и ни одна сила не имеет идентифицируемого источника. Любая точка зрения позволяет нам описывать природу, но точка зрения в инерциальной системе отсчета является самой простой в том смысле, что все силы имеют происхождение и объяснения.
Резюме
Концептуальные вопросы
Если вы хотите уменьшить напряжение (которое связано с центростремительной силой) на высокоскоростных шинах, вы бы использовали шины большого или малого диаметра? Объяснять.
Определить центростремительную силу. Может ли любой тип силы (например, напряжение, сила тяжести, трение и т. д.) быть центростремительной силой? Может ли любая комбинация сил быть центростремительной силой?
Показать раствор
Если центростремительная сила направлена к центру, почему вы чувствуете, что вас «отбрасывает» от центра, когда автомобиль движется по кривой? Объяснять.
Гонщики обычно срезают углы, как показано ниже (Путь 2). Объясните, как это позволяет выполнять кривую с наибольшей скоростью.
Показать решение
Во многих парках развлечений есть аттракционы с вертикальными петлями, как показано ниже. В целях безопасности вагоны крепятся к рельсам таким образом, что они не могут упасть. Если автомобиль перевернется с нужной скоростью, центростремительная сила будет обеспечена только гравитацией. Какая другая сила действует и каково ее направление, если:
Если автомобиль перевернется с нужной скоростью, центростремительная сила будет обеспечена только гравитацией. Какая другая сила действует и каково ее направление, если:
(a) Автомобиль выходит из-под контроля на скорости, превышающей эту?
(б) Автомобиль переезжает через верх на скорости ниже этой?
Что приводит к удалению воды с одежды в центробежной сушилке?
Показать раствор
Когда фигурист образует круг, какая сила отвечает за его поворот? Используйте диаграмму свободного тела в своем ответе.
Предположим, ребенок едет на карусели на расстоянии примерно посередине между ее центром и краем. У нее есть коробка для завтрака, покоящаяся на вощеной бумаге, так что между ней и каруселью очень мало трения. По какому пути, показанному ниже, пойдет коробка для завтрака, когда она отпустит ее? Ланч-бокс оставляет след в пыли на карусели. Эта тропа прямая, изогнутая влево или изогнутая вправо? Поясните свой ответ.
Показать решение
Чувствуете ли вы, что вас бросает в обе стороны, когда вы преодолеваете поворот, который идеально подходит для скорости вашего автомобиля? Как направлена сила, действующая на вас со стороны автокресла?
Предположим, что масса движется по круговой траектории на столе без трения, как показано ниже. В земной системе отсчета нет центробежной силы, оттягивающей массу от центра вращения, но есть сила, натягивающая веревку, прикрепляющую массу к гвоздю. Используя понятия, связанные с центростремительной силой и третьим законом Ньютона, объясните, какая сила растягивает струну, определяя ее физическое происхождение.
Показать решение
При смыве унитаза или сливе воды из раковины вода (и другой материал) начинает вращаться вокруг слива по пути вниз. Предполагая отсутствие начального вращения и поток, первоначально направленный прямо к стоку, объясните, чем вызвано вращение и какое направление оно имеет в Северном полушарии. (Обратите внимание, что это небольшой эффект, и в большинстве туалетов вращение вызвано направленными струями воды.) Изменится ли направление вращения, если вода будет нагнетаться в канализацию?
(Обратите внимание, что это небольшой эффект, и в большинстве туалетов вращение вызвано направленными струями воды.) Изменится ли направление вращения, если вода будет нагнетаться в канализацию?
Автомобиль поворачивает и натыкается на лед с очень низким коэффициентом кинетической фантастики. Автомобиль соскальзывает с дороги. Опишите путь автомобиля при выезде с дороги.
Показать раствор
В одном из аттракционов в парке аттракционов участники входят в большую вертикальную бочку и встают у стены на ее горизонтальном полу. Ствол раскручивается, и пол падает. Всадники чувствуют, как будто они прижаты к стене силой, похожей на силу гравитации. Это сила инерции, ощущаемая и используемая гонщиками для объяснения событий во вращающейся системе отсчета ствола. Объясните в инерциальной системе отсчета (Земля почти один), что прижимает всадников к стене, и определите все силы, действующие на них. 9{2} [/латекс]. С кем вы согласны и почему?
Показать раствор
Невращающаяся система отсчета, расположенная в центре Солнца, является почти инерциальной. Почему это не совсем инерциальная система отсчета?
Почему это не совсем инерциальная система отсчета?
Задачи
(a) Ребенок массой 22,0 кг катается на игровой карусели, которая вращается со скоростью 40,0 об/мин. Какая центростремительная сила действует, если он находится на расстоянии 1,25 м от его центра? б) Какая центростремительная сила действует, если карусель вращается со скоростью 3,00 об/мин и находится на расстоянии 8,00 м от ее центра? в) Сравните каждую силу с ее весом.
Показать раствор
Рассчитайте центростремительную силу на конце лопасти ветряной турбины радиусом 100 м, вращающейся со скоростью 0,5 об/с. Предположим, что масса равна 4 кг.
Каков идеальный угол крена для плавного поворота радиусом 1,20 км на шоссе с ограничением скорости 105 км/ч (около 65 миль/ч) при условии, что все едут с ограничением?
Показать раствор
Какова идеальная скорость для прохождения кривой радиусом 100,0 м с виражом под углом [latex] 20,0\text{°} [/latex]?
(a) Каков радиус бобслейного поворота с креном [латекс] 75,0\text{°} [/латекс] и скоростью 30,0 м/с при идеальном крене? б) Рассчитайте центростремительное ускорение. в) Вам кажется, что это ускорение велико?
в) Вам кажется, что это ускорение велико?
Показать раствор
Частью езды на велосипеде является наклон под правильным углом при выполнении поворота, как показано ниже. Чтобы быть устойчивым, сила, действующая на землю, должна быть на линии, проходящей через центр тяжести. Сила, действующая на велосипедное колесо, может быть разделена на две перпендикулярные составляющие: трение параллельно дороге (которое должно обеспечивать центростремительную силу) и вертикальную нормальную силу (которая должна равняться весу системы). (a) Покажите, что [латекс] \тета [/латекс] (в соответствии с приведенным определением) связан со скоростью 9{2}\текст{/}рг). [/latex] (b) Рассчитайте [latex] \theta [/latex] для поворота со скоростью 12,0 м/с и радиусом 30,0 м (как в гонке).
Если автомобиль движется по виражу со скоростью ниже идеальной, необходимо трение, чтобы предотвратить скольжение внутрь поворота (проблема на обледенелых горных дорогах).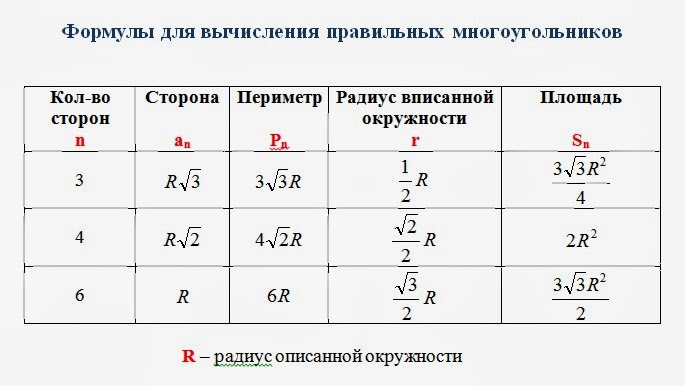 (a) Рассчитайте идеальную скорость для прохождения кривой радиусом 100,0 м с уклоном [latex] 15,0\text{°} [/latex]. б) Каков минимальный коэффициент трения, необходимый для того, чтобы испуганный водитель мог пройти ту же кривую на скорости 20,0 км/ч?
(a) Рассчитайте идеальную скорость для прохождения кривой радиусом 100,0 м с уклоном [latex] 15,0\text{°} [/latex]. б) Каков минимальный коэффициент трения, необходимый для того, чтобы испуганный водитель мог пройти ту же кривую на скорости 20,0 км/ч?
Показать раствор
Современные американские горки имеют вертикальные петли, как показано здесь. Радиус кривизны вверху меньше, чем по бокам, поэтому центростремительное ускорение вниз вверху будет больше, чем ускорение свободного падения, и пассажиры будут плотно прижаты к своим сиденьям. а) Какова скорость американских горок в верхней части петли, если радиус кривизны в этой точке равен 15,0 м, а ускорение автомобиля вниз равно 1,50 г 9{3}\,\text{кг} [/латекс].
Ребенок массой 40,0 кг находится в вагоне американских горок, который движется по кольцу радиусом 7,00 м. В точке А скорость автомобиля 10,0 м/с, а в точке В скорость 10,5 м/с. Предположим, что ребенок не держится и не пристегнут ремнем безопасности. а) С какой силой автокресло действует на ребенка в точке А? б) Какова сила воздействия автокресла на ребенка в точке В? в) Какая минимальная скорость необходима, чтобы удержать ребенка на своем месте в точке А?
а) С какой силой автокресло действует на ребенка в точке А? б) Какова сила воздействия автокресла на ребенка в точке В? в) Какая минимальная скорость необходима, чтобы удержать ребенка на своем месте в точке А?
Автомобиль огибает кривую радиусом 65 м без уклона. Если коэффициент трения покоя между дорогой и автомобилем равен 0,70, какова максимальная скорость, с которой автомобиль проходит кривую без проскальзывания?
Показать раствор
Автомобильная дорога с уклоном предназначена для движения транспорта со скоростью 90,0 км/ч. Радиус кривой 310 м. Какой угол наклона шоссе?
Глоссарий
- изогнутая кривая
- поворот на дороге с наклоном, позволяющим транспортному средству преодолевать поворот
- центростремительная сила
- любая результирующая сила, вызывающая равномерное круговое движение
- Сила Кориолиса
- сила инерции, вызывающая кажущееся отклонение движущихся объектов, если смотреть на них во вращающейся системе отсчета
- идеальный банкинг
- наклон кривой на дороге, когда угол наклона позволяет транспортному средству преодолевать кривую на определенной скорости без помощи трения между шинами и дорогой; чистая внешняя сила, действующая на транспортное средство, равна горизонтальной центростремительной силе при отсутствии трения
- сила инерции
- сила, не имеющая физического происхождения
- неинерциальная система отсчета
- ускоренная система отсчета
Калькулятор центростремительной силы
Автор Wojciech Sas, PhD кандидат
Отзыв Стивена Вудинга
Последнее обновление: 02 октября 2022 г.
- Что такое центростремительная сила? Уравнение центростремительной силы
- Единицы измерения центростремительной силы
- Центростремительная и центробежная силы. В чем разница между центростремительным и центробежным?
- Как найти центростремительную силу с помощью калькулятора центростремительной силы?
- Центростремительная сила и принцип сохранения энергии
- Часто задаваемые вопросы
Добро пожаловать в калькулятор центростремительной силы. Этот простой в использовании инструмент поможет вам найти ответы на самые распространенные и интригующие вопросы о центростремительной силе . Задумывались ли вы когда-нибудь:
- Что такое центростремительная сила?
- Как рассчитать центростремительную силу?
- Как найти центростремительную силу, действующую на тело, движущееся по окружности?
- Центростремительная сила против центробежной силы – в чем разница?
Если да, то это правильное место для начала! Давайте вместе прочитаем статью, чтобы узнать об определении центростремительной силы и единицах измерения центростремительной силы. Вы также можете найти пару примеров центростремительной силы для самостоятельного расчета .
Вы также можете найти пару примеров центростремительной силы для самостоятельного расчета .
Что такое центростремительная сила? Уравнение центростремительной силы
В книжном определении центростремительной силы говорится, что — это сила, действующая на любой объект, движущийся по криволинейной траектории. Направление силы всегда параллельно радиусу кривизны r .
Обычно мы имеем дело с примерами центростремительной силы, когда говорим о круговом движении . Это самый простой тип нелинейного движения. В этом случае радиус кривизны, естественно, равен радиусу окружности. Проверьте калькулятор кругового движения Omni для более подробного объяснения с примерами!
Формулу центростремительной силы можно записать так:
F = m × v² / r ,
где:
-
F– центростремительная сила; -
m– масса объекта; -
v— его скорость; и -
r– радиус кривизны (окружности).
Согласно второму закону Ньютона, a = v² / r — это формула центростремительного ускорения.
Взгляните на диаграмму центростремительной силы, чтобы понять, что такое определение центростремительной силы:
Мы также можем использовать калькулятор угловой скорости, чтобы переписать уравнение центростремительной силы, заменив скорость угловой скоростью ω :
F = m × ω² × r .
Единицы измерения центростремительной силы
Поскольку центростремительная сила — это сила, она имеет ту же единицу измерения, что и другие силы в физике . Итак, , что такое единица центростремительной силы?
- Единицей центростремительной силы в системе СИ является Ньютон,
Н; - Британской единицей центростремительной силы является фунтал,
pdl; - Английской инженерной единицей центростремительной силы является фунт-сила,
lbf; - Единицей центростремительной силы в СГС является дина,
dy.
Однако, используя наш калькулятор центростремительной силы, вам не нужно беспокоиться о переводе единиц силы. Вы можете изменить их автоматически одним щелчком мыши!
Аналогично, единицей центростремительного ускорения является м/с² .
Центростремительная и центробежная сила. В чем разница между центростремительным и центробежным?
На первый взгляд может показаться, что между центростремительной и центробежной силой нет никакой разницы. В нашем калькуляторе центробежной силы используется точно такое же уравнение, как и для центростремительной :
F = m × v²/r .
Решающим фактором, который помогает нам различать эти два понятия, является система отсчета . Представьте круговое движение, например, ребенок на карусели:
В инерциальной системе отсчета (родитель наблюдает за ребенком на расстоянии), присутствует только одна сила, изменяющая направление движения – центростремительная сила;
В неинерциальной системе отсчета (точка зрения ребенка), существуют две соответствующие силы одинаковых величин, которые уравновешивают друг друга .
 Еще раз, есть центростремительная сила, действующая к центру вращения. Вторая – центробежная сила – представитель силы инерции.
Еще раз, есть центростремительная сила, действующая к центру вращения. Вторая – центробежная сила – представитель силы инерции.
Как видите, центростремительная сила присутствует в обеих системах отсчета, а центробежная проявляется только в неинерциальной.
Не всегда очевидно, имеем ли мы дело с инерциальной или неинерциальной системой отсчета. Как отличить их? Давайте посмотрим на две диаграммы со сравнением центростремительной и центробежной силы:
Как найти центростремительную силу с помощью калькулятора центростремительной силы?
Имея в виду теорию, давайте попробуем решить несколько примеров центростремительной силы.
Как рассчитать центростремительную силу, действующую на автомобиль, движущийся по круговой трассе? Масса автомобиля
2 т, скорость45 км/ч, радиус пути10 м:- Прежде чем приступить к вычислениям, переведем массу в килограммы и поменяем единицы измерения скорости с
км/чнам/с.
2 т = 2000 кг,45 км/ч = 12,5 м/с; - Примените уравнение центростремительной силы,
F = m × v² / r = 2000 × (12,5)² / 10 = 31 250 Н; - Мы также можем записать решение, используя экспоненциальную запись,
F = 3,125×10⁴ Н, или с соответствующим суффиксом,F = 31,25 кН.
- Прежде чем приступить к вычислениям, переведем массу в килограммы и поменяем единицы измерения скорости с
Найдем скорость объекта, который движется по окружности радиусом
r = 5 футов, когда центростремительная сила равна3,6 пдл. Его масса2 фунта:- Измените формулу центростремительной силы, чтобы получить квадрат скорости. Для этого умножьте обе части уравнения на
rи разделите наm; -
v² = F × r / m = 3,6 × 5/2 = 9; - Извлеките квадратный корень из предыдущего результата, чтобы получить скорость,
v = √9 = 3 фут/с; - Мы также можем переписать результат с другой единицей измерения.
 После округления до трех значащих цифр скорость равна
После округления до трех значащих цифр скорость равна 0,914 м/с.
- Измените формулу центростремительной силы, чтобы получить квадрат скорости. Для этого умножьте обе части уравнения на
Всякий раз, когда вы заблудились или просто хотите проверить результаты, не стесняйтесь использовать наш калькулятор центростремительной силы. Это следует в точности тем же шагам, что и в этих примерах центростремительной силы, так что вы можете оценить любую из переменных уравнения центростремительной силы !
Центростремительная сила и принцип сохранения энергии
Мы также можем переписать определение центростремительной силы так, чтобы направление силы всегда было равно перпендикулярно движению .
Теперь вспомним определение произведения:
W = F · s .
Если угол между перемещением перемещения с и силой F равен 90° , то работа равна нулю, поэтому никакая дополнительная энергия не поступает и не выходит из системы . Каковы последствия?
Каковы последствия?
Если на объект действует только центростремительная сила, полная энергия системы сохраняется . Одними из самых известных примеров такого рода являются планетные системы. Вот почему планеты веками обращаются вокруг Солнца по стабильным орбитам.
Часто задаваемые вопросы
Как рассчитать центростремительную силу?
Чтобы вычислить центростремительную силу для объекта, движущегося в круговом движении , необходимо:
- Найти квадрат его линейной скорости ,
v². - Умножьте это значение на его массу ,
м. - Разделить все на радиус круга ,
r.
В чем разница между центростремительной и центробежной силой?
Центростремительная сила заставляет объект двигаться по криволинейной траектории, и она указывает на центр вращения . Центробежная сила — это кажущаяся сила , ощущаемая телом, движущимся по криволинейной траектории, и она указывает вне кривизны .
Центробежная сила — это кажущаяся сила , ощущаемая телом, движущимся по криволинейной траектории, и она указывает вне кривизны .
Как центростремительная сила влияет на круговое движение?
Центростремительная сила перпендикулярна скорости и меняет свое направление, не изменяя своей величины . Если это единственная сила, действующая на объект, это приводит к равномерному круговому движению.
Что вызывает центростремительную силу?
В зависимости от ситуации в качестве центростремительной силы могут выступать разные силы:
- Гравитационная сила – для Луны или спутников, вращающихся вокруг Земли;
- Фрикционные – для автомобиля или конькобежца, совершающего поворот;
- Натяжение – для шарика на резьбе;
- Контактная сила – для человека на американских горках или в самолете.

Какая сила вызывает центростремительное движение Земли?
Гравитационное притяжение вызывает центростремительное движение Земли. Земля движется вокруг Солнца из-за гравитационной силы, притягивающей эти два тела. Центростремительная сила указывает на Солнце, которое изменяет направление скорости Земли и приводит к эллиптическому движению .
Какая связь между центростремительной силой и массой?
Центростремительная сила пропорциональна массе . Удвоение массы удваивает центростремительную силу. Точно так же деление массы на коэффициент десять уменьшает центростремительную силу в десять раз.
Почему для кругового движения необходима центростремительная сила?
Чтобы двигаться по кругу, нам нужно приложить центростремительную силу, которая изменяет направление скорости . В противном случае, согласно первому закону Ньютона, объект двигался бы прямолинейно с постоянной скоростью, если бы не было результирующей силы .
Wojciech SAS, кандидат PhD
Масса (M)
Радиус (R)
Тангенциальная скорость (V)
Угловая скорость (ω)
Центральная сила (F)
Centraptal Accellator AcceLator Accellator AcceLator AcceLator Accelal AcceLatorsal Accellatorsal AcceLatorsal AcceLator.
Посмотрите 19 похожих калькуляторов вращательного и периодического движения 🌎
Угловое ускорениеУгловое смещениеУгловая частота… Еще 16
Равномерное круговое движение
Равномерное круговое движениеОбзор:
Объект, движущийся по окружности радиусом r
с постоянной скоростью v ускоряется.
направление вектора его скорости все время меняется, но величина
вектор скорости остается постоянным. Вектор ускорения не может иметь
компонента в направлении вектора скорости, так как такая компонента
вызвать изменение скорости. Поэтому вектор ускорения должен быть
перпендикулярно вектору скорости в любой точке окружности. Этот
ускорение называется радиальным ускорением
или центростремительное ускорение, и оно указывает
к центру круга. Величина центростремительной
вектор ускорения равен с = v 2 /r.
Величина центростремительной
вектор ускорения равен с = v 2 /r.
Какова сила при различных обстоятельствах?
Решим несколько задач, исследуя этот вопрос.
Проблема:
Груз массой 3 кг, прикрепленный к легкой нити, вращается по горизонтальной поверхности без трения. стол. Радиус окружности равен 0,8 м, а струна может выдержать массу 25 кг до разрыва. Какой диапазон скоростей может иметь масса перед струной перерывы?
Решение:
- Рассуждение:
Масса, прикрепленная к нити, вращается по горизонтали, стол без трения.
Предположим, что масса вращается с постоянной скоростью. это ускорение. Направление ускорения в сторону центр круга, а его величина v 2 /r. В струне есть напряжение. Нить натягивает массу с силой F, направленной к центру окружности. Этот сила F отвечает за центростремительное ускорение, F = мв 2 /р.
Струна может выдержать до разрыва массу 25 кг, т. е.
может позволить массе до 25 кг висеть на веревке рядом с
поверхность земли. Максимальное натяжение струны
поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н.
е.
может позволить массе до 25 кг висеть на веревке рядом с
поверхность земли. Максимальное натяжение струны
поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н.
Учитывая F max = 245 Н и F = mv 2 /r, мы можем найти v max . - Детали расчета:
v макс. 2 = F макс. об/мин = (250 Н)(0,8 м)/(3кг). v max = 8,1 м/с.
Проблема:
Монета, помещенная на расстоянии 30 см от центра вращающегося горизонтального поворотного стола
когда его скорость 50 см/с.
а) Какая сила обеспечивает центростремительное ускорение, когда монета неподвижна?
относительно поворотного стола?
б) Каков коэффициент статического трения между монетой и поворотным столом?
Решение:
- Рассуждение:
Когда монета покоится относительно вращающегося поворотного стола, сила статическое трение между монетой и поворотным столом обеспечивает центростремительное ускорение.
Сила трения покоя имеет максимальное значение f с = μ с Н = μ с мг.
Настройка μ с мг = mv 2 /r, мы можем решить для μ s . - Детали расчета:
(а) Сила трения покоя между монетой и поворотным столом обеспечивает центростремительное ускорение.
(b) Величина максимального сила трения покоя равна f с = μ с Н. Это максимальная сила трения покоя равна mv 2 /r при v = 0,5 м/с. Имеем μ с N = μ с mg = mv 2 /r,
или μ с = v 2 /(rg) = (0,5 м/с) 2 /(0,3 м 9,8 м/с 2 ) = 0,085.
Проблема:
Рассмотрим конический маятник с грузом массой 80 кг на проволоке длиной 10 м, образующей угол.
θ = 5 o с вертикалью. Определить
(а) горизонтальная и вертикальная составляющая силы, действующей со стороны проволоки на
маятник и
(b) центростремительное ускорение боба.
Решение:
- Рассуждение:
Диаграмма свободного тела боба показана справа.
Боб не меняет своего вертикального положения, y = константа, v y = a y = 0. Вертикальный компонент T должен иметь величина мг.
Горизонтальная составляющая Т обеспечивает центростремительное (радиальное) ускорение а р . - Детали расчета:
(a) Вертикальный компонент T должен иметь величина мг.
Tcos(5 o ) = мг, T = (80 кг 9,8 м/с 2 )/cos(5 или ) = 787 N
Величина горизонтальной составляющей T равна Tsin(5 o ) = 68,6 Н. Горизонтальная составляющая силы направлена к центру круг.(b) Tsin(5 o ) = ma r , a r = (68,6 Н)/(80 кг) = 0,857 м/с 2 .
Скорость боба находится из a r = v 2 /r, v = (a r r) ½ .
Так как r = (10 м)*sin(5 o ), имеем v = 0,86 м/с.
Проблема:
Автомобиль массой 1800 кг преодолевает неровность на дороге, идущей по дуге окружности.
радиусом 42 м.
а) С какой силой дорога действует на автомобиль при прохождении автомобиля?
наивысшая точка горки, если автомобиль движется со скоростью 16 м/с?
б) С какой максимальной скоростью может двигаться автомобиль, проезжая через этот горб?
потеря связи с дорогой?
Решение:
- Рассуждение:
Показана схема свободного кузова автомобиля.Единственными силами, действующими на автомобиль, движущийся с постоянной скоростью, являются сила тяжести и нормальная сила, действующая на дорогу. Если эти силы равны по величине, автомобиль не разгоняется. Если автомобиль движется по дуга окружности, то она ускоряется. Ускорение равно r = v 2 /р. Следовательно, гравитационная сила должна иметь большую величины, чем нормальная сила.

- Детали расчета:
Нам нужно
мг – n = mv 2 /r, или n = m(g – v 2 /r).
n = (1800 кг)(9,8 м/с 2 – (16 м/с) 2 /(42 m)) = 6669 N(b) Автомобиль теряет контакт с дорогой, когда n становится равным нулю. Затем дорога больше не поддерживает машину. Это происходит, когда g – v 2 /r = 0, или v 2 = gr = 411,6 м 2 /с 2 , v = 20,3 РС.
Модуль 5: Вопрос 1
Чувствуете ли вы, что вас бросает в обе стороны, когда вы преодолеваете кривую, которая идеально накрен для скорости вашего автомобиля? Как направлена сила, приложенная на вас возле автокресла?
Обсудите это со своими однокурсниками на форуме!
Гравитация
Массивные объекты обладают инерцией. Требуется сила, чтобы изменить их состояние
движение. Все массивные объекты взаимодействуют через сила гравитации . Частица массой m 1 действует с силой
F 12 на частицу массой m 2 . Закон тяготения Ньютона дает эту силу как
Частица массой m 1 действует с силой
F 12 на частицу массой m 2 . Закон тяготения Ньютона дает эту силу как
F 12 = (-G m 1 m 2 /r 12 2 )
( р 12 / р 12 ).
Здесь r 12 — расстояние между частицами 1
и 2, и ( r 12 /r 12 ) является
Единичный вектор , указывающий от частицы 1 к частице
2.
G — гравитационная постоянная, G = 6,67*10 -11 Нм 2 /кг 2 .
Сила F 21 , действующая на частицу массой m 2 действует на частицу массой m 1 , равно – F 12 , по третьему закону Ньютона. Сила тяжести всегда привлекательный.
Точка в объекте, от которой расстояние r 12 равно
измеряется его центр масс. Масса m 1 притягивает массу m 2 ,
и масса m 2 притягивает массу m 1 . Центр
масса каждого тела притягивается к центру масс другого
объект.
Центр
масса каждого тела притягивается к центру масс другого
объект.
Взвешивание земли
Радиус Земли R = 6368 км. Если вы подниметесь на гору высотой 1000 м,
ваше расстояние от центра земли изменится на (1/6368) * 100 % = 0,016 %
а величина гравитационной силы, действующей на вас, изменится на (1/6368) 2 *100
% = 2,4*10 -6 %. Для всех объектов вблизи поверхности земли
расстояние от центра почти постоянно, а величина
Поэтому вектор гравитационной силы приблизительно постоянен. За малым
расстояния, когда кривизной земной поверхности можно пренебречь,
направление вектора гравитационной силы также почти постоянно. Это указывает
прямо вниз к центру земли.
Сила тяжести, действующая на тело массой m на поверхности земли, равна
величина F = мг. Используя закон всемирного тяготения Ньютона, мы пишем GMm/R 2 =
мг, где М — масса Земли. Таким образом, мы имеем M = gR 2 /G.
Используя R = 6,4*10 6 м, находим M = (9,8 м/с 2 )(6,4*10 6 м) 2 /(6,67*10 -11 Н·м 2 /кг 2 ) =
6*10 24 кг.
Орбитальный
Гравитационное притяжение между объектом и землей притягивает объект к центру земли. Когда объект вращается вокруг Земли, направление силы тяжести на объекте постоянно меняется. радиус Земли настолько велик, что Земля кажется в некоторых местах плоской наблюдатель, стоящий на поверхности. Когда проблема касается только расстояний, которые намного меньше радиуса Земли, мы часто пренебрегаем кривизной земной поверхности и предположим, что сила гравитации направлена в одну и ту же направление вниз везде.
Ссылка: Спутник как снаряд
Предположим, что вблизи поверхности земли в
x-направление, как показано на рисунке выше. Первоначально он ускоряется только в
Y-направление. Но по мере движения объекта направление ускорения
изменения. Если начальная скорость объектов достаточно высока, мы должны принять
изменение направления силы учитывать при расчете объектов
траектория. Объект на круговой орбите вокруг Земли находится
постоянно падает к центру земли. Это постоянно
ускорение. Но пока он движется по криволинейной траектории, поверхность
Земля изгибается в сторону от объекта так, что расстояние между Землей и
объект остается постоянным.
Это постоянно
ускорение. Но пока он движется по криволинейной траектории, поверхность
Земля изгибается в сторону от объекта так, что расстояние между Землей и
объект остается постоянным.
Сила тяжести всегда направлена к центру объекта. круговой орбите и отвечает за центростремительное ускорение объект.
F = mv 2 /r
Для объекта у поверхности земли F = mg и r = 6,4*10 6 м. Скорость орбитального объекта находится из mg = mv 2 /r, v 2 = gr = (9,8 м/с 2 )(6,4*10 6 м). У нас v = 7919 м/с, или примерно 8000 м/с. Требуется объект t = 2πr/v = (6,28*6,4*10 6 м)/(7919 м/с) = 5075 с = 84 мин, чтобы совершить полный оборот по орбите.
Если тот же объект двигался по круговой орбите с большим радиусом, сила
силы тяжести на объекте будет меньше. Поскольку мы удваиваем расстояние от
центра земли сила тяжести уменьшается в 1/4 раза.
центростремительное ускорение v 2 /r уменьшается в 1/4 раза. Этот
означает, что v 2 должен уменьшиться в 1/2 раза. Имеем v = 5600 м/с
а для совершения оборота по орбите требуется 14355 с = 240 мин.
Этот
означает, что v 2 должен уменьшиться в 1/2 раза. Имеем v = 5600 м/с
а для совершения оборота по орбите требуется 14355 с = 240 мин.
Объектов на геосинхронных орбитах совершить полный оборот за 24 часа или 86400 с. Следовательно, их скорость равна v = 2πr/(86400 с). Запись GMm/r 2 = mv 2 /r = m(2πr/(86400 с)) 2 /r, или r 3 = GM(86400s) 2 /(4π). мы можем решить это уравнение для радиуса геосинхронной орбиты. При М = 6*10 24 кг имеем r=42260 км. Геосинхронный спутник вращается вокруг 42260 км – 6400 км = 35860 км над поверхностью земли. Радиус его орбиты в 6,6 раза больше радиуса Земли.
Луна совершает один оборот вокруг Земли за 27,3 дня. Мы можем найти расстояние до Луну таким же образом мы нашли расстояние до геосинхронного спутника. Расстояние от Земли до Луны 384400 км.
Проблема:
Когда падающий метеор находится на расстоянии над земной поверхностью в 3 раза больше Радиус Земли, каково ускорение ее свободного падения под действием силы тяжести приложенная к нему сила?
Решение:
- Рассуждение:
Сила, действующая на метеор, равна F = ma = GMm/r 2 .



 1 Кинематика
1 Кинематика
 1 Электростатика
1 Электростатика
 5 Излучение и спектры
5 Излучение и спектры
 11.2019, 23:53
11.2019, 23:53  ..
..

 11.2019, 09:27
11.2019, 09:27  11.2019, 10:15
11.2019, 10:15  .. Набирал поздно вечером и скопировал не то условие…
.. Набирал поздно вечером и скопировал не то условие… 11.2019, 12:01
11.2019, 12:01  11.2019, 12:48
11.2019, 12:48  11.2019, 15:06
11.2019, 15:06  Но кривизна (и радиус оной) — это дифференциальная геометрия, вроде бы. Не знаю уж, вносит ли тут физика что-то своё.
Но кривизна (и радиус оной) — это дифференциальная геометрия, вроде бы. Не знаю уж, вносит ли тут физика что-то своё.
 ..
..

 Еще раз, есть центростремительная сила, действующая к центру вращения. Вторая – центробежная сила – представитель силы инерции.
Еще раз, есть центростремительная сила, действующая к центру вращения. Вторая – центробежная сила – представитель силы инерции.
 После округления до трех значащих цифр скорость равна
После округления до трех значащих цифр скорость равна 
 е.
может позволить массе до 25 кг висеть на веревке рядом с
поверхность земли. Максимальное натяжение струны
поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н.
е.
может позволить массе до 25 кг висеть на веревке рядом с
поверхность земли. Максимальное натяжение струны
поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н. 


