Физика формула времени: Скорость и путь при равноускоренном движении — урок. Физика, 9 класс.

Расчет скорости, пути и времени движения

Урок 10. Физика 7 класс ФГОС

На этом уроке мы научимся применять полученные знания на практике. Изучая механическое движение, мы познакомились с несколькими формулами, которые позволяют рассчитать путь и время движения. Нас ждет пять задач различной сложности. А в конце урока мы попытаемся вывести алгоритм решения задач на движение.

Конспект урока “Расчет скорости, пути и времени движения”

Расчёт пути и времени движения

«Движение – это жизнь»

Аристотель

В данной теме будем применять приобретённые знания о механическом движении на практике. Прежде чем начать решать задачи, вспомним, необходимые определения. Путь – это физическая величина, равная длине траектории, по которой двигалось тело, в течение данного промежутка времени. Путь является скалярной величиной, то есть, не имеет направления. Скорость при равномерном движении – это величина, равная отношению пройденного пути к промежутку времени, за который этот путь пройден.

                                                              

Скорость является векторной величиной, то есть, характеризуется как числовым значением, так и направлением.

Средняя скорость при неравномерном движении – это величина, равная отношению всего пройденного пути к общему времени в пути.

                                                  

Задача 1. Какой путь пройдет автомобиль, двигаясь равномерно со скоростью 75 км/ч за 20 минут?

В первую очередь, необходимо научиться правильно оформлять задачи по физике. При решении любой задачи нужно писать «дано». То есть, в левой части листа необходимо записать слово «дано», после которого ставится двоеточие, а дальше в столбик перечисляете все исходные данные, которые указаны в условии задачи.

В нашем случае – это скорость и время в пути. После этого, нужно очеркнуть данные и ниже (уже под линией) записать, что необходимо найти. В задаче спрашивается, какой путь пройдет автомобиль. Дальше приступаем непосредственно к решению задачи.

А теперь обратите внимание вот на что: скорость в условии задачи дана в км/ч, то есть, сколько километров автомобиль проходит за час. А время в условии дано в минутах. Поэтому, прежде чем делать вычисления, необходимо перевести минут в часы.

В общем и целом, этот способ правильный. Но, чтобы не запутаться с единицами измерения, можно (и даже нужно) переводить данные в систему СИ сразу после того, как записано «дано». Напомним, что для перевода км/ч в м/с или м/с в км/ч необходимо

                                                      1 м/с = 3,6 км/ч

                                                    1 км/ч = 1/3,6 м/с

Время в системе СИ измеряется в секундах. В одной минуте шестьдесят секунд, поэтому, чтобы перевести минуты в секунды, нужно минуты умножить на 60.

После того, как перевели все данные в систему СИ, необходимо очеркнуть и эту колонку, а правее пишитсяе само решение. Решение и ответ будут одинаковыми. Однако рекомендуется переводить данные в систему СИ.

Задача 2. Мотоциклист проехал 5 км вдвое быстрее, чем следующие 7 км. Найдите его среднюю скорость, если общее время в пути составило 10 минут.

Получившееся выражение, в котором остались, только те величины, которые были даны изначально, называется расчетной формулой. Только в расчетную формулу необходимо подставлять числовые значения, а до этого, все делается в буквенном виде.

Задача 3. Самолет взлетел, после чего пролетел 120 км на определенной высоте, а потом приземлился. Известно, что пути, пройденные в процессе взлета и посадки равны 120 км каждый. Во время взлета и посадки, скорость самолета была равна 200 м/с, а во время остального пути – 250 м/с. Какое время самолет затратил на весь путь? Какова средняя скорость?

Сразу хочется обратить ваше внимание на распространенную ошибку. Среднюю скорость нельзя находить как среднее арифметическое разных скоростей на разных участках движения. В этом можно убедиться с помощью простых расчетов: если подсчитать среднюю скорость, как среднее арифметическое скоростей, то получим 216,7 м/с. Этот результат неправильный. Теперь подсчитаем среднюю скорость как отношение всего пройденного пути к общему времени в пути. В результате получим 214,3 м/с. Получается вроде небольшая разница. В результате неверных расчётов за каждую секунду, пройденное расстояние увеличивается на 2,4 м/с. Поэтому, при неверном расчете за час пройденное расстоянии будет больше на 8,6 км, а это существенно.

Задача 4. Средняя скорость движения велосипедиста равна 8 м/с. Известно, что первую часть своего пути велосипедист проехал за 3 минуты. За какое время велосипедист проехал вторую часть, если общий путь составил 2 км?

Задача 5. Определите по графику скорость равномерного движения тела.

Здесь, конечно, никаких данных, кроме самого графика нет, поэтому, «дано» писать не нужно.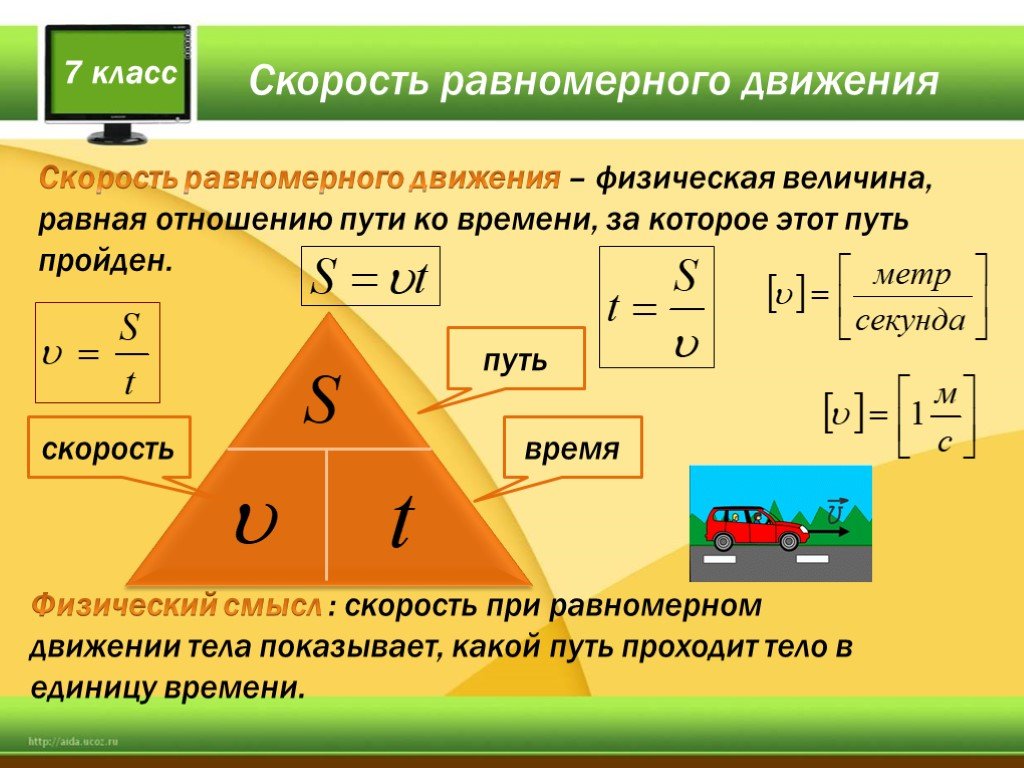 В таких заданиях, в первую очередь нужно посмотреть на оси графика: какие величины они обозначают и в каких единицах измеряются. Вертикальная ось – обозначает пройденный путь в метрах, а горизонтальная ось – время в минутах. Значит, это график зависимости пройденного пути от времени. При равномерном движении скорость постоянна, значит, можно путь, пройденный за определенный промежуток времени, разделить на это время и, таким образом, найти скорость. Для наибольшей точности желательно найти точку, на графике, наиболее близкую к пересечению клеточек. Когда нашли такую точку, смотрим на соответствующие координаты, то есть, на значения пути и времени. Для этого из точки опускаем перпендикуляры на обе оси. Теперь, когда получили значение координат, можно определить скорость.

Основные выводы:

В качестве итогов урока, рассмотрим общий алгоритм решения задач на движение.

Предыдущий урок 9 Скорость тела.

Равномерное и неравномерное движение

Следующий урок 11 Инерция

Получите полный комплект видеоуроков, тестов и презентаций Физика 7 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Страница не найдена – РОО “Ассоциация победителей олимпиад”

Ваши ФИО*

Ваш email*

Ваш номер телефона*

Какой предмет вы хотели бы преподавать?*

Расскажите кратко о своих олимпиадных достижениях*

Приложите резюме*

Объём файлов не должен превышать 20 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt

Please leave this field empty.

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

Ваша электронная почта*

Из какого вы региона?*

Расскажите, как мы могли бы сотрудничать*

Please leave this field empty.

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО*

Ваша электронная почта*

Ваш номер телефона*

Образовательное учреждение*

Расскажите кратко, какая у вас сложилась ситуация с олимпиадным движением в школе и какого результата вы ожидаете от сотрудничества с АПО*

Please leave this field empty.

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

Ваш email

Каким предметом вы интересуетесь

Выберите наиболее подходящий статус Статус не выбранУченикРодительПредставитель школыПедагог

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО ученика

Дата рождения ученика

Класс

Образовательное учреждение

Город образовательного учреждения

ФИО родителя

Телефон родителя

Email родителя

Выберите группу Группа не выбрана

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО ученика

Дата рождения ученика

Класс

Образовательное учреждение

Город образовательного учреждения

ФИО родителя

Телефон родителя

Email родителя

Выберите группу Группа не выбрана

Мотивационное письмо Объём файла не должен превышать 2 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО

Телефон

Email

Образовательное учреждение

Город образовательного учреждения

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО

Телефон

Email

Проект / отдел

Должность

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО ребенка

Название образовательного учреждения

Город образовательного учреждения

ФИО родителя

Телефон родителя

Email родителя

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

Войти

---

Родитель

Буду покупать курсы для своего ребёнка Зарегистрироваться

---

Обучающийся

Сам буду проходить курсы Зарегистрироваться

---

Представитель школы

Буду заказывать услуги для своего образовательного учреждения и контролировать их исполнение Зарегистрироваться

---

Слушатель КПК

Буду проходить курсы повышения квалификации для учителей Зарегистрироваться

Период | Определение, символ, формулы и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полета на Луну до управления космосом — мы изучаем широкий спектр тем, которые питают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Связанный контент

3.

S: Движение по прямой (краткое содержание)

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5369

• OpenStax
• OpenStax

Основные термины

ускорение свободного падения	ускорение объекта под действием силы тяжести
среднее ускорение	скорость изменения скорости; изменение скорости во времени
средняя скорость	общее пройденное расстояние, деленное на прошедшее время
средняя скорость	смещение, деленное на время, в течение которого происходит смещение
смещение	изменение положения объекта
пройденное расстояние	общая длина пути, пройденного между двумя позициями
истекшее время	разница между временем окончания и временем начала
свободное падение	состояние движения, которое является результатом только гравитационной силы
мгновенное ускорение	ускорение в определенный момент времени
мгновенная скорость	абсолютное значение мгновенной скорости
мгновенная скорость	скорость в определенный момент или момент времени
кинематика	описание движения через такие свойства, как положение, время, скорость и ускорение
позиция	местоположение объекта в определенное время
полный водоизмещение	сумма индивидуальных перемещений за заданный период времени
задача преследования двух тел	задача кинематики, в которой неизвестные вычисляются путем одновременного решения кинематических уравнений для двух движущихся объектов

Ключевые уравнения

Рабочий объем	$$\Delta x = x_{f} – x_{i}$$
Полный водоизмещение	$$\Delta x_{Всего} = \sum \Delta x_{i}$$
Средняя скорость	$$\bar{v} = \frac{\Delta x}{\Delta t} = \frac{x_{2} – x_{1}}{t_{2} – t_{1}}$$
Мгновенная скорость	$$v(t) = \frac{dx(t)}{dt}$$
Средняя скорость	$$\bar{s} = \frac{Total\; расстояние}{Прошло\; время}$$
Мгновенная скорость	$$Мгновенно\; скорость = |v(t)|$$
Среднее ускорение	$$\bar{a} = \frac{\Delta v}{\Delta t} = \frac{v_{f} – x_{0}}{t_{f} – t_{0}}$$
Мгновенное ускорение	$$a(t) = \frac{dv(t)}{dt}$$
Позиция по средней скорости 9{2} – 2 г(г – г_{0})$$ 90 174
Скорость от ускорения	$$v(t) = \int a(t)dt + C_{1}$$
Положение по скорости	$$x(t) = \int v(t)dt + C_{2}$$

Резюме

3.

1 Положение, перемещение и средняя скорость

• Кинематика — это описание движения без учета его причин. В этой главе оно ограничивается движением по прямой линии, называемым одномерным движением.
• Смещение — это изменение положения объекта. Единицей перемещения в СИ является метр. Смещение имеет направление, а также величину.
• Пройденное расстояние — это общая длина пути, пройденного между двумя позициями.
• Время измеряется изменениями. Время между двумя точками положения x ₁ и x ₂ равно \(\Delta\)t = t ₂ − t ₁ . Прошедшее время для события равно \(\Delta\)t = t _f – t ₀ , где t _f — конечное время, а t ₀ — начальное время. Начальное время часто принимается равным нулю.
• Средняя скорость \(\bar{v}\) определяется как смещение, деленное на прошедшее время. Если x ₁ , t ₁ и x ₂ , t ₂ являются двумя точками времени положения, средняя скорость между этими точками равна

\[\bar{v} = \frac{\Delta x}{\Delta t} = \frac{x_{2} – x_{1}}{t_{2} – t_{1}} \ldotp\ ]

3.

2 Мгновенная скорость и скорость

• Мгновенная скорость является непрерывной функцией времени и дает скорость в любой момент времени во время движения частицы. Мы можем рассчитать мгновенную скорость в определенный момент времени, взяв производную функции положения, которая дает нам функциональную форму мгновенной скорости v(t).
• Мгновенная скорость является вектором и может быть отрицательным.
• Мгновенная скорость находится путем взятия абсолютного значения мгновенной скорости, и оно всегда положительное.
• Средняя скорость равна общему пройденному расстоянию, деленному на прошедшее время.
• Наклон графика зависимости положения от времени в определенный момент времени дает мгновенную скорость в этот момент времени.

3.3 Среднее и мгновенное ускорение

• Ускорение – это скорость изменения скорости. Ускорение — это вектор; оно имеет как величину, так и направление. Единицей ускорения в системе СИ является метр в секунду в квадрате.
• Ускорение может быть вызвано изменением величины или направления скорости, или и тем, и другим.
• Мгновенное ускорение a(t) является непрерывной функцией времени и дает ускорение в любой конкретный момент времени во время движения. Он рассчитывается из производной функции скорости. Мгновенное ускорение — это наклон графика зависимости скорости от времени.
• Отрицательное ускорение (иногда называемое замедлением) — это ускорение в отрицательном направлении в выбранной системе координат.

3.4 Движение с постоянным ускорением

• При анализе одномерного движения с постоянным ускорением определите известные величины и выберите соответствующие уравнения для решения неизвестных. Для решения неизвестных необходимо одно или два кинематических уравнения, в зависимости от известных и неизвестных величин.
• Задачи преследования двух тел всегда требуют одновременного решения двух уравнений для неизвестных.

3.

5 Свободное падение

• Объект в свободном падении испытывает постоянное ускорение, если сопротивлением воздуха можно пренебречь.
• На Земле все свободно падающие объекты имеют ускорение g из-за силы тяжести, которое в среднем составляет g = 9,81 м/с ² .
• Для объектов в свободном падении направление вверх обычно считается положительным для смещения, скорости и ускорения.

3.6 Нахождение скорости и перемещения по ускорению

• Интегральное исчисление дает нам более полную формулировку кинематики.
• Если ускорение a(t) известно, мы можем использовать интегральное исчисление для получения выражений для скорости v(t) и положения x(t).
• Если ускорение постоянно, интегральные уравнения сводятся к уравнению 3.12 и уравнению 3.13 для движения с постоянным ускорением.

Авторы и авторство

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими сотрудничающими авторами.