Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
1. Найти время полета тела на определенной высоте
hв – высота на восходящем участке траектории
hн – высота на нисходящем участке траектории
t – время в момент которого тело находится на высоте hв или hн
Vo – начальная скорость тела
α – угол под которым брошено тело
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула для определения значения времени, за которое тело поднялось на определенную высоту, на восходящем участке траектории
Формула для определения значения времени, за которое тело поднялось на определенную высоту, на нисходящем участке траектории
Таким образом, одному значению высоты будет соответствовать два значения времени, одно при подъеме, второе при падении.
2. Найти время полета тела пролетевшее определенное расстояние
S – расстояние пройденное по горизонтали
t – время за которое тело прошло расстояние S
Vo – начальная скорость тела
Vx – проекция начальной скорости на ось OX
Vy
α – угол под которым брошено тело
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула для определения значения времени, за которое пройдено определенное расстояние
3. Значение времени при максимальных значениях высоты и дальности
Smax – максимальная дальность по горизонтали
hmax – максимальная высота
tmax – время всего полета
th – время
Vo – начальная скорость тела
Vx – проекция начальной скорости на ось OX
Vy – проекция начальной скорости на ось OY
α – угол под которым брошено тело
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула для определения значения времени, затраченное на весь полет, если известна начальная скорость или ее проекции
Формула для определения значения времени, на максимальной высоте
Т. к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно – время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту
к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно – время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту
Формула скорости свободного падения в физике
Задание. Одно тело бросили вертикально вверх с начальной скоростью равной $v_0.$ В этот же момент времени вертикально вниз с начальной скоростью $v_0$ бросили второе тело. Высота, с которой бросили это тело равно высоте максимального подъема первого тела. Какова скорость первого и второго тел в момент встречи этих двух тел? Тела считайте материальными точками, сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
За основу решения задачи примем уравнение для скорости движения тела в поле тяжести Земли:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(2.1\right).\]Для первого тела уравнение (2.1) в проекции на ось Y будет иметь вид:
\[v_1=v_0-gt\ \left(2.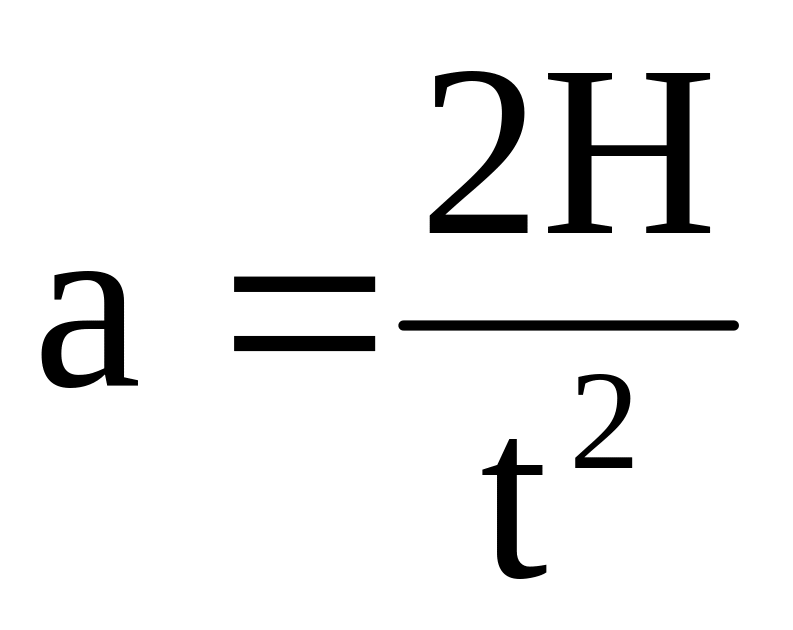 2_0}{2g}=v_0+\frac{v_0}{4}=\frac{5}{4}v_0.\]
2_0}{2g}=v_0+\frac{v_0}{4}=\frac{5}{4}v_0.\]Ответ. $v_1=\frac{3}{4}v_0,$ $v_2=\frac{5}{4}v_0$
Свободное падение тел
Ускорение свободного падения
Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.
Ускорение свободного паденияУскорение свободного падения – ускорение, с которым все тела падают на Землю.
Ускорение свободного падения приблизительно равно 9,81 мс2 и обозначается буквой g. Иногда, когда точность принципиально не важна, ускорение свободного падения округляют до 10 мс2.
Земля – не идеальный шар, и в различных точках земной поверхности, в зависимости от координат и высоты над уровнем моря, значение g варьируется. Так, самое большое ускорение свободного падения – на полюсах (≈9,83 мс2), а самое малое – на экваторе (≈9,78 мс2).
Свободное падение тела
Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его.
Свободное падение – прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать.
h=v0+gt22.
Так как начальна скорость равна нулю, перепишем:
h=gt22.
Отсюда находится выражение для времени падения тела с высоты h:
t=2hg.
Принимая во внимание, что v=gt, найдем скорость тела в момент падения, то есть максимальную скорость:
v=2hg·g=2hg.
Движение тела, брошенного вертикально вверх
Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:
v=v0-gt.
Подставив v=0, найдем время подъема тела на максимальную высоту:
t=v0g.
Время падения совпадает со временем подъема, и тело вернется на Землю через t=2v0g.
Максимальная высота подъема тела, брошенного вертикально:
h=v022g.
Нужна помощь преподавателя?
Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.
На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.
Первый график – это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.
Второй график – движение тела, брошенного вертикально вверх с начальной скоростью v0=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.
Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.
Движение тела, брошенного под углом к горизонту
С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.
Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения – v0y. Движение вдоль оси OX – равномерное и прямолинейное, с начальной скоростью v0x.
Условия для движения вдоль оси ОХ:
x0=0; v0x=v0cosα; ax=0.
Условия для движения вдоль оси OY:
y0=0; v0y=v0sinα; ay=-g.
Приведем формулы для движения тела, брошенного под углом к горизонту.
Время полета тела:
t=2v0sinαg.
Дальность полета тела:
L=v02sin2αg.
Максимальная дальность полета достигается при угле α=45°.
Lmax=v02g.
Максимальная высота подъема:
h=v02sin2α2g.
Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука – баллистика.
Потенциальная энергия — урок.
 Физика, 8 класс.
Физика, 8 класс.Обрати внимание!
Потенциальная энергия присуща всем телам, которые обладают потенциальной способностью совершать работу.
Потенциальной энергией обладает тело, которое поднято на некоторую высоту над поверхностью земли.
Пример:
Яблоко висит на ветке на определённой высоте над землёй. Пока яблоко находится на высоте, оно обладает потенциальной способностью упасть и совершить работу.
За уровень отсчёта можно принять не только уровень поверхности земли, но и любую другую поверхность, на которой значение потенциальной энергии принимается равным нулю.
Пол в помещении может находиться выше поверхности земли, однако тела, находящиеся в этом помещении, не могут упасть ниже уровня пола, поэтому принимается, что на полу потенциальная энергия тел равна \(нулю\).
Потенциальной энергией обладают все тела, которые подняты на определённую высоту.
Обрати внимание!
Потенциальная энергия тела, поднятого над землёй, прямо пропорциональна массе \(m\), ускорению свободного падения \(g\) и высоте нахождения тела над землёй \(h\).
Эти величины объединяются формулой:
Eпот=m⋅g⋅h.
Потенциальной энергией обладают как неподвижные, так и движущиеся тела.
Пример:
Самолёт, который летит на определённой высоте, тоже обладает потенциальной энергией.
С увеличением высоты расположения тела линейно увеличивается и его потенциальная энергия. Если высота увеличится в \(2\) раза, тогда и потенциальная энергия увеличится в \(2\) раза.
Зависимость потенциальной энергии от высоты можно изобразить на графике, где предполагается, что масса тела постоянна и равна \(2\) кг.
При увеличении массы тела линейно увеличивается также и его потенциальная энергия. Если масса увеличится в \(2\) раза, тогда и потенциальная энергия увеличится в \(2\) раза.
Пример:
Тело, падая с высоты, обладает способностью совершать работу. В Латвии именно потенциальная энергия воды обеспечивает население электроэнергией. Большую часть энергии, произведённой акционерным обществом «Латвэнерго», получают на трёх крупнейших в стране гидроэлектростанциях, которые в среднем производят \(70\) % от общего объёма производимой электроэнергии.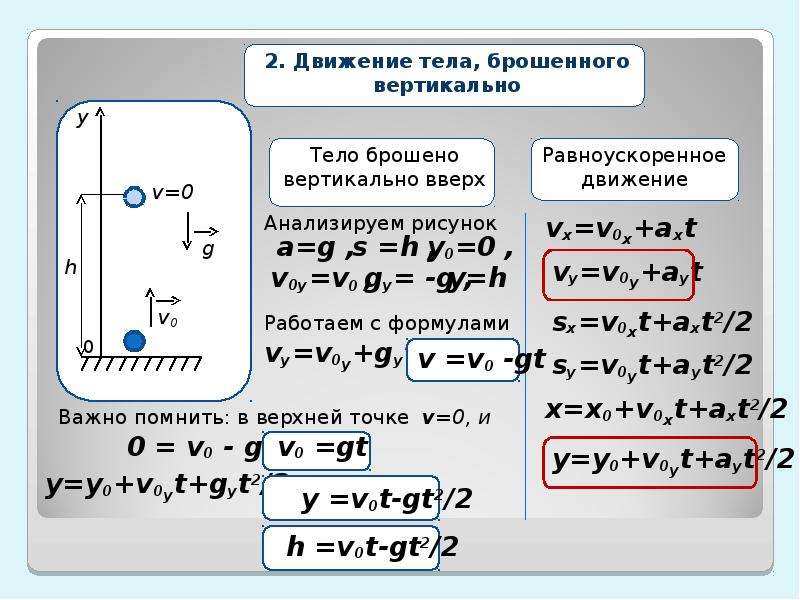 Гидроэлектростанции используют потенциальную энергию воды для того, чтобы преобразовать её в энергию вращения лопастей турбины генераторов и далее — в электрическую энергию. Чтобы обеспечить эффективное производство электроэнергии на гидроэлектростанции, необходимо обеспечить оптимальную разность уровней перед плотиной и за ней, а также оптимальную скорость протекания водной массы. Во время паводков заметно увеличивается масса воды, увеличивается её напор и сила, которая может вращать генератор, а в результате уменьшения водной массы, уменьшается и разность её уровней, что может привести к снижению эффективности производства электроэнергии или сделать его меньшим по сравнению с оптимальными условиями.
Гидроэлектростанции используют потенциальную энергию воды для того, чтобы преобразовать её в энергию вращения лопастей турбины генераторов и далее — в электрическую энергию. Чтобы обеспечить эффективное производство электроэнергии на гидроэлектростанции, необходимо обеспечить оптимальную разность уровней перед плотиной и за ней, а также оптимальную скорость протекания водной массы. Во время паводков заметно увеличивается масса воды, увеличивается её напор и сила, которая может вращать генератор, а в результате уменьшения водной массы, уменьшается и разность её уровней, что может привести к снижению эффективности производства электроэнергии или сделать его меньшим по сравнению с оптимальными условиями.
Потенциальной энергией обладают также тела, которые упруго деформированы.
Если тело деформировать в пределах упругой деформации, тогда после снятия внешней действующей силы тело возвращается в первоначальное состояние и при этом может совершать работу.
В качестве упругого тела можно использовать пружину или резинку.
Обрати внимание!
Потенциальная энергия упруго растянутой пружины прямо пропорциональна коэффициенту жёсткости пружины (k) и квадрату величины абсолютной деформации пружины Δx.
Определяют потенциальную энергию упруго растянутой пружины по формуле:
Eпот=k⋅Δx22.
Чем более жёсткую пружину или резинку используют, тем больше её потенциальная энергия при одном и том же абсолютном удлинении.
При увеличении коэффициента жёсткости пружины в \(2\) раза, её потенциальная энергия увеличивается также в \(2\) раза.
Чем больше деформация пружины или резинки, тем больше её потенциальная энергия при одном и том же коэффициенте жёсткости.
При увеличении абсолютного удлинения пружины в \(2\) раза, её потенциальная энергия увеличивается в \(4\) раза.
Ускорение свободного падения, формулы. Почему тела в вакууме падают одинаково
Тестирование онлайн
Свободное падение. Ускорение
Свободным падение будем называть движение предметов вертикально вниз или вертикально вверх. Это равноускоренное движение, но особый его вид. Для этого движения справедливы все формулы и законы равноускоренного движения.
Это равноускоренное движение, но особый его вид. Для этого движения справедливы все формулы и законы равноускоренного движения.
Если тело летит вертикально вниз, то оно ускоряется, в этом случае вектор скорости (направлен вертикально вниз) совпадает с вектором ускорения. Если тело летит вертикально вверх, то оно замедляется, в этом случае вектор скорости (направлен вверх) не совпадает с направлением ускорения. Вектор ускорения при свободном падении всегда направлен вертикально вниз.
Ускорение при свободном падении тел является постоянной величиной.
Это означает какое бы тело не летело вверх или вниз, его скорость будет изменяться одинаково. НО с одной оговоркой, если силой сопротивления воздуха можно пренебречь.
Ускорение свободного падения принято обозначать буквой, отличной от ускорения. Но ускорение свободного падения и ускорение это одна и та же физическая величина и имеют они одинаковый физический смысл. Участвуют одинаково в формулах для равноускоренного движения.
Знак “+” в формулах пишем, когда тело летит вниз (ускоряется), знак “-” – когда тело летит вверх (замедляется)
Всем известно из школьных учебников физики, что в вакууме камушек и перышко летят одинаково. Но мало кто понимает, почему же в вакууме тела разной массы приземляются одновременно. Как ни крути, будь они в вакууме или в воздухе масса у них разная. Ответ прост. Сила, которая заставляет тела падать (сила тяжести), вызываемая гравитационным полем Земли у этих тел разная. У камня она больше (так как у камня больше масса), у перышка она меньше. Но здесь нет зависимости: чем больше сила, тем больше ускорение! Сравним, действуем с одинаковой силой на тяжелый шкаф и легкую тумбочку. Под действием этой силы тумбочка будет перемещаться быстрее. А для того, чтобы шкаф и тумбочка двигались одинаково, на шкаф необходимо воздействовать сильнее, чем на тумбочку. То же самое проделывает Земля. Более тяжелые тела она притягивает с большей силой, чем легкие. И эти силы так распределяются между массами, что все они в результате падают в вакууме одновременно, независимо от массы.
Отдельно рассмотрим вопрос о возникающем сопротивлении воздуха. Возьмем два одинаковых листа бумаги. Один из них скомкаем и одновременно отпустим из рук. Скомканный лист упадет на землю раньше. Здесь разное время падения не связано с массой тела и силой тяжести, а обусловлено сопротивлением воздуха.
Рассмотрим падение тела с некоторой высоты h без начальной скорости. Если координатную ось ОУ направить вверх, совместив начало координат с поверхностью Земли, получим основные характеристики этого движения.
Тело, брошенное вертикально вверх, движется равноускоренно с ускорением свободного падения. В этом случае векторы скорости и ускорения направлены в противоположные стороны, а модуль скорости с течением времени уменьшается.
ВАЖНО! Так как подъем тела до максимальной высоты и последующее падение до уровня земли абсолютно симметричные движения (с одним и тем же ускорением, просто одно замедленное, а другое — ускоренное), то скорость, с которой приземлится тело, будет равна скорости, с которой его подбросили. При этом время подъема тела до максимальной высоты будет равно времени падения тела с этой высоты до уровня земли. Таким образом, все время полета составит двойное время подъема или падения. Скорость тела на одном и том же уровне при подъеме и при падении так же будет одинаковой.
При этом время подъема тела до максимальной высоты будет равно времени падения тела с этой высоты до уровня земли. Таким образом, все время полета составит двойное время подъема или падения. Скорость тела на одном и том же уровне при подъеме и при падении так же будет одинаковой.
Главное запомнить
1) Направление ускорения при свободном падении тела;
2) Численное значение ускорения свободного падения;
3) Формулы
Вывести формулу для определения времени падения тела с некоторой высоты h без начальной скорости.
Вывести формулу для определения времени подъема тела до максимальной высоты, брошенного с начальной скоростью v0
Вывести формулу для определения максимальной высоты подъема тела, брошенного вертикально вверх с начальной скоростью v0
Барометрическая формула | Физика
Движение молекул связано с тепловым состоянием тела. Чем более нагрето тело, тем оживленнее беспорядочное движение молекул. Термин «беспорядочное движение молекул» с полным правом может быть заменен термином «тепловое движение молекул».
Термин «беспорядочное движение молекул» с полным правом может быть заменен термином «тепловое движение молекул».
Вследствие хаотического движения молекулы, разлетаясь во все стороны, должны бы равномерно распределиться в предоставленном им объеме. Почему же воздух, окружающий Землю, не разлетается по всему мировому пространству? Его удерживает притяжение к Земле. Это притяжение нарушает равномерное распределение молекул в мировом пространстве. С другой стороны, если бы не тепловое движение, то все молекулы упали бы на Землю. В результате борьбы этих двух тенденций — падения вниз и стремления равномерно рассеяться в окружающем пространстве — в атмосфере наблюдается некоторое распределение плотности воздуха по высоте. Молекулы сосредоточены гуще в нижних слоях и реже в верхних. Математическое выражение этой закономерности дается формулой, называемой барометрической:
Здесь ρ – плотность воздуха на высоте h, ρ0 – плотность воздуха при h = 0, m – масса молекулы, T — абсолютная температура воздуха, k — так называемая постоянная Больцмана (k = 1,38 * 10-23 Дж/К). Описываемая барометрической формулой функция ρ есть показательная функция; ее основание выражается числом e = 2,71828… Такие показательные функции называют экспоненциальными. Заметим, что приведенная формула является упрощенной. Во-первых, как известно, воздух состоит из нескольких различных газов – азота, кислорода, водорода и др. Молекулы разных газов имеют разные массы. Чем легче газ, тем медленнее уменьшается с высотой его плотность. Во-вторых, в барометрической формуле предполагается, что температура воздуха одинакова на всех рассматриваемых высотах. Известно, однако, что температура воздуха с высотой понижается. В-третьих, надо учитывать также, что ускорение g зависит от высоты. Наконец, приведенная выше формула не учитывает ветра и конвекционных потоков воздуха, которые могут весьма заметно влиять на плотность воздуха.
Описываемая барометрической формулой функция ρ есть показательная функция; ее основание выражается числом e = 2,71828… Такие показательные функции называют экспоненциальными. Заметим, что приведенная формула является упрощенной. Во-первых, как известно, воздух состоит из нескольких различных газов – азота, кислорода, водорода и др. Молекулы разных газов имеют разные массы. Чем легче газ, тем медленнее уменьшается с высотой его плотность. Во-вторых, в барометрической формуле предполагается, что температура воздуха одинакова на всех рассматриваемых высотах. Известно, однако, что температура воздуха с высотой понижается. В-третьих, надо учитывать также, что ускорение g зависит от высоты. Наконец, приведенная выше формула не учитывает ветра и конвекционных потоков воздуха, которые могут весьма заметно влиять на плотность воздуха.
Тем не менее барометрической формулой можно пользоваться как приближенной формулой, которая правильно передает основную закономерность в уменьшении плотности воздуха с высотой. Эту формулу применяют по отношению к определенному типу газа и при этом рассматривают относительно небольшие высоты.
Эту формулу применяют по отношению к определенному типу газа и при этом рассматривают относительно небольшие высоты.
Подчеркнем, что описываемое барометрической формулой распределение плотности по высоте оказывается неизменным, сколько бы времени мы ни наблюдали (ветер не принимается во внимание). Молекулы воздуха находятся все время в движении, сталкиваются, перемещаются из одних точек пространства в другие; тем не менее в среднем их число в единице объема на данной высоте остается неизменным.
Рассмотренный закон распределения оказывается применимым не только к нижним слоям атмосферы Земли, но и к растворам, содержащим множество мелких частичек во взвешенном состоянии. Французский физик Перрен, изучавший броуновское движение, производил опыты с эмульсией спиртового раствора смолы гуммигута или мастики в воде. Предварительно жидкость подвергалась многократному центрифугированию для получения эмульсии, состоящей из очень мелких зернышек одинакового размера. Капля эмульсии помещалась в стеклянную кюветку и рассматривалась в микроскоп через маленькую диафрагму. Тогда в поле зрения можно было пересчитать видимые частицы. Изменяя высоту подвижной части микроскопа, можно получать четкие изображения частиц в разных слоях эмульсии, расположенных на разных глубинах кюветки (рис. 74). В каждом из этих слоев и подсчитывались зерна эмульсии. Чтобы исключить случайность, брали для каждого слоя среднее значение из нескольких тысяч измерений. Применяя к этому распределению барометрическую формулу, Перрен смог определить число молекул в 1 моль любого газа.
Тогда в поле зрения можно было пересчитать видимые частицы. Изменяя высоту подвижной части микроскопа, можно получать четкие изображения частиц в разных слоях эмульсии, расположенных на разных глубинах кюветки (рис. 74). В каждом из этих слоев и подсчитывались зерна эмульсии. Чтобы исключить случайность, брали для каждого слоя среднее значение из нескольких тысяч измерений. Применяя к этому распределению барометрическую формулу, Перрен смог определить число молекул в 1 моль любого газа.
Полученное значение очень мало отличается от значения, определенного при помощи других способов. В настоящее время число молекул в 1 моль любого газа считают равным 6,02 * 1023. Это число называют числом Авогадро. Известно, что 1 моль газа при нормальных условиях занимает объем 22,4 л. Отсюда легко определить и число молекул в 1 см3 газа при нормальных условиях:
Нет, конечно, необходимости объяснять, что найденное число передает только порядок количества молекул, т. е. оно приведено так же округленно, как, скажем, число, характеризующее плотность населения какого-нибудь города.
е. оно приведено так же округленно, как, скажем, число, характеризующее плотность населения какого-нибудь города.
Использование опорных схем при решении задач по физике. 7-й класс
Многие учащиеся в силу своих способностей не могут выводить уравнения связей, поэтому я использую им в помощь опорные схемы. Опоры помогают не запоминать специально, а выводить уравнения для вычислений, способствуют развитию мыслительных способностей, направлены на закрепление, обобщение и применение изученного материала. Рекомендую учащимся нарисовать в тетради треугольники или их можно также изготовить из плотной бумаги.
Каждая схема представляет собой
равносторонний треугольник, длина стороны
которого равна 5 – 6 см. Боковые стороны
треугольника делим пополам, соединяем их между
собой. Середину основания соединяем с серединой
полученного отрезка. Получаем малый треугольник
и две трапеции, в которые вписываем обозначение
физических величин.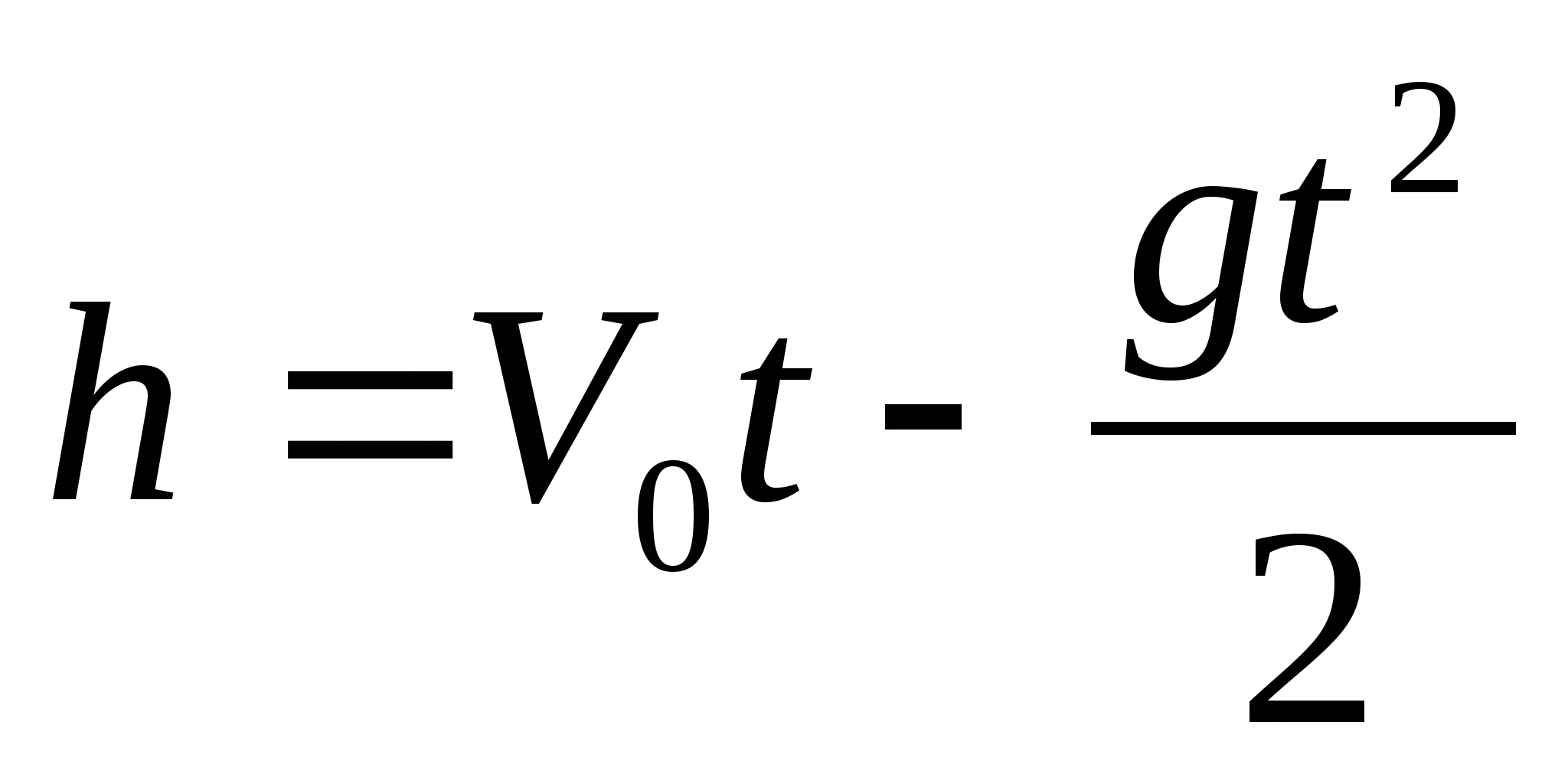
Для нахождения расстояния на основе скорости и времени используется треугольник (а), в малый треугольник которого записано обозначение расстояния (S), а в трапециях – скорости (v) и времени (t).
Для вычисления массы, зная ее объем и плотность, можно воспользоваться треугольником (б), в малый треугольник которого записано обозначение массы (m), а в трапециях – объема (V) и плотности вещества ().
Для расчетов веса тела используется треугольник (в): в малый треугольник вписывается обозначение веса тела (P), а в трапециях – массы тела (m) и ускорения свободного падения (g).
Для вычисления силы тяжести применяется
соответствующий треугольник (г). В малый
треугольник вписано обозначение силы тяжести (Fтяж),
а в трапеции – массы (m) и ускорения
свободного падения (g).
Для нахождения давления на дно и стенки сосуда используем несколько иной вариант (д). В равностороннем треугольнике находим середины боковых сторон, соединяем их между собой. В получившийся малый треугольник записываем обозначение давления (p). Полученную трапецию делим таким образом, чтобы получилось две трапеции и прямоугольник. В получившиеся трапеции вписываем обозначения плотности () и высоты (h), а в прямоугольник ? ускорения свободного падения (g)
Рекомендую использовать эти опоры на этапе закрепления знаний и умений по решению задач, во время самостоятельной работы. Однако первое их использование должно производится с комментарием учителя.
Алгоритм нахождения физических величин по треугольникам (а, б, в, г):
- Закрыть обозначение величины, которую необходимо найти.
- Если известные величины вписаны в трапеции, то
их необходимо перемножить.

- Если известные величины вписаны в малый треугольник, то величину, стоящую над разделительной линией, нужно разделить на величину, стоящую под разделительной линией.
Задача: Расстояние между поселками 8 км. Сколько времени будет идти пешеход между данными поселками, если скорость пешехода 5 км/ч?
Учитель: Что нам известно из условия задачи?
Ученик: Расстояние и скорость.
Учитель: Что нужно найти?
Ученик: Время, которое пешеход потратит пешеход, чтобы преодолеть расстояние между поселками.
Учитель: Вспомните, как обозначаются расстояние и скорость.
Ученик: S – расстояние, ? – скорость.
Учитель: Запишите данные условия задачи.
Ученик: (один на доске, остальные в тетрадях):
| Дано: | Решение: |
Учитель: Используя схему и алгоритм к ней,
запишите формулу нахождения времени.
Ученик: Воспользуемся треугольником (а): .
Учитель: Проведите вычисления:
Ученик: .
Учитель: Выразите данное время, для удобства в часах и минутах. Запишите ответ задачи.
Ученик: Так как 1 час = 60 мин, а в условии задачи 1,6 ч, тогда t = 1,6 ч = 1,6 • 60 мин = 96 мин = = 1ч 36 мин.
Ответ: t = 1 ч 36 мин.
Задача: Кубик имеет размер ребра 1 см. Взвешивание на весах показало, что его масса 400 мг. Из какого материала изготовлен кубик?
Учитель: Что нам известно из условия задачи? Что нужно найти?
Ученик: Известно ребро куба, его масса. Нужно узнать из какого материала изготовлен кубик, т.е. плотность данного тела.
Учитель: Выпишите данные условия задачи. Используя схему и алгоритм к ней, запишите формулу для нахождения плотности вещества.
| Дано: | Решение: |
Ученик: Воспользуемся треугольником (б): .
Учитель: Что нужно знать, чтобы найти плотность?
Ученик: Нужно знать объем куба.
Учитель: Как найти объем куба?
Ученик: V = a 3, где а = 1 см, V = 1 см3.
Учитель: Вычислите плотность по данной формуле, выразив массу кубика в граммах.
Ученик: 400 мг = 400 : 1000 г = 0,4 г; .
Учитель: Вам нужно найти, из какого материала изготовлен кубик?
Ученик: Воспользуемся таблицей плотности твердых тел:
| Твердое тело | , кг/м3 | , г/см3 |
| Дуб (сухой) | 700 | 0,70 |
| Сосна | 400 | 0,40 |
| Пробка | 240 | 0,24 |
Ответ: Данный кубик изготовлен из сосны.
Алгоритм для расчетов, связанных с давлением на дно и стенки сосуда по треугольнику (д):
Закрыть величину, которую необходимо найти.
Для вычисления p нужно величины стоящие под разделительной линией: ?, g, h перемножить. Получаем уравнение:
р = • g • h.
3. Для вычисления:
а) нужно величину стоящую над разделительной линией р делим на произведение величин стоящих под разделительной линией и получаем уравнение:
;
б) g поступаем аналогично пункту а) и получаем уравнение:
;
в) h поступаем аналогично пункту а) и получаем уравнение:
.
Задача: В фильтр для очистки воды налита вода. Какова высота емкости для воды, если давление в сосуде 1,5 кПа?
Учитель: Что нам известно из условия задачи и что нужно найти?
Ученик: Известно давление воды, а также постоянные величины плотность воды и ускорение свободного падения. Найти высоту сосуда.
Учитель: Запишите данные условия задачи.
Ученик:
| Дано: | Решение: |
Ученик: р = 1,5 кПа = 1,5 • 1000 Па = 1500Па.
Учитель: Используя схему и алгоритм к ней, запишите формулу для нахождения высоты сосуда. Выполните вычисления.
Ученик: Воспользуемся треугольником (д): .
Ответ: Высота сосуда 15 см.
Задача: Наибольшая глубина реки 5 м. Какое давление будет испытывать спасатель, если он опустится на дно?
Учитель: Что нам известно из условия задачи? Что нужно найти?
Ученик: Известна глубина реки и постоянные величины: плотность воды и ускорение свободного падения. Найти какое давление оказывает вода на спасателя.
Учитель: Запишите данные условия задачи.
Ученик:
| Дано: | Решение: |
Учитель: Используя схему и алгоритм к ней, запишите формулу для нахождения давления. Произведите вычисления и запишите ответ задачи.
Ученик: Воспользуемся треугольником (д): р = •g • h .
р = 1000 кг/м3 • 9,8 н/кг • 5 м 50000 Пa 50 кПа.
Ответ: р = 50 кПа.
Ниже приведены разноуровневые задачи для самостоятельного закрепления.
а) уровень:
- Какая скорость больше 20 м/с или 72 км/ч?
- Автомобиль проехал 180 км за 2 часа. Какова средняя скорость поезда?
- Человек шел 1,5 часа со скоростью 6 км/ч. Какой путь он прошел?
b) уровень:
- Скорость пули автомата Калашникова 715 м/с. Какое расстояние пролетит пуля за 0,5 мин?
- Нарушил ли правила водитель, если установлен знак 40 км/ч, а участок дороги в 100 м он проехал за 10 с?
- Шарик в нашем опыте скатился по желобу за 3 с. Какова средняя скорость движения шарика по желобу, если его длина 45 см?
с) уровень:
- Покупатель купил 3 л меда. Какова масса мёда?
- Водитель заправил 40 л бензина. На сколько увеличилась масса автомобиля?
- Сколько кирпичей можно погрузить в пятитонный автомобиль, если объем одного кирпича 2 дм3 и уложены в вровень с бортами?
- Ширина одной реки 10 м, а другой 100 м. Одинаковое ли давление будет испытывать пловец, если он опустится на глубину 3 м в первую реку и на глубину 3 м во вторую реку?
Алгоритм для решения задач:
- Прочитайте текст задачи.
- Запишите условие и требования задачи с помощью общепринятых обозначений.
- Переведите величины, если это необходимо, в систему СИ.
- Выберите нужный треугольник и выразите из него требуемую величину.
- Определите, все ли данные вам известны из треугольника, если необходимо произведите дополнительные вычисления.
- Произведите вычисления по данной формуле.
- Запишите ответ.
Использование рассмотренных опорных схем показало, что они положительно влияют на обучение всех учащихся, но особенно тех, которые вначале испытывают затруднения при выполнении различных заданий.
Такой подход заинтересовывает учащихся, так как подобная организация учебного процесса развивает их мыслительные способности: заставляет их быть внимательными, учит анализировать; создает каждому учащемуся радость успеха, и у них исчезает чувство беспомощности.
Мяч брошен вертикально вверх
Расскажите о Physicsteacher.in
Движение вверх, а затем движение шара вниз, когда мяч брошен вертикально вверх – это то, что мы обсудим здесь, а также выведем уравнения вертикального движения. Итак, начнем с основ кинематики вертикального движения.
Что происходит, когда мяч брошен вертикально вверх?
Когда мяч брошен вертикально вверх, он начинает свое вертикальное движение с начальной скоростью.
По мере того, как мяч движется вверх по вертикали, его скорость постепенно уменьшается под действием силы тяжести земли, действующей в направлении, противоположном движению мяча.
Другими словами, при движении вверх мяч движется с запаздыванием. И, наконец, на высоте скорость мяча обращается в ноль.
Затем он снова начинает вертикально падать вниз, и на этот раз его скорость постепенно увеличивается под действием силы тяжести.
Во время движения вниз мяч совпадает с направлением силы тяжести, и в результате мяч с ускорением опускается вниз и достигает земли.
Какие важные формулы или указатели относятся к вертикальному движению?
Важные формулы и указатели для вертикального движения включают:
1> достигнутая максимальная высота,
2> время, необходимое для движения вверх и вниз,
3> ускорение мяча в разных точках,
4> скорость мяча в разных точках. примеры,
5> силы, действующие на мяч,
6> формула или уравнение вертикального движения
7> кинетическая энергия и потенциальная энергия шара при вертикальном движении
Мы найдем все это в этом посте.2 + 2gH… .. (vi)
Список формул, относящихся к мячу, брошенному вертикально вверх [набор формул]
Если мяч брошен вертикально вверх с начальной скоростью V 0 , то вот набор формул для вашего быстрого ознакомления.
1) Достигнутая максимальная высота =
H = V 0 2 / (2 г)
2) Скорость в наивысшей точке = 0
3) Время движения вверх = V 0 / g
4) Время движения вниз =
В 0 / г
5) Общее время движения в воздухе = (2 В 0 ) / г
6) Ускорение мяча = ускорение свободного падения (g ) действующие вниз, к центру земли [без учета сопротивления воздуха]
7) Силы, действующие на мяч = Гравитация (сила тяжести, создаваемая землей)
[без учета сопротивления воздуха]
Решение проблем с использованием этих формул
Мяч бросается вертикально вверх со скоростью 49 м / с. Рассчитайте максимальную высоту и время, необходимое для достижения максимальной высоты.
H = U 2 / (2g) = (49 2 ) / (2 x 9,8) = 122,5 м
T = U / g = 49 / 9,8 = 5 сек
Мяч бросается вертикально вверх со скоростью 20 м / с. рассчитать максимальную высоту и время, необходимое для достижения максимальной высоты.
H = U 2 / (2g) = (20 2 ) / (2 x 9,8) = 20,4 м
T = U / g = 20 / 9,8 = 2,04 с
Мяч брошен вертикально вверх. он возвращается на 6 секунд позже. Скорость, с которой он был брошен:
Время, необходимое для достижения максимальной высоты = 6/2 = 3 секунды
Мы знаем, T = U / g
или, U = gT
U = 10 x 3 м / с = 30 м / с
Скажем, мяч брошен вертикально вверх с некоторой скоростью, скажем v1 , которую мы будем рассматривать как начальную скорость для восходящего пути.
По прошествии определенного периода времени t, мяч достигает высоты, за которой он больше не может двигаться вверх, и останавливается там, т.е. его скорость на этой высоте становится равной нулю.
Высота, на которой скорость становится равной нулю, что является максимальной высотой , когда мяч пошел вверх, скажем, H .
И для этого восходящего движения конечная скорость v2 равна 0 , потому что шар остановился в конце этого восходящего движения.
Почему брошенный вверх объект падает после достижения точки?
Когда объект бросается с определенной начальной скоростью (скажем, V), он приобретает кинетическую энергию в момент броска.
По мере того, как он движется вверх от своего исходного положения (откуда он был брошен) и набирает высоту, его потенциальная энергия возрастает.
Это происходит потому, что потенциальная энергия (PE) прямо пропорциональна высоте объекта. (PE = mgh, где h – высота).
Теперь, исходя из закона разговора об энергии, мы можем сказать, что рост PE происходит за счет преобразования некоторой формы энергии.2.
По мере увеличения высоты скорость падает, что приводит к снижению KE и соответствующему увеличению PE.
В какой-то момент KE становится равным нулю. В этот момент скорость становится равной нулю.
Это называется наивысшей точкой вертикального движения вверх. После этого мяч начинает падать вниз.
Другими словами, мы можем сказать, что KE, использованная брошенным объектом, подвергается коррозии под отрицательным влиянием противоположно направленной силы тяжести (гравитационная сила, обусловленная землей).
Влияние отрицательное, потому что сила тяжести тянет вниз, в то время как мяч пытается двигаться вверх.
Через некоторое время, когда весь KE обнуляется, мяч останавливается. А потом начинает падать к поверхности земли.
Во всех приведенных выше обсуждениях мы считали сопротивление воздуха незначительным.
** Те, кто знает о космической скорости, могут прочитать сообщение об этом здесь: Escape Velocity
Какие силы действуют на мяч, брошенный вверх?
Учитывая, что сопротивление воздуха или сила сопротивления незначительны, единственная сила, действующая на мяч, – это сила тяжести i.2, и его направление будет вниз, к центру Земли.
Совершенно очевидно, что после броска вверх скорость мяча постепенно уменьшается, т.е. на мяч действует отрицательное ускорение. Ускорение отрицательное, потому что это ускорение направлено вниз, в то время как мяч движется вверх.
И из-за этого отрицательного ускорения скорость мяча постепенно уменьшается. И да. Как сказано выше, это ускорение есть не что иное, как ускорение , вызванное силой тяжести , вызванное гравитационным притяжением или силой, действующей со стороны земли на шар.2.
См. Здесь , как ускорение свободного падения зависит от высоты и глубины относительно поверхности земли.
Выведите уравнение времени, необходимого мячу для достижения максимальной высоты во время восходящего движения.
Поскольку это ускорение , вызванное силой тяжести (g), работает противоположно восходящей скорости, мы должны использовать отрицательный знак в формуле ниже, используемой для восходящего движения мяча.
Мы знаем, что значение g в СИ равно 9.8 м / сек.
Используя одно из уравнений движения,
v2 = v1 – gt …………………… (i)
Поскольку v2 = 0 (в самой высокой точке скорость становится равной нулю), то мы можем записать предыдущее уравнение следующим образом:
0 = v1 – gt
или, t = v1 / g ……………………. (Ii)
Итак, из уравнения (ii), время , необходимое мячу для достижения максимальной высоты , выражается как
= (Начальная скорость, с которой мяч отбрасывается вертикально вверх) / (ускорение свободного падения)….. (iii)
Так, например, если мяч брошен вертикально вверх со скоростью 98 м / с, то для достижения максимальной высоты потребуется = 98 / 9,8 = 10 секунд.
Вывести формулу максимальной высоты, достигаемой при движении вверх, когда мяч подбрасывается вертикально вверх?
И максимальная достигнутая высота H получается по формуле:
v2 2 = v1 2 -2gH (при отрицательном ускорении) ……………… (iii)
Поскольку v2 = 0, ( в наивысшей точке скорость становится равной нулю ), поэтому мы можем переписать уравнение iii как:
0 = v1 2 – 2gH
или H = v1 2 / 2g (уравнение максимальной высоты) ……….(iv)
Следовательно, если мяч брошен вертикально вверх со скоростью 98 м / с, максимальная высота, которой он достигнет, будет = (98 x 98) / (2 x 9,8) метр = 490 метров.
Каковы скорость и ускорение мяча, когда он достигает наивысшей точки?
Просто резюмирую ответ здесь, хотя мы уже рассмотрели это в разделе выше.
Скорость в наивысшей точке равна нулю, поскольку мяч на мгновение останавливается там, прежде чем начать свое движение вниз.
И ускорение , действующее на мяч в этой точке, – это ускорение свободного падения (g), и на этот раз оно считается положительным, то есть вниз, поскольку мяч теперь готов к свободному падению. (без учета сопротивления воздуха)
Движение мяча внизКаково ускорение мяча, брошенного вертикально вверх при движении вниз?
Когда мяч достигает максимальной высоты, он начинает свободное падение на землю.
Сила, приложенная к нему, снова является силой тяжести, и на этот раз он имеет положительное ускорение, то есть следует в том же направлении, что и ускорение , вызванное гравитацией (g)
Какова скорость
мяча перед тем, как он коснется земли ?И один важный момент , во время падения вниз величина скорости мяча непосредственно перед тем, как коснуться земли , будет такой же, как величина скорости, с которой он был брошен вверх (здесь v1).Мы докажем это математически здесь:
Здесь, когда мяч падает вертикально вниз, он падает на ту же высоту H (здесь H = v1 2 / 2g , как указано в уравнении iv)
Во время этого смещения вниз начальная скорость равна конечной скорости движения вверх, то есть v2. И мы знаем, что v2 = 0.
И во время движения вниз конечная скорость равна v3. Эта скорость достигается за счет вертикально падающего шара непосредственно перед касанием земли.
Мы должны выяснить выражение этой версии v3. Кроме того, мы должны узнать время, которое потребовалось (скажем, T) для этого падения.
v3 2 = v2 2 + 2 g H = 0 + 2 g (v1 2 / 2g) = v1 2
т.е. v3 = v1 ……………. (V)
Итак, мы можем сказать, что при падении вниз величина скорости мяча непосредственно перед касанием земли будет такой же, как величина скорости, с которой он был брошен вверх (здесь v1).
Найдите формулу периода времени для движения вниз, когда мяч брошен вертикально вверх
Можно доказать, что время, необходимое для движения вниз, или время, необходимое мячу для падения с самой высокой точки и достижения земли, такое же, как время, необходимое для движения вверх = v1 / g
Давайте докажем это здесь математически:
(см. Диаграмму выше для движения вниз)
v3 = v2 + g T
или, v3 = 0 + g T
так, T = v3 / g = v1 / g ( из уравнения v выше ) …………. (vi)
Итак, Время нисходящего движения (T) = Время восходящего движения (t) = v1 / g
Это означает, что время нисходящего движения = время восходящего движения
Общее время, необходимое для движения вверх и вниз
Итак (из уравнений ii и vi) для вертикально брошенного объекта общее время , затраченное на его движение вверх и вниз = t + T = 2v1 / g ………. (Vii)
Полный пример:
Скажем, мяч брошен вертикально вверх со скоростью 98 м / с. Итак, v1 = 98 м / с
1) Максимальная высота, достигаемая им, будет = v1 2 / 2g = (98 x98) / (2 x 9.8) метр = 490 метров.
2) Время, необходимое для достижения наивысшей точки = v1 / g = 98 / 9,8 секунды = 10 секунд
3) Скорость в наивысшей точке = 0
4) Время, необходимое для достижения земли при падении с самой высокой точки = v1 / g = 98 / 9,8 секунды = 10 секунд
5) Общее время, затраченное на движение вверх и вниз = 10 сек + 10 сек = 20 сек.
6) Скорость непосредственно перед касанием земли = такая же, как и начальная скорость метания = 98 м / с
Предлагаемое и похожее сообщение
Поделиться сейчас:
Надеюсь, вам понравился этот пост.Теперь вы можете поделиться им как можно чаще, используя кнопки социальных сетей на странице.
Модель падающего объекта
Объект называется свободно падающим телом, если его бросают или роняют вертикально с начальной скоростью, и тогда на его движение влияет только сила тяжести.
Положение любого свободно падающего тела определяется начальной скоростью и начальной высотой.
Если час высота, измеренная в футах, т это количество секунд, в течение которых объект упал с начальной высоты час 0 с начальной скоростью или скоростью v 0 (дюйм / сек), тогда модель высоты падающего объекта: час ( т ) знак равно – 16 т 2 + v 0 т + час 0
Значок « – 16 т 2 Термин происходит от ускорения из-за силы тяжести, притягивающей объект к земле.Скорость объекта в определенный момент времени т дан кем-то: v ( т ) знак равно – 32 т + v 0
Когда объект подбрасывается вверх с земли с определенной начальной скоростью, начальная высота равна нулю, а когда объект падает с начальной высоты, начальная скорость равна нулю.Если значение час находится в метрах и s в метрах / сек, ускорение свободного падения в метрах / сек равно 4.9 , уравнение принимает следующий вид: час ( т ) знак равно – 4.9 т 2 + v 0 т + час 0 а затем скорость объекта в конкретный момент времени т дан кем-то: v ( т ) знак равно – 9.8 т + v 0
Пример 1:
Мяч бросается вертикально вверх с начальной скоростью 80 фут / сек. Как высоко будет мяч после 3 секунды?
т знак равно 3 а также v 0 знак равно 80 фут / сек
Так:
час знак равно – 16 ( 3 ) 2 + 80 ( 3 )
знак равно – 144 + 240
знак равно 96 футов
Пример 2:
Объект падает с высоты 120 ноги.Если предположить, что сопротивления воздуха нет, сколько времени нужно, чтобы достичь земли?
Если час измеряется в футах, т – количество секунд, в течение которых объект упал, и час 0 – начальная высота, с которой объект был сброшен, тогда модель высоты падающего объекта:
час знак равно – 16 т 2 + час 0
Обратите внимание, что начальная скорость здесь равна нулю.
Заменять 0 для час а также 120 для час 0 в модели. 0 знак равно – 16 т 2 + 120
Решите уравнение для т .
0 – 120 знак равно – 16 т 2 + 120 – 120
– 120 знак равно – 16 т 2
– 120 – 16 знак равно – 16 т 2 – 16
7.5 знак равно т 2
Извлекаем квадратный корень:
т знак равно 7,5
≈ ± 2,74
С т представляет время, оно не может быть отрицательным.
Следовательно, объект достигнет земли примерно за 2.74 секунд.
Эти уравнения упрощены. Они игнорируют сопротивление воздуха, а гравитационная постоянная является приблизительной. Также эта модель работает только для поверхности Земли (на уровне моря). Модель на других планетах будет другой, потому что у них другая сила тяжести. Например, на поверхности Луны с час в метрах и v 0 в м / сек модель падающего объекта час знак равно – 0.8 т 2 + v 0 т + час 0 .
Калькулятор движения снаряда
Движение снаряда (горизонтальная траектория) вычислитель находит начальную и конечную скорость, начальную и конечная высота, максимальная высота, горизонтальное расстояние, продолжительность полета, время до достичь максимальной высоты, а также параметров угла пуска и посадки снаряда движение в физике.Кроме того, для снаряда построены следующие графики. движение.
– Высота (или вертикальное положение) в зависимости от времени
– Вертикальная скорость в зависимости от времени
– Горизонтальное положение в зависимости от высоты (или вертикальное положение)
– Горизонтальная скорость в зависимости от времени
– Горизонтальное положение в зависимости от угла
В расчетах не учитывается влияние сопротивления воздуха. Формулы движения снаряда, используемые для расчетов, приведены в «Списке уравнений». раздел.
Примечание. Используйте точку “.” как десятичный разделитель.
Примечание *: вектор силы тяжести отрицателен в направлении вниз.
| РЕЗУЛЬТАТЫ | |||
| Параметр | 1 st Решение | 2 nd Решение (если существует) | Отряд |
| Начальная скорость (V 0 ) | [РС] | ||
| Начальная горизонтальная скорость (V 0x ) | |||
| Начальная вертикальная скорость (V 0y ) | |||
| Конечная скорость (V f ) | |||
| Конечная горизонтальная скорость (V fx ) | |||
| Конечная вертикальная скорость (V fy ) | |||
| Начальная высота (y 0 ) | [м] | ||
| Конечная высота (y f ) | |||
| Максимальная высота (h) | |||
| Горизонтальное расстояние (l) | |||
| Продолжительность полета (т) | [s] | ||
| Время достичь Максимум.Высота (т х ) | |||
| Угол пуска (α 0 ) | [град] | ||
| Посадочный угол (α f ) | |||
Примечание. Округление по умолчанию составляет 5 знаков после запятой.
Движение снаряда: Движение снаряда – это форма движения, которая имеет место в двух измерениях. Форма движения – парабола.
Уравнения скорости гравитации для падающих объектов, Рон Куртус
SfC Home> Физика> Гравитация>
от Рона Куртуса
Когда вы бросаете объект с некоторой высоты над землей, он имеет нулевую начальную скорость.Простые уравнения позволяют вычислить скорость падающий объект достигает через заданный период времени и его скорость при заданном смещении. Уравнения предполагают, что сопротивление воздуха незначительно.
Примеры демонстрируют применение уравнений.
Вопросы, которые могут у вас возникнуть:
- Какое уравнение для скорости в данный момент времени?
- Какое уравнение определяет скорость достижения заданного смещения?
- Какие примеры этих уравнений?
Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц
Скорость относительно времени
Общее уравнение гравитации для скорости относительно времени:
v = GT + v i
( Подробную информацию о выводе см. В разделе «Вывод уравнений скорости-времени для гравитации». )
Поскольку начальная скорость v i = 0 для объекта, который просто падает, уравнение сводится к:
v = gt
где
- v – вертикальная скорость объекта в метрах в секунду (м / с) или футах в секунду (фут / с)
- g – ускорение свободного падения (9.8 м / с 2 или 32 фут / с 2 )
- t – время в секундах, в течение которого объект упал
Скорость падающего объекта как функция времени или смещения
Скорость относительно смещения
Общее уравнение гравитации для скорости относительно смещения:
v = ± √ (2gy + v i 2 )
где
- ± означает плюс-минус
- √ (2gy + v i 2 ) – квадратный корень из величины (2gy + v i 2 )
- y – вертикальное смещение в метрах (м) или футах (футах)
( См. Раздел «Вывод уравнений силы тяжести смещения и скорости») для получения подробной информации.)
Поскольку v i = 0, y положительно, потому что оно ниже начальной точки. Кроме того, против отрицательно и положительно. Применяется только член + из ± .
Таким образом, уравнение скорости падающего объекта после того, как он прошел определенное перемещение, имеет вид:
v = √ (2gy)
Примеры
Следующие примеры иллюстрируют применение уравнений.
За данный момент
Какой будет скорость объекта после 3-х секундного падения?
Решение
Подставить в уравнение:
v = gt
Если вы используете г = 9,8 м / с 2 , v = (9,8 м / с 2 ) * (3 с) = 29,4 м / с.
Если вы используете г = 32 фут / с 2 , v = (32 фут / с 2 ) * (3 с) = 96 фут / с.
Для заданного водоизмещения
Какова скорость объекта после того, как он упал на 100 футов?
Решение
Поскольку y находится в футах, g = 32 фут / с 2 . Подставляем в уравнение:
v = √ (2gy)
v = √ [2 * (32 фут / с 2 ) * (100 футов)]
v = √ (6400 футов 2 / с 2 )
v = 80 фут / с
Сводка
Существуют простые уравнения для падающих объектов, которые позволяют вычислить скорость, которую объект достигает для данного перемещения или времени.Уравнения:
v = gt
v = √ (2gy)
Будь чемпионом
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Гравитационные ресурсы
Падающие тела – Physics Hypertextbook
Уравнения падающего тела – Википедия
Расчет силы тяжести – Земля – Калькулятор
Кинематические уравнения и свободное падение – Физический класс
Книги
(Примечание: Школа чемпионов может получать комиссионные от покупки книг)
Книги с самым высоким рейтингом по простой науке о гравитации
Книги с самым высоким рейтингом по продвинутой физике гравитации
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_equations_falling_velocity.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Гравитационные темы
Уравнения скорости тяжести падающих предметов
Квадратичный Проблемы со словами: Движение снаряда (стр. 1 из 3) Ячейки: Снаряд движение, Общие проблемы со словами, Макс. / мин. проблемы Для наших целей «снаряд» – это любой объект, который бросают, стреляют или роняют.Обычно объект двигаясь прямо вверх или прямо вниз.
Какая высота (вверху уровень земли), когда объект врезается в землю? Ну, очевидно, ноль. Вот и ищу момент когда высота с = 0.Ставлю с равным нулю, и решаем: Затем т = 6 или т = 2. Второе решение за две секунды до запуска, что не имеет смысла в данном контекст. (На графике это имеет смысл, потому что линия пересекает x – ось в 2, но отрицательное время не сработает в этой проблеме со словом.) Итак, “ t = 2 “является посторонним решение, и я проигнорирую его. Обратите внимание на строительство уравнение высоты в задаче выше. Начальная высота пуска составляла 58,8 метров, а постоянный член составил «58,8». Начальная скорость (стартовая скорость) 19,6 м / с. м / с, а коэффициент при линейном члене составил «19,6». Это всегда верно для этих проблем с движением снаряда вверх / вниз. (Если у вас есть упражнение с боковыми движениями, уравнение будет иметь другое форма, но они всегда дают вы это уравнение.) Начальная скорость – это коэффициент для среднего члена, а начальная скорость высота – постоянный член. А коэффициент главный член происходит от силы тяжести. Этот коэффициент отрицательно, так как сила тяжести тянет вниз, и значение будет либо «4,9» (если ваши единицы измерения “метры”) или “16” (если ваши единицы – «футы»). В общем, формат: s ( t ) = GT 2 + v 0 t + час 0 …где “ г ” вот “4.9” или “16” выводится из значения силы тяжести (технически это половина силы тяжести, но вам, вероятно, не нужно знать это правильно сейчас), “ v 0 ” (“vee-naught” или “vee-sub-zero”) – начальная скорость, и “ h 0 ” (“aitch-naught” или “aitch-sub-zero”) – начальная рост. Запомните это уравнение (или, по крайней мере, его значение), потому что вам может потребоваться это знать на тесте.
Хм … Не дали мне уравнение на этот раз.Но это нормально, потому что я могу создать уравнение из информации, что они сделали дай мне. Начальная высота 80 футов над землей и начальная скорость 64 фут / с. Поскольку мои единицы измерения – футы, тогда число для гравитации будет 16, и мое уравнение: Они хотят, чтобы я нашел максимальная высота. Для такой отрицательной квадратичной функции максимум будет быть в вершине перевернутой параболы.Так что они действительно хотят меня найти вершину. Из графика Я знаю, как найти вершину; в этом случае вершина находится в точке (2, 144): Но что это за вершина скажи мне? Согласно моему уравнению, я вставляю значения времени и извлекаю значения высоты, поэтому ввод “2” должно быть время и на выходе “144” должен быть рост. авторское право Элизабет Стапель 2004-2011 Все права защищены
Мои единицы на этот раз «метров», поэтому гравитационное число будет «4,9». Поскольку объект стартовал на уровне земли, начальная высота была 0. Тогда мое уравнение: Поскольку это отрицательный квадратичный, график представляет собой перевернутую параболу.Я могу найти двоих раз, когда объект ровно 34,3 метров, и я знаю, что объект будет выше 34,3 метров все время между ними. Почему «два раза» и как знаю ли я, что промежуток времени находится между этими двумя временами? Поскольку первый раз будет, когда объект пройдет высоту 34,3 метров на пути к максимальной высоте, и второй раз, когда быть, когда он превысит 34,3 метров, когда он снова падает на землю.Итак, я должен решить следующее: Тогда объект находится на 34,3 метра через одну секунду после запуска (поднимается) и снова через семь секунд после запуск (возвращаясь вниз). Вычитая, чтобы найти разницу, я нахожу что: Не удивляйтесь, если многие ваших упражнений выполняются так же “аккуратно”, как и в приведенных выше примерах. имеют. Многие учебники по-прежнему тщательно разрабатывают упражнения, так что вы можете решить с помощью факторизации (то есть, быстро выполнив алгебру).Тем не мение, сильная зависимость от калькуляторов приводит к тому, что все больше текстов создают “интересные” (то есть излишне сложные) упражнения, поэтому некоторые (или все) ваши упражнения могут включать в себя гораздо больше беспорядочных вычислений, чем было показано здесь. Если да, внимательно изучите эти “аккуратные” примеры, пока не получите совершенно уверены, что вы следуете рассуждениям.
Наша начальная высота запуска будет то же самое: мы оба стартуем со 160 футов над землей.И число силы тяжести, поскольку мы работаем в ногах, будет быть 16. Моя начальная скорость равна нулю, так как я только что уронил книгу, но мой приятель Скорость Германа – минус 48, негатив проистекает из того факта, что он выбросил свою книгу на а не вверх. Итак, наши уравнения “высоты”: В каждом случае мне нужно найти время, чтобы книги достигли нулевой высоты («ноль» «на уровне земли»), поэтому: шахта: 0
= 16 т 2 + 160, т 2 10 = 0,
так т = sqrt (10) Я проигнорирую негатив значения времени.Его книга попадает в воду через две секунды, а моя попадает в после sqrt (10) секунд, или примерно через 3,16 секунд. То есть: Время от времени они станьте умнее и поместите проблему “снаряда” в другую среду. Уравнение останется прежним по структуре, но вам, возможно, придется учитывать для другого значения силы тяжести.
Чтобы составить моё уравнение для В этом упражнении нужно иметь в виду, что значение коэффициента « г » из уравнения “движения снаряда” выше составляет половину значения силы тяжести. В физике есть – «универсальная гравитационная постоянная» G ; тогда каждый объект проявляет свою собственную гравитационную силу, которая связана с собственной массе и универсальной постоянной G .В формуле “движение снаряда” “ g ” составляет половину значения гравитационной силы для этого конкретного тело. Например, гравитационная сила на Земле направлена вниз 32. фут / с 2 , но мы использовали “16” в уравнении. Так “ г ” для моего уравнения на этот раз будет 98 2 = 49. Тогда: Затем т = 0 или t = 3.Первое решение представляет, когда мяч был запущен, поэтому второе решение – это один я хочу. Примечание: на Земле это было бы требуется чуть больше девяти секунд, чтобы мяч упал на землю. Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>
|
Калькулятор максимальной высоты – Движение снаряда
когда тело брошено или выброшено в воздух, по диагонали около поверхности земли, затем оно движется вдоль криволинейная траектория постоянного ускорения, направленная к центру Земли.Путь этого объект называется движением снаряда.
Максимальная высота снаряда – это когда снаряд достигает 0 вертикальной скорости. Так что вертикальная составляющая вектора скорости будет направлена вниз. Горизонтальное смещение снаряд – это дальность полета снаряда, которая зависит от начальной скорости объекта.
При запуске объекта с земли (начальная высота = 0)
ч макс = В o ² * sin (α) ² / (2 * g)
При запуске объекта с высоты (начальная высота> 0)
ч макс = h + V o ² * sin (α) ² / (2 * g)
Где:
V o – начальная скорость
α – угол вылета
h – начальная высота
h max – максимальная высота
Пример
Вопрос: Самолет пожарного направляет пожарный шланг вверх, в сторону пожара в небоскребе.Вода выходя из шланга со скоростью 38 м / сек. Если пожарный держит шланг под углом 58,5 °. Рассчитайте максимальную высоту потока воды.
Решение:
Капля воды, покидающая шланг, рассматривается как летящий объект.
Начальная скорость V o = 38 м / с
Угол вылета α = 58,5 °
ускорение свободного падения g = 9.8 м / сек²
Максимальная высота h max = V o ² * sin (α) ² / (2 * g)
= ((38) ² x sin58,5 °) / (2 x 9,8)
= (1444 х 0,852) / (19,6)
= 1230,288 / 19,6
= 62,76
Следовательно, максимальная высота выхода воды из шланга будет 62,76 м.
Physicscalc.Com имеет различные калькуляторы физических концепций, такие как вычислители волн, вычислители вращательного и периодического движения, оптику, механику жидкости и т. д.Просто возьми помощь необходимого калькулятора, чтобы быстро найти результат.
Практика применения формул движения снаряда – видео и стенограмма урока
Горизонтальное и вертикальное движение
Чтобы решить проблемы с движением снаряда, мы должны помнить о нескольких вещах. Во-первых, горизонтальная скорость снаряда должна оставаться постоянной, поскольку сила тяжести действует только в вертикальном направлении. Это приводит нас к следующим формулам:
Верхнее уравнение говорит нам, что горизонтальное ускорение равно нулю.Следовательно, горизонтальная скорость в любой момент времени постоянна и равна начальной горизонтальной скорости, как показано во втором уравнении. В нижней формуле x , горизонтальное расстояние перемещения, равно начальному горизонтальному расстоянию, xo , плюс произведение горизонтальной скорости, vo , и времени прохождения, t .
Как насчет вертикального направления? Итак, поскольку теперь мы должны учитывать силу тяжести, направленную вниз, формулы выглядят следующим образом:
Вертикальное ускорение имеет постоянное значение минус g , где g – ускорение свободного падения, 9.8 метров в секунду на нашей планете. Вторая формула говорит нам, что конечная вертикальная скорость, vy , равна начальной вертикальной скорости, vo , минус g , умноженное на t .
В третьем уравнении у нас есть окончательное вертикальное положение, y , равное исходному вертикальному положению, yo , плюс vyo умноженное на t минус половина умноженное на g умноженное на t в квадрате . Конечный квадрат вертикальной скорости, vy в квадрате, равен квадрату начальной вертикальной скорости, vo в квадрате, минус 2, умноженное на g, умноженное на величину y , минус yo .
Убрав эти потенциально скучные, но все же важные вещи, давайте перейдем к некоторым интересным примерам. Просто убедитесь, что вы попробовали каждую проблему самостоятельно, прежде чем увидеть решение, которое предлагает этот урок. Это неспроста называется практикой!
Тренировочная задача с пушечным ядром
Представьте, что вы стреляете пушечным ядром с 60-метрового холма по земле внизу. Предположим, что скорость пушечного ядра составляет 25 м / с, что оно выстреливается под углом 40 градусов по отношению к горизонтали, и что вы гарантировали, что под землей никого нет.
Рассчитайте горизонтальное расстояние, которое оно пройдет, его максимальную высоту и общее время пути до того, как ядро упадет на землю, как показано на следующем рисунке:
Для каждого неизвестного, которое мы решаем (время, максимальная высота и общий горизонтальный диапазон), хитрость заключается в том, чтобы выбрать уравнение, которое содержит только одно неизвестное. Вы можете видеть, что в нашем примере есть несколько разных известных вещей:
Общее время в пути можно рассчитать с помощью этого уравнения, поскольку оно содержит неизвестные t , но не неизвестные x или hmax :
Вставка 60 для начальной вертикальной высоты, 25-кратного синуса 40 градусов для начальной вертикальной скорости и 9.8 для г , получаем квадратное уравнение:
После решения квадратного уравнения вы должны получить t равно 5,5 секунды.
Чтобы вычислить максимальную высоту, нам сначала нужно использовать приведенное ниже уравнение для вычисления времени, t , которое потребуется для достижения вертикального пика:
Установка нуля для конечной вертикальной скорости, 25-кратного синуса 40 градусов для начальной вертикальной скорости и 9.8 для г :
Получаем t равно 1,64 секунды.
Теперь мы можем использовать эту формулу, чтобы найти максимальную высоту, где y равно hmax . Опять же:
Вставка т ,
По нашим расчетам, максимальная высота составляет 73,2 метра.
Наконец, мы вычисляем пройденное горизонтальное расстояние, x , по следующей формуле:
Подключение к общему времени в пути, 5.5 секунд и горизонтальную составляющую скорости, нижний индекс v x ноль , в уравнение:
Мы получаем пройденное горизонтальное расстояние x , равное 105 метрам.
Практическое задание Эйфелевой башни
Представьте, что вы бросаете монету со смотровой площадки Эйфелевой башни на высоте 276 метров над землей. (На самом деле не пытайтесь это делать в реальной жизни, это действительно может кому-то навредить!) Предположим, что сопротивление воздуха незначительно.Сколько времени потребуется, чтобы монета ударилась о землю и какова будет ее конечная скорость при соприкосновении с землей?
Опять же, давайте разберемся, что мы знаем с самого начала, а что не знаем. Это поможет нам понять, что делать в первую очередь. Вот что мы знаем и чего не знаем:
Итак, учитывая наши предыдущие формулы вертикального движения, что мы можем сделать с этими известными и неизвестными? Использование следующей формулы имеет наибольший смысл, поскольку она помогает нам решить для t , а без t мы не сможем решить для vy .Итак, мы используем следующую формулу, где мы знаем все, кроме t :
Мы используем наши знания: ноль для конечной высоты, 276 для начальной высоты и ноль для начальной вертикальной скорости, как вы можете видеть здесь:
Решая для времени, вы должны получить t равно 7,5 секунды.
Как насчет окончательной вертикальной скорости при ударе монеты о землю? Поскольку теперь мы знаем t , мы можем использовать показанное здесь уравнение, чтобы решить эту проблему! Вот необходимое нам уравнение:
Мы подставляем наши знания, ноль для начальной вертикальной скорости и 7.5 секунд для т ,
, чтобы получить конечную скорость 73,5 метра в секунду. Обратите внимание, что мы также могли использовать здесь уравнение:
, чтобы получить тот же результат.
Краткое содержание урока
Если вы провели эти эксперименты правильно, никто не должен был пострадать! Также не помешает пересмотреть некоторые вещи.Напомним, что движение снаряда – это движение, при котором объект движется в пространстве только под действием силы тяжести. Этот движущийся объект может иметь любой размер, форму и состав материала и называется снарядом . Мы использовали два набора формул: первый для анализа движения по оси x ,
и второй для анализа движения по оси y .
