Электродинамика, формулы. Основные формулы электродинамики Основные формулы электродинамики таблица
Шпаргалка с формулами по физике для ЕГЭ
Шпаргалка с формулами по физике для ЕГЭ
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
А потом вордовский файл , который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ –υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.

- Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 – Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 – Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 – t / T
- Энергия связи атомных ядер
E CB =(Zm p +Nm n -Mя)∙c 2
СТО
- t=t 1 /√1-υ 2 /c 2
- ℓ=ℓ 0 ∙√1-υ 2 /c 2
- υ 2 =(υ 1 +υ)/1+ υ 1 ∙υ/c 2
- Е = mс 2
Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
При изучении темы “Постоянный ток” необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца При изучении “Магнетизма” необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.
Электрические и магнитные явления связаны особой формой существования материи – электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.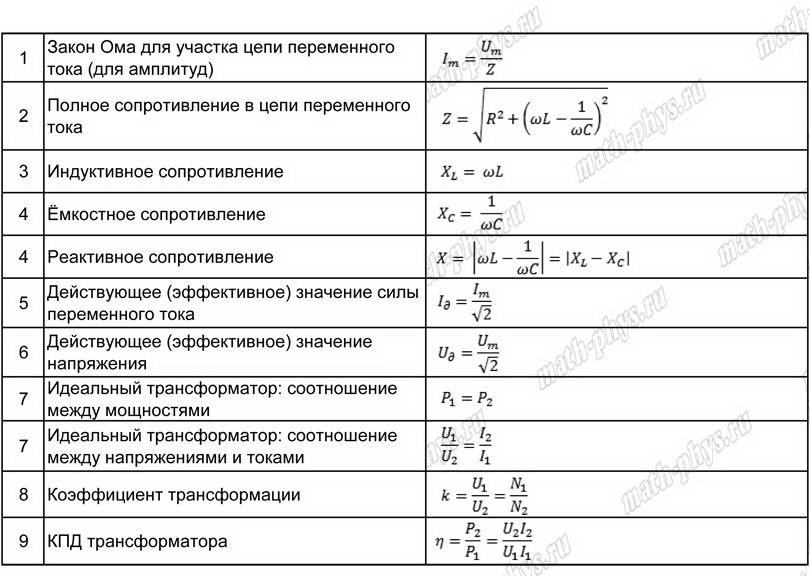
Таблица основных формул электричества и магнетизма
Физические законы, формулы, переменные | Формулы электричество и магнетизм | ||||||||
Закон Кулона: | |||||||||
Напряженность электрического поля: где Ḟ – сила, действующая на заряд q 0 , находящийся в данной точке поля. | |||||||||
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями | |||||||||
Потенциал электрического поля: где W – потенциальная энергия заряда
q
0 . | |||||||||
Потенциал поля точечного заряда на расстоянии r от заряда: | |||||||||
По принципу суперпозиции полей, напряженность: | |||||||||
Потенциал: где Ē i и ϕ i – напряженность и потенциал в данной точке поля, создаваемый i-м зарядом. | |||||||||
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ 1 в точку с потенциалом ϕ 2 : | |||||||||
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля: | |||||||||
Электроемкость уединенного проводника: | |||||||||
Электроемкость конденсатора: | |||||||||
Электроемкость плоского конденсатора: где S – площадь пластины (одной) конденсатора, d – расстояние между пластинами. | |||||||||
Энергия заряженного конденсатора: | |||||||||
Сила тока: | |||||||||
Плотность тока: где S – площадь поперечного сечения проводника. | |||||||||
Сопротивление проводника: l – длина проводника; S – площадь поперечного сечения. | |||||||||
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС: Где ε – ЭДС источника тока, R и r – внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи: | |||||||||
Закон Джоуля-Ленца 1) для однородного участка цепи постоянного тока: 2) для участка цепи с изменяющимся со временем током: | |||||||||
Мощность тока: | |||||||||
Связь магнитной индукции и напряженности магнитного поля: где B – вектор магнитной индукции, | |||||||||
Магнитная индукция (индукция магнитного поля): 2) поля бесконечно длинного прямого тока 3) поля, созданного отрезком проводника с током |
Электродинамика – это раздел физики, изучающий теорию электромагнитного поля, а также взаимодействие между электрическими зарядами. Электродинамика стала еще одной ступенью бурного развития физики. Имеются формулы по электродинамике, а также шпоры и задачи по электродинамике.
Как наука зародилась в результате многочисленных открытий и экспериментов. Разделом электродинамики, изучающим взаимодействия и электрические поля покоящихся электрических зарядов, является электростатика.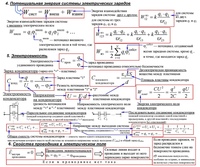
Классическая электродинамика
Электродинамика развивалась бурными темпами, многие известные ученые внесли свой вклад в развитие электродинамики. В 1785 г. французским физиком Ш. Кулоном был экспериментально установлен закон взаимодействия двух неподвижных точечных зарядов. Кулон Шарль Огюстен В 1820 г. датский физик Х. Эрстед показал, что ток, текущий по проводам, создает вокруг себя магнитное поле. Эрстед Ханс Христиан В 1831 г. М.Фарадей открыл электромагнитную индукцию. Фарадей Майкл Электродинамика – наука, занимающаяся изучением электромагнитного поля. Это поле проявляет себя посредством силового взаимодействия с теми частицами вещества, которые имеют электрический заряд. привлекла английского ученого Дж. Максвелла. Основываясь на опытных данных, он предложил уравнения, достаточные для описания всех электромагнитных явлений.Учебник скачать бесплатно с сайта
Название: Электродинамика и распространение радиоволн
Закон Кулона:
где F – сила электростатического взаимодействия между двумя заряженными телами;
q 1 , q 2 – электрические заряды тел;
ε – относительная, диэлектрическая проницаемость среды;
ε 0 =8,85·10 -12 Ф/м – электрическая постоянная;
r – расстояние между двумя заряженными телами.
Линейная плотность заряда:
где dq – элементарныйзаряд, приходящийся на участок длины dl.
Поверхностная плотность заряда:
где dq – элементарныйзаряд, приходящийся на поверхность ds.
Объемная плотность заряда:
где dq – элементарныйзаряд, в объеме dV.
Напряженность электрического поля:
где F – сила действующая на заряд q .
Теорема Гаусса:
где Е – напряженность электростатического поля;
dS – вектор, модуль которого равен площади пронизываемой поверхности, а направление совпадает с направлением нормали к площадке;
q – алгебраическая сумма заключенных внутри поверхности dS зарядов.
Теорема о циркуляции вектора напряженности:
Потенциал электростатического поля:
где W p – потенциальная энергия точечного заряда q .
Потенциал точечного заряда:
Напряженность поля точечного заряда:
.
Напряженность поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром:
где τ – линейная плотность заряда;
r – расстояние от нити или оси цилиндра до точки, напряженность поля в которой определяется.
Напряженность поля, создаваемого бесконечной равномерной заряженной плоскостью:
где σ – поверхностная плотность заряда.
Связь потенциала с напряженностью в общем случае:
E= – gradφ= .
Связь потенциала с напряженностью в случае однородного поля:
E = ,
где d – расстояние между точками с потенциалами φ 1 и φ 2 .
Связь потенциала с напряженностью в случае поля, обладающего центральной или осевой симметрией:
Работа сил поля по перемещению заряда q из точки поля с потенциалом φ 1 в точку с потенциалом φ 2:
A=q(φ 1 – φ 2).
Электроемкость проводника:
где q – заряд проводника;
φ – потенциал проводника при условии, что в бесконечности потенциал проводника принимается равным нулю.
Электроемкость конденсатора:
где q – заряд конденсатора;
U – разность потенциалов между пластинами конденсатора.
Электроемкость плоского конденсатора:
где ε – диэлектрическая проницаемость диэлектрика, расположенного между пластинами;
d – расстояние между пластинами;
S – суммарная площадь пластин.
Электроемкость батареи конденсаторов:
б) при параллельном соединении:
Энергия заряженного конденсатора:
,
где q – заряд конденсатора;
U – разность потенциалов между пластинами;
C – электроемкость конденсатора.
Сила постоянного тока:
где dq – заряд, протекший через поперечное сечение проводника за время dt .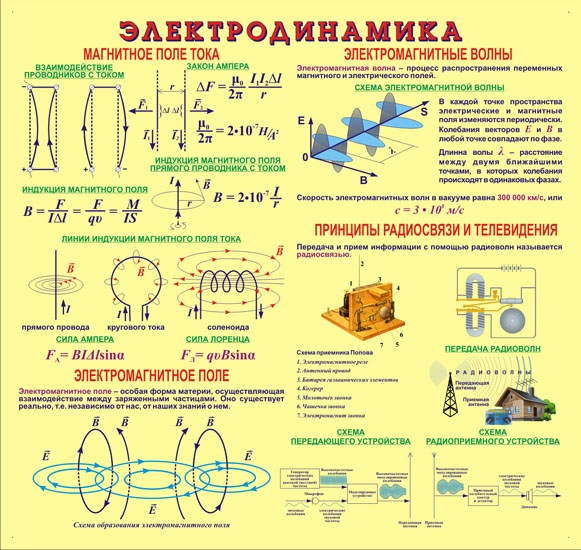
Плотность тока:
где I – сила тока в проводнике;
S – площадь проводника.
Закон Ома для участка цепи, не содержащего ЭДС:
где I – сила тока на участке;
U
R – сопротивление участка.
Закон Ома для участка цепи, содержащего ЭДС:
где I – сила тока на участке;
U – напряжение на концах участка;
R – полное сопротивление участка;
ε – ЭДС источника.
Закон Ома для замкнутой (полной) цепи:
где I – сила тока в цепи;
R – внешнее сопротивление цепи;
r – внутреннее сопротивление источника;
ε – ЭДС источника.
Законы Кирхгофа:
2. ,
где – алгебраическая сумма сил токов, сходящихся в узле;
– алгебраическая сумма падений напряжений в контуре;
– алгебраическая сумма ЭДС в контуре.
Сопротивление проводника:
где R – сопротивление проводника;
ρ – удельное сопротивление проводника;
l – длина проводника;
S
Проводимость проводника:
где G – проводимость проводника;
γ – удельная проводимость проводника;
l – длина проводника;
S – площадь поперечного сечения проводника.
Сопротивление системы проводников:
а) при последовательном соединении:
а) при параллельном соединении:
Работа тока:
,
где A – работа тока;
U – напряжение;
I – сила тока;
R – сопротивление;
t – время.
Мощность тока:
.
Закон Джоуля – Ленца
где Q – количество выделившейся теплоты.
Закон Ома в дифференциальной форме:
j =γE ,
где j – плотность тока;
γ – удельная проводимость;
E – напряженность электрического поля.
Связь магнитной индукции с напряженность магнитного поля:
B =μμ 0 H ,
где B – вектор магнитной индукции;
μ– магнитная проницаемость;
H – напряженность магнитного поля.
Закон Био – Савара – Лапласа:
,
где dB – индукция магнитного поля, создаваемая проводником в некоторой точке;
μ – магнитная проницаемость;
μ 0 =4π·10 -7 Гн/м – магнитная постоянная;
I – сила тока в проводнике;
dl – элемент проводника;
r – радиус-вектор, проведенный из элемента dl проводника в точку, в которой определяется индукция магнитного поля.
Закон полного тока для магнитного поля (теорема о циркуляции вектора B ):
,
где n – число проводников с токами, охватываемых контуром L произвольной формы.
Магнитная индукция в центре кругового тока:
где R – радиус кругового витка.
Магнитная индукция на оси кругового тока:
,
где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока:
где r 0 – расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля соленоида:
B= μμ 0 nI,
где n – отношение числа витков соленоида к его длине.
Сила Ампера:
dF =I,
где dF – сила Ампера;
I – сила тока в проводнике;
dl – длина проводника;
B – индукция магнитного поля.
Сила Лоренца:
F =qE +q [v B ],
где F – сила Лоренца;
q – заряд частицы;
E – напряженность электрического поля;
v – скорость частицы;
B – индукция магнитного поля.
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности:
Φ=B n S ,
где Φ –магнитный поток;
B n – проекция вектора магнитной индукции на вектор нормали;
S – площадь контура;
б) в случае неоднородного магнитного поля и произвольной проекции:
Потокосцепления (полный поток) для тороида и соленоида:
где Ψ – полный поток;
N – число витков;
Φ – магнитный поток, пронизывающий один виток.
Индуктивность контура:
Индуктивность соленоида:
L= μμ 0 n 2 V,
где L – индуктивность соленоида;
μ – магнитная проницаемость;
μ 0 – магнитная постоянная;
n – отношение числа витков к его длине;
V – объем соленоида.
Закон электромагнитной индукции Фарадея:
где ε i – ЭДС индукции;
– изменение полного потока в единицу времени.
Работа по перемещению замкнутого контура в магнитном поле:
A=I ΔΦ,
где A – работа по перемещению контура;
I – сила тока в контуре;
ΔΦ – изменение магнитного потока, пронизывающего контур.
ЭДС самоиндукции:
Энергия магнитного поля:
Объемная плотность энергии магнитного поля:
,
где ω – объемная плотность энергии магнитного поля;
B – индукция магнитного поля;
H – напряженность магнитного поля;
μ – магнитная проницаемость;
μ 0 – магнитная постоянная.
3.2. Понятия и определения
? Перечислите свойства электрического заряда.
1. Существуют заряды двух типов – положительные и отрицательные.
2. Одноименные заряды отталкиваются, разноименные притягиваются.
3.Заряды обладают свойством дискретности – все кратны наименьшему элементарному.
4. Заряд инвариантен, его величина не зависит от системы отсчета.
5. Заряд аддитивен – заряд системы тел равен сумме зарядов всех тел системы.
6. Полный электрический заряд замкнутой системы есть величина постоянная
7. Неподвижный заряд – источник электрического поля, движущийся заряд – источник магнитного поля.
? Сформулируйте закон Кулона.
Сила взаимодействия двух точечных неподвижных зарядов пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними. Направлена сила вдоль линии, соединяющей заряды.
? Что такое электрическое поле? Напряженность электрического поля? Сформулируйте принцип суперпозиции напряженности электрического поля.
Электрическое поле – вид материи, связанный с электрическими зарядами и передающий действие одних зарядов на другие. Напряженность – силовая характеристика поля, равная силе, действующий на единичный положительный заряд, помещенный в данную точку поля. Принцип суперпозиции – напряженность поля, создаваемая системой точечных зарядов, равна векторной сумме напряженностей поля каждого заряда.
Напряженность – силовая характеристика поля, равная силе, действующий на единичный положительный заряд, помещенный в данную точку поля. Принцип суперпозиции – напряженность поля, создаваемая системой точечных зарядов, равна векторной сумме напряженностей поля каждого заряда.
? Что называют силовыми линиями напряженности электростатического поля? Перечислите свойства силовых линий.
Линия, касательная в каждой точке которых совпадает с направлением вектора напряженности поля называется силовой. Свойства силовые линии – начинаются на положительных, заканчиваются на отрицательных зарядах, не прерываются, не пересекаются друг с другом.
? Дайте определение электрического диполя. Поле диполя.
Система из двух равных по модулю, противоположных по знаку точечных электрических зарядов, расстояние между которыми мало по сравнению с расстоянием до точек, где наблюдается действие этих зарядов.Вектор напряженности имеет направление, противоположное вектору электрического момента диполя (который, в свою очередь, направлен от отрицательного заряда к положительному).
? Что такое потенциал электростатического поля? Сформулируйте принцип суперпозиции потенциала.
Скалярная величина, численно равная отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к величине этого заряда. Принцип суперпозиции – потенциал системы точечных зарядов в некоторой точке пространства равен алгебраической сумме потенциалов, которые создали бы по отдельности эти заряды в этой же точке пространства.
? Какова связь между напряженностью и потенциалом?
E =- (E -напряженность поля в данной точке поля, j – потенциал в этой точке.)
? Определите понятие «поток вектора напряженности электрического поля». Сформулируйте электростатическую теорему Гаусса.
Для произвольной замкнутой поверхности поток вектора напряженности E электрического поля Ф Е = . Теорема Гаусса:
= (здесь Q i – заряды, охваченные замкнутой поверхностью). Справедлива для замкнутой поверхности любой формы.
Справедлива для замкнутой поверхности любой формы.
? Какие вещества называют проводниками? Как распределены заряды и электростатическое поле в проводнике? Что такое электростатическая индукция?
Проводники -вещества, в которых под действием электрического поля могут двигаться упорядоченно свободные заряды. Под действием внешнего поля заряды перераспределяются, создавая собственное поле, равное по модулю внешнему и направленное противоположно. Поэтому результирующая напряженность внутри проводника равна 0.
Электростатическая индукция – вид электризации, при котором под действием внешнего электрического поля происходит перераспределение зарядов между частями данного тела.
? Что такое электроемкость уединенного проводника, конденсатора. Как определить емкость плоского кондесатора, батареи конденсаторов, соединенных последовательно, параллельно? Единица измерения электроемкости.
Уединенный проводник: где С –емкость, q – заряд, j – потенциал. Единица измерения – фарад [Ф ]. (1 Ф – емкость проводника, у которого потенциал возрастает на 1 В при сообщении проводнику заряда 1 Кл).
Единица измерения – фарад [Ф ]. (1 Ф – емкость проводника, у которого потенциал возрастает на 1 В при сообщении проводнику заряда 1 Кл).
Емкость плоского конденсатора . Последовательное соединение: . Параллельное соединение: С общ =С 1 +С 2 +…+С n
? Какие вещества называют диэлектриками? Какие типы диэлектриков вы знаете? Что такое поляризация диэлектриков?
Диэлектрики – вещества, в которых при обычных условиях нет свободных электрических зарядов. Существуют диэлектрики полярные, неполярные, сегнетоэлектрики. Поляризацией называется процесс ориентации диполей под воздействием внешнего электрического поля.
? Что такое вектор электрического смещения? Cформулируйте постулат Максвелла.
Вектор электрического смещения D характеризует электростатическое поле, создаваемое свободными зарядами (т.е. в вакууме), но при таком распределении в пространстве, какое имеется при наличии диэлектрика. Постулат Максвелла: . Физический смысл – выражает закон создания электрических полей действием зарядов в произвольных средах.
Постулат Максвелла: . Физический смысл – выражает закон создания электрических полей действием зарядов в произвольных средах.
? Сформулируйте и поясните граничные условия для электростатического поля.
При переходе электрического поля через границу раздела двух диэлектрических сред вектор напряженности и смещения скачкообразно меняются по величине и направлению. Соотношения, характеризующие эти изменения, называются граничными условиями. Их 4:
(3), (4)
? Как определяется энергия электростатического поля? Плотность энергии?
Энергия W= (E- напряженность поля, e-диэлектрическая проницаемость, e 0 -электрическая постоянная, V – объем поля), плотность энергии
? Определите понятие «электрический ток». Виды токов. Характеристики электрического тока. Какое условие необходимо для его возникновения и существования?
Ток – упорядоченное движение заряженных частиц. Виды – ток проводимости, упорядоченное движение свободных зарядов в проводнике, конвекционный – возникает при перемещении в пространстве заряженного макроскопического тела. Для возникновения и существования тока необходимо наличие заряженных частиц, способных перемещаться упорядоченно, и наличие электрического поля, энергия которого восполняясь, расходовалась бы на это упорядоченное движение.
Виды – ток проводимости, упорядоченное движение свободных зарядов в проводнике, конвекционный – возникает при перемещении в пространстве заряженного макроскопического тела. Для возникновения и существования тока необходимо наличие заряженных частиц, способных перемещаться упорядоченно, и наличие электрического поля, энергия которого восполняясь, расходовалась бы на это упорядоченное движение.
? Приведите и поясните уравнение непрерывности. Сформулируйте условие стационарности тока в интегральной и дифференциальной формах.
Уравнение непрерывности . Выражает в дифференциальной форме закон сохранения заряда. Условие стационарности (постоянства) тока в интегральной форме: и дифференциальной – .
? Запишите закон Ома в интегральной и дифференциальной формах.
Интегральная форма – (I –ток, U – напряжение, R -сопротивление). Дифференциальная форма – (j -плотность тока, g- удельная электрическая проводимость, E – напряженность поля в проводнике).
? Что такое сторонние силы? ЭДС?
Сторонние силы разделяют заряды на положительные и отрицательные. ЭДС- отношение работы по перемещению заряда вдоль всей замкнутой цепи к его величине
? Как определяется работа и мощность тока?
При перемещении заряда q по электрической цепи, на концах которой действует напряжение U , электрическим полем совершается работа , мощность тока (t-время)
? Сформулируйте правила Кирхгофа для разветвленных цепей. Какие законы сохранения заложены в правилах Кирхгофа? Сколько независимых уравнений надо составить на основе первого и второго законов Кирхгофа?
1. Алгебраическая сумма токов, сходящихся в узле, равна 0.
2. В любом произвольно выбранном замкнутом контуре алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС, встречающихся в этом контуре. Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Число уравнений в сумме должно быть равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС).
Число уравнений в сумме должно быть равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС).
? Электрический ток в газе. Процессы ионизации и рекомбинации. Понятие о плазме.
Электрический ток в газах – направленное движение свободных электронов и ионов. При нормальных условиях газы – диэлектрики, проводниками становятся после ионизации. Ионизация – процесс образования ионов путем отделения электронов от молекул газа. Происходит вследствие воздействия внешнего ионизатора – сильного нагрева, рентгеновского или ультрафиолетового облучения, бомбардировки электронами. Рекомбинация – процесс, обратный ионизации. Плазма – представляет собой полностью или частично ионизированный газ, в котором концентрации положительных и отрицательных зарядов равны.
? Электрический ток в вакууме. Термоэлектронная эмиссия.
Носители тока в вакууме – электроны, вылетевшие вследствие эмиссии с поверхности электродов. Термоэлектронная эмиссия – испускание электронов нагретыми металлами.
Термоэлектронная эмиссия – испускание электронов нагретыми металлами.
? Что вы знаете о явлении сверхпроводимости?
Явление, при котором сопротивление некоторых чистых металлов (олово, свинец, алюминий) падает до нуля при температурах, близких к абсолютному нулю.
? Что вы знаете об электрическом сопротивлении проводников? Что такое удельное сопротивление, зависимость его от температуры, удельная электрическая проводимость? Что вы знаете о последовательном и параллельном соединении проводников. Что такое шунт, дополнительное сопротивление?
Сопротивление – величина, прямо пропорциональная длине проводника l и обратно пропорциональная площади S поперечного сечения проводника: (r-удельное сопротивление). Проводимость- величина, обратная сопротивлению. Удельное сопротивление (сопротивление проводника длиной 1 м сечением 1 м 2). Удельное сопротивление зависит от температуры , здесь a – температурный коэффициент, R и R 0 , r и r 0 –сопротивления и удельные сопротивления при t и 0 0 С. Параллельное – , последовательное R=R 1 +R 2 +…+R n . Шунт- резистор, подключаемый параллельно электроизмерительному прибору, для отведения части электрического тока, чтобы расширить пределы измерений.
Параллельное – , последовательное R=R 1 +R 2 +…+R n . Шунт- резистор, подключаемый параллельно электроизмерительному прибору, для отведения части электрического тока, чтобы расширить пределы измерений.
? Магнитное поле. Какие источники могут создавать магнитное поле?
Магнитное поле – особый вид материи, посредством которой взаимодействуют движущиеся электрические заряды. Причина существования постоянного магнитного поля неподвижный проводник с постоянным электрическим током, или постоянные магниты.
? Сформулируйте закон Ампера. Как взаимодействуют проводники, по которым ток течет в одном (противоположном) направлении?
На проводник с током действует сила Ампера, равная .
B – магнитная индукция, I- ток в проводнике, Dl –длина участка проводника, a-угол между магнитной индукцией и участком проводника. В одном направлении -притягиваются, в противоположном – отталкиваются.
? Дайте определение силы Ампера. Как определить ее направление?
Это сила, действующая на проводник с током, помещенный в магнитное поле. Направление определяем так: ладонь левой руки располагаем так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца были направлены по току в проводнике. Отогнутый большой палец покажет направление силы Ампера.
? Поясните движение заряженных частиц в магнитном поле. Что такое сила Лоренца? Как находится ее направление?
Движущаяся заряженная частица создает свое собственное магнитное поле. Если ее поместить во внешнее магнитное поле, то взаимодействие полей проявится в возникновении силы, действующей на частицу со стороны внешнего поля – силы Лоренца. Направление – по правилу левой руки. Для положительного заряда- вектор B входит в ладонь левой руки, четыре пальца направлены по движению положительного заряда (вектору скорости), отогнутый большой палец показывает направление силы Лоренца. На отрицательный заряд та же сила действует в обратном направлении.
На отрицательный заряд та же сила действует в обратном направлении.
(q -заряд, v -скорость, B – индукция, a- угол между направлением скорости и магнитной индукции).
? Рамка с током в однородном магнитном поле. Как определяется магнитный момент?
Магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая ее определенным образом. Вращающий момент определяется формулой: M =p m xB , где p m – вектор магнитного момента рамки с током, равный ISn (ток на площадь поверхности контура, на единичную нормаль к контуру), B -вектор магнитной индукции, количественная характеристика магнитного поля.
? Что такое вектор магнитной индукции? Как определить его направление? Как графически изображают магнитное поле?
Вектор магнитной индукции – это силовая характеристика магнитного поля. Магнитное поле наглядно изображают с помощью силовых линий. В каждой точке поля касательная к силовой линии совпадает с направлением вектора магнитной индукции.
Магнитное поле наглядно изображают с помощью силовых линий. В каждой точке поля касательная к силовой линии совпадает с направлением вектора магнитной индукции.
? Сформулируйте и поясните закон Био – Савара – Лапласа.
Закон Био – Савара – Лапласа позволяет рассчитать для проводника с током I магнитную индукцию поля dB , создаваемого в произвольной точке поля dl проводника: (здесь m 0 -магнитная постоянная, m-магнитная проницаемость среды). Направление вектора индукции определяется по правилу правого винта, если поступательное движение винта соответствует направлению тока в элементе.
? Сформулируйте принцип суперпозиции для магнитного поля.
Принцип суперпозиции – магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
? Поясните основные характеристики магнитного поля: магнитный поток, циркуляция магнитного поля, магнитная индукция.
Магнитным потоком Ф через какую-либо поверхность S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и косинус угла a между векторами B и n (внешней нормалью к поверхности). Циркуляцией вектора B по заданному замкнутому контуру называется интеграл вида , где dl – вектор элементарной длины контура. Теорема о циркуляции вектора B : циркуляция вектора B по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром. Вектор магнитной индукции – это силовая характеристика магнитного поля. Магнитное поле наглядно изображают с помощью силовых линий. В каждой точке поля касательная к силовой линии совпадает с направлением вектора магнитной индукции.
? Запишите и прокомментируйте условие соленоидальности магнитного поля интегральной и дифференциальной формах.
Векторные поля, в которых отсутствуют источники и стоки, называют соленоидальными. Условие соленоидальности магнитного поля в интегральной форме: и дифференциальной форме:
? Магнетики. Виды магнетиков. Феромагнетики и их свойства. Что такое гистерезис?
Вещество является магнетиком, если оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками.Намагничивающиеся во внешнем магнитном поле по направлению поля – парамагнетиками. Эти два класса называют слабомагнитными веществами. Сильномагнитные вещества, намагниченные даже при отсутствии внешнего магнитного поля, называют ферромагнетиками. Магнитный гистерезис – различие в значениях намагниченности ферромагнетика при одной и той же напряженности Н намагничивающего поля в зависимости от значения предварительной намагниченности. Такая графическая зависимость называется петлей гистерезиса.
? Сформулируйте и поясните закон полного тока в интегральной и дифференциальной формах (основные ур-я магнитостатики в веществе).
? Что такое электромагнитная индукция? Сформулируйте и поясните основной закон электромагнитной индукции (закон Фарадея). Сформулируйте правило Ленца.
Явление возникновения электродвижущей силы (ЭДС индукции) в проводнике, находящемся в переменном магнитном поле или движущемся в постоянном в постоянном магнитном поле называют электромагнитной индукцией. Закон Фарадея: какова бы не была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре ЭДС
Знак минус определяется правилом Ленца – индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.
? В чем заключается явление самоиндукции? Что такое индуктивность, единицы измерения? Токи при замыкании и размыкании электрической цепи.
Возникновение ЭДС индукции в проводящем контуре под действием собственного магнитного поля при его изменении, происходящем в результате изменения в проводнике силы тока. Индуктивность – коэффициент пропорциональности, зависящий от формы и размеров проводника или контура, [Гн]. В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи. Поэтому величина силы тока не может меняться мгновенно (механический аналог – инертность).
? Явление взаимной индукции. Коэффициент взаимной индукции.
Если два неподвижных контура расположены близко друг к другу, то при изменении силы тока в одном контуре, возникает ЭДС в другом контуре. Это явление называется взаимной индукцией. Коэффициенты пропорциональности L 21 и L 12 называют взаимной индуктивностью контуров, они равны.
? Запишите уравнения Максвелла в интегральной форме. Поясните их физический смысл.
; ;
; .
Из теории Максвелла следует, что электрическое и магнитное поле нельзя рассматривать как независимые – изменение во времени одного приводит к изменению другого.
? Энергия магнитного поля. Плотность энергии магнитного поля.
Энергия , L –индуктивность, I – сила тока.
Плотность , В – магнитная индукция, Н – напряженность магнитного поля, V -объем.
? Принцип относительности в электродинамике
Общие закономерности электромагнитных полей описываются уравнениями Максвелла. В релятивистской электродинамике установлено, что релятивистская инвариантность этих уравнений имеет место только при условии относительности электрических и магнитных полей, т.е. при зависимости характеристик этих полей от выбора инерциальных систем отсчета. В подвижной системе электрическое поле такое же, как в неподвижной, но в подвижной системе имеется магнитное поле, которого в неподвижной системе нет.
Колебания и волны
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 –υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ –υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 – Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 – Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
Основные формулы и методические рекомендации по решению задач на электростатику
«Решение задач — это практическое искусство,
подобно плаванию, или катанию на лыжах,
или игре на пианино: вы можете научиться этому,
только практикуясь. .. если вы захотите научиться
.. если вы захотите научиться
плавать, то вынуждены будете зайти в воду,
а если вы захотите стать человеком,
хорошо решающим задачи, вы вынуждены их решать»
Д. Пойа
Данная тема посвящена рассмотрению общих методов решения задач по физике, а также повторим основные формулы и величины электростатики - одного из разделов электродинамики.
В этом разделе будет рассматриваться всё, что связано с электродинамикой, а в конце курса будут рассмотрены колебания и волны. Напомним, что электродинамикой, в общем случае, называется наука, посвящённая решению любых задач, связанных с изучением электромагнитного поля, его взаимодействия с электрически заряженными телами, а также с телами, обладающими магнитными свойствами.
Известно, что электродинамика разбита на несколько разделов.
В данном курсе будет рассмотрена, в первую очередь, электростатика. Электростатика
изучает взаимодействие неподвижных электрических зарядов. Далее перейдём к
изучению законов постоянного тока: здесь будут
рассматриваться электрические цепи, а также различные характеристики
электрического тока. Следующий раздел будет посвящен основам магнитостатики
– то есть, изучению взаимодействия постоянных токов посредством создаваемых ими
магнитных полей.
Далее перейдём к
изучению законов постоянного тока: здесь будут
рассматриваться электрические цепи, а также различные характеристики
электрического тока. Следующий раздел будет посвящен основам магнитостатики
– то есть, изучению взаимодействия постоянных токов посредством создаваемых ими
магнитных полей.
В последнем разделе будут рассмотрены решения задач на электромагнитную индукцию. Напомним, что электромагнитная индукция – это явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Рассмотрим методические рекомендации по решению физических задач. Конечно, не существует универсального способа решения любой задачи, поэтому дадим лишь самые общие рекомендации. Однако, следует заметить, что прежде чем решать задачи, необходимо изучить и понять теорию, относящуюся к данной теме.
Методические рекомендации по решению задач.
1) Внимательно прочесть условия задачи, мысленно представляя ситуацию, описанную в ней. Очень часто ученики делают ошибки из-за того, что не вникли в условие задачи. Для примера рассмотрим простую задачу: Точечный заряд, равный 300 мкКл, переместился из одной точки в другую, потенциал в которой ниже на 0,5 В. Найдите работу, совершенную электрическим полем, предполагая, что это поле однородно.
2) Записать условие задачи в кратком форме (то есть, записать «дано»). Также, необходимо уметь извлекать данные из литературных выражений: например, в задаче следует предположить, что поле однородно, то есть, модуль, и направление вектора напряжённости остаются постоянными в каждой точке поля. И, конечно, необходимо указать в «дано» искомую величину.
3) Перевести значения всех физических величин в СИ. Иногда, в
этом нет необходимости, но, тем не менее, все вычисления должны производиться с
величинами, имеющими соответствующие единицы измерения.
4) Сделать рисунок, чертеж или схему. На рисунке показать все векторные величины. Почти в любой задаче имеет смысл начертить вспомогательный рисунок.
5) Выяснить, какими физическими законами можно описать данную задачу. Если в закон входят векторные величины, то надо записать уравнение, выражающее закон в векторном виде.
6) Выбрать направления координатных осей и записать векторные соотношения в проекциях на оси координат в виде скалярных уравнений.
7) Оценить количество неизвестных физических величин, вошедших в уравнения и составить столько же уравнений, которые образуют систему уравнений. Решить полученную систему уравнений и выразить искомую величину в общем виде.
8) Проверить правильность решения с помощью обозначений единиц физических величин.
9) Подставить в общее решение числовые значения физических величин и произвести вычисления.
10) Оценить реальность полученного результата и записать
ответ в единицах СИ или в тех единицах, которые заданы в условии задачи.
11) Записать ответ, обязательно указав единицы измерения величины, записанной вами в ответе. Иногда, полезно проверить, есть ли другие способы решения данной задачи.
|
ДАНО: q = 300 мкКл Dj = –5 В |
СИ 3×10–6 Кл |
РЕШЕНИЕ |
|
A = ? |
Ответ: работа электрического поля составила 1,5 мкДж.
Основные формулы электростатики.
|
Формула |
Описание формулы |
|
|
Сила
взаимодействия двух точечных зарядов q1
и q2, находящихся на расстоянии r, где k = 9×109 Н×м2/Кл2
– коэффициент пропорциональности, e –
диэлектрическая проницаемость среды. |
|
Напряжённость поля точечного заряда q на расстоянии r от заряда. |
|
|
Принцип суперпозиции полей, где E1, E2, En – напряженность поля, создаваемого соответственно зарядами q1, q2, qn. |
|
|
Потенциал точечного заряда q, где А – работа электрического поля по переносу заряда. |
|
|
Разность потенциалов или электрическое напряжение между двумя точками. |
|
|
Работа электрического поля по переносу заряда. |
|
|
Электроёмкость конденсатора |
|
|
Электроёмкость плоского конденсатора |
|
|
Потенциальная энергия заряженного конденсатора |
|
|
Закон сохранения электрического заряда |
Методические рекомендации по решению задач на
электростатику.
1. Сделать схематический рисунок, обозначив на нём точечные заряды и силы, действующие на интересующий заряд. Также, при необходимости, обозначить линии напряжённости или эквипотенциальные поверхности, относящиеся к решению задачи.
2. Выбрать систему отсчёта (например, обозначить нулевой потенциал или нулевой энергетический уровень).
3. Составить на основании законов электростатики систему уравнений в векторном виде для всех интересующих зарядов (или полей). А затем в скалярной форме, спроецировав на координатные оси векторные уравнения.
4. Решить полученную систему уравнений относительно искомых величин в общем виде, убедиться в соответствии единиц измерения и произвести вычисления.
Электрическая энергия 10 класс онлайн-подготовка на Ростелеком Лицей
Электрическая энергия
Электрический ток может быть использован для передачи энергии. Источник напряжения переводит какой-то другой тип энергии в энергию электрического тока, а в приборах энергия электрического тока вновь переходит в другой тип. Таким образом, электрическая энергия может быть переведена в другой тип энергии: механическую, тепловую, световую или химическую. Например, в работе утюга, чайника, лампочки, электродвигателя или аккумулятора.
Источник напряжения переводит какой-то другой тип энергии в энергию электрического тока, а в приборах энергия электрического тока вновь переходит в другой тип. Таким образом, электрическая энергия может быть переведена в другой тип энергии: механическую, тепловую, световую или химическую. Например, в работе утюга, чайника, лампочки, электродвигателя или аккумулятора.
Как вычислить энергию электрического тока?
Рассмотрим аккумулятор, подключенный к резистору. Вся энергия источника в этом случае переходит в тепловую. Тепло, которое выделяется на резисторе, может быть вычислено по формуле:
Q=IU △ t
Перепишем эту формулу в другом виде, используя закон Ома:
I = UR → U = IR
Q = IU△t = I2R△t
Q = I2R△t
Эта формула выражает закон Джоуля-Ленца: тепло, выделившееся на проводнике, равно произведению квадрата тока, протекающего через проводник, сопротивления проводника и времени, в течении которого течет ток.
Таким образом, мы имеем две формулы для энергии электрического поля:
W = A△t = IU – наиболее общая формула для мощности источника
W = Q△t = I2R – формула для тепловой мощности, выделяющейся на проводнике
В случае постоянного тока, когда вся энергия переходит в тепловую, эти формулы эквивалентны. Но в общем случае, при переменном токе, между ними есть существенная разница.
Например, рассмотрим, параллельное соединение двух проводников. Это могут быть две лампочки, подключенные в бытовую сеть. На каком проводнике выделится больше тепла, на большем или на меньшем?
Т.е. 100-ватная лампочка имеет меньшее сопротивление, чем 50-ватная. Рассмотрим теперь последовательное соединение двух сопротивлений. Например, этими сопротивлениями могут быть лампочка и подводящие провода.
Wr = I2r
WR = I2R
WrWR=rR
Более сложный пример: вы подсоединяете удлинитель в розетку, и подключаете к нему холодильник, стиральную машину, чайник и утюг. 2 R . Т.к. ток через подводящий провод в N раз больший, то мощность, выделяемая источником, равна INU, т.е. примерно в N раз больше. Т.е. чем больше утюгов вы подключите, тем больше источнику потребуется работать.
2 R . Т.к. ток через подводящий провод в N раз больший, то мощность, выделяемая источником, равна INU, т.е. примерно в N раз больше. Т.е. чем больше утюгов вы подключите, тем больше источнику потребуется работать.
2. При большом количестве утюгов тепло, выделяющееся на подводящем проводе, оказывается немалым. Допустим, сопротивление подводящего провода r. Тогда на нем выделится тепловая мощность (IN)2 Rr. Т.е. мощность будет пропорциональна N2.
3. Если сопротивление подводящих проводов слишком велико, то выделяющаяся теплота превысит некоторое пороговое значение.
При подключении большого числа электроприборов или мощных электроприборов стоит помнить о том, что подводящие провода должны быть достаточно толстыми, чтобы выдержать эту нагрузку.
Формулы по физике необходимые для сдачи егэ. Формулы по физике, которые рекомендуется выучить и хорошо освоить для успешной сдачи ЕГЭ
Абсолютно необходимы для того, чтобы человек, решивший изучать эту науку, вооружившись ими, мог чувствовать себя в мире физики как рыба в воде. Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Расположение физических формул в специализированных учебниках распределяется обычно по соответствующим разделам среди текстовой информации, поэтому их поиск там может отнять довольно-таки много времени, а тем более, если они вдруг понадобятся Вам срочно!
Представленные ниже шпаргалки по физике содержат все основные формулы из курса физики , которые будут полезны учащимся школ и вузов.
Все формулы школьного курса по физике с сайта http://4ege.ru
I. Кинематика скачать
1. Основные понятия
2. Законы сложения скоростей и ускорений
3. Нормальное и тангенциальное ускорения
4. Типы движений
4.1. Равномерное движение
4.1.1. Равномерное прямолинейное движение
4.1.2. Равномерное движение по окружности
4.2. Движение с постоянным ускорением
4.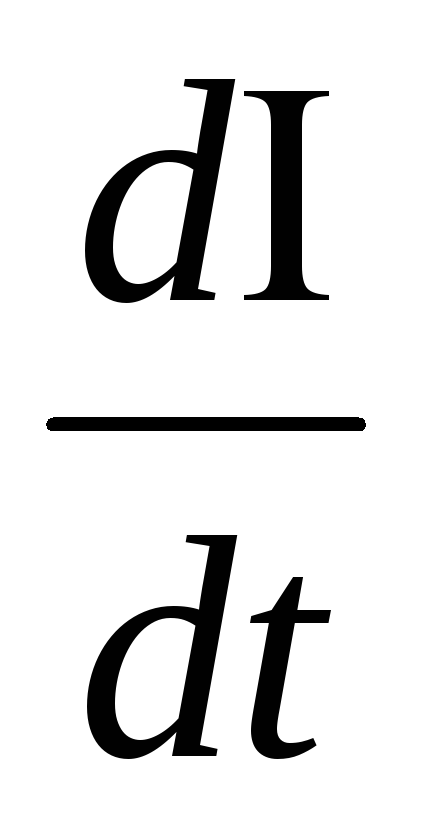 2.1. Равноускоренное движение
2.1. Равноускоренное движение
4.2.2. Равнозамедленное движение
4.3. Гармоническое движение
II. Динамика скачать
1. Второй закон Ньютона
2. Теорема о движении центра масс
3. Третий закон Ньютона
4. Силы
5. Гравитационная сила
6. Силы, действующие через контакт
III. Законы сохранения. Работа и мощность скачать
1. Импульс материальной точки
2. Импульс системы материальных точек
3. Теорема об изменении импульса материальной точки
4. Теорема об изменении импульса системы материальных точек
5. Закон сохранения импульса
6. Работа силы
7. Мощность
8. Механическая энергия
9. Теорема о механической энергии
10. Закон сохранения механической энергии
11. Диссипативные силы
12. Методы вычисления работы
13. Средняя по времени сила
IV. Статика и гидростатика скачать
1. Условия равновесия
2. Вращающий момент
3. Неустойчивое равновесие, устойчивое равновесие, безразличное равновесие
4. Центр масс, центр тяжести
5. Сила гидростатического давления
Сила гидростатического давления
6. Давлением жидкости
7. Давление в какой-либо точке жидкости
8, 9. Давление в однородной покоящейся жидкости
10. Архимедова сила
V. Тепловые явления скачать
1. Уравнение Менделеева-Клапейрона
2. Закон Дальтона
3. Основное уравнение МКТ
4. Газовые законы
5. Первый закон термодинамики
6. Адиабатический процесс
7. КПД циклического процесса (теплового двигателя)
8. Насыщенный пар
VI. Электростатика скачать
1. Закон Кулона
2. Принцип суперпозиции
3. Электрическое поле
3.1. Напряженность и потенциал электрического поля, созданного одним точечным зарядом Q
3.2. Напряженность и потенциал электрического поля, созданного системой точечных зарядов Q1, Q2, …
3.3. Напряженность и потенциал электрического поля, созданного равномерно заряженным по поверхности шаром
3.4. Напряженность и потенциал однородного электрического поля, (созданного равномерно заряженной плоскотью или плоским конденсатором)
4. Потенциальная энергия системы электрических зарядов
Потенциальная энергия системы электрических зарядов
5. Электроемкость
6. Свойства проводника в электрическом поле
VII. Постоянный ток скачать
1. Упорядоченная скорость
2. Сила тока
3. Плотность тока
4. Закон Ома для участка цепи, не содержащего ЭДС
5. Закон Ома для участка цепи, содержащего ЭДС
6. Закон Ома для полной (замкнутой) цепи
7. Последовательное соединение проводников
8. Параллельное соединение проводников
9. Работа и мощность электрического тока
10. КПД электрической цепи
11. Условие выделения максимальной мощности на нагрузке
12. Закон Фарадея для электролиза
VIII. Магнитные явления скачать
1. Магнитное поле
2. Движение зарядов в магнитном поле
3. Рамка с током в магнитном поле
4. Магнитные поля, создаваемые различными токами
5. Взаимодействие токов
6. Явление электромагнитной индукции
7. Явление самоиндукции
IX. Колебания и волны скачать
1. Колебания, определения
2. Гармонические колебания
3.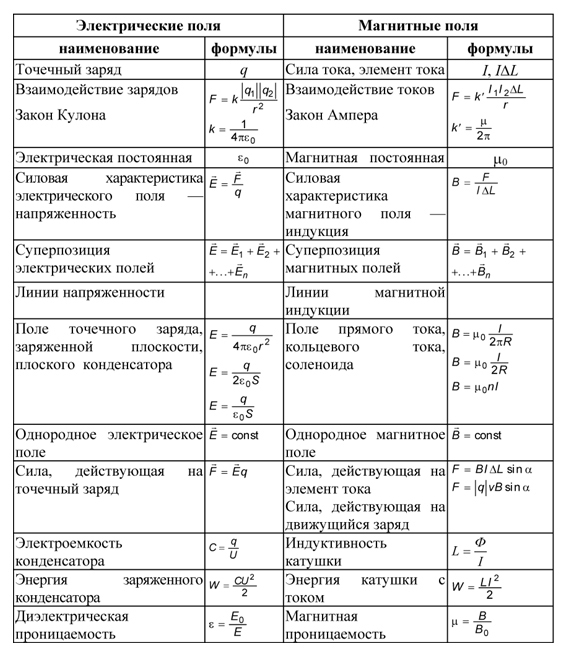 Простейшие колебательные системы
Простейшие колебательные системы
4. Волна
X. Оптика скачать
1. Закон отражения
2. Закон преломления
3. Линза
4. Изображение
5. Возможные случаи расположения предмета
6. Интерференция
7. Дифракция
Большая шпаргалка по физике . Все формулы изложены в компактном виде с небольшими комментариями. Шпаргалка также содержит полезные константы и прочую информацию. Файл содержит следующие разделы физики:
Механика (кинематика, динамика и статика)
Молекулярная физика. Свойства газов и жидкостей
Термодинамика
Электрические и электромагнитные явления
Электродинамика. Постоянный ток
Электромагнетизм
Колебания и волны. Оптика. Акустика
Квантовая физика и теория относительности
Маленькая шпора по физике . Все самое необходимое для экзамена. Нарезка основных формул по физике на одной странице. Не очень эстетично, зато практично. 🙂
Единый Государственный Экзамен охватывает информацию по всему курсу физики с 7 по 11 класс. Однако если некоторые формулы по физике для ЕГЭ неплохо запоминаются сами по себе, над другими приходится поработать. Мы рассмотрим некоторые формулы, которые полезны для решения различных задач.
Однако если некоторые формулы по физике для ЕГЭ неплохо запоминаются сами по себе, над другими приходится поработать. Мы рассмотрим некоторые формулы, которые полезны для решения различных задач.
Кинематика
Начнем традиционно с кинематики. Частая ошибка здесь – неверное вычисление средней скорости неравномерного прямолинейного движения. В данном случае задачи пытаются решать с помощью среднего арифметического. Однако все не так просто. Среднее арифметическое – только частный случай. А для нахождения средней скорости движения существует полезная формула:
где S – весь путь, пройденный телом за определенное время t.
Молекулярно-Кинетическая Теория (МКТ)
МКТ может поставить множество коварных «ловушек» для невнимательного школьника. Чтобы избежать этого, нужно свободно владеть формулами по физике для ЕГЭ в этой области.
Начнем с закона Менделеева-Клапейрона, использующегося для идеальных газов. Он звучит так:
где p –давление газа,
V – занимаемый им объем,
n – количество газа,
R – универсальная газовая постоянная,
T – температура.
Обратите внимание на примеры задач с применением этого закона.
Все представляют себе, что такое влажность. Значения относительной влажности ежедневно сообщаются в СМИ. На экзамене же пригодится формула: здесь ф – относительная влажность воздуха,
ρ – плотность водяного пара, находящегося в воздухе,
ρ0 – плотность насыщенного пара при конкретной температуре.
Эта последняя величина – табличное значение, поэтому оно должно быть в условии задачи.
Термодинамика
Термодинамика – отрасль, достаточно близкая к МКТ, поэтому многие понятия пересекаются. Термодинамика базируется на двух своих началах. Практически каждая задача этой области требует знание и применение первого начала термодинамики, выраженного формулой
Это формулируется следующим образом:
Количество теплоты Q, которое было получено системой, расходуется на совершение работы A над внешними телами и изменение ΔU внутренней энергии данной системы.
Сила Архимеда
Напоследок поговорим о поведении погруженных в жидкость тел. Очевидно, что на каждое из них действует сила тяжести, направленная вертикально вниз. Но в жидкости все тела весят меньше. Это обусловливается частичным компенсированием силы тяжести противоположно направленной силой Архимеда. Ее значение равно Таким образом, эта сила, старающаяся вытолкнуть тело из жидкости, зависит от плотности той самой жидкости и объема погруженной в нее части тела. Сила Архимеда действует и в газах, но вследствие ничтожности плотности газов ею обыкновенно пренебрегают.
Очевидно, что на каждое из них действует сила тяжести, направленная вертикально вниз. Но в жидкости все тела весят меньше. Это обусловливается частичным компенсированием силы тяжести противоположно направленной силой Архимеда. Ее значение равно Таким образом, эта сила, старающаяся вытолкнуть тело из жидкости, зависит от плотности той самой жидкости и объема погруженной в нее части тела. Сила Архимеда действует и в газах, но вследствие ничтожности плотности газов ею обыкновенно пренебрегают.
ЕГЭ проверяет знания школьника в различных областях физики. Формулы для ЕГЭ по физике способствуют успешному решению задач (можно воспользоваться ) и общему пониманию основных физических процессов.
Как правило, именно математику, а не физику принято считать королевой точных наук. Мы полагаем, что это утверждение спорно, ведь технический прогресс невозможен без знания физики и её развития. Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Секреты подготовки
Возможно, это связано с кажущейся сложностью предмета или популярностью профессий гуманитарного и управленческого профиля, но в 2016 году только 24 % всех абитуриентов приняли решение сдавать физику, в 2017 – лишь 16 %. Такие статистические данные невольно заставляют задуматься, не слишком ли завышены требования или просто уровень интеллекта в стране падает. Почему-то не верится, что так мало школьников 11 класса желают стать:
- инженерами;
- ювелирами;
- авиаконструкторами;
- геологами;
- пиротехниками;
- экологами,
- технологами на производстве и т.д.
Знание формул и законов физики в равной степени необходимо для разработчиков интеллектуальных систем, вычислительной техники, оборудования и вооружения. При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
Те ученики, которые исправно посещали все уроки физики вплоть до последнего звонка, знают, что в период с 5 по 11 класс изучается около 450 формул. Выделить из этих четырех с половиной сотен хотя бы 50 крайне сложно, поскольку все они важны. Подобного мнения, очевидно, также придерживаются разработчики Кодификатора. Тем не менее, если вы одарены необыкновенно и не ограничены во времени, вам хватит 19 формул, ведь при желании из них можно вывести все остальные. За основу мы решили взять главные разделы:
- механику;
- физику молекулярную;
- электромагнетизм и электричество;
- оптику;
- физику атомную.
Очевидно, что подготовка к ЕГЭ должна быть ежедневной, но если по каким-то причинам вы приступили к изучению всего материала лишь сейчас, настоящее чудо может совершить экспресс-курс, предлагаемый нашим центром. Надеемся, эти 19 формул также будут вам полезны:
Вы, наверное, заметили, что некоторые формулы по физике для сдачи ЕГЭ остались без пояснений? Мы предоставляем вам самим их изучить и открыть для себя законы, по которым абсолютно всё вершится в этом мире.
Шпаргалка с формулами по физике для ЕГЭ
Шпаргалка с формулами по физике для ЕГЭ
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
А потом вордовский файл , который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 –υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ –υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 – Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 – Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 – t / T
- Энергия связи атомных ядер
E CB =(Zm p +Nm n -Mя)∙c 2
СТО
- t=t 1 /√1-υ 2 /c 2
- ℓ=ℓ 0 ∙√1-υ 2 /c 2
- υ 2 =(υ 1 +υ)/1+ υ 1 ∙υ/c 2
- Е = mс 2
Простейшие физические формулы.
 Расширенная PDF версия документа “Все главные формулы по школьной физике”
Расширенная PDF версия документа “Все главные формулы по школьной физике”Размер: px
Начинать показ со страницы:
Транскрипт1
Формулы по физике, которые рекомендуется выучить и хорошо освоить для успешной сдачи ЕГЭ. Версия: 0.92 β. Составитель: Ваулин Д.Н. Литература: 1. Пёрышкин А.В. Физика 7 класс. Учебник для общеобразовательных учреждений. 13-е издание, стереотипное. Москва. Дрофа Пёрышкин А.В. Физика 8 класс. Учебник для общеобразовательных учреждений. 12-е издание, стереотипное. Москва. Дрофа Пёрышкин А.В., Гутник Е.М. Физика 9 класс. Учебник для общеобразовательных учреждений. 14-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я. и др. Физика. Механика 10 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Молекулярная физика. Термодинамика 10 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 13-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З., Слободсков Б.А. Физика. Электродинамика классы. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Колебания и волны 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Оптика. Квантовая физика 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Жирным выделены формулы, которые стоит учить, когда уже отлично освоены не выделенные жирным формулы. 7 класс. 1. Средняя скорость: 2. Плотность: 3. Закон Гука: 4. Сила тяжести:
Москва. Дрофа Мякишев Г.Я., Синяков А.З., Слободсков Б.А. Физика. Электродинамика классы. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Колебания и волны 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Оптика. Квантовая физика 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Жирным выделены формулы, которые стоит учить, когда уже отлично освоены не выделенные жирным формулы. 7 класс. 1. Средняя скорость: 2. Плотность: 3. Закон Гука: 4. Сила тяжести:
2
5. Давление: 6. Давление столба жидкости: 7. Архимедова сила: 8. Механическая работа: 9. Мощность совершения работы: 10. Момент силы: 11. Коэффициент полезного действия (КПД) механизма: 12. Потенциальная энергия при постоянном: 13. Кинетическая энергия: 8 класс. 14. Количество теплоты необходимое для нагревания: 15. Количество теплоты, выделяемое при сгорании: 16. Количество теплоты необходимое для плавления:
Количество теплоты, выделяемое при сгорании: 16. Количество теплоты необходимое для плавления:
3 17. Относительная влажность воздуха: 18. Количество теплоты необходимое для парообразования: 19. КПД теплового двигателя: 20. Полезная работа теплового двигателя: 21. Закон сохранения заряда: 22. Сила тока: 23. Напряжение: 24. Сопротивление: 25. Общее сопротивление последовательного соединения проводников: 26. Общее сопротивление параллельного соединения проводников: 27. Закон Ома для участка цепи:
4 28. Мощность электрического тока: 29. Закон Джоуля-Ленца: 30. Закон отражения света: 31. Закон преломления света: 32. Оптическая сила линзы: 9 класс. 33. Зависимость скорости от времени при равноускоренном движении: 34. Зависимость радиус вектора от времени при равноускоренном движении: 35. Второй закон Ньютона: 36. Третий закон Ньютона: 37. Закон всемирного тяготения:
5
38. Центростремительное ускорение: 39. Импульс: 40. Закон изменения энергии: 41. Связь периода и частоты: 42. Связь длинны волны и частоты: 43. Закон изменения импульса: 44. Закон Ампера: 45. Энергия магнитного поля тока: 46. Формула трансформатора: 47. Действующее значение тока: 48. Действующее значение напряжения:
Связь длинны волны и частоты: 43. Закон изменения импульса: 44. Закон Ампера: 45. Энергия магнитного поля тока: 46. Формула трансформатора: 47. Действующее значение тока: 48. Действующее значение напряжения:
6 49. Заряд конденсатора: 50. Электроёмкость плоского конденсатора: 51. Общая ёмкость параллельно соединённых конденсаторов: 52. Энергия электрического поля конденсатора: 53. Формула Томпсона: 54. Энергия фотона: 55. Поглощение фотона атомом: 56. Связь массы и энергии: 1. Поглощённая доза излучения: 2. Эквивалентная доза излучения:
7 57. Закон радиоактивного распада: 10 класс. 58. Угловая скорость: 59. Связь скорости с угловой: 60. Закон сложения скоростей: 61. Сила трения скольжения: 62. Сила трения покоя: 3. Сила сопротивления среды: [ 63. Потенциальная энергия растянутой пружины: 4. Радиус вектор центра масс:
8
64. Количество вещества: 65. Уравнение Менделеева-Клапейрона: 66. Основное уравнение молекулярно кинетической теории: 67. Концентрация частиц: 68. Связь между средней кинетической энергией частиц и температурой газа: 69. Внутренняя энергия газа: 70. Работа газа: 71. Первое начало термодинамики: 72. КПД машины Карно: 5. Тепловое линейное расширение: 6. Тепловое объёмное расширение:
Связь между средней кинетической энергией частиц и температурой газа: 69. Внутренняя энергия газа: 70. Работа газа: 71. Первое начало термодинамики: 72. КПД машины Карно: 5. Тепловое линейное расширение: 6. Тепловое объёмное расширение:
9 73. Закон Кулона: 74. Напряжённость электрического поля: 75. Напряжённость электрического поля точечного заряда: 7. Поток напряжённости электрического поля: 8. Теорема Гаусса: 76. Потенциальная энергия заряда при постоянном: 77. Потенциальная энергия взаимодействия тел: 78. Потенциальная энергия взаимодействия зарядов: 79. Потенциал: 80. Разность потенциалов: 81. Связь напряжённости однородного электрического поля и напряжения:
10
82. Общая электроёмкость последовательно соединённых конденсаторов: 83. Зависимость удельного сопротивления от температуры: 84. Первое правило Кирхгофа: 85. Закон Ома для полной цепи: 86. Второе правило Кирхгофа: 87. Закон Фарадея: 11 класс. 9. Закон Био-Савара-Лапласа: 10. Магнитная индукция бесконечного провода: 88. Сила Лоренца:
Сила Лоренца:
11 89. Магнитный поток: 90. Закон электромагнитной индукции: 91. Индуктивность: 92. Зависимость величины, изменяющейся по гармоническому закону от времени: 93. Зависимость скорости изменения величины, изменяющейся по гармоническому закону от времени: 94. Зависимость ускорения изменения величины, изменяющейся по гармоническому закону от времени: 95. Период колебаний нитяного маятника: 96. Период колебаний пружинного маятника: 11. Емкостное сопротивление: 12. Индуктивное сопротивление:
12 13. Сопротивление для переменного тока: 97. Формула тонкой линзы: 98. Условие интерференционного максимума: 99. Условие интерференционного минимума: 14. Преобразования Лоренца координат: 15. Преобразования Лоренца времени: 16. Релятивистский закон сложения скоростей: 100. Зависимость массы тела от скорости: 17. Релятивистская связь между энергией и импульсом:
13 101. Уравнение фотоэффекта: 102. Красная граница фотоэффекта: 103. Длина волны Де Бройля:
Программа вступительных испытаний по учебному предмету «Физика» для лиц, имеющих общее среднее образование, для получения высшего образования І ступени, 2018 год 1 УТВЕРЖДЕНО Приказ Министра образования
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «АНГАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» УТВЕРЖДАЮ “чебной работе II. В. Истомина 2016 г. ПРОГРАММА ВСТУПИТЕЛЬНОГО
В. Истомина 2016 г. ПРОГРАММА ВСТУПИТЕЛЬНОГО
2 6. Количество заданий в одном варианте теста 30. Часть А 18 заданий. Часть В 12 заданий. 7. Структура теста Раздел 1. Механика 11 заданий (36,7 %). Раздел 2. Основы молекулярно-кинетической теории и
УТВЕРЖДЕНО Приказ Министра образования Республики Беларусь от 30.10.2015 817 Программы вступительных испытаний в учреждения образования для лиц, имеющих общее среднее образование, для получения высшего
1/5 ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ФИЗИКА 1. МЕХАНИКА КИНЕМАТИКА Механическое движение и его виды. Относительность механического движения. Скорость. Ускорение. Равномерное движение. Прямолинейное равноускоренное
1. Общие положения Программа предназначена для подготовки к вступительному испытанию по физике для поступающих на факультет физики и ИКТ Чеченского государственного университета. Вступительный экзамен
Код: Содержание: 1. МЕХАНИКА 1.1. КИНЕМАТИКА 1.1.1. Механическое движение и его виды 1. 1.2. Относительность механического движения 1.1.3. Скорость 1.1.4. Ускорение 1.1.5. Равномерное движение 1.1.6. Прямолинейное
1.2. Относительность механического движения 1.1.3. Скорость 1.1.4. Ускорение 1.1.5. Равномерное движение 1.1.6. Прямолинейное
ПРОГРАММА ЭЛЕМЕНТОВ СОДЕРЖАНИЯ И ТРЕБОВАНИЙ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЙ ДЛЯ ПРОВЕДЕНИЯ В 2014 ГОДУ ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ПО ФИЗИКЕ Программа элементов содержания по
ПРОГРАММА СОБЕСЕДОВАНИЯ ПО ДИСЦИПЛИНЕ «ФИЗИКА» Физика и методы научного познания Предмет физики. Физика как наука. Научные методы познания окружающего мира и их отличия от других методов познания. Физика
СПЕЦИФИКАЦИЯ теста по учебному предмету «Физика» для проведения централизованного тестирования в 2017 году 1. Назначение теста объективное оценивание уровня подготовки лиц, имеющих общее среднее образование
СПЕЦИФИКАЦИЯ теста по учебному предмету «Физика» для проведения централизованного тестирования в 2018 году 1. Назначение теста объективное оценивание уровня подготовки лиц, имеющих общее среднее образование
Оглавление Основные положения. .. 3 1. МЕХАНИКА… 3 2. МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ… 4 3. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ… 4 4. КОЛЕБАНИЯ И ВОЛНЫ… 5 5. ОПТИКА… 5 6. КВАНТОВАЯ ФИЗИКА… 6 СПИСОК
.. 3 1. МЕХАНИКА… 3 2. МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ… 4 3. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ… 4 4. КОЛЕБАНИЯ И ВОЛНЫ… 5 5. ОПТИКА… 5 6. КВАНТОВАЯ ФИЗИКА… 6 СПИСОК
1 Общие положения Настоящая программа составлена на основе действующих учебных программ для средней школы, колледжа и техникума. При проведении собеседования основное внимание обращается на понимание абитуриентами
Спецификация теста по предмету физика для Единого национального тестирования и комплексного тестирования (Утвержден для использования в Едином национальном тестировании и комплексном тестировании с 2018
ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ (БАКАЛАВРИАТ/СПЕЦИАЛИТЕТ) ПО ОБЩЕОБРАЗОВАТЕЛЬНОЙ ДИСЦИПЛИНЕ «ФИЗИКА» Программа составлена на основе Федерального государственного образовательного стандарта среднего общего
«УТВЕРЖДАЮ» Руководитель Федеральной службы по надзору в сфере образования и науки «СОГЛАСОВАНО» Председатель Научнометодического совета ФИПИ по физике Единый государственный экзамен по ФИЗИКЕ Кодификатор
По предмету: Физика, 11 класс 2017 г. СОДЕРЖАНИЕ 1. Перечень диагностических работ 2. Количественные показатели 3. Общие результаты 3.1. Результаты на уровне региона 3.2. Распределение по баллам 3.3. Результаты
СОДЕРЖАНИЕ 1. Перечень диагностических работ 2. Количественные показатели 3. Общие результаты 3.1. Результаты на уровне региона 3.2. Распределение по баллам 3.3. Результаты
НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ «АССОЦИАЦИЯ МОСКОВСКИХ ВУЗОВ» ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОДЕЗИИ И КАРТОГРАФИИ НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ
УТВЕРЖДЕНО Приказ Министра образования Республики Беларусь 03.12.2018 836 Билеты для проведения экзамена в порядке экстерната при освоении содержания образовательной программы среднего образования по учебному
ПРОГРАММА ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ ПО ФИЗИКЕ В первом столбце указан код раздела, которому соответствуют крупные блоки содержания. Во втором столбце приводится код элемента содержания, для которого создаются
ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ПО ФИЗИКЕ САНКТ-ПЕТЕРБУРГ 2014 ГОД 1. Механическое движение. Относительность движения. Системы отсчета.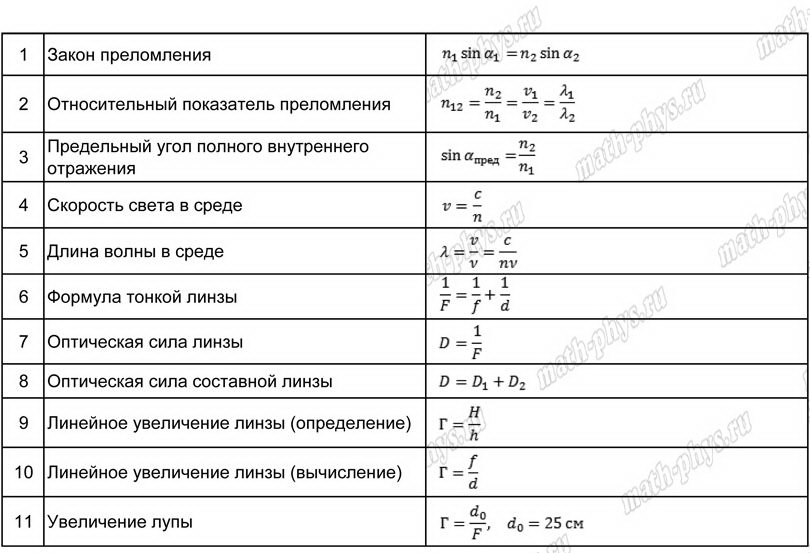 Материальная точка. 2. Траектория. Путь и перемещение. 3. Равномерное
Материальная точка. 2. Траектория. Путь и перемещение. 3. Равномерное
Министерство образования и науки Краснодарского края государственное бюджетное профессиональное образовательное учреждение Краснодарского края “Краснодарский информационно- технологический техникум” Тематический
Подготовка к ЕГЭ по физике (4 месяца) Перечень лекций, тестов и заданий. Дата начала Дата завершения Блок 0 Введение В.1 Скалярные и векторные величины. В.2 Сложение и вычитание векторов. В.3 Умножение
Введение………………………………. 8 Руководство по использованию диска…………….. 8 Установка программы……………………. 8 Работа с программой……………………. 11 От издательства…………………………
Негосударственное образовательное учреждение высшего образования «Кубанский социально-экономический институт (КСЭИ)» ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ПО ФИЗИКЕ для абитуриентов, поступающих в вуз Рассмотрено
ПРОГРАММА ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ ПО ФИЗИКЕ В ФГБОУ ВО «ПГУ» В 2016 ГОДУ СОДЕРЖАНИЕ ПРОГРАММЫ 1 МЕХАНИКА 1. 1 КИНЕМАТИКА 1.1.1 Механическое движение и его виды 1.1.2 Относительность механического движения
1 КИНЕМАТИКА 1.1.1 Механическое движение и его виды 1.1.2 Относительность механического движения
ПРОГРАММА ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ ПО ФИЗИКЕ для поступающих в Московский государственный университет геодезии и картографии. Программа составлена в соответствии с типовой программой по физике средней
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный строительный университет»
Вопросы к экзаменационным билетам по дисциплине Физика Билет 1 1. Физика и метод научного познания. Современная физическая картина мира. 2. Магнитное поле. Магнитное взаимодействие. Вектор магнитной индукции.
«УТВЕРЖДАЮ» Директор Федерального института педагогических измерений «СОГЛАСОВАНО» Председатель Научнометодического совета ФИПИ по физике Единый государственный экзамен по ФИЗИКЕ Кодификатор элементов
Тематика тестовых задач по физике для 11 класса Механика Кинематика: 1.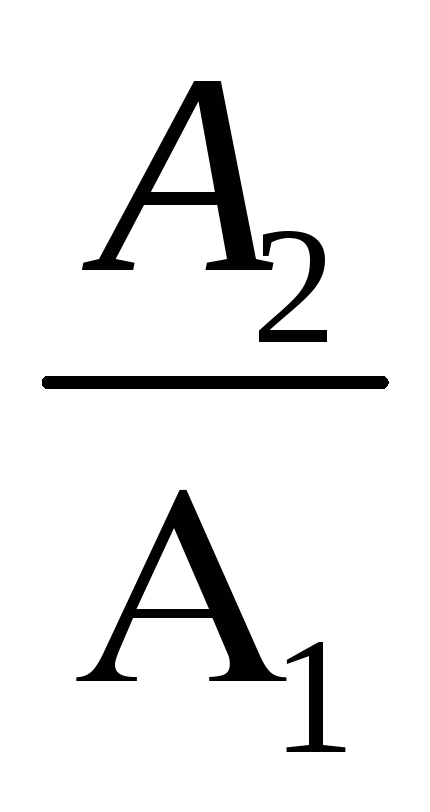 Кинематика прямолинейного движения материальной точки. Путь и перемещение. Скорость и ускорение. Сложение скоростей. Прямолинейное
Кинематика прямолинейного движения материальной точки. Путь и перемещение. Скорость и ускорение. Сложение скоростей. Прямолинейное
ÓÄÊ 373:53 ÁÁÊ 22.3ÿ72 Í34 Макет подготовлен при содействии ООО «Айдиономикс» В оформлении обложки использованы элементы дизайна: Tantoon Studio, incomible / Istockphoto / Thinkstock / Fotobank.ru Í34
ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОГРАММА ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА ПО ФИЗИКЕ Составитель: Профессор, к.т.н. Першенков П.П. Пенза 2014 Механика 1. Прямолинейное равномерное движение. Вектор. Проекции
МИНИСТЕРСТВО ОБОРОНЫ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное казённое военное образовательное учреждение высшего образования Краснодарское высшее военное авиационное училище лётчиков имени Героя
189 УТВЕРЖДЕНО Приказ Министра образования Республики Беларусь от 30.10.2018 765 Программа вступительных испытаний по учебному предмету «Физика» для лиц, имеющих общее среднее образование, для получения
Программа вступительных испытаний по учебному предмету «Физика» для лиц, имеющих общее среднее образование, для получения высшего образования І ступени или среднего специального образования, 2019 год ПОЯСНИТЕЛЬНАЯ
Контрольные работы по физике 29 группа 4 семестр Решаем один из предложенных вариантов в каждой контрольной работе.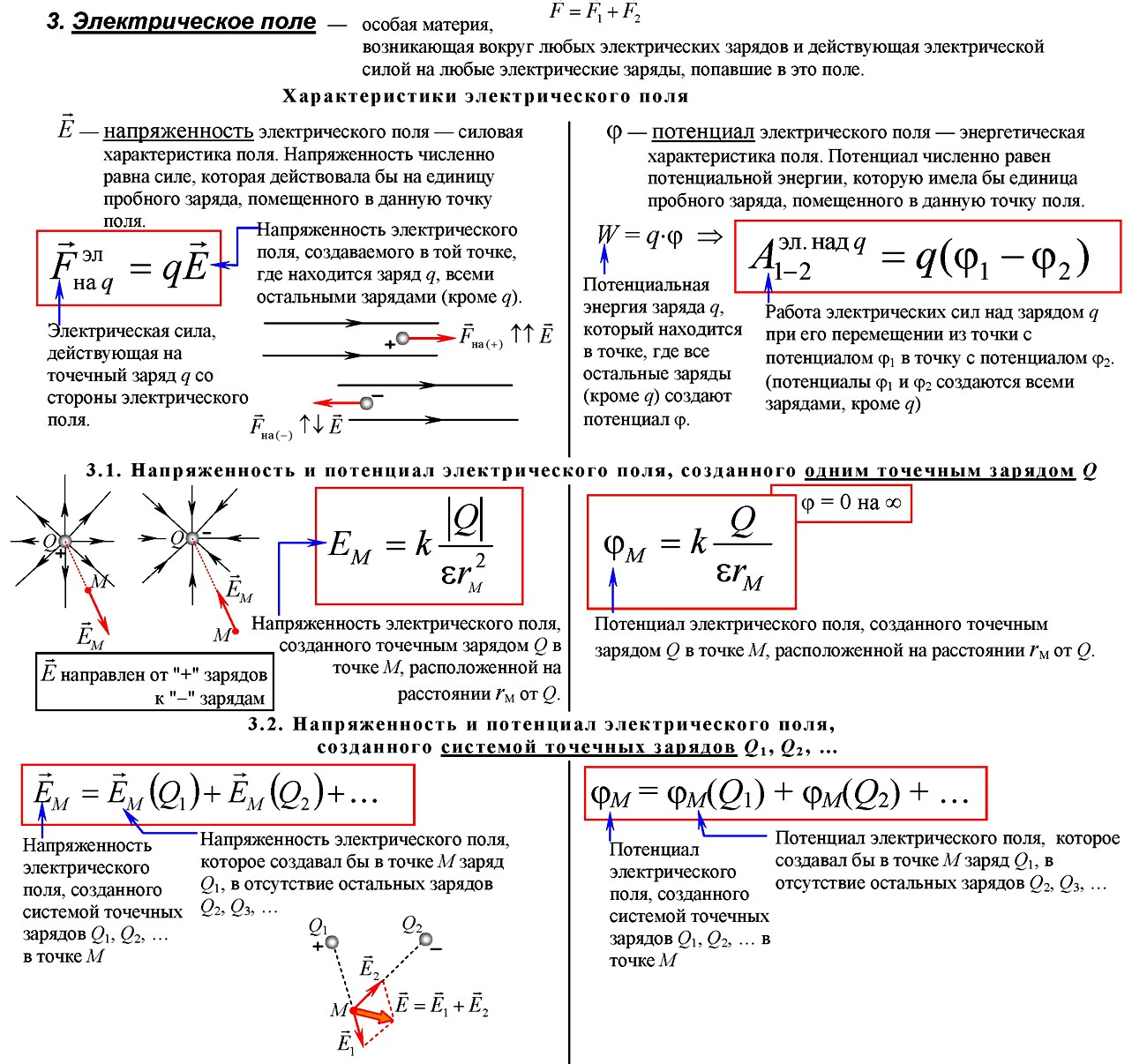 Контрольная работа 11 Механические колебания. Упругие волны. Вариант 1 1. Материальная
Контрольная работа 11 Механические колебания. Упругие волны. Вариант 1 1. Материальная
Программа к вступительному испытанию по общеобразовательному предмету «Физика» при поступлении в Сыктывкарский лесной институт Программа предназначена для подготовки к массовой письменной проверке знаний
Федеральное государственное автономное учреждение высшего профессионального образования Национальный исследовательский университет «Высшая школа экономики» Программа вступительного испытания по физике
Пояснительная записка Программный материал рассчитан для учащихся 11 классов на 1 учебный час в неделю, всего 34 часа. Настоящая программа позволяет более глубоко и осмысленно изучать практические и теоретические
ФГБОУ ВПО «Петербургский государственный университет путей сообщения Императора Александра I» Программа вступительного испытания по физике для поступающих на обучение по программам бакалавриата и специалитета
ПРОГРАММА ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА ПО ФИЗИКЕ для абитуриентов, поступающих в ФГБОУ ВО Смоленскую ГСХА в 2017 году Программа для вступительного испытания по физике Раздел 1.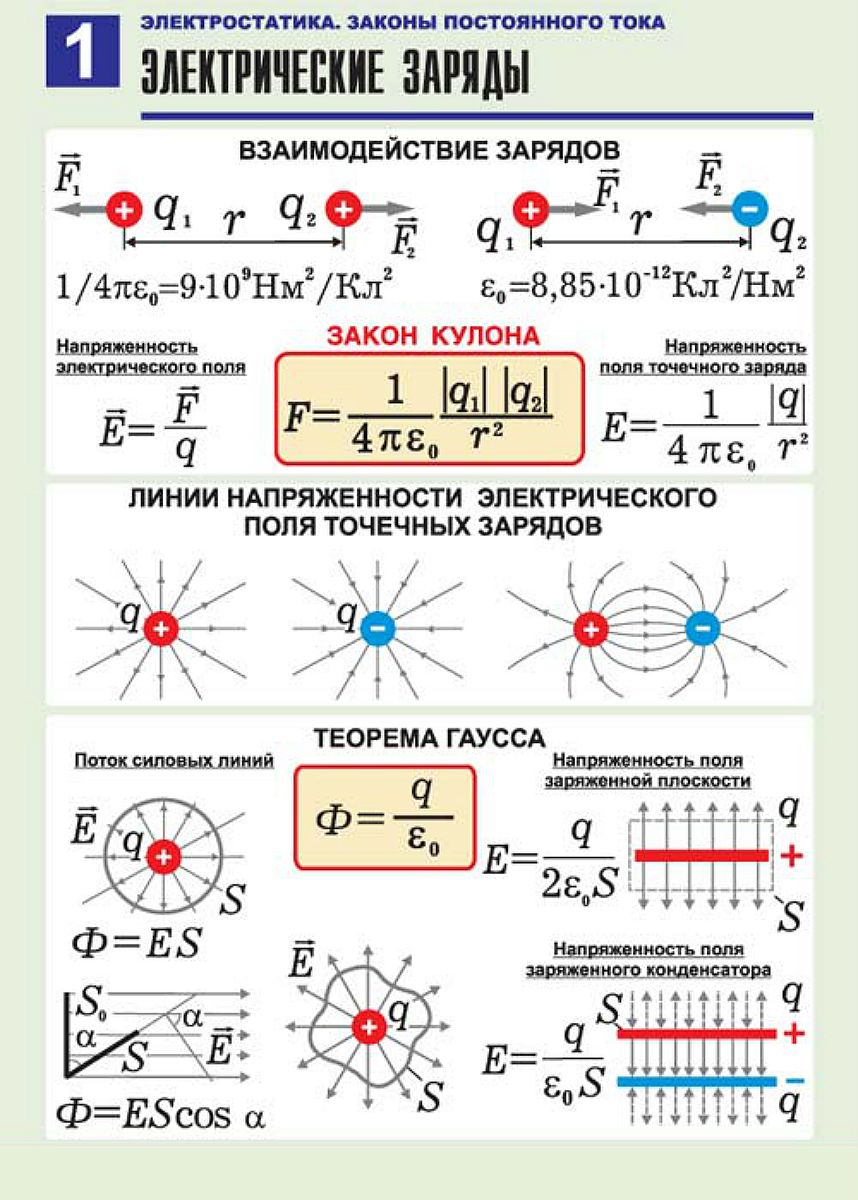 Перечень элементов содержания,
Перечень элементов содержания,
Занят ия Наименование разделов и дисциплин 1 Механическое движение. Относительность механического движения. Система отсчёта. Материальная точка. Траектория. Путь. Вектор перемещения и его проекции. Прямолинейное
Аннотация к рабочей программе по физике 7 класс (базовый уровень) Рабочая программа по физике 7 класса составлена на основании ФЗ РФ 273 от компонента государственного стандарта основного общего образования
1 семестр Введение. 1 Основные науки о природе. Естественнонаучный метод познания. Раздел 1. Механика. Тема 1.1. Кинематика твёрдого тела 2 Относительность механического движения. Системы отсчета. Характеристики
2 ификатор элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для проведения единого государственного экзамена по ФИЗИКЕ Единый государственный экзамен по
ПРОГРАММА ПО ФИЗИКЕ При проведении экзаменов по физике основное внимание должно быть обращено на понимание экзаменующимся сущности физический явлений и законов, на умение истолковать смысл физических величин
Программа по физике для поступающих в ОАНО ВПО ВУиТ Вступительные испытания по физике проводятся в форме письменной работы (тестирования) и собеседования, с помощью которой проверяются знания учащихся,
Министерство образования и науки Российской Федерации федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский политехнический университет Петра Великого»
ЭКЗАМЕНАЦИОННЫЕ БИЛЕТЫ ГОСУДАРСТВЕННОЙ ИТОГОВОЙ АТТЕСТАЦИИ ПО ФИЗИКЕ ПО ОБРАЗОВАТЕЛЬНЫМ ПРОГРАММАМ ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ Билет 1 1. Что изучает физика. Физические явления. Наблюдения, опыты. 2.
Что изучает физика. Физические явления. Наблюдения, опыты. 2.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ Учреждение образования «Брестский государственный технический университет» ПРОГРАММА собеседования для иностранных абитуриентов по предмету «ФИЗИКА» Разработана:
Аннотация к рабочим программам по физике Класс: 10 Уровень изучения учебного материала: базовый. УМК, учебник: Рабочая программа по физике для 10-11 классов составлена на основе Федерального компонента
Методы научного познания Эксперимент и теория в процессе познания мира. Моделирование явлений. Физические законы и пределы их применения. Роль математики в физике. Принципы причинности и соответствия.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Аннотация к контрольно-оценочному средству по учебному предмету «Физика» 1. Общие положения. Контрольно-оценочные средства (КОС) предназначены для контроля и оценки образовательных достижений обучающихся,
Общие положения. Контрольно-оценочные средства (КОС) предназначены для контроля и оценки образовательных достижений обучающихся,
При составлении программы следующие правовые документы 10-11классы были использованы федеральный компонент государственного стандарта среднего (полного) общего образования по физике, утвержденный в 2004
Раздел 1. Планируемые результаты. Личностные: в ценностно-ориентированной сфере чувство гордости за российскую физическую науку, отношение к физике как элементу общечеловеческой культуры, гуманизм, положительное
Е.Н. Бурцева, В.А. Пивень, Т.Л. Шапошникова, Л.Н. Терновая ОСНОВЫ ЭЛЕМЕНТАРНОЙ ФИЗИКИ (базовый уровень) Учебное пособие Краснодар 2012 УДК 53 ББК 22.3 Б91 Рецензенты: Е.Н. Тумаев, доктор физико-математических
0 Пояснительная записка. Программа по физике для 10 11 классов составлена на основе авторской программы: Физика 10 11 класс Г.Я. Мякишев М.:Дрофа,-2010г. и ориентирована на использование учебно-методического
Тема Дата Количество часов Календарно-тематическое планирование По физике 10 класс (профильный уровень) Требования к знаниям Форма контроля ФИЗИКА И МЕТОДЫ НАУЧНОГО ПОЗНАНИЯ 1 ФИЗИЧЕСКИЕ ЗАКОНЫ И ТЕОРИИ
Шпаргалка с формулами по физике для ЕГЭ
Шпаргалка с формулами по физике для ЕГЭ
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
Для начала картинка, которую можно распечатать в компактном виде.
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
А потом вордовский файл , который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 –υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ –υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 – Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 – Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 – t / T
- Энергия связи атомных ядер
E CB =(Zm p +Nm n -Mя)∙c 2
СТО
- t=t 1 /√1-υ 2 /c 2
- ℓ=ℓ 0 ∙√1-υ 2 /c 2
- υ 2 =(υ 1 +υ)/1+ υ 1 ∙υ/c 2
- Е = mс 2
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 –υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ –υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 – Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 – Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
Абсолютно необходимы для того, чтобы человек, решивший изучать эту науку, вооружившись ими, мог чувствовать себя в мире физики как рыба в воде.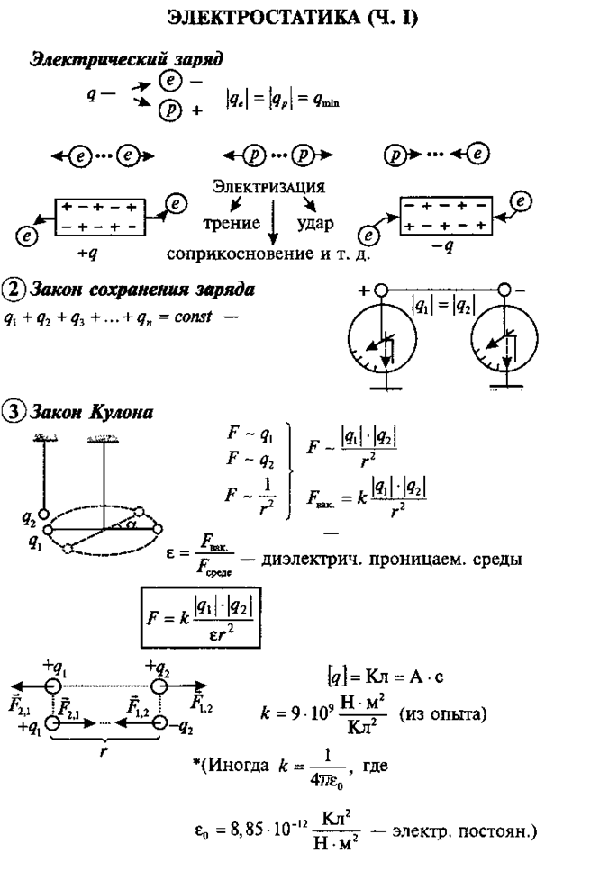 Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Расположение физических формул в специализированных учебниках распределяется обычно по соответствующим разделам среди текстовой информации, поэтому их поиск там может отнять довольно-таки много времени, а тем более, если они вдруг понадобятся Вам срочно!
Представленные ниже шпаргалки по физике содержат все основные формулы из курса физики , которые будут полезны учащимся школ и вузов.
Все формулы школьного курса по физике с сайта http://4ege.ru
I. Кинематика скачать
1. Основные понятия
2. Законы сложения скоростей и ускорений
3. Нормальное и тангенциальное ускорения
4. Типы движений
4.1. Равномерное движение
4.1.1. Равномерное прямолинейное движение
4.1.2. Равномерное движение по окружности
4.2. Движение с постоянным ускорением
4. 2.1. Равноускоренное движение
2.1. Равноускоренное движение
4.2.2. Равнозамедленное движение
4.3. Гармоническое движение
II. Динамика скачать
1. Второй закон Ньютона
2. Теорема о движении центра масс
3. Третий закон Ньютона
4. Силы
5. Гравитационная сила
6. Силы, действующие через контакт
III. Законы сохранения. Работа и мощность скачать
1. Импульс материальной точки
2. Импульс системы материальных точек
3. Теорема об изменении импульса материальной точки
4. Теорема об изменении импульса системы материальных точек
5. Закон сохранения импульса
6. Работа силы
7. Мощность
8. Механическая энергия
9. Теорема о механической энергии
10. Закон сохранения механической энергии
11. Диссипативные силы
12. Методы вычисления работы
13. Средняя по времени сила
IV. Статика и гидростатика скачать
1. Условия равновесия
2. Вращающий момент
3. Неустойчивое равновесие, устойчивое равновесие, безразличное равновесие
4. Центр масс, центр тяжести
5. Сила гидростатического давления
Сила гидростатического давления
6. Давлением жидкости
7. Давление в какой-либо точке жидкости
8, 9. Давление в однородной покоящейся жидкости
10. Архимедова сила
V. Тепловые явления скачать
1. Уравнение Менделеева-Клапейрона
2. Закон Дальтона
3. Основное уравнение МКТ
4. Газовые законы
5. Первый закон термодинамики
6. Адиабатический процесс
7. КПД циклического процесса (теплового двигателя)
8. Насыщенный пар
VI. Электростатика скачать
1. Закон Кулона
2. Принцип суперпозиции
3. Электрическое поле
3.1. Напряженность и потенциал электрического поля, созданного одним точечным зарядом Q
3.2. Напряженность и потенциал электрического поля, созданного системой точечных зарядов Q1, Q2, …
3.3. Напряженность и потенциал электрического поля, созданного равномерно заряженным по поверхности шаром
3.4. Напряженность и потенциал однородного электрического поля, (созданного равномерно заряженной плоскотью или плоским конденсатором)
4. Потенциальная энергия системы электрических зарядов
Потенциальная энергия системы электрических зарядов
5. Электроемкость
6. Свойства проводника в электрическом поле
VII. Постоянный ток скачать
1. Упорядоченная скорость
2. Сила тока
3. Плотность тока
4. Закон Ома для участка цепи, не содержащего ЭДС
5. Закон Ома для участка цепи, содержащего ЭДС
6. Закон Ома для полной (замкнутой) цепи
7. Последовательное соединение проводников
8. Параллельное соединение проводников
9. Работа и мощность электрического тока
10. КПД электрической цепи
11. Условие выделения максимальной мощности на нагрузке
12. Закон Фарадея для электролиза
VIII. Магнитные явления скачать
1. Магнитное поле
2. Движение зарядов в магнитном поле
3. Рамка с током в магнитном поле
4. Магнитные поля, создаваемые различными токами
5. Взаимодействие токов
6. Явление электромагнитной индукции
7. Явление самоиндукции
IX. Колебания и волны скачать
1. Колебания, определения
2. Гармонические колебания
3. Простейшие колебательные системы
Простейшие колебательные системы
4. Волна
X. Оптика скачать
1. Закон отражения
2. Закон преломления
3. Линза
4. Изображение
5. Возможные случаи расположения предмета
6. Интерференция
7. Дифракция
Большая шпаргалка по физике . Все формулы изложены в компактном виде с небольшими комментариями. Шпаргалка также содержит полезные константы и прочую информацию. Файл содержит следующие разделы физики:
Механика (кинематика, динамика и статика)
Молекулярная физика. Свойства газов и жидкостей
Термодинамика
Электрические и электромагнитные явления
Электродинамика. Постоянный ток
Электромагнетизм
Колебания и волны. Оптика. Акустика
Квантовая физика и теория относительности
Маленькая шпора по физике . Все самое необходимое для экзамена. Нарезка основных формул по физике на одной странице. Не очень эстетично, зато практично. 🙂
Связь между квантовой физикой и уравнениями Максвелла в модели атома водорода
Габриэль Д. Пуччини. «Электродинамика при возможной альтернативе преобразованию Лоренца». Основы писем по физике. 16(5), 481-494, январь 2017 г. DOI: 10.1023/BFopl0000012778.72452.6f.
Пуччини. «Электродинамика при возможной альтернативе преобразованию Лоренца». Основы писем по физике. 16(5), 481-494, январь 2017 г. DOI: 10.1023/BFopl0000012778.72452.6f.
И.Т. Кинзер, Дж. Фукаи. «Сила Вебера и уравнение Максвелла». Нашел. физ. лат. 9(5), с.457. 1996. DOI: 10.1007/BF021
.Т.К. Саркар, М. Салазар-Пальма. «Оригинальное представление Максвеллом электромагнитной теории и ее эволюции», в Hand Book of Antenna Technologies. Спрингер, Сингапур. 2015. DOI: org/10.1007/978-9814560.
А.Л. Шаляпин, В.И. Стукалов. Введение в классическую электродинамику и атомную физику. Екатеринбург. УМС. 490p 2006. (на русском языке).
В.М. Бернштейн. «Эволюция электродинамики Гаусса – Вебера, квантовая механика без волновой теории», в сб. Фундаментальные проблемы естествознания и техники.30р. Санкт-Петербург, 2000. (на русском языке).
Ф.Ф. Менде, А.С. Дубровин. Альтернативная идеология электродинамики. Монография, Москва, 218с. 2016. (на русском языке).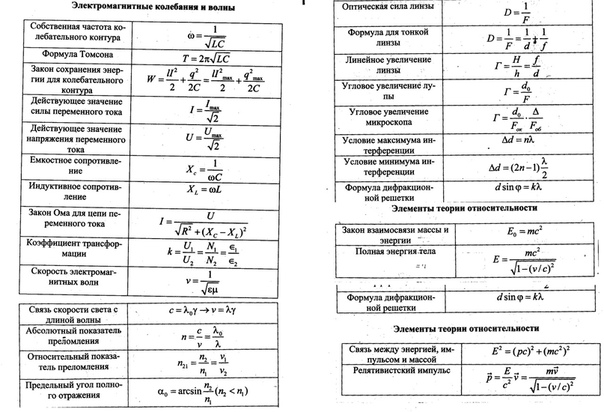
Р. П. Фейнман, Р. Б. Лейгтон, М. Сэндс. Фейнмановские лекции по физике. Массачусетс, Лондон, том. 2, 1964.
Л-М. Мукала, Т. Нсонго. «Максвеллоподобная теория, объединяющая обычные поля». Научно-исследовательский журнал технических наук. об. 6(2), 20-26, февраль 2017.
р.П. Фейнман. КЭД – странная теория света и материи. Мемориальные лекции. Аликс Г. Маутнер. Издательство Принстонского университета. 1985.
Ю.Э. Хорошавцев. «Размышление о квантовой механике, исходя из принципа сохранения энтропии в атомном масштабе». Журнал математических исследований. ISSN 1916 – 9795. Том. 11(3), 1–16, 2019. DOI: 10.5539/jmr.v11n3pxx.
Фрэнсис С. Джонсон, Брюс Л. Крагин, Ричард Ходжес. «Плотность электромагнитного импульса и вектор Пойнтинга в статических полях».Американский журнал физики. 1994. DOI: org/101119/1.17738.
С.М. Ким, Грег. Гбур. «Сохранение углового момента в частично когерентных волновых полях». физ. Версия A (86), октябрь 2012 г.
Р. Пфайфер, Т. Ниеминен, Н. Хекенберг. «Импульс электромагнитной волны в диэлектрической среде». Обзоры современной физики. 79(4), 2007.
Пфайфер, Т. Ниеминен, Н. Хекенберг. «Импульс электромагнитной волны в диэлектрической среде». Обзоры современной физики. 79(4), 2007.
Ю.Э. Хорошавцев. «Мнимые векторы в механике и электродинамике». Вестник инженеров-строителей.ISSN 1999 – 5571, 4(9), 115-117, декабрь 2006 г. (на русском языке).
Дэвид Р. Джексон. Справочник по электротехнике. Под редакцией: Вай-Кай-Чен, Academic Press. 2005.
Р. П. Фейнман, Р. Б. Лейгтон, М. Сэндс. Фейнмановские лекции по физике. Аддисон – издательство Wesley, Массачусетс, Лондон, Vol. 3, 1963.
Мэтью Д. Швардс. Квантовая теория поля и стандартная модель. University Press, Кембридж, Нью-Йорк, 1-е издание.Март 2014 г. DOI: doi.org/10.5281/zenodo.2578864.
Т. Д. Кароцци, Дж. Э. С. Бергман, Р.Л. Карлссон. «Комплексная теорема Пойнтинга как закон сохранения». Препринт. 2005.
Джеральд Кайзер. «Завершение сложной теоремы Пойнтинга: сохранение реактивной энергии за реактивное время», в Центре сигналов и волн, Портленд.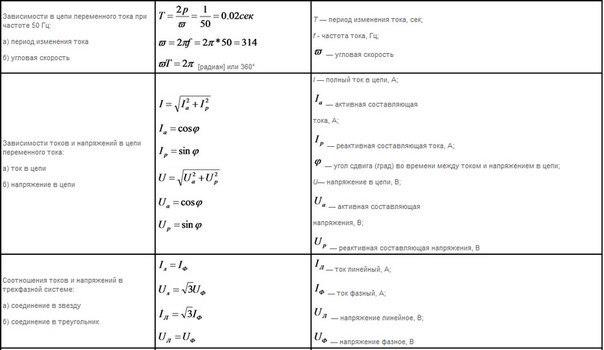 Декабрь 2014 г.
Декабрь 2014 г.
Игнасио Кампос Хименес, Х.А. Э. Роа Нери. «О теореме Пойнтинга». Европейский журнал физики.13(3), 117, июль 2000 г. DOI: 10.1088/0143-0807/13/3/003.
Л.Д. Ландау и Э. М. Лифшиц. Квантовая механика: Нерелятивистская теория. об. 3, 3-е изд. 1977.
Электродинамика, формулы. Электромагнетизм
Электродинамика Это наука о свойствах и законах особого вида материи – электромагнитного поля, которое взаимодействует между электрически заряженными телами или частицами.
Квантовая электродинамика (КЭД) – квантовая полевая теория электромагнитных взаимодействий; наиболее развитая часть квантовой теории поля. Классическая электродинамика учитывает только непрерывные свойства электромагнитного поля, в то время как квантовая электродинамика основана на представлении о том, что электромагнитное поле обладает и разрывными (дискретными) свойствами, носителями которых являются кванты поля – фотоны. Взаимодействие электромагнитного излучения с заряженными частицами рассматривается в квантовой электродинамике как поглощение и испускание фотонов частицами.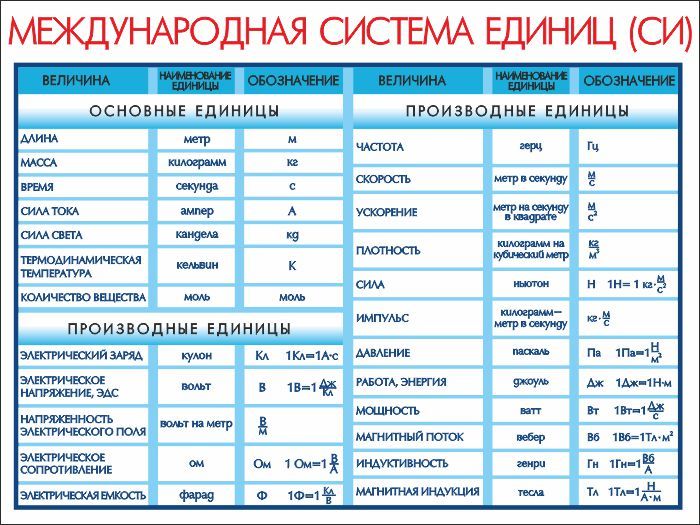
2.Характеристики электромагнитного поля
Электромагнитное поле – Э = Н / Кл = Б / М
Э = Ф / q – отношение силы, действующей со стороны поля, к величине этого заряда.
D – индукция электрического поля – называется вектором, пропорциональным вектору напряженности, но не зависящим от свойств среды
D знак равно 𝞮 Е ; 𝞮 = 𝞮 0 𝞮 ’ 0 = 8.85*10 -12 Ф/м
В- вектор магнитной индукции = Н/А*м = 1Тл поля к проводнику с током, к току в проводнике и его длине . Б =
| Ф |/ Я * л (США) Н – напряженность магнитного поля (А/м) = 80 эрстед =) 80 Гаусс, называется вектором, параллельным вектору индукции, но не зависящим от свойств среды. Н = 1 / мк, где мк = мк 0* м’
Н = 1 / мк, где мк = мк 0* м’
3.Векторные поля. Интегральные и дифференциальные характеристики векторного поля
4 теорема Ostrograd-Gauss и STOKS
5.Law подвеска
6 Gauss’s Теорема
7
7.Vector Flow
8 Уравнения непрерывности
9.Ток смещения
10 Закона полного тока
11.law непрерывности магнитного потока
12. Контакты
13 Законы о Джоле-Ленце в дифференциальной форме
количество тепла, выделяемого на единицу времени в проводнике с сопротивлением r при прочности тока I, по закону Джоуля-Ленца, равно:
Применяя этот закон к бесконечно малому цилиндру, ось которого совпадает с направлением тока, получим
Учитывая, что – объем бесконечно малого цилиндра, а – количество теплоты, выделяющееся в единице объема в единицу времени, находим
,
Где выражено в ваттах на кубический метр. Учитывая, что j 2 = j * j и используя выражение для j, можно записать отношение в виде:
Учитывая, что j 2 = j * j и используя выражение для j, можно записать отношение в виде:
Это равенство выражает закон Джоуля-Ленца в дифференциальной форме.
14. Полная система уравнений Максвелла в веществе
В среде внешние электрические и магнитные поля вызывают поляризацию и намагниченность вещества, которые макроскопически описываются вектором поляризации P и вектором намагниченности M вещества соответственно, и вызваны появлением связанных зарядов и токов.В результате поле в среде оказывается суммой внешних полей и полей, вызванных связанными зарядами и токами.
Поляризация P и намагниченность вещества M связаны с векторами напряженности и индукции электрического и магнитного полей следующими соотношениями:
Следовательно, выражая векторы D и H через E, B и, можно получить математически эквивалентную систему уравнений Максвелла:
Здесь индекс обозначает свободные заряды и токи.Уравнения Максвелла в таком виде являются фундаментальными в том смысле, что они не зависят от модели электромагнитного устройства материи. Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в, а затем в Р, М и, следовательно, в D, В сложную микроскопическую природу электромагнитного поля в среде.
Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в, а затем в Р, М и, следовательно, в D, В сложную микроскопическую природу электромагнитного поля в среде.
Определение 1
Электродинамика — огромная и важная область физики, изучающая классические, неквантовые свойства электромагнитного поля и движения положительно заряженных магнитных зарядов, взаимодействующих между собой с помощью этого поля.
Рис. 1. Кратко об электродинамике. Author24 – онлайн обмен студенческими работами
Электродинамика представлена широким кругом разнообразных постановок задач и их грамотных решений, приближенных методов и частных случаев, которые объединены в единое целое общими исходными законами и уравнениями. Последние, составляющие основную часть классической электродинамики, подробно представлены в формулах Максвелла. В настоящее время ученые продолжают изучение принципов этого направления в физике, построение каркаса его взаимосвязей с другими научными направлениями.
Закон Кулона в электродинамике обозначается так: $ F = \ frac (kq1q2) (r2) $, где $ k = \ frac (9 \ cdot 10 (H \ cdot m)) (Cl) $. Уравнение напряженности электрического поля записывается так: $E = \frac(F)(q)$, а поток вектора индукции магнитного поля $∆Ф = В∆S\cos(a)$.
В электродинамике в первую очередь изучаются свободные заряды и зарядовые системы, которые способствуют активации непрерывного энергетического спектра. Классическому описанию электромагнитного взаимодействия способствует то, что оно эффективно уже в низкоэнергетическом пределе, когда энергетический потенциал частиц и фотонов мал по сравнению с энергией покоя электрона.
В таких ситуациях часто не происходит аннигиляции заряженных частиц, так как происходит лишь постепенное изменение состояния их неустойчивого движения в результате обмена большим количеством фотонов низкой энергии.
Примечание 1
Однако даже при высоких энергиях частиц в среде, несмотря на значительную роль флуктуаций, электродинамика может успешно использоваться для всестороннего описания среднестатистических, макроскопических характеристик и процессов.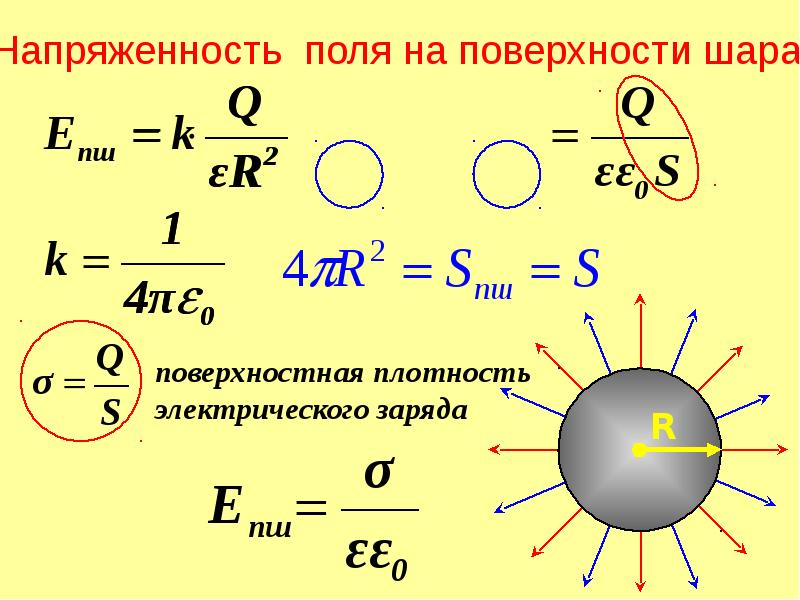
Основные уравнения электродинамики
Основными формулами, описывающими поведение электромагнитного поля и его непосредственное взаимодействие с заряженными телами, являются уравнения Максвелла, определяющие вероятные действия свободного электромагнитного поля в среде и вакууме, а также общая генерация поля источниками.
Среди этих положений в физике можно выделить:
- Теорема Гаусса для электрического поля – предназначена для определения генерации электростатического поля положительными зарядами;
- гипотеза о замкнутости силовых линий – способствует взаимодействию процессов внутри самого магнитного поля;
- Закон индукции Фарадея – устанавливает генерацию электрических и магнитных полей переменными свойствами окружающей среды.
В общем, теорема Ампера – Максвелла представляет собой уникальное представление о циркуляции линий в магнитном поле с постепенным добавлением токов смещения, введенное самим Максвеллом, точно определяет преобразование магнитного поля движущимися зарядами и переменное действие электрического поля.
Заряд и сила в электродинамике
В электродинамике взаимодействие силы и заряда электромагнитного поля исходит из следующего совместного определения электрического заряда $q$, энергии $E$ и магнитного $B$ полей, которые утвержден в качестве фундаментального физического закона на основании всей совокупности экспериментальных данных.Формула для силы Лоренца (в рамках идеализации точечного заряда, движущегося с определенной скоростью) записывается с заменой скорости $v$.
Проводники часто содержат огромное количество зарядов, поэтому эти заряды достаточно хорошо компенсируются: количество положительных и отрицательных зарядов всегда равно друг другу. Следовательно, полная электрическая сила, постоянно действующая на проводник, также равна нулю. В результате магнитные силы, действующие на отдельные заряды в проводнике, не компенсируются, так как при наличии тока скорости зарядов всегда различны.Уравнение действия проводника с током в магнитном поле можно записать так: $ G = | v ⃗ | s\cos(a)$
Если в качестве тока исследовать не жидкость, а полноценный и устойчивый поток заряженных частиц, то весь энергетический потенциал, проходящий линейно через площадь в $1s$, будет силой тока равно: $ I = ρ | \ век (в) | s\cos(a)$, где $ρ$ — плотность заряда (в единице объема в общем потоке).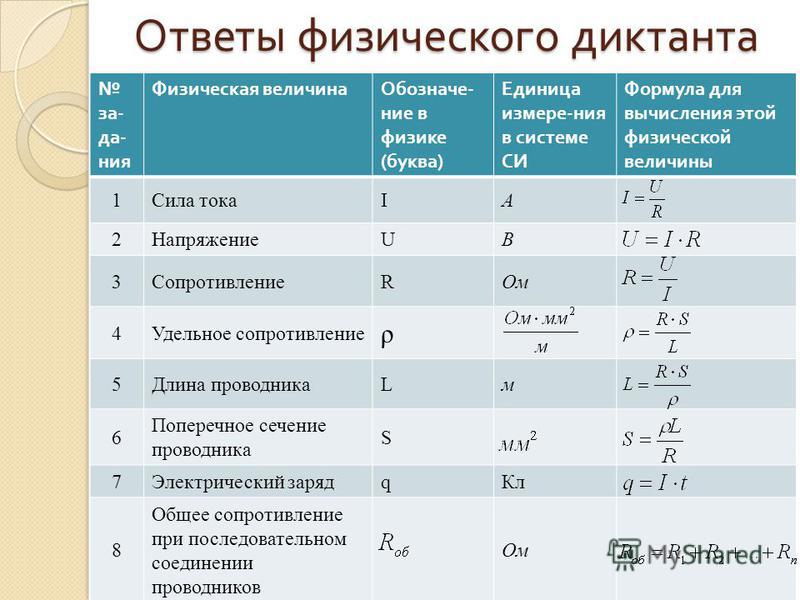
Примечание 2
Если магнитное и электрическое поле систематически изменяются от точки к точке на конкретном участке, то в выражениях и формулах для парциальных течений, как и в случае жидкости, средние значения $E⃗$ и $B⃗$ при сайт обязательны.
Особое положение электродинамики в физике
Значимое положение электродинамики в современной науке подтверждается известной работой А. Эйнштейна, в которой подробно изложены принципы и основы специальной теории относительности. Научная работа выдающегося ученого называется «К электродинамике движущихся тел» и включает в себя огромное количество важных уравнений и определений.
Электродинамика как отдельная область физики состоит из следующих разделов:
- учение о поле неподвижных, но электрически заряженных физических тел и частиц;
- учение о свойствах электрического тока;
- учение о взаимодействии магнитного поля и электромагнитной индукции;
- учение об электромагнитных волнах и колебаниях.

Все вышеперечисленные разделы объединены в одно целое теоремой Д. Максвелла, который не только создал и представил стройную теорию электромагнитного поля, но и описал все его свойства, доказав его реальное существование. Работа именно этого ученого показала научному миру, что известные в то время электрические и магнитные поля являются всего лишь проявлением единого электромагнитного поля, функционирующего в разных системах отсчета.
Существенная часть физики посвящена изучению электродинамики и электромагнитных явлений.Эта область во многом претендует на статус отдельной науки, так как не только исследует все законы электромагнитных взаимодействий, но и подробно их описывает с помощью математических формул. Глубокие и многолетние исследования электродинамики открыли новые пути использования электромагнитных явлений на практике на благо всего человечества.
Электродинамика — раздел физики, изучающий теорию электромагнитного поля, а также взаимодействие между электрическими зарядами. Электродинамика стала еще одним этапом бурного развития физики. Есть формулы по электродинамике, а также шпоры и задачи по электродинамике.
Электродинамика стала еще одним этапом бурного развития физики. Есть формулы по электродинамике, а также шпоры и задачи по электродинамике.
Как родилась наука в результате многочисленных открытий и экспериментов. Раздел электродинамики, изучающий взаимодействия и электрические поля покоящихся электрических зарядов, — электростатика.
Классическая электродинамика
Электродинамика развивалась быстрыми темпами, многие известные ученые внесли свой вклад в развитие электродинамики.В 1785 г. французский физик К. Кулон экспериментально установил закон взаимодействия двух неподвижных точечных зарядов. Кулон Шарль Огюстен В 1820 году датский физик Г. Эрстед показал, что ток, протекающий по проводам, создает вокруг себя магнитное поле. Эрстед Ганс Христиан В 1831 г. М. Фарадей открыл электромагнитную индукцию. Фарадей Майкл Электродинамика — наука, изучающая электромагнитное поле. Это поле проявляется через силовое взаимодействие с теми частицами материи, которые имеют электрический заряд. привлек английский ученый Дж. Максвелл. На основе эмпирических данных он предложил уравнения, достаточные для описания всех электромагнитных явлений.
привлек английский ученый Дж. Максвелл. На основе эмпирических данных он предложил уравнения, достаточные для описания всех электромагнитных явлений. Учебное пособие скачать бесплатно с сайта
Название: Электродинамика и распространение радиоволн
Сессия приближается, и нам пора переходить от теории к практике. На выходных мы сели и подумали, что многие студенты хотели бы иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего.Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что самым жестоким образом зазубрено накануне, такая подборка сослужит отличную службу.
Большинство задач обычно относят к трем наиболее популярным областям физики. Это Механика , Термодинамика и Молекулярная физика , Электричество … Давайте их возьмем!
Основные формулы физики – динамика, кинематика, статика
Начнем с самого простого.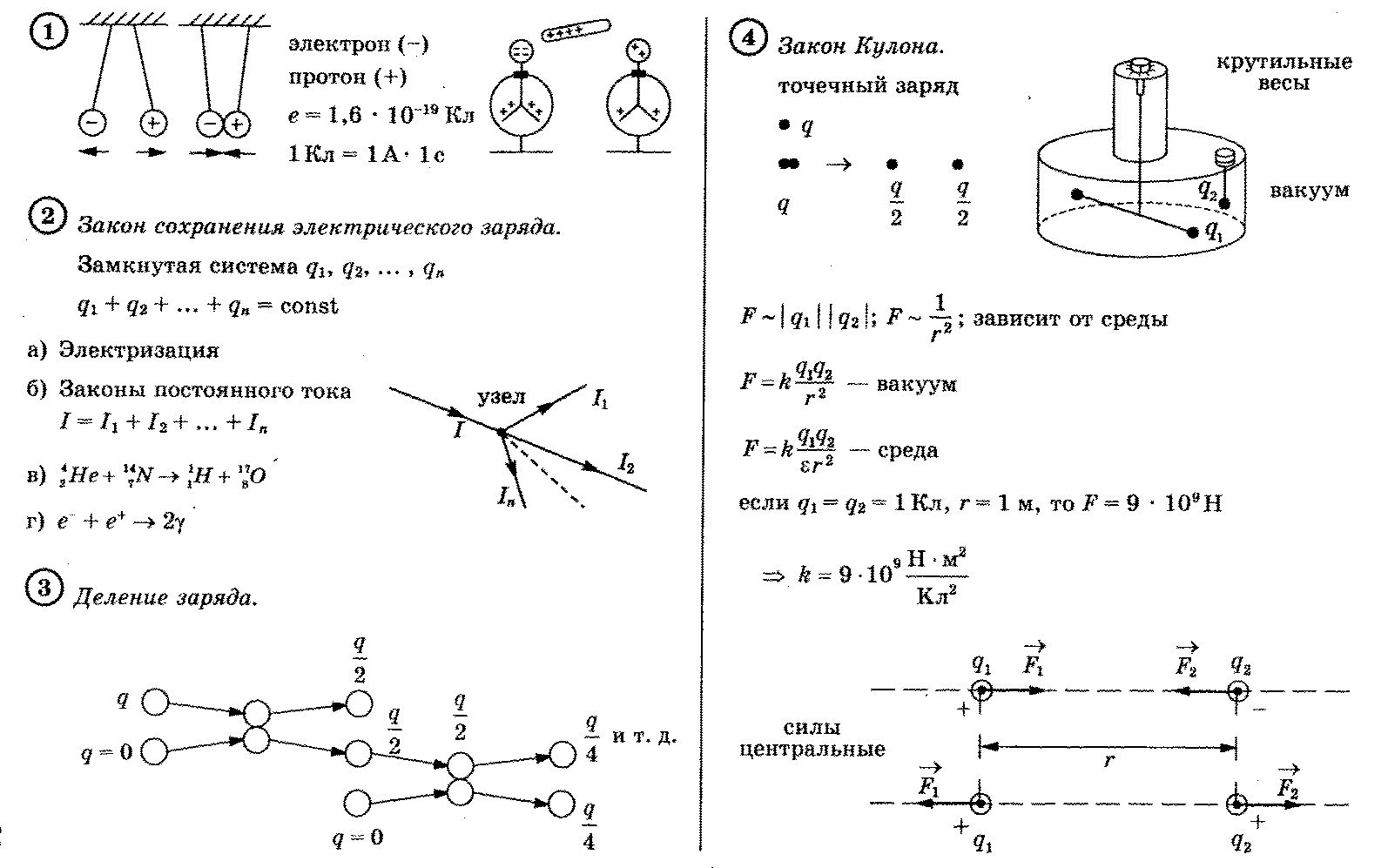 Старое доброе любимое прямое и плавное движение.
Старое доброе любимое прямое и плавное движение.
Кинематические формулы:
Конечно, не будем забывать о движении по кругу, а потом перейдем к динамике и законам Ньютона.
После динамики пора рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда мы без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами для колебаний и волн и перейдем к молекулярной физике и термодинамике.
КПД, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка. 10% на любая работа .
Основные физические формулы: электричество
Пора переходить к электричеству, хотя термодинамика его меньше любит. Начнем с электростатики.
И, под барабанную дробь, заканчиваем формулами закона Ома, электромагнитной индукции и электромагнитных колебаний.
Вот и все. Конечно, можно привести целую гору формул, но это бесполезно. Когда формул слишком много, можно легко запутаться, а потом и вовсе расплавить мозг. Мы надеемся, что наша шпаргалка по основным формулам физики поможет вам решить ваши любимые задачи быстрее и эффективнее. А если хотите что-то уточнить или не нашли нужной формулы: спросите у специалистов студенческая служба … Наши авторы держат в голове сотни формул и щелкают задачи как орешки.Свяжитесь с нами, и вскоре любая задача станет для вас непосильной.
Шпаргалка с формулами по физике к ЕГЭ
и не только (могут понадобиться 7, 8, 9, 10 и 11 классы).
Во-первых, картинка, которую можно распечатать в компактном виде.
Механика
- Давление P = F / S
- Плотность ρ = м/В
- Давление на глубине жидкости P = ρ ∙ g ∙ h
- Сила тяжести Fт = мг
- 5. Архимедова сила Fa = ρ w ∙ g ∙ Vт
- Уравнение движения для равноускоренного движения
Х = Х 0 + υ 0 ∙ t + (а ∙ t 2) / 2 S = ( υ 2 – υ 0 2) / 2а S = ( υ + υ 0) ∙ т/2
- Уравнение скорости равноускоренного движения υ = υ 0 + а∙т
- Ускорение a = ( υ – υ 0) / т
- Круговая скорость υ = 2πR / Т
- Центростремительное ускорение a = υ 2 / Р
- Связь между периодом и частотой ν = 1 / T = ω / 2π
- II Закон Ньютона F = ma
- Закон Гука Fy = -kx
- Закон всемирного тяготения F = G∙M∙m/R 2
- Вес тела, движущегося с ускорением a P = m (g + a)
- Вес тела, движущегося с ускорением a ↓ P = m (g-a)
- Сила трения Ffr = мкН
- Импульс тела p = m υ
- Импульс силы Ft = ∆p
- Момент силы M = F ∙ ℓ
- Потенциальная энергия тела, поднятого над землей Ep = mgh
- Потенциальная энергия упруго деформированного тела Ep = kx 2/2
- Кинетическая энергия тела Ek = m υ 2/2
- Работа A = F ∙ S ∙ cosα
- Мощность N = A / t = F ∙ υ
- Эффективность η = Ар/Аз
- Период колебаний математического маятника T = 2π√ℓ/g
- Период колебаний пружинного маятника T = 2 π √m/k
- Уравнение гармонических колебаний X = Xmax ∙ cos ωt
- Связь между длиной волны, ее скоростью и периодом λ = υ Т
Молекулярная физика и термодинамика
- Количество вещества ν = N / Na
- Молярная масса М = m/ν
- Ср.
 род.энергия молекул одноатомного газа Ek = 3/2 ∙ kT
род.энергия молекул одноатомного газа Ek = 3/2 ∙ kT - Основное уравнение МКТ P = nkT = 1/3nm 0 υ 2
- Закон Гей – Люссака (изобарический процесс) V / T = const
- Закон Шарля (изохорический процесс) P/T = const
- Относительная влажность φ = P / P 0 ∙ 100%
- Междунар. энергия идеальна. одноатомный газ U = 3/2∙M/µ∙RT
- Работа с газом A = P ∙ ΔV
- Закон Бойля-Мариотта (изотермический процесс) PV = const
- Количество теплоты при нагреве Q = Cm (T 2 -T 1)
- Количество теплоты при плавлении Q = λm
- Количество теплоты при испарении Q = Lm
- Количество теплоты при сгорании топлива Q = qm
- Уравнение состояния идеального газа PV = m / M ∙ RT
- Первый закон термодинамики ΔU = A + Q
- КПД тепловых двигателей η = (Q 1 – Q 2) / Q 1
- Эффективность идеальна.двигателей (цикл Карно) η = (T 1 – T 2) / T 1
Электростатика и электродинамика – формулы физики
- Закон Кулона F = k ∙ q 1 ∙ q 2 / R 2
- Напряженность электрического поля E = F/q
- Напряженность электронного поля точечного заряда E = k ∙ q / R 2
- Поверхностная плотность заряда σ = q/S
- Напряженность электронного поля бесконечной плоскости E = 2πkσ
- Диэлектрическая проницаемость ε = E 0 / E
- Потенциальная энергия взаимодействия.
 заряды Вт = k ∙ q 1 q 2 / R
заряды Вт = k ∙ q 1 q 2 / R - Потенциал φ = Вт/q
- Потенциал точечного заряда φ = k ∙ q / R
- Напряжение U = A/q
- Для однородного электрического поля U = E ∙ d
- Электрическая мощность C = q/U
- Электрическая емкость плоского конденсатора C = S ∙ ε ∙ ε 0/д
- Энергия заряженного конденсатора Вт = qU/2 = q²/2С = CU²/2
- Ток I = q/t
- Сопротивление проводника R = ρ ∙ ℓ / S
- Закон Ома для участка цепи I = U/R
- Законы последнего.соединения I 1 = I 2 = I, U 1 + U 2 = U, R 1 + R 2 = R
- Параллельные законы соед. U 1 = U 2 = U, I 1 + I 2 = I, 1 / R 1 + 1 / R 2 = 1 / R
- Мощность электрического тока P = I ∙ U
- Закон Джоуля-Ленца Q = I 2 Rt
- Закон Ома для полной цепи I = ε / (R + r)
- Ток короткого замыкания (R = 0) I = ε / r
- Вектор магнитной индукции B = Fmax / ℓ ∙ I
- Ампер-сила Fa = IBℓsin α
- Сила Лоренца Fl = Bqυsin α
- Магнитный поток Ф = BSсos α Ф = LI
- Закон электромагнитной индукции Ei = ΔФ / Δt
- ЭДС индукции в проводнике движения Ei = Bℓ υ sinα
- ЭДС самоиндукции Esi = -L ∙ ΔI / Δt
- Энергия магнитного поля катушки Wm = LI 2/2
- Период колебаний кол.
 контур T = 2π ∙ √LC
контур T = 2π ∙ √LC - Индуктивное сопротивление X L = ωL = 2πLν
- Емкостное сопротивление Xc = 1/ωC
- Действующее значение тока Id = Imax / √2,
- Действующее значение напряжения Uд = Umax / √2
- Полное сопротивление Z = √ (Xc-X L) 2 + R 2
Оптика
- Закон преломления света n 21 = n 2 / n 1 = υ 1 / υ 2
- Показатель преломления n 21 = sin α / sin γ
- Формула тонкой линзы 1/F = 1/d + 1/f
- Оптическая сила линзы D = 1/F
- максимальная помеха: Δd = kλ,
- мин. помеха: Δd = (2k + 1) λ / 2
- Дифференциальная решетка d ∙ sin φ = k λ
Квантовая физика
- Ф-ля Эйнштейн для фотоэффекта hν = Aout + Ek, Ek = U s e
- Красная граница фотоэффекта ν к = Aвых/ч
- Импульс фотона P = mc = h/λ = E/s
Атомно-ядерная физика
Электродинамика – обзор | ScienceDirect Topics
§76 Электродинамика движущихся диэлектриков
Движение среды приводит к взаимодействию электрического и магнитного полей. Такие явления для проводников обсуждались в § 63; теперь мы обсудим их для диэлектриков. Здесь мы практически имеем дело с явлениями, происходящими в движущихся средах при наличии внешних электрических или магнитных полей. Следует подчеркнуть, что они никак не связаны с появлением полей в результате самого движения (§§ 36, 64).
Такие явления для проводников обсуждались в § 63; теперь мы обсудим их для диэлектриков. Здесь мы практически имеем дело с явлениями, происходящими в движущихся средах при наличии внешних электрических или магнитных полей. Следует подчеркнуть, что они никак не связаны с появлением полей в результате самого движения (§§ 36, 64).
Отправной точкой в § 63 были формулы, дающие преобразование поля при изменении системы отсчета. Там достаточно было знать общие формулы преобразования электрического и магнитного полей в вакууме, усреднение которых дает сразу формулы преобразования E и B .В диэлектриках задача значительно сложнее, так как электромагнитное поле описывается большим числом величин.
При движении макроскопических тел скорости обычно малы по сравнению со скоростью света. Однако для получения необходимых приближенных формул преобразования проще всего воспользоваться точными релятивистскими формулами, справедливыми для всех скоростей.
В электродинамике поля в вакууме компоненты векторов электрического и магнитного полей e и h фактически являются компонентами антисимметричного четырехмерного тензора (или четырехмерного тензора) второго ранга (см. Поля , §23).То же самое верно для E и B , которые являются средними значениями e и h . Таким образом, существует четырехтензор F µv , компоненты которого задаются формулой†
(76.1)Fµv=(0ExEyEz−Ex0−BzBy−EzBz0−Bx−Ez−ByBy0),Fµv=(0−Ex−Ey −EzEx0−BzByEyBz0−BxEz−ByBx0).
С помощью этого тензора первые два уравнения Максвелла
(76.2)div B=0,curl E=−(1/c)∂B/∂t,
можно записать в четырехмерной форме
(76.3)∂Fλµ∂χv+∂Fµv∂χλ+∂Fvλ∂xµ=0.
Это показывает релятивистскую инвариантность уравнений. Применимость уравнений (76.2) к движущимся телам очевидна, так как они получаются непосредственно из точных микроскопических уравнений Максвелла заменой e и h их усредненными значениями E и B .
Вторая пара уравнений Максвелла
(76.4)div D=0,curl H=(1/c)∂D/∂t
также сохраняет свой вид в движущихся средах.Это видно из рассуждений, приведенных в § 75, в которых мы использовали только общие свойства тел (например, что полный заряд равен нулю), одинаково справедливые для движущихся и покоящихся тел. Однако отношения между D и E и B и H не обязательно должны быть такими же, как в покоящихся телах.
Поскольку они справедливы для тел как в состоянии покоя, так и в движении, уравнения (76.4) не должны изменяться преобразованием Лоренца. Для поля в вакууме векторы D и H такие же, как E и B , а релятивистская инвариантность второй пары уравнений Максвелла проявляется в том, что их также можно записать в виде четырехмерную форму, используя тот же тензор F λμ : ∂ F λμ / ∂ x μ = 0 (см. 1, § 1).Отсюда ясно, что для обеспечения релятивистской инвариантности уравнений (76.4) необходимо, чтобы компоненты векторов D и H преобразовывались как компоненты четырехтензора, в точности подобного F мкВ , которое мы обозначим через H мкВ : (76,5)Hµv=(0DxDyDz-Dx0-HzHy-DyHz0-Hx-Dz-HyHx0),Hµv=(0-Dx-Dy-HzDyHz-00Hz −HxDz−HyHx0). Используя этот тензор, мы можем записать уравнения (76.4) в виде (76.6)∂Hλµ/∂χµ=0. Выяснив, что величины E, D, H, B образуют четырехмерные тензоры, мы установили и закон их перехода из одной системы отсчета в другую. Однако нас скорее интересуют соотношения между величинами в движущейся среде, которые обобщают соотношения D = εE и B = μ H , справедливые в покоящейся среде. Обозначим через u μ 4-вектор скорости среды; его компоненты связаны с трехмерной скоростью v соотношением uµ=(1√(1−v2/c2). Из этого четырехвектора и четырехтензоров F мкВ и H мкВ мы образуем комбинации, которые становятся E и D в покоящейся среде. Этими комбинациями являются четырехвекторы F λμ u μ и H λμ u μ ; для v = 0 их временные компоненты равны нулю, а их пространственные компоненты равны E и D соответственно.Таким образом, четырехмерное обобщение уравнения D = εE равно † (76,7)Hλμuμ=εFλμuμ. Аналогично, мы видим, что обобщением B = μ H является четырехмерное уравнение (76.8)Fλμuv+Fμvuλ+Fvλ=μ(Hλμuv+Hμvuλ+Hvλuμ). Возвращаясь от четырехмерных к трехмерным обозначениям, мы получаем из этих двух уравнений векторные соотношения‡ (76.9)D+v×H/c=ε(E+v×B/c).B +E×v/c=μ(H+D×v/c). Эти формулы, впервые выведенные Г. Минковским (1908 г.), являются точными в том смысле, что еще не сделано никаких предположений относительно величины скорости. Если отношение v/c считать малым, уравнения можно решить для D и B с точностью до членов первого порядка, чтобы получить (76.10)D=εE+(εμ−1)v×H /c, (76,11)B=µH+(εµ-1)E×v/c. Эти формулы вместе с уравнениями Максвелла (76.2) и (76.4) составляют основу электродинамики движущихся диэлектриков. Граничные условия для уравнений Максвелла также несколько изменены. Из уравнений div D = 0, div B = 0 по-прежнему следует непрерывность нормальных компонент индукций: (76.12)Dn1=Dn2,Bn1=Bn2. Условия на тангенциальные составляющие полей проще всего получить при переходе от неподвижной системы отсчета K к другой, K′ , движущейся вместе с рассматриваемым элементом поверхности, скорость которого по нормали n обозначим через v n . (76.13)n×(E2−E1)=vn(B2−B1)/c,n×(h3−h2)=−vn(D2−D1)/c.} Если сюда подставить выражения (76.10) и (76.11) и пренебрегая членами более высокого порядка в v/c , получаем −vn(ε2−ε1)Et/c.} В этом приближении нет необходимости различать значения H и E на двух сторонах поверхности в правых частях уравнений (76.14). Если тело движется так, что его поверхность движется по касательной к самой себе (т.г. тело вращения, вращающееся вокруг своей оси), то v n = 0. Задача 1. Диэлектрический шар равномерно вращается в вакууме в однородном постоянном магнитном поле . Определить результирующее электрическое поле вблизи шара. Решение . При расчете результирующего электрического поля магнитное поле можно принять таким же, как и для покоящегося шара, так как учет обратного влияния изменения магнитного поля дал бы поправки более высокого порядка малости.Внутри сферы магнитное поле имеет однородное значение H(i)=3 /(2+µ); ср. (8.2). Поскольку вращение стационарное, результирующее электрическое поле постоянно и, как любое статическое электрическое поле, имеет потенциал: E = − град φ. Вне сферы потенциал удовлетворяет уравнению Δφ ( e ) = 0; внутри сферы оно удовлетворяет (1)Δφ(i)=2(εμ−1)Ω·H(i)/cε, , где Ω — угловая скорость. (2)−ε[∂φ(i)∂r]r=a+εµ−1ca[Ω·H(i) −(Ω·n)(H(i)·n)]=−[∂φ(e)dr]r=a. Здесь a — радиус сферы, а n — единичный радиальный вектор. Из-за симметрии сферы требуемое электрическое поле определяется только двумя постоянными векторами, Ω и . Из компонент этих векторов можно составить билинейный скаляр · Ω и билинейный тензор iΩk+ kΩi−23δik ·Ω, след которого равен нулю.Соответственно потенциал поля вне сферы ищем в виде с D ii = 0), электрический квадрупольный тензор момента сферы (см. Филдс , § 41). В φ ( e ) не может появиться член постоянной формы / r , поскольку такой член дал бы ненулевой полный электрический поток через поверхность, окружающую сферу, тогда как сфера не заряжена. (4)φ(i)=r22a5Diknink+εµ−13cεΩ·H(i)(r2−a2). Первый член является решением однородного уравнения Δφ = 0, а коэффициент выбран так, чтобы обеспечить непрерывность потенциала и, следовательно, E f на поверхности сферы. Подставляя (3) и (4) в (2), получаем (5)Dik=−a5c3(εµ−1)(3+2ε)(2+µ)[ iΩk+ kΩi−23δik ·Ω]. Таким образом, вблизи вращающейся сферы образуется квадрупольное электрическое поле, а квадрупольный момент сферы определяется формулой (5).В частности, если ось вращения (ось z) параллельна внешнему полю, D ik имеет только диагональные компоненты Dzz=−a5c4(εµ−1)(3+2ε)(2 +μ) ·Ω,Dxx=Dyy=−12Dzz. Аналогично, квадрупольное магнитное поле возникает вблизи сферы, вращающейся в однородном электрическом поле. Магнитный квадрупольный момент определяется выражением (5), если изменить знак и заменить ε, μ, на μ, ε, F соответственно. Задача 2. Решение . Магнитное поле внутри шара однородно и выражается через постоянную намагниченность M уравнениями . 3, H ( i ) = – 4π M /3.Вторая из формул (76.9) в этом случае не имеет места, так как формула B = µH неверна для покоящегося ферромагнетика; из первого из (76.9) имеем внутри сферы D=εE+εv×B/c−v×H/c=εE+4π(2ε+1)v×M/3c. Потенциал результирующего электрического поля вне сферы удовлетворяет уравнению Δ φ ( e ) = 0 , а внутри сферы – Δ φ ( i ) 1 1 + 1) МОм/ 3 сε. Граничное условие непрерывности D n на поверхности сферы дает φ(e)∂r]r=a. , где θ — угол между нормалью n и направлением Ω и M (ось z). Из граничного условия получаем следующие выражения для электрического квадрупольного момента вращающейся сферы: – полный магнитный момент шара.Для металлического шара мы должны взять ε → ∞, что дает Dzz=−4ΩMa2/3c. Сто пятьдесят лет назад Джеймс Клерк Максвелл представил набор уравнений, описывающих практически любое проявление электромагнетизма. Можно ли найти такие же компактные описания — и стоит ли искать — в каждой области физики? «Самым значительным событием девятнадцатого века будет считаться открытие Максвеллом законов электродинамики.Гражданская война в США отойдет на задний план…» В 1861 году Джеймс Клерк Максвелл опубликовал первую часть своей статьи из четырех частей «О физических силовых линиях» в «Философском журнале » . Максвелл показал, что электричество, магнетизм и свет — три явления, которые кажутся столь разными в своем проявлении, — являются разными аспектами одного и того же явления. Более того, Максвелл предложил набор всего из нескольких уравнений, чтобы кратко описать то, что мы сегодня знаем как электромагнетизм. Несмотря на все разносторонние последствия и разветвления работы Максвелла, возможно, это компактное описание электромагнетизма в едином наборе уравнений заставляет нас, физиков, так гордиться уравнениями Максвелла. Максвелл изначально свел весь объем работ по электричеству и магнетизму в 20 уравнений; Оливеру Хевисайду приписывают то, что он сжал их в четыре уравнения в частных производных, которые сейчас обычно появляются. Но уравнения Максвелла также содержат очень практические рекомендации. Если экспериментальное открытие или новая теория, описывающая явления в области уравнений Максвелла, противоречат им, то это открытие либо революционно, либо — что более вероятно — ошибочно. Эта пробная функция тем более примечательна, если вы задумаетесь, насколько далеки современные проблемы, которые мы решаем, решая уравнения Максвелла, от мира, в котором Максвелл жил и работал. Это прекрасно выразил Макс Планк в 1931 году на праздновании столетия клерка Максвелла в Кембриджском университете ( Nature 128 , 604–607; 1931): «Теория электродинамики [Максвелла] изначально была основанный на совершенно особых представлениях о механической природе эфира, в соответствии с тем, что в его время механическое понимание природы считалось почти само собой разумеющимся, получив сильную поддержку благодаря открытию закона сохранения энергии. Точно так же, как у нас есть памятник Максвеллу, на который можно опереться, приятно знать, что существует компактный набор законов термодинамики или постулатов специальной теории относительности.Эти основные уравнения, законы или аксиомы сами по себе не могут дать ясного представления о множестве явлений, которыми они управляют. Тем не менее, они указывают, как далеко мы можем отклониться: как только в данной области достигнуты реальные границы, требуется серьезный пересмотр. (Известно, что тот факт, что уравнения Максвелла не согласуются с ньютоновской механикой, привел к формулировке специальной теории относительности.) Однако не в каждой области физики имеется такой базис. Точно так же в обширной области «сложности» мы регулярно поражаемся тому, как механизмы, лежащие в основе, скажем, социальной сети, также участвуют в функционировании метаболизма живого существа. Можем ли мы и здесь отбросить первоначальный контекст и найти лишь несколько общих руководящих принципов? Могут ли эти принципы, в свою очередь, помочь нам понять, что вообще представляет собой сложная система? Может быть много других областей, которых не хватает, но они могли бы выиграть от компактной основы. Или есть? Действительно ли каждая область нуждается в аксиоматической основе, из которой можно вывести все? Взглянув на математику, например, можно утверждать, что важная аксиоматизация геометрии Гильбертом, основанная на 20 (первоначально 21) предположениях, не имеет большого значения для повседневного практика. Итак, как далеко мы можем или должны продвинуться в духе, который сияет в наследии Максвелла? twitter.com/naturephysics Не усложнять?. Nature Phys 7, 441 (2011). https://doi.org/10.1038/nphys2024 Загрузить цитату Любой, с кем вы поделитесь следующей ссылкой, сможет прочитать этот контент: Извините, ссылка для общего доступа в настоящее время недоступна доступны для этой статьи. Предоставлено инициативой Springer Nature SharedIt по обмену контентом. В этой главе мы познакомимся с электродвижущей силой, законом Ома и законом Фарадея.
наряду с электромагнитной индукцией, индуктивностью и энергией в магнитном поле.Мы
напишите уравнения Максвелла в вакууме и веществе. В конце этой главы мы представляем
проблема, связанная с понятием магнитного заряда; раскрываем его роль в конкретном
преобразование двойственности и его связь с инвариантностью максвелловского
уравнения. Дан ток I , протекающий через резистор с сопротивлением R , мощность указана как При заданном магнитном потоке генерируемая электродвижущая сила (ЭДС) равна , где поток определяется выражением Энергия, запасенная в магнитном поле, равна Также энергия, запасенная в индукторе с индуктивностью I , определяется как Закон Гаусса Дифференциальная форма Интегральная форма Без имени Дифференциальная форма Интегральная форма Закон Фарадея Дифференциальная форма Интегральная форма Закон Ампера-Максвелла Дифференциальная форма Интегральная форма Задача 1.1. Две концентрические сферы радиусов и , с , разделены материалом с проводимостью , где – постоянная с соответствующими единицами. Приблизить Уменьшить Сбросить размер изображения Скачать рисунок: Fields
Fields vc√(1−v2/c2)).
vc√(1−v2/c2)). }
}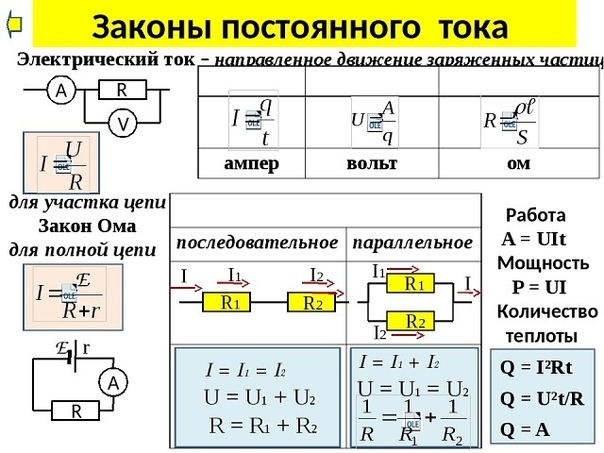 Обычные условия, а именно, что E’ t и H’ t непрерывны, выполняются в системе K’. По формулам релятивистского преобразования (см. Поля , §24) они эквивалентны непрерывности тангенциальных компонент векторов E + v×B /c и H − v×D / c . Взяв компоненты перпендикулярно n и используя уравнения (76.12), получим требуемые граничные условия:
Обычные условия, а именно, что E’ t и H’ t непрерывны, выполняются в системе K’. По формулам релятивистского преобразования (см. Поля , §24) они эквивалентны непрерывности тангенциальных компонент векторов E + v×B /c и H − v×D / c . Взяв компоненты перпендикулярно n и используя уравнения (76.12), получим требуемые граничные условия: Только в этом случае граничные условия (76.13) или (76.14) сводятся к обычным условиям, что E t и H t быть непрерывным.
Только в этом случае граничные условия (76.13) или (76.14) сводятся к обычным условиям, что E t и H t быть непрерывным. ЗАДАЧИ
 Последнее уравнение получается из div D = 0 заменой D выражением (76.10) с v = Ω × r. Условие непрерывности нормальной составляющей D на поверхности сферы дает
Последнее уравнение получается из div D = 0 заменой D выражением (76.10) с v = Ω × r. Условие непрерывности нормальной составляющей D на поверхности сферы дает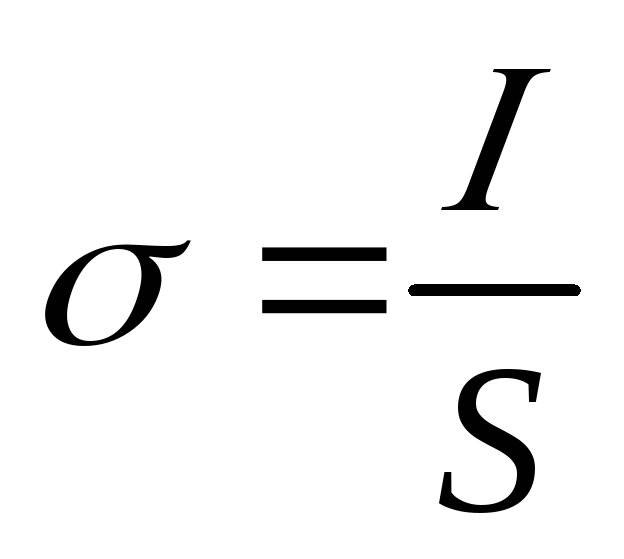 Потенциал поля внутри сферы ищется в виде
Потенциал поля внутри сферы ищется в виде Намагниченный шар равномерно вращается в вакууме вокруг своей оси, параллельной направлению намагниченности.Определите результирующее электрическое поле вблизи сферы.†
Намагниченный шар равномерно вращается в вакууме вокруг своей оси, параллельной направлению намагниченности.Определите результирующее электрическое поле вблизи сферы.† Ищем φ ( e ) и φ ( i ) в виде 4π(2ε+1)9cεMΩ(r2−a2).
Ищем φ ( e ) и φ ( i ) в виде 4π(2ε+1)9cεMΩ(r2−a2). Все просто? | Физика природы
 Статья описывает математическую физику электромагнетизма и должна была стать важной вехой в науке. По словам Ричарда Фейнмана: «С точки зрения истории человечества — скажем, через десять тысяч лет — не может быть никаких сомнений в том, что самым значительным событием девятнадцатого века будет считаться открытие Максвеллом законы электродинамики.Гражданская война в США отойдет на второй план по сравнению с этим важным научным событием того же десятилетия».
Статья описывает математическую физику электромагнетизма и должна была стать важной вехой в науке. По словам Ричарда Фейнмана: «С точки зрения истории человечества — скажем, через десять тысяч лет — не может быть никаких сомнений в том, что самым значительным событием девятнадцатого века будет считаться открытие Максвеллом законы электродинамики.Гражданская война в США отойдет на второй план по сравнению с этим важным научным событием того же десятилетия». Действительно, используя тензорную нотацию (или, альтернативно, геометрическую алгебру, как обсуждает Марк Бьюкенен на странице 442 этого выпуска), эти четыре уравнения можно свернуть в одно, выкристаллизовав их в монолитный монумент культовой красоты. Одно уравнение, чтобы управлять всем электромагнетизмом.
Действительно, используя тензорную нотацию (или, альтернативно, геометрическую алгебру, как обсуждает Марк Бьюкенен на странице 442 этого выпуска), эти четыре уравнения можно свернуть в одно, выкристаллизовав их в монолитный монумент культовой красоты. Одно уравнение, чтобы управлять всем электромагнетизмом. Но после того, как с помощью таких механических представлений Максвелл нашел свои электромагнитные дифференциальные уравнения и осознал степень их эффективности, он, не колеблясь, отбросил механические интерпретации дифференциальных уравнений как незначительную принадлежность, чтобы сделать их независимыми и придать своей теории чистую и возвышенную форму».
Но после того, как с помощью таких механических представлений Максвелл нашел свои электромагнитные дифференциальные уравнения и осознал степень их эффективности, он, не колеблясь, отбросил механические интерпретации дифференциальных уравнений как незначительную принадлежность, чтобы сделать их независимыми и придать своей теории чистую и возвышенную форму». Это может быть наиболее очевидным в квантовой механике, которая, как широко считается, основана на специальных аксиомах.В последнее десятилетие квантово-информационное сообщество стремилось наложить теоретико-информационные ограничения на квантовую теорию ( Nature Phys. 1 , 2–4; 2005) — эта попытка также обсуждается в обзоре книги. на странице 443 этого номера. Хотя, опять же, аксиоматическая основа квантовой механики может не сразу привести нас к новым открытиям, она может предложить более интуитивное понимание квантовой механики и сделать некоторые загадочные открытия, о которых обычно сообщают в лабораториях и в теоретической работе, менее удивительными и легкими. понять.
Это может быть наиболее очевидным в квантовой механике, которая, как широко считается, основана на специальных аксиомах.В последнее десятилетие квантово-информационное сообщество стремилось наложить теоретико-информационные ограничения на квантовую теорию ( Nature Phys. 1 , 2–4; 2005) — эта попытка также обсуждается в обзоре книги. на странице 443 этого номера. Хотя, опять же, аксиоматическая основа квантовой механики может не сразу привести нас к новым открытиям, она может предложить более интуитивное понимание квантовой механики и сделать некоторые загадочные открытия, о которых обычно сообщают в лабораториях и в теоретической работе, менее удивительными и легкими. понять.
Об этой статье
Процитировать эту статью
Поделиться этой статьей

Уравнения Максвелла — Электродинамика — глава книги
1.1.1. Закон Ома
1.1.2. Закон нагрева Джоуля
1.1.3. Правило потока для движущей электродвижущей силы
1.
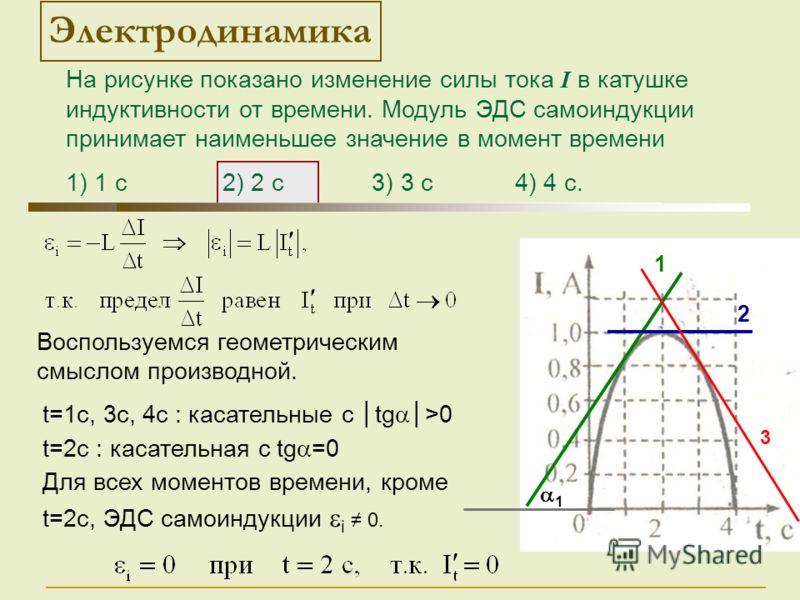 1.4. Магнитная энергия
1.4. Магнитная энергия 1.1.5. Уравнения Максвелла
 Найдите сопротивление этого
материал, если потенциал между сферами .
Найдите сопротивление этого
материал, если потенциал между сферами .
Решение 1.1. Начиная с плотности тока, мы имеем
Обратите внимание, что наш ток будет зависеть только от так
Таким образом,
и решение для поля дает
Учитывая
, мы имеем
Поскольку закон Ома гласит , мы видим, что сопротивление равно
Задача 1.2. Два длинных цилиндра радиусами и, с, разделены неизвестным материалом проводимости.Они поддерживаются при электрическом потенциале с током I , текущим от одного к другому в
длина . Найдите проводимость.
Найдите проводимость.
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешениемРешение 1.2. Начнем с расчета электрического поля между цилиндрами при радиус , с между радиусами и . Считаем заряд на единицу длины внутреннего цилиндра. Закон Гаусса состояний
Левая часть уравнения равна
В то время как прилагаемый заряд равен просто
Отсюда следует, что
А электрическое поле равно
Помните, что тогда ток рассчитывается как
Электрический потенциал равен
Подставляя из тока получаем .Вернемся к электрическому потенциалу
Следовательно, проводимость равна
Вот как мы можем определить тип материала, измерив
ток и разность потенциалов и, конечно же, геометрические размеры , и .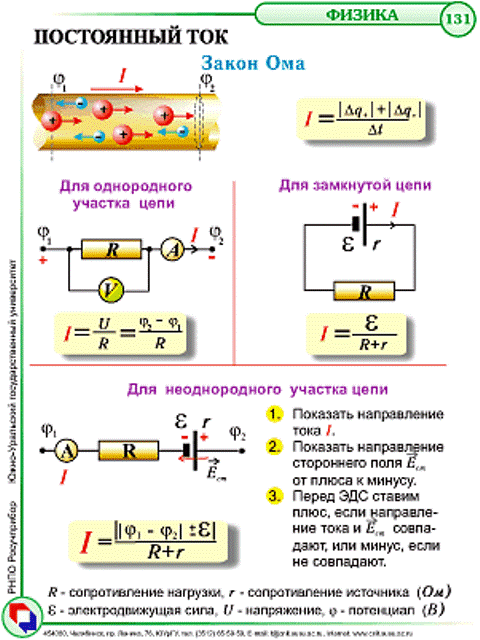
Задача 1.3. Токопроводящий стержень массы скользит без трения по двум параллельным проводящим рельсам, расположенным на расстояние, соединенное резистором.Система помещена в однородное магнитное поле, за пределы страницы.
Решение 1.3.
Задача 1.4. Рассмотрим путь ниже, который состоит из двух параллельных проводящих рельсов, разделенных
расстоянием и двумя металлическими стержнями массы; все это находится в магнитном поле, направленном на страницу.Первоначально правый такт (такт 2), который
сопротивление , удерживается на месте, в то время как левый бар (бар 1) движется к бару
2 со скоростью. В момент времени оба стержня могут свободно перемещаться. Найдите минимальное расстояние между брусками в момент времени, при котором бруски не столкнутся.
В момент времени оба стержня могут свободно перемещаться. Найдите минимальное расстояние между брусками в момент времени, при котором бруски не столкнутся.
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешениемРешение 1.4. В момент времени в контуре протекает ток I . Из
мы видим, что этот ток течет по часовой стрелке. Это создает силу на каждый бар, имеющий величину
На баре 1 эта сила направлена влево; и на такте 2 это сила направлена вправо. Это означает, что при , бар 1 будет замедляться, а бар 2 ускоряться. Это приводит к ток, зависящий от времени, который определяется как
и теперь будет зависеть от скоростей обоих стержней,
Следовательно,
Теперь мы можем проанализировать движение каждого стержня. Для бара 1 сила равна
слева. Таким образом,
Для бара 1 сила равна
слева. Таким образом,
Для бара 2 имеем
Мы можем переписать их как
и
, где
Примечание
так
где константа. При имеем и . Таким образом, и . Теперь мы можем использовать это для решения для ,
Перестановка дает
, а интегрирование дает
, где и – константы. Теперь мы можем решить для ,
Так как , у нас есть
Следовательно,
Используя это, мы можем решить для ,
Теперь мы можем использовать и решить для .Решение для ,
и ,
где и – константы. Вовремя , . Следовательно,
Итак,
Теперь нужно решить ,
Так как мы не хотим, чтобы столбики сталкивались, нам нужно
, поэтому
Следовательно, чтобы бруски не столкнулись, мы должны есть
Задача 1. 5. Рассмотрим приведенный ниже провод, состоящий из круглой петли радиусом и резистора с сопротивлением .Круглая часть помещена в магнитное поле, направленное в
страница с , где константа. Найдите полную энергию, рассеиваемую резистором при .
5. Рассмотрим приведенный ниже провод, состоящий из круглой петли радиусом и резистора с сопротивлением .Круглая часть помещена в магнитное поле, направленное в
страница с , где константа. Найдите полную энергию, рассеиваемую резистором при .
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешениемРешение 1.5. Изменяющееся магнитное поле индуцирует ЭДС в петле, которая задана на
Это означает, что ток в контуре равен
Мы знаем, что мощность равна
, поэтому общая энергия равна
Используя наш ток, мы имеем
Следовательно, общая энергия, рассеиваемая резистором, равна
Задача 1.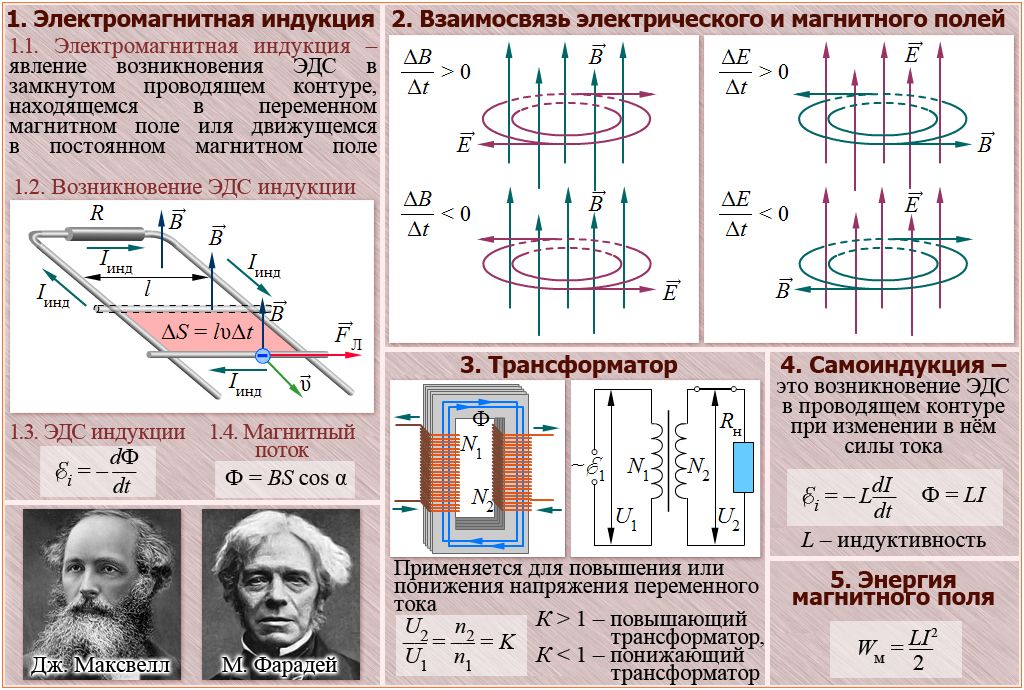 6.
6.
Решение 1.6.
Задача 1.7. Рассмотрим петлю из провода радиусом ниже, расположенную над длинным прямым проводом, по которому течет ток с .Найти индуцированную электродвижущую силу (ЭДС) в контуре, если его центр расположен над проводом.
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешениемРешение 1.7. Электродвижущая сила определяется выражением
, где поток равен
Мы знаем, что магнитное поле, создаваемое длинным проводом, равно
Если мы рассмотрим петлю в плоскости zs , мы получим
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешениемМы видим, что уравнение цикла равно
.
И у нас также есть
Таким образом,
Чтобы показать, как ограничено z , мы можем переписать нашу окружность уравнение как
Следовательно, наш поток равен
, а наша электродвижущая сила равна
.Задача 1.8. Прямоугольная петля со сторонами и помещена в плоскость xz и подвергается воздействию неоднородное зависящее от времени магнитное поле вида , где – постоянная. Найдите электродвижущую силу, индуцируемую в контуре.
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешением Решение 1. 8. Начнем с правила потока для движущейся электродвижущей силы.
сила
8. Начнем с правила потока для движущейся электродвижущей силы.
сила
где поток определяется как
В нашем случае поток можно рассчитать следующим образом:
Следовательно, электродвижущая сила равна
Задача 1.9. Рассмотрим цепь с батареей, обеспечивающей постоянную электродвижущую силу, резистором с сопротивлением и соленоидом полного сопротивления.Найдите силу тока в цепи и определите время после замыкания. цепь, в которой ток достигнет своего конечного равновесного значения.
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешением Решение 1.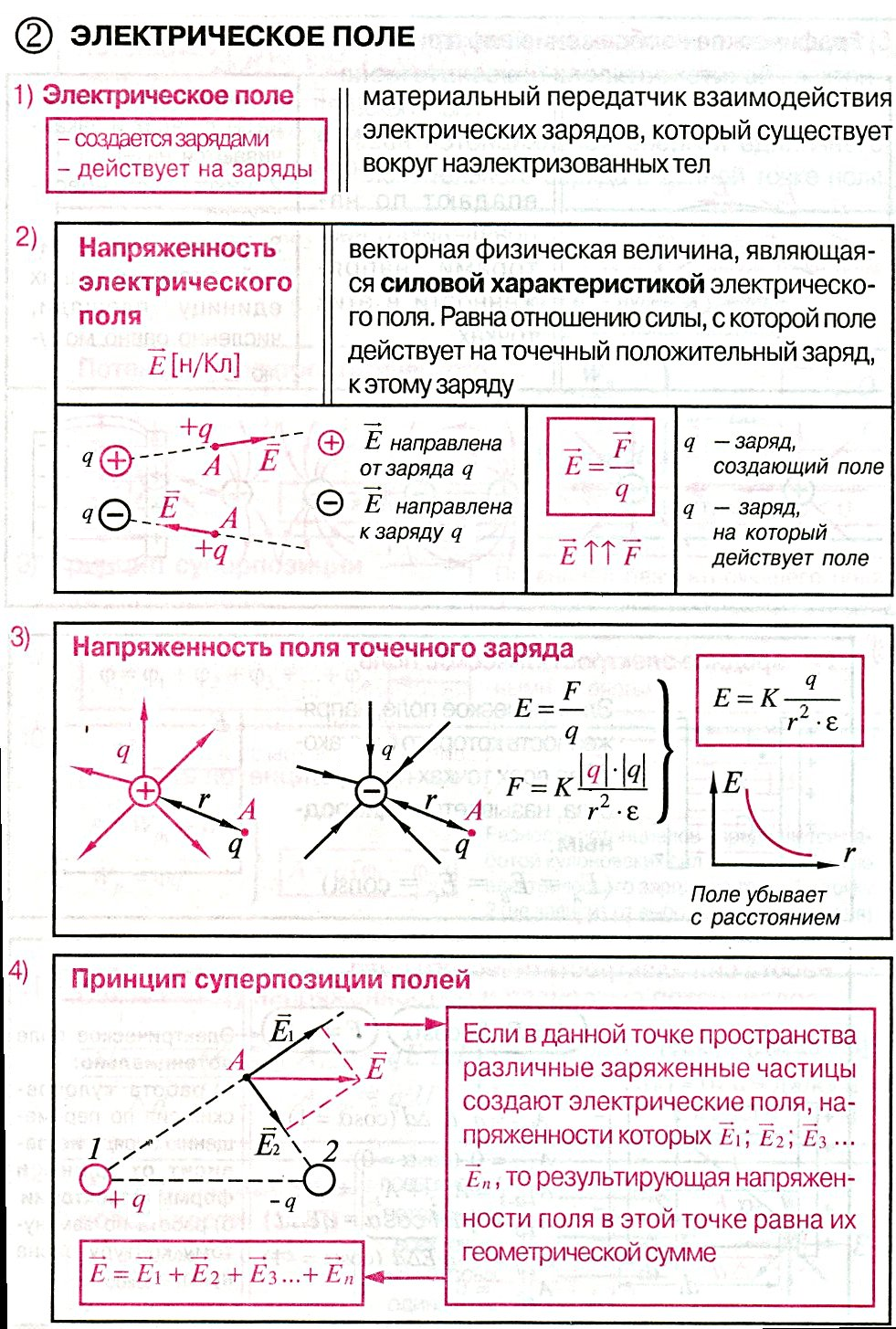 9. Закон Кирхгофа в схеме:
9. Закон Кирхгофа в схеме:
Решение дифференциального уравнения первого порядка:
где – постоянная, получаемая из начальных условий. Начиная с at , у нас есть , поэтому
Следовательно,
Когда
Найдем время t необходимое для того, чтобы схема достичь текущего
Обратите внимание, что , где – постоянная времени.
Например, для .
Задача 1.10. Найдите удельную индуктивность бесконечно длинного коаксиального кабеля радиусом , по которому течет ток, как показано на рисунке. Используйте энергетические расчеты.
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешением Решение 1. 10. Самоиндукция связана с энергией как
10. Самоиндукция связана с энергией как
Рассчитаем энергию конфигурации
Далее нам нужно найти магнитное поле. Из закона Ампера единственный значительный (область ненулевого магнитного поля) для радиуса между и .
где вложенный ток. Левая часть равна
Отсюда
Энергия цилиндрической оболочки длиной , радиусом с и толщиной d с равно:
Мы получаем полную энергию, интегрируя по с из а до б
Вернуться к полному сопротивлению на единицу длины:
Задача 1.11. По длинному полому проводу (внутренний радиус , внешний радиус ) течет ток в одном направлении, пропорциональный его
расстояние от оси. Затем этот ток возвращается по поверхности провода. Если
общий обратный ток равен , найдите индуктивность провода по длине.
Затем этот ток возвращается по поверхности провода. Если
общий обратный ток равен , найдите индуктивность провода по длине.
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешениемРешение 1.11. Учитывая, что полная энергия определяется выражением
, нахождение магнитного поля позволит нам решить приведенное выше уравнение за . Напомним, что поле задано числом
.Обратите внимание, что у нас есть для и . Следовательно, мы имеем магнитное поле только для . Плотность тока в этой области может быть записана как
Тогда мы имеем
Мы также можем решить, учитывая, что
поэтому
Тогда наш замкнутый ток равен
Возвращаясь к нашему магнитному полю, мы имеем have
Теперь мы можем использовать это, чтобы найти общую энергию, используя
, где . Следовательно,
Следовательно,
Теперь, рассматривая
, мы видим, что индуктивность на длину равна
Задача 1.12. Медленно меняющийся бесконечный поверхностный ток течет по xy -плоскости. Найдите индуцированный электрическое поле.
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешениемРешение 1.12. Используя
, мы можем увидеть, как этот ток создает поле
Теперь мы можем использовать
, чтобы найти поле. Глядя на xz -плоскость имеем
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешением, где направляется со страницы для и на страницу для . При первом рассмотрении мы имеем
При первом рассмотрении мы имеем
Кроме того,
Следовательно,
Аналогично, для мы имеем
Мы можем проверить их, рассматривая
Для ,
и для ,
, как и ожидалось.
Проблема 1.13 Рассмотрим приведенную ниже схему, состоящую из соленоида с числом витков на длину, расположенного в центре квадратного контура и соединенного с ним. стороны.Ось соленоида перпендикулярна плоскости петли. Контур содержит источник и резистор. Найдите ток, который течет, если и подключен в момент времени.
Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешением Решение 1. 13. Поле соленоида определяется как
13. Поле соленоида определяется как
Это переменное поле индуцирует ЭДС в цепи
Это противодействует электродвижущей силе источника, поэтому ток равен определяется как
Некоторая перестановка дает,
Теперь мы можем решить это дифференциальное уравнение для получения,
Задача 1.14. Рассмотрим проводящую сферическую оболочку радиуса , которая вращается вокруг оси z- с угловым скорость . Оболочка помещена в однородное магнитное поле.
(a)
Покажите, что электродвижущая сила, возникающая между «северным полюсом» и «южным полюсом», равна нуль.(b)
Как насчет электродвижущей силы между «северным полюсом» и «параллельным 45′?Приблизить Уменьшить Сбросить размер изображения
Скачать рисунок:
Стандартное изображение Изображение с высоким разрешением
Решение 1.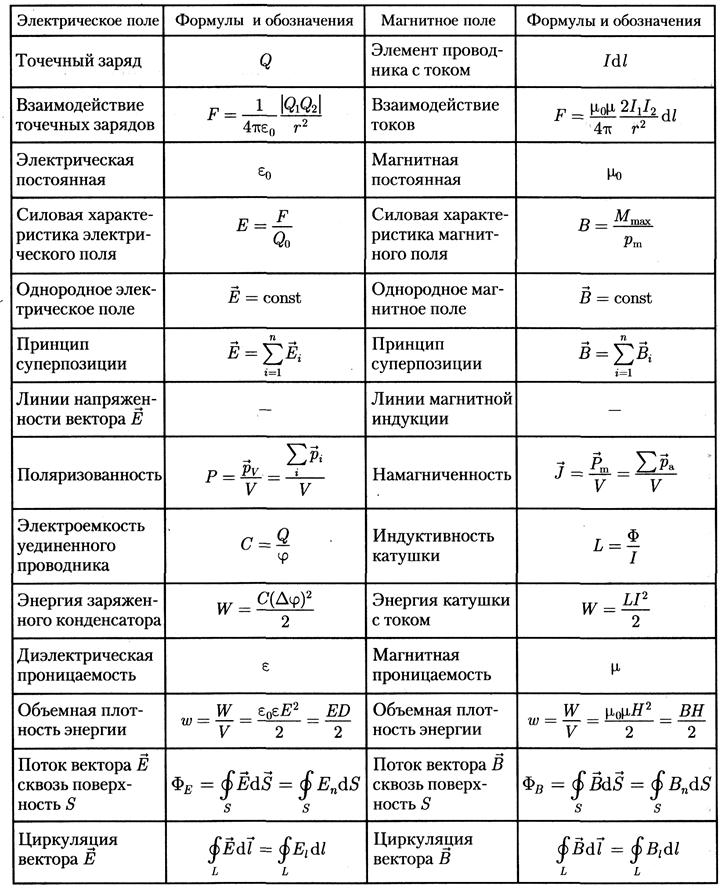 14.
14.
Задача 1.15. Сравните отношение тока проводимости к току смещения для двух решения диэлектрических проницаемостей и , имеющих удельные сопротивления и , на частоте . Учтите, что оба решения обладают проницаемостью. Рассмотрим плоский конденсатор, погруженный в каждый тип воды. раствора и приложенным напряжением .
Решение 1.15. Ток проводимости определяется как
Для плоского конденсатора электрическое поле определяется на
Ток смещения равен
Следовательно, отношение амплитуд двух токов
Теперь, если мы сравним два водных раствора
Задача 1. 16. Докажите, что уравнения Максвелла с магнитным зарядом (a)–(d) и закон силы
уравнения (e) инвариантны относительно преобразования двойственности (*).
16. Докажите, что уравнения Максвелла с магнитным зарядом (a)–(d) и закон силы
уравнения (e) инвариантны относительно преобразования двойственности (*).
(а)
(б)
(в)
(г)
(д)
Преобразование двойственности (*)
Решение 1.16.
Задача 1. 17. Рассмотрим бесконечно длинный прямой провод, по которому течет медленно меняющийся ток. Можно показать (Griffiths 1999, пример 7.9), что наведенный электрический ток
поле задается
17. Рассмотрим бесконечно длинный прямой провод, по которому течет медленно меняющийся ток. Можно показать (Griffiths 1999, пример 7.9), что наведенный электрический ток
поле задается
, где константа по отношению к . Если , покажите, что это удовлетворяет уравнениям Максвелла и найдите и .
Решение 1.17. Мы можем видеть, что этот ток приводит к магнитному полю
Начиная с
, как и ожидалось. Теперь, чтобы проверить закон Фарадея,
Мы можем видеть, что правая часть дается как
Левая часть дается как
с
Таким образом,
Поскольку не зависит от (или или, если на то пошло) ,
Также,
Следовательно,
как и ожидалось.Теперь мы можем использовать закон Гаусса, чтобы найти ,
Здесь мы имеем
, используя тот же аргумент, что и раньше. Кроме того,
Кроме того,
Следовательно, , что ожидается из контекста примера. Наконец, мы будем используйте закон Ампера, чтобы найти .
Начиная с левой стороны,
Следовательно,
где
Тогда плотность тока равна
Обратите внимание, что это, как и , зависит от константы (относительно пространства), которая зависит от всей истории текущего .
Задача 1.18. Используйте уравнения Максвелла и закон силы Лоренца, чтобы вывести закон Кулона для двух сборы за плату.
Решение 1.18. Закон силы гласит
Поскольку магнитного поля нет,
Теперь мы можем рассмотреть закон Гаусса,
Мы можем взять интеграл по всему пространству с обеих сторон
Правая часть будет просто
Применяя дивергенцию теорема в левой части дает
Объединив все, мы получим
или
. Подставив это в закон силы, мы получим
Подставив это в закон силы, мы получим
, что в точности соответствует закону Кулона.
Электродинамика на основе уравнений Максвелла (уровень бакалавриата)
Этот курс предназначен для всех, кто хочет узнать о теоретической электродинамике!
Немного математики в колледже (основные производные и векторная алгебра) — это все, что вам нужно знать!
Несколько концепций электродинамики, таких как заряды, электромагнитные волны, электрические и магнитные поля, преподаются уже в старшей школе. Однако понять их истинное происхождение на самом деле не представляется возможным.Для этого Максвелл сформулировал 4 уравнения, на основе которых можно объяснить большинство явлений современной электродинамики: электростатику, магнитостатику, а также задачи, зависящие от времени, и свет как электромагнитную волну.
Однако я думаю, что этот теоретический подход часто преподается либо слишком расплывчато, либо со слишком сильным акцентом на математике. Вместо того, чтобы смотреть случайные видео на Youtube или проходить сотни часов университетских курсов, я думаю, что курсы Udemy — это хорошая платформа для целенаправленного обучения.
Вместо того, чтобы смотреть случайные видео на Youtube или проходить сотни часов университетских курсов, я думаю, что курсы Udemy — это хорошая платформа для целенаправленного обучения.
Приглашаем вас присоединиться к этому тщательно подготовленному курсу, который научит вас 101 электродинамике и включает викторины, слайды, упражнения, а также учебник по математическим предпосылкам!
Почему я?
Меня зовут Бёрге Гёбель, и я постдокторант, занимаюсь электродинамикой и квантовой теорией. В настоящее время я занимаюсь исследованием возникающей электродинамики особых магнитных текстур. Я не забыл время, когда я узнал об электродинамике и до сих пор помню проблемы, которые были у меня и других студентов.Я усовершенствовал свои навыки консультанта в качестве наставника бакалавров, магистров и аспирантов в области теоретической физики.
Этот курс для вас …
… если вы собираетесь посещать университетский курс по электродинамике и хотите быть хорошо подготовленным
.
 .. или если вы хотите пройти курс теоретической физики, не сталкиваясь с жесткой математикой других тем
.. или если вы хотите пройти курс теоретической физики, не сталкиваясь с жесткой математикой других тем… или если у вас есть общее представление о зарядах, электромагнитных волнах, магнитных и электрических полях, но вы хотите узнать их истинное происхождение
… или если вы просто хотите тщательно освежить память перед экзаменами 🙂
Темы
Мы начнем с математических предпосылок и ранних физических явлений, которые привели к нашему современному пониманию электродинамики. Например, мы узнаем о комплексных числах, операторе набла, зарядах, магнитных моментах, а также об электрическом и магнитном полях. Затем введем уравнения Максвелла. Эти четыре уравнения составляют основу всего этого курса и позволяют вывести все явления, которые мы обсуждаем, такие как закон Ампера, закон Кулона и закон Био-Савара.
Начнем с частного случая вакуума, где отсутствуют заряды и токи: Здесь возбуждениями являются электромагнитные волны или, другими словами, свет. Мы выводим электрические и магнитные поля и обсуждаем возможные поляризации света.
Мы выводим электрические и магнитные поля и обсуждаем возможные поляризации света.
После этого мы оставляем вакуум, но рассматриваем задачи, не зависящие от времени. Эта область теоретической физики называется электростатикой и магнитостатикой. Мы решаем интересные задачи, такие как расчет электрического поля заряженной сферы, разность напряжений на конденсаторе, магнитное поле вокруг провода или дальнее поле диполя.
Наконец, рассмотрим самый общий случай: задачи, зависящие от времени. Как мы увидим, мы можем полагаться на наши предыдущие результаты для статического случая с некоторыми изменениями. Кроме того, я покажу вам, как все наши результаты лишь незначительно меняются, когда мы рассматриваем электродинамику в материи, например, в куске металла.
Я надеюсь, что вы взволнованы, и я любезно приветствую вас на нашем курсе!
Электромагнитные волны
Электромагнитные волны Электромагнитные (ЭМ) волны меняют электрические и магнитные поля,
перенос энергии и импульса
через пространство. ЭМ волны являются решениями уравнений Максвелла, которые
основные уравнения электродинамики. ЭМ-волнам не нужна среда, они могут проходить через пустые
космос. Синусоидальные плоские волны являются одним из видов электромагнитных волн.
Не все ЭМ
волны представляют собой синусоидальные плоские волны, но все электромагнитные волны можно рассматривать как линейные
суперпозиция синусоидальных плоских волн, распространяющихся в произвольных направлениях.
Самолет ЭМ
волна, бегущая в направлении x, имеет форму
ЭМ волны являются решениями уравнений Максвелла, которые
основные уравнения электродинамики. ЭМ-волнам не нужна среда, они могут проходить через пустые
космос. Синусоидальные плоские волны являются одним из видов электромагнитных волн.
Не все ЭМ
волны представляют собой синусоидальные плоские волны, но все электромагнитные волны можно рассматривать как линейные
суперпозиция синусоидальных плоских волн, распространяющихся в произвольных направлениях.
Самолет ЭМ
волна, бегущая в направлении x, имеет форму
| E(x,t) = E max cos(kx – ωt + φ), B (x,t) = B max cos(kx – ωt + φ). E — вектор электрического поля, B — магнитное
вектор поля ЭМ волны. Для электромагнитных волн E и B всегда перпендикулярны друг другу и перпендикулярны
направление распространения. Направление распространения – это направление
из E x B . Если для волны, бегущей в направлении х, E = E j , то B = Б к и j x k = i .электромагнитный волны – поперечные волны. |
Волновое число k = 2π/λ, где λ — длина волны. Частота волны f равна f = ω/2π, ω — угловая частота. Скорость любой периодической волны равна произведение его длины волны и частоты.
v = λf.
Скорость любых электромагнитных волн в свободном пространстве это скорость света c = 3*10 8 РС.Электромагнитные волны могут иметь любую длину волны λ или частоту f как пока λf = c.
Когда электромагнитные волны распространяются через среду, скорость волн в
среда v = c/n(λ свободный ), где n(λ свободный ) индекс
преломления среды. Показатель преломления n является свойством
среды, а это зависит от длины волны λ свободной ЭМ волны. Если среда поглощает часть энергии
переносится волной, то n(λ свободное ) равно
комплексное число. Для воздуха n почти равно 1 для всех длин волн.
Когда электромагнитная волна распространяется из одной среды с показателем преломления n 1 в другую среду с другим показателем преломления n 2 , то его
Частота остается той же, что и , но меняются его скорость и длина волны. Для воздуха
n почти равно 1,
Для воздуха n почти равно 1 для всех длин волн.
Когда электромагнитная волна распространяется из одной среды с показателем преломления n 1 в другую среду с другим показателем преломления n 2 , то его
Частота остается той же, что и , но меняются его скорость и длина волны. Для воздуха
n почти равно 1,
| Электромагнитные волны классифицируются по
их частота f или, что то же самое, в соответствии с их длиной волны λ = c/f.Видимый свет имеет
диапазон длин волн от ~400 нм до ~700 нм. Фиолетовый свет имеет
длина волны ~400 нм, частота ~7,5*10 14 Гц. красный
свет имеет длину волны ~700 нм и частоту ~4,3*10 14 Гц. Видимый свет составляет лишь небольшую часть полного электромагнитного
спектр. Электромагнитные волны с более короткими длинами волн и более высокими частотами
включают ультрафиолетовое излучение, рентгеновское излучение и гамма-излучение. |
Поляризация
| Поляризация — явление, свойственное поперечным волнам. Продольные волны
Например, звук не может быть поляризован. Свет и другие электромагнитные волны
поперечные волны, состоящие из взаимно перпендикулярных флуктуирующих электрических и
магнитные поля.На диаграмме справа электромагнитная волна распространяется в
х, электрическое поле колеблется в плоскости ху, а магнитное
поле колеблется в плоскости xz. Линия описывает электрическое поле
вектор по мере распространения волны. Для линейно поляризованной электромагнитной волны, распространяющейся в направлении x, угол, который электрическое поле образует с осью y, уникален. | |
Неполяризованная электромагнитная волна, распространяющаяся в направлении x, представляет собой
суперпозиция многих волн.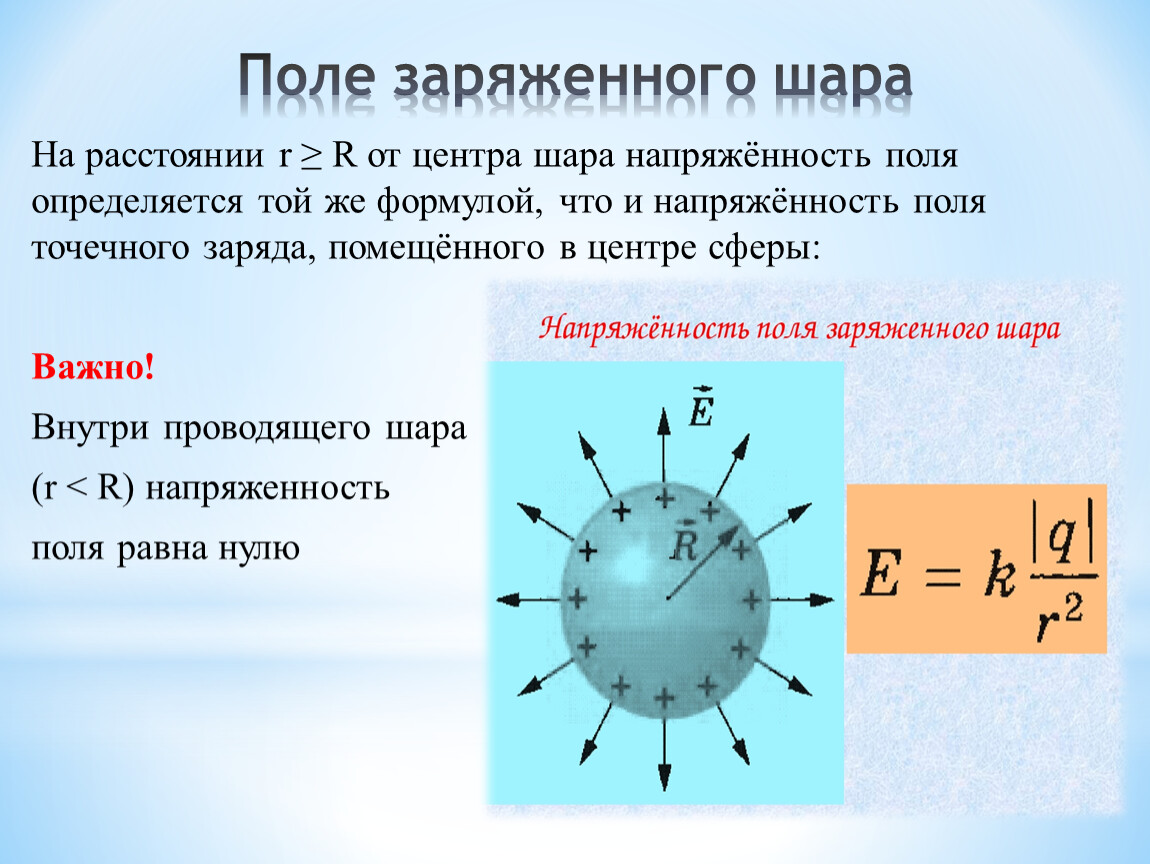 Для каждой из этих волн вектор электрического поля
перпендикулярна оси x, но составляет угол с осью y
разные для разных волн. Для неполяризованного света, путешествующего в
x-направление E y и E z случайным образом меняются во времени
это намного короче, чем нужно для наблюдения. Для каждой из этих волн вектор электрического поля
перпендикулярна оси x, но составляет угол с осью y
разные для разных волн. Для неполяризованного света, путешествующего в
x-направление E y и E z случайным образом меняются во времени
это намного короче, чем нужно для наблюдения.Схема на свет изображает неполяризованный свет. Естественный свет, как правило, неполяризован. |
Перенос электромагнитных волн энергия через пространство.В свободном пространстве эта энергия переносится волной со скоростью c. Величина потока энергии S – это количество энергии, которое пересекает единицу площади перпендикулярно направлению распространения волны в единицу времени. Это дается
S = EB/(μ 0 ) = E 2 / (μ 0 c),
, так как для электромагнитных волн B = E/c. Единицы S: Дж/(м 2 с).
μ 0 — константа, называемая проницаемостью свободного пространства, μ 0 = 4π*10 -7 Н/Д 2 .
Примечание:
Энергия , переносимая электромагнитной волной
пропорциональна квадрату амплитуды, E 2 ,
волна.
Вектор Пойнтинга – это вектор потока энергии. Это назван в честь Джон Генри Пойнтинг. Его направлением является направление распространения волны, т. е. направление, в котором транспортируется энергия.
S = (1/μ 0 ) E x B.
Энергия на единицу площади в единицу времени — это мощность на единицу площади. S представляет мощность на единицу площади в электромагнитной волне. Если электромагнитная волна падает на площадь A , где она поглощается, то мощность, передаваемая в эту область, равна P = S ∙ А .
Среднее по времени значение вектора Пойнтинга равно
называется освещенностью или интенсивностью.Излучение является средним
энергии на единицу площади в единицу времени.
=
ЭМ волна также транспорт импульс. Поток импульса равен S /с. То величина потока импульса S / c – это количество импульса, пересекающего единицу площади, перпендикулярной направлению распространения волны в единицу времени. Если электромагнитная волна падает на площадь A , где она поглощается, импульс передается в эту область в направлении, перпендикулярном площадь в единицу времени равна dp perp /dt = (1/c) S ∙ A .
Следовательно, изменяется импульс объекта, поглощающего излучение. Скорость изменение равно dp perp /dt = (1/c)SA perp , где A perp площадь поперечного сечения объекта перпендикулярно направлению распространения электромагнитной волны. Импульс объекта изменяется, если на него действует сила.
F perp = dp perp /dt = (1/c)SA perp
— сила, с которой излучение действует на объект, поглощающий
излучение. Разделив обе части этого уравнения на A perp ,
находим радиационное давление
(сила на единицу площади) P = (1/c)S. Если
излучение отражается, а не поглощается, тогда его импульс меняет направление.
То
Поэтому радиационное давление на объект, отражающий излучение, в два раза больше
радиационное давление на объект, который поглощает излучение.
Разделив обе части этого уравнения на A perp ,
находим радиационное давление
(сила на единицу площади) P = (1/c)S. Если
излучение отражается, а не поглощается, тогда его импульс меняет направление.
То
Поэтому радиационное давление на объект, отражающий излучение, в два раза больше
радиационное давление на объект, который поглощает излучение.
Фотоны
Электромагнитные волны переносят энергию и импульс через пространство.То энергия и импульс, переносимые электромагнитной волной, не являются непрерывно распределяется по фронту волны. Энергия и импульс передаются фотонами дискретными порциями. Фотоны — это частицы света. Свет «квантуется». Фотоны всегда движутся со скоростью света. Энергия каждый фотон равен E = hf = hc/λ. Импульс каждого фотона равен E/c = hf/c = h/λ.
(ч = 6,626*10 -34 Дж с = 4,136*10 -15 эВ с
единица энергии: 1 эВ = 1.6*10 -19 Дж
полезный продукт: hc = 1240 эВ нм)
Так что же такое электромагнитная волна, волна или поток фотонов? Каковы наши современные представления о природе свет и другие электромагнитные волны?
Квантовая механика рассматривает фотоны как кванты или пакеты энергии. Но эти
кванты ведут себя совсем не так, как макроскопические частицы. Для макроскопической частицы мы
предположим, что мы можем измерить его положение и скорость в любое время с помощью
произвольная точность и аккуратность.Учитывая, что мы сделали это, мы можем предсказать
с произвольной точностью и аккуратностью его последующего движения. Но для любого фотона
мы можем только предсказать вероятность того, что
фотон будет находиться в заданной позиции. Эту вероятность можно вычислить
используя волновое уравнение для электромагнитных волн. Где волновое уравнение
предсказывает высокую интенсивность света , вероятность велика, и
там, где он предсказывает низкую интенсивность света, вероятность мала.
Но эти
кванты ведут себя совсем не так, как макроскопические частицы. Для макроскопической частицы мы
предположим, что мы можем измерить его положение и скорость в любое время с помощью
произвольная точность и аккуратность.Учитывая, что мы сделали это, мы можем предсказать
с произвольной точностью и аккуратностью его последующего движения. Но для любого фотона
мы можем только предсказать вероятность того, что
фотон будет находиться в заданной позиции. Эту вероятность можно вычислить
используя волновое уравнение для электромагнитных волн. Где волновое уравнение
предсказывает высокую интенсивность света , вероятность велика, и
там, где он предсказывает низкую интенсивность света, вероятность мала.
.



 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC

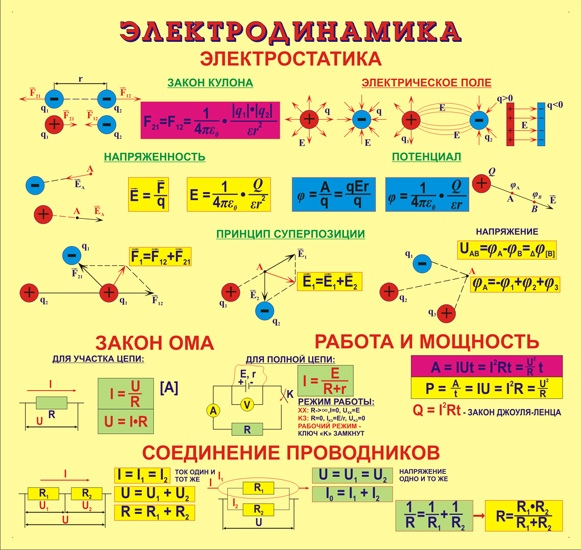
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC
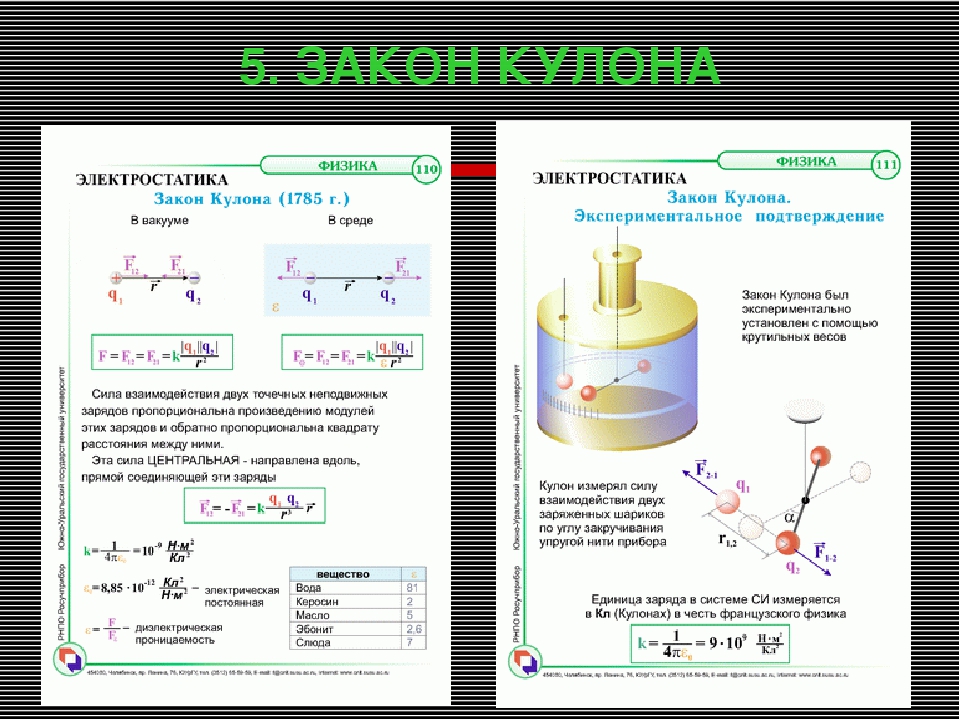 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2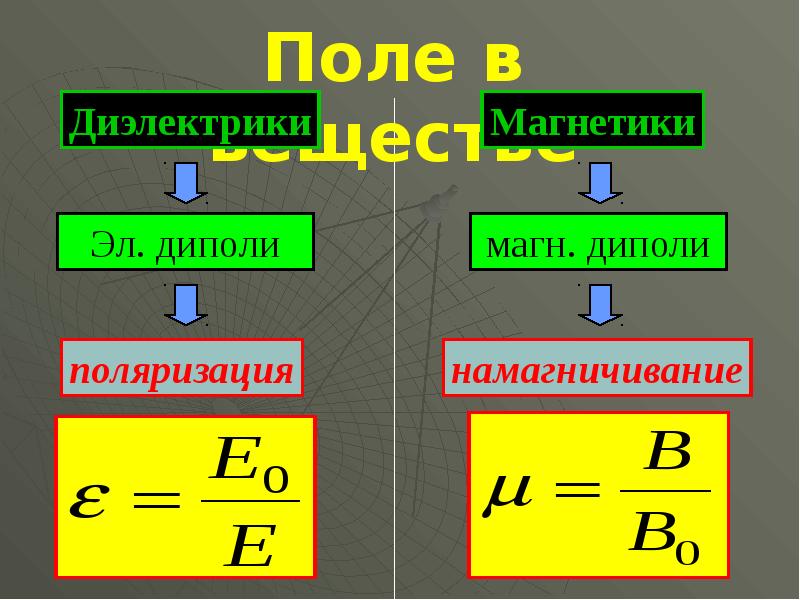 контура T=2π ∙√LC
контура T=2π ∙√LC
 род.энергия молекул одноатомного газа Ek = 3/2 ∙ kT
род.энергия молекул одноатомного газа Ek = 3/2 ∙ kT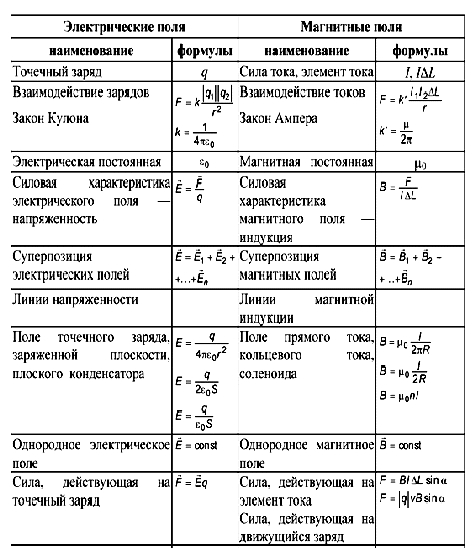 заряды Вт = k ∙ q 1 q 2 / R
заряды Вт = k ∙ q 1 q 2 / R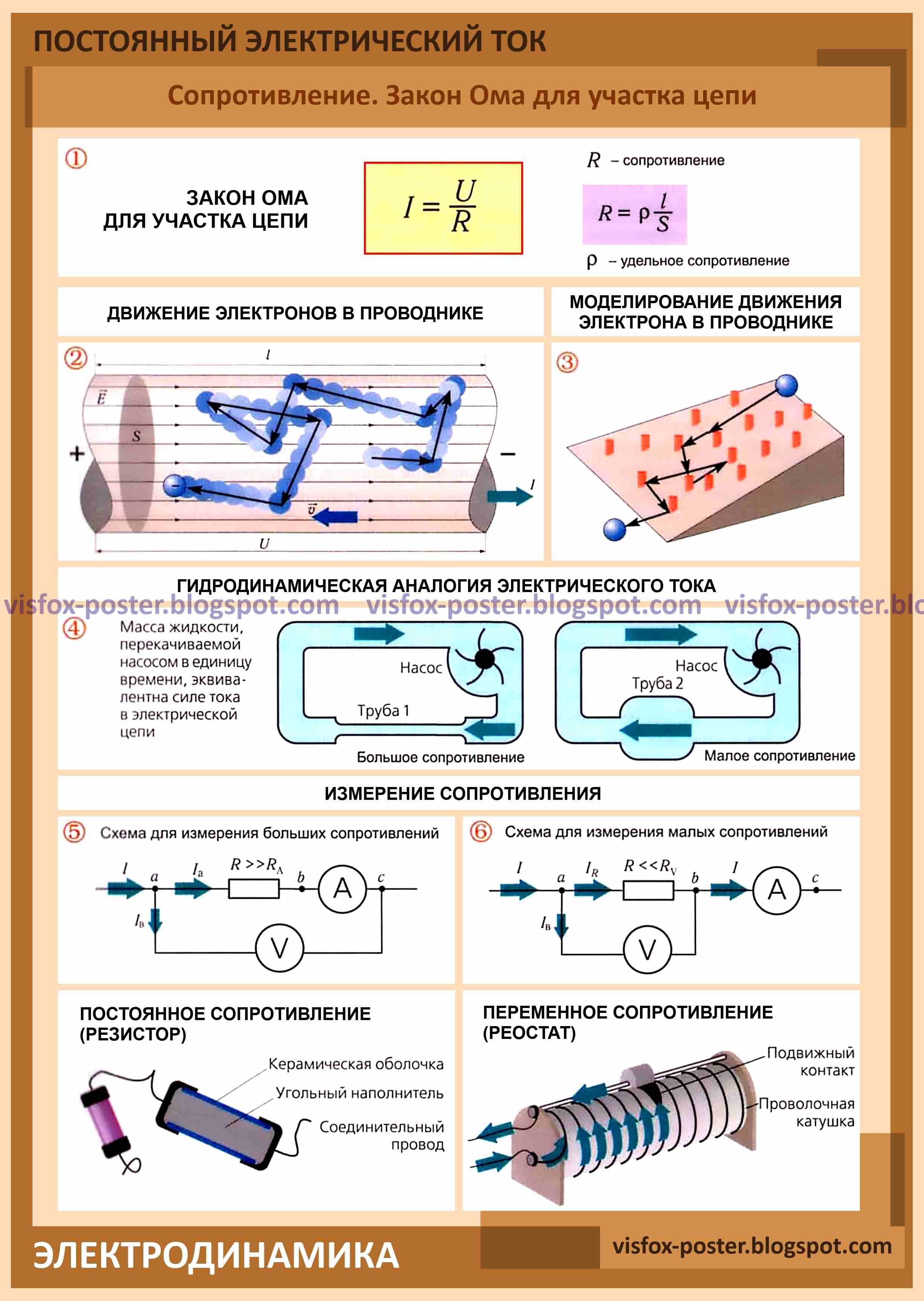 контур T = 2π ∙ √LC
контур T = 2π ∙ √LC .. или если вы хотите пройти курс теоретической физики, не сталкиваясь с жесткой математикой других тем
.. или если вы хотите пройти курс теоретической физики, не сталкиваясь с жесткой математикой других тем
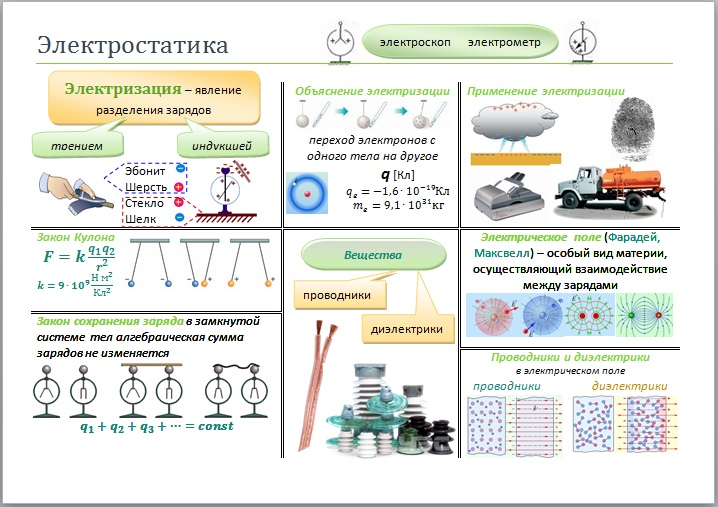 электромагнитные волны с
более длинные волны и более низкие частоты включают инфракрасный свет, микроволны и
радио- и телевизионные волны.
электромагнитные волны с
более длинные волны и более низкие частоты включают инфракрасный свет, микроволны и
радио- и телевизионные волны.