Физика формулы электродинамика: Электродинамика, формулы - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Электродинамика, формулы

Определение 1

Электродинамика – это огромная и важная область физики, в которой исследуются классические, неквантовые свойства электромагнитного поля и движения положительно заряженных магнитных зарядов, взаимодействующих друг с другом с помощью этого поля.

Рисунок 1. Коротко про электродинамику. Автор24 — интернет-биржа студенческих работ

Электродинамика представляется широким комплексом разнообразных постановок задач и их грамотных решений, приближенных способов и частных случаев, которые объединены в одно целое общими начальными законами и уравнениями. Последние, составляя основную часть классической электродинамики, подробно представлены в формулах Максвелла. В настоящее время ученые продолжают изучать принципы указанной области в физике, скелет ее построения взаимоотношения с другими научными направлениями.

Закон Кулона в электродинамике обозначается таким образом: $F= \frac {kq1q2} {r2}$, где $k= \frac {9 \cdot 10 (H \cdot m)} {Кл}$.

Уравнение напряженности электрического поля записывается так: $E= \frac {F}{q}$, а поток вектора индукции магнитного поля $∆Ф=В∆S \cos {a}$.

В электродинамике в первую очередь изучаются свободные заряды и системы зарядов, которые содействуют активизации непрерывного энергетического спектра. Классическому описанию электромагнитного взаимодействия благоприятствует то, что оно является эффективным уже в низкоэнергетическом пределе, когда энергетический потенциал частиц и фотонов мал по сравнению с энергией покоя электрона.

В таких ситуациях зачастую отсутствует аннигиляция заряженных частиц, так как присутствует только постепенное изменение состояния их нестабильного движения в итоге обмена большим количеством низкоэнергетических фотонов.

Замечание 1

Однако и при высоких энергиях частиц в среде, несмотря на существенную роль флуктуации, электродинамика может быть использована с успехом для комплексного описания среднестатистических, макроскопических характеристик и процессов.

Основные уравнения электродинамики

Основными формулами, которые описывают поведение электромагнитного поля и его прямое взаимодействие с заряженными телами, являются уравнения Максвелла, определяющие вероятные действия свободного электромагнитного поля в среде и вакууме, а также общую генерацию поля источниками.

Среди этих положений в физике возможно выделить:

теорема Гаусса для электрического поля – предназначена для определения генерации электростатического поля положительными зарядами;
гипотеза замкнутости силовых линий – содействует взаимодействию процессов внутри самого магнитного поля;
закон индукции Фарадея – устанавливает генерацию электрического и магнитного поля переменными свойствами окружающей среды.

В целом, теорема Ампера — Максвелла — это уникальная идея о циркуляции линий в магнитном поле с постепенным добавлением токов смещения, введенных самим Максвеллом, точно определяет трансформацию магнитного поля движущимися зарядами и переменным действием электрического поля.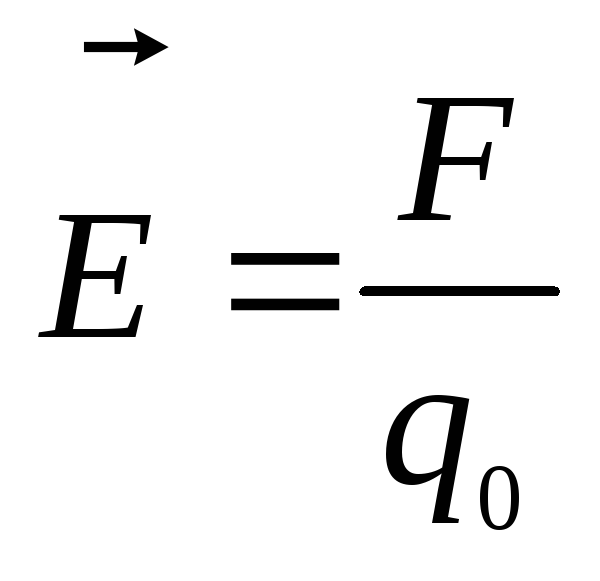

Заряд и сила в электродинамике

В электродинамике взаимодействие силы и заряда электромагнитного поля исходит из следующего совместного определения электрического заряда $q$, энергии $E$ и магнитного $B$ полей, которые утверждаются в качестве основополагающего физического закона, основанного на всей совокупности экспериментальных данных. Формулу для силы Лоренца (в пределах идеализации точечного заряда, движущегося с определенной скоростью), записывают с заменой скорости $v$.

В проводниках зачастую содержится огромное количество зарядов, следовательно, эти заряды достаточно хорошо скомпенсированы: число положительных и отрицательных зарядов всегда равны между собой. Следовательно, суммарная электрическая сила, которая постоянно действует на проводник, равна также нулю. Магнитные же силы, функционирующие на отдельных зарядов в проводнике, в итоге не компенсируются, ведь при наличии тока скорости движения зарядов всегда различны. Уравнение действия проводника с током в магнитном поле можно записать так: $G = |v ⃗ |s \cos{a} $

Если исследовать не жидкость, а полноценный и стабильный поток заряженных частиц в качестве тока, то весь энергетический потенциал, проходящий линейно через площадку за $1с$,— и будет являться силой тока, равной: $I = ρ| \vec {v} |s \cos{a} $, где $ρ$ — плотность заряда (в единице объема в общем потоке).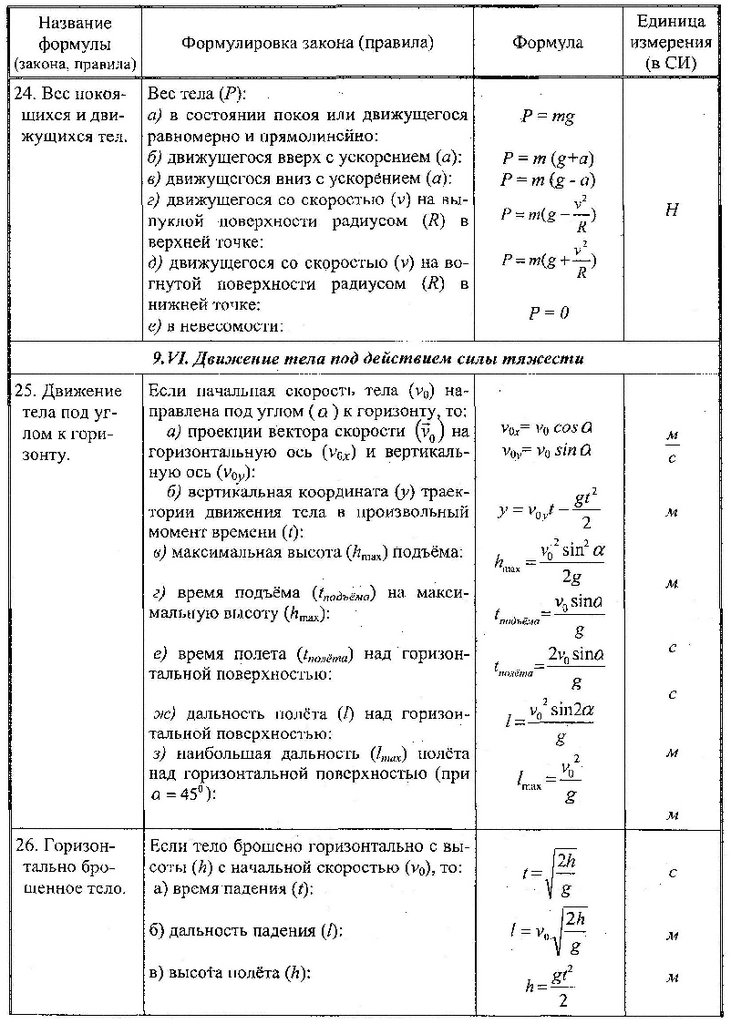

Замечание 2

Если магнитное и электрическое поле систематически меняется от точки к точке на конкретной площадке, то в выражениях и формулах для частичных потоков, как и в случае с жидкостью, в обязательном порядке проставляются средние показатели $E ⃗ $и $B ⃗$ на площадке.

Особое положение электродинамике в физике

Значимое положение электродинамики в современной науке возможно подтвердить посредством известного произведения А. Эйнштейна, в котором были детально изложены принципы и основы специальной теории относительности. Научный труд выдающегося ученого называется «К электродинамике подвижных тел», и включает в себя огромное количество важных уравнений и определений.

Как отдельная область физики электродинамика состоит из таких разделов:

учение о поле неподвижных, но электрически заряженных физических тел и частиц;

учение о свойствах электрического тока;
учение о взаимодействии магнитного поля и электромагнитной индукции;
учение об электромагнитных волнах и колебаниях.

Все вышеуказанные разделы в одно целое объединяет теорема Д. Максвелла, который не только создал и представил стройную теорию электромагнитного поля, но и описал все его свойства, доказав его реальное существование. Работа именно этого ученого показала научному миру, что известные на тот момент электрическое и магнитное поля являются всего лишь проявлением единого электромагнитного поля, функционирующего в различных системах отсчета.

Существенная часть физики посвящена изучению электродинамики и электромагнитных явлений. Эта область в значительной мере претендует на статус отдельной науки, так как она не только исследует все закономерности электромагнитных взаимодействий, но и детально описывает их посредством математических формул. Глубокие и многолетние исследования электродинамики открыли новые пути для использования электромагнитных явлений на практике, для блага всего человечества.

Электродинамика (установление соответствия между графиками, физическими величинами и формулами) | ЕГЭ по физике

3. 1. Основные понятия и законы электростатики

Закон Кулона:
сила взаимодействия двух точечных неподвижных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними:

Коэффициент пропорциональности в этом законе

В СИ коэффициент k записывается в виде

где ε₀ = 8, 85 · 10⁻¹² Ф/м (электрическая постоянная).

Точечными зарядами называют такие заряды, расстояния между которыми гораздо больше их размеров.
Электрические заряды взаимодействуют между собой с помощью электрического поля. Для качественного описания электрического поля используется силовая характеристика, которая называется «напряжённостью электрического поля» (E). Напряжённость электрического поля равна отношению силы, действующей на пробный заряд, помещённый в некоторую точку поля, к величине этого заряда:

Направление вектора напряжённости совпадает с направлением силы, действующей на положительный пробный заряд. [E]=B/м. Из закона Кулона и определения напряжённости поля следует, что напряжённость поля точечного заряда

где q — заряд, создающий поле; r — расстояние от точки, где находится заряд, до точки, где создаётся поле.
Если электрическое поле создаётся не одним, а несколькими зарядами, то для нахождения напряжённости результирующего поля используется принцип суперпозиции электрических полей: напряжённость результирующего поля равна векторной сумме напряжённостей полей, созданных каждым из зарядов — источников в отдельности:

Работа электрического поля при перемещении заряда: найдём работу перемещения положительного заряда силами Кулона в однородном электрическом поле. Пусть поле перемещает заряд q из точки 1 в точку 2:

В электрическом поле работа не зависит от формы траектории, по которой перемещается заряд. Из механики известно, что если работа не зависит от формы траектории, то она равна изменению потенциальной энергии с противоположным знаком:

Отсюда следует, что

Потенциалом электрического поля называют отношение потенциальной энергии заряда в поле к этому заряду:

Запишем работу поля в виде

Здесь U = ϕ₁ − ϕ₂ — разность потенциалов в начальной и конечной точках траектории. Разность потенциалов называют также напряжением

Часто наряду с понятием «разность потенциалов» вводят понятие «потенциал некоторой точки поля». Под потенциалом точки подразумевают разность потенциалов между данной точкой и некоторой заранее выбранной точкой поля. Эту точку можно выбирать в бесконечности, тогда говорят о потенциале относительной бесконечности.
Потенциал поля точечного заряда подсчитывается по формуле

Проекция напряжённости электрического поля на какую-нибудь ось и потенциал связаны соотношением

3.2. Электроёмкость. Конденсаторы. Энергия электрического поля

Электроёмкостью тела называют величину отношения

Формула для подсчёта ёмкости плоского конденсатора имеет вид:

где S — площадь обкладок, d — расстояние между ними.
Конденсаторы можно соединять в батареи. При параллельном соединении ёмкость батареи C равна сумме ёмкостей конденсаторов:

Разности потенциалов между обкладками одинаковы, а заряды прямо пропорциональны ёмкостям.
При последовательном соединении величина, обратная ёмкости батареи, равна сумме обратных ёмкостей, входящих в батарею:

Заряды на конденсаторах одинаковы, а разности потенциалов обратно пропорциональны ёмкостям.
Заряженный конденсатор обладает энергией. Энергию заряженного конденсатора можно подсчитать по любой из следующих формул:

3.3. Основные понятия и законы постоянного тока

Электрический ток — направленное движение электрических зарядов. В разных веществах носителями заряда выступают элементарные частицы разного знака. За положительное направление тока принято направление движения положительных зарядов. Количественно электрический ток характеризуют его силой. Это заряд, прошедший за единицу времени через поперечное сечение проводника:

Закон Ома для участка цепи имеет вид:

Коэффициент пропорциональности R, называемый электрическим сопротивлением, является характеристикой проводника [R]=Ом. Сопротивление проводника зависит от его геометрии и свойств материала:

где l — длина проводника, ρ — удельное сопротивление, S — площадь поперечного сечения. ρ является характеристикой материала и его состояния. [ρ] = Ом·м.
Проводники можно соединять последовательно. Сопротивление такого соединения находится как сумма сопротивлений:

При параллельном соединении величина, обратная сопротивлению, равна сумме обратных сопротивлений:

Для того чтобы в цепи длительное время протекал электрический ток, в составе цепи должны содержаться источники тока. Количественно источники тока характеризуют их электродвижущей силой (ЭДС). Это отношение работы, которую совершают сторонние силы при переносе электрических зарядов по замкнутой цепи, к величине перенесённого заряда:

Если к зажимам источника тока подключить нагрузочное сопротивление R, то в получившейся замкнутой цепи потечёт ток, силу которого можно подсчитать по формуле

Это соотношение называют законом Ома для полной цепи.

Электрический ток, пробегая по проводникам, нагревает их, совершая при этом работу

где t — время, I — сила тока, U — разность потенциалов, q — прошедший заряд.

Закон Джоуля-Ленца:

3.4. Основные понятия и законы магнитостатики

Характеристикой магнитного поля является магнитная индукция ➛B. Поскольку это вектор, то следует определить и направление этого вектора, и его модуль. Направление вектора магнитной индукции связано с ориентирующим действием магнитного поля на магнитную стрелку. За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Направление вектора магнитной индукции прямолинейного проводника с токам можно определить с помощью правила буравчика:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения рукоятки буравчика совпадает с направлением вектора магнитной индукции.

Модулем вектора магнитной индукции назовём отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током , к произведению силы тока на длину этого участка:

Единица магнитной индукции называется тесла (1 Тл)

Магнитным потоком Φ через поверхность контура площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь этой поверхности и на косинус угла между вектором магнитной индукции ➛B и нормалью к поверхности ➛n:

Единицей магнитного потока является вебер (1 Вб).
На проводник с током, помещённый в магнитное поле, действует сила Ампера

Закон Ампера:
на отрезок проводника с током силой I и длиной l, помещённый в однородное магнитное поле с индукцией ➛B , действует сила, модуль которой равен произведению модуля вектора магнитной индукции на силу тока, на длину участка проводника, находящегося в магнитном поле, и на синус угла между направлением вектора ➛B и проводником с током:

Направление силы Ампера определяется с помощью правила левой руки:
если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а четыре вытянутых пальца указывали бы направление тока, то отогнутый на 90° большой палец укажет направление силы Ампера.
На электрический заряд, движущийся в магнитном поле, действует сила Лоренца. Модуль силы Лоренца, действующей на положительный заряд, равен произведению модуля заряда на модуль вектора магнитной индукции и на синус угла между вектором магнитной индукции и вектором скорости движущегося заряда:

Направление силы Лоренца определяется с помощью правила левой руки: если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда, то отогнутый на 90° большой палец покажет направление силы Лоренца, действующей на заряд. Для отрицательно заряженной частицы сила Лоренца направлена против направления большого пальца.

3.5. Основные понятия и законы электромагнитной индукции

Если замкнутый проводящий контур пронизывается меняющимся магнитным потоком, то в этом контуре возникает ЭДС и электрический ток.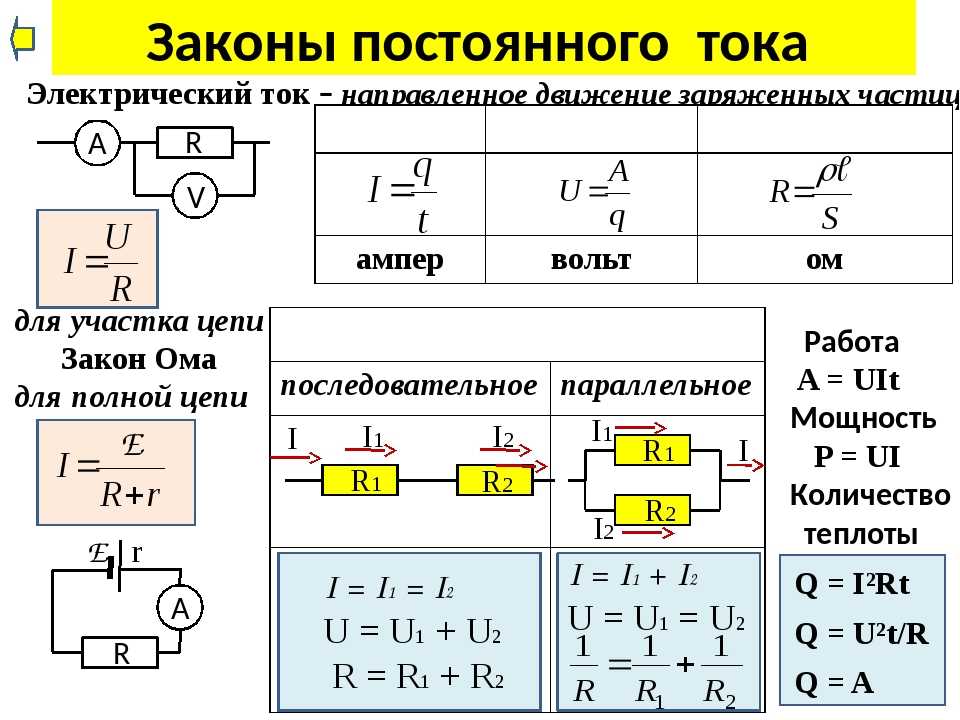 Эту ЭДС называют ЭДС электромагнитной индукции, а ток — индукционным. Явление их возникновения называют электромагнитной индукцией. ЭДС индукции можно подсчитать по основному закону электромагнитной индукции или по закону Фарадея:

Знак «−» связан с направлением индукционного тока. Оно определяется по правилу Ленца:
индукционный ток имеет такое направление, что его действие противодействует причине, вызвавшей появление этого тока.
Магнитный поток, пронизывающий контур, прямо пропорционален току, протекающему в этом контуре:

Коэффициент пропорциональности L зависит от геометрии контура и называется индуктивностью, или коэффициентом самоиндукции этого контура. [L] = 1 Гн

Энергию магнитного поля тока можно подсчитать по формуле

где L — индуктивность проводника, создающего поле; I — ток, текущий по этому проводнику

3.6. Электромагнитные колебания и волны

Колебательным контуром называется электрическая цепь, состоящая из последовательно соединённых конденсатора с ёмкостью C и катушки с индуктивностью L (см.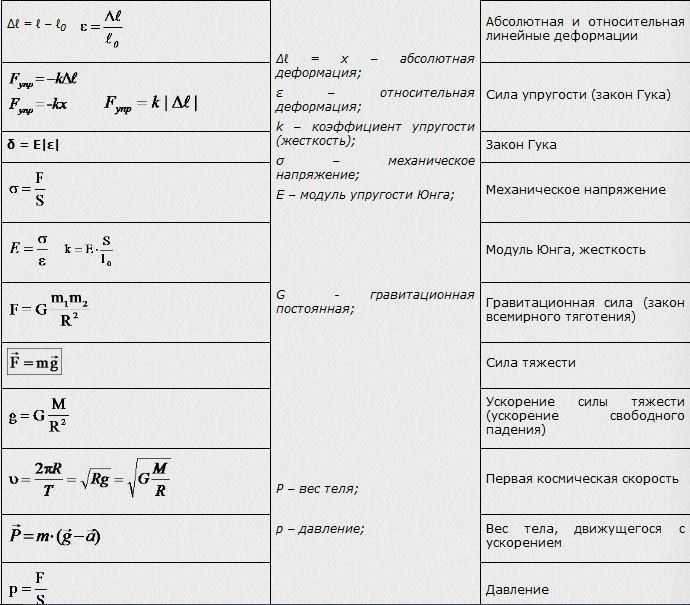

рис. 7).

Для свободных незатухающих колебаний в контуре циклическая частота определяется формулой

Период свободных колебаний в контуре определяется формулой Томсона:

Если в LC-контур последовательно с L, C и R включить источник переменного напряжения, то в цепи возникнут вынужденные электрические колебания. Такие колебания принято называть переменным электрическим током
В цепь переменного тока можно включать три вида нагрузки — конденсатор, резистор и катушку индуктивности.

Конденсатор оказывает переменному току сопротивление, которое можно посчитать по формуле

Ток, текущий через конденсатор, по фазе опережает напряжение на π/2 или на четверть периода, а напряжение отстаёт от тока на такой же фазовый угол.

Катушка индуктивности оказывает переменному току сопротивление, которое можно посчитать по формуле

Ток, текущий через катушку индуктивности, по фазе отстаёт от напряжения на π/2 или на четверть периода. Напряжение опережает ток на такой же фазовый угол.

Трансформатором называется устройство, предназначенное для преобразования переменных токов. Трансформатор состоит из замкнутого стального сердечника, на который надеты две катушки. Катушка, которая подключается к источнику переменного напряжения, называется первичной обмоткой, а катушка, которая подключается к потребителю, называется вторичной обмоткой. Отношение напряжения на первичной обмотке и вторичной обмотке трансформатора равно отношению числа витков в этих обмотках:

Если K > 1, трансформатор понижающий, если K

Практика: решай 18 задание и тренировочные варианты ЕГЭ по физике

Физика – 10 класс. Электродинамика. Формулы. III.

150. Закон сохранения заряда: .

151. Закон Кулона: , .

152. Напряжённость электростатического поля: .

153.Напряженность электростатического

поля точечного заряда: .

154. Принцип суперпозиции электростатических

полей:

155. Напряженность электростатического поля

заряженной проводящей сферы: .

156.Напряженность электростатического поля

равномерно заряженной бесконечной сферы: .

157. Относительная диэлектрическая

проницаемость вещества:

158. .Закон Кулона в веществе: .

159. Напряжённость поля точечного .

заряда в веществе:

160.Напряжённость поля диполя .

в вакууме:

161. Напряжённость поля диполя

в веществе: .

162. Потенциал электростатического

поля и энергия точечного заряда

в поле: , .

163. Принцип суперпозиции

Электростатического поля: .

164. Разность потенциалов (напряжение) .

165. работа при перемещении заряда

в поле: .

166. Единица измерения напряжения:

167. Потенциал поля точечного заряда

в вакууме: .

168. Потенциал поля точечного заряда

в веществе: .

169. Связь разности потенциалов с

напряжённостью однородного

электростатического поля: ( .

170. Ёмкость уединённого проводника: .

171.Электроёмкость уединённой

сферы: .

172.Электроёмкость конденсатора: .

173. Электроёмкость плоского конденсатора: .

174. Энергия заряженного конденсатора: . или .

175. Ёмкость и заряд батареи параллельно

соединённых конденсаторов, напряжение:

176.Формула для вычисления ёмкости,

батареи, последовательно соединённых

конденсаторов:

177. Распределение заряда и напряжения

при последовательном соединении

конденсаторов:

178. Сила постоянного электрического тока: .

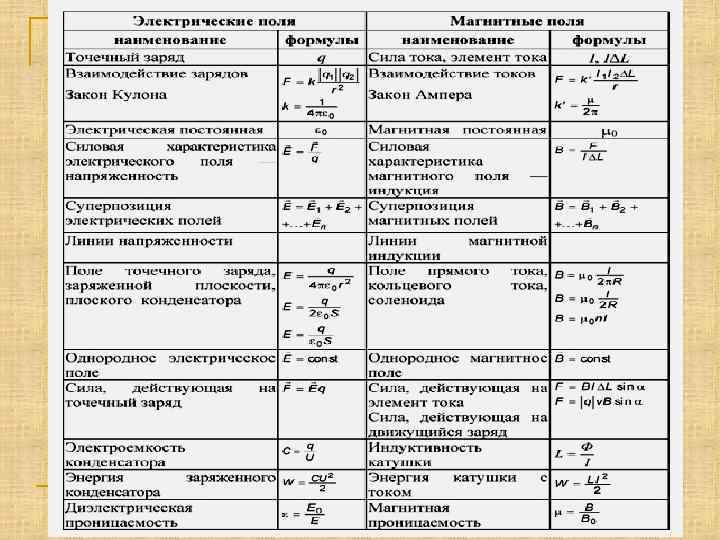
179. Плотность постоянного электрического тока: .

180. ЭДС источника постоянного

электрического тока: .

181. Напряжение на концах

проводника :

182. Закон Ома для участка цепи: .

183. Сопротивление проводника: .

184. Сопротивление, напряжение и

сила тока при последовательном

соединении проводников:

185. Сопротивление, напряжение и ,

и сила в ветвях тока при

параллельном соединении

проводников:

186.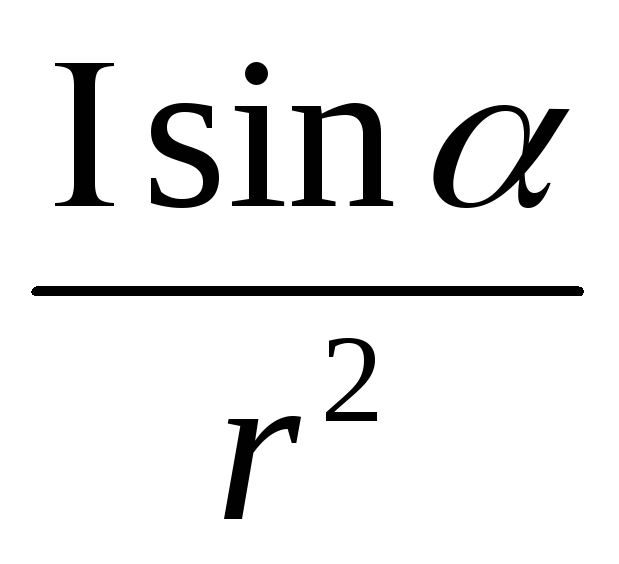 Сопротивленеи шунта амперметра: .

187. Сопротивление шунта вольтметра: .

188.Формулы работы и мощности

постоянного тока:

189. Формулы работы и мощности постоянного тока

при параллельном соединении: . .

190. Формулы работы и мощности постоянного тока

при последовательном соединении: . .

191.Закон Джоуля – Ленца: .

192. Закон Ома для полной цепи: .

193.Падение напряжения на внешнем .

участке цепи:

194.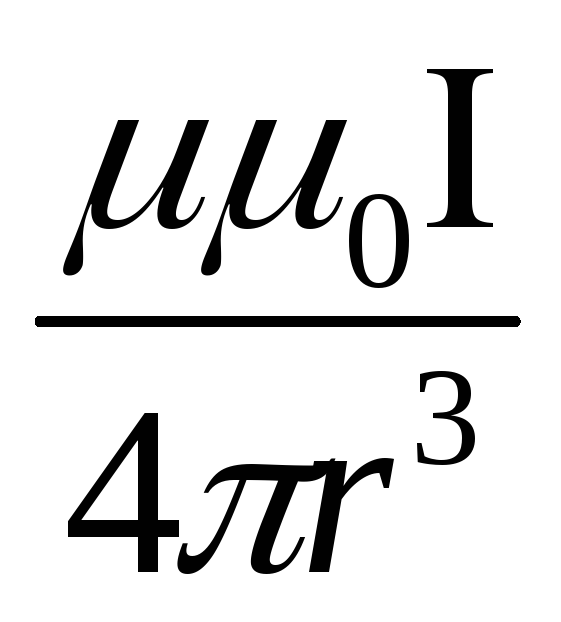 Падение напряжения на внутреннем

участке цепи: .

195. Сила тока при коротком .

замыкании:

196. Зависимость удельного сопротивления

от температуры: .

197. Температурный коэффициент

сопротивления: .

198. Первое правило Кирхгофа: .

199. Второе правило Кирхгофа: .

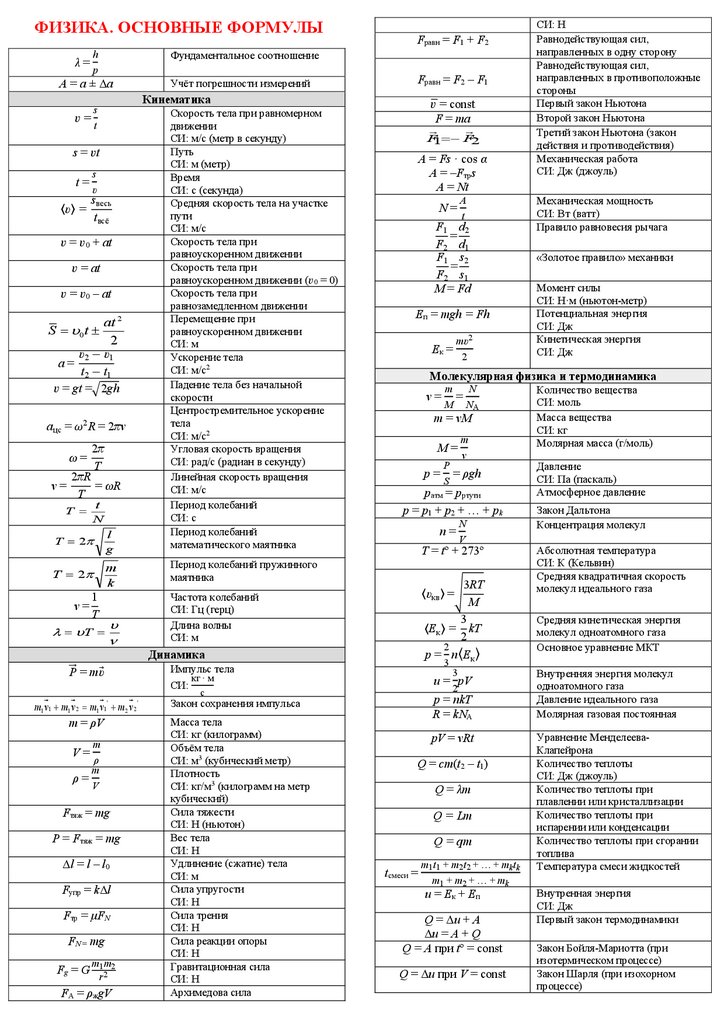
200. ЭДС и внутреннее сопротивление

батареи, последовательно соединённых

источников тока: , .

201. ЭДС и внутреннее сопротивление

батареи, параллельно соединённых

одинаковых источников тока: , .

202. Закон Фарадея: .

203. Химический эквивалент вещества: .

204.Связь электрохимического эквивалента

вещества с его химическим эквивалентом: .

205.Постоянная Фарадея :

206.Модуль вектора магнитной индукции: .

207. Сила Ампера: .

208.Сила Лоренца: .

209. Напряжение в Эффекте Холла: .

210. Разность потенциалов, возникающая на

концах проводника длины , движущегося в

магнитном поле со скоростью :

211. Магнитная индукция в

в веществе: .

212. Магнитная восприимчивость

вещества: .

213.Магнитная проницаемость

вещества:

214. Магнитный поток: .

215. Модуль ЭДС индукции: , = .

216. Закон Фарадея:

217. Сила индукционного тока

в контуре: .

218. ЭДС индукции в катушке

Из витков:

219. Магнитный поток, создаваемый .

током в замкнутом контуре:

220. ЭДС самоиндукции: = или

221. Энергия магнитного поля: .

222. Максимальная энергия .

электрического поля в

колебательном контуре:

223. Максимальная энергия .

электрического поля в

колебательном контуре:

224. Энергия электромагнитного поля

в колебательном контуре:

225. Уравнение колебаний

в колебательном контуре:

, если то .

226. Формула Томсона: .

227.Напряжение и сила , .

переменного тока:

228.Мгновенная мощность

переменного тока:

229.Средняя за период мощность .

переменного тока:

230. Эффективное (действующее) .

значение силы тока:

231. Эффективное (действующее)

значение напряжения переменного

тока: .

232. Индуктивное сопротивление: .

233. Ёмкостное сопротивление:

234. Напряжение в цепи переменного тока: .

235.Закон Ома для цепи переменного тока: .

236. Полное сопротивление цепи переменного тока: .

237. Условие резонанса в цепи переменного тока: или .

238. ЭДС генератора переменного тока: .

239. Коэффициент трансформации: .

240. Повышающий трансформатор: , , .

241. Понижающий трансформатор: , , .

242.Частота переменного тока в .

генераторе с пар полюсами:

243. Уравнение бегущей гармонической ,

электромагнитной волны:

244. Энергия, переносимая

электромагнитной волной: .

245. Плотность потока

электромагнитного излучения:

246. Зависимость интенсивности излучения

от расстояния до источника: .

формулы физики ЭЛЕКТРОДИНАМИКА | Материал для подготовки к ЕГЭ (ГИА) по физике (11 класс) на тему:

Формула	Название формулы	Физические величины
ЭЛЕКТРОСТАТИКА
	Закон сохранения электрического заряда	q – электрический заряд (Кл, Кулон) – напряженность (В/м) – сила кулоновского взаимодействия (Н, Ньютон) , U – потенциал, разность потенциалов (В, Вольт) , работа сторонних сил по перемещению электрического заряда (Дж, Джоуль) – Энергия заряда в однородном поле (Дж, Джоуль) С – Электроемкость (Ф, Фарад) d – расстояние (м, метр) S – площадь обкладок конденсатора (м2) r – расстояние между электрическими зарядами, (м) -электрическая постоянная – коэффициент пропорциональности в законе Кулона – диэлектрическая проницаемость среды
	Принцип суперпозиции полей
	Закон Кулона
	Напряженность поля
	Потенциал точечного заряда
	Разность потенциалов
	Энергия заряда в однородном поле
	Электроемкость
	Электроемкость плоского конденсатора
	Потенциальная энергия плоского конденсатора
	Коэффициент пропорциональности в законе Кулона
ЭЛЕКТРОДИНАМИКА
	Сила тока	I – сила тока (А, Ампер) U – напряжение (В, Вольт) R – сопротивление (Ом) – удельное сопротивление проводника (Ом∙м) l – длина проводника (м, метр) S – площадь поперечного сечения проводника (м2) – ЭДС (В, Вольт) Q – количество теплоты (Дж, Джоуль) А – работа (Дж, Джоуль) Р – мощность (Вт, Ватт) t – время (с, секунда) r – внутреннее сопротивление (Ом)
	Напряжение
	Закон Ома
	Сопротивление
	Закон Джоуля-Ленца
	Мощность электрического тока
	Закон Ома для полной цепи
	ЭДС источника
	Напряжение на внешней цепи
	КПД источника тока
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ
	Сила тока	I – сила тока (А, Ампер) U – напряжение (В, Вольт) R – сопротивление (Ом) С – Электроемкость (Ф, Фарад) q – электрический заряд (Кл, Кулон)
	Напряжение
	Сопротивление
	Сопротивление при N одинаковых резисторах
	Электрический заряд
	Электроемкость
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ
	Сила тока	I – сила тока (А, Ампер) U – напряжение (В, Вольт) R – сопротивление (Ом) С – Электроемкость (Ф, Фарад) q – электрический заряд (Кл, Кулон)
	Напряжение
	Сопротивление
	Сопротивление при N одинаковых резисторах
	Электрический заряд
	Электроемкость
МАГНИТНОЕ ПОЛЕ
	Сила Ампера	– вектор магнитной индукции (Тл, Тесла) m – масса частицы (кг) r – радиус описанной окружности (м, метр) – скорость (м/с)
	Сила Лоренца
	Радиус описанной окружности при движении частицы в магнитном поле
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
	Магнитный поток	– Энергия электромагнитного поля (Дж, Джоуль) L – индуктивность катушки (Гн, Генри) – длина проводника (м, метр) – магнитный поток (Вб, Вебер) – сила тока (А, ампер) – время (с, секунда)
	Магнитный поток
	ЭДС самоиндукции
	ЭДС индукции в движущемся проводнике
	Энергия электромагнитного поля

Формулы и буквенные обозначения по физике.

Основные физические величины, их буквенные обозначения в физике. Производные физические величины

В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования. Кроме указанных… … Википедия

Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия

Список знаковых систем (систем обозначений и т.п.), используемых человеческой цивилизацией, за исключением письменностей, для которых имеется отдельный список. Содержание 1 Критерии включения в список 2 Математика … Википедия

Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8& … Википедия

Дирак, Поль Адриен Морис Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8 августа 1902(… Википедия

Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz … Википедия

У этого термина существуют и другие значения, см.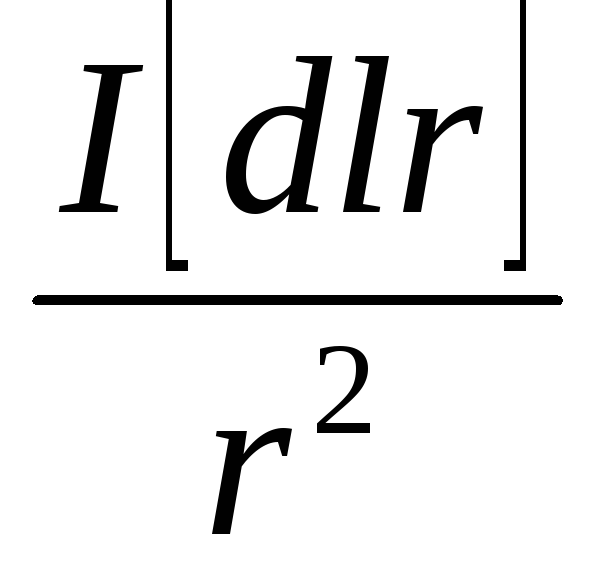 Мезон (значения). Мезон (от др. греч. μέσος средний) бозон сильного взаимодействия. В Стандартной модели, мезоны это составные (не элементарные) частицы, состоящие из чётного… … Википедия

Ядерная физика … Википедия

Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации… … Википедия

Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации часто… … Википедия

Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.

Физика и основные физические величины

Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.

Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике.

Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:

длина,
масса,
время,
сила тока,
температура,
количество вещества,
сила света.

Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль.

Производные физические величины

Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.

Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.

Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.

СИ: общие сведения

Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.

Заключение

Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.

Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?

Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.

Что обозначает прописная буква N в физике?

Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.

Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).

Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).

Что такое N в физике, помимо уже указанных величин? Это может быть:

постоянная Авогадро;

увеличение оптического прибора;

концентрация вещества;

число Дебая;

полная мощность излучения.

Что может обозначать строчная буква n в физике?

Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:

показатель преломления, причем он может быть абсолютным или относительным;

нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;

частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).

Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.

Какая физическая величина может быть обозначена n и N?

Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.

Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.

Формулы, в которых фигурирует прописная N

Первая из них определяет мощность, которая равна отношению работы ко времени:

В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :

Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.

Чтобы определить электрический заряд, потребуется формула:

Еще одна формула с N в физике – частота колебаний.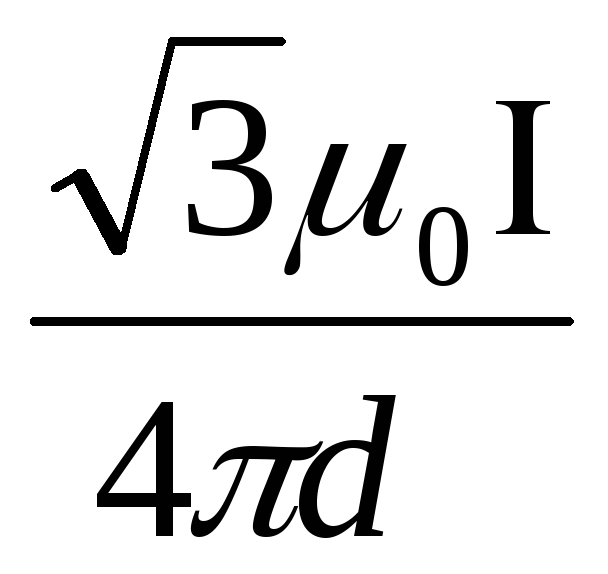 Чтобы ее сосчитать, нужно их число разделить на время:

Появляется буква «эн» в формуле для периода обращения:

Формулы, в которых встречается строчная n

В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.

Так, для абсолютного показателя преломления формула записывается следующим образом:

Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.

Формула для относительного показателя преломления несколько сложнее:

n 21 = v 1: v 2 = n 2: n 1 ,

где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.

Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.

Чему равно n в физике, если это показатель преломления?

Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.

Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.

Задача на мощность

№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.

Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.

Выбор формул. Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.

Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.

Ответ. Мощность трактора равна 20 000 Вт.

Задачи на показатель преломления

№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.

В СИ переводить данные не требуется.

При выборе формул остановиться нужно на этой: n = с: v.

Решение. Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.

Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.

№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.

Нужно ли переводить в СИ? Скорости даны во внесистемных единицах.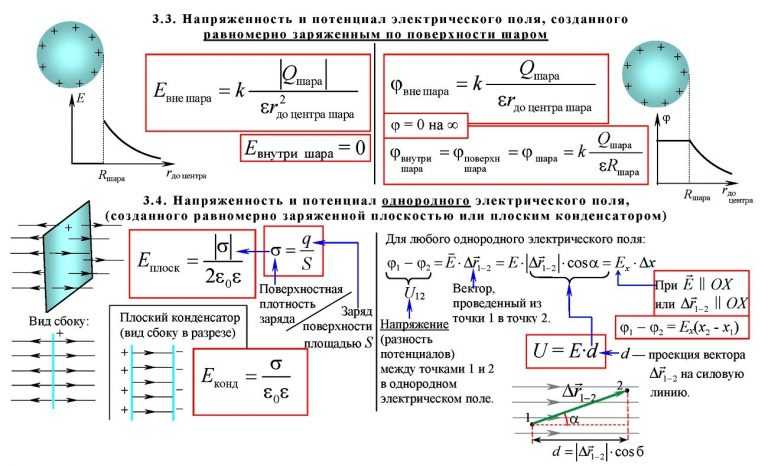 Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.

Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.

Решение. В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).

Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.

Ответ. Значение угла преломления — 26º.

Задачи на период обращения

№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.

Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.

Подбор формул . Период вращения и число оборотов связаны формулой Т = t: N.

Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.

Ответ. Число оборотов лопастей мельницы равно 720.

№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?

Все данные приведены с СИ, поэтому переводить ничего не нужно.

Необходимая формула : частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.

Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.

Ответ. Винт самолета совершает 3000 оборотов за 120 с.

Подведем итоги

Когда ученику в задаче по физике встречается формула, содержащая n или N, ему нужно разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение. Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.

Шпаргалка с формулами по физике для ЕГЭ

и не только (может понадобиться 7, 8, 9, 10 и 11 классам).

Для начала картинка, которую можно распечатать в компактном виде.

Механика

Давление Р=F/S
Плотность ρ=m/V
Давление на глубине жидкости P=ρ∙g∙h
Сила тяжести Fт=mg
5. Архимедова сила Fa=ρ ж ∙g∙Vт
Уравнение движения при равноускоренном движении

X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 –υ 0 2) /2а S=(υ +υ 0) ∙t /2

Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
Ускорение a=(υ –υ 0)/t
Скорость при движении по окружности υ =2πR/Т
Центростремительное ускорение a=υ 2 /R
Связь периода с частотой ν=1/T=ω/2π
II закон Ньютона F=ma
Закон Гука Fy=-kx
Закон Всемирного тяготения F=G∙M∙m/R 2
Вес тела, движущегося с ускорением а Р=m(g+a)
Вес тела, движущегося с ускорением а↓ Р=m(g-a)
Сила трения Fтр=µN
Импульс тела p=mυ
Импульс силы Ft=∆p
Момент силы M=F∙ℓ
Потенциальная энергия тела, поднятого над землей Eп=mgh
Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
Кинетическая энергия тела Ek=mυ 2 /2
Работа A=F∙S∙cosα
Мощность N=A/t=F∙υ
Коэффициент полезного действия η=Aп/Аз
Период колебаний математического маятника T=2π√ℓ/g
Период колебаний пружинного маятника T=2 π √m/k
Уравнение гармонических колебаний Х=Хmax∙cos ωt
Связь длины волны, ее скорости и периода λ= υ Т

Молекулярная физика и термодинамика

Количество вещества ν=N/ Na
Молярная масса М=m/ν
Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT
Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
Закон Гей – Люссака (изобарный процесс) V/T =const
Закон Шарля (изохорный процесс) P/T =const
Относительная влажность φ=P/P 0 ∙100%
Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
Работа газа A=P∙ΔV
Закон Бойля – Мариотта (изотермический процесс) PV=const
Количество теплоты при нагревании Q=Cm(T 2 -T 1)
Количество теплоты при плавлении Q=λm
Количество теплоты при парообразовании Q=Lm
Количество теплоты при сгорании топлива Q=qm
Уравнение состояния идеального газа PV=m/M∙RT
Первый закон термодинамики ΔU=A+Q
КПД тепловых двигателей η= (Q 1 – Q 2)/ Q 1
КПД идеал. двигателей (цикл Карно) η= (Т 1 – Т 2)/ Т 1

Электростатика и электродинамика – формулы по физике

Закон Кулона F=k∙q 1 ∙q 2 /R 2
Напряженность электрического поля E=F/q
Напряженность эл. поля точечного заряда E=k∙q/R 2
Поверхностная плотность зарядов σ = q/S
Напряженность эл. поля бесконечной плоскости E=2πkσ
Диэлектрическая проницаемость ε=E 0 /E
Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
Потенциал φ=W/q
Потенциал точечного заряда φ=k∙q/R
Напряжение U=A/q
Для однородного электрического поля U=E∙d
Электроемкость C=q/U
Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
Сила тока I=q/t
Сопротивление проводника R=ρ∙ℓ/S
Закон Ома для участка цепи I=U/R
Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
Мощность электрического тока P=I∙U
Закон Джоуля-Ленца Q=I 2 Rt
Закон Ома для полной цепи I=ε/(R+r)
Ток короткого замыкания (R=0) I=ε/r
Вектор магнитной индукции B=Fmax/ℓ∙I
Сила Ампера Fa=IBℓsin α
Сила Лоренца Fл=Bqυsin α
Магнитный поток Ф=BSсos α Ф=LI
Закон электромагнитной индукции Ei=ΔФ/Δt
ЭДС индукции в движ проводнике Ei=Вℓυ sinα
ЭДС самоиндукции Esi=-L∙ΔI/Δt
Энергия магнитного поля катушки Wм=LI 2 /2
Период колебаний кол. контура T=2π ∙√LC
Индуктивное сопротивление X L =ωL=2πLν
Емкостное сопротивление Xc=1/ωC
Действующее значение силы тока Iд=Imax/√2,
Действующее значение напряжения Uд=Umax/√2
Полное сопротивление Z=√(Xc-X L) 2 +R 2

Оптика

Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
Показатель преломления n 21 =sin α/sin γ
Формула тонкой линзы 1/F=1/d + 1/f
Оптическая сила линзы D=1/F
max интерференции: Δd=kλ,
min интерференции: Δd=(2k+1)λ/2
Диф.решетка d∙sin φ=k λ

Квантовая физика

Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
Красная граница фотоэффекта ν к = Aвых/h
Импульс фотона P=mc=h/ λ=Е/с

Физика атомного ядра

Закон радиоактивного распада N=N 0 ∙2 – t / T
Энергия связи атомных ядер

Основные формулы и методические рекомендации по решению задач на волны

Урок 35.

Видеоуроки. Решение задач по физике. Электродинамика.

В завершении курса, мы затронем волновые явления. Данное видео повторяет основные величины и формулы, без которых нельзя решать задачи на волновые явления.

Конспект урока “Основные формулы и методические рекомендации по решению задач на волны”

«Во всём мне хочется

дойти до самой сути…»

Борис Пастернак

Данная тема посвящена рассмотрению основных формул и методических рекомендаций по решению задач на волны.

Волна – это изменение некоторой совокупности физических величин, таких как характеристики физического поля или материальной среды, которое способно перемещаться, удаляясь от места их возникновения, или колебаться внутри ограниченных областей пространства. Говоря более простым языком, волна – это явление распространения в пространстве с течением времени изменения физической величины, переносящее с собой энергию.

Например, как известно, если качнуть поплавок на воде, то от него пойдут круги – это и есть волны, которые переносят энергию, сообщённую вами поплавку за счёт действия сил упругости.

Все волны обладают определёнными свойствами. Это поглощение, рассеяние, отражение, преломление, интерференция, дифракция, дисперсия и поляризация. Интерференция и дифракция являются доказательствами волновой природы того или иного процесса. Иными словами, если наблюдается явление дифракции или интерференции, значит, мы имеем дело с волновыми процессами.

Основными характеристиками волн являются: длина волны, частота волны и скорость волны.

Длина волны – это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. Частота – это количество колебаний точки в пространстве, совершённых за единицу времени. Под скоростью волны понимается скорость её распространения, то есть, та скорость, с которой волна переносит энергию. Например, скорость электромагнитной волны в вакууме равна скорости света.

Теперь рассмотрим классификацию волн. Волны могут быть упругими или электромагнитными. Под упругими волнами понимаются механические волны, то есть, волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия сил упругости. Электромагнитная волна – это распространяющееся в пространстве изменение состояния электромагнитного поля. Иногда говорят «распространяющиеся в пространстве возмущения электромагнитного поля».

Кроме того, волны классифицируются на продольные и поперечные. Продольные волны возникают при колебаниях частиц параллельно направлению распространения волны (то есть, направлению её скорости). Например, звуковые волны являются продольными.

В поперечных волнах, колебания частиц происходят перпендикулярно направлению распространения волны. Например, свет является поперечной волной. Также, волны могут иметь смешанный тип, характеризующийся формой волнового фронта. Волны могут быть плоскими, сферическими, цилиндрическими и даже спиральными. Остановимся отдельно на плоской волне.

Плоская волна – это волна, волновые поверхности которой представляют собой параллельные друг другу плоскости, причём колебания происходят в направлении нормали к поверхности. Например, если взять жестяной лист за один конец и качнуть его в руках, то мы получим плоскую волну.

Сведём в таблицу основные формулы волновых явлений.

Формула	Описание формулы
	Длина волны, распространяющейся со скоростью , период колебаний которой равен .
	Скорость распространения волны длиной 𝜆 с частотой 𝜈.
	Скорость распространения электромагнитной волныв электрической среде с проницаемостью и/или магнитной среде с проницаемостью , где с – скорость света в вакууме.
	Разность фаз между колебаниями точек на расстояниях x₁ и x₂ от источника волны.
	Уравнение бегущей волны, описывающее смещение всех точек волновой поверхности в зависимости от смещения и времени , где – амплитуда колебаний, – циклическая частота, – скорость распространения волны.
	Расстояние от радиолокатора доя объекта, от которой луч радиолокатора вернулся на полотно за время t, где с – скорость света.
	Интенсивность электромагнитной волны, где – плотность энергии

Методические рекомендации по решению задач на применение общего уравнения бегущей волны

1. Записать общее уравнение бегущей волны.

2. Если в задаче есть заданное уравнение волны, сопоставить его с общим уравнением и определить необходимые параметры волны.

3. Если в задаче даны характеристики волны, составить соответствующее уравнение, опираясь на них.

Методические рекомендации по решению задач на нахождение длины, частоты или скорости волны

1. Записать уравнение, описывающее связь длины волны со скоростью её распространения.

2. При необходимости использовать формулы, описывающие взаимосвязь между линейной частотой, периодом и циклической частотой.

3.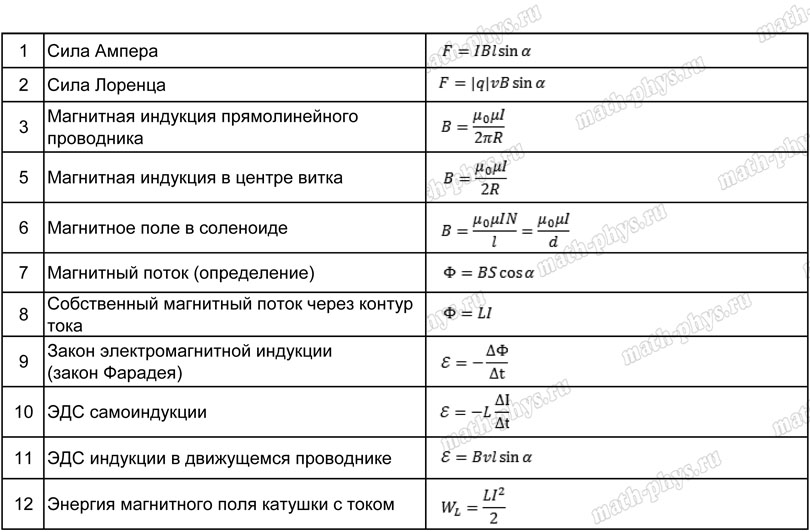 На основании применённых формул составить систему уравнений и решить её относительно искомых величин.

Предыдущий урок 34 Трансформаторы

Следующий урок 36 Длина волны. Связь длины волны со скоростью её распространения. Уравнение волны

Получите полный комплект видеоуроков, тестов и презентаций Видеоуроки. Решение задач по физике. Электродинамика.

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Электромагнетизм | Физика для идиотов

Содержание

1 Все это
2 Основы
3 Перемещение вещей
4 Схемы
- 4. 1 Что есть что?
- 4,2 ампер, вольт и ом (ох!)
5 Глубокий конец
- 5.1 Закон Гаусса
  - 5,1,1 Заряженное кольцо
- 5.2 Закон GAUSS для магнитизма
- 5.2 Закон GAUSS для магнитизма
- 5,2 GAUSS.0014
- 5.4 Закон Ампера-Максвелла
6 Другая форма глубокого конца
7 Еще одна форма глубокого конца

Для электромагнетизма все, что вам нужно знать, это то, что происходит, когда у вас есть + или – заряды, что происходит, когда они приближаются и что происходит, когда они перемещаются. Вот и все! Для всех неквантовых ЭМ нужны всего 5 формул. 4 уравнения Максвелла и уравнение Лоренца описывают все электричество, магнетизм, свет, звук, излучение, фактически большую часть физики:

(1)

(2)

(3)

(4)

(5)

Насколько плохой может быть тема, если вы можете описать ее всего с помощью 5 уравнений, вы, вероятно, сможете уместить их все на обратной стороне пивной подставки. Теперь, когда вы увидели заключение, мы можем перейти к началу и подробно прочитать всю историю. Если вы не изучаете университетский курс, вы можете не знать точно, что означает или делает уравнение, но этот сайт объяснит их позже, сначала давайте вернемся к основам.

Заряд бывает двух типов: положительный и отрицательный, и измеряется в кулонах (C). Если у вас есть заряд сам по себе, он излучает поле во всех направлениях. Поле от заряда представлено буквой E, как и в E-электричестве. Если вы поместите другой заряд в поле, оно испытает силу. Одноименные заряды отталкиваются, а разноименные притягиваются. Чем больше заряд, тем сильнее сила, и чем дальше заряды, тем слабее сила, как и следовало ожидать. Это отношение может быть представлено законом Кулона;

s — это два заряда и расстояние между ними в квадрате. Другой бит — это просто константа, которая примерно равна

00000. (Точный вывод этого закона можно найти здесь). Из них вы можете видеть, что сила равна полю, умноженному на любой заряд, который вы приложили.

Используя это, вы можете вычислить поле или силу между частицами, атомами или чем-то еще, имеющим заряд, при условии, что они не движутся. Как только вы начинаете движение заряда, происходят другие вещи.

Как только заряд начинает двигаться, он создает другое поле. Новое поле — это магнетизм, и оно представлено буквой B, как в B-магматизме?

Причина, по которой это B, просто в том, что он был вторым в алфавитном списке:

Электромагнитный векторный потенциал: A
Магнитная индукция: B
Суммарный электрический ток: C
Электрический рабочий объем: D
Электродвижущая сила: E
Механическая сила: F
Скорость в точке: G
Сила магнитного поля: H

(это также объясняет, откуда H, для тех, кто заинтересован).

Итак, теперь ваша частица, или атом, или что-то еще имеет 2 выходных поля. Полное уравнение, описывающее, как оба поля действуют на частицу, выглядит так:

, известное как сила Лоренца. Символ не означает умножения, в данном контексте он означает перекрестное произведение. По сути, это короткий способ записи «умножить на синус угла между». Это потому, что поле толкает в 90°, в каком бы направлении он ни указывал И в каком бы направлении вы ни двигались. Теперь, если вы не выполняете ЭМ выше уровня A, вы можете забыть все о направлениях и углах и просто написать

Если мы расширим вышеизложенное выражение у нас есть

Но мы уже можем описать один из этих битов, это просто закон Кулона. Кроме того, на уровне A или ниже ситуация, вероятно, будет упрощена, поэтому вам нужно будет рассматривать только поля и отдельно. Таким образом, вам, вероятно, придется использовать только одну из следующих двух формул,

Очевидно, это сила и заряд, а также два ранее описанных поля и скорость движущегося заряда. Электрическое поле измеряется в единицах СИ ньютонов на кулон () или, что эквивалентно, вольт на метр (). Магнитное поле измеряется в единицах СИ Тесла (Тл), что эквивалентно Веберам на квадратный метр () или вольт-секундам на квадратный метр ()

Теперь я не большой поклонник схем, никогда не был, теперь, надеюсь, я’ Я буду достаточно профессионален, чтобы моя неприязнь к ним не отразилась в этом разделе, но если это произойдет, я заранее извиняюсь. Если я действительно начну бороться со своей ненавистью, мне, возможно, придется вызвать второго писателя

Цепи A в основном просто серия движущихся зарядов со случайным объектом или устройством, которые влияют на поток. Теперь, когда я скажу, что электроны движутся вокруг, большинство людей подумает, что их скорость близка к скорости света, но это неправильно. Настоящие электроны движутся ОЧЕНЬ медленно, это волна движется быстро. Как сказано выше, одинаковые заряды отталкиваются, поэтому поместите один электрон рядом с другим, и они разойдутся. С током в проводе у вас в основном есть трубка электронов, и вы добавляете один к одному из концов, это заставляет следующий электрон двигаться вниз, который, в свою очередь, толкает следующий и так далее.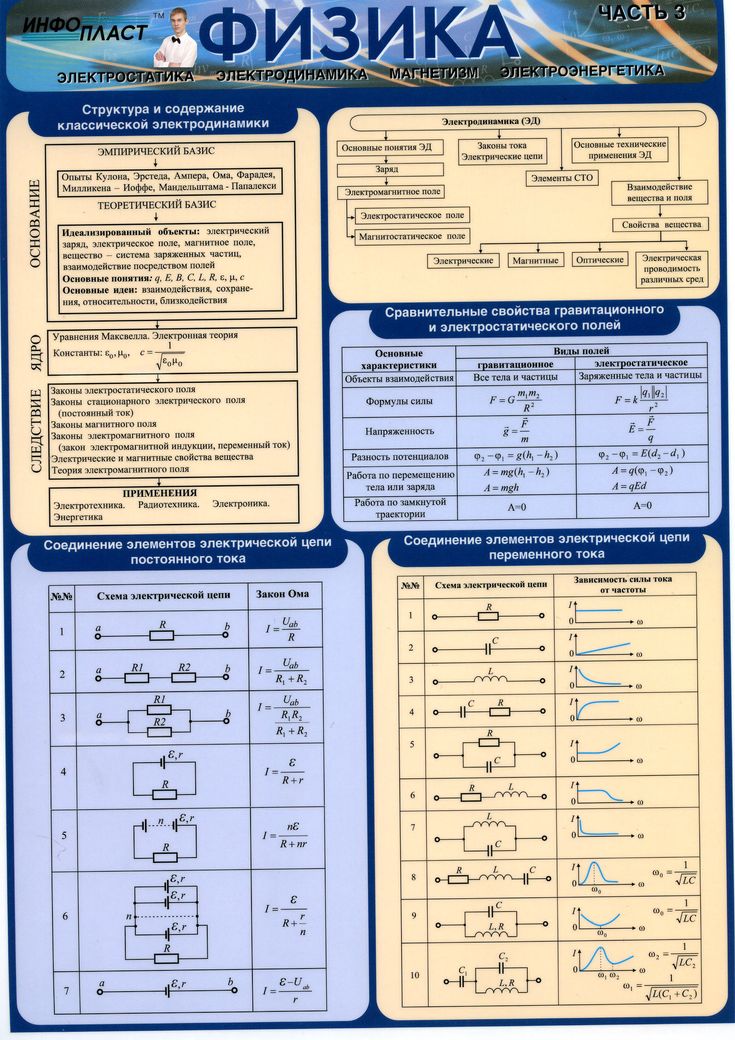 Таким образом, у вас есть эффект мексиканской волны, который движется быстро, но сами электроны движутся медленно.

Схемы обычно содержат всевозможные объекты и устройства в зависимости от того, для чего они предназначены, и в зависимости от того, как вы их настроите в схеме, зависит, как вы будете выполнять все свои расчеты.

Что есть что?

Если вы установите все компоненты в замкнутый цикл, например

, то мы скажем, что все компоненты находятся в серии . Если вы настроите их с путями ветвления, такими как

, тогда мы скажем, что компоненты находятся в Параллельный . Вы также можете создавать цепи, которые представляют собой смесь последовательных и параллельных секций, например,

Ампер, Вольт и Ом (о боже!) (А). Амперы эквивалентны количеству заряда, прошедшего за определенное время, поэтому 2 кулона за 6 секунд будут эквивалентны 0,3А. Это, как и большинство вещей в физике, можно выразить в красивой формуле, которую вы должны выучить:

Еще одна важная идея в цепях — напряжение или разность потенциалов. Вольты – это в основном разница электрического потенциала в двух разных точках. Электрический потенциал между двумя точками определяется как

, где расстояние между и . Это в основном поле, умноженное на расстояние.

Другой важной идеей, когда речь заходит о цепях, является сопротивление. Сопротивление в основном является мерой того, какое сопротивление противостоит электрическому току. Почти все объекты или устройства в цепи вызывают сопротивление, и для расчета общего сопротивления в цепи вы используете одно или несколько из этих правил

Одним из наиболее важных и фундаментальных уравнений в цепях является закон Ома, и он связывает ток, напряжение и сопротивление.

Вот оно. Классический ЭМ не идет дальше этого. Эти 4 являются фундаментальным уравнением для ВСЕХ полей в ЭМ. Это может занять некоторое время, чтобы прийти в себя, но как только вы это сделаете, все должно иметь смысл.

Если вы не знаете об интеграции и дифференциации, я предлагаю вам перейти к разделу «Интеграция» или «Дифференциация», я попытаюсь объяснить это здесь, но в основном сосредоточусь на физике.

Закон Гаусса

Хорошо, тогда сначала у нас есть Закон Гаусса.

Это говорит о том, что интеграл электрического поля через замкнутую область равен общему заряду внутри области, деленному на . является константой, называемой «Проницаемость свободного пространства», и проявляется во всей физике вместе с «Проницаемостью свободного пространства». Это уравнение означает, что вы можете взять ЛЮБУЮ замкнутую поверхность и найти поле, проходящее через нее, при условии, что вы можете заниматься математикой. Обычно вы не можете. Однако есть ряд случаев, когда это приятно и легко. Случаи, когда поле равномерно выходит прямо через поверхность. Случаев

A Сферическая поверхность вокруг точки или сферы
A Цилиндрическая поверхность вокруг бесконечной проволоки
A Регулярная поверхность на сечении бесконечной плоскости

Я допускаю, что это звучит расплывчато и абстрактно, поэтому я продемонстрирую это с помощью диаграммы.

Это поверхности Гаусса. В основном с этими поверхностями все, что вы пытаетесь сделать, это облегчить жизнь. Вы просто убедитесь, что поверхность всегда находится на одном и том же расстоянии от источника заряда и что поле всегда проходит на 90 градусов. Затем вы можете решить интеграл с закрытыми глазами, это так просто. Левая часть закона Гаусса равна Е, умноженной на поверхность выбранной вами формы.

Сферическая поверхность становится , где радиус сферы.
Цилиндрическая поверхность становится , где и — длина и радиус цилиндра.
Обычная поверхность становится , где площадь выше и ниже бесконечной поверхности (вам нужен коэффициент 2, так как поле идет выше и ниже поверхности на 90 градусов).

Таким образом, закон Гаусса для сферы принимает вид

Который ранее был представлен как закон Кулона, теперь вы знаете, откуда он взялся. Закон Гаусса для бесконечной линии заряда всего лишь

. Если у вас есть бесконечная линия заряда, то общий заряд на ней бесконечен, и нет никакого способа узнать, какая часть этого бесконечного заряда будет у вас внутри вашей гауссовой поверхности. Вот тут-то и возникает значение заряда на единицу длины, поэтому, если = 4 см и у вас есть 5 метров, то заряд составляет всего 20С. Вот и все, просто значение заряда.

Для бесконечной поверхности закон Гаусса становится

Еще раз был добавлен новый символ, но он такой же, как и раньше. это просто плата за единицу площади, поэтому, если = 5 см и у вас есть площадь 100 м, общая стоимость составляет 500 C.

Заряженное кольцо

Допустим, у вас есть заряженное кольцо, и вам нужно знать создаваемое им поле. Мы снова будем использовать один из самых важных инструментов в физике, упрощая задачу. Во-первых, мы будем смотреть только на поле вдоль оси кольца, иначе все становится слишком сложным и не стоит усилий. Теперь давайте просто возьмем очень маленькую часть кольца и скажем, что это сфера. На самом деле это не так, но чем меньше мы делаем секцию, тем больше мы можем сделать ее похожей на точечный заряд. Итак, у вас есть что-то вроде этого

Вы хотите найти поле в точке по оси от кольца полного заряда и радиуса. Маленькая квадратная часть вверху — это то, что вы принимаете за заряженную сферу. Теперь мы не знаем, сколько заряда находится в этом маленьком разделе, поскольку вы можете сделать его любого размера, который вы хотите, поэтому мы просто называем заряд небольшим количеством . Итак, теперь у нас есть

Теперь, если подумать, каждый бит кольца выше оси, толкающей вниз, будет иметь такой же бит ниже оси, толкающей вверх. Это также будет одинаково для левой и правой и всех других частей кольца. Таким образом, вся сила от кольца будет действовать только вдоль оси. Чтобы отработать только этот бит, нам нужно использовать некоторый триггер. Нам нужно умножить поле на , чтобы получить осевую составляющую.

Как вы можете знать или не знать, также может быть описано (используя SOH CAH TOA) следующим соотношением для нашей ситуации: Итак, теперь у нас есть

Однако мы можем не знать, что это такое. Мы знаем радиус диска , и расстояние мы от диска, . Используя немного старого Пифагора, мы можем переписать в терминах и

Итак, теперь наше уравнение выглядит так

Теперь мы хотим избавиться от этого , поэтому мы интегрируем

Теперь мы знаем из диаграммы в начале, что общий заряд на диске равен , поэтому, если мы сложим все маленькие биты общего должно быть , так что интеграл просто .

Вот оно, поле с заряженного диска. Все, что вам нужно, это поле с точки зрения и некоторые знания триггеров, и вы сможете это реализовать. Я мог бы просто дать вам окончательное решение, но таким образом вы сможете увидеть, откуда оно взялось, а затем, если вы его забудете, вы сможете разработать его из первых принципов, как указано выше.

Закон Гаусса для магнетизма

Это красиво и просто, но имеет некоторые важные последствия. Закон Гаусса для магнетизма:

Он похож на обычный закон Гаусса в том смысле, что он описывает поле, на этот раз магнитное поле, . Он говорит, что интеграл от B по замкнутой поверхности равен нулю. Ничего такого. Каждая линия поля, выходящая за пределы поверхности, имеет эквивалент, входящий внутрь. Общего поля не существует. Это означает, что невозможно получить источники Магнитного поля. В то время как электроны и протоны являются источником поля, от которого расходятся или сходятся силовые линии, магнитного аналога не существует. Линии магнитного поля всегда представляют собой замкнутые петли, без начала и без конца. Это, конечно, не помешало людям подготовиться на случай, если мы найдем магнитный монополь.

Это уравнение может показаться красивым, и так оно и есть, но само по себе оно совершенно бесполезно. Обычно результат 0 в физике очень важен, он означает, что может происходить что-то особенное, здесь он показывает, что магнитных монополей не существует.

Закон Фарадея

Теперь все становится сложнее, здесь у нас есть закон Фарадея,

Я проведу вас через каждую часть, чтобы показать вам, что это на самом деле означает. Сначала у нас есть левая сторона, которая проста. Это так же, как закон Гаусса, только интеграл по другой вещи. Вместо того, чтобы находить полное поле через поверхность, теперь мы находим полное поле вокруг замкнутого контура. Это все, что отличается от левой стороны, больше никаких поверхностей, только замкнутые петли. Теперь о правой стороне. Во-первых, у нас есть минус, отметив, что это сложно. Почему он там, будет объяснено позже. Далее у нас есть еще один интеграл, и он выглядит ужасно. Символ в основном означает небольшое изменение. Так является изменением , и является изменением , где является временем. Целое – это скорость изменения , насколько оно изменяется () в данный момент времени (). И это интегрируется по области. это область внутри замкнутого контура, если вы нарисуете какую-нибудь случайную волнистую вещь, убедившись, что линия не пересекается и соединяется сама с собой, тогда длина вокруг линии будет вашей, а область внутри линии — вашей. Простой да? Таким образом, общая сумма по циклу просто равна минусу изменения в цикле.

Что произойдет, если нет ? Ну нет , значит , ноль, что делает интеграл равным 0, значит нет . Что произойдет, если у вас есть константа ? Что ж, снова равно 0. Значит, равно нулю, что делает интеграл равным 0, так что снова нет . Вы можете создать поле только из меняющегося поля.

Значение знака минус связано с тем, что поля создают поля, а поля создают поля (как показано в законах Фарадея и Ампера). Если бы минуса не было, то поля продолжали бы накапливаться и накапливаться, в конечном итоге давая бесконечную энергию, а это недопустимо!

Закон Ампера-Максвелла

Последним из уравнений Максвелла является закон Ампера-Максвелла. Как первые два закона были похожи, так и последние два, в этом порядке для них есть шаблон, который может облегчить их запоминание. над областью, над областью, вокруг петли и теперь, наконец, вокруг петли. Уравнение:

Левая часть, простая, интеграл от B по замкнутому контуру. Правая сторона, не так просто. Сначала давайте проигнорируем немного, я вернусь к этому. В остальном он очень похож на закон Фарадея. У вас есть еще одно изменяющееся поле, интегрированное в область, но на этот раз это . На этот раз вместо умножения на минус 1 вы умножаете на . Опять же, это две очень важные величины в физике, по отдельности и вместе взятые. Они находятся в самом сердце ЭМ. Таким образом, ваше магнитное поле вокруг контура просто равно изменяющемуся полю Е, проходящему через него раз на , но тогда вам придется немного добавить. Это бит. Это просто ток, проходящий через петлю за время , потому что, как сказано в разделе «Перемещение вещей», если у вас есть движущийся заряд, то есть ток, вы получаете магнитное поле. Таким образом, вы должны добавить два бита вместе. Красный.

Помимо написания приведенных выше уравнений Максвелла в так называемой интегральной форме, вы также можете записать их в дифференциальной форме, например: упрощение. И интегральная форма, и дифференциальная форма являются векторными уравнениями, и они избавляют вас от необходимости выписывать полные 8 уравнений Максвелла для полей и во всех трех измерениях.

. также компактизируйте четыре векторных уравнения Максвелла в два тензорных уравнения, например так: Они определены как

(6)

(7)

где – скорость света. То и просто скажу где в векторе или матрице смотреть, но сбивает с толку у некоторых начало с 0, так и (не путать с кубом). То же самое с , так и

Формулы физики

Закон Кулона		Q = электрический заряд r ₂₁ = расстояние от Q ₁ до Q ₂ к = 8,99 х 10 ⁹ Н·м ² /C ²
Диэлектрическая проницаемость свободного пространства ε ₀
Электрическое поле
Электрическое поле точечного заряда Q ₁
Суперпозиция электрических поля от множества точечных зарядов
Электрический поток Φ _E через закрытую поверхность
Закон Гаусса
Равномерное распределение заряда для нитей, поверхностей и объемов
Ускорение заряженного частица массой m и зарядом q в электрическом поле
Дипольный момент p электрический диполь
Крутящий момент на электрическом диполе в электрическом поле
Работа по перемещению испытательного заряда q от r ₁ до r ₂ в электрическом поле точечный заряд Q
Потенциальная энергия испытания заряд q при наличии точечного заряда В
Работа по перемещению испытательного заряда q от P ₁ до P ₂ в произвольном электрическом поле
Изменение потенциальной энергии на переместить тестовый заряд q с P ₁ на P ₂ в произвольном электрическом поле
Разность электрических потенциалов
Электрический потенциал при r точечного заряда Q со ссылкой на ∞
Электрический потенциал на P системы N точечные заряды
Потенциальная энергия произвольная система точечных зарядов Q _i
Электрический потенциал при перпендикулярное расстояние a от бесконечного, равномерно заряженного провода с линейная плотность заряда λ
Электрическое поле проводника поверхность с плотностью заряда σ
Электрический ток I
Закон Ома
Омические потери или Джоулев нагрев
Плотность тока
Проводимость σ
Удельное сопротивление ρ
Закон Ома
Сопротивление провода площадь поперечного сечения A и длина ℓ
Температурная зависимость удельное сопротивление для большинства проводников
Резисторы серии
Резисторы параллельно
Правило соединения Кирхгофа
Правило петли Кирхгофа
Емкость С
Емкость C А конденсатор с параллельными пластинами с площадью поверхности A , разделение пластин d , и диэлектрическая проницаемость κ
Накопленная энергия U в конденсатор
Параллельные конденсаторы
Конденсаторы серии
Диэлектрическая проницаемость κ
Плотность энергии в электрическом поле
Закон магнитной силы
Закон Био-Савара
Магнитная индукция на оси тока I в кольце радиусом и
Магнитный дипольный момент токовая петля
Закон Гаусса для магнитного поля Поля
Закон об амперах
Магнитная индукция от тока I на длинном прямом проводе
Магнитная индукция в соленоид
Движение перпендикулярно однородное магнитное поле B
Закон силы Лоренца
Сила на токоведущей провод
Крутящий момент в токовой петле в магнитное поле B

Индуцированная электродвижущая сила
Электродвижущая сила генератор, вращающийся с угловой скоростью ω
Крутящий момент простой электродвигатель мотор
Электродвижущая сила, приводящая в движение простой электродвигатель
Ток смещения I _d
Закон Ампре-Максвелла
RC-цепь (разрядка)
RC-цепь (зарядка)
Самоиндукция L
Самоиндукция соленоида

электростатика – Вопрос по двум формулам классической электродинамики Джексона

$\begingroup$

Я читаю $Classical$ $Электродинамику$ Джексона, и есть две форума, которые вызывают у меня некоторые проблемы. Что происходит, так это то, что если я комбинирую эти формулы определенным образом, я могу вывести некоторые абсурдные результаты. Поясню: 93 х’ = \textbf{E}(\textbf{х}) \конец{выравнивание*} где я использовал аналогичные расчеты, как указано выше.

Вывод будет $$A\textbf{E}(\textbf{x})=\textbf{E}(A\textbf{x})=\textbf{E}(\textbf{x}).$$ Поскольку ортогональная матрица $A$ была произвольной, это верно для всех ортогональных $A$ и, следовательно, всегда $\textbf{E}(\textbf{x})=0$ в случае, если $\rho$ радиально симметричен. Но разве это не абсурд и совершенно неправильно? Где ошибка в моем рассуждении?

электростатика
электрические поля 9{3/2}} $$ и аналогично для $y$ и $z$.
Проблема в вашем заключении в том, что вы забыли включить $A$ в $\nabla_x$, который не равен $\nabla_{(Ax)}$.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Уравнения Максвелла: предсказание и наблюдение электромагнитных волн
Цель обучения
К концу этого раздела вы сможете:
- Переформулировать уравнения Максвелла.
Рис. 1. Джеймс Клерк Максвелл, физик 19-го века, разработал теорию, объясняющую взаимосвязь между электричеством и магнетизмом, и правильно предсказал, что видимый свет вызывается электромагнитными волнами. (кредит: Г. Дж. Стодарт)
Шотландец Джеймс Клерк Максвелл (1831–1879) считается величайшим физиком-теоретиком 19 века. (См. рис. 1.) Хотя он умер молодым, Максвелл не только сформулировал полную электромагнитную теорию, представленную уравнениями Максвелла , но также разработал кинетическую теорию газов и внес значительный вклад в понимание цветового зрения и природы Сатурна. кольца.
Максвелл объединил всю работу, проделанную блестящими физиками, такими как Эрстед, Кулон, Гаусс и Фарадей, и добавил свои собственные идеи для разработки всеобъемлющей теории электромагнетизма. Уравнения Максвелла перефразированы здесь словами, потому что их математическая формулировка выходит за рамки этого текста. Однако уравнения иллюстрируют, как простые на первый взгляд математические утверждения могут изящно объединять и выражать множество понятий — вот почему математика — это язык науки.
Уравнения Максвелла
1. Линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Электрическое поле определяется как сила на единицу заряда пробного заряда, а величина силы связана с электрической постоянной ε ₀ , также известной как диэлектрическая проницаемость свободного пространства. Из первого уравнения Максвелла мы получаем специальную форму закона Кулона, известную как закон Гаусса для электричества.
2. Линии магнитного поля непрерывны, не имеют ни начала, ни конца. Известно, что магнитных монополей не существует. Сила магнитной силы связана с магнитной постоянной μ ₀ , также известной как проницаемость свободного пространства. Это второе уравнение Максвелла известно как закон Гаусса для магнетизма.
3. Изменяющееся магнитное поле индуцирует электродвижущую силу (ЭДС) и, следовательно, электрическое поле. Направление ЭДС противоположно изменению. Это третье уравнение Максвелла представляет собой закон индукции Фарадея и включает в себя закон Ленца.
4. Магнитные поля генерируются движущимися зарядами или изменяющимися электрическими полями. Это четвертое уравнение Максвелла включает в себя закон Ампера и добавляет еще один источник магнетизма — изменяющиеся электрические поля.
Уравнения Максвелла охватывают основные законы электричества и магнетизма. Что не так очевидно, так это симметрия, которую Максвелл ввел в свою математическую структуру. Особенно важно добавление им гипотезы о том, что изменяющиеся электрические поля создают магнитные поля. Это в точности аналогично (и симметрично) закону индукции Фарадея, о чем давно подозревали, но прекрасно вписывается в уравнения Максвелла.
Симметрия проявляется в природе в самых разных ситуациях. В современных исследованиях симметрия играет важную роль в поиске субатомных частиц с использованием массивных многонациональных ускорителей частиц, таких как новый Большой адронный коллайдер в ЦЕРНе.
Установление связей: объединение сил
Полная и симметричная теория Максвелла показала, что электрические и магнитные силы не являются отдельными, а являются разными проявлениями одного и того же — электромагнитной силы. Это классическое объединение сил является одним из мотивов нынешних попыток объединить четыре основных взаимодействия в природе — гравитационное, электрическое, сильное и слабое ядерное взаимодействие.
Поскольку изменяющиеся электрические поля создают относительно слабые магнитные поля, их было нелегко обнаружить во времена гипотезы Максвелла. Однако Максвелл понял, что колеблющиеся заряды, подобные зарядам в цепях переменного тока, создают изменяющиеся электрические поля. Он предсказал, что эти меняющиеся поля будут распространяться от источника подобно волнам, создаваемым в озере прыгающей рыбой.
Волны, предсказанные Максвеллом, будут состоять из колеблющихся электрических и магнитных полей, определяемых как электромагнитная волна (ЭМ-волна). Электромагнитные волны могли бы воздействовать на заряды на большом расстоянии от их источника, и поэтому их можно было бы обнаружить. Максвелл рассчитал, что электромагнитные волны будут распространяться со скоростью, определяемой уравнением 98\text{ м/с}\\[/latex]
, что равно скорости света. Фактически Максвелл пришел к выводу, что свет представляет собой электромагнитную волну с такой длиной волны, что ее можно обнаружить глазом.
Должны существовать и другие длины волн — еще неизвестно, существуют ли они. Если это так, то теория и замечательные предсказания Максвелла подтвердятся, что станет величайшим триумфом физики со времен Ньютона. Экспериментальная проверка пришла через несколько лет, но не раньше смерти Максвелла.
Наблюдения Герца
Немецкий физик Генрих Герц (1857–1894) первым сгенерировал и обнаружил в лаборатории определенные типы электромагнитных волн. Начиная с 1887 года он провел серию экспериментов, которые не только подтвердили существование электромагнитных волн, но и подтвердили, что они распространяются со скоростью света.
Гц использовалась схема AC RLC (резистор-индуктор-конденсатор), которая резонирует на известной частоте [латекс]f_0=\frac{1}{2\pi\sqrt{LC}}\\[/latex] и подключил его к проволочной петле, как показано на рис. 2. Высокое напряжение, индуцированное через зазор в петле, вызывало искры, которые были видимым свидетельством тока в цепи и помогали генерировать электромагнитные волны.
Через лабораторию Герц прикрепил еще один контур к другому контуру RLC , который можно было настроить (как шкала на радио) на ту же резонансную частоту, что и первый, и, таким образом, можно было настроить на прием электромагнитных волн. В этой петле также был зазор, через который генерировались искры, что давало убедительные доказательства того, что электромагнитные волны были получены.
Рис. 2. Аппарат, использованный Герцем в 1887 г. для генерации и обнаружения электромагнитных волн. РЛК цепь, подключенная к первому контуру, вызывала искрение через разрыв в проволочном контуре и генерировала электромагнитные волны. Искры через щель во втором контуре, расположенном поперек лаборатории, свидетельствовали о том, что волны были получены.
Герц также изучал отражение, преломление и интерференцию генерируемых им электромагнитных волн, подтверждая их волновой характер. Он смог определить длину волны по интерференционным картинам, а зная их частоту, рассчитать скорость распространения по уравнению v = fλ (скорость — или скорость — равна частоте, умноженной на длину волны). Таким образом, Герц смог доказать, что электромагнитные волны распространяются со скоростью света. Единица СИ для частоты, герц (1 Гц = 1 цикл/сек), названа в его честь.
Резюме раздела
- Электромагнитные волны состоят из осциллирующих электрических и магнитных полей и распространяются со скоростью света c . Они были предсказаны Максвеллом, который также показал, что
  [латекс]\displaystyle{c}=\frac{1}{\sqrt{{\mu }_{0}{\epsilon}_{0}}}\\[ /латекс],
  , где μ ₀ является проницаемостью свободного пространства, а ε ₀ является диэлектрической проницаемостью свободного пространства.
- Предсказание Максвелла об электромагнитных волнах явилось результатом его формулировки полной и симметричной теории электричества и магнетизма, известной как уравнения Максвелла.
- Эти четыре уравнения перефразированы в этом тексте, а не представлены в числовом виде, и охватывают основные законы электричества и магнетизма. Первый — это закон Гаусса для электричества, второй — закон Гаусса для магнетизма, третий — закон индукции Фарадея, включая закон Ленца, и четвертый — закон Ампера в симметричной формулировке, добавляющий еще один источник магнетизма — изменяющиеся электрические поля.
Задачи и упражнения
1. Убедитесь, что правильное значение скорости света c получается при вводе в уравнение числовых значений проницаемости и диэлектрической проницаемости свободного пространства (μ ₀ и ε ₀ ) [latex]c=\frac{1}{\sqrt{{\mu}_{0}{\epsilon}_{0}}}\\[/latex].
2. Покажите, что при вводе единиц СИ для μ ₀ и ε ₀ в правой части уравнения в приведенной выше задаче единицами измерения являются м/с.
Глоссарий
электромагнитные волны: излучение в форме волн электрической и магнитной энергии
уравнения Максвелла: набор из четырех уравнений, составляющих полную всеобъемлющую теорию электромагнетизма

RLC электрическая цепь, включающая резистор, конденсатор и катушку индуктивности

герц: единица СИ, обозначающая частоту электромагнитной волны в циклах в секунду

скорость света: в вакууме, таком как космос, скорость света постоянна 3 × 10 источник, производящий электрический ток

линии электрического поля: набор воображаемых линий, которые проходят между источником электричества и заряженными объектами в окружающей области, со стрелками, направленными от положительно заряженных объектов к отрицательно заряженным объектам. Чем больше линий в узоре, тем сильнее электрическое поле в этой области

линии магнитного поля: набор непрерывных воображаемых линий, которые выходят из противоположных магнитных полюсов и входят в них. Плотность линий указывает на величину магнитного поля

Электромагнитные волны

Электромагнитные (ЭМ) волны представляют собой изменение электрических и магнитных полей, перенос энергии и импульса через пространство. ЭМ волны являются решениями уравнений Максвелла, которые основные уравнения электродинамики. ЭМ-волнам не нужна среда, они могут проходить через пустые пространство. Синусоидальные плоские волны являются одним из видов электромагнитных волн. Не все ЭМ волны представляют собой синусоидальные плоские волны, но все электромагнитные волны можно рассматривать как линейные суперпозиция синусоидальных плоских волн, распространяющихся в произвольных направлениях. Самолет ЭМ волна, бегущая в направлении x, имеет форму

E(x,t) = E _max cos(kx – ωt + φ), B (x,t) = B _max cos(kx – ωt + φ).

E — вектор электрического поля, B — магнитное поле. вектор поля ЭМ волны. Для электромагнитных волн E и B всегда перпендикулярны друг другу и перпендикулярны направление распространения. Направление распространения – это направление из Е х В .

Если для волны, бегущей в направлении x, E = E j , то B = Б к и j x k = i . электромагнитный волны – поперечные волны.

Волновое число k = 2π/λ, где λ — длина волны. Частота волны f равна f = ω/2π, ω — угловая частота. Скорость любой периодической волны равна произведение его длины волны и частоты.

v = λf.

Скорость любых электромагнитных волн в свободном пространстве скорость света c = 3*10 ⁸ РС. Электромагнитные волны могут иметь любую длину волны λ или частоту f как пока λf = c.

Когда электромагнитные волны распространяются через среду, скорость волн в среда v = c/n(λ _{свободный} ), где n(λ _{свободный} ) индекс преломления среды. Показатель преломления n является свойством среды, и зависит от длины волны λ _{бесплатно} ЭМ волны. Если среда поглощает часть энергии переносится волной, то n(λ _{свободное} ) равно комплексное число. Для воздуха n почти равно 1 для всех длин волн. Когда электромагнитная волна распространяется из одной среды с показателем преломления n ₁ в другую среду с другим показателем преломления n ₂ , то его Частота остается той же, что и , но меняются его скорость и длина волны. Для воздуха n почти равно 1,

Электромагнитный спектр

Электромагнитные волны классифицируются по их частота f или, что то же самое, в соответствии с их длиной волны λ = c/f.

Видимый свет имеет диапазон длин волн от ~400 нм до ~700 нм. Фиолетовый свет имеет длина волны ~400 нм, частота ~7,5*10 ¹⁴ Гц. Красный свет имеет длину волны ~700 нм и частоту ~4,3*10 ¹⁴ Гц.

Видимый свет составляет лишь небольшую часть полного электромагнитного спектр. Электромагнитные волны с более короткими длинами волн и более высокими частотами включают ультрафиолетовое излучение, рентгеновское излучение и гамма-излучение. электромагнитные волны с более длинные волны и более низкие частоты включают инфракрасный свет, микроволны и радио- и телевизионные волны.

Поляризация

Поляризация — явление, свойственное поперечным волнам. Продольные волны Например, звук не может быть поляризован. Свет и другие электромагнитные волны поперечные волны, состоящие из взаимно перпендикулярных флуктуирующих электрических и магнитные поля.

На диаграмме справа электромагнитная волна распространяется в х, электрическое поле колеблется в плоскости ху, а магнитное поле колеблется в плоскости xz. Линия описывает электрическое поле вектор по мере распространения волны.

Для линейно поляризованной электромагнитной волны, распространяющейся в направлении x, угол, который электрическое поле образует с осью y, уникален.

Неполяризованная электромагнитная волна, распространяющаяся в направлении x, представляет собой суперпозиция многих волн. Для каждой из этих волн вектор электрического поля перпендикулярна оси x, но составляет угол с осью y разные для разных волн. Для неполяризованного света, путешествующего в х-направление E _y и E _z случайным образом меняются во времени. это намного короче, чем нужно для наблюдения.

Схема на свет изображает неполяризованный свет. Естественный свет, как правило, неполяризован.

Перенос электромагнитных волн энергия через пространство. В свободном пространстве эта энергия переносится волной со скоростью c. Величина потока энергии S – это количество энергии, пересекает единицу площади перпендикулярно направлению распространения волны в единицу времени. Это дается

S = EB/(µ ₀ ) = E ² /(µ ₀ c),

, так как для электромагнитных волн B = E/c. Единицы S: Дж/(м ² с). μ ₀ — константа, называемая проницаемостью свободного пространства, μ ₀ = 4π*10 ^-7 Н/Д ² .

Примечание:
Энергия , переносимая электромагнитной волной пропорциональна квадрату амплитуды, E ² , волна.

Вектор Пойнтинга является вектором потока энергии. Это назван в честь Джон Генри Пойнтинг. Его направлением является направление распространения волны, т. е. направление, в котором транспортируется энергия.

S = (1/μ ₀ ) E x B.

Энергия на единицу площади в единицу времени — это мощность на единицу площади. S представляет мощность на единицу площади в электромагнитной волне. Если электромагнитная волна падает на площадь 90 295 A 90 296, где она поглощается, то мощность, передаваемая в эту область, равна P = S ∙ A .

Среднее по времени значение вектора Пойнтинга равно называется освещенность или интенсивность. Излучение является средним энергии на единицу площади в единицу времени. ~~= 2 >/(μ ₀ с) = E _max ² /(2μ ₀ c).~~

ЭМ волна также транспорт импульс. Поток импульса равен S /с. величина потока импульса S / c – это количество импульса, пересекающего единицу площади, перпендикулярной направлению распространения волны в единицу времени. Если электромагнитная волна падает на площадь А где это поглощается, импульс передается в эту область в направлении, перпендикулярном площадь в единицу времени равна dp _perp /dt = (1/c) S ∙ A .

Следовательно, изменяется импульс объекта, поглощающего излучение. Скорость изменение равно dp _perp /dt = (1/c)SA _perp , где A _perp площадь поперечного сечения объекта перпендикулярно направлению распространения электромагнитной волны. Импульс объекта изменяется, если на него действует сила.

~~F _perp = dp _perp /dt = (1/c)SA _perp~~

— сила, с которой излучение действует на объект, поглощающий излучение. Разделив обе части этого уравнения на A _perp , находим радиационное давление (сила на единицу площади) P = (1/c)S. Если излучение отражается, а не поглощается, тогда его импульс меняет направление. Поэтому радиационное давление на объект, отражающий излучение, в два раза больше радиационное давление на объект, который поглощает излучение.

~~Фотоны~~

Электромагнитные волны переносят энергию и импульс через пространство. энергия и импульс, переносимые электромагнитной волной, не являются непрерывно распределяется по фронту волны. Энергия и импульс передаются фотонами дискретными порциями. Фотоны — это частицы света. Свет «квантуется». Фотоны всегда движутся со скоростью света. Энергия каждый фотон равен E = hf = hc/λ. Импульс каждого фотона равен E/c = hf/c = h/λ.

(ч = 6,626*10 ^-34 Дж с = 4,136*10 ^-15 эВ с
единица энергии: 1 эВ = 1,6*10 ^-19 Дж
полезный продукт: hc = 1240 эВ нм)

Так что же такое электромагнитная волна, волна или поток фотонов? Каковы наши современные представления о природе свет и другие электромагнитные волны?

Квантовая механика рассматривает фотоны как кванты или пакеты энергии. Но эти кванты ведут себя совсем не так, как макроскопические частицы. Для макроскопической частицы мы предположим, что мы можем измерить его положение и скорость в любое время с помощью произвольная точность и аккуратность. Учитывая, что мы сделали это, мы можем предсказать с произвольной точностью и аккуратностью его последующего движения. Но для любого фотона мы можем только предсказать вероятность того, что фотон будет находиться в заданной позиции. Эту вероятность можно вычислить используя волновое уравнение для электромагнитных волн. Где волновое уравнение предсказывает высокую интенсивность света , вероятность велика, и там, где он предсказывает низкую интенсивность света, вероятность мала.

Электромагнетизм с использованием геометрической алгебры в сравнении с компонентами

Электромагнетизм с использованием геометрической алгебры в сравнении с компонентами
1  Введение
Сегодняшняя задача состоит в том, чтобы сравнить несколько более сложных и менее изощренные способы выражения законов электромагнетизма. В частности, мы сравниваем геометрическую алгебру, обычные векторы и компоненты вектора.
Мы делаем это в духе принципа соответствия: всякий раз, когда вы изучаете новый формализм, вы должны проверить, что он согласуется с то, что вы уже знаете.
Этот документ также доступен в PDF формат. Вы можете найти это выгодным, если ваш браузер не может отображать стандартные математические символы HTML.
* Содержание
1. Введение
2 Предварительный просмотр
3  Вектора
4  Компоненты
5 Электромагнетизм с использованием геометрической алгебры
6  Заряд, сила и энергия
6.1 Сохранение заряда
6.2 Закон силы Лоренца
6.3 Лагранжева плотность
6.4 Вектор Пойнтинга
6.5 Тензор энергии-импульса
7 Векторный потенциал
7.1 Основная идея
7.2 D=3 по сравнению с D=4
7.3 Калибровочная инвариантность
7.4 Уравнение Максвелла в терминах векторного потенциала
8  Геометрическая алгебра – общие замечания
8.1  Обзор
8.2 Без украшений
8.3 Нет перекрестного произведения
8. 4 Нет хиральности
8.5 Несколько подходов
9 ловушек, которых следует избегать
9.1  Определение скалярного произведения
9.2 Единица Псевдоскаляр
9.3 Экспоненты; Квадрат против нормы в квадрате
9.4 Скалярный продукт не обязательно коммутативен
10 Дополнительные примечания
10.1  Подробнее об обозначениях
10.2 Коэффициенты c
11 Приложение: плоские волны
11.1 Бегущие волны
11.2 Соотношение фаз бегущей волны
11.3 Соотношение фаз стоячей волны
11.4 Изображение пространства-времени
12 Ссылки
2 Предварительный просмотр
Как мы увидим в разделе 5, уравнения Максвелла для электромагнитное поле может быть записано в удивительно компактном и элегантная форма:
∇ F =
1
c є ₀
6 (1)
где J вектор в пространстве-времени, представляющий заряд и ток, F — бивектор, представляющий электромагнитное поле. это стоит изучить формализм геометрической алгебры (также известной как алгебра Клиффорда) просто чтобы увидеть этот результат.
Также интересно применить принцип соответствия, посмотреть как это уравнение воспроизводит результаты, которые могут быть более знакомы в другие формы. Поэтому давайте сделаем шаг назад и повторим прозаическое непространственно-временная негеометрическая версия уравнения Максвелла.
3  Вектора
Мы начнем с записи уравнений Максвелла в терминах векторных полей в три измерения, а именно:
∇ · Е =
∇ × E =
c ² ∇ × B =
∇ · B = 0
             (2)
Эти уравнения имеют несколько глубоких симметрий. Мы можем сделать некоторые из симметрии более очевидны, сделав несколько поверхностных изменений. причины этого будут объяснены в данный момент.
9
∇ · E =
1
c є ₀
cρ
∇ × cB −   E
= 1
07
2 9
c є ₀
j
∇ · cB = 0
∇ × E + (3)
Эти уравнения инвариантны относительно вращений в трех Габаритные размеры. их явно инвариант , потому что они имеют был записан в векторной системе счисления. Мы еще не указали основу для трехмерного пространства, поэтому, если Алиса использует систему отсчета, которая то, что повернуто относительно системы отсчета Боба, уравнение 3 не только означает одно и то же для них обоих, оно выглядит так же, дословно.
Напротив, эти уравнения обладают релятивистской инвариантностью, т.е. Манифест , а не . Координата t появляется явно. Если Алиса использует систему отсчета, которая движется относительно системы отсчета Боба кадре, они не смогут договориться о значении t. Для этого материи, они не смогут договориться о значениях E-поля и B-поле.
Конечно, несогласие с координатами и несогласие с полями в конце концов отменяется, поэтому Алиса и Боб в конце концов договоритесь о том, что предсказывают уравнения, что произойдет физически.
Следовательно, уравнение 3 представляет собой промежуточный уровень изощренность: явная инвариантность относительно вращений, но неявная инвариантность по отношению к бустам.
При переходе от уравнения 2 к уравнению 3 мы добавили факторы c в стратегических местах. Это помогает составить уравнения более явно симметричны. Конкретно:
Везде, где появляется t, мы устроили так появляется ct, а не только t. Обоснование в том, что ct имеет те же размеры, что и x, y и z. Чтобы сказать то же самое с другой стороны, в пространстве-времени партнером x, y и z не является t. а скорее кт.
Точно так же партнером j является не ρ, а скорее cρ. В пространстве-времени cρ представляет собой определенное количество заряда, в одном пространственном положении и течет в будущее, тогда как j представляет заряд, перетекающий из одного пространственного положения в другое.
И последнее, но не менее важное: подходящим партнером для E является не B, а скорее КБ. В каждом месте, где появляется Б, мы устроили вещи, поэтому появляется комбинация cB, а не только B. Этот это просто упражнение в алгебраической перестановке, и оно не меняет смысл уравнений. Причина в том, что cB имеет те же размеры, что и у E, и расположение вещей таким образом делает уравнения более явно симметричны. (были предложения от Гаусс и другие рассматривают cB как «то самое» магнитное поле, но мы отказываемся от этого, так как это отклонялось бы от общепринятого значение терминов.)
Несколько дополнительных замечаний:
Уравнения Максвелла бесполезны без уравнения Лоренца. действующее законодательство, как обсуждалось в разделе 6.2.
Как всегда, µ ₀ є ₀ c ² = 1.
Эти уравнения верны в любой системе единиц, включая СИ среди прочих. (В некоторых системах единиц возможно сформулировать менее общие, но более компактные уравнения, возможно, установив c=1 и/или настройка 4πє ₀ =1. Эти компактные составы согласуются с уравнением 3. Они являются следствием уравнение 3 … а не наоборот. Мы будем придерживаться более общая формулировка в этом документе. Это немного меньше элегантный, но значительно более практичный. Также преобразование из более общую форму в какую-то менее общую форму значительно легче, чем порок наоборот Подробную информацию о единицах измерения и т. д. см. в ссылке 1 и ссылка 2. )
4  Компоненты
Мы можем построить еще менее сложное выражение, выбрав основе и выписав компоненты:
∇ _i E _i =
  є _ijk ∇ _j cB _k − E _i
=
1
C є ₀
j _i
  ∇ _i cB _i = 0
  є _ijk ∇ _j E _K+ CB _I
= 0
(4)
См. раздел 10.1 для получения информации об используемых обозначениях. здесь.
Выражение вещей в таких компонентах иногда удобно для вычислений, но скрывает инвариантность к вращению. Если Алиса использует систему отсчета, повернутую относительно системы Боба, они не смогут договориться о том, что означает x _i или что означает E _i. Конечно инвариантность к вращению все еще существует; оно просто стало непроявленным.
5 Электромагнетизм с использованием геометрической алгебры
Геометрическая алгебра (также известная как алгебра Клиффорда) имеет много преимущества, как обсуждалось в разделе 8. Оказывается, мы может записать уравнения Максвелла в легко запоминающейся форме
∇ F =
1
c є ₀
6 (5)
, который содержит все значение менее сложной версии, уравнение 3, как мы продемонстрируем через мгновение.
Преимущество этого выражения в том, что оно явно лоренцево. инвариант (включая повышения, а также вращения). Сравните это с уравнение 3, в котором лоренц-инвариантность не проявляется.
В целом, лучший подход — решать практические проблемы путем прямое обращение к уравнению 1. Некоторые примеры можно найти в раздел 11 и ссылка 3.
Однако это не основная цель данного документа. Вместо этого мы хотим вывести менее сложные уравнения Максвелла (уравнение 3) начиная с уравнения 1. Это можно считать тестом или применение принципа соответствия.
Для начала нам нужно установить соответствие между 3-мерный электрический ток j и соответствующий четырехмерный вектор текущий J. То есть,
J = c ρ γ ₀ + j ^k γ _k (6)
где мы выбрали систему отсчета, в которой γ ₀ , γ ₁ , γ ₂ и γ ₃ — ортонормированный базис векторы. В частности, γ ₀ — времяподобный базисный вектор. Мы см., что ρ имеет отношение к непрерывности потока заряда в направление раз , как обычный трехмерный ток j представляет собой течение в пространственноподобных направлениях. Видеть ссылка 4, чтобы узнать больше об идее сохранение и непрерывность потока.
Нам также нужно знать, как F связана с старомодные поля E и B. В любом конкретном кадре

Ф = (E + i cB) γ ₀

, где i — единичный псевдоскаляр (уравнение 45). Мы можем расширить это как:
F = E γ ₀   −  cB γ ₁ γ ₂ γ ₃
= E ^k γ _k γ ₀   −  cB ^k γ _k γ ₁ γ ₂ γ ₃
             (8)
где E ^k и B ^k — компоненты обычного электрического поля и магнитное поле, измеренное в выбранной нами системе отсчета.
Это уравнение имеет довольно интересную структуру. Это говорит нам, что мы следует рассматривать электромагнитное поле как бивектор. В любой В данном репере этот бивектор F имеет два вклада: один вклад представляет собой бивектор, имеющий одно ребро во времениподобном направлении, связанный с E, а другой вклад является бивектором имеющий оба ребра в пространственноподобных направлениях, связанных с cB.
Мы интенсивно используем центральную функцию Клиффорда. Алгебра, а именно умение умножать векторы. Это умножение подчиняется обычным ассоциативным и дистрибутивным законам, но не общий коммутативный. ¹ В частности, потому что наши базисные векторы γ _µ ортогональны, каждый из них антикоммутирует с остальными:
γ _µ γ _ν = – γ _ν γ _µ для всех µ ≠ ν (9)
и условие нормализации ² в D=1+3 требует знака минус во времениподобном составная часть:
γ ₀ γ ₀ = −1, γ ₁ γ ₁ = +1, γ ₂ γ ₂ = +1, γ ₃ γ ₃ = +1 (10)
Теперь все, что нам нужно сделать, это подставить уравнение 7 в уравнение 1 и поверните рукоятку.
Будет 12 терминов с участием E, потому что E состоит из трех компонентов Е ^k , а оператор производной имеет четыре компоненты ∇ ^µ . Точно так же будет 12 терминов с участием B.
+∇ ¹ E ^{1 +∇ ¹ E ¹} +∇ E ^{1 +∇ E ^{1 +∇ E ^{1. ¹ γ ₀ γ ₁ γ ₂}}}
∇ F = +∇ ⁰ E ¹ γ ₁ +∇ ¹ E ¹
   +∇ ³ E ¹ γ ₀ γ ₃ γ ₁
+∇ ⁰ E ² γ ₂    +∇ ¹ E ² γ ₀ γ ₁ γ ₂    +∇ ² E ² γ ₀    −∇ ³ E ² γ ₀ γ ₂ γ ₃
+∇ ⁰ E ³ γ ₃    −∇ ¹ E ³ γ ₀ γ ₃ γ ₁    +∇ ² E ³ γ ₀ γ ₂ γ ₃    +∇ ³ E ³ γ ₀

−∇ ⁰ cB ¹ γ ₀ γ ₂ γ ₃    −∇ ¹ cB ¹ γ ₁ γ ₂ γ ₃    −∇ ² cB ¹ γ ₃    +∇ ³ cB ¹ γ ₂
−∇ ⁰ cB ² γ ₀ γ ₃ γ ₁    + ∇ ¹ КБ ² γ ₃    −∇ ² cB ² γ ₁ γ ₂ γ ₃    −∇ ³ cB ² γ ₁
−∇ ⁰ cB ³ γ ₀ γ ₁ γ ₂    −∇ ¹ cB ³ γ ₂    +∇ ² CB ³ γ ₁ -∇ ³ CB ³ γ ₁ γ ₂ γ ₃
(11)
Давайте обсудим, что это значит. Начнем с девяти терминов выделен синим цветом. Шесть терминов, включающих cB, являются компонентами из ∇ × cB. Точно так же три члена, включающие E, являются компоненты +∇ ⁰ E, что совпадает с −(∂/c∂t) E. Каждый из этих членов включает ровно один из пространственноподобные базисные векторы (γ ₁ , γ ₂ и γ ₃ ), поэтому мы имеем дело со старым добрым вектором в пространстве D=3. RHS уравнение 1 имеет вектор, который соответствует этому, а именно D=3 плотность тока. Таким образом, синие термины говорят нам, что ∇ × cB − (∂/c∂t) E = (1/cє ₀ ) j, что хорошо согласуется с уравнением 3.
Далее рассмотрим девять членов, выделенных красным. Шесть терминов с участием E являются компонентами ∇ × E. Аналогично, три члена, включающие cB, являются компонентами −∇ ⁰ cB, т.е. то же, что +(∂/c∂t) cB. Эти девять терминов — все тривекторы с проекцией во времениподобном направлении (γ ₀ ). Поскольку в правой части уравнения 1 нет тривекторных членов, мы должны заключить, что сумма этих красных членов равна нулю, т. е. ∇ × E + (∂/c∂t) cB = 0, что также согласуется с уравнение 3.
Три черных члена, включающих букву E, совпадают с фигурой, похожей на время J и скажите нам, что ∇ · E = (1/є ₀ ) ρ. Три черных термины, включающие cB, говорят нам, что ∇ · cB = 0. ³
Позвольте мне сказать несколько слов о том, как это было рассчитано. Это действительно было совершенно механически, просто следуя формализму. Рассмотрим термин +∇ ² cB ³ γ ₁ в последней строке. Мы начали с выражение ∇ F, имеющее два множителя, поэтому рассматриваемый термин будет иметь два множителя: ∇ ² γ ₂ и −cB ³ γ ₃ γ ₁ γ ₂ γ ₃ , что объединить, чтобы получить −∇ ² γ ₂ cB ³ γ ₃ γ ₁ γ ₂ γ ₃ . Все, что нам нужно сделать, это переставьте векторы γ, чтобы привести это к стандартной форме. Потяните скаляры на передний план и переставляем первые два вектора с помощью уравнение 9, чтобы получить +∇ ² cB ³ γ ₃ γ ₂ γ ₁ γ ₂ γ ₃ . Переставить снова чтобы получить −∇ ² cB ³ γ ₃ γ ₁ γ ₂ γ ₂ γ ₃ что сокращает использование уравнение 10 до −∇ ² cB ³ γ ₃ γ ₁ γ ₃ . Затем еще один перестановка и еще одно сокращение, и дело сделано.
Единственная часть, которая требовала принятия решения, это запись γ ₀ γ ₃ γ ₁ в местах, где я мог бы написать −γ ₀ γ ₁ γ ₃ . Это только косметика; это заставляет знаки попадать в красивый узор, так что это легче чтобы увидеть соответствие со старомодным перекрестным произведением. Мы может сделать это более элегантным и менее произвольным, если мы скажем правило состоит в том, чтобы записать все псевдовекторы, используя базис {i γ _µ для µ=0,1,2,3}, где i – единичный псевдоскаляр (уравнение 45).
После того, как вычисления были сделаны, решение о том, как раскрасить термины, заняло некоторое суждение, но незначительное, потому что термины естественным образом разделяются по мере того, как векторы и тривекторы, пространственноподобные и времениподобные.
6  Заряд, сила и энергия
6.1 Сохранение заряда
Предварительный просмотр: Наша цель — доказать, что заряд сохраняется, т. е. что ∇·J=0. Мы не собираемся предполагать сохранение; мы собирается доказать, что сохранение уже гарантировано как следствие уравнения 1, уравнения Максвелла. Мы сделаем что, взяв расхождение обеих частей уравнения.
Предыстория: нам понадобится математическая лемма, которая утверждает дивергенция дивергенции бивектора всегда равна нулю. Чтобы вывести Для этого рассмотрим произвольный бивектор W. Предположим временно, что W представляет собой простую лопасть, т. е. W = a γ ₅ γ ₆ . Тогда расхождение равно
∇ · W = ∇ · a γ ₅ γ ₆                    90 0006
70006
= ⟨∇ a γ ₅ γ ₆ ⟩ ₁
= ∇ ⁵ γ ₅ a γ ₅ γ ₆ + ∇ ⁶ γ ₆ a γ ₅ γ ₆
= ∇ ⁵ a γ ₆ − ∇ ⁶ a γ ₅
             (12)
, где во второй строке мы использовали общее правило, что точка продукт является низкокачественной частью полного геометрического продукта. На В последней строке мы временно предположили, что γ ₅ и γ ₆ равны пространственноподобны, но мы увидим, что это допущение излишне.
Возьмем теперь дивергенцию дивергенции.
∇ · (∇ · W) = ∇ · (∇ ⁵ a γ ₆ − ∇ ⁶ a γ ₅ )
= ⟨∇ (∇ ⁵ a γ ₆ − ∇ ⁶ a γ ₅ )⟩ ₀
= ∇ ⁶ γ ₆ ∇ ⁵ а γ ₆ − ∇ ⁵ γ ₅ ∇ ⁶ a γ ₅
= ∇ ⁶ ∇ ⁵ a − ∇ ⁵ ∇ ⁶ а
= 0
             (13)
В последней строке мы использовали тот факт, что различные компоненты операторы градиента коммутируют друг с другом.
Теперь мы отказываемся от предположения, что наши базисные векторы времениподобны. Ты следует проверить, что на самом деле не имеет значения, являются ли γ ₅ и γ ₆ пространственноподобны или времениподобны. Подсказка: более полный расчет даст нам:
∇ · (∇ · W) = ∇ ⁶ ∇ ⁵ a γ ₅ ² γ ₆ ² − ∇ ⁵ ∇ ⁶ a γ ₅ ² γ ₆ ²
=
5
5
             (14)
Теперь отменим предположение, что W — лезвие. По дистрибутиву закону, если ∇·(∇·W) равно нулю для любого лезвия класса = 2, это равен нулю для любой суммы таких лопастей, т. е. для любого бивектора вообще. Мы заключить во всей общности:
∇ · (∇ · W) = 0      (для любого бивектора W)
             (15)
В качестве другой леммы для любого бивектора всегда можно написать
0005
∇W = ⟨∇W⟩ ₁+⟨∇W⟩ ₃
=
∇·W + ∇∧W
             (16)
Это позволяет нам разделить ∇F следующим образом:
(17а)9
∇F = ∇·F + ∇∧F
6
∇·F =
1
C є ₀
J
9 (17б) ∇∧F = нечто      (во всей общности)      (17с) = 0      (при условии отсутствия монополий)      (17д)
Для целей этого раздела все, что нам нужно, это уравнение 17b. Это класс = 1 часть Максвелла уравнение. Нам не нужно предполагать отсутствие монополий. Нам не нужно ничего знать о тривекторной части Уравнение Максвелла. Нам не нужно уравнение 17d или даже уравнение 17c.
Используя нашу лемму (уравнение 15), мы можем записать
∇ · J = Cє ₀ ∇ · (∇ · F)
= 00006 = 00005 = 00006
             (18)
Разумеется, мы используем четырехмерное расхождение. Нуль дивергенция выражает непрерывность мировых линий в пространстве-времени. За объяснение того, почему это правильный способ выразить идею сохранение с точки зрения непрерывности потока, см. ссылку 4.
6.2  Закон силы Лоренца
Как отмечалось выше, наша теория электромагнетизма была бы неполной. без закона силы Лоренца.
Старомодный способ записи закона силы Лоренца:
p = q(E + × cB) (19)
где p — импульс, q — заряд, v — заряд. обычная трехмерная скорость.
Как и практически любое уравнение с перекрестными произведениями, уравнение 19можно улучшить, переписав его с помощью геометрического Алгебра вместо:
p = q u · F (20)
где τ – собственное время, u = dx/dτ является 4-мерным собственным скорость, ⁴ p = m u — импульс, m — инвариантная масса. Здесь p и u — векторы в пространстве-времени D=1+3. Это релятивистски правильное обобщение уравнение 19.
Уравнение 20, в отличие от предыдущих уравнений, включает точку товар. В частности, он включает скалярное произведение вектора с бивектор. Такие вещи не так просто вычислить, как точку. произведение между двумя векторами, но их по-прежнему достаточно легко вычислить. вычислить в терминах геометрического произведения. В общем, точка продукт является частью самого низкого качества полного геометрического продукта, так как обсуждалось в ссылке 5. В случае вектора с точками бивектора, имеем:
A · (B∧C) = ⟨A (B∧C)⟩ ₁
= ½⟨ABC – ACBB⟩ ₁ .
             (21)
Это означает, что мы просто формируем геометрическое произведение и выбрасываем все, кроме оценки = 1 часть. Другой способ обращения с «vector dot bivector»:
A·(B∧C) = (A·B)C − (A·C)B
             (22)
, который можно считать своего рода «распределительным законом» для распределение точечного оператора по клиновому оператору. Уравнение 22 говорит нам, что произведение A·(B∧C) является вектор, лежащий в плоскости, натянутой на B и C.
Следующие примеры полезны для проверки правильности из предыдущих уравнений:
γ ₁ ·(γ ₁ ∧γ ₁ ) = 0
γ ₁ ·(γ ₁ ∧γ ₂) = γ ₂
γ ₂ · (γ ₁ ∧γ ₂65).
γ ₃ ·(γ ₁ ∧γ ₂ ) = 0
             (23)
Чтобы сказать то же самое в геометрических (а не в алгебраических) терминах, вы может визуализировать произведение вектора на бивектор как следующим образом:
Отбросить компонент вектора, перпендикулярный к плоскости бивектора. Держите проекцию в самолет.
Результат (скалярное произведение) будет в плоскости и перпендикулярно проекции. Его длина будет равна величине бивектор, умноженный на величину проекции.
Пример закона Лоренца в действии показан на рисунок 1, для случая электромагнитного поля бивектор (F), однородный в пространстве, ориентированный чисто в плоскости бумаги. Показанная на рисунке циклотронная орбита соответствует движение положительного пробного заряда с некоторой начальной скоростью, свободное сил, отличных от указанного электромагнитного поля.
Рисунок 1. Закон Лоренца
Этот результат легко понять. Если частица движется в направлении красного вектора, он испытает сила в синем направлении. Если частица движется в синем направлении, на нее будет действовать сила, противоположная красной направление.
Подводя итог: магнитная часть закона силы Лоренца равна очень легко запомнить:
Бивектор поля в плоскости бумаги
приводит к циклотронной орбите в плоскости бумаги.
На движение, перпендикулярное бивектору поля, поле не влияет.
Вышеизложенное применяется, если поле F уже выражено в современных термы, как бивектор. Теперь, в духе этого документа, мы пересматриваем ситуацию, чтобы продемонстрировать соответствие между идеей бивектора и старомодные идеи, такие как вектор электрического поля и псевдовектор магнитного поля.
Бивектор, показанный на рисунке 1, является чисто пространственным, поэтому он должно соответствовать магнитному полю, электрическое поле в нашем случае отсутствует. точка зрения. Псевдовектор магнитного поля перпендикулярен в газету, направлено из газет. Вы можете проверить с помощью правило правой силы, что циклотронная орбита, показанная на рисунок 1 верен для положительного пробного заряда, движущегося в такое магнитное поле.
Забавно проверить общий случай, для любого F, который известен в термины старомодного вектора электрического поля и магнитного поля псевдовектор, как в уравнении 7 или уравнении 8. Как предложенное уравнением 20, мы должны взять скалярное произведение u с обеими частями нашего выражения для F. Соответствие принцип предполагает, что мы должны восстановить старомодный 3-вектор вариант силового закона, т. е. уравнение 19. Выполнить скалярного произведения, мы могли бы просто повернуть рукоятку… но на самом деле мы вряд ли нужно делать какую-либо работу вообще. Скалярный продукт в u · F использует подмножество полного геометрического произведения u F, а именно плоскость векторные (оценка=1) условия. См. уравнение 18 в ссылке 6. Мы можно избежать некоторой работы, потому что u F имеет ту же структуру, что и ∇ F – это просто геометрическое произведение некоторого вектора на F – так что мы можно просто повторно использовать уравнение 11, заменив ∇ на u везде. Тогда мы отбрасываем все тривекторные члены, и что остается точечный продукт.
В нерелятивистском пределе времениподобная составляющая скорости равно единице плюс пренебрежимо малые члены более высокого порядка. Итак, синие термины в уравнении 11 дают нам обычное уравнение Лоренца для пространственноподобные компоненты изменения импульса: 1 E + v × B.
Черные члены, включающие E, дают нам бонус: они сообщают нам мощность (т. е. скорость работы, т. е. производная по времени кинетической энергия), а именно v · E.
6.3 Плотность лагранжиана
Рассмотрим горм электромагнитного поля, а именно горм(F) ≡ ⟨FF ^{^∼} ⟩ ₀ . Вы можете легко подтвердите это:
⟨FF ^{^∼} ⟩ ₀ = (cB) ² – E ² (24)
Это скаляр, лоренц-инвариантный скаляр. Это полезно в количество способов, не последним из которых является тот факт, что −є ₀ ((cB) ² − E ² ) – плотность лагранжиана для электромагнитное поле.
6.4 Вектор Пойнтинга
Давайте продолжим искать выражения, связанные с энергией, включающие F. Раздел 6.3 дает нам подсказку, где искать; лагранжева плотность — это не «эта» плотность энергии, а ее меньше всего имеет размерность плотности энергии.
Из старомодного электромагнетизма мы знаем, что должен существовать плотность энергии, которая соответствует квадрату напряженности поля. Этот говорит нам о количестве энергии на единицу объема. По старинке В терминах плотность энергии равна ½ є ₀ (E ² + c ² B ² ).
Существует также вектор Пойнтинга, который сообщает нам количество энергии расход на единицу площади поверхности в единицу времени. В старомодными терминами, это c є ₀ E×cB. .
Итак, без дополнительной мотивации, мы используем задним числом 20/20, чтобы утверждать, что F γ ₀ F будет интересно. Следуя духу этого документ, давайте проверим это утверждение, вычислив F γ ₀ F с точки зрения старомодных полей E и B, и видя, что мы получить. Подставляем вместо F уравнение 7 и превращаем рукоятка:
99999999999999999999999999999969 9000 +E ^K9 9000 +. 0365   γ _j −  γ _j   γ _k ) γ ₁ γ ₂ γ ₃
F γ ₀ F = (E ^k γ _k γ ₀   −  cB ^j γ _j γ ₁ γ ₂ γ ₃ ) γ ₀ (E ^k γ _k γ ₀   −  cB ^j γ _j γ ₁ γ ₂ γ 3 ₎
= E ^k γ _k γ ₀ γ ₀ E ^j γ _j γ ₀
− E ^k γ _k γ ₀ γ ₀ cB ^j γ _j γ ₁ γ ₂ γ ₃ − cB ^k γ _k γ ₁ γ ₂ γ ₃ γ ₀ E ^j γ _j γ ₀
+ cB ^k γ _k γ ₁ γ ₂ γ ₃ γ ₀ cB ^j γ _j γ ₁ γ ₂ γ ₃
= − E ^k γ _k E ^j γ _j γ ₀
+E ^K γ _K CB ^J γ _J γ ₁ γ ₂ γ ₁ γ ₂ γ ₁ γ ₂ γ ₁ γ ₂ γ ₁ γ ₂ γ ₁ γ ₂ γ ₁ γ ₂. − cB ^k γ _k γ ₁ γ ₂ γ ₃   E ^j γ _j
+ cB ^k γ _k γ ₁ γ ₂ γ ₃ cB ^j γ _j γ ₁ γ ₂ γ ₃ γ ₀
= − E ^k γ _k E ^j γ _j γ ₀
+E ^K γ _K CB ^J γ _J γ _{J γ _J γ _{1 γ _J γ _{9 γ _J γ ₁ γ _j γ _{j γ _J γ _{j .
− cB ^j γ _j γ ₁ γ ₂ γ ₃   E ^k γ _k}}}}}
− cB ^k γ _k cB ^j γ _j γ ₀
= – E · E γ ₀
+E ^K
− c ² B·B γ ₀
= − (E·E + c ² B·B) γ ₀
− 2 (E×cB ) ^к γ _к
             (25)
При переходе со второй строки на третью мы использовали тот факт, что (γ ₀ ) ² = −1. Мы также использовали тот факт, что γ ₀ γ _k = − γ ₀ γ _k для всех k ∈ {1,2,3}. С другой стороны, (γ ₁ γ ₂ γ ₃ )γ _k = +γ _k (γ ₁ γ ₂ γ ₃ ). То есть, когда мы ездим γ _к по трем факторам в (γ ₁ γ ₂ γ ₃ ), мы берем только два множителя −1, а не три, так как для одного из факторы, индекс этого фактора будет соответствовать индексу k, и γ _k, очевидно, коммутирует сам с собой.
На следующем этапе мы использовали тот факт, что (γ ₁ γ ₂ γ ₃ ) ² = −1. Мы также изменили некоторые фиктивные индексы.
Итак, мы видим, что нас особенно должно интересовать количество
T(γ ₀ ) := −½ є ₀ F γ ₀ F
=
є ₀ ⎡
⎢
⎢
⎢
⎣
(E ²+C ² B ²)/2
(E ).0004 (E×cB) ₂
(E×cB) ₃
⎤
⎥
⎥
⎥
⎦
             (26)
Пространственная часть T(γ ₀ ) старомодна. трехмерный вектор Пойнтинга (кроме отсутствующего множителя c), а времяподобная компонента представляет собой соответствующую энергию плотность.
Хотя это T(γ ₀ )-вектор имеет четыре компонента, это не хорошо себя лоренц-ковариантный четырехвектор. На самом деле это только один столбец объекта 4 × 4, а именно тензор энергии-импульса, T. Записав T(γ ₀ ) через E и B (как во второй строке уравнения 26) имеет смысл только в той системе отсчета, где E и B определены. Кроме того, если вы хотите подключить T(γ ₀ ) вектору Пойнтинга в данной системе отсчета, γ ₀ не может быть любым базисный вектор, но должен быть 4-скоростью самой системы отсчета, т.е. единичный вектор в направлении времени в данном кадре.
В более общем смысле количество
T(a) := −½ є ₀ F a F (27)
представляет поток [энергии, импульса] через гиперповерхность перпендикулярно вектору а. Более общий взгляд на это представлено в разделе 6. 5.
6.5 Тензор энергии-импульса
Тензор энергии-импульса T для электромагнитного поля (в вакуум) имеет следующие матричные элементы:
T _µν = F γ _µ F γ _ν              (28)
для любого набора базисных векторов {γ _{µ }} Уравнение 26 и уравнение 27 можно понимать как частные случаи уравнение 28.
7 Векторный потенциал
7.1 Основная идея
В четырех измерениях бивектор электромагнитного поля F всегда может быть записана как внешняя производная квазивекторного потенциала А. И наоборот, мы можем интегрировать электромагнитное поле, чтобы найти разность потенциалов между точкой P и точкой Q.
F = DA
= ∇∧A
             (29)
Это неявно определяет, что мы подразумеваем под А. Однако А не является определяется однозначно, как обсуждалось в разделе 7.3. Более того, даже хотя A выглядит так, как будто это четырехвектор, это не так.
7.2 D=3 по сравнению с D=4
В электростатике в любой выбранной системе отсчета электрическая поле всегда можно записать как производную некоторого потенциала ϕ. Этот ϕ называется скалярным потенциалом или электростатический потенциал.
И наоборот, вы всегда можете интегрировать электростатическое поле, чтобы найти разность потенциалов между любыми двумя точками.
В нестатических ситуациях в трех измерениях электрическое поле в общем случае не может быть записан как производная любого скаляра потенциал. В частности, рассмотрим электрическое поле внутри бетатроне, или в обычном трансформаторе, или в контуре заземления, или в радиоволна. Лоток E отличен от нуля:
∇×E ≡ *(∇∧E)     [in D=3]
≠ 0     [when the magnetic поле меняется]
             (30)
Достаточно доказать, что:
Е ≠ ∇ϕ      для любого ϕ     [при изменении магнитного поля]
             (31)
Это говорит нам о том, что любая попытка интегрировать E для нахождения скаляра разность потенциалов между точкой P и точкой Q не пройдёт; в интеграл будет зависеть от пути из P в Q, а не только от конечные точки.
Также, сколько стоит:
9003 =
E ≠ ∇∧ϕ      для любого ϕ      заряд      присутствует заряд
             (32)
Электростатический потенциал несколько связан с векторным следующим образом: Внешне привлекательно писать:
☠     А = [ϕ/c, A _x, A _Y, A _Z] (потенциал Four-Vector-Ish) (Четырех-вектор) (33а)
☠      ϕ = c A ₀
90 005 0 0 6 (33б)
Однако имейте в виду, что уравнение 33a — это мошенничество, потому что оно определяет объект, который не четырехвектор. Он имеет четыре компонентов, но этого недостаточно, чтобы сделать его хорошо себя 4-вектор. Он не ведет себя должным образом по отношению к Лоренцу преобразования.
Это не трагедия, потому что потенциалы не наблюдаемый. Единственное, что имеет значение, это отличие от . между двумя потенциалами, и это оказывается хорошим поведением для по следующей причине:
Грубо говоря, если вы начинаете с векторного потенциала в определенного калибра, а затем перейти к другой системе отсчета, вы получите векторный потенциал с тем же физическим смыслом г. в некоторых другой винтообразный калибр . Если вы попытаетесь вычислить A, оценив его в один кадр, а затем преобразовать его в другой кадр, вы почти конечно, получите неправильное значение для A. Однако, когда вы вычисляете любое физически наблюдаемый, датчик выпадает, так что вы можете в конечном итоге с правильная физика.
В частности, ключевое уравнение 29 в порядке. электромагнитное поле F является хорошим бивектором. Внешний вид производная на правой стороне аннулирует все без исключения калибровочные поля.
В любом случае, если вы выберете конкретную систему отсчета и конкретной калибровке, то вы можете думать о ϕ/c как о времяподобная компонента A.
В этот момент вы должны спросить себя, как можно ∇∧(поле) не равно нулю в трех измерениях, но равно нулю в четыре измерения? Как это не нарушает переписку принцип? Как это не противоречит утверждению, сделанному в ссылке 7, что пространство-время Минковского очень и очень похоже на Евклидово пространство?
Ответ заключается в том, что когда мы переключаемся с трех измерений на четыре, мы переопределить среднее через «поле», «потенциал» и «клин» товар. В четырех измерениях внешняя производная вектора имеет больше терминов. Используя принцип соответствия, мы можем объяснить это с точки зрения старых полей E и B следующим образом: когда мы вычислить ∇∧F, производную по времени B-компоненты отменяет пространственные производные Е-компоненты.
Это ловушка для неосторожных. Не позволяйте вашему опыту с D=3 отравить свою интуицию насчет D=4. Рассмотрим контраст:
В D=3 важно помнить, что «поле» (E) вообще говоря, не является производной какого-либо потенциала. В D=4 мы можем всегда пишите «поле» (F) как F = dA.
Для некоторых задач существует естественная система отсчета, которая имеет огромное практическое значение. Для некоторых задач можно Фрейм-независимый пространственно-временной подход прост, удобен, мощен, и элегантный.
Например, если вы имеете дело с трансформаторами или контурами заземления, вам очень заботятся об электрическом поле в корпусе устройства. тот факт, что это поле нельзя записать как градиент какого-либо потенциал важен. См. ссылку 8 для предложений по как визуализировать происходящее.
7.3 Калибровочная инвариантность
Векторный потенциал неявно определяется уравнением 29. Однако для любого заданного поля F вы не знаете является ли векторный потенциал A или A + λ′, поскольку мы можно написать:
F = ∇∧(A + λ′)
             (34)
для любого векторного поля λ′ такого, что
∇∧λ′ = 0
             (35)
В частности, мы можем использовать градиент любого скалярного поля λ:
λ′ = ∇λ
             (36)
, который гарантированно сработает, поскольку ∇∧∇(что угодно) автоматически ноль. Остерегайтесь непоследовательной терминологии: Иногда λ называется «калибровочным полем», а иногда λ′ называется калибровочным полем.
7.4  Уравнение Максвелла в терминах векторного потенциала
Тот факт, что мы можем записать бивектор электромагнитного поля в виде производная векторного поля связана с отсутствием тривекторные члены в правой части уравнения Максвелла (уравнение 1). В частности, поскольку ∇ — вектор, мы всегда можем напишите:
∇F = ∇·F (Vector Piece)
+ ∇∧F (Piect Trivector)
(37) (37) (37) (37).
Уравнение 37 – математическое тождество, действительное для любого F, который вы можете придумать. Применив его к электромагнитному поля, в частности, и подставляя уравнение 29, мы получить:
∇F = ∇·∇∧A      (vector piece)
+ ∇∧∇∧A      (трещотка)
             (38)
Итак, мы не могли бы написать F = ∇∧A, если бы не знали, что ∇∧F было нулем, так как ∇∧∇∧A автоматически ноль. Действительно, ∇∧∇∧(что угодно) есть автоматически обнуляется; см. уравнение 17.
Объединив эти идеи, мы видим, что другой способ записи Уравнение Максвелла:
∇·∇∧ A =
1
c є ₀ 9J 1 1 (39)
или аналогичный:
∇ ² A =
1
c є ₀
Дж (40)
были ∇ ² называется даламберовской или (эквивалентно) четырехмерный лапласиан. Это точечный продукт производной оператор сам с собой.
В некоторых ссылках одна и та же идея выражается другим символом:
□ ² A =
1
c є ₀
Дж (41)
Остерегайтесь, что в других ссылках используется простой неквадрат □ для представляют Даламбера. По идее они резервируют ∇ ² для представления трехмерного лапласиана и используйте □ ² для представляют собой четырехмерное обобщение. Однако в этом документ, мы предполагаем, что все векторы четырехмерны, если только иное не указано; например, p – четырехимпульс, A – четырехвекторный потенциал, ∇ — четырехмерный градиент, et так далее.
8 Геометрическая алгебра. Общие замечания
8.1 Обзор
Геометрическая алгебра имеет ряд огромных преимуществ. Он обеспечивает унифицированный вид внутренних продуктов, внешних продуктов, D = 2 Flatland, D = 3 пространство, D=1+3 пространство-время, векторы, тензоры, комплексные числа, кватернионы, спиноры, вращения, отражения, повышения и многое другое. Этот может показаться слишком хорошим, чтобы быть правдой, но это действительно работает.
Если вам нужно введение в геометрическую алгебру, см. ссылка 9, ссылка 10 и другие ссылки в раздел 12. Так же, как я не включил вводное обсуждение операторов дивергенции и скручивания в уравнении 3, я не буду включить вводное обсуждение геометрической алгебры здесь. Есть Нет смысла дублировать то, что есть в ссылках. Особенно, ссылка 10 обсуждает электромагнетизм с использованием D = 3 Clifford Алгебра, которой легче следовать, чем обсуждение D=4 здесь, но результаты не такие простые и элегантные, как уравнение 1. расчет здесь хоть и не особо сложен, но и не претендует быть совсем элементарным.
8.2  Без украшений
В геометрической алгебре принято не различать векторы с помощью полужирный шрифт или другие украшения. Это целесообразно, поскольку Алгебра Клиффорда оперирует мультивекторами и рассматривает все мультивекторы практически одинаково. Мультивекторы могут быть скалярами, векторами, бивекторами, псевдовекторами, псевдоскаляры — или линейные комбинации вышеперечисленных.
8.3  Без перекрестного произведения
Обратите внимание, что в уравнении 1 нет оператора перекрестного произведения. или уравнение 20. Это хорошо. Кросс-произведения – это проблема. Они не существуют в двух измерениях, они хуже, чем бесполезны в четырех измерениях, и даже не на 100% заслуживают доверия в трех измерениях. Габаритные размеры. Например, рассмотрим вращающийся объект и его вектор углового момента r × p. Если вы посмотрите на объект в зеркало, вектор углового момента обратный. Вы не можете нарисовать изображение вращающегося объекта и его вектор углового момента и ожидать, что изображение будет инвариантным относительно отражений.
Насколько я могу судить, каждая физическая формула, включающая векторное произведение можно улучшить, переписав его, используя вместо этого продукт клина.
Для вращающегося объекта векторное произведение r × p является вектором ориентированы по оси вращения, а клиновое изделие r ∧ p — площадь, ориентированная в плоскости вращения. Понятие «ось вращения» не переносимо на D=2 или D=4, но концепция «плоскости вращения» прекрасно работает во всех измерениях.
Если вы думаете, что перекрестные произведения — это проблема, подождите, пока вы не увидите Эйлера углы. Они определяются только по отношению к конкретному базису. Жалко представлять вращения так, как это не вращательно инвариант. Геометрическая алгебра исправляет это.
8.4 Нет хиральности
Обратите внимание, что алгебра Клиффорда не требует правила правой руки. В уравнение 10, времениподобный вектор отличается от пространственноподобный вектор, но в противном случае это уравнение и уравнение 9 одинаково относиться ко всем базисным векторам; переименование или их повторный заказ не имеет значения.
В D=3 или D=1+3 единичный псевдоскаляр (уравнение 45) является киральным; то есть для его построения требуется правило правой руки. Аксиомы Алгебра Клиффорда иногда допускает, но никогда не требует построения такой твари. Законы электромагнетизма полностью левый/правый симметричный. Магнитный член в уравнении 7 содержит B, который является хиральным, потому что он был определен с помощью старомодного перекрестное произведение … но тот же термин содержит множитель i, который делает общее выражение симметричным влево/вправо. Было бы лучше записать магнитное поле как бивектор для начала (как в ссылка 3), поэтому уравнения проявят внутренняя левая/правая симметрия физических законов.
8.5 Несколько подходов
Существует три разных подхода к определению F-подобного количество как часть формулировки геометрической алгебры электромагнетизм.
Подход бивектор + бивектор, используемый здесь, например, в уравнение 7.
Метод вектор + аксиально-векторный, как используется, например. в ссылка 10.
Скалярно-векторный подход, используемый в например ссылка 11.
Каждый подход непротиворечив, и большинство уравнений, таких как уравнение 1, одинаковы во всех системах.
Преимущество бивекторного + бивекторного подхода заключается в том, что он дом в пространстве-времени», т. е. рассматривает x и t одинаково, и относится к B и E одинаково (насколько это возможно). Это позволяет легко и интуитивно рисовать бивекторные диаграммы сортировка, используемая в ссылке 3.
9  подводных камней, которых следует избегать
9.1 Определение скалярного произведения
Возможно, вы привыкли расширять скалярное произведение как
А·Б  ?=? А ₁ B ₁ + A ₂ B ₂ + A ₃ B ₃ (42)
как будто это определение скалярного произведения. .. но это не то определение, и вы получите неверный ответ, если попробуете соответствующая вещь в неевклидовом пространстве, таком как пространство-время. Так что вы должны сделать вместо этого, чтобы расширить
A = A ^µ γ _µ = A ⁰ γ ₀ + A ¹ γ ₁ + А ² γ ₂ + А ³ γ ₃ (43)
, где γ _µ — базисные векторы. Такое расширение является всегда легально. Именно это определяет компоненты A ^µ . верхние индексы на A обозначают компоненты A; они не экспоненты. Нижние индексы у γ не указывают компоненты; они просто обозначают, о каком из базисных векторов идет речь. Это возможно, но не особенно полезно думать о γ ₀ как нулевая компонента некоторого «вектора векторов»; на всякий случай помни что γ ₀ является вектором самому себе.
Когда вы берете скалярное произведение A·B, разложение уравнение 43 (и аналогичное расширение для B) дает вам шестнадцать членов, так как скалярное произведение распределяется по дополнение обычным способом. Двенадцать недиагональных членов исчезают, поскольку они включают в себя такие вещи, как γ ₁ .γ ₂ и базис векторы взаимно ортогональны. Итак, нам остается
А·Б = A ⁰ B ⁰ γ ₀ .γ ₀+A ¹ B ¹ γ _{.
+ A ² B ² γ ₂ .γ ₂ + A ³ B ³ γ ₃ .γ ₃}
= − А ⁰ Б ⁰+A ¹ B ¹+A ² B ²+A ³ B ³
(44)
, где член A ₀ B ₀ имеет знак минус, потому что γ ₀ ² равно -1.
9.2 Псевдоскаляр единиц
Еще одна вещь, на которую следует обратить внимание при чтении геометрической алгебры литература касается использования символа я для единицы псевдоскаляр:
i := γ ₀ γ ₁ γ ₂ γ ₃ (45)
Хорошо иметь символ для единицы псевдоскаляра, и выбор i обладает некоторыми интригующими свойствами, вытекающими из того факта, что i ² = −1, но есть ловушка: у вас может возникнуть соблазн рассматривать i как скаляр, но это не так. Скаляры коммутируют со всем, тогда как это i антикоммутирует с векторами (и всеми мультивекторами нечетной степени). Это коварным, потому что в D=3 единичный псевдоскаляр коммутирует с все. По этим причинам мы в основном избегали использования i в Основная часть этой заметки.
9.3 Экспоненты; Квадрат в сравнении с нормой в квадрате
Логическая непротиворечивость требует, чтобы при использовании надстрочных индексов в качестве степени, они должны обозначать простые степени:
M ² := MM
M ³ := MMM
etc.
             (46)
для любого многовекторного M. Однако наблюдается неблагоприятная тенденция для некоторых авторов писать M ², когда они имеют в виду MM ^{^∼}, где M ^{^∼} — это , обратное числа M, образованное записью в обратном порядке. упорядочить все векторы, составляющие M; например обратная сторона уравнение 7 говорит нам, что F ^{^∼} = γ ₀ (E+cBi).
Это коварно, потому что для скаляров и векторов MM ^{^∼} = MM; различие важно только для объектов класса 2 и выше.
Я рекомендую писать MM ^{^∼} всякий раз, когда вы имеете в виду MM ^{^∼} . Много авторы испытывают искушение придумать для этого стенографию — возможно, М ² , |М| ² , или ||М|| ² – но по моему опыту такие вещи гораздо больше проблем, чем они стоят. Вам нужно быть особенно осторожны в случае, когда задействованы времениподобные векторы, поскольку мм ^{^∼} вполне может быть отрицательным. В таком случае любое обозначение, которое предполагает, что MM ^{^∼} является квадратом чего-либо просто просит беда.
Родственная и очень важная идея – горм объекта М, определяется как скалярная часть MM ^{^∼} , т. е. ⟨MM ^{^∼} ⟩ ₀ . (Мы видели хороший физический пример, а именно горм электромагнитного поля, в разделе 6.3.)
9.4 Скалярное произведение не обязательно коммутативно
Скалярное произведение вектора на бивектор является антикоммутативным, так что будьте осторожны, когда пишете закон силы Лоренца:
u · F = − F · u (47)
Это коварно, потому что скалярное произведение коммутативно при действии на двух векторах или на «почти» любой комбинации мультивекторов. Это антикоммутативны только в тех случаях, когда один из них имеет нечетную степень, а у другого крупнее даже комплектация. То есть, в общем,
A · B = (−1) ^{мин(r,s)|r−s|} Б · А (48)
, где r — степень A, а s — степень B. Это результат может показаться несколько нелогичным, но это легко доказать; сравните уравнение 22 в ссылке 6.
10  Дополнительные примечания
10.
1  Подробнее об обозначениях
Вы можете думать о x ₁ как о направлении X, x ₂ как Y-направление и x ₃ как Z-направление, но для большинства целей мы предпочитаем обозначение {x ₁ x ₂ x ₃ } вместо обозначения {X Y Z}. Мы будем использовать x ⁰ и t почти взаимозаменяемо. Есть неустроенные вопросы о t по сравнению с ct, как обсуждалось в разделе 10.2.
Мы используем правило суммирования Эйнштейна, которое требует подразумеваемое суммирование по повторяющимся фиктивным индексам, так что, например.
∇ _k E _k := ∇ ₁ E ₁ + ∇ ₂ E ₂ + ∇ _{6 4 3} (49)
Индексы с латинскими буквами проходят через значения 1,2,3, а индексы с греческими буквами индексы переходят значения 0,1,2,3.
По определению того, что мы подразумеваем под компонентом, мы можем расширить ∇ оператор по компонентам
∇ = ∇ ^мкм γ _мкм (50)
Естественно ∇ ¹ = (∂/∂x ¹ ) и аналогично для x ² и x ³ , но вы должны быть осторожны со знаком минус в
∇ ⁰ = −(∂/∂x ⁰ ) (51)
Обратите внимание, что уравнение 50 выражает вектор через компоненты, умноженные на базисные векторы, в отличие от уравнения 51 который выражает только один компонент.
Вот как мне нравится запоминать, куда идет знак минус. Представьте себе скалярное поле f(x), т. е. некоторый безразмерный скаляр как функция положения. Позиции измеряются в дюймах. Длина вектор градиента ∇f равен , а не измеряется в тех же единицах, что и длина векторов положения. На самом деле он будет иметь размеры обратное дюймов. Так что в этом духе мы можем написать
∇ = + + + (52)
Мы можем легко вычислить обратные величины γ _µ векторов в соответствии с уравнением 10, в результате чего:
∇ = − γ ₀ + γ ₁ + γ ₂ + γ ₃ (53)
, которое имеет решающий знак минус перед первым членом и имеет базисные векторы в числителях, которым они обычно принадлежат.
Мы используем є _ijk, который является Levi-Civita полностью антисимметричный символ: он равен +1, когда ijk — циклический перестановка 123, равна -1, когда ijk является нечетной перестановкой 123, и ноль в противном случае (а именно, когда один из индексов равен один из других).
10.2 Факторы c
В области электромагнетизма, когда мы выходим за пределы от начального до среднего или профессионального уровня уровне принято измерять время в единицах длины, поэтому что скорость света равна c=1 в выбранных единицах.
Это разумный выбор. Однако это должно оставаться выбором, а не обязательство. Нам должно быть позволено выбирать старомодные единицы измерения. время, если мы хотим. Иногда существуют неизвращенные причины выбор c≠1 — например, при проверке соответствия принцип, как мы делаем в этом документе.
Это вызывает трудности, поскольку в литературе некоторые ключевые формулы беспечно предполагают c=1, и если вы хотите вернуться назад и обобщить формулы так, чтобы они работали даже при c≠1, это не всегда очевидно, как это сделать. Это «обычно» очевидно, но не всегда.
В частности, рассмотрим горм вектора (т.е. 4-вектора) R, который определяет положение в пространстве-времени. Для любого вектора R степени = 1 горм равно скалярному произведению, R·R. Для вектора положения мы можно записать горму в терминах компонентов, а именно −c ² t ² + х ² + у ² + я ² . Если исключить множитель c ², получится выражение неверное, действительно размерно необоснованное … если только c = 1. Работая в обратном направлении от обычного определения скалярного произведения, Нам известно, что вектор положения равен R = [c t, x, y, z], а не просто [t, х, у, г].
Аналогичный аргумент говорит нам, что 4-вектор [энергии, импульса] равен [E, c p _x , c p _y , c p _z ] не просто [E, p _x, p _y, p _z].
Терминология в этой области – ловушка для неосторожных. Вы должны быть тщательно различать «время» (а именно t) и «время». времениподобная компонента вектора положения» (а именно, ct).
Иногда предлагается, чтобы скалярное произведение (т.е. метрика) переопределен, чтобы включить явные факторы c, которые позволили бы вектор положения можно записать просто как [t, x, y, z]. я не делаю рекомендую это, потому что, хотя это полезно для позиционных 4-векторов, это совершенно бесполезно для 4-векторов [энергии, импульса].
11  Приложение: плоские волны
11.1  Бегущие волны
В качестве скромного применения уравнения 1 попробуем найти некоторые решения для него. Следуя духу этого документа, мы подчеркнет простоту, а не элегантность. Мы сформулируем проблема в современных четырехмерных терминах, но таким образом, чтобы поддерживать контакт со старыми трехмерными концепциями, зависящими от фрейма, такими как E и B. Также ограничимся рассмотрением плоских волн в свободном пространство.
В свободном пространстве нет ни заряда, ни тока, поэтому уравнение 1 упрощается до:
∇ F = 0 (54)
Запишем простой анзац (уравнение 55), а затем покажите, что это действительно так. решить уравнение 54.
F = E(ky−vt)γ _{0 6 _{γ
+ D(ky−vt)γ ₂ γ ₀ − cB(ky−vt)γ ₁ γ ₂}}
= + D(Φ)γ ₂ γ ₀ − cB(Φ)γ ₁ γ ₂
             (55)
где F — бивектор электромагнитного поля, E, D и B — простые скалярные функции одного скалярного аргумента с пока еще неопределенный физический смысл, а Φ — скалярная фаза:
Φ := ky − vt
k = +1     for propagation in the +y direction
k = −1     для распространения в направлении −y
             (56)
Вот некоторые мотивы, которые могут сделать этот анзац менее загадочным:
Когда k=+1, запись фазы как функции y−vt является стандартный способ создания чего-то, что держит форму при путешествуя в направлении +y со скоростью v. Вы можете убедиться, что все, что происходит в [t,y] = [0,0], также происходит в [t,y] = [t ₁, vt ₁].
Точно так же, когда k=−1, запись фазы как функции из −y−vt создает что-то, что движется в направлении −y в точке скорость v.
Правая часть уравнения 55 является наиболее общей бивектор, который можно записать в 1+3-мерном пространстве-времени без упоминая γ ₃ .
Если мы сделаем снимок в любой момент времени, мы обнаружим, что каждый самолет параллельно плоскости xz проходит волновой фронт. То есть каждый такой плоскость представляет собой контур постоянной фазы. Это потому, что, по построение, контур постоянного t и постоянного y. Фаза зависит от t и y, но не от x или z. Это то, что мы хотели бы ожидать плоской волны, бегущей в направлении y.
Использование правила цепочки.
=
= кЭ’
             (57)
Соответствующие заявления могут быть сделаны о B и D . .. просто подайте заявку цепное правило соответствующим образом. Здесь E′ произносится как «E Prime» и обозначает полную производную от E с относительно скалярной фазы Φ.
Поскольку в уравнении 55 три члена, принимая производная дает нам шесть членов; три для времениподобной части градиент и три для пространственноподобной части. Подключение и Упрощение бита дает нам:
∇F = (−∂/∂CT) Eγ ₀ γ ₁ γ ₀ γ ₁ γ ₀ γ ₁ γ ₀ γ ₁ γ ₀ γ ₁ γ ₀ γ ₁ γ ₀ + (−∂/∂ct)Dγ ₀ γ ₂ γ ₀ − (−∂/∂ct)cBγ ₀ γ ₁ γ ₂
+(∂/∂y) Eγ ₂ γ ₁ γ ₀ + (∂/∂y)Dγ ₂ γ ₂ γ ₀ – (∂/∂y) CBγ ₂ γ ₁ γ ₂
= (v/c) Eriou +  (v/c)D’γ ₀ γ ₂ γ ₀ − (v/c)cB′γ ₀ γ ₁ γ ₂
+KE′ ₂ γ ₁ γ ₀ γ ₁ γ ₀ γ ₁ γ ₀ γ ₁. + kD’γ ₂ γ _D γ ₀ – KCB′γ ₂ γ ₁ γ ₂
= (V/C) E’RING ₁ + (v/c)D′γ ₂ − (v/c)cB’γ ₀ γ ₁ γ ₂
− kE′γ ₀ γ ₁ γ ₂ − kD’γ ₀ + kcB′γ ₁
             (58)
Из уравнения 54 мы знаем, что это должно быть равно нулю. Каждая компонента вектора должна отдельно равняться нулю. Следовательно:
E′ =    from the trivector part

D′ = 0    from the γ ₀ (timelike) part

cB′ =    из γ ₁ (пространственноподобной) части
             (59)
Дополнительные сведения об этих результатах см. в разделе 11.2. А пока давайте объединим эти результаты, чтобы получить согласованность требование для E’:
E′ = (v ² /c ² ) E’
             (60)
, где мы использовали тот факт, что k ² =1.
Первое, что мы узнаем из уравнения 60, это что электромагнитная плоская волна в свободном пространстве должна распространяться на скорость |v|=c. Это неизбежное следствие теории Максвелла. уравнение в свободном пространстве, уравнение 54.
Во-вторых, мы узнаем, что для любой волны, распространяющейся в требуемой скорости, волновая функция может иметь любую форму, поэтому пока она является дифференцируемой функцией своего аргумента, т.е. дифференцируемая функция фазы Φ. Следует подчеркнуть что мы не предполагали, что E является синусоидальным или даже периодическим. Любой функция E(Φ), о которой вы можете думать, если она дифференцируема, является приемлемой волновой функцией для плоской волны в свободном пространстве. Даже изолированная вспышка, как показано на рисунке 2, может быть решение уравнения 54. Метка движется слева направо со скоростью света; на рисунке показан только снимок снято в момент времени t=0.
Рис. 2. Моментальный снимок изолированного сообщения
Третье, что мы узнаем из уравнения 60 в сочетании с уравнение 59 заключается в том, что после того, как мы выбрали E, тогда cB ограничено уравнением 59. То есть в каждой точке пространство-время, E = −kcB + g, где g — некоторая постоянная интегрирования. Это г не очень интересно. Она постоянна во всем пространстве и время, и представляет собой некоторый однородный, нераспространяющийся фон поле. Это не влияет на распространяющуюся волну; волна просто распространяется мимо него.
Это завершает задачу по поиску некоторого решения.
Посмотрим, сможем ли мы найти еще несколько решений.
Прежде всего, мы знаем, что уравнения Максвелла инвариантны относительно пространственноподобные вращения, поэтому мы знаем, что должны существовать плоские волны распространяется в любом направлении, а не только в направлении y. Любой повернутый версия нашего решения является другим решением.
Во-вторых, легко проверить, что множитель γ ₁ в уравнение 55 не играло никакой важной роли в расчет; в основном это просто сопровождало поездку. Мы могли бы легко замените его на γ ₃ и тем самым получить другое решение, распространяется в том же направлении, что и предыдущее решение, но линейно от него не зависит. Это явление называется поляризация . Анзац в уравнении 55 равен поляризованы в направлении γ ₁. Вы можете убедиться, что вектор поляризации должен быть перпендикулярен направлению распространение; в противном случае уравнение 55 не работать как решение уравнения 54.
Мы не будем это доказывать, но утверждаем, что теперь у нас есть все ингредиенты необходимо построить наиболее общее решение для плоских волн в свободном space: сначала выберите направление распространения. Затем выберите основу для вектора поляризации, т.е. два единичных вектора в плоскости перпендикулярно направлению распространения. Тогда подумайте о двух произвольные дифференцируемые функции фазы, по одной для каждой компоненты вектор поляризации. Наконец, возьмем произвольные суперпозиции все выше.
Касательное замечание: хотя анзац в уравнении 55 содержит три члена, тот факт, что E=kcB и D=0 означает, что его можно записать в виде одной лопасти, то есть бивектора, который это просто произведение двух векторов. Specifically:
F = E(Φ) γ ₁ (γ ₀ − kγ ₂ )
             (61)
Структура здесь, как и для любой бегущей плоской волны, проста. Там три фактора: скалярная функция E(Φ), задающая форма волны, умноженная на пространственноподобный вектор, представляющий поляризация, умноженная на нулевой вектор, представляющий направление распространение.
Общая электромагнитная плоская волна представляет собой не одну лопасть, а можно записать в виде суммы лопаток этой формы. Даже в более общем плане есть много волн, которые не являются плоскими волнами.
11.2 Соотношение фаз бегущей волны
Как отмечалось в разделе 11.1, существует строгое соответствие между электрической частью и магнитной частью в электромагнитном бегущая плоская волна. Для метки (или чего-либо еще), бегущей влево справа
E′ = −cB′     поточечно везде в пространстве и времени
             (62)
Это иногда выражается словами «поле E» и «поле cB». находятся «в фазе». (Такое выражение имеет больше смысла для синусоидальные волны, чем для всплесков.)
Между тем, для вспышек (или чего-либо еще), бегущих справа налево,
E′ = +cB’     поточечно везде в пространстве и времени
             (63)
То есть опять существует строгая зависимость между Е и cB . .. но соотношение в уравнении 63 такое отношение диаметрально противоположное уравнение 62. Одно из них сдвинуто по фазе на 180 градусов. с другим.
Если вы рассматриваете суперпозицию левого пятна и правая вспышка, все понятие «отношения фаз» уходит в прошлое. из окна. У вас могут быть места, где E равно нулю, но cB равно нулю. не, или наоборот, или как угодно, а местные отношения между E и cB будет сильно меняться в зависимости от пространства и время. Конкретный тип суперпозиции рассматривается в раздел 11.3.
11.3 Соотношение фаз стоячей волны
Стоячую волну можно рассматривать как суперпозицию равные и противоположные бегущие волны. В частности, начнем с синусоидальные волны
E ₁ = cos(ct − y)
E ₂ = cos(ct + y)
E = E ₁ + E ₂
cB ₁ = −E ₁
cB ₂ = +E ₂
CB = CB ₁ +CB CB ₁ +CB ₂
= -E ₁+E ₂
(64)
В любом конкретном месте y волна является синусоидальной функцией время. Выбор другого места просто меняет фазу. Давайте применить тождество тригонометрической суммы углов:
Е ₁ = COS (CT) COS (Y)+SIN (CT) SIN (Y)
E ₂ = COS (CT) COS (y) − sin(ct) sin(y)
E = E ₁ + E ₂
E = 2 cos(ct ) cos(y)
cB = −E ₁ + E ₂
= −2 sin(ct) sin(y)
(65)
Итак, как рекламировалось выше, мы видим, что в большинстве мест, т.е. место, где cos(y) и sin(y) отличны от нуля – Поле E и поле B сдвинуты по фазе на 90 градусов для положения стоя. волна. (Они находятся в фазе бегущей волны, как обсуждалось в раздел 11.2.)
11.4 Пространство-время Изображение
Этот раздел ограничен случаем, когда k=+1; то есть волна распространяется в направлении +y. Также примем постоянную интегрирование g равно нулю. Поэтому E = cB везде.
Метка, которую мы видели на рисунке 2, снова изображена на рисунок 3. Первый изображал две переменные, а именно E в зависимости от y (при постоянном t). Последний изображает три переменных, а именно t, y и E. Значение E представлено по близости линий тока. Вы можете видеть это спереди половина метки (большие значения y) поле E в два раза больше как в задней половине метки.
Рисунок 3. Излучение: линии потока в пространстве-времени.
Тот факт, что E = cB, соответствует тому факту, что при каждом точка в пространстве-времени, количество линий потока на единицу расстояния в времяподобное направление равно количеству линий потока на единицу расстояние в пространственноподобном направлении. Пример этого изображен двумя маленькими синими стрелками на рисунке. Каждая стрелка не только пересекает одинаковое количество линий потока, он пересекает одни и те же линии потока.
Как видите, это прямое следствие геометрии пространство-время, и тот факт, что волна распространяется со скоростью v=с.
Как показано фиолетовыми линиями, контуры постоянной фазы проходят от с юго-запада на северо-восток. Фаза увеличивается к югу и востоку. Возрастание фазы к югу соответствует временному периоду, а фаза, возрастающая к востоку, соответствует пространственному периоду то есть длина волны. Обратите внимание, что любая попытка измерить период или длина волны полностью зависит от кадра. Некоторые свойства волны (например, общее количество циклов) не зависят от кадра, но другие свойства (такие как период, частота, длина волны и волновое число) обязательно зависит от фрейма.
На рисунке 3 направления x и z не совпадают. видимый. Если бы мы сделали более сложную схему, из другого В перспективе бивектор электромагнитного поля F будет представлены трубками . Величина F соответствует количество труб на единицу площади.
12  Номера по каталогу
1.
Статья в Википедии: «Система сантиметр-грамм-секунда единиц»
http://en.wikipedia.org/wiki/CGS
2.
У. Э. Бейлис и Г. У. Ф. Дрейк,
«Единицы и константы»
в Справочнике атомной молекулярной и оптической физики AIP 1996
http://www.atomwave.org/rmparticle/ao%20refs/aifm%20refs%20sorted%20by%20topic/other %20atom%20optics%20reviews/drakepdf/DRAKE01.PDF
3.
Джон Денкер,
«Бивектор магнитного поля длинного прямого провода»
www.av8n.com/physics/straight-wire.htm
4.
Джон Денкер
«Сохранение в связи с непрерывностью и постоянством»
www.av8n.com/physics/conservation-continuity.htm
5.
Джон Денкер,
«Введение в алгебру Клиффорда»
www.av8n.com/physics/clifford-intro. htm
6.
Ричард Э. Харк,
«Введение в математику пространственно-временной алгебры»
http://www.harke.org/ps/intro.ps.gz
7.
Джон Денкер,
«Добро пожаловать в пространство-время»
www.av8n.com/physics/spacetime-welcome.htm
8.
Джон Денкер,
«Визуализация поля, которое не является градиентом какого-либо потенциала»
www.av8n.com/physics/non-grady.htm
9.
Стивен Галл, Энтони Ласенби и Крис Доран,
«Геометрическая алгебра пространства-времени»
http://www.mrao.cam.ac.uk/~clifford/introduction/intro/intro.html
10.
Дэвид Хестенес,
«Лекция с медалью Эрстеда 2002: Реформирование математического языка физики»
Аннотация: http://geocalc.clas.asu.edu/html/Overview.html Полная статья: http://geocalc.clas.asu.edu/pdf/OerstedMedalLecture.pdf
11.
WE Baylis,
Электродинамика, современный геометрический подход
Биркхойзер, Бостон (1999).
1
Возможно, вы знакомы с матрицей умножение, которое имеет многие из тех же аксиом, что и геометрическое Алгебра, включая ассоциативный закон, распределительный закон и некоммутативное умножение. Но аналогия не идеальна: произведение двух матриц есть другая матрица, тогда как геометрическое произведение двух векторов не является другим вектором: это может быть скаляр (сила, умноженная на расстояние = работа) или бивектор (сила, умноженная на расстояние = крутящий момент) или, возможно, их комбинация, но это не будет правильный вектор.
2
Некоторые другие авторы используют обратное соглашение, в котором γ ₀ γ ₀ = +1 и все другие равны −1. Это не имеет большого значения; физика работает из того же, используя любое соглашение. Но соглашение, используемое здесь делает немного легче увидеть соответствие со старым добрым D=3 вектора.

Электродинамика, формулы

Основные уравнения электродинамики

Заряд и сила в электродинамике

Особое положение электродинамике в физике

Электродинамика (установление соответствия между графиками, физическими величинами и формулами) | ЕГЭ по физике

Физика – 10 класс. Электродинамика. Формулы. III.

формулы физики ЭЛЕКТРОДИНАМИКА | Материал для подготовки к ЕГЭ (ГИА) по физике (11 класс) на тему:

Формулы и буквенные обозначения по физике.

Физика и основные физические величины

Производные физические величины

СИ: общие сведения

Заключение

Что обозначает прописная буква N в физике?

Что может обозначать строчная буква n в физике?

Какая физическая величина может быть обозначена n и N?

Формулы, в которых фигурирует прописная N

Формулы, в которых встречается строчная n

Чему равно n в физике, если это показатель преломления?

Задача на мощность

Задачи на показатель преломления

Задачи на период обращения

Подведем итоги

Электростатика и электродинамика – формулы по физике

Основные формулы и методические рекомендации по решению задач на волны

Урок 35.

Конспект урока “Основные формулы и методические рекомендации по решению задач на волны”

Получите полный комплект видеоуроков, тестов и презентаций Видеоуроки. Решение задач по физике. Электродинамика.

Электромагнетизм | Физика для идиотов

00000. (Точный вывод этого закона можно найти здесь). Из них вы можете видеть, что сила равна полю, умноженному на любой заряд, который вы приложили.

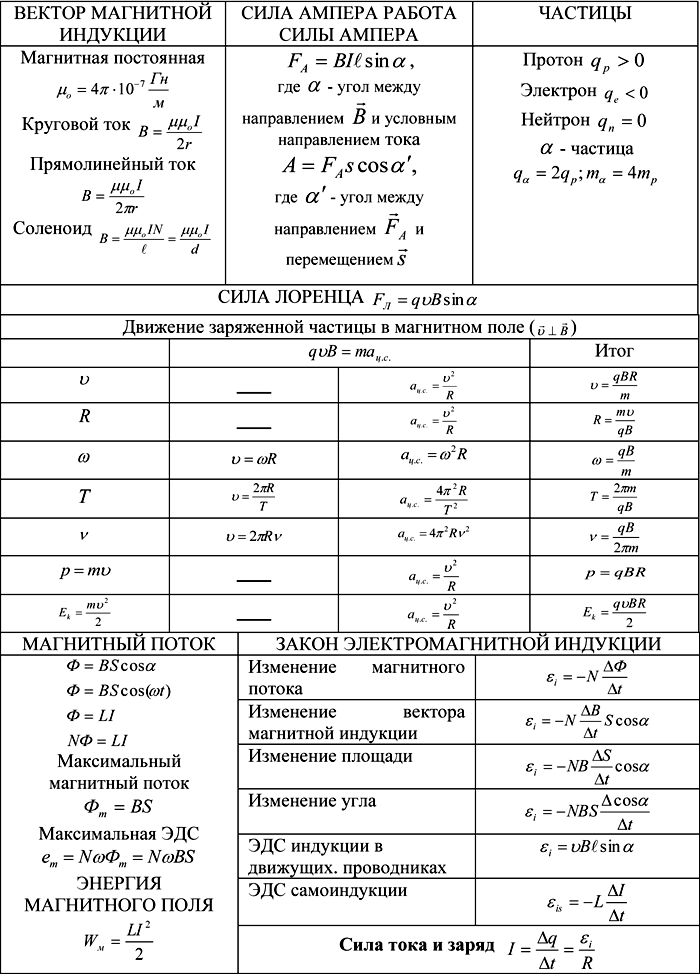Что есть что?

Закон Гаусса

Заряженное кольцо

Закон Гаусса для магнетизма

Закон Фарадея

Закон Ампера-Максвелла

Формулы физики

электростатика – Вопрос по двум формулам классической электродинамики Джексона

Твой ответ

Зарегистрируйтесь или войдите в систему

Опубликовать как гость

Опубликовать как гость

Уравнения Максвелла: предсказание и наблюдение электромагнитных волн

Цель обучения

Уравнения Максвелла

Установление связей: объединение сил

Наблюдения Герца

Резюме раздела

Задачи и упражнения

Глоссарий

Электромагнитные волны

Электромагнетизм с использованием геометрической алгебры в сравнении с компонентами

1 Введение

* Содержание

2 Предварительный просмотр

6 (1)

3 Вектора

2 9

07

4 Компоненты

5 Электромагнетизм с использованием геометрической алгебры

6 (5)

6 Заряд, сила и энергия

6.1 Сохранение заряда

70006

5

5

6

6.2 Закон силы Лоренца

6.3 Плотность лагранжиана

6.4 Вектор Пойнтинга

6.5 Тензор энергии-импульса

7 Векторный потенциал

7.1 Основная идея

7.2 D=3 по сравнению с D=4

90 005 0 0 6 (33б)

7.3 Калибровочная инвариантность

7.4 Уравнение Максвелла в терминах векторного потенциала

8 Геометрическая алгебра. Общие замечания

8.1 Обзор

8.2 Без украшений