Решебник по физике за 9 класс А.В.Перышкин, Е.М.ГутникЗадачи, предлагаемые для повторения и при 3 часах физики в неделю
Решебники и ГДЗ
Начните вводить часть условия (например, могут ли, чему равен или найти):
- 1. Для каждого из векторов, изображенных на рисунке 191, определите: а) координаты начала и конца; б) проекции на ось у; в) модули проекций на ось у, г) модули векторов.
- 2. На рисунке 192 векторы а и с перпендикулярны оси X, а векторы b и d параллельны ей. Выразите проекции ах, bх, сх и dx через модули этих векторов или соответствующие числа.
- 3. На рисунке 193 изображена траектория движения шарика, переместившегося из точки А в точку В. Определите: а) координаты начального и конечного положений шарика; б) проекции sx и sy перемещения шарика; в) модули |sх| и |sy| проекций перемещения; г) модул
- 4. Катер переместился относительно пристани из точки А(-8; —2) в точку В(4; 3).
Сделайте чертеж, совместив начало координат с пристанью и указав на нем точки А и В. Определите перемещение катера АВ. Мог ли путь, проделанный катером, быть больше совершенно - 5. Известно, что для определения координаты прямолинейно движущегося тела используется уравнение х = х0 + sx. Докажите, что координата тела при его прямолинейном равномерном движении для любого момента времени определяется с помощью уравнения х = х0 + vxt
- 6. Запишите уравнение для определения координаты тела, движущегося прямолинейно со скоростью 5 м/с вдоль оси X, если в момент начала наблюдения его координата была равна 3 м.
- 7. Два поезда — пассажирский и товарный — движутся по параллельным путям. Относительно здания вокзала движение пассажирского поезда описывается уравнением xп= 260 – 10t, а товарного — уравнением хт = -100 + 8t. Приняв вокзал и поезда за материальные точки
- 8. Туристы сплавляются на плоту по реке. На рисунке 194 показано. как меняется со временем координата плота относительно места стоянки туристов (точки О). Начало наблюдения совпадает с моментом спуска плота на воду и началом движения. Где плот был спущен
- 9. Мальчик съезжает с горы на санках, двигаясь из состояния покоя прямолинейно и равноускоренно. За первые 2 с после начала движения его скорость возрастает до 3 м/с. Через какой промежуток времени от начала движения скорость мальчика станет равной 4,5 м/
- 10. Преобразуйте формулу к виду:
- 11. Исходя из того, что выведите формулу
- 12. На рисунке 27 показаны положения шарика через каждую 0,1с его равноускоренного падения из состояния покоя. Координаты всех шести положений отмечены черточками по правому краю линейки. Пользуясь рисунком, определите среднюю скорость шарика за первые 0,
- 13. Два лифта — обычный и скоростной — одновременно приходят в движение и в течение одного и того же промежутка времени движутся равноускоренно. Во сколько раз путь, который пройдет за это время скоростной лифт, больше пути, пройденного обычным лифтом, ес
- 15. Автомобиль движется прямолинейно вдоль оси X. Уравнение зависимости проекции вектора скорости автомобиля от времени в СИ выглядит так: vx = 10 + 0,5t. Определите модуль и направление начальной скорости и ускорения автомобиля. Как меняется модуль векто
- 16. От удара клюшкой шайба приобрела начальную скорость 5 м/с и стала скользить по льду с ускорением 1 м/с2. Запишите уравнение зависимости проекции вектора скорости шайбы от времени и постройте соответствующий этому уравнению график.
- 17. Известно, что для определения координаты прямолинейно движущегося тела используется уравнение Докажите, что координата тела при его прямолинейном равноускоренном движении для любого момента времени определяется с помощью уравнения
- 18. Лыжник скатывается с горы, двигаясь прямолинейно с постоянным ускорением 0,1 м/с2. Напишите уравнения, выражающие зависимость от времени координаты и проекции вектора скорости движения лыжника, если его начальные координата и скорость равны нулю.
- 19. Велосипедист движется по шоссе прямолинейно со скоростью, модуль которой равен 40 км/ч относительно земли. Параллельно ему движется автомобиль. Что можно сказать о модуле вектора скорости и направлении движения автомобиля относительно земли, если отно
- 20. Скорость катера относительно воды в реке в 5 раз больше скорости течения воды относительно берега. Рассматривая движение катера относительно берега, определите, во сколько раз быстрее катер движется по течению, чем против него.
- 21. Мальчик держит в руках шарик массой 3,87 г и объемом 3 ⋅ 10-3 м3. Что произойдет с этим шариком, если его выпустить из рук?
- 22. Стальной шар равномерно катится по горизонтальной поверхности и сталкивается с неподвижным алюминиевым шаром, в результате чего алюминиевый шар получает некоторое ускорение.
- 23. Пусть МЗ и RЗ— соответственно масса и радиус земного шара, g0 — ускорение свободного падения на поверхности Земли, a g — на высоте h. Исходя из формул выведите формулу:
- 24. На рисунке 196 изображены равные по массе шарики 1 и 2, привязанные к нитям длиной к и 2к соответственно и движущиеся по окружностям с одинаковой по модулю скоростью v. Сравните центростремительные ускорения, с которыми движутся шарики, и силу натяжен
- 25. Исходя из формулы для определения центростремительного ускорения при движении по окружности и формулы выведенной вами при решении задачи 23, получите следующую формулу для расчета первой космической скорости на высоте h над поверхностью Земли:
- 26. Среднее значение радиуса Земли равно 6400 км, а ускорение свободного падения у земной поверхности равно 9,8 м/с2. Пользуясь только этими данными, вычислите первую космическую скорость на высоте 3600 км над поверхностью Земли.
- 27. Постройте график зависимости проекции вектора скорости от времени для тела, свободно падающего в течение 4 с (v0 = 0, считать g= 10 м/с2).
- 28. Тело массой 0,3 кг свободно падает из состояния покоя в течение 3 с. На сколько увеличивается его импульс за первую секунду падения? за вторую секунду падения?
- 29. С помощью графика, построенного вами при решении задачи 27, покажите, что импульс свободно падающего тела за равные промежутки времени меняется на одну и ту же величину.
- 30. Алюминиевый и медный шарики одинакового объема свободно падают из состояния покоя с одной и той же высоты в течение 2,5 с. Импульс какого из шариков будет больше и во сколько раз к концу первой секунды падения? к концу второй секунды падения? Ответы о
- 31. Два одинаковых бильярдных шара, двигаясь вдоль одной прямой, сталкиваются друг с другом. Перед столкновением проекция вектора скорости первого шара на ось X была равна 0,2 м/с, а второго — 0,1 м/с. Определите проекцию вектора скорости второго шара пос
- 32. Решите предыдущую задачу для случая, при котором v1x = 0,2 м/с, v2x= -0,1 м/с, v’1x = -0,1 м/с (где v1x и v2x — проекции векторов скорости соответственно 1-го и 2-го шаров до их столкновения, a v’1x — проекция вектора скорости 1-го шара после столкнов
- 33. Используя данные и результат решения задачи 32, покажите, что при столкновении шаров выполняется закон сохранения полной механической энергии.
- 34. На рисунке 197 показано, как меняется с течением времени проекция вектора скорости одной из точек сидения качелей. С какой частотой происходит это изменение? Какова частота изменения скорости любой другой точки качелей, совершающей колебания?
- 35. Струна арфы совершает гармонические колебания с частотой 40 Гц. Постройте график зависимости координаты от времени для средней точки струны, амплитуда колебаний которой равна 3 мм. (Для построения графика рекомендуем разметить ось t так, как показано
- 36. Как добиться звучания одного из двух одинаковых камертонов на резонаторных ящиках, не дотрагиваясь до него? Как при этом следует расположить отверстия резонаторных ящиков по отношению друг к другу? Ответы поясните.
- 37. Качели периодически подталкивают рукой, т. е. действуют на них вынуждающей силой. На рисунке 199 изображен график зависимости амплитуды установившихся колебаний качелей от частоты данной вынуждающей силы. Пользуясь этим графиком, определите: а) При ка
- 38. На рисунке 200 изображен проводник АВ длиной 10 см и массой 2 г, помещенный в однородное магнитное поле с индукцией 4 • 10 2 Тл перпендикулярно линиям магнитной индукции. По проводнику протекает электрический ток (подводимый по тонким проводам, на кот
- 39. В камеру Вильсона, помещенную в однородное магнитное поле, влетает электрон и движется по дуге окружности (см. белую штриховую линию на рисунке 201). Под действием какой силы меняется направление скорости электрона? В какой точке он влетел в камеру?
- 40. Известно, что сила F, с которой однородное магнитное поле с индукцией В действует на частицу с зарядом е, движущуюся со скоростью о перпендикулярно линиям магнитной индукции, определяется по формуле: F = Bev. По дуге окружности какого радиуса будет дв
- 41. В результате какого радиоактивного распада углерод 146C превращается в азот 147N?
- 42. При бомбардировке ядер алюминия 2713Al нейтронами из образовавшегося ядра выбрасывается α-частица. Напишите уравнение этой реакции.
- 43. Пользуясь законом сохранения массового и зарядового чисел, заполните пропуск в записи следующей ядерной реакции: В 105B+ … → 73Li + 42He.
- 44. Какой химический элемент образуется в результате α-распада изотопа урана 23892U? Запишите эту реакцию.
- 45. В результате какого числа β-распадов ядро атома тория 23490Th превращается в ядро атома урана 23892U?
Сделайте чертеж, совместив начало координат с пристанью и указав на нем точки А и В. Определите перемещение катера АВ. Мог ли путь, проделанный катером, быть больше совершенно
Начало наблюдения совпадает с моментом спуска плота на воду и началом движения. Где плот был спущен
На рисунке 195 представлен график зависимости проекции скорости лифта при разгоне от времени. Перечертите этот график в тетрадь и в тех же координатных осях постройте аналогичный график для скоростного лифта, ускорение которого в 3 раза больше, чем об
Лыжник скатывается с горы, двигаясь прямолинейно с постоянным ускорением 0,1 м/с2. Напишите уравнения, выражающие зависимость от времени координаты и проекции вектора скорости движения лыжника, если его начальные координата и скорость равны нулю.
Решите предыдущую задачу для случая, при котором v1x = 0,2 м/с, v2x= -0,1 м/с, v’1x = -0,1 м/с (где v1x и v2x — проекции векторов скорости соответственно 1-го и 2-го шаров до их столкновения, a v’1x — проекция вектора скорости 1-го шара после столкнов
По дуге окружности какого радиуса будет двШкольные формулы по физике 7-11 классы
- формат docx
- размер 97.99 КБ
- добавлен 07 декабря 2009 г.
Все школьные формулы по механике, молекулярной физике,
термодинамике, электродинамике, оптике, квантовой физике и т.
д.
Смотрите также
Шпаргалка
- формат pdf
- размер 1.58 МБ
- добавлен 21 января 2012 г.
М.: РИОР, 2009. – 32 с. В шпаргалке приведены все основные формулы и определения по физике. Рекомендуется всем изучающим и сдающим физику в школах, средних и высших учебных заведениях.
Шпаргалка
- формат jpg
- размер 149.22 КБ
- добавлен 14 января 2011 г.
Здесь представлены самые основные формулы, которые могут понадобиться студенту при сдачи экзамена по физике. Разделы: кинематика, динамика, электростатика, квантовая физика, ядерная физика и другие.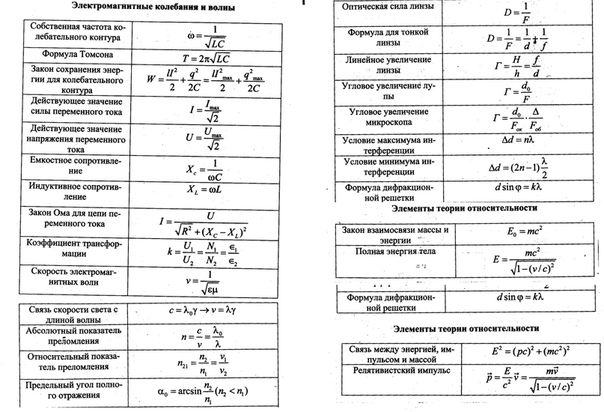
Один этот самый лист.
software
- формат exe
- размер 91.13 КБ
- добавлен 12 июля 2010 г.
Программа, выводящая на экран формулы по физике. Бета-версия. Доступна только кинематика. NNSoft, 2006 г. Разработки для Pocket PC. Разделы: Кинематика; Динамика, Законы Сохранения; Статика, гидростатика; Мех. Колебания. Волны.; МКТ; термодинамика.rn
- формат pdf
- размер 1.95 МБ
- добавлен 06 октября 2011 г.
На 10 страницах приведены всё основные формулы по физике. Может пригодиться студенту при подготовке к экзамену, контрольной работе или просто для освежения памяти по следующим разделам: Кинематика.
Динамика. Законы сохранения. Работа и мощность. Статика и гидростатика. Тепловые явления. Электростатика. Постоянный ток. Магнитные явления. Колебания и волны. Оптика.
Шпаргалка
- формат doc
- размер 128.54 КБ
- добавлен 30 октября 2011 г.
Выписки на 9 листах из книги “Краткий справочник по физике” Гридасов А.Ю. Новосибирск 1997 г. Файл содержит формулы из курса физики, которые будут полезны учащимся старших классов школ и младших курсов вузов. Все формулы изложены в компактном виде с небольшими комментариями. Файл также содержит полезные константы и прочую информацию.
Шпаргалка
- формат doc
- размер 136. 87 КБ
- добавлен 24 января 2009 г.
87 КБФормулы по курсу физики: Механике, молекулярной физике и термодинамике, электричеству и магнетизму, колебаниям и волнам, оптике, квантовой природе излучения, элементам квантовой физики атомов, молекул и твёрдых тел, элементам физики атомного ядра и элементарных частиц.
- формат jpg
- размер 1.15 МБ
- добавлен 27 мая 2009 г.
Формулы – Шпоры по физике сделаны специально для мобильного телефона или графического калькулятора. (калькулятор должен иметь флешь память и читать jpg формат) Есть формулы по: Кинематике. Динамике. Законах сохранения энергии. Механика жидкостей. Основах МКТ. Термодинамике. Колебаниях и волнах. Электростатике. Постоянном электрическом токе. Индукции.
Электромагнитным колебаниям. Оптике. Ядерным реакциям. Квантовой физике. Основам СТО.rn
- формат doc
- размер 120.56 КБ
- добавлен 11 декабря 2007 г.
Шпора по физике. Готова к распечатке. Содержит формулы по темам: кинематика, движение под углом к горизонту, криволинейное движение, механика жидкостей и газов, свойства газов, молекулярно-кинетическая теория, электричество и магнетизм и так далее.
Шпаргалка
- формат doc
- размер 2.24 МБ
- добавлен 22 февраля 2011 г.
Полный сборник по физике, включающий в себя основные формулы, законы и определения. Данный сборник(глоссарий предназначен для студентов технического факультета).
Рассмотрены следующие темы: Механика. Динамика. Молекулярный физика и термодинамика. Электричество и магнетизм. Оптика.
- формат jpg, htm
- размер 17.33 МБ
- добавлен 22 октября 2009 г.
Шпоры по Физике. Буквы, используемые для обозначения величин Методика решения задач по физике Векторы Основные положения, законы и формулы Механика Кинематика Динамика Статика Простые механизмы Жидкости и газы Молекулярная физика Термодинамика Электростатика Электричество Магнитное поле Колебания и волны Оптика Элементы теории относительности Квантовая физика Атомная и ядерная физика Приложения Шкала электромагнитных волн…
CBSE Class 6, 7, 8 ,9, 10, 12
Перейти к содержимому
CBSE Class 7, 8 ,9, 10, 12 Математика Все важные формулы и темы s B Формула – Вывод, применение и часто задаваемые вопросы
Формула отношений и функций
Введение, типы, примеры задач и важные часто задаваемые вопросы
Отмеченная цена и часто задаваемые вопросы
9 Формула уксуса – Объяснение, структура, свойства, сравнение, реакция и часто задаваемые вопросы Математическая формула CBSE Class 11
Принцип математической индукции CBSE Class 10 Math Formula
Математическая формула 9 класса CBSE
Системы счисления Математическая формула CBSE класса 8
Визуализация объемных фигур CBSE Class 7 Math Formula 9
CBSE Class 6 Math Formula
Физика
Математика
Химия
Физика 90 667
Связанное содержание
9.
3 Простые машины — физикаРаздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать простые и сложные машины
- Расчет механического преимущества и эффективности простых и сложных машин
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
- (C) описывать простые и сложные механизмы и решать задачи, связанные с простыми механизмами;
- (D) определяют входную работу, выходную работу, механическое преимущество и эффективность машин.
Кроме того, Руководство по физике для средней школы рассматривает содержание этого раздела лабораторной работы под названием «Работа и энергия», а также следующие стандарты:
- (6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
- (Д) продемонстрировать и применить законы сохранения энергии и сохранения импульса в одном измерении.
Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:Основные термины раздела
| сложная машина | выход эффективности | идеальное механическое преимущество | наклонная плоскость | входная работа |
| рычаг | механическое преимущество | выходная работа | шкив | винт |
| простая машина | клин | колесо и ось |
Поддержка учителей
Поддержка учителей
В этом разделе вы примените то, что узнали о работе, чтобы найти механические преимущества и эффективность простых машин.
[BL][OL] Спросите учащихся, что они знают о машинах и работе. Развейте любые заблуждения о том, что машины сокращают объем работы. Следите за тем, чтобы учащиеся не приравнивали машины и двигатели, запрашивая (и, при необходимости, предоставляя) примеры машин без двигателя. Объясните, что простые машины часто держат в руках и что они снижают силу, а не работают.
[AL] Запросить напоминание формулы W = f d . Объясните, что произведение силы на расстояние имеет решающее значение для понимания простых механизмов. Поскольку объем работы не меняется, срок f d не меняется, но сила может уменьшаться при увеличении расстояния. Это основной принцип всех простых машин.
Простые машины
Простые машины облегчают работу, но не уменьшают ее объем. Почему простые машины не могут изменить объем выполняемой вами работы? Напомним, что в закрытых системах общее количество энергии сохраняется.
Машина не может увеличить количество энергии, которую вы в нее вкладываете. Итак, чем полезна простая машина? Хотя она не может изменить объем выполняемой вами работы, простая машина может изменить величину силы, которую вы должны приложить к объекту, и расстояние, на котором вы прикладываете силу. В большинстве случаев для уменьшения силы, которую необходимо приложить для выполнения работы, используется простая машина. Обратной стороной является то, что вы должны приложить силу на большее расстояние, потому что произведение силы и расстояния, f d (что равно работе) не изменяется.
Давайте посмотрим, как это работает на практике. На рис. 9.8(а) рабочий использует своего рода рычаг, чтобы приложить небольшое усилие на большом расстоянии, в то время как монтировка тянет гвоздь с большой силой на небольшом расстоянии. На рис. 9.8(b) показано, как математически работает рычаг. Сила усилия, приложенная в точке F e , поднимает груз (сила сопротивления), который давит вниз в точке F р .
Треугольный стержень называется точкой опоры; часть рычага между точкой опоры и F e – плечо усилия, L e ; а часть слева – это рычаг сопротивления, L r . Механическое преимущество — это число, которое говорит нам, во сколько раз простая машина увеличивает силу усилия. Идеальное механическое преимущество, IMA , представляет собой механическое преимущество совершенной машины без потери полезной работы, вызванной трением между движущимися частями. Уравнение для IMA показан на рис. 9.8(b).
Рисунок 9,8 а) Рычаг представляет собой разновидность рычага. (b) Идеальное механическое преимущество равно длине плеча усилия, деленному на длину плеча сопротивления рычага.
В общем, IMA = сила сопротивления, F r , деленная на силу усилия, F e .
IMA также равняется расстоянию, на котором прикладывается усилие, d e , деленное на расстояние, которое проходит груз, d r .
IMA=FrFe=dedrIMA=FrFe=dedr
Возвращаясь к сохранению энергии, для любой простой машины работа, вложенная в машину, Вт i равна работе, производимой машиной, Вт или . Объединив это с информацией из предыдущих абзацев, мы можем написать
. Wi=WoFede=FrdrIf Fe
Уравнения показывают, как простая машина может производить тот же объем работы, уменьшая величину усилия за счет увеличения расстояния, на котором действует усилие.
Смотреть физику
Введение в механические преимущества
В этом видеоролике показано, как рассчитать IMA рычага тремя различными методами: (1) по силе усилия и силе сопротивления; (2) от длин плеч рычагов, и; (3) от расстояния, на котором приложена сила, и расстояния, на которое перемещается груз.
Поддержка учителей
Поддержка учителей
Начало этого видео может вызвать больше путаницы, чем просветления. Он показывает вывод с использованием триггерных функций, который выходит за рамки этой главы. Заинтересованные студенты могут захотеть пройти через это. Большинству учащихся следует пропустить последние две-три минуты, в которых объясняются основы расчета IMA рычага по различным соотношениям. Обзор W = f d .
Физика часов: введение в механические преимущества. В этом видео представлены простые машины, механическое преимущество и моменты.
Нажмите, чтобы просмотреть содержимое
Двое детей разного веса катаются на качелях. Как они располагаются относительно точки опоры (точки опоры), чтобы сохранять равновесие?
Более тяжелый ребенок сидит ближе к точке опоры.
Более тяжелый ребенок сидит дальше от точки опоры.
Оба ребенка сидят на равном расстоянии от точки опоры.
Поскольку оба имеют разный вес, они никогда не будут сбалансированы.
Некоторые рычаги прикладывают большое усилие к короткому рычагу. Это приводит к тому, что на конце рычага сопротивления действует меньшая сила на большем расстоянии. Примерами этого типа рычага являются бейсбольные биты, молотки и клюшки для гольфа. В другом типе рычага точка опоры находится на конце рычага, а груз — посередине, как в конструкции тачки.
Поддержка учителей
Поддержка учителей
[AL]Скажите учащимся, что есть еще два класса рычагов с различным расположением нагрузки, точки опоры и усилия. Попросите их сначала попытаться нарисовать их. После того, как они с вашей помощью или без вас обнаружат три типа, спросите, могут ли они придумать примеры типов, не показанных на рис. 9.8.
Простая машина, показанная на рис. 9.9, называется колесом и осью . На самом деле это форма рычага. Разница в том, что рычаг усилия может вращаться по полному кругу вокруг точки опоры, которая является центром оси. Сила, приложенная к внешней стороне колеса, вызывает большее усилие, приложенное к веревке, обернутой вокруг оси. Как показано на рисунке, идеальное механическое преимущество рассчитывается путем деления радиуса колеса на радиус оси. Любое устройство с кривошипным приводом является примером колеса и оси.
Рисунок
9,9
Сила, приложенная к колесу, действует на его ось.
Поддержка учителей
Поддержка учителей
[BL][OL] Посмотрите, уловили ли учащиеся идею о том, что колесо и ось на самом деле являются разновидностью рычага. Покажите им, что это больше похоже на рычаг, если колесо заменить рукояткой. Приведите несколько примеров: лебедка с ручным приводом, рулевое колесо, дверная ручка и т. д. Спросите их, почему рулевые колеса имели больший диаметр до изобретения гидроусилителя руля.
[AL] Объясните, что колеса транспортных средств на самом деле не являются простыми механизмами в том смысле, в каком они изображены на рис. 9.9. Ось транспортного средства не работает под нагрузкой. Потери энергии на трение уменьшаются, но ничего не поднимается.
Наклонная плоскость и клин — две формы одной и той же простой машины. Клин — это просто две наклонные плоскости, расположенные спиной к спине. На рис. 9.10 показаны простые формулы для расчета IMA s этих машин.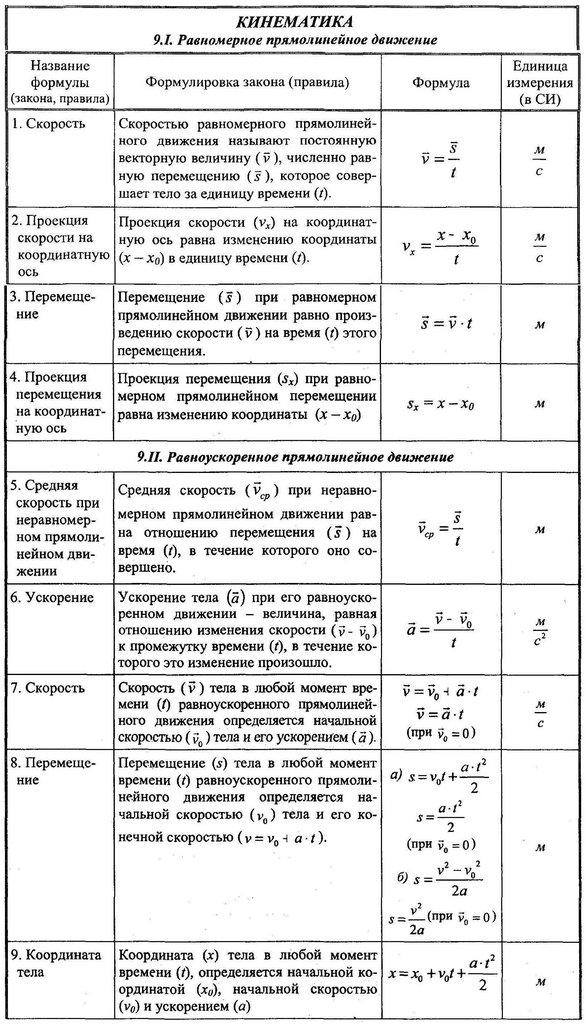
Все наклонные мощеные поверхности для ходьбы или вождения представляют собой наклонные плоскости. Ножи и головки топоров являются примерами клиньев.
Рисунок 9.10 Слева показана наклонная плоскость, справа – клин.
Поддержка учителей
Поддержка учителей
[BL][OL] Расскажите о сходстве и различиях наклонных плоскостей и клиньев. Обратите внимание, что при использовании наклонной плоскости груз перемещается, а при использовании клина груз неподвижен, а машина движется. Объясните, почему в этих машинах на трение обычно теряется больше энергии, чем в других простых машинах.
Винт, показанный на рис. 9.11, на самом деле представляет собой рычаг, прикрепленный к круглой наклонной плоскости. Шурупы по дереву (конечно) также являются примерами шурупов. Рычажная часть этих винтов представляет собой отвертку. В формуле для IMA расстояние между резьбами винтов называется шагом и имеет символ P .
Рисунок 9.11 Показанный здесь винт используется для подъема очень тяжелых предметов, например, угла автомобиля или дома на небольшое расстояние.
Поддержка учителей
Поддержка учителей
[BL][OL] Предложите выделить винт в отдельный тип простой машины, возможно, потому, что он выглядит совсем иначе, чем он есть на самом деле — наклонная плоскость, которую иногда поворачивает рычаг. Объясните, что комбинированное механическое преимущество может быть большим. Устройства, подобные показанному на рис. 9.10, используются для подъема автомобилей и даже домов. Предложите учащимся сравнить этот шуруп с шурупом для дерева и круглой лестницей.
[AL] Спросите учащихся, чем сила, прикладываемая шурупом, отличается от силы, приложенной шурупом на рис. 9..10. Попросите объяснить 2 ππ в уравнении для IMA .
На рис. 9.12 показаны три различные системы шкивов. Из всех простых машин механическое преимущество легче всего рассчитать для шкивов.
Просто посчитайте количество канатов, поддерживающих груз. Это IMA . И снова мы должны применять силу на более длинном расстоянии, чтобы умножить силу. Чтобы поднять груз на 1 метр с помощью шкивной системы, нужно потянуть N метров веревки. Системы шкивов часто используются для подъема флагов и оконных жалюзи и являются частью механизма строительных кранов.
Рисунок 9.12 Здесь показаны три системы шкивов.
Поддержка учителей
Поддержка учителей
[BL][OL] Расчет шкива IMA кажется слишком простым, чтобы быть правдой, но это так. Попросите учащихся попытаться понять, почему IMA — это просто N . Скажите им, что просмотр видео должен прояснить этот момент. Шкивы когда-то видели на парусных кораблях и фермах, где они использовались для подъема тяжелых грузов.
Выступ, который вы, возможно, видели на конце старых крыш сарая, — это место, где когда-то был прикреплен шкив. Таким образом, тюки сена можно было поднять на сеновал, не промокнув. Шкивы все еще можно увидеть в использовании, чаще всего на больших строительных кранах.
Смотреть физику
Механические преимущества наклонных плоскостей и шкивов
В первой части этого видео показано, как рассчитать IMA систем шкивов. В последней части показано, как рассчитать IMA наклонной плоскости.
Поддержка учителей
Поддержка учителей
Прежде чем смотреть видео, ознакомьтесь с тем, что вы узнали о IMA наклонных плоскостей и систем шкивов. Напомните учащимся, что для идеальной машины работа в = работа и что Вт = f d .
На видео показано как найти ф с и д с.
Проверка захвата
Как можно использовать систему шкивов, чтобы поднять легкий груз на большую высоту?
- Уменьшить радиус шкива.
- Увеличить количество шкивов.
- Уменьшите количество канатов, поддерживающих груз.
- Увеличьте количество канатов, поддерживающих груз.
Сложная машина представляет собой комбинацию двух или более простых машин. Кусачки на рис. 9.13 соединить два рычага и два клина. Велосипеды включают в себя колеса и оси, рычаги, винты и шкивы. Автомобили и другие транспортные средства представляют собой комбинации многих машин.
Рисунок 9.13 Кусачки для проволоки – это обычная сложная машина.
Поддержка учителей
Поддержка учителей
[BL][OL] Убедитесь, что учащиеся понимают, что сложная машина представляет собой просто комбинацию простых машин и все еще довольно проста .
Не позволяйте им путать этот термин со сложными машинами, такими как компьютеры. Обратите внимание, что IMA отдельных простых машин в сложной машине обычно умножаются, потому что выходная сила одной машины становится входной силой другой машины. В качестве дополнительного развлечения предложите учащимся найти в Интернете Машина Руба Голдберга .
Расчет механического преимущества и эффективности простых машин
В общем, IMA = сила сопротивления, F r , деленная на силу усилия, F e . IMA также равняется расстоянию, на которое прикладывается усилие, d e , деленному на расстояние, которое проходит груз, d r .
IMA=FrFe=dedrIMA=FrFe=dedr
Вернитесь к обсуждениям каждой простой машины для конкретных уравнений для IMA для каждого типа машины.
Никакие простые или сложные машины не обладают фактическими механическими преимуществами, рассчитанными по уравнениям IMA . В реальной жизни часть прикладной работы всегда заканчивается напрасной тратой тепла из-за трения между движущимися частями. И входная работа ( W i ), и выходная работа ( W o ) являются результатом действия силы 9.0005 F , действующий на расстоянии, d .
Wi=FidianandWo=FodoWi=FidianandWo=Fodo
Выходная эффективность машины — это просто работа на выходе, деленная на работу на входе, и обычно умножается на 100, так что это выражается в процентах.
% эффективности=WoWi×100% эффективности=WoWi×100
Посмотрите на изображения простых машин и подумайте, какая из них будет иметь наибольшую эффективность. Эффективность связана с трением, а трение зависит от гладкости поверхностей и от площади соприкасающихся поверхностей.
Как смазка повлияет на эффективность простой машины?
Поддержка учителей
Поддержка учителей
[BL][OL] Повторить материал о переходе механической энергии в теплоту и законе сохранения энергии. Объясните, каким образом тепловые потери из-за трения гарантируют, что Вт o всегда будет меньше, чем Вт i , предотвращая достижение КПД 100%.
Рабочий пример
Эффективность рычага
Входная сила в 11 Н, действующая на плечо усилия рычага, перемещается на 0,4 м, что поднимает груз массой 40 Н, опирающийся на плечо сопротивления, на расстояние 0,1 м. Каков КПД машины?
Стратегия
Составьте уравнение для эффективности простой машины, % КПД = WoWi × 100, % КПД = WoWi × 100, и рассчитайте Вт o и Вт i .
Оба рабочих значения являются продуктом Fd .
Решение
Wi=FidiWi=Fidi = (11)(0,4) = 4,4 Дж и Wo=FodoWo=Fodo = (40)(0,1) = 4,0 Дж, тогда % эффективности=WoWi×100=4,04,4×100= 91% % эффективность=WoWi×100=4,04,4×100=91%
Обсуждение
КПД реальных машин всегда будет меньше 100 процентов из-за работы, которая преобразуется в недоступное тепло за счет трения и сопротивления воздуха. W o и W i всегда можно рассчитать как силу, умноженную на расстояние, хотя эти величины не всегда так очевидны, как в случае с рычагом.
Поддержка учителей
Поддержка учителей
Совет для преподавателя. При расчете эффективности достаточно легко понять, что такое сила входа и выхода: сила, которую вы прикладываете, — это сила входа, а вес поднимаемого объекта — сила выхода. Входное и выходное расстояния легче увидеть для рычага, наклонной плоскости и клина.
Остальные три не так очевидны. Для системы шкивов входное расстояние — это расстояние, на которое вы тянете веревку, а выходное расстояние — это расстояние, на которое поднимается груз. Для колеса и оси входное расстояние — это окружность колеса, а выходное расстояние — это окружность оси. Для винта входное расстояние — это длина окружности, к которой приложена сила, а выходное расстояние — это расстояние между витками резьбы.
Практические задачи
11.
(кредит: модификация работы OdysseyWare Inc.)Рисунок 9.14
Наклонная плоскость длиной 5 м и высотой 2 м используется для загрузки большого ящика в кузов грузовика. Что такое IMA наклонной плоскости?
0,4
2,5
0,4\,\текст{м}
2.
5\,\текст{м}
5\,\текст{м}12.
Если система шкивов может поднять груз 200 Н с усилием 52 Н и имеет КПД почти 100 %, сколько канатов поддерживает груз?
- Требуется 1 веревка, поскольку фактическое механическое преимущество составляет 0,26.
- Требуется 1 веревка, потому что фактическое механическое преимущество составляет 3,80.
- Требуется 4 веревки, потому что фактическое механическое преимущество составляет 0,26.
- Требуется 4 веревки, потому что фактическое механическое преимущество составляет 3,80.
Проверьте свое понимание
13.
Правда или ложь — КПД простой машины всегда меньше 100 %, потому что некоторая малая часть вложенной работы всегда преобразуется в тепловую энергию за счет трения.
- Правда
- Ложь
14.