Магнетизм – Физика – Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Сила Ампера
К оглавлению…
Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем. Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл).
где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.
Для определения направления силы Ампера обычно используют правило «Левой руки»: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).
Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.
Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.
Момент сил, действующих на рамку с током
Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера.
где: S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции (нормаль – вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.
Сила Лоренца
К оглавлению…
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле  Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:
Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:
Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет
Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:
Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:
Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R.
Теория о магнитном поле
К оглавлению…
Магнитное взаимодействие токов
Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером.
где: μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:
μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2.
Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:
где: μ – магнитная проницаемость вещества (об этом чуть ниже).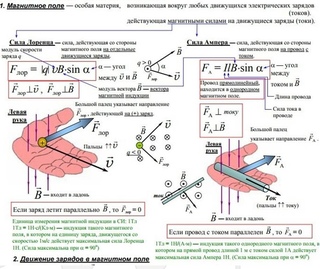
Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй – на юг. Отсюда название полюсов: северный (N) и южный (S). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой
Вектор магнитной индукции
Вектор магнитной индукции – векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику. Обозначается В, единица измерения – 1 Тесла. 1 Тл – очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Обозначается В, единица измерения – 1 Тесла. 1 Тл – очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.
Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:
В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки»
В случае прямого тока линии магнитной индукции – окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.
Вектора магнитной индукции направлены по касательной к окружности.
Соленоид – намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I. Магнитное поле соленоида подобно полю прямого постоянного магнита. Внутри соленоида длиной
Линии магнитного поля имеют вид замкнутых линий – это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.
Магнитные свойства вещества
Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ, для которой верно следующее:
Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики – кислород, платина, магний – несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков – железо, никель, кобальт – μ >> 1. Например, у железа μ ≈ 25000.
В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики – кислород, платина, магний – несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков – железо, никель, кобальт – μ >> 1. Например, у железа μ ≈ 25000.
Магнитный поток. Электромагнитная индукция
К оглавлению…
Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:
где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).
Единица магнитного потока в системе СИ называется Вебером (Вб).
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции εинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.
- Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
- Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
При решении задач важно сразу определить за счет чего меняется магнитный поток.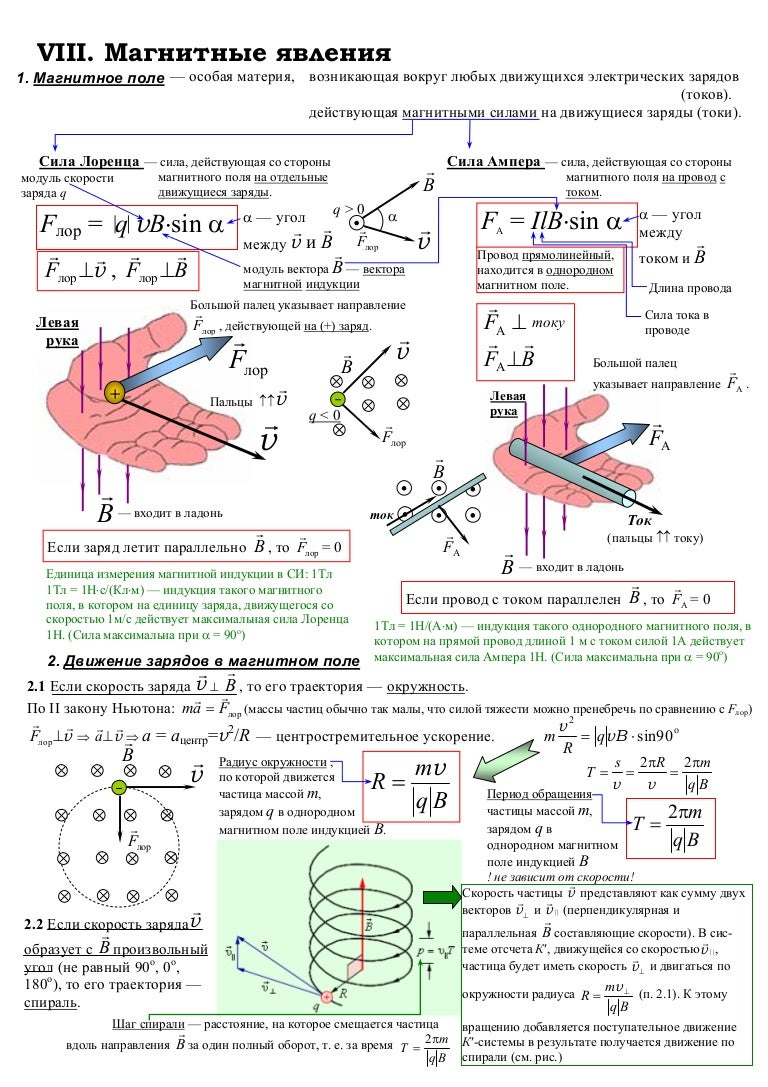 Возможно три варианта:
Возможно три варианта:
- Меняется магнитное поле.
- Меняется площадь контура.
- Меняется ориентация рамки относительно поля.
При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Движение проводника в магнитном поле
К оглавлению…
При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:
где: α – угол, который измеряется между направлением скорости и вектора магнитной индукции.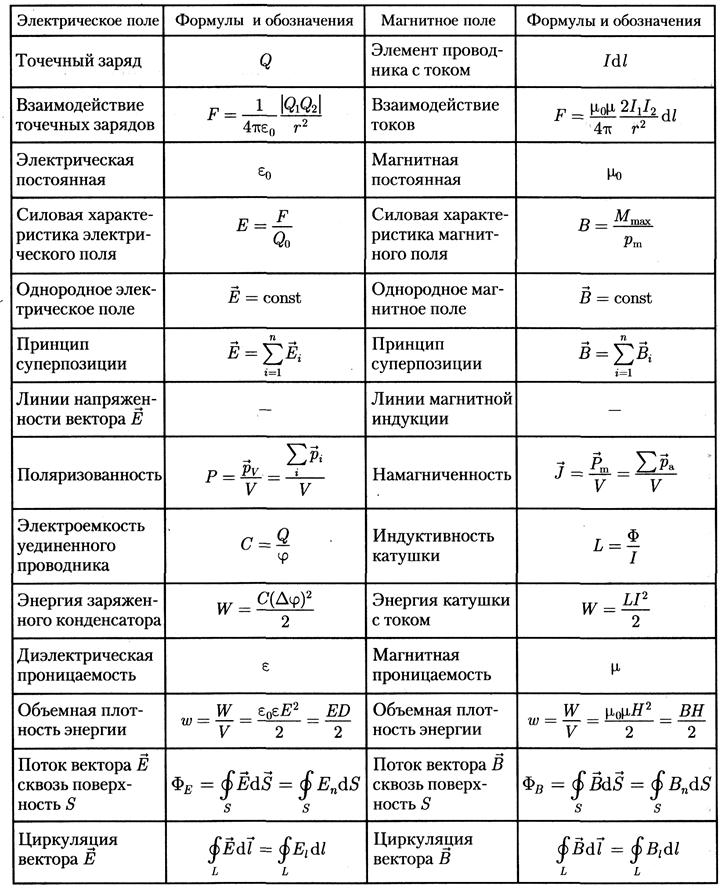 В неподвижных частях контура ЭДС не возникает.
В неподвижных частях контура ЭДС не возникает.
Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω, то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:
Индуктивность. Самоиндукция. Энергия магнитного поля
К оглавлению…
Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).
Единица индуктивности в СИ называется Генри (Гн).
Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:
где: n – концентрация витков на единицу длины катушки:
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:
Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):
Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):
Правило Ленца
К оглавлению. ..
..
Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.
Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.
Все формулы по магнетизму физика. Основные формулы по физике
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл ) . По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про .
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса.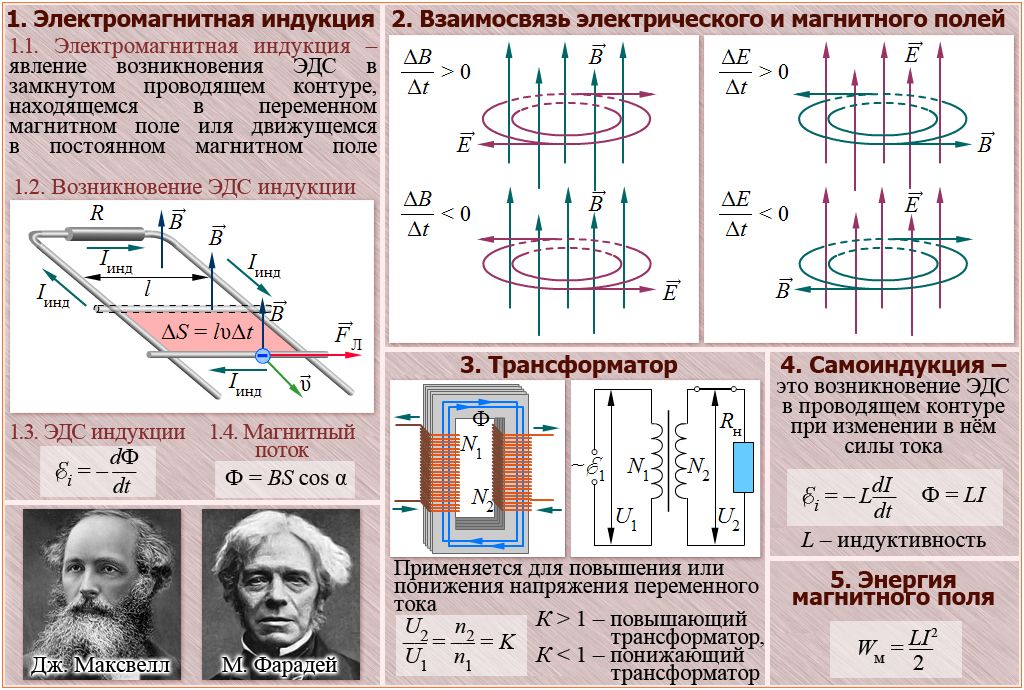 Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки . Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B . Если мы поместим в него проводник длиной l , по которому течет ток силой I , то поле будет действовать на проводник с силой:
Это и есть сила Ампера . Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца . Здесь важно отметить слово «движущийся» , так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v , а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. – это катушка, то есть множество круговых витков с током.
Пусть их количество – N , а длина самого соленоилда – l . Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на
Магнитный поток и ЭДС
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф .
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В .
При изменении магнитного потока через контур в контуре индуцируется ЭДС , равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила , вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн) . На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики « электричество и магнетизм» , однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в
Электричество и магнетизм формулы.
Закон Кулона
1. закон Кулона
2 . напряженность электрического поля
напряженность электрического поля
3. модуль напряженности поля точечного заряда
4 . принцип суперпозиции
5. -вектор электрического момента диполя – дипольный момент
6.
2. Теорема Гаусса
7
8.
9. теорема Гаусса
10. теорема Гаусса
11.
12. – дивергенция поля
13
Потенциал электростатического поля
14. -работа сил электростатического поля по перемещению пробного заряда q в электрическом поле точечного заряда Q
15. – интегральный признак потенциальности электростатического поля
16. – приращение потенциала электростатического поля
17 . – убыль потенциала электростатического поля
18 . – нормировка потенциала (выбор начала отсчета)
19 . – принцип суперпозиции для
20. – квазистатическая работа сил поля при перемещении
по произвольному пути из т. 1 в т.2
1 в т.2
21. – локальное соотношение между и
22. – потенциал точечного заряда
23. – потенциал диполя
24. – дифференциальный оператор Гамильтона («набла») в полярной системе координат
25 . – оператор Лапласа или лапласиан
26. – уравнение Лапласа
27. – уравнение Пуассона
4. Энергия в электростатике.
28. – энергия электростатического взаимодействия зарядов друг с другом
29 . – полная электростатическая энергия заряженного тела
30. – объемная плотность энергии (энергия, локализованная в единичном объеме)
31. – энергия взаимодействия точечного диполя с внешним полем
5. Проводники электростатике
32. – поле вблизи поверхности проводника
33. – электроемкость уединенного проводника
34. – емкость плоского конденсатора
35 . – емкость сферического конденсатора, образованного сферическими проводящими поверхностями радиусов а и b
– емкость сферического конденсатора, образованного сферическими проводящими поверхностями радиусов а и b
36 . – энергия конденсатора
6. Электростатическое поле в диэлектриках
37. , – диэлектрическая восприимчивость вещества
38. – поляризованность (электрический дипольный момент единицы объема вещества)
39. – связь между напряженностью и поляризованностью
40 . теорема Гаусса для вектора в интегральной форме
41. – теорема Гаусса для вектора в дифференциальной форме
42. – граничные условия для вектора
43. – теорема Гаусса для вектора в диэлектриках
44 . – электрическое смещение
45. – интегральная и локальная теорема Гаусса для вектора
46. – граничные условия для вектора , где – поверхностная плотность сторонних зарядов
47. – связь и для изотропных сред
Постоянный ток
48. – сила тока
49 . – заряд, проходящий через сечение проводника
50. – уравнение непрерывности (закон сохранения заряда)
51. – уравнение непрерывности в дифференциальной форме
52 . – разность потенциалов для проводника, в котором не действуют сторонние силы, отождествляется с падением напряжения
53. – закон Ома
54. – закон Джоуля -Ленца
55. – сопротивление провода из однородного материала одинаковой толщины
56. – закон Ома в дифференциальной форме
57 . – величина, обратная удельному сопротивлению называется удельной электрической проводимостью
58 . – закон Джоуля –Ленца в дифференциальной форме
59. -интегральная форма закона Ома с учетом поля сторонних сил для участка цепи, содержащего ЭДС.
60 . – первый закон Кирхгофа. Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю.
61. -второй закон Кирхгофа. Сумма напряжений вдоль любого замкнутого контура цепи равна алгебраической сумме ЭДС, действующих в этом контуре.
62 . – удельная тепловая мощность тока в неоднородной проводящей среде
Закон Био-Савара
63 . – сила Лоренца
64 . – если в некоторой системе отсчета электромагнитное поле является электрическим
(т.е. ), то в другой системе отсчета , движущейся относительно К со скоростью , компоненты электромагнитного поля отличны от нуля и связаны соотношением 64
65 . – если в некоторой системе отсчета электрически заряженное тело имеет скорость , то электрическая и магнитная компоненты электромагнитного поля, создаваемого его зарядом, связаны в этой системе отсчета соотношением
66 . – если в некоторой системе отсчета электромагнитное поле является магнитным (), то в любой другой системе отсчета, движущейся со скоростью относительно первой, компоненты и электромагнитного поля отличны от нуля и связаны соотношением
67. – индукция магнитного поля движущегося заряда
68 . – магнитная постоянная
6.
2. Теорема Гаусса
7 . – поток поля через произвольную поверхность
8. – принцип аддитивности потоков
9. теорема Гаусса
10. теорема Гаусса
11. – дифференциальный оператор Гамильтона («набла»)в декартовой системе координат
12. – дивергенция поля
13 . локальная (дифференциальная) теорема Гаусса
Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем . Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл). Если в магнитное поле с индукцией B поместить проводник длиной l с током I , то на него будет действовать сила, называемая силой Ампера , которая вычисляется по формуле:
где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.
Для определения направления силы Ампера обычно используют правило «Левой руки» : если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).
Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.
Момент сил, действующих на рамку с током
Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера. Вращательный момент сил Ампера равен:
где: S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции (нормаль – вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.
Сила Лоренца
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I , находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца . Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B , двигающуюся со скоростью v , вычисляется по следующей формуле:
Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет отрицательный заряд, то направление силы Лоренца, найденное по правилу левой руки, надо будет заменить на противоположное.
Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает . Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:
Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R .
Теория о магнитном поле
Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I 1 и I 2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:
где: μ 0 – постоянная величина, которую называют магнитной постоянной . Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:
μ 0 = 4π ·10 –7 H/A 2 ≈ 1,26·10 –6 H/A 2 .
Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:
где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:
Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй – на юг. Отсюда название полюсов: северный (N ) и южный (S ). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N ) и южный (красным цветом или буквой S ). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.
Вектор магнитной индукции
Вектор магнитной индукции – векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику. Обозначается В , единица измерения – 1 Тесла. 1 Тл – очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.
Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:
В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки» : если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:
В случае прямого тока линии магнитной индукции – окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.
Соленоид – намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):
Линии магнитного поля имеют вид замкнутых линий – это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.
Магнитные свойства вещества
Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ , для которой верно следующее:
Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики – кислород, платина, магний – несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков – железо, никель, кобальт – μ >> 1. Например, у железа μ ≈ 25000.
Магнитный поток. Электромагнитная индукция
Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:
где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции ε инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.
- Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
- Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:
- Меняется магнитное поле.
- Меняется площадь контура.
- Меняется ориентация рамки относительно поля.
При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S , вращающемся с угловой скоростью ω в магнитном поле с индукцией В :
Движение проводника в магнитном поле
При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:
где: α – угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.
Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω , то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:
Индуктивность. Самоиндукция. Энергия магнитного поля
Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ , пронизывающий контур или катушку с током, пропорционален силе тока I :
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).
Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:
где: n – концентрация витков на единицу длины катушки:
ЭДС самоиндукции , возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:
Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия W м магнитного поля катушки с индуктивностью L , создаваемого током I , может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI ):
Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):
Правило Ленца
Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.
На этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Формула индукции магнитного поля, B
Направлением вектора магнитной индукции считают направление на север магнитной стрелки, которая может свободно вращаться в магнитном поле. Такое же направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре.
Модуль вектора магнитной индукции можно установить, используя силу, которая действует на проводники с током, помещенные в магнитное поле (силу Ампера). Тогда модуль вектора равен частному от деления максимальной силы (), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ():
Рассматривая силу Лоренца, которая действует на заряженную частицу, движущуюся в магнитном поле, получают формулу для магнитной индукции в виде:
где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.
Формулой, которая определяет величину вектора магнитной индукции в данной точке магнитного поля, считают так же следующее выражение:
где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля. Вращающий момент (M), действующий на контур с током I в однородном магнитном поле можно вычислить как:
где S – площадь, которую обтекает ток I. Следует помнить, что максимальный вращающий момент получается тогда, когда плоскость контура параллельна линиям магнитной индукции поля ().
Принцип суперпозиции магнитных полей
Если магнитное поле получается в результат наложения нескольких магнитных полей то, магнитная индукция поля (), может быть найдена как векторная сумма магнитных индукций отдельных полей ():
Закон Био-Савара-Лапласа, как формула для вычисления величины индукции магнитного поля
Закон Био-Савара – Лапласа является одним из распространенных законов, который позволяет вычислить вектор магнитной индукции () в любой точке магнитного поля, создаваемого в вакууме элементарным проводником с током:
где I – сила тока; – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связывает формула:
где – относительная магнитная проницаемость вещества.
Частные случаи формул для вычисления модуля вектора магнитной индукции
Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):
где R – радиус витка.
Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:
где r – расстояние от оси проводника до точки, в которой рассматривается поле.
В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:
где n – количество витков соленоида на единицу длины; I – сила тока в витке.
Примеры решения задач по теме «Индукция магнитного поля»
Формула магнитной индукции, B
Формулы определяющие величину вектора магнитной индукции получают, используя выражение для силы Ампера, силы Лоренца и применяя понятие вращающего момента.
Формула величины вектора магнитной индукции
Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение:
где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля.
При помощи силы Ампера величина вектора магнитной индукции задана как:
где модуль равен пределу отношения величины силы (), с которой магнитное поле действует на бесконечно малый проводник с током, к силе тока (I) умноженной на длину этого проводника (), если длина проводника стремится к нулю. Как известно кроме величины вектор магнитной индукции имеет направление. В данном случае перпендикулярен к направлению силы и перпендикулярен направлению элемента проводника. Если рассматривать вращение из конца вектора магнитной индукции по кратчайшему расстоянию от направления силы к направлению тока, оно должно идти против часовой стрелки.
Используя силу Лоренца, получают формулу для магнитной индукции в виде:
где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.
Закон Био-Савара-Лапласа
Данный закон предоставляет нам возможность вычислить вектор магнитной индукции () в любой точке магнитного поля, которое создается в вакууме элементарным проводником с током:
где I – сила тока; – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связывает формула:
где – относительная магнитная проницаемость вещества.
Частные случаи формул для вычисления величины вектора магнитной индукции
Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):
где R – радиус витка.
Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:
где r – расстояние от оси проводника до точки, в которой рассматривается поле.
В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:
где n – количество витков соленоида на единицу длины; I – сила тока в витке.
Принцип суперпозиции
Магнитная индукция поля (), которое является наложением нескольких полей, находится как векторная сумма магнитных индукций отдельных полей ():
Примеры решения задач по теме «Магнитная индукция»
основные формулы, законы и правила
Магнитное поле — это форма материи, окружающей движущиеся электрические заряды. Магнитное поле окружает проводники с током.
Силовой характеристикой магнитного поля является магнитная индукция.
Магнитная индукция
— это величина, равная отношению максимального момента силы, вращающей контур с током в магнитном поле, к силе тока в этом контуре и его площади:Другое определение магнитной индукции: магнитная индукция — это величина, равная отношению максимальной силы, действующей на проводник с током в магнитном поле, к силе тока в нем и длине этого проводника в магнитном поле:
Магнитная индукция — векторная величина. Вектор магнитной индукции совпадает по направлению с положительной нормалью
к плоскости контура. Занаправление положительной нормали п принято направление поступательного движения правого винта (буравчика), когда его головка вращается по току в контуре (рис. 208).
Правым винтом может служить ваша правая рука. Если свернуть четыре пальца правой руки в направлении тока в контуре, то большой палец, отставленный на 90°, покажет направление положительной нормали и вектора магнитной индукции.
Единица магнитной индукции в СИ — тесла (Тл).
Магнитное поле изображают графически с помощью магнитных силовых линий или линий вектора магнитной индукции.
В природе не существует магнитных зарядов, поэтому линии вектора магнитной индукции всегда замкнуты.
Магнитное поле является вихревым, в отличие от потенциального электростатического поля, линии которого всегда разомкнуты, т. к. начинаются и оканчиваются на электрических зарядах. Линии вектора магнитной индукции охватывают проводники с током. Линии вектора магнитной индукции поля прямого тока представляют собой концентрические окружности с центром на проводнике с током (рис. 209). Их направление можно определить с помощью правого винта (или с помощью вашей правой руки: если большой палец правой руки направить по направлению тока в проводнике, то четыре загнутых пальца покажут направление линии магнитной индукции). По мере удаления от проводника с током индукция магнитного поля этого тока уменьшается.
Магнитное поле, в каждой точке которого вектор магнитной индукции одинаков, называется однородным. Линии магнитной индукции однородного поля представляют собой прямые, расположенные на одинаковом расстоянии друг от друга. Чем гуще они располагаются, тем больше магнитная индукция.
Примером однородного магнитного поля является магнитное поле внутри длинного соленоида — катушки с током (рис. 210).
Линии магнитной индукции выходят из северного полюса N и входят в его южный полюс S.
Магнитное поле полосового магнита (рис. 211) наибольшее на его полюсах, а в центре его магнитная индукция равна нулю.
Если в однородное поле внести контур с током, расположив его плоскость параллельно линиям магнитной индукции, то на стороны контура, перпендикулярным линиям магнитной индукции, будет действовать пара сил Ампера, которая создаст максимальный вращающий момент сил
, равный произведению индукции магнитного поля, силы тока в ней и ее площади:Если плоскость контура расположена под углом к линиям вектора индукции однородного магнитного поля, то момент сил определяет формула
Здесь
— угол между вектором индукции магнитного поля и нормалью к плоскости рамки.Момент сил, вращающих контур с током в однородном магнитном поле, равен произведению индукции этого поля, силы тока в контуре, площади контура и синуса угла между векторами магнитной индукции и нормали к плоскости контура.
Если плоскость контура перпендикулярна линиям вектора магнитной индукции, то вращающий момент сил равен 0, а силы Ампера действуют в плоскости контура, деформируя его.
Направление силы Ампера можно определить по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в ладонь, а четыре вытянутых пальца направить по току в проводнике, то большой палец, отставленный на 90 , покажет направление силы Ампера, действующей на этот проводник в данном магнитном поле (рис. 212).
Если проводник с током расположить параллельно магнитным линиям, то сила Ампера на него действовать не будет.
Сила Ампера
Величину силы Ампера определяет закон Ампера: сила F, действующая на проводник с током в однородном магнитном поле, равна произведению магнитной индукции этого поля В, силы тока в проводнике I, длины проводника в магнитном поле I и синуса угла а между направлением магнитного поля и направлением тока в проводнике:
Сила, с которой магнитное поле действует на движущийся в нем заряд, называется силой Лоренца.
Сила ЛоренцаСила Лоренца
действующая на заряд q, движущийся в однородном магнитном поле, равна произведению индукции этого поля В на заряд, на скорость его движения v и на синус угла между направлением магнитного поля и направлением движения зарядаОпределить направление силы Лоренца можно тоже по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления движения отрицательного заряда), то большой палец, отставленный на 90″, покажет направление силы Лоренца.
Заряженная частица, влетевшая в однородное магнитное поле перпендикулярно его магнитным линиям, движется равномерно по окружности, охватывающей магнитные линии.
При этом сила Лоренца направлена по радиусу к центру окружности.
На рис. 213 положительно заряженная частица с зарядом q, влетевшая в направлении, показанном вектором v в однородное магнитное поле индукцией В, направленном за чертеж, движется вокруг магнитных линий против часовой стрелки.
Если заряженная частица влетает в магнитное поле под углом к магнитным линиям, то она станет двигаться по винтовой линии (рис. 214), вращаясь по окружности с линейной скоростью, равной нормальной составляющей
вектора скорости usin а, и одновременно перемещаясьравномерно вдоль линий вектора индукции магнитного поля с тангенциальной составляющей vcos а вектора скорости
.Расстояние х, которое она пролетит вдоль магнитной линии за один оборот, называется шагом винта. Поскольку вдоль магнитной линии частица движется с постоянной скоростью и, то шаг винта равен
Здесь Т — период, т.е. время одного оборота частицы вокруг магнитных линий.
Сила Лоренца всегда перпендикулярна вектору скорости и, следовательно, вектору перемещения заряда, поэтому она работы перемещения заряда в магнитном поле не совершает, вследствие чего кинетическая энергия заряда, движущегося в магнитном поле под действием силы Лоренца, не изменяется.
Если заряженная частица движется одновременно в электрическом и магнитном полях (т.е. в электромагнитном поле), то на нее действует обобщенная сила Лоренца, равная векторной сумме силы Лоренца, действующей на нее со стороны магнитного поля, и силы Кулона, действующей со стороны электрического поля.
Пусть в однородном магнитном поле индукцией находится некоторая площадка S (рис. 215).
Магнитный поток Ф, создаваемый однородным магнитным полем сквозь некоторую площадку, равен произведению индукции этого магнитного поля В на величину площадки S и на косинус угла а между вектором магнитной индукции и нормалью
к площадке.Если площадка S расположена перпендикулярно магнитным линиям однородного поля, то магнитный поток, пересекающий ее, максимален:
Если площадка S расположена параллельно магнитным линиям, то они ее не пересекают, поэтому магнитный поток через площадку в этом случае равен нулю.
Магнитный потокМагнитный поток — скалярная алгебраическая величина, т.е. он может быть положителен и отрицателен, поскольку косинус угла может быть больше и меньше нуля.
Если магнитный поток пересекает замкнутую поверхность (представьте ее в виде надутого воздушного шарика), то, поскольку все магнитные линии непрерывны и замыкаются сами на себя, число входящих в эту поверхность магнитных линий, создающих отрицательный поток, будет равно числу выходящих магнитных линий, создающих численно такой же по модулю, но положительный поток. Поэтому полный поток вектора магнитной индукции сквозь замкнутую поверхность равен нулю. Это важное свойство магнитного поля свидетельствует об отсутствии в природе магнитных зарядов и вихревом характере магнитного поля.
Единица магнитного потока в СИ — вебер (Вб).
Когда магнитный поток сквозь площадь, ограниченную проводящим контуром, изменяется, в этом контуре возникает индукционный ток.
Правило Ленца: индукционный ток всегда направлен так, что своим магнитным полем он противодействует изменению магнитного потока, вызвавшего этот ток.
Обратимся к рис. 216, а). Когда магнитный поток сквозь контур, создаваемый внешним по отношению к контуру магнитным полем индукцией
, нарастает , индукционный ток в контуре направлен так, что его магнитное поле индукцией (на рис. 216, а) оно изображено штриховыми стрелками), антинаправлено внешнему магнитному полю, противодействуя увеличению магнитного потока. Отметим, что направление тока связано с направлением своего магнитного поля правилом правого винта — буравчика. Когда же магнитный поток, создаваемый внешним магнитным полем индукцией убывает (рис. 216, б), индукционный ток в контуре изменяет свое направление на противоположное и при этом его магнитное поле оказывается сонаправленным с внешним полем . Теперь магнитное поле индукционного тока противодействует убыли магнитного потока, создаваемого внешним магнитным полем сквозь контур, поддерживая его.Явление возникновения индукционного тока в контуре при изменении магнитного потока, пересекающего этот контур, называется электромагнитной индукцией. По закону Ома сила индукционного тока
прямо пропорциональна ЭДС индукции и обратно пропорциональна сопротивлению контура В:Закон ФарадеяЗакон Фарадея для электромагнитной индукции: ЭДС электромагнитной индукции, возникающая в контуре при всяком изменении магнитного потока, пересекающего этот контур, равна скорости изменения магнитного потока, взятой со знаком минус,
Здесь
— ЭДС индукции в контуре, — скорость изменения магнитного потока, пересекающего контур, N — число витков в контуре (безразмерное).Эта формула справедлива, когда магнитный поток изменяется монотонно, т.е. когда за равные промежутки времени
он изменяется на одинаковую величину и ЭДС индукции постоянна. Если же магнитный поток изменяется произвольно, то увеличиваясь, то уменьшаясь, что бывает при вращении контура в магнитном поле, то пользоваться этой формулой для определения мгновенного значения ЭДС индукции нельзя, по ней можно определить только среднее значение ЭДС индукции.При произвольном изменении магнитного потока сквозь контур ЭДС индукции равна первой производной магнитного потока по времени, взятой со знаком минус:
Здесь
— первая производная магнитного потока по времени.Знак минус в этих формулах объясняется правилом Ленца.
Если контур, пересекаемый переменным магнитным потоком, содержит не один, а N витков, то ЭДС индукции в нем будет в N раз больше, чем в одном витке. При этом предыдущие формулы примут вид:
ЭДС индукции, возникающая в проводнике, движущемся поступательно в однородном магнитном поле под углом к магнитным линиям, равна произведению индукции этого поля на скорость проводника, на его длину в этом поле и на синус угла между вектором индукции магнитного и вектором скорости проводника:
ЭДС индукции
, возникающая в контуре, вращающемся равномерно в однородном магнитном поле, равна произведению угловой скорости контура на индукцию В магнитного поля, на площадь контура S и на синус угла а между вектором магнитной индукции и нормалью к плоскости контура:В случае, когда плоскость контура параллельна магнитным линиям, угол
. Тогда ЭДС индукции в контуре будет максимальна.Если контур содержит N витков, то ЭДС индукции в нем в N раз больше, чем в одном витке:
Явление возникновения ЭДС индукции и индукционного тока в контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции.
Магнитный поток Ф сквозь катушку (или контур любой иной формы) прямо пропорционален силе тока в ней, т.е. между этими величинами существует прямо пропорциональная зависимость:
Здесь L — коэффициент пропорциональности между током и связанным с ним магнитным потоком. Он называется коэффициентом самоиндукции контура или его индуктивностью. Величина индуктивности зависит от формы и размеров самого контура, а также от магнитных свойств среды, и постоянна для данного контура. Индуктивность контура — скалярная положительная величина. Она не зависит от наличия или отсутствия тока в нем. Индуктивность катушек заводского изготовления указывается в их паспорте.
Единица индуктивности в СИ — генри (Гн).
ЭДС самоиндукции
, возникающая в контуре при изменении тока в нем, прямо пропорциональна скорости изменения силы тока в контуре, взятой со знаком «минус»:Здесь
—скорость изменения силы тока, т.е. изменение силы тока за единицу времени.Если ток в контуре изменяется произвольно, то пользоваться этой формулой для определения мгновенной ЭДС самоиндукции нельзя, по ней можно определить лишь среднее значение ЭДС самоиндукции за время
. Для определения мгновенного значения ЭДС самоиндукции в этом случае надо пользоваться формулойМгновенная ЭДС самоиндукции прямо пропорциональна первой производной силы тока по времени, взятой со знаком «минус».
Магнитное поле, как и всякое силовое поле, обладает энергией.
Энергия магнитного поля катушки с током соленоида равна половине произведения индуктивности этого соленоида на квадрат силы тока в нем:
Поскольку магнитное поле размыто по пространству, то, чтобы охарактеризовать его энергетические свойства, вводят величину, равную энергии магнитного поля в единице объема пространства, занятого этим полем. Эта величина называется объемной плотностью энергии магнитного поля
.Объемная плотность энергии магнитного поля
равна отношению энергии магнитного поля к объему V пространства, занятого им:Объемная плотность энергии магнитного поля прямо пропорциональна квадрату магнитной индукции этого поля и обратно пропорциональна относительной магнитной проницаемости окружающей среды:
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Магнитная индукция, магнитный поток: определение, формулы, смысл
Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.
Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается.
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.
Васильев Дмитрий Петрович
Профессор электротехники СПбГПУ
Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки – именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.
Магнитный поток
Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.
Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.
Магнитометры, используемые для ее измерения, называют теслометрами.
Абрамян Евгений Павлович
Доцент кафедры электротехники СПбГПУ
Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).
После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.
Магнитное поле. Силы – материалы для подготовки к ЕГЭ по Физике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: сила Ампера, сила Лоренца.В отличие от электрического поля, которое действует на любой заряд, магнитное поле действует только на движущиеся заряженные частицы. При этом оказывается, что сила зависит не только от величины, но и от направления скорости заряда.
Сила Лоренца
Сила, с которой магнитное поле действует на заряженную частицу, называется силой Лоренца. Опыт показывает, что вектор силы Лоренца находится следующим образом.
1. Абсолютная величина силы Лоренца равна:
(1)
Здесь — абсолютная величина заряда, — скорость заряда, — индукция магнитного поля, — угол между векторами и .
2. Сила Лоренца перпендикулярна обоим векторам и . Иными словами, вектор перпендикулярен плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля.
Остаётся выяснить, в какое полупространство относительно данной плоскости направлена сила Лоренца.
3. Взаимное расположение векторов , и для положительного заряда показано на рис. 1.
Рис. 1. Сила Лоренца
Направление силы Лоренца определяется в данном случае по одному из двух альтернативных правил.
Правило часовой стрелки. Сила Лоренца направлена туда, глядя откуда кратчайший поворот вектора скорости частицы v к вектору магнитной индукции B виден против часовой стрелки.
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление скорости частицы, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Лоренца.
Для отрицательного заряда направление силы Лоренца меняется на противоположное.
Всё вышеперечисленное является обобщением опытных фактов. Формула (1) позволяет связать размерность индукции магнитного поля с размерностями других физических величин:
Сила Ампера
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.
Происхождение силы Ампера легко понять. Ведь ток в металле является направленным движением электронов, а на каждый электрон действует сила Лоренца. Все эти силы Лоренца, действующие на свободные электроны, имеют одинаковое направление и одинаковую величину; они складываются друг с другом и дают результирующую силу Ампера.
Направление силы Ампера определяется по тем же двум правилам, сформулированным выше.
Правило часовой стрелки . Сила Ампера направлена туда, глядя откуда кратчайший поворот тока к полю виден против часовой стрелки .
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление тока, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Ампера .
Взаимное расположение тока, поля и силы Ампера указано на рис. 2.
Рис. 2. Сила Ампера
На этом рисунке проводник имеет длину , а угол между направлениями тока и поля равен . Мы сейчас выведем выражение для абсолютной величины силы Ампера.
На каждый свободный электрон действует сила Лоренца:
где — скорость направленного движения свободных электронов в проводнике.
Пусть — число свободных электронов в данном проводнике, — их концентрация (число в единице объёма). Тогда:
где — объём проводника, — площадь его поперечного сечения. Получаем:
Мы не случайно выделили скобками четыре сомножителя. Ведь это есть не что иное, как сила тока: (вспомните выражение силы тока через скорость направленного движения свободных зарядов!). В результате приходим к окончательной формуле для силы Ампера:
(2)
Хорошую возможность поупражняться в нахождении направлений магнитного поля и силы Ампера даёт взаимодействие параллельных токов. Оказывается, два параллельных провода отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают (рис. 3).
Рис. 3. Взаимодействие параллельных токов
Обязательно убедитесь в этом самостоятельно! Делаем так. Сначала берём произвольную точку на первом проводе и определяем направление магнитного поля, создаваемого в этой точке вторым проводом (правило вам известно — см. предыдущий листок>). Ну а затем находим направление силы Ампера, действующей на первый провод со стороны магнитного поля второго провода.
Рамка с током в магнитном поле
В листках по термодинамике мы говорили о важности циклически работающих машин: они снабжают нас энергией. Понимание законов термодинамики позволило сконструировать тепловые двигатели, которые исправно служат нам и по сей день.
Понимание же законов электромагнетизма дало возможность создать циклическую машину другого типа — электродвигатель.
Мы рассмотрим один из элементов электродвигателя — рамку с током в магнитном поле. Разобравшись в её поведении, мы сможем уловить основную идею функционирования электродвигателя.
Пусть прямоугольная рамка может вращаться вокруг горизонтальной оси (рис. 4, слева). Рамка находится в вертикальном однородном магнитном поле . Ток течёт по рамке в направлении ; это направление показано соответствующими стрелками.
Рис. 4. Рамка с током в магнитном поле
Вектор называется вектором нормали; он перпендикулярен плоскости рамки и направлен туда, глядя откуда ток кажется циркулирующим против часовой стрелки. (Иными словами, вектор сонаправлен с вектором индукции магнитного поля, которое создаётся током в рамке.) Поворот рамки измеряется углом между векторами и .
Теперь определим направления сил Ампера, которые действуют на рамку со стороны магнитного поля. Эти силы расставлены на рисунке; вот вам ещё одно упражнение на правило часовой стрелки (левой руки) — обязательно проверьте правильность указанных направлений!
Силы и , приложенные к сторонам и , действуют вдоль оси вращения. Они лишь растягивают рамку и не вызывают её вращение.
Куда более интересны силы и , приложеные соответственно к сторонам и . Они лежат в горизонтальной плоскости и перпендикулярны оси вращения. Эти силы вращают рамку в направлении по часовой стрелке, если смотреть справа (рис. 4, правая часть). Вычислим момент этой пары сил относительно оси вращения рамки.
Пусть длина стороны равна . Тогда
Пусть длина стороны равна . Плечо силы , как видно из рис. 4 (справа) равно:
Таким же будет плечо силы . Отсюда получаем момент сил, вращающий рамку:
Теперь заметим, что — площадь рамки. Окончательно имеем:
(3)
В этой формуле площадь служит единственной геометрической характеристикой рамки.Это наводит на мысль, что только площадь рамки и существенна в выражении для вращающего момента. И действительно, можно доказать (разбивая рамку на бесконечно узкие полоски, неотличимые от прямоугольников), что формула (3) справедлива для рамки любой формы с площадью .
Как видно из формулы (3), максимальный вращающий момент равен:
Эта максимальная величина момента достигается при , то есть когда плоскость рамки параллельна магнитному полю.
Вращающий момент становится равным нулю при и . Оба этих положения по-своему интересны.
При плоскость рамки перпендикулярна полю, а векторы и направлены в разные стороны. Данное положение является положением неустойчивого равновенсия: стоит хоть немного шевельнуть рамку, как силы Ампера начнут её вращать в том же направлении, поворачивая вектор к вектору (убедитесь!).
При плоскость рамки также перпендикулярна полю, а векторы и сонаправлены. Это — положение устойчивого равновенсия: при отклонении рамки возникает вращающий момент, стремящийся вернуть рамку назад (убедитесь!). Начнутся колебания рамки, постепенно затухающие из-за трения. В конце концов рамка остановится в положении ; в этом положении вектор индукции магнитного поля рамки сонаправлен с вектором индукции внешнего магнитного поля (вот почему при намагничивании вещества элементарные токи ориентируются так, что их поля направлены в сторону внешнего магнитного поля). Полезное сопоставление: рамка занимает такое положение, что её положительная нормаль ориентируется в том же направлении, что и северный конец стрелки компаса, помещённой в это магнитное поле.
Таким образом, поведение рамки в магнитном поле становится ясным: если отклонить рамку от положения устойчивого равновесия и отпустить, то рамка будет совершать колебания. С точки зрения совершения механической работы это не очень хорошо: если намотать нить на ось вращения и подвесить к нити груз, то груз будет то подниматься, то опускаться.
Но вот если исхитриться и заставить ток менять направление в нужные моменты, то вместо колебаний рамки начнётся её непрерывное вращение и, соответственно, непрерывный подъём подвешенного груза. Тогда-то и получится полноценный электродвигатель; идея с переменой направления тока реализуется с помощью коллектора и щёток.
Формула магнитного поля
Когда электрический ток проходит по проводу, вокруг него образуется магнитное поле. Силовые линии магнитного поля образуют концентрические круги вокруг провода. Направление магнитного поля зависит от направления тока. Его можно определить с помощью «правила правой руки», указав большим пальцем правой руки в направлении тока. Направление линий магнитного поля – это направление ваших согнутых пальцев. Величина магнитного поля зависит от силы тока и расстояния от провода, несущего заряд.В формулу входит константа. Это называется проницаемостью свободного пространства и имеет значение. Единица магнитного поля – тесла, т.
.B = величина магнитного поля (тесла, Тл)
= проницаемость свободного пространства ()
I = величина электрического тока (Амперы, А)
r = расстояние (м)
Формула магнитного поля Вопросы:
1) Какова величина магнитного поля на расстоянии 0,10 м от провода, несущего 3.00 ток? Если у тока есть векторное направление вне страницы (или экрана), каково направление магнитного поля?
Ответ: Величину магнитного поля можно рассчитать по формуле:
Величина магнитного поля составляет 6,00 x 10 -6 Тл, что также можно записать как (микротесла).
Направление магнитного поля можно определить с помощью «правила правой руки», указав большим пальцем правой руки в направлении тока. Направление линий магнитного поля – это направление ваших согнутых пальцев. У тока есть векторное направление за пределы страницы, поэтому ваши пальцы будут сгибаться против часовой стрелки. Поэтому силовые линии магнитного поля направлены против часовой стрелки, образуя круги вокруг провода.
2) Если величина магнитного поля 2.00 м от провода составляет 10,0 нТл (нано-Тесла), какова величина электрического тока, переносимого по проводу? Если силовые линии магнитного поля образуют круги по часовой стрелке в плоскости страницы (или экрана), каково направление вектора электрического тока?
Ответ: Величину электрического тока можно рассчитать, переставив формулу магнитного поля:
Величина магнитного поля указывается в нано-Тесла. Приставка «нано» означает 10 -9 и т. Д.Таким образом, величина магнитного поля на указанном расстоянии составляет:
.B = 10,0 нТл
Величина тока в проводе:
Величина электрического тока в проводе 0,100А.
Направление электрического тока можно определить с помощью «правила правой руки».Линии магнитного поля образуют круги по часовой стрелке в плоскости страницы, поэтому представьте, что вы сгибаете правую руку так, чтобы пальцы указывали по часовой стрелке. Для этого ваш большой палец должен указывать на страницу (или экран). Следовательно, электрический ток направлен внутрь страницы (или экрана).
Расчет магнитных полей и сил
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Электромагнитная сила – Гипертекст по физике
Обсуждение
введение
Магнетизм – это сила, с которой движущиеся заряды действуют друг на друга.Это формальное определение основано на этом простом уравнении.
F B = q v × B
Напомним, что электричество (по сути) – это сила, с помощью которой заряды действуют друг на друга. Поскольку эта сила существует независимо от того, движутся ли заряды, ее иногда называют электростатической силой. Можно сказать, что магнетизм – это электродинамическая сила, но это случается редко. Комбинация электрических и магнитных сил на заряженном объекте известна как сила Лоренца .
F = q ( E + v × B )
Для большого заряда…
| F B = q | v × B | ||||
| F B = q | d x | × В = | dq | ℓ × B | |
| дт | дт | ||||
| F B = I | ℓ × B | ||||
Эта формула магнитной силы, действующей на токоведущий провод, является основой эксперимента, который использовался для определения ампер с 1948 по 2019 год.
Ампер – это постоянный ток, который, если его поддерживать в двух прямых параллельных проводниках бесконечной длины, с незначительным круглым поперечным сечением и помещать на расстоянии одного метра в вакууме, создавал бы между этими проводниками силу, равную 2 × 10 −7. ньютона на метр длины
МБПМ, 1948 г.
Используя закон Ампера, мы вывели формулу для силы магнитного поля, окружающего длинный прямой провод с током…
Подставьте это выражение в формулу магнитной силы.(Поскольку два провода параллельны, поле одного встречает другой под прямым углом, и перекрестное произведение сводится к прямому умножению.) Решение для силы на единицу длины, как описано в эксперименте…
| F B | = | I ℓ × B | ||
| Ф В | = | Iℓ | мкм 0 I | |
| 2π r | ||||
| Ф В | = | мкм 0 I 2 | ||
| ℓ | 2π r | |||
Устанавливает необычно точное значение проницаемости свободного пространства (необычно точное для физической константы).Подставьте значения для измерений, описанных в эксперименте BIPM, в последнее полученное нами уравнение…
| = | ||
| (2 × 10 -7 Н) | = | мкм 0 (1 А) 2 |
| (1 м) | 2π (1 м) |
и решите для проницаемости свободного пространства…
| мкм 0 = | 2π (1 м) (2 × 10 −7 Н) | |
| (1 м) (1 А) 2 | ||
| мкм 0 = | 4π × 10 −7 НЕТ 2 | |
Возвращение к формуле для магнитной силы на проводе с током приводит к следующему определению напряженности магнитного поля и ее единицы, тесла.
| d F B = I d ℓ × B | ⇒ | .В = | Ф В | ⇒ | . ⎡ ⎢ ⎣ | Т = | N | ⎤ ⎥ ⎦ |
| Iℓ | Am |
Третья линейка для правой / левой руки
Электронно-лучевая трубка: цветной телевизор (цветной монитор), осциллограф,
масс-спектрометр
циклотрон
космическая погода, сияние, радиационные пояса Ван Аллена
электродвигатель
Электромагнитный рельсовый пистолет
ядерный магнитный резонанс?
Магнитное поле: определение, причины, формула, единицы и измерения (с примерами)
Обновлено 28 декабря 2020 г.
Ли Джонсон
Поля окружают нас повсюду.Будь то гравитационное поле, вызванное массой Земли, или электрические поля, создаваемые заряженными частицами, такими как электроны, невидимые поля есть повсюду, представляющие потенциалы и невидимые силы, способные перемещать объекты с соответствующими характеристиками.
Например, электрическое поле в области означает, что заряженный объект может отклониться от своего первоначального пути, когда он входит в область, а гравитационное поле из-за массы Земли удерживает вас на поверхности Земли, если вы этого не сделаете. некоторые работают над преодолением его влияния.
Магнитные поля являются причиной магнитных сил, а объекты, которые оказывают магнитные силы на другие объекты, делают это, создавая магнитное поле. Магнитные поля можно обнаружить по отклонению стрелок компаса, которые совпадают с силовыми линиями (магнитный север стрелки указывает на магнитный юг). Если вы изучаете электричество и магнетизм, изучение магнитных полей и магнитной силы станет важным шагом на вашем пути.
Что такое магнитное поле?
В физике в целом поля – это векторы со значениями в каждой области пространства, которые говорят вам, насколько сильным или слабым является эффект в этой точке, а также направление эффекта.Например, объект с массой, такой как солнце, создает гравитационное поле, и в результате на другие объекты с массой, попадающие в это поле, действует сила. Вот как гравитационное притяжение Солнца удерживает Землю на орбите вокруг себя.
Дальше в солнечной системе, например, на орбите Урана, действует та же сила, но сила намного ниже. Он всегда направлен прямо на солнце; Если вы представите себе набор стрел, окружающих Солнце, все они указывают на него, но с большей длиной на близких расстояниях (более сильная сила) и меньшей длиной на больших расстояниях (более слабая сила), вы в основном вообразили гравитационное поле в Солнечной системе.
Таким же образом, объекты с зарядом создают электрические поля, а движущиеся заряды создают магнитных полей , которые могут вызывать магнитную силу в соседнем заряженном объекте или других магнитных материалах.
Эти поля немного сложнее по форме, чем гравитационные поля, поскольку они имеют петлевые силовые линии магнитного поля, которые выходят из положительного (или северного полюса) и заканчиваются на отрицательном (или южном полюсе), но заполняют та же основная роль.Они похожи на силовые линии, которые говорят вам, как будет вести себя объект, помещенный в определенное место. Вы можете четко визуализировать это, используя железные опилки, которые будут совпадать с внешним магнитным полем.
Магнитные поля всегда дипольные поля , поэтому магнитных монополей нет. Обычно магнитные поля обозначаются буквой B , но если магнитное поле проходит через магнитный материал, он может поляризоваться и генерировать собственное магнитное поле.Это второе поле вносит вклад в первое поле, и их комбинация обозначается буквой H , где
H = \ frac {B} {\ mu_m} \ text {и} \ mu_m = K_m \ mu_0
, где μ 0 = 4π × 10 – 7 Гн / м (т.е. магнитная проницаемость свободного пространства), а K м – относительная проницаемость рассматриваемого материала.
Величина магнитного поля, проходящего через данную область, называется магнитным потоком.Плотность магнитного потока связана с локальной напряженностью поля. Поскольку магнитные поля всегда диполярны, чистый магнитный поток через замкнутую поверхность равен 0. (Любые силовые линии, выходящие из поверхности, обязательно входят в нее снова, сокращаясь.)
Единицы измерения и измерения
Единица измерения магнитного поля в системе СИ. сила – тесла (Тл), где:
1 тесла = 1 Тл = 1 кг / А с 2 = 1 В с / м 2 = 1 Н / А м
Еще одна широко используемая единица измерения магнитного поля сила – это гаусс (G), где:
Тесла – довольно большая единица, поэтому во многих практических ситуациях более полезным выбором будет гаусс – например, магнит на холодильник будет иметь силу около 100 G, а Магнитное поле Земли на поверхности Земли составляет около 0.5 G.
Причины возникновения магнитных полей
Электричество и магнетизм фундаментально взаимосвязаны, поскольку магнитные поля генерируются движущимся зарядом (например, электрическими токами) или изменяющимися электрическими полями, в то время как изменяющееся магнитное поле создает электрическое поле.
В стержневом магните или подобном магнитном объекте магнитное поле возникает в результате выравнивания нескольких магнитных «доменов», которые, в свою очередь, создаются движением заряженных электронов вокруг ядер их атомов.Эти движения создают небольшие магнитные поля внутри домена. В большинстве материалов домены будут иметь случайное выравнивание и компенсировать друг друга, но в некоторых материалах магнитные поля в соседних доменах выравниваются, и это создает более крупномасштабный магнетизм.
Магнитное поле Земли также создается движущимся зарядом, но в данном случае это движение расплавленного слоя, окружающего ядро Земли, которое создает магнитное поле. Это объясняется теорией динамо , которая описывает, как вращающаяся электрически заряженная жидкость генерирует магнитное поле.Внешнее ядро Земли содержит постоянно движущееся жидкое железо с электронами, движущимися через жидкость и генерирующими магнитное поле.
Солнце также обладает магнитным полем, и объяснение того, как это работает, очень похоже. Однако разные скорости вращения различных частей Солнца (то есть жидкообразного материала на разных широтах) со временем приводят к спутыванию силовых линий, а также ко многим явлениям, связанным с Солнцем, таким как солнечные вспышки и солнечные пятна. , и примерно 11-летний солнечный цикл.Солнце имеет два полюса, как стержневой магнит, но движение солнечной плазмы и постепенно возрастающая солнечная активность заставляют магнитные полюса переворачиваться каждые 11 лет.
Формулы магнитного поля
Магнитные поля из-за разного расположения движущихся зарядов должны быть получены индивидуально, но есть много стандартных формул, которые вы можете использовать, чтобы вам не приходилось каждый раз «изобретать колесо». Вы можете получить формулы практически для любого расположения движущегося заряда, используя закон Био-Савара или закон Ампера-Максвелла.Однако полученные формулы для простых схем электрического тока настолько широко используются и цитируются, что вы можете просто рассматривать их как «стандартные формулы», а не выводить их каждый раз из закона Био-Савара или Ампера-Максвелла.
Магнитное поле прямолинейного тока определяется по закону Ампера (более простая форма закона Ампера-Максвелла) как:
B = \ frac {μ_0 I} {2 π r}
Где μ 0 определено ранее, I – ток в амперах, а r – расстояние от провода, на котором измеряется магнитное поле.
Магнитное поле в центре токовой петли определяется выражением:
B = \ frac {μ_0 I} {2 R}
Где R – радиус петли, а другие символы – как определено ранее.
Наконец, магнитное поле соленоида определяется выражением:
B = μ_0 \ frac {N} {L} I
Где N – количество витков, а L – длина соленоида. Магнитное поле соленоида в основном сосредоточено в центре катушки.
Примеры расчетов
Обучение использованию этих уравнений (и подобных им) – это главное, что вам нужно сделать при вычислении магнитного поля или результирующей магнитной силы, поэтому пример каждого из них поможет вам решить проблемы, с которыми вы, вероятно, столкнетесь.
Для длинного прямого провода, по которому течет ток 5 ампер (т. Е. I = 5 А), какова напряженность магнитного поля на расстоянии 0,5 м от провода?
Используя первое уравнение с I = 5 A и r = 0.{−4} \ text {T} \ end {align}
Другой пример расчета магнитного поля может работать немного по-другому – например, сообщая вам поле в центре соленоида и ток, но запрашивая N / Коэффициент L – но пока вы знакомы с уравнениями, у вас не будет проблем с ответом на них.
11.3: Магнитные поля и линии
Мы обрисовали в общих чертах свойства магнитов, описали их поведение и перечислили некоторые области применения магнитных свойств.Несмотря на то, что не существует таких вещей, как изолированные магнитные заряды, мы все же можем определить притяжение и отталкивание магнитов как основанное на поле. В этом разделе мы определяем магнитное поле, определяем его направление на основе правила правой руки и обсуждаем, как рисовать силовые линии магнитного поля.
Определение магнитного поля
Магнитное поле определяется силой, которую испытывает заряженная частица, движущаяся в этом поле, после того, как мы учтем гравитационные и любые дополнительные электрические силы, возможные на заряд.Величина этой силы пропорциональна величине заряда q , скорости заряженной частицы v и величине приложенного магнитного поля. Направление этой силы перпендикулярно как направлению движущейся заряженной частицы, так и направлению приложенного магнитного поля. Основываясь на этих наблюдениях, мы определяем напряженность магнитного поля B на основе магнитной силы \ (\ vec {F} \) на заряде q , движущемся со скоростью, как перекрестное произведение скорости и магнитного поля, то есть
\ [\ vec {F} = q \ vec {v} \ times \ vec {B}.\ label {eq1} \]
Фактически, именно так мы определяем магнитное поле \ (\ vec {B} \) – в терминах силы, действующей на заряженную частицу, движущуюся в магнитном поле. Величина силы определяется из определения перекрестного произведения, поскольку оно относится к величине каждого из векторов. Другими словами, величина силы удовлетворяет
\ [F = qv \, B \ sin \, \ theta \ label {eq2} \]
, где θ – угол между скоростью и магнитным полем.{-5} \, T \) или \ (0.5 \, G \).
Стратегия решения проблем: направление магнитного поля по правилу правой руки
Направление магнитной силы \ (\ vec {F} \) перпендикулярно плоскости, образованной \ (\ vec {v} \) и \ (\ vec {B} \), как определено правой частью . rule-1 (или RHR-1), которое показано на рисунке \ (\ PageIndex {1} \).
- Сориентируйте правую руку так, чтобы пальцы сгибались в плоскости, определяемой векторами скорости и магнитного поля.
- Правой рукой проведите пальцами от скорости к магнитному полю под наименьшим возможным углом.
- Магнитная сила направлена туда, куда указывает ваш большой палец.
- Если заряд был отрицательным, измените направление на противоположное. Рисунок \ (\ PageIndex {1} \): Магнитные поля действуют на движущиеся заряды. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной b \ (\ vec {v} \) и \ (\ vec {B} \), и следует правилу правой руки-1 (RHR-1 ) как показано.Величина силы пропорциональна \ (q, \, v, \, B, \) и синусу угла между \ (\ vec {v} \) и \ (\ vec {B} \).
Примечание
Посетите этот веб-сайт для дополнительной практики с направлением магнитных полей.
На статические заряды не действует магнитная сила. Однако на заряды, движущиеся под углом к магнитному полю, действует магнитная сила. Когда заряды неподвижны, их электрические поля не влияют на магниты. Однако, когда заряды движутся, они создают магнитные поля, которые действуют на другие магниты.4 м / с \)?
Рисунок \ (\ PageIndex {2} \): Магнитные силы на альфа-частицу, движущуюся в однородном магнитном поле. Поле на каждом рисунке одинаковое, но скорость разная.Стратегия
Нам дан заряд, его скорость, сила и направление магнитного поля. Таким образом, мы можем использовать уравнение \ (\ vec {F} = q \ vec {v} \ times \ vec {B} \) или \ (F = qv \, B sin \, \ theta \) для вычисления силы. Направление силы определяется RHR-1.
Решение
- Во-первых, чтобы определить направление, начните с того, что пальцы будут указывать в положительном направлении x .{-14} N \, \ hat {j} \]
- Во-первых, чтобы определить направленность, начните с того, что пальцы будут указывать в отрицательном направлении y . Проведите пальцами вверх в направлении магнитного поля, как в предыдущей задаче. Ваш большой палец должен быть открыт в отрицательном направлении x . Это должно соответствовать математическому ответу. Чтобы вычислить силу, мы используем заданные заряд, скорость и магнитное поле, а также определение магнитной силы в форме перекрестного произведения для вычисления: \ [\ vec {F} = q \ vec {v} \ times \ vec { B} = (3.{-14} Н. \]
- Поскольку скорость и магнитное поле параллельны друг другу, нет никакой ориентации вашей руки, которая приведет к направлению силы. Следовательно, сила, действующая на этот движущийся заряд, равна нулю. Это подтверждается перекрестным произведением. Когда вы пересекаете два вектора, указывающих в одном направлении, результат равен нулю.
- Во-первых, чтобы определить направление, ваши пальцы могут указывать в любом направлении; однако вы должны поднять пальцы вверх в направлении магнитного поля.o. \] Величину силы также можно рассчитать с помощью уравнения \ ref {eq2}. Однако скорость в этом вопросе состоит из трех компонентов. Компонентой скорости z можно пренебречь, потому что она параллельна магнитному полю и, следовательно, не создает силы. Величина скорости вычисляется из компонентов x и y . Угол между скоростью в плоскости xy и магнитным полем в плоскости z составляет 90 градусов.{-14} N \]
Значение
Перекрестное произведение в этой формуле дает третий вектор, который должен быть перпендикулярен двум другим. Другие физические величины, такие как угловой момент, также имеют три вектора, которые связаны между собой перекрестным произведением. Обратите внимание, что типичные значения силы в задачах магнитной силы намного больше, чем сила тяжести. Следовательно, для изолированного заряда магнитная сила является доминирующей силой, управляющей движением заряда.{-15} N \)
Представление магнитных полей
Представление магнитных полей с помощью силовых линий очень полезно для визуализации силы и направления магнитного поля. Как показано на рисунке \ (\ PageIndex {3} \), каждая из этих линий образует замкнутый цикл, даже если это не показано ограничениями пространства, доступного для рисунка. Силовые линии выходят из северного полюса (N), огибают южный полюс (S) и проходят через стержневой магнит обратно к северному полюсу.
У линий магнитного поля есть несколько жестких правил:
- Направление магнитного поля касается силовой линии в любой точке пространства. Маленький компас укажет направление линии поля.
- Сила поля пропорциональна близости линий. Она точно пропорциональна количеству линий на единицу площади, перпендикулярной линиям (называемой плотностью площади).
- Силовые линии магнитного поля никогда не могут пересекаться, а это означает, что поле уникально в любой точке пространства.
- Линии магнитного поля непрерывны, образуют замкнутые контуры без начала и конца. Они направлены от северного полюса к южному полюсу.
Последнее свойство связано с тем, что северный и южный полюса не могут быть разделены. Это явное отличие от силовых линий электрического поля, которые обычно начинаются с положительных зарядов и заканчиваются отрицательными зарядами или на бесконечности. Если бы изолированные магнитные заряды (называемые магнитными монополями ) существовали, то силовые линии магнитного поля начинались бы и заканчивались на них.
Рис. \ (\ PageIndex {3} \): Линии магнитного поля определяются так, чтобы они имели направление, в котором указывает маленький компас при размещении в определенном месте в поле. Сила поля пропорциональна близости (или плотности) линий. Если бы можно было исследовать внутреннюю часть магнита, было бы обнаружено, что силовые линии образуют непрерывные замкнутые контуры. Чтобы уместиться в разумном пространстве, некоторые из этих рисунков могут не показывать замыкание петель; однако, если бы было предоставлено достаточно места, петли были бы закрыты.11,5: Магнитная сила на проводнике с током
Движущиеся заряды испытывают силу в магнитном поле. Если эти движущиеся заряды находятся в проводе, то есть если по проводу течет ток, на провод также должна воздействовать сила. Однако, прежде чем обсуждать силу, действующую на ток со стороны магнитного поля, мы сначала исследуем магнитное поле, создаваемое электрическим током. Здесь мы изучаем два отдельных эффекта, которые тесно взаимодействуют: провод с током создает магнитное поле, а магнитное поле оказывает силу на провод с током.
Магнитные поля, создаваемые электрическим током
Обсуждая исторические открытия в области магнетизма, мы упомянули открытие Эрстеда о том, что провод, по которому проходит электрический ток, вызывает отклонение расположенного рядом компаса. Было установлено, что электрические токи создают магнитные поля. (Эта связь между электричеством и магнетизмом более подробно обсуждается в Источниках магнитных полей.)
Стрелка компаса рядом с проволокой испытывает силу, которая выравнивает касательную иглы к окружности вокруг проволоки.Следовательно, токоведущий провод создает кольцевые петли магнитного поля. Чтобы определить направление магнитного поля, создаваемого проводом, мы используем второе правило правой руки. В RHR-2 ваш большой палец указывает в направлении тока, в то время как ваши пальцы охватывают провод, указывая в направлении создаваемого магнитного поля (рисунок \ (\ PageIndex {1} \)). Если магнитное поле попадало на вас или выходило за пределы страницы, мы обозначаем это точкой. Если магнитное поле попадало на страницу, мы обозначаем это знаком ×.
Эти символы получены с учетом векторной стрелки: стрелка, направленная на вас, с вашей точки зрения будет выглядеть как точка или кончик стрелки. Стрелка, направленная от вас, с вашей точки зрения будет выглядеть как крест или знак ×. Составной эскиз магнитных кругов показан на рисунке \ (\ PageIndex {1} \), где показано, что напряженность поля уменьшается по мере удаления от провода петлями, которые расположены дальше друг от друга.
Рисунок \ (\ PageIndex {1} \): (a) Когда провод находится в плоскости бумаги, поле перпендикулярно бумаге.Обратите внимание на символы, используемые для поля, указывающего внутрь (например, хвоста стрелки), и поля, указывающего наружу (например, кончика стрелки). (б) Длинный и прямой провод создает поле с силовыми линиями магнитного поля, образующими кольцевые петли.Расчет магнитной силы
Электрический ток – это упорядоченное движение заряда. Следовательно, провод с током в магнитном поле должен испытывать силу, создаваемую этим полем. Чтобы исследовать эту силу, давайте рассмотрим бесконечно малое сечение провода, как показано на рисунке \ (\ PageIndex {3} \).Длина и площадь поперечного сечения секции равны дл и A соответственно, поэтому ее объем равен \ (V = A \ cdot dl \). Проволока сформирована из материала, который содержит n носителей заряда в единице объема, поэтому количество носителей заряда в секции составляет \ (nA \ cdot dl \). Если носители заряда движутся со скоростью дрейфа \ (\ vec {v} _d \), ток I в проводе равен (от тока и сопротивления)
\ [I = neAv_d. \]
Магнитная сила на любом отдельном носителе заряда равна \ (e \ vec {v} _d \ times \ vec {B} \), поэтому общая магнитная сила \ (d \ vec {F} \) на \ (nA \ cdot dl \) носителей заряда в сечении провода
\ [d \ vec {F} = (nA \ cdot dl) e \ vec {v} _d \ times \ vec {B}.\]
Мы можем определить dl как вектор длиной dl , указывающий вдоль \ (\ vec {v} _d \), что позволяет нам переписать это уравнение как
\ [d \ vec {F} = neAv_dd \ vec {l} \ times \ vec {B}, \] или
\ [d \ vec {F} = Id \ vec {l} \ times \ vec {B}. \ label {11.12} \]
Это сила магнитного поля на отрезке провода. Обратите внимание, что на самом деле это результирующая сила, действующая со стороны поля на сами носители заряда. Направление этой силы задается RHR-1, где вы указываете пальцами в направлении тока и сгибаете их к полю.Затем ваш большой палец указывает в направлении силы.
Рисунок \ (\ PageIndex {2} \): бесконечно малое сечение токоведущего провода в магнитном поле.Чтобы определить магнитную силу \ (\ vec {F} \) на проводе произвольной длины и формы, мы должны интегрировать уравнение \ ref {11.12} по всему проводу. Если сечение провода прямое, а B однородный, дифференциалы уравнения становятся абсолютными величинами, что дает нам
\ [\ vec {F} = I \ vec {l} \ times \ vec {B}.\]
Это сила, действующая на прямой провод с током в однородном магнитном поле.
Пример \ (\ PageIndex {1} \): уравновешивание гравитационных и магнитных сил на проводе с током
Провод длиной 50 см и массой 10 г подвешен в горизонтальной плоскости с помощью пары гибких проводов (рисунок \ (\ PageIndex {3} \)). Затем на проволоку действует постоянное магнитное поле величиной 0,50 Тл, которое направлено, как показано. Каковы величина и направление тока в проводе, необходимые для снятия напряжения в опорных выводах?
Рисунок \ (\ PageIndex {3} \): (a) Проволока, подвешенная в магнитном поле.(б) Схема свободного тела для проволоки.Стратегия
Из диаграммы свободного тела на рисунке, натяжения в опорных выводах стремятся к нулю, когда гравитационная и магнитная силы уравновешивают друг друга. Используя RHR-1, мы обнаруживаем, что магнитная сила направлена вверх. Затем мы можем определить ток I , приравняв две силы.
Решение
Приравняйте две силы веса и магнитной силы к проводу:
\ [мг = IlB.2)} {(0,50 \, m) (0,50 \, T)} = 0,39 \, A. \]
Значение
Это сильное магнитное поле создает значительную силу на длине провода, чтобы противодействовать весу провода.
Пример \ (\ PageIndex {2} \): расчет магнитной силы на токопроводящем проводе
По длинному жесткому проводу, проложенному вдоль оси y , проходит ток 5,0 А, протекающий в положительном направлении y . (а) Если постоянное магнитное поле величиной 0.30 Тл направлено вдоль положительной оси x , какова сила магнитного поля на единицу длины провода? (b) Если постоянное магнитное поле 0,30 Тл направлено на 30 градусов от оси + x к оси + y , какова магнитная сила на единицу длины на проводе?
Стратегия
Магнитная сила, действующая на провод с током в магнитном поле, определяется выражением \ (\ vec {F} = I \ vec {l} \ times \ vec {B} \). Что касается части а, поскольку ток и магнитное поле перпендикулярны в этой задаче, мы можем упростить формулу, чтобы дать нам величину и найти направление через RHR-1.Угол θ равен 90 градусам, что означает \ (sin \, \ theta = 1. \). Кроме того, длину можно разделить на левую часть, чтобы найти силу на единицу длины. Для части b текущая длина, умноженная на длину, записывается в обозначении единичного вектора, а также магнитное поле. После взятия перекрестного произведения направленность очевидна по результирующему единичному вектору.
Решение
- Начнем с общей формулы магнитной силы на проводе. Мы ищем силу на единицу длины, поэтому мы делим ее на длину, чтобы вывести ее в левую часть.Мы также устанавливаем \ (sin \, \ theta \). Таким образом, решением будет \ [F = IlB \, sin \, \ theta \] \ [\ frac {F} {l} = (5.0 \, A) (0.30 \, T) \] \ [\ frac {F} {l} = 1,5 \, Н / м. \] Направленность: Укажите пальцами в положительном направлении y и согните пальцы в положительном направлении x . Ваш большой палец будет указывать в направлении \ (- \ vec {k} \). Следовательно, с учетом направленности решение будет \ [\ frac {\ vec {F}} {l} = -1,5 \ vec {k} \, Н / м. \]
- Текущее значение, умноженное на длину, и магнитное поле записываются в виде единичного вектора.o) \ hat {i} \] \ [\ vec {F} / l = -1.30 \ hat {k} \, Н / м. \]
Значение
Это большое магнитное поле создает значительную силу на небольшой длине провода. По мере того, как угол магнитного поля становится более близким к току в проводе, на него действует меньшая сила, как видно из сравнения частей a и b.
Упражнение \ (\ PageIndex {1} \)
Прямой гибкий медный провод погружается в магнитное поле, направленное внутрь страницы.(a) Если ток в проводе течет в направлении + x , в каком направлении будет изгибаться провод? (b) В какую сторону изгибается провод, если ток течет в направлении – x -?
Решение
а. наклоняется вверх; б. наклоняется вниз
Пример \ (\ PageIndex {3} \): сила на круглом проводе
Круговая токовая петля радиусом R , по которой проходит ток I , размещена в плоскости xy . Постоянное однородное магнитное поле прорезает петлю параллельно оси y (рисунок \ (\ PageIndex {4} \)).Найдите магнитную силу на верхней половине петли, нижней половине петли и общую силу на петле.
Рисунок \ (\ PageIndex {4} \): петля из провода, по которой течет ток в магнитном поле.Стратегия
Магнитная сила на верхнем контуре должна быть записана в терминах дифференциальной силы, действующей на каждый сегмент контура. Если мы интегрируем по каждому дифференциальному элементу, мы решаем общую силу на этом участке петли. Сила, действующая на нижнюю петлю, определяется аналогичным образом, а общая сила складывается из этих двух сил.
Решение
Дифференциальное усилие на произвольном отрезке проволоки, расположенном на верхнем кольце, составляет:
\ [dF = I B \, sin \, \ theta \, dl, \], где \ (\ theta \) – угол между направлением магнитного поля (+ y ) и отрезком провода. Дифференциальный сегмент расположен на том же радиусе, поэтому, используя формулу длины дуги, мы имеем:
\ [dl = Rd \ theta \]
\ [dF = IBR \, sin \, \ theta \, d \ theta. \]
Чтобы найти силу на отрезке, мы интегрируем по верхней половине круга от 0 до \ (\ pi \).0 sin \, \ theta \, d \ theta = IBR (-cos 0 + cos \ pi) = -2 IBR. \]
Чистая сила – это сумма этих сил, равная нулю.
Значение
Полная сила на любом замкнутом контуре в однородном магнитном поле равна нулю. Несмотря на то, что каждая часть петли имеет силу, действующую на нее, результирующая сила, действующая на систему, равна нулю. (Обратите внимание, что на петле есть чистый крутящий момент, который мы рассмотрим в следующем разделе.)
Электромагнитные силы и поля
Стержневой магнит притягивает к своим концам железные предметы, называемые полюсами .Один конец – это северный полюс , а другой – южный полюс . Если стержень подвешен так, чтобы он мог свободно двигаться, магнит выровняется так, чтобы его северный полюс указывал на географический север Земли. Подвешенный стержневой магнит действует как компас в магнитном поле Земли. Если два стержневых магнита приблизить друг к другу, одинаковые полюса будут отталкиваться друг от друга, а разные полюса притянутся друг к другу. (Примечание: согласно этому определению, магнитный полюс под северным географическим полюсом Земли является южным полюсом магнитного поля Земли.)
Это магнитное притяжение или отталкивание можно объяснить как влияние одного магнита на другой, или можно сказать, что один магнит создает в области вокруг себя магнитное поле , которое воздействует на другой магнит. Магнитное поле в любой точке – это вектор. Направление магнитного поля ( B ) в указанной точке – это направление, в котором северный конец стрелки компаса указывает в этом положении. Линии магнитного поля , аналогичные силовым линиям электрического поля, описывают силу, действующую на магнитные частицы, находящиеся внутри поля.Железные опилки будут выровнены, чтобы обозначить структуру силовых линий магнитного поля.
Сила движущегося заряда
Если заряд движется через магнитное поле под углом, он испытывает силу. Уравнение задается следующим образом: F = q v × B или F = qvB sin θ, где q – заряд, B – магнитное поле, v – скорость и θ – угол между направлениями магнитного поля и скорости; таким образом, используя определение перекрестного произведения, определение магнитного поля равно
Магнитное поле выражается в единицах СИ как тесла (Тл), которую также называют Вебером на квадратный метр:
Направление F определяется по правилу правой руки, показанному на рисунке 1.
| ||
Чтобы найти направление силы, действующей на заряд, плоской рукой направьте большой палец в направлении скорости положительного заряда, а пальцы – в направлении магнитного поля.Направление силы вне ладони. (Если движущийся заряд отрицательный, укажите большим пальцем в направлении, противоположном его направлению движения.) Математически эта сила является перекрестным произведением вектора скорости и вектора магнитного поля.
Если скорость заряженной частицы перпендикулярна однородному магнитному полю, сила всегда будет направлена к центру круга радиусом r , как показано на рисунке 2. x символизирует магнитное поле в плоскость бумаги – хвост стрелки.(Точка символизирует вектор, выходящий из плоскости бумаги – кончик стрелки.)
| ||
Магнитная сила обеспечивает центростремительное ускорение:
или
Радиус пути пропорционален массе заряда.Это уравнение лежит в основе работы масс-спектрометра , который может разделять одинаково ионизированные атомы немного разных масс. Однократно ионизированным атомам придаются равные скорости, и поскольку их заряды одинаковы и они проходят через один и тот же B , они будут двигаться немного разными путями и затем могут быть разделены.
Сила, действующая на проводник с током
Заряды, удерживаемые в проводах, также могут испытывать силу в магнитном поле.Ток (I) в магнитном поле ( B ) испытывает силу ( F ), заданную уравнением F = I l × B или F = IlB sin θ, где l – длина провода, представленная вектором, указывающим в направлении тока.
