Карта сайта || Филиал КузГТУ г.Прокопьевск
|
|
Закон сохранения момента импульса – формула и примеры
4.
6
Средняя оценка: 4.6
Всего получено оценок: 131.
4.6
Средняя оценка: 4.6
Всего получено оценок: 131.
Важнейшим свойством Природы являются Законы сохранения, которые являются следствием однородности пространства и времени. Законы сохранения применимы ко многим величинам, одной из которых является момент импульса. Рассмотрим этот случай подробнее.
Импульс для вращательного движения
Одной из мер механического движения тела является импульс. Для поступательного движения импульс материальной точки определяется произведением ее скорости на массу:
$$\overrightarrow p = \overrightarrow v m$$
Рис. 1. Импульс материальной точки.Вращательное движение отличается от поступательного тем, что в таком движении все величины зависят от положения оси вращения, и результаты движения изменяются в зависимости от расстояния до нее (радиуса вращения).
Поэтому во вращательном движении все линейные величины заменяются угловыми величинами, зависящими от радиуса.
2$ – момент инерции материальной точки массой $m$, вращающейся по траектории радиуса $R$.
Момент импульса считается положительным, если движение происходит вдоль выбранного направления (обычно против часовой стрелки), и отрицательным, если движение происходит против него.
Сохранение момента импульса
Импульс – это величина, подчиняющаяся Законам сохранения. Для вращательного движения Закон также остается в силе. Закон сохранения момента импульса гласит:
Для замкнутой системы суммарный момент импульсов всех материальных точек остается постоянным во времени.
То есть, также, как и для поступательного движения, момент импульса системы может изменяться только лишь при внешнем воздействии на нее.
Вне этих воздействий могут меняться составляющие момента импульса, но не сам момент импульса. Например, при упругом столкновении двух материальных точек равной массы, они могут полностью изменить направление вращения, и, таким образом, момент импульса каждой поменяет знак.
Вращение любого тела рано или поздно прекращается в результате трения. Однако, Закон сохранения момента импульса здесь не нарушается, поскольку система не замкнута. Момент импульса уменьшается за счет того, что энергия вращающегося тела уходит, превращаясь во внутреннюю энергию трущихся поверхностей.
Закон сохранения момента импульса, также, как и Закон сохранения импульса для поступательного движения – это следствие симметрии пространства, то есть, равноправия всех точек пространства для физических законов.
Рис. 2. Законы сохранения и их связь с симметрией.Формула Закона сохранения момента импульса записывается следующим образом:
$$L_1+L_2+…+L_n=const$$
Проявления сохранения момента импульса
Закон сохранения момента импульса, как и Закон сохранения импульса для поступательного движения, достаточно часто проявляется в окружающем нас мире.
Однако, если для поступательного движения наиболее частым примером сохранения импульса являются столкновения тел, то для вращательного движения более интересны события, связанные с изменением момента инерции вращающихся тел.
Поскольку момент инерции тела зависит от его геометрии, то при изменении формы момент инерции тела практически всегда изменяется, и может уменьшиться без изменения общей его массы (если более тяжелые части тела переместятся ближе к оси вращения). А поскольку момент импульса вращающегося тела остается постоянным, то при уменьшении момента инерции неминуемо должна увеличиться угловая скорость, хотя, никакого внешнего воздействия на тело не происходит.
Для наблюдения данного явления используется опыт со скамьей Жуковского. Человек на вращающейся платформе может изменять скорость ее вращения, сводя или разводя руки (для увеличения эффекта в руки берутся гантели):
Тот же механизм лежит в основе пируэтов, выполняемых фигуристами.
Угловая скорость вращения резко увеличивается, когда они прижимают разведенные руки к груди.
Что мы узнали?
Закон сохранения момента импульса гласит, что сумма моментов импульсов в замкнутой системе остается постоянной во времени. Данный Закон – это следствие симметрии пространства. Его проявления можно наблюдать в изменении скорости вращения тел при изменении их формы.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 131.
А какая ваша оценка?
Вращательная инерция – главы физики колледжа 1-17
10 Вращательное движение и угловой момент
Резюме
- Понять взаимосвязь между силой, массой и ускорением.
- Изучите вращающее действие силы.
- Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, линейным ускорением и угловым ускорением.
Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 1. На самом деле ваша интуиция надежно предсказывает многие из задействованных факторов . Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Рисунок 1.
Для вращения велосипедного колеса требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше. Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу[латекс]\boldsymbol{F}[/латекс]к точечной массе[латекс]\жирныйсимвол{м}[ /latex], который находится на расстоянии[latex]\boldsymbol{r}[/latex] от точки вращения, как показано на рисунке 2. Поскольку сила перпендикулярна [latex]\boldsymbol{r},[/latex] ускорение[латекс]\boldsymbol{a=\frac{F}{m}}[/latex]получено в направлении[латекс]\boldsymbol{F}.[/latex]Мы можем изменить это уравнение так, что[ латекс]\boldsymbol{F=ma}[/latex]а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что [латекс]\boldsymbol{a=r\omega},[/latex]и подставим это выражение в [латекс]\boldsymbol{F=ma},[/latex]получив 92}[/latex]называется вращательная инерция или момент инерции точки массы[latex]\boldsymbol{m}[/latex]расстояние[latex]\boldsymbol{r}[/latex]от центр вращения.
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.
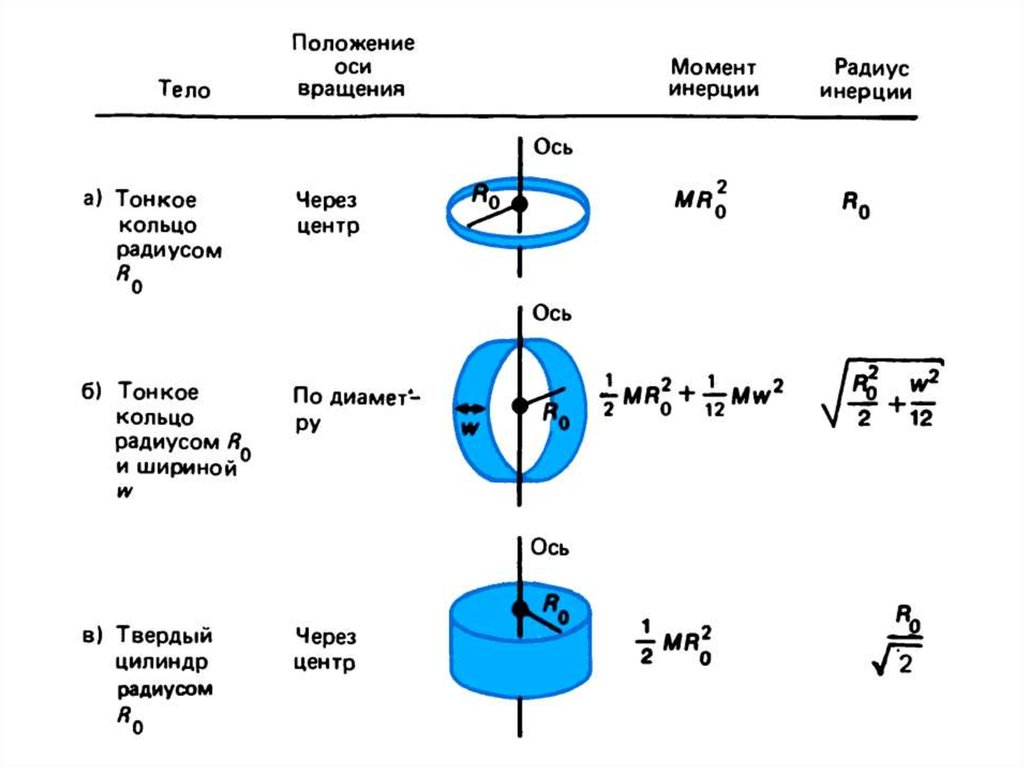
Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. 2, мы должны распространить идею инерции вращения на все типы объектов. Чтобы расширить наше понятие инерции вращения, мы определяем 92},[/latex],где[латекс]\boldsymbol{M}[/латекс]это его общая масса, а[латекс]\boldsymbol{R}[/латекс]его радиус.
2}[/latex]), как мы могли бы ожидать от его определения.
Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением составляет
.[латекс] \boldsymbol{\textbf{net}\tau=I\alpha}[/латекс]
или
[латекс]\boldsymbol{\alpha\:=}[/латекс][латекс]\boldsymbol{\frac{\textbf{net}\tau}{I}},[/latex]
, где net[latex]\boldsymbol{\tau}[/latex] — общий крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в [латекс]\boldsymbol{\tau=I\alpha},\:\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}}[/latex] является аналогом вращения Ньютона. второй закон и очень широко применимы. Это уравнение действительно справедливо для любой крутящий момент, примененный к любому объекту относительно любой оси .
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение.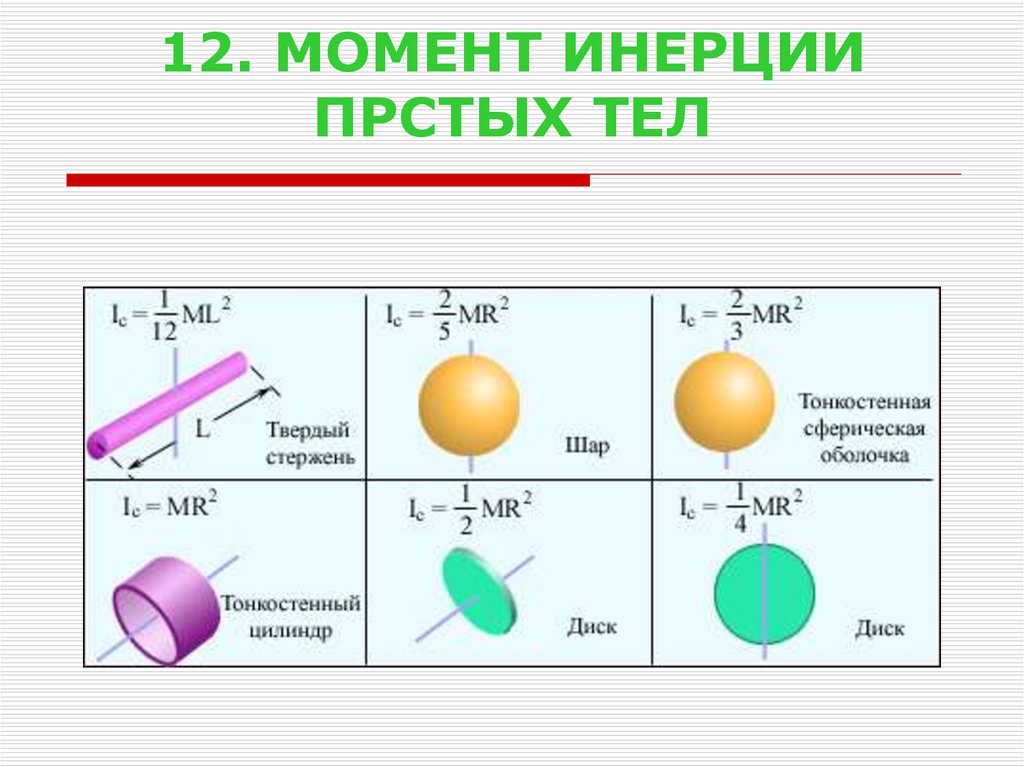
Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.
ЭКСПЕРИМЕНТ ДЛЯ ДОМА
Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо.
(Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ ДЛЯ ДИНАМИКИ ВРАЩЕНИЯ
- Изучите ситуацию, чтобы определить, что крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
- Определить интересующую систему .
- Нарисуйте свободную диаграмму тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
- Применить [латекс]\boldsymbol{\textbf{net}\tau=I\alpha},\:\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}},[/latex ] вращательный эквивалент второго закона Ньютона для решения задачи . Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
- Как всегда, проверьте решение, чтобы убедиться, что оно разумно .
Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ
В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.
Рисунок 3. Некоторые инерции вращения.Пример 1. Расчет влияния распределения масс на карусель
Рассмотрим отца, толкающего игровую карусель на рис. 4. Он прикладывает силу 250 Н к краю карусели весом 50,0 кг. круговой, который имеет радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.
Стратегия
Угловое ускорение задается непосредственно выражением [латекс]\boldsymbol{\alpha=\frac{\textbf{net}\tau}{I}}:[/latex]
[латекс]\boldsymbol {\alpha\:=}[/latex][latex]\boldsymbol{\frac{\tau}{I}}.[/latex]
Чтобы найти [латекс]\boldsymbol{\alpha},[/latex ] мы должны сначала вычислить крутящий момент[латекс]\boldsymbol{\tau}[/латекс](который одинаков в обоих случаях) и момент инерции[латекс]\жирныйсимвол{I}[/латекс](который больше в второй случай). Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трением можно пренебречь, так что 92}}.[/latex]
Решение для (b)
Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели -круглый. Чтобы найти общий момент инерции[latex]\boldsymbol{I},[/latex]мы сначала находим момент инерции ребенка[latex]\boldsymbol{I _{\textbf{c}}}[/latex], рассматривая ребенок должен быть эквивалентен точечной массе на расстоянии 1,25 м от оси.
2}.[/латекс] 92}}.[/latex]
Обсуждение
Угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, и только 8,89 рад/с, когда на ней находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
- Чем дальше приложена сила от оси вращения, тем больше угловое ускорение; угловое ускорение обратно пропорционально массе.
- Если мы воздействуем силой[латекс]\boldsymbol{F}[/латекс] на точечную массу[латекс]\boldsymbol{m}[/латекс], находящуюся на расстоянии[латекс]\жирныйсимвол{r}[/латекс ]от точки вращения и поскольку сила перпендикулярна[латекс]\boldsymbol{r},[/латекс]ускорение[латекс]\boldsymbol{a = F/m}[/латекс]получается в направлении[ латекс]\boldsymbol{F}. [/latex]Мы можем изменить это уравнение так, что
[латекс]\boldsymbol{F = ma},[/латекс]
, а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что [latex]\boldsymbol{a = r\alpha},[/latex]и подставим это выражение в [latex]\boldsymbol{F=ma},[/latex]получив
[латекс]\boldsymbol{F=г-н\альфа}[/латекс]
- Крутящий момент — это вращающая способность силы. В этом случае, поскольку [латекс]\boldsymbol{F}[/latex]перпендикулярен [латексу]\boldsymbol{r},[/latex]крутящий момент равен просто [латекс]\boldsymbol{\tau=rF}.[/ латекс] Если мы умножим обе части приведенного выше уравнения на [латекс]\boldsymbol{r},[/латекс] мы получим крутящий момент в левой части. То есть, 92}.[/латекс]
- Общая взаимосвязь между крутящим моментом, моментом инерции и угловым ускорением такова:
[латекс]\boldsymbol{\tau=I\alpha}[/латекс]
или
[латекс]\boldsymbol{\alpha=}[/латекс][латекс]\boldsymbol{\frac{\textbf{net}\tau}{I}}[/latex]
[/latex]Мы можем изменить это уравнение так, что- крутящий момент
- поворотная эффективность силы
- инерция вращения
- сопротивление изменению вращения. Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex]и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции
Момент инерции
Момент инерции — это причудливый способ сказать, насколько сложно что-то вращать. Чем больше момент инерции, тем труднее его крутить. Когда вы что-то крутите, это не просто движение одного большого куска. На самом деле он состоит из множества мелких кусочков. Каждая часть имеет разное расстояние от центра вращения. Момент инерции зависит от того, как все эти части расположены вокруг центра. В физике мы обычно просто делаем вид, что вся масса находится в одном месте в центре объекта.
Уравнение момента инерции
Момент, мы используем причудливую массу того, насколько далеко он находится от центра вращения. Уравнение выглядит так: I = Σmr². I — момент инерции, измеренный в килограммах на квадратный метр (кг·м2), m — масса, измеренная в килограммах (кг), и r — расстояние по перпендикуляру к оси вращения, измеренное в метрах (м). Но, если предположить, что вся масса сосредоточена в одной точке, можно использовать более простое уравнение. На рисунке показано, как далеко точка находится от центра вращения.
Диаграмма, показывающая расстояние оси вращения r
Откуда взялся момент инерции?
Закон Ньютона гласит, что когда на объект действует сила, он начинает двигаться в том же направлении, что и эта сила. Уравнение выглядит так: Ft = m x at. Ft — результирующая сила, m — масса объекта, at — поступательное ускорение. Для вещей, которые вращаются, мы используем другой вид силы, называемый крутящим моментом. Это зависит от того, как сильно вы нажимаете на него и как далеко от центра вы нажимаете. Но вместо ускорения мы используем нечто, называемое угловым ускорением, которое зависит от того, как быстро он вращается и как далеко он находится от центра. Момент инерции подобен массе для вращения вещей. Это противоположно массе в обычном уравнении силы, так что вот так: I = 1/м. И, как и обычная сила, крутящий момент также пропорционален моменту инерции и угловому ускорению. Итак, уравнение для крутящего момента T = I x α. Если что-то имеет больший момент инерции, его будет труднее крутить.
Примеры расчета момента инерции
Момент инерции показывает, насколько трудно заставить что-либо вращаться или остановить его вращение. Это зависит от того, сколько вещей есть и как они распределены вокруг оси вращения. Когда вы добавляете больше материала к вращающемуся объекту или раздвигаете его дальше от оси, момент инерции увеличивается, и его становится труднее вращать или останавливать. С другой стороны, если вы убираете предмет или приближаете его к оси, момент инерции становится меньше, и крутиться или останавливаться становится легче. Момент инерции специфичен для каждого объекта и его формы, и он различен для каждой оси вращения. Итак, момент инерции — ключевое понятие, помогающее нам понять, как вещи движутся и взаимодействуют в окружающем нас мире.
Изображения
Инерция вращенияМомент инерции
Как рассчитать момент инерции?
Момент инерции можно рассчитать как сумму произведения отдельных масс объекта и их соответствующего квадрата перпендикулярного расстояния до оси вращения.