способы нахождения, формула, единицы измерения, свойства объема тела
Содержание:
- Понятие объема тела
- Свойства объема тела
- Как вычислить объем тела: все формулы
- Примеры решения задач
- Задания для самостоятельной работы
Содержание
- Понятие объема тела
- Свойства объема тела
- Как вычислить объем тела: все формулы
- Примеры решения задач
- Задания для самостоятельной работы
Понятие объема тела
Объем является количественным параметром пространства, занятого телом или веществом.
Термин объема можно рассматривать совместно с понятием вместимости. Это обозначение для объема какого-то внутреннего пространства сосуда, коробки и тому подобного. Объем тела, как и вместимость некой емкости, зависит от таких характеристик, как:
- форма;
- линейные размеры.
Главным свойством объема принято считать аддитивность.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Аддитивность означает равенство объема какого-либо тела сумме объемов частей этого тела, которые не пересекаются между собой.
Согласно СИ, единицей измерения объема является метр кубический (м³). В процессе решения задач можно встретить единицы измерения объемов тел в виде см³, дм³, или литров. В иностранной литературе также используются указания объемов веществ, находящихся в жидком или сыпучем состоянии, в таких единицах измерения, как, например, галлон, баррель и другие.
Величина объема используется при составлении различных уравнений и неравенств. При этом данный параметр обозначают с помощью буквы V. Это сокращение от латинского слова volume, которое в переводе означает объем или наполнение.
Свойства объема тела
В процессе решения разнообразных задач по физике, алгебре и геометрии целесообразно использовать свойства, которыми обладает объем тела. Перечислим основные из них:
- Объем тела не может быть отрицательной величиной.
- В том случае, когда некое геометрическое тело состоит из определенного количества геометрических тел, не обладающих едиными внутренними точками, объем такого тела складывается из объемов составляющих его тел.
- Объем фигуры в виде куба с ребром, значение которого равно единице измерения длины, равен единице.
- Аналогичные друг другу геометрические тела обладают одинаковыми объемами.
- В том случае, когда тело имеет объем V1 и расположено в другом теле с объемом V2, справедливо следующее соотношение: \(V1<V2
\).

Таким образом, первый шар имеет площадь поверхности, которая в 25 раз больше по сравнению с аналогичной характеристикой второго шара.
Ответ: 25.
Задача 2
На рисунке изображены конусы. Назовем их \(K_1\) и \(K_2\).
Полная поверхность \(K_1\) по площади относится к площади полной поверхности \(K_2\) как 4:1.
Фигура \(K_1\) обладает радиусом, который в 4 раза больше образующей \(K_1\) и в 2 раза больше радиуса \(K_2\).
Требуется вычислить, как относится образующая \(K_2\) к образующей \(K_1.\)
Источник: shkolkovo.netРешение
Представим, что образующая конуса равна 1, а радиус основания обозначим, как R. Тогда можно записать следующее соотношение:
\(S=\pi R (R+l)\)
Запишем отношения площадей полной поверхности заданных конусов:
\(\dfrac41=\dfrac{\pi \,R_1\cdot (R_1+l_1)}{\pi \, R_2\cdot (R_2+l_2)}\)
Согласно условию задачи, имеем:
\(R_1=4l_1, R_2=\frac12R_1=2l_1\)
В результате:
\(\dfrac41=\dfrac{4l_1\cdot (4l_1+l_1)}{2l_1\cdot (2l_1+l_2)} \quad\Rightarrow\quad \dfrac{l_2}{l_1}=\dfrac12=0,5\)
Ответ: 0,5.

Задача 3
Даны два прямоугольных параллелепипеда. Объем первой фигуры равен 105. Известно, что первый параллелепипед по высоте превышает второй в 7 раз. Ширина второй фигуры в 2 раза больше по сравнению с аналогичным параметром первой фигуры. Первый параллелепипед длиннее в три раза, чем второй. Необходимо вычислить объем, который имеет второй параллелепипед.
Решение
Обозначим высоту, ширину и длину геометрических фигур с помощью букв а, b, с соответственно. Вспомним формулу, по которой можно найти объем прямоугольного параллелепипеда:
V=abc
Применительно к нашей задаче, запишем:
\(\dfrac{105}{V_2}=\dfrac{V_1}{V_2}=\dfrac{a_1b_1c_1}{a_2b_2c_2}\)
Известно, что:
\(a_1=7a_2, b_2=2b_1, c_1=3c_2\)
В результате:
\(\dfrac{105}{V_2}=\dfrac{7a_2\cdot b_1\cdot 3c_2}{a_2\cdot 2b_1\cdot c_2}= \dfrac{7\cdot 3}2 \quad\Rightarrow\quad V_2=\dfrac{105\cdot 2}{21}=10\)
Ответ: 10.

Задача 4
Даны два конуса. Площадь боковой поверхности первой геометрической фигуры относится к площади боковой поверхности второй фигуры как 3:7. Первый конус обладает радиусом, который относится к радиусу второго конуса, как 15:7. Необходимо определить, как относится образующая первого конуса к образующей второго конуса.
Решение
Составим формулу для расчета площади боковой поверхности конуса:
\(S=\pi Rl\)
Запишем отношения площадей боковых поверхностей для первого и второго конусов:
\(\dfrac 37=\dfrac{S_1}{S_2}=\dfrac{\pi R_1\,l_1}{\pi R_2\,l_2}\)
Зная, что отношение радиусов двух геометрических фигур равно 15:7, получим:
\(\frac{R_1}{R_2}=\frac{15}7, то \dfrac37=\dfrac {15}7\cdot \dfrac{l_1}{l_2} \quad\Rightarrow\quad \dfrac{l_1}{l_2}=\dfrac37\cdot \dfrac7{15}=\dfrac15=0,2\)
Ответ: 0,2.
Задача 5
Имеется пара шаров.

Таким образом, потребуется долить в емкость:
\(600-75=525 \ {\small{\text{грамм}}}\)
Ответ: 525.
Задача 7
Изображена четырехугольная пирамида. Ее высота равна h. Отметим точку сбоку на ребре геометрической фигуры так, чтобы она была удалена на \frac13h от плоскости основания. Данную точку пересекает плоскость, которая параллельна плоскости основания и отделяет от пирамиды аналогичную фигуру меньшего размера. Объем начальной пирамиды равен 54. Требуется вычислить объем меньшей пирамиды, которая получилась в результате.
Решение
Назовем точку, через которую проведена плоскость, A’ на ребре AS. Параллельность плоскости и основания является причиной пересечения боковых граней по прямым A’B’, \ B’C’, \ C’D’, \ D’A’, параллельным соответственно AB, \ BC, \ CD, \ DA. В этом случае SA’B’C’D’ является правильной четырехугольной пирамидой.
 3 \quad\Rightarrow\quad \dfrac{R_1}{R_2}=\sqrt[3]{343}=7\)
3 \quad\Rightarrow\quad \dfrac{R_1}{R_2}=\sqrt[3]{343}=7\)Сделаем вывод, что радиус первого шара в 7 раз больше по сравнению с радиусом второго шара.
Ответ: 7.
Задание 3
На рисунке изображены два цилиндра. Первый из них обладает площадью боковой поверхности, равной 16. Радиус второй фигуры больше в 4 раза по сравнению с радиусом первой фигуры. Второй цилиндр ниже, чем первый цилиндр, в 5 раз. Требуется вычислить площадь боковой поверхности второго цилиндра.
Решение
Запишем формулу для вычисления площади боковой поверхности цилиндра, которую уже проходили ранее:
\(S=2\pi RH\)
Составим отношение площадей боковых поверхностей двух фигур:
\(\dfrac{16}{S_2}=\dfrac{S_1}{S_2}=\dfrac{2\pi \,R_1\,H_1}{2\pi \,R_2\,H_2}= \dfrac{R_1}{R_2}\cdot \dfrac{H_1}{H_2}\)
В результате:
\(R_2=4R_1, H_1=5H_2\)
Таким образом:
\(\dfrac{16}{S_2}=\dfrac{R_1}{4R_1}\cdot \dfrac{5H_2}{H_2}= \dfrac14\cdot 5=\dfrac54\)
Получим, что:
\(S_2=\dfrac{16\cdot 4}5=12,8\)
Ответ: 12,8.
 3=27\)
3=27\)В результате объем первого шара в 27 раз больше по сравнению с объемом второго шара.
Ответ: 27.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Расчет массы и объема тела
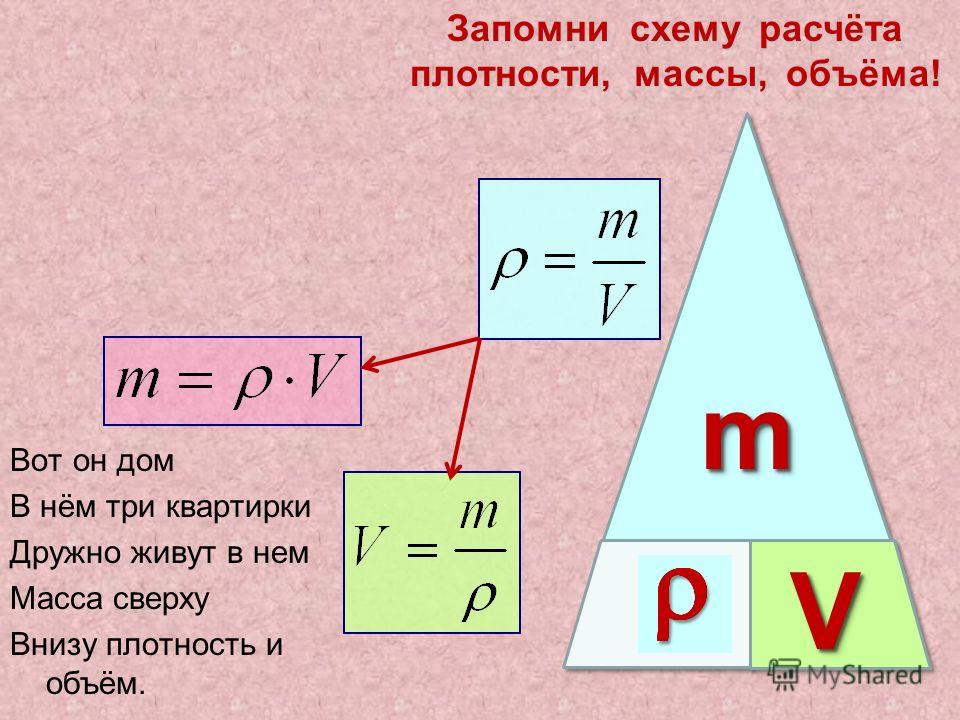
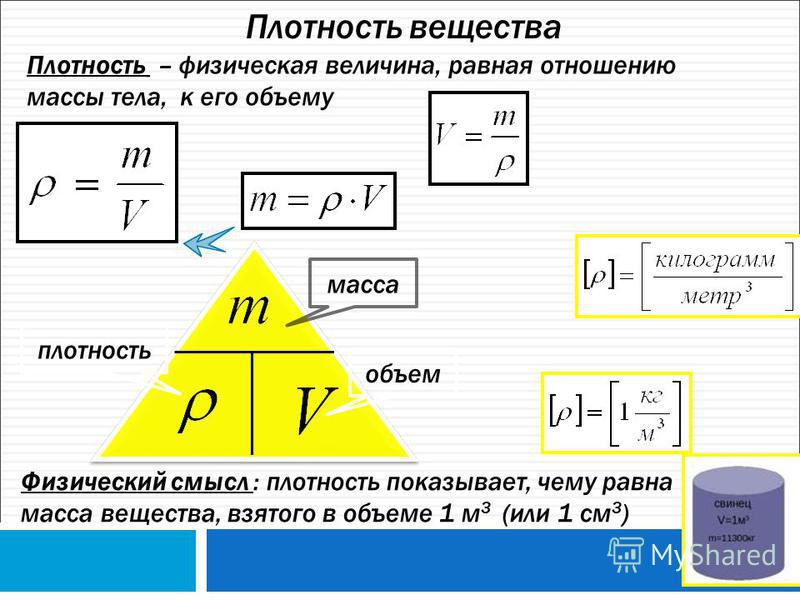
Для того чтобы определить плотность вещества, надо массу тела разделить на его объем:
(10.1)
Массу тела можно определить с помощью весов. А как найти объем тела?
Если тело имеет форму прямоугольного параллелепипеда (рис. 24), то его объем находится по формуле
V = аbс.
Если же у него какая-то другая форма, то его объем можно найти методом, который был открыт древнегреческим ученым Архимедом в III в. до н. э.
Архимед родился в Сиракузах на острове Сицилия. Его отец, астроном Фидий, был родственником Гиерона, ставшего в 270 г. до н. э. царем города, в котором они жили.
До нас дошли не все сочинения Архимеда. О многих его открытиях стало известно благодаря более поздним авторам, в сохранившихся трудах которых описываются его изобретения.
 Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
«Что касается Архимеда, то изо всех его многочисленных и разнообразных открытий то открытие, о котором я расскажу, представляется мне сделанным с безграничным остроумием.Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания вес короны оказался соответствующим выданному весу золота.После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну.
 Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».
Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».Затем, пишет Витрувий, Архимед взял сосуд, доверху наполненный водой, и опустил в него золотой слиток, равный по весу короне. Измерив объем вытесненной воды, он снова наполнил сосуд водой и опустил в него корону. Объем воды, вытесненной короной, оказался больше объема воды, вытесненной золотым слитком. Больший объем короны означал, что в ней присутствует менее плотное, чем золото, вещество. Поэтому опыт, проделанный Архимедом, показал, что часть золота была похищена.
Итак, для определения объема тела, имеющего неправильную форму, достаточно измерить объем воды, вытесняемой данным телом. Располагая измерительным цилиндром (мензуркой), это сделать несложно.
В тех случаях, когда известны масса и плотность тела, его объем можно найти по формуле, вытекающей из формулы (10.
 1):
1):(10.2)
Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность.
Если, наоборот, объем тела известен, то, зная, из какого вещества оно состоит, можно найти его массу:
m = ρV. (10.3)
Чтобы определить массу тела, надо плотность тела умножить на его объем.
1. Какие способы определения объема вы знаете? 2. Что вам известно об Архимеде? 3. Как можно найти массу тела по его плотности и объему?
Экспериментальное задание. Возьмите кусок мыла, имеющий форму прямоугольного параллелепипеда, на котором обозначена его масса. Проделав необходимые измерения, определите плотность мыла.Формулы объема – объяснение, единицы измерения, примеры решений и часто задаваемые вопросы
- Формула
- Формула объема
Что такое объем?
Дата последнего обновления: 17 апреля 2023 г.

•
Всего просмотров: 237 тыс.
•
Просмотров сегодня: 3,07 тыс.
объем предмета. Кроме того, если объект полый, то известно, что его внутренняя часть пуста. Полая часть может быть заполнена воздухом или жидкостью. В этом случае объем вещества, которым можно заполнить внутреннее пространство, даст вместимость любой емкости.
Таким образом, объем объекта может быть определен как мера занимаемого им пространства, или объем объекта как объем вещества, которое может вместить его внутренняя часть. Здесь единицей измерения любого из двух является кубическая единица.
Единицы объема
Объем измеряется в «кубических» единицах. Объем любой заданной фигуры — это количество кубиков, необходимых для ее полного заполнения, например, кубиков в коробке.
Объем куба равен сторона х сторона х сторона. Поскольку все стороны квадрата равны, это может быть просто длина одной стороны в кубе.

Если предположить, что у квадрата одна сторона равна 4 дюймам, объем будет 4 дюйма умножить на 4 дюйма x 4 дюйма, или 64 кубических дюйма. (Кубические дюймы также могут быть записаны в 3.)
Некоторые формулы для нахождения объемов основных геометрических фигур: 0048
Формула объема
Переменные
Прямоугольный Сплошной или кубовидный
В = Д × Ш × В
Д = Длина
Ш = Ширина
В = Высота
V = a 3
a = длина края или стороны
Цилиндр
V = π r 2
4 r = радиус круглого основания7 3 hh = высота
Призма
V = B × h
B = площадь основания, (B = сторона 2 или длина.
h 1 9092 5 = высота 1 ширина)
ширина)Сфера
V = (4⁄3)π r 3
r = радиус сферы
⁄3) × Ш × В
B = площадь основания,
h = высота пирамиды
Круговой конус правый
V = (1⁄3)πr 2 h
r = высота 19048 9043 90 90 90 круглого основания 90 3
Квадратный или прямоугольный Пирамида
V = (1⁄3) × длина × ширина × высота
l = длина основания,
w = ширина основания,
h = высота (от основания до кончика)
Эллипсоид
V = (4⁄3) × π × a × b × c
a, b, c = полуоси эллипсоида 3 ⁄ (6 √2)
a = Длина края
Решенные примеры
Вопрос 1) Размеры прямоугольного резервуара для воды даны как 2 м 75 см, 1 м 80 см 0 и 1.
 Сколько литров воды можно налить в бак данных размеров?
Сколько литров воды можно налить в бак данных размеров?Решение) Как мы знаем, что 1м = 100см.
Размеры резервуара: 2 м 75 см, 1 м 80 см и 1 м 40 см.
Мы можем записать это как 275 см, 180 см, 140 см
Теперь мы знаем, что объем прямоугольного параллелепипеда равен, Объем = l × b × h 3
Поскольку 1000 см = 1 литр
Таким образом, V = 6930 литров
Следовательно, бак может вместить 6930 литров воды.
Недавно обновленные страницы
Диагональ квадратной формулы — значение, вывод и решенные примеры
Формула дисперсионного анализа — определение, полная форма, статистика и примеры
Средняя формула — методы отклонения, решенные примеры и часто задаваемые вопросы
Формула процентной доходности — APY, атомная экономика и решенная Пример
Формула серии – определение, примеры решения и часто задаваемые вопросы
Формула площади поверхности квадратной пирамиды – определение и вопросы
Формула диагонали квадрата – значение, вывод и примеры решения
Формула дисперсионного анализа — определение, полная форма, статистика и примеры
Формула среднего — методы отклонения, примеры решений и часто задаваемые вопросы
Формула процентного выхода — APY, атомная экономика и пример решения
Формула серии — определение, примеры решения и часто задаваемые вопросы
Площадь поверхности квадратной пирамиды Формула – определение и вопросы
Актуальные темы
Объем: определение, примеры и формула
Сколько места занимает ручка или слон? Сколько места вы занимаете? Мы часто можем ссылаться на объем объекта, но что такое объем, как мы измеряем объемы и какие единицы измерения мы используем для описания объема?
Определение объема
Хотя объем чего-либо является интуитивно понятным понятием, может быть трудно точно описать, что такое объем.
 Ниже приводится возможное описание тома.
Ниже приводится возможное описание тома.Объем объекта является мерой объема трехмерного пространства, которое он занимает.
Это означает, что объем слона больше объема комара.
Один из способов представить объем — это спросить, сколько кубиков сахара поместилось бы внутри предмета, если бы он был полым. Если объект \(1\) гипотетически будет содержать \(200\) кубиков сахара, а объект \(2\) будет содержать \(400\), то объем объекта \(2\) вдвое больше объема объекта \( 1\).
Другой (неисчисляемый, но более точный) способ представления объема — сколько воды поместилось бы внутри объекта, если бы он был полым. Если вы наполните водой два предмета и предмет \(1\) в два раза тяжелее предмета \(2\), то предмет \(1\) будет в два раза больше по объему, чем предмет \(2\).
Так же, как масса, заряд и форма, объем является физическим свойством объекта.
Формула для объема
Не существует общей формулы для объема объектов (если мы не хотим использовать исчисление), но давайте рассмотрим очень простой объект: прямоугольный параллелепипед.
 Это трехмерная версия прямоугольника, см. рисунок ниже.
Это трехмерная версия прямоугольника, см. рисунок ниже.Прямоугольный параллелепипед со сторонами a , b и c , Арьян ван Дензен – StudySmarter Originals.
Длина сторон равна \(a\), \(b\) и \(c\). Если мы удвоим \(a\), то внутри прямоугольного параллелепипеда поместится в два раза больше кубиков сахара, чем раньше, потому что у нас фактически есть две копии исходного прямоугольного параллелепипеда друг над другом. Это означает, что объем прямоугольного параллелепипеда удвоится, если мы удвоим длину \(a\). То же самое касается длин \(b\) и \(c\). Эти длины являются единственными факторами, влияющими на объем прямоугольного параллелепипеда, потому что они содержат всю информацию, необходимую для определения этого объекта. Таким образом, объем \(V _{\text{rc}}\) прямоугольного кубоида должен быть постоянным, умноженным на произведение длины всех сторон, \(abc\). Бывает, что константа равна \(1\), поэтому наша формула принимает вид:
\[V_{\text{r.
 3\), потому что куб — это просто прямоугольный параллелепипед с \(a=b=c\).
3\), потому что куб — это просто прямоугольный параллелепипед с \(a=b=c\).Измерение объемов
Мы также можем использовать воду для измерения объема объектов на практике. Мы начинаем с полностью заполненного прямоугольно-кубовидного резервуара с водой и опускаем наш объект в воду. Часть воды будет переливаться в этом процессе, потому что вода должна освободить место для объекта внутри резервуара. Это количество комнаты является объемом объекта. Если теперь мы снова вытащим объект из воды, уровень воды в резервуаре упадет, потому что мы удалили объем нашего объекта из резервуара. Незаполненная часть бака теперь имеет тот же объем, что и объект, потому что мы только что вынули объект из бака! Эта незаполненная часть бака будет иметь форму прямоугольного параллелепипеда, поэтому этот объем легко измерить по формуле, которую мы приводили ранее. Вуаля, этот измеренный объем и есть объем нашего объекта. См. иллюстрацию ниже для схематического представления этого процесса.
 93\). Это \(8000\,\mathrm{L}\).
93\). Это \(8000\,\mathrm{L}\).Вычисление объемов
Существуют формы, для которых достаточно легко вычислить объем, т.е. без необходимости использования какой-либо сложной математики, такой как исчисление, каждый раз, когда вы сталкиваетесь с такой формой.
Пирамиды имеют основание и высоту, перпендикулярную этому основанию, см. рисунок ниже для иллюстрации. Если основание пирамиды имеет площадь \(A\), а пирамида имеет высоту \(h\), то объем \(V\) пирамиды всегда определяется выражением \(V=Ah/3\) . 93\).
Примеры объемов в физике
Объем объектов важен во многих вопросах физики.
Знание объема газа (например, газа, находящегося в закрытом сосуде) необходимо для заключения о его плотности, давлении и температуре. Если мы сожмем газ до меньшего объема, его давление возрастет: он будет отталкивать нас.
Попробуйте сжать закрытую бутылку с водой. Вы не уйдете очень далеко, потому что уменьшение объема воздуха в бутылке вызовет увеличение давления, отталкивающего вас.





 3 \quad\Rightarrow\quad \dfrac{R_1}{R_2}=\sqrt[3]{343}=7\)
3 \quad\Rightarrow\quad \dfrac{R_1}{R_2}=\sqrt[3]{343}=7\) 3=27\)
3=27\) Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю: Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».
Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)». 1):
1):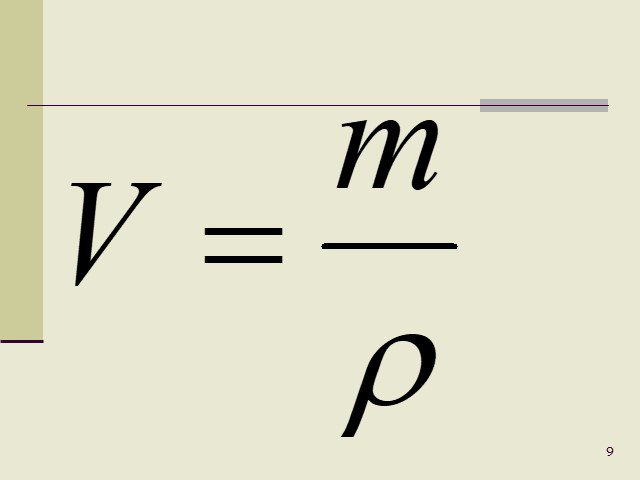

 ширина)
ширина) Сколько литров воды можно налить в бак данных размеров?
Сколько литров воды можно налить в бак данных размеров? Ниже приводится возможное описание тома.
Ниже приводится возможное описание тома.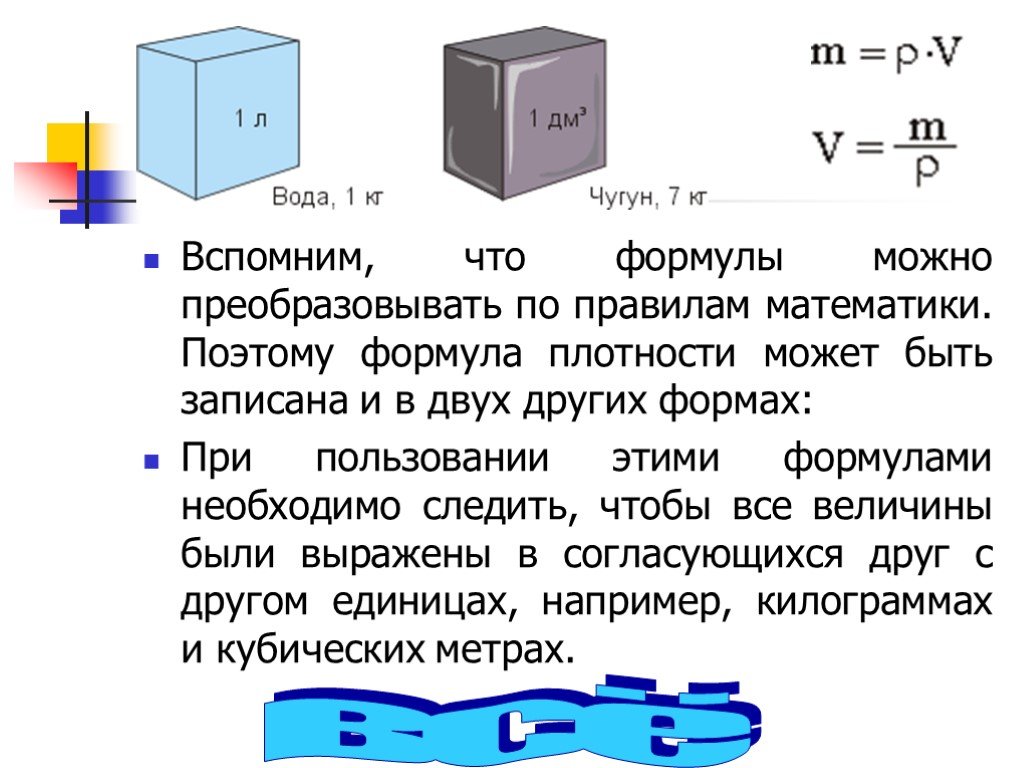 Это трехмерная версия прямоугольника, см. рисунок ниже.
Это трехмерная версия прямоугольника, см. рисунок ниже. 3\), потому что куб — это просто прямоугольный параллелепипед с \(a=b=c\).
3\), потому что куб — это просто прямоугольный параллелепипед с \(a=b=c\). 93\). Это \(8000\,\mathrm{L}\).
93\). Это \(8000\,\mathrm{L}\).